No CrossRef data available.
Published online by Cambridge University Press: 24 April 2023
Large deviations of the largest and smallest eigenvalues of 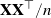 $\mathbf{X}\mathbf{X}^\top/n$ are studied in this note, where
$\mathbf{X}\mathbf{X}^\top/n$ are studied in this note, where 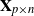 $\mathbf{X}_{p\times n}$ is a
$\mathbf{X}_{p\times n}$ is a 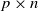 $p\times n$ random matrix with independent and identically distributed (i.i.d.) sub-Gaussian entries. The assumption imposed on the dimension size p and the sample size n is
$p\times n$ random matrix with independent and identically distributed (i.i.d.) sub-Gaussian entries. The assumption imposed on the dimension size p and the sample size n is 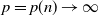 $p=p(n)\rightarrow\infty$ with
$p=p(n)\rightarrow\infty$ with 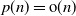 $p(n)={\mathrm{o}}(n)$. This study generalizes one result obtained in [3].
$p(n)={\mathrm{o}}(n)$. This study generalizes one result obtained in [3].