1 Introduction
Ever since Sullivan’s translation of Ahlfors’ finiteness theorem into a solution of a long-standing open problem on wandering domains in the 1980s [Reference Sullivan43], many more connections between the theory of Kleinian groups and the study of dynamics of rational functions on ![]() $\widehat {\mathbb {C}}$ have been discovered. These analogies between the two branches of conformal dynamics, which are commonly known as Sullivan’s dictionary, not only provide a conceptual framework for understanding the connections but motivate research in each field as well.
$\widehat {\mathbb {C}}$ have been discovered. These analogies between the two branches of conformal dynamics, which are commonly known as Sullivan’s dictionary, not only provide a conceptual framework for understanding the connections but motivate research in each field as well.
In this article, we extend this dictionary by establishing a strikingly explicit correspondence between
• Kissing reflection groups: groups generated by reflections along the circles of finite circle packings
 $\mathcal {P}$ (see Section 3) and
$\mathcal {P}$ (see Section 3) and• Critically fixed anti-rational maps: proper anti-holomorphic self-maps of
 $\widehat {\mathbb {C}}$ with all critical points fixed (see Section 4).
$\widehat {\mathbb {C}}$ with all critical points fixed (see Section 4).
This correspondence can be expressed by a combinatorial model: a simple plane graph ![]() $\Gamma $. Throughout this article, a plane graph will mean a planar graph together with an embedding in
$\Gamma $. Throughout this article, a plane graph will mean a planar graph together with an embedding in ![]() $\widehat {\mathbb {C}}$. We say that two plane graphs are isomorphic if the underlying graph isomorphism is induced by an orientation-preserving homeomorphism of
$\widehat {\mathbb {C}}$. We say that two plane graphs are isomorphic if the underlying graph isomorphism is induced by an orientation-preserving homeomorphism of ![]() $\widehat {\mathbb {C}}$. A graph
$\widehat {\mathbb {C}}$. A graph ![]() $\Gamma $ is said to be k-connected if
$\Gamma $ is said to be k-connected if ![]() $\Gamma $ contains more than k vertices and remains connected if any
$\Gamma $ contains more than k vertices and remains connected if any ![]() $k-1$ vertices and their corresponding incident edges are removed. Our first result shows the following.
$k-1$ vertices and their corresponding incident edges are removed. Our first result shows the following.
Theorem 1.1. The following three sets are in natural bijective correspondence:
•
 $\{2$-connected simple plane graphs
$\{2$-connected simple plane graphs  $\Gamma $ with
$\Gamma $ with  $d+1$ vertices up to isomorphism of plane graphs
$d+1$ vertices up to isomorphism of plane graphs $\}$,
$\}$,•
 $\{$Kissing reflection groups G of rank
$\{$Kissing reflection groups G of rank  $d+1$ with connected limit set up to QC conjugacy
$d+1$ with connected limit set up to QC conjugacy $\}$,
$\}$,•
 $\{$Critically fixed anti-rational maps
$\{$Critically fixed anti-rational maps  $\mathcal {R}$ of degree d up to Möbius conjugacy
$\mathcal {R}$ of degree d up to Möbius conjugacy $\}$.
$\}$.
Moreover, if ![]() $G_\Gamma $ and
$G_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ correspond to the same plane graph
$\mathcal {R}_\Gamma $ correspond to the same plane graph ![]() $\Gamma $, then the limit set
$\Gamma $, then the limit set ![]() $\Lambda (G_\Gamma )$ is homeomorphic to the Julia set
$\Lambda (G_\Gamma )$ is homeomorphic to the Julia set ![]() $\mathcal {J}(\mathcal {R}_\Gamma )$ via a dynamically natural map.
$\mathcal {J}(\mathcal {R}_\Gamma )$ via a dynamically natural map.
The correspondence between graphs and kissing reflection groups comes from the well-known circle packing theorem (see Theorem 2.1): given a kissing reflection group G with corresponding circle packing ![]() $\mathcal {P}$, the plane graph
$\mathcal {P}$, the plane graph ![]() $\Gamma $ associated to G in Theorem 1.1 is the contact graph of the circle packing
$\Gamma $ associated to G in Theorem 1.1 is the contact graph of the circle packing ![]() $\mathcal {P}$. The
$\mathcal {P}$. The ![]() $2$-connectedness condition for
$2$-connectedness condition for ![]() $\Gamma $ is equivalent to the connectedness condition for the limit set of G (see Figure 1.1).
$\Gamma $ is equivalent to the connectedness condition for the limit set of G (see Figure 1.1).

Figure 1.1 An example of the correspondence.
On the other hand, given a critically fixed anti-rational map ![]() $\mathcal {R}$, we consider the union
$\mathcal {R}$, we consider the union ![]() $\mathscr {T}$ of all fixed internal rays in the invariant Fatou components (each of which necessarily contains a fixed critical point of
$\mathscr {T}$ of all fixed internal rays in the invariant Fatou components (each of which necessarily contains a fixed critical point of ![]() $\mathcal {R}$), known as the Tischler graph (cf. [Reference Tischler46]). Roughly speaking, Tischler graphs are to critically fixed (anti-)rational maps what Hubbard trees are to postcritically finite (anti-)polynomials: both are forward invariant graphs containing the postcritical points. We show that the planar dual of
$\mathcal {R}$), known as the Tischler graph (cf. [Reference Tischler46]). Roughly speaking, Tischler graphs are to critically fixed (anti-)rational maps what Hubbard trees are to postcritically finite (anti-)polynomials: both are forward invariant graphs containing the postcritical points. We show that the planar dual of ![]() $\mathscr {T}$ is a
$\mathscr {T}$ is a ![]() $2$-connected simple plane graph. The plane graph
$2$-connected simple plane graph. The plane graph ![]() $\Gamma $ we associate to
$\Gamma $ we associate to ![]() $\mathcal {R}$ in Theorem 1.1 is the planar dual
$\mathcal {R}$ in Theorem 1.1 is the planar dual ![]() $\mathscr {T}^{\vee }$ of
$\mathscr {T}^{\vee }$ of ![]() $\mathscr {T}$ (see Figure 1.1).
$\mathscr {T}$ (see Figure 1.1).
In the special case when ![]() $\Gamma $ is the planar dual of a triangulation of
$\Gamma $ is the planar dual of a triangulation of ![]() $\widehat {\mathbb {C}}$, the existence of the critically fixed anti-rational map
$\widehat {\mathbb {C}}$, the existence of the critically fixed anti-rational map ![]() $\mathcal {R}_\Gamma $ was proved in [Reference Lodge, Lyubich, Merenkov and Mukherjee24].
$\mathcal {R}_\Gamma $ was proved in [Reference Lodge, Lyubich, Merenkov and Mukherjee24].
We remark that the correspondence between ![]() $G_\Gamma $ and
$G_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ through the plane graph
$\mathcal {R}_\Gamma $ through the plane graph ![]() $\Gamma $ is dynamically natural. Indeed, we associate, following [Reference Lodge, Lyubich, Merenkov and Mukherjee24, §4], a map
$\Gamma $ is dynamically natural. Indeed, we associate, following [Reference Lodge, Lyubich, Merenkov and Mukherjee24, §4], a map ![]() $\mathcal {N}_\Gamma $ to the group
$\mathcal {N}_\Gamma $ to the group ![]() $G_\Gamma $ with the properties that
$G_\Gamma $ with the properties that ![]() $\mathcal {N}_\Gamma $ and
$\mathcal {N}_\Gamma $ and ![]() $G_\Gamma $ have the same grand orbits (cf. [Reference Nielsen33, Reference Bowen and Series2]) and the homeomorphism between
$G_\Gamma $ have the same grand orbits (cf. [Reference Nielsen33, Reference Bowen and Series2]) and the homeomorphism between ![]() $\Lambda (G_\Gamma )$ and
$\Lambda (G_\Gamma )$ and ![]() $\mathcal {J}(\mathcal {R}_\Gamma )$ conjugates
$\mathcal {J}(\mathcal {R}_\Gamma )$ conjugates ![]() $\mathcal {N}_\Gamma $ to
$\mathcal {N}_\Gamma $ to ![]() $\mathcal {R}_\Gamma $. See Subsection 4.3 for more details.
$\mathcal {R}_\Gamma $. See Subsection 4.3 for more details.
The asymmetry between the QC conjugacies on the group side and Möbius conjugacies on the anti-rational map side is artificial. Since the dynamical correspondence is between the limit set and the Julia set, Theorem 1.1 yields a bijection between quasiconformal conjugacy classes of kissing reflection groups (of rank ![]() $d+1$) with connected limit set and hyperbolic components having critically fixed anti-rational maps (of degree d) as centres.
$d+1$) with connected limit set and hyperbolic components having critically fixed anti-rational maps (of degree d) as centres.
The geometric mating problems
In complex dynamics, polynomial mating is an operation first introduced by Douady in [Reference Douady5] that takes two suitable polynomials ![]() $P_1$ and
$P_1$ and ![]() $P_2$ and constructs a richer dynamical system by carefully pasting together the boundaries of their filled Julia sets to obtain a copy of the Riemann sphere, together with a rational map R from this sphere to itself (see Definition 4.16 for the precise formulation). It is natural and important to understand which pairs of polynomials can be mated and which rational maps are matings of two polynomials. The analogous question in the Kleinian group setting can be formulated in terms of Cannon–Thurston maps for degenerations in the quasi-Fuchsian space (see [Reference Hubbard14] and Subsection 3.3 for related discussions). The correspondence in Theorem 1.1 allows us to explicitly characterise kissing reflection groups and critically fixed anti-rational maps that arise as matings.
$P_2$ and constructs a richer dynamical system by carefully pasting together the boundaries of their filled Julia sets to obtain a copy of the Riemann sphere, together with a rational map R from this sphere to itself (see Definition 4.16 for the precise formulation). It is natural and important to understand which pairs of polynomials can be mated and which rational maps are matings of two polynomials. The analogous question in the Kleinian group setting can be formulated in terms of Cannon–Thurston maps for degenerations in the quasi-Fuchsian space (see [Reference Hubbard14] and Subsection 3.3 for related discussions). The correspondence in Theorem 1.1 allows us to explicitly characterise kissing reflection groups and critically fixed anti-rational maps that arise as matings.
We say that a simple plane graph ![]() $\Gamma $ with n vertices is outerplanar if it has a face with all n vertices on its boundary. It is said to be Hamiltonian if there exists a Hamiltonian cycle; that is, a closed path visiting every vertex exactly once.
$\Gamma $ with n vertices is outerplanar if it has a face with all n vertices on its boundary. It is said to be Hamiltonian if there exists a Hamiltonian cycle; that is, a closed path visiting every vertex exactly once.
Theorem 1.2. Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph. Let
$2$-connected simple plane graph. Let ![]() $G_\Gamma $ and
$G_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ be a kissing reflection group and a critically fixed anti-rational map associated with
$\mathcal {R}_\Gamma $ be a kissing reflection group and a critically fixed anti-rational map associated with ![]() $\Gamma $. Then the following hold true:
$\Gamma $. Then the following hold true:
•
 $\Gamma $ is outerplanar
$\Gamma $ is outerplanar  $\Leftrightarrow \mathcal {R}_\Gamma $ is a critically fixed anti-polynomial
$\Leftrightarrow \mathcal {R}_\Gamma $ is a critically fixed anti-polynomial  $\Leftrightarrow G_\Gamma $ is a function group.
$\Leftrightarrow G_\Gamma $ is a function group.•
 $\Gamma $ is Hamiltonian
$\Gamma $ is Hamiltonian  $\Leftrightarrow \mathcal {R}_\Gamma $ is a mating of two polynomials
$\Leftrightarrow \mathcal {R}_\Gamma $ is a mating of two polynomials  $\Leftrightarrow G_\Gamma $ is a mating of two function groups
$\Leftrightarrow G_\Gamma $ is a mating of two function groups  $\Leftrightarrow G_\Gamma $ is in the closure of the quasiconformal deformation space of the regular ideal polygon reflection group.
$\Leftrightarrow G_\Gamma $ is in the closure of the quasiconformal deformation space of the regular ideal polygon reflection group.
It is known that a rational map may arise as the geometric mating of more than one pair of polynomials (in other words, the decomposition/unmating of a rational map into a pair of polynomials is not necessarily unique). This phenomenon was first observed in [Reference Wittner48] and is referred to as shared matings (see [Reference Rees39]). In our setting, we actually prove that each Hamiltonian cycle of ![]() $\Gamma $ gives an unmating of
$\Gamma $ gives an unmating of ![]() $\mathcal {R}_\Gamma $ into two anti-polynomials. Thus, we get many examples of shared matings coming from different Hamiltonian cycles in the associated graphs.
$\mathcal {R}_\Gamma $ into two anti-polynomials. Thus, we get many examples of shared matings coming from different Hamiltonian cycles in the associated graphs.
We now address the converse question of mateability in terms of laminations. Let us first note that the question of mateability for kissing reflection groups can be answered using Thurston’s double limit theorem and the hyperbolisation theorem. In the reflection group setting, possible degenerations in the quasi-Fuchsian space (of the regular ideal polygon reflection group) are listed by a pair of geodesic laminations on the two conformal boundaries which are invariant under some orientation-reversing involution ![]() $\sigma $ (see Subsection 3.3). All of these
$\sigma $ (see Subsection 3.3). All of these ![]() $\sigma $-invariant laminations turn out to be multicurves on the associated conformal boundaries. A pair of simple closed curves is said to be parallel if they are isotopic under the natural orientation-reversing identification of the two conformal boundary components. A pair of laminations is said to be nonparallel if no two components are parallel. If we lift a multicurve to the universal cover, we get two invariant laminations on the circle. Then they are are nonparallel if and only if the two laminations share no common leaf under the natural identification of the two copies of the circle. Thurston’s hyperbolisation theorem asserts that in our setting, the degeneration along a pair of laminations exists if and only if this pair is nonparallel.
$\sigma $-invariant laminations turn out to be multicurves on the associated conformal boundaries. A pair of simple closed curves is said to be parallel if they are isotopic under the natural orientation-reversing identification of the two conformal boundary components. A pair of laminations is said to be nonparallel if no two components are parallel. If we lift a multicurve to the universal cover, we get two invariant laminations on the circle. Then they are are nonparallel if and only if the two laminations share no common leaf under the natural identification of the two copies of the circle. Thurston’s hyperbolisation theorem asserts that in our setting, the degeneration along a pair of laminations exists if and only if this pair is nonparallel.
For a marked anti-polynomial, we can also associate a lamination via the Bötthcher coordinate at infinity. As before, we say a pair of (anti-polynomial) laminations is nonparallel if they share no common leaf under the natural identification of the two copies of the circle. When we glue two filled Julia sets using the corresponding laminations, the resulting topological space may not be a ![]() $2$-sphere. We call this a Moore obstruction. We prove the following more general mateability theorem for postcritically finite anti-polynomials, which in particular answers the question of mateability of two critically fixed anti-polynomials.
$2$-sphere. We call this a Moore obstruction. We prove the following more general mateability theorem for postcritically finite anti-polynomials, which in particular answers the question of mateability of two critically fixed anti-polynomials.
Theorem 1.3. Let ![]() $P_1$ and
$P_1$ and ![]() $P_2$ be two marked anti-polynomials of equal degree
$P_2$ be two marked anti-polynomials of equal degree ![]() $d\geq 2$, where
$d\geq 2$, where ![]() $P_1$ is critically fixed and
$P_1$ is critically fixed and ![]() $P_2$ is postcritically finite, hyperbolic. Then there is an anti-rational map R that is the geometric mating of
$P_2$ is postcritically finite, hyperbolic. Then there is an anti-rational map R that is the geometric mating of ![]() $P_1$ and
$P_1$ and ![]() $P_2$ if and only if there is no Moore obstruction.
$P_2$ if and only if there is no Moore obstruction.
Consequently, if both ![]() $P_1$ and
$P_1$ and ![]() $P_2$ are critically fixed, then they are geometrically mateable if and only if the corresponding laminations are nonparallel.
$P_2$ are critically fixed, then they are geometrically mateable if and only if the corresponding laminations are nonparallel.
Acylindrical manifolds and gasket sets
A circle packing is a connected collection of (oriented) circles in ![]() $\widehat {\mathbb {C}}$ with disjoint interiors. We say that a closed set
$\widehat {\mathbb {C}}$ with disjoint interiors. We say that a closed set ![]() $\Lambda $ is a round gasket if
$\Lambda $ is a round gasket if
•
 $\Lambda $ is the closure of some infinite circle packing; and
$\Lambda $ is the closure of some infinite circle packing; and• the complement of
 $\Lambda $ is a union of round disks which is dense in
$\Lambda $ is a union of round disks which is dense in  $\widehat {\mathbb {C}}$.
$\widehat {\mathbb {C}}$.
We will call a homeomorphic copy of a round gasket a gasket.
Many examples of kissing reflection groups and critically fixed anti-rational maps have gasket limit sets and Julia sets (see Figure 1.2). The correspondence allows us to classify all of these examples (cf. [Reference Kontorovich and Nakamura17, Theorem 28] and [Reference Keen, Maskit and Series16]).

Figure 1.2 Critically fixed anti-rational maps associated to Platonic solids. The Fatou components are coloured according to their grand orbit. The Tischler graph ![]() $\mathscr {T}$, which is the planar dual of
$\mathscr {T}$, which is the planar dual of ![]() $\Gamma $, is visible in the figures by connecting the centres of critical fixed Fatou components.
$\Gamma $, is visible in the figures by connecting the centres of critical fixed Fatou components.
Theorem 1.4. Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph. Then
$2$-connected simple plane graph. Then
![]() $G_\Gamma $ has gasket limit set
$G_\Gamma $ has gasket limit set ![]() $\iff \mathcal {R}_\Gamma $ has gasket Julia set
$\iff \mathcal {R}_\Gamma $ has gasket Julia set ![]() $\iff \Gamma $ is
$\iff \Gamma $ is ![]() $3$-connected.
$3$-connected.
The ![]() $3$-connectedness for the graph
$3$-connectedness for the graph ![]() $\Gamma $ also has a characterisation purely in terms of the inherent structure of the hyperbolic
$\Gamma $ also has a characterisation purely in terms of the inherent structure of the hyperbolic ![]() $3$-manifold associated with
$3$-manifold associated with ![]() $G_\Gamma $. Given a kissing reflection group
$G_\Gamma $. Given a kissing reflection group ![]() $G_\Gamma $, the index
$G_\Gamma $, the index ![]() $2$ subgroup
$2$ subgroup ![]() $\widetilde {G}_\Gamma $ consisting of orientation-preserving elements is a Kleinian group. We say that
$\widetilde {G}_\Gamma $ consisting of orientation-preserving elements is a Kleinian group. We say that ![]() $G_\Gamma $ is acylindrical if the hyperbolic
$G_\Gamma $ is acylindrical if the hyperbolic ![]() $3$-manifold for
$3$-manifold for ![]() $\widetilde {G}_\Gamma $ is acylindrical (see Subsection 3.2 for the precise definitions). We show the following.
$\widetilde {G}_\Gamma $ is acylindrical (see Subsection 3.2 for the precise definitions). We show the following.
Theorem 1.5. Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph. Then
$2$-connected simple plane graph. Then
![]() $G_\Gamma $ is acylindrical
$G_\Gamma $ is acylindrical ![]() $\iff \Gamma $ is
$\iff \Gamma $ is ![]() $3$-connected.
$3$-connected.
Parameter space implications of the dictionary
We now briefly mention some natural questions regarding parameter spaces of anti-rational maps raised by the aforementioned dictionary between kissing reflection groups and critically fixed anti-rational maps.
Acylindrical manifolds play an important role in 3-dimensional geometry and topology. Relevant to our discussion, Thurston proved that the deformation space of an acylindrical ![]() $3$-manifold is bounded [Reference Thurston45] (this is famously known as Thurston’s compactness theorem). The analogue of deformation spaces in holomorphic dynamics is hyperbolic components. The analogy established in Theorems 1.4 and 1.5 leads one to ask whether there is a counterpart of Thurston’s compactness theorem for hyperbolic components of critically fixed anti-rational maps with gasket Julia sets (see [Reference McMullen, Bott and Jaffe29, Question 5.3] for the corresponding question in the convex cocompact setting). In a forthcoming paper, a suitably interpreted boundedness result will be proved for the hyperbolic components under consideration [Reference Lodge, Luo and Mukherjee23].
$3$-manifold is bounded [Reference Thurston45] (this is famously known as Thurston’s compactness theorem). The analogue of deformation spaces in holomorphic dynamics is hyperbolic components. The analogy established in Theorems 1.4 and 1.5 leads one to ask whether there is a counterpart of Thurston’s compactness theorem for hyperbolic components of critically fixed anti-rational maps with gasket Julia sets (see [Reference McMullen, Bott and Jaffe29, Question 5.3] for the corresponding question in the convex cocompact setting). In a forthcoming paper, a suitably interpreted boundedness result will be proved for the hyperbolic components under consideration [Reference Lodge, Luo and Mukherjee23].
In [Reference Hatcher and Thurston13], Hatcher and Thurston studied the topology of the moduli space of marked circle packings with n circles in ![]() $\mathbb {C}$. In particular, they showed that the map that sends a marked circle packing to the centres of the circles yields a homotopy equivalence between the moduli space of marked circle packings and the configuration space of n marked points in
$\mathbb {C}$. In particular, they showed that the map that sends a marked circle packing to the centres of the circles yields a homotopy equivalence between the moduli space of marked circle packings and the configuration space of n marked points in ![]() $\mathbb {C}$. Motivated by this statement, one may ask whether the union of the closures of the hyperbolic components of degree d critically fixed anti-rational maps have a nontrivial topology. This question will be answered affirmatively in a future work, drawing exact parallels between contact structures of quasiconformal deformation spaces of kissing reflection groups and the corresponding hyperbolic component closures [Reference Lodge, Luo and Mukherjee23].
$\mathbb {C}$. Motivated by this statement, one may ask whether the union of the closures of the hyperbolic components of degree d critically fixed anti-rational maps have a nontrivial topology. This question will be answered affirmatively in a future work, drawing exact parallels between contact structures of quasiconformal deformation spaces of kissing reflection groups and the corresponding hyperbolic component closures [Reference Lodge, Luo and Mukherjee23].
We now summarise these correspondences in the following table.Footnote 1

Notes and references
Aspects of Sullivan’s dictionary were already anticipated by Fatou [Reference Fatou8, p. 22]. Part of the correspondence in Theorem 1.1 was recently established in [Reference Lodge, Lyubich, Merenkov and Mukherjee24] where the Tischler graphs were assumed to be triangulations. A classification of critically fixed anti-rational maps has also been obtained in [Reference Geyer9]. There is also a connection between Kleinian reflection groups, anti-rational maps and Schwarz reflections of quadrature domains explained in [Reference Lee, Lyubich, Makarov and Mukherjee21, Reference Lodge, Lyubich, Merenkov and Mukherjee24, Reference Lazebnik, Makarov and Mukherjee19, Reference Lazebnik, Makarov and Mukherjee20]. In the holomorphic setting, critically fixed rational maps have been studied in [Reference Cordwell, Gilbertson, Nuechterlein, Pilgrim and Pinella4, Reference Hlushchanka11].
Many critically fixed anti-rational maps have large symmetry groups. The examples corresponding to the five platonic solids are listed in Figure 1.2. The counterparts in the holomorphic setting were constructed in [Reference Doyle and McMullen7] (see also [Reference Buff3, Reference Hu, Jimenez and Muzician12]).
The connections between number-theoretic problems for circle packings and equidistribution results for Kleinian groups can be found in [Reference Kontorovich and Oh18, Reference Oh, Shah, Aravinda, Farrell and Lafont34, Reference Kontorovich and Nakamura17].
Some questions
The dictionary between kissing reflection groups and critically fixed anti-rational maps raises some natural questions. Let us fix a ![]() $2$-connected simple plane graph
$2$-connected simple plane graph ![]() $\Gamma $.
$\Gamma $.
• Although the limit and Julia sets
 $\Lambda (G_\Gamma )$ and
$\Lambda (G_\Gamma )$ and  $\mathcal {J}(\mathcal {R}_\Gamma )$ are homeomorphic, the dynamically natural homeomorphism is not a quasisymmetry because it sends parabolic fixed points to repelling ones. In fact, we believe that there is no quasiconformal homeomorphism of the sphere carrying one to the other. In the case when
$\mathcal {J}(\mathcal {R}_\Gamma )$ are homeomorphic, the dynamically natural homeomorphism is not a quasisymmetry because it sends parabolic fixed points to repelling ones. In fact, we believe that there is no quasiconformal homeomorphism of the sphere carrying one to the other. In the case when  $\Gamma $ is
$\Gamma $ is  $3$-connected, this follows from the observation that the boundaries of two components of the domain of discontinuity of
$3$-connected, this follows from the observation that the boundaries of two components of the domain of discontinuity of  $G_\Gamma $ touch at a cusp (with zero angle), while the boundaries of two Fatou components of
$G_\Gamma $ touch at a cusp (with zero angle), while the boundaries of two Fatou components of  $\mathcal {R}_\Gamma $ touch at a repelling (pre-) fixed point (with a positive angle). However, in general, we do not know how to rule out the existence of ‘exotic’ quasiconformal homeomorphisms between
$\mathcal {R}_\Gamma $ touch at a repelling (pre-) fixed point (with a positive angle). However, in general, we do not know how to rule out the existence of ‘exotic’ quasiconformal homeomorphisms between  $\Lambda (G_\Gamma )$ and
$\Lambda (G_\Gamma )$ and  $\mathcal {J}(\mathcal {R}_\Gamma )$. Moreover, since the quasisymmetry group of a fractal is a quasiconformal invariant, it will be interesting to know the quasisymmetry groups of
$\mathcal {J}(\mathcal {R}_\Gamma )$. Moreover, since the quasisymmetry group of a fractal is a quasiconformal invariant, it will be interesting to know the quasisymmetry groups of  $\Lambda (G_\Gamma )$ and
$\Lambda (G_\Gamma )$ and  $\mathcal {J}(\mathcal {R}_\Gamma )$. Note that according to [Reference Lodge, Lyubich, Merenkov and Mukherjee24], the quasisymmetry groups of these two fractals are isomorphic when the dual of
$\mathcal {J}(\mathcal {R}_\Gamma )$. Note that according to [Reference Lodge, Lyubich, Merenkov and Mukherjee24], the quasisymmetry groups of these two fractals are isomorphic when the dual of  $\Gamma $ is an unreduced triangulation.
$\Gamma $ is an unreduced triangulation.• Our proof of the existence of a homeomorphism between
 $\Lambda (G_\Gamma )$ and
$\Lambda (G_\Gamma )$ and  $\mathcal {J}(\mathcal {R}_\Gamma )$ only makes use of the conformal dynamics of the group and the anti-rational map on
$\mathcal {J}(\mathcal {R}_\Gamma )$ only makes use of the conformal dynamics of the group and the anti-rational map on  $\widehat {\mathbb {C}}$. One would like to know whether there is a direct
$\widehat {\mathbb {C}}$. One would like to know whether there is a direct  $3$-dimensional interpretation of this result.
$3$-dimensional interpretation of this result.
Structure of the article
We collect various known circle packing theorems in Section 2. Based on this, we prove the connection between kissing reflection groups and simple plane graphs in Section 3. In particular, the group part of Theorem 1.1, Theorem 1.2, Theorem 1.4 and Theorem 1.5 is proved in Proposition 3.4, Propositions 3.18, 3.20, 3.21, Proposition 3.10 and Proposition 3.6, respectively.
Critically fixed anti-rational maps are studied in Section 4. The anti-rational map part of Theorem 1.1 is proved in Proposition 4.10. Once this is established, the anti-rational map part of Theorem 1.2 and Theorem 1.4 follow from their group counterparts as explained in Corollary 4.17. Theorem 1.3 is proved in Proposition 4.23 and Corollary 4.24.
2 Circle Packings
In this article, a circle packing ![]() $\mathcal {P}$ is a connected finite collection of (oriented) circles in
$\mathcal {P}$ is a connected finite collection of (oriented) circles in ![]() $\widehat {\mathbb {C}}$ with disjoint interiors. Unless stated otherwise, the circle packings in this article are assumed to contain at least three circles. The combinatorics of configuration of a circle packing can be described by its contact graph
$\widehat {\mathbb {C}}$ with disjoint interiors. Unless stated otherwise, the circle packings in this article are assumed to contain at least three circles. The combinatorics of configuration of a circle packing can be described by its contact graph ![]() $\Gamma $: we associate a vertex to each circle and two vertices are connected by an edge if and only if the two associated circles intersect. The embedding of the circles in
$\Gamma $: we associate a vertex to each circle and two vertices are connected by an edge if and only if the two associated circles intersect. The embedding of the circles in ![]() $\widehat {\mathbb {C}}$ determines the isomorphism class of its contact graph as a plane graph. It can also be checked easily that the contact graph of a circle packing is simple. This turns out to be the only constraint for the graph (See [Reference Thurston44, Chapter 13]).
$\widehat {\mathbb {C}}$ determines the isomorphism class of its contact graph as a plane graph. It can also be checked easily that the contact graph of a circle packing is simple. This turns out to be the only constraint for the graph (See [Reference Thurston44, Chapter 13]).
Theorem 2.1. Circle Packing Theorem
Every connected simple plane graph is isomorphic to the contact graph of some circle packing.
The definition of contact graphs can be easily generalised to an infinite collection of circles with disjoint interiors. In this article, an infinite circle packing ![]() $\mathcal {P}$ is an infinite collection of (oriented) circles in
$\mathcal {P}$ is an infinite collection of (oriented) circles in ![]() $\hat {\mathbb {C}}$ with disjoint interiors, whose contact graph is connected.
$\hat {\mathbb {C}}$ with disjoint interiors, whose contact graph is connected.
k-connected graphs
A graph ![]() $\Gamma $ is said to be k-connected if
$\Gamma $ is said to be k-connected if ![]() $\Gamma $ contains more than k vertices and remains connected if any
$\Gamma $ contains more than k vertices and remains connected if any ![]() $k-1$ vertices and their corresponding incident edges are removed. A graph is
$k-1$ vertices and their corresponding incident edges are removed. A graph is ![]() $\Gamma $ is said to be polyhedral if
$\Gamma $ is said to be polyhedral if ![]() $\Gamma $ is the
$\Gamma $ is the ![]() $1$-skeleton of a convex polyhedron. According to Steinitz’s theorem, a graph is polyhedral if and only if it is
$1$-skeleton of a convex polyhedron. According to Steinitz’s theorem, a graph is polyhedral if and only if it is ![]() $3$-connected and planar.
$3$-connected and planar.
Given a polyhedral graph, we have a stronger version of the circle packing theorem [Reference Schramm40] (cf. midsphere for canonical polyhedron).
Theorem 2.2. Circle Packing Theorem for polyhedral graphs
Suppose ![]() $\Gamma $ is a polyhedral graph; then there is a pair of circle packings whose contact graphs are isomorphic to
$\Gamma $ is a polyhedral graph; then there is a pair of circle packings whose contact graphs are isomorphic to ![]() $\Gamma $ and its planar dual. Moreover, the two circle packings intersect orthogonally at their points of tangency.
$\Gamma $ and its planar dual. Moreover, the two circle packings intersect orthogonally at their points of tangency.
This pair of circle packings is unique up to Möbius transformations.
Marked contact graphs
In many situations, it is better to work with a marking on the graph as well as the circle packing. A marking of a graph ![]() $\Gamma $ is a choice of the graph isomorphism
$\Gamma $ is a choice of the graph isomorphism
where ![]() $\mathscr {G}$ is the underlying abstract graph of
$\mathscr {G}$ is the underlying abstract graph of ![]() $\Gamma $. We will refer to the pair
$\Gamma $. We will refer to the pair ![]() $(\Gamma , \phi )$ as a marked graph.
$(\Gamma , \phi )$ as a marked graph.
Given two marked plane graphs ![]() $(\Gamma _1, \phi _1)$ and
$(\Gamma _1, \phi _1)$ and ![]() $(\Gamma _2, \phi _2)$ with the same underlying abstract graph
$(\Gamma _2, \phi _2)$ with the same underlying abstract graph ![]() $\mathscr {G}$, we say that they are equivalent if
$\mathscr {G}$, we say that they are equivalent if  $\phi _2\circ \phi _1^{-1}:\Gamma _1 \longrightarrow \Gamma _2$ is an isomorphism of plane graphs.
$\phi _2\circ \phi _1^{-1}:\Gamma _1 \longrightarrow \Gamma _2$ is an isomorphism of plane graphs.
Similarly, a circle packing ![]() $\mathcal {P}$ is said to be marked if the associated contact graph is marked.
$\mathcal {P}$ is said to be marked if the associated contact graph is marked.
3 Kissing Reflection Groups
Let ![]() $\Gamma $ be a marked connected simple plane graph. By the circle packing theorem,
$\Gamma $ be a marked connected simple plane graph. By the circle packing theorem, ![]() $\Gamma $ is (isomorphic to) the contact graph of some marked circle packing
$\Gamma $ is (isomorphic to) the contact graph of some marked circle packing
We define the kissing reflection group associated to this circle packing ![]() $\mathcal {P}$ as
$\mathcal {P}$ as
where ![]() $g_i$ is the reflection along the circle
$g_i$ is the reflection along the circle ![]() $C_i$.
$C_i$.
We denote the group of all Möbius automorphisms of ![]() $\widehat {\mathbb {C}}$ by
$\widehat {\mathbb {C}}$ by  $\textrm {Aut}^+(\widehat {\mathbb {C}})$ and the group of all Möbius and anti-Möbius automorphisms of
$\textrm {Aut}^+(\widehat {\mathbb {C}})$ and the group of all Möbius and anti-Möbius automorphisms of ![]() $\widehat {\mathbb {C}}$ by
$\widehat {\mathbb {C}}$ by  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$. Note that since a kissing reflection group is a discrete subgroup of
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$. Note that since a kissing reflection group is a discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$, definitions of limit set and domain of discontinuity can be easily extended to kissing reflection groups. We shall use
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$, definitions of limit set and domain of discontinuity can be easily extended to kissing reflection groups. We shall use ![]() $\widetilde {G}_{\mathcal {P}}$ to denote the index 2 subgroup of
$\widetilde {G}_{\mathcal {P}}$ to denote the index 2 subgroup of ![]() $G_{\mathcal {P}}$ consisting of orientation-preserving elements. Note that
$G_{\mathcal {P}}$ consisting of orientation-preserving elements. Note that ![]() $\widetilde {G}_{\mathcal {P}}$ lies on the boundary of Schottky groups.
$\widetilde {G}_{\mathcal {P}}$ lies on the boundary of Schottky groups.
We remark that if ![]() $\mathcal {P}'$ is another circle packing realising
$\mathcal {P}'$ is another circle packing realising ![]() $\Gamma $, since the graph
$\Gamma $, since the graph ![]() $\Gamma $ is marked, there is a canonical identification of the circle packing
$\Gamma $ is marked, there is a canonical identification of the circle packing ![]() $\mathcal {P}'$ with
$\mathcal {P}'$ with ![]() $\mathcal {P}$. This gives a canonical isomorphism between the kissing reflection groups
$\mathcal {P}$. This gives a canonical isomorphism between the kissing reflection groups ![]() $G_{\mathcal {P}'}$ and
$G_{\mathcal {P}'}$ and ![]() $G_{\mathcal {P}}$, which is induced by a quasiconformal map. We refer to
$G_{\mathcal {P}}$, which is induced by a quasiconformal map. We refer to ![]() $\Gamma $ as the contact graph associated to
$\Gamma $ as the contact graph associated to ![]() $G_{\mathcal {P}}$.
$G_{\mathcal {P}}$.
3.1 Limit set and domain of discontinuity of kissing reflection groups
Let ![]() $\mathcal {P} = \{C_1,\ldots , C_n\}$ be a marked circle packing and
$\mathcal {P} = \{C_1,\ldots , C_n\}$ be a marked circle packing and ![]() $D_i$ be the associated open disks for
$D_i$ be the associated open disks for ![]() $C_i$. Let P be the set consisting of points of tangency for the circle packing
$C_i$. Let P be the set consisting of points of tangency for the circle packing ![]() $\mathcal {P}$. Let
$\mathcal {P}$. Let
 $$ \begin{align*}\Pi = \widehat{\mathbb{C}}\setminus\left(\bigcup_{i=1}^n D_i \cup P\right). \end{align*} $$
$$ \begin{align*}\Pi = \widehat{\mathbb{C}}\setminus\left(\bigcup_{i=1}^n D_i \cup P\right). \end{align*} $$Then ![]() $\Pi $ is a fundamental domain of the action of
$\Pi $ is a fundamental domain of the action of ![]() $G_{\mathcal {P}}$ on the domain of discontinuity
$G_{\mathcal {P}}$ on the domain of discontinuity ![]() $\Omega (G_{\mathcal {P}})$. Denote
$\Omega (G_{\mathcal {P}})$. Denote  $\Pi = \bigcup _{i=1}^k \Pi _i$ where
$\Pi = \bigcup _{i=1}^k \Pi _i$ where ![]() $\Pi _i$ is a component of
$\Pi _i$ is a component of ![]() $\Pi $. Note that when the limit set of
$\Pi $. Note that when the limit set of ![]() $G_{\mathcal {P}}$ is connected, each component of the domain of discontinuity is simply connected (that is, a conformal disk) and each component
$G_{\mathcal {P}}$ is connected, each component of the domain of discontinuity is simply connected (that is, a conformal disk) and each component ![]() $\Pi _i$ is a closed ideal polygon in the corresponding component of the domain of discontinuity bounded by arcs of finitely many circles in the circle packing.
$\Pi _i$ is a closed ideal polygon in the corresponding component of the domain of discontinuity bounded by arcs of finitely many circles in the circle packing.
Since ![]() $G_{\mathcal {P}}$ is a free product of finitely many copies of
$G_{\mathcal {P}}$ is a free product of finitely many copies of ![]() $\mathbb {Z}/2\mathbb {Z}$, each element
$\mathbb {Z}/2\mathbb {Z}$, each element ![]() $g \in G_{\mathcal {P}}$ admits a shortest expression
$g \in G_{\mathcal {P}}$ admits a shortest expression ![]() $g = g_{i_1} \ldots g_{i_l}$ (
$g = g_{i_1} \ldots g_{i_l}$ (![]() $i_r\neq i_{r+1}$, for
$i_r\neq i_{r+1}$, for ![]() $r\in \{1,\cdots , l-1\}$) with respect to the standard generating set
$r\in \{1,\cdots , l-1\}$) with respect to the standard generating set ![]() $S = \{g_1,\ldots , g_n\}$. The integer l is called the length of the group element g, thought of as a word in terms of the generators.
$S = \{g_1,\ldots , g_n\}$. The integer l is called the length of the group element g, thought of as a word in terms of the generators.
The following lemma follows directly by induction.
Lemma 3.1. Let ![]() $g=g_{i_1} \ldots g_{i_l}$ be an element of length l, then
$g=g_{i_1} \ldots g_{i_l}$ be an element of length l, then ![]() $g\cdot \Pi \subseteq \overline {D}_{i_1}$.
$g\cdot \Pi \subseteq \overline {D}_{i_1}$.
We set  $\Pi ^1:= \bigcup _{i=1}^n g_i\cdot \Pi $ and
$\Pi ^1:= \bigcup _{i=1}^n g_i\cdot \Pi $ and 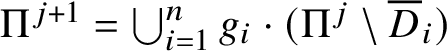 $\Pi ^{j+1} = \bigcup _{i=1}^n g_i\cdot (\Pi ^j\setminus \overline {D}_i)$. For consistency, we also set
$\Pi ^{j+1} = \bigcup _{i=1}^n g_i\cdot (\Pi ^j\setminus \overline {D}_i)$. For consistency, we also set ![]() $\Pi ^0:= \Pi $. We call
$\Pi ^0:= \Pi $. We call ![]() $\Pi ^l$ the tiling of level l. The following lemma justifies this terminology.
$\Pi ^l$ the tiling of level l. The following lemma justifies this terminology.
 $$ \begin{align*}\Pi^{l} = \bigcup_{\vert g\vert = l} g\cdot \Pi.\end{align*} $$
$$ \begin{align*}\Pi^{l} = \bigcup_{\vert g\vert = l} g\cdot \Pi.\end{align*} $$Proof. We will prove this by induction. The base case is satisfied by the definition of ![]() $\Pi ^1$. Assume that
$\Pi ^1$. Assume that  $\Pi ^{j} = \bigcup _{\vert g\vert = j} g\cdot \Pi $. Let
$\Pi ^{j} = \bigcup _{\vert g\vert = j} g\cdot \Pi $. Let ![]() $g = g_{i_1}g_{i_2} \ldots g_{i_{j+1}}$ be of length
$g = g_{i_1}g_{i_2} \ldots g_{i_{j+1}}$ be of length ![]() $j+1$. Note that
$j+1$. Note that ![]() $i_1 \neq i_2$. By Lemma 3.1,
$i_1 \neq i_2$. By Lemma 3.1, ![]() $g_{i_2}g_{i_3} \ldots g_{i_{j+1}}\cdot \Pi $ does not intersect
$g_{i_2}g_{i_3} \ldots g_{i_{j+1}}\cdot \Pi $ does not intersect ![]() $\overline {D}_{i_1}$; thus,
$\overline {D}_{i_1}$; thus, ![]() $g\cdot \Pi \subseteq g_{i_1} \cdot (\Pi ^j\setminus \overline {D}_{i_1})$. So
$g\cdot \Pi \subseteq g_{i_1} \cdot (\Pi ^j\setminus \overline {D}_{i_1})$. So 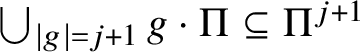 $\bigcup _{\vert g\vert = j+1} g\cdot \Pi \subseteq \Pi ^{j+1}$. The reverse inclusion can be proved similarly.
$\bigcup _{\vert g\vert = j+1} g\cdot \Pi \subseteq \Pi ^{j+1}$. The reverse inclusion can be proved similarly.
Since the domain of discontinuity is the union of tiles of all levels, Lemma 3.2 implies that
 $$ \begin{align*}\Omega(G_{\mathcal{P}}) = \bigcup_{g\in G_{\mathcal{P}}} g\cdot \Pi = \bigcup_{i=0}^\infty \Pi^i. \end{align*} $$
$$ \begin{align*}\Omega(G_{\mathcal{P}}) = \bigcup_{g\in G_{\mathcal{P}}} g\cdot \Pi = \bigcup_{i=0}^\infty \Pi^i. \end{align*} $$ Similarly, we set  $\mathcal {D}^i = \widehat {\mathbb {C}} \setminus \bigcup _{j=0}^i\Pi ^j$. We remark that
$\mathcal {D}^i = \widehat {\mathbb {C}} \setminus \bigcup _{j=0}^i\Pi ^j$. We remark that ![]() $\mathcal {D}^i$ is neither open nor closed: it is a finite union of open disks together with the orbit of P under the group elements of length up to i on the boundaries of these disks.
$\mathcal {D}^i$ is neither open nor closed: it is a finite union of open disks together with the orbit of P under the group elements of length up to i on the boundaries of these disks.
Let ![]() $\overline {\mathcal {D}^i}$ be its closure. Note that each
$\overline {\mathcal {D}^i}$ be its closure. Note that each ![]() $\overline {\mathcal {D}^i}$ is a union of closed disks for some (possibly disconnected) finite circle packing. Indeed,
$\overline {\mathcal {D}^i}$ is a union of closed disks for some (possibly disconnected) finite circle packing. Indeed,
 $$ \begin{align*}\overline{\mathcal{D}^0} = \overline{\widehat{\mathbb{C}}\setminus\Pi^0} = \bigcup_{i=1}^n \overline{D}_i \end{align*} $$
$$ \begin{align*}\overline{\mathcal{D}^0} = \overline{\widehat{\mathbb{C}}\setminus\Pi^0} = \bigcup_{i=1}^n \overline{D}_i \end{align*} $$is the union of the closed disks corresponding to the original circle packing ![]() $\mathcal {P}$. By induction, we have that at level
$\mathcal {P}$. By induction, we have that at level ![]() $i+1$,
$i+1$,
 $$ \begin{align} \overline{\mathcal{D}^{i+1}} = \bigcup_{j=1}^n g_j \cdot \overline{\mathcal{D}^i\setminus\overline{D}_j} \end{align} $$
$$ \begin{align} \overline{\mathcal{D}^{i+1}} = \bigcup_{j=1}^n g_j \cdot \overline{\mathcal{D}^i\setminus\overline{D}_j} \end{align} $$is the union of the images of the level i disks outside of ![]() $\overline {D}_j$ under
$\overline {D}_j$ under ![]() $g_j$.
$g_j$.
We also note that the sequence ![]() $\overline {\mathcal {D}}^i$ is nested and thus the limit set
$\overline {\mathcal {D}}^i$ is nested and thus the limit set
 $$ \begin{align*}\Lambda(G_{\mathcal{P}}) = \bigcap_{i=0}^\infty \mathcal{D}^i = \bigcap_{i=0}^\infty \overline{\mathcal{D}^i}. \end{align*} $$
$$ \begin{align*}\Lambda(G_{\mathcal{P}}) = \bigcap_{i=0}^\infty \mathcal{D}^i = \bigcap_{i=0}^\infty \overline{\mathcal{D}^i}. \end{align*} $$Therefore, we have the following expansive property of the group action on ![]() $\Lambda (G_{\mathcal {P}})$.
$\Lambda (G_{\mathcal {P}})$.
Lemma 3.3. Let ![]() $r_n$ be the maximum spherical diameter of the disks in
$r_n$ be the maximum spherical diameter of the disks in ![]() $\mathcal {D}^n$. Then
$\mathcal {D}^n$. Then ![]() $r_n \to 0$.
$r_n \to 0$.
Proof. Otherwise, we can construct a sequence of nested disks of radius bounded from below implying that the limit set contains a disk, which is a contradiction.
We now prove the group part of Theorem 1.1.
Proposition 3.4. The kissing reflection group ![]() $G_{\mathcal {P}}$ has connected limit set if and only if the contact graph
$G_{\mathcal {P}}$ has connected limit set if and only if the contact graph ![]() $\Gamma $ of
$\Gamma $ of ![]() $\mathcal {P}$ is
$\mathcal {P}$ is ![]() $2$-connected.
$2$-connected.
Proof. If ![]() $\Gamma $ is not
$\Gamma $ is not ![]() $2$-connected, then there exists a circle (say
$2$-connected, then there exists a circle (say ![]() $C_1$) such that the circle packing becomes disconnected once we remove it. Then we see
$C_1$) such that the circle packing becomes disconnected once we remove it. Then we see ![]() $\mathcal {D}^1 \subseteq \widehat {\mathbb {C}}$ is disconnected by Equation 3.1. This forces the limit set to be disconnected as well (see Figure 3.1).
$\mathcal {D}^1 \subseteq \widehat {\mathbb {C}}$ is disconnected by Equation 3.1. This forces the limit set to be disconnected as well (see Figure 3.1).
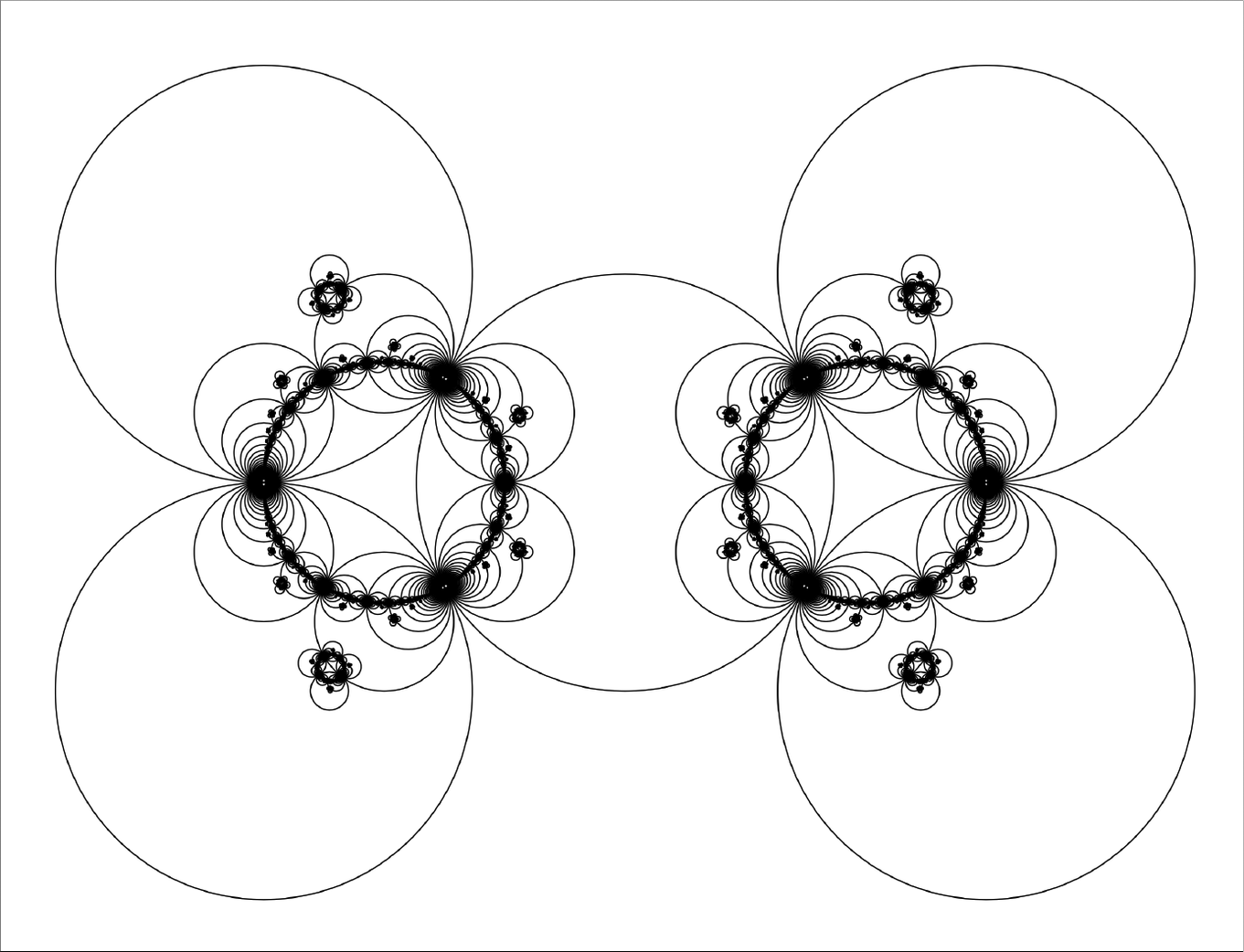
Figure 3.1 A disconnected limit set for a kissing reflection group G with non-![]() $2$-connected contact graph. G is generated by reflections along the five visible large circles in the figure.
$2$-connected contact graph. G is generated by reflections along the five visible large circles in the figure.
On the other hand, if ![]() $\Gamma $ is
$\Gamma $ is ![]() $2$-connected, then
$2$-connected, then ![]() $\mathcal {D}^1$ is connected by Equation 3.1. Now by induction and Equation 3.1 again,
$\mathcal {D}^1$ is connected by Equation 3.1. Now by induction and Equation 3.1 again, ![]() $\mathcal {D}^i$ is connected for all i. Thus,
$\mathcal {D}^i$ is connected for all i. Thus,  $\Lambda (G_{\mathcal {P}}) = \bigcap _{i=0}^\infty \mathcal {D}^i$ is also connected.
$\Lambda (G_{\mathcal {P}}) = \bigcap _{i=0}^\infty \mathcal {D}^i$ is also connected.
Proposition 3.4 and the definition of kissing reflection groups show that the association of a ![]() $2$-connected simple plane graph with a kissing reflection group with connected limit set is well defined and surjective. To verify that this is indeed injective, we remark that if
$2$-connected simple plane graph with a kissing reflection group with connected limit set is well defined and surjective. To verify that this is indeed injective, we remark that if ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {P}'$ are two circle packings associated to two contact graphs that are nonisomorphic as plane graphs, then the closures of the fundamental domains
$\mathcal {P}'$ are two circle packings associated to two contact graphs that are nonisomorphic as plane graphs, then the closures of the fundamental domains ![]() $\overline {\Pi }$ and
$\overline {\Pi }$ and ![]() $\overline {\Pi '}$ are not homeomorphic. Note that the touching patterns of different components of
$\overline {\Pi '}$ are not homeomorphic. Note that the touching patterns of different components of ![]() $\Pi $ or
$\Pi $ or ![]() $\Pi '$ completely determine the structures of the pairing cylinders of the associated
$\Pi '$ completely determine the structures of the pairing cylinders of the associated ![]() $3$-manifolds at the cusps (See [Reference Marden25, §2.6]). This means that the conformal boundaries of
$3$-manifolds at the cusps (See [Reference Marden25, §2.6]). This means that the conformal boundaries of ![]() $\mathbb {H}^3/\widetilde {G}_{\mathcal {P}}$ and
$\mathbb {H}^3/\widetilde {G}_{\mathcal {P}}$ and ![]() $\mathbb {H}^3/\widetilde {G}_{\mathcal {P}'}$ with the pairing cylinder structures are not the same. Thus, the two kissing reflection groups
$\mathbb {H}^3/\widetilde {G}_{\mathcal {P}'}$ with the pairing cylinder structures are not the same. Thus, the two kissing reflection groups ![]() $G_{\mathcal {P}}$ and
$G_{\mathcal {P}}$ and ![]() $G_{\mathcal {P}'}$ are not quasiconformally isomorphic.
$G_{\mathcal {P}'}$ are not quasiconformally isomorphic.
3.2 Acylindrical kissing reflection groups
Recall that ![]() $\widetilde {G}_{\mathcal {P}}$ is the index
$\widetilde {G}_{\mathcal {P}}$ is the index ![]() $2$ subgroup of
$2$ subgroup of ![]() $G_{\mathcal {P}}$ consisting of orientation-preserving elements. We set
$G_{\mathcal {P}}$ consisting of orientation-preserving elements. We set
to be the associated ![]() $3$-manifold with boundary. Note that the boundary
$3$-manifold with boundary. Note that the boundary
is a finite union of punctured spheres. Each punctured sphere corresponds to the double of a component of ![]() $\Pi $.
$\Pi $.
Let F be a face of ![]() $\Gamma $. Then it corresponds to a component
$\Gamma $. Then it corresponds to a component ![]() $\Pi _F$ of
$\Pi _F$ of ![]() $\Pi $, which also corresponds to a component
$\Pi $, which also corresponds to a component ![]() $R_F$ of
$R_F$ of ![]() $\partial \mathcal {M}(G_{\mathcal {P}})$. More precisely, there is a unique component
$\partial \mathcal {M}(G_{\mathcal {P}})$. More precisely, there is a unique component ![]() $\Omega _F$ of
$\Omega _F$ of ![]() $\Omega (G_{\mathcal {P}})$ containing
$\Omega (G_{\mathcal {P}})$ containing ![]() $\Pi _F$ and
$\Pi _F$ and
where ![]() $\text {stab}(\Omega _F)$ is the stabiliser of
$\text {stab}(\Omega _F)$ is the stabiliser of ![]() $\Omega _F$ in
$\Omega _F$ in ![]() $\widetilde {G}_{\mathcal {P}}$.
$\widetilde {G}_{\mathcal {P}}$.
A compact ![]() $3$-manifold
$3$-manifold ![]() $M^3$ with boundary is called acylindrical if
$M^3$ with boundary is called acylindrical if ![]() $M^3$ contains no essential cylinders and is boundary incompressible. Here an essential cylinder C in
$M^3$ contains no essential cylinders and is boundary incompressible. Here an essential cylinder C in ![]() $M^3$ is a closed cylinder C such that
$M^3$ is a closed cylinder C such that ![]() $C\cap \partial M^3 = \partial C$, the boundary components of C are not homotopic to points in
$C\cap \partial M^3 = \partial C$, the boundary components of C are not homotopic to points in ![]() $\partial M^3$ and C is not homotopic into
$\partial M^3$ and C is not homotopic into ![]() $\partial M^3$.
$\partial M^3$. ![]() $M^3$ is said to be boundary incompressible if the inclusion
$M^3$ is said to be boundary incompressible if the inclusion ![]() is injective for every component R of
is injective for every component R of ![]() $\partial M^3$. (We refer the reader to [Reference Marden26, §3.7, §4.7] for detailed discussions.)
$\partial M^3$. (We refer the reader to [Reference Marden26, §3.7, §4.7] for detailed discussions.)
Our manifold ![]() $\mathcal {M}(G_{\mathcal {P}})$ is not a compact manifold as there are parabolic elements (cusps) in
$\mathcal {M}(G_{\mathcal {P}})$ is not a compact manifold as there are parabolic elements (cusps) in ![]() $\widetilde {G}_{\mathcal {P}}$. Thurston [Reference Thurston45] introduced the notion of pared manifolds to work with Kleinian groups with parabolic elements. In our setting, we can also use an equivalent definition without introducing pared manifolds. To start the definition, we note that for a geometrically finite group, associated with the conjugacy class of a rank 1 cusp, there is a pair of punctures
$\widetilde {G}_{\mathcal {P}}$. Thurston [Reference Thurston45] introduced the notion of pared manifolds to work with Kleinian groups with parabolic elements. In our setting, we can also use an equivalent definition without introducing pared manifolds. To start the definition, we note that for a geometrically finite group, associated with the conjugacy class of a rank 1 cusp, there is a pair of punctures ![]() $p_1, p_2$ on
$p_1, p_2$ on ![]() $\partial M^3$. If
$\partial M^3$. If ![]() $c_1, c_2$ are small circles in
$c_1, c_2$ are small circles in ![]() $\partial M$ retractable to
$\partial M$ retractable to ![]() $p_1, p_2$, then there is a pairing cylinder C in
$p_1, p_2$, then there is a pairing cylinder C in ![]() $M^3$, which is a cylinder bounded by
$M^3$, which is a cylinder bounded by ![]() $c_1$ and
$c_1$ and ![]() $c_2$ (see [Reference Marden25, §2.6], [Reference Marden26, p. 125]).
$c_2$ (see [Reference Marden25, §2.6], [Reference Marden26, p. 125]).
Definition 3.5. A kissing reflection group ![]() $G_{\mathcal {P}}$ is said to be acylindrical if
$G_{\mathcal {P}}$ is said to be acylindrical if ![]() $\mathcal {M}(G_{\mathcal {P}})$ is boundary incompressible and every essential cylinder is homotopic to a pairing cylinder.
$\mathcal {M}(G_{\mathcal {P}})$ is boundary incompressible and every essential cylinder is homotopic to a pairing cylinder.
Note that ![]() $\mathcal {M}(G_{\mathcal {P}})$ is boundary incompressible if and only if each component of
$\mathcal {M}(G_{\mathcal {P}})$ is boundary incompressible if and only if each component of ![]() $\Omega (G_{\mathcal {P}})$ is simply connected if and only if the limit set
$\Omega (G_{\mathcal {P}})$ is simply connected if and only if the limit set ![]() $\Lambda (G_{\mathcal {P}})$ is connected. We also note that the acylindrical condition is a quasiconformal invariant and hence does not depend on the choice of the circle packing
$\Lambda (G_{\mathcal {P}})$ is connected. We also note that the acylindrical condition is a quasiconformal invariant and hence does not depend on the choice of the circle packing ![]() $\mathcal {P}$ realising a simple connected plane graph
$\mathcal {P}$ realising a simple connected plane graph ![]() $\Gamma $. In the remainder of this section, we shall prove the following characterisation of acylindrical kissing Kleinian reflection groups.
$\Gamma $. In the remainder of this section, we shall prove the following characterisation of acylindrical kissing Kleinian reflection groups.
Proposition 3.6. The kissing reflection group ![]() $G_{\mathcal {P}}$ is acylindrical if and only if the contact graph
$G_{\mathcal {P}}$ is acylindrical if and only if the contact graph ![]() $\Gamma $ of
$\Gamma $ of ![]() $\mathcal {P}$ is
$\mathcal {P}$ is ![]() $3$-connected.
$3$-connected.
This proposition will be proved after the following lemmas. Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph and
$2$-connected simple plane graph and ![]() $\mathcal {P} = \{C_1,\ldots , C_n\}$ be a realisation of
$\mathcal {P} = \{C_1,\ldots , C_n\}$ be a realisation of ![]() $\Gamma $. Let
$\Gamma $. Let ![]() $G_{\mathcal {P}}$ be the kissing reflection group, with generators
$G_{\mathcal {P}}$ be the kissing reflection group, with generators ![]() $g_1,\ldots , g_n$ given by reflections along
$g_1,\ldots , g_n$ given by reflections along ![]() $C_1,\ldots , C_n$. Note that a face F of
$C_1,\ldots , C_n$. Note that a face F of ![]() $\Gamma $ corresponds to a component
$\Gamma $ corresponds to a component ![]() $R_F$ of
$R_F$ of ![]() $\partial \mathcal {M}(G_{\mathcal {P}})$.
$\partial \mathcal {M}(G_{\mathcal {P}})$.
Any two nonadjacent vertices ![]() $v, w$ of the face F give rise to an essential simple closed curve
$v, w$ of the face F give rise to an essential simple closed curve ![]() $\widetilde {\gamma }^F_{vw}$ on
$\widetilde {\gamma }^F_{vw}$ on ![]() $R_F$ (a simple closed curve on a surface is essential if it is not homotopic to a point or a puncture). More precisely, let
$R_F$ (a simple closed curve on a surface is essential if it is not homotopic to a point or a puncture). More precisely, let ![]() $g_v, g_w$ be the reflections associated to the two vertices; then
$g_v, g_w$ be the reflections associated to the two vertices; then ![]() $g_vg_w \in \text {stab}(\Omega _F)$ is a loxodromic element under the uniformisation of
$g_vg_w \in \text {stab}(\Omega _F)$ is a loxodromic element under the uniformisation of ![]() $R_F$ which gives the simple closed curve
$R_F$ which gives the simple closed curve ![]() $\widetilde {\gamma }^F_{vw}$ on
$\widetilde {\gamma }^F_{vw}$ on ![]() $R_F$. Note that
$R_F$. Note that ![]() $g_vg_w$ itself may not be loxodromic as the vertices
$g_vg_w$ itself may not be loxodromic as the vertices ![]() $v,w$ may be adjacent in some other faces. If this is the case, then we have an accidental parabolic element (see [Reference Marden26, p. 198, Section 3, Problem 17]).
$v,w$ may be adjacent in some other faces. If this is the case, then we have an accidental parabolic element (see [Reference Marden26, p. 198, Section 3, Problem 17]).
We first prove the following graph-theoretic lemma.
Lemma 3.7. Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph. If
$2$-connected simple plane graph. If ![]() $\Gamma $ is not
$\Gamma $ is not ![]() $3$-connected, then there exist two vertices
$3$-connected, then there exist two vertices ![]() $v, w$ so that
$v, w$ so that ![]() $v, w$ lie on the intersection of the boundaries of two faces
$v, w$ lie on the intersection of the boundaries of two faces ![]() $F_1$ and
$F_1$ and ![]() $F_2$. Moreover, they are nonadjacent for at least one of the two faces.
$F_2$. Moreover, they are nonadjacent for at least one of the two faces.
Proof. As ![]() $\Gamma $ is not
$\Gamma $ is not ![]() $3$-connected, there exist two vertices
$3$-connected, there exist two vertices ![]() $v, w$ so that
$v, w$ so that ![]() $\Gamma \setminus \{v, w\}$ is disconnected. Let
$\Gamma \setminus \{v, w\}$ is disconnected. Let ![]() $F_1,\ldots , F_k$ be the list of faces that contain v as a vertex. Since
$F_1,\ldots , F_k$ be the list of faces that contain v as a vertex. Since ![]() $\Gamma $ is plane, we may assume that the faces
$\Gamma $ is plane, we may assume that the faces ![]() $F_i$ are ordered around v counterclockwise. Since
$F_i$ are ordered around v counterclockwise. Since ![]() $\Gamma $ is plane and
$\Gamma $ is plane and ![]() $2$-connected, each face
$2$-connected, each face ![]() $F_i$ is a Jordan domain. Let
$F_i$ is a Jordan domain. Let ![]() $v_{i,0} = v, v_{i,1},\ldots , v_{i, j_i}$ be the vertices of
$v_{i,0} = v, v_{i,1},\ldots , v_{i, j_i}$ be the vertices of ![]() $F_i$ ordered counterclockwise. Since the faces
$F_i$ ordered counterclockwise. Since the faces ![]() $F_i$ are ordered counterclockwise, we have that
$F_i$ are ordered counterclockwise, we have that ![]() $v_{i,j_i} = v_{i+1, 1}$. We remark that there might be additional identifications. Then
$v_{i,j_i} = v_{i+1, 1}$. We remark that there might be additional identifications. Then
form a (potentially non-simple) cycle C (see Figure 3.2). Since ![]() $\Gamma $ is
$\Gamma $ is ![]() $2$-connected,
$2$-connected, ![]() $\Gamma \setminus \{w\}$ is connected. Thus, in particular, any vertex p is connected to
$\Gamma \setminus \{w\}$ is connected. Thus, in particular, any vertex p is connected to ![]() $C\setminus \{w\}$ in
$C\setminus \{w\}$ in ![]() $\Gamma \setminus \{w\}$. Thus, if
$\Gamma \setminus \{w\}$. Thus, if ![]() $w \notin C$ or w only appears once in C, then
$w \notin C$ or w only appears once in C, then ![]() $C\setminus \{w\}$ is connected. This would imply that
$C\setminus \{w\}$ is connected. This would imply that ![]() $\Gamma \setminus \{v,w\}$ is connected, which is a contradiction. Therefore, w must appear at least twice in the cycle C. Since each face is a Jordan domain, w must appear on the boundaries of at least two faces
$\Gamma \setminus \{v,w\}$ is connected, which is a contradiction. Therefore, w must appear at least twice in the cycle C. Since each face is a Jordan domain, w must appear on the boundaries of at least two faces ![]() $F_{i_1}$ and
$F_{i_1}$ and ![]() $F_{i_2}$.
$F_{i_2}$.

Figure 3.2 A schematic of the potentially non-simple cycle around v.
Since ![]() $\Gamma $ is simple, w is adjacent to v in at most two faces, in which case
$\Gamma $ is simple, w is adjacent to v in at most two faces, in which case ![]() $w = v_{i,j_i} = v_{i+1,1}$; that is, it contributes to only one point in C. Therefore, there exists a face on which w is not adjacent to v. This proves the lemma.
$w = v_{i,j_i} = v_{i+1,1}$; that is, it contributes to only one point in C. Therefore, there exists a face on which w is not adjacent to v. This proves the lemma.
We can now prove one direction of Proposition 3.6.
Lemma 3.8. If ![]() $G_{\mathcal {P}}$ is acylindrical, then
$G_{\mathcal {P}}$ is acylindrical, then ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$-connected.
$3$-connected.
Proof. Note that ![]() $\Gamma $ must be
$\Gamma $ must be ![]() $2$-connected as
$2$-connected as ![]() $\Lambda (G_{\mathcal {P}})$ is connected (by the boundary incompressibility condition). We will prove the contrapositive and assume that
$\Lambda (G_{\mathcal {P}})$ is connected (by the boundary incompressibility condition). We will prove the contrapositive and assume that ![]() $\Gamma $ is not
$\Gamma $ is not ![]() $3$-connected. Let
$3$-connected. Let ![]() $v,w$ be the two vertices given by Lemma 3.7. There are two cases.
$v,w$ be the two vertices given by Lemma 3.7. There are two cases.
If ![]() $v, w$ are nonadjacent vertices in two faces
$v, w$ are nonadjacent vertices in two faces ![]() $F_1, F_2$, then
$F_1, F_2$, then ![]() $g_vg_w$ gives a pair of essential simple closed curves on
$g_vg_w$ gives a pair of essential simple closed curves on ![]() $R_{F_1}$ and
$R_{F_1}$ and ![]() $R_{F_2}$ in
$R_{F_2}$ in ![]() $\partial \mathcal {M}(G_{\mathcal {P}})$. This pair bounds an essential cylinder (see the Cylinder Theorem in [Reference Marden26, §3.7]), which is not homotopic to a pairing cylinder of two punctures (see
$\partial \mathcal {M}(G_{\mathcal {P}})$. This pair bounds an essential cylinder (see the Cylinder Theorem in [Reference Marden26, §3.7]), which is not homotopic to a pairing cylinder of two punctures (see ![]() $g_Cg_{C''}$ in Figure 3.4).
$g_Cg_{C''}$ in Figure 3.4).

Figure 3.3 The limit set of a kissing reflection group G with a ![]() $3$-connected contact graph.
$3$-connected contact graph.
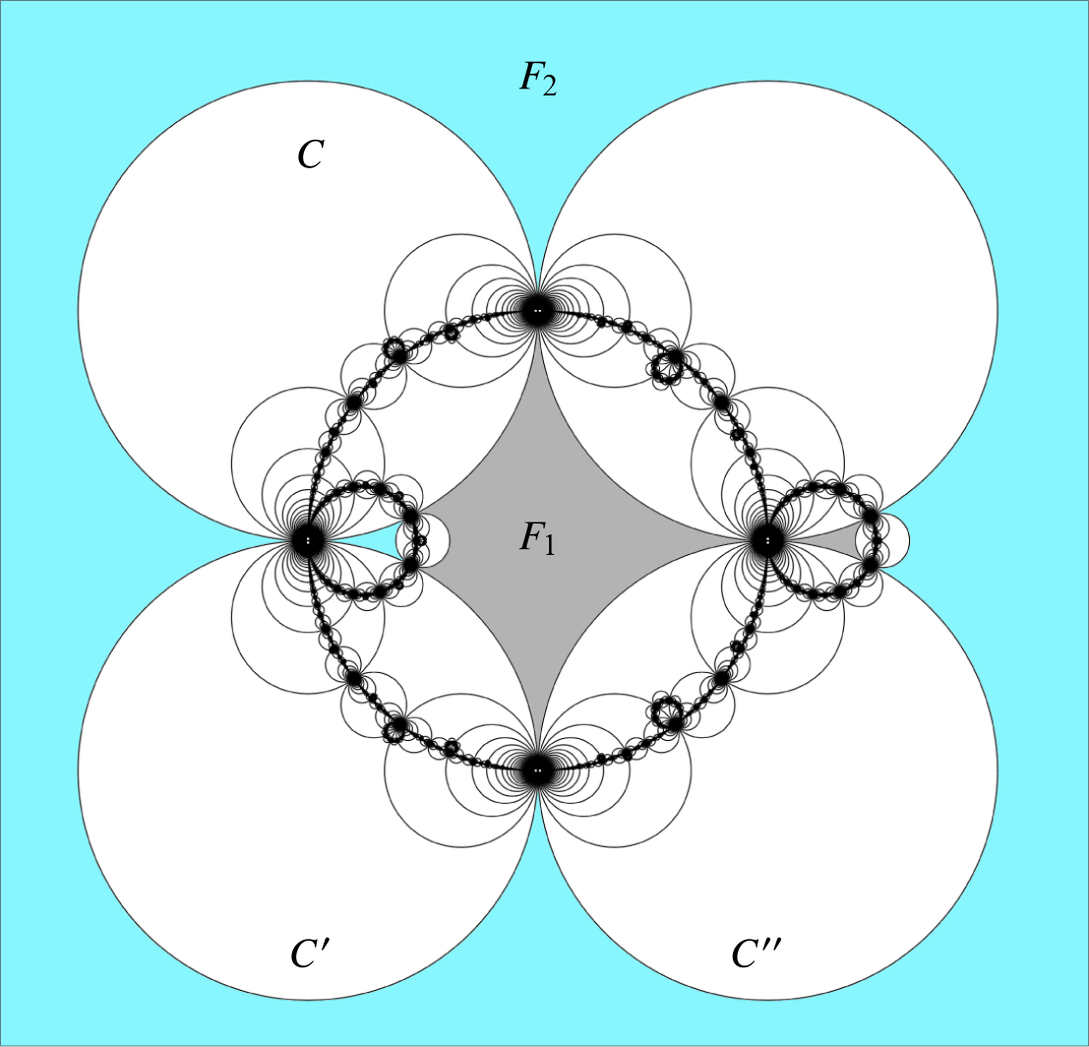
Figure 3.4 The limit set of a kissing reflection group G with Hamiltonian but non-![]() $3$-connected contact graph. The unique Hamiltonian cycle of the associated contact graph
$3$-connected contact graph. The unique Hamiltonian cycle of the associated contact graph ![]() $\Gamma $ divides the fundamental domain
$\Gamma $ divides the fundamental domain ![]() $\Pi (G)$ into two parts
$\Pi (G)$ into two parts ![]() $\Pi ^\pm $, which are shaded in grey and blue. With appropriate markings, G is the mating of two copies of the group H shown in Figure 3.6.
$\Pi ^\pm $, which are shaded in grey and blue. With appropriate markings, G is the mating of two copies of the group H shown in Figure 3.6.
If ![]() $v, w$ are nonadjacent vertices in
$v, w$ are nonadjacent vertices in ![]() $F_1$ but adjacent vertices in
$F_1$ but adjacent vertices in ![]() $F_2$, then
$F_2$, then ![]() $g_vg_w$ corresponds to an essential simple closed curve in
$g_vg_w$ corresponds to an essential simple closed curve in ![]() $R_{F_1}$ and a simple closed curve homotopic to a puncture in
$R_{F_1}$ and a simple closed curve homotopic to a puncture in ![]() $R_{F_2}$. Then
$R_{F_2}$. Then ![]() $g_vg_w$ is an accidental parabolic and the two curves bound an essential cylinder which is not homotopic to a pairing cylinder (see
$g_vg_w$ is an accidental parabolic and the two curves bound an essential cylinder which is not homotopic to a pairing cylinder (see ![]() $g_Cg_{C'}$ in Figure 3.4).
$g_Cg_{C'}$ in Figure 3.4).
Therefore, in either case, ![]() $G_{\mathcal {P}}$ is cylindrical.
$G_{\mathcal {P}}$ is cylindrical.
Gasket limit set
Recall that a closed set ![]() $\Lambda $ is a round gasket if
$\Lambda $ is a round gasket if
•
 $\Lambda $ is the closure of some infinite circle packing; and
$\Lambda $ is the closure of some infinite circle packing; and• the complement of
 $\Lambda $ is a union of round disks which is dense in
$\Lambda $ is a union of round disks which is dense in  $\widehat {\mathbb {C}}$.
$\widehat {\mathbb {C}}$.
We call a homeomorphic copy of a round gasket a gasket. See Section 2 for our definition of infinite circle packings.
If ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$-connected, then
$3$-connected, then ![]() $\Gamma $ is a polyhedral graph. Let
$\Gamma $ is a polyhedral graph. Let ![]() $\Gamma ^{\vee }$ be the planar dual of
$\Gamma ^{\vee }$ be the planar dual of ![]() $\Gamma $. Then Theorem 2.2 gives a (unique) pair of circle packings
$\Gamma $. Then Theorem 2.2 gives a (unique) pair of circle packings ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {P}^{\vee }$ whose contact graphs are isomorphic to
$\mathcal {P}^{\vee }$ whose contact graphs are isomorphic to ![]() $\Gamma $ and
$\Gamma $ and ![]() $\Gamma ^{\vee }$ (respectively) as plane graphs such that
$\Gamma ^{\vee }$ (respectively) as plane graphs such that ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {P}^{\vee }$ intersect orthogonally at their points of tangency (see Figure 3.3). Let
$\mathcal {P}^{\vee }$ intersect orthogonally at their points of tangency (see Figure 3.3). Let ![]() $G_{\mathcal {P}}$ be the kissing reflection group associated with
$G_{\mathcal {P}}$ be the kissing reflection group associated with ![]() $\mathcal {P}$. Since the circle packing
$\mathcal {P}$. Since the circle packing ![]() $\mathcal {P}^{\vee }$ is dual to
$\mathcal {P}^{\vee }$ is dual to ![]() $\mathcal {P}$, we have that
$\mathcal {P}$, we have that
 $$ \begin{align*}\bigcup_{g\in G_{\mathcal{P}}} \bigcup_{C\in \mathcal{P}^{\vee}} g\cdot C \end{align*} $$
$$ \begin{align*}\bigcup_{g\in G_{\mathcal{P}}} \bigcup_{C\in \mathcal{P}^{\vee}} g\cdot C \end{align*} $$is an infinite circle packing and the limit set is the closure
 $$ \begin{align*}\Lambda(G_{\mathcal{P}}) = \overline{\bigcup_{g\in G_{\mathcal{P}}} \bigcup_{C\in \mathcal{P}^{\vee}} g\cdot C}. \end{align*} $$
$$ \begin{align*}\Lambda(G_{\mathcal{P}}) = \overline{\bigcup_{g\in G_{\mathcal{P}}} \bigcup_{C\in \mathcal{P}^{\vee}} g\cdot C}. \end{align*} $$Since ![]() $\Lambda (G_{\mathcal {P}})$ is nowhere dense and the complement is a union of round disks, we conclude that
$\Lambda (G_{\mathcal {P}})$ is nowhere dense and the complement is a union of round disks, we conclude that ![]() $\Lambda (G_{\mathcal {P}})$ is a round gasket.
$\Lambda (G_{\mathcal {P}})$ is a round gasket.
Note that each component of ![]() $\Omega (G_{\mathcal {P}})$ is of the form
$\Omega (G_{\mathcal {P}})$ is of the form ![]() $g\cdot D$ where
$g\cdot D$ where ![]() $g\in G_{\mathcal {P}}$ and D is a disk in the dual circle packing
$g\in G_{\mathcal {P}}$ and D is a disk in the dual circle packing ![]() $\mathcal {P}^{\vee }$. By induction, we have the following.
$\mathcal {P}^{\vee }$. By induction, we have the following.
Lemma 3.9. If ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$-connected, then the closure of any two different components of
$3$-connected, then the closure of any two different components of ![]() $\Omega (G_{\mathcal {P}})$ only intersect at cusps.
$\Omega (G_{\mathcal {P}})$ only intersect at cusps.
We have the following characterisation of gasket limit set for kissing reflection groups.
Proposition 3.10. Let ![]() $\Gamma $ be a simple plane graph; then
$\Gamma $ be a simple plane graph; then ![]() $\Lambda (G_{\mathcal {P}})$ is a gasket if and only if
$\Lambda (G_{\mathcal {P}})$ is a gasket if and only if ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$-connected.
$3$-connected.
Proof. Indeed, from the above discussion, if ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$ connected, then
$3$ connected, then ![]() $\Lambda (G_{\mathcal {P}})$ is a gasket.
$\Lambda (G_{\mathcal {P}})$ is a gasket.
Conversely, if ![]() $\Gamma $ is not
$\Gamma $ is not ![]() $2$-connected, then
$2$-connected, then ![]() $\Lambda (G_{\mathcal {P}})$ is disconnected by Proposition 3.4, so it is not a gasket. On the other hand, if
$\Lambda (G_{\mathcal {P}})$ is disconnected by Proposition 3.4, so it is not a gasket. On the other hand, if ![]() $\Gamma $ is
$\Gamma $ is ![]() $2$-connected but not
$2$-connected but not ![]() $3$-connected, by Lemma 3.7 we have two vertices
$3$-connected, by Lemma 3.7 we have two vertices ![]() $v, w$ so that
$v, w$ so that ![]() $v,w$ lie on the intersection of the boundaries of two faces
$v,w$ lie on the intersection of the boundaries of two faces ![]() $F_1$ and
$F_1$ and ![]() $F_2$. If
$F_2$. If ![]() $v, w$ are nonadjacent vertices in both
$v, w$ are nonadjacent vertices in both ![]() $F_1$ and
$F_1$ and ![]() $F_2$, then the corresponding components
$F_2$, then the corresponding components ![]() $\Omega _{F_1}$ and
$\Omega _{F_1}$ and ![]() $\Omega _{F_2}$ touch at two points corresponding to the two fixed points of the loxodromic element
$\Omega _{F_2}$ touch at two points corresponding to the two fixed points of the loxodromic element ![]() $g_vg_w$ (see
$g_vg_w$ (see ![]() $g_Cg_{C''}$ in Figure 3.4). Thus,
$g_Cg_{C''}$ in Figure 3.4). Thus, ![]() $\Lambda (G_{\mathcal {P}})$ is not a gasket. If
$\Lambda (G_{\mathcal {P}})$ is not a gasket. If ![]() $v, w$ are nonadjacent vertices in
$v, w$ are nonadjacent vertices in ![]() $F_1$ but adjacent vertices in
$F_1$ but adjacent vertices in ![]() $F_2$, then
$F_2$, then ![]() $g_vg_w$ gives an accidental parabolic element. The corresponding component
$g_vg_w$ gives an accidental parabolic element. The corresponding component ![]() $\Omega _{F_1}$ is not a Jordan domain as the unique fixed point of the parabolic element
$\Omega _{F_1}$ is not a Jordan domain as the unique fixed point of the parabolic element ![]() $g_vg_w$ corresponds to two points on the ideal boundary of
$g_vg_w$ corresponds to two points on the ideal boundary of ![]() $\Omega _{F_1}$ (see
$\Omega _{F_1}$ (see ![]() $g_Cg_{C'}$ in Figure 3.4). Therefore,
$g_Cg_{C'}$ in Figure 3.4). Therefore, ![]() $\Lambda (G_{\mathcal {P}})$ is not a gasket.
$\Lambda (G_{\mathcal {P}})$ is not a gasket.
In the course of the proof, we have actually derived the following characterisation which is worth mentioning.
Proposition 3.11. Let ![]() $\mathcal {P}$ be a circle packing whose contact graph
$\mathcal {P}$ be a circle packing whose contact graph ![]() $\Gamma $ is not
$\Gamma $ is not ![]() $3$-connected and
$3$-connected and ![]() $G_{\mathcal {P}}$ be the associated kissing reflection group; then either
$G_{\mathcal {P}}$ be the associated kissing reflection group; then either
• there exists a component of
 $\Omega (G_{\mathcal {P}})$ which is not a Jordan domain; or
$\Omega (G_{\mathcal {P}})$ which is not a Jordan domain; or• there exist two components of
 $\Omega (G_{\mathcal {P}})$ whose closures touch at least at two points.
$\Omega (G_{\mathcal {P}})$ whose closures touch at least at two points.
We are now able to prove the other direction of Proposition 3.6.
Lemma 3.12. If ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$-connected, then
$3$-connected, then ![]() $G_{\mathcal {P}}$ is acylindrical.
$G_{\mathcal {P}}$ is acylindrical.
Proof. Since ![]() $\Gamma $ is
$\Gamma $ is ![]() $3$-connected, it follows that the closures of any two different components of
$3$-connected, it follows that the closures of any two different components of ![]() $\Omega (G_{\mathcal {P}})$ intersect only at cusps. This means that there are no essential cylinder other than the pairing cylinders of the rank one cusps. So
$\Omega (G_{\mathcal {P}})$ intersect only at cusps. This means that there are no essential cylinder other than the pairing cylinders of the rank one cusps. So ![]() $G_{\mathcal {P}}$ is acylindrical.
$G_{\mathcal {P}}$ is acylindrical.
We remark that the unique configuration of pairs of circle packings given in Theorem 2.2 gives a kissing reflection group with totally geodesic boundary. This unique point in the deformation space of acylindrical manifolds is guaranteed by a theorem of McMullen [Reference McMullen28].
3.3 Deformation spaces of kissing reflection groups
Throughout this section, we will use bold symbols, such as ![]() $\mathbf {G}, \mathbf {G}_\Gamma $, to represent the base point for the corresponding deformation spaces. We use regular symbols G to represent the image of a representation in the deformation spaces. If the group is a kissing reflection group, we also use
$\mathbf {G}, \mathbf {G}_\Gamma $, to represent the base point for the corresponding deformation spaces. We use regular symbols G to represent the image of a representation in the deformation spaces. If the group is a kissing reflection group, we also use ![]() $G_{\mathcal {P}}$ if we want to emphasise the corresponding circle packing
$G_{\mathcal {P}}$ if we want to emphasise the corresponding circle packing ![]() $\mathcal {P}$.
$\mathcal {P}$.
Definition of  $\textrm {AH}(\mathbf {G})$
$\textrm {AH}(\mathbf {G})$
Let ![]() $\mathbf {G}$ be a finitely generated discrete subgroup of
$\mathbf {G}$ be a finitely generated discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$. A representation (that is, a group homomorphism)
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$. A representation (that is, a group homomorphism)  $\xi : \mathbf {G} \longrightarrow \textrm {Aut}^\pm (\widehat {\mathbb {C}})$ is said to be weakly type-preserving
$\xi : \mathbf {G} \longrightarrow \textrm {Aut}^\pm (\widehat {\mathbb {C}})$ is said to be weakly type-preserving
1. if
 $\xi (g) \in \textrm {Aut}^+(\widehat {\mathbb {C}})$ if and only if
$\xi (g) \in \textrm {Aut}^+(\widehat {\mathbb {C}})$ if and only if  $g\in \textrm {Aut}^+(\widehat {\mathbb {C}})$ and
$g\in \textrm {Aut}^+(\widehat {\mathbb {C}})$ and2. if
 $g \in \textrm {Aut}^+(\widehat {\mathbb {C}})$, then
$g \in \textrm {Aut}^+(\widehat {\mathbb {C}})$, then  $\xi (g)$ is parabolic whenever g is parabolic.
$\xi (g)$ is parabolic whenever g is parabolic.
Note that a weakly type-preserving representation may send a loxodromic element to a parabolic one.
Definition 3.13. Let ![]() $\mathbf {G}$ be a finitely generated discrete subgroup of
$\mathbf {G}$ be a finitely generated discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$.
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$.
 $$ \begin{align*} \textrm{AH}(\mathbf{G}) &:= \lbrace\xi: \mathbf{G}\longrightarrow G\ \textrm{is a weakly type-preserving isomorphism to} \\ & \textrm{a discrete subgroup}\ G\ \textrm{of}\ \textrm{Aut}^\pm(\widehat{\mathbb{C}})\rbrace / \sim,\; \end{align*} $$
$$ \begin{align*} \textrm{AH}(\mathbf{G}) &:= \lbrace\xi: \mathbf{G}\longrightarrow G\ \textrm{is a weakly type-preserving isomorphism to} \\ & \textrm{a discrete subgroup}\ G\ \textrm{of}\ \textrm{Aut}^\pm(\widehat{\mathbb{C}})\rbrace / \sim,\; \end{align*} $$where ![]() $\xi _1\sim \xi _2$ if there exists a Möbius transformation M such that
$\xi _1\sim \xi _2$ if there exists a Möbius transformation M such that
![]() $\textrm {AH}(\mathbf {G})$ inherits the quotient topology of algebraic convergence. Indeed, we say that a sequence of weakly type-preserving representations
$\textrm {AH}(\mathbf {G})$ inherits the quotient topology of algebraic convergence. Indeed, we say that a sequence of weakly type-preserving representations ![]() $\{\xi _n\}$ converges to
$\{\xi _n\}$ converges to ![]() $\xi $ algebraically if
$\xi $ algebraically if ![]() $\{\xi _n(g_i)\}$ converges to
$\{\xi _n(g_i)\}$ converges to ![]() $\xi (g_i)$ as elements of
$\xi (g_i)$ as elements of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ for (any) finite generating set
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ for (any) finite generating set ![]() $\{g_i\}$.
$\{g_i\}$.
Quasiconformal deformation space of  $\mathbf {G}$
$\mathbf {G}$
Recall that a Kleinian group is said to be geometrically finite if it has a finite-sided fundamental polyhedron. We say a finitely generated discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ is geometrically finite if the index
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ is geometrically finite if the index ![]() $2$ subgroup is geometrically finite.
$2$ subgroup is geometrically finite.
Let ![]() $\mathbf {G}$ be a finitely generated, geometrically finite, discrete subgroup of
$\mathbf {G}$ be a finitely generated, geometrically finite, discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$. A group G is called a quasiconformal deformation of
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$. A group G is called a quasiconformal deformation of ![]() $\mathbf {G}$ if there is a quasiconformal map
$\mathbf {G}$ if there is a quasiconformal map ![]() $F: \widehat {\mathbb {C}} \longrightarrow \widehat {\mathbb {C}}$ that induces an isomorphism
$F: \widehat {\mathbb {C}} \longrightarrow \widehat {\mathbb {C}}$ that induces an isomorphism ![]() $\xi : \mathbf {G} \longrightarrow G$ such that
$\xi : \mathbf {G} \longrightarrow G$ such that ![]() $F \circ g(z) = \xi (g) \circ F(z)$ for all
$F \circ g(z) = \xi (g) \circ F(z)$ for all ![]() $g\in \mathbf {G}$ and
$g\in \mathbf {G}$ and ![]() $z\in \widehat {\mathbb {C}}$. Such a group G is necessarily geometrically finite and discrete. The map F is uniquely determined (up to normalisation) by its Beltrami differential on the domain of discontinuity
$z\in \widehat {\mathbb {C}}$. Such a group G is necessarily geometrically finite and discrete. The map F is uniquely determined (up to normalisation) by its Beltrami differential on the domain of discontinuity ![]() $\Omega (\mathbf {G})$ (See [Reference Marden26, §5.1.2, Theorem 3.13.5]).
$\Omega (\mathbf {G})$ (See [Reference Marden26, §5.1.2, Theorem 3.13.5]).
We define the quasiconformal deformation space of ![]() $\mathbf {G}$ as
$\mathbf {G}$ as
By definition, ![]() $\mathcal {QC}(\mathbf {G}) \subseteq \textrm {AH}(\mathbf {G})$.
$\mathcal {QC}(\mathbf {G}) \subseteq \textrm {AH}(\mathbf {G})$.
Kissing reflection groups
The above discussion is quite general and applies to any Kleinian (reflection) group. In the following, we will specialise to the case of a kissing reflection group.
Recall that different realisations of a fixed marked, connected simple plane graph ![]() $\Gamma $ as circle packings
$\Gamma $ as circle packings ![]() $\mathcal {P}$ give canonically isomorphic kissing reflection groups
$\mathcal {P}$ give canonically isomorphic kissing reflection groups ![]() $G_{\mathcal {P}}$. Thus, the algebraic/quasiconformal deformation spaces of all such
$G_{\mathcal {P}}$. Thus, the algebraic/quasiconformal deformation spaces of all such ![]() $G_{\mathcal {P}}$ can be canonically identified. However, in order to study these deformation spaces, it will be convenient to fix a (marked) circle packing realisation
$G_{\mathcal {P}}$ can be canonically identified. However, in order to study these deformation spaces, it will be convenient to fix a (marked) circle packing realisation ![]() $\mathcal {P}$ of the (marked) graph
$\mathcal {P}$ of the (marked) graph ![]() $\Gamma $ and use the associated kissing reflection group
$\Gamma $ and use the associated kissing reflection group
as the base point. With this choice, we can and will use the notation ![]() $\textrm {AH}(\Gamma )$ and
$\textrm {AH}(\Gamma )$ and ![]() $\mathcal {QC}(\Gamma )$ to denote
$\mathcal {QC}(\Gamma )$ to denote ![]() $\textrm {AH}(\mathbf {G}_\Gamma )$ and
$\textrm {AH}(\mathbf {G}_\Gamma )$ and ![]() $\mathcal {QC}(\mathbf {G}_\Gamma )$, respectively.
$\mathcal {QC}(\mathbf {G}_\Gamma )$, respectively.
Now let ![]() $\Gamma _0$ be a simple plane graph. The goal of this section is to describe the algebraic deformation space
$\Gamma _0$ be a simple plane graph. The goal of this section is to describe the algebraic deformation space ![]() $\textrm {AH}(\Gamma _0)$ and the closure
$\textrm {AH}(\Gamma _0)$ and the closure ![]() $\overline {\mathcal {QC}(\Gamma _0)}$ (of the quasiconformal deformation space) in
$\overline {\mathcal {QC}(\Gamma _0)}$ (of the quasiconformal deformation space) in ![]() $\textrm {AH}(\Gamma _0)$.
$\textrm {AH}(\Gamma _0)$.
In line with the convention introduced above, we choose a circle packing ![]() $\{\mathbf {C}_1,\ldots , \mathbf {C}_n\}$ realising
$\{\mathbf {C}_1,\ldots , \mathbf {C}_n\}$ realising ![]() $\Gamma _0$ and denote the reflection along
$\Gamma _0$ and denote the reflection along ![]() $\mathbf {C}_i$ as
$\mathbf {C}_i$ as ![]() $\rho _i$. Let
$\rho _i$. Let ![]() $\mathbf {G}_{\Gamma _0}$ be the kissing reflection group generated by the reflections
$\mathbf {G}_{\Gamma _0}$ be the kissing reflection group generated by the reflections ![]() $\rho _i$. We remark that since we will be working with deformation spaces for several contact graphs, we use
$\rho _i$. We remark that since we will be working with deformation spaces for several contact graphs, we use ![]() $\mathbf {G}_{\Gamma _0}$ to emphasise that the contact graph is
$\mathbf {G}_{\Gamma _0}$ to emphasise that the contact graph is ![]() $\Gamma _0$.
$\Gamma _0$.
Let G be a discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ and let
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ and let ![]() $\xi : \mathbf {G}_{\Gamma _0}\longrightarrow G$ be a weakly type-preserving isomorphism. Since the union of the circles
$\xi : \mathbf {G}_{\Gamma _0}\longrightarrow G$ be a weakly type-preserving isomorphism. Since the union of the circles ![]() $\mathbf {C}_1,\ldots , \mathbf {C}_n$ is connected, for each
$\mathbf {C}_1,\ldots , \mathbf {C}_n$ is connected, for each ![]() $\rho _i$ there exists
$\rho _i$ there exists ![]() $\rho _j$ so that
$\rho _j$ so that ![]() $\rho _i\circ \rho _j$ is parabolic. This implies that no
$\rho _i\circ \rho _j$ is parabolic. This implies that no ![]() $\xi (\rho _i)$ is the antipodal map. Hence,
$\xi (\rho _i)$ is the antipodal map. Hence, ![]() $\xi (\rho _i)$ is also a circular reflection. Assume that
$\xi (\rho _i)$ is also a circular reflection. Assume that ![]() $\xi (\rho _i)$ is the reflection along some circle
$\xi (\rho _i)$ is the reflection along some circle ![]() $C_i$. If
$C_i$. If ![]() $\rho _i \circ \rho _j$ is parabolic, then
$\rho _i \circ \rho _j$ is parabolic, then ![]() $\xi (\rho _i) \circ \xi (\rho _{j})$ is also parabolic. Thus,
$\xi (\rho _i) \circ \xi (\rho _{j})$ is also parabolic. Thus, ![]() $C_i$ is tangent to
$C_i$ is tangent to ![]() $C_j$ as well. This motivates the following definition.
$C_j$ as well. This motivates the following definition.
Definition 3.14. Let ![]() $\Gamma $ be a simple plane graph with the same number of vertices as
$\Gamma $ be a simple plane graph with the same number of vertices as ![]() $\Gamma _0$. We say that
$\Gamma _0$. We say that ![]() $\Gamma $ abstractly dominates
$\Gamma $ abstractly dominates ![]() $\Gamma _0$, denoted by
$\Gamma _0$, denoted by ![]() $\Gamma \geq _{a} \Gamma _0$, if there exists an embedding
$\Gamma \geq _{a} \Gamma _0$, if there exists an embedding ![]() $\psi : \Gamma _0 \longrightarrow \Gamma $ as abstract graphs (that is, if there exists a graph isomorphism between
$\psi : \Gamma _0 \longrightarrow \Gamma $ as abstract graphs (that is, if there exists a graph isomorphism between ![]() $\Gamma _0$ and a subgraph of
$\Gamma _0$ and a subgraph of ![]() $\Gamma $).
$\Gamma $).
We say that ![]() $\Gamma $ dominates
$\Gamma $ dominates ![]() $\Gamma _0$, denoted by
$\Gamma _0$, denoted by ![]() $\Gamma \geq \Gamma _0$, if there exists an embedding
$\Gamma \geq \Gamma _0$, if there exists an embedding ![]() $\psi : \Gamma _0 \longrightarrow \Gamma $ as plane graphs (that is, if there exists a graph isomorphism between
$\psi : \Gamma _0 \longrightarrow \Gamma $ as plane graphs (that is, if there exists a graph isomorphism between ![]() $\Gamma _0$ and a subgraph of
$\Gamma _0$ and a subgraph of ![]() $\Gamma $ that extends to an orientation-preserving homeomorphism of
$\Gamma $ that extends to an orientation-preserving homeomorphism of ![]() $\widehat {\mathbb {C}}$).
$\widehat {\mathbb {C}}$).
We also define
and
In other words, a simple plane graph ![]() $\Gamma $ abstractly dominates
$\Gamma $ abstractly dominates ![]() $\Gamma _0$ if
$\Gamma _0$ if ![]() $\Gamma $ (as an abstract graph) can be constructed from
$\Gamma $ (as an abstract graph) can be constructed from ![]() $\Gamma _0$ by introducing new edges, and it dominates
$\Gamma _0$ by introducing new edges, and it dominates ![]() $\Gamma _0$ if one can do this while respecting the plane structure.
$\Gamma _0$ if one can do this while respecting the plane structure.
We emphasise that the graph ![]() $\Gamma $ is always assumed to be planar, but the embedding
$\Gamma $ is always assumed to be planar, but the embedding ![]() $\psi $ may not respect the plane structure in
$\psi $ may not respect the plane structure in ![]() $\mathrm {Emb}_a(\Gamma _0)$ (see Figure 3.5). We also remark that an element
$\mathrm {Emb}_a(\Gamma _0)$ (see Figure 3.5). We also remark that an element ![]() $(\Gamma , \psi )$ is identified with
$(\Gamma , \psi )$ is identified with ![]() $(\Gamma ', \psi ')$ in
$(\Gamma ', \psi ')$ in ![]() $\mathrm {Emb}_a(\Gamma _0)$ or
$\mathrm {Emb}_a(\Gamma _0)$ or ![]() $\mathrm {Emb}_p(\Gamma _0)$ if
$\mathrm {Emb}_p(\Gamma _0)$ if ![]() $\psi '\circ \psi ^{-1}$ extends to an isomorphism between
$\psi '\circ \psi ^{-1}$ extends to an isomorphism between ![]() $\Gamma $ and
$\Gamma $ and ![]() $\Gamma '$ as plane graphs.
$\Gamma '$ as plane graphs.

Figure 3.5 The graph on the left abstractly dominates the graph on the right, but no embedding of the right graph into the left graph respects the plane structure.
We have the following lemma.
Lemma 3.15. Let G be a discrete subgroup of  $\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ and let
$\textrm {Aut}^\pm (\widehat {\mathbb {C}})$ and let ![]() $\xi :\mathbf {G}_{\Gamma _0}\longrightarrow G$ be a weakly type-preserving isomorphism. Then the simple plane graph
$\xi :\mathbf {G}_{\Gamma _0}\longrightarrow G$ be a weakly type-preserving isomorphism. Then the simple plane graph ![]() $\Gamma $ associated with G abstractly dominates
$\Gamma $ associated with G abstractly dominates ![]() $\Gamma _0$.
$\Gamma _0$.
Conversely, if ![]() $\Gamma $ is a simple plane graph abstractly dominating
$\Gamma $ is a simple plane graph abstractly dominating ![]() $\Gamma _0$ and G is a kissing reflection group associated with
$\Gamma _0$ and G is a kissing reflection group associated with ![]() $\Gamma $, then there exists a weakly type-preserving isomorphism
$\Gamma $, then there exists a weakly type-preserving isomorphism ![]() $\xi :\mathbf {G}_{\Gamma _0}\longrightarrow G$.
$\xi :\mathbf {G}_{\Gamma _0}\longrightarrow G$.
Proof. Let ![]() $G= \xi (\mathbf {G}_{\Gamma _0})$ be a discrete faithful weakly type-preserving representation, then the reflections
$G= \xi (\mathbf {G}_{\Gamma _0})$ be a discrete faithful weakly type-preserving representation, then the reflections ![]() $\xi (\rho _i)$ along
$\xi (\rho _i)$ along ![]() $C_i$ generate G. If there were a nontangential intersection between some
$C_i$ generate G. If there were a nontangential intersection between some ![]() $C_i$ and
$C_i$ and ![]() $C_j$, it would introduce a new relation between
$C_j$, it would introduce a new relation between ![]() $\xi (\rho _i)$ and
$\xi (\rho _i)$ and ![]() $\xi (\rho _j)$ by discreteness of G (cf. [Reference Vinberg and Shvartsman47, Chapter 5, Subsection 1.1]), which would contradict the assumption that
$\xi (\rho _j)$ by discreteness of G (cf. [Reference Vinberg and Shvartsman47, Chapter 5, Subsection 1.1]), which would contradict the assumption that ![]() $\xi $ is an isomorphism. Similarly, if there were circles
$\xi $ is an isomorphism. Similarly, if there were circles ![]() $C_i, C_j, C_k$ touching at a point, then discreteness would give a new relation among
$C_i, C_j, C_k$ touching at a point, then discreteness would give a new relation among ![]() $\xi (\rho _i)$,
$\xi (\rho _i)$, ![]() $\xi (\rho _j)$ and
$\xi (\rho _j)$ and ![]() $\xi (\rho _k)$, which would again lead to a contradiction. The above observations combined with the discussion preceding Definition 3.14 imply that
$\xi (\rho _k)$, which would again lead to a contradiction. The above observations combined with the discussion preceding Definition 3.14 imply that ![]() $\{C_1,\ldots , C_n\}$ is a circle packing with associated contact graph
$\{C_1,\ldots , C_n\}$ is a circle packing with associated contact graph ![]() $\Gamma $ abstractly dominating
$\Gamma $ abstractly dominating ![]() $\Gamma _0$.
$\Gamma _0$.
Conversely, assume that G is a kissing reflection group associated with a simple plane graph ![]() $\Gamma $ abstractly dominating
$\Gamma $ abstractly dominating ![]() $\Gamma _0$. Let
$\Gamma _0$. Let ![]() $C_i$ be the circle corresponding to
$C_i$ be the circle corresponding to ![]() $\mathbf {C}_i$ under a particular embedding of
$\mathbf {C}_i$ under a particular embedding of ![]() $\Gamma _0$ into
$\Gamma _0$ into ![]() $\Gamma $ (as abstract graphs) and
$\Gamma $ (as abstract graphs) and ![]() $g_i$ be the reflection along
$g_i$ be the reflection along ![]() $C_i$. Defining
$C_i$. Defining ![]() $\xi :\mathbf {G}_{\Gamma _0}\longrightarrow G$ by
$\xi :\mathbf {G}_{\Gamma _0}\longrightarrow G$ by ![]() $\xi (\rho _i) = g_i$, it is easy to check that
$\xi (\rho _i) = g_i$, it is easy to check that ![]() $\xi $ is a weakly type-preserving isomorphism.
$\xi $ is a weakly type-preserving isomorphism.
Note that for kissing reflection groups, the double of the polyhedron bounded by the half-planes associated to the circles ![]() $C_i$ is a fundamental polyhedron for the action of the index two Kleinian group on
$C_i$ is a fundamental polyhedron for the action of the index two Kleinian group on ![]() $\mathbb {H}^3$. Thus, we have the following corollary which is worth mentioning.
$\mathbb {H}^3$. Thus, we have the following corollary which is worth mentioning.
Corollary 3.16. Every group in ![]() $\textrm {AH}(\Gamma _0)$ is geometrically finite.
$\textrm {AH}(\Gamma _0)$ is geometrically finite.
Let ![]() $(\Gamma , \psi ) \in \mathrm {Emb}_p(\Gamma _0)$ (respectively in
$(\Gamma , \psi ) \in \mathrm {Emb}_p(\Gamma _0)$ (respectively in ![]() $\mathrm {Emb}_a(\Gamma _0)$). Let us fix a circle packing
$\mathrm {Emb}_a(\Gamma _0)$). Let us fix a circle packing ![]() $C_{1,\Gamma }, \ldots , C_{n, \Gamma }$ realising
$C_{1,\Gamma }, \ldots , C_{n, \Gamma }$ realising ![]() $\Gamma $, where
$\Gamma $, where ![]() $C_{i,\Gamma }$ corresponds to
$C_{i,\Gamma }$ corresponds to ![]() $\mathbf {C}_i$ under the embedding
$\mathbf {C}_i$ under the embedding ![]() $\psi $ of
$\psi $ of ![]() $\Gamma _0$. Let
$\Gamma _0$. Let ![]() $g_i$ be the associated reflection along
$g_i$ be the associated reflection along ![]() $C_{i, \Gamma }$ and
$C_{i, \Gamma }$ and ![]() $\mathbf {G}_\Gamma = \langle g_1,\ldots , g_{n}\rangle $. Then Lemma 3.15 shows that
$\mathbf {G}_\Gamma = \langle g_1,\ldots , g_{n}\rangle $. Then Lemma 3.15 shows that
 $$ \begin{align*} \xi_{(\Gamma,\psi)}: \mathbf{G}_{\Gamma_0} &\longrightarrow \mathbf{G}_\Gamma\\ \rho_i &\mapsto g_i \end{align*} $$
$$ \begin{align*} \xi_{(\Gamma,\psi)}: \mathbf{G}_{\Gamma_0} &\longrightarrow \mathbf{G}_\Gamma\\ \rho_i &\mapsto g_i \end{align*} $$is a weakly type-preserving isomorphism. Thus, ![]() $\mathcal {QC}(\Gamma )= \mathcal {QC}(\mathbf {G}_\Gamma )$ can be embedded in
$\mathcal {QC}(\Gamma )= \mathcal {QC}(\mathbf {G}_\Gamma )$ can be embedded in ![]() $\textrm {AH}(\Gamma _0)= \textrm {AH}(\mathbf {G}_{\Gamma _0})$. Indeed, if
$\textrm {AH}(\Gamma _0)= \textrm {AH}(\mathbf {G}_{\Gamma _0})$. Indeed, if ![]() $\xi : \mathbf {G}_\Gamma \longrightarrow G$ represents an element in
$\xi : \mathbf {G}_\Gamma \longrightarrow G$ represents an element in ![]() $\mathcal {QC}(\Gamma )$, then
$\mathcal {QC}(\Gamma )$, then
is a weakly type-preserving isomorphism. It can be checked that the map ![]() $\xi \mapsto \xi \circ \xi _{(\Gamma ,\psi )}$ gives an embedding of
$\xi \mapsto \xi \circ \xi _{(\Gamma ,\psi )}$ gives an embedding of ![]() $\mathcal {QC}(\Gamma )$ into
$\mathcal {QC}(\Gamma )$ into ![]() $\textrm {AH}(\Gamma _0)$. We shall identify the space
$\textrm {AH}(\Gamma _0)$. We shall identify the space ![]() $\mathcal {QC}(\Gamma )$ with its image in
$\mathcal {QC}(\Gamma )$ with its image in ![]() $\textrm {AH}(\Gamma _0)$ under this embedding.
$\textrm {AH}(\Gamma _0)$ under this embedding.
 $$ \begin{align*}\textrm{AH}(\Gamma_0) = \bigcup_{(\Gamma, \psi) \in \mathrm{Emb}_a(\Gamma_0)} \mathcal{QC}(\Gamma) \end{align*} $$
$$ \begin{align*}\textrm{AH}(\Gamma_0) = \bigcup_{(\Gamma, \psi) \in \mathrm{Emb}_a(\Gamma_0)} \mathcal{QC}(\Gamma) \end{align*} $$and
 $$ \begin{align*}\overline{\mathcal{QC}(\Gamma_0)} = \bigcup_{(\Gamma, \psi) \in \mathrm{Emb}_p(\Gamma_0)} \mathcal{QC}(\Gamma). \end{align*} $$
$$ \begin{align*}\overline{\mathcal{QC}(\Gamma_0)} = \bigcup_{(\Gamma, \psi) \in \mathrm{Emb}_p(\Gamma_0)} \mathcal{QC}(\Gamma). \end{align*} $$The proof of this proposition will be furnished after a discussion of pinching deformations. Once the connection with pinching deformation is established, the result can be derived from [Reference Ohshika35].
The perspective of pinching deformation
For the general discussion of pinching deformations, let us fix an arbitrary ![]() $2$-connected simple plane graph
$2$-connected simple plane graph ![]() $\Gamma $, a circle packing
$\Gamma $, a circle packing ![]() $\mathcal {P}$ with contact graph isomorphic to
$\mathcal {P}$ with contact graph isomorphic to ![]() $\Gamma $ and the associated kissing reflection group
$\Gamma $ and the associated kissing reflection group ![]() $\mathbf {G}= G_{\mathcal {P}}$, which we think of as the base point of the quasiconformal deformation space
$\mathbf {G}= G_{\mathcal {P}}$, which we think of as the base point of the quasiconformal deformation space ![]() $\mathcal {QC}(\Gamma )$. Since
$\mathcal {QC}(\Gamma )$. Since ![]() $\Gamma $ is the only graph appearing in this discussion (until the proof Proposition 3.17), we omit the subscript ‘
$\Gamma $ is the only graph appearing in this discussion (until the proof Proposition 3.17), we omit the subscript ‘![]() $\Gamma $’ from the base point
$\Gamma $’ from the base point ![]() $\mathbf {G}$.
$\mathbf {G}$.
Let F be a face of ![]() $\Gamma $ and
$\Gamma $ and ![]() $R_F$ be the associated component of
$R_F$ be the associated component of ![]() $\partial \mathcal {M}(\mathbf {G})$. Let
$\partial \mathcal {M}(\mathbf {G})$. Let ![]() $C\in \mathcal {P}$ be a circle on the boundary of
$C\in \mathcal {P}$ be a circle on the boundary of ![]() $\Pi _F$. Then the reflection along C descends to an anti-conformal involution on
$\Pi _F$. Then the reflection along C descends to an anti-conformal involution on ![]() $R_F$, which we shall denote as
$R_F$, which we shall denote as
Note that different choices of the circle descend to the same involution. It is known that for boundary incompressible geometrically finite Kleinian groups, the quasiconformal deformation space is the product of the Teichmüller spaces of the components of the conformal boundary (see [Reference Marden26, Theorem 5.1.3]):
 $$ \begin{align*}\mathcal{QC}(\widetilde{\mathbf{G}}) = \prod_{F \text{ face of } \Gamma} \textrm{Teich} (R_F), \end{align*} $$
$$ \begin{align*}\mathcal{QC}(\widetilde{\mathbf{G}}) = \prod_{F \text{ face of } \Gamma} \textrm{Teich} (R_F), \end{align*} $$where ![]() $\widetilde {\mathbf {G}}$ is the index two subgroup of
$\widetilde {\mathbf {G}}$ is the index two subgroup of ![]() $\mathbf {G}$ consisting of orientation-preserving elements.
$\mathbf {G}$ consisting of orientation-preserving elements.
We denote by ![]() $\textrm {Teich}^{\sigma _F} (R_F) \subseteq \textrm {Teich} (R_F)$ those elements corresponding to
$\textrm {Teich}^{\sigma _F} (R_F) \subseteq \textrm {Teich} (R_F)$ those elements corresponding to ![]() $\sigma _F$-invariant quasiconformal deformations of
$\sigma _F$-invariant quasiconformal deformations of ![]() $R_F$. Then
$R_F$. Then
 $$ \begin{align*}\mathcal{QC}(\mathbf{G}) = \prod_{F \text{ face of } \Gamma} \textrm{Teich}^{\sigma_F} (R_F). \end{align*} $$
$$ \begin{align*}\mathcal{QC}(\mathbf{G}) = \prod_{F \text{ face of } \Gamma} \textrm{Teich}^{\sigma_F} (R_F). \end{align*} $$Indeed, any element in ![]() $\prod _{F \text { face of } \Gamma } \textrm {Teich}^{\sigma _F} (R_F)$ is uniquely determined by the associated Beltrami differential on
$\prod _{F \text { face of } \Gamma } \textrm {Teich}^{\sigma _F} (R_F)$ is uniquely determined by the associated Beltrami differential on ![]() $\Pi _F$, which can be pulled back by
$\Pi _F$, which can be pulled back by ![]() $\mathbf {G}$ to produce a
$\mathbf {G}$ to produce a ![]() $\mathbf {G}$-invariant Beltrami differential on
$\mathbf {G}$-invariant Beltrami differential on ![]() $\widehat {\mathbb {C}}$. Such a Beltrami differential can be uniformised by the measurable Riemann mapping theorem.
$\widehat {\mathbb {C}}$. Such a Beltrami differential can be uniformised by the measurable Riemann mapping theorem.
Recall that ![]() $\Pi _F$ is an ideal polygon. Note that the component of
$\Pi _F$ is an ideal polygon. Note that the component of ![]() $\Omega (\mathbf {G})$ containing
$\Omega (\mathbf {G})$ containing ![]() $\Pi _F$ is simply connected and hence
$\Pi _F$ is simply connected and hence ![]() $\Pi _F$ inherits the hyperbolic metric from the corresponding component of
$\Pi _F$ inherits the hyperbolic metric from the corresponding component of ![]() $\Omega (\mathbf {G})$. Then
$\Omega (\mathbf {G})$. Then ![]() $R_F$ is simply the double of
$R_F$ is simply the double of ![]() $\Pi _F$. We claim that the only
$\Pi _F$. We claim that the only ![]() $\sigma _F$-invariant geodesics are those simple closed curves
$\sigma _F$-invariant geodesics are those simple closed curves ![]() $\widetilde {\gamma }^F_{vw}$ on
$\widetilde {\gamma }^F_{vw}$ on ![]() $R_F$ (see the discussion following Proposition 3.6 for the definition of
$R_F$ (see the discussion following Proposition 3.6 for the definition of ![]() $\widetilde {\gamma }^F_{vw}$), where
$\widetilde {\gamma }^F_{vw}$), where ![]() $v,w$ are two nonadjacent vertices on the boundary of F. Indeed, any
$v,w$ are two nonadjacent vertices on the boundary of F. Indeed, any ![]() $\sigma _F$-invariant geodesic would intersect the boundary of the ideal polygon perpendicularly and the
$\sigma _F$-invariant geodesic would intersect the boundary of the ideal polygon perpendicularly and the ![]() $\widetilde {\gamma }^F_{vw}$ are the only geodesics satisfying this property. We denote the associated geodesic arc in
$\widetilde {\gamma }^F_{vw}$ are the only geodesics satisfying this property. We denote the associated geodesic arc in ![]() $\Pi _F$ by
$\Pi _F$ by ![]() $\gamma ^F_{vw}$.
$\gamma ^F_{vw}$.
We define a multicurve on a surface as a disjoint union of simple closed curves, such that no two components are homotopic. It is said to be weighted if a nonnegative number is assigned to each component. We shall identify two multicurves if they are homotopic to each other.
Let ![]() $\mathcal {T}$ be a triangulation of F obtained by adding new edges connecting the vertices of F. Since each additional edge in this triangulation connects two nonadjacent vertices of F, we can associate a multicurve
$\mathcal {T}$ be a triangulation of F obtained by adding new edges connecting the vertices of F. Since each additional edge in this triangulation connects two nonadjacent vertices of F, we can associate a multicurve  $\widetilde {\alpha }^F_{\mathcal {T}}$ on
$\widetilde {\alpha }^F_{\mathcal {T}}$ on ![]() $R_F$ consisting of all
$R_F$ consisting of all ![]() $\widetilde {\gamma }^F_{vw}$, where
$\widetilde {\gamma }^F_{vw}$, where ![]() $vw$ is a new edge in
$vw$ is a new edge in ![]() $\mathcal {T}$. A marking of the graph
$\mathcal {T}$. A marking of the graph ![]() $\Gamma $ also gives a marking of the multicurve. We use
$\Gamma $ also gives a marking of the multicurve. We use  $\alpha ^F_{\mathcal {T}}$ to denote the multi-arc in the hyperbolic ideal polygon
$\alpha ^F_{\mathcal {T}}$ to denote the multi-arc in the hyperbolic ideal polygon ![]() $\Pi _F$. Since
$\Pi _F$. Since ![]() $\mathcal {T}$ is a triangulation, the multicurve
$\mathcal {T}$ is a triangulation, the multicurve  $\widetilde {\alpha }^F_{\mathcal {T}}$ yields a pants decomposition of the punctured sphere
$\widetilde {\alpha }^F_{\mathcal {T}}$ yields a pants decomposition of the punctured sphere ![]() $R_F$ such that the boundary components of every pair of pants are punctures or simple closed curves in
$R_F$ such that the boundary components of every pair of pants are punctures or simple closed curves in  $\widetilde {\alpha }^F_{\mathcal {T}}$. Thus, the complex structures of these pairs of pants are uniquely determined by the lengths of the marked multicurve
$\widetilde {\alpha }^F_{\mathcal {T}}$. Thus, the complex structures of these pairs of pants are uniquely determined by the lengths of the marked multicurve  $\widetilde {\alpha }^F_{\mathcal {T}}$ (cf. [Reference Imayoshi and Taniguchi15, Theorem 3.5]). Since
$\widetilde {\alpha }^F_{\mathcal {T}}$ (cf. [Reference Imayoshi and Taniguchi15, Theorem 3.5]). Since ![]() $R_F$ is invariant under the anti-conformal involution
$R_F$ is invariant under the anti-conformal involution ![]() $\sigma _F$, the surface
$\sigma _F$, the surface ![]() $R_F$ is uniquely determined by the complex structures of the above pairs of pants and hence by the lengths of the marked multicurve
$R_F$ is uniquely determined by the complex structures of the above pairs of pants and hence by the lengths of the marked multicurve  $\widetilde {\alpha }^F_{\mathcal {T}}$. If F has m sides, then any triangulation of F has
$\widetilde {\alpha }^F_{\mathcal {T}}$. If F has m sides, then any triangulation of F has ![]() $m-3$ additional edges. Thus, we have the analogue of Fenchel–Nielsen coordinates on
$m-3$ additional edges. Thus, we have the analogue of Fenchel–Nielsen coordinates on
by assigning to each element of ![]() $\textrm {Teich}^{\sigma _F} (R_F)$ the lengths of the marked multicurve
$\textrm {Teich}^{\sigma _F} (R_F)$ the lengths of the marked multicurve  $\widetilde {\alpha }^F_{\mathcal {T}}$ (or, equivalently, the lengths of the marked multi-arc
$\widetilde {\alpha }^F_{\mathcal {T}}$ (or, equivalently, the lengths of the marked multi-arc  $\alpha ^F_{\mathcal {T}}$). Note that with these lengths, the multi-arcs and the multicurves become weighted. Note that different triangulations yield different coordinates. We also remark that unlike classical Fenchel–Nielsen coordinates on Teichmüller spaces, Fenchel–Nielsen coordinates on
$\alpha ^F_{\mathcal {T}}$). Note that with these lengths, the multi-arcs and the multicurves become weighted. Note that different triangulations yield different coordinates. We also remark that unlike classical Fenchel–Nielsen coordinates on Teichmüller spaces, Fenchel–Nielsen coordinates on ![]() $\textrm {Teich}^{\sigma _F} (R_F)$ do not contain twist parameters precisely due to the
$\textrm {Teich}^{\sigma _F} (R_F)$ do not contain twist parameters precisely due to the ![]() $\sigma _F-$invariance of quasiconformal deformations (cf. [Reference Imayoshi and Taniguchi15, §3.2]).
$\sigma _F-$invariance of quasiconformal deformations (cf. [Reference Imayoshi and Taniguchi15, §3.2]).
In order to degenerate in ![]() $\textrm {Teich}^{\sigma _F} (R_F)$, the length of some arc
$\textrm {Teich}^{\sigma _F} (R_F)$, the length of some arc ![]() $\gamma ^F_{vw}$ must shrink to
$\gamma ^F_{vw}$ must shrink to ![]() $0$. The above discussion implies that the closure of
$0$. The above discussion implies that the closure of ![]() $\textrm {Teich}^{\sigma _F} (R_F)$ in the Thurston compactification consists only of weighted
$\textrm {Teich}^{\sigma _F} (R_F)$ in the Thurston compactification consists only of weighted ![]() $\sigma _F$-invariant multicurves
$\sigma _F$-invariant multicurves ![]() $\widetilde {\alpha }^F$. If
$\widetilde {\alpha }^F$. If ![]() $S_k \in \textrm {Teich}^{\sigma _F} (R_F)$ converges to a weighted
$S_k \in \textrm {Teich}^{\sigma _F} (R_F)$ converges to a weighted ![]() $\sigma _F$-invariant multicurve
$\sigma _F$-invariant multicurve ![]() $\widetilde {\alpha }^F$, then we say that
$\widetilde {\alpha }^F$, then we say that ![]() $S_k$ is a pinching deformation on
$S_k$ is a pinching deformation on ![]() $\widetilde {\alpha }^F$. More generally, we say that
$\widetilde {\alpha }^F$. More generally, we say that ![]() $G_k \in \mathcal {QC}(\mathbf {G})$ is a pinching deformation on
$G_k \in \mathcal {QC}(\mathbf {G})$ is a pinching deformation on ![]() $\widetilde {\alpha } = \bigcup \widetilde {\alpha }^F$ if for each face F, the conformal boundary associated to F is a pinching deformation on
$\widetilde {\alpha } = \bigcup \widetilde {\alpha }^F$ if for each face F, the conformal boundary associated to F is a pinching deformation on ![]() $\widetilde {\alpha }^F$.
$\widetilde {\alpha }^F$.
Given two curves ![]() $\widetilde {\gamma }^F_{vw} \subseteq R_F$ and
$\widetilde {\gamma }^F_{vw} \subseteq R_F$ and ![]() $\widetilde {\gamma }^{F'}_{ut} \subseteq R_{F'}$, we say that they are parallel if they are homotopic in the
$\widetilde {\gamma }^{F'}_{ut} \subseteq R_{F'}$, we say that they are parallel if they are homotopic in the ![]() $3$-manifold
$3$-manifold ![]() $\mathcal {M}(G_{\mathcal {P}})$. Since the curve
$\mathcal {M}(G_{\mathcal {P}})$. Since the curve ![]() $\widetilde {\gamma }^F_{vw}$ corresponds to the element
$\widetilde {\gamma }^F_{vw}$ corresponds to the element ![]() $g_vg_w$, we get that
$g_vg_w$, we get that ![]() $\widetilde {\gamma }^F_{vw}$ and
$\widetilde {\gamma }^F_{vw}$ and ![]() $\widetilde {\gamma }^{F'}_{ut}$ are parallel if and only if (possibly after switching the order)
$\widetilde {\gamma }^{F'}_{ut}$ are parallel if and only if (possibly after switching the order) ![]() $v=u$ and
$v=u$ and ![]() $w=t$. Note that in this case,
$w=t$. Note that in this case, ![]() $g_vg_w \in \text {stab}(\Omega _F) \cap \text {stab}(\Omega _{F'})$ and
$g_vg_w \in \text {stab}(\Omega _F) \cap \text {stab}(\Omega _{F'})$ and ![]() $v, w$ are on the common boundaries of F and
$v, w$ are on the common boundaries of F and ![]() $F'$. (See, for example, Figure 3.4 where
$F'$. (See, for example, Figure 3.4 where ![]() $v, w$ correspond to the circles
$v, w$ correspond to the circles ![]() $C, C''$, where the curve
$C, C''$, where the curve ![]() $\widetilde {\gamma }^{F_1}_{vw}$ is parallel with
$\widetilde {\gamma }^{F_1}_{vw}$ is parallel with ![]() $\widetilde {\gamma }^{F_2}_{vw}$.)
$\widetilde {\gamma }^{F_2}_{vw}$.)
Let ![]() $\widetilde {\alpha } = \bigcup \widetilde {\alpha }^F$ be a union of
$\widetilde {\alpha } = \bigcup \widetilde {\alpha }^F$ be a union of ![]() $\sigma _F$-invariant multicurves. We say that
$\sigma _F$-invariant multicurves. We say that ![]() $\widetilde {\alpha }$ is a nonparallel multicurve if no two components are parallel. We note that nonparallel multicurves
$\widetilde {\alpha }$ is a nonparallel multicurve if no two components are parallel. We note that nonparallel multicurves ![]() $\widetilde {\alpha }$ for
$\widetilde {\alpha }$ for ![]() $\mathbf {G}$ are in one-to-one correspondence with the simple plane graphs that dominate
$\mathbf {G}$ are in one-to-one correspondence with the simple plane graphs that dominate ![]() $\Gamma $. Indeed, any multicurve
$\Gamma $. Indeed, any multicurve ![]() $\widetilde {\alpha } = \bigcup \widetilde {\alpha }^F$ corresponds to a plane graph that dominates
$\widetilde {\alpha } = \bigcup \widetilde {\alpha }^F$ corresponds to a plane graph that dominates ![]() $\Gamma $. The nonparallel condition is equivalent to the condition that the graph is simple.
$\Gamma $. The nonparallel condition is equivalent to the condition that the graph is simple.
We now apply the general discussion carried out above to prove Proposition 3.17.
Proof of Proposition 3.17
The first equality follows from Lemma 3.15.
We first show  $ \bigcup _{(\Gamma , \psi ) \in \mathrm {Emb}_p(\Gamma _0)} \mathcal {QC}(\Gamma ) \subseteq \overline {\mathcal {QC}(\Gamma _0)}$. Let
$ \bigcup _{(\Gamma , \psi ) \in \mathrm {Emb}_p(\Gamma _0)} \mathcal {QC}(\Gamma ) \subseteq \overline {\mathcal {QC}(\Gamma _0)}$. Let ![]() $\Gamma $ be a simple plane graph that dominates
$\Gamma $ be a simple plane graph that dominates ![]() $\Gamma _0$ with embedding
$\Gamma _0$ with embedding ![]() $\psi :\Gamma _0 \longrightarrow \Gamma $ as plane graphs. It follows from the discussion on pinching deformations that there exists a nonparallel multicurve
$\psi :\Gamma _0 \longrightarrow \Gamma $ as plane graphs. It follows from the discussion on pinching deformations that there exists a nonparallel multicurve ![]() $\widetilde \alpha \subseteq \partial \mathcal {M}(\mathbf {G}_{\Gamma _0})$ associated to
$\widetilde \alpha \subseteq \partial \mathcal {M}(\mathbf {G}_{\Gamma _0})$ associated to ![]() $\Gamma $. We complete
$\Gamma $. We complete ![]() $\Gamma $ to a triangulation
$\Gamma $ to a triangulation ![]() $\mathcal {T}$ by adding edges. As before,
$\mathcal {T}$ by adding edges. As before, ![]() $\mathcal {T}$ gives a
$\mathcal {T}$ gives a ![]() $\sigma $-invariant multicurve
$\sigma $-invariant multicurve  $\widetilde {\beta }\subseteq \partial \mathcal {M}(\mathbf {G}_{\Gamma _0})$ which contains
$\widetilde {\beta }\subseteq \partial \mathcal {M}(\mathbf {G}_{\Gamma _0})$ which contains ![]() $\widetilde {\alpha }$. We set
$\widetilde {\alpha }$. We set ![]() $\widetilde {\beta } = \widetilde {\alpha } \sqcup \widetilde {\alpha }'$. Then the lengths of the multicurve
$\widetilde {\beta } = \widetilde {\alpha } \sqcup \widetilde {\alpha }'$. Then the lengths of the multicurve ![]() $\widetilde {\alpha }'$ give a parametrisation of
$\widetilde {\alpha }'$ give a parametrisation of ![]() $\mathcal {QC}(\Gamma )$ and the lengths of the multicurve
$\mathcal {QC}(\Gamma )$ and the lengths of the multicurve ![]() $\widetilde {\beta }$ give a parametrisation of
$\widetilde {\beta }$ give a parametrisation of ![]() $\mathcal {QC}(\Gamma _0)$. Now given any element
$\mathcal {QC}(\Gamma _0)$. Now given any element  $\vec {l}=(l_\gamma : \gamma \in \widetilde {\alpha }') \in \mathcal {QC}(\Gamma )$, we show that it can be realised as the algebraic limit of a sequence in
$\vec {l}=(l_\gamma : \gamma \in \widetilde {\alpha }') \in \mathcal {QC}(\Gamma )$, we show that it can be realised as the algebraic limit of a sequence in ![]() $\mathcal {QC}(\Gamma _0)$.
$\mathcal {QC}(\Gamma _0)$.
Such a construction is standard and follows directly from [Reference Ohshika35, Theorem 5.1] (see also [Reference Maskit27]). For completeness, we sketch the proof here. Let ![]() $G \in \mathcal {QC}(\Gamma _0)$ be so that the length of the multicurve
$G \in \mathcal {QC}(\Gamma _0)$ be so that the length of the multicurve ![]() $\widetilde {\alpha }'$ is
$\widetilde {\alpha }'$ is ![]() $\vec {l}$. We assume that
$\vec {l}$. We assume that ![]() $\widetilde {\beta }$ is realised by hyperbolic geodesics in
$\widetilde {\beta }$ is realised by hyperbolic geodesics in ![]() $\partial \mathcal {M}(G)$. Let
$\partial \mathcal {M}(G)$. Let ![]() $A \subseteq \partial \mathcal {M}(G)$ be an
$A \subseteq \partial \mathcal {M}(G)$ be an ![]() $\epsilon $-neighbourhood of
$\epsilon $-neighbourhood of ![]() $\widetilde {\alpha }$. We choose
$\widetilde {\alpha }$. We choose ![]() $\epsilon $ small enough so that A is disjoint from
$\epsilon $ small enough so that A is disjoint from ![]() $\widetilde {\alpha }'$ and each component contains only one component of
$\widetilde {\alpha }'$ and each component contains only one component of ![]() $\widetilde {\alpha }$. We construct a sequence of quasiconformal deformations supported on A so that the modulus of each annulus in A tends to infinity while
$\widetilde {\alpha }$. We construct a sequence of quasiconformal deformations supported on A so that the modulus of each annulus in A tends to infinity while ![]() $\widetilde {\alpha }$ remains as core curves. Since the multicurve
$\widetilde {\alpha }$ remains as core curves. Since the multicurve ![]() $\widetilde {\alpha }$ is nonparallel, Thurston’s hyperbolisation theorem guarantees a convergent subsequence (see [Reference Ohshika35] for more details). This algebraic limit is a kissing reflection group. By construction, the contact graph of such a limiting kissing reflection group is
$\widetilde {\alpha }$ is nonparallel, Thurston’s hyperbolisation theorem guarantees a convergent subsequence (see [Reference Ohshika35] for more details). This algebraic limit is a kissing reflection group. By construction, the contact graph of such a limiting kissing reflection group is ![]() $\Gamma $ and the lengths of
$\Gamma $ and the lengths of ![]() $\widetilde {\alpha }'$ is
$\widetilde {\alpha }'$ is ![]() $\vec {l}$.
$\vec {l}$.
Conversely, if a sequence of quasiconformal deformations ![]() $\xi _n:\mathbf {G}_{\Gamma _0}\longrightarrow G_n$ of
$\xi _n:\mathbf {G}_{\Gamma _0}\longrightarrow G_n$ of ![]() $\mathbf {G}_{\Gamma _0}$ converges to
$\mathbf {G}_{\Gamma _0}$ converges to ![]() $\xi _\infty :\mathbf {G}_{\Gamma _0} \longrightarrow G$ algebraically, then G is a kissing reflection group. Since
$\xi _\infty :\mathbf {G}_{\Gamma _0} \longrightarrow G$ algebraically, then G is a kissing reflection group. Since ![]() $\{\xi _n(g_i)\}$ converges, where
$\{\xi _n(g_i)\}$ converges, where ![]() $g_i$ are the standard generators, the contact graph for G dominates
$g_i$ are the standard generators, the contact graph for G dominates ![]() $\Gamma _0$. The embedding
$\Gamma _0$. The embedding ![]() $\psi : \Gamma _0 \longrightarrow \Gamma $ (respecting the plane structure) comes from the identification of the generators.
$\psi : \Gamma _0 \longrightarrow \Gamma $ (respecting the plane structure) comes from the identification of the generators.
3.4 Quasi-Fuchsian space and mating locus
The above discussion applies to the special case of quasi-Fuchsian space. This space is related to the mating locus for critically fixed anti-rational maps.
Let ![]() $\Gamma _d$ be the marked
$\Gamma _d$ be the marked ![]() $d+1$-sided polygonal graph; that is,
$d+1$-sided polygonal graph; that is, ![]() $\Gamma _d$ contains
$\Gamma _d$ contains ![]() $d+1$ vertices
$d+1$ vertices ![]() $v_1,\ldots , v_{d+1}$ with edges
$v_1,\ldots , v_{d+1}$ with edges ![]() $v_iv_{i+1}$ where indices are understood modulo
$v_iv_{i+1}$ where indices are understood modulo ![]() $d+1$. We choose the most symmetric circle packing
$d+1$. We choose the most symmetric circle packing ![]() $\mathcal {P}_d$ realising
$\mathcal {P}_d$ realising ![]() $\Gamma _d$. More precisely, consider the ideal
$\Gamma _d$. More precisely, consider the ideal ![]() $(d+1)$-gon in
$(d+1)$-gon in ![]() $\mathbb {D}\cong \mathbb {H}^2$ with vertices at the
$\mathbb {D}\cong \mathbb {H}^2$ with vertices at the ![]() $(d+1)$-st roots of unity. The edges of this ideal
$(d+1)$-st roots of unity. The edges of this ideal ![]() $(d+1)$-gon are arcs of
$(d+1)$-gon are arcs of ![]() $d+1$ circles and we label these circles as
$d+1$ circles and we label these circles as ![]() $\mathcal {P}_d := \{\mathbf {C}_1,\ldots , \mathbf {C}_{d+1}\}$, where we index them counterclockwise such that
$\mathcal {P}_d := \{\mathbf {C}_1,\ldots , \mathbf {C}_{d+1}\}$, where we index them counterclockwise such that ![]() $\mathbf {C}_1$ passes through
$\mathbf {C}_1$ passes through ![]() $1$ and
$1$ and ![]() $e^{2\pi i/(d+1)}$. Let
$e^{2\pi i/(d+1)}$. Let ![]() $\mathbf {G}_d$ be the kissing reflection group associated to
$\mathbf {G}_d$ be the kissing reflection group associated to ![]() $\mathcal {P}_d$. Note that
$\mathcal {P}_d$. Note that ![]() $\widetilde {\mathbf {G}}_d$ is a Fuchsian group. We remark that since any embedding of the polygonal graph
$\widetilde {\mathbf {G}}_d$ is a Fuchsian group. We remark that since any embedding of the polygonal graph ![]() $\Gamma _d$ into a graph
$\Gamma _d$ into a graph ![]() $\Gamma $ abstractly dominating
$\Gamma $ abstractly dominating ![]() $\Gamma _d$ respects the plane structure, we have that
$\Gamma _d$ respects the plane structure, we have that ![]() $\textrm {AH}(\Gamma _d)=\overline {\mathcal {QC}(\Gamma _d)}$.
$\textrm {AH}(\Gamma _d)=\overline {\mathcal {QC}(\Gamma _d)}$.
Recall that a graph ![]() $\Gamma $ is said to be Hamiltonian if there exists a cycle which passes through each vertex exactly once. Since a simple plane graph with
$\Gamma $ is said to be Hamiltonian if there exists a cycle which passes through each vertex exactly once. Since a simple plane graph with ![]() $d+1$ vertices is Hamiltonian if and only if it dominates
$d+1$ vertices is Hamiltonian if and only if it dominates ![]() $\Gamma _d$, the following proposition follows immediately from Proposition 3.17.
$\Gamma _d$, the following proposition follows immediately from Proposition 3.17.
Proposition 3.18. Let ![]() $\Gamma $ be a simple plane graph with
$\Gamma $ be a simple plane graph with ![]() $d+1$ vertices; then any kissing reflection group G with contact graph
$d+1$ vertices; then any kissing reflection group G with contact graph ![]() $\Gamma $ is in the closure
$\Gamma $ is in the closure ![]() $\overline {\mathcal {QC}(\Gamma _d)}$ if and only if
$\overline {\mathcal {QC}(\Gamma _d)}$ if and only if ![]() $\Gamma $ is Hamiltonian.
$\Gamma $ is Hamiltonian.
Let ![]() $\Gamma $ be a marked Hamiltonian simple plane graph with a Hamiltonian cycle
$\Gamma $ be a marked Hamiltonian simple plane graph with a Hamiltonian cycle ![]() $C = (v_1,\ldots ,v_{d+1})$. Let
$C = (v_1,\ldots ,v_{d+1})$. Let ![]() $G:=\langle g_1,\ldots , g_{d+1}\rangle $ be a kissing reflection group with contact graph
$G:=\langle g_1,\ldots , g_{d+1}\rangle $ be a kissing reflection group with contact graph ![]() $\Gamma $. The Hamiltonian cycle divides the fundamental domain
$\Gamma $. The Hamiltonian cycle divides the fundamental domain ![]() $\Pi \subseteq \widehat {\mathbb {C}}$ into two parts and we denote them as
$\Pi \subseteq \widehat {\mathbb {C}}$ into two parts and we denote them as ![]() $\Pi ^+$ and
$\Pi ^+$ and ![]() $\Pi ^-$, where we assume that the Hamiltonian cycle is positively oriented on the boundary of
$\Pi ^-$, where we assume that the Hamiltonian cycle is positively oriented on the boundary of ![]() $\Pi ^+$ and negatively oriented on the boundary of
$\Pi ^+$ and negatively oriented on the boundary of ![]() $\Pi ^-$ (see Figure 3.4). We denote
$\Pi ^-$ (see Figure 3.4). We denote
 $$ \begin{align*}\Omega^\pm := \bigcup_{g\in G} g\cdot \Pi^\pm. \end{align*} $$
$$ \begin{align*}\Omega^\pm := \bigcup_{g\in G} g\cdot \Pi^\pm. \end{align*} $$Since each ![]() $\Omega ^\pm $ is G-invariant, we have
$\Omega ^\pm $ is G-invariant, we have ![]() $\Lambda (G) = \partial \Omega ^+ = \partial \Omega ^-$.
$\Lambda (G) = \partial \Omega ^+ = \partial \Omega ^-$.
As in Subsection 3.1, set
 $$ \begin{align*}\Pi^{1,\pm} = \bigcup_{i=1}^{d+1} g_i \cdot \Pi^\pm,\ \textrm{and}\quad \Pi^{j+1,\pm} = \bigcup_{i=1}^{d+1} g_i \cdot \left(\Pi^{j,\pm} \setminus \overline{D}_i\right).\end{align*} $$
$$ \begin{align*}\Pi^{1,\pm} = \bigcup_{i=1}^{d+1} g_i \cdot \Pi^\pm,\ \textrm{and}\quad \Pi^{j+1,\pm} = \bigcup_{i=1}^{d+1} g_i \cdot \left(\Pi^{j,\pm} \setminus \overline{D}_i\right).\end{align*} $$For consistency, we also set ![]() $\Pi ^{0, \pm } = \Pi ^\pm $. Then the arguments of the proof of Lemma 3.2 show that
$\Pi ^{0, \pm } = \Pi ^\pm $. Then the arguments of the proof of Lemma 3.2 show that
 $$ \begin{align*}\Pi^{l,\pm} = \bigcup_{\vert g\vert = l} g\cdot \Pi^\pm. \end{align*} $$
$$ \begin{align*}\Pi^{l,\pm} = \bigcup_{\vert g\vert = l} g\cdot \Pi^\pm. \end{align*} $$Lemma 3.19. The closures ![]() $\overline {\Omega ^+}$ and
$\overline {\Omega ^+}$ and ![]() $\overline {\Omega ^-}$ are connected.
$\overline {\Omega ^-}$ are connected.
Proof. We shall prove by induction that the closures  $\overline {\bigcup _{i=0}^n \Pi ^{i,+}}$ and
$\overline {\bigcup _{i=0}^n \Pi ^{i,+}}$ and  $\overline {\bigcup _{i=0}^n \Pi ^{i,+}\setminus \overline {D}_j}$ are connected for all n and j.
$\overline {\bigcup _{i=0}^n \Pi ^{i,+}\setminus \overline {D}_j}$ are connected for all n and j.
Indeed, the base case is true as ![]() $\overline {\Pi ^+}$ and
$\overline {\Pi ^+}$ and  $\overline {\Pi ^+ \setminus \overline {D}_j}$ are connected for all j. Assume that
$\overline {\Pi ^+ \setminus \overline {D}_j}$ are connected for all j. Assume that  $\overline {\bigcup _{i=0}^n \Pi ^{i,+}}$ and
$\overline {\bigcup _{i=0}^n \Pi ^{i,+}}$ and  $\overline {\bigcup _{i=0}^n \Pi ^{i,+}\setminus \overline {D}_j}$ are connected for all j. Note that
$\overline {\bigcup _{i=0}^n \Pi ^{i,+}\setminus \overline {D}_j}$ are connected for all j. Note that
 $$ \begin{align*}\overline{\bigcup_{i=0}^{n+1} \Pi^{i,+}} = \overline{\Pi^{+} \cup \bigcup_{j=1}^{d+1} g_j \cdot \left(\bigcup_{i=0}^n \Pi^{i,+} \setminus \overline{D}_j\right)}. \end{align*} $$
$$ \begin{align*}\overline{\bigcup_{i=0}^{n+1} \Pi^{i,+}} = \overline{\Pi^{+} \cup \bigcup_{j=1}^{d+1} g_j \cdot \left(\bigcup_{i=0}^n \Pi^{i,+} \setminus \overline{D}_j\right)}. \end{align*} $$By the induction hypothesis,  $\overline {g_j \cdot (\bigcup _{i=0}^n \Pi ^{i,+} \setminus \overline {D}_j)}$ is connected. Since each
$\overline {g_j \cdot (\bigcup _{i=0}^n \Pi ^{i,+} \setminus \overline {D}_j)}$ is connected. Since each
 $$ \begin{align*}\overline{g_j \cdot \left(\bigcup_{i=0}^n \Pi^{i,+} \setminus \overline{D}_j\right)} \end{align*} $$
$$ \begin{align*}\overline{g_j \cdot \left(\bigcup_{i=0}^n \Pi^{i,+} \setminus \overline{D}_j\right)} \end{align*} $$intersects ![]() $\overline {\Pi ^{+}}$ along an arc of
$\overline {\Pi ^{+}}$ along an arc of ![]() $C_j = \partial D_j$, we have that
$C_j = \partial D_j$, we have that  $\overline {\bigcup _{i=0}^{n+1} \Pi ^{i,+}}$ is also connected.
$\overline {\bigcup _{i=0}^{n+1} \Pi ^{i,+}}$ is also connected.
Similarly,
 $$ \begin{align*}\overline{\bigcup_{i=0}^{n+1} \Pi^{i,+}\setminus \overline{D}_j} = \overline{\Pi^+ \cup \bigcup_{k\neq j} g_k \cdot \left(\bigcup_{i=0}^n \Pi^{i,+} \setminus \overline{D}_k\right)} \end{align*} $$
$$ \begin{align*}\overline{\bigcup_{i=0}^{n+1} \Pi^{i,+}\setminus \overline{D}_j} = \overline{\Pi^+ \cup \bigcup_{k\neq j} g_k \cdot \left(\bigcup_{i=0}^n \Pi^{i,+} \setminus \overline{D}_k\right)} \end{align*} $$is connected for any j.
Connectedness of ![]() $\overline {\Omega ^-}$ is proved in the same way.
$\overline {\Omega ^-}$ is proved in the same way.
Matings of function kissing reflection groups
We say that a kissing reflection group G with connected limit set is a function kissing reflection group if there is a component ![]() $\Omega _0$ of
$\Omega _0$ of ![]() $\Omega (G)$ invariant under G. This terminology was traditionally used in complex analysis as one can construct Poincaré series, differentials and functions on it.
$\Omega (G)$ invariant under G. This terminology was traditionally used in complex analysis as one can construct Poincaré series, differentials and functions on it.
We say that a simple plane graph ![]() $\Gamma $ with n vertices is outerplanar if it has a face with all n vertices on its boundary. We also call this face the outer face. Note that a
$\Gamma $ with n vertices is outerplanar if it has a face with all n vertices on its boundary. We also call this face the outer face. Note that a ![]() $2$-connected outerplanar graph is Hamiltonian with a unique Hamiltonian cycle. The following proposition characterises function kissing reflection groups in terms of their contact graphs.
$2$-connected outerplanar graph is Hamiltonian with a unique Hamiltonian cycle. The following proposition characterises function kissing reflection groups in terms of their contact graphs.
Proposition 3.20. A kissing reflection group G is a function group if and only if its contact graph ![]() $\Gamma $ is 2-connected and outerplanar.
$\Gamma $ is 2-connected and outerplanar.
Proof. If ![]() $\Gamma $ is outerplanar, then let
$\Gamma $ is outerplanar, then let ![]() $\Omega _F$ be the component of
$\Omega _F$ be the component of ![]() $\Omega (G)$ associated to the outer face F. It is easy to see that the standard generating set fixes
$\Omega (G)$ associated to the outer face F. It is easy to see that the standard generating set fixes ![]() $\Omega _F$, so
$\Omega _F$, so ![]() $\Omega _F$ is invariant under G.
$\Omega _F$ is invariant under G.
Conversely, assume that ![]() $\Gamma $ is not outerplanar. Since
$\Gamma $ is not outerplanar. Since ![]() $\Pi $ is a fundamental domain of the action of G on
$\Pi $ is a fundamental domain of the action of G on ![]() $\Omega (G)$, any G-invariant component of
$\Omega (G)$, any G-invariant component of ![]() $\Omega (G)$ must correspond to some face of
$\Omega (G)$ must correspond to some face of ![]() $\Gamma $. Let F be a face of
$\Gamma $. Let F be a face of ![]() $\Gamma $. Since
$\Gamma $. Since ![]() $\Gamma $ is not outerplanar, there exists a vertex v which is not on the boundary of F. Thus,
$\Gamma $ is not outerplanar, there exists a vertex v which is not on the boundary of F. Thus, ![]() $g_v \cdot \Pi _F$ is not in
$g_v \cdot \Pi _F$ is not in ![]() $\Omega _F$ and hence
$\Omega _F$ and hence ![]() $\Omega _F$ is not invariant under G.
$\Omega _F$ is not invariant under G.
For a function kissing reflection group G, we set ![]() $\Omega _b := \Omega (G)\setminus \Omega _0$, where
$\Omega _b := \Omega (G)\setminus \Omega _0$, where ![]() $\Omega _0$ is G-invariant. Similarly, we shall use the notation
$\Omega _0$ is G-invariant. Similarly, we shall use the notation ![]() $\Pi _b := \Pi \cap \Omega _b$ (see Figure 3.6) and
$\Pi _b := \Pi \cap \Omega _b$ (see Figure 3.6) and  $\Pi ^i_b := \Pi ^i \cap \Omega _b$, for
$\Pi ^i_b := \Pi ^i \cap \Omega _b$, for ![]() $i\geq 0$ (see Lemma 3.2). We call the closure
$i\geq 0$ (see Lemma 3.2). We call the closure ![]() $\overline {\Omega _b} = \widehat {\mathbb {C}} \setminus \Omega _0$ the filled limit set for the function kissing reflection group G and denote it by
$\overline {\Omega _b} = \widehat {\mathbb {C}} \setminus \Omega _0$ the filled limit set for the function kissing reflection group G and denote it by ![]() $\mathcal {K}(G)$.
$\mathcal {K}(G)$.
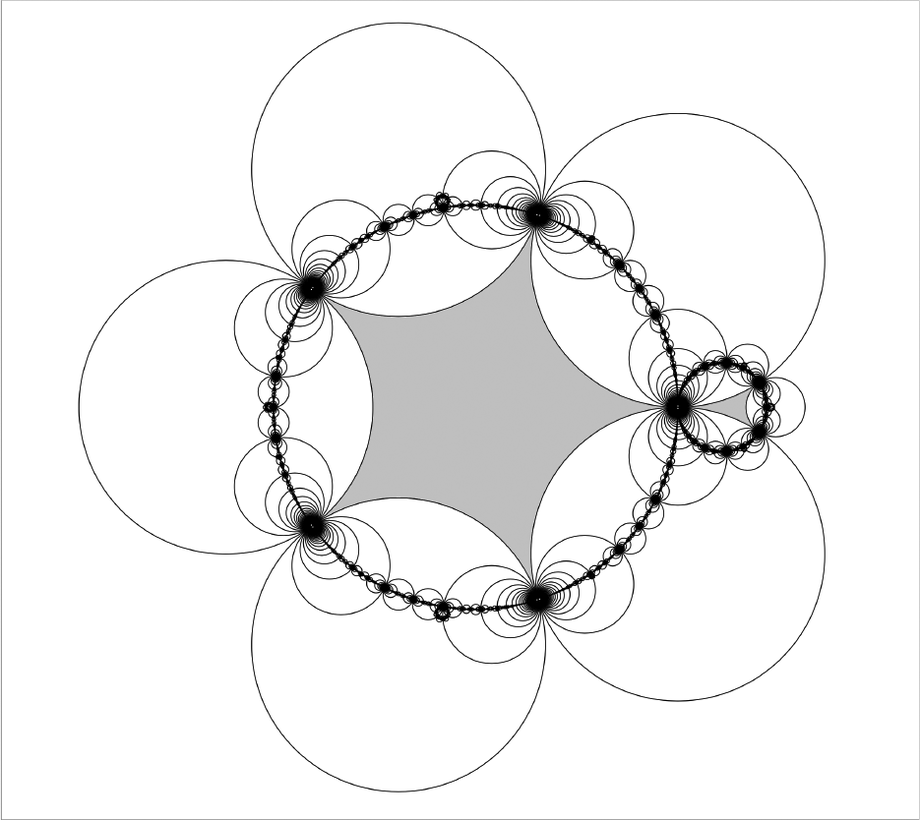
Figure 3.6 The limit set of a function kissing reflection group H with an outerplanar contact graph. The grey region represents the part ![]() $\Pi _b$ of the fundamental domain
$\Pi _b$ of the fundamental domain ![]() $\Pi (H)$ corresponding to the non-outer faces of
$\Pi (H)$ corresponding to the non-outer faces of ![]() $\Gamma (H)$. The kissing reflection group G shown in Figure 3.4 can be constructed by pinching a simple closed curve for H.
$\Gamma (H)$. The kissing reflection group G shown in Figure 3.4 can be constructed by pinching a simple closed curve for H.
Let ![]() $G^\pm $ be two function kissing reflection groups with the same number of vertices in their contact graphs. We say that a kissing reflection group G is a geometric mating of
$G^\pm $ be two function kissing reflection groups with the same number of vertices in their contact graphs. We say that a kissing reflection group G is a geometric mating of ![]() $G^+$ and
$G^+$ and ![]() $G^-$ if we have
$G^-$ if we have
• a decomposition
 $\Omega (G) = \Omega ^+(G) \sqcup \Omega ^-(G)$ with
$\Omega (G) = \Omega ^+(G) \sqcup \Omega ^-(G)$ with  $\Lambda (G) = \partial \Omega ^+(G) = \partial \Omega ^-(G)$;
$\Lambda (G) = \partial \Omega ^+(G) = \partial \Omega ^-(G)$;• weakly type-preserving isomorphisms
 $\phi ^\pm : G^\pm \longrightarrow G$;
$\phi ^\pm : G^\pm \longrightarrow G$;• continuous surjections
 $\psi ^{\pm }: \mathcal {K}(G^\pm ) \longrightarrow \overline {\Omega ^\pm (G)}$ which are conformal between the interior
$\psi ^{\pm }: \mathcal {K}(G^\pm ) \longrightarrow \overline {\Omega ^\pm (G)}$ which are conformal between the interior  $\mathring {\mathcal {K}}(G^\pm )$ and
$\mathring {\mathcal {K}}(G^\pm )$ and  $\Omega ^\pm (G)$ such that for any
$\Omega ^\pm (G)$ such that for any  $g\in G^\pm $,
$g\in G^\pm $,  $\psi ^\pm \circ g|_{\mathcal {K}(G^\pm )} = \phi ^\pm (g) \circ \psi ^\pm $.
$\psi ^\pm \circ g|_{\mathcal {K}(G^\pm )} = \phi ^\pm (g) \circ \psi ^\pm $.
Note that by the semi-conjugacy relation, the sets ![]() $\Omega ^\pm (G)$ are
$\Omega ^\pm (G)$ are ![]() $G-$invariant. We shall now complete the proof of the group part of Theorem 1.2.
$G-$invariant. We shall now complete the proof of the group part of Theorem 1.2.
Proposition 3.21. A kissing reflection group G is a geometric mating of two function kissing reflection groups if and only if the contact graph ![]() $\Gamma (G)$ of G is Hamiltonian.
$\Gamma (G)$ of G is Hamiltonian.
Proof. If G is a geometric mating of ![]() $G^\pm $, then we have a decomposition
$G^\pm $, then we have a decomposition ![]() $\Omega (G) = \Omega ^+(G) \sqcup \Omega ^-(G)$ with
$\Omega (G) = \Omega ^+(G) \sqcup \Omega ^-(G)$ with ![]() $\Lambda (G) = \partial \Omega ^+(G) = \partial \Omega ^-(G)$. This gives a decomposition of
$\Lambda (G) = \partial \Omega ^+(G) = \partial \Omega ^-(G)$. This gives a decomposition of ![]() $\Pi (G) = \Pi ^+ \sqcup \Pi ^-$ and thus a decomposition of the contact graph
$\Pi (G) = \Pi ^+ \sqcup \Pi ^-$ and thus a decomposition of the contact graph ![]() $\Gamma (G) = \Gamma ^+ \cup \Gamma ^-$. More precisely, the vertex sets of
$\Gamma (G) = \Gamma ^+ \cup \Gamma ^-$. More precisely, the vertex sets of ![]() $\Gamma ^\pm $ coincide with that of
$\Gamma ^\pm $ coincide with that of ![]() $\Gamma (G)$ and there is an edge in
$\Gamma (G)$ and there is an edge in ![]() $\Gamma ^\pm $ connecting two vertices if and only if the point of intersection of the corresponding two circles lies in
$\Gamma ^\pm $ connecting two vertices if and only if the point of intersection of the corresponding two circles lies in ![]() $\partial \Pi ^\pm $. Since the action of
$\partial \Pi ^\pm $. Since the action of ![]() $G^\pm $ on
$G^\pm $ on ![]() $\mathcal {K}(G^\pm )$ is semi-conjugate to G on
$\mathcal {K}(G^\pm )$ is semi-conjugate to G on ![]() $\overline {\Omega ^\pm (G)}$, it follows that
$\overline {\Omega ^\pm (G)}$, it follows that ![]() $\Gamma ^\pm $ is isomorphic to
$\Gamma ^\pm $ is isomorphic to ![]() $\Gamma (G^\pm )$ as plane graphs. Thus, the intersection of
$\Gamma (G^\pm )$ as plane graphs. Thus, the intersection of ![]() $\Gamma ^+$ and
$\Gamma ^+$ and ![]() $\Gamma ^-$ (which is the common boundary of the outer faces of
$\Gamma ^-$ (which is the common boundary of the outer faces of ![]() $\Gamma ^+$ and
$\Gamma ^+$ and ![]() $\Gamma ^-$) gives a Hamiltonian cycle for
$\Gamma ^-$) gives a Hamiltonian cycle for ![]() $\Gamma (G)$.
$\Gamma (G)$.
Conversely, if ![]() $\Gamma (G)$ is Hamiltonian, then a Hamiltonian cycle yields a decomposition
$\Gamma (G)$ is Hamiltonian, then a Hamiltonian cycle yields a decomposition ![]() $\Gamma (G) = \Gamma ^+ \cup \Gamma ^-$, where
$\Gamma (G) = \Gamma ^+ \cup \Gamma ^-$, where ![]() $\Gamma ^+$ and
$\Gamma ^+$ and ![]() $\Gamma ^-$ are outerplanar graphs with vertex sets equal to that of
$\Gamma ^-$ are outerplanar graphs with vertex sets equal to that of ![]() $\Gamma (G)$. We construct function kissing reflection groups
$\Gamma (G)$. We construct function kissing reflection groups ![]() $G^\pm $ with contact graphs
$G^\pm $ with contact graphs ![]() $\Gamma (G^\pm ) = \Gamma ^\pm $. Note that we have a natural embedding of
$\Gamma (G^\pm ) = \Gamma ^\pm $. Note that we have a natural embedding of ![]() $\Gamma (G^\pm )$ into
$\Gamma (G^\pm )$ into ![]() $\Gamma (G)$ (as plane graphs), which gives an identification of vertices and non-outer faces. Thus, we have weakly type-preserving isomorphisms
$\Gamma (G)$ (as plane graphs), which gives an identification of vertices and non-outer faces. Thus, we have weakly type-preserving isomorphisms ![]() $\phi ^\pm : G^\pm \longrightarrow G$ coming from the identification of vertices and Proposition 3.17. By quasiconformal deformation, we may assume that for each non-outer face
$\phi ^\pm : G^\pm \longrightarrow G$ coming from the identification of vertices and Proposition 3.17. By quasiconformal deformation, we may assume that for each non-outer face ![]() $F\in \Gamma (G^\pm )$, the associated conformal boundary component
$F\in \Gamma (G^\pm )$, the associated conformal boundary component ![]() $R_F(G^\pm )\subseteq \partial \mathcal {M}(G^\pm )$ is conformally equivalent to the corresponding conformal boundary component
$R_F(G^\pm )\subseteq \partial \mathcal {M}(G^\pm )$ is conformally equivalent to the corresponding conformal boundary component ![]() $R_F(G)\subseteq \partial \mathcal {M}(G)$.
$R_F(G)\subseteq \partial \mathcal {M}(G)$.
The existence of the desired continuous map ![]() $\psi ^+$ can be derived from a more general statement on the existence of Cannon–Thurston maps (see [Reference Mj and Series32, Theorem 4.2]). For completeness and making the proof self-contained, we give an explicit construction of
$\psi ^+$ can be derived from a more general statement on the existence of Cannon–Thurston maps (see [Reference Mj and Series32, Theorem 4.2]). For completeness and making the proof self-contained, we give an explicit construction of ![]() $\psi ^+: \mathcal {K}(G^+) \longrightarrow \overline {\Omega ^+(G)}$. This construction is done in levels: we start with a homeomorphism
$\psi ^+: \mathcal {K}(G^+) \longrightarrow \overline {\Omega ^+(G)}$. This construction is done in levels: we start with a homeomorphism
 $$ \begin{align*}\psi^+_0: \overline{\Pi^{0}_b(G^+)} \longrightarrow \overline{\Pi^{0, +}}.\end{align*} $$
$$ \begin{align*}\psi^+_0: \overline{\Pi^{0}_b(G^+)} \longrightarrow \overline{\Pi^{0, +}}.\end{align*} $$This can be chosen to be conformal on the interior as the associated conformal boundaries are assumed to be conformally equivalent. Assuming that
 $$ \begin{align*}\psi^+_i: \overline{\bigcup_{j=0}^i \Pi^{j}_b(G^+)} \longrightarrow \overline{\bigcup_{j=0}^i \Pi^{j,+}}\end{align*} $$
$$ \begin{align*}\psi^+_i: \overline{\bigcup_{j=0}^i \Pi^{j}_b(G^+)} \longrightarrow \overline{\bigcup_{j=0}^i \Pi^{j,+}}\end{align*} $$is constructed, we extend ![]() $\psi ^+_i$ to
$\psi ^+_i$ to ![]() $\psi ^+_{i+1}$ by setting
$\psi ^+_{i+1}$ by setting
if  $z\in \Pi ^{i+1}_b(G^+) \cap D_k$. It is easy to check by induction that
$z\in \Pi ^{i+1}_b(G^+) \cap D_k$. It is easy to check by induction that ![]() $\psi ^+_{i+1}$ is a homeomorphism which is conformal on the interior (see Figure 3.4 and Figure 3.6).
$\psi ^+_{i+1}$ is a homeomorphism which is conformal on the interior (see Figure 3.4 and Figure 3.6).
Let  $P^{0}(G^+) := \overline {\Pi ^{0}_b(G^+)}\setminus \Pi ^{0}_b(G^+)$; then
$P^{0}(G^+) := \overline {\Pi ^{0}_b(G^+)}\setminus \Pi ^{0}_b(G^+)$; then ![]() $P^{0}(G^+)$ consists of cusps where various components of
$P^{0}(G^+)$ consists of cusps where various components of  $\Pi ^{0}_b(G^+)$ touch. Let
$\Pi ^{0}_b(G^+)$ touch. Let  $P^{\infty }(G^+):= \bigcup _{g\in G^+} g\cdot P^{0}(G^+)$. Then
$P^{\infty }(G^+):= \bigcup _{g\in G^+} g\cdot P^{0}(G^+)$. Then ![]() $P^{\infty }(G^+)$ is dense in
$P^{\infty }(G^+)$ is dense in ![]() $\Lambda (G^+)$. We define
$\Lambda (G^+)$. We define ![]() $P^{\infty , +}$ similarly (where,
$P^{\infty , +}$ similarly (where,  $P^{0,+}:=\overline {\Pi ^{0,+}}\setminus \Pi ^{0,+}$) and note that
$P^{0,+}:=\overline {\Pi ^{0,+}}\setminus \Pi ^{0,+}$) and note that ![]() $P^{\infty , +}$ is dense in
$P^{\infty , +}$ is dense in ![]() $\partial \Omega ^+(G) = \Lambda (G)$.
$\partial \Omega ^+(G) = \Lambda (G)$.
Note that  $\psi ^+_i = \psi ^+_j$ on
$\psi ^+_i = \psi ^+_j$ on ![]() $P^{i}(G^+)$ for all
$P^{i}(G^+)$ for all ![]() $j \geq i$. Thus, we have a well-defined limit
$j \geq i$. Thus, we have a well-defined limit ![]() $\psi ^+ : P^{\infty }(G^+) \longrightarrow P^{\infty , +}$. We claim that
$\psi ^+ : P^{\infty }(G^+) \longrightarrow P^{\infty , +}$. We claim that ![]() $\psi ^+$ is uniformly continuous on
$\psi ^+$ is uniformly continuous on ![]() $P^{\infty }(G^+)$. For an arbitrary
$P^{\infty }(G^+)$. For an arbitrary ![]() $\epsilon>0$, there exists N such that all disks in
$\epsilon>0$, there exists N such that all disks in ![]() $\mathcal {D}^N(G)$ have spherical diameter
$\mathcal {D}^N(G)$ have spherical diameter ![]() $< \epsilon $ by Lemma 3.3. Choose
$< \epsilon $ by Lemma 3.3. Choose ![]() $\delta $ so that any two nonadjacent disks in
$\delta $ so that any two nonadjacent disks in ![]() $\mathcal {D}^N(G^+)$ are separated in spherical metric by
$\mathcal {D}^N(G^+)$ are separated in spherical metric by ![]() $\delta $. Then if
$\delta $. Then if ![]() $x,y \in P^{\infty }(G^+)$ with
$x,y \in P^{\infty }(G^+)$ with ![]() $d(x,y) < \delta $, they must lie in two adjacent disks of
$d(x,y) < \delta $, they must lie in two adjacent disks of ![]() $\mathcal {D}^N(G^+)$. Thus,
$\mathcal {D}^N(G^+)$. Thus, ![]() $\psi ^+_i(x)$ and
$\psi ^+_i(x)$ and ![]() $\psi ^+_i(y)$ (whenever defined) lie in two adjacent disks of
$\psi ^+_i(y)$ (whenever defined) lie in two adjacent disks of ![]() $\mathcal {D}^N(G)$ for all
$\mathcal {D}^N(G)$ for all ![]() $i\geq N$. Hence,
$i\geq N$. Hence, ![]() $d(\psi ^+_i(x), \psi ^+_i(y)) < 2\epsilon $ for all
$d(\psi ^+_i(x), \psi ^+_i(y)) < 2\epsilon $ for all ![]() $i \geq N$. This shows that
$i \geq N$. This shows that ![]() $\psi ^+$ is uniformly continuous on
$\psi ^+$ is uniformly continuous on ![]() $P^{\infty }(G^+)$.
$P^{\infty }(G^+)$.
Thus, we have a continuous extension ![]() $\psi ^+: \mathcal {K}(G^+) \longrightarrow \overline {\Omega ^+(G)}$. It is easy to check that
$\psi ^+: \mathcal {K}(G^+) \longrightarrow \overline {\Omega ^+(G)}$. It is easy to check that ![]() $\psi ^+$ is surjective, conformal on the interior and equivariant with respect to the actions of
$\psi ^+$ is surjective, conformal on the interior and equivariant with respect to the actions of ![]() $G^+$ and G.
$G^+$ and G.
The same proof gives the construction for ![]() $\psi ^-$. This shows that G is a geometric mating of
$\psi ^-$. This shows that G is a geometric mating of ![]() $G^+$ and
$G^+$ and ![]() $G^-$.
$G^-$.
Note that from the proof of Proposition 3.21, we see that each (marked) Hamiltonian cycle H gives a decomposition of the graph ![]() $\Gamma = \Gamma ^+ \cup \Gamma ^-$ and hence an unmating of a kissing reflection group. From the pinching perspective as in the proof of Proposition 3.17, this (marked) Hamiltonian cycle also gives a pair of nonparallel multicurves. This pair of multicurves can be constructed explicitly from the decomposition of
$\Gamma = \Gamma ^+ \cup \Gamma ^-$ and hence an unmating of a kissing reflection group. From the pinching perspective as in the proof of Proposition 3.17, this (marked) Hamiltonian cycle also gives a pair of nonparallel multicurves. This pair of multicurves can be constructed explicitly from the decomposition of ![]() $\Gamma $. Indeed, each edge in
$\Gamma $. Indeed, each edge in ![]() $\Gamma ^\pm - H$ gives a pair of nonadjacent vertices in H. The corresponding
$\Gamma ^\pm - H$ gives a pair of nonadjacent vertices in H. The corresponding ![]() $\sigma $-invariant curve comes from these nonadjacent vertices in H. If a marking is not specified on H, this pair of multicurves is defined only up to simultaneous change of coordinates on the two conformal boundaries.
$\sigma $-invariant curve comes from these nonadjacent vertices in H. If a marking is not specified on H, this pair of multicurves is defined only up to simultaneous change of coordinates on the two conformal boundaries.
3.5 Nielsen maps for kissing reflection groups
Let ![]() $\Gamma $ be a simple plane graph and
$\Gamma $ be a simple plane graph and ![]() $G_\Gamma $ be a kissing reflection group with contact graph
$G_\Gamma $ be a kissing reflection group with contact graph ![]() $\Gamma $. Recall that
$\Gamma $. Recall that  $\overline {\mathcal {D}} = \bigcup _{j=1}^n \overline {D_j}$ is defined as the union of the closure of the disks for the associated circle packing. We define the Nielsen map
$\overline {\mathcal {D}} = \bigcup _{j=1}^n \overline {D_j}$ is defined as the union of the closure of the disks for the associated circle packing. We define the Nielsen map ![]() $\mathcal {N}_\Gamma : \overline {\mathcal {D}} \longrightarrow \widehat {\mathbb {C}}$ by
$\mathcal {N}_\Gamma : \overline {\mathcal {D}} \longrightarrow \widehat {\mathbb {C}}$ by
 $$ \begin{align*}\mathcal{N}_\Gamma(z) = g_j(z) \text{ if } z\in \overline{D_j}. \end{align*} $$
$$ \begin{align*}\mathcal{N}_\Gamma(z) = g_j(z) \text{ if } z\in \overline{D_j}. \end{align*} $$ Let us now assume that ![]() $\Gamma $ is
$\Gamma $ is ![]() $2$-connected; then the limit set
$2$-connected; then the limit set ![]() $\Lambda (G_\Gamma )$ is connected. Thus, each component of
$\Lambda (G_\Gamma )$ is connected. Thus, each component of ![]() $\Omega (G_\Gamma )$ is a topological disk. Let F be a face with
$\Omega (G_\Gamma )$ is a topological disk. Let F be a face with ![]() $d+1$ sides of
$d+1$ sides of ![]() $\Gamma $ and let
$\Gamma $ and let ![]() $\Omega _F$ be the component of
$\Omega _F$ be the component of ![]() $\Omega (G)$ containing
$\Omega (G)$ containing ![]() $\Pi _F$. By a quasiconformal deformation, we can assume that the restriction of
$\Pi _F$. By a quasiconformal deformation, we can assume that the restriction of ![]() $G_\Gamma $ on
$G_\Gamma $ on ![]() $\Omega _F$ is conformally conjugate to the regular ideal
$\Omega _F$ is conformally conjugate to the regular ideal ![]() $d+1$-gon reflection group on
$d+1$-gon reflection group on ![]() $\mathbb {D} \cong \mathbb {H}^2$.
$\mathbb {D} \cong \mathbb {H}^2$.
For the regular ideal ![]() $d+1$-gon reflection group
$d+1$-gon reflection group ![]() $\mathbf {G}_d$ (whose associated contact graph is
$\mathbf {G}_d$ (whose associated contact graph is ![]() $\Gamma _d$), the
$\Gamma _d$), the ![]() $d+1$ disks yield a Markov partition for the action of the Nielsen map
$d+1$ disks yield a Markov partition for the action of the Nielsen map ![]() $\mathcal {N}_d\equiv \mathcal {N}_{\Gamma _d}$ on the limit set
$\mathcal {N}_d\equiv \mathcal {N}_{\Gamma _d}$ on the limit set ![]() $\Lambda (\mathbf {G}_d)=\mathbb {S}^1$. The diameters of the preimages of these disks under
$\Lambda (\mathbf {G}_d)=\mathbb {S}^1$. The diameters of the preimages of these disks under ![]() $\mathcal {N}_d$ shrink to
$\mathcal {N}_d$ shrink to ![]() $0$ uniformly by Lemma 3.3 and hence the Nielsen map
$0$ uniformly by Lemma 3.3 and hence the Nielsen map ![]() $\mathcal {N}_d$ is topologically conjugate to
$\mathcal {N}_d$ is topologically conjugate to ![]() $z\mapsto \overline {z}^d$ on
$z\mapsto \overline {z}^d$ on ![]() $\mathbb {S}^1$ (cf. [Reference Lodge, Lyubich, Merenkov and Mukherjee24, §4]).
$\mathbb {S}^1$ (cf. [Reference Lodge, Lyubich, Merenkov and Mukherjee24, §4]).
Therefore, the Nielsen map ![]() $\mathcal {N}_\Gamma $ is topologically conjugate to
$\mathcal {N}_\Gamma $ is topologically conjugate to ![]() $\overline {z}^d$ on the ideal boundary of
$\overline {z}^d$ on the ideal boundary of ![]() $\Omega _F$. This allows us to replace the dynamics of
$\Omega _F$. This allows us to replace the dynamics of ![]() $\mathcal {N}_\Gamma $ on
$\mathcal {N}_\Gamma $ on ![]() $\Omega _F$ by
$\Omega _F$ by ![]() $\overline {z}^d$ for every face of
$\overline {z}^d$ for every face of ![]() $\Gamma $ and obtain a globally defined orientation-reversing branched covering
$\Gamma $ and obtain a globally defined orientation-reversing branched covering ![]() $\mathcal {G}_\Gamma : \widehat {\mathbb {C}}\longrightarrow \widehat {\mathbb {C}}$.
$\mathcal {G}_\Gamma : \widehat {\mathbb {C}}\longrightarrow \widehat {\mathbb {C}}$.
More precisely, let ![]() $\phi :\mathbb {D} \longrightarrow \Omega _F$ be a conformal conjugacy between
$\phi :\mathbb {D} \longrightarrow \Omega _F$ be a conformal conjugacy between ![]() $\mathcal {N}_d$ and
$\mathcal {N}_d$ and ![]() $\mathcal {N}_\Gamma $, which extends to a topological conjugacy from the ideal boundary
$\mathcal {N}_\Gamma $, which extends to a topological conjugacy from the ideal boundary ![]() $\mathbb {S}^1 = I(\mathbb {D}) = \partial \mathbb {D}$ onto
$\mathbb {S}^1 = I(\mathbb {D}) = \partial \mathbb {D}$ onto ![]() $I(\Omega _F)$. Let
$I(\Omega _F)$. Let ![]() $\psi : \overline {\mathbb {D}} \longrightarrow \overline {\mathbb {D}}$ be an arbitrary homeomorphic extension of the topological conjugacy between
$\psi : \overline {\mathbb {D}} \longrightarrow \overline {\mathbb {D}}$ be an arbitrary homeomorphic extension of the topological conjugacy between  $\overline {z}^d\vert _{\mathbb {S}^1}$ and
$\overline {z}^d\vert _{\mathbb {S}^1}$ and ![]() $\mathcal {N}_d\vert _{\mathbb {S}^1}$ fixing
$\mathcal {N}_d\vert _{\mathbb {S}^1}$ fixing ![]() $1$. We define
$1$. We define
 $$ \begin{align} \mathcal{G}_\Gamma :=\left\{\begin{array}{ll} \mathcal{N}_\Gamma & \mbox{on}\ \overline{\mathcal{D}}\setminus \bigcup_{F} \Omega_F, \\ (\phi\circ\psi) \circ m_{-d} \circ (\phi\circ\psi)^{-1} & \mbox{on}\ \Omega_F, \end{array}\right. \end{align} $$
$$ \begin{align} \mathcal{G}_\Gamma :=\left\{\begin{array}{ll} \mathcal{N}_\Gamma & \mbox{on}\ \overline{\mathcal{D}}\setminus \bigcup_{F} \Omega_F, \\ (\phi\circ\psi) \circ m_{-d} \circ (\phi\circ\psi)^{-1} & \mbox{on}\ \Omega_F, \end{array}\right. \end{align} $$where ![]() $m_{-d}(z) = \overline {z}^d$.
$m_{-d}(z) = \overline {z}^d$.
The map ![]() $\overline {z}^d$ has
$\overline {z}^d$ has ![]() $d+1$ invariant rays in
$d+1$ invariant rays in ![]() $\mathbb {D}$ connecting
$\mathbb {D}$ connecting ![]() $0$ with
$0$ with ![]() $e^{2\pi i \cdot \frac {j}{d+1}}$ by radial line segments. We shall refer to these rays as internal rays. For each
$e^{2\pi i \cdot \frac {j}{d+1}}$ by radial line segments. We shall refer to these rays as internal rays. For each ![]() $\Omega _F$, we let
$\Omega _F$, we let ![]() $\mathscr {T}_F$ be the image of the union of these
$\mathscr {T}_F$ be the image of the union of these ![]() $d+1$ internal rays (under
$d+1$ internal rays (under ![]() $\phi \circ \psi $), and we call the image of
$\phi \circ \psi $), and we call the image of ![]() $0$ the centre of
$0$ the centre of ![]() $\Omega _F$. This graph
$\Omega _F$. This graph ![]() $\mathscr {T}_F$ is a deformation retract of
$\mathscr {T}_F$ is a deformation retract of ![]() $\Pi _F$ fixing the ideal points. Thus, each ray of
$\Pi _F$ fixing the ideal points. Thus, each ray of ![]() $\Omega _F$ lands exactly at a cusp where two circles of the circle packing touch. We define
$\Omega _F$ lands exactly at a cusp where two circles of the circle packing touch. We define
 $$ \begin{align} \mathscr{T}(\mathcal{G}_\Gamma) := \bigcup_F \overline{\mathscr{T}_F} \end{align} $$
$$ \begin{align} \mathscr{T}(\mathcal{G}_\Gamma) := \bigcup_F \overline{\mathscr{T}_F} \end{align} $$and endow it with a simplicial structure such that the centres of the faces are vertices. Then ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ is the planar dual to the plane graph
$\mathscr {T}(\mathcal {G}_\Gamma )$ is the planar dual to the plane graph ![]() $\Gamma $. We will now see that
$\Gamma $. We will now see that ![]() $\mathcal {G}_\Gamma $ acts as a ‘reflection’ on each face of
$\mathcal {G}_\Gamma $ acts as a ‘reflection’ on each face of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$.
$\mathscr {T}(\mathcal {G}_\Gamma )$.
Lemma 3.22. Let P be an open face of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$; then
$\mathscr {T}(\mathcal {G}_\Gamma )$; then ![]() $\mathcal {G}_\Gamma $ is a homeomorphism sending P to the interior of its complement.
$\mathcal {G}_\Gamma $ is a homeomorphism sending P to the interior of its complement.
Proof. Since ![]() $\Gamma $ is
$\Gamma $ is ![]() $2$-connected, the complement of
$2$-connected, the complement of ![]() $\overline {P}$ is connected, so P is a Jordan domain. Since P contains no critical point and
$\overline {P}$ is connected, so P is a Jordan domain. Since P contains no critical point and ![]() $\mathcal {G}_\Gamma (\partial P) = \partial P$, it follows that
$\mathcal {G}_\Gamma (\partial P) = \partial P$, it follows that ![]() $\mathcal {G}_\Gamma $ sends P homeomorphically to the interior of its complement.
$\mathcal {G}_\Gamma $ sends P homeomorphically to the interior of its complement.
We shall see in the next section that this branched covering ![]() $\mathcal {G}_\Gamma $ is topologically conjugate to a critically fixed anti-rational map R and this dual graph
$\mathcal {G}_\Gamma $ is topologically conjugate to a critically fixed anti-rational map R and this dual graph ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ is the Tischler graph associated with R.
$\mathscr {T}(\mathcal {G}_\Gamma )$ is the Tischler graph associated with R.
4 Critically Fixed Anti-rational Maps
In this section, we shall show how critically fixed anti-rational maps are related to circle packings and kissing reflection groups. As a corollary of our study, we obtain a classification of critically fixed anti-rational maps in terms of the combinatorics of planar duals of Tischler graphs. A classification of these maps in terms of combinatorial properties of Tischler graphs was given independently by Geyer in a recent work [Reference Geyer9]. For the purpose of establishing a dynamical correspondence between critically fixed anti-rational maps and kissing reflection groups, planar duals of Tischler graphs turn out to be a more natural combinatorial invariant.
The arguments employed in Subsection 4.1, where we investigate the structure (of planar duals) of Tischler graphs, parallel those used in the proof of [Reference Geyer9, Theorem 4.3]. On the other hand, [Reference Geyer9, §6] uses purely topological means to construct Thurston maps for the realisation part of the classification theorem; while we use the branched cover ![]() $\mathcal {G}_\Gamma $ of Subsection 3.5, which is cooked up from Nielsen maps of kissing reflection groups (see Subsection 4.2).
$\mathcal {G}_\Gamma $ of Subsection 3.5, which is cooked up from Nielsen maps of kissing reflection groups (see Subsection 4.2).
We define an anti-polynomial P of degree d as
where ![]() $a_i\in \mathbb {C}$ and
$a_i\in \mathbb {C}$ and ![]() $a_d \neq 0$. An anti-rational map R of degree d is the ratio of two anti-polynomials
$a_d \neq 0$. An anti-rational map R of degree d is the ratio of two anti-polynomials
 $$ \begin{align*}R(z) = \frac{P(z)}{Q(z)} \end{align*} $$
$$ \begin{align*}R(z) = \frac{P(z)}{Q(z)} \end{align*} $$where P and Q have no common zeroes and the maximum degree of P and Q is d. An anti-rational map of degree d is an orientation-reversing branched covering of ![]() $\widehat {\mathbb {C}}$. It is said to be critically fixed if all of its critical points are fixed. The Julia set and Fatou set of anti-rational maps can be defined as in the rational setting.
$\widehat {\mathbb {C}}$. It is said to be critically fixed if all of its critical points are fixed. The Julia set and Fatou set of anti-rational maps can be defined as in the rational setting.
4.1 Tischler graph of critically fixed anti-rational maps
Let R be a critically fixed anti-rational map of degree d. Let ![]() $c_1,\cdots , c_k$ be the distinct critical points of R and the local degree of R at
$c_1,\cdots , c_k$ be the distinct critical points of R and the local degree of R at ![]() $c_i$ be
$c_i$ be ![]() $m_i$ (
$m_i$ (![]() $i=1,\cdots , k$). Since R has
$i=1,\cdots , k$). Since R has ![]() $(2d-2)$ critical points counting multiplicity, we have that
$(2d-2)$ critical points counting multiplicity, we have that
 $$ \begin{align*}\displaystyle\sum_{i=1}^k (m_i-1)=2d-2\ \implies\ \displaystyle\sum_{i=1}^k m_i=2d+k-2. \end{align*} $$
$$ \begin{align*}\displaystyle\sum_{i=1}^k (m_i-1)=2d-2\ \implies\ \displaystyle\sum_{i=1}^k m_i=2d+k-2. \end{align*} $$ Suppose that ![]() $U_i$ is the invariant Fatou component containing
$U_i$ is the invariant Fatou component containing ![]() $c_i$ (
$c_i$ (![]() $i=1,\cdots , k$). Then
$i=1,\cdots , k$). Then ![]() $U_i$ is a simply connected domain such that
$U_i$ is a simply connected domain such that ![]() $R\vert _{U_i}$ is conformally conjugate to
$R\vert _{U_i}$ is conformally conjugate to ![]() $\overline {z}^{m_i}\vert _{\mathbb {D}}$ [Reference Milnor31, Theorem 9.3]. This defines internal rays in
$\overline {z}^{m_i}\vert _{\mathbb {D}}$ [Reference Milnor31, Theorem 9.3]. This defines internal rays in ![]() $U_i$ and R maps the internal ray at angle
$U_i$ and R maps the internal ray at angle ![]() $\theta \in \mathbb {R}/\mathbb {Z}$ to the one at angle
$\theta \in \mathbb {R}/\mathbb {Z}$ to the one at angle ![]() $-m_i\theta \in \mathbb {R}/\mathbb {Z}$. It follows that there are
$-m_i\theta \in \mathbb {R}/\mathbb {Z}$. It follows that there are ![]() $(m_i+1)$ fixed internal rays in
$(m_i+1)$ fixed internal rays in ![]() $U_i$. A straightforward adaptation of [Reference Milnor31, Theorem 18.10] now implies that all of these fixed internal rays land at repelling fixed points on
$U_i$. A straightforward adaptation of [Reference Milnor31, Theorem 18.10] now implies that all of these fixed internal rays land at repelling fixed points on ![]() $\partial U_i$.
$\partial U_i$.
We define the Tischler graph ![]() $\mathscr {T}$ of R as the union of the closures of the fixed internal rays of R.
$\mathscr {T}$ of R as the union of the closures of the fixed internal rays of R.
Lemma 4.1. R has exactly ![]() $(d+2k-1)$ distinct fixed points in
$(d+2k-1)$ distinct fixed points in ![]() $\widehat {\mathbb {C}}$ of which
$\widehat {\mathbb {C}}$ of which ![]() $(d+k-1)$ lie on the Julia set of R.
$(d+k-1)$ lie on the Julia set of R.
Proof. Note that R has no neutral fixed point and exactly k attracting fixed points. The count of the total number of fixed points of R now follows from the Lefschetz fixed point theorem (see [Reference Lee and Makarov22, Lemma 6.1]).
Lemma 4.2. The fixed internal rays of R land pairwise.
Proof. As R is a local orientation-reversing diffeomorphism in a neighbourhood of the landing point of each internal ray, it follows that at most two distinct fixed internal rays may land at a common point.
Note that the total number of fixed internal rays of R is
 $$ \begin{align*}\displaystyle\sum_{i=1}^k (m_i+1)=2(d+k-1), \end{align*} $$
$$ \begin{align*}\displaystyle\sum_{i=1}^k (m_i+1)=2(d+k-1), \end{align*} $$while there are only ![]() $(d+k-1)$ landing points available for these rays by Lemma 4.1. Since no more than two fixed internal rays can land at a common fixed point, the result follows.
$(d+k-1)$ landing points available for these rays by Lemma 4.1. Since no more than two fixed internal rays can land at a common fixed point, the result follows.
In our setting, it is more natural to put a simplicial structure on ![]() $\mathscr {T}$ so that the vertices correspond to the critical points of R. We will refer to the repelling fixed points on
$\mathscr {T}$ so that the vertices correspond to the critical points of R. We will refer to the repelling fixed points on ![]() $\mathscr {T}$ as the midpoints of the edges. To distinguish an edge of
$\mathscr {T}$ as the midpoints of the edges. To distinguish an edge of ![]() $\mathscr {T}$ from an arc connecting a vertex and a midpoint, we will call the latter an internal ray of
$\mathscr {T}$ from an arc connecting a vertex and a midpoint, we will call the latter an internal ray of ![]() $\mathscr {T}$.
$\mathscr {T}$.
Corollary 4.3. The valence of the critical point ![]() $c_i$ (as a vertex of
$c_i$ (as a vertex of ![]() $\mathscr {T}$) is
$\mathscr {T}$) is ![]() $(m_i+1)$ (
$(m_i+1)$ (![]() $i=1,\cdots , k$). The repelling fixed points of R are in bijective correspondence with the edges of
$i=1,\cdots , k$). The repelling fixed points of R are in bijective correspondence with the edges of ![]() $\mathscr {T}$.
$\mathscr {T}$.
The proof of Lemma 4.2 implies the following (see [Reference Hlushchanka11, Corollary 6] for the same statement in the holomorphic setting).
Corollary 4.4. Each fixed point of R lies on (the closure of) a fixed internal ray.
We are now ready to establish the key properties of the Tischler graph of a critically fixed anti-rational map that will be used in the combinatorial classification of such maps.
Lemma 4.5. The faces of ![]() $\mathscr {T}$ are Jordan domains.
$\mathscr {T}$ are Jordan domains.
Proof. Let F be a face of the Tischler graph ![]() $\mathscr {T}$. Then a component of the ideal boundary
$\mathscr {T}$. Then a component of the ideal boundary ![]() $I(F)$ consists of a sequence of edges
$I(F)$ consists of a sequence of edges ![]() $e_1,\ldots , e_m$ of
$e_1,\ldots , e_m$ of ![]() $\mathscr {T}$, oriented counterclockwise viewed from F. Note that a priori,
$\mathscr {T}$, oriented counterclockwise viewed from F. Note that a priori, ![]() $e_i$ may be equal to
$e_i$ may be equal to ![]() $e_j$ in
$e_j$ in ![]() $\mathscr {T}$ for different i and j.
$\mathscr {T}$ for different i and j.
Consider the graph T whose vertices are components of ![]() $\widehat {\mathbb {C}}\setminus \overline {F}$ and two vertices
$\widehat {\mathbb {C}}\setminus \overline {F}$ and two vertices ![]() $U, V$ are connected by an edge if there is a path in
$U, V$ are connected by an edge if there is a path in ![]() $\widehat {\mathbb {C}}\setminus F$ connecting
$\widehat {\mathbb {C}}\setminus F$ connecting ![]() $U,V$ and not passing through other components. Then T is a finite union of trees. Since each vertex (of
$U,V$ and not passing through other components. Then T is a finite union of trees. Since each vertex (of ![]() $\mathscr {T}$) has valence at least
$\mathscr {T}$) has valence at least ![]() $3$, we have that
$3$, we have that ![]() $e_i\neq e_{i+1}$. This also implies that two adjacent components
$e_i\neq e_{i+1}$. This also implies that two adjacent components ![]() $U,V$ either share a common boundary vertex or there exists an edge of
$U,V$ either share a common boundary vertex or there exists an edge of ![]() $\mathscr {T}$ connecting them. Let U be a component of
$\mathscr {T}$ connecting them. Let U be a component of ![]() $\widehat {\mathbb {C}}\setminus \overline {F}$. If
$\widehat {\mathbb {C}}\setminus \overline {F}$. If ![]() $e_i, e_j$ are a pair of adjacent edges of
$e_i, e_j$ are a pair of adjacent edges of ![]() $\partial U$ but
$\partial U$ but ![]() $e_i, e_j$ are not adjacent on the ideal boundary
$e_i, e_j$ are not adjacent on the ideal boundary ![]() $I(F)$, then there exists a component V of
$I(F)$, then there exists a component V of ![]() $\widehat {\mathbb {C}}\setminus \overline {F}$ ‘attached’ to U through the vertex
$\widehat {\mathbb {C}}\setminus \overline {F}$ ‘attached’ to U through the vertex ![]() $v = e_i \cap e_j$ (see Figure 4.1). Therefore, the number of pairs of adjacent edges of
$v = e_i \cap e_j$ (see Figure 4.1). Therefore, the number of pairs of adjacent edges of ![]() $\partial U$ that are not adjacent on the ideal boundary
$\partial U$ that are not adjacent on the ideal boundary ![]() $I(F)$ equals to the valence of U in T. Choose U to be an end point of T and let
$I(F)$ equals to the valence of U in T. Choose U to be an end point of T and let ![]() $S = \partial U$.
$S = \partial U$.

Figure 4.1 An a priori possible schematic of a component of the boundary of F.
Since R is orientation-reversing and each edge of ![]() $\mathscr {T}$ is invariant under the map, R reflects the two sides near each open edge of S. Thus, there is a connected component V of
$\mathscr {T}$ is invariant under the map, R reflects the two sides near each open edge of S. Thus, there is a connected component V of ![]() $R^{-1}(U)$ with
$R^{-1}(U)$ with ![]() $\partial V \cap \partial U \neq \emptyset $ and
$\partial V \cap \partial U \neq \emptyset $ and ![]() $V \cap F \neq \emptyset $. It is easy to see from the local dynamics of
$V \cap F \neq \emptyset $. It is easy to see from the local dynamics of ![]() $\overline {z}^{m_i}$ at the origin that near a critical point, R sends the region bounded by two adjacent edges of
$\overline {z}^{m_i}$ at the origin that near a critical point, R sends the region bounded by two adjacent edges of ![]() $\mathscr {T}$ to its complement. Therefore, by our choice of U, we have
$\mathscr {T}$ to its complement. Therefore, by our choice of U, we have ![]() $\partial U \subseteq \partial V$. Since
$\partial U \subseteq \partial V$. Since ![]() $\partial F$ is R-invariant,
$\partial F$ is R-invariant, ![]() $V \cap \partial F = \emptyset $. Thus,
$V \cap \partial F = \emptyset $. Thus, ![]() $V \subseteq F$ and V contains no critical points of R. As U is a disk, the Riemann–Hurwitz formula now implies that V is a disk and R is a homeomorphism from
$V \subseteq F$ and V contains no critical points of R. As U is a disk, the Riemann–Hurwitz formula now implies that V is a disk and R is a homeomorphism from ![]() $\partial V$ to
$\partial V$ to ![]() $\partial U$. Therefore,
$\partial U$. Therefore, ![]() $\partial U = \partial V$ and
$\partial U = \partial V$ and ![]() $V = F$; so F is a Jordan domain.
$V = F$; so F is a Jordan domain.
In particular, we have the following.
Corollary 4.6. The Tischler graph ![]() $\mathscr {T}$ is connected.
$\mathscr {T}$ is connected.
In fact, the Tischler graph gives a topological model for the map R.
Corollary 4.7. Let F be a face of ![]() $\mathscr {T}$ and
$\mathscr {T}$ and  $F^c = \overline {\widehat {\mathbb {C}}\setminus F}$ be the closure of its complement. Then
$F^c = \overline {\widehat {\mathbb {C}}\setminus F}$ be the closure of its complement. Then ![]() $R: \overline {F} \longrightarrow F^c$ is an orientation-reversing homeomorphism.
$R: \overline {F} \longrightarrow F^c$ is an orientation-reversing homeomorphism.
Lemma 4.8. Let ![]() $F_1, F_2$ be two faces of
$F_1, F_2$ be two faces of ![]() $\mathscr {T}$; then the boundaries share at most one edge.
$\mathscr {T}$; then the boundaries share at most one edge.
Proof. Suppose that ![]() $F_1$ and
$F_1$ and ![]() $F_2$ share two or more edges. For
$F_2$ share two or more edges. For ![]() $i=1,2$, let
$i=1,2$, let ![]() $\gamma _i$ be the hyperbolic geodesic arc in
$\gamma _i$ be the hyperbolic geodesic arc in ![]() $\mathring {F_i}$ connecting the two midpoints of the edges and let
$\mathring {F_i}$ connecting the two midpoints of the edges and let ![]() $\gamma = \gamma _1 \cup \gamma _2$. Since each vertex has valence at least
$\gamma = \gamma _1 \cup \gamma _2$. Since each vertex has valence at least ![]() $3$, we see that
$3$, we see that ![]() $\gamma $ is essential in
$\gamma $ is essential in  $\widehat {\mathbb {C}}\setminus V(\mathscr {T}) = \widehat {\mathbb {C}}\setminus P(R)$ (that is,
$\widehat {\mathbb {C}}\setminus V(\mathscr {T}) = \widehat {\mathbb {C}}\setminus P(R)$ (that is, ![]() $\gamma $ is not homotopic to a point or a puncture of the surface
$\gamma $ is not homotopic to a point or a puncture of the surface 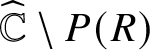 $\widehat {\mathbb {C}}\setminus P(R)$), where
$\widehat {\mathbb {C}}\setminus P(R)$), where ![]() $P(R)$ stands for the postcritical set of R and
$P(R)$ stands for the postcritical set of R and ![]() $V(\mathscr {T})$ denotes the vertex set of the graph
$V(\mathscr {T})$ denotes the vertex set of the graph ![]() $\mathscr {T}$. By Corollary 4.7, there exists
$\mathscr {T}$. By Corollary 4.7, there exists ![]() $\gamma '$ homotopic to
$\gamma '$ homotopic to ![]() $\gamma $ in
$\gamma $ in  $\widehat {\mathbb {C}}\setminus P(R)$ such that
$\widehat {\mathbb {C}}\setminus P(R)$ such that ![]() $R: \gamma ' \longrightarrow \gamma $ is a homeomorphism. This gives a Thurston obstruction (more precisely, a Levy cycle) for the anti-rational map R (see the discussion in Subsection 4.2 on Thurston’s theory for rational maps), which is a contradiction. Hence, the supposition that
$R: \gamma ' \longrightarrow \gamma $ is a homeomorphism. This gives a Thurston obstruction (more precisely, a Levy cycle) for the anti-rational map R (see the discussion in Subsection 4.2 on Thurston’s theory for rational maps), which is a contradiction. Hence, the supposition that ![]() $F_1$ and
$F_1$ and ![]() $F_2$ share two or more edges is false.
$F_2$ share two or more edges is false.
The following result, where we translate the above properties of the Tischler graph to a simple graph-theoretic property of its planar dual, plays a crucial role in the combinatorial classification of critically fixed anti-rational maps.
Lemma 4.9. Let ![]() $\Gamma $ be the planar dual of the Tischler graph
$\Gamma $ be the planar dual of the Tischler graph ![]() $\mathscr {T}$ of a critically fixed anti-rational map R. Then
$\mathscr {T}$ of a critically fixed anti-rational map R. Then ![]() $\Gamma $ is simple and
$\Gamma $ is simple and ![]() $2$-connected.
$2$-connected.
Proof. By Lemma 4.8, no two faces of ![]() $\mathscr {T}$ share two edges on their boundary. Hence, the dual graph contains no multi-edge. Again, as each face of
$\mathscr {T}$ share two edges on their boundary. Hence, the dual graph contains no multi-edge. Again, as each face of ![]() $\mathscr {T}$ is a Jordan domain by Lemma 4.5, the dual graph contains no self-loop. Therefore,
$\mathscr {T}$ is a Jordan domain by Lemma 4.5, the dual graph contains no self-loop. Therefore, ![]() $\Gamma $ is simple.
$\Gamma $ is simple.
The fact that each face of ![]() $\mathscr {T}$ is a Jordan domain also implies that the complement of the closure of each face is connected. So the dual graph
$\mathscr {T}$ is a Jordan domain also implies that the complement of the closure of each face is connected. So the dual graph ![]() $\Gamma $ remains connected upon deletion of any vertex. In other words,
$\Gamma $ remains connected upon deletion of any vertex. In other words, ![]() $\Gamma $ is
$\Gamma $ is ![]() $2$-connected.
$2$-connected.
4.2 Constructing critically fixed anti-rational maps from graphs
Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph and
$2$-connected simple plane graph and ![]() $G_\Gamma $ be an associated kissing reflection group. In Subsection 3.5, we constructed a topological branched covering
$G_\Gamma $ be an associated kissing reflection group. In Subsection 3.5, we constructed a topological branched covering ![]() $\mathcal {G}_\Gamma $ from the Nielsen map of
$\mathcal {G}_\Gamma $ from the Nielsen map of ![]() $G_\Gamma $. In the remainder of this section, we will use this branched covering
$G_\Gamma $. In the remainder of this section, we will use this branched covering ![]() $\mathcal {G}_\Gamma $ to promote Lemma 4.9 to a characterisation of Tischler graphs of critically fixed anti-rational maps.
$\mathcal {G}_\Gamma $ to promote Lemma 4.9 to a characterisation of Tischler graphs of critically fixed anti-rational maps.
Proposition 4.10. A plane graph ![]() $\mathcal {T}$ is the Tischler graph of a critically fixed anti-rational map R if and only if the dual (plane) graph
$\mathcal {T}$ is the Tischler graph of a critically fixed anti-rational map R if and only if the dual (plane) graph ![]() $\Gamma $ is simple and
$\Gamma $ is simple and ![]() $2$-connected. Moreover, R is topologically conjugate to
$2$-connected. Moreover, R is topologically conjugate to ![]() $\mathcal {G}_\Gamma $.
$\mathcal {G}_\Gamma $.
We will first introduce some terminology. A postcritically finite branched covering (possibly orientation-reversing) of a topological ![]() $2$-sphere
$2$-sphere ![]() $\mathbb {S}^2$ is called a Thurston map. We denote the postcritical set of a Thurston map f by
$\mathbb {S}^2$ is called a Thurston map. We denote the postcritical set of a Thurston map f by ![]() $P(f)$. Two Thurston maps f and g are equivalent if there exist two orientation-preserving homeomorphisms
$P(f)$. Two Thurston maps f and g are equivalent if there exist two orientation-preserving homeomorphisms ![]() $h_0,h_1:(\mathbb {S}^2,P(f))\to (\mathbb {S}^2,P(g))$ so that
$h_0,h_1:(\mathbb {S}^2,P(f))\to (\mathbb {S}^2,P(g))$ so that ![]() $h_0\circ f = g\circ h_1$, where
$h_0\circ f = g\circ h_1$, where ![]() $h_0$ and
$h_0$ and ![]() $h_1$ are isotopic relative to
$h_1$ are isotopic relative to ![]() $P(f)$.
$P(f)$.
A set of pairwise disjoint, nonisotopic, essential, simple closed curves ![]() $\Sigma $ on
$\Sigma $ on ![]() $\mathbb {S}^2\setminus P(f)$ is called a curve system. A curve system
$\mathbb {S}^2\setminus P(f)$ is called a curve system. A curve system ![]() $\Sigma $ is called f-stable if for every curve
$\Sigma $ is called f-stable if for every curve ![]() $\sigma \in \Sigma $, all of the essential components of
$\sigma \in \Sigma $, all of the essential components of ![]() $f^{-1}(\sigma )$ are homotopic rel
$f^{-1}(\sigma )$ are homotopic rel ![]() $P(f)$ to curves in
$P(f)$ to curves in ![]() $\Sigma $. We associate to an f-stable curve system
$\Sigma $. We associate to an f-stable curve system ![]() $\Sigma $ the Thurston linear transformation
$\Sigma $ the Thurston linear transformation
defined as
 $$ \begin{align*}f_\Sigma(\sigma) = \sum_{\sigma' \subseteq f^{-1}(\sigma)} \frac{1}{\deg(f: \sigma' \rightarrow \sigma)}[\sigma']_\Sigma, \end{align*} $$
$$ \begin{align*}f_\Sigma(\sigma) = \sum_{\sigma' \subseteq f^{-1}(\sigma)} \frac{1}{\deg(f: \sigma' \rightarrow \sigma)}[\sigma']_\Sigma, \end{align*} $$where ![]() $\sigma \in \Sigma $ and
$\sigma \in \Sigma $ and ![]() $[\sigma ']_\Sigma $ denotes the element of
$[\sigma ']_\Sigma $ denotes the element of ![]() $\Sigma $ isotopic to
$\Sigma $ isotopic to ![]() $\sigma '$, if it exists. The curve system is called irrreducible if
$\sigma '$, if it exists. The curve system is called irrreducible if ![]() $f_\Sigma $ is irreducible as a linear transformation. It is said to be a Thurston obstruction if the spectral radius
$f_\Sigma $ is irreducible as a linear transformation. It is said to be a Thurston obstruction if the spectral radius ![]() $\lambda (f_\Sigma ) \geq 1$.
$\lambda (f_\Sigma ) \geq 1$.
Similarly, an arc ![]() $\lambda $ in
$\lambda $ in ![]() $\mathbb {S}^2\setminus P(f)$ is an embedding of
$\mathbb {S}^2\setminus P(f)$ is an embedding of ![]() $(0,1)$ in
$(0,1)$ in ![]() $\mathbb {S}^2\setminus P(f)$ with endpoints in
$\mathbb {S}^2\setminus P(f)$ with endpoints in ![]() $P(f)$. It is said to be essential if it is not contractible in
$P(f)$. It is said to be essential if it is not contractible in ![]() $\mathbb {S}^2$ fixing the two endpoints. A set of pairwise nonisotopic essential arcs
$\mathbb {S}^2$ fixing the two endpoints. A set of pairwise nonisotopic essential arcs ![]() $\Lambda $ is called an arc system. The Thurston linear transformation
$\Lambda $ is called an arc system. The Thurston linear transformation ![]() $f_\Lambda $ is defined in a similar way, and we say that it is irreducible if
$f_\Lambda $ is defined in a similar way, and we say that it is irreducible if ![]() $f_\Lambda $ is irreducible as a linear transformation.
$f_\Lambda $ is irreducible as a linear transformation.
The next proposition allows us to directly apply Thurston’s topological characterisation theorem for rational maps (see [Reference Douady and Hubbard6, Theorem 1]) to the study of orientation-reversing Thurston maps (see [Reference Geyer9, Theorem 3.9] for an intrinsic topological characterisation theorem for anti-rational maps). It is proved by considering the second iterate of Thurston’s pullback map on the Teichmüller space of ![]() $\mathbb {S}^2\setminus P(f)$. The reader is referred to [Reference Douady and Hubbard6] for the definition of hyperbolic orbifold, but this is the typical case as any map with more than four postcritical points has hyperbolic orbifold.
$\mathbb {S}^2\setminus P(f)$. The reader is referred to [Reference Douady and Hubbard6] for the definition of hyperbolic orbifold, but this is the typical case as any map with more than four postcritical points has hyperbolic orbifold.
Proposition 4.11. [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Proposition 6.1] Let f be an orientation-reversing Thurston map so that ![]() $f\circ f$ has hyperbolic orbifold. Then f is equivalent to an anti-rational map if and only if
$f\circ f$ has hyperbolic orbifold. Then f is equivalent to an anti-rational map if and only if ![]() $f\circ f$ is equivalent to a rational map if and only if
$f\circ f$ is equivalent to a rational map if and only if ![]() $f\circ f$ has no Thurston obstruction. Moreover, if f is equivalent to an anti-rational map, the map is unique up to Möbius conjugacy.
$f\circ f$ has no Thurston obstruction. Moreover, if f is equivalent to an anti-rational map, the map is unique up to Möbius conjugacy.
For a curve system ![]() $\Sigma $ (respectively an arc system
$\Sigma $ (respectively an arc system ![]() $\Lambda $), we set
$\Lambda $), we set ![]() $\widetilde {\Sigma }$ (respectively
$\widetilde {\Sigma }$ (respectively ![]() $\widetilde {\Lambda }$) as the union of those components of
$\widetilde {\Lambda }$) as the union of those components of ![]() $f^{-1}(\Sigma )$ (respectively
$f^{-1}(\Sigma )$ (respectively ![]() $f^{-1}(\Lambda )$) which are isotopic relative to
$f^{-1}(\Lambda )$) which are isotopic relative to ![]() $P(f)$ to elements of
$P(f)$ to elements of ![]() $\Sigma $ (respectively
$\Sigma $ (respectively ![]() $\Lambda $). We will use
$\Lambda $). We will use ![]() $\Sigma \cdot \Lambda $ to denote the minimal intersection number between them. We will be using the following theorem excerpted and paraphrased from [Reference Pilgrim and Tan38, Theorem 3.2].
$\Sigma \cdot \Lambda $ to denote the minimal intersection number between them. We will be using the following theorem excerpted and paraphrased from [Reference Pilgrim and Tan38, Theorem 3.2].
Theorem 4.12. [Reference Pilgrim and Tan38, Theorem 3.2] Let f be an orientation-preserving Thurston map, ![]() $\Sigma $ an irreducible Thurston obstruction in
$\Sigma $ an irreducible Thurston obstruction in ![]() $(\mathbb {S}^2, P(f))$ and
$(\mathbb {S}^2, P(f))$ and ![]() $\Lambda $ an irreducible arc system in
$\Lambda $ an irreducible arc system in ![]() $(\mathbb {S}^2, P(f))$. Assume that
$(\mathbb {S}^2, P(f))$. Assume that ![]() $\Sigma $ intersect
$\Sigma $ intersect ![]() $\Lambda $ minimally; then either
$\Lambda $ minimally; then either
•
 $\Sigma \cdot \Lambda = 0$; or
$\Sigma \cdot \Lambda = 0$; or•
 $\Sigma \cdot \Lambda \neq 0$ and for each
$\Sigma \cdot \Lambda \neq 0$ and for each  $\lambda \in \Lambda $, there is exactly one connected component
$\lambda \in \Lambda $, there is exactly one connected component  $\lambda '$ of
$\lambda '$ of  $f^{-1}(\lambda )$ such that
$f^{-1}(\lambda )$ such that  $\lambda ' \cap \widetilde {\Sigma } \neq \emptyset $. Moreover, the arc
$\lambda ' \cap \widetilde {\Sigma } \neq \emptyset $. Moreover, the arc  $\lambda '$ is the unique component of
$\lambda '$ is the unique component of  $f^{-1}(\lambda )$ which is isotopic to an element of
$f^{-1}(\lambda )$ which is isotopic to an element of  $\Lambda $.
$\Lambda $.
With these preparations, we are now ready to show that ![]() $\mathcal {G}_\Gamma $ is equivalent to an anti-rational map. The proof is similar to [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Proposition 6.2].
$\mathcal {G}_\Gamma $ is equivalent to an anti-rational map. The proof is similar to [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Proposition 6.2].
Lemma 4.13. Let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph. Then
$2$-connected simple plane graph. Then ![]() $\mathcal {G}_\Gamma $ is equivalent to a critically fixed anti-rational map
$\mathcal {G}_\Gamma $ is equivalent to a critically fixed anti-rational map ![]() $\mathcal {R}_\Gamma $.
$\mathcal {R}_\Gamma $.
Proof. It is easy to verify that ![]() $\mathcal {G}_\Gamma \circ \mathcal {G}_\Gamma $ has hyperbolic orbifold, except when
$\mathcal {G}_\Gamma \circ \mathcal {G}_\Gamma $ has hyperbolic orbifold, except when ![]() $\Gamma =\Gamma _d$, in which case
$\Gamma =\Gamma _d$, in which case ![]() $\mathcal {G}_\Gamma $ has only two fixed critical points, each of which is fully branched and
$\mathcal {G}_\Gamma $ has only two fixed critical points, each of which is fully branched and ![]() $\mathcal {G}_\Gamma $ is equivalent to
$\mathcal {G}_\Gamma $ is equivalent to ![]() $\overline {z}^d$. Thus, by Proposition 4.11, we will prove the lemma by showing that there is no Thurston obstruction for
$\overline {z}^d$. Thus, by Proposition 4.11, we will prove the lemma by showing that there is no Thurston obstruction for ![]() $\mathcal {G}_\Gamma \circ \mathcal {G}_\Gamma $.
$\mathcal {G}_\Gamma \circ \mathcal {G}_\Gamma $.
We will assume that there is a Thurston obstruction ![]() $\Sigma $ and arrive at a contradiction. After passing to a subset, we may assume that
$\Sigma $ and arrive at a contradiction. After passing to a subset, we may assume that ![]() $\Sigma $ is irreducible. Isotoping the curve system
$\Sigma $ is irreducible. Isotoping the curve system ![]() $\Sigma $, we may assume that
$\Sigma $, we may assume that ![]() $\Sigma $ intersects the graph
$\Sigma $ intersects the graph ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ minimally (see Subsection 3.5 for the definition of
$\mathscr {T}(\mathcal {G}_\Gamma )$ minimally (see Subsection 3.5 for the definition of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$). Let
$\mathscr {T}(\mathcal {G}_\Gamma )$). Let ![]() $\lambda $ be an edge in
$\lambda $ be an edge in ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$; then
$\mathscr {T}(\mathcal {G}_\Gamma )$; then ![]() $\Lambda = \{\lambda \}$ is an irreducible arc system. Let
$\Lambda = \{\lambda \}$ is an irreducible arc system. Let ![]() $\widetilde {\Sigma }$ be the union of those components of
$\widetilde {\Sigma }$ be the union of those components of  $\mathcal {G}_\Gamma ^{-2}(\Sigma )$ which are isotopic to elements of
$\mathcal {G}_\Gamma ^{-2}(\Sigma )$ which are isotopic to elements of ![]() $\Sigma $.
$\Sigma $.
We claim that ![]() $\widetilde {\Sigma }$ does not intersect
$\widetilde {\Sigma }$ does not intersect 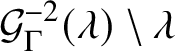 $\mathcal {G}_\Gamma ^{-2}(\lambda ) \setminus \lambda $. Indeed, applying Theorem 4.12, we are led to the following two cases. In the first case, we have
$\mathcal {G}_\Gamma ^{-2}(\lambda ) \setminus \lambda $. Indeed, applying Theorem 4.12, we are led to the following two cases. In the first case, we have ![]() $\Sigma \cdot \lambda = 0$; hence,
$\Sigma \cdot \lambda = 0$; hence,  $\mathcal {G}_\Gamma ^{-2}(\Sigma )$ cannot intersect
$\mathcal {G}_\Gamma ^{-2}(\Sigma )$ cannot intersect  $\mathcal {G}_\Gamma ^{-2}(\lambda )$ and the claim follows. In the second case, since
$\mathcal {G}_\Gamma ^{-2}(\lambda )$ and the claim follows. In the second case, since ![]() $\mathcal {G}_\Gamma (\lambda ) = \lambda $, we conclude that
$\mathcal {G}_\Gamma (\lambda ) = \lambda $, we conclude that ![]() $\lambda $ is the unique component of
$\lambda $ is the unique component of  $\mathcal {G}_\Gamma ^{-2}(\lambda )$ isotopic to
$\mathcal {G}_\Gamma ^{-2}(\lambda )$ isotopic to ![]() $\lambda $. Thus, the only component of
$\lambda $. Thus, the only component of  $\mathcal {G}_\Gamma ^{-2}(\lambda )$ intersecting
$\mathcal {G}_\Gamma ^{-2}(\lambda )$ intersecting ![]() $\widetilde {\Sigma }$ is
$\widetilde {\Sigma }$ is ![]() $\lambda $, so the claim follows.
$\lambda $, so the claim follows.
Applying this argument on all the edges of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$, we conclude that
$\mathscr {T}(\mathcal {G}_\Gamma )$, we conclude that ![]() $\widetilde {\Sigma }$ does not intersect
$\widetilde {\Sigma }$ does not intersect  $\mathcal {G}_\Gamma ^{-2}(\mathscr {T}(\mathcal {G}_\Gamma )) \setminus \mathscr {T}(\mathcal {G}_\Gamma )$.
$\mathcal {G}_\Gamma ^{-2}(\mathscr {T}(\mathcal {G}_\Gamma )) \setminus \mathscr {T}(\mathcal {G}_\Gamma )$.
Let F be a face of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ with vertices of
$\mathscr {T}(\mathcal {G}_\Gamma )$ with vertices of ![]() $\partial F$ denoted by
$\partial F$ denoted by ![]() $v_1, \ldots , v_k$ counterclockwise. Denote
$v_1, \ldots , v_k$ counterclockwise. Denote ![]() $e_i \subseteq \partial F$ be the open edge connecting
$e_i \subseteq \partial F$ be the open edge connecting ![]() $v_i, v_{i+1}$. We claim that the graph obtained by removing the boundary edges of F
$v_i, v_{i+1}$. We claim that the graph obtained by removing the boundary edges of F
 $$ \begin{align*}\mathscr{T}_{F}:=\mathscr{T}(\mathcal{G}_\Gamma) \setminus \bigcup_{i=1}^k e_i \end{align*} $$
$$ \begin{align*}\mathscr{T}_{F}:=\mathscr{T}(\mathcal{G}_\Gamma) \setminus \bigcup_{i=1}^k e_i \end{align*} $$is still connected. Since ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ is connected, any vertex v is connected to the set
$\mathscr {T}(\mathcal {G}_\Gamma )$ is connected, any vertex v is connected to the set ![]() $\{v_1,\ldots , v_k\}$ in
$\{v_1,\ldots , v_k\}$ in ![]() $\mathscr {T}_{F}$. Thus, it suffices to show that
$\mathscr {T}_{F}$. Thus, it suffices to show that ![]() $v_i$ and
$v_i$ and ![]() $v_{i+1}$ are connected in
$v_{i+1}$ are connected in ![]() $\mathscr {T}_{F}$ for all i. As the planar dual
$\mathscr {T}_{F}$ for all i. As the planar dual ![]() $\Gamma $ of
$\Gamma $ of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ is
$\mathscr {T}(\mathcal {G}_\Gamma )$ is ![]() $2$-connected and has no self-loop, each face of
$2$-connected and has no self-loop, each face of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ is a Jordan domain. Hence, there exists a face
$\mathscr {T}(\mathcal {G}_\Gamma )$ is a Jordan domain. Hence, there exists a face ![]() $F_i\neq F$ of
$F_i\neq F$ of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ sharing
$\mathscr {T}(\mathcal {G}_\Gamma )$ sharing ![]() $e_i$ on the boundary with F. Moreover, since
$e_i$ on the boundary with F. Moreover, since ![]() $\Gamma $ has no multi-edge, the boundaries of any two faces of
$\Gamma $ has no multi-edge, the boundaries of any two faces of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ intersect at most at one edge. Thus,
$\mathscr {T}(\mathcal {G}_\Gamma )$ intersect at most at one edge. Thus, ![]() $\partial F_i \cap \partial F = e_i \cup \{v_i, v_{i+1}\}$. Hence,
$\partial F_i \cap \partial F = e_i \cup \{v_i, v_{i+1}\}$. Hence, ![]() $v_i$ and
$v_i$ and ![]() $v_{i+1}$ are connected by a path in
$v_{i+1}$ are connected by a path in ![]() $\partial F_i \setminus e_i \subseteq \mathscr {T}_{F}$, and this proves the claim.
$\partial F_i \setminus e_i \subseteq \mathscr {T}_{F}$, and this proves the claim.
Therefore, by Lemma 3.22, we deduce that
 $$ \begin{align*}(\mathcal{G}_\Gamma^{-1} (\mathscr{T}(\mathcal{G}_\Gamma)) \setminus \mathscr{T}(\mathcal{G}_\Gamma)) \cup V(\mathscr{T}(\mathcal{G}_\Gamma)) \end{align*} $$
$$ \begin{align*}(\mathcal{G}_\Gamma^{-1} (\mathscr{T}(\mathcal{G}_\Gamma)) \setminus \mathscr{T}(\mathcal{G}_\Gamma)) \cup V(\mathscr{T}(\mathcal{G}_\Gamma)) \end{align*} $$is connected. Thus,  $(\mathcal {G}_\Gamma ^{-2}(\mathscr {T}(\mathcal {G}_\Gamma )) \setminus \mathscr {T}(\mathcal {G}_\Gamma )) \cup V(\mathscr {T}(\mathcal {G}_\Gamma ))$ is a connected graph containing the postcritical set
$(\mathcal {G}_\Gamma ^{-2}(\mathscr {T}(\mathcal {G}_\Gamma )) \setminus \mathscr {T}(\mathcal {G}_\Gamma )) \cup V(\mathscr {T}(\mathcal {G}_\Gamma ))$ is a connected graph containing the postcritical set ![]() $P(\mathcal {G}_\Gamma \circ \mathcal {G}_\Gamma ) = V(\mathscr {T}(\mathcal {G}_\Gamma ))$. This forces
$P(\mathcal {G}_\Gamma \circ \mathcal {G}_\Gamma ) = V(\mathscr {T}(\mathcal {G}_\Gamma ))$. This forces ![]() $\Sigma $ to be empty, which is a contradiction.
$\Sigma $ to be empty, which is a contradiction.
Therefore, ![]() $\mathcal {G}_\Gamma $ is equivalent to an anti-rational map
$\mathcal {G}_\Gamma $ is equivalent to an anti-rational map ![]() $\mathcal {R}_\Gamma $. Since
$\mathcal {R}_\Gamma $. Since ![]() $\mathcal {G}_\Gamma $ is critically fixed, so is
$\mathcal {G}_\Gamma $ is critically fixed, so is ![]() $\mathcal {R}_\Gamma $.
$\mathcal {R}_\Gamma $.
Let ![]() $h_0, h_1:(\mathbb {S}^2,P(\mathcal {G}_\Gamma ))\to (\mathbb {S}^2,P(\mathcal {R}_\Gamma ))$ be two orientation-preserving homeomorphisms so that
$h_0, h_1:(\mathbb {S}^2,P(\mathcal {G}_\Gamma ))\to (\mathbb {S}^2,P(\mathcal {R}_\Gamma ))$ be two orientation-preserving homeomorphisms so that ![]() $h_0\circ \mathcal {G}_\Gamma = \mathcal {R}_\Gamma \circ h_1$ where
$h_0\circ \mathcal {G}_\Gamma = \mathcal {R}_\Gamma \circ h_1$ where ![]() $h_0$ and
$h_0$ and ![]() $h_1$ are isotopic relative to
$h_1$ are isotopic relative to ![]() $P(\mathcal {G}_\Gamma ) = V(\mathscr {T}(\mathcal {G}_\Gamma ))$.
$P(\mathcal {G}_\Gamma ) = V(\mathscr {T}(\mathcal {G}_\Gamma ))$.
We now use a standard pullback argument to prove the following.
Lemma 4.14. ![]() $h_0(\mathscr {T}(\mathcal {G}_\Gamma ))$ is isotopic to the Tischler graph
$h_0(\mathscr {T}(\mathcal {G}_\Gamma ))$ is isotopic to the Tischler graph ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$.
$\mathscr {T}(\mathcal {R}_\Gamma )$.
Proof. Let ![]() $\alpha $ be an edge of
$\alpha $ be an edge of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$; then
$\mathscr {T}(\mathcal {G}_\Gamma )$; then ![]() $\mathcal {G}_\Gamma (\alpha ) = \alpha $. Consider the sequence of homeomorphisms
$\mathcal {G}_\Gamma (\alpha ) = \alpha $. Consider the sequence of homeomorphisms ![]() $h_i$ with
$h_i$ with
Each ![]() $h_i$ is normalised so that it carries
$h_i$ is normalised so that it carries ![]() $P(\mathcal {G}_\Gamma )$ to
$P(\mathcal {G}_\Gamma )$ to ![]() $P(\mathcal {R}_\Gamma )$. Note by induction,
$P(\mathcal {R}_\Gamma )$. Note by induction, ![]() $\beta _i = h_i(\alpha )$ is isotopic to
$\beta _i = h_i(\alpha )$ is isotopic to ![]() $\beta _0$ relative to the endpoints. Applying isotopy, we may assume that there is a decomposition
$\beta _0$ relative to the endpoints. Applying isotopy, we may assume that there is a decomposition ![]() $\beta _0 = \beta _0^- + \gamma _0 + \beta _0^+$, where
$\beta _0 = \beta _0^- + \gamma _0 + \beta _0^+$, where ![]() $\beta _0^\pm $ are two internal rays and
$\beta _0^\pm $ are two internal rays and ![]() $\gamma _0$ does not intersect any invariant Fatou component. Then every
$\gamma _0$ does not intersect any invariant Fatou component. Then every ![]() $\beta _i = \beta _i^- + \gamma _i + \beta _i^+$ has such a decomposition, too.
$\beta _i = \beta _i^- + \gamma _i + \beta _i^+$ has such a decomposition, too.
Note that ![]() $\mathcal {R}_\Gamma (\gamma _{i+1}) = \gamma _{i}$ and
$\mathcal {R}_\Gamma (\gamma _{i+1}) = \gamma _{i}$ and ![]() $\mathcal {R}_\Gamma :\gamma _{i+1}\to \gamma _{i}$ is injective for each i. Since
$\mathcal {R}_\Gamma :\gamma _{i+1}\to \gamma _{i}$ is injective for each i. Since ![]() $\mathcal {R}_\Gamma $ is hyperbolic and the curves
$\mathcal {R}_\Gamma $ is hyperbolic and the curves ![]() $\gamma _i$ are uniformly bounded away from the postcritical point set of
$\gamma _i$ are uniformly bounded away from the postcritical point set of ![]() $\mathcal {R}_\Gamma $, we conclude that the sequence of curves
$\mathcal {R}_\Gamma $, we conclude that the sequence of curves ![]() $\{\gamma _i\}$ shrinks to a point. Thus, if
$\{\gamma _i\}$ shrinks to a point. Thus, if ![]() $\beta $ is a limit of
$\beta $ is a limit of ![]() $\beta _i$ in the Hausdorff topology, then
$\beta _i$ in the Hausdorff topology, then ![]() $\beta $ is a union of two internal rays and it is isotopic to
$\beta $ is a union of two internal rays and it is isotopic to ![]() $\beta _0$. Therefore,
$\beta _0$. Therefore, ![]() $h_0(\alpha )$ is isotopic to an edge of
$h_0(\alpha )$ is isotopic to an edge of ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$.
$\mathscr {T}(\mathcal {R}_\Gamma )$.
Since this is true for every edge of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ and
$\mathscr {T}(\mathcal {G}_\Gamma )$ and ![]() $h_0$ is an orientation-preserving homeomorphism, by counting the valence at every critical point, we conclude that
$h_0$ is an orientation-preserving homeomorphism, by counting the valence at every critical point, we conclude that ![]() $h_0(\mathscr {T}(\mathcal {G}_\Gamma ))$ is isotopic to
$h_0(\mathscr {T}(\mathcal {G}_\Gamma ))$ is isotopic to ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$.
$\mathscr {T}(\mathcal {R}_\Gamma )$.
Therefore, after performing isotopy, we may assume that ![]() $h_0$ restricts to a homeomorphism between the graphs
$h_0$ restricts to a homeomorphism between the graphs ![]() $h_0: \mathscr {T}(\mathcal {G}_\Gamma ) \longrightarrow \mathscr {T}(\mathcal {R}_\Gamma )$. By lifting,
$h_0: \mathscr {T}(\mathcal {G}_\Gamma ) \longrightarrow \mathscr {T}(\mathcal {R}_\Gamma )$. By lifting, ![]() $h_1: \mathscr {T}(\mathcal {G}_\Gamma ) \longrightarrow \mathscr {T}(\mathcal {R}_\Gamma )$ is also a homeomorphism. Let F be a face of
$h_1: \mathscr {T}(\mathcal {G}_\Gamma ) \longrightarrow \mathscr {T}(\mathcal {R}_\Gamma )$ is also a homeomorphism. Let F be a face of ![]() $\Gamma $. By our construction of
$\Gamma $. By our construction of ![]() $\mathcal {G}_\Gamma $ (see Equation 3.2),
$\mathcal {G}_\Gamma $ (see Equation 3.2), ![]() $\mathcal {G}_\Gamma $ is conjugate to
$\mathcal {G}_\Gamma $ is conjugate to ![]() $\bar {z}^{d_F}$ on the corresponding component
$\bar {z}^{d_F}$ on the corresponding component ![]() $\Omega _F$, where
$\Omega _F$, where ![]() $d_F + 1$ is the number of edges in the ideal boundary of the face F. Since
$d_F + 1$ is the number of edges in the ideal boundary of the face F. Since ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ is constructed by taking the union over all faces of the fixed internal rays under such conjugacies (see Equation 3.3), the dynamics of
$\mathscr {T}(\mathcal {G}_\Gamma )$ is constructed by taking the union over all faces of the fixed internal rays under such conjugacies (see Equation 3.3), the dynamics of ![]() $\mathcal {G}_\Gamma $ and
$\mathcal {G}_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ on each edge of
$\mathcal {R}_\Gamma $ on each edge of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ and
$\mathscr {T}(\mathcal {G}_\Gamma )$ and ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$ are conjugate. Therefore, after further isotoping
$\mathscr {T}(\mathcal {R}_\Gamma )$ are conjugate. Therefore, after further isotoping ![]() $h_0$, we may assume that
$h_0$, we may assume that
gives a conjugacy between ![]() $\mathcal {G}_\Gamma $ and
$\mathcal {G}_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ from
$\mathcal {R}_\Gamma $ from ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ to
$\mathscr {T}(\mathcal {G}_\Gamma )$ to ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$. Hence, both
$\mathscr {T}(\mathcal {R}_\Gamma )$. Hence, both ![]() $h_0$ and
$h_0$ and ![]() $h_1$ send a face of
$h_1$ send a face of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ homomorphically to the corresponding face of
$\mathscr {T}(\mathcal {G}_\Gamma )$ homomorphically to the corresponding face of ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$.
$\mathscr {T}(\mathcal {R}_\Gamma )$.
As an application of the above, we will show that the dynamics on the limit set and Julia set are topologically conjugate (cf. [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Theorem 6.11]).
Lemma 4.15. There is a homeomorphism ![]() $h: \Lambda (G_\Gamma ) \longrightarrow \mathcal {J}(\mathcal {R}_\Gamma )$ satisfying
$h: \Lambda (G_\Gamma ) \longrightarrow \mathcal {J}(\mathcal {R}_\Gamma )$ satisfying ![]() $h\circ \mathcal {G}_\Gamma = \mathcal {R}_\Gamma \circ h$.
$h\circ \mathcal {G}_\Gamma = \mathcal {R}_\Gamma \circ h$.
Proof. Let ![]() $P^0$ consist of the points of tangency of the circle packing,
$P^0$ consist of the points of tangency of the circle packing,  $P^{i+1} := \mathcal {G}_\Gamma ^{-1}(P^i)$ and
$P^{i+1} := \mathcal {G}_\Gamma ^{-1}(P^i)$ and ![]() $P^\infty := \bigcup _{i=0}^\infty P^i$. Then
$P^\infty := \bigcup _{i=0}^\infty P^i$. Then ![]() $P^\infty $ corresponds to the
$P^\infty $ corresponds to the ![]() $G_\Gamma $ orbit of the cusps and hence is dense in
$G_\Gamma $ orbit of the cusps and hence is dense in ![]() $\Lambda (G_\Gamma )$. Let
$\Lambda (G_\Gamma )$. Let ![]() $Q^0 := h_0(P^0)$, which is also the set of repelling fixed points of
$Q^0 := h_0(P^0)$, which is also the set of repelling fixed points of ![]() $\mathcal {R}_\Gamma $ and
$\mathcal {R}_\Gamma $ and  $Q^{i+1} := \mathcal {R}_\Gamma ^{-1}(Q^i)$. Then
$Q^{i+1} := \mathcal {R}_\Gamma ^{-1}(Q^i)$. Then ![]() $Q^\infty := \bigcup _{i=0}^\infty Q^i$ is dense in
$Q^\infty := \bigcup _{i=0}^\infty Q^i$ is dense in ![]() $\mathcal {J}(\mathcal {R}_\Gamma )$.
$\mathcal {J}(\mathcal {R}_\Gamma )$.
Recall that for each face F of ![]() $\Gamma $, the dynamics of
$\Gamma $, the dynamics of ![]() $\mathcal {G}_\Gamma $ (respectively of
$\mathcal {G}_\Gamma $ (respectively of ![]() $\mathcal {R}_\Gamma $) on the corresponding component of
$\mathcal {R}_\Gamma $) on the corresponding component of ![]() $\Omega (G_\Gamma )$ (respectively on the corresponding critically fixed Fatou component of
$\Omega (G_\Gamma )$ (respectively on the corresponding critically fixed Fatou component of ![]() $\mathcal {R}_\Gamma $) can be uniformised to
$\mathcal {R}_\Gamma $) can be uniformised to ![]() $\overline {z}^d$ on
$\overline {z}^d$ on ![]() $\mathbb {D}$. Let
$\mathbb {D}$. Let ![]() $\Pi $ be the closed ideal
$\Pi $ be the closed ideal ![]() $d+1$-gon in
$d+1$-gon in ![]() $\mathbb {D}$ with ideal vertices at the fixed points of
$\mathbb {D}$ with ideal vertices at the fixed points of ![]() $\overline {z}^d$ on
$\overline {z}^d$ on ![]() $\mathbb {S}^1$. Let
$\mathbb {S}^1$. Let ![]() $\mathcal {L}_{\mathcal {G}, F}$ and
$\mathcal {L}_{\mathcal {G}, F}$ and ![]() $\mathcal {L}_{\mathcal {R},F}$ be the image of
$\mathcal {L}_{\mathcal {R},F}$ be the image of ![]() $\Pi $ under the uniformising map in the dynamical plane of
$\Pi $ under the uniformising map in the dynamical plane of ![]() $\mathcal {G}_\Gamma $ and
$\mathcal {G}_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ respectively and
$\mathcal {R}_\Gamma $ respectively and ![]() $\mathcal {L}_{\mathcal {G}}$ and
$\mathcal {L}_{\mathcal {G}}$ and ![]() $\mathcal {L}_{\mathcal {R}}$ be the union over all faces.
$\mathcal {L}_{\mathcal {R}}$ be the union over all faces.
Let  $\mathcal {E}^0 := \widehat {\mathbb {C}}\setminus \overline {\mathcal {L}_{\mathcal {G}}}$ and
$\mathcal {E}^0 := \widehat {\mathbb {C}}\setminus \overline {\mathcal {L}_{\mathcal {G}}}$ and ![]() $\mathcal {H}^0 := \widehat {\mathbb {C}}\setminus \overline {\mathcal {L}_{\mathcal {R}}}$. Inductively, let
$\mathcal {H}^0 := \widehat {\mathbb {C}}\setminus \overline {\mathcal {L}_{\mathcal {R}}}$. Inductively, let  $\mathcal {E}^{i+1} := \mathcal {G}_\Gamma ^{-1}(\mathcal {E}^i)$ and
$\mathcal {E}^{i+1} := \mathcal {G}_\Gamma ^{-1}(\mathcal {E}^i)$ and  $\mathcal {H}^{i+1} := \mathcal {R}_\Gamma ^{-1}(\mathcal {H}^i)$. Note that these sets are the analogues of
$\mathcal {H}^{i+1} := \mathcal {R}_\Gamma ^{-1}(\mathcal {H}^i)$. Note that these sets are the analogues of ![]() $\mathcal {D}^{i}$ for kissing reflection groups. Since
$\mathcal {D}^{i}$ for kissing reflection groups. Since ![]() $\mathcal {G}_\Gamma $ (respectively
$\mathcal {G}_\Gamma $ (respectively ![]() $\mathcal {R}_\Gamma $) sends a face of
$\mathcal {R}_\Gamma $) sends a face of ![]() $\mathscr {T}(\mathcal {G}_\Gamma )$ (respectively a face of
$\mathscr {T}(\mathcal {G}_\Gamma )$ (respectively a face of ![]() $\mathscr {T}(\mathcal {R}_\Gamma )$) to its complement univalently, our construction guarantees that
$\mathscr {T}(\mathcal {R}_\Gamma )$) to its complement univalently, our construction guarantees that  $\overline {\mathcal {E}^1} \subseteq \overline {\mathcal {E}^0}$ and
$\overline {\mathcal {E}^1} \subseteq \overline {\mathcal {E}^0}$ and  $\overline {\mathcal {H}^1} \subseteq \overline {\mathcal {H}^0}$. Inductively, we see that
$\overline {\mathcal {H}^1} \subseteq \overline {\mathcal {H}^0}$. Inductively, we see that  $\{\overline {\mathcal {E}^{i}}\}$ and
$\{\overline {\mathcal {E}^{i}}\}$ and  $\{\overline {\mathcal {H}^i}\}$ are nested sequences of closed sets. Thus, we have
$\{\overline {\mathcal {H}^i}\}$ are nested sequences of closed sets. Thus, we have
 $$ \begin{align*}\Lambda(G_\Gamma) = \bigcap_{i=0}^\infty \overline{\mathcal{E}^{i}} \end{align*} $$
$$ \begin{align*}\Lambda(G_\Gamma) = \bigcap_{i=0}^\infty \overline{\mathcal{E}^{i}} \end{align*} $$and
 $$ \begin{align*}\mathcal{J}(\mathcal{R}_\Gamma) = \bigcap_{i=0}^\infty \overline{\mathcal{H}^{i}}. \end{align*} $$
$$ \begin{align*}\mathcal{J}(\mathcal{R}_\Gamma) = \bigcap_{i=0}^\infty \overline{\mathcal{H}^{i}}. \end{align*} $$ Since ![]() $\mathcal {R}_\Gamma $ is hyperbolic and
$\mathcal {R}_\Gamma $ is hyperbolic and ![]() $\mathcal {H}^i$ contains no critical value, the diameters of the components of
$\mathcal {H}^i$ contains no critical value, the diameters of the components of ![]() $\mathcal {H}^{i}\cap \mathcal {J}(\mathcal {R}_\Gamma )$ shrink to
$\mathcal {H}^{i}\cap \mathcal {J}(\mathcal {R}_\Gamma )$ shrink to ![]() $0$ uniformly. On the other hand, since
$0$ uniformly. On the other hand, since ![]() $ \mathcal {G}_\Gamma = \mathcal {N}_\Gamma $ on
$ \mathcal {G}_\Gamma = \mathcal {N}_\Gamma $ on ![]() $\Lambda (G_\Gamma )$, the diameters of the components of
$\Lambda (G_\Gamma )$, the diameters of the components of ![]() $\mathcal {E}^{i}\cap \Lambda (G_\Gamma )$ shrink to
$\mathcal {E}^{i}\cap \Lambda (G_\Gamma )$ shrink to ![]() $0$ uniformly by Lemma 3.3.
$0$ uniformly by Lemma 3.3.
After isotoping ![]() $h_0$, we may assume that
$h_0$, we may assume that ![]() $h_0 (\mathcal {E}^0) = \mathcal {H}^0$. We consider the pullback sequence
$h_0 (\mathcal {E}^0) = \mathcal {H}^0$. We consider the pullback sequence ![]() $\{h_i\}$ with
$\{h_i\}$ with
where each ![]() $h_i$ carries
$h_i$ carries ![]() $P(\mathcal {G}_\Gamma )$ to
$P(\mathcal {G}_\Gamma )$ to ![]() $P(\mathcal {R}_\Gamma )$. Since we have assumed
$P(\mathcal {R}_\Gamma )$. Since we have assumed ![]() $h_0 = h_1$ on
$h_0 = h_1$ on ![]() $P^0$, inductively, we have
$P^0$, inductively, we have ![]() $h_j = h_i$ on
$h_j = h_i$ on ![]() $P_i$ and
$P_i$ and ![]() $h_j(P^i) = Q^i$ for all
$h_j(P^i) = Q^i$ for all ![]() $j\geq i$. We define
$j\geq i$. We define ![]() $h(x) := \lim h_i(x)$ for
$h(x) := \lim h_i(x)$ for ![]() $x\in P^\infty $.
$x\in P^\infty $.
Then a similar argument as in the proof of Proposition 3.21 implies that h is uniformly continuous on ![]() $P^\infty $. Indeed, given
$P^\infty $. Indeed, given ![]() $\epsilon>0$, we can choose N so that the diameter of any component of
$\epsilon>0$, we can choose N so that the diameter of any component of ![]() $\mathcal {H}^N\cap \mathcal {J}(\mathcal {R}_\Gamma )$ is less than
$\mathcal {H}^N\cap \mathcal {J}(\mathcal {R}_\Gamma )$ is less than ![]() $ \epsilon $. We choose
$ \epsilon $. We choose ![]() $\delta $ so that any two nonadjacent components of
$\delta $ so that any two nonadjacent components of ![]() $\mathcal {E}^N\cap \Lambda (G_\Gamma )$ are at least
$\mathcal {E}^N\cap \Lambda (G_\Gamma )$ are at least ![]() $\delta $ distance away. If
$\delta $ distance away. If ![]() $x,y\in P^\infty $ are at most
$x,y\in P^\infty $ are at most ![]() $\delta $ distance apart, they lie in two adjacent components of
$\delta $ distance apart, they lie in two adjacent components of ![]() $\mathcal {E}^N$, so
$\mathcal {E}^N$, so ![]() $h_j(x), h_j(y)$ lie in two adjacent components of
$h_j(x), h_j(y)$ lie in two adjacent components of ![]() $\mathcal {H}^N$ for all
$\mathcal {H}^N$ for all ![]() $j\geq N$. Hence,
$j\geq N$. Hence, ![]() $d(h_j(x), h_j(y)) < 2\epsilon $.
$d(h_j(x), h_j(y)) < 2\epsilon $.
Since ![]() $P^\infty $ and
$P^\infty $ and ![]() $Q^\infty $ are dense on
$Q^\infty $ are dense on ![]() $\Lambda (G_\Gamma )$ and
$\Lambda (G_\Gamma )$ and ![]() $\mathcal {J}(\mathcal {R}_\Gamma )$ (respectively), we get a unique continuous extension
$\mathcal {J}(\mathcal {R}_\Gamma )$ (respectively), we get a unique continuous extension
Applying the same argument on the sequence  $\{h_j^{-1}\}$, we get the continuous inverse of h. Thus, h is a homeomorphism. Since h conjugates
$\{h_j^{-1}\}$, we get the continuous inverse of h. Thus, h is a homeomorphism. Since h conjugates ![]() $\mathcal {G}_\Gamma $ to
$\mathcal {G}_\Gamma $ to ![]() $\mathcal {R}_\Gamma $ on
$\mathcal {R}_\Gamma $ on ![]() $P^\infty $, it also conjugates
$P^\infty $, it also conjugates ![]() $\mathcal {G}_\Gamma $ to
$\mathcal {G}_\Gamma $ to ![]() $\mathcal {R}_\Gamma $ on
$\mathcal {R}_\Gamma $ on ![]() $\Lambda (G_\Gamma )$.
$\Lambda (G_\Gamma )$.
We are now ready to prove Proposition 4.10 (cf. [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Proposition 6.13]).
Proof of Proposition 4.10
By Lemma 4.9, the dual graph of a Tischler graph (of a critically fixed anti-rational map) is ![]() $2$-connected simple and plane.
$2$-connected simple and plane.
Conversely, given any ![]() $2$-connected simple plane graph
$2$-connected simple plane graph ![]() $\Gamma $, by Lemma 4.13 and Lemma 4.14 we can construct a critically fixed anti-rational map
$\Gamma $, by Lemma 4.13 and Lemma 4.14 we can construct a critically fixed anti-rational map ![]() $\mathcal {R}_\Gamma $ whose Tischler graph is the planar dual of
$\mathcal {R}_\Gamma $ whose Tischler graph is the planar dual of ![]() $\Gamma $.
$\Gamma $.
It remains to show that ![]() $\mathcal {G}_\Gamma $ and
$\mathcal {G}_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ are topologically conjugate. Let h be the topological conjugacy on
$\mathcal {R}_\Gamma $ are topologically conjugate. Let h be the topological conjugacy on ![]() $\Lambda (G_\Gamma )$ produced in Lemma 4.15. Let U be a critically fixed component
$\Lambda (G_\Gamma )$ produced in Lemma 4.15. Let U be a critically fixed component ![]() $\mathcal {G}_\Gamma $. Then by construction, there exists
$\mathcal {G}_\Gamma $. Then by construction, there exists ![]() $\Phi : \mathbb {D}\longrightarrow U$ conjugating
$\Phi : \mathbb {D}\longrightarrow U$ conjugating ![]() $m_{-d}(z) = \overline {z}^d$ to
$m_{-d}(z) = \overline {z}^d$ to ![]() $\mathcal {G}_\Gamma $. The map extends to a semiconjugacy between
$\mathcal {G}_\Gamma $. The map extends to a semiconjugacy between ![]() $\mathbb {S}^1$ and
$\mathbb {S}^1$ and ![]() $\partial U$.
$\partial U$.
Similarly, let V be the corresponding critically fixed Fatou component of ![]() $\mathcal {R}_\Gamma $. Then we have
$\mathcal {R}_\Gamma $. Then we have ![]() $\Psi : \mathbb {D}\longrightarrow V$ conjugating
$\Psi : \mathbb {D}\longrightarrow V$ conjugating ![]() $m_{-d}(z) = \overline {z}^d$ to
$m_{-d}(z) = \overline {z}^d$ to ![]() $\mathcal {R}_\Gamma $, which extends to a semiconjugacy. Note that there are
$\mathcal {R}_\Gamma $, which extends to a semiconjugacy. Note that there are ![]() $d+1$ different choices of such a conjugacy, and we may choose one so that
$d+1$ different choices of such a conjugacy, and we may choose one so that ![]() $h\circ \Phi = \Psi $ on
$h\circ \Phi = \Psi $ on ![]() $\mathbb {S}^1$. Thus, we can extend the topological conjugacy h to all of U by setting
$\mathbb {S}^1$. Thus, we can extend the topological conjugacy h to all of U by setting ![]() $h:= \Psi \circ \Phi ^{-1}$.
$h:= \Psi \circ \Phi ^{-1}$.
In this way, we obtain a homeomorphic extension of h to all critically fixed components of ![]() $\mathcal {G}_\Gamma $. Lifting these extensions to all of the preimages of the critically fixed components of
$\mathcal {G}_\Gamma $. Lifting these extensions to all of the preimages of the critically fixed components of ![]() $\mathcal {G}_\Gamma $, we get a map defined on
$\mathcal {G}_\Gamma $, we get a map defined on ![]() $\widehat {\mathbb {C}}$. Since the diameters of the preimages of the critically fixed components (of
$\widehat {\mathbb {C}}$. Since the diameters of the preimages of the critically fixed components (of ![]() $\mathcal {G}_\Gamma $) as well as the corresponding Fatou components (of
$\mathcal {G}_\Gamma $) as well as the corresponding Fatou components (of ![]() $\mathcal {R}_\Gamma $) go to
$\mathcal {R}_\Gamma $) go to ![]() $0$ uniformly, we conclude that all of these extensions paste together to yield a global homeomorphism, which is our desired topological conjugacy.
$0$ uniformly, we conclude that all of these extensions paste together to yield a global homeomorphism, which is our desired topological conjugacy.
In light of Proposition 4.10, we see that the association of the isomorphism class of a ![]() $2$-connected simple plane graph to the Möbius conjugacy class of a critically fixed anti-rational map is well defined and surjective. To verify that this is indeed injective, we remark that if two (plane) graphs
$2$-connected simple plane graph to the Möbius conjugacy class of a critically fixed anti-rational map is well defined and surjective. To verify that this is indeed injective, we remark that if two (plane) graphs ![]() $\Gamma $ and
$\Gamma $ and ![]() $\Gamma '$ are isomorphic as plane graphs, then the associated Tischler graphs are also isomorphic as plane graphs. This means that the corresponding pair of critically fixed anti-rational maps are Thurston equivalent. Thus, by Thurston’s rigidity result, they are Möbius conjugate.
$\Gamma '$ are isomorphic as plane graphs, then the associated Tischler graphs are also isomorphic as plane graphs. This means that the corresponding pair of critically fixed anti-rational maps are Thurston equivalent. Thus, by Thurston’s rigidity result, they are Möbius conjugate.
As in the kissing reflection group setting, we define a geometric mating of two (anti-)polynomials as follows.
Definition 4.16. We say that a rational map (or an anti-rational map) R is a geometric mating of two polynomials (or two anti-polynomials) ![]() $P^\pm $ with connected Julia sets if we have
$P^\pm $ with connected Julia sets if we have
• a decomposition of the Fatou set
 $\mathcal {F}(R) = \mathcal {F}^+ \sqcup \mathcal {F}^-$ with
$\mathcal {F}(R) = \mathcal {F}^+ \sqcup \mathcal {F}^-$ with  $\mathcal {J}(R) = \partial \mathcal {F}^+ = \partial \mathcal {F}^-$; and
$\mathcal {J}(R) = \partial \mathcal {F}^+ = \partial \mathcal {F}^-$; and• two continuous surjections from the filled Julia sets
 $\psi ^\pm : \mathcal {K}(P^\pm ) \to \overline {\mathcal {F}^\pm }$ that are conformal between
$\psi ^\pm : \mathcal {K}(P^\pm ) \to \overline {\mathcal {F}^\pm }$ that are conformal between  $\operatorname {\mathrm {Int}}{\mathcal {K}}(P^\pm )$ and
$\operatorname {\mathrm {Int}}{\mathcal {K}}(P^\pm )$ and  $\mathcal {F}^\pm $
$\mathcal {F}^\pm $
so that
As a corollary, we have the following.
1. A critically fixed anti-rational map R is an anti-polynomial if and only if the dual graph
 $\Gamma $ of
$\Gamma $ of  $\mathscr {T}(R)$ is outerplanar.
$\mathscr {T}(R)$ is outerplanar.2. A critically fixed anti-rational map R is a geometric mating of two anti-polynomials if and only if the dual graph
 $\Gamma $ of
$\Gamma $ of  $\mathscr {T}(R)$ is Hamiltonian.
$\mathscr {T}(R)$ is Hamiltonian.3. A critically fixed anti-rational map R has a gasket Julia set if and only if the dual graph
 $\Gamma $ of
$\Gamma $ of  $\mathscr {T}(R)$ is
$\mathscr {T}(R)$ is  $3$-connected.
$3$-connected.
Proof. The first statement follows from Proposition 4.10 as the graph ![]() $\Gamma $ is outerplanar if and only if there is a vertex in the dual graph
$\Gamma $ is outerplanar if and only if there is a vertex in the dual graph ![]() $\Gamma ^\vee =\mathscr {T}(R)$ with maximal valence if and only if R has a fully branched fixed critical point.
$\Gamma ^\vee =\mathscr {T}(R)$ with maximal valence if and only if R has a fully branched fixed critical point.
For the second statement, let ![]() $\Gamma $ be a
$\Gamma $ be a ![]() $2$-connected simple plane graph. Let
$2$-connected simple plane graph. Let ![]() $G_\Gamma $ be an associated kissing reflection group and
$G_\Gamma $ be an associated kissing reflection group and ![]() $\mathcal {G}_\Gamma $ and
$\mathcal {G}_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ be the associated branched covering and anti-rational map. By Proposition 4.10,
$\mathcal {R}_\Gamma $ be the associated branched covering and anti-rational map. By Proposition 4.10, ![]() $\mathcal {G}_\Gamma $ and
$\mathcal {G}_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ are topologically conjugated by h.
$\mathcal {R}_\Gamma $ are topologically conjugated by h.
If ![]() $\mathcal {R}_\Gamma $ is a geometric mating of two anti-polynomials
$\mathcal {R}_\Gamma $ is a geometric mating of two anti-polynomials ![]() $P^\pm $ which are necessarily critically fixed, then the conjugacy gives a decomposition of
$P^\pm $ which are necessarily critically fixed, then the conjugacy gives a decomposition of ![]() $\Omega (G_\Gamma ) = \Omega ^+\sqcup \Omega ^-$. It is not hard to check that the
$\Omega (G_\Gamma ) = \Omega ^+\sqcup \Omega ^-$. It is not hard to check that the ![]() $\Gamma $-actions on
$\Gamma $-actions on ![]() $\overline {\Omega ^\pm }$ are conjugate to the actions of the function kissing reflection groups
$\overline {\Omega ^\pm }$ are conjugate to the actions of the function kissing reflection groups ![]() $G^\pm $ on their filled limit sets, where
$G^\pm $ on their filled limit sets, where ![]() $G^\pm $ correspond to
$G^\pm $ correspond to ![]() $P^\pm $. Thus,
$P^\pm $. Thus, ![]() $G_\Gamma $ is a geometric mating of the two function kissing reflection groups
$G_\Gamma $ is a geometric mating of the two function kissing reflection groups ![]() $G^\pm $, so
$G^\pm $, so ![]() $\Gamma $ is Hamiltonian by Proposition 3.21.
$\Gamma $ is Hamiltonian by Proposition 3.21.
Conversely, if ![]() $\Gamma $ is Hamiltonian, then
$\Gamma $ is Hamiltonian, then ![]() $G_\Gamma $ is a geometric mating of two function kissing reflection groups
$G_\Gamma $ is a geometric mating of two function kissing reflection groups ![]() $G^\pm $ and we get a decomposition of
$G^\pm $ and we get a decomposition of ![]() $\Omega (G_\Gamma )$ by Proposition 3.21. The conjugacy h transports this decomposition to the anti-rational map setting. One can now check directly that
$\Omega (G_\Gamma )$ by Proposition 3.21. The conjugacy h transports this decomposition to the anti-rational map setting. One can now check directly that ![]() $\mathcal {R}_\Gamma $ is a geometric mating of the anti-polynomials
$\mathcal {R}_\Gamma $ is a geometric mating of the anti-polynomials ![]() $P^\pm $ that are associated to the function kissing reflection groups
$P^\pm $ that are associated to the function kissing reflection groups ![]() $G^\pm $.
$G^\pm $.
The third statement follows immediately from Propositions 4.10 and 3.10.
Remark 4.18. The Hubbard tree of a critically fixed anti-polynomial P is a strict subset of ![]() $\mathscr {T}(P)\cap \mathcal {K}(P)$, where
$\mathscr {T}(P)\cap \mathcal {K}(P)$, where ![]() $\mathcal {K}(P)$ is the filled Julia set of P (cf. [Reference Lazebnik, Makarov and Mukherjee20, §5]).
$\mathcal {K}(P)$ is the filled Julia set of P (cf. [Reference Lazebnik, Makarov and Mukherjee20, §5]).
Remark 4.19. It is not hard to see that the existence of a Hamiltonian cycle for ![]() $\mathscr {T}(R)^{\vee }$ is equivalent to the existence of an equator for R in the sense of [Reference Meyer30, Definition 4.1]. This gives an alternative proof of the second statement of Corollary 4.17 (cf. [Reference Meyer30, Theorem 4.2]).
$\mathscr {T}(R)^{\vee }$ is equivalent to the existence of an equator for R in the sense of [Reference Meyer30, Definition 4.1]. This gives an alternative proof of the second statement of Corollary 4.17 (cf. [Reference Meyer30, Theorem 4.2]).
4.3 Dynamical correspondence
Let ![]() $G_\Gamma $ and
$G_\Gamma $ and ![]() $\mathcal {R}_\Gamma $ be a kissing reflection group and a critically fixed anti-rational map associated to a
$\mathcal {R}_\Gamma $ be a kissing reflection group and a critically fixed anti-rational map associated to a ![]() $2$-connected simple plane graph
$2$-connected simple plane graph ![]() $\Gamma $. Here we summarise the correspondence between various dynamical objects associated with the group and the anti-rational map.
$\Gamma $. Here we summarise the correspondence between various dynamical objects associated with the group and the anti-rational map.
• Markov partitions for limit and Julia sets: The associated circle packing
 $\mathcal {P}$ gives a Markov partition for the group dynamics on the limit set (more precisely, for the action of the Nielsen map
$\mathcal {P}$ gives a Markov partition for the group dynamics on the limit set (more precisely, for the action of the Nielsen map  $\mathcal {N}_\Gamma $ on
$\mathcal {N}_\Gamma $ on  $\Lambda (G_\Gamma )$). On the other side, the faces of the Tischler graph determine a Markov partition for the action of
$\Lambda (G_\Gamma )$). On the other side, the faces of the Tischler graph determine a Markov partition for the action of  $\mathcal {R}_\Gamma $ on the Julia set. The topological conjugacy respects this pair of Markov partitions and the itineraries of points with respect to the corresponding Markov partitions.
$\mathcal {R}_\Gamma $ on the Julia set. The topological conjugacy respects this pair of Markov partitions and the itineraries of points with respect to the corresponding Markov partitions.• Cusps and repelling fixed points: The orbits of parabolic fixed points of
 $G_\Gamma $ bijectively correspond to pairs of adjacent vertices or, equivalently, to the edges of
$G_\Gamma $ bijectively correspond to pairs of adjacent vertices or, equivalently, to the edges of  $\Gamma $. On the other side, the repelling fixed points of
$\Gamma $. On the other side, the repelling fixed points of  $\mathcal {R}_\Gamma $ are in bijective correspondence with the edges of the Tischler graph
$\mathcal {R}_\Gamma $ are in bijective correspondence with the edges of the Tischler graph  $\mathscr {T} = \Gamma ^\vee $ and thus also with the edges of
$\mathscr {T} = \Gamma ^\vee $ and thus also with the edges of  $\Gamma $. They are naturally identified by the topological conjugacy.
$\Gamma $. They are naturally identified by the topological conjugacy.•
 $\boldsymbol {\sigma }$-Invariant curves and
$\boldsymbol {\sigma }$-Invariant curves and $\boldsymbol {2}$-cycles: Each
$\boldsymbol {2}$-cycles: Each  $\sigma $-invariant simple closed curve on the conformal boundary
$\sigma $-invariant simple closed curve on the conformal boundary  $\partial \mathcal {M}(G_\Gamma )$ corresponds to a pair of nonadjacent vertices on a face of
$\partial \mathcal {M}(G_\Gamma )$ corresponds to a pair of nonadjacent vertices on a face of  $\Gamma $ (see the discussion on pinching deformations after Proposition 3.17 for the definition of the involution
$\Gamma $ (see the discussion on pinching deformations after Proposition 3.17 for the definition of the involution  $\sigma $). On the other side, the above Markov partition for
$\sigma $). On the other side, the above Markov partition for  $\mathcal {R}_\Gamma \vert _{\mathcal {J}(\mathcal {R}(\Gamma ))}$ shows that each
$\mathcal {R}_\Gamma \vert _{\mathcal {J}(\mathcal {R}(\Gamma ))}$ shows that each  $2$-cycle on the ideal boundary of an invariant Fatou component corresponds to a pair of nonadjacent vertices on the associated face of
$2$-cycle on the ideal boundary of an invariant Fatou component corresponds to a pair of nonadjacent vertices on the associated face of  $\Gamma $. These
$\Gamma $. These  $\sigma $-invariant curves and
$\sigma $-invariant curves and  $2$-cycles are naturally identified by the topological conjugacy. We remark that it is possible that a
$2$-cycles are naturally identified by the topological conjugacy. We remark that it is possible that a  $\sigma $-invariant curve yields an accidental parabolic element, in which case the corresponding
$\sigma $-invariant curve yields an accidental parabolic element, in which case the corresponding  $2$-cycle on the ideal boundary of the invariant Fatou component coalesces and gives rise to a repelling fixed point of
$2$-cycle on the ideal boundary of the invariant Fatou component coalesces and gives rise to a repelling fixed point of  $\mathcal {R}_\Gamma $. This happens if and only if the two corresponding vertices are adjacent in
$\mathcal {R}_\Gamma $. This happens if and only if the two corresponding vertices are adjacent in  $\Gamma $.
$\Gamma $.• Question mark conjugacy: If we choose our group
 $G_\Gamma $ so that each conformal boundary is the double of a suitable regular ideal polygon, then the restriction of the homeomorphism h of Lemma 4.15 between the boundary of an invariant Fatou component and the boundary of the corresponding component of
$G_\Gamma $ so that each conformal boundary is the double of a suitable regular ideal polygon, then the restriction of the homeomorphism h of Lemma 4.15 between the boundary of an invariant Fatou component and the boundary of the corresponding component of  $\Omega (G_\Gamma )$ gives a homeomorphism between the ideal boundaries
$\Omega (G_\Gamma )$ gives a homeomorphism between the ideal boundaries  $\phi :\mathbb {S}^1\longrightarrow \mathbb {S}^1$ that conjugates
$\phi :\mathbb {S}^1\longrightarrow \mathbb {S}^1$ that conjugates  $\overline {z}^e$ to the Nielsen map
$\overline {z}^e$ to the Nielsen map  $\mathcal {N}_e$ of the regular ideal
$\mathcal {N}_e$ of the regular ideal  $(e+1)$-gon reflection group. This conjugacy
$(e+1)$-gon reflection group. This conjugacy  $\phi $ is a generalisation of the Minkowski question mark function (see [Reference Lee, Lyubich, Makarov and Mukherjee21, §3.2, §5.4.2] [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Remark 9.1]).
$\phi $ is a generalisation of the Minkowski question mark function (see [Reference Lee, Lyubich, Makarov and Mukherjee21, §3.2, §5.4.2] [Reference Lodge, Lyubich, Merenkov and Mukherjee24, Remark 9.1]).• Function groups and anti-polynomials: If
 $G_\Gamma $ is a function kissing reflection group (of rank
$G_\Gamma $ is a function kissing reflection group (of rank  $d+1$), then it can be constructed by pinching a
$d+1$), then it can be constructed by pinching a  $\sigma $-invariant multicurve
$\sigma $-invariant multicurve  $\alpha $ on one component of
$\alpha $ on one component of  $\partial \mathcal {M}(\mathbf {G}_d)$ (recall that
$\partial \mathcal {M}(\mathbf {G}_d)$ (recall that  $\mathbf {G}_d$ is the regular ideal polygon group of rank
$\mathbf {G}_d$ is the regular ideal polygon group of rank  $d+1$). Under the natural orientation-reversing identification of the two components of
$d+1$). Under the natural orientation-reversing identification of the two components of  $\partial \mathcal {M}(\mathbf {G}_d)$, the multicurve
$\partial \mathcal {M}(\mathbf {G}_d)$, the multicurve  $\alpha $ gives a
$\alpha $ gives a  $\sigma $-invariant multicurve
$\sigma $-invariant multicurve  $\alpha '$ on the component of
$\alpha '$ on the component of  $\partial \mathcal {M}(G_\Gamma )$ associated to the
$\partial \mathcal {M}(G_\Gamma )$ associated to the  $G_\Gamma $-invariant domain
$G_\Gamma $-invariant domain  $\Omega _0\subseteq \Omega (G_\Gamma )$. The multicurve
$\Omega _0\subseteq \Omega (G_\Gamma )$. The multicurve  $\alpha '$ consists precisely of the simple closed curves corresponding to the accidental parabolics of
$\alpha '$ consists precisely of the simple closed curves corresponding to the accidental parabolics of  $G_\Gamma $. On the other side, the corresponding
$G_\Gamma $. On the other side, the corresponding  $2$-cycles on the ideal boundary of the unbounded Fatou component (that is, the basin of infinity) generate the lamination for the Julia set of the anti-polynomial
$2$-cycles on the ideal boundary of the unbounded Fatou component (that is, the basin of infinity) generate the lamination for the Julia set of the anti-polynomial  $R_\Gamma $.
$R_\Gamma $.• Quasi-Fuchsian closure and mating: If
 $G_\Gamma $ lies in the closure of the quasi-Fuchsian deformation space of
$G_\Gamma $ lies in the closure of the quasi-Fuchsian deformation space of  $\mathbf {G}_d$, then
$\mathbf {G}_d$, then  $G_\Gamma $ is obtained by pinching two nonparallel
$G_\Gamma $ is obtained by pinching two nonparallel  $\sigma $-invariant multicurves
$\sigma $-invariant multicurves  $\alpha ^+$ and
$\alpha ^+$ and  $\alpha ^-$ on the two components of
$\alpha ^-$ on the two components of  $\partial \mathcal {M}(\mathbf {G}_d)$; equivalently,
$\partial \mathcal {M}(\mathbf {G}_d)$; equivalently,  $G_\Gamma $ is a mating of two function kissing reflection groups
$G_\Gamma $ is a mating of two function kissing reflection groups  $G^+$ and
$G^+$ and  $G^-$. On the other side, the critically fixed anti-rational map
$G^-$. On the other side, the critically fixed anti-rational map  $\mathcal {R}_\Gamma $ is a mating of the critically fixed anti-polynomials
$\mathcal {R}_\Gamma $ is a mating of the critically fixed anti-polynomials  $P^+$ and
$P^+$ and  $P^-$, which correspond to the groups
$P^-$, which correspond to the groups  $G^+$ and
$G^+$ and  $G^-$ (respectively). The topological conjugacy between
$G^-$ (respectively). The topological conjugacy between  $\mathcal {N}_\Gamma \vert _{\Lambda (G_\Gamma )}$ and
$\mathcal {N}_\Gamma \vert _{\Lambda (G_\Gamma )}$ and  $\mathcal {R}_\Gamma \vert _{\mathcal {J}(\mathcal {R}_\Gamma )}$ is induced by the circle homeomorphism that conjugates
$\mathcal {R}_\Gamma \vert _{\mathcal {J}(\mathcal {R}_\Gamma )}$ is induced by the circle homeomorphism that conjugates  $\mathcal {N}_d$ to
$\mathcal {N}_d$ to  $\overline {z}^d$.
$\overline {z}^d$.
4.4 Mating of two anti-polynomials
In this subsection, we shall discuss the converse question of mateablity in terms of laminations. Let
be a monic centred anti-polynomial with connected Julia set. We denote the filled Julia set by ![]() $\mathcal {K}(P)$. There is a unique Böttcher coordinate
$\mathcal {K}(P)$. There is a unique Böttcher coordinate
with derivative ![]() $1$ at infinity that conjugates
$1$ at infinity that conjugates ![]() $\overline {z}^d$ to P. We shall call a monic centred anti-polynomial equipped with this preferred Böttcher coordinate a marked anti-polynomial. Note that when the Julia set is connected, this marking is equivalent to an affine conjugacy class of anti-polynomials together with a choice of Böttcher coordinate at infinity. If we further assume that the Julia set is locally connected, the map
$\overline {z}^d$ to P. We shall call a monic centred anti-polynomial equipped with this preferred Böttcher coordinate a marked anti-polynomial. Note that when the Julia set is connected, this marking is equivalent to an affine conjugacy class of anti-polynomials together with a choice of Böttcher coordinate at infinity. If we further assume that the Julia set is locally connected, the map ![]() $\psi $ extends to a continuous semi-conjugacy
$\psi $ extends to a continuous semi-conjugacy ![]() $\psi :\mathbb {S}^1 \longrightarrow \mathcal {J}(P)$ between
$\psi :\mathbb {S}^1 \longrightarrow \mathcal {J}(P)$ between ![]() $\overline {z}^d$ and P. This semi-conjugacy gives rise to a
$\overline {z}^d$ and P. This semi-conjugacy gives rise to a ![]() $\overline {z}^d$-invariant lamination on the circle
$\overline {z}^d$-invariant lamination on the circle ![]() $\mathbb {S}^1$ for the marked anti-polynomial. The coordinate on
$\mathbb {S}^1$ for the marked anti-polynomial. The coordinate on ![]() $\mathbb {S}^1\cong \mathbb {R}/\mathbb {Z}$ will be called external angle. The image of
$\mathbb {S}^1\cong \mathbb {R}/\mathbb {Z}$ will be called external angle. The image of ![]() $\{re^{2\pi i\theta }\in \mathbb {C}: r\geq 1\}$ under
$\{re^{2\pi i\theta }\in \mathbb {C}: r\geq 1\}$ under ![]() $\psi $ will be called an external ray at angle
$\psi $ will be called an external ray at angle ![]() $\theta $ and will be denoted by
$\theta $ and will be denoted by ![]() $R(\theta )$. If
$R(\theta )$. If ![]() $x\in \mathcal {J}(P)$ is the intersection of two external rays, then x is a cut-point of
$x\in \mathcal {J}(P)$ is the intersection of two external rays, then x is a cut-point of ![]() $\mathcal {J}(P)$ (equivalently, a cut-point of
$\mathcal {J}(P)$ (equivalently, a cut-point of ![]() $\mathcal {K}(P)$).
$\mathcal {K}(P)$).
If we denote ![]() as the complex plane together with the circle at infinity, then a marked anti-polynomial extends continuously to
as the complex plane together with the circle at infinity, then a marked anti-polynomial extends continuously to ![]() by the formula
by the formula ![]() $P(\infty , w) = (\infty , \overline {w}^d)$.
$P(\infty , w) = (\infty , \overline {w}^d)$.
Let P and Q be two marked degree d anti-polynomials. To distinguish the two domains ![]() , we denote them by
, we denote them by ![]() $\mathbb {C}_P$ and
$\mathbb {C}_P$ and ![]() $\mathbb {C}_Q$. The quotient
$\mathbb {C}_Q$. The quotient
 $$\begin{align*}\mathbb{S}^2_{P,Q}:=(\mathbb{C}_P\cup\mathbb{C}_Q)/\{(\infty_P,w)\sim(\infty_Q,\overline{w})\}\end{align*}$$
$$\begin{align*}\mathbb{S}^2_{P,Q}:=(\mathbb{C}_P\cup\mathbb{C}_Q)/\{(\infty_P,w)\sim(\infty_Q,\overline{w})\}\end{align*}$$defines a topological sphere. Denote the equivalence class of ![]() $(\infty _P,w)$ by
$(\infty _P,w)$ by ![]() $(\infty ,w)$ and define the equator of
$(\infty ,w)$ and define the equator of  $\mathbb {S}^2_{P,Q}$ to be the set
$\mathbb {S}^2_{P,Q}$ to be the set ![]() $\{(\infty ,w): w\in \mathbb {S}^1\}$. The formal mating of P and Q is the degree d branched cover
$\{(\infty ,w): w\in \mathbb {S}^1\}$. The formal mating of P and Q is the degree d branched cover  $P\bot \!\! \! {\bot } Q:\mathbb {S}^2_{f,g}\to \mathbb {S}^2_{f,g}$ defined by the formula
$P\bot \!\! \! {\bot } Q:\mathbb {S}^2_{f,g}\to \mathbb {S}^2_{f,g}$ defined by the formula
 $$\begin{align*}(P\bot \!\! \! {\bot} Q)(z) = \begin{cases} P(z) & z\in\mathbb{C}_P, \\ (\infty,\overline{z}^d) & \text{for }(\infty,z), \\ Q(z) & z\in\mathbb{C}_Q. \end{cases}\end{align*}$$
$$\begin{align*}(P\bot \!\! \! {\bot} Q)(z) = \begin{cases} P(z) & z\in\mathbb{C}_P, \\ (\infty,\overline{z}^d) & \text{for }(\infty,z), \\ Q(z) & z\in\mathbb{C}_Q. \end{cases}\end{align*}$$ Suppose that P and Q have connected and locally connected Julia sets. The closure in  $\mathbb {S}^2_{P,Q}$ of the external ray at angle
$\mathbb {S}^2_{P,Q}$ of the external ray at angle ![]() $\theta $ in
$\theta $ in ![]() $\mathbb {C}_P$ is denoted
$\mathbb {C}_P$ is denoted ![]() $R_P(\theta )$ and, likewise, the closure of the external ray at angle
$R_P(\theta )$ and, likewise, the closure of the external ray at angle ![]() $\theta $ in
$\theta $ in ![]() $\mathbb {C}_Q$ is denoted
$\mathbb {C}_Q$ is denoted ![]() $R_Q(\theta )$. Then
$R_Q(\theta )$. Then ![]() $R_P(\theta )$ and
$R_P(\theta )$ and ![]() $R_Q(-\theta )$ are rays in
$R_Q(-\theta )$ are rays in  $\mathbb {S}^2_{P,Q}$ that share a common endpoint
$\mathbb {S}^2_{P,Q}$ that share a common endpoint ![]() $(\infty ,e^{2\pi i\theta })$. The extended external ray at angle
$(\infty ,e^{2\pi i\theta })$. The extended external ray at angle ![]() $\theta $ in
$\theta $ in  $\mathbb {S}^2_{P,Q}$ is defined as
$\mathbb {S}^2_{P,Q}$ is defined as ![]() $R(\theta ):=R_P(\theta )\cup R_Q(-\theta )$. Each extended external ray intersects each of
$R(\theta ):=R_P(\theta )\cup R_Q(-\theta )$. Each extended external ray intersects each of ![]() $\mathcal {K}(P)$,
$\mathcal {K}(P)$, ![]() $\mathcal {K}(Q)$ and the equator at exactly one point.
$\mathcal {K}(Q)$ and the equator at exactly one point.
We define the ray equivalence ![]() $\sim _{ray}$ as the smallest equivalence relation on
$\sim _{ray}$ as the smallest equivalence relation on  $\mathbb {S}^2_{P,Q}$ so that two points
$\mathbb {S}^2_{P,Q}$ so that two points  $x,y\in \mathbb {S}^2_{P,Q}$ are equivalent if there exists
$x,y\in \mathbb {S}^2_{P,Q}$ are equivalent if there exists ![]() $\theta $ so that
$\theta $ so that ![]() $x,y\in R(\theta )$. A ray equivalence class
$x,y\in R(\theta )$. A ray equivalence class ![]() $\gamma $ can be considered as an embedded graph: the vertices are the points in
$\gamma $ can be considered as an embedded graph: the vertices are the points in ![]() $\gamma \cap (\mathcal {K}(P)\cup \mathcal {K}(Q))$ and the edges are the external extended rays in
$\gamma \cap (\mathcal {K}(P)\cup \mathcal {K}(Q))$ and the edges are the external extended rays in ![]() $\gamma $. We also denote by
$\gamma $. We also denote by ![]() $[x]$ the ray equivalence class of x. The diameter of a ray equivalence class is computed with respect to the graph metric. The vertex set of a ray equivalence class
$[x]$ the ray equivalence class of x. The diameter of a ray equivalence class is computed with respect to the graph metric. The vertex set of a ray equivalence class ![]() $[x]$ has a natural partition consisting of the two sets
$[x]$ has a natural partition consisting of the two sets ![]() $[x]\cap \mathcal {K}(P)$ and
$[x]\cap \mathcal {K}(P)$ and ![]() $[x]\cap \mathcal {K}(Q)$, and using this partition
$[x]\cap \mathcal {K}(Q)$, and using this partition ![]() $[x]$ is seen to be a bipartite graph.
$[x]$ is seen to be a bipartite graph.
An equivalence relation ![]() $\sim $ on
$\sim $ on ![]() $\mathbb {S}^2$ is said to be Moore-unobstructed if the quotient
$\mathbb {S}^2$ is said to be Moore-unobstructed if the quotient ![]() $\mathbb {S}^2/{\sim }$ is homeomorphic to
$\mathbb {S}^2/{\sim }$ is homeomorphic to ![]() $\mathbb {S}^2$. The following theorem is due to A. Epstein (see [Reference Petersen and Meyer36, Proposition 4.12]).
$\mathbb {S}^2$. The following theorem is due to A. Epstein (see [Reference Petersen and Meyer36, Proposition 4.12]).
Proposition 4.20. Let P and Q be two anti-polynomials of equal degree ![]() $d\geq 2$ with connected and locally connected Julia sets. If the equivalence classes of
$d\geq 2$ with connected and locally connected Julia sets. If the equivalence classes of ![]() $\sim _{ray}$ are ray-trees having uniformly bounded diameter, then
$\sim _{ray}$ are ray-trees having uniformly bounded diameter, then  $\mathbb {S}^2_{P,Q}/{\sim _{ray}}$ is Moore-unobstructed.
$\mathbb {S}^2_{P,Q}/{\sim _{ray}}$ is Moore-unobstructed.
We remark that the proof of this theorem uses Moore’s theorem. It is originally stated only for polynomials, but the proof extends identically to the case of anti-polynomials. There is also a partial converse of the above statement which we will not be using here.
For a critically fixed anti-polynomial P, we have the following description of the cut-points of ![]() $\mathcal {K}(P)$. The result directly follows from the dynamical correspondence between function kissing reflection groups and critically fixed anti-polynomials discussed in Subsection 4.3.
$\mathcal {K}(P)$. The result directly follows from the dynamical correspondence between function kissing reflection groups and critically fixed anti-polynomials discussed in Subsection 4.3.
Lemma 4.21. Let P be a critically fixed anti-polynomial. Then any cut-point of ![]() $\mathcal {K}(P)$ is eventually mapped to a repelling fixed point that is the landing point of a
$\mathcal {K}(P)$ is eventually mapped to a repelling fixed point that is the landing point of a ![]() $2$-cycle of external rays.
$2$-cycle of external rays.
An extended external ray that contains a repelling fixed point of a critically fixed anti-polynomial is called a principal ray. The ray equivalence class of a principal ray is called a principal ray class. In our setting, the Moore obstructions can be detected simply by looking at these principal ray classes.
Lemma 4.22. Let P and Q be two marked anti-polynomials of equal degree ![]() $d\geq 2$, where P is critically fixed and Q is postcritically finite and hyperbolic.
$d\geq 2$, where P is critically fixed and Q is postcritically finite and hyperbolic.
1. If a principal ray equivalence class of
 $\sim _{ray}$ contains more than one cut-point of
$\sim _{ray}$ contains more than one cut-point of  $\mathcal {K}(P)$, it must contain a 2-cycle or a 4-cycle.
$\mathcal {K}(P)$, it must contain a 2-cycle or a 4-cycle.2. The equivalence
 $\sim _{ray}$ is Moore-obstructed if and only if some principal ray equivalence class contains a 2-cycle or a 4-cycle.
$\sim _{ray}$ is Moore-obstructed if and only if some principal ray equivalence class contains a 2-cycle or a 4-cycle.
Proof. We first note that since the second iterate of a postcritically finite anti-polynomial is a postcritically finite holomorphic polynomial with the same Julia set, it follows from [Reference Milnor31, §9, §19] that the Julia sets of ![]() $P, Q$ are connected and locally connected.
$P, Q$ are connected and locally connected.
Let ![]() $x\in \mathcal {K}(P)$ be a repelling fixed point whose ray equivalence class
$x\in \mathcal {K}(P)$ be a repelling fixed point whose ray equivalence class ![]() $[x]$ contains more than one cut-point of
$[x]$ contains more than one cut-point of ![]() $\mathcal {K}(P)$. Each point of
$\mathcal {K}(P)$. Each point of ![]() $\mathcal {J}(P)$ is the landing point of one or two rays. Since
$\mathcal {J}(P)$ is the landing point of one or two rays. Since ![]() $[x]$ is connected, there must be cut-points
$[x]$ is connected, there must be cut-points ![]() $w',z'\in [x]$ in
$w',z'\in [x]$ in ![]() $\mathcal {K}(P)$ so that
$\mathcal {K}(P)$ so that ![]() $w'\sim _{ray} z'$ with
$w'\sim _{ray} z'$ with ![]() $w'$ and
$w'$ and ![]() $z'$ having graph distance two. Let
$z'$ having graph distance two. Let ![]() $\gamma $ be the union of the two rays realising the connection between
$\gamma $ be the union of the two rays realising the connection between ![]() $w'$ and
$w'$ and ![]() $z'$. For some iterate j, we have from Lemma 4.21 that
$z'$. For some iterate j, we have from Lemma 4.21 that ![]() $(P\bot \!\! \! {\bot } Q)^j(w')$ and
$(P\bot \!\! \! {\bot } Q)^j(w')$ and ![]() $(P\bot \!\! \! {\bot } Q)^j(z')$ are fixed points, which we denote w and z respectively. The graph distance between w and z is either 0 or 2. In the former case,
$(P\bot \!\! \! {\bot } Q)^j(z')$ are fixed points, which we denote w and z respectively. The graph distance between w and z is either 0 or 2. In the former case, ![]() $w=z$, and since Q is hyperbolic and hence a local homeomorphism on
$w=z$, and since Q is hyperbolic and hence a local homeomorphism on ![]() $\mathcal {J}(Q)$, we have that
$\mathcal {J}(Q)$, we have that ![]() $(P\bot \!\! \! {\bot } Q)^j(\gamma )$ is a 2-cycle. Since x is a fixed point, its ray class is forward invariant, so
$(P\bot \!\! \! {\bot } Q)^j(\gamma )$ is a 2-cycle. Since x is a fixed point, its ray class is forward invariant, so ![]() $(P\bot \!\! \! {\bot } Q)^j(\gamma )$ must be contained in
$(P\bot \!\! \! {\bot } Q)^j(\gamma )$ must be contained in ![]() $[x]$. This yields a 2-cycle in
$[x]$. This yields a 2-cycle in ![]() $[x]$.
$[x]$.
Suppose now that ![]() $w\neq z$. There then exist two extended external rays
$w\neq z$. There then exist two extended external rays ![]() $\alpha _z$ and
$\alpha _z$ and ![]() $\alpha _w$ that land at z and w and share a common endpoint
$\alpha _w$ that land at z and w and share a common endpoint ![]() $v\in \mathcal {K}(Q)$. Let
$v\in \mathcal {K}(Q)$. Let ![]() $\gamma $ be the concatenation of these two rays. Each of
$\gamma $ be the concatenation of these two rays. Each of ![]() $\alpha _z,\alpha _w$ must have dynamical period 2 since they land at fixed cut-points of P. If v is a fixed point, then the graph
$\alpha _z,\alpha _w$ must have dynamical period 2 since they land at fixed cut-points of P. If v is a fixed point, then the graph ![]() $\alpha _w\cup (P\bot \!\! \! {\bot } Q)(\alpha _w)$ is a cycle of length
$\alpha _w\cup (P\bot \!\! \! {\bot } Q)(\alpha _w)$ is a cycle of length ![]() $2$ for
$2$ for ![]() $\sim _{ray}$. If v has period
$\sim _{ray}$. If v has period ![]() $2$, then
$2$, then ![]() $\gamma \cup (P\bot \!\! \! {\bot } Q)(\gamma )$ is a cycle of length
$\gamma \cup (P\bot \!\! \! {\bot } Q)(\gamma )$ is a cycle of length ![]() $4$ for
$4$ for ![]() $\sim _{ray}$. As argued before, either of these cycles must be in
$\sim _{ray}$. As argued before, either of these cycles must be in ![]() $[x]$. This concludes the proof of statement 1.
$[x]$. This concludes the proof of statement 1.
If a principal ray equivalence contains a cycle, it is immediate that ![]() ${\sim _{ray}}$ is Moore-obstructed. Now assume that no principal ray equivalence class contains a
${\sim _{ray}}$ is Moore-obstructed. Now assume that no principal ray equivalence class contains a ![]() $2$-cycle or a
$2$-cycle or a ![]() $4$-cycle. This means that the diameter of a principal ray equivalence class is bounded by
$4$-cycle. This means that the diameter of a principal ray equivalence class is bounded by ![]() $4$ as there can be at most one cut-point of
$4$ as there can be at most one cut-point of ![]() $\mathcal {K}(P)$ in this class. Any principal ray equivalence class must evidently be a tree.
$\mathcal {K}(P)$ in this class. Any principal ray equivalence class must evidently be a tree.
Now let ![]() $z\in \mathcal {J}(P)$. If there is no cut-point in the equivalence class
$z\in \mathcal {J}(P)$. If there is no cut-point in the equivalence class ![]() $[z]$, then
$[z]$, then ![]() $[z]$ is a tree and has diameter at most
$[z]$ is a tree and has diameter at most ![]() $2$. Otherwise, by Lemma 4.21, it is eventually mapped to a principal ray equivalence class. Since both P and Q are hyperbolic, the map
$2$. Otherwise, by Lemma 4.21, it is eventually mapped to a principal ray equivalence class. Since both P and Q are hyperbolic, the map ![]() $P\bot \!\! \! {\bot } Q$ is a local homeomorphism on
$P\bot \!\! \! {\bot } Q$ is a local homeomorphism on ![]() $\mathcal {J}(P)$ and
$\mathcal {J}(P)$ and ![]() $\mathcal {J}(Q)$. Since all of the principal ray equivalence classes are trees, in particular, simply connected, any component of its preimage under
$\mathcal {J}(Q)$. Since all of the principal ray equivalence classes are trees, in particular, simply connected, any component of its preimage under ![]() $P\bot \!\! \! {\bot } Q$ is homeomorphic to it. Thus, by induction, we conclude that
$P\bot \!\! \! {\bot } Q$ is homeomorphic to it. Thus, by induction, we conclude that ![]() $[z]$ is a tree and has diameter at most
$[z]$ is a tree and has diameter at most ![]() $4$. Now by Proposition 4.20, the mating is Moore-unobstructed.
$4$. Now by Proposition 4.20, the mating is Moore-unobstructed.
We now prove that for a large class of pairs of anti-polynomials, the absence of Moore obstruction is equivalent to the existence of geometric mating.
Proposition 4.23. Let P and Q be marked anti-polynomials of equal degree ![]() $d\geq 2$, where P is critically fixed and Q is postcritically finite and hyperbolic. There is an anti-rational map that is the geometric mating of P and Q if and only if
$d\geq 2$, where P is critically fixed and Q is postcritically finite and hyperbolic. There is an anti-rational map that is the geometric mating of P and Q if and only if ![]() $\sim _{ray}$ is not Moore-obstructed.
$\sim _{ray}$ is not Moore-obstructed.
Proof. The only if part of the statement is immediate. To prove the if part, we will first show that the absence of Moore obstruction can be promoted to the absence of Thurston obstruction. Note that the only case where ![]() $(P\bot \!\! \! {\bot } Q)^{2}$ has nonhyperbolic orbifold is when P and Q are both power maps, in which case the conclusion of the theorem is immediate. Thus, we assume for the remainder of the proof that
$(P\bot \!\! \! {\bot } Q)^{2}$ has nonhyperbolic orbifold is when P and Q are both power maps, in which case the conclusion of the theorem is immediate. Thus, we assume for the remainder of the proof that ![]() $(P\bot \!\! \! {\bot } Q)^{2}$ has hyperbolic orbifold.
$(P\bot \!\! \! {\bot } Q)^{2}$ has hyperbolic orbifold.
Suppose ![]() $(P\bot \!\! \! {\bot } Q)^{2}$ has a Thurston obstruction
$(P\bot \!\! \! {\bot } Q)^{2}$ has a Thurston obstruction ![]() $\Gamma $. We may assume that
$\Gamma $. We may assume that ![]() $\Gamma $ is irreducible. Since Q has no Thurston obstruction, there is some edge
$\Gamma $ is irreducible. Since Q has no Thurston obstruction, there is some edge ![]() $\lambda $ in the Hubbard tree
$\lambda $ in the Hubbard tree ![]() $H_P$ so that
$H_P$ so that ![]() $\Gamma \cdot \lambda \neq 0$. Note that
$\Gamma \cdot \lambda \neq 0$. Note that ![]() $\lambda $ is an irreducible arc system consisting of one arc, so it follows from [Reference Shishikura and Tan42, Theorem 3.9] that
$\lambda $ is an irreducible arc system consisting of one arc, so it follows from [Reference Shishikura and Tan42, Theorem 3.9] that ![]() $\Gamma $ must also be a Levy cycle consisting of one essential curve
$\Gamma $ must also be a Levy cycle consisting of one essential curve ![]() $\gamma $.
$\gamma $.

Figure 4.2 Two cubic anti-polynomials together with all rays that have period 2 or smaller. The first map is a critically fixed anti-polynomial so that the 1/8 and 5/8 rays co-land. The second map is produced by tuning the first map with basilicas so that the pairs ![]() $(0/1,3/4)$ and
$(0/1,3/4)$ and ![]() $(1/2,1/4)$ co-land. The unique principal ray equivalence class has no cycle. Their mating is depicted below using the software [Reference Bartholdi1].
$(1/2,1/4)$ co-land. The unique principal ray equivalence class has no cycle. Their mating is depicted below using the software [Reference Bartholdi1].

Since ![]() $P\bot \!\! \! {\bot } Q$ is hyperbolic, the Levy cycle is not degenerate (as defined in [Reference Shishikura and Tan42,
$P\bot \!\! \! {\bot } Q$ is hyperbolic, the Levy cycle is not degenerate (as defined in [Reference Shishikura and Tan42, ![]() $\S$1]). Thus, there is a periodic ray class that contains a cycle [Reference Shishikura and Tan42, Theorem 1.4(2)]. By the hypothesis that there is no Moore obstruction, no such periodic ray class exists. This is a contradiction and so no Thurston obstruction exists for
$\S$1]). Thus, there is a periodic ray class that contains a cycle [Reference Shishikura and Tan42, Theorem 1.4(2)]. By the hypothesis that there is no Moore obstruction, no such periodic ray class exists. This is a contradiction and so no Thurston obstruction exists for ![]() $(P\bot \!\! \! {\bot } Q)^{2}$. By Proposition 4.11, it follows that
$(P\bot \!\! \! {\bot } Q)^{2}$. By Proposition 4.11, it follows that ![]() $P\bot \!\! \! {\bot } Q$ is also unobstructed and Thurston equivalent to a rational map.
$P\bot \!\! \! {\bot } Q$ is also unobstructed and Thurston equivalent to a rational map.
Having shown that ![]() $P\bot \!\! \! {\bot } Q$ has no Thurston obstruction, the Rees–Shishikura theorem (which extends directly to orientation-reversing maps) implies that the geometric mating of P and Q exists [Reference Shishikura41, Theorem 1.7].
$P\bot \!\! \! {\bot } Q$ has no Thurston obstruction, the Rees–Shishikura theorem (which extends directly to orientation-reversing maps) implies that the geometric mating of P and Q exists [Reference Shishikura41, Theorem 1.7].
Recall that a pair of laminations on ![]() $\mathbb {S}^1$ for marked anti-polynomials is said to be nonparallel if they share no common leaf under the natural orientation-reversing identification of the two copies of
$\mathbb {S}^1$ for marked anti-polynomials is said to be nonparallel if they share no common leaf under the natural orientation-reversing identification of the two copies of ![]() $\mathbb {S}^1$. This is equivalent to saying that the ray equivalence classes contain no 2-cycle. We immediately have the following corollary from Lemma 4.22 and Proposition 4.23.
$\mathbb {S}^1$. This is equivalent to saying that the ray equivalence classes contain no 2-cycle. We immediately have the following corollary from Lemma 4.22 and Proposition 4.23.
Corollary 4.24. A marked critically fixed anti-polynomial P and a marked postcritically finite, hyperbolic anti-polynomial Q are geometrically mateable if and only if the principal ray equivalence classes contain no ![]() $2$-cycles or
$2$-cycles or ![]() $4$-cycles.
$4$-cycles.
Two marked critically fixed anti-polynomials P and Q are geometrically mateable if and only if their laminations are nonparallel.
Proof. The first statement is immediate.
To see the second one, we note that according to Lemma 4.21, the lamination of a marked critically fixed anti-polynomial is generated by the period ![]() $2$ cycles of rays landing at the repelling fixed points (which are cut-points). In light of this, it is easy to see that for two marked critically fixed anti-polynomials, no principal ray equivalence class contains a
$2$ cycles of rays landing at the repelling fixed points (which are cut-points). In light of this, it is easy to see that for two marked critically fixed anti-polynomials, no principal ray equivalence class contains a ![]() $4$-cycle. The second statement now follows from this observation and the first statement.
$4$-cycle. The second statement now follows from this observation and the first statement.
Acknowledgements
The authors thank Curt McMullen for useful suggestions. They also thank Mikhail Hlushchanka for stimulating discussions. The authors are grateful to the anonymous referee for their valuable input. The third author thanks the Institute for Mathematical Sciences and Simons Center for Geometry and Physics at Stony Brook University for their hospitality during part of the work on this project. The third author was supported by an endowment from Infosys Foundation and SERB research grant SRG/2020/000018.
Conflict of interest
None.






























