2. MH370 FLIGHT FACTS

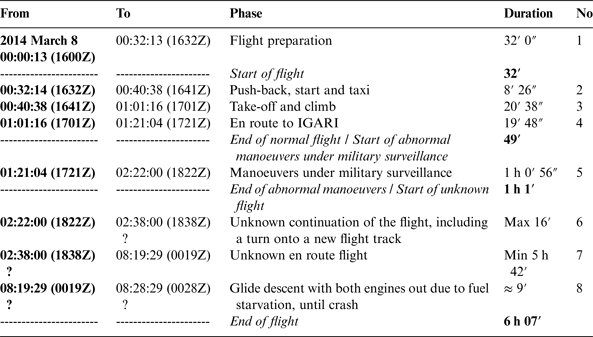
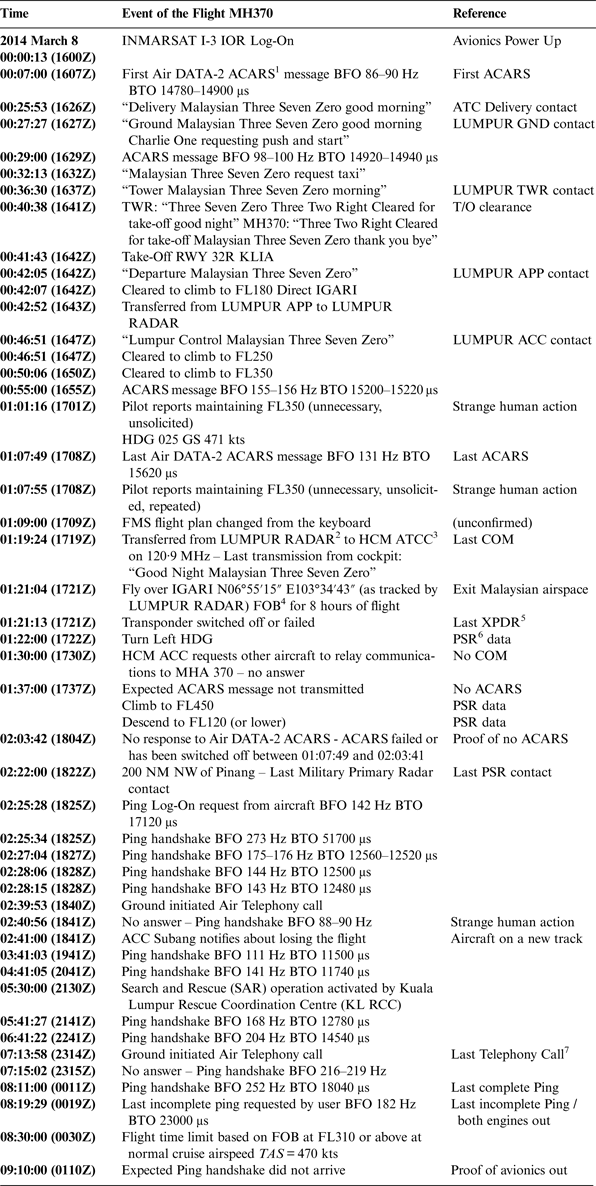
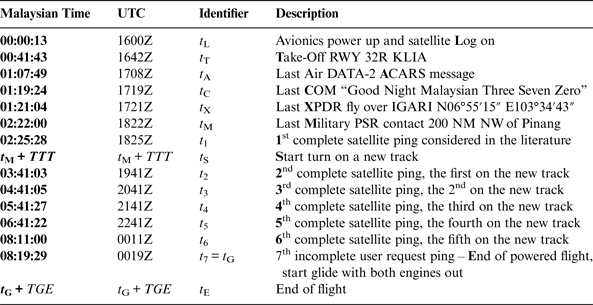
Malaysian Airlines 370 took off with 239 Persons On Board (POB) (227 passengers out of the capacity of 282 and 12 members of crew). The initial flight plan was from Kuala Lumpur International (KLIA) to Beijing Capital International Airport (ZBAA). The ETA (Estimated Time of Arrival at planned destination (UTC)) was 2230Z and ETE (Estimated Time En route (estimated duration of flight in hours and minutes)) was 05:49. The fuel load was 49,100 kg, enough for over eight hours of flight. The MH370 flight phases are described in Table 1. Table 2 provides a detailed sequence of known facts about the flight, including the seven relevant ping exchanges between the INMARSAT-3 Indian Ocean Region (IOR) satellite and the SATCOM transceiver, which allow the calculation of the flight trajectory. The key moments of the flight are defined in Table 3.

Table 1. MH370 Flight Phases.

Table 2. Sequence of Known Facts about MH370.

¹ ACARS: Aircraft Communications Addressing and Reporting System, automated bidirectional system for technical and operational messages between aircraft and a ground communication network or a satellite communication network

² ACC Subang, Malaysia

³ ACC Ho Chi Mingh, Vietnam

⁴ FOB: Fuel on Board

⁵ XPRD: Secondary Surveillance Transponder

⁶ PSR: Primary Surveillance Radar (military)

⁷ Not answered, but the subsequent ping proved aircraft to be in operational status.

Table 3. Key moments of the MH370 flight.

The signal delay is called BTO (Burst Timing Offset) and it is caused by the time the radio waves take to travel from the satellite ground station to the satellite to the aircraft and back. Based on this, the instantaneous distance between the satellite and the aircraft (range) may be calculated for each ping exchange. The calculations presented in this paper rely mainly on these BTOs.

The locus of the points within a certain range is a sphere with the centre in the satellite position, with the range as the radius. This sphere may be intersected with the surface parallel to the ellipsoid or the geoid, at an altitude above the geoid, which corresponds with the presumed flight level of the aircraft. This is in fact the isobaric surface for level flight, corresponding to the local meteorological data. The intersection yields a curve very close to a circle. At the given moment of the ping, the position of the aircraft is somewhere on that quasi-circle.

The shift in carrier frequency is called BFO (Burst Frequency Offset). It is caused by the Doppler-Fizeau effect due to the relative speed between the aircraft and the satellite. In the calculations below, the BFO values were not used, and this is a major difference between this method and other methods used until now and known to the authors (Ashton et al., Reference Ashton, Schuster-Bruce, Colledge and Dickinson2014; Hradecky, Reference Hradecky2014). The reason for avoiding the use of BFO values is that the problem of relative speed is geometrically ill conditioned in this case, especially in the first half of the flight.

3. CALCULATION OF QUASI-CIRCLES

This paper models the Earth as the WGS-84 ellipsoid. The ranges define quasi-circles at the intersection between the isobaric surface that the aircraft levels on, and the sphere with the centre in the satellite antenna position and the BTO-based range as the radius.

The INMARSAT-3 satellites are five satellites in 36,000 km high geostationary orbit (N0°), as follows: AOR-W at a longitude of W54°, AOR-E at W15·5°, I-3 at 25°E, IOR (the satellite used by MH370) at E64·5°, and POR at E178°. INMARSAT-3 IOR has an orbit inclined at 1·66°. This inclination gives a wobble movement with a period of T = 24 hours. The actual orbital altitude of IOR at t ₆ was: 35,794 km, as compared to the target of 35,786 km Above Mean Sea Level (AMSL). Although geostationary, the actual position of the IOR satellite moved slightly during the MH370 flight.

In the Earth-Centred-Earth-Fixed (ECEF) frame, the system of equations used to calculate the seven quasi-circles (see Figure 8) are the WGS-84 rotation ellipsoid equations and the satellite-centred sphere equations:

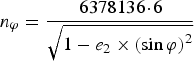(1)$$n_\varphi = \displaystyle{{6378136\! \cdot\! 6} \over {\sqrt {1 - e_2 \times \left( {\sin \varphi} \right)^2}}} $$

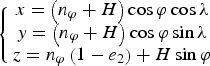(2)$$\left\{ {\matrix{ {x = \left( {n_\varphi + H} \right)\cos \varphi \cos \lambda} \cr {y = \left( {n_\varphi + H} \right)\cos \varphi \sin \lambda} \cr {z = n_\varphi \left( {1 - e_2} \right) + H\sin \varphi} \cr}} \right.$$

(3)$$\sqrt {\left( {x - x_{SAT}} \right)^2 + \left( {y - y_{SAT}} \right)^2 + \left( {z - z_{SAT}} \right)^2} - Range_{satellite\; to\; aircraft} = 0$$

From (Ashton et al., Reference Ashton, Schuster-Bruce, Colledge and Dickinson2014):

(4)$$Range_{satellite\; to\; aircraft} = \displaystyle{1 \over 2}c \cdot (BTO - bias) - Range_{satellite\; to\; Perth\; GES} $$

(5)$$bias = - 495679\; \mu s$$

The Equations (2) in x, y, z are substituted in Equation (3), providing a way to calculate longitude λ as a function of latitude ϕ. The seven quasi-circles correspond to the seven pings, illustrated in Figure 8, which occurred at the times t ₁ to t ₇ (see Table 3). However, the first complete satellite ping considered in the literature was not used in this paper, because the initialisation of the problem is uncertain, so less weight should be given to the starting point. Consequently, the work presented in this paper relies on the last six quasi-circles only. As a confirmation of this selection of quasi-circles, the contribution of the six pings to the total inconsistency of the trajectory is well balanced. The individual contribution of the first ping to the total inconsistency would have been disproportionately larger than the contributions of the other pings.

4. SOLVING TRAJECTORY EQUATIONS

The authors independently calculated the MH370 trajectory based on the following data:

1. 1. Flight trajectory until the last known position P_18_22 as recorded by the military primary radars (N 6° 36′ 15″ E 96° 33′ 14″) (Malaysian Gov., 2014; Hradecky, Reference Hradecky2014).

2. 2. The set of recorded INMARSAT (INMARSAT, 2014) satellite pings (signal handshake delays and carrier frequency drift) (Malaysian Gov., 2014, Hradecky, Reference Hradecky2014).

3. 3. The wind vector field, isobaric surface height and air temperature in the wider area at the moment of the flight, retrieved from the National Oceanic and Atmospheric Administration (NOAA) 2014). Interpolations in time, position, and flight levels were used for the best local current estimate of the wind velocity and the air temperature.

4. 4. The Boeing 777-200ER flight performance and systems (Boeing, 1992a). A Boeing 777-200ER flight simulator based on a dynamic model was developed by the authors (Section 5).

5. 5. The Boeing 777-200ER FMS (Flight Management System) specifications (Bulfer and Gifford, Reference Bulfer and Gifford1999).

6. 6. The WGS-84 ellipsoid shape approximation of the Earth.

7. 7. The INMARSAT-3 IOR satellite orbital data (Malaysian Gov., 2014).

The unknowns of this problem and the space of solutions are considered in the following subsections (see Figure 1).

Figure 1. MH370 trajectory problem unknowns: TTT, TK, FL, and M.

4.6. Trajectory Equations

Given the above considerations, the space of solutions was reduced from 34,056,000 initial possible solutions down to 42,240 possible trajectories, as summarised in Table 4 and illustrated in Figure 1 by underlined text.

Table 4. The subspace of solutions for refined search.

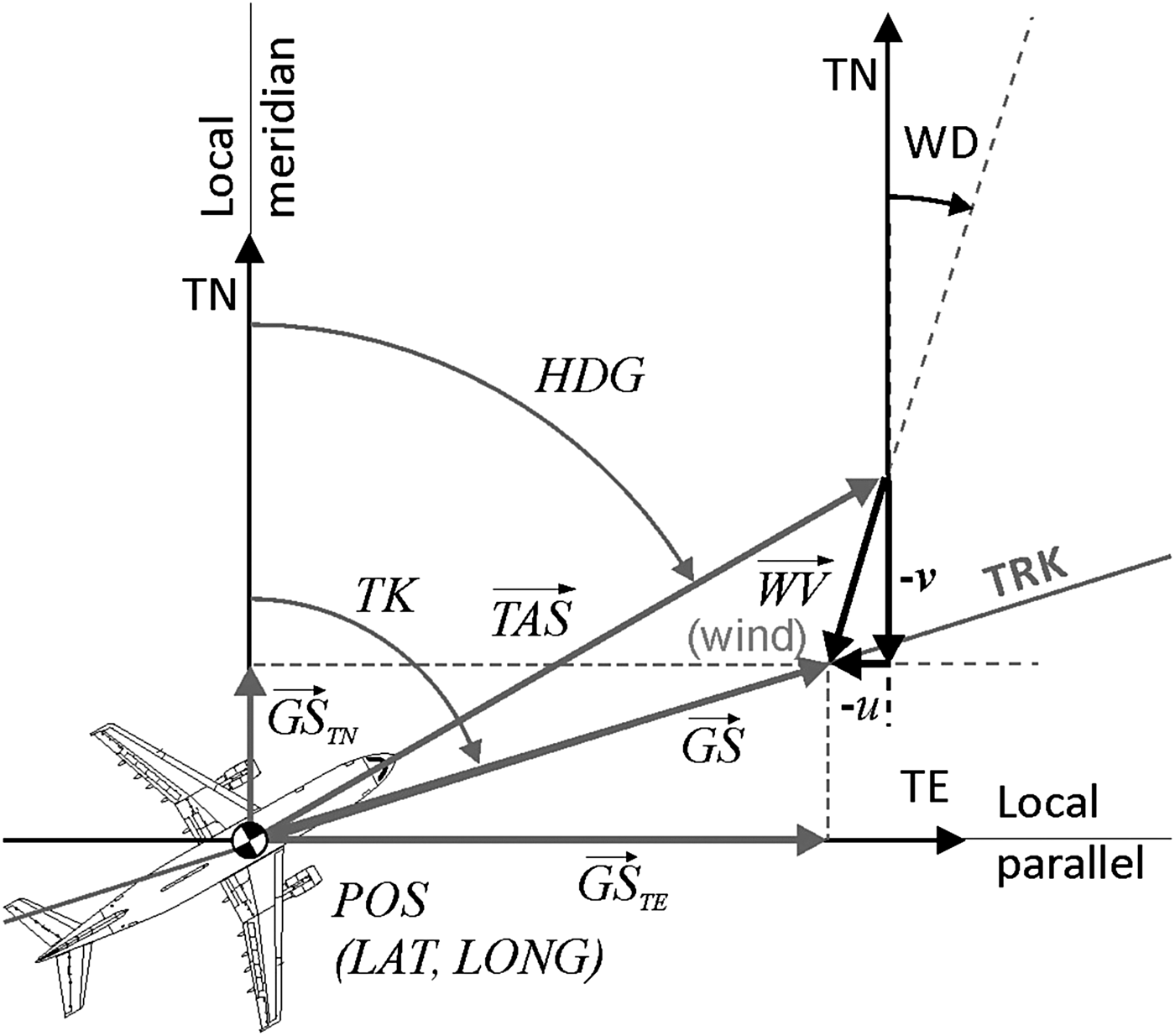
Considering the True North (u) and the True East (v) components of the local horizontal wind velocity vector retrieved from the NOAA records, the speed triangle system of trigonometric equations is the following (see Figure 2):

(6)$$\left\{ {\matrix{ {TAS \cdot \cos HDG + v = GS\; \cdot \cos TK} \cr {TAS\; \cdot \sin HDG + u = GS \cdot \sin TK} }} \right.$$

The solution of the system is the following:

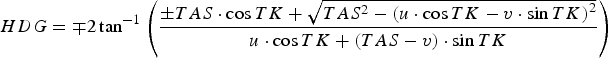(7)$$HDG = \mp 2\tan ^{ - 1} \left( {\displaystyle{{ \pm TAS \cdot \cos TK + \sqrt {TAS^2 - \left( {u \cdot \cos TK - v \cdot \sin TK} \right)^2}} \over {u \cdot \cos TK + \left( {TAS - v} \right) \cdot \sin TK}}} \right)$$

(8)$$GS = v \cdot \cos TK + u \cdot \sin TK \mp \sqrt {TAS^2 - \left( {u \cdot \cos TK - v \cdot \sin TK} \right)^2} $$

Figure 2. Local wind triangle solved at each time step in the course of flight simulation.

The system of six equations that result from the data (the time delays BTO of the six relevant pings) is over determined, and it was solved so as to minimise the quadratic sum of errors, which was considered as the inconsistency of the solution (Ε). The inconsistency was calculated and used as an optimisation criterion to refine the search to the most plausible solution:

(9)$${\rm \varepsilon} = \sqrt {\sum \nolimits_1^6 d_i ^2} = min$$

Each of the six errors d _i is the distance between the aircraft at the moment of each of the six pings, and the closest point belonging to the respective quasi-circle.

The flight was simulated using a Runge-Kutta IV method with a time step of 10 seconds, integrating the local speed triangle (Figure 2) and the dynamic flight simulator equations. At the moments of the pings, the position resulting from the simulation was compared to the position resulting from the radio transmission by calculating the distance d _i between the two. The quadratic sum of distances d _i was minimised using a complete search optimisation method. All calculations were done by a MATLAB application written by the authors.

The wind velocity and air temperature were retrieved from the NOAA world weather database (NOAA, 2014), with a granulation of 0·5° of latitude and longitude. Linear interpolation of latitude and longitude was used between the nodes. Vertically, the data are presented for the following isobaric surfaces: 10, 20, 30, 50, 70, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750, 800, 850, 900, 925, 950, 975, and 1000 mbar. These isobars are converted into flight levels using the ISA model, and linear interpolation was used between the isobaric surfaces.

5. THE DYNAMIC MODEL FLIGHT SIMULATOR

For the purpose of this research, a Boeing 777-200ER flight simulator was developed. The simulator is based on a dynamic model i.e. considers the mass of the aircraft and calculates the fuel flow at each time step. The simulator served three separate goals:

• • To integrate the flight trajectory, the current mass of the aircraft, and the fuel consumption. By comparing the fuel consumption to the known fuel on board in the first stage of the flight, one can determine the approximate moment of fuel exhaust. This is compared to t _G, which results from optimisation (see Table 7).

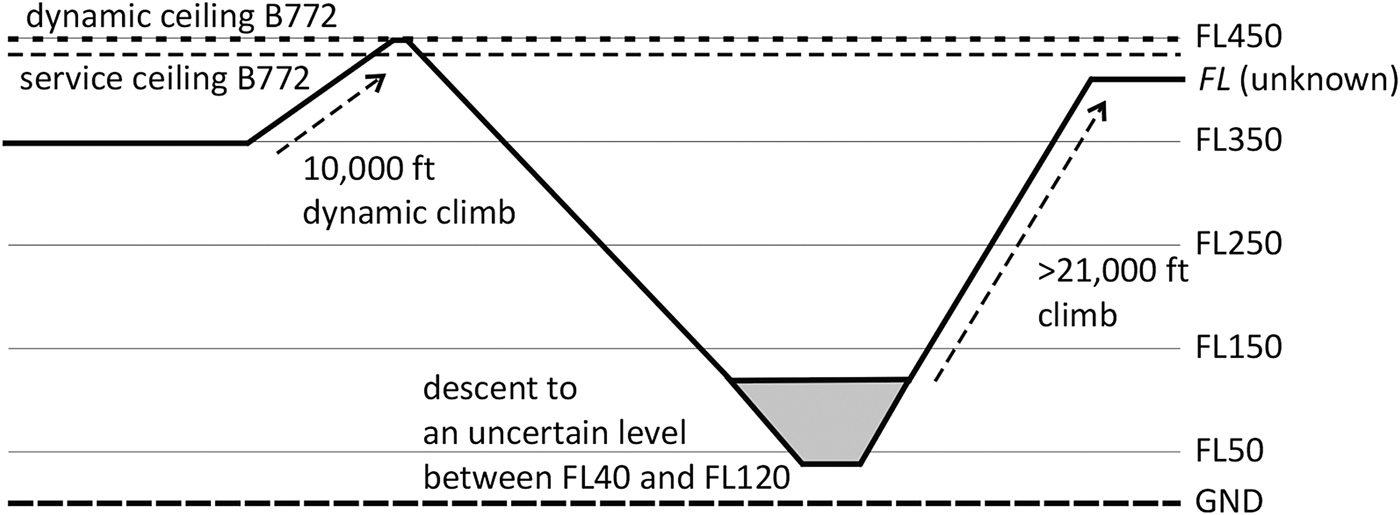
• • To calculate the fuel consumption of a dynamic climb to FL450, a descent to FL120 or below, and a climb back to an unknown cruise FL (Figure 3). These manoeuvres were recorded by the military primary surveillance radars, so the exact levels or details of the manoeuvres are not known. Instead of a simulator based on a time step integration, the authors used a method based on energy and aircraft climb / descent efficiency to calculate the fuel consumed by it.

  

  Figure 3. The flight profile of the MH370 under military primary radar surveillance.

• • To simulate the final glide descent portion, since the start of glide descent (t _G) until crash (t _E).

The equations of the simulator are the following:

(10)$$TAS = M \cdot a $$

(11)$${C_L} = {C_{L\alpha }} \cdot \left( {\alpha - {\alpha _{CL0}}} \right) $$

(12)$$C_D = C_{D0} + K_2 \cdot C_L ^2 $$

(13)$$L = \displaystyle{{\rho _0} \over 2} \cdot TAS^2 \cdot S \cdot C_L $$

(14)$$D = \displaystyle{{\rho _0} \over 2} \cdot TAS^2 \cdot S \cdot C_D $$

(15)$$T = \displaystyle{D \over {{\rm cos}\left( {\alpha + \tau} \right)}}$$

(16)$$T \cdot {\rm sin}\left( {\alpha + \tau } \right) + L = m \cdot g \cdot {\rm cos}\left( \phi \right)$$

The coefficients used for Boeing 777 are as presented in Table 5.

Table 5. Aerodynamic Coefficients for Boeing 777 (Pereira, Reference Pereira2011).

Simulation of the fuel consumption between the last ACARS message and last military primary radar contact was done with the following equations:

(17)$$F{F_{avg}} \cdot \left( {{t_M} - {t_A}} \right) + F{C_{\Delta E}} = F{C_{total}} $$

(18)$$FC_{\Delta E} = \displaystyle{{\Delta E_p + \Delta E_c} \over {s \cdot eff}}$$

The efficiency eff of the engines was calibrated based on the FOB at engine start and FOB at the moment of the last ACARS message (A). The taxi fuel consumption was calculated using the following formula:

(19)$$\displaystyle{\,f \over {\sqrt {T_{amb}}}} = a_{taxi} + b_{taxi} \cdot t_{taxi} + c_{taxi} \cdot na $$

where a _taxi = −0·1223 b _taxi = 0·0335 c _taxi = 0·1385 are the coefficients for a Boeing 777, na is the number of accelerations during taxi (it is considered to be at least two) and the ambient temperature in Kuala Lumpur in March during night was assumed to be T _amb = 297·15 K (Khadilkar, Reference Khadilkar2011). The taxi fuel consumption which results from the above equation is f = 457·8 kg. The remaining FOB at take-off is 49100–457·8 = 48612 kg. Knowing the FOB broadcast by the last ACARS message (43,800 kg) and considering an average fuel flow of FF _avg = 6406 kg/h and the specific energy of Jet A-1, s = 43·02 MJ/kg, the resultant efficiency of the engines is 32·32%. In this case, both the kinematic and the potential energy of the aircraft change. Using the calibrated engine efficiency, the resulting fuel consumption between the last ACARS message (A) and last military primary surveillance radar contact (M) is approximately 10,000 kg, depending on the FL to which the aircraft is considered to have climbed for the long cruise flight towards the south. For example, if the aircraft climbs to FL390, the calculated fuel consumption for the last ACARS – last primary radar contact segment is FC _total = 10065·3 kg. In this case only the change in potential energy is considered (calculated with an average mass) and only at the climb regions. It is supposed that the fuel economy during the descending portions of the flight is balanced by the higher consumption in the dense air.

Simulation of fuel flow during the long cruise flight is based on Boeing (1992a) and Filippone (Reference Filippone2006). Using the calculated thrust and the mass of the aircraft, the following polynomial equation was defined (coefficients are given in Table 6):

(20)$$FF/ENG = {\,p_{0\comma0}} + {\,p_{1\comma0}} \cdot m + {\,p_{0\comma1}} \cdot T$$

Simulation of the final glide descent with both engines out in the time interval TGD presumed 9 minutes is presented in Pleter and Constantinescu (Reference Pleter and Constantinescu2014).

Table 6. Equation (20) Coefficients.

During the cruise flight, TK is kept constant by small turns, which compensate for crosswind. However, in the glide descent region, the simulation keeps a constant HDG instead of TK, and these turns are no longer performed, as illustrated in the inset in Figure 8. This is consistent with the expected behaviour of the automated systems. By keeping a constant HDG, the local crosswind slightly drifted the aircraft during the gliding descent.

6. ANALYSIS OF RESULTS

The multimodal optimisation using ε as a criterion (inconsistency to be minimised) yields the most probable trajectories and the most probable values of the unknowns TTT, TK, and M. The unknown FL is considered a parameter, because the problem is not sensitive with respect to the geometric FL. Just two TK ranges came out to be consistent: the Southern track around 190° (true) and the Northern track of around 336°. The Southern track fits better (a very low inconsistency, 38 solutions between 16 and 25 km), whereas the Northern track does not fit so well (zero solutions under 30 km).

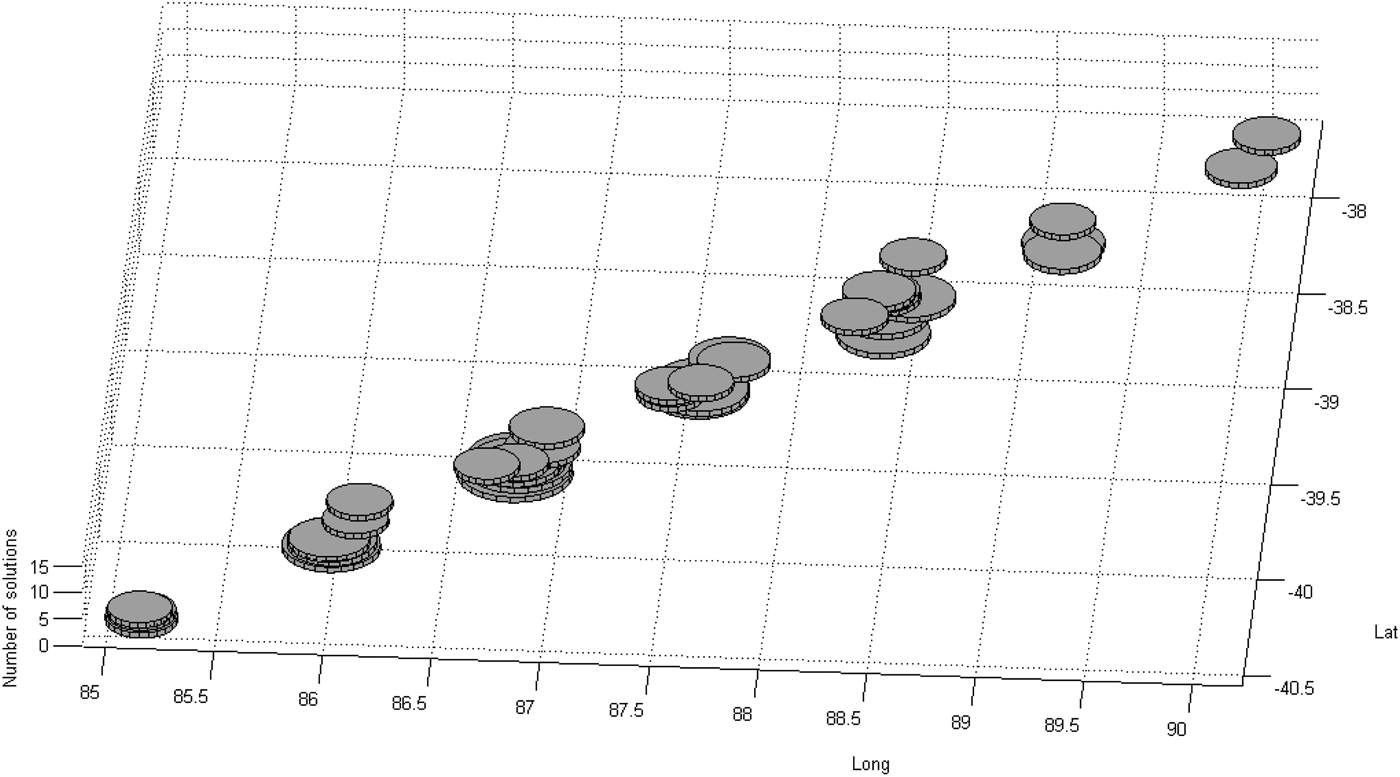
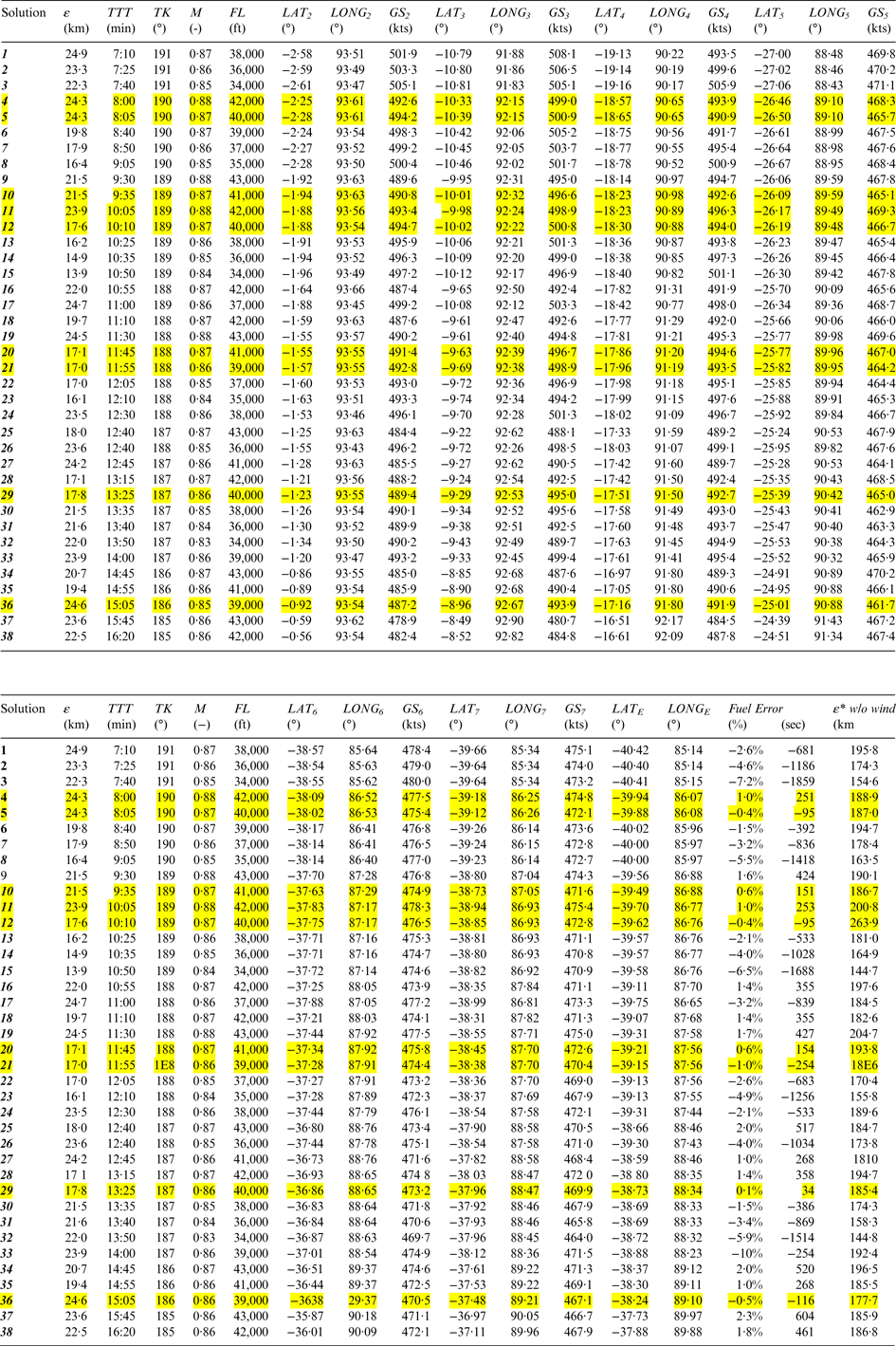
The multimodal optimisation yields the set of all solutions with a certain minimum probability instead of a single most probable solution. Given the nature of the problem and the scarcity of data coming from a unique source, this approach adds more value than the initial search done by the same authors for the most probable trajectory (Pleter and Constantinescu, Reference Pleter and Constantinescu2014). Thus all trajectories with an overall inconsistency lower than 25 km were considered as potential solutions, and they are represented in Tables 7 and 8, and in Figures 4 to 6. The threshold of 25 km is remarkably low as compared to the total length of the trajectory (almost 6,000 km). There are 38 consistent solutions (with ε ⩽ 25 km), and they are analysed in Table 7 and in the subsequent Figures. In Figure 4 all the 38 consistent solutions were represented as cylinders. The diameter of the cylinder is the inverse function of the inconsistency, i.e. consistency (1/ε).

Figure 4. Position of the end of flight (E) for each of the 38 consistent solutions.

Figure 5. The locus of the end of flight positions (E*) for solution 11 considering a constant angular velocity turn during glide descent; the circles represent the possible points of impact for each respective angular velocity.

Figure 6. The end of flight point (E) for each of the 38 consistent solutions (discs); the weighted average of these points is represented by a light colour disc; the transparent areas resulting from the turning glide descent model (Figure 5) were positioned on the calculated end of flight points to give a probable area of impact; the ellipses on the 7^th arc represent the most probable areas of impact.

Table 7. Consistent MH370 trajectory solutions and the corresponding positions of the end of flight (E) – solutions in yellow are confirmed by the available fuel criterion, with a fuel error ≤ 1%.

Table 8. Flight level distribution of the consistent MH370 trajectory solutions.

The most consistent solutions presented in Table 7 have a remarkably low inconsistency, of ε < 17 km. Column “Fuel error” in Table 7 (second part) compares the top of descent (t _G) calculated with the optimisation method based on the satellite pings and the top of descent (t _G*) calculated with the integration of the fuel flow until the moment of fuel exhaust. The relative error ranges between −7·2% and +2·3%. For nine solutions (represented in yellow), the relative time error stays within ±1% (254 seconds of flight in absolute value), which is remarkable, given the inherent uncertainty caused by the manoeuvres before the last turn. Moreover, these small relative errors are symmetrically distributed in the range of the consistent solutions. Such a distribution appears to validate the results of the optimisation. The relative time error filter discards the lower FL solutions, such as solutions 3, 15, and 32. Also, this filter discards the lower M solutions, such as 8 and 26. Given the double validation, from the optimisation and the fuel burn simulation, solutions at the upper end of the FL and M scales stand out, e.g. solution 11.

The places where the flight might have ended in the 38 most probable scenarios are represented in Figures 4 and 5. The places seem clustered in seven isolated groups, but the gaps between these groups might be equally interesting for searching. The solution-clustering phenomenon is probably a consequence of selecting integer values for TK. In reality, TK could have very well been a rational number, in the case of the third hypothesis of the FMS programming presented above, a “DIRECT TO” a distant point given by LAT and LONG. Figure 8 illustrates the whole simulated trajectory, which corresponds to one of the solutions (11). The last portion of this trajectory is made visible at a better scale in the inset.

These 38 end of flight points were calculated assuming that the glide descent was flown with a constant heading (no turn). Since the probability of a turn due to the initial thrust asymmetry is high (ATSB, 2014a; 2014b - MH370 - Definition of Underwater Search Areas), and the rate of turn (the angular velocity) is not known, a locus of all potential end of flight points (E*) was developed and illustrated in Figure 5. All trajectories in Figure 5 correspond to the end of flight point of Solution 11, and are all turning trajectories with incremental angular velocities. The circles at the end of each same-length orthodrome trajectory represent potential points of impact with the water.

In reality, the turn could have been with variable angular velocity. The fixed angular velocity model in Figure 5 however includes in the envelope of the E* points all possible impact points. In Figure 6, for each cluster of E solutions, the corresponding E* envelope was represented as a transparent area. Out of this area, the ellipses on the seventh arch illustrate the spiral dive, which could be a higher probability impact area.

In Table 8 the same 38 solutions were placed on their FLs, making it obvious that the fuel burn criterion favours the higher FLs solutions (in yellow). Flying in a denser atmosphere, although geometrically consistent with the BTOs, would have fuel starved the engines much earlier than the moment t _G, which is known.

For the same solution 11, the simulated ground speed variation over the entire flight was represented in Figure 9. The ground speed is calculated as the vector addition between the horizontal component of the true airspeed and the local wind velocity. For a possible validation of such a trajectory with a method based on BFO, Table 9 indicates the ground speed in the seven moments of the seven pings, decomposed in the ECEF framework.

Table 9. Solution 11 ground speed decomposed in ECEF reference for the seven quasi-circles.

The inclusion of the wind vector field in simulating the flight increased the relevance, as shown in Table 7. The inconsistency of the best-fit trajectories is between 6 and 15 times worse in cases where the wind vector field is not used. This validates the simulation and the use of the proper wind vector field, which is one of the few certain facts regarding this flight.