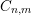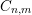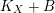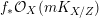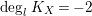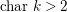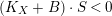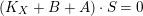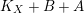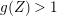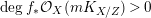1 Introduction
Iitaka conjecture
Let
![]() $X$
be a normal projective variety over a field
$X$
be a normal projective variety over a field
![]() $k$
,
$k$
,
![]() $L$
a Cartier divisor on
$L$
a Cartier divisor on
![]() $X$
, and
$X$
, and
![]() $N(L)$
the set of all positive integers
$N(L)$
the set of all positive integers
![]() $m$
such that the linear system
$m$
such that the linear system
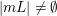 $|mL|\neq \emptyset$
. For an integer
$|mL|\neq \emptyset$
. For an integer
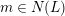 $m\in N(L)$
, let
$m\in N(L)$
, let
![]() $\unicode[STIX]{x1D6F7}_{|mL|}$
be the rational map defined by
$\unicode[STIX]{x1D6F7}_{|mL|}$
be the rational map defined by
![]() $|mL|$
. The Kodaira dimension
$|mL|$
. The Kodaira dimension
![]() $\unicode[STIX]{x1D705}(L)$
is defined as
$\unicode[STIX]{x1D705}(L)$
is defined as
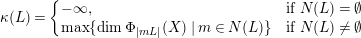 $$\begin{eqnarray}\unicode[STIX]{x1D705}(L)=\left\{\begin{array}{@{}ll@{}}-\infty , & \text{if }N(L)=\emptyset \\ \max \{\dim \unicode[STIX]{x1D6F7}_{|mL|}(X)\mid m\in N(L)\} & \text{if}~N(L)\neq \emptyset \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(L)=\left\{\begin{array}{@{}ll@{}}-\infty , & \text{if }N(L)=\emptyset \\ \max \{\dim \unicode[STIX]{x1D6F7}_{|mL|}(X)\mid m\in N(L)\} & \text{if}~N(L)\neq \emptyset \end{array}\right.\end{eqnarray}$$
If
![]() $L$
is a
$L$
is a
![]() $\mathbb{Q}$
-Cartier divisor,
$\mathbb{Q}$
-Cartier divisor,
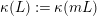 $\unicode[STIX]{x1D705}(L):=\unicode[STIX]{x1D705}(mL)$
for any natural number
$\unicode[STIX]{x1D705}(L):=\unicode[STIX]{x1D705}(mL)$
for any natural number
![]() $m$
so that
$m$
so that
![]() $mL$
is Cartier. This does not depend on the choice of
$mL$
is Cartier. This does not depend on the choice of
![]() $m$
.
$m$
.
Throughout this paper, a contraction is a projective morphism
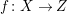 $f:X\rightarrow Z$
between varieties such that
$f:X\rightarrow Z$
between varieties such that
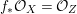 $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$
. The following conjecture due to Iitaka (in characteristic zero) is of fundamental importance in the classification theory of algebraic varieties.
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{Z}$
. The following conjecture due to Iitaka (in characteristic zero) is of fundamental importance in the classification theory of algebraic varieties.
Conjecture 1.1. (
 $C_{n,m}$
)
$C_{n,m}$
)
Let
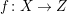 $f:X\rightarrow Z$
be a contraction between smooth projective varieties of dimension
$f:X\rightarrow Z$
be a contraction between smooth projective varieties of dimension
![]() $n,m$
respectively, over an algebraically closed field
$n,m$
respectively, over an algebraically closed field
![]() $k$
. Assume the generic fiber
$k$
. Assume the generic fiber
![]() $F$
is smooth. Then
$F$
is smooth. Then
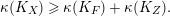 $$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})\geqslant \unicode[STIX]{x1D705}(K_{F})+\unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})\geqslant \unicode[STIX]{x1D705}(K_{F})+\unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
One can formulate a more general problem when
![]() $F$
is not smooth either by assuming it is geometrically integral with a resolution or by considering
$F$
is not smooth either by assuming it is geometrically integral with a resolution or by considering
![]() $F$
as a variety over the function field of
$F$
as a variety over the function field of
![]() $Z$
(for example, see Corollary 1.3).
$Z$
(for example, see Corollary 1.3).
Over the field of complex numbers, the conjecture has been studied by Kawamata [Reference Kawamata22, Reference Kawamata23, Reference Kawamata25], Kollár [Reference Kollár29], Viehweg [Reference Viehweg43, Reference Viehweg44, Reference Viehweg44], Birkar [Reference Birkar3], Chen and Hacon [Reference Chen and Hacon12], Cao and Pǎun [Reference Cao and Pǎun8], and so forth. We refer to [Reference Chen and Zhang13] for a collection of results over
![]() $\mathbb{C}$
. In positive characteristic, Chen and Zhang proved the conjecture for fibrations of relative dimension one [Reference Chen and Zhang13], and Patakfalvi proved it when
$\mathbb{C}$
. In positive characteristic, Chen and Zhang proved the conjecture for fibrations of relative dimension one [Reference Chen and Zhang13], and Patakfalvi proved it when
![]() $Z$
is of general type and the generic geometric fiber satisfies certain properties [Reference Patakfalvi36, Theorem 1.1] (see also [Reference Patakfalvi37, Corollary 4.6]).
$Z$
is of general type and the generic geometric fiber satisfies certain properties [Reference Patakfalvi36, Theorem 1.1] (see also [Reference Patakfalvi37, Corollary 4.6]).
In this paper, we prove:
Theorem 1.2. Conjecture
![]() $C_{n,m}$
holds when
$C_{n,m}$
holds when
![]() $n=3$
,
$n=3$
,
![]() $k=\bar{\mathbb{F}}_{p}$
, and
$k=\bar{\mathbb{F}}_{p}$
, and
![]() $p>5$
.
$p>5$
.
Note that the smoothness of
![]() $X_{\unicode[STIX]{x1D702}}$
implies that
$X_{\unicode[STIX]{x1D702}}$
implies that
![]() $f$
is separable [Reference Liu31, Section 3.2.2]. The case
$f$
is separable [Reference Liu31, Section 3.2.2]. The case
![]() $C_{3,2}$
follows from [Reference Chen and Zhang13], so the main result here is
$C_{3,2}$
follows from [Reference Chen and Zhang13], so the main result here is
![]() $C_{3,1}$
. Our main tools are the log minimal model program for
$C_{3,1}$
. Our main tools are the log minimal model program for
![]() $3$
-folds developed recently by Hacon, Xu, and Birkar [Reference Birkar5, Reference Hacon and Xu16, Reference Xu47], birational geometry of log surfaces over nonclosed fields (see below), and the semi-positivity results of Patakfalvi [Reference Patakfalvi37]. The reason for the restriction
$3$
-folds developed recently by Hacon, Xu, and Birkar [Reference Birkar5, Reference Hacon and Xu16, Reference Xu47], birational geometry of log surfaces over nonclosed fields (see below), and the semi-positivity results of Patakfalvi [Reference Patakfalvi37]. The reason for the restriction
![]() $k=\bar{\mathbb{F}}_{p}$
is that it is often easier to prove semi-ampleness of divisors over finite fields; for example, if
$k=\bar{\mathbb{F}}_{p}$
is that it is often easier to prove semi-ampleness of divisors over finite fields; for example, if
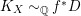 $K_{X}{\sim}_{\mathbb{Q}}f^{\ast }D$
for some
$K_{X}{\sim}_{\mathbb{Q}}f^{\ast }D$
for some
![]() $D\equiv 0$
on
$D\equiv 0$
on
![]() $Z$
, then
$Z$
, then
![]() $D{\sim}_{\mathbb{Q}}0$
is automatic over
$D{\sim}_{\mathbb{Q}}0$
is automatic over
![]() $k=\bar{\mathbb{F}}_{p}$
but the same conclusion would perhaps require substantial effort over other fields; this is a major issue also in characteristic zero [Reference Kawamata22].
$k=\bar{\mathbb{F}}_{p}$
but the same conclusion would perhaps require substantial effort over other fields; this is a major issue also in characteristic zero [Reference Kawamata22].
Since resolution theory holds in dimension three in positive characteristics, we get
Corollary 1.3. Let
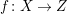 $f:X\rightarrow Z$
be a contraction, from a smooth projective three- dimensional variety to a smooth projective curve over
$f:X\rightarrow Z$
be a contraction, from a smooth projective three- dimensional variety to a smooth projective curve over
 $\bar{\mathbb{F}}_{p},p>5$
. Let
$\bar{\mathbb{F}}_{p},p>5$
. Let
![]() $\tilde{F}$
be a smooth model of the generic geometric fiber of
$\tilde{F}$
be a smooth model of the generic geometric fiber of
![]() $f$
. Then
$f$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})\geqslant \unicode[STIX]{x1D705}(K_{\tilde{F}})+\unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})\geqslant \unicode[STIX]{x1D705}(K_{\tilde{F}})+\unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
Log surfaces over nonclosed fields
Let
![]() $X\rightarrow Z$
be a contraction between normal varieties and let
$X\rightarrow Z$
be a contraction between normal varieties and let
![]() $F$
be its generic fiber. As is well known, in char
$F$
be its generic fiber. As is well known, in char
![]() $p>0$
,
$p>0$
,
![]() $F$
may not be smooth even if
$F$
may not be smooth even if
![]() $X$
and
$X$
and
![]() $Z$
are smooth. Actually
$Z$
are smooth. Actually
![]() $F$
may even be geometrically nonreduced. This creates difficulties because proofs in birational geometry are often based on induction and in this case we cannot simply apply induction and lift information from
$F$
may even be geometrically nonreduced. This creates difficulties because proofs in birational geometry are often based on induction and in this case we cannot simply apply induction and lift information from
![]() $F$
to
$F$
to
![]() $X$
. On the other hand,
$X$
. On the other hand,
![]() $F$
has nice properties if we think of it as a variety over the function field of
$F$
has nice properties if we think of it as a variety over the function field of
![]() $Z$
without passing to the algebraic closure of this function field. For example, if
$Z$
without passing to the algebraic closure of this function field. For example, if
![]() $X$
is smooth, then
$X$
is smooth, then
![]() $F$
is regular. In particular, relevant to this paper is the case in which
$F$
is regular. In particular, relevant to this paper is the case in which
![]() $X$
is a
$X$
is a
![]() $3$
-fold and
$3$
-fold and
![]() $Z$
is a curve. So it is natural for us to consider surfaces over a not necessarily algebraically closed field
$Z$
is a curve. So it is natural for us to consider surfaces over a not necessarily algebraically closed field
![]() $k$
.
$k$
.
It is easy to define pairs, singularities, minimal models, and so forth over an arbitrary field. See Sections 2.4 and 2.5 for more details.
Theorem 1.4. Let
![]() $(X,B)$
be a projective dlt pair of dimension two over a field
$(X,B)$
be a projective dlt pair of dimension two over a field
![]() $k$
where
$k$
where
![]() $B$
is a
$B$
is a
![]() $\mathbb{Q}$
-boundary. Then we can run an LMMP on
$\mathbb{Q}$
-boundary. Then we can run an LMMP on
 $K_{X}+B$
which ends with a log minimal model or a Mori fiber space.
$K_{X}+B$
which ends with a log minimal model or a Mori fiber space.
Theorem 1.5. Let
![]() $(X,B)$
be a projective klt pair of dimension two over a field
$(X,B)$
be a projective klt pair of dimension two over a field
![]() $k$
where
$k$
where
![]() $B$
is a
$B$
is a
![]() $\mathbb{Q}$
-boundary. Assume
$\mathbb{Q}$
-boundary. Assume
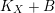 $K_{X}+B$
is nef and that
$K_{X}+B$
is nef and that
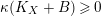 $\unicode[STIX]{x1D705}(K_{X}+B)\geqslant 0$
. Then
$\unicode[STIX]{x1D705}(K_{X}+B)\geqslant 0$
. Then
 $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
These results were proved by Tanaka [Reference Tanaka41] not long ago. Actually he proves more general statements; in particular, he proves 1.5 without the assumption
 $\unicode[STIX]{x1D705}(K_{X}+B)\geqslant 0$
. We give a self-contained proof of the above theorems. Our proof of 1.4 is perhaps the same as that in [Reference Tanaka41] which closely follows Keel’s techniques [Reference Keel26]. However, our proof of 1.5 seems to be different from his. He relies on another paper [Reference Tanaka40] but our proof is short and direct which follows Mumford’s ideas [Reference Mumford33] and uses a result of Totaro [Reference Totaro42]. In fact we worked out these proofs before [Reference Tanaka41] appeared.
$\unicode[STIX]{x1D705}(K_{X}+B)\geqslant 0$
. We give a self-contained proof of the above theorems. Our proof of 1.4 is perhaps the same as that in [Reference Tanaka41] which closely follows Keel’s techniques [Reference Keel26]. However, our proof of 1.5 seems to be different from his. He relies on another paper [Reference Tanaka40] but our proof is short and direct which follows Mumford’s ideas [Reference Mumford33] and uses a result of Totaro [Reference Totaro42]. In fact we worked out these proofs before [Reference Tanaka41] appeared.
Relative good minimal models of
 $3$
-folds
$3$
-folds
As mentioned earlier our motivation for considering surfaces over nonclosed fields is to treat
![]() $3$
-folds over curves.
$3$
-folds over curves.
Theorem 1.6. Let
![]() $(X,B)$
be a projective klt pair of dimension three where
$(X,B)$
be a projective klt pair of dimension three where
![]() $B$
is a
$B$
is a
![]() $\mathbb{Q}$
-boundary, and
$\mathbb{Q}$
-boundary, and
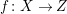 $f:X\rightarrow Z$
be a contraction onto a curve, over
$f:X\rightarrow Z$
be a contraction onto a curve, over
![]() $\bar{\mathbb{F}}_{p}$
with
$\bar{\mathbb{F}}_{p}$
with
![]() $p>5$
. Let
$p>5$
. Let
![]() $F$
be the generic fiber of
$F$
be the generic fiber of
![]() $f$
. If
$f$
. If
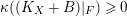 $\unicode[STIX]{x1D705}((K_{X}+B)|_{F})\geqslant 0$
, then
$\unicode[STIX]{x1D705}((K_{X}+B)|_{F})\geqslant 0$
, then
![]() $(X,B)$
has a good log minimal model over
$(X,B)$
has a good log minimal model over
![]() $Z$
.
$Z$
.
Actually the proof of the theorem works over any algebraically closed field of char
![]() $p>5$
except when
$p>5$
except when
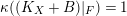 $\unicode[STIX]{x1D705}((K_{X}+B)|_{F})=1$
. In this case we make use of the fact that any nef and big divisor on a surface over
$\unicode[STIX]{x1D705}((K_{X}+B)|_{F})=1$
. In this case we make use of the fact that any nef and big divisor on a surface over
![]() $\bar{\mathbb{F}}_{p}$
is semi-ample.
$\bar{\mathbb{F}}_{p}$
is semi-ample.
As far as Theorem 1.2 is concerned we only need special cases of 1.6 which in turn only needs special cases of 1.5. We only need the case when
![]() $B=0$
and
$B=0$
and
![]() $F$
is smooth, or when
$F$
is smooth, or when
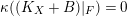 $\unicode[STIX]{x1D705}((K_{X}+B)|_{F})=0$
but
$\unicode[STIX]{x1D705}((K_{X}+B)|_{F})=0$
but
![]() $F$
admits a contraction onto an elliptic curve. See Remark 3.17 for some more detailed explanations.
$F$
admits a contraction onto an elliptic curve. See Remark 3.17 for some more detailed explanations.
2 Preliminaries
We follow Kollár [Reference Kollár27] to define canonical sheaves and divisors, adjunction, pairs, singularities, and so forth which we discuss below.
2.1 Relative canonical sheaves
Let
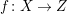 $f:X\rightarrow Z$
be a morphism of schemes where
$f:X\rightarrow Z$
be a morphism of schemes where
![]() $Z$
is regular and excellent, and
$Z$
is regular and excellent, and
![]() $X$
is pure dimensional and of finite type over
$X$
is pure dimensional and of finite type over
![]() $Z$
. Let
$Z$
. Let
![]() $S$
be a closed subscheme of
$S$
be a closed subscheme of
![]() $X$
and
$X$
and
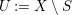 $U:=X\setminus S$
. Assume that
$U:=X\setminus S$
. Assume that
-
∙ codimension of
 $S$
in
$S$
in
 $X$
is at least
$X$
is at least
 $2$
; and
$2$
; and -
∙
 $U$
is a locally closed local complete intersection in some
$U$
is a locally closed local complete intersection in some
 $\mathbb{P}_{Z}^{n}$
.
$\mathbb{P}_{Z}^{n}$
.
Let
![]() ${\mathcal{I}}$
be the ideal sheaf of the closure of
${\mathcal{I}}$
be the ideal sheaf of the closure of
![]() $U$
in
$U$
in
![]() $\mathbb{P}_{Z}^{n}$
and let
$\mathbb{P}_{Z}^{n}$
and let
 $j:U\rightarrow X$
be the inclusion map of
$j:U\rightarrow X$
be the inclusion map of
![]() $U$
in
$U$
in
![]() $X$
. Now define the relative canonical sheaf as
$X$
. Now define the relative canonical sheaf as
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{X/Z}=j_{\ast }((\unicode[STIX]{x1D714}_{\mathbb{P}_{Z}^{n}/Z}\otimes (\det {\mathcal{I}}/{\mathcal{I}}^{2})^{\vee })|_{U}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{X/Z}=j_{\ast }((\unicode[STIX]{x1D714}_{\mathbb{P}_{Z}^{n}/Z}\otimes (\det {\mathcal{I}}/{\mathcal{I}}^{2})^{\vee })|_{U}).\end{eqnarray}$$
Note that
![]() ${\mathcal{I}}/{\mathcal{I}}^{2}$
is locally free on
${\mathcal{I}}/{\mathcal{I}}^{2}$
is locally free on
![]() $U$
. Moreover,
$U$
. Moreover,
![]() $\unicode[STIX]{x1D714}_{\mathbb{P}_{Z}^{n}/Z}$
is as usual defined to be
$\unicode[STIX]{x1D714}_{\mathbb{P}_{Z}^{n}/Z}$
is as usual defined to be
 ${\mathcal{O}}_{\mathbb{P}_{Z}^{n}}(-n-1)$
.
${\mathcal{O}}_{\mathbb{P}_{Z}^{n}}(-n-1)$
.
2.2 Relative canonical sheaves and divisors of normal schemes
Let
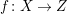 $f:X\rightarrow Z$
be a quasi-projective morphism of schemes where
$f:X\rightarrow Z$
be a quasi-projective morphism of schemes where
![]() $Z$
is regular and excellent, and
$Z$
is regular and excellent, and
![]() $X$
is integral and normal. The set of regular points of
$X$
is integral and normal. The set of regular points of
![]() $X$
is an open subset
$X$
is an open subset
![]() $U$
of
$U$
of
![]() $X$
by definition of excellent schemes (cf. [Reference Bruns and Herzog7, p. 382]). Let
$X$
by definition of excellent schemes (cf. [Reference Bruns and Herzog7, p. 382]). Let
![]() $S$
be any closed subscheme of
$S$
be any closed subscheme of
![]() $X$
containing the singular points and such that the codimension of
$X$
containing the singular points and such that the codimension of
![]() $S$
in
$S$
in
![]() $X$
is at least
$X$
is at least
![]() $2$
. Such an
$2$
. Such an
![]() $S$
exists because
$S$
exists because
![]() $X$
is normal. If we embed
$X$
is normal. If we embed
![]() $U$
as a locally closed subscheme into some
$U$
as a locally closed subscheme into some
![]() $\mathbb{P}_{Z}^{n}$
, then
$\mathbb{P}_{Z}^{n}$
, then
![]() $U$
is a locally closed local complete intersection because
$U$
is a locally closed local complete intersection because
![]() $U$
is regular (cf. [Reference Bruns and Herzog7, Proposition 2.2.4]). Therefore, we can define the relative canonical sheaf
$U$
is regular (cf. [Reference Bruns and Herzog7, Proposition 2.2.4]). Therefore, we can define the relative canonical sheaf
![]() $\unicode[STIX]{x1D714}_{X/Z}$
as in the previous subsection. Under this situation, this sheaf is of the form
$\unicode[STIX]{x1D714}_{X/Z}$
as in the previous subsection. Under this situation, this sheaf is of the form
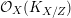 ${\mathcal{O}}_{X}(K_{X/Z})$
for some divisor
${\mathcal{O}}_{X}(K_{X/Z})$
for some divisor
![]() $K_{X/Z}$
which we refer to as the canonical divisor of
$K_{X/Z}$
which we refer to as the canonical divisor of
![]() $X$
over
$X$
over
![]() $Z$
(when
$Z$
(when
![]() $Z$
is the spectrum of a field, we usually drop
$Z$
is the spectrum of a field, we usually drop
![]() $Z$
and just write
$Z$
and just write
![]() $\unicode[STIX]{x1D714}_{X}$
and
$\unicode[STIX]{x1D714}_{X}$
and
![]() $K_{X}$
if the ground field is obvious from the context).
$K_{X}$
if the ground field is obvious from the context).
If
![]() $Y\rightarrow Z$
is another quasi-projective morphism from a normal integral scheme
$Y\rightarrow Z$
is another quasi-projective morphism from a normal integral scheme
![]() $Y$
with
$Y$
with
![]() $K_{Y/Z}$
being
$K_{Y/Z}$
being
![]() $\mathbb{Q}$
-Cartier, and if we are given a
$\mathbb{Q}$
-Cartier, and if we are given a
![]() $Z$
-morphism
$Z$
-morphism
 $h:X\rightarrow Y$
, then we let
$h:X\rightarrow Y$
, then we let
 $K_{X/Y}=K_{X/Z}-h^{\ast }K_{Y/Z}$
, which is compatible with the definition of above paragraph if
$K_{X/Y}=K_{X/Z}-h^{\ast }K_{Y/Z}$
, which is compatible with the definition of above paragraph if
![]() $Y$
is regular.
$Y$
is regular.
Now assume that
![]() $Z$
is integral and let
$Z$
is integral and let
![]() $F$
be the generic fiber of
$F$
be the generic fiber of
![]() $X\rightarrow Z$
. Let
$X\rightarrow Z$
. Let
![]() $V$
and
$V$
and
![]() $T$
be the inverse images of
$T$
be the inverse images of
![]() $U$
and
$U$
and
![]() $S$
under the morphism
$S$
under the morphism
![]() $F\rightarrow X$
. Then
$F\rightarrow X$
. Then
![]() $F$
is normal,
$F$
is normal,
![]() $V$
is regular, and the codimension of
$V$
is regular, and the codimension of
![]() $T$
in
$T$
in
![]() $F$
is at least
$F$
is at least
![]() $2$
. We consider
$2$
. We consider
![]() $F$
with its natural scheme structure over
$F$
with its natural scheme structure over
![]() $K$
, the function field of
$K$
, the function field of
![]() $Z$
. By the definition of canonical sheaves,
$Z$
. By the definition of canonical sheaves,
![]() $\unicode[STIX]{x1D714}_{V}$
is the pullback of
$\unicode[STIX]{x1D714}_{V}$
is the pullback of
![]() $\unicode[STIX]{x1D714}_{U/Z}$
. Therefore,
$\unicode[STIX]{x1D714}_{U/Z}$
. Therefore,
![]() $K_{V}$
is the pullback of
$K_{V}$
is the pullback of
![]() $K_{U/Z}$
. Moreover, if
$K_{U/Z}$
. Moreover, if
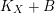 $K_{X}+B$
is
$K_{X}+B$
is
![]() $\mathbb{Q}$
-Cartier for some
$\mathbb{Q}$
-Cartier for some
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $B$
, then we can write
$B$
, then we can write
 $K_{F}+B_{F}$
for the pullback of
$K_{F}+B_{F}$
for the pullback of
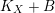 $K_{X}+B$
to
$K_{X}+B$
to
![]() $F$
where
$F$
where
![]() $B_{F}$
is canonically determined by
$B_{F}$
is canonically determined by
![]() $B$
: more precisely,
$B$
: more precisely,
![]() $B_{F}$
is the closure of the pullback of
$B_{F}$
is the closure of the pullback of
![]() $B|_{U}$
to
$B|_{U}$
to
![]() $V$
.
$V$
.
2.3 Intersection theory
For a short introduction to intersection theory on a proper scheme
![]() $X$
over a field
$X$
over a field
![]() $k$
, see [Reference Kollár and Mori28, Section 1.5]. Note that intersection numbers depend on the ground field
$k$
, see [Reference Kollár and Mori28, Section 1.5]. Note that intersection numbers depend on the ground field
![]() $k$
. For a detailed treatment of intersection theory on regular surfaces, see [Reference Liu31, Chapter 9]. Although [Reference Liu31] does not seem to treat the Riemann–Roch formula, it holds on regular projective surfaces. More precisely, if
$k$
. For a detailed treatment of intersection theory on regular surfaces, see [Reference Liu31, Chapter 9]. Although [Reference Liu31] does not seem to treat the Riemann–Roch formula, it holds on regular projective surfaces. More precisely, if
![]() $X$
is a regular surface projective over a field
$X$
is a regular surface projective over a field
![]() $k$
and if
$k$
and if
![]() $L$
is a Cartier divisor, then
$L$
is a Cartier divisor, then
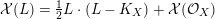 $$\begin{eqnarray}{\mathcal{X}}(L)={\textstyle \frac{1}{2}}L\cdot (L-K_{X})+{\mathcal{X}}({\mathcal{O}}_{X})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}(L)={\textstyle \frac{1}{2}}L\cdot (L-K_{X})+{\mathcal{X}}({\mathcal{O}}_{X})\end{eqnarray}$$
where
![]() $K_{X}$
means the relative canonical divisor of
$K_{X}$
means the relative canonical divisor of
![]() $X$
over
$X$
over
![]() $k$
, and
$k$
, and
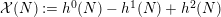 ${\mathcal{X}}(N):=h^{0}(N)-h^{1}(N)+h^{2}(N)$
for any divisor (or sheaf)
${\mathcal{X}}(N):=h^{0}(N)-h^{1}(N)+h^{2}(N)$
for any divisor (or sheaf)
![]() $N$
which also depends on the ground field
$N$
which also depends on the ground field
![]() $k$
. The formula can be proved as in the case of smooth surfaces over algebraically closed fields. The main point is that it can be reduced to Riemann–Roch on curves which holds in a quite general setting (cf. [Reference Liu31, Section 7.3]). See [Reference Tanaka41, Section 1.3] for a complete proof.
$k$
. The formula can be proved as in the case of smooth surfaces over algebraically closed fields. The main point is that it can be reduced to Riemann–Roch on curves which holds in a quite general setting (cf. [Reference Liu31, Section 7.3]). See [Reference Tanaka41, Section 1.3] for a complete proof.
2.4 Pairs and singularities
Let
![]() $k$
be a field. A pair
$k$
be a field. A pair
![]() $(X,B)$
over
$(X,B)$
over
![]() $k$
consists of a normal quasi-projective variety
$k$
consists of a normal quasi-projective variety
![]() $X$
over
$X$
over
![]() $k$
and an
$k$
and an
![]() $\mathbb{Q}$
-Weil divisor
$\mathbb{Q}$
-Weil divisor
![]() $B$
with coefficients in
$B$
with coefficients in
![]() $[0,1]$
such that
$[0,1]$
such that
 $K_{X}+B$
is
$K_{X}+B$
is
![]() $\mathbb{Q}$
-Cartier. We usually refer to
$\mathbb{Q}$
-Cartier. We usually refer to
![]() $B$
as a
$B$
as a
![]() $\mathbb{Q}$
-boundary. See [Reference Kollár27, Definitions 1.5 and 2.8] for definitions in more general settings.
$\mathbb{Q}$
-boundary. See [Reference Kollár27, Definitions 1.5 and 2.8] for definitions in more general settings.
For any projective birational morphism
 $f:W\rightarrow X$
from a normal variety
$f:W\rightarrow X$
from a normal variety
![]() $W$
, we can write
$W$
, we can write
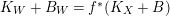 $K_{W}+B_{W}=f^{\ast }(K_{X}+B)$
for some unique
$K_{W}+B_{W}=f^{\ast }(K_{X}+B)$
for some unique
![]() $\mathbb{Q}$
-Weil divisor
$\mathbb{Q}$
-Weil divisor
![]() $B_{W}$
. For a prime divisor
$B_{W}$
. For a prime divisor
![]() $D$
on
$D$
on
![]() $W$
we define the log discrepancy
$W$
we define the log discrepancy
 $a(D,X,B)$
to be
$a(D,X,B)$
to be
![]() $1-b$
where
$1-b$
where
![]() $b$
is the coefficient of
$b$
is the coefficient of
![]() $D$
in
$D$
in
![]() $B_{W}$
. We say
$B_{W}$
. We say
![]() $(X,B)$
is lc (resp. klt) if
$(X,B)$
is lc (resp. klt) if
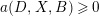 $a(D,X,B)\geqslant 0$
(resp.
$a(D,X,B)\geqslant 0$
(resp.
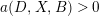 $a(D,X,B)>0$
) for any
$a(D,X,B)>0$
) for any
![]() $D$
on any such
$D$
on any such
![]() $W$
. On the other hand, we say
$W$
. On the other hand, we say
![]() $(X,B)$
is dlt if there is a closed subset
$(X,B)$
is dlt if there is a closed subset
![]() $Z\subset X$
of codimension at least two such that
$Z\subset X$
of codimension at least two such that
 $a(D,X,B)>0$
for any
$a(D,X,B)>0$
for any
![]() $D$
whose image in
$D$
whose image in
![]() $X$
is inside
$X$
is inside
![]() $Z$
and such that outside
$Z$
and such that outside
![]() $Z$
we have:
$Z$
we have:
![]() $X$
is regular and
$X$
is regular and
![]() $\text{Supp}\,B$
has simple normal crossing singularities.
$\text{Supp}\,B$
has simple normal crossing singularities.
We say
![]() $f$
is a log resolution of
$f$
is a log resolution of
![]() $(X,B)$
if
$(X,B)$
if
![]() $W$
is regular and
$W$
is regular and
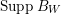 $\text{Supp}\,B_{W}$
has simple normal crossing singularities. Log resolutions exist when
$\text{Supp}\,B_{W}$
has simple normal crossing singularities. Log resolutions exist when
 $\dim X=2$
[Reference Shafarevich38] or if
$\dim X=2$
[Reference Shafarevich38] or if
![]() $k$
is algebraically closed and
$k$
is algebraically closed and
 $\dim X\leqslant 3$
; in these situations one can check whether
$\dim X\leqslant 3$
; in these situations one can check whether
![]() $(X,B)$
is lc or klt by looking at one log resolution. Moreover, if
$(X,B)$
is lc or klt by looking at one log resolution. Moreover, if
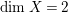 $\dim X=2$
, then a minimal resolution of
$\dim X=2$
, then a minimal resolution of
![]() $X$
exists.
$X$
exists.
2.5 Minimal models and Mori fiber spaces
Let
![]() $(X,B)$
be an lc pair and
$(X,B)$
be an lc pair and
![]() $(Y,B_{Y})$
be a
$(Y,B_{Y})$
be a
![]() $\mathbb{Q}$
-factorial dlt pair, over a field
$\mathbb{Q}$
-factorial dlt pair, over a field
![]() $k$
, equipped with projective morphisms
$k$
, equipped with projective morphisms
![]() $X\rightarrow Z$
and
$X\rightarrow Z$
and
![]() $Y\rightarrow Z$
and a birational map
$Y\rightarrow Z$
and a birational map
 $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$
commuting with these morphisms such that
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$
commuting with these morphisms such that
 $\unicode[STIX]{x1D719}_{\ast }B=B_{Y}$
and such that
$\unicode[STIX]{x1D719}_{\ast }B=B_{Y}$
and such that
![]() $\unicode[STIX]{x1D719}^{-1}$
does not contract divisors. Assume in addition that
$\unicode[STIX]{x1D719}^{-1}$
does not contract divisors. Assume in addition that
 $$\begin{eqnarray}a(D,X,B)\leqslant a(D,Y,B_{Y})\end{eqnarray}$$
$$\begin{eqnarray}a(D,X,B)\leqslant a(D,Y,B_{Y})\end{eqnarray}$$
for any prime divisor
![]() $D$
on birational models of
$D$
on birational models of
![]() $X$
with strict inequality if
$X$
with strict inequality if
![]() $D$
is on
$D$
is on
![]() $X$
and exceptional/
$X$
and exceptional/
![]() $Y$
. We say
$Y$
. We say
![]() $(Y,B_{Y})$
is a log minimal model of
$(Y,B_{Y})$
is a log minimal model of
![]() $(X,B)$
over
$(X,B)$
over
![]() $Z$
if
$Z$
if
 $K_{Y}+B_{Y}$
is nef
$K_{Y}+B_{Y}$
is nef
![]() $/Z$
. We say
$/Z$
. We say
![]() $(Y,B_{Y})$
is a Mori fiber space of
$(Y,B_{Y})$
is a Mori fiber space of
![]() $(X,B)$
over
$(X,B)$
over
![]() $Z$
if there is a
$Z$
if there is a
 $K_{Y}+B_{Y}$
-negative extremal contraction
$K_{Y}+B_{Y}$
-negative extremal contraction
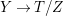 $Y\rightarrow T/Z$
with
$Y\rightarrow T/Z$
with
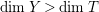 $\dim Y>\dim T$
.
$\dim Y>\dim T$
.
2.6 Minimal models of 3-folds
For
![]() $3$
-folds we have the following result.
$3$
-folds we have the following result.
Theorem 2.7. Let
![]() $(X,B)$
be a projective klt pair of dimension three and
$(X,B)$
be a projective klt pair of dimension three and
![]() $X\rightarrow Z$
a contraction to projective variety, over an algebraically closed field
$X\rightarrow Z$
a contraction to projective variety, over an algebraically closed field
![]() $k$
of char
$k$
of char
![]() $p>5$
.
$p>5$
.
-
(1) If
 $K_{X}+B$
is pseudo-effective over
$K_{X}+B$
is pseudo-effective over
 $Z$
, then
$Z$
, then
 $(X,B)$
has a log minimal model over
$(X,B)$
has a log minimal model over
 $Z$
.
$Z$
. -
(2) If
 $K_{X}+B$
is not pseudo-effective over
$K_{X}+B$
is not pseudo-effective over
 $Z$
, then
$Z$
, then
 $(X,B)$
has a Mori fiber space over
$(X,B)$
has a Mori fiber space over
 $Z$
.
$Z$
. -
(3) If
 $K_{X}+B$
is nef over
$K_{X}+B$
is nef over
 $Z$
, and
$Z$
, and
 $K_{X}+B$
or
$K_{X}+B$
or
 $B$
is big over
$B$
is big over
 $Z$
, then
$Z$
, then
 $K_{X}+B$
is semi-ample over
$K_{X}+B$
is semi-ample over
 $Z$
.
$Z$
.
Part (1) is proved in [Reference Hacon and Xu16] for canonical singularities, and in [Reference Birkar5] in general. Part (2) is proved in [Reference Cascini, Tanaka and Xu11] for terminal singularities, and in [Reference Birkar and Waldron6] in general. Part (3) is proved in various forms in [Reference Birkar5, Reference Birkar and Waldron6, Reference Xu47].
2.8 Adjunction
Let
![]() $X$
be a normal projective variety over a field
$X$
be a normal projective variety over a field
![]() $k$
. Let
$k$
. Let
![]() $B\geqslant 0$
be a
$B\geqslant 0$
be a
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
such that
$X$
such that
 $K_{X}+B$
is
$K_{X}+B$
is
![]() $\mathbb{Q}$
-Cartier. Let
$\mathbb{Q}$
-Cartier. Let
![]() $S$
be a component of
$S$
be a component of
![]() $\left\lfloor B\right\rfloor$
. Then we can write the pullback of
$\left\lfloor B\right\rfloor$
. Then we can write the pullback of
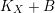 $K_{X}+B$
to the normalization
$K_{X}+B$
to the normalization
![]() $S^{\unicode[STIX]{x1D708}}$
as
$S^{\unicode[STIX]{x1D708}}$
as
 $K_{S^{\unicode[STIX]{x1D708}}}+B_{S^{\unicode[STIX]{x1D708}}}$
where the different
$K_{S^{\unicode[STIX]{x1D708}}}+B_{S^{\unicode[STIX]{x1D708}}}$
where the different
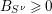 $B_{S^{\unicode[STIX]{x1D708}}}\geqslant 0$
is canonically determined. If
$B_{S^{\unicode[STIX]{x1D708}}}\geqslant 0$
is canonically determined. If
![]() $(X,B)$
is lc outside a codimension
$(X,B)$
is lc outside a codimension
![]() ${\geqslant}3$
subset of
${\geqslant}3$
subset of
![]() $X$
, then
$X$
, then
![]() $B_{S^{\unicode[STIX]{x1D708}}}$
is a boundary. See [Reference Kollár27, Proposition 4.5] for more details.
$B_{S^{\unicode[STIX]{x1D708}}}$
is a boundary. See [Reference Kollár27, Proposition 4.5] for more details.
2.9 Varieties over
 $\bar{\mathbb{F}}_{p}$
$\bar{\mathbb{F}}_{p}$
Varieties over finite fields enjoy some special properties which we exploit. For example, any numerically trivial divisor on a projective variety over
![]() $\bar{\mathbb{F}}_{p}$
is torsion [Reference Keel26]. Another example is this:
$\bar{\mathbb{F}}_{p}$
is torsion [Reference Keel26]. Another example is this:
Theorem 2.10. [Reference Tanaka39, Theorem 0.1 and 0.2]
Let
![]() $X$
be a normal projective surface over
$X$
be a normal projective surface over
![]() $\bar{\mathbb{F}}_{p}$
. Let
$\bar{\mathbb{F}}_{p}$
. Let
![]() $\unicode[STIX]{x1D6E5}$
be an effective
$\unicode[STIX]{x1D6E5}$
be an effective
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
. If
$X$
. If
 $K_{X}+\unicode[STIX]{x1D6E5}$
is pseudo-effective, then there exists a minimal model
$K_{X}+\unicode[STIX]{x1D6E5}$
is pseudo-effective, then there exists a minimal model
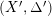 $(X^{\prime },\unicode[STIX]{x1D6E5}^{\prime })$
of
$(X^{\prime },\unicode[STIX]{x1D6E5}^{\prime })$
of
![]() $(X,\unicode[STIX]{x1D6E5})$
, and
$(X,\unicode[STIX]{x1D6E5})$
, and
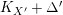 $K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }$
is semi-ample.
$K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }$
is semi-ample.
2.11 Semi-positivity of direct images of pluricanonical sheaves
The following result is extracted from [Reference Patakfalvi37, 1.5, 1.6, 1.7 and the paragraph below 1.7]. It holds in a more general form but this is all we need in this paper.
Theorem 2.12. [Reference Patakfalvi37]
Let
 $f:X\rightarrow Z$
be a surjective morphism from a normal projective variety to a smooth projective curve over an algebraically closed field
$f:X\rightarrow Z$
be a surjective morphism from a normal projective variety to a smooth projective curve over an algebraically closed field
![]() $k$
. Assume
$k$
. Assume
![]() $K_{X}$
is
$K_{X}$
is
![]() $\mathbb{Q}$
-Cartier and that general fibers are strongly
$\mathbb{Q}$
-Cartier and that general fibers are strongly
![]() $F$
-regular.
$F$
-regular.
-
∙ If
 $K_{X}$
is nef over
$K_{X}$
is nef over
 $Z$
and
$Z$
and
 $K_{X}$
is semi-ample on the generic fiber of
$K_{X}$
is semi-ample on the generic fiber of
 $f$
, then
$f$
, then
 $K_{X/Z}$
is nef.
$K_{X/Z}$
is nef. -
∙ If
 $K_{X}$
is ample over
$K_{X}$
is ample over
 $Z$
, then
$Z$
, then
 $f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is a nef vector bundle for any sufficiently divisible natural number
$f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is a nef vector bundle for any sufficiently divisible natural number
 $m$
.
$m$
.
We apply the theorem only when
![]() $X$
is a
$X$
is a
![]() $3$
-fold and general fibers have canonical singularities.
$3$
-fold and general fibers have canonical singularities.
2.13 Varieties with elliptic fibrations
For fibrations whose general fibers are elliptic curves, we can use a weak canonical bundle formula which allows us to do induction.
Theorem 2.14. Let
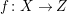 $f:X\rightarrow Z$
be a contraction between smooth projective varieties over an algebraically closed field
$f:X\rightarrow Z$
be a contraction between smooth projective varieties over an algebraically closed field
![]() $k$
such that the geometric generic fiber is a smooth elliptic curve. Then
$k$
such that the geometric generic fiber is a smooth elliptic curve. Then
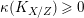 $\unicode[STIX]{x1D705}(K_{X/Z})\geqslant 0$
.
$\unicode[STIX]{x1D705}(K_{X/Z})\geqslant 0$
.
Proof. This follows from [Reference Chen and Zhang13, 3.2]. ◻
2.15 Nef divisors with Kodaira dimension one
Lemma 2.16. Let
![]() $X$
be a normal surface projective over a field
$X$
be a normal surface projective over a field
![]() $k$
. Let
$k$
. Let
![]() $L$
be a nef
$L$
be a nef
![]() $\mathbb{Q}$
-divisor with
$\mathbb{Q}$
-divisor with
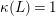 $\unicode[STIX]{x1D705}(L)=1$
. Then
$\unicode[STIX]{x1D705}(L)=1$
. Then
![]() $L$
is semi-ample.
$L$
is semi-ample.
Proof. Let
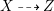 $X{\dashrightarrow}Z$
be the rational map defined by the linear system
$X{\dashrightarrow}Z$
be the rational map defined by the linear system
![]() $|mL|$
for some sufficiently divisible
$|mL|$
for some sufficiently divisible
![]() $m>0$
. Then
$m>0$
. Then
 $\dim Z=1$
. We can replace
$\dim Z=1$
. We can replace
![]() $X$
with the normalization of the graph of
$X$
with the normalization of the graph of
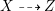 $X{\dashrightarrow}Z$
; hence, assume
$X{\dashrightarrow}Z$
; hence, assume
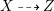 $X{\dashrightarrow}Z$
is a morphism. We can in addition assume
$X{\dashrightarrow}Z$
is a morphism. We can in addition assume
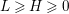 $L\geqslant H\geqslant 0$
where
$L\geqslant H\geqslant 0$
where
![]() $H$
is the pullback of some ample
$H$
is the pullback of some ample
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $Z$
. Since
$Z$
. Since
![]() $L$
is not big, its support does not intersect the generic fiber of
$L$
is not big, its support does not intersect the generic fiber of
![]() $X\rightarrow Z$
.
$X\rightarrow Z$
.
Let
![]() $F$
be a fiber of
$F$
be a fiber of
![]() $X\rightarrow Z$
which has a common component with
$X\rightarrow Z$
which has a common component with
![]() $L$
. Let
$L$
. Let
![]() $a$
be the smallest rational number such that
$a$
be the smallest rational number such that
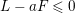 $L-aF\leqslant 0$
near
$L-aF\leqslant 0$
near
![]() $F$
. Then
$F$
. Then
![]() $L-aF$
has no common component with
$L-aF$
has no common component with
![]() $F$
; otherwise there would be two components
$F$
; otherwise there would be two components
![]() $C,D$
of
$C,D$
of
![]() $F$
such that
$F$
such that
![]() $C$
intersects
$C$
intersects
![]() $D$
,
$D$
,
![]() $C$
is not a component of
$C$
is not a component of
![]() $L-aF$
but
$L-aF$
but
![]() $D$
is a component of
$D$
is a component of
![]() $L-aF$
which implies
$L-aF$
which implies
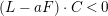 $(L-aF)\cdot C<0$
, a contradiction. These arguments show that
$(L-aF)\cdot C<0$
, a contradiction. These arguments show that
![]() $L$
is the pullback of some
$L$
is the pullback of some
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $Z$
which is necessarily ample, hence
$Z$
which is necessarily ample, hence
![]() $L$
is semi-ample. ◻
$L$
is semi-ample. ◻
2.17 Generically trivial divisors
We recall a result of Kawamata adapted to char
![]() $p>0$
.
$p>0$
.
Lemma 2.18. [Reference Birkar and Waldron6, Lemma 5.6]
Let
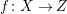 $f:X\rightarrow Z$
be a contraction between normal projective varieties over an algebraically closed field
$f:X\rightarrow Z$
be a contraction between normal projective varieties over an algebraically closed field
![]() $k$
and
$k$
and
![]() $L$
a nef
$L$
a nef
![]() $/Z$
$/Z$
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
such that
$X$
such that
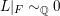 $L|_{F}{\sim}_{\mathbb{Q}}0$
where
$L|_{F}{\sim}_{\mathbb{Q}}0$
where
![]() $F$
is the generic fiber of
$F$
is the generic fiber of
![]() $f$
. Assume
$f$
. Assume
 $\dim Z\leqslant 3$
if
$\dim Z\leqslant 3$
if
![]() $k$
has char
$k$
has char
![]() $p>0$
. Then there exist a diagram
$p>0$
. Then there exist a diagram

with
![]() $\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}$
projective birational, and a
$\unicode[STIX]{x1D719},\unicode[STIX]{x1D713}$
projective birational, and a
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D$
on
$D$
on
![]() $Z^{\prime }$
such that
$Z^{\prime }$
such that
 $\unicode[STIX]{x1D719}^{\ast }L{\sim}_{\mathbb{Q}}{f^{\prime }}^{\ast }D$
.
$\unicode[STIX]{x1D719}^{\ast }L{\sim}_{\mathbb{Q}}{f^{\prime }}^{\ast }D$
.
2.19 Easy additivity of Kodaira dimensions
The following result is well-known to experts [Reference Fujita15, Propostion 1].
Lemma 2.20. Let
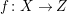 $f:X\rightarrow Z$
be a contraction between normal varieties projective over a field
$f:X\rightarrow Z$
be a contraction between normal varieties projective over a field
![]() $k$
. Let
$k$
. Let
![]() $D$
be an effective
$D$
be an effective
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $X$
and
$X$
and
![]() $H$
a big
$H$
a big
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $Z$
. Then
$Z$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(D+f^{\ast }H)\geqslant \unicode[STIX]{x1D705}(D|_{F})+\dim Z\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(D+f^{\ast }H)\geqslant \unicode[STIX]{x1D705}(D|_{F})+\dim Z\end{eqnarray}$$
where
![]() $F$
is the generic fiber of
$F$
is the generic fiber of
![]() $f$
.
$f$
.
Proof. Since
![]() $D$
is effective, it is enough to prove the statement with
$D$
is effective, it is enough to prove the statement with
![]() $H$
replaced by any positive multiple and
$H$
replaced by any positive multiple and
![]() $D$
replaced by
$D$
replaced by
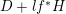 $D+lf^{\ast }H$
for some
$D+lf^{\ast }H$
for some
![]() $l>0$
. If
$l>0$
. If
![]() $V\rightarrow X$
is a morphism, we denote the pullback of
$V\rightarrow X$
is a morphism, we denote the pullback of
![]() $D$
to
$D$
to
![]() $V$
by
$V$
by
![]() $D_{V}$
(similar notation for other divisors). Let
$D_{V}$
(similar notation for other divisors). Let
![]() $m$
be a sufficiently divisible natural number and let
$m$
be a sufficiently divisible natural number and let
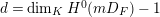 $d=\dim _{K}H^{0}(mD_{F})-1$
where
$d=\dim _{K}H^{0}(mD_{F})-1$
where
![]() $K$
is the function field of
$K$
is the function field of
![]() $Z$
. Let
$Z$
. Let
![]() $S$
be the normalization of the image of
$S$
be the normalization of the image of
 $\unicode[STIX]{x1D719}_{mD_{F}}:F{\dashrightarrow}\mathbb{P}_{K}^{d}$
whose dimension is equal to
$\unicode[STIX]{x1D719}_{mD_{F}}:F{\dashrightarrow}\mathbb{P}_{K}^{d}$
whose dimension is equal to
![]() $\unicode[STIX]{x1D705}(D_{F})$
. Moreover,
$\unicode[STIX]{x1D705}(D_{F})$
. Moreover,
![]() $\unicode[STIX]{x1D719}_{mD_{F}}$
induces a (not unique) map
$\unicode[STIX]{x1D719}_{mD_{F}}$
induces a (not unique) map
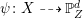 $\unicode[STIX]{x1D713}:X{\dashrightarrow}\mathbb{P}_{Z}^{d}$
over
$\unicode[STIX]{x1D713}:X{\dashrightarrow}\mathbb{P}_{Z}^{d}$
over
![]() $Z$
which restricts to
$Z$
which restricts to
![]() $\unicode[STIX]{x1D719}_{mD_{F}}$
. Let
$\unicode[STIX]{x1D719}_{mD_{F}}$
. Let
![]() $T$
be the normalization of the image of
$T$
be the normalization of the image of
![]() $\unicode[STIX]{x1D713}$
. Let
$\unicode[STIX]{x1D713}$
. Let
![]() $Y$
be the normalization of the graph of
$Y$
be the normalization of the graph of
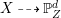 $X{\dashrightarrow}\mathbb{P}_{Z}^{d}$
and
$X{\dashrightarrow}\mathbb{P}_{Z}^{d}$
and
![]() $G$
the generic fiber of
$G$
the generic fiber of
![]() $Y\rightarrow Z$
. We have induced morphisms
$Y\rightarrow Z$
. We have induced morphisms
![]() $Y\rightarrow T$
,
$Y\rightarrow T$
,
![]() $G\rightarrow S$
, and
$G\rightarrow S$
, and
![]() $G\rightarrow F$
.
$G\rightarrow F$
.
Let
![]() $A$
on
$A$
on
![]() $\mathbb{P}_{Z}^{d}$
be the pullback of a hyperplane via the projection
$\mathbb{P}_{Z}^{d}$
be the pullback of a hyperplane via the projection
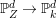 $\mathbb{P}_{Z}^{d}\rightarrow \mathbb{P}_{k}^{d}$
. Perhaps after changing
$\mathbb{P}_{Z}^{d}\rightarrow \mathbb{P}_{k}^{d}$
. Perhaps after changing
![]() $D$
up to
$D$
up to
![]() $\mathbb{Q}$
-linear equivalence we can assume
$\mathbb{Q}$
-linear equivalence we can assume
 $mD_{G}\geqslant A_{G}$
. Thus replacing
$mD_{G}\geqslant A_{G}$
. Thus replacing
![]() $D$
with
$D$
with
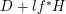 $D+lf^{\ast }H$
for some
$D+lf^{\ast }H$
for some
![]() $l$
we can assume
$l$
we can assume
 $mD_{Y}\geqslant A_{Y}$
. Therefore, we may replace
$mD_{Y}\geqslant A_{Y}$
. Therefore, we may replace
![]() $X$
with
$X$
with
![]() $T$
and replace
$T$
and replace
![]() $D$
with
$D$
with
![]() $A_{T}$
. But then the statement is trivial in this case because we can assume
$A_{T}$
. But then the statement is trivial in this case because we can assume
 $A+f^{\ast }H$
is ample. ◻
$A+f^{\ast }H$
is ample. ◻
2.21 Covering Theorem
Theorem 2.22. [Reference Iitaka21, Theorem 10.5]
Let
 $f:X\rightarrow Y$
be a proper surjective morphism between smooth complete varieties. If
$f:X\rightarrow Y$
be a proper surjective morphism between smooth complete varieties. If
![]() $D$
is a Cartier divisor on
$D$
is a Cartier divisor on
![]() $Y$
and
$Y$
and
![]() $E$
an effective
$E$
an effective
![]() $f$
-exceptional divisor on
$f$
-exceptional divisor on
![]() $X$
, then
$X$
, then
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(f^{\ast }D+E)=\unicode[STIX]{x1D705}(D).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(f^{\ast }D+E)=\unicode[STIX]{x1D705}(D).\end{eqnarray}$$
Here by
![]() $f$
-exceptional we mean: for any prime divisor
$f$
-exceptional we mean: for any prime divisor
![]() $P$
on
$P$
on
![]() $Y$
, there is a prime divisor
$Y$
, there is a prime divisor
![]() $Q$
on
$Q$
on
![]() $X$
mapping onto
$X$
mapping onto
![]() $P$
such that
$P$
such that
![]() $Q$
is not a component of
$Q$
is not a component of
![]() $E$
.
$E$
.
3 Log surfaces over nonclosed fields
In this section,
![]() $k$
will denote a field which is not necessarily algebraically closed. Shafarevich [Reference Shafarevich38] studied the minimal model theory of regular surfaces over nonclosed fields and Dedekind rings (see also [Reference Liu31]), and Manin [Reference Manin32] and Iskovskikh [Reference Iskovskikh20] treated the special case of rational surfaces. None of them seems to have discussed the abundance problem. If
$k$
will denote a field which is not necessarily algebraically closed. Shafarevich [Reference Shafarevich38] studied the minimal model theory of regular surfaces over nonclosed fields and Dedekind rings (see also [Reference Liu31]), and Manin [Reference Manin32] and Iskovskikh [Reference Iskovskikh20] treated the special case of rational surfaces. None of them seems to have discussed the abundance problem. If
![]() $k$
is perfect (e.g., when char
$k$
is perfect (e.g., when char
![]() $k=0$
) or if the surface is smooth over
$k=0$
) or if the surface is smooth over
![]() $k$
, then one can often reduce problems to the algebraically closed case by passing to the algebraic closure. But our main point here is that we can actually prove many things by working over
$k$
, then one can often reduce problems to the algebraically closed case by passing to the algebraic closure. But our main point here is that we can actually prove many things by working over
![]() $k$
rather than the algebraic closure when char
$k$
rather than the algebraic closure when char
![]() $k>0$
.
$k>0$
.
3.1 Curves with negative canonical divisor
As a preparation we collect some results about curves.
Lemma 3.2. Let
![]() $X$
be a local complete intersection integral projective curve over a field
$X$
be a local complete intersection integral projective curve over a field
![]() $k$
, and let
$k$
, and let
 $l=H^{0}({\mathcal{O}}_{X})$
. Assume that
$l=H^{0}({\mathcal{O}}_{X})$
. Assume that
 $\deg _{k}K_{X}<0$
. Then
$\deg _{k}K_{X}<0$
. Then
-
(i)
 $\text{Pic}^{0}(X)=0$
;
$\text{Pic}^{0}(X)=0$
; -
(ii)
 $X$
is a conic over
$X$
is a conic over
 $l$
, and
$l$
, and
 $\deg _{l}K_{X}=-2$
;
$\deg _{l}K_{X}=-2$
; -
(iii) if
 $X$
is normal and
$X$
is normal and
 $\text{char}~k>2$
, then
$\text{char}~k>2$
, then
 $X_{\bar{l}}\cong \mathbb{P}_{\bar{l}}^{1}$
.
$X_{\bar{l}}\cong \mathbb{P}_{\bar{l}}^{1}$
.
Proof. By assumption
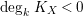 $\deg _{k}K_{X}<0$
, we get
$\deg _{k}K_{X}<0$
, we get
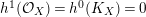 $h^{1}({\mathcal{O}}_{X})=h^{0}(K_{X})=0$
which implies
$h^{1}({\mathcal{O}}_{X})=h^{0}(K_{X})=0$
which implies
 $p_{a}(X)\leqslant 0$
. Then (i) and (ii) follow from [Reference Liu31, Chapter 9, Proposition 3.16], and (iii) is [Reference Cascini, Tanaka and Xu11, Lemma 6.5]. ◻
$p_{a}(X)\leqslant 0$
. Then (i) and (ii) follow from [Reference Liu31, Chapter 9, Proposition 3.16], and (iii) is [Reference Cascini, Tanaka and Xu11, Lemma 6.5]. ◻
3.3 Reduced boundary of dlt pairs
Lemma 3.4. Assume
![]() $(X,B)$
is a
$(X,B)$
is a
![]() $\mathbb{Q}$
-factorial dlt pair of dimension two over a field
$\mathbb{Q}$
-factorial dlt pair of dimension two over a field
![]() $k$
. Then every irreducible component of
$k$
. Then every irreducible component of
![]() $\left\lfloor B\right\rfloor$
is regular.
$\left\lfloor B\right\rfloor$
is regular.
Proof. Let
![]() $S$
be a component of
$S$
be a component of
![]() $\left\lfloor B\right\rfloor$
and let
$\left\lfloor B\right\rfloor$
and let
![]() $x\in S$
be a closed point. As
$x\in S$
be a closed point. As
![]() $(X,S)$
is plt,
$(X,S)$
is plt,
![]() $S$
is regular at
$S$
is regular at
![]() $x$
by [Reference Kollár27, 3.35]. ◻
$x$
by [Reference Kollár27, 3.35]. ◻
Proposition 3.5. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() $\mathbb{Q}$
-factorial dlt pair of dimension two projective over a field
$\mathbb{Q}$
-factorial dlt pair of dimension two projective over a field
![]() $k$
where
$k$
where
![]() $B$
is a
$B$
is a
![]() $\mathbb{Q}$
-boundary. Assume
$\mathbb{Q}$
-boundary. Assume
![]() $S$
is a component of
$S$
is a component of
![]() $\left\lfloor B\right\rfloor$
and
$\left\lfloor B\right\rfloor$
and
![]() $A$
is an ample
$A$
is an ample
![]() $\mathbb{Q}$
-divisor such that
$\mathbb{Q}$
-divisor such that
-
∙
 $(K_{X}+B)\cdot S<0$
;
$(K_{X}+B)\cdot S<0$
; -
∙
 $(K_{X}+B+A)\cdot S=0$
; and
$(K_{X}+B+A)\cdot S=0$
; and -
∙
 $K_{X}+B+A$
is nef and big.
$K_{X}+B+A$
is nef and big.
Then there is a birational morphism
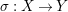 $\unicode[STIX]{x1D70E}:X\rightarrow Y$
with
$\unicode[STIX]{x1D70E}:X\rightarrow Y$
with
![]() $Y$
normal and projective, whose exceptional locus is equal to
$Y$
normal and projective, whose exceptional locus is equal to
![]() $S$
, and the resulting pair
$S$
, and the resulting pair
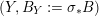 $(Y,B_{Y}:=\unicode[STIX]{x1D70E}_{\ast }B)$
is
$(Y,B_{Y}:=\unicode[STIX]{x1D70E}_{\ast }B)$
is
![]() $\mathbb{Q}$
-factorial dlt. Moreover,
$\mathbb{Q}$
-factorial dlt. Moreover,
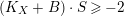 $(K_{X}+B)\cdot S\geqslant -2$
.
$(K_{X}+B)\cdot S\geqslant -2$
.
Proof. By perturbing the coefficients of
![]() $B$
(i.e., by replacing
$B$
(i.e., by replacing
![]() $B$
with
$B$
with
![]() $B-P$
and replacing
$B-P$
and replacing
![]() $A$
with
$A$
with
![]() $A+P$
for some appropriate
$A+P$
for some appropriate
![]() $P$
) we can assume
$P$
) we can assume
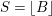 $S=\left\lfloor B\right\rfloor$
. Since
$S=\left\lfloor B\right\rfloor$
. Since
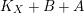 $K_{X}+B+A$
is nef and big, we can write
$K_{X}+B+A$
is nef and big, we can write
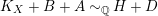 $K_{X}+B+A{\sim}_{\mathbb{Q}}H+D$
where
$K_{X}+B+A{\sim}_{\mathbb{Q}}H+D$
where
![]() $H$
is ample and
$H$
is ample and
![]() $D\geqslant 0$
. Since
$D\geqslant 0$
. Since
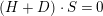 $(H+D)\cdot S=0$
,
$(H+D)\cdot S=0$
,
![]() $S$
is a component of
$S$
is a component of
![]() $D$
and
$D$
and
![]() $S^{2}<0$
. Let
$S^{2}<0$
. Let
![]() $\unicode[STIX]{x1D716}>0$
be a small rational number such that
$\unicode[STIX]{x1D716}>0$
be a small rational number such that
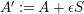 $A^{\prime }:=A+\unicode[STIX]{x1D716}S$
is ample. Then
$A^{\prime }:=A+\unicode[STIX]{x1D716}S$
is ample. Then
![]() $S$
is the only curve on
$S$
is the only curve on
![]() $X$
such that
$X$
such that
 $(K_{X}+B+A^{\prime })\cdot S<0$
. Let
$(K_{X}+B+A^{\prime })\cdot S<0$
. Let
![]() $t$
be the smallest real number such that
$t$
be the smallest real number such that
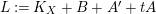 $L:=K_{X}+B+A^{\prime }+tA$
is nef. We want to show
$L:=K_{X}+B+A^{\prime }+tA$
is nef. We want to show
![]() $L$
is semi-ample and that
$L$
is semi-ample and that
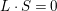 $L\cdot S=0$
. If char
$L\cdot S=0$
. If char
![]() $k=0$
, the last sentence and the other claims of the proposition can be reduced to the algebraically closed case by passing to the algebraic closure. So we assume char
$k=0$
, the last sentence and the other claims of the proposition can be reduced to the algebraically closed case by passing to the algebraic closure. So we assume char
![]() $k>0$
.
$k>0$
.
By definition
![]() $L$
is nef and big but not ample; then there is a curve
$L$
is nef and big but not ample; then there is a curve
![]() $C$
with
$C$
with
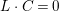 $L\cdot C=0$
by Nakai–Moishezon criterion [Reference Debarre14, Theorem 1.21], which implies
$L\cdot C=0$
by Nakai–Moishezon criterion [Reference Debarre14, Theorem 1.21], which implies
![]() $t$
is a rational number. Actually
$t$
is a rational number. Actually
![]() $C=S$
by construction.
$C=S$
by construction.
By Lemma 3.4,
![]() $S$
is regular. Then by adjunction (2.8) we can write
$S$
is regular. Then by adjunction (2.8) we can write
 $K_{S}+B_{S}=(K_{X}+B)|_{S}$
where
$K_{S}+B_{S}=(K_{X}+B)|_{S}$
where
![]() $B_{S}\geqslant 0$
. Since
$B_{S}\geqslant 0$
. Since
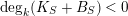 $\deg _{k}(K_{S}+B_{S})<0$
, we have
$\deg _{k}(K_{S}+B_{S})<0$
, we have
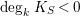 $\deg _{k}K_{S}<0$
. This implies
$\deg _{k}K_{S}<0$
. This implies
 $\text{Pic}^{0}(S)=0$
by Lemma 3.2. Therefore,
$\text{Pic}^{0}(S)=0$
by Lemma 3.2. Therefore,
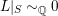 $L|_{S}{\sim}_{\mathbb{Q}}0$
which implies that
$L|_{S}{\sim}_{\mathbb{Q}}0$
which implies that
![]() $L$
is semi-ample [Reference Keel26], so it defines a birational contraction
$L$
is semi-ample [Reference Keel26], so it defines a birational contraction
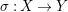 $\unicode[STIX]{x1D70E}:X\rightarrow Y$
contracting exactly
$\unicode[STIX]{x1D70E}:X\rightarrow Y$
contracting exactly
![]() $S$
so that
$S$
so that
![]() $L_{Y}$
is ample where
$L_{Y}$
is ample where
![]() $L_{Y}$
is the pushdown of
$L_{Y}$
is the pushdown of
![]() $L$
.
$L$
.
The dlt property of
![]() $(Y,B_{Y})$
is obvious once we show
$(Y,B_{Y})$
is obvious once we show
![]() $Y$
is
$Y$
is
![]() $\mathbb{Q}$
-factorial where
$\mathbb{Q}$
-factorial where
![]() $B_{Y}$
is the pushdown of
$B_{Y}$
is the pushdown of
![]() $B$
. Let
$B$
. Let
![]() $R_{Y}$
be a prime divisor on
$R_{Y}$
be a prime divisor on
![]() $Y$
and
$Y$
and
![]() $R$
its birational transform on
$R$
its birational transform on
![]() $X$
. There is
$X$
. There is
![]() $s\geqslant 0$
such that
$s\geqslant 0$
such that
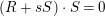 $(R+sS)\cdot S=0$
. Since
$(R+sS)\cdot S=0$
. Since
![]() $L$
is the pullback of an ample divisor on
$L$
is the pullback of an ample divisor on
![]() $Y$
, the divisor
$Y$
, the divisor
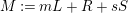 $M:=mL+R+sS$
is nef and big on
$M:=mL+R+sS$
is nef and big on
![]() $X$
, and
$X$
, and
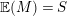 $\mathbb{E}(M)=S$
for any
$\mathbb{E}(M)=S$
for any
![]() $m\gg 0$
. Moreover,
$m\gg 0$
. Moreover,
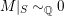 $M|_{S}{\sim}_{\mathbb{Q}}0$
, so by [Reference Keel26, Theorem 0.2],
$M|_{S}{\sim}_{\mathbb{Q}}0$
, so by [Reference Keel26, Theorem 0.2],
![]() $M$
is semi-ample, thus it is the pullback of some ample divisor
$M$
is semi-ample, thus it is the pullback of some ample divisor
![]() $M_{Y}$
on
$M_{Y}$
on
![]() $Y$
. But then
$Y$
. But then
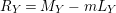 $R_{Y}=M_{Y}-mL_{Y}$
is
$R_{Y}=M_{Y}-mL_{Y}$
is
![]() $\mathbb{Q}$
-Cartier. This shows
$\mathbb{Q}$
-Cartier. This shows
![]() $Y$
is
$Y$
is
![]() $\mathbb{Q}$
-factorial. Finally
$\mathbb{Q}$
-factorial. Finally
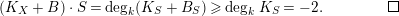 $$\begin{eqnarray}(K_{X}+B)\cdot S=\deg _{k}(K_{S}+B_{S})\geqslant \deg _{k}K_{S}=-2.\square\end{eqnarray}$$
$$\begin{eqnarray}(K_{X}+B)\cdot S=\deg _{k}(K_{S}+B_{S})\geqslant \deg _{k}K_{S}=-2.\square\end{eqnarray}$$
3.6 Base point freeness
Proposition 3.7. Let
![]() $(X,B)$
be a klt pair of dimension two projective over a field
$(X,B)$
be a klt pair of dimension two projective over a field
![]() $k$
where
$k$
where
![]() $B$
is a
$B$
is a
![]() $\mathbb{Q}$
-boundary. Assume
$\mathbb{Q}$
-boundary. Assume
![]() $L$
is a nef and big
$L$
is a nef and big
![]() $\mathbb{Q}$
-divisor so that
$\mathbb{Q}$
-divisor so that
 $L-(K_{X}+B)$
is nef. Then
$L-(K_{X}+B)$
is nef. Then
![]() $L$
is semi-ample.
$L$
is semi-ample.
Proof. If char
![]() $k=0$
, we can pass to the algebraic closure of
$k=0$
, we can pass to the algebraic closure of
![]() $k$
in which case the theorem is well-known. So we assume char
$k$
in which case the theorem is well-known. So we assume char
![]() $k>0$
.
$k>0$
.
Since
![]() $L$
is nef and big, by [Reference Keel26, Theorem 1.9], there exist a birational morphism
$L$
is nef and big, by [Reference Keel26, Theorem 1.9], there exist a birational morphism
![]() $X\rightarrow V$
to a proper algebraic space
$X\rightarrow V$
to a proper algebraic space
![]() $V$
and a reduced divisor
$V$
and a reduced divisor
![]() $D$
on
$D$
on
![]() $X$
such that, the exceptional locus is equal to
$X$
such that, the exceptional locus is equal to
![]() $D$
, and that
$D$
, and that
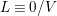 $L\equiv 0/V$
.
$L\equiv 0/V$
.
Let
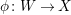 $\unicode[STIX]{x1D719}:W\rightarrow X$
be a log resolution of
$\unicode[STIX]{x1D719}:W\rightarrow X$
be a log resolution of
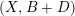 $(X,B+D)$
. Let
$(X,B+D)$
. Let
![]() $\unicode[STIX]{x1D6E5}_{W}$
be the sum of the birational transform of
$\unicode[STIX]{x1D6E5}_{W}$
be the sum of the birational transform of
![]() $B_{V}$
plus the reduced exceptional divisor of
$B_{V}$
plus the reduced exceptional divisor of
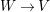 $W\rightarrow V$
where
$W\rightarrow V$
where
![]() $B_{V}$
is the pushdown of
$B_{V}$
is the pushdown of
![]() $B$
on
$B$
on
![]() $V$
. Let
$V$
. Let
![]() $R_{W}$
be an ample divisor on
$R_{W}$
be an ample divisor on
![]() $W$
and let
$W$
and let
![]() $L_{W}$
be the pullback of
$L_{W}$
be the pullback of
![]() $L$
. Also let
$L$
. Also let
 $G=L-(K_{X}+B)$
and
$G=L-(K_{X}+B)$
and
![]() $G_{W}$
be its pullback. Fix
$G_{W}$
be its pullback. Fix
![]() $m\gg 0$
and let
$m\gg 0$
and let
![]() $t$
be the smallest number such that
$t$
be the smallest number such that
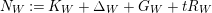 $$\begin{eqnarray}N_{W}:=K_{W}+\unicode[STIX]{x1D6E5}_{W}+G_{W}+tR_{W}\end{eqnarray}$$
$$\begin{eqnarray}N_{W}:=K_{W}+\unicode[STIX]{x1D6E5}_{W}+G_{W}+tR_{W}\end{eqnarray}$$
is nef. Note that by construction,
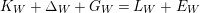 $K_{W}+\unicode[STIX]{x1D6E5}_{W}+G_{W}=L_{W}+E_{W}$
where
$K_{W}+\unicode[STIX]{x1D6E5}_{W}+G_{W}=L_{W}+E_{W}$
where
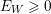 $E_{W}\geqslant 0$
and its support is equal to the exceptional locus of
$E_{W}\geqslant 0$
and its support is equal to the exceptional locus of
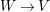 $W\rightarrow V$
. Moreover,
$W\rightarrow V$
. Moreover,
![]() $N_{W}$
is nef and big but not ample, so by [Reference Cascini, McKernan and Mustaţă10], there is a curve
$N_{W}$
is nef and big but not ample, so by [Reference Cascini, McKernan and Mustaţă10], there is a curve
![]() $S$
with
$S$
with
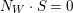 $N_{W}\cdot S=0$
. Since
$N_{W}\cdot S=0$
. Since
 $(K_{W}+\unicode[STIX]{x1D6E5}_{W}+G_{W})\cdot S<0$
,
$(K_{W}+\unicode[STIX]{x1D6E5}_{W}+G_{W})\cdot S<0$
,
 $E_{W}\cdot S<0$
, hence
$E_{W}\cdot S<0$
, hence
![]() $S$
is a component of
$S$
is a component of
![]() $E_{W}$
which is contracted over
$E_{W}$
which is contracted over
![]() $V$
, so it is a component of
$V$
, so it is a component of
![]() $\unicode[STIX]{x1D6E5}_{W}$
. In addition,
$\unicode[STIX]{x1D6E5}_{W}$
. In addition,
![]() $t$
is a rational number and
$t$
is a rational number and
 $(K_{W}+\unicode[STIX]{x1D6E5}_{W})\cdot S<0$
. Therefore, by Proposition 3.5,
$(K_{W}+\unicode[STIX]{x1D6E5}_{W})\cdot S<0$
. Therefore, by Proposition 3.5,
![]() $S$
can be contracted by a birational morphism
$S$
can be contracted by a birational morphism
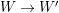 $W\rightarrow W^{\prime }$
with an induced morphism
$W\rightarrow W^{\prime }$
with an induced morphism
 $W^{\prime }\rightarrow V$
. Continuing this process gives an LMMP on
$W^{\prime }\rightarrow V$
. Continuing this process gives an LMMP on
 $K_{W}+\unicode[STIX]{x1D6E5}_{W}$
over
$K_{W}+\unicode[STIX]{x1D6E5}_{W}$
over
![]() $V$
. It terminates with some model
$V$
. It terminates with some model
![]() $Y$
on which
$Y$
on which
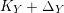 $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
is nef
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
is nef
![]() $/V$
.
$/V$
.
Since
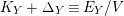 $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}\equiv E_{Y}/V$
,
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}\equiv E_{Y}/V$
,
![]() $E_{Y}$
is nef over
$E_{Y}$
is nef over
![]() $V$
and since
$V$
and since
![]() $E_{Y}$
is exceptional over
$E_{Y}$
is exceptional over
![]() $V$
, we deduce
$V$
, we deduce
![]() $E_{Y}=0$
by the negativity lemma (which holds over arbitrary fields). Therefore,
$E_{Y}=0$
by the negativity lemma (which holds over arbitrary fields). Therefore,
![]() $Y=V$
because
$Y=V$
because
![]() $E_{Y}$
contains all the exceptional curves of
$E_{Y}$
contains all the exceptional curves of
![]() $Y\rightarrow V$
. Thus
$Y\rightarrow V$
. Thus
![]() $V$
is projective and
$V$
is projective and
![]() $\mathbb{Q}$
-factorial. Now
$\mathbb{Q}$
-factorial. Now
![]() $L_{V}$
is ample and it pulls back to
$L_{V}$
is ample and it pulls back to
![]() $L$
, hence
$L$
, hence
![]() $L$
is semi-ample. ◻
$L$
is semi-ample. ◻
Proposition 3.8. Let
![]() $(X,B)$
be a klt pair of dimension two projective over a field
$(X,B)$
be a klt pair of dimension two projective over a field
![]() $k$
where
$k$
where
![]() $B$
is a
$B$
is a
![]() $\mathbb{Q}$
-boundary. Assume
$\mathbb{Q}$
-boundary. Assume
![]() $L$
is a nef
$L$
is a nef
![]() $\mathbb{Q}$
-divisor so that
$\mathbb{Q}$
-divisor so that
 $L-(K_{X}+B)$
is nef and big, and
$L-(K_{X}+B)$
is nef and big, and
![]() $L$
is not numerically trivial. Then
$L$
is not numerically trivial. Then
![]() $L$
is semi-ample.
$L$
is semi-ample.
Proof. By Proposition 3.7, we can assume
![]() $L$
is not big. Moreover, replacing
$L$
is not big. Moreover, replacing
![]() $X$
with its minimal resolution we can assume
$X$
with its minimal resolution we can assume
![]() $X$
is regular. Let
$X$
is regular. Let
 $G:=L-(K_{X}+B)$
. By the Riemann–Roch theorem for regular surfaces (see 2.3), for any sufficiently divisible natural number
$G:=L-(K_{X}+B)$
. By the Riemann–Roch theorem for regular surfaces (see 2.3), for any sufficiently divisible natural number
![]() $m$
we have
$m$
we have
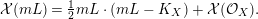 $$\begin{eqnarray}{\mathcal{X}}(mL)={\textstyle \frac{1}{2}}mL\cdot (mL-K_{X})+{\mathcal{X}}({\mathcal{O}}_{X}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}(mL)={\textstyle \frac{1}{2}}mL\cdot (mL-K_{X})+{\mathcal{X}}({\mathcal{O}}_{X}).\end{eqnarray}$$
Since
![]() $G$
is big and
$G$
is big and
![]() $L$
is not numerically trivial,
$L$
is not numerically trivial,
 $L\cdot G>0$
, and since
$L\cdot G>0$
, and since
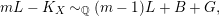 $$\begin{eqnarray}mL-K_{X}{\sim}_{\mathbb{Q}}(m-1)L+B+G,\end{eqnarray}$$
$$\begin{eqnarray}mL-K_{X}{\sim}_{\mathbb{Q}}(m-1)L+B+G,\end{eqnarray}$$
 $L\cdot (mL-K_{X})>0$
, hence
$L\cdot (mL-K_{X})>0$
, hence
![]() ${\mathcal{X}}(mL)$
is large when
${\mathcal{X}}(mL)$
is large when
![]() $m$
is large. This implies
$m$
is large. This implies
 $h^{0}(mL)\geqslant 2$
for such
$h^{0}(mL)\geqslant 2$
for such
![]() $m$
because
$m$
because
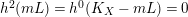 $h^{2}(mL)=h^{0}(K_{X}-mL)=0$
. Therefore,
$h^{2}(mL)=h^{0}(K_{X}-mL)=0$
. Therefore,
![]() $L$
is semi-ample by Lemma 2.16. ◻
$L$
is semi-ample by Lemma 2.16. ◻
3.9 Running the LMMP
Proof of Theorem 1.4.
The proof is broken into several steps.
Step 1. Assume
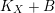 $K_{X}+B$
is pseudo-effective but not nef. First suppose
$K_{X}+B$
is pseudo-effective but not nef. First suppose
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial (we see in the next step that this is automatically satisfied). Let
$\mathbb{Q}$
-factorial (we see in the next step that this is automatically satisfied). Let
![]() $H$
be an ample divisor on
$H$
be an ample divisor on
![]() $X$
and let
$X$
and let
![]() $t$
be the smallest number such that
$t$
be the smallest number such that
 $L=K_{X}+B+tH$
is nef. Obviously
$L=K_{X}+B+tH$
is nef. Obviously
![]() $L$
is nef and big. Moreover,
$L$
is nef and big. Moreover,
![]() $t$
is rational which can be seen as in the proof of Proposition 3.5. Although we can apply Proposition 3.7 to deduce that
$t$
is rational which can be seen as in the proof of Proposition 3.5. Although we can apply Proposition 3.7 to deduce that
![]() $L$
is semi-ample and defines a contraction but we want to modify the situation so that the contraction contracts only one curve. Pick a curve
$L$
is semi-ample and defines a contraction but we want to modify the situation so that the contraction contracts only one curve. Pick a curve
![]() $C$
such that
$C$
such that
 $L\cdot C=0$
. Let
$L\cdot C=0$
. Let
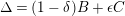 $\unicode[STIX]{x1D6E5}=(1-\unicode[STIX]{x1D6FF})B+\unicode[STIX]{x1D716}C$
for certain small rational numbers
$\unicode[STIX]{x1D6E5}=(1-\unicode[STIX]{x1D6FF})B+\unicode[STIX]{x1D716}C$
for certain small rational numbers
![]() $\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF}>0$
so that
$\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF}>0$
so that
![]() $(X,\unicode[STIX]{x1D6E5})$
is klt,
$(X,\unicode[STIX]{x1D6E5})$
is klt,
 $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
, and
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
, and
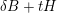 $\unicode[STIX]{x1D6FF}B+tH$
is ample. Now let
$\unicode[STIX]{x1D6FF}B+tH$
is ample. Now let
![]() $t^{\prime }$
be the smallest number such that
$t^{\prime }$
be the smallest number such that
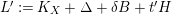 $L^{\prime }:=K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}B+t^{\prime }H$
is nef. Then
$L^{\prime }:=K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}B+t^{\prime }H$
is nef. Then
![]() $t<t^{\prime }$
because
$t<t^{\prime }$
because
![]() $C^{2}<0$
, so
$C^{2}<0$
, so
![]() $L^{\prime }$
is nef and big, and
$L^{\prime }$
is nef and big, and
 $\unicode[STIX]{x1D6FF}B+t^{\prime }H$
is ample. Note that
$\unicode[STIX]{x1D6FF}B+t^{\prime }H$
is ample. Note that
![]() $C$
is the only curve satisfying
$C$
is the only curve satisfying
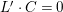 $L^{\prime }\cdot C=0$
.
$L^{\prime }\cdot C=0$
.
Now by Proposition 3.7,
![]() $L^{\prime }$
is semi-ample and it defines a nontrivial birational contraction
$L^{\prime }$
is semi-ample and it defines a nontrivial birational contraction
![]() $X\rightarrow Y$
contracting
$X\rightarrow Y$
contracting
![]() $C$
with
$C$
with
 $(K_{X}+B)\cdot C<0$
. Let
$(K_{X}+B)\cdot C<0$
. Let
![]() $R_{Y}$
be a prime divisor on
$R_{Y}$
be a prime divisor on
![]() $Y$
and
$Y$
and
![]() $R$
its birational transform on
$R$
its birational transform on
![]() $X$
. Let
$X$
. Let
![]() $r$
be the number such that
$r$
be the number such that
 $(R+rC)\cdot C=0$
. If
$(R+rC)\cdot C=0$
. If
![]() $m>0$
is sufficiently large, then
$m>0$
is sufficiently large, then
 $L^{\prime \prime }:=mL^{\prime }+R+rC$
is nef and big. Moreover, applying 3.7 to
$L^{\prime \prime }:=mL^{\prime }+R+rC$
is nef and big. Moreover, applying 3.7 to
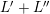 $L^{\prime }+L^{\prime \prime }$
shows that
$L^{\prime }+L^{\prime \prime }$
shows that
![]() $L^{\prime \prime }$
is the pullback of an ample divisor on
$L^{\prime \prime }$
is the pullback of an ample divisor on
![]() $Y$
, hence
$Y$
, hence
![]() $R_{Y}$
is
$R_{Y}$
is
![]() $\mathbb{Q}$
-Cartier. Therefore,
$\mathbb{Q}$
-Cartier. Therefore,
![]() $Y$
is
$Y$
is
![]() $\mathbb{Q}$
-factorial and
$\mathbb{Q}$
-factorial and
![]() $(Y,B_{Y})$
is dlt. Now replace
$(Y,B_{Y})$
is dlt. Now replace
![]() $(X,B)$
with
$(X,B)$
with
![]() $(Y,B_{Y})$
and repeat the argument.
$(Y,B_{Y})$
and repeat the argument.
Step 2. In this step we show that the dlt property of
![]() $(X,B)$
implies
$(X,B)$
implies
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial. Since the pair is dlt, there is a log resolution
$\mathbb{Q}$
-factorial. Since the pair is dlt, there is a log resolution
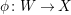 $\unicode[STIX]{x1D719}:W\rightarrow X$
such that the log discrepancy
$\unicode[STIX]{x1D719}:W\rightarrow X$
such that the log discrepancy
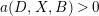 $a(D,X,B)>0$
for every curve
$a(D,X,B)>0$
for every curve
![]() $D$
contracted by
$D$
contracted by
![]() $\unicode[STIX]{x1D719}$
. Fix
$\unicode[STIX]{x1D719}$
. Fix
![]() $m\gg 0$
. By Bertini Theorem (similar argument as in [Reference Xu47, Proposition 2.3]), there exists a divisor
$m\gg 0$
. By Bertini Theorem (similar argument as in [Reference Xu47, Proposition 2.3]), there exists a divisor
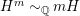 $H^{m}{\sim}_{\mathbb{Q}}mH$
on
$H^{m}{\sim}_{\mathbb{Q}}mH$
on
![]() $X$
such that
$X$
such that
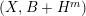 $(X,B+H^{m})$
is dlt. Let
$(X,B+H^{m})$
is dlt. Let
![]() $\unicode[STIX]{x1D6E4}_{W}$
on
$\unicode[STIX]{x1D6E4}_{W}$
on
![]() $W$
be the sum of the birational transform of
$W$
be the sum of the birational transform of
 $B+H^{m}$
and the reduced exceptional divisor of
$B+H^{m}$
and the reduced exceptional divisor of
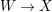 $W\rightarrow X$
. Then
$W\rightarrow X$
. Then
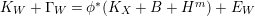 $K_{W}+\unicode[STIX]{x1D6E4}_{W}=\unicode[STIX]{x1D719}^{\ast }(K_{X}+B+H^{m})+E_{W}$
where
$K_{W}+\unicode[STIX]{x1D6E4}_{W}=\unicode[STIX]{x1D719}^{\ast }(K_{X}+B+H^{m})+E_{W}$
where
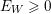 $E_{W}\geqslant 0$
is contracted over
$E_{W}\geqslant 0$
is contracted over
![]() $X$
. Then applying a similar procedure as above, we can run an LMMP for
$X$
. Then applying a similar procedure as above, we can run an LMMP for
 $K_{W}+\unicode[STIX]{x1D6E4}_{W}$
. Since
$K_{W}+\unicode[STIX]{x1D6E4}_{W}$
. Since
![]() $m\gg 0$
, by projection formula the curves
$m\gg 0$
, by projection formula the curves
![]() $C$
contracted by the LMMP intersect
$C$
contracted by the LMMP intersect
![]() $\unicode[STIX]{x1D719}^{\ast }H$
trivially, and by Proposition 3.5, such curves are contracted by
$\unicode[STIX]{x1D719}^{\ast }H$
trivially, and by Proposition 3.5, such curves are contracted by
![]() $\unicode[STIX]{x1D719}$
. In other words, the LMMP is over
$\unicode[STIX]{x1D719}$
. In other words, the LMMP is over
![]() $X$
. The LMMP contracts
$X$
. The LMMP contracts
![]() $E_{W}$
so it ends with
$E_{W}$
so it ends with
![]() $X$
which means
$X$
which means
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial. This and the previous step together prove the theorem when
$\mathbb{Q}$
-factorial. This and the previous step together prove the theorem when
 $K_{X}+B$
is pseudo-effective.
$K_{X}+B$
is pseudo-effective.
Step 3. From now on we assume
 $K_{X}+B$
is not pseudo-effective. If there is a curve
$K_{X}+B$
is not pseudo-effective. If there is a curve
![]() $C$
such that
$C$
such that
 $(K_{X}+B)\cdot C<0$
and such that there is a birational morphism
$(K_{X}+B)\cdot C<0$
and such that there is a birational morphism
![]() $X\rightarrow Y$
with exceptional divisor equal to
$X\rightarrow Y$
with exceptional divisor equal to
![]() $C$
, then we replace
$C$
, then we replace
![]() $(X,B)$
with
$(X,B)$
with
![]() $(Y,B_{Y})$
. So we can assume there is no such
$(Y,B_{Y})$
. So we can assume there is no such
![]() $C$
.
$C$
.
Pick an ample divisor
![]() $A$
and let
$A$
and let
![]() $t$
be the smallest number such that
$t$
be the smallest number such that
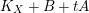 $K_{X}+B+tA$
is pseudo-effective. By the last paragraph
$K_{X}+B+tA$
is pseudo-effective. By the last paragraph
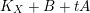 $K_{X}+B+tA$
is nef: otherwise, we can run an LMMP for
$K_{X}+B+tA$
is nef: otherwise, we can run an LMMP for
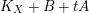 $K_{X}+B+tA$
which is also an LMMP for
$K_{X}+B+tA$
which is also an LMMP for
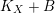 $K_{X}+B$
contracting some curve
$K_{X}+B$
contracting some curve
![]() $C$
, a contradiction.
$C$
, a contradiction.
If
 $\unicode[STIX]{x1D70C}(X)=1$
, then we already have a Mori fiber space. So assume
$\unicode[STIX]{x1D70C}(X)=1$
, then we already have a Mori fiber space. So assume
 $\unicode[STIX]{x1D70C}(X)>1$
. Then there is another ample divisor
$\unicode[STIX]{x1D70C}(X)>1$
. Then there is another ample divisor
![]() $H$
such that
$H$
such that
![]() $A$
is not numerically equivalent to
$A$
is not numerically equivalent to
![]() $hH$
for any number
$hH$
for any number
![]() $h$
. Let
$h$
. Let
![]() $s$
be the smallest number such that
$s$
be the smallest number such that
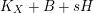 $K_{X}+B+sH$
is pseudo-effective. Arguing as above,
$K_{X}+B+sH$
is pseudo-effective. Arguing as above,
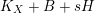 $K_{X}+B+sH$
is nef. By our choice of
$K_{X}+B+sH$
is nef. By our choice of
![]() $A$
and
$A$
and
![]() $H$
both
$H$
both
 $K_{X}+B+tA$
and
$K_{X}+B+tA$
and
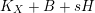 $K_{X}+B+sH$
cannot be numerically trivial at the same time. We may assume
$K_{X}+B+sH$
cannot be numerically trivial at the same time. We may assume
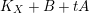 $K_{X}+B+tA$
is not numerically trivial.
$K_{X}+B+tA$
is not numerically trivial.
Step 4. In this step we assume
![]() $t$
is a rational number. By Proposition 3.8,
$t$
is a rational number. By Proposition 3.8,
 $K_{X}+B+tA$
is semi-ample defining a contraction
$K_{X}+B+tA$
is semi-ample defining a contraction
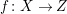 $f:X\rightarrow Z$
onto
$f:X\rightarrow Z$
onto
![]() $Z$
of dimension one. Assume there is a fiber
$Z$
of dimension one. Assume there is a fiber
![]() $F$
of
$F$
of
![]() $f$
which is not irreducible. Let
$f$
which is not irreducible. Let
![]() $C$
be a component of
$C$
be a component of
![]() $F$
. Then
$F$
. Then
![]() $C^{2}<0$
. We can find a
$C^{2}<0$
. We can find a
![]() $\mathbb{Q}$
-boundary
$\mathbb{Q}$
-boundary
![]() $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
![]() $(X,\unicode[STIX]{x1D6E5})$
is klt,
$(X,\unicode[STIX]{x1D6E5})$
is klt,
 $K_{X}+\unicode[STIX]{x1D6E5}$
is pseudo-effective, and
$K_{X}+\unicode[STIX]{x1D6E5}$
is pseudo-effective, and
 $(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
. So we can contract
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot C<0$
. So we can contract
![]() $C$
. But since
$C$
. But since
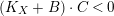 $(K_{X}+B)\cdot C<0$
, this contradicts the first paragraph of Step 3. Therefore, we can assume all the fibers of
$(K_{X}+B)\cdot C<0$
, this contradicts the first paragraph of Step 3. Therefore, we can assume all the fibers of
![]() $f$
are irreducible. But this means
$f$
are irreducible. But this means
![]() $f$
is extremal and so
$f$
is extremal and so
![]() $f$
is a Mori fiber space.
$f$
is a Mori fiber space.
Step 5. Finally we show
![]() $t$
is indeed a rational number. Assume not. We derive a contradiction. Let
$t$
is indeed a rational number. Assume not. We derive a contradiction. Let
 $L=K_{X}+B+tA$
. We can assume
$L=K_{X}+B+tA$
. We can assume
![]() $A$
is an effective
$A$
is an effective
![]() $Q$
-divisor. For each sufficiently divisible natural number
$Q$
-divisor. For each sufficiently divisible natural number
![]() $m$
, let
$m$
, let
![]() $a_{m}$
be the number so that
$a_{m}$
be the number so that
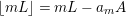 $\left\lfloor mL\right\rfloor =mL-a_{m}A$
. Since
$\left\lfloor mL\right\rfloor =mL-a_{m}A$
. Since
![]() $t$
is not rational, there is an infinite set
$t$
is not rational, there is an infinite set
![]() $\unicode[STIX]{x1D6F1}$
of such
$\unicode[STIX]{x1D6F1}$
of such
![]() $m$
so that the
$m$
so that the
![]() $a_{m}$
form a strictly decreasing sequence with
$a_{m}$
form a strictly decreasing sequence with
 $\lim _{m\in \unicode[STIX]{x1D6F1}}a_{m}=0$
. On the other hand, for each
$\lim _{m\in \unicode[STIX]{x1D6F1}}a_{m}=0$
. On the other hand, for each
![]() $m\in \unicode[STIX]{x1D6F1}$
, let
$m\in \unicode[STIX]{x1D6F1}$
, let
![]() $a_{m}^{\prime }$
be the number so that
$a_{m}^{\prime }$
be the number so that
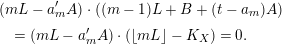 $$\begin{eqnarray}\displaystyle & & \displaystyle (mL-a_{m}^{\prime }A)\cdot ((m-1)L+B+(t-a_{m})A)\nonumber\\ \displaystyle & & \displaystyle \quad =(mL-a_{m}^{\prime }A)\cdot (\left\lfloor mL\right\rfloor -K_{X})=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (mL-a_{m}^{\prime }A)\cdot ((m-1)L+B+(t-a_{m})A)\nonumber\\ \displaystyle & & \displaystyle \quad =(mL-a_{m}^{\prime }A)\cdot (\left\lfloor mL\right\rfloor -K_{X})=0.\nonumber\end{eqnarray}$$
Since
 $\lim _{m\in \unicode[STIX]{x1D6F1}}a_{m}=0$
and
$\lim _{m\in \unicode[STIX]{x1D6F1}}a_{m}=0$
and
![]() $L^{2}=0$
, we can see
$L^{2}=0$
, we can see
 $$\begin{eqnarray}\lim _{m\in \unicode[STIX]{x1D6F1}}a_{m}^{\prime }=\lim _{m\in \unicode[STIX]{x1D6F1}}\frac{mL\cdot ((m-1)L+B+(t-a_{m})A)}{A\cdot ((m-1)L+B+(t-a_{m})A)}=\frac{L\cdot (B+tA)}{A\cdot L}>0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\in \unicode[STIX]{x1D6F1}}a_{m}^{\prime }=\lim _{m\in \unicode[STIX]{x1D6F1}}\frac{mL\cdot ((m-1)L+B+(t-a_{m})A)}{A\cdot ((m-1)L+B+(t-a_{m})A)}=\frac{L\cdot (B+tA)}{A\cdot L}>0.\end{eqnarray}$$
Thus we can assume
 $$\begin{eqnarray}(mL-a_{m}A)\cdot (\left\lfloor mL\right\rfloor -K_{X})>\unicode[STIX]{x1D70F}(m-1)A\cdot L\end{eqnarray}$$
$$\begin{eqnarray}(mL-a_{m}A)\cdot (\left\lfloor mL\right\rfloor -K_{X})>\unicode[STIX]{x1D70F}(m-1)A\cdot L\end{eqnarray}$$
for some
![]() $\unicode[STIX]{x1D70F}>0$
independent of
$\unicode[STIX]{x1D70F}>0$
independent of
![]() $m$
. Therefore,
$m$
. Therefore,
 $$\begin{eqnarray}{\mathcal{X}}(\left\lfloor mL\right\rfloor )={\textstyle \frac{1}{2}}(mL-a_{m}A)\cdot (\left\lfloor mL\right\rfloor -K_{X})+{\mathcal{X}}({\mathcal{O}}_{X})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}(\left\lfloor mL\right\rfloor )={\textstyle \frac{1}{2}}(mL-a_{m}A)\cdot (\left\lfloor mL\right\rfloor -K_{X})+{\mathcal{X}}({\mathcal{O}}_{X})\end{eqnarray}$$
is large when
![]() $m\in \unicode[STIX]{x1D6F1}$
is large. This in turn implies
$m\in \unicode[STIX]{x1D6F1}$
is large. This in turn implies
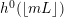 $h^{0}(\left\lfloor mL\right\rfloor )$
is large for such
$h^{0}(\left\lfloor mL\right\rfloor )$
is large for such
![]() $m$
. Take a divisor
$m$
. Take a divisor
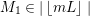 $M_{1}\in |\left\lfloor mL\right\rfloor |$
. Then
$M_{1}\in |\left\lfloor mL\right\rfloor |$
. Then
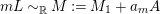 $mL{\sim}_{\mathbb{R}}M:=M_{1}+a_{m}A$
. If
$mL{\sim}_{\mathbb{R}}M:=M_{1}+a_{m}A$
. If
![]() $C$
is a component of
$C$
is a component of
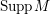 $\text{Supp}M$
, then
$\text{Supp}M$
, then
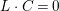 $L\cdot C=0$
which means
$L\cdot C=0$
which means
![]() $t$
is a rational number, a contradiction. ◻
$t$
is a rational number, a contradiction. ◻
3.10 Mori fiber spaces
Proposition 3.11. Let
![]() $(X,B)$
be a dlt pair of dimension two projective over a field
$(X,B)$
be a dlt pair of dimension two projective over a field
![]() $k$
. Assume
$k$
. Assume
 $f:X\rightarrow Z$
is a Mori fiber structure for
$f:X\rightarrow Z$
is a Mori fiber structure for
![]() $(X,B)$
where
$(X,B)$
where
 $\dim Z=1$
. Then the geometric general fibers of
$\dim Z=1$
. Then the geometric general fibers of
![]() $f$
are conics and if char
$f$
are conics and if char
![]() $k>2$
they are smooth rational curves. In particular, if
$k>2$
they are smooth rational curves. In particular, if
![]() $F$
is a general fiber, then
$F$
is a general fiber, then
 $(K_{X}+B)\cdot F\geqslant -2$
.
$(K_{X}+B)\cdot F\geqslant -2$
.
Proof. Let
![]() $F$
be the generic fiber of
$F$
be the generic fiber of
![]() $f$
which is a regular curve since
$f$
which is a regular curve since
![]() $X$
is regular in codimension one. Since
$X$
is regular in codimension one. Since
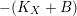 $-(K_{X}+B)$
is ample over
$-(K_{X}+B)$
is ample over
![]() $Z$
,
$Z$
,
![]() $-K_{F}$
is ample. On the other hand, since
$-K_{F}$
is ample. On the other hand, since
![]() $f$
is a contraction,
$f$
is a contraction,
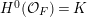 $H^{0}({\mathcal{O}}_{F})=K$
where
$H^{0}({\mathcal{O}}_{F})=K$
where
![]() $K$
is the function field of
$K$
is the function field of
![]() $Z$
. The assertions follow from Lemma 3.2 straightforwardly. ◻
$Z$
. The assertions follow from Lemma 3.2 straightforwardly. ◻
3.12 Curves of canonical type
Let
![]() $X$
be a regular surface projective over a field
$X$
be a regular surface projective over a field
![]() $k$
. A connected divisor
$k$
. A connected divisor
 $D=\sum _{1}^{r}d_{i}D_{i}\geqslant 0$
is called a curve of canonical type if
$D=\sum _{1}^{r}d_{i}D_{i}\geqslant 0$
is called a curve of canonical type if
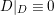 $D|_{D}\equiv 0$
and
$D|_{D}\equiv 0$
and
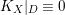 $K_{X}|_{D}\equiv 0$
. It is called indecomposable if there is no prime number dividing all the
$K_{X}|_{D}\equiv 0$
. It is called indecomposable if there is no prime number dividing all the
![]() $d_{i}$
. The following result was proved by Mumford [Reference Mumford33, p. 332]. Although he assumes the ground field to be algebraically closed his proof works for arbitrary fields. We give the proof for convenience (see also [Reference Badescu2, Theorem 7.8]).
$d_{i}$
. The following result was proved by Mumford [Reference Mumford33, p. 332]. Although he assumes the ground field to be algebraically closed his proof works for arbitrary fields. We give the proof for convenience (see also [Reference Badescu2, Theorem 7.8]).
Proposition 3.13. Let
![]() $D$
be an indecomposable curve of canonical type. Let
$D$
be an indecomposable curve of canonical type. Let
![]() $L$
be a Cartier divisor on
$L$
be a Cartier divisor on
![]() $D$
such that
$D$
such that
![]() $L\equiv 0$
. If
$L\equiv 0$
. If
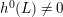 $h^{0}(L)\neq 0$
, then
$h^{0}(L)\neq 0$
, then
![]() $L\sim 0$
.
$L\sim 0$
.
Proof. Assume
 $\unicode[STIX]{x1D6FC}\in H^{0}(L)$
is nonzero. Then
$\unicode[STIX]{x1D6FC}\in H^{0}(L)$
is nonzero. Then
![]() $\unicode[STIX]{x1D6FC}|_{D_{i}}$
is either nowhere vanishing or everywhere vanishing because
$\unicode[STIX]{x1D6FC}|_{D_{i}}$
is either nowhere vanishing or everywhere vanishing because
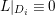 $L|_{D_{i}}\equiv 0$
. Since
$L|_{D_{i}}\equiv 0$
. Since
![]() $D$
is connected, either
$D$
is connected, either
![]() $\unicode[STIX]{x1D6FC}$
is nowhere vanishing on
$\unicode[STIX]{x1D6FC}$
is nowhere vanishing on
![]() $D$
or
$D$
or
 $\unicode[STIX]{x1D6FC}|_{\text{Supp}\,D}=0$
. The former implies
$\unicode[STIX]{x1D6FC}|_{\text{Supp}\,D}=0$
. The former implies
![]() $L$
is generated by global sections which in turn implies
$L$
is generated by global sections which in turn implies
![]() $L\sim 0$
. So it is enough to treat the latter. Let
$L\sim 0$
. So it is enough to treat the latter. Let
![]() $n_{i}$
be the order of vanishing of
$n_{i}$
be the order of vanishing of
![]() $\unicode[STIX]{x1D6FC}$
along
$\unicode[STIX]{x1D6FC}$
along
![]() $D_{i}$
. Let
$D_{i}$
. Let
 $N=\sum n_{i}D_{i}$
. Then by assumption
$N=\sum n_{i}D_{i}$
. Then by assumption
 $0<N<D$
.
$0<N<D$
.
We claim that for every component
![]() $D_{i}$
such that
$D_{i}$
such that
![]() $n_{i}<d_{i}$
,
$n_{i}<d_{i}$
,
![]() $-N|_{D_{i}}$
is nef. Granted this claim, since
$-N|_{D_{i}}$
is nef. Granted this claim, since
![]() $D$
is connected we have that
$D$
is connected we have that
![]() $n_{i}>0$
for every
$n_{i}>0$
for every
 $i\in \{1,2,\ldots ,r\}$
. Let
$i\in \{1,2,\ldots ,r\}$
. Let
![]() $a$
be the smallest rational number such that
$a$
be the smallest rational number such that
 $aN-D\geqslant 0$
. Then
$aN-D\geqslant 0$
. Then
 $aN-D=0$
because otherwise, since
$aN-D=0$
because otherwise, since
![]() $D$
is connected, there will exist a component
$D$
is connected, there will exist a component
![]() $D_{i}$
of
$D_{i}$
of
![]() $D$
such that
$D$
such that
![]() $D_{i}$
is not contained in
$D_{i}$
is not contained in
 $aN-D$
,
$aN-D$
,
![]() $n_{i}<d_{i}$
and
$n_{i}<d_{i}$
and
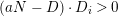 $(aN-D)\cdot D_{i}>0$
, which contradicts that
$(aN-D)\cdot D_{i}>0$
, which contradicts that
![]() $-N|_{D_{i}}$
is nef. Since the
$-N|_{D_{i}}$
is nef. Since the
![]() $d_{i}$
have no common factor,
$d_{i}$
have no common factor,
![]() $N=D$
. So
$N=D$
. So
![]() $\unicode[STIX]{x1D6FC}=0$
, a contradiction.
$\unicode[STIX]{x1D6FC}=0$
, a contradiction.
The claim follows from local analysis. Assume
![]() $n_{i}<d_{i}$
, say for
$n_{i}<d_{i}$
, say for
![]() $i=1$
. Consider the exact sequence
$i=1$
. Consider the exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{D_{1}}(L-n_{1}D_{1})\rightarrow {\mathcal{O}}_{(n_{1}+1)D_{1}}(L)\rightarrow {\mathcal{O}}_{n_{1}D_{1}}(L)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{D_{1}}(L-n_{1}D_{1})\rightarrow {\mathcal{O}}_{(n_{1}+1)D_{1}}(L)\rightarrow {\mathcal{O}}_{n_{1}D_{1}}(L)\rightarrow 0.\end{eqnarray}$$
Since
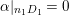 $\unicode[STIX]{x1D6FC}|_{n_{1}D_{1}}=0$
by definition of
$\unicode[STIX]{x1D6FC}|_{n_{1}D_{1}}=0$
by definition of
![]() $n_{1}$
, the section
$n_{1}$
, the section
 $\unicode[STIX]{x1D6FC}|_{(n_{1}+1)D_{1}}$
is the image of a section
$\unicode[STIX]{x1D6FC}|_{(n_{1}+1)D_{1}}$
is the image of a section
![]() $\unicode[STIX]{x1D6FD}$
of
$\unicode[STIX]{x1D6FD}$
of
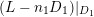 $(L-n_{1}D_{1})|_{D_{1}}$
. If
$(L-n_{1}D_{1})|_{D_{1}}$
. If
![]() $P$
is the zero divisor of
$P$
is the zero divisor of
![]() $\unicode[STIX]{x1D6FD}$
, then a local computation of intersection numbers shows that
$\unicode[STIX]{x1D6FD}$
, then a local computation of intersection numbers shows that
 $P\geqslant (N-n_{1}D_{1})|_{D_{1}}$
. More precisely, let
$P\geqslant (N-n_{1}D_{1})|_{D_{1}}$
. More precisely, let
![]() $v\in D_{1}$
be a closed point, let
$v\in D_{1}$
be a closed point, let
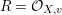 $R={\mathcal{O}}_{X,v}$
, and let
$R={\mathcal{O}}_{X,v}$
, and let
![]() $f_{i}$
be a local equation of
$f_{i}$
be a local equation of
![]() $D_{i}$
near
$D_{i}$
near
![]() $v$
. Then locally considering
$v$
. Then locally considering
![]() $\unicode[STIX]{x1D6FC}$
as an element of
$\unicode[STIX]{x1D6FC}$
as an element of
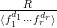 $\frac{R}{\langle f_{1}^{d_{1}}\cdots f_{r}^{d_{r}}\rangle }$
, it is easy to see that
$\frac{R}{\langle f_{1}^{d_{1}}\cdots f_{r}^{d_{r}}\rangle }$
, it is easy to see that
![]() $\unicode[STIX]{x1D6FC}$
is represented by
$\unicode[STIX]{x1D6FC}$
is represented by
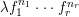 $\unicode[STIX]{x1D706}f_{1}^{n_{1}}\cdots f_{r}^{n_{r}}$
for some
$\unicode[STIX]{x1D706}f_{1}^{n_{1}}\cdots f_{r}^{n_{r}}$
for some
![]() $\unicode[STIX]{x1D706}\in R$
, and that
$\unicode[STIX]{x1D706}\in R$
, and that
![]() $\unicode[STIX]{x1D6FD}$
is represented by
$\unicode[STIX]{x1D6FD}$
is represented by
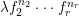 $\unicode[STIX]{x1D706}f_{2}^{n_{2}}\cdots f_{r}^{n_{r}}$
which gives the equation of
$\unicode[STIX]{x1D706}f_{2}^{n_{2}}\cdots f_{r}^{n_{r}}$
which gives the equation of
![]() $P$
near
$P$
near
![]() $v$
. Therefore, from
$v$
. Therefore, from
 $$\begin{eqnarray}\text{length}_{R/\langle f_{1}\rangle }\frac{R}{\langle f_{1},\unicode[STIX]{x1D706}f_{2}^{n_{2}}\cdots f_{r}^{n_{r}}\rangle }\geqslant \text{length}_{R}\frac{R}{\langle f_{1},f_{2}^{n_{2}}\cdots f_{r}^{n_{r}}\rangle }\end{eqnarray}$$
$$\begin{eqnarray}\text{length}_{R/\langle f_{1}\rangle }\frac{R}{\langle f_{1},\unicode[STIX]{x1D706}f_{2}^{n_{2}}\cdots f_{r}^{n_{r}}\rangle }\geqslant \text{length}_{R}\frac{R}{\langle f_{1},f_{2}^{n_{2}}\cdots f_{r}^{n_{r}}\rangle }\end{eqnarray}$$
we deduce that locally near
![]() $v$
we have
$v$
we have
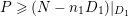 $P\geqslant (N-n_{1}D_{1})|_{D_{1}}$
because the left hand side of the displayed formula is the coefficient of
$P\geqslant (N-n_{1}D_{1})|_{D_{1}}$
because the left hand side of the displayed formula is the coefficient of
![]() $v$
in
$v$
in
![]() $P$
and the right hand side is nothing but the local intersection number
$P$
and the right hand side is nothing but the local intersection number
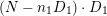 $(N-n_{1}D_{1})\cdot D_{1}$
at
$(N-n_{1}D_{1})\cdot D_{1}$
at
![]() $v$
which is in turn equal to the coefficient of
$v$
which is in turn equal to the coefficient of
![]() $v$
in
$v$
in
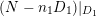 $(N-n_{1}D_{1})|_{D_{1}}$
. As
$(N-n_{1}D_{1})|_{D_{1}}$
. As
 $P\sim (L-n_{1}D_{1})|_{D_{1}}$
, we deduce that
$P\sim (L-n_{1}D_{1})|_{D_{1}}$
, we deduce that
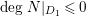 $\deg N|_{D_{1}}\leqslant 0$
. ◻
$\deg N|_{D_{1}}\leqslant 0$
. ◻
Proposition 3.14. Let
![]() $D$
be an indecomposable curve of canonical type. Then the arithmetic genus
$D$
be an indecomposable curve of canonical type. Then the arithmetic genus
 $p_{a}(D)=1$
and
$p_{a}(D)=1$
and
![]() $K_{D}\sim 0$
.
$K_{D}\sim 0$
.
Proof. By definition of curves of canonical type
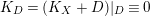 $K_{D}=(K_{X}+D)|_{D}\equiv 0$
. By [Reference Liu31, Chapter 7, Corollary 3.31],
$K_{D}=(K_{X}+D)|_{D}\equiv 0$
. By [Reference Liu31, Chapter 7, Corollary 3.31],
 $0=\deg _{k}K_{D}=2(p_{a}(D)-1)$
. Thus
$0=\deg _{k}K_{D}=2(p_{a}(D)-1)$
. Thus
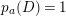 $p_{a}(D)=1$
which means
$p_{a}(D)=1$
which means
 ${\mathcal{X}}({\mathcal{O}}_{D})=0$
, hence
${\mathcal{X}}({\mathcal{O}}_{D})=0$
, hence
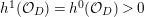 $h^{1}({\mathcal{O}}_{D})=h^{0}({\mathcal{O}}_{D})>0$
. So by duality
$h^{1}({\mathcal{O}}_{D})=h^{0}({\mathcal{O}}_{D})>0$
. So by duality
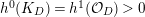 $h^{0}(K_{D})=h^{1}({\mathcal{O}}_{D})>0$
which implies
$h^{0}(K_{D})=h^{1}({\mathcal{O}}_{D})>0$
which implies
![]() $K_{D}\sim 0$
by Proposition 3.13. ◻
$K_{D}\sim 0$
by Proposition 3.13. ◻
Proposition 3.15. Assume char
![]() $k>0$
. Let
$k>0$
. Let
![]() $D$
be an indecomposable curve of canonical type such that
$D$
be an indecomposable curve of canonical type such that
![]() $D|_{D}$
is torsion. Then
$D|_{D}$
is torsion. Then
![]() $D$
is semi-ample on
$D$
is semi-ample on
![]() $X$
.
$X$
.
Proof. Let
![]() $r$
be the order of
$r$
be the order of
![]() $D|_{D}$
in
$D|_{D}$
in
![]() $\text{Pic}(D)$
. First we want to show
$\text{Pic}(D)$
. First we want to show
 $rD|_{rD}\sim 0$
. This is trivially true if
$rD|_{rD}\sim 0$
. This is trivially true if
![]() $r=1$
, so assume
$r=1$
, so assume
![]() $r>1$
. Assume we already know
$r>1$
. Assume we already know
 $rD|_{lD}\sim 0$
for some
$rD|_{lD}\sim 0$
for some
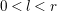 $0<l<r$
. Consider the exact sequence
$0<l<r$
. Consider the exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{D}(rD-lD)\rightarrow {\mathcal{O}}_{(l+1)D}(rD)\rightarrow {\mathcal{O}}_{lD}(rD)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{D}(rD-lD)\rightarrow {\mathcal{O}}_{(l+1)D}(rD)\rightarrow {\mathcal{O}}_{lD}(rD)\rightarrow 0.\end{eqnarray}$$
Now
 $h^{0}({\mathcal{O}}_{D}(rD-lD))=0$
by Proposition 3.13, and since
$h^{0}({\mathcal{O}}_{D}(rD-lD))=0$
by Proposition 3.13, and since
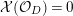 ${\mathcal{X}}({\mathcal{O}}_{D})=0$
, by Riemann–Roch we get
${\mathcal{X}}({\mathcal{O}}_{D})=0$
, by Riemann–Roch we get
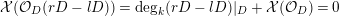 $$\begin{eqnarray}{\mathcal{X}}({\mathcal{O}}_{D}(rD-lD))=\deg _{k}(rD-lD)|_{D}+{\mathcal{X}}({\mathcal{O}}_{D})=0\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}({\mathcal{O}}_{D}(rD-lD))=\deg _{k}(rD-lD)|_{D}+{\mathcal{X}}({\mathcal{O}}_{D})=0\end{eqnarray}$$
which implies
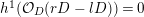 $h^{1}({\mathcal{O}}_{D}(rD-lD))=0$
. So any nowhere vanishing section of
$h^{1}({\mathcal{O}}_{D}(rD-lD))=0$
. So any nowhere vanishing section of
 ${\mathcal{O}}_{lD}(rD)$
lifts to
${\mathcal{O}}_{lD}(rD)$
lifts to
 ${\mathcal{O}}_{(l+1)D}(rD)$
which shows
${\mathcal{O}}_{(l+1)D}(rD)$
which shows
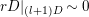 $rD|_{(l+1)D}\sim 0$
. Inductively one shows
$rD|_{(l+1)D}\sim 0$
. Inductively one shows
 $rD|_{rD}\sim 0$
. Finally applying [Reference Totaro42, Lemma 4.1], we deduce
$rD|_{rD}\sim 0$
. Finally applying [Reference Totaro42, Lemma 4.1], we deduce
![]() $D$
is semi-ample. ◻
$D$
is semi-ample. ◻
3.16 Abundance
Proof of Theorem 1.5.
We can assume
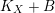 $K_{X}+B$
is not big by Proposition 3.7. Replacing
$K_{X}+B$
is not big by Proposition 3.7. Replacing
![]() $X$
with its minimal resolution we can assume
$X$
with its minimal resolution we can assume
![]() $X$
is regular. By assumption
$X$
is regular. By assumption
 $m(K_{X}+B)\sim M$
for some integer
$m(K_{X}+B)\sim M$
for some integer
![]() $m>0$
and
$m>0$
and
![]() $M$
is an effective Cartier divisor. Let
$M$
is an effective Cartier divisor. Let
![]() $n$
be a sufficiently large natural number. We can run an LMMP on
$n$
be a sufficiently large natural number. We can run an LMMP on
 $K_{X}+nM$
because
$K_{X}+nM$
because
 $$\begin{eqnarray}K_{X}+nM\sim (1+nm)\left(K_{X}+\frac{nm}{1+nm}B\right)\end{eqnarray}$$
$$\begin{eqnarray}K_{X}+nM\sim (1+nm)\left(K_{X}+\frac{nm}{1+nm}B\right)\end{eqnarray}$$
and because
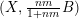 $(X,\frac{nm}{1+nm}B)$
is klt. Moreover, we claim that
$(X,\frac{nm}{1+nm}B)$
is klt. Moreover, we claim that
![]() $M$
is numerically trivial on each step of the LMMP and the nefness of
$M$
is numerically trivial on each step of the LMMP and the nefness of
![]() $M$
is preserved in the process. Indeed assume the first step of the LMMP is a birational contraction
$M$
is preserved in the process. Indeed assume the first step of the LMMP is a birational contraction
![]() $X\rightarrow Z$
contracting a curve
$X\rightarrow Z$
contracting a curve
![]() $E$
. Then
$E$
. Then
 $\deg _{k}K_{E}=(K_{X}+E)\cdot E<0$
, hence by Lemma 3.2, if setting
$\deg _{k}K_{E}=(K_{X}+E)\cdot E<0$
, hence by Lemma 3.2, if setting
 $l=H^{0}({\mathcal{O}}_{E})$
then
$l=H^{0}({\mathcal{O}}_{E})$
then
 $$\begin{eqnarray}-2=\deg _{l}K_{E}=\deg _{l}(K_{X}+E)|_{E}\end{eqnarray}$$
$$\begin{eqnarray}-2=\deg _{l}K_{E}=\deg _{l}(K_{X}+E)|_{E}\end{eqnarray}$$
which implies
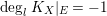 $\deg _{l}K_{X}|_{E}=-1$
. Thus from
$\deg _{l}K_{X}|_{E}=-1$
. Thus from
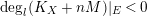 $\deg _{l}(K_{X}+nM)|_{E}<0$
we deduce
$\deg _{l}(K_{X}+nM)|_{E}<0$
we deduce
 $M\cdot E=0$
, because otherwise,
$M\cdot E=0$
, because otherwise,
 $\deg _{l}M|_{E}\geqslant 1$
since
$\deg _{l}M|_{E}\geqslant 1$
since
![]() $M$
is Cartier, this is impossible since we have assumed
$M$
is Cartier, this is impossible since we have assumed
![]() $n\gg 0$
. On the other hand, if
$n\gg 0$
. On the other hand, if
![]() $X\rightarrow Z$
is a Mori fiber space, then we stop the LMMP and in this case
$X\rightarrow Z$
is a Mori fiber space, then we stop the LMMP and in this case
 $M\equiv 0/Z$
by Proposition 3.11 and calculations similar to those above. Applying this argument to every step of the LMMP proves the claim. Note that the regularity of
$M\equiv 0/Z$
by Proposition 3.11 and calculations similar to those above. Applying this argument to every step of the LMMP proves the claim. Note that the regularity of
![]() $X$
is also preserved by the LMMP because the LMMP is a
$X$
is also preserved by the LMMP because the LMMP is a
![]() $K_{X}$
-MMP; hence
$K_{X}$
-MMP; hence
![]() $X$
remains with terminal singularities which implies regularity.
$X$
remains with terminal singularities which implies regularity.
Replacing
![]() $X$
with the end product of the LMMP we can assume either
$X$
with the end product of the LMMP we can assume either
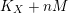 $K_{X}+nM$
is nef or that there is a Mori fiber structure
$K_{X}+nM$
is nef or that there is a Mori fiber structure
![]() $X\rightarrow Z$
so that
$X\rightarrow Z$
so that
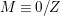 $M\equiv 0/Z$
. First assume
$M\equiv 0/Z$
. First assume
 $K_{X}+nM$
is nef. There is a divisor
$K_{X}+nM$
is nef. There is a divisor
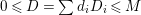 $0\leqslant D=\sum d_{i}D_{i}\leqslant M$
such that
$0\leqslant D=\sum d_{i}D_{i}\leqslant M$
such that
![]() $D$
is connected, the
$D$
is connected, the
![]() $d_{i}$
have no common prime factor, and
$d_{i}$
have no common prime factor, and
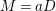 $M=aD$
in a neighborhood of
$M=aD$
in a neighborhood of
![]() $D$
for some number
$D$
for some number
![]() $a$
. In particular,
$a$
. In particular,
![]() $D$
is nef. We show
$D$
is nef. We show
![]() $D$
is an indecomposable curve of canonical type. It is enough to show
$D$
is an indecomposable curve of canonical type. It is enough to show
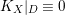 $K_{X}|_{D}\equiv 0$
because
$K_{X}|_{D}\equiv 0$
because
![]() $M$
not being big implies
$M$
not being big implies
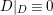 $D|_{D}\equiv 0$
. Since
$D|_{D}\equiv 0$
. Since
![]() $M$
is not big and since
$M$
is not big and since
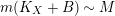 $m(K_{X}+B)\sim M$
, we deduce
$m(K_{X}+B)\sim M$
, we deduce
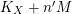 $K_{X}+n^{\prime }M$
is not big for any
$K_{X}+n^{\prime }M$
is not big for any
![]() $n^{\prime }$
. Therefore,
$n^{\prime }$
. Therefore,
 $(K_{X}+nM+M)^{2}=0$
from which we deduce
$(K_{X}+nM+M)^{2}=0$
from which we deduce
 $(K_{X}+nM)\cdot M=0$
, hence
$(K_{X}+nM)\cdot M=0$
, hence
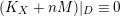 $(K_{X}+nM)|_{D}\equiv 0$
, so
$(K_{X}+nM)|_{D}\equiv 0$
, so
 $K_{X}|_{D}\equiv 0$
.
$K_{X}|_{D}\equiv 0$
.
In order to apply Proposition 3.15 we need to show
![]() $D|_{D}$
is torsion. By construction,
$D|_{D}$
is torsion. By construction,
 $B|_{D}\equiv 0$
which implies
$B|_{D}\equiv 0$
which implies
 $B=bD$
in some neighborhood of
$B=bD$
in some neighborhood of
![]() $D$
because
$D$
because
![]() $D$
is connected, where
$D$
is connected, where
![]() $b<1$
is a rational number. Taking positive integer
$b<1$
is a rational number. Taking positive integer
![]() $m^{\prime }$
so that
$m^{\prime }$
so that
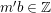 $m^{\prime }b\in \mathbb{Z}$
we get
$m^{\prime }b\in \mathbb{Z}$
we get
 $$\begin{eqnarray}\displaystyle 0 & {\sim} & \displaystyle m^{\prime }K_{D}=m^{\prime }(K_{X}+D)|_{D}=m^{\prime }(K_{X}+B+D)|_{D}-m^{\prime }B|_{D}\nonumber\\ \displaystyle & {\sim} & \displaystyle (a+m^{\prime })D|_{D}-m^{\prime }bD|_{D}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & {\sim} & \displaystyle m^{\prime }K_{D}=m^{\prime }(K_{X}+D)|_{D}=m^{\prime }(K_{X}+B+D)|_{D}-m^{\prime }B|_{D}\nonumber\\ \displaystyle & {\sim} & \displaystyle (a+m^{\prime })D|_{D}-m^{\prime }bD|_{D}\nonumber\end{eqnarray}$$
which implies
![]() $D|_{D}$
is torsion because
$D|_{D}$
is torsion because
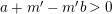 $a+m^{\prime }-m^{\prime }b>0$
. Therefore,
$a+m^{\prime }-m^{\prime }b>0$
. Therefore,
![]() $D$
is semi-ample, hence
$D$
is semi-ample, hence
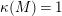 $\unicode[STIX]{x1D705}(M)=1$
which implies
$\unicode[STIX]{x1D705}(M)=1$
which implies
![]() $M$
is semi-ample by Lemma 2.16.
$M$
is semi-ample by Lemma 2.16.
Now assume we have a Mori fiber structure
![]() $X\rightarrow Z$
with
$X\rightarrow Z$
with
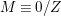 $M\equiv 0/Z$
. If
$M\equiv 0/Z$
. If
![]() $F$
is the generic fiber, then
$F$
is the generic fiber, then
 $M|_{F}\sim 0$
. This implies
$M|_{F}\sim 0$
. This implies
![]() $M$
is the pullback of some effective divisor
$M$
is the pullback of some effective divisor
![]() $N$
on
$N$
on
![]() $Z$
. Either
$Z$
. Either
![]() $N$
is ample or
$N$
is ample or
![]() $N=0$
, hence in any case
$N=0$
, hence in any case
![]() $M$
is semi-ample. ◻
$M$
is semi-ample. ◻
Remark 3.17. Here we explain what we need from this section for the proof of Theorem 1.2. We need Theorem 1.5 for the proof of Theorem 1.6. In turn we use Theorem 1.6 in the proofs of Corollary 4.1 and Proposition 5.3 (steps 1 and 5) in two situations: when (1)
![]() $F$
is smooth and when (2)
$F$
is smooth and when (2)
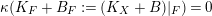 $\unicode[STIX]{x1D705}(K_{F}+B_{F}:=(K_{X}+B)|_{F})=0$
and there is a surjective map
$\unicode[STIX]{x1D705}(K_{F}+B_{F}:=(K_{X}+B)|_{F})=0$
and there is a surjective map
![]() $F\rightarrow C$
onto an elliptic curve defined over the function field
$F\rightarrow C$
onto an elliptic curve defined over the function field
![]() $K$
of
$K$
of
![]() $Z$
and such that
$Z$
and such that
 $K_{F}+B_{F}$
is big over
$K_{F}+B_{F}$
is big over
![]() $C$
. In each case it is enough to know that
$C$
. In each case it is enough to know that
 $K_{F}+B_{F}$
is semi-ample. In case (1), we can pass to the algebraic closure
$K_{F}+B_{F}$
is semi-ample. In case (1), we can pass to the algebraic closure
![]() $\bar{K}$
and deduce that
$\bar{K}$
and deduce that
 $K_{F}+B_{F}$
is semi-ample. In case (2),
$K_{F}+B_{F}$
is semi-ample. In case (2),
 $m(K_{F}+B_{F})\sim M_{F}\geqslant 0$
for some
$m(K_{F}+B_{F})\sim M_{F}\geqslant 0$
for some
![]() $m>0$
, and using the map
$m>0$
, and using the map
![]() $F\rightarrow C$
it is relatively easy to show
$F\rightarrow C$
it is relatively easy to show
 $M_{F}=0$
: if not then each connected component of
$M_{F}=0$
: if not then each connected component of
![]() $M_{F}$
is irreducible; let
$M_{F}$
is irreducible; let
![]() $D$
be the reduction of such a component; then there is one such
$D$
be the reduction of such a component; then there is one such
![]() $D$
which maps onto
$D$
which maps onto
![]() $C$
and one can show that
$C$
and one can show that
![]() $D$
is an elliptic curve with
$D$
is an elliptic curve with
 $K_{F}\cdot D=0$
and
$K_{F}\cdot D=0$
and
![]() $D|_{D}$
torsion; one then applies Proposition 3.15 to deduce that
$D|_{D}$
torsion; one then applies Proposition 3.15 to deduce that
![]() $D$
is semi-ample, hence
$D$
is semi-ample, hence
 $\unicode[STIX]{x1D705}(M_{F})\geqslant 1$
, a contradiction.
$\unicode[STIX]{x1D705}(M_{F})\geqslant 1$
, a contradiction.
4 Relative good minimal models of
 $3$
-folds
$3$
-folds
Proof of Theorem 1.6.
By [Reference Birkar5],
![]() $(X,B)$
has a log minimal model over
$(X,B)$
has a log minimal model over
![]() $Z$
. Replacing
$Z$
. Replacing
![]() $(X,B)$
with the minimal model, we can assume
$(X,B)$
with the minimal model, we can assume
 $K_{X}+B$
is nef
$K_{X}+B$
is nef
![]() $/Z$
. Let
$/Z$
. Let
![]() $F$
be the generic fiber of
$F$
be the generic fiber of
![]() $X\rightarrow Z$
and let
$X\rightarrow Z$
and let
 $K_{F}+B_{F}=(K_{X}+B)|_{F}$
. Then
$K_{F}+B_{F}=(K_{X}+B)|_{F}$
. Then
![]() $(F,B_{F})$
is klt and
$(F,B_{F})$
is klt and
 $K_{F}+B_{F}$
is nef with
$K_{F}+B_{F}$
is nef with
 $\unicode[STIX]{x1D705}(K_{F}+B_{F})\geqslant 0$
. By Theorem 1.5,
$\unicode[STIX]{x1D705}(K_{F}+B_{F})\geqslant 0$
. By Theorem 1.5,
 $K_{F}+B_{F}$
is semi-ample.
$K_{F}+B_{F}$
is semi-ample.
If
 $\unicode[STIX]{x1D705}(K_{F}+B_{F})=0$
, then
$\unicode[STIX]{x1D705}(K_{F}+B_{F})=0$
, then
 $K_{F}+B_{F}{\sim}_{\mathbb{Q}}0$
, hence
$K_{F}+B_{F}{\sim}_{\mathbb{Q}}0$
, hence
 $K_{X}+B{\sim}_{\mathbb{Q}}0/Z$
, by Lemma 2.18. On the other hand, if
$K_{X}+B{\sim}_{\mathbb{Q}}0/Z$
, by Lemma 2.18. On the other hand, if
 $\unicode[STIX]{x1D705}(K_{F}+B_{F})=2$
, then
$\unicode[STIX]{x1D705}(K_{F}+B_{F})=2$
, then
 $K_{X}+B$
is big
$K_{X}+B$
is big
![]() $/Z$
, hence it is semi-ample over
$/Z$
, hence it is semi-ample over
![]() $Z$
by Theorem 2.7. So we assume
$Z$
by Theorem 2.7. So we assume
 $\unicode[STIX]{x1D705}(K_{F}+B_{F})=1$
.
$\unicode[STIX]{x1D705}(K_{F}+B_{F})=1$
.
Since
 $K_{F}+B_{F}$
is semi-ample and
$K_{F}+B_{F}$
is semi-ample and
 $\unicode[STIX]{x1D705}(K_{F}+B_{F})=1$
, there is a diagram
$\unicode[STIX]{x1D705}(K_{F}+B_{F})=1$
, there is a diagram

where
![]() $\unicode[STIX]{x1D719}$
is birational,
$\unicode[STIX]{x1D719}$
is birational,
![]() $S$
is a smooth projective surface, and
$S$
is a smooth projective surface, and
 $\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)|_{G}{\sim}_{\mathbb{Q}}0$
on the generic fiber
$\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)|_{G}{\sim}_{\mathbb{Q}}0$
on the generic fiber
![]() $G$
of
$G$
of
![]() $g$
. By Lemma 2.18, we can actually assume
$g$
. By Lemma 2.18, we can actually assume
 $\unicode[STIX]{x1D719}^{\ast }(K_{X}+B){\sim}_{\mathbb{Q}}0/S$
. So
$\unicode[STIX]{x1D719}^{\ast }(K_{X}+B){\sim}_{\mathbb{Q}}0/S$
. So
 $\unicode[STIX]{x1D719}^{\ast }(K_{X}+B){\sim}_{\mathbb{Q}}g^{\ast }D$
for some
$\unicode[STIX]{x1D719}^{\ast }(K_{X}+B){\sim}_{\mathbb{Q}}g^{\ast }D$
for some
![]() $\mathbb{Q}$
-Cartier
$\mathbb{Q}$
-Cartier
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D$
on
$D$
on
![]() $S$
. On the other hand, let
$S$
. On the other hand, let
![]() $H$
be an ample divisor on
$H$
be an ample divisor on
![]() $Z$
. Then since
$Z$
. Then since
![]() $D$
is nef and big over
$D$
is nef and big over
![]() $Z$
,
$Z$
,
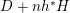 $D+nh^{\ast }H$
is nef and big for any
$D+nh^{\ast }H$
is nef and big for any
![]() $n\gg 0$
. Since we are working over
$n\gg 0$
. Since we are working over
![]() $\bar{\mathbb{F}}_{p}$
,
$\bar{\mathbb{F}}_{p}$
,
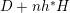 $D+nh^{\ast }H$
is semi-ample (this follows from [Reference Keel26]) which implies
$D+nh^{\ast }H$
is semi-ample (this follows from [Reference Keel26]) which implies
![]() $D$
is semi-ample over
$D$
is semi-ample over
![]() $Z$
from which we deduce
$Z$
from which we deduce
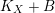 $K_{X}+B$
is semi-ample over
$K_{X}+B$
is semi-ample over
![]() $Z$
. ◻
$Z$
. ◻
Corollary 4.1. Let
![]() $W$
be a smooth projective
$W$
be a smooth projective
![]() $3$
-fold over an algebraically closed field
$3$
-fold over an algebraically closed field
![]() $k$
of char
$k$
of char
![]() $p>5$
. Assume
$p>5$
. Assume
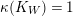 $\unicode[STIX]{x1D705}(K_{W})=1$
. If
$\unicode[STIX]{x1D705}(K_{W})=1$
. If
![]() $X$
is a minimal model of
$X$
is a minimal model of
![]() $W$
, then the Iitaka fibration
$W$
, then the Iitaka fibration
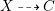 $X{\dashrightarrow}C$
is a morphism where
$X{\dashrightarrow}C$
is a morphism where
![]() $C$
is a smooth projective curve, and
$C$
is a smooth projective curve, and
 $K_{X}{\sim}_{\mathbb{Q}}0/C$
.
$K_{X}{\sim}_{\mathbb{Q}}0/C$
.
Proof. Denote by
 $g:W{\dashrightarrow}C$
the Iitaka fibration, which is assumed to be a morphism by blowing up
$g:W{\dashrightarrow}C$
the Iitaka fibration, which is assumed to be a morphism by blowing up
![]() $W$
. Let
$W$
. Let
 $r:Y\rightarrow C$
be a minimal model of
$r:Y\rightarrow C$
be a minimal model of
![]() $W$
over
$W$
over
![]() $C$
which has at most terminal singularities. Let
$C$
which has at most terminal singularities. Let
![]() $R$
be the generic fiber of
$R$
be the generic fiber of
![]() $r$
. Since
$r$
. Since
![]() $Y$
is regular in codimension two,
$Y$
is regular in codimension two,
![]() $R$
is a regular surface. Since
$R$
is a regular surface. Since
 $\unicode[STIX]{x1D705}(K_{W})=1$
and since
$\unicode[STIX]{x1D705}(K_{W})=1$
and since
![]() $g$
is the Iitaka fibration of
$g$
is the Iitaka fibration of
![]() $K_{W}$
,
$K_{W}$
,
 $\unicode[STIX]{x1D705}(K_{R})=0$
. Moreover, as
$\unicode[STIX]{x1D705}(K_{R})=0$
. Moreover, as
![]() $K_{Y}$
is nef over
$K_{Y}$
is nef over
![]() $C$
,
$C$
,
![]() $K_{R}$
is nef too. Therefore, by Theorem 1.5,
$K_{R}$
is nef too. Therefore, by Theorem 1.5,
 $K_{R}{\sim}_{\mathbb{Q}}0$
. This implies
$K_{R}{\sim}_{\mathbb{Q}}0$
. This implies
 $K_{Y}{\sim}_{\mathbb{Q}}0/C$
as
$K_{Y}{\sim}_{\mathbb{Q}}0/C$
as
![]() $K_{Y}$
is nef over
$K_{Y}$
is nef over
![]() $C$
, by Lemma 2.18. Thus
$C$
, by Lemma 2.18. Thus
![]() $K_{Y}$
is the pullback of an ample
$K_{Y}$
is the pullback of an ample
![]() $\mathbb{Q}$
-divisor on
$\mathbb{Q}$
-divisor on
![]() $C$
. In particular, this means that
$C$
. In particular, this means that
![]() $Y$
is a minimal model of
$Y$
is a minimal model of
![]() $W$
globally, not just over
$W$
globally, not just over
![]() $C$
.
$C$
.
From the above arguments, we have that
![]() $K_{Y}$
is semi-ample. So if
$K_{Y}$
is semi-ample. So if
![]() $X$
is a minimal model of
$X$
is a minimal model of
![]() $W$
, then
$W$
, then
![]() $K_{X}$
is semi-ample too by a standard argument using the negativity lemma, the pullback of
$K_{X}$
is semi-ample too by a standard argument using the negativity lemma, the pullback of
![]() $K_{X}$
and
$K_{X}$
and
![]() $K_{Y}$
coincide on any common resolution of
$K_{Y}$
coincide on any common resolution of
![]() $X$
and
$X$
and
![]() $Y$
(cf. [Reference Birkar4, Remark 2.7]). Therefore, the Iitaka fibration
$Y$
(cf. [Reference Birkar4, Remark 2.7]). Therefore, the Iitaka fibration
 $X{\dashrightarrow}C$
is a morphism, and
$X{\dashrightarrow}C$
is a morphism, and
 $K_{X}{\sim}_{\mathbb{Q}}0/C$
as claimed. ◻
$K_{X}{\sim}_{\mathbb{Q}}0/C$
as claimed. ◻
5 Kodaira dimensions
In this section we prove some results on Kodaira dimensions which will be used in the proof of Theorem 1.2.
Proposition 5.1. Let
 $f:X\rightarrow Z$
be a contraction from a smooth projective variety onto a smooth projective curve over an algebraically closed field
$f:X\rightarrow Z$
be a contraction from a smooth projective variety onto a smooth projective curve over an algebraically closed field
![]() $k$
of char
$k$
of char
![]() $p>0$
. Assume there is an integer
$p>0$
. Assume there is an integer
![]() $m>1$
such that
$m>1$
such that
 $f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is a nonzero nef vector bundle. If either
$f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is a nonzero nef vector bundle. If either
-
(1)
 $g(Z)>1$
; or
$g(Z)>1$
; or -
(2)
 $g(Z)=1$
and
$g(Z)=1$
and
 $\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})>0$
;
$\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})>0$
;
then
 $\unicode[STIX]{x1D705}(K_{X})\geqslant \unicode[STIX]{x1D705}(K_{F})+1$
where
$\unicode[STIX]{x1D705}(K_{X})\geqslant \unicode[STIX]{x1D705}(K_{F})+1$
where
![]() $F$
denotes the generic fiber.
$F$
denotes the generic fiber.
Proof. (1) Since
 $f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is nef,
$f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is nef,
 $f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})\otimes {\mathcal{O}}_{Z}(P)$
is ample where
$f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})\otimes {\mathcal{O}}_{Z}(P)$
is ample where
![]() $P$
is a closed point on
$P$
is a closed point on
![]() $Z$
. So for sufficiently divisible positive integer
$Z$
. So for sufficiently divisible positive integer
![]() $l$
, the sheaf
$l$
, the sheaf
 $S^{l}(f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})\otimes {\mathcal{O}}_{Z}(P))$
is globally generated. Considering the natural homomorphism
$S^{l}(f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})\otimes {\mathcal{O}}_{Z}(P))$
is globally generated. Considering the natural homomorphism
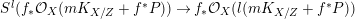 $S^{l}(f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z}+f^{\ast }P))\rightarrow f_{\ast }{\mathcal{O}}_{X}(l(mK_{X/Z}+f^{\ast }P))$
which is nonzero, we conclude that the divisor
$S^{l}(f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z}+f^{\ast }P))\rightarrow f_{\ast }{\mathcal{O}}_{X}(l(mK_{X/Z}+f^{\ast }P))$
which is nonzero, we conclude that the divisor
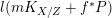 $l(mK_{X/Z}+f^{\ast }P)$
is linearly equivalent to an effective Cartier divisor.
$l(mK_{X/Z}+f^{\ast }P)$
is linearly equivalent to an effective Cartier divisor.
As
 $g(Z)>1$
, we can write
$g(Z)>1$
, we can write
 $K_{Z}\sim P+N$
where
$K_{Z}\sim P+N$
where
![]() $N$
is an effective divisor. Then
$N$
is an effective divisor. Then
 $$\begin{eqnarray}lmK_{X}\sim l(mK_{X/Z}+f^{\ast }P)+(m-1)lf^{\ast }P+lmN.\end{eqnarray}$$
$$\begin{eqnarray}lmK_{X}\sim l(mK_{X/Z}+f^{\ast }P)+(m-1)lf^{\ast }P+lmN.\end{eqnarray}$$
Applying Lemma 2.20 we are done in this case.
(2) Let
 $r=\text{rank }f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
. Let
$r=\text{rank }f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
. Let
![]() $d>r$
be an integer not divisible by
$d>r$
be an integer not divisible by
![]() $p$
. With
$p$
. With
![]() $Z$
seen as an abelian variety, the morphism
$Z$
seen as an abelian variety, the morphism
 $Z^{\prime }=Z\xrightarrow[{}]{\times d}Z$
is an étale cover of degree
$Z^{\prime }=Z\xrightarrow[{}]{\times d}Z$
is an étale cover of degree
![]() $d^{2}$
by [Reference Mumford34, Section 6]. Consider the base change
$d^{2}$
by [Reference Mumford34, Section 6]. Consider the base change
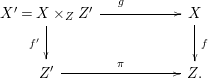
Since
![]() $\unicode[STIX]{x1D70B}$
is flat, we have
$\unicode[STIX]{x1D70B}$
is flat, we have
 $K_{X^{\prime }/Z^{\prime }}=g^{\ast }K_{X/Z}$
by [Reference Hartshorne18, Theorem 8.7] and
$K_{X^{\prime }/Z^{\prime }}=g^{\ast }K_{X/Z}$
by [Reference Hartshorne18, Theorem 8.7] and
 $f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})\cong \unicode[STIX]{x1D70B}^{\ast }f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
by [Reference Hartshorne19, Proposition 9.3]. By Riemann–Roch for vector bundles over a curve, we have
$f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})\cong \unicode[STIX]{x1D70B}^{\ast }f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
by [Reference Hartshorne19, Proposition 9.3]. By Riemann–Roch for vector bundles over a curve, we have
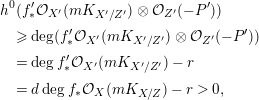 $$\begin{eqnarray}\displaystyle & & \displaystyle h^{0}(f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})\otimes {\mathcal{O}}_{Z^{\prime }}(-P^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \deg (f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})\otimes {\mathcal{O}}_{Z^{\prime }}(-P^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad =\deg f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})-r\nonumber\\ \displaystyle & & \displaystyle \quad =d\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})-r>0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle h^{0}(f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})\otimes {\mathcal{O}}_{Z^{\prime }}(-P^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \deg (f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})\otimes {\mathcal{O}}_{Z^{\prime }}(-P^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad =\deg f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }/Z^{\prime }})-r\nonumber\\ \displaystyle & & \displaystyle \quad =d\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})-r>0,\nonumber\end{eqnarray}$$
where
![]() $P^{\prime }\in Z^{\prime }$
is a closed point. So
$P^{\prime }\in Z^{\prime }$
is a closed point. So
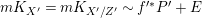 $mK_{X^{\prime }}=mK_{X^{\prime }/Z^{\prime }}\sim {f^{\prime }}^{\ast }P^{\prime }+E$
for some effective divisor
$mK_{X^{\prime }}=mK_{X^{\prime }/Z^{\prime }}\sim {f^{\prime }}^{\ast }P^{\prime }+E$
for some effective divisor
![]() $E$
on
$E$
on
![]() $X^{\prime }$
. Then
$X^{\prime }$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})=\unicode[STIX]{x1D705}(K_{X^{\prime }})=\unicode[STIX]{x1D705}(K_{X^{\prime }}+{f^{\prime }}^{\ast }P^{\prime })\geqslant \unicode[STIX]{x1D705}(K_{F^{\prime }})+1=\unicode[STIX]{x1D705}(K_{F})+1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})=\unicode[STIX]{x1D705}(K_{X^{\prime }})=\unicode[STIX]{x1D705}(K_{X^{\prime }}+{f^{\prime }}^{\ast }P^{\prime })\geqslant \unicode[STIX]{x1D705}(K_{F^{\prime }})+1=\unicode[STIX]{x1D705}(K_{F})+1\end{eqnarray}$$
by Lemma 2.20 where
![]() $F^{\prime }$
is the generic fiber of
$F^{\prime }$
is the generic fiber of
![]() $f^{\prime }$
. ◻
$f^{\prime }$
. ◻
Proposition 5.2. Let
 $f:X\rightarrow Z$
be a contraction from a normal
$f:X\rightarrow Z$
be a contraction from a normal
![]() $\mathbb{Q}$
-factorial projective variety to an elliptic curve over
$\mathbb{Q}$
-factorial projective variety to an elliptic curve over
![]() $\bar{\mathbb{F}}_{p}$
. Assume that
$\bar{\mathbb{F}}_{p}$
. Assume that
 $f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})$
is a nonzero nef vector bundle for some
$f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})$
is a nonzero nef vector bundle for some
![]() $l>0$
. Then
$l>0$
. Then
 $\unicode[STIX]{x1D705}(K_{X})\geqslant 0$
.
$\unicode[STIX]{x1D705}(K_{X})\geqslant 0$
.
Proof. If
 $\deg f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})>0$
, then
$\deg f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})>0$
, then
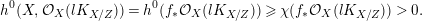 $$\begin{eqnarray}h^{0}(X,{\mathcal{O}}_{X}(lK_{X/Z}))=h^{0}(f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))\geqslant \unicode[STIX]{x1D712}(f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))>0.\end{eqnarray}$$
$$\begin{eqnarray}h^{0}(X,{\mathcal{O}}_{X}(lK_{X/Z}))=h^{0}(f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))\geqslant \unicode[STIX]{x1D712}(f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))>0.\end{eqnarray}$$
So we can assume
 $\deg f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})=0$
. By [Reference Atiyah1, Part II, Theorem 5], the vector bundle
$\deg f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})=0$
. By [Reference Atiyah1, Part II, Theorem 5], the vector bundle
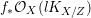 $f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})$
can be decomposed into a direct sum
$f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})$
can be decomposed into a direct sum
 $\bigoplus _{i}V_{i}\otimes L_{i}$
where
$\bigoplus _{i}V_{i}\otimes L_{i}$
where
![]() $V_{i}$
are nef indecomposable vector bundles with
$V_{i}$
are nef indecomposable vector bundles with
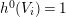 $h^{0}(V_{i})=1$
and
$h^{0}(V_{i})=1$
and
![]() $L_{i}$
are line bundles with
$L_{i}$
are line bundles with
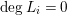 $\deg L_{i}=0$
. Since we work over
$\deg L_{i}=0$
. Since we work over
![]() $\bar{\mathbb{F}}_{p}$
,
$\bar{\mathbb{F}}_{p}$
,
![]() $L_{1}$
is torsion, say of order
$L_{1}$
is torsion, say of order
![]() $n$
. We have a cover
$n$
. We have a cover
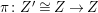 $\unicode[STIX]{x1D70B}:Z^{\prime }\cong Z\rightarrow Z$
between elliptic curves induced by the dual map
$\unicode[STIX]{x1D70B}:Z^{\prime }\cong Z\rightarrow Z$
between elliptic curves induced by the dual map
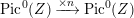 $\text{Pic}^{0}(Z)\xrightarrow[{}]{\times n}\text{Pic}^{0}(Z)$
. Then
$\text{Pic}^{0}(Z)\xrightarrow[{}]{\times n}\text{Pic}^{0}(Z)$
. Then
 $\unicode[STIX]{x1D70B}^{\ast }L_{1}\sim {\mathcal{O}}_{Z^{\prime }}$
, and
$\unicode[STIX]{x1D70B}^{\ast }L_{1}\sim {\mathcal{O}}_{Z^{\prime }}$
, and
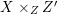 $X\times _{Z}Z^{\prime }$
is integral since
$X\times _{Z}Z^{\prime }$
is integral since
![]() $\unicode[STIX]{x1D70B}$
is flat and
$\unicode[STIX]{x1D70B}$
is flat and
![]() $f$
is separable. Let
$f$
is separable. Let
![]() $X^{\prime }$
be the normalization of the fiber product
$X^{\prime }$
be the normalization of the fiber product
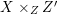 $X\times _{Z}Z^{\prime }$
. Consider the natural morphisms
$X\times _{Z}Z^{\prime }$
. Consider the natural morphisms
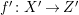 $f^{\prime }:X^{\prime }\rightarrow Z^{\prime }$
and
$f^{\prime }:X^{\prime }\rightarrow Z^{\prime }$
and
 $\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow X$
. Then we have a natural inclusion
$\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow X$
. Then we have a natural inclusion
 $\unicode[STIX]{x1D70B}^{\ast }f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})\subseteq f_{\ast }^{\prime }({\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))$
by [Reference Hartshorne19, Proposition 9.3]. So
$\unicode[STIX]{x1D70B}^{\ast }f_{\ast }{\mathcal{O}}_{X}(lK_{X/Z})\subseteq f_{\ast }^{\prime }({\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))$
by [Reference Hartshorne19, Proposition 9.3]. So
 $f_{\ast }^{\prime }({\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))$
contains
$f_{\ast }^{\prime }({\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))$
contains
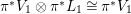 $\unicode[STIX]{x1D70B}^{\ast }V_{1}\otimes \unicode[STIX]{x1D70B}^{\ast }L_{1}\cong \unicode[STIX]{x1D70B}^{\ast }V_{1}$
. Hence
$\unicode[STIX]{x1D70B}^{\ast }V_{1}\otimes \unicode[STIX]{x1D70B}^{\ast }L_{1}\cong \unicode[STIX]{x1D70B}^{\ast }V_{1}$
. Hence
 $$\begin{eqnarray}h^{0}(X^{\prime },{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))=h^{0}(Z^{\prime },f_{\ast }^{\prime }({\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z})))\geqslant h^{0}(Z^{\prime },\unicode[STIX]{x1D70B}^{\ast }V_{1})\geqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}h^{0}(X^{\prime },{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))=h^{0}(Z^{\prime },f_{\ast }^{\prime }({\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z})))\geqslant h^{0}(Z^{\prime },\unicode[STIX]{x1D70B}^{\ast }V_{1})\geqslant 1.\end{eqnarray}$$
By Theorem 2.22, we have
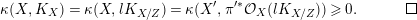 $$\begin{eqnarray}\unicode[STIX]{x1D705}(X,K_{X})=\unicode[STIX]{x1D705}(X,lK_{X/Z})=\unicode[STIX]{x1D705}(X^{\prime },{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))\geqslant 0.\square\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(X,K_{X})=\unicode[STIX]{x1D705}(X,lK_{X/Z})=\unicode[STIX]{x1D705}(X^{\prime },{\unicode[STIX]{x1D70B}^{\prime }}^{\ast }{\mathcal{O}}_{X}(lK_{X/Z}))\geqslant 0.\square\end{eqnarray}$$
Proposition 5.3. Let
 $f:X\rightarrow Z$
be a contraction from a projective
$f:X\rightarrow Z$
be a contraction from a projective
![]() $3$
-fold with
$3$
-fold with
![]() $\mathbb{Q}$
-factorial terminal singularities to an elliptic curve over
$\mathbb{Q}$
-factorial terminal singularities to an elliptic curve over
![]() $\bar{\mathbb{F}}_{p}$
with
$\bar{\mathbb{F}}_{p}$
with
![]() $p>5$
. Assume that
$p>5$
. Assume that
![]() $K_{X}$
is big over
$K_{X}$
is big over
![]() $Z$
and that the generic fiber of
$Z$
and that the generic fiber of
![]() $f$
is smooth. Then
$f$
is smooth. Then
 $\unicode[STIX]{x1D705}(X)\geqslant 2$
.
$\unicode[STIX]{x1D705}(X)\geqslant 2$
.
Proof. We break the proof into several steps.
Step 1. By Theorem 2.7, there is a minimal model
![]() $Y$
of
$Y$
of
![]() $X$
over
$X$
over
![]() $Z$
. Since
$Z$
. Since
![]() $Y$
has terminal singularities, the generic fiber of
$Y$
has terminal singularities, the generic fiber of
![]() $Y\rightarrow Z$
is also smooth. Replacing
$Y\rightarrow Z$
is also smooth. Replacing
![]() $X$
with
$X$
with
![]() $Y$
, we can assume
$Y$
, we can assume
![]() $K_{X}$
is nef
$K_{X}$
is nef
![]() $/Z$
. Since
$/Z$
. Since
![]() $Z$
is an elliptic curve,
$Z$
is an elliptic curve,
![]() $K_{X}$
is actually globally nef by the cone theorem [Reference Birkar and Waldron6, Theorem 1.1], because otherwise there will exist a rational curve
$K_{X}$
is actually globally nef by the cone theorem [Reference Birkar and Waldron6, Theorem 1.1], because otherwise there will exist a rational curve
![]() $\unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6E4}$
such that
 $K_{X}\cdot \unicode[STIX]{x1D6E4}<0$
, and
$K_{X}\cdot \unicode[STIX]{x1D6E4}<0$
, and
![]() $\unicode[STIX]{x1D6E4}$
must be contained one fiber of
$\unicode[STIX]{x1D6E4}$
must be contained one fiber of
![]() $f$
since
$f$
since
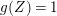 $g(Z)=1$
, which, however, contradicts that
$g(Z)=1$
, which, however, contradicts that
![]() $X$
is minimal over
$X$
is minimal over
![]() $Z$
.
$Z$
.
Step 2. Let
![]() $X^{\prime }$
be the relative canonical model of
$X^{\prime }$
be the relative canonical model of
![]() $X$
over
$X$
over
![]() $Z$
which exists by Theorem 2.7. So
$Z$
which exists by Theorem 2.7. So
![]() $K_{X^{\prime }}$
is ample over
$K_{X^{\prime }}$
is ample over
![]() $Z$
. Since the geometric generic fiber
$Z$
. Since the geometric generic fiber
![]() $X_{\bar{\unicode[STIX]{x1D702}}}$
of
$X_{\bar{\unicode[STIX]{x1D702}}}$
of
![]() $f$
is smooth, the geometric generic fiber
$f$
is smooth, the geometric generic fiber
![]() $X_{\bar{\unicode[STIX]{x1D702}}}^{\prime }$
of
$X_{\bar{\unicode[STIX]{x1D702}}}^{\prime }$
of
![]() $f^{\prime }$
coincides with the canonical model of
$f^{\prime }$
coincides with the canonical model of
![]() $X_{\bar{\unicode[STIX]{x1D702}}}$
, and has canonical singularities which are strongly
$X_{\bar{\unicode[STIX]{x1D702}}}$
, and has canonical singularities which are strongly
![]() $F$
-regular since
$F$
-regular since
 $\text{char}k=p>5$
by [Reference Hara17]. Therefore, by Theorem 2.12,
$\text{char}k=p>5$
by [Reference Hara17]. Therefore, by Theorem 2.12,
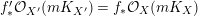 $f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }})=f_{\ast }{\mathcal{O}}_{X}(mK_{X})$
is a nef vector bundle for any sufficiently divisible
$f_{\ast }^{\prime }{\mathcal{O}}_{X^{\prime }}(mK_{X^{\prime }})=f_{\ast }{\mathcal{O}}_{X}(mK_{X})$
is a nef vector bundle for any sufficiently divisible
![]() $m>0$
.
$m>0$
.
If
 $\unicode[STIX]{x1D708}(K_{X})=3$
, then
$\unicode[STIX]{x1D708}(K_{X})=3$
, then
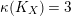 $\unicode[STIX]{x1D705}(K_{X})=3$
, so there is nothing to prove. On the other hand, if
$\unicode[STIX]{x1D705}(K_{X})=3$
, so there is nothing to prove. On the other hand, if
 $f_{\ast }{\mathcal{O}}_{X}(mK_{X})$
is nef with
$f_{\ast }{\mathcal{O}}_{X}(mK_{X})$
is nef with
 $\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X})>0$
for some
$\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X})>0$
for some
![]() $m>0$
, then we are done by applying Proposition 5.1 to a resolution of
$m>0$
, then we are done by applying Proposition 5.1 to a resolution of
![]() $X$
. So in the following we assume
$X$
. So in the following we assume
 $\unicode[STIX]{x1D708}(K_{X})=2$
and that
$\unicode[STIX]{x1D708}(K_{X})=2$
and that
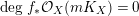 $\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X})=0$
for any sufficiently divisible positive integer
$\deg f_{\ast }{\mathcal{O}}_{X}(mK_{X})=0$
for any sufficiently divisible positive integer
![]() $m$
.
$m$
.
Step 3. Applying Proposition 5.2 and Step 2, we find a positive integer
![]() $l$
and a divisor
$l$
and a divisor
![]() $M\geqslant 0$
such that
$M\geqslant 0$
such that
 $lK_{X}\sim M$
and that
$lK_{X}\sim M$
and that
 $f_{\ast }{\mathcal{O}}_{X}(klK_{X})$
is nef for any
$f_{\ast }{\mathcal{O}}_{X}(klK_{X})$
is nef for any
![]() $k\geqslant 1$
. We prove that
$k\geqslant 1$
. We prove that
![]() $K_{X}|_{M}$
is semi-ample.
$K_{X}|_{M}$
is semi-ample.
Let
![]() $T$
be a horizontal
$T$
be a horizontal
![]() $/Z$
component of
$/Z$
component of
![]() $M$
. We show that
$M$
. We show that
![]() $K_{X}|_{T}$
is semi-ample. Take the normalization
$K_{X}|_{T}$
is semi-ample. Take the normalization
![]() $S\rightarrow T$
, and let
$S\rightarrow T$
, and let
![]() $C\subset S$
be the reduction of the conductor. Write
$C\subset S$
be the reduction of the conductor. Write
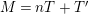 $M=nT+T^{\prime }$
where
$M=nT+T^{\prime }$
where
![]() $T$
is not a component of
$T$
is not a component of
![]() $T^{\prime }$
. By adjunction [Reference Keel26, 5.3], we have
$T^{\prime }$
. By adjunction [Reference Keel26, 5.3], we have
 $$\begin{eqnarray}\left.\left(K_{X}+\frac{M}{n}\right)\right|_{S}{\sim}_{\mathbb{Q}}K_{S}+C+D\end{eqnarray}$$
$$\begin{eqnarray}\left.\left(K_{X}+\frac{M}{n}\right)\right|_{S}{\sim}_{\mathbb{Q}}K_{S}+C+D\end{eqnarray}$$
where
![]() $D$
is a canonically defined effective
$D$
is a canonically defined effective
![]() $\mathbb{Q}$
-divisor and
$\mathbb{Q}$
-divisor and
![]() $|_{S}$
means pullback to
$|_{S}$
means pullback to
![]() $S$
. Then
$S$
. Then
![]() $K_{X}|_{S}$
is semi-ample on
$K_{X}|_{S}$
is semi-ample on
![]() $S$
by Theorem 2.10.
$S$
by Theorem 2.10.
We want to argue that semi-ampleness of
![]() $K_{X}|_{S}$
implies semi-ampleness of
$K_{X}|_{S}$
implies semi-ampleness of
![]() $K_{X}|_{T}$
. Since
$K_{X}|_{T}$
. Since
![]() $K_{X}$
is nef and
$K_{X}$
is nef and
 $K_{X}^{3}=0$
, we have
$K_{X}^{3}=0$
, we have
 $K_{X}^{2}\cdot T=0$
, that is,
$K_{X}^{2}\cdot T=0$
, that is,
 $(K_{X}|_{T})^{2}=0$
, thus
$(K_{X}|_{T})^{2}=0$
, thus
 $(K_{X}|_{S})^{2}=0$
.
$(K_{X}|_{S})^{2}=0$
.
If
 $\unicode[STIX]{x1D708}(K_{X}|_{S})=0$
, then
$\unicode[STIX]{x1D708}(K_{X}|_{S})=0$
, then
 $K_{X}|_{S}{\sim}_{\mathbb{Q}}0$
, that is, the associated map is trivial, hence
$K_{X}|_{S}{\sim}_{\mathbb{Q}}0$
, that is, the associated map is trivial, hence
![]() $K_{X}|_{T}$
is semi-ample by [Reference Keel26, Corollary 2.14].
$K_{X}|_{T}$
is semi-ample by [Reference Keel26, Corollary 2.14].
If
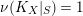 $\unicode[STIX]{x1D708}(K_{X}|_{S})=1$
. We denote by
$\unicode[STIX]{x1D708}(K_{X}|_{S})=1$
. We denote by
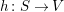 $h:S\rightarrow V$
the map associated to
$h:S\rightarrow V$
the map associated to
![]() $K_{X}|_{S}$
and denote by
$K_{X}|_{S}$
and denote by
![]() $H$
a general fiber, which has genus
$H$
a general fiber, which has genus
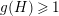 $g(H)\geqslant 1$
because it dominates
$g(H)\geqslant 1$
because it dominates
![]() $Z$
. As
$Z$
. As
 $K_{X}|_{S}\cdot H=0$
, we have
$K_{X}|_{S}\cdot H=0$
, we have
 $(K_{S}+C+D)\cdot H=0$
, hence
$(K_{S}+C+D)\cdot H=0$
, hence
 $$\begin{eqnarray}0\leqslant \deg K_{H}=(K_{S}+H)\cdot H=K_{S}\cdot H=-(C+D)\cdot H\leqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant \deg K_{H}=(K_{S}+H)\cdot H=K_{S}\cdot H=-(C+D)\cdot H\leqslant 0.\end{eqnarray}$$
Therefore,
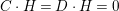 $C\cdot H=D\cdot H=0$
, and
$C\cdot H=D\cdot H=0$
, and
![]() $H$
is smooth with arithmetic genus
$H$
is smooth with arithmetic genus
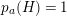 $p_{a}(H)=1$
. Applying [Reference Keel26, Corollary 2.14] again, we conclude that
$p_{a}(H)=1$
. Applying [Reference Keel26, Corollary 2.14] again, we conclude that
![]() $K_{X}|_{T}$
is semi-ample, and the associated map
$K_{X}|_{T}$
is semi-ample, and the associated map
 $\bar{h}:T\rightarrow \bar{V}$
is an elliptic fibration. In particular, this means that no component of
$\bar{h}:T\rightarrow \bar{V}$
is an elliptic fibration. In particular, this means that no component of
![]() $T^{\prime }$
intersects the general fibers of
$T^{\prime }$
intersects the general fibers of
![]() $\bar{h}$
.
$\bar{h}$
.
Let
![]() $R_{0}$
be the union of the vertical
$R_{0}$
be the union of the vertical
![]() $/Z$
components of
$/Z$
components of
![]() $M$
. Then since
$M$
. Then since
![]() $K_{X}$
is
$K_{X}$
is
![]() $f$
-semi-ample by Theorem 2.7, the restriction
$f$
-semi-ample by Theorem 2.7, the restriction
![]() $K_{X}|_{R_{0}}$
is semi-ample. Let
$K_{X}|_{R_{0}}$
is semi-ample. Let
![]() $R\leqslant M$
be a reduced divisor containing
$R\leqslant M$
be a reduced divisor containing
![]() $R_{0}$
and assume that
$R_{0}$
and assume that
![]() $K_{X}|_{R}$
is semi-ample. If
$K_{X}|_{R}$
is semi-ample. If
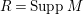 $R=\text{Supp}\,M$
, then
$R=\text{Supp}\,M$
, then
![]() $K_{X}|_{M}$
is semi-ample by [Reference Keel26, Lemma 1.4]. If not, pick a horizontal
$K_{X}|_{M}$
is semi-ample by [Reference Keel26, Lemma 1.4]. If not, pick a horizontal
![]() $/Z$
component
$/Z$
component
![]() $T$
of
$T$
of
![]() $M$
which is not a component of
$M$
which is not a component of
![]() $R$
. As noted above,
$R$
. As noted above,
![]() $K_{X}|_{T}$
is semi-ample defining a contraction
$K_{X}|_{T}$
is semi-ample defining a contraction
 $\bar{h}:T\rightarrow \bar{V}$
such that, either
$\bar{h}:T\rightarrow \bar{V}$
such that, either
 $\bar{V}=\text{spec}~k$
, or
$\bar{V}=\text{spec}~k$
, or
 $\dim \bar{V}=1$
and general fibers of
$\dim \bar{V}=1$
and general fibers of
![]() $\bar{h}$
do not intersect any component of
$\bar{h}$
do not intersect any component of
![]() $R$
. Applying [Reference Keel26, Corollary 2.12], we deduce that
$R$
. Applying [Reference Keel26, Corollary 2.12], we deduce that
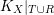 $K_{X}|_{T\cup R}$
is semi-ample. Inductively, we extend
$K_{X}|_{T\cup R}$
is semi-ample. Inductively, we extend
![]() $R$
to the support of
$R$
to the support of
![]() $M$
.
$M$
.
Step 4. In this step we prove
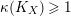 $\unicode[STIX]{x1D705}(K_{X})\geqslant 1$
. Consider the following exact sequence
$\unicode[STIX]{x1D705}(K_{X})\geqslant 1$
. Consider the following exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{X}((k-1)M)\rightarrow {\mathcal{O}}_{X}(kM)\rightarrow {\mathcal{O}}_{M}(kM)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{X}((k-1)M)\rightarrow {\mathcal{O}}_{X}(kM)\rightarrow {\mathcal{O}}_{M}(kM)\rightarrow 0.\end{eqnarray}$$
For
![]() $k\geqslant 2$
, by assumptions in Step 2, both
$k\geqslant 2$
, by assumptions in Step 2, both
 $f_{\ast }{\mathcal{O}}_{X}(kM)$
and
$f_{\ast }{\mathcal{O}}_{X}(kM)$
and
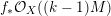 $f_{\ast }{\mathcal{O}}_{X}((k-1)M)$
are nef vector bundles with
$f_{\ast }{\mathcal{O}}_{X}((k-1)M)$
are nef vector bundles with
 $$\begin{eqnarray}\deg f_{\ast }{\mathcal{O}}_{X}(kM)=\deg f_{\ast }{\mathcal{O}}_{X}((k-1)M)=0.\end{eqnarray}$$
$$\begin{eqnarray}\deg f_{\ast }{\mathcal{O}}_{X}(kM)=\deg f_{\ast }{\mathcal{O}}_{X}((k-1)M)=0.\end{eqnarray}$$
If
 $$\begin{eqnarray}h^{0}(f_{\ast }{\mathcal{O}}_{X}(kM))=h^{0}(f_{\ast }{\mathcal{O}}_{X}((k-1)M))=1\end{eqnarray}$$
$$\begin{eqnarray}h^{0}(f_{\ast }{\mathcal{O}}_{X}(kM))=h^{0}(f_{\ast }{\mathcal{O}}_{X}((k-1)M))=1\end{eqnarray}$$
for all
![]() $k\geqslant 2$
, then
$k\geqslant 2$
, then
 $h^{1}(f_{\ast }{\mathcal{O}}_{X}((k-1)M))=1$
for such
$h^{1}(f_{\ast }{\mathcal{O}}_{X}((k-1)M))=1$
for such
![]() $k$
by Riemann–Roch, and by taking cohomology of the exact sequence (5.3.1), we conclude that
$k$
by Riemann–Roch, and by taking cohomology of the exact sequence (5.3.1), we conclude that
 $h^{0}({\mathcal{O}}_{M}(kM))\leqslant 1$
. However, this contradicts semi-ampleness of
$h^{0}({\mathcal{O}}_{M}(kM))\leqslant 1$
. However, this contradicts semi-ampleness of
![]() $M|_{M}$
and the property
$M|_{M}$
and the property
 $\unicode[STIX]{x1D708}(M|_{M})\geqslant 1$
. Therefore,
$\unicode[STIX]{x1D708}(M|_{M})\geqslant 1$
. Therefore,
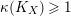 $\unicode[STIX]{x1D705}(K_{X})\geqslant 1$
.
$\unicode[STIX]{x1D705}(K_{X})\geqslant 1$
.
Step 5. Assume
 $\unicode[STIX]{x1D705}(K_{X})=1$
. We derive a contradiction. Let
$\unicode[STIX]{x1D705}(K_{X})=1$
. We derive a contradiction. Let
 $W\rightarrow X$
be a resolution so that the Iitaka fibration
$W\rightarrow X$
be a resolution so that the Iitaka fibration
 $W\rightarrow C$
is a morphism. By Corollary 4.1, the induced map
$W\rightarrow C$
is a morphism. By Corollary 4.1, the induced map
 $X{\dashrightarrow}C$
is a morphism and
$X{\dashrightarrow}C$
is a morphism and
 $K_{X}{\sim}_{\mathbb{Q}}0/C$
. In particular,
$K_{X}{\sim}_{\mathbb{Q}}0/C$
. In particular,
 $\unicode[STIX]{x1D708}(K_{X})=1$
which contradicts the assumption
$\unicode[STIX]{x1D708}(K_{X})=1$
which contradicts the assumption
 $\unicode[STIX]{x1D708}(K_{X})=2$
. ◻
$\unicode[STIX]{x1D708}(K_{X})=2$
. ◻
6 Proof of Theorem 1.2
Proof of Theorem 1.2.
We can assume
 $\unicode[STIX]{x1D705}(K_{Z})\geqslant 0$
and
$\unicode[STIX]{x1D705}(K_{Z})\geqslant 0$
and
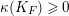 $\unicode[STIX]{x1D705}(K_{F})\geqslant 0$
. As pointed out in the introduction
$\unicode[STIX]{x1D705}(K_{F})\geqslant 0$
. As pointed out in the introduction
![]() $C_{3,2}$
follows from [Reference Chen and Zhang13], so we assume
$C_{3,2}$
follows from [Reference Chen and Zhang13], so we assume
![]() $n=3$
and
$n=3$
and
![]() $m=1$
. Replacing
$m=1$
. Replacing
![]() $X$
with a minimal model over
$X$
with a minimal model over
![]() $Z$
, we can assume
$Z$
, we can assume
![]() $K_{X}$
is
$K_{X}$
is
![]() $\text{nef}/Z$
. Of course
$\text{nef}/Z$
. Of course
![]() $X$
may not be smooth any more but it has
$X$
may not be smooth any more but it has
![]() $\mathbb{Q}$
-factorial terminal singularities. The generic fiber stays smooth by the arguments in Step 1 of the proof of Theorem 5.3.
$\mathbb{Q}$
-factorial terminal singularities. The generic fiber stays smooth by the arguments in Step 1 of the proof of Theorem 5.3.
If
 $\unicode[STIX]{x1D705}(K_{F})=0$
, then by Theorem 1.6 and Lemma 2.18,
$\unicode[STIX]{x1D705}(K_{F})=0$
, then by Theorem 1.6 and Lemma 2.18,
 $K_{X/Z}{\sim}_{\mathbb{Q}}f^{\ast }M$
for some
$K_{X/Z}{\sim}_{\mathbb{Q}}f^{\ast }M$
for some
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $M$
. Moreover, by Theorem 2.12,
$M$
. Moreover, by Theorem 2.12,
![]() $K_{X/Z}$
is nef, hence
$K_{X/Z}$
is nef, hence
 $\deg M\geqslant 0$
which implies
$\deg M\geqslant 0$
which implies
 $\unicode[STIX]{x1D705}(M)\geqslant 0$
as we are working over
$\unicode[STIX]{x1D705}(M)\geqslant 0$
as we are working over
![]() $\bar{\mathbb{F}}_{p}$
. Thus
$\bar{\mathbb{F}}_{p}$
. Thus
 $\unicode[STIX]{x1D705}(K_{X/Z})\geqslant 0$
and
$\unicode[STIX]{x1D705}(K_{X/Z})\geqslant 0$
and
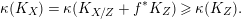 $$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})=\unicode[STIX]{x1D705}(K_{X/Z}+f^{\ast }K_{Z})\geqslant \unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X})=\unicode[STIX]{x1D705}(K_{X/Z}+f^{\ast }K_{Z})\geqslant \unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
If
 $\unicode[STIX]{x1D705}(K_{F})=1$
, then
$\unicode[STIX]{x1D705}(K_{F})=1$
, then
![]() $K_{F}$
is semi-ample by Theorem 1.5. We claim that the geometric generic fiber of the Iitaka fibration
$K_{F}$
is semi-ample by Theorem 1.5. We claim that the geometric generic fiber of the Iitaka fibration
 $I:F\rightarrow C$
is a smooth elliptic curve. Indeed, denote by
$I:F\rightarrow C$
is a smooth elliptic curve. Indeed, denote by
 $\bar{F}=F\otimes _{K(Z)}\overline{K(Z)}$
the geometric generic fiber of
$\bar{F}=F\otimes _{K(Z)}\overline{K(Z)}$
the geometric generic fiber of
![]() $f$
. Since
$f$
. Since
 $\text{char}~k=p>5$
, the geometric generic fiber of the Iitaka fibration
$\text{char}~k=p>5$
, the geometric generic fiber of the Iitaka fibration
 $\bar{I}:\bar{F}\rightarrow \bar{C}$
is a smooth elliptic curve by [Reference Badescu2, Theorem 7.18]. For any sufficiently divisible positive integer
$\bar{I}:\bar{F}\rightarrow \bar{C}$
is a smooth elliptic curve by [Reference Badescu2, Theorem 7.18]. For any sufficiently divisible positive integer
![]() $n$
, since
$n$
, since
 $H^{0}(\bar{F},nK_{\bar{F}})\cong H^{0}(F,nK_{F})\otimes _{K(Z)}\overline{K(Z)}$
, we see that
$H^{0}(\bar{F},nK_{\bar{F}})\cong H^{0}(F,nK_{F})\otimes _{K(Z)}\overline{K(Z)}$
, we see that
 $\bar{I}:\bar{F}\rightarrow \bar{C}$
coincides with the base change of the morphism
$\bar{I}:\bar{F}\rightarrow \bar{C}$
coincides with the base change of the morphism
 $I:F\rightarrow C$
via
$I:F\rightarrow C$
via
 $\text{spec}~\overline{K(Z)}\rightarrow \text{spec}~K(Z)$
. Thus the geometric generic fiber of
$\text{spec}~\overline{K(Z)}\rightarrow \text{spec}~K(Z)$
. Thus the geometric generic fiber of
![]() $I$
is a smooth elliptic curve.
$I$
is a smooth elliptic curve.
Considering the relative Iitaka fibration, blowing up
![]() $X$
if necessary, with the help of Theorem 1.6 and Lemma 2.18, we get a smooth resolution of
$X$
if necessary, with the help of Theorem 1.6 and Lemma 2.18, we get a smooth resolution of
 $\unicode[STIX]{x1D70E}:X^{\prime }\rightarrow X$
and a smooth surface
$\unicode[STIX]{x1D70E}:X^{\prime }\rightarrow X$
and a smooth surface
![]() $Y$
fitting into the following commutative diagram
$Y$
fitting into the following commutative diagram

such that
-
∙ the geometric generic fiber of
 $h$
is a smooth elliptic curve;
$h$
is a smooth elliptic curve; -
∙
 $\unicode[STIX]{x1D70E}^{\ast }K_{X}{\sim}_{\mathbb{Q}}h^{\ast }D$
where
$\unicode[STIX]{x1D70E}^{\ast }K_{X}{\sim}_{\mathbb{Q}}h^{\ast }D$
where
 $D$
is a
$D$
is a
 $g$
-big divisor on
$g$
-big divisor on
 $Y$
.
$Y$
.
By flattening trick (cf. [Reference Viehweg46, Lemma 7.3]), we can assume that every
![]() $h$
-exceptional divisor is also
$h$
-exceptional divisor is also
![]() $\unicode[STIX]{x1D70E}$
-exceptional. By Theorem 2.14, we have effective vertical (w.r.t.
$\unicode[STIX]{x1D70E}$
-exceptional. By Theorem 2.14, we have effective vertical (w.r.t.
![]() $h$
) divisors
$h$
) divisors
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}$
on
$D_{2}$
on
![]() $X^{\prime }$
such that
$X^{\prime }$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}^{\ast }K_{X}+D_{1}{\sim}_{\mathbb{Q}}K_{X^{\prime }}{\sim}_{\mathbb{Q}}h^{\ast }K_{Y}+D_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}^{\ast }K_{X}+D_{1}{\sim}_{\mathbb{Q}}K_{X^{\prime }}{\sim}_{\mathbb{Q}}h^{\ast }K_{Y}+D_{2}.\end{eqnarray}$$
Then
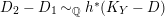 $D_{2}-D_{1}{\sim}_{\mathbb{Q}}h^{\ast }(K_{Y}-D)$
. So there exists a
$D_{2}-D_{1}{\sim}_{\mathbb{Q}}h^{\ast }(K_{Y}-D)$
. So there exists a
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $Y$
such that
$Y$
such that
 $D_{1}-D_{2}=h^{\ast }\unicode[STIX]{x1D6E5}$
. We can write that
$D_{1}-D_{2}=h^{\ast }\unicode[STIX]{x1D6E5}$
. We can write that
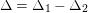 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}-\unicode[STIX]{x1D6E5}_{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}-\unicode[STIX]{x1D6E5}_{2}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
are effective divisors on
$\unicode[STIX]{x1D6E5}_{2}$
are effective divisors on
![]() $Y$
having no common components, thus are supported in
$Y$
having no common components, thus are supported in
![]() $h(D_{1})$
and
$h(D_{1})$
and
![]() $h(D_{2})$
, respectively. It follows that
$h(D_{2})$
, respectively. It follows that
 $$\begin{eqnarray}h^{\ast }D{\sim}_{\mathbb{ Q}}h^{\ast }(K_{Y}+\unicode[STIX]{x1D6E5}_{2}-\unicode[STIX]{x1D6E5}_{1})~\text{and thus}~D_{2}-D_{1}{\sim}_{\mathbb{Q}}h^{\ast }(\unicode[STIX]{x1D6E5}_{2}-\unicode[STIX]{x1D6E5}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}h^{\ast }D{\sim}_{\mathbb{ Q}}h^{\ast }(K_{Y}+\unicode[STIX]{x1D6E5}_{2}-\unicode[STIX]{x1D6E5}_{1})~\text{and thus}~D_{2}-D_{1}{\sim}_{\mathbb{Q}}h^{\ast }(\unicode[STIX]{x1D6E5}_{2}-\unicode[STIX]{x1D6E5}_{1}).\end{eqnarray}$$
Therefore,
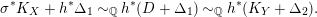 $$\begin{eqnarray}\unicode[STIX]{x1D70E}^{\ast }K_{X}+h^{\ast }\unicode[STIX]{x1D6E5}_{1}{\sim}_{\mathbb{Q}}h^{\ast }(D+\unicode[STIX]{x1D6E5}_{1}){\sim}_{\mathbb{Q}}h^{\ast }(K_{Y}+\unicode[STIX]{x1D6E5}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}^{\ast }K_{X}+h^{\ast }\unicode[STIX]{x1D6E5}_{1}{\sim}_{\mathbb{Q}}h^{\ast }(D+\unicode[STIX]{x1D6E5}_{1}){\sim}_{\mathbb{Q}}h^{\ast }(K_{Y}+\unicode[STIX]{x1D6E5}_{2}).\end{eqnarray}$$
Consider the pair
![]() $(Y,\unicode[STIX]{x1D6E5}_{2})$
. By Theorem 2.10, we obtain a minimal model
$(Y,\unicode[STIX]{x1D6E5}_{2})$
. By Theorem 2.10, we obtain a minimal model
 $(Y^{\prime },\unicode[STIX]{x1D6E5}^{\prime })$
of
$(Y^{\prime },\unicode[STIX]{x1D6E5}^{\prime })$
of
![]() $(Y,\unicode[STIX]{x1D6E5}_{2})$
such that
$(Y,\unicode[STIX]{x1D6E5}_{2})$
such that
 $K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }$
is semi-ample. Denote by
$K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }$
is semi-ample. Denote by
 $\unicode[STIX]{x1D707}:Y\rightarrow Y^{\prime }$
the natural morphism. There exists an effective
$\unicode[STIX]{x1D707}:Y\rightarrow Y^{\prime }$
the natural morphism. There exists an effective
![]() $\unicode[STIX]{x1D707}$
-exceptional divisor
$\unicode[STIX]{x1D707}$
-exceptional divisor
![]() $E$
such that
$E$
such that
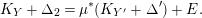 $$\begin{eqnarray}K_{Y}+\unicode[STIX]{x1D6E5}_{2}=\unicode[STIX]{x1D707}^{\ast }(K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })+E.\end{eqnarray}$$
$$\begin{eqnarray}K_{Y}+\unicode[STIX]{x1D6E5}_{2}=\unicode[STIX]{x1D707}^{\ast }(K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })+E.\end{eqnarray}$$
Since
 $D+\unicode[STIX]{x1D6E5}_{1}{\sim}_{\mathbb{Q}}K_{Y}+\unicode[STIX]{x1D6E5}_{2}$
and
$D+\unicode[STIX]{x1D6E5}_{1}{\sim}_{\mathbb{Q}}K_{Y}+\unicode[STIX]{x1D6E5}_{2}$
and
![]() $D$
is nef and
$D$
is nef and
![]() $g$
-big, we have
$g$
-big, we have
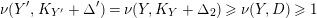 $$\begin{eqnarray}\unicode[STIX]{x1D708}(Y^{\prime },K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })=\unicode[STIX]{x1D708}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{2})\geqslant \unicode[STIX]{x1D708}(Y,D)\geqslant 1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(Y^{\prime },K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })=\unicode[STIX]{x1D708}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{2})\geqslant \unicode[STIX]{x1D708}(Y,D)\geqslant 1\end{eqnarray}$$
where the first “
![]() $=$
” is obtained by the proof of [Reference Cascini, Hacon, Mustaţǎ and Schwede9, Proposition 2.7] and the fact that
$=$
” is obtained by the proof of [Reference Cascini, Hacon, Mustaţǎ and Schwede9, Proposition 2.7] and the fact that
 $\unicode[STIX]{x1D707}_{\ast }({\mathcal{O}}_{Y}(\llcorner nE\lrcorner ))={\mathcal{O}}_{Y^{\prime }}$
for any integer
$\unicode[STIX]{x1D707}_{\ast }({\mathcal{O}}_{Y}(\llcorner nE\lrcorner ))={\mathcal{O}}_{Y^{\prime }}$
for any integer
![]() $n>0$
. So
$n>0$
. So
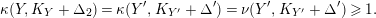 $$\begin{eqnarray}\unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{2})=\unicode[STIX]{x1D705}(Y^{\prime },K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })=\unicode[STIX]{x1D708}(Y^{\prime },K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })\geqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{2})=\unicode[STIX]{x1D705}(Y^{\prime },K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })=\unicode[STIX]{x1D708}(Y^{\prime },K_{Y^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })\geqslant 1.\end{eqnarray}$$
Observe that every component of
![]() $h^{\ast }\unicode[STIX]{x1D6E5}_{1}$
is either contained in
$h^{\ast }\unicode[STIX]{x1D6E5}_{1}$
is either contained in
![]() $D_{1}$
or
$D_{1}$
or
![]() $h$
-exceptional, thus is
$h$
-exceptional, thus is
![]() $\unicode[STIX]{x1D70E}$
-exceptional. Then applying Theorem 2.22, we conclude that
$\unicode[STIX]{x1D70E}$
-exceptional. Then applying Theorem 2.22, we conclude that
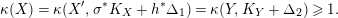 $$\begin{eqnarray}\unicode[STIX]{x1D705}(X)=\unicode[STIX]{x1D705}(X^{\prime },\unicode[STIX]{x1D70E}^{\ast }K_{X}+h^{\ast }\unicode[STIX]{x1D6E5}_{1})=\unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{2})\geqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(X)=\unicode[STIX]{x1D705}(X^{\prime },\unicode[STIX]{x1D70E}^{\ast }K_{X}+h^{\ast }\unicode[STIX]{x1D6E5}_{1})=\unicode[STIX]{x1D705}(Y,K_{Y}+\unicode[STIX]{x1D6E5}_{2})\geqslant 1.\end{eqnarray}$$
If
 $g(Z)=1$
, then we are done by the above inequality.
$g(Z)=1$
, then we are done by the above inequality.
So assume that
 $g(Z)\geqslant 2$
. If
$g(Z)\geqslant 2$
. If
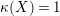 $\unicode[STIX]{x1D705}(X)=1$
, then by Corollary 4.1
$\unicode[STIX]{x1D705}(X)=1$
, then by Corollary 4.1
![]() $K_{X}$
is semi-ample, and the Iitaka fibration
$K_{X}$
is semi-ample, and the Iitaka fibration
 $I:X\rightarrow C$
is a morphism. Let
$I:X\rightarrow C$
is a morphism. Let
![]() $G$
be a general fiber of
$G$
be a general fiber of
![]() $I$
, which is integral since
$I$
, which is integral since
![]() $I$
is separable [Reference Badescu2, Lemma 7.2]. Then
$I$
is separable [Reference Badescu2, Lemma 7.2]. Then
![]() $G$
is dominant over
$G$
is dominant over
![]() $Z$
and
$Z$
and
 $K_{G}{\sim}_{\mathbb{Q}}0$
. Let
$K_{G}{\sim}_{\mathbb{Q}}0$
. Let
![]() $\tilde{G}$
be a smooth resolution of
$\tilde{G}$
be a smooth resolution of
![]() $G$
. By the construction above, the divisor
$G$
. By the construction above, the divisor
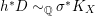 $h^{\ast }D{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70E}^{\ast }K_{X}$
is semi-ample, and induces a morphism coinciding with the composite morphism
$h^{\ast }D{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D70E}^{\ast }K_{X}$
is semi-ample, and induces a morphism coinciding with the composite morphism
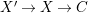 $X^{\prime }\rightarrow X\rightarrow C$
. Since
$X^{\prime }\rightarrow X\rightarrow C$
. Since
 $h:X^{\prime }\rightarrow Y$
is fibered by elliptic curves, we conclude that the Stein factorization of the natural morphism
$h:X^{\prime }\rightarrow Y$
is fibered by elliptic curves, we conclude that the Stein factorization of the natural morphism
![]() $\tilde{G}\rightarrow Z$
induces an elliptic fibration
$\tilde{G}\rightarrow Z$
induces an elliptic fibration
![]() $\tilde{G}\rightarrow \tilde{Z}$
with
$\tilde{G}\rightarrow \tilde{Z}$
with
 $g(\tilde{Z})\geqslant 2$
, hence
$g(\tilde{Z})\geqslant 2$
, hence
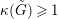 $\unicode[STIX]{x1D705}(\tilde{G})\geqslant 1$
. However, this contradicts that
$\unicode[STIX]{x1D705}(\tilde{G})\geqslant 1$
. However, this contradicts that
 $K_{G}{\sim}_{\mathbb{Q}}0$
.
$K_{G}{\sim}_{\mathbb{Q}}0$
.
Finally assume
 $\unicode[STIX]{x1D705}(K_{F})=2$
. If
$\unicode[STIX]{x1D705}(K_{F})=2$
. If
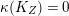 $\unicode[STIX]{x1D705}(K_{Z})=0$
we apply Proposition 5.3. But if
$\unicode[STIX]{x1D705}(K_{Z})=0$
we apply Proposition 5.3. But if
 $\unicode[STIX]{x1D705}(K_{Z})=1$
, we replace
$\unicode[STIX]{x1D705}(K_{Z})=1$
, we replace
![]() $X$
with its canonical model over
$X$
with its canonical model over
![]() $Z$
so that
$Z$
so that
![]() $K_{X}$
is ample over
$K_{X}$
is ample over
![]() $Z$
, and we use Theorem 2.12 to deduce
$Z$
, and we use Theorem 2.12 to deduce
 $f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is a nef vector bundle for sufficiently divisible integer
$f_{\ast }{\mathcal{O}}_{X}(mK_{X/Z})$
is a nef vector bundle for sufficiently divisible integer
![]() $m>0$
as in the proof of 5.3; next we apply Proposition 5.1 to a resolution of
$m>0$
as in the proof of 5.3; next we apply Proposition 5.1 to a resolution of
![]() $X$
. ◻
$X$
. ◻
Proof of Corollary 1.3.
By [Reference Badescu2, Corollary 7.3]
![]() $f$
has integral generic geometric fiber. Let
$f$
has integral generic geometric fiber. Let
![]() $F$
be the generic fiber of
$F$
be the generic fiber of
![]() $f$
, let
$f$
, let
 $F_{1}=F\times _{K(Z)}K(Z)^{1/p^{\infty }}$
, and let
$F_{1}=F\times _{K(Z)}K(Z)^{1/p^{\infty }}$
, and let
 $\tilde{F}_{1}\rightarrow F_{1}$
be a desingularization. Since
$\tilde{F}_{1}\rightarrow F_{1}$
be a desingularization. Since
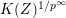 $K(Z)^{1/p^{\infty }}$
is perfect,
$K(Z)^{1/p^{\infty }}$
is perfect,
![]() $\tilde{F}_{1}$
is smooth over
$\tilde{F}_{1}$
is smooth over
 $K(Z)^{1/p^{\infty }}$
by [Reference Liu31, Chapter 4 Corollary 3.33]. Therefore, there exists a natural number
$K(Z)^{1/p^{\infty }}$
by [Reference Liu31, Chapter 4 Corollary 3.33]. Therefore, there exists a natural number
![]() $e$
such that
$e$
such that
![]() $\tilde{F}_{1}$
can be descent to
$\tilde{F}_{1}$
can be descent to
![]() $\tilde{F}_{2}$
, which is a desingularization of
$\tilde{F}_{2}$
, which is a desingularization of
 $F_{2}=F\times _{K(Z)}K(Z)^{1/p^{e}}$
and smooth over
$F_{2}=F\times _{K(Z)}K(Z)^{1/p^{e}}$
and smooth over
 $K(Z)^{1/p^{e}}$
.
$K(Z)^{1/p^{e}}$
.
Denote by
 $F^{e}:Z^{\prime }\rightarrow Z$
the
$F^{e}:Z^{\prime }\rightarrow Z$
the
![]() $e$
th absolute Frobenius iteration. Then
$e$
th absolute Frobenius iteration. Then
 $X\times _{Z}Z^{\prime }$
is integral since
$X\times _{Z}Z^{\prime }$
is integral since
![]() $F^{e}$
is flat and
$F^{e}$
is flat and
![]() $f$
is separable. We have the following commutative diagram
$f$
is separable. We have the following commutative diagram

where
 $\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X\times _{Z}Z^{\prime }$
is a resolution. By the above argument, the generic fiber
$\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X\times _{Z}Z^{\prime }$
is a resolution. By the above argument, the generic fiber
![]() $F^{\prime }$
of
$F^{\prime }$
of
![]() $f^{\prime }$
is a smooth curve over
$f^{\prime }$
is a smooth curve over
![]() $K(Z^{\prime })$
. By Theorem 1.2,
$K(Z^{\prime })$
. By Theorem 1.2,
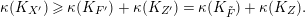 $$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X^{\prime }})\geqslant \unicode[STIX]{x1D705}(K_{F^{\prime }})+\unicode[STIX]{x1D705}(K_{Z^{\prime }})=\unicode[STIX]{x1D705}(K_{\tilde{F}})+\unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}(K_{X^{\prime }})\geqslant \unicode[STIX]{x1D705}(K_{F^{\prime }})+\unicode[STIX]{x1D705}(K_{Z^{\prime }})=\unicode[STIX]{x1D705}(K_{\tilde{F}})+\unicode[STIX]{x1D705}(K_{Z}).\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D70E}=g\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
be the natural composite morphism. By [Reference Chen and Zhang13, Theorem 2.4], there exists an effective
$\unicode[STIX]{x1D70E}=g\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
be the natural composite morphism. By [Reference Chen and Zhang13, Theorem 2.4], there exists an effective
![]() $\unicode[STIX]{x1D70E}$
-exceptional divisor
$\unicode[STIX]{x1D70E}$
-exceptional divisor
![]() $E$
on
$E$
on
![]() $X^{\prime }$
such that
$X^{\prime }$
such that
 $$\begin{eqnarray}K_{X^{\prime }/Z^{\prime }}\leqslant \unicode[STIX]{x1D70E}^{\ast }K_{X/Z}+E.\end{eqnarray}$$
$$\begin{eqnarray}K_{X^{\prime }/Z^{\prime }}\leqslant \unicode[STIX]{x1D70E}^{\ast }K_{X/Z}+E.\end{eqnarray}$$
Thus
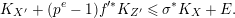 $$\begin{eqnarray}K_{X^{\prime }}+(p^{e}-1){f^{\prime }}^{\ast }K_{Z^{\prime }}\leqslant \unicode[STIX]{x1D70E}^{\ast }K_{X}+E.\end{eqnarray}$$
$$\begin{eqnarray}K_{X^{\prime }}+(p^{e}-1){f^{\prime }}^{\ast }K_{Z^{\prime }}\leqslant \unicode[STIX]{x1D70E}^{\ast }K_{X}+E.\end{eqnarray}$$
We can assume
![]() $K_{Z^{\prime }}$
is effective, thus
$K_{Z^{\prime }}$
is effective, thus
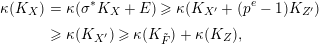 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}(K_{X}) & = & \displaystyle \unicode[STIX]{x1D705}(\unicode[STIX]{x1D70E}^{\ast }K_{X}+E)\geqslant \unicode[STIX]{x1D705}(K_{X^{\prime }}+(p^{e}-1)K_{Z^{\prime }})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D705}(K_{X^{\prime }})\geqslant \unicode[STIX]{x1D705}(K_{\tilde{F}})+\unicode[STIX]{x1D705}(K_{Z}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}(K_{X}) & = & \displaystyle \unicode[STIX]{x1D705}(\unicode[STIX]{x1D70E}^{\ast }K_{X}+E)\geqslant \unicode[STIX]{x1D705}(K_{X^{\prime }}+(p^{e}-1)K_{Z^{\prime }})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D705}(K_{X^{\prime }})\geqslant \unicode[STIX]{x1D705}(K_{\tilde{F}})+\unicode[STIX]{x1D705}(K_{Z}),\nonumber\end{eqnarray}$$
where the first “
![]() $=$
” is from Theorem 2.22. ◻
$=$
” is from Theorem 2.22. ◻
Acknowledgments
We would like to thank Burt Totaro for answering our questions regarding the results in his paper [Reference Totaro42]. We would also like to thank the referee for reading the paper carefully and for giving us many helpful comments.