Introduction
In mass-balance studies, accurate data on accumulation and ablation are needed to reach correct conclusions. However, it is often difficult to obtain accurate field data on snow accumulation since the accumulation rate may vary substantially over short distances. Precipitated snow is strongly affected by snowdrift, and hence an originally smooth snow cover can be redistributed into a complicated accumulation pattern. Radar soundings along continuous profiles provide detailed information on spatial variability in snow accumulation (Reference Holmlund, Richardson and JanssonHolmlund and Richardson, 1995; Reference Kohler, Moore, Kennett, Engeset and ElvehøyKohler and others, 1997; Reference Richardson, Aarholt, Hamran, Holmlund and IsakssonRichardson and others, 1997; Reference Holmgren, Sturm, Yankielun and KohHolmgren and others, 1998).
In this paper, we analyze the spatial variability in snow-layer depths along an overland traverse performed in 1996-97 in central Dronning Maud Land (DML), East Antarctica. Snow-radar data were collected continuously along a 500 km traverse which started at -2400 m a.s.l., approximately following the ice divide towards Dome F for 500 km, and ended at 3450 m a.s.l. (Fig. 1). Shallow firn cores (10-20 m long) were drilled at 11 sites (Reference Winther and WintherWinther and others, 1997). At the coring sites, an additional radar profile (1-5 km long) crossing the traverse route was sounded to evaluate the representativeness of the core. In this paper we also provide an example of a grid-net radar survey, which was designed to make a detailed evaluation of the spatial representativeness of a core. This survey was performed around the drilling site of a 100 m long ice core obtained in a near-coastal area in western DML in 1997-98 (Reference Holmlund, Stenberg, Karlöf, Nyman, Gjerde, Thomassen and Grön-lundHolmlund and others, 1999).
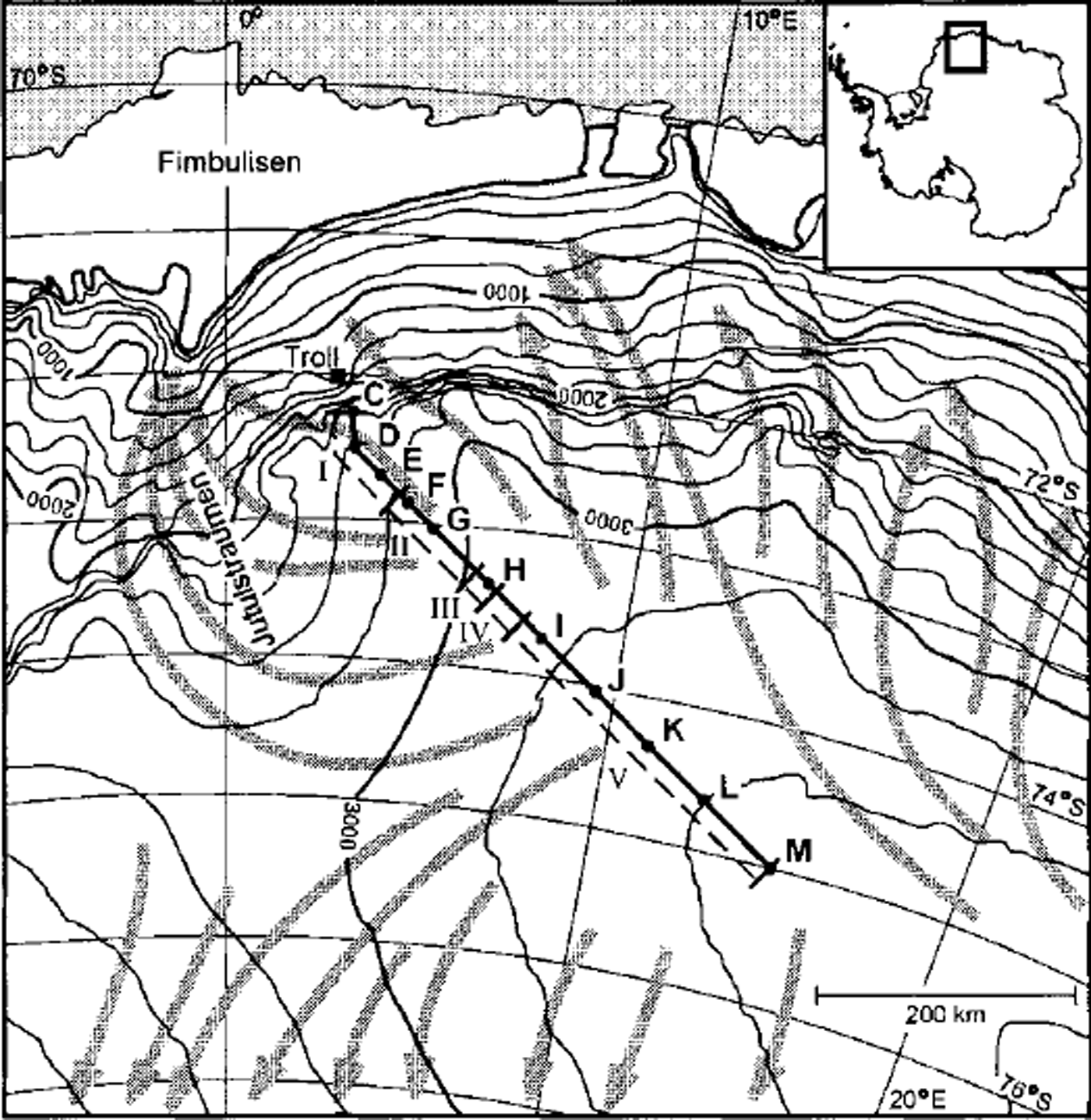
Fig. 1. Location map. The traverse route is marked with a solid line, and firn-coring sites are marked with letters. Sections I-V along the traverse are referred to in the text. North of sections I and II, approximately at the 2000 m level, there is a nunatak range that delimits the polar plateau from the coastal area. The arrows indicate modelled streamlines for general surface winds in the area (from Reference Parish and BromwichParish and Bromwich, 1987). The figure is redrawn from a satellite image map (1:2000000; If AG, 1997).
Equipment
The radar used is a Frequency Modulated Continuous Wave (FM-CW) synthetic pulse system (Reference Hamran and AarholtHamran and Aarholt, 1993; Reference Hamran, Gjessing, Hjelmstad and AarholtHamran and others, 1995). It transmits a series of CW signals in which 201 frequencies are transmitted in sequence, and data are post-processed from frequency domain to time domain using an inverse fast Fourier transform (IFFT). A high dynamic range is obtained by a long effective integration time in the receiver, and improved vertical resolution is gained by applying an increased number of samples in the IFFT. We performed soundings at 800-2300 MHz, with log-periodic antennae (AEL APN-106AA) mounted on a Hagglunds all-terrain carrier.
Differential global positioning system (GPS) measurements (dual-frequency P-code GPS), with an estimated accuracy of 2m, were performed along the traverse. The reference GPS receiver was located at Troll station (Fig. 1). Complementary positions were recorded by single-point GPS measurements with a horizontal accuracy of ±200 m.
Methods
The snow-radar methods are described in detail by Reference Richardson, Aarholt, Hamran, Holmlund and IsakssonRichardson and others (1997). In the present study we merely provide an outline of these methods, with the following improvements and additions: (1) depth-density depth-wave-speed, and depth-travel-time relations were fitted to exponential functions instead of polynomials, and were used in the depth computations; (2) data points on snow-layer depth were interpolated at fixed distance intervals (additional); and (3) statistics on snow-layer depths were computed for individual radar recordings (additional). The mapped snow layers have not been dated, and we therefore dealt only with snow-layer depths and not absolute accumulation rates.
Radar travel times were translated into depth values by an empirical relation between firn density and electromagnetic wave speed (Reference Richardson, Aarholt, Hamran, Holmlund and IsakssonRichardson and others, 1997). The radar recordings cover continuous profiles with a horizontal resolution of ∼5m (Fig. 2). The stratigraphic features in the snowpack detectable by radar are caused by layers of different dielectric properties. The dielectric properties of dry snow are affected by several parameters, of which the most important is density (e.g. Reference Tiuri, Sihvola, Nyfors and HallikainenTiuri and others, 1984; Reference Kovacs, Gow and MoreyKovacs and others, 1995; Reference MatzlerMäzler, 1996). Snow with divergent dielectric properties may form at the surface during periods with exceptional climatic or atmospheric conditions, such as intense storms, extremely high insolation, high temperatures or atmospheric deposition of impurities. In line with Reference Vaughan, Corr, Doake and WaddingtonVaughan and others (1999), we assume that layers yielding a strong radar reflection are isochronous. Snow layers were identified using the characteristic position in the layer sequence as well as the layer-reflection intensity relative to other layers in the sequence. The depth-density relation for the snowpack was established from 11 firn cores (Fig. 3), retrieved with a Polar Ice Coring Office (PICO) drill (3 in (7.62 cm) diameter core barrel). The depth-density relation has often been described by exponential equations (e.g. Reference BaderBader, 1954; Reference Alley, Bolzan and WhillansAlley and others, 1982; Reference West, Winebrenner, Tsang and RottWest and others, 1996), and we choose to describe the relation with the function
where ρ is density expressed in kg m−3 and z is depth below snow surface expressed in metres. The constants a, b and c are determined by fitting p(z) to the data using the least-squares method. We found that the density profiles are displaced towards lower densities with increasing altitude. Therefore we decided to divide the study area into two regions, each with a characteristic density profile: a low-altitude region (cores C-H and Equation (2)) and a high-altitude region (cores I -M and Equation (3)).
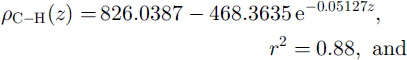
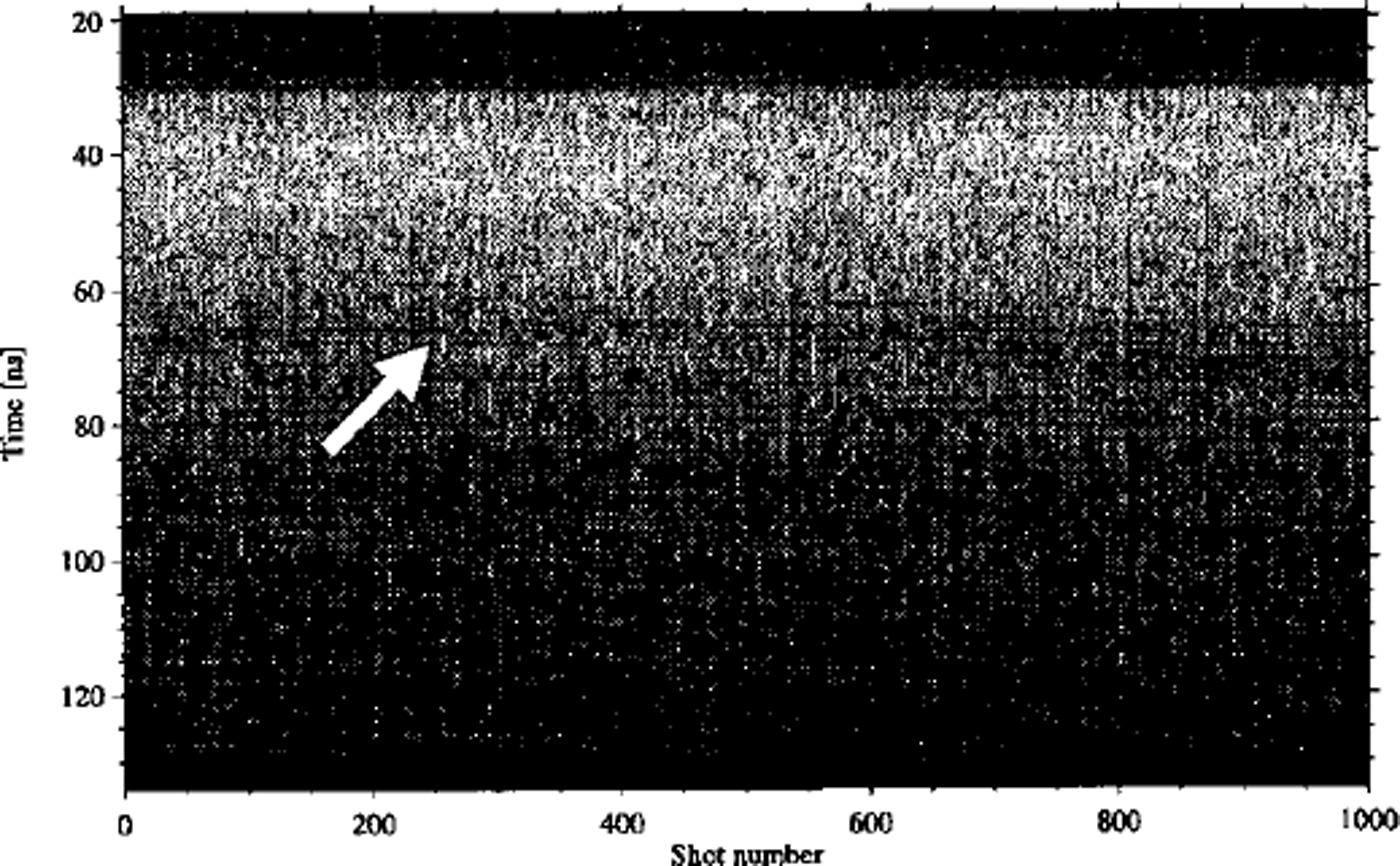
Fig. 2. A 5 km long radar recording retrieved at 3250 m a.s.l. The vertical tine-scale corresponds to a maximum depth of ∼11m. The arrow indicates the snow layer that was mapped in this section.
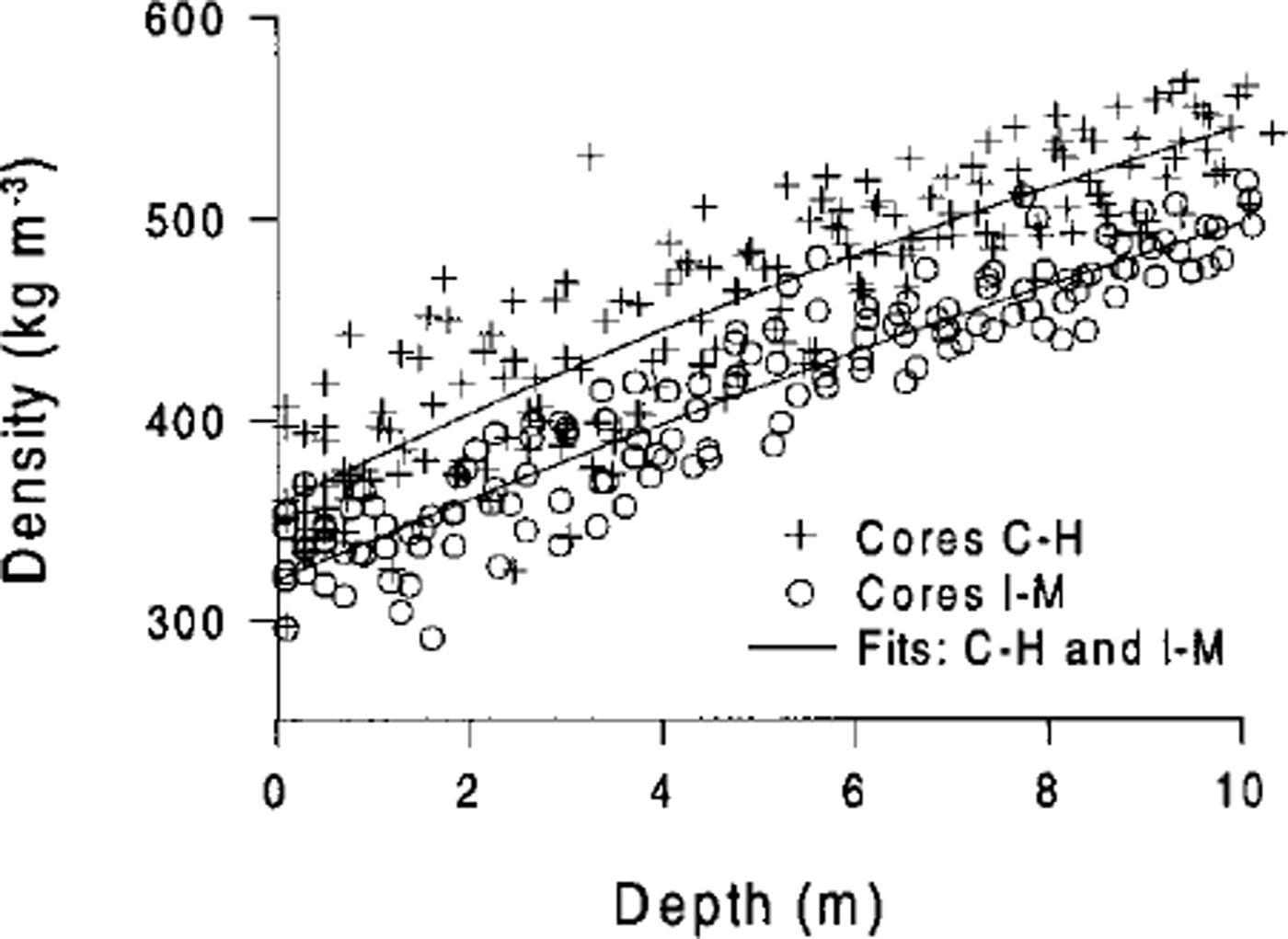
Fig. 3. The depth-density data from 11 coring sites (see Fig. 1) indicate decreasing density values towards higher altitudes. The area was divided into two density regions (cores C-H and I-M), and exponential functions describing the depth-density relation were fitted to the data.
According to Equations (2) and (3), densities are 7-11% lower in the high-altitude than in the low-altitude region. Wave speed (v) is determined by the dielectric constant (ε), described by
where c0 is the speed of electromagnetic waves in a vacuum. The dielectric constant is composed of a real and an imaginary part. In dry snow and firn the imaginary part is negligible (Reference MatzlerMazier, 1987). In Antarctic firn, which is here considered dry, the real part of the dielectric constant, ε’, can be described as a function of density:
(Reference Kovacs, Gow and MoreyKovacs and others, 1995). A simplified model for the ray-path geometry was adopted, which neglects ray-path refraction within the snowpack. Errors resulting from this simplification decrease with increasing reflection depth (Reference Richardson, Aarholt, Hamran, Holmlund and IsakssonRichardson and others, 1997), and in order to escape such errors, travel times yielding reflection depths of < 1 m were omitted from the dataset. The upper 10 m of the snowpack was divided into 0.1 m thick depth sections for which the wave speeds were calculated using Equations (2-5). Least-squares exponential fits were used to describe wave-speed variations with depth for the two regions (C-H and I-M). The two-way travel-time was computed for 28 selected reflection depths between 1 and 15 m, and an exponential equation was applied to fit the reflection-depth-travel-time data using the least-squares method, giving
where reflection depths, zrC-H and zrI-M, are given in metres, and travel times, t, in nanoseconds (ns). Applying Equations (6) and (7) to an arbitrary travel time for each region yields only a 2.5-3.0% difference in reflection depth for 1-10 m depths. This small difference indicates that two density regions are sufficient for the study area; further division would not have changed the results significantly.
At coring sites, the snow-layer depths were translated into mw.e., which is an appropriate unit for interpretation of accumulation rates obtained from cores. For this translation, we derived cumulative density profiles from the density functions (2) and (3):
where and pcI_M(z) denote the cumulative density (kg m−3) in the G-H and the I -M region, respectively.
For each digitised radar recording, data points were interpolated to fixed distance intervals of 20 m. A distance interval of 20 m or less was required to maintain a proper shape of the digitised travel-time record. For each radar recording, snow-layer mean depth and standard deviation were computed, and minimum and maximum depths were recorded. Furthermore, the standard deviation was computed for layer depths through recording sequences when the same layer could be identified in several subsequent radar recordings. We expressed standard deviation as a percentage of the mean depth in order to obtain comparable standard deviation values for snow layers of different ages. The standard deviation describes the data dispersion in metres around the mean depth for the mapped layers. At a specific locality an old snow layer will have a larger mean depth than a young layer. The depth variations of the older layer contain the data dispersion accumulated over more years, and thus the depth variations of the older layer will yield a higher standard deviation than those of the younger layer, even though both layers describe the same variability. By expressing the standard deviation in per cent of the mean depth, we escape this problem.
The positions of radar profiles and the ice-sheet topography were mapped in detail along the traverse. The GPS logging interval was 15 s, corresponding to a travel distance of approximately 40 m. Unfortunately the radar periodically interfered with the GPS receiver, resulting in interrupted satellite contact or large uncertainties in GPS data. As a complement, single-point GPS measurements were logged at ∼ 5 km intervals for positioning of the radar recordings. Positions for ice-sheet elevation were measured from another vehicle (dual frequency P-code GPS), without disturbance from the radar.
Results
Figure 4 presents results from the radar soundings complemented with surface elevations and firn-core accumulation rates along the traverse route. When several snow layers are present in the radar data they follow the same undulating pattern, depicting matching rising and dipping features. It was not possible to find a snow layer that could be identified throughout the traverse; instead we mapped different layers in different areas. Based on the distribution of snow-layer depths in Figure 4, we divided the profile into five characteristic sections (I-V; Fig. 4). In section I (2400-2840 m a.s.l.), the snow stratigraphy is well developed and easily interpreted. The general snow-layer pattern shows a pronounced trend of decreasing snow accumulation towards the south and higher altitudes. In section II (2840-3030 m a.s.l.) the interpretation was very difficult and the identification of specific layers was ambiguous. The stratigraphy is more or less diffuse, with few distinguishable layers, and we could not identify the snow layers that were mapped in section I. The radar data indicate that parts of section II are exposed to net erosion. In sections III-V (above 3030 m a.s.l.), the snow stratigraphy was distinct and easily interpreted, presenting no problems of snow-layer identification. In section III (3030-3080 m a.s.l.), the snow layering does not show any clear trend, but in section IV (3080-3140 m a.s.l.) it shows a strong trend of increasing accumulation with increasing elevation. In section V (above 3140m a.s.l.), the layering indicates a slight trend of decreasing accumulation with increasing altitude.
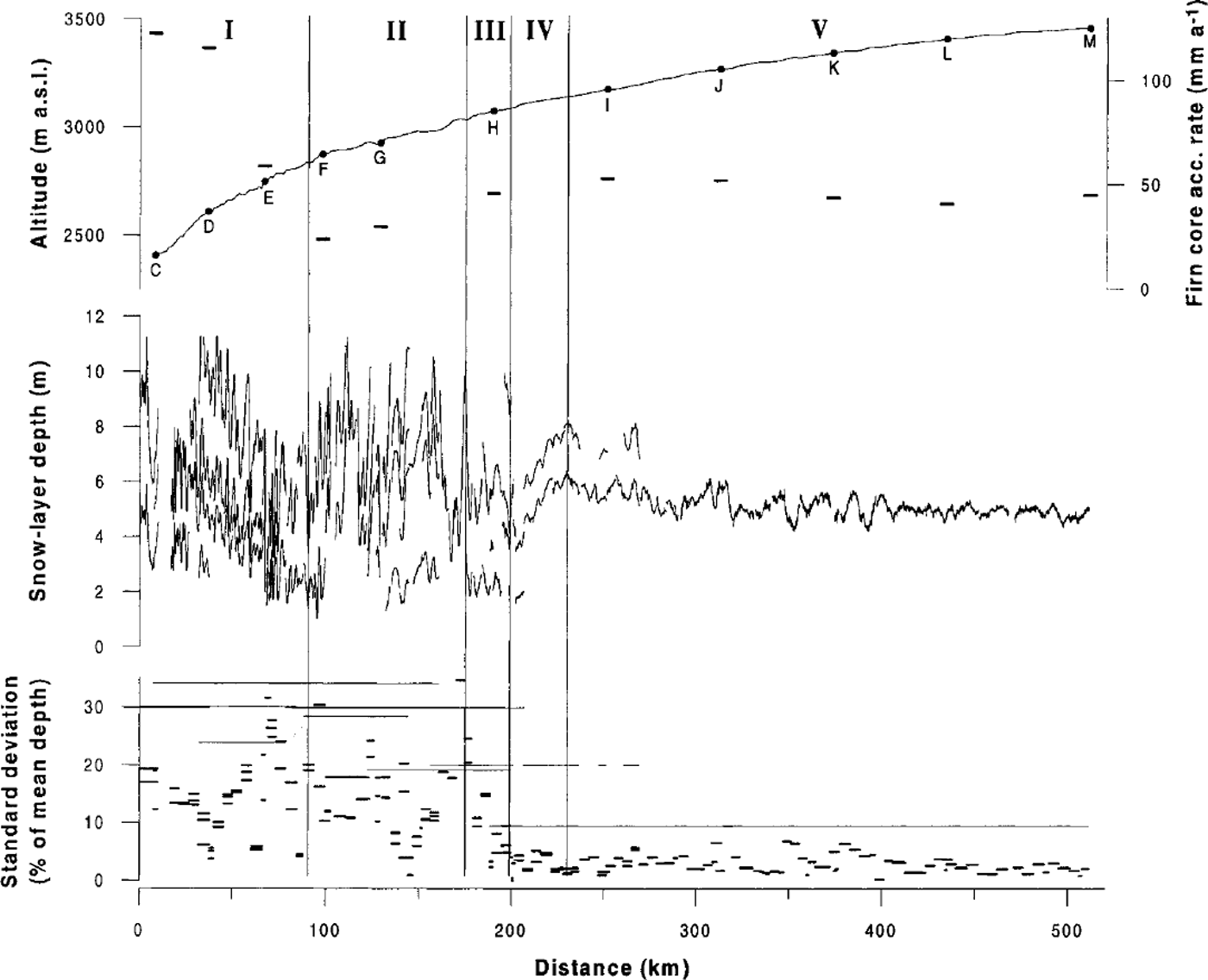
Fig. 4. The upper graph shows the ice-sheet surface altitude, the coring locations C-M with average accumulation rates between 1965 and 1997 (horizontal bars) and the characteristic sections I-V.The accumulation data are taken from Reference Van den BroekeVan den Broeke and others (1999). The middle graph shows the depths of snow layers mapped by radar, and the lower graph shows the spatial variability in snow-layer depths as standard deviation, expressed as percentage of the mean depth. Short thick bars indicate the variability of layers from individual 5 km recordings. Thin lines show the variability of longer sequences of the same layer.
The lower graph in Figure 4 shows the variability in snow-layer depths described as standard deviation values. The standard deviation values range from a few per cent up to ∼ 35% of the mean depth. High variability occurs at altitudes below 3080 m a.s.l. (sections I III) where the standard deviation values are scattered, with some 5 km segments having high and some having low standard deviation. Above 3080 m a.s.l. (sections IV and V), the variability is very low, with the standard deviation values well aggregated. Generally, the layer depths in the long recording sequences show a higher standard deviation than the individual 5 km segments.
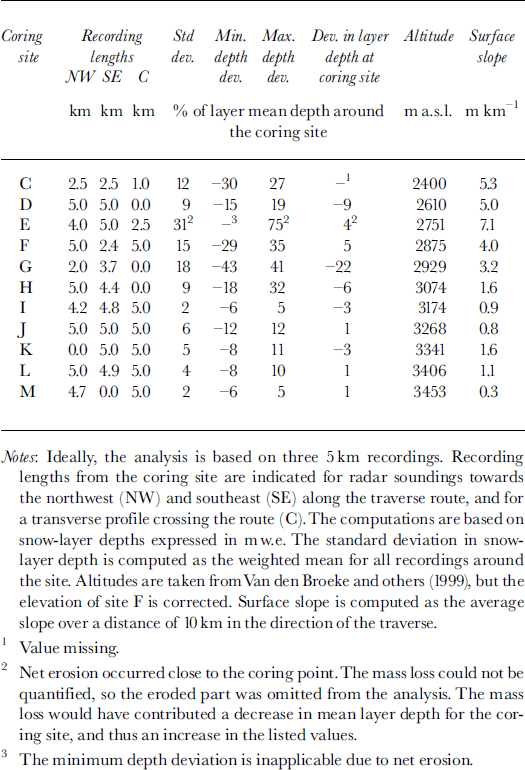
Table 1 shows the spatial variability in snow-layer depths around coring sites, and the representativeness of the firn cores. The variability is indicated by the standard deviation values, complemented by the minimum and maximum depth deviations from the mean depth around each core. At the specific point where each core was drilled, the deviation in snow-layer depth from the mean layer depth around the coring site indicates the representativeness of the core. The standard deviation is 2-31% of the coring-site mean depth, while recorded minimum and maximum depths deviate by 5-75% from the coring-site mean. At the coring points, the snow-layer depths deviate by 1-22% from the mean depths around the coring sites. The surface slope is 0.3-7.1 m km"1.
Table 1. Spatial variability in snow-layer depths and representativeness of firn cores
Results from the grid-net survey in western DML (73° 10’ S, 13°20’ E), covering an area of 15 km x 20 km, are shown in Figure 5. For this part of the study, radar profiles were sounded at 700-1100 MHz with a sampling interval of ∼ 2 5 m. A constant wave speed was assumed for a simplified depth calculation. The mean depth of the mapped snow layer is 20 m. The spatial pattern of the net accumulation is irregular, with snow-layer depths varying between 40% and 240% of the layer depth at the drilling site. The snow-layer depths have a standard deviation of 21 % of the mean depth. At the coring site, the snow-layer depth is 10% less than the mean depth for the studied area.
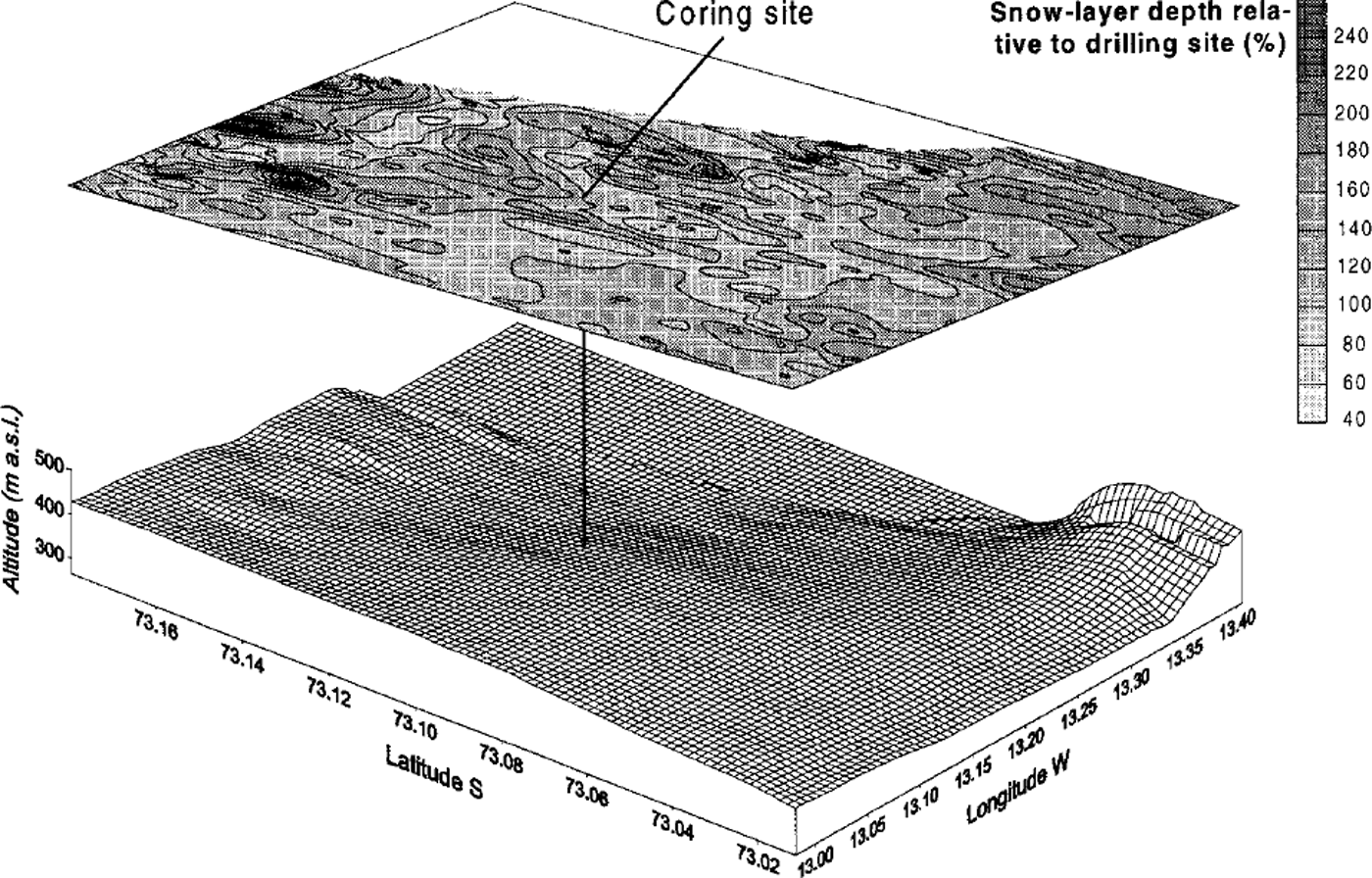
Fig. 5. Spatial variability in snow-layer depths and surface topography around a near-coastal coring site in western DML, deduced by radar soundings in a detailed grid. At this site a 100 m long core was obtained in 1997-98. The surface topography is exaggerated by a factor of 10. The maps were interpolated with a gridcell size of 200 mx200 m.
Discussion
Accumulation pattern along the traverse
Radar soundings of the top 10 m of the snowpack may cover some decades of accumulated snow in the study area, and hence they yield information on the recent net accumulation pattern. The snow layers mapped along the traverse route provide a good picture of the regional net accumulation pattern (Fig. 4). The radar data agree with the accumulation rates obtained from the firn cores, but they also contribute important additional information on the accumulation between the coring sites. In stratigraphic cross sections with several distinguishable snow layers, individual layers follow the same undulating pattern, indicating that the general net accumulation pattern has been stable over recent decades (Figs 2 and 4). This is in accordance with previous studies in western DML (e.g. Reference Isaksson and KarlenIsaksson and Karlen, 1994; Reference Richardson, Aarholt, Hamran, Holmlund and IsakssonRichardson and others, 1997). The marked trend of decreasing net accumulation with increasing altitude in section I is probably related to the relatively steep surface slope (Fig. 4; Table 1) and the closeness to the nunatak range that delimits the polar plateau from the lower coastal area. Near the Antarctic coast, the precipitation is mainly caused by adiabatic cooling of the air as it rises due to steep topography (Reference King and TurnerKing and Turner, 1997). The highest accumulation occurs at the steepest slopes and is generally related to frontal cyclonic systems (Reference BromwichBromwich, 1988). However, most major weather systems do not penetrate into the Antarctic interior. The pronounced trend of decreasing net accumulation in section I could thus partly be explained by a relatively strong influence of coastal cyclonic systems in the lowest parts, which decreases towards higher elevations. On the polar plateau most precipitation occurs from isolated clouds or optically very thin clouds yielding "clear-sky" precipitation. It has been suggested that orographic lifting of maritime air is important in increasing the air-moisture content for production of "clear-sky" precipitation over the Antarctic interior (Reference BromwichBromwich, 1988). It is likely that such a process is most important close to the orographic barrier, which in our case would contribute to the higher accumulation rates close to the nunataks. The slight trend of decreasing net accumulation in section V (Fig. 4) is probably related to the capacity of air to retain moisture, which decreases with decreasing temperature and thus increasing elevation (e.g. Reference RobinRobin, 1977).
According to the discussion above, we would expect decreasing accumulation rates with increasing surface elevation and with increasing distance from the orographic barrier near the coast. The net accumulation in sections II-IV deviates from this pattern. This is most likely because of an uneven redistribution of snow through erosion and deposition. The disturbed snow layering and the occurrence of net erosion in section II indicate windy conditions with intense redistribution of the snow cover. In the Antarctic interior, near-surface wind flow is mainly driven by katabatic forcing, with katabatic winds mainly governed by the terrain slope and the surface inversion strength (Reference Parish and BromwichParish and Bromwich, 1987). The ice-sheet surface slope along the profile (Fig. 4; Table 1) does not suggest a stronger katabatic flow in section II than in other sections along the traverse. Reference Parish and BromwichParish and Bromwich (1987) modelled general katabatic surface winds over the entire Antarctic continent, and their low-level streamline map (arrows in Fig. 1) provides useful information for the interpretation of the observed accumulation pattern. In section I, the wind streamlines point towards the nunatak range in the northwest, but from section II, the streamlines are first directed towards west-southwest, then turn north to drain along the surface trough of Jutulstraumen. Stronger katabatic winds and more efficient erosion in section II could thus be explained by higher wind speeds associated with the smooth surface topography of Jutulstraumen, compared with section I where the air drains across rough nunataks. It is likely that sections III and IVare also affected by relatively high erosion. However, the influence of erosion decreases towards the south, explaining the strong trend of increasing accumulation with increasing elevation in section IV.
Spatial variability along the traverse
The variability in snow-layer depths (Fig. 4) indicates significantly changed conditions around 3080 m a.s.l. At higher elevations (sections IV and V), the standard deviation was generally < 10% of the mean depth, indicating a very smooth net accumulation pattern. At elevations below 3080 m, the accumulation pattern varied much more, with standard deviation values up to 35% of the mean depth. The change in spatial variability around 3080 m a.s.l. cannot be explained by the surface elevation or the distance to open sea. There seems to be a correlation between spatial variability and surface slope along the traverse (Table 1), but the slope cannot explain the abrupt transition around 3080 m a.s.l. However, the decrease in variability coincides with a clear decline in surface relief, as the surface topography becomes smoother around the initiation of section IV just above 3000 m a.s.l. (Fig. 4). Here the ice thickness is -2700 m (unpublished radar data from Alfred Wegener Institute, EPICA pre-site survey 1995-96). The smoother surface topography and more even accumulation pattern above 3080 m a.s.l. could be due to the ice thickness being too great to reflect bed topography in the topography of the ice-sheet surface, or wind speed not being high enough for efficient erosion. Most likely an interaction between several components causes this transition. Understanding of the spatial variability in accumulation rate in the studied area would be greatly improved by regional-scale modelling of wind regimes, such as that initiated by Reference Van den BroekeVan den Broeke and others (1999), but at higher resolution.
Spatial variability around the firn cores
Around coring sites G, D, F, G and H (sections I III) the variability was relatively high, with a standard deviation of 9-18% of the mean depth, and minimum and maximum depths deviated by 15-43% from the mean. For coring site G, which had the highest variability, the core could have been drilled on a spot where the accumulation rate was as much as 4 3% lower than the mean value for this area. The high variability around coring site G is also reflected in the low representativeness of the core, which shows that the accumulation rate obtained from laboratory analysis of core G underestimates the mean accumulation by 22%. In spite of the relatively high spatial variability around coring sites D, Fand H, the representativeness of these cores was high. The cores yield accumulation rates that deviate by 5-9% from the mean accumulation rate. Around coring site E, the variability was exceptionally high for the polar plateau, because net erosion occurred close to the coring point. As we could not quantify the mass loss, we excluded the eroded part from the computations (see comments in Table 1). The standard deviation was 31% and the recorded maximum depth deviated by 75% from the mean. However, the representativeness of core E was surprisingly good, and the accumulation rate of the core deviated by only 4% from the mean. Goring sites I -M (sectionV) were characterised by low spatial variability with a standard deviation of 2-6%, and recorded minimum and maximum depths deviated by only 5-12 % from the mean depth. The representativeness of these cores was very high, the cores yielding accumulation rates that deviate by only 1-3% from the mean values around the sites. Table 1 shows that radar data contribute important information on accumulation that complements the detailed point data obtained from firn cores.
Spatial variability around the 100 m long core and design of variability surveys
At the coring site for the 100 m long core in western DML, we interpolated a map of the accumulation pattern and surface topography, and determined the spatial variability and the representativeness of the core (Fig. 5). We regard the variability around the coring site as relatively low (std dev. 21%), considering that the core was drilled in a near-coastal area. The spatial representativeness of the core is relatively high. It underestimates the mean accumulation rate for the mapped 300 km2 area by 10%. According to Figure 5, there is a strong correlation between surface topography and accumulation rate.
The best way to determine the spatial variability around a coring site, and the representativeness of the core, is to analyze snow-layer depth variations in a detailed grid net as seen in Figure 5. However, this kind of survey raises some important questions. How large an area should be analyzed around a core in order to determine its spatial representativeness? At what resolution should the maps be interpolated? At what scale does the variability become part of a regional trend? To achieve comparable representativeness values for various cores, it is important that the surveys are of similar size and resolution. Figure 4 shows that the spatial variability was generally higher for long sequences of a specific snow layer than with separate 5 km recordings. This is related to the fact that the longer sequences contain regional trends. As an example, we interpolated a trend for sectionV and subtracted this trend from the data before computing statistics, which resulted in a decrease in the standard deviation from 0.4 to 0.3 m. The best way to exclude possible regional trends from the variability data may be to start by surveying along extended profiles to determine general trends, and to subtract these trends from the data before computing the spatial variability.
Conclusions
Three major characteristic regions describe the general net accumulation pattern along a 500 km long traverse on the polar plateau. From the nunatak range at 2400-2840 m a.s.l., there is a clear trend of decreasing accumulation with increasing altitude. At 2840-3140 m a.s.l., erosion rates are relatively high. In the lowest part of this section (2840-3030ma.s.l) the snow stratigraphy is disturbed, with focal areas of net erosion, indicating that this region is exposed to strong winds. At 3140-3450 m a.s.l., there was a slight trend of decreasing net accumulation with increasing elevation.
The spatial variability in snow-layer depths varies between different sections of the traverse. At elevations below 3080 m, the variability is high with standard deviation values up to 35% of the snow-layer mean depth, while above 3080 ma.s.l. the variability is low, with standard deviation values of < 10% of the mean depth. The marked change in variability around 3080 m a.s.l. coincides with a change in ice-sheet surface relief, with a shift to an extremely smooth topography at higher elevations. Around firn-coring sites, the standard deviation is 2-31% of the mean depth. The minimum and maximum snow-layer depths deviate by up to 75% from the mean depth around the coring sites, which is a surprisingly high deviation for the polar plateau. In general, the representativeness of the firn cores is high. However, the core with the lowest representativeness was drilled at a point where the accumulation rate is 22% lower than the mean accumulation around the coring site. This demonstrates the importance of determining the spatial representativeness of cores and of making radar pre-site surveys prior to drilling.
Around the coring site for a 100 m long core, radar soundings were performed over a detailed grid. At this site there is a strong correlation between surface topography and accumulation rate. The study shows that the core underestimates the mean accumulation rate for a surrounding 300 km2 area by 10%. The best way to determine the spatial variability and the representativeness of a core is to make surveys in a detailed grid around the coring site, and to produce a net accumulation map. Before the spatial variability is analyzed, regional trends in net accumulation could be excluded from the data.
The complex wind pattern which is reflected in the radar data on snow-layer thickness along the 500 km traverse cannot be explained by any single physical parameter such as distance to open sea, surface elevation or slope. The combined effect of several parameters probably explains the observed complicated accumulation pattern. More detailed studies with modelling of wind regimes on a regional scale based on accurate high-resolution digital elevation models would increase our understanding of wind conditions and accumulation patterns on the polar plateau.
Acknowledgements
We would like to express our thanks to everyone who helped with this work. In particular, we would like to thank E. Aarholt,T. Eiken, Hewlett-Packard, P.Jansson, J.-O. Naslund, S. Onarheim and R. Pettersson. This work is a contribution to the "European Project for Ice Coring in Antarctica" (EPICA), a joint European Science Foundation/European Commission (EC) scientific programme, funded by the EC under the Environment and Climate Programme (1994-98) contract ENV4-CT95-0074 and by national contributions from Belgium, Denmark, France, Germany, Italy, The Netherlands, Norway, Sweden, Switzerland and the U.K. This is EPICA publication No. 9.








