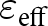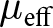Introduction
In recent years, there has been a great deal of attention devoted toward metamaterial, and the related research lab moved from being simply a theoretical concept to a field with developed and marketed applications. It is an engineered material having negative permittivity (ε) or permeability (μ) or both negative ε and μ simultaneously [Reference Ziolkowski and Engheta1]. Due to these unique electromagnetic (EM) properties, it supports backward waves [Reference Belov2], inverse Snell’s law [Reference Schroden, Mohammed, Christopher and Andreas3], opposite group and phase velocity [Reference Wang and Cheng4], inverse Doppler’s effect [Reference Xie, Zhu, Zhang, Zhijiang and Wang5], etc., which are not found in naturally occurring materials. They are formed by the combination of different materials such as metals and substrate. Different materials are arranged in repeating patterns, at scales that are smaller than the wavelength of the influenced phenomena. Metamaterials achieve their characteristics not from the single material but from the arrangement of repeating pattern structure. Their shape, geometry, size, and arrangement lead to smart properties which are capable of manipulating EM waves: blocking, absorbing, enhancing, or bending waves [Reference Holloway, Kuester, Gordon, O'Hara, Booth and Smith6].
For the first time, Jagdish Chander Bose at the end of nineteenth century in the year 1898 performed some experiments that became the seed work for today’s dynamic field of metamaterials [Reference Cheng, Luo and Chen7]. In 1914, Lindell continued the work by embedding artificial chiral elements in a host medium [Reference Zhang, Tian, Zhang and Zhang8]. Thereafter in 1948, Kock tailored the effective medium properties, i.e., effective permittivity (![]() ${\varepsilon _{{\textrm{eff}}}}$) and effective permeability (
${\varepsilon _{{\textrm{eff}}}}$) and effective permeability (![]() ${\mu _{{\textrm{eff}}}}$) by periodically arranging the conducting disks, strips, and spheres [Reference Fang and Zhang9]. In 1968, Veselago theoretically explained the wave propagation in a double negative (DNG) material and concluded that
${\mu _{{\textrm{eff}}}}$) by periodically arranging the conducting disks, strips, and spheres [Reference Fang and Zhang9]. In 1968, Veselago theoretically explained the wave propagation in a double negative (DNG) material and concluded that ![]() ${\varepsilon _{{\textrm{eff}}}}$ and
${\varepsilon _{{\textrm{eff}}}}$ and ![]() ${\mu _{{\textrm{eff}}}}$ and the refractive index (η) are negative with less than zero values [Reference Niesler, Gansel, Fischbach and Wegener10]. He explored that the direction of phase velocity is opposite to the direction of Poynting vector in a DNG material. However, this extraordinary finding could not be verified until Sir John Pendry et al. in 1999 [Reference Xiong, Chen, Cheng and Luo11] postulated that the artificially engineered structures such as split-ring resonator (SRR) with negative effective material properties can be constructed. Based on this concept, the existence of first DNG material was experimentally demonstrated by Smith et al., and this type of material is also named as left-handed material [Reference Fluhler12]. In the demonstration, Smith et al. used a periodic array of SRR and continuous wire, to provide simultaneously negative value of
${\mu _{{\textrm{eff}}}}$ and the refractive index (η) are negative with less than zero values [Reference Niesler, Gansel, Fischbach and Wegener10]. He explored that the direction of phase velocity is opposite to the direction of Poynting vector in a DNG material. However, this extraordinary finding could not be verified until Sir John Pendry et al. in 1999 [Reference Xiong, Chen, Cheng and Luo11] postulated that the artificially engineered structures such as split-ring resonator (SRR) with negative effective material properties can be constructed. Based on this concept, the existence of first DNG material was experimentally demonstrated by Smith et al., and this type of material is also named as left-handed material [Reference Fluhler12]. In the demonstration, Smith et al. used a periodic array of SRR and continuous wire, to provide simultaneously negative value of ![]() ${\varepsilon _{{\textrm{eff}}}}$ and
${\varepsilon _{{\textrm{eff}}}}$ and ![]() ${\mu _{{\textrm{eff}}}}$. Since then, these artificially engineered materials, i.e., metamaterials, became the theme of investigation for the researchers worldwide.
${\mu _{{\textrm{eff}}}}$. Since then, these artificially engineered materials, i.e., metamaterials, became the theme of investigation for the researchers worldwide.
Metamaterials have a wide range of potential applications in EM (ranging from low microwave to optical frequencies), including controllable “smart” surfaces [Reference Zhiren, Cheng, Luo, Chen and Xiangcheng13], miniaturized cavity resonators [Reference Watts, Liu and Padilla14], novel wave-guiding structures [Reference Cheng, Qian, Luo, Chen and Cheng15], angular-independent surfaces [Reference Caloz, Okabe, Iwai and Itoh16], biomedical devices [Reference Lai, Itoh and Caloz17], terahertz switches [Reference Cheng, Qian, Luo, Chen and Cheng15], fluid-tunable frequency-agile materials [Reference Watts, Liu and Padilla14], radar cross section (RCS) reduction [Reference Kaur, Upadhyaya and Palandoken18], EM compatibility in electronic devices [Reference Kaur and Upadhyaya19], antennas [Reference Xiong, Hong, Luo and Zhong20], chip-less RFID [Reference Landy, Sajuyigbe, Mock, Smith and Padilla21], solar cells [Reference Hoffman, Alekseyev, Howard, Franz, Wasserman, Podolskiy and Gmachl22], cloaking [Reference Mendhe and Prasad Kosta23], phase modulators [Reference Mendhe and Prasad Kosta23], thermal emitters [Reference Melik, Unal, Perkgoz, Puttlitz and Demir24], power imaging [Reference Luh25], bolometers [Reference Bliss and Forsythe26], photo-detectors [Reference Gil, Bonache and Martin27], artificial magnetic conductors [Reference Chen, Willie, Zide, Gossard, Taylor and Averitt28], and metamaterial absorber (MA) [Reference Enoch, Tayeb, Sabouroux, Guerin and Vincent29].
This article presents an angle-independent wideband metamaterial microwave absorber (MMA). The proposed structure consists of outer (rectangular SRR [RSSR]) and inner (circular SSR [CSRR]) geometry. The structure is a three-layer design in which top and bottom surfaces are made up of copper, and middle layer consists of FR-4 substrate. The resonate surface is designed to achieve maximum absorption in the range of 6.11–13.52 GHz. The bandwidth of absorption achieved is 7.41 GHz. In the range of interest, three different peaks are considered having maximum absorption with respect to other points. At three different peaks, electric and current distribution are plotted to show the absorption phenomenon. The metamaterial behavior is satisfied by using effective parameters ![]() ${\varepsilon _{{\textrm{eff}}}}$ and
${\varepsilon _{{\textrm{eff}}}}$ and ![]() ${\mu _{{\textrm{eff}}}}$. Normal and oblique incidence are plotted to verify angle-independent phenomenon. The simulation of the proposed structure is carried out using commercially available ANSYS HFSS 19.1v. The simulated structure is fabricated and measured inside the anechoic chamber. Finally, the proposed and already reported MMA are compared to find the novelty of the structure [Reference Cheng and Zhao30–Reference Ranjan, Barde, Choubey, Sinha and Kumar Mahto36]. It is observed that the proposed structure is novel in terms of uniquely used resistors in congestion with two circular slotted rings, which is compact in size and has larger bandwidth. The proposed MMA finds practical applications in RCS reduction, terrestrial communication, keyless entry system, space communication, radar, and baby monitor.
${\mu _{{\textrm{eff}}}}$. Normal and oblique incidence are plotted to verify angle-independent phenomenon. The simulation of the proposed structure is carried out using commercially available ANSYS HFSS 19.1v. The simulated structure is fabricated and measured inside the anechoic chamber. Finally, the proposed and already reported MMA are compared to find the novelty of the structure [Reference Cheng and Zhao30–Reference Ranjan, Barde, Choubey, Sinha and Kumar Mahto36]. It is observed that the proposed structure is novel in terms of uniquely used resistors in congestion with two circular slotted rings, which is compact in size and has larger bandwidth. The proposed MMA finds practical applications in RCS reduction, terrestrial communication, keyless entry system, space communication, radar, and baby monitor.
Structure design
The unit cell of the proposed MMA consists of outer and inner structures. The outer structure is an RSRR, and the inner structure is CSRR. The lumped resistors are connected to the outer and inner structures. The geometry of the structure is made up of three layers. The top and bottom layers are made up of copper (Cu, conductivity σ = 5 × 107 S/m, thickness = 0.035 mm). The middle layer is made up of FR-4 (ε r = 4.4, loss tangent δ = 0.02, thickness = 3.2 mm) substrate acting as a dielectric medium. The three-layer geometry is portrayed in Fig. 1. The overall dimension of the structure is 14 mm × 14 mm × 3.2 mm, as shown in Fig. 2. The top resonating structure is designed in such a way that maximum absorption and angle independence are achieved for C and X band frequency applications.

Figure 1. Schematic diagram of proposed MA.

Figure 2. Front view of proposed MA unit cell.
Simulation and parametric analysis
The MMA proposed in this article is simulated using commercially available ANSYS HFSS 19.1 v. The maximum absorption is achieved by optimizing the geometry with respect to height of substrate, inner resistance, and outer resistance. The height of the substrate varies from 0.8 to 4.8 mm in the step size of 0.8 mm, and for substrate height equal to 3.2 mm maximum absorption is achieved as shown in Fig. 3. Second, the outer value of resistance varies from 50 to 150 Ω in the step size of 20 Ω, and for 110 Ω maximum absorption is achieved as shown in Fig. 4. Finally, the inner value of resistance varies from 105 to 185 Ω in the step size of 20 Ω, and for 145 Ω maximum absorption is achieved as shown in Fig. 5.

Figure 3. Absorptivity for different cases—height of the substrate.

Figure 4. Absorptivity for different cases—outer resistance.

Figure 5. Absorptivity for different cases—inner resistance.
After varying the parameters, i.e., height of substrate, outer resistance, and inner resistance, the wideband absorptivity A(ω) is obtained when height of substrate equals 3.2 mm, outer resistance equals 110 Ω, and inner resistance equals 145 Ω.
Wideband absorptivity A(ω) is calculated from Eq. (1), which depends upon reflected (![]() ${S_{11}}$) and transmitted (
${S_{11}}$) and transmitted (![]() ${S_{21}}$) power, but as the lower layer is completely covered with copper, the transmitted power in Eq. (1) is zero and absorptivity completely depends upon reflected power given by Eq. (2). The absorptivity of the structure can be increased by minimizing the reflected power from the surface.
${S_{21}}$) power, but as the lower layer is completely covered with copper, the transmitted power in Eq. (1) is zero and absorptivity completely depends upon reflected power given by Eq. (2). The absorptivity of the structure can be increased by minimizing the reflected power from the surface.
The proposed geometry obtains wideband absorption of 7.41 GHz ranging from 6.11 GHz to 13.52 GHz above 0.9 absorptivity with three absorption peaks at 6.76, 11.15, and 13.07 GHz as shown in Fig. 6.

Figure 6. Absorptivity vs frequency plot.
Absorption mechanism
The unit cell of the proposed MMA is considered a homogeneous medium for the absorption mechanism process. The normalized impedance can be evaluated by Eq. (3).
 \begin{equation}Z = \sqrt {{{{{\left( {1 + {S_{11}}} \right)}^2} - S_{21}^2} \over {{{\left( {1 - {S_{11}}} \right)}^2} - S_{21}^2}}} \end{equation}
\begin{equation}Z = \sqrt {{{{{\left( {1 + {S_{11}}} \right)}^2} - S_{21}^2} \over {{{\left( {1 - {S_{11}}} \right)}^2} - S_{21}^2}}} \end{equation} In Eq. (3), transmitted power (![]() ${S_{21}}$) is absent because the bottom layer is completely covered with conducting material; due to this, no incident wave will be transmitted from the structure. Therefore, Eq. (3) is now modified as Eq. (4).
${S_{21}}$) is absent because the bottom layer is completely covered with conducting material; due to this, no incident wave will be transmitted from the structure. Therefore, Eq. (3) is now modified as Eq. (4).
 \begin{equation}Z = {{\left( {1 + {S_{11}}} \right)} \over {\left( {1 - {S_{11}}} \right)}}\end{equation}
\begin{equation}Z = {{\left( {1 + {S_{11}}} \right)} \over {\left( {1 - {S_{11}}} \right)}}\end{equation} For analysis purpose and to calculate the exact normalized impedance, transmitted power (![]() ${S_{21}}$) plays an important role. To calculate
${S_{21}}$) plays an important role. To calculate ![]() ${S_{21}}$ the small portion from the bottom conducting layer is etched from all the four corner in such a way that absorption curve remains the same. The normalized impedance curve obtained after the process of etching is portrayed in Fig. 7. From Fig. 7 it is observed that in the range of interest real part is approaching toward unity while imaginary part is approaching toward zero, which confirms that proper impedance matching is achieved for the proposed structure.
${S_{21}}$ the small portion from the bottom conducting layer is etched from all the four corner in such a way that absorption curve remains the same. The normalized impedance curve obtained after the process of etching is portrayed in Fig. 7. From Fig. 7 it is observed that in the range of interest real part is approaching toward unity while imaginary part is approaching toward zero, which confirms that proper impedance matching is achieved for the proposed structure.

Figure 7. Simulated normal impedance.
The real and imaginary parts approach toward 1 and 0, respectively, as shown in Fig. 7, which is due to the fact that effective parameters, i.e., ![]() ${\varepsilon _{{\textrm{eff}}}}$ and
${\varepsilon _{{\textrm{eff}}}}$ and ![]() ${\mu _{{\textrm{eff}}}}$ are changing very rapidly at the wide range of absorption frequency, which is the region of interest. This can be proven by the observation from Figs. 8 and 9, respectively.
${\mu _{{\textrm{eff}}}}$ are changing very rapidly at the wide range of absorption frequency, which is the region of interest. This can be proven by the observation from Figs. 8 and 9, respectively.

Figure 8. Simulated real part of permittivity and permeability.

Figure 9. Simulated imaginary part of permittivity and permeability.
The refractive index (![]() $\eta $) is calculated using Eq. (5) and plotted in Fig. 10. The
$\eta $) is calculated using Eq. (5) and plotted in Fig. 10. The ![]() $\eta $ changes abruptly due to resonance conditions at a particular value or range of
$\eta $ changes abruptly due to resonance conditions at a particular value or range of ![]() $\varepsilon $ and
$\varepsilon $ and ![]() $ \mu $.
$ \mu $.
 \begin{equation}\eta = {1 \over {kd}}{\textrm{co}}{{\textrm{s}}^{ - 1}}\left[ {{1 \over {2{S_{21}}}}\left( {1 - S_{21}^2 - S_{11}^2} \right)} \right]\end{equation}
\begin{equation}\eta = {1 \over {kd}}{\textrm{co}}{{\textrm{s}}^{ - 1}}\left[ {{1 \over {2{S_{21}}}}\left( {1 - S_{21}^2 - S_{11}^2} \right)} \right]\end{equation}
Figure 10. Refractive index vs frequency.
The absorption mechanism can be properly explained from the electric field and current distribution at the top and bottom surface of the proposed structure. To simulate the plot fields, three different frequencies are considered in the region of interest. The three different frequencies are 6.76, 11.15, and 13.07 GHz with absorptivities of 0.94, 0.94, and 0.99, respectively.
The current distribution plot shows that the current flowing at top and bottom surface is anti-parallel to each other, as shown in Fig. 11. Due to circulating current, magnetic excitation is created perpendicular to magnetic field. Electric field is induced due to electric excitation, as shown in Fig. 12; due to this strong EM, resonance occurs which maximizes the absorption.

Figure 11. Current distribution: (a) top and (b) bottom surfaces at 6.76, 11.15, and 13.07 GHz of proposed MA.

Figure 12. Electric field distribution: (a) top and (b) bottom surfaces at 6.76, 11.15, and 13.07 GHz of proposed MA.
Metasurface analysis under normal and oblique incidence
The angle independence of MMA is observed by analyzing the structure under normal and oblique (TE and TM) incidence. The electric field direction is fixed, and the wave vector and magnetic field direction are changed to analyze the absorption. Under normal incidence, the structure is rotated from horizontal polarization (![]() $\phi = 0^\circ $) to a vertical polarization (
$\phi = 0^\circ $) to a vertical polarization (![]() $\phi = {90^ \circ }$), and the reflection coefficient is measured at every
$\phi = {90^ \circ }$), and the reflection coefficient is measured at every ![]() $15^\circ $ increments. When the polarization angle changes the absorptivity remains the same. Therefore, the proposed MMA is angle independent as shown in Fig. 13 as simulated and Fig. 14 as measured.
$15^\circ $ increments. When the polarization angle changes the absorptivity remains the same. Therefore, the proposed MMA is angle independent as shown in Fig. 13 as simulated and Fig. 14 as measured.

Figure 13. Simulated absorptivity curve under normal incidence.

Figure 14. Measured absorptivity curve under normal incidence.
The structure is further examined under oblique incidence of wave. The proposed structure is investigated at different angles from 0° to 90° at each 15° increments for both TE and TM polarization, and the absorptivity curves are plotted in Figs. 15 and 16, respectively. It is observed that absorptivity response degrades as angle of incidence increases.

Figure 15. Absorptivity curve under oblique incidence for TE polarization.

Figure 16. Absorptivity curve under oblique incidence for TM polarization.
The proposed and already reported MMA are compared with respect to size of unit cell, bandwidth, and thickness in Table 1. It is observed from the table that the proposed structure is compact in terms of size and has larger bandwidth.
Table 1. Comparison between proposed and already published metamaterial absorber articles

Measurement setup
The proposed MMA was fabricated on FR-4 substrate having an overall dimension of 140 cm × 140 cm, containing 10 × 10 unit cells as depicted in Fig. 17. The backside of FR-4 sheet has been covered with copper. The measurement of absorptivity under normal incidence is carried out inside an anechoic chamber with the help of vector network analyzer. The setup consists of two horn antennas acting as a transmitter and receiver. The complete setup for measurement is replicated in Fig. 18. The simulation and measurement results for absorptivity are shown in Fig. 19. and a close agreement between the simulation and measured results is observed.

Figure 17. Fabricated 140 cm × 140 cm sheet.

Figure 18. Experimental setup inside anechoic chamber.

Figure 19. Simulated and measured absorptivity plot.
Conclusion
The MMA reported in this article is angle-independent wideband absorber. The structure is simulated on FR-4 substrate having overall dimension of 14 mm × 14 mm × 3.2 mm. The unit cell of proposed MMA consists of outer and inner structure associated with lumped resistors. The outer structure consists of RSRR, whereas inner structure consists of CSRR. The structure is made up of three layers, in which top and bottom layer is made up of copper acting as a conducting material. The middle layer is made up of FR-4 acting as a dielectric substrate. The resonating structure at the top is design in such a way so that wideband absorption is achieved in the range from 6.11 to 13.52 GHz. The wideband absorption within the range is approaching almost toward unity having bandwidth of 7.41 GHz. Three different peaks are considered in the range of interest having maximum absorption of 0.94, 0.94, and 0.99 at frequencies of 6.76, 11.15, and 13.07 GHz, respectively. The structure is analyzed using the effective parameters, i.e., effective permittivity (![]() ${\varepsilon _{{\textrm{eff}}}}$) and effective permeability (
${\varepsilon _{{\textrm{eff}}}}$) and effective permeability (![]() ${\mu _{{\textrm{eff}}}}$), to satisfy that structure is acting as a metamaterial. Electric field and current distribution are plotted at three different peaks to prove the mechanism of wideband absorption. Normal and oblique incidence are plotted to satisfy that structure is behaving as an angle independent. The simulated structure is fabricated on FR-4 substrate and measured inside an anechoic chamber. Finally, to prove the novelty of the work, the proposed structure is compared with the already reported MMA. The proposed MMA finds practical applications in RCS reduction, terrestrial communication, keyless entry system, space communication, radar, and baby monitor.
${\mu _{{\textrm{eff}}}}$), to satisfy that structure is acting as a metamaterial. Electric field and current distribution are plotted at three different peaks to prove the mechanism of wideband absorption. Normal and oblique incidence are plotted to satisfy that structure is behaving as an angle independent. The simulated structure is fabricated on FR-4 substrate and measured inside an anechoic chamber. Finally, to prove the novelty of the work, the proposed structure is compared with the already reported MMA. The proposed MMA finds practical applications in RCS reduction, terrestrial communication, keyless entry system, space communication, radar, and baby monitor.
Competing interest
The authors report no conflict of interest.

Chetan Barde was born in Jabalpur, India, in 1986. He received his B.E. degree in electronics and communication engineering from RGPV University, Bhopal, India, in 2008 and M.Tech degree in nanotechnology from the VIT University, Vellore, India, in 2013. He received Ph.D. degree from the National Institute of Technology, Jamshedpur, India. Currently, he is working in Indian Institute of Information Technology Bhagalpur, Bihar, India. His research interest includes ZOR antenna, metamaterials and their applications, and electromagnetic wave absorbers.

Neelesh Kumar Gupta was born in Bhopal, India. He received his B.E. degree in electronics and communication engineering and M.Tech degree from RGPV University, Bhopal, India. He received Ph.D. degree from National Institute of Technology, Bhopal, India. Currently, he is working in the Department of Electronics and Communication Engineering, Ajay Kumar Garg Engineering College, Ghaziabad, Uttar Pradesh, India. His research interest includes ZOR antenna, metamaterials and its applications, and electromagnetic wave absorbers.

Prakash Ranjan was born in Vaishali, India, in 1982. He received his B.E. degree in electronics and communication engineering from Anna University, Chennai, India, in 2009, and M.Tech degree in electronics and communication engineering from the YMCA University, Haryana, India, in 2012. In 2019, he completed his Ph.D. at the National Institute of Technology, Jamshedpur, India, and subsequently, joined the Department of Electronics and Communication Engineering, Indian Institute of Information Technology, Bhagalpur, as Assistant Professor. He is a graduate student member of IEEE. His research interest includes metasurfaces, metamaterials and its applications, electromagnetic wave absorbers, ZOR antenna, and soft computing optimization techniques.

Komal Roy is pursuing her Ph.D., from National Institute of Technology, Jamshedpur, India. Her research interest includes ZOR antenna, metamaterials and its applications, and electromagnetic wave absorbers.

Rashmi Sinha was born in Ranchi, India, in 1972. She received her B.Sc. and M.Sc. degrees in electrical engineering from the National Institute of Technology, Jamshedpur, India, in 1995 and 2000, respectively. She did her Ph.D. from the same institute. In 1997, she joined the Department of Electronic and Communication Engineering, NIT Jamshedpur, India. Her current research interest includes antenna design, signal processing, communication and soft computing. She is a member of IEEE, and a life member of the Institute of Engineers (India).