1 INTRODUCTION
Several studies based on different techniques and data revealed the non-steady state and asymmetrical structure of our Galaxy. The Milky Way Galaxy is still evolving under the effects of internal and external forces. After the discovery of the accretion of the Sagittarius dwarf galaxy (Ibata, Gilmore & Irwin Reference Ibata, Gilmore and Irwin1994), researchers drew their attention to the Galactic streams. Sagittarius stream (Majewski et al. Reference Majewski, Skrutskie, Weinberg and Ostheimer2003) is associated with the Sagittarius dwarf galaxy. However, there are Galactic streams whose origins are not yet known. Some of them are tidal debris and some of them originate from the accretion. Galactic warp and dynamical interaction of the thick disc with the Galactic long bar can be associated with some of the Galactic streams (Williams et al. Reference Williams2013, and the references therein). The presence of some of the streams are revealed by their large-scale stellar over-densities. Monoceros stream (Newberg et al. Reference Newberg2002; Yanny et al. Reference Yanny2003) outward from the Sun and Hercules thick disc cloud (Larsen & Humphreys Reference Larsen and Humphreys1996; Parker, Humphreys, & Larsen Reference Parker, Humphreys and Larsen2003; Parker, Humphreys, & Beers Reference Parker, Humphreys and Beers2004; Larsen, Humphreys, & Cabanela Reference Larsen, Humphreys and Cabanela2008) inward from the Sun are examples for these over-density structures. Helmi stream (Helmi et al. Reference Helmi, White, de Zeeuw and Zhao1999) and the recent Aquarius stream (Williams et al. Reference Williams2011) are also two notable streams.
Star count analysis is one of the procedures used to reveal the complex structure of the Galaxy. Bilir et al. (Reference Bilir, Karaali, Ak, Yaz and Hamzaoğlu2006) showed that the scale heights and the scale lengths of the thin and thick discs are Galactic longitude dependent. In Ak et al. (Reference Ak, Bilir, Karaali and Buser2007a,Reference Ak, Bilir, Karaali, Buser and Cabrera-Laversb), the metallicities for relatively short vertical distances (z < 2.5 kpc) show systematic fluctuations with Galactic longitude which was interpreted as the flare effect of the disc. A more comprehensive study was carried out by Bilir et al. (Reference Bilir, Cabrera-Lavers, Karaali, Ak, Yaz and López-Corredoira2008) who showed that the thin and thick disc scale heights as well as the axis ratio of the halo varies with Galactic longitude. The variation of these parameters were explained with the gravitational effect of the Galactic long bar. A similar work is carried out by Yaz & Karaali (Reference Yaz and Karaali2010) in intermediate latitudes of the Galaxy where the variations of the thin and thick disc scale heights were explained with the effect of the disc flare and disc long bar.
The velocity distribution in the UV plane is also complex, i.e. it differs from a smooth Schwarzschild distribution. This has been proven for the solar neighbourhood (Dehnen Reference Dehnen1998) and the recent studies revealed that the same case holds also for the solar suburb (Antoja et al. Reference Antoja2012). The complex structure is probably created by the Galactic long bar and spiral arms. Dissolving open clusters and perturbative effect of the disc by merger events can also be used for the explanation of the complexity (Williams et al. Reference Williams2013). Siebert et al. (Reference Siebert2011) showed that the radial velocities (V R) estimated via the RAdial Velocity Experiment (RAVE; Steinmetz et al. Reference Steinmetz2006) data are non-zero and also, they have a small gradient, i.e. dV R/dR < −3 kms− 1 kpc− 1. A similar result based on RAVE red clump (RC) stars has been cited in Casetti-Dinescu et al. (Reference Casetti-Dinescu, Girard, Korchagin and van Altena2011). Siebert et al. (Reference Siebert2012) used density-wave models to show that the radial streaming originates from the resonance effect of the spiral arms, and reproduced the gradient just mentioned. Probably, the most comprehensive study is that of Williams et al. (Reference Williams2013) which is based on the stars from the internal release of RAVE data in October 2011. Beyond a detailed error analysis, Williams et al. (Reference Williams2013) confirmed the radial gradient dV R/dR < −3 kms− 1 kpc− 1 and they revealed the different behaviour of the vertical velocities, V Z, of the RC stars in opposite regions of R ~ 8 kpc in the (R, Z) plane. Also, Williams et al. (Reference Williams2013) argued that the Hercules thick disc cloud (Larsen & Humphreys Reference Larsen and Humphreys1996; Parker et al. Reference Parker, Humphreys and Larsen2003; Larsen et al. Reference Larsen, Humphreys and Cabanela2008) is an important phenomenon which causes the variation of the stellar velocities. Parker et al. (Reference Parker, Humphreys and Larsen2003) gave the Galactic coordinates of the thick disc cloud as 20° ⩽ l ⩽ 55°, 25° ⩽ b ⩽ 45°, 305° ⩽ l ⩽ 340° and − 45° ⩽ b ⩽ −25°. Larsen et al. (Reference Larsen, Humphreys and Cabanela2008) stated that the centre of the over-density region ranges from (X, Y, Z) = (6.5, −2.2, 1.5) to (X, Y, Z) = (6.5, 0.3, 1.5) kpc, and that there is a clear excess of stars in quadrant Q 1 over quadrant Q 4 in the range l = 25° − 45° and b = 30° − 40°.
In this study, we intend to contribute to the discussions of the complexity of the Milky Way Galaxy by investigating the variation of the space velocity components of 6 610 RC stars. The difference between the procedures in the literature and ours is the application of a series of constraints in our work, i.e. (1) we used the space velocity components instead of the cylindrical coordinates; (2) we applied corrections for the differential rotation to our velocities; (3) we investigated the variation of the velocities for three Galactic populations, thin and thick discs, halo and their combinations; (4) we investigated the lag of the sample stars relative to the local standard of rest of the stars; and (5) we investigated the variation of the velocities in terms of z min and z max instead of current positions which covers the effect of long-lived internal and external forces. The paper is organised as follows. The data are given in Section 2. Section 3 is devoted to the distribution of the velocity components for stars relative to several parameters: (i) vertical distance, i.e. for stars above and below the Galactic plane separately, (ii) Galactocentric distance and (iii) Galactic longitude. The distribution of the velocity dispersions for different velocities is also given in this section. Finally, a discussion of the results and a short conclusion is presented in Section 4.
2 DATA
The data of 6 781 RC stars are taken from Bilir et al. (Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012). They used the RAVE Data Release 3 (DR3, Siebert et al. Reference Siebert2011) survey and applied a series of constraints to 83 072 radial velocity measurements to identify 7 985 RC stars among them. Also, they carried out the following evaluations to obtain the final sample of RC stars: the proper motions of 7 846 stars were taken from RAVE DR3 while the 139 stars which were not available in this catalogue were provided from the PPMXL catalogue of Roeser, Demleitner, & Schilbach (Reference Roeser, Demleitner and Schilbach2010). Distances were obtained by combining the apparent KS magnitude of the star in question and the absolute magnitude M KS = −1.54 ± 0.04 mag, adopted for all RC stars (Groenewegen Reference Groenewegen2008), while the E(B − V) reddening was obtained iteratively by using published methodology (cf. Coşkunoğlu et al. Reference Coşkunoğlu2011, and the references therein). The apparent KS magnitudes were de-reddened by means of the equations in Fiorucci & Munari (Reference Fiorucci and Munari2003). Distribution of the RC stars in Equatorial and Galactic coordinates is given in Figure 1.

Figure 1. Distribution of RAVE DR3 RC stars in the (a) Equatorial and (b) Galactic coordinates.
Bilir et al. (Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012) combined the distances with the RAVE DR3 radial velocities and available proper motions, applying the algorithms and transformation matrices of Johnson & Soderblom (Reference Johnson and Soderblom1987) to obtain the Galactic space velocity components (U, V, W) of the sample stars. In the calculations, epoch J2000 was adopted as described in the International Celestial Reference System of the Hipparcos and Tycho-2 catalogues (ESA 1997). The transformation matrices use the notation of right-handed system. Hence, U, V and W are the components of a velocity vector of a star with respect to the Sun, where U is positive towards the Galactic centre (l = 0°, b = 0°), V is positive in the direction of the Galactic rotation (l = 90°, b = 0°) and W is positive towards the North Galactic Pole (b = 90°).
Bilir et al. (Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012) adopted the value of the rotation speed of the Sun as 222.5 km s− 1. Correction for differential Galactic rotation is necessary for accurate determination of the U, V and W velocity components. The effect is proportional to the projection of the distance to the stars on to the Galactic plane, i.e. the W velocity component is not affected by Galactic differential rotation (Mihalas & Binney Reference Mihalas and Binney1981). They applied the procedure of Mihalas & Binney (Reference Mihalas and Binney1981) to the distribution of the sample stars and estimated the first-order Galactic differential rotation corrections for the U and V velocity components of the sample stars. The U, V and W velocities were reduced to local standard of rest (LSR) by adopting the solar LSR velocities in Coşkunoğlu et al. (Reference Coşkunoğlu2011), (U⊙, V⊙, W⊙) = (8.83, 14.19, 6.57) km s− 1. We will use the symbols U lsr, V lsr and W lsr for them, hereafter. The uncertainties of the space velocities U err, V err and W err (Figure 2) were computed by propagating the uncertainties of the proper motions, distances and radial velocities, again using an algorithm by Johnson & Soderblom (Reference Johnson and Soderblom1987). Then, the error for the total space motion of a star follows from the equation

Figure 2. Distribution of the errors of the space velocity components U (upper panel), V (middle panel) and W (lower panel) for the sample used in this study. The medians, means and the standard deviations are also stated in the panels, respectively.
Bilir et al. (Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012) removed the RC stars with total space velocity errors larger than the mean errors (⟨S err⟩ = 39 km s− 1) plus the standard deviation (σ = 36 km s− 1), i.e. S err > 75 km s− 1, thus the sample reduced to 6 781 stars. Also in this study, 171 RC stars that are very close to Galactic plane (− 10° ⩽ b ⩽ +10°) were excluded from the sample of Bilir et al. (Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012). These stars are in the calibration fields, so their properties such as age may be different from the general Galactic population we intend to study here. Thus, the final sample used in this study reduced to 6 610. The large errors originate from the proper motions. The proper motions of 706 stars with S err > 75 km s− 1 is μtoterr ⩽ 10 mas yr− 1 and those of 498 stars is μtoterr > 10 mas yr− 1. The distance histogram of the RC stars (Figure 3) shows that those with large errors, S err > 75 km s− 1, are located at large distances. A proper motion error of 10 mas yr− 1 corresponds to 50 km s− 1 at 1 kpc, and correspondingly more if further away. Hence, omitting RC stars with S err > 75 km s− 1 removed the space velocity components with large errors. Also, distance and radial velocity errors may affect the space velocity components. However, in our study, they are small, i.e. distances are based on the absolute magnitude M Ks = −1.54 ± 0.04 mag (Groenewegen Reference Groenewegen2008), where the error is rather small, and RAVE group gives a median radial velocity error of 1.2 km s− 1 (Siebert et al. Reference Siebert2011). The distribution of the sample stars in the (X, Y) and (X, Z) planes and their space velocity components (U, V) and (W, V) are plotted in Figures 4 and 5, respectively. Both figures involve the sample stars as well as the rejected ones. The RC stars with S err > 75 km s− 1 (blue colour) can be located at the outermost region of Figure 4, i.e. their X, Y and Z coordinates are larger than the sample stars (grey colour), while the RC stars close to the Galactic plane, |b| < 10°, occupy the central part of the figure, as expected. The positions of the sample stars and the stars close to the Galactic plane in Figure 5 are almost the same as in Figure 4. However, the stars with errors S err > 75 km s− 1 – and with large distances – are concentrated in the central part of the diagram giving the indication that their (relatively) large errors reduced their space velocity components to smaller values.

Figure 3. Distance histogram of the RC stars. Upper panel corresponds to all RC stars (N = 7 985), while the lower one is drawn for the final sample (N = 6 610). The middle panel corresponds to the RC stars with large proper motion errors (μtoterr > 10 mas yr− 1) and large distances (d > 1 kpc, right histogram, N= 1 204), and those close to the Galactic plane (|b| ⩽ 10°, left histogram, N = 171).

Figure 4. Distribution of the sample stars (grey colour) and rejected ones: stars with S err > 75 km s− 1 (blue colour) and stars close to the Galactic plane (red colour) in the (X, Y) and (X, Z) planes. RC stars with errors S err > 75 km s− 1 dominate the outermost region of the diagram.

Figure 5. Distribution of the sample stars (grey colour) and rejected ones: stars with S err > 75 km s− 1 (blue colour) and stars close to the Galactic plane (red colour) in two panels of space velocity components: (a) (V lsr, U lsr) and (b) (V lsr, W lsr).
We used standard gravitational potentials described in the literature (Miyamoto & Nagai Reference Miyamoto and Nagai1975; Hernquist Reference Hernquist1990; Johnston, Spergel, & Hernquist Reference Johnston, Spergel and Hernquist1995; Dinescu, Girard, & van Altena Reference Dinescu, Girard and van Altena1999) to estimate orbital elements of each of the sample stars. The orbital elements for a star used in our work are the mean of the corresponding orbital elements calculated over 15 orbital periods of that specific star. The orbital integration typically corresponds to 3 Gyr and is sufficient to evaluate the orbital elements of solar suburb stars (Coşkunoğlu et al. Reference Coşkunoğlu, Ak, Bilir, Karaali, Önal, Yaz, Gilmore and Seabroke2012; Bilir et al. Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012; Duran et al. Reference Duran, Ak, Bilir, Karaali, Ak, Bostancı and Coşkunoğlu2013).
First, we performed the test-particle integration in a Milky Way potential which consists of a logarithmic halo to determine a possible orbit in the form below:
with v 0 = 186 km s− 1 and d = 12 kpc. The disc is represented by a Miyamoto-Nagai potential (Miyamoto & Nagai Reference Miyamoto and Nagai1975):
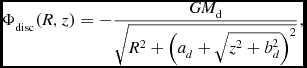 \begin{eqnarray}
\Phi _{\rm disc}(R,z)=-\frac{G M_{\rm d}}{ \sqrt{R^{2} + \left( a_d + \sqrt{z^{2}+b_d^{2}} \right)^{2}}},
\end{eqnarray}
\begin{eqnarray}
\Phi _{\rm disc}(R,z)=-\frac{G M_{\rm d}}{ \sqrt{R^{2} + \left( a_d + \sqrt{z^{2}+b_d^{2}} \right)^{2}}},
\end{eqnarray}
with M d = 1011 M ⊙, ad = 6.5 kpc and bd = 0.26 kpc. Finally, the bulge is modelled as a Hernquist potential (Hernquist Reference Hernquist1990):
using M b = 3.4 × 1010 M ⊙ and c = 0.7 kpc. The superposition of these components gives quite a good representation of the Milky Way. The circular speed at the solar radius is 222.5 km s− 1. P LSR = 2.18 × 108 yr is the orbital period of the LSR and Vc = 222.5 km s− 1 denotes the circular rotational velocity at the solar Galactocentric distance, R 0 = 8 kpc.
For our kinematic analysis, we are interested in the mean radial Galactocentric distance (Rm ) as a function of the stellar population and the orbital shape. Williams et al. (Reference Williams2011) have analyzed the radial orbital eccentricities of RAVE sample of thick-disc stars, to test thick-disc formation models. Here, we consider the vertical orbital eccentricity, ev for population analysis. Rm is defined as the arithmetic mean of the final perigalactic (Rp ) and apogalactic (Ra ) distances, and z max and z min are the final maximum and minimum values of the z coordinates, respectively, to the Galactic plane, where ev is defined as follows:
where Rm = (Ra + Rp )/2 (Pauli Reference Pauli, Gerdjikov and Tsvetkov2005).
3 DISTRIBUTION OF THE SPACE VELOCITY COMPONENTS
3.1 Distribution of the space velocity components above and below the Galactic plane
We adopted the vertical orbital eccentricities and the procedure in Bilir et al. (Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012) and separated all the sample into three populations, thin disc (ev ⩽ 0.12), thick disc (0.12 < ev ⩽ 0.25) and halo (ev > 0.25). We carried out the same evaluation for the RC stars above and below the Galactic plane. The Galactic latitudes of these sub-samples are b > 10° and b < −10°, respectively, due to the restriction explained in Section 2. The space velocity components and their corresponding dispersions for three categories are given in Table 1. The number of stars for the thin disc are in majority, while those for the halo are in minority, as expected for a sample of stars in the solar suburb. The data confirm another expectation of us, i.e. the numerical values for a specific velocity component are different for different populations. One can see in Table 1 that there is a symmetrical distribution relative to the Galactic plane for only two parameters, i.e. the space velocity component V lsr and its total dispersion σtot. The number of stars below the Galactic plane is larger than the ones above, due to the observational strategy of RAVE, 3 801 and 2 809 stars respectively. Hence, the errors of the space velocity components for the stars with b < −10° are less than the corresponding ones with b > 10°.
Table 1. The space velocity components relative to the LSR velocities (U lsr, V lsr, W lsr) and their dispersions (σ U , σ V , σ W , σtot), for the RC stars above (b > 10°) and below (b < −10°) the Galactic plane in terms of vertical eccentricity ev . N denotes the number of stars and σtot is the total space velocity dispersion. The errors of the space velocity components are the mean of the errors of the corresponding stars, while those for the dispersions are the standard errors.

3.2 Distribution of the space velocity components relative to the Galactocentric radial distance in different z min and z max intervals
We estimated the space velocity components of the sample stars relative to Rm in different z min and z max intervals. The ranges of these parameters are 4 < Rm ⩽ 11, − 2.5 ⩽ z min ⩽ 0 and 0 < z max ⩽ 2.5 kpc. The results are given in Table 2. The distributions of the space velocity components are given in Figure 6. In the following, we discuss the trends in each space velocity component.
Table 2. The space velocity components relative to the LSR velocities (U lsr, V lsr, W lsr) and their space velocity dispersions (σ U , σ V , σ W , σtot) for the RC stars in terms of mean Galactocentric radial distance (Rm ) for five z min and five z max intervals. N denotes the number of RC stars in the Rm range stated on the same line. Errors as defined in Table 1.


Figure 6. Distribution of the space velocity components relative to the LSR velocities, U lsr, V lsr, W lsr, in terms of mean Galactocentric radial distance Rm , for five z min and five z max intervals. The figures in the top panel indicate the number of stars. The error bars are also shown in the diagram.
3.2.1 U lsr
The variation of the space velocity component U lsr is given at the top panel of Figure 6. When we consider the errors, the general trend is a flat distribution. However, there are different distributions in some z min/z max intervals, such as − 1 < z min ⩽ −0.5 and − 0.5 < z min ⩽ 0 kpc where a small increase in U lsr can be detected at ~ 7.5 kpc. Whereas, the numerical value of U lsr in the interval 1.5 < z max ⩽ 2 kpc at distance Rm ~ 7.5 kpc gives the indication of a change in the trend, i.e. the decreasing velocity component in the distance interval 5 < Rm < 7.5 kpc flattens at larger Rm distances. A different figure is related to the extreme intervals, − 2.5 ⩽ z min ⩽ −2 and 2 < z max ⩽ 2.5 kpc, where U lsr is an increasing function of Rm . However, the number of stars in these intervals are small.
3.2.2 V lsr
The middle panel in Figure 6 shows that there is a smooth variation of the velocity component V lsr with respect to Rm for all z min and z max intervals. Also, there is a slight indication (at least for the smallest values in each interval) that V lsr values for the RC stars for b < −10° increases with decreasing distance to the Galactic plane, while they increase gradually with increasing distance to the Galactic plane for b > 10°. This argument has been confirmed by the mean of V lsr velocity components in z min and z max intervals. Figure 7 shows that there is almost a symmetrical distribution of the mean V lsr velocity components with respect to z min and z max for all RC stars. That is the V lsr velocity component values are highest in the Galactic plane and they become relatively lower with higher Galactic latitudes. This is what we expect from the Jeans equations, V lsr decreases as the asymmetrical drift increases and asymmetric drift increases with velocity dispersion (cf. Binney & Tremaine Reference Binney and Tremain1998). The symmetric shape of the curve in this figure is also a general property of stellar Galactic orbits, i.e. z min ≈ −z max, due to symmetry of the Galactic potential relative to the Galactic plane.

Figure 7. Diagram of the mean V lsr space velocity components for five z min and five z max distances. The error bars are also shown in the diagram.
3.2.3 W lsr
The distribution of the space velocity component W lsr is given in the lower panel of Figure 6. The distribution is rather flat in all z min and z max intervals, except in the intervals − 2.5 ⩽ z min ⩽ −2 and 1.5 < z max ⩽ 2 kpc where in the first interval there is a concave shape with a minimum at ~ 7.5 kpc and where there is an extended peak covering the Galactocentric distances larger than Rm ~ 7.5 kpc following the flat distribution in shorter distances, Rm ⩽ 7.5 kpc. While W lsr increases with Rm distance monotonously in the interval 2 < z max ⩽ 2.5 kpc. We omit the first bin in this interval which contains only five stars.
3.3 Distribution of the space velocity components relative to the Galactic longitude in different z min and z max intervals
In this section, we discuss the distribution of the space velocity components relative to the Galactic longitude. However, we stress that we cannot discuss motions in all four quadrants on equal footing, as RAVE observed only stars in the southern celestial hemisphere. We evaluated the mean of the space velocity components U lsr, V lsr and W lsr, for four quadrants, Q 1(0° ⩽ l ⩽ 90°), Q 2(90° < l ⩽ 180°), Q 3(180° < l ⩽ 270°) and Q 4(270° < l ⩽ 360°) of the Galaxy (Table 3) and plotted them in Figure 8. We discuss the most striking features of the space velocity components in the following.
Table 3. The mean space velocity components relative to the LSR velocities (U lsr, V lsr, W lsr) for four quadrants and for five z min and five z max intervals. N and ⟨l⟩ denote the number of stars and the mean longitude for the corresponding quadrant. Errors as defined in Table 1.


Figure 8. Distribution of the space velocity components relative to the LSR velocities, U lsr, V lsr, W lsr, in terms of Galactic longitude, for five z min and five z max intervals. The figures in the top panel indicate the number of stars. The error bars are also shown in the diagram.
3.3.1 U lsr
Distribution of the U lsr space velocity components relative to the quadrants are plotted at the top panel in Figure 8. Two features can be detected in z min and z max intervals: (i) there are systematic differences between the space velocity components in the quadrants Q 1, Q 3 and Q 4, U lsr being larger in Q 3 than ones in Q 1 and Q 4 in all z min and z max intervals, except 2 < z max ⩽ 2.5 kpc; (ii) the U lsr space velocity component corresponding to the data in Q 1 decreases monotonously with increasing distance to the Galactic plane in the ranges − 1.5 < z min ⩽ 0 and 0 < z max ⩽ 1.5 kpc and it increases at relatively extreme distances.
3.3.2 V lsr
The middle panel of Figure 8 shows that, for z min intervals, the V lsr space velocity component for a given Qi (i= 1, 3, 4) increases with increasing z min, i.e. a result stated in Section 3.2.1. That is the V lsr space velocity components attain their larger values at lower Galactic latitudes. Any numerical value of V lsr which does not obey this argument is related to the number of stars used for its evaluation and consequently its error. As an example, we give the V lsr values and the number of stars for the intervals − 1.5 < z min ⩽ −1, − 2 < z min ⩽ −1.5, and − 2.5 ⩽ z min ⩽ −2 kpc, for the quadrant Q 1, i.e. V lsr = −27.7 ± 20.08 km s− 1, N = 246; V lsr = −14.54 ± 22.62 km s− 1, N = 103; and V lsr = −23.32 ± 27.12 km s− 1, N = 57, respectively. The numerical value of V lsr for the first z min interval obeys the argument just cited, whereas those for the other two z min intervals with higher errors and less number of stars do not. For z max intervals, the same case holds only for the Q 3 and Q 4, while the behaviour of the V lsr space velocity component for Q 1 is in the opposite sense. We cannot consider the V lsr space velocity component for Q 2 due to absence of stars for this quadrant.
3.3.3 W lsr
Distribution of the W lsr space velocity components relative to the quadrants are plotted in the lower panel of Figure 8. The behaviours of W lsr for stars in two quadrants are rather interesting. In Q 1, W lsr is positive in three z max intervals, 0 < z max ⩽ 0.5, 0.5 < z max ⩽ 1 and 1 < z max ⩽ 1.5 kpc, while it is negative in all five z min intervals. That is, the RC stars above the Galactic plane in Q 1 move towards the direction of North Galactic Pole, whereas those below the Galactic plane in the same quadrant move in the opposite direction. The number of stars in the intervals 1.5 < z max ⩽ 2 and 2 < z max ⩽ 2.5 kpc which do not obey the argument just stated are only N = 16 and 6, respectively. However, the case is reverse for the RC stars in quadrant Q 3, i.e. W lsr is negative in the same z max intervals, 0 < z max ⩽ 0.5, 0.5 < z max ⩽ 1 and 1 < z max ⩽ 1.5 kpc, while it is positive in three z min intervals: − 2 < z min ⩽ −1.5, − 1.5 < z min ⩽ −1, − 1 < z min ⩽ −0.5 kpc. That is, the RC stars above and below the Galactic plane in the z max and z min intervals cited move towards the Galactic plane.
The errors of the U lsr and W lsr are larger than the absolute values of the corresponding space velocities. Hence, the behaviours of these velocity components are probably more complicated than we detected. RAVE observed only stars in the southern celestial hemisphere. Hence, the number of stars with z max distances are relatively smaller than the corresponding ones with z min ones, which causes larger errors.
3.4 Distribution of the space velocity dispersions
We estimated the dispersions of the space velocity components for the sample stars as a function of Rm in different z min and z max intervals. The ranges of Rm , z min and z max are 4 ⩽ Rm ⩽ 11, − 2.5 ⩽ z min ⩽ 0 and 0 < z max ⩽ 2.5 kpc, respectively. The results are given in Table 2 and Figure 9. The RC stars at extreme Galactocentric distances, 4 ⩽ Rm ⩽ 5 and 10 < Rm ⩽ 11 kpc, are small in number. The number of stars are also relatively small for − 2.5 ⩽ z min ⩽ − 2 and 2 < z max ⩽ 2.5 kpc intervals, and their errors are large. In our discussions below, we will give less weight to the bins corresponding to small number of stars and relatively large errors.

Figure 9. Distribution of the dispersions of space velocity components relative to the LSR velocities, σ U , σ V , σ W , σtot, in terms of mean Galactocentric radial distance Rm , for five z min and five z max intervals. The figures in the top panel indicate the number of stars. The error bars are also shown in the diagram.
The distribution of the σ U dispersion is almost flat in − 0.5 < z min ⩽ 0 and 0 < z max ⩽ 0.5 kpc intervals, while there is a positive (but small) gradient in other z min and z max intervals, i.e. σ U increases with increasing Rm . That is, the distribution of σ U is different between the ranges close to the Galactic plane and the further ones.
The distribution of the σ V dispersion is also flat in − 0.5 < z min ⩽ 0 and 0 < z max ⩽ 0.5 kpc intervals. However, one can detect a small gradient in some of the other z min and z max intervals, such as − 1.5 < z min ⩽ − 1 and 0.5 < z max ⩽ 1 kpc.
The trend of the distribution of the dispersion σ W is almost the same as σ U and σ V in the intervals − 0.5 < z min ⩽ 0 and 0 < z max ⩽ 0.5 kpc, while there is a gradient in the distribution of σ W in the other z min and z max intervals. Additionally, this gradient is in opposite sense cited for σ U velocity dispersion, i.e. σ W decreases with increasing Rm distance.
The general aspect of the distribution of each space velocity dispersion, σ U , σ V , σ W and σtot, in Figure 9 gives the indication of a parabolic function with its vertex at the Galactic plane: the space velocity dispersions are small in two intervals, − 0.5 < z min ⩽ 0 and 0 < z max ⩽ 0.5 kpc, but gradually, they become larger in the z min and z max intervals corresponding to larger distances from the Galactic plane. The small gradients in the z min and z max intervals encouraged us to estimate the mean space velocity dispersion in these intervals and plotted them versus corresponding mean z min and z max values. Figure 10 shows that a Gaussian distribution fits to each of the space velocity dispersion, i.e. σ U , σ V , σ W , σtot. Also, the smooth distribution of the velocity dispersions reveals that the thin and thick discs are kinematically continuous components of the Galaxy. Actually, the majority of our sample consists of the thin and thick disc RC stars, and there is a smooth transition between the small (thin disc) and relatively large (thick disc) space velocity dispersion in Figure 10. As stated in Section 3.2.2., the symmetric shapes of the curves in this figure are also a general property of stellar Galactic orbits, i.e. z min ≈ −z max and the symmetric of the Galactic potential relative to the Galactic plane.

Figure 10. Mean dispersions of the space velocity components, σ U , σ V , σ W and σtot, for five z min and five z max intervals.
4 SUMMARY AND DISCUSSION
We used the space velocity components and their dispersions of 6 610 RC stars and investigated their distribution relative to vertical distance, Galactocentric radial distance and Galactic longitude. The total error of the space velocity components is restricted with S err ⩽ 75 km s− 1, and space velocity components are corrected with differential rotation, to obtain reliable data. Also, we investigated the variation of the space velocity components in terms of z min and z max distances instead of z, which covers the effect of long-lived internal and external forces.
In our distance calculations, we adopted a single value of absolute value, M KS = −1.54 mag (Groenewegen Reference Groenewegen2008). It has been cited in the literature (cf. Williams et al. Reference Williams2013) that the use of a single value does not compromise the results considerably. The proper motions of all RC stars are taken from RAVE DR3, except those of 139 stars which were not available in this catalogue and which were provided from the PPMXL, as cited in Section 2. Different proper motion catalogues such as SPM4 and UCAC3 could be used as well. However, different proper motions change only the predicted values of the space velocity components but not the trends of their distributions. Additionally, the difference between the values of a given space velocity component predicted by two different proper motion catalogue is not large (cf. Williams et al. Reference Williams2013). We omitted the RC stars with total error S err > 75 km s− 1 in their space velocities where most of these errors originate from the proper motions. The proper motions of 706 stars with S err > 75 km s− 1 is μtoterr ⩽ 10 mas and those of 498 stars is μtoterr > 10 mas. The distances are based on a single absolute magnitude with an error of ± 0.04 mag, and RAVE group gives a median radial velocity error of 1.2 km s− 1 (Siebert et al. Reference Siebert2011). Hence, the effect of the distance errors and radial velocity should be much smaller than the one for proper motion.
The space velocity components and their dispersions for different populations, i.e. thin and thick discs and halo, are different as expected. The space velocity components for RC stars above (b > 10°) and below (b < −10°) the Galactic plane are compatible only for V lsr of the thin disc.
The V lsr space velocity component is vertical distance (z min and z max) and Rm dependent. There is a smooth variation relative to Rm . The mean of the V lsr space velocity components for 10 z min and z max intervals could be fitted to a Gaussian distribution with a minimum point at the Galactic plane, a result expected from the Jeans equations, i.e. V lsr decreases as the asymmetric drift increases and asymmetric drift increases with space velocity dispersion (Binney & Tremaine Reference Binney and Tremain1998).
The general trend of the space velocity component U lsr is a flat distribution in terms of Rm for most of the z min and z max intervals. However, there are some intervals where the trend changes at ~ 7.5 kpc. Also, the distribution in the extreme intervals, − 2.5 ⩽ z min ⩽ − 2 and 2 < z max ⩽ 2.5 kpc is an increasing function. However, the number of stars in these intervals are relatively small corresponding to larger errors.
The distribution of the space velocity component W lsr is also flat, again with some exceptions, i.e. there is a concave shape with a minimum at Rm ~ 7.5 kpc in the interval − 2.5 ⩽ z min ⩽ −2 kpc, and an extended peak covering distances larger than Rm ~ 7.5 kpc, following the flat distribution in shorter distances. The distribution of W lsr is an increasing function in the extreme interval, 2 < z max ⩽ 2.5, similar to U lsr.
The behaviours of the space velocity components are different in four quadrants (Figure 11). The upper panel of Figure 11 shows that the space velocity components U lsr estimated for the RC stars in the quadrant Q 3 (180° < l ⩽ 270°) are larger than the ones estimated for the RC stars in quadrants Q 1 (0° ⩽ l ⩽ 90°) and Q 4 (270° < l ⩽ 360°) for all z min and z max intervals, except the interval 2 < z max ⩽ 2.5 kpc which is not valid for Q 4. We will see in the following that z min and z max intervals which involve small number of stars, such as in the present case where the number of stars is only N = 15, show exceptions due to corresponding large errors. Different U lsr space velocity components indicate different lag for the RC stars in different quadrants. The U lsr velocity components for quadrants Q 1 and Q 4 attain their maximum values at small distances to the Galactic plane, while its distribution for the quadrant Q 3 gives the indication of a double peak distribution. In our analysis, we give less weight to the (relatively) extreme z min and z max intervals due to larger errors, as mentioned above in this paragraph.
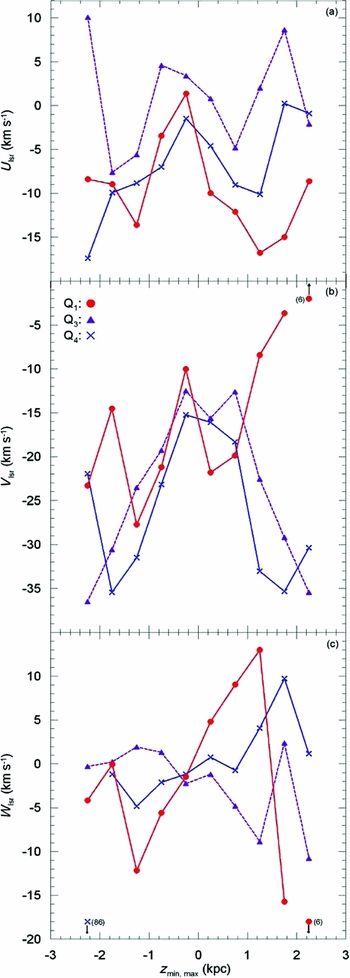
Figure 11. Distribution of the space velocity components relative to the LSR velocities, U lsr, V lsr, W lsr, for three quadrants: Q 1(0° ⩽ l ⩽ 90°), Q 3(180° < l ⩽ 270°) and Q 4(270° < l ⩽ 360°) shown with different symbols, for five z min and five z max distances. Figures in the parenthesis indicate the (small) number of stars for which the errors are large.
The space velocity component V lsr shows almost a similar distribution in terms of z min and z max distances in the quadrants Q 3 and Q 4 (middle panel), i.e. V lsr attains its (relative algebraic) large numerical values in − 0.5 < z min ⩽ 0 and 0 < z max ⩽ 1 kpc intervals, then it decreases gradually with larger distances from the Galactic plane. That is, the lag for the space velocity component in the direction to the Galactic rotation increases from the Galactic plane to larger vertical distances. However, the same case does not hold for V lsr estimated for the RC stars in the quadrant Q 1, i.e. the distribution of V lsr shows two minima and three maxima in the interval formed by combining five z min and five z max intervals. Especially, V lsr is a monotonous increasing function in the z max intervals, starting from a minimum point in 0 < z max ⩽ 0.5 kpc interval which also contradicts with the maximum V lsr space velocity components estimated in the quadrants Q 3 and Q 4.
In the case of the space velocity component W lsr, the similarity exists for the RC stars in the quadrants Q 1 and Q 4, as explained in the following. The numerical values of W lsr for the quadrants Q 1 and Q 4 are negative for all z min intervals, while they are positive for Q 1 in three z max intervals, 0 < z max ⩽ 0.5, 0.5 < z max ⩽ 1 and 1 < z max ⩽ 1.5 kpc. However, the number of stars in the other two z max intervals where W lsr is not positive, are only 16 and 6. W lsr is positive for Q 4 for four z max intervals, and its numerical value in the fifth z max interval, 0.5 < z max ⩽ 1 kpc, is only − 0.73 km s− 1. The overall picture for the space velocity component in the quadrants Q 1 and Q 4 (in the inward direction relative to the Sun) is that RC stars above the Galactic plane move in the direction to the North Galactic Pole, whereas those below the Galactic plane move in the opposite direction, they show a rarefaction. The distribution of the space velocity component W lsr in the quadrant Q 3 is different than the ones in the quadrants Q 1 and Q 4, i.e. W lsr is positive (or close to zero) in four z min intervals and negative in four z max intervals. That is, in the case of quadrant Q 3 (in the outward direction), RC stars above and below the Galactic plane move towards the Galactic plane, they show a compression. We could not consider the quadrant Q 2 due to absence of stars in the z max intervals and only 94 stars in the z min intervals. Also, we stress (again) that we cannot discuss motions in three quadrants on equal footing, as RAVE observed only stars in the southern celestial hemisphere.
Our results confirm the complex structure of our Galaxy. It is non-homogeneous, in non-steady state, and asymmetric. The rarefaction and the compression of the RC stars in different quadrants were detected also in Williams et al. (Reference Williams2013). However, their procedure is different. In Williams et al. (Reference Williams2013), two opposite features were based on the Galactocentric radial distance, i.e. inward of Ro = 8.5 kpc stars show a rarefaction, while outward of Ro kpc they show a compression. In Bilir et al. (Reference Bilir, Cabrera-Lavers, Karaali, Ak, Yaz and López-Corredoira2008), the Galactic longitude dependence of the scale heights of the thin and thick discs were explained with the gravitational effect of the Galactic long bar (see also, Cabrera-Lavers et al. Reference Cabrera-Lavers, Bilir, Ak, Yaz and López-Corredoira2007). Hence, the features detected in our study probably originate from the Galactic long bar, rather than any other event such as an accretion. The vertical distances, z min and z max, used in this study correspond to a long-lived time scale. Hence, any event related to the gradients of the space velocity components should be also long lived. Also this argument favours the Galactic long bar.
However, we do not argue that all the features mentioned above can be explained with only one event. Differences between the lags for the U lsr space velocity components of the stars at the same vertical distance but in different quadrants, such as Q 1, Q 3 and Q 4, need alternative events.
5 CONCLUSION
The distributions of the space velocity components U lsr, V lsr and W lsr, relative to the vertical distance z max/z min, Galactocentric distance R and Galactic longitude l show that the Milky Way galaxy has a non-homogeneous, non-steady state and asymmetric structure. The Galactic long bar is the probable origin of many, but not all, of the features detected.
ACKNOWLEDGEMENTS
We are grateful to the anonymous reviewer who improved our paper by his/her comments and suggestions. This work has been supported in part by the Scientific and Technological Research Council (TÜBİTAK) 112T120. Funding for RAVE has been provided by the Australian Astronomical Observatory; the Leibniz-Institut fuer Astrophysik Potsdam (AIP); the Australian National University; the Australian Research Council; the French National Research Agency; the German Research Foundation; the European Research Council (ERC-StG 240271 Galactica); the Istituto Nazionale di Astrofisica at Padova; The Johns Hopkins University; the National Science Foundation of the USA (AST-0908326); the W. M. Keck Foundation; the Macquarie University; the Netherlands Research School for Astronomy; the Natural Sciences and Engineering Research Council of Canada; the Slovenian Research Agency; the Swiss National Science Foundation; the Science & Technology Facilities Council of the UK; Opticon; Strasbourg Observatory; and the Universities of Groningen, Heidelberg and Sydney.
The RAVE website is at http://www.rave-survey.org. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of the SIMBAD, NASA's Astrophysics Data System Bibliographic Services and the NASA/IPAC ExtraGalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.

















