Introduction
This paper reports the description and the crystal structure of letnikovite-(Ce) [Russian Cyrillic: летниковит-(Ce)], ideally (Na□)Ca2Ce2[Si7O17(OH)]F4(H2O)4, a new mineral from the well-known Darai-Pioz alkaline massif, Tien-Shan Mountains, Central Tajikistan. Letnikovite-(Ce) is a sheet-silicate mineral with large channels and potentially can be used as a model for synthesis of microporous materials of industrial interest. Single-crystal X-ray diffraction studies revealed a single [Si7O17(OH)]7– sheet of five-membered and ten-membered rings of SiO4 and SiO3(OH) tetrahedra that has never been described in minerals (Hawthorne et al., Reference Hawthorne, Uvarova and Sokolova2019). The mineral is named for Professor Felix Artem'evich Letnikov (Russian Cyrillic: Феликс Артемьевич Летников) (born October 3rd, 1934, Polotsk, USSR), Academician of the Russian Academy of Sciences, a prominent geologist working on the petrology and geochemistry of Precambrian rocks. Professor Letnikov has had a major impact on the principal areas of his work and has made a significant contribution to the organisation of science in Siberia. The new mineral and its name (symbol Lkv-Ce) have been approved by the Commission on New Minerals, Nomenclature and Classification, International Mineralogical Association (IMA2022–132, Agakhanov et al., Reference Agakhanov, Sokolova, Cámara, Karpenko, Hawthorne, Pautov, Kasatkin, Pekov and Agakhanova2023). The holotype material is deposited in the systematic collection of the Fersman Mineralogical Museum, Moscow, Russia, catalogue number 98145.
Occurrence and associated minerals
Letnikovite-(Ce) was found in the moraine of the Darai-Pioz glacier in the upper reaches of the Darai-Pioz River, Tien-Shan mountains, near the junction of the Turkestansky, Zeravshansky and Alaisky ranges (39°30′N 70°40′E). This area is in the Rasht (formerly Garm) district, Central Tajikistan. The alkaline Darai-Pioz massif belongs to the Upper Paleozoic Alaysky (Matchaisky) intrusive complex. Information on the geology of the Darai-Pioz massif can be found in Pautov et al. (Reference Pautov, Agakhanov, Karpenko, Uvarova, Sokolova and Hawthorne2019) with reference to relevant earlier publications.
Letnikovite-(Се) was found in boulders (up to 2 m) of quartz rock, 90–95% medium- to coarse-grained quartz of ice-like appearance (quartz grains vary from 2 mm to 2 cm) characteristic for moraine deposits of the Darai-Pioz glacier. The following subordinate and accessory minerals are present: large (up to 10 cm across) golden-brown tabular and lamellar crystals of polylithionite, pink plates of sogdianite–sugilite, pale-yellow to orange aggregates and tabular crystals of reedmergnerite, black crystals of aegirine, orange–brown semi-transparent lentil-like crystals of stillwellite-(Се), grass-green or yellowish-green semi-transparent and transparent crystals of leucosphenite, dark-green crystals of turkestanite and aggregates of large white grains of microcline. Also common are fine-grained brown or greyish-brown aggregates of Mn-bearing pectolite, quartz, Sr-bearing fluorite, aegirine and a variety of rare minerals; letnikovite-(Ce) occurs in these pectolite-rich aggregates (Fig. 1a). Associated minerals are quartz, fluorite, pectolite, baratovite, aegirine, leucosphenite, neptunite, reedmergnerite, orlovite, sokolovaite, mendeleevite-(Ce), odigitriaite, pekovite, zeravshanite, kirchhoffite and garmite. Letnikovite-(Ce) occurs in a peralkaline pegmatite oversaturated with silica (silexite-like) and was formed at a late, probably hydrothermal, stage of the pegmatite.

Figure 1. Back-scatter electron images of polished sections with letnikovite-(Ce) [Lkv-Ce] in association with mendeleevite-(Ce) [Mdl-Ce], pectolite [Pct], fluorite [Fl] and quartz [Qz]: (a) the grain used for Raman spectroscopy, determination of micro-indentation hardness and reflectance spectra; (b) a microprobe mount with a grain that was deposited as holotype material (#98145) at the Fersman Mineralogical Museum.
Physical properties
Letnikovite-(Ce) occurs as isolated prismatic grains up to 0.1 mm long and up to 0.03 mm thick in a quartz–pectolite aggregate (Fig. 1a,b). The mineral is colourless and has a white streak and a vitreous lustre. Letnikovite-(Ce) does not fluoresce under cathode rays or ultraviolet light. The mineral is brittle, cleavage is {001} perfect, the fracture is stepped along the cleavage plane and uneven across this direction; no parting was observed. The average micro-indentation hardness is VHN50 = 239 kg/mm2 (with a range of 193–266). Although micro-indentation and Mohs hardness are different hardness measurements (Broz et al., Reference Broz, Cook and Whitney2006), the first representing the resistance to indentation and the second one the resistance to scratch, the present value of micro-indentation hardness corresponds roughly to a Mohs hardness of ~4. Measurements were done on the PMT-3 instrument, calibrated on NaCl at a loading of 50 g. The calculated density, D calc., is 2.847 g/cm3.
Macroscopically, the crystals do not show twinning. However, because of the microscopic twinning, the 2V value and optic sign could not be determined. Letnikovite-(Ce) is nonpleochroic. In reflected light, letnikovite-(Ce) is grey. Bireflectance is weak, ΔR = 0.8% (589 nm). When observed in air, internal reflections were not seen, and anisotropy is not visible. Reflectance values were measured with a UMSP-50 Opton microspectrophotometer using the Opton SiC standard 474251 (with a spectral slot width of 10 nm) and are given in Table 1.
Table 1. Reflectance values (%) for letnikovite-(Ce).*

* The values required by the COM are given in bold.
Raman spectroscopy
The Raman spectrum of letnikovite-(Ce) (Fig. 2a,b) was obtained at room temperature from a randomly oriented crystal (polished section, 70 × 30 μm size) using a Thermo DXR2xi Raman imaging confocal microscope with a green laser (532 nm). The output power of the laser beam was 5 mW (at 50% power), holographic diffraction grating with 4000 lines per cm, spectral resolution was 2 cm–1, and the range was from 50 to 6000 cm–1. The diameter of the focal spot on the sample was 2 μm. The back-scattered Raman signal was collected with a 100× objective; the signal acquisition time for a single scan from 50–6000 cm–1 was 0.5 s and the signal was averaged over 1000 scans. For the range 50–1800 cm–1 the signal acquisition time was 2.0 s and the signal was averaged over 30 scans. The spectrum was processed using Omnic software (Thermo Scientific™). Letnikovite-(Ce) shows intensive luminescence from 100 to 3500 cm–1, and background subtraction was applied.

Figure 2. Background-subtracted Raman spectrum of letnikovite-(Ce): (a) the ‘fingerprint’ region from 50–1800 cm–1; and (b) the principal O–H stretching region from 3000–3800 cm–1.
On the basis of data for some ring silicates with Na, Ca and rare earth elements (REE) (Sitarz et al., Reference Sitarz, Mozgawa and Handke1998; Frost and Xi, Reference Frost and Xi2012; Tobbens et al., Reference Tobbens, Kahlenberg, Kaindl, Sartory and Konzett2008), we assign the bands at 1107 and 952 cm–1 to Si–O stretching vibrations, and those at 667 and 693 cm–1 are attributed to O–Si–O bending modes. Raman bands of lower frequency (500–100 cm–1, Fig. 2a) are assigned to Me–O stretching vibrations and collective lattice vibrations and translational and deformation modes, including the intense band at 464 cm–1 which probably corresponds to a Ca–O stretching mode (Frost and Xi, Reference Frost and Xi2012).
From 3000–3700 cm–1 (Fig. 2b), there are several broad peaks (3233, 3402 and 3553 cm–1) corresponding to stretching modes of H2O and OH groups.
Chemical composition
The chemical composition of letnikovite-(Ce) was determined using a JEOL 773 electron-microprobe (EDS mode, an accelerating voltage of 20 kV, a beam current of 2 nA and a beam diameter of 5 μm; Fersman Mineralogical Museum). The following standards were used: microcline USNM 143966 (Si; K); albite 107 (Na); SrTiO3 (Sr); CsTbP4O12 (Cs); ilmenite USNM 96189 (Fe); anorthite USNM 137041 (Ca); diopside USNM 11773 (Mg); LaPO4 (La); CePO4 (Ce); PrPO4 (Pr); NdPO4 (Nd); SmPO4 (Sm); EuPO4 (Eu); GdPO4 (Gd); and MgF2 (F).
The data (5 analyses) were reduced and corrected by the PAP method of Pouchou and Pichoir (Reference Pouchou, Pichoir and Armstrong1985). The chemical composition of letnikovite-(Ce) is the mean of five determinations and is given in Table 2. The empirical formula calculated on 7 Si atoms per formula unit (apfu) is Na0.72K0.14Cs0.04Ca2.10Sr0.55Mg0.28Pb0.05Fe0.04(Ce0.71Nd0.33La0.14Pr0.10Eu0.02Gd0.01)Σ1.31Si7O21.84F3.81H8.58, Z = 4. The structural formula based on refined site-occupancies (see below) is (Na0.72Ca0.16□1.12)Σ2(Cs0.04□0.96)Σ1(Ca1.83□0.17)Σ2(Mg0.28Fe0.04□0.68)Σ1(Ln 3+1.31Sr0.55Ca0.09Pb0.05)Σ2[Si7O17(OH)]F3.81(H2O)3.79, where Ln 3+1.31 = (Ce0.71Nd0.33La0.14Pr0.10Eu0.02Gd0.01)Σ1.31. The simplified formula is (Na,□)2Ca2(Ln 3+,Sr)2[Si7O17(OH)]F4(H2O)4, where Ce is the dominant lanthanoid and (□,Cs) and (□,Mg) are omitted as □ > 70%. The ideal formula of letnikovite-(Ce), (Na□)Ca2Ce2[Si7O17(OH)]F4(H2O)4 (see below), requires (wt.%) Na2O 3.04, CaO 11.03, Ce2O3 32.28, SiO2 41.36, F 7.47, H2O 7.97, O ≡ F –3.15, total 100.00.
Table 2. Chemical composition and unit formula for letnikovite-(Ce).

* Formula calculated on 7 Si apfu; Esd = estimated standard deviation.
** H2O calculated from structure-refinement results: H2O = 3.79 pfu and OH = 1.0 pfu.
Powder X-ray diffraction
Powder X-ray diffraction data were obtained by collapsing single-crystal experimental data into two dimensions. Data (in Å for MoKα) are listed in Table 3. Unit-cell parameters are therefore the same as from the single-crystal data (Table 4).
Table 3. Simulated powder X-ray diffraction data (d in Å) * for letnikovite-(Ce).

* Powder data were obtained by collapsing single-crystal X-ray diffraction data into two dimensions.
Intensities are listed for reflections with I est. ≥ 20; the eight strongest peaks are marked in bold.
Table 4. Miscellaneous structure-refinement data for letnikovite-(Ce).

*Twin components are related by the transformation matrix ($\bar{1}$![]() 0 0, 0 $\bar{1}$
0 0, 0 $\bar{1}$![]() 0, 1 0 1).
0, 1 0 1).
X-ray single-crystal data collection and structure solution and refinement
X-ray single-crystal data for letnikovite-(Ce) were collected from a twinned crystal with a Rigaku Oxford Diffraction diffractometer equipped with a Mo micro-source X-ray tube and a Dectris Pilatus-200 K detector, controlled by the Crysalis-Pro™ software (Rigaku Oxford Diffraction, 2018). The intensities of reflections with –13 ≤ h ≤ 13, –41 ≤ k ≤ 41 and –25 ≤ l ≤ 25 were collected with a frame width of 0.5° and a frame time of 40 s up to 2θ ≤ 81.34°, and an empirical absorption correction (SCALE3 ABSPACK, Rigaku Oxford Diffraction, 2018) was applied. There were few observed reflections at high 2θ, and refinement of the structure was done for 2θ ≤ 54°, –9 ≤ h ≤ 9, –29 ≤ k ≤ 29 and –17 ≤ l ≤ 17. The observed lattice is metrically orthorhombic F with the following cell parameters obtained from the monoclinic cell via the transformation matrix $\bar{1}$![]() 00/102/010: a = 7.473, b = 26.852 and c = 22.920 Å. However, a tentative structure solution in space group F222 yielded wrong coordination geometries as well as ill-defined anisotropic displacement parameters. The monoclinic cell with half-cell volume led to a much more satisfactory solution. The crystal-structure solution by direct methods and refinement were done with the Bruker SHELXTL Version 5.1 software (Sheldrick, Reference Sheldrick2015) in space group C2/m. We refined the structure as two components related by the TWIN matrix ($\bar{1}$
00/102/010: a = 7.473, b = 26.852 and c = 22.920 Å. However, a tentative structure solution in space group F222 yielded wrong coordination geometries as well as ill-defined anisotropic displacement parameters. The monoclinic cell with half-cell volume led to a much more satisfactory solution. The crystal-structure solution by direct methods and refinement were done with the Bruker SHELXTL Version 5.1 software (Sheldrick, Reference Sheldrick2015) in space group C2/m. We refined the structure as two components related by the TWIN matrix ($\bar{1}$![]() 0 0, 0 $\bar{1}$
0 0, 0 $\bar{1}$![]() 0, 1 0 1). The crystal structure of letnikovite-(Ce) was refined to R 1 = 4.20%, the twin ratio being 0.502(5):0.498(5) (Table 4). Details of data collection and structure refinement are given in Table 4. The occupancies of six cation sites were refined with the following scattering curves: M1 site: Ce; M(2,3) sites: Ca; M4 site: Mg; A1 and A2 sites: Na and Cs, respectively. The occupancies of the X(1–4) and W(1–5) anion sites were refined with the scattering curves of F and O, respectively. Refinement of the X2 and W1 site-occupancies converged to integer values (within 3 e.s.d.) and were subsequently fixed at full occupancy. Scattering curves for neutral atoms were taken from the International Tables for Crystallography (Wilson, Reference Wilson1992). Final atom coordinates and equivalent displacement parameters are given in Table 5, selected interatomic distances and angles in Table 6, refined site-scattering values and assigned site-populations in Table 7, and bond-valence values in Tables 8 and 9. A list of observed and calculated structure factors and a Crystallographic Information File (CIF) have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary Material (see below). The sturcture diagrams were drawn using Atoms 6.4 software (Dowty, Reference Dowty2016).
0, 1 0 1). The crystal structure of letnikovite-(Ce) was refined to R 1 = 4.20%, the twin ratio being 0.502(5):0.498(5) (Table 4). Details of data collection and structure refinement are given in Table 4. The occupancies of six cation sites were refined with the following scattering curves: M1 site: Ce; M(2,3) sites: Ca; M4 site: Mg; A1 and A2 sites: Na and Cs, respectively. The occupancies of the X(1–4) and W(1–5) anion sites were refined with the scattering curves of F and O, respectively. Refinement of the X2 and W1 site-occupancies converged to integer values (within 3 e.s.d.) and were subsequently fixed at full occupancy. Scattering curves for neutral atoms were taken from the International Tables for Crystallography (Wilson, Reference Wilson1992). Final atom coordinates and equivalent displacement parameters are given in Table 5, selected interatomic distances and angles in Table 6, refined site-scattering values and assigned site-populations in Table 7, and bond-valence values in Tables 8 and 9. A list of observed and calculated structure factors and a Crystallographic Information File (CIF) have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary Material (see below). The sturcture diagrams were drawn using Atoms 6.4 software (Dowty, Reference Dowty2016).
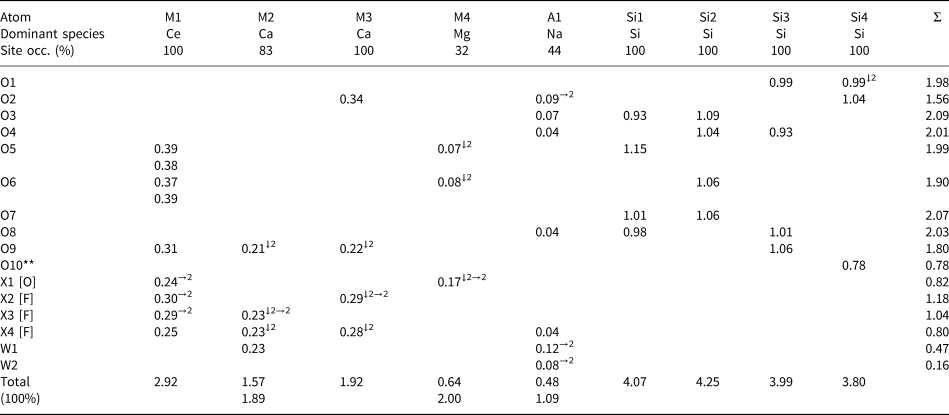
Table 5. Atom coordinates, site occupancies (Site occ., %) and anisotropic displacement parameters (Å2) for letnikovite-(Ce).

* For composition of the M(1–4) and A(1,2) sites see Table 7; X1 = [(H2O),F]; X2 = F, X(3,4) = [F,(H2O)]; W(1–5) = O atoms of H2O groups; **U iso.
Table 6. Selected interatomic distances (Å) and angles (°) in letnikovite-(Ce).

φ = O, F, H2O and OH.
Symmetry codes: a: –x, y, –z + 1; b: –x + 1, y, –z + 1; c: x+½, y–½, z; d: x+½, –y+½, z; e: –x+½, –y+½, –z + 1; f: –x+½, y–½, –z + 1; g: –x+3/2, –y+½, –z + 1; h: –x+3/2, y–½, –z + 1; i: x–½, y+½, z; j: x+½, y+½, z + 1; k: x, –y + 1, z; l: x, y, z; m: –x, y, –z; n: x, y, z–1; o: x–½, y+½, z–1; p: –x+½, y+½, –z + 1; q: x, –y + 1, z–1; r: –x, –y + 1, –z + 1; s: x–½, –y–½, z; t: –x + 2, –y, –z + 1; u: –x + 1, –y, –z.
Table 7. Refined site-scattering and assigned site-populations for letnikovite-(Ce).

φ = O, F, OH and H2O.
* Ln 3+1.31 = Ce0.71Nd0.33La0.14Pr0.10Eu0.02Gd0.01 [76.76 epfu]; fav = 58.60 el. (fav = average scattering curve for Ln3+1.31).
** Site scattering was refined, adjusted in accord with chemical analysis (Table 2), and then fixed at the last stages of the refinement.
Table 8. Bond-valence values (vu) for anions in letnikovite-(Ce).
*Bond-valence parameters (vu) are from Brown (Reference Brown, O'Keeffe and Navrotsky1981); bonds to oxygen were used for O(1–10), X1 and W(1,2); bonds to fluorine were used for X(2–4); occupancies of cation sites were taken into account for all calculations; the last row gives bond-valence sums for M2, M4 and A1 where the corresponding sites are 100% occupied.
**See discussion in the text on the contribution of hydrogen bonding to the bond-valence sum at O10.
Table 9. Bond-valence values (vu) for the O2 and X(1,3,4) anions involved in short-range order in letnikovite-(Ce)*.

* Bond-valence parameters (vu) are from Brown (Reference Brown, O'Keeffe and Navrotsky1981); anion curves are shown in square brackets for each atom.
** There are O–O distances [O2–W1 and O2–W3, Table 6] suitable for possible hydrogen bonding which can add ~0.3 vu in total to the bond-valence sum of 1.38 vu at O2. With the bond-valence sum of 1.68 vu, O2 = O atom.
Site-population assignment
Firstly, we assign Si to four tetrahedrally coordinated Si sites, with <Si–O> = 1.619 Å (Tables 5, 6).
Next considered are the four M sites in the heteropolyhedral sheet (Table 5). At the [9]-coordinated M1 site, the refined scattering is 104.5 electrons per formula unit (epfu), the highest value for the M sites; the mean bond length <M1–φ> = 2.539 Å (φ = O, F and H2O). In accord with the grand mean bond length <[9]Ce3+–O> = 2.553 Å observed in inorganic structures (Gagné, Reference Gagné2018), we assign heavy scatters: REE = Ln 3+1.31, where Ce is the dominant lanthanoid (Ln = lanthanoids) and minor Pb: 0.05 apfu, plus Sr: 0.55 apfu and minor Ca: 0.09 apfu, to the M1 site [[9]Ce3+: r = 1.196 Å, [9]Sr: r = 1.31, [9]Pb: r = 1.35 Å, [9]Ca2+: r = 1.18 Å, Shannon (Reference Shannon1976)] (Tables 5–7). There is a good agreement between refined and calculated site-scattering for the M1 site: 104.5 and 103.56 epfu, respectively (Table 7). On the basis of the refined site-scattering values and observed bond distances, we assign Ca0.83□0.17 and Ca1.0 apfu to the M2 and M3 sites, respectively (Table 7). The remaining M4 octahedron is the smallest polyhedron, and the refined scattering at the M4 site is 4.4 epfu, the lowest value for the M sites. Therefore, we allocate all the available Mg and Fe2+ to the M4 site, and the composition of the site is Mg0.28Fe2+0.04□0.68 apfu.
The interstitial A1 and A2 sites have refined site-scattering values of 11.0 and 2.2 epfu, respectively, with a sum of 13.2 epfu (Table 7). The cations to be assigned to these sites are Na, Ca and Cs, with a total scattering of 13.32 epfu (Table 2). The A1 polyhedron is smaller (mean bond distance of 2.546 Å), whereas the A2 polyhedron is larger, with <A2–φ> = 3.65 Å. Therefore, we assign all the available Na and Ca to the A1 site, which yields 11.12 epfu, in good agreement with the refined value of 11.0(4) epfu. Cs is the largest cation left to be assigned, and we allocate it to the A2 site. Hence a vacancy is dominant at the A2 site (Table 7).
Description of the structure
Cation sites
The crystal structure contains three groups of cation sites: M sites of the heteropolyhedral sheet, Si sites of the Si–O–OH sheet, and interstitial A1 and A2 sites.
Heteropolyhedral sheet
There are four cation sites in the heteropolyhedral sheet: the Ce-dominant M1 site, the Ca-dominant M(2,3) sites, and the □-dominant M4 site (Fig. 3a,b). The M1 site is occupied by Ln 1.31Sr0.55Ca0.09Pb0.05 apfu, where Ce is the dominant lanthanoid. The M1 atom is coordinated by nine anions: five O atoms and four X(1–4) anions where X = F and H2O (Tables 5–7) (see discussion on short-range order below). The ideal composition of the M1 site is Ce2 apfu. The M2 site is occupied by Ca at 83%, its composition is Ca0.83□0.17 pfu, ideally Ca1.0 apfu. The M2 atom is coordinated by seven anions: two O atoms, four X(3,4) anions and an H2O group at the W1 site (Tables 6, 7). The M3 site is fully occupied by Ca, its ideal composition is Ca1.0 apfu. The M3 atom is coordinated by seven anions: three O atoms and four X(2,4) anions (Tables 6, 7). The M4 site is occupied by Mg0.28Fe2+0.04□0.68 pfu, its ideal composition is □1.0 pfu. Ideally, cations of the heteropolyhedral sheet, M 2Ca +M 3Ca + M 1Ce2 + M 4□, sum to [Ca2Ce2]10+ apfu (Table 7).

Figure 3. Short-range order (SRO) arrangements in the heteropolyhedral sheet, ideally [Ca2Ce2F4(H2O)2]7+: (a) SRO-68%, the M4 site is vacant, and the X1 site is occupied by an H2O group; (b) SRO-32%, the M4 site is occupied by Mg plus minor Fe2+, the X1 site is occupied by F, and M4 octahedra share edges and vertices with M1 and M2 polyhedra. The [9]-coordinated Ce-dominant M1 polyhedra are green, [7]-coordinated Ca-dominant M(1,2) polyhedra are pink, Mg-dominant M4 octahedra are purple, the vacant M4 site is shown as a white circle with a purple rim; H2O groups and F atoms are shown as large red and small yellow spheres, respectively.
Si–O–OH sheet
In the Si–O–OH sheet (Fig. 4a,b), there are four Si(1–4) tetrahedrally coordinated sites occupied by Si with a <Si–O> distance of 1.619 Å (Tables 5, 6). We consider the Si–O–OH sheet as a complex anion (see below).

Figure 4. A single [Si7O17(OH)]7– sheet of five-membered and ten-membered rings of SiO4 and SiO3(OH) tetrahedra parallel to (001): (a) in the lower sheet at z ≈ 0.69, SiO3(OH) tetrahedra are oriented upward along c; (b) in the upper sheet at z ≈ 1.21, SiO3(OH) tetrahedra of the upper sheet are oriented downward along c; upward looking SiO3(OH) tetrahedra belong to the lower sheet and indicate the relative orientations of the two sheets. Si tetrahedra are orange, OH groups are shown as small turquoise spheres.
Interstitial sites
In letnikovite-(Ce), there are two interstitial sites: A1 and A2. They occur in the large channels between two Si–O–OH sheets (Fig. 5a,b). The A1 site is coordinated by three basal O atoms of Si tetrahedra, two H2O groups at the W(1,2) sites and an X4 anion (Table 6, Fig. 6a,b). It is ~50% occupied by Na0.72Ca0.16□1.12 pfu, and <A1–φ> = 2.546 Å (Table 7). We write the ideal composition of the A1 site as (Na□) pfu. The A2 site occurs in the centre of the channel (Fig. 5a) and is dominantly vacant. The A2 site is coordinated by eight basal oxygen atoms of Si tetrahedra on both sides of the channel and three H2O groups at the W(2,4) sites in the centre of the channel (Table 6, Fig. 7). It is occupied at 4% by Cs: Cs0.04□0.96 pfu, and <A2–φ> = 3.65 Å (Table 7). We write the ideal composition of the A2 site as □ pfu. Ideally, interstitial cations, A 1(Na□) +A 2□, sum to (Na□)1+ pfu.

Figure 5. Letnikovite-(Ce): (a) general view of the crystal structure; (b) linkage of a heteropolyhedral sheet and a single Si–O–OH sheet. Inset on the right from (a) shows possible hydrogen bonds between OH groups of two Si4 tetrahedra in the upper and lower Si–O–OH sheets along c. Legend as in Fig. 3, Si tetrahedra are orange, OH groups are shown as small turquoise spheres; interstitial cations, [7]Na at the A1 site (44% occupancy) and [11]Cs at the A2 site (4% occupancy) are shown as blue and pale-orange spheres; H2O groups at partly occupied W(2–5) sites in between two Si–O–OH sheets are shown as large red spheres.

Figure 6. Short-range order arrangements related to the A1 site occupied by Na at 44% and W2 site occupied by H2O at 44%: (a) SRO-44%, the A1 site is 100% occupied by Na and the [7]-coordinated A1 polyhedra link via vertices occupied by H2O groups at the W1 and W2 sites; (b) SRO-56%, the A1 and W2 sites are vacant. Legend as in Fig. 5, the O atom at the O2 site is shown as a small white sphere.

Figure 7. The [11]Cs at the A2 site. Legend as in Fig. 5.
Cations of the heteropolyhedral sheet and interstitial complex ideally sum to (Ca2Ce2)10+ + (Na□)+ = [(Na□)Ca2Ce2]11+.
Anion sites
Si–O–OH sheet
There are 10 anion sites, O(1–10), occupied by O atoms which form the tetrahedral coordination of the Si(1–4) atoms (Tables 5, 6). O(1, 3–9) receive bond valences of 1.80–2.09 vu (valence units) (Table 8) and hence are O atoms. The three SiO4 tetrahedra, Si1, Si2 and Si3, are similar in size: with <Si–O> = 1.62, 1.60 and 1.624 Å, respectively. The Si4 tetrahedron, with <Si4–φ> = 1.644 Å, has one long Si4–O10 distance of 1.71 Å, and O10 receives a bond valence of 0.78 vu (Table 8), hence O10 is an oxygen atom of an OH group [φ = O and OH]. Therefore, the Si4 tetrahedron has the composition SiO3(OH).
Note that for two O atoms of Si tetrahedra, Table 8 gives significantly low bond-valence sums: 1.56 vu (instead of ~2 vu) for O2 and 0.78 vu (instead of ~1.2 vu) for O10, an O atom of an OH group. The O2 atom is a common vertex for the M3 [Ca] and A1 [Na, 44% occupancy] polyhedra and Si4 tetrahedron. Consider short-range order (SRO) arrangements for O2. SRO-1 (44%) occurs where the O2 atom receives bond-valence contributions from the M3 [Ca], A1 [where the A1 site is 100% occupied by Na] and Si4, with a total sum of 1.78 vu (Table 9), hence O2 is an O atom (Fig. 6a). SRO-2 (56%) occurs where the O2 atom receives bond-valence contributions from M3 [Ca] and Si4 but does not receive a bond-valence contribution from A1 [□] [the A1 site is 56% vacant, Tables 5, 7], hence the bond-valence sum at O2 is 1.38 vu (Table 9). However, O2 can receive an additional bond-valence contribution of 0.30 vu via hydrogen bonding from O atoms of H2O groups at the W1 and W3 sites (Fig. 6b). Distances O2–W1 = 2.83 Å and O2–W3 = 3.11 Å (Table 5) are suitable for hydrogen bonding. Hence at SRO-2 (56%), the bond-valence sum at O2 is 1.38 + 0.30 = 1.68 vu and O2 is an O atom.
The O10 atom receives 0.78 vu from Si4 (Table 8) and, possibly, bond-valence contributions from (1) O10′ related by the inversion centre [O10–O10′ = 2.88 Å, 0.15 vu] and (2) an O atom of an H2O group at the W1 site [O10–W1 = 2.60 Å, 0.25 vu] (Table 5): 0.78 + 0.15 + 0.25 = 1.18 vu, a common value for the bond-valence sum at the O atom of an OH group.
Si(1–4) and O(1–10) atoms form a distinct complex Si–O–OH oxyanion, [Si7O17(OH)]7– per formula unit.
Heteropolyhedral sheet
The M(1–4) cations of the heteropolyhedral sheet are coordinated by O atoms shared with the Si–O–OH sheet, X(1–4) anions and an H2O group at the W1 site (Tables 5, 6; Fig. 3a,b). The X(1–4) sites give 5 apfu, and the W1 site gives 1 apfu. Consider the four X(1–4) sites. The X2 anion receives four bond-valence contributions from the M1 and M3 cations which occur at fully occupied sites: these four contributions sum to 1.18 vu (Table 8) and X2 is a F atom (Fig. 3a, Table 7). The three X(1,3,4) anions are involved in short-range order, and their compositions vary (Tables 5–7). For example, the X1 anion is bonded to the M1 and M4 atoms in the polyhedral sheet. The M1 site is fully occupied, mainly by REE; the M4 site is occupied by Mg and minor Fe2+ at 32% (Table 7). Consider SRO-1(68%), where the M4 site is vacant (Fig. 3a): the X1 anion receives 0.48 vu, i.e. two bond-valence contributions from two M1 cations (Table 9), and X1 is an H2O group. Consider SRO-2 (32%), where the M4 site is occupied by Mg plus minor Fe2+ (Fig. 3b): the X1 anion receives bond-valence contributions from the M1 and M4 atoms, summing to 1.22 vu (Table 9), and X1 is a F atom. Hence the composition of the X1 site is (H2O)0.68F0.32 pfu (Table 7), ideally (H2O)1.0 pfu. Similarly, the compositions of the X3 and X4 sites are F0.83(H2O)0.17 pfu and F1.66(H2O)0.34 pfu (ideally F and F2 apfu) (Table 7). Ideal compositions of the four X(1–4) sites, X 1H2O +X 2F + X 3F + X 4F2, sum to [F4(H2O)]4– pfu. The W1 site is 100%-occupied by H2O groups, giving (H2O)1.0 pfu. Hence the ideal composition of the anions/H2O groups of the heteropolyhedral sheet not shared with the Si–O–OH sheet is X(1–4)[F4(H2O)]4– + W 1(H2O) = [F4(H2O)2]4– pfu.
Interstitial complex
In the interstitial complex, the four W(2–5) sites are partly occupied by H2O groups: W2 and W3 at 44 and 19%, and W4 and W5 at 16 and 23% (Table 5). The O atoms of H2O groups at the W(2,4) sites are ligands of the A(1,2) cations: A1 [W2] and A2 [W(2,4)] (Table 6). H2O groups at the W(3,5) sites occur in the large channels of the structure (Fig. 5a). The W(2–5) sites give (H2O)1.60 pfu, ideally (H2O)2 pfu.
The complex Si–O–OH anion, and the simple anions of the heteropolyhedral sheet and interstitial complex (charge is given in brackets), [Si7O17(OH)] (7–) + [F4(H2O)2] [X(1–4),W1] (4–) + (H2O)2 [W(2–5)] (0), sum to [Si7O17(OH)]F4(H2O)4, with a total charge of 11–. The presence of OH and H2O groups is in accord with the Raman spectrum (Fig. 2b).
General topology of the crystal structure
In the crystal structure of letnikovite-(Ce), the main structural unit is a layer of the central heteropolyhedral Ca–Ce sheet and two adjacent identical Si–O–OH sheets. The heteropolyhedral sheet parallel to (001) is composed of [9]-coordinated Ce-dominant M1 polyhedra, [7]-coordinated Ca-dominant M(2,3) polyhedra and vacancy-dominant M4 octahedra which share common edges and common vertices (Fig. 3a,b). We sum the cation and anion parts of the heteropolyhedral sheet to derive its ideal composition: [Ca2Ce2]10+ + [F4(H2O)2]4– = [Ca2Ce2F4(H2O)2]6+. The Si–O–OH sheet is composed of SiO4 and SiO3(OH) tetrahedra in the ratio 6:1, Si tetrahedra form five-membered [Si5O15]10– and ten-membered [Si10O33(OH)2]28– rings in the ratio 2:1 (Fig. 4a,b). In a sheet, ribbons of ten-membered and five-membered rings extend along [100]. Rings of tetrahedra share common vertices to form a single [Si7O17(OH)]7– sheet parallel to (001). This is the first occurrence of a single [Si7O17(OH)]7– sheet with a new topology that has not been found in any mineral (Hawthorne et al., Reference Hawthorne, Uvarova and Sokolova2019) and we call it the ‘letnikovite’ sheet. Two equivalent single sheets related by a mirror plane occur at z ≈ 0.69 and z ≈ 1.21 and connect via hydrogen bonding between OH groups of the two SiO3(OH) tetrahedra (Fig. 5a, inset). Polyhedra of the central Ca–Ce sheet share common vertices with two adjacent Si–O–OH sheets to form a layer of composition {Ca2Ce2[Si7O17(OH)]F4(H2O)2}1– (Fig. 5a,b). The layers are stacked along [001] and link via (1) cations at the interstitial A(1,2) sites and H2O groups, and (2) hydrogen bonding between OH groups of the Si–O–OH sheets and H2O groups of the Ca–Ce sheets. This type of linkage yields wide channels along [100] (Fig. 5a). Along [100], the interstitial A1 and A2 sites (Figs. 6, 7) are partly occupied by Na (44%) and Cs (4%), respectively. We sum cation and anion parts of the interstitial complex to derive its ideal composition: (Na□)1+ + (H2O)2 = [(Na□)(H2O)2]1+.
The general structural formula of letnikovite-(Ce)
On the basis of the SREF results and bond-valence calculations, we write the ideal formula of letnikovite-(Ce) as the sum of the cation and anion components: [(Na□)Ca2Ce2]11+ + {[Si7O17(OH)]F4(H2O)4}11– = (Na□)Ca2Ce2[Si7O17(OH)]F4(H2O)4, Z = 4. The simplified formula is (Na,□)2Ca2(Ln 3+,Sr)2[Si7O17(OH)]F4(H2O)4, where Ce is the dominant lanthanoid. The validity of the ideal formula is supported by the good agreement between the total charges for cations in the ideal and empirical formulae: 1+ (Na□) + 10+ (Ca2Ce2) = 11+ versus 1.08+ (□2.08Na0.72Ca0.16Cs0.04) + 9.61+ (Ca1.92Ln 1.31Sr0.55Mg0.28Pb0.05Fe2+0.04□0.85) = 10.69+.
Above, we wrote the ideal formulae of letnikovite-(Ce) on the basis of the sum of the cation and anion components. Here, we write the ideal structural formula and ideal formula of letnikovite-(Ce) (Z = 4) on the basis of ideal compositions of cation and anion sites, A 1(Na□), A 2□, M 2Ca, M 3Ca, M 1Ce2, M 4□, [Si7O17(OH)], X 2F, X 3F, X 4F2, X 1H2O,W 1H2O, W (2–5)(H2O)2, as (Na□)□Ca2Ce2□[Si7O17(OH)][F4(H2O)](H2O)(H2O)2 and (Na□)Ca2Ce2[Si7O17(OH)]F4(H2O)4, respectively.
Relation to other sheet silicates
We can remotely relate letnikovite-(Ce) to nekoite, Ca3Si6O15⋅7H2O (Alberti and Galli, Reference Alberti and Galli1980), okenite, Ca10Si18O46⋅18H2O (Merlino, Reference Merlino1983), and zeravshanite, Cs4Na2Zr3[Si18O45](H2O)2 (Uvarova et al., Reference Uvarova, Sokolova, Hawthorne, Pautov and Agakhanov2004; Pautov et al., Reference Pautov, Agakhanov, Uvarova, Sokolova and Hawthorne2004), silicate minerals with a single sheet of five-membered rings and eight-membered rings of SiO4 tetrahedra; the composition of this sheet is (Si6O15)6–. In zeravshanite, the Si–O sheet is folded, hence Uvarova et al. (Reference Uvarova, Sokolova, Hawthorne, Pautov and Agakhanov2004) wrote its composition as (Si18O45)18–. In a Si–O–OH sheet in letnikovite-(Ce), ribbons of ten-membered rings and five-membered rings are parallel to [100], a = 7.4726(3) Å. In nekoite, okenite and zeravshanite, ribbons of eight-membered rings and five-membered rings are parallel to: [001], c = 7.339 Å (nekoite); [010], b = 7.28 Å (okenite) and [010], b = 7.5464 Å (zeravshanite).
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1180/mgm.2023.65.
Acknowledgements
We thank reviewers Oleg Siidra and two anonymous reviewers and Associate Editor Owen Missen for helpful comments. FCH was supported by Discovery grants from the Natural Sciences and Engineering Research Council of Canada.
Competing interests
The authors declare none.


















