Introduction

In general, thermistors, when used as temperature measuring devices, are used singly 0rin pairs in some impedance net, that net being driven by some power supply, and also having an output which is monitored by a detector. Frequently the thermistor is placed at the end of a transmission line.

Errors in precision and accuracy enter from numerous sources: from thermistor drift, from the power supply or its configuration, from the detector, impedance net or transmission line, and from the calibration fit (Reference BeckBeck, 1956;Reference Misener and Thompson Misener and Thompson, 1952; Reference Muller and Stolton Muller and Stolton, 1953; Reference FenwalFenwal, 1968[a]). It is the intent of this paper to examine instrumental parameters, and to discuss how they may be used or determined, in order to optimize the precision with which the resistance of a given thermistor in a fixed situation can be determined. These parameters include: thermistor self-heating, nominal thermistor resistance, range of application, and resolution of the detector. This examination applies equally both to the calibration of the sensor and to field measurements using it since both conditions can be completely described.

Thermistor Characteristics

Manufacturers of thermistors generally provide figures for their thermistors that indicate the ability of the device to dissipate power P into the surrounding medium. This “dissipation constant” D_c is specifically defined as the amount of power required to raise the temperature of the thermistor 1 deg above the ambient temperature T. More conveniently

where Δ T is the magnitude of thermistor self-healing. In ice, for spherical thermistors (Reference Carslaw and JaegerCarslaw and Jaeger, 1959),

where k _i is the thermal conductivity of ice and r _t is the radius of the thermistor. Equation (I) clearly depends on the environment of the thermistor. Manufacturers’ figures are usually given for the thermistor in still air. In ice D _c is at least a factor of three greater, and although increases in D _c will improve the measurement precision, a factor of three in D _c results in no more than 1.5 dB improvement in precision. Hence, for the examples used here, manufacturers’ figures will be used.

Thermistors have negative thermal coefficients of resistivity, which shall be called R T. For most thermistors

and this figure will be used in all of the examples (Reference Jessop and JudgeJessop and Judge, 1974).

The “time constant” of a thermistor, as defined by some manufacturers is the time required for a thermistor to change its temperature 63% of the amount of temperature change of a value impressed upon it in a step change (Reference FenwalFenwal, 1968[b]). For a given thermistor, this may vary from fractions of seconds to minutes as a function of environment. For steady-state temperature measurements, a more useful time constant would be the time required for a thermistor to reach 63% of ΔT above T, from the initiation of power, but because of the effects of environment on D _c and hence ΔT, and also consideration of the fact that the two constants as defined here are probably closely related, the latter time constant is almost certainly indeterminable, especially if the thermistor were deployed in a bore hole in ice.

The best that should be said about a thermistor being used to measure a steady-state temperature is that the temperature it measures is between T and T+ ΔT. It is necessary, then, that the allowable error due to self-heating must be the full value of ΔT, and that in most cases this will not be reached. It may be possible to determine D _c by measuring resistance R as a function of P for large values of P, but the advantage of knowing D _c accurately is offset by the relatively large P required to take advantage of the information.

Bridges

The simplest type of resistance-measuring device consists of a current source driving the unknown resistance. A voltmeter then measures the voltage drop across the resistance. A measure of the signal available is dV/dR. In this case

All analog ohmmeters and digital ohmmeters work in this fashion. The difficulties involved in taking this approach is that analog meters rarely have enough dynamic range or precision to be useful as high-precision instruments, and the long-term linearity and short-term thermal stability of digital meters are generally not good enough for the overall accuracy to approach the resolving capability of the instrument. This is particularly the case when different instruments are used for calibration and field measurements.

Null detectors have the advantage that they do not require the dynamic range or linearity of the “ohmmeter” type of instrument. However, they may still be thermally sensitive, and they often cannot be used for long-term unattended measurements. This is a problem if measurements continuous in time are required over a large temperature range. For making single measurements of steady-state or slowly varying temperatures, null detectors are well suited. A typical configuration is a Wheatstone bridge with the four arms equal. In this case if the bridge voltage is V _B

If power dissipated in the thermistor is the same in both eases

and ratios of signal to power may be compared. It follows that the ratio of signal to power voltage for the first case is twice that for the second case. Difficulties in constructing relatively noiseless current sources would probably counter the advantages of one case over the other. For this reason the null detector will be considered here.

Resolution

Let ΔT* be the desired temperature resolution. Then

where ΔR is the necessary resolution in terms of resistance. From Equations (5) and (7)

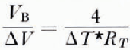
where ΔV is the required voltage resolution of the detector.

Power from the bridge due to Johnson noise is ideally

where V _n is noise voltage, k is Boltzmannàs constant, T is the absolute temperature, and B is the bandwidth of the detector. A convenient measure of the quality of the detector may be defined as the noise figure

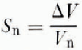
where ΔV now represents the detectoràs best resolving ability. Recall from Equation (6) that

From Equations (6), (8), (9) and (10)

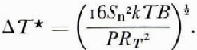
But from Equation (1)

a minimum of the sum of ΔT and ΔT* occurs at

It follows from Equations (11), (12) and (13) that

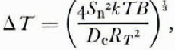
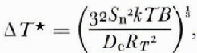
Equations (14), (15) and (16) are useful for determining the optimum resolution of any system as the parameters approach the ideal. More realistically it would be convenient to have an expression for the optimum in terms of the detector resolution ΔV. From Equations (9), (10), (14), (15) and (16)

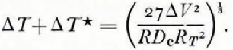
From Equations (17), (18) and (19) detector parameters and power levels may be optimized, and overall accuracies known. Consider for example a thermistor with D _c= I mW deg^-1 which is to be operated at 10 kΩ. Suppose our detector has an input noise voltage of I μ.V. Then

ΔT+ ΔT* ≈ 0.001 deg.

Here signal power has been assumed to be equal to noise power. Generally it would be desirable to have signal-to-noise ratios of at least 10 dB, Then

ΔT+ ΔT* ≈ 0.002 3 deg.

If a D.C. bridge is used with a good detector (e.g. Analog Devices chopper amp. Model 260K) it would have input noise on the order of 1 μV P-P with a bandwidth to 10 Hz. Since a reasonable response time is desirable, a bandwidth of 5 Hz is minimal. Input noise voltage drift of 0.I μV deg-1 would boost effective input voltage noise to about 3.5 μV. This would boost a usable ΔV to 12 μV, and in our example

ΔT+ ΔT* ≈ 0.005 4 deg.

This may be considered a practical limiting accuracy for a thermistor with D _c = 1 mW deg^-1 and R = 10 kΩ, when driven by a D.C. system.

Other difficulties involved in using a D.C, system arise from thermal voltage offsets, and from the proximity of 50 Hz or 60 Hz sources. The first may be helped by selecting a chopper- stabilized detector or similar detector designed for thermal immunity and by careful circuit design. The second, which may be large enough to obscure measurements in spite of a sharp roll-off, should be helped by using good shielding and grounding (the most likely mechanism would be that the transmission line, acting like an antenna, would provide sufficient commonmode signal to overload the detector input).

It is possible to obtain amplifiers which operate at audio frequencies, that have considerably less input noise voltage per unit bandwidth than D.C. amplifiers. Detectors, either phase-locked, or simple, are easily designed. Bandwidths may be limited to less than 100 Hz, which will keep input noise voltage well below the best available D.C. detectors. For systems where extremely high precision is necessary, the designer may consider using an A.C. voltage source to feed his bridge. However, new design problems accompany the choice of an A.C. source. The operating frequency should be kept as low as possible. The reason is twofold: first, since a low bandwidth is desirable, a low center frequency would minimize the need for a large Q; second and predominant, the effects of stray reactance in the bridge, and particularly in the transmission line to the thermistor, would be minimized. Below 100 Hz flicker noise predominates and all the difficulties of D.C. bridges ensue (Reference Letzter and WebsterLetzter and Webster, 1970).

Line effects

It is usually possible to determine the resistance of the transmission line being used, or at least get an estimate well within the required accuracy. This may then be corrected for when determining the actual thermistor resistance. If a three- or four-wire transmission line is used, the problem can be eliminated entirely (Reference JessopJessop, 1964).

It is desirable to know what is the maximum capacitance C of the transmission line which will still permit a null of amplitude ΔV. If C is sufficiently small, then its effect is to shift the phase of the current, amplitude changes being second order. The constraint on C is

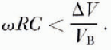
If the detector is phase-locked then the observed resistance R _o is related to the actual resistance R _a by

To a first approximation

provided the transmission line is short (this error will usually be sufficiently small that an estimate of C will yield a correction ΔR of sufficient accuracy). For long transmission lines null information may be coded into a frequency-modulated or pulse-coded signal (private communication from R. Goodman). Numerous sophisticated measurement systems exist, some of which combine D.C . and A.C. bridge power (Reference BeckBeck, 1963; Reference Greenhill and WhiteheadGreen hill and Whitehead, 1949).

Evaluation Of Digital Multimeters

On the basis of Equation (12) and the relation of ΔT* to P (from Equations (9), (10) and(11)

It is possible to evaluate and compare measurement systems for a given R and D _c (Reference GarfinkelGarfinkel, 1974)

Fig. 1. Errors in temperature measurement as a function of power to a Fenwal GB34P2 thermistor, for seven digital voltmeters. The diagonal line represents thermistor self-heating. The thin error bars represent the meter accuracy. The thick error bars represent the meter resolution. The numbers indicate the points plotted from Table I.

The following digital multimeters have been evaluated in Figure I and Table I as thermistor measurement systems with respect to thermistor self-heating, displayed precision, guaranteed acccuracy, each when used with a Fenwal GB34P2 thermistor--10 kΩ < R < 15 kΩ, D _c = 1 mW deg^-1. Only the Systron Donner 7205 compares in accuracy with a bridge and chopper-stabilized null detector. However other meters may provide equivalent accuracy for thermistors with different values of R and D _c.