Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T05:20:21.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of Glacier de Saint-Sorlin, French Alps, and equilibrium-line altitude during the Little Ice Age

Published online by Cambridge University Press:  08 September 2017

Louis Lliboutry
Louis Lliboutry*
Affiliation:
3 Avenue de la Foy, 38700 Corenc, France
Rights & Permissions [Opens in a new window]

Abstract

Glacier de Saint-Sorlin, French Alps, left terminal moraines at 1.3, 2.9 and 3.7 km ahead of the present terminus. According to proxy data and to historical maps, these were formed in the 19th, 18th and 17th centuries, respectively. A plateau at 2700–2625 m was then surrounded by ice but never became an accumulation area. This fact shows that the equilibrium-line altitude (ELA) on the glacier never dropped below 2300 m. The following simple models apply sufficiently to yield reliable estimations of past ELA: (1) a uniform and constant vertical gradient of the mass balance, down to the terminus; and (2) a plane bed, with a slope of 8.5° and a uniform width. Then in a steady situation the accumulation–area ratio is 1/2. Compared to the mean for 1956–72, at the onset of the Little Ice Age the balances were higher by 3.75 m ice a−1, and the ELA was 400 m lower. Correlations between 1956–72 balances and meteorological data suggest that during the melting season the 0°C isotherm was about 800 m lower, while the winter precipitation at low altitudes did not change. These correlations may have been different in the past, but an equal lowering of the ELA and of the 0°C isotherm, as assumed by several authors, seems excluded.

Type
Research Article
Information
Journal of Glaciology , Volume 48 , Issue 160 , 2002 , pp. 118 - 124
Copyright
Copyright © The Author(s) 2002

1. Introduction

Since 1957, annual field observations and measurements have been made on Glacier de Saint-Sorlin, French Alps. After 1962 they were made by the Laboratoire de Glaciologie, Grenoble, but since the activity of this laboratory has shifted to the analysis of polar ice cores, many observations from Glacier de Saint-Sorlin have gone unpublished. This paper deals with the extension of the glacier during the Little Ice Age.

Unlike most other Alpine glaciers, because of a peculiar orography, Glacier de Saint-Sorlin has left terminal moraines up to 3.7 km ahead of its present terminus, making it easy to distinguish several advances of decreasing amplitude. Moreover, past balances and past equilibrium-line altitudes (ELAs) can be roughly estimated. Of course, these estimates are not as precise as those based on field data. One must rely on a kind of “uniformitarian principle”: suggested balances and rates of advance or retreat in the past are acceptable if similar values have been measured in recent times on some mountain glaciers. This philosophy is normal in any historical work. The interest of this paper is mainly tutorial: it shows that, in favourable cases, even very crude models allow us to narrow the range of possibilities and to disprove published assertions that are not grounded on a sound model.

2. Geographical Description

Glacier de Saint-Sorlin, the largest glacier of Grandes Rousses, is the nearest to Grenoble, France (Fig. 1). It is located 6.4 km (as the crow flies) from Col de la Croix de Fer (2068 m), accessible in summer from Grenoble (300 m) by 76 km of good road. Off-road vehicles can go further, to Grand Lac (2450 m). Since 1967, when a bulldozer opened a track, those with tracked vehicles can reach a Centre National de la Recherche Scientifique (CNRS) Alpine hut on a knob of rock at the glacier margin (Fig. 2), called here the “diffluence knob”.

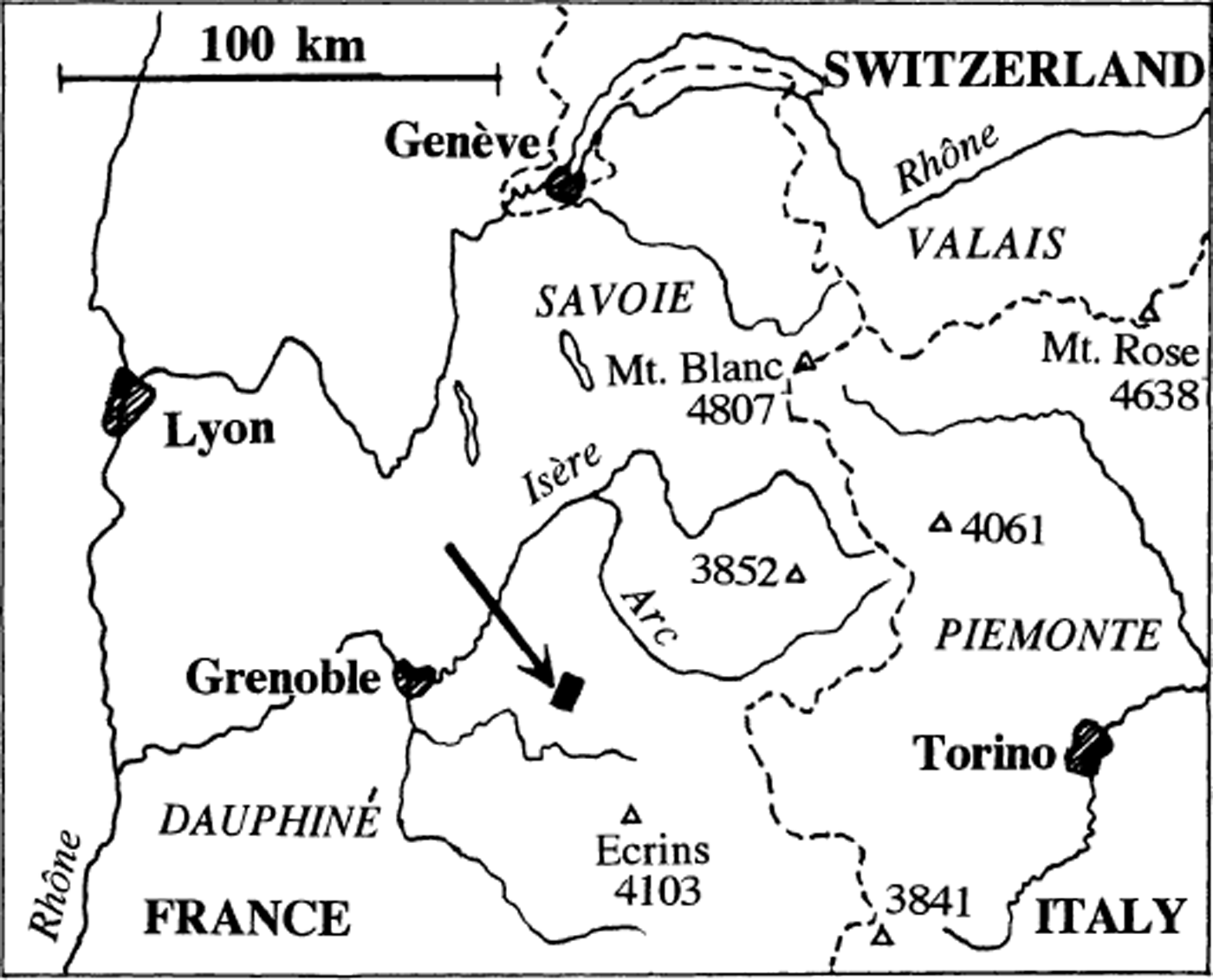
Fig. 1. Location map. Figure 2 is a map of the black rectangle indicated by an arrow.

Fig. 2. Simplified reproduction of Plan directeur, with glaciers as they were in 1908 (the site of the CNRS hut on the “diffluence knob” was then ice-covered). During the 1920 advance, the limits of Glacier de Saint-Sorlin were about the same. Direction of the geographical North (GN) and scale are given in the centre of the glacier. Lambert coordinates, used in all French maps, are X = x + 901000 m and Y = y + 325000 m. × × × × ; oldest moraine (mid-17th century); + + + +: middle moraine (18th century). Both were drawn from hyperstereoscopic examination of Institut Géographique National aerial pictures (mission Bonneville–Saint-Jean-de-Maurienne 1956, pictures 265–267, and mission La Grave 1960, pictures 090–091)– – – – : last moraine (1860, trimline), drawn from field observation.

Glacier de Saint-Sorlin collects most of the solid precipitation falling in a cirque of 5 km2, lying entirely above 2700 m. This cirque is delimited on the west by the end of the Grandes Rousses ridge, running over 4.0 km from Etendard (3468 m); and on the east by a short ridge 2.4 km long, also of hard metamorphic rock, starting from Petit Sauvage (3161 m). Between Etendard and Petit Sauvage, whose summits are 1.2 km apart, a saddle of snow, Col des Quirlies (2998 m in 1972), offers an easy way, without bergschrunds, to the neighbouring Glacier des Quirlies. In contrast to most other glaciers in the Western Alps, the land in front of the glacier does not descend rapidly to low altitudes.

Glacier de Saint-Sorlin may be divided into three parts:

  1. 1. On the west, >1 km2 in horizontal projection, a steep part with a rather uniform slope (about 22°), descending from the western ridge (3400 m) to 2800 m. The winter accumulation here is low because it is a leeward slope for the winds bringing snow (Reference Lliboutry and EchevinLliboutry and Echevin, 1975). There are patches which are ablation zones, and at the summit of Etendard some ground with a moderate slope remains unglaciated.The stream of ice from this western part is therefore small.

  2. 2. The southeast part, about 0.6 km2, ranging from 3100 to 2900 m and with an average slope of 17°, which is the main accumulation area.

  3. 3. The central and lower part, covering about 1.5 km2, which is almost entirely an ablation zone. It slopes gently north-northeast from Col des Quirlies, ending as a wide ice ramp. In 1971 the lowest point was at 2636 m, 2.6 km from Col des Quirlies. Flat, recently deglaciated ground, with a slope of about 6°, extends down to about 2400 m.

Beyond the glacier, the torrent (Rieu Blanc) flows down a steep valley carved by erosion, joining the Arc river in Savoy.

3. Terminal Moraines

From a few days of field observations, C. Jacob (in Reference Flusin, Jacob and OffnerFlusin and others, 1909) recognized three systems of terminal moraines on the opposite side of Grandes Rousses:

  1. 1. the oldest and lowest moraines of the Holocene, reaching 1800 m at l’Alpe d’Huez, the ski resort, corresponding to the stade (stage) du Plateau des Brandes;

  2. 2. middle moraines (stade des Petites Rousses);

  3. 3. the youngest moraines, the trimline of 1905 (stade du glacier des Rousses).

Downstream of Glacier de Saint-Sorlin these three systems (Fig. 2) can be recognized today by hyper-stereoscopic examination of aerial pictures. Jacob missed the middle system and attributed the lowest moraines to the middle stage.

The oldest moraines (1900–2000 m) are found on the north and east shores of Grand Lac, and in the Rieu Blanc valley, near the mountain hut César Durand and Chalets de la Balme. Ice could not cross a pass at 2535 m between the two watersheds at the north foot of Aiguille Rousse de Bramant (2665–2642 m): there was an ice divide at its south foot, on a pass at 2474 m.

The middle moraine system shows two tongues going down eastward into tributaries of the Rieu Blanc valley, with termini at 2290 and 2350 m, respectively. A third tongue, further south, from which Rieu Blanc started, was on a cliff top at 2300 m. The first map of the area was made in 1730 by Sardinian cartographers; it only gives the points where torrents emerged from glaciers (Reference MouginMougin, 1927). It confirms the existence of the three termini in the Rieu Blanc watershed at that time, but we do not know whether this was before or after the deposition of the terminal moraine.

At the lee of the diffluence knob, there is an undulating plateau, sloping northward from 2700 to 2625 m, called Planpré by Reference Flusin, Jacob and OffnerFlusin and others (1909). On its eastern side, at 2650 m, I found a surprising terrace of humus-rich fine earth, without sand or gravel. It probably formed as a bog at the glacier margin.Whether it corresponds to the oldest morainic system as drawn in Figure 2, or to the middle one is unknown.

The youngest advance, marked by a trimline and a moraine about 1 m high, can be accurately drawn in the Rieu Blanc watershed, with the lowest point at 2400 m. It crosses Planpré between its two small lakes, at 2665 m. In the valley of Lacs de Bramant the trimline reaches the shore of Lac Tournant, but it is blurred and no terminal moraine is found there.

The ages of these three morainic systems can only be inferred from the well-known story of other Alpine glaciers. A comprehensive review of original documents is found in LeRoy Ladurie (1967). It may be summarized as follows. The second half of the 16th century had many very cold winters and often cool summers. In 1570 a medieval goldmine of the Hohe Tauern was already covered by 20 m of ice, and in 1588 Grindelwaldgletscher knocked over its terminal moraine. In 1599, Vernagtferner, Tirol, advanced and dammed the Rofenthal. Mer de Glace (then called Glacier des Bois) invaded the valley of Chamonix, destroying several hamlets, in 1600 and again in 1628–30 and 1641–44. In the mid-17 th century, 50 km south of Glacier de Saint-Sorlin, Glaciers Blanc and Noir advanced into a meadow, Pré de Madame Carle (Reference MouginMougin, 1927). Our conclusion is that the oldest moraines (Jacob’s stage of Plateau des Brandes) date from the first half of the 17 th century.

After a moderate recession during the second half of the 17th century, Alpine glaciers were again very extended throughout the 18th century, especially in the periods 1700–40 and 1770–80. The middle moraines of Saint-Sorlin correspond to these advances. The last advances of Alpine glaciers were in 1818–25, and their strong, long-lasting retreat began in 1860. Glacier de Saint-Sorlin indeed advanced between 1909 and 1923 (Reference AllixAllix, 1927; Reference MouginMougin, 1927), but no terminal moraine was left. Thus the last morainic system is from about 1860. One century later, the ground that had been left bare still had sparse vegetation. Since a thick meadow covers Planpré (giving it its name), this plateau was not covered by ice during the 18th century, and probably never during the whole Little Ice Age.

4. Past ela and Past Mass Balances

4.1. A model for the mass balances

The estimation of past mass balances is grounded on (a) a model for the mass balances; (b) a rough model for the glacier geometry; and (c) the assumption that when the terminus began to recede and the moraines were deposited, the glacier had reached steady state.

The model for the mass balance of Glacier de Saint-Sorlin has three ingredients:

  1. (1) Each year, the mass balances vary from their respective averages during the period of observation by about the same amount. This fact has been well established for the period 1956–73 by Reference LliboutryLliboutry (1974) and Reference Lliboutry and EchevinLliboutry and Echevin (1975). In Reference LliboutryLliboutry (1974) the balance (in m ice a−1 and with a changed sign) at site j for year t was denoted bjt. Its mean value for 1956–72 was denoted αj, and the uniform variation of all the bjt for year t was denoted βt. A “linear statistical model” for the balance is:

(1)

where rjt (the residual) is a random term with a centred Gaussian distribution. In the present paper the sign of balances will not be changed, and indexes will be dropped, with −αj and −βt being denoted and Δb, respectively. Moreover residuals will not be considered. Thus Equation (1) reads:

(2)

  1. (2) The mean annual balance at a given site, , is a function of altitude, aspect, slope and curvature of the surface. It may be modelled as a function of altitude only by averaging all its values at a given altitude z (in practice, all the known values within a narrow range of altitudes). Note that b(z) or is not the result of a regression between two random variables. Instead, b may be considered a random variable, but the altitude z of the ablation stake where b is measured cannot, since it is chosen by the observer. To obtain b(z) all the range of altitudes must be divided into brackets of equal size, a mean balance calculated for each bracket, and the same weight given to each bracket, whatever the number of stakes within it.

    Results are given in Figure 3. Up to about 3000 m, b is more or less a linear function of altitude, and the family of straight lines b(z) are parallel (they differ by Δb, which is independent of the site, hence of altitude). At higher altitudes, b(z) decreases, as may be expected from the observations reported in section 2. This result falsifies Reference FinsterwalderFinsterwalder’s (1954) rule of thumb that b(z) is a parabola with its summit at the highest point of the glacier. In fact, below 3000 m , a constant termed the activity coefficient. (The concept of an activity coefficient becomes fuzzy or even misleading for other kinds of glaciers.) Equation (2) may be written, and b M denoting the values at z M = 3000 m of and b, respectively:

(3)

For the years 1956–73, , and c = 0.0098 m ice a−1 and m−1 of elevation.

  1. (3) Whereas ingredients (1) and (2) are based on data, the third ingredient is an assumption. It is assumed that the mass-balance model above was also valid during the Little Ice Age, although the climate had changed and the glacier extended to lower altitudes. This is a first application of the “uniformitarian principle” mentioned in the introduction.

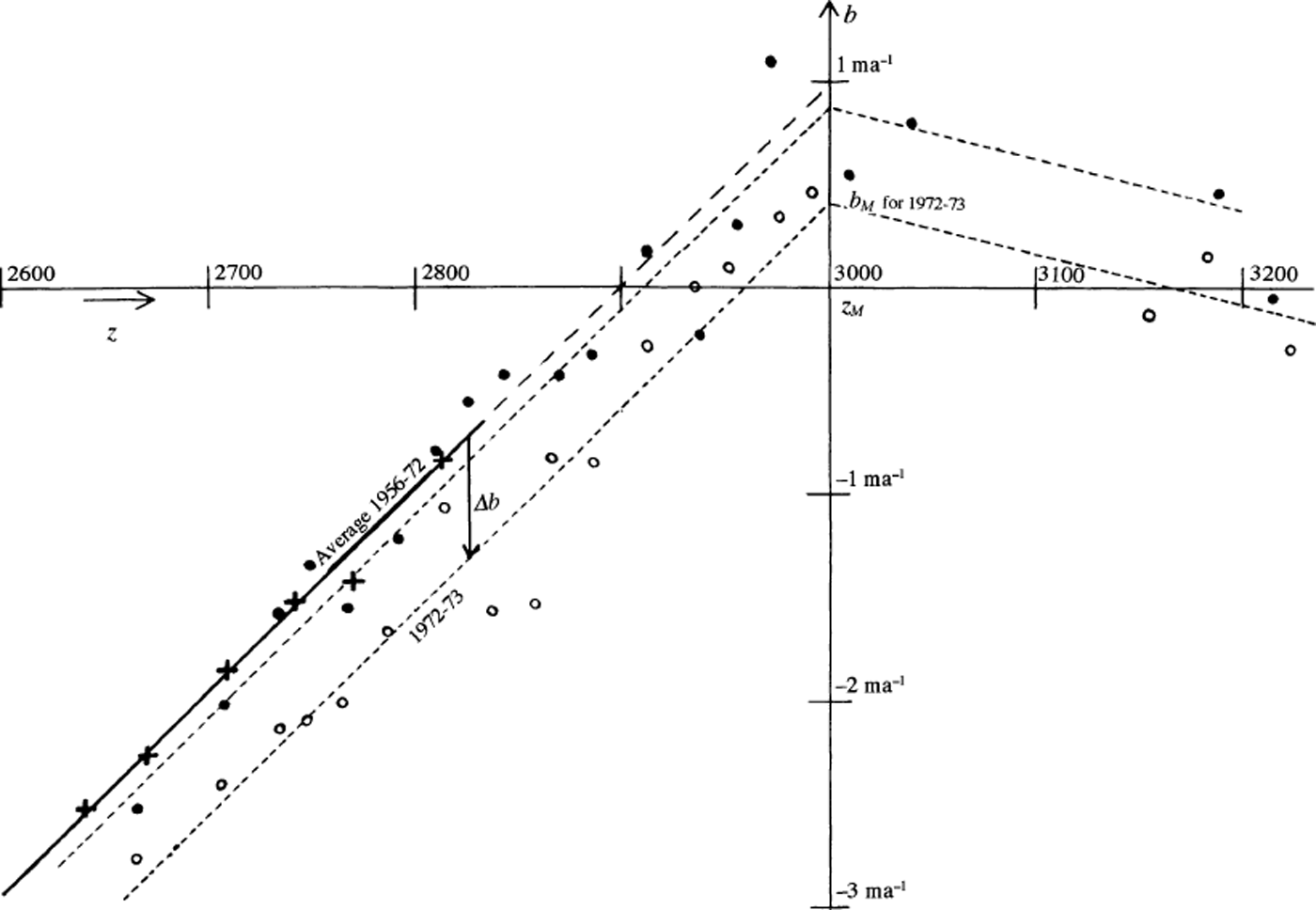
Fig. 3. Measured mass balances on Glacier de Saint-Sorlin, in m ice a−1. Crosses and thick line: average 1956–72; dots: data for 1971/72; small circles: datafor 1972/73; dashes: assumed models for these two measurement years.

4.2. A two-dimensional model of the glacier, and ELA in steady state

Consider a glacier of uniform width on a plane bed with slope β, which flows from z = z M to z = z T. The balance given by the model above is zero at the ELA (z = z EL), and thus:

(4)

At the terminus the balance is:

(5)

When the glacier is steady (then z T will be denoted z ST), the volumetric discharge per unit width (q) is α ≈ β, denoting the surface slope:

(6)

Then q(z) has a maximum value at the ELA, where it amounts to

(7)

and it is zero at z = z ST. From Equation (6):

(8)

Comparing with Equation (4), the accumulation–area ratio (AAR) in the steady state is

(9)

and the balance at the steady terminus is

(10)

4.3. Shear stress and thickness at the ELA, in steady state

With this model, in steady state, at the ELA all velocities are parallel to the bed and to the glacier surface, which has a slope equal to that of the bed, β. The state of stress is simple shear. With ρg denoting the volumetric weight of ice (ρg = 8820 Pa m−1), the shear stress parallel to the bed, at distance ζ to the surface, is approximately:

(11)

In particular, h EL denoting the glacier thickness at the ELA, the friction on the bed there is:

(12)

τxz causes a strain rate in the bulk of the glacier which causes the forward velocity (u) to vary with ζ. The stress–strain-rate relationship for temperate glacier ice is well known from laboratory experiments (Reference LliboutryLliboutry, 1987). The results below indicate that during the Little Ice Age, Glacier de Saint-Sorlin, at the ELA at least, remained temperate. This kind ofice can be modelled as an isotropic power-law viscous fluid, with Glen’s exponent n = 3. In the case of simple shear, the rheological law reads:

(13)

with B = 440 MPa−3 a−1 (Reference LliboutryLliboutry, 1987, p.451).The velocity at any depth at the ELA (u EL), the surface velocity at the ELA (u SEL) and the discharge of ice per unit width at the ELA (q EL) can be inferred. Since there is no precise law that allows one to infer the annual sliding velocity (U EL) from the friction τ b (Reference LliboutryLliboutry, 2002), some value of the former must be assumed. It is:

(14)

On the other hand, in steady state, q EL is given by Equation (7). Comparing with Equation (14), h EL is obtained, and thus τ b and u SEL.

4.4. Application of the model, and comments

Glacier de Saint-Sorlin roughly fits the model above, with tan β = 0.15, except in its upper part. The accumulation zone extends above 3000 m, while in the model it ends there. The accumulation zone of the real glacier below 3000 m is smaller than in the model, but the discharge at 3000 m is substantial, whereas in the model it is zero. These differences should more or less cancel each other, making the model roughly valid. We assume that a steady state was reached in 1908–20 and during the formation of the three systems of moraines (in the first half of the 17th century, in the 18th century and around 1860). All the calculated estimations are given in Table 1.

Table 1. Steady states of Glacier de Saint-Sorlin

The maximum value of b M, when the lowest moraines were deposited, is 4.75 m a−1 (Δb = 3.75 m a−1). It may be compared with the balance for 1954–71 at 3550 m on Mer de Glace, which was 3.57 m a−1 (Reference Vallon, Petit and FabreVallon and others, 1976). Since in all actual mountain glaciers 0.7 < τ b < 1.4 bar, according to the uniformitarian principle, U EL should be in the range 20–40 m a−1. During this maximum extension h EL = 116 ± 5 m and u SEL = 75.3 ±1.4 m a−1. This rise of u SEL, which is currently about 10 m a−1 , is less than the increase from 17 to 280 m a−1 observed at Vernagtferner, Tirol, in 1899 (Reference FinsterwalderFinsterwalder, 1924), and similar to the rise from about 30 to 125 m a−1 at Hintereisferner, Tirol, in 1919 (Reference HessHess, 1924), or from 5 to 30 m a−1 at Glacier de Gébroulaz, Vanoise, between 1910 and 1920 (Reference Reynaud and VallonReynaud and Vallon, 1983).

Vegetation and the very old humus-rich terrace seem to show that during the 17th- and 18th-century advances, an accumulation zone did not form on the Planpré plateau. According to the estimations in Table 1, the ELA was 20 m lower than Planpré in the 18th century, and 150 m lower during the 17th-century advance. These values are insufficient for a glacier to develop: 400 m lower is necessary, according to the following facts. The mean number of days per year with snow cover on the ground increases with altitude, reaching 365 at the “365 level”. Data for the period 1891–1949 in the Davos (Central Alps) area yield a 365 level at 3200 m, whereas the ELA on glaciers was at 2800 m at this time (Reference ZinggZingg, 1958). Russian authors also confirm that a 400 m depression is a minimum (Reference LliboutryLliboutry, 1965, p.439–440).

›C. Jacob (in Reference Flusin, Jacob and OffnerFlusin and others, 1909), by assuming the AAR to be 0.75 (Brückner’s rule of thumb), suggested that the ELA during the 19th-, 18th- and 17th-century advances was 2895, 2600 and 2100 m respectively. Brückner’s rule, drawn from glaciers whose ablation zone is a narrow valley glacier, obviously does not apply here. It predicts that in the 17th century Planpré was glaciated, contrary to field evidence, and that the ELA in 1860 was about the same as in 1956–72 (2900 m), when the glacier was continuously receding.

4.5. Advances and retreats between steady situations

Past advances and retreats of Glacier de Saint-Sorlin at a shorter time-scale are unknown. Reference Jóhannesson, Raymond and WaddingtonJόhannesson and others (1989) assume “a specified sliding distribution” through climatic changes, which is dubious, and their numerical simulations assume a horizontal bed, which is a singular case, inappropriate for mountain glaciers.

Near the terminus, all velocity comes from sliding. Sliding velocities should have varied considerably because of changes in meltwater input at the glacier sole and in glacier extension, which modify all subglacial water pressures. The fastest seasonal sliding velocities observed today at Glacier de Saint-Sorlin, in summer, are about 30 m a−1. At this pace, the oldest advance of about 3 km would have taken one century. But an advance with velocities increasing to 150–300 m a−1 as observed in Tirol, and thus an advance of 3 km in 10–20 years, cannot be excluded.

As for retreat rates, an upper limit is obtained by assuming that near the terminus the sliding velocity was almost zero, and that the dihedral angle of the ice edge was the same as today: α – β = 8.5°. Assume that this was the case during some period between 1860 and 1908, during which balances were the same as the average for 1956–72. The terminus was at z T ≈ 2500 m, and thus, from Equation (3), b T ≈ −4.0 m a−1. It follows a retreat rate −b T cotan (α − β) ≈ 26.8 m a−1. A retreat by 540 m between the termini of 1860 and 1908 would then have occurred in just 20 years. A lower limit of the retreat rate is obviously 540/48 = 11.2 m a−1, similar to that measured in the years 1969–73 (10.4 m a−1).

5. Climatic Changes that have Provided the Estimated Δb

5.1. Actual correlations

Reference MartinMartin (1974) compared the annual balances at Glacier de Saint-Sorlin and nearby Glacier de Sarennes from 1956 to 1972 (b in m of water this time) to the precipitation at Le Chazelet (1780 m; 16 km southeast of the glacier) during 1 year preceding balance measurements, and the mean temperature (in °C) during the melting season (May–August) at Saint-Sorlin-d’Arves (1550 m; 8 km northeast of the glacier). He found the following good correlation (r 2 = 0.734) between the annual deviations from their mean values (Δb, ΔP and ΔT, respectively):

(15)

For Glacier de Sarennes the correlation is still better (r 2 = 0.887):

(16)

Later, Reference MartinMartin (1978) compared the annual balances at Glacier de Sarennes with meteorological data at Lyon–Bron airport (196 m; 130 km west-northwest of the glacier). Longer records allowed him to determine explicative variables almost independent of each other: the precipitation from October to May (P 10–5) (accumulation period on the glacier), the mean of the daily maximum temperatures in July and August (Θ7–8) (which explains 58% of the variance), and the precipitation in June (P 6) which is well correlated with the June mean temperature. Balances are very sensitive to snowfalls in June, because they raise the albedo of the glacier when levels of solar radiation are highest. He found the following good correlation (r 2 = 0.77):

(17)

5.2. Suggested climatic changes

The correlation between ablation and summer temperature has changed during the last 20 years (Reference Vincent and VallonVincent and Vallon, 1997). Contrary to their explanation, I think that summers became cloudier after the construction of the Grandmaison dam nearby, on the windward side. Thus it may be a local effect, which does not falsify the assumption that Martin’s correlations more or less held in the past.

According to Equation (15), the largest value, Δb = 3.75 m ice = 3.37 m water (Table 1), might be explained, for instance, by the credible changes ΔP = 0.52 m and ΔT = −5.0°C. In this case, the 0°C isotherm during the melting season would be 800 m lower and the ELA 400 m lower. For the same change in balance, alternate changes in ΔT and ΔP are possible. For example, Equation (15) yields ΔT = −2.5°C and ΔP = 1.09 m. However, to assume that annual precipitation was twice the present value is unrealistic, given the persistence of the same cultivation during the Little Ice Age. On the other hand, according to Equation (17), the Δb = 3.37 m water may be explained, for instance, by maximum July and August temperatures 6°C lower than today, June precipitation larger by 0. 22 m, and no change at all in winter precipitation.

6. Conclusion

The first step in estimating the climatic changes of the Little Ice Age must be to estimate the changes in the annual balances, known to be about the same at any altitude and over a wide area (Reference ReynaudReynaud, 1980). Glacier de Saint-Sorlin is well suited for this estimation because (1) old terminal moraines are distinct from each other, while elsewhere they are often superimposed; (2) Planpré plateau, where a glacier never developed, gives a lower limit for the ELA; (3) the two dimensional model of a glacier on an inclined plane bed is realistic enough for rough estimations.

Assuming the activity index is independent of altitude and a constant, this model leads to very simple relations: in steady state, the balances at the head and at the terminus are opposite, and the AAR is 1/2. Assuming that the glacier was steady when the terminal moraines were built, and again in 1908–20, the corresponding increases in the balance, compared to its average in 1956–72, are 1.42–3.75 m ice a−1. Although sliding velocities are unknown, past thicknesses and surface velocities at the ELA can be estimated.

Next, changes in temperature and precipitation that caused these balances can be suggested. Although they are much more conjectural, they should be taken into account when investigating climatic changes during the last six centuries. Equal variations of the ELA and of the mean 0°C isotherm are excluded.

Acknowledgements

This paper benefited from comments by referees M. Pelto and M. Funk, by the Scientific Editor N. Glasser and by the co-Chief Editor Matthew Sturm.

References

Allix, A. 1927. Observations glaciologiques faites en Dauphiné jusqu’en 1924. Glacier de Saint-Sorlin. Études Glaciologiques 6 (Paris, Ministère de l’Agriculture. Direction Générale des Eaux et Forêts. Service d’Étude des Grandes Forces Hydrauliques. Région des Alpes), 1–26, 30–31, 74–77, 116, 134.Google Scholar
Finsterwalder, S. 1924. Mechanism der Gletscherbewegung und Gletschertextur. Z. Gletscherkd., 13.Google Scholar
Flusin, G., Jacob, C. and Offner, J.. 1909. Études glaciaires, géographiques et botaniques dans le massif des Grandes Rousses: rapport des campagnes de 1905 et 1906. Paris, Ministére de I’Agriculture. Direction Générale des Eaux et Forêts. Service d’Étude des Grandes Forces Hydrauliques. Region des Alpes. (Études Glaciologiques 1.)Google Scholar
Hess, H. 1924. Der Hintereisferner 1893 bis 1922, ein Beitrag zur Lösung des Problems der Gletscherbewegung. Z. Gletscherkd., 13(4–5), 145–204.Google Scholar
Jóhannesson, T., Raymond, C. and Waddington, E.. 1989.Time-scale for adjustment of glaciers to changes in mass balance. J. Glaciol, 35(121), 355–369.Google Scholar
Le Roy Ladurie, E. 1967. Histoire du climat depuis l’an mil. Paris, Flammarion. (Nouvelle Bibliothèque Scientifique.)Google Scholar
Lliboutry, L. 1965. Traité de glaciologie. Tome II: Glaciers, variations du climat, sols gelés. Paris, Masson et Cie.Google Scholar
Lliboutry, L. 1974. Multivariate statistical analysis of glacier annual balances. J Glaciol., 13(69), 371–392.Google Scholar
Lliboutry, L. A. 1987. Very slow flows of solids: basics of modeling in geodynamics and glaciology. Dordrecht, etc., Martinus Nijhoff Publishers.Google Scholar
Lliboutry, L. 2002. Velocities, strain rates, stresses, crevassing and faulting on Glacier de Saint-Sorlin, French Alps, 1957–76. J. Glaciol, 48(160), 125–141.Google Scholar
Lliboutry, L. and Echevin, M.. 1975. Mesure des bilans annuels en zone d’accumulation. Z. Gletscherkd. Glazialgeol., 10(1–2), 1974, 71–88.Google Scholar
Martin, S. 1974. Correlation bilans de masse annuels — facteurs météorologiques dans les Grandes Rousses. Z. Gletscherkd. Glazialgeol., 10, 89–100.Google Scholar
Martin, S. 1978. Analyse et reconstitution de la serie des bilans annuels du Glacier de Sarennes, sa relation avec les fluctuations du niveau de trois glaciers du Massif du Mont-Blanc (Bossons, Argentiére, Mer de Glace). Z. Gletscherkd. Glazialgeol., 13(1–2), 1977, 127–153.Google Scholar
Mougin, P. 1927. Variations historiques des glaciers des Grandes Rousses. Études Glaciologiques 6 (Paris, Ministère de l’Agriculture. Direction Générale des Eaux et Forêts. Service d’Édes Grandes Forces Hydrauliques. Région des Alpes), 139–149.Google Scholar
Reynaud, L. 1980. Can the linear balance model be extended to the whole Alps? International Association of Hydrological Sciences Publication 126 (Riederalp Workshop 1978 — World Glacier Inventory), 273–284.Google Scholar
Reynaud, L. and Vallon, M.. 1983. Analyse et synthése des mesures glaciologiques effectuées sur le glacier de Gébroulaz, massif de la Vanoise, France. Tav. Sci. Parc Nat. Vanoise 13, 9–29.Google Scholar
Vallon, M., Petit, J.-R. and Fabre, B.. 1976. Study of an ice core to the bedrock in the accumulation zone of an Alpine glacier. J. Glaciol., 17(75), 13–28.Google Scholar
Vincent, C. and Vallon, M.. 1997. Meteorological controls on glacier mass balance: empirical relations suggested by measurements on glacier de Sarennes, France. J. Glaciol., 43(143), 131–137.Google Scholar
Zingg, Th. 1958. Das Raumgewicht der Schneedecke. Actes Soc. Helvétique Sci. Natur. 138.Google Scholar
Figure 0

Fig. 1. Location map. Figure 2 is a map of the black rectangle indicated by an arrow.

Figure 1

Fig. 2. Simplified reproduction of Plan directeur, with glaciers as they were in 1908 (the site of the CNRS hut on the “diffluence knob” was then ice-covered). During the 1920 advance, the limits of Glacier de Saint-Sorlin were about the same. Direction of the geographical North (GN) and scale are given in the centre of the glacier. Lambert coordinates, used in all French maps, are X = x + 901000 m and Y = y + 325000 m. × × × × ; oldest moraine (mid-17th century); + + + +: middle moraine (18th century). Both were drawn from hyperstereoscopic examination of Institut Géographique National aerial pictures (mission Bonneville–Saint-Jean-de-Maurienne 1956, pictures 265–267, and mission La Grave 1960, pictures 090–091)– – – – : last moraine (1860, trimline), drawn from field observation.

Figure 2

Fig. 3. Measured mass balances on Glacier de Saint-Sorlin, in m ice a−1. Crosses and thick line: average 1956–72; dots: data for 1971/72; small circles: datafor 1972/73; dashes: assumed models for these two measurement years.

Figure 3

Table 1. Steady states of Glacier de Saint-Sorlin