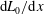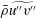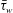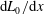1 Introduction
Introduced by Rotta (Reference Rotta1950), Clauser (Reference Clauser1954) and Townsend (Reference Townsend1956b
), the concept of self-similar equilibrium boundary layers is one of the most successful approaches to understand turbulent boundary layers (TBLs) with pressure gradients (PGs) in incompressible flow. The equilibrium character of the flow largely excludes Reynolds-number effects and reproducibly defines the history of the boundary layer. Since PG effects are unambiguously correlated with the reaction of the turbulent flow in equilibrium conditions, scaling laws can be derived, mapping the streamwise-evolving boundary layer to one unique solution. According to Smits & Dussauge (Reference Smits and Dussauge2006), these ‘scaling laws give a unifying framework to our knowledge, and their derivation and validation is one of the important tasks of turbulence research’. Nearly all conclusions about the quantitative influence of PGs on TBLs have therefore been obtained from equilibrium cases, and the expectation of how a TBL spatially evolves in various flow conditions has been shaped by investigation of this special class of flows. Although the idea of self-similarity appears clear and simple, the multiscale nature of turbulent flows leads to difficulties. In its classical definition in the case of zero pressure gradient (ZPG), the TBL is split into two regions, an inner layer mainly affected by viscous forces and an outer layer more affected by turbulent forces. Different regions thus have different scales, i.e. the length scale in the inner layer is based on viscosity (
$\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
), leading to the
$y^{+}$
scaling, and in the outer layer on scales such as the boundary-layer thickness, leading to the outer scaling. With only one set of a local length and velocity scale, self-similarity can only be achieved either for the inner or the outer layer, but not for the entire boundary layer.
Owing to the increased interest in flows with PGs, also the definition of canonical cases for PG TBLs has been subjected to many discussions in the past 20 years. Even if the principal ideas founded by Rotta (Reference Rotta1950) and Clauser (Reference Clauser1954) are the most common definitions of self-similar equilibrium boundary layers for PG TBLs still today, a lot of progress has been made in the derivation and/or the interpretation of new and partly more complete definitions. A detailed distinction between the terms ‘self-similarity’ and ‘equilibrium’ will be given in § 2.1. Since different analyses start with different assumptions on the type of self-similarity that should be obtained, some similarity conditions are more restrictive than others (see also George & Castillo Reference George and Castillo1993; Maciel, Rossignol & Lemay Reference Maciel, Rossignol and Lemay2006). Fundamental questions are still open, such as the ‘correct’ choice of the length and velocity scales that characterize the outer layer of incompressible PG TBLs, as their choice has not been conclusively clarified (see e.g. Maciel et al. Reference Maciel, Wei, Gungor and Simens2018). In addition to the definition of self-similarity for PG TBLs itself, also the extent to which those equilibrium boundary layers represent the general case is controversially discussed. A more detailed introduction to the theory of incompressible equilibrium flow is given in § 2 of this study.
In addition to Reynolds-number effects, the concept of compressible self-similarity also has to eliminate compressibility effects due to a varying Mach number in the streamwise direction, if streamwise collapse of local flow-field profiles should be obtained. Supersonic PG TBLs additionally consist of both sub- and supersonic parts, which are expanded and compressed oppositely to each other in their spatial evolution (Smits & Dussauge Reference Smits and Dussauge2006). The growth of the compressible boundary layer is therefore strongly dependent on local conditions and often differs from intuition based on subsonics. Moreover, the adiabatic wall temperature is continuously altering in the streamwise direction and the recovery factor cannot readily be assumed to be constant any more. All these effects render the prediction of the compressible PG TBL intricate. In fact, not much is known about the conditions of compressible turbulent self-similarity (see also Wenzel et al. Reference Wenzel, Gibis, Kloker and Rist2019), despite its importance for the understanding of compressible TBLs in general, and many questions are still open. To what extent can self-similarity be achieved in the compressible regime? What are the properties of this condition? If the momentum boundary layer can reach a self-similar state, does this also hold for the energy boundary layer, and, if so, what are the relevant properties? To what extent and how are incompressible approaches for the choice of characteristic scales transferable to the compressible regime?
1.1 Objectives of this study
Using the direct numerical simulation (DNS) data presented in the first part of this series Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019), where an inner scaling is mostly employed, the main goal of the present second part is to investigate both the conditions and the limits of streamwise self-similarity for the outer layer of compressible TBLs. For this purpose, a self-similarity analysis is performed for the compressible Favre-averaged two-dimensional turbulent boundary-layer equations by using the same methodical approach as for the incompressible regime. Thereby the properties and relevant parameters for (approximate) self-similarity for the outer layer of compressible TBLs are derived and discussed. On this basis, the most commonly used incompressible scaling laws for the outer layer are extended to compressible flows. All results are then evaluated in outer scaling and discussed using the DNS data.
The study herein is structured as follows. For better understanding of the detailed self-similarity analysis in § 3, the features known so far of self-similarity for the incompressible and also the compressible regime are summarized in § 2. In the results (§ 4) the analysis is applied on the DNS database, while concluding remarks are summarized in § 5.
2 Previous work
In this study, a distinction between the concepts of self-similarity and flow equilibrium is needed, since both are the starting points for theoretical investigations related to the self-similarity of PG TBLs. Both terms are briefly introduced before the previous work is summarized.
In the following, Reynolds averages are denoted by an overbar,
$\bar{f}$
, and density-weighted Favre averages by a tilde,
$\tilde{f}=\overline{\unicode[STIX]{x1D70C}f}/\bar{\unicode[STIX]{x1D70C}}$
; fluctuations around Reynolds and Favre averages are denoted by single and double primes,
$f^{\prime }=f-\bar{f}$
and
$f^{\prime \prime }=f-\tilde{f}$
, respectively.
2.1 Distinction between equilibrium and self-similarity
According to George & Castillo (Reference George and Castillo1993) and Maciel et al. (Reference Maciel, Rossignol and Lemay2006), flow equilibrium implies that all terms in the boundary-layer equations must maintain their relative weight as the flow spatially evolves, which means that ‘the balance of the turbulent kinetic energy is virtually unaffected by the nature of flow in adjacent regions’ (Townsend Reference Townsend1961). Self-similarity (or self-preservation), on the other hand, implies that the (most important) statistical properties of a flow only depend on local length and velocity scales. Thus, if normalized by an appropriately chosen set of local scales like the skin-friction velocity
$u_{\unicode[STIX]{x1D70F}}$
or the displacement thickness
$\unicode[STIX]{x1D6FF}^{\ast }$
, for instance, the boundary-layer solution is invariant to the Reynolds number, which means that local flow-field profiles can be collapsed for various streamwise positions (Maciel et al.
Reference Maciel, Rossignol and Lemay2006).
Therefore, the concept of flow equilibrium is a definition of flow history in general without being limited to any particular type of self-similarity – whatever such flow may look like. Conversely, if a flow is found to be self-similar in the streamwise direction, then it is in equilibrium regardless of the similarity assumptions (Maciel et al.
Reference Maciel, Rossignol and Lemay2006). Note that both the terms equilibrium and self-similarity have often been used equivocally in history without being further distinguished (the Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}$
predicting self-similarity of TBLs is traditionally known as an ‘equilibrium parameter’).
2.2 Introduction to incompressible equilibrium layers
This section is subdivided into two parts: a first part introducing the conditions of self-similarity and a second part summarizing the appropriate choice of scaling parameters.
2.2.1 Self-similarity of incompressible turbulent boundary layers
Based on a theory for the outer layer of ‘traditional’ equilibrium boundary layers, Rotta (Reference Rotta1950) and Clauser (Reference Clauser1956) defined an equilibrium TBL as one where the pressure-gradient parameter
$\unicode[STIX]{x1D6FD}$
(Rotta–Clauser parameter) with the wall shear stress
$\bar{\unicode[STIX]{x1D70F}}_{w}$
and the far-field pressure
$p_{e}$
(subscripts ‘
$e$
’ and ‘
$w$
’ are quantities at the boundary-layer edge and the wall, respectively),
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\frac{\unicode[STIX]{x1D6FF}^{\ast }}{\bar{\unicode[STIX]{x1D70F}}_{w}}\frac{\text{d}p_{e}}{\text{d}x}=\frac{\unicode[STIX]{x1D6FF}^{\ast }}{\unicode[STIX]{x1D70C}u_{\unicode[STIX]{x1D70F}}^{2}}\frac{\text{d}p_{e}}{\text{d}x},\end{eqnarray}$$
is constant in the streamwise direction and the edge velocity
$u_{e}(x)$
follows a power-law distribution. Thus, if scaled with an appropriately chosen set of local length and velocity scales (see § 2.2.3), local mean-flow profiles should be independent of the streamwise position. In the same years, Townsend (Reference Townsend1956a
,Reference Townsend
b
) extended Clauser’s analysis by defining equilibrium layers as those where the local turbulence production and dissipation balance, which justifies the use of eddy-viscosity and mixing-length-type arguments.
Especially the limit of separating boundary layers for strong adverse pressure gradients (APGs), however, represented an inconsistency in classical theory since
$\unicode[STIX]{x1D6FD}$
tends to infinity if the wall shear stress
$\bar{\unicode[STIX]{x1D70F}}_{w}$
tends to zero. Since the concept of self-similarity should apply to all PG cases regardless of the PG strength, however, particular attention was paid to the case of separating flow. This led to a self-similarity analysis of half-power laws for the separated case (Stratford Reference Stratford1959) and its combination with the law of the wall for weak PG cases (see Townsend Reference Townsend1961; Mellor & Gibson Reference Mellor and Gibson1966; McDonald Reference McDonald1969; Perry & Schofield Reference Perry and Schofield1973; Skote & Henningson Reference Skote and Henningson2002). The main results of these studies have been developments in the definition of valid scales (see § 2.2.3), as well as in the discussion of generalized versions of a law of the wall.
Related to the definition of self-similarity itself, further theories have been presented, among others, by Kader & Yaglom (Reference Kader and Yaglom1978) for so-called ‘moving-equilibrium’ TBLs, or the analysis of Perry, Marusic & Jones (Reference Perry, Marusic and Jones2002) using a wake formulation.
More recently, an additional theory has been presented by George & Castillo (Reference George and Castillo1993) and extended by Maciel et al. (Reference Maciel, Rossignol and Lemay2006) for the inner and outer layers of the PG TBL which provides ‘another look at the equilibrium boundary layer’.
2.2.2 Recent work on the definition of self-similarity
By assuming general ansatz functions for all
$x$
- and
$y$
-dependent quantities in the two-dimensional boundary-layer equations, George & Castillo (Reference George and Castillo1993) concluded that all TBLs are in a state of equilibrium if the incompressible (subscript ‘
$inc$
’) pressure-gradient parameter
$\unicode[STIX]{x1D6EC}_{inc}$
using the boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99}$
,
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{inc}=\frac{\unicode[STIX]{x1D6FF}_{99}}{\text{d}\unicode[STIX]{x1D6FF}_{99}/\text{d}x}\frac{\text{d}p_{e}/\text{d}x}{\unicode[STIX]{x1D70C}\,\bar{u}_{e}^{2}}=-\frac{\unicode[STIX]{x1D6FF}_{99}}{\text{d}\unicode[STIX]{x1D6FF}_{99}/\text{d}x}\frac{\text{d}\bar{u}_{e}/\text{d}x}{\bar{u}_{e}},\end{eqnarray}$$
is constant in the streamwise direction. Additionally, many other conditions have been derived for various boundary-layer quantities, which all have to be fulfilled in the case of streamwise equilibrium in a strict sense. Based on the analysis, the velocity scale
$U_{0}$
and the Reynolds-stress scales
$R_{ij}$
of the outer region of TBLs for instance have to evolve such that
$$\begin{eqnarray}\frac{U_{0}}{u_{e}}=\text{const.},\quad \frac{R_{uu}}{u_{e}^{2}}=\text{const.},\quad \frac{R_{vv}}{u_{e}^{2}}=\text{const.},\quad \frac{R_{uv}}{\displaystyle u_{e}^{2}\,\frac{\text{d}\unicode[STIX]{x1D6FF}_{99}}{\text{d}x}}=\text{const}.\end{eqnarray}$$
It has been concluded therefore that the scales which characterize the turbulent flow in the outer region of the boundary layer have to be
$u_{e}$
,
$u_{e}^{2}$
and
$u_{e}^{2}\,\text{d}\unicode[STIX]{x1D6FF}_{99}/\text{d}x$
. In consecutive papers Castillo & George (Reference Castillo and George2001) and Castillo, Wang & George (Reference Castillo, Wang and George2004) extended the theory for the outer layer and suggested that there are only three possible values for the pressure-gradient parameter
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D703}}$
, if built by the momentum thickness
$\unicode[STIX]{x1D703}$
instead of
$\unicode[STIX]{x1D6FF}_{99}$
, see (2.2), each one for favourable pressure gradients (FPGs), ZPGs and APGs. Further extensions to incorporate the incompressible thermal boundary layers can be found in Araya & Castillo (Reference Araya and Castillo2013).
A generalized version of the previous similarity analysis for arbitrary scales was conducted by Maciel et al. (Reference Maciel, Rossignol and Lemay2006). It has been shown that the (generalized) pressure-gradient parameter
$\unicode[STIX]{x1D6EC}_{inc}$
can be reduced to
$\unicode[STIX]{x1D6FD}$
, if time-scale arguments are assumed to be valid and are additionally taken into account. Both the Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}$
and the classical theory of equilibrium flows therefore have been argued to remain valid without respective extensions. Furthermore, it has been noted that, even though
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D703}}$
is often observed to be in three value ranges, there are more than three self-similar profiles.
2.2.3 Discussion on length and velocity scales
The scales are of essential importance for the physical understanding of self-similarity itself. Only if chosen appropriately can a collapse of flow-field profiles extracted at various streamwise positions be achieved.
In analogy to ZPG cases, early studies traditionally use the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
as a velocity scale for the outer layer of PG TBLs, but, in contrast to the inner layer, in combination with the boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99}$
as outer length scale. More complex approaches, such as
$\unicode[STIX]{x1D6E5}=\int _{0}^{e}((u_{e}-\bar{u})/u_{\unicode[STIX]{x1D70F}})\,\text{d}y=\unicode[STIX]{x1D6FF}^{\ast }u_{e}/u_{\unicode[STIX]{x1D70F}}$
, have been proposed by Clauser (Reference Clauser1956), for instance. The choice of the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
, however, has often been questioned in the literature since its definition fails for flows with strong APGs approaching separation, among others. In the study by Mellor & Gibson (Reference Mellor and Gibson1966), the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
therefore has only been used as the velocity scale for low PG cases, but a new pressure-gradient velocity
$u_{p}$
has been derived for strong PG cases. A combination of both friction and PG scales has been proposed by Skote, Henningson & Henkes (Reference Skote, Henningson and Henkes1998), for example. Additional approaches are given by Perry & Schofield (Reference Perry and Schofield1973), among others, who proposed a maximum-shear-stress-based velocity scale and a new length scale.
In contrast to wall-shear-stress-based velocity scales, also the boundary-layer-edge velocity
$u_{e}$
has often been assumed to be a valid velocity scale for the outer layer of PG TBLs (see Castillo & George Reference Castillo and George2001; Kitsios et al.
Reference Kitsios, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2016, Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017). However, the use of this scale is often disputed, as it contradicts the classical theory for ZPG boundary layers (Panton Reference Panton2005); it is argued that both
$u_{\unicode[STIX]{x1D70F}}$
and
$u_{e}$
cannot be characteristic scales for the outer layer simultaneously. Therefore,
$u_{e}$
is assumed to be inconsistent within the asymptotic limits for the Reynolds stresses and therefore not a valid scale.
Zagarola & Smits (Reference Zagarola and Smits1998) derived a new outer-velocity scale
$u_{ZS}=u_{e}\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
, which is proportional to the average deficit of mass flow rate caused by the presence of a wall. It has been shown by Panton (Reference Panton2005) that the Zagarola–Smits (ZS) velocity
$u_{ZS}$
is equivalent to using higher-order theory and is consistent with traditional scaling arguments. By contrast, George (Reference George2006) claims that the ZS scale can also be made consistent with the edge scaling, depending on which theory is correct. Based on validation with experimental data, Castillo & George (Reference Castillo and George2001) further argued that the ZS scale removes the level of dependence from both the upstream conditions and the Reynolds number for a large number of cases, although not completely.
A comparison between the most commonly used length and velocity scales (friction velocity, pressure velocity, ZS and wake scaling) has been presented recently by Maciel et al. (Reference Maciel, Wei, Gungor and Simens2018) for general, non-equilibrium PG TBLs. In agreement with other studies, by Castillo et al. (Reference Castillo, Wang and George2004) or Maciel et al. (Reference Maciel, Rossignol and Lemay2006) for instance, they consistently concluded that both
$u_{ZS}$
and
$\unicode[STIX]{x1D6FF}_{99}$
are an excellent set of scales for equilibrium and non-equilibrium incompressible TBLs.
2.3 Introduction to compressible equilibrium layers
Although it can be expected that the compressible PG TBL can also be characterized by a certain degree of self-similarity due to the close relation between the incompressible Reynolds-averaged and Favre-averaged turbulent boundary-layer equations, there is no comparable theory for compressible flows as the one provided by Rotta (Reference Rotta1950) and Clauser (Reference Clauser1954) for incompressible flows. The lack of sufficiently accurate data seems to be one of the major issues in the analysis, theory and their verification of compressible PG TBLs; quantities like the wall shear stress
$\bar{\unicode[STIX]{x1D70F}}_{w}$
, turbulent velocity and heat-flux fluctuations or boundary-layer thicknesses are difficult to measure (Smits & Dussauge Reference Smits and Dussauge2006). For any kind of self-similarity analyses, however, these data are of essential importance to validate critical assumptions. The closest experimental realization of compressible equilibrium can be found in the work by Thomas (Reference Thomas1974).
Most arguments related to the possible self-similarity of compressible PG TBLs are therefore based on Morkovin’s hypothesis, which essentially states that compressible boundary layers ‘follow the incompressible pattern’. Compressible PG TBLs are therefore expected to be characterized by the same boundary-layer structure and it can be assumed that extended, but similarly motivated, scaling arguments used in incompressible flows still also work for compressible flows. To compare different sets of compressible experiments, definitions that are close to the incompressible Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}=(L/\bar{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
with an arbitrary length scale
$L$
are commonly used to characterize pressure-gradient influences. While the displacement thickness
$\unicode[STIX]{x1D6FF}^{\ast }$
is usually used for the length scale
$L$
, also the kinematic (incompressible) displacement thickness
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
or the momentum thickness
$\unicode[STIX]{x1D703}$
as well as an inner-layer pressure-gradient parameter
$(\bar{\unicode[STIX]{x1D708}}_{w}/(\bar{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{3}))(\text{d}p_{e}/\text{d}x)$
can be found in the literature (Fernholz, Finley & Mikulla Reference Fernholz, Finley and Mikulla1981). It is often mentioned, however, that none of these definitions contains the influence of the wall-normal PG, which is often mentioned to be important with increasing Mach numbers, especially for cases with wall curvature (see Fernholz et al.
Reference Fernholz, Dussauge, Finley, Smits and Reshotko1989; Smith & Smits Reference Smith and Smits1995).
Like for the condition of self-similarity, also the definition of appropriate scales is largely based on incompressible arguments. Therefore, the compressible profiles are mostly scaled in their pseudo-incompressible Morkovin- or van-Driest-transformed representation with the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
. There have been nearly no tests of different characteristic scales in compressible flow. Since the experimental accuracy in compressible flow is usually not sufficient to be used to verify advanced scaling arguments, the traditional scalings are commonly used (Smits & Dussauge Reference Smits and Dussauge2006).
3 Self-similarity analysis for the outer layer of compressible TBLs
In this section a self-similarity theory is presented for compressible TBLs. After introducing the principal method in § 3.1, the self-similarity analysis is given in § 3.2 and discussed in § 3.3. The construction of characteristic scales is given in § 3.4.
3.1 Methodology
The analysis is performed for general characteristic scales of the velocity
$U_{0}$
, mass flux
$F_{0}$
and total enthalpy
$G_{0}$
and a single length scale
$L_{0}$
characterizing the growth of the velocity, the mass-flux and the energy boundary layers simultaneously. Thus, the similarity analysis itself only provides templates for conditions that must be fulfilled by possible characteristic scales in case of self-similarity; consequently, without the specific choice of scales, the results are not applicable to real flow data. In analogy to the analysis of incompressible TBLs, such as by George & Castillo (Reference George and Castillo1993), Castillo et al. (Reference Castillo, Wang and George2004), Maciel et al. (Reference Maciel, Rossignol and Lemay2006) and Kitsios et al. (Reference Kitsios, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2016, Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017), see § 2.2.2, a separation-of-variables approach is used for the present analysis. Every quantity
$\unicode[STIX]{x1D6F9}(x,y)$
of the compressible two-dimensional boundary-layer equations is hereby assumed to consist of a combination of ansatz functions; for example,
$\unicode[STIX]{x1D6F9}(x,y)=\unicode[STIX]{x1D6F7}(x)\unicode[STIX]{x1D719}(\unicode[STIX]{x1D702})$
, where
$\unicode[STIX]{x1D6F7}(x)$
and
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D702})$
depend only on either the streamwise position
$x$
or the wall-normal position
$\unicode[STIX]{x1D702}=y/L_{0}(x)$
. All ansatz functions are plugged into the compressible boundary-layer equations, which then are rearranged into terms solely depending on either
$x$
or
$\unicode[STIX]{x1D702}$
. By assuming that all
$x$
-dependent parts have to be proportional to each other or are negligibly small in self-similar flows, conditions for equilibrium can be derived. It is emphasized that these conditions can also be contradictory, which would imply that exact self-similarity cannot be achieved for the outer layer of compressible PG TBLs.
The basic procedure is analogous to incompressible approaches, but some differences need to be mentioned. The self-similarity analysis of compressible TBLs must simultaneously take into account the spatial evolution of the velocity (kinematic), the mass-flux and the energy boundary layers. Since these do not necessarily evolve proportionally to each other in the streamwise direction, each boundary layer should be characterized by an individual length scale
$L_{0}(x)$
. However, both the assumption of one length scale for each type of boundary layer and the assumption of only a single general length scale
$L_{0}(x)$
for all three boundary layers does not significantly alter the results (see § A.1). A similar approach has been used for compressible turbulent jets by Smits & Dussauge (Reference Smits and Dussauge2006), which only considers the momentum equation by assuming that the energy equation behaves similarly (
$Pr_{t}=1$
). For a more generalized theory, a single general length scale
$L_{0}(x)$
is used first as in Maciel et al. (Reference Maciel, Rossignol and Lemay2006). The findings obtained are then supplemented in a few points by an analysis with multiple length scales given in § A.1.
This work assumes a two-layer structure and focuses on the outer layer, since PG influences are small on the inner layer for moderate PGs; see part 1 of the series.
3.2 Self-similarity analysis
By using the simplified
$y$
-momentum equation
$\bar{p}=p_{e}-\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
with the far-field pressure
$p_{e}$
(see Wenzel et al.
Reference Wenzel, Gibis, Kloker and Rist2019), the Favre-averaged boundary-layer equations for two-dimensional flows are written as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}\tilde{u} }{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}\tilde{v}}{\unicode[STIX]{x2202}y}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\tilde{u} \frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}x}+\bar{\unicode[STIX]{x1D70C}}\tilde{v}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}y}=-\frac{\unicode[STIX]{x2202}p_{e}}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left[\bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}y}-\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}\right]-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}[\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}-\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bar{\unicode[STIX]{x1D70C}}\tilde{u} \frac{\unicode[STIX]{x2202}\tilde{h}_{0}}{\unicode[STIX]{x2202}x}+\bar{\unicode[STIX]{x1D70C}}\tilde{v}\frac{\unicode[STIX]{x2202}\tilde{h}_{0}}{\unicode[STIX]{x2202}y}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left[-\tilde{u} \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}-\frac{1}{2}\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 3}}-\frac{1}{2}\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}u^{\prime \prime }}-\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }h^{\prime \prime }}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left[-\tilde{u} \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}-\frac{1}{2}\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 3}}-\frac{1}{2}\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}v^{\prime \prime }}-\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime }h^{\prime \prime }}+\tilde{u} \bar{\unicode[STIX]{x1D707}}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}y}+\bar{k}\frac{\unicode[STIX]{x2202}\tilde{T}}{\unicode[STIX]{x2202}y}\right],\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}$
is the dynamic viscosity and
$k$
is the thermal conductivity. The general form of the momentum equation resembles the momentum equation as used in Townsend (Reference Townsend1956b
). To avoid the explicit appearance of a PG term in the energy equation, a total-enthalpy formulation is used. Note that more turbulent terms are kept compared to their common definitions (cf. Smits & Dussauge Reference Smits and Dussauge2006), since terms like
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
and
$\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
are not necessarily negligible in the case of strong APGs, for instance. Only the turbulent dissipation terms
$\text{d}(\tilde{v}\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}})/\text{d}y$
and
$\text{d}(\tilde{v}\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }})/\text{d}x$
are omitted.
3.2.1 Outer-layer ansatz functions
For the self-similarity of the outer layer, all quantities in (3.1)–(3.3) are represented by commonly used functional forms:
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\tilde{u} =F_{e}(x)+F_{0}(x)f(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{u} =U_{e}(x)+U_{0}(x)f_{u}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{h}_{0}=G_{e}(x)+G_{0}(x)g(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}=-R_{uv}(x)r_{uv}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}=R_{uu}(x)r_{uu}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}=R_{vv}(x)r_{vv}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\textstyle \frac{1}{2}}\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 3}}=R_{u3}(x)r_{u3}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\textstyle \frac{1}{2}}\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}v^{\prime \prime }}=R_{u2v}(x)r_{u2v}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\textstyle \frac{1}{2}}\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}u^{\prime \prime }}=R_{v2u}(x)r_{v2u}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\textstyle \frac{1}{2}}\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 3}}=R_{v3}(x)r_{v3}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }h^{\prime \prime }}=R_{uh}(x)r_{uh}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime }h^{\prime \prime }}=R_{vh}(x)r_{vh}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D707}}=M(x)m(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y=L_{0}(x)\unicode[STIX]{x1D702}, & \displaystyle\end{eqnarray}$$
where the subscript ‘
$e$
’ is the quantity at the boundary-layer edge and the subscript ‘
$0$
’ is a characteristic scale. Analogously to the incompressible analysis by Townsend (Reference Townsend1956b
), the mean-flow quantities (3.4)–(3.6) are chosen in a generalized defect-law form like
$f_{u}(\unicode[STIX]{x1D702})=(\tilde{u} -U_{e})/U_{0}(x)$
, which resembles
$f_{u}(y/\unicode[STIX]{x1D6FF}_{99})=(\tilde{u} -U_{e})/u_{\unicode[STIX]{x1D70F}}$
for the velocity, for instance. The defect form for the mass flux is deduced from its incompressible limit, and for the total enthalpy it is chosen analogous to temperature profiles in incompressible studies (Tennekes & Lumley Reference Tennekes and Lumley1972). Their verification with DNS results is part of § 4. All turbulent terms (3.7)–(3.15) and the viscosity (3.16) are represented analogously to the analysis of George & Castillo (Reference George and Castillo1993) as products of an
$x$
-dependent and an
$\unicode[STIX]{x1D702}$
-dependent quantity. In contrast to most previous incompressible analyses, where the displacement thickness
$\unicode[STIX]{x1D6FF}^{\ast }$
is anticipated as length scale
$L_{0}(x)$
for the outer scaling (Townsend Reference Townsend1956b
; Castillo et al.
Reference Castillo, Wang and George2004; Kitsios et al.
Reference Kitsios, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2016, Reference Kitsios, Sekimoto, Atkinson, Sillero, Borrell, Gungor, Jiménez and Soria2017),
$L_{0}(x)$
is not yet specified in (3.17) for the present study as in Maciel et al. (Reference Maciel, Rossignol and Lemay2006), which allows its variation in the following.
It is also mentioned that the direct specification of functional forms for velocity, mass flux and total enthalpy implicitly includes the equation of state. Thus, as long as all functional forms are fulfilled, this analysis is independent of the fluid used.
3.2.2 Expansion of momentum and energy equation
In the following, all terms of the boundary-layer
$x$
-momentum (3.2) and energy equation (3.3) are replaced by the functional forms (3.4)–(3.17). Therefore, the continuity equation (3.1) is used to substitute the mass flux in the
$y$
-direction,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}\tilde{v}}{\unicode[STIX]{x2202}y}=-\frac{\unicode[STIX]{x2202}\bar{\unicode[STIX]{x1D70C}}\tilde{u} }{\unicode[STIX]{x2202}x}=-\frac{\unicode[STIX]{x2202}F_{e}}{\unicode[STIX]{x2202}x}-F_{0}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}-\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}x}f,\end{eqnarray}$$
which then is replaced in (3.2) and (3.3) by
$$\begin{eqnarray}\displaystyle \bar{\unicode[STIX]{x1D70C}}\tilde{v} & = & \displaystyle -L_{0}\frac{\unicode[STIX]{x2202}F_{e}}{\unicode[STIX]{x2202}x}\unicode[STIX]{x1D702}-F_{0}\int _{0}^{y}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\,\text{d}y-\frac{\unicode[STIX]{x2202}F_{0}}{\unicode[STIX]{x2202}x}\int _{0}^{y}f\,\text{d}y\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -L_{0}\frac{\unicode[STIX]{x2202}F_{e}}{\unicode[STIX]{x2202}x}\unicode[STIX]{x1D702}+F_{0}\frac{\unicode[STIX]{x2202}L_{0}}{\unicode[STIX]{x2202}x}\unicode[STIX]{x1D702}f-\frac{\unicode[STIX]{x2202}L_{0}F_{0}}{\unicode[STIX]{x2202}x}F,\end{eqnarray}$$
where
$F(\unicode[STIX]{x1D702})=\int _{0}^{\unicode[STIX]{x1D702}}f\,\text{d}\unicode[STIX]{x1D702}$
. If all terms are split into only
$x$
- and
$\unicode[STIX]{x1D702}$
-dependent parts, the expanded
$x$
-momentum equation reads
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{0}U_{0}-U_{0}\frac{\text{d}F_{0}}{\text{d}x}\right]F\frac{\text{d}f_{u}}{\text{d}\unicode[STIX]{x1D702}}+\left[F_{0}\frac{\text{d}U_{0}}{\text{d}x}\right]ff_{u}+\left[F_{0}\frac{\text{d}U_{e}}{\text{d}x}\right]f\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[F_{e}\frac{\text{d}U_{0}}{\text{d}x}\right]f_{u}+\left[F_{e}\frac{\text{d}U_{e}}{\text{d}x}\right]1+\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{e}U_{0}-U_{0}\frac{\text{d}F_{e}}{\text{d}x}\right]\unicode[STIX]{x1D702}\frac{\text{d}f_{u}}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[\frac{\text{d}R_{uu}}{\text{d}x}\right]r_{uu}+\left[-\frac{\text{d}R_{vv}}{\text{d}x}\right]r_{vv}+\left[-\frac{R_{uv}}{L_{0}}\right]\frac{\text{d}r_{uv}}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{uu}\right]\unicode[STIX]{x1D702}\frac{\text{d}r_{uu}}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{vv}\right]\unicode[STIX]{x1D702}\frac{\text{d}r_{vv}}{\text{d}\unicode[STIX]{x1D702}}=\left[-\frac{\text{d}p_{e}}{\text{d}x}\right]1+\left[\frac{MU_{0}}{L_{0}^{2}}\right]\frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}\left(m\frac{\text{d}f_{u}}{\text{d}\unicode[STIX]{x1D702}}\right),\end{eqnarray}$$
and the expanded energy equation
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{e}G_{0}-G_{0}\frac{\text{d}F_{e}}{\text{d}x}\right]\unicode[STIX]{x1D702}\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{0}G_{0}-G_{0}\frac{\text{d}F_{0}}{\text{d}x}\right]F\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D702}}+\left[F_{0}\frac{\text{d}G_{0}}{\text{d}x}\right]fg\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[F_{0}\frac{\text{d}G_{e}}{\text{d}x}\right]f+\left[F_{e}\frac{\text{d}G_{0}}{\text{d}x}\right]g+\left[F_{e}\frac{\text{d}G_{e}}{\text{d}x}\right]1\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[\frac{\text{d}R_{uu}U_{0}}{\text{d}x}\right]f_{u}r_{uu}+\left[\frac{\text{d}R_{uu}U_{e}}{\text{d}x}\right]r_{uu}+\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{uu}U_{0}\right]\unicode[STIX]{x1D702}\frac{\text{d}f_{u}r_{uu}}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{uu}U_{e}\right]\unicode[STIX]{x1D702}\frac{\text{d}r_{uu}}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{R_{uv}U_{0}}{L_{0}}\right]\frac{\text{d}f_{u}r_{uv}}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{R_{uv}U_{e}}{L_{0}}\right]\frac{\text{d}r_{uv}}{\text{d}\unicode[STIX]{x1D702}}+\left[\frac{\text{d}R_{hu}}{\text{d}x}\right]r_{hu}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{hu}\right]\unicode[STIX]{x1D702}\frac{\text{d}r_{hu}}{\text{d}\unicode[STIX]{x1D702}}+\left[\frac{R_{hv}}{L_{0}}\right]\frac{\text{d}r_{hv}}{\text{d}\unicode[STIX]{x1D702}}+\left[\frac{\text{d}R_{u3}}{\text{d}x}\right]r_{u3}+\left[\frac{R_{u2v}}{L_{0}}\right]\frac{\text{d}r_{u2v}}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{u3}\right]\unicode[STIX]{x1D702}\frac{\text{d}r_{u3}}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{v2u}\right]\unicode[STIX]{x1D702}\frac{\text{d}r_{v2u}}{\text{d}\unicode[STIX]{x1D702}}+\left[\frac{\text{d}R_{v2u}}{\text{d}x}\right]r_{v2u}+\left[\frac{R_{v3}}{L_{0}}\right]\frac{\text{d}r_{v3}}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left[\frac{MU_{0}^{2}}{L_{0}^{2}}-\frac{MU_{0}^{2}}{PrL_{0}^{2}}\right]\frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}\left(mf_{u}\frac{\text{d}f_{u}}{\text{d}\unicode[STIX]{x1D702}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left[\frac{MU_{0}U_{e}}{L_{0}^{2}}-\frac{MU_{0}U_{e}}{PrL_{0}^{2}}\right]\frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}\left(m\frac{\text{d}f_{u}}{\text{d}\unicode[STIX]{x1D702}}\right)+\left[\frac{G_{0}M}{PrL_{0}^{2}}\right]\frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}\left(m\frac{\text{d}g}{\text{d}\unicode[STIX]{x1D702}}\right).\end{eqnarray}$$
All
$x$
-dependent terms denote the weight of a term with respect to the streamwise evolution and are written in square brackets
$[~~]$
.
3.2.3 Equilibrium of the
$x$
-momentum equation – mean flow
If self-similar solutions exist for the
$x$
-momentum equation (3.21), all
$x$
-dependent parts of each term have to be in equilibrium and hence proportional to each other or negligibly small. Thus, the convective terms imply that
$$\begin{eqnarray}\displaystyle & \displaystyle \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{e}U_{0}-U_{0}\frac{\text{d}F_{e}}{\text{d}x}\right]\sim \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{0}U_{0}-U_{0}\frac{\text{d}F_{0}}{\text{d}x}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[F_{0}\frac{\text{d}U_{0}}{\text{d}x}\right]\sim \left[F_{0}\frac{\text{d}U_{e}}{\text{d}x}\right]\sim \left[F_{e}\frac{\text{d}U_{0}}{\text{d}x}\right]\sim \left[F_{e}\frac{\text{d}U_{e}}{\text{d}x}\right], & \displaystyle\end{eqnarray}$$
which leads to the condition
$$\begin{eqnarray}\displaystyle & \displaystyle F_{0}\sim F_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{0}\sim U_{e}, & \displaystyle\end{eqnarray}$$
which is further discussed in § 3.3.3. From the convective and the pressure terms it can be further concluded that
$$\begin{eqnarray}\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{0}U_{0}-U_{0}\frac{\text{d}F_{0}}{\text{d}x}\right]\sim \left[F_{0}\frac{\text{d}U_{0}}{\text{d}x}\right]\sim \left[\frac{\text{d}p_{e}}{\text{d}x}\right],\end{eqnarray}$$
which results in three conditions. The first one is:
$$\begin{eqnarray}F_{0}\frac{\text{d}U_{0}}{\text{d}x}\sim \frac{\text{d}p_{e}}{\text{d}x}.\end{eqnarray}$$
By using
$U_{0}\sim U_{e}$
and
$F_{0}\sim F_{e}$
from (3.26) and (3.25), this condition yields
$F_{e}(\text{d}U_{e}/\text{d}x)\sim \text{d}p_{e}/\text{d}x$
, or, replaced by physical quantities,
$(\bar{\unicode[STIX]{x1D70C}}\tilde{u} )_{e}(\text{d}\tilde{u} _{e}/\text{d}x)\sim \text{d}p_{e}/\text{d}x$
. This is a true statement in our case since it resembles the
$x$
-momentum equation in (3.2) if evaluated at the edge of the boundary layer, where all
$y$
-derivatives tend to zero and turbulent fluctuations are negligible. The second condition relates the spatial evolution of the mass-flux, velocity and length scales:
$$\begin{eqnarray}\frac{1}{L_{0}}\frac{\text{d}L_{0}}{\text{d}x}\sim \frac{1}{F_{0}}\frac{\text{d}F_{0}}{\text{d}x}\sim \frac{1}{U_{0}}\frac{\text{d}U_{0}}{\text{d}x}.\end{eqnarray}$$
Thus, if the length scale or the velocity scale has a distribution of
$L_{0}=a(x-x_{0})^{n}$
, for instance (if
$\text{d}L_{0}/\text{d}x=\text{const.}$
,
$n=1$
), all quantities
$U_{0}$
,
$G_{0}$
and
$F_{0}$
have to evolve according to a similar power law. With
$(\text{d}L_{0}/\text{d}x)/L_{0}=\text{d}(\ln L_{0})/\text{d}x$
, the third condition is the compressible pressure-gradient boundary-layer growth parameter:
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{c}\sim \frac{L_{0}}{\displaystyle F_{e}U_{e}\frac{\text{d}L_{0}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}\sim \frac{L_{0}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}=\frac{1}{\displaystyle F_{0}U_{0}\frac{\text{d}\ln (L_{0})}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}=\text{const.}\end{eqnarray}$$
Its definition is nearly identical to the generalized, Reynolds-averaged one found for incompressible boundary layers (2.2) by Castillo et al. (Reference Castillo, Wang and George2004):
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{inc}=\frac{L_{0}}{\displaystyle \unicode[STIX]{x1D70C}U_{e}^{2}\frac{\text{d}L_{0}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x},\end{eqnarray}$$
if the boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99}$
is replaced by an arbitrary length scale
$L_{0}$
.
3.2.4 Equilibrium of the energy equation – mean flow
Analogously, the process is repeated for the mean-flow terms of the energy equation (3.22). To relate the edge and characteristic scales, two types of convective terms are used,
$$\begin{eqnarray}\displaystyle & \displaystyle \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{e}G_{0}-G_{0}\frac{\text{d}F_{e}}{\text{d}x}\right]\sim \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{0}G_{0}-G_{0}\frac{\text{d}F_{0}}{\text{d}x}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left[F_{0}\frac{\text{d}G_{0}}{\text{d}x}\right]\sim \left[F_{0}\frac{\text{d}G_{e}}{\text{d}x}\right]\sim \left[F_{e}\frac{\text{d}G_{0}}{\text{d}x}\right]\sim \left[F_{e}\frac{\text{d}G_{e}}{\text{d}x}\right], & \displaystyle\end{eqnarray}$$
which leads to a similar condition as in the momentum equation,
$F_{0}\sim F_{e}$
and
$G_{0}\sim G_{e}$
. Since the total enthalpy at the edge
$G_{e}$
is a constant, but the characteristic total enthalpy scale
$G_{0}$
varies in the streamwise direction,
$G_{e}\sim G_{0}$
can only be fulfilled if either
$G_{e}=0$
or
$G_{0}=0$
. Therefore, by assuming a constant stagnation enthalpy
$G_{e}$
in the free stream, the reference zero for the total enthalpy
$G_{e}$
is adjusted such that
$G_{e}=0$
. Using
$F_{e}\sim F_{0}$
and
$G_{e}=0$
on the weight of the convective terms,
$$\begin{eqnarray}\left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{e}G_{0}-G_{0}\frac{\text{d}F_{e}}{\text{d}x}\right]\sim \left[F_{0}\frac{\text{d}G_{0}}{\text{d}x}\right],\end{eqnarray}$$
returns a condition similar to (3.29),
$$\begin{eqnarray}\frac{1}{F_{0}}\frac{\text{d}F_{0}}{\text{d}x}\sim \frac{1}{L_{0}}\frac{\text{d}L_{0}}{\text{d}x}\sim \frac{1}{G_{0}}\frac{\text{d}G_{0}}{\text{d}x}.\end{eqnarray}$$
This again defines the relation between the scaling quantities, which implies a similar evolution of the characteristic total enthalpy defect scale as found for the momentum boundary layer.
3.2.5 Equilibrium of the turbulent terms
From the split momentum equation (3.21), the following conditions can be derived for the turbulent terms:
$$\begin{eqnarray}\left[\frac{\text{d}R_{uu}}{\text{d}x}\right]\sim \left[-\frac{\text{d}R_{vv}}{\text{d}x}\right]\sim \left[-\frac{R_{uv}}{L_{0}}\right]\sim \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{uu}\right]\sim \left[\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{vv}\right]\sim \left[\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{0}U_{0}\right].\end{eqnarray}$$
With (3.27), the turbulent stresses of the momentum equation scale for equilibrium boundary layers as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{uu}}{F_{0}U_{0}}\sim \frac{R_{uu}}{F_{e}U_{e}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{vv}}{F_{0}U_{0}}\sim \frac{R_{vv}}{F_{e}U_{e}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{uv}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}}\sim \frac{R_{uv}}{\displaystyle F_{e}U_{e}\frac{\text{d}L_{0}}{\text{d}x}}=\text{const}. & \displaystyle\end{eqnarray}$$
Note that the definition of turbulent scales like
$R_{uu}$
also allows the additional choice of a case-dependent scaling constant termed
$C_{M}$
in the following, such that
$R_{uu}=C_{M}F_{0}U_{0}$
, for instance. Their further use and choice will be discussed in the results in § 4.
From the split energy equation (3.22), the conditions for the turbulent terms are
$$\begin{eqnarray}\displaystyle \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{hu}\right] & {\sim} & \displaystyle \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{u3}\right]\sim \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{uu}U_{0}\right]\sim \left[-\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}R_{v2u}\right]\nonumber\\ \displaystyle & {\sim} & \displaystyle \left[\frac{\text{d}U_{0}R_{uu}}{\text{d}x}\right]\sim \left[\frac{\text{d}R_{hu}}{\text{d}x}\right]\sim \left[\frac{\text{d}R_{u3}}{\text{d}x}\right]\sim \left[\frac{\text{d}R_{v2u}}{\text{d}x}\right]\sim \left[\frac{R_{hv}}{L_{0}}\right]\nonumber\\ \displaystyle & {\sim} & \displaystyle \left[\frac{R_{u2v}}{L_{0}}\right]\sim \left[\frac{R_{u3}}{L_{0}}\right]\sim \left[-\frac{R_{uv}U_{0}}{L_{0}}\right]\sim \left[\frac{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}{L_{0}}F_{e}G_{0}\right].\end{eqnarray}$$
Finally, if identical scaling of the Favre stresses, e.g.
$R_{uu}$
, is assumed for the energy and the momentum equations, see (3.37)–(3.39), the following conditions can be derived:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{uu}U_{0}}{F_{0}G_{0}}\sim \frac{R_{uu}}{F_{0}U_{0}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{uv}U_{0}}{\displaystyle F_{0}G_{0}\frac{\text{d}L_{0}}{\text{d}x}}\sim \frac{R_{uv}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{u3}}{F_{0}G_{0}}\sim \frac{R_{u3}}{F_{0}U_{0}^{2}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{v2u}}{F_{0}G_{0}}\sim \frac{R_{v2u}}{F_{0}U_{0}^{2}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{hu}}{F_{0}G_{0}}\sim \frac{R_{hu}}{F_{0}U_{0}^{2}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{hv}}{\displaystyle F_{0}G_{0}\frac{\text{d}L_{0}}{\text{d}x}}\sim \frac{R_{hv}}{\displaystyle F_{0}U_{0}^{2}\frac{\text{d}L_{0}}{\text{d}x}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{u2v}}{\displaystyle F_{0}G_{0}\frac{\text{d}L_{0}}{\text{d}x}}\sim \frac{R_{u2v}}{\displaystyle F_{0}U_{0}^{2}\frac{\text{d}L_{0}}{\text{d}x}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{R_{v3}}{\displaystyle F_{0}G_{0}\frac{\text{d}L_{0}}{\text{d}x}}\sim \frac{R_{v3}}{\displaystyle F_{0}U_{0}^{2}\frac{\text{d}L_{0}}{\text{d}x}}=\text{const}. & \displaystyle\end{eqnarray}$$
Similarly to the momentum equation, a case-dependent scaling constant
$C_{E}$
can be introduced, such that
$R_{hu}=C_{E}F_{0}G_{0}$
, for instance; see § 4.
3.2.6 Viscous terms
In the outer layer, viscous terms are usually neglected. If they are included, the similarity condition for the viscous terms in the momentum equation (3.21) is
$$\begin{eqnarray}\frac{M}{F_{e}L_{0}}\frac{1}{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}=\text{const.},\end{eqnarray}$$
with the first part being the inverse of the Reynolds number computed with the outer length scale
$L_{0}$
. For the energy equation, the diffusion terms return the similarity conditions
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{MG_{0}}{F_{0}U_{0}^{2}L_{0}}\frac{1}{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{MG_{0}}{PrF_{0}U_{0}^{2}L_{0}}\frac{1}{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}=\text{const.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{M}{PrF_{0}L_{0}}\frac{1}{\displaystyle \frac{\text{d}L_{0}}{\text{d}x}}=\text{const.}, & \displaystyle\end{eqnarray}$$
which are essentially identical to the ones for the momentum equation in (3.49) if
$Pr=\text{const.}$
; see § 3.3.5 for further discussions.
3.3 Discussion
The first point is related to the ansatz functions (3.4)–(3.17), which have been defined a priori to represent all quantities of the compressible turbulent boundary-layer equations. These functions already assume both the self-similarity of the quantity as well as the shape of its particular wall-normal distribution (a defect-law relation, for instance). All conditions derived thus rely on the validity of the chosen ansatz functions and break if these are not appropriately chosen; their validation with DNS data is part of § 4.
The second point is related to the interpretation of the conditions revealed, like the PG condition in (3.30). For a PG parameter, for example, it is desirable that self-similar flows with different similarity solutions are uniquely characterized by the PG-parameter value, which is not the case for the condition derived. If the PG condition is directly used as a PG parameter in incompressible studies, for instance, see (3.31),
$\unicode[STIX]{x1D6EC}_{inc}$
tends towards similar values for self-similar cases with different APG strength, meaning that the
$\unicode[STIX]{x1D6EC}_{inc}$
value is not unique. Therefore, it is important to mention that the conditions revealed only impose requirements on the construction of possible parameters, but leave degrees of freedom in the additional consideration of case-dependent constants like
$C_{M}$
and
$C_{E}$
mentioned in § 3.2.5.
The third point is related to the conditions resulting from the analysis like
$U_{0}\sim U_{e}$
in (3.26), for instance. Although some of these conditions are less important than others in practice, see also § 4, true self-similarity can only be determined for the outer layer, if all conditions derived are fulfilled in a strict sense. Furthermore, the generality of the product ansatz for the turbulent stresses might allow solutions that real turbulence might not be able to realize. Therefore, the most important conditions, namely the PG parameter
$\unicode[STIX]{x1D6EC}_{c}$
(3.30), the conditions of
$F_{0}/F_{e}=\text{const.}$
(3.25) and
$U_{0}/U_{e}=\text{const.}$
(3.26), the coupling of the momentum and energy equations and the results for the viscous terms, are discussed in more detail in the following.
3.3.1 Towards a relation between
$\unicode[STIX]{x1D6EC}_{c}$
and
$\unicode[STIX]{x1D6FD}$
As supposed by the analysis, the self-similar state of the compressible PG TBL is predicted by the pressure-gradient boundary-layer evolution parameter
$\unicode[STIX]{x1D6EC}_{c}$
. If the traditional Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FF}^{\ast }/\bar{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
is written in a generalized form after Maciel et al. (Reference Maciel, Rossignol and Lemay2006) with
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim F_{0}U_{0}$
by
$\unicode[STIX]{x1D6FD}=(L_{0}/(F_{0}U_{0}))(\text{d}p_{e}/\text{d}x)$
, its formulation only differs from
$\unicode[STIX]{x1D6EC}_{c}$
by the additional consideration of
$\text{d}L_{0}/\text{d}x$
:
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{c}=\frac{\unicode[STIX]{x1D6FD}}{\text{d}L_{0}/\text{d}x}=\text{const.},\end{eqnarray}$$
which raises the question about the influence of
$\text{d}L_{0}/\text{d}x$
and thus the significance of both
$\unicode[STIX]{x1D6EC}_{c}$
and
$\unicode[STIX]{x1D6FD}$
. As the significance of
$\text{d}L_{0}/\text{d}x$
is very difficult to quantify especially for experimental results, its influence on low-Reynolds-number flows is still unclear. By taking various arguments into account, Maciel et al. (Reference Maciel, Rossignol and Lemay2006), for instance, argued that
$\text{d}L_{0}/\text{d}x$
should be constant for self-similar boundary layers in a strict case. For the ZPG TBL, however, which can be regarded as the simplest self-similar spatially evolving TBL,
$\text{d}L_{0}/\text{d}x$
is not constant, especially for finite Reynolds numbers, if the length scale is assumed to be the boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99}$
or other commonly used length scales. Therefore, it will be an important part of the results section to compare the significance of
$\unicode[STIX]{x1D6EC}_{c}$
and
$\unicode[STIX]{x1D6FD}$
as well as the influence of
$\text{d}L_{0}/\text{d}x$
for the investigated data.
Note that the choice of
$\text{d}L_{0}/\text{d}x=\text{const.}$
has often been implicitly assumed in older studies (Townsend Reference Townsend1956b
; Mellor & Gibson Reference Mellor and Gibson1966) by setting the turbulent characteristic scales a priori. For instance, in Townsend (Reference Townsend1956b
), all turbulent stresses were assumed to scale according to each other as
$R_{ij}=F_{0}U_{0}$
, which can only be fulfilled if
$\text{d}L_{0}/\text{d}x=\text{const.}$
; compare (3.37)–(3.39).
3.3.2 Towards the length scale
$L_{0}$
The presented analysis was performed for a universal length scale
$L_{0}$
that characterizes the spatial evolution of the velocity, mass-flux and energy boundary layers at the same time. If, in contrast, a separate length scale is used for each boundary layer in the analysis, as shown in § A.1, the Rotta–Clauser parameter yields
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\frac{L_{0,K}}{F_{0}U_{0}}\frac{\text{d}p_{e}}{\text{d}x},\end{eqnarray}$$
where the length scale
$L_{0,K}$
is associated with the velocity (kinematic) boundary layer. Thus, if the mass-flux and the velocity boundary layers do not evolve strictly similarly and the generalized Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}$
, for instance, is still a valid indicator for self-similarity, the approximated state of self-similarity is better predicted by using a kinematic length scale like the incompressible displacement thickness
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
rather than with a mass-flux scale like the compressible displacement thickness
$\unicode[STIX]{x1D6FF}^{\ast }$
in the compressible regime. This finding is already confirmed in part 1 of this study by using DNS data (see Wenzel et al.
Reference Wenzel, Gibis, Kloker and Rist2019).
3.3.3 Towards the conditions
$U_{0}\sim U_{e}$
and
$F_{0}\sim F_{e}$
The condition derived from (3.26) is analogous to incompressible analyses (Townsend Reference Townsend1956a
; Mellor & Gibson Reference Mellor and Gibson1966) and imposes
$U_{0}/U_{e}=\text{const.}$
for all Reynolds numbers. In Castillo & George (Reference Castillo and George2001) it is assumed that
$U_{0}/U_{e}=\text{const.}$
can reach a finite constant value, whereas Maciel et al. (Reference Maciel, Rossignol and Lemay2006) postulate that the ratio will approach zero in the asymptotic limit. Therefore, according to Maciel et al. (Reference Maciel, Rossignol and Lemay2006), the obvious choice of
$U_{0}=U_{e}$
is questionable, since
$U_{e}$
is not expected to correctly scale turbulent stresses. However, as noted by Mellor & Gibson (Reference Mellor and Gibson1966), the variation of self-similar solutions was found to be not sensitive with regard to variations in
$u_{\unicode[STIX]{x1D70F}}/U_{e}$
for which
$U_{0}/U_{e}$
is not constant, which also explains the success of related scales. Analogous to the condition for the velocity scale
$U_{0}/U_{e}=\text{const.}$
, (3.25) poses the condition on the mass flux as
$F_{0}/F_{e}=\text{const.}$
and thus on the density
$\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D70C}_{e}=\text{const.}$
, if
$U_{0}/U_{e}=\text{const.}$
is assumed. The condition
$\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D70C}_{e}=\text{const.}$
directly involves compressibility effects and can only be fulfilled either for ZPG cases where the local Mach number does not alter, or in the asymptotic limit for
$x\rightarrow \infty$
. The sensitivity of self-similar solutions to a non-constancy of
$F_{0}/F_{e}$
is evaluated in § 4 by using the DNS data. Nevertheless, it seems clear from this discussion that the conditions of self-similarity can only be achieved approximately in the compressible regime.
3.3.4 Towards the connection between the momentum and energy equation
Two conditions have been found for all Favre stresses
$R_{ij}$
from the momentum and energy equation, see e.g. (3.37) and (3.41). Since both conditions have to be proportional to each other for each stress, see e.g. (3.41) for
$R_{uu}$
, the characteristic total enthalpy has to be proportional to the characteristic kinetic energy,
$G_{0}\sim U_{0}^{2}$
. This relation couples the streamwise evolution of the energy equation with that of the momentum equation. Hence, the enthalpy scale can be set as
$G_{0}=cU_{0}^{2}/2$
with
$c$
being a constant. In self-similar boundary layers with
$U_{e}\sim U_{0}$
, the recovery factor
$r$
in the Crocco–Busemann relation with the total enthalpy at the wall
$H_{w}$
and edge
$H_{e}$
of the boundary layer
$H_{w}=H_{e}+(r-1)U_{e}(x)^{2}/2$
is therefore a constant in the streamwise direction.
For non-adiabatic walls, the modified Crocco–Busemann or Walz relation
$\tilde{h}_{0}-H_{w}=(\bar{q}_{w}/\bar{\unicode[STIX]{x1D70F}}_{w})\tilde{u}$
has to be used, where
$\bar{q}_{w}$
is the wall-normal heat flux at the wall. Thus, by assuming that this relation is capable of describing the streamwise evolution of the flow and that the analysis can be transferred to non-adiabatic conditions, the results can be extended to flows with wall heat flux. (Note that the turbulent boundary-layer equations are strictly speaking only derived for adiabatic conditions in this study.) Thus, if subjected to non-zero wall heat flux, self-similar solutions can only be possible if the heat flux is
$\bar{q}_{w}(x)/\bar{\unicode[STIX]{x1D70F}}_{w}(x)\sim U_{e}(x)$
. This is subject of further investigation.
3.3.5 Viscous terms
If
$\text{d}L_{0}/\text{d}x$
is assumed to be (approximately) constant for equilibrium boundary layers, the condition
$M/(F_{e}L_{0})=Re^{-1}=\text{const.}$
in (3.49) is only true for
$Re^{-1}\rightarrow 0$
and thus
$x\rightarrow \infty$
. Consequently, an exact self-similarity of the viscous terms is not possible. Note that the condition
$G_{0}\sim U_{0}^{2}$
is also recovered for the viscous stresses, which hence does not lead to any additional contradiction in the analysis.
3.4 Scales
The analysis in the previous section has been conducted for a general set of scales
$F_{0}$
,
$U_{0}$
and
$G_{0}$
(by using a single length scale
$L_{0}$
). If flow data should be analysed, these scales must somehow be associated with boundary-layer quantities. However, especially in the case of self-preserving flows, there are multiple possible choices for these scales for the outer layer, as introduced in § 2.2.3 for incompressible flows. Nevertheless, some guidelines on the appropriate choice of valid scalings can be made to obtain a consistent set of scales.
3.4.1 Definition of length scales
Following the ideas of Clauser (Reference Clauser1954) and Maciel et al. (Reference Maciel, Rossignol and Lemay2006), the integral of appropriately scaled flow-field profiles should be identical for different streamwise positions and thus can be associated with a length scale
$L_{0}$
. Thus, three different length scales
$L_{0,F}$
,
$L_{0,K}$
and
$L_{0,G}$
can be generally defined for the compressible regime, one for the mass-flux, one for the kinematic and one for the energy boundary layer, respectively (in contrast to only one in the incompressible case):
$$\begin{eqnarray}L_{0,F}=\int _{0}^{\unicode[STIX]{x1D6FF}_{e}}\frac{F_{e}-\bar{\unicode[STIX]{x1D70C}}\tilde{u} }{F_{0}}\,\text{d}y=\unicode[STIX]{x1D6FF}^{\ast }\frac{F_{e}}{F_{0}},\end{eqnarray}$$
$$\begin{eqnarray}L_{0,K}=\int _{0}^{\unicode[STIX]{x1D6FF}_{e}}\frac{U_{e}-\tilde{u} }{U_{0}}\,\text{d}y=\unicode[STIX]{x1D6FF}_{K}^{\ast }\frac{U_{e}}{U_{0}}\end{eqnarray}$$
or
$$\begin{eqnarray}L_{0,G}=\int _{0}^{\unicode[STIX]{x1D6FF}_{e}}\left|\frac{\tilde{h}_{0}-H_{e}}{G_{0}}\right|\,\text{d}y=\unicode[STIX]{x1D6FF}_{H}\frac{|H_{w}-H_{e}|}{G_{0}},\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}^{\ast }=\int _{0}^{\unicode[STIX]{x1D6FF}_{e}}\left(1-\frac{\bar{\unicode[STIX]{x1D70C}}\tilde{u} }{\unicode[STIX]{x1D70C}_{e}U_{e}}\right)\,\text{d}y, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}_{K}^{\ast }=\int _{0}^{\unicode[STIX]{x1D6FF}_{e}}\left(1-\frac{\tilde{u} }{U_{e}}\right)\,\text{d}y, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}_{H}=\int _{0}^{\unicode[STIX]{x1D6FF}_{e}}\left|\frac{\tilde{h}_{0}-H_{e}}{H_{w}-H_{e}}\right|\,\text{d}y. & \displaystyle\end{eqnarray}$$
For the mass-flux and velocity length scales,
$L_{0,F}$
and
$L_{0,K}$
, respectively, both the compressible
$\unicode[STIX]{x1D6FF}^{\ast }$
and the kinematic
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
displacement thicknesses are used. For the total-enthalpy profiles, the use of an enthalpy thickness
$\unicode[STIX]{x1D6FF}_{H}$
is the simplest possible, consistent option. The absolute value of the integrand is used to avoid a negative defect in the outer layer (see figure 5) reducing the length scale
$L_{0,G}$
. Note that the method can also be adapted to using integral length scales with a similar form as the momentum thickness (see Maciel et al.
Reference Maciel, Rossignol and Lemay2006).
3.4.2 Determination of scales
In the self-similarity analysis introduced so far, the spatial growth and thus the length scales of the mass-flux boundary layer
$L_{0,F}$
(3.55), the kinematic boundary layer
$L_{0,K}$
(3.56) and the energy boundary layer
$L_{0,G}$
(3.56) are represented by a single length scale
$L_{0}$
only, yielding
$$\begin{eqnarray}L_{0}=L_{0,F}=L_{0,K}=L_{0,G}.\end{eqnarray}$$
Equations (3.55)–(3.57) and (3.61) thus represent a basic system to generate a consistent set of scales, if one of the four unknowns (
$L_{0}$
,
$U_{0}$
,
$F_{0}$
or
$G_{0}$
) is predefined.
Table 1. Consistent sets of compressible characteristic scales. RC, Rotter–Clauser; ZS, Zagarola–Smits.
In the following, four consistent sets of scales are introduced, which all are intended to extend the most commonly used incompressible sets of scales to the compressible regime. It is explicitly pointed out that this selection is by no means complete or definitive, since a great variety of sets should at least approximately work for the special case of equilibrium flows; see § 4. However, it was found that using consistent scales based on a valid velocity scale leads to the best results, as most terms in the momentum equation scale with a kinematic length scale
$L_{0,K}$
(see § A.1 for a more detailed examination).
The chosen sets of scales are summarized in table 1, and the ideas behind them are discussed briefly below.
Edge scaling. In the incompressible analysis of George & Castillo (Reference George and Castillo1993), the velocity at the edge of the boundary layer
$U_{e}$
is used as the characteristic velocity scale
$U_{0}$
. This scaling is a result of the condition
$U_{e}\sim U_{0}$
, see (3.26), with the assumption that the ratio does not approach zero. Derived from (3.55)–(3.57) and (3.61), the remaining scales are determined as
$L_{0,e}=\unicode[STIX]{x1D6FF}_{K}^{\ast }$
,
$F_{0,e}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })F_{e}$
and
$G_{0,e}=|H_{w}-H_{e}|\unicode[STIX]{x1D6FF}_{H}/\unicode[STIX]{x1D6FF}_{K}^{\ast }$
.
Friction scaling. For flows approximating ZPG conditions, Clauser (Reference Clauser1954), Mellor & Gibson (Reference Mellor and Gibson1966) and Townsend (Reference Townsend1956b
) used the skin-friction velocity
$u_{\unicode[STIX]{x1D70F}}$
as a velocity scale
$U_{0}$
. With the same arguments, the characteristic velocity scale is chosen to depend on
$u_{\unicode[STIX]{x1D70F}}$
with
$U_{0,\unicode[STIX]{x1D70F}}=\sqrt{(\bar{\unicode[STIX]{x1D70C}}_{w}/\unicode[STIX]{x1D70C}_{e})(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}^{\ast })}u_{\unicode[STIX]{x1D70F}}$
, yielding a characteristic length scale of
$L_{0,\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6FF}_{K}^{\ast }U_{e}/U_{0,\unicode[STIX]{x1D70F}}$
. The definition of
$U_{0,\unicode[STIX]{x1D70F}}$
is constructed to allow the Favre stresses
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u_{i}^{\prime \prime }u_{j}^{\prime \prime }}$
to be scaled by
$F_{0,\unicode[STIX]{x1D70F}}U_{0,\unicode[STIX]{x1D70F}}=\bar{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2}$
, which almost resembles Morkovin’s scaling. The corresponding mass-flux and enthalpy scales are then
$F_{0,\unicode[STIX]{x1D70F}}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })\unicode[STIX]{x1D70C}_{e}U_{0,\unicode[STIX]{x1D70F}}$
and
$G_{0,\unicode[STIX]{x1D70F}}=(H_{0,w}-H_{0,e})\unicode[STIX]{x1D6FF}_{H}/L_{0,\unicode[STIX]{x1D70F}}$
. Note that also other options for the velocity scale, such as
$(\bar{\unicode[STIX]{x1D70C}}_{w}/\unicode[STIX]{x1D70C}_{e})u_{\unicode[STIX]{x1D70F}}$
, essentially yield a similar result, but simply using
$u_{\unicode[STIX]{x1D70F}}$
does not work within the chosen framework, as the Favre stresses would be scaled with the edge density (
$F_{0}U_{0}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })\unicode[STIX]{x1D70C}_{e}u_{\unicode[STIX]{x1D70F}}^{2}$
).
Rotta–Clauser (RC) scaling. The RC scaling is designed to match the Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{RC}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\bar{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)=(L_{0}/(F_{0}U_{0}))(\text{d}p_{e}/\text{d}x)$
and can be interpreted as a variant of the friction scaling. The velocity scale results in
$U_{0,RC}=((\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}^{\ast })(U_{e}\bar{\unicode[STIX]{x1D70F}}_{w}/\unicode[STIX]{x1D70C}_{e}))^{1/3}$
, the mass-flux scale in
$F_{0,RC}=(\unicode[STIX]{x1D70C}_{e}\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })U_{0,RC}$
and the enthalpy scale in
$G_{0,RC}=|H_{w}-H_{e}|\unicode[STIX]{x1D6FF}_{H}/L_{0,RC}$
. The length scale results in
$L_{0,RC}=\unicode[STIX]{x1D6FF}_{K}^{\ast }U_{e}/U_{0,RC}$
.
Zagarola–Smits (ZS) scaling. The ZS scaling, after Zagarola & Smits (Reference Zagarola and Smits1998), has as characteristic length scale the boundary-layer thickness
$L_{0,ZS}=\unicode[STIX]{x1D6FF}_{99}$
. The velocity scale yields
$U_{0,ZS}=U_{e}\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
, and is the average defect of the profile. The corresponding mass-flux and enthalpy scales are
$F_{0,ZS}=F_{e}\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
and
$G_{0,ZS}=|H_{w}-H_{e}|\unicode[STIX]{x1D6FF}_{H}/\unicode[STIX]{x1D6FF}_{99}$
, respectively.
4 Results
The DNS presented in part 1 for both moderate APG and FPG cases have been especially designed to achieve compressible near-equilibrium TBLs; see Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019) for details. Furthermore, sub- and supersonic inflow Mach numbers are used to allow for a meaningful comparison between the (quasi-)incompressible/subsonic and the compressible/supersonic regimes. It is the objective of this section to analyse these data with respect to the theory presented so far. For this purpose, important parameters and conditions discussed in § 3 are first examined, before the streamwise self-similarity of flow profiles is investigated in more detail for the outer layer. Local flow-field profiles are therefore extracted at 10 equidistant streamwise positions, all of which are in regions of estimated self-similarity where
$\unicode[STIX]{x1D6FD}_{K}$
is approximately constant (see Wenzel et al.
Reference Wenzel, Gibis, Kloker and Rist2019). By normalization with all scaling sets derived in § 3.4, both their scaling success as well as the DNS’s state of self-similarity is assessed.
Table 2. Summarized properties of DNS results presented by Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019) in the domain of interest. Given parameters are the kinematic Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{K}$
and parameters evaluated at the beginning (‘
$1$
’) and the end (‘
$2$
’) of the region of interest, where
$\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\bar{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
is almost constant. Here
$M_{e}$
is the local Mach number,
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D6FF}_{99,av}$
is the spatial extent of the region of interest in averaged boundary-layer thicknesses (‘
$av$
’),
$\unicode[STIX]{x1D6FF}_{99,2}/\unicode[STIX]{x1D6FF}_{99,1}$
is the ratio of local boundary-layer thickness, and
$Re_{\unicode[STIX]{x1D703}}$
is the corresponding Reynolds number. Prefix
$i$
is for almost incompressible and
$c$
for compressible cases.
It is emphasized that the successful collapse of local flow-field profiles is crucial, as it is a necessary condition for the meaningfulness of the self-similarity analysis derived and the self-similar state of the computed data; for further discussion see § 4.5.1. If no collapse can be achieved, the reason cannot be clearly attributed to a lacking quality of data, to a misleading choice of characteristic scales or to wrong assumptions for ansatz functions plugged in to the self-similarity analysis, for instance.
4.1 Summary of DNS data
A summary of the most important flow-field properties is given in table 2 for all cases used in the following. According to Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019), all cases are denoted to be either APG, ZPG or FPG with a prefix
$i$
for almost incompressible and
$c$
for compressible cases. In the following, only regions of approximate self-similarity are considered, where
$\unicode[STIX]{x1D6FD}_{K}$
is approximately constant. For the subsonic cases, this region is located between
$150\leqslant x/\unicode[STIX]{x1D6FF}_{99,0}\leqslant 310$
; for the supersonic cases between
$250\leqslant x/\unicode[STIX]{x1D6FF}_{99,0}\leqslant 480$
; the beginning and the end of these regions are denoted by the index ‘
$1$
’ and ‘
$2$
’, respectively. The boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99,av}$
used in table 2 is the averaged one over the region of interest.
In the following, results of the subsonic cases are plotted in red, the supersonic cases in blue and the supersonic FPG case in cyan. The strength of the PGs is distinguished by different line styles: all ZPG cases are depicted as solid lines, the PG cases by different types of non-solid lines; the dashes of a line style become shorter for increasing pressure-gradient strength and thus rising
$\unicode[STIX]{x1D6FD}_{K}$
values.
4.2 Parameters
To estimate the success of the characteristic scalings, the most important conditions derived in the self-similarity in § 3 are evaluated in this section. In all related figures, the
$x$
-coordinate is normalized by the boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99,0}$
at the inlet of the domain (
$Re_{\unicode[STIX]{x1D703}}\approx 300$
) and is denoted by
$x^{\ast }$
.
4.2.1 Validity of characteristic scales
The characteristic scales have to be proportional to the flow-field values determined at the edge of the boundary layer, yielding
$$\begin{eqnarray}U_{0}\sim U_{e},\quad F_{0}\sim F_{e},\quad G_{0}\sim U_{0}^{2}.\end{eqnarray}$$
Hence, the ratios of
$U_{0}/U_{e}$
,
$F_{0}/F_{e}$
and
$G_{0}/U_{0}^{2}$
should be constant for self-similar flows. For all four sets of scaling, the respective conditions are given in figure 1(a–d).
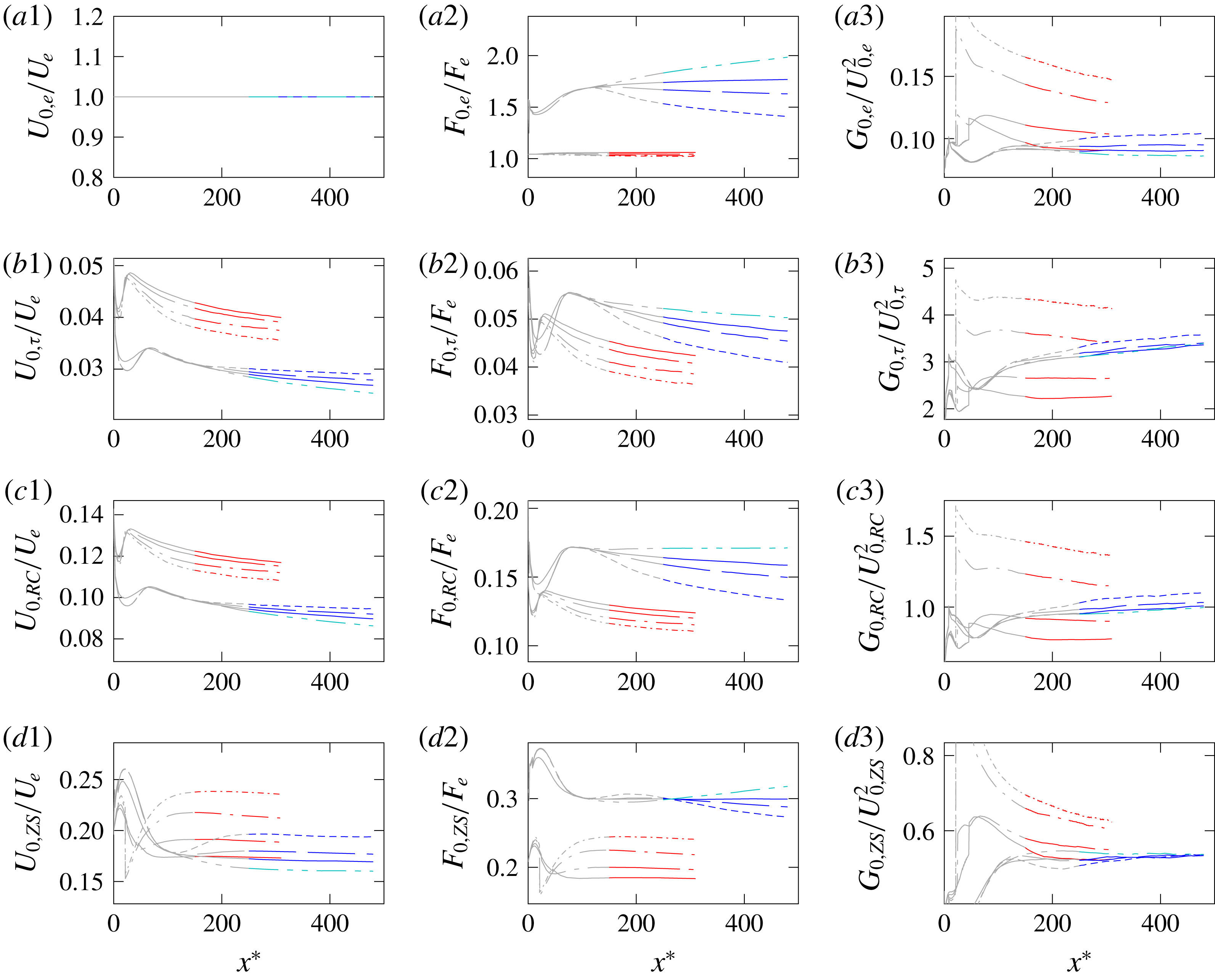
Figure 1. Plots of
$U_{0}/U_{e}$
(column 1),
$F_{0}/F_{e}$
(column 2) and
$G_{0}/U_{0}^{2}$
(column 3) for different scalings: (a) edge scaling, (b) friction scaling, (c) RC scaling and (d) ZS scaling. Grey lines denote the induction regions where
$\unicode[STIX]{x1D6FD}_{K}$
is not yet constant. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
Depicted in the first two columns, at first the conditions
$U_{0}/U_{e}=\text{const.}$
and
$F_{0}/F_{e}=\text{const.}$
are discussed. For the edge scaling in figure 1(a1), the condition for the velocity
$U_{0,e}=U_{e}$
gives a true statement. The corresponding mass-flux scale in figure 1(a2) has to be
$F_{0,e}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })F_{e}\neq F_{e}$
, yielding the false statement
$F_{0,e}\nsim F_{e}$
for supersonic cases; these vary by approximately
$10\,\%$
in figure 1(a2). Note that the scales could also have been chosen to fulfil
$F_{0}/F_{e}=\text{const.}$
, which lead to
$U_{0,e}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}^{\ast })U_{e}$
and thus to
$U_{0,e}\nsim U_{e}$
if
$F_{0}=F_{e}$
, for instance. Since the scaling success is better for velocity-based scalings as already discussed in § 3.3.2, these have been chosen to best fulfil the
$U_{0}/U_{e}=\text{const.}$
condition. An exemplary comparison between the two approaches for local velocity profiles is depicted in the appendix; see § A.2 later. Both for the friction scaling in figure 1(b1) and (b2) and the RC scaling in figure 1(c1) and (c2), it is evident that both ratios
$U_{0}/U_{e}$
and
$F_{0}/F_{e}$
are not constant and exhibit slight negative drifts. For the ZS scaling in figure 1(d1) and (d2) in contrast, almost the same behaviour is reproduced as for the edge scaling in figure 1(a1) and (a2).
Depicted in the third column of figure 1, the condition
$G_{0}\sim U_{0}^{2}$
relates the evolution of the characteristic kinetic energy
$U_{0}^{2}$
to the defect total enthalpy
$G_{0}$
. Consistently for all scalings in figure 1
$(a3{-}d3)$
, the distributions for all supersonic cases are approximately constant for all PGs (slightly better for the edge and ZS scales) and exhibit only small variations between different cases. For the subsonic cases, the differences for the various PG strengths are larger and the distributions are not as constant as for the supersonic cases. Since the statement
$G_{0}\sim U_{0}^{2}$
is closely related to a constant recovery factor
$r$
in the Walz relation as discussed in § 3.3.4, also the recovery factor of the subsonic PG cases is not as constant as for the supersonic cases, as depicted and discussed in Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019). But recall that the recovery factor becomes meaningless for Mach numbers approaching zero.
4.2.2 Similarity parameter
Both the compressible pressure-gradient boundary-layer growth parameter
$\unicode[STIX]{x1D6EC}_{c}=(L_{0}\,\text{d}p_{e}/\text{d}x)/(U_{0}F_{0}\,\text{d}L_{0}/\text{d}x)$
and the generalized Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}=(L_{0}\,\text{d}p_{e}/\text{d}x)/(U_{0}F_{0})$
are depicted in figures 2(a) and 2(b), respectively. For the
$\unicode[STIX]{x1D6EC}_{c}$
distributions, the
$\text{d}L_{0}/\text{d}x$
distributions have been smoothed by applying a Savitzky–Golay filter to the
$L_{0}$
distributions. Note that
$\unicode[STIX]{x1D6FD}_{RC}$
corresponds to
$\unicode[STIX]{x1D6FD}_{K}$
in Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019).
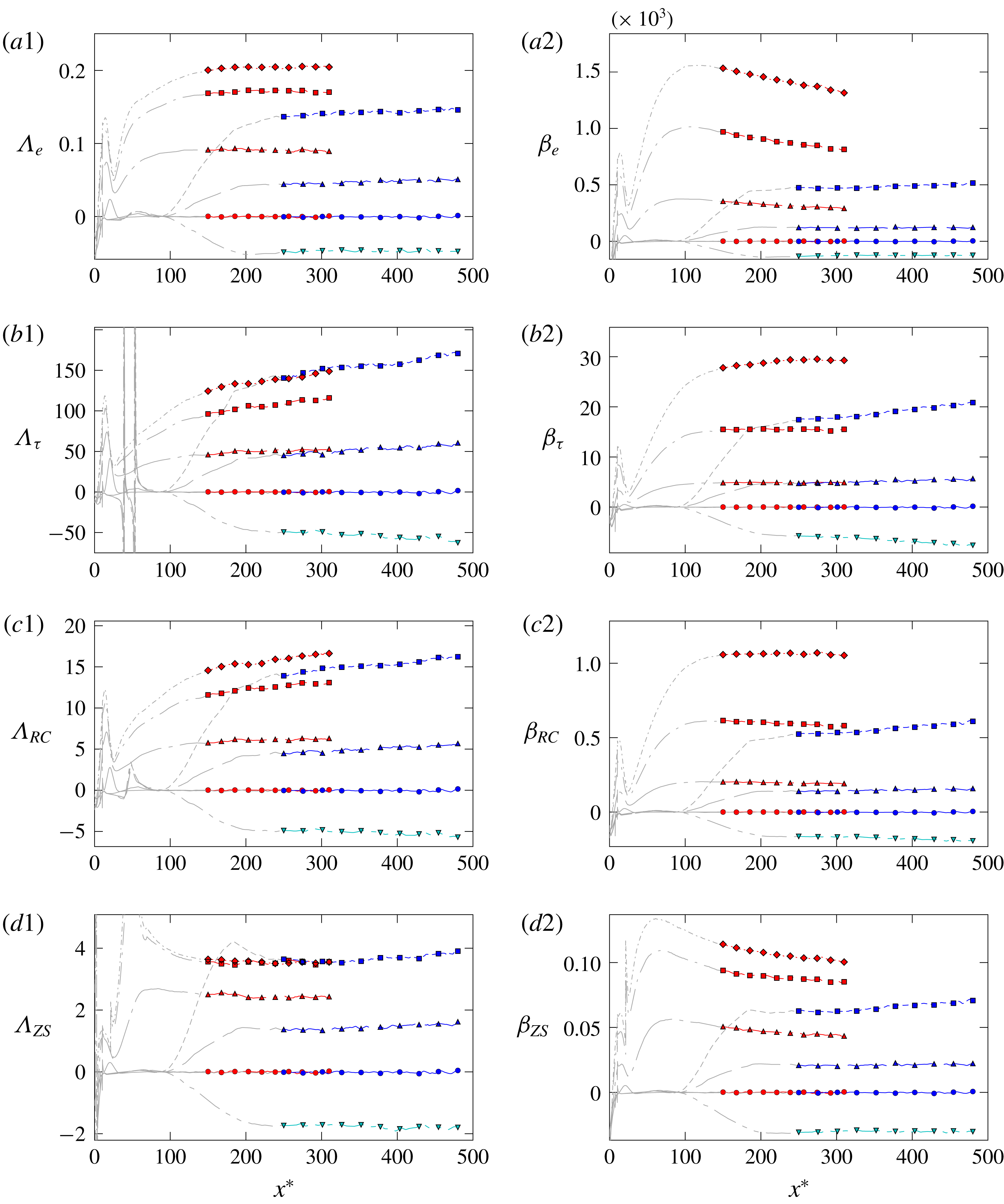
Figure 2. Plots of PG boundary-layer-growth parameter
$\unicode[STIX]{x1D6EC}_{c}$
(column 1) and PG parameter
$\unicode[STIX]{x1D6FD}$
(column 2) for different scalings: (a) edge scaling, (b) friction scaling, (c) RC scaling and (d) ZS scaling. Symbols mark positions where local profiles are extracted in the following; cases with the same
$\unicode[STIX]{x1D6FD}_{K}$
have the same symbol type. Grey lines denote the induction regions, where
$\unicode[STIX]{x1D6FD}_{K}$
is not yet constant. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
The compressible
$\unicode[STIX]{x1D6EC}_{c}$
parameter converges towards an almost constant state for the edge and ZS scalings for both the compressible and incompressible scales in the domain of interest, see figure 2(a1) and (d1). The friction and RC scales in figure 2(b1) and (c1), in contrast, show visible variations, becoming pronounced with increasing PG strength. For the
$\unicode[STIX]{x1D6FD}$
distributions in figure 2(a2–d2), the supersonic cases exhibit a comparable behaviour as for
$\unicode[STIX]{x1D6EC}_{c}$
in figure 2(a1–d1) for all scalings. For the subsonics the trend is reversed;
$\unicode[STIX]{x1D6FD}$
is almost constant for the friction and RC scales in figure 2(b2) and (c2) and visibly decreasing for the edge and ZS scales in figure 2(a2) and (d2).
Implied by the visible differences between both
$\unicode[STIX]{x1D6EC}_{c}$
and
$\unicode[STIX]{x1D6FD}$
, which only differ by the additional consideration of
$\text{d}L_{0}/\text{d}x$
, the assumption of
$\text{d}L_{0}/\text{d}x\approx \text{const.}$
is only approximately fulfilled for our data and is expected to have significant influences on the scaling success. Its consequences are discussed in the following. It is emphasized that the various scalings shift the relative position of sub- and supersonic cases with respect to each other and thus do not allow a consistent comparison between PG strengths for compressible and incompressible cases for different parameters.
4.3 Self-similarity of mean-flow profiles
In the following, the streamwise self-similarity of the Favre-averaged mass-flux, velocity and total-enthalpy distributions is investigated for the outer layer. Local flow-field profiles are extracted at 10 equidistant streamwise positions, all of which are located in regions of estimated self-similarity for each case; see the symbols in figure 2. Extracted at these 10 positions, the corresponding flow-field profiles are given as grey lines in the background of all following plots, their mean value as coloured lines in the foreground. All flow variables are depicted in the four different scalings introduced, see (3.4)–(3.17), and plotted in their defect formulation versus
$y/\unicode[STIX]{x1D6FF}_{99}$
.
4.3.1 Mean velocity profiles
$\tilde{u}$
The mean velocity profiles are shown in figure 3. Represented in the edge scaling in figure 3
$(a)$
, the velocity-defect profile
$1-\tilde{u} /\tilde{u} _{e}$
approximately corresponds to the integrand of the incompressible displacement thickness
$1-\bar{u}/\bar{u}_{e}$
and thus characterizes the velocity defect. Whereas higher APGs lead to higher defects and thus less full profiles compared to ZPGs, FPGs lead to fuller profiles. A comparison between compressible and incompressible profiles shows comparable, but not identical, distributions for cases with similar
$\unicode[STIX]{x1D6FD}_{K}$
values; see e.g. the two ZPG cases. For both the friction scaling in figure 3
$(b)$
and the
$RC$
scaling in figure 3
$(c)$
, the sub- and supersonic counterparts are further separated from each other. Like for the edge scaling in figure 3
$(a)$
, the ZS scaling in figure 3
$(d)$
corresponds to the integrand of the incompressible displacement thickness, but is additionally scaled by
$\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}_{99}$
such that profiles for the various PGs are pushed more closely together; however, they do not collapse.
Figure 3. Mean velocity profiles for different characteristic velocity scales: (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
Figure 4. Mean mass-flux profiles for different characteristic mass-flux scales: (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
The edge scaling in figure 3(a) shows an impressive collapse for both the sub- and supersonic cases, meaning that all 10 grey lines for successive
$x$
positions of each case collapse under the corresponding coloured lines. For the friction scaling in figure 3(b) and also the RC scaling in figure 3(c), the collapse is noticeably worse, meaning that the 10 grey lines of each case slightly scatter. The extent of this scattering is comparable for all cases. For the ZS scaling in figure 3(d), the collapse of each of the 10 streamwise profiles is as good as for the edge scaling in figure 3
$(a)$
.
It is interesting to see that the scaling success of the velocity profiles is well correlated with the constancy of the condition
$U_{0}\sim U_{e}$
and the
$\unicode[STIX]{x1D6EC}_{c}$
parameter tested in figures 1(a1–d1) and 2(a1–d1), respectively. While both conditions are well fulfilled for both the edge and ZS scalings, which excellently scale the spatially evolving kinematic boundary layers, they exhibit slight deviations for the friction and RC scalings. The conditions
$U_{0}\sim U_{e}$
and
$\unicode[STIX]{x1D6EC}_{c}=\text{const.}$
derived in the analysis are therefore expected to be meaningful indicators for a good set of scales. For the
$\unicode[STIX]{x1D6FD}$
parameters (figure 2(a1–d1)), in contrast, which only differ from
$\unicode[STIX]{x1D6EC}_{c}$
by not including
$\text{d}L_{0}/\text{d}x$
, the inverse trends can be found. The
$\unicode[STIX]{x1D6FD}$
distributions are more constant for the friction and RC scalings, which, however, do not scale the spatially evolving boundary layers to the same degree as the edge and ZS scalings. Thus, it might be expected that both friction-based scales are slightly influenced by
$\text{d}L_{0}/\text{d}x$
values not being perfectly constant for the low Reynolds numbers investigated, which are eliminated in the calculation of
$\unicode[STIX]{x1D6FD}$
. For higher Reynolds numbers, where
$\text{d}L_{0}/\text{d}x$
becomes more constant by a reduced growth of the boundary layer, the scaling success of both friction-based scalings is expected to increase; see § 4.5.3 for a detailed discussion.
4.3.2 Mean mass-flux profiles
$\bar{\unicode[STIX]{x1D70C}}\tilde{u}$
In figure 4 the Favre-averaged mass-flux profiles are shown. Since density variations are weak for the subsonic cases, their profiles are virtually identical to the velocity profiles discussed above. For the supersonic cases, in contrast, differences can be observed in the boundary-layer edge region where the mass-flux boundary-layer thickness is somewhat increased; see for instance the ZPG cases.
Figure 5. Mean total enthalpy profiles for different characteristic enthalpy scales: (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red line: ——,
$iZPG$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
Nevertheless, the edge scaling in figure 4(a) and the ZS scaling in figure 4(d) work excellently for both the sub- and supersonic cases in accordance with the velocity profiles discussed before. For the friction scaling in figure 4(b) and the RC scaling in figure 4(c), the collapse of the 10 profiles for each case is slightly worse. Note that the scaling success of the edge and ZS scalings was not necessarily expected for the supersonic cases, since their
$F_{0}/F_{e}$
ratios have no longer been found to be constant in figure 1(a2) and 1(d2). Hence also the DNS results indicate that large parts of the boundary layer scale much better with kinematic than with mass-flux quantities.
4.3.3 Mean total-enthalpy profiles
$\tilde{h}_{0}$
Lastly, the total enthalpy profiles
$\tilde{h}_{0}$
are shown in figure 5. Since the total enthalpy decreases near the wall, i.e. has a large deficit there, a (smaller) localized negative deficit peak (at higher velocity) rises in the outer part of the boundary layer balancing the deficit near the wall. Note that the absolute magnitude of the total enthalpy defect goes to zero for zero Mach number. For subsonic APG cases, normalized defect profiles can indeed be calculated but describe absolute values of negligible size and thus may be misinterpreted and are omitted here. For the supersonic cases, the outer peak is larger than for the subsonic ZPG case, but no clear influence of the PG strength is visible.
An assessment of the scaling quality, and thus the collapse of the respective 10 grey lines behind their corresponding coloured averaged line, does not show the same quality as for the mass-flux and the velocity profiles before. However, the self-similarity of the total-enthalpy profiles requires the self-similarity both of the mass-flux profiles and of the coupling mechanism between mass flux and enthalpy, and thus self-similarity is much more difficult to achieve for the total enthalpy. With this in mind, the given distributions still indicate approximate self-similarity in the outer layer of the total-enthalpy profiles. In the inner layer below roughly
$y/\unicode[STIX]{x1D6FF}_{99}\approx 0.15$
, the plotted profiles appear to be
$x$
-dependent for both the ZPG and PG cases. As previously seen in the relations
$G_{0}\sim U_{0}^{2}$
in figure 1(a3–d3) and the recovery factors in part 1 (see Wenzel et al.
Reference Wenzel, Gibis, Kloker and Rist2019), all supersonic profiles are nearly identical.
4.4 Self-similarity of turbulent terms
Besides the mean-flow profiles discussed before, also the profiles of the turbulent-fluctuation terms have to collapse for the derived scalings. However, as has often been observed, this is more difficult to achieve in general than collapsing the mean-flow profiles even for the ZPG case; see Maciel et al. (Reference Maciel, Rossignol and Lemay2006) for instance.
For the mean-flow profiles discussed in the previous section, compressible and quasi-incompressible cases have been found to be scaled to different similarity profiles for similar
$\unicode[STIX]{x1D6FD}_{K}$
values; compare the sub- and supersonic ZPG profiles in figure 3 for instance. For the turbulent terms, however, the shear-stress distributions
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u_{i}^{\prime \prime }u_{j}^{\prime \prime }}$
have been found to be almost Mach-number-invariant if normalized by the local wall shear stress
$\bar{\unicode[STIX]{x1D70F}}_{w}$
(Morkovin’s scaling) in part 1 (see Wenzel et al.
Reference Wenzel, Gibis, Kloker and Rist2019). Thus, by a suitable selection of the constants
$C_{M}$
and
$C_{E}$
introduced in § 3.2.5, this behaviour is utilized to remove the Mach-number dependence of the initial profile for various cases. To this end the constant
$C_{M}$
is chosen as
$$\begin{eqnarray}C_{M}=\left.\frac{\bar{\unicode[STIX]{x1D70F}}_{w}}{F_{0}U_{0}}\right|_{ref}=\text{const.},\end{eqnarray}$$
which resembles Morkovin’s scaling for the Favre stresses,
$$\begin{eqnarray}r_{u_{i}u_{j}}(\unicode[STIX]{x1D702})=\frac{\bar{\unicode[STIX]{x1D70C}}\widetilde{u_{i}^{\prime \prime }u_{j}^{\prime \prime }}}{C_{M}F_{0}U_{0}}=\frac{\bar{\unicode[STIX]{x1D70C}}\widetilde{u_{i}^{\prime \prime }u_{j}^{\prime \prime }}}{F_{0}U_{0}}\left.\frac{F_{0}U_{0}}{\bar{\unicode[STIX]{x1D70F}}_{w}}\right|_{ref}.\end{eqnarray}$$
The subscript ‘
$ref$
’ denotes a selectable position in the domain. For the turbulent heat fluxes, it has been found that the constant
$C_{E}$
, chosen as
$$\begin{eqnarray}C_{E}=\left.\frac{\bar{\unicode[STIX]{x1D70F}}_{w}U_{0}}{F_{0}G_{0}}\right|_{ref}=\text{const.},\end{eqnarray}$$
scales the turbulent heat fluxes to a similar order of magnitude for the sub- and supersonic flows. For all scalings, the constants
$C_{M}$
and
$C_{E}$
are evaluated for the initial profile in the domain of self-similarity. Since the friction scaling has already been designed to reproduce Morkovin’s scaling,
$C_{M}$
equals one for this case.
4.4.1 Favre stresses
The
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
Favre stress is shown in figure 6. As discussed in Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019), a second peak is forming in the outer layer of the boundary layers for increasing PG strength besides the inner peak. This peak is localized at around
$y/\unicode[STIX]{x1D6FF}_{99}\approx 0.4$
for the highest subsonic PG. As a consequence of the additional consideration of
$C_{M}$
and thus Morkovin’s scaling, sub- and supersonic cases are directly comparable for similar
$\unicode[STIX]{x1D6FD}_{K}$
values. Note that, in contrast to the mass-flux profiles in figure 4, both sub- and supersonic Favre-stress distributions tend to zero at the same
$y/\unicode[STIX]{x1D6FF}_{99}$
. This further supports the expectation that the Favre stresses are closely coupled to the kinematic boundary layer and thus scale with a kinematic rather than a mass-flux-related length scale.
Figure 6. Favre stress
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
in (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
An excellent collapse for the outer layer of the subsonic cases is achieved for both the edge and ZS scalings in figure 6
$(a)$
and
$(d)$
, respectively. For the supersonic cases, the 10 respective lines of each case differ slightly, meaning that the scaling success is slightly worse. Recall, however, that also the
$\unicode[STIX]{x1D6FD}_{K}$
distributions (equivalent to
$\unicode[STIX]{x1D6FD}_{RC}$
in figure 2) of the supersonic cases are somewhat less constant compared to the subsonic ones. Additionally, the region of interest is larger for some supersonic cases if measured in
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D6FF}_{99,av}$
and compared for the same
$\unicode[STIX]{x1D6FD}_{K}$
; see table 2. For both the friction and RC scalings in figure 6
$(b)$
and
$(c)$
, respectively, the scaling success is comparable to the edge and ZS scalings for the ZPG cases. With increasing APG strength, it worsens somewhat for both the sub- and supersonic cases, whereas for the FPG case it is better. For high APGs, the results for the RC scaling are slightly better than for the friction scaling.
Figure 7. Same as figure 6, but for Favre stress
$\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
.
The
$\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
Favre stress is depicted in figure 7. As already discussed in Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019), this stress is directly coupled to the mean-pressure distribution
$\bar{p}=p_{e}-\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
and thus directly depends on the wall-normal PG. In contrast to the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
stress, the profile has only a single peak, which is widened and moved further outside towards the boundary-layer edge for increasing PG strength. All sets of scales show a similar behaviour as for the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
distributions discussed before.
Figure 8. Favre stress
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
in (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
The
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
Favre stress is depicted in figure 8. This stress is directly linked to the shear-stress evolution and hence represents the most important stress for turbulence modelling. Its shape is comparable to that of
$\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
by only exhibiting one peak, which is widened and moved further outside with increasing PG strength. In contrast to the other stresses, the self-similarity analysis has revealed a scaling of
$F_{0}U_{0}(\text{d}L_{0}/\text{d}x)$
instead of
$F_{0}U_{0}$
, see (3.39). Although
$\text{d}L_{0}/\text{d}x$
is often expected to be constant for self-similar flows, its value drifts slightly due to the low Reynolds numbers in the DNS data, and thus has a visible effect on the scaling success. The smoothed
$\text{d}L_{0}/\text{d}x$
term is therefore included for the scalings in figure 8. However, the additional inclusion of
$\text{d}L_{0}/\text{d}x$
makes the comparison of different PG cases difficult, since
$\text{d}L_{0}/\text{d}x$
depends on the PG strength and on the Mach and Reynolds numbers. Note that the effect of smoothing
$\text{d}L_{0}/\text{d}x$
is only small for the edge and ZS scalings. For the friction and RC scalings, smoothing eliminates some outliers due to noise in
$\text{d}L_{0}/\text{d}x$
. To ensure comparability between different PG cases for
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
as well as between
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
and other stresses,
$\text{d}L_{0}/\text{d}x$
is normalized to one concerning the streamwise mean of
$\text{d}L_{0}/\text{d}x$
of every PG case.
The trend of the scaling quality is in principle the same as for the previous plots, although the spread for the friction and RC scalings in figure 8(b,c) is larger. To estimate the influence of
$\text{d}L_{0}/\text{d}x$
in the scaling success, the same plot without including
$\text{d}L_{0}/\text{d}x$
is given in figure 13 in § A.3 for comparison. Note that the scaling success is thereby significantly improved for the friction and RC scalings, as the neglect of
$\text{d}L_{0}/\text{d}x$
balances the implicit dependence on
$\text{d}L_{0}/\text{d}x$
for both scales. As this is at the core of the discrepancies between Townsend (Reference Townsend1956b
), George & Castillo (Reference George and Castillo1993) and Maciel et al. (Reference Maciel, Rossignol and Lemay2006), its implications are discussed in § 4.5.3.
4.4.2 Turbulent heat fluxes
The turbulent heat flux
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }u^{\prime \prime }}$
is shown in figure 9. Besides the inner peak, an outer peak forms for increasing APG strength. With the same arguments as for the total enthalpy profiles in § 4.3.3, the subsonic cases are omitted except for the ZPG case.
Figure 9. Turbulent heat flux
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }u^{\prime \prime }}$
in (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red line: ——,
$iZPG$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
Figure 10. Same as figure 9, but for turbulent heat flux
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }v^{\prime \prime }}$
.
Both the distributions as well as the respective streamwise scaling success resemble those of the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
distributions shown in figure 6. It is noted that sub- and supersonic ZPG cases are only matched by the additional consideration of
$C_{E}$
for the edge scaling in figure 9
$(a)$
, and with slightly worse success also for the ZS scaling in figure 9
$(d)$
. Note that the definition of
$C_{E}$
is mainly based on arguments related to Morkovin’s scaling, which, however, cannot necessarily be assumed to still work for the turbulent heat fluxes. The scaling quality is approximately the same for all four scalings.
The turbulent heat flux
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }v^{\prime \prime }}$
is shown in figure 10. Combined with the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
profile (figure 8),
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }v^{\prime \prime }}$
is usually employed to define the turbulent Prandtl number in combination with the wall-normal gradients of streamwise velocity and temperature of the mean flow. Like for the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
stress, the similarity analysis has revealed
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }v^{\prime \prime }}$
to be scaled by also taking
$\text{d}L_{0}/\text{d}x$
into account, see (3.46). As the concept of the turbulent Prandtl number assumes, the distributions of
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }v^{\prime \prime }}$
are indeed very similar to those of
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
. The scaling quality is comparable for all sets of scaling, comparable as for
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }u^{\prime \prime }}$
.
4.5 Discussion
All statements made in this section are, strictly speaking, only reliable for the Mach- and Reynolds-number ranges investigated. On the other hand, there is no decisive factor rendering their extrapolation not plausible.
4.5.1 Assessment of DNS data
The collapse of local flow-field profiles extracted from the DNS data is crucial for this study, as it validates the meaningfulness of both the self-similarity analysis as well as the self-similar state of the computed flow field. However, this state is not simple to warrant. For example, excellent scaling results were found for the edge scaling, but a different choice of PG distributions could have made another scaling more successful; recall that all PG distributions in the DNS have been aimed at yielding constant
$\unicode[STIX]{x1D6FD}_{K}$
. For this reason, the ZPG cases are of particular importance, since these can be assumed to be in equilibrium without being calibrated to any PG distribution. Hence they provide the most clear measure for the ‘pure’ scaling success of every particular scaling set. Thus, as long as the PG cases show the same trends as the ZPG cases, like comparable distributions of
$U_{0}/U_{e}$
in figure 2 for instance, the results can be stated to be conclusive.
4.5.2 Conditions for the characteristic scales
In the self-similarity analysis, § 3.2, conditions were derived for a valid set of scales for self-similar flows. The characteristic scales have to be proportional to the flow-field properties at the boundary-layer edge,
$U_{0}\sim U_{e}$
,
$F_{0}\sim F_{e}$
, and the PG parameter
$\unicode[STIX]{x1D6EC}_{c}$
has to be constant in the streamwise direction, among others. The scales of the kinetic energy and the total enthalpy should develop according to
$U_{0}^{2}\sim G_{0}$
.
By testing different sets of scales, it has been shown that both conditions are well fulfilled for the edge and ZS scalings. The scaling success of the friction and RC scalings is slightly weaker; especially, the constancy of
$U_{0}/U_{e}$
is not as well fulfilled. For both, however, the evolution becomes increasingly constant for increasing Reynolds numbers, suggesting that the scaling success becomes increasingly better. As further discussed in § 4.5.3 and demonstrated in § A.4, the friction scaling can be improved by a ‘low-Reynolds-number’ correction. The limiting behaviour of
$U_{0}/U_{e}$
cannot be safely extrapolated from the available data. Hence, both the conditions
$U_{0}\sim U_{e}$
and
$\unicode[STIX]{x1D6EC}_{c}=\text{const.}$
seem to be a meaningful measure of the quality for a scaling set. As a result of the varying density of the supersonic cases in the streamwise direction, the ratio
$F_{0}/F_{e}$
is only poorly fulfilled for all sets, which, however, has no visible effect on the scaling success. The condition of
$U_{0}^{2}\sim G_{0}$
is approximately fulfilled for all supersonic cases.
4.5.3 On the influence of
$\text{d}L_{0}/\text{d}x$
In contrast to the classical theory, many terms in the self-similarity analysis presented in § 3.2 are scaled by the additional consideration of
$\text{d}L_{0}/\text{d}x$
. While this term is mostly neglected or set constant in classical works, its inclusion yields visible influences on the results presented due to the ‘low’ Reynolds numbers investigated.
Compared to the generalized
$\unicode[STIX]{x1D6FD}$
parameter introduced by Maciel et al. (Reference Maciel, Rossignol and Lemay2006) for instance,
$\unicode[STIX]{x1D6EC}_{c}$
only differs by additionally taking
$\text{d}L_{0}/\text{d}x$
into account,
$\unicode[STIX]{x1D6EC}_{c}=\unicode[STIX]{x1D6FD}/(\text{d}L_{0}/\text{d}x)$
. While
$\unicode[STIX]{x1D6EC}_{c}$
is almost constant and
$\unicode[STIX]{x1D6FD}$
is not for the well-behaving edge and ZS scalings, the opposite applies for the slightly weaker-performing friction and RC scalings;
$\unicode[STIX]{x1D6FD}$
(and thus
$\unicode[STIX]{x1D6FD}_{RC}=\unicode[STIX]{x1D6FD}_{K}$
) is almost constant and
$\unicode[STIX]{x1D6EC}_{c}$
is not. Furthermore, if
$\text{d}L_{0}/\text{d}x$
is taken into account for the scaling of
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
as proposed by the self-similarity analysis, an excellent scaling success is determined for the edge and ZS scalings. If neglected, on the other hand, an excellent agreement is determined for the friction and RC scalings. Consequently, it seems reasonable to assume that the
$\text{d}L_{0}/\text{d}x$
term is already implicitly included in the friction-based scales and hence does not have to be re-accounted for in the definition of
$\unicode[STIX]{x1D6EC}_{c}$
or the scaling of
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
for the friction-based scaling sets for instance. Both observations are discussed in the following.
In classical incompressible theory, the velocity scale can be derived from the wall shear stress and the streamwise evolution of the Favre shear stress
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}\sim F_{0}U_{0}\sim \bar{\unicode[STIX]{x1D70C}}_{w}U_{0}^{2}$
, which results in
$U_{0}=\sqrt{\bar{\unicode[STIX]{x1D70F}}_{w}/\bar{\unicode[STIX]{x1D70C}}_{w}}=u_{\unicode[STIX]{x1D70F}}$
for friction-based scalings. From part 1 of this study and with (3.39), in contrast, it is, however, reasonable to assume
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70F}}_{w}\sim \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}\sim F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}\end{eqnarray}$$
in the streamwise direction. Therefore, if
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim F_{0}U_{0}(\text{d}L_{0}/\text{d}x)\sim \bar{\unicode[STIX]{x1D70C}}_{w}U_{0}^{2}(\text{d}L_{0}/\text{d}x)$
is assumed, the velocity scale yields
$$\begin{eqnarray}U_{0}=\sqrt{\bar{\unicode[STIX]{x1D70F}}_{w}/\bar{\unicode[STIX]{x1D70C}}_{w}}/\sqrt{\text{d}L_{0}/\text{d}x}=u_{\unicode[STIX]{x1D70F}}/\sqrt{\text{d}L_{0}/\text{d}x},\end{eqnarray}$$
instead of just using
$U_{0}=u_{\unicode[STIX]{x1D70F}}$
. The additional consideration of
$\text{d}L_{0}/\text{d}x$
can hence be interpreted as a ‘low-Reynolds-number’ correction of
$U_{0}=u_{\unicode[STIX]{x1D70F}}$
. With the same arguments, a compressible ‘low-Reynolds-number’ corrected version is derived and tested in § A.4 for the compressible regime. Its scaling success yields almost perfect results, which are essentially the same as for the edge scaling (implying
$U_{e}\sim u_{\unicode[STIX]{x1D70F}}/\sqrt{\text{d}L_{0}/\text{d}x}$
).
Like for the velocity scale, also the PG parameter can be associated with the influence of
$\bar{\unicode[STIX]{x1D70F}}_{w}$
. If
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim F_{0}U_{0}$
is assumed, the traditional Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\bar{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
yields for a general set of scales
$\unicode[STIX]{x1D6FD}=(L_{0}/(F_{0}U_{0}))(\text{d}p_{e}/\text{d}x)$
, implying
$\unicode[STIX]{x1D6EC}_{c}\sim \unicode[STIX]{x1D6FD}/(\text{d}L_{0}/\text{d}x)$
. If, on the other hand,
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim F_{0}U_{0}(\text{d}L_{0}/\text{d}x)$
is assumed,
$\unicode[STIX]{x1D6FD}_{K}$
can be directly associated with
$\unicode[STIX]{x1D6EC}_{c}$
using
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{K}=\frac{\unicode[STIX]{x1D6FF}_{K}^{\ast }}{\bar{\unicode[STIX]{x1D70F}}_{w}}\frac{\text{d}p_{e}}{\text{d}x}\sim \frac{L_{0}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}\sim \unicode[STIX]{x1D6EC}_{c}.\end{eqnarray}$$
In its traditional definition, therefore,
$\unicode[STIX]{x1D6FD}_{K}$
fulfils the definition of
$\unicode[STIX]{x1D6EC}_{c}$
and thus still indicates the state of self-similarity, even if
$\text{d}L_{0}/\text{d}x$
cannot be assumed constant.
4.5.4 Towards the interpretation of
$\unicode[STIX]{x1D6EC}_{c}$
A clear requirement for a meaningful PG parameter is the comparability of different PG strengths, connecting sub- and supersonic PG cases. It is desirable that flows with identical shear-stress distributions (or identical Favre-stress distributions) are characterized by an identical value of the PG parameter. For all scaling sets tested, this is only achieved for
$\unicode[STIX]{x1D6FD}_{K}$
(
$\unicode[STIX]{x1D6FD}_{RC}$
), see figure 2(c2). For the
$\unicode[STIX]{x1D6EC}_{c}$
distributions, see figure 2(a1–d1), only the constancy of the respective values is found as a criterion for self-similarity; the particular
$\unicode[STIX]{x1D6EC}_{c}$
values of cases with similar shear-stress distributions, however, differ. If
$\unicode[STIX]{x1D6EC}_{c}$
is interpreted as
$\unicode[STIX]{x1D6EC}_{c}=\unicode[STIX]{x1D6FD}/(\text{d}L_{0}/\text{d}x)$
, where both
$\unicode[STIX]{x1D6FD}$
and
$\text{d}L_{0}/\text{d}x$
are strongly influenced by the PG, the behaviour of
$\unicode[STIX]{x1D6EC}_{c}$
is sometimes misleading: different cases with different flow profiles are ‘characterized’ by identical
$\unicode[STIX]{x1D6EC}_{c}$
values; see figure 2(b1–d1) for example.
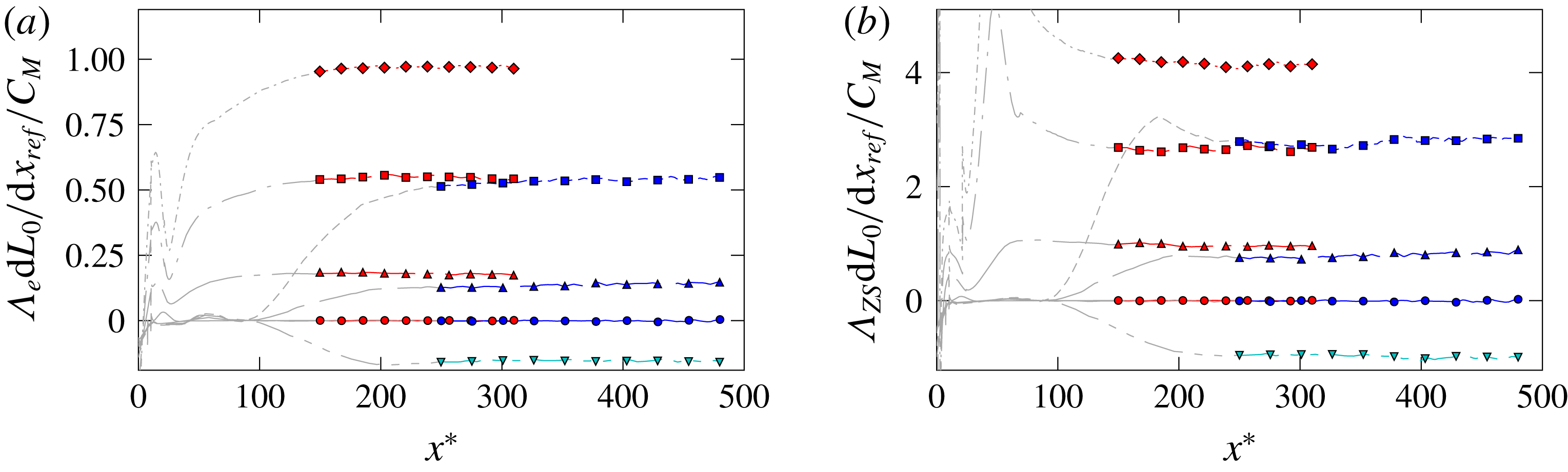
Figure 11. Pressure-gradient boundary-layer growth parameter
$\unicode[STIX]{x1D6EC}_{c}$
computed according to (4.8) for the (a) edge and (b) ZS scalings. Identical symbols denote cases with similar
$\unicode[STIX]{x1D6FD}_{K}$
values. Red: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
To obtain a characterizing behaviour of
$\unicode[STIX]{x1D6EC}_{c}$
, two modifications are proposed. Whereas the additional consideration of
$C_{M}$
(see (4.2)) eliminates the Mach-number dependence of
$\unicode[STIX]{x1D6EC}_{c}$
and thus ensures comparability for cases with similar shear-stress distributions, the case dependence of
$\text{d}L_{0}/\text{d}x$
is reduced by normalization to one at a reference position. A modified
$\unicode[STIX]{x1D6EC}_{c}$
parameter is therefore calculated as
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{c}=\frac{\displaystyle L_{0}\frac{\text{d}p_{e}}{\text{d}x}}{\displaystyle C_{M}U_{0}F_{0}\left.\frac{\text{d}L_{0}}{\text{d}x}\right|_{O1}}\quad \text{with }\left.\frac{\text{d}L_{0}}{\text{d}x}\right|_{O1}=\frac{\text{d}L_{0}}{\text{d}x}\frac{1}{\displaystyle \left.\frac{\text{d}L_{0}}{\text{d}x}\right|_{ref}}.\end{eqnarray}$$
For both the edge and ZS scalings, typical results are given in figure 11. The reference position in chosen in such a way that the resulting streamwise average of
$(\text{d}L_{0}/\text{d}x)|_{O1}$
is approximately one, e.g.
$(1/(x_{2}-x_{1}))\int _{x1}^{x_{2}}(\text{d}L_{0}/\text{d}x)|_{O1}\,\text{d}x\approx 1$
, where
$x_{1}$
and
$x_{2}$
are the bounds of the region of interest. Like for
$\unicode[STIX]{x1D6FD}_{K}$
in figure 2(c2), the
$\unicode[STIX]{x1D6EC}_{c}$
distributions now become equal again for cases with similar PG influence (note the symbols).
4.5.5 Assessment of self-similarity for compressible flow
If self-similarity should be determined for compressible flow, streamwise scale invariance must be fulfilled for all Reynolds numbers in a strict sense.
By the appropriate choice of characteristic scales, the distributions of turbulent mean fluctuation have been successfully collapsed for cases with similar
$\unicode[STIX]{x1D6FD}_{K}$
values. Since the (quasi-)incompressible APG cases are the limit of the compressible APG cases for
$Re\rightarrow \infty$
, and both are collapsed on a similarity solution, a high degree of self-similarity can be expected for the turbulent terms in the compressible regime. For the mean-flow profiles, however, compressible and incompressible cases could not be directly related to each other with the outer scaling investigated here. The limiting behaviour of the supersonic cases for
$Re\rightarrow \infty$
therefore cannot be deduced unambiguously from the available data. The violation of the condition
$F_{0}\sim F_{e}$
, for instance, does not seem to have any visible influence on the scaling success in the investigated Reynolds-number range, but it is expected for the presented scales that this does not hold for
$Re\rightarrow \infty$
. The reason is that van Driest’s transformation, which would allow a comparison (at least to a certain degree; see Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018)) between compressible and incompressible cases, cannot simply be built in to the self-similarity framework presented. In contrast to Morkovin’s scaling, van Driest’s transformation represents a
$y$
-dependent scaling that cannot be built in as a simple scaling factor. This does not mean that there are no modified techniques that could incorporate adequate compressibility transformations.
5 Conclusions
The main objective of this study is to investigate the properties of self-similarity for the outer layer of compressible turbulent boundary layers with pressure gradient. Based on the compressible turbulent boundary-layer equations, a self-similarity analysis is presented whose results are validated using the compressible DNS data presented in Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019).
5.1 Results of the self-similarity analysis
The analysis is performed for general characteristic scales of the velocity
$U_{0}$
, mass flux
$F_{0}$
and total enthalpy
$G_{0}$
and a single length scale
$L_{0}$
characterizing the growth of the velocity, the mass-flux and the energy boundary layers simultaneously. It has been shown that using a single length scale yields essentially the same restrictions as characterizing each boundary layer by its own length scale.
In summary, the main findings of the analysis are that the ratios
$U_{0}/U_{e}$
,
$F_{0}/F_{e}$
and
$G_{0}/U_{0}^{2}$
as well as the compressible pressure-gradient boundary-layer evolution parameter
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{c}=\frac{\displaystyle L_{0}\frac{\text{d}p_{e}}{\text{d}x}}{\displaystyle C_{M}U_{0}F_{0}\left.\frac{\text{d}L_{0}}{\text{d}x}\right|_{O1}}\quad \text{with }\left.\frac{\text{d}L_{0}}{\text{d}x}\right|_{O1}=\frac{\text{d}L_{0}}{\text{d}x}\frac{1}{\displaystyle \left.\frac{\text{d}L_{0}}{\text{d}x}\right|_{ref}}\end{eqnarray}$$
have to be constant in the streamwise direction for self-similar flows. By introducing a constant
$C_{M}=\bar{\unicode[STIX]{x1D70F}}_{w}/(U_{0}F_{0})|_{ref}$
motivated by the Morkovin scaling and a normalization of the
$\text{d}L_{0}/\text{d}x$
term,
$\unicode[STIX]{x1D6EC}_{c}$
values become comparable for PG cases with similar shear-stress distributions, no matter whether the flow is incompressible or compressible.
5.2 On the validity of characteristic scales and the influence of
$\text{d}L_{0}/\text{d}x$
Four sets for the compressible scales
$U_{0}$
,
$F_{0}$
,
$G_{0}$
and
$L_{0}$
are proposed and tested. These are aimed at being compressible extensions of the incompressible edge scaling, friction scaling, Zagarola–Smits (ZS) scaling and a newly constructed Rotta–Clauser (RC) scaling. The latter yields the Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{K}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\bar{\unicode[STIX]{x1D70F}}_{w})(\text{d}p_{e}/\text{d}x)$
if the RC scales are plugged into the generalized form of
$\unicode[STIX]{x1D6FD}=(L_{0}\,\text{d}p_{e}/\text{d}x)/(U_{0}F_{0})$
introduced by Maciel et al. (Reference Maciel, Rossignol and Lemay2006);
$\unicode[STIX]{x1D6FF}_{K}^{\ast }$
is the kinematic (incompressible) displacement thickness for the compressible flow. All scales are constructed on velocity-based arguments and are identical to the incompressible scales in the incompressible limit. Consequently, all findings gained apply equally to the incompressible regime. To estimate the scaling success of the proposed sets, the collapse of flow-field profiles extracted at various streamwise positions and normalized by the respective scalings has been assessed.
For the turbulent terms, compressible and incompressible distributions are collapsed by the additional consideration of
$C_{M}$
for cases with the same shear-stress distributions. If the edge scaling or ZS scaling is applied, local flow profiles are excellently collapsed into a single profile in the Reynolds-number range considered. For the friction and RC scalings, in contrast, the scaling success is not that perfect. This holds for both the Favre stresses and the turbulent heat fluxes. In contrast to the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime 2}}$
and
$\bar{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime \prime 2}}$
stresses, the analysis reveals the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
stress (and also
$\bar{\unicode[STIX]{x1D70C}}\widetilde{h^{\prime \prime }v^{\prime \prime }}$
) to be scaled by incorporating
$\text{d}L_{0}/\text{d}x$
. While this term is usually neglected in related studies, the inclusion of
$\text{d}L_{0}/\text{d}x$
has brought remarkable improvements for the edge and ZS scalings in the considered Reynolds-number range. Note that this is not the case for the friction and RC scalings, since the
$\text{d}L_{0}/\text{d}x$
term is already implicitly included in the velocity scale
$U_{0}$
. If the
$\text{d}L_{0}/\text{d}x$
term is incorporated in the velocity scale, as exemplarily tested for the friction scaling, a ‘low-Reynolds-number’ correction is achieved (
$U_{0}=u_{\unicode[STIX]{x1D70F}}/\sqrt{\text{d}L_{0}/\text{d}x}$
instead of
$U_{0}=u_{\unicode[STIX]{x1D70F}}$
for incompressible flow); the scaling success is comparable to the edge scaling and ZS scaling. The proven scaling quality of
$u_{\unicode[STIX]{x1D70F}}$
at high Reynolds numbers known from the literature (see e.g. Panton Reference Panton2005) can therefore hold also for the low Reynolds numbers investigated here, but only by a reinterpretation of
$u_{\unicode[STIX]{x1D70F}}$
as a velocity scale for the outer layer.
Concerning the mean flow, local profiles can be excellently collapsed using the edge or ZS scaling in the Reynolds-number range considered. This holds for the velocity, the mass-flux and (to a slightly lesser extent) the total-enthalpy distributions. In comparison, the friction and RC scalings exhibit a slight Reynolds-number-dependent drift, which, however, can be eliminated by the incorporation of
$\text{d}L_{0}/\text{d}x$
. In contrast to the turbulent stresses, compressible and incompressible mean-flow profiles do not collapse for comparable shear-stress distributions.
Related to the relevance of the conditions
$U_{0}/U_{e}$
,
$F_{0}/F_{e}$
,
$G_{0}/U_{0}^{2}$
and
$\unicode[STIX]{x1D6EC}_{c}$
being constants for the individual scalings, only
$F_{0}/F_{e}$
seems to be of minor importance for the scaling success. For stronger Mach-number variations in the streamwise direction, however, a visible influence is expected. All other conditions are well fulfilled for the well-working edge and ZS scales. Note that
$G_{0}/U_{0}^{2}=\text{const.}$
is only meaningful for the supersonic cases.
5.3 Validity of the traditional Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{K}$
In comparison to the generalized Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}=(L_{0}/(U_{0}F_{0}))(\text{d}p_{e}/\text{d}x)$
,
$\unicode[STIX]{x1D6EC}_{c}$
only differs by the additional inclusion of
$\text{d}L_{0}/\text{d}x$
, namely by dividing
$\unicode[STIX]{x1D6FD}$
by
$\text{d}L_{0}/\text{d}x$
. For the data investigated,
$\text{d}L_{0}/\text{d}x$
is noticeably non-constant due to the low Reynolds number considered. Hence, for the well-behaving edge and ZS scalings, where the equilibrium state with self-similarity is documented by a constant
$\unicode[STIX]{x1D6EC}_{c}$
, the generalized
$\unicode[STIX]{x1D6FD}$
is not a good indicator for self-similarity. However, if the traditional Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{K}$
is built by assuming
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim F_{0}U_{0}(\text{d}L_{0}/\text{d}x)$
as supposed by the analysis and the data,
$\unicode[STIX]{x1D6FD}_{K}$
can be directly associated with
$\unicode[STIX]{x1D6EC}_{c}$
using
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{K}=\frac{\unicode[STIX]{x1D6FF}_{K}^{\ast }}{\bar{\unicode[STIX]{x1D70F}}_{w}}\frac{\text{d}p_{e}}{\text{d}x}\sim \frac{L_{0}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}\sim \unicode[STIX]{x1D6EC}_{c}.\end{eqnarray}$$
The simpler to determine, commonly used Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}_{K}$
in its traditional definition is therefore fulfilling the definition of
$\unicode[STIX]{x1D6EC}_{c}$
and thus still indicates the state of self-similarity, even if
$\text{d}L_{0}/\text{d}x$
cannot be assumed constant. This reinterpretation of
$\unicode[STIX]{x1D6FD}_{K}$
as a valid parameter of the form
$\unicode[STIX]{x1D6EC}_{c}$
thus forms a direct bridge between Clauser’s (Reference Clauser1954) and George & Castillo’s (Reference George and Castillo1993) self-similarity analyses, which have so far not been satisfactorily linked to each other even in the incompressible regime. Note that the pressure-gradient distributions for the DNS in Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019) were chosen to yield constant
$\unicode[STIX]{x1D6FD}_{K}$
. Like for
$\unicode[STIX]{x1D6EC}_{c}$
in (5.1), the influence of various PG strengths in compressible and incompressible cases can be also directly compared using
$\unicode[STIX]{x1D6FD}_{K}$
, which thus represents a characterizing parameter also for general compressible turbulent boundary layers.
5.4 Limits and potential of self-similarity for compressible turbulent boundary layers
Finally, although
$F_{0}/F_{e}$
is not fulfilled and compressibility influences on the achievable self-similarity are expected at some point, self-similarity can be achieved to a very high degree in the compressible regime. Using our data, it was possible to show that an impressive scaling success can be achieved at least over 30 boundary-layer thicknesses with suitable compressible scaling sets; note that this range is by far unique in related incompressible studies discussed in the literature. Thus the concept of self-similarity, widely used in the incompressible regime, represents also an extremely valuable tool for the consistent, systematic investigation of compressible turbulent boundary layers with pressure gradients.
Acknowledgements
The financial support by the Deutsche Forschungsgemeinschaft (DFG) under reference nos RI680/31-1, RI680/34-1 and RI680/38-1, and the provision of computational resources on the Cray XC40 by the Federal High Performance Computing Center Stuttgart (HLRS) under grant GCS_Lamt (LAMTUR), ID = 44026, are gratefully acknowledged, as well as fruitful discussions within the DFG Collaborative Research Center SFB/TRR 40, initiated by sub-project A4.
Appendix A
A.1 Multiple length scales
Even though multiple length scales will essentially recover the identical conditions for equilibrium, they are helpful in understanding how to choose certain parameters in more general cases. Therefore, the ansatz functions are chosen as
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{\unicode[STIX]{x1D70C}}\tilde{u} =F_{e}(x)+F_{0}(x)f(\unicode[STIX]{x1D713}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{u} =U_{e}(x)+U_{0}(x)f_{u}(\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{h}_{0}=G_{e}(x)+G_{0}(x)g(\unicode[STIX]{x1D703}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y=L_{0,F}(x)\unicode[STIX]{x1D713}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y=L_{0,K}(x)\unicode[STIX]{x1D702}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y=L_{0,G}(x)\unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$
where quantities with a subscript ‘
$e$
’ denote the edge scales and with subscript ‘
$0$
’ the characteristic scale. In the above,
$L_{0,F}$
is the characteristic length scale for the mass flux
$\bar{\unicode[STIX]{x1D70C}}\tilde{u}$
,
$L_{0,K}$
is the kinematic length scale and
$L_{0,G}$
is the energy length scale.
Considering only the mean-flow terms results in the split momentum equation
$$\begin{eqnarray}\displaystyle & & \displaystyle \left[\frac{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0,F}}{\text{d}x}}{L_{0,K}}\right]\unicode[STIX]{x1D713}f(\unicode[STIX]{x1D713})\frac{\text{d}f_{u}(\unicode[STIX]{x1D702})}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{\displaystyle L_{0,F}U_{0}\frac{\text{d}F_{e}}{\text{d}x}}{L_{0,K}}\right]\unicode[STIX]{x1D713}\frac{\text{d}f_{u}(\unicode[STIX]{x1D702})}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[-\frac{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0,K}}{\text{d}x}}{L_{0,K}}\right]\unicode[STIX]{x1D702}f(\unicode[STIX]{x1D713})\frac{\text{d}f_{u}(\unicode[STIX]{x1D702})}{\text{d}\unicode[STIX]{x1D702}}+\left[-\frac{\displaystyle F_{e}U_{0}\frac{\text{d}L_{0,K}}{\text{d}x}}{L_{0,K}}\right]\unicode[STIX]{x1D702}\frac{\text{d}f_{u}(\unicode[STIX]{x1D702})}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[-\frac{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0,F}}{\text{d}x}}{L_{0,K}}-\frac{\displaystyle L_{0,F}U_{0}\frac{\text{d}F_{0}}{\text{d}x}}{L_{0,K}}\right]F(\unicode[STIX]{x1D713})\frac{\text{d}f_{u}(\unicode[STIX]{x1D702})}{\text{d}\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[F_{0}\frac{\text{d}U_{0}}{\text{d}x}\right]f(\unicode[STIX]{x1D713})f_{u}(\unicode[STIX]{x1D702})+\left[F_{0}\frac{\text{d}U_{e}}{\text{d}x}\right]f(\unicode[STIX]{x1D713})+\left[F_{e}\frac{\text{d}U_{0}}{\text{d}x}\right]f_{u}(\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[F_{e}\frac{\text{d}U_{e}}{\text{d}x}\right]1+\text{turbulent terms}+\text{viscous terms}=\left[\frac{\text{d}p_{e}}{\text{d}x}\right]1.\end{eqnarray}$$
Using the same arguments as in § 3.2, this recovers identical conditions as in the analysis with one length scale
$L_{0}$
, for example:
$$\begin{eqnarray}\displaystyle & \displaystyle F_{e}\sim F_{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{e}\sim U_{0}. & \displaystyle\end{eqnarray}$$
From (A 7), the condition
$\text{d}L_{0,K}/\text{d}x\sim \text{d}L_{0,F}/\text{d}x$
can be derived, leading to
$L_{0,K}\sim L_{0,F}+\text{const.}$
if integrated. If it is further assumed that
$L_{0,K}$
and
$L_{0,F}$
become proportional to each other in the incompressible limit, it is reasonable to assume
$\text{const}.=0$
. Similarly with the energy equation, for the three length scales the condition
$$\begin{eqnarray}L_{0,K}\sim L_{0,F}\sim L_{0,G}\end{eqnarray}$$
is obtained, implying that the multiple length-scale analysis leads to essentially the same conditions as the analysis with only a single length scale.
Nevertheless, some additional remarks are possible. In the momentum equation (A 7), almost all terms are scaled by the kinematic length scale
$L_{0,K}$
, which thus can be interpreted to be the most relevant length scale. The length scale
$L_{0,K}$
assumed in the analysis in § 3.2 as the only length scale simultaneously characterizing the growth of the velocity, the mass-flux and the energy boundary layers, thus often can be more associated with a kinematic
$L_{0,K}$
rather than a mass-flux length scale
$L_{0,F}$
.
As done for the single length scale in (3.30), for instance, the pressure-gradient boundary-layer evolution parameter yields
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{c}\sim \frac{L_{0,K}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0,K}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}\sim \frac{L_{0,K}}{\displaystyle F_{0}U_{0}\frac{\text{d}L_{0,F}}{\text{d}x}}\frac{\text{d}p_{e}}{\text{d}x}=\text{const.}\end{eqnarray}$$
By assuming
$\text{d}L_{0,K}/\text{d}x=\text{const.}$
, the generalized Rotta–Clauser parameter
$\unicode[STIX]{x1D6FD}$
yields
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\frac{L_{0,K}}{F_{0}U_{0}}\frac{\text{d}p_{e}}{\text{d}x}.\end{eqnarray}$$
A.2 Scaling comparison: edge velocity or edge mass flux
In the edge scaling introduced in § 3.4.2 and summarized in table 1, the edge velocity
$U_{e}$
is used as characteristic velocity scale. For the mass flux, this leads to the condition
$F_{0,e}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })F_{e}$
, which is a false statement for compressible flows; see figure 1(a2). In contrast, also the choice of
$F_{0}=F_{e}$
seems reasonable, which in turn leads to the false statement for the velocity scale,
$U_{0,e}=(\unicode[STIX]{x1D6FF}_{K}^{\ast }/\unicode[STIX]{x1D6FF}^{\ast })U_{e}$
. The remaining scales are
$L_{e}=\unicode[STIX]{x1D6FF}^{\ast }$
and
$G_{0,e}=|H_{w}-H_{e}|\unicode[STIX]{x1D6FF}_{H}/\unicode[STIX]{x1D6FF}^{\ast }$
.
Figure 12. Mean velocity profiles for variations of the edge scales: (a) velocity-based edge scaling and (b) mass-flux-based edge scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
To compare the scaling quality of both scaling sets, the scaling success is exemplarily tested for the velocity profiles in figure 12 as introduced in § 4.3. It is obvious that the velocity-based set of scales is superior to the mass-flux-based one for which the compressible cases are not appropriately scaled.
A.3 Favre stress
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
without regarding
$\text{d}L_{0}/\text{d}x$
According to figure 8 the Favre stress
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
is given in figure 13, but without taking the
$\text{d}L_{0}/\text{d}x$
term in the normalization into account; see (3.39). While this neglect leads to a significant worsening for the edge and ZS scalings compared to figure 8, it leads to an almost perfect and thus significantly improved scaling success for the friction and RC scalings compared to figure 8. As already mentioned in the discussion of figure 2, for example, this indicates the conclusion that the
$\text{d}L_{0}/\text{d}x$
term is already implicitly included in the definition of both shear-stress-motivated scales; see also § 4.5.3 and § A.4.
Figure 13. Favre stress
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
without regarding
$\text{d}L_{0}/\text{d}x$
in the scaling in (a) edge scaling, (b) friction scaling, (c) RC scaling, and (d) ZS scaling. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
A.4 Low-Reynolds-number correction for the friction scaling
As exemplarily demonstrated for the
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
Favre stress in § A.3, the inclusion of the
$\text{d}L_{0}/\text{d}x$
term noticeably influences the scaling success at the Reynolds numbers investigated. It is additionally shown that
$\text{d}L_{0}/\text{d}x$
is already implicitly included in the friction-based scaling sets; if it is neglected, the scaling success for
$\bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
is virtually perfect, see figure 13(b). Consequently, by additionally incorporating
$\text{d}L_{0}/\text{d}x$
in its construction, a ‘low-Reynolds-number correction’ can be proposed for the friction scaling (the same would also be possible for the RC scaling).
From part 1 of this study (see Wenzel et al.
Reference Wenzel, Gibis, Kloker and Rist2019), it is reasonable to assume
$\bar{\unicode[STIX]{x1D70F}}_{w}\sim \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}$
in the streamwise direction. With (3.39) and
$F_{0}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })\unicode[STIX]{x1D70C}_{e}U_{0}$
from (3.55) and (3.56), the wall shear stress is proportional to
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70F}}_{w}\sim \bar{\unicode[STIX]{x1D70C}}\widetilde{u^{\prime \prime }v^{\prime \prime }}\sim F_{0}U_{0}\frac{\text{d}L_{0}}{\text{d}x}\sim \frac{\unicode[STIX]{x1D6FF}^{\ast }}{\unicode[STIX]{x1D6FF}_{K}^{\ast }}\unicode[STIX]{x1D70C}_{e}U_{0}^{2}\frac{\text{d}L_{0}}{\text{d}x}.\end{eqnarray}$$
Using
$\bar{\unicode[STIX]{x1D70F}}_{w}=\bar{\unicode[STIX]{x1D70C}}_{w}u_{\unicode[STIX]{x1D70F}}^{2}$
, a possible ‘low-Reynolds-number’ corrected (subscript ‘
$lR$
’) friction velocity scale
$U_{0,\unicode[STIX]{x1D70F}_{lR}}$
can be defined as
$$\begin{eqnarray}U_{0,\unicode[STIX]{x1D70F}_{lR}}=\sqrt{\frac{\unicode[STIX]{x1D6FF}_{K}^{\ast }}{\unicode[STIX]{x1D6FF}^{\ast }}\frac{\bar{\unicode[STIX]{x1D70C}}_{w}}{\displaystyle \unicode[STIX]{x1D70C}_{e}}\frac{1}{\displaystyle \frac{\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}}{\text{d}x}}}u_{\unicode[STIX]{x1D70F}},\end{eqnarray}$$
which only differs by the additional inclusion of
$\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}/\text{d}x$
from the friction velocity scale
$U_{0,\unicode[STIX]{x1D70F}}$
in table 1. With the friction length scale
$L_{0,\unicode[STIX]{x1D70F}_{lR}}=\unicode[STIX]{x1D6FF}_{K}^{\ast }(U_{e}/U_{0,\unicode[STIX]{x1D70F}_{lR}})$
and the assumption of
$U_{e}/U_{0,\unicode[STIX]{x1D70F}_{lR}}=\text{const.}$
,
$\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}/\text{d}x$
results in
$$\begin{eqnarray}\frac{\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}}{\text{d}x}=\frac{\displaystyle \text{d}\left(\unicode[STIX]{x1D6FF}_{K}^{\ast }\frac{U_{e}}{U_{0,\unicode[STIX]{x1D70F}_{lR}}}\right)}{\text{d}x}\sim \frac{\text{d}\unicode[STIX]{x1D6FF}_{K}^{\ast }}{\text{d}x}.\end{eqnarray}$$
The remaining mass-flux scale is
$F_{0,\unicode[STIX]{x1D70F}_{lR}}=(\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{K}^{\ast })\unicode[STIX]{x1D70C}_{e}U_{0,\unicode[STIX]{x1D70F}_{lR}}$
, and the enthalpy scale is
$G_{0,\unicode[STIX]{x1D70F}_{lR}}=|H_{w}-H_{e}|\unicode[STIX]{x1D6FF}_{H}/L_{0,\unicode[STIX]{x1D70F}_{lR}}$
. It should be mentioned, however, that the calculation of this scale is numerically demanding due to the sensitivity of
$\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}/\text{d}x$
; especially, the distributions of the turbulent stresses are greatly scattered by its additional incorporation. Furthermore, since the
$\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}/\text{d}x$
term is not implicitly included in the ‘low-Reynolds-number’ corrected friction scale any more, the self-similar state is more predicted by the
$\unicode[STIX]{x1D6EC}_{c}$
distribution like for the edge scaling and not by
$\unicode[STIX]{x1D6FD}_{K}$
like for the friction scaling.
Figure 14. Scaling success for ‘low-Reynolds-number’ corrected friction scaling. (a) Self-similarity conditions according to figure 1: (a1)
$U_{0}/U_{e}$
, (a2)
$F_{0}/F_{e}$
, and (a3)
$G_{0}/U_{0}^{2}$
. (b) Mean-velocity profiles and (c) mean mass-flux profiles according to figures 3 and 4, respectively. Grey lines: profiles extracted at 10 streamwise positions. Coloured lines: average profiles. Red lines: ——,
$iZPG$
; —— –,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.19}$
; — – —,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=0.58}$
; –
$\cdot$
–
$\cdot$
–
$\cdot$
–,
$iAPG_{\unicode[STIX]{x1D6FD}_{K}=1.05}$
. Blue lines: ——,
$cZPG$
; —— –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.15}$
; – – – – –,
$cAPG_{\unicode[STIX]{x1D6FD}_{K}=0.55}$
. Cyan line: — – – —,
$cFPG_{\unicode[STIX]{x1D6FD}_{K}=-0.18}$
.
In the same representation as in figure 1, the streamwise evolution of the
$U_{0,\unicode[STIX]{x1D70F}_{lR}}/U_{e}$
,
$F_{0,\unicode[STIX]{x1D70F}_{lR}}/F_{e}$
and
$G_{0,\unicode[STIX]{x1D70F}_{lR}}/U_{0,\unicode[STIX]{x1D70F}_{lR}}^{2}$
conditions are depicted in figure 14(a). According to figures 3 and 4, the streamwise collapse of the mean-velocity and mass-flux profiles are tested in figures 14(b) and 14(c), respectively. In order to retain comparability between different PG cases,
$\text{d}L_{0,\unicode[STIX]{x1D70F}_{lR}}/\text{d}x$
is normalized to one according to (4.8). As can be seen from figure 14, the ‘low-Reynolds-number’ corrected friction scale yields essentially the same scaling success as the edge and ZS scalings in the results section of this study, although slightly suffering from inaccuracies in the computation of
$\text{d}L_{0}/\text{d}x$
, especially for stronger PGs.
Open access
