1. Introduction

In 1956 the Cambridge Austerdalsbre Expedition was studying the formation of wave ogives at the foot of the Odinsbre ice fall in Norway. ^{1 ,} Reference Nye ^{2 ,} Reference Nye ³ For this purpose a line of 23 stakes running longitudinally down the glacier was set up (Fig. 1), and the changes in the distances between the stakes were measured over a period of one month. It was then possible to deduce the longitudinal strain-rate in the ice as a function of the distance down the glacier; this was the main purpose of the experiment and the results are fully described in reference 3. The present paper is concerned with some additional measurements made on the stake system. Besides finding out the longitudinal component of strain-rate we wanted to have some information about the other components of the strain-rate tensor at a few representative points down the stake line. We therefore set up the five squares of stakes shown in Fig. 1 centerd on Stakes 3, B, C, D and E. By measuring the sides and diagonals of these square patterns at intervals over a period of one month it was possible to calculate with considerable accuracy all components of the rate of strain tensor at the five center points. The number of quantities measured at each square is greater than the number of unknowns to be derived from them, and the method used to calculate the strain-rate components from the data may be of some interest.

Fig. 1 Map of the stake system at the foot of the Odinsbre ice fall showing the measured intervals, the directions and magnitudes of the principal stresses, the horizontal component of velocity, the directions of maximum surface slope and the positions of the crevasses

Having obtained the strain-rate components we proceed to calculate the principal strain-rates and, by using the measured flow law of ice, the principal stresses. It so happened that the main stake line skirted the edge of an extensive crevassed area on its western side. It is therefore possible to compare the direction of the crevasses with the direction of the principal strain-rates, and to see whether the crevasses are associated with tensile stresses. Although the experiment can be used for this test of the theory of crevasse formation, it was not specifically designed for the purpose; if it had been, a different location would have been chosen.

2. Measurements

The relation of the stake line to the ice fall is shown in the map which appears in Fig. 1 of reference 3; Figs. 13, 14 and 15 of the same paper show photographs of the stake system. The method of making the measurements on the squares has already been described in reference 3 and the details need not be repeated here. In brief, all the intervals shown by dotted lines in Fig. 1 of the present paper were measured three or four times in August 1956; certain corrections were applied, and the average rate of stretching

of each interval over the month was computed. is defined by the equation

where l ₁ and l ₂ are the initial and final lengths of a stake interval and Δt is the time interval.

3. Reduction of Results

Fig. 2a shows a square pattern of five stakes. Ideally, the outline is a perfect square with one stake in the center. The x axis is along one diagonal and points down the glacier; the z axis is along the other diagonal, and the y axis is normal to the glacier surface. The measurements give 8 values of

corresponding to the 8 stake intervals a ₁, a ₂, b ₁, b ₂, c ₁, c ₂, d ₁, d ₂. We first reduce these 8 values to 4 by averaging the intervals a ₁ and a ₂, b ₁ and b ₂, c ₁ and c ₂, d ₁ and d ₂. We then have the values of corresponding to the four directions θ = 0, 45, 90, 135°, where θ is measured clockwise from Oz (Fig. 2b). The averaging process takes account of the variation of the strain-rate tensor over the area of the square, so far as this is possible by linear interpolation, and the 4 values of obtained all now refer to the point at the center of the square. The problem is to deduce from these four values the best values of the 3 components of the strain-rate tensor. An immediate check on consistency comes from the fact that theoretically

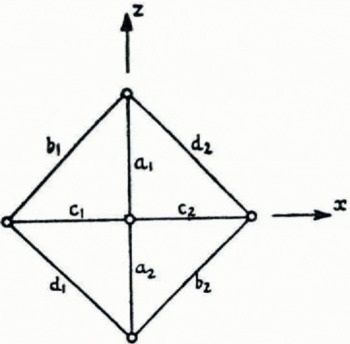
Fig. 2a Ideal stake pattern

Fig. 2b

If the object had been simply to measure strain-rates, we could have dispensed with the stake at the center;

for the two diagonals of the square could have been measured directly, instead of by averaging the values for a ₁, a ₂ and c ₁, c ₂. However, we wanted to make theodolite measurements of the absolute velocity of the point at the center of the square, and we therefore retained the central stake for this purpose.

In fact it was not always possible to make the arrays as near to perfect squares as we should have liked, because the geometrically correct position of one or more of the stakes turned out to be in a crevasse. The resulting compromise meant that the angles were not quite 45° and 90°. The worst case was the square centerd on C, where the angles of the various pairs of intervals at the mean survey date, measured clockwise from the direction C-CE, were

When averaged, these give

If the axis of reference is now rotated anticlockwise by 0.5° we obtain

and the greatest misalignment in angle from the ideal values 0, 45, 90, 135° is 3°. We accordingly place Oz at 0.5° anticlockwise from the line C-CE; Ox is placed at right angles to Oz.

This case has been chosen for illustration because it is the worst. The corresponding angles for the other four squares are given in the Appendix set out in the same way. Corresponding to the misalignment of 3° noted above for Square C, the misalignments for the other four squares 3, B, D and E were 1.5, 1, 2 and 0° respectively.

The procedure is, accordingly, first to choose the x and z axes for each square in such a way as to make the directions a, b, c, d, as close as possible to 0, 45, 90 and 135°. We then assume that the measured values correspond exactly to these ideal directions. The 8 measured strain-rates

for each square are set out in columns 2, 3, 4, 5 of Table I. Each square is denoted by the number or letter of the stake at its center. The 8 strain-rates are given in the order:

Corresponding values are then averaged in the next line of the table to give

and at the center of the square. As a preliminary test of consistency is compared with ; the greatest disagreement is found to be 0.017 yr.⁻¹ (column 8). It is interesting to notice that this is very much less than the difference between the strain-rates measured on parallel intervals of the same square, which in one case (Square 3, θ = 45°) is as much as 0.572 yr.⁻¹. The differences between parallel intervals are due to the very high gradients of the strain-rate components in the area under observation. The figures underline the importance of reducing the observations so that, so far as is possible by linear interpolation, they all refer to a single point, the center of the square.

The principle of least squares is now used to deduce the best values of the 3 strain-rate components

from and . The problem is essentially to find the best solution to 4 simultaneous linear equations involving 3 unknowns. The standard methodReference Topping ¹² is used, namely, to form the normal equations and to solve them. An exactly analogous problem arises in crystal physics when one wishes to deduce the components of some tensor property of a crystal from a number of measurements made in different crystallographic directions. W. L. Bond has shown Reference Nye ⁴ that the crystal physics problem may be very conveniently solved by matrix methods, and it happens that the numerical example of Bond’s method given in Reference Nyereference 4 applies exactly to the present case. The directions of the x and z axes and the sense of θ in the present paper have therefore been chosen so as to agree with the notation of the numerical example (x and z corresponding to x ₁ and x ₃). We shall not repeat the matrix calculations here but shall merely quote the result: the best values of are given by

(

is the component of shear strain-rate as usually defined, that is, the rate of decrease in angle between two lines in the ice that are instantaneously parallel to Ox and Oz; is the corresponding tensor component of strain-rate.) Equations (2) are readily interpreted. Thus is obtained by giving a weight of 3/4 to the direct measurement and a weight of 1/4 to . A similar interpretation applies to . We also see that is derived entirely from and ; this is as it should be, because the measured values of and can give no information on the shear strain-rate component.

For illustration we may take the square centerd on Stake 3. The value of

measured directly, that is was −0.935 yr.⁻¹, but this is corrected with the help of the other three measurements to −0.931 yr.⁻¹. Similarly the direct measurement of , that is , is corrected from +0.273 yr.⁻¹ to +0.277 yr.⁻¹. The value of comes out to be −0.224 yr.⁻¹.

The residuals v, say, of the four measured values can be calculatedReference Nye ⁴ by a further matrix multiplication. For Square 3 this gives v =+0·004, −0·004, +0·004, −0·004 yr.⁻¹ respectively. The four residuals always have the same absolute values, and it is not in practice necessary to go through the matrix multiplication each time to obtain them. The absolute value of v is simply the amount by which the value of

or measured directly is corrected by the least-squares procedure (it is also one quarter of the figure shown in the last column of Table I). The standard error in each of the four measured values isReference Topping ¹² , and by standard methods it can be shown that the standard error in and is , and in is .

Thus our result for Square 3 is

with a standard error of about ±0.007 yr.⁻¹. The corresponding results obtained by using the same procedure on the other squares are given in Table II.

Since the y axis is perpendicular to the upper surface of the glacier, which is free from shear tractions, Oy will be a principal axis of stress. If we assume that the principal axes of the strain-rate tensor are parallel to those of the stress tensor, it follows that Oy is also a principal axis of strain-rate, and therefore that

. Denoting the principal strain-rate corresponding to Oy by , and making the assumption that each element of ice remains unchanged in volume (see Section 5), we have

calculated from this equation is given in column 3 of Table III.

We now calculate the magnitudes and directions of the principal strain-rates

, in the xz plane, from the equations:

where ϕ is the angle between Oz and the principal axis nearest to it, in the sense defined in Fig. 2b. This principal axis will be that of the algebraically greater principal strain-rate

if , and the algebraically lesser principal strain-rate if . Since for all five squares, ϕ is the angle between and Oz. The results are given in columns 2, 4 and 5 of Table III.

Our determination of the strain-rate tensor at the centers of the five squares is now complete.

4. Calculation of the Stresses

We may now deduce the stresses from the strain-rates by using the results of laboratory experiments on the flow of ice, but in doing so it is necessary to make some further assumptions. There are certain restrictions on what can be assumed, and GlenReference Glen ⁵ has recently given a rather general discussion of the problem. For the present application it is reasonable to make the mathematically simplest set of assumptions as discussed in reference 6. This includes, among others, the assumptions that the flow is independent of a superposed hydrostatic pressure, and that the material is isotropic and incompressible.

If σ ₁, σ ₂, σ ₃, are the principal components of stress (positive when tensile), the hydrostatic stress σ is defined by

and the principal stress deviators σ′₁, σ′₂, σ′₃ by

An effective shear stress τ, equal to

times the octahedral shear stress,Footnote * is defined by

and an effective strain-rate

by

It is assumed that there exists a functional relation

, called the flow law. Then it is shownReference Nye ⁶ that, under the assumptions of the theory,

may be thought of as an effective viscosity, which varies according to the three dimensional state of stress and strain-rate in an element.

If we take the flow law given by Glen’s experimentsReference Glen ⁷ in uniaxial compression at −0.02° C. we find (p. 129 of Reference Nyereference 6)

where

is in yr.⁻¹ and τ is in bars, or

This theory can now be applied to the strain-rates measured on the squares of stakes. We first calculate

from (10), then τ from (13), then , and hence σ′, σ′₂, σ′₃ from (11). These results are given in Table III.

Finally we put a σ ₂ = 0 (leaving atmospheric pressure out of account); hence

and

The values of the hydrostatic pressure σ and the principal stresses σ ₁, and σ ₃ calculated from these equations are given in Table III.

The map in Fig. 1 shows the magnitudes and directions of the principal stresses so obtained. The date of the map is 23 August 1956. On the other hand, the foregoing calculations give the directions of principal stress relative to the stake line at the mean survey date, 12 August 1956. This introduces a small difficulty because the stake line, particularly in the upper parts, rotated slightly between the two dates. The directions of principal stress have been inserted on the map for 23 August by assuming that they remained fixed relative to the stake line between 12 and 23 August.

5. Correlation with the Crevasses

Fig. 1 shows the positions and directions of the crevasses in the neighbourhood of the stake line. From Stake 10 to Stake B the stake line marks the edge of a very heavily crevassed area which lies on its western side (see the photographs in Figs. 13 and 14 of reference 2). This crevassed area continues up the ice fall from Stake B, but its eastern boundary in this region is to the west of the stake line; thus it leaves an area from Stake 4 to Stake 1 where clearly defined crevasses are absent. There is nevertheless very considerable relief of the surface from Stake 3 to Stake 1, for this is the beginning of the ice fall proper.

An attempt has been made in Fig. 1 to indicate the nature of the crevasses. Many of them were far from being sharp fissures in the ice; in many places they could better be described as a series of parallel sharp ridges with either sharp or rather rounded depressions between them. Many of the crevasses in fact appeared to be old ones, much modified by ablation.

The presence of crevasses within the area of a square raises the question of what stress and strain-rate it is that has been measured, for the crevasses must introduce local inhomogeneities into the stress and strain-rate field. Now the depth of the crevasses was always less, and in nearly all cases very much less, than the distances between the stakes. We picture the upper crevassed layer of ice as resting on an unbroken continuous layer at a depth of a few metres, and it is the strain-rate of this under-layer that is being measured (provided we neglect the changes of strain-rate with depth caused by large-scale bending of the iceReference Nye ³ ). If the inhomogeneities introduced by the crevasses had affected the measurements seriously, the test of consistency

would not have been satisfied.

Similar considerations hold for the validity of the equation

. Crevasses may be opening or closing within the area of a square, and the volume enclosed by the crevasses may be changing. given by the equation is then not even an average of the fluctuating strain-rate in the upper crevassed layer. It is, however, properly interpreted as the strain-rate of the continuous under-layer (with the same proviso as before).

According to theoretical ideas (for example, reference 9 and 10) crevasses should only appear when at least one of the principal stresses in the surface is tensile; and if one principal stress is tensile and the other is compressive the crevasses, if any, should be perpendicular to the tensile stress component. The extent of the agreement with these predictions may be judged from Fig. 1.

We may first note that at all five measured points any crevasses present in the neighbourhood are perpendicular to the algebraically greatest (most tensile) principal stress, and in this respect the theory is well obeyed. A similar result was found by WardReference Ward ¹³ on Highway Glacier, Baffin Island. MeierReference Meier ¹⁴ found, as a result of a very extensive and systematic experiment on the Saskatchewan Glacier, that “the major crevasse systems are related in orientation [i.e. perpendicular] to the greatest principal strain-rate although there is some suggestion of slight differences in angle”. Meier suggests very plausible reasons why small differences should be expected.

As regards the sign of the algebraically greatest principal stress in the present experiment the matter is less clear-cut. One notices that the stress in question is compressive at 3, very slightly tensile at B, definitely compressive at C, definitely tensile at D, and very slightly compressive at E. To judge whether the signs of the borderline results at B and E are significant we may note that

, whose sign decides whether the principal stress σ is tensile or not, has the value +0.009±0.002 yr.⁻¹ at B and −0.004±0.003 yr.⁻¹ at E. Thus the stress of +0.06 bars at B is probably genuinely tensile, but the sign of the stress of −0.04 bars at E is more doubtful. That there should be borderline results at B and E is not unexpected, since these points lie at the edge of crevassed areas, and one would therefore expect a criterion for crevasse formation to be only just satisfied, or only just not satisfied.

At 3 clearly defined crevasses are absent and the two principal stresses are compressive, in accord with the theory. Near D there are crevasses and one principal stress is tensile, also in accord with the theory. The situation at C is unexpected; there are crevasses close by but they run perpendicular to a compressive stress of 1.47 bars. It is unlikely that the transverse gradient of stress ∂σ ₃/∂z is sufficient to turn the compressive stress into a tension in such a short distance; nor is there any obvious tensile region up glacier from C where the crevasses might have formed; this case remains puzzling.

Thus the theoretical prediction that the crevasses should be perpendicular to the algebraically greatest principal stress is very well verified—but the experiment is inconclusive on the question of the magnitude of the stress necessary to form crevasses.

Since many of the crevasses appear to be old and since the velocity of the ice in this area is between 0.9 and 0.4 m./day, it is interesting that there is such a good correlation between crevasse directions and principal stress directions. One would rather have expected to find a correlation between the crevasses at a particular point and the principal stress directions, not at this point but at the point higher up the glacier where the crevasses were formed. This correlation is not easy to make, however, because one would have to allow for the fact that the general flow of the ice will cause a crevasse to rotate after it is formed.

As we have already mentioned, the experiment was not designed to test the theory of crevasse formation, and in setting out the stake line we were more concerned to avoid crevasses than to include them. This is why the measured points are on the edge rather than in the center of a crevasse field. There is no reason, however, why similar stake patterns should not be used in an experiment designed specifically to test crevasse theory.

Acknowledgements

I should like to thank the many members of the expedition in 1956 who helped in setting up the stake system and in surveying it. Mr. W. H. Ward developed the drilling equipment and the technique for inserting the stakes,Reference Ward ¹¹ and Dr. J. W. Glen supervised much of the survey work. The map of the crevasses which forms part of Fig. 1 was made by Mr. A. Morrison.

The expedition acknowledges the help given by many organizations, and the financial help given by the Royal Society, Cambridge University, the Mount Everest Foundation, Trinity College, Cambridge, the Royal Geographical Society, the Tennant Fund of Cambridge University, and the University College of Swansea. I myself am indebted to Bristol University for a grant.

MS. received 5 December 1958