1. INTRODUCTION
GPS has been developed for both high-precision and safety-critical applications. However, GPS positioning results can be degraded by error sources such as multipath and propagation errors. To meet the required accuracy and integrity, a stochastic model, which describes the GPS measurement quality, has been applied for weighting measurements in the position solution and estimating bounds on position errors in integrity monitoring systems (Jin and Jong, Reference Jin and Jong1996; Pullen et al., Reference Pullen, Walter and Enge2002; Lee, Reference Lee2005; Aquino et al., Reference Aquino, Monico, Dodson, Marques, Franceschi, Alfonsi, Romano and Andreotti2009). Extensive studies have been carried out to derive a suitable stochastic model.
GPS error sources such as propagation and multipath errors are closely related to the satellite elevation, therefore the relationship between the satellite elevation and the precision of GPS code observations can be used to estimate the standard deviation of code measurement errors. Examples of these stochastic models include the exponential function of satellite elevation in early studies (Euler and Goad, Reference Euler and Goad1991; Jin and Jong, Reference Jin and Jong1996) and the modified functions of satellite elevation, such as the cosine and the sine functions (Jin et al., Reference Jin, Wang and Park2005).
Obstacles such as bushes and tall buildings often cause large multipath errors. Signal-to-Noise Ratio (SNR) is related to the multipath error, so SNR, instead of the satellite elevation has also been proposed for estimating the noise level. Examples of a SNR-based model can be found in Hartinger and Brunner (Reference Hartinger and Brunner1999) and Satirapod and Wang (Reference Satirapod and Wang2000). Satirapod and Wang (Reference Satirapod and Wang2000) argued that both the satellite elevation-based and the SNR-based models can be used as quality indicators of phase measurements, but they do not always reflect reality.
Despite arguments about the choice of the stochastic model, the satellite elevation-dependent pseudorange noise model for three receiver types has been specified by the Minimum Aviation System Performance Standards (MASPS) (McGraw et al., Reference McGraw, Murphy, Brenner, Pullen and Van2000; RTCA, 2000). Adopted by the International Civil Aviation Organization (ICAO), the model has been used in Ground-Based Augmentation Systems (GBAS).
The measurement noise level is assumed to be determined by the satellite elevation angle or SNR in the above models. In low latitude areas, unfortunately, ionospheric disturbances happen frequently, and result in an increased measurement noise level and the frequent loss of lock on GPS signals. The extreme effects of ionospheric disturbances on GPS integrity and availability, such as the loss of lock and smoothing time are evaluated in Seo et al. (Reference Seo, Walter and Enge2011). The receiver can track the satellite during some periods of disturbances but still suffers from a high noise level, and the distribution of the pseudorange noise has non-Gaussian tails (Datta-Barua et al., Reference Datta-Barua, Doherty and Delay2003; Chen et al., Reference Chen, Gao, Hu and Chen2008; Aquino et al., Reference Aquino, Monico, Dodson, Marques, Franceschi, Alfonsi, Romano and Andreotti2009). That is, the true sigma of noise frequently exceeds the assumed sigma from the noise model. In this case, the accuracy is degraded, and the integrity is not guaranteed. Thus the knowledge about the noise level under ionospheric disturbances in history is critical for improving the GPS performance. A previous effort is to use a S4-based stochastic model (Aquino et al., Reference Aquino, Monico, Dodson, Marques, Franceschi, Alfonsi, Romano and Andreotti2009). However, there are two factors that may limit the model from being widely used. The scintillation indices, S4 or σ φ, are provided by a specially designed GPS receiver rather than a commercial receiver. In addition, the performance of this method depends on the scintillation prediction model.
The purpose of this paper is to present a statistical technique for mitigating the effects of ionosphere disturbances on GPS accuracy and integrity based on ROTI. ROTI has been proposed for indicating ionospheric disturbances in previous studies (Pi et al., Reference Pi, Mannucci, Lindqwister and Ho1997; Ma and Maruyama, Reference Ma and Maruyama2006), and the index can be derived from a dual frequency receiver rather than the specially designed receiver. With both the ROTI and the satellite elevation being incorporated, a modified stochastic model is proposed to reduce the effect of the disturbed observation on the positioning accuracy. To mitigate the effects on GPS integrity, on the other hand, the inflated standard deviations for different ionospheric conditions are also presented. The stochastic model and the inflated standard deviation presented in the paper are believed to be applicable since the model is summarized from large amounts of GPS data collected from low latitudes in 2001, when solar activity reached its maximum.
In Section 2, calculations of the code noise and ROTI, together with the traditional stochastic model are presented, and the strategy for grouping observations by ROTI is described. The overview of GPS data used in this paper is introduced in Section 3. In Section 4, the relationship between ionosphere activity and the noise level is investigated using long-term GPS data collected from low-latitude areas. The modified stochastic model and the inflated standard deviations are developed in the investigation. Finally, conclusions are presented in Section 5.
2. GROUPING OBSERVATIONS BY IONOSPHERIC DISTURBANCE
2.1. Pseudorange Noise Observable
From dual frequency code observations, P 1, P 2, the ionosphere-free linear combination can be formed to cancel the ionospheric delay:
$$\eqalign{& P_3 = \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} P_1 - \displaystyle{{\,f_2^2} \over {\,f_1^2 - f_2^2}} P_2 \cr & \;\;\;\; = \sqrt {(x_u - x^s )^2 + (y_u - y^s )^2 + (z_u - z^s )^2} + dt_u - dt^s + T + \varepsilon _3} $$where P 3 is the ionosphere-free code measurement, f 1 and f 2 are two GPS frequencies, (x u, yu, zu) denotes the receiver position, (xs, ys , zs) is the satellite position, dt u is the receiver clock error, dts is the satellite clock error, T is the tropospheric delay and ε 3 is the noise term of the combination.
The variance of the ionosphere-free observable noise can be obtained by using the law of the error propagation:
$$\sigma _{\varepsilon _3} ^2 = (c_1, c_2 )\left( {\matrix{ {\sigma _{\varepsilon _1} ^2} & {\sigma _{\varepsilon _1, \varepsilon _2} ^2} \cr {\sigma _{\varepsilon _2, \varepsilon _1} ^2} & {\sigma _{\varepsilon _2} ^2} \cr}} \right)\left( \matrix{c_1 \cr c_2 } \right)$$where c 1 are c 2 are constants, and defined as: 
$c_1 = \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} $ and 
$c_2 = \displaystyle{{\,f_2^2} \over {\,f_1^2 - f_2^2}} $; 
$\sigma _{\varepsilon _1} ^2, \sigma _{\varepsilon _2} ^2 $ are variance of the noise on P 1, P 2 respectively; 
$\sigma _{\varepsilon _1, \varepsilon _2} ^2 $ and 
$\sigma _{\varepsilon _2, \varepsilon _1} ^2 $ are covariance of the P1 noise and the P2 noise.
In this paper, the noise levels on two frequencies are assumed to be identical and statistically independent. Specifically, the covariance is assumed to be zero (
$\sigma _{\varepsilon _1, \varepsilon _2} ^2 = 0$,
$\sigma _{\varepsilon _2, \varepsilon _1} ^2 = 0$), and 
$\sigma _{\varepsilon _1} ^2 $ is assumed to be equal with 
$\sigma _{\varepsilon _2} ^2 $. So the variance of the noise (
$\sigma _{\varepsilon _1} ^2, \sigma _{\varepsilon _2} ^2 $) absorbs the covariance, and the obtained sigma of code noise is increased under these assumptions. The noise level of the ionosphere-free code measurement is expressed as:
$$\sigma _{\varepsilon _3} = \sqrt {(c_1 )^2 + (c_2 )^2} \sigma _{noise} $$where σ noise is the pseudorange noise standard deviation on each frequency. In this paper, the ionosphere-free combination noise is estimated first, and then the standard deviation of the pseudorange noise is calculated by using Equation (3).
To calculate the noise term ε 3, other terms on the right side of Equation (1), including the receiver position, satellite orbit and clock correction, should be determined.
2.1.1. The receiver position
The receiver position is surveyed precisely in this study. It should be noted that the height of the antenna should be considered because the offset of the antenna can reach the metre level in some stations.
2.1.2. The satellite orbit and clock
The satellite position, (xs, ys, zs), is calculated from International GNSS Service (IGS) final precise orbit products. The accuracy of satellite position can reach 3–5 cm due to recent developments in orbit determination. The satellite clock error dts is estimated from the IGS precise clock files.
2.1.3. The tropospheric delay
Without the proper compensation, tropospheric delay can introduce more than 20 m in the range domain. In this study, the Hopfield model was used to estimate the tropospheric delay.
2.1.4. The receiver clock error
After eliminating above terms, the remaining unknowns are the receiver clock error and the noise term, as shown on the left side of Equation (4):
$$dt_u + \varepsilon _3 = P_3 - \sqrt {(x_u - x^s )^2 + (y_u - y^s )^2 + (z_u - z^s )^2} + dt^s - T$$Equation (4) is a measurement to one satellite from a receiver, and a number of such equations can be obtained from several satellite measurements at the same epoch. Assuming that the noise ε 3 is zero-mean normal distributed, the receiver clock error dt u can be estimated by averaging the right side of Equation (4) from different observations at the same epoch. After eliminating the receiver clock error from the ionosphere-free code measurement P 3, the ionosphere-free combination noise ε 3 is obtained.
Some outliers, such as receiver failures and bad IGS data, can deteriorate the estimation of the noise. These outliers are detected and screened out before the further analysis in this study. Multipath effects introduce large errors when the satellite elevation angle is small, so a satellite elevation cut-off of 15° is applied to reduce the multipath errors.
2.2. ROTI
The scintillation indices such as “S4” have been widely used to quantify ionospheric disturbances. However, the ionospheric indices are provided by a specially designed GPS receiver, and are not available when using a commercial GPS receiver. Alternatively, ROTI has also been developed and used for indicating ionospheric disturbances. GPS dual-frequency carrier phase measurements, L1 and L2, are combined to form the geometry-free observable:
$$L_4 = L_1 - L_2 $$where L 4 is the geometry-free combination in metres. Differencing two consecutive epochs of the geometry-free measurement (L 4) for the same satellite leads to the temporal difference of TEC. ROTI is defined as the standard deviation of the temporal difference in five minutes for each satellite along the path (Pi et al., Reference Pi, Mannucci, Lindqwister and Ho1997; Chen et al., Reference Chen, Gao, Hu and Chen2008).
An example of ROTI together with the ionosphere-free combination noise ε 3 at station HKKT is shown in Figure 1. Details about the stations are given in Section 3. The different colours indicate different satellites. Both ROTI and the ionosphere-free noise increased from 2000 to 0200 local time. The largest noise could reach five metres during the period.
Figure 1. Diurnal variation of (a) ROTI and (b) ionosphere-free noise ε 3 on Day 69 2001.
2.3. Traditional Stochastic Model
Proposed by Euler and Goad (Reference Euler and Goad1991), the model assumes that the pseudorange noise level is the exponential function of the satellite elevation angle. The model is expressed as (RTCA, 2000; McGraw et al., Reference McGraw, Murphy, Brenner, Pullen and Van2000):
$$\sigma _{noise} = a_0 + a_1 e^{ - \theta /\theta _c}, 5{\char "000B0} \leqslant \theta \leqslant 90 {\char "000B0} $$where θ is the satellite elevation angle, and a 0, a 1 and θ c are coefficients of the model.
Three coefficients in the above stochastic model are specified in the RTCA/DO-253 (RCTA, 2000) according to the type of receiver. Because geodetic receivers are used in this study, the noise standard deviation of 0·1472 m can be obtained from the specification when the satellite elevation angle is assigned to 5°. From the traditional model, the standard deviation of the ionosphere-free combination noise (ε 3) is 0·4383 in case the of the 5° satellite elevation angle.
In Figure 1, the noise caused by the ionospheric disturbances could reach as large as five metres. The noise during the period of ionospheric disturbances is much larger, and could be as large as ten times the sigma using the traditional stochastic model.
2.4. Pseudorange Noise Level Estimation
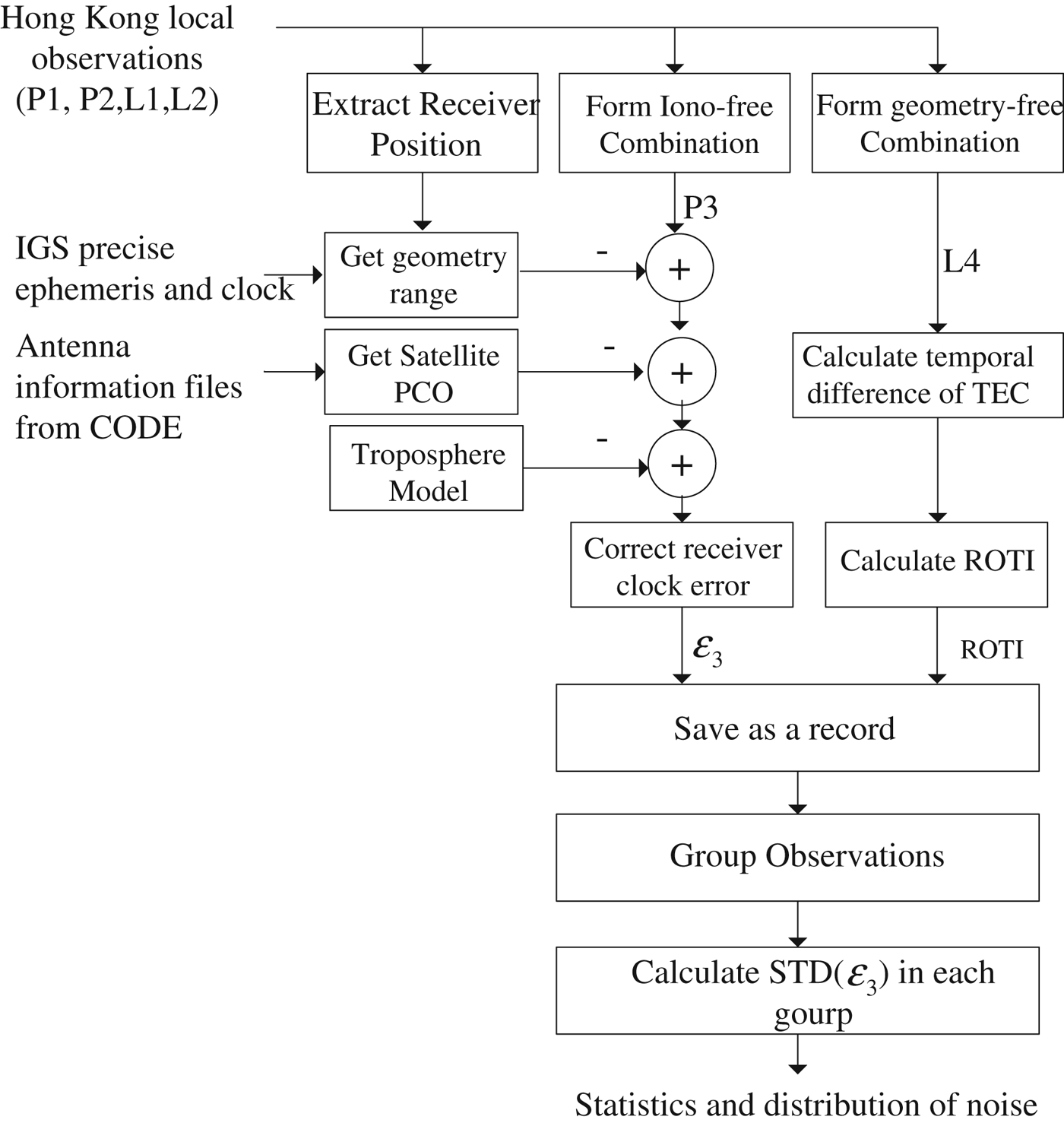
GPS observations collected in Hong Kong were used for this research. Details about the Hong Kong reference stations are included in the next section. Precise orbit and clock products were downloaded from the IGS website and used to obtain the noise. The observations including P1, P2, L1, L2 were processed in two flows, one is the noise calculation based on P1 and P2, the other ROTI estimation based on L1 and L2.
As shown in Figure 2, the flow on the left is to calculate the ionosphere-free combination noise (Section 2.1), and the one on the right of figure is to estimate ROTI (Section 2.2). For each satellite measurement, the ionosphere-free combination noise and ROTI are obtained. The results are then stored as a record in a database that is designed especially for the management of large amounts of GPS data. Based on this database, tools are developed for different purposes, such as data searching and displaying results, as well as the correlation analysis.
Figure 2. Evaluating the noise level under different ionosphere conditions.
In a previous study (Ma and Maruyama, Reference Ma and Maruyama2006), the ionosphere fluctuations are grouped into five classes according to ROTI. The grouping method of this research is very similar to the previous one. Considering that GPS receivers in Hong Kong collect data at five second intervals, observations are grouped according to: Quiet for 0 <ROTI <0.1; Moderate I for 0.1⩽ ROTI < 0.25; Moderate II for 0.25 ⩽ ROTI < 0.5 and Severe for ROTI ⩾ 0.5. Then the noise level in each group is derived, and the relationship between the ionosphere activities and the level of the pseudorange noise can also be analysed.
3. DATA OVERVIEW
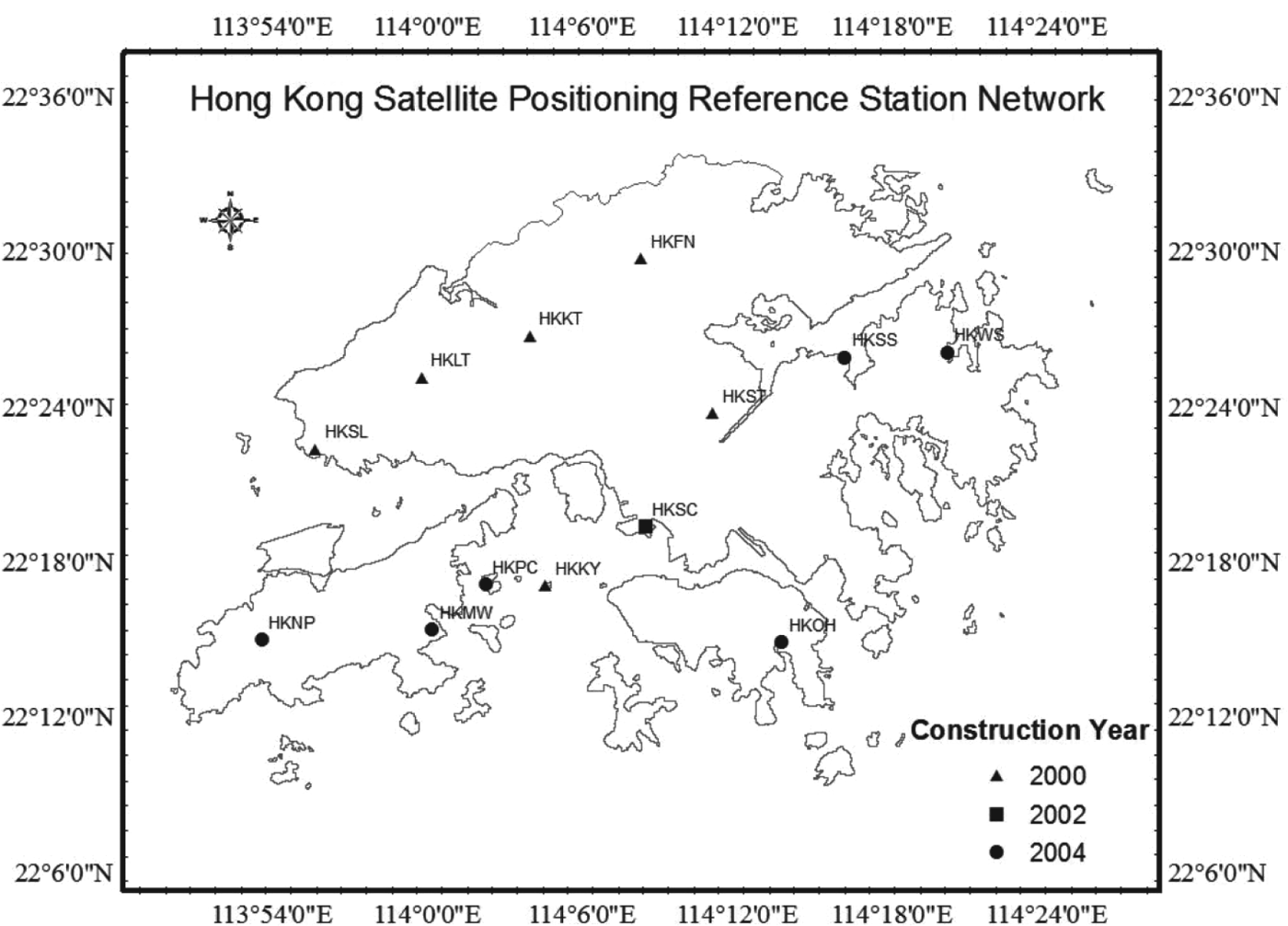
Hong Kong is located in the low-latitude area where ionospheric disturbances happen frequently, especially during the period of the solar maximum (Chen et al., Reference Chen, Gao, Hu and Chen2008). Long term GPS data from the active network in Hong Kong are available. From huge amounts of historical data during the last 11-year solar cycle, the characteristics of the ionosphere can be drawn and the effects of the ionospheric disturbances on GPS can also be evaluated. The number of Continuously Operating Reference Stations (CORS) increased from six in 2001 to 13 now. The dense network provides more details about the characteristics of the ionosphere in the region. Locations of Hong Kong reference stations are shown in Figure 3.
Figure 3. Locations of Hong Kong reference stations.
4. RESULTS
4.1. Pseudorange Noise Standard Deviation
GPS data collected from five stations in 2001 during the solar maximum are used to investigate the statistical properties of the pseudorange noise. The same type of receiver is installed in these stations that are denoted as triangles in Figure 3. Table 1 summarises the classification results together with the noise level in each group. It should be noted that σ noise denotes the code noise level of each GPS frequency, and it is calculated from 
$\sigma _{\varepsilon _3} $ based on Equation (3).
Table 1. Standard deviations of pseudorange noise under different ionosphere conditions in 2001.
The standard deviation of the pseudorange noise under the Quiet condition is 0·141 m, and the value agrees with the type B noise level specified MASPS. More importantly, the pseudorange noise level increases with ROTI. The noise level under the Severe condition reaches 0·304 m, which is as much as twice that under the quiet condition. The total percentage of the disturbance occurrence is 0·87%.
Satellite elevation dependent functions have been used to estimate the pseudorange noise level in previous studies, current software and specifications. To evaluate effects of both the satellite elevation and the ionospheric disturbance on the pseudorange noise level, the observations in each group are divided into several bins according to the corresponding satellite elevation angle. Then, the standard deviation of the pseudorange noise for every bin can be calculated, and shown as the dot in Figure 4. Finally, the traditional model (RTCA, 2000) is fitted for each ionosphere condition, which is denoted by the curve in Figure 4. The coefficients of the curves are shown in Table 2. For the comparison purpose, the noise levels for the type B receiver in the MASPS specification are shown as circles. From the figure, it is concluded that the standard deviation of the pseudorange noise is dependent on effects of both the ionospheric condition and the satellite elevation angle. Curves in Figure 4 and coefficients in Table 2 constitute the proposed stochastic model in which both ROTI and the satellite elevation angle are incorporated.
Figure 4. The modified stochastic model in which both the satellite elevation angle and the ionosphere disturbance level are incorporated.
Table 2. Coefficients of the modified stochastic model.
The modified stochastic model is statistically calculated from huge amounts of GPS data, and it can be used in the least squares method for weighting observations. A test was carried out for assessing the proposed model. Dual frequency pseudorange measurements collected on 15 March 2001 from HKKT station were processed for single point positioning in which precise orbit and clock products from IGS were used for estimating the orbit and the clock errors. Two strategies were applied for weighting measurements: the equal weight solution in which measurements are equally weighted for positioning, and our proposed weighting method based on the modified stochastic model. A comparison of the positioning error between the two strategies is shown in Figure 5. It can be observed that GPS measurements are affected by the ionospheric disturbances during two periods, from 2245 to 2310 local time and from 0010 to 0025 local time. During the period of disturbances, the positioning results from equal weight strategy vibrated rapidly. By using our proposed model during disturbances, the positioning error was reduced significantly.
Figure 5. Variation of (a) ROTI and (b) Vertical positioning error.
A further investigation was carried out to verify the consistency of the noise levels across five stations. The same type of GPS receivers are installed in these stations. Figure 6 shows the noise standard deviations in five stations under different ionospheric conditions. It can be concluded that the noise levels are similar for stations HKKT, HKKY, HKLT and HKSL. The small fluctuations may be attributed to the difference of ionosphere conditions between stations or the multipath caused errors. A larger noise level is observed at HKST station when compared to other stations.
Figure 6. Standard deviations of code noise for five stations under different ionosphere conditions.
Results in Table 1 and Table 2 are statistically calculated from huge amounts of GPS data (in the order of 108), and they can be used in the weighted least-squares method for weighting measurements. However, they cannot be used directly for the integrity purpose because it must be guaranteed that the standard deviation in each group overbounds actual noise distribution. The following section investigates the distribution of noise under four ionospheric disturbance classes.
4.2. Overbounding Tails of Noise Distribution
To show the noise distribution under each group, observations are divided into bins with the equal bin size of 1 cm. The relative frequency can be calculated according to:
$$f_j = \displaystyle{{c_j} \over {c_{total}}} $$where: the subscript j is the bin index, c j is the measurement number in the jth bin and c total is the total measurements number for the group.
Figure 7 shows the relative frequency histogram of the ionosphere-free noise (ε 3) under the Quiet condition. It can be observed that the relative frequency of the tail is much smaller than that of the middle point, so the tails of distribution could not be shown clearly. An alternative figure is developed. The apparent Probability Density Function (PDF) is developed by dividing the relative frequency by the bin size. Figure 8 shows the apparent PDF of noise shown as red dots in a logarithm scale:
$$F_j = \log _{10} (\,f_j /s_{bin} )$$where s bin represents the bin size.
Figure 7. Relative frequency histogram of noise (ε 3) under ionosphere Quiet condition.
Figure 8. Noise (ε 3) distribution and the bound under ionosphere Quiet condition.
The solid curve in Figure 8 denotes a normal distribution with the standard deviation given in Table 1. Compared with 1σ distribution, the true noise distribution, represented by red dots, has non-Gaussian tails at both sides. Thus standard deviations given in Table 1 are still not enough to overbound the true noise distribution.
The sigma inflation method has been developed and used in Lee (Reference Lee2005) to overbound non-Gaussian tails in the GBAS correction errors. The main idea of the inflation strategy is to find an inflated normal distribution in which the PDF is larger than non-Gaussian tails at both sides. The sigma inflation strategy is applied for overbounding non-Gaussian tails in noise distribution, shown as the dot-dash curve in Figure 8.
Distributions of the ionosphere-free combination noise (ε 3) under other ionosphere conditions, Moderate I, Moderate II and Severe, are given in Figure 9. It can be concluded from Figure 8 and Figure 9 that the noise distribution of the Quiet group is almost a Gaussian one, and the noise distribution of the Moderate group or the Severe group has heavy non-Gaussian tails. So during the period of ionospheric disturbances, the noise distribution is characterised by the more abnormal behaviour.
Figure 9. Noise (ε 3) Distribution and the bound under (a) Moderate I (b) Moderate II (c) Severe ionosphere conditions.
Table 3 summarizes inflation factors and the standard deviations after overbounding. It can be seen that the inflated sigma increases when ionospheric disturbances become more severe. Multiplying the standard deviation in Table 1 by the corresponding inflation factor, one can get the noise sigma bound.
Table 3. Inflation factors and standard deviations for different ionospheric condtions.
In integrity monitoring systems, the real time observations are classified into four classes by ROTI. For each observation, the noise standard deviation and the inflated noise standard deviation can be obtained from Table 1 and Table 2 respectively. In case of ionospheric disturbances, using a large sigma of the noise leads to a large protection level. When ionospheric disturbances are quiet, the availability of the navigation system is not affected. In this way, the integrity can thus be assured while maximizing the availability of the navigation system.
In this research, the sample size in each year is in the order of 108. Compared with the 10−9 integrity risk requirement, the size seems insufficient. However, ionospheric disturbances are related to solar activity (11-year cycle), and the data used in this research is in the solar peak year (2001) in the previous cycle. So the inflation for insufficient data size is not a necessity for the sigma of noise for this research.
5. CONCLUSIONS
The ionospheric disturbances affect GPS performance in terms of accuracy and integrity, especially over equatorial regions. This paper develops a novel solution that can successfully mitigate the effects of the ionospheric disturbances on GPS accuracy and integrity using a commercial dual frequency receiver. ROTI, which can be derived from the receiver, is used to categorize the measurements into different groups. Based on the groups, the effects of ionospheric disturbances are investigated using GPS data collected from the same type of receivers in low latitude regions in 2001. The results from long-term GPS data processing include two parts: the modified noise model for weighting measurements to improve the positioning accuracy and inflated standard deviations of noise for the integrity monitoring.
Under the Quiet ionospheric disturbance condition, the pseudorange noise standard deviation is 0·141 metres, and the calculated result agrees with the specification. The occurrence rate of ionospheric disturbances in Hong Kong reached 0·87% in 2001. During the period of ionospheric disturbances, the noise level increases, and can be more than twice that under the Quiet condition.
Taking into account both effects of the satellite elevation and the ionospheric disturbance, a modified stochastic model for weighting observations is developed. In the model, the noise level is determined by not only the satellite elevation but also the ROTI. The more severe the ionospheric disturbance is, the larger noise level that can be obtained, and the less weight is given for the measurement. Therefore the effects of ionospheric disturbances on GPS accuracy can be mitigated by using the modified model. The test shows that the model can effectively mitigate the effects of the ionospheric disturbance on the GPS accuracy. Further comparisons between stations show that the same type of receivers installed at different locations have different noise levels. The difference of the noise levels may be caused by effects of the multipath or the ionospheric condition because these stations are separated by tens of kilometres.
To mitigate the effects of non-Gaussian tails on GPS integrity, the noise standard deviations used in integrity monitoring systems should overbound the actual noise distribution. The sigma inflation method is used to overbound the noise in this paper, and inflation factors for different ionospheric conditions are also recommended. When the ionosphere is quiet, the availability of the navigation system can be guaranteed by the small protection level that is calculated from small noise sigma. In cases of ionospheric disturbances, however, the inflated sigma, leads to the larger protection level, and the integrity of navigation system can thus be ensured. Therefore, by using the inflated sigma in this paper, one can achieve the integrity risk requirement while maximising the availability of the navigation system.
It is believed that this technique together with the results in this paper can be used to mitigate the effects of ionospheric disturbances because: (i) ROTI is available for the dual frequency receiver, and can be used for indexing the ionospheric disturbance; (ii) the model in this paper is summarized from GPS data collected over low latitude regions in 2001, and large amounts of GPS data guarantee the applicability of the stochastic model.
ACKNOWLEDGEMENTS
The research was substantially funded by Hong Kong RGC General Research fund (A/C: PolyU 5131/10E).
