Introduction

Reliable dating is a condition for proper interpretation of the environmental records retrieved from ice sheets by ice-core drilling, and also for interpretation of the internal reflection horizons in ice sheets revealed by radio echo-sounding, and believed to be isochrones, i.e. surfaces of equal age. A whole lot of experimental methods for ice-core dating are now available, e.g. dating by seasonal variations of stable isotopes, microparticles, chemical constituents, electrical conductivity (Reference Hammer, Oeschger and LangwayHammer, 1989), dating by means of reference horizons (Reference Hammer, Oeschger and LangwayHammer, 1989), or dating by radioactive isotopes (Reference Stauffer, Oeschger and LangwayStauffer, 1989).

However, theoretical dating of ice cores by means of ice-dynamic modeling is also a useful dating method, for example, for establishing preliminary time-scales for core-sampling purposes, and for providing a reference to which ice-core results can be compared (Reference ReehReeh and others, 1985; Reference Reeh, Oeschger and LangwayReeh, 1988,1989). Moreover, dating by ice-dynamic models seems to be the only practicable method for determining the age of the internal reflection horizons.

In general, the age of an “ice particle” at a given depth in an ice sheet is calculated by first determining the path of the particle from the site of deposition on the surface and then calculating the time taken by the particle to travel along this path from the surface to its present position. This requires modeling of the dynamic and thermal histories of the ice sheet during the entire period elapsed since the ice particle was deposited at the surface. This again pre-supposes past up-stream histories of accumulation rate, ice thickness, ice temperature, and ice flow-law parameters to be known or calculated. Therefore, theoretical dating of ice over long time spans, during which significant changes in the above-mentioned quantities have occurred, requires application of non-steady-state models. However, when dealing only with the upper layers of the ice sheets, dating by steady-state models may be acceptable. To what depth, or rather how far back in time, steady-state flow-model dating is acceptable depends mainly on the size of the ice mass. For the large Antarctic and Greenland ice sheets, the limit is c, 10 000 year, i.e. back to the termination of the last ice age, prior to which time substantial changes in accumulation rate, and also perhaps in flow pattern and ice thickness, have occurred (see discussion byReference Reeh and Bleil Reeh (in press)). For smaller ice caps, the age limit is more like 1000–1500 year (Reference Reeh, Oeschger and LangwayReeh, 1989).

Theoretical ice-core dating (or, equivalently, calculation of the annual layer-thickness profile) can be approached in two rather different ways:

a. By applying simple models for which analytical solutions are possible. The models applied so far have been subject to rather severe restrictions such as assuming steady state, two-dimensional flow, constant ice thickness, and accumulation rate in the direction of flow

(e.g. Haefeli, 1963; Reference Dansgaard and JohnsenDansgaard and Johnsen, 1969;Reference Philberth and Federer Philberth and Federer, 1971;Reference Paterson and Waddington Paterson and Waddington, 1984). The assumptions imply that the thickness of the annual layers and therefore also the age-depth profiles do not vary horizontally. To reflect this fact, these models will be denoted “sandwich” models.

b. By applying numerical models, which take into account up-stream variations in accumulation rate, ice thickness, and horizontal convergence-divergence of the flow, in some cases even non-stationarity (e.g.Reference Budd Budd, 1969; Reference Radok, Barry, Jenssen, Keen, Kiladis and Mclnnes Radok and others, 1982; Reference Robin de and Robin de Robin, 1983; Reference Reeh and GundestrupReeh and others, 1985; Reference Huybrechts and OerlemansHuybrechts and Oerlemans, 1988;Reference Reeh, and and Paterson Reeh and Paterson, 1988).

The aim of the present work is to develop models for the age-depth relationship in ice sheets which are still simple enough that solutions can be obtained by analytical methods, but which go a step further than “sandwich” models. The models will be used to study how horizontal convergence-divergence of the flow, and up-stream variations in accumulation rate and ice thickness, influence the age-depth relationship in general. Moreover, for specific dating purposes, models will be developed that can be used to date the layers in the upper part of an ice sheet.

Coordinate System, Ice Flux, And Velocity Profile

The coordinate system adopted in this work is the one used by Reeh

(1988), i.e. the x-axis is horizontal, follows the flow line, and is oriented in the direction of flow, which direction is assumed not to change with depth. The y-axis is also horizontal and directed transverse to the flow line, and the z-axis is vertical and positive upwards (see Fig. 1). The radius of curvature of the surface-elevation contours at their intersection with the flow line is denoted R. R is positive for diverging flow and negative for converging flow.

Fig. 1. a. Shows horizontal curvilinear coordinate axes x and y along flow lines and surface-elevation contours, respectively. R is radius of curvature of the elevation contour at the point of intersection with the flow line. b. Shows a vertical section along the flow line. c. Shows transformed vertical section along the flow line.

The velocity component in the x-direction is denoted u.

Due to the definition of the flow line, the y-component of the velocity is zero. The upper and lower surfaces of the ice sheet are denoted S(x) and B(x), respectively, while H(x) = S(x) - B(x) denotes ice thickness.

The ice-volume flux per unit width

(1)

where `a = a _S + a _B −∂H/∂t, and a_s and a_B are net mass balances (positive for accumulation, negative for ablation) at the ice-sheet surface and base, respectively, and ∂H/∂t is the rate of change of ice thickness. Here, we shall deal with an ice sheet in steady state without melting-refrcezing at the base. Consequently, ∂H/∂t = 0 and a_B = 0. The non-steady-state situation and the case of basal melting- refreezing will be dealt with in papers in preparation. ForEquation (1) to hold, the ice-sheet material must be assumed to be incompressible. In consequence, ice-equivalent thicknesses are used in the calculations.

The solution of the differential Equation (1) is

(2)

where C is an arbitrary constant to be determined by a boundary condition, specifying q(x) for one value of x.

The assumption made byReference Reeh, and and Paterson Reeh (1988) that the shape of the horizontal velocity-depth profile varies only slowly with x is also adopted in this work. This assumption allows the horizontal velocity component to be written

(3)

where 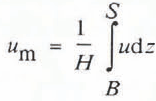is the depth-averaged velocity, and

(4)

is a dimensionless vertical coordinate, standardized to the range 0–1. Φ(Z̃) is the shape function of the horizontal velocity-depth profile, and is subject to the condition ι

Particle Paths

Consider the path of the “ice particle” P, which at time t = t₁ is situated at the ice-sheet surface at point (x_RS₁ ) (see Fig. 2). Since the ice sheet is assumed to be in steady state, the particle path is stationary and coincident with a flow line. At time t = t₂ the

“ice particle” has moved to the section at x₂ and is located at distance h above the ice-sheet base.

Mass conservation requires that the mass flux into a flow tube at section 1 (see Fig. 2) must equal the mass

flux out of the flow tube at section 2. Therefore, denoting the variable width of the flow tube by W, we get

(5)

Substituting for u by means of Equation (3) and introducing the function 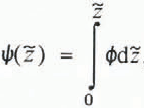Equation (5) may be rewritten о

(6)

where h̃ = h/H₂

The change in W along the flow line is determined by the differential equation dW/dx = W/R, from which by integration

(7)

Combining Equations (6) and (7), we get

(8)

When solved with respect to

(9)

this equation determines the path followed by the particle that was originally deposited at the ice-sheet surface at section 1. When solved with respect to

(10)

the original surface position of the particle, now located at section 2 at the distance h above the base, is determined.

Fig. 2. Flow tube illustrating mass conservation.

To illustrate the use of Equation (8), consider the case of plane flow

(R = ∞) with constant accumulation rate a and ice thickness H. Taking the origin of the x-axis at the ice divide, we get q(x) = ax and Equation (8), therefore, is reduced to

(11)

Further, if it is assumed that the horizontal velocity does not vary with depth (column flow), which means that Φ(Z̃) = 1, and consequently, it follows from Equation (11) that

(12)

which shows that, in this case, the particle paths are hyperbolas with the ice divide and the ice-sheet base as asymptotes, a result already deduced by Haefeli (1963).

Isochrones, Age Profiles, And Annual Layer-Thickness Profiles

The time taken by a particle to travel along the path from the surface at section 1 to its location deep in the ice sheet at section 2 is calculated as follows.

Since, by definition, u_m(x) = q(x)/H(x), Equation (3) can be rewritten

(13)

where the notation Φ(h(x₁,x)) indicates that the value of the shape function φ should be determined at the varying heights (as determined from Equation (9)) attained by the particle during its motion along the path. Hence, from Equation (13)

(14)

where x ₁ is to be considered a constant. By substituting in this equation for x ₁ by means of

Equation (10) (after the integration has been carried out), the age-depth profile at section 2 will be expressed in terms of x ₂ and h̃

(15)

On the other hand, for a fixed value of t = t ₀ and x₂considered a variable, Equation (15) also determines the equation of the t ₀ year old isochrone, i.e. the internal surface consisting of those particles that formed the free, upper surface of the ice sheet i₀ years ago.

From the age-depth profile, the annual, layer-thickness profile is simply determined by the expression

(16)

where τ is 1 year.

Sandwich-model flow

As mentioned previously, sandwich-model flow is characterized by constant accumulation rate a and ice thickness H along the flow line. According to Equation (11), the h-x ₁-x relationship then becomes from which, by differentiation,

Using this expression, and q(x) = ax. Equation (14) may be reduced to

(17)

which is equivalent to an equation derived by Reference Philberth and FedererPhilberth and Federer (1971).

The annual layer-thickness profile is derived by means of Equations (16) and (17):

(18)

where λ_s is the annual Jayer thickness at the surface.

If we put (column flow), Equations (17) and (18) can be further simplified to t = (H/a)log(H/h) and λ/λ _S = h/H, which are the well-known logarithmic age profile, respectively, the linear annual layer-thickness profile deduced by Haefeli (1963).

Modified column flow

The assumption of a uniform vertical strain-rate variation with depth in the ice sheet leads to substantial simplifications in ice-flow modeling. However, it is a poor approximation to the real strain-rate variation below a certain depth in the ice sheet. Generally, the strain-rate decreases towards the ice-sheet base, where it approaches zero if the base is horizontal and the ice is frozen to it. To account for this fact, Reference Dansgaard and JohnsenDansgaard and Johnsen (1969) introduced a model with φ constant down to some distance I above the base and from there decreasing linearly to zero at the base (see Fig. 3). This model, which is a substantial improvement compared to the constant vertical strain-rate model, still has the advantage of being simple, particularly when considering only the upper part of the ice sheet above the bend in the strain-rate profile. The ratio f of the surface strain-rate to the depth-averaged strain-rate (which is equal to the ratio of the horizontal surface velocity to the depth-averaged horizontal ^velocity) can be expressed in terms of the relative distance l̃ = l/H

Fig. 3. Dansgaard-Johnsen shape function φ for the depth distribution of horizontal velocity and vertical strain-rate (modified column flow).

(19)

For Z̃ > l̃ the profile functions Φ(Z̃) and become

(19)

Figure 4 shows a section along a flow line through the upper layers of the ice sheet. At x₁ the thickness of the surface layer is

.After t years, the segment AB has moved to the position A’ B’ at x₂ . Since the

horizontal velocities are assumed not to vary with depth, the line segment A’B’ is still vertical and represents the thickness λ(x₂,h) of the t year old annual layer at section 2. Mass-conservation considerations for the corresponding flow tube, with due account also of the changing flow-tube width, therefore leads to

(21)

Fig. 4. Verlicai section along the flow line illustrating the deformation and displacement of an annual layer.

Combining this equation with Equations (3), (6), (19), and (20), and using the fact that λ(x ₁, H ₁) = τa(x ₁) and that u_m(x) = q(x)/H(x) we find

(22)

which determines the annual layer-thickness profile along the vertical through x₂ as a function of h̃, x₁ and x₂ Substituting for

.V₁ by means of Equation (10) will give the layer-thickness profile in terms of h̃ and x₂ , only.

From Equation (22) the age-depth profile is obtained by means of the equation

(23)

It should be stressed that Equations (22) and (23) are deduced with the assumption that the vertical velocity does not vary with depth at least not in the part of the ice sheet containing the flow tube shown in Figure 4. In the case of a depth-dependent horizontal velocity profile, points A’ and

B’ will be displaced horizontally with respect to each other, and the simple relationship expressed by Equation (21), which is vital for the deduction of Equations (22) and (23), does not hold.

Idealized Ice Sheets

The purpose of this section is to illustrate how the age and annual layer-thickness profiles are influenced by diverging horizontal flow and by non-uniform distributions of up-stream accumulation rate and ice thickness. This is done by considering some simple, idealized ice-sheet models. Since column flow will be pre-supposed in all examples, the expressions and diagrams displayed in this section are not meant to be used for practical ice-dating purposes, but are meant merely to illustrate some general features. Equations that can actually be used to date the layers in the upper part of an ice sheet will be displayed in the following section.

Ice flux

The divergence of the flow near a dome is determined by the variation of the radius of curvature of the elevation-contour lines at their points of intersection with the flow lines. A simple variation that allows for various degrees of divergence is as follows:

(24)

where x is a coordinate along the flow line with origin at the dome (see Fig. 5).

Fig. 5. Horizontal flow pattern near an ice ridge or dome, a. Shows plane flow near a horizontal ridge (m = 0). b. Shows radial flow near a circular dome (m = 1). c. Shows flow near an el Uptically shaped dome. (1): m > 1; (2): 0 < m <1.

m = 0 coresponds to plane flow, m = 1 corresponds to radial flow from a circular dome, and high values of m correspond to even stronger divergence of the flow (see Fig. 5).

Using Equation (24) for R(x) and a linear variation of the accumulation rate according to the equation

(25)

the ice flux, as determined from Equation (2), becomes

(26)

since q = 0 at the dome x = 0).

For column flow, , and Equation (8) therefore becomes

(27)

where α = a₁/a₀

Plane, ideal plastic ice sheet with uniform accumulation-rate distribution

The influence on the time-scale of a non-uniform ice-thickness distribution will be illustrated by considering an ice-thickness variation according to the equation H = where H₀ is the ice thickness at the divide (x = 0), and L is the half-width of the ice sheet. This thickness variation corresponds to that of an ideal plastic ice sheet on a horizontal base (Reference OrowanOrowan, 1949). Moreover, the flow is assumed to be plane flow (R = ∞, m = 0), and the accumulation-rate distribution is assumed to be uniform (α = 0). Therefore, Equation (27) is reduced to

(28)

The column-flow assumption also implies that f = 1 in Equation (22). Consequently, the annual layer-thickness profile is determined by Equation (22) to be

where λ_s is the annual layer thickness at the surface of the ice sheet at section 2. From Equation (28), we get x₁ = x₂h̃, which, when substituted into the equation above, gives

(29)

The age profile is determined by means of Equation (23) as

ι

from which

(30)

where t₀ = −(H₀/a₀)log(h̃) is the age profile at the ice divide. In Figure 6, λ/λ _S and (a_o/H₂)t are shown as functions of ft for various values of x₂/L.

Figure 6 shows that the annual layer-thickness profiles become more and more concave-down with increasing distance from the ice divide. This means that, generally, the annual layers are thinner than corresponding to sandwich-model flow with the local accumulation rate and ice thickness. For example, for x₂/L = 0.9, the layers half-way down the ice sheet are less than half as thick as they would be if the up-stream ice thickness was constant and equal to the local thickness. The reason for the decreased layer thicknesses is that flow with decreasing ice thickness in the direction of flow causes increased strain-rates (thinning rates) of the layers. On the other hand, increasing ice thickness in the flow direction has the effect of increasing the layer thicknesses due to decreased strain-rates, and consequently leads to annual layer-thickness profiles that are concave-up.

Fig. 6. Ideal plastic ice sheet with plane flow and constant accumulation rale. Dimensionless layer thickness and age versus fractional height above the base, parameterized for various values of the fractional distance from the ice divide (x₂/L).

In terms of the age-depth profile, this means that decreasing/increasing ice thickness in the direction of flow causes an older/younger age in a given relative height above the base than if the up-stream ice thickness were constant.

Ice sheet with constant thickness and linearly varying accumulation rate

The influence on the age-depth profile of a nonuniform accumulation-rate distribution will be illustrated by considering an ice sheet with constant thickness H₀ , and a linear variation of the accumulation rate according to the equation a = a₀ + a₁x. Since f = 1 (column flow), the annual layer-thickness profile, as determined from Equation (22), therefore becomes

(31)

where α = a₁/a₀

Assuming the flow to be plane flow (R = ∞, m = 0), Equation (27) is reduced to

(32)

which, when solved with respect to αx₁ , yields

Combining this equation with Equation (31), we find

(33)

The age-depth profile is determined by means of Equation

(23) as

from which

(35)

where t₀ = −(H₀/a₀)log(h̃) is the time-scale at the ice divide (x₂ = 0).

In Figure 7, λ/λ _S and (a₂/H₀)t are shown as functions of h̃ for various values of a₂/a₀ where a₂ denotes a(x₂).

Fig. 7. Constant-thickness ice sheet with plane flow and linearly varying accumulation rate. Dimensionless layer thickness and age versus fractional height above the base, parameterized for various values of the ratio (a₂/a₀ ) between the local accumulation rate and the accumulation rate at the ice divide.

Figure 7 shows that, depending on whether the accumulation rate increases (a₂/a₀ > 1) or decreases (a₂/a₀ > 1) in the direction of flow, the annual layer-thickness profiles are concave-down, respectively concave-up. The degree of curvature of the profiles increases for a₂/a₀ → 0 as well as for a₂/a₀ → ∞

In terms of the age-depth profile, this means that increasing/decreasing accumulation rate in the direction of flow will tend to increase/decrease the age of the ice in a given height above the base when compared to the case of a constant accumulation rate equal to the local value. This is clearly illustrated in the lower panel of Figure 7.

Diverging flow

It is clear from Equations (22) and (23) that divergence/convergence does not enter the expressions for the layer-thickness and age profiles directly. Therefore, divergence/convergence has only an indirect influence on these profiles through the influence on the variation of the ice flux along the flow line, manifesting itself in the h̃−x₁−x₂ relationship given by Equation (27).

To see an effect, therefore, at least one of the quantities (accumulation rate or ice thickness) must vary along the flow line. Here we consider the case of uniform accumulation rate (α = 0) and a linear ice-thickness variation

(35)

Then, Equation (27) is reduced to

(36)

Combining this equation with Equations (22) and (23), the annual layer-thickness profile, respectively, the age profile is found to be

(37)

and

(38)

where t₀ = −(H₀/a₀)log(h̃) is the age profile at the ice divide.

In Figure 8, λ/λ _S and (a₀/H₂)t are shown for the case of

βx₂ = 1 (corresponding to a doubling of the ice thickness over the distance х₂)) for various values of the divergence parameter m. The figure shows that the larger the divergence, the less is the influence of up-stream ice-thickness variations. This is understandable, since increased divergence causes decreasing horizontal flow velocities, and therefore causes the particle paths to originate from locations closer to the site considered.

Ice sheet with diverging flow

Fig. 8. Ice sheet with constant accumulation rate, linearly varying ice thickness, and diverging flow. Dimensionless layer thickness and age versus fractional height above the base, parameterized for various values of the divergence parameter (m). Local ice thickness is twice the thickness at the dome.

Dating Of The Upper Layers

In this section, expressions will be deduced for the layer-thickness and age profiles in the upper part of an ice sheet. Strain-rates are assumed to be constant down to a certain level (modified column flow), and the expressions deduced are only valid in the part of the ice sheet above this level. Accumulation rate, ice thickness, and radius of curvature of the surface-contour lines are all assumed to vary linearly along the flow line. The origin of the x-axis is most conveniently put at the section where layer-thickness and age profiles are to be calculated, i.e. х₂ = 0 (see Fig. 2).

With a = a₀(1 + αx), H = H₀(1 + βx), and R= R₀ + x the ice flux per unit width, as determined from Equation (2), becomes

(39)

where q₀ = u_mH₀ is the ice flux per unit width at x = 0 (the profile location).

For modified column flow, , where the fractional depth

d̃ = d/H has been introduced instead of h̃ − 1 This substitution results in simpler mathematical expressions. Note that, according to the definition, d̃ is a negative quantity. Also, x₁ is negative due to choosing the origin of the x-axis at section 2.

Now, by means of Equation (8), we get

(40)

As illustrated by the examples in the previous section, it is a condition for obtaining analytical solutions for the λ and age profiles that Equation (40) can be solved explicitly with respect to

x₁ Since Equation (40) is of the third order in x₁ , this requirement is obviously fulfilled. However, the analytical expressions are greatly simplified if Equation (40) can be reduced to be of the second order in x₁ This is the case if either α = 0 (constant accumulation rate), or if R = ∞ (plane flow). For these two cases, Equation (40) may be solved with respect to x₁ to give

(41)

where K = R₀ if α = 0, and K = 1/α if R = ∞

From Equations (22) and (23), the λ profile, respectively the age profile can be expressed as

(42)

and

(43)

Plane flow

Substituting in Equations (42) and (43) for x₁ , by means of Equation (41) with K = 1/α, we obtain

(44)

and

(45)

where c = 2q₀α/a₀

From Equation (45) the age profile is obtained by integration: For

с < 1:

(46(a))

For c = 1

(46(b))

For c > 1

(46(c))

It appears from Equations (44) and (46) that, if β = α, i.e. if the ice thickness and the accumulation rate display similar variations (relatively speaking) along the flow line, then their influence on the λ and age profiles cancels out. Consequently, we get a linear variation with depth of the annual layer thickness, respectively a logarithmic variation with depth of the age, i.e. exactly the same λ and age profiles that would result in the case of constant accumulation rate and ice thickness.

Equations (44) and (46) do not apply in the case of α = 0. In this case, the expressions for the λ and age profiles become

(47)

and

(48)

where c₁ = βq₀/a₀

Diverging/converging flow with uniform accumulation rate

In this case, we have K = R₀ in Equation (41), and Equations (42) and (43) therefore yield

(49)

and for c₂ < 1:

(50(a))

for c = 1

(50(b))

For c > 1

(50(c))

Equations (49) and (50) do not apply for the case of R₀ = ∞, in which case Equations (47) and (48) should be used.

Application To Greenland Drill-Hole Locations

In order to use the expressions for the λ and age profiles, the following information is required: ice thickness, accumulation rate, and ice flux at the location where the profiles are to be calculated. Furthermore, the gradients of ice thickness and accumulation rate, and the convergence/ divergence of the flow must be known as far up-stream as to the original surface location of the oldest (the deepest) layer to be dated. The distance to this site (.x₁ ) may not be known in advance, but it can be calculated from Equation (40). Therefore, some trial and error may be needed for the actual dating.

Also, the profile factor f (the ratio of horizontal surface velocity to the depth-averaged velocity) must be estimated. This is straightforward in the few cases where the velocity-depth profile has been measured in a deep hole. If only the surface velocity u_s has been measured, the f factor can be estimated as ƒ = H₀u_s/q₀ , where H₀ is ice thickness and q₀ is the ice flux per unit width calculated by integrating Equation (1) with the starting point at an ice dome or ice divide.

For the Greenland ice sheet, a simpler approach can be used for estimating f. Deformation measurements in the deep bore hole at Dye 3 on the south Greenland ice sheet has shown that the horizontal velocity at a depth corresponding to the transition from ice deposited in the present post-glacial period (the Holocene) to ice deposited in the last glacial period (the Wisconsinan) constitutes more than 80% of the surface velocity (Reference Hansen and GundestrupHansen and Gundestrup, 1988). Moreover, at the same depth, there is a sharp change in the vertical gradient of the velocity profile from large values below the transition to rather small values above. This is, in part, due to a combination of high shear stresses and high ice temperatures in the bottom part of the ice sheet, but the effect is enhanced due to the fact that the Wisconsinan ice deforms 3–4 times more readily than Holocene ice, probably due to a much increased micro-particle content (Reference Hansen and GundestrupHansen and Gundestrup, 1988).

Model calculations (to be presented elsewhere) indicate that the Dye 3 velocity profile is typical for the slope regions of the Greenland ice sheet. This suggests that a modified column-flow model with constant strain-rate down to the Holocene/Wisconsinan transition (dated to 10 750 ± 150 years BP. by Reference Hammer, Clausen and TauberHammer and others (1986)) is an acceptable approximation in connection with dating of the Holocene ice in Greenland. Since the depth to the transition may not be known in advance, the dating may require application of a trial-and-error procedure. The temporal variations of accumulation rate and ice thickness of the interior regions of the Greenland ice sheet during the Holocene have been discussed byReference Reeh and Bleil Reeh (in press). It is concluded that accumulation rates may have varied by about

Table I Dye 3 Data

Comments: * Vertical distances reduced by a 24 m correction for low firn densities.

^† where year is the transverse strain-rate (Reference Drew and WhillansDrew and Whillans, 1984).

^± The β value calculated by means of the mean thickness gradient given byReference Reeh and Gundestrup Reeh and Gundestrup (1985) is 3.0 ×

10⁻⁶. This gradient was calculated from profile data along an estimated straight flow line from Dye 3 to the up-stream ice ridge. The actual flow line bends to the south, and the β value given in the table is a better estimate of β along the actual flow line.

10%, and that ice-thickness variations were probably even less as indicated by total gas-content analyses on core ice from Dye 3 and Camp Century (Reference Herron and LangwayHerron and Langway, 1987). Therefore, steady state seems to be an acceptable approximation for the interior regions of the Greenland ice sheet during the Holocene.

Dye 3

At the Dye 3 deep-drilling site on the south Greenland ice sheet (lat.

65°11’N., 43° 49’W.) all the information needed as input to the model is known. Furthermore, the age-depth profile has been determined experimentally down to the Holocene/Wisconsinan transition, thus providing a unique possibility for checking the results of the model calculations (see Table I).

The gradients α and β are determined over a 45 km section up-stream of Dye 3, corresponding to the calculated distance to the site of origin at the surface of the ice found at 1760 m ice-equivalent depth in the core.

The large (negative) value of R₀ suggests that the corresponding small convergence of the flow in the Dye 3 region will only have a modest influence on the time-scale. Therefore, Equations

(46a, b, c) which are valid for plane flow have been applied for calculating the age-depth profile. This profile is shown in Figure 8, together with the experimentally determined age-depth profile

(Reference Dansgaard, Clausen, Dahl–Jensen, Gundestrup, Hammer, Ghazi and FantechiDansgaard and others, 1986;Reference Hammer, Clausen and Tauber Hammer and others, 1986). For comparison, age-depth profiles for “sandwich-model” flow (α = 0, β = 0), for flow with constant ice thickness (β = 0), and for flow with constant accumulation rate (α = 0), are also shown in the figure.

It appears from the figure that the best fit to the

“experimental” time-scale is provided by the full model.

This is further illustrated in Table II which shows that the full model predicts the time-scale back to 10 750 B.P. with a root-mean-square

(RMS) relative deviation of only c. 3%, whereas the other models have RMS values between 5 and 10%. Also, the full model gives the best prediction of the age (t ₁₇₆₀) at the Holocene/Wisconsinan transition with a deviation (Δt₁₇₆₀) of only −200 years, compared to deviations between +340 and −1840 years for the other models. Table II also shows that the accumulation-rate variation has a larger influence on the age-depth profile than has the ice-thickness variation. Furthermore, Table Il demonstrates the previously mentioned fact that, when the accumulation-rate and ice-thickness gradients have the same sign, they counteract each other as regards their influence on the age-depth profile.

Fig. 9. Age-depth profiles for Dye 3. Curves labeled 1–4 are calculated with the following up-stream distributions of accumulation rate (a) and ice thickness (H): (1) Linear a and H. (2) Linear a and constant H. (3) Constant a and linear H. (4) Constant a and H. Points marked by asterisks are “observed” ages according to Dansgaard and others (1986) and Reference Hammer, Clausen and TauberHammer and others (1986).

Table II. Dye 3. Comparison of experimental and calculated ages

The superiority of the full model compared to the sandwich model is further illustrated in Figure 10, in which the theoretical layer-thickness profiles for these models are compared to the measured annual layer thicknesses in the (true) depth interval 1650–1780 m (Reference Hammer, Clausen and TauberHammer and others, 1986). The full model gives a reasonable fit to the measurements, whereas the layers calculated by means of the sandwich model are 30–40% too thick.

Fig. 10. Comparison of measured layer-thickness profile (step curve, heavy bars, and points marked by asterisksJ at the Holocene/Pleistocene transition in the Dye 3 core with calculated layer-thickness profiles. Full line: calculation with linear distributions of accumulation rate (a) and ice thickness (H). Dashed line: calculation with constant of a and H (sandwich model). Modified fromReference Hammer, Clausen and Tauber Hammer and others (1986).

Finally, the error introduced by neglecting the small convergence of the flow near Dye 3 is evaluated by calculating the age at the 1760 m ice-equivalent depth by means of Equations (50a, b, c). The difference between this age and the age calculated with constant accumulation rate, but with neglect of the convergence (last row in Table II), is only 50 years, confirming that the influence of the convergence on the age-depth profile is negligible.

Model calculations with 2% changes in accumulation rate, respectively surface velocity (the likely maximum errors), resulted in changes in t ₁₇₆₀ of only about 50 years.

Milcent

Milcent (lat. 70°18’N., long. 45°35’W.) is located approximately midway between the ice divide and the ice margin on the EGIG profile line in central West Greenland. Along the EGIG profile, which closely follows a flow line, accumulation-rate, ice-thickness, and surface-velocity data are available (see Table III).

Since only an intermediate drilling down to c. 400 m has been undertaken at Milcent (Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and ReehHammer and others, 1978), neither the f factor nor the depth d₀ to the Holocene/ Wisconsinan transition are known. These quantities, therefore, must be found by trial and error, i.e. the depth d₀ is estimated, and the f factor and the ice flux are subsequently calculated from the expressions ƒ = 2/(1 + d̃₀), respectively q₀ = u_sH₀/ƒ, and finally, the age is calculated from the expressions given in the previous sections. Calculations with d₀ = 1730, 1740, and 1750 m gave ages of 10 570, 10 740, and 10 910 years B.P., respectively, suggesting that d₀ ~1740 m. This depth was therefore used to calculate the age-depth profiles by means of Equations (46) and (48), which apply to the case of plane flow, which is a very good aproximation for the EGIG line, as indicated by the locally straight and parallel surface-elevation contours (Radok and others, 1982). The ice-thickness and accumulation variations are due to a good approximation linear, with only minor deviations from the linear trend lines (Reference BensonBenson, 1962; Reference Quervain deQuervain and others, 1969; Reference GudmandsenGudmandsen, 1973).

In Figure 11, age-depth profiles are displayed for the full model, for sandwich-model flow, for flow with constant accumulation rate, and for flow with constant ice thickness. With increasing depth, the differences between the age-depth profiles become much larger than at Dye 3. This is due to the large horizontal surface velocity up-stream of Milcent, which causes the ice to originate from sites far up-stream (up to about 190 km) of Milcent, where accumulation rates and ice thicknesses are much different from the values at Milcent. Also, the increasing trend in accumulation rate and the decreasing trend in ice thickness in the direction of flow tend to influence the age-depth profile in the same manner, in contrast to what is the case for Dye 3, where the two trends partly counter-balance each other.

Fig. 11. Age-depth profiles for Milcent. Curves labeled 1–4 are calculated with the following up-stream distributions of accumulation rate (a) unci ice thickness (H): (1) Linear a and H. (2) Linear a and constant H. (3) Constant a and linear H. (4) Constant a and H. Point marked by an asterisk is an “observed” age according toReference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and Reeh Hammer and others (1978).

The large differences between the predicted ages are illustrated by the calculated ages at the 1740 m ice-equivalent depth. The ages are 10 740, 9010, 8040, and 6950 years BP., respectively for the full model, the model

Table III. Milcent data

Comment: *Vertical ice depth reduced by a 20 m correction for low firn densities. considering only accumulation-rate variations, the model considering only ice-thickness variations, and the sandwich model. The very different ages illustrate the importance of taking into account gradients in accumulation rate and ice thickness in theoretical ice-sheet dating.

Dating of the 398 m ice core drilled at Milcent gave an age of 796 years B.P. at the bottom of the drill hole (Hammer and others, 1978). At this level, all four models predict ages that deviate less than 3% from the experimentally obtained age.

Camp Century

Camp Century (lat. 77°10’N., long. 61°08’W.) is also a location for a deep drilling on the Greenland ice sheet. Accumulation rate and ice thickness up-stream of Camp Century can be estimated from the data available, and the surface velocity is also known (see Table IV).

Table IV. Camp century data

Comments: *Vertical distances reduced by a 20 m correction for low firn densities.

Bore-hole deformation measurements, however, are not consistent with the surface velocity (Reference Gundestrup, Clausen, Hansen and RandGundestrup and others, 1987), so that neither the f factor nor the ice flux can be reliably calculated from the measurements. On the other hand, the ice core has been experimentally dated down to the Holocene/Wisconsinan transition, which allows checking of theoretical time-scales.

However, unfortunately, the attempts to establish a time-scale for Camp Century by means of the simple models developed in previous sections have been rather unsuccessful. All the model calculations gave ages around 8000 years at a depth corresponding to the Holocene/ Wisconsinan transition, and predicted the ice from this depth to originate from approximately IOkm up-stream of Camp Century.

Camp Century is located on a local ridge with a strongly divergent flow pattern, which cannot be described well enough by a linear variation of the radius of curvature as prescribed in the present models. Due to the strong divergence, the velocity decreases much more slowly in the up-stream direction than in the case of less divergent flow. This means that 10 750 year old ice originates from a location c 30 km up-stream of Camp Century (and not 10 km, as predicted by the simple models). 30 km up-stream, the accumulation rates are significantly less than, and ice thicknesses significantly greater than at Camp Century. Calculations (to be presented elsewhere) with the more advanced flow model described by Reeh (1988), taking into account the strong divergence of the flow up-stream of Camp Century, give an age of 10 500 years for ice at 1138m depth (the Holocene/Wisconsinan transition). Moreover, the horizontal velocity profile calculated by means of this more advanced model exhibits a sharp bend at the depth of the Holocene/Wisconsinan transition, and the velocity at this depth constitutes c. 85% of the surface velocity, indicating that the simple models do not break down because of the assumption of modified column flow but rather because divergence is not correctly accounted for.

The conclusion that a simple model based on the assumption of modified column flow cannot be used for dating the ice at Camp Century is apparently contradicted byReference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and Reeh Hammer and others (1978), who used such a model to date successfully the Camp Century ice core back to the Holocene/Wisconsinan transition. However, Reference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and ReehHammer and others (1978) estimated the depth to the bend in the velocity profile to be d = 938 m by means of a least-squares fit of the theoretical, annual layer-thickness profile to the observed annual layer-thickness profile. Even though this value of d gives a very good fit to the layer-thickness profile, it probably has not much to do with the position of the bend point in the horizontal velocity profile, which according to the above-mentioned model study should rather be put 200 m deeper (as is also indicated by the, unfortunately rather uncertain, observed velocity profile presented in figure 4 of Reference Gundestrup, Clausen, Hansen and RandGundestrup and others (1987)).

The conclusion, therefore, must be that theReference Hammer, Clausen, Dansgaard, Gundestrup, Johnsen and Reeh Hammer and others (1978) dating of the Camp Century record is basically due to curve-fitting and cannot be considered a flow-model dating. This, of course, does not make the Hammer and others' time-scale less useful for providing dates along the Camp Century core.

Concluding Remarks

The simple models developed in this study have been used to illustrate how up-stream variations in accumulation rate and ice thickness, and horizontal convergence/ divergence of the flow, have an influence on the age and annual layer-thickness profiles in an ice sheet. Generally, a decrease/increase of the accumulation rate and an increase/ decrease of the ice thickness in the up-stream direction (i.e. opposite to the flow direction) results in older/younger ice at a given depth in the ice sheet than would result if the up-stream accumulation rate and ice thickness were constant along the flow line.

Convergence/divergence of the up-stream flow will decrease/increase the effect of accumulation-rate and ice-thickness gradients, whereas convergence/divergence has no influence at all on the age and layer-thickness profiles if the up-stream accumulation rate and ice thickness are constant.

A modified column-flow model, i.e. a model for which the strain-rate profile (or, equivalently, the horizontal velocity profile) is constant down to the depth corresponding to the Holocene/Wisconsinan transition 10 750 year B.P., seems to work well for dating the ice back to c. 10 000 year B.P. at sites in the slope regions of the Greenland ice sheet. As illustrated by the Milcent location of the western slope of the central Greenland ice sheet, the neglect of up-stream accumulation-rate and ice-thickness gradients may lead to dating errors as large as 3000’4000 years for c. 10 000 year old ice.

However, even if these gradients are taken into account, the simple model fails to give acceptable ages for 10 000 year old ice at locations on slightly sloping ice ridges with strongly divergent flow, as for example the Camp Century location. The main reason for this failure is that the site of origin of the ice cannot be determined accurately enough by the simple models, if the flow is strongly divergent. Another limitation to applying the simple models is that, at their present stage of development, they cannot handle the case of an up-stream accumulation-rate gradient simultaneously with convergence/divergence of the flow.

With these limitations, the models are believed to be useful for ice-sheet dating at locations where the available data or the required accuracy do not justify application of elaborate numerical models. Even though some of the formulae given in the previous sections may look rather complicated, they can easily be worked out on a pocket calculator, and will in many cases be a sensible alternative to using numerical flow models.

In conclusion, it should once more be pointed out that it does not make sense to use steady-state flow-model dating of Greenland or Antarctic ice older than 10 00011 000 years, because, prior to that time, substantial accumulation-rate changes had taken place, and there may also have been significant changes in ice thickness and flow pattern. For smaller ice caps, problems with steady-state model dating may already arise at an age of a few thousand years (Reference Reeh, Oeschger and LangwayReeh, 1989).