Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-16T22:07:18.571Z Has data issue: false hasContentIssue false
  • English
  • Français

MAXIMAL STABLE QUOTIENTS OF INVARIANT TYPES IN NIP THEORIES

Part of: Model theory

Published online by Cambridge University Press:  25 October 2023

KRZYSZTOF KRUPIŃSKI Open the ORCID record for KRZYSZTOF KRUPIŃSKI [Opens in a new window]  and
ADRIÁN PORTILLO Open the ORCID record for ADRIÁN PORTILLO [Opens in a new window]
KRZYSZTOF KRUPIŃSKI*
Affiliation:
INSTYTUT MATEMATYCZNY UNIWERSYTETU WROCŁAWSKIEGO PL. GRUNWALDZKI 2, 50-384 WROCŁAW, POLAND E-mail: [email protected]
ADRIÁN PORTILLO
Affiliation:
INSTYTUT MATEMATYCZNY UNIWERSYTETU WROCŁAWSKIEGO PL. GRUNWALDZKI 2, 50-384 WROCŁAW, POLAND E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a NIP theory T, a sufficiently saturated model 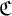${\mathfrak C}$ of T, and an invariant (over some small subset of 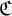${\mathfrak C}$) global type p, we prove that there exists a finest relatively type-definable over a small set of parameters from 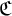${\mathfrak C}$ equivalence relation on the set of realizations of p which has stable quotient. This is a counterpart for equivalence relations of the main result of [2] on the existence of maximal stable quotients of type-definable groups in NIP theories. Our proof adapts the ideas of the proof of this result, working with relatively type-definable subsets of the group of automorphisms of the monster model as defined in [3].

Keywords

stable quotienthyperimaginaryinvariant type

MSC classification

Primary: 03C45: Classification theory, stability and related concepts
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben-Yaacov, I., Simplicity in compact abstract theories . Journal of Mathematical Logic , vol. 03 (2003), no. 02, pp. 163–191.Google Scholar
Haskel, M. and Pillay, A., On maximal stable quotients of definable groups in $NIP$ theories, this Journal, vol. 83 (2018), no. 1, pp. 117–122.Google Scholar
Hrushovski, E., Krupiński, K., and Pillay, A., On first order amenability, preprint, 2021, arXiv:2004.08306v2 [math.LO].Google Scholar
Krupiński, K., Newelski, L., and Simon, P., Boundedness and absoluteness of some dynamical invariants in model theory . Journal of Mathematical Logic , vol. 19 (2019), no. 02, p. 1950012.CrossRefGoogle Scholar
Krupiński, K., Pillay, A., and Rzepecki, T., Topological dynamics and the complexity of strong types . Israel Journal of Mathematics , vol. 228 (2018), pp. 863–932.Google Scholar
Krupiński, K. and Portillo, A., On stable quotients . Notre Dame Journal of Formal Logic , vol. 63 (2022), no. 3, pp. 373–394.Google Scholar
Onshuus, A. and Peterzil, Y., A note on stable sets, groups, and theories with NIP . Mathematical Logic Quarterly , vol. 53 (2007), no. 3, pp. 295–300.Google Scholar