1 INTRODUCTION
Since the inherent size and dimensionality of the data given by the observation such as the Sloan Digital Sky Survey (SDSS; York et al. Reference York2000), numerous methods have been developed in order to classify the spectra in an automatic way. The principal component analysis (PCA) is among the most widely used techniques. In Deeming (Reference Deeming1964), the PCA was first introduced to astronomical spectral data processing. The author investigated the application of PCA in classifying late-type giants. Connolly et al. (Reference Connolly, Szalay, Bershady, Kinney and Calzetti1995) discussed the application of PCA in the classification of optical and UV galaxy spectra. They found that the galaxy spectral types can be described in terms of one parameter family: the angle of the first two eigenvectors given by PCA. They also found that the PCA projection for galaxy spectra correlates well with star formation rate. Yip et al. (Reference Yip2004b), using PCA, studied the properties of the quasar spectra from SDSS with various redshifts.
Schematically, PCA attempts to explain most of the variation in the original multivariate data by a small number of components called principal components (PCs). The PCs are the linear combination of the original variables, and the PC coefficients (loadings) measure the importance of the corresponding variables in constructing the PCs. However, if there are too many variables, we may not know which variables are more important than others. In that case, the PCs may be difficult to interpret and explain. Different methods have been introduced to improve the interpretability of the PCs. The sparse principal component analysis (SPCA) has been proved to be a good solution to this problem. The SPCA attempts to give the sparse vectors, which will be used as PC coefficients. In sparse vectors, the components that correspond to the non-important variables will be reduced to zero. Then, the variables which are important in constructing PCs will become apparent. Using this way, the sparse PCA improves the interpretability of the PCs.
The SPCA method may originate from Cadima & Jolliffe (Reference Cadima and Jolliffe1995), in which the authors attempted to get the sparse principal components (SPCs) by a simple axis rotation. The following works, such as sparse PCA (SPCA; Zou, Hastie, & Tibshirani Reference Zou, Hastie and Tibshirani2006), direct approach of sparse PCA (DSPCA; d’Aspremont et al. Reference d’Aspremont, EI Ghaoui, Jordan and Lanckriet2007) and greedy search sparse PCA (GSPCA; Moghaddam, Weiss, & Avidan Reference Moghaddam, Weiss, Avidan, Scholkopf, Platt and Hoffman2007), show that the SPCA can be approached in different ways. In Sriperumbudur, Torres, & Gert (Reference Sriperumbudur, Torres and Lankriet2011), the authors introduced a sparse PCA algorithm, which they called the DCPCA (sparse PCA using a difference convex program) algorithm. Using an approximation that is related to the negative log-likelihood of a Student's t-distribution, in Sriperumbudur, Torres, & Gert (Reference Sriperumbudur, Torres and Lankriet2011), the authors present a solution of the generalised eigenvalue problems by invoking the majorisation–minimisation method. As an application of this method, a sparse PCA method called DCPCA (see Table 1) is proposed.
Table 1. The algorithm of DCPCA.

a A is the covariance matrix.
b Sn + is the set of positive semidefinite matrices of size n × n defined over R.
c X is an n-dimensional column vector.
To classify the spectra accurately and efficiently, various methods have been introduced to the spectral data processing. In Zhao, Hu, & Zhao (Reference Zhao, Hu and Zhao2005), Zhao et al. (Reference Zhao, Wang, Luo and Zhan2009), and Liu, Liu, & Zhao (Reference Liu, Liu and Zhao2006), the authors proposed several methods of feature lines extraction based on the wavelet transform. They first applied the wavelet transform to the data set and then used some techniques including sparse representation to extract the feature lines of spectra. In Weaver & Torres-Dodgen (Reference Weaver and Torres-Dodgen1997), the artificial neural networks (ANN) was applied in the problem of automatically classifying stellar spectra of all temperature and luminosity classes. In Singh, Gulati, & Gupta (Reference Singh, Gulati and Gupta1998), the PCA+ANN method was used in the stellar classification problem. A recently developed pattern classifier called support vector machine (SVM) has been used for separating quasars from large survey data bases (Gao, Zhang, & Zhao Reference Gao, Zhang and Zhao2008).
Compared with PCA, the SPCA method has not been widely studied in the spectral classification problem. In this paper, we will apply DCPCA, a recently developed sparse PCA technique, to extract the feature lines of cataclysmic variables’ spectra. We will make a comparison between the sparse eigenvector derived by DCPCA and the eigenvector given by PCA. We then apply this algorithm to reduce the dimension of the spectra and then use SVM for classification. This method (DCPCA+SVM) provides us with a new automatic classification method which can be reliably applied to a large-scale data set. The practical detail of this method will be given in Section 4. In the following, the sparse eigenvector given by DCPCA will be called sparse eigenspectrum (SES) and the eigenvector given by PCA called eigenspectrum (ES). The principal component given by SES will be called SPC.
The paper is organised as follows. In Section 2, we will give a brief introduction to the sparse algorithm DCPCA. In Section 3, we will give an introduction to cataclysmic variables (CVs). In Section 4, DCPCA will be used for feature extraction and then applied to reduce the dimension of the spectra to be classified. The advantage of this approach over the PCA will then be discussed. In Section 5, we consider the effect of parameter variation and present the practical technique about the reliable and valid applications of DCPCA. Section 6 concludes the work.
2 DCPCA: A BRIEF REVIEW
In this section, we will give a brief review of DCPCA for the sake of completeness. As for detailed description of DCPCA, as well as its application in the gene data, we refer the reader to Sriperumbudur, Torres, & Gert (Reference Sriperumbudur, Torres and Lankriet2011).
Let
Problem (1) is a special case of the following sparse generalised eigenvector problem (GEV):
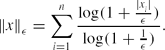 \begin{equation*}
\Vert x\Vert _\epsilon = \sum \limits _{i=1}^n\frac{\log (1+\frac{|x_i|}{\epsilon })}{\log (1+\frac{1}{\epsilon })}.
\end{equation*}
\begin{equation*}
\Vert x\Vert _\epsilon = \sum \limits _{i=1}^n\frac{\log (1+\frac{|x_i|}{\epsilon })}{\log (1+\frac{1}{\epsilon })}.
\end{equation*}
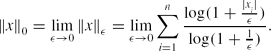 \begin{equation*}
\Vert x\Vert _0=\lim \limits _{\epsilon \rightarrow 0}\Vert x\Vert _\epsilon =\lim \limits _{\epsilon \rightarrow 0}\sum \limits _{i=1}^n\frac{\log (1+\frac{|x_i|}{\epsilon })}{\log (1+\frac{1}{\epsilon })}.
\end{equation*}
\begin{equation*}
\Vert x\Vert _0=\lim \limits _{\epsilon \rightarrow 0}\Vert x\Vert _\epsilon =\lim \limits _{\epsilon \rightarrow 0}\sum \limits _{i=1}^n\frac{\log (1+\frac{|x_i|}{\epsilon })}{\log (1+\frac{1}{\epsilon })}.
\end{equation*}
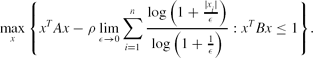 \begin{equation}
\max \limits _{x}\Bigg\lbrace x^TAx-\rho \lim \limits _{\epsilon \rightarrow 0}\sum \limits _{i=1}^n\frac{\log \big(1+\frac{|x_i|}{\epsilon }\big)}{\log \big(1+\frac{1}{\epsilon }\big)}: x^TBx\le 1\Bigg\rbrace.
\end{equation}
\begin{equation}
\max \limits _{x}\Bigg\lbrace x^TAx-\rho \lim \limits _{\epsilon \rightarrow 0}\sum \limits _{i=1}^n\frac{\log \big(1+\frac{|x_i|}{\epsilon }\big)}{\log \big(1+\frac{1}{\epsilon }\big)}: x^TBx\le 1\Bigg\rbrace.
\end{equation}
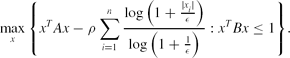 \begin{equation}
\max \limits _{x}\Bigg\lbrace x^TAx-\rho \sum \limits _{i=1}^n\frac{\log \big(1+\frac{|x_i|}{\epsilon }\big)}{\log \big(1+\frac{1}{\epsilon }\big)}: x^TBx\le 1\Bigg\rbrace.
\end{equation}
\begin{equation}
\max \limits _{x}\Bigg\lbrace x^TAx-\rho \sum \limits _{i=1}^n\frac{\log \big(1+\frac{|x_i|}{\epsilon }\big)}{\log \big(1+\frac{1}{\epsilon }\big)}: x^TBx\le 1\Bigg\rbrace.
\end{equation}
Let
![]() $\rho _\epsilon = {\rho }/{\log (1+\frac{1}{\epsilon })}$
. We can then reduce the above problem into the following d.c. problem:
$\rho _\epsilon = {\rho }/{\log (1+\frac{1}{\epsilon })}$
. We can then reduce the above problem into the following d.c. problem:
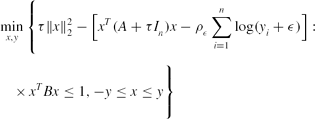 \begin{eqnarray}
&&\min \limits _{x,y}\Bigg\lbrace \tau \Vert x\Vert _2^2-\big[x^T(A+\tau I_n)x-\rho _\epsilon \sum \limits _{i=1}^n\log (y_i+\epsilon )\big]: \nonumber\\
&&\quad\times\, x^TBx\le 1, -y\le x\le y\Bigg\rbrace
\end{eqnarray}
\begin{eqnarray}
&&\min \limits _{x,y}\Bigg\lbrace \tau \Vert x\Vert _2^2-\big[x^T(A+\tau I_n)x-\rho _\epsilon \sum \limits _{i=1}^n\log (y_i+\epsilon )\big]: \nonumber\\
&&\quad\times\, x^TBx\le 1, -y\le x\le y\Bigg\rbrace
\end{eqnarray}
 \begin{eqnarray}
&& g((x,y),(z,w)):=\tau \Vert x\Vert _2^2-z^T(A+\tau I_n)z+\quad\rho _\epsilon \sum \limits _{i=1}^n\log (\epsilon +w_i)\nonumber\\
&&\quad-2(x-z)^T(A+\tau I_n)z+\rho _\epsilon \sum \limits _{i=1}^n\frac{y_i-w_i}{w_i+\epsilon },
\end{eqnarray}
\begin{eqnarray}
&& g((x,y),(z,w)):=\tau \Vert x\Vert _2^2-z^T(A+\tau I_n)z+\quad\rho _\epsilon \sum \limits _{i=1}^n\log (\epsilon +w_i)\nonumber\\
&&\quad-2(x-z)^T(A+\tau I_n)z+\rho _\epsilon \sum \limits _{i=1}^n\frac{y_i-w_i}{w_i+\epsilon },
\end{eqnarray}
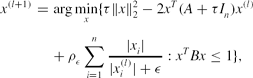 \begin{eqnarray}
x^{(l+1)}&=&\arg \min \limits _{x}\lbrace \tau \Vert x\Vert _2^2-2x^T(A+\tau I_n)x^{(l)}\nonumber\\
&& +\,\rho _\epsilon \sum \limits _{i=1}^n\frac{|x_i|}{|x_i^{(l)}|+\epsilon }:x^TBx\le 1\rbrace ,
\end{eqnarray}
\begin{eqnarray}
x^{(l+1)}&=&\arg \min \limits _{x}\lbrace \tau \Vert x\Vert _2^2-2x^T(A+\tau I_n)x^{(l)}\nonumber\\
&& +\,\rho _\epsilon \sum \limits _{i=1}^n\frac{|x_i|}{|x_i^{(l)}|+\epsilon }:x^TBx\le 1\rbrace ,
\end{eqnarray}
Briefly, the sparse PCA problem can be considered as a special case of the generalised eigenvector problem (GEV). By some approximate techniques, the GEV problem can be transformed to a continuous optimisation problem (COP) which can be solved in various ways. In the DCPCA algorithm, the COP is first formulated as a d.c. program. Then by the M-M algorithm, a generalisation of the well-known expectation–maximisation algorithm, the problem is finally solved.
Using DCPCA, we can get the first sparse eigenvector of the covariance matrix A, and then obtain the following r (r = 1, 2, …, m − 1), leading eigenvectors of A through the deflation method given in Table 2.
Table 2. The algorithm of iterative.

a A is the covariance matrix.
3 A BRIEF INTRODUCTION TO CATACLYSMIC VARIABLES
CVs are binary stars. The three main types of CVs are novae, dwarf novae, and magnetic CVs, each of which has various subclasses. The canonical model of the system consists of a white dwarf star and a low-mass red dwarf star, and the white dwarf star accretes material from the red one via the accretion disk. Because of thermal instabilities in the accretion disk, some of these systems may occasionally outburst and become several magnitudes brighter for a few days to a few weeks at most.
The spectra of CVs in an outburst phase have obvious Balmer absorption lines. A typical spectrum of CVs is given by Figure 1. The observation of 20 CVs and related objects by Li et al. presented us with the characteristics of the CVs spectra. They classified the spectra into the following three groups (Li, Liu, & Hu Reference Li, Liu and Hu1999):
-
• Spectrum with emission lines, including the hydrogen Balmer emission lines, neutral helium lines, and ionised helium lines, sometimes Fe ii lines and C iii/N iii lines. They are quiet dwarf nova or nova-like variables;
-
• Spectrum with the H emission lines, whose Balmer lines are absorption lines with emission nuclear core, sometimes with neutral helium lines. They are dwarf nova or nova-like variables in the outburst phase;
-
• Spectrum with Balmer lines, which have pure absorption spectra composed of helium lines, or emission nuclear in low quantum number of Balmer lines. They are probably dwarf stars in the outburst phase.

Figure 1. Spectrum of a cataclysmic variable star.
The observation of the CVs has a long history. Initial studies concentrated on the optical part of the spectrum. Thanks to the development of astronomical techniques and instruments, e.g., multi-fiber and multi-aperture spectrographs, adaptive optics, etc., it becomes possible for the multi-wavelength studies of the spectrum to gain the maximum information about this binary system. From 2001 to 2006, Szkody et al. had been using SDSS to search for CVs. These studies provide us with a sample of 208 CVs spectra (Szkody et al. Reference Szkody2002, Reference Szkody2003, Reference Szkody2004, Reference Szkody2005, Reference Szkody2006, Reference Szkody2007), which has the statistical significance for the following research.
In the following, we will first apply the DCPCA method to extract the characteristic lines of these spectra of CVs. Then, the DCPCA+SVM method will be applied to the automatic classification of CVs. The results show that this algorithm can effectively extract the spectral information of the celestial target, which approves that the method can be applied to the automatic classification system.
4 EXPERIMENT
4.1 Data preprocessing
The spectral data, each of which has 3,522 feature components, have been sky subtracted and flux normalised, and cover the wavelength range 3,800–9,000
![]() $\mathring{\text{A}}$
. Suppose the spectral data set is given by
$\mathring{\text{A}}$
. Suppose the spectral data set is given by
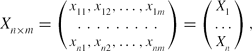 \begin{equation*}
X_{n\times m}=\left(\begin{array}{cccc}x_{11},x_{12},\dots ,x_{1m}\\
\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill \\
x_{n1},x_{n2},\dots ,x_{nm} \end{array}\right)=\left(\begin{array}{c}X_1\\
\dots \\
X_n \end{array}\right),
\end{equation*}
\begin{equation*}
X_{n\times m}=\left(\begin{array}{cccc}x_{11},x_{12},\dots ,x_{1m}\\
\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill\dotfill \\
x_{n1},x_{n2},\dots ,x_{nm} \end{array}\right)=\left(\begin{array}{c}X_1\\
\dots \\
X_n \end{array}\right),
\end{equation*}
Suppose that the SES Yi of length n has r non-zero elements, then the sparsity of Yi is defined as

Figure 2. Sparsity of the first SES versus parameter ρ by using two different initial vectors x
(0) = x
1 and x
(0) = x
2, where
![]() $x_1=(\frac{1}{\sqrt{3,522}},\dots ,\frac{1}{\sqrt{3,522}})^T$
and
$x_1=(\frac{1}{\sqrt{3,522}},\dots ,\frac{1}{\sqrt{3,522}})^T$
and
![]() $x_2=(\frac{1}{\sqrt{1,000}}, \dots , \frac{1}{\sqrt{1,000}},0,\dots ,0)^T$
. Both x
(0) satisfy (x
(0))
T
x
(0) = 1. The red diamond represents the result obtained by using x
1, and the blue diamond represents the result obtained by using x
2. This figure shows that the sparsity will change with the increase of ρ. Moreover, for a given sparsity, the corresponding ρ will vary with the change of the initial vector x
(0). Other x
(0) will lead to a similar conclusion. For simplicity, we will not give any further discussion on the effect of different x
(0).
$x_2=(\frac{1}{\sqrt{1,000}}, \dots , \frac{1}{\sqrt{1,000}},0,\dots ,0)^T$
. Both x
(0) satisfy (x
(0))
T
x
(0) = 1. The red diamond represents the result obtained by using x
1, and the blue diamond represents the result obtained by using x
2. This figure shows that the sparsity will change with the increase of ρ. Moreover, for a given sparsity, the corresponding ρ will vary with the change of the initial vector x
(0). Other x
(0) will lead to a similar conclusion. For simplicity, we will not give any further discussion on the effect of different x
(0).
4.2 Feature extraction using DCPCA
PCA has been used with great success to derive the eigenspectra for the galaxy classification system. The redshift measurement of galaxies and QSOs has also used the eigenspectrum basis defined by a PCA of some QSO and galaxy spectra with known redshifts. In this section, the DCPCA is first applied to derive the feature lines of CVs, then to get the SESs of CVs spectra, which provides a different approach to the feature extraction procedure. The experiment results show that this method is effective and reliable. The orientation of the eigenspectra given in the figures of this section will be arbitrary.
-
1. Feature lines extraction. In this scheme, the DCPCA is applied to derive the feature lines of CVs spectra. The original spectra and the corresponding feature lines derived by DCPCA are given by Figure 3. As we can see, the spectral components around the feature lines have been extracted successfully, in the meantime, the remaining components have been reduced to zero.
-
2. Feature extraction. The sample of CVs spectra data X 208×3,522 we used in this scheme are the 208 spectra observed in Szkody et al. (Reference Szkody2002, Reference Szkody2003, Reference Szkody2004, Reference Szkody2005, Reference Szkody2006, Reference Szkody2007). Let S 3,522×3,522 be the corresponding covariance matrix of X 208×3,522. We then apply the DCPCA algorithm to S 3,522×3,522 to get the SESs.
The first three SESs, and their comparison with the corresponding eigenspectra given by PCA, are given by Figures 4–6. As we have seen from these three figures, the non-essential parts of the spectra have been gradually reduced to zero by DCPCA. They illustrate the performance of the sparse algorithm DCPCA in feature extraction. Four obvious emission lines, i.e. Balmer and He ii lines, which we used to identify CVs, have been derived successfully. Thus, the spectral features in the SES given by DCPCA are obvious and can be interpreted easily. Nevertheless, as shown in Figures 4–6, it is difficult for us to recognise the features in the PCA eigenspectra. This confirms that SES is more interpretable than ES.

Figure 3. (a) Original spectrum of CVs and (b) feature lines extracted by DCPCA.

Figure 4. The first eigenspectra given by PCA and DCPCA. (a) The first eigenspectrum given by PCA; the first SES with sparsity (b) h = 0.0009, (c) h = 0.1911, and (d) h = 0.9609. Panels (a–d) show that the difference between eigenspectra given by PCA and DCPCA gradually becomes apparent. Panels (a) and (b) can be considered as the same figure (the sum of their difference is less than 0.03). The differences between (a) and (c–d) are apparent. These SESs are chosen from the 101 SESs obtained by using the method given by Section 4.1.

Figure 5. The second eigenspectra given by PCA and DCPCA. (a) The second eigenspectrum given by PCA; the second SES with sparsity (b) h = 0, (c) h = 0.2348, and (d) h = 0.9171. The differences between panels (a) and (b–d) are apparent. The SESs are chosen from the 101 SESs obtained by using the method given by Section 4.1.

Figure 6. The third eigenspectra given by PCA and DCPCA. (a) The third eigenspectrum given by PCA; (b) the third SES with sparsity (b) h = 0, (c) h = 0.2641, and (d) h = 0.9645. The differences between panels (a) and (b–d) are apparent. The SESs are chosen from the 101 SESs obtained by using the method given by Section 4.1.
As we have seen, the non-essential parts of the spectra now are reduced to the zero elements of SESs. However, if there are too many zero elements in SESs, the spectral features will disappear. Then, it is crucial for us to determine the optimal sparsity for the SESs. The optimal sparsity should have the following properties: the SES with this sparsity retains the features of the spectra and, at the same time, it has the minimum number of the non-zero elements.
In order to determine the optimal value of sparsity, we plot the eigenspectra with different sparsity and then compare them. As shown in Figure 7, the sparsity of the eigenspectrum between 0.95 and 0.98 is optimal. If the sparsity is below 0.95, there are still some redundant non-zero elements in the SES. If the sparsity is above 0.98, some important spectral features will disappear.

Figure 7. The first sparse eigenspectra with various sparsity. The spectral features will disappear if sparsity is above 0.98, while the redundant elements of the spectrum have not been reduced to zero if sparsity is below 0.95.
4.3 Classification of CVs based on DCPCA
4.3.1 A review of support vector machine
The SVM, which is proposed by Vapnik and his fellowships in 1995 (Vapnik Reference Vapnik1995) is a machine learning algorithm based on statistical learning theory and structural risk minimisation (Christopher Reference Burges1998). It mainly deals with two-category classification problems, and also regression problems. Suppose that we have a training data set
SVM has been proved to be efficient and reliable in the object classification. In our experiments, DCPCA is applied to reduce the size of spectra from 3,522 to 3 sparse PCs and then SVM is used for an automatic classification. The comparison of this method with the related PCA+SVM method will then be presented.
When we apply SVM to the classification problem, the parameter σ in the Gaussian kernel function needs to be determined. In our experiments, for the sake of simplicity, we make a priori choice of using σ = 1. We will show in Section 4.3.2 that the classification results are almost independent of the value of σ. Since the choice of σ has no direct influence on our conclusion, this is not discussed further. However, it is worth noting here that there is extensive literature on how to choose an appropriate kernel parameter for each particular data set (Ishida & de Souza Reference Ishida and de Souza2012).
4.3.2 Classification using SVM
As the PCA method has been used as a dimensionality reduction tool in spectral classification, we may wonder whether the DCPCA can be used to accomplish the same task. In this section, the following two methods will be applied to the CVs separation problem:
-
• DCPCA+SVM.
-
• PCA+SVM.
The spectral data we used are provided by the Data Release 7 of SDSS. The detailed information of these spectra is given in Table 3. The data set is randomly divided into two equal parts: D1 and D2. Then, 208 CVs spectra are randomly divided into two equal parts: C1 and C2. The data D1+C1 will be used for training and D2+C2 for testing. The final classification results will be represented by the classification accuracy r, which is defined by
Table 3. Information of the spectral data.

1. DCPCA+SVM. In this scheme, the SVM is applied to the first three dimension data which are obtained by the first three SESs with various sparsity. We will investigate the relationship between the classification result and the sparsity of the SES. We will show that the classification results will not decrease with the increase of sparsity.
The procedure of the experiment is given in Table 4. The first two DCPCA-projected dimensions of the CVs spectra data are given in Figure 8(b). The two-dimensional representation of the classification result is given in Figures 9(a) and (b). For clarity, we will show the CVs and non-CVs in the test set in two different plots (Figures 9 a and b). We also plot the decision boundary given by SVM in training. The objects of the test set located on one side of the decision boundary will be classified as CVs, and others will be classified as non-CVs. As we can see, the CVs have been generally well separated in the two-dimensional projected space. The classification results obtained by using the first three PCs (including using 1 PC, 2 PCs, and 3 PCs), which are obtained by the first three SESs with various sparsity, are shown in Figure 10. From Figure 10, we find that the classification accuracies have not decreased with the increase of sparsity. Therefore, we conclude that, while reducing most of the elements into zero, DCPCA retains the most important characteristics of the spectra in the SESs.
Table 4. Experiment using DCPCA+SVM.


Figure 8. Two-dimensional projection of 208 CV spectra given by (a) PCA and (b) DCPCA.

Figure 9. Result of DCPCA+SVM. SPC1 represents the first sparse principal component computed with DCPCA, and SPC2 is the second principal component. The sparsity of the SESs which are applied to get SPC1 and SPC2 is 0.9749. The training set is represented by the red star (CVs), green circles (non-CVs). The decision boundary of SVM is applied to classify the CVs and non-CVs in the test set. (a) CVs test sample points (blue diamond) are superimposed to the training set. (b) Non-CVs test sample points (blue dots) are superimposed to the training set. This figure and the following figure (Figure 11) are merely two-dimensional illustrations to show the projected spread of points. This particular configuration is not used in the classification.

Figure 10. Classification accuracy versus sparsity of the SESs. It shows that the classification results using four SPCs, which are obtained by the first four SESs, are similar to those using three SPCs. Thus, the discussion about the relationship between classification results and the sparsity is limited on the first three SESs.

Figure 11. Result of PCA+SVM. PC1 represents the first principal component computed with PCA, and PC2 is the second principal component. The training set is represented by the red star (CVs) and green circles (non-CVs). The decision boundary of SVM is applied to classify the CVs and non-CVs in the test set. (a) CVs test sample points (blue diamond) are superimposed to the training set. (b) Non-CVs test sample points (blue dots) are superimposed to the training set. This figure is merely two-dimensional illustrations to show the projected spread of points. This particular configuration is not used in the classification.
Four SESs with various sparsity have been used in the experiment. As shown in Figure 10, the results have not been improved significantly. Thus, we limit our discussion to the first three SESs for clarity.
2. PCA+SVM. In this scheme, first, PCA is applied to reduce the spectral data into 1–11 dimensions, and then the SVM method is used for automatic classification. The procedure of the experiment is given in Table 5. The first two PCA-projected dimensions of the CVs spectra are given in Figure 8(a). The two-dimensional representation of the classification results is given in Figure 11, in which the CVs and non-CVs points in the test set are represented as Figure 9. The classification accuracies for varying dimensions of feature vectors are given by Table 6.
Table 5. Experiment using PCA+SVM.
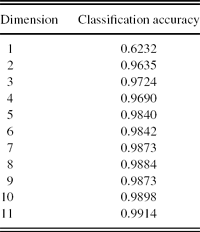
Table 6. Classification accuracy of PCA+SVM.

3. Comparison of DCPCA+SVM and PCA+SVM. In this scheme, we will compare the performance of ES with that of SES in classification.
First, we perform DCPCA+SVM by using the first four SESs with various sparsity, and then compare the performance with that of PCA+SVM. The comparison of these two methods is given by Figure 12. Though the DCPCA+SVM results will vary with the increase of the sparsity, we find that DCPCA+SVM has separated the CVs with great success from other objects, and its performance is comparable with that of PCA+SVM.

Figure 12. Classification results’ comparison between PCA+SVM and DCPCA+SVM. The dot line represents the classification accuracy based on PCA. Classification accuracies using (a) the first SES with various sparsity, (b) the first two eigenspectra (SESs) with various sparsity, (c) the first three SESs with various sparsity, and (d) the first four SESs with various sparsity. Panels (a–d) show that the SESs perform similar to eigenspectra in the classification, though most of the elements in SESs are zero.
Second, we perform DCPCA+SVM by using the first 11 SESs with the optimum sparsity (the average sparsity is 0.9781), and then make a comparison with PCA+SVM. The results are given in Figure 13. We find that when we use the optimum SESs (SES with the optimum sparsity), DCPCA+SVM performs better than PCA+SVM.

Figure 13. Classification results of DCPCA+SVM and PCA+SVM obtained by using the first 11 PCs. The SPCs used in DCPCA+SVM are obtained by the optimal SESs (the SESs with the sparsity lie within the optimum interval). The average sparsity of the first 11 SESs used in experiment is 0.9781. It also shows that the first three SPCs are enough for a good result, and the classification accuracies are not improved significantly if we use more than three SPCs.
Figures 12 and 13 show that the performance of DCPCA+SVM is comparable with that of PCA+SVM. When we use the optimum SESs (the average sparsity is 0.9781), DCPCA+SVM performs better than PCA+SVM. Thus, we conclude that the SESs contain significant amounts of classification information, especially the optimum SESs. Furthermore, both figures show that the classification accuracies using more than three SESs are not improved significantly than using the first three SESs, which is consistent with the result given in Figure 10.
In order to minimise the influence of random factors, the experiments have been repeated 10 times, and the classification accuracies given above are the average values. The effect of varying σ in the Gaussian kernel has been studied (see Figure 14). We find that the classification results are almost independent of the value of σ.

Figure 14. Classification results of SVM by using first two SESs with various sparsity versus σ in the Gaussian kernel. Sparsity of the first two SESs is (a) 0.004, (b) 0.5647, (c) 0.9299, and (d) 0.9848. Panels (a–d) show that the classification results are almost independent of σ. The results of using other numbers of SESs are similar.
5 DISCUSSION
Besides the parameters in Algorithm 1, there are three parameters that need to be determined in our experiment: the σ in the Gaussian kernel, the optimal sparsity h of the SESs, and the number of the PCs we used in DCPCA+SVM. As discussed in Section 4.3.1 and shown in Figure 14, the variation of σ has no direct influence on the classification result. So, we set σ = 1 in the experiment. In the DCPCA+SVM experiment in Section 4.3.2, only the first three SPCs with various sparsity are utilised, because more SPCs will not improve the classification accuracy significantly, as shown in Figures 10 and 13.
For the sparsity h of the SES, we find in Section 4.2 that h whose value is in the range of 0.95–0.98 is optimal. To verify the conclusion, we will compare the performance of these SESs in the DCPCA+SVM experiment. Namely, the SESs with various sparsity will be applied to get the sparse principal components (SPCs), which will be used in the DCPCA+SVM experiment, and in turn, the performance of these SPCs will be utilised to evaluate these SESs. The SESs are divided into three groups: the SESs with sparsity between 0.95 and 0.98 (SES1), SESs with sparsity above 0.98 (SES2), and SESs with sparsity lower than 0.95 (SES3). Then, these SESs will be used in the DCPCA+SVM experiment. The experiment results are shown in Figure 15. We find that the classification results using SES1 are obviously better than those using SES2 and SES3, which confirms that the sparsity between 0.95 and 0.98 is optimal.

Figure 15. Classification accuracy versus sparsity. The SESs are divided into three groups: SESs with sparsity between 0.95 and 0.98 (SES1), SESs with sparsity above 0.98 (SES2), and SESs with sparsity below 0.95 (SES3). Then these SESs are utilised to get the SPC groups: SPC1, SPC2, and SPC3. These SPCs will then be used in the DCPCA+SVM experiment as in Section 4.3.2. (a) The result of SPC1+SVM versus the result of SPC2+SVM, and (b) the result of SPC3+SVM versus the average result of SPC1+SVM. Panel (a) shows that when the sparsity is above 0.98, the classification result will be unstable. Panels (a) and (b) show that the classification results using SPC1 are significantly better than those using SPC2 and SPC3. It implies that SES1 performs better than SES2 and SES3 in the classification. For the sake of simplicity, we use the first SPC in the classification. The classification results of using other numbers of SPCs are similar.
Despite DCPCA is reliable in extracting spectral features, it is worth noting that it may take a long time to determine a suitable ρ with which we can obtain a required SES. As shown in Figure 2, the sparsity of the SES depends on the value of the parameter ρ. However, using the method specified in Section 4.1, we can get the optimal SES (the sparsity of which lies within the optimum interval) quickly. Thus, there is no need to determine the optimum ρ (by which we can get the optimal SES) in application. Moreover, as shown in Figure 2, for a given sparsity, the corresponding ρ will vary with the change of the initial vector x (0). It makes no sense for us to determine the optimum ρ. Though the vector x (0) can also affect the final results, we will not discuss it further for simplicity.
Using the method proposed in Section 4.1, we can obtain 101 different SESs corresponding to each eigenspectrum given by PCA (i.e., we can obtain 101 SESs with various sparsity corresponding to the first eigenspectrum of PCA, 101 SESs with various sparsity corresponding to the second eigenspectrum of PCA, etc.). All SESs used in the experiment and shown in figures are chosen from these SESs. It is difficult to obtain the SESs with exactly the same sparsity. For example, the sparsity of the first optimum SES is 0.9759, while that of the second one is 0.9739. In fact, we will not have to obtain the SESs with exactly the same sparsity. We just need to obtain the SESs with the sparsity lying in some interval, such as the optimum interval 0.95–0.98. Thus, if we use more than one SES but provide only one sparsity in the experiment, this sparsity is the average value. For example, we used the first 11 optimum SESs in Figure 13.Since these optimum SESs possess different sparsity, we only provide the average sparsity 0.9781 in the figure.
6 CONCLUSION
In this paper, we first demonstrate the performance of the DCPCA algorithm in the feature lines extraction by applying it to the CVs spectra data. Then, we present an application of this algorithm in the classification of CVs spectra. In the classification experiments, we first use the DCPCA to reduce the dimension of the spectra, and then use SVM to classify the CVs from other objects. The result comparing with the traditional PCA+SVM method shows that the reduction of the number of features used by classifier does not necessarily lead to a deterioration of the separation rate. Compared with PCA, the sparse PCA method has not been widely applied in the spectral data processing. Nonetheless, the demonstrations given here have shown the perspective of the sparse PCA method in this route. We find that
-
1. DCPCA is reliable in extracting the feature of spectra. Compared with the eigenspectra given by PCA, SESs are more interpretable. Thus, the spectral feature of CVs can be well described by the SES whose number of non-zero elements is dramatically smaller than the number usually considered necessary.
-
2. Changing σ in Gaussian has no direct influence on our conclusion.
-
3. The sparsity of SESs between 0.95 and 0.98 is optimum.
-
4. When we use SESs with the optimum sparsity (the average sparsity is 0.9781), DCPCA+SVM will perform better than PCA+SVM.
-
5. The parameter ρ has a direct influence on the sparsity of SES. However, it is not necessary for us to determine the optimum ρ. Using the method given in Section 4.1, we can get the optimal SES without any prior knowledge of the optimal ρ.
ACKNOWLEDGMENTS
We thank the referee for a thorough reading and valuable comments. This work is supported by the National Natural Science Foundation of China (grants 10973021 and 11078013).
APPENDIX: PRINCIPAL COMPONENT ANALYSIS
Consider a data set
























