2 Features of nonlinear compression with the use of KDP

All the aspects of nonlinear compression (spectrum broadening, pulse shortening, and peak intensity increase) were considered in detail in Ref. [Reference Khazanov, Mironov and Mourou3] as a function of two key parameters: the В-integral (Equation (1)) and the dimensionless parameter of nonlinear medium dispersion

(2) \begin{align}D=L\frac{k_2}{T_{\mathrm{F}}^2},\end{align}

where T _F is the full width at half maximum (FWHM) duration of the input Fourier-transform-limited (FTL) Gaussian pulse. The parameters B and D characterize nonlinearity and dispersion and have a simple physical meaning: B is the ratio of the medium length L to the nonlinear length (the length at which a nonlinear phase equal to 1 is accumulated) and D is the ratio of L to the dispersion length L _d = T _F ²/k ₂. The KDP crystal at the wavelength λ = 910 nm has a very small value of k ₂ = 11.3 fs²/mm. Hereinafter, we use the Sellmeier equation from Ref. [Reference Zernike30]. Moreover, k ₂ reduces with growing λ and at λ = 985 nm changes its sign. Consequently, not only group velocity dispersion k ₂ but also the next, third-order dispersion (TOD) should be taken into account. For silica, the value of k ₂ is much higher (28 fs²/mm). However, as we show in the following, at large B values the effect of TOD is even more significant.

With allowance for TOD, the laser pulse propagation in a medium with Kerr nonlinearity is described by the equation

(3) \begin{align}\frac{\partial a}{\partial \xi }\,{-}\,\frac{i\cdot D}{2}\frac{\partial^2a}{\partial {\eta}^2}\,{+}\,\frac{T}{6}\frac{\partial^3a}{\partial {\eta}^3}\,{=}-iB\left({\left|a\right|}^2\cdot a\,{-}\,\frac{2\cdot i}{\unicode{x3c0} \cdot N}\,\frac{\partial}{\partial \eta}\left({\left|a\right|}^2\cdot a\right)\right)\!,\end{align}

where ξ=z/L, z is the longitudinal coordinate, L is the thickness of the plate, η=(t-z/u)/T _F, 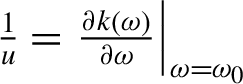$\frac{1}{u}={\left.\frac{\partial k\left(\omega \right)}{\partial \omega}\right|}_{\omega ={\omega}_0}$ , a=A/A ₁₀ is the complex amplitude of the field normalized to the value at the input boundary (A ₁₀), T=Lk ₃/T _F ³ is the dimensionless parameter TOD, 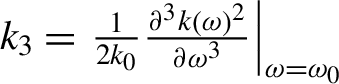${k}_3={\left.\frac{1}{2{k}_0}\frac{\partial^3k{\left(\omega \right)}^2}{\partial {\omega}^3}\right|}_{\omega ={\omega}_0}$ , k(ω)=n(ω)ω/с is the wave vector, k ₀ =k(ω₀), N=T _F/τ, and τ =2π/ω₀ is the period of the optical field. At the input of the nonlinear medium, let there be a Gaussian FTL pulse

(4) \begin{align}a\left(t,z=0\right)={e}^{-2\cdot \ln (2)\cdot \frac{t^2}{T_{\mathrm{F}}^2}}.\end{align}

CMs introduce a quadratic spectral phase; thereby the field amplitude of the output (compressed) pulse a _out is defined by

(5) \begin{align}{a}_{\mathrm{out}}(t)={F}^{-1}\left({e}^{-\frac{i\alpha \cdot {\Omega}^2}{2}}\cdot F\left(a\left(t,z=L\right)\right)\right).\end{align}

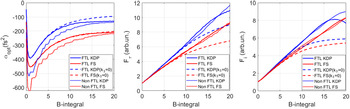
where Ω = ω – ω₀, α is the parameter of CM dispersion, and F and F ^–1 are the direct and inverse Fourier transforms. The quantity α_opt designates the value of α at which the compressed pulse intensity I _out is maximal, and hence, the intensity increase factor F _i = I _out/I _in is also maximal. The numerical modeling (Equations (3)–(5)) was performed for KDP and silica with the parameters given in Table 1. Values of B were varied from 0 to 20 by changing the input pulse intensity I _in. Here B = 10 corresponds to an intensity of 0.79 TW/cm² for KDP and 1.18 TW/cm² for silica. Curves for α_opt(B) are plotted in Figure 1(a). The dashed curves for k ₃ = 0 are given for comparison. Analogous curves for F _τ = τ_in/τ_o and F _i at α = α_opt are plotted in Figures 1(b) and 1(c).

Table 1 The parameters of numerical modeling.

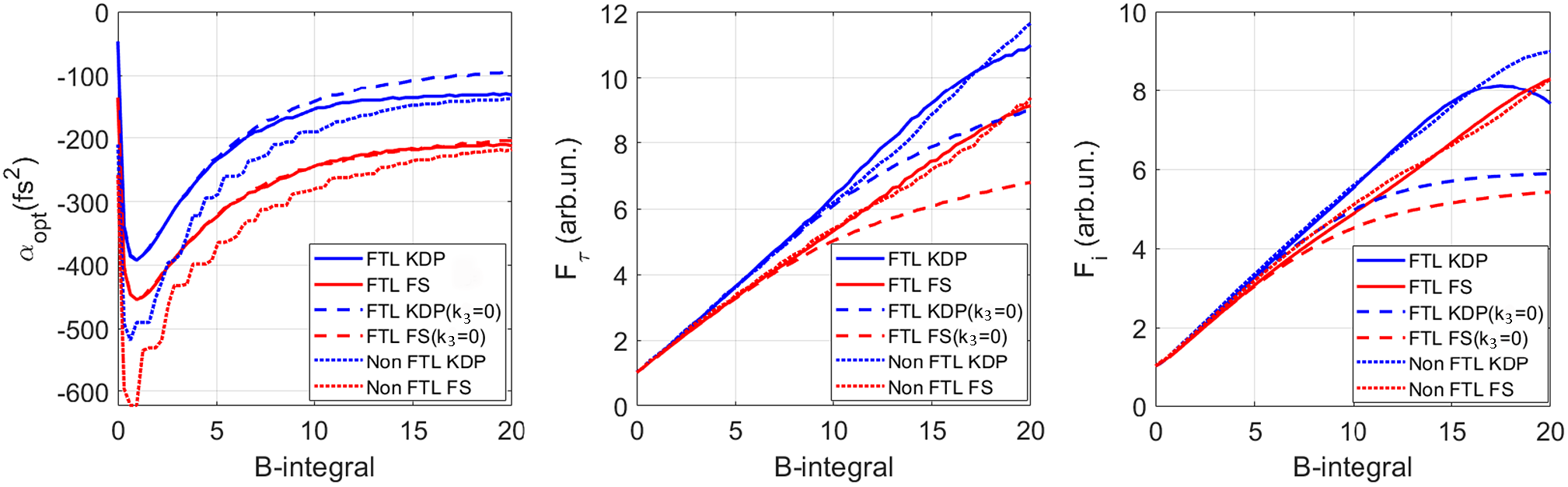
Figure 1 Curves for (a) α_opt(B), (b) F _τ(B), and (c) F _i(B) for α = α_opt for KDP (blue) and silica (red): FTL pulse at k ₃ ≠ 0 (solid curves) and k ₃ = 0 (dashed curves); non-Gaussian FTL pulse, the spectrum and autocorrelation function of which are presented in Figure 3(a) (dotted curves). FTL, Fourier-transform-limited.

It is clear from Figure 1(a) that at large B the allowance for TOD in KDP (in contrast to silica) results in an increase in the absolute value of α_opt, which should be taken into consideration when planning experiments. In addition, with TOD taken into account, both F _τ and F _i become much larger for both KDP and silica. This is quite unexpected. Physically this is explained by the fact that at SPM the pulse acquires not only a positive quadratic spectral phase that is compensated by the negative quadratic dispersion of CMs, but also a negative cubic spectral phase that is partially compensated for by the positive cubic dispersion of the medium. As the values of T are identical for KDP and silica (see Table 1), the effect of TOD on these media is approximately the same (see Figures 1(a)–1(c)).

3 Experimental results

The schematic diagram of the experiment is shown in Figure 2. After reflection from the last diffraction grating of the compressor, the PEARL laser beam (central wavelength of about 910 nm) with a pulse energy of up to 18 J, a duration of 55–67 fs, and a diameter of 18 cm propagated 2.5 m in free space for self-filtering^[ Reference Mironov, Lozhkarev, Ginzburg, Yakovlev, Luchinin, Shaykin, Khazanov, Babin, Novikov, Fadeev, Sergeev and Mourou ^{18 ]}. After that, the beam was propagated in a 4-mm-thick homemade KDP crystal with angles of optical axes θ = φ = 0. The output surface had an anti-reflecting coating. We used the reflection from the input uncoated surface to measure the spectrum and the autocorrelation function (ACF) of the input pulse. The measurements were made for a small part of the beam with a diameter of 1 cm. After free propagation over a distance of 6 m, the beam was reflected from CMs with a diameter of 20 cm manufactured by UltraFast Innovations GmbH (reflection coefficient >99%, bandwidth >200 nm). We used mirrors with sum dispersion α = −100 fs², −200 fs², and −250 fs². In addition, in the experiments with α = −200 fs² and −250 fs² we placed a 1-mm-thick silica plate before the autocorrelator to introduce additional dispersion α = +28 fs², which is equivalent to the sum CMs dispersion α = −172 fs² and −222 fs², respectively.

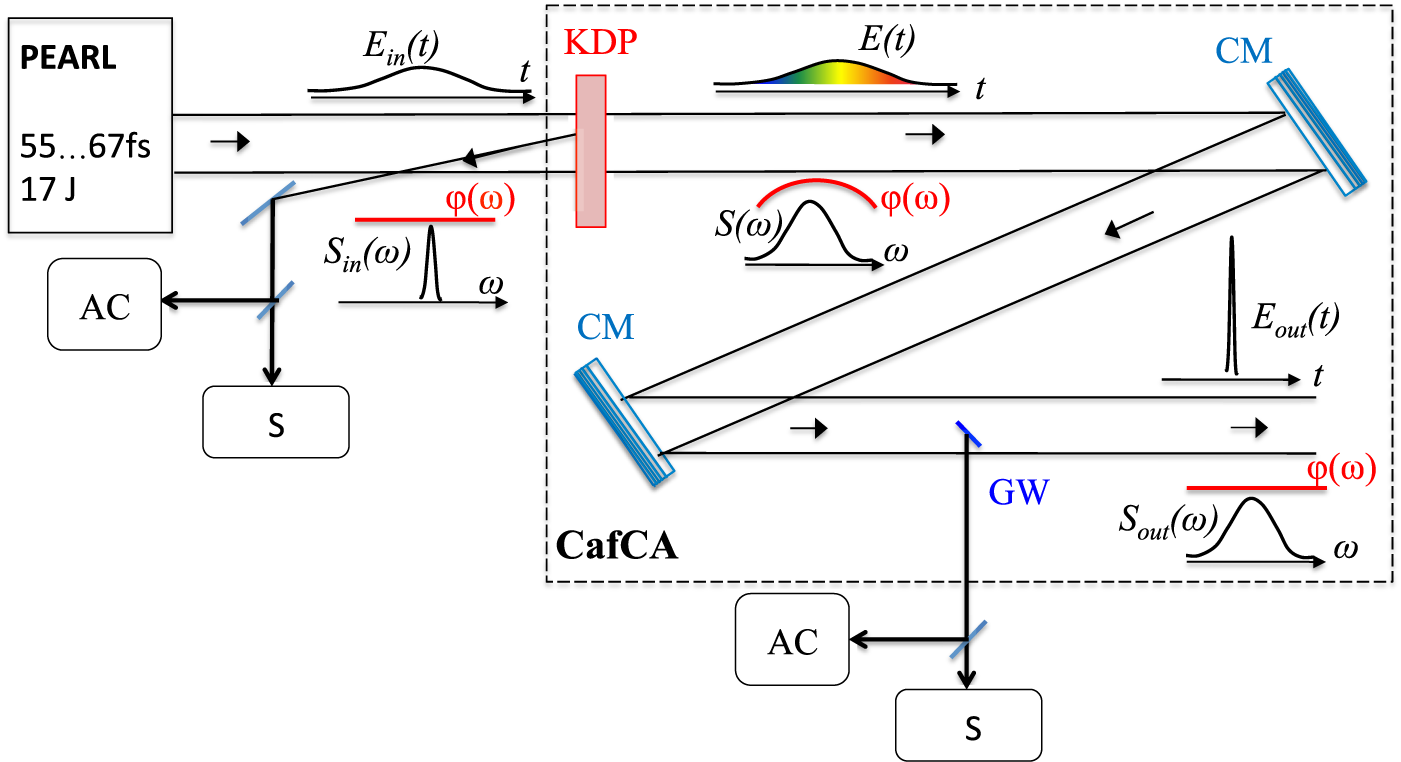
Figure 2 Schematic of the experiment. CM, chirped mirror; GW, small-aperture glass wedge; AC, autocorrelator; S, spectrometer.

To measure the parameters of the output (compressed) pulse, a glass wedge (GW) with an aperture of 1 cm × 2 cm and a matt back surface was placed in the beam path. The beam reflected from the first surface of the wedge was directed to the spectrometer and the autocorrelator. The position of the wedge within the beam aperture corresponded to the place where the ACF and the spectrum of the input beam were measured, which made it possible to measure the characteristics of the input and output pulses in a single shot. We used 1.42 as a decorrelation factor to calculate the pulse duration from the autocorrelation function.

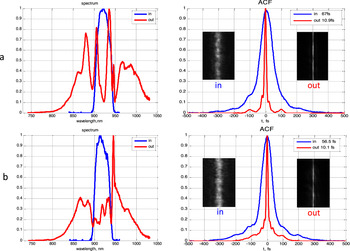
Typical measurement results are presented in Figure 3 for two shots at α = −200 fs². The output pulse spectra have characteristic narrow peaks arising because the input pulses are not FTL (see Ref. [Reference Ginzburg, Kochetkov, Yakovlev, Mironov, Shaykin and Khazanov23] for details). Note that the measured output pulse spectrum is bounded at the longwave side by the spectrometer bandwidth (1030 nm).

Figure 3 Measured input (blue) and output (red) spectra and ACF for two typical shots: (a) B = 13, τ_in = 67 fs, τ_out = 10.9 fs and (b) B = 14, τ_in = 57 fs, τ_out = 10.1 fs.

An yoptimal value of CMs dispersion α_opt depends on B (see Figure 1(a)). The curves for the minimal duration of a compressed pulse τ_out as a function of α for two ranges B = 5, …, 9 and B = 11, …, 19 are plotted in Figure 4. Analogous curves for 5-mm-thick and 3-mm-thick silica^[ Reference Ginzburg, Yakovlev, Zuev, Korobeynikova, Kochetkov, Kuzmin, Mironov, Shaykin, Shaikin, Khazanov and Mourou ^{15 ,} Reference Ginzburg, Yakovlev, Zuev, Korobeynikova, Kochetkov, Kuzmin, Mironov, Shaykin, Shaikin and Khazanov ^{20 ]} are also presented in this figure. Note that these are qualitative data, as a different number of shots were made for different values of α. Nevertheless, some conclusions follow from Figure 4. First, the value of α_opt decreases with a decrease in the parameter D: α_opt is maximal for 5-mm-thick silica (D = 0.037 at τ_in = 61 fs) and minimal for KDP (D = 0.01 at τ_in = 61 fs). The difference is not very large for large values of B, but is significant for small B. This fully agrees with Figure 1(a). Second, the absolute values of α_opt obtained experimentally are larger than those predicted theoretically (see Figure 1(a)). The reason is that the pulse used in experiments was not an FTL pulse. The absolute value of α_opt for such pulses is much larger than for FTL pulses, which was first noted in Ref. [Reference Mironov, Ginzburg, Yakovlev, Kochetkov, Shaykin, Khazanov and Mourou11]. To illustrate this fact, we presented in Figure 1(a) an α_opt(B) curve for a KDP crystal for the case when the input pulse has the spectrum and ACF shown in Figure 3(a): the dotted blue curve is lower than the solid curve. Third, from the viewpoint of minimal pulse duration, KDP, although slightly, is preferable to silica: 10 versus 11 fs at large values of B and 13 versus 16 fs at small B. This also agrees with the results of numerical modeling (see Figure 1).

Figure 4 Experimental minimal compressed pulse duration τ_out for KDP (L = 4 mm), silica (L = 5 mm), and silica (L = 3 mm^[ Reference Ginzburg, Yakovlev, Zuev, Korobeynikova, Kochetkov, Kuzmin, Mironov, Shaykin, Shaikin, Khazanov and Mourou ^{15 ,} Reference Ginzburg, Yakovlev, Zuev, Korobeynikova, Kochetkov, Kuzmin, Mironov, Shaykin, Shaikin and Khazanov ^{20 ]}) for two ranges of B values. The curves are plotted to make the figure more illustrative.

The experimental data for τ_in=55, …, 67 fs obtained at α = −200 fs² are presented in Figure 5. The peak power P _out for a compressed pulse with τ_out = 10 fs was 1.5 PW (we took into account the 20% losses associated with a lower intensity at the beam periphery and the respective larger τ_out). Despite the spread in the values in Figure 5, we can claim that at α = −200 fs² there exists an optimal value of the B-integral (of the order of 15) at which τ_out is minimal and F _τ is maximal. With a further increase in B, the input pulse spectrum is broadened but, despite this fact, τ_out increases as |α_opt| is already less than 200 fs², that is, CMs have redundant dispersion, as a result of which the output pulse is negatively chirped. At the same time, Figure 5 demonstrates that in a wide range of B-integral values from 11 to 19, for the same CMs set (α = −200 fs²), all the shots are within the interval of τ_out from 9.3 to 13.6 fs and F _τ from 4.6 to 7. From the practical point of view, this spread is not very large and can be made even less if the input pulse has more stable duration and spectral phase.

Despite the huge values of the B-integral, no damage was observed either in KDP or in CMs, that is, small-scale self-focusing was not a significant issue. One of the reasons for this is a significant shift of the maximum of the increment of self-focusing instability to the region of high spatial frequencies, which results in a reduced noise power in the region of the maximal increment due to a decrease in the spectral density of the noise^[ Reference Ginzburg, Kochetkov, Mironov, Potemkin, Silin and Khazanov ^{31 ]} and beam self-filtering at free propagation^[ Reference Mironov, Lozhkarev, Ginzburg, Yakovlev, Luchinin, Shaykin, Khazanov, Babin, Novikov, Fadeev, Sergeev and Mourou ^{18 ,} Reference Mironov, Lozhkarev, Luchinin, Shaykin and Khazanov ^{19 ,} Reference Ginzburg, Kochetkov, Mironov, Potemkin, Silin and Khazanov ^{31 ,} Reference Ginzburg, Kochetkov, Potemkin and Khazanov ^{32 ]}. Another possible reason is the convective nature of the self-focusing instability at pulse duration commensurate with 10 field periods^[ Reference Balakin, Litvak, Mironov and Skobelev ^{33 ,} Reference Balakin, Kim, Litvak, Mironov and Skobelev ^{34 ]}. The suppression of small-scale self-focusing is discussed in more detail in Ref. [Reference Khazanov, Mironov and Mourou3].

Note that further power scaling may be limited by damage threshold which strongly depends on the polishing and coating quality. Being a water-soluble crystal, KDP requires more efforts for both polishing and coating compared with silica. In addition, there could be crystal degradation effects on a longer term. This could limit the use of KDP in high peak power femtosecond lasers with high repetition rate.

Figure 5 Output pulse duration τ_out (blue) and pulse compression factor F _τ = τ_in/τ_out (red) at α = −200 fs²; τ_in = 55, …, 67 fs.

Thus, we have experimentally demonstrated that KDP can give results similar to (τ_in/τ_out > 6), and even a little better (τ_out = 10 fs) than those we have recently obtained with silica^[ Reference Ginzburg, Yakovlev, Kochetkov, Kuzmin, Mironov, Shaikin, Shaykin and Khazanov ^{17 ]}, with the superiority of KDP being still more pronounced for small B-integrals (B = 5, …, 9) (see Figure 4). In addition, KDP has a number of other advantages. First, for KDP the α_opt values are smaller (Figures 1(a) and 4). This allows a smaller number of mirrors to be used or the same number of mirrors but with lower dispersion, which are easier to produce. Second, for KDP the value of α_opt changes less with the variation of the B-integral (Figure 4). This makes it possible to use one set of CMs for a wide range of intensities, as demonstrated in Figure 5. Third, KDP anisotropy enables controlling linear and nonlinear properties of the material by choosing crystal orientation that is determined by the angles θ and φ. Like in any uniaxial crystal, the linear refractive index (and, hence, k ₂ and k ₃) of an ordinary wave depends neither on θ nor on φ. However, similarly to any tetragonal crystal of $\overline{4}22$ symmetry, n ₂ does not depend on θ, but is dependent on φ^[ Reference Banks, Feit and Perry ^{35 ]}, and n ₂ maxima and minima are, respectively, at φ = 0+πm/2 and φ = π/4+πm/2 (m is an integer). Thus, for example, by rotating a z-cut crystal (θ = 0) around the z-axis it is possible to continuously change the В-integral by about a factor of 1.5: n ₂(θ = 0, φ = 0) = 4.6 × 10^–16 cm²/W, and n ₂(θ = 0, φ = π/4) = 3.3 × 10^–16 cm²/W^[ Reference Kulagin, Ganeev, Tugushev, Ryasnyansky and Usmanov ^{36 ]}. Still more opportunities are provided by an extraordinary wave for which k ₂ and k ₃ depend on θ, and n ₂ depends on both θ and φ. The n ₂(θ, φ) function can be found in Ref. [Reference Kulagin, Ganeev, Tugushev, Ryasnyansky and Usmanov35]. The functions k ₂(θ) and k ₃(θ) can be readily obtained from the known expression for n _e(θ) and from the Sellmeier equations^[ Reference Zernike ^{30 ]}. Thus, for an extraordinary wave, dispersion and nonlinearity can be controlled independently by varying θ and φ, respectively. Note that it is also possible to use a KDP crystal isomorph: a DKDP crystal whose dispersion strongly differs from KDP dispersion^[ Reference Lozhkarev, Freidman, Ginzburg, Khazanov, Palashov, Sergeev and Yakovlev ^{37 ]}. The optimization of the parameters k ₂, k ₃, and n ₂ will be considered in a separate paper.