3.1. IFG Module Architecture

Figure 5 shows the architecture of an ABIA IFG module and its interfaces. This module is designed to provide CIF and WIF alerts in real-time (i.e., in accordance with the specified TTC and TTW requirements in all relevant flight phases). IFG module inputs are from the GNSS receiver and other aircraft sensors. The GNSS and Sensors Layer (GSL) passes the aircraft Position, Velocity, Time (PVT) and attitude (Euler angles) data (from the on board Inertial Navigation Systems, Air Data Computer, etc.), GNSS data (raw measurements and PVT) and the Flight Control System (FCS) actuators data to the Data Extraction Layer (DEL). At this stage, the required Navigation and Flight Dynamics (NFD) and GNSS Constellation Data (GCD) are extracted, together with the relevant information from an aircraft Three-Dimensional Model (3DM) and from a Terrain and Objects Database (TOD). The 3DM database is a detailed geometric model of the aircraft built in a Computer Aided Three-dimensional Interactive Application (CATIA). The TOD uses a Digital Terrain Elevation Database (DTED) and additional man-made objects data to obtain a detailed map of the surfaces neighbouring the aircraft.

Figure 5. IFG module architecture.

In the Integrity Processing Layer (IPL) the Doppler Analysis Module (DAM) calculates the Doppler shift by processing the NFD and GCD inputs. The Multipath Analysis Module (MAM) processes the 3DM, TOD, GNSS Constellation Simulator (GCS) and A/C Navigation/Dynamics Simulator (ADS) inputs to determine multipath contributions from the aircraft (wings/fuselage) and from the terrain/objects close to the aircraft. The Obscuration Analysis Module (OAM) receives inputs from the 3DM, GCS and ADS, and computes the GNSS antenna(e) obscuration matrices corresponding to the various aircraft manoeuvres. The Signal Analysis Module (SAM) calculates the link budget of the direct GNSS signals received by the aircraft in the presence of atmospheric propagation disturbances Carrier-to-Noise (C/N₀), as well as the applicable Radio Frequency (RF) interference (Jamming-to Signal [J/S]) levels. The Integrity Flags Layer (IFL) uses a set of predefined CIF/WIF threshold parameters to trigger the generation of both caution and warning flags associated with antenna obscuration, Doppler shift, multipath, carrier, interference and satellite geometry degradations.

3.2. Antenna Obscuration Analysis

Due to the manoeuvres of the aircraft, the wings, tail and fuselage will obscure some satellites during the flight. Figure 6 shows the structure of the OAM.

Figure 6. GNSS antenna obscuration analysis.

A Three Degrees of Freedom (3-DOF) model with variable mass was developed to calculate the trajectory of the aircraft (i.e., position, velocity and attitude (Euler angles)) during the different flight phases. Taking into account the aircraft shape (CATIA 3-D model), the aircraft flight dynamics (pitch, roll and yaw variations) and the geometric displacement of the GNSS satellites in view, the Antenna Obscuration Matrices (AOM) are generated for the different flight conditions. An example of the TORNAO-IDS AOM obtained with 50° bank angle is shown in Figure 7.

Figure 7. TORNADO-IDS upper antenna (centrally mounted) AOM (Bank=+50°).

Besides the AOM, other factors influence the satellite visibility. In general, a satellite is geometrically visible to the GNSS receiver only if its elevation in the antenna frame is above the Earth horizon and the antenna elevation mask. It should be noted that even high performance avionics GNSS antennae have gain patterns that are typically below -3 dB at about 5 degrees elevation and, as a consequence, their performance becomes marginal below this limit (Figure 8).

Figure 8. High quality antenna gain pattern (L1 frequency).

In order to determine if a satellite is obscured, the Line of Sight (LOS) of the satellite with respect to the antenna phase centre has to be determined. To calculate the satellite azimuth and elevation with respect to the antenna a transformation matrix between the Earth Centred Earth Fixed (ECEF) and antenna frames must be applied. This is obtained from:

(5)$${\rm T}_{\rm E}^{\rm a} = {\rm T}_{\rm b}^{\rm a} *{\rm T}_{\rm N}^{\rm b} *{\rm T}_{\rm E}^{\rm N} $$

where:

T_b^a

is the transformation matrix between the aircraft body frame and the antenna frame,

T_N^b

is the transformation matrix from the East-North-Up (ENU) frame to body frame and

T_E^N

is the ECEF to ENU transformation matrix.

As an example, Figure 9 shows the trajectory of an aircraft during a Turning Descent Manoeuvre (TDM) lasting 300 seconds.

Figure 9. Turning descent manoeuvre.

Figure 10 shows the combined Global Positioning System (GPS)/GALILEO satellite visibility during the same flight phase. During the manoeuvre, the number of satellites in view varies from 7 to 16.

Figure 10. Satellite Visibility (TDM).

TORNADO-IDS flight trials showed that the signal losses due to antenna obscuration can be reduced by introducing constraints to the aircraft initial heading for left and right turns (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). In particular, it was found that the satellite losses are minimised by reducing the number of left turns performed with the initial heading ranging from North-East to South-East, and the number of right turns performed with the initial heading between South-West and North-West. This fact can be explained by considering a typical northern hemisphere mid-latitude sky plot shown in Figure 11.

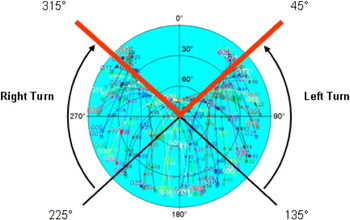
Figure 11. GPS sky-plot (northern hemisphere mid-latitude).

Since in the northern hemisphere/mid-latitudes the majority of satellites are available in the azimuth range 45 to 315 degrees, a left turn with an initial heading in the range 45 to 135 degrees would be prone to GPS data losses, due to the reduced number of satellites available in the direction of the turn. Similar considerations apply for right turns performed with an initial heading in the range 225 to 315 degrees.

3.3. GNSS Signal and Interference Analysis

The received signal strength is affected by a number of factors including transmitter and receiver characteristics, propagation losses and interferences. In our case, the SAM combines the various factors contributing to the GNSS link budget and signal degradations due to interference. Multipath induced effects are considered separately. The SAM module takes inputs from the GCS and NFD modules, and computes both C/N₀ and J/S. The ratio of total carrier power to noise C/N₀) in dB-Hz is the most generic representation of received signal strength. This is given by:

(6)$$\displaystyle{{\rm C} \over {{\rm N}_0}} = {\rm P}_{\rm t} + {\rm G}_{\rm t} + {\rm G}_{\rm r} + {\rm L}_{\rm s} - {\rm L}_{\rm a} - {\rm L}_{\rm r} - \sigma _{\rm m} - {\rm N}_{\rm f} $$

where:

P_T

is the transmitted power level (dBw);

G_t

is the satellite antenna gain (dBic);

G_r

is the receiver antenna gain toward the satellite (dBic);

L_s

is the free space loss (dB);

L_a

is the atmospheric attenuation in dry-air (dB);

L_r

is the rainfall attenuation (dB);

σ _m

is the tropospheric fading (dB) and;

N_f

is the receiver noise figure (dB).

The link budget calculated from Equation (6) only refers to the direct GNSS signal received from a satellite. Multipath effects, which are due to the geometric and reflective characteristics of the environment surrounding the GNSS antenna are not included in this calculation and are discussed separately. The L-band antenna onboard GPS satellites is designed to radiate the composite L-band signals to the users on and near the Earth. As shown in Figure 12, the GPS satellite viewing angle from edge-to-edge of the Earth is about 27·7° (Boithias, Reference Boithias1982). The satellite antenna is designed to illuminate the Earth's surface with an almost uniform signal strength. The path loss of the signal is a function of the distance from the antenna phase centre to the surface of the Earth. The path loss is least when the satellite is directly overhead and is most at the edge of the coverage area.

Figure 12. GPS Satellite Antenna Coverage.

The difference in signal strength caused by this variation in path length is about 2·1 dB [6] and the satellite antenna gain can be approximated by:

(7)$${\rm G}_{\rm t} = 2{\cdot}5413*\sin {\rm E} - 2{\cdot}5413$$

where E is the elevation angle. Similarly, the avionics antenna gain pattern shown in Figure 8 can be approximated by:

(8)$${\rm G}_{\rm r} = 9\cdot8756*\sin {\rm E} - 4\cdot7567$$

GNSS signal frequencies (L-band) are sufficiently high to keep the ionospheric delay effects relatively small. On the other hand, they are not so high as to suffer severe propagation losses even in rainy conditions. However, the atmosphere causes small but non-negligible effects that must be taken into account. The major effects that the atmosphere has on GNSS signals include those detailed in (Parkinson and Spilker, Reference Parkinson and Spilker1996):

• • Ionospheric group delay/carrier phase advance;

• • Tropospheric group delay;

• • Ionospheric scintillation;

• • Tropospheric attenuation;

• • Tropospheric scintillation.

The first two effects have a significant impact on GNSS data accuracy but do not directly affect the received signal strength (C/N₀). Ionospheric scintillation is due to irregularities in the electron density of the Earth's ionosphere (scale size from hundreds of metres to kilometres), producing a variety of local diffraction and refraction effects. These effects cause short-term signal fading which can severely stress the tracking capabilities of a GNSS receiver. Signal enhancements can also occur for very short periods, but these are not really useful from the GNSS receiver perspective. Atmospheric scintillation effects are more significant in the equatorial and sub-equatorial regions and tend to be less of a factor at European and North-American latitudes. Unfortunately, at the moment, there is little we can do to estimate ionospheric scintillation effects and no efficient algorithms are available for integration in the ABIA system. Tropospheric attenuation in the GNSS frequency bands is dominated by oxygen and the effects of other chemical species can be neglected for most applications. Oxygen attenuation (A) is in the order of 0·035 dB for a satellite at zenith and its variation with elevation angle (E) can be approximated by (Parkinson and Spilker, Reference Parkinson and Spilker1996):

(9)$${\rm A(E)} \cong \displaystyle{{0{\cdot}07} \over {\sin {\rm E} + 0{\cdot}043}}\; (\rm dB) \quad {\rm for}\; 3 \lt E \lt 10\; {deg} $$

(10)$${\rm A(E)} \cong \displaystyle{{0{\cdot}035} \over {\sin {\rm E}}}\; (\rm dB) \quad {\rm for} \ {\bf E} \lt 10\; {deg} $$

These formulae provide acceptable results only if E>3 degrees. However, since several other errors affect measurements from satellites with elevations below 5°, a software mask is typically employed in avionics GNSS receivers to exclude these satellites form the navigation computations (Sabatini and Palmerini, Reference Sabatini and Palmerini2008). Tropospheric rainfall attenuation has a minor effect in the GNSS frequency bands. For instance, at a frequency of 2 GHz the attenuation for high rainfall rates is less than 0·01 dB/km (rainfall attenuation below 2 GHz is even less). Tropospheric scintillation is caused by irregularities (primarily turbulence) causing variations of the refractive index. This effect varies with time, frequency and elevation angle. For small omnidirectional antennas, such as GNSS antennas, the CCIR provided the following expression for the long-term rms amplitude scintillation (Boithias, Reference Boithias1982):

(11)$${\rm \sigma} _{\rm m} = 0{\cdot}025{\rm f}^{0{\cdot}58} (\csc {\bf E})^{ - 0{\cdot}85} {\rm \;} \quad ({\rm dB})$$

where f is the frequency in GHz.

The Noise Figure (N_f) is related to the system noise temperature (T_sys) in Kelvin as follows (Davenport and Root, Reference Davenport and Root1987):

(12)$${\rm N}_{\rm f} = 10\log \left( {1 + \displaystyle{{{\rm T}_{{\rm sys}}} \over {{\rm T}_0}}} \right)\quad ({\rm db})$$

where T₀=290 K=24·6 dB-K.

T_sys for antenna plus receiver can be computed using the Friis formula (Friis, Reference Friis1944). Typical N_f values for state-of-the-art GPS receivers are between 2 and 4 dB. Intentional and unintentional RF interference (jamming) can result in degraded navigation accuracy or complete loss of the GNSS receiver tracking. Jammers can be classified into three broad categories: Narrowband Jammers (NBJ), Spread Spectrum Jammers (SSJ) and Wideband Gaussian Jammers (WGJ). Fortunately, a number of effective jamming detection and anti-jamming (filtering and suppression) techniques have been developed for military GNSS applications and some of them are now available for civil use as well (Ward, Reference Ward1994). The J/S performance of a GNSS receiver at its tracking threshold can be evaluated by the following equation (Kaplan and Hegarty, Reference Kaplan and Hegarty2006):

(13)$$\displaystyle{{\rm J} \over {\rm S}} = 10\log {\rm QR}_{\rm c} \left[ {\displaystyle{1 \over {10^{0.1({\rm C}/{\rm N}_0 )_{{\rm MIN}}}}} - \displaystyle{1 \over {10^{0.1({\rm C}/{\rm N}_0 )}}}} \right]$$

where:

Q

is the processing gain adjustment factor (1 for NBJ, 1·5 for SSJ and 2 for WGJ);

R_c

is the code chipping rate (chips/s);

$({\textstyle{{\rm C} \over {{\rm N}_0}}} )_{{\rm MIN}} $$

is the receiver tracking threshold (dB-Hz).

Since the weak limit in an avionics receiver is the carrier tracking loop threshold (typically the Phase Lock Loop [PLL]), this threshold is usually substituted for $({\textstyle{{\rm C} \over {{\rm N}_0}}} )_{{\rm MIN}} $. During the flight test activities performed on TORNADO-IDS with unaided C/A code avionics receivers, it was found that in all the dynamics conditions explored and in the absence of jamming, a $({\textstyle{{\rm C} \over {{\rm N}_0}}} )$ of 25 dB-Hz was sufficient to keep tracking the satellites. As an example, using this 25 dB-Hz tracking threshold, we can calculate the J/S performance of the TORNDO-IDS GPS receiver considering one of the satellites tracked during the descent manoeuvre illustrated in Figure 9. As shown in Figure 13, during this manoeuvre, the C/N₀ for Pseudo Random Noise (PRN) PRN-14 was about 37 dB-Hz.

Figure 13. Calculated C/N₀ for PRN-14.

Table 1 shows the corresponding J/S calculations, assuming (C/N_o)_MIN=25 dB-Hz. Using these J/S values, the minimum range in metres from a jamming source can be calculated from:

(14)$${\rm R}_{{\rm min}} = \displaystyle{{\lambda _j} \over {4\pi}} \left( {10^{\textstyle{{{\rm ERP}_{{\rm tj}} - {\rm P}_{{\rm rj}} + {\rm G}_{{\rm rj}} - {\rm L}_{{\rm rf}}} \over {20}}}} \right)$$

where:

ERP_tj

is the effective radiated power of the jammer (dBw).

j

is the wavelength of jammer frequency (m).

P_rj

is the received (incident) jamming power level at threshold=${\textstyle{{\rm J} \over {\rm S}}}$+P_rs (dBw).

P_rs

is the minimum received (incident) signal power (dBw).

G_rj

is the GNSS antenna gain toward jammer (dBic).

L_rf

is the jammer power attenuation due to receiver front-end filtering (dB).

3.4. Doppler Shift Analysis

Doppler shift is the change in frequency of the received signal that is experienced when the observer (aircraft) moves relative to the signal source (satellite). The Doppler shift of the n^th satellite signal frequency is given by:

(15)$${\rm \Delta f}_n = {\rm f}\left( {\displaystyle{{{\rm v}_{\rm i} - {\rm v}_{\rm u}} \over {\rm c}}} \right)\cos \alpha _{\rm n} $$

where:

v_i

is the satellite velocity.

v_u

is the aircraft velocity.

c

is the speed of light.

f

is the GNSS signal frequency.

α _n

is the angle between the aircraft velocity and the n^th satellite LOS vector.

During the initial phases of the GPS-TSPI flight test campaign (Sabatini and Palmerini, Reference Sabatini and Palmerini2008), it was noted that, even in high dynamics avionics receivers, the reacquisition time after loss of one or more satellite signals could be up to 40 seconds, depending on flight conditions and satellite constellations (Figure 14). Therefore, we investigated how the Doppler shift could affect the receiver's capability to track the carrier phase and rapidly reacquire the signal after a loss. Doppler shift directly affects the signal acquisition time of the receiver, both in terms of frequency of the code and frequency of the carrier. In general, acquisition time increases in the presence of Doppler shift. Considering the case of one satellite tracked, the Doppler shift is due to the relative velocity of the satellite and the receiver (i.e., the difference between the projections of the velocity vectors along the satellite-receiver direction). The worst case is, therefore, that of an aircraft flying along the LOS to the satellite, in which the full velocity vector of the aircraft must be used to determine the relative velocity. Analysis of receiver data recorded during several flights and up to speeds of 500 knots highlighted that the Doppler effect causes a frequency shift, with respect to the carrier frequency L1, which reaches a maximum value of about 15 KHz. This value is low if compared with the GPS signal bandwidth and the high dynamic characteristics of the carrier tracking loops internal to the avionics receiver guarantee that neither the data accuracy is degraded nor the carrier phase is lost because of Doppler shift. Nevertheless, the coupling between such a frequency shift and the signal reacquisition strategy of the receiver can significantly affect the time necessary to get data after a signal loss, even when a good satellite configuration is available.

Figure 14. Doppler shift and signal acquisition in an avionics receiver.

Table 1. J/S calculations for 25 dB-Hz tracking threshold.

3.5. Multipath Analysis

Multipath is caused by the interference of multiple reflections (from the ground and the aircraft structure) with the direct signal transmitted by the satellite, and represents a major source of error in GNSS observations. The level and characteristics of multipath depend on the geometry of the environment surrounding the antenna, the reflectivity of nearby objects/terrain and the satellite elevation angle. In order to build a reliable multipath model, a combination of signal analysis and geometric ray-tracing methods was adopted. To start, we use the aircraft 3D CATIA model to identify the geometric characteristics of the multipath signal and study the Signal-to-Noise ratio variations in the presence of multipath (S/N_m).

From Figure 15, the S/N_m and phase error for a single refection can be represented as a function of direct and multipath signal amplitudes and the multipath relative phase is β (Ward, Reference Ward1994):

(16)$$\displaystyle{{\rm S} \over {{\rm N}_{\rm m}}} = {\rm A}_{\rm c}^2 = {\rm A}_{\rm d}^2 + {\rm A}_{\rm m}^2 + 2{\rm A}_{\rm d} {\rm A}_{\rm m} \cos \beta $$

(17)$$\tan (\delta _\phi ) = \displaystyle{{{\rm A}_{\rm m} \sin \beta} \over {{\rm A}_{\rm d} + {\rm A}_{\rm m} \cos \beta}} $$

where:

A_d

is the direct signal amplitude.

A_m

is the multipath signal amplitude.

β

is the phase of the multipath.

Figure 16 shows that both the multipath phase β and the multipath amplitude affect the received signal. Therefore, we require a multipath model to simulate these two factors, considering the reflections from the airframe and from the ground. In our research, we adopted the Aeronautical Multipath Channel (AMC) model developed during the ESA-SDS research (Steingass, Reference Steingass2004).

Figure 15. Phase of GNSS signal.

Figure 16. Variation of A_c as function of the angle β.

Figure 17 illustrates the overall structure of the AMC model. Let h(t, τ) be the impulse response of the multipath channel model. Then h(t, τ) is given by (Steingass, Reference Steingass2004):

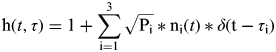(18)$${\rm h(}t,\tau {\rm )} = 1 + \mathop \sum \limits_{{\rm i} = 1}^3 \sqrt {{\rm P}_{\rm i}} *{\rm n}_{\rm i} (t)*\delta ({\rm t} - \tau _{\rm i} )$$

Figure 17. AMC model structure.

where:

P_i is the Echo Power of the i^th path.

The signal n_i(t) is a noise signal with Power i, and a power spectral density N(f):

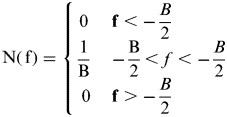(19)$${\rm N(\,f)} = \left\{ {\matrix{ {0\;} & {{\bf f} \lt - \displaystyle{B \over 2}} \hfill \cr {\displaystyle{1 \over {\rm B}}\;} & { - \displaystyle{{\rm B} \over 2} \lt f \lt - \displaystyle{B \over 2}}\hfill \cr 0& {{\bf f} \gt - \displaystyle{B \over 2}} \hfill \cr}} \right.$$

where B is the noise bandwidth.

From the multipath channel model in Figure 18, the wing reflection, the fuselage reflection and the ground-echo are the main components of the multipath signal.

Figure 18. Geometric reflection model.

Figure 18 shows the geometric reflection model. The incoming wave is emitted from point T, R is the receiver location and S is the reflection point. V is a defined point on the reflecting surface and n stands for a unit vector normal to the surface.

In ray-tracing, the reflection point S and the defined point V should satisfy the equation:

(20)$$({\rm S} - {\rm V}) \times {\rm n} = 0$$

and the line equation connecting T and R_image:

(21)$${\rm S} = {\rm T} + {\rm t} \times ({\rm R}_{{\rm image}} - {\rm T})$$

where t is a parameter between 0 and 1.

Combining Equations (20) and (21):

(22)$${\rm S} = {\rm T} + \displaystyle{{{\rm n} \times {\rm V} - {\rm n} \times {\rm T}} \over {{\rm n} \times ({\rm R}_{{\rm image}} - {\rm T})}}({\rm R}_{{\rm image}} - {\rm T})$$

The corresponding extra path length L_mS, due to specular reflection, is then:

(23)$${\rm L}_{{\rm mS}} = \left| {{\rm T} - {\rm S}} \right| + \left| {{\rm R} - {\rm S}} \right| - \left| {{\rm T} - {\rm R}} \right|$$

In our wing reflection model, the wing is assumed to be flat. By Gaussian Doppler Spectrum theory, the power of the wing echo spectrum is assumed to be (Braasch, Reference Braasch1992):

(24)$${\rm P}_{{\rm Gr}({\rm dB})} = 20{\rm *log}\left( {\displaystyle{1 \over {\sqrt {2{\rm \pi \sigma} ^2}}} {\rm *e}^{ - {\textstyle{{{\rm f}^2} \over {2{\rm \sigma} ^2}}}}} \right)$$

where the deviation σ=3·8 Hz.

The wing reflection signal delay can be calculated from:

(25)$${\rm \tau} _{{\rm wing}} ({\rm t}) = \displaystyle{{2{\rm *L*sin}({\rm E})} \over {{\rm C}_0}} $$

where:

L

is the antenna height from the wing.

E

is the elevation angle (degrees).

C₀

is the speed of light.

The fuselage is assumed to be a cylinder and the power of the fuselage echo spectrum is given by:

(26)$${\rm P}_{{\rm proc}} ({\rm dB}) = 20{\rm *log}_{10} \left[ {k_1 *e^{(k_2 *|f|\; )} - SNR - k_3} \right]$$

where k₁, k₂ and k₃ are the fuselage geometric coefficients described in (Steingass and Lehner, Reference Steingass and Lehner2004).

Previous research showed that the fuselage reflection characteristics change very little by increasing the fuselage radius. For easier implementation of the fuselage reflection model, a 2-dimensional polynomial function of 4^th order was fitted to each parameter (mean, b₂, b₃). As an example, considering the TORNADO-IDS upper antenna located on the fuselage at a height of L_fuselage=0·05 metres, the fuselage reflection time delay is τ _fuselage=1·7×10⁻¹⁰ s. Ground reflection becomes important only during the landing phase, when the aircraft is in close proximity of the terrain. As before, assuming a Gaussian distributed ground reflection amplitude with zero mean, the ground-echo power can be described by Equation (24). Assuming that the terrain is flat:

(27)$$\tau _{{\rm ground}} ({\rm t}) = \displaystyle{{2*{\rm h}*\sin ({\rm E})} \over {{\rm C}_0}} $$

where:

h

is the aircraft altitude.

E

is the elevation angle.

This basic ground-echo model can be expanded to take into account various terrain and man-made building geometries. As discussed in (Parkinson and Spilker, Reference Parkinson and Spilker1996), GPS receivers can effectively reject most of the multipath signal if the differential delay Δτ>1·5 μs for the C/A code and 0·15 μs for the P(Y) code. As a consequence, the region of potential ground-echo multipath problems for the C/A code is:

(28)$${\rm h}*\sin ({\rm E}) \lt (1{\cdot}5\,\mu s)*{\rm C}_0 = 448{\cdot}5\,{\rm m}$$

Simulation and test activities performed on various military aircraft showed that, above this threshold, the fuselage reflections are normally the main contributors to the airframe multipath. In particular, it was found that the airframe multipath ranging error budget can be minimised by placing the GNSS antenna 5 centimetres (or more) above the highest point on the aircraft fuselage. Applying this criterion to the TORNADO-IDS antenna installation, the airframe multipath error associated to each satellite remained below 2 metres in all relevant flight conditions and aircraft-satellite relative geometries. To investigate the effects of ground-echo multipath on the TORNADO-IDS GPS receiver, flight test activities were performed with satellite elevation angles between 5° and 90° and bank/pitch angles exceeding 45°. In these conditions, it was observed that no significant ground-echo multipath is present for altitudes above 500 feet Above Ground Level (AGL). As this value is much lower that the theoretical threshold established by Equation (28), it was concluded that the signal attenuation due to ground reflectivity was responsible for the reduced susceptibility to ground-echo multipath. Nevertheless, reducing the aircraft altitude below 500 feet AGL and performing attitude manoeuvres exceeding 45°, significant ground-echo multipath errors were experienced. In particular, it was observed that the effect of ground-echo signals translated into a sudden increase of the multipath ranging error of up to two orders of magnitude with respect to the airframe multipath errors alone. During a low-level TORNADO-IDS flight trial, it was found that the ground-multipath ranging error reached a value of about 140 metres when the aircraft was flying at an altitude of 300 feet AGL over flat terrain with a roll angle exceeding 45°. It must be pointed out, however, that such particular flight conditions are only likely to be encountered in military aircraft and some UAV applications. Due to the flight profile requirements and manoeuvring constraints of typical airliners, the ground multipath contributions can be normally neglected in these cases. According to the Standard Multipath Error Model (SMEM) research (Murphy et al., Reference Murphy, Friedman, Booth, Geren, Molloy, Clark and Burns2004) and experimental validation activities performed in the United States on various types of civil airliners (Booth et al., Reference Booth, Murphy and Liu2000), the airframe multipath ranging error (multipath) associated to a satellite observation can be calculated directly as a function of the satellite elevation angle:

(29)$$\sigma_{\rm multipath} = 0{\cdot}13 + 0{\cdot}53{\rm e}^{(\rm - E/10)} $$

This model was endorsed by the International Civil Aviation Organisation (ICAO) GNSS panel (Booth et al., Reference Booth, Murphy and Liu2000) and included in the Minimum Operational Performance Standards (MOPS) for the Local Area Augmentation System (RTCA, 2004) and for the Wide Area Augmentation System (RTCA, 2006). Further research is currently in progress at CSV-RSV, NGI and CU on other airframe types, including general aviation aircraft and various classes of UAVs. For small UAV platforms, multipath effects associated with low-level flight in urban environments is also being investigated. Preliminary results obtained with small-size UAVs show that multipath ranging errors in excess of 100 metres are possible when the vehicle flies in proximity of large buildings. Further research is needed to corroborate these initial findings and to obtain useful models for the various classes of UAV platforms considered for the ABIA development.