Introduction
GaN plays an important role in today’s optoelectronics. This is mainly due to its large band gap (3.4 eV for hexagonal GaN) which makes blue light emission possible. Many devices like blue light emitting diodes or lasers are based on hexagonal GaN (see [Reference Nakamura and Fasol1] for an overview), although recently the first light emitting diodes using cubic GaN have been constructed [Reference Yang, Zheng, Li, Wang, Xu, Wang and Hu2,Reference As and Lischka3].
Electronic states in the band gap induced by extended defects can significantly alter the optical performance. This fact becomes extremely important in laser devices, where parasitic components in the emission spectrum are highly undesirable. Moreover, point defects could be trapped in the stress field of extended defects giving rise to charge accumulation in their vicinity. The resulting electrostatic field can lead to electron scattering which will severely affect the electron mobility (see Look and Sizelove [Reference Look and Sizelove4] for a recent model in hexagonal GaN). Therefore, there is considerable interest in understanding the microstructure of extended defects in GaN and their interaction with point defects.
In this paper we discuss a variety of line defects in hexagonal GaN. We discuss the line defects in their pure form as well as the interaction with point defects which are likely to be trapped in the stress field. In addition first results on dislocations in cubic GaN are presented.
For our calculations we used two different methods to obtain geometries, energetics and electrical properties of the examined structures: AIMPRO, an ab initio local density-functional (LDF) pseudopotential method and SCC-DFTB, a self-consistent charge density-functional tight-binding method. On the one hand the AIMPRO method allows accurate determination of the electronic structure. The SCC-DFTB method on the other hand can be applied to larger supercells and thus makes possible the calculation of formation energies of extended defects. Details of both methods and their application to GaN and oxygen related defect complexes in GaN have been given previously [Reference Elsner, Jones, Sitch, Porezag, Elstner, Frauenheim, Heggie, Öberg and Briddon5-Reference Elsner, Jones, Haugk, Frauenheim, Heggie, Öberg and Briddon7].
Dislocations in Hexagonal GaN
Threading Screw Dislocations
Threading screw dislocations in hexagonal material have a Burgers vector parallel to the dislocation line [0001]. The smallest screw dislocations have thus elementary Burgers vectors ±c. Since they nucleate in the early stages of growth at the sapphire interface and thread to the surface of the crystallites, screw dislocations are believed to arise from the collisions of islands during growth [Reference Ning, Chien and Pirouz8]. At a screw dislocation the surface is rough and has a high energy which favours the nucleation of islands. They are thus vital for the growth process.
We consider first a screw dislocation with a full core [Reference Elsner, Jones, Sitch, Porezag, Elstner, Frauenheim, Heggie, Öberg and Briddon5]. This type has been observed by Xin et al. [Reference Xin, Pennycook, Browning, Nelist, Sivananthan, Omnes, Beaumont, Faurie and Gibart9] using high resolution Z-contrast imaging. Both the AMIPRO and the SCC-DFTB method found heavily distorted bond lengths (by as much as 0.4 Å) yielding deep gap states ranging from 0.9 to 1.6 eV above the valence band maximum, VBM, and shallow gap states at 0.2 eV below the conduction band minimum, CBM. An analysis of these gap states revealed that the states above the VBM are localised on N core atoms, whereas the states below CBM are localised on core atoms but have mixed Ga and N character. Therefore the full-core screw dislocation is electrically active and could act as a non-radiative centre [Reference Elsner, Jones, Sitch, Porezag, Elstner, Frauenheim, Heggie, Öberg and Briddon5]. Similarly one could expect that dislocations of mixed type would also have deep states in the gap as a result of the distortion arising from their screw component. Indeed atomic force microscopy in combination with CL imaging has shown that threading dislocations with a screw component act as nonradiative combination sites [Reference Rosner, Carr, Ludowise, Girlami and Erikson10].
A calculation in a supercell containing a full-core screw dipole consisting of two dislocations with [0001] and -[0001], which are symmetrically equivalent, gave a high line energy of 4.88 eV/Å which is due to the strong distortion of the bonds of the core atoms.
Similar calculations were then carried out with the hexagonal core of the screw dislocation removed giving a core with a narrow opening of approximately 7.2 Å (see Fig. 1). The atoms on the walls adopt three fold coordinations similar to those found on the (10−10) surface. Thus Ga (N) atoms develop sp2 (p3) hybridisations which lower the surface energy and clear the gap of deep states. We found shallow gap states which are induced by the distortion arising from the Burgers vector. This was verified by comparison with the undistorted (10−10) surface which shows no shallow states.

Figure 1 Left: Top view (in [0001] ) of the relaxed core of the open-core screw dislocation. The three fold coordinated atoms 1 (Ga) and 2 (N) adopt a hybridisation similar to the (10−10) surface atoms. Right: TEM image of a nanopipe containing a dislocation with a screw component. During growth the nanopipe closes leaving the dislocation with an opening of three rows (approx. 8 Å) wide. Z. Liliental-Weber [Reference Liliental-Weber11].
The distortion in the open-core screw dislocation (maximum of 0.2 Å) is significantly less than that in the full-core screw dislocation. It is therefore not surprising that the calculated line energy of 4.55 eV/Å is lower than the line energy of the full-core screw dislocation. The energy required to form the surface at the wall is compensated by the energy gained by reducing the strain. However, a further opening gave a higher line energy and we conclude that the equilibrium diameter is approximately 7.2 Å. This opening has also been observed by Liliental-Weber et al. [Reference Liliental-Weber11] who found some of the screw dislocations to have holes which are three atomic rows wide (see Fig. 1).
A theoretical approach to predict the opening of a screw dislocation was deduced by Frank [Reference Frank12]. By balancing the elastic dislocation strain energy released by the formation of a hollow core against the energy of the resulting free surfaces, he showed that, for isotropic linear elasticity and a cylindrical core, the equilibrium core radius is

where γ; is the surface energy, μ is the shear modulus and b is the Burgers vector. For a rough estimate of the equilibrium radius, we use the theoretical value for the surface energy of {10−10} facets which we found to be γ= 121 meV/Å2. Taking μ = 8·1010 Nm−2 as an upper limit and b = 0.5 nm for the Burgers vector of an elementary screw dislocation yields 0.2 nm as the equilibrium radius. It is unlikely, that isotropic elasticity theory can describe the severely distorted full core and give precise quantitative values. Nevertheless our calculated value of 7.2 Å is reasonably close.
Oxygen and the Formation of Nanopipes
Nanopipes in hexagonal GaN thread along the c-axis and have hexagonal cross sections, i.e. they are enclosed by {10−10} type walls (see Fig. 2). The first suggestion was that they were the manifestation of screw dislocations with empty cores as discussed long ago by Frank [Reference Frank12]. However, as shown above neither ab initio calculations nor Frank's theorem support the idea that in GaN the core of a screw dislocation with Burgers vector equal to c is open with a large diameter. Liliental-Weber et al. [Reference Liliental-Weber, Chen, Ruvimov and Washburn13] found the diameters and densities of nanotubes to be increased in the presence of impurities, e.g. O, Mg, In and Si, and argued that these impurities decorate the {10−10} walls of the nanotubes inhibiting overgrowth. O being the main source of unintentional doping in GaN, we will now discuss how O can cause the formation of nanopipes.

Figure 2 Left: High resolution Z-contrast image along [0001] of a nanopipe. Y. Xin unpublished. Right: Suggested mechanism for the formation of a nanopipe (area No. 0). Three hexagons (No. 1,2,3) are growing together. As the surface to bulk ratio at edges (No. 4,5,6) is very large, they grow out quickly leaving a nanopipe (area No. 0) with {10−10} type facets.
There is experimental evidence that oxygen acts as a donor in bulk GaN [Reference Wetzel, Suski, Ager, Weber, Haller, Fischer, Meyer, Molnar and Perlin14] and total energy calculations show that O sits on a N site [Reference Neugebauer and Walle15]. Since the internal surfaces of screw dislocations are very similar to those of the low energy (10−10) surface, we investigated [Reference Elsner, Jones, Haugk, Gutierrez, Frauenheim, Heggie, Öberg and Briddon16] the likely surface sites for oxygen replacing N atoms. We found that the energy of a neutral ON defect is 0.8 eV lower at the relaxed (10−10) surface. This shows that there is a tendency for O to segregate to the surface. The added oxygen has an additional electron occupying a state near the CBM. The defect has therefore a high energy and would attract acceptors resulting in a neutral complex. One possible acceptor, other than added dopants, would be a gallium vacancy (VGa) which acts as a triple acceptor and has been calculated to have a low formation energy in n-type GaN [Reference Neugebauer and Walle17,Reference Bougulawski, Briggs and Bernholc18]. Consequently, we suppose that the surface oxygen concentration could be sufficiently large, and the oxygen atoms sufficiently mobile, that the three N neighbours of VGa at the (10-10) surface are replaced by O forming the VGa−(ON)3 defect.
Our calculations [Reference Elsner, Jones, Haugk, Gutierrez, Frauenheim, Heggie, Öberg and Briddon16] showed that VGa−(ON)3 is more stable at the surface than in the bulk by 2.15 eV. Two O neighbours of the surface vacancy lie below the surface and each is bonded to three Ga neighbours, but the surface O is bonded to only two subsurface Ga atoms in a normal oxygen bridge site. The defect is electrically inactive with the O atoms passivating the vacancy in the same way asVH4 in Si.
The question then arises as to the influence of the defect on the growth of the material. Growth over the defect must proceed by adding a Ga atom to the vacant site but this leaves three electrons in shallow levels near the conduction band resulting in a very high energy. This suggests that the defect can stabilise the surface and thus inhibit growth. From this we can conclude that such defects lead to the formation of nanopipes if we assume that during growth of the epilayers, either nanopipes with very large radii are formed which gradually shrink when their surfaces grow out, or there is a rapid drift of oxygen to a pre-existing nanopipe. In either case the concentration of oxygen and VGa−(ON)3 defects increases at the walls of the nanopipe. The maximum concentration of this defect would be reached if 50 % (100 %) of the first (second) layer N atoms were replaced by O and further growth then would be prevented. It is, however, likely that far less than the maximum concentration is necessary to stabilise the surface and make further shrinkage of the nanopipe impossible. Provided oxygen could diffuse to the surface fast enough, the diameter and density of the holes would be related to the initial density of oxygen atoms in the bulk. This model requires that the walls of the nanopipe are coated with oxygen although the initial stages of formation of the pipe are obscure.
In conclusion, we have shown that oxygen tends to segregate to the (10-10) surface and forms stable and chemically inert VGa−(ON)3 defects. These defects increase in concentration when the internal surfaces grow out. When a critical concentration of the order of a monolayer is reached, further growth is prevented. This model leads to nanopipes with (10-10) walls coated with GaO and supports the suggestions of Liliental-Weber et al. that nanopipes are linked to the presence of impurities [Reference Liliental-Weber, Chen, Ruvimov and Washburn13].
Threading Edge Dislocations
Pure edge dislocations lie on {10-10} planes and b = a = [Reference Nakamura and Fasol1−210]/3 is their Burgers vector. They are a dominant species of dislocation, occurring at extremely high densities of approximately 108 − 1011 cm−2 in hexagonal GaN grown by MOCVD on (0001) sapphire and in analogy to screw dislocations are thought to arise from the collisions of islands during growth [Reference Ning, Chien and Pirouz8].
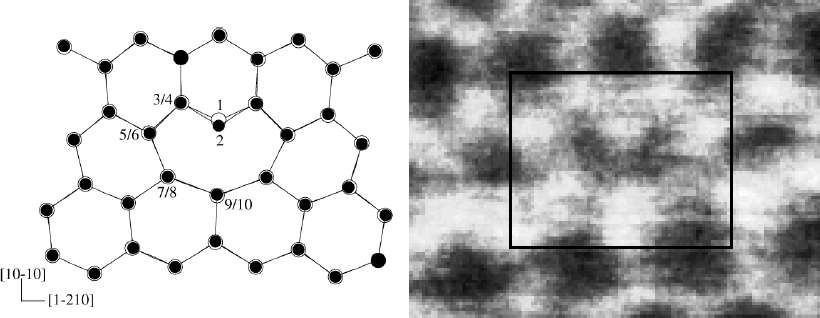
The relaxed core of the threading edge dislocation is shown in Fig. 3. The corresponding bond lengths and bond angles of the most distorted atoms are given in Table I. With respect to the perfect lattice the distance between columns (1/2) and (3/4) [and the equivalent on the right] is 9 % contracted while the distance between columns (9/10) and (7/8) [and the equivalent on the right] is 13 % stretched. This atomic geometry for the threading edge dislocation has recently been confirmed by Xin et al. [Reference Xin, Pennycook, Browning, Nelist, Sivananthan, Omnes, Beaumont, Faurie and Gibart9] using atomic resolution Z-contrast imaging. Consistent with our calculation they determined a contraction (stretching) of 15±10 % of the distances between the columns at the dislocation core. Our calculations show that in a manner identical to the (10−10) surface, the three-fold coordinated Ga (N) atoms (no. 1 and 2 in Fig. 3) relax towards sp2 (p3) leading to empty Ga dangling bonds pushed towards the CBM, and filled lone pairs on N atoms lying near the VBM. Thus using the SCC-DFTB method we find full-core threading edge dislocations to induce no deep states into the band gap and conclude that in their pure form they should not be charged. Concerning the electrical properties of full-core edge dislocations it should be noted that using plane-wave scf calculations Wright et al.. [Reference Wright and Gossner19] found the full core edge dislocation to possess states below the CBM (0.75 eV). However, recent Monte Carlo calculations for different background dopant densities based on scf plane-wave energy calculations by Wright and co-workers [Reference Leung, Wright and Stechel20] have shown no significant charge accumulation at the full-core threading edge dislocation even in heavily n-doped material.
Table I. Bond lengths, min-max (average) in Å and bond angles, min-max (average) in ° for the most distorted atoms at the core of the threading edge dislocation b=1/3[1−210]). Atom numbers refer to Fig. 3.


Figure 3 Left: Top view (along [0001]) of the relaxed core of the threading edge dislocation (b=1/3[Reference Nakamura and Fasol1−210]). The three fold coordinated atoms 1 (Ga) and 2 (N) adopt a hybridisation similar to the (10−10) surface atoms. The distance between columns (1/2) and (3/4) is contracted by 9 % while the distance between columns (7/8) and (9/10) is stretched by 13 %. Right: High resolution Z-contrast image of a threading edge dislocation looking down [0001]. The bright dots are atomic columns of alternating Ga and N atoms. The dislocation core is shown in the boxed region. Y. Xin et al. [Reference Xin, Pennycook, Browning, Nelist, Sivananthan, Omnes, Beaumont, Faurie and Gibart9].
From a supercell calculation, we obtain a line energy of 2.19 eV/Å for the threading edge dislocation. We note that this line energy is considerably lower than the one found for the screw dislocation with a narrow opening. This can be interpreted by noting that the edge dislocation has a smaller number of three fold coordinated atoms than the open-core screw dislocation as well as a smaller elastic strain energy. The latter arises from the smaller Burgers vector and from the smaller energy factor k = (1-ν)−1 for edge dislocations where ν is the Poissons ratio (for screw dislocations k is equal to 1).
In analogy to the open-core screw dislocations we have investigated whether the energy of the threading edge dislocation could be lowered by removing the most distorted core atoms (see Fig. 3). However, removal of either the columns of atoms (9,10), or the columns (1,2), (3,4), (5,6), (7,8) and their equivalents on the right, leads to considerably higher line energies. This implies that, in contrast with screw dislocations, which as discussed above can exist with a variety of cores, the threading edge dislocations should exist with a full core. Recent experimental results (Z-contrast imaging and EELS) by Xin et al. [Reference Xin, James, Arslan, Sivananthan, Browning, Pennycook, Omnes, Beaumont, Faurie and Gibart21] show that the vast majority of edge dislocations have indeed a full core independent of the type of doping.
Deep Acceptors Trapped at Threading Edge Dislocations
The VGa −(ON)3 defect considered above in the context of the formation of nanotubes is electrically inactive at a (10−10) surface site but defects like VGa −(ON)2 and VGa −ON act as single and double acceptors, respectively. If these were trapped in the strain field of a dislocation, then we would expect the dislocation to appear electrically active [Reference Elsner, Jones, Haugk, Frauenheim, Heggie, Öberg and Briddon7]. We expect the energy of VGa −(ON)n to be much lower at the dislocation core than in the bulk. This is because a neighbouring pair of three-fold coordinated Ga and N atoms are removed from the core and an O atom is inserted into the N site. The oxygen atom then lies in bridge site between two Ga atoms in a normal bonding configuration. Also other positions near to the dislocation core are found to be energetically favourable. Indeed, assuming Ga-rich growth conditions, O in equilibrium with Ga2O3 and n-type material our calculations find the resulting formation energies of these defects at the dislocation core and in the dislocation stress field to be significantly lower than in bulk material (see [Reference Elsner, Jones, Haugk, Frauenheim, Heggie, Öberg and Briddon7] for more details). Thus the core of the dislocation will spontaneously oxidise if oxygen is mobile. In any event, we anticipate that electrically active donor and acceptor pairs will be trapped at the core and in the dislocation stress field possibly giving rise to a negatively charged dislocation line in n-type material. This is in agreement with temperature-dependent Hall-effect measurements [Reference Look and Sizelove4].
Dislocations in Cubic GaN
The 60°-Shuffle-Dislocation
We now investigate the properties of dislocations in cubic GaN. Our results are limited to possible models for 60°-shuffle-dislocations. Indeed, 60°-dislocations have recently been observed in MBE grown GaN on (001) GaAs by TEM [Reference Kaiser22].
60°-dislocations are dislocations of mixed edge and screw character with a Burgers vector inclined at an angle of 60° to the direction of the dislocation line. In zincblende lattices we distinguish the glide and the shuffle type. Here only the latter is discussed.
Figure 4 (left) shows the projection of the relaxed 60°-shuffle-dislocation with nitrogen core. The dislocation lies along [Reference Nakamura and Fasol1-Reference Rosner, Carr, Ludowise, Girlami and Erikson10] thus normal to the projection plane. Bond lengths and bond angles of the three-fold coordinated nitrogen core atom (atom (1) in Fig. 4 (left)) are given in Table II. With respect to the prefect lattice the bonds between the core atom (1) and its next gallium neighbours (2/3) are 7 % contracted while those between (4), (5), (6), (7) and (8) are 7 % stretched. Although the three-fold coordinated nitrogen core atoms (1) relax along -[111] they are still sp3 hybridised. We therefore expect the dangling bonds of those atoms to induce deep gap states. Indeed our calculations show acceptor-like states giving rise to a partially filled band 0.3 eV above the VBM. This band is approximately 0.3 eV wide.
Table II. Bond lengths, min-max (average) in Å and bond angles, min-max (average) in ° for the nitrogen core atom of the 60°-shuffle-dislocation. Atom numbers refer to Fig. 4 (left).


Figure 4 Left: 60°-shuffle-dislocation with nitrogen core. Right: 60°-shuffle-dislocation with gallium core.
The relaxed core of the gallium core 60°-shuffle-dislocation is shown in Fig. 4 (right). The dislocation lies along [Reference Nakamura and Fasol1-Reference Rosner, Carr, Ludowise, Girlami and Erikson10] thus normal to the projection plane. The corresponding bond angles of all three-fold coordinated atoms are given in Table III. Unlike the nitrogen core the gallium core shows a reconstruction where Ga − N bonds are broken (between columns (5/6) and (7/8)) and the whole core structure is heavily distorted. Of the three-fold coordinated atoms every second atom along the dislocation line ([Reference Nakamura and Fasol1-Reference Rosner, Carr, Ludowise, Girlami and Erikson10] direction) is distorted inwards (see columns (1/2), (5/6) and (7/8) in Fig. 4). Table IV lists the distances between the three-fold atoms. As for the nitrogen core we find a partially filled band, this time 0.4 eV above the VBM and 0.3 eV wide. Additionally a very narrow band exists at mid-gap position..
Up to now the lack of detailed experimental TEM or Z-contrast data on dislocations in cubic GaN prevents a direct comparison and evaluation of our models.
Table III. Bond angles, min-max (average) in ° for all three-fold coordinated atoms of the 60°-shuffle-dislocation with gallium core. Atom numbers refer to Fig. 4 (right).

Table IV. Distances in Å between the three-fold coordinated atoms of the 60°-shuffle-dislocation with gallium core. Atom numbers refer to Fig. 4 (right).

Interaction of Impurities with the Nitrogen Core 60°-Shuffle-Dislocation
We investigated the interaction of impurities like the nitrogen vacancy, oxygen and carbon with the nitrogen core 60°-shuffle-dislocation. The calculations show that ON, VN and CN are stable in the dislocation core (at position (1) in Fig. 4 (left)). The formation energies of the neutral charge states of VN and ON in the dislocation core are lower than in the bulk (4.4 and 2.2 eV respectively). For CN no difference in formation energy was found. This means VN and ON are bound to the core and CN is not. We thus conclude that oxygen and nitrogen vacancies are likely to be accumulated at the nitrogen core of the 60°-shuffle-dislocation.
To learn about the effects of oxygen on the electronic structure, we increased the oxygen concentration from 1/4 to 3/4 of all core atoms at position (1) and found no significant change in the energetic position or width of the dislocation-induced band. However, oxygen seems to be able to passivate the electrical activity by filling up the dislocation band at least in n-type material.
To get deeper insights here, further investigations have to include different charge states of the defects as well as charge accumulations at the dislocations themselves.
Summary
We have presented calculations for a variety of line defects threading along the c-axis in hexagonal GaN. We found full-core screw dislocations to have a large distortion of the bonds at the dislocation core resulting in deep states in the band gap. Open-core screw dislocations and in particular threading edge dislocations, which occur at very high densities, have a core structure similar to (10−10) surfaces and therefore do not induce deep acceptor states in their impurity-free form.
Oxygen-related defect complexes, some of which are electrically active, are found to possess very low formation energies at the core and in the stress field of threading edge dislocations in hexagonal material. One specific oxygen related defect complex, VGa − (ON)3 is believed to be responsible for the formation of nanopipes in hexagonal GaN.
In cubic GaN we found the 60°-shuffle-dislocation to be electrically active. Similarly to dislocations in hexagonal material the 60°-shuffle-dislocation is likely to trap point defects and impurities which could alter the electrical properties.
Acknowledgements
The authors would like to thank A.F. Wright, A. Mühlig, Z. Liliental-Weber and Y. Xin for useful and stimulating discussions.