Impact Statement
Atmospheric chemistry regulates the abundance and variability of nearly all atmospheric pollutants and many greenhouse gases. These chemical processes are understood to be the result of a highly coupled system of reactions between a large number of chemical species. To model these processes, scientists have developed various “chemical mechanisms,” which are mathematical and computational representations of this chemical reaction system. These mechanisms are fundamentally composed of individual chemical reactions that are coupled together in a highly nonlinear manner. This coupling process leads to an emergent structure in the system of chemical interactions. To date, that emergent structure has not been well characterized. This work addresses that research gap through the application of novel graph theoretical analyses. By enumerating mechanism motifs or patterns of interaction in the mechanism, we are able to quantify the higher-order structure present in multiple different atmospheric chemical mechanisms. Our analysis provides a novel quantification of emergent structure in chemical mechanisms and a new set of tools for comparing different atmospheric chemical mechanisms currently in use.
1. Introduction
Chemical reaction-driven variability in the composition of the atmosphere is a fundamental control on the modern environmental challenges of air pollution and climate change. These reactions are the dominant source of most pollution in urban areas and the primary loss process for many important greenhouse gases (Seinfeld and Pandis, Reference Seinfeld and Pandis2016). As such, a detailed understanding of atmospheric chemical processes is necessary to understand the driving factors behind these modern environmental crises.
In nature, atmospheric chemistry involves at least tens of thousands of chemical species and hundreds of thousands of reactions. To gain an understanding in light of this complexity, a variety of mathematical methods are used to model the chemical reactions in the atmosphere. These methods most commonly take the form of parameterized systems of coupled differential equations that define the chemical dynamics, which are then studied by solving the system from a given initial condition using various integration methods (e.g., Damian et al., Reference Damian, Sandu, Damian, Potra and Carmichael2002). In conjunction with these approaches, recent work has demonstrated the potential for methods from the graph theory literature to provide valuable complementary information on the structure and dynamics of chemical reactions in the atmosphere (Silva et al., Reference Silva, Burrows, Evans and Halappanavar2021; Wiser et al., Reference Wiser, Place, Sen, Pye, Yang and Westervelt2023).
These graph methods are based on analysis of chemical mechanisms—which are statements of all relevant chemical reactions thought to occur in the atmosphere. These mechanisms are treated as a graph (or a network), where chemical species and reactions can be represented as nodes, and their interactions are represented as edges in a graph. Graph analysis of these mechanisms has led to useful scientific results in the atmospheric chemical sciences. Recent work by Silva et al. (Reference Silva, Burrows, Evans and Halappanavar2021) demonstrated that insights gained from graph theoretical analysis of these mechanisms are consistent with those from traditional differential equations-based methods. Dobrijevic et al. (Reference Dobrijevic, Parisot and Dutour1995) used graph methods to identify important reactions in the chemical mechanisms of planetary atmospheres. Wiser et al. (Reference Wiser, Place, Sen, Pye, Yang and Westervelt2023) applied novel graph reduction techniques to develop new atmospheric chemical mechanisms for use in global atmospheric models.
These chemical mechanisms are all broadly designed with similar basic building blocks—a set of reactants reacting to form a set of products. Those products and reactants can then participate in further reactions, ultimately creating the highly coupled system present in most atmospheric chemical mechanisms. The emergent structure and dynamics of this complex and highly coupled chemical system can be difficult to characterize. This challenge arises due to the fact that the behavior of any individual chemical species is not fundamentally representative of the behavior of the overall chemical system. Instead, the emergent properties of the entire mechanism arise due to the coupling of species to each other. These complex couplings of species are represented as connectivity (or network structure) in a graph (Wilson, Reference Wilson2010).
Many methods exist to study the connectivity in graphs (e.g., Estrada, Reference Estrada2016). Here, we focus on so-called “motifs” present in the chemical mechanisms. Motifs are statistically significant repeating patterns of connectivity (also known as graphlets or subgraphs) within the larger graph structure, sometimes termed “fundamental building blocks” of complex systems (e.g., Milo et al., Reference Milo, Shen-Orr, Itzkovitz, Kashtan, Chklovskii and Alon2002; Masoudi-Nejad et al., Reference Masoudi-Nejad, Schreiber and Kashani2012). Tracking the relative abundance of a particular motif in a graph can yield insight into larger-scale graph connectivity patterns, and ultimately, the properties of the system being modeled by the graph (Yeger-Lotem et al., Reference Yeger-Lotem, Sattath, Kashtan, Itzkovitz, Milo and Pinter2004; Gonen and Shavitt, Reference Gonen, Shavitt, Avrachenkov, Donato and Litvak2009; Simmons et al., Reference Simmons, Cirtwill, Baker, Wauchope, Dicks, Stouffer and Sutherland2019; Blokhuis et al., Reference Blokhuis, Lacoste and Nghe2020). For example, Milo et al. (Reference Milo, Shen-Orr, Itzkovitz, Kashtan, Chklovskii and Alon2002) demonstrated how motifs represent basic processes in graphs of complex systems like food webs, neural circuitry, and gene transcription networks. Alon (Reference Alon2007) reviews the use of these motifs for studying gene and protein transcription networks, demonstrating how a motif-based graph analysis can help characterize the function of processes in these networks. In a chemical context, Tyson and Novák (Reference Tyson and Novák2010) study motifs in graphs of biochemical reactions, finding that the statistically significant motifs correspond to chemical regulation processes in the system. Blokhuis et al. (Reference Blokhuis, Lacoste and Nghe2020) derive motifs necessary for catalysis and autocatalysis in chemical reaction mechanisms, underscoring the key role characterizing graph motifs can play in the chemical sciences.
In this work, we explored network motifs across atmospheric chemical mechanisms of varying complexity. For each mechanism, we counted all motifs containing three nodes and compared their abundance to a structurally similar randomized baseline. Our results illustrate key emergent structural properties of these mechanisms and help explain differences in the dynamical predictions of these three representations of the atmospheric chemical system.
2. Graph representation of atmospheric chemical mechanisms
Chemical reaction mechanisms can be represented as a graph in a variety of ways (Sakamoto et al., Reference Sakamoto, Kawakami and Yoshikawa1988; Bajczyk et al., Reference Bajczyk, Dittwald, Wołos, Szymkuć and Grzybowski2018; Wiser et al., Reference Wiser, Place, Sen, Pye, Yang and Westervelt2023). As a brief overview, a graph G = (V, E), is a pair consisting of a set of unique entities represented as nodes or vertices in V, and a set of binary relations on nodes represented as edges in E. A directed graph is a graph where edges are directed or ordered between nodes. A bipartite graph is a graph where the node set can be partitioned into two subsets, such that edges can only exist between nodes in each subset and never within nodes of the same subset. Here, we use the directed bipartite “species-reaction graph” framework (Feinberg, Reference Feinberg and Feinberg2019; Silva et al., Reference Silva, Burrows, Evans and Halappanavar2021). In a species reaction graph, there are two classes of nodes: species and reactions. Species nodes are connected to reaction nodes with a directed edge, representing reactions the species participates in as a reactant. Reaction nodes are connected to species that are a product of that reaction by a directed edge. This is summarized in Figure 1 for a hypothetical bimolecular reaction: A + B → C + D.

Figure 1. Sample graph of a single bimolecular reaction.
While the species reaction graph in Figure 1 contains edges with directional arrows pointing only in one direction, these edges can be bidirectional. Bidirectional (or “reciprocal”) edges do occur in atmospheric chemical mechanisms, where they are often used to approximate several chemical reactions in one reaction step. An analog to Figure 1 with these bidirectional edges is shown in the Supplementary Material (Figure S1).
We explored three different gas-phase chemical mechanisms in this work: the master chemical mechanism (MCM) v3.3, the GEOS-Chem v12.6 Tropchem chemical mechanism, and the Super-Fast mechanism. Each of these mechanisms aims to reproduce the dynamics of the atmospheric chemical system, though they are designed for very different use cases. The MCM is designed to represent chemical reactions in the atmosphere at a very high level of detail. It has 5833 chemical species and 17,224 reactions (Jenkin et al., Reference Jenkin, Saunders, Wagner and Pilling2003; Saunders et al., Reference Saunders, Jenkin, Derwent and Pilling2003; Bloss et al., Reference Bloss, Wagner, Jenkin, Volkamer, Bloss and Lee2005). The MCM is very computationally expensive and is primarily used as a 1-D box model to simulate chemical timescales of hours to days (Jenkin et al., Reference Jenkin, Saunders and Pilling1997). The GEOS-Chem mechanism represents an intermediate complexity chemical mechanism, with approximately 195 chemical species and 417 reactions (Mao et al., Reference Mao, Paulot, Jacob, Cohen, Crounse and Wennberg2013; Sherwen et al., Reference Sherwen, Schmidt, Evans, Carpenter, Großmann and Eastham2016; Travis et al., Reference Travis, Jacob, Fisher, Kim, Marais and Zhu2016). GEOS-Chem is typically used to simulate the 3D composition of the atmosphere on regional to global scales, for timescales of up to several years (Bey et al., Reference Bey, Jacob, Yantosca, Logan, Field and Fiore2001). The Super-Fast mechanism is a highly parameterized simplified mechanism with 18 chemical species and 20 reactions (Cameron-Smith et al., Reference Cameron-Smith, Lamarque, Connell, Chuang and Vitt2006). The orders of magnitude reduction in complexity make Super-Fast the least computationally expensive mechanism studied here, enabling use cases in global 3D climate models with simulation timescales of decades to centuries (Cameron-Smith et al., Reference Cameron-Smith, Lamarque, Connell, Chuang and Vitt2006; Brown-Steiner et al., Reference Brown-Steiner, Selin, Prinn, Tilmes, Emmons, Lamarque and Cameron-Smith2018). In the graph representation of these mechanisms, Super-Fast has 38 nodes and 81 edges, the GEOS-Chem mechanism has 612 nodes and 2444 edges, and the MCM has 23,057 nodes and 57,245 edges. Full visualization and an initial graph theoretical comparison of the bipartite graphs of these three mechanisms can be found in Silva et al. (Reference Silva, Burrows, Evans and Halappanavar2021).
3. Motif counting
Motifs are repeating patterns of connectivity (also known as subgraphs or graphlets) within a larger graph. Here, we investigate the smallest possible set of motifs, those containing only three nodes. As in other studies of motifs (Milo et al., Reference Milo, Shen-Orr, Itzkovitz, Kashtan, Chklovskii and Alon2002; Masoudi-Nejad et al., Reference Masoudi-Nejad, Schreiber and Kashani2012), we require a motif to have at least two edges (i.e., no isolated nodes). Additionally, since the networks we are studying are all bipartite graphs, there cannot be a 3-node motif with three edges (i.e., a complete triangle), as that would require either species to interconnect or reactions to interconnect. With those qualifications, there are six potential combinations of nodes and edges that form motifs, each distinguished by the directionality of the edges. These six different combinations are often referred to as “isomorphism classes” in the literature (e.g., Milo et al., Reference Milo, Shen-Orr, Itzkovitz, Kashtan, Chklovskii and Alon2002; Pržulj, Reference Pržulj2007), a term that we will use for the remainder of this manuscript. For each isomorphism class, there are two different subgraphs, one where the apex is a species (“species-centered”) and one where the apex is a reaction (“reaction-centered”). All possible three-node motifs for directed bipartite graphs, along with what they represent in chemical mechanisms, are shown in Figure 2. Example graphs containing an isomorphism class with bidirectional edges (i.e., those in classes 3, 5, and 6) are shown in the Supplementary Material (Figure S1).
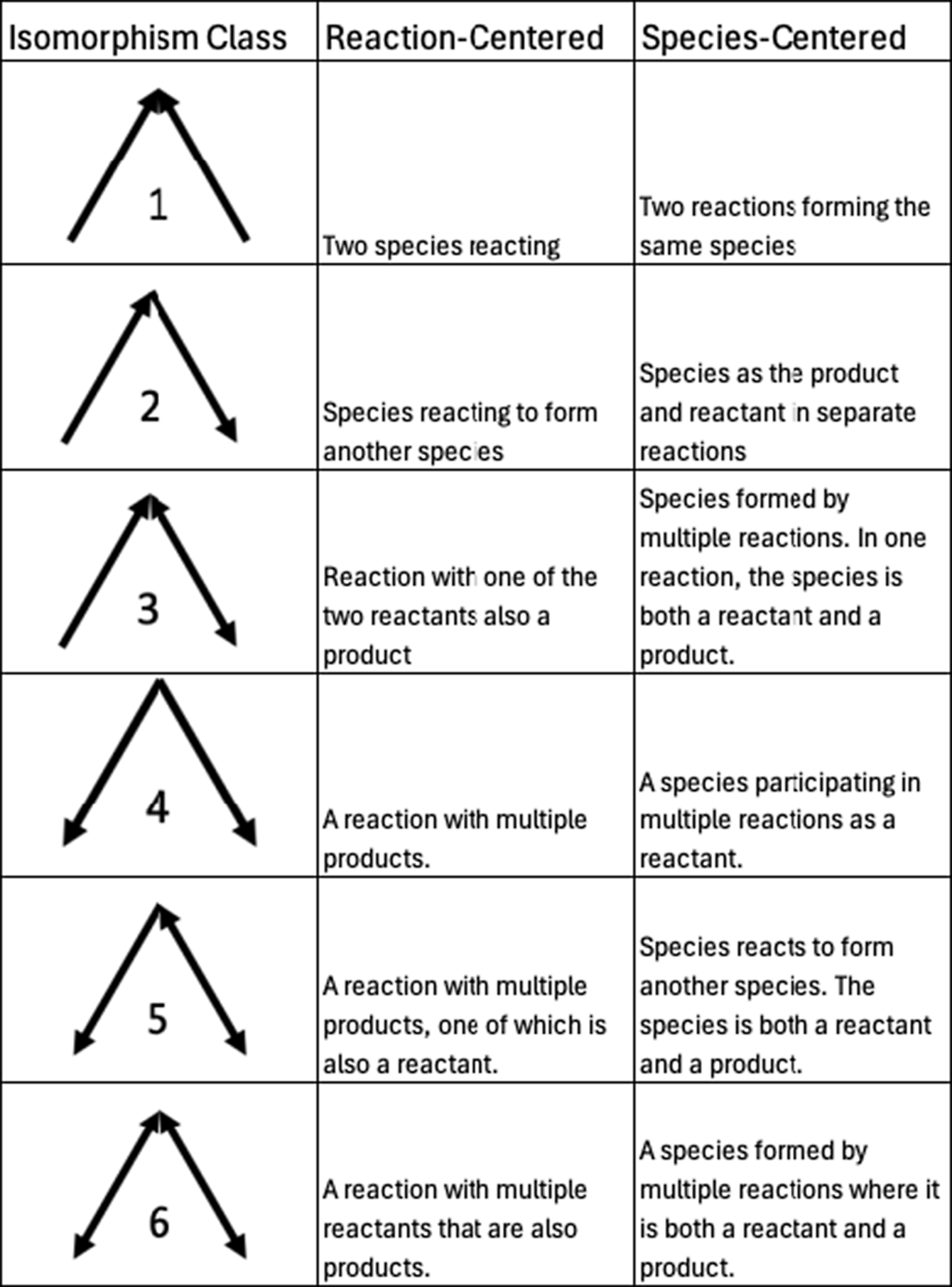
Figure 2. All possible 3-node motif isomorphism classes are studied in this work, along with species- and reaction-centered chemical explanations.
As a baseline example of motif counting, all motifs in the bimolecular reaction in Figure 1 are shown in Figure 3. Isomorphism class 1 appears once in this graph, as the two species react. Isomorphism class 2 appears four times, from reactants reacting to form products. Lastly, isomorphism class 4 appears once as the reaction produces multiple products. In a bipartite reaction with n products, isomorphism class 1 appears once, isomorphism class 2 scales as 2n, and isomorphism class 4 scales as n(n − 1)/2. Given that scaling, and so long as there are fewer than five products, a bimolecular reaction graph will have more class 2 motifs than class 4, and only one class 1 motif.
We use the igraph software package (Csardi and Nepusz, Reference Csardi and Nepusz2006) in this work for all graph analysis tasks, including motif counting.
4. Results and discussion
We count and intercompare the motif prevalence in the Super-Fast, GEOS-Chem, and MCM chemical mechanisms. The total motif counts are summarized in the histograms in Figure 4. This motif count scales with the size of the mechanisms, with the large MCM having upwards of 5 orders of magnitude more total motifs than the compact Super-Fast mechanism.

Figure 4. Distribution of motifs for all six isomorphism classes across all three chemical mechanisms studied in this work.
In general, isomorphism classes 1, 2, and 4 are the most common in all three mechanisms. These are the basic building blocks of a bimolecular reaction and are all present in a basic bimolecular reaction with two products, A + B → C + D, as shown in Figure 3. The other three classes (classes 3, 5, and 6) present in Figure 4 all have bidirectional edges, indicating reciprocal reactions (reactions where some subset of reactants are also products). These are substantially less common because reciprocal reactions are so rare in these reaction mechanisms. Our prior work quantified that only up to 10% of edges are bidirectional (Silva et al., Reference Silva, Burrows, Evans and Halappanavar2021).
A bimolecular reaction generally contributes more motifs in isomorphism class 2 than classes 1 or 4. These mechanisms are dominantly composed of bimolecular reactions, where there are 18 bimolecular reactions (90% of all reactions) in the Super-Fast mechanism, 346 (83%) in the GEOS-Chem mechanism, and 9794 (57%) in the MCM. The Super-Fast motif distribution is consistent with this bimolecular reaction motif occurrence pattern. However, the most common isomorphism class in the GEOS-Chem and MCM graphs is isomorphism class 1. Isomorphism class 1 is only present once in any bimolecular reaction and scales with the number of reactants in a reaction as m(m − 1)/2, where m is the number of reactants. Since most reactions have a reasonably small number of unique reactants (e.g., ~2), the only way isomorphism class 1 can dominate in the mechanism arises from the connectivity pattern in the graph—namely that many chemical species are reactants and products in more than one reaction.
Certain species in the chemical mechanisms participate in an outsized fraction of all chemical reactions. We investigate what fraction of the motif pattern in Figure 4 is related to the species that participate in the most reactions (i.e., with highest degree), namely the HOx (OH and HO2) and NOx (NO and NO2) chemical families. These chemical families represent four species that are highly connected in these graphs, participating in the bulk of the individual chemical reactions (Silva et al., Reference Silva, Burrows, Evans and Halappanavar2021). The fraction of each isomorphism class attributable to motifs centered on HOx and NOx is shown in Figure 5. Motifs centered on the HOx and NOx chemical families represent more than 50% of most isomorphism classes. As the mechanism complexity increases, the fraction of motif classes centered on the HOx and NOx chemical families increases. The MCM shows nearly 100% of the isomorphism classes containing bidirectional edges (classes 3, 5, and 6) are centered on the HOx and NOx chemical families. This indicates that in the MCM, and to a lesser extent GEOS-Chem, nearly all reactions wherein a reactant is also a product are reactions that involve at least one of: OH, HO2, NO, or NO2 as that reactant.

Figure 5. The fraction of isomorphism classes centered on the HOx and NOx chemical families.
We further assess the motif prevalence in the graphs by comparison to the motif prevalence of structurally similar but randomly generated baseline graphs. For a useful 1:1 comparison, these random baselines must retain similar properties as the original graph being studied. To that end, we generated random graphs that were bipartite, had the same number of nodes and edges, and the same degree distribution of chemical species (both in and out degree) as the original chemical mechanism graphs. This was done by randomly shuffling graph edges such that all species nodes have randomly selected reaction nodes as neighbors. We use this edge-shuffling method in lieu of other random graph generative models (e.g., Watts and Strogatz, Reference Watts and Strogatz1998; Chung and Lu, Reference Chung and Lu2002) to strictly maintain many of the node level connectivity patterns that are characteristic of atmospheric chemical mechanisms (e.g., highly connected oxidants, Silva et al. Reference Silva, Burrows, Evans and Halappanavar2021). We generated 1000 of these random graphs for each of the three chemical mechanisms studied in this work and counted the motifs in each of these baselines. Once the random baseline graphs were generated and motifs counted, we calculated the statistical significance of the motif prevalence through a standard z-score. We consider any motif isomorphism class with a z-score of greater than or equal to 1.96 (p ≤ 0.05) to be statistically significant.
The motif prevalence z-scores are summarized in Figure 6. Since the size of the three mechanisms studied here varies across several orders of magnitude, the direct comparison of z-scores across mechanisms is not meaningful. As such, we normalize them to the z-score associated with the first isomorphism class. Non-normalized z-scores are shown in the Supplementary Material (Figure S2).

Figure 6. The scaled z-score of the isomorphism class prevalence in each of the three mechanisms is compared to a random baseline. Transparent bars are not statistically significant.
For each of the three mechanisms, the first isomorphism class has the largest associated z-score and is positive (i.e., more likely to occur than in a random baseline graph). This is consistent with the design of these mechanisms wherein multiple chemical compounds react, and multiple reactions form the same compound. Put another way, most chemical species in atmospheric chemical mechanisms participate in multiple chemical reactions. The agreement in prevalence direction and significance across all three chemical mechanisms disappears beyond the first isomorphism class. The MCM and Super-Fast mechanisms all have motif prevalence z-scores that agree directionally, but not all of the Super-Fast z-scores are significant, in contrast to the MCM. Across all three mechanisms, in some cases, the z-score may be in a similar direction (e.g., class 2, 3, and 5), but not all mechanisms have significant class prevalence or wildly different magnitudes. In other cases, the z-score direction may change entirely between chemical mechanisms, as in isomorphism class 4, which is more likely to occur than random in the Super-Fast and MCM mechanisms but less likely in the GEOS-Chem mechanism. The divergent behavior of the GEOS-Chem mechanism with respect to classes 2 and 4 is particularly noteworthy. Along with isomorphism class 1, these are the fundamental three motifs present in a bimolecular reaction and are explicitly added to the mechanisms during construction (see Figure 3). Class 2 is either a species reacting to form another species or species as the product and reactant in separate reactions. In the GEOS-Chem mechanism, isomorphism class 2 is not statistically significantly represented in the connectivity pattern. Isomorphism Class 4, which represents a reaction with multiple products or species participating in multiple reactions as a reactant, is statistically significantly less likely to occur than random in GEOS-Chem, fully opposite from the other two mechanisms. The emergent structure of chemical interactions in these mechanisms differ substantially, despite the fact that all three mechanisms are dominantly composed of biomolecular reactions.
5. A simple model relating motif prevalence to chemical dynamics
Motifs represent fundamental coupling within chemical mechanisms. Since that coupling governs the dynamics of the chemical system, the results in Section 4 raise the question of how differences in motif prevalence impact the dynamics of the three different mechanisms. The three mechanisms investigated here were selected in part because they are so different—they simulate different chemistry, have different species and rate constants, and have very different use cases. As such, attributing any differences in mechanism dynamics to motif prevalence is challenging.
To address this challenge, we use randomly generated graph baselines for the Super-Fast chemical mechanism to illustrate how differences in motif prevalence can lead to differences in dynamical behavior. We convert 1000 random Super-Fast graphs into the system of ODEs they represent and integrate them forward in time. It is important to note that while these random graphs are structurally similar to the true chemical mechanism graph, they do have key differences—principally among them that these graphs are randomly generated, and prior work has shown that chemical mechanisms are decidedly nonrandom (Silva et al., Reference Silva, Burrows, Evans and Halappanavar2021). Further, the randomized reactions are not necessarily chemically plausible—we do not require notions of conservation laws present in the random graphs (e.g., Liu et al., Reference Liu, Sturm, Bharadwaj, Silva and Tegmark2024), and we do not limit the number of connected components in the graphs. Given these caveats, we treat these random mechanism baselines only as an interesting simple model for atmospheric chemical dynamics and leave the generation of random mechanism graphs that are structurally distinct but dynamically consistent to future work. We integrate the random ODEs forward in time with all species having initial concentrations of 10 (arbitrary units) and all reaction rates equal to 1 (arbitrary units). Integration is done using a forward Euler integration scheme for 500 timesteps with a stepsize of 0.0001.
The process by which we generate randomized baseline graphs preserves many of the node-level graph properties (e.g., in- and out-degree distribution). This preservation means that each random graph still has compounds that participate in an outsized fraction of reactions as a product or a reactant. We label the compound that is most connected (e.g., has the highest degree) in the random graphs in this way a “pseudo-oxidant.” We plot the average concentration of this pseudo-oxidant in the random graphs as a function of time in Figure 7. For each isomorphism class, we additionally plot the average concentration of this pseudo-oxidant for the subset of random graphs with motif prevalence in the top or bottom 5th percentile across random samples. For all three concentration trajectories, we estimate the standard error of the mean as the standard deviation divided by the square root of the number of samples.

Figure 7. The mean pseudo-oxidant concentration with time across 1000 random Super-Fast baseline graphs (black line). The mean concentration for the 95%ile and 5%ile for each isomorphism class are shown in red and blue lines, respectively. The standard error of the mean estimate is shown in the shaded areas.
Across all of these isomorphism classes, there are two broad categories. The first is those where increased prevalence of the class leads to a slower reduction in pseudo-oxidant concentrations and decreased prevalence of the class leads to a faster concentration reduction. Isomorphism classes 1, 2, and 4 are in this first category. The second is the opposite, where increased prevalence of the class leads to a faster reduction in pseudo-oxidant concentrations, and decreased prevalence of the class leads to a slower concentration reduction. The remaining isomorphism classes 3, 5, and 6 are in this second category. For each isomorphism class after 500 timesteps, the mean pseudo-oxidant concentration is always statistically different from the 95th percentile motif prevalence class and usually different from the 5th percentile class at the 95% confidence interval. The two exceptions are for isomorphism classes 1 and 3, where the pseudo-oxidant concentration for 5th percentile class prevalence is not different than the mean after 500 timesteps.
There are several isomorphism classes that were identified as particularly interesting in the motif prevalence analysis associated with Figure 6, and we highlight the associated pseudo-oxidant behavior in Figure 7 for those classes here. The increased prevalence of isomorphism class 1 is consistent across all three mechanisms, and it arises from two species reacting or two reactions forming the same species in the mechanism. In Figure 7, the increased prevalence of isomorphism class 1 dynamically helps maintain the abundance of this pseudo-oxidant in the atmosphere. The prevalence of isomorphism class 4 is statistically significant for all three mechanisms – underrepresented in GEOS-Chem and overrepresented relative to the baseline in the Super-Fast and MCM graphs. This class comes from reactions with multiple products or species that participate in multiple reactions as a reactant. Dynamically, increased isomorphism class 4 prevalence is associated with a slower pseudo-oxidant loss. In the case of the GEOS-Chem mechanism with reduced prevalence of isomorphism class 4, this simple model indicates that the pseudo-oxidant loss would be modestly faster.
In the three real chemical mechanisms, the pseudo-oxidant analog is OH. Prior work has found different OH concentrations when simulated using these mechanisms (e.g., Brown-Steiner et al., Reference Brown-Steiner, Selin, Prinn, Tilmes, Emmons, Lamarque and Cameron-Smith2018; Wolfe et al., Reference Wolfe, Marvin, Roberts, Travis and Liao2016), though a detailed intercomparison of OH chemical dynamics in these mechanisms has not yet been completed. What is known is that the direction and magnitude of the differences in OH concentrations are strongly dependent on the atmospheric chemical state and cannot be trivially attributed to motif prevalence alone.
6. Summary and broader implications
The higher-order structure in atmospheric chemical mechanisms arises due to the coupling of chemical species through chemical reactions. We quantified this emergent structure by exploring repeating patterns of connectivity known as graph motifs. We counted all 3-node motifs in three mechanisms of varying complexity: the MCM, GEOS-Chem, and the Super-Fast chemical mechanisms. These chemical mechanisms are largely constructed through coupling many individual (largely bimolecular) reactions together. That signature of bimolecular chemistry is present to some degree in the motif counts for each mechanism. However, we find substantial differences in motif class counts across the three mechanisms studie here. The total motif abundance in each mechanism is more complex than simply chaining a series of bimolecular reactions together, consistent with the high degree of chemical coupling and complexity present in atmospheric chemical mechanisms.
Overall, these results point to the fact that while there are some similarities between these chemical mechanisms (they are all simulating the same general system), higher-order structural analysis indicates that they are fundamentally different. This is consistent with the notion that these chemical mechanisms have different patterns of chemical interactions and represent a different set of underlying chemical dynamics (e.g., Brown-Steiner et al., Reference Brown-Steiner, Selin, Prinn, Tilmes, Emmons, Lamarque and Cameron-Smith2018).
Graph structural analysis can provide key insight to enable detailed comparison and diagnosis of system behavior across the atmospheric and environmental sciences. Future work integrating additional processes into these graph mechanism representations (e.g., photolysis, heterogeneous chemistry, etc.) and work further exploring the direct connection between graph structural properties and dynamical system behavior would be valuable. This would provide additional context for interpreting the implications of the differences shown in this comparative analysis.
Supplementary material
The supplementary material for this article can be found at http://doi.org/10.1017/eds.2024.30.
Acknowledgments
We are grateful for the feedback on this work provided by Tori Barber and the helpful reviews of two anonymous reviewers. S.J.S. would like to acknowledge Hey Bear Sensory for providing childcare, which enabled the writing of this paper. M.M.H. was funded in part by the US DOE Exascale Computing Project’s (ECP) (17-SC-20-SC) ExaGraph codesign center at Pacific Northwest National Laboratory.
Author contribution
Conceptualization: S.J.S. Methodology: S.J.S.; M.H. Data curation: S.J.S. Data visualization: S.J.S. Writing original draft: S.J.S.; M.H. All authors approved the final submitted draft.
Competing interest
None declared.
Data availability statement
Replication data and code can be found on Zenodo, https://doi.org/10.5281/zenodo.10652025.
Ethical standard
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
This research was supported by NSF Grant Number AGS-2228923.











Comments
Dear Editor,
I am writing to submit our paper titled “Graph Characterization of Higher Order Structure in Atmospheric Chemical Reaction Mechanisms ” for consideration in Environmental Data Science. The manuscript focuses on using modern graph theoretical methods to understand emergent structures within atmospheric chemical mechanisms.
In this work, we address the need to characterize the structure of interactions in chemical mechanisms and assess the differences between the structural characteristics of different mechanisms. We quantify patterns of interaction in the mechanism through counting so-called “motifs”. These are statistically significant small patterns of connectivity (i.e., subgraphs), that have been shown in prior work to provide useful information on the structure and function of complex networks. Our findings reveal distinct motif distributions across different types of atmospheric chemical mechanisms, providing a novel framework for intercomparison and structural assessment.
We believe that our research contributes significantly to the field of atmospheric chemistry and data science by offering novel insights into the emergent structural of chemical mechanisms. This sort of analysis has never been done before in this application space, and the results provide important information for contextualizing mechanism differences.
Thank you for considering our work for publication.
Sam Silva, Ph.D.