1. Introduction
A graphon is a symmetric measurable function W from
![]() $[0,1]^2$
to [0,1], where symmetric here means that
$[0,1]^2$
to [0,1], where symmetric here means that
![]() $W(x,y) = W(y,x)$
for all
$W(x,y) = W(y,x)$
for all
![]() $(x,y) \in [0,1]^2$
. Very roughly, this may be seen as a continuous analogue of a graph. The homomorphism density
$(x,y) \in [0,1]^2$
. Very roughly, this may be seen as a continuous analogue of a graph. The homomorphism density
![]() $t_H(W)$
of a graph H in a graphon W is then given by
$t_H(W)$
of a graph H in a graphon W is then given by
 \[t_H(W) = \mathbb{E} \left[\prod_{ij \in E(H)} W(x_i, x_j)\right] = \int_{[0,1]^{v(H)}} \prod_{ij \in E(H)} W(x_i, x_j) \ d\mu^{v(H)},\]
\[t_H(W) = \mathbb{E} \left[\prod_{ij \in E(H)} W(x_i, x_j)\right] = \int_{[0,1]^{v(H)}} \prod_{ij \in E(H)} W(x_i, x_j) \ d\mu^{v(H)},\]
where
![]() $\mu$
is the Lebesgue measure on [0,1]. Our concern in this paper will be with the following question: for which ordered pairs of graphs (H, H
′) is it the case that H dominates H
′, in the sense that
$\mu$
is the Lebesgue measure on [0,1]. Our concern in this paper will be with the following question: for which ordered pairs of graphs (H, H
′) is it the case that H dominates H
′, in the sense that
for all graphons W?
This question has been studied both implicitly and explicitly for decades. For instance, a celebrated conjecture of Sidorenko [
Reference Sidorenko17, Reference Sidorenko18
] says that H dominates
![]() $K_2$
if and only if H is bipartite. The necessity of the bipartiteness condition is simple to verify, but its sufficiency is a difficult problem which has attracted a great deal of attention in recent years [
Reference Conlon, Fox and Sudakov2, Reference Conlon, Kim, Lee and Lee3, Reference Conlon and Lee5–Reference Coregliano and Razborov7, Reference Kim, Lee and Lee11, Reference Li and Szegedy14, Reference Szegedy22
].
$K_2$
if and only if H is bipartite. The necessity of the bipartiteness condition is simple to verify, but its sufficiency is a difficult problem which has attracted a great deal of attention in recent years [
Reference Conlon, Fox and Sudakov2, Reference Conlon, Kim, Lee and Lee3, Reference Conlon and Lee5–Reference Coregliano and Razborov7, Reference Kim, Lee and Lee11, Reference Li and Szegedy14, Reference Szegedy22
].
One of the oldest results in this direction is a result of Godsil that first appeared in a paper of Erdős and Simonovits [
Reference Erdős and Simonovits8
]. If we write
![]() $P_n$
for the path with n vertices, his result says that
$P_n$
for the path with n vertices, his result says that
![]() $P_n$
dominates
$P_n$
dominates
![]() $P_m$
whenever
$P_m$
whenever
![]() $2 \leq m \leq n$
and n is odd. That is, even-length paths dominate all of their connected subgraphs and this easily extends to all subgraphs. In what follows, we will refer to a graph H with this property, that H dominates H
′ for all subgraphs H
′ of H with at least one edge, as a dominating graph.
$2 \leq m \leq n$
and n is odd. That is, even-length paths dominate all of their connected subgraphs and this easily extends to all subgraphs. In what follows, we will refer to a graph H with this property, that H dominates H
′ for all subgraphs H
′ of H with at least one edge, as a dominating graph.
The only other graphs known to have this property are the weakly norming graphs whose study was initiated by Lovász [ Reference Lovász15 ] and Hatami [ Reference Hatami10 ]. The fact that all weakly norming graphs are dominating was proved by Hatami [ Reference Hatami10 ]. Until quite recently, only a handful of weakly norming graphs were known [ Reference Hatami10, Reference Lovász16 ], but a much broader collection of examples was found by the authors [ Reference Conlon and Lee4 ], who showed how to associate a family of weakly norming graphs to any finite reflection group. The purpose of this paper is to show that the family of dominating graphs is broader still. In particular, we will show that both previous families of examples, weakly norming graphs and even-length paths, can be placed within a common framework.
One of the main results in [ Reference Conlon and Lee4 ] says that if there is a sequence of what we might call reflections, each of which takes a subgraph J of a graph H and produces another subgraph J ′, that starts with a single edge and ends with H, then H is weakly norming. The corresponding result here allows a second operation, which we call relocation, and says that if, through a sequence of reflections and relocations, one can start with a single edge and get to a graph H, then H is dominating. In [ Reference Conlon and Lee4 ], our results can be neatly packaged in terms of what we call reflection graphs. Unfortunately, there seems to be no such clean statement here. Instead, we will apply our reflection/relocation mechanism to produce a variety of examples, each derived in some way from a reflection group. For now, we illustrate our results with just one family of examples, which, by a recent result of Sidorenko [ Reference Sidorenko20 ], are known to not be weakly norming. Recall that the 1-subdivision of a graph H is the graph obtained by replacing each edge of H by a path with two edges.
Theorem 1·1. The 1-subdivision of the complete bipartite graph
![]() $K_{t,t}$
is dominating.
$K_{t,t}$
is dominating.
The rest of the paper is organised as follows. In the next section, we prove some necessary conditions for a graph H to dominate another graph H ′, thereby also giving some conditions that must be satisfied by any dominating graph. In Section 3, we describe our reflection/relocation mechanism and show that it produces dominating graphs. We then use this mechanism in Section 4 to find new examples of dominating graphs, including those mentioned in Theorem 1·1. We talk about applications of the domination property in Section 5, before concluding with some further remarks and open problems.
2. Necessary conditions for domination
As we remarked in the introduction, any dominating graph must be bipartite. Here we establish some more necessary conditions. First, we show that any connected dominating graph must be 1-balanced, in the sense that
![]() ${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
for every subgraph H
′ of H. The proof is essentially due to Hatami [
Reference Hatami10
], who proved an analogous result for weakly norming graphs.
${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
for every subgraph H
′ of H. The proof is essentially due to Hatami [
Reference Hatami10
], who proved an analogous result for weakly norming graphs.
Proposition 2·1. Let H and H
′ be connected graphs. If H dominates H
′, then
![]() ${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
.
${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
.
Proof. For
![]() $1 \leq k \leq n$
, let
$1 \leq k \leq n$
, let
![]() $I_{n,k}$
be the square-shaped subset
$I_{n,k}$
be the square-shaped subset
![]() $\{(x,y)\;:\;(k-1)/n<x,y<k/n\}$
of the unit square and let W be the block graphon given by
$\{(x,y)\;:\;(k-1)/n<x,y<k/n\}$
of the unit square and let W be the block graphon given by
![]() $W =\sum_{k=1}^n \mathbf{1}_{I_{n,k}}$
. Then, since both H and H
′ are connected,
$W =\sum_{k=1}^n \mathbf{1}_{I_{n,k}}$
. Then, since both H and H
′ are connected,
Thus, the domination inequality
![]() $t_H(W)^{1/e(H)}\geq t_{H^{\prime}}(W)^{1/e(H^{\prime})}$
can be rewritten as
$t_H(W)^{1/e(H)}\geq t_{H^{\prime}}(W)^{1/e(H^{\prime})}$
can be rewritten as
which yields the desired inequality
![]() ${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
.
${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
.
Corollary 2·2. If H is a connected dominating graph, then
![]() ${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
for every subgraph H
′ of H.
${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
for every subgraph H
′ of H.
Proof. By Proposition 2·1, we may assume that H
′ is not connected. Let
![]() $F_1,F_2,\dots,F_t$
be the connected components of H
′ and let
$F_1,F_2,\dots,F_t$
be the connected components of H
′ and let
![]() $d_i\;:\!=\;{e(F_i)}/({v(F_i)-1})$
. Then
$d_i\;:\!=\;{e(F_i)}/({v(F_i)-1})$
. Then
and, hence,
![]() ${e(H^{\prime})}/({v(H^{\prime})-1})$
is smaller than a convex combination of the
${e(H^{\prime})}/({v(H^{\prime})-1})$
is smaller than a convex combination of the
![]() $d_i$
. Therefore, there must be a component
$d_i$
. Therefore, there must be a component
![]() $F_j$
with
$F_j$
with
![]() $d_j>{e(H^{\prime})}/({v(H^{\prime})-1})$
. Hence, since, by Proposition 2·1,
$d_j>{e(H^{\prime})}/({v(H^{\prime})-1})$
. Hence, since, by Proposition 2·1,
![]() ${e(H)}/({v(H) - 1}) \geq {e(F)}/({v(F) - 1})$
for every connected F, we have
${e(H)}/({v(H) - 1}) \geq {e(F)}/({v(F) - 1})$
for every connected F, we have
![]() ${e(H)}/({v(H) - 1})\geq d_j$
, which implies that
${e(H)}/({v(H) - 1})\geq d_j$
, which implies that
![]() ${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
for every subgraph H
′.
${e(H)}/({v(H) - 1}) \geq {e(H^{\prime})}/({v(H^{\prime}) - 1})$
for every subgraph H
′.
As pointed out in [
Reference Garbe, Hladký and Lee9
], this result is not true if H is not connected, as may be seen by considering the weakly norming, and hence dominating, graph consisting of two disjoint copies of
![]() $K_{1,2}$
and the subgraph consisting of a single copy of
$K_{1,2}$
and the subgraph consisting of a single copy of
![]() $K_{1,2}$
.
$K_{1,2}$
.
Our second condition states that every connected dominating graph has the property that every vertex on the smaller side of the bipartition has the same degree. The proof is again similar to a result of Hatami [
Reference Hatami10
], who showed that every connected weakly norming graph is bi-regular, i.e., all vertices on the same side of the bipartition have the same degree. This stronger property does not necessarily hold for dominating graphs, since, as we shall see, there are many examples, including even-length paths and the example
![]() $C_6^+$
in Figure 1, which are not bi-regular.
$C_6^+$
in Figure 1, which are not bi-regular.

Fig. 1. The graph
![]() $C_6^+$
, which is dominating but not weakly norming.
$C_6^+$
, which is dominating but not weakly norming.
Proposition 2·3. Let H be a connected dominating graph with bipartition
![]() $A\cup B$
. If
$A\cup B$
. If
![]() $|A|\leq|B|$
, then every vertex
$|A|\leq|B|$
, then every vertex
![]() $v\in A$
must have the same degree. Moreover, the maximum degree
$v\in A$
must have the same degree. Moreover, the maximum degree
![]() $\Delta$
of H is attained by the vertices in A.
$\Delta$
of H is attained by the vertices in A.
Proof. Let
![]() $\varepsilon<1/2$
be positive and let I and J be the two disjoint intervals
$\varepsilon<1/2$
be positive and let I and J be the two disjoint intervals
![]() $[0,\varepsilon)$
and
$[0,\varepsilon)$
and
![]() $[\varepsilon,1]$
, respectively. Denote by W the graphon
$[\varepsilon,1]$
, respectively. Denote by W the graphon
![]() $\mathbf{1}_{I\times J}+\mathbf{1}_{J\times I}$
. Denote by S the star with
$\mathbf{1}_{I\times J}+\mathbf{1}_{J\times I}$
. Denote by S the star with
![]() $\Delta$
leaves, which is clearly a subgraph of H. Then
$\Delta$
leaves, which is clearly a subgraph of H. Then
Since
![]() $\varepsilon<1/2$
,
$\varepsilon<1/2$
,
![]() $t_S(W)\geq \varepsilon/2^{\Delta}$
, so the inequality
$t_S(W)\geq \varepsilon/2^{\Delta}$
, so the inequality
![]() $t_H(W)\geq t_S(W)^{e(H)/\Delta}$
, which holds since H is dominating, gives
$t_H(W)\geq t_S(W)^{e(H)/\Delta}$
, which holds since H is dominating, gives
But this gives a contradiction for
![]() $\varepsilon$
sufficiently small unless
$\varepsilon$
sufficiently small unless
![]() $|A|\leq e(H)/\Delta$
. On the other hand,
$|A|\leq e(H)/\Delta$
. On the other hand,
![]() $e(H)\leq \Delta |A|$
. Therefore,
$e(H)\leq \Delta |A|$
. Therefore,
![]() $e(H)=\Delta|A|$
, which means that every vertex in A has degree
$e(H)=\Delta|A|$
, which means that every vertex in A has degree
![]() $\Delta$
.
$\Delta$
.
As a corollary, we note that if the two sides of the bipartition of a connected dominating graph H have the same size, i.e.,
![]() $|A|=|B|$
, then the graph must be regular.
$|A|=|B|$
, then the graph must be regular.
The reason we have largely focused on connected dominating graphs is because of the following result, which says that the components of any dominating graph must all be the same. This generalises, and gives a simpler proof of, a similar result for weakly norming graphs proved by Garbe, Hladký and Lee [ Reference Garbe, Hladký and Lee9 ].
Lemma 2·4. A graph without isolated vertices is dominating if and only if each of its components is the same dominating graph.
Proof. It easy to check that the disjoint union of multiple copies of the same dominating graph is dominating, so we will focus on the opposite direction. To this end, let H be a dominating graph with no isolated vertices and at least two components and write
![]() $H = H_1 \cup H_2$
, where
$H = H_1 \cup H_2$
, where
![]() $H_1$
is a single component and
$H_1$
is a single component and
![]() $H_2$
is the union of the remaining components. Then
$H_2$
is the union of the remaining components. Then
![]() $t_H(W)^{1/e(H)} \geq t_{H_1}(W)^{1/e(H_1)}$
is equivalent to
$t_H(W)^{1/e(H)} \geq t_{H_1}(W)^{1/e(H_1)}$
is equivalent to
![]() $t_{H_2}(W)^{1/e(H_2)} \geq t_{H_1}(W)^{1/e(H_1)}$
, where we used that
$t_{H_2}(W)^{1/e(H_2)} \geq t_{H_1}(W)^{1/e(H_1)}$
, where we used that
![]() $t_H(W)= t_{H_1}(W) t_{H_2}(W)$
. Similarly,
$t_H(W)= t_{H_1}(W) t_{H_2}(W)$
. Similarly,
![]() $t_H(W)^{1/e(H)} \geq t_{H_2}(W)^{1/e(H_2)}$
is equivalent to
$t_H(W)^{1/e(H)} \geq t_{H_2}(W)^{1/e(H_2)}$
is equivalent to
![]() $t_{H_1}(W)^{1/e(H_1)} \geq t_{H_2}(W)^{1/e(H_2)}$
. Hence, if H is dominating, we must have that
$t_{H_1}(W)^{1/e(H_1)} \geq t_{H_2}(W)^{1/e(H_2)}$
. Hence, if H is dominating, we must have that
![]() $t_{H_1}(W)^{1/e(H_1)} = t_{H_2}(W)^{1/e(H_2)}$
for all W. But this is the same as saying that
$t_{H_1}(W)^{1/e(H_1)} = t_{H_2}(W)^{1/e(H_2)}$
for all W. But this is the same as saying that
![]() $t_{H_1}(W)^{e(H_2)} = t_{H_2}(W)^{e(H_1)}$
for all W, which in turn implies that
$t_{H_1}(W)^{e(H_2)} = t_{H_2}(W)^{e(H_1)}$
for all W, which in turn implies that
![]() $t_{e(H_2) H_1}(W) = t_{e(H_1) H_2}(W)$
for all W. But, by [
Reference Lovász16
, theorem 5·29], this implies that
$t_{e(H_2) H_1}(W) = t_{e(H_1) H_2}(W)$
for all W. But, by [
Reference Lovász16
, theorem 5·29], this implies that
![]() $e(H_2) H_1 = e(H_1) H_2$
, so
$e(H_2) H_1 = e(H_1) H_2$
, so
![]() $H_2$
must be a union of copies of
$H_2$
must be a union of copies of
![]() $H_1$
. To verify that
$H_1$
. To verify that
![]() $H_1$
is itself dominating, suppose that
$H_1$
is itself dominating, suppose that
![]() $H = rH_1$
and consider the subgraph
$H = rH_1$
and consider the subgraph
![]() $H^{\prime} = rH^{\prime}_1$
, where
$H^{\prime} = rH^{\prime}_1$
, where
![]() $H^{\prime}_1$
is a subgraph of
$H^{\prime}_1$
is a subgraph of
![]() $H_1$
. Then, since H is dominating,
$H_1$
. Then, since H is dominating,
 \begin{align*} t_{H_1}(W)^{1/e(H_1)} &= t_{rH_1}(W)^{1/re(H_1)} = t_H(W)^{1/e(H)} \\ &\geq t_{H^{\prime}}(W)^{1/e(H^{\prime})} = t_{rH^{\prime}_1}(W)^{1/re(H^{\prime}_1)} = t_{H^{\prime}_1}(W)^{1/e(H^{\prime}_1)}\end{align*}
\begin{align*} t_{H_1}(W)^{1/e(H_1)} &= t_{rH_1}(W)^{1/re(H_1)} = t_H(W)^{1/e(H)} \\ &\geq t_{H^{\prime}}(W)^{1/e(H^{\prime})} = t_{rH^{\prime}_1}(W)^{1/re(H^{\prime}_1)} = t_{H^{\prime}_1}(W)^{1/e(H^{\prime}_1)}\end{align*}
for all W, implying that
![]() $H_1$
is indeed dominating.
$H_1$
is indeed dominating.
3. Layered percolation
Given a connected graph H, we say that an automorphism
![]() $\phi$
of H is a cut involution if the following conditions hold:
$\phi$
of H is a cut involution if the following conditions hold:
-
(i)
 $\phi$
is an involution, that is,
$\phi$
is an involution, that is,
 $\phi = \phi^{-1}$
;
$\phi = \phi^{-1}$
; -
(ii) the fixed point set
 $F_\phi = \{v \in V(H) \;:\; \phi(v) = v\}$
is a vertex cut of H;
$F_\phi = \{v \in V(H) \;:\; \phi(v) = v\}$
is a vertex cut of H; -
(iii)
 $V(H) \setminus F_\phi$
is the disjoint union of sets
$V(H) \setminus F_\phi$
is the disjoint union of sets
 $L_\phi$
and
$L_\phi$
and
 $R_\phi$
, where there are no edges between
$R_\phi$
, where there are no edges between
 $L_\phi$
and
$L_\phi$
and
 $R_\phi$
and they are mapped to one another under
$R_\phi$
and they are mapped to one another under
 $\phi$
.Footnote 1
$\phi$
.Footnote 1
The cut involution group
![]() $W_H$
is then the group of automorphisms of H generated by its cut involutions.
$W_H$
is then the group of automorphisms of H generated by its cut involutions.
Suppose now that a particular choice for
![]() $L_\phi$
and
$L_\phi$
and
![]() $R_\phi$
has been made for each cut involution
$R_\phi$
has been made for each cut involution
![]() $\phi$
of H. We define the left-folding map
$\phi$
of H. We define the left-folding map
![]() $\phi^+: V(H) \rightarrow V(H)$
of a cut involution
$\phi^+: V(H) \rightarrow V(H)$
of a cut involution
![]() $\phi$
of H by
$\phi$
of H by
 \begin{align*} {}\phi^+(v)= {}\begin{cases} {} {}\phi(v) \;&\textrm{ if }v\in R_\phi\\[5pt] {} {}v &\textrm{ if }v\in L_\phi\cup F_\phi {}\end{cases}\end{align*}
\begin{align*} {}\phi^+(v)= {}\begin{cases} {} {}\phi(v) \;&\textrm{ if }v\in R_\phi\\[5pt] {} {}v &\textrm{ if }v\in L_\phi\cup F_\phi {}\end{cases}\end{align*}
and, similarly, define the right-folding map
![]() $\phi^-$
by swapping the roles of
$\phi^-$
by swapping the roles of
![]() $L_\phi$
and
$L_\phi$
and
![]() $R_\phi$
. For brevity, we refer to both the left- and right-folding maps as half-folding maps of
$R_\phi$
. For brevity, we refer to both the left- and right-folding maps as half-folding maps of
![]() $\phi$
. The conjugate
$\phi$
. The conjugate
![]() $\overline{\psi}$
of a half-folding map
$\overline{\psi}$
of a half-folding map
![]() $\psi$
is then the other half-folding map defined by the same cut involution.
$\psi$
is then the other half-folding map defined by the same cut involution.
If J is an edge subset of H and
![]() $\phi$
is a cut involution of H, we define two edge sets
$\phi$
is a cut involution of H, we define two edge sets
![]() $J^+(\phi)$
and
$J^+(\phi)$
and
![]() $J^-(\phi)$
by
$J^-(\phi)$
by
That is,
![]() $J^+(\phi)$
is the graph formed by copying the edges of J from the left half onto the right half, while
$J^+(\phi)$
is the graph formed by copying the edges of J from the left half onto the right half, while
![]() $J^-(\phi)$
copies the edges from the right half onto the left half. The maps
$J^-(\phi)$
copies the edges from the right half onto the left half. The maps
![]() $J \mapsto J^+(\phi)$
and
$J \mapsto J^+(\phi)$
and
![]() $J \mapsto J^-(\phi)$
are the ‘reflections’ mentioned in the introduction. In what follows, we will sometimes abuse notation slightly by writing
$J \mapsto J^-(\phi)$
are the ‘reflections’ mentioned in the introduction. In what follows, we will sometimes abuse notation slightly by writing
![]() $J(\phi^+)$
for
$J(\phi^+)$
for
![]() $J^+(\phi)$
and
$J^+(\phi)$
and
![]() $J(\phi^-)$
for
$J(\phi^-)$
for
![]() $J^-(\phi)$
.
$J^-(\phi)$
.
Let
![]() $J_0,J_1,J_2,\dots$
be a sequence of edge subsets of H. We say that it is a folding sequence in H if, for each
$J_0,J_1,J_2,\dots$
be a sequence of edge subsets of H. We say that it is a folding sequence in H if, for each
![]() $i\geq 1$
,
$i\geq 1$
,
![]() $J_i=J_{i-1}(\psi_i)$
for some half-folding map
$J_i=J_{i-1}(\psi_i)$
for some half-folding map
![]() $\psi_{i}$
, calling the corresponding sequence of half-folding maps
$\psi_{i}$
, calling the corresponding sequence of half-folding maps
![]() $(\psi_i)_{i=1}^N$
the signature of the folding sequence. If a finite folding sequence
$(\psi_i)_{i=1}^N$
the signature of the folding sequence. If a finite folding sequence
![]() $J_0,J_1,\dots,J_N$
in a graph H starts from a set
$J_0,J_1,\dots,J_N$
in a graph H starts from a set
![]() $J_0$
consisting of a single edge and ends with
$J_0$
consisting of a single edge and ends with
![]() $J_N=E(H)$
, then we call it a percolating sequence. The reason for these definitions is that such folding sequences allow us to keep track of repeated applications of the Cauchy–Schwarz inequality. Indeed, a simple application of the Cauchy–Schwarz inequality gives
$J_N=E(H)$
, then we call it a percolating sequence. The reason for these definitions is that such folding sequences allow us to keep track of repeated applications of the Cauchy–Schwarz inequality. Indeed, a simple application of the Cauchy–Schwarz inequality gives
where here we identify the edge sets
![]() $J_i$
,
$J_i$
,
![]() $J_i^+(\phi)$
and
$J_i^+(\phi)$
and
![]() $J_i^-(\phi)$
with their corresponding subgraphs. With this terminology in place, we may recall one of the main results in [
Reference Conlon and Lee4
], which says that if there is a percolating sequence in a graph H, then, through appropriate repeated applications of (1), we have that H is weakly norming.
$J_i^-(\phi)$
with their corresponding subgraphs. With this terminology in place, we may recall one of the main results in [
Reference Conlon and Lee4
], which says that if there is a percolating sequence in a graph H, then, through appropriate repeated applications of (1), we have that H is weakly norming.
Theorem 3·1 (Conlon--Lee). If there exists a percolating sequence
![]() $J_0,J_1,\dots,J_N$
, then H is weakly norming.
$J_0,J_1,\dots,J_N$
, then H is weakly norming.
The aim of this section is to prove a multilayered variant of this result whose conclusion is that a particular graph H is dominating. Suppose that
![]() $H_1,H_2,\dots,H_k$
are edge-disjoint subgraphs of H that partition the edge set E(H). We say that
$H_1,H_2,\dots,H_k$
are edge-disjoint subgraphs of H that partition the edge set E(H). We say that
![]() $H_1,H_2,\dots,H_k$
are layers of the graph H if there is a nontrivial subset
$H_1,H_2,\dots,H_k$
are layers of the graph H if there is a nontrivial subset
![]() $\Phi$
of the set of cut involutions of H such that
$\Phi$
of the set of cut involutions of H such that
![]() $\phi(e) \in E(H_i)$
for all
$\phi(e) \in E(H_i)$
for all
![]() $\phi \in \Phi$
,
$\phi \in \Phi$
,
![]() $i \in [k]$
and
$i \in [k]$
and
![]() $e \in E(H_i)$
. A layered percolating sequence for H (with respect to
$e \in E(H_i)$
. A layered percolating sequence for H (with respect to
![]() $H_1,H_2,\dots,H_k$
, though we typically omit this) is then a folding sequence
$H_1,H_2,\dots,H_k$
, though we typically omit this) is then a folding sequence
![]() $J_0,J_1,\dots,J_N$
with signature
$J_0,J_1,\dots,J_N$
with signature
![]() $(\psi_i)_{i=1}^N$
such that
$(\psi_i)_{i=1}^N$
such that
![]() $J_0$
consists of k edges
$J_0$
consists of k edges
![]() $e_1,e_2,\dots,e_k$
, where
$e_1,e_2,\dots,e_k$
, where
![]() $e_i\in E(H_i)$
for each
$e_i\in E(H_i)$
for each
![]() $i\in [k]$
,
$i\in [k]$
,
![]() $J_N=E(H)$
and each
$J_N=E(H)$
and each
![]() $\psi_i$
is a half-folding map associated to a cut involution
$\psi_i$
is a half-folding map associated to a cut involution
![]() $\phi_i \in \Phi$
. The k edges
$\phi_i \in \Phi$
. The k edges
![]() $e_1,e_2,\dots,e_k$
that form
$e_1,e_2,\dots,e_k$
that form
![]() $J_0$
are called the seeds of the layered percolating sequence. In particular, if there is a layered percolating sequence for H, then each
$J_0$
are called the seeds of the layered percolating sequence. In particular, if there is a layered percolating sequence for H, then each
![]() $H_i$
is edge-transitive under the group of automorphisms of H generated by the set of layer-preserving cut involutions
$H_i$
is edge-transitive under the group of automorphisms of H generated by the set of layer-preserving cut involutions
![]() $\Phi$
.
$\Phi$
.
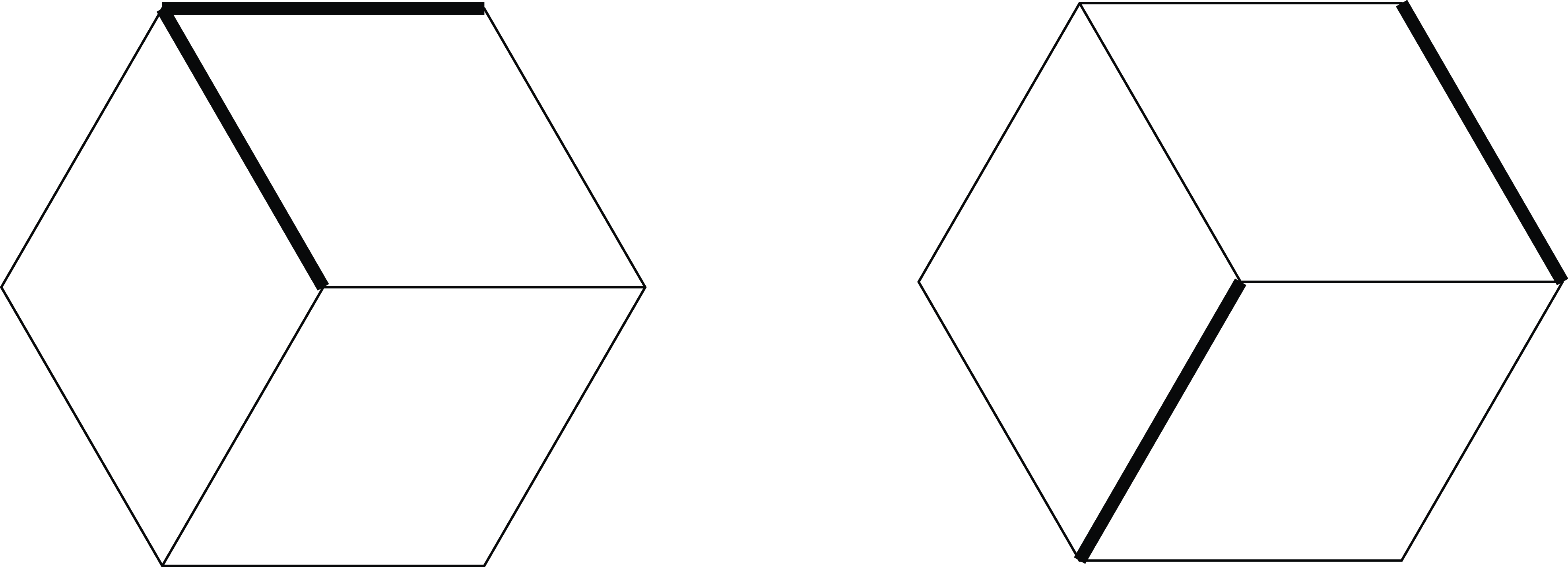
Fig. 2. Different choices for
![]() $J_0$
in
$J_0$
in
![]() $C_6^+$
.
$C_6^+$
.
Example 3·2. On the left-hand side of Figure 2, the two thick edges represent one possible choice for
![]() $J_0$
in a layered percolating sequence for
$J_0$
in a layered percolating sequence for
![]() $C_6^+$
. More precisely, the layers of the partition are the outer cycle
$C_6^+$
. More precisely, the layers of the partition are the outer cycle
![]() $C_6$
and the star
$C_6$
and the star
![]() $K_{1,3}$
of edges adjacent to the central vertex. The inner edge percolates to cover the star
$K_{1,3}$
of edges adjacent to the central vertex. The inner edge percolates to cover the star
![]() $K_{1,3}$
, while the outer edge percolates to cover the cycle
$K_{1,3}$
, while the outer edge percolates to cover the cycle
![]() $C_6$
. Moreover, as required for a layered percolating sequence, they percolate together to cover the entire graph J. In contrast, the choice of thick edges on the right-hand side of Figure 2 does not produce a layered percolating sequence. To see this, note that any cut involution that places the two edges in opposite halves will delete one of the two edges when we reflect.
$C_6$
. Moreover, as required for a layered percolating sequence, they percolate together to cover the entire graph J. In contrast, the choice of thick edges on the right-hand side of Figure 2 does not produce a layered percolating sequence. To see this, note that any cut involution that places the two edges in opposite halves will delete one of the two edges when we reflect.
For
![]() $I\subseteq [k]$
, let
$I\subseteq [k]$
, let
![]() $H_I = \cup_{i \in I} H_i$
be the subgraph obtained by taking the union of all the edges in the layers
$H_I = \cup_{i \in I} H_i$
be the subgraph obtained by taking the union of all the edges in the layers
![]() $H_i$
with
$H_i$
with
![]() $i\in I$
. As the second case in Example 3·2 above shows, even if a layered percolating sequence exists, there may also be k-edge subsets F spanning all the layers such that following the percolating sequence starting with F does not lead to the whole set E(H). This is a potential problem in generalising Theorem 3·1. However, we now show that, even if this happens, the folding sequence does always end with
$i\in I$
. As the second case in Example 3·2 above shows, even if a layered percolating sequence exists, there may also be k-edge subsets F spanning all the layers such that following the percolating sequence starting with F does not lead to the whole set E(H). This is a potential problem in generalising Theorem 3·1. However, we now show that, even if this happens, the folding sequence does always end with
![]() $E(H_I)$
for some
$E(H_I)$
for some
![]() $I\subseteq [k]$
.
$I\subseteq [k]$
.
Lemma 3·3. Let H be a graph with layers
![]() $H_1, \dots, H_k$
and let
$H_1, \dots, H_k$
and let
![]() $J_0, J_1,\dots,J_N$
be a layered percolating sequence of H with signature
$J_0, J_1,\dots,J_N$
be a layered percolating sequence of H with signature
![]() $(\psi_i)_{i=1}^N$
. Then every folding sequence
$(\psi_i)_{i=1}^N$
. Then every folding sequence
![]() $F_0,F_1,\dots,F_N$
with the same signature satisfies
$F_0,F_1,\dots,F_N$
with the same signature satisfies
![]() $F_N=E(H_I)$
with
$F_N=E(H_I)$
with
![]() $I= J_0\cap F_0$
.
$I= J_0\cap F_0$
.
Proof. Let
![]() $F_{i,j}\;:\!=\;F_i\cap E(H_j)$
. Then
$F_{i,j}\;:\!=\;F_i\cap E(H_j)$
. Then
![]() $F_{i,j}=F_{i-1,j}(\psi_i)$
, by considering the restriction of the signature
$F_{i,j}=F_{i-1,j}(\psi_i)$
, by considering the restriction of the signature
![]() $(\psi_i)_{i=1}^N$
to
$(\psi_i)_{i=1}^N$
to
![]() $E(H_j)$
. Suppose that there is
$E(H_j)$
. Suppose that there is
![]() $e_j\in J_0\cap F_0\cap E(H_j)$
, i.e.,
$e_j\in J_0\cap F_0\cap E(H_j)$
, i.e.,
![]() $F_{0,j}\supseteq J_0\cap E(H_j)=\{e_j\}$
. Then, by induction,
$F_{0,j}\supseteq J_0\cap E(H_j)=\{e_j\}$
. Then, by induction,
for each
![]() $i=1,2,\dots,N$
. In particular,
$i=1,2,\dots,N$
. In particular,
![]() $F_{N,j}=E(H_j)$
.
$F_{N,j}=E(H_j)$
.
Suppose now that
![]() $J_0\cap F_{0,j}$
is empty. Let
$J_0\cap F_{0,j}$
is empty. Let
![]() $\overline{F}=E(H_j)\setminus F$
for
$\overline{F}=E(H_j)\setminus F$
for
![]() $F\subseteq E(H_j)$
. It then follows that
$F\subseteq E(H_j)$
. It then follows that
In particular,
![]() $\overline{F_{i,j}}=\overline{F_{i-1,j}(\psi)}=\overline{F_{i-1,j}}(\psi)$
and, therefore,
$\overline{F_{i,j}}=\overline{F_{i-1,j}(\psi)}=\overline{F_{i-1,j}}(\psi)$
and, therefore,
![]() $\overline{F_{0,j}},\overline{F_{1,j}},\dots,\overline{F_{N,j}}$
is again a folding sequence with signature
$\overline{F_{0,j}},\overline{F_{1,j}},\dots,\overline{F_{N,j}}$
is again a folding sequence with signature
![]() $(\psi_i)_{i=1}^N$
. Thus, by repeating the argument above,
$(\psi_i)_{i=1}^N$
. Thus, by repeating the argument above,
![]() $\overline{F_{N,j}}=E(H_j)$
since
$\overline{F_{N,j}}=E(H_j)$
since
![]() $J_0\cap \overline{F_{0,j}}$
is nonempty. That is,
$J_0\cap \overline{F_{0,j}}$
is nonempty. That is,
![]() $F_{N,j}$
is empty.
$F_{N,j}$
is empty.
To summarise,
![]() $F_{N,j}$
is either the whole of
$F_{N,j}$
is either the whole of
![]() $E(H_j)$
or empty, depending on whether
$E(H_j)$
or empty, depending on whether
![]() $J_0\cap F_{0,j}$
is nonempty or empty. Thus,
$J_0\cap F_{0,j}$
is nonempty or empty. Thus,
![]() $F_N=E(H_I)$
with
$F_N=E(H_I)$
with
![]() $I=J_0\cap F_0$
.
$I=J_0\cap F_0$
.
At first glance, this lemma seems to be something of a dead end. Starting from a given subgraph
![]() $F_0$
, we set out to cover the entire graph, but instead only managed to cover some of its layers. It is at this point that we need to introduce our second operation. Suppose that we have a layered percolating sequence in H whose set of seeds is K. Given a nonempty
$F_0$
, we set out to cover the entire graph, but instead only managed to cover some of its layers. It is at this point that we need to introduce our second operation. Suppose that we have a layered percolating sequence in H whose set of seeds is K. Given a nonempty
![]() $I\subsetneq [k]$
, a subgraph H
′ of H is said to be a relocation of
$I\subsetneq [k]$
, a subgraph H
′ of H is said to be a relocation of
![]() $H_I$
if it dominates
$H_I$
if it dominates
![]() $H_I$
and contains more than
$H_I$
and contains more than
![]() $|I|$
seeds from K. We then say that the layers can be relocated if, for any nonempty
$|I|$
seeds from K. We then say that the layers can be relocated if, for any nonempty
![]() $I \subsetneq [k]$
, there is a relocation H
′ of
$I \subsetneq [k]$
, there is a relocation H
′ of
![]() $H_I$
. In particular, if there is always a subgraph isomorphic to
$H_I$
. In particular, if there is always a subgraph isomorphic to
![]() $H_I$
in H that contains more than
$H_I$
in H that contains more than
![]() $|I|$
seeds, then the layers can be relocated. The rough idea is that after each relocation step we can apply the folding sequence to the relocation to fill more layers of H, which can in turn be relocated.
$|I|$
seeds, then the layers can be relocated. The rough idea is that after each relocation step we can apply the folding sequence to the relocation to fill more layers of H, which can in turn be relocated.
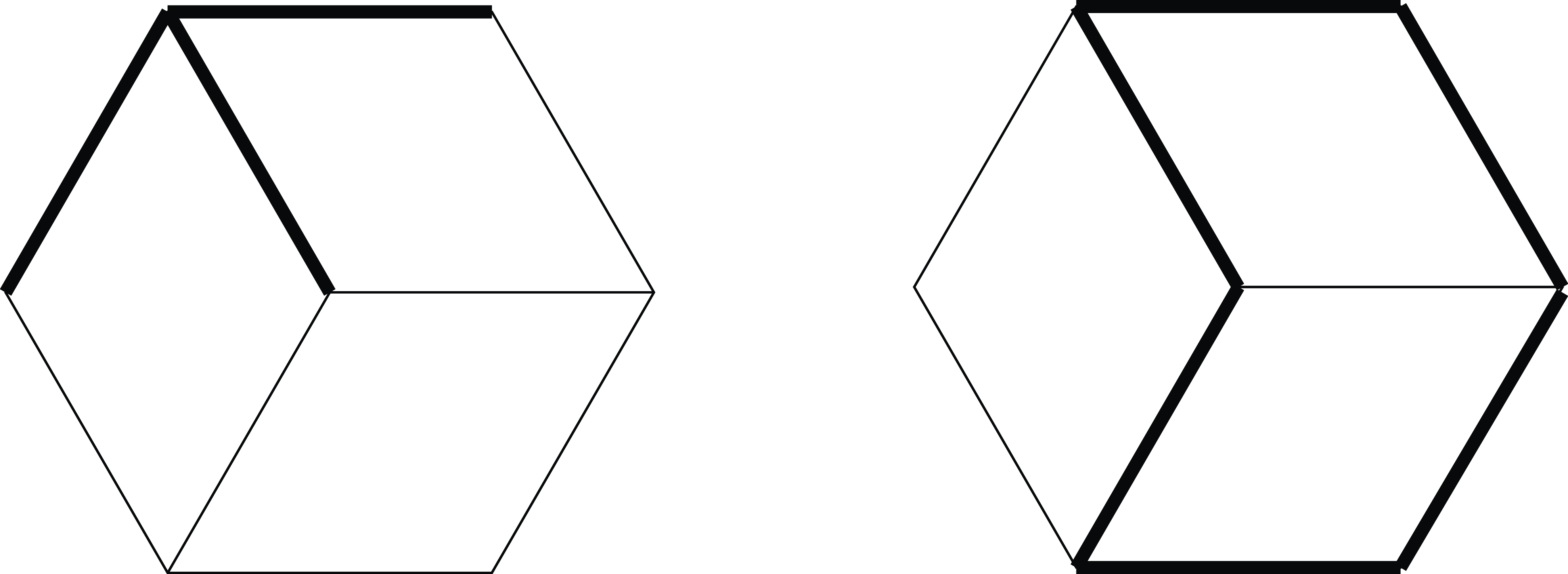
Fig. 3. Relocations of the inner star
![]() $K_{1,3}$
and the outer cycle
$K_{1,3}$
and the outer cycle
![]() $C_6$
in
$C_6$
in
![]() $C_6^+$
.
$C_6^+$
.
Example 3·4. As shown in Figure 3, the layers of
![]() $C_6^+$
, in this case a copy of
$C_6^+$
, in this case a copy of
![]() $K_{1,3}$
and a copy of
$K_{1,3}$
and a copy of
![]() $C_6$
, can both be relocated to include the set
$C_6$
, can both be relocated to include the set
![]() $J_0$
on the left-hand side of Figure 2.
$J_0$
on the left-hand side of Figure 2.
The main result of this section is now the following.
Theorem 3·5. Suppose that H is a graph with layers
![]() $H_1, \dots, H_k$
. If there exists a layered percolating sequence for H and the layers can be relocated, then H is dominating.
$H_1, \dots, H_k$
. If there exists a layered percolating sequence for H and the layers can be relocated, then H is dominating.
Proof. The case
![]() $k=1$
is a corollary of Theorem 3·1, so we may assume
$k=1$
is a corollary of Theorem 3·1, so we may assume
![]() $k>1$
. Let F be an arbitrary nonempty edge subset of H and let
$k>1$
. Let F be an arbitrary nonempty edge subset of H and let
![]() $\Psi\;:\!=\;(\psi_i)_{i=1}^N$
be the signature of a layered percolating sequence
$\Psi\;:\!=\;(\psi_i)_{i=1}^N$
be the signature of a layered percolating sequence
![]() $J_0, J_1,\dots,J_N$
. Note that, since each layer is edge transitive, we may assume
$J_0, J_1,\dots,J_N$
. Note that, since each layer is edge transitive, we may assume
![]() $F\cap J_0$
is nonempty.
$F\cap J_0$
is nonempty.
We now define a rooted tree
![]() $\mathcal{T}(F;\;\Psi)$
of depth
$\mathcal{T}(F;\;\Psi)$
of depth
![]() $N+1$
which encodes which graphs are obtained through iterations of (1) and relocations. The vertices of
$N+1$
which encodes which graphs are obtained through iterations of (1) and relocations. The vertices of
![]() $\mathcal{T}(F;\;\Psi)$
are labelled by edge subsets of H with the root labelled by the initial edge subset F. Each vertex at depth
$\mathcal{T}(F;\;\Psi)$
are labelled by edge subsets of H with the root labelled by the initial edge subset F. Each vertex at depth
![]() $d \lt N$
, labelled with J, say, has two children with labels
$d \lt N$
, labelled with J, say, has two children with labels
![]() $J(\psi_{d+1})$
and
$J(\psi_{d+1})$
and
![]() $J(\overline{\psi_{d+1}})$
. If, at depth N, a vertex has label
$J(\overline{\psi_{d+1}})$
. If, at depth N, a vertex has label
![]() $J=E(H_I)$
for some nonempty
$J=E(H_I)$
for some nonempty
![]() $I\subsetneq [k]$
, then it has a unique child labelled by its relocation J
′. Otherwise, it has a unique child labelled by the same J as the parent. We now abuse notation slightly by using J to denote both an edge subset of H and the corresponding subgraph. With this convention, each parent J relates to its children
$I\subsetneq [k]$
, then it has a unique child labelled by its relocation J
′. Otherwise, it has a unique child labelled by the same J as the parent. We now abuse notation slightly by using J to denote both an edge subset of H and the corresponding subgraph. With this convention, each parent J relates to its children
![]() $J(\psi)$
and
$J(\psi)$
and
![]() $J(\overline{\psi})$
or its only child J
′ through the inequalities
$J(\overline{\psi})$
or its only child J
′ through the inequalities
In either case, the sum of the size of the edge set times the corresponding exponent is the same on both sides, i.e.,
![]() $|J|=\tfrac{1}{2}|J(\psi)|+\tfrac{1}{2}|J(\overline{\psi})|$
and
$|J|=\tfrac{1}{2}|J(\psi)|+\tfrac{1}{2}|J(\overline{\psi})|$
and
![]() $|J|=|J'|\cdot |J|/|J'|$
. This is therefore an invariant throughout the entire process.
$|J|=|J'|\cdot |J|/|J'|$
. This is therefore an invariant throughout the entire process.
Denote by
![]() $F_{1},\dots,F_{2^d}$
the edge subsets that label the vertices at depth
$F_{1},\dots,F_{2^d}$
the edge subsets that label the vertices at depth
![]() $d\le N$
. Because we applied inequality (1) iteratively at each depth, we have the bound
$d\le N$
. Because we applied inequality (1) iteratively at each depth, we have the bound
 \begin{align*} t_{F}(W) \leq \prod_{i=1}^{2^d} t_{F_{i}}(W)^{1/2^d},\end{align*}
\begin{align*} t_{F}(W) \leq \prod_{i=1}^{2^d} t_{F_{i}}(W)^{1/2^d},\end{align*}
where
![]() $\sum_{j=1}^{2^d}2^{-d}|F_{j}|=|F|$
. When
$\sum_{j=1}^{2^d}2^{-d}|F_{j}|=|F|$
. When
![]() $d=N$
, by Lemma 3·3, each
$d=N$
, by Lemma 3·3, each
![]() $F_{j}$
is equal to
$F_{j}$
is equal to
![]() $E(H_{I_j})$
for some
$E(H_{I_j})$
for some
![]() $I_j\subseteq [k]$
and, moreover, at least one of the
$I_j\subseteq [k]$
and, moreover, at least one of the
![]() $I_j$
is nonempty, since
$I_j$
is nonempty, since
![]() $J_0\cap F$
was nonempty. Then the single child of any
$J_0\cap F$
was nonempty. Then the single child of any
![]() $F_j$
with
$F_j$
with
![]() $I_j\neq\emptyset$
is the relocation
$I_j\neq\emptyset$
is the relocation
![]() $F_j'$
of
$F_j'$
of
![]() $F_j$
, which, unless
$F_j$
, which, unless
![]() $I_j=[k]$
, contains more than
$I_j=[k]$
, contains more than
![]() $|I_j|$
seeds. If
$|I_j|$
seeds. If
![]() $I_j$
is either empty or [k], then no relocation is possible. Thus, at depth
$I_j$
is either empty or [k], then no relocation is possible. Thus, at depth
![]() $N+1$
, the corresponding inequality is
$N+1$
, the corresponding inequality is
 \begin{align} t_{F}(W) \leq \prod_{i=1}^{2^N} t_{F_{i}'}(W)^{\alpha_i},\end{align}
\begin{align} t_{F}(W) \leq \prod_{i=1}^{2^N} t_{F_{i}'}(W)^{\alpha_i},\end{align}
where
![]() $F^{\prime}_i$
is the label of the unique child of
$F^{\prime}_i$
is the label of the unique child of
![]() $F_i$
,
$F_i$
,
![]() $\alpha_i = |F_i|/|F^{\prime}_i|2^N$
and
$\alpha_i = |F_i|/|F^{\prime}_i|2^N$
and
![]() $\sum_{i=1}^{2^N} \alpha_i |F^{\prime}_i| = |F|$
.
$\sum_{i=1}^{2^N} \alpha_i |F^{\prime}_i| = |F|$
.
We now expand this tree by adding the tree
![]() $\mathcal{T}(F^{\prime}_j;\;\Psi)$
starting from each leaf. Once again, one of the leaves is equal to a relocation of some
$\mathcal{T}(F^{\prime}_j;\;\Psi)$
starting from each leaf. Once again, one of the leaves is equal to a relocation of some
![]() $E(H_J)$
, which, unless
$E(H_J)$
, which, unless
![]() $J=[k]$
, contains more than
$J=[k]$
, contains more than
![]() $|J|$
seeds. Thus, for each
$|J|$
seeds. Thus, for each
![]() $j=1,2,\dots, 2^N$
,
$j=1,2,\dots, 2^N$
,
 \begin{align*} t_{F_j'}(W) \leq \prod_{i=1}^{2^N} t_{F_{i,j}^{(2)}}(W)^{\alpha_{i,j}},\end{align*}
\begin{align*} t_{F_j'}(W) \leq \prod_{i=1}^{2^N} t_{F_{i,j}^{(2)}}(W)^{\alpha_{i,j}},\end{align*}
where
![]() $\sum_{i=1}^{2^N} \alpha_{i,j} |F_{i,j}^{(2)}| = |F^{\prime}_j|$
. Hence, combined with (2), we have that
$\sum_{i=1}^{2^N} \alpha_{i,j} |F_{i,j}^{(2)}| = |F^{\prime}_j|$
. Hence, combined with (2), we have that
 \begin{align*} t_{F}(W) \leq \prod_{i=1}^{2^{2N}} t_{F_{i}^{(2)}}(W)^{\beta_i},\end{align*}
\begin{align*} t_{F}(W) \leq \prod_{i=1}^{2^{2N}} t_{F_{i}^{(2)}}(W)^{\beta_i},\end{align*}
where
![]() $F_{i}^{(2)}$
is a reindexing of the
$F_{i}^{(2)}$
is a reindexing of the
![]() $F_{i,j}^{(2)}$
’s and
$F_{i,j}^{(2)}$
’s and
![]() $\sum_{i=1}^{2^{2N}} \beta_i |F_{i}^{(2)}| = |F|$
. We continue to iterate this process, noting that, each time we iterate, we increase the maximum number of seeds in the graphs that appear in the corresponding upper bound for F, until it reaches k. Therefore, if we iterate
$\sum_{i=1}^{2^{2N}} \beta_i |F_{i}^{(2)}| = |F|$
. We continue to iterate this process, noting that, each time we iterate, we increase the maximum number of seeds in the graphs that appear in the corresponding upper bound for F, until it reaches k. Therefore, if we iterate
![]() $k-3$
more times, we must obtain a bound of the form
$k-3$
more times, we must obtain a bound of the form
 \begin{align} t_{F}(W) \leq \prod_{i=1}^{N_k} t_{K_{i}}(W)^{\rho_i},\end{align}
\begin{align} t_{F}(W) \leq \prod_{i=1}^{N_k} t_{K_{i}}(W)^{\rho_i},\end{align}
where
![]() $N_k=2^{(k-1)N}$
,
$N_k=2^{(k-1)N}$
,
![]() $\sum_{i=1}^{N_k} \rho_i|K_{i}|=|F|$
and at least one of the
$\sum_{i=1}^{N_k} \rho_i|K_{i}|=|F|$
and at least one of the
![]() $K_j$
, say
$K_j$
, say
![]() $K_1$
, is equal to E(H). Since the choice of F was arbitrary, each
$K_1$
, is equal to E(H). Since the choice of F was arbitrary, each
![]() $K_j$
also satisfies
$K_j$
also satisfies
 \begin{align*} t_{K_j}(W) \leq \prod_{i=1}^{N_k} t_{K_{i}^{(j)}}(W)^{\rho_{i,j}}\end{align*}
\begin{align*} t_{K_j}(W) \leq \prod_{i=1}^{N_k} t_{K_{i}^{(j)}}(W)^{\rho_{i,j}}\end{align*}
for some
![]() $\rho_{i,j}$
with
$\rho_{i,j}$
with
![]() $\sum_{i=1}^{N_k} \rho_{i,j} |K_{i}^{(j)}| = |K_j|$
. Note that if
$\sum_{i=1}^{N_k} \rho_{i,j} |K_{i}^{(j)}| = |K_j|$
. Note that if
![]() $K_j$
equals either
$K_j$
equals either
![]() $\emptyset$
or E(H), then so do all of its descendants
$\emptyset$
or E(H), then so do all of its descendants
![]() $K_{i}^{(j)}$
, while if
$K_{i}^{(j)}$
, while if
![]() $K_j$
is neither
$K_j$
is neither
![]() $\emptyset$
nor E(H), then at least one of its descendants, say
$\emptyset$
nor E(H), then at least one of its descendants, say
![]() $K_{1}^{(j)}$
, is equal to E(H). Substituting this back into (3) yields, after a suitable relabelling, that
$K_{1}^{(j)}$
, is equal to E(H). Substituting this back into (3) yields, after a suitable relabelling, that
 \begin{align*} t_{F}(W) \leq \prod_{i=1}^{N_k^2} t_{K_{i}}(W)^{\sigma_i},\end{align*}
\begin{align*} t_{F}(W) \leq \prod_{i=1}^{N_k^2} t_{K_{i}}(W)^{\sigma_i},\end{align*}
where
![]() $\sum_{i=1}^{N_k^2} \sigma_i |K_i| = |F|$
and the proportion of the
$\sum_{i=1}^{N_k^2} \sigma_i |K_i| = |F|$
and the proportion of the
![]() $K_j$
which are equal to neither
$K_j$
which are equal to neither
![]() $\emptyset$
nor E(H) has dropped to at most a
$\emptyset$
nor E(H) has dropped to at most a
![]() $(1 - 1/N_k)$
-factor of what it was. Repeating this process, we see that the proportion of
$(1 - 1/N_k)$
-factor of what it was. Repeating this process, we see that the proportion of
![]() $K_j$
which are equal to neither
$K_j$
which are equal to neither
![]() $\emptyset$
nor E(H) converges to 0 and the proportion which are equal to E(H) converges to some limit
$\emptyset$
nor E(H) converges to 0 and the proportion which are equal to E(H) converges to some limit
![]() $\gamma$
. But then we must have that
$\gamma$
. But then we must have that
![]() $\gamma e(H) = e(F)$
and
$\gamma e(H) = e(F)$
and
![]() $t_F(W) \leq t_H(W)^\gamma$
, which together yield the required domination inequality.
$t_F(W) \leq t_H(W)^\gamma$
, which together yield the required domination inequality.
When applying Theorem 3·5, there are two conditions to check: the existence of layered percolating sequences and the possibility of relocations. While verifying the second condition can be a little ad hoc, there is an approach to finding graphs with layered percolating sequences that builds on our earlier work [ Reference Conlon and Lee4 ] connecting weakly norming graphs and reflection groups. We will be rather terse here, but we refer the reader to [ Reference Conlon and Lee4 ] for a more comprehensive introduction to reflection groups.
Let
![]() $\mathcal{W}$
be a finite reflection group with S a set of simple reflections and let
$\mathcal{W}$
be a finite reflection group with S a set of simple reflections and let
![]() $\mathcal{W}_1,\mathcal{W}_2,\dots,\mathcal{W}_k$
be subgroups of
$\mathcal{W}_1,\mathcal{W}_2,\dots,\mathcal{W}_k$
be subgroups of
![]() $\mathcal{W}$
generated by subsets
$\mathcal{W}$
generated by subsets
![]() $S_1,S_2,\dots,S_k$
of S, respectively. Then the
$S_1,S_2,\dots,S_k$
of S, respectively. Then the
![]() $(S_1,\dots,S_k;\;S,\mathcal{W})$
-reflection hypergraph, shown in [
Reference Conlon and Lee4
] to be weakly norming, is the k-partite k-uniform hypergraph whose parts are the cosets of
$(S_1,\dots,S_k;\;S,\mathcal{W})$
-reflection hypergraph, shown in [
Reference Conlon and Lee4
] to be weakly norming, is the k-partite k-uniform hypergraph whose parts are the cosets of
![]() $\mathcal{W}_i$
for each
$\mathcal{W}_i$
for each
![]() $i = 1, \dots, k$
, with an edge for every k-tuple of the form
$i = 1, \dots, k$
, with an edge for every k-tuple of the form
![]() $(w\mathcal{W}_1,w\mathcal{W}_2,\dots,w\mathcal{W}_k)$
with
$(w\mathcal{W}_1,w\mathcal{W}_2,\dots,w\mathcal{W}_k)$
with
![]() $w \in \mathcal{W}$
. If we now replace each hyperedge
$w \in \mathcal{W}$
. If we now replace each hyperedge
![]() $(w\mathcal{W}_1,w\mathcal{W}_2,\dots,w\mathcal{W}_k)$
by a
$(w\mathcal{W}_1,w\mathcal{W}_2,\dots,w\mathcal{W}_k)$
by a
![]() $(k-1)$
-star centred at
$(k-1)$
-star centred at
![]() $w\mathcal{W}_i$
, we obtain a bipartite graphFootnote 2 between the cosets of
$w\mathcal{W}_i$
, we obtain a bipartite graphFootnote 2 between the cosets of
![]() $\mathcal{W}_i$
and the union of the cosets of
$\mathcal{W}_i$
and the union of the cosets of
![]() $\mathcal{W}_1,\dots, \mathcal{W}_{i-1}, \mathcal{W}_{i+1}, \dots,\mathcal{W}_k$
, which we call the
$\mathcal{W}_1,\dots, \mathcal{W}_{i-1}, \mathcal{W}_{i+1}, \dots,\mathcal{W}_k$
, which we call the
![]() $(S_1,\dots,S_k;\;i,S,\mathcal{W})$
-graph. Since the induced subgraph of this graph between the cosets of
$(S_1,\dots,S_k;\;i,S,\mathcal{W})$
-graph. Since the induced subgraph of this graph between the cosets of
![]() $\mathcal{W}_i$
and
$\mathcal{W}_i$
and
![]() $\mathcal{W}_j$
, for each
$\mathcal{W}_j$
, for each
![]() $j\neq i$
, is the
$j\neq i$
, is the
![]() $(S_i,S_j;\;S,\mathcal{W})$
-reflection graph and the set of reflections
$(S_i,S_j;\;S,\mathcal{W})$
-reflection graph and the set of reflections
![]() $t\in\mathcal{W}$
give cut involutions of these graphs (see [
Reference Conlon and Lee4
, corollary 4·9]), the graph naturally has layers.
$t\in\mathcal{W}$
give cut involutions of these graphs (see [
Reference Conlon and Lee4
, corollary 4·9]), the graph naturally has layers.
Example 3·6. Let
![]() $\mathcal{W}$
be the symmetric group on the three elements
$\mathcal{W}$
be the symmetric group on the three elements
![]() $\{1,2,3\}$
and let
$\{1,2,3\}$
and let
![]() $S=\{\sigma_{12},\sigma_{23}\}$
, where
$S=\{\sigma_{12},\sigma_{23}\}$
, where
![]() $\sigma_{ij}$
is the permutation that swaps i and j. Then the graph
$\sigma_{ij}$
is the permutation that swaps i and j. Then the graph
![]() $C_6^+$
in Figure 1 is isomorphic to the
$C_6^+$
in Figure 1 is isomorphic to the
![]() $(S_1,S_2,S_3;\;1,S,\mathcal{W})$
-graph with
$(S_1,S_2,S_3;\;1,S,\mathcal{W})$
-graph with
![]() $S_1=\{\sigma_{12}\}$
,
$S_1=\{\sigma_{12}\}$
,
![]() $S_2=\{\sigma_{23}\}$
and
$S_2=\{\sigma_{23}\}$
and
![]() $S_3=S$
.
$S_3=S$
.
Theorem 3·7. Let H be the
![]() $(S_1,S_2,\dots,S_k;\;i,S,\mathcal{W})$
-graph. Then there exists a layered percolating sequence
$(S_1,S_2,\dots,S_k;\;i,S,\mathcal{W})$
-graph. Then there exists a layered percolating sequence
![]() $J_0,J_1,\dots, J_N$
such that
$J_0,J_1,\dots, J_N$
such that
![]() $J_0$
is the edge set of the
$J_0$
is the edge set of the
![]() $(k-1)$
-star induced on
$(k-1)$
-star induced on
![]() $\{\mathcal{W}_1,\dots,\mathcal{W}_k\}$
.
$\{\mathcal{W}_1,\dots,\mathcal{W}_k\}$
.
We omit the proof, which is virtually identical to that of [ Reference Conlon and Lee4 , theorem 1·2].
4. Constructions of dominating graphs
We now construct various examples of dominating graphs. Our first such family is as follows and already includes our running example
![]() $J = C_6^+$
from Figure 1.
$J = C_6^+$
from Figure 1.
Theorem 4·1. Suppose that H is a reflection graph with one side A in its bipartition of order a and regular of degree d. If
![]() $d\geq a-1$
, then the graph
$d\geq a-1$
, then the graph
![]() $H_A^+$
formed by joining a new vertex to each vertex in A is dominating.
$H_A^+$
formed by joining a new vertex to each vertex in A is dominating.
Proof. Suppose that H is the
![]() $(S_1,S_2;\;S,\mathcal{W})$
-reflection graph, where A is the family of all cosets of the form
$(S_1,S_2;\;S,\mathcal{W})$
-reflection graph, where A is the family of all cosets of the form
![]() $w\mathcal{W}_1$
. Let
$w\mathcal{W}_1$
. Let
![]() $S_3=S$
, so that
$S_3=S$
, so that
![]() $\mathcal{W}_3=\mathcal{W}$
. Then
$\mathcal{W}_3=\mathcal{W}$
. Then
![]() $H_A^+$
is the
$H_A^+$
is the
![]() $(S_1,S_2,S_3;\;1,S,\mathcal{W})$
-graph and, hence, by Theorem 3·7, there exists a layered percolating sequence starting with two edges that form a star centred at
$(S_1,S_2,S_3;\;1,S,\mathcal{W})$
-graph and, hence, by Theorem 3·7, there exists a layered percolating sequence starting with two edges that form a star centred at
![]() $v\in A$
. In fact, any such 2-star does the job, because of the edge-transitivity of each layer.
$v\in A$
. In fact, any such 2-star does the job, because of the edge-transitivity of each layer.
By Theorem 3·5, it remains to show that the layers can be relocated. Let
![]() $v_0$
be the vertex adjacent to all the vertices in A and let B be the other side of the bipartition of H to A. First observe that the layer isomorphic to the
$v_0$
be the vertex adjacent to all the vertices in A and let B be the other side of the bipartition of H to A. First observe that the layer isomorphic to the
![]() $(S_1,S_2;\;S,\mathcal{W})$
-graph H can be relocated by using the vertex
$(S_1,S_2;\;S,\mathcal{W})$
-graph H can be relocated by using the vertex
![]() $v_0$
. Concretely, we may replace any
$v_0$
. Concretely, we may replace any
![]() $b\in B$
and its incident edges by
$b\in B$
and its incident edges by
![]() $v_0$
and the edges between
$v_0$
and the edges between
![]() $v_0$
and the neighbours of b, since
$v_0$
and the neighbours of b, since
![]() $v_0$
is adjacent to all vertices in A. Provided
$v_0$
is adjacent to all vertices in A. Provided
![]() $d \geq 2$
(the easy case where
$d \geq 2$
(the easy case where
![]() $d = 1$
can be dealt with separately), this relocation contains two seeds that form a 2-star centred on A, whereas H only contained one seed. The other layer between
$d = 1$
can be dealt with separately), this relocation contains two seeds that form a 2-star centred on A, whereas H only contained one seed. The other layer between
![]() $v_0$
and A is just a copy of an a-star centred at
$v_0$
and A is just a copy of an a-star centred at
![]() $v_0$
. This star can easily be relocated to another a-star centred in A containing more seeds than the star centred at
$v_0$
. This star can easily be relocated to another a-star centred in A containing more seeds than the star centred at
![]() $v_0$
, where we use that each
$v_0$
, where we use that each
![]() $v\in A$
has degree
$v\in A$
has degree
![]() $d+1\geq a$
in
$d+1\geq a$
in
![]() $H_A^+$
.
$H_A^+$
.
This theorem adds many more examples of dominating graphs besides
![]() $C_6^+$
. For instance, Figure 4 shows the dominating graphs obtained by adding a vertex to four vertex-disjoint copies of
$C_6^+$
. For instance, Figure 4 shows the dominating graphs obtained by adding a vertex to four vertex-disjoint copies of
![]() $K_{1,4}$
, the 1-subdivision of
$K_{1,4}$
, the 1-subdivision of
![]() $K_4$
and the 3-dimensional cube.
$K_4$
and the 3-dimensional cube.
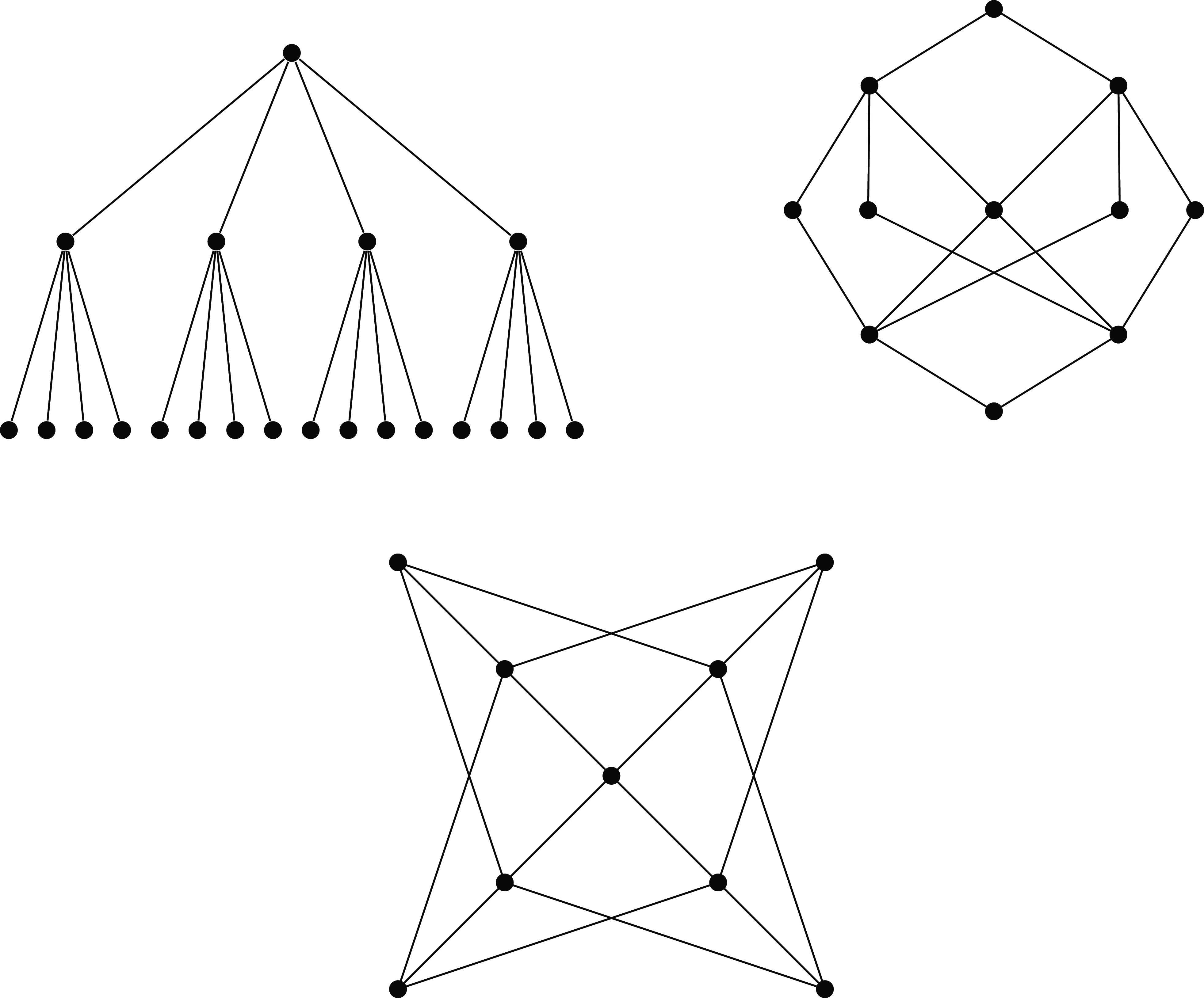
Fig. 4. Examples of
![]() $H_A^+$
.
$H_A^+$
.
For a graph H, the
![]() $K_{2,t}$
-replacement of H is the graph obtained by replacing each edge with a copy of
$K_{2,t}$
-replacement of H is the graph obtained by replacing each edge with a copy of
![]() $K_{2,t}$
, identifying the edge’s endpoints with the two vertices on one side of the corresponding copy of
$K_{2,t}$
, identifying the edge’s endpoints with the two vertices on one side of the corresponding copy of
![]() $K_{2,t}$
. In particular, the
$K_{2,t}$
. In particular, the
![]() $K_{2,1}$
-replacement of H is just the 1-subdivision of H. Alternatively, the
$K_{2,1}$
-replacement of H is just the 1-subdivision of H. Alternatively, the
![]() $K_{2,t}$
-replacement can be viewed as replacing each edge of H by t multiedges and then 1-subdividing this multigraph. When we form the
$K_{2,t}$
-replacement can be viewed as replacing each edge of H by t multiedges and then 1-subdividing this multigraph. When we form the
![]() $K_{2,t}$
-replacement of a graph, the side of the bipartition that corresponds to the original set of vertices is typically smaller. Thus, by Proposition 2·3, for this graph to be dominating, the original graph H must be regular. We now prove a sort of converse to this observation, showing that if H is a regular reflection graph, then the
$K_{2,t}$
-replacement of a graph, the side of the bipartition that corresponds to the original set of vertices is typically smaller. Thus, by Proposition 2·3, for this graph to be dominating, the original graph H must be regular. We now prove a sort of converse to this observation, showing that if H is a regular reflection graph, then the
![]() $K_{2,t}$
-replacement of H is dominating.
$K_{2,t}$
-replacement of H is dominating.
Theorem 4·2. The
![]() $K_{2,t}$
-replacement of a connected regular reflection graph H is dominating.
$K_{2,t}$
-replacement of a connected regular reflection graph H is dominating.
Proof. Suppose that
![]() $A\cup B$
is the bipartition of H. Let H
′ be the
$A\cup B$
is the bipartition of H. Let H
′ be the
![]() $K_{2,t}$
-replacement of H and let
$K_{2,t}$
-replacement of H and let
![]() $A'\cup B'$
be its bipartition, where
$A'\cup B'$
be its bipartition, where
![]() $A'=V(H)$
and B
′ is the disjoint union of t copies of E(H). An edge in H
′ then represents an incidence between the corresponding vertex and edge in H.
$A'=V(H)$
and B
′ is the disjoint union of t copies of E(H). An edge in H
′ then represents an incidence between the corresponding vertex and edge in H.
For a vertex
![]() $b\in B'$
, let
$b\in B'$
, let
![]() $E_b$
be the set of vertices in B
′ that have the same two neighbours as b, i.e., the set of all copies of the same edge in H as b. For each
$E_b$
be the set of vertices in B
′ that have the same two neighbours as b, i.e., the set of all copies of the same edge in H as b. For each
![]() $b'\in E_b$
, there exists a cut involution
$b'\in E_b$
, there exists a cut involution
![]() $\phi_{b,b'}$
of H
′ that fixes all other vertices, but maps b and b
′ to each other. Moreover, the cut involutions
$\phi_{b,b'}$
of H
′ that fixes all other vertices, but maps b and b
′ to each other. Moreover, the cut involutions
![]() $\phi$
of H extend naturally to cut involutions
$\phi$
of H extend naturally to cut involutions
![]() $\phi'$
of H
′ where
$\phi'$
of H
′ where
![]() $\phi'(v)=\phi(v)$
for
$\phi'(v)=\phi(v)$
for
![]() $v\in V(H)=A'$
and
$v\in V(H)=A'$
and
![]() $\phi'(u)$
is the jth copy of
$\phi'(u)$
is the jth copy of
![]() $\phi(e)$
if
$\phi(e)$
if
![]() $u\in B'$
is the jth copy of
$u\in B'$
is the jth copy of
![]() $e\in E(H)$
. Together, these cut involutions easily show that the two isomorphic induced subgraphs on
$e\in E(H)$
. Together, these cut involutions easily show that the two isomorphic induced subgraphs on
![]() $A\cup B'$
and
$A\cup B'$
and
![]() $B\cup B'$
are layers in H
′.
$B\cup B'$
are layers in H
′.
We claim that any two edges ab and bc with
![]() $a \in A$
,
$a \in A$
,
![]() $b \in B'$
and
$b \in B'$
and
![]() $c \in B$
give an appropriate
$c \in B$
give an appropriate
![]() $J_0$
for a layered percolating sequence. Indeed, by using the cut involutions
$J_0$
for a layered percolating sequence. Indeed, by using the cut involutions
![]() $\phi_{b,b'}$
for every pair (b, b
′), where b
′ is a copy of the same H-edge as b, one obtains a folding sequence
$\phi_{b,b'}$
for every pair (b, b
′), where b
′ is a copy of the same H-edge as b, one obtains a folding sequence
![]() $J_0,J_1,\dots,J_{t-1}$
, where
$J_0,J_1,\dots,J_{t-1}$
, where
![]() $J_{t-1}$
contains all edges of the forms ab
′ and b
′
c with
$J_{t-1}$
contains all edges of the forms ab
′ and b
′
c with
![]() $b' \in E_b$
. If we then use the standard percolating sequence for H given by [
Reference Conlon and Lee4
, theorem 4·12], we obtain a layered percolating sequence.
$b' \in E_b$
. If we then use the standard percolating sequence for H given by [
Reference Conlon and Lee4
, theorem 4·12], we obtain a layered percolating sequence.
By Theorem 3·7, it remains to check that the layers can be relocated. Recall that the two layers are the induced subgraphs on
![]() $A\cup B'$
and
$A\cup B'$
and
![]() $B\cup B'$
, respectively, which are isomorphic copies of
$B\cup B'$
, respectively, which are isomorphic copies of
![]() $|A|$
disjoint td-stars, where d is the degree of a vertex in the regular graph H. To relocate the layer on
$|A|$
disjoint td-stars, where d is the degree of a vertex in the regular graph H. To relocate the layer on
![]() $A\cup B'$
, we replace a vertex
$A\cup B'$
, we replace a vertex
![]() $a\in A$
by a vertex
$a\in A$
by a vertex
![]() $b\in B$
. Then the td-star centred at a is replaced by another td-star that shares t leaves with each of the d different td-stars centred at the neighbours of b in H. Let J be this edge-disjoint (but not vertex-disjoint) union of
$b\in B$
. Then the td-star centred at a is replaced by another td-star that shares t leaves with each of the d different td-stars centred at the neighbours of b in H. Let J be this edge-disjoint (but not vertex-disjoint) union of
![]() $d+1$
different td-stars. Then J consists of d copies of
$d+1$
different td-stars. Then J consists of d copies of
![]() $K_{2,t}$
such that the two-vertex side of each
$K_{2,t}$
such that the two-vertex side of each
![]() $K_{2,t}$
consists of a vertex
$K_{2,t}$
consists of a vertex
![]() $v\in A$
and b, where v and b are adjacent in H, and
$v\in A$
and b, where v and b are adjacent in H, and
![]() $t(d-1)$
pendant leaves attached to each
$t(d-1)$
pendant leaves attached to each
![]() $v\in A$
. The induced subgraph on
$v\in A$
. The induced subgraph on
![]() $A\setminus\{a\}\cup\{b\}\cup B'$
is the disjoint union of J and
$A\setminus\{a\}\cup\{b\}\cup B'$
is the disjoint union of J and
![]() $|A|-d-1$
further td-stars. Theorem 2·7 in [
Reference Lee12
] now implies that
$|A|-d-1$
further td-stars. Theorem 2·7 in [
Reference Lee12
] now implies that
where S denotes the td-star. Thus, J dominates a td-star and, moreover, it contains two seeds. It is then simple to conclude that the induced subgraph on
![]() $A\setminus\{a\}\cup\{b\}\cup B'$
is a relocation of the layer induced on
$A\setminus\{a\}\cup\{b\}\cup B'$
is a relocation of the layer induced on
![]() $A\cup B'$
.
$A\cup B'$
.
In particular, this result clearly implies our Theorem 1·1, since the complete bipartite graphs
![]() $K_{t,t}$
are themselves regular reflection graphs. For more examples, suppose
$K_{t,t}$
are themselves regular reflection graphs. For more examples, suppose
![]() $r < t$
and consider the bipartite graph between the set of r-subsets and the set of
$r < t$
and consider the bipartite graph between the set of r-subsets and the set of
![]() $(t-r)$
-subsets of [t] where two sets are connected if and only if the smaller of the two sets is contained in the larger one. This family of bipartite Kneser graphs, as they are known, includes
$(t-r)$
-subsets of [t] where two sets are connected if and only if the smaller of the two sets is contained in the larger one. This family of bipartite Kneser graphs, as they are known, includes
![]() $K_{t,t}$
with a perfect matching removed and the middle layer graph. They are all regular reflection graphs and so, by Theorem 4·2, their 1-subdivisions, and all their
$K_{t,t}$
with a perfect matching removed and the middle layer graph. They are all regular reflection graphs and so, by Theorem 4·2, their 1-subdivisions, and all their
![]() $K_{2,t}$
-replacements, are dominating.
$K_{2,t}$
-replacements, are dominating.
We have already seen that some trees are dominating, including even-length paths and the example shown in Figure 4, but there are more examples. A perfect d-regular tree is a tree T rooted at a vertex r such that r has d children, every vertex other than r or the leaves has
![]() $d-1$
children and every leaf is at the same distance from r. In particular, every path of length 2k is a 2-regular tree of depth k. Thus, the following theorem generalises Godsil’s result on even-length paths.
$d-1$
children and every leaf is at the same distance from r. In particular, every path of length 2k is a 2-regular tree of depth k. Thus, the following theorem generalises Godsil’s result on even-length paths.
Theorem 4·3. Every perfect d-regular tree T is dominating.
Proof. We proceed by induction on the depth k of the tree. As the statement is simple for
![]() $k = 1$
, we may assume that T has depth k and any subgraph of the perfect d-regular tree of depth
$k = 1$
, we may assume that T has depth k and any subgraph of the perfect d-regular tree of depth
![]() $k-1$
is dominated by that tree. Since it is clear that T has layered percolating sequences, with the edges of any shortest path from the root r to a leaf serving as the seeds, it will suffice to show that the layers can be relocated. The layers here are just the bipartite graphs between the vertices of depths i and
$k-1$
is dominated by that tree. Since it is clear that T has layered percolating sequences, with the edges of any shortest path from the root r to a leaf serving as the seeds, it will suffice to show that the layers can be relocated. The layers here are just the bipartite graphs between the vertices of depths i and
![]() $i+1$
for
$i+1$
for
![]() $0 \leq i < k$
, so if we have a union of at most
$0 \leq i < k$
, so if we have a union of at most
![]() $k-1$
layers, then each of the connected components of the resulting graph is a subgraph of the perfect d-regular tree of depth
$k-1$
layers, then each of the connected components of the resulting graph is a subgraph of the perfect d-regular tree of depth
![]() $k-1$
, so they and their union are dominated by this tree. But this tree is easily seen to be isomorphic to a subgraph of T that includes a shortest path from r to the leaves, so the layers can indeed be relocated.
$k-1$
, so they and their union are dominated by this tree. But this tree is easily seen to be isomorphic to a subgraph of T that includes a shortest path from r to the leaves, so the layers can indeed be relocated.
To close this section, we note that, unlike weakly norming graphs (see [
Reference Hatami10
]), the family of dominating graphs is not closed under taking (bipartite) tensor products. For example, consider the tensor product
![]() $C_6^+ \times C_6^+$
, where the two copies of
$C_6^+ \times C_6^+$
, where the two copies of
![]() $C_6^+$
are oriented the opposite way. Then each side of the bipartition of
$C_6^+$
are oriented the opposite way. Then each side of the bipartition of
![]() $C_6^+ \times C_6^+$
has vertices with two distinct degrees and so, by Lemma 2·3, the graph cannot be dominating. However, as shown by the following lemma, which says that blowups of dominating graphs are again dominating, some tensor products are still allowed.
$C_6^+ \times C_6^+$
has vertices with two distinct degrees and so, by Lemma 2·3, the graph cannot be dominating. However, as shown by the following lemma, which says that blowups of dominating graphs are again dominating, some tensor products are still allowed.
Lemma 4·4. If H is a dominating graph, then so is
![]() $H \times K_{m,m}$
for any integer
$H \times K_{m,m}$
for any integer
![]() $m \geq 1$
.
$m \geq 1$
.
We will only sketch the proof of this lemma, working throughout in the language of graphs rather than graphons. Suppose then that J is a subgraph of
![]() $H \times K_{m,m}$
and we would like to show that
$H \times K_{m,m}$
and we would like to show that
![]() $t_J(G) \leq t_{H \times K_{m,m}}(G)$
for all graphs G. The first step is to show that there exist subgraphs
$t_J(G) \leq t_{H \times K_{m,m}}(G)$
for all graphs G. The first step is to show that there exist subgraphs
![]() $J_1, \dots, J_t$
of H and positive real numbers
$J_1, \dots, J_t$
of H and positive real numbers
![]() $\alpha_1, \dots, \alpha_t$
with
$\alpha_1, \dots, \alpha_t$
with
![]() $\sum_{i=1}^t \alpha_i = 1$
such that
$\sum_{i=1}^t \alpha_i = 1$
such that
![]() $t_J(G) \leq \prod_{i=1}^t t_{J_i \times K_{m,m}}(G)^{\alpha_i}$
. For this, we consider an edge
$t_J(G) \leq \prod_{i=1}^t t_{J_i \times K_{m,m}}(G)^{\alpha_i}$
. For this, we consider an edge
![]() $e = (u,v)$
of H such that J contains an edge of the form
$e = (u,v)$
of H such that J contains an edge of the form
![]() $(e, \cdot)$
. Then, if we fix all vertices in
$(e, \cdot)$
. Then, if we fix all vertices in
![]() $H \times K_{m,m}$
except those of the form
$H \times K_{m,m}$
except those of the form
![]() $(u, \cdot)$
and
$(u, \cdot)$
and
![]() $(v, \cdot)$
and use the fact that
$(v, \cdot)$
and use the fact that
![]() $K_{m,m}$
has a percolating sequence, we can show that
$K_{m,m}$
has a percolating sequence, we can show that
![]() $t_J(G) \leq \prod_{i=1}^{s} t_{B_{i}}(G)^{\beta_{i}}$
, where each
$t_J(G) \leq \prod_{i=1}^{s} t_{B_{i}}(G)^{\beta_{i}}$
, where each
![]() $B_{i}$
is a subgraph of
$B_{i}$
is a subgraph of
![]() $H \times K_{m,m}$
which includes either all or none of the edges in
$H \times K_{m,m}$
which includes either all or none of the edges in
![]() $e \times K_{m,m}$
and the
$e \times K_{m,m}$
and the
![]() $\beta_{i}$
are positive real numbers with
$\beta_{i}$
are positive real numbers with
![]() $\sum_{i=1}^{s} \beta_{i} = 1$
. Repeating this process for all edges
$\sum_{i=1}^{s} \beta_{i} = 1$
. Repeating this process for all edges
![]() $e = (u,v)$
of H such that J contains an edge of the form
$e = (u,v)$
of H such that J contains an edge of the form
![]() $(e, \cdot)$
implies that
$(e, \cdot)$
implies that
![]() $t_J(G) \leq \prod_{i=1}^t t_{F_i}(G)^{\alpha_i}$
, where each
$t_J(G) \leq \prod_{i=1}^t t_{F_i}(G)^{\alpha_i}$
, where each
![]() $F_i$
is a subgraph of
$F_i$
is a subgraph of
![]() $H \times K_{m,m}$
which includes either all or none of the edges in
$H \times K_{m,m}$
which includes either all or none of the edges in
![]() $e \times K_{m,m}$
for all
$e \times K_{m,m}$
for all
![]() $e \in E(H)$
and
$e \in E(H)$
and
![]() $\alpha_1, \dots, \alpha_t$
are positive real numbers with
$\alpha_1, \dots, \alpha_t$
are positive real numbers with
![]() $\sum_{i=1}^t \alpha_i = 1$
. But then each
$\sum_{i=1}^t \alpha_i = 1$
. But then each
![]() $F_i$
is of the form
$F_i$
is of the form
![]() $J_i \times K_{m,m}$
, giving exactly the inequality we require.
$J_i \times K_{m,m}$
, giving exactly the inequality we require.
The second step is to show that
![]() $J_i \times K_{m,m}$
is dominated by
$J_i \times K_{m,m}$
is dominated by
![]() $H \times K_{m,m}$
for each
$H \times K_{m,m}$
for each
![]() $J_i$
. For this, given a graph G, consider the auxiliary graph
$J_i$
. For this, given a graph G, consider the auxiliary graph
![]() $G^*$
whose vertex set A is the set of (not necessarily distinct) ordered m-tuples in G with an edge between a and a
′ if there is a homomorphic copy of
$G^*$
whose vertex set A is the set of (not necessarily distinct) ordered m-tuples in G with an edge between a and a
′ if there is a homomorphic copy of
![]() $K_{m,m}$
between a and a
′ in G. Then, since H is dominating,
$K_{m,m}$
between a and a
′ in G. Then, since H is dominating,
as required. Combining the results of the two steps then completes the proof.
We note that the same proof works with
![]() $K_{m,m}$
replaced by any other vertex-transitive reflection graph, such as an even cycle or a hypercube. Moreover, a similar result also holds for
$K_{m,m}$
replaced by any other vertex-transitive reflection graph, such as an even cycle or a hypercube. Moreover, a similar result also holds for
![]() $H \times K_{m,n}$
with
$H \times K_{m,n}$
with
![]() $m \neq n$
or even with
$m \neq n$
or even with
![]() $K_{m,n}$
replaced by any other reflection graph, but one needs to assume that H satisfies an appropriate bipartite version of the domination property (which is indeed satisfied by all of our examples) for the proof to go through.
$K_{m,n}$
replaced by any other reflection graph, but one needs to assume that H satisfies an appropriate bipartite version of the domination property (which is indeed satisfied by all of our examples) for the proof to go through.
5. Applications of the domination property
5·1. Sidorenko’s conjecture
Building on earlier work applying entropy techniques to Sidorenko’s conjecture [ Reference Conlon, Kim, Lee and Lee3, Reference Kim, Lee and Lee11, Reference Li and Szegedy14, Reference Szegedy22 ], it was shown in [ Reference Conlon and Lee4 , section 5] that weakly norming graphs can be used as building blocks to produce a family of graphs satisfying the conjecture. The proof of that result only relied on the fact that weakly norming graphs are dominating, so it easily extends to dominating graphs. To say more, we need some definitions.
A tree decomposition of a graph H is a pair
![]() $(\mathcal{F}, \mathcal{T})$
consisting of a family
$(\mathcal{F}, \mathcal{T})$
consisting of a family
![]() $\mathcal{F}$
of vertex subsets of H and a tree
$\mathcal{F}$
of vertex subsets of H and a tree
![]() $\mathcal{T}$
on
$\mathcal{T}$
on
![]() $\mathcal{F}$
such that:
$\mathcal{F}$
such that:
-
(1)
 $\bigcup_{X\in\mathcal{F}}X=V(H)$
;
$\bigcup_{X\in\mathcal{F}}X=V(H)$
; -
(2) for each
 $e \in E(H)$
, there is a set
$e \in E(H)$
, there is a set
 $X \in \mathcal{F}$
such that X contains e;
$X \in \mathcal{F}$
such that X contains e; -
(3) for
 $X,Y,Z\in \mathcal{F}$
,
$X,Y,Z\in \mathcal{F}$
,
 $X\cap Y\subseteq Z$
whenever Z lies on the path from X to Y in
$X\cap Y\subseteq Z$
whenever Z lies on the path from X to Y in
 $\mathcal{T}$
.
$\mathcal{T}$
.
Given a graph H and an induced subgraph J, a J-decomposition of a graph H is a tree decomposition
![]() $(\mathcal{F},\mathcal{T})$
of H satisfying the following two extra conditions:
$(\mathcal{F},\mathcal{T})$
of H satisfying the following two extra conditions:
-
(1) each induced subgraph H[X],
 $X \in \mathcal{F}$
, is isomorphic to J;
$X \in \mathcal{F}$
, is isomorphic to J; -
(2) for every pair
 $X,Y\in \mathcal{F}$
which are adjacent in
$X,Y\in \mathcal{F}$
which are adjacent in
 $\mathcal{T}$
, there is an isomorphism between the two copies H[X] and H[Y] of J that fixes
$\mathcal{T}$
, there is an isomorphism between the two copies H[X] and H[Y] of J that fixes
 $X \cap Y$
.
$X \cap Y$
.
We say that a graph is J-decomposable if it admits a J-decomposition. Our application of the domination property to Sidorenko’s conjecture is now as follows.
Theorem 5·1. If J is a dominating graph, then every J-decomposable graph H satisfies Sidorenko’s conjecture. That is, for any graphon W,
![]() $t_H(W)\geq t_{K_2}(W)^{e(H)}$
.
$t_H(W)\geq t_{K_2}(W)^{e(H)}$
.
As in [ Reference Conlon and Lee4 ], we expect that entropy techniques can be used to broaden this class further, but we have chosen not to pursue this direction here.
5·2. The Erdős–Simonovits conjecture
The supersaturation conjecture of Erdős and Simonovits [
Reference Simonovits21
] is often cited as an equivalent formulation of Sidorenko’s conjecture, but it is in fact stronger for sparse graphs. Recall that
![]() $\textrm{ex}(n,H)$
is the largest number of edges in an H-free graph with n vertices. Their conjecture is then as follows.
$\textrm{ex}(n,H)$
is the largest number of edges in an H-free graph with n vertices. Their conjecture is then as follows.
Conjecture 5·2 (Erdős-Simonovits). Let H be a bipartite graph. Then there exist positive constants c and C such that every n-vertex graph G with at least
![]() $C\cdot \textrm{ex}(n,H)$
edges contains at least
$C\cdot \textrm{ex}(n,H)$
edges contains at least
![]() $c\cdot n^{v(H)}p^{e(H)} $
copies of H, where
$c\cdot n^{v(H)}p^{e(H)} $
copies of H, where
![]() $p=t_{K_2}(G)$
.
$p=t_{K_2}(G)$
.
In full generality, this conjecture is known for only a handful of special cases. However, here we show that dominating graphs do satisfy the conjecture to some nontrivial extent. In the proof below, we will use the notation
![]() $\textrm{Hom}(H,G)$
to denote the set of homomorphisms from a graph H to another graph G. In particular, if G has n vertices,
$\textrm{Hom}(H,G)$
to denote the set of homomorphisms from a graph H to another graph G. In particular, if G has n vertices,
![]() $t_H(G) = |\textrm{Hom}(H,G)|/n^{v(H)}$
.
$t_H(G) = |\textrm{Hom}(H,G)|/n^{v(H)}$
.
Theorem 5·3. Let H be a bipartite graph with maximum degree
![]() $\Delta$
. If H dominates
$\Delta$
. If H dominates
![]() $H\setminus v$
for each
$H\setminus v$
for each
![]() $v\in V(H)$
and each
$v\in V(H)$
and each
![]() $H\setminus v$
satisfies Sidorenko’s conjecture, then there exist positive constants c and C such that every n-vertex graph with at least
$H\setminus v$
satisfies Sidorenko’s conjecture, then there exist positive constants c and C such that every n-vertex graph with at least
![]() $Cn^{2-1/\Delta}$
edges contains at least
$Cn^{2-1/\Delta}$
edges contains at least
![]() $cn^{v(H)}p^{e(H)}$
copies of H, where
$cn^{v(H)}p^{e(H)}$
copies of H, where
![]() $p=t_{K_2}(G)$
.
$p=t_{K_2}(G)$
.
Proof. Suppose, for the sake of contradiction, that there are no such constants
![]() $c,C>0$
. That is, given any
$c,C>0$
. That is, given any
![]() $c,C>0$
, there exists an n-vertex graph G with
$c,C>0$
, there exists an n-vertex graph G with
![]() $e(G)\geq Cn^{2-1/\Delta}$
such that at least a
$e(G)\geq Cn^{2-1/\Delta}$
such that at least a
![]() $(1-c)$
-proportion of the homomorphic copies of H in G are degenerate. As each degenerate copy of H is contained in a homomorphic copy of
$(1-c)$
-proportion of the homomorphic copies of H in G are degenerate. As each degenerate copy of H is contained in a homomorphic copy of
![]() $H\setminus v$
for some
$H\setminus v$
for some
![]() $v\in V(H)$
, it follows that
$v\in V(H)$
, it follows that
Let H
′ be the subgraph of H that attains the maximum value of
![]() $|\textrm{Hom}(H\setminus v,G)|$
amongst all
$|\textrm{Hom}(H\setminus v,G)|$
amongst all
![]() $H\setminus v$
for
$H\setminus v$
for
![]() $v\in V(H)$
. In particular,
$v\in V(H)$
. In particular,
![]() $v(H)|\textrm{Hom}(H^{\prime},G)|\geq (1-c)|\textrm{Hom}(H,G)|$
. Dividing both sides by
$v(H)|\textrm{Hom}(H^{\prime},G)|\geq (1-c)|\textrm{Hom}(H,G)|$
. Dividing both sides by
![]() $n^{v(H)}$
then gives
$n^{v(H)}$
then gives
![]() $({v(H)}/{n})t_{H^{\prime}}(G)\geq (1-c)t_{H}(G)$
. Combining this with the domination inequality
$({v(H)}/{n})t_{H^{\prime}}(G)\geq (1-c)t_{H}(G)$
. Combining this with the domination inequality
![]() $t_{H}(G)\geq t_{H^{\prime}}(G)^{e(H)/e(H^{\prime})}$
and the Sidorenko inequality
$t_{H}(G)\geq t_{H^{\prime}}(G)^{e(H)/e(H^{\prime})}$
and the Sidorenko inequality
![]() $t_{H^{\prime}}(G)\geq t_{K_2}(G)^{e(H^{\prime})}$
gives
$t_{H^{\prime}}(G)\geq t_{K_2}(G)^{e(H^{\prime})}$
gives
where the final inequality used
![]() $e(H)-e(H^{\prime})\leq \Delta$
. Therefore,
$e(H)-e(H^{\prime})\leq \Delta$
. Therefore,
![]() $p\leq \left({v(H)}/({1-c})\right)^{1/\Delta} n^{-1/\Delta}$
. Now choosing
$p\leq \left({v(H)}/({1-c})\right)^{1/\Delta} n^{-1/\Delta}$
. Now choosing
![]() $c=1/2$
and
$c=1/2$
and
![]() $C=3v(H)$
yields the desired contradiction.
$C=3v(H)$
yields the desired contradiction.
6. Concluding remarks
Which graphs are dominating? Following [ Reference Conlon and Lee4 ], it is reasonable to conjecture that a graph is weakly norming if and only if it has a percolating sequence, but we suspect that there is no such clean characterisation for dominating graphs. However, there are several interesting questions whose answers would help to clarify the nature of this family.
For instance, is it the case that every dominating graph arises through our reflection/relocation mechanism? And, if so, is it the case that they can all be associated in some nontrivial way to a reflection group? It is a little hard to make these questions more precise, but perhaps there is some example we missed that answers both in the negative.
We have already seen that there are dominating graphs, such as our running example
![]() $C_6^+$
, which are not edge transitive. This again sets them apart from weakly norming graphs, since Sidorenko [
Reference Sidorenko19
] has shown that any weakly norming graph must be edge transitive. However, all of our bi-regular examples are edge transitive. It would be interesting to decide if this is a more general phenomenon.
$C_6^+$
, which are not edge transitive. This again sets them apart from weakly norming graphs, since Sidorenko [
Reference Sidorenko19
] has shown that any weakly norming graph must be edge transitive. However, all of our bi-regular examples are edge transitive. It would be interesting to decide if this is a more general phenomenon.
It would also be interesting to decide whether there are examples other than trees where we need to look at three or more distinct layers (or, alternatively, where we need to relocate two or more times) to confirm the domination property. For both Theorem 4·1 and 4·2, we use only two layers and, despite searching extensively, we did not find any interesting examples with more layers. A related problem is to find an example of a dominating graph which has more than two distinct degrees on the larger side or, which would be more interesting, to show that no such graph exists.
Finally, as with our work on weakly norming graphs, most of the concepts and results in this paper extend to hypergraphs. We will not go into this in any depth here, but many of the same questions can also be asked in this more general context.
Strong domination. We say that a graph H strongly dominates another graph H ′ if
for any bounded symmetric measurable function W from
![]() $[0,1]^2$
to
$[0,1]^2$
to
![]() $\mathbb{R}$
. That is, W is no longer required to take positive values. This is in line with the distinction between norming and weakly norming graphs in [
Reference Hatami10
]. We then say that a graph H is strongly dominating if it strongly dominates all of its subgraphs. As in [
Reference Conlon and Lee4
], our results here have analogues in the strongly dominating case. For instance, the analogue of Theorem 3·5 holds provided all of our reflections and relocations correspond to strong domination inequalities. In practice, this means that all of our cut involutions must be stable, meaning that the fixed set of the involution is an independent (or stable) set. However, besides the family of norming graphs themselves (see [
Reference Lee and Sidorenko13
] for an in-depth study of which reflection graphs are norming), the only strongly dominating graphs we were able to identify are even-length paths. It would be interesting to find more.
$\mathbb{R}$
. That is, W is no longer required to take positive values. This is in line with the distinction between norming and weakly norming graphs in [
Reference Hatami10
]. We then say that a graph H is strongly dominating if it strongly dominates all of its subgraphs. As in [
Reference Conlon and Lee4
], our results here have analogues in the strongly dominating case. For instance, the analogue of Theorem 3·5 holds provided all of our reflections and relocations correspond to strong domination inequalities. In practice, this means that all of our cut involutions must be stable, meaning that the fixed set of the involution is an independent (or stable) set. However, besides the family of norming graphs themselves (see [
Reference Lee and Sidorenko13
] for an in-depth study of which reflection graphs are norming), the only strongly dominating graphs we were able to identify are even-length paths. It would be interesting to find more.
These notions also suggest the study of which graphs have the strong Sidorenko property, that H strongly dominates
![]() $K_2$
, i.e.,
$K_2$
, i.e.,
for all bounded symmetric measurable functions
![]() $W\;:\;[0, 1]^2 \to \mathbb{R}$
. Clearly, any such graph must be bipartite. If H has the stronger property that it strongly dominates
$W\;:\;[0, 1]^2 \to \mathbb{R}$
. Clearly, any such graph must be bipartite. If H has the stronger property that it strongly dominates
![]() $K_{1,2}$
, then H must also be positive, in the sense that
$K_{1,2}$
, then H must also be positive, in the sense that
![]() $t_H(W) \geq 0$
for all W (see [
Reference Antolín Camarena, Csóka, Hubai, Lippner and Lovász1
] for more on positive graphs, including a tantalising conjecture about their structure). To show this, suppose that
$t_H(W) \geq 0$
for all W (see [
Reference Antolín Camarena, Csóka, Hubai, Lippner and Lovász1
] for more on positive graphs, including a tantalising conjecture about their structure). To show this, suppose that
![]() $t_H(W) < 0$
and choose some W
′ such that
$t_H(W) < 0$
and choose some W
′ such that
![]() $t_H(W') > 0$
. Then there exists
$t_H(W') > 0$
. Then there exists
![]() $p > 0$
such that
$p > 0$
such that
![]() $t_H(W + pW') = 0$
. However, unless
$t_H(W + pW') = 0$
. However, unless
![]() $W + p W'$
averages to zero along almost every fibre, a situation which an appropriate choice of W
′ avoids, we must have
$W + p W'$
averages to zero along almost every fibre, a situation which an appropriate choice of W
′ avoids, we must have
![]() $t_{K_{1,2}}(W+pW') > 0$
, contradicting the assumption that H strongly dominates
$t_{K_{1,2}}(W+pW') > 0$
, contradicting the assumption that H strongly dominates
![]() $K_{1,2}$
. We believe that a similar conclusion should hold if we only know that H strongly dominates
$K_{1,2}$
. We believe that a similar conclusion should hold if we only know that H strongly dominates
![]() $K_2$
, namely, that once we delete any isolated edges from H, the remaining graph H
′ should be positive.
$K_2$
, namely, that once we delete any isolated edges from H, the remaining graph H
′ should be positive.
It is tempting also to conjecture a converse, saying that any positive bipartite graph has the strong Sidorenko property. Unfortunately, this is false. Indeed, the disjoint union 2H of two copies of H is always positive, but it does not have the strong Sidorenko property unless H itself does. It remains a tantalising problem to classify, or at least formulate a reasonable conjecture about, those graphs which do have the strong Sidorenko property.
Other domination inequalities. Given a graph H and a vertex x, the graph
![]() $H_x(k)$
is the subgraph induced by all vertices of distance at most k from x. If H is vertex transitive, then we may omit the subscript x. We make the following conjecture.
$H_x(k)$
is the subgraph induced by all vertices of distance at most k from x. If H is vertex transitive, then we may omit the subscript x. We make the following conjecture.
Conjecture 6·1. Suppose that H is a vertex-transitive reflection graph with diameter d. Then
![]() $H(\ell)$
dominates H(k) for all
$H(\ell)$
dominates H(k) for all
![]() $1 \leq k \leq \ell \leq d$
.
$1 \leq k \leq \ell \leq d$
.
Why believe this conjecture? For one thing, it holds when H is an even cycle, as follows easily from the fact that even-length paths are dominating. But, less obviously, it also holds when H is the n-dimensional cube
![]() $Q_n$
. This again follows from our reflection/relocation mechanism. Indeed, if we label the vertices of the cube with the subsets of [n], then, for x the empty set, H(k) consists of all subsets of [n] with at most k elements. If we relocate H(k) by moving each vertex S to
$Q_n$
. This again follows from our reflection/relocation mechanism. Indeed, if we label the vertices of the cube with the subsets of [n], then, for x the empty set, H(k) consists of all subsets of [n] with at most k elements. If we relocate H(k) by moving each vertex S to
![]() $S \triangle \{i\}$
for some i and then percolate, this increases the number of layers by one. Iterating then gives the result.
$S \triangle \{i\}$
for some i and then percolate, this increases the number of layers by one. Iterating then gives the result.
Observe that
![]() $Q_3(2) = C_6^+$
is dominating, as is
$Q_3(2) = C_6^+$
is dominating, as is
![]() $Q_n(2)$
for any n, but
$Q_n(2)$
for any n, but
![]() $Q_n(\ell)$
is generally not. However, the fact that
$Q_n(\ell)$
is generally not. However, the fact that
![]() $Q_n(\ell)$
dominates
$Q_n(\ell)$
dominates
![]() $Q_n(k)$
for all
$Q_n(k)$
for all
![]() $1 \leq k \leq \ell$
may be seen as a near miss. Conjecture 6.1 is then just asking to what extent this phenomenon generalises. Note that the fact that H is vertex transitive allows for easy relocations, but it also seems to be a necessary condition, as such relocations are not always possible in non-vertex-transitive reflection graphs such as the 1-subdivision of an octahedron.
$1 \leq k \leq \ell$
may be seen as a near miss. Conjecture 6.1 is then just asking to what extent this phenomenon generalises. Note that the fact that H is vertex transitive allows for easy relocations, but it also seems to be a necessary condition, as such relocations are not always possible in non-vertex-transitive reflection graphs such as the 1-subdivision of an octahedron.
Acknowledgements
DC is supported by NSF Award DMS-2054452. JL is supported by the National Research Foundation of Korea (NRF) Grant 2022R1C1C1010300, Samsung STF Grant SSTF-BA2201-02 and IBS-R029-C4.













