DNA structure in the RecA filament: B-like, but with a separation every three bases
RecA family proteins pair two DNAs of the same sequence and promote their strand exchange during homologous recombination (Shibata et al., Reference Shibata, Dasgupta, Cunningham and Radding1979). This universal process plays important roles in DNA metabolism, such as formation of chromosome pairs at meiosis, and repair of stalled replication forks and double-strand breaks (Alberts et al., Reference Alberts, Johnson, Lewis, Raff, Roberts and Walter2002).
RecA initially binds single-stranded DNA (ssDNA) with high cooperativity, forming a nucleoprotein filament (DiCapua et al., Reference DiCapua, Engel, Stasiak and Koller1982; Howard-Flanders et al., Reference Howard-Flanders, West and Stasiak1984). This filament selectively binds double-stranded DNA (dsDNA) with the same or similar sequence, and aligns the two sequences for strand exchange. The test for homology involves a direct interaction between the two DNAs. The structure of ssDNA in the RecA filament has been determined by X-ray crystallography (Chen et al., Reference Chen, Yang and Pavletich2008). Each RecA monomer covers three bases, which are arranged in a very similar manner as the bases in B-form dsDNA: stacked, perpendicularly oriented, and immobilized (Chabbert et al., Reference Chabbert, Lami and Takahashi1991; Norden et al., Reference Norden, Elvingson, Kubista, Sjoberg, Ryberg, Ryberg, Mortensen and Takahashi1992; Chen et al., Reference Chen, Yang and Pavletich2008). In this configuration, the ssDNA is ready to pair with the incoming DNA. However, the ssDNA is elongated 1.5-fold due to intercalation of RecA amino acid residues every three bases (Chen et al., Reference Chen, Yang and Pavletich2008). The role of this DNA elongation has been discussed (Bosaeus et al., Reference Bosaeus, Reymer, Beke-Somfai, Brown, Takahashi, Wittung-Stafshede, Rocha and Norden2017; Stavans, Reference Stavans2018), but its importance remains unclear. Hence, the mechanism by which RecA family proteins search for and recognize homologous DNA remains to be clarified.
Minimum size of homology for the RecA reaction
One important question is whether RecA tests for homology between two DNAs one nucleotide at a time or several nucleotides at once, and if the latter, how many nucleotides are tested. The answer could provide a clue about the mechanism of homology recognition: if the effective recognition size is three nucleotides, then recognition could be achieved by a single protomer of RecA, and the incoming B-form dsDNA could easily pair with the stacked B-form DNA. By contrast, if the effective recognition size is greater than three, the incoming dsDNA must be deformed, most probably via elongation, to pair with the first DNA because the latter is stretched 1.5-fold by a separation every three bases. Determination of this effective size would also be useful for understanding the basis of rapid homology searching by RecA family proteins (Fulconis et al., Reference Fulconis, Dutreix and Viovy2005; Kates-Harbeck et al., Reference Kates-Harbeck, Tilloy and Prentiss2013; Jiang and Prentiss, Reference Jiang and Prentiss2014). Short-sequence homology can exist in any DNA, trapping RecA at non-target DNA and slowing the search. On the other hand, examination of long sequence requires DNAs to be geometrically rearranged in order to be paired, which would certainly take time and decrease search speed.
Hsieh et al. demonstrated that a sequence identity of eight bases is sufficient for the strand-exchange reaction between two oligonucleotides in vitro (Hsieh et al., Reference Hsieh, Camerini-Otero and Camerini-Otero1992). Prentiss and colleagues showed that the presence of mismatch bases affects RecA-promoted ssDNA/dsDNA pair formation. Five matches over 20 bases are not sufficient for pair formation (Danilowicz et al., Reference Danilowicz, Yang, Kelley, Prevost and Prentiss2015); accordingly, those authors proposed that the initial homology test involves eight bases. Using a single-molecule approach, Ragunathan et al. (Reference Ragunathan, Liu and Ha2012) observed that a sequence match of as few as six bases is sufficient for homology recognition.
These results, however, did not show that all of the nucleotides are recognized at the same time. For instance, recognition could start with as little as one nucleotide before testing of the second nucleotide. When a six–eight contiguous nucleotide match is achieved, the complex is stable enough to be detected and to allow the strand exchange reaction to proceed. To determine real recognition size, i.e. the number of nucleotides to be tested at once, it is necessary to analyze the pairing rate (association rate).
Analysis of the mismatch effect on the association step
In this study, we analyzed the effect of mismatch bases (sequence heterogeneity) on the association rate of dsDNA with RecA/ssDNA complex filament (i.e. the pairing rate). We previously observed that the presence of mismatch bases decreases the association rate (Bazemore et al., Reference Bazemore, FoltaStogniew, Takahashi and Radding1997). Because strand exchange can start at any point in the DNA, the presence of mismatch bases eliminates some potential starting points, decreasing the number of possible associations and proportionally slowing the overall association rate.
Under this hypothesis, and if RecA recognizes homology one nucleotide at a time, there are l possible starting points (where l is the size of the DNA in nucleotide) in the absence of a mismatch, and one mismatch nucleotide abolishes one possible starting point for pairing (Fig. 1). If the recognition is made two nucleotides at a time, one mismatch base abolishes two starting points among (l − 1) possibilities (Fig. 1). In general, when the recognition size is n nucleotides, one mismatch abolishes n possible starting points among (l − n + 1) possibilities. If we assume that a mismatch of one base among n bases completely prevents initiation of pairing at the site, we can compute the decrease in the number of starting points with the increase in number of mismatches (m) by using the following formula:
where N 0 is the number of starting points in the absence of mismatch; l the length of DNA; n the recognition size; and m the number of mismatches. If a mismatch does not completely abolish initiation at the site, but only by x%, the formula will be N/N 0 = ((l − n + 1) − n × m × x/100)/(l − n + 1).

Fig. 1. The reduction in the number of possible pairing initiations due to one mismatch base is a function of recognition size. The presence of one mismatch base (x) abolishes some initiation possibilities (dotted line) upon the recognition size.
However, we cannot apply these formula when the distance between mismatches is smaller than the recognition size, because some of the starting sites that were abolished by one mismatch overlapped with those that were abolished by a neighboring mismatch (see supplement Fig. S1).
The pairing rate decreases proportionally with the number of mismatch bases
In our previous experiments, we used a DNA of 83 bases in length (l = 83). Mismatch bases were spread throughout the DNA sequence, and the distance between mismatch bases was greater than six bases (Bazemore et al., Reference Bazemore, FoltaStogniew, Takahashi and Radding1997). Therefore, we need not consider the case of more than two mismatches in one section if n < 7, and can apply the formula above to compute the decrease in the number of pairing sites (Fig. 2). In the case of n > 7, we cannot apply the formula and manually counted possible starting points to generate theoretical curves. We then compared these theoretical curves with the experimental data. The data show that the rate decreases linearly with the number of mismatches (Fig. 2), indicating that a mismatch at any position abolishes the number of starting points in a similar manner. This supports the hypothesis that homologous recognition can occur at any point along the DNA with almost identical efficiency. This mechanism increases the probability of initiation relative to a situation in which the reaction can start only at one well-determined position. Thus, the observed mechanism contributes to rapid search for homologous sequence.
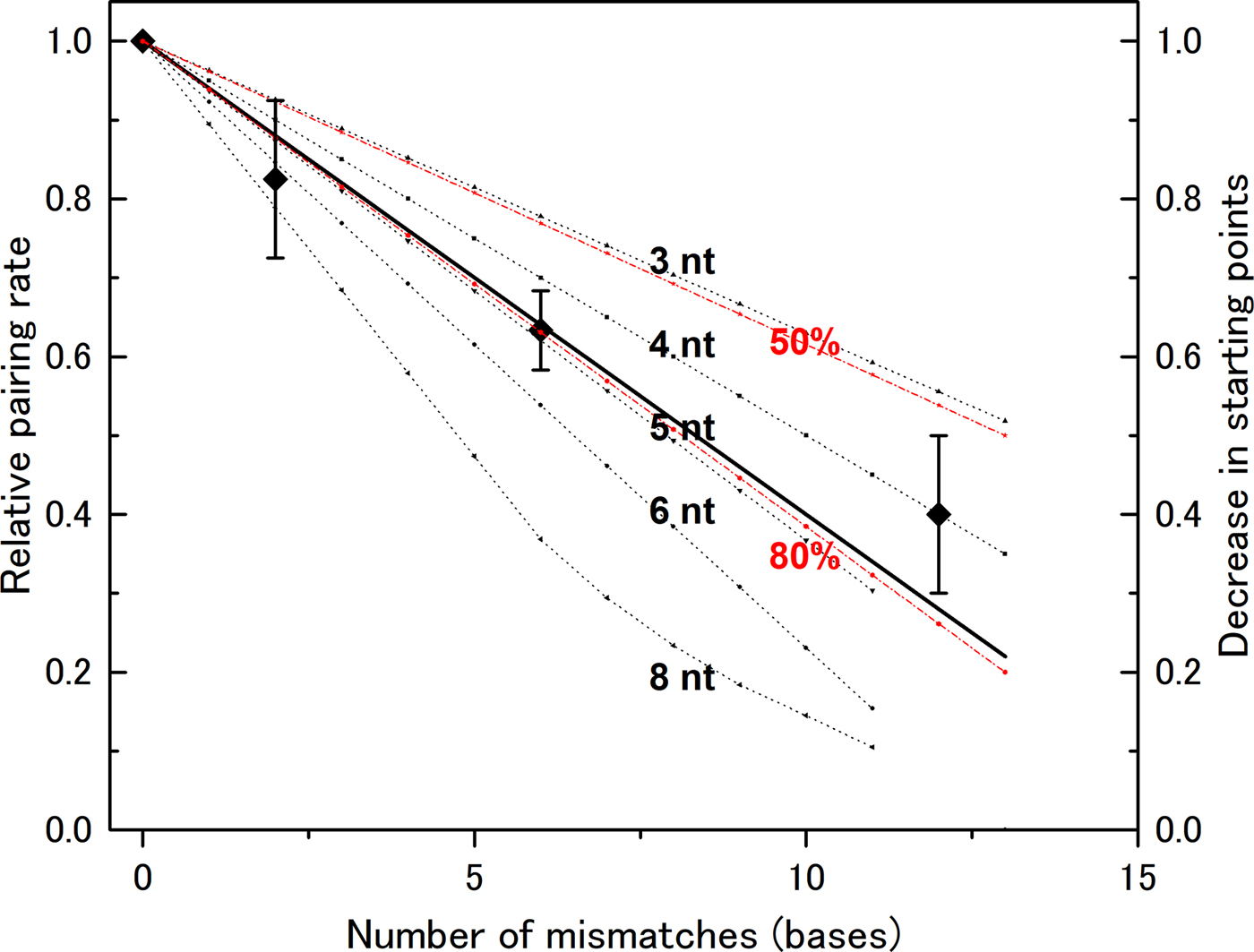
Fig. 2. Recognition size influences the effect of mismatch bases on the DNA-pairing rate. The reduction in the pairing rate as a function of the number of mismatch bases was computed for various recognition sizes (noted in the figure), and the data were compared with experimental data obtained by Bazemore et al. (Reference Bazemore, FoltaStogniew, Takahashi and Radding1997). In the case of n = 8, the computed curve is not linear because the regions affected by two mismatches can overlap when the number of mismatches becomes large. The theoretical curves for recognition sizes of six bases and pairing prevention of 80 or 50% per mismatch are also shown (in red).
A recognition size of five or six nucleotides fits the experimental data
The experimental data fit closely with curves for n = 5 ± 1. If we assume that a single mismatch does not completely abolish the starting point, but instead prevents it 80% of the time, the computed curve for n = 6 becomes almost the same as the one for n = 5 and fits closely with the experimental data (Fig. 2). By contrast, the theoretical curve with 50% pairing inhibition does not fit the experimental data. The size determined in this manner is slightly smaller than the sizes obtained by other methods, but is clearly larger than three bases. Recent analysis of a non-polymerizing RecA mutant showed that dimer formed by covalent linking can promote DNA pair formation while its monomer form cannot (Shinohara et al., Reference Shinohara, Arai, Iikura, Kasagi, Masuda-Ozawa, Yamaguchi, Suzuki-Nagata, Shibata and Mikawa2018). Since each RecA monomer covers three bases, this observation suggests that pair formation requires more than a three base match but less than a six base match, which is compatible with our results. According to the analysis by Fulconis et al. (Reference Fulconis, Dutreix and Viovy2005), a recognition size of five or six bases permits efficient search homology.
These results indicate that dsDNA is deformed, probably via elongation, at the early step of reaction to pair with the primary bound elongated ssDNA. Supporting this idea, Prentiss et al. observed that differential extension of dsDNA facilitates the pairing step (Danilowicz et al., Reference Danilowicz, Peacock-Villada, Vlassakis, Facon, Feinstein, Kleckner and Prentiss2014). Because stretching of free dsDNA is slow, RecA must promote this stretching.
The observation that an almost complete match of five or six bases is required for the recognition suggests that recognition is not based on thermodynamic stability. The absence of one base pair from five or six base pairs decreases binding energy by only about 20%. This cannot explain the rigorous discrimination observed in the experiments. Therefore, selection of homologous DNA must be made kinetically rather than thermodynamically, and some factor other than simple Watson–Crick hydrogen bonding may be involved.
In the case of Rad51, a eukaryotic homolog of RecA, Anand et al. (Reference Anand, Beach, Li and Haber2017) demonstrated that the presence of single-nucleotide mismatch every eight bases decreases the efficiency of homologous recombination repair by 15% relative to the completely matched situation, but that significant repair occurs even in the presence of one mismatch every six bases. On the basis of this finding, they proposed that the effective recognition size is six to eight bases. Based on single-molecule observation in vitro, Qi et al. proposed a recognition size of eight bases (Qi et al., Reference Qi, Redding, Lee, Gibb, Kwon, Niu, Gaines, Sung and Greene2015). Thus, the minimum size of the homology that Rad51 requires to start the reaction is similar to that RecA requires. These results suggest that Rad51 searches for homologous DNA in a similar manner to that of RecA, although so far no kinetic analysis of the pairing step has been performed.
Outlook
We estimated the size of homology required RecA to start DNA pair formation. The results revealed that the incoming dsDNA must be elongated, with de-stacking of some bases. Base de-stacking probably plays some role in searching for or recognizing homology. Interestingly, a similar situation is observed for the selection of complementary nucleotides by DNA polymerase. The crystal structure of DNA polymerase reveals that the base of the template DNA that is opposite to incoming complementary nucleotide, and thus involved in the selection, is not stacked on one of the neighboring bases (Kool, Reference Kool2001). Weakening the base-stacking interaction might increase the accuracy of complementary base selection to permit a particular orientation.
Our analysis also demonstrates that the selection of homologous DNA is not achieved thermodynamically, but kinetically. Selection requires some factor besides Watson–Crick hydrogen bonding, because the latter is weak at long distances and therefore could not play a major role in the association step. Furthermore, the energetic difference due to one mismatch over five or six nucleotides is too small to ensure stringent selection. Kool and colleagues showed that the selection of complementary nucleotide by DNA polymerase does not require hydrogen-bond formation with the template DNA base (Kool, Reference Kool2001). Watson–Crick hydrogen bonding is certainly important for stability, but some other structural factors such as nucleobase shape may play a more important role in the selection of the complementary base. It would be worthwhile to determine whether this is also the case for other biological processes involving nucleic acid/nucleic acid interaction, such as the replication, transcription, translation, and regulation by siRNA and miRNA.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0033583518000094.
Author ORCIDs
Masayuki Takahashi 0000-0002-1856-5312.
Acknowledgements
We would like to thank Professors James Haber (Brandies University, Waltham, USA) and Hiroshi Iwasaki (Tokyo Institute of Technology, Tokyo, Japan), and Dr. Chantal Prevost (CNRS, Paris, France) for valuable discussions.




