Article contents
A first-passage-place problem for integrated diffusion processes
Published online by Cambridge University Press: 22 May 2023
Abstract
Let 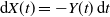 ${\mathrm{d}} X(t) = -Y(t) \, {\mathrm{d}} t$, where Y(t) is a one-dimensional diffusion process, and let
${\mathrm{d}} X(t) = -Y(t) \, {\mathrm{d}} t$, where Y(t) is a one-dimensional diffusion process, and let 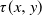 $\tau(x,y)$ be the first time the process (X(t), Y(t)), starting from (x, y), leaves a subset of the first quadrant. The problem of computing the probability
$\tau(x,y)$ be the first time the process (X(t), Y(t)), starting from (x, y), leaves a subset of the first quadrant. The problem of computing the probability 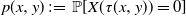 $p(x,y)\,:\!=\, \mathbb{P}[X(\tau(x,y))=0]$ is considered. The Laplace transform of the function p(x, y) is obtained in important particular cases, and it is shown that the transform can at least be inverted numerically. Explicit expressions for the Laplace transform of
$p(x,y)\,:\!=\, \mathbb{P}[X(\tau(x,y))=0]$ is considered. The Laplace transform of the function p(x, y) is obtained in important particular cases, and it is shown that the transform can at least be inverted numerically. Explicit expressions for the Laplace transform of 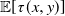 $\mathbb{E}[\tau(x,y)]$ and of the moment-generating function of
$\mathbb{E}[\tau(x,y)]$ and of the moment-generating function of 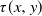 $\tau(x,y)$ can also be derived.
$\tau(x,y)$ can also be derived.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by



