Introduction

Calculation of an avalanche impact pressure is one of the most important problems in engineering practice. Much has been written about this problem (see, e.g., Reference MellorMellor, 1975; Reference Lang and BrownLang and Brown, 1980; Reference Salm, Burkard and GublerSalm and others, 1990; Reference HákonardóttirHákonardóttir, 2004). Most of the authors have ignored snow compressibility and the possibility of compression shock waves, though it is known that snow density is changed by flow impact against an obstacle.

The effect of snow compressibility was taken into account by Reference Briukhanov and OuraBriukhanov and others (1967), Reference Gonor and Pik-PichakGonor and Pik-Pichak (1983) and Reference Eglit, Kulibaba and NaaimEglit and others (2007). Reference Briukhanov and OuraBriukhanov and others (1967) dealt with stationary overflow of a wedge by an avalanche; Reference Eglit, Kulibaba and NaaimEglit and others (2007) considered a non-stationary process of impact against a wall but ignored the influence of the flow boundaries, so the problem is one-dimensional. Reference Gonor and Pik-PichakGonor and Pik-Pichak (1983) presented a numerical solution of the two-dimensional (2-D) problem of a dense avalanche impact against a wall, taking account of the flow boundaries, but they ignored gravity, so they could not calculate the maximum flow height at the wall. This paper presents a numerical solution to a time-dependent 2-D problem of an avalanche impact against a wall, taking account of both compressibility and gravity. The assumed equations of state for moving snow differ from those used by Reference Gonor and Pik-PichakGonor and Pik-Pichak (1983) since here we consider low-density dry avalanches with densities <100 kgm^–3. In these avalanches the average spacing between centers of snow/ice particles is sufficiently large (Reference Eglit, Kulibaba and NaaimEglit and others, 2007) that particles do not have permanent contacts with each other, and the flow of snow–air mixture behaves like a flow of a mixture of two gases (air and gas of particles). The equations of state for low-density avalanches that follow from this assumption were proposed by Reference Briukhanov and OuraBriukhanov and others (1967) and Reference Eglit, Kulibaba and NaaimEglit and others (2007).

Statement of the Problem

Consider a 2-D avalanche flow, where both the flow and the obstacle are wide, and lateral movement is ignored. The flow velocity is u ₀ and its depth is H. The air pressure is p ₀, and the flow density at the upper surface is ρ ₀. Note that the pressure and the density inside the flow depend on the depth, due to gravity and compressibility of the moving snow. At an instant t = 0 the flow meets a high solid wall. The wall is perpendicular to the local slope, and its height is larger than the incoming flow height (see Fig. 1). After the impact the flow starts to pile up at the wall, and a shock wave appears, moving upstream and interacting with the flow boundaries. We are interested in the pressure, density and velocity distributions in the flow after the impact, and particularly in the pressure and the flow height at the wall.

Fig. 1. A sketch of the flow after impact.

The continuity, momentum and energy equations are:

Here t is time, x and y are coordinates along the slope and normal to it, respectively, g is the gravitational acceleration, u and v are the velocity components, and ρ, p and e are the flow density, pressure and the internal energy density,

respectively. The impact process is assumed to be adiabatic, and shear stresses are neglected. The following equation may be used instead of Equation (4):

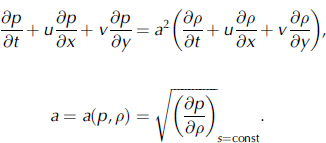
Here a is the sound velocity in an avalanche flow. Equation (5) is true on condition that the flow is adiabatic (the entropy s is constant).

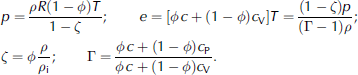
Systems (1–4) or (1–3), (5) are not complete. Equations of state are needed for a complete system. For low-density avalanches the following equations of state are assumed (see Reference Eglit, Kulibaba and NaaimEglit and others, 2007):

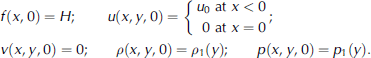
Here R is the gas constant for air, ϕ and ζ are the mass and the volume fractions of ice in the ice–air mixture, respectively, T is the flow absolute temperature, ρ _i is the density of ice, c is the specific capacity of ice, c _V and c _P are specific capacities of air at constant volume and at constant pressure, respectively, and ⌈ is the ratio of specific capacities of the mixture at constant volume and at constant pressure. The

formula for the sound speed is

We also need to write the initial and boundary conditions. Let the equation of the upper surface of the flow be y = f(x,t), where f is an unknown fucntion of the time t and the coordinate along the slope x (see Fig. 1). The wall is located at x = 0. Consider the part of the flow between x = –X and x = 0 (see Fig. 1). The domain where the differential equations should be solved is –X ≤ x ≤ 0; 0 ≤ y ≤ f (x,t): The initial conditions are

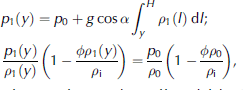
The density ρ ₁(y) and the pressure p ₁(y) in the incoming avalanche flow depend on the depth due to gravity and compressibility. If the density and pressure in the flow upper layer are ρ ₀, p ₀ then ρ ₁(y) and p ₁(y) are calculated by the relations

with α the slope angle near the wall, and l the integration variable. These relations follow from the assumptions that before the impact the pressure across the flow obeys the hydrostatic law, and the temperature is constant.

Let us write the boundary conditions. Supposing that the disturbances from the wall do not reach the left boundary x = –X during the time period under consideration, we have

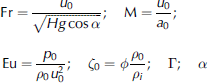
The impermeability condition at the bottom (y = 0) is v(x,0,t) = 0 and at the wall (x=0) is u(0,y,t) = 0: We assume that the flow does not reach the top of the wall during the time period studied.

The dynamic and kinematics conditions at the upper free surface of the flow are p(x, f (x, t) t) = p ₀; [∂f (x, t)]=∂t+ u(x, f (x, t), t)[∂f (x, t)]=∂x=v(x, f (x, t), t): The problem can be written in dimensionless form introducing dimensionless variables

Here a ₀ = a ₍p0, ρ ₀) is the sound speed in the avalanche surface layer before impact. When the problem is formulated in dimensionless form, the following dimensionless parameters enter the equations and boundary conditions:

which are the Froude number, the Mach number, the Euler number, the volume concentration of ice in the top layer of an avalanche before impact, the mixture specific heat ratio and the slope angle at the location of the wall, respectively. Note that the Euler number Eu can be calculated by M, ζ ₀ and Γ.

Numerical Method

At first we transformed the equations introducing the new variables t ⁰, x', y' t' = t̄; x' = x̄; y' = ȳ=[f̄ (x̄, t̄)]: With the new variables the equations have a more complicated form. However, they are convenient because the flow domain is transformed into a rectangle –X̄ X ≤ x' ≤ 0; 0 ≤ y' ≤ 1: Calculations were made using a finite-difference method based on the McCormack scheme for internal nodes and on the Kentzer method for points at the upper free surface (Reference Anderson, Tannehill and PletcherAnderson and others, 1984). The Courant condition determined the value of the step in time. A special smoothing procedure was used to decrease oscillations in the domains of shocks (Reference Zhmakin, Popov and FursenkoZhmakin and others, 1977). However, we could not get rid of some numerical oscillations at the very beginning of the process. The software was successfully tested on the known gas-dynamics analytical solution to the problem of an impact of an infinite gas flow against an infinite wall. Horizontal flows (α = 0) with different values of M, ζ ₀, ⌈ and Fr were studied. The following values of the flow parameters were taken as a basic variant:

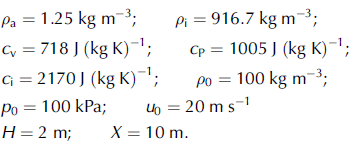
These parameter values give a ₀ = 33.5 ms^–1, p _W = 1.96p ₀, where p _W is the value of the impact pressure at the base of the wall, calculated by the formula for a direct shock wave (Reference Eglit, Kulibaba and NaaimEglit and others, 2007), and

Results of Calculations

The results of the calculations presented in Reference Briukhanov and OuraFigures 2–8 were obtained for the values of dimensionless parameters (Equation (8)). Figure 2 shows the behavior of the pressure at the wall at three levels above the ground in time. Oscillations seen for dimensionless time less than 0.6 are numerical, not physical (corresponding to the values (7) of the input-parameters dimensional time t < 0.03 s. The impact pressure at the base of the wall is constant until dimensionless time is almost equal to 1, i.e. until the moment when the rarefaction wave originating at the top boundary of the flow reaches the base. This maximum value of the impact pressure is equal to p _W, so the formulas proposed by Reference Eglit, Kulibaba and NaaimEglit and others (2007) can be used to estimate the maximum value of the impact pressure. The distribution of the pressure at the ground near the wall is plotted in Figure 3. A frontal shock wave moving upstream is easily distinguished. Note that there arise zones where the pressure is less than the atmospheric pressure. We can see an analogous effect in Figure 4, where the distributions of the pressure along the wall at three moments of time are given. The pressure, velocity and density fields inside the flow at different instants after impact are shown in Figures 5–8. The shape of the flow-free surface is seen in Figures 5 and 6. A hydraulic jump can be noticed in the flow after a certain time interval (see Fig. 6). The height of the jump is less than that in an incompressible flow. If the flow of an incompressible fluid with velocity u ₀ = 20ms^–1 and initial depth H = 2 m strikes a high wall, then, according to the shallow-water theory, the height of the jump is 14.1 m, while in our calculations it is about 12.5 m. This is connected to compressibility of the snow and is in accordance with results of granular flow measurements (see Reference HákonardóttirHákonardóttir, 2004). Figure 9 and Table 1 demonstrate the dependence of the dimensionless pressure coefficient c _D defined by

Fig. 2. Dimensionless pressure at the wall vs dimensionless time at three levels above the ground.

Fig. 3. Dimensionless pressure at the ground in front of the wall at different instants. For the values (7) of the flow parameters, dimensionless time values 0.17, 0.84 and 4.19 correspond to dimensional time values 0.01 s, 0.05 s and 0.25 s respectively.

Fig. 4. Distribution of dimensionless pressure along the wall at different instants. For the values (7) of the flow parameters dimensionless time values 0.17, 0.84 and 4.19 correspond to dimensional time values 0.01 s, 0.05 s and 0.25 s respectively.

Fig. 5. The shape of the flow and the dimensionless pressure distribution inside the flow at dimensionless time 0.84.

Fig. 6. The shape of the flow and the dimensionless pressure distribution inside the flow at dimensionless time 4.19.

Fig. 7. The dimensionless velocity field at dimensionless time 4.19.

Fig. 8. The dimensionless density distribution in the flow at dimensionless time 4.19.

Fig. 9. The pressure coefficient c _D vs the flow Mach number. The curve approximates the calculated values; small points show the values of c _D calculated at different values of the Froude number (see Table 1).

on the initial flow parameters. Here p _max is the maximum value of the pressure at the base of the wall. In calculations we varied the values of the input dimensionless parameters by changing the initial velocity, initial flow density and initial flow depth at constant values of the other parameters (7). Figure 9 shows that c _D depends mainly on the flow Mach number M (especially at large values of M), since at fixed value of the Mach number and strong variation (up to two times) of the Froude number the values of c _D vary slightly. Calculations show that the latter variations in c _D are caused by variations of static pressure due to variations of the flow height. The static component of c _D is much less than the dynamic component in the studied flows. Table 1 presents the values of the ratios of the maximum pressure and density at the base of the wall to the initial pressure and density in the flow surface layer

at various values of the flow parameters. The density in the bottom part of the flow just after impact may be significantly larger than (up to 2.3 times) the initial flow density.

Conclusions

The two-dimensional problem of an avalanche impact against a high wall is studied in this paper, taking account of snow compressibility, gravity and the influence of flow boundaries. It is shown that compression shocks and rarefaction waves appear in the flow at impact. A frontal shock wave moves upstream. Both zones with high pressure and zones with low pressure can be observed on the wall surface, as well as on the flow bottom and inside the flow.

The shape of the flow and the dimensionless pressure distribution inside the flow at dimensionless time 4.19.

A hydraulic jump is formed in the flow after a certain time interval. The height of the jump is less than that in an incompressible flow.

Maximum pressure values are found at the first moment of impact at the base of the wall.

The pressure on the upper part of the wall (more than four times higher for initial flow depths) differs from atmospheric pressure by not more than 5% during the studied time interval.

The maximum snow height at the wall is less than that calculated by shallow-water theory, but is still overestimated by the present theory because friction is not taken into account. Taking account of friction is a task for future work.

The maximum value of the pressure coefficient depends mainly on the Mach number of the flow. The Mach number should therefore be respected in physical models of the impact process.

The static component of the maximum pressure on the wall is much less than the dynamic component for the studied flows.

The density varies inside the flow after impact, due to shock and rarefaction waves. The maximum density increase depends on the avalanche velocity and may be up to 2.3.

Only low-density avalanches are considered in this paper. However, the software can easily be modified to study the impact of dense avalanches by replacing an equation of state by an equation suitable for modeling the behavior of dense snow.

Direct comparison of the results of our calculations with measurements in natural and laboratory avalanches is not possible at present, mainly because data are lacking on the density behavior at impact. Density measurement sensors have been installed at some avalanche test sites (Reference Sovilla, Schaer and RammerSovilla and others, 2008), but the data are not yet available. Another cause of difficulty in directly comparing this theory with measurements is the following: This paper deals with situations when the incoming flow depth is lower than the height of the wall. Such situations, which are common for laboratory flows (Hákonard\ó ttir, 2004) and occur in nature (high dams and walls), have not yet been studied in detail for natural flows. Impact pressure is usually measured on small obstacles fully submerged into the flow (e.g. Reference Gauer, Lied and KristensenGauer and others, 2008; Reference Sovilla, Schaer and RammerSovilla and others, 2008). Mathematical modeling of impact against small obstacles is a task for the future. However, we believe that some important features of the impact phenomena described in this paper are common for phenomena of different spatial scales for different time intervals and should be taken into account in studying the process of avalanche impact against an obstacle.