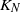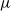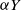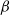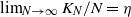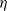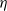1. Introduction
The model described in the abstract aims to quantify the role of migration in the propagation of epidemics on the simplest possible migration model, namely a closed network of
![]() $\cdot/M/\infty$
queues, and for the simplest epidemic process, namely the susceptible–infected–susceptible (SIS) model. The thermodynamic limit discussed in the abstract is considered in order to further simplify the problem.
$\cdot/M/\infty$
queues, and for the simplest epidemic process, namely the susceptible–infected–susceptible (SIS) model. The thermodynamic limit discussed in the abstract is considered in order to further simplify the problem.
The epidemic interpretation of the SIS thermodynamic model is as follows: individuals move from place (station) to place, where places are indexed by, say,
![]() $\mathbb Z$
. The overall density of individuals is
$\mathbb Z$
. The overall density of individuals is
![]() $\eta$
(i.e., the mean number of individuals per station is
$\eta$
(i.e., the mean number of individuals per station is
![]() $\eta$
). An individual stays at a place for an independent random time which is exponentially distributed with parameter
$\eta$
). An individual stays at a place for an independent random time which is exponentially distributed with parameter
![]() $\mu$
. The last parameter can be seen as the migration rate. The departure rate of individuals from a given place is hence
$\mu$
. The last parameter can be seen as the migration rate. The departure rate of individuals from a given place is hence
![]() $\lambda=\mu \eta$
. When it leaves a place, an individual migrates to a place chosen independently and ‘at random’. At each station, individuals are subject to the SIS dynamics with parameters
$\lambda=\mu \eta$
. When it leaves a place, an individual migrates to a place chosen independently and ‘at random’. At each station, individuals are subject to the SIS dynamics with parameters
![]() $(\alpha,\beta)$
. Infections and recoveries take place in stations and conditionally on the state of the stations.
$(\alpha,\beta)$
. Infections and recoveries take place in stations and conditionally on the state of the stations.
In order to answer the question of the abstract, we first consider the problem of a single open station of the M/M/
![]() $\infty$
type, referred to as the M/M/
$\infty$
type, referred to as the M/M/
![]() $\infty$
SIS reactor. The input features two types of customers, infected and susceptible. The customer states change according to the mechanisms described in the abstract. The question is about the steady state of this queue. Of particular interest to us is the proportion
$\infty$
SIS reactor. The input features two types of customers, infected and susceptible. The customer states change according to the mechanisms described in the abstract. The question is about the steady state of this queue. Of particular interest to us is the proportion
![]() $p_o$
of infected customers in the stationary output point process of this reactor in the steady state. This system has its steady state with a joint generating function characterized as a solution of a second-order wave-type partial differential equation (PDE) for which we have found no closed-form solution. We nevertheless derive several structural properties of this open system, which are of independent interest.
$p_o$
of infected customers in the stationary output point process of this reactor in the steady state. This system has its steady state with a joint generating function characterized as a solution of a second-order wave-type partial differential equation (PDE) for which we have found no closed-form solution. We nevertheless derive several structural properties of this open system, which are of independent interest.
The connection of the SIS reactor with the problem of the abstract is the following: Fix all parameters
![]() $\lambda,\mu,\alpha,$
and
$\lambda,\mu,\alpha,$
and
![]() $\beta$
of the thermodynamic limit as defined in the abstract. If the latter has a non-degenerate steady state (namely a steady state with survival), then there must exist a
$\beta$
of the thermodynamic limit as defined in the abstract. If the latter has a non-degenerate steady state (namely a steady state with survival), then there must exist a
![]() $0<p<1$
such that the open system with infected proportion p in input has a proportion of infected in output,
$0<p<1$
such that the open system with infected proportion p in input has a proportion of infected in output,
![]() $p_o$
, equal to p in the steady state. Conversely, if the SIS reactor has a stationary regime where
$p_o$
, equal to p in the steady state. Conversely, if the SIS reactor has a stationary regime where
![]() $p_o(p)=p$
, for some
$p_o(p)=p$
, for some
![]() $p=p^*>0$
, then the thermodynamic limit has a stationary regime where the epidemic persists for appropriate initial conditions. In addition, it will be shown that if the SIS reactor admits no p such that
$p=p^*>0$
, then the thermodynamic limit has a stationary regime where the epidemic persists for appropriate initial conditions. In addition, it will be shown that if the SIS reactor admits no p such that
![]() $p_o(p)=p$
, then for all initial conditions, when time tends to infinity, the proportion of infected customers tends to 0 in the thermodynamic limit. This is why we study the conditions on the parameters
$p_o(p)=p$
, then for all initial conditions, when time tends to infinity, the proportion of infected customers tends to 0 in the thermodynamic limit. This is why we study the conditions on the parameters
![]() $\lambda,\mu,\alpha,$
and
$\lambda,\mu,\alpha,$
and
![]() $\beta$
under which such a p exists, a situation that we will call survival, as well as conditions under which no such p exists, a situation that we call weak extinction.
$\beta$
under which such a p exists, a situation that we will call survival, as well as conditions under which no such p exists, a situation that we call weak extinction.
More precisely, we prove that the SIS thermodynamic limit admits the following phase transition diagram: fix all parameters other than
![]() $\eta$
; there exists a non-degenerate function
$\eta$
; there exists a non-degenerate function
![]() $\eta_c(\alpha,\beta,\mu)$
such that, for
$\eta_c(\alpha,\beta,\mu)$
such that, for
![]() $\eta\le\eta_c$
, there is strong extinction, whereas for
$\eta\le\eta_c$
, there is strong extinction, whereas for
![]() $\eta>\eta_c$
, there is survival. We also derive bounds on the steady states of both the single open station model and the thermodynamic model. For instance, we give bounds on
$\eta>\eta_c$
, there is survival. We also derive bounds on the steady states of both the single open station model and the thermodynamic model. For instance, we give bounds on
![]() $\eta_c$
and
$\eta_c$
and
![]() $p^*$
for the latter. Some of these bounds are established under a hypothesis of negative correlation which is substantiated by simulation but not proved at this stage.
$p^*$
for the latter. Some of these bounds are established under a hypothesis of negative correlation which is substantiated by simulation but not proved at this stage.
All the structural results on the SIS reactor are proved. All the results on the thermodynamic limit are proved under the assumption that the limits defining them exist—which we conjecture. This will be referred to as the thermodynamic propagation of chaos ansatz.
We also study the following variants of the SIS reactor:
-
• The departure-on-change-of-state (DOCS) reactor, where the infection rate is the same as above, but where (a) an infection immediately leads to a departure, and (b) a recovery immediately leads to a departure. This problem is simpler in that the associated PDE can be solved.
-
• The averaged-infection-rate (AIR) reactor, where (a) the infection rate of any susceptible is constant (rather than proportional to the actual number of infected), and (b) the recovery mechanism is as in the SIS case. This last model is a product-form Jackson network and admits a simple product-form solution.
In contrast to the plain SIS case, the stationary regimes of these two other open systems admit closed-form expressions. These two open-loop models in turn lead to thermodynamic limits. More precisely, the DOCS reactor leads to the DOCS thermodynamic limit, where customers leave the station as soon as they change their state and are immediately routed to another station chosen at random while keeping their new state. The AIR reactor leads to the AIR thermodynamic limit, which is a closed network (similar to the plain SIS thermodynamic limit) where, in any station, susceptible customers get infected with a rate that is proportional to the mean number of infected customers in all stations. The closed-form solutions alluded to above are used to quantify the phase diagram of the last two thermodynamic limits.
The AIR system is conjectured to provide bounds to the plain SIS system. These bounds are in the following sense. Consider two thermodynamic limits A and A
′ with the same parameters
![]() $\alpha,\beta,\mu$
and with varying
$\alpha,\beta,\mu$
and with varying
![]() $\eta$
. System A will be said to have more infection in mean than system A
′ if the mean number of infected customers is greater in A than in A
′ in steady state. Assume that system A (resp. A
′) admits a critical value
$\eta$
. System A will be said to have more infection in mean than system A
′ if the mean number of infected customers is greater in A than in A
′ in steady state. Assume that system A (resp. A
′) admits a critical value
![]() $\eta_c$
(resp.
$\eta_c$
(resp.
![]() $\eta^{\prime}_c$
) such that if
$\eta^{\prime}_c$
) such that if
![]() $\eta>\eta_c$
(resp.
$\eta>\eta_c$
(resp.
![]() $\eta>\eta^{\prime}_c$
), then there is survival, whereas otherwise there is extinction. System A
′ will be said to be safer than system A if
$\eta>\eta^{\prime}_c$
), then there is survival, whereas otherwise there is extinction. System A
′ will be said to be safer than system A if
![]() $\eta^{\prime}_c\ge \eta_c$
. If A has more infection in mean than A
′, then A
′ is safer than A. The converse is not true in general. It will be proved that, under a certain negative correlation conjecture which is backed by simulation, DOCS is safer than AIR. There is numerical evidence that plain SIS can be safer than DOCS, or vice versa, depending on the parameters.
$\eta^{\prime}_c\ge \eta_c$
. If A has more infection in mean than A
′, then A
′ is safer than A. The converse is not true in general. It will be proved that, under a certain negative correlation conjecture which is backed by simulation, DOCS is safer than AIR. There is numerical evidence that plain SIS can be safer than DOCS, or vice versa, depending on the parameters.
The main probabilistic tools used in the paper are stochastic comparison, coupling, the rate conservation principle (RCP), various classes of Markov processes with both discrete and continuous state spaces, mean-field limits, and branching processes. The PDEs alluded to above are instrumental for finding solutions to the Kolmogorov equations of the generating functions of the discrete-state-space Markov chains in question.
The paper is structured as follows. A summary of the models (single-station models and thermodynamic limit models) is given in Section 2, so as to make navigation between them easier. The open SIS reactor is studied in Section 3. Its stationary generating function satisfies a wave-type PDE for which we have not found a closed-form solution so far. We then establish rate conservation equations which are useful throughout the paper. Section 4 discusses the DOCS open reactor and Section 5 the AIR open reactor. Both models can be solved in closed form. The wave-type PDE of the DOCS reactor has a closed-form solution, whereas the AIR reactor reduces to a product-form queueing network for which an explicit solution is already known. The closed-form expressions provide bounds on the SIS dynamics. Section 6 gathers results on the thermodynamic mean-field limit of the SIS dynamics. The analysis is based on structural properties of the open SIS reactor. The main result is a characterization of the structure of the phase diagram. The same is done in Sections 7 and 8 for the AIR and the DOCS thermodynamic limits, respectively. Section 9 gives a probabilistic interpretation for the phase transition thresholds in terms of branching conditions. Finally, Section 10 gathers additional numerical observations based on discrete event simulation.
The appendix contains the proofs of several central and auxiliary results. The extended arXiv version of the paper [Reference Baccelli, Foss and Shneer2] contains further material and in particular inequalities that would follow from the conjectured property of anti-association (negative correlation) of certain random variables in this SIS dynamics.
We conclude this introduction with a brief overview of the relevant literature. In the absence of mobility, the problem has been extensively studied in the particle system literature [Reference Liggett11], where the model is referred to as the contact process. This literature contains a large corpus of results on the phase diagrams of infinite graphs with finite degrees such as grids and regular trees. The problem has also been studied on finite deterministic graphs, where the main question is that of the separation between logarithmic and exponential growth of the time till extinction with respect to the size of the graph. There is also a series of studies of SIS epidemic models on populations partitioned into households and, in particular, on their correlation structure and time to extinction; see e.g. [Reference Donnelli5] and [Reference Britton and Neal4] and references therein.
The SIS dynamics has also been extensively studied on finite random graphs. For overviews on this class of questions, see e.g. [Reference Pastor-Satorras, Castellano, Van Mieghem and Vespignani14] and [Reference Newman13]. Moment closure techniques [Reference Kuehn10, Reference Krishnarajah, Cook, Marion and Gibson9] provide an important tool in this context. The contact process has also been studied on infinite random graphs with unbounded degrees. The supercritical Bienaymé–Galton–Watson tree was studied in [Reference Pemantle15], where it was shown that some critical values can be degenerate. It has also been extensively studied on Euclidean point processes [Reference Ganesan7, Reference Hao8, Reference Ménard and Singh12].
The analysis of the case with mobility is more recent. The situation where agents perform a random walk on a finite graph and agents meeting at a given point of the graph may infect each other was studied in [Reference Figueiredo, Iacobelli and Shneer6]. The situation where agents form a Poisson point process and migrate in the Euclidean plane was studied in [Reference Baccelli and Ramesan3], which proposed a computational framework based on moment closure techniques for evaluating the role of mobility in the propagation of epidemics.
The queueing model studied here may be seen as a discrete version of the model in [Reference Baccelli and Ramesan3], or as a thermodynamic limit of that of [Reference Figueiredo, Iacobelli and Shneer6].

Figure 1. On the left, the SIS reactor. On the right, the AIR reactor with parameter y.
2. The models
2.1. The open models
All models in this subsection feature an open queueing system with two types of customers. There are two independent Poisson external arrival point processes: that of susceptible customers, with intensity
![]() $\lambda q$
, and that of infected customers, with intensity
$\lambda q$
, and that of infected customers, with intensity
![]() $\lambda p$
, with
$\lambda p$
, with
![]() $q=1-p$
.
$q=1-p$
.
2.1.1. The plain SIS reactor
The SIS reactor features a single M/M/
![]() $\infty$
-type station (that will be referred to as a reactor). Service times of all customers in this queue are exponential with parameter
$\infty$
-type station (that will be referred to as a reactor). Service times of all customers in this queue are exponential with parameter
![]() $\mu$
. While waiting in the reactor, each susceptible customer becomes infected with the instantaneous rate
$\mu$
. While waiting in the reactor, each susceptible customer becomes infected with the instantaneous rate
![]() $\alpha n$
when there are n infected customers, and each infected customer recovers and becomes susceptible with rate
$\alpha n$
when there are n infected customers, and each infected customer recovers and becomes susceptible with rate
![]() $\beta$
. It is because of this interaction that we call the queue a reactor (see the left panel of Figure 1).
$\beta$
. It is because of this interaction that we call the queue a reactor (see the left panel of Figure 1).
Let X (resp. Y) denote the number of susceptible (resp. infected) customers in the steady state of the SIS reactor. By classical arguments, one gets that for all
![]() $0\le x\le 1$
,
$0\le x\le 1$
,
![]() $0\le y\le 1$
, the joint generating function
$0\le y\le 1$
, the joint generating function
![]() $\Phi(x,y)={\mathbb{E}}\big[x^Xy^Y\big]$
satisfies the PDE
$\Phi(x,y)={\mathbb{E}}\big[x^Xy^Y\big]$
satisfies the PDE
The term in
![]() $\Phi_{xy}(x,y)$
, which comes from the infection rate in XY, allows one to link this equation to the one-dimensional wave equation.
$\Phi_{xy}(x,y)$
, which comes from the infection rate in XY, allows one to link this equation to the one-dimensional wave equation.
Remark 1. The one-dimensional wave equation reads
![]() $U_{tt} = c^2 U_{zz},$
with c velocity, t time, and z space. The last PDE leads (after a change of variables) to a relation between second derivatives of the form
$U_{tt} = c^2 U_{zz},$
with c velocity, t time, and z space. The last PDE leads (after a change of variables) to a relation between second derivatives of the form
![]() $\Psi_{xx}= \left(\frac y x\right)^2 \Psi_{yy}$
plus additional lower-order terms—that is, a velocity of
$\Psi_{xx}= \left(\frac y x\right)^2 \Psi_{yy}$
plus additional lower-order terms—that is, a velocity of
![]() $\frac y x$
when interpreting x as time and y as space. In this sense, the wave equation satisfied by the joint generating function involves a velocity that is not determined by the parameters of the dynamics but only by the variables of the joint generating function.
$\frac y x$
when interpreting x as time and y as space. In this sense, the wave equation satisfied by the joint generating function involves a velocity that is not determined by the parameters of the dynamics but only by the variables of the joint generating function.
2.1.2. The AIR reactor
The AIR model features a network of two M/M/
![]() $\infty$
stations. All infected arrivals are routed to the second station (that of the infected). The service rate in this station is
$\infty$
stations. All infected arrivals are routed to the second station (that of the infected). The service rate in this station is
![]() $\nu=\mu+\beta$
. When a customer leaves this station, it leaves the network with probability
$\nu=\mu+\beta$
. When a customer leaves this station, it leaves the network with probability
![]() $\frac{\mu}{\mu +\beta}$
and is routed to the first station otherwise. All susceptible customers are routed to the first station (that of the susceptible). At time t, the service rate in this station is
$\frac{\mu}{\mu +\beta}$
and is routed to the first station otherwise. All susceptible customers are routed to the first station (that of the susceptible). At time t, the service rate in this station is
![]() $\mu + y(t) \alpha$
, where y(t) is a positive deterministic function that can be fixed at will. When a customer leaves this station, it leaves the network with probability
$\mu + y(t) \alpha$
, where y(t) is a positive deterministic function that can be fixed at will. When a customer leaves this station, it leaves the network with probability
![]() $\frac{\mu}{\mu + y(t) \alpha}$
and is routed to the second station with probability
$\frac{\mu}{\mu + y(t) \alpha}$
and is routed to the second station with probability
![]() $\frac{y(t) \alpha}{\mu + y(t) \alpha}$
. This is depicted in the right panel of Figure 1. The main difference from the SIS reactor is that the infection rate of a susceptible is a state-independent deterministic function here. In particular, when y(t) is constant, we will not need the PDE here but will rather use the theory of product-form queueing networks (see Section 5).
$\frac{y(t) \alpha}{\mu + y(t) \alpha}$
. This is depicted in the right panel of Figure 1. The main difference from the SIS reactor is that the infection rate of a susceptible is a state-independent deterministic function here. In particular, when y(t) is constant, we will not need the PDE here but will rather use the theory of product-form queueing networks (see Section 5).
2.1.3. The averaging mean-field limit of the SIS reactor
The averaging mean-field limit of the plain SIS model is defined as the following limit of open networks. Consider a system with K stations. Each station is an M/M/
![]() $\infty$
queue with service rate
$\infty$
queue with service rate
![]() $\mu$
and arrival rate
$\mu$
and arrival rate
![]() $\lambda$
. Each arrival is independently declared infected with probability p and susceptible otherwise. In each station, an infected customer turns susceptible with rate
$\lambda$
. Each arrival is independently declared infected with probability p and susceptible otherwise. In each station, an infected customer turns susceptible with rate
![]() $\beta$
, and a susceptible customer turns infected with rate
$\beta$
, and a susceptible customer turns infected with rate
![]() $\frac \alpha K \sum_{k=1}^K Y_k(t),$
where
$\frac \alpha K \sum_{k=1}^K Y_k(t),$
where
![]() $Y_k(t)$
is the number of infected nodes in station k at time t. So in this model, which is depicted in the left panel of Figure 4, conditionally on the state, the infection rate of a susceptible in a station is proportional to the empirical mean of the number of infected customers in all stations (rather than to the number of infected customers in the same station in the SIS reactor). The averaging mean-field limit of SIS is obtained by letting
$Y_k(t)$
is the number of infected nodes in station k at time t. So in this model, which is depicted in the left panel of Figure 4, conditionally on the state, the infection rate of a susceptible in a station is proportional to the empirical mean of the number of infected customers in all stations (rather than to the number of infected customers in the same station in the SIS reactor). The averaging mean-field limit of SIS is obtained by letting
![]() $K\to \infty$
. The empirical mean in question then converges to a constant, which is also the mean number of infected customers in the typical station. When it exists, this limit features a typical station which is an AIR model with the constraint that
$K\to \infty$
. The empirical mean in question then converges to a constant, which is also the mean number of infected customers in the typical station. When it exists, this limit features a typical station which is an AIR model with the constraint that
![]() $y(.)$
must be such that
$y(.)$
must be such that
![]() $y(t)={\mathbb{E}}_{y(.)}[Y(t)]$
for all t, where
$y(t)={\mathbb{E}}_{y(.)}[Y(t)]$
for all t, where
![]() ${\mathbb{P}}_{y(.)}$
is the distribution at time t of the system with parameter
${\mathbb{P}}_{y(.)}$
is the distribution at time t of the system with parameter
![]() $y(.)$
, and Y(t) is the number of infected customers at time t in the AIR station. The construction of such a system is discussed in Appendix D. A single AIR station where
$y(.)$
, and Y(t) is the number of infected customers at time t in the AIR station. The construction of such a system is discussed in Appendix D. A single AIR station where
![]() $y(.)={\mathbb{E}}_{y(.)}[Y(t)]$
will be referred to as an AIR averaging mean-field (AIR-AMF) reactor.
$y(.)={\mathbb{E}}_{y(.)}[Y(t)]$
will be referred to as an AIR averaging mean-field (AIR-AMF) reactor.
2.1.4. The DOCS reactor
The DOCS model features a single station as in the SIS case. The infection mechanism of the SIS model is replaced by a simultaneous infection and departure mechanism with the following characteristics: if the number of infected is Y(t), each susceptible gets infected with rate
![]() $\alpha Y(t)$
and, upon infection, it immediately leaves the system for good. There is also a ‘natural’ departure rate of susceptible customers, denoted by
$\alpha Y(t)$
and, upon infection, it immediately leaves the system for good. There is also a ‘natural’ departure rate of susceptible customers, denoted by
![]() $\mu$
. The total departure rate of infected customers is hence
$\mu$
. The total departure rate of infected customers is hence
![]() $\nu=\mu+\beta$
, since when an infected customer recovers, it immediately leaves the system. Equivalently, the total departure rate is
$\nu=\mu+\beta$
, since when an infected customer recovers, it immediately leaves the system. Equivalently, the total departure rate is
![]() $\mu+\beta$
, and upon departure, the infected customer keeps its state with probability
$\mu+\beta$
, and upon departure, the infected customer keeps its state with probability
![]() $\mu/(\mu+\beta)$
or swaps to susceptible with the complementary probability. See the left panel of Figure 2.
$\mu/(\mu+\beta)$
or swaps to susceptible with the complementary probability. See the left panel of Figure 2.

Figure 2. On the left, the DOCS reactor. On the right, the prelimit routing DOCS network with two stations.
In fact, if one just needs to determine
![]() ${\mathbb{E}} (X)$
in the DOCS reactor, the state of departing customers does not matter. Therefore, we may (and will) analyze a more general scheme where there are no recoveries but a general departure rate
${\mathbb{E}} (X)$
in the DOCS reactor, the state of departing customers does not matter. Therefore, we may (and will) analyze a more general scheme where there are no recoveries but a general departure rate
![]() $\nu$
of infected customers, and where
$\nu$
of infected customers, and where
![]() $\nu$
and
$\nu$
and
![]() $\mu$
are not linked as above.
$\mu$
are not linked as above.
The associated PDE for the stationary generating function of the general DOCS reactor is
Remark 2. A wave-type equation shows up in the DOCS and the plain SIS systems, whereas it does not in the AIR model. This comes from the nonlinear infection rate of the form
![]() $\alpha XY$
whenever the state is (X, Y). This leads to the
$\alpha XY$
whenever the state is (X, Y). This leads to the
![]() $\frac{\partial}{\partial x}$
and
$\frac{\partial}{\partial x}$
and
![]() $\frac{\partial}{\partial y}$
terms in the corresponding PDEs, which in turn lead to the corresponding wave equations. In contrast, in the AIR system, this nonlinearity is replaced by the linear rate
$\frac{\partial}{\partial y}$
terms in the corresponding PDEs, which in turn lead to the corresponding wave equations. In contrast, in the AIR system, this nonlinearity is replaced by the linear rate
![]() $\alpha X{\mathbb{E}}[Y]$
, with
$\alpha X{\mathbb{E}}[Y]$
, with
![]() ${\mathbb{E}}[Y]$
seen as a parameter determined by a nonlinear relationship, which explains why the wave equation does not show up.
${\mathbb{E}}[Y]$
seen as a parameter determined by a nonlinear relationship, which explains why the wave equation does not show up.
2.2. The routing mean-field limit of the DOCS reactor
The DOCS routing reactor, which will be essential below, is a variant of the DOCS reactor. It is based on a DOCS routing mean-field limit, which should not be confused with the DOCS thermodynamic limit (defined in Subsection 2.3 below). This routing mean-field limit is defined as follows. Consider first a network made of N DOCS reactors, as depicted in the right panel of Figure 2. For this network, the state variables in station
![]() $1\le n \le N$
will be denoted by
$1\le n \le N$
will be denoted by
![]() $\widehat X_n(t)$
and
$\widehat X_n(t)$
and
![]() $\widehat Y_n(t)$
. Each station is a
$\widehat Y_n(t)$
. Each station is a
![]() $\cdot$
/M/
$\cdot$
/M/
![]() $\infty$
station with service rate
$\infty$
station with service rate
![]() $\mu$
and external arrival rate
$\mu$
and external arrival rate
![]() $\lambda$
. There is an external Poisson arrival process to each station, and each external arrival is independently declared infected with probability p and susceptible otherwise. In each station, an infected customer turns susceptible with rate
$\lambda$
. There is an external Poisson arrival process to each station, and each external arrival is independently declared infected with probability p and susceptible otherwise. In each station, an infected customer turns susceptible with rate
![]() $\beta$
. But rather than staying in the station (as in SIS), this newly susceptible customer instantaneously leaves, and rather than leaving for good as in the DOCS open reactor, it joins another station chosen at random and independently among the N stations. Similarly, in station n, a susceptible customer turns infected with rate
$\beta$
. But rather than staying in the station (as in SIS), this newly susceptible customer instantaneously leaves, and rather than leaving for good as in the DOCS open reactor, it joins another station chosen at random and independently among the N stations. Similarly, in station n, a susceptible customer turns infected with rate
![]() $\alpha \widehat Y_n(t)$
at time t. But rather than staying in this station, the newly infected customer instantaneously joins another station chosen at random and independently among the N stations.
$\alpha \widehat Y_n(t)$
at time t. But rather than staying in this station, the newly infected customer instantaneously joins another station chosen at random and independently among the N stations.

Figure 3. On the left, a closed network of three SIS reactors. On the right, the SIS TL.

Figure 4. On the left, a closed network of three AIR reactors. On the right, the AIR TL.
When N tends to infinity, we get the DOCS routing mean-field limit, which is a system with both external arrivals and internal customer routing. Again, the existence of this limit will not be discussed in the present paper. In the steady state of this limit, the overall arrival point process of infected customers in a typical station is Poisson with rate
![]() $\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]$
(sum of external and internal rates), and that of susceptible customers is independent and Poisson with rate
$\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]$
(sum of external and internal rates), and that of susceptible customers is independent and Poisson with rate
![]() $\lambda q +\beta {\mathbb{E}}[\widehat Y]$
(sum of external and internal rates again). Here
$\lambda q +\beta {\mathbb{E}}[\widehat Y]$
(sum of external and internal rates again). Here
![]() $\widehat X$
and
$\widehat X$
and
![]() $\widehat Y$
represent the stationary state variables of a typical station in this limit. Here and in what follows, we use a hat on these variables to distinguish them from those of the DOCS reactor.
$\widehat Y$
represent the stationary state variables of a typical station in this limit. Here and in what follows, we use a hat on these variables to distinguish them from those of the DOCS reactor.
We will use the term routing DOCS reactor to refer to the typical station in question, namely a station which behaves as a DOCS reactor but where, in addition to an external infected (resp. susceptible) Poisson input point process of intensity
![]() $\lambda p(t)$
(resp.
$\lambda p(t)$
(resp.
![]() $\lambda q(t)$
), there is an additional ‘re-routing’ infected (resp. susceptible) Poisson point process of intensity
$\lambda q(t)$
), there is an additional ‘re-routing’ infected (resp. susceptible) Poisson point process of intensity
![]() $\alpha {\mathbb{E}}\big[\widehat X(t)\widehat Y(t)\big]$
(resp.
$\alpha {\mathbb{E}}\big[\widehat X(t)\widehat Y(t)\big]$
(resp.
![]() $\beta {\mathbb{E}}[X(t)]$
).
$\beta {\mathbb{E}}[X(t)]$
).
For all
![]() $0\le x\le 1$
,
$0\le x\le 1$
,
![]() $0\le y\le 1$
, in steady state, the joint generating function
$0\le y\le 1$
, in steady state, the joint generating function
![]() $\widehat\Phi(x,y)={\mathbb{E}}\big[x^{\widehat X}y^{\widehat Y}\big]$
satisfies the PDE
$\widehat\Phi(x,y)={\mathbb{E}}\big[x^{\widehat X}y^{\widehat Y}\big]$
satisfies the PDE
This PDE is an instance of the DOCS PDE in (2) with the following specific parameters:
![]() $\lambda q$
is replaced by
$\lambda q$
is replaced by
![]() $\lambda q+\beta {\mathbb{E}}[\widehat Y]$
,
$\lambda q+\beta {\mathbb{E}}[\widehat Y]$
,
![]() $\lambda p$
by
$\lambda p$
by
![]() $\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]$
, and
$\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]$
, and
![]() $\nu$
is taken equal to
$\nu$
is taken equal to
![]() $\mu + \beta$
.
$\mu + \beta$
.
Here are a few observations on the routing DOCS models. Consider first the prelimit model with N stations. Consider the whole system as a single system. Any customer has an exponential lifetime in the queue with parameter
![]() $\mu$
. During its lifetime, an individual changes state but stays in the system. Since the total arrival rate to the system is
$\mu$
. During its lifetime, an individual changes state but stays in the system. Since the total arrival rate to the system is
![]() $\lambda N$
, the total number of customers in the stationary regime is Poisson with parameter (and mean)
$\lambda N$
, the total number of customers in the stationary regime is Poisson with parameter (and mean)
![]() $\lambda N/\mu$
. Because of the symmetry, the mean number of all customers in any station is hence
$\lambda N/\mu$
. Because of the symmetry, the mean number of all customers in any station is hence
![]() $\lambda/\mu$
. Letting N tend to infinity and noting that uniform integrability holds, we conclude that the mean number of customers stays equal to
$\lambda/\mu$
. Letting N tend to infinity and noting that uniform integrability holds, we conclude that the mean number of customers stays equal to
![]() $\lambda/\mu$
in the infinite system too. For all fixed N, in the stationary regime, the pairs of
$\lambda/\mu$
in the infinite system too. For all fixed N, in the stationary regime, the pairs of
![]() $(\widehat X,\widehat Y)$
vectors at different stations form an exchangeable family of dependent random vectors, with all coordinates summing up to a Poisson random variable.
$(\widehat X,\widehat Y)$
vectors at different stations form an exchangeable family of dependent random vectors, with all coordinates summing up to a Poisson random variable.
2.3. The thermodynamic limits
2.3.1. Definition
The thermodynamic limits pertain to a family of closed networks as illustrated for SIS in the left panel of Figure 3 or for DOCS in the left panel of Figure 5.
They are all infinite-dimensional Markov systems. They can also be seen as certain nonlinear Markov processes (see Appendix D). Consequently, a wide range of asymptotic behaviors are possible for any given initial condition. For instance the dynamics could, e.g., converge to a stationary measure, or be periodic, or admit an attractor.
In this paper, for all cases considered, we assume that the thermodynamic limit exists and satisfies the following properties on any compact of time: (i) stations have independent dynamics; (ii) in each station, the arrival point process of susceptible (resp. infected) customers is (possibly non-homogeneous) Poisson, with these two processes being independent. This set of properties will be referred to as the thermodynamic propagation of chaos ansatz.

Figure 5. On the left, a closed network with two DOCS stations. At a fork, routing decisions are up or down with probability 1/2. On the right, the DOCS TL.
2.3.2. Examples
In all examples below, the prelimit is a closed system of N stations. Each station is again a
![]() $\cdot$
/M/
$\cdot$
/M/
![]() $\infty$
queue with departure rate
$\infty$
queue with departure rate
![]() $\mu$
. There is a total of
$\mu$
. There is a total of
![]() $K_N$
customers, and we assume that
$K_N$
customers, and we assume that
![]() $\lim_{N\to \infty} K_N/N= \lambda/\mu\,:\!=\,\eta$
. Here
$\lim_{N\to \infty} K_N/N= \lambda/\mu\,:\!=\,\eta$
. Here
![]() $\eta$
and
$\eta$
and
![]() $\lambda$
are positive constants representing the mean population per station and the arrival rate in a station, respectively. The routing is independent and uniform at random to all stations.
$\lambda$
are positive constants representing the mean population per station and the arrival rate in a station, respectively. The routing is independent and uniform at random to all stations.
Plain SIS. We will call the SIS thermodynamic limit (SIS TL) the infinite-dimensional system obtained by letting N tend to infinity, assuming
![]() $K_N$
behaves as described above. This limit is illustrated in the right panel of Figure 3.
$K_N$
behaves as described above. This limit is illustrated in the right panel of Figure 3.
AIR. The AIR thermodynamic limit (AIR TL) is best described as the following variant of the closed system of the abstract, which is depicted in the left panel of Figure 4. There are N stations, with state variables
![]() $\widetilde X_n$
and
$\widetilde X_n$
and
![]() $\widetilde Y_n$
. In any station, each susceptible customer swaps to infected with the instantaneous rate
$\widetilde Y_n$
. In any station, each susceptible customer swaps to infected with the instantaneous rate
![]() $\alpha \frac 1 N \sum_{k=1}^N \widetilde Y_k$
if there are
$\alpha \frac 1 N \sum_{k=1}^N \widetilde Y_k$
if there are
![]() $\widetilde Y_k$
infected customers in station k, whereas each infected customer recovers and becomes susceptible with rate
$\widetilde Y_k$
infected customers in station k, whereas each infected customer recovers and becomes susceptible with rate
![]() $\beta$
. Letting
$\beta$
. Letting
![]() $N\to \infty$
, one gets a variant of the SIS TL (again assumed to hold here), where stations are independent. In this limit, which is depicted in the right panel of Figure 4, each station behaves as an AIR AMF reactor (with
$N\to \infty$
, one gets a variant of the SIS TL (again assumed to hold here), where stations are independent. In this limit, which is depicted in the right panel of Figure 4, each station behaves as an AIR AMF reactor (with
![]() $y(t)={\mathbb{E}}[\widetilde Y(t)]$
) with the following constraint on the parameters: the external arrival rate of susceptible customers is equal to
$y(t)={\mathbb{E}}[\widetilde Y(t)]$
) with the following constraint on the parameters: the external arrival rate of susceptible customers is equal to
![]() $\mu {\mathbb{E}}[\widetilde X(t)]$
, and that of infected customers is
$\mu {\mathbb{E}}[\widetilde X(t)]$
, and that of infected customers is
![]() $\mu {\mathbb{E}}[\widetilde Y(t)]$
.
$\mu {\mathbb{E}}[\widetilde Y(t)]$
.
DOCS. The DOCS thermodynamic limit (DOCS TL) features a closed queueing network with N DOCS stations and a total of
![]() $K_N$
customers, as illustrated in the left panel of Figure 5. If station n has
$K_N$
customers, as illustrated in the left panel of Figure 5. If station n has
![]() $X_n$
susceptible and
$X_n$
susceptible and
![]() $Y_n$
infected customers, each susceptible customer swaps to infected with the instantaneous rate
$Y_n$
infected customers, each susceptible customer swaps to infected with the instantaneous rate
![]() $\alpha Y_n$
; upon infection, it simultaneously leaves this station and is routed to one of the N stations chosen at random. Similarly, each infected customer becomes susceptible with rate
$\alpha Y_n$
; upon infection, it simultaneously leaves this station and is routed to one of the N stations chosen at random. Similarly, each infected customer becomes susceptible with rate
![]() $\beta$
; upon recovery, it simultaneously leaves and is routed to a station chosen at random. In addition, as in the closed SIS network model, each customer (infected or susceptible) also leaves the station with a departure rate
$\beta$
; upon recovery, it simultaneously leaves and is routed to a station chosen at random. In addition, as in the closed SIS network model, each customer (infected or susceptible) also leaves the station with a departure rate
![]() $\mu$
and is then also routed to a station chosen at random. We let N tend to infinity and assume that
$\mu$
and is then also routed to a station chosen at random. We let N tend to infinity and assume that
![]() $K_N$
is such that the total input rate to a station tends to
$K_N$
is such that the total input rate to a station tends to
![]() $\lambda$
(or equivalently that the density of customers is
$\lambda$
(or equivalently that the density of customers is
![]() $\eta$
). Then, in the limit when it exists, each station behaves as a routing DOCS reactor as defined in Subsection 2.2, with the additional consistency property that, in the latter, the external infected arrival rate
$\eta$
). Then, in the limit when it exists, each station behaves as a routing DOCS reactor as defined in Subsection 2.2, with the additional consistency property that, in the latter, the external infected arrival rate
![]() $\lambda p^*(t)$
should match the external infected departure rate
$\lambda p^*(t)$
should match the external infected departure rate
![]() $\mu {\mathbb{E}}\big[\widehat Y(t)\big]$
, and similarly,
$\mu {\mathbb{E}}\big[\widehat Y(t)\big]$
, and similarly,
![]() $\lambda q^*(t)$
should be equal to
$\lambda q^*(t)$
should be equal to
![]() $\mu {\mathbb{E}}\big[\widehat X(t)\big]$
. This fixed point, which characterizes the stationary distribution of the DOCS TL, is illustrated on the right in Figure 5.
$\mu {\mathbb{E}}\big[\widehat X(t)\big]$
. This fixed point, which characterizes the stationary distribution of the DOCS TL, is illustrated on the right in Figure 5.
2.3.3. Survival versus extinction
Below, for all thermodynamic limits, we assume that propagation of chaos holds. We will show that under this assumption, the dynamics of the infinite-dimensional Markov systems in question can be reduced to that of a finite-dimensional nonlinear Markov process.
Definition 1. In any thermodynamic limit, we will say that there is survival if the associated Markov system has a steady-state distribution with a fraction
![]() $0<p<1$
of susceptible customers. We will say that there is weak extinction if there exists no such p. We will say that there is strong extinction if, for all initial conditions, the associated Markov system converges to a regime without infected customers.
$0<p<1$
of susceptible customers. We will say that there is weak extinction if there exists no such p. We will say that there is strong extinction if, for all initial conditions, the associated Markov system converges to a regime without infected customers.
Remark 3. Weak extinction does not mean that the epidemic vanishes in the infinite-dimensional system as time tends to infinity. It only means that there is no initial condition for the associated infinite-dimensional Markov system to converge to a limiting regime with a positive fraction of infected customers.
Remark 4. As in many other models, survival in the thermodynamic limit should translate to the fact that the time to extinction in the prelimit at
![]() $N<\infty$
grows exponentially in N, where N is as defined in the abstract.
$N<\infty$
grows exponentially in N, where N is as defined in the abstract.
3. SIS reactor analysis
3.1. Preliminary observations
It is easy to check from the PDE (1) that
![]() $\Phi(z,z)= e^{-\frac \lambda \mu (1-z)}.$
A direct probabilistic argument also gives that
$\Phi(z,z)= e^{-\frac \lambda \mu (1-z)}.$
A direct probabilistic argument also gives that
![]() $X+Y\sim Pois (\lambda/\mu)$
.
$X+Y\sim Pois (\lambda/\mu)$
.
We were not able to solve this PDE. This is why we resort to other techniques based on the RCP [Reference Baccelli and Brémaud1]. A variety of conservation equations will be discussed. These are of independent interest and will also be used in what follows.
3.2. First-order relations
The simplest first-order relation states that the rate of arrivals,
![]() $\lambda$
, should match the rate of departures, namely
$\lambda$
, should match the rate of departures, namely
![]() $\mu {\mathbb{E}}[X+Y]$
. Note that there is no reason for the rate of arrivals of infected customers,
$\mu {\mathbb{E}}[X+Y]$
. Note that there is no reason for the rate of arrivals of infected customers,
![]() $\lambda p$
, to match that of departures of infected customers, namely
$\lambda p$
, to match that of departures of infected customers, namely
![]() $\mu {\mathbb{E}}[Y]$
. This also holds for susceptible customers.
$\mu {\mathbb{E}}[Y]$
. This also holds for susceptible customers.
Lemma 1. The following relation holds:
Proof. We get this relation by differentiating the PDE (1) with respect to y and taking
![]() $x=y=1$
.
$x=y=1$
.
This has a simple RCP interpretation. We recognize in the left-hand side of (4) the increase rate of the mean number of infected customers in steady state (due to arrivals and infections), whereas the right-hand side is the mean decrease rate of the same quantity due to recoveries and departures from the reactor.
Also note that by differentiating the PDE (1) with respect to x and taking
![]() $x=y=1$
, we get
$x=y=1$
, we get
This equation is actually the same as that in the lemma (using the fact that
![]() ${\mathbb{E}}[X]+{\mathbb{E}}[Y]=\frac \lambda \mu$
).
${\mathbb{E}}[X]+{\mathbb{E}}[Y]=\frac \lambda \mu$
).
3.3. Second-order relations
Lemma 2. The following relations hold:
and
Proof. The first relation is obtained by differentiating the PDE (1) with respect to y twice and taking
![]() $x=y=1$
, the second by differentiating the PDE with respect to x twice and taking
$x=y=1$
, the second by differentiating the PDE with respect to x twice and taking
![]() $x=y=1$
.
$x=y=1$
.
3.4. Higher-order relations
Lemma 3.
For all non-negative integers m and n, the RCP relation for
![]() $X^mY^n$
reads
$X^mY^n$
reads
 \begin{eqnarray}& & \hspace{-1cm}\lambda p {\mathbb{E}}[X^m\left((Y+1)^n-Y^n\right)] +\lambda q {\mathbb{E}}[\!\left((X+1)^m-X^m\right)Y^n]\nonumber \\& +\, &\beta {\mathbb{E}}[Y\left((X+1)^m(Y-1)^n-X^mY^n\right)] +\alpha {\mathbb{E}}[XY\left((X-1)^m(Y+1)^n-X^mY^n\right)]\nonumber \\& +\, &\mu {\mathbb{E}}[X\left((X-1)^m-X^m\right)Y^n ]+\mu {\mathbb{E}}[YX^m\left((Y-1)^n-Y^n\right)]=0.\end{eqnarray}
\begin{eqnarray}& & \hspace{-1cm}\lambda p {\mathbb{E}}[X^m\left((Y+1)^n-Y^n\right)] +\lambda q {\mathbb{E}}[\!\left((X+1)^m-X^m\right)Y^n]\nonumber \\& +\, &\beta {\mathbb{E}}[Y\left((X+1)^m(Y-1)^n-X^mY^n\right)] +\alpha {\mathbb{E}}[XY\left((X-1)^m(Y+1)^n-X^mY^n\right)]\nonumber \\& +\, &\mu {\mathbb{E}}[X\left((X-1)^m-X^m\right)Y^n ]+\mu {\mathbb{E}}[YX^m\left((Y-1)^n-Y^n\right)]=0.\end{eqnarray}
The proof is based on Equations (54), (55), and (56) in Appendix A.
4. DOCS reactor analysis
4.1. Preliminary observations
We start with a few observations on this system:
-
• By either a simple probabilistic argument or a direct analytical derivation based on the PDE, we get that
 $\Phi(1,y)=e^{-\theta(1-y)}$
; that is, Y is Poisson with mean
$\Phi(1,y)=e^{-\theta(1-y)}$
; that is, Y is Poisson with mean
 $\theta=\frac{\lambda p}{\nu}$
(the Y process is that of an autonomous M/M/
$\theta=\frac{\lambda p}{\nu}$
(the Y process is that of an autonomous M/M/
 $\infty$
queue with input rate
$\infty$
queue with input rate
 $\lambda$
and service rate
$\lambda$
and service rate
 $\nu$
).
$\nu$
). -
• Here, the random variable
 $X+Y$
has no reason to be Poisson.
$X+Y$
has no reason to be Poisson. -
• The stationary output rate of infected customers,
 $\nu {\mathbb{E}}[Y]$
, should match the input rate of infected customers (
$\nu {\mathbb{E}}[Y]$
, should match the input rate of infected customers (
 $\lambda p$
). This is because the infected customers evolve as those of an M/M/
$\lambda p$
). This is because the infected customers evolve as those of an M/M/
 $\infty$
queue.
$\infty$
queue. -
• The stationary depletion rate of susceptible customers,
 $\mu {\mathbb{E}}[X]+ \alpha {\mathbb{E}}[XY]$
, should match the increase rate of susceptible customers (
$\mu {\mathbb{E}}[X]+ \alpha {\mathbb{E}}[XY]$
, should match the increase rate of susceptible customers (
 $\lambda q$
). This is because the susceptible customers evolve as in a stationary queue.
$\lambda q$
). This is because the susceptible customers evolve as in a stationary queue.
We summarize the last two observations in the following conservation equations:
4.2. Analytical solution
By differentiating Equation (2) with respect to x and taking
![]() $x=1$
, we get
$x=1$
, we get
or equivalently, the function
![]() $\Psi(y)\,:\!=\, \Phi_x(1,y)$
satisfies the ordinary differential equation (ODE)
$\Psi(y)\,:\!=\, \Phi_x(1,y)$
satisfies the ordinary differential equation (ODE)
This can be rewritten as the first-order ODE
with
Notice that the coefficients of this first-order ODE have a singularity at
One can nevertheless work out the solution of this ODE for y in a neighborhood of 1 not including
![]() $y^*$
. The homogeneous equation has for a solution
$y^*$
. The homogeneous equation has for a solution
Hence, when looking for a solution of the form
![]() $\Psi(y)=T(y) a(y)$
, we get that
$\Psi(y)=T(y) a(y)$
, we get that
Hence
An expansion shows that for u in a right neighborhood of
![]() $y^*$
,
$y^*$
,
![]() $e^{-\int_1^u h(z) dz}\sim K (u-y^*)^{b}$
with K a constant and
$e^{-\int_1^u h(z) dz}\sim K (u-y^*)^{b}$
with K a constant and
Hence the integral
is well defined and finite despite the singularity of g at
![]() $y^*$
. This integral must match
$y^*$
. This integral must match
![]() $\Psi(1)$
. Indeed, if this were not the case, the function
$\Psi(1)$
. Indeed, if this were not the case, the function
![]() $\Psi$
would have a singularity at
$\Psi$
would have a singularity at
![]() $y^*$
, which is not possible. Hence
$y^*$
, which is not possible. Hence
that is,
Using the fact that
with
![]() $y^*=\frac \nu{\nu +\alpha}$
, we get that
$y^*=\frac \nu{\nu +\alpha}$
, we get that
That is,
 \begin{eqnarray}{\mathbb{E}}[X] & \,=\, & \frac {\lambda q} { (\nu+\alpha)\left(\frac{\alpha}{\nu+\alpha}\right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}} }\times \nonumber \\ & &\int_{\frac{\nu }{\nu+\alpha}}^1e^{-\frac{\lambda p \alpha}{\nu(\nu +\alpha)} (1-u)}\left( u-\frac \nu {\nu+\alpha} \right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}-1}du .\end{eqnarray}
\begin{eqnarray}{\mathbb{E}}[X] & \,=\, & \frac {\lambda q} { (\nu+\alpha)\left(\frac{\alpha}{\nu+\alpha}\right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}} }\times \nonumber \\ & &\int_{\frac{\nu }{\nu+\alpha}}^1e^{-\frac{\lambda p \alpha}{\nu(\nu +\alpha)} (1-u)}\left( u-\frac \nu {\nu+\alpha} \right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}-1}du .\end{eqnarray}
Applying the change of variables
![]() $u= t \frac{\alpha}{\nu +\alpha} + \frac{\nu}{\nu +\alpha}$
, we get
$u= t \frac{\alpha}{\nu +\alpha} + \frac{\nu}{\nu +\alpha}$
, we get
4.3. Analysis of the routing DOCS reactor
Compared to the SIS reactor, the routing DOCS reactor (defined in Subsection 2.2) features much faster migration. This is because the natural departures (those happening with rate
![]() $\mu$
regardless of the state) are complemented by departures that are caused by a change of state. Because of the nature of the mean-field model, this goes with an increased arrival rate of both infected and susceptible customers, in that ‘external’ arrivals (those happening with rate
$\mu$
regardless of the state) are complemented by departures that are caused by a change of state. Because of the nature of the mean-field model, this goes with an increased arrival rate of both infected and susceptible customers, in that ‘external’ arrivals (those happening with rate
![]() $\lambda p(t)$
for infected and rate
$\lambda p(t)$
for infected and rate
![]() $\lambda q(t)$
for susceptible customers) are complemented by ‘internal’ arrivals (with respective rates
$\lambda q(t)$
for susceptible customers) are complemented by ‘internal’ arrivals (with respective rates
![]() $\alpha {\mathbb{E}}\big[\widehat X(t)\widehat Y(t)\big]$
for infected and
$\alpha {\mathbb{E}}\big[\widehat X(t)\widehat Y(t)\big]$
for infected and
![]() $\beta {\mathbb{E}}\big[\widehat Y(t)\big]$
for susceptible customers). As we shall see (Lemma 4 below), this accelerated migration (in and out) preserves the mean queue size in steady state when it exists.
$\beta {\mathbb{E}}\big[\widehat Y(t)\big]$
for susceptible customers). As we shall see (Lemma 4 below), this accelerated migration (in and out) preserves the mean queue size in steady state when it exists.
4.3.1. Stationary regime of the routing DOCS reactor
An important question is whether there exists a stationary regime for this reactor. A necessary condition is that there exists a probabilistic solution to the PDE (2) satisfying the above consistency equations. If this is the case, it follows from the observations preceding the remark of Subsection 2.2 and the results of Subsection 4.1 that
![]() $\widehat Y$
is Poisson with parameter
$\widehat Y$
is Poisson with parameter
The random variable
![]() $\widehat X+\widehat Y$
has no reason to be Poisson and the two terms of the sum have no reason to be independent. In fact we will see later on that they are neither Poisson nor independent.
$\widehat X+\widehat Y$
has no reason to be Poisson and the two terms of the sum have no reason to be independent. In fact we will see later on that they are neither Poisson nor independent.
4.3.2. First-order rate conservation
Assuming that the routing DOCS reactor has a stationary regime, one can apply the rate conservation equations to this system. The first-order RCP, which says that the input and output rates coincide, reads
for susceptible customers and
for infected ones. Note that these match the first-order relations of the SIS reactor.
Lemma 4. In the stationary regime of the DOCS routing mean-field model, one also has
Proof. The result is obtained by adding up the last two equations.
The fact that the mean total population is the same as in the SIS model is remarkable, as here, and in contrast to the SIS reactor,
![]() $\widehat X +\widehat Y$
is not Poisson.
$\widehat X +\widehat Y$
is not Poisson.
4.3.3. Higher-order rate conservation
The setting is that of the last subsection. The RCP for
![]() $\widehat Y(\widehat Y-1)$
reads
$\widehat Y(\widehat Y-1)$
reads
Note that it is similar to (6), except that
![]() ${\mathbb{E}}[XY^2]$
is replaced by
${\mathbb{E}}[XY^2]$
is replaced by
![]() ${\mathbb{E}}[\widehat X\widehat Y] {\mathbb{E}}[\widehat Y]$
. Similarly, the RCP for
${\mathbb{E}}[\widehat X\widehat Y] {\mathbb{E}}[\widehat Y]$
. Similarly, the RCP for
![]() $\widehat X(\widehat X-1)$
reads
$\widehat X(\widehat X-1)$
reads
which is similar to (7), except that
![]() $\beta {\mathbb{E}}[XY]$
is replaced by
$\beta {\mathbb{E}}[XY]$
is replaced by
![]() $\beta {\mathbb{E}}[\widehat X] {\mathbb{E}}[\widehat Y]$
. Finally, the RCP for
$\beta {\mathbb{E}}[\widehat X] {\mathbb{E}}[\widehat Y]$
. Finally, the RCP for
![]() $\widehat X \widehat Y$
reads
$\widehat X \widehat Y$
reads
Note that the complexity of the last two equations remains similar to that of the corresponding equations in the initial system.
5. AIR reactor analysis
5.1. The reactor
Thanks to the linearity of the rates, the AIR queueing network defined in Section 2 has a product-form distribution in steady state which is the product of two Poisson distributions, with parameter
![]() $\frac {\lambda_1}{\mu}$
in station 1 and
$\frac {\lambda_1}{\mu}$
in station 1 and
![]() $\frac {\lambda_2}{\mu}$
in station 2. Direct computations based on the traffic equations
$\frac {\lambda_2}{\mu}$
in station 2. Direct computations based on the traffic equations
give that
We also have
![]() $x=\frac {\lambda_1}{\mu+\alpha y}=\frac \lambda \mu -y$
, with x the mean queue size in station 1.
$x=\frac {\lambda_1}{\mu+\alpha y}=\frac \lambda \mu -y$
, with x the mean queue size in station 1.
5.2. The averaging mean-field case
Consider the averaging mean-field limit when it exists. Denote by
![]() $\widetilde X$
the stationary number of susceptible customers in the typical station and by
$\widetilde X$
the stationary number of susceptible customers in the typical station and by
![]() $\widetilde Y$
the stationary number of infected ones in this system. By arguments similar to those in Subsection 3.2, these state variables satisfy the relations
$\widetilde Y$
the stationary number of infected ones in this system. By arguments similar to those in Subsection 3.2, these state variables satisfy the relations
where the independence comes from the fact that in the limit, the infection rate is constant and equal to
![]() $\alpha y=\alpha {\mathbb{E}}[\widetilde Y]$
. Using this and the fact that
$\alpha y=\alpha {\mathbb{E}}[\widetilde Y]$
. Using this and the fact that
![]() ${\mathbb{E}}[\widetilde X]=\frac \lambda \mu -y$
, one gets
${\mathbb{E}}[\widetilde X]=\frac \lambda \mu -y$
, one gets
Thus, in the averaging mean-field version of the SIS reactor,
 \begin{equation} {\mathbb{E}}[\widetilde X] = \frac{\mu +\beta+\alpha \frac \lambda \mu-\sqrt{(\mu +\beta+\alpha \frac \lambda \mu )^2 -4\alpha\lambda \left(q+\frac \beta \mu \right)}}{2\alpha}\end{equation}
\begin{equation} {\mathbb{E}}[\widetilde X] = \frac{\mu +\beta+\alpha \frac \lambda \mu-\sqrt{(\mu +\beta+\alpha \frac \lambda \mu )^2 -4\alpha\lambda \left(q+\frac \beta \mu \right)}}{2\alpha}\end{equation}
and
 \begin{equation} {\mathbb{E}}[\widetilde Y] = \frac \lambda \mu -\frac{\mu +\beta+\alpha \frac \lambda \mu-\sqrt{(\mu +\beta+\alpha \frac \lambda \mu )^2 -4\alpha\lambda \left(q+\frac \beta \mu \right)}}{2\alpha}.\end{equation}
\begin{equation} {\mathbb{E}}[\widetilde Y] = \frac \lambda \mu -\frac{\mu +\beta+\alpha \frac \lambda \mu-\sqrt{(\mu +\beta+\alpha \frac \lambda \mu )^2 -4\alpha\lambda \left(q+\frac \beta \mu \right)}}{2\alpha}.\end{equation}
6. SIS TL analysis
The natural parameters of the SIS TL are
![]() $(\eta,\mu,\alpha,\beta)$
with
$(\eta,\mu,\alpha,\beta)$
with
![]() $\eta$
the density parameter (that is, the mean number of customers per station, whatever their state),
$\eta$
the density parameter (that is, the mean number of customers per station, whatever their state),
![]() $\mu$
the motion rate,
$\mu$
the motion rate,
![]() $\alpha$
the infection rate, and
$\alpha$
the infection rate, and
![]() $\beta$
the recovery rate. Note that the arrival rate in a station (whatever the state) is then
$\beta$
the recovery rate. Note that the arrival rate in a station (whatever the state) is then
![]() $\lambda=\eta \mu$
. Another natural parameterization is hence
$\lambda=\eta \mu$
. Another natural parameterization is hence
![]() $(\lambda,\mu,\alpha,\beta)$
.
$(\lambda,\mu,\alpha,\beta)$
.
6.1. Fixed-point equations for the SIS reactor
If this thermodynamic model admits a stationary regime, then there exists, in the open-loop SIS reactor with parameters
![]() $\eta,\mu,\alpha,\beta$
, a value of p, say
$\eta,\mu,\alpha,\beta$
, a value of p, say
![]() $p^*$
, such that, for this value of p, the external arrival rate
$p^*$
, such that, for this value of p, the external arrival rate
![]() $\lambda p$
of infected customers matches the external departure rate of infected customers, namely
$\lambda p$
of infected customers matches the external departure rate of infected customers, namely
![]() $\lambda p^*=\mu {\mathbb{E}}[Y]$
(or equivalently
$\lambda p^*=\mu {\mathbb{E}}[Y]$
(or equivalently
![]() $g(p^*)=p^*$
). Similarly, we should also have
$g(p^*)=p^*$
). Similarly, we should also have
![]() $\lambda q^*= \mu {\mathbb{E}}[X]$
.
$\lambda q^*= \mu {\mathbb{E}}[X]$
.
Note that since the total arrival rate of infected customers,
![]() $\lambda p^* +\alpha {\mathbb{E}}[XY]$
, necessarily matches the total departure rate of infected customers,
$\lambda p^* +\alpha {\mathbb{E}}[XY]$
, necessarily matches the total departure rate of infected customers,
![]() $(\mu+\beta) {\mathbb{E}}[Y]$
, the fact that
$(\mu+\beta) {\mathbb{E}}[Y]$
, the fact that
![]() $\lambda p^*=\mu {\mathbb{E}}[Y]$
is equivalent to the fact that
$\lambda p^*=\mu {\mathbb{E}}[Y]$
is equivalent to the fact that
![]() $\alpha {\mathbb{E}}[XY] = \beta {\mathbb{E}}[Y]$
.
$\alpha {\mathbb{E}}[XY] = \beta {\mathbb{E}}[Y]$
.
6.1.1. Arrival versus departure rate of infected customers
Let
![]() $p_o$
denote the proportion of infected customers in the departure process of the SIS reactor in steady state, namely
$p_o$
denote the proportion of infected customers in the departure process of the SIS reactor in steady state, namely
![]() $ p_o= {\mathbb{E}}[Y] \frac \mu \lambda.$
Here is another representation of
$ p_o= {\mathbb{E}}[Y] \frac \mu \lambda.$
Here is another representation of
![]() $p_0$
obtained by considering departures within the first busy cycle of an M/M/
$p_0$
obtained by considering departures within the first busy cycle of an M/M/
![]() $\infty$
queue (i.e., the cycle starting when the queue moves from empty to busy and ending at the next event of this type). By the strong law of large numbers,
$\infty$
queue (i.e., the cycle starting when the queue moves from empty to busy and ending at the next event of this type). By the strong law of large numbers,
![]() $p_o$
may be represented as
$p_o$
may be represented as
![]() $p_o = \frac{{\mathbb{E}} D_I(T)}{{\mathbb{E}} D(T)}$
, where T is the duration of a typical busy cycle, D(T) the number of customers served within the cycle, and
$p_o = \frac{{\mathbb{E}} D_I(T)}{{\mathbb{E}} D(T)}$
, where T is the duration of a typical busy cycle, D(T) the number of customers served within the cycle, and
![]() $D_I(T)$
the number of customers departed from the system in the infected state within the cycle.
$D_I(T)$
the number of customers departed from the system in the infected state within the cycle.
Let us fix strictly positive parameters
![]() $\mu,\alpha$
, and
$\mu,\alpha$
, and
![]() $\beta$
and consider
$\beta$
and consider
![]() $p_o$
as a function of p and
$p_o$
as a function of p and
![]() $\eta$
only, say
$\eta$
only, say
![]() $p_o=g(p,\eta)$
. If
$p_o=g(p,\eta)$
. If
![]() $\eta$
is fixed too, then we write g(p) instead of
$\eta$
is fixed too, then we write g(p) instead of
![]() $g(p,\eta)$
. Clearly,
$g(p,\eta)$
. Clearly,
![]() $g(0)=0$
and
$g(0)=0$
and
![]() $g(1)<1$
.
$g(1)<1$
.
The next lemmas are proved in Appendix B.
Lemma 5.
The function g is an increasing, strictly concave, and differentiable function on
![]() $[0, 1]$
.
$[0, 1]$
.
Lemma 6.
Depending on the parameters
![]() $\eta$
,
$\eta$
,
![]() $\mu$
,
$\mu$
,
![]() $\alpha$
, and
$\alpha$
, and
![]() $\beta$
, either there is only one solution
$\beta$
, either there is only one solution
![]() $p=0$
to the equation
$p=0$
to the equation
or there are exactly two solutions,
![]() $p=0$
and
$p=0$
and
![]() $p^*\equiv p^*(\eta,\mu,\alpha,\beta)\in (0, 1)$
. Let g′(0) denote the right derivative of the function g(p) at 0, which exists by the previous lemma. Then
$p^*\equiv p^*(\eta,\mu,\alpha,\beta)\in (0, 1)$
. Let g′(0) denote the right derivative of the function g(p) at 0, which exists by the previous lemma. Then
![]() $p^*$
exists if and only if
$p^*$
exists if and only if
![]() $g^{\prime}(0)>1$
.
$g^{\prime}(0)>1$
.
6.1.2. Main results on fixed point
In this subsection, we consider
![]() $p_o$
as a function of the two parameters p and
$p_o$
as a function of the two parameters p and
![]() $\eta$
, i.e.
$\eta$
, i.e.
![]() $p_o= g(p,\eta)$
. The proof of the following lemma is given in Appendix B.
$p_o= g(p,\eta)$
. The proof of the following lemma is given in Appendix B.
Lemma 7.
The function
![]() $\eta \to g^{\prime}(0,\eta)$
is strictly increasing.
$\eta \to g^{\prime}(0,\eta)$
is strictly increasing.
Corollary 1. There exists a function
![]() $\eta_c^{(s)}(\alpha,\beta,\mu)=\eta_c(\alpha,\beta,\mu) \in [0,\infty)\cup \{\infty\}$
such that
$\eta_c^{(s)}(\alpha,\beta,\mu)=\eta_c(\alpha,\beta,\mu) \in [0,\infty)\cup \{\infty\}$
such that
Proof. These results follow directly from the previous lemmas.
6.2. Bounds
In this subsection, we provide sufficient conditions for the existence and the non-existence of solutions
![]() $p^*>0$
to the equation
$p^*>0$
to the equation
![]() $p_o(p)=p$
. We also show that
$p_o(p)=p$
. We also show that
![]() $\eta_c^{(s)}$
is finite and strictly positive.
$\eta_c^{(s)}$
is finite and strictly positive.
Lemma 8.
Fix the set of parameters
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
, and
$\beta$
, and
![]() $\mu$
. For
$\mu$
. For
![]() $\eta$
(or equivalently
$\eta$
(or equivalently
![]() $\lambda$
) large enough, there exists
$\lambda$
) large enough, there exists
![]() $p_1 > 0$
such that if
$p_1 > 0$
such that if
![]() $0<p < p_1$
, then the fraction of infected customers of the output is larger than that of the input, namely
$0<p < p_1$
, then the fraction of infected customers of the output is larger than that of the input, namely
![]() $p_{o} > p$
.
$p_{o} > p$
.
Proof. An infected individual is guaranteed to leave infected if it departs before it recovers. The probability of this is
![]() $\mu/(\mu+\beta)$
. A susceptible individual (referred to as the target individual in what follows in this paragraph) is guaranteed to leave infected if (a) an infected individual (referred to as such in what follows in this paragraph) arrives before the target susceptible individual departs (the probability of this is
$\mu/(\mu+\beta)$
. A susceptible individual (referred to as the target individual in what follows in this paragraph) is guaranteed to leave infected if (a) an infected individual (referred to as such in what follows in this paragraph) arrives before the target susceptible individual departs (the probability of this is
![]() $\lambda p/(\lambda p + \mu)$
); then (b) the infected individual infects the target individual before the departure of either of them and before the recovery of the infected one (the probability of this is
$\lambda p/(\lambda p + \mu)$
); then (b) the infected individual infects the target individual before the departure of either of them and before the recovery of the infected one (the probability of this is
![]() $\alpha/(\alpha+2\mu+\beta)$
); and then either (c) the target individual departs before its own recovery (the probability of this is
$\alpha/(\alpha+2\mu+\beta)$
); and then either (c) the target individual departs before its own recovery (the probability of this is
![]() $\mu/(\mu+\beta)$
), or (c′) the target individual recovers before the departure of either one and before the recovery of the infected one (the probability of this is
$\mu/(\mu+\beta)$
), or (c′) the target individual recovers before the departure of either one and before the recovery of the infected one (the probability of this is
![]() $\beta/(2\mu+2\beta)$
) but gets infected by the infected one again, and so on. Thus,
$\beta/(2\mu+2\beta)$
) but gets infected by the infected one again, and so on. Thus,
where
Note that
![]() $p_o>p$
follows if the right-hand side of (29) is strictly bigger than p, which is equivalent to
$p_o>p$
follows if the right-hand side of (29) is strictly bigger than p, which is equivalent to
![]() $\frac{\mu}{\mu+\beta} + (1-p) \cdot \frac{\lambda \kappa}{\lambda p+\mu} >1$
, or to
$\frac{\mu}{\mu+\beta} + (1-p) \cdot \frac{\lambda \kappa}{\lambda p+\mu} >1$
, or to
![]() $(1-p)\frac{\lambda \kappa}{\lambda p+\mu} > \frac{\beta}{\mu+\beta}.$
$(1-p)\frac{\lambda \kappa}{\lambda p+\mu} > \frac{\beta}{\mu+\beta}.$
Assume that, for some
![]() $C>1$
,
$C>1$
,
then
![]() $p_o > p$
for
$p_o > p$
for
![]() $ p < p_1 \equiv \frac{C-1}{\lambda/\mu +C}, $
so that there exists a
$ p < p_1 \equiv \frac{C-1}{\lambda/\mu +C}, $
so that there exists a
![]() $p^*>0$
solving
$p^*>0$
solving
![]() $p_o(p)=p$
.
$p_o(p)=p$
.
Corollary 2.
It follows from Lemma 8 that for all
![]() $\alpha,\beta,\mu$
, the value of
$\alpha,\beta,\mu$
, the value of
![]() $\eta_c^{(s)}$
in Corollary 1 is finite, and more precisely
$\eta_c^{(s)}$
in Corollary 1 is finite, and more precisely
with
![]() $\kappa$
defined in (30).
$\kappa$
defined in (30).
Here is another observation.
Lemma 9.
Fix the set of parameters
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
, and
$\beta$
, and
![]() $\mu$
. For
$\mu$
. For
![]() $\eta$
(or equivalently
$\eta$
(or equivalently
![]() $\lambda$
) small enough,
$\lambda$
) small enough,
![]() $p_{o} < p$
for all p.
$p_{o} < p$
for all p.
Proof. An individual is guaranteed to leave the system as susceptible in one of two scenarios. In the first scenario, it arrives as susceptible, finds no infected individuals in the system upon its arrival, and leaves before the arrival of an infected individual. The probability of this is
![]() $ (1-p) {\mathbb{P}}(Y=0) \frac{\mu}{\mu+\lambda p}$
, which can be bounded from below by
$ (1-p) {\mathbb{P}}(Y=0) \frac{\mu}{\mu+\lambda p}$
, which can be bounded from below by
 \begin{align*}& (1-p)(1-{\mathbb{E}}(Y)) \left(1-\frac{\lambda p}{\mu+\lambda p}\right) = (1-p)\left(1-p_{o} \frac{\lambda}{\mu}\right)\left(1-p\frac{\lambda}{\mu}\right)\\ & \ge \left(1-p\left(1+\frac{\lambda}{\mu}\right)\right)\left(1-p_{o} \frac{\lambda}{\mu}\right) \ge 1-p\left(1+\frac{\lambda}{\mu}\right) -p_{o} \frac{\lambda}{\mu}.\end{align*}
\begin{align*}& (1-p)(1-{\mathbb{E}}(Y)) \left(1-\frac{\lambda p}{\mu+\lambda p}\right) = (1-p)\left(1-p_{o} \frac{\lambda}{\mu}\right)\left(1-p\frac{\lambda}{\mu}\right)\\ & \ge \left(1-p\left(1+\frac{\lambda}{\mu}\right)\right)\left(1-p_{o} \frac{\lambda}{\mu}\right) \ge 1-p\left(1+\frac{\lambda}{\mu}\right) -p_{o} \frac{\lambda}{\mu}.\end{align*}
Finally, for a fixed
![]() $\mu$
and a small
$\mu$
and a small
![]() $\varepsilon>0$
, one can take
$\varepsilon>0$
, one can take
![]() $\lambda \le \varepsilon \mu$
so that the above is bounded from below by
$\lambda \le \varepsilon \mu$
so that the above is bounded from below by
![]() $ 1-p(1+\varepsilon) - \varepsilon p_{o}.$
$ 1-p(1+\varepsilon) - \varepsilon p_{o}.$
In the second scenario, an individual arrives infected, finds no other individual in the system, recovers before any other individual arrives and then leaves before any infected individual arrives. The probability of this is
With the choice of small
![]() $\lambda$
already made, the above is bounded from below by
$\lambda$
already made, the above is bounded from below by
where
![]() $c = \beta/(\beta+\mu)$
. Combining the two scenarios, we conclude
$c = \beta/(\beta+\mu)$
. Combining the two scenarios, we conclude
or equivalently
as long as
![]() $\varepsilon < c/(2+3c)$
.
$\varepsilon < c/(2+3c)$
.
From the proof of Lemma 9, one gets the following bound.
Corollary 3.
For all
![]() $\alpha,\beta,\mu$
, the value of
$\alpha,\beta,\mu$
, the value of
![]() $\eta_c^{(s)}$
in Corollary 1 is strictly positive, and more precisely
$\eta_c^{(s)}$
in Corollary 1 is strictly positive, and more precisely
Remark 5. Note that the last lower bound does not depend on
![]() $\alpha$
. This may look surprising at first glance. The fact that this bound holds even for
$\alpha$
. This may look surprising at first glance. The fact that this bound holds even for
![]() $\alpha =\infty$
can be explained as follows. For any fixed
$\alpha =\infty$
can be explained as follows. For any fixed
![]() $\eta >0$
, in the M/M/
$\eta >0$
, in the M/M/
![]() $\infty$
queue, there are busy cycles with only one customer. The smaller
$\infty$
queue, there are busy cycles with only one customer. The smaller
![]() $\eta$
is, the closer to 1 is the probability
$\eta$
is, the closer to 1 is the probability
![]() $\mu/(\lambda+\mu)$
that a typical busy cycle will have only one customer to be served. Call such a cycle a 1-cycle. If a customer enters the queue as infected and if it is served in a 1-cycle, it has a chance close to
$\mu/(\lambda+\mu)$
that a typical busy cycle will have only one customer to be served. Call such a cycle a 1-cycle. If a customer enters the queue as infected and if it is served in a 1-cycle, it has a chance close to
![]() $\beta/(\beta+\mu)$
of recovering before leaving the queue; and if it susceptible, it leaves the queue susceptible after service in a 1-cycle queue. So
$\beta/(\beta+\mu)$
of recovering before leaving the queue; and if it susceptible, it leaves the queue susceptible after service in a 1-cycle queue. So
![]() $p_0>p$
uniformly in all values of
$p_0>p$
uniformly in all values of
![]() $\alpha$
, for all
$\alpha$
, for all
![]() $\eta$
sufficiently small.
$\eta$
sufficiently small.
6.3. Survival versus extinction
The limiting system has only three parameters. Indeed, one can always take, say,
![]() $\beta=1$
by a time rescaling, so that only the other three parameters remain. Consider the parameterization
$\beta=1$
by a time rescaling, so that only the other three parameters remain. Consider the parameterization
![]() $(\alpha,\mu,\eta)$
and the associated positive orthant.
$(\alpha,\mu,\eta)$
and the associated positive orthant.
6.3.1. Phase diagram in
 $\eta$
$\eta$
The following two results rely on the definitions of extinction and survival given in Definition 1. They show that the SIS TL admits a simple phase diagram with respect to
![]() $\eta$
, with critical value equal to
$\eta$
, with critical value equal to
![]() $\eta_c^{(s)}$
as defined above.
$\eta_c^{(s)}$
as defined above.
Theorem 1.
If the SIS thermodynamic propagation of chaos ansatz holds, then, in the SIS TL, there exists a constant
![]() $\eta_c$
such that there is survival if
$\eta_c$
such that there is survival if
![]() $\eta > \eta_c^{(s)}$
.
$\eta > \eta_c^{(s)}$
.
Proof. From Corollary 1, if
![]() $\eta > \eta_c^{(s)}$
, there exists
$\eta > \eta_c^{(s)}$
, there exists
![]() $p^*>0$
such that
$p^*>0$
such that
![]() $g(p^*)=p^*$
. If the ansatz holds, take as initial distribution in the nonlinear Markov representation of the SIS TL the law of the open SIS reactor with infected input rate
$g(p^*)=p^*$
. If the ansatz holds, take as initial distribution in the nonlinear Markov representation of the SIS TL the law of the open SIS reactor with infected input rate
![]() $p=p^*$
. This distribution is a stationary distribution of this system.
$p=p^*$
. This distribution is a stationary distribution of this system.
Theorem 2.
If the SIS thermodynamic propagation of chaos ansatz holds, then, in the SIS TL, there is strong extinction if
![]() $\eta \le \eta_c^{(s)}$
.
$\eta \le \eta_c^{(s)}$
.
Proof. The proof is given in Appendix E.
Remark 6. Theorem 1 only shows that there exists an initial distribution
![]() ${\mathcal P}^*$
of the SIS TL that makes this limiting system stationary. A stronger result is proved in Corollary 6 in the appendix: for all initial distributions which are stochastically larger than
${\mathcal P}^*$
of the SIS TL that makes this limiting system stationary. A stronger result is proved in Corollary 6 in the appendix: for all initial distributions which are stochastically larger than
![]() ${\mathcal P}^*$
, the distribution of the SIS TL converges to
${\mathcal P}^*$
, the distribution of the SIS TL converges to
![]() ${\mathcal P}^*$
as time tends to infinity.
${\mathcal P}^*$
as time tends to infinity.
6.3.2. Phase diagrams in
 $\alpha$
and in
$\alpha$
and in
 $\beta$
$\beta$
Consider the SIS reactor. Fix all parameters except
![]() $\alpha$
(resp.
$\alpha$
(resp.
![]() $\beta$
) and consider
$\beta$
) and consider
![]() $0<\alpha_1<\alpha_2$
(resp.
$0<\alpha_1<\alpha_2$
(resp.
![]() $0<\beta_2<\beta_1$
). It is shown in Appendix C that there exists a coupling of the two associated models such that
$0<\beta_2<\beta_1$
). It is shown in Appendix C that there exists a coupling of the two associated models such that
![]() $X_1(t)+Y_1(t)=X_2(t)+Y_2(t)\,=\!:\,N(t)$
and
$X_1(t)+Y_1(t)=X_2(t)+Y_2(t)\,=\!:\,N(t)$
and
![]() $Y_1(t)\le Y_2(t)$
almost surely (a.s.), for all
$Y_1(t)\le Y_2(t)$
almost surely (a.s.), for all
![]() $t\ge 0$
, given that the two models start from the same initial condition
$t\ge 0$
, given that the two models start from the same initial condition
![]() $X_1(0)=X_2(0)$
and
$X_1(0)=X_2(0)$
and
![]() $Y_1(0)=Y_2(0)$
a.s.
$Y_1(0)=Y_2(0)$
a.s.
Consider now a finite closed network of SIS reactors with N stations and
![]() $K_N$
customers. It is shown in Appendix C that the same monotonicity properties hold.
$K_N$
customers. It is shown in Appendix C that the same monotonicity properties hold.
By arguments similar to those used with respect to
![]() $\eta$
, we have the following result.
$\eta$
, we have the following result.
Theorem 3.
If the SIS thermodynamic propagation of chaos ansatz holds, then, in the SIS TL, there exists a constant
![]() $\alpha_c^{(s)}$
(resp.
$\alpha_c^{(s)}$
(resp.
![]() $\beta_c^{(s)}$
) such that there is survival if
$\beta_c^{(s)}$
) such that there is survival if
![]() $\alpha > \alpha_c^{(s)}$
(resp.
$\alpha > \alpha_c^{(s)}$
(resp.
![]() $\beta < \beta_c^{(s)}$
) and strong extinction otherwise.
$\beta < \beta_c^{(s)}$
) and strong extinction otherwise.
6.3.3. Other phase diagrams
Phase diagrams with respect to
![]() $\mu$
will only be discussed numerically in Section 10. An example of a question of interest is whether there is a simple (monotonic as above) phase diagram with respect to
$\mu$
will only be discussed numerically in Section 10. An example of a question of interest is whether there is a simple (monotonic as above) phase diagram with respect to
![]() $\mu$
when
$\mu$
when
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
, and
$\beta$
, and
![]() $\eta$
are fixed.
$\eta$
are fixed.
6.4. First- and second-order relations in the thermodynamic limit
In the thermodynamic limit, the first-order relation of Lemma 1 simplifies to
Consider now the second-order relations of Lemma 2. Equation (6) can be rewritten as
or equivalently
 \begin{align} (\mu + \beta ) ({\mathbb{E}}[Y^2] -{\mathbb{E}}[Y]^2 -{\mathbb{E}}[Y]) & = \alpha {\mathbb{E}}[XY] {\mathbb{E}}\left[Y \frac {\alpha XY}{{\mathbb{E}}[\alpha XY]}\right] -\beta{\mathbb{E}}[Y]\nonumber \\& = \beta {\mathbb{E}}[Y]({\mathbb{E}}_I^0[Y^-]-{\mathbb{E}}[Y]).\end{align}
\begin{align} (\mu + \beta ) ({\mathbb{E}}[Y^2] -{\mathbb{E}}[Y]^2 -{\mathbb{E}}[Y]) & = \alpha {\mathbb{E}}[XY] {\mathbb{E}}\left[Y \frac {\alpha XY}{{\mathbb{E}}[\alpha XY]}\right] -\beta{\mathbb{E}}[Y]\nonumber \\& = \beta {\mathbb{E}}[Y]({\mathbb{E}}_I^0[Y^-]-{\mathbb{E}}[Y]).\end{align}
Similarly, (7) can be rewritten as
or equivalently
 \begin{eqnarray}&& \mu \left({\mathbb{E}}[X^2] -{\mathbb{E}}[X]^2-{\mathbb{E}}[X]\right) (\alpha+\beta) {\mathbb{E}}[XY] -\alpha{\mathbb{E}}[XY] {\mathbb{E}}\left[X \frac {\alpha XY}{{\mathbb{E}}[\alpha XY]}\right]\nonumber\\ & =\, & {\mathbb{E}}[XY] \alpha \left( 1 + \frac{\beta}{\alpha} - {\mathbb{E}}_I^0[X^-]\right) = {\mathbb{E}}[XY] \alpha \left(\frac{\beta}{\alpha} - {\mathbb{E}}_I^0[X^+]\right).\end{eqnarray}
\begin{eqnarray}&& \mu \left({\mathbb{E}}[X^2] -{\mathbb{E}}[X]^2-{\mathbb{E}}[X]\right) (\alpha+\beta) {\mathbb{E}}[XY] -\alpha{\mathbb{E}}[XY] {\mathbb{E}}\left[X \frac {\alpha XY}{{\mathbb{E}}[\alpha XY]}\right]\nonumber\\ & =\, & {\mathbb{E}}[XY] \alpha \left( 1 + \frac{\beta}{\alpha} - {\mathbb{E}}_I^0[X^-]\right) = {\mathbb{E}}[XY] \alpha \left(\frac{\beta}{\alpha} - {\mathbb{E}}_I^0[X^+]\right).\end{eqnarray}
Similarly, Equation (57) can be simplified to
whereas (58) can be simplified to
7. AIR TL analysis
Let
Theorem 4.
Under the AIR TL propagation of chaos ansatz, if
![]() $\eta \le \eta_c^{(a)}$
, then there is weak extinction, whereas if
$\eta \le \eta_c^{(a)}$
, then there is weak extinction, whereas if
![]() $\eta> \eta_c^{(a)}$
, there is survival. In addition, if there is survival, in the stationary regime of the thermodynamic limit,
$\eta> \eta_c^{(a)}$
, there is survival. In addition, if there is survival, in the stationary regime of the thermodynamic limit,
![]() ${\mathbb{E}}[\widetilde X] = \frac \beta \alpha$
,
${\mathbb{E}}[\widetilde X] = \frac \beta \alpha$
,
![]() ${\mathbb{E}}[\widetilde Y]= \eta - \frac \beta \alpha$
,
${\mathbb{E}}[\widetilde Y]= \eta - \frac \beta \alpha$
,
![]() $1-\widetilde p^*= \widetilde q^* = \frac{\beta}{\eta \alpha}$
, and
$1-\widetilde p^*= \widetilde q^* = \frac{\beta}{\eta \alpha}$
, and
![]() $ \widetilde X$
and
$ \widetilde X$
and
![]() $\widetilde Y$
are independent and Poisson. In addition, the departure rate from a station is
$\widetilde Y$
are independent and Poisson. In addition, the departure rate from a station is
![]() $\lambda=\eta \mu$
.
$\lambda=\eta \mu$
.
If there is extinction, in the stationary regime,
![]() ${\mathbb{E}}[\widetilde X] = \frac \beta \alpha $
,
${\mathbb{E}}[\widetilde X] = \frac \beta \alpha $
,
![]() ${\mathbb{E}}[\widetilde Y]= 0$
,
${\mathbb{E}}[\widetilde Y]= 0$
,
![]() $ 1-\widetilde p^*= \widetilde q^* = 1$
, and
$ 1-\widetilde p^*= \widetilde q^* = 1$
, and
![]() $ \widetilde X$
is Poisson. In addition, the departure rate from a station is
$ \widetilde X$
is Poisson. In addition, the departure rate from a station is
![]() $\lambda=\eta \mu$
.
$\lambda=\eta \mu$
.
Proof. Assuming existence of the thermodynamic limit and its convergence to a stationary distribution, the result is immediate from plugging in
![]() $y=p \eta$
in (25).
$y=p \eta$
in (25).
The AIR phase diagram is hence quite explicit. We have
![]() $\eta_c= \frac{\beta}{\alpha}$
, which does not depend on
$\eta_c= \frac{\beta}{\alpha}$
, which does not depend on
![]() $\mu$
. In addition, the following continuity property holds: when
$\mu$
. In addition, the following continuity property holds: when
![]() $\eta\downarrow \eta_c$
,
$\eta\downarrow \eta_c$
,
![]() ${\mathbb{E}}[\widetilde Y] \downarrow 0$
. Similar statements can be formulated with respect to any parameter other than
${\mathbb{E}}[\widetilde Y] \downarrow 0$
. Similar statements can be formulated with respect to any parameter other than
![]() $\eta$
.
$\eta$
.
8. DOCS TL analysis
Since the behavior of a station in the DOCS TL is a specific instance of that of a station in the routing mean-field model, the following two results hold on the former: (i) The assumption that the ‘external’ arrival rate is
![]() $\lambda$
is equivalent to the assumption that the mean number of customers (of both types) in a station in steady state is
$\lambda$
is equivalent to the assumption that the mean number of customers (of both types) in a station in steady state is
![]() $\frac{\lambda}{\mu}$
(see Equation (20)). By symmetry, this is equivalent to assuming that
$\frac{\lambda}{\mu}$
(see Equation (20)). By symmetry, this is equivalent to assuming that
![]() $\lim_{N\to \infty} K_N/N= \lambda/\mu\,:\!=\,\eta$
in the DOCS TL. (ii) The condition
$\lim_{N\to \infty} K_N/N= \lambda/\mu\,:\!=\,\eta$
in the DOCS TL. (ii) The condition
![]() $\lambda p^*= \mu {\mathbb{E}}[\widehat Y]$
is equivalent to
$\lambda p^*= \mu {\mathbb{E}}[\widehat Y]$
is equivalent to
![]() $\alpha {\mathbb{E}}[\widehat X \widehat Y]= \beta {\mathbb{E}}[\widehat Y]$
in view of (19). In words, in the DOCS TL, the stationary rate of ‘in-station’ infections matches the stationary rate of ‘in-station’ recoveries.
$\alpha {\mathbb{E}}[\widehat X \widehat Y]= \beta {\mathbb{E}}[\widehat Y]$
in view of (19). In words, in the DOCS TL, the stationary rate of ‘in-station’ infections matches the stationary rate of ‘in-station’ recoveries.
8.1. Analytical solution
In this section we use p in place of
![]() $p^*$
to lighten the notation.
$p^*$
to lighten the notation.
8.1.1. Rate conservation equations
As shown above, in the thermodynamic limit, we have
(in words, the rate of ‘natural’ migration of infected customers matches that of ‘external’ arrivals of infected customers),
(in words, the rate of ‘natural’ migration of susceptible customers matches that of ‘external’ arrivals of susceptible customers), and
(in words, the rate of ‘infections’ matches that of ‘recoveries’).
It follows that
that is,
![]() $\widehat \theta=\frac{\lambda p}{\mu}$
, which is consistent with (42).
$\widehat \theta=\frac{\lambda p}{\mu}$
, which is consistent with (42).
As for second-order relations, when using the fact that
![]() $\widehat Y$
is Poisson, one gets that (21) brings no information, whereas (22) leads to
$\widehat Y$
is Poisson, one gets that (21) brings no information, whereas (22) leads to
and (23) to
8.1.2. Analytic treatment based on the DOCS ODE solution
The explicit solution of the open DOCS model is now used to analyze this thermodynamic limit. We recall that, in the DOCS TL, each station behaves as an open DOCS reactor with susceptible input rate
infected input rate
and susceptible departure rate
![]() $\nu=\mu +\beta$
. Hence, it follows from (16) that
$\nu=\mu +\beta$
. Hence, it follows from (16) that
Since
![]() $\mu {\mathbb{E}}[\widehat X]= \lambda q$
, we have the following.
$\mu {\mathbb{E}}[\widehat X]= \lambda q$
, we have the following.
Proposition 1. In the DOCS TL, q satisfies the fixed-point relation
where the right-hand side is the analytic expression for
![]() $\frac{{\mathbb{E}}[\widehat X]}\eta$
in this context.
$\frac{{\mathbb{E}}[\widehat X]}\eta$
in this context.
8.1.3. Monotonicity and convexity properties
Here we study the properties of the right-hand side of Equation (48) with respect to various parameters.
We consider the dependence on
![]() $\eta$
first. Rewriting the right-hand side of Equation (48) as
$\eta$
first. Rewriting the right-hand side of Equation (48) as
one gets that this right-hand side is a strictly decreasing function of
![]() $\eta$
when all other parameters are fixed.
$\eta$
when all other parameters are fixed.
The dependence on
![]() $\mu$
is more complicated. The integrand in the right-hand side of (48) is a monotone increasing function of
$\mu$
is more complicated. The integrand in the right-hand side of (48) is a monotone increasing function of
![]() $\mu$
since
$\mu$
since
![]() $\frac{(\mu+\beta)\alpha}{\mu(\mu+\beta+\alpha)^2}$
as a function of
$\frac{(\mu+\beta)\alpha}{\mu(\mu+\beta+\alpha)^2}$
as a function of
![]() $\mu$
is decreasing. However, the coefficient
$\mu$
is decreasing. However, the coefficient
![]() $\frac{q\mu+p\beta}{\mu+\alpha+\beta}$
is equal to
$\frac{q\mu+p\beta}{\mu+\alpha+\beta}$
is equal to
![]() $q+ \frac{p\beta - q (\alpha+\beta)}{\mu+\alpha+\beta}$
, which is either an increasing or decreasing function of
$q+ \frac{p\beta - q (\alpha+\beta)}{\mu+\alpha+\beta}$
, which is either an increasing or decreasing function of
![]() $\mu$
, depending on the sign of
$\mu$
, depending on the sign of
![]() $p\beta - q (\alpha+\beta)$
.
$p\beta - q (\alpha+\beta)$
.
Consider now the dependence in p. Clearly,
is a positive and strictly decreasing function of p, when all other parameters
![]() $\eta,\mu,\alpha,\beta$
are fixed. The quantity
$\eta,\mu,\alpha,\beta$
are fixed. The quantity
is positive, since
are two strictly positive functions, and finite since
![]() $\lim_{t\to 0} t^r \log t = 0$
for any
$\lim_{t\to 0} t^r \log t = 0$
for any
![]() $r>0$
.
$r>0$
.
Furthermore, the numerator
![]() $q\mu + p\beta$
in the prefactor of the right-hand side of (49) may be represented as
$q\mu + p\beta$
in the prefactor of the right-hand side of (49) may be represented as
![]() $\mu + p(\beta-\mu)$
, which is strictly positive. Hence, if
$\mu + p(\beta-\mu)$
, which is strictly positive. Hence, if
![]() $\beta\le \mu$
, the function in the right-hand side of (48) is strictly decreasing since its derivative with respect to p is
$\beta\le \mu$
, the function in the right-hand side of (48) is strictly decreasing since its derivative with respect to p is
and strictly convex since its second derivative is
In particular,
 \begin{eqnarray} D(0) & \,=\, & \frac{\beta}{\mu}-1 -\eta\left( \frac{\alpha(\mu+\beta)}{\mu(\mu+\alpha +\beta)} + \frac{\alpha^2}{(\mu+\alpha+\beta)(2\mu+\alpha +\beta)} \right)\nonumber\\ & \equiv\, &\frac{\beta}{\mu}-1- \eta \cdot \frac{\alpha}{\mu}\left(1+\frac{\alpha}{2\mu+\beta}\right)^{-1}. \end{eqnarray}
\begin{eqnarray} D(0) & \,=\, & \frac{\beta}{\mu}-1 -\eta\left( \frac{\alpha(\mu+\beta)}{\mu(\mu+\alpha +\beta)} + \frac{\alpha^2}{(\mu+\alpha+\beta)(2\mu+\alpha +\beta)} \right)\nonumber\\ & \equiv\, &\frac{\beta}{\mu}-1- \eta \cdot \frac{\alpha}{\mu}\left(1+\frac{\alpha}{2\mu+\beta}\right)^{-1}. \end{eqnarray}
8.2. Phase diagram
Let
Here is an analogue of Corollary 1 for DOCS.
Lemma 10. In the DOCS TL, if
![]() $\beta\le \mu$
, then
$\beta\le \mu$
, then
Proof. The left-hand side and the right-hand side of (48) coincide at
![]() $p=0$
, where both are equal to 1. At
$p=0$
, where both are equal to 1. At
![]() $p=1$
, the left-hand side of (48) is 0, whereas the right-hand side of (48) is positive. By (51), we have
$p=1$
, the left-hand side of (48) is 0, whereas the right-hand side of (48) is positive. By (51), we have
![]() $D(0)<-1$
if and only if
$D(0)<-1$
if and only if
![]() $\eta > \eta_c^{(d)}$
. When
$\eta > \eta_c^{(d)}$
. When
![]() $\beta\le \mu$
, the right-hand side of (48) is a decreasing and convex function of p. Hence, if the first derivative of the right-hand side of (48) at 0 is less than
$\beta\le \mu$
, the right-hand side of (48) is a decreasing and convex function of p. Hence, if the first derivative of the right-hand side of (48) at 0 is less than
![]() $-1$
, then there is exactly one positive solution to (48), whereas if it is greater than or equal to
$-1$
, then there is exactly one positive solution to (48), whereas if it is greater than or equal to
![]() $-1$
, there is no such solution.
$-1$
, there is no such solution.
In the general case, there is at least one positive solution if the first derivative of the right-hand side of (48) at 0 is less than
![]() $-1$
.
$-1$
.
Theorem 5.
Under the DOCS thermodynamic propagation of chaos ansatz, if
![]() $\eta\le\eta_c^{(d)}$
, then there is weak extinction, whereas if
$\eta\le\eta_c^{(d)}$
, then there is weak extinction, whereas if
![]() $\eta>\eta_c^{(d)}$
, then there is survival.
$\eta>\eta_c^{(d)}$
, then there is survival.
Note that the statement on weak extinction in the last theorem is only proved under the assumption
![]() $\beta\le \mu$
. There is numerical evidence that it also holds without this condition.
$\beta\le \mu$
. There is numerical evidence that it also holds without this condition.
8.3. Interpretation of the results
Monotonicity. In DOCS, two contradictory phenomena are present:
-
1. A larger motion rate implies smaller population density, which lowers local epidemic spread.
-
2. A larger motion rate implies more global dissemination of the epidemic.
This possibly explains the following facts:
-
(a) The quantity
 $\eta_c^{(d)}$
is decreasing in
$\eta_c^{(d)}$
is decreasing in
 $\mu$
(the motion rate); that is, if the population density per reactor is fixed, then increasing motion makes the system less safe. This is because only the phenomenon 2 is at play; the phenomenon 1 is blocked in this setting where
$\mu$
(the motion rate); that is, if the population density per reactor is fixed, then increasing motion makes the system less safe. This is because only the phenomenon 2 is at play; the phenomenon 1 is blocked in this setting where
 $\eta$
is fixed.
$\eta$
is fixed. -
(b) The quantity
 $\lambda_c^{(d)}$
is increasing in
$\lambda_c^{(d)}$
is increasing in
 $\mu$
; that is, if the overall arrival rate in a reactor is fixed, then increasing motion leads to a safer system. In this case the phenomena 1 and 2 compete and our formula shows that the phenomenon 1 (or locality) dominates.
$\mu$
; that is, if the overall arrival rate in a reactor is fixed, then increasing motion leads to a safer system. In this case the phenomena 1 and 2 compete and our formula shows that the phenomenon 1 (or locality) dominates.
9. On the thresholds of the thermodynamic limits
Here is first a general observation on the connections between the properties of the open reactors and the thresholds (with respect to
![]() $\eta$
) of the thermodynamic limits. We have shown that survival in a thermodynamic limit is guaranteed as soon as the derivative at 0 of the
$\eta$
) of the thermodynamic limits. We have shown that survival in a thermodynamic limit is guaranteed as soon as the derivative at 0 of the
![]() $p\to p_0(p)$
function of the associated reactor is more than 1. Classical busy-cycle arguments show that the latter derivative can in turn be reinterpreted as the mean number of susceptible customers that a single infected customer arriving in the open reactor infects before leaving the reactor, given that the latter has only susceptible customers upon the arrival in question. This is precisely the
$p\to p_0(p)$
function of the associated reactor is more than 1. Classical busy-cycle arguments show that the latter derivative can in turn be reinterpreted as the mean number of susceptible customers that a single infected customer arriving in the open reactor infects before leaving the reactor, given that the latter has only susceptible customers upon the arrival in question. This is precisely the
![]() $R_0$
parameter of epidemiologists. For SIS, the result is stronger: there is survival if the mean number of susceptible customers that a single infected customer infects is more than 1 and strong extinction otherwise. Of course, this mean number depends on the system considered. For AIR, the evaluation of this mean number is based on an averaging over the geometries of the random environments that a customer sees. For SIS or DOCS the evaluation takes the random and dynamic nature of the environment into account.
$R_0$
parameter of epidemiologists. For SIS, the result is stronger: there is survival if the mean number of susceptible customers that a single infected customer infects is more than 1 and strong extinction otherwise. Of course, this mean number depends on the system considered. For AIR, the evaluation of this mean number is based on an averaging over the geometries of the random environments that a customer sees. For SIS or DOCS the evaluation takes the random and dynamic nature of the environment into account.
We now make some further observations on the thermodynamic limit thresholds in terms of the last mean value (or
![]() $R_0$
) interpretation when the scales of the
$R_0$
) interpretation when the scales of the
![]() $(\lambda,\mu)$
or the
$(\lambda,\mu)$
or the
![]() $(\alpha,\beta)$
parameters, respectively, are changed.
$(\alpha,\beta)$
parameters, respectively, are changed.
Consider first a family of thermodynamic limits for DOCS indexed by n, and assume that
![]() $\lambda_n$
and
$\lambda_n$
and
![]() $\mu_n$
both tend to infinity in such a way that the limit of the ratio
$\mu_n$
both tend to infinity in such a way that the limit of the ratio
![]() $\lambda_n/\mu_n$
is a positive constant
$\lambda_n/\mu_n$
is a positive constant
![]() $\eta$
, whereas
$\eta$
, whereas
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
stay constant. Then
$\beta$
stay constant. Then
![]() $\eta_c^{(d,n)}$
tends to
$\eta_c^{(d,n)}$
tends to
![]() $\eta_c^{(a)}=\beta/\alpha$
. Here is a probabilistic interpretation of this fact. Take a unique infected customer in a large closed network of DOCS reactors, and assume that apart from this infected customer, the system contains only susceptible customers. As
$\eta_c^{(a)}=\beta/\alpha$
. Here is a probabilistic interpretation of this fact. Take a unique infected customer in a large closed network of DOCS reactors, and assume that apart from this infected customer, the system contains only susceptible customers. As
![]() $\mu$
is very large, the infected customer travels very fast and visits many stations before recovering. The mean number of customers it infects before recovering is
$\mu$
is very large, the infected customer travels very fast and visits many stations before recovering. The mean number of customers it infects before recovering is
![]() $N\,:\!=\, \eta \alpha/\beta$
. This formula uses that fact that the recovery time has mean
$N\,:\!=\, \eta \alpha/\beta$
. This formula uses that fact that the recovery time has mean
![]() $1/\beta$
, the infection rate is
$1/\beta$
, the infection rate is
![]() $\alpha$
, and some homogenization takes place over the population of susceptible customers seen before recovery, due to fast motion. In this limit (
$\alpha$
, and some homogenization takes place over the population of susceptible customers seen before recovery, due to fast motion. In this limit (
![]() $\lambda$
and
$\lambda$
and
![]() $\mu$
high), the condition
$\mu$
high), the condition
![]() $\eta < \eta_c^{(d)}$
is then equivalent to the branching criticality condition
$\eta < \eta_c^{(d)}$
is then equivalent to the branching criticality condition
![]() $N < 1$
, which is that of AIR. The argument should extend to SIS: under the same assumptions, the threshold for SIS
$N < 1$
, which is that of AIR. The argument should extend to SIS: under the same assumptions, the threshold for SIS
![]() $\eta_c^{(s)}$
should tend to
$\eta_c^{(s)}$
should tend to
![]() $\eta_c^{(a)}=\beta/\alpha$
as well.
$\eta_c^{(a)}=\beta/\alpha$
as well.
Consider now a family of DOCS TLs, also indexed by n, and where
![]() $\beta_n$
and
$\beta_n$
and
![]() $\alpha_n$
both tend to infinity in such a way that the limit of the ratio
$\alpha_n$
both tend to infinity in such a way that the limit of the ratio
![]() $\beta_n/\alpha_n$
is a positive constant
$\beta_n/\alpha_n$
is a positive constant
![]() $\kappa$
, whereas
$\kappa$
, whereas
![]() $\lambda$
and
$\lambda$
and
![]() $\mu$
stay constant. It is easy to see that
$\mu$
stay constant. It is easy to see that
![]() $\eta_c^{(d)}$
tends to
$\eta_c^{(d)}$
tends to
![]() $1+\kappa$
. The condition
$1+\kappa$
. The condition
![]() $\eta> \eta_c^{(d)}$
then reads
$\eta> \eta_c^{(d)}$
then reads
![]() $M\,:\!=\, \eta \alpha/(\alpha+\beta) > 1$
; that is, it is again like a branching condition stating that the mean number M of customers infected by a single infected customer is more than 1. Indeed, a single infected customer arriving at a station finds a mean of
$M\,:\!=\, \eta \alpha/(\alpha+\beta) > 1$
; that is, it is again like a branching condition stating that the mean number M of customers infected by a single infected customer is more than 1. Indeed, a single infected customer arriving at a station finds a mean of
![]() $\eta$
susceptible customers. For a tagged susceptible customer, start two exponential clocks, one of parameter
$\eta$
susceptible customers. For a tagged susceptible customer, start two exponential clocks, one of parameter
![]() $\alpha$
(for its own infection), and one of parameter
$\alpha$
(for its own infection), and one of parameter
![]() $\beta$
(for the departure of the infected customer). The chance that the tagged customer gets infected is hence
$\beta$
(for the departure of the infected customer). The chance that the tagged customer gets infected is hence
![]() $\alpha/(\alpha+\beta)$
. This justifies the interpretation of M. Now each infected customer then immediately leaves for another queue far away, where its fate is the same and independent. This justifies the branching (independence) interpretation. Note that
$\alpha/(\alpha+\beta)$
. This justifies the interpretation of M. Now each infected customer then immediately leaves for another queue far away, where its fate is the same and independent. This justifies the branching (independence) interpretation. Note that
![]() $\mu$
has disappeared because it is negligible with respect to
$\mu$
has disappeared because it is negligible with respect to
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
. This interpretation is specific to DOCS.
$\beta$
. This interpretation is specific to DOCS.
10. Comparison and numerical results
10.1. Comparison of plain SIS TL and AIR TL
We conjecture that, in the stationary regime of the SIS TL, there is a negative correlation between X and Y. This negative correlation property is substantiated by simulation but unproved at this stage. It is proved in the arXiv version of this paper [Reference Baccelli, Foss and Shneer2] that if this negative correlation property holds, then
![]() $\eta_c^{(s)}\ge \eta_c^{(a)}$
, that is, SIS is safer than AIR. A potential interpretation is as follows: replacing the infection rate
$\eta_c^{(s)}\ge \eta_c^{(a)}$
, that is, SIS is safer than AIR. A potential interpretation is as follows: replacing the infection rate
![]() $\alpha Y$
by
$\alpha Y$
by
![]() $\alpha {\mathbb{E}}[Y]$
at the same time decreases the infection rate when Y is large and increases it when Y is small. In the thermodynamic limit, this last fact dominates and makes it more likely for the epidemic to survive in AIR than in plain SIS.
$\alpha {\mathbb{E}}[Y]$
at the same time decreases the infection rate when Y is large and increases it when Y is small. In the thermodynamic limit, this last fact dominates and makes it more likely for the epidemic to survive in AIR than in plain SIS.
10.2. Comparison of plain SIS TL and DOCS TL
In this subsection, we use a mix of simulation and analysis to compare
![]() $\eta_c$
in the thermodynamic limits of SIS and DOCS. The main conclusion is that depending on the parameters, either SIS or DOCS may be safer. The evaluation of
$\eta_c$
in the thermodynamic limits of SIS and DOCS. The main conclusion is that depending on the parameters, either SIS or DOCS may be safer. The evaluation of
![]() $\lambda_c^{(s)}$
is based on Theorems 1 and 2. The simulation of
$\lambda_c^{(s)}$
is based on Theorems 1 and 2. The simulation of
![]() $\eta_c^{(s)}$
is based on its characterization in Corollary 1 in terms of the derivative at 0 of the function
$\eta_c^{(s)}$
is based on its characterization in Corollary 1 in terms of the derivative at 0 of the function
![]() $p_0(p)$
. For DOCS, we use the evaluation of
$p_0(p)$
. For DOCS, we use the evaluation of
![]() $\lambda_c^{(d)}$
in Lemma 10.
$\lambda_c^{(d)}$
in Lemma 10.
Figure 6 features a situation where both
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
are moderate. We observe that
$\beta$
are moderate. We observe that
![]() $\eta_c^{(d)}< \eta_c^{(s)}$
, or equivalently, SIS is safer than DOCS.
$\eta_c^{(d)}< \eta_c^{(s)}$
, or equivalently, SIS is safer than DOCS.

Figure 6. Comparison of
![]() $\eta_c^{(s)}$
and
$\eta_c^{(s)}$
and
![]() $\eta_c^{(d)}$
for
$\eta_c^{(d)}$
for
![]() $\mu=1$
,
$\mu=1$
,
![]() $\beta=1$
, and
$\beta=1$
, and
![]() $\alpha=1$
.
$\alpha=1$
.
The left panel of Figure 7 features a situation where
![]() $\alpha$
is large and
$\alpha$
is large and
![]() $\beta$
moderate. We observe that
$\beta$
moderate. We observe that
![]() $\eta_c^{(s)}< \eta_c^{(d)}$
, or equivalently, DOCS is safer than SIS. One possible explanation is that although the mean population in each system is the same, in DOCS, in any station with infection present, infected customers leave immediately, which is safer than the SIS case where they stay and infect all other susceptible customers present in the station.
$\eta_c^{(s)}< \eta_c^{(d)}$
, or equivalently, DOCS is safer than SIS. One possible explanation is that although the mean population in each system is the same, in DOCS, in any station with infection present, infected customers leave immediately, which is safer than the SIS case where they stay and infect all other susceptible customers present in the station.

Figure 7. Left: comparison of
![]() $\eta_c^{(s)}$
and
$\eta_c^{(s)}$
and
![]() $\eta_c^{(d)}$
for
$\eta_c^{(d)}$
for
![]() $\mu=1$
,
$\mu=1$
,
![]() $\beta=1$
, and
$\beta=1$
, and
![]() $\alpha=20$
; Right: comparison of
$\alpha=20$
; Right: comparison of
![]() $\eta_c^{(s)}$
and
$\eta_c^{(s)}$
and
![]() $\eta_c^{(d)}$
for
$\eta_c^{(d)}$
for
![]() $\mu=1$
,
$\mu=1$
,
![]() $\beta=10$
, and
$\beta=10$
, and
![]() $\alpha=1$
. On the left it is not clear which curve is higher at low values of
$\alpha=1$
. On the left it is not clear which curve is higher at low values of
![]() $\lambda$
, but it is clear that the curve corresponding to DOCS is lower for high values of
$\lambda$
, but it is clear that the curve corresponding to DOCS is lower for high values of
![]() $\lambda$
and that, crucially, it reaches 1 later than the curve for SIS. On the right it is clear that the curve corresponding to DOCS reaches 1 earlier than that corresponding to SIS. The curves in both panels are produced by simulation, and for DOCS we also provide the exact curve that follows from our analytical results.
$\lambda$
and that, crucially, it reaches 1 later than the curve for SIS. On the right it is clear that the curve corresponding to DOCS reaches 1 earlier than that corresponding to SIS. The curves in both panels are produced by simulation, and for DOCS we also provide the exact curve that follows from our analytical results.
One can observe in Figure 6 that the curve corresponding to the derivative at
![]() $p=0$
for DOCS is higher (resp. lower) than that for SIS for low (resp. high) values of
$p=0$
for DOCS is higher (resp. lower) than that for SIS for low (resp. high) values of
![]() $\lambda$
and, crucially, reaches 1 at a lower value of
$\lambda$
and, crucially, reaches 1 at a lower value of
![]() $\lambda$
. Both curves are produced by simulation. We also present the exact curve for DOCS that follows from our analytic results; this can be observed to agree with simulations.
$\lambda$
. Both curves are produced by simulation. We also present the exact curve for DOCS that follows from our analytic results; this can be observed to agree with simulations.
The right panel of Figure 7 features a situation where
![]() $\beta$
is large and
$\beta$
is large and
![]() $\alpha$
moderate. Here SIS is safer than DOCS again. The interpretation is that although the mean number of individuals per station is the same in either case, in DOCS any station with many infected customers is more quickly depleted because of their fast recovery.
$\alpha$
moderate. Here SIS is safer than DOCS again. The interpretation is that although the mean number of individuals per station is the same in either case, in DOCS any station with many infected customers is more quickly depleted because of their fast recovery.
10.3. Comparison of SIS-DOCS TL and AIR TL
It follows directly from the expressions for
![]() $\eta_c$
in both cases that
$\eta_c$
in both cases that
![]() $\eta_c^{(d)}>\eta_c^{(a)}$
. This can be rephrased by saying that DOCS is safer than AIR. A possible interpretation is again that extinction happens when Y fluctuates to small values throughout all reactors of a large system. Fixing Y to its means as in AIR, in the thermodynamic limit, makes these fluctuations less likely. This possibly explains why the AIR system is less safe than the DOCS system.
$\eta_c^{(d)}>\eta_c^{(a)}$
. This can be rephrased by saying that DOCS is safer than AIR. A possible interpretation is again that extinction happens when Y fluctuates to small values throughout all reactors of a large system. Fixing Y to its means as in AIR, in the thermodynamic limit, makes these fluctuations less likely. This possibly explains why the AIR system is less safe than the DOCS system.

Figure 8. Graphs of the derivative at
![]() $p=0$
of g(p) in the SIS reactor as function of
$p=0$
of g(p) in the SIS reactor as function of
![]() $\mu$
when
$\mu$
when
![]() $\eta$
,
$\eta$
,
![]() $\alpha$
, and
$\alpha$
, and
![]() $\beta$
are fixed. On the left,
$\beta$
are fixed. On the left,
![]() $\eta=\alpha=\beta=1$
; on the right,
$\eta=\alpha=\beta=1$
; on the right,
![]() $\eta=3$
,
$\eta=3$
,
![]() $\alpha=5$
,
$\alpha=5$
,
![]() $\beta=1$
.
$\beta=1$
.
10.4. Phase diagram in
 $\mu$
$\mu$
For the SIS reactor and SIS TL, we have already characterized the phase diagrams: they turn out to be of the threshold type (survival in one interval, extinction in another). Another interesting question is what such a phase diagram looks like in
![]() $\mu$
. More specifically, one may be interested in fixing
$\mu$
. More specifically, one may be interested in fixing
![]() $\eta$
,
$\eta$
,
![]() $\alpha$
, and
$\alpha$
, and
![]() $\beta$
and asking for which values of
$\beta$
and asking for which values of
![]() $\mu$
the epidemic survives and for which it does not.
$\mu$
the epidemic survives and for which it does not.
We have shown that, in order to answer such a question, one needs to examine the derivative at
![]() $p=0$
of the function g(p). Our findings were based on the monotonicity of this derivative with respect to the relevant parameters.
$p=0$
of the function g(p). Our findings were based on the monotonicity of this derivative with respect to the relevant parameters.
Numerical evidence shows that such monotonicity with respect to
![]() $\mu$
does not always hold. Indeed, Figure 8 contains graphs of the derivative as a function of
$\mu$
does not always hold. Indeed, Figure 8 contains graphs of the derivative as a function of
![]() $\mu$
, when the other parameters are fixed, in two scenarios. On the right,
$\mu$
, when the other parameters are fixed, in two scenarios. On the right,
![]() $\eta=3$
,
$\eta=3$
,
![]() $\alpha=5$
,
$\alpha=5$
,
![]() $\beta=1$
, and one can observe the absence of monotonicity and convexity. On the left, however, when
$\beta=1$
, and one can observe the absence of monotonicity and convexity. On the left, however, when
![]() $\eta=\alpha=\beta=1$
, it appears that the derivative is monotone. This evidence suggests that the phase diagram in
$\eta=\alpha=\beta=1$
, it appears that the derivative is monotone. This evidence suggests that the phase diagram in
![]() $\mu$
may be more complicated than in the case of other parameters. This is in line with what was observed in [Reference Baccelli and Ramesan3]. We plan to address the subject further in future research.
$\mu$
may be more complicated than in the case of other parameters. This is in line with what was observed in [Reference Baccelli and Ramesan3]. We plan to address the subject further in future research.
11. Conclusion and future research
We have rigorously proved the structure of the phase diagram of the SIS model under the assumption that the Poisson hypothesis holds. Future research on the basic model will consist in first proving the Poisson hypothesis (ansatz). Another key objective on the basic SIS model will be to establish the phase diagram for parameters other than population density. It would be nice to complement this with computational results like those established for the AIR and DOCS variants of the model. Several further variants of the basic model can also be considered, such as SIRS-type models where individuals go through a recovery phase (where they cannot be infected) before becoming susceptible again. We will also study further spatial SIS dynamics. Other basic queueing models, for instance finite-capacity queues, can also be considered. In fact, such epidemics can be devised on virtually all queueing network models in the literature.
Appendix A. Rate conservation
One can rewrite (6) as
Let I denote the stationary infection epoch point process. Its intensity is
![]() $a_i = \alpha {\mathbb{E}}[XY]$
, and by Papangelou’s theorem [Reference Baccelli and Brémaud1],
$a_i = \alpha {\mathbb{E}}[XY]$
, and by Papangelou’s theorem [Reference Baccelli and Brémaud1],
with
![]() ${\mathbb{E}}^0_{I}$
denoting expectation with respect to the Palm probability with respect to I [Reference Baccelli and Brémaud1]. Hence the left-hand side of the last equality is
${\mathbb{E}}^0_{I}$
denoting expectation with respect to the Palm probability with respect to I [Reference Baccelli and Brémaud1]. Hence the left-hand side of the last equality is
![]() $\lambda p {\mathbb{E}} [Y] + a_i {\mathbb{E}}^0_{I}[ Y]$
, in which we recognize half of the increase rate of
$\lambda p {\mathbb{E}} [Y] + a_i {\mathbb{E}}^0_{I}[ Y]$
, in which we recognize half of the increase rate of
![]() ${\mathbb{E}}[Y(Y-1)]$
. Let
${\mathbb{E}}[Y(Y-1)]$
. Let
![]() $M_i$
denote the point process of recovery or departures of infected customers. The right-hand side of (53) can be rewritten as
$M_i$
denote the point process of recovery or departures of infected customers. The right-hand side of (53) can be rewritten as
with
![]() $d_i$
the intensity of
$d_i$
the intensity of
![]() $M_i$
and the same Palm probability notation as above. This is twice the decrease rate of
$M_i$
and the same Palm probability notation as above. This is twice the decrease rate of
![]() $Y(Y-1)$
. Hence (6) is nothing else than the RCP for
$Y(Y-1)$
. Hence (6) is nothing else than the RCP for
![]() $\frac 1 2 Y(Y-1)$
.
$\frac 1 2 Y(Y-1)$
.
The RCP for
![]() $Y^2$
in turn reads
$Y^2$
in turn reads
Similarly, we can rewrite (7) as
or equivalently
By the same arguments, the right-hand side is half the decrease rate of the second factorial moment of X due to infection and departures. The left-hand side is half the increase rate of the same quantity due to arrivals of susceptible customers and recoveries of infected customers. This equation is hence the RCP for
![]() $\frac 1 2 X(X-1)$
. The RCP for
$\frac 1 2 X(X-1)$
. The RCP for
![]() $X^2$
reads
$X^2$
reads
If we differentiate the PDE with respect to x and y (or y and x) and taking
![]() $x=y=1$
, we get
$x=y=1$
, we get
It is easy to check that inserting the two relations from the last lemma into the equation above does not give anything new. It just confirms that
![]() $X+Y$
is Poisson-
$X+Y$
is Poisson-
![]() $\lambda/\mu$
. It is easy to check that this is in fact the RCP for XY.
$\lambda/\mu$
. It is easy to check that this is in fact the RCP for XY.
Remark 7. Using the Palm interpretation given above, and PASTA, it is easy to check that (6) can be rewritten as
with
![]() $\mu_i=\mu{\mathbb{E}}[Y]$
the exogenous departure rate in this queue,
$\mu_i=\mu{\mathbb{E}}[Y]$
the exogenous departure rate in this queue,
![]() $a_s=\beta{\mathbb{E}}[Y]$
the recovery rate, and
$a_s=\beta{\mathbb{E}}[Y]$
the recovery rate, and
![]() $a_i=\alpha{\mathbb{E}}[XY]$
the infection rate. This is nothing but the classical property that, in the ‘infected queue’, the Palm expectation of the number of customers just before arrivals coincides with the Palm expectation of the number of customers just after departures. Similarly, (7) reads
$a_i=\alpha{\mathbb{E}}[XY]$
the infection rate. This is nothing but the classical property that, in the ‘infected queue’, the Palm expectation of the number of customers just before arrivals coincides with the Palm expectation of the number of customers just after departures. Similarly, (7) reads
with similar notation.
Corollary 4. The following relations hold:
and
 \begin{eqnarray}& & \hspace{-1.6cm} \frac \lambda \mu\left(\lambda p +\frac {\mu +\beta} {\mu\alpha} (2\mu(\mu q+\beta) -\lambda \alpha)\right)-\left(\lambda p +\mu+\beta +\frac 2 \alpha (\mu+\beta)^2\right) {\mathbb{E}} [X] \nonumber \\& & +(\mu+\beta) {\mathbb{E}}[X^2] =-\alpha {\mathbb{E}}\big[ XY^2\big].\end{eqnarray}
\begin{eqnarray}& & \hspace{-1.6cm} \frac \lambda \mu\left(\lambda p +\frac {\mu +\beta} {\mu\alpha} (2\mu(\mu q+\beta) -\lambda \alpha)\right)-\left(\lambda p +\mu+\beta +\frac 2 \alpha (\mu+\beta)^2\right) {\mathbb{E}} [X] \nonumber \\& & +(\mu+\beta) {\mathbb{E}}[X^2] =-\alpha {\mathbb{E}}\big[ XY^2\big].\end{eqnarray}
Proof. Use (4) to eliminate
![]() ${\mathbb{E}}[XY]$
in each of the relations of Lemma 2. Use also the relations
${\mathbb{E}}[XY]$
in each of the relations of Lemma 2. Use also the relations
![]() ${\mathbb{E}}[X]+{\mathbb{E}}[Y]= \frac \lambda \mu $
and
${\mathbb{E}}[X]+{\mathbb{E}}[Y]= \frac \lambda \mu $
and
![]() $ {\mathbb{E}}[X^2] + 2{\mathbb{E}}[XY] + {\mathbb{E}}[Y^2] = \frac {\lambda^2} {\mu^2} + \frac \lambda \mu $
to get the second relation.
$ {\mathbb{E}}[X^2] + 2{\mathbb{E}}[XY] + {\mathbb{E}}[Y^2] = \frac {\lambda^2} {\mu^2} + \frac \lambda \mu $
to get the second relation.
Appendix B. Proofs of Lemmas 5, 6, and 7
Proof of Lemma 5. The proof consists of four steps: monotonicity, concavity, strict concavity, and differentiability.
Below, to make the proof more transparent, we use the notation
![]() $N_I(t)$
instead of X(t) and
$N_I(t)$
instead of X(t) and
![]() $N_S(t)$
instead of Y(t). In addition, the properties are expressed with respect to
$N_S(t)$
instead of Y(t). In addition, the properties are expressed with respect to
![]() $\lambda=\eta\mu$
rather than
$\lambda=\eta\mu$
rather than
![]() $\eta$
. Since
$\eta$
. Since
![]() $\mu$
is a constant, this is equivalent.
$\mu$
is a constant, this is equivalent.
(1) Monotonicity. Consider the typical busy cycle. Assume that the first customer arrives at an empty system at time 0 and let
![]() $T>0$
be the first time when the system becomes empty again. We have to show that the mean number of infected customers that depart from the system within the time interval [0, T] is an increasing function of p.
$T>0$
be the first time when the system becomes empty again. We have to show that the mean number of infected customers that depart from the system within the time interval [0, T] is an increasing function of p.
For that, we consider two models, with input probabilities of being infected p and
![]() $\widehat{p}>p$
. For the input probability p and for
$\widehat{p}>p$
. For the input probability p and for
![]() $0\le t \le T$
, we denote by N(t) the total number of customers at time
$0\le t \le T$
, we denote by N(t) the total number of customers at time
![]() $t>0$
, by
$t>0$
, by
![]() $N_I(t)$
the number of infected customers, and by
$N_I(t)$
the number of infected customers, and by
![]() $N_S(t)$
the number of susceptible customers. Clearly,
$N_S(t)$
the number of susceptible customers. Clearly,
![]() $N(t)=N_I(t)+N_S(t)$
. Let
$N(t)=N_I(t)+N_S(t)$
. Let
![]() $\widehat{N}(t)$
,
$\widehat{N}(t)$
,
![]() $\widehat{N}_I(t)$
, and
$\widehat{N}_I(t)$
, and
![]() $\widehat{N}_S(t)$
by the corresponding processes related to probability
$\widehat{N}_S(t)$
by the corresponding processes related to probability
![]() $\widehat{p}$
, with
$\widehat{p}$
, with
![]() $\widehat{N}(t)=\widehat{N}_I(t)+\widehat{N}_S(t)$
for
$\widehat{N}(t)=\widehat{N}_I(t)+\widehat{N}_S(t)$
for
![]() $t\ge 0$
.
$t\ge 0$
.
We produce a coupling of the two models such that, for all
![]() $0\le t\le T$
,
$0\le t\le T$
,
![]() $N(t)=\widehat{N}(t)$
a.s., while
$N(t)=\widehat{N}(t)$
a.s., while
![]() $\widehat{N}_I(t)\ge N_I(t)$
and, therefore,
$\widehat{N}_I(t)\ge N_I(t)$
and, therefore,
![]() $\widehat{N}_S(t)\le N_S(t)$
. Thus, for the total numbers of departures of infected customers within the first busy cycle, we get
$\widehat{N}_S(t)\le N_S(t)$
. Thus, for the total numbers of departures of infected customers within the first busy cycle, we get
![]() $D_I(T) \le \widehat{D}_I(T)$
a.s. Moreover, we will show that
$D_I(T) \le \widehat{D}_I(T)$
a.s. Moreover, we will show that
![]() ${\mathbb{P}}(D_I(T) < \widehat{D}_I(T))>0$
.
${\mathbb{P}}(D_I(T) < \widehat{D}_I(T))>0$
.
Let
![]() $t_n$
,
$t_n$
,
![]() $n\ge 1$
, be exponential-
$n\ge 1$
, be exponential-
![]() $\lambda$
random variables; let
$\lambda$
random variables; let
![]() $\sigma_{n,j}$
,
$\sigma_{n,j}$
,
![]() $n,j\ge 1$
, be exponential-
$n,j\ge 1$
, be exponential-
![]() $\mu$
random variables; let
$\mu$
random variables; let
![]() $a_{n,i,j}$
be exponential-
$a_{n,i,j}$
be exponential-
![]() $\alpha$
random variables; let
$\alpha$
random variables; let
![]() $b_{n,j}$
be exponential-
$b_{n,j}$
be exponential-
![]() $\beta$
random variables; and let
$\beta$
random variables; and let
![]() $u_{n}$
have a uniform distribution in the interval (0, 1). We assume all these random variables to be mutually independent.
$u_{n}$
have a uniform distribution in the interval (0, 1). We assume all these random variables to be mutually independent.
We introduce embedded epochs
![]() $T_0=0<T_1< T_2 < \ldots < T_{\psi}=T$
, where
$T_0=0<T_1< T_2 < \ldots < T_{\psi}=T$
, where
![]() $\psi$
is a random natural number representing the total number of events (jumps) that occur in both systems. This is not restrictive, as some of these events will be fictitious in either system. Both processes
$\psi$
is a random natural number representing the total number of events (jumps) that occur in both systems. This is not restrictive, as some of these events will be fictitious in either system. Both processes
![]() $(N_S(t),N_I(t))$
and
$(N_S(t),N_I(t))$
and
![]() $(\widehat{N}_S(t),\widehat{N}_I(t))$
are piecewise constant and may make jumps only at time instants
$(\widehat{N}_S(t),\widehat{N}_I(t))$
are piecewise constant and may make jumps only at time instants
![]() $T_n$
. We assume the processes to be right-continuous, and customers to be numbered in each group at any time, in a way that we will make precise in due time.
$T_n$
. We assume the processes to be right-continuous, and customers to be numbered in each group at any time, in a way that we will make precise in due time.
At time
![]() $T_0=0$
, we let
$T_0=0$
, we let
and
Then we evaluate the values of the processes recursively: that is, we produce both time
![]() $T_{n+1}$
and their values at time
$T_{n+1}$
and their values at time
![]() $T_{n+1}$
given time
$T_{n+1}$
given time
![]() $T_n$
, their values at time
$T_n$
, their values at time
![]() $T_n$
, and the values of
$T_n$
, and the values of
![]() $t_{n+1}$
,
$t_{n+1}$
,
![]() $u_{n+1}$
,
$u_{n+1}$
,
![]() $\{\sigma_{n+1,j}\}_{j\ge 1}$
,
$\{\sigma_{n+1,j}\}_{j\ge 1}$
,
![]() $\{a_{n+1,i,j}\}_{i,j\ge 1}$
,
$\{a_{n+1,i,j}\}_{i,j\ge 1}$
,
![]() $\{b_{n+1,j}\}_{j\ge 1}$
.
$\{b_{n+1,j}\}_{j\ge 1}$
.
Assume we have introduced both processes up to time
![]() $T_n$
and shown that
$T_n$
and shown that
![]() $\widehat{N}_I(T_n)\ge N_I(T_n)$
and
$\widehat{N}_I(T_n)\ge N_I(T_n)$
and
![]() $\widehat{N}(T_n)=N(T_n)$
. Assume that
$\widehat{N}(T_n)=N(T_n)$
. Assume that
![]() $\sigma_{n+1,j}$
,
$\sigma_{n+1,j}$
,
![]() $1\le j \le N(T_n)$
, are the remaining service times of all present customers, where customers numbered
$1\le j \le N(T_n)$
, are the remaining service times of all present customers, where customers numbered
![]() $1,\ldots,N_I(T_n)$
are infected in both systems, customers numbered
$1,\ldots,N_I(T_n)$
are infected in both systems, customers numbered
![]() $N_I(T_n)+1,\ldots,\widehat{N}_I(T_n)$
are susceptible in the first system and infected in the second system, and customers numbered
$N_I(T_n)+1,\ldots,\widehat{N}_I(T_n)$
are susceptible in the first system and infected in the second system, and customers numbered
![]() $\widehat{N}_I(T_n)+1, \ldots,N(T_n)$
are susceptible in both systems. Assume that the random variables
$\widehat{N}_I(T_n)+1, \ldots,N(T_n)$
are susceptible in both systems. Assume that the random variables
![]() $b_{n+1,j}$
, for
$b_{n+1,j}$
, for
![]() $j=N_I(T_n)+1,\ldots,\widehat{N}_I(T_n)$
, represent the recovery times for the corresponding infected customers in the second system, and that for
$j=N_I(T_n)+1,\ldots,\widehat{N}_I(T_n)$
, represent the recovery times for the corresponding infected customers in the second system, and that for
![]() $j=1,\ldots, N_I(T_n)$
they represent the recovery times for customers that are infected in both systems. Assume that if customer j is infected and customer i is susceptible at time
$j=1,\ldots, N_I(T_n)$
they represent the recovery times for customers that are infected in both systems. Assume that if customer j is infected and customer i is susceptible at time
![]() $T_n$
, then
$T_n$
, then
![]() $a_{n+1,j,i}$
is the instant when j may infect i.
$a_{n+1,j,i}$
is the instant when j may infect i.
Consider the random sets of integers
![]() $C_1(n) = \{j\,:\, 1\le j \le N_I(T_n)\}$
,
$C_1(n) = \{j\,:\, 1\le j \le N_I(T_n)\}$
,
![]() $C_2(n) = \{j\,:\, N_I(T_n)< j \le \widehat{N}_I(T_n)\}$
, and
$C_2(n) = \{j\,:\, N_I(T_n)< j \le \widehat{N}_I(T_n)\}$
, and
![]() $C_3(n) = \{j\,:\, \widehat{N}_I(T_n)< j \le N(T_n)\}$
. For
$C_3(n) = \{j\,:\, \widehat{N}_I(T_n)< j \le N(T_n)\}$
. For
![]() $k=1,2,3$
, let
$k=1,2,3$
, let
where
![]() $\min_{\emptyset} = \infty$
, by convention. Next, for
$\min_{\emptyset} = \infty$
, by convention. Next, for
![]() $k,l=1,2,3$
, let
$k,l=1,2,3$
, let
Finally, let
Therefore,
![]() $\theta_{n+1}$
is the next time instant when something happens in any of the systems—either the arrival of a new customer, the departure of a present customer, the recovery of a present customer, or the infection of one present customer by another one. Then
$\theta_{n+1}$
is the next time instant when something happens in any of the systems—either the arrival of a new customer, the departure of a present customer, the recovery of a present customer, or the infection of one present customer by another one. Then
If
![]() $\theta_{n+1}=t_{n+1}$
, i.e. a new customer arrives, then
$\theta_{n+1}=t_{n+1}$
, i.e. a new customer arrives, then
and
![]() $N(T_{n+1})=\widehat{N}(T_{n+1})=N(T_n)+1$
,
$N(T_{n+1})=\widehat{N}(T_{n+1})=N(T_n)+1$
,
If
![]() $\theta_{n+1}= \min_{1\le k\le 3} \Sigma_{n+1,k}$
, then one of the present customers departs. If
$\theta_{n+1}= \min_{1\le k\le 3} \Sigma_{n+1,k}$
, then one of the present customers departs. If
![]() $\Sigma_{n+1,1}$
is the smallest among the three, then there is a departure of a customer that is infected in both systems. Therefore,
$\Sigma_{n+1,1}$
is the smallest among the three, then there is a departure of a customer that is infected in both systems. Therefore,
![]() $D_I(T_{n+1})=D_I(T_n)+1$
,
$D_I(T_{n+1})=D_I(T_n)+1$
,
![]() $\widehat{D}_I(T_{n+1})=\widehat{D}_I(T_n)+1$
,
$\widehat{D}_I(T_{n+1})=\widehat{D}_I(T_n)+1$
,
![]() $D_S(T_{n+1})=D_S(T_n)$
,
$D_S(T_{n+1})=D_S(T_n)$
,
![]() $\widehat{D}_S(T_{n+1})=\widehat{D}_S(T_n)$
, and
$\widehat{D}_S(T_{n+1})=\widehat{D}_S(T_n)$
, and
![]() $N_I(T_{n+1})=$
$N_I(T_{n+1})=$
![]() $N_I(T_n)-1$
,
$N_I(T_n)-1$
,
![]() $\widehat{N}_I(T_{n+1})=\widehat{N}_I(T_n)-1$
,
$\widehat{N}_I(T_{n+1})=\widehat{N}_I(T_n)-1$
,
![]() $N_S(T_{n+1})=N_S(T_n)$
,
$N_S(T_{n+1})=N_S(T_n)$
,
![]() $\widehat{N}_S(T_{n+1})=\widehat{N}_S(T_n)$
. By the symmetry, if
$\widehat{N}_S(T_{n+1})=\widehat{N}_S(T_n)$
. By the symmetry, if
![]() $\sigma_{n+1,3}$
is the smallest, then there is a departure of a customer that is susceptible in both systems. Therefore,
$\sigma_{n+1,3}$
is the smallest, then there is a departure of a customer that is susceptible in both systems. Therefore,
![]() $D_S(T_{n+1})=D_S(T_n)+1$
,
$D_S(T_{n+1})=D_S(T_n)+1$
,
![]() $\widehat{D}_S(T_{n+1})=\widehat{D}_S(T_n)+1$
,
$\widehat{D}_S(T_{n+1})=\widehat{D}_S(T_n)+1$
,
![]() $D_I(T_{n+1})=D_I(T_n)$
,
$D_I(T_{n+1})=D_I(T_n)$
,
![]() $\widehat{D}_I(T_{n+1})=\widehat{D}_I(T_n)$
, and
$\widehat{D}_I(T_{n+1})=\widehat{D}_I(T_n)$
, and
![]() $N_S(T_{n+1})=N_S(T_n)-1$
,
$N_S(T_{n+1})=N_S(T_n)-1$
,
![]() $\widehat{N}_S(T_{n+1})=\widehat{N}_S(T_n)-1$
,
$\widehat{N}_S(T_{n+1})=\widehat{N}_S(T_n)-1$
,
![]() $N_I(T_{n+1})=N_I(T_n)$
,
$N_I(T_{n+1})=N_I(T_n)$
,
![]() $\widehat{N}_I(T_{n+1})=\widehat{N}_I(T_n)$
.
$\widehat{N}_I(T_{n+1})=\widehat{N}_I(T_n)$
.
Next, if
![]() $\Sigma_{n+1,2}$
is the smallest, then this means that the strict inequality
$\Sigma_{n+1,2}$
is the smallest, then this means that the strict inequality
![]() $N_I(T_n)<\widehat{N}_I(T_n)$
holds and there is a departure of a customer that is susceptible in the first system and infected in the second. Then
$N_I(T_n)<\widehat{N}_I(T_n)$
holds and there is a departure of a customer that is susceptible in the first system and infected in the second. Then
![]() $D_I(T_{n+1})=D_I(T_n)$
,
$D_I(T_{n+1})=D_I(T_n)$
,
![]() $\widehat{D}_I(T_{n+1})=\widehat{D}_I(T_n)+1$
,
$\widehat{D}_I(T_{n+1})=\widehat{D}_I(T_n)+1$
,
![]() $D_S(T_{n+1})=D_S(T_n)+1$
,
$D_S(T_{n+1})=D_S(T_n)+1$
,
![]() $\widehat{D}_S(T_{n+1})=\widehat{D}_S(T_n)$
, and
$\widehat{D}_S(T_{n+1})=\widehat{D}_S(T_n)$
, and
![]() $N_I(T_{n+1})=N_I(T_n)$
,
$N_I(T_{n+1})=N_I(T_n)$
,
![]() $\widehat{N}_I(T_{n+1})=\widehat{N}_I(T_n)-1$
,
$\widehat{N}_I(T_{n+1})=\widehat{N}_I(T_n)-1$
,
![]() $N_S(T_{n+1})=N_S(T_n)-1$
,
$N_S(T_{n+1})=N_S(T_n)-1$
,
![]() $\widehat{N}_S(T_{n+1})=\widehat{N}_S(T_n)$
. One can see that in all three cases
$\widehat{N}_S(T_{n+1})=\widehat{N}_S(T_n)$
. One can see that in all three cases
Similarly, if
![]() $\theta_{n+1} = \min_{k=1,2} B_{n+1,k}$
, then the numbers of departures do not change, and either (a) there is a simultaneous recovery of a customer that was infected in both systems, or (b) there was a customer that was susceptible in the first system and infected in the second, it has recovered in the second system, and nothing has changed in the first system. Again, one can see that the needed inequalities (62) continue to hold.
$\theta_{n+1} = \min_{k=1,2} B_{n+1,k}$
, then the numbers of departures do not change, and either (a) there is a simultaneous recovery of a customer that was infected in both systems, or (b) there was a customer that was susceptible in the first system and infected in the second, it has recovered in the second system, and nothing has changed in the first system. Again, one can see that the needed inequalities (62) continue to hold.
Finally, if
![]() $\theta_{n+1} = \min (A_{n+1,2,3}, A_{n+1,1,3},A_{n+1,1,2})$
, then the number of departures stays the same and there are again three scenarios. If
$\theta_{n+1} = \min (A_{n+1,2,3}, A_{n+1,1,3},A_{n+1,1,2})$
, then the number of departures stays the same and there are again three scenarios. If
![]() $A_{n+1,2,3}$
is the smallest among the three, then the set
$A_{n+1,2,3}$
is the smallest among the three, then the set
![]() $C_2(n)$
of customers that are susceptible in the first system and infected in the second system at time
$C_2(n)$
of customers that are susceptible in the first system and infected in the second system at time
![]() $T_n$
is non-empty, one of them has infected one of the susceptible customers in the second system, and nothing has changed in the first system. Therefore, the number of susceptible customers in the second system decreases and the number of susceptible customers in the first system stays the same. Thus, the needed inequalities (62) continue to hold. If
$T_n$
is non-empty, one of them has infected one of the susceptible customers in the second system, and nothing has changed in the first system. Therefore, the number of susceptible customers in the second system decreases and the number of susceptible customers in the first system stays the same. Thus, the needed inequalities (62) continue to hold. If
![]() $A_{n+1,1,2}$
is the smallest, then the set
$A_{n+1,1,2}$
is the smallest, then the set
![]() $C_2(n)$
is non-empty again, so we have strict inequality
$C_2(n)$
is non-empty again, so we have strict inequality
![]() $N_S(T_n)>\widehat{N}_S(T_n)$
, and at time
$N_S(T_n)>\widehat{N}_S(T_n)$
, and at time
![]() $T_{n+1}$
, one of customers from this set becomes infected in the first system, while nothing changes in the second system. Therefore,
$T_{n+1}$
, one of customers from this set becomes infected in the first system, while nothing changes in the second system. Therefore,
as required. If
![]() $A_{n+1,1,3}$
is the smallest, then one of the customers that is susceptible at time
$A_{n+1,1,3}$
is the smallest, then one of the customers that is susceptible at time
![]() $T_n$
in both systems becomes infected in both systems. So the required inequalities continue to hold.
$T_n$
in both systems becomes infected in both systems. So the required inequalities continue to hold.
This completes the proof of the fact that
![]() $D_I(t)\le \widehat{D}_I(t)$
at any time
$D_I(t)\le \widehat{D}_I(t)$
at any time
![]() $0<t<T$
and, in particular,
$0<t<T$
and, in particular,
![]() $D_I\equiv D_I(T) \le \widehat{D}_I\equiv \widehat{D}_I(T)$
a.s. It is left to show that the inequality may be strict with positive probability. However, this is almost obvious:
$D_I\equiv D_I(T) \le \widehat{D}_I\equiv \widehat{D}_I(T)$
a.s. It is left to show that the inequality may be strict with positive probability. However, this is almost obvious:
where the events on the right are independent and of positive probabilities.
Remark 8. The monotonicity property discussed above can be extended in two ways:
-
1. Rather than comparing the two systems in a busy cycle, one compares them over the whole time half-axis. For this, one has to start the two systems at time
 $T_0=0$
with the same total population
$T_0=0$
with the same total population
 $N(T_0)=\widehat{N}(T_0)$
and with more infected customers in the dominating system than in the dominated one, i.e., with
$N(T_0)=\widehat{N}(T_0)$
and with more infected customers in the dominating system than in the dominated one, i.e., with
 $N_I(T_0)\le \widehat{N}_I(T_0)$
a.s. Based on the same arguments, one proves by induction over the overall jump times
$N_I(T_0)\le \widehat{N}_I(T_0)$
a.s. Based on the same arguments, one proves by induction over the overall jump times
 $\{T_n\}$
that in the coupling described above, for all t,
$\{T_n\}$
that in the coupling described above, for all t,
 $N(t)= \widehat{N}(t)$
a.s. and
$N(t)= \widehat{N}(t)$
a.s. and
 $N_I(t)\le \widehat{N}_I(t)$
a.s.
$N_I(t)\le \widehat{N}_I(t)$
a.s. -
2. The setting of the previous item can be extended to the situation where, rather than having constant fractions of the Poisson arrivals, p and
 $\widehat p$
, that are infected in the two systems, with
$\widehat p$
, that are infected in the two systems, with
 $p\le \widehat p$
, one has deterministic time-varying fractions p(t) and
$p\le \widehat p$
, one has deterministic time-varying fractions p(t) and
 $\widehat p(t)$
of the Poisson arrivals which are infected in the two systems, with
$\widehat p(t)$
of the Poisson arrivals which are infected in the two systems, with
 $p(.)\le\widehat p(.)$
. In this case we again have that, if
$p(.)\le\widehat p(.)$
. In this case we again have that, if
 $N_I(T_0)\le \widehat{N}_I(T_0)$
a.s., then in the same coupling,
$N_I(T_0)\le \widehat{N}_I(T_0)$
a.s., then in the same coupling,
 $N(t)= \widehat{N}(t)$
a.s. and
$N(t)= \widehat{N}(t)$
a.s. and
 $N_I(t)\le \widehat{N}_I(t)$
a.s. for all t.
$N_I(t)\le \widehat{N}_I(t)$
a.s. for all t.
(2) Concavity. We now introduce a slightly different coupling that allows us to consider simultaneously models with different parameters.
From now on, we do not enumerate customers. Instead, we consider a countable number
![]() ${\mathcal Z}$
of ‘locations’ for them that coincide with ‘servers’. More precisely, we assume that an arriving customer chooses an empty server at random and stays there until its departure from the system.
${\mathcal Z}$
of ‘locations’ for them that coincide with ‘servers’. More precisely, we assume that an arriving customer chooses an empty server at random and stays there until its departure from the system.
We continue to consider a single busy cycle on the time interval [0, T]. We again denote by
![]() $T_0<T_1<T_2<\ldots$
the time instants when the state of the systems may change. Hence, the state of the system Z(t) at time t is a collection of pairs
$T_0<T_1<T_2<\ldots$
the time instants when the state of the systems may change. Hence, the state of the system Z(t) at time t is a collection of pairs
![]() $\{ (z,c_z(t)), z\in{\mathcal Z}\}$
, where z is a server and
$\{ (z,c_z(t)), z\in{\mathcal Z}\}$
, where z is a server and
![]() $c_z$
is its ‘color’. Here
$c_z$
is its ‘color’. Here
![]() $c_z(t) ={\bf n}$
(where ‘n’ means ‘no color’) if server z is empty at time t, and
$c_z(t) ={\bf n}$
(where ‘n’ means ‘no color’) if server z is empty at time t, and
![]() $c_z(t)$
has one of several other colors otherwise. (The meanings of these colors will be explained in due time.) Let
$c_z(t)$
has one of several other colors otherwise. (The meanings of these colors will be explained in due time.) Let
![]() ${\mathcal N}(t) = \{z \,:\, c_z(t) \ne {\bf n} \}$
be the set of occupied servers, and let
${\mathcal N}(t) = \{z \,:\, c_z(t) \ne {\bf n} \}$
be the set of occupied servers, and let
![]() $N(t) = \sum_{z\in {\mathcal z}} {\mathbf I} (c_z(t)\ne{\bf n})$
denote its cardinality.
$N(t) = \sum_{z\in {\mathcal z}} {\mathbf I} (c_z(t)\ne{\bf n})$
denote its cardinality.
We introduce the following sequences of random variables:
-
•
 $\{u_n\}_{n\ge 0}$
are uniformly distributed in (0, 1);
$\{u_n\}_{n\ge 0}$
are uniformly distributed in (0, 1); -
•
 $\{t_n\}_{n\ge 1}$
are exponential-
$\{t_n\}_{n\ge 1}$
are exponential-
 $\lambda$
;
$\lambda$
; -
•
 $\{\sigma_{n,z}\}_{n\ge 0, z\in{\mathcal Z}}$
are exponential-
$\{\sigma_{n,z}\}_{n\ge 0, z\in{\mathcal Z}}$
are exponential-
 $\mu$
;
$\mu$
; -
•
 $\{b_{n,z}\}_{n\ge 0, z\in {\mathcal Z}}$
are exponential-
$\{b_{n,z}\}_{n\ge 0, z\in {\mathcal Z}}$
are exponential-
 $\beta$
;
$\beta$
; -
•
 $\{a_{n,z,v}\}_{n\ge 0, z,v\in {\mathcal Z}, z\ne v}$
are exponential-
$\{a_{n,z,v}\}_{n\ge 0, z,v\in {\mathcal Z}, z\ne v}$
are exponential-
 $\alpha$
.
$\alpha$
.
We assume that all these random variables are mutually independent.
Let
![]() $T_0=0$
. Introduce recursively
$T_0=0$
. Introduce recursively
![]() $\{\theta_k\}$
and
$\{\theta_k\}$
and
![]() $T_k=\sum_1^k \theta_j$
. Let
$T_k=\sum_1^k \theta_j$
. Let
![]() ${\mathcal N}_k = {\mathcal N} (T_k+0)$
. For
${\mathcal N}_k = {\mathcal N} (T_k+0)$
. For
![]() $n\ge 1$
, assuming that
$n\ge 1$
, assuming that
![]() $T_{n-1}$
is defined, we let
$T_{n-1}$
is defined, we let
![]() $\Sigma_n = \min_{z\in {\mathcal N}_{n-1}} \sigma_{n,z}$
,
$\Sigma_n = \min_{z\in {\mathcal N}_{n-1}} \sigma_{n,z}$
,
![]() $B_n = \min_{z\in {\mathcal N}_{n-1}} b_{n,z}$
,
$B_n = \min_{z\in {\mathcal N}_{n-1}} b_{n,z}$
,
![]() $A_n = \min_{z,v\in {\mathcal N}_{n-1}, z\ne v} a_{n,z,v}$
. Then let
$A_n = \min_{z,v\in {\mathcal N}_{n-1}, z\ne v} a_{n,z,v}$
. Then let
Now we are ready to define a ‘three-color’ process. Let
![]() $p\ge 0$
,
$p\ge 0$
,
![]() $q\ge 0$
,
$q\ge 0$
,
![]() $r>0$
be numbers that sum up to 1,
$r>0$
be numbers that sum up to 1,
![]() $p+r+q=1$
. We assume that each arriving customer gets the red color with probability p, the magenta color with probability r, and the green color with probability q. It occupies a server (that gets the same color as the customer).
$p+r+q=1$
. We assume that each arriving customer gets the red color with probability p, the magenta color with probability r, and the green color with probability q. It occupies a server (that gets the same color as the customer).
We assume the process to be piecewise constant between time instants
![]() $T_n$
. We introduce coloring by induction.
$T_n$
. We introduce coloring by induction.
At time
![]() $T_0=0$
, we color the arriving customer magenta if
$T_0=0$
, we color the arriving customer magenta if
![]() $u_0\le r$
, red if
$u_0\le r$
, red if
![]() $r<u_0\le r+p$
, and green if
$r<u_0\le r+p$
, and green if
![]() $u_0>r+p$
, and we assume that the customer keeps its color within the time interval
$u_0>r+p$
, and we assume that the customer keeps its color within the time interval
![]() $(T_0,T_1]$
.
$(T_0,T_1]$
.
Assume that coloring is done up to time
![]() $T_n$
. Proceed with coloring for the time interval
$T_n$
. Proceed with coloring for the time interval
![]() $(T_n,T_{n+1}]$
.
$(T_n,T_{n+1}]$
.
If
![]() $\theta_n=t_n$
, then we place an arriving customer at one of the empty servers and color the customer magenta if
$\theta_n=t_n$
, then we place an arriving customer at one of the empty servers and color the customer magenta if
![]() $u_n\le r$
, red if
$u_n\le r$
, red if
![]() $r<u_n\le r+p$
, and green if
$r<u_n\le r+p$
, and green if
![]() $u_n>r+p$
.
$u_n>r+p$
.
If
![]() $\theta_n=\sigma_{n,z}$
for some
$\theta_n=\sigma_{n,z}$
for some
![]() $z\in {\mathcal N}_n$
, then customer z leaves the system and the corresponding server becomes idle (‘no color’).
$z\in {\mathcal N}_n$
, then customer z leaves the system and the corresponding server becomes idle (‘no color’).
If
![]() $\theta_n = \beta_{n,z}$
for some
$\theta_n = \beta_{n,z}$
for some
![]() $z\in {\mathcal N}_n$
, then customer z becomes green, regardless of what color it had before.
$z\in {\mathcal N}_n$
, then customer z becomes green, regardless of what color it had before.
If
![]() $\theta_n = A_n$
, then we have to consider three cases. At time
$\theta_n = A_n$
, then we have to consider three cases. At time
![]() $T_n$
, let
$T_n$
, let
![]() ${\mathcal N}_{n,m}, \ {\mathcal N}_{n,r}, \ {\mathcal N}_{n,g}$
be the sets of magenta, red, and green customers, where clearly
${\mathcal N}_{n,m}, \ {\mathcal N}_{n,r}, \ {\mathcal N}_{n,g}$
be the sets of magenta, red, and green customers, where clearly
Let
![]() $N_{n,m}$
,
$N_{n,m}$
,
![]() $N_{n,r}$
, and
$N_{n,r}$
, and
![]() $N_{n,g}$
be the corresponding cardinalities. If
$N_{n,g}$
be the corresponding cardinalities. If
![]() $\theta_n = a_{n,z,v}$
for some
$\theta_n = a_{n,z,v}$
for some
![]() $z\in {\mathcal N}_{n,g}$
, then (since green means susceptible) there is no new infection and all colors stay the same (one could say that this is a ‘false coloring’).
$z\in {\mathcal N}_{n,g}$
, then (since green means susceptible) there is no new infection and all colors stay the same (one could say that this is a ‘false coloring’).
If
![]() $\theta_n = a_{n,z,v}$
for some
$\theta_n = a_{n,z,v}$
for some
![]() $z\in {\mathcal N}_{n,r}$
, then customer v (and the corresponding server) becomes red, whatever color it had before.
$z\in {\mathcal N}_{n,r}$
, then customer v (and the corresponding server) becomes red, whatever color it had before.
Finally, if
![]() $\theta_n = a_{n,z,v}$
for some
$\theta_n = a_{n,z,v}$
for some
![]() $z\in {\mathcal N}_{n,m}$
, then customer v (and the corresponding server) becomes magenta if it was either magenta or green before—or remains red if it was red before.
$z\in {\mathcal N}_{n,m}$
, then customer v (and the corresponding server) becomes magenta if it was either magenta or green before—or remains red if it was red before.
Thus, we have defined the three-color dynamics within the busy cycle.
As a result of the proposed coupling construction, one can observe the following.
-
1. If we do not distinguish between (i.e. we ‘merge’) the green and magenta colors (and recolor them as ‘new green’), then we get the two-color susceptible–infected model considered earlier, with the probability of green arrivals
 $r+q$
and the probability of red arrivals p; call this model the
$r+q$
and the probability of red arrivals p; call this model the
 $(p, r+q)$
model.
$(p, r+q)$
model. -
2. If we do not distinguish between (i.e. we ‘merge’) the magenta and red colors (and recolor them as ‘new red’), then we get the two-color susceptible–infected model considered earlier, with the probability of green arrivals q and the probability of red arrivals
 $r+p$
; call this model the
$r+p$
; call this model the
 $(r+p,q)$
model.
$(r+p,q)$
model.
This means that, for
![]() $0\le t\le T$
, the random variable
$0\le t\le T$
, the random variable
![]() $N_m(t)$
represents the ‘excess’ of the number of ‘red’ customers in the
$N_m(t)$
represents the ‘excess’ of the number of ‘red’ customers in the
![]() $(r+p,q)$
model in comparison with the
$(r+p,q)$
model in comparison with the
![]() $(p,r+q)$
model.
$(p,r+q)$
model.
Assume now that
![]() $q>0$
and consider the three-color
$q>0$
and consider the three-color
![]() $(r,\widehat{p},\widehat{q})$
-model with
$(r,\widehat{p},\widehat{q})$
-model with
![]() $\widehat{p}>p$
and
$\widehat{p}>p$
and
![]() $r+\widehat{p}+\widehat{q}=1$
. Let
$r+\widehat{p}+\widehat{q}=1$
. Let
![]() $\widehat{\mathcal N}_m(t)$
be the set of magenta customers at time t in this model and
$\widehat{\mathcal N}_m(t)$
be the set of magenta customers at time t in this model and
![]() $\widehat{N}_m(t)$
its cardinality. Then straightforward induction arguments show that
$\widehat{N}_m(t)$
its cardinality. Then straightforward induction arguments show that
![]() $\widehat{\mathcal N}_m(t) \subseteq {\mathcal N}_m(t)$
and, therefore,
$\widehat{\mathcal N}_m(t) \subseteq {\mathcal N}_m(t)$
and, therefore,
![]() $\widehat{N}_m(t)\le N_m(t)$
a.s., for any
$\widehat{N}_m(t)\le N_m(t)$
a.s., for any
![]() $0\le t \le T$
. In turn, this implies that the total number of departures within the first cycle of magenta customers in the corresponding systems, call them
$0\le t \le T$
. In turn, this implies that the total number of departures within the first cycle of magenta customers in the corresponding systems, call them
![]() $D_m(T)$
and
$D_m(T)$
and
![]() $\widehat{D}_m(T)$
, satisfy
$\widehat{D}_m(T)$
, satisfy
![]() $D_m(T) \ge \widehat{D}_m(T)$
a.s. Recall the notation
$D_m(T) \ge \widehat{D}_m(T)$
a.s. Recall the notation
![]() $p_o=g(p)$
. Then
$p_o=g(p)$
. Then
 \begin{eqnarray*} & & g(p) = \frac{{\mathbb{E}} D_g(T)}{{{\mathbb{E}} D(T)}}, \qquad g(p+r) = \frac{{\mathbb{E}}(D_g(T)+D_m(T))}{{{\mathbb{E}} D(T)}}, \\ & & g(\widehat{p}) = \frac{{\mathbb{E}} \widehat{D}_g(T)}{{{\mathbb{E}} D(T)}}, \qquad g(\widehat{p}+r) = \frac{{\mathbb{E}}(\widehat{D}_g(T)+\widehat{D}_m(T))}{{{\mathbb{E}} D(T)}},\end{eqnarray*}
\begin{eqnarray*} & & g(p) = \frac{{\mathbb{E}} D_g(T)}{{{\mathbb{E}} D(T)}}, \qquad g(p+r) = \frac{{\mathbb{E}}(D_g(T)+D_m(T))}{{{\mathbb{E}} D(T)}}, \\ & & g(\widehat{p}) = \frac{{\mathbb{E}} \widehat{D}_g(T)}{{{\mathbb{E}} D(T)}}, \qquad g(\widehat{p}+r) = \frac{{\mathbb{E}}(\widehat{D}_g(T)+\widehat{D}_m(T))}{{{\mathbb{E}} D(T)}},\end{eqnarray*}
where, as before,
![]() ${{\mathbb{E}} D(T)}$
is the mean number of customers served in the first busy cycle (which is the same as the total number of departures within the cycle). Since
${{\mathbb{E}} D(T)}$
is the mean number of customers served in the first busy cycle (which is the same as the total number of departures within the cycle). Since
we get the required concavity.
(3) Strict concavity. It is enough to consider the latter coupling construction and to justify that, for any
![]() $r>0$
and any
$r>0$
and any
![]() $0\le p <\widehat{p} \le 1-r$
,
$0\le p <\widehat{p} \le 1-r$
,
![]() ${\mathbb{P}} (D_m(T)>\widehat{D}_m(T))>0$
. One can see that this strict inequality holds on the following event, which has strictly positive probability:
${\mathbb{P}} (D_m(T)>\widehat{D}_m(T))>0$
. One can see that this strict inequality holds on the following event, which has strictly positive probability:
The latter means that the following sequence of events occurs:
-
• The first customer gets the magenta color in both three-color systems.
-
• Then the second customer appears and gets the green color in the first system and red in the second.
-
• Then the second customer attempts to recolor the first one. This does not work in the first system, where we continue to have one green and one magenta; however, the attempt is successful in the second system, where we get two reds.
-
• Finally, the first customer leaves the system and then the second leaves the system; this ends the busy cycle.
One can see that
![]() $D_m(T)=1>\widehat{D}_m(T)=0$
on the event (63).
$D_m(T)=1>\widehat{D}_m(T)=0$
on the event (63).
(4) Differentiability. Let
![]() $h>0$
be small. For
$h>0$
be small. For
![]() $p>0$
, introduce a four-color model with the colors green, violet, magenta, and red. Consider the second coupling construction introduced in the subsection ‘Concavity’ above. If we have an arrival at time
$p>0$
, introduce a four-color model with the colors green, violet, magenta, and red. Consider the second coupling construction introduced in the subsection ‘Concavity’ above. If we have an arrival at time
![]() $T_n$
, then the new customer is colored green if
$T_n$
, then the new customer is colored green if
![]() $u_n<p-h$
, violet if
$u_n<p-h$
, violet if
![]() $p-h\le u_n < p$
, magenta if
$p-h\le u_n < p$
, magenta if
![]() $p\le u_n < p+h$
, and red if
$p\le u_n < p+h$
, and red if
![]() $u_n \ge p+h$
. Let
$u_n \ge p+h$
. Let
![]() $A_v$
be the event that there is only one violet arrival and no magenta arrival in the (first) busy cycle, and
$A_v$
be the event that there is only one violet arrival and no magenta arrival in the (first) busy cycle, and
![]() $A_m$
that there is only one magenta arrival and no violet arrival. These events have equal probabilities that are of order
$A_m$
that there is only one magenta arrival and no violet arrival. These events have equal probabilities that are of order
![]() $ch+o(h)$
, where
$ch+o(h)$
, where
![]() $c={\mathbb{E}} \nu$
and
$c={\mathbb{E}} \nu$
and
![]() $\nu$
is the mean number of arrivals within a busy cycle; there appear only (at most) three colors (green, violet, and red) on the event
$\nu$
is the mean number of arrivals within a busy cycle; there appear only (at most) three colors (green, violet, and red) on the event
![]() $A_v$
and, similarly, at most three colors (green, magenta, and red) on the event
$A_v$
and, similarly, at most three colors (green, magenta, and red) on the event
![]() $A_m$
. Moreover, the dynamics of the process on the events
$A_m$
. Moreover, the dynamics of the process on the events
![]() $A_v$
and
$A_v$
and
![]() $A_m$
are identical, with the obvious swap of violet and magenta customers. Therefore, the mean number
$A_m$
are identical, with the obvious swap of violet and magenta customers. Therefore, the mean number
![]() ${\mathbb{E}} (D_v(T)\ | A_v)$
of violet departures given the event
${\mathbb{E}} (D_v(T)\ | A_v)$
of violet departures given the event
![]() $A_v$
coincides with the mean number
$A_v$
coincides with the mean number
![]() ${\mathbb{E}} (D_m(T) \ | A_m)$
of magenta departures given the event
${\mathbb{E}} (D_m(T) \ | A_m)$
of magenta departures given the event
![]() $A_m$
. Furthermore, the event that there are two or more violet and/or magenta arrivals has probability
$A_m$
. Furthermore, the event that there are two or more violet and/or magenta arrivals has probability
![]() $O(h^2)=o(h)$
. Since
$O(h^2)=o(h)$
. Since
 \begin{align*}& g(p)-g(p-h) = \frac{{\mathbb{E}} D_v(T)}{{\mathbb{E}} D(T)} = ch \cdot \frac{{\mathbb{E}} (D_v(T)\ | A_v))}{{\mathbb{E}} D(T)} + o(h)\\ &=ch \cdot \frac{{\mathbb{E}} (D_m(T)\ | A_m))}{{\mathbb{E}} D(T)} + o(h) = \frac{{\mathbb{E}} D_m(T)}{{\mathbb{E}} D(T)} +o(h) =g(p+h)-g(p) + o(h),\end{align*}
\begin{align*}& g(p)-g(p-h) = \frac{{\mathbb{E}} D_v(T)}{{\mathbb{E}} D(T)} = ch \cdot \frac{{\mathbb{E}} (D_v(T)\ | A_v))}{{\mathbb{E}} D(T)} + o(h)\\ &=ch \cdot \frac{{\mathbb{E}} (D_m(T)\ | A_m))}{{\mathbb{E}} D(T)} + o(h) = \frac{{\mathbb{E}} D_m(T)}{{\mathbb{E}} D(T)} +o(h) =g(p+h)-g(p) + o(h),\end{align*}
we get
By letting h tend to infinity, we obtain the desired differentiability of the function g at the point p.
Proof of Lemma
6. The proof follows from the following arguments: when
![]() $p=1$
, we have
$p=1$
, we have
![]() $p_o<1$
, and if
$p_o<1$
, and if
![]() $p=0$
, then
$p=0$
, then
![]() $p_o=0$
. The function
$p_o=0$
. The function
![]() $p_o=g(p)$
is monotone increasing, strictly concave, and differentiable. If the right derivative g′(0) is less than or equal to 1, then there is no other solution to
$p_o=g(p)$
is monotone increasing, strictly concave, and differentiable. If the right derivative g′(0) is less than or equal to 1, then there is no other solution to
![]() $p=p_o$
within (0, 1). If
$p=p_o$
within (0, 1). If
![]() $g^{\prime}(0)>1$
, there is exactly one other solution, say
$g^{\prime}(0)>1$
, there is exactly one other solution, say
![]() $p^*$
, to the fixed-point equation
$p^*$
, to the fixed-point equation
![]() $p=g(p) \equiv p_o$
, such that
$p=g(p) \equiv p_o$
, such that
![]() $0<p^*<1$
.
$0<p^*<1$
.
Proof of Lemma
7. Let
![]() $0<\widehat{\lambda}<\lambda$
. By the splitting theorem for Poisson processes, a Poisson-
$0<\widehat{\lambda}<\lambda$
. By the splitting theorem for Poisson processes, a Poisson-
![]() $\widehat{\lambda}$
process may be obtained from a Poisson-
$\widehat{\lambda}$
process may be obtained from a Poisson-
![]() $\lambda$
process through independent and identically distributed thinning of points with acceptance probability
$\lambda$
process through independent and identically distributed thinning of points with acceptance probability
![]() $r=\widehat{\lambda}/\lambda$
.
$r=\widehat{\lambda}/\lambda$
.
Consider the first busy cycle of length T for the infinite-server queue with input rate
![]() $\lambda$
; call it ‘system 1’. Let
$\lambda$
; call it ‘system 1’. Let
![]() $D\equiv D(T)$
be the number of customers that are served in/depart from system 1 within the time interval [0, T]. Then in ‘system 2’ with input rate
$D\equiv D(T)$
be the number of customers that are served in/depart from system 1 within the time interval [0, T]. Then in ‘system 2’ with input rate
![]() $\widehat{\lambda}$
, the total number
$\widehat{\lambda}$
, the total number
![]() $\widehat{D}$
of departures within [0, T] has a conditional binomial distribution Bin(D, r); i.e., given any value
$\widehat{D}$
of departures within [0, T] has a conditional binomial distribution Bin(D, r); i.e., given any value
![]() $D=k$
, we have
$D=k$
, we have
![]() $\widehat{D} \sim Bin (k,r)$
. Then
$\widehat{D} \sim Bin (k,r)$
. Then
![]() ${\mathbb{E}} \widehat{D} = r {\mathbb{E}} D$
.
${\mathbb{E}} \widehat{D} = r {\mathbb{E}} D$
.
Let
![]() $D_I$
be the total number of infected departures from system 1 and
$D_I$
be the total number of infected departures from system 1 and
![]() $\widehat{D}_I$
from system 2, within the time interval [0, T]. Clearly,
$\widehat{D}_I$
from system 2, within the time interval [0, T]. Clearly,
![]() $ D_I\ge \widehat{D}_I$
a.s.
$ D_I\ge \widehat{D}_I$
a.s.
We have
![]() $G(h,\lambda) =\frac{{\mathbb{E}} D_I}{{\mathbb{E}}D}$
and
$G(h,\lambda) =\frac{{\mathbb{E}} D_I}{{\mathbb{E}}D}$
and
![]() $G(h,\widehat{\lambda}) =\frac{{\mathbb{E}} \widehat{D}_I}{r{\mathbb{E}}D}$
.
$G(h,\widehat{\lambda}) =\frac{{\mathbb{E}} \widehat{D}_I}{r{\mathbb{E}}D}$
.
For small h, given D, the total number of arrivals of infected customers within [0, T] to system 1 is 0 with probability
![]() $1-hD +o(h)$
, 1 with probability
$1-hD +o(h)$
, 1 with probability
![]() $hD+o(h)$
, and more than 1 with probability o(h). Let
$hD+o(h)$
, and more than 1 with probability o(h). Let
![]() $\kappa_i=1$
if the ith arrival is infected and
$\kappa_i=1$
if the ith arrival is infected and
![]() $\kappa_i=0$
otherwise (here
$\kappa_i=0$
otherwise (here
![]() ${\mathbb{P}} (\kappa_i=1)=h$
). Let
${\mathbb{P}} (\kappa_i=1)=h$
). Let
![]() $\zeta_i=1$
if the ith arrival to system 1 is selected for system 2 and
$\zeta_i=1$
if the ith arrival to system 1 is selected for system 2 and
![]() $\zeta_i=0$
otherwise (here
$\zeta_i=0$
otherwise (here
![]() ${\mathbb{P}}(\zeta_i=1)=r$
). Then
${\mathbb{P}}(\zeta_i=1)=r$
). Then
 $${\mathbb{E}} D_I = \sum_k {\mathbb{P}} (D=k)\sum_{i=1}^k {\mathbb{P}} (A_{k,i}){\mathbb{E}}\left(D_I \ | \ D=k, A_{k,i} \right)= h C_{\lambda} +o(h),$$
$${\mathbb{E}} D_I = \sum_k {\mathbb{P}} (D=k)\sum_{i=1}^k {\mathbb{P}} (A_{k,i}){\mathbb{E}}\left(D_I \ | \ D=k, A_{k,i} \right)= h C_{\lambda} +o(h),$$
where
![]() $C_{\lambda} = \sum_k {\mathbb{P}} (D=k)\sum_{i=1}^k{\mathbb{E}}\left(D_I \ | \ D=k, A_{k,i} \right)$
and, for
$C_{\lambda} = \sum_k {\mathbb{P}} (D=k)\sum_{i=1}^k{\mathbb{E}}\left(D_I \ | \ D=k, A_{k,i} \right)$
and, for
![]() $1\le i \le k$
,
$1\le i \le k$
,
![]() $A_{k,i }= \{ \kappa_i=1, \kappa_j=0 \ \mbox{for all} \ 1\le j \le k, \ j\neq i\}.$
Next,
$A_{k,i }= \{ \kappa_i=1, \kappa_j=0 \ \mbox{for all} \ 1\le j \le k, \ j\neq i\}.$
Next,
 \begin{align*} {\mathbb{E}} \widehat{D}_I &= \sum_k {\mathbb{P}} (D=k) {\mathbb{E}}\left( \sum_{i=1}^k\widehat{D}_I {\mathbf I} (A_{k,i}){\mathbf I}(\zeta_i=1) \ | \ D=k\right) + o(h)\\&\le\sum_k {\mathbb{P}} (D=k) {\mathbb{E}}\left( \sum_{i=1}^kD_I {\mathbf I} (A_{k,i}){\mathbf I}(\zeta_i=1) \ | \ D=k\right) + o(h)= r {\mathbb{E}} D_I + o(h),\end{align*}
\begin{align*} {\mathbb{E}} \widehat{D}_I &= \sum_k {\mathbb{P}} (D=k) {\mathbb{E}}\left( \sum_{i=1}^k\widehat{D}_I {\mathbf I} (A_{k,i}){\mathbf I}(\zeta_i=1) \ | \ D=k\right) + o(h)\\&\le\sum_k {\mathbb{P}} (D=k) {\mathbb{E}}\left( \sum_{i=1}^kD_I {\mathbf I} (A_{k,i}){\mathbf I}(\zeta_i=1) \ | \ D=k\right) + o(h)= r {\mathbb{E}} D_I + o(h),\end{align*}
and we get the needed monotonicity. In fact, there is strict inequality in the second line above, since the event
![]() $\{ D=2, \kappa_1=1, \kappa_2=0, \zeta_1=0, \zeta_2=1\}$
has positive probability and, assuming the occurrence in system 1 of the sequence of events that (1) customer 1 infects customer 2, (2) customer 1 leaves, and (3) customer 2 leaves, we get
$\{ D=2, \kappa_1=1, \kappa_2=0, \zeta_1=0, \zeta_2=1\}$
has positive probability and, assuming the occurrence in system 1 of the sequence of events that (1) customer 1 infects customer 2, (2) customer 1 leaves, and (3) customer 2 leaves, we get
![]() $D_I=2$
in the first system while
$D_I=2$
in the first system while
![]() $\widehat{D}_I=0$
in the second system.
$\widehat{D}_I=0$
in the second system.
Appendix C. Monotonicity in
 $\alpha$
and
$\alpha$
and
 $\beta$
$\beta$
The construction of the coupling for the SIS reactor is as follows. The two processes are piecewise constant and may change their states (jump) only at embedded epochs
![]() $T_0=0<T_1<T_2<\ldots$
. Let
$T_0=0<T_1<T_2<\ldots$
. Let
![]() $X_{i,n}=X_i(T_n+0)$
and
$X_{i,n}=X_i(T_n+0)$
and
![]() $Y_{i,n}=Y_i(T_n+0)$
, for
$Y_{i,n}=Y_i(T_n+0)$
, for
![]() $i=1,2$
and
$i=1,2$
and
![]() $n=0, 1,2,\ldots$
. Furthermore, let
$n=0, 1,2,\ldots$
. Furthermore, let
![]() $N_n=X_{1,n}+Y_{2,n}$
. At each time
$N_n=X_{1,n}+Y_{2,n}$
. At each time
![]() $T_n+0$
, we set an exponential clock of rate
$T_n+0$
, we set an exponential clock of rate
![]() $\lambda$
,
$\lambda$
,
![]() $N_n$
clocks of rate
$N_n$
clocks of rate
![]() $\mu$
,
$\mu$
,
![]() $N_n$
clocks of rate
$N_n$
clocks of rate
![]() $\beta$
, and
$\beta$
, and
![]() $N_n(N_n-1)$
clocks of rate
$N_n(N_n-1)$
clocks of rate
![]() $\alpha_2$
. We equip all customers,
$\alpha_2$
. We equip all customers,
![]() $i=1,\ldots,N_n$
, with a
$i=1,\ldots,N_n$
, with a
![]() $\mu$
–clock and a
$\mu$
–clock and a
![]() $\beta$
-clock, and all pairs of customers, say (i, j), with an
$\beta$
-clock, and all pairs of customers, say (i, j), with an
![]() $\alpha$
-clock. All clocks are mutually independent.
$\alpha$
-clock. All clocks are mutually independent.
Let
![]() $T_{n+1}$
be the time when the first of these clocks rings. If this is the
$T_{n+1}$
be the time when the first of these clocks rings. If this is the
![]() $\lambda$
-clock, then a new customer arrives and it (simultaneously) becomes either I, with probability p, or S, with probability
$\lambda$
-clock, then a new customer arrives and it (simultaneously) becomes either I, with probability p, or S, with probability
![]() $q=1-p$
. If it is the ith
$q=1-p$
. If it is the ith
![]() $\mu$
-clock, then the ith customer leaves both systems simultaneously. If it is the ith
$\mu$
-clock, then the ith customer leaves both systems simultaneously. If it is the ith
![]() $\beta$
-clock, then the ith customer becomes S in both systems, regardless of its earlier state. And if it is the (i, j)th
$\beta$
-clock, then the ith customer becomes S in both systems, regardless of its earlier state. And if it is the (i, j)th
![]() $\alpha$
-clock, then, in the second system (that with infection parameter
$\alpha$
-clock, then, in the second system (that with infection parameter
![]() $\alpha_2$
), the jth customer becomes I if the ith customer is I, regardless of the history, and does not change its state if the ith was S. In the first system (with infection parameter
$\alpha_2$
), the jth customer becomes I if the ith customer is I, regardless of the history, and does not change its state if the ith was S. In the first system (with infection parameter
![]() $\alpha_1$
), if the ith customer is I, then the jth customer becomes I with probability
$\alpha_1$
), if the ith customer is I, then the jth customer becomes I with probability
![]() $\alpha_1/\alpha_2$
, and keeps its earlier state (no jump) in all other cases.
$\alpha_1/\alpha_2$
, and keeps its earlier state (no jump) in all other cases.
With this coupling, direct induction arguments provide the claimed monotonicity.
A similar coupling construction holds for the closed system with the following simplifications and modifications: here
![]() $N(t)\equiv N$
, for any t; there is no
$N(t)\equiv N$
, for any t; there is no
![]() $\lambda$
-clock; the ringing of a
$\lambda$
-clock; the ringing of a
![]() $\mu$
-clock means that the corresponding customer moves at random to any of N stations, and we assume that in both systems, customers move to the same stations; when an
$\mu$
-clock means that the corresponding customer moves at random to any of N stations, and we assume that in both systems, customers move to the same stations; when an
![]() $\alpha$
-clock rings that corresponds to the pair of customers (i, j), the jth customer becomes I if i and j are located at the same station.
$\alpha$
-clock rings that corresponds to the pair of customers (i, j), the jth customer becomes I if i and j are located at the same station.
Appendix D. The thermodynamic limits as nonlinear Markov processes
In the transient thermodynamic limit of SIS, at time t, a station has a Poisson arrival process of infected (resp. susceptible) customers with an intensity equal to
![]() $\mu {\mathbb{E}} [Y(t)]$
(resp.
$\mu {\mathbb{E}} [Y(t)]$
(resp.
![]() $\mu {\mathbb{E}}[X(t)]$
), where Y(t) (resp. X(t)) is the the number of infected (resp. susceptible) customers in the station at time t. The aim of this section is to show that this can be described in terms of a nonlinear Markov dynamics.
$\mu {\mathbb{E}}[X(t)]$
), where Y(t) (resp. X(t)) is the the number of infected (resp. susceptible) customers in the station at time t. The aim of this section is to show that this can be described in terms of a nonlinear Markov dynamics.
This is best explained when looking first at a discrete-time version of the problem. Time is slotted with increments of duration h. At time
![]() $k=0$
, choose an initial condition in the infinite-dimensional thermodynamic limit. The latter consists of a product-form distribution of customers over stations, with a fixed joint distribution
$k=0$
, choose an initial condition in the infinite-dimensional thermodynamic limit. The latter consists of a product-form distribution of customers over stations, with a fixed joint distribution
![]() ${\mathcal P}_0$
of infected and susceptible customers in any given station, such that the sum of the two coordinates is Poisson-
${\mathcal P}_0$
of infected and susceptible customers in any given station, such that the sum of the two coordinates is Poisson-
![]() $\eta$
. The number of infected (resp. susceptible) arrivals in time slot 1 is Poisson with parameter
$\eta$
. The number of infected (resp. susceptible) arrivals in time slot 1 is Poisson with parameter
![]() $h\mu {\mathbb{E}} [Y_0]$
(resp.
$h\mu {\mathbb{E}} [Y_0]$
(resp.
![]() $h\mu {\mathbb{E}} [X_0]$
), where the expectations are with respect to
$h\mu {\mathbb{E}} [X_0]$
), where the expectations are with respect to
![]() ${\mathcal P}_0$
. In addition, each of the
${\mathcal P}_0$
. In addition, each of the
![]() $Y_0$
infected customers tosses a three-face die with respective weights
$Y_0$
infected customers tosses a three-face die with respective weights
If the outcome is 1, the customer stays and keeps its SIS state. If the outcome is 2, it stays and changes its SIS state. If the outcome is 3, it leaves. Similarly, conditionally on
![]() $Y_0$
, each of the
$Y_0$
, each of the
![]() $X_0$
infected customers tosses a three-face die with respective weights
$X_0$
infected customers tosses a three-face die with respective weights
If the outcome is 1, the customer stays and keeps its SIS state. If the outcome is 2, it stays and changes its SIS state. If the outcome is 3, it leaves. All these define a state
![]() $(X_1,Y_1)$
. Let
$(X_1,Y_1)$
. Let
![]() ${\mathcal P}_1$
be the distribution of
${\mathcal P}_1$
be the distribution of
![]() $(X_1,Y_1)$
.
$(X_1,Y_1)$
.
The construction for all k is then obtained by induction. Assume the triple
![]() $(X_k,Y_k, {\mathcal P}_k)$
is well defined. By applying the same dynamics to this triple, one gets at the same time a state
$(X_k,Y_k, {\mathcal P}_k)$
is well defined. By applying the same dynamics to this triple, one gets at the same time a state
![]() $(X_{k+1},Y_{k+1})$
and a distribution
$(X_{k+1},Y_{k+1})$
and a distribution
![]() ${\mathcal P}_{k+1}$
.
${\mathcal P}_{k+1}$
.
The key observations are then the following: (a) once the sequence of distributions
![]() $\{{\mathcal P}_k\}$
is determined, one can then see the evolution of
$\{{\mathcal P}_k\}$
is determined, one can then see the evolution of
![]() $\{(X_k,Y_k)\}$
as that of a standard discrete-time discrete-space nonlinear Markov chain. (b) A stationary distribution is a distribution
$\{(X_k,Y_k)\}$
as that of a standard discrete-time discrete-space nonlinear Markov chain. (b) A stationary distribution is a distribution
![]() ${\mathcal P}$
such that if
${\mathcal P}$
such that if
![]() ${\mathcal P}_0={\mathcal P}$
, then
${\mathcal P}_0={\mathcal P}$
, then
![]() ${\mathcal P}_1={\mathcal P}$
. (c) By tightness arguments, this can be extended to the continuous-time case by letting
${\mathcal P}_1={\mathcal P}$
. (c) By tightness arguments, this can be extended to the continuous-time case by letting
![]() $h\to 0$
.
$h\to 0$
.
Appendix E. Proof of Theorem 2
Below,
![]() $p^*$
is the maximum root of the fixed-point equation
$p^*$
is the maximum root of the fixed-point equation
![]() $p=g(p)$
for the plain SIS reactor. This means that if
$p=g(p)$
for the plain SIS reactor. This means that if
![]() $g^{\prime}(0)\le 1$
, then
$g^{\prime}(0)\le 1$
, then
![]() $p^*=0$
, whereas if
$p^*=0$
, whereas if
![]() $g^{\prime}(0)>1$
, then
$g^{\prime}(0)>1$
, then
![]() $p^*$
is positive and there are two solutions to the fixed-point equation.
$p^*$
is positive and there are two solutions to the fixed-point equation.
Consider an M/M/
![]() $\infty$
system in the stationary regime on the time horizon
$\infty$
system in the stationary regime on the time horizon
![]() $[0,\infty)$
, with input rate
$[0,\infty)$
, with input rate
![]() $\lambda$
and service rate
$\lambda$
and service rate
![]() $\mu$
. The number of customers in the system at any time t, N(t), has a Poisson distribution with parameter
$\mu$
. The number of customers in the system at any time t, N(t), has a Poisson distribution with parameter
![]() $\eta = \lambda/\mu$
.
$\eta = \lambda/\mu$
.
Monotonicity. Consider the SIS reactor with a Poisson input point process with a time-varying intensity like that discussed in Remark 8. Consider two variants of customer ‘coloring’ at time 0 and of input rates. In the first variant, there are initially Y(0) infected customers and the input point process of infected customers has an intensity equal to
![]() $\lambda p(.)$
, while in the second variant there are initially
$\lambda p(.)$
, while in the second variant there are initially
![]() $\widehat Y(0)$
infected customers and the intensity of infected customers is
$\widehat Y(0)$
infected customers and the intensity of infected customers is
![]() $\lambda \widehat p(.)$
. Here p(t) and
$\lambda \widehat p(.)$
. Here p(t) and
![]() $\widehat p(t)$
are two given deterministic functions.
$\widehat p(t)$
are two given deterministic functions.
The next result follows from the monotonicity property established in Appendix B—more precisely, see Remark 8.
Lemma 11.
If
![]() $Y(0)\le\widehat Y(0)$
a.s. and
$Y(0)\le\widehat Y(0)$
a.s. and
![]() $p(.)\le\widehat p(.)$
, then, under an appropriate coupling, for all t,
$p(.)\le\widehat p(.)$
, then, under an appropriate coupling, for all t,
![]() $Y(t)\le \widehat Y(t)$
a.s.
$Y(t)\le \widehat Y(t)$
a.s.
In what follows, ‘by simple monotonicity arguments’ means ‘by applying Lemma 11 ′.
The upper process. We introduce an SIS model with a varying fraction of infected customers in the input process and instantaneous extra infections along the lines described in Remark 8.
Recall that we consider a total population dynamics which is that of an M/M/
![]() $\infty$
system in the stationary regime on the time horizon
$\infty$
system in the stationary regime on the time horizon
![]() $[0,\infty)$
, with input rate
$[0,\infty)$
, with input rate
![]() $\lambda$
and service rate
$\lambda$
and service rate
![]() $\mu$
.
$\mu$
.
Consider now the following infection/recovery mechanism. We introduce recursively deterministic times
![]() $T^{(0)}=0<T^{(1)}<T^{(2)}<\ldots$
and probabilities
$T^{(0)}=0<T^{(1)}<T^{(2)}<\ldots$
and probabilities
![]() $p^{(1)}=1>p^{(2)}> \ldots$
such that
$p^{(1)}=1>p^{(2)}> \ldots$
such that
-
(i)
 $p^{(n)}\downarrow p^*$
as
$p^{(n)}\downarrow p^*$
as
 $n\to\infty$
;
$n\to\infty$
; -
(ii) for any
 $n=1,2,\ldots$
, each customer that arrives in the system within the time interval
$n=1,2,\ldots$
, each customer that arrives in the system within the time interval
 $(T^{(n-1)},T^{(n)})$
is infected with probability
$(T^{(n-1)},T^{(n)})$
is infected with probability
 $p^{(n)}$
and susceptible otherwise, independently of everything else;
$p^{(n)}$
and susceptible otherwise, independently of everything else; -
(iii) for any
 $n=1,2,\ldots$
, at time
$n=1,2,\ldots$
, at time
 $T^{(n-1)}$
, all customers present in the system become infected instantaneously.
$T^{(n-1)}$
, all customers present in the system become infected instantaneously.
In more detail, with
![]() $n=1,2,\ldots$
, we introduce recursively processes
$n=1,2,\ldots$
, we introduce recursively processes
![]() $(\widehat{X}^{(n)}(t),\widehat{Y}^{(n)}(t))$
, for
$(\widehat{X}^{(n)}(t),\widehat{Y}^{(n)}(t))$
, for
![]() $t\ge T^{(n-1)}$
, and then let
$t\ge T^{(n-1)}$
, and then let
First we assume that, at time
![]() $T^{(0)}=0$
, all customers that are present in the system are infected, and that, starting from time 0, all arriving customers are infected too (i.e., each is infected with probability
$T^{(0)}=0$
, all customers that are present in the system are infected, and that, starting from time 0, all arriving customers are infected too (i.e., each is infected with probability
![]() $p^{(1)}=1$
). We have a time-homogeneous and irreducible Markov jump process on a countable state space, which is clearly aperiodic and positive recurrent. Therefore, there exists a unique stationary distribution which is the limit in law obtained for any initial state, and the speed of convergence to this stationary distribution is exponential. In the stationary regime, the output rate of infected customers is
$p^{(1)}=1$
). We have a time-homogeneous and irreducible Markov jump process on a countable state space, which is clearly aperiodic and positive recurrent. Therefore, there exists a unique stationary distribution which is the limit in law obtained for any initial state, and the speed of convergence to this stationary distribution is exponential. In the stationary regime, the output rate of infected customers is
![]() $p_o^{(1)}$
, which is strictly less than
$p_o^{(1)}$
, which is strictly less than
![]() $p^{(1)}=1$
. In particular, if one denotes by
$p^{(1)}=1$
. In particular, if one denotes by
![]() $\big(\widehat{X}^{(1)}(t),\widehat{Y}^{(1)}(t)\big)$
the state process in this dynamics, one has
$\big(\widehat{X}^{(1)}(t),\widehat{Y}^{(1)}(t)\big)$
the state process in this dynamics, one has
![]() ${\mathbb{E}} \widehat{Y}^{(1)}(t) \to p^{(1)}_o \eta$
exponentially fast, as
${\mathbb{E}} \widehat{Y}^{(1)}(t) \to p^{(1)}_o \eta$
exponentially fast, as
![]() $t\to\infty$
.
$t\to\infty$
.
Let
![]() $\delta \in (0, 1)$
be arbitrarily small. We choose time
$\delta \in (0, 1)$
be arbitrarily small. We choose time
![]() $T^{(1)}$
as
$T^{(1)}$
as
Then let
![]() $p^{(2)}=p^{(1)}_o+\delta \big(p^{(1)}-p^{(1)}_o\big)/2$
. By (64), this completes the description of the dynamics of the process
$p^{(2)}=p^{(1)}_o+\delta \big(p^{(1)}-p^{(1)}_o\big)/2$
. By (64), this completes the description of the dynamics of the process
![]() $\big(\widehat{X}(t), \widehat{Y}(t)\big)$
within the first time slot
$\big(\widehat{X}(t), \widehat{Y}(t)\big)$
within the first time slot
![]() $[T^{(0)},T^{(1)})$
. Note that, by monotonicity and convexity of the function
$[T^{(0)},T^{(1)})$
. Note that, by monotonicity and convexity of the function
![]() $p_o = g(p)$
, we get
$p_o = g(p)$
, we get
![]() $p^{(1)}_0>p^*$
.
$p^{(1)}_0>p^*$
.
Assume we have introduced the processes
![]() $\big(\widehat{X}^{(i)}(t),\widehat{Y}^{(i)}(t)\big)$
on the time intervals
$\big(\widehat{X}^{(i)}(t),\widehat{Y}^{(i)}(t)\big)$
on the time intervals
![]() $[T^{(i-1)},\infty)$
, for
$[T^{(i-1)},\infty)$
, for
![]() $i=1,\ldots,n-1$
, and therefore have defined the process
$i=1,\ldots,n-1$
, and therefore have defined the process
![]() $\big(\widehat{X}(t), \widehat{Y}(t)\big)$
on the interval
$\big(\widehat{X}(t), \widehat{Y}(t)\big)$
on the interval
![]() $[0,T^{(n-1)})$
via (64). At the beginning of the nth time slot (at time
$[0,T^{(n-1)})$
via (64). At the beginning of the nth time slot (at time
![]() $T^{(n-1)}$
), we change all customers present in the system to infected and assume that, starting from this time, each arriving customer is either infected with probability
$T^{(n-1)}$
), we change all customers present in the system to infected and assume that, starting from this time, each arriving customer is either infected with probability
![]() $p^{(n)}>p^*$
, or susceptible otherwise. Then, starting from time
$p^{(n)}>p^*$
, or susceptible otherwise. Then, starting from time
![]() $T^{(n-1)}$
, our system again behaves as an irreducible time-homogeneous Markov jump process whose distribution converges exponentially fast to its unique stationary distribution with output fraction of infected customers
$T^{(n-1)}$
, our system again behaves as an irreducible time-homogeneous Markov jump process whose distribution converges exponentially fast to its unique stationary distribution with output fraction of infected customers
![]() $p^{(n)}_o $
, which is strictly bigger than
$p^{(n)}_o $
, which is strictly bigger than
![]() $p^*$
(thanks again to monotonicity and convexity of the function g). We denote this process by
$p^*$
(thanks again to monotonicity and convexity of the function g). We denote this process by
![]() $(\widehat{X}^{(n)}(t),\widehat{Y}^{(n)}(t))$
,
$(\widehat{X}^{(n)}(t),\widehat{Y}^{(n)}(t))$
,
![]() $t\ge T^{(n-1)}$
. Then we let
$t\ge T^{(n-1)}$
. Then we let
and
![]() $p^{(n+1)}=p^{(n)}_o+\delta \big(p^{(n)}-p^{(n)}_o\big)\cdot 2^{-n}$
. This completes the description of the process
$p^{(n+1)}=p^{(n)}_o+\delta \big(p^{(n)}-p^{(n)}_o\big)\cdot 2^{-n}$
. This completes the description of the process
![]() $(\widehat{X}(t),\widehat{Y}(t))$
within the nth time slot
$(\widehat{X}(t),\widehat{Y}(t))$
within the nth time slot
![]() $[T^{(n-1)},T^{(n)})$
. Again, thanks to monotonicity and convexity of the function
$[T^{(n-1)},T^{(n)})$
. Again, thanks to monotonicity and convexity of the function
![]() $p_o = g(p)$
, we get
$p_o = g(p)$
, we get
![]() $p^{(n)}_o> p^{(n+1)}_o>p^*$
.
$p^{(n)}_o> p^{(n+1)}_o>p^*$
.
Thus, we have defined the process
![]() $(\widehat{X}(t),\widehat{Y}(t))$
for all
$(\widehat{X}(t),\widehat{Y}(t))$
for all
![]() $t\ge 0$
. It is left to explain the convergence (i). We know that there is no solution to the equation
$t\ge 0$
. It is left to explain the convergence (i). We know that there is no solution to the equation
![]() $p_0=g(p)$
bigger than
$p_0=g(p)$
bigger than
![]() $p^*$
, and the monotone sequences
$p^*$
, and the monotone sequences
![]() $p^{(n)}$
and
$p^{(n)}$
and
![]() $p^{(n)}_o$
converge to the same limit which is a solution to this fixed-point equation. The fact that this is the maximal solution proves the result.
$p^{(n)}_o$
converge to the same limit which is a solution to this fixed-point equation. The fact that this is the maximal solution proves the result.
Comparison of the upper process and the thermodynamic limit process.
As shown in Appendix D, under the propagation of chaos ansatz, the dynamics of any station in the SIS TL can be seen as a nonlinear Markov jump process (X(t), Y(t)) with a certain fraction
![]() $p^*(t)$
of infected customers at time t (the fraction such that at any time t,
$p^*(t)$
of infected customers at time t (the fraction such that at any time t,
![]() $\lambda p^*(t)=\mu {\mathbb{E}} Y(t)$
).
$\lambda p^*(t)=\mu {\mathbb{E}} Y(t)$
).
By construction,
![]() ${X}(t)+{Y}(t)=N(t)$
for all
${X}(t)+{Y}(t)=N(t)$
for all
![]() $t\ge 0$
, where N(t) is the Poisson process describing the dynamics of the stationary M/M/
$t\ge 0$
, where N(t) is the Poisson process describing the dynamics of the stationary M/M/
![]() $\infty$
system and also
$\infty$
system and also
![]() $N(t)= \widehat{X}(t)+\widehat{Y}(t)$
a.s. (where the latter are the state variables in the upper system described above).
$N(t)= \widehat{X}(t)+\widehat{Y}(t)$
a.s. (where the latter are the state variables in the upper system described above).
Proposition 2.
For all
![]() $t\ge 0$
, in a proper coupling,
$t\ge 0$
, in a proper coupling,
![]() $Y(t) \le \widehat{Y}(t)$
a.s. Therefore,
$Y(t) \le \widehat{Y}(t)$
a.s. Therefore,
![]() $\limsup_{t\to\infty}{\mathbb{E}} Y(t) \le p^*.$
$\limsup_{t\to\infty}{\mathbb{E}} Y(t) \le p^*.$
Proof. First, by simple monotonicity arguments,
![]() $Y(t) \le \widehat{Y}^{(1)}(t)$
a.s. for all
$Y(t) \le \widehat{Y}^{(1)}(t)$
a.s. for all
![]() $t\ge 0$
. In particular,
$t\ge 0$
. In particular,
![]() ${\mathbb{E}} Y(t)/\eta \le p^{(2)}$
for all
${\mathbb{E}} Y(t)/\eta \le p^{(2)}$
for all
![]() $t\ge T^{(1)}$
. Consider now the time interval
$t\ge T^{(1)}$
. Consider now the time interval
![]() $[T^{(1)}, \infty)$
and compare the processes
$[T^{(1)}, \infty)$
and compare the processes
![]() $(\widehat{X}^{(2)}(t),\widehat{Y}^{(2)}(t))$
and (X(t), Y(t)) within this interval. By construction, at the initial time
$(\widehat{X}^{(2)}(t),\widehat{Y}^{(2)}(t))$
and (X(t), Y(t)) within this interval. By construction, at the initial time
![]() $T^{(1)}$
of this time period,
$T^{(1)}$
of this time period,
![]() $\widehat{Y}^{(2)}(T^{(1)})\ge Y(T^{(1)})$
a.s., and for all
$\widehat{Y}^{(2)}(T^{(1)})\ge Y(T^{(1)})$
a.s., and for all
![]() $t\ge T^{(1)}$
, the input rate of infected customers in the auxiliary upper process is bigger than that in the thermodynamic limit. Then it follows from simple sample-path arguments that
$t\ge T^{(1)}$
, the input rate of infected customers in the auxiliary upper process is bigger than that in the thermodynamic limit. Then it follows from simple sample-path arguments that
![]() $Y(t)\le \widehat{Y}^{(2)}(t)$
a.s. for all
$Y(t)\le \widehat{Y}^{(2)}(t)$
a.s. for all
![]() $t\ge T^{(1)}$
, and in particular,
$t\ge T^{(1)}$
, and in particular,
![]() ${\mathbb{E}}(Y(t)) \le {\mathbb{E}} \widehat{Y}^{(2)}(t)$
, where the right-hand side is smaller than
${\mathbb{E}}(Y(t)) \le {\mathbb{E}} \widehat{Y}^{(2)}(t)$
, where the right-hand side is smaller than
![]() $p_1^{(3)}$
, for all
$p_1^{(3)}$
, for all
![]() $t\ge T^{(3)}$
.
$t\ge T^{(3)}$
.
The induction argument implies that for any
![]() $n=1,2,\ldots$
and any
$n=1,2,\ldots$
and any
![]() $k\le n$
and
$k\le n$
and
![]() $t\ge T^{(n-1)}$
, the following inequalities hold a.s.:
$t\ge T^{(n-1)}$
, the following inequalities hold a.s.:
![]() $Y(t) \le \widehat{Y}^{(k)}(t)$
, and therefore
$Y(t) \le \widehat{Y}^{(k)}(t)$
, and therefore
![]() $Y(t) \le \widehat Y(t)$
. It is left to show that
$Y(t) \le \widehat Y(t)$
. It is left to show that
![]() $\lim p^{(k)}=p^*$
. However, this is clear since
$\lim p^{(k)}=p^*$
. However, this is clear since
![]() $p^*$
is the maximal solution to the equation
$p^*$
is the maximal solution to the equation
![]() $p=g(p)$
and, by convexity, all
$p=g(p)$
and, by convexity, all
![]() $p^{(k)}>p^*$
since
$p^{(k)}>p^*$
since
![]() $p^{(k)}_0 = g(p^{(k)})<p^{(k)}$
.
$p^{(k)}_0 = g(p^{(k)})<p^{(k)}$
.
Corollary 5.
If
![]() $g^{\prime}(0)\le 1$
, then there is extinction of the infection process in that
$g^{\prime}(0)\le 1$
, then there is extinction of the infection process in that
![]() $\lim_{t\to\infty} {\mathbb{E}} {Y}(t)=0$
, for all initial distributions of infected customers in the system.
$\lim_{t\to\infty} {\mathbb{E}} {Y}(t)=0$
, for all initial distributions of infected customers in the system.
The next corollary follows from simple monotonicity arguments. Before stating it, we recall the following result on the fixed point of the SIS reactor. Assume
![]() $g^{\prime}(0)>0$
, which implies that
$g^{\prime}(0)>0$
, which implies that
![]() $p^*>0$
. Any SIS reactor is a time-homogeneous Markov process
$p^*>0$
. Any SIS reactor is a time-homogeneous Markov process
![]() $(\widetilde X(t),\widetilde Y(t))$
with a countable state space, which is irreducible, positive recurrent, and ergodic. In particular, for
$(\widetilde X(t),\widetilde Y(t))$
with a countable state space, which is irreducible, positive recurrent, and ergodic. In particular, for
![]() $p=p^*$
, for all initial conditions
$p=p^*$
, for all initial conditions
![]() $(\widetilde X(0),\widetilde Y(0))$
, this Markov process converges to a limiting stationary Markov process with
$(\widetilde X(0),\widetilde Y(0))$
, this Markov process converges to a limiting stationary Markov process with
![]() $\mu {\mathbb{E}} \widetilde Y= p^*\lambda$
. Denote this last stationary process by
$\mu {\mathbb{E}} \widetilde Y= p^*\lambda$
. Denote this last stationary process by
![]() $\{(\widetilde X^*(t),\widetilde Y^*(t))\}_t$
. This last process can be used to build a specific example
$\{(\widetilde X^*(t),\widetilde Y^*(t))\}_t$
. This last process can be used to build a specific example
![]() $(X^*(t), Y^*(t),{\mathcal P}^*_t)$
,
$(X^*(t), Y^*(t),{\mathcal P}^*_t)$
,
![]() $t\ge 0$
, of the nonlinear Markov chain of Appendix D, where the initial distribution
$t\ge 0$
, of the nonlinear Markov chain of Appendix D, where the initial distribution
![]() ${\mathcal P}^*_0$
is that of
${\mathcal P}^*_0$
is that of
![]() $(\widetilde X^*(0),\widetilde Y^*(0))$
. This distribution is invariant for this nonlinear dynamics. By this, we mean that it makes the Markov chain homogeneous and stationary, with an input rate of infected customers which is constant, equal to
$(\widetilde X^*(0),\widetilde Y^*(0))$
. This distribution is invariant for this nonlinear dynamics. By this, we mean that it makes the Markov chain homogeneous and stationary, with an input rate of infected customers which is constant, equal to
![]() $\lambda p^*$
, and equal to the mean output rate of infected customers.
$\lambda p^*$
, and equal to the mean output rate of infected customers.
Corollary 6.
Consider the process
![]() $Y^*(t)$
defined above. Then
$Y^*(t)$
defined above. Then
![]() $\widehat{Y}(t)\ge Y^*(t)$
a.s. for all
$\widehat{Y}(t)\ge Y^*(t)$
a.s. for all
![]() $t\ge 0$
, and
$t\ge 0$
, and
![]() ${\mathbb{P}}(\widehat{Y}(t)=Y^*(t)) \to 1$
as
${\mathbb{P}}(\widehat{Y}(t)=Y^*(t)) \to 1$
as
![]() $t\to\infty$
, where
$t\to\infty$
, where
![]() $\widehat{Y}(t)$
is the upper process of Proposition 2.
$\widehat{Y}(t)$
is the upper process of Proposition 2.
Consider the nonlinear Markov process Y(t) defined in Appendix D with any initial distribution such that
![]() ${Y}(0) \ge Y^*(0)$
a.s., with
${Y}(0) \ge Y^*(0)$
a.s., with
![]() $Y^*(.)$
defined above. Then
$Y^*(.)$
defined above. Then
![]() $\widehat{Y}(t)\ge {Y}(t)\ge Y^*(t)$
a.s. and
$\widehat{Y}(t)\ge {Y}(t)\ge Y^*(t)$
a.s. and
![]() ${\mathbb{P}} (\widehat{Y}(t)= {Y}(t) = Y^*(t)) \to 1$
.
${\mathbb{P}} (\widehat{Y}(t)= {Y}(t) = Y^*(t)) \to 1$
.
The only thing to comment upon is the last statement. It follows from the facts that all Y-variables are integer-valued and that the monotone convergence of integer-valued random variables is necessarily also a coupling (or total variation) convergence.
Funding information
The work of the first author was supported by the ERC NEMO grant, under the European Union’s Horizon 2020 research and innovation program, grant agreement no. 788851 to INRIA.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.