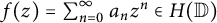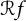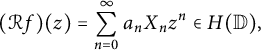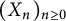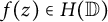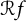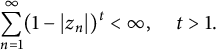1 Introduction and main results
It has been folklore since the early history of random analytic functions
$(\mathcal {R} f)(z)= \sum _{k=0}^{\infty } \pm a_k z^k$
that the behaviors of
$\mathcal {R} f$
exhibit often a dichotomy according to whether the coefficients
$\{a_k\}_{k=0}^{\infty }$
are square-summable or not. In principle, if
$\sum |a_k|^2<\infty $
, then
$\mathcal {R} f$
behaves reasonably well, and otherwise, wildly.
Relevant to the theme in this note are geometric conditions on the zero sequence
$\{z_n\}_{n=1}^{\infty }$
of an analytic function over the unit disk, among which the best known one is perhaps the Blaschke condition, i.e.,
$$ \begin{align*}\sum_{n=1}^{\infty} (1-|z_n|)<\infty.\end{align*} $$
For functions in the Hardy space
$H^p(\mathbb {D}) \ (p>0)$
over the unit disk, the zero sets are characterized as those sequences satisfying the Blaschke condition [Reference Duren4].
In the random setting, Littlewood’s theorem from 1930 [Reference Littlewood10] implies that
$$ \begin{align*}(\mathcal{R}f)(z)=\sum_{n=0}^\infty \pm a_n z^n \in H^p(\mathbb{D})\end{align*} $$
almost surely for all
$p>0$
if
$f(z)=\sum _{n=0}^{\infty }a_n z^n \in H^2(\mathbb {D})$
. It follows that the zero sequence of
$\mathcal {R} f$
satisfies the Blaschke condition almost surely. A converse statement holds as well, due to Nazarov, Nishry, and Sodin, who showed in 2013 [Reference Nazarov, Nishry and Sodin12] that if
$f\notin H^2(\mathbb {D})$
, then
$$ \begin{align*}\sum_{n=1}^{\infty}(1-|z_n(\omega)|)=\infty\end{align*} $$
almost surely, where
$\{z_n(\omega )\}_{n=1}^{\infty }$
is the zero sequence of
$\mathcal {R} f$
.
The purpose of this note is two-fold: firstly, we hope to gain more insight into the square-summable case, for which the quantity
$\sum (1-|z_n(\omega )|)$
, as well as another notion
$L(\mathcal {R} f)$
(see (1) below), defines an a.s. finite random variable whose quantitative property is of interests to us; secondly, and perhaps more importantly, we hope to gain more insight for the failure of the Blaschke condition in the non-square-summable territory for which much less is known in the literature.
Definition 1.1. A function
$f(z)\in H(\mathbb {D})$
is said to be in the class
$\mathfrak {B} _t~(t\ge 1)$
if its zero set
$\{z_n\}_{n=1}^{\infty }$
satisfies the
$B_t$
-condition:
$$ \begin{align*} \sum_{n=1}^{\infty}(1-|z_n|)^t<\infty. \end{align*} $$
Remark. We shall use the class
$\mathfrak {B}_1$
and the Blaschke class interchangeably.
We shall indeed treat three kinds of randomization methods in this note.
Definition 1.2. A random variable X is called Bernoulli if
$\mathbb {P}(X=1)=\mathbb {P}(X=-1)=\frac {1}{2}$
, Steinhaus if it is uniformly distributed on the unit circle, and by
$N(0,1)$
, we mean the law of a Gaussian variable with zero mean and unit variance. Moreover, for
$X\in \{\text {Bernoulli, Steinhaus, } N(0,1)\}$
, a standard X sequence is a sequence of independent, identically distributed X variables, denoted by
$\{\epsilon _n\}_{n\geq 0}$
,
$\{e^{2\pi i\alpha _n}\}_{n\geq 0}$
and
$\{\xi _n\}_{n\geq 0}$
, respectively. Lastly, a standard random sequence
$\{X_n\}_{n\geq 0}$
refers to either a standard Bernoulli, Steinhaus, or Gaussian
$N(0,1)$
sequence.
Theorem 1.3. Let
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
,
$\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
$\{X_k\}_{k=0}^{\infty }$
is a standard random sequence, and let
$\{z_n(\omega )\}_{n=1}^{\infty }$
be the zero sequence of
$\mathcal {R} f$
, repeated according to multiplicity and ordered by nondecreasing modules. Then the following statements are equivalent for any
$t>1$
:
-
(i)
$\mathcal {R} f\in \mathfrak {B}_t$
a.s.
$;$
-
(ii)
$\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_n(\omega )|)^t)<\infty ;$
-
(iii)
$\int _0^1 (\log (\sum _{k=0}^{\infty } |a_k|^2 r^{2k}))(1-r)^{t-2}dr<\infty .$
Corollary 1.4. Let
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
and
$\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
$\{X_k\}_{k\geq 0}$
is a standard random sequence. Then
$\mathcal {R} f\in \mathfrak {B}_2$
almost surely if and only if
$$ \begin{align*}\int_0^1 \log\big(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}\big)dr<\infty.\end{align*} $$
As a complement, for
$t=1$
, we obtain more information when
$f \in H^2$
as follows. Let
$$ \begin{align} L(f):=\lim_{r\rightarrow1^-}\frac{1}{2\pi}\int_0^{2\pi}\log|f(re^{i\theta})|d\theta.\end{align} $$
We observe that
$L(f)$
is not really a measure of the size of f, since, for any g nonvanishing on
$\mathbb {D}$
with
$g(0)=1$
, one has
$L(fg)=L(f)$
. By Theorem 2.3 in [Reference Duren4], both
$$ \begin{align*}\sum (1-|z_n(\omega)|) \quad \text{ and} \quad L(\mathcal{R} f)\end{align*} $$
are a.s. finite random variables if and only if
$f\in H^2$
. Next, we obtain quantitative estimates for these two random variables, which complement the known results on the classical Blaschke condition.
Theorem 1.5. Let
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
,
$\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
$\{X_k\}_{k=0}^{\infty }$
is a standard random sequence, and let
$\{z_n(\omega )\}_{n=1}^{\infty }$
be the zero sequence of
$\mathcal {R} f$
, repeated according to multiplicity and ordered by nondecreasing modules. Then the following statements are equivalent:
-
(i)
$f\in H^2;$
-
(ii)
$\mathcal {R} f\in \mathfrak {B}_1$
a.s.
$;$
-
(iii)
$\mathbb {E}\left (\sum _{n=1}^{\infty }\left (1-|z_{n}(w)|\right )\right )<\infty ;$
-
(iv)
$\mathbb {E}\left (e^{L(\mathcal {R} f)}\right )<\infty .$
The rest of this note is devoted to the proofs of Theorems 1.3 and 1.5, ending with remarks on the zero sets of random analytic functions in the Bergman spaces.
2 Preliminaries
In this section, we introduce a key tool needed for our proofs. We motivate the estimate in [Reference Nazarov, Nishry and Sodin12] for Rademacher random variables by considering first the easier case of a standard Gaussian sequence
$\{X_k\}_{k\geq 0}$
. For
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
, we assume
$|a_0|=1$
and set
$$ \begin{align*}\widehat{F}_r(\theta)=\mathcal{R} f(re^{i\theta})/(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})^{\frac{1}{2}}.\end{align*} $$
Then, for any
$r\in (0,1)$
, we rewrite
$$ \begin{align*} \widehat{F}_r(\theta)=\sum _{k=0}^{\infty} \widehat{a}_k(r) X_k e^{ik\theta}, \end{align*} $$
which is a random Fourier series satisfying the condition
$\sum _{k=0}^{\infty } |\widehat {a}_k(r)|^2=1$
. Consequently, for each
$\theta $
, the random variable
$ \widehat {F}_r(\theta )$
is a standard complex-valued Gaussian variable. In particular,
$\mathbb {E}(|\log |\widehat {F}_{r}(\theta )||)$
is a positive constant (which can be estimated by
$\sqrt {\frac {2}{\pi }}\int _0^{\infty }|\log x|e^{-x^2/2}dx \thickapprox 0.87928$
). Now, the following equation, together with Theorem 2.3 in [Reference Duren4], implies that the zeros of
$\mathcal {R} f$
satisfy the standard Blaschke condition almost surely if and only if
$f\in H^2$
:
$$ \begin{align*} \int_0^{2\pi}\log|\mathcal{R} f(r e^{i\theta})|\frac{d\theta}{2\pi} =\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}) +\int_0^{2\pi}\log |\widehat{F}_{r}(\theta) |\frac{d\theta}{2\pi}. \end{align*} $$
Then, for the Rademacher case, the remarkable estimate of Nazarov, Nishry, and Sodin [Reference Nazarov, Nishry and Sodin12, Corollary 1.2] provides a uniform bound for
$r \in (0,1)$
:
$$ \begin{align} \mathbb{E}\left(\frac{1}{2\pi}\int_{0}^{2\pi}\left|\log|\widehat{F}_{r}(\theta)|\right|d\theta\right)\leq C< \infty. \end{align} $$
For the Steinhaus case, by [Reference Offord13, Reference Ullrich16, Reference Ullrich17], one has indeed
$$ \begin{align*}\sup_{\theta \in [0,2\pi]} \mathbb{E}(|\log |\widehat{F}_{r}(\theta)||) < \infty. \end{align*} $$
In particular, the estimate (2) holds for all three standard randomization methods.
3 Proof of Theorem 1.3
Motivated by Theorem 2 in [Reference Heilper5], we have the following.
Lemma 3.1. Let
$\{z_n\}_{n=1}^{\infty }$
be the zero sequence of a function
$f\in H(\mathbb {D})$
and let
$t>1$
be a real number. Then
$\sum _{n=1}^{\infty }(1-|z_n|)^t<\infty $
if and only if
$$ \begin{align} \sup_{0\leq r<1}\int_{|z|<r}(\log |f(z)|)(1-|z|)^{t-2}dA(z)<\infty, \end{align} $$
where
$dA$
denotes the area measure on
$\mathbb {D}$
.
Proof Since
$(\log |z|)(1-|z|)^{t-2}$
is area-integrable, without loss of generality, we assume
$|f(0)|=1$
. Assume first that
$\sum _{n=1}^{\infty }(1-|z_n|)^t<\infty $
, where
$\{z_n\}_{n=1}^{\infty }$
are repeated according to multiplicity and ordered by nondecreasing modules. The counting function
$n(r)$
denotes the number of zeros of
$f(z)$
in the disk
$|z|<r$
. Denote by
$N(r):=\int _{0}^{r}\frac {n(s)}{s}ds$
the integrated counting function. By using integration-by-parts, twice, one has
$$ \begin{align} \nonumber &\frac{1}{2\pi}\int_{|z|<r}(\log |f(z)|)(1-|z|)^{t-2}dA(z) \\ &\quad=C_1(r)\int_0^r N(s)(1-s)^{t-2}ds \\ \nonumber &\quad=\frac{C_1(r)}{t-1}\bigg[-N(r)(1-r)^{t-1}+C_2(r)\int_0^r (1-s)^{t-1}n(s)ds\bigg]\\ \nonumber &\quad=\frac{C_1(r)}{t-1}\bigg[-N(r)(1-r)^{t-1}-\frac{C_2(r)}{t}n(r)(1-r)^{t}+\frac{C_2(r)}{t}\sum_{|z_n|<r}(1-|z_n|)^t\bigg], \end{align} $$
where
$C_1(r)$
is bounded because of the monotonicity of
$\int _0^{2\pi } \log |f(re^{i\theta })|d\theta $
in r and
$C_2(r)$
is bounded since
$n(s)$
vanishes when s is small. Then, the necessity follows by letting
$r\rightarrow 1^-$
.
Now, we assume (3). Then by Jensen’s formula, we have
$\int _0^1 N(r)(1-r)^{t-2}dr<\infty $
. The monotonicity of
$N(r)$
yields
$N(r)=o\left (\frac {1}{(1-r)^{t-1}}\right )$
. Since
$n(s)$
is nondecreasing, we obtain
$$ \begin{align*} (r-r^2)n(r^2)\leq\int_{r^2}^r n(s)ds=o\left(\frac{1}{(1-r)^{t-1}}\right), \end{align*} $$
which implies
$n(r)=o\left (\frac {1}{(1-r)^t}\right )$
. This, together with (4), yields the sufficiency. The proof is complete now.
Proof of Theorem 1.3
We shall show that (i)
$\Leftrightarrow $
(iii) and (iii)
$\Rightarrow $
(ii) since (ii)
$\Rightarrow $
(i) is trivial. Firstly, we consider (i)
$\Leftrightarrow $
(iii). As above, we may assume
$|f(0)|=1$
. Set
$\widehat {F}_r(\theta )=\mathcal {R} f(re^{i\theta })/(\sum _{k=0}^{\infty } |a_k|^2 r^{2k})^{\frac {1}{2}}$
. We observe that
$$ \begin{align*} &\frac{1}{2\pi}\int_{|z|<s} (\log|\mathcal{R} f(z)|)(1-|z|)^{t-2} dA(z)\\ &\quad=C_1(s)\bigg\{\frac{1}{2}\int_0^s(\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr\\ &\qquad\qquad\quad+\frac{1}{2\pi}\int_0^s\int_0^{2\pi}(\log|\widehat{F}_r(\theta)|)(1-r)^{t-2}d\theta dr\bigg\}, \end{align*} $$
where
$C_1(s)$
is bounded by the monotonicity of
$ \int _0^{2\pi }\log |\mathcal {R} f(re^{i\theta })|d\theta $
in r. By the estimate (2), for any
$t>1$
and
$s\in [0,1]$
, we obtain
$$ \begin{align} \mathbb{E}\left(\frac{1}{2\pi}\int_0^s\int_{0}^{2\pi}\left|\log|\widehat{F}_{r}(\theta)|\right|(1-r)^{t-2}d\theta dr\right) \leq C, \end{align} $$
where C is an absolute constant. Therefore, we obtain
$$ \begin{align*} \sup_{0\leq s<1}\int_{|z|<s} (\log|\mathcal{R} f(z)|)(1-|z|)^{t-2} dA(z)<\infty \quad \text{a.s.} \end{align*} $$
if and only if
$$ \begin{align*} \int_0^1 (\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr<\infty. \end{align*} $$
This, together with Lemma 3.1, proves (i)
$\Leftrightarrow $
(iii). Next, (iii)
$\Rightarrow $
(ii). By Jensen’s formula,
$$ \begin{align*} N_{\mathcal{R}f}(r) =\frac{1}{2}\log\left(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}\right)+\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta-\log|X_{0}|. \end{align*} $$
Integrating with respect to r over
$(0,1)$
and taking the expectation give us
$$ \begin{align*} \mathbb{E}&\left(\int_0^1 N_{\mathcal{R}f}(r)(1-r)^{t-2}dr\right)\\ &\quad=\frac{1}{2}\int_0^1 (\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr\\ &\qquad+\mathbb{E}\left(\frac{1}{2\pi}\int_0^1\int_{0}^{2\pi}(\log|\widehat{F}_{r}(\theta)|) (1-r)^{t-2}d\theta dr\right) -\frac{\mathbb{E}(\log|X_{0}|)}{t-1}. \end{align*} $$
Then (5), together with the assumption (iii), yields that
$\mathbb {E}(\int _0^1 N_{\mathcal {R}f}(r)(1-r)^{t-2}dr)$
is finite. Therefore,
$\int _0^1 N_{\mathcal {R}f}(r)(1-r)^{t-2} dr<\infty $
a.s. By the monotonicity of
$N_{\mathcal {R}f}(r)$
, we have
$N_{\mathcal {R}f}(r)=o\left (\frac {1}{(1-r)^{t-1}}\right )$
a.s. Further, since
$n_{\mathcal {R}f}(s)$
is nondecreasing, we get
$$ \begin{align} (r-r^2)n_{\mathcal{R}f}(r^2)\leq\int_{r^2}^r n_{\mathcal{R}f}(s)ds=o\bigg(\frac{1}{(1-r)^{t-1}}\bigg)\quad \text{a.s.} \end{align} $$
Thus,
$n_{\mathcal {R}f}(r)=o\left (\frac {1}{(1-r)^t}\right )$
a.s. Then we use integration-by-parts twice to obtain
$$ \begin{align*} \sum_{n=1}^{\infty}(1-|z_n(\omega)|)^t =&\int_0^1 (1-r)^t dn_{\mathcal{R}f}(r) \leq t\int_0^1 \frac{(1-r)^{t-1}}{r}n_{\mathcal{R}f}(r) dr\\ =&t(t-1)\int_0^1 N_{\mathcal{R}f}(r)(1-r)^{t-2}dr, \end{align*} $$
which implies that
$\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_n(\omega )|)^t)<\infty $
and completes the proof.
4 Proof of Theorem 1.5
Let
$\{X_k\}_{k=0}^{\infty }$
be a standard random sequence. By the Kolmogorov 0-1 law [Reference Cinlar3, Theorem 5.12, p. 86] and Theorem 2.3 in [Reference Duren4], one has
$ \mathbb {P} (\mathcal {R} f\in \mathfrak {B}_1)\in \{0,1\}, $
for any
$ f\in H(\mathbb {D}).$
By [Reference Nazarov, Nishry and Sodin12], this probability is one if and only if
$ f \in H^2$
. So Theorem 1.5 complements their result.
Let X be a measurable space, with
$\nu $
a probability measure on it. Assume that g is a measurable function on X such that
$||g||_{L^{p_0}(X, d\nu )}<\infty $
for some
$p_0>0$
. Then by [Reference Rudin14, p. 71], we know that
$$ \begin{align*}\exp\left(\int_X \log|g|d\nu\right)=\lim_{p\rightarrow0^+}||g||_{L^p(X, d\nu)}. \end{align*} $$
Hence, for any
$f\in H(\mathbb {D})$
,
$$ \begin{align*}e^{L(f)}=\lim_{r\rightarrow1^-}\lim_{p\rightarrow0^+}||f_r||_p,\end{align*} $$
where
$f_r(z)=f(rz), \ (0<r<1)$
. The double limit above is not commutative, and there exists
$f \in H(\mathbb {D})$
such that
$$ \begin{align*}e^{L(f)}<\infty \quad \text{but} \quad \lim_{p\rightarrow0^+}||f||_{H^p}=\infty.\end{align*} $$
Actually, for both terms to be finite, respectively, one has
$$ \begin{align*}e^{L(f)}<\infty\Longleftrightarrow f\in \mathfrak{B}_1 \quad \text{and}\quad \lim _{p\rightarrow0^+}||f||_{H^p}<\infty\Longleftrightarrow f\in \cup_{p>0}H^p.\end{align*} $$
Here, the first equivalence follows from Theorem 2.3 in [Reference Duren4]. We observe that, however, if
$f\in \cup _{p>0}H^p$
, then
$$ \begin{align} \lim_{r\rightarrow1^-}\lim_{p\rightarrow0^+}||f_r||_p=\lim_{p\rightarrow0^+}\lim_{r\rightarrow1^-}||f_r||_p. \end{align} $$
Indeed, by the canonical factorization theorem [Reference Duren4, p. 24], one can easily prove the following equality which leads to (7):
$$ \begin{align*}\lim_{r\rightarrow1^-}\frac{1}{2\pi}\int_0^{2\pi}\log|f(re^{i\theta})|d\theta =\frac{1}{2\pi}\int_0^{2\pi}\log|f(e^{i\theta})|d\theta.\end{align*} $$
It is curious to us that, despite its apparently simple looking, this equality is not recorded in the literature, up to the best of our knowledge. For several related statements, one can consult pages 17, 22, 23, 26 in [Reference Duren4]. We summarize the above discussion as the following lemma.
Lemma 4.1. If
$f\in \cup _{p>0}H^p$
, then
$\lim _{p\rightarrow 0^+}||f||_{H^p}=e^{L(f)}$
.
Remark. The polynomial version of Lemma 4.1 is well-known [Reference Borwein and Erdélyi1], and useful in number theory, in connection with the so-called Mahler measure
$M(g)$
[Reference McKee and Smyth11, Reference Smyth15], which is defined for a polynomial g with complex coefficients by
$\log M(g)=\frac {1}{2\pi }\int _0^{2\pi }\log |g(e^{i\theta })|d\theta $
. An application of the Jensen formula shows that
$M(g)=|a_n| \prod _{j=1}^n \text {max}(1, |z_j|),$
where
$a_n$
is the leading coefficient of g, and
$\{z_j\}_{j=1}^n$
the complex roots. It is an elementary fact that
$M(g)=\lim _{p\rightarrow 0^+}||g||_p.$
We are now ready to prove Theorem 1.5.
Proof of Theorem 1.5
(iii)
$\Rightarrow $
(ii) and (iv)
$\Rightarrow $
(ii) are trivial. For (i)
$\Rightarrow $
(ii), if
$f \in H^2$
, then it follows from Littlewood’s theorem (see [Reference Kahane8, p. 54], [Reference Littlewood9, Reference Littlewood10]) that
$\mathcal {R} f \in \mathfrak {B}_1$
almost surely since
$\mathfrak {B}_1$
contains
$H^p$
for every
$p>0$
. Now, for (i)
$\Rightarrow $
(iii), without loss of generality, we assume
$|a_0|=1$
. Recall that
$\widehat {F}_r(\theta )=\mathcal {R} f(re^{i\theta })/(\sum _{k=0}^{\infty } |a_k|^2 r^{2k})^{\frac {1}{2}}$
. By Jensen’s formula,
$$ \begin{align*} N_{\mathcal{R}f}(r) &=\frac{1}{2\pi}\int_{0}^{2\pi}\log|\mathcal{R}f(re^{i\theta})|d\theta-\log|\mathcal{R}f(0)|\\ &=\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})+\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta-\log|X_{0}|. \end{align*} $$
Taking the expectation yields
$$ \begin{align*} \mathbb{\mathbb{E}}(N_{\mathcal{R}f}(r)) =\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})+\mathbb{E}\left(\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta\right) -\mathbb{E}(\log|X_{0}|). \end{align*} $$
Since
$f\in H^{2}$
, by the estimate (2), we know that
$\lim _{r\rightarrow 1^-}\mathbb {E}(N_{\mathcal {R}f}(r))$
is finite. This, together with Fubini’s theorem, yields that
$\int _{0}^{1}\mathbb {E}(n_{\mathcal {R}f}(t))dt$
is finite, which is, in turn, equivalent to that
$\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_{n}(\omega )|))$
is finite by applying integration-by-parts and Fubini’s theorem to
$\sum _{n=1}^{\infty }(1-|z_{n}(\omega )|)=\int _0^1 (1-t)dn_{\mathcal {R}f}(t).$
Next, we show (i)
$\Rightarrow $
(iv). According to Littlewood’s theorem and Lemma 4.1, if
$f\in H^2$
, then
$e^{L(\mathcal {R} f)}=\lim _{p\rightarrow 0^+}||\mathcal {R} f||_{H^p}$
a.s. Taking the expectation yields
$$ \begin{align*} \mathbb{E} e^{L(\mathcal{R} f)}=\mathbb{E}(\lim _{p\rightarrow0^+}||\mathcal{R} f||_{H^p})\leq \mathbb{E}(||\mathcal{R} f||_{H^2})\leq(\sum_{k=0}^{\infty} |a_k|^2)^{\frac{1}{2}}<\infty, \end{align*} $$
as desired, where the second inequality is due to an application of Jensen’s inequality.
It remains to show (ii)
$\Rightarrow $
(i). Recall that
$\mathcal {R} f\in \mathfrak {B}_1$
a.s. if and only if
$L(\mathcal {R} f)<\infty $
a.s. We observe that
$$ \begin{align*} L(\mathcal{R} f)=\lim_{r\rightarrow1^-}\frac{1}{2}\log(\sum_{k=0}^{\infty}|a_k|^2 r^{2k}) +\lim_{r\rightarrow1^-}\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta. \end{align*} $$
The limit
$\lim _{r\to 1^-}\frac {1}{2\pi }\int _{0}^{2\pi }\log |\widehat {F}_{r}(\theta )|d\theta $
exists since
$L(\mathcal {R} f)$
is finite almost surely and
$\sum _{k=0}^{\infty } |a_k|^2 r^{2k}$
increases monotonically with r. By Fatou’s lemma and (2), we get
$$ \begin{align*} \lim_{r\rightarrow1^-}\bigg|\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta\bigg|<\infty \quad\text{a.s.}, \end{align*} $$
which yields
$f\in H^2$
.
As an application, from Theorem 1.5, one can easily deduce the following, since both statements are equivalent to
$f \in H^2$
. It is of interests to us to find a direct proof for this result, which, however, eludes our repeated efforts. The corresponding deterministic statement is clearly false.
Corollary 4.2. Let
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
and
$\{X_k\}_{k=0}^{\infty }$
be a standard random sequence. Then
$$ \begin{align*} L(\mathcal{R} f)<\infty \quad \text{a.s.}\quad\Longleftrightarrow \quad L^+(\mathcal{R} f)<\infty \quad \text{a.s.}, \end{align*} $$
where
$L^+(f):=\lim _{r\rightarrow 1^-}\frac {1}{2\pi }\int _{0}^{2\pi }\log ^+|f(re^{i\theta })|d\theta .$
5 The Bergman spaces
In 1974, Horowitz showed that the zero sets of the Bergman space
$A^p$
, for any
$p>0$
, satisfy the following for any
$\varepsilon>0$
[Reference Horowitz6]:
$$ \begin{align} \sum_{n=1}^{\infty} (1-|z_n|)\bigg(\log\frac{1}{1-|z_n|}\bigg)^{-1-\varepsilon}<\infty. \end{align} $$
Let
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in A^p$
for some
$p>0$
. By [Reference Cheng, Fang and Liu2],
$\mathcal {R} f\in A^q $
almost surely for some
$q>0$
, hence, the zero set
$\{z_n(\omega )\}_{n=1}^{\infty }$
of
$\mathcal {R} f$
satisfies (8) almost surely. We have conjectured the following for
$\mathcal {R} f$
when
$f \in A^p$
:
$$ \begin{align} \sum_{n=1}^{\infty} (1-|z_n(\omega)|)\bigg(\log\frac{1}{1-|z_n(\omega)|}\bigg)^{-1}<\infty\quad \text{a.s.} \quad ? \end{align} $$
This is negated below.
By arguing similarly as in the proof of Lemma 3.1, we obtain that the zero set
$\{z_{n}\}_{n=1}^{\infty }$
of
$f\in H(\mathbb {D})$
satisfies
$$ \begin{align} \sum_{n=1}^{\infty}\left(1-|z_{n}|\right)\left(\log\frac{1}{1-|z_{n}|}\right)^{-1}<\infty \end{align} $$
if and only if
$$ \begin{align} \int_{\mathbb{D}}(\log|f(z)|) (1-|z|)^{-1}\left(\log\frac{e}{1-|z|}\right)^{-2}dA(z)<\infty. \end{align} $$
Moreover, arguments similar to those in the proof of Theorem 1.3, yield a random version that the zero set
$\{z_{n}(\omega )\}_{n=1}^{\infty }$
of
$\mathcal {R} f$
satisfies (10) almost surely if and only if
$$ \begin{align} \int_0^1 \big(\log ( \sum_{k=0}^{\infty} |a_k|^2 r^{2k}) \big) (1-r)^{-1} \left(\log\frac{e}{1-r}\right)^{-2} dr<\infty. \end{align} $$
In order to negate (9), it suffices to find
$f\in A^p$
such that (12) fails. Let
$$ \begin{align*}f_t(z)=\sum_{n=1}^{\infty} 2^{nt} z^{2^n}, \quad 0<t<1/p\end{align*} $$
be a lacunary series. By [Reference Jevtić, Vukotić and Arsenović7, Theorem 8.1.1],
$f_t \in A^p$
if and only if
$t<1/p$
. Set
$g_t(r) = \sum _{n=1}^{\infty } 2^{2nt} r^{2^{n+1}}$
. We claim that if
$t>0$
, then
$$ \begin{align} g_t(r) \asymp \left(\frac{1}{1-r}\right)^{2t}. \end{align} $$
Let
$r_N=1-\frac {1}{2^N}$
. By monotonicity in r, it suffices to show that
$$ \begin{align*} g_t(r_N)= \sum_{n=1}^{\infty} 2^{2nt} r_N^{2^{n+1}} \asymp 2^{2Nt}. \end{align*} $$
Note that
$r_N^{2^{n+1}} $
is bounded above and below when
$1\leq n \leq N$
. Hence,
$$ \begin{align*}\sum_{n=1}^{N} 2^{2nt} r_N^{2^{n+1}} \asymp \sum_{n=1}^{N} 2^{2nt} \asymp 2^{2Nt}.\end{align*} $$
Additionally,
$$ \begin{align*} \sum_{n=N+1}^{\infty}2^{2nt} r_N^{2^{n+1}} \lesssim \sum_{n=N+1}^{\infty} 2^{2nt} e^{-2^{n+1-N}} \lesssim 2^{2Nt}. \end{align*} $$
Therefore, the assertion (13) follows, and we deduce that (12) fails for
$f_t$
.
Acknowledgments
The authors would like to thank the anonymous referee for careful reading of the manuscript and for his/her insightful comments and suggestions which helped to make the paper more readable. The authors also thank Prof. Pham Trong Tien for his valuable discussion.
