1. Introduction
Supraglacial lake dynamics have become an increasingly important factor in ice-sheet response to climate change, because lakes have been implicated in ice-shelf disintegration (e.g. Reference Scambos, Hulbe and FahnestockScambos and others, 2003) and influenced grounded ice-sheet flow through their impact on subglacial hydrology. When lakes on ice sheets suddenly drain (e.g. Reference DasDas and others, 2008; Reference DoyleDoyle and others, 2013; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013), the subglacial drainage system receives a pulse of water that, in turn, contributes to both temporary and longer-term changes in ice velocity (Reference BartholomewBartholomew and others, 2011; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference Banwell, Willis and ArnoldBanwell and others, 2013; Reference JoughinJoughin and others, 2013). Within the ablation zone of the Greenland ice sheet (GrIS), supraglacial lakes form in surface depressions controlled by the interplay between bedrock topography and ice flow (Reference Echelmeyer, Clarke and HarrisonEchelmeyer and others, 1991; Reference Darnell, Amundson, Cathles and MacAyealDarnell and others, 2013; Reference SergienkoSergienko, 2013). This means that processes unrelated to climate change (i.e. bedrock characteristics and ice-flow physics) determine the areal distribution, maximum depth and volume of the lakes.
In contrast, lakes on floating ice shelves do not depend on the ice/bedrock interaction to define their location, geometry and volume. Instead, lakes on ice shelves inhabit various surface depressions that arise from a variety of processes (e.g. basal crevassing (Reference McGrath, Steffen, Rajaram, Scambos, Abdalati and RignotMcGrath and others, 2012), grounding zone flow-stripe development (Reference Glasser and GudmundssonGlasser and Gudmundsson, 2012) and intermittent suture-zone voids (Reference GlasserGlasser and others, 2009)). Lakes on ice shelves are also products of the viscoelastic flexure of the ice, and can represent a surface load that can suddenly change when fractures develop through the ice shelf, causing lake drainage through hydrofracture (Reference Van der VeenVan der Veen, 1998, Reference Van der Veen2007; Reference MacAyeal and SergienkoMacAyeal and Sergienko, 2013).
Among the impacts of supraglacial lakes on both grounded and floating ice, none are so powerfully linked to ice-sheet change as those leading to the sudden collapse of the Larsen B ice shelf (LBIS), Antarctica, in 2002 (e.g. Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000, Reference Scambos, Hulbe and Fahnestock2003; Reference Van den BroekeVan den Broeke, 2005; Reference VaughanVaughan, 2008). During the decades leading up to the collapse, the number of lakes on the central portion of the ice shelf gradually grew from near zero to ~3000 (Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000; Reference Glasser and ScambosGlasser and Scambos, 2008). However, just days prior to the disintegration, the majority of the ~3000 lakesdrained, suggesting that the sudden, coordinated movement of surface water to the ocean below may have been a contributing proximal trigger to the collapse (Reference Scambos, Hulbe and FahnestockScambos and others, 2003). The loss of the majority of the LBIS resulted in a reduction of the buttressing forces that act to reduce ice flow across grounding lines shared with the ice shelf. Following the break-up event, a sustained speed-up of land-to-sea ice flow of glaciers that were previously buttressed by the ice shelf was observed (Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000, Reference Scambos, Bohlander, Shuman and Skvarca2004; Reference Sergienko and MacAyealSergienko and MacAyeal, 2005; Reference Van den BroekeVan den Broeke, 2005; Reference Glasser and ScambosGlasser and Scambos, 2008; Reference Glasser, Scambos, Bohlander, Truffer, Pettit and DaviesGlasser and others, 2011; Reference Rott, Müller, Nagler and FloricioiuRott and others, 2011). Thus, as with the acceleration of GrIS flow, the inland ice of Antarctica can also accelerate in response to lake drainage, but by a different mechanism.
However, while ground-based studies of supraglacial lakes on the GrIS are abundant, relatively little ground-based research has been directed toward study of supraglacial lakes on Antarctic ice shelves. Antarctic lakes are harder to study because they are either more remote (relative to logistics centres) or have themselves disappeared as the ice shelves on which they resided no longer exist.
In the present study, we endeavour to strengthen the link between the relatively plentiful research directed to lakes on the GrIS and the relatively unstudied lakes on the present and recently collapsed ice shelves of Antarctica. The first step in establishing this link is to determine parallels and contrasts between spatial patterns, shapes, surface areas and depths of lakes on the land-terminating Paakitsoq region of the GrIS and on the former LBIS. Our study is conducted through the analysis of Landsat 7 Enhanced Thematic Mapper Plus (ETM+) imagery acquired for both regions.
In addition to improving our overall understanding of supraglacial lakes on ice shelves, this study will help to establish whether or not surface-routing and lake-filling models which are already in existence for the GrIS (e.g. Reference Banwell, Arnold, Willis, Tedesco and AhlstrømBanwell and others, 2012a; Reference Leeson, Shepherd, Palmer, Sundal and FettweisLeeson and others, 2012) are transferable to Antarctic ice shelves. Finally, our work will establish idealized properties of supraglacial lake geometries; an important first step in the development of numerical model studies of lakes on ice sheets and ice shelves.
2. Methods
In this section we describe the analytical process that was undertaken for both the LBIS, and for a similar-sized (~3000 km2) area of grounded ice in the Paakitsoq region of the GrIS, northeast of Jakobshavn Isbræ (Reference BanwellBanwell and others, 2012b, their fig. 1). Two Landsat 7 ETM+ images were analysed for this study. For the LBIS, we chose the image dated 21 February 2000 (scene ID: L71216106_ 10620000221), as this is the most cloud-free image available within 2 years of the break-up event. This image also forms the basis of a prior study of lake patterning and morphology on the LBIS (Reference Glasser and ScambosGlasser and Scambos, 2008), and thus serves as a fiduciary representation of the state of the LBIS 2 years prior to its collapse. For Paakitsoq, Greenland, we used the cloud-free image dated 7 July 2001 (scene ID: L71009011_01120010707). We note that the two images are from periods of time during the melt season that do not coincide with either ‘time of maximum lake volume’ or ‘end of season’ or any other benchmark, but are rather snapshots of time that represent the best available information.
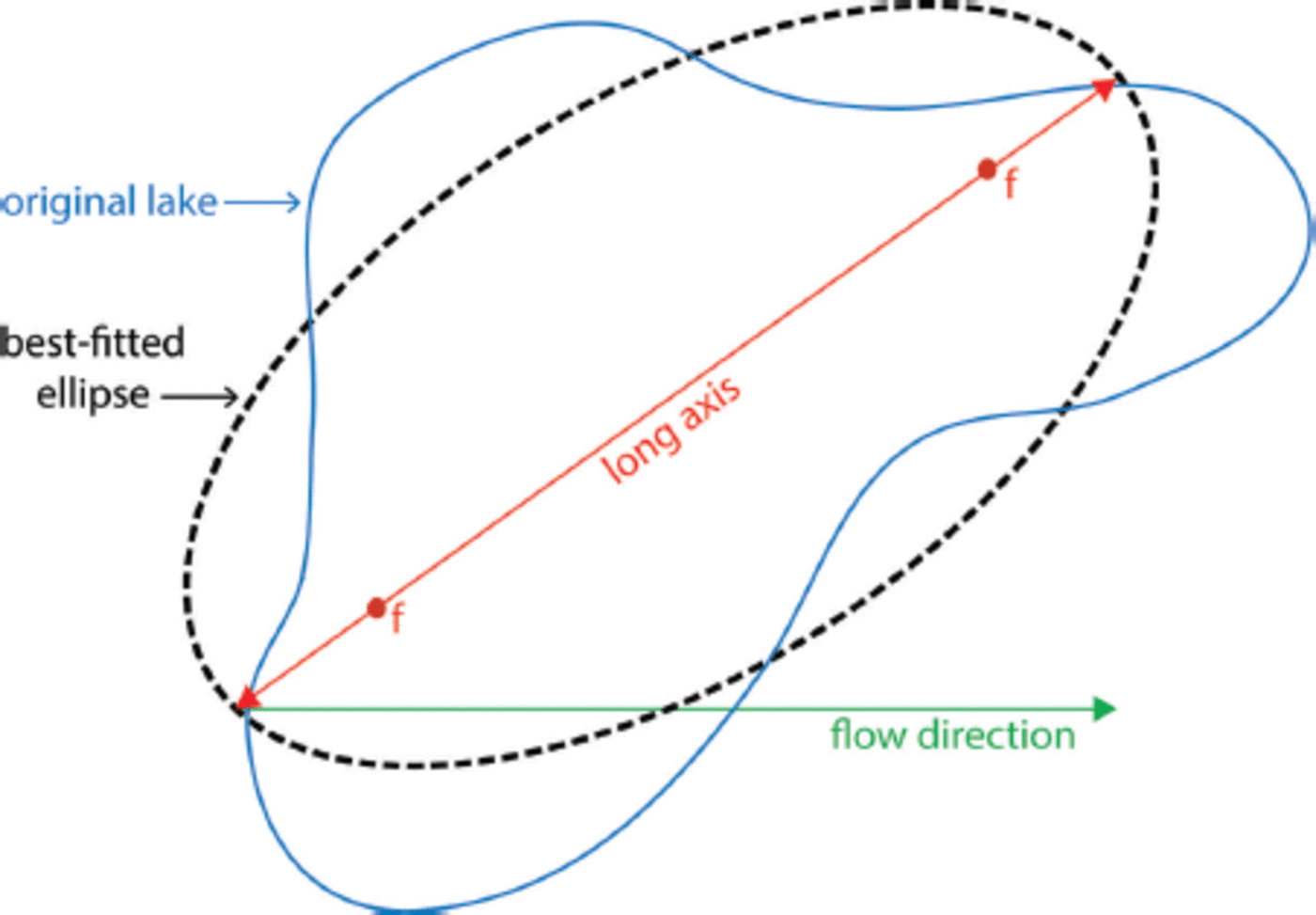
Fig. 1. Schematic of optimal fit of an ellipse (with f indicating the foci) to the outline of a previously identified lake. The ellipse and original lake are equal in area. The angle between the long axis of the ellipse and the flow direction (either clockwise or anticlockwise) determines the ellipse orientation.
2.1. Lake boundaries and area
Image pixels were classified into ‘lake-covered’ or ‘bare ice/ snow’ using Landsat image reflectance data, following Reference Box and SkiBox and Ski (2007). Each Landsat band was first converted from digital numbers to radiance and then from radiance to reflectance using the equations of Reference Chander, Markham and HelderChander and others (2009). Then, to make this classification, the blue/red ratio of reflectance (involving Landsat bands 1 and 3; 450-515 and 630-690 nm, respectively) was evaluated from the Landsat image. As this ratio increases toward the lake centres, where water is deepest, and decreases towards the edges, where water is most shallow, it was necessary to carefully identify the value of this ratio corresponding to bare ice at lake edges. Based on experimental results, and on known areas of lakes on the GrIS, Reference Box and SkiBox and Ski (2007) suggest that the threshold value of blue/red ratio of reflectance should be in the range 1.05-1.25 at the edges of lakes. Further to the study by Reference Box and SkiBox and Ski (2007), we found that the algorithm needs to be adapted to avoid problems associated with floating lake ice on lake surfaces. Unless these areas were masked, negative lake depths were found, due to the high reflectance of the ice compared to the open water.
Once the pixels representing flooded areas had been established, the ‘bwboundaries’ function in MATLAB was used to identify lake boundaries. Subsequently, the ‘regionprops’ function in MATLAB was used to identify the number of pixels (i.e. surface areas of lakes) within the closed edges as a means of determining lake area.
2.2. Lake depth
Supraglacial lake depths were estimated using a method developed by Reference Sneed and HamiltonSneed and Hamilton (2007), originally applied to Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) (VNIR1, 520–600 nm) imagery, but also applicable to Landsat 7 ETM+ imagery (band 2; 525–605nm) (Reference Sneed and HamiltonSneed and Hamilton, 2011). The approach for extracting water depth and lake-bottom albedo is based on the Beer–Lambert law (Reference Ingle and CrouchIngle and Crouch, 1988), which describes the attenuation of radiation through a water column:
where I(z,λ) is the water-leaving spectral intensity at some depth, I(0λ) is the spectral intensity at zero depth, Kλ is the spectral attenuation and z is depth. Written in terms of reflectance, and inverted to logarithmic form (Reference PhilpotPhilpot, 1989), z is determined by
where Ad is the bottom or substrate albedo (reflectance), R∞ is the reflectance for optically deep water, Rw is the reflectance of some pixel of interest and g is given by
where Kd is the diffuse attenuation coefficient for down-welling light, a is the beam absorption coefficient and D u is an upwelling light distribution function or the reciprocal of the upwelling average cosine (Reference MobleyMobley, 1994).
To determine Ad we took the mean reflectance value of the ring of pixels around the lake that are barely covered with water (i.e. those adjacent to the water-covered pixels, as detected by the blue/red ratio of reflectance). Although Reference Sneed and HamiltonSneed and Hamilton (2007) used the same Ad for their entire region of interest, as our region is larger we chose to calculate a unique Ad for each lake. For the LBIS, values for Ad ranged from 0.30 to 0.79 (with a mean value of 0.68), and for Paakitsoq, values for Ad ranged from 0.17 to 0.76 (with a mean value of 0.66).
To determine R∞ , the reflectance from optically deep water where the influence of bottom reflectance is nil, we used the value of reflectance from water that is deeper than ~40 m in the image. It was necessary to take care when selecting pixels that were far from shorelines, to ensure that R∞ estimates were not biased by water that was too shallow, turbid water or pixels containing floating ice.
This approach assumes that the substrate (bottom) of the lake is homogeneous, the impact of suspended or dissolved organic or inorganic matter in the water column is negligible on absorption, there is no inelastic scattering (e.g. Raman scattering or fluorescence) and that the lake surface is not significantly roughened due to wind (Reference Sneed and HamiltonSneed and Hamilton, 2007). Once the depth of each ‘flooded’ pixel had been calculated, the ‘regionprops’ function in MATLAB was again used to determine the ‘MaxIntensity’ (i.e. the maximum lake depth) and the ‘MeanIntensity’ (i.e. the mean lake depth) for each of the identified lakes.
2.3. Lake shape, orientation and eccentricity
Once lake edges, and thus areas, had been delineated (following Reference Box and SkiBox and Ski, 2007), and depths had been established (following Reference Sneed and HamiltonSneed and Hamilton, 2007), the MATLAB ‘regionprops’ function was used to obtain other lake properties. As illustrated in Figure 1, this function works by best-fitting ellipses to the identified lakes. Lake properties which this function is able to diagnose include: (1) eccentricity (i.e. the ratio from 0 to 1 of the distance between the foci of the ellipse and its long axis length, where 0 indicates that the ellipse is a circle and 1 indicates a line segment), (2) orientation (from 0° to 90° from the average ice-flow direction on the ice shelf/sheet in either a clockwise or anticlockwise direction) and (3) solidity (from 0 to 1, denoting the proportion of the pixels in the convex hull of the lake that are also bound within the lake itself; lakes with sinuous boundaries tend to have low solidity, circular lakes have a solidity of 1).
2.4. Algorithm validation
Using the same 21 February 2000 image, Reference Glasser and ScambosGlasser and Scambos (2008) produced a detailed structural glaciological analysis of overall changes in surface structures on the LBIS prior to its collapse in late February 2002. Although this study, which used manual digitization, identified general patterns of lake positions, areas and shapes of supraglacial lakes, it did not perform a quantitative analysis of these properties and, importantly, did not analyse lake depth. Thus, in our study, we also statistically analyse the shape files of lakes used in the Reference Glasser and ScambosGlasser and Scambos (2008) study, in order to compare, and thus validate, the results of our study using an automated algorithm.
3. Results
3.1. Larsen B lake patterns and characteristics
The most appropriate value for the blue/red band threshold for the LBIS to appropriately discriminate bare ice/snow from water is found to be 1.2, which results in the identification of 3227 lakes, as shown in Figure 2. This threshold value is chosen because it produces a pattern of lakes on the ice-shelf surface that is most similar to the pattern of lakes identified visually on the Landsat image and documented by Reference Glasser and ScambosGlasser and Scambos (2008) (also see Section 3.2). If a slightly lower threshold value of 1.1 is chosen, only 272 separate flooded areas are identified, as the majority of the entire surface of the LBIS is erroneously classified as lake-covered. If a slightly higher threshold value of 1.3 is chosen, only 1419 lakes are identified, and the small lakes, in particular, are no longer identified.

Fig. 2. Depths of lakes on the Larsen B ice shelf using reflectance of the 2 1 February 2000 Landsat image. Although some lake depths are >4m, for visualization purposes 4m is plotted as the maximum depth here. Three areas, a, b and c, are enlarged to show varying lake characteristics and patterns across the ice-shelf surface. Marginal areas, which can be grounded ice, bare land surface or ocean surface, are shaded grey.
As also recognized by Reference Glasser and ScambosGlasser and Scambos (2008), we identify a variety of different ‘domains’ on the ice-shelf surface, each displaying different lake characteristics. We have highlighted lakes within three areas of these domains in Figure 2. In area a of Figure 2, we see fairly linearly shaped lakes, with their long axis diverging from the mean ice-flow direction from west to east. This is indicative of ice-flow divergence where fast-flowing glaciers enter the ice shelf from the west. Although lake depths generally vary from ~1 to ~4m here, the deepest identified lake on the ice shelf also falls within this region; calculated to be 6.8 m at its deepest point. In area b of Figure 2, longitudinal features, which are aligned roughly parallel with ice flow, dominate. These features are up to 30 km in length and 2-3 m in depth. Thus, compared to area a, ice flow in this region is likely to be convergent rather than divergent along the flow direction. In area c of Figure 2, we see lakes that are fairly circular (i.e. their eccentricity is close to 1) and have a larger mean area than the majority of lakes on the ice shelf. We suggest that these characteristics are due to slower ice flow in this region (for additional information on structural features of the LBIS related to flow, as well as the area of the LBIS that disintegrated, refer to Reference Glasser and ScambosGlasser and Scambos, 2008). Through an increased lifespan, lakes would be able to undergo more enlargement by bottom ablation than other lakes on the ice shelf. The majority of the lakes in this area are also covered with floating ice (seen as white areas in Fig. 2c). Although the outer rings of open, lake-ice-free water of the lakes are calculated to be from ~0.5 to ~1.5 m in depth, we cannot calculate the depth of the central, probably deepest, regions because of the ice cover.
Over the entire ice shelf, we calculate the mean lake area to be 0.10 km2 (with standard deviation, = 0.29 km2) and the total surface area covered by lakes to be 315 km2. This is 5.3% of the total area of ice shelf analysed, with a mean lake density of 0.55 km–2. We calculate that lakes covered ~10% of the 3200 km2 of ice shelf which disintegrated in a 35 day period beginning on 31 January 2002 (Reference Scambos, Bohlander, Shuman and SkvarcaScambos and others, 2004). As we discuss below, this larger percentage of lake cover constitutes one of the most important differences between lakes on the LBIS and lakes on the GrIS.
The mean lake depth on the LBIS is calculated to be 0.82 m (a = 0.56 m), and the mean maximum lake depth is 1.6 m (a = 0.99 m) (Fig. 3). The mean eccentricity is 0.84 (a = 0.13 m), the mean solidity is 0.80 (a = 0.14) and the average mean orientation of the long axis of ellipses (best-fitted to the lakes) is 46° away from the flow direction (a = 28°). The latter assumes that the average flow direction is from west to east (Reference Vieli, Payne, Du and ShepherdVieli and others, 2006, their fig. 5).
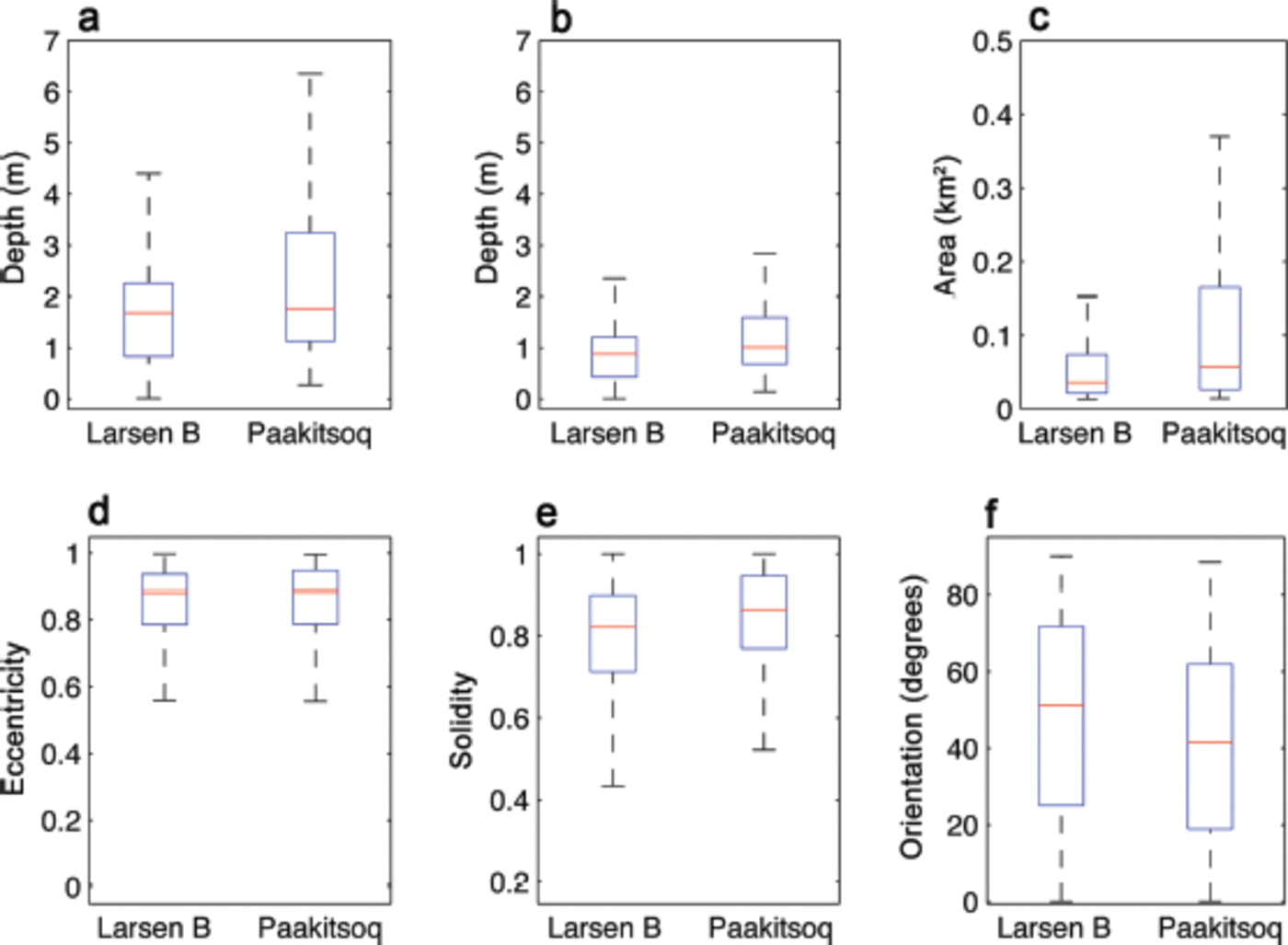
Fig. 3. Plots showing (a) maximum depth, (b) mean depth, (c) mean area, (d) eccentricity, (e) solidity and (f) orientation from the mean flow direction, of lakes on both the LBIS (N = 3227) and at Paakitsoq (N = 239) in order to clearly capture the scale and differences between the two lake systems. On each box the red mark is the median and the edges of the box are the 25th and 75th percentiles (q 1 and q 3, respectively). The length of the whiskers (dotted lines) is equal to q 3 + 1.5(q 3 – q 1).
Using the mean lake depth (0.82 m), the total number of lakes on the LBIS (3227), the average lake area (0.1 km2) and the assumption that the ice shelf has a uniform thickness of 200 m (Sandhager and others, 2005), we calculate that there are 5.2 x108MJ of potential energy stored on the surface as free water (equivalent to 8.7 x 104MJ km–2). This calculation is useful, as it gives an indication of the amount of energy available for the drainage of lakes by hydrofracture, the process that was probably the main driver behind the disintegration of the ice shelf (Reference Scambos, Hulbe and FahnestockScambos and others, 2003, Reference Scambos2009).
3.2. Comparison to results of the Glasser and Scambos (2008) study
Reference Glasser and ScambosGlasser and Scambos (2008) identified 2696 supraglacial lakes (their ‘meltwater ponds’); 16% fewer than the number of lakes identified in our study. Reference Glasser and ScambosGlasser and Scambos (2008) also calculated that individual lakes had a slightly higher mean area of 0.13 km2, and in total they calculated that lakes on the LBIS covered a slightly higher surface area of 365 km2. However, although we calculate that lakes are on average ~30% smaller than the lakes identified by Reference Glasser and ScambosGlasser and Scambos (2008), as we identify ~16% more lakes on the LBIS we calculate that the total surface area of lake coverage is only ~12% less than that calculated by Reference Glasser and ScambosGlasser and Scambos (2008).
3.3. Comparison with a land-terminating region of the GrIS
Compared to the threshold value for the blue/red ratio for the LBIS, a slightly higher threshold value of 1.4 is required for the Paakitsoq region of the GrIS. Using this threshold value, we identified 239 lakes, as shown in Figure 4 (note a different depth scale than Fig. 1). Threshold values <1.4 for Paakitsoq result in large, dispersed areas of the ablation zone being erroneously classified as lakes. Threshold values >1.4 for Paakitsoq meant that the wispy, linear water features, observed to link lakes in the areas of higher elevation within the region studied (Fig. 4, area b), were no longer identified as flooded areas.

Fig. 4. Depths of lakes in the Paakitsoq region, West Greenland (see Reference BanwellBanwell and others, 2012b, for location figure) using reflectance of the 7 July 2001 Landsat image. Two areas, a and b, are highlighted, in order to show varying lake characteristics and patterns across the ice-sheet surface. Marginal areas of bare land surface are shaded grey.
Figure 3 compares the values of key lake properties between the LBIS and the Paakitsoq region. Compared to lakes on the LBIS, lakes in the Paakitsoq region have a larger mean area of 0.15 km2 ( = 0.24 km2). However, we calculate that lakes only cover ~1% of the ice surface compared to 5.3% for the LBIS. The mean lake density in the Paakitsoq region is thus only 0.07 km–2. This constitutes one of the major differences between lakes on grounded ice and floating ice we have identified in the comparison.
Lakes in the Paakitsoq region are also generally deeper than lakes on the LBIS, with a mean depth of 1.3 m (σ = 0.97 m) and a mean maximum depth of 2.5 m (σ = 1.9 m) (Fig. 3 and 4). The deepest identified lake in the region, calculated to have a maximum depth of 9.0 m, is shown in area a of Figure 4. Overall, lake depths across the Paakitsoq region show more variation than the lakes on the LBIS (Fig. 3). With regard to the lake orientations, LBIS lakes are on average orientated 46° away from the dominant ice-flow direction, whereas the average orientation of Paakitsoq lakes from the dominant flow direction (east to west) is 37° (σ = 24°). The calculated solidity for the Paakitsoq lakes is 0.83 (σ = 0.15), which is 4% higher than the value for the LBIS lakes (i.e. Paakitsoq lakes are more convex than LBIS lakes).
4. Discussion
When average values for lake properties identified in our study are compared to those of lakes identified by Reference Glasser and ScambosGlasser and Scambos (2008), it is encouraging that the total number of lakes and the average area of those lakes are of the same order of magnitude for both studies. There are, however, some minor discrepancies. For example, we identify 16% more lakes than Reference Glasser and ScambosGlasser and Scambos (2008), and those lakes are on average 30% smaller. Thus, it is likely that the analysis of Reference Glasser and ScambosGlasser and Scambos (2008) may have grouped together into one large lake what our automated algorithm identified as a collection of nearby smaller lakes.
The automated algorithm used in our study extends the Reference Glasser and ScambosGlasser and Scambos (2008) study by also calculating lake depths. Reference Glasser and ScambosGlasser and Scambos (2008) state that, although supraglacial lakes are generally aligned along the local topographic slope (which is roughly aligned perpendicular to the general ice-flow direction), some surface water features are longitudinal in form and are aligned parallel to the downslope direction. Although they suggest that these features could be interpreted as meltwater streams, as have been observed on the Amery Ice Shelf, Antarctica (Reference PhillipsPhillips, 1998), such a deduction does not agree with all other observations. For example, as we calculate these features to be ~2m or more deep (Fig. 2, area b, displayed in light green), we suggest that they are unlikely to all be meltwater streams, as many do not reach the eastern edge of the ice shelf and thus there is not an obvious outflow point for a large quantity of water to leave the ice shelf (unless outflow is accommodated by a moulin). Additionally, as the ice-shelf surface slope is minimal (i.e. the ice thickness change from grounding line to ice front is ~50 m (Reference Sandhäger, Rack and JansenSandhäger and others, 2005, their fig. 2), implying a 5m change in ~50 km, or a slope of 10–4), it seems unlikely that there could be a substantial volume of flowing water across the ice-shelf surface. Thus, although some meltwater has been observed to leave the LBIS as waterfalls (personal communication from T. Scambos, 2013), this runoff into the ocean is likely to be only a small fraction of the summer surface melt volume.
The standard deviations and interquartile ranges of mean lake depth, maximum lake depth and lake area are generally higher in the Paakitsoq region, indicating that Paakitsoq lakes have more variable depths and areas than LBIS lakes (Fig. 3). The reason for this is likely to be primarily related to the substantial elevation gradient in the Paakitsoq region: from ~400 m at the ice margin to 1500 m inland, compared to an almost negligible elevation gradient on the floating LBIS. Consequentially, on the GrIS, increased melt as summer progresses not only causes existing lakes to grow, but also results in lake formation at higher elevations as the ablation zone expands (Reference LiangLiang and others, 2012; Reference FitzpatrickFitzpatrick and others, 2013). Conversely, the standard deviations of eccentricity, orientation and solidity are found to be comparable between the two regions. This is because these lake properties are affected by elevation to a much lesser extent than lake depth and area.
The mean depth of Paakitsoq lakes is calculated to be 0.48 m more than for lakes on the LBIS, and the mean maximum depth of Paakitsoq lakes is calculated to be 0.90 m more than LBIS lakes (Fig. 3). Additionally, Paakitsoq lakes are on average 0.05 km2 larger than LBIS lakes. A less striking difference between lakes in the two regions concerns their average orientation. We calculate that Paakitsoq lakes are orientated at a lower angle (378) to the average ice flow direction than the LBIS lakes (468). These differences are thought to be due to a variety of different reasons, discussed below.
We suggest that the differences in average lake depth and area are partially due to the higher surface melt rates on the GrIS. Owing to its size and elevation, the Antarctic ice sheet creates its own climate with an important influence on the surrounding ocean (Reference Rignot and ThomasRignot and Thomas, 2002; Reference BromwichBromwich and others, 2013). Furthermore, once a lake exists, it enlarges not only by receiving meltwater from the surrounding ice surface, but also due to a positive albedo feedback process, whereby bottom-lake ablation is enhanced by up to 170% compared to bare ice, as modelled by Reference Lüthje, Pedersen, Reeh and GreuellLüthje and others (2006), and up to 135%, as observed by Reference TedescoTedesco and others (2012).
The other reason for the differences in average lake depth, area and orientation between the two locations relates to the two fundamentally different ways in which supraglacial lakes on land-terminating regions of the GrIS and on Antarctic ice shelves initially form and subsequently interact with one another. At Paakitsoq, supraglacial lakes form in surface depressions that are controlled by the underlying bedrock topography (Reference Box and SkiBox and Ski, 2007; Reference Lampkin and VanderbergLampkin and Vanderberg, 2011) and by spatial variations in the degree of basal ice lubrication and sliding velocity (Reference GudmundssonGudmundsson, 2003). This causes the majority of lakes on the GrIS to remain in fixed locations interannually (Reference Thomsen, Thorning and BraithwaiteThomsen and others, 1988; Reference Echelmeyer, Clarke and HarrisonEchelmeyer and others, 1991; Reference Selmes and Murray Tand JamesSelmes and others, 2011), and thus the average orientation and volume of lakes in a specific region of the GrIS will depend on the average patterns of bed topography and basal friction in that region. Additionally, if lakes on the GrIS overflow, lakes in downstream catchments may receive extra water, and thus surface catchment areas of lakes on the GrIS may enlarge through the melt season (Reference Banwell, Arnold, Willis, Tedesco and AhlstrømBanwell and others, 2012a).
Conversely, undulations and depressions on ice shelves, which may fill to form lakes, are produced and influenced by an entirely different combination of processes. To date, only a few studies have focused on improving our understanding of lake formation processes on ice shelves. One such study is by Reference LaBarbera and MacAyealLaBarbera and MacAyeal (2011), who suggest that supraglacial lakes on ice shelves form in the depressions of a viscous-buckling wave associated with compressive ice-shelf stresses. This idea is thought to be associated with a previously described ice-shelf phenomenon known as ‘pressure rolls’ (Reference Hattersley-SmithHattersley-Smith, 1957; Reference Collins and McCraeCollins and McCrae, 1985). As various studies have also concluded, when supraglacial lakes accumulate water, they begin to flex the ice shelf downward, causing further deepening and attraction of surrounding meltwater runoff patterns (Reference Hattersley-SmithHattersley-Smith, 1957; Reference MacAyeal and SergienkoMacAyeal and Sergienko, 2013). However, due to the minimal surface slope of ice shelves compared to the steep surface slope of the GrIS, only relatively small catchment areas are likely to develop on ice shelves.
Further to these ideas, we speculate that surface undulations on ice shelves may form as ice crosses the sudden break in slope at the grounding line, as here it is likely to experience some degree of flexure, buckling or fracturing. For example, ice-covered lakes and dolines were observed near the grounding line of the Lambert/Amery Ice Shelf by Reference Hambrey and DowdeswellHambrey and Dowdeswell (1994). It is also here (i.e. near the Antarctic Peninsula mountains) where surface melting is likely to be highest, owing to a föhn effect and/or runoff from darker, ice-free areas. As the ice subsequently converges away from the grounding line and out onto the ice shelf and towards the ice front, these undulations, which were probably parallel to the grounding line (if the ice-flow direction was perpendicular to the grounding line), may undergo strain and thus rotation in response to the convergence of ice flow and the resultant stress field. We suggest that it is the combination of these processes that assist in producing lakes on the LBIS which are relatively shallow and uniform in depth, and have an average orientation of 46° to the general ice-flow direction.
5. Conclusions
Compared to lakes at Paakitsoq, a land-terminating region of the GrIS, lakes on the floating LBIS show less variance in their mean depths and areas. It is therefore conceivable that the majority of lakes on the LBIS all reached a critical volume to drain by hydrofracture at a similar time, enabling the rapid break-up of the ice shelf in March 2002. Compared to lakes at Paakitsoq, lakes on the LBIS have a greater spatial density, and also cover a greater proportion of the total surface area of the ice on which the lakes are localized (~5.3% cf. ~1.0%). This greater density is probably due to the almost negligible large-scale elevation change across the surface of the ice shelf (~25 m) compared to a change of ~1100 m at Paakitsoq. As a consequence of the low variability of the surface elevation of the LBIS, it seems feasible that supraglacial lakes are hydrologically isolated (i.e. where water does not overflow from basins of different elevation) and simply grow in place by enhanced surface ablation associated with the reduced albedo of standing water.
Finally, if we consider the transferability of existing surface-routing and lake-filling models (e.g. Reference Banwell, Arnold, Willis, Tedesco and AhlstrømBanwell and others, 2012a; Reference Leeson, Shepherd, Palmer, Sundal and FettweisLeeson and others, 2012) to Antarctic ice shelves, we conclude that ice shelves are likely to be too flat to enable the widespread movement of meltwater across the surface and the filling of surface depressions to be coherently modelled. This is likely to mean that lakes on ice shelves can be modelled more simplistically, as features that derive their water from local drainage basins that are relatively static in size and shape. Additionally, existing surface-routing and lake-filling models assume static ice topography. Although this is a good assumption for the GrIS, where lake positions are relatively constant interannually, this is not a reasonable assumption for Antarctic ice shelves, where lakes move concurrently with ice flow and where lake water constitutes a surface load that introduces vertical flexure.
Acknowledgements
We acknowledge the support of the US National Science Foundation under grant ANT-0944248. We also thank the scientific editor, Weili Wang, and two anonymous referees for careful reviews that helped to improve an earlier draft of the paper.






