1. Introduction
This paper describes the results of a series of experiments investigating the form of the wind velocity boundary layer over a snow surface, with and without drift. This information is essential to help calculate the energy balance at the snow surface and also to assess mass movement of snow by wind. The process of drift is important both over relatively flat terrain, such as Antarctic regions, where it contributes to mass balance, and also in mountainous terrain, where accumulation on steep slopes can contribute to the danger of avalanches.
The velocity boundary layer over a surface is often described by a log-law, where the wind speed at a particular height is a function of the surface friction velocity, u*, and aerodynamic roughness length, z0 (Reference StullStull, 1988). The parameters u* and z0 are then used to model the fluxes of heat and water vapour from the surface, which are important, not only for snowpack development (Reference Marks and DozierMarks and Dozier, 1992; Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others, 2002b), but also for mass-balance calculations (Reference ClineCline, 1997; Reference Liston and SturmListon and Sturm, 1998; Reference Box and BromwichBox and others, 2004).
Aerodynamically rough, solid surfaces have roughness lengths independent of u* (Reference SchlichtingSchlichting and Gersten, 2003). The same does not always hold over granular surfaces, such as snow or sand; above the threshold friction velocity, u*t, particles will be entrained and transported by drift. At low wind speeds, this drift will be predominantly saltation, where particles follow parabolic paths over the surface (Reference BagnoldBagnold, 1941, p. 10–37). These drifting particles increase the aerodynamic roughness of the surface. Reference OwenOwen (1964) summarized earlier research relating to the aerodynamic effects of drifting particles, and developed a theoretical framework to explain this effect. Together, these suggest two regimes for flow over granular surfaces: a region where u* ≥ u*t and z0 is constant, and another where u* ≤ u*t and z0 increases when measured above the drifting material. Implementing this in a model then requires z0 over the stable surface, u*t and the dependence of z0 on u* when u* ≥ u*t.
Current models of the boundary layer over snow vary in their treatment of z0. In some cases it is assumed constant (Reference ClineCline, 1997; Reference Li and PomeroyLi and Pomeroy, 1997b; Reference Reijmer, Meijgaard and van den BroekeReijmer and others, 2003; Reference Garen and MarksGaren and Marks, 2005; Reference Kunstmann and StadlerKunstmann and Stadler, 2005) and in others it is affected by snowdrift (Reference Liston and SturmListon and Sturm, 1998; Reference Lehning, Doorschot and BarteltLehning and others, 2000). For large-scale climate modelling over large regions, assuming a fixed u*t and/or z0 may be valid because surface conditions only change within narrow bands, but models can still be significantly influenced by z0 (e.g. Reference Reijmer, Meijgaard and van den BroekeReijmer and others, 2003).
Field measurements (Reference Stearns, Weidner, Bromwich and StearnsStearns and Weidner, 1993; Reference Bintanja and van den BroekeBintanja and Van den Broeke, 1995; Reference Andreas, Jordan, Guest, Persson, Grachev and FairallAndreas and others, 2004) of the boundary layer over snow-covered ice do show an increase in z0 with u*, but their results do not distinguish between periods with or without drift and do not include surface snow characterization. Reference Oura, Kobayashi and KobayashiOura and others (1967) and Kobaya-shi (1969, 1972) measured z0 over snow with and without drift, and noted a dependency of z 0 upon the presence of drift. Oura and others measured identical z0 during snowfall and over a non-drifting snow surface, showing that it is drifting particles that increase z0, not just the presence of particles in the air from precipitation. Results from Reference KönigKönig (1985) include details of the degree of drift over an ice sheet, but give no information about the snow surface or transport rates. Reference Doorschot, Lehning and VrouweDoorschot and others (2004) report some characteristics of the local snow cover during field measurements of u*t and z0, but these were in mountainous terrain. Unfortunately, none of these studies allow terrain, surface and saltation influences to be separated.
Reference BagnoldBagnold (1941, p. 57–76) measured boundary layers over still and drifting sand and provided much of the groundwork for current steady-state models of sand drift (e.g. Reference SørensenSørensen, 1991). The same physical basis has been applied to models of snowdrift, such as SnowTran-3D (Reference Liston and SturmListon and Sturm, 1998) and the snowdrift index in SNOWPACK (a snow-cover development simulator; Reference Lehning, Doorschot and BarteltLehning and others, 2000). In SnowTran-3D, u*t is constant, while in SNOWPACK it is calculated from a modified version of Reference SchmidtSchmidt’s (1980) drift threshold algorithm, which estimates u*t from snow characteristics. Other models of drifting snow have been developed from first principles (Reference DoorschotDoorschot and Lehning, 2002), while Reference Shao and LiShao and Li (1999) and Reference Nemoto and NishimuraNemoto and Nishimura (2004) coupled large-eddy simulations using the Navier–Stokes equations with Lagrangian particle treatment to model snow and sand transport, respectively. Drift prediction models using weather station data have also been developed for meteorological services (Reference Li and PomeroyLi and Pomeroy, 1997a, b), but these tend to consider drift as a probabilistic event and relate conditions to a measurement height, rather than surface conditions u* and z0.
No study that we are aware of has related the form of the velocity boundary layer over a flat snow surface to the snow itself, or repeatedly measured u*t and snow characteristics together. This is easier in a wind tunnel than in field experiments, as mean flow is, by definition, in one direction and the boundary layer which is formed is only influenced by snow of known characteristics. There are no additional effects from terrain or atmospheric stability which could influence results.
We describe a series of experiments designed to measure boundary layer flow over natural snow under controlled conditions in a wind tunnel at the Swiss Federal Institute for Snow and Avalanche Research SLF in Davos, Switzerland. An overview of the theory of boundary layer flow over snow is given, and then compared to first measurements from the wind tunnel. The influence of weather and snow properties on measured boundary layer friction velocities and roughness lengths up to and at the drift threshold is examined. Finally several algorithms for u*t (Reference BagnoldBagnold, 1941; Reference SchmidtSchmidt, 1980; Reference Li and PomeroyLi and Pomeroy, 1997a) are compared to our results.
2. Theory
The time-averaged, turbulent, neutrally stratified, velocity boundary layer over an immobile rough surface can be described by a log-law. This describes a logarithmic profile, where the velocity, u, at a height z is a function of the surface roughness length, z0, and the friction velocity, u*, so that

where K is the von Kármán constant, taken here as 0.41 (for a review of experimental results, see Reference GarrattGarratt, 1994, p. 289) and u * and z0 can be determined from velocity and height measurements. This result depends on the validity of the loglaw profile and the accuracy of the measurements.
Surfaces are generally divided into three hydraulic regimes, depending on the height to which wall roughness penetrates the different regions of the boundary layer, and the influence they have on the drag. Wall roughness elements can be characterized according to their size relative to the wall layer thickness, δv, where δv = v/u* with v the kinematic viscosity. If the roughness elements of size d are similar in size to the wall layer thickness, i.e. δv/d ≈ 1, the elements are submerged in the viscous sub-layer of the boundary layer. In this case, the roughness elements do not affect the wall drag and the wall is considered hydraulically smooth. The limit to this regime is d/δv = 5 (Reference SchlichtingSchlichting and Gersten, 2003, p. 522). As d/δv increases, the roughness elements project out of the viscous sub-layer but do not reach the boundary with the overlap layer of the boundary layer until z = 70δv. This is known as the transitional flow regime and occurs while 5 ≤ d/δv ≤ 70; viscous forces still influence the drag, and hence z 0 is a function of u *. As d/δv increases further, and elements penetrate into the overlap layer, the roughness elements directly influence the wall drag. The drag is independent of the flow Reynolds number, and hence z 0 (which is an expression of the surface drag coefficient) is independent of u*. This is known as the hydraulically rough regime; thus fully rough flow requires that surface roughness elements have a size d ≥ 70δ v.
Reference SchlichtingSchlichting and Gersten (2003, p. 530) give z0 = d/25 in the fully rough regime when the wall is covered with densely packed sand grains over a solid surface. This can be used to calculate a roughness Reynolds number, Re* = z0u*/v, where the rough regime is Re* > 2.8. By comparison, Reference Greeley and IversenGreeley and Iversen (1985, p.43) give d/30 ≤ z0 ≤ d/8, depending on the distribution of sand on the surface, and hence the start of the rough regime is in the range 2.33 < Re* < 8.75. Reference AndreasAndreas (1987) and Reference Bintanja and van den BroekeBintanja and Van den Broeke (1995) assume that the rough region is Re* ≥ 2.5. Given the uncertainty about the onset of the fully rough regime in terms of Re*, it seems more sensible to use the definition of the rough regime starting at d ≥ 70δv.
In the wind tunnel at –10°C and 835 hPa, v is approximately 1.48 × 10–5m2s–1. The typical u* is 0.3 ms–1. This gives a wall layer thickness Sv = 50mm, and requires that the roughness elements project at least 3.45mm into the flow from a solid surface to reach the overlap region of the boundary layer. The surface of the snow is uneven and often permeable, and so occasional snow particles may protrude into the overlap region, causing a rough surface where z0 is independent of u*.
The surface roughness length is also affected by the presence of drifting snow particles. Reference OwenOwen (1964) provided a theoretical basis for the influence of drifting particles on the flow above the saltating layer. His hypothesis was that the roughness of a drifting surface should increase compared to the stable surface so the velocity at a height z is given by

where D’ is a constant and g is the acceleration due to gravity, 9.81 ms–2. Equating this to the more familiar form in Equation (1) gives
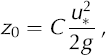
where the constant C is exp(— D’K). From a survey of data in the literature, Reference OwenOwen (1964) found D’ to be 9.7, i.e. C = 0.021 over sand and soil. A literature survey by Reference TablerTabler (1980) gave 0.011 ≤ C ≤ 0.028 for smooth snow covers with long fetch. Konig (1985) found C = 0.012 over snow-covered ice, while Reference Bintanja and van den BroekeBintanja and Van den Broeke (1995) measured C = 0.032 under similar conditions. Reference Liston and SturmListon and Sturm (1998) used C = 0.12 for flow over ‘topographically variable’ terrain. Reference CharnockCharnock (1955) is often referenced in place of Owen, as his equation has the same form but was developed to explain z0 over waves, not saltating surfaces.
At the onset of saltation, Equations (2) and (1) must both apply. Therefore, z0 before drift (if it is constant) can be used to calculate u*t from Equation (3). For u* > u*t, the minimum z0 which is seen by measurements above the saltation layer is given by Equation (3). Owen’s relationship gives the minimum z0 because topographic influences could increase the apparent z0 at a given u*, as was observed by Reference Doorschot, Lehning and VrouweDoorschot and others (2004).
The total mass flux, Q, from a loose surface has been measured for sand by Reference BagnoldBagnold (1941, p. 69–70) and Reference Shao and RaupachShao and Raupach (1992), and for snow by Reference Nishimura, Sugiura, Nemoto and MaenoNishimura and others, (1998), Reference Nishimura and HuntNishimura and Hunt (2000) and Reference Nishimura and NemotoNishimura and Nemoto (2005) and results give a relationship of the form:

where a is a constant. From dimensional considerations, a is given by αmppd/g, where pp is the density of the particle and am is some constant for a particular surface.
Drift in the wind tunnel is measured using a snow particle counter (SPC). SPC measurements in the wind tunnel do not cover the entire saltation layer. The SPC measures the flux over a 2.5mm high window, positioned 50mm above the snow surface, and so the effect of moving the saltating cloud past the SPC has to be included. Separating the mass flux at a height z into a total mass flux Q(u*) and a profile function ϕ(u*, z) which defines the form of the drifting flux with height, we can define a general form of the mass flux at a height q(z) as a function of u * and z, which for u * ≥ u*t is given by
From the definition of saltation, there is zero horizontal mass flux at the ground and at z = ∞, implying a maximum at a given height. Reference Pomeroy and GrayPomeroy and Gray (1990) give the height of maximum mass flux (hs) as ![]() . This gives hs = 12mm at u*
= 0.4m s–1. Our SPC is at 50 mm. Various experiments (Reference Budd, Dingle, Radok and RubinBudd and others, 1966; Reference SchmidtSchmidt, 1982; Reference Maeno, Nishimura, Sugiura and KosugiMaeno and others, 1995; Reference Nishimura, Sugiura, Nemoto and MaenoNishimura and others, 1998; Reference Nishimura and HuntNishimura and Hunt, 2000) have shown that the horizontal mass flux of drifting snow decays exponentially with height. This observed decay, with no near-ground maximum, may show the limits of measurement resolution or the influence of other snow transport processes. To fit our measurements, we use a parameterization of horizontal mass flux decay with increasing height. This parameterization, described as a profile function, is valid above the height of maximum transport, and was used to fit measurement data by Reference Nishimura and HuntNishimura and Hunt (2000).
. This gives hs = 12mm at u*
= 0.4m s–1. Our SPC is at 50 mm. Various experiments (Reference Budd, Dingle, Radok and RubinBudd and others, 1966; Reference SchmidtSchmidt, 1982; Reference Maeno, Nishimura, Sugiura and KosugiMaeno and others, 1995; Reference Nishimura, Sugiura, Nemoto and MaenoNishimura and others, 1998; Reference Nishimura and HuntNishimura and Hunt, 2000) have shown that the horizontal mass flux of drifting snow decays exponentially with height. This observed decay, with no near-ground maximum, may show the limits of measurement resolution or the influence of other snow transport processes. To fit our measurements, we use a parameterization of horizontal mass flux decay with increasing height. This parameterization, described as a profile function, is valid above the height of maximum transport, and was used to fit measurement data by Reference Nishimura and HuntNishimura and Hunt (2000).
If the measurement height is z and the characteristic height of the saltation system is L and the integral over 0 ≤ z ≤ ∞ is 1, allowing the profile function to scale the total mass flux, the profile function is given by
The characteristic height, L, can be estimated from conservation of energy. If a particle leaves a surface with a vertical velocity pu*, where p is some constant, conservation of energy dictates that it will reach a height given by (1 /2g)(pu*)2, if external forces are zero. The parameter 2/p2 is defined as A, where A is a dimensionless parameter for a single experiment. Hence, L is given by

Reference Nishimura and HuntNishimura and Hunt (2000) report A = 0.45 for drifting 0.48mm diameter snow, decreasing to 0.13–0.16 for drifting ice particles.
Substituting Equations (4) and (6) into Equation (5) and then substituting L from Equation (7) gives the mass flux at a single height when u* > u*t as

The only unknowns, then, are a and u*t , which can be calculated from measurements of u * and q(z) using regression. We take λ = 0.45, but an example fit shown in Figure 3 shows that even when A is changed to 0.3 or 0.6 the influence on the mass flux is minimal. Using a fixed value of A improves the stability of the regression, as only two values, a and u*, have to be found.
At the threshold, the total aerodynamic forces acting on a particle are just sufficient to remove a snow particle from the snow surface. Reference BagnoldBagnold (1941, p.86) equated the moments due to aerodynamic forces on a grain and a grain’s immersed weight, to calculate the threshold u*, and showed that

where pice is the density of ice (917 kg m–3), pair is the density of air, d is the grain diameter and A is the threshold parameter. Bagnold stated that for a Reynolds number of the form Re*d = u*d/v, the threshold parameter for sand in air is constant at 0.1 for Re*d > 3.5, a behaviour reported for other spherical or granular materials by Reference Greeley and IversenGreeley and Iversen (1985, p. 78).
Reference SchmidtSchmidt (1980) suggested a formulation for u*t for snow which used both the snow bulk properties and microstructure. Reference Lehning, Doorschot and BarteltLehning and others (2000) reformulated that relationship to give:

The dimensionless constants A and B are 0.009 and 0.0135, respectively, SP is the sphericity, N3 is the mean number of bonds per particle (also known as three-dimensional coordination number), db is the bond diameter and σ is a reference shear stress set to 300 Pa. Equation (10) calculates the shear required to cause drift, which is equal to the sum of a particle mass and a shear acting on a bond. The mass term is given by Apicegd(SP + 1), and the shearing term by ![]() .
.
An alternative approach was taken by Reference Li and PomeroyLi and Pomeroy (1997a), who gave a parameterization of the threshold 10m wind speed using the air temperature as the predictive variable. Based on a fit to observations in the Canadian Prairies, Li and Pomeroy proposed that
where T a is the air temperature (°C) measured 2m above the surface and ut(10) is a threshold wind speed at 10m above the surface.
3. Method
The SLF wind tunnel is situated 1650m a.s.l. in the Flüelatal, above Davos, Graubünden, Switzerland. The tunnel is housed in a converted Swiss Army bunker, and snowfalls are collected outside the bunker in trays. These trays are then moved intact into the bunker with as little disturbance as possible, allowing the behaviour of a natural snowpack to be investigated. Trays are used for experiments when they contain 0.06–0.16m depth of undisturbed snow. One test reported here uses sieved depth hoar (see Table 1); all others use snow naturally deposited by precipitation.
Table 1. Weather conditions and snow characterization for wind tunnel tests. RH: relative humidity; SMP: SnowMicroPen; SP: sphericity; DN: dendricity

The wind tunnel is 14m long, with a 1 × 1m crosssection. The tunnel operates in suction, drawing air from outside the bunker through a honeycomb, nets and a 4 : 1 contraction into the tunnel. Spires mounted on the floor downstream of the contraction create large-scale vortices. These are followed by regular roughness elements for 4m and then fine-fibred, long-pile carpet for 4m. This gives a logarithmic boundary layer approximately 0.25m deep. This is followed by 4m of fresh snow in trays. The height of the snow trays is adjusted so that the top of the snow coincides with the uppermost fibres of the carpet. The trays are open in the streamwise direction, allowing uninterrupted boundary layer development. A sketch of the tunnel is shown in Figure 1.

Fig. 1. Schematic view of the wind tunnel experiment. Anemometers are at 0.05 and 0.1m above the snow at the start of the experiment. An SPC is at 0.05m above the snow at the same streamwise position.
The bunker is shaded from the sun by mountains from December to March, and is not heated. The tunnel was run before each experiment to draw air into the building and cool the tunnel. The building, tunnel, outside air and snow cover are therefore in thermal equilibrium.
During the experiments described here, free-stream wind speeds (and hence u*) were increased incrementally in the range 3–18ms–1 over ~30min, and the resulting velocity profiles and drift were measured. Free-stream wind speeds were left constant for 3–4 min between each gradual increase in speed. These constant-speed intervals are described as measurement ‘plateaux’. Ambient temperature, humidity and pressure were measured at the tunnel inlet at 1 Hz.
Initial measurements of the boundary layer were made in 2005 using two Schiltknecht MiniAir propellor-type anemometers (‘MiniAirs’) at 5 and 10cm above the snow surface. The MiniAir velocity time series were filtered to remove transients from increasing the wind tunnel speed, but keeping the plateaux when the wind speed was kept constant. Equation (1) was used to calculate u* and z0 from the mean velocity profile during the plateaux. The vertical position of these sensors increased as erosion occurred, but was unknown because of the lack of a suitable sensor. Therefore z0 from the MiniAirs can only be used before the start of drift. The calculated u* after the start of drift should still be valid as the vertical separation between the anemometers is fixed by their support, although at some point the air velocity at the lower anemometer will be influenced by drift (Reference BagnoldBagnold, 1941). Measurement plateaux were discarded once friction velocity started to decrease while the velocity at the highest anemometer increased.
A detailed boundary layer velocity profile was measured during experiments in 2006 using a total pressure rake. The rake had ten total pressure probes from ~25 to 250mm above the surface, arranged to give four probes below the SPC and the rest above. It was positioned 0.30m upstream from the MiniAirs and SPC. The exact height was calculated from the known position of the total pressure probes on their supporting aerofoil and the position of the aerofoil above the snow surface. A static pressure measurement was obtained from the static pressure port of a pitot-static tube on the tunnel centre line. This was subtracted from the total pressure measurements to give a dynamic pressure, Pdyn. The air density, pair, was calculated from the tunnel static pressure, and temperature and humidity at the inlet to the test section using the equation of state. The velocity at each point on the rake is then given by ![]() . Rake velocity profiles were only measured during the plateaux when the tunnel motor speed was kept constant.
. Rake velocity profiles were only measured during the plateaux when the tunnel motor speed was kept constant.
Drift was measured using a Niigaata Electric SPC-S7 optical SPC, positioned 5 cm above the snow at the same fetch as the anemometers. The SPC records the number of particles in 32 equivalent-diameter classes passing through the detector every second. The SPC detects particle diameters dSPC in the range 80 ≤ dSPC ≤ 500mm in a detector plane 2.5mm high and 25mm wide, oriented perpendicular to the main flow in the tunnel.
A potential drawback of the wind tunnel arrangement is that the surface is by necessity ‘patchy’. That is, sections of differing surface roughness (roughness elements, carpet and then snow) follow each other. A boundary layer which develops over a surface of a specific roughness length and then encounters a second surface roughness will adapt to the new roughness. This adaptation takes the form of an internal boundary layer growing from the upstream edge of the second patch. The interface height of the internal boundary layer, z i, is a function of the roughness length of the second surface, in this case snow, and the fetch, x, over which the internal boundary layer develops. Reference AryaArya (2001, p. 326–327) reports that experimental data show

where a¡ is an empirical constant, 0.35 ≤ a¡ ≤ 0.75. The highest anemometer was mounted 0.1m above the surface after fetch x = 3 m; in the worst case ai = 0.35 and the smallest roughness length at which zi ≥ 0.1m is z0 = 2.4 × 10–5m. Roughness lengths smaller than this were therefore rejected as being improbable, as they would require the upper anemometer to be above the interface.
Snow was characterized before the start of drift using several methods. A basic ‘field’ style classification was made of grain type, snow temperature and snow density (Reference ColbeckColbeck and others, 1990). High-spatial-resolution vertical penetrometer readings were taken before experiments using a SnowMicroPen (SMP; Reference Schneebeli, Pielmeier and JohnsonSchneebeli and others, 1999). Twodimensional image processing of photomicrographs of at least 30 snow particles allowed characterization by objective criteria such as diameter, dendricity and sphericity. Drift is usually observed after 5–10min during experiments, depending on the threshold velocity. Comparing measurements of surface particle diameter and snow density just before experiments start, and then after the start of drift, shows that any changes during this short time are too small to detect. Temperatures measured by thermocouples in the snow and free stream typically differed by less than 2 K, which minimizes the turbulent fluxes of sensible heat to and from the snowpack and so reduces metamorphosis.
Grain characteristics are determined from image processing of digitized photomicrographs. The mean diameter of a particle is taken as the mean distance through its centroid to diametrically opposing points every 2° around the circumference. The mean particle diameter for an experiment is the numerical average of all mean diameters measured from the images, denoted d1. Sphericity, SP, and dendricity, DN, of particles are defined from images using the definitions of Reference Lesaffre, Pougatch and MartinLesaffre and others (1998).
The process of snow metamorphosis results in a change of DN from 1 for new snow towards zero for older snow. We distinguish between the two major processes of metamorphosis by describing snow with DN ≤ 0.5 and SP ≥ 0.5 as snow which is becoming rounded, and snow with DN ≤ 0.5 and SP ≤ 0.5 as snow which is becoming faceted (Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others, 2002b, fig. 8).
4. The Boundary Layer Over Snow
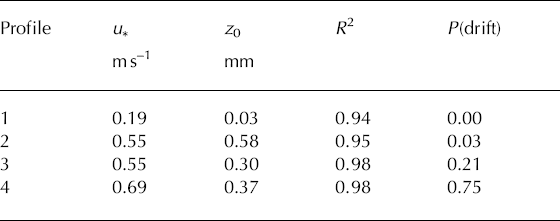
Example velocity profiles from the rake are plotted in Figure 2. From this plot it is apparent that the lower boundary layer velocities follow the log-law, as they are linear to more than 0.10m above the snow surface. In this region they are described by Equation (1) with R2 ≥ 0.8. The resulting u* and z0 for the profiles are given in Table 2. Drift during the measurement plateaux is described by the probability of drift at the SPC, defined as the number of 1 s intervals during which drift was measured, divided by the duration of the plateau. Both MiniAir anemometers are in the region z ≤ 0.1 m, at least until drift starts, and this confirms that we can apply Equation (1) to those measurements to calculate u* and z0. As more data were taken from the anemometers than the rake, all further data presented here use u* and z0 calculated from the MiniAir data.

Fig. 2. Velocity profiles over snow. Profiles were measured by dynamic pressure rake over snow on 2 March 2006. Different markers indicate different measurement plateaux. Filled points show data fitted using the log-law (Equation (1)). The fit is limited to z ≤ 0.1 m. Drift occurs in plateaux 2–4, and data are limited to 0.05 ≤ z ≤ 0.1 m. The calculated u* and z0 are summarized in Table 2.
Table 2. Fits to the velocity profiles shown in Figure 2. Velocity data are fitted using Equation (1). R2 is the value of the coefficient of determination for the fit. P(drift) is the probability of drift in that plateau
4.1. Drift threshold
The mass flux of drifting snow during an experiment is plotted in Figure 3. This shows the friction velocity obtained from the MiniAirs, and the mean mass flux measured by the SPC during each plateau. Instead of a subjective assessment of the drift threshold, either from data (Reference Doorschot, Lehning and VrouweDoorschot and others, 2004) or from observations in the tunnel (Reference Liu, Dong and WangLiu and others, 2006), we use the plateau-averaged u* and plateau-averaged SPC mass flux qSPC to estimate the threshold. An example of a fit to experimental data using Equation (8) is given in Figure 3, which also demonstrates the reason for this method. If the threshold had been defined as the first point where drift was detected, the threshold would have been at u* < 0.32 ms–1, and would have been defined by a single data point. However, a visual inspection of the whole data series does suggest a threshold at u* ≈ 0.3m s–1. This is also the value found by regression through the whole data series. The threshold is then defined in terms relevant to mass movement, not by a single measurement or a small number of drifting particles.

Fig. 3. Drifting-snow mass flux as a function of u*. Snow mass flux is averaged over measurement plateaux during measurements on 9 March 2005. Data are fitted using Equation (8). Three different values of λ were tested, and u*t = 0.30 ms–1 in each case. The number beside each data point is the total number of observed particles at each point.
Because u*t is obtained from a fit to Equation (8), it does not correspond directly to a measurement plateau, and thus has no z0 measurement associated with it. The threshold roughness length, z0t, is taken as the linearly interpolated value of z0 from the measurements immediately around the threshold. Data are bracketed in the range [u*t] and [z0t] using the friction velocities and roughness lengths measured during the neighbouring measurements. Ambient conditions at the onset of drift were taken as the mean values in these plateaux.
Table 3 details the friction velocity and roughness length at the threshold. A threshold wind speed at 10m above the surface, ut(10) is calculated from z0t and u*t using Equation (1). In Figure 4, z0 is plotted against u* up to and including the drift threshold. The roughness lengths before the threshold are values measured during the course of the experiment. Equation (3) is also plotted with C = 0.021 and shows that u*t measured in the wind tunnel is generally 10–20% higher than would be expected for the measured z 0, compared to sand and soil measurements. Another set of measurements was made during summer 2005, using low-density, open-celled foam in place of snow. Repeated measurements over the foam, which had a roughness length similar to snow, showed that the uncertainty in z0 for u*t ≤ 0.4 ms–1 could be greater than 50%. Owen’s model therefore lies within the uncertainty range of all but two data points. Threshold friction velocities obtained for each experiment are not exact because there may be some drift below the height of the SPC at u* ≤ u*t. There is also the chance that the SPC simply misses drifting particles at this height as it only occupies 2.5% of the channel width, although this is unlikely given the time at the plateau.

Fig. 4. Values of z0 and u* up to and including the drift threshold. Each thin line shows one experiment. Wind velocities were measured by anemometers at two heights. The model for drifting sand and soil of Reference OwenOwen (1964) (Equation (3)) is also shown.
Table 3. Boundary layer characteristics at saltation threshold for wind tunnel tests

The value of z 0t measured in the wind tunnel is generally lower than field measurements. It is two orders of magnitude lower than those measured over fresh snow by Reference Doorschot, Lehning and VrouweDoorschot and others (2004) in an Alpine landscape and almost two orders of magnitude lower than those measured at Ice Station Weddell, Antarctica, by Reference Andreas, Jordan and MakshtasAndreas and others (2005). Our measured z0t are an order of magnitude lower than z0 measured during the Surface Heat Budget of the Arctic Ocean field experiment (SHEBA; Reference Andreas, Jordan, Guest, Persson, Grachev and FairallAndreas and others, 2004). Reference Bintanja and van den BroekeBintanja and Van den Broeke (1995) measured z0 typically 1–2 orders of magnitude higher than our threshold levels. Reference Bintanja and van den BroekeBintanja and Van den Broeke (1995, fig. 3) show a lower limit to measured data at z0 = 0.016u2/g. Note that they used Reference CharnockCharnock’s (1955) relationship for breaking waves, that is, the form in Equation (3). This gives C = 0.032, and a lower limit to z 0 which is 50% higher than our measurements. Reference Pomeroy and GrayPomeroy and Gray (1990) found C = 0.1203, giving z0 some six times greater than ours. Higher values in natural settings compared to the wind tunnel are probably a result of the experimental set-up; the tunnel floor is relatively smooth compared to natural flat surfaces, where topology, sastrugi, vegetation or other obstructions would increase z0.
4.2. Pre-threshold roughness lengths
Pre-threshold u* and z0 normalized by u*t and z0t are shown in Figure 5. A linear regression fitted by least squares to the data shows that z0 is almost constant as u* increases towards the threshold value, so that z0/zot = 0.04u*/u*t + 0.94. The regression is heavily influenced by one test with a comparatively high u*t (17 January 2005). Removing test data gives z0/z0t = —0.34u*/u*t + 1.3. The 95% confidence interval for both cases includes the line z0/z0t, suggesting that it is highly likely that z0 for a particular snow surface is independent of u* until the start of drift. This will be further investigated by systematic measurements of u* and z0 over analogous materials.

Fig. 5. Values of z0 and u* shown in Figure 4 normalized by the saltation threshold values for each experiment.
4.3. Influence of weather and snow characteristics
The drift threshold conditions of 15 snow samples have been measured. This gives a dataset of some 9 different snow types, ambient temperatures from –16 to 0°C and particle diameters ranging from 0.1 to 3 mm. The ambient conditions and snow characterization for the tests are summarized in Table 1 and compared to threshold conditions in Figure 6. Coefficients of determination from linear regressions are also given.

Fig. 6. Influence of ambient conditions and snow properties on saltation threshold conditions.
Aerodynamic roughness over surfaces covered in arrays of objects is partly determined by the particle profile presented to the wind, and partly by the particle spacing (Reference Wooding, Bradley and MarshallWooding and others, 1973). These may be functions of snow particle diameter and density. Reference Magono and LeeMagono and Lee (1966) showed that cloud temperature and humidity change the form of fresh snow particles, so we might also expect weather conditions to influence z 0t.
From Figure 6 e–h there is no indication of a link between the ambient conditions, snow properties and z0t. This is probably because we cannot account for the effect of differences between cloud conditions, which drive the formation of snow crystals, and the near-ground conditions measured here.
The highest observed correlation is between u *t and the snow density, where R2 = 0.91, but this could be spurious, given the strong influence on the resulting fit of the high density and u*t of just one test (17 January 2005). The next highest correlation, R2 = 0.51, was seen between u*t and d1, and may also be prone to influence from one test more than others. However, both the snow density and particle diameter are tested for their use as predictor variables for u*t in section 5. A low correlation (R2 = 0.21) was obtained between u*t and the ambient temperature. Reference Kirchner, Michot, Narita and SuzukiKirchner and others (2001) show that strain rates at which an ice matrix behaves as a ductile material are higher at high temperatures than lower temperatures. Assuming strain rates at the snow surface are similar in all drift experiments, this would mean that a warmer surface is less likely to fail and eject a particle, so that warmer surfaces would be expected to have higher u *t. There is a trend toward this in Figure 6a, but again the small size of the dataset limits the reliability of a simple linear regression.
4.4. Surface penetration resistance
Snow surface penetration resistance was measured before experiments using a SMP. Figure 7 shows the mean force applied by the SMP compared to the threshold shear, ![]() . The mean force is measured when the SMP tip is 4–5mm into the snow, and represents complete immersion of the SMP tip. The SMP measures the total force required to break contact points and move grains within the snow. Aerodynamic entrainment at the surface during saltation is also a process where bonds are broken, so a correlation might be expected. The shear required to start drift does tend to increase with penetration resistance, although with low correlation (R2 = 0.27). This suggests that a linear regression is too simplistic a model.
. The mean force is measured when the SMP tip is 4–5mm into the snow, and represents complete immersion of the SMP tip. The SMP measures the total force required to break contact points and move grains within the snow. Aerodynamic entrainment at the surface during saltation is also a process where bonds are broken, so a correlation might be expected. The shear required to start drift does tend to increase with penetration resistance, although with low correlation (R2 = 0.27). This suggests that a linear regression is too simplistic a model.

Fig. 7. Surface penetration resistance compared to threshold aerodynamic shear stress. Penetration resistance is measured by SMP.
4.5. Airborne grain sizes
Grain sizes of airborne snow were measured by the SPC at 0.05m above the snow surface. Reference Budd, Dingle, Radok and RubinBudd and others (1966), Reference SchmidtSchmidt (1982) and Reference Nishimura and NemotoNishimura and Nemoto (2005) demonstrate that the size distribution of airborne grains can be fitted using a two-parameter gamma-distribution function, where the probability of observing a grain of diameter d is given by
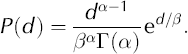
The mean grain diameter is given by the product αβ.
Figure 8 compares the mean grain diameter seen on the surface with that detected by the SPC. The mean drifting grains seen immediately after the drift threshold by the SPC were typically of diameter 100–175 mm. These were calculated from SPC records using Equation (13). They do not correlate with surface grain sizes, as given in Table 1. This is surprising as the grain size and snow density affect the threshold, but the drifting particles are ultimately similar.

Fig. 8. Comparison of diameters of airborne and surface snow particles. Airborne particle diameters are calculated using a fit to SPC data (Equation (13)). Surface particle diameters are measured from images.
Reference SchmidtSchmidt (1982) and Reference Nishimura and NemotoNishimura and Nemoto (2005) also measured drift on flat surfaces after snowfall. They measured drifting particles with mean diameters in the range 100–200mm, using similar equipment to ours, although they did not relate these back to a characterization of the snow on the ground. Our fetch is only 3 m, compared to several hundred or thousand metres in field experiments, but observed particle diameters are very similar. This suggests either that particles are rapidly fracturing before they reach the detector, or that smaller ice particles are selectively entrained from the snow surface. Simulations using the model of Reference Doorschot, Lehning and VrouweDoorschot and others (2004) show that the jump length of a 150mm diameter particle, reaching 5 cm above the surface of fresh snow, is of the order of 1 m. If particles are rebounding from the surface on every impact, the particles are likely to have had three jumps before reaching the detector. This number of impacts may be enough to reduce the size of the particles seen during the characterization to the size of particles at the SPC, giving the relationship seen in Figure 8, but we cannot track individual particles through the tunnel to investigate this. For lowdensity snow at velocities only slightly higher than the threshold, aerodynamic entrainment might be expected to dominate over rebound (Reference DoorschotDoorschot, 2002). Because smaller particles have smaller bonds to their neighbours and lower mass, and are therefore easier to entrain from the surface, it is most likely that it is the smaller particles which move at the drift threshold.
This size discrepancy has implications for snow transport in mountainous regions. During a storm all sizes of particles are moved, both from the surface and the snow which has not yet reached the ground. This may result in increased deposition of snow on lee slopes, causing ‘wind slab’. This may be combined with an extra impulse normal to the surface from wind eddies, which would further increase packing of deposits, independent of exposition, raising the density of the slab. In comparison, when significant wind first occurs after a snowfall, smaller particles or broken crystals are apparently entrained and transported. As these are then deposited back into the snow, this would probably cause an increased density at the surface of the snow, a ‘wind crust’ (see Reference ColbeckColbeck and others, 1990). Experiments in the wind tunnel have not yet been able to reproduce a significant wind crust, although surface erosion features, such as striations, have been observed.
5. Comparison to Threshold Algorithms
Experiments by Reference BagnoldBagnold (1941) and Reference Greeley and IversenGreeley and Iversen (1985) measured the threshold friction velocity of spherical and angular particles such as sand, clover seeds and nut shells. However, snow is not spherical. A solution to this is to convert the shapes measured using image processing to a circle with equivalent aerodynamic properties. The diameter of the equivalent circle is the hydraulic diameter, dh. The hydraulic diameter is calculated as dh = ![]() , where
, where ![]() is the mean area and p the mean perimeter of the snow in a sample.
is the mean area and p the mean perimeter of the snow in a sample.
Results from our measurements comparing dh with u*t are shown in Figure 9, and show that the measured threshold, u tt, is well predicted using Equation (9) with A = 0.18. The smallest particle size observed on the surface was dh = 0.26 mm, and the lowest threshold friction velocity was 0.28 ms–1. Taking u as 1.48 × 10–5 Pa s at-10°C and 83.5 kPa ambient pressure, the lowest particle Reynolds number was 4.9 at the start of saltation. Measurements from Reference Greeley and IversenGreeley and Iversen (1985, fig. 3.6) show that the threshold parameter, A, is constant for Re*d ≥ 5 at 0.1 for noncohesive, granular materials.

Fig. 9. Measurements of u*t as a function of surface particle hydraulic diameter, dh. The lines are Equation (9) (Reference BagnoldBagnold, 1941) with threshold parameter 4 = 0.1 (solid line) and 4 = 0.2 (dashed line).
Schmidt’s algorithm (Equation (10)) was developed for cohesive ice particles, but the parameters have been tuned for snow from field observations of drift, and hence we use the diameter of the snow calculated from image processing, d I. Image processing is also used to calculate the mapped sphericity, SP. Air density is obtained from measured temperature and pressure during the test. The bond diameter, d b, and three-dimensional coordination number, N3, must be estimated or measured. Reference Brown, Edens and BarberBrown and others (1999) assumed db = d/10 for fresh snow, increasing to 0.15–0.30 after 7 days of isothermal metamorphosis. Reference KeelerKeeler (1969) found db ≤ d/20 for snow 2 days old, but reported no data for snow younger than this. We assume a range of 0.1 ≤ db/d1 ≤ 0.4, with no correction for density or age, and use this to bracket our prediction. The correlation given in Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others (2002a) is used to calculate N3 from the bulk density of the snow, ps:

Equation (14) gives N3 = 1.53 for snow of density 50 kg m–3, increasing to 1.78 at 100 kgm–3. Reference Brown, Edens and BarberBrown and others (1999) assume N3 = 2.5.
Figure 10a shows that u *t is well predicted where it was assumed db = dI/10, and so the bond strength is predicted to be lowest. Predictions using the mean values lead to significant over-prediction. Figure 10b shows the calculated u*t if A = 0.023 and B = 3.45 × 10–3 in Equation (10). These constants are implemented in SNOWPACK 9.1. The predicted range of u *t has reduced, and predictions assuming the smallest bond sizes agree well with the measured values. Uncertainty remains in both cases, though, as db is unknown. From Equation (10), db and d of the surface particles are more important for calculating the threshold friction velocity than the sphericity, SP.

Fig. 10. Comparison of predicted and measured u*t. (a) Reference SchmidtSchmidt (1980) formulation; and (b) SNOWPACK 9.1 formulation. Circles show predictions assuming d 1/d b = 10, and squares assume d 1/d b = 2.5. The cases where the calculated and measured thresholds are identical are shown with dotted lines.
A comparison with Reference Li and PomeroyLi and Pomeroy (1997a) requires an air temperature at 2 m, which is unknown. Assuming that in the wind tunnel there is negligible temperature gradient normal to the surface, Ta approximates to the temperature at the inlet to the test section. A comparison between Equation (11) and ut(10) calculated from the wind tunnel threshold results is shown in Figure 11. Data from the wind tunnel suggest that at temperatures near 0°C, Equation (11) under-predicts the threshold. The original data in Reference Li and PomeroyLi and Pomeroy (1997a) show that at —5 < Ta < 0, the 95% confidence interval extends over the range 3 < ut(10) < 14 ms–1, which leaves only one of our data points as an outlier. Given that the dataset used to obtain Equation (11) is based on 6 years of hourly data from 16 weather stations, it is unreasonable to propose a new set of coefficients based on just 15 wind tunnel data points.

Fig. 11. Drift threshold wind speeds at 10m above the surface as a function of air temperature. Wind tunnel data are extrapolated from measured u*t and z0t. The dashed line shows Equation (11) (Reference Li and PomeroyLi and Pomeroy, 1997a).
Our data are not inconsistent with Equation (11), but it appears that the predictive power of a statistical analysis is limited in comparison to the approaches of Reference SchmidtSchmidt (1980) and Reference BagnoldBagnold (1941). Figures 6, 9 and 10 strongly suggest that directly measured snow size and density information is a more useful predictor for the drift threshold velocity than temperature some distance above the snow surface.
6. Conclusions
A wind tunnel for measuring boundary layer profiles over natural snow under controlled conditions has been commissioned at SLF in Davos. Drift threshold conditions have been measured during a series of experiments with smooth, fresh snow and compared to measured snow properties and characteristics. A routine has been developed to automatically recognize the drift threshold from boundary layer data and point measurements of drifting-snow mass flux. The threshold u* were found to vary between 0.27 and 0.69m s–1. Roughness lengths at the threshold varied from 0.04 to 0.13 mm, and the range of both u* and z0 may increase as more snow samples are tested.
Wind-tunnel values of z0 are smaller than most field measurements, although similar to lowest values measured over Antarctic snow-covered ice with minimal topographical influences. As u* increased toward u*t, z0 was found to change slightly, and we expect that a larger dataset will show that a particular snow surface generally has a constant z 0 until the onset of drift, as with sand or other rough surfaces. The roughness length at the drift threshold was well predicted using the approach of Reference OwenOwen (1964), with C = 0.021, as has been found for sand and soil. Two measurements, one with depth hoar and the other with highly broken particles, show lower z0t than expected. The reason for this difference is not clear.
Threshold algorithms based on force balance (Reference BagnoldBagnold, 1941) show that the drift threshold for new and decomposing snow is well predicted using the particle hydraulic diameter and A ≈0.18. This is 80% greater than found for non-cohesive, granular material such as sand. The threshold friction velocity predicted by Schmidt’s algorithm using mean particle form information from photomicrographs was found to be ≈100% larger than the observed mean value in the wind tunnel. A modified formulation as used in SNOWPACK 9.1 over-predicted the threshold by ≈50%. The predicted threshold using both formulations is strongly influenced by the presumed bond size. However, assuming small bond sizes in both formulations resulted in good agreement. Models based on Schmidt’s algorithm can bound u*t only if the coordination number, particle and bond diameter are accurately described by models which reflect the variation found in a snowpack. A third threshold model using wind speeds at 10m above the surface was also compared to our data (Reference Li and PomeroyLi and Pomeroy, 1997a). Results lie within the confidence interval of that correlation, which was originally developed from data obtained from weather stations in the Canadian Prairies.
Grain sizes measured by an SPC at 0.05m above the snow surface directly after the start of drift were fitted using a gamma distribution. This gave a mean particle diameter in the range 100–175 mm, independent of the surface particle size. The airborne particle diameter is the same as has been found in field experiments both in Antarctica and in Wyoming, USA. Threshold wind speeds at 10m above the surface, predicted assuming a log-law wind profile and our measured u*t and z0t, are similar to those found over flat terrain in Canada. Taken together this indicates that despite the short fetch in the wind tunnel, our results mirror those found in natural conditions.
We now intend to further develop our wind tunnel to validate drifting-snow models (Reference DoorschotDoorschot and Lehning, 2002; Reference Nemoto and NishimuraNemoto and Nishimura, 2004) and to investigate roughness lengths with drift.
Acknowledgements
This work was partially financed by the Swiss National Foundation. C. Fierz advised us on snow characterization and SNOWPACK, and all in the Snow Physics group at SLF helped with interpreting snow data. T. Exner, R. Grant, D. Ambühl, V. Smith, A. Craig and the SLF Workshop were invaluable for help preparing the wind tunnel and the techniques we applied. We thank K. Nishimura and M. Reference Nishimura and NemotoNemoto for their assistance in January 2005. J. McElwaine helped develop our threshold regression technique. The scientific editor, R. Naruse, and two anonymous reviewers provided valuable suggestions for improvements to this paper. Niigata Electric provided an SPC-S7.


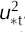 . The influence of macroscopic objects on the roughness length is shown by the lower values measured over the smooth and flat snow surface of the wind tunnel (0.04 ≤ z
. The influence of macroscopic objects on the roughness length is shown by the lower values measured over the smooth and flat snow surface of the wind tunnel (0.04 ≤ z













