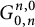1 Introduction
The well-known Riemann hypothesis asserts that all nontrivial zeros of the Riemann zeta function
![]() $\zeta (s)$
lie on the line
$\zeta (s)$
lie on the line
![]() $\Re (s) =1/2$
. In 1916, Riesz [Reference Riesz23] showed that a necessary and sufficient criterion for the Riemann hypothesis is the bound
$\Re (s) =1/2$
. In 1916, Riesz [Reference Riesz23] showed that a necessary and sufficient criterion for the Riemann hypothesis is the bound
for any
![]() ${\delta }>0$
. Around the same time, Hardy and Littlewood [Reference Hardy and Littlewood14] established that the bound
${\delta }>0$
. Around the same time, Hardy and Littlewood [Reference Hardy and Littlewood14] established that the bound
 $$ \begin{align} \displaystyle\sum\limits_{n=1}^{\infty}\frac{\mu(n)}{n}e^{-x/n^2} = O_{\delta}\big(x^{-\frac{1}{4}+\delta}\big) {,} \end{align} $$
$$ \begin{align} \displaystyle\sum\limits_{n=1}^{\infty}\frac{\mu(n)}{n}e^{-x/n^2} = O_{\delta}\big(x^{-\frac{1}{4}+\delta}\big) {,} \end{align} $$
for any
![]() ${\delta }>0$
is equivalent to the Riemann hypothesis. Various variants of Riesz-type criteria have been given in the literature, for instance, for Dirichlet L-functions and in the setting of primitive Hecke forms by Dixit, Roy, and Zaharescu in [Reference Dixit, Roy and Zaharescu13] and [Reference Dixit, Roy and Zaharescu12], respectively; by Dixit, Gupta, and Vatwani [Reference Dixit, Gupta and Vatwani9] for the Dedekind zeta function; and by Banerjee and Kumar [Reference Banerjee and Kumar3] for L-functions associated with primitive Maass cusp forms over the congruence subgroup
${\delta }>0$
is equivalent to the Riemann hypothesis. Various variants of Riesz-type criteria have been given in the literature, for instance, for Dirichlet L-functions and in the setting of primitive Hecke forms by Dixit, Roy, and Zaharescu in [Reference Dixit, Roy and Zaharescu13] and [Reference Dixit, Roy and Zaharescu12], respectively; by Dixit, Gupta, and Vatwani [Reference Dixit, Gupta and Vatwani9] for the Dedekind zeta function; and by Banerjee and Kumar [Reference Banerjee and Kumar3] for L-functions associated with primitive Maass cusp forms over the congruence subgroup
![]() $\Gamma _0(N)$
. In [Reference Kühn, Robles and Roy16], Kühn, Robles, and Roy obtained a generalized Riesz-type criterion involving functions which are reciprocal under a certain Hankel transformation. Their result holds for L-functions in the reduced Selberg class of degree one. Recently, Agarwal, Maji, and Garg [Reference Agarwal, Garg and Maji1] obtained a generalization of (1.1) and (1.2) by giving criteria involving the sum
$\Gamma _0(N)$
. In [Reference Kühn, Robles and Roy16], Kühn, Robles, and Roy obtained a generalized Riesz-type criterion involving functions which are reciprocal under a certain Hankel transformation. Their result holds for L-functions in the reduced Selberg class of degree one. Recently, Agarwal, Maji, and Garg [Reference Agarwal, Garg and Maji1] obtained a generalization of (1.1) and (1.2) by giving criteria involving the sum
![]() $ \sum \limits _{n=1}^{\infty }\frac {\mu (n)}{n^k}e^{-x/n^2}, $
where
$ \sum \limits _{n=1}^{\infty }\frac {\mu (n)}{n^k}e^{-x/n^2}, $
where
![]() $k\ge 1$
is a real number. In forthcoming work, they also obtain analogs of this for Dirichlet L-functions.
$k\ge 1$
is a real number. In forthcoming work, they also obtain analogs of this for Dirichlet L-functions.
In this paper, we obtain Riesz-type criteria for the grand Riemann hypothesis (GRH) for a broad class of L-functions. More precisely, we obtain criteria which are sufficient for GRH and applicable to functions
![]() $F(s)$
satisfying axioms of the Selberg class
$F(s)$
satisfying axioms of the Selberg class
![]() $\mathcal S$
without imposing the Ramanujan hypothesis for the coefficients of
$\mathcal S$
without imposing the Ramanujan hypothesis for the coefficients of
![]() $F(s)$
. On the other hand, we also obtain necessary criteria for GRH which apply to functions in a subclass of the Selberg class, which we denote as
$F(s)$
. On the other hand, we also obtain necessary criteria for GRH which apply to functions in a subclass of the Selberg class, which we denote as
![]() $\mathcal S^*$
. Essentially, elements of
$\mathcal S^*$
. Essentially, elements of
![]() $\mathcal {S^*}$
have a polynomial Euler product and a functional equation involving Gamma functions evaluated on shifts of rational multiples of s. It is expected that this subclass does not exclude any important examples. In fact,
$\mathcal {S^*}$
have a polynomial Euler product and a functional equation involving Gamma functions evaluated on shifts of rational multiples of s. It is expected that this subclass does not exclude any important examples. In fact,
![]() $\mathcal S^*$
is conjectured to be
$\mathcal S^*$
is conjectured to be
![]() $\mathcal {S}$
. This result is stated as Theorem 2.4.
$\mathcal {S}$
. This result is stated as Theorem 2.4.
Some key features of our result are as follows. The number of
![]() $\Gamma $
-factors of the type
$\Gamma $
-factors of the type
![]() $\Gamma ({\alpha } s+{\beta }) ({\alpha }>0)$
in the functional equation of
$\Gamma ({\alpha } s+{\beta }) ({\alpha }>0)$
in the functional equation of
![]() $F(s)$
, for which
$F(s)$
, for which
![]() ${\beta }=0$
, plays an important role in our results. This parameter is denoted
${\beta }=0$
, plays an important role in our results. This parameter is denoted
![]() $j_F$
later in the paper and statements of our results are different depending on whether
$j_F$
later in the paper and statements of our results are different depending on whether
![]() $j_F$
is zero or nonzero. Another feature is that we incorporate the degree of the L-function in a new way in order to generalize the kernel of (1.2). It is clear that the natural analog of
$j_F$
is zero or nonzero. Another feature is that we incorporate the degree of the L-function in a new way in order to generalize the kernel of (1.2). It is clear that the natural analog of
![]() $\mu (n)$
is the coefficient appearing in the Dirichlet series of
$\mu (n)$
is the coefficient appearing in the Dirichlet series of
![]() $1/F(s)$
, denoted by
$1/F(s)$
, denoted by
![]() $b_F(n)$
. However, the kernel
$b_F(n)$
. However, the kernel
![]() $e^{-x/n^2} $
of (1.2) should be thought of as the function
$e^{-x/n^2} $
of (1.2) should be thought of as the function
![]() $\exp (-y^2)$
evaluated on
$\exp (-y^2)$
evaluated on
![]() $\sqrt {x}/ n$
. We generalize this to a function
$\sqrt {x}/ n$
. We generalize this to a function
![]() $Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}\big ( (\sqrt {x}/n)^{d_F} \big )$
(see (2.5) and (2.6)), where
$Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}\big ( (\sqrt {x}/n)^{d_F} \big )$
(see (2.5) and (2.6)), where
![]() $d_F$
is the degree of the L-function
$d_F$
is the degree of the L-function
![]() $F(s)$
and
$F(s)$
and
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta }$
are parameters explicitly arising from the functional equation of
$\boldsymbol {\alpha }, \boldsymbol {\beta }$
are parameters explicitly arising from the functional equation of
![]() $F(s)$
. The presence of the degree
$F(s)$
. The presence of the degree
![]() $d_F$
in the exponent of the argument is a key factor which was not obvious from existing results and plays a crucial role in our theorems. The function
$d_F$
in the exponent of the argument is a key factor which was not obvious from existing results and plays a crucial role in our theorems. The function
![]() $Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
(see (2.5)) can essentially (up to a possible residue term) be viewed as an inverse Mellin transform of the product of Gamma factors arising in the functional equation of
$Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
(see (2.5)) can essentially (up to a possible residue term) be viewed as an inverse Mellin transform of the product of Gamma factors arising in the functional equation of
![]() $F(s)$
. Indeed, this is a natural and apt generalization if we interpret the function
$F(s)$
. Indeed, this is a natural and apt generalization if we interpret the function
![]() $\exp ({-y^2})$
appearing in (1.2) as the inverse Mellin transform of the factor
$\exp ({-y^2})$
appearing in (1.2) as the inverse Mellin transform of the factor
![]() $\Gamma (s/2)$
which arises in the functional equation of
$\Gamma (s/2)$
which arises in the functional equation of
![]() $\zeta (s)$
. Our methods rely on obtaining nontrivial estimates (up to a residue term) for
$\zeta (s)$
. Our methods rely on obtaining nontrivial estimates (up to a residue term) for
![]() $Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
as well as its derivative by exploiting the close connection between
$Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
as well as its derivative by exploiting the close connection between
![]() $Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
and the Meijer G-function. These are given in Lemmas 3.5 and 3.6.
$Z_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
and the Meijer G-function. These are given in Lemmas 3.5 and 3.6.
Moreover, along the lines of [Reference Dixit, Roy and Zaharescu13], we introduce an additional parameter z by inserting a
![]() $\cosh $
term. This allows for greater flexibility, enabling us to obtain a sufficient criterion for the case when all but finitely many zeros of
$\cosh $
term. This allows for greater flexibility, enabling us to obtain a sufficient criterion for the case when all but finitely many zeros of
![]() $F(s)$
lie on the critical line. This result (Theorem 2.5) is valid for any element
$F(s)$
lie on the critical line. This result (Theorem 2.5) is valid for any element
![]() $F(s)$
satisfying assumptions of the Selberg class without necessarily satisfying the Ramanujan hypothesis. Our results which do not require the Ramanujan hypothesis on the coefficients of the L-function are thus valid for a larger class of L-functions, for instance, Artin L-functions and automorphic L-functions (associated with automorphic representations of
$F(s)$
satisfying assumptions of the Selberg class without necessarily satisfying the Ramanujan hypothesis. Our results which do not require the Ramanujan hypothesis on the coefficients of the L-function are thus valid for a larger class of L-functions, for instance, Artin L-functions and automorphic L-functions (associated with automorphic representations of
![]() $\mathrm {GL}(n)$
over number fields).
$\mathrm {GL}(n)$
over number fields).
The intuition behind such equivalent criteria for the Riemann hypothesis lies in what are known as identities of Ramanujan–Hardy–Littlewood type. In particular, the criterion (1.2) was motivated via a striking modular transformation obtained by Ramanujan, involving infinite series of the Möbius function [Reference Ramanujan22] (see also [Reference Berndt4, p. 468, Entry 37]). This identity was later corrected by Hardy and Littlewood [Reference Hardy and Littlewood14, p. 156, Section 2.5] to give the following.
Theorem 1.1 (Ramanujan–Hardy–Littlewood)
Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two positive numbers such that
$\beta $
be two positive numbers such that
![]() $\alpha \beta =\pi $
. Assume that the series
$\alpha \beta =\pi $
. Assume that the series
![]() $\sum _{\rho }\left (\Gamma {\left (\frac {1-\rho }{2}\right )}/\zeta ^{'}(\rho )\right )x^{\rho }$
converges for every positive real x, where
$\sum _{\rho }\left (\Gamma {\left (\frac {1-\rho }{2}\right )}/\zeta ^{'}(\rho )\right )x^{\rho }$
converges for every positive real x, where
![]() $\rho $
runs through the nontrivial zeros of
$\rho $
runs through the nontrivial zeros of
![]() $\zeta (s)$
, and that the nontrivial zeros of
$\zeta (s)$
, and that the nontrivial zeros of
![]() $\zeta (s)$
are simple. Then
$\zeta (s)$
are simple. Then
 $$ \begin{align} &\sqrt{\alpha}\sum_{n=1}^{\infty}\frac{\mu(n)}{n}e^{-\alpha^2/n^2}-\sqrt{\beta}\sum_{n=1}^{\infty}\frac{\mu(n)}{n}e^{-\beta^2/n^2}=-\frac{1}{2\sqrt{\beta}}\sum_{\rho}\frac{\Gamma{\left(\frac{1-\rho}{2}\right)}}{\zeta^{'}(\rho)}\beta^{\rho}. \end{align} $$
$$ \begin{align} &\sqrt{\alpha}\sum_{n=1}^{\infty}\frac{\mu(n)}{n}e^{-\alpha^2/n^2}-\sqrt{\beta}\sum_{n=1}^{\infty}\frac{\mu(n)}{n}e^{-\beta^2/n^2}=-\frac{1}{2\sqrt{\beta}}\sum_{\rho}\frac{\Gamma{\left(\frac{1-\rho}{2}\right)}}{\zeta^{'}(\rho)}\beta^{\rho}. \end{align} $$
Such identities can be viewed as encoding relations between arithmetical and analytic pieces of information about the relevant L-function. In this case, the left-hand side contains arithmetical information about
![]() $\zeta (s)$
due to the Möbius function, whereas the right-hand side pertains to analytic information involving the nontrivial zeros of
$\zeta (s)$
due to the Möbius function, whereas the right-hand side pertains to analytic information involving the nontrivial zeros of
![]() $\zeta (s)$
.
$\zeta (s)$
.
Showing the convergence of the series on the right-hand side is nontrivial. While it is widely believed that the series is rapidly convergent, what is currently known is that it is convergent under a certain bracketing of the terms. More precisely, this bracketing means that for some positive constant c, the terms for which
are included in the same bracket (see [Reference Titchmarsh25, p. 220]). It also turns out that convergence under such bracketing is enough to prove (1.3) [Reference Hardy and Littlewood14, p. 158], [Reference Titchmarsh25, p. 220].
There exist several generalizations of (1.3) in various settings. In [Reference Dixit, Roy and Zaharescu12], Dixit, Roy, and Zaharescu obtained such an analog for Hecke forms. In [Reference Roy, Zaharescu and Zaki24], Roy, Zaharescu, and Zaki obtained a result of the type (1.3) where the Möbius function is replaced by a convolution of Dirichlet characters with the Möbius function. Further results of this kind have also been obtained by Dixit [Reference Dixit7, Reference Dixit8], Kühn, Robles, and Roy [Reference Kühn, Robles and Roy16], Dixit, Roy, and Zaharescu [Reference Dixit, Roy and Zaharescu13], Agarwal, Garg, and Maji [Reference Agarwal, Garg and Maji1], Dixit, Gupta, and Vatwani [Reference Dixit, Gupta and Vatwani9], etc. In this paper, we prove a very general such identity for L-functions satisfying axioms of the Selberg class other than the Ramanujan hypothesis. This result is stated as Theorem 2.1. By taking specific examples of L-functions in
![]() $\mathcal {S}$
, we not only recover many existing such identities in the literature, but also obtain elegant new transformations involving special values of Meijer G-functions of the type
$\mathcal {S}$
, we not only recover many existing such identities in the literature, but also obtain elegant new transformations involving special values of Meijer G-functions of the type
![]() $ {G^{n , 0}_{0 , n}}$
, where
$ {G^{n , 0}_{0 , n}}$
, where
![]() $n \in \mathbb N$
. Some such consequences are given in Corollaries 2.2 and 2.3.
$n \in \mathbb N$
. Some such consequences are given in Corollaries 2.2 and 2.3.
The paper is organized as follows. We first define the Selberg class of L-functions and then proceed to state our main results in Section 2. In Section 3, we give some preliminary lemmas which will be needed in our proofs. In Section 4, we prove Theorem 2.1, which is our analog of the Ramanujan–Hardy–Littlewood identity for the Selberg class. In Section 5, we give proofs of the transformations that arise as special cases of Theorem 2.1. Section 6 is devoted to proving Riesz-type criteria for the GRH for our general L-functions.
2 Statements of results
In 1991, Selberg introduced a general class
![]() $\mathcal {S}$
of Dirichlet series satisfying certain axioms. A Dirichlet series
$\mathcal {S}$
of Dirichlet series satisfying certain axioms. A Dirichlet series
![]() $F(s)$
is defined to be in
$F(s)$
is defined to be in
![]() $\mathcal {S}$
if it satisfies the following conditions:
$\mathcal {S}$
if it satisfies the following conditions:
-
(i) (Dirichlet series)
 $F(s)$
can be expressed as a Dirichlet series which is absolutely convergent in the region Re
$F(s)$
can be expressed as a Dirichlet series which is absolutely convergent in the region Re $$ \begin{align*} F\left(s\right)\mathrm{=}\sum^{\mathrm{\infty }}_{n{=1}}{\frac{a_F\left(n\right)}{n^s}}, \end{align*} $$
$$ \begin{align*} F\left(s\right)\mathrm{=}\sum^{\mathrm{\infty }}_{n{=1}}{\frac{a_F\left(n\right)}{n^s}}, \end{align*} $$
 $ (s)> 1$
, with
$ (s)> 1$
, with
 $ a_F (1) = 1 $
.
$ a_F (1) = 1 $
.
-
(ii) (Analytic continuation) There exists a nonnegative integer
 $ m $
, such that
$ m $
, such that
 $(s-1)^m F(s)$
is an entire function of finite order.
$(s-1)^m F(s)$
is an entire function of finite order. -
(iii) (Functional equation) Using the notation
 $\bar {\Phi }(s)=\overline {\Phi (\bar {s})}$
,
$\bar {\Phi }(s)=\overline {\Phi (\bar {s})}$
,
 $F(s)$
satisfies a functional equation of the type (2.1)where
$F(s)$
satisfies a functional equation of the type (2.1)where $$ \begin{align} {\Phi}(s)=\omega \bar{\Phi}(1-s), \end{align} $$
where
$$ \begin{align} {\Phi}(s)=\omega \bar{\Phi}(1-s), \end{align} $$
where $$ \begin{align*} {\Phi}(s)=Q^s F({s}) \prod_{i=1}^q \Gamma\left(\alpha_i s+\beta_i \right) = \gamma_F(s)F(s) \: (\text{say}), \end{align*} $$
$$ \begin{align*} {\Phi}(s)=Q^s F({s}) \prod_{i=1}^q \Gamma\left(\alpha_i s+\beta_i \right) = \gamma_F(s)F(s) \: (\text{say}), \end{align*} $$
 $\ Q>0, \ \alpha _i>0$
,
$\ Q>0, \ \alpha _i>0$
,
 $q\in \mathbb {N}$
and
$q\in \mathbb {N}$
and
 $\beta _i$
,
$\beta _i$
,
 $\omega $
are complex numbers with
$\omega $
are complex numbers with
 $\Re (\beta _i)\geq 0$
and
$\Re (\beta _i)\geq 0$
and
 $|\omega |=1$
.
$|\omega |=1$
.
-
(iv) (Euler product) For
 $\Re (s)>1$
, we have where
$\Re (s)>1$
, we have where $$ \begin{align*} F\left(s\right)={\prod_p }F_p\left(s\right), \end{align*} $$
$$ \begin{align*} F\left(s\right)={\prod_p }F_p\left(s\right), \end{align*} $$
 $F_p \left (s\right ){=}\exp \left ( \sum ^{{\infty }}_{j{=1}}{\frac {g({p^j})}{p^{js}}}\right ) $
, with
$F_p \left (s\right ){=}\exp \left ( \sum ^{{\infty }}_{j{=1}}{\frac {g({p^j})}{p^{js}}}\right ) $
, with
 $g({p^j})\ll p^{j\theta }$
for some
$g({p^j})\ll p^{j\theta }$
for some
 $\theta < {1\over 2}$
.
$\theta < {1\over 2}$
.
-
(v) (Ramanujan hypothesis) For every
 $ \epsilon> 0$
,
$ \epsilon> 0$
,  $$ \begin{align*} a_F\left(n\right)\ll_{\epsilon }n^{\epsilon }. \end{align*} $$
$$ \begin{align*} a_F\left(n\right)\ll_{\epsilon }n^{\epsilon }. \end{align*} $$
Many well-known functions such as the Riemann zeta function, Dirichlet L-functions, Dedekind zeta functions associated with algebraic number fields, etc. are elements of the Selberg class. The function
![]() $\gamma _F(s)$
in axiom (iii) is called the
$\gamma _F(s)$
in axiom (iii) is called the
![]() $\gamma $
-factor of F. This may not be unique, for instance, by application of the duplication formula for any of the
$\gamma $
-factor of F. This may not be unique, for instance, by application of the duplication formula for any of the
![]() $\Gamma $
-functions involved. However, it is known that the
$\Gamma $
-functions involved. However, it is known that the
![]() $\gamma $
-factor is unique up to a constant (see [Reference Conrey and Ghosh5, Theorem 2.1]). The information in (iii) can be summarized by denoting
$\gamma $
-factor is unique up to a constant (see [Reference Conrey and Ghosh5, Theorem 2.1]). The information in (iii) can be summarized by denoting
![]() $(Q,\boldsymbol {\alpha , \beta },w)$
as the data of F, where
$(Q,\boldsymbol {\alpha , \beta },w)$
as the data of F, where
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
are vectors given by
$\boldsymbol {\beta }$
are vectors given by
![]() $\boldsymbol {\alpha }=(\alpha _1,\alpha _2,\ldots , \alpha _q)$
and
$\boldsymbol {\alpha }=(\alpha _1,\alpha _2,\ldots , \alpha _q)$
and
![]() $\boldsymbol {\beta }=(\beta _1,\beta _2,\ldots , \beta _q)$
. We will also use
$\boldsymbol {\beta }=(\beta _1,\beta _2,\ldots , \beta _q)$
. We will also use
![]() $\boldsymbol {\bar {\beta }}$
to denote
$\boldsymbol {\bar {\beta }}$
to denote
![]() $(\bar {{\beta }}_1, \bar {{\beta }}_2, \ldots , \bar {{\beta }}_q)$
. The data of F is thus not uniquely determined in general. One defines the degree
$(\bar {{\beta }}_1, \bar {{\beta }}_2, \ldots , \bar {{\beta }}_q)$
. The data of F is thus not uniquely determined in general. One defines the degree
![]() $d_F$
of
$d_F$
of
![]() $F\in \mathcal {S}$
as
$F\in \mathcal {S}$
as
 $$ \begin{align*} d_F=2\sum_{i=1 }^{q}\alpha_i. \end{align*} $$
$$ \begin{align*} d_F=2\sum_{i=1 }^{q}\alpha_i. \end{align*} $$
It is well known that
![]() $d_F$
is an invariant, that is, the degree of F is uniquely determined by the function
$d_F$
is an invariant, that is, the degree of F is uniquely determined by the function
![]() $F(s)$
. We note that due to the Euler product (axiom (iv)), any
$F(s)$
. We note that due to the Euler product (axiom (iv)), any
![]() $F\in \mathcal {S}$
does not vanish in the region
$F\in \mathcal {S}$
does not vanish in the region
![]() $\Re (s)>1$
(see, for instance, [Reference Conrey and Ghosh5, Lemma 2.1]). Hence, there is an arithmetic function
$\Re (s)>1$
(see, for instance, [Reference Conrey and Ghosh5, Lemma 2.1]). Hence, there is an arithmetic function
![]() $b_F(n)$
such that for
$b_F(n)$
such that for
![]() $\Re (s)>1$
,
$\Re (s)>1$
,
 $$ \begin{align*} {1\over F(s)}=\sum_{n=1}^{\infty} {b_F(n)\over n^s}. \end{align*} $$
$$ \begin{align*} {1\over F(s)}=\sum_{n=1}^{\infty} {b_F(n)\over n^s}. \end{align*} $$
In order to understand the analog of the Riemann hypothesis for
![]() $F\in \mathcal {S}$
, some discussion of zeros of F is necessary. The zeros of F in the region
$F\in \mathcal {S}$
, some discussion of zeros of F is necessary. The zeros of F in the region
![]() $\Re (s)<0$
are called trivial zeros. Using the functional equation, it is easy to see that the trivial zeros of
$\Re (s)<0$
are called trivial zeros. Using the functional equation, it is easy to see that the trivial zeros of
![]() $F(s)$
are located at the poles of the
$F(s)$
are located at the poles of the
![]() $\gamma $
-factors
$\gamma $
-factors
![]() $\gamma _F$
. More precisely, the trivial zeros occur at
$\gamma _F$
. More precisely, the trivial zeros occur at
 $$ \begin{align*} \left\{s={-m-\beta_i \over \alpha_i}:m\in \mathbb{N}\cup\{0\}\right\}_{i=1}^q \cap\{s:\Re(s)<0\}. \end{align*} $$
$$ \begin{align*} \left\{s={-m-\beta_i \over \alpha_i}:m\in \mathbb{N}\cup\{0\}\right\}_{i=1}^q \cap\{s:\Re(s)<0\}. \end{align*} $$
The other zeros of F occur inside the critical strip
![]() $0\leq \Re (s)\leq 1$
. All such zeros except at
$0\leq \Re (s)\leq 1$
. All such zeros except at
![]() $s=0$
are called the nontrivial zeros of F. The case
$s=0$
are called the nontrivial zeros of F. The case
![]() $s=0$
is more delicate. It is often possible for F to have a zero at
$s=0$
is more delicate. It is often possible for F to have a zero at
![]() $s=0$
. Let
$s=0$
. Let
If we put
![]() $s=0$
into the functional equation of F, then the
$s=0$
into the functional equation of F, then the
![]() $\gamma $
-factors on either side are entire except for poles coming from factors of the type
$\gamma $
-factors on either side are entire except for poles coming from factors of the type
![]() $\Gamma ({\alpha }_is+{\beta }_i)$
whenever
$\Gamma ({\alpha }_is+{\beta }_i)$
whenever
![]() ${\beta }_i$
happens to be zero. Let
${\beta }_i$
happens to be zero. Let
![]() $j_F$
be the number of components of
$j_F$
be the number of components of
![]() $\boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q)$
which are zero, that is,
$\boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q)$
which are zero, that is,
In order to ensure that
![]() $j_F$
is well defined for a given
$j_F$
is well defined for a given
![]() $F\in \mathcal {S}$
, we adopt the convention that
$F\in \mathcal {S}$
, we adopt the convention that
![]() $\gamma _F$
is of the form
$\gamma _F$
is of the form
![]() $ {Q^s}\prod _{i=1}^q \Gamma \left (\alpha _i s+\beta _i \right )$
, with q being the least such integer. That is, if
$ {Q^s}\prod _{i=1}^q \Gamma \left (\alpha _i s+\beta _i \right )$
, with q being the least such integer. That is, if
![]() $\gamma ^{\prime }_F= {Q^s}\prod _{i=1}^{q'} \Gamma \left (\alpha ^{\prime }_i s+\beta ^{\prime }_i \right )$
is any other admissible
$\gamma ^{\prime }_F= {Q^s}\prod _{i=1}^{q'} \Gamma \left (\alpha ^{\prime }_i s+\beta ^{\prime }_i \right )$
is any other admissible
![]() $\gamma $
-factor for F, then we have
$\gamma $
-factor for F, then we have
![]() $q'\geq q.$
Thus,
$q'\geq q.$
Thus,
![]() $F(s)$
has a zero of order
$F(s)$
has a zero of order
![]() $j_F-k_F$
at
$j_F-k_F$
at
![]() $s=0$
. Moreover, note that for F satisfying axiom
$s=0$
. Moreover, note that for F satisfying axiom
![]() $(ii)$
of
$(ii)$
of
![]() $\mathcal {S}$
, we must have
$\mathcal {S}$
, we must have
![]() $j_F\geq k_F$
since F cannot have a pole at
$j_F\geq k_F$
since F cannot have a pole at
![]() $s=0$
. For instance, for the Dedekind zeta function
$s=0$
. For instance, for the Dedekind zeta function
![]() $\zeta _{\mathbb {K}}(s)$
, associated with a number field
$\zeta _{\mathbb {K}}(s)$
, associated with a number field
![]() $\mathbb {K}$
, one sees that
$\mathbb {K}$
, one sees that
![]() $k_F=1$
, while
$k_F=1$
, while
![]() $j_F=r_1+r_2$
, where
$j_F=r_1+r_2$
, where
![]() $r_1$
and
$r_1$
and
![]() $2r_2$
are the number of real and imaginary embeddings of
$2r_2$
are the number of real and imaginary embeddings of
![]() $\mathbb {K}$
into
$\mathbb {K}$
into
![]() $\mathbb {C}$
, respectively. Thus,
$\mathbb {C}$
, respectively. Thus,
![]() $\zeta _{\mathbb {K}}(s)$
has a zero at
$\zeta _{\mathbb {K}}(s)$
has a zero at
![]() $s=0$
, whenever
$s=0$
, whenever
![]() $r_1+r_2-1>0$
. The GRH conjectures that all the nontrivial zeros of F lie on the critical line
$r_1+r_2-1>0$
. The GRH conjectures that all the nontrivial zeros of F lie on the critical line
![]() $\Re (s)={1\over 2}$
.
$\Re (s)={1\over 2}$
.
We now set up some notation. The line integral
![]() $\int _{c-i\infty }^{c+i\infty }$
will be denoted as
$\int _{c-i\infty }^{c+i\infty }$
will be denoted as
![]() $\int _{(c)}$
. We also define a parameter
$\int _{(c)}$
. We also define a parameter
![]() $c_F$
depending on the data of F as follows:
$c_F$
depending on the data of F as follows:
 $$ \begin{align} c_F = \left\lbrace \begin{array}{ll} \min \limits_{1\le i\le q} \left\{ \frac{1}{2{\alpha}_i} \right\}, & \text{if } \Re(\beta_i)=0 \ \forall \ 1\leq i\leq q, \\ {\min \limits_{1\le i\le q \atop {\Re ({\beta}_i)\neq 0}}} \left\{ \frac{\Re ({\beta}_i)}{{\alpha}_i} \right\}, & \text{otherwise}. \end{array} \right. \end{align} $$
$$ \begin{align} c_F = \left\lbrace \begin{array}{ll} \min \limits_{1\le i\le q} \left\{ \frac{1}{2{\alpha}_i} \right\}, & \text{if } \Re(\beta_i)=0 \ \forall \ 1\leq i\leq q, \\ {\min \limits_{1\le i\le q \atop {\Re ({\beta}_i)\neq 0}}} \left\{ \frac{\Re ({\beta}_i)}{{\alpha}_i} \right\}, & \text{otherwise}. \end{array} \right. \end{align} $$
It is clear that there are no trivial zeros of F to the right of
![]() $\Re (s)=-c_F$
. Define for
$\Re (s)=-c_F$
. Define for
![]() $-c_F <c<0$
and
$-c_F <c<0$
and
![]() $x>0$
,
$x>0$
,
 $$ \begin{align} Z_{ \boldsymbol{\alpha,\beta} }(x) :=\frac{1}{2 \pi i} \int\limits_{(c)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){x^{ - s}} ds}, \end{align} $$
$$ \begin{align} Z_{ \boldsymbol{\alpha,\beta} }(x) :=\frac{1}{2 \pi i} \int\limits_{(c)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){x^{ - s}} ds}, \end{align} $$
and
 $$ \begin{align} \mathcal{P} _{\boldsymbol{\alpha,\beta} ,z}(y):=\sum\limits_{n = 1}^\infty \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\sqrt{y} }{n}} \right)^{d_F}\right)\cosh\left({\sqrt{y}z}\over n\right), \end{align} $$
$$ \begin{align} \mathcal{P} _{\boldsymbol{\alpha,\beta} ,z}(y):=\sum\limits_{n = 1}^\infty \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\sqrt{y} }{n}} \right)^{d_F}\right)\cosh\left({\sqrt{y}z}\over n\right), \end{align} $$
for
![]() $y>0$
and
$y>0$
and
![]() $z\in \mathbb {C}$
. The exponent
$z\in \mathbb {C}$
. The exponent
![]() $d_F$
introduced here in the definition of the kernel
$d_F$
introduced here in the definition of the kernel
![]() $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
will play a key role in what follows.
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
will play a key role in what follows.
Our first result is a modular relation for functions F in the Selberg class. We will denote the derivative of
![]() $F(s)$
with respect to s by
$F(s)$
with respect to s by
![]() $F'(s)$
.
$F'(s)$
.
Theorem 2.1 Let F satisfy axioms (i)–(iv) of the class
![]() $\mathcal {S}$
. For every positive real x, assume the convergence of the series
$\mathcal {S}$
. For every positive real x, assume the convergence of the series
 $$ \begin{align*} \sum\limits_{\rho} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1- \bar{\rho})+\beta_i \right)}{\overline{F'({\rho})}}x^{\bar{\rho}}, \end{align*} $$
$$ \begin{align*} \sum\limits_{\rho} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1- \bar{\rho})+\beta_i \right)}{\overline{F'({\rho})}}x^{\bar{\rho}}, \end{align*} $$
where
![]() $\rho $
runs through the nontrivial zeros of
$\rho $
runs through the nontrivial zeros of
![]() $F(s)$
. Suppose that each nontrivial zero of
$F(s)$
. Suppose that each nontrivial zero of
![]() $F(s)$
is simple. Let
$F(s)$
is simple. Let
![]() $\eta , \nu>0$
be such that
$\eta , \nu>0$
be such that
![]() $\eta \nu ={1\over Q^2}$
. Let
$\eta \nu ={1\over Q^2}$
. Let
![]() $r= {j_F-k_F}$
, where
$r= {j_F-k_F}$
, where
![]() $k_F, j_F$
are as defined in (2.2), (2.3), respectively. Then, for
$k_F, j_F$
are as defined in (2.2), (2.3), respectively. Then, for
![]() $r>0$
, we have
$r>0$
, we have
 $$ \begin{align} \omega\sqrt{\eta}& \sum_{n=1}^{\infty} {b_{F}(n)\over n}Z_{\boldsymbol{\alpha,\beta} }\left(\eta \over n\right)-{\sqrt{\nu} }\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}Z_{\boldsymbol{\alpha,\overline{\beta}}}\left(\nu \over n\right)\nonumber\\& = -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho}) +\beta_i \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}}\nonumber\\&\quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}(s-1)^r \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+\beta_i \right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=1}\nonumber\\& \quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}s^r \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+\beta_i \right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=0}. \end{align} $$
$$ \begin{align} \omega\sqrt{\eta}& \sum_{n=1}^{\infty} {b_{F}(n)\over n}Z_{\boldsymbol{\alpha,\beta} }\left(\eta \over n\right)-{\sqrt{\nu} }\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}Z_{\boldsymbol{\alpha,\overline{\beta}}}\left(\nu \over n\right)\nonumber\\& = -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho}) +\beta_i \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}}\nonumber\\&\quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}(s-1)^r \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+\beta_i \right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=1}\nonumber\\& \quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}s^r \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+\beta_i \right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=0}. \end{align} $$
If
![]() $r = 0$
, we have the following more simplified relation:
$r = 0$
, we have the following more simplified relation:
 $$ \begin{align*} \omega\sqrt{\eta} \sum_{n=1}^{\infty} {b_{F}(n)\over n}Z_{\boldsymbol{\alpha,\beta} }\left(\eta \over n\right)-{\sqrt{\nu} }\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}Z_{\boldsymbol{\alpha,\overline{\beta}}}\left(\nu \over n\right) = -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho}) +\beta_i \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}}. \end{align*} $$
$$ \begin{align*} \omega\sqrt{\eta} \sum_{n=1}^{\infty} {b_{F}(n)\over n}Z_{\boldsymbol{\alpha,\beta} }\left(\eta \over n\right)-{\sqrt{\nu} }\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}Z_{\boldsymbol{\alpha,\overline{\beta}}}\left(\nu \over n\right) = -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho}) +\beta_i \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}}. \end{align*} $$
A straightforward consequence of Theorem 2.1 is that the classical result of Ramanujan, Hardy, and Littlewood follows as a special case since, for
![]() $F(s)=\zeta (s)$
, we have
$F(s)=\zeta (s)$
, we have
![]() $Z_{\boldsymbol {{\alpha },{\beta }}}(x) =Z_{(1/2),(0)}(x)$
, which equals
$Z_{\boldsymbol {{\alpha },{\beta }}}(x) =Z_{(1/2),(0)}(x)$
, which equals
![]() $2(e^{-x^2}-1)$
. Moreover, when F is the Dedekind zeta function of a number field
$2(e^{-x^2}-1)$
. Moreover, when F is the Dedekind zeta function of a number field
![]() $ {\mathbb {K}}$
, it is easy to check that
$ {\mathbb {K}}$
, it is easy to check that
 $$ \begin{align*} \boldsymbol{{\alpha}}=(\underbrace{\substack{{1\over 2},\ldots,{1\over 2}}}_{r_1\text{ times}},\underbrace{1,\ldots, 1}_{r_2\text{ times}}), \quad \boldsymbol{{\beta}}=(0,\ldots, 0) \quad \text{and} \quad Z_{\boldsymbol{{\alpha},{\beta}}}(x)=\frac{1}{2 \pi i} \int_{(c)} {{\Gamma ^{{r_1}}}\left( {\frac{s}{2}} \right){\Gamma ^{{r_2}}}\left( s \right){x^{ - s}}ds}, \end{align*} $$
$$ \begin{align*} \boldsymbol{{\alpha}}=(\underbrace{\substack{{1\over 2},\ldots,{1\over 2}}}_{r_1\text{ times}},\underbrace{1,\ldots, 1}_{r_2\text{ times}}), \quad \boldsymbol{{\beta}}=(0,\ldots, 0) \quad \text{and} \quad Z_{\boldsymbol{{\alpha},{\beta}}}(x)=\frac{1}{2 \pi i} \int_{(c)} {{\Gamma ^{{r_1}}}\left( {\frac{s}{2}} \right){\Gamma ^{{r_2}}}\left( s \right){x^{ - s}}ds}, \end{align*} $$
where
![]() $-{1\over 2}<c<0$
and
$-{1\over 2}<c<0$
and
![]() $r_1$
,
$r_1$
,
![]() $2r_2$
are the number of real and complex embeddings of
$2r_2$
are the number of real and complex embeddings of
![]() $ {\mathbb {K}}$
, respectively. It thus follows that a special case of Theorem 2.1 yields Theorem
$ {\mathbb {K}}$
, respectively. It thus follows that a special case of Theorem 2.1 yields Theorem
![]() $ {1.3}$
and Corollary 3.2 of [Reference Dixit, Gupta and Vatwani9].
$ {1.3}$
and Corollary 3.2 of [Reference Dixit, Gupta and Vatwani9].
We now state more nontrivial consequences of Theorem 2.1 among which are certain elegant transformations involving special values of the Meijer G-function (defined in (3.3)). In particular, special values of Meijer G-functions of the type
![]() $ {G^{n , 0}_{0 , n}}$
for
$ {G^{n , 0}_{0 , n}}$
for
![]() $n=1,2,3,\ldots $
come into play. Some interesting such special values involve the modified Bessel function of the second kind, which we proceed to define below.
$n=1,2,3,\ldots $
come into play. Some interesting such special values involve the modified Bessel function of the second kind, which we proceed to define below.
The Bessel function of the first kind of order
![]() $\nu $
is defined by [Reference Watson26, p. 40]
$\nu $
is defined by [Reference Watson26, p. 40]
 $$ \begin{align*} J_{\nu}(z)&:=\sum_{m=0}^{\infty}\frac{(-1)^m(z/2)^{2m+\nu}}{m!\Gamma(m+1+\nu)} \hspace{9mm} (z,\nu\in\mathbb{C}). \end{align*} $$
$$ \begin{align*} J_{\nu}(z)&:=\sum_{m=0}^{\infty}\frac{(-1)^m(z/2)^{2m+\nu}}{m!\Gamma(m+1+\nu)} \hspace{9mm} (z,\nu\in\mathbb{C}). \end{align*} $$
The modified Bessel functions of the first and second kinds of order
![]() $\nu $
are defined by [Reference Watson26, pp. 77–78]
$\nu $
are defined by [Reference Watson26, pp. 77–78]
 $$ \begin{align*} I_{\nu}(z)&:= \begin{cases} e^{-\frac{1}{2}\pi\nu i}J_{\nu}(e^{\frac{1}{2}\pi i}z), & \text{if }-\pi<\text{ arg }z\leq\frac{\pi}{2},\\ e^{\frac{3}{2}\pi\nu i}J_{\nu}(e^{-\frac{3}{2}\pi i}z), & \text{if }\frac{\pi}{2}<\text{ arg }z\leq \pi, \end{cases}\\ K_{\nu}(z)&:=\frac{\pi}{2}\frac{I_{-\nu}(z)-I_{\nu}(z)}{\sin\nu\pi}, \end{align*} $$
$$ \begin{align*} I_{\nu}(z)&:= \begin{cases} e^{-\frac{1}{2}\pi\nu i}J_{\nu}(e^{\frac{1}{2}\pi i}z), & \text{if }-\pi<\text{ arg }z\leq\frac{\pi}{2},\\ e^{\frac{3}{2}\pi\nu i}J_{\nu}(e^{-\frac{3}{2}\pi i}z), & \text{if }\frac{\pi}{2}<\text{ arg }z\leq \pi, \end{cases}\\ K_{\nu}(z)&:=\frac{\pi}{2}\frac{I_{-\nu}(z)-I_{\nu}(z)}{\sin\nu\pi}, \end{align*} $$
respectively, with
![]() $K_n(z)$
defined by
$K_n(z)$
defined by
![]() $\lim _{\nu \to n}K_{\nu }(z)$
if n is an integer.
$\lim _{\nu \to n}K_{\nu }(z)$
if n is an integer.
We state some special values of the Meijer G-function which are relevant in the context of Theorem 2.1:
 $$ \begin{align} {G^{4 , 0}_{0 , 4}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 4} \ b+{2\over 4}\ b+{3\over 4} \end{matrix} \right| z \right) &={\sqrt{2}\pi^{3\over 2}}z^be^{-4 {z}^{1/4}}, \end{align} $$
$$ \begin{align} {G^{4 , 0}_{0 , 4}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 4} \ b+{2\over 4}\ b+{3\over 4} \end{matrix} \right| z \right) &={\sqrt{2}\pi^{3\over 2}}z^be^{-4 {z}^{1/4}}, \end{align} $$
 $$ \begin{align} {G^{4 , 0}_{0 , 4}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 2} \ 2b-c\ c \end{matrix} \right| z \right) &=8{\sqrt{\pi}}z^b K_{2c-2b}(2\sqrt{2} (-z)^{1/4} )K_{2c-2b}\left({2\sqrt{2}\sqrt{z}\over (-z)^{1/4}}\right).\nonumber\\ \end{align} $$
$$ \begin{align} {G^{4 , 0}_{0 , 4}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 2} \ 2b-c\ c \end{matrix} \right| z \right) &=8{\sqrt{\pi}}z^b K_{2c-2b}(2\sqrt{2} (-z)^{1/4} )K_{2c-2b}\left({2\sqrt{2}\sqrt{z}\over (-z)^{1/4}}\right).\nonumber\\ \end{align} $$
Using the identity (2.8), one can derive the following transformation. We give the proof in Section 5.
Corollary 2.2 Let
![]() $F\in \mathcal {S}$
with data
$F\in \mathcal {S}$
with data
![]() $(Q, \boldsymbol {\alpha ,\beta }, \omega )$
, where
$(Q, \boldsymbol {\alpha ,\beta }, \omega )$
, where
![]() $\boldsymbol {\alpha }=(4)$
and
$\boldsymbol {\alpha }=(4)$
and
![]() $\boldsymbol {\beta }=({\beta }_1)$
. For every positive real x, assume the convergence of the series
$\boldsymbol {\beta }=({\beta }_1)$
. For every positive real x, assume the convergence of the series
 $$ \begin{align*} \sum_{\rho} \frac{\Gamma\left(4(1-\bar{\rho}) + \bar {\beta}_1 \right)}{\overline{F'({\rho})}}x^{\bar{\rho}}, \end{align*} $$
$$ \begin{align*} \sum_{\rho} \frac{\Gamma\left(4(1-\bar{\rho}) + \bar {\beta}_1 \right)}{\overline{F'({\rho})}}x^{\bar{\rho}}, \end{align*} $$
where
![]() $\rho $
runs through the nontrivial zeros of
$\rho $
runs through the nontrivial zeros of
![]() $F(s)$
. Suppose that each nontrivial zero of
$F(s)$
. Suppose that each nontrivial zero of
![]() $F(s)$
is simple. Let
$F(s)$
is simple. Let
![]() $\eta , \nu>0$
be such that
$\eta , \nu>0$
be such that
![]() $\eta \nu ={1\over Q^2}$
. For the case
$\eta \nu ={1\over Q^2}$
. For the case
![]() ${\beta }_1=0$
, we let
${\beta }_1=0$
, we let
![]() $r=1-k_F$
, where
$r=1-k_F$
, where
![]() $k_F$
is as defined in (2.2). Then, for
$k_F$
is as defined in (2.2). Then, for
![]() $r>0$
, we have
$r>0$
, we have
 $$ \begin{align} {\omega\sqrt{\eta}\over 4}& \sum_{n=1}^{\infty} {b_{F}(n)\over n}\left(e^{-\left( {\eta \over n}\right)^{1/4} }-{1}\right)-{\sqrt{\nu} \over 4}\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}\left(e^{-\left( {\nu \over n}\right)^{1/4} }-{1}\right)\nonumber\\ &= -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\Gamma\left(4(1-\bar{\rho}) \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}} - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}(s-1)^r \frac{\Gamma\left(4(1-s) \right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=1}\nonumber\\ & \quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}s^r \frac{\Gamma\left(4(1-s)\right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=0}. \end{align} $$
$$ \begin{align} {\omega\sqrt{\eta}\over 4}& \sum_{n=1}^{\infty} {b_{F}(n)\over n}\left(e^{-\left( {\eta \over n}\right)^{1/4} }-{1}\right)-{\sqrt{\nu} \over 4}\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}\left(e^{-\left( {\nu \over n}\right)^{1/4} }-{1}\right)\nonumber\\ &= -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\Gamma\left(4(1-\bar{\rho}) \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}} - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}(s-1)^r \frac{\Gamma\left(4(1-s) \right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=1}\nonumber\\ & \quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}s^r \frac{\Gamma\left(4(1-s)\right)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=0}. \end{align} $$
When
![]() $r=0,$
the same identity holds without the last two residue terms appearing. When
$r=0,$
the same identity holds without the last two residue terms appearing. When
![]() ${\beta }_1\neq 0$
, we let
${\beta }_1\neq 0$
, we let
![]() $r=-k_F$
. Then
$r=-k_F$
. Then
![]() $r=0$
is the only possibility. We then have
$r=0$
is the only possibility. We then have
 $$ \begin{align} &{\omega\sqrt{\eta}\over 4} \sum_{n=1}^{\infty} {b_{F}(n)\over n} \left(\eta \over n \right)^{\bar{{\beta}}_1/ 4}e^{-\left( {\eta \over n}\right)^{1/4} }-{\sqrt{\nu} \over 4}\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}& \left(\nu \over n \right)^{\bar{{\beta}}_1/ 4}e^{-\left( {\nu \over n}\right)^{1/4} }\nonumber\\& \quad = -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\Gamma\left(4(1-\bar{\rho})+\bar{\beta_1} \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}}. \end{align} $$
$$ \begin{align} &{\omega\sqrt{\eta}\over 4} \sum_{n=1}^{\infty} {b_{F}(n)\over n} \left(\eta \over n \right)^{\bar{{\beta}}_1/ 4}e^{-\left( {\eta \over n}\right)^{1/4} }-{\sqrt{\nu} \over 4}\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}& \left(\nu \over n \right)^{\bar{{\beta}}_1/ 4}e^{-\left( {\nu \over n}\right)^{1/4} }\nonumber\\& \quad = -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\Gamma\left(4(1-\bar{\rho})+\bar{\beta_1} \right)}{\overline{F'({\rho})}}\nu^{\bar{\rho}}. \end{align} $$
The identity (2.9) yields the following transformation involving the modified Bessel function of the second kind.
Corollary 2.3 Let
![]() $F\in \mathcal {S}$
with data
$F\in \mathcal {S}$
with data
![]() $(Q,(1,1,1,1),(0,{1\over 2},-C,C),\omega )$
, where C is a nonzero real constant. For every positive real x, assume the convergence of the series
$(Q,(1,1,1,1),(0,{1\over 2},-C,C),\omega )$
, where C is a nonzero real constant. For every positive real x, assume the convergence of the series
 $$ \begin{align*} \sum_{\rho} \frac{\Gamma(1-\bar{\rho}) \Gamma\left({3\over 2}-\bar{\rho} \right) \Gamma(1-C-\bar{\rho}) \Gamma(C+1-\bar{\rho}) }{\overline{F'({\rho})}}x^{\bar{\rho}}, \end{align*} $$
$$ \begin{align*} \sum_{\rho} \frac{\Gamma(1-\bar{\rho}) \Gamma\left({3\over 2}-\bar{\rho} \right) \Gamma(1-C-\bar{\rho}) \Gamma(C+1-\bar{\rho}) }{\overline{F'({\rho})}}x^{\bar{\rho}}, \end{align*} $$
where
![]() $\rho $
runs through the nontrivial zeros of
$\rho $
runs through the nontrivial zeros of
![]() $F(s)$
. Suppose that each nontrivial zero of
$F(s)$
. Suppose that each nontrivial zero of
![]() $F(s)$
is simple. Let
$F(s)$
is simple. Let
![]() $\eta , \nu>0$
be such that
$\eta , \nu>0$
be such that
![]() $\eta \nu ={1\over Q^2}$
. Let
$\eta \nu ={1\over Q^2}$
. Let
![]() $r= {1-k_F}$
, where
$r= {1-k_F}$
, where
![]() $k_F$
is as defined in (2.2). Then, for
$k_F$
is as defined in (2.2). Then, for
![]() $r>0$
, we have
$r>0$
, we have
 $$ \begin{align} \omega\sqrt{\eta}& \sum_{n=1}^{\infty} {b_{F}(n)\over n}\left(8{\sqrt{\pi}} K_{2C}\left(2\sqrt{2} \left( {-{\eta\over n}} \right)^{1/4} \right)K_{2C}\left({2\sqrt{2}\sqrt{{\eta\over n}}\over \left( {-{\eta\over n}} \right)^{1/4} }\right)+{\pi\sqrt{\pi}\over C\sin \pi C}\right)\nonumber\\ &\quad-{\sqrt{\nu} }\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}\left(8{\sqrt{\pi}} K_{2C}\left(2\sqrt{2} \left( {-{\nu\over n}} \right)^{1/4} \right)K_{2C}\left({2\sqrt{2}\sqrt{{\nu\over n}}\over \left( {-{\nu\over n}} \right)^{1/4} }\right)+{\pi\sqrt{\pi}\over C\sin \pi C}\right)\nonumber\\ &= -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\Gamma(1-\bar{\rho}) \Gamma\left({3\over 2}-\bar{\rho} \right) \Gamma(1-C-\bar{\rho}) \Gamma(1+C-\bar{\rho}) }{\overline{F'({\rho})}}\nu^{\bar{\rho}} \nonumber\\ & \quad- {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}(s-1)^r \frac{\Gamma(1-s) \Gamma\left({3\over 2}-s \right) \Gamma(1-C-s) \Gamma(1+C-s)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=1}\nonumber\\ & \quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}s^r \frac{\Gamma(1-s) \Gamma\left({3\over 2}-s \right) \Gamma(1-C-s) \Gamma(1+C-s)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=0}.\nonumber\\[-24pt] \end{align} $$
$$ \begin{align} \omega\sqrt{\eta}& \sum_{n=1}^{\infty} {b_{F}(n)\over n}\left(8{\sqrt{\pi}} K_{2C}\left(2\sqrt{2} \left( {-{\eta\over n}} \right)^{1/4} \right)K_{2C}\left({2\sqrt{2}\sqrt{{\eta\over n}}\over \left( {-{\eta\over n}} \right)^{1/4} }\right)+{\pi\sqrt{\pi}\over C\sin \pi C}\right)\nonumber\\ &\quad-{\sqrt{\nu} }\sum_{n=1}^{\infty} {\overline{b_{F}(n)}\over n}\left(8{\sqrt{\pi}} K_{2C}\left(2\sqrt{2} \left( {-{\nu\over n}} \right)^{1/4} \right)K_{2C}\left({2\sqrt{2}\sqrt{{\nu\over n}}\over \left( {-{\nu\over n}} \right)^{1/4} }\right)+{\pi\sqrt{\pi}\over C\sin \pi C}\right)\nonumber\\ &= -{1\over \sqrt{\nu} }\sum_{\rho} \frac{\Gamma(1-\bar{\rho}) \Gamma\left({3\over 2}-\bar{\rho} \right) \Gamma(1-C-\bar{\rho}) \Gamma(1+C-\bar{\rho}) }{\overline{F'({\rho})}}\nu^{\bar{\rho}} \nonumber\\ & \quad- {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}(s-1)^r \frac{\Gamma(1-s) \Gamma\left({3\over 2}-s \right) \Gamma(1-C-s) \Gamma(1+C-s)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=1}\nonumber\\ & \quad - {1\over \sqrt{\nu}(r-1)!}{d^{r-1}\over ds^{r-1}}s^r \frac{\Gamma(1-s) \Gamma\left({3\over 2}-s \right) \Gamma(1-C-s) \Gamma(1+C-s)}{\overline{F(\bar{s})}}\nu^{s}\bigg|_{s=0}.\nonumber\\[-24pt] \end{align} $$
When
![]() $r=0,$
the same identity holds without the last two residue terms appearing.
$r=0,$
the same identity holds without the last two residue terms appearing.
Similarly, the identities (2.13) given below can be used to recover Corollaries 3.4 and 3.3 of [Reference Dixit, Gupta and Vatwani9], respectively.
 $$ \begin{align} {G^{1 , 0}_{0 , 1}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \end{matrix} \right| z \right) =e^{-z}z^b, \qquad \qquad {G^{2 , 0}_{0 , 2}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 2} \end{matrix} \right| z \right) =\sqrt{\pi}z^be^{-2\sqrt{z}}. \end{align} $$
$$ \begin{align} {G^{1 , 0}_{0 , 1}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \end{matrix} \right| z \right) =e^{-z}z^b, \qquad \qquad {G^{2 , 0}_{0 , 2}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 2} \end{matrix} \right| z \right) =\sqrt{\pi}z^be^{-2\sqrt{z}}. \end{align} $$
It is also possible to obtain more such transformations involving special values of
![]() $ {G^{n , 0}_{0 , n}} $
for other values of n, for instance, using any of the following identities:
$ {G^{n , 0}_{0 , n}} $
for other values of n, for instance, using any of the following identities:
 $$ \begin{align*} & {G^{2 , 0}_{0 , 2}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ c \end{matrix} \right| z \right) =2z^{{1\over 2}(b+c)}K_{b-c}(2\sqrt{z}), \qquad {G^{3 , 0}_{0 , 3}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 3} \ b+{2\over 3} \end{matrix} \right| z \right) ={2\pi\over \sqrt{3}}z^be^{-3 {z}^{1/ 3}}, \\ & {G^{5 , 0}_{0 , 5}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 5} \ b+{2\over 5}\ b+{3\over 5}\ b+{4\over 5} \end{matrix} \right| z \right) ={4\pi^{ 2}\over\sqrt{5}}z^be^{-5 {z}^{1/ 5}}. \end{align*} $$
$$ \begin{align*} & {G^{2 , 0}_{0 , 2}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ c \end{matrix} \right| z \right) =2z^{{1\over 2}(b+c)}K_{b-c}(2\sqrt{z}), \qquad {G^{3 , 0}_{0 , 3}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 3} \ b+{2\over 3} \end{matrix} \right| z \right) ={2\pi\over \sqrt{3}}z^be^{-3 {z}^{1/ 3}}, \\ & {G^{5 , 0}_{0 , 5}}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ b \ b+{1\over 5} \ b+{2\over 5}\ b+{3\over 5}\ b+{4\over 5} \end{matrix} \right| z \right) ={4\pi^{ 2}\over\sqrt{5}}z^be^{-5 {z}^{1/ 5}}. \end{align*} $$
Since the proofs follow analogously to those of Corollaries 2.2 and 2.3, we do not delve into them here.
Our next main result gives Riesz-type criteria for the GRH, applicable to a general class of L-functions. Before stating this, we make some remarks about certain additional conditions that we need to impose on our L-function
![]() $F(s)$
.
$F(s)$
.
The first such condition pertains to (iv) of the Selberg class axioms. From the perspective of known examples, in particular, automorphic L-functions, it is natural to restrict
![]() $1\over F_p (s)$
to be a polynomial in
$1\over F_p (s)$
to be a polynomial in
![]() $p^{-s}$
of degree independent of p (see, for instance, [Reference Conrey and Ghosh5]). Axiom (iv) may thus be strengthened to axiom (iv)
$p^{-s}$
of degree independent of p (see, for instance, [Reference Conrey and Ghosh5]). Axiom (iv) may thus be strengthened to axiom (iv)
![]() $'$
given below. We say that F has polynomial Euler product if it satisfies the following:
$'$
given below. We say that F has polynomial Euler product if it satisfies the following:
(iv)
![]() $'$
(Polynomial Euler product) For
$'$
(Polynomial Euler product) For
![]() $\Re (s)>1$
, we have
$\Re (s)>1$
, we have
 $$ \begin{align*} F(s)=\prod_p\prod_{i=1}^{n}\left( 1-{\gamma_i(p)\over p^s}\right)^{-1} , \end{align*} $$
$$ \begin{align*} F(s)=\prod_p\prod_{i=1}^{n}\left( 1-{\gamma_i(p)\over p^s}\right)^{-1} , \end{align*} $$
where
![]() $\gamma _i(p)$
are complex numbers. It is conjectured that all L-functions in the Selberg class have a polynomial Euler product. It is well known that under (iv)
$\gamma _i(p)$
are complex numbers. It is conjectured that all L-functions in the Selberg class have a polynomial Euler product. It is well known that under (iv)
![]() $'$
, the axiom (v) is equivalent to the bound
$'$
, the axiom (v) is equivalent to the bound
for all primes p and
![]() $i=1,\ldots ,m$
(see, for instance, [Reference Aistleitner and Pańkowski2, p. 347]).
$i=1,\ldots ,m$
(see, for instance, [Reference Aistleitner and Pańkowski2, p. 347]).
In all known examples of L-functions from
![]() $\mathcal {S}$
, it is possible to find a normalization such that in axiom (iii), one has all
$\mathcal {S}$
, it is possible to find a normalization such that in axiom (iii), one has all
![]() ${\alpha }_i$
’s to be rational numbers. In fact, Conrey and Ghosh observed that one could take
${\alpha }_i$
’s to be rational numbers. In fact, Conrey and Ghosh observed that one could take
![]() ${\alpha }_i={1\over 2}$
for all i (cf. [Reference Conrey and Ghosh5, p. 12]). We thus formulate a subclass of functions called
${\alpha }_i={1\over 2}$
for all i (cf. [Reference Conrey and Ghosh5, p. 12]). We thus formulate a subclass of functions called
![]() $\mathcal {S}^*$
satisfying axioms (i)–(iii), (iv)
$\mathcal {S}^*$
satisfying axioms (i)–(iii), (iv)
![]() $'$
, (v), with the additional restriction that in the data
$'$
, (v), with the additional restriction that in the data
![]() $(Q,\boldsymbol {{\alpha },{\beta }},w)$
of F, all the components of
$(Q,\boldsymbol {{\alpha },{\beta }},w)$
of F, all the components of
![]() $\boldsymbol {{\alpha }}$
are rational numbers.
$\boldsymbol {{\alpha }}$
are rational numbers.
We do not appear to exclude any known examples of important L-functions under these new hypotheses. Indeed, it is conjectured that
![]() $\mathcal {S}^*=\mathcal {S}$
. Our next result gives Riesz-type criteria for the GRH in this setting.
$\mathcal {S}^*=\mathcal {S}$
. Our next result gives Riesz-type criteria for the GRH in this setting.
Theorem 2.4 Let F satisfy axioms (i)–(iv) of the class
![]() $\mathcal {S}$
. Let
$\mathcal {S}$
. Let
![]() $j_F$
be as defined in (2.3). Then the following hold.
$j_F$
be as defined in (2.3). Then the following hold.
-
(a) If
 $F\in \mathcal {S^*}$
and
$F\in \mathcal {S^*}$
and
 $j_F=0$
, then the GRH for
$j_F=0$
, then the GRH for
 $F(s)$
implies that
$F(s)$
implies that
 $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)={O}_{F,{\delta }, z}\left ( y^{-\frac {1}{4}+\delta } \right )$
as
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)={O}_{F,{\delta }, z}\left ( y^{-\frac {1}{4}+\delta } \right )$
as
 $y\to {\infty} $
, for any
$y\to {\infty} $
, for any
 ${\delta }>0$
.
${\delta }>0$
. -
(b) Let
 $\epsilon>0$
. If
$\epsilon>0$
. If
 $F\in \mathcal {S^*}$
and
$F\in \mathcal {S^*}$
and
 $j_F\neq 0$
, then the GRH for
$j_F\neq 0$
, then the GRH for
 $F(s)$
implies that (2.15)as
$F(s)$
implies that (2.15)as $$ \begin{align} \mathcal{P} _{\boldsymbol{\alpha,\beta} ,0}(y)+ \sum_{n=1}^{[y ^{{1\over 2}-\epsilon}] -1}{b_F(n) \over n} {\operatorname{Res}\limits_{s=0} } \prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)\left({\sqrt{y}\over n} \right)^{-d_Fs} \ll_{F,{\delta}} y^{-\frac{1}{4}+\delta} \end{align} $$
$$ \begin{align} \mathcal{P} _{\boldsymbol{\alpha,\beta} ,0}(y)+ \sum_{n=1}^{[y ^{{1\over 2}-\epsilon}] -1}{b_F(n) \over n} {\operatorname{Res}\limits_{s=0} } \prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)\left({\sqrt{y}\over n} \right)^{-d_Fs} \ll_{F,{\delta}} y^{-\frac{1}{4}+\delta} \end{align} $$
 $y\to {\infty} $
for any
$y\to {\infty} $
for any
 ${\delta }>0$
.
${\delta }>0$
.
-
(c) The estimate
 $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,0}(y)={O}_{F,{\delta }}\left ( y^{-\frac {1}{4}+\delta } \right )$
as
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,0}(y)={O}_{F,{\delta }}\left ( y^{-\frac {1}{4}+\delta } \right )$
as
 $y\to {\infty} $
for any
$y\to {\infty} $
for any
 ${\delta }>0$
implies the GRH for
${\delta }>0$
implies the GRH for
 $F(s).$
$F(s).$
Part
![]() $(c)$
is valid for the larger class of functions satisfying axioms (i)–(iv) of the Selberg class. We remark that our result gives an equivalent condition for the GRH when
$(c)$
is valid for the larger class of functions satisfying axioms (i)–(iv) of the Selberg class. We remark that our result gives an equivalent condition for the GRH when
![]() $F\in \mathcal {S^*}$
satisfies
$F\in \mathcal {S^*}$
satisfies
![]() $j_F=0$
, namely, we show that, in this case, GRH is equivalent to the estimate
$j_F=0$
, namely, we show that, in this case, GRH is equivalent to the estimate
![]() $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,0}(y)\ll _{F,{\delta }}\left ( y^{-\frac {1}{4}+\delta } \right )$
. The role of
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,0}(y)\ll _{F,{\delta }}\left ( y^{-\frac {1}{4}+\delta } \right )$
. The role of
![]() $j_F$
(and hence the data of F) is a new feature of our result, and has not been recorded explicitly before.
$j_F$
(and hence the data of F) is a new feature of our result, and has not been recorded explicitly before.
Until this point, we have not made use of the flexibility offered by the parameter z in the definition (2.6) of
![]() $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
. This parameter allows us to give a criterion for an “almost” GRH phenomenon as follows. This is a generalization of Theorem 1.1(b) of [Reference Dixit, Roy and Zaharescu13].
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
. This parameter allows us to give a criterion for an “almost” GRH phenomenon as follows. This is a generalization of Theorem 1.1(b) of [Reference Dixit, Roy and Zaharescu13].
Theorem 2.5 Let F satisfy axioms (i)–(iv) of the class
![]() $\mathcal {S}$
. If
$\mathcal {S}$
. If
![]() $z \ne 0$
and
$z \ne 0$
and
![]() $\arg z \ne \pm {\pi \over 2}$
, then the estimate
$\arg z \ne \pm {\pi \over 2}$
, then the estimate
![]() $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)={O}_{F, {\delta }}\left ( y^{-\frac {1}{4}+\delta } \right )$
, as
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)={O}_{F, {\delta }}\left ( y^{-\frac {1}{4}+\delta } \right )$
, as
![]() $y\to {\infty} $
for any
$y\to {\infty} $
for any
![]() ${\delta }>0$
implies that
${\delta }>0$
implies that
![]() $F(s)$
has at most finitely many nontrivial zeros of the critical line.
$F(s)$
has at most finitely many nontrivial zeros of the critical line.
Remark We note that the Ramanujan bound (axiom (v)) for
![]() $F(s)$
will be used only in the proofs of parts (a) and (b) of Theorem 2.4. In particular, it is used to conclude that GRH implies square root cancellation in the summatory function of
$F(s)$
will be used only in the proofs of parts (a) and (b) of Theorem 2.4. In particular, it is used to conclude that GRH implies square root cancellation in the summatory function of
![]() $b_F(n)$
, which is in turn used to derive the estimate (6.2).
$b_F(n)$
, which is in turn used to derive the estimate (6.2).
3 Preliminary results
Throughout this section, let
![]() $F\in \mathcal {S}$
. Let us consider
$F\in \mathcal {S}$
. Let us consider
It is well known that as
![]() $T\to \infty $
,
$T\to \infty $
,
![]() $N_F(T)$
satisfies the asymptotic formula (see [Reference Mukhopadhyay and Srinivas20, p. 264])
$N_F(T)$
satisfies the asymptotic formula (see [Reference Mukhopadhyay and Srinivas20, p. 264])
where
![]() $d_F$
is the degree of F and
$d_F$
is the degree of F and
![]() $C=C(F)$
is some constant. This, in particular, gives
$C=C(F)$
is some constant. This, in particular, gives
From (3.1), one can conclude that the number of zeros of
![]() $F(s)$
in the critical strip between the horizontal lines Im
$F(s)$
in the critical strip between the horizontal lines Im
![]() $(s)=T+1$
and Im
$(s)=T+1$
and Im
![]() $(s)=T-1$
is
$(s)=T-1$
is
![]() ${O}(\log T)$
.
${O}(\log T)$
.
Another result that will be used repeatedly in our proofs is the following well-known estimate for the Gamma function.
Lemma 3.1 (Stirling’s formula, [Reference Copson6])
For
![]() $s=\sigma +it$
with
$s=\sigma +it$
with
![]() $C\leq \sigma \leq D$
, we have as
$C\leq \sigma \leq D$
, we have as
![]() $|t| \to \infty $
,
$|t| \to \infty $
,
 $$ \begin{align} |\Gamma(s)|=(2\pi)^{\frac{1}{2}}|t|^{\sigma-\tfrac{1}{2}}e^{-\frac{1}{2}\pi |t|}\left(1+O\left(\frac{1}{|t|}\right)\right). \end{align} $$
$$ \begin{align} |\Gamma(s)|=(2\pi)^{\frac{1}{2}}|t|^{\sigma-\tfrac{1}{2}}e^{-\frac{1}{2}\pi |t|}\left(1+O\left(\frac{1}{|t|}\right)\right). \end{align} $$
The Meijer G-function is defined as [Reference Luke18, p. 143]
 $$ \begin{align} G_{p,q}^{m,n}\left( \left. \begin{matrix} a_1 & \ldots & a_p\\ b_1 & \ldots & b_q \end{matrix} \right| z \right)=\frac{1}{2 \pi i}\int\limits_L\frac{\Pi_{j=1}^m \Gamma(b_j-s) \Pi_{j=1}^n \Gamma(1-a_j+s)}{\Pi_{j=m+1}^{q} \Gamma(1-b_j+s) \Pi_{j=n+1}^{p} \Gamma(a_j-s)} z^sds, \end{align} $$
$$ \begin{align} G_{p,q}^{m,n}\left( \left. \begin{matrix} a_1 & \ldots & a_p\\ b_1 & \ldots & b_q \end{matrix} \right| z \right)=\frac{1}{2 \pi i}\int\limits_L\frac{\Pi_{j=1}^m \Gamma(b_j-s) \Pi_{j=1}^n \Gamma(1-a_j+s)}{\Pi_{j=m+1}^{q} \Gamma(1-b_j+s) \Pi_{j=n+1}^{p} \Gamma(a_j-s)} z^sds, \end{align} $$
where L is a curve from
![]() $-i{\infty} $
to
$-i{\infty} $
to
![]() $i{\infty} $
which separates the poles of the factors
$i{\infty} $
which separates the poles of the factors
![]() $\Gamma (b_j-s)$
from those of the factors
$\Gamma (b_j-s)$
from those of the factors
![]() $\Gamma (1-a_j+s)$
. For more details, we refer the reader to [Reference Luke18, p. 143].
$\Gamma (1-a_j+s)$
. For more details, we refer the reader to [Reference Luke18, p. 143].
Recall the definitions (2.5) and (2.6) of
![]() ${Z_{\boldsymbol {{\alpha },{\beta }}}(x)}$
and
${Z_{\boldsymbol {{\alpha },{\beta }}}(x)}$
and
![]() $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
, respectively. We will prove some preliminary results about these functions.
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
, respectively. We will prove some preliminary results about these functions.
Lemma 3.2 Let
![]() $0 <\mathrm {Re}(s)<{1 \over 2}$
,
$0 <\mathrm {Re}(s)<{1 \over 2}$
,
![]() $\boldsymbol {{\alpha }}=({\alpha }_1,\ldots , {\alpha }_q), \ \boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q),$
with
$\boldsymbol {{\alpha }}=({\alpha }_1,\ldots , {\alpha }_q), \ \boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q),$
with
![]() ${\alpha }_i>0$
and
${\alpha }_i>0$
and
![]() $\Re ({\beta }_i)>0$
for each i. Then
$\Re ({\beta }_i)>0$
for each i. Then
 $$ \begin{align} \int_{0}^{\infty}y^{-s-1}\mathcal{P} _{\boldsymbol{\alpha,\beta} ,z}(y)dy=\frac{2 }{d_F F(2s+1)}\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!} {\prod_{i=1}^q\Gamma\left({2\alpha_i\over d_F} (t-s)+\bar{\beta_i} \right)}. \end{align} $$
$$ \begin{align} \int_{0}^{\infty}y^{-s-1}\mathcal{P} _{\boldsymbol{\alpha,\beta} ,z}(y)dy=\frac{2 }{d_F F(2s+1)}\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!} {\prod_{i=1}^q\Gamma\left({2\alpha_i\over d_F} (t-s)+\bar{\beta_i} \right)}. \end{align} $$
Proof Let
Substituting y by
![]() ${x\over n^2}$
, we have
${x\over n^2}$
, we have
Multiplying both sides by
![]() $a_F(n)$
and summing over all n, we obtain from (2.6)
$a_F(n)$
and summing over all n, we obtain from (2.6)
 $$ \begin{align*} &F(2s+1)\phi (s,\boldsymbol{\alpha,\beta} ,z)\\& \quad =\sum\limits_{n = 1}^\infty\int_{0}^{\infty}{x^{-s-1}a_F(n)\over n}\sum\limits_{m = 1}^\infty \frac{{b_F(m)}}{m}{Z_{{\alpha},{\beta}}}\left( \left({\frac{\sqrt{x} }{mn}}\right)^{d_F} \right) \cosh\left({\sqrt{x}z\over nm}\right) dx\nonumber \\& \quad =\sum\limits_{n = 1}^\infty\int_{0}^{\infty}{x^{-s-1}a_F(n)\over n}\sum\limits_{m = 1}^\infty \frac{{b_F(m)}}{m}\sum_{t=0}^{{\infty}}{z^{2t}x^t\over m^{2t}n^{2t}(2t)!} \frac{1}{2 \pi i}\\& \qquad \times \int\limits_{(c)} \prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right){\left( {\frac{\sqrt{x} }{mn}} \right)^{ -d_F s'}}ds' dx, \end{align*} $$
$$ \begin{align*} &F(2s+1)\phi (s,\boldsymbol{\alpha,\beta} ,z)\\& \quad =\sum\limits_{n = 1}^\infty\int_{0}^{\infty}{x^{-s-1}a_F(n)\over n}\sum\limits_{m = 1}^\infty \frac{{b_F(m)}}{m}{Z_{{\alpha},{\beta}}}\left( \left({\frac{\sqrt{x} }{mn}}\right)^{d_F} \right) \cosh\left({\sqrt{x}z\over nm}\right) dx\nonumber \\& \quad =\sum\limits_{n = 1}^\infty\int_{0}^{\infty}{x^{-s-1}a_F(n)\over n}\sum\limits_{m = 1}^\infty \frac{{b_F(m)}}{m}\sum_{t=0}^{{\infty}}{z^{2t}x^t\over m^{2t}n^{2t}(2t)!} \frac{1}{2 \pi i}\\& \qquad \times \int\limits_{(c)} \prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right){\left( {\frac{\sqrt{x} }{mn}} \right)^{ -d_F s'}}ds' dx, \end{align*} $$
using the series expansion for
![]() $\cosh (x)$
. Applying the Weierstrass M-test and the Lebesgue dominated convergence theorem, one can show that
$\cosh (x)$
. Applying the Weierstrass M-test and the Lebesgue dominated convergence theorem, one can show that
 $$ \begin{align} &F(2s+1)\phi (s,\boldsymbol{\alpha,\beta} ,z)\nonumber\\& \quad =\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!} \int_{0}^{\infty}{x^{-s+t-1}}\frac{1}{2 \pi i} \int\limits_{(c)} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right)}{F(2t+1-d_Fs')}\sum\limits_{n = 1}^\infty{a_F(n)\over n^{2t+1-d_Fs'}}{\left( {{\sqrt{x} }} \right)^{ - d_Fs'}}ds' dx\nonumber \\& \quad =\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!}\int_{0}^{\infty}{x^{-s+t-1}}\frac{1}{2 \pi i} \int\limits_{(c)} {\prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right)}{\left( {{\sqrt{x} }} \right)^{ - d_Fs'}}ds' dx.\nonumber\\ \end{align} $$
$$ \begin{align} &F(2s+1)\phi (s,\boldsymbol{\alpha,\beta} ,z)\nonumber\\& \quad =\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!} \int_{0}^{\infty}{x^{-s+t-1}}\frac{1}{2 \pi i} \int\limits_{(c)} \frac{\prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right)}{F(2t+1-d_Fs')}\sum\limits_{n = 1}^\infty{a_F(n)\over n^{2t+1-d_Fs'}}{\left( {{\sqrt{x} }} \right)^{ - d_Fs'}}ds' dx\nonumber \\& \quad =\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!}\int_{0}^{\infty}{x^{-s+t-1}}\frac{1}{2 \pi i} \int\limits_{(c)} {\prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right)}{\left( {{\sqrt{x} }} \right)^{ - d_Fs'}}ds' dx.\nonumber\\ \end{align} $$
Substituting
![]() $s'$
by
$s'$
by
![]() ${-2w\over d_F}$
, we have
${-2w\over d_F}$
, we have
 $$ \begin{align} &\frac{1}{2 \pi i} \! \int_{0}^{\infty} \!\!\! {x^{-s+t-1}} \!\! \int\limits_{(c)} \! {\prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right)}{{{{x} }} ^{ - d_Fs' \over 2}}ds' dx\nonumber\\& \quad =\frac{2}{d_F2 \pi i} \int_{0}^{\infty}\!\!\!\! {x^{-s+t-1}} \!\!\!\! \int\limits_{{\left( -cd_F\over 2\right) }} \! {\prod_{i=1}^q\Gamma\left(- \tfrac{2\alpha_i w} { d_F}+\bar{\beta_i} \right)}{x} ^{w}dw dx\nonumber\\& \quad = {2\over d_F}{\prod_{i=1}^q\Gamma\left({2\alpha_i\over d_F} (t-s)+\bar{\beta_i} \right)}, \end{align} $$
$$ \begin{align} &\frac{1}{2 \pi i} \! \int_{0}^{\infty} \!\!\! {x^{-s+t-1}} \!\! \int\limits_{(c)} \! {\prod_{i=1}^q\Gamma\left(\alpha_i s'+\bar{\beta_i} \right)}{{{{x} }} ^{ - d_Fs' \over 2}}ds' dx\nonumber\\& \quad =\frac{2}{d_F2 \pi i} \int_{0}^{\infty}\!\!\!\! {x^{-s+t-1}} \!\!\!\! \int\limits_{{\left( -cd_F\over 2\right) }} \! {\prod_{i=1}^q\Gamma\left(- \tfrac{2\alpha_i w} { d_F}+\bar{\beta_i} \right)}{x} ^{w}dw dx\nonumber\\& \quad = {2\over d_F}{\prod_{i=1}^q\Gamma\left({2\alpha_i\over d_F} (t-s)+\bar{\beta_i} \right)}, \end{align} $$
upon replacing x by
![]() $\frac {1}{x}$
and using the Mellin inversion theorem [Reference McLachlan19, pp. 341–343]. Combining (3.5) and (3.6) completes the proof.
$\frac {1}{x}$
and using the Mellin inversion theorem [Reference McLachlan19, pp. 341–343]. Combining (3.5) and (3.6) completes the proof.
Lemma 3.3 For
![]() $-c_F<c<0$
and
$-c_F<c<0$
and
![]() $x>0$
, we have
$x>0$
, we have
Proof Let us write
![]() $\bar {\beta }_i=a_i+ib_i$
. Using the functional equation of
$\bar {\beta }_i=a_i+ib_i$
. Using the functional equation of
![]() $\Gamma $
, we have from (2.5),
$\Gamma $
, we have from (2.5),
 $$ \begin{align*} Z_{\boldsymbol{\alpha,\beta} }(x) & =\frac{1}{2 \pi i} \int_{c-i\infty}^{c+i\infty} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i}+1 \right)\over\prod_{i=1}^q\left(\alpha_i s+\bar{\beta_i} \right) }{x^{ - s}}ds\\ & =\frac{1}{2 \pi i} \int_{-\infty}^{\infty} {\prod_{i=1}^q\Gamma\left(\alpha_ic +a_i +1+i({\alpha}_it-b_i) \right)\over\prod_{i=1}^q\left(\alpha_ic +a_i +i({\alpha}_it-b_i) \right) }{x^{ -c-it}}dt. \end{align*} $$
$$ \begin{align*} Z_{\boldsymbol{\alpha,\beta} }(x) & =\frac{1}{2 \pi i} \int_{c-i\infty}^{c+i\infty} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i}+1 \right)\over\prod_{i=1}^q\left(\alpha_i s+\bar{\beta_i} \right) }{x^{ - s}}ds\\ & =\frac{1}{2 \pi i} \int_{-\infty}^{\infty} {\prod_{i=1}^q\Gamma\left(\alpha_ic +a_i +1+i({\alpha}_it-b_i) \right)\over\prod_{i=1}^q\left(\alpha_ic +a_i +i({\alpha}_it-b_i) \right) }{x^{ -c-it}}dt. \end{align*} $$
It can be seen that
 $$ \begin{align*} 1+|t|&\ll_F|\alpha_ic +a_i| +|{\alpha}_it-b_i|\\ &\ll_{F} |\alpha_ic +a_i +i({\alpha}_it-b_i)|, \end{align*} $$
$$ \begin{align*} 1+|t|&\ll_F|\alpha_ic +a_i| +|{\alpha}_it-b_i|\\ &\ll_{F} |\alpha_ic +a_i +i({\alpha}_it-b_i)|, \end{align*} $$
using the Cauchy–Schwarz inequality. Using this for the denominator and Stirling’s formula for the numerator, we get
 $$ \begin{align*} Z_{\boldsymbol{\alpha,\beta} }(x)&\ll_F \int_{-{\infty}}^{{\infty}}\frac{\prod_{i=1}^q\left( |{\alpha}_it-b_i|^{{\alpha}_ic+a_i+{1\over 2}}e^{-{\pi\over 2}|{\alpha}_it-b_i|}\right) }{(1+|t|)^{q}}x^{-c}dt. \end{align*} $$
$$ \begin{align*} Z_{\boldsymbol{\alpha,\beta} }(x)&\ll_F \int_{-{\infty}}^{{\infty}}\frac{\prod_{i=1}^q\left( |{\alpha}_it-b_i|^{{\alpha}_ic+a_i+{1\over 2}}e^{-{\pi\over 2}|{\alpha}_it-b_i|}\right) }{(1+|t|)^{q}}x^{-c}dt. \end{align*} $$
Noting that the exponent
![]() ${\alpha }_ic+a_i+{1\over 2}$
is positive in the region
${\alpha }_ic+a_i+{1\over 2}$
is positive in the region
![]() $-c_F<c<0$
due to the choice of
$-c_F<c<0$
due to the choice of
![]() $c_F$
(see (2.4)), it is easy to see that
$c_F$
(see (2.4)), it is easy to see that
![]() $ Z_{\boldsymbol {\alpha ,\beta } }(x)\ll _Fx^{-c}, $
as needed.
$ Z_{\boldsymbol {\alpha ,\beta } }(x)\ll _Fx^{-c}, $
as needed.
Lemma 3.4 For
![]() $-c_F<c<0$
and
$-c_F<c<0$
and
![]() $x>0$
, we have
$x>0$
, we have
where
![]() $Z^{\prime }_{\boldsymbol {\alpha ,\beta } }(x)$
denotes the derivative of
$Z^{\prime }_{\boldsymbol {\alpha ,\beta } }(x)$
denotes the derivative of
![]() $ Z_{\boldsymbol {\alpha ,\beta } }\left ( { x}\right )$
with respect to its argument x.
$ Z_{\boldsymbol {\alpha ,\beta } }\left ( { x}\right )$
with respect to its argument x.
Proof The proof follows in exactly the same manner as that of Lemma 3.3.
For
![]() $x\in \mathbb {R} $
and
$x\in \mathbb {R} $
and
![]() $1<d<1+c_F$
, we define the following function which is closely related to the function
$1<d<1+c_F$
, we define the following function which is closely related to the function
![]() ${Z}_{\boldsymbol {\alpha ,\beta } }(x)$
defined in (2.5). Let
${Z}_{\boldsymbol {\alpha ,\beta } }(x)$
defined in (2.5). Let
 $$ \begin{align*} \tilde{Z}_{{\boldsymbol{\alpha,\beta}}}(x) :=\frac{1}{2 \pi i} \int\limits_{(d)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){x^{ - s}}ds}. \end{align*} $$
$$ \begin{align*} \tilde{Z}_{{\boldsymbol{\alpha,\beta}}}(x) :=\frac{1}{2 \pi i} \int\limits_{(d)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){x^{ - s}}ds}. \end{align*} $$
The advantage of using
![]() $\tilde {Z}_{{\boldsymbol {\alpha ,\beta }}}(x)$
is that one is able to obtain better upper bounds for this function by relating it to the Meijer G-function. Moreover,
$\tilde {Z}_{{\boldsymbol {\alpha ,\beta }}}(x)$
is that one is able to obtain better upper bounds for this function by relating it to the Meijer G-function. Moreover,
![]() $\tilde {Z}_{{\boldsymbol {\alpha ,\beta }}}(x)$
differs from
$\tilde {Z}_{{\boldsymbol {\alpha ,\beta }}}(x)$
differs from
![]() ${Z}_{{\boldsymbol {\alpha ,\beta }}}(x)$
only by a residue term. More precisely, using Cauchy’s residue theorem to shift the line of integration from c to d, we have
${Z}_{{\boldsymbol {\alpha ,\beta }}}(x)$
only by a residue term. More precisely, using Cauchy’s residue theorem to shift the line of integration from c to d, we have
 $$ \begin{align} {Z}_{\boldsymbol{\alpha,\beta} }\left(x \right) =\tilde{Z}_{\boldsymbol{\alpha,\beta} }\left(x \right)-\operatorname{Res}_{s=0} \prod_{i=1}^{q}\Gamma\left({\alpha}_is+\bar{\beta_i} \right){\left(x \right)^{ -s}}. \end{align} $$
$$ \begin{align} {Z}_{\boldsymbol{\alpha,\beta} }\left(x \right) =\tilde{Z}_{\boldsymbol{\alpha,\beta} }\left(x \right)-\operatorname{Res}_{s=0} \prod_{i=1}^{q}\Gamma\left({\alpha}_is+\bar{\beta_i} \right){\left(x \right)^{ -s}}. \end{align} $$
In what follows, we show exponential decay as
![]() $x\to \infty $
for both
$x\to \infty $
for both
![]() $\tilde {Z}_{\boldsymbol {\alpha ,\beta } }\left ( { x}\right )$
as well as
$\tilde {Z}_{\boldsymbol {\alpha ,\beta } }\left ( { x}\right )$
as well as
![]() $\tilde {Z}^{\prime }_{\boldsymbol {\alpha ,\beta } }\left ( { x}\right )$
(its derivative with respect to x). These results are used when
$\tilde {Z}^{\prime }_{\boldsymbol {\alpha ,\beta } }\left ( { x}\right )$
(its derivative with respect to x). These results are used when
![]() $\tilde {Z}_{\boldsymbol {\alpha ,\beta }}$
arises from the data of a function F in the class
$\tilde {Z}_{\boldsymbol {\alpha ,\beta }}$
arises from the data of a function F in the class
![]() $\mathcal {S}^*$
defined preceding Theorem 2.4.
$\mathcal {S}^*$
defined preceding Theorem 2.4.
Lemma 3.5 Let
![]() $\boldsymbol {{\alpha }}=({\alpha }_1,\ldots , {\alpha }_q), \ \boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q),$
with
$\boldsymbol {{\alpha }}=({\alpha }_1,\ldots , {\alpha }_q), \ \boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q),$
with
![]() ${\alpha }_i>0$
and
${\alpha }_i>0$
and
![]() $\Re ({\beta }_i)>0$
for all i. Assume that each component of
$\Re ({\beta }_i)>0$
for all i. Assume that each component of
![]() $\boldsymbol {{\alpha }}$
is rational, say
$\boldsymbol {{\alpha }}$
is rational, say
![]() ${\alpha }_i={m_i\over n_i}$
with
${\alpha }_i={m_i\over n_i}$
with
![]() $(m_i, n_i)=1$
. Let L be the lcm
$(m_i, n_i)=1$
. Let L be the lcm
![]() $[n_1, \ldots , n_q]$
. Denote the positive integer
$[n_1, \ldots , n_q]$
. Denote the positive integer
![]() ${\alpha }_i L$
by
${\alpha }_i L$
by
![]() $k_i$
. Using the notation
$k_i$
. Using the notation
 $$ \begin{align} C_1=\frac{ L d_F}{ 2\left({ \prod_{i=1}^qk_i^{k_i} }\right)^{2/ Ld_F}}, \quad C_2= \frac{2}{d_F} ,\quad C_3={1-q\over 2}+\sum_{i=1}^{q}\bar{{\beta}_i}, \end{align} $$
$$ \begin{align} C_1=\frac{ L d_F}{ 2\left({ \prod_{i=1}^qk_i^{k_i} }\right)^{2/ Ld_F}}, \quad C_2= \frac{2}{d_F} ,\quad C_3={1-q\over 2}+\sum_{i=1}^{q}\bar{{\beta}_i}, \end{align} $$
we have as
![]() $x\to \infty $
,
$x\to \infty $
,
Proof We have from the definition
 $$ \begin{align*} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&=\frac{1}{2 \pi i} \int\limits_{(d)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){x^{ - s}}ds}, \end{align*} $$
$$ \begin{align*} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&=\frac{1}{2 \pi i} \int\limits_{(d)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){x^{ - s}}ds}, \end{align*} $$
where
![]() $d>0$
. The change of variable
$d>0$
. The change of variable
![]() $s=Lz$
gives
$s=Lz$
gives
 $$ \begin{align*} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&=\frac{L}{2 \pi i} \int\limits_{\left( d/L\right) } {\prod_{i=1}^q\Gamma\left(k_iz+\bar{\beta_i} \right){x^{ -z L}}dz}. \end{align*} $$
$$ \begin{align*} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&=\frac{L}{2 \pi i} \int\limits_{\left( d/L\right) } {\prod_{i=1}^q\Gamma\left(k_iz+\bar{\beta_i} \right){x^{ -z L}}dz}. \end{align*} $$
Using the Gauss multiplication formula, we have
 $$ \begin{align*} \Gamma\left(k_i\left(z+{\bar{\beta_i}\over k_i} \right)\right)=(2\pi)^{1-k_i \over 2}k_i^{k_i\left(z+{\bar{\beta_i}\over k_i} \right)-{1\over 2}}\prod_{j=1}^{k_i}\Gamma\left(z+{\bar{\beta_i}\over k_i} +{j-1\over k_i}\right). \end{align*} $$
$$ \begin{align*} \Gamma\left(k_i\left(z+{\bar{\beta_i}\over k_i} \right)\right)=(2\pi)^{1-k_i \over 2}k_i^{k_i\left(z+{\bar{\beta_i}\over k_i} \right)-{1\over 2}}\prod_{j=1}^{k_i}\Gamma\left(z+{\bar{\beta_i}\over k_i} +{j-1\over k_i}\right). \end{align*} $$
Thus,
![]() $\tilde {Z}_{\boldsymbol {\alpha ,\beta } }(x)$
equals
$\tilde {Z}_{\boldsymbol {\alpha ,\beta } }(x)$
equals
 $$ \begin{align*} \frac{L}{2 \pi i}(2\pi)^{{q \over 2}-{1\over 2}\sum_{i=1}^{q}k_i}\left( \prod_{i=1}^qk_i^{{\bar{\beta_i}} -{1\over 2}}\right) \int\limits_{\left( d/ L\right) } \left({x^{ L}\over \prod_{i=1}^qk_i^{k_i} }\right)^{-z} {\prod_{i=1}^q\prod_{j=1}^{k_i}\Gamma\left(z+{\bar{\beta_i}\over k_i} +{j-1\over k_i}\right)dz}. \end{align*} $$
$$ \begin{align*} \frac{L}{2 \pi i}(2\pi)^{{q \over 2}-{1\over 2}\sum_{i=1}^{q}k_i}\left( \prod_{i=1}^qk_i^{{\bar{\beta_i}} -{1\over 2}}\right) \int\limits_{\left( d/ L\right) } \left({x^{ L}\over \prod_{i=1}^qk_i^{k_i} }\right)^{-z} {\prod_{i=1}^q\prod_{j=1}^{k_i}\Gamma\left(z+{\bar{\beta_i}\over k_i} +{j-1\over k_i}\right)dz}. \end{align*} $$
The above expression agrees with that for a Meijer G-function. In particular, since
![]() $d/L>0$
, the line of integration does separate the poles as prescribed in (3.3). Putting
$d/L>0$
, the line of integration does separate the poles as prescribed in (3.3). Putting
 $$ \begin{align} b_{ij}={\bar{\beta_i}\over k_i} +{j-1\over k_i}, \quad \ 1\leq j\leq k_i, \ 1\leq i\leq q, \end{align} $$
$$ \begin{align} b_{ij}={\bar{\beta_i}\over k_i} +{j-1\over k_i}, \quad \ 1\leq j\leq k_i, \ 1\leq i\leq q, \end{align} $$
and
![]() $w={x^{ L}\over \prod _{i=1}^qk_i^{k_i} }$
, we find that
$w={x^{ L}\over \prod _{i=1}^qk_i^{k_i} }$
, we find that
 $$ \begin{align} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&= {L}(2\pi)^{{q \over 2}-{1\over 2}\sum_{i=1}^{q}k_i}\left( \prod_{i=1}^qk_i^{{\bar{\beta_i}} -{1\over 2}}\right) \frac{1}{2 \pi i}\int\limits_{\left( d/ L\right) } w^{-z} {\prod_{i=1}^q\prod_{j=1}^{k_i}\Gamma\left(z+b_{ij}\right)dz}\nonumber\\ &= {L}(2\pi)^{{q \over 2}-{1\over 2}\sum_{i=1}^{q}k_i}\left( \prod_{i=1}^qk_i^{{\bar{\beta_i}} -{1\over 2}}\right) G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| w \right). \end{align} $$
$$ \begin{align} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&= {L}(2\pi)^{{q \over 2}-{1\over 2}\sum_{i=1}^{q}k_i}\left( \prod_{i=1}^qk_i^{{\bar{\beta_i}} -{1\over 2}}\right) \frac{1}{2 \pi i}\int\limits_{\left( d/ L\right) } w^{-z} {\prod_{i=1}^q\prod_{j=1}^{k_i}\Gamma\left(z+b_{ij}\right)dz}\nonumber\\ &= {L}(2\pi)^{{q \over 2}-{1\over 2}\sum_{i=1}^{q}k_i}\left( \prod_{i=1}^qk_i^{{\bar{\beta_i}} -{1\over 2}}\right) G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| w \right). \end{align} $$
We now use an asymptotic relation for the Meijer G-function from [Reference Luke18, p. 180]. One can compute that in our case,
![]() ${\sigma } =\sum _{k=1}^{q}k_i$
and
${\sigma } =\sum _{k=1}^{q}k_i$
and
![]() $\theta ={1\over {\sigma }}\left (\sum _{i=1}^{q}\bar {\beta _i}+{1-q \over 2}\right )$
, where
$\theta ={1\over {\sigma }}\left (\sum _{i=1}^{q}\bar {\beta _i}+{1-q \over 2}\right )$
, where
![]() ${\sigma }$
and
${\sigma }$
and
![]() $\theta $
are defined as per the notation on page 180 of [Reference Luke18]. We get
$\theta $
are defined as per the notation on page 180 of [Reference Luke18]. We get
 $$ \begin{align} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&\ll_F G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| w \right)\nonumber\\ &\ll_F \frac{(2\pi)^{\sum k_i-1 \over 2}}{\sqrt{\sum k_i}} \exp\left( -\sum k_i w^{1/ \sum k_i}\right) w^\theta \\ &\ll_F \exp\left( -\sum k_i \left({x^{ L}\over \prod_{i=1}^qk_i^{k_i} }\right)^{1/\sum k_i}\right) x^{ L {\left(\sum_{i=1}^{q}\bar{\beta_i}+{1-q \over 2}\right)}/\sum k_i}.\nonumber \end{align} $$
$$ \begin{align} \tilde{Z}_{\boldsymbol{\alpha,\beta} }(x)&\ll_F G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| w \right)\nonumber\\ &\ll_F \frac{(2\pi)^{\sum k_i-1 \over 2}}{\sqrt{\sum k_i}} \exp\left( -\sum k_i w^{1/ \sum k_i}\right) w^\theta \\ &\ll_F \exp\left( -\sum k_i \left({x^{ L}\over \prod_{i=1}^qk_i^{k_i} }\right)^{1/\sum k_i}\right) x^{ L {\left(\sum_{i=1}^{q}\bar{\beta_i}+{1-q \over 2}\right)}/\sum k_i}.\nonumber \end{align} $$
Observing that
 $$ \begin{align*} \sum_{i=1}^q k_i = \sum_{i=1}^q \alpha_i L = {Ld_F \over 2 }, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^q k_i = \sum_{i=1}^q \alpha_i L = {Ld_F \over 2 }, \end{align*} $$
we complete the proof.
Lemma 3.6 Let
![]() $\boldsymbol {{\alpha }}=({\alpha }_1,\ldots , {\alpha }_q), \ \boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q),$
with
$\boldsymbol {{\alpha }}=({\alpha }_1,\ldots , {\alpha }_q), \ \boldsymbol {{\beta }}=({\beta }_1,\ldots , {\beta }_q),$
with
![]() ${\alpha }_i>0$
and
${\alpha }_i>0$
and
![]() $\Re ({\beta }_i)>0$
for all i. Assume that each component of
$\Re ({\beta }_i)>0$
for all i. Assume that each component of
![]() $\boldsymbol {{\alpha }}$
is rational, say
$\boldsymbol {{\alpha }}$
is rational, say
![]() ${\alpha }_i={m_i\over n_i}$
with
${\alpha }_i={m_i\over n_i}$
with
![]() $(m_i, n_i)=1$
. Let L be the lcm
$(m_i, n_i)=1$
. Let L be the lcm
![]() $[n_1, \ldots , n_q]$
. Denoting the positive integer
$[n_1, \ldots , n_q]$
. Denoting the positive integer
![]() ${\alpha }_i L$
by
${\alpha }_i L$
by
![]() $k_i$
, we define
$k_i$
, we define
![]() $C_i$
’s as in (3.8). Then as
$C_i$
’s as in (3.8). Then as
![]() $x\to \infty $
, we have
$x\to \infty $
, we have
where
![]() $C_4=\max \{0, C_2-1\}$
.
$C_4=\max \{0, C_2-1\}$
.
Proof We will use the identity (12) from Luke [Reference Luke18, p. 151], which gives after some simplification
 $$ \begin{align} {d\over dz}\left(G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| z \right)\right) = {b_{11}\over z}G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| z \right)-{1\over z}G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{11}+1, b^{*}_{i,j} \end{matrix} \ \ \bigg| z \right), \end{align} $$
$$ \begin{align} {d\over dz}\left(G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| z \right)\right) = {b_{11}\over z}G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| z \right)-{1\over z}G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{11}+1, b^{*}_{i,j} \end{matrix} \ \ \bigg| z \right), \end{align} $$
where the
![]() $b_{ij}$
’s are as defined in (3.9) and
$b_{ij}$
’s are as defined in (3.9) and
![]() $b^{*}_{ij}$
denotes the same sequence as
$b^{*}_{ij}$
denotes the same sequence as
![]() $b_{ij}$
without the first term
$b_{ij}$
without the first term
![]() $b_{11}$
. From (3.10), letting
$b_{11}$
. From (3.10), letting
![]() $z={x^{ L}\over \prod _{i=1}^qk_i^{k_i} }$
and
$z={x^{ L}\over \prod _{i=1}^qk_i^{k_i} }$
and
![]() $L_1= {L}(2\pi )^{{q \over 2}-{1\over 2}\sum _{i=1}^{q}k_i}\left ( \prod _{i=1}^qk_i^{{\bar {\beta _i}} -{1\over 2}}\right )$
, we have
$L_1= {L}(2\pi )^{{q \over 2}-{1\over 2}\sum _{i=1}^{q}k_i}\left ( \prod _{i=1}^qk_i^{{\bar {\beta _i}} -{1\over 2}}\right )$
, we have
 $$ \begin{align*} \tilde{Z}^{\prime}_{\boldsymbol{\alpha,\beta} }(x)&=L_1 {d\over dz}\left(G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\& b_{i,j} \end{matrix} \ \ \bigg| z \right)\right){dz\over dx} \\&= {{Lx^{ L-1}\over \prod_{i=1}^qk_i^{k_i} }} {b_{11}\over z}L_1 G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| z \right)- {{Lx^{ L-1}\over \prod_{i=1}^qk_i^{k_i} }} {1\over z} L_1 G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{11}+1, b^{*}_{i,j} \end{matrix} \ \bigg| z \right), \end{align*} $$
$$ \begin{align*} \tilde{Z}^{\prime}_{\boldsymbol{\alpha,\beta} }(x)&=L_1 {d\over dz}\left(G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\& b_{i,j} \end{matrix} \ \ \bigg| z \right)\right){dz\over dx} \\&= {{Lx^{ L-1}\over \prod_{i=1}^qk_i^{k_i} }} {b_{11}\over z}L_1 G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{i,j} \end{matrix} \ \ \bigg| z \right)- {{Lx^{ L-1}\over \prod_{i=1}^qk_i^{k_i} }} {1\over z} L_1 G_{0 \ , \ \ \sum k_i}^{ \sum k_i, \ 0}\left(\!\!\!\!\!\!\!\begin{matrix} &\rule{0.5cm}{0.05cm} \\ & b_{11}+1, b^{*}_{i,j} \end{matrix} \ \bigg| z \right), \end{align*} $$
using (3.12). For the first term above, we use (3.10) followed by Lemma 3.5. For the second term, following the notation of [Reference Luke18, p. 180], the parameter
![]() $\sigma = \sum k_i $
while
$\sigma = \sum k_i $
while
![]() $\theta $
takes the value
$\theta $
takes the value
![]() ${1\over \sum k_i}\left (\sum _{i=1}^{q}\bar {\beta _i}+1+{1-q \over 2}\right )$
. We then apply the estimate (3.11). We have thus obtained
${1\over \sum k_i}\left (\sum _{i=1}^{q}\bar {\beta _i}+1+{1-q \over 2}\right )$
. We then apply the estimate (3.11). We have thus obtained
 $$ \begin{align*} \tilde{Z}^{\prime}_{\boldsymbol{\alpha,\beta} }(x)&\ll_F\left({\bar{{\beta}_1}\over k_1}\exp \big( {-C_1x^{C_2}} \big) x^{C_2C_3} +{L\over x} \exp \big( {-C_1x^{C_2}} \big) x^{C_2(C_3+1)}\right)\nonumber\\ &\ll_F \exp \big( {-C_1x^{C_2}} \big) x^{C_2C_3+C_4}.\\[-38pt] \end{align*} $$
$$ \begin{align*} \tilde{Z}^{\prime}_{\boldsymbol{\alpha,\beta} }(x)&\ll_F\left({\bar{{\beta}_1}\over k_1}\exp \big( {-C_1x^{C_2}} \big) x^{C_2C_3} +{L\over x} \exp \big( {-C_1x^{C_2}} \big) x^{C_2(C_3+1)}\right)\nonumber\\ &\ll_F \exp \big( {-C_1x^{C_2}} \big) x^{C_2C_3+C_4}.\\[-38pt] \end{align*} $$
4 Ramanujan–Hardy–Littlewood-type identity for Selberg class
Before giving the proof of Theorem 2.1, we prove the following results. We will first derive an approximate formula for
![]() ${F'\over F }(s)$
in terms of zeros
${F'\over F }(s)$
in terms of zeros
![]() $\rho $
of F which are near s. This is a generalization of Theorem 9.6(A) of [Reference Titchmarsh25].
$\rho $
of F which are near s. This is a generalization of Theorem 9.6(A) of [Reference Titchmarsh25].
Lemma 4.1 Let F satisfy axioms (i)–(iv) of the class
![]() $\mathcal {S}$
. If
$\mathcal {S}$
. If
![]() $\rho =\beta +i\gamma $
runs through zeros of
$\rho =\beta +i\gamma $
runs through zeros of
![]() $F(s)$
,
$F(s)$
,
 $$ \begin{align} \frac{F' (s)}{F (s)} ={ \sum_{|t-\gamma| \leq 1} \frac{1}{s-\rho}}+{O_F}(\log t), \end{align} $$
$$ \begin{align} \frac{F' (s)}{F (s)} ={ \sum_{|t-\gamma| \leq 1} \frac{1}{s-\rho}}+{O_F}(\log t), \end{align} $$
uniformly for
![]() $\sigma \in [-c_F,1+c_F]$
, where
$\sigma \in [-c_F,1+c_F]$
, where
![]() $s={\sigma }+it$
and
$s={\sigma }+it$
and
![]() $c_F$
is as defined in (2.4).
$c_F$
is as defined in (2.4).
Proof Let
![]() $s=\sigma +it$
with
$s=\sigma +it$
with
![]() $t>2$
and
$t>2$
and
![]() $\sigma \in [-c_F,1+c_F]$
. We will use Lemma
$\sigma \in [-c_F,1+c_F]$
. We will use Lemma
![]() $(\alpha )$
on page 56 of [Reference Titchmarsh25] with
$(\alpha )$
on page 56 of [Reference Titchmarsh25] with
![]() $f(s)=F(s)$
,
$f(s)=F(s)$
,
![]() $s_0=2+it$
and
$s_0=2+it$
and
![]() $r=4(2+c_F)$
. Then, from Lemma 3.4 (in particular, (5) and (9)) of [Reference Dixit and Murty11], it is clear that the hypothesis
$r=4(2+c_F)$
. Then, from Lemma 3.4 (in particular, (5) and (9)) of [Reference Dixit and Murty11], it is clear that the hypothesis
 $$ \begin{align*} \left|{f(s)\over f(s_0)}\right|<e^M, \end{align*} $$
$$ \begin{align*} \left|{f(s)\over f(s_0)}\right|<e^M, \end{align*} $$
holds with
![]() $M=A\log t$
for some constant A depending on F. Lemma
$M=A\log t$
for some constant A depending on F. Lemma
![]() $(\alpha )$
of [Reference Titchmarsh25, p. 56] then yields
$(\alpha )$
of [Reference Titchmarsh25, p. 56] then yields
 $$ \begin{align} {F'(s)\over F(s)}=\sum_{ \rho :|\rho-s_0|\leq {2(2+c_F)}}{1\over s-\rho}+O_F(\log t) \end{align} $$
$$ \begin{align} {F'(s)\over F(s)}=\sum_{ \rho :|\rho-s_0|\leq {2(2+c_F)}}{1\over s-\rho}+O_F(\log t) \end{align} $$
for
![]() $|\sigma -2|\leq {r\over 4}$
, and so, in particular, for
$|\sigma -2|\leq {r\over 4}$
, and so, in particular, for
![]() $-c_F\leq \sigma \leq 1+c_F$
due to the choice of r. We would like to replace the main term in (4.2) by
$-c_F\leq \sigma \leq 1+c_F$
due to the choice of r. We would like to replace the main term in (4.2) by
 $$ \begin{align} \sum_{ \rho :|\gamma-t|\leq 1}{1\over s-\rho}, \end{align} $$
$$ \begin{align} \sum_{ \rho :|\gamma-t|\leq 1}{1\over s-\rho}, \end{align} $$
where
![]() $\gamma $
refers to the ordinate of the zero
$\gamma $
refers to the ordinate of the zero
![]() $\rho $
. Indeed, the sum in (4.2) runs over more number of terms than in (4.3), but since
$\rho $
. Indeed, the sum in (4.2) runs over more number of terms than in (4.3), but since
![]() $|\rho -s_0|\leq 4+2c_F$
implies
$|\rho -s_0|\leq 4+2c_F$
implies
![]() $|\gamma -t|\leq 4+2c_F$
, this difference is atmost
$|\gamma -t|\leq 4+2c_F$
, this difference is atmost
by (3.1). This completes the proof.
Lemma 4.2 Let F satisfy axioms (i)–(iv) of the class
![]() $\mathcal {S}$
. Suppose that the degree of F is
$\mathcal {S}$
. Suppose that the degree of F is
![]() $d_F$
. Let
$d_F$
. Let
![]() $A_1>0$
be a sufficiently small constant. Let
$A_1>0$
be a sufficiently small constant. Let
![]() $T\rightarrow \infty $
through values such that
$T\rightarrow \infty $
through values such that
![]() $|T-\gamma |>\exp { \left (-A_1 \gamma / \log \gamma \right )}$
for every ordinate
$|T-\gamma |>\exp { \left (-A_1 \gamma / \log \gamma \right )}$
for every ordinate
![]() $\gamma $
of a zero of
$\gamma $
of a zero of
![]() $F(s)$
. Then, for
$F(s)$
. Then, for
![]() $\sigma \in [-c_F,1+c_F ]$
, where
$\sigma \in [-c_F,1+c_F ]$
, where
![]() $c_F$
is as defined in (2.4), we have
$c_F$
is as defined in (2.4), we have
where
![]() $0<A_2 < {\pi d_F\over 4}$
.
$0<A_2 < {\pi d_F\over 4}$
.
Proof Our starting point for the proof is (4.1), which holds uniformly for
![]() $s=\sigma +it$
with
$s=\sigma +it$
with
![]() $\sigma \in [-c_F, 1+c_F]$
. Integrating (4.1) with respect to s from
$\sigma \in [-c_F, 1+c_F]$
. Integrating (4.1) with respect to s from
![]() ${1+c_F} +it$
to
${1+c_F} +it$
to
![]() $z=\sigma ' + it$
, where
$z=\sigma ' + it$
, where
![]() $\sigma ' \in [-c_F,{1+c_F}]$
, and t does not equal the ordinate of any zero of
$\sigma ' \in [-c_F,{1+c_F}]$
, and t does not equal the ordinate of any zero of
![]() $F(s)$
, we get
$F(s)$
, we get
 $$ \begin{align} \log F (z) - \log F \left({{1+c_F}} +it \right)&=\bigg[{\sum_{|t-\gamma| \leq 1} \log (s-\rho) } \bigg]_{{{1+c_F}} +it} ^{{z}} +{O}_F(\log t) \nonumber\\&={\sum_{|t-\gamma| \leq 1} \log (z-\rho) }-{\sum_{|t-\gamma| \leq 1} \log \left( {{1+c_F}}+it-\rho\right) } +{O}_F(\log t). \end{align} $$
$$ \begin{align} \log F (z) - \log F \left({{1+c_F}} +it \right)&=\bigg[{\sum_{|t-\gamma| \leq 1} \log (s-\rho) } \bigg]_{{{1+c_F}} +it} ^{{z}} +{O}_F(\log t) \nonumber\\&={\sum_{|t-\gamma| \leq 1} \log (z-\rho) }-{\sum_{|t-\gamma| \leq 1} \log \left( {{1+c_F}}+it-\rho\right) } +{O}_F(\log t). \end{align} $$
Since
![]() $\log \left ({1+c_F}+it-\rho \right ) $
is bounded when
$\log \left ({1+c_F}+it-\rho \right ) $
is bounded when
![]() $|t-\gamma |\leq 1$
, and the number of terms in the second sum above is
$|t-\gamma |\leq 1$
, and the number of terms in the second sum above is
![]() $\ll \log t$
from (3.1), we obtain
$\ll \log t$
from (3.1), we obtain
Moreover,
 $$ \begin{align*} | F\left({1+c_F}+it\right)|\leq \sum_{n=1}^{\infty}\frac{|a(n)|}{n^{1+c_F}}, \end{align*} $$
$$ \begin{align*} | F\left({1+c_F}+it\right)|\leq \sum_{n=1}^{\infty}\frac{|a(n)|}{n^{1+c_F}}, \end{align*} $$
which is bounded due to absolute convergence of
![]() $F(s)$
to the right of
$F(s)$
to the right of
![]() $\Re (s)=1$
. Consequently, (4.4) yields
$\Re (s)=1$
. Consequently, (4.4) yields
Since Re
![]() $(s-\rho )$
is bounded, taking real parts on both sides, we obtain
$(s-\rho )$
is bounded, taking real parts on both sides, we obtain
 $$ \begin{align*} \log |F (s)| &={\sum_{|t-\gamma| \leq 1} \log |s-\rho| }+{O}_F(\log t)\\ &\geq {\sum_{|t-\gamma| \leq 1} \log |t-\gamma| }+{O}_F(\log t). \end{align*} $$
$$ \begin{align*} \log |F (s)| &={\sum_{|t-\gamma| \leq 1} \log |s-\rho| }+{O}_F(\log t)\\ &\geq {\sum_{|t-\gamma| \leq 1} \log |t-\gamma| }+{O}_F(\log t). \end{align*} $$
Let
![]() $A_1$
be a sufficiently small constant to be chosen later. We now let
$A_1$
be a sufficiently small constant to be chosen later. We now let
![]() $s=\sigma + iT$
, where
$s=\sigma + iT$
, where
![]() $T\to \infty $
through values such that
$T\to \infty $
through values such that
![]() $|T-\gamma |> \exp \left (-A_1\gamma / \log \gamma \right )$
for every ordinate
$|T-\gamma |> \exp \left (-A_1\gamma / \log \gamma \right )$
for every ordinate
![]() $\gamma $
of a zero of
$\gamma $
of a zero of
![]() $F(s)$
. Then the above inequality yields
$F(s)$
. Then the above inequality yields
 $$ \begin{align} \log |F (\sigma + iT)| \geq -{\sum_{|T-\gamma| \leq 1}{ A_1 \gamma \over \log\gamma }} +{O}_F(\log T). \end{align} $$
$$ \begin{align} \log |F (\sigma + iT)| \geq -{\sum_{|T-\gamma| \leq 1}{ A_1 \gamma \over \log\gamma }} +{O}_F(\log T). \end{align} $$
From (3.1), we see that
 $$ \begin{align} {\sum_{|T-\gamma| \leq 1} {A_1 \gamma \over \log\gamma }} \leq \sum_{|T-\gamma| \leq 1} A_1 \frac{T+1}{\log(T-1)} \leq C_1A_1T, \end{align} $$
$$ \begin{align} {\sum_{|T-\gamma| \leq 1} {A_1 \gamma \over \log\gamma }} \leq \sum_{|T-\gamma| \leq 1} A_1 \frac{T+1}{\log(T-1)} \leq C_1A_1T, \end{align} $$
for some absolute constant
![]() $C_1>0$
. Equations (4.5) and (4.6) imply that
$C_1>0$
. Equations (4.5) and (4.6) imply that
for some absolute constant
![]() $C_2>0$
. Choosing
$C_2>0$
. Choosing
![]() $A_1$
sufficiently small so that
$A_1$
sufficiently small so that
![]() $C_2A_1< {\pi d_F\over 4}$
completes the proof.
$C_2A_1< {\pi d_F\over 4}$
completes the proof.
4.1 Proof of Theorem 2.1
From (2.5), we have
 $$ \begin{align*} \sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}{Z_{\boldsymbol{{\alpha},{\beta}}}}\left( {\frac{\eta }{n}} \right)} &= \sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}\frac{1}{{2\pi i}}\int\limits_{(c)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){{\left( {\frac{\eta }{n}} \right)}^{ - s}}ds} } \\ & = \frac{1}{2\pi i} \int\limits_{(c)} \prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)\sum\limits_{n = 1}^\infty\frac{b_F(n)}{n^{1-s}}{ {\eta }}^{ - s}ds \\ & = \frac{1}{{2\pi i}}\int\limits_{\left( {c} \right)} {\frac{\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)}{{F(1 - s)}}{\eta ^{ - s}}ds}. \end{align*} $$
$$ \begin{align*} \sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}{Z_{\boldsymbol{{\alpha},{\beta}}}}\left( {\frac{\eta }{n}} \right)} &= \sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}\frac{1}{{2\pi i}}\int\limits_{(c)} {\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){{\left( {\frac{\eta }{n}} \right)}^{ - s}}ds} } \\ & = \frac{1}{2\pi i} \int\limits_{(c)} \prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)\sum\limits_{n = 1}^\infty\frac{b_F(n)}{n^{1-s}}{ {\eta }}^{ - s}ds \\ & = \frac{1}{{2\pi i}}\int\limits_{\left( {c} \right)} {\frac{\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)}{{F(1 - s)}}{\eta ^{ - s}}ds}. \end{align*} $$
In the second step above, we have interchanged the order of integration and summation by using Stirling’s formula (3.2). Using the functional equation (2.1), we obtain
 $$ \begin{align} \sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}{Z_{\boldsymbol{{\alpha},{\beta}}}}\left( {\frac{\eta }{n}} \right)} &= \frac{\bar{\omega}}{{2\pi i}}\int\limits_{\left( {c} \right)} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds. \end{align} $$
$$ \begin{align} \sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}{Z_{\boldsymbol{{\alpha},{\beta}}}}\left( {\frac{\eta }{n}} \right)} &= \frac{\bar{\omega}}{{2\pi i}}\int\limits_{\left( {c} \right)} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds. \end{align} $$
We first assume that
![]() $r=j_F-k_F>0$
. As seen in Figure 1, we consider the rectangular contour
$r=j_F-k_F>0$
. As seen in Figure 1, we consider the rectangular contour
![]() $\mathscr {C}$
with sides
$\mathscr {C}$
with sides
![]() $\left [c -iT, d-iT \right ], \left [d-iT, d + iT \right ], \left [d + iT, c+iT \right ]$
, and
$\left [c -iT, d-iT \right ], \left [d-iT, d + iT \right ], \left [d + iT, c+iT \right ]$
, and
![]() $ \left [c+iT, c-iT \right ] $
, where
$ \left [c+iT, c-iT \right ] $
, where
![]() $T>0$
and
$T>0$
and
![]() $1<d<1+c_F $
. From the choice of
$1<d<1+c_F $
. From the choice of
![]() $c_F$
as given in (2.4) and the discussion preceding it, it is clear that the only possible poles inside
$c_F$
as given in (2.4) and the discussion preceding it, it is clear that the only possible poles inside
![]() $\mathscr {C}$
, for the
$\mathscr {C}$
, for the
![]() $\Gamma $
-factors appearing in the integrand of (4.7) are at
$\Gamma $
-factors appearing in the integrand of (4.7) are at
![]() $s=1$
, coming from those factors for which
$s=1$
, coming from those factors for which
![]() ${\beta }_i=0$
. As there are
${\beta }_i=0$
. As there are
![]() $j_F$
such factors and F has a pole of order
$j_F$
such factors and F has a pole of order
![]() $k_F$
at
$k_F$
at
![]() $s=1$
, this yields a pole of order
$s=1$
, this yields a pole of order
![]() $j_F-k_F$
at
$j_F-k_F$
at
![]() $s=1$
for the integrand in (4.7). Again from the discussion preceding (2.4),
$s=1$
for the integrand in (4.7). Again from the discussion preceding (2.4),
![]() $F(s)$
has a zero of order
$F(s)$
has a zero of order
![]() $j_F-k_F$
at
$j_F-k_F$
at
![]() $s=0$
, thereby giving a pole of same order for our integrand at
$s=0$
, thereby giving a pole of same order for our integrand at
![]() $s=0$
.
$s=0$
.

Figure 1: The contour
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Finally, we also have simple poles at conjugates of nontrivial zeros of
![]() $F(s)$
. Applying Cauchy’s residue theorem gives
$F(s)$
. Applying Cauchy’s residue theorem gives
 $$ \begin{align} &\frac{1}{{2\pi i}}\left[\hspace{5pt} {\int\limits_{ c - iT}^{d - iT} {+\int\limits_{d - iT}^{d + iT} {+\int\limits_{d + iT}^{ c + iT} {+\int\limits_{ c + iT}^{ c - iT} {} } } } } \hspace{5pt}\right] \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds \nonumber\\& \quad =\sum\limits_\rho {\bar{\omega}} Q^{1-2\bar{\rho}}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho})+{\beta_i} \right)}{\overline{{F'({\rho})}}}{\eta ^{ - \bar{\rho}}} \nonumber\\& \qquad + {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{s}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 0}} \nonumber\\& \qquad + {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{\left( {s - 1} \right)}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 1}}. \end{align} $$
$$ \begin{align} &\frac{1}{{2\pi i}}\left[\hspace{5pt} {\int\limits_{ c - iT}^{d - iT} {+\int\limits_{d - iT}^{d + iT} {+\int\limits_{d + iT}^{ c + iT} {+\int\limits_{ c + iT}^{ c - iT} {} } } } } \hspace{5pt}\right] \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds \nonumber\\& \quad =\sum\limits_\rho {\bar{\omega}} Q^{1-2\bar{\rho}}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho})+{\beta_i} \right)}{\overline{{F'({\rho})}}}{\eta ^{ - \bar{\rho}}} \nonumber\\& \qquad + {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{s}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 0}} \nonumber\\& \qquad + {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{\left( {s - 1} \right)}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 1}}. \end{align} $$
By Lemma 4.2, Stirling’s formula (3.2) and the definition of
![]() $d_F$
, as
$d_F$
, as
![]() $|T|\to \infty $
,
$|T|\to \infty $
,
 $$ \begin{align*} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}=O\left(e^{\left( A_2- {\pi d_F\over4}\right)|T| } \right). \end{align*} $$
$$ \begin{align*} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}=O\left(e^{\left( A_2- {\pi d_F\over4}\right)|T| } \right). \end{align*} $$
Since
![]() $A_2 < {\pi d_F \over 4}$
, we conclude that the integrals along the horizontal line segments in (4.8) go to zero as
$A_2 < {\pi d_F \over 4}$
, we conclude that the integrals along the horizontal line segments in (4.8) go to zero as
![]() $|T|\to \infty $
.
$|T|\to \infty $
.
Derivation of the second integral on the left-hand side of (4.8) is as follows. Using
![]() $\eta \nu ={1\over Q^2}$
,
$\eta \nu ={1\over Q^2}$
,
 $$ \begin{align*} \frac{1}{{2\pi i}} \int\limits_{d - iT}^{d + iT} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds&=\frac{1}{{2\pi i}} \int\limits_{d - iT}^{d + iT} \bar{\omega} Q\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\nu ^s}ds. \end{align*} $$
$$ \begin{align*} \frac{1}{{2\pi i}} \int\limits_{d - iT}^{d + iT} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds&=\frac{1}{{2\pi i}} \int\limits_{d - iT}^{d + iT} \bar{\omega} Q\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\nu ^s}ds. \end{align*} $$
Putting
![]() $s=1-u$
and
$s=1-u$
and
![]() $c'=1-d$
, we obtain
$c'=1-d$
, we obtain
 $$ \begin{align*} \frac{1}{{2\pi i}} \int\limits_{d - iT}^{d + iT} \bar{\omega} Q\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\nu ^s}ds&=-\frac{\bar{\omega} Q}{{2\pi i}} \int\limits_{c' + iT}^{c' - iT} \frac{\prod_{i=1}^q\Gamma\left(\alpha_iu+{\beta_i} \right)}{\overline{{F(1-\bar{u})}}}{\nu ^{1-u}} du \\ &=\frac{\bar{\omega} Q}{{2\pi i}} \int\limits_{c' - iT}^{c' + iT} {\prod_{i=1}^q\Gamma\left(\alpha_iu+{\beta_i} \right)}\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n^{1-u}}{\nu ^{1-u}} du \\ &=\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n}\frac{\bar{\omega} Q\nu}{{2\pi i}} \int\limits_{c' - iT}^{c' + iT} {\prod_{i=1}^q\Gamma\left(\alpha_iu+{\beta_i} \right)}{\left(\nu \over n \right) ^{-u}} du, \end{align*} $$
$$ \begin{align*} \frac{1}{{2\pi i}} \int\limits_{d - iT}^{d + iT} \bar{\omega} Q\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\nu ^s}ds&=-\frac{\bar{\omega} Q}{{2\pi i}} \int\limits_{c' + iT}^{c' - iT} \frac{\prod_{i=1}^q\Gamma\left(\alpha_iu+{\beta_i} \right)}{\overline{{F(1-\bar{u})}}}{\nu ^{1-u}} du \\ &=\frac{\bar{\omega} Q}{{2\pi i}} \int\limits_{c' - iT}^{c' + iT} {\prod_{i=1}^q\Gamma\left(\alpha_iu+{\beta_i} \right)}\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n^{1-u}}{\nu ^{1-u}} du \\ &=\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n}\frac{\bar{\omega} Q\nu}{{2\pi i}} \int\limits_{c' - iT}^{c' + iT} {\prod_{i=1}^q\Gamma\left(\alpha_iu+{\beta_i} \right)}{\left(\nu \over n \right) ^{-u}} du, \end{align*} $$
where the second equality is valid as
![]() $\Re (1-\bar {u})=d>1$
. As
$\Re (1-\bar {u})=d>1$
. As
![]() $T\to \infty $
, since
$T\to \infty $
, since
![]() $-c_F<c'<0$
, using (2.5), we obtain
$-c_F<c'<0$
, using (2.5), we obtain
 $$ \begin{align} \frac{1}{{2\pi i}} \int\limits_{(d)} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds=\bar{\omega} Q\nu\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n}Z_{\boldsymbol{\alpha,\bar{\beta}}} \left(\nu \over n \right). \end{align} $$
$$ \begin{align} \frac{1}{{2\pi i}} \int\limits_{(d)} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}ds=\bar{\omega} Q\nu\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n}Z_{\boldsymbol{\alpha,\bar{\beta}}} \left(\nu \over n \right). \end{align} $$
Letting
![]() $T\to \infty $
in (4.8) and using (4.7) and (4.9), we get
$T\to \infty $
in (4.8) and using (4.7) and (4.9), we get
 $$ \begin{align*} &-\sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}{Z_{\boldsymbol{\alpha,\beta}}}\left( {\frac{\eta }{n}} \right)} +\bar{\omega} Q\nu\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n}Z_{\boldsymbol{\alpha,\bar{\beta}}} \left(\nu \over n \right) \\& \quad =\sum\limits_\rho {\bar{\omega}} Q^{1-2\bar{\rho}}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho})+{\beta_i} \right)}{\overline{{F'({\rho})}}}{\eta ^{ - \bar{\rho}}}\nonumber\\& \qquad + {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{s}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 0}} \\& \qquad+ {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{\left( {s - 1} \right)}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 1}}. \end{align*} $$
$$ \begin{align*} &-\sum\limits_{n = 1}^\infty {\frac{{b_F(n)}}{n}{Z_{\boldsymbol{\alpha,\beta}}}\left( {\frac{\eta }{n}} \right)} +\bar{\omega} Q\nu\sum_{n=1}^{\infty}{\overline{b_F(n)}\over n}Z_{\boldsymbol{\alpha,\bar{\beta}}} \left(\nu \over n \right) \\& \quad =\sum\limits_\rho {\bar{\omega}} Q^{1-2\bar{\rho}}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-\bar{\rho})+{\beta_i} \right)}{\overline{{F'({\rho})}}}{\eta ^{ - \bar{\rho}}}\nonumber\\& \qquad + {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{s}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 0}} \\& \qquad+ {\left. {\frac{1}{{(r - 1)!}}\frac{{{d^{r - 1}}}}{{d{s^{r - 1}}}}{{\left( {s - 1} \right)}^r} \bar{\omega} Q^{1-2s}\frac{\prod_{i=1}^q\Gamma\left(\alpha_i(1-s)+{\beta_i} \right)}{\overline{{F(\bar{s})}}}{\eta ^{ - s}}} \right|{}_{s = 1}}. \end{align*} $$
Multiplying both sides by
![]() $-\omega \sqrt {\eta } $
and using the fact
$-\omega \sqrt {\eta } $
and using the fact
![]() $\eta \nu ={1\over Q^2}$
, we get the required result (2.7).
$\eta \nu ={1\over Q^2}$
, we get the required result (2.7).
For
![]() $r\leq 0$
, it is easy to see that last two terms on the right-hand side of (4.8) do not appear, but the remainder of the proof remains unchanged. This completes the proof.
$r\leq 0$
, it is easy to see that last two terms on the right-hand side of (4.8) do not appear, but the remainder of the proof remains unchanged. This completes the proof.
5 Proofs of Corollaries 2.2 and 2.3
In this section, we prove some consequences of Theorem 2.1.
5.1 Proof of Corollary 2.2
We will use the notation set up in the statement of Lemma 3.5. From the data of F, we have
![]() $q=1$
,
$q=1$
,
![]() $\boldsymbol {\alpha }=(4)$
,
$\boldsymbol {\alpha }=(4)$
,
![]() $\boldsymbol {\beta } = ({\beta }_1)$
, and hence,
$\boldsymbol {\beta } = ({\beta }_1)$
, and hence,
![]() $L=1$
and
$L=1$
and
![]() $k_1=4$
. The sequence
$k_1=4$
. The sequence
![]() $b_{ij}$
of (3.9) is given by
$b_{ij}$
of (3.9) is given by
![]() $ b_{1,j} =( \bar {{\beta }_1} + j-1 )/ 4$
with
$ b_{1,j} =( \bar {{\beta }_1} + j-1 )/ 4$
with
![]() $ j =1, \ldots , 4. $
We express
$ j =1, \ldots , 4. $
We express
![]() ${Z}_{{(4),(\beta _1)} }(x)$
in terms of
${Z}_{{(4),(\beta _1)} }(x)$
in terms of
![]() $\tilde {Z}_{{(4),(\beta _1)} }(x)$
using (3.7) and then write
$\tilde {Z}_{{(4),(\beta _1)} }(x)$
using (3.7) and then write
![]() $\tilde {Z}_{{(4),(\beta _1)} }(x)$
in terms of the Meijer G-function using (3.10) to obtain
$\tilde {Z}_{{(4),(\beta _1)} }(x)$
in terms of the Meijer G-function using (3.10) to obtain
 $$ \begin{align*} {Z}_{{(4),(\beta_1)} }(x) &= \begin{cases} (2\pi)^{-{3\over 2}} \frac{4^{\bar{{\beta}}_1}} {2} G^{4 , 0}_{0 , 4}\Bigg( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ {\bar{{\beta}_1}\over 4} \ {\bar{{\beta}_1}\over 4}+{1\over 4} \ {\bar{{\beta}_1}\over 4}+{2\over 4}\ {\bar{{\beta}_1}\over 4}+{3\over 4} \end{matrix} \right| {x \over 4^4} \Bigg),& \text{if } \bar{{\beta}}_1 \neq 0,\\ {(2\pi)^{-{3\over 2}} } {1 \over 2}G^{4 , 0}_{0 , 4}\Bigg( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ 0 \ {1\over 4} \ {2\over 4}\ {3\over 4} \end{matrix} \right| {x \over 4^4} \Bigg)-{1\over 4},& \text{if } \bar{{\beta}}_1 = 0. \end{cases} \end{align*} $$
$$ \begin{align*} {Z}_{{(4),(\beta_1)} }(x) &= \begin{cases} (2\pi)^{-{3\over 2}} \frac{4^{\bar{{\beta}}_1}} {2} G^{4 , 0}_{0 , 4}\Bigg( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ {\bar{{\beta}_1}\over 4} \ {\bar{{\beta}_1}\over 4}+{1\over 4} \ {\bar{{\beta}_1}\over 4}+{2\over 4}\ {\bar{{\beta}_1}\over 4}+{3\over 4} \end{matrix} \right| {x \over 4^4} \Bigg),& \text{if } \bar{{\beta}}_1 \neq 0,\\ {(2\pi)^{-{3\over 2}} } {1 \over 2}G^{4 , 0}_{0 , 4}\Bigg( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ 0 \ {1\over 4} \ {2\over 4}\ {3\over 4} \end{matrix} \right| {x \over 4^4} \Bigg)-{1\over 4},& \text{if } \bar{{\beta}}_1 = 0. \end{cases} \end{align*} $$
For this special value of the Meijer G-function, (2.8) gives
 $$ \begin{align*} {Z}_{{(4),(\beta_1)} }(x)= \begin{cases} {1\over 4}x^{\bar{{\beta}}_1/ 4}e^{- {x}^{1/4} },& \text{if } {\beta}_1 \neq 0,\\ {1\over 4}e^{-x^{1/4} }-{1\over 4}, & \text{if } {\beta}_1 = 0. \end{cases} \end{align*} $$
$$ \begin{align*} {Z}_{{(4),(\beta_1)} }(x)= \begin{cases} {1\over 4}x^{\bar{{\beta}}_1/ 4}e^{- {x}^{1/4} },& \text{if } {\beta}_1 \neq 0,\\ {1\over 4}e^{-x^{1/4} }-{1\over 4}, & \text{if } {\beta}_1 = 0. \end{cases} \end{align*} $$
Substituting these values into Theorem 2.1, we obtain (2.10) and (2.11), respectively, as desired.
5.2 Proof of Corollary 2.3
Again, following the notation of Lemma 3.5, in this case, we have
![]() $q=4$
,
$q=4$
,
![]() $L=1,$
and
$L=1,$
and
![]() $k_i=1 $
for
$k_i=1 $
for
![]() $1\le i \le 4$
. Calculating the residue term of (3.7), it can be seen that
$1\le i \le 4$
. Calculating the residue term of (3.7), it can be seen that
We note that the sequence
![]() $b_{ij}$
of (3.9) is now given by
$b_{ij}$
of (3.9) is now given by
![]() $ \left \lbrace b_{i,1} \right \rbrace _{i=1}^4 = \{0, 1/2, -C, C \}. $
Using 3.10, we have
$ \left \lbrace b_{i,1} \right \rbrace _{i=1}^4 = \{0, 1/2, -C, C \}. $
Using 3.10, we have
 $$ \begin{align} \tilde{Z }_{(1,1,1,1),(0,{1 \over 2},-C,C) }\left(x \right) = G^{4 , 0}_{0 , 4}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ 0 \ {1\over 2} \ -C\ C \end{matrix} \right| x \right). \end{align} $$
$$ \begin{align} \tilde{Z }_{(1,1,1,1),(0,{1 \over 2},-C,C) }\left(x \right) = G^{4 , 0}_{0 , 4}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ 0 \ {1\over 2} \ -C\ C \end{matrix} \right| x \right). \end{align} $$
Putting
![]() $b=0$
and
$b=0$
and
![]() $c=C$
in (2.9), we get
$c=C$
in (2.9), we get
 $$ \begin{align} G^{4 , 0}_{0 , 4}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ 0 \ {1\over 2} \ -C\ C \end{matrix} \right| z \right)&=8{\sqrt{\pi}} K_{2C}(2\sqrt{2}(-z)^{1/4} )K_{2C}\left({2\sqrt{2}\sqrt{z}\over (-z)^{1/4}}\right). \end{align} $$
$$ \begin{align} G^{4 , 0}_{0 , 4}\left( \left. \begin{matrix} \rule{.4cm}{.2mm} \\ 0 \ {1\over 2} \ -C\ C \end{matrix} \right| z \right)&=8{\sqrt{\pi}} K_{2C}(2\sqrt{2}(-z)^{1/4} )K_{2C}\left({2\sqrt{2}\sqrt{z}\over (-z)^{1/4}}\right). \end{align} $$
Using the reflection formula to simplify the residue term in (5.1) and combining it with (5.2) and (5.3), we obtain
 $$ \begin{align*} {Z}_{{(1,1,1,1),(0,{1\over 2},-C,C)} }\left(x \right) &=8{\sqrt{\pi}} K_{2C}(2\sqrt{2} ({-x})^{1/4} )K_{2C}\left({2\sqrt{2}\sqrt{x}\over ({-x})^{1/4}}\right)+{\pi\sqrt{\pi}\over C\sin \pi C}. \end{align*} $$
$$ \begin{align*} {Z}_{{(1,1,1,1),(0,{1\over 2},-C,C)} }\left(x \right) &=8{\sqrt{\pi}} K_{2C}(2\sqrt{2} ({-x})^{1/4} )K_{2C}\left({2\sqrt{2}\sqrt{x}\over ({-x})^{1/4}}\right)+{\pi\sqrt{\pi}\over C\sin \pi C}. \end{align*} $$
6 Riesz-type criteria for Selberg class
6.1 Proof of Theorem 2.4
For
![]() $F\in \mathcal {S^*}$
, consider the summatory function of the coefficients of
$F\in \mathcal {S^*}$
, consider the summatory function of the coefficients of
![]() $F(s)^{-1}$
, given by
$F(s)^{-1}$
, given by
It can be checked that
![]() $F\in \mathcal {S^*}$
is contained in the general class of L-functions constructed on page 94 of Iwaniec–Kowalski [Reference Iwaniec and Kowalski15]. In particular, axiom (iv)
$F\in \mathcal {S^*}$
is contained in the general class of L-functions constructed on page 94 of Iwaniec–Kowalski [Reference Iwaniec and Kowalski15]. In particular, axiom (iv)
![]() $'$
and the inequality (2.14) play a crucial role here. We may thus apply Proposition 5.14 of [Reference Iwaniec and Kowalski15] to obtain that GRH implies the bound
$'$
and the inequality (2.14) play a crucial role here. We may thus apply Proposition 5.14 of [Reference Iwaniec and Kowalski15] to obtain that GRH implies the bound
for any
![]() ${\delta }>0$
, as
${\delta }>0$
, as
![]() $x\to \infty $
. Let us define
$x\to \infty $
. Let us define
 $$ \begin{align*} M_F(h, N)=\sum_{n=h}^{N}{b_F(n)\over n}. \end{align*} $$
$$ \begin{align*} M_F(h, N)=\sum_{n=h}^{N}{b_F(n)\over n}. \end{align*} $$
Applying partial summation to (6.1), one can deduce that as
![]() $h\to \infty $
, we have under GRH
$h\to \infty $
, we have under GRH
for any
![]() ${\delta }>0$
, uniformly for any
${\delta }>0$
, uniformly for any
![]() $N\geq h$
. If
$N\geq h$
. If
![]() $N<h$
, we interpret
$N<h$
, we interpret
![]() $M_F (h,N)$
to be zero. We now commence the proof of Theorem 2.4.
$M_F (h,N)$
to be zero. We now commence the proof of Theorem 2.4.
6.1.1 Proof of Theorem 2.4(a)
Let
![]() $\epsilon>0$
be sufficiently small. From (2.6), we may write
$\epsilon>0$
be sufficiently small. From (2.6), we may write
 $$ \begin{align} \mathcal{P} _{\boldsymbol{\alpha,\beta} ,z}(\nu^2)&=\sum\limits_{n = 1}^\infty \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)\cosh\left({\nu z}\over n\right)\nonumber\\ &=\left[ \sum\limits_{n = 1}^{h-1}+\sum\limits_{n = h}^{\infty} \right] \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)\cosh\left({\nu z}\over n\right)\nonumber\\ &=: P_1+P_2, \text{(say),} \end{align} $$
$$ \begin{align} \mathcal{P} _{\boldsymbol{\alpha,\beta} ,z}(\nu^2)&=\sum\limits_{n = 1}^\infty \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)\cosh\left({\nu z}\over n\right)\nonumber\\ &=\left[ \sum\limits_{n = 1}^{h-1}+\sum\limits_{n = h}^{\infty} \right] \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)\cosh\left({\nu z}\over n\right)\nonumber\\ &=: P_1+P_2, \text{(say),} \end{align} $$
where h equals the greatest integer less than or equal to
![]() $\nu ^{1-\epsilon }$
, that is,
$\nu ^{1-\epsilon }$
, that is,
![]() $h =[\nu ^{1-\epsilon }]$
. We first consider the partial sum of
$h =[\nu ^{1-\epsilon }]$
. We first consider the partial sum of
![]() $P_2$
, given by
$P_2$
, given by
 $$ \begin{align} P_2(N) &:= \sum\limits_{n = h}^{N}\frac{{b_F(n)}}{n}{Z_{\boldsymbol{\alpha,\beta} }}\left( \left( {\frac{\nu }{n}} \right)^{d_F} \right) \cosh \left(\frac{\nu z}{n} \right) \nonumber\\ &= \sum_{ n=h }^N\left( M_{F}(h,n)-M_F(h,n-1)\right) {Z_{\boldsymbol{\alpha,\beta} }} \left( \left( {\frac{\nu }{n}} \right)^{d_F}\right) \cosh \left(\frac{\nu z}{n} \right) \nonumber\\ &=\sum_{ n=h }^{N-1} M_F(h,n) \left( f(n)-f(n+1) \right) + M_{F}{(h,N)}f(N), \end{align} $$
$$ \begin{align} P_2(N) &:= \sum\limits_{n = h}^{N}\frac{{b_F(n)}}{n}{Z_{\boldsymbol{\alpha,\beta} }}\left( \left( {\frac{\nu }{n}} \right)^{d_F} \right) \cosh \left(\frac{\nu z}{n} \right) \nonumber\\ &= \sum_{ n=h }^N\left( M_{F}(h,n)-M_F(h,n-1)\right) {Z_{\boldsymbol{\alpha,\beta} }} \left( \left( {\frac{\nu }{n}} \right)^{d_F}\right) \cosh \left(\frac{\nu z}{n} \right) \nonumber\\ &=\sum_{ n=h }^{N-1} M_F(h,n) \left( f(n)-f(n+1) \right) + M_{F}{(h,N)}f(N), \end{align} $$
where
 $$ \begin{align*} f(t) := Z_{\boldsymbol{\alpha,\beta} }\left( \left( {\frac{\nu }{t}} \right)^{d_F}\right) \cosh \left(\frac{\nu z}{t} \right). \end{align*} $$
$$ \begin{align*} f(t) := Z_{\boldsymbol{\alpha,\beta} }\left( \left( {\frac{\nu }{t}} \right)^{d_F}\right) \cosh \left(\frac{\nu z}{t} \right). \end{align*} $$
Using Lemma 3.3 and the bounds (6.2) and
![]() $\cosh (xz) \ll _z 1$
as
$\cosh (xz) \ll _z 1$
as
![]() $x \to 0$
, we find that
$x \to 0$
, we find that
 $$ \begin{align*} M_F(h,N) f(N) \ll_{{\delta}, F,z} h^{-\frac{1}{2}+{\delta}} \left( \frac{N}{\nu} \right)^{cd_F}, \end{align*} $$
$$ \begin{align*} M_F(h,N) f(N) \ll_{{\delta}, F,z} h^{-\frac{1}{2}+{\delta}} \left( \frac{N}{\nu} \right)^{cd_F}, \end{align*} $$
where
![]() $-c_F<c <0$
. Letting
$-c_F<c <0$
. Letting
![]() $N \to \infty $
, the above expression goes to zero, so that (6.4) yields
$N \to \infty $
, the above expression goes to zero, so that (6.4) yields
 $$ \begin{align} P_2 &=\sum_{ n=h }^{\infty } M_F(h,n) \left( f(n)-f(n+1) \right) \qquad\ \ \quad\qquad\end{align} $$
$$ \begin{align} P_2 &=\sum_{ n=h }^{\infty } M_F(h,n) \left( f(n)-f(n+1) \right) \qquad\ \ \quad\qquad\end{align} $$
 $$ \begin{align} &= \left[\sum_{ n=h }^{[C\nu] }+ \sum_{ n=[C\nu] }^{\infty } \right] M_F(h,n) \left(f(n)- f(n+1)\right) \nonumber\\ &=: P_3+P_4 \quad \text{ (say)}. \end{align} $$
$$ \begin{align} &= \left[\sum_{ n=h }^{[C\nu] }+ \sum_{ n=[C\nu] }^{\infty } \right] M_F(h,n) \left(f(n)- f(n+1)\right) \nonumber\\ &=: P_3+P_4 \quad \text{ (say)}. \end{align} $$
Here, C is a constant to be chosen later and
![]() $[C\nu ]$
denotes the greatest integer less than or equal to
$[C\nu ]$
denotes the greatest integer less than or equal to
![]() $C\nu $
. Using the mean value theorem, there exists
$C\nu $
. Using the mean value theorem, there exists
![]() $\lambda _n \in (n, n+1)$
such that
$\lambda _n \in (n, n+1)$
such that
 $$ \begin{align} {f(n+1)-f(n) } &= f'(\lambda_n)\nonumber \\ &= -\frac{d_F \nu^{d_F}}{\lambda_n^{d_F+1}} Z^{\prime}_{\boldsymbol{\alpha,\beta} }\left(\kern-1.2pt \left(\kern-1pt {\frac{\nu }{\lambda_n}} \right)^{d_F}\right) \cosh \left(\kern-1pt\frac{\nu z}{\lambda_n} \kern-1pt\right) -\frac{\nu z}{\lambda_n^{2}} Z_{\boldsymbol{\alpha,\beta} }\left(\kern-1pt \left(\kern-1pt {\frac{\nu }{\lambda_n}} \kern-1pt\right)^{d_F}\right) \sinh \left(\kern-1pt\frac{\nu z}{\lambda_n} \kern-1pt\right). \end{align} $$
$$ \begin{align} {f(n+1)-f(n) } &= f'(\lambda_n)\nonumber \\ &= -\frac{d_F \nu^{d_F}}{\lambda_n^{d_F+1}} Z^{\prime}_{\boldsymbol{\alpha,\beta} }\left(\kern-1.2pt \left(\kern-1pt {\frac{\nu }{\lambda_n}} \right)^{d_F}\right) \cosh \left(\kern-1pt\frac{\nu z}{\lambda_n} \kern-1pt\right) -\frac{\nu z}{\lambda_n^{2}} Z_{\boldsymbol{\alpha,\beta} }\left(\kern-1pt \left(\kern-1pt {\frac{\nu }{\lambda_n}} \kern-1pt\right)^{d_F}\right) \sinh \left(\kern-1pt\frac{\nu z}{\lambda_n} \kern-1pt\right). \end{align} $$
We will estimate
![]() $f(n)-f(n+1)$
in two different ranges of n, as relevant for
$f(n)-f(n+1)$
in two different ranges of n, as relevant for
![]() $P_3$
and
$P_3$
and
![]() $P_4$
in what follows.
$P_4$
in what follows.
At this point, the assumption that
![]() $j_F=0$
plays a crucial role. Indeed, when
$j_F=0$
plays a crucial role. Indeed, when
![]() $j_F=0$
, one sees from (3.7) that
$j_F=0$
, one sees from (3.7) that
![]() $Z_{\boldsymbol {\alpha ,\beta } }$
is the same as
$Z_{\boldsymbol {\alpha ,\beta } }$
is the same as
![]() $\tilde Z_{\boldsymbol {\alpha ,\beta } }$
. Thus, for
$\tilde Z_{\boldsymbol {\alpha ,\beta } }$
. Thus, for
![]() $\nu /\lambda _n$
sufficiently large, we can apply Lemmas 3.5 and 3.6. Since
$\nu /\lambda _n$
sufficiently large, we can apply Lemmas 3.5 and 3.6. Since
![]() $n\leq \lambda _n \ll n$
, this means that in the range
$n\leq \lambda _n \ll n$
, this means that in the range
![]() $n \le [C\nu ]$
, for sufficiently small C, we have
$n \le [C\nu ]$
, for sufficiently small C, we have
 $$ \begin{align} |f(n)-f(n+1)| \ll_{F,z,C} \exp\left(-C_1 \left( \frac{\nu}{n} \right)^2 + \frac{\nu |\Re(z)| }{n} \right) \left(\frac{\nu}{n}\right)^{2C_3+d_FC_4} \left( \frac{\nu^{d_F}}{n^{d_F+1}} + \frac{\nu}{n^2} \right), \end{align} $$
$$ \begin{align} |f(n)-f(n+1)| \ll_{F,z,C} \exp\left(-C_1 \left( \frac{\nu}{n} \right)^2 + \frac{\nu |\Re(z)| }{n} \right) \left(\frac{\nu}{n}\right)^{2C_3+d_FC_4} \left( \frac{\nu^{d_F}}{n^{d_F+1}} + \frac{\nu}{n^2} \right), \end{align} $$
where
![]() $C_i$
’s are as defined in (3.8). Here, we have used the fact that
$C_i$
’s are as defined in (3.8). Here, we have used the fact that
![]() $d_FC_2=2$
and that
$d_FC_2=2$
and that
![]() $\cosh (xz)$
and
$\cosh (xz)$
and
![]() $\sinh (xz)$
are trivially of the order
$\sinh (xz)$
are trivially of the order
![]() $\exp (x \Re (z))$
. Using the above estimate and (6.2) in (6.6), we obtain
$\exp (x \Re (z))$
. Using the above estimate and (6.2) in (6.6), we obtain
 $$ \begin{align} P_3\ll_{{\delta}, F,z, C} \sum_{n=h}^{[C\nu]} \frac{h^{-{1 \over 2} +{\delta}}}{n}\exp\left(-C_1 \left( \frac{\nu}{n} \right)^2 + \frac{\nu \left|\Re(z)\right| }{n} \right) \left(\frac{\nu}{n}\right)^{2C_3+d_FC_4 + d_F}. \end{align} $$
$$ \begin{align} P_3\ll_{{\delta}, F,z, C} \sum_{n=h}^{[C\nu]} \frac{h^{-{1 \over 2} +{\delta}}}{n}\exp\left(-C_1 \left( \frac{\nu}{n} \right)^2 + \frac{\nu \left|\Re(z)\right| }{n} \right) \left(\frac{\nu}{n}\right)^{2C_3+d_FC_4 + d_F}. \end{align} $$
Keeping in mind that
![]() $C_1>0$
, it can be seen that the argument of
$C_1>0$
, it can be seen that the argument of
![]() $\exp $
is negative if
$\exp $
is negative if
![]() $n < C_1\nu / |\Re z|$
. In the range of n applicable to
$n < C_1\nu / |\Re z|$
. In the range of n applicable to
![]() $P_3$
, it is enough to ensure that
$P_3$
, it is enough to ensure that
We choose C to be sufficiently small, say
![]() $ C= {C_1}/({MC_1+|\Re z|}), $
where
$ C= {C_1}/({MC_1+|\Re z|}), $
where
![]() $M>0$
is a sufficiently large fixed constant, so that (6.8) and (6.10) are both satisfied. Writing
$M>0$
is a sufficiently large fixed constant, so that (6.8) and (6.10) are both satisfied. Writing
![]() $2C_3+d_FC_4+d_F$
as
$2C_3+d_FC_4+d_F$
as
![]() $C_5$
, (6.9) then gives
$C_5$
, (6.9) then gives
 $$ \begin{align} P_3 &\ll_{{\delta}, F, z, C} h^{-{1\over 2} +{\delta}} \sum_{ n=h}^{[C\nu]} \frac{\nu ^{C_5}}{n^{C_5+1}} \ll_{{\delta}, F, z, C} h^{-{1\over 2} +{\delta}} \nu ^{C_5} \int_{h}^{C\nu} \frac{1}{t^{C_5+1}} dt. \end{align} $$
$$ \begin{align} P_3 &\ll_{{\delta}, F, z, C} h^{-{1\over 2} +{\delta}} \sum_{ n=h}^{[C\nu]} \frac{\nu ^{C_5}}{n^{C_5+1}} \ll_{{\delta}, F, z, C} h^{-{1\over 2} +{\delta}} \nu ^{C_5} \int_{h}^{C\nu} \frac{1}{t^{C_5+1}} dt. \end{align} $$
Thus, we obtain
for any
![]() $\delta>0$
, keeping in mind that h was chosen to be
$\delta>0$
, keeping in mind that h was chosen to be
![]() $[\nu ^{1-\epsilon }]$
.
$[\nu ^{1-\epsilon }]$
.
We now turn to
![]() $P_4$
. Since the range of n is now
$P_4$
. Since the range of n is now
![]() $n> [C\nu ]$
, we will use Lemmas 3.3 and 3.4 to bound
$n> [C\nu ]$
, we will use Lemmas 3.3 and 3.4 to bound
![]() $Z_{\boldsymbol {\alpha ,\beta } }$
and
$Z_{\boldsymbol {\alpha ,\beta } }$
and
![]() $Z^{\prime }_{\boldsymbol {\alpha ,\beta } }$
, respectively. Moreover, we have
$Z^{\prime }_{\boldsymbol {\alpha ,\beta } }$
, respectively. Moreover, we have
![]() $\cosh (xz) \ll _z 1$
and
$\cosh (xz) \ll _z 1$
and
![]() $\sinh (xz) \ll _z x$
when
$\sinh (xz) \ll _z x$
when
![]() $x>0$
is bounded above by some absolute constant. Applying all this to (6.7) gives, for
$x>0$
is bounded above by some absolute constant. Applying all this to (6.7) gives, for
![]() $n> [C\nu ]$
,
$n> [C\nu ]$
,
 $$ \begin{align*} f(n) - f(n+1) &\ll_{F,z,C} \frac{\nu^{d_F}}{n^{d_F+1}} \left( \frac{\nu}{n} \right)^{(-c-1)d_F} + \frac{\nu}{n^2}\left( \frac{\nu}{n} \right)^{-cd_F+1} \\ &\ll_{F,z,C} \frac{1}{n} \left( \frac{\nu}{n} \right)^{-cd_F+2}. \end{align*} $$
$$ \begin{align*} f(n) - f(n+1) &\ll_{F,z,C} \frac{\nu^{d_F}}{n^{d_F+1}} \left( \frac{\nu}{n} \right)^{(-c-1)d_F} + \frac{\nu}{n^2}\left( \frac{\nu}{n} \right)^{-cd_F+1} \\ &\ll_{F,z,C} \frac{1}{n} \left( \frac{\nu}{n} \right)^{-cd_F+2}. \end{align*} $$
Again, from (6.6), we have
 $$ \begin{align} P_4 &\ll_{\epsilon, F,z,C}h^{-{1 \over 2} +\epsilon} \sum_{ n=h }^\infty \frac{\nu^{-cd_F+2} }{n^{-cd_F+3}} \ll_{{\delta}, F,z,C} h^{-{1\over 2} +{\delta}}, \end{align} $$
$$ \begin{align} P_4 &\ll_{\epsilon, F,z,C}h^{-{1 \over 2} +\epsilon} \sum_{ n=h }^\infty \frac{\nu^{-cd_F+2} }{n^{-cd_F+3}} \ll_{{\delta}, F,z,C} h^{-{1\over 2} +{\delta}}, \end{align} $$
for any
![]() ${\delta }>0$
, in the same manner as done for
${\delta }>0$
, in the same manner as done for
![]() $P_3$
in (6.11). Combining (6.6), (6.12), and (6.13), we obtain that, for any
$P_3$
in (6.11). Combining (6.6), (6.12), and (6.13), we obtain that, for any
![]() ${\delta }>0$
,
${\delta }>0$
,
We now consider the first series of (6.3). Again, since
![]() $j_F=0$
, we have
$j_F=0$
, we have
![]() $Z_{\boldsymbol {\alpha ,\beta } } = \tilde Z_{\boldsymbol {\alpha ,\beta } }$
. Moreover, we have assumed
$Z_{\boldsymbol {\alpha ,\beta } } = \tilde Z_{\boldsymbol {\alpha ,\beta } }$
. Moreover, we have assumed
![]() $F\in \mathcal S^*$
, which means that Lemma 3.5 can be applied. This bound gives
$F\in \mathcal S^*$
, which means that Lemma 3.5 can be applied. This bound gives
 $$ \begin{align*} P_1 \ll \sum\limits_{n = 1}^{h-1}{|b_F(n)| \over n}\exp \left(-C_1\left(\nu\over n\right)^{2} + \frac{\nu|\Re z| }{n} \right)\left(\nu\over n\right)^{2C_3}. \end{align*} $$
$$ \begin{align*} P_1 \ll \sum\limits_{n = 1}^{h-1}{|b_F(n)| \over n}\exp \left(-C_1\left(\nu\over n\right)^{2} + \frac{\nu|\Re z| }{n} \right)\left(\nu\over n\right)^{2C_3}. \end{align*} $$
Here, we have used the trivial bound
![]() $\cosh (\nu z/n) \ll \exp ( \nu |\Re z|/n )$
. Since
$\cosh (\nu z/n) \ll \exp ( \nu |\Re z|/n )$
. Since
![]() $b_F$
is the inverse of
$b_F$
is the inverse of
![]() $a_F$
under Dirichlet convolution, using induction one can derive the following relation for any prime p and
$a_F$
under Dirichlet convolution, using induction one can derive the following relation for any prime p and
![]() $m \in \mathbb N$
,
$m \in \mathbb N$
,
 $$ \begin{align*} b_F(p^m) = - \sum_{j=1}^{m} a_F(p^j) b_F(p^{m-j}). \end{align*} $$
$$ \begin{align*} b_F(p^m) = - \sum_{j=1}^{m} a_F(p^j) b_F(p^{m-j}). \end{align*} $$
Using the Ramanujan bound (axiom (v)) for
![]() $a_F(n)$
and induction on m, it follows that axiom (v) is also true for
$a_F(n)$
and induction on m, it follows that axiom (v) is also true for
![]() $b_F$
on prime powers. As
$b_F$
on prime powers. As
![]() $b_F(n)$
is multiplicative, this gives
$b_F(n)$
is multiplicative, this gives
![]() $b_F(n) \ll _{\delta } n^{\delta }$
for any
$b_F(n) \ll _{\delta } n^{\delta }$
for any
![]() ${\delta }>0$
. Hence, we may write
${\delta }>0$
. Hence, we may write
 $$ \begin{align*} P_1 & \ll \sum\limits_{n = 1}^{h-1}\left(\nu\over n\right)^{2C_3}\exp \left(-{\nu\over n}\left( C_1{\nu\over n} -{|\Re z|}\right)\right). \end{align*} $$
$$ \begin{align*} P_1 & \ll \sum\limits_{n = 1}^{h-1}\left(\nu\over n\right)^{2C_3}\exp \left(-{\nu\over n}\left( C_1{\nu\over n} -{|\Re z|}\right)\right). \end{align*} $$
We choose the parameter
![]() $\nu $
to satisfy
$\nu $
to satisfy
![]() $\nu ^{\epsilon /2}>{|\Re z|\over C_1}$
. Then, for n in the range specified by the above sum and
$\nu ^{\epsilon /2}>{|\Re z|\over C_1}$
. Then, for n in the range specified by the above sum and
![]() $ h = [\nu ^{1-\epsilon }]$
, we have
$ h = [\nu ^{1-\epsilon }]$
, we have
![]() $C_1{\nu \over n} -{|\Re z|}\geq C_1\left ( {\nu \over h} -{\nu ^{\epsilon /2}}\right ) \gg C_1\nu ^\epsilon $
. Hence, one has
$C_1{\nu \over n} -{|\Re z|}\geq C_1\left ( {\nu \over h} -{\nu ^{\epsilon /2}}\right ) \gg C_1\nu ^\epsilon $
. Hence, one has
 $$ \begin{align} P_1&\ll\sum\limits_{n = 1}^{h-1} \exp \left(-{\nu\over h} C_1{\nu^\epsilon}\right)\left(\nu\over n\right)^{2C_3} \ll \sum\limits_{n = 1}^{h-1} \exp \left(- C_1{\nu^{2\epsilon}}\right)\left(\nu\over n\right)^{2C_3} \ll \exp \left(-c{\nu^{2\epsilon}}\right), \end{align} $$
$$ \begin{align} P_1&\ll\sum\limits_{n = 1}^{h-1} \exp \left(-{\nu\over h} C_1{\nu^\epsilon}\right)\left(\nu\over n\right)^{2C_3} \ll \sum\limits_{n = 1}^{h-1} \exp \left(- C_1{\nu^{2\epsilon}}\right)\left(\nu\over n\right)^{2C_3} \ll \exp \left(-c{\nu^{2\epsilon}}\right), \end{align} $$
for some constant
![]() $c>0$
. Combining (6.14), (6.15), replacing
$c>0$
. Combining (6.14), (6.15), replacing
![]() $\nu ^2$
by y, and letting
$\nu ^2$
by y, and letting
![]() $y\to \infty $
, we obtain the required bound for
$y\to \infty $
, we obtain the required bound for
![]() $\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
.
$\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)$
.
6.1.2 Proof of Theorem 2.4(b)
Whenever
![]() $j_F\neq 0$
,
$j_F\neq 0$
,
![]() $ {Z_{\boldsymbol { {\alpha },{\beta }} }}$
and
$ {Z_{\boldsymbol { {\alpha },{\beta }} }}$
and
![]() $ {\tilde Z_{\boldsymbol { {\alpha },{\beta }} }}$
differ by the residue term given in (3.7). We first write
$ {\tilde Z_{\boldsymbol { {\alpha },{\beta }} }}$
differ by the residue term given in (3.7). We first write
![]() $\mathcal {P}_{\boldsymbol {{\alpha },{\beta }},0}(\nu ^2) = P_1+P_2$
as in (6.3). Using (6.5) and (6.7), keeping in mind that
$\mathcal {P}_{\boldsymbol {{\alpha },{\beta }},0}(\nu ^2) = P_1+P_2$
as in (6.3). Using (6.5) and (6.7), keeping in mind that
![]() $z=0$
, we can write
$z=0$
, we can write
 $$ \begin{align*} P_2= \sum_{n=h}^{\infty} -\frac{d_F\nu^{d_F}}{\lambda_n^{d_F+1}} M_F(h, n) {Z^{\prime}_{\boldsymbol{ {\alpha},{\beta}} }}\left( \left( \nu \over \lambda_n \right)^{d_F} \right). \end{align*} $$
$$ \begin{align*} P_2= \sum_{n=h}^{\infty} -\frac{d_F\nu^{d_F}}{\lambda_n^{d_F+1}} M_F(h, n) {Z^{\prime}_{\boldsymbol{ {\alpha},{\beta}} }}\left( \left( \nu \over \lambda_n \right)^{d_F} \right). \end{align*} $$
The primary departure here from the proof of part (a) given above is that due to the nontrivial residue term in (3.7), we no longer have an exponential decay bound for
![]() $Z^{\prime }_{\boldsymbol { {\alpha },{\beta }} }$
. We resort to Lemma 3.4 instead. This along with (6.2) (which is true because of GRH) yields
$Z^{\prime }_{\boldsymbol { {\alpha },{\beta }} }$
. We resort to Lemma 3.4 instead. This along with (6.2) (which is true because of GRH) yields
 $$ \begin{align*} P_2 \ll_{{\delta}, F} h^{-{1\over 2}+{\delta}} \sum_{ n=h}^\infty \frac{\nu^{d_F}}{n^{d_F+1}} \left( \frac{\nu}{n} \right)^{(-c-1)d_F} \ll_{{\delta}, F} h^{-{1\over 2}+{\delta}} \sum_{ n=h}^\infty \frac{\nu^{-cd_F}}{n^{-cd_F+1}}. \end{align*} $$
$$ \begin{align*} P_2 \ll_{{\delta}, F} h^{-{1\over 2}+{\delta}} \sum_{ n=h}^\infty \frac{\nu^{d_F}}{n^{d_F+1}} \left( \frac{\nu}{n} \right)^{(-c-1)d_F} \ll_{{\delta}, F} h^{-{1\over 2}+{\delta}} \sum_{ n=h}^\infty \frac{\nu^{-cd_F}}{n^{-cd_F+1}}. \end{align*} $$
Using the integral test as done in (6.11), we find that
![]() $P_2 \ll _{{\delta }, F} h^{-{1\over 2}+{\delta }}, $
for any
$P_2 \ll _{{\delta }, F} h^{-{1\over 2}+{\delta }}, $
for any
![]() ${\delta }>0$
.
${\delta }>0$
.
Turning to
![]() $P_1$
, we have
$P_1$
, we have
 $$ \begin{align} P_1&=\sum\limits_{n = 1}^{h-1} \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)\nonumber\\ &=\sum\limits_{n = 1}^{h-1} \frac{{b_F(n)}}{n}{\tilde{Z}_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)-\sum\limits_{n = 1}^{h-1} \frac{{b_F(n)}}{n}\operatorname{Res}_{s=0}\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){\left( {\frac{\nu }{n}} \right)^{-d_Fs}}. \end{align} $$
$$ \begin{align} P_1&=\sum\limits_{n = 1}^{h-1} \frac{{b_F(n)}}{n}{Z_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)\nonumber\\ &=\sum\limits_{n = 1}^{h-1} \frac{{b_F(n)}}{n}{\tilde{Z}_{\boldsymbol{ {\alpha},{\beta}} }}\left(\left( {\frac{\nu }{n}} \right)^{d_F}\right)-\sum\limits_{n = 1}^{h-1} \frac{{b_F(n)}}{n}\operatorname{Res}_{s=0}\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right){\left( {\frac{\nu }{n}} \right)^{-d_Fs}}. \end{align} $$
The first sum of (6.16) satisfies the bound (6.15) as done in the proof of part (a), and is thus negligible compared to
![]() $P_2$
. Note that the assumption
$P_2$
. Note that the assumption
![]() $F\in \mathcal S^*$
is used here. Using
$F\in \mathcal S^*$
is used here. Using
![]() $h =[\nu ^{1-\epsilon } ]$
and replacing
$h =[\nu ^{1-\epsilon } ]$
and replacing
![]() $\nu ^2$
by y, the second term becomes
$\nu ^2$
by y, the second term becomes
 $$ \begin{align*} \sum_{n=1}^{[y ^{{1\over 2}-\epsilon}] -1}{b_F(n) \over n}\operatorname{Res}\limits_{s=0}\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)\left({\sqrt{y}\over n} \right)^{-d_Fs}. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{[y ^{{1\over 2}-\epsilon}] -1}{b_F(n) \over n}\operatorname{Res}\limits_{s=0}\prod_{i=1}^q\Gamma\left(\alpha_i s+\bar{\beta_i} \right)\left({\sqrt{y}\over n} \right)^{-d_Fs}. \end{align*} $$
Hence, GRH implies the estimate (2.15).
6.1.3 Proof of Theorem 2.4(c)
As
![]() $z\to 0$
, only the
$z\to 0$
, only the
![]() $t=0$
term survives in (3.4). Thus, for
$t=0$
term survives in (3.4). Thus, for
![]() $0 < \Re (s)<1/2$
, we have
$0 < \Re (s)<1/2$
, we have
 $$ \begin{align*} {F(2s+1)} \int_{0}^{\infty}y^{-s-1}\mathcal{P} _{\boldsymbol{\alpha,\beta} ,0}(y)dy={2\over d_F }{\prod_{i=1}^{q}\Gamma\left( -{2{\alpha}_is\over d_F}+\bar {\beta}_i \right) }. \end{align*} $$
$$ \begin{align*} {F(2s+1)} \int_{0}^{\infty}y^{-s-1}\mathcal{P} _{\boldsymbol{\alpha,\beta} ,0}(y)dy={2\over d_F }{\prod_{i=1}^{q}\Gamma\left( -{2{\alpha}_is\over d_F}+\bar {\beta}_i \right) }. \end{align*} $$
We will try to extend this identity to a larger region of the complex plane. The right-hand side has no poles in the region
![]() $\Re (s) \le 0$
except for a pole of order
$\Re (s) \le 0$
except for a pole of order
![]() $j_F$
at
$j_F$
at
![]() $s=0$
. Since
$s=0$
. Since
![]() $F(2s+1)$
has a pole of order
$F(2s+1)$
has a pole of order
![]() $k_F$
at
$k_F$
at
![]() $s=0$
, let us multiply both sides by
$s=0$
, let us multiply both sides by
![]() $s^\ell $
where
$s^\ell $
where
![]() $\ell =\max [k_F,j_F]$
. This gives
$\ell =\max [k_F,j_F]$
. This gives
 $$ \begin{align} s^\ell {F(2s+1)} \int_{0}^{\infty}y^{-s-1}\mathcal{P} _{\boldsymbol{\alpha,\beta} ,0}(y)dy= {2 s^\ell \over d_F }{\prod_{i=1}^{q}\Gamma\left( -{2{\alpha}_is\over d_F}+\bar {\beta}_i \right) }. \end{align} $$
$$ \begin{align} s^\ell {F(2s+1)} \int_{0}^{\infty}y^{-s-1}\mathcal{P} _{\boldsymbol{\alpha,\beta} ,0}(y)dy= {2 s^\ell \over d_F }{\prod_{i=1}^{q}\Gamma\left( -{2{\alpha}_is\over d_F}+\bar {\beta}_i \right) }. \end{align} $$
We next partition the above integral as
The assumed bound
![]() $\mathcal {P}_{\boldsymbol {\alpha ,\beta },0 }(y) \ll _{F, {\delta }} y^{-{1\over 4} + {\delta }}$
, implies that
$\mathcal {P}_{\boldsymbol {\alpha ,\beta },0 }(y) \ll _{F, {\delta }} y^{-{1\over 4} + {\delta }}$
, implies that
![]() $I_2$
is integrable in the region
$I_2$
is integrable in the region
![]() $-{1\over 4} < \Re (s)$
. In order to analyze
$-{1\over 4} < \Re (s)$
. In order to analyze
![]() $I_1$
, we apply (2.6) and the bound of Lemma 3.3 to
$I_1$
, we apply (2.6) and the bound of Lemma 3.3 to
![]() $Z_{\boldsymbol {\alpha ,\beta }}\left ( (\sqrt y/ n)^{d_F} \right )$
. It can then be seen that
$Z_{\boldsymbol {\alpha ,\beta }}\left ( (\sqrt y/ n)^{d_F} \right )$
. It can then be seen that
![]() $I_1$
is integrable for
$I_1$
is integrable for
![]() $\Re (s) < -cd_F/2$
, where
$\Re (s) < -cd_F/2$
, where
![]() $-c_F<c<0$
. It thus follows that I is analytic for
$-c_F<c<0$
. It thus follows that I is analytic for
![]() $\Re (s) \in (-1/4, \epsilon )$
for
$\Re (s) \in (-1/4, \epsilon )$
for
![]() $\epsilon>0$
sufficiently small. As both sides of the identity (6.17) are analytic in this region, by the principle of analytic continuation, (6.17) holds for an extended region of
$\epsilon>0$
sufficiently small. As both sides of the identity (6.17) are analytic in this region, by the principle of analytic continuation, (6.17) holds for an extended region of
![]() $\mathbb C$
, in particular, for
$\mathbb C$
, in particular, for
![]() $-{1\over 4}<\Re (s)\le 0$
.
$-{1\over 4}<\Re (s)\le 0$
.
Since the right-hand side of (6.17) does not vanish in the region
![]() $-{1\over 4} <\Re s<0$
and the integral I is analytic here, we see that
$-{1\over 4} <\Re s<0$
and the integral I is analytic here, we see that
![]() $F(2s+1)$
does not vanish in this region. This implies the nonvanishing of
$F(2s+1)$
does not vanish in this region. This implies the nonvanishing of
![]() $F(s)$
in
$F(s)$
in
![]() ${1\over 2}<\Re (s)<1$
as needed.
${1\over 2}<\Re (s)<1$
as needed.
6.1.4 Proof of Theorem 2.5
Let
![]() $z\ne 0 $
,
$z\ne 0 $
,
![]() $\arg z \ne \pm {\pi /2}$
be fixed. Let
$\arg z \ne \pm {\pi /2}$
be fixed. Let
![]() $s=\sigma {+iT}$
, and
$s=\sigma {+iT}$
, and
![]() $\bar {{\beta }_i}=\delta _i+i\gamma _i$
for
$\bar {{\beta }_i}=\delta _i+i\gamma _i$
for
![]() $i=1, \ldots , q$
. From (3.4), we have, for
$i=1, \ldots , q$
. From (3.4), we have, for
![]() $0< \Re s <1/2$
,
$0< \Re s <1/2$
,
 $$ \begin{align} s^{k_F} &F(2s+1) \phi(s,\boldsymbol {\alpha}, \boldsymbol {\beta}, z ) ={2 s^{k_F} \over d_F}\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!}{\prod_{i=1}^q\Gamma\left({2\alpha_i\over d_F} (t-s)+\bar{\beta_i} \right)}, \end{align} $$
$$ \begin{align} s^{k_F} &F(2s+1) \phi(s,\boldsymbol {\alpha}, \boldsymbol {\beta}, z ) ={2 s^{k_F} \over d_F}\sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!}{\prod_{i=1}^q\Gamma\left({2\alpha_i\over d_F} (t-s)+\bar{\beta_i} \right)}, \end{align} $$
where
![]() $ \phi (s,\boldsymbol {\alpha }, \boldsymbol {\beta }, z ) = \int _{0}^{\infty }y^{-s-1}\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)dy$
, and
$ \phi (s,\boldsymbol {\alpha }, \boldsymbol {\beta }, z ) = \int _{0}^{\infty }y^{-s-1}\mathcal {P} _{\boldsymbol {\alpha ,\beta } ,z}(y)dy$
, and
![]() $k_F$
is the order of the pole of
$k_F$
is the order of the pole of
![]() $F(s)$
at
$F(s)$
at
![]() $s=1$
. We will first extend this identity to the region
$s=1$
. We will first extend this identity to the region
![]() $-1/4< \Re (s)\le 0$
. Using Stirling’s formula (3.2), as
$-1/4< \Re (s)\le 0$
. Using Stirling’s formula (3.2), as
![]() $|T|\to \infty $
, the product of Gamma factors above can be written as
$|T|\to \infty $
, the product of Gamma factors above can be written as
 $$ \begin{align} (2\pi)^{q/2} \left( 1+O_{F} \left( \frac{1}{ |T|}\right) \right) \prod_{i=1}^q\bigg( \bigg|{2\alpha_iT\over d_F}-\gamma_i \bigg|^{{2\alpha_i(t-\sigma)\over d_F}+\delta_i-{1\over 2}} e^{-{\pi\over 2}\big| {2\alpha_iT\over d_F}-\gamma_i \big|}\bigg). \end{align} $$
$$ \begin{align} (2\pi)^{q/2} \left( 1+O_{F} \left( \frac{1}{ |T|}\right) \right) \prod_{i=1}^q\bigg( \bigg|{2\alpha_iT\over d_F}-\gamma_i \bigg|^{{2\alpha_i(t-\sigma)\over d_F}+\delta_i-{1\over 2}} e^{-{\pi\over 2}\big| {2\alpha_iT\over d_F}-\gamma_i \big|}\bigg). \end{align} $$
In particular, using (6.19), it is easy to check that the radius of convergence of the power series on the right-hand side of (6.18) is infinite. Using the assumed bound
![]() $\mathcal P_{\boldsymbol {\alpha }, \boldsymbol {\beta }, z} (y) \ll _{F, {\delta }} y^{- {1\over 4} + {\delta }}$
, the integral
$\mathcal P_{\boldsymbol {\alpha }, \boldsymbol {\beta }, z} (y) \ll _{F, {\delta }} y^{- {1\over 4} + {\delta }}$
, the integral
![]() $ \phi (s,\boldsymbol {\alpha }, \boldsymbol {\beta }, z ) $
can be shown to be analytic in the region
$ \phi (s,\boldsymbol {\alpha }, \boldsymbol {\beta }, z ) $
can be shown to be analytic in the region
![]() $\Re (s) \in (-1/4,\epsilon )$
for
$\Re (s) \in (-1/4,\epsilon )$
for
![]() $\epsilon>0$
sufficiently small, exactly as done in the proof of Theorem 2.4(c) above. Moreover, the factor
$\epsilon>0$
sufficiently small, exactly as done in the proof of Theorem 2.4(c) above. Moreover, the factor
![]() $s^{k_F} F(2s+1)$
is entire. From the principle of analytic continuation, we see that (6.18) holds in
$s^{k_F} F(2s+1)$
is entire. From the principle of analytic continuation, we see that (6.18) holds in
![]() $-1/4 < \Re (s)\le 0$
.
$-1/4 < \Re (s)\le 0$
.
We now consider
![]() $s=\sigma {+iT}$
, where
$s=\sigma {+iT}$
, where
![]() $-1/4 < \sigma < 0$
. Plugging (6.19) into (6.18), we obtain for
$-1/4 < \sigma < 0$
. Plugging (6.19) into (6.18), we obtain for
![]() $ s^{k_F} F(2s+1)\phi (s, \boldsymbol {\alpha }, \boldsymbol {\beta }, z)$
, the main term
$ s^{k_F} F(2s+1)\phi (s, \boldsymbol {\alpha }, \boldsymbol {\beta }, z)$
, the main term
 $$ \begin{align} &{2 s^{k_F}(2\pi)^{q/2}\over d_F}\prod_{i=1}^q\bigg( \bigg|{2\alpha_iT\over d_F}-\gamma_i \bigg|^{-{2\alpha_i \sigma \over d_F}+\delta_i-{1\over 2}} e^{-{\pi\over 2} \big| {2\alpha_iT\over d_F}- \gamma_i \big|}\bigg) \sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!}\prod_{i=1}^q\left| {2\alpha_iT\over d_F} - \gamma_i \right|{}^{2\alpha_i t\over d_F} \nonumber\\ = &{2 s^{k_F}(2\pi)^{q/2}\over d_F}\prod_{i=1}^q\bigg( \bigg|{2\alpha_iT\over d_F}-\gamma_i \bigg|^{-{2\alpha_i \sigma \over d_F}+\delta_i-{1\over 2}} e^{-{\pi\over 2} \big| {2\alpha_iT\over d_F}- \gamma_i \big|}\bigg) \cosh\left(z \prod_{i=1}^q\left|{2\alpha_iT\over d_F}- \gamma_i\right|{}^{\alpha_i\over d_F}\right), \end{align} $$
$$ \begin{align} &{2 s^{k_F}(2\pi)^{q/2}\over d_F}\prod_{i=1}^q\bigg( \bigg|{2\alpha_iT\over d_F}-\gamma_i \bigg|^{-{2\alpha_i \sigma \over d_F}+\delta_i-{1\over 2}} e^{-{\pi\over 2} \big| {2\alpha_iT\over d_F}- \gamma_i \big|}\bigg) \sum_{t=0}^{{\infty}}{z^{2t}\over(2t)!}\prod_{i=1}^q\left| {2\alpha_iT\over d_F} - \gamma_i \right|{}^{2\alpha_i t\over d_F} \nonumber\\ = &{2 s^{k_F}(2\pi)^{q/2}\over d_F}\prod_{i=1}^q\bigg( \bigg|{2\alpha_iT\over d_F}-\gamma_i \bigg|^{-{2\alpha_i \sigma \over d_F}+\delta_i-{1\over 2}} e^{-{\pi\over 2} \big| {2\alpha_iT\over d_F}- \gamma_i \big|}\bigg) \cosh\left(z \prod_{i=1}^q\left|{2\alpha_iT\over d_F}- \gamma_i\right|{}^{\alpha_i\over d_F}\right), \end{align} $$
using the Taylor series for
![]() $\cosh (z)$
. The error term involved is
$\cosh (z)$
. The error term involved is
![]() $O_F(1/|T|)$
times the absolute value of (6.20). Note that if
$O_F(1/|T|)$
times the absolute value of (6.20). Note that if
![]() $\arg z = \pm {\pi \over 2}$
, then the argument of
$\arg z = \pm {\pi \over 2}$
, then the argument of
![]() $\cosh $
above is purely imaginary, which would mean that the
$\cosh $
above is purely imaginary, which would mean that the
![]() $\cosh $
term is bounded since
$\cosh $
term is bounded since
![]() $\cosh z= \cos (iz)$
. Thus, we see that if
$\cosh z= \cos (iz)$
. Thus, we see that if
![]() $z\ne 0$
and
$z\ne 0$
and
![]() $\arg z \ne \pm {\pi \over 2}$
, then as
$\arg z \ne \pm {\pi \over 2}$
, then as
![]() $T\to \infty $
, the
$T\to \infty $
, the
![]() $\cosh $
term is unbounded. This means that as
$\cosh $
term is unbounded. This means that as
![]() $T \to \infty $
, the expression (6.20) tends to infinity in absolute value. Hence, there must exist a sufficiently large value
$T \to \infty $
, the expression (6.20) tends to infinity in absolute value. Hence, there must exist a sufficiently large value
![]() $T_{F,z}$
of T, such that for
$T_{F,z}$
of T, such that for
![]() $T>T_{F,z}$
, the expression (6.20) is nonzero. Since
$T>T_{F,z}$
, the expression (6.20) is nonzero. Since
![]() $s^{k_F}\phi (s, \boldsymbol {\alpha }, \boldsymbol {\beta }, z)$
is analytic in this region, we must have that
$s^{k_F}\phi (s, \boldsymbol {\alpha }, \boldsymbol {\beta }, z)$
is analytic in this region, we must have that
![]() $F(2s+1)$
does not vanish for
$F(2s+1)$
does not vanish for
![]() $s={\sigma }+iT$
with
$s={\sigma }+iT$
with
![]() ${\sigma } \in (-1/4,0)$
and
${\sigma } \in (-1/4,0)$
and
![]() $T> T_{F,z}$
. This means that any zeros of
$T> T_{F,z}$
. This means that any zeros of
![]() $F(s)$
in the critical strip which are of the line
$F(s)$
in the critical strip which are of the line
![]() $\Re (s)=1/2$
must lie in a vertical strip of fixed height. As the number of such zeros is finite, this proves the result.
$\Re (s)=1/2$
must lie in a vertical strip of fixed height. As the number of such zeros is finite, this proves the result.
7 Concluding remarks
We make some remarks regarding potential directions of further investigation here. Theorem 2.1 and Corollaries 2.2, 2.3, each assume the convergence of a certain series. It is possible that this assumption can be weakened by assuming convergence under the kind of bracketing given by (1.4). This may be feasible along the lines of the treatment in the classical case.
Indeed, it may even be possible to prove such “bracketed convergence” as has been done for the Riemann zeta function. This is a nontrivial question, which we have not attempted to resolve here.
Another natural question is whether some of the hypotheses assumed to prove Riesz-type criteria for our L-functions can be eliminated. While it is known that the Euler product axiom and the Ramanujan hypothesis are crucial in order to consider GRH (see, for instance, [Reference Perelli21, pp. 27–28]), it is worth asking whether the polynomial Euler product assumption can be dispensed with. One can also enquire whether Ramanujan–Hardy–Littlewood type identities are valid for larger classes of L-functions, for instance, the Lindelöf class [Reference Dixit and Murty10, Reference Kumar Murty17].
In line with Lemmas 3.5 and 3.6, it is possible to obtain nontrivial estimates for higher derivatives of
![]() $\tilde {Z}_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
, which may find useful applications in related problems.
$\tilde {Z}_{\boldsymbol {\alpha }, \boldsymbol {\beta }}(x)$
, which may find useful applications in related problems.
Acknowledgment
The authors are grateful to the referee for reading this paper and making encouraging comments. The authors express their sincere thanks to Atul Dixit, Bibekananda Maji, and Ankush Goswami for helpful conversations at various stages of this paper.