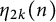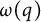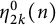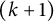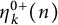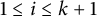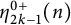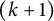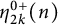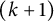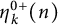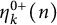1 Introduction and statement of results
This paper is concerned with combinatorial interpretations and asymptotic formulas for the symmetrized positive moments of odd ranks of odd Durfee symbols and k-marked Durfee symbols. Odd Durfee symbols and k-marked Durfee symbols were first introduced by Andrews [Reference Andrews2] in 2007, and were used to give a natural combinatorial explanation to an identity associated with Watson’s third-order mock theta function
![]() $\omega (q)$
[Reference Watson11], which is defined as
$\omega (q)$
[Reference Watson11], which is defined as
 $$\begin{align*}\omega(q):=\sum_{n=0}^\infty\frac{q^{2n(n+1)}}{(q;q^2)_{n+1}^2},\end{align*}$$
$$\begin{align*}\omega(q):=\sum_{n=0}^\infty\frac{q^{2n(n+1)}}{(q;q^2)_{n+1}^2},\end{align*}$$
where
 $$\begin{align*}(a;q)_n:=\prod_{m=0}^{n-1}(1-aq^m).\end{align*}$$
$$\begin{align*}(a;q)_n:=\prod_{m=0}^{n-1}(1-aq^m).\end{align*}$$
Definition 1.1 (Odd Durfee symbols)
An odd Durfee symbol of n is a two-rowed array with a subscript
 $$ \begin{align*} (\alpha,\beta)_d:=\left(\alpha_1\ \alpha_2\ \ldots\ \alpha_s\atop \beta_1\ \beta_2\ \ldots\ \beta_t\right)_d, \end{align*} $$
$$ \begin{align*} (\alpha,\beta)_d:=\left(\alpha_1\ \alpha_2\ \ldots\ \alpha_s\atop \beta_1\ \beta_2\ \ldots\ \beta_t\right)_d, \end{align*} $$
where
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
are all positive odd numbers,
$\beta _i$
are all positive odd numbers,
![]() $2d+1\geq \alpha _1\geq \alpha _2\geq \cdots \geq \alpha _s>0$
,
$2d+1\geq \alpha _1\geq \alpha _2\geq \cdots \geq \alpha _s>0$
,
![]() $2d+1\geq \beta _1\geq \beta _2\geq \cdots \geq \beta _t>0$
and
$2d+1\geq \beta _1\geq \beta _2\geq \cdots \geq \beta _t>0$
and
![]() $n=\sum _{i=1}^s\alpha _i+\sum _{i=1}^t\beta _i+2d^2+2d+1$
.
$n=\sum _{i=1}^s\alpha _i+\sum _{i=1}^t\beta _i+2d^2+2d+1$
.
Here, we use the rephrased version of the definition of odd Durfee symbols due to the work of Ji [Reference Ji9].
Recall that
![]() $q\omega (q)$
is also the generating function for partitions in which at least all but one instance of the largest part is one of a pair of consecutive nonnegative integers. It is trivial to see that the summation of two consecutive nonnegative integers is odd, and conversely that every odd number is a sum of two consecutive integers. We also observe that any odd positive integer can been decomposed into some
$q\omega (q)$
is also the generating function for partitions in which at least all but one instance of the largest part is one of a pair of consecutive nonnegative integers. It is trivial to see that the summation of two consecutive nonnegative integers is odd, and conversely that every odd number is a sum of two consecutive integers. We also observe that any odd positive integer can been decomposed into some
![]() $2$
’s and one
$2$
’s and one
![]() $1$
. Then there is a simple bijection between the set of partitions of n in which at least all but one instance of the largest part is one of a pair of consecutive nonnegative integers and the set of odd Durfee symbols of n. For example, the partition
$1$
. Then there is a simple bijection between the set of partitions of n in which at least all but one instance of the largest part is one of a pair of consecutive nonnegative integers and the set of odd Durfee symbols of n. For example, the partition
![]() $8+(4+3)+(3+2)+(3+2)+(1+0)+(1+0)$
can been seen as “odd Ferrers diagram”
$8+(4+3)+(3+2)+(3+2)+(1+0)+(1+0)$
can been seen as “odd Ferrers diagram”

of shape
![]() $(8,4,3,3,1,1)$
. The top row of
$(8,4,3,3,1,1)$
. The top row of
![]() $1$
’s represents 8; the second row is
$1$
’s represents 8; the second row is
![]() $(4+3)$
; the third row is
$(4+3)$
; the third row is
![]() $(3+2)$
as is the fourth row; the last two rows represent
$(3+2)$
as is the fourth row; the last two rows represent
![]() $(1+0)$
. As it shown, this odd Ferrers diagram has a Durfee square of size
$(1+0)$
. As it shown, this odd Ferrers diagram has a Durfee square of size
![]() $3$
indicated by the dotted lines. Then we see that it is mapped to the odd Durfee symbol:
$3$
indicated by the dotted lines. Then we see that it is mapped to the odd Durfee symbol:
 $$\begin{align*}\left( \begin{array}{ccccc} 3& 1&1&1&1\\ 5& 1&1&& \\ \end{array} \right)_2. \end{align*}$$
$$\begin{align*}\left( \begin{array}{ccccc} 3& 1&1&1&1\\ 5& 1&1&& \\ \end{array} \right)_2. \end{align*}$$
Analogues to ordinary rank of partitions, Andrews [Reference Andrews2] defined odd rank of an odd Durfee symbol to be the number of entries in the top row minus the number of entries in the bottom row. Let
![]() $N^0(m,n)$
denote the number of odd Durfee symbols of n with odd rank m. According to this definition, it is easy to see that
$N^0(m,n)$
denote the number of odd Durfee symbols of n with odd rank m. According to this definition, it is easy to see that
![]() $N^0(m,n)=N^0(-m,n)$
. Wang [Reference Wang10] showed that
$N^0(m,n)=N^0(-m,n)$
. Wang [Reference Wang10] showed that
![]() $N^0(m,n)=0$
for
$N^0(m,n)=0$
for
![]() $n\equiv m\pmod 2$
. Denote the number of odd Durfee symbols of n with odd rank congruent to a modulo b by
$n\equiv m\pmod 2$
. Denote the number of odd Durfee symbols of n with odd rank congruent to a modulo b by
![]() $N^0(a,b;n)$
. Wang [Reference Wang10] also obtained some generating functions for
$N^0(a,b;n)$
. Wang [Reference Wang10] also obtained some generating functions for
![]() $N^0(a,b;cn+d),$
where
$N^0(a,b;cn+d),$
where
![]() $c\in \{2,4,8\}$
, and thus derived many congruences for odd rank modulo powers of
$c\in \{2,4,8\}$
, and thus derived many congruences for odd rank modulo powers of
![]() $2$
.
$2$
.
In order to study the relations between cranks and ranks of partitions, Atkin and Garvan [Reference Atkin and Garvan3] considered the kth moment of the rank which is defined by
Here,
![]() $N(m,n)$
denotes the number of partitions of n with ordinary rank m. Andrews [Reference Andrews2] found that there is a rich combinatorial and enumerative structure related to the moments of ranks. He defined the kth symmetrized moment of rank as
$N(m,n)$
denotes the number of partitions of n with ordinary rank m. Andrews [Reference Andrews2] found that there is a rich combinatorial and enumerative structure related to the moments of ranks. He defined the kth symmetrized moment of rank as
 $$\begin{align*}\eta_k(n):=\sum_{m=-\infty}^\infty\binom{m+\lfloor\frac{k}{2}\rfloor}{k}N(m,n),\end{align*}$$
$$\begin{align*}\eta_k(n):=\sum_{m=-\infty}^\infty\binom{m+\lfloor\frac{k}{2}\rfloor}{k}N(m,n),\end{align*}$$
and discovered that
![]() $\eta _{2k}(n)$
counts
$\eta _{2k}(n)$
counts
![]() $(k+1)$
-marked Durfee symbols of n. For our purpose, we do not give the definitions of Durfee symbols and k-marked Durfee symbols here. Bringmann et al. [Reference Bringmann, Lovejoy and Osburn5] introduced two-parameter generalizations of k-marked Durfee symbols and the kth symmetrized rank moment and studied automorphic properties of their generating functions. In 2014, Chen, Ji, and Shen [Reference Chen, Ji and Shen7] defined the kth symmetrized positive moment
$(k+1)$
-marked Durfee symbols of n. For our purpose, we do not give the definitions of Durfee symbols and k-marked Durfee symbols here. Bringmann et al. [Reference Bringmann, Lovejoy and Osburn5] introduced two-parameter generalizations of k-marked Durfee symbols and the kth symmetrized rank moment and studied automorphic properties of their generating functions. In 2014, Chen, Ji, and Shen [Reference Chen, Ji and Shen7] defined the kth symmetrized positive moment
![]() $\overline {\eta }_k(n)$
of ranks of partitions of n by
$\overline {\eta }_k(n)$
of ranks of partitions of n by
 $$\begin{align*}\overline{\eta}_k(n):=\sum_{m=1}^\infty\binom{m+\lfloor\frac{k-1}{2}\rfloor}{k}N(m,n).\end{align*}$$
$$\begin{align*}\overline{\eta}_k(n):=\sum_{m=1}^\infty\binom{m+\lfloor\frac{k-1}{2}\rfloor}{k}N(m,n).\end{align*}$$
They also gave a combinatorial interpretation of
![]() $\overline {\eta }_k(n)$
. More precisely, for
$\overline {\eta }_k(n)$
. More precisely, for
![]() $1\leq i\leq k+1$
,
$1\leq i\leq k+1$
,
![]() $\overline {\eta }_{2k-1}(n)$
counts those
$\overline {\eta }_{2k-1}(n)$
counts those
![]() $(k+1)$
-marked Durfee symbols of n with the ith rank equal to 0;
$(k+1)$
-marked Durfee symbols of n with the ith rank equal to 0;
![]() $\overline {\eta }_{2k}(n)$
counts those
$\overline {\eta }_{2k}(n)$
counts those
![]() $(k+1)$
-marked Durfee symbols of n with the ith rank being positive.
$(k+1)$
-marked Durfee symbols of n with the ith rank being positive.
Furthermore, Andrews [Reference Andrews2] considered the symmetrized kth moment function of odd ranks of odd Durfee symbols
 $$\begin{align*}\eta_k^0(n):=\sum_{m=-\infty}^\infty\binom{m+\lfloor\frac{k}{2}\rfloor}{k}N^0(m,n),\end{align*}$$
$$\begin{align*}\eta_k^0(n):=\sum_{m=-\infty}^\infty\binom{m+\lfloor\frac{k}{2}\rfloor}{k}N^0(m,n),\end{align*}$$
and showed that
![]() $\eta _{2k}^0(n)$
is equal to the number of
$\eta _{2k}^0(n)$
is equal to the number of
![]() $(k+1)$
-marked odd Durfee symbols of n. It is the right time to give the definition of k-marked odd Durfee symbols.
$(k+1)$
-marked odd Durfee symbols of n. It is the right time to give the definition of k-marked odd Durfee symbols.
Definition 1.2 (k-marked odd Durfee symbols)
A k-marked odd Durfee symbol of n is composed of k-pairs of partitions into odd parts with the subscript, which is defined as
 $$\begin{align*}\eta^0:=\left(\alpha^k,\alpha^{k-1},\ldots,\alpha^1\atop \beta^k,\beta^{k-1},\ldots,\beta^1\right)_d,\end{align*}$$
$$\begin{align*}\eta^0:=\left(\alpha^k,\alpha^{k-1},\ldots,\alpha^1\atop \beta^k,\beta^{k-1},\ldots,\beta^1\right)_d,\end{align*}$$
where
![]() $\alpha ^i$
(resp.
$\alpha ^i$
(resp.
![]() $\beta ^i$
) are all partitions with odd parts and
$\beta ^i$
) are all partitions with odd parts and
![]() $\sum _{i=1}^k(|\alpha ^i|+|\beta ^i|)+2d^2+2d+1$
=n. Furthermore, the partitions
$\sum _{i=1}^k(|\alpha ^i|+|\beta ^i|)+2d^2+2d+1$
=n. Furthermore, the partitions
![]() $\alpha ^i$
and
$\alpha ^i$
and
![]() $\beta ^i$
must satisfy the following three conditions:
$\beta ^i$
must satisfy the following three conditions:
-
(i) For
 $1\leq i< k$
,
$1\leq i< k$
,
 $\alpha ^i$
must be non-empty partition, while
$\alpha ^i$
must be non-empty partition, while
 $\alpha ^k$
and
$\alpha ^k$
and
 $\beta ^i$
could be empty;
$\beta ^i$
could be empty; -
(ii)
 $\beta _1^{i-1}\leq \alpha _1^{i-1}\leq \beta _{\ell (\beta ^i)}^i$
for
$\beta _1^{i-1}\leq \alpha _1^{i-1}\leq \beta _{\ell (\beta ^i)}^i$
for
 $2\leq i\leq k$
;
$2\leq i\leq k$
; -
(iii)
 $\beta ^k_1$
,
$\beta ^k_1$
,
 $\alpha _1^k\leq 2d+1$
,
$\alpha _1^k\leq 2d+1$
,
where
![]() $\alpha _1^i$
(resp.
$\alpha _1^i$
(resp.
![]() $\beta _1^i$
) is the largest part of the partition
$\beta _1^i$
) is the largest part of the partition
![]() $\alpha ^i$
(resp.
$\alpha ^i$
(resp.
![]() $\beta ^i$
) and
$\beta ^i$
) and
![]() $\alpha _{l(\alpha ^i)}^i$
(resp.
$\alpha _{l(\alpha ^i)}^i$
(resp.
![]() $\beta _{l(\beta ^i)}^i$
) is the smallest part of the partition
$\beta _{l(\beta ^i)}^i$
) is the smallest part of the partition
![]() $\alpha ^i$
(resp.
$\alpha ^i$
(resp.
![]() $\beta ^i$
), and
$\beta ^i$
), and
![]() $\ell (\beta )$
denotes the number of parts of the partition
$\ell (\beta )$
denotes the number of parts of the partition
![]() $\beta $
. Moreover, the ith odd rank of
$\beta $
. Moreover, the ith odd rank of
![]() $\eta ^0$
is defined as
$\eta ^0$
is defined as
 $$\begin{align*}r_i(\eta^0):=\left\{ \begin{array}{ll} \ell(\alpha^i)-\ell(\beta^i)-1, & \text{for }1\leq i<k, \\ \ell(\alpha^k)-\ell(\beta^k), & \text{for }i=k. \end{array} \right. \end{align*}$$
$$\begin{align*}r_i(\eta^0):=\left\{ \begin{array}{ll} \ell(\alpha^i)-\ell(\beta^i)-1, & \text{for }1\leq i<k, \\ \ell(\alpha^k)-\ell(\beta^k), & \text{for }i=k. \end{array} \right. \end{align*}$$
Some open problems and conjectures proposed by Andrews in [Reference Andrews2] have since driven the study of this combinatorial structure. For example, Bringmann [Reference Bringmann4] gave effective asymptotic formulas for the symmetrized second moment functions
![]() $\eta _2(n)$
and
$\eta _2(n)$
and
![]() $\eta ^0_2(n)$
. Namely, we have
$\eta ^0_2(n)$
. Namely, we have
 $$ \begin{align*} \eta_2(n)=&\sum_{k=1}^{\lfloor\sqrt{n}\rfloor}A_k(n)\bigg[ -\frac{3}{2(24n-1)^{\frac{1}{4}}}I_{1/2}\bigg(\frac{\pi}{6k}\sqrt{24n-1}\bigg)+\frac{\pi (24n-1)^{\frac{1}{4}}}{12k}\\ &\ \times I_{-1/2}\bigg(\frac{\pi}{6k}\sqrt{24n-1}\bigg)+\frac{\pi}{12k(24n-1)^{\frac{3}{4}}} I_{3/2}\bigg(\frac{\pi}{6k}\sqrt{24n-1}\bigg)\bigg]+O(n^{1+\epsilon}), \end{align*} $$
$$ \begin{align*} \eta_2(n)=&\sum_{k=1}^{\lfloor\sqrt{n}\rfloor}A_k(n)\bigg[ -\frac{3}{2(24n-1)^{\frac{1}{4}}}I_{1/2}\bigg(\frac{\pi}{6k}\sqrt{24n-1}\bigg)+\frac{\pi (24n-1)^{\frac{1}{4}}}{12k}\\ &\ \times I_{-1/2}\bigg(\frac{\pi}{6k}\sqrt{24n-1}\bigg)+\frac{\pi}{12k(24n-1)^{\frac{3}{4}}} I_{3/2}\bigg(\frac{\pi}{6k}\sqrt{24n-1}\bigg)\bigg]+O(n^{1+\epsilon}), \end{align*} $$
and
 $$ \begin{align*} \eta_2^0(n)=-\frac{i}{\sqrt{2}}\sum_{k=1\atop k odd}^{\lfloor\sqrt{n}\rfloor}A^0_k(n)&\bigg[ -\frac{3\pi^2(3n-1)^{\frac{1}{4}}}{4}I_{-1/2}\bigg(\frac{\pi}{3k}\sqrt{3n-1}\bigg)\\ &+\frac{\pi (3n-1)^{\frac{3}{4}}}{16k} I_{-3/2}\bigg(\frac{\pi}{3k}\sqrt{3n-1}\bigg)\bigg]+O(n^{2+\epsilon}), \end{align*} $$
$$ \begin{align*} \eta_2^0(n)=-\frac{i}{\sqrt{2}}\sum_{k=1\atop k odd}^{\lfloor\sqrt{n}\rfloor}A^0_k(n)&\bigg[ -\frac{3\pi^2(3n-1)^{\frac{1}{4}}}{4}I_{-1/2}\bigg(\frac{\pi}{3k}\sqrt{3n-1}\bigg)\\ &+\frac{\pi (3n-1)^{\frac{3}{4}}}{16k} I_{-3/2}\bigg(\frac{\pi}{3k}\sqrt{3n-1}\bigg)\bigg]+O(n^{2+\epsilon}), \end{align*} $$
where
![]() $A_k^0(n)$
is a certain Kloosterman type summation and the function
$A_k^0(n)$
is a certain Kloosterman type summation and the function
![]() $I_k(x)$
is the usual I-Bessel function of order k. Alfes et al. [Reference Alfes, Bringmann and Lovejoy1] introduced two-parameter generalizations of
$I_k(x)$
is the usual I-Bessel function of order k. Alfes et al. [Reference Alfes, Bringmann and Lovejoy1] introduced two-parameter generalizations of
![]() $(k+1)$
-marked odd Durfee symbols and the
$(k+1)$
-marked odd Durfee symbols and the
![]() $2k$
th symmetrized odd rank moment and studied automorphic properties of their generating functions. With the help of Mittag-Leffler decomposition and Wright’s variant of the Hardy–Ramanujan circle method, Bringmann and Mahlburg [Reference Bringmann and Mahlburg6] found an asymptotic formula of the symmetrized positive moments
$2k$
th symmetrized odd rank moment and studied automorphic properties of their generating functions. With the help of Mittag-Leffler decomposition and Wright’s variant of the Hardy–Ramanujan circle method, Bringmann and Mahlburg [Reference Bringmann and Mahlburg6] found an asymptotic formula of the symmetrized positive moments
![]() $\eta _k^+(n)$
of ranks of partitions, where
$\eta _k^+(n)$
of ranks of partitions, where
 $$\begin{align*}\eta_k^+(n):=\sum_{m=1}^\infty\binom{m+\lfloor\frac{k-1}{2}\rfloor}{k} N(m,n).\end{align*}$$
$$\begin{align*}\eta_k^+(n):=\sum_{m=1}^\infty\binom{m+\lfloor\frac{k-1}{2}\rfloor}{k} N(m,n).\end{align*}$$
If the kth symmetrized positive moment
![]() $\eta ^{0+}_k(n)$
of odd ranks of odd Durfee symbols of n is given by
$\eta ^{0+}_k(n)$
of odd ranks of odd Durfee symbols of n is given by
 $$\begin{align*}\eta_k^{0+}(n):=\sum_{m=1}^\infty\binom{m+\lfloor\frac{k-1}{2}\rfloor}{k} N^0(m,n),\end{align*}$$
$$\begin{align*}\eta_k^{0+}(n):=\sum_{m=1}^\infty\binom{m+\lfloor\frac{k-1}{2}\rfloor}{k} N^0(m,n),\end{align*}$$
it is natural to ask which combinatorial structure counted by
![]() $\eta ^{0+}_k(n)$
and study the asymptotic behavior of
$\eta ^{0+}_k(n)$
and study the asymptotic behavior of
![]() $\eta ^{0+}_k(n)$
.
$\eta ^{0+}_k(n)$
.
One of main objectives of this paper is to give an combinatorial interpretation of
![]() $\eta ^{0+}_{k}(n)$
in terms of k-marked Durfee symbols. Denote the number of k-marked odd Durfee symbols of n with the ith odd rank equal to
$\eta ^{0+}_{k}(n)$
in terms of k-marked Durfee symbols. Denote the number of k-marked odd Durfee symbols of n with the ith odd rank equal to
![]() $m_i$
by
$m_i$
by
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
. Andrews [Reference Andrews2] showed that
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
. Andrews [Reference Andrews2] showed that
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
is symmetric with respect to
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
is symmetric with respect to
![]() $m_1,m_2,\ldots ,m_k$
for
$m_1,m_2,\ldots ,m_k$
for
![]() $k\geq 2$
. Moreover, Ji [Reference Ji9] found the following relation:
$k\geq 2$
. Moreover, Ji [Reference Ji9] found the following relation:
 $$\begin{align*}D_k^0(m_1,m_2,\ldots,m_k;n)=\sum_{j=0}^\infty\binom{j+k-2}{k-2}N^0\left(\sum_{i=1}^k|m_i|+2j+k-1,n\right).\end{align*}$$
$$\begin{align*}D_k^0(m_1,m_2,\ldots,m_k;n)=\sum_{j=0}^\infty\binom{j+k-2}{k-2}N^0\left(\sum_{i=1}^k|m_i|+2j+k-1,n\right).\end{align*}$$
With the aid of symmetry of
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
and the relation above, we find the following combinatorial interpretations of
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
and the relation above, we find the following combinatorial interpretations of
![]() $\eta ^{0+}_{k}(n)$
.
$\eta ^{0+}_{k}(n)$
.
Theorem 1.3 For any
![]() $k\geq 1$
and fixed
$k\geq 1$
and fixed
![]() $i\geq 1$
, we have:
$i\geq 1$
, we have:
-
(1)
 $\eta ^{0+}_{2k-1}(n)$
is equal to the number of
$\eta ^{0+}_{2k-1}(n)$
is equal to the number of
 $(k+1)$
-marked odd Durfee symbols of n with the ith odd rank equal to zero;
$(k+1)$
-marked odd Durfee symbols of n with the ith odd rank equal to zero; -
(2)
 $\eta ^{0+}_{2k}(n)$
is equal to the number of
$\eta ^{0+}_{2k}(n)$
is equal to the number of
 $(k+1)$
-marked odd Durfee symbols of n with the ith odd rank being positive.
$(k+1)$
-marked odd Durfee symbols of n with the ith odd rank being positive.
Notice that the generating function of the odd rank function
![]() $N^0(m,n)$
of odd Durfee symbols is
$N^0(m,n)$
of odd Durfee symbols is
 $$ \begin{align} R^0(w;q):=&\sum_{n=1}^\infty\sum_{m=-\infty}^\infty N^0(m,n)w^mq^n\nonumber\\[5pt] =&\sum_{n= 0}^\infty\frac{q^{2n(n+1)+1}}{(wq;q^2)_{n+1}(w^{-1}q;q^2)_{n+1}}\nonumber\\[5pt] =&\frac{1}{(q^2;q^2)_\infty}\sum_{n=-\infty}^\infty\frac{(-1)^nq^{3n^2+3n+1}}{1-wq^{2n+1}}. \end{align} $$
$$ \begin{align} R^0(w;q):=&\sum_{n=1}^\infty\sum_{m=-\infty}^\infty N^0(m,n)w^mq^n\nonumber\\[5pt] =&\sum_{n= 0}^\infty\frac{q^{2n(n+1)+1}}{(wq;q^2)_{n+1}(w^{-1}q;q^2)_{n+1}}\nonumber\\[5pt] =&\frac{1}{(q^2;q^2)_\infty}\sum_{n=-\infty}^\infty\frac{(-1)^nq^{3n^2+3n+1}}{1-wq^{2n+1}}. \end{align} $$
The last identity is equivalent to Watson’s first identity on page 66 of [Reference Watson11]. By expanding the summand of (1.1), we find that for any m,
Using this generating function (1.2) of
![]() $N^0(m,n)$
and the combinatorial interpretation of
$N^0(m,n)$
and the combinatorial interpretation of
![]() $\eta ^{0+}_{r}(n)$
in Theorem 1.3, we obtain the following generating functions of
$\eta ^{0+}_{r}(n)$
in Theorem 1.3, we obtain the following generating functions of
![]() $\eta ^{0+}_{r}(n)$
.
$\eta ^{0+}_{r}(n)$
.
Theorem 1.4 For any
![]() $r\geq 1$
, we have
$r\geq 1$
, we have
 $$ \begin{align} \sum_{n=0}^\infty\eta^{0+}_{r}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+3n+1+(2n+1)\lfloor\frac{r+1}{2}\rfloor}}{(1-q^{2n+1})^{r+1}}. \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty\eta^{0+}_{r}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+3n+1+(2n+1)\lfloor\frac{r+1}{2}\rfloor}}{(1-q^{2n+1})^{r+1}}. \end{align} $$
Although Wright’s approach is lesser-known, and gives much weaker results than Hardy and Ramanujan in the study of the coefficients of modular forms, it is powerful enough to provide an asymptotic expansion for the coefficients and flexible enough that it applies to nonmodular generating functions such as the symmetrized positive odd rank moments. Let
![]() $I_\ell $
denote the usual I-Bessel function of order
$I_\ell $
denote the usual I-Bessel function of order
![]() $\ell $
. The Dirichlet beta function
$\ell $
. The Dirichlet beta function
![]() $\beta (s)$
(also known as the Catalan beta function) is defined as
$\beta (s)$
(also known as the Catalan beta function) is defined as
 $$\begin{align*}\beta(s):=\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^s},\end{align*}$$
$$\begin{align*}\beta(s):=\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^s},\end{align*}$$
where we assume
![]() $\mathrm {Re}(s)>0$
. Based on the generating function of
$\mathrm {Re}(s)>0$
. Based on the generating function of
![]() $\eta ^{0+}_{r}(n)$
in Theorem 1.4, we apply Wright’s variant of the Hardy–Ramanujan circle method to study the asymptotic behavior of the symmetrized positive moments.
$\eta ^{0+}_{r}(n)$
in Theorem 1.4, we apply Wright’s variant of the Hardy–Ramanujan circle method to study the asymptotic behavior of the symmetrized positive moments.
Theorem 1.5 Suppose that
![]() $r\geq 2$
. As
$r\geq 2$
. As
![]() $N\rightarrow \infty $
,
$N\rightarrow \infty $
,
 $$ \begin{align*} \eta^{0+}_r(N)= \lambda_rN^{\frac{2r-1}{4}}I_{r-\frac{1}{2}}\left(\pi \sqrt{\frac{N}{3}}\right) +\mu_rN^{\frac{2r-3}{4}}I_{r-\frac{3}{2}}\left(\pi \sqrt{\frac{N}{3}}\right)+O\left(N^{\frac{2r-5}{4}}e^{\frac{\pi \sqrt{N}}{\sqrt{3}}}\right), \end{align*} $$
$$ \begin{align*} \eta^{0+}_r(N)= \lambda_rN^{\frac{2r-1}{4}}I_{r-\frac{1}{2}}\left(\pi \sqrt{\frac{N}{3}}\right) +\mu_rN^{\frac{2r-3}{4}}I_{r-\frac{3}{2}}\left(\pi \sqrt{\frac{N}{3}}\right)+O\left(N^{\frac{2r-5}{4}}e^{\frac{\pi \sqrt{N}}{\sqrt{3}}}\right), \end{align*} $$
where the constants
![]() $\lambda _r$
and
$\lambda _r$
and
![]() $\mu _r$
are given by
$\mu _r$
are given by
Utilizing the well-known asymptotic formula for the modified Bessel functions:
we obtain the following asymptotic formula of symmetrized positive moments of odd ranks.
Corollary 1.6 Suppose that
![]() $r\geq 2$
. As
$r\geq 2$
. As
![]() $N\rightarrow \infty $
,
$N\rightarrow \infty $
,
Remark 1.7 It should be noted that the asymptotic formula for
![]() $\eta ^{0+}_r(N)$
in Corollary 1.6 also holds for
$\eta ^{0+}_r(N)$
in Corollary 1.6 also holds for
![]() $r=1$
, although the proof is simpler, but slightly different from those for
$r=1$
, although the proof is simpler, but slightly different from those for
![]() $r\geq 2$
in the proof of Theorem 1.5.
$r\geq 2$
in the proof of Theorem 1.5.
This paper is organized as follows: In Section 2, we first define the kth symmetrized positive moment
![]() $\eta _k^{0+}(n)$
of odd ranks by
$\eta _k^{0+}(n)$
of odd ranks by
 $$\begin{align*}\eta^{0+}_{k}(n):=\sum_{m=1}^\infty\binom{m+\left\lfloor\frac{k-1}{2}\right\rfloor}{k}N^0(m,n).\end{align*}$$
$$\begin{align*}\eta^{0+}_{k}(n):=\sum_{m=1}^\infty\binom{m+\left\lfloor\frac{k-1}{2}\right\rfloor}{k}N^0(m,n).\end{align*}$$
Then we prove that for all
![]() $1\leq i\leq k+1$
,
$1\leq i\leq k+1$
,
![]() $\eta _{2k-1}^{0+}(n)$
is equal to the number of
$\eta _{2k-1}^{0+}(n)$
is equal to the number of
![]() $(k+1)$
-marked Durfee symbols of n with the ith odd rank equal to zero and
$(k+1)$
-marked Durfee symbols of n with the ith odd rank equal to zero and
![]() $\eta _{2k}^{0+}(n)$
is equal to the number of
$\eta _{2k}^{0+}(n)$
is equal to the number of
![]() $(k+1)$
-marked Durfee symbols of n with the ith odd rank being positive, which are stated in Theorem 1.3. In Section 3, we show that the generating function, given in Theorem 1.4, of
$(k+1)$
-marked Durfee symbols of n with the ith odd rank being positive, which are stated in Theorem 1.3. In Section 3, we show that the generating function, given in Theorem 1.4, of
![]() $\eta _{k}^{0+}(n) (k\geq 1)$
is
$\eta _{k}^{0+}(n) (k\geq 1)$
is
 $$\begin{align*}\sum_{n=0}^\infty\eta^{0+}_{k}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+3n+1+(2n+1)\left\lfloor\frac{k+1}{2}\right\rfloor}}{(1-q^{2n+1})^{k+1}}.\end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty\eta^{0+}_{k}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+3n+1+(2n+1)\left\lfloor\frac{k+1}{2}\right\rfloor}}{(1-q^{2n+1})^{k+1}}.\end{align*}$$
In Section 4, we first study the asymptotic behavior of the generating function of
![]() $\eta _{k}^{0+}(n)$
, and then use Wright’s variant of the Hardy–Ramanujan circle method to obtain an asymptotic formula for
$\eta _{k}^{0+}(n)$
, and then use Wright’s variant of the Hardy–Ramanujan circle method to obtain an asymptotic formula for
![]() $\eta _{k}^{0+}(n) (k\geq 2)$
in Corollary 1.6:
$\eta _{k}^{0+}(n) (k\geq 2)$
in Corollary 1.6:
as n tends to infinity in which
![]() $\beta (k)$
is the Dirichlet beta function.
$\beta (k)$
is the Dirichlet beta function.
2 Combinatorial interpretations for
 $\eta ^{0+}_k(n)$
$\eta ^{0+}_k(n)$
Motivated the work of Chen, Ji, and Shen [Reference Chen, Ji and Shen7], we consider the kth symmetrized positive moment
![]() $\eta ^{0+}_k(n)$
of odd ranks of odd Durfee symbols of n. Before giving combinatorial interpretations of
$\eta ^{0+}_k(n)$
of odd ranks of odd Durfee symbols of n. Before giving combinatorial interpretations of
![]() $\eta ^{0+}_{k}(n)$
, we need some definitions and related results. Denote the number of k-marked odd Durfee symbols of n with the ith odd rank equal to
$\eta ^{0+}_{k}(n)$
, we need some definitions and related results. Denote the number of k-marked odd Durfee symbols of n with the ith odd rank equal to
![]() $m_i$
by
$m_i$
by
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
. Andrews [Reference Andrews2] showed that
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
. Andrews [Reference Andrews2] showed that
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
is symmetric in
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
is symmetric in
![]() $m_1,m_2,\ldots ,m_k$
for
$m_1,m_2,\ldots ,m_k$
for
![]() $k\geq 2$
. Ji [Reference Ji9] found the following relation between
$k\geq 2$
. Ji [Reference Ji9] found the following relation between
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
and
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
and
![]() $N^0(m,n)$
.
$N^0(m,n)$
.
Theorem 2.1 [Reference Ji9, Theorem 4.9] For
![]() $k\geq 2$
, we have
$k\geq 2$
, we have
 $$ \begin{align} D_k^0(m_1,m_2,\ldots,m_k;n)=\sum_{j=0}^\infty\binom{j+k-2}{k-2}N^0\left(\sum_{i=1}^k|m_i|+2j+k-1,n\right). \end{align} $$
$$ \begin{align} D_k^0(m_1,m_2,\ldots,m_k;n)=\sum_{j=0}^\infty\binom{j+k-2}{k-2}N^0\left(\sum_{i=1}^k|m_i|+2j+k-1,n\right). \end{align} $$
Note that
![]() $\binom {j+k-2}{k-2}$
is the number of nonnegative integer solutions to
$\binom {j+k-2}{k-2}$
is the number of nonnegative integer solutions to
![]() $t_1+t_2+\cdots +t_{k-1}=j$
. Then we find that the identity (2.1) is equivalent to
$t_1+t_2+\cdots +t_{k-1}=j$
. Then we find that the identity (2.1) is equivalent to
 $$ \begin{align} D_k^0(m_1,m_2,\ldots,m_k;n) =\sum_{t_1,\ldots,t_{k-1}=0}^{\infty}N^0\left(\sum_{i=1}^k|m_i|+2\sum_{i=1}^{k-1}t_i+k-1,n\right). \end{align} $$
$$ \begin{align} D_k^0(m_1,m_2,\ldots,m_k;n) =\sum_{t_1,\ldots,t_{k-1}=0}^{\infty}N^0\left(\sum_{i=1}^k|m_i|+2\sum_{i=1}^{k-1}t_i+k-1,n\right). \end{align} $$
Based on this relation above, we give the combinatorial interpretations of
![]() $\eta ^{0+}_{k}(n)$
in Theorem 1.3.
$\eta ^{0+}_{k}(n)$
in Theorem 1.3.
Proof of Theorem 1.3
(1) Since
![]() $D_k^0(m_1,m_2,\ldots ,m_k;n)$
is symmetric, it suffices to show that
$D_k^0(m_1,m_2,\ldots ,m_k;n)$
is symmetric, it suffices to show that
 $$\begin{align*}\sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty D_{k+1}^0(0,m_2,m_3,\ldots,m_{k+1};n)=\eta^{0+}_{2k-1}(n).\end{align*}$$
$$\begin{align*}\sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty D_{k+1}^0(0,m_2,m_3,\ldots,m_{k+1};n)=\eta^{0+}_{2k-1}(n).\end{align*}$$
From the relation (2.2), we derive that
 $$ \begin{align} &\sum_{m_2,m_3,\ldots,m_{k+1} =-\infty}^\infty D^0_{k+1}(0,m_2,m_3,\ldots,m_{k+1};n)\\[5pt]\nonumber &\qquad=\sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty \sum_{t_1,\ldots,t_{k-1}=0}^{\infty}N^0\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^{k}t_i+k,n\right). \end{align} $$
$$ \begin{align} &\sum_{m_2,m_3,\ldots,m_{k+1} =-\infty}^\infty D^0_{k+1}(0,m_2,m_3,\ldots,m_{k+1};n)\\[5pt]\nonumber &\qquad=\sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty \sum_{t_1,\ldots,t_{k-1}=0}^{\infty}N^0\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^{k}t_i+k,n\right). \end{align} $$
For fixed k and n, let
![]() $c_k(n)$
denote the number of integer solutions to the equation
$c_k(n)$
denote the number of integer solutions to the equation
where
![]() $t_i\geq 0$
for
$t_i\geq 0$
for
![]() $1\leq i\leq k$
. Then the generating function of
$1\leq i\leq k$
. Then the generating function of
![]() $c_k(n)$
is
$c_k(n)$
is
 $$ \begin{align*} \sum_{n=0}^\infty c_k(n)q^n&=(1+2q+2q^2+2q^3+\ldots)^k(1+q^2+q^4+q^6+\ldots)^k\\[5pt] &=\left(\frac{1+q}{1-q}\right)^k\left(\frac{1}{1-q^2}\right)^k=\frac{1}{(1-q)^{2k}}\\[5pt] &=\sum_{n=0}^\infty\binom{n+2k-1}{2k-1}q^n. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty c_k(n)q^n&=(1+2q+2q^2+2q^3+\ldots)^k(1+q^2+q^4+q^6+\ldots)^k\\[5pt] &=\left(\frac{1+q}{1-q}\right)^k\left(\frac{1}{1-q^2}\right)^k=\frac{1}{(1-q)^{2k}}\\[5pt] &=\sum_{n=0}^\infty\binom{n+2k-1}{2k-1}q^n. \end{align*} $$
Therefore, the identity (2.3) is equivalent to
 $$ \begin{align} \sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty D^0_{k+1}(0,m_2,m_3,\ldots,m_{k+1};n) =\sum_{m=0}^\infty \binom{m+k-1}{2k-1}N^0(m,n), \end{align} $$
$$ \begin{align} \sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty D^0_{k+1}(0,m_2,m_3,\ldots,m_{k+1};n) =\sum_{m=0}^\infty \binom{m+k-1}{2k-1}N^0(m,n), \end{align} $$
which is equal to
![]() $\overline {\eta }_{2k-1}(n)$
.
$\overline {\eta }_{2k-1}(n)$
.
(2) It suffices to show that
 $$ \begin{align*} &\sum_{m_1=1\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^{+\infty}D_{k+1}^0(m_1,m_2,\ldots,m_{k+1};n)\\[5pt] &\qquad=\sum_{m_1=1\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^{+\infty}\sum_{t_1,\ldots,t_k=0}^\infty N^0\left(m_1+\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i+k,n\right). \end{align*} $$
$$ \begin{align*} &\sum_{m_1=1\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^{+\infty}D_{k+1}^0(m_1,m_2,\ldots,m_{k+1};n)\\[5pt] &\qquad=\sum_{m_1=1\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^{+\infty}\sum_{t_1,\ldots,t_k=0}^\infty N^0\left(m_1+\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i+k,n\right). \end{align*} $$
For fixed k and n, let
![]() $c_k(n)$
denote the number of integer solutions to the equation
$c_k(n)$
denote the number of integer solutions to the equation
where
![]() $m_1$
is a positive integer and
$m_1$
is a positive integer and
![]() $t_i\geq 0$
for
$t_i\geq 0$
for
![]() $0\leq i\leq k$
. Then the generating function of
$0\leq i\leq k$
. Then the generating function of
![]() $c_k(n)$
is
$c_k(n)$
is
It follows that
 $$ \begin{align*} \sum_{m_1=1\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^{\infty}D_{k+1}^0(m_1,m_2,\ldots,m_{k+1};n) =\sum_{m=0}^\infty \binom{m+k-1}{2k} N^0(m,n), \end{align*} $$
$$ \begin{align*} \sum_{m_1=1\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^{\infty}D_{k+1}^0(m_1,m_2,\ldots,m_{k+1};n) =\sum_{m=0}^\infty \binom{m+k-1}{2k} N^0(m,n), \end{align*} $$
which is equal to
![]() $\eta ^{0+}_{2k}(n)$
.
$\eta ^{0+}_{2k}(n)$
.
3 Generating functions of
 $\eta ^{0+}_k(n)$
$\eta ^{0+}_k(n)$
In this section, we use the generating function of
![]() $N^0(m,n)$
to calculate the generating functions of
$N^0(m,n)$
to calculate the generating functions of
![]() $D_{k+1}(0,m_2,\ldots ,m_{k+1};n)$
and
$D_{k+1}(0,m_2,\ldots ,m_{k+1};n)$
and
![]() $D_{k+1}(m_1,m_2,\ldots ,m_{k+1};n) (m_1>0)$
. Then we obtain the generating functions of
$D_{k+1}(m_1,m_2,\ldots ,m_{k+1};n) (m_1>0)$
. Then we obtain the generating functions of
![]() $\eta ^{0+}_{2k-1}(n)$
and
$\eta ^{0+}_{2k-1}(n)$
and
![]() $\eta ^{0+}_{2k}(n)$
.
$\eta ^{0+}_{2k}(n)$
.
Theorem 3.1 For
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
 $$ \begin{align*} &\sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty \sum_{n=0}^\infty D_{k+1}^0(0,m_2,\ldots,m_{k+1};n)x_1^{m_2}\ldots x_k^{m_{k+1}}q^n\\[5pt] &\qquad =\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty(-1)^n \frac{q^{3n^2+3n+1+k(2n+1)}}{\prod_{j=1}^k(1-x_jq^{2n+1})(1-x_j^{-1}q^{2n+1})}. \end{align*} $$
$$ \begin{align*} &\sum_{m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty \sum_{n=0}^\infty D_{k+1}^0(0,m_2,\ldots,m_{k+1};n)x_1^{m_2}\ldots x_k^{m_{k+1}}q^n\\[5pt] &\qquad =\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty(-1)^n \frac{q^{3n^2+3n+1+k(2n+1)}}{\prod_{j=1}^k(1-x_jq^{2n+1})(1-x_j^{-1}q^{2n+1})}. \end{align*} $$
Proof Define
 $$\begin{align*}G_k(x_1,\ldots,x_k;q):=\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty \sum_{n=0}^\infty D_{k+1}^0(0,m_2,\ldots,m_{k+1};n)x_1^{m_2}\ldots x_k^{m_{k+1}}q^n.\end{align*}$$
$$\begin{align*}G_k(x_1,\ldots,x_k;q):=\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty \sum_{n=0}^\infty D_{k+1}^0(0,m_2,\ldots,m_{k+1};n)x_1^{m_2}\ldots x_k^{m_{k+1}}q^n.\end{align*}$$
With the help of the generating function (1.2) of
![]() $N^0(m,n)$
and the relation (2.2), we find that
$N^0(m,n)$
and the relation (2.2), we find that
 $$ \begin{align*} &G_k(x_1,\ldots,x_k;q)\\[5pt] &\qquad=\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty\sum_{t_1,\ldots,t_k=0}^\infty x_1^{m_2}x_2^{m_3}\ldots x_k^{m_{k+1}} \sum_{n=0}^\infty N^0\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i+k,n\right)q^n\\[5pt] &\qquad =\frac{1}{(q^2;q^2)_\infty}\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty\sum_{t_1,\ldots,t_k=0}^\infty x_1^{m_2}\ldots x_k^{m_{k+1}}\\[5pt] &\qquad\qquad\qquad\times\sum_{n=0}^\infty (-1)^nq^{3n^2+3n+1+\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i+k\right)(2n+1)}\\[5pt] &\qquad=\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty (-1)^nq^{3n^2+3n+1+k(2n+1)}\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty\\[5pt] &\qquad\qquad\qquad\times\sum_{t_1,\ldots,t_k=0}^\infty x_1^{m_2}\ldots x_k^{m_{k+1}}q^{(2n+1)\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i\right).} \end{align*} $$
$$ \begin{align*} &G_k(x_1,\ldots,x_k;q)\\[5pt] &\qquad=\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty\sum_{t_1,\ldots,t_k=0}^\infty x_1^{m_2}x_2^{m_3}\ldots x_k^{m_{k+1}} \sum_{n=0}^\infty N^0\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i+k,n\right)q^n\\[5pt] &\qquad =\frac{1}{(q^2;q^2)_\infty}\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty\sum_{t_1,\ldots,t_k=0}^\infty x_1^{m_2}\ldots x_k^{m_{k+1}}\\[5pt] &\qquad\qquad\qquad\times\sum_{n=0}^\infty (-1)^nq^{3n^2+3n+1+\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i+k\right)(2n+1)}\\[5pt] &\qquad=\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty (-1)^nq^{3n^2+3n+1+k(2n+1)}\sum_{m_2,\ldots,m_{k+1}=-\infty}^\infty\\[5pt] &\qquad\qquad\qquad\times\sum_{t_1,\ldots,t_k=0}^\infty x_1^{m_2}\ldots x_k^{m_{k+1}}q^{(2n+1)\left(\sum_{i=2}^{k+1}|m_i|+2\sum_{i=1}^kt_i\right).} \end{align*} $$
Applying the formula
 $$\begin{align*}\sum_{a=-\infty}^\infty\sum_{b=0}^\infty x^aq^{(2n+1)(|a|+2b)}=\frac{1}{(1-xq^{2n+1})(1-x^{-1}q^{2n+1})}\end{align*}$$
$$\begin{align*}\sum_{a=-\infty}^\infty\sum_{b=0}^\infty x^aq^{(2n+1)(|a|+2b)}=\frac{1}{(1-xq^{2n+1})(1-x^{-1}q^{2n+1})}\end{align*}$$
repeatedly, we find that
 $$\begin{align*}G_k(x_1,\ldots,x_k;q)=\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty (-1)^n\frac{q^{3n^2+3n+1+k(2n+1)}}{\prod_{j=1}^k(1-x_jq^{2n+1})(1-x_j^{-1}q^{2n+1})}.\end{align*}$$
$$\begin{align*}G_k(x_1,\ldots,x_k;q)=\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty (-1)^n\frac{q^{3n^2+3n+1+k(2n+1)}}{\prod_{j=1}^k(1-x_jq^{2n+1})(1-x_j^{-1}q^{2n+1})}.\end{align*}$$
Setting
![]() $x_i=1 (1\leq i\leq k)$
in Theorem 3.1 and using Theorem 1.3, we derive the following generating function of
$x_i=1 (1\leq i\leq k)$
in Theorem 3.1 and using Theorem 1.3, we derive the following generating function of
![]() $\eta ^{0+}_{2k-1}(n)$
.
$\eta ^{0+}_{2k-1}(n)$
.
Theorem 3.2 For
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
 $$\begin{align*}\sum_{n=0}^\infty\eta^{0+}_{2k-1}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+(2k+3)n+k+1}}{(1-q^{2n+1})^{2k}}.\end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty\eta^{0+}_{2k-1}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+(2k+3)n+k+1}}{(1-q^{2n+1})^{2k}}.\end{align*}$$
Similar to the proof of Theorem 3.1, one may obtain the generating function of
![]() $D_{k+1}^0(m_1,m_2,\ldots ,m_{k+1};n)$
.
$D_{k+1}^0(m_1,m_2,\ldots ,m_{k+1};n)$
.
Theorem 3.3 For
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
 $$ \begin{align*} &\sum_{m_1>0\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty \sum_{n=0}^\infty D_{k+1}^0(m_1,m_2,\ldots,m_{k+1};n)x_1^{m_1}\ldots x_{k+1}^{m_{k+1}}q^n\\[5pt] &\qquad=\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty(-1)^n \frac{x_1q^{3n^2+3n+1+k(2n+1)}}{(1-x_1q^{2n+1}) \prod_{j=2}^{k+1}(1-x_jq^{2n+1})(1-x_j^{-1}q^{2n+1})}. \end{align*} $$
$$ \begin{align*} &\sum_{m_1>0\atop m_2,m_3,\ldots,m_{k+1}=-\infty}^\infty \sum_{n=0}^\infty D_{k+1}^0(m_1,m_2,\ldots,m_{k+1};n)x_1^{m_1}\ldots x_{k+1}^{m_{k+1}}q^n\\[5pt] &\qquad=\frac{1}{(q^2;q^2)_\infty}\sum_{n=0}^\infty(-1)^n \frac{x_1q^{3n^2+3n+1+k(2n+1)}}{(1-x_1q^{2n+1}) \prod_{j=2}^{k+1}(1-x_jq^{2n+1})(1-x_j^{-1}q^{2n+1})}. \end{align*} $$
Setting
![]() $x_i=1 (1\leq i\leq k+1)$
in Theorem 3.3 and using Theorem 1.3, we obtain the following generating function of
$x_i=1 (1\leq i\leq k+1)$
in Theorem 3.3 and using Theorem 1.3, we obtain the following generating function of
![]() $\eta ^{0+}_{2k}(n)$
.
$\eta ^{0+}_{2k}(n)$
.
Theorem 3.4 For
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
 $$\begin{align*}\sum_{n=0}^\infty\eta^{0+}_{2k}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+(2k+3)n+k+1}}{(1-q^{2n+1})^{2k+1}}.\end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty\eta^{0+}_{2k}(n)q^n=\frac{1}{(q^2;q^2)_\infty} \sum_{n=0}^\infty \frac{(-1)^nq^{3n^2+(2k+3)n+k+1}}{(1-q^{2n+1})^{2k+1}}.\end{align*}$$
4 Asymptotic behavior for
 $\eta ^{0+}_k(n)$
$\eta ^{0+}_k(n)$
In this section, we apply Wright’s variant of the Hardy–Ramanujan circle method to study the asymptotic behavior of the symmetrized positive moments. Throughout this section, we set
![]() $q=e^{2\pi i\tau }$
with
$q=e^{2\pi i\tau }$
with
![]() $\tau =x+iy\in \mathcal {H}$
, where
$\tau =x+iy\in \mathcal {H}$
, where
![]() $\mathcal {H}$
denotes the upper half complex plane.
$\mathcal {H}$
denotes the upper half complex plane.
4.1 Asymptotic behavior of generating functions
Now, we use these generating functions of symmetrized positive moments of odd ranks to study the asymptotic behavior analytically. For convenience, we define a “false” Appell-type sum by
 $$ \begin{align} S_{r}(q):=\sum_{n=0}^\infty\frac{(-1)^nq^{3n^2+(2\lfloor\frac{r}{2}\rfloor+3)n +\lfloor\frac{r}{2}\rfloor+1}}{(1-q^{2n+1})^{r}}. \end{align} $$
$$ \begin{align} S_{r}(q):=\sum_{n=0}^\infty\frac{(-1)^nq^{3n^2+(2\lfloor\frac{r}{2}\rfloor+3)n +\lfloor\frac{r}{2}\rfloor+1}}{(1-q^{2n+1})^{r}}. \end{align} $$
For
![]() $r\geq 1$
, we set
$r\geq 1$
, we set
From the factor
![]() $\frac {1}{(q^2;q^2)_\infty }$
, we see that the dominant poles are at
$\frac {1}{(q^2;q^2)_\infty }$
, we see that the dominant poles are at
![]() $q=\pm 1$
. Since the asymptotic behavior of
$q=\pm 1$
. Since the asymptotic behavior of
![]() $\frac {1}{(q^2;q^2)_\infty }$
can be easily understood through modular transformations, the asymptotic behavior of
$\frac {1}{(q^2;q^2)_\infty }$
can be easily understood through modular transformations, the asymptotic behavior of
![]() $F_r(q)$
is reduced to study that of
$F_r(q)$
is reduced to study that of
![]() $S_{r+1}(q)$
near the dominant poles
$S_{r+1}(q)$
near the dominant poles
![]() $q=\pm 1$
.
$q=\pm 1$
.
4.2 Bounds near the dominate poles
To investigate the asymptotic behavior of
![]() $S_r(q)$
at the poles
$S_r(q)$
at the poles
![]() $q=1$
and
$q=1$
and
![]() $q=-1$
, we need the Mittag-Leffler partial fraction decomposition (for example, see [Reference Bringmann and Mahlburg6, Equation (3.1)]) as follows:
$q=-1$
, we need the Mittag-Leffler partial fraction decomposition (for example, see [Reference Bringmann and Mahlburg6, Equation (3.1)]) as follows:
 $$ \begin{align} \left(\frac{e^{\pi iw}}{1-e^{2\pi iw}}\right)^r=&\frac{1}{(-2\pi iw)^r}+\sum_{0<j<r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-2\pi iw)^j}\nonumber\\[5pt] &\quad+\sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-2\pi i)^j} \sum_{m\geq1}(-1)^{mr}\left[\frac{1}{(w-m)^j}+\frac{1}{(w+m)^j}\right], \end{align} $$
$$ \begin{align} \left(\frac{e^{\pi iw}}{1-e^{2\pi iw}}\right)^r=&\frac{1}{(-2\pi iw)^r}+\sum_{0<j<r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-2\pi iw)^j}\nonumber\\[5pt] &\quad+\sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-2\pi i)^j} \sum_{m\geq1}(-1)^{mr}\left[\frac{1}{(w-m)^j}+\frac{1}{(w+m)^j}\right], \end{align} $$
where
![]() $w\in \mathbb {C}$
and
$w\in \mathbb {C}$
and
![]() $\alpha _j$
are certain constants. In particular,
$\alpha _j$
are certain constants. In particular,
![]() $\alpha _r=1$
.
$\alpha _r=1$
.
We start with investigating
![]() $S_r(q)$
near
$S_r(q)$
near
![]() $q=1$
. Setting
$q=1$
. Setting
![]() $w=(2n+1)\tau $
, we see that
$w=(2n+1)\tau $
, we see that
 $$ \begin{align} S_{r}(q)=&\sum_{n=0}^\infty(-1)^nq^{3n^2+\bigg(2\lfloor\frac{r}{2}\rfloor+3-r\bigg)n+\lfloor\frac{r}{2}\rfloor-\frac{r}{2}+1} \bigg[\frac{1}{(-2\pi i(2n+1)\tau)^r}\nonumber\\[5pt] &+\sum_{0<j<r\atop j\equiv r \pmod2}\frac{\alpha_j}{(-2\pi i(2n+1)\tau)^j}\\[5pt] &+\sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-2\pi i)^j} \sum_{m\geq1}(-1)^{rm}\bigg(\frac{1}{((2n+1)\tau-m)^j}+\frac{1}{((2n+1)\tau+m)^j}\bigg)\bigg].\nonumber \end{align} $$
$$ \begin{align} S_{r}(q)=&\sum_{n=0}^\infty(-1)^nq^{3n^2+\bigg(2\lfloor\frac{r}{2}\rfloor+3-r\bigg)n+\lfloor\frac{r}{2}\rfloor-\frac{r}{2}+1} \bigg[\frac{1}{(-2\pi i(2n+1)\tau)^r}\nonumber\\[5pt] &+\sum_{0<j<r\atop j\equiv r \pmod2}\frac{\alpha_j}{(-2\pi i(2n+1)\tau)^j}\\[5pt] &+\sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-2\pi i)^j} \sum_{m\geq1}(-1)^{rm}\bigg(\frac{1}{((2n+1)\tau-m)^j}+\frac{1}{((2n+1)\tau+m)^j}\bigg)\bigg].\nonumber \end{align} $$
Now, we first consider the contribution from the first bracketed term in (4.3) for
![]() $r\geq 3$
and
$r\geq 3$
and
![]() $|x|\leq y=\frac {1}{4\sqrt {3N}}$
. To this end, we define
$|x|\leq y=\frac {1}{4\sqrt {3N}}$
. To this end, we define
Then the first term of
![]() $S_r(q)$
in (4.3) can be expressed as
$S_r(q)$
in (4.3) can be expressed as
![]() $(-2\pi i\tau )^{-r}g_r(\tau )$
. Thus, it is sufficient to study the functions
$(-2\pi i\tau )^{-r}g_r(\tau )$
. Thus, it is sufficient to study the functions
![]() $g_j(\tau )$
. For convenience, we set
$g_j(\tau )$
. For convenience, we set
![]() $a:=2\left \lfloor \frac {r}{2}\right \rfloor +3-r$
and
$a:=2\left \lfloor \frac {r}{2}\right \rfloor +3-r$
and
![]() $b:=\left \lfloor \frac {r}{2}\right \rfloor -\frac {r}{2}+1$
. If
$b:=\left \lfloor \frac {r}{2}\right \rfloor -\frac {r}{2}+1$
. If
![]() $j\geq 1$
, then
$j\geq 1$
, then
![]() $g_{j}(\tau )$
is convergent at
$g_{j}(\tau )$
is convergent at
![]() $\tau =0$
, and
$\tau =0$
, and
where
![]() $\beta (j)$
is the Dirichlet beta function. Notice that if
$\beta (j)$
is the Dirichlet beta function. Notice that if
![]() $j\geq 2$
, then
$j\geq 2$
, then
![]() $g_j$
is absolutely (and uniformly) convergent for all
$g_j$
is absolutely (and uniformly) convergent for all
![]() $|q|\leq 1$
, since
$|q|\leq 1$
, since
 $$\begin{align*}|g_j(\tau)|\leq\sum_{n=0}^\infty\frac{1}{(2n+1)^j}=\frac{2^j-1}{2^j}\zeta(j).\end{align*}$$
$$\begin{align*}|g_j(\tau)|\leq\sum_{n=0}^\infty\frac{1}{(2n+1)^j}=\frac{2^j-1}{2^j}\zeta(j).\end{align*}$$
Here,
![]() $\zeta (j)$
denotes the Riemann
$\zeta (j)$
denotes the Riemann
![]() $\zeta $
-function. We will apply Taylor’s theorem to obtain lower-order asymptotic terms in
$\zeta $
-function. We will apply Taylor’s theorem to obtain lower-order asymptotic terms in
![]() $g_j$
, and make use of the fact that the resulting derivatives can be expressed recursively using
$g_j$
, and make use of the fact that the resulting derivatives can be expressed recursively using
 $$ \begin{align*} \frac{1}{2\pi i}\frac{\partial}{\partial\tau}g_j(\tau)=&\frac{3}{4}g_{j-2}(\tau)+\frac{a-3}{2}g_{j-1}(\tau) +\frac{1}{4}g_j(\tau),\\[5pt] \left(\frac{1}{2\pi i}\right)^2\frac{\partial^2}{\partial\tau^2}g_j(\tau) =&\frac{9}{16}g_{j-4}(\tau)+\frac{3(a-3)}{4}g_{j-3}(\tau)\\[5pt] &+\frac{2 a^2-18 a+12 b+27}{8}g_{j-2}(\tau)\\[5pt] &+\frac{a-3}{4} g_{j-1}(\tau)+\frac{1}{16}g_{j}(\tau). \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi i}\frac{\partial}{\partial\tau}g_j(\tau)=&\frac{3}{4}g_{j-2}(\tau)+\frac{a-3}{2}g_{j-1}(\tau) +\frac{1}{4}g_j(\tau),\\[5pt] \left(\frac{1}{2\pi i}\right)^2\frac{\partial^2}{\partial\tau^2}g_j(\tau) =&\frac{9}{16}g_{j-4}(\tau)+\frac{3(a-3)}{4}g_{j-3}(\tau)\\[5pt] &+\frac{2 a^2-18 a+12 b+27}{8}g_{j-2}(\tau)\\[5pt] &+\frac{a-3}{4} g_{j-1}(\tau)+\frac{1}{16}g_{j}(\tau). \end{align*} $$
We use Taylor’s theorem for
![]() $j\geq 6$
and get the following truncated expansion:
$j\geq 6$
and get the following truncated expansion:
A simple calculation shows that for
![]() $j\geq 6$
,
$j\geq 6$
,
and
Additionally, we should individually consider the small value of j, that is,
![]() $-1\leq j\leq 1$
. Here, we make use of Zagier’s technical tool [Reference Zagier13, Proposition 3] to study the asymptotic expansions of series such as
$-1\leq j\leq 1$
. Here, we make use of Zagier’s technical tool [Reference Zagier13, Proposition 3] to study the asymptotic expansions of series such as
![]() $g_{j}$
. Bringmann and Mahlburg [Reference Bringmann and Mahlburg6] gave a generalization of Zagier’s result.
$g_{j}$
. Bringmann and Mahlburg [Reference Bringmann and Mahlburg6] gave a generalization of Zagier’s result.
Lemma 4.1 [Reference Bringmann and Mahlburg6, Proposition A.1]
Suppose that
![]() $f(t)$
is a smooth function on the positive reals and has the asymptotic expansion
$f(t)$
is a smooth function on the positive reals and has the asymptotic expansion
 $$\begin{align*}f(t)=\sum_{n=0}^sb_nt^n+O(t^{S+1}),\end{align*}$$
$$\begin{align*}f(t)=\sum_{n=0}^sb_nt^n+O(t^{S+1}),\end{align*}$$
for any
![]() $S\geq 0$
, as
$S\geq 0$
, as
![]() $t\rightarrow 0^+$
. Assume also that
$t\rightarrow 0^+$
. Assume also that
![]() $f(t)$
and all of its derivatives are of rapid decay at infinity and that
$f(t)$
and all of its derivatives are of rapid decay at infinity and that
![]() $I_f:=\int _{0}^\infty f(u)du$
converges. Then we have the following asymptotic expansion:
$I_f:=\int _{0}^\infty f(u)du$
converges. Then we have the following asymptotic expansion:
 $$\begin{align*}\sum_{m=0}^\infty f((m+a)t)=\frac{I_f}{t}-\sum_{n=0}^sb_n\frac{B_{n+1}(a)}{n+1}t^n,\end{align*}$$
$$\begin{align*}\sum_{m=0}^\infty f((m+a)t)=\frac{I_f}{t}-\sum_{n=0}^sb_n\frac{B_{n+1}(a)}{n+1}t^n,\end{align*}$$
where
![]() $B_n(x)$
is the nth Bernoulli polynomial, defined by
$B_n(x)$
is the nth Bernoulli polynomial, defined by
![]() $\frac {te^{xt}}{e^t-1}=\sum _{n\geq 0}B_n(x)\frac {t^n}{n!}$
.
$\frac {te^{xt}}{e^t-1}=\sum _{n\geq 0}B_n(x)\frac {t^n}{n!}$
.
Now, we aim to prove that
![]() $g_j(\tau ) (-1\leq j\leq 1)$
can be uniformly bounded in a neighborhood of
$g_j(\tau ) (-1\leq j\leq 1)$
can be uniformly bounded in a neighborhood of
![]() $\tau =0$
with
$\tau =0$
with
![]() $|x|\leq y$
. With the aid of Lemma 4.1, we first deal with the case of
$|x|\leq y$
. With the aid of Lemma 4.1, we first deal with the case of
![]() $j=0$
.
$j=0$
.
Proposition 4.2 Suppose that
![]() $y=\frac {1}{4\sqrt {3N}}$
and
$y=\frac {1}{4\sqrt {3N}}$
and
![]() $|x|\leq y$
. Then
$|x|\leq y$
. Then
Proof Observe that
We separate the odd terms and even terms, and consider only the real part, as the imaginary part can be treated in the same way. We have
 $$ \begin{align*} &\mathrm{Re}(g_0(\tau))\\[5pt] =&\cos\bigg(2\pi\bigg (b-\frac{a^2}{12}\bigg)x\bigg)e^{-2\pi y(b-a^2/12)}\sum_{n=0}^\infty\bigg[e^{-24\pi y(n+a/12)^2}\cos\bigg(24\pi x(n+a/12)^2\bigg)\\&\qquad\qquad-e^{-24\pi y(n+\frac{a+6}{12})^2}\cos\bigg(24\pi x\bigg(n+\frac{a+6}{12}\bigg)^2\bigg)\bigg]\\[5pt] =&\cos(2\pi (b-a^2/12)x)e^{-2\pi y(b-a^2/12)}\sum_{n\geq0}\bigg(f_{\frac{x}{y}}((n+a/12)\sqrt{y})- f_{\frac{x}{y}}\bigg(\bigg(n+\frac{a+6}{12}\bigg)\sqrt{y}\bigg)\bigg), \end{align*} $$
$$ \begin{align*} &\mathrm{Re}(g_0(\tau))\\[5pt] =&\cos\bigg(2\pi\bigg (b-\frac{a^2}{12}\bigg)x\bigg)e^{-2\pi y(b-a^2/12)}\sum_{n=0}^\infty\bigg[e^{-24\pi y(n+a/12)^2}\cos\bigg(24\pi x(n+a/12)^2\bigg)\\&\qquad\qquad-e^{-24\pi y(n+\frac{a+6}{12})^2}\cos\bigg(24\pi x\bigg(n+\frac{a+6}{12}\bigg)^2\bigg)\bigg]\\[5pt] =&\cos(2\pi (b-a^2/12)x)e^{-2\pi y(b-a^2/12)}\sum_{n\geq0}\bigg(f_{\frac{x}{y}}((n+a/12)\sqrt{y})- f_{\frac{x}{y}}\bigg(\bigg(n+\frac{a+6}{12}\bigg)\sqrt{y}\bigg)\bigg), \end{align*} $$
where
Note that
![]() $f_v(t)$
is an even function, and thus its Taylor series at
$f_v(t)$
is an even function, and thus its Taylor series at
![]() $t=0$
only has even powers of t as follows:
$t=0$
only has even powers of t as follows:
It is easy to see that
converges and has a uniform bound, since
Therefore, we apply Zagier’s lemma to
![]() $\mathrm {Re}(g_0(\tau ))$
and obtain the asymptotic expansion
$\mathrm {Re}(g_0(\tau ))$
and obtain the asymptotic expansion
 $$ \begin{align*} \mathrm{Re}(g_0(\tau))=&\left(y^{-\frac{1}{2}}I_f-B_1\left(\frac{a}{12}\right)+O_{\frac{x}{y}}(y)-\left(y^{-\frac{1}{2}}I_f-B_1\left(\frac{a+6}{12}\right)+O_{\frac{x}{y}}(y)\right)\right) \\ &\qquad\cdot\cos\left(2\pi (b-a^2/12)x\right)e^{-2\pi y(b-a^2/12)}. \end{align*} $$
$$ \begin{align*} \mathrm{Re}(g_0(\tau))=&\left(y^{-\frac{1}{2}}I_f-B_1\left(\frac{a}{12}\right)+O_{\frac{x}{y}}(y)-\left(y^{-\frac{1}{2}}I_f-B_1\left(\frac{a+6}{12}\right)+O_{\frac{x}{y}}(y)\right)\right) \\ &\qquad\cdot\cos\left(2\pi (b-a^2/12)x\right)e^{-2\pi y(b-a^2/12)}. \end{align*} $$
Since
![]() $|\frac {x}{y}|\leq 1$
, we see that
$|\frac {x}{y}|\leq 1$
, we see that
The proof of the case
![]() $j=-1$
is similar as that of
$j=-1$
is similar as that of
![]() $j=0$
.
$j=0$
.
We turn to deal with the case for
![]() $j=1$
.
$j=1$
.
Proposition 4.3 Suppose that
![]() $y=\frac {1}{4\sqrt {3N}}$
and
$y=\frac {1}{4\sqrt {3N}}$
and
![]() $|x|\leq y$
. Then
$|x|\leq y$
. Then
Proof We first define
Then it follows that
![]() $g_1(\tau )=q^{b-\frac {a^2}{12}}\cdot \widetilde {g_1}(\tau )$
. As above, we split
$g_1(\tau )=q^{b-\frac {a^2}{12}}\cdot \widetilde {g_1}(\tau )$
. As above, we split
![]() $\widetilde {g_1}(\tau )$
into odd terms and even terms, and consider only the real part, as the imaginary part is treated identically. So we have
$\widetilde {g_1}(\tau )$
into odd terms and even terms, and consider only the real part, as the imaginary part is treated identically. So we have
 $$ \begin{align} \mathrm{Re}(\widetilde{g_1}(\tau))=\sum_{n\geq0}&\bigg(\frac{e^{-24\pi y(n+a/12)^2}\cos(24\pi x(n+a/12)^2)}{4n+1}\nonumber\\ &-\frac{e^{-24\pi y\bigg(n+(a+6)/12\bigg)^2}\cos(24\pi x(n+(a+6)/12)^2)}{4n+3}\bigg). \end{align} $$
$$ \begin{align} \mathrm{Re}(\widetilde{g_1}(\tau))=\sum_{n\geq0}&\bigg(\frac{e^{-24\pi y(n+a/12)^2}\cos(24\pi x(n+a/12)^2)}{4n+1}\nonumber\\ &-\frac{e^{-24\pi y\bigg(n+(a+6)/12\bigg)^2}\cos(24\pi x(n+(a+6)/12)^2)}{4n+3}\bigg). \end{align} $$
In order to combine these two terms, we write
If the big-O term is inserted into (4.7), the sum is absolutely and uniformly convergent, so we may discard this error term without affecting the overall convergence.
Here, we present two trivial but useful estimates:
 $$ \begin{align*} |\cos(x+a)-\cos(x)|&\leq \min\{|a|,2\},\ \text{for}\quad x,a\in\mathbb{R},\\[5pt] |1-e^{-x}|&\leq \min\{x,1\},\quad \text{for}\quad x\geq0. \end{align*} $$
$$ \begin{align*} |\cos(x+a)-\cos(x)|&\leq \min\{|a|,2\},\ \text{for}\quad x,a\in\mathbb{R},\\[5pt] |1-e^{-x}|&\leq \min\{x,1\},\quad \text{for}\quad x\geq0. \end{align*} $$
To apply these bounds, we rewrite the second term of (4.7) in the following way:
 $$ \begin{align} &\frac{e^{-24\pi y\left(n+\frac{a+6}{12}\right)^2}\cos\left(24\pi x\left(n+\frac{a+6}{12}\right)^2\right)}{4n+1}\nonumber\\[5pt] =&\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\left(e^{-24\pi y\left(n+\frac{a+3}{12}\right)}-1\right)\cos\left(24\pi x\left(n+\frac{a+6}{12}\right)^2\right)\\[5pt] &\quad+\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\left(\cos\left(24\pi x\left(n+\frac{a+6}{12}\right)^2\right)-\cos\left(24\pi x\left(n+\frac{a}{12}\right)^2\right)\right)\nonumber\\[5pt] &\quad+\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\cos\left(24\pi x\left(n+\frac{a}{12}\right)^2\right).\nonumber \end{align} $$
$$ \begin{align} &\frac{e^{-24\pi y\left(n+\frac{a+6}{12}\right)^2}\cos\left(24\pi x\left(n+\frac{a+6}{12}\right)^2\right)}{4n+1}\nonumber\\[5pt] =&\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\left(e^{-24\pi y\left(n+\frac{a+3}{12}\right)}-1\right)\cos\left(24\pi x\left(n+\frac{a+6}{12}\right)^2\right)\\[5pt] &\quad+\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\left(\cos\left(24\pi x\left(n+\frac{a+6}{12}\right)^2\right)-\cos\left(24\pi x\left(n+\frac{a}{12}\right)^2\right)\right)\nonumber\\[5pt] &\quad+\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\cos\left(24\pi x\left(n+\frac{a}{12}\right)^2\right).\nonumber \end{align} $$
The contribution of the first pair of terms in (4.8) to the sum in (4.7) is asymptotically bounded by
 $$ \begin{align*} &\sum_{n\geq0}\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\min\left\{1,24\pi y\left(n+\frac{a+3}{12}\right)\right\}\\[5pt] &\quad\ll y\sum_{0\leq n\leq \frac{1}{24\pi y}-\frac{a+3}{12}}e^{-n^2y}+\sum_{n\geq\frac{1}{24\pi y}-\frac{a+3}{12}}n^{-1}e^{-n^2y}\\[5pt] &\quad\ll\sqrt{y}+y\sum_{n\geq\frac{1}{24\pi y}-\frac{a+3}{12}}e^{-n^2y}\ll\sqrt{y}. \end{align*} $$
$$ \begin{align*} &\sum_{n\geq0}\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\min\left\{1,24\pi y\left(n+\frac{a+3}{12}\right)\right\}\\[5pt] &\quad\ll y\sum_{0\leq n\leq \frac{1}{24\pi y}-\frac{a+3}{12}}e^{-n^2y}+\sum_{n\geq\frac{1}{24\pi y}-\frac{a+3}{12}}n^{-1}e^{-n^2y}\\[5pt] &\quad\ll\sqrt{y}+y\sum_{n\geq\frac{1}{24\pi y}-\frac{a+3}{12}}e^{-n^2y}\ll\sqrt{y}. \end{align*} $$
For the second pair of terms in (4.8), we note that
![]() $|x|\leq y$
and obtain that
$|x|\leq y$
and obtain that
 $$ \begin{align*} &\sum_{n\geq0}\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\min\left\{2,24\pi |x|\left(n+\frac{a+3}{12}\right)\right\}\\[5pt] &\quad\leq\sum_{n\geq0}\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\min\left\{2,24\pi y\left(n+\frac{a+3}{12}\right)\right\} \ll\sqrt{y}. \end{align*} $$
$$ \begin{align*} &\sum_{n\geq0}\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\min\left\{2,24\pi |x|\left(n+\frac{a+3}{12}\right)\right\}\\[5pt] &\quad\leq\sum_{n\geq0}\frac{e^{-24\pi y\left(n+\frac{a}{12}\right)^2}}{4n+1}\min\left\{2,24\pi y\left(n+\frac{a+3}{12}\right)\right\} \ll\sqrt{y}. \end{align*} $$
Since the third term in (4.8) cancels the first term in (4.7), and the real part is bounded overall, we complete the proof.
The second bracketed term in (4.3) is a finite summation on j. Employing the following simple uniform bound:
 $$ \begin{align} g_j(\tau)\ll \sum_{n=0}^{\infty}\frac{e^{-Cn^2y}}{(2n+1)^j}\ll \begin{cases} 1, & \text{if }j\geq 2, \\ 1+\frac{1}{\sqrt{y}}\ll N^{\frac{1}{4}}, & \text{if }j=1, \end{cases} \end{align} $$
$$ \begin{align} g_j(\tau)\ll \sum_{n=0}^{\infty}\frac{e^{-Cn^2y}}{(2n+1)^j}\ll \begin{cases} 1, & \text{if }j\geq 2, \\ 1+\frac{1}{\sqrt{y}}\ll N^{\frac{1}{4}}, & \text{if }j=1, \end{cases} \end{align} $$
for some constants C, we conclude that the contribution of the second bracketed term is absorbed into the error term.
The final bracketed term in (4.3) is also a finite summation on j. Noticing the constraint
![]() $|x|\leq y$
, we easily deduce that for
$|x|\leq y$
, we easily deduce that for
![]() $m\in \mathbb {Z}\backslash \{0\}$
,
$m\in \mathbb {Z}\backslash \{0\}$
,
So when
![]() $j>1$
, we see that
$j>1$
, we see that
 $$ \begin{align} &\sum_{n=0}^{\infty}(-1)^nq^{3n^2+an+b}\sum_{m\geq1}(-1)^{mr}\left(\frac{1}{((2n+1)\tau-m)^j}+\frac{1}{((2n+1)\tau+m)^j}\right)\nonumber\\[5pt] &\quad\ll\sum_{m\geq1}m^{-j}\sum_{n\geq0}e^{-6\pi n^2y}\ll y^{-1/2}\ll N^{\frac{1}{4}}. \end{align} $$
$$ \begin{align} &\sum_{n=0}^{\infty}(-1)^nq^{3n^2+an+b}\sum_{m\geq1}(-1)^{mr}\left(\frac{1}{((2n+1)\tau-m)^j}+\frac{1}{((2n+1)\tau+m)^j}\right)\nonumber\\[5pt] &\quad\ll\sum_{m\geq1}m^{-j}\sum_{n\geq0}e^{-6\pi n^2y}\ll y^{-1/2}\ll N^{\frac{1}{4}}. \end{align} $$
Moreover, for
![]() $j=1,$
we have
$j=1,$
we have
 $$\begin{align*}\frac{1}{(2n+1)\tau-m}+\frac{1}{(2n+1)\tau+m}\ll \frac{(2n+1)\tau}{m^2}.\end{align*}$$
$$\begin{align*}\frac{1}{(2n+1)\tau-m}+\frac{1}{(2n+1)\tau+m}\ll \frac{(2n+1)\tau}{m^2}.\end{align*}$$
Thus, the corresponding contribution can be bounded by
As a consequence, combining equations (4.4)–(4.6) and (4.9)–(4.11) with Propositions 4.2 and 4.3, we could determine the first terms in the asymptotic expansion of
![]() $S_r(q)$
near
$S_r(q)$
near
![]() $q=1$
.
$q=1$
.
Proposition 4.4 Assume
![]() $r\geq 3$
,
$r\geq 3$
,
![]() $|x|\leq y=\frac {1}{4\sqrt {3N}}$
. As
$|x|\leq y=\frac {1}{4\sqrt {3N}}$
. As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
with
 $$ \begin{align*} c_r&=\beta(r)\quad \text{for}\ r\geq 3, \\ d_r&=\frac{3}{4}\beta(r-2)+\frac{a-3}{2}\beta(r-1)+\frac{1}{4}\beta(r)\quad \text{for}\ r\geq 3. \end{align*} $$
$$ \begin{align*} c_r&=\beta(r)\quad \text{for}\ r\geq 3, \\ d_r&=\frac{3}{4}\beta(r-2)+\frac{a-3}{2}\beta(r-1)+\frac{1}{4}\beta(r)\quad \text{for}\ r\geq 3. \end{align*} $$
Corollary 4.5 Assume that
![]() $r\geq 2$
,
$r\geq 2$
,
![]() $y=\frac {1}{4\sqrt {3N}}$
, and
$y=\frac {1}{4\sqrt {3N}}$
, and
![]() $|x|\leq y$
. As
$|x|\leq y$
. As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
where
Proof Recall the modular inversion formula for Dedekind’s eta-function, which states that
Then we have
Combining this with Proposition 4.4, we find that
 $$ \begin{align*} \frac{1}{(q^2;q^2)_\infty}S_{r+1}(q)&=\sqrt{-2i\tau}e^{\frac{\pi i}{24\tau}}\left(1-\frac{-2\pi i\tau}{12}+O(N^{-1})\right)\\ &\qquad\qquad\cdot \left(c_{r+1}(-2\pi i\tau)^{-r-1}-d_{r+1}(-2\pi i\tau)^{-r}+O(N^{\frac{r+1}{2}-1})\right)\\ &=c_{r+1}^*(-2\pi i\tau)^{-\frac{1}{2}-r}e^{\frac{\pi i}{24\tau}}+d_{r+1}^*(-2\pi i\tau)^{\frac{1}{2}-r}e^{\frac{\pi i}{24\tau}}+ O\left(N^{\frac{2r-3}{4}}e^{\pi\sqrt{\frac{N}{12}}}\right). \end{align*} $$
$$ \begin{align*} \frac{1}{(q^2;q^2)_\infty}S_{r+1}(q)&=\sqrt{-2i\tau}e^{\frac{\pi i}{24\tau}}\left(1-\frac{-2\pi i\tau}{12}+O(N^{-1})\right)\\ &\qquad\qquad\cdot \left(c_{r+1}(-2\pi i\tau)^{-r-1}-d_{r+1}(-2\pi i\tau)^{-r}+O(N^{\frac{r+1}{2}-1})\right)\\ &=c_{r+1}^*(-2\pi i\tau)^{-\frac{1}{2}-r}e^{\frac{\pi i}{24\tau}}+d_{r+1}^*(-2\pi i\tau)^{\frac{1}{2}-r}e^{\frac{\pi i}{24\tau}}+ O\left(N^{\frac{2r-3}{4}}e^{\pi\sqrt{\frac{N}{12}}}\right). \end{align*} $$
Now, we turn to investigate the asymptotic behavior of
![]() $F_r(q)$
near
$F_r(q)$
near
![]() $q=-1$
.
$q=-1$
.
Proposition 4.6 Assume that
![]() $r\geq 1$
,
$r\geq 1$
,
![]() $y=\frac {1}{4\sqrt {3N}}$
, and
$y=\frac {1}{4\sqrt {3N}}$
, and
![]() $|x-\frac {1}{2}|\leq y$
. As
$|x-\frac {1}{2}|\leq y$
. As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
Proof By setting
![]() $z:=\tau -\frac {1}{2}=x-\frac {1}{2}+iy$
and
$z:=\tau -\frac {1}{2}=x-\frac {1}{2}+iy$
and
![]() $Q:=e^{2\pi iz}=-q$
, we derive that
$Q:=e^{2\pi iz}=-q$
, we derive that
 $$ \begin{align*} S_r(q) &= S_r(-Q) =\sum_{n\geq0}(-1)^{n}\frac{(-Q)^{3n^2+\left(2\left\lfloor\frac{r}{2}\right\rfloor+3\right)n+\left\lfloor\frac{r}{2}\right\rfloor+1}}{\left(1-(-Q)^{2n+1}\right)^r}\\[5pt] &=\sum_{n\geq0}(-1)^{n+\left\lfloor\frac{r}{2}\right\rfloor+1}\frac{Q^{3n^2+\left(2\left\lfloor\frac{r}{2}\right\rfloor+3\right)n+\left\lfloor\frac{r}{2}\right\rfloor+1}}{(1+Q^{2n+1})^r}. \end{align*} $$
$$ \begin{align*} S_r(q) &= S_r(-Q) =\sum_{n\geq0}(-1)^{n}\frac{(-Q)^{3n^2+\left(2\left\lfloor\frac{r}{2}\right\rfloor+3\right)n+\left\lfloor\frac{r}{2}\right\rfloor+1}}{\left(1-(-Q)^{2n+1}\right)^r}\\[5pt] &=\sum_{n\geq0}(-1)^{n+\left\lfloor\frac{r}{2}\right\rfloor+1}\frac{Q^{3n^2+\left(2\left\lfloor\frac{r}{2}\right\rfloor+3\right)n+\left\lfloor\frac{r}{2}\right\rfloor+1}}{(1+Q^{2n+1})^r}. \end{align*} $$
We recall that
![]() $a=2\left \lfloor \frac {r}{2}\right \rfloor +3-r$
and
$a=2\left \lfloor \frac {r}{2}\right \rfloor +3-r$
and
![]() $b=\left \lfloor \frac {r}{2}\right \rfloor -\frac {r}{2}+1$
, and then obtain that
$b=\left \lfloor \frac {r}{2}\right \rfloor -\frac {r}{2}+1$
, and then obtain that
 $$ \begin{align*} S_r(q)=\sum_{n\geq0}(-1)^{n+\left\lfloor\frac{r}{2}\right\rfloor+1}Q^{3n^2+an+b}\frac{Q^{(n+\frac{1}{2})r}}{(1+Q^{2n+1})^r}. \end{align*} $$
$$ \begin{align*} S_r(q)=\sum_{n\geq0}(-1)^{n+\left\lfloor\frac{r}{2}\right\rfloor+1}Q^{3n^2+an+b}\frac{Q^{(n+\frac{1}{2})r}}{(1+Q^{2n+1})^r}. \end{align*} $$
By setting
![]() $w:=(2n+1)z+\frac {1}{2}$
in (4.2), we find that
$w:=(2n+1)z+\frac {1}{2}$
in (4.2), we find that
 $$ \begin{align*} &\frac{i^re^{\pi i(2n+1)rz}}{\left(1+e^{2\pi i(2n+1)z}\right)^r}\\ &\quad = \sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-\pi i)^j\left((4n+2)z+1\right)^j} +\sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-\pi i)^j}\sum_{m\geq1}(-1)^{rm}\\ &\qquad\times\left(\frac{1}{((4n+2)z+1-2m)^j}+\frac{1}{((4n+2)z+1+2m)^j}\right). \end{align*} $$
$$ \begin{align*} &\frac{i^re^{\pi i(2n+1)rz}}{\left(1+e^{2\pi i(2n+1)z}\right)^r}\\ &\quad = \sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-\pi i)^j\left((4n+2)z+1\right)^j} +\sum_{0<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-\pi i)^j}\sum_{m\geq1}(-1)^{rm}\\ &\qquad\times\left(\frac{1}{((4n+2)z+1-2m)^j}+\frac{1}{((4n+2)z+1+2m)^j}\right). \end{align*} $$
We first consider the contribution of the final term. It is clear that for
![]() $m\in \mathbb {Z}$
(note that
$m\in \mathbb {Z}$
(note that
![]() $z=(x-\frac {1}{2})+iy$
and
$z=(x-\frac {1}{2})+iy$
and
![]() $|x-\frac {1}{2}|\leq y$
),
$|x-\frac {1}{2}|\leq y$
),
Notice that for
![]() $j>1$
,
$j>1$
,
 $$\begin{align*}\sum_{m\geq1}(-1)^m\left(\frac{1}{(1-2m)^j}+\frac{1}{(1+2m)^j}\right)\ll\sum_{m\geq1}m^{-j}\ll 1.\end{align*}$$
$$\begin{align*}\sum_{m\geq1}(-1)^m\left(\frac{1}{(1-2m)^j}+\frac{1}{(1+2m)^j}\right)\ll\sum_{m\geq1}m^{-j}\ll 1.\end{align*}$$
If r is odd, then, for the case
![]() $j=1$
, we have
$j=1$
, we have
 $$ \begin{align*} &\frac{1}{(4n+2)z+1}+\sum_{m\geq1}(-1)^m \left(\frac{1}{(4n+2)z+1-2m}+\frac{1}{(4n+2)z+1+2m}\right)\\[5pt] =&\sum_{m\geq1}(-1)^m\left(\frac{1}{(4n+2)z+1-2m}-\frac{1}{(4n+2)z-1+2m}\right)\\[5pt] =&\sum_{m\geq1}(-1)^m\frac{4m-2}{(4n+2)^2z^2-(2m-1)^2}. \end{align*} $$
$$ \begin{align*} &\frac{1}{(4n+2)z+1}+\sum_{m\geq1}(-1)^m \left(\frac{1}{(4n+2)z+1-2m}+\frac{1}{(4n+2)z+1+2m}\right)\\[5pt] =&\sum_{m\geq1}(-1)^m\left(\frac{1}{(4n+2)z+1-2m}-\frac{1}{(4n+2)z-1+2m}\right)\\[5pt] =&\sum_{m\geq1}(-1)^m\frac{4m-2}{(4n+2)^2z^2-(2m-1)^2}. \end{align*} $$
By splitting this fraction into two terms:
 $$\begin{align*}\frac{4m-2}{(4n+2)^2z^2-(2m-1)^2}=(4m-2) \left(\frac{1}{(4n+2)^2z^2-(2m-1)^2}+\frac{1}{(2m-1)^2}\right)-\frac{2}{2m-1},\end{align*}$$
$$\begin{align*}\frac{4m-2}{(4n+2)^2z^2-(2m-1)^2}=(4m-2) \left(\frac{1}{(4n+2)^2z^2-(2m-1)^2}+\frac{1}{(2m-1)^2}\right)-\frac{2}{2m-1},\end{align*}$$
and noting that
 $$ \begin{align*} &\left|\frac{1}{(4n+2)^2z^2-(2m-1)^2}+\frac{1}{(2m-1)^2}\right|\\[5pt] &\quad=\left|\frac{(4n+2)^2z^2}{((4n+2)^2z^2-(2m-1)^2)(2m-1)^2}\right|\leq \frac{2(4n+2)^2y^2}{(2m-1)^4}. \end{align*} $$
$$ \begin{align*} &\left|\frac{1}{(4n+2)^2z^2-(2m-1)^2}+\frac{1}{(2m-1)^2}\right|\\[5pt] &\quad=\left|\frac{(4n+2)^2z^2}{((4n+2)^2z^2-(2m-1)^2)(2m-1)^2}\right|\leq \frac{2(4n+2)^2y^2}{(2m-1)^4}. \end{align*} $$
Therefore, we derive that
 $$ \begin{align*} &\sum_{m\geq1}(-1)^m\frac{4m-2}{(4n+2)^2z^2-(2m-1)^2}\\ &\quad\leq 4(4n+2)^2y^2\left|\sum_{m\geq1}\frac{1}{(2m-1)^3}\right|+\left|\sum_{m\geq1}\frac{(-1)^k}{2k-1}\right|\\ &\quad\leq\frac{\pi^3(2n+1)^2y^2}{2}+\frac{\pi}{4}. \end{align*} $$
$$ \begin{align*} &\sum_{m\geq1}(-1)^m\frac{4m-2}{(4n+2)^2z^2-(2m-1)^2}\\ &\quad\leq 4(4n+2)^2y^2\left|\sum_{m\geq1}\frac{1}{(2m-1)^3}\right|+\left|\sum_{m\geq1}\frac{(-1)^k}{2k-1}\right|\\ &\quad\leq\frac{\pi^3(2n+1)^2y^2}{2}+\frac{\pi}{4}. \end{align*} $$
Moreover, we observe that
 $$\begin{align*}\sum_{1<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-\pi i)^j\left((4n+2)z+1\right)^j}\ll1.\end{align*}$$
$$\begin{align*}\sum_{1<j\leq r\atop j\equiv r\pmod2}\frac{\alpha_j}{(-\pi i)^j\left((4n+2)z+1\right)^j}\ll1.\end{align*}$$
Therefore, we have
 $$ \begin{align*} \frac{i^re^{\pi i(2n+1)rz}}{\left(1+e^{2\pi i(2n+1)z}\right)^r} \ll1+ \frac{\pi^3(2n+1)^2y^2}{2}+\frac{\pi}{4}+1\ll \frac{\pi^3(2n+1)^2y^2}{2}. \end{align*} $$
$$ \begin{align*} \frac{i^re^{\pi i(2n+1)rz}}{\left(1+e^{2\pi i(2n+1)z}\right)^r} \ll1+ \frac{\pi^3(2n+1)^2y^2}{2}+\frac{\pi}{4}+1\ll \frac{\pi^3(2n+1)^2y^2}{2}. \end{align*} $$
Thus, by using Lemma 4.1, we find that the contribution of the final term to
![]() $S_r(q)$
can be bound by
$S_r(q)$
can be bound by
 $$\begin{align*}S_r(q)=\sum_{n\geq 0}(-1)^{n+\lfloor\frac{r}{2}\rfloor+1}Q^{3n^2+an+b} \frac{Q^{(n+\frac{1}{2})r}}{(1+Q^{2n+1})^r} \ll\sum_{n\geq 1}(2n+1)^2y^2e^{-6\pi yn^2}\ll 1, \end{align*}$$
$$\begin{align*}S_r(q)=\sum_{n\geq 0}(-1)^{n+\lfloor\frac{r}{2}\rfloor+1}Q^{3n^2+an+b} \frac{Q^{(n+\frac{1}{2})r}}{(1+Q^{2n+1})^r} \ll\sum_{n\geq 1}(2n+1)^2y^2e^{-6\pi yn^2}\ll 1, \end{align*}$$
which completes the proof.
Corollary 4.7 Assume that
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $y=\frac {1}{4\sqrt {3N}}$
, and
$y=\frac {1}{4\sqrt {3N}}$
, and
![]() $|x-1/2|\leq y$
. As
$|x-1/2|\leq y$
. As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
Proof We note that
and the proof follows.
4.3 Bounds away from the dominate poles
Finally, there is a position to estimate the asymptotic behavior of
![]() $F_r(q)$
away from the dominate poles
$F_r(q)$
away from the dominate poles
![]() $q=\pm 1$
.
$q=\pm 1$
.
Proposition 4.8 For
![]() $r\geq 0$
and
$r\geq 0$
and
![]() $y>0$
with
$y>0$
with
![]() $y\leq |x|\leq \frac {1}{2}-y$
,
$y\leq |x|\leq \frac {1}{2}-y$
,
Proof From the Taylor expansion, we see that
So we have
 $$ \begin{align*} |S_r(q)|\leq \frac{|q|^{\lfloor\frac{r}{2}\rfloor+1}}{(1-|q|)^r} \sum_{n\geq0}|q|^{3n^2+\left(2\lfloor\frac{r}{2}\rfloor+3\right)n} \ll \frac{1}{y^r}\cdot y^{-1/2}=y^{-r-1/2}, \end{align*} $$
$$ \begin{align*} |S_r(q)|\leq \frac{|q|^{\lfloor\frac{r}{2}\rfloor+1}}{(1-|q|)^r} \sum_{n\geq0}|q|^{3n^2+\left(2\lfloor\frac{r}{2}\rfloor+3\right)n} \ll \frac{1}{y^r}\cdot y^{-1/2}=y^{-r-1/2}, \end{align*} $$
where the final summation follows through a comparison with a Gaussian integral.
Corollary 4.9 Assume that
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $y=\frac {1}{4\sqrt {3N}}$
, and
$y=\frac {1}{4\sqrt {3N}}$
, and
![]() $y\leq |x|\leq \frac {1}{2}-y$
. As
$y\leq |x|\leq \frac {1}{2}-y$
. As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
Proof From [Reference Jang and Kim8, Equation (4.4)], we know that
 $$\begin{align*}\left|\frac{1}{(q^2;q^2)_\infty}\right|\ll \sqrt{2y}\exp\left[\frac{1}{y} \left(\frac{\pi}{24}-\frac{1}{4\pi}\left(1-\frac{1}{\sqrt{2}}\right)\right)\right]. \end{align*}$$
$$\begin{align*}\left|\frac{1}{(q^2;q^2)_\infty}\right|\ll \sqrt{2y}\exp\left[\frac{1}{y} \left(\frac{\pi}{24}-\frac{1}{4\pi}\left(1-\frac{1}{\sqrt{2}}\right)\right)\right]. \end{align*}$$
Combined with Proposition 4.8, this gives the claimed expression.
4.4 The circle method
Now, we apply Wright’s variant of the Hardy–Ramanujan circle method. Cauchy’s theorem gives an integral representation for the coefficients of
![]() $F_r(q)$
, namely,
$F_r(q)$
, namely,
 $$ \begin{align} \eta_r^{0+}(N)=\frac{1}{2\pi i}\int_{\mathcal{C}}\frac{F_{r}(q)}{q^{N+1}}dq=\int_{-\frac{1}{2}}^{\frac{1}{2}} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx, \end{align} $$
$$ \begin{align} \eta_r^{0+}(N)=\frac{1}{2\pi i}\int_{\mathcal{C}}\frac{F_{r}(q)}{q^{N+1}}dq=\int_{-\frac{1}{2}}^{\frac{1}{2}} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx, \end{align} $$
where the contour is the counterclockwise traversal of the circle
![]() $\mathcal {C}:=\{|q|=e^{-\frac {\pi }{2\sqrt {3N}}}\}$
. We sperate (4.14) into three ranges
$\mathcal {C}:=\{|q|=e^{-\frac {\pi }{2\sqrt {3N}}}\}$
. We sperate (4.14) into three ranges
 $$ \begin{align*} \eta_r^{0+}(N)=&\int_{|x|\leq y} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx\\[5pt] &+\int_{y\leq|x|\leq\frac{1}{2}-y} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx\\[5pt] &+\int_{|x-\frac{1}{2}|\leq y} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx\\[5pt] =:&\mathcal{I}_1+\mathcal{I}_2+\mathcal{I}_3, \end{align*} $$
$$ \begin{align*} \eta_r^{0+}(N)=&\int_{|x|\leq y} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx\\[5pt] &+\int_{y\leq|x|\leq\frac{1}{2}-y} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx\\[5pt] &+\int_{|x-\frac{1}{2}|\leq y} F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}dx\\[5pt] =:&\mathcal{I}_1+\mathcal{I}_2+\mathcal{I}_3, \end{align*} $$
where
![]() $y=\frac {1}{4\sqrt {3N}}$
.
$y=\frac {1}{4\sqrt {3N}}$
.
Next, we will show that the integral
![]() $\mathcal {I}_1$
contributes the main term and the integrals
$\mathcal {I}_1$
contributes the main term and the integrals
![]() $\mathcal {I}_2$
and
$\mathcal {I}_2$
and
![]() $\mathcal {I}_3$
are absorbed in the error term.
$\mathcal {I}_3$
are absorbed in the error term.
We first evaluate the integral
![]() $\mathcal {I}_1$
and aim to rewrite the integral
$\mathcal {I}_1$
and aim to rewrite the integral
![]() $\mathcal {I}_1$
in terms of Bessel functions up to an error term. To this end, we need to introduce an auxiliary function, which is defined by Wright [Reference Wright12],
$\mathcal {I}_1$
in terms of Bessel functions up to an error term. To this end, we need to introduce an auxiliary function, which is defined by Wright [Reference Wright12],
where
![]() $M>0$
is fixed and
$M>0$
is fixed and
![]() $u\in \mathbb {R}^+$
. Adopting the similar approach of [Reference Bringmann and Mahlburg6, Lemma 4.2], one may find that the auxiliary function
$u\in \mathbb {R}^+$
. Adopting the similar approach of [Reference Bringmann and Mahlburg6, Lemma 4.2], one may find that the auxiliary function
![]() $P_s(u)$
can be rewritten in terms of the I-Bessel function up to an error term.
$P_s(u)$
can be rewritten in terms of the I-Bessel function up to an error term.
Lemma 4.10 Assume that
![]() $u=\pi \sqrt {\frac {N}{6}}$
. As
$u=\pi \sqrt {\frac {N}{6}}$
. As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
With the help of this lemma, we can evaluate the integral
![]() $\mathcal {I}_1$
.
$\mathcal {I}_1$
.
Proposition 4.11 Assume that
![]() $r\geq 2$
. As
$r\geq 2$
. As
![]() $N\rightarrow \infty $
,
$N\rightarrow \infty $
,
 $$\begin{align*}\mathcal{I}_1-c_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{1}{2}-r}I_{r-\frac{1}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)+d_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{3}{2}-r}I_{r-\frac{3}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)\ll N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}.\end{align*}$$
$$\begin{align*}\mathcal{I}_1-c_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{1}{2}-r}I_{r-\frac{1}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)+d_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{3}{2}-r}I_{r-\frac{3}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)\ll N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}.\end{align*}$$
Proof By making the change of variables
![]() $v=1-i4\sqrt {3N}x$
, we arrive at
$v=1-i4\sqrt {3N}x$
, we arrive at
 $$ \begin{align*} \mathcal{I}_1=&\int_{1-i}^{1+i}\frac{1}{i4\sqrt{3N}}\bigg(c_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{-\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}v}}\\[5pt] &\qquad\quad+d_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}v}}+O\bigg(N^{\frac{2r-3}{4}}e^{\pi\sqrt{\frac{N}{12}}}\bigg)\bigg)e^{\frac{\pi \sqrt{N}v}{2\sqrt{3}}}\mathrm{d}v\\[5pt] =&\frac{1}{i4\sqrt{3N}}\int_{1-i}^{1+i}\bigg[c_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{-\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}(v+v^{-1})}+d_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}(v+v^{-1})}\bigg]\mathrm{d}v\\[5pt] &\qquad\quad+O\bigg(N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}\bigg)\\[5pt] =&c_{r+1}^*\bigg(\frac{\pi}{2\sqrt{3N}}\bigg)^{\frac{1}{2}-r}P_{-\frac{1}{2}-r} \bigg(\pi\sqrt{\frac{N}{12}}\bigg)+d_{r+1}^*\bigg(\frac{\pi}{2\sqrt{3N}}\bigg)^{\frac{3}{2}-r}P_{\frac{1}{2}-r} \bigg(\pi\sqrt{\frac{N}{12}}\bigg)\\[5pt] &\qquad\quad+O\bigg(N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}\bigg). \end{align*} $$
$$ \begin{align*} \mathcal{I}_1=&\int_{1-i}^{1+i}\frac{1}{i4\sqrt{3N}}\bigg(c_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{-\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}v}}\\[5pt] &\qquad\quad+d_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}v}}+O\bigg(N^{\frac{2r-3}{4}}e^{\pi\sqrt{\frac{N}{12}}}\bigg)\bigg)e^{\frac{\pi \sqrt{N}v}{2\sqrt{3}}}\mathrm{d}v\\[5pt] =&\frac{1}{i4\sqrt{3N}}\int_{1-i}^{1+i}\bigg[c_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{-\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}(v+v^{-1})}+d_{r+1}^*\bigg(\frac{\pi v}{2\sqrt{3N}}\bigg)^{\frac{1}{2}-r}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}(v+v^{-1})}\bigg]\mathrm{d}v\\[5pt] &\qquad\quad+O\bigg(N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}\bigg)\\[5pt] =&c_{r+1}^*\bigg(\frac{\pi}{2\sqrt{3N}}\bigg)^{\frac{1}{2}-r}P_{-\frac{1}{2}-r} \bigg(\pi\sqrt{\frac{N}{12}}\bigg)+d_{r+1}^*\bigg(\frac{\pi}{2\sqrt{3N}}\bigg)^{\frac{3}{2}-r}P_{\frac{1}{2}-r} \bigg(\pi\sqrt{\frac{N}{12}}\bigg)\\[5pt] &\qquad\quad+O\bigg(N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}\bigg). \end{align*} $$
By applying Lemma 4.10, we conclude that
 $$ \begin{align*} \mathcal{I}_1=&c_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{1}{2}-r}I_{r-\frac{1}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)+d_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{3}{2}-r}I_{r-\frac{3}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)\\[5pt] &\qquad\quad+O\left(N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{I}_1=&c_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{1}{2}-r}I_{r-\frac{1}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)+d_{r+1}^*\left(\frac{\pi}{2\sqrt{3N}}\right)^{\frac{3}{2}-r}I_{r-\frac{3}{2}} \left(\pi\sqrt{\frac{N}{3}}\right)\\[5pt] &\qquad\quad+O\left(N^{\frac{2r-5}{4}}e^{\pi\sqrt{\frac{N}{3}}}\right). \end{align*} $$
We now turn to the integrals
![]() $\mathcal {I}_2$
and
$\mathcal {I}_2$
and
![]() $\mathcal {I}_3$
and find that they are exponentially smaller than the main asymptotic terms.
$\mathcal {I}_3$
and find that they are exponentially smaller than the main asymptotic terms.
Proposition 4.12 As
![]() $N\rightarrow \infty $
, we have
$N\rightarrow \infty $
, we have
Proof
 $$ \begin{align*}|\mathcal{I}_2|\leq& \int_{\frac{1}{4\sqrt{3N}}\leq|x|\leq\frac{1}{2}-\frac{1}{4\sqrt{3N}}} \left|F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}\right|\mathrm{d}x\\[5pt] \ll&N^{\frac{r+1}{2}}e^{\sqrt{3N}\left(\frac{\pi}{6}-\frac{1}{\pi}\left(1-\frac{1}{\sqrt{2}}\right)\right)} e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}}=N^{\frac{r+1}{2}}e^{\pi \sqrt{\frac{N}{3}}-\frac{\sqrt{3N}}{\pi}(1-\frac{\sqrt{2}}{2})}. \end{align*} $$
$$ \begin{align*}|\mathcal{I}_2|\leq& \int_{\frac{1}{4\sqrt{3N}}\leq|x|\leq\frac{1}{2}-\frac{1}{4\sqrt{3N}}} \left|F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}\right|\mathrm{d}x\\[5pt] \ll&N^{\frac{r+1}{2}}e^{\sqrt{3N}\left(\frac{\pi}{6}-\frac{1}{\pi}\left(1-\frac{1}{\sqrt{2}}\right)\right)} e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}}=N^{\frac{r+1}{2}}e^{\pi \sqrt{\frac{N}{3}}-\frac{\sqrt{3N}}{\pi}(1-\frac{\sqrt{2}}{2})}. \end{align*} $$
For the integral
![]() $\mathcal {I}_3$
, we have
$\mathcal {I}_3$
, we have
 $$ \begin{align*} |\mathcal{I}_3|=&\int_{|x-\frac{1}{2}|\leq \frac{1}{4\sqrt{3N}}}\left|F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}\right|\mathrm{d}x\\[5pt]\ll&N^{-\frac{1}{4}}e^{\pi\sqrt{\frac{N}{12}}}\int_{|x-\frac{1}{2}|\leq \frac{1}{4\sqrt{3N}}}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}}\mathrm{d}x\\[5pt]\ll& N^{-\frac{3}{4}}e^{\pi\sqrt{\frac{N}{3}}}. \end{align*} $$
$$ \begin{align*} |\mathcal{I}_3|=&\int_{|x-\frac{1}{2}|\leq \frac{1}{4\sqrt{3N}}}\left|F_r(e^{2\pi ix-\frac{\pi}{2\sqrt{3N}}})e^{-2\pi iNx+\frac{\pi \sqrt{N}}{2\sqrt{3}}}\right|\mathrm{d}x\\[5pt]\ll&N^{-\frac{1}{4}}e^{\pi\sqrt{\frac{N}{12}}}\int_{|x-\frac{1}{2}|\leq \frac{1}{4\sqrt{3N}}}e^{\frac{\pi \sqrt{N}}{2\sqrt{3}}}\mathrm{d}x\\[5pt]\ll& N^{-\frac{3}{4}}e^{\pi\sqrt{\frac{N}{3}}}. \end{align*} $$
Combining with Propositions 4.11 and 4.12, we obtain the following asymptotic formula.
Theorem 4.13 Assume that
![]() $r\geq 2$
. As
$r\geq 2$
. As
![]() $N\rightarrow \infty $
,
$N\rightarrow \infty $
,
 $$\begin{align*}\eta_r^{0+}(N)-c_{r+1}^*\left(\frac{\pi }{2\sqrt{3N}}\right)^{\frac{1}{2}-r} I_{r-\frac{1}{2}}\left(\pi \sqrt{\frac{N}{3}}\right)-d_{r+1}^*\left(\frac{\pi }{2\sqrt{3N}}\right)^{\frac{3}{2}-r}I_{r-\frac{3}{2}}\left(\pi \sqrt{\frac{N}{3}}\right)\ll N^{\frac{2r-5}{4}}e^{\frac{\pi \sqrt{N}}{\sqrt{3}}}.\end{align*}$$
$$\begin{align*}\eta_r^{0+}(N)-c_{r+1}^*\left(\frac{\pi }{2\sqrt{3N}}\right)^{\frac{1}{2}-r} I_{r-\frac{1}{2}}\left(\pi \sqrt{\frac{N}{3}}\right)-d_{r+1}^*\left(\frac{\pi }{2\sqrt{3N}}\right)^{\frac{3}{2}-r}I_{r-\frac{3}{2}}\left(\pi \sqrt{\frac{N}{3}}\right)\ll N^{\frac{2r-5}{4}}e^{\frac{\pi \sqrt{N}}{\sqrt{3}}}.\end{align*}$$
This completes the proof of Theorem 1.5.
Acknowledgment
The author is very grateful to the anonymous reviewers for their carefully reading and valuable suggestions which greatly improved this work.
Funding
This research is supported by the Natural Science Foundation of Chongqing (Grant No. cstc2020jcyj-msxmX0591), the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202200614), and the Research Startup Foundation of Chongqing University of Posts and Telecommunications (A2020-32).