Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-16T16:25:03.910Z Has data issue: false hasContentIssue false
  • English
  • Français

A RIGIDITY PROPERTY OF PLURIHARMONIC MAPS FROM PROJECTIVE MANIFOLDS

Part of: Variational problems in infinite-dimensional spaces

Published online by Cambridge University Press:  13 October 2022

CHE-HUNG HUANG Open the ORCID record for CHE-HUNG HUANG [Opens in a new window]
CHE-HUNG HUANG*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose M is a complex projective manifold of dimension 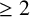$\geq 2$, V is the support of an ample divisor in M and U is an open set in M that intersects each irreducible component of V. We show that a pluriharmonic map 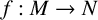$f:M\to N$ into a Kähler manifold N is holomorphic whenever $f\vert _{V\,\cap \, U}$ is holomorphic.

Keywords

harmonic mappings

MSC classification

Primary: 58E20: Harmonic maps , etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 166 - 168
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Griffiths, P. and Harris, J., Principles of Algebraic Geometry (Wiley, Hoboken, NJ, 1978).Google Scholar
Gromov, M., ‘Super stable Kählerian horseshoe?’, in: Essays in Mathematics and Its Applications (eds. Pardalos, P. M. and Rassias, T. M.) (Springer, Berlin–Heidelberg, 2012), 151–229.CrossRefGoogle Scholar
Ohnita, Y. and Udagawa, S., ‘Stablility, complex-analyticity and constancy of pluriharmonic maps from compact Kähler manifolds’, Math. Z. 205 (1990), 629–644.CrossRefGoogle Scholar
Sampson, J. H., ‘Some properties and applications of harmonic mappings’, Ann. Sci. Éc. Norm. Supér. (4) 11 (1978), 211–228.CrossRefGoogle Scholar
Siu, Y.-T., ‘The complex-analyticity of harmonic maps and the strong rigidity of compact Kähler manifolds’, Ann. of Math. (2) 112 (1980), 73–111.CrossRefGoogle Scholar
Toledo, D., ‘Hermitian curvature and plurisubharmonicity of energy on Teichmüller space’, Geom. Funct. Anal. 22 (2012), 1015–1032.CrossRefGoogle Scholar