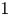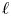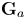Introduction
Let ![]() $K$ be a local field of positive characteristic and let
$K$ be a local field of positive characteristic and let ![]() $E$ be a Drinfeld module of finite residual characteristic over
$E$ be a Drinfeld module of finite residual characteristic over ![]() $\operatorname {Spec} K$ (cf. § 2.3 and see § 2.4 for the terminology). Pick a separable closure
$\operatorname {Spec} K$ (cf. § 2.3 and see § 2.4 for the terminology). Pick a separable closure ![]() $K^s/K$. We investigate the action of the inertia subgroup
$K^s/K$. We investigate the action of the inertia subgroup ![]() $I_K \subset \operatorname {Gal}(K^s/K)$ on the Tate modules
$I_K \subset \operatorname {Gal}(K^s/K)$ on the Tate modules ![]() $T_\mathfrak {p} E$. This parallels the study of local monodromy in the
$T_\mathfrak {p} E$. This parallels the study of local monodromy in the ![]() $\ell$-adic cohomology theory.
$\ell$-adic cohomology theory.
In the ![]() $\ell$-adic theory one assumes that the prime
$\ell$-adic theory one assumes that the prime ![]() $\ell$ is different from the residual characteristic of the base field. By way of analogy we suppose that the prime
$\ell$ is different from the residual characteristic of the base field. By way of analogy we suppose that the prime ![]() $\mathfrak {p}$ is different from the residual characteristic
$\mathfrak {p}$ is different from the residual characteristic ![]() $\bar {\mathfrak {p}}$ of the Drinfeld module
$\bar {\mathfrak {p}}$ of the Drinfeld module ![]() $E$. The case
$E$. The case ![]() $\mathfrak {p} = \bar {\mathfrak {p}}$ belongs to a function field analogue of Fontaine's theory, and is the subject of a separate study.
$\mathfrak {p} = \bar {\mathfrak {p}}$ belongs to a function field analogue of Fontaine's theory, and is the subject of a separate study.
Even under the assumption ![]() $\mathfrak {p} \ne \bar {\mathfrak {p}}$ the local monodromy of Drinfeld modules is much more complicated than that of algebraic varieties. The good reduction criterion of Takahashi implies that the image of the wild inertia in
$\mathfrak {p} \ne \bar {\mathfrak {p}}$ the local monodromy of Drinfeld modules is much more complicated than that of algebraic varieties. The good reduction criterion of Takahashi implies that the image of the wild inertia in ![]() $\operatorname {GL}(T_\mathfrak {p} E)$ is infinite unless
$\operatorname {GL}(T_\mathfrak {p} E)$ is infinite unless ![]() $E$ has potential good reduction.
$E$ has potential good reduction.
However, there is a limit on the ramification. Recall that the inertia subgroup ![]() $I_K$ carries a descending filtration by closed normal subgroups
$I_K$ carries a descending filtration by closed normal subgroups ![]() $I_K^{u}$,
$I_K^{u}$, ![]() $u \in \mathbf {Q}_{\geqslant 0}$, the ramification filtration in upper numbering.
$u \in \mathbf {Q}_{\geqslant 0}$, the ramification filtration in upper numbering.
Theorem 1 Let ![]() $E$ be a Drinfeld module of finite residual characteristic
$E$ be a Drinfeld module of finite residual characteristic ![]() $\bar {\mathfrak {p}}$ over
$\bar {\mathfrak {p}}$ over ![]() $\operatorname {Spec} K$. Then there is a rational number
$\operatorname {Spec} K$. Then there is a rational number ![]() $u\geqslant 0$ such that for every prime
$u\geqslant 0$ such that for every prime ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$ the ramification subgroup
$\mathfrak {p}\ne \bar {\mathfrak {p}}$ the ramification subgroup ![]() $I_K^{u}$ acts trivially on the Tate module
$I_K^{u}$ acts trivially on the Tate module ![]() $T_\mathfrak {p} E$.
$T_\mathfrak {p} E$.
The author first deduced this result from a ![]() $z$-adic analogue of Grothendieck's
$z$-adic analogue of Grothendieck's ![]() $\ell$-adic monodromy theorem. The
$\ell$-adic monodromy theorem. The ![]() $z$-adic monodromy theorem applies in the generality of arbitrary
$z$-adic monodromy theorem applies in the generality of arbitrary ![]() $A$-motives, and will be published in a forthcoming article. A direct and less technically involved proof of Theorem 1 was found by Richard Pink after some discussions with the current author. In this paper, the author would like to present a revision of Pink's argument (Theorem 3.2.4(1)) together with related results.
$A$-motives, and will be published in a forthcoming article. A direct and less technically involved proof of Theorem 1 was found by Richard Pink after some discussions with the current author. In this paper, the author would like to present a revision of Pink's argument (Theorem 3.2.4(1)) together with related results.
Replacing ![]() $K$ by a finite separable extension we are free to assume that the Drinfeld module
$K$ by a finite separable extension we are free to assume that the Drinfeld module ![]() $E$ has stable reduction. This means that
$E$ has stable reduction. This means that ![]() $E$ is an analytic quotient of a Drinfeld module
$E$ is an analytic quotient of a Drinfeld module ![]() $D$ of good reduction by a period lattice
$D$ of good reduction by a period lattice ![]() $\varLambda \subset D(K^s)$, cf. § 4.1. Let us further assume that the lattice
$\varLambda \subset D(K^s)$, cf. § 4.1. Let us further assume that the lattice ![]() $\varLambda$ is defined over
$\varLambda$ is defined over ![]() $K$, which is to say,
$K$, which is to say, ![]() $\varLambda \subset D(K)$. Then the action of the inertia group
$\varLambda \subset D(K)$. Then the action of the inertia group ![]() $I_K$ on
$I_K$ on ![]() $T_\mathfrak {p} E$ factors through the maximal abelian quotient
$T_\mathfrak {p} E$ factors through the maximal abelian quotient ![]() $I_K^{\text {ab}}$. By the Hasse–Arf theorem the induced ramification filtration of
$I_K^{\text {ab}}$. By the Hasse–Arf theorem the induced ramification filtration of ![]() $I_K^{\text {ab}}$ is integrally indexed, so we can make the following definition.
$I_K^{\text {ab}}$ is integrally indexed, so we can make the following definition.
Definition The local conductor ![]() $\operatorname {\mathfrak {f}}(E/K)$ is the least integer
$\operatorname {\mathfrak {f}}(E/K)$ is the least integer ![]() $m\geqslant 0$ such that the ramification subgroup
$m\geqslant 0$ such that the ramification subgroup ![]() $\smash {I_K^{{\text {ab}},m+1}}$ acts trivially on
$\smash {I_K^{{\text {ab}},m+1}}$ acts trivially on ![]() $T_\mathfrak {p} E$ for all
$T_\mathfrak {p} E$ for all ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$.
$\mathfrak {p}\ne \bar {\mathfrak {p}}$.
The conductor is zero if and only if ![]() $\varLambda = 0$, i.e. if the Drinfeld module
$\varLambda = 0$, i.e. if the Drinfeld module ![]() $E$ has good reduction. Otherwise, the conductor is a positive integer that is prime to
$E$ has good reduction. Otherwise, the conductor is a positive integer that is prime to ![]() $p$. An important property of the conductor is its invariance under isogenies.
$p$. An important property of the conductor is its invariance under isogenies.
The conductor is hard to compute, and we can do it only for special period lattices (Theorem 4.1.13). In general, we can bound the conductor from above by a more amenable invariant.
In the following, let us denote by ![]() $A$ the chosen coefficient ring of our Drinfeld modules, cf. § 2.3. This ring is a Dedekind domain over
$A$ the chosen coefficient ring of our Drinfeld modules, cf. § 2.3. This ring is a Dedekind domain over ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$ with finite group of units. The period lattice
$\mathbf {F}_{\hspace {-1.5pt} q}$ with finite group of units. The period lattice ![]() $\varLambda$ carries a natural structure of a finitely generated projective
$\varLambda$ carries a natural structure of a finitely generated projective ![]() $A$-module.
$A$-module.
Poonen [Reference PoonenPoo95] introduced the notion of canonical local height. This provides the period lattice ![]() $\varLambda$ with a natural norm. Building on the work of Taguchi [Reference TaguchiTag93, § 4] we develop a theory of normed
$\varLambda$ with a natural norm. Building on the work of Taguchi [Reference TaguchiTag93, § 4] we develop a theory of normed ![]() $A$-lattices in function field arithmetic (§ 1) and, in particular, define the volume of such lattices.
$A$-lattices in function field arithmetic (§ 1) and, in particular, define the volume of such lattices.
Theorem 2 Let ![]() $E$ be a Drinfeld
$E$ be a Drinfeld ![]() $A$-module of stable reduction over
$A$-module of stable reduction over ![]() $\operatorname {Spec} K$ with the local period lattice
$\operatorname {Spec} K$ with the local period lattice ![]() $\varLambda$ defined over
$\varLambda$ defined over ![]() $K$. Let
$K$. Let ![]() $r$ be the rank of
$r$ be the rank of ![]() $E$. Then we have an inequality
$E$. Then we have an inequality
where ![]() $\operatorname {vol}(\varLambda )$ is the volume of the period lattice,
$\operatorname {vol}(\varLambda )$ is the volume of the period lattice, ![]() $s = r - \operatorname {rank}_A(\varLambda )$ and
$s = r - \operatorname {rank}_A(\varLambda )$ and ![]() $C$ is an effective constant that depends only on
$C$ is an effective constant that depends only on ![]() $A$.
$A$.
To prove this bound we set up a correspondence between normed ![]() $A$-lattices and systems of vector bundles on the compactification of the curve
$A$-lattices and systems of vector bundles on the compactification of the curve ![]() $\operatorname {Spec} A$. For such bundles one has a classical criterion of global generation via Castelnuovo–Mumford regularity. Translated to the setting of lattices this gives a volume bound on norms of generators, and the conductor inequality follows.
$\operatorname {Spec} A$. For such bundles one has a classical criterion of global generation via Castelnuovo–Mumford regularity. Translated to the setting of lattices this gives a volume bound on norms of generators, and the conductor inequality follows.
The bound of Theorem 2 is effective in the following sense: there is an algorithm which calculates ![]() $\operatorname {vol}(\varLambda )$ from the
$\operatorname {vol}(\varLambda )$ from the ![]() $\tau$-polynomials defining the Drinfeld module
$\tau$-polynomials defining the Drinfeld module ![]() $E$. This will be demonstrated in a forthcoming article.
$E$. This will be demonstrated in a forthcoming article.
Asayama and Huang [Reference Asayama and HuangAH24, Reference HuangHua24] introduced the notion of a conductor for Drinfeld modules of rank ![]() $2$ and proved a version of Szpiro's conjecture under additional assumptions. It would be interesting to know the precise relation between the conductor of Asayama and Huang and the conductor of this paper.
$2$ and proved a version of Szpiro's conjecture under additional assumptions. It would be interesting to know the precise relation between the conductor of Asayama and Huang and the conductor of this paper.
Last but not least, we study the image of inertia in ![]() $\operatorname {GL}(T_\mathfrak {p} E)$. The following result can be seen as a local open image theorem for Drinfeld modules with period lattices of rank
$\operatorname {GL}(T_\mathfrak {p} E)$. The following result can be seen as a local open image theorem for Drinfeld modules with period lattices of rank ![]() $1$.
$1$.
Theorem 3 Let ![]() $E$ be a Drinfeld module of finite residual characteristic
$E$ be a Drinfeld module of finite residual characteristic ![]() $\bar {\mathfrak {p}}$ and rank
$\bar {\mathfrak {p}}$ and rank ![]() $r$ over
$r$ over ![]() $\operatorname {Spec} K$. Suppose that the local period lattice of
$\operatorname {Spec} K$. Suppose that the local period lattice of ![]() $E$ has rank
$E$ has rank ![]() $1$. Then for each prime
$1$. Then for each prime ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$ the image of inertia in
$\mathfrak {p}\ne \bar {\mathfrak {p}}$ the image of inertia in ![]() $\operatorname {GL}(T_\mathfrak {p} E)$ is commensurable with a closed algebraic subgroup
$\operatorname {GL}(T_\mathfrak {p} E)$ is commensurable with a closed algebraic subgroup ![]() $U \cong (\mathbf {G}_a)^{\times (r-1)}$.
$U \cong (\mathbf {G}_a)^{\times (r-1)}$.
Let ![]() $V$ be a local
$V$ be a local ![]() $\ell$-adic Galois representation. The
$\ell$-adic Galois representation. The ![]() $\ell$-adic monodromy theorem of Grothendieck implies that the image of inertia in
$\ell$-adic monodromy theorem of Grothendieck implies that the image of inertia in ![]() $\operatorname {GL}(V)$ is commensurable with a closed algebraic subgroup
$\operatorname {GL}(V)$ is commensurable with a closed algebraic subgroup ![]() $U \cong (\mathbf {G}_a)^{\times d}$, but the dimension
$U \cong (\mathbf {G}_a)^{\times d}$, but the dimension ![]() $d$ can only be
$d$ can only be ![]() $0$ or
$0$ or ![]() $1$. Theorem 3 shows that in the case of Drinfeld modules the dimension
$1$. Theorem 3 shows that in the case of Drinfeld modules the dimension ![]() $d$ can be as large as
$d$ can be as large as ![]() $\dim (V) - 1$.
$\dim (V) - 1$.
The situation with Drinfeld modules that have period lattices of rank at least ![]() $2$ is made complicated by the presence of nontrivial endomorphisms. Still one expects that a suitable local open image theorem holds in all cases. This is a subject of current research.
$2$ is made complicated by the presence of nontrivial endomorphisms. Still one expects that a suitable local open image theorem holds in all cases. This is a subject of current research.
Finally, let us discuss the proofs of Theorems 1, 2 and 3. Replacing ![]() $K$ with a finite separable extension we are free to assume that the Drinfeld module
$K$ with a finite separable extension we are free to assume that the Drinfeld module ![]() $E$ is an analytic quotient of a Drinfeld module
$E$ is an analytic quotient of a Drinfeld module ![]() $D$ of good reduction by a period lattice
$D$ of good reduction by a period lattice ![]() $\varLambda \subset D(K)$. For each prime
$\varLambda \subset D(K)$. For each prime ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$ we then have a short exact sequence of
$\mathfrak {p}\ne \bar {\mathfrak {p}}$ we then have a short exact sequence of ![]() $G_K$-modules
$G_K$-modules
with ![]() $A_\mathfrak {p}$ the
$A_\mathfrak {p}$ the ![]() $\mathfrak {p}$-adic completion of
$\mathfrak {p}$-adic completion of ![]() $A$. The inertia group
$A$. The inertia group ![]() $I_K$ acts trivially on the first and the last module. Consequently, the action of
$I_K$ acts trivially on the first and the last module. Consequently, the action of ![]() $I_K$ on
$I_K$ on ![]() $T_\mathfrak {p} E$ differs from the identity by a homomorphism
$T_\mathfrak {p} E$ differs from the identity by a homomorphism ![]() $I_K \to \operatorname {Hom}_A(\varLambda,\,T_\mathfrak {p} D)$. This homomorphism can be equally seen as a pairing
$I_K \to \operatorname {Hom}_A(\varLambda,\,T_\mathfrak {p} D)$. This homomorphism can be equally seen as a pairing
In the exact same way as in the theory of abelian varieties, this pairing turns out to be the restriction to ![]() $\varLambda$ of a certain universal pairing
$\varLambda$ of a certain universal pairing
the ![]() $\mathfrak {p}$-adic Kummer pairing of
$\mathfrak {p}$-adic Kummer pairing of ![]() $D$.
$D$.
The Kummer pairing from the theory of abelian varieties factors through the tame quotient of the inertia group ![]() $I_K$. This quotient group is procyclic of order prime to the residual characteristic
$I_K$. This quotient group is procyclic of order prime to the residual characteristic ![]() $p$ of
$p$ of ![]() $K$. By contrast, the Kummer pairing of the Drinfeld module
$K$. By contrast, the Kummer pairing of the Drinfeld module ![]() $D$ factors through the maximal quotient
$D$ factors through the maximal quotient ![]() $J_K = I_K^{\text {ab}}/(I_K^{\text {ab}})^{\times p}$ that is abelian of exponent
$J_K = I_K^{\text {ab}}/(I_K^{\text {ab}})^{\times p}$ that is abelian of exponent ![]() $p$. Unlike the tame quotient, the induced ramification filtration on
$p$. Unlike the tame quotient, the induced ramification filtration on ![]() $J_K$ is nontrivial and, in fact, has a break at every positive integer that is prime to
$J_K$ is nontrivial and, in fact, has a break at every positive integer that is prime to ![]() $p$.
$p$.
We study how the Kummer pairing of ![]() $D$ interacts with the ramification filtration on
$D$ interacts with the ramification filtration on ![]() $J_K$. We prove that for each element
$J_K$. We prove that for each element ![]() $\lambda \in D(K)$ the homomorphism
$\lambda \in D(K)$ the homomorphism ![]() $[\lambda, \,)_{}\colon J_K \to T_\mathfrak {p} D$ vanishes on a sufficiently deep ramification subgroup
$[\lambda, \,)_{}\colon J_K \to T_\mathfrak {p} D$ vanishes on a sufficiently deep ramification subgroup ![]() $J_K^u$ with
$J_K^u$ with ![]() $u$ bounded from above by the Poonen height of
$u$ bounded from above by the Poonen height of ![]() $\lambda$, see Theorem 3.2.4. This property of the Kummer pairing implies Theorems 1 and 2.
$\lambda$, see Theorem 3.2.4. This property of the Kummer pairing implies Theorems 1 and 2.
We also prove that the homomorphism ![]() $[\lambda, \,)_{}\colon J_K \to T_\mathfrak {p} D$ has open image provided that
$[\lambda, \,)_{}\colon J_K \to T_\mathfrak {p} D$ has open image provided that ![]() $\lambda$ is not contained in the subset of integral elements
$\lambda$ is not contained in the subset of integral elements ![]() $D(\mathcal {O}_K)$, see Theorem 3.3.2. This property implies Theorem 3.
$D(\mathcal {O}_K)$, see Theorem 3.3.2. This property implies Theorem 3.
The Stacks Project
We will use The Stacks Project [Sta] as a source for algebraic geometry. References to The Stacks Project have the form [St: ![]() $wxyz$] where ‘
$wxyz$] where ‘![]() $wxyz$’ is a combination of letters and numbers. The corresponding item is located at https://stacks.math.columbia.edu/tag/
$wxyz$’ is a combination of letters and numbers. The corresponding item is located at https://stacks.math.columbia.edu/tag/ ![]() $wxyz$.
$wxyz$.
1. Normed lattices
Recall that a lattice in the sense of geometry of numbers is a finitely generated free ![]() $\mathbf {Z}$-module
$\mathbf {Z}$-module ![]() $L$ equipped with a positive-definite quadratic form
$L$ equipped with a positive-definite quadratic form ![]() $q\colon L \to \mathbf {R}_{\geqslant 0}$. The induced norm
$q\colon L \to \mathbf {R}_{\geqslant 0}$. The induced norm ![]() $\|\cdot \| = \sqrt {q(\cdot )}$ is homogeneous with respect to the archimedean absolute value: we have
$\|\cdot \| = \sqrt {q(\cdot )}$ is homogeneous with respect to the archimedean absolute value: we have ![]() $\|a v\| = |a| \cdot \|v\|$ for all integers
$\|a v\| = |a| \cdot \|v\|$ for all integers ![]() $a \in \mathbf {Z}$ and vectors
$a \in \mathbf {Z}$ and vectors ![]() $v \in L$.
$v \in L$.
We shall transfer the notion of a normed lattice to the setting of function fields. To this end we draw upon an informal analogy between the pair ![]() $(\mathbf {Q}, \infty )$ consisting of the field of rational numbers
$(\mathbf {Q}, \infty )$ consisting of the field of rational numbers ![]() $\mathbf {Q}$ and its unique archimedean place, and the pair
$\mathbf {Q}$ and its unique archimedean place, and the pair ![]() $(F, \infty )$ consisting of a global function field
$(F, \infty )$ consisting of a global function field ![]() $F$ and an arbitrarily chosen place
$F$ and an arbitrarily chosen place ![]() $\infty$.
$\infty$.
The ring ![]() $\mathbf {Z}$ is the set of elements
$\mathbf {Z}$ is the set of elements ![]() $x\in \mathbf {Q}$ which are regular away from
$x\in \mathbf {Q}$ which are regular away from ![]() $\infty$ and the field
$\infty$ and the field ![]() $\mathbf {R}$ is the completion of
$\mathbf {R}$ is the completion of ![]() $\mathbf {Q}$ at
$\mathbf {Q}$ at ![]() $\infty$. In the same way, the pair
$\infty$. In the same way, the pair ![]() $(F, \infty )$ determines a Dedekind domain
$(F, \infty )$ determines a Dedekind domain ![]() $A$ and a locally compact field
$A$ and a locally compact field ![]() $F_\infty$. One can consider the pair of rings
$F_\infty$. One can consider the pair of rings ![]() $A\subset F_\infty$ as a function field equivalent of the pair
$A\subset F_\infty$ as a function field equivalent of the pair ![]() $\mathbf {Z}\subset \mathbf {R}$.
$\mathbf {Z}\subset \mathbf {R}$.
Inspired by this observation we define an ![]() $A$-lattice as a finitely generated projective
$A$-lattice as a finitely generated projective ![]() $A$-module
$A$-module ![]() $\varLambda$ equipped with a norm
$\varLambda$ equipped with a norm ![]() $\|\cdot \|\colon \varLambda \to \mathbf {R}_{\geqslant 0}$ which is homogeneous with respect to a fixed
$\|\cdot \|\colon \varLambda \to \mathbf {R}_{\geqslant 0}$ which is homogeneous with respect to a fixed ![]() $\infty$-adic absolute value on
$\infty$-adic absolute value on ![]() $F_\infty$ and induces the discrete topology on
$F_\infty$ and induces the discrete topology on ![]() $\varLambda$. The study of normed lattices in function field arithmetic was initiated by Taguchi [Reference TaguchiTag93, § 4]. We develop the theory further by relating normed lattices to vector bundles on the smooth projective curve
$\varLambda$. The study of normed lattices in function field arithmetic was initiated by Taguchi [Reference TaguchiTag93, § 4]. We develop the theory further by relating normed lattices to vector bundles on the smooth projective curve ![]() $X$ which has
$X$ which has ![]() $F$ as the field of rational functions.
$F$ as the field of rational functions.
As is the case for ![]() $\mathbf {Z}$-lattices the norm of an
$\mathbf {Z}$-lattices the norm of an ![]() $A$-lattice
$A$-lattice ![]() $\varLambda$ extends uniquely to a norm on the ‘real’ vector space
$\varLambda$ extends uniquely to a norm on the ‘real’ vector space ![]() $V_\infty = F_\infty \otimes _A \varLambda$ but this result is rather subtle. One then defines the volume of the lattice
$V_\infty = F_\infty \otimes _A \varLambda$ but this result is rather subtle. One then defines the volume of the lattice ![]() $\varLambda$ as a normalized volume of its fundamental domain in the locally compact vector space
$\varLambda$ as a normalized volume of its fundamental domain in the locally compact vector space ![]() $V_\infty$. The relation between lattices and vector bundles leads to a bound on norms of generators in terms of the volume (Theorem 1.6.4).
$V_\infty$. The relation between lattices and vector bundles leads to a bound on norms of generators in terms of the volume (Theorem 1.6.4).
In [Reference TaguchiTag93, § 4] Taguchi defined the discriminant of a lattice. At the moment it is not clear what is the precise relation between the volume as defined in this paper and the discriminant of Taguchi.
1.1 Normed vector spaces
As a preparation for the theory of lattices let us review some properties of normed vector spaces following [Reference Bosch, Güntzer and RemmertBGR84, Ch. 2]. We fix a field ![]() $F$ and an absolute value
$F$ and an absolute value ![]() $|\cdot |\colon F \to \mathbf {R}_{\geqslant 0}$ that arises from a nontrivial discrete valuation. Let
$|\cdot |\colon F \to \mathbf {R}_{\geqslant 0}$ that arises from a nontrivial discrete valuation. Let ![]() $R = \{ x \in F, |x| \leqslant 1 \}$ be the corresponding ring of integers. We denote its maximal ideal by
$R = \{ x \in F, |x| \leqslant 1 \}$ be the corresponding ring of integers. We denote its maximal ideal by ![]() $\mathfrak {p}$.
$\mathfrak {p}$.
Let ![]() $V$ be a finite-dimensional
$V$ be a finite-dimensional ![]() $F$-vector space. Recall that a
$F$-vector space. Recall that a ![]() $\mathfrak {p}$-adic norm on
$\mathfrak {p}$-adic norm on ![]() $V$ is a map
$V$ is a map ![]() $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ with the following properties:
$\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ with the following properties:
(
 ${\rm V} _{\!1 }$)
${\rm V} _{\!1 }$)  $\|v\| = 0$ if and only if
$\|v\| = 0$ if and only if  $v = 0$;
$v = 0$;(
 ${\rm V} _{\!2 }$)
${\rm V} _{\!2 }$)  $\|v + v'\| \leqslant \max \{ \|v\|, \|v'\| \}$;
$\|v + v'\| \leqslant \max \{ \|v\|, \|v'\| \}$;(
 ${\rm V} _{\!3 }$)
${\rm V} _{\!3 }$)  $\|x v\| = |x| \cdot \|v\|$ for all
$\|x v\| = |x| \cdot \|v\|$ for all  $x \in F$.
$x \in F$.
We have ![]() $\|{-}v\| = \|v\|$ by the homogeneity property (
$\|{-}v\| = \|v\|$ by the homogeneity property (![]() ${\rm V}_{\!3}$), so the ultrametric inequality (
${\rm V}_{\!3}$), so the ultrametric inequality (![]() ${\rm V}_{\!2}$) becomes an equality when
${\rm V}_{\!2}$) becomes an equality when ![]() $\|v\|\ne \|v'\|$.
$\|v\|\ne \|v'\|$.
Let ![]() $\pi \in F$ be a uniformizer and set
$\pi \in F$ be a uniformizer and set ![]() $\varepsilon := |\pi |$. Observe that
$\varepsilon := |\pi |$. Observe that ![]() $\varepsilon \in (0, 1)$.
$\varepsilon \in (0, 1)$.
Lemma 1.1.1 The image of the norm function ![]() $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ has the form
$\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ has the form
where ![]() $r_1, r_2, \dotsc, r_m \in (\varepsilon,\:1]$ is a sequence of real numbers,
$r_1, r_2, \dotsc, r_m \in (\varepsilon,\:1]$ is a sequence of real numbers, ![]() $m\leqslant \dim V$.
$m\leqslant \dim V$.
Proof. The set of values ![]() $|F^\times | = \varepsilon ^{\mathbf {Z}}$ is a subgroup of
$|F^\times | = \varepsilon ^{\mathbf {Z}}$ is a subgroup of ![]() $\mathbf {R}^\times$, so the claim follows by [Reference Bosch, Güntzer and RemmertBGR84, Prop. 2.1.4/2].
$\mathbf {R}^\times$, so the claim follows by [Reference Bosch, Güntzer and RemmertBGR84, Prop. 2.1.4/2].
The ultrametric inequality (![]() ${\rm V}_{\!2}$) and the homogeneity property (
${\rm V}_{\!2}$) and the homogeneity property (![]() ${\rm V}_{\!3}$) imply that the balls
${\rm V}_{\!3}$) imply that the balls
are ![]() $R$-submodules of
$R$-submodules of ![]() $V$ such that:
$V$ such that:
 $({\rm B} _{ 1 } )$
$({\rm B} _{ 1 } )$  $x\,B(V,\,r) = B(V,\,|x|\,r)$ for every scalar
$x\,B(V,\,r) = B(V,\,|x|\,r)$ for every scalar  $x \in F^\times$;
$x \in F^\times$; $({\rm B} _{ 2 } )$
$({\rm B} _{ 2 } )$  $F \otimes _{R} B(V,\,r) = V$.
$F \otimes _{R} B(V,\,r) = V$.
Lemma 1.1.2 For each pair of real numbers ![]() $r' > r > 0$ the quotient
$r' > r > 0$ the quotient ![]() $R$-module
$R$-module ![]() $B(V,\,r')/B(V,\,r)$ has finite length.
$B(V,\,r')/B(V,\,r)$ has finite length.
Proof. It suffices to prove the claim for ![]() $r = r'\varepsilon ^n$ with any integer
$r = r'\varepsilon ^n$ with any integer ![]() $n>0$. The
$n>0$. The ![]() $R$-module
$R$-module ![]() $B(V,\,r')$ is torsion-free by construction and has finite rank by property
$B(V,\,r')$ is torsion-free by construction and has finite rank by property ![]() $({\rm B}_2)$. We also have
$({\rm B}_2)$. We also have ![]() $B(V,\,r) = \mathfrak {p}^nB(V,\,r')$ by property
$B(V,\,r) = \mathfrak {p}^nB(V,\,r')$ by property ![]() $({\rm B}_1)$. Invoking Lemma 3 of [Reference PoonenPoo95, § 5] we conclude that the
$({\rm B}_1)$. Invoking Lemma 3 of [Reference PoonenPoo95, § 5] we conclude that the ![]() $R/\mathfrak {p}^n$-module
$R/\mathfrak {p}^n$-module ![]() $B(V,\,r')/B(V,\,r)$ is finitely generated and, thus, has finite length.
$B(V,\,r')/B(V,\,r)$ is finitely generated and, thus, has finite length.
Each norm endows the vector space ![]() $V$ with a topology by means of the fundamental system
$V$ with a topology by means of the fundamental system ![]() $\{B(V,\,r)\}_{r>0}$. Lemma 1.1.1 implies that this system is the same as the system of open balls
$\{B(V,\,r)\}_{r>0}$. Lemma 1.1.1 implies that this system is the same as the system of open balls ![]() $\{ v \in V, \|v\| < r \}$.
$\{ v \in V, \|v\| < r \}$.
It is important to note that, in general, the norm topology on ![]() $V$ can be coarser than the canonical
$V$ can be coarser than the canonical ![]() $\mathfrak {p}$-adic topology. An explicit construction of such norms is given in Example 1.1.7. From Lemma 1.1.2 we directly have the following result.
$\mathfrak {p}$-adic topology. An explicit construction of such norms is given in Example 1.1.7. From Lemma 1.1.2 we directly have the following result.
Corollary 1.1.3 A norm on ![]() $V$ induces the canonical
$V$ induces the canonical ![]() $\mathfrak {p}$-adic topology if and only if for each real number
$\mathfrak {p}$-adic topology if and only if for each real number ![]() $r > 0$ the
$r > 0$ the ![]() $R$-module
$R$-module ![]() $B(V,\,r)$ is finitely generated.
$B(V,\,r)$ is finitely generated.
To increase flexibility we will need the notion of a seminorm which is a map ![]() $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ satisfying the conditions (
$\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ satisfying the conditions (![]() ${\rm V}_{\!2}$) and (
${\rm V}_{\!2}$) and (![]() ${\rm V}_{\!3}$). The following claim is easy to check.
${\rm V}_{\!3}$). The following claim is easy to check.
Lemma 1.1.4 For each seminorm ![]() $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ the following hold.
$\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ the following hold.
(1) The kernel
 $H = \{ v \in V, \:\|v\| = 0 \}$ is an
$H = \{ v \in V, \:\|v\| = 0 \}$ is an  $F$-vector subspace of
$F$-vector subspace of  $V$.
$V$.(2) The map
 $\|\cdot \|$ factors through the quotient homomorphism
$\|\cdot \|$ factors through the quotient homomorphism  $V \twoheadrightarrow V/H$ and induces a norm on
$V \twoheadrightarrow V/H$ and induces a norm on  $V/H$.
$V/H$.
Next we give a criterion for the norm on ![]() $V$ to induce the canonical
$V$ to induce the canonical ![]() $\mathfrak {p}$-adic topology. Let
$\mathfrak {p}$-adic topology. Let ![]() $\smash {F_{\mathfrak {p}}}$ be the
$\smash {F_{\mathfrak {p}}}$ be the ![]() $\mathfrak {p}$-adic completion of the field
$\mathfrak {p}$-adic completion of the field ![]() $F$.
$F$.
Theorem 1.1.5 Each norm on the vector space ![]() $V$ extends uniquely to a seminorm on the
$V$ extends uniquely to a seminorm on the ![]() $\mathfrak {p}$-adic completion
$\mathfrak {p}$-adic completion ![]() $\smash {V_{\mathfrak {p}}} = \smash {F_{\mathfrak {p}}}\otimes _{F} V$, and such an extension is a norm if and only if the original norm induces the
$\smash {V_{\mathfrak {p}}} = \smash {F_{\mathfrak {p}}}\otimes _{F} V$, and such an extension is a norm if and only if the original norm induces the ![]() $\mathfrak {p}$-adic topology on
$\mathfrak {p}$-adic topology on ![]() $V$.
$V$.
Proof. It follows from Proposition 1 of [Reference BourbakiBou81, II, § 1, n![]() ${}^\circ$1] that every seminorm is continuous with respect to the
${}^\circ$1] that every seminorm is continuous with respect to the ![]() $\mathfrak {p}$-adic topology on
$\mathfrak {p}$-adic topology on ![]() $\smash {V_{\mathfrak {p}}}$ and the analytic topology on
$\smash {V_{\mathfrak {p}}}$ and the analytic topology on ![]() $\mathbf {R}_{\geqslant 0}$. Since the vector space
$\mathbf {R}_{\geqslant 0}$. Since the vector space ![]() $V$ is
$V$ is ![]() $\mathfrak {p}$-adically dense in
$\mathfrak {p}$-adically dense in ![]() $\smash {V_{\mathfrak {p}}}$ we conclude that the sought extension is unique.
$\smash {V_{\mathfrak {p}}}$ we conclude that the sought extension is unique.
Let ![]() ${V_{\rho }}$ be the completion of the normed vector space
${V_{\rho }}$ be the completion of the normed vector space ![]() $V$ as in [Reference Bosch, Güntzer and RemmertBGR84, § 2.1.3]. This is a normed
$V$ as in [Reference Bosch, Güntzer and RemmertBGR84, § 2.1.3]. This is a normed ![]() $\smash {F_{\mathfrak {p}}}$-vector space by construction. The proof of [Reference Bosch, Güntzer and RemmertBGR84, Prop. 2.3.3/6] shows that the natural morphism
$\smash {F_{\mathfrak {p}}}$-vector space by construction. The proof of [Reference Bosch, Güntzer and RemmertBGR84, Prop. 2.3.3/6] shows that the natural morphism ![]() $\smash {V_{\mathfrak {p}}} \twoheadrightarrow {V_{\rho }}$ is surjective. Taking the composition of the norm on
$\smash {V_{\mathfrak {p}}} \twoheadrightarrow {V_{\rho }}$ is surjective. Taking the composition of the norm on ![]() ${V_{\rho }}$ with the surjection
${V_{\rho }}$ with the surjection ![]() $\smash {V_{\mathfrak {p}}} \twoheadrightarrow {V_{\rho }}$ we obtain the desired seminorm on the vector space
$\smash {V_{\mathfrak {p}}} \twoheadrightarrow {V_{\rho }}$ we obtain the desired seminorm on the vector space ![]() $\smash {V_{\mathfrak {p}}}$.
$\smash {V_{\mathfrak {p}}}$.
The seminorm on ![]() $\smash {V_{\mathfrak {p}}}$ is a norm if and only if the surjection
$\smash {V_{\mathfrak {p}}}$ is a norm if and only if the surjection ![]() $\smash {V_{\mathfrak {p}}}\twoheadrightarrow {V_{\rho }}$ is an isomorphism. According to [Reference Bosch, Güntzer and RemmertBGR84, Prop. 2.3.3/6] the latter happens if and only if the norm topology on
$\smash {V_{\mathfrak {p}}}\twoheadrightarrow {V_{\rho }}$ is an isomorphism. According to [Reference Bosch, Güntzer and RemmertBGR84, Prop. 2.3.3/6] the latter happens if and only if the norm topology on ![]() $V$ is the canonical
$V$ is the canonical ![]() $\mathfrak {p}$-adic topology, as claimed.
$\mathfrak {p}$-adic topology, as claimed.
Corollary 1.1.6 Suppose that the field ![]() $F$ is
$F$ is ![]() $\mathfrak {p}$-adically complete. Then the norm topology on
$\mathfrak {p}$-adically complete. Then the norm topology on ![]() $V$ is the canonical
$V$ is the canonical ![]() $\mathfrak {p}$-adic topology.
$\mathfrak {p}$-adic topology.
The behaviour of ![]() $\mathfrak {p}$-adic norms in Theorem 1.1.5 resembles the behaviour of real-valued quadratic forms on a finite-dimensional
$\mathfrak {p}$-adic norms in Theorem 1.1.5 resembles the behaviour of real-valued quadratic forms on a finite-dimensional ![]() $\mathbf {Q}$-vector space
$\mathbf {Q}$-vector space ![]() $V$. Every such form
$V$. Every such form ![]() $q$ extends uniquely to the real vector space
$q$ extends uniquely to the real vector space ![]() $V_\infty = \mathbf {R}\otimes _{\mathbf {Q}} V$. If the form
$V_\infty = \mathbf {R}\otimes _{\mathbf {Q}} V$. If the form ![]() $q$ takes strictly positive values on
$q$ takes strictly positive values on ![]() $V\smallsetminus \{0\}$ then it is positive-semidefinite, and the map
$V\smallsetminus \{0\}$ then it is positive-semidefinite, and the map ![]() $v \mapsto q(v)^{1/2}$ is an archimedean seminorm on
$v \mapsto q(v)^{1/2}$ is an archimedean seminorm on ![]() $V_\infty$. This seminorm is a norm if and only if the form
$V_\infty$. This seminorm is a norm if and only if the form ![]() $q$ is positive-definite. Comparing with Theorem 1.1.5, we conclude that the property of inducing the
$q$ is positive-definite. Comparing with Theorem 1.1.5, we conclude that the property of inducing the ![]() $\mathfrak {p}$-adic topology can be understood as a form of positive-definiteness for
$\mathfrak {p}$-adic topology can be understood as a form of positive-definiteness for ![]() $\mathfrak {p}$-adic norms.
$\mathfrak {p}$-adic norms.
As an offshoot of Theorem 1.1.5 we get a description of all norms that fail to induce the ![]() $\mathfrak {p}$-adic topology on
$\mathfrak {p}$-adic topology on ![]() $V$.
$V$.
Example 1.1.7 Suppose that ![]() $\dim V \geqslant 2$, and that the field
$\dim V \geqslant 2$, and that the field ![]() $F$ is not
$F$ is not ![]() $\mathfrak {p}$-adically complete. Pick a nonzero subspace
$\mathfrak {p}$-adically complete. Pick a nonzero subspace ![]() $H \subset \smash {V_{\mathfrak {p}}}$ which is totally irrational in the sense that
$H \subset \smash {V_{\mathfrak {p}}}$ which is totally irrational in the sense that ![]() $H \cap V = \{0\}$. Pick a norm on the quotient
$H \cap V = \{0\}$. Pick a norm on the quotient ![]() $\smash {V_{\mathfrak {p}}}/H$. The natural morphism
$\smash {V_{\mathfrak {p}}}/H$. The natural morphism ![]() $V\hookrightarrow \smash {V_{\mathfrak {p}}}/H$ is injective by construction, so we obtain a norm on
$V\hookrightarrow \smash {V_{\mathfrak {p}}}/H$ is injective by construction, so we obtain a norm on ![]() $V$ by composition with the chosen norm on
$V$ by composition with the chosen norm on ![]() $\smash {V_{\mathfrak {p}}}/H$.
$\smash {V_{\mathfrak {p}}}/H$.
Theorem 1.1.5 implies that the norm topology on ![]() $V$ is not
$V$ is not ![]() $\mathfrak {p}$-adic as otherwise the subspace
$\mathfrak {p}$-adic as otherwise the subspace ![]() $H$ will be zero. It follows by Corollary 1.1.3 that the balls
$H$ will be zero. It follows by Corollary 1.1.3 that the balls ![]() $B(V,\,r)$ are not finitely generated as
$B(V,\,r)$ are not finitely generated as ![]() $R$-modules. Theorem 1.1.5 also implies that varying the choices of
$R$-modules. Theorem 1.1.5 also implies that varying the choices of ![]() $H$ and of the norm on
$H$ and of the norm on ![]() $\smash {V_{\mathfrak {p}}}/H$ one obtains every norm on
$\smash {V_{\mathfrak {p}}}/H$ one obtains every norm on ![]() $V$ that does not induce the
$V$ that does not induce the ![]() $\mathfrak {p}$-adic topology.
$\mathfrak {p}$-adic topology.
1.2 The setting
From now on we fix a global function field ![]() $F$ and a place
$F$ and a place ![]() $\infty$ of
$\infty$ of ![]() $F$. We will use the following notation:
$F$. We will use the following notation:
–
 $\kappa \subset F$ is the ring of elements which are regular at all places;
$\kappa \subset F$ is the ring of elements which are regular at all places;–
 $A \subset F$ is the ring of elements which are regular outside
$A \subset F$ is the ring of elements which are regular outside  $\infty$;
$\infty$;–
 $\mathcal {O}_{F,\infty } \subset F$ is the ring of elements which are regular at
$\mathcal {O}_{F,\infty } \subset F$ is the ring of elements which are regular at  $\infty$;
$\infty$;–
 $F_\infty$ is the
$F_\infty$ is the  $\infty$-adic completion of
$\infty$-adic completion of  $F$;
$F$;–
 $\kappa _\infty$ is the residue field of
$\kappa _\infty$ is the residue field of  $F_\infty$ (and of
$F_\infty$ (and of  $\mathcal {O}_{F,\infty }$);
$\mathcal {O}_{F,\infty }$);–
 $c = |\kappa _\infty |$ is the cardinality of this residue field.
$c = |\kappa _\infty |$ is the cardinality of this residue field.
Fix an ![]() $\infty$-adic absolute value
$\infty$-adic absolute value ![]() $|\cdot |_\infty \colon F_\infty \to \mathbf {R}_{\geqslant 0}$ such that
$|\cdot |_\infty \colon F_\infty \to \mathbf {R}_{\geqslant 0}$ such that ![]() $|\pi |_\infty ^{-1} = c$ for a uniformizer
$|\pi |_\infty ^{-1} = c$ for a uniformizer ![]() $\pi \in F_\infty$. Although our theory works with any normalization, this particular choice leads to better-looking formulas.
$\pi \in F_\infty$. Although our theory works with any normalization, this particular choice leads to better-looking formulas.
The ring ![]() $\kappa$ is a finite field, called the field of constants of
$\kappa$ is a finite field, called the field of constants of ![]() $F$. The ring
$F$. The ring ![]() $A$ is a Dedekind domain of finite type over
$A$ is a Dedekind domain of finite type over ![]() $\kappa$. We will refer to
$\kappa$. We will refer to ![]() $A$ as the coefficient ring and it will serve us as an analogue of the ring of integers
$A$ as the coefficient ring and it will serve us as an analogue of the ring of integers ![]() $\mathbf {Z}$. The local field
$\mathbf {Z}$. The local field ![]() $F_\infty$ will play the role of the field of real numbers
$F_\infty$ will play the role of the field of real numbers ![]() $\mathbf {R}$.
$\mathbf {R}$.
1.3 Lattices
Let ![]() $\varLambda$ be a finitely generated projective
$\varLambda$ be a finitely generated projective ![]() $A$-module. An
$A$-module. An ![]() $\infty$-adic norm on
$\infty$-adic norm on ![]() $\varLambda$ is a map
$\varLambda$ is a map ![]() $\|\cdot \|\colon \varLambda \to \mathbf {R}_{\geqslant 0}$ such that:
$\|\cdot \|\colon \varLambda \to \mathbf {R}_{\geqslant 0}$ such that:
(Λ 1)
 $\|\lambda \| = 0$ if and only if
$\|\lambda \| = 0$ if and only if  $\lambda = 0$;
$\lambda = 0$;(Λ 2)
 $\|\lambda + \lambda '\| \leqslant \max \{ \|\lambda \|, \|\lambda '\| \}$;
$\|\lambda + \lambda '\| \leqslant \max \{ \|\lambda \|, \|\lambda '\| \}$;(Λ 3)
 $\|a\lambda \| = |a|_\infty \|\lambda \|$ for all
$\|a\lambda \| = |a|_\infty \|\lambda \|$ for all  $a \in A$.
$a \in A$.
Following the construction in [Reference Bosch, Güntzer and RemmertBGR84, § 2.1.3] every such norm extends uniquely to an ![]() $\infty$-adic norm on the rational vector space
$\infty$-adic norm on the rational vector space
We will apply the considerations of § 1.1 to the normed vector space ![]() $V$. By analogy with § 1.1 we define the following subsets of
$V$. By analogy with § 1.1 we define the following subsets of ![]() $\varLambda$:
$\varLambda$:
This time ![]() $B(\varLambda,\,r)$ is merely a
$B(\varLambda,\,r)$ is merely a ![]() $\kappa$-vector space.
$\kappa$-vector space.
Lemma 1.3.1 For each pair of real numbers ![]() $r' > r > 0$ the subspace
$r' > r > 0$ the subspace ![]() $B(\varLambda,\,r)$ has finite index in
$B(\varLambda,\,r)$ has finite index in ![]() $B(\varLambda,\,r')$.
$B(\varLambda,\,r')$.
Proof. By construction, ![]() $B(\varLambda,\,s) = \varLambda \cap B(V,\,s)$ for all
$B(\varLambda,\,s) = \varLambda \cap B(V,\,s)$ for all ![]() $s > 0$. We thus have an inclusion of
$s > 0$. We thus have an inclusion of ![]() $\kappa$-vector spaces
$\kappa$-vector spaces
and the claim follows from Lemma 1.1.2.
We are ready for the main definition of this section.
Definition 1.3.2 An ![]() $A$-lattice is a finitely generated projective
$A$-lattice is a finitely generated projective ![]() $A$-module
$A$-module ![]() $\varLambda$ supplied with an
$\varLambda$ supplied with an ![]() $\infty$-adic norm
$\infty$-adic norm ![]() $\|\cdot \|$ that induces the discrete topology on
$\|\cdot \|$ that induces the discrete topology on ![]() $\varLambda$.
$\varLambda$.
In other words there is a real number ![]() $\varepsilon >0$ such that every nonzero lattice vector
$\varepsilon >0$ such that every nonzero lattice vector ![]() $\lambda$ satisfies
$\lambda$ satisfies ![]() $\|\lambda \| \geqslant \varepsilon$. By Lemma 1.3.1 this holds if and only if the subsets
$\|\lambda \| \geqslant \varepsilon$. By Lemma 1.3.1 this holds if and only if the subsets ![]() $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$ are finite for every
$\{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$ are finite for every ![]() $r > 0$.
$r > 0$.
A norm can induce a non-discrete topology on ![]() $\varLambda$. All such norms are described in Example 1.1.7 above.
$\varLambda$. All such norms are described in Example 1.1.7 above.
The discreteness condition of Definition 1.3.2 can be seen as a function field analogue of positive-definiteness. Let ![]() $q$ be a real-valued quadratic form on a finitely generated free
$q$ be a real-valued quadratic form on a finitely generated free ![]() $\mathbf {Z}$-module
$\mathbf {Z}$-module ![]() $L$. Suppose that the form
$L$. Suppose that the form ![]() $q$ takes strictly positive values on
$q$ takes strictly positive values on ![]() $L \smallsetminus \{0\}$. Then
$L \smallsetminus \{0\}$. Then ![]() $q$ is positive-semidefinite as a quadratic form on the real vector space
$q$ is positive-semidefinite as a quadratic form on the real vector space ![]() $\mathbf {R}\otimes _{\mathbf {Z}} L$, and is positive-definite if and only if for each real number
$\mathbf {R}\otimes _{\mathbf {Z}} L$, and is positive-definite if and only if for each real number ![]() $r > 0$ the set
$r > 0$ the set ![]() $\{v \in L, \,q(v) \leqslant r \}$ is finite, cf. Lemma 9.5 of [Reference SilvermanSil09, VIII.9].
$\{v \in L, \,q(v) \leqslant r \}$ is finite, cf. Lemma 9.5 of [Reference SilvermanSil09, VIII.9].
Theorem 1.3.3 Let ![]() $\varLambda$ be a lattice. Then the norm on
$\varLambda$ be a lattice. Then the norm on ![]() $\varLambda$ extends to a unique
$\varLambda$ extends to a unique ![]() $\infty$-adic norm on the vector space
$\infty$-adic norm on the vector space ![]() $V_\infty = F_\infty \otimes _A \varLambda$.
$V_\infty = F_\infty \otimes _A \varLambda$.
Proof. We have observed previously that the norm on ![]() $\varLambda$ extends uniquely to an
$\varLambda$ extends uniquely to an ![]() $\infty$-adic norm on the rational vector space
$\infty$-adic norm on the rational vector space ![]() $V = F\otimes _A \varLambda$. By Theorem 1.1.5 the norm on
$V = F\otimes _A \varLambda$. By Theorem 1.1.5 the norm on ![]() $V$ extends to a unique seminorm on
$V$ extends to a unique seminorm on ![]() $V_\infty$. Let
$V_\infty$. Let ![]() $H$ be the kernel of this seminorm and consider the quotient vector space
$H$ be the kernel of this seminorm and consider the quotient vector space ![]() $W = V_\infty /H$. The seminorm on
$W = V_\infty /H$. The seminorm on ![]() $V_\infty$ is the composite of the surjection
$V_\infty$ is the composite of the surjection ![]() $V_\infty \twoheadrightarrow W$ and a norm on
$V_\infty \twoheadrightarrow W$ and a norm on ![]() $W$.
$W$.
The lattice ![]() $\varLambda$ injects into the quotient vector space
$\varLambda$ injects into the quotient vector space ![]() $W$. By assumption, the sets
$W$. By assumption, the sets ![]() $B(\varLambda,\,r)$ are finite for all
$B(\varLambda,\,r)$ are finite for all ![]() $r > 0$ so
$r > 0$ so ![]() $\varLambda$ is discrete in
$\varLambda$ is discrete in ![]() $W$ with respect to the norm topology. As the field
$W$ with respect to the norm topology. As the field ![]() $F_\infty$ is
$F_\infty$ is ![]() $\infty$-adically complete it follows by Corollary 1.1.6 that the norm topology on
$\infty$-adically complete it follows by Corollary 1.1.6 that the norm topology on ![]() $W$ is the canonical
$W$ is the canonical ![]() $\infty$-adic topology. The fact that
$\infty$-adic topology. The fact that ![]() $\varLambda$ is discrete in
$\varLambda$ is discrete in ![]() $W$ thus implies that
$W$ thus implies that ![]() $\operatorname {rank} \varLambda \leqslant \dim W$. As
$\operatorname {rank} \varLambda \leqslant \dim W$. As ![]() $\operatorname {rank}\varLambda = \dim V_\infty$ we deduce that
$\operatorname {rank}\varLambda = \dim V_\infty$ we deduce that ![]() $H = 0$.
$H = 0$.
Corollary 1.3.4 Let ![]() $\varLambda$ be a lattice, and consider the rational vector space
$\varLambda$ be a lattice, and consider the rational vector space ![]() $V = F\otimes _A \varLambda$ with the induced norm. Then for each real number
$V = F\otimes _A \varLambda$ with the induced norm. Then for each real number ![]() $r > 0$ the ball
$r > 0$ the ball ![]() $B(V,\,r)$ is finitely generated as a module over the ring
$B(V,\,r)$ is finitely generated as a module over the ring ![]() $\mathcal {O}_{F,\infty }$.
$\mathcal {O}_{F,\infty }$.
1.4 Lattices and vector bundles
We shall relate lattices to vector bundles on the smooth projective curve ![]() $X$ over
$X$ over ![]() $\operatorname {Spec} \kappa$ which compactifies the affine curve
$\operatorname {Spec} \kappa$ which compactifies the affine curve ![]() $Y = \operatorname {Spec} A$. By construction we have
$Y = \operatorname {Spec} A$. By construction we have ![]() $X\smallsetminus Y = \{\infty \}$. Let us denote by
$X\smallsetminus Y = \{\infty \}$. Let us denote by ![]() $\mathcal {O}_X({-}\infty )$ the ideal sheaf of the reduced closed subscheme
$\mathcal {O}_X({-}\infty )$ the ideal sheaf of the reduced closed subscheme ![]() $\{\infty \} \subset X$.
$\{\infty \} \subset X$.
Pick a lattice ![]() $\varLambda$, set
$\varLambda$, set ![]() $V = F\otimes _A \varLambda$, and let
$V = F\otimes _A \varLambda$, and let ![]() $\mathcal {E}_{\varLambda }$ be the locally free sheaf on the curve
$\mathcal {E}_{\varLambda }$ be the locally free sheaf on the curve ![]() $Y$ induced by the
$Y$ induced by the ![]() $A$-module
$A$-module ![]() $\varLambda$. Let
$\varLambda$. Let ![]() $r > 0$ be a real number.
$r > 0$ be a real number.
Definition 1.4.1 The quasi-coherent sheaf ![]() $\mathcal {E}_{\varLambda, r}$ on the curve
$\mathcal {E}_{\varLambda, r}$ on the curve ![]() $X$ is constructed by gluing the locally free sheaf
$X$ is constructed by gluing the locally free sheaf ![]() $\mathcal {E}_{\varLambda }$ to the
$\mathcal {E}_{\varLambda }$ to the ![]() $\mathcal {O}_{F,\infty }$-module
$\mathcal {O}_{F,\infty }$-module ![]() $B(V,\,r)$ via the canonical isomorphism
$B(V,\,r)$ via the canonical isomorphism
Theorem 1.4.2 The sheaf ![]() $\mathcal {E}_{\varLambda, r}$ has the following properties.
$\mathcal {E}_{\varLambda, r}$ has the following properties.
(1) The sheaf
 $\mathcal {E}_{\varLambda, r}$ is locally free of finite rank.
$\mathcal {E}_{\varLambda, r}$ is locally free of finite rank.(2)
 $H^0(X,\:\mathcal {E}_{\varLambda, r}) = \{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$.
$H^0(X,\:\mathcal {E}_{\varLambda, r}) = \{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$.(3) For every
 $i \in \mathbf {Z}$ we have
$i \in \mathbf {Z}$ we have  $\mathcal {E}_{\varLambda, r}(i\infty ) = \mathcal {E}_{\varLambda, r c^i}$.
$\mathcal {E}_{\varLambda, r}(i\infty ) = \mathcal {E}_{\varLambda, r c^i}$.
Proof. Property (1) follows from Corollary 1.3.4 and property (2) is immediate. To show property (3) note that the locally free sheaf ![]() $\mathcal {E}_{\varLambda, r}(i\infty )$ is obtained by gluing the sheaves induced by the modules
$\mathcal {E}_{\varLambda, r}(i\infty )$ is obtained by gluing the sheaves induced by the modules ![]() $\varLambda$ and
$\varLambda$ and ![]() $\pi ^{-i} B(V,\,r)$ with
$\pi ^{-i} B(V,\,r)$ with ![]() $\pi$ a uniformizer of
$\pi$ a uniformizer of ![]() $\mathcal {O}_{F,\infty }$. The claim follows since
$\mathcal {O}_{F,\infty }$. The claim follows since ![]() $\pi ^{-i} B(V,\,r) = B(V,\,r c^i)$.
$\pi ^{-i} B(V,\,r) = B(V,\,r c^i)$.
Combining Theorem 1.4.2 with Lemma 1.1.1 we obtain a correspondence between lattices and systems of vector bundles.
Corollary 1.4.3 There is a one-to-one correspondence between ![]() $A$-lattices and pairs which consist of (i) a strictly increasing chain of locally free sheaves
$A$-lattices and pairs which consist of (i) a strictly increasing chain of locally free sheaves
on the complete curve ![]() $X$ such that
$X$ such that ![]() $\mathcal {E}_i|_Y = \mathcal {E}_{i+1}|_Y$ for all
$\mathcal {E}_i|_Y = \mathcal {E}_{i+1}|_Y$ for all ![]() $i \in \{1, \dotsc, m -1 \}$, and (ii) a sequence of real numbers
$i \in \{1, \dotsc, m -1 \}$, and (ii) a sequence of real numbers
The ![]() $A$-module
$A$-module ![]() $\varLambda = H^0(Y,\mathcal {E}_i)$ is finitely generated projective and is independent of the choice of
$\varLambda = H^0(Y,\mathcal {E}_i)$ is finitely generated projective and is independent of the choice of ![]() $i$. It carries a filtration by
$i$. It carries a filtration by ![]() $\kappa$-vector spaces
$\kappa$-vector spaces ![]() $H^0(X,\mathcal {E}_i(j\infty ))$ with
$H^0(X,\mathcal {E}_i(j\infty ))$ with ![]() $i \in \{1,\dotsc,m\}$ and
$i \in \{1,\dotsc,m\}$ and ![]() $j \in \mathbf {Z}$. For each element
$j \in \mathbf {Z}$. For each element ![]() $\lambda \in \varLambda$ we set
$\lambda \in \varLambda$ we set
It is easy to check that the function ![]() $\|\cdot \|$ is a norm on
$\|\cdot \|$ is a norm on ![]() $\varLambda$. The normed module
$\varLambda$. The normed module ![]() $\varLambda$ is a lattice since the vector spaces
$\varLambda$ is a lattice since the vector spaces ![]() $H^0(X,\mathcal {E}_i(j\infty ))$ are finite-dimensional.
$H^0(X,\mathcal {E}_i(j\infty ))$ are finite-dimensional.
1.5 The volume
Let ![]() $\varLambda$ be a lattice, and consider the vector space
$\varLambda$ be a lattice, and consider the vector space ![]() $V_\infty = F_\infty \otimes _A \varLambda$ with the induced norm. By Corollary 1.1.6 the norm topology on
$V_\infty = F_\infty \otimes _A \varLambda$ with the induced norm. By Corollary 1.1.6 the norm topology on ![]() $V_\infty$ is the canonical
$V_\infty$ is the canonical ![]() $\infty$-adic topology. For each real number
$\infty$-adic topology. For each real number ![]() $r > 0$ the ball
$r > 0$ the ball ![]() $B(V_\infty,\,r)$ is thus compact and open, and we can make the following definition.
$B(V_\infty,\,r)$ is thus compact and open, and we can make the following definition.
Definition 1.5.1 The ![]() $r$-normalized volume of
$r$-normalized volume of ![]() $\varLambda$ is defined by the formula
$\varLambda$ is defined by the formula
where ![]() $\mu$ is the unique translation-invariant Haar measure on
$\mu$ is the unique translation-invariant Haar measure on ![]() $V_\infty$ satisfying
$V_\infty$ satisfying ![]() $\mu (B(V_\infty,\,r)) = 1$. In the case
$\mu (B(V_\infty,\,r)) = 1$. In the case ![]() $r = 1$ we will use the simplified notation:
$r = 1$ we will use the simplified notation:
Denoting by ![]() $n$ the rank of the lattice
$n$ the rank of the lattice ![]() $\varLambda$ we have an equality for every integer
$\varLambda$ we have an equality for every integer ![]() $i$:
$i$:
This results from the fact that ![]() $\mu (B(V_\infty,\,r c^i)) = c^{ni} \,\mu (B(V_\infty,\,r))$ for every translation-invariant Haar measure
$\mu (B(V_\infty,\,r c^i)) = c^{ni} \,\mu (B(V_\infty,\,r))$ for every translation-invariant Haar measure ![]() $\mu$.
$\mu$.
In the following we denote by ![]() $\chi$ the Euler characteristic of coherent sheaves on the curve
$\chi$ the Euler characteristic of coherent sheaves on the curve ![]() $X\to \operatorname {Spec}\kappa$.
$X\to \operatorname {Spec}\kappa$.
Lemma 1.5.2 We have ![]() $\operatorname {vol}(\varLambda,\,r) = {|\kappa |}^{-\chi (\mathcal {E}_{\varLambda, r})}$.
$\operatorname {vol}(\varLambda,\,r) = {|\kappa |}^{-\chi (\mathcal {E}_{\varLambda, r})}$.
Proof. The cohomology of the locally free sheaf ![]() $\mathcal {E}_{\varLambda, r}$ is computed by a Čech complex
$\mathcal {E}_{\varLambda, r}$ is computed by a Čech complex
concentrated in degrees ![]() $0$ and
$0$ and ![]() $1$. We rewrite this complex as follows:
$1$. We rewrite this complex as follows:
Thus, for every translation-invariant Haar measure ![]() $\mu$ on
$\mu$ on ![]() $V_\infty$ we have an equality:
$V_\infty$ we have an equality:
The claim follows.
As in the case of ![]() $\mathbf {Z}$-lattices we can compute the volume of an
$\mathbf {Z}$-lattices we can compute the volume of an ![]() $A$-lattice via the absolute value of a determinant. In the following formula, we treat the respective wedge products as elements of one-dimensional
$A$-lattice via the absolute value of a determinant. In the following formula, we treat the respective wedge products as elements of one-dimensional ![]() $F_\infty$-vector space
$F_\infty$-vector space ![]() $\det (V_\infty )$. Their quotient is a well-defined element of
$\det (V_\infty )$. Their quotient is a well-defined element of ![]() $F_\infty ^\times$.
$F_\infty ^\times$.
Lemma 1.5.3 Pick a basis ![]() $v_1, \dotsc, v_n$ of the free module
$v_1, \dotsc, v_n$ of the free module ![]() $B(V_\infty,\,r)$ and pick vectors
$B(V_\infty,\,r)$ and pick vectors ![]() $\lambda _1,\dotsc,\lambda _n$ generating a submodule of finite index
$\lambda _1,\dotsc,\lambda _n$ generating a submodule of finite index ![]() $e$ in
$e$ in ![]() $\varLambda$. Then
$\varLambda$. Then
 \[ \operatorname{vol}(\varLambda,\,r) = \frac{{|\kappa|}^{(g-1)n}}{e} \biggl|\frac{\lambda_1 \wedge \dotsb \wedge \lambda_n}{v_1 \wedge \dotsb \wedge v_n} \biggr|_\infty, \]
\[ \operatorname{vol}(\varLambda,\,r) = \frac{{|\kappa|}^{(g-1)n}}{e} \biggl|\frac{\lambda_1 \wedge \dotsb \wedge \lambda_n}{v_1 \wedge \dotsb \wedge v_n} \biggr|_\infty, \]
where ![]() $g$ is the genus of the coefficient field
$g$ is the genus of the coefficient field ![]() $F$.
$F$.
Proof The product ![]() $s = \lambda _1 \wedge \dotsb \wedge \lambda _n$ is a rational section of the invertible sheaf
$s = \lambda _1 \wedge \dotsb \wedge \lambda _n$ is a rational section of the invertible sheaf ![]() $\det (\mathcal {E}_{\varLambda, r})$. Its order at the point
$\det (\mathcal {E}_{\varLambda, r})$. Its order at the point ![]() $\infty$ equals
$\infty$ equals
where ![]() $v_\infty \colon F_\infty ^\times \twoheadrightarrow \mathbf {Z}$ is the normalized
$v_\infty \colon F_\infty ^\times \twoheadrightarrow \mathbf {Z}$ is the normalized ![]() $\infty$-adic valuation. Hence,
$\infty$-adic valuation. Hence,
The claim then follows from Lemma 1.5.2 and Riemann–Roch formula.
Theorem 1.5.4 Let ![]() $\varLambda$ be a lattice of rank
$\varLambda$ be a lattice of rank ![]() $n$ and let
$n$ and let ![]() $r > 0$ be a real number. Then for all integers
$r > 0$ be a real number. Then for all integers ![]() $i \gg 0$ we have an equality:
$i \gg 0$ we have an equality:
Moreover, for all integers ![]() $i$ we have a lower bound:
$i$ we have a lower bound:
Proof. Let ![]() $i$ be a non-negative integer. Consider a natural short exact sequence of sheaves on the curve
$i$ be a non-negative integer. Consider a natural short exact sequence of sheaves on the curve ![]() $X$:
$X$:
The coherent sheaf ![]() $\mathcal {F}$ is concentrated at the point
$\mathcal {F}$ is concentrated at the point ![]() $\infty$ and has length
$\infty$ and has length ![]() $n i$ as an
$n i$ as an ![]() $\mathcal {O}_{X,\infty }$-module. We thus have an equality
$\mathcal {O}_{X,\infty }$-module. We thus have an equality
By construction we have ![]() $H^0(X,\:\mathcal {E}_{\varLambda, r}(i\infty )) = \{\lambda \in \varLambda,\:\|\lambda \| \leqslant r c^i\}$. Hence, Lemma 1.5.2 implies that
$H^0(X,\:\mathcal {E}_{\varLambda, r}(i\infty )) = \{\lambda \in \varLambda,\:\|\lambda \| \leqslant r c^i\}$. Hence, Lemma 1.5.2 implies that
The cohomology group ![]() $H^1(X,\:\mathcal {E}_{\varLambda, r}(i\infty ))$ vanishes for
$H^1(X,\:\mathcal {E}_{\varLambda, r}(i\infty ))$ vanishes for ![]() $i \gg 0$ as the invertible sheaf
$i \gg 0$ as the invertible sheaf ![]() $\mathcal {O}_X(\infty )$ is ample. The first claim of the theorem follows. To prove the second claim note that
$\mathcal {O}_X(\infty )$ is ample. The first claim of the theorem follows. To prove the second claim note that ![]() $c^{ni} \,\operatorname {vol}(\varLambda,\,r)^{-1} = \operatorname {vol}(\varLambda,\,r c^i)^{-1}$ for each integer
$c^{ni} \,\operatorname {vol}(\varLambda,\,r)^{-1} = \operatorname {vol}(\varLambda,\,r c^i)^{-1}$ for each integer ![]() $i$. It is thus enough to treat the case
$i$. It is thus enough to treat the case ![]() $i = 0$ which follows from the displayed formula above.
$i = 0$ which follows from the displayed formula above.
Corollary 1.5.5 Every lattice ![]() $\varLambda$ of rank
$\varLambda$ of rank ![]() $n$ contains a nonzero vector of norm at most
$n$ contains a nonzero vector of norm at most ![]() $c\cdot {\operatorname {vol}(\varLambda )}^{1/n}$.
$c\cdot {\operatorname {vol}(\varLambda )}^{1/n}$.
1.6 A bound on norms of generators
We would like to find a real number ![]() $r > 0$ such that the subset
$r > 0$ such that the subset ![]() $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$ generates the lattice
$\{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$ generates the lattice ![]() $\varLambda$. To this end, we will employ the correspondence between lattices and vector bundles. We will use supplementary notation:
$\varLambda$. To this end, we will employ the correspondence between lattices and vector bundles. We will use supplementary notation:
–
 $g$ is the genus of the smooth projective curve
$g$ is the genus of the smooth projective curve  $X\to \operatorname {Spec}\kappa$;
$X\to \operatorname {Spec}\kappa$;–
 $f = [\kappa _\infty :\kappa ]$.
$f = [\kappa _\infty :\kappa ]$.
The invertible sheaf ![]() $\mathcal {O}_X(\infty )$ has degree
$\mathcal {O}_X(\infty )$ has degree ![]() $f$. Let us also pick an auxiliary integer
$f$. Let us also pick an auxiliary integer ![]() $h$ such that the twist
$h$ such that the twist ![]() $\mathcal {O}_X(h\infty )$ is very ample. We will utilize a classical criterion for global generation of coherent sheaves on curves.
$\mathcal {O}_X(h\infty )$ is very ample. We will utilize a classical criterion for global generation of coherent sheaves on curves.
Lemma 1.6.1 Let ![]() $\mathcal {E}$ be a coherent sheaf on the curve
$\mathcal {E}$ be a coherent sheaf on the curve ![]() $X$. If
$X$. If ![]() $H^1(X,\mathcal {E}) = 0$, then the sheaf
$H^1(X,\mathcal {E}) = 0$, then the sheaf ![]() $\mathcal {E}(h\infty )$ is globally generated.
$\mathcal {E}(h\infty )$ is globally generated.
Proof. Let ![]() $\iota \colon X \hookrightarrow \mathbf {P}^N$ be the closed embedding defined by global sections of
$\iota \colon X \hookrightarrow \mathbf {P}^N$ be the closed embedding defined by global sections of ![]() $\mathcal {O}_X(h\infty )$. The coherent sheaf
$\mathcal {O}_X(h\infty )$. The coherent sheaf ![]() $\iota _*(\mathcal {E})$ is
$\iota _*(\mathcal {E})$ is ![]() $1$-regular in the sense of Castelnuovo–Mumford [St: 08A3]. Hence, the sheaf
$1$-regular in the sense of Castelnuovo–Mumford [St: 08A3]. Hence, the sheaf ![]() $\iota _*(\mathcal {E})(1) = \iota _*(\mathcal {E}(h\infty ))$ is globally generated [St: 08A8].
$\iota _*(\mathcal {E})(1) = \iota _*(\mathcal {E}(h\infty ))$ is globally generated [St: 08A8].
Lemma 1.6.2 Let ![]() $\mathcal {E}$ be a locally free sheaf of rank
$\mathcal {E}$ be a locally free sheaf of rank ![]() $n$ on the curve
$n$ on the curve ![]() $X$. Set
$X$. Set
Suppose that the sheaf ![]() $\mathcal {E}$ is an iterated extension of invertible sheaves of degree at most
$\mathcal {E}$ is an iterated extension of invertible sheaves of degree at most ![]() $2g - 2$. Then the sheaf
$2g - 2$. Then the sheaf ![]() $\mathcal {E}(i\infty )$ is globally generated.
$\mathcal {E}(i\infty )$ is globally generated.
Proof. Write the degrees of invertible sheaves in the form ![]() $(2g - 2) - e_j$ with
$(2g - 2) - e_j$ with ![]() $e_j \geqslant 0$. We have
$e_j \geqslant 0$. We have ![]() $\deg \mathcal {E} = (2g-2)n - \sum e_j$ so that
$\deg \mathcal {E} = (2g-2)n - \sum e_j$ so that
Hence, the sheaf ![]() $\mathcal {E}' = \mathcal {E}((i-h)\infty )$ is an iterated extension of invertible sheaves of degree at least
$\mathcal {E}' = \mathcal {E}((i-h)\infty )$ is an iterated extension of invertible sheaves of degree at least ![]() $2g-1$. Induction on the number of invertible sheaves implies that
$2g-1$. Induction on the number of invertible sheaves implies that ![]() $H^1(X,\,\mathcal {E}') = 0$ so the sheaf
$H^1(X,\,\mathcal {E}') = 0$ so the sheaf ![]() $\mathcal {E}'(h\infty )$ is globally generated by Lemma 1.6.1.
$\mathcal {E}'(h\infty )$ is globally generated by Lemma 1.6.1.
Lemma 1.6.3 Let ![]() $\mathcal {E}$ be a locally free sheaf of rank
$\mathcal {E}$ be a locally free sheaf of rank ![]() $n$ on the curve
$n$ on the curve ![]() $X$. Set
$X$. Set
Suppose that ![]() $H^0(X,\,\mathcal {E}) = 0$. Then the sheaf
$H^0(X,\,\mathcal {E}) = 0$. Then the sheaf ![]() $\mathcal {E}(i\infty )$ is globally generated.
$\mathcal {E}(i\infty )$ is globally generated.
Proof. Let ![]() $\Omega$ be the canonical sheaf of the curve
$\Omega$ be the canonical sheaf of the curve ![]() $X\to \operatorname {Spec}\kappa$ and set
$X\to \operatorname {Spec}\kappa$ and set ![]() $\mathcal {F} = \mathcal {E}^* \otimes \Omega$. Serre duality shows that
$\mathcal {F} = \mathcal {E}^* \otimes \Omega$. Serre duality shows that ![]() $H^1(X,\,\mathcal {F}) = 0$ so the sheaf
$H^1(X,\,\mathcal {F}) = 0$ so the sheaf ![]() $\mathcal {F}(h\infty )$ is globally generated by Lemma 1.6.1. Dualizing and twisting we get an embedding
$\mathcal {F}(h\infty )$ is globally generated by Lemma 1.6.1. Dualizing and twisting we get an embedding ![]() $\mathcal {E}(-h\infty ) \hookrightarrow \Omega ^{\oplus m}$,
$\mathcal {E}(-h\infty ) \hookrightarrow \Omega ^{\oplus m}$, ![]() $m \gg 0$. Hence the sheaf
$m \gg 0$. Hence the sheaf ![]() $\mathcal {E}' = \mathcal {E}(-h\infty )$ is an iterated extension of invertible subsheaves
$\mathcal {E}' = \mathcal {E}(-h\infty )$ is an iterated extension of invertible subsheaves ![]() $\mathcal {L} \subset \Omega$. Every such subsheaf has degree at most
$\mathcal {L} \subset \Omega$. Every such subsheaf has degree at most ![]() $2g - 2$. Lemma 1.6.2 implies that the sheaf
$2g - 2$. Lemma 1.6.2 implies that the sheaf ![]() $\mathcal {E}'((i+h)\infty ) = \mathcal {E}(i\infty )$ is globally generated with
$\mathcal {E}'((i+h)\infty ) = \mathcal {E}(i\infty )$ is globally generated with
The claim follows since ![]() $\deg \mathcal {E}' = \deg \mathcal {E} - f h n$.
$\deg \mathcal {E}' = \deg \mathcal {E} - f h n$.
Theorem 1.6.4 Let ![]() $\varLambda$ be a lattice of rank
$\varLambda$ be a lattice of rank ![]() $n$. Suppose that every nonzero vector of
$n$. Suppose that every nonzero vector of ![]() $\varLambda$ has norm at least
$\varLambda$ has norm at least ![]() $1$. Then the
$1$. Then the ![]() $A$-module
$A$-module ![]() $\varLambda$ is generated by the subset
$\varLambda$ is generated by the subset
with ![]() $C = {|\kappa |}^{3g + 2f - 1}$.
$C = {|\kappa |}^{3g + 2f - 1}$.
Proof. Consider the locally free sheaf ![]() $\mathcal {E} = \mathcal {E}_{\varLambda, 1}$. We have
$\mathcal {E} = \mathcal {E}_{\varLambda, 1}$. We have
Thus ![]() $H^0(X,\mathcal {E}({-}\infty )) = 0$ by our assumption on the length of nonzero lattice vectors. Invoking the Riemann–Roch formula, we deduce that
$H^0(X,\mathcal {E}({-}\infty )) = 0$ by our assumption on the length of nonzero lattice vectors. Invoking the Riemann–Roch formula, we deduce that
Hence, by Lemma 1.6.3 the sheaf ![]() $\mathcal {E}((i-1)\infty )$ is globally generated when
$\mathcal {E}((i-1)\infty )$ is globally generated when
To ensure that the invertible sheaf ![]() $\mathcal {O}_X(h\infty )$ is very ample it is enough to take any integer
$\mathcal {O}_X(h\infty )$ is very ample it is enough to take any integer ![]() $h$ such that
$h$ such that ![]() $f h\geqslant 2g + 1$. We thus have an estimate
$f h\geqslant 2g + 1$. We thus have an estimate ![]() $f h\leqslant 2g + f$, and the sheaf
$f h\leqslant 2g + f$, and the sheaf ![]() $\mathcal {E}(j\infty )$ is globally generated for an integer
$\mathcal {E}(j\infty )$ is globally generated for an integer ![]() $j$ such that
$j$ such that
In particular, the ![]() $A$-module
$A$-module ![]() $\varLambda = H^0(Y,\:\mathcal {E}(j\infty ))$ is generated by the subset
$\varLambda = H^0(Y,\:\mathcal {E}(j\infty ))$ is generated by the subset
Since ![]() $c = {|\kappa |}^{f}$, we obtain an estimate
$c = {|\kappa |}^{f}$, we obtain an estimate
The result follows as ![]() ${|\kappa |}^{-\chi (\mathcal {E})} = \operatorname {vol}(\varLambda )$ by Lemma 1.5.2.
${|\kappa |}^{-\chi (\mathcal {E})} = \operatorname {vol}(\varLambda )$ by Lemma 1.5.2.
In the case ![]() $A=\kappa [t]$ the estimate of Theorem 1.6.4 is sharp in all ranks. The lattice
$A=\kappa [t]$ the estimate of Theorem 1.6.4 is sharp in all ranks. The lattice ![]() $A^{\oplus n}$ with the supremum norm has volume
$A^{\oplus n}$ with the supremum norm has volume ![]() ${|\kappa |}^{-n}$, is generated by vectors of norm
${|\kappa |}^{-n}$, is generated by vectors of norm ![]() $1$ and has no nonzero vectors of norm strictly less than
$1$ and has no nonzero vectors of norm strictly less than ![]() $1$.
$1$.
2. Preliminaries concerning Drinfeld modules
Fix a field ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality
$\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality ![]() $q < \infty$. Let
$q < \infty$. Let ![]() $K$ be a field over
$K$ be a field over ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$. In the following, we will refer to
$\mathbf {F}_{\hspace {-1.5pt} q}$. In the following, we will refer to ![]() $K$ as the base field. Pick a separable closure
$K$ as the base field. Pick a separable closure ![]() $K^s/K$ and let
$K^s/K$ and let ![]() $G_K$ be the corresponding absolute Galois group.
$G_K$ be the corresponding absolute Galois group.
2.1 Twisted polynomials
Let ![]() $K[\tau ]$ be the twisted polynomial ring. This is the ring of polynomials in a formal variable
$K[\tau ]$ be the twisted polynomial ring. This is the ring of polynomials in a formal variable ![]() $\tau$ with coefficients in
$\tau$ with coefficients in ![]() $K$ and with the multiplication subject to the rule
$K$ and with the multiplication subject to the rule ![]() $\tau \,\alpha = \alpha ^q\,\tau$ for all
$\tau \,\alpha = \alpha ^q\,\tau$ for all ![]() $\alpha \in K$. The elements of
$\alpha \in K$. The elements of ![]() $K[\tau ]$ will be referred to as
$K[\tau ]$ will be referred to as ![]() $\tau$-polynomials.
$\tau$-polynomials.
The ring ![]() $K[\tau ]$ is the endomorphism ring of the
$K[\tau ]$ is the endomorphism ring of the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme
$\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme ![]() $\mathbf {G}_a$ over
$\mathbf {G}_a$ over ![]() $\operatorname {Spec} K$ with the element
$\operatorname {Spec} K$ with the element ![]() $\tau$ corresponding to the
$\tau$ corresponding to the ![]() $q$-Frobenius. This interpretation allows us to evaluate
$q$-Frobenius. This interpretation allows us to evaluate ![]() $\tau$-polynomials at points of
$\tau$-polynomials at points of ![]() $\mathbf {G}_a$.
$\mathbf {G}_a$.
Lemma 2.1.1 Let ![]() $V$ be a finite-dimensional Galois-stable
$V$ be a finite-dimensional Galois-stable ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-vector subspace of
$\mathbf {F}_{\hspace {-1.5pt} q}$-vector subspace of ![]() $K^s$ and let
$K^s$ and let ![]() $f\colon V \to K^s$ be a Galois-equivariant
$f\colon V \to K^s$ be a Galois-equivariant ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-linear map. Set
$\mathbf {F}_{\hspace {-1.5pt} q}$-linear map. Set ![]() $n = \dim V$ and suppose that
$n = \dim V$ and suppose that ![]() $n > 0$. Then the following hold.
$n > 0$. Then the following hold.
(1) There is a unique
 $\tau$-polynomial of the form
which satisfies
$\tau$-polynomial of the form
which satisfies \[ \varphi = a_0 + a_1 \tau + \dotsb + a_{n-1} \tau^{n-1}, \quad a_i \in K, \]
\[ \varphi = a_0 + a_1 \tau + \dotsb + a_{n-1} \tau^{n-1}, \quad a_i \in K, \]
 $\varphi (v) = f(v)$ for all
$\varphi (v) = f(v)$ for all  $v \in V$.
$v \in V$.(2) The coefficients
 $a_i$ are determined by the equation
where
$a_i$ are determined by the equation
where \[ \begin{pmatrix} v_1 & v_1^q & \dotsb & v_1^{q^{n-1}} \\ v_2 & v_2^q & \dotsb & v_2^{q^{n-1}} \\ & & \dotsb & \\ v_n & v_n^q & \dotsb & v_n^{q^{n-1}} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix} = \begin{pmatrix} f(v_1) \\ f(v_2) \\ \vdots \\ f(v_n) \end{pmatrix}, \]
\[ \begin{pmatrix} v_1 & v_1^q & \dotsb & v_1^{q^{n-1}} \\ v_2 & v_2^q & \dotsb & v_2^{q^{n-1}} \\ & & \dotsb & \\ v_n & v_n^q & \dotsb & v_n^{q^{n-1}} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix} = \begin{pmatrix} f(v_1) \\ f(v_2) \\ \vdots \\ f(v_n) \end{pmatrix}, \]
 $v_1, \dotsc, v_n$ is a basis of
$v_1, \dotsc, v_n$ is a basis of  $V$.
$V$.
Proof. The determinant of the square matrix in part (2) is the Moore determinant ![]() $M(v_1,\dotsc,v_n)$, see [Reference PapikianPap23, Definition 3.1.17]. This determinant is nonzero because the elements
$M(v_1,\dotsc,v_n)$, see [Reference PapikianPap23, Definition 3.1.17]. This determinant is nonzero because the elements ![]() $v_1, \dotsc, v_n$ are
$v_1, \dotsc, v_n$ are ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-linearly independent. Hence, the solution vector is uniquely determined.
$\mathbf {F}_{\hspace {-1.5pt} q}$-linearly independent. Hence, the solution vector is uniquely determined.
Consider the polynomial ![]() $\varphi = a_0 + a_1 \tau + \dotsb + a_{n-1} \tau ^{n-1}$. By construction, we have
$\varphi = a_0 + a_1 \tau + \dotsb + a_{n-1} \tau ^{n-1}$. By construction, we have ![]() $\varphi (v_i) = f(v_i)$ for all
$\varphi (v_i) = f(v_i)$ for all ![]() $i \in \{1,\dotsc,n\}$ which implies by linearity that
$i \in \{1,\dotsc,n\}$ which implies by linearity that ![]() $\varphi (v) = f(v)$ for all
$\varphi (v) = f(v)$ for all ![]() $v \in V$. It remains to show that the coefficients of
$v \in V$. It remains to show that the coefficients of ![]() $\varphi$ are Galois-invariant and, thus, belong to the subfield
$\varphi$ are Galois-invariant and, thus, belong to the subfield ![]() $K\subset K^s$.
$K\subset K^s$.
Apply an automorphism ![]() $g \in G_K$ to both sides of the matrix equation in part (2). Since the map
$g \in G_K$ to both sides of the matrix equation in part (2). Since the map ![]() $f$ is Galois-equivariant, it follows that the polynomial
$f$ is Galois-equivariant, it follows that the polynomial
satisfies ![]() $({}^g \varphi )(g v_i) = f(g v_i)$ for all
$({}^g \varphi )(g v_i) = f(g v_i)$ for all ![]() $i$. The set
$i$. The set ![]() $g v_1, \dotsc, g v_n$ is yet another basis of
$g v_1, \dotsc, g v_n$ is yet another basis of ![]() $V$ so the linearity implies that
$V$ so the linearity implies that ![]() $({}^g \varphi )(v) = f(v)$ for all
$({}^g \varphi )(v) = f(v)$ for all ![]() $v \in V$. In particular,
$v \in V$. In particular, ![]() $({}^g \varphi )(v_i) = f(v_i)$ for all
$({}^g \varphi )(v_i) = f(v_i)$ for all ![]() $i$. Since the matrix equation in part (2) has a unique solution, we deduce that
$i$. Since the matrix equation in part (2) has a unique solution, we deduce that ![]() ${}^g \varphi = \varphi$, and the claim follows.
${}^g \varphi = \varphi$, and the claim follows.
2.2 Artin–Schreier theory
Let ![]() $E$ be an
$E$ be an ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme over
$\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme over ![]() $\operatorname {Spec} K$ which is isomorphic to
$\operatorname {Spec} K$ which is isomorphic to ![]() $\mathbf {G}_a$. Consider a separable isogeny
$\mathbf {G}_a$. Consider a separable isogeny ![]() $\varphi \colon E \to E$, i.e. an
$\varphi \colon E \to E$, i.e. an ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-linear morphism that induces an isomorphism of the tangent spaces at zero. Let
$\mathbf {F}_{\hspace {-1.5pt} q}$-linear morphism that induces an isomorphism of the tangent spaces at zero. Let ![]() $V$ be the kernel of
$V$ be the kernel of ![]() $\varphi$ viewed as a morphism of sheaves on the small étale site of
$\varphi$ viewed as a morphism of sheaves on the small étale site of ![]() $\operatorname {Spec} K$. The sheaf
$\operatorname {Spec} K$. The sheaf ![]() $V$ corresponds to the
$V$ corresponds to the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-vector space of roots
$\mathbf {F}_{\hspace {-1.5pt} q}$-vector space of roots
equipped with the natural Galois action. The short exact sequence of sheaves
induces a long exact sequence of cohomology that terminates in a surjective boundary homomorphism
The boundary homomorphism ![]() $\partial _\varphi$ sends
$\partial _\varphi$ sends ![]() $x \in E(K)$ to the class of the cocycle
$x \in E(K)$ to the class of the cocycle ![]() $g \mapsto g y - y$ with
$g \mapsto g y - y$ with ![]() $y \in E(K^s)$ any element satisfying
$y \in E(K^s)$ any element satisfying ![]() $\varphi (y) = x$.
$\varphi (y) = x$.
We will refer to ![]() $\partial _\varphi$ as the Artin–Schreier homomorphism of the isogeny
$\partial _\varphi$ as the Artin–Schreier homomorphism of the isogeny ![]() $\varphi$. We will use the shorthand
$\varphi$. We will use the shorthand ![]() $\partial _q$ to denote the Artin–Schreier homomorphism of the isogeny
$\partial _q$ to denote the Artin–Schreier homomorphism of the isogeny ![]() $\tau - 1\colon \mathbf {G}_a \to \mathbf {G}_a$ with kernel the constant sheaf
$\tau - 1\colon \mathbf {G}_a \to \mathbf {G}_a$ with kernel the constant sheaf ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$.
$\mathbf {F}_{\hspace {-1.5pt} q}$.
Suppose that the sheaf ![]() $V$ is constant or, equivalently, that the
$V$ is constant or, equivalently, that the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-vector space
$\mathbf {F}_{\hspace {-1.5pt} q}$-vector space ![]() $V$ is contained in
$V$ is contained in ![]() $E(K)$. Then the cohomology group
$E(K)$. Then the cohomology group ![]() $H^1(K,\:V)$ coincides with the
$H^1(K,\:V)$ coincides with the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-vector space of continuous homomorphisms
$\mathbf {F}_{\hspace {-1.5pt} q}$-vector space of continuous homomorphisms ![]() $G_K\to V$. In this case, we will often write the Artin–Schreier boundary homomorphism
$G_K\to V$. In this case, we will often write the Artin–Schreier boundary homomorphism ![]() $\partial _\varphi$ in the form of a pairing
$\partial _\varphi$ in the form of a pairing
We will use the shorthand ![]() $[\ ,\ )_{q}$ for the pairing of the isogeny
$[\ ,\ )_{q}$ for the pairing of the isogeny ![]() $\tau -1$.
$\tau -1$.
Lemma 2.2.1 Let ![]() $\varphi \colon \mathbf {G}_a \to \mathbf {G}_a$ be a separable isogeny with kernel
$\varphi \colon \mathbf {G}_a \to \mathbf {G}_a$ be a separable isogeny with kernel ![]() $V$. Then for every Galois-equivariant epimorphism
$V$. Then for every Galois-equivariant epimorphism ![]() $f\colon V \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} q}$, there is a scaling factor
$f\colon V \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} q}$, there is a scaling factor ![]() $u \in K$ which makes the following square commutative.
$u \in K$ which makes the following square commutative.

The factor ![]() $u$ is computed via Moore determinants:
$u$ is computed via Moore determinants:
The terms in this formula have the following meaning:
–
 $\alpha$ is the top coefficient of the
$\alpha$ is the top coefficient of the  $\tau$-polynomial
$\tau$-polynomial  $\varphi$;
$\varphi$;–
 $v \in V$ is an element such that
$v \in V$ is an element such that  $f(v) = 1$;
$f(v) = 1$;–
 $w_1, \dotsc, w_n \in V$ is a basis of the hyperplane
$w_1, \dotsc, w_n \in V$ is a basis of the hyperplane  $\ker (f) \subset V$.
$\ker (f) \subset V$.
The value of ![]() $u$ is independent of choices of
$u$ is independent of choices of ![]() $v$ and
$v$ and ![]() $w_1,\dotsc,w_n$.
$w_1,\dotsc,w_n$.
The factor ![]() $u$ of Lemma 2.2.1 is unique provided that
$u$ of Lemma 2.2.1 is unique provided that ![]() $H^1(K,\,\mathbf {F}_{\hspace {-1.5pt} p}) \ne 0$.
$H^1(K,\,\mathbf {F}_{\hspace {-1.5pt} p}) \ne 0$.
Proof of Lemma 2.2.1 As a first step we shall prolong the morphism ![]() $f\colon V \to \mathbf {F}_{\hspace {-1.5pt} q}$ to the following morphism of short exact sequences of sheaves.
$f\colon V \to \mathbf {F}_{\hspace {-1.5pt} q}$ to the following morphism of short exact sequences of sheaves.

By Lemma 2.1.1(1) there is a unique polynomial ![]() $\psi _0 \in K[\tau ]$ of degree strictly less than
$\psi _0 \in K[\tau ]$ of degree strictly less than ![]() $\dim V = n + 1$ which makes the left square commutative. The composite
$\dim V = n + 1$ which makes the left square commutative. The composite ![]() $(\tau - 1) \psi _0$ vanishes on the
$(\tau - 1) \psi _0$ vanishes on the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-vector subspace
$\mathbf {F}_{\hspace {-1.5pt} q}$-vector subspace ![]() $V \subset K^s$, and is thus divisible by the polynomial
$V \subset K^s$, and is thus divisible by the polynomial ![]() $\varphi$ on the right [Reference PapikianPap23, Corollary 3.1.16]. We get the existence of the polynomial
$\varphi$ on the right [Reference PapikianPap23, Corollary 3.1.16]. We get the existence of the polynomial ![]() $\psi _1$. By construction,
$\psi _1$. By construction, ![]() $\deg \psi _0 \leqslant n$ and
$\deg \psi _0 \leqslant n$ and ![]() $\deg \varphi = n+1$ so the relation
$\deg \varphi = n+1$ so the relation
implies that the polynomial ![]() $\psi _1 = u$ is constant, and that
$\psi _1 = u$ is constant, and that
where the element ![]() $\beta$ is the top coefficient of the polynomial
$\beta$ is the top coefficient of the polynomial ![]() $\psi _0$. This coefficient is computed by Lemma 2.1.1(2) which yields the Moore determinant formula for
$\psi _0$. This coefficient is computed by Lemma 2.1.1(2) which yields the Moore determinant formula for ![]() $u$.
$u$.
2.3 Drinfeld modules
Fix a global function field ![]() $F$ over
$F$ over ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$ and a place
$\mathbf {F}_{\hspace {-1.5pt} q}$ and a place ![]() $\infty$ of
$\infty$ of ![]() $F$. As in § 1.2 this determines a coefficient ring
$F$. As in § 1.2 this determines a coefficient ring ![]() $A$, i.e. the subring of
$A$, i.e. the subring of ![]() $F$ consisting of elements which are regular outside
$F$ consisting of elements which are regular outside ![]() $\infty$. We will freely use the notation and the terminology of § 1.2 with respect to coefficient rings and related objects.
$\infty$. We will freely use the notation and the terminology of § 1.2 with respect to coefficient rings and related objects.
For us a Drinfeld ![]() $A$-module over
$A$-module over ![]() $\operatorname {Spec} K$ is an
$\operatorname {Spec} K$ is an ![]() $A$-module scheme
$A$-module scheme ![]() $E$ such that the underlying
$E$ such that the underlying ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme is isomorphic to
$\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme is isomorphic to ![]() $\mathbf {G}_a$, and the multiplication morphism
$\mathbf {G}_a$, and the multiplication morphism ![]() $a\colon E \to E$ is an isogeny of degree strictly greater than
$a\colon E \to E$ is an isogeny of degree strictly greater than ![]() $1$ for at least one element
$1$ for at least one element ![]() $a \in A$.
$a \in A$.
Subject to a choice of an ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-linear isomorphism
$\mathbf {F}_{\hspace {-1.5pt} q}$-linear isomorphism ![]() $E \xrightarrow {\smash {{ {\sim }}}} \mathbf {G}_a$ the data of an
$E \xrightarrow {\smash {{ {\sim }}}} \mathbf {G}_a$ the data of an ![]() $A$-module structure on
$A$-module structure on ![]() $E$ amounts to a morphism of
$E$ amounts to a morphism of ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-algebras
$\mathbf {F}_{\hspace {-1.5pt} q}$-algebras ![]() $\varphi \colon A \to K[\tau ]$, and one recovers the more common definition of a Drinfeld module.
$\varphi \colon A \to K[\tau ]$, and one recovers the more common definition of a Drinfeld module.
Let ![]() $\operatorname {Lie}_E$ be the tangent space of
$\operatorname {Lie}_E$ be the tangent space of ![]() $E$ at zero. This is a vector space of dimension
$E$ at zero. This is a vector space of dimension ![]() $1$ over the base field
$1$ over the base field ![]() $K$. The action of
$K$. The action of ![]() $A$ on
$A$ on ![]() $\operatorname {Lie}_E$ determines a morphism
$\operatorname {Lie}_E$ determines a morphism ![]() $\iota _E\colon A \to K$, the characteristic homomorphism of the Drinfeld module
$\iota _E\colon A \to K$, the characteristic homomorphism of the Drinfeld module ![]() $E$. The characteristic of
$E$. The characteristic of ![]() $E$ is the ideal
$E$ is the ideal ![]() $\ker (\iota _E) \subset A$.
$\ker (\iota _E) \subset A$.
Let ![]() $\mathfrak {n} \subset A$ be a proper ideal which is not divisible by the characteristic of
$\mathfrak {n} \subset A$ be a proper ideal which is not divisible by the characteristic of ![]() $E$. The
$E$. The ![]() $\mathfrak {n}$-torsion of
$\mathfrak {n}$-torsion of ![]() $E$ is most naturally represented by the
$E$ is most naturally represented by the ![]() $A/\mathfrak {n}$-module
$A/\mathfrak {n}$-module
We will use a modified definition which makes it easier to form inverse systems.
Definition 2.3.1 We have ![]() $E[\mathfrak {n}\rangle = \operatorname {Hom}_A(\mathfrak {n}^{-1}/A, E(K^s))$.
$E[\mathfrak {n}\rangle = \operatorname {Hom}_A(\mathfrak {n}^{-1}/A, E(K^s))$.
The ![]() $A/\mathfrak {n}$-module
$A/\mathfrak {n}$-module ![]() $E[\mathfrak {n}\rangle$ inherits an action of the absolute Galois group
$E[\mathfrak {n}\rangle$ inherits an action of the absolute Galois group ![]() $G_K$ from
$G_K$ from ![]() $E(K^s)$. As the
$E(K^s)$. As the ![]() $A/\mathfrak {n}$-module
$A/\mathfrak {n}$-module ![]() $\mathfrak {n}^{-1}/A$ is free of rank
$\mathfrak {n}^{-1}/A$ is free of rank ![]() $1$ a choice of its generator gives rise to a
$1$ a choice of its generator gives rise to a ![]() $G_K$-equivariant isomorphism of
$G_K$-equivariant isomorphism of ![]() $A/\mathfrak {n}$-modules:
$A/\mathfrak {n}$-modules:
An inclusion of ideals ![]() $\mathfrak {n}'\subset \mathfrak {n}$ induces a surjection
$\mathfrak {n}'\subset \mathfrak {n}$ induces a surjection ![]() $E[\mathfrak {n}'\rangle \twoheadrightarrow E[\mathfrak {n}\rangle$, and the resulting morphism
$E[\mathfrak {n}'\rangle \twoheadrightarrow E[\mathfrak {n}\rangle$, and the resulting morphism ![]() $A/\mathfrak {n} \otimes _{A/\mathfrak {n}'} E[\mathfrak {n}'\rangle \xrightarrow {\smash {{ {\sim }}}} E[\mathfrak {n}\rangle$ is an isomorphism.
$A/\mathfrak {n} \otimes _{A/\mathfrak {n}'} E[\mathfrak {n}'\rangle \xrightarrow {\smash {{ {\sim }}}} E[\mathfrak {n}\rangle$ is an isomorphism.
Lemma 2.3.2 We have a Galois-equivariant short exact sequence of ![]() $A$-modules which is natural in the ideal
$A$-modules which is natural in the ideal ![]() $\mathfrak {n}$ and the Drinfeld module
$\mathfrak {n}$ and the Drinfeld module ![]() $E$:
$E$:
The first arrow is given by the composition with the quotient map ![]() $\mathfrak {n}^{-1} \twoheadrightarrow \mathfrak {n}^{-1}/A$ and the second arrow is the evaluation at
$\mathfrak {n}^{-1} \twoheadrightarrow \mathfrak {n}^{-1}/A$ and the second arrow is the evaluation at ![]() $1 \in \mathfrak {n}^{-1}$.
$1 \in \mathfrak {n}^{-1}$.
Proof. We only need to prove the exactness on the right. Suppose that ![]() $\mathfrak {n} = (a)$ for some
$\mathfrak {n} = (a)$ for some ![]() $a \in A$. The isogeny
$a \in A$. The isogeny ![]() $a\colon E \to E$ is separable since the ideal
$a\colon E \to E$ is separable since the ideal ![]() $\mathfrak {n}$ is not divisible by the characteristic of
$\mathfrak {n}$ is not divisible by the characteristic of ![]() $E$. Hence, the morphism
$E$. Hence, the morphism ![]() $a\colon E(K^s) \twoheadrightarrow E(K^s)$ is surjective, and we get the claim.
$a\colon E(K^s) \twoheadrightarrow E(K^s)$ is surjective, and we get the claim.
In the general case the ideal ![]() $\mathfrak {n}^i$ is principal for all sufficiently divisible integers
$\mathfrak {n}^i$ is principal for all sufficiently divisible integers ![]() $i > 0$ since the Picard group of the scheme
$i > 0$ since the Picard group of the scheme ![]() $\operatorname {Spec} A$ is finite. The claim results from the naturality of our sequence with respect to the ideal
$\operatorname {Spec} A$ is finite. The claim results from the naturality of our sequence with respect to the ideal ![]() $\mathfrak {n}$.
$\mathfrak {n}$.
Definition 2.3.3 The Kummer boundary homomorphism
is the boundary homomorphism arising from the sequence of Lemma 2.3.2. When the ![]() $\mathfrak {n}$-torsion of
$\mathfrak {n}$-torsion of ![]() $E$ is rational we will write it in the form of a pairing:
$E$ is rational we will write it in the form of a pairing:
The map ![]() $\partial _{\mathfrak {n}}$ can be also called the Artin–Schreier homomorphism but this name is less common in the literature.
$\partial _{\mathfrak {n}}$ can be also called the Artin–Schreier homomorphism but this name is less common in the literature.
Lemma 2.3.4 The homomorphism ![]() $\partial _{\mathfrak {n}}$ has the following description:
$\partial _{\mathfrak {n}}$ has the following description:
(1) For each
 $x \in E(K)$ there is an
$x \in E(K)$ there is an  $A$-module homomorphism
$A$-module homomorphism  $f\colon \mathfrak {n}^{-1} \to E(K^s)$ such that
$f\colon \mathfrak {n}^{-1} \to E(K^s)$ such that  $f(1) = x$.
$f(1) = x$.(2) The cohomology class
 $\partial _{\mathfrak {n}}(x)$ is represented by a cocycle given by the formula
$\partial _{\mathfrak {n}}(x)$ is represented by a cocycle given by the formula  $g \mapsto g \circ f - f$ where the right-hand side is seen as a morphism from the quotient
$g \mapsto g \circ f - f$ where the right-hand side is seen as a morphism from the quotient  $\mathfrak {n}^{-1}/A$.
$\mathfrak {n}^{-1}/A$.
Proof. This follows from Lemma 2.3.2 by elementary properties of group cohomology.
Lemma 2.3.5 For each proper principal ideal ![]() $(a) = \mathfrak {a}$ of the ring
$(a) = \mathfrak {a}$ of the ring ![]() $A$ which is not divisible by the characteristic of
$A$ which is not divisible by the characteristic of ![]() $E$ we have a commutative diagram
$E$ we have a commutative diagram

where ![]() $\partial _{a}$ is the Artin–Schreier boundary homomorphism of the separable isogeny
$\partial _{a}$ is the Artin–Schreier boundary homomorphism of the separable isogeny ![]() $a\colon E \to E$, and
$a\colon E \to E$, and ![]() $\text {ev}_{a}\colon E[\mathfrak {a}\rangle \xrightarrow {\smash {{ {\sim }}}} E[a]$ is an isomorphism defined by the formula
$\text {ev}_{a}\colon E[\mathfrak {a}\rangle \xrightarrow {\smash {{ {\sim }}}} E[a]$ is an isomorphism defined by the formula ![]() $x\mapsto x(a^{-1})$.
$x\mapsto x(a^{-1})$.
Proof. We have the following commutative diagram.

The claim follows by naturality of boundary homomorphisms.
2.4 Drinfeld modules over local fields
In this section our base field ![]() $K$ is assumed to be local. We denote by
$K$ is assumed to be local. We denote by ![]() $\mathcal {O}_K$ the ring of integers of
$\mathcal {O}_K$ the ring of integers of ![]() $K$ and by
$K$ and by ![]() $\mathfrak {p}_K$ the maximal ideal of
$\mathfrak {p}_K$ the maximal ideal of ![]() $\mathcal {O}_K$.
$\mathcal {O}_K$.
Pick a coefficient ring ![]() $A$ over
$A$ over ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$. Let
$\mathbf {F}_{\hspace {-1.5pt} q}$. Let ![]() $E$ be a Drinfeld
$E$ be a Drinfeld ![]() $A$-module over
$A$-module over ![]() $\operatorname {Spec} K$ and let
$\operatorname {Spec} K$ and let ![]() $\iota _E\colon A \to K$ be its characteristic homomorphism.
$\iota _E\colon A \to K$ be its characteristic homomorphism.
Definition 2.4.1 The Drinfeld module ![]() $E$ has finite residual characteristic when
$E$ has finite residual characteristic when ![]() $\iota _E(A) \subset \mathcal {O}_K$. The residual characteristic
$\iota _E(A) \subset \mathcal {O}_K$. The residual characteristic ![]() $\bar {\mathfrak {p}}$ of
$\bar {\mathfrak {p}}$ of ![]() $E$ is the ideal
$E$ is the ideal
This ideal is maximal because the residue field ![]() $\mathcal {O}_K/\mathfrak {p}_K$ is finite.
$\mathcal {O}_K/\mathfrak {p}_K$ is finite.
The analogous situation for abelian varieties is when the base field ![]() $K$ is a non-archimedean local field. The residual characteristic of an abelian variety is just the residual characteristic of the field
$K$ is a non-archimedean local field. The residual characteristic of an abelian variety is just the residual characteristic of the field ![]() $K$.
$K$.
From now on we suppose that the Drinfeld module ![]() $E$ has finite residual characteristic. It will be convenient for us to assemble the
$E$ has finite residual characteristic. It will be convenient for us to assemble the ![]() $\mathfrak {p}$-adic Tate modules
$\mathfrak {p}$-adic Tate modules ![]() $T_\mathfrak {p} E$,
$T_\mathfrak {p} E$, ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$, into a single object.
$\mathfrak {p}\ne \bar {\mathfrak {p}}$, into a single object.
Definition 2.4.2 The ring of restricted integral adeles is defined by the formula
where ![]() $\mathfrak {n} \subset A$ runs over proper ideals that are prime to
$\mathfrak {n} \subset A$ runs over proper ideals that are prime to ![]() $\bar {\mathfrak {p}}$.
$\bar {\mathfrak {p}}$.
We have a natural isomorphism ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}} = \prod _{\mathfrak {p}\ne \bar {\mathfrak {p}}} A_\mathfrak {p}$ where
${A}_{\text {ad},\bar {\mathfrak {p}}} = \prod _{\mathfrak {p}\ne \bar {\mathfrak {p}}} A_\mathfrak {p}$ where ![]() $A_\mathfrak {p}$ is the
$A_\mathfrak {p}$ is the ![]() $\mathfrak {p}$-adic completion of
$\mathfrak {p}$-adic completion of ![]() $A$. Compared with the ring of integral adeles of the function field
$A$. Compared with the ring of integral adeles of the function field ![]() $F$, the ring
$F$, the ring ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$ does not include the factors at the places
${A}_{\text {ad},\bar {\mathfrak {p}}}$ does not include the factors at the places ![]() $\bar {\mathfrak {p}}$ and
$\bar {\mathfrak {p}}$ and ![]() $\infty$.
$\infty$.
Definition 2.4.3 The restricted adelic Tate module ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is defined by the formula
${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is defined by the formula
where ![]() $\mathfrak {n} \subset A$ runs over proper ideals that are prime to
$\mathfrak {n} \subset A$ runs over proper ideals that are prime to ![]() $\bar {\mathfrak {p}}$ and the transition maps are induced by inclusions of the ideals.
$\bar {\mathfrak {p}}$ and the transition maps are induced by inclusions of the ideals.
The Tate module ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is a free module over the ring
${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is a free module over the ring ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$ and its rank coincides with the rank of the Drinfeld module
${A}_{\text {ad},\bar {\mathfrak {p}}}$ and its rank coincides with the rank of the Drinfeld module ![]() $E$. The Galois action on
$E$. The Galois action on ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is
${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$-linear. We have a natural
${A}_{\text {ad},\bar {\mathfrak {p}}}$-linear. We have a natural ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$-linear Galois-equivariant isomorphism:
${A}_{\text {ad},\bar {\mathfrak {p}}}$-linear Galois-equivariant isomorphism:
Lemma 2.4.4 Consider the inclusion-ordered family ![]() $\mathcal {F}$ of proper principal ideals
$\mathcal {F}$ of proper principal ideals ![]() $\mathfrak {a} \subset A$ that are prime to the residual characteristic
$\mathfrak {a} \subset A$ that are prime to the residual characteristic ![]() $\bar {\mathfrak {p}}$. Then the natural homomorphism
$\bar {\mathfrak {p}}$. Then the natural homomorphism
is an isomorphism.
Proof. For each proper ideal ![]() $\mathfrak {n}\not \subset \bar {\mathfrak {p}}$ there is a non-constant element
$\mathfrak {n}\not \subset \bar {\mathfrak {p}}$ there is a non-constant element ![]() $a \in \mathfrak {n} \smallsetminus \bar {\mathfrak {p}}$. Then
$a \in \mathfrak {n} \smallsetminus \bar {\mathfrak {p}}$. Then ![]() $(a) \in \mathcal {F}$, and as
$(a) \in \mathcal {F}$, and as ![]() $(a) \subset \mathfrak {n}$ we conclude that the family
$(a) \subset \mathfrak {n}$ we conclude that the family ![]() $\mathcal {F}$ is initial in the family of all proper ideals not contained in
$\mathcal {F}$ is initial in the family of all proper ideals not contained in ![]() $\bar {\mathfrak {p}}$. The claim follows.
$\bar {\mathfrak {p}}$. The claim follows.
3. The local Kummer pairing
Fix a finite field ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality
$\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality ![]() $q$ and characteristic
$q$ and characteristic ![]() $p$. In this section our base field
$p$. In this section our base field ![]() $K/\mathbf {F}_{\hspace {-1.5pt} q}$ is assumed to be local. We denote by
$K/\mathbf {F}_{\hspace {-1.5pt} q}$ is assumed to be local. We denote by ![]() $\mathcal {O}_K\subset K$ the ring of integers and by
$\mathcal {O}_K\subset K$ the ring of integers and by ![]() $\mathfrak {p}_K \subset \mathcal {O}_K$ the maximal ideal. As usual we fix a separable closure
$\mathfrak {p}_K \subset \mathcal {O}_K$ the maximal ideal. As usual we fix a separable closure ![]() $K^s/K$ and denote by
$K^s/K$ and denote by ![]() $G_K$ the corresponding absolute Galois group.
$G_K$ the corresponding absolute Galois group.
3.1 Ramification subgroups
Let ![]() $I_K$ be the inertia subgroup of the absolute Galois group
$I_K$ be the inertia subgroup of the absolute Galois group ![]() $G_K$, and let
$G_K$, and let ![]() $P_K$ be the wild inertia subgroup.
$P_K$ be the wild inertia subgroup.
Definition 3.1.1 We denote by ![]() $J_K$ the maximal quotient of
$J_K$ the maximal quotient of ![]() $I_K$ that is abelian of exponent
$I_K$ that is abelian of exponent ![]() $p$:
$p$:
The quotient group ![]() $I_K/P_K$ is procyclic of order prime to
$I_K/P_K$ is procyclic of order prime to ![]() $p$, so the fact that
$p$, so the fact that ![]() $P_K$ is a pro-
$P_K$ is a pro-![]() $p$ group implies that the surjection
$p$ group implies that the surjection ![]() $I_K \twoheadrightarrow I_K/P_K$ is split. As the group
$I_K \twoheadrightarrow I_K/P_K$ is split. As the group ![]() $J_K$ is abelian
$J_K$ is abelian ![]() $p$-torsion we conclude that the canonical morphism
$p$-torsion we conclude that the canonical morphism ![]() $P_K \twoheadrightarrow J_K$ is surjective.
$P_K \twoheadrightarrow J_K$ is surjective.
The inertia subgroup ![]() $I_K$ carries a decreasing separated exhaustive filtration by closed normal subgroups
$I_K$ carries a decreasing separated exhaustive filtration by closed normal subgroups ![]() $I_K^{u}$,
$I_K^{u}$, ![]() $u \in \mathbf {Q}_{\geqslant 0}$, the ramification filtration in upper numbering [Reference SerreSer68, Chapitre IV, § 3, Remarque 1, p. 83]. The wild inertia subgroup
$u \in \mathbf {Q}_{\geqslant 0}$, the ramification filtration in upper numbering [Reference SerreSer68, Chapitre IV, § 3, Remarque 1, p. 83]. The wild inertia subgroup ![]() $P_K$ is the closure of the subgroup
$P_K$ is the closure of the subgroup ![]() $\bigcup _{u > 0} I_K^{u}$.
$\bigcup _{u > 0} I_K^{u}$.
The ramification filtration of ![]() $I_K$ induces a filtration of
$I_K$ induces a filtration of ![]() $J_K$. As the group
$J_K$. As the group ![]() $J_K$ is abelian the Hasse–Arf theorem implies that the induced filtration is integrally indexed: for each
$J_K$ is abelian the Hasse–Arf theorem implies that the induced filtration is integrally indexed: for each ![]() $u\geqslant 0$ the subgroup
$u\geqslant 0$ the subgroup ![]() $J_K^u$ coincides with
$J_K^u$ coincides with ![]() $J_K^m$,
$J_K^m$, ![]() $m = \lceil u \rceil$.
$m = \lceil u \rceil$.
Lemma 3.1.2 For every integer ![]() $m \geqslant 0$ such that
$m \geqslant 0$ such that ![]() $m \equiv 0\pmod {p}$ we have
$m \equiv 0\pmod {p}$ we have
Proof. Let ![]() $L\subset K^s$ be a finite Galois extension of
$L\subset K^s$ be a finite Galois extension of ![]() $K$ with Galois group
$K$ with Galois group ![]() $G$ and upper index ramification filtration
$G$ and upper index ramification filtration ![]() $\{ G^u \}_{u\geqslant 0}$. Suppose that the inertia group
$\{ G^u \}_{u\geqslant 0}$. Suppose that the inertia group ![]() $G^0$ is abelian
$G^0$ is abelian ![]() $p$-torsion. We need to show that
$p$-torsion. We need to show that ![]() $G^{pi} = G^{pi+1}$ for each
$G^{pi} = G^{pi+1}$ for each ![]() $i \geqslant 0$.
$i \geqslant 0$.
We are free to assume that ![]() $\smash {G^0} = G$. The group
$\smash {G^0} = G$. The group ![]() $G$ is abelian, so we have the reciprocity morphism
$G$ is abelian, so we have the reciprocity morphism ![]() $\omega \colon K^\times \twoheadrightarrow G$ of local class field theory. This morphism transforms the
$\omega \colon K^\times \twoheadrightarrow G$ of local class field theory. This morphism transforms the ![]() $n$-unit filtration
$n$-unit filtration ![]() $\smash {\{U_K^{(n)}\}_{n\geqslant 0}}$ to the ramification filtration. For each
$\smash {\{U_K^{(n)}\}_{n\geqslant 0}}$ to the ramification filtration. For each ![]() $i \geqslant 0$ the
$i \geqslant 0$ the ![]() $p$th power map induces a morphism
$p$th power map induces a morphism
This is surjective since the residue field of ![]() $K$ is perfect. Our claim follows.
$K$ is perfect. Our claim follows.
3.2 Local pairing
Fix a Drinfeld ![]() $A$-module
$A$-module ![]() ${D}$ over
${D}$ over ![]() $\operatorname {Spec} \mathcal {O}_K$. By this we mean not only that
$\operatorname {Spec} \mathcal {O}_K$. By this we mean not only that ![]() ${D}$ can be defined by a homomorphism
${D}$ can be defined by a homomorphism ![]() $\varphi \colon A \to \mathcal {O}_K[\tau ]$ but also that the reduction of
$\varphi \colon A \to \mathcal {O}_K[\tau ]$ but also that the reduction of ![]() $\varphi$ modulo
$\varphi$ modulo ![]() $\mathfrak {p}_K$ is a Drinfeld module of the same rank as over
$\mathfrak {p}_K$ is a Drinfeld module of the same rank as over ![]() $K$.
$K$.
The Drinfeld module ![]() ${D}$ has finite residual characteristic, denoted by
${D}$ has finite residual characteristic, denoted by ![]() $\bar {\mathfrak {p}}$ as usual. Let
$\bar {\mathfrak {p}}$ as usual. Let ![]() $K^\textit {ur}\subset K^s$ be the maximal unramified extension and let
$K^\textit {ur}\subset K^s$ be the maximal unramified extension and let ![]() $\mathfrak {n}\subset A$ be a proper ideal not divisible by
$\mathfrak {n}\subset A$ be a proper ideal not divisible by ![]() $\bar {\mathfrak {p}}$. Since
$\bar {\mathfrak {p}}$. Since ![]() ${D}$ is a Drinfeld module over
${D}$ is a Drinfeld module over ![]() $\operatorname {Spec}\mathcal {O}_K$ the
$\operatorname {Spec}\mathcal {O}_K$ the ![]() $\mathfrak {n}$-torsion of
$\mathfrak {n}$-torsion of ![]() ${D}$ is contained in
${D}$ is contained in ![]() ${D}(K^\textit {ur})$. Hence, by § 2.3 we have the Kummer pairing
${D}(K^\textit {ur})$. Hence, by § 2.3 we have the Kummer pairing ![]() $[\ ,\ )_{\mathfrak {n}}\colon {D}(K^\textit {ur}) \times I_K \to {D}[\mathfrak {n}\rangle$.
$[\ ,\ )_{\mathfrak {n}}\colon {D}(K^\textit {ur}) \times I_K \to {D}[\mathfrak {n}\rangle$.
Definition 3.2.1 The local restricted adelic Kummer pairing
is the limit of the Kummer pairings ![]() $[\ ,\ )_{\mathfrak {n}}$ over the inclusion-ordered system of proper ideals
$[\ ,\ )_{\mathfrak {n}}$ over the inclusion-ordered system of proper ideals ![]() $\mathfrak {n}$ not divisible by the residual characteristic
$\mathfrak {n}$ not divisible by the residual characteristic ![]() $\bar {\mathfrak {p}}$.
$\bar {\mathfrak {p}}$.
Since the Tate module ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}}{D}$ is
${T}_{\text {ad},\bar {\mathfrak {p}}}{D}$ is ![]() $p$-torsion the pairing
$p$-torsion the pairing ![]() $[\ ,\ )_{\text {ad}}$ factors through the maximal quotient
$[\ ,\ )_{\text {ad}}$ factors through the maximal quotient ![]() $J_K = I_K^{\text {ab}}/(I_K^{\text {ab}})^{\times p}$ that is abelian of exponent
$J_K = I_K^{\text {ab}}/(I_K^{\text {ab}})^{\times p}$ that is abelian of exponent ![]() $p$.
$p$.
Let ![]() $v\colon K \twoheadrightarrow \mathbf {Z} \cup \{\infty \}$ be the normalized valuation of the base field
$v\colon K \twoheadrightarrow \mathbf {Z} \cup \{\infty \}$ be the normalized valuation of the base field ![]() $K$. Every isomorphism of
$K$. Every isomorphism of ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-module schemes
$\mathbf {F}_{\hspace {-1.5pt} q}$-module schemes ![]() ${D} \xrightarrow {\smash {{ {\sim }}}} \mathbf {G}_a$ over
${D} \xrightarrow {\smash {{ {\sim }}}} \mathbf {G}_a$ over ![]() $\operatorname {Spec} \mathcal {O}_K$ induces a valuation function on
$\operatorname {Spec} \mathcal {O}_K$ induces a valuation function on ![]() ${D}(K)$ by transport of structure from
${D}(K)$ by transport of structure from ![]() $\mathbf {G}_a(K) = K$. The result is independent of choices because the choices differ by multiplication by an integral unit on the side of
$\mathbf {G}_a(K) = K$. The result is independent of choices because the choices differ by multiplication by an integral unit on the side of ![]() $\mathbf {G}_a$. We denote the resulting valuation function by
$\mathbf {G}_a$. We denote the resulting valuation function by ![]() $v$ as well.
$v$ as well.
Definition 3.2.2 For every ![]() $\lambda \in {D}(K)$ we set
$\lambda \in {D}(K)$ we set
Poonen [Reference PoonenPoo95] introduced the notion of canonical local height on the ![]() $A$-module
$A$-module ![]() ${D}(K)$. Since the Drinfeld module
${D}(K)$. Since the Drinfeld module ![]() ${D}$ has good reduction, Proposition 4(4) of [Reference PoonenPoo95, § 3] implies that the map
${D}$ has good reduction, Proposition 4(4) of [Reference PoonenPoo95, § 3] implies that the map ![]() $\|\cdot \|\colon {D}(K) \to \mathbf {Z}_{\geqslant 0}$ is exactly the canonical local height. This map satisfies the ultrametric inequality:
$\|\cdot \|\colon {D}(K) \to \mathbf {Z}_{\geqslant 0}$ is exactly the canonical local height. This map satisfies the ultrametric inequality:
However, ![]() $\|\lambda \| = 0$ for every
$\|\lambda \| = 0$ for every ![]() $\lambda \in {D}(\mathcal {O}_K)$ so the height
$\lambda \in {D}(\mathcal {O}_K)$ so the height ![]() $\|\cdot \|$ is only a seminorm on
$\|\cdot \|$ is only a seminorm on ![]() ${D}(K)$. This seminorm is
${D}(K)$. This seminorm is ![]() $\infty$-adic in the following sense.
$\infty$-adic in the following sense.
Lemma 3.2.3 For each ![]() $\lambda \in {D}(K)$ and each
$\lambda \in {D}(K)$ and each ![]() $a \in A$ we have an equality
$a \in A$ we have an equality
where ![]() $s$ is the rank of the Drinfeld module
$s$ is the rank of the Drinfeld module ![]() ${D}$.
${D}$.
The map ![]() $x \mapsto |x|_\infty ^s$ is an
$x \mapsto |x|_\infty ^s$ is an ![]() $\infty$-adic absolute value on the local field
$\infty$-adic absolute value on the local field ![]() $F_\infty$ albeit its normalization differs from the one of § 1.2 when
$F_\infty$ albeit its normalization differs from the one of § 1.2 when ![]() $s > 1$.
$s > 1$.
Proof of Lemma 3.2.3 This follows from Proposition 2 and Proposition 4(4) of [Reference PoonenPoo95]. For the reader's convenience let us give a direct argument. The claim is clear when ![]() $a = 0$ and holds when
$a = 0$ and holds when ![]() $\|\lambda \| = 0$ since
$\|\lambda \| = 0$ since ![]() ${D}(\mathcal {O}_K)$ is an
${D}(\mathcal {O}_K)$ is an ![]() $A$-submodule of
$A$-submodule of ![]() ${D}(K)$. We are thus free to assume that
${D}(K)$. We are thus free to assume that ![]() $a \ne 0$ and
$a \ne 0$ and ![]() $\|\lambda \| > 0$.
$\|\lambda \| > 0$.
We identify the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme
$\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme ![]() ${D}$ with
${D}$ with ![]() $\mathbf {G}_a$ over
$\mathbf {G}_a$ over ![]() $\operatorname {Spec} \mathcal {O}_K$. The induced
$\operatorname {Spec} \mathcal {O}_K$. The induced ![]() $A$-module scheme structure is described by a homomorphism
$A$-module scheme structure is described by a homomorphism ![]() $\varphi \colon A \to \mathcal {O}_K[\tau ]$. Write
$\varphi \colon A \to \mathcal {O}_K[\tau ]$. Write ![]() $\varphi (a) = \alpha _0 + \alpha _1 \tau + \dotsb + \alpha _n \tau ^n$ with
$\varphi (a) = \alpha _0 + \alpha _1 \tau + \dotsb + \alpha _n \tau ^n$ with ![]() $\alpha _n \ne 0$. The top coefficient
$\alpha _n \ne 0$. The top coefficient ![]() $\alpha _n$ is a unit since
$\alpha _n$ is a unit since ![]() ${D}$ is a Drinfeld module over
${D}$ is a Drinfeld module over ![]() $\operatorname {Spec} \mathcal {O}_K$. Hence,
$\operatorname {Spec} \mathcal {O}_K$. Hence, ![]() $v(\alpha _n \lambda ^{q^n}) = q^n v(\lambda )$. Combining this with the estimates
$v(\alpha _n \lambda ^{q^n}) = q^n v(\lambda )$. Combining this with the estimates ![]() $v(\alpha _i \lambda ^{q^i}) \geqslant q^i v(\lambda )$,
$v(\alpha _i \lambda ^{q^i}) \geqslant q^i v(\lambda )$, ![]() $i < n$, and the assumption
$i < n$, and the assumption ![]() $v(\lambda ) < 0$ we deduce an equality
$v(\lambda ) < 0$ we deduce an equality
The degree ![]() $n$ of the polynomial
$n$ of the polynomial ![]() $\varphi (a)$ is expressed by a formula
$\varphi (a)$ is expressed by a formula
where ![]() $v_\infty$ is the normalized valuation of the local field
$v_\infty$ is the normalized valuation of the local field ![]() $F_\infty$. The absolute value of § 1.2 is given by the formula
$F_\infty$. The absolute value of § 1.2 is given by the formula
As ![]() $|\kappa _\infty | = q^{[\kappa _\infty :\mathbf {F}_{\hspace {-1.5pt} q}]}$ we deduce that
$|\kappa _\infty | = q^{[\kappa _\infty :\mathbf {F}_{\hspace {-1.5pt} q}]}$ we deduce that ![]() $q^n = |a|_\infty ^s$ and the claim follows.
$q^n = |a|_\infty ^s$ and the claim follows.
Theorem 3.2.4 Let ![]() $\lambda \in {D}(K)$ be an element, and consider the homomorphism
$\lambda \in {D}(K)$ be an element, and consider the homomorphism
Then the following hold.
(1) This homomorphism vanishes on the ramification subgroup
 $J^{\|\lambda \|+1}_K$. In particular, it vanishes altogether when
$J^{\|\lambda \|+1}_K$. In particular, it vanishes altogether when  $\|\lambda \| = 0$.
$\|\lambda \| = 0$.(2) If the height
 $\|\lambda \|$ is prime to
$\|\lambda \|$ is prime to  $p$, then the homomorphism
$p$, then the homomorphism  $[\lambda,\ )_{\text {ad}}$ maps the ramification subgroup
$[\lambda,\ )_{\text {ad}}$ maps the ramification subgroup  $\smash {J^{\|\lambda \|}_K}$ surjectively onto
$\smash {J^{\|\lambda \|}_K}$ surjectively onto  ${T}_{\text {ad},\bar {\mathfrak {p}}} {D}$.
${T}_{\text {ad},\bar {\mathfrak {p}}} {D}$.
Proof. By Lemmas 2.4.4 and 2.3.5 it is enough to prove the claims for every homomorphism ![]() $[\lambda,\ )_{a}\colon J_K \to {D}[a]$ where
$[\lambda,\ )_{a}\colon J_K \to {D}[a]$ where ![]() $a \in A$ runs over non-constant elements that are prime to the residual characteristic
$a \in A$ runs over non-constant elements that are prime to the residual characteristic ![]() $\bar {\mathfrak {p}}$ of
$\bar {\mathfrak {p}}$ of ![]() ${D}$.
${D}$.
The height ![]() $\|\lambda \|$, the group
$\|\lambda \|$, the group ![]() $J_K$ and the homomorphism
$J_K$ and the homomorphism ![]() $[\lambda,\ )_{a}$ remain unchanged when we replace the base field
$[\lambda,\ )_{a}$ remain unchanged when we replace the base field ![]() $K$ by an unramified extension. As the Drinfeld module
$K$ by an unramified extension. As the Drinfeld module ![]() ${D}$ has good reduction and the element
${D}$ has good reduction and the element ![]() $a$ is prime to
$a$ is prime to ![]() $\bar {\mathfrak {p}}$ we are free to assume that the torsion module
$\bar {\mathfrak {p}}$ we are free to assume that the torsion module ![]() ${D}[a]$ is contained in
${D}[a]$ is contained in ![]() ${D}(K)$, and consequently in
${D}(K)$, and consequently in ![]() ${D}(\mathcal {O}_K)$.
${D}(\mathcal {O}_K)$.
An ![]() $\mathbf {F}_{\hspace {-1.5pt} p}$-vector subspace
$\mathbf {F}_{\hspace {-1.5pt} p}$-vector subspace ![]() $V\subset {D}[a]$ is zero if and only if
$V\subset {D}[a]$ is zero if and only if ![]() $f(V) = 0$ for each nonzero linear form
$f(V) = 0$ for each nonzero linear form ![]() $f\colon {D}[a] \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} p}$. Likewise
$f\colon {D}[a] \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} p}$. Likewise ![]() $V = {D}[a]$ if and only if
$V = {D}[a]$ if and only if ![]() $f(V) = \mathbf {F}_{\hspace {-1.5pt} p}$ for every such form
$f(V) = \mathbf {F}_{\hspace {-1.5pt} p}$ for every such form ![]() $f$. It is thus enough to prove our claims after composing the homomorphism
$f$. It is thus enough to prove our claims after composing the homomorphism ![]() $[\lambda,\ )_{a}$ with every
$[\lambda,\ )_{a}$ with every ![]() $f$.
$f$.
From now on we identify the ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme
$\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme ![]() ${D}$ with
${D}$ with ![]() $\mathbf {G}_a$ over
$\mathbf {G}_a$ over ![]() $\operatorname {Spec} \mathcal {O}_K$. The resulting
$\operatorname {Spec} \mathcal {O}_K$. The resulting ![]() $A$-module scheme structure on
$A$-module scheme structure on ![]() $\mathbf {G}_a$ is given by a homomorphism
$\mathbf {G}_a$ is given by a homomorphism ![]() $\varphi \colon A \to \mathcal {O}_K[\tau ]$.
$\varphi \colon A \to \mathcal {O}_K[\tau ]$.
Let ![]() $f\colon {D}[a] \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} p}$ be a nonzero linear form. According to Lemma 2.2.1 there is an element
$f\colon {D}[a] \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} p}$ be a nonzero linear form. According to Lemma 2.2.1 there is an element ![]() $u \in \mathbf {G}_a(K)$ such that
$u \in \mathbf {G}_a(K)$ such that
This element is given by a formula with Moore determinants ![]() $M(-)$:
$M(-)$:
Here ![]() $\alpha$ is the top coefficient of the polynomial
$\alpha$ is the top coefficient of the polynomial ![]() $\varphi (a)$ and
$\varphi (a)$ and ![]() $w_1, \dotsc,w_n,v$ is a suitable
$w_1, \dotsc,w_n,v$ is a suitable ![]() $\mathbf {F}_{\hspace {-1.5pt} p}$-basis of
$\mathbf {F}_{\hspace {-1.5pt} p}$-basis of ![]() ${D}[a]$.
${D}[a]$.
By our assumption ![]() ${D}$ is a Drinfeld module over
${D}$ is a Drinfeld module over ![]() $\operatorname {Spec}\mathcal {O}_K$. This implies that the top coefficient
$\operatorname {Spec}\mathcal {O}_K$. This implies that the top coefficient ![]() $\alpha$ is an integral unit. Since
$\alpha$ is an integral unit. Since ![]() $a$ is prime to the residual characteristic the torsion module
$a$ is prime to the residual characteristic the torsion module ![]() ${D}[a] \subset {D}(\mathcal {O}_K)$ maps injectively to
${D}[a] \subset {D}(\mathcal {O}_K)$ maps injectively to ![]() ${D}(k)$ where
${D}(k)$ where ![]() $k$ is the residue field of
$k$ is the residue field of ![]() $\mathcal {O}_K$. In particular, the image of the basis
$\mathcal {O}_K$. In particular, the image of the basis ![]() $w_1,\dotsc,w_n,v$ in
$w_1,\dotsc,w_n,v$ in ![]() ${D}(k)$ remains
${D}(k)$ remains ![]() $\mathbf {F}_{\hspace {-1.5pt} p}$-linearly independent. Hence, the corresponding Moore determinants are nonzero. We conclude that the element
$\mathbf {F}_{\hspace {-1.5pt} p}$-linearly independent. Hence, the corresponding Moore determinants are nonzero. We conclude that the element ![]() $u$ is an integral unit. It follows that
$u$ is an integral unit. It follows that ![]() $v(u\lambda ) = v(\lambda )$.
$v(u\lambda ) = v(\lambda )$.
Consider the Artin–Schreier polynomial ![]() $X^p - X = u\lambda$. The Galois group
$X^p - X = u\lambda$. The Galois group ![]() $G$ of its splitting field is the image of the absolute Galois group under the homomorphism
$G$ of its splitting field is the image of the absolute Galois group under the homomorphism ![]() $[u\lambda,\ )_{p}$. The upper index ramification filtration of
$[u\lambda,\ )_{p}$. The upper index ramification filtration of ![]() $G$ is given by images of absolute ramification subgroups:
$G$ is given by images of absolute ramification subgroups:
This filtration was calculated by Hasse (see Thomas [Reference ThomasTho05], Proposition 2.1 and the following paragraph). Set ![]() $b = \max \{0,\,-v(u\lambda )\}$. Then the subgroups
$b = \max \{0,\,-v(u\lambda )\}$. Then the subgroups ![]() $G^{i}$ vanish for
$G^{i}$ vanish for ![]() $i > b$, and if the integer
$i > b$, and if the integer ![]() $b$ is prime to
$b$ is prime to ![]() $p$, then
$p$, then ![]() $G^{b} = G = \mathbf {F}_{\hspace {-1.5pt} p}$. Our theorem follows since
$G^{b} = G = \mathbf {F}_{\hspace {-1.5pt} p}$. Our theorem follows since ![]() $v(u\lambda ) = v(\lambda )$ as shown previously.
$v(u\lambda ) = v(\lambda )$ as shown previously.
3.3 Open image theorem
The following arguments involve passage from the base field ![]() $K$ to a finite separable extension
$K$ to a finite separable extension ![]() $L$. On account of this we have to fix a few conventions. First, it will be more convenient for us to view the homomorphism
$L$. On account of this we have to fix a few conventions. First, it will be more convenient for us to view the homomorphism ![]() $[\lambda,\ )_{\text {ad}}$ as a morphism from the inertia subgroup
$[\lambda,\ )_{\text {ad}}$ as a morphism from the inertia subgroup ![]() $I_K$ rather than its quotient
$I_K$ rather than its quotient ![]() $J_K$.
$J_K$.
Second, we need to be careful with the canonical local height on the ![]() $A$-module
$A$-module ![]() ${D}(L)$. This involves the normalized valuation of
${D}(L)$. This involves the normalized valuation of ![]() $L$ and so differs from the height on the submodule
$L$ and so differs from the height on the submodule ![]() ${D}(K)$ by an integer factor, the ramification index of
${D}(K)$ by an integer factor, the ramification index of ![]() $L/K$. We will denote the height on
$L/K$. We will denote the height on ![]() ${D}(L)$ by
${D}(L)$ by ![]() $\|\cdot \|_{L}$.
$\|\cdot \|_{L}$.
Lemma 3.3.1 Let ![]() $\lambda \in {D}(K) \smallsetminus {D}(\mathcal {O}_K)$ be an element, and suppose that the homomorphism
$\lambda \in {D}(K) \smallsetminus {D}(\mathcal {O}_K)$ be an element, and suppose that the homomorphism ![]() $[\lambda,\ )_{\text {ad}}\colon I_K \to {T}_{\text {ad},\bar {\mathfrak {p}}} {D}$ is not surjective. Then there are:
$[\lambda,\ )_{\text {ad}}\colon I_K \to {T}_{\text {ad},\bar {\mathfrak {p}}} {D}$ is not surjective. Then there are:
– a non-constant element
 $a \in A$ prime to the residual characteristic
$a \in A$ prime to the residual characteristic  $\bar {\mathfrak {p}}$ of
$\bar {\mathfrak {p}}$ of  ${D}$;
${D}$;– a finite separable extension
 $L/K$; and
$L/K$; and– an element
 $\lambda ' \in {D}(L)\smallsetminus {D}(\mathcal {O}_L)$;
$\lambda ' \in {D}(L)\smallsetminus {D}(\mathcal {O}_L)$;
such that
Here ![]() $v_p\colon \mathbf {Q} \twoheadrightarrow \mathbf {Z}\cup \{\infty \}$ denotes the normalized
$v_p\colon \mathbf {Q} \twoheadrightarrow \mathbf {Z}\cup \{\infty \}$ denotes the normalized ![]() $p$-adic valuation.
$p$-adic valuation.
Proof. Lemmas 2.4.4 and 2.3.5 imply that there is a non-constant element ![]() $a \not \in \bar {\mathfrak {p}}$ such that the homomorphism
$a \not \in \bar {\mathfrak {p}}$ such that the homomorphism ![]() $[\lambda,\ )_{a}\colon I_K \to {D}[a]$ is not surjective.
$[\lambda,\ )_{a}\colon I_K \to {D}[a]$ is not surjective.
The height ![]() $\|\lambda \|$, the inertia group
$\|\lambda \|$, the inertia group ![]() $I_K$ and the homomorphism
$I_K$ and the homomorphism ![]() $[\lambda,\ )_{a}$ remain unchanged when we replace the base field
$[\lambda,\ )_{a}$ remain unchanged when we replace the base field ![]() $K$ by an unramified extension. We are thus free to assume that the torsion scheme
$K$ by an unramified extension. We are thus free to assume that the torsion scheme ![]() ${D}[a]$ is constant or, in other words, that all the
${D}[a]$ is constant or, in other words, that all the ![]() $K^s$-points of
$K^s$-points of ![]() ${D}[a]$ are defined over the field
${D}[a]$ are defined over the field ![]() $K$. Under this assumption the homomorphism
$K$. Under this assumption the homomorphism ![]() $[\lambda,\ )_{a}$ is defined on the absolute Galois group
$[\lambda,\ )_{a}$ is defined on the absolute Galois group ![]() $G_K$, see § 2.2. Its kernel determines a finite abelian
$G_K$, see § 2.2. Its kernel determines a finite abelian ![]() $p$-torsion extension
$p$-torsion extension ![]() $L/K$.
$L/K$.
Let ![]() $I \subset {D}[a]$ be the image of the inertia subgroup
$I \subset {D}[a]$ be the image of the inertia subgroup ![]() $I_K$. The ramification index
$I_K$. The ramification index ![]() $e$ of the extension
$e$ of the extension ![]() $L/K$ equals the cardinality of
$L/K$ equals the cardinality of ![]() $I$. By our choice of the absolute value
$I$. By our choice of the absolute value ![]() $|\cdot |_\infty$ in § 1.2 we have an equality
$|\cdot |_\infty$ in § 1.2 we have an equality ![]() $|A/(a)| = |a|_\infty$. Thus, the torsion module
$|A/(a)| = |a|_\infty$. Thus, the torsion module ![]() ${D}[a]$ has cardinality
${D}[a]$ has cardinality ![]() $|a|_\infty ^s$, and the assumption
$|a|_\infty ^s$, and the assumption ![]() $I \ne {D}[a]$ implies that
$I \ne {D}[a]$ implies that ![]() $e < |a|_\infty ^s$.
$e < |a|_\infty ^s$.
By construction there is an element ![]() $\lambda ' \in {D}(L)$ such that
$\lambda ' \in {D}(L)$ such that ![]() $a \lambda ' = \lambda$. We have
$a \lambda ' = \lambda$. We have ![]() $\|\lambda \|_{L} = e \, \|\lambda \|_{K}$ so Lemma 3.2.3 shows that
$\|\lambda \|_{L} = e \, \|\lambda \|_{K}$ so Lemma 3.2.3 shows that
The integers ![]() $e$ and
$e$ and ![]() $|a|_\infty$ are powers of
$|a|_\infty$ are powers of ![]() $p$ so the strict inequality
$p$ so the strict inequality ![]() $e < |a|_\infty ^s$ implies a strict inequality of
$e < |a|_\infty ^s$ implies a strict inequality of ![]() $p$-adic valuations
$p$-adic valuations ![]() $v_p(\|\lambda '\|_{L}) < v_p(\|\lambda \|_{K})$ as claimed.
$v_p(\|\lambda '\|_{L}) < v_p(\|\lambda \|_{K})$ as claimed.
Theorem 3.3.2 For each element ![]() $\lambda \in {D}(K) \smallsetminus {D}(\mathcal {O}_K)$ the homomorphism
$\lambda \in {D}(K) \smallsetminus {D}(\mathcal {O}_K)$ the homomorphism ![]() $[\lambda,\ )_{\text {ad}}\colon I_K \to {T}_{\text {ad},\bar {\mathfrak {p}}} {D}$ has open image.
$[\lambda,\ )_{\text {ad}}\colon I_K \to {T}_{\text {ad},\bar {\mathfrak {p}}} {D}$ has open image.
Proof. Suppose that the homomorphism is not surjective. Invoking Lemma 3.3.1 we obtain a non-constant element ![]() $a \in A\smallsetminus \bar {\mathfrak {p}}$, a finite separable extension
$a \in A\smallsetminus \bar {\mathfrak {p}}$, a finite separable extension ![]() $L/K$ and an element
$L/K$ and an element ![]() $\lambda ' \in {D}(L)$ such that
$\lambda ' \in {D}(L)$ such that ![]() $a \lambda ' = \lambda$. As the pairing
$a \lambda ' = \lambda$. As the pairing ![]() $[\ ,\ )_{\text {ad}}$ is
$[\ ,\ )_{\text {ad}}$ is ![]() $A$-linear in the first argument we deduce that
$A$-linear in the first argument we deduce that
The right-hand side has finite index in ![]() $[\lambda, I_K)_{\text {ad}}$. Hence, it is enough to prove the theorem with
$[\lambda, I_K)_{\text {ad}}$. Hence, it is enough to prove the theorem with ![]() $\lambda$ replaced by
$\lambda$ replaced by ![]() $\lambda '$ and
$\lambda '$ and ![]() $K$ replaced by
$K$ replaced by ![]() $L$.
$L$.
Lemma 3.3.1 also shows that we have a strict inequality of ![]() $p$-adic valuations:
$p$-adic valuations:
The height ![]() $\|\cdot \|_{L}$ takes only integer values, so the valuation
$\|\cdot \|_{L}$ takes only integer values, so the valuation ![]() $v_p(\|\lambda '\|_{L})$ is bounded below by zero. Hence, after repeating our argument finitely many times we arrive at a situation where the homomorphism
$v_p(\|\lambda '\|_{L})$ is bounded below by zero. Hence, after repeating our argument finitely many times we arrive at a situation where the homomorphism ![]() $[\lambda ',\ )_{\text {ad}}$ is onto.
$[\lambda ',\ )_{\text {ad}}$ is onto.
4. Applications
We retain the notation and the conventions of § 3. In particular, our base field ![]() $K$ is a local field over a finite field
$K$ is a local field over a finite field ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality
$\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality ![]() $q$ and characteristic
$q$ and characteristic ![]() $p$. We fix a separable closure
$p$. We fix a separable closure ![]() $K^s/K$, denote by
$K^s/K$, denote by ![]() $G_K$ the corresponding absolute Galois group, by
$G_K$ the corresponding absolute Galois group, by ![]() $I_K$ the inertia subgroup and by
$I_K$ the inertia subgroup and by ![]() $J_K$ the maximal quotient of
$J_K$ the maximal quotient of ![]() $I_K$ that is abelian of exponent
$I_K$ that is abelian of exponent ![]() $p$; see § 3.1
$p$; see § 3.1
4.1 The conductor of a Drinfeld module
Let ![]() $A$ be a coefficient ring over
$A$ be a coefficient ring over ![]() $\mathbf {F}_{\hspace {-1.5pt} q}$ and let
$\mathbf {F}_{\hspace {-1.5pt} q}$ and let ![]() $E$ be a Drinfeld
$E$ be a Drinfeld ![]() $A$-module of stable reduction over
$A$-module of stable reduction over ![]() $\operatorname {Spec} K$. Drinfeld's theory of Tate uniformization [Reference DrinfeldDri74, § 7] represents
$\operatorname {Spec} K$. Drinfeld's theory of Tate uniformization [Reference DrinfeldDri74, § 7] represents ![]() $E$ as an analytic quotient of a Drinfeld module
$E$ as an analytic quotient of a Drinfeld module ![]() ${D}$ over
${D}$ over ![]() $\operatorname {Spec}\mathcal {O}_K$ by a Galois-invariant lattice
$\operatorname {Spec}\mathcal {O}_K$ by a Galois-invariant lattice ![]() $\varLambda \subset {D}(K^s)$, a finitely generated projective
$\varLambda \subset {D}(K^s)$, a finitely generated projective ![]() $A$-submodule which is discrete with respect to the adic topology. We thus have an analytic morphism
$A$-submodule which is discrete with respect to the adic topology. We thus have an analytic morphism ![]() $e_\varLambda \colon {D} \to E$ extending to a short exact sequence:
$e_\varLambda \colon {D} \to E$ extending to a short exact sequence:
This sequence is determined functorially by the Drinfeld module ![]() $E$. We will refer to
$E$. We will refer to ![]() $\varLambda$ as the period lattice of
$\varLambda$ as the period lattice of ![]() $E$ and to
$E$ and to ![]() $e_\varLambda$ as the exponential map of
$e_\varLambda$ as the exponential map of ![]() $\varLambda$. A detailed exposition of Tate uniformization theory can be found in a recent book by Papikian [Reference PapikianPap23, § 6.2].
$\varLambda$. A detailed exposition of Tate uniformization theory can be found in a recent book by Papikian [Reference PapikianPap23, § 6.2].
Throughout this section we make an additional assumption: the lattice ![]() $\varLambda$ is defined over
$\varLambda$ is defined over ![]() $K$, which is to say,
$K$, which is to say, ![]() $\varLambda \subset {D}(K)$. We will study the action of inertia on the Tate modules of
$\varLambda \subset {D}(K)$. We will study the action of inertia on the Tate modules of ![]() $E$.
$E$.
Lemma 4.1.1 The Drinfeld modules ![]() ${D}$ and
${D}$ and ![]() $E$ have the same characteristic homomorphism.
$E$ have the same characteristic homomorphism.
Proof. The proof follows since the exponential ![]() $e_\varLambda$ induces an isomorphism of tangent spaces
$e_\varLambda$ induces an isomorphism of tangent spaces ![]() $\operatorname {Lie}_{D} \xrightarrow {\smash {{ {\sim }}}} \operatorname {Lie}_E$.
$\operatorname {Lie}_{D} \xrightarrow {\smash {{ {\sim }}}} \operatorname {Lie}_E$.
Lemma 4.1.2 For each proper ideal ![]() $\mathfrak {n}\subset A$ that is not divisible by the characteristic of
$\mathfrak {n}\subset A$ that is not divisible by the characteristic of ![]() $E$ we have a Galois-equivariant short exact sequence of
$E$ we have a Galois-equivariant short exact sequence of ![]() $A/\mathfrak {n}$-modules:
$A/\mathfrak {n}$-modules:
The homomorphism ![]() $\delta _{\mathfrak {n}}$ has the following description.
$\delta _{\mathfrak {n}}$ has the following description.
(1) For each
 $x \in E[\mathfrak {n}\rangle$ there is an
$x \in E[\mathfrak {n}\rangle$ there is an  $A$-module morphism
$A$-module morphism  $\tilde {x}\colon \mathfrak {n}^{-1} \to {D}(K^s)$ which lifts
$\tilde {x}\colon \mathfrak {n}^{-1} \to {D}(K^s)$ which lifts  $x$ in the sense that
$x$ in the sense that  $e_\varLambda \circ \tilde {x}$ equals the composite of
$e_\varLambda \circ \tilde {x}$ equals the composite of  $x$ and the quotient morphism
$x$ and the quotient morphism  $\mathfrak {n}^{-1} \twoheadrightarrow \mathfrak {n}^{-1}/A$.
$\mathfrak {n}^{-1} \twoheadrightarrow \mathfrak {n}^{-1}/A$.(2) The residue class
 $\delta _{\mathfrak {n}}(x)$ is represented by the element
$\delta _{\mathfrak {n}}(x)$ is represented by the element  $\tilde {x}(1) \in \varLambda$ where
$\tilde {x}(1) \in \varLambda$ where  $\tilde {x}$ is a lift of
$\tilde {x}$ is a lift of  $x$.
$x$.(3) Given a representative
 $\lambda$ of the residue class
$\lambda$ of the residue class  $\delta _{\mathfrak {n}}(x)$ one can pick a lift
$\delta _{\mathfrak {n}}(x)$ one can pick a lift  $\tilde {x}$ such that
$\tilde {x}$ such that  $\tilde {x}(1) = \lambda$.
$\tilde {x}(1) = \lambda$.
Proof. Consider a commutative diagram

with the vertical arrows given by ![]() $A$-module multiplication. The bottom row of this diagram is exact by construction and the top row is exact since the
$A$-module multiplication. The bottom row of this diagram is exact by construction and the top row is exact since the ![]() $A$-module
$A$-module ![]() $\mathfrak {n}$ is flat.
$\mathfrak {n}$ is flat.
Consider the natural isomorphism ![]() $\mathfrak {n}\otimes _A M \xrightarrow {\smash {{ {\sim }}}} \operatorname {Hom}_A(\mathfrak {n}^{-1},\:M)$. Under this isomorphism the multiplication map
$\mathfrak {n}\otimes _A M \xrightarrow {\smash {{ {\sim }}}} \operatorname {Hom}_A(\mathfrak {n}^{-1},\:M)$. Under this isomorphism the multiplication map ![]() $\mathfrak {n} \otimes _A M \to M$ is transformed to the evaluation map
$\mathfrak {n} \otimes _A M \to M$ is transformed to the evaluation map ![]() $f \mapsto f(1)$. Hence, the middle vertical arrow in the diagram above is surjective by Lemma 2.3.2, and our claims follow from the snake lemma.
$f \mapsto f(1)$. Hence, the middle vertical arrow in the diagram above is surjective by Lemma 2.3.2, and our claims follow from the snake lemma.
Lemma 4.1.1 implies that Drinfeld modules ![]() ${D}$ and
${D}$ and ![]() $E$ have the same residual characteristic. As usual, we denote this characteristic by
$E$ have the same residual characteristic. As usual, we denote this characteristic by ![]() $\bar {\mathfrak {p}}$. Consider the restricted adelic Tate module
$\bar {\mathfrak {p}}$. Consider the restricted adelic Tate module ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ and let
${T}_{\text {ad},\bar {\mathfrak {p}}} E$ and let ![]() $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ be the group of its automorphisms as an
$\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ be the group of its automorphisms as an ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$-module. The action of the inertia subgroup
${A}_{\text {ad},\bar {\mathfrak {p}}}$-module. The action of the inertia subgroup ![]() $I_K$ gives rise to the (local) restricted adelic monodromy representation
$I_K$ gives rise to the (local) restricted adelic monodromy representation
Similarly, for each prime ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$ we have the
$\mathfrak {p}\ne \bar {\mathfrak {p}}$ we have the ![]() $\mathfrak {p}$-adic monodromy representation
$\mathfrak {p}$-adic monodromy representation ![]() $\rho _{\mathfrak {p}}\colon I_K \to \operatorname {GL}(T_\mathfrak {p} E)$. The representation
$\rho _{\mathfrak {p}}\colon I_K \to \operatorname {GL}(T_\mathfrak {p} E)$. The representation ![]() $\rho _{\mathfrak {p}}$ is the composite of
$\rho _{\mathfrak {p}}$ is the composite of ![]() $\rho$ and the projection
$\rho$ and the projection ![]() $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E) \to \operatorname {GL}(T_\mathfrak {p} E)$.
$\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E) \to \operatorname {GL}(T_\mathfrak {p} E)$.
Taking the limit of sequences of Lemma 4.1.2 we obtain a short exact sequence of Galois representations:

As the Drinfeld module ![]() ${D}$ has good reduction we have at our disposal the local adelic Kummer pairing
${D}$ has good reduction we have at our disposal the local adelic Kummer pairing
Lemma 4.1.3 The monodromy representation ![]() $\rho$ factors as a composition
$\rho$ factors as a composition
where the second arrow is given by the formula ![]() $f \mapsto 1 + {T}_{\text {ad},\bar {\mathfrak {p}}}(e_\varLambda ) \circ f \circ \delta _{\text {ad}}$.
$f \mapsto 1 + {T}_{\text {ad},\bar {\mathfrak {p}}}(e_\varLambda ) \circ f \circ \delta _{\text {ad}}$.
Proof. Let ![]() $\mathfrak {n} \subset A$ be a proper ideal not divisible by
$\mathfrak {n} \subset A$ be a proper ideal not divisible by ![]() $\bar {\mathfrak {p}}$ and let
$\bar {\mathfrak {p}}$ and let ![]() $x \in E[\mathfrak {n}\rangle$ be an element. Pick a representative
$x \in E[\mathfrak {n}\rangle$ be an element. Pick a representative ![]() $\lambda$ of the residue class
$\lambda$ of the residue class ![]() $\delta _{\mathfrak {n}}(x)$. We need to show that for each automorphism
$\delta _{\mathfrak {n}}(x)$. We need to show that for each automorphism ![]() $g \in I_K$ one has
$g \in I_K$ one has
Let ![]() $\tilde {x}\colon \mathfrak {n}^{-1} \to {D}(K^s)$ be a lift of
$\tilde {x}\colon \mathfrak {n}^{-1} \to {D}(K^s)$ be a lift of ![]() $x$. By Lemma 4.1.2(3) we are free to assume that
$x$. By Lemma 4.1.2(3) we are free to assume that ![]() $\tilde {x}(1) = \lambda$. Lemma 2.3.4 shows that
$\tilde {x}(1) = \lambda$. Lemma 2.3.4 shows that
Hence, ![]() $e_\varLambda \circ [\lambda, g)_{\mathfrak {n}} = g \circ x - x$, and we are done.
$e_\varLambda \circ [\lambda, g)_{\mathfrak {n}} = g \circ x - x$, and we are done.
Corollary 4.1.4 The monodromy representation ![]() $\rho$ factors through the maximal quotient
$\rho$ factors through the maximal quotient ![]() $J_K = I_K^{{\text {ab}}} / (I_K^{{\text {ab}}})^{\times p}$ that is abelian of exponent
$J_K = I_K^{{\text {ab}}} / (I_K^{{\text {ab}}})^{\times p}$ that is abelian of exponent ![]() $p$.
$p$.
Remark 4.1.5 Similar reasoning applies to abelian varieties over a non-archimedean local field ![]() $K$. Raynaud proved that:
$K$. Raynaud proved that:
– every abelian variety over
 $K$ has potentially semistable reduction [Reference Grothendieck and RaynaudGR72, § 3];
$K$ has potentially semistable reduction [Reference Grothendieck and RaynaudGR72, § 3];– an abelian variety
 $E$ of semistable reduction is a rigid analytic quotient of a semiabelian variety
$E$ of semistable reduction is a rigid analytic quotient of a semiabelian variety  $D$ of good reduction by a lattice
$D$ of good reduction by a lattice  $\varLambda$ (see [Reference Grothendieck and RaynaudGR72, § 14]).
$\varLambda$ (see [Reference Grothendieck and RaynaudGR72, § 14]).
The Galois action on the lattice ![]() $\varLambda$ is always unramified [Reference Grothendieck and RaynaudGR72, § 3, Cor. 3.8]. Consequently, for each prime
$\varLambda$ is always unramified [Reference Grothendieck and RaynaudGR72, § 3, Cor. 3.8]. Consequently, for each prime ![]() $\ell$ different from the residual characteristic the
$\ell$ different from the residual characteristic the ![]() $\ell$-adic monodromy representation
$\ell$-adic monodromy representation ![]() $\rho _\ell \colon I_K \to \operatorname {GL}(T_\ell E)$ is expressed in terms of the Kummer pairing of
$\rho _\ell \colon I_K \to \operatorname {GL}(T_\ell E)$ is expressed in terms of the Kummer pairing of ![]() $D$ in the same way as in our Lemma 4.1.3. One deduces that
$D$ in the same way as in our Lemma 4.1.3. One deduces that ![]() $\rho _\ell$ is unipotent of level at most 2, and that
$\rho _\ell$ is unipotent of level at most 2, and that ![]() $\rho _\ell (P_K) = \{1\}$.
$\rho _\ell (P_K) = \{1\}$.
Let us return to the setting of Drinfeld modules. Following § 3.2 we consider Poonen's canonical local height ![]() $\|\cdot \|$ on the
$\|\cdot \|$ on the ![]() $A$-module
$A$-module ![]() ${D}(K)$. We have seen that with a suitable normalization of the absolute value this height is an
${D}(K)$. We have seen that with a suitable normalization of the absolute value this height is an ![]() $\infty$-adic seminorm. Remarkably, this restricts to a proper norm on every period lattice
$\infty$-adic seminorm. Remarkably, this restricts to a proper norm on every period lattice ![]() $\varLambda$.
$\varLambda$.
Lemma 4.1.6 The induced height ![]() $\|\cdot \|\colon \varLambda \to \mathbf {Z}_{\geqslant 0}$ has the following properties:
$\|\cdot \|\colon \varLambda \to \mathbf {Z}_{\geqslant 0}$ has the following properties:
(1)
 $\|\lambda \| = 0$ if and only if
$\|\lambda \| = 0$ if and only if  $\lambda = 0$;
$\lambda = 0$;(2)
 $\|\lambda + \lambda '\| \leqslant \max \{\|\lambda \|, \:\|\lambda '\| \}$;
$\|\lambda + \lambda '\| \leqslant \max \{\|\lambda \|, \:\|\lambda '\| \}$;(3)
 $\|a\lambda \| = |a|_\infty ^s \, \|\lambda \|$ for all
$\|a\lambda \| = |a|_\infty ^s \, \|\lambda \|$ for all  $a \in A$;
$a \in A$;(4) the subset
 $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant b\}$ is finite for every
$\{\lambda \in \varLambda,\:\|\lambda \| \leqslant b\}$ is finite for every  $b > 0$.
$b > 0$.
The exponent ![]() $s$ in property (3) is the rank of the Drinfeld module
$s$ in property (3) is the rank of the Drinfeld module ![]() ${D}$.
${D}$.
Proof. Properties (2) and (3) hold for the ambient seminorm and property (4) follows since the lattice ![]() $\varLambda$ is discrete in
$\varLambda$ is discrete in ![]() ${D}(K)$. We only need to check the first property. Note that
${D}(K)$. We only need to check the first property. Note that ![]() $\|\lambda \| = 0$ if and only if
$\|\lambda \| = 0$ if and only if ![]() $\lambda \in {D}(\mathcal {O}_K)$. The
$\lambda \in {D}(\mathcal {O}_K)$. The ![]() $A$-module
$A$-module ![]() $\varLambda ' = \varLambda \cap {D}(\mathcal {O}_K)$ is finite since
$\varLambda ' = \varLambda \cap {D}(\mathcal {O}_K)$ is finite since ![]() $\varLambda$ is discrete in
$\varLambda$ is discrete in ![]() ${D}(K)$. Hence,
${D}(K)$. Hence, ![]() $\varLambda '$ is torsion, and thus zero as the enclosing module
$\varLambda '$ is torsion, and thus zero as the enclosing module ![]() $\varLambda$ is torsion-free.
$\varLambda$ is torsion-free.
This fits to our definition of a normed lattice (Definition 1.3.2) with a caveat: the homogeneity property (3) holds for a differently normalized ![]() $\infty$-adic absolute value. When necessary we will correct for this discrepancy by considering the norm
$\infty$-adic absolute value. When necessary we will correct for this discrepancy by considering the norm ![]() $\|\cdot \|^{{1}/{s}}$.
$\|\cdot \|^{{1}/{s}}$.
Theorem 4.1.7 Let ![]() $E$ be a Drinfeld module of stable reduction over
$E$ be a Drinfeld module of stable reduction over ![]() $\operatorname {Spec} K$ with period lattice
$\operatorname {Spec} K$ with period lattice ![]() $\varLambda$ defined over
$\varLambda$ defined over ![]() $K$. Then there is an integer
$K$. Then there is an integer ![]() $m\geqslant 0$ such that the monodromy representation
$m\geqslant 0$ such that the monodromy representation ![]() $\rho \colon J_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ maps the ramification subgroup
$\rho \colon J_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ maps the ramification subgroup ![]() $\smash {J^{m}_K}$ to
$\smash {J^{m}_K}$ to ![]() $1$. Explicitly, if the period lattice
$1$. Explicitly, if the period lattice ![]() $\varLambda$ is generated by elements
$\varLambda$ is generated by elements ![]() $\lambda _1, \dotsc, \lambda _n$, then one can take
$\lambda _1, \dotsc, \lambda _n$, then one can take
Proof. By Theorem 3.2.4(1) each homomorphism ![]() $[\lambda _i,\ )_{\text {ad}}$ vanishes on the subgroup
$[\lambda _i,\ )_{\text {ad}}$ vanishes on the subgroup ![]() $\smash {J^{m}_K}$. Since the Kummer pairing is
$\smash {J^{m}_K}$. Since the Kummer pairing is ![]() $A$-linear in the first argument it follows that the homomorphism
$A$-linear in the first argument it follows that the homomorphism ![]() $[\lambda,\ )_{\text {ad}}$ vanishes on
$[\lambda,\ )_{\text {ad}}$ vanishes on ![]() $\smash {J^{m}_K}$ for all
$\smash {J^{m}_K}$ for all ![]() $\lambda \in \varLambda$. Lemma 4.1.3 implies the result.
$\lambda \in \varLambda$. Lemma 4.1.3 implies the result.
In view of Theorem 4.1.7 the following definition makes sense.
Definition 4.1.8 The conductor ![]() $\operatorname {\mathfrak {f}}(E/K)$ is the least integer
$\operatorname {\mathfrak {f}}(E/K)$ is the least integer ![]() $m\geqslant 0$ such that
$m\geqslant 0$ such that ![]() $\rho (J_K^{m+1}) = 1$.
$\rho (J_K^{m+1}) = 1$.
Lemma 4.1.9 We have ![]() $\operatorname {\mathfrak {f}}(E/K) = 0$ if and only if the Drinfeld module
$\operatorname {\mathfrak {f}}(E/K) = 0$ if and only if the Drinfeld module ![]() $E$ has good reduction.
$E$ has good reduction.
Proof. We have ![]() $J_K^0 = J_K^1$ by Lemma 3.1.2 so
$J_K^0 = J_K^1$ by Lemma 3.1.2 so ![]() $\operatorname {\mathfrak {f}}(E/K) = 0$ if and only if the inertia group
$\operatorname {\mathfrak {f}}(E/K) = 0$ if and only if the inertia group ![]() $I_K$ acts trivially on
$I_K$ acts trivially on ![]() $T_\mathfrak {p} E$ for all
$T_\mathfrak {p} E$ for all ![]() $\mathfrak {p}\ne \bar {\mathfrak {p}}$. The claim thus follows from Takahashi's good reduction criterion [Reference TakahashiTak82].
$\mathfrak {p}\ne \bar {\mathfrak {p}}$. The claim thus follows from Takahashi's good reduction criterion [Reference TakahashiTak82].
The invariant ![]() $\operatorname {\mathfrak {f}}(E/K)$ relates to conductors of torsion point extensions in the following way. For each proper ideal
$\operatorname {\mathfrak {f}}(E/K)$ relates to conductors of torsion point extensions in the following way. For each proper ideal ![]() $\mathfrak {n}$ that is prime to
$\mathfrak {n}$ that is prime to ![]() $\bar {\mathfrak {p}}$ consider the extension
$\bar {\mathfrak {p}}$ consider the extension ![]() $K_\mathfrak {n}\subset K^s$ generated by the
$K_\mathfrak {n}\subset K^s$ generated by the ![]() $\mathfrak {n}$-torsion points of
$\mathfrak {n}$-torsion points of ![]() $E$, which is to say, the group
$E$, which is to say, the group ![]() $\operatorname {Gal}(K^s/K_\mathfrak {n})$ is the kernel of the torsion points representation
$\operatorname {Gal}(K^s/K_\mathfrak {n})$ is the kernel of the torsion points representation ![]() $G_K \to \operatorname {GL}(E[\mathfrak {n}])$. Let
$G_K \to \operatorname {GL}(E[\mathfrak {n}])$. Let ![]() ${K_\mathfrak {n}}^{\kern -.9ex\circ }\subset K_\mathfrak {n}$ be the maximal unramified subextension.
${K_\mathfrak {n}}^{\kern -.9ex\circ }\subset K_\mathfrak {n}$ be the maximal unramified subextension.
Lemma 4.1.10 The extensions ![]() $K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ are abelian and their conductors are related to
$K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ are abelian and their conductors are related to ![]() $\operatorname {\mathfrak {f}}(E/K)$ as follows. If
$\operatorname {\mathfrak {f}}(E/K)$ as follows. If ![]() $\operatorname {\mathfrak {f}}(E/K) \ne 0$, then we have an equality
$\operatorname {\mathfrak {f}}(E/K) \ne 0$, then we have an equality
If ![]() $\operatorname {\mathfrak {f}}(E/K) = 0$, then
$\operatorname {\mathfrak {f}}(E/K) = 0$, then ![]() $\operatorname {\mathfrak {f}}(K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }) = 0$ for all
$\operatorname {\mathfrak {f}}(K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }) = 0$ for all ![]() $\mathfrak {n}$.
$\mathfrak {n}$.
Proof. The Galois representation ![]() $E[\mathfrak {n}]$ and
$E[\mathfrak {n}]$ and ![]() $E[\mathfrak {n}\rangle$ are non-canonically isomorphic, cf. § 2.3. Thus, the Galois group of the extension
$E[\mathfrak {n}\rangle$ are non-canonically isomorphic, cf. § 2.3. Thus, the Galois group of the extension ![]() $K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ is the image of the absolute inertia subgroup
$K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ is the image of the absolute inertia subgroup ![]() $I_K$ under the torsion points representation
$I_K$ under the torsion points representation ![]() $G_K \to \operatorname {GL}(E[\mathfrak {n}\rangle )$. The latter is obtained from the adelic Tate module representation by reduction modulo the ideal
$G_K \to \operatorname {GL}(E[\mathfrak {n}\rangle )$. The latter is obtained from the adelic Tate module representation by reduction modulo the ideal ![]() $\mathfrak {n}{A}_{\text {ad},\bar {\mathfrak {p}}}$. Hence, the extension
$\mathfrak {n}{A}_{\text {ad},\bar {\mathfrak {p}}}$. Hence, the extension ![]() $K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ is abelian by Corollary 4.1.4. When this extension is nontrivial its conductor and its highest break in upper numbering
$K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ is abelian by Corollary 4.1.4. When this extension is nontrivial its conductor and its highest break in upper numbering ![]() $b(K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ })$ are related in the following way:
$b(K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ })$ are related in the following way:
see [Reference SerreSer67, § 4.2, Proposition 1]. In view of this formula our claim is immediate.
The normalization of the conductor ![]() $\operatorname {\mathfrak {f}}(E/K)$ thus differs by
$\operatorname {\mathfrak {f}}(E/K)$ thus differs by ![]() $1$ from the one of local class field theory. In our case this choice leads to better-looking formulas.
$1$ from the one of local class field theory. In our case this choice leads to better-looking formulas.
Lemma 4.1.11 The conductor ![]() $\operatorname {\mathfrak {f}}(E/K)$ is either zero or a positive integer that is prime to
$\operatorname {\mathfrak {f}}(E/K)$ is either zero or a positive integer that is prime to ![]() $p$.
$p$.
Proof. If ![]() $m \geqslant 0$ is an integer that is divisible by
$m \geqslant 0$ is an integer that is divisible by ![]() $p$, then we have
$p$, then we have ![]() $J_K^{m} = J_K^{m+1}$ by Lemma 3.1.2.
$J_K^{m} = J_K^{m+1}$ by Lemma 3.1.2.
Lemma 4.1.12 The conductor is an isogeny invariant.
Proof. We have to be careful as we do not fix the characteristic homomorphism of our Drinfeld modules. In addition, in this proof it will be more convenient to represent Drinfeld modules by homomorphisms ![]() $A \to K[\tau ]$.
$A \to K[\tau ]$.
Let ![]() $\varphi, \psi \colon A \to K[\tau ]$ be Drinfeld modules and let
$\varphi, \psi \colon A \to K[\tau ]$ be Drinfeld modules and let ![]() $f\colon \varphi \to \psi$ be an isogeny, i.e. a nonzero element of
$f\colon \varphi \to \psi$ be an isogeny, i.e. a nonzero element of ![]() $K[\tau ]$ satisfying
$K[\tau ]$ satisfying ![]() $f \varphi (a) = \psi (a) f$ for all
$f \varphi (a) = \psi (a) f$ for all ![]() $a \in A$. Write
$a \in A$. Write ![]() $f = g\,\tau ^n$ with
$f = g\,\tau ^n$ with ![]() $g \in K[\tau ]$ having nonzero constant coefficient. We have a well-defined homomorphism
$g \in K[\tau ]$ having nonzero constant coefficient. We have a well-defined homomorphism
One checks easily that ![]() $\varphi '$ is a Drinfeld module. The identity
$\varphi '$ is a Drinfeld module. The identity ![]() $f \, \varphi (a) = \psi (a) f$ implies that
$f \, \varphi (a) = \psi (a) f$ implies that ![]() $g \varphi '(a) = \psi (a) g$ so
$g \varphi '(a) = \psi (a) g$ so ![]() $g$ is an isogeny from
$g$ is an isogeny from ![]() $\varphi '$ to
$\varphi '$ to ![]() $\psi$. Likewise
$\psi$. Likewise ![]() $\tau ^n$ is an isogeny from
$\tau ^n$ is an isogeny from ![]() $\varphi$ to
$\varphi$ to ![]() $\varphi '$.
$\varphi '$.
As the constant coefficient of ![]() $g$ is nonzero it follows that the characteristic homomorphisms of
$g$ is nonzero it follows that the characteristic homomorphisms of ![]() $\varphi '$ and
$\varphi '$ and ![]() $\psi$ are the same. The characteristic homomorphisms
$\psi$ are the same. The characteristic homomorphisms ![]() $\chi _\varphi$ and
$\chi _\varphi$ and ![]() $\chi _{\varphi '}$ are related by the formula
$\chi _{\varphi '}$ are related by the formula
where ![]() $\sigma \colon K \to K$ is the
$\sigma \colon K \to K$ is the ![]() $q$th power map. In particular, if
$q$th power map. In particular, if ![]() $\varphi$ has finite residual characteristic, then so do
$\varphi$ has finite residual characteristic, then so do ![]() $\varphi '$ and
$\varphi '$ and ![]() $\psi$, and the residual characteristics of
$\psi$, and the residual characteristics of ![]() $\varphi$,
$\varphi$, ![]() $\varphi '$ and
$\varphi '$ and ![]() $\psi$ coincide. We will denote these residual characteristics by
$\psi$ coincide. We will denote these residual characteristics by ![]() $\bar {\mathfrak {p}}$ as usual.
$\bar {\mathfrak {p}}$ as usual.
Next, suppose that ![]() $\varphi$ has stable reduction. It then follows by Lemma 6.1.5(1) of [Reference PapikianPap23] that
$\varphi$ has stable reduction. It then follows by Lemma 6.1.5(1) of [Reference PapikianPap23] that ![]() $\varphi '$ also has stable reduction. Suppose further that
$\varphi '$ also has stable reduction. Suppose further that ![]() $\psi$ also has stable reduction. By Theorem 6.2.12 of [Reference PapikianPap23] the isogeny
$\psi$ also has stable reduction. By Theorem 6.2.12 of [Reference PapikianPap23] the isogeny ![]() $g$ induces a Galois-equivariant injective morphism of period lattices
$g$ induces a Galois-equivariant injective morphism of period lattices ![]() $g\colon \varLambda _{\varphi '} \hookrightarrow \varLambda _\psi$. Assuming that
$g\colon \varLambda _{\varphi '} \hookrightarrow \varLambda _\psi$. Assuming that ![]() $\varLambda _\psi \subset K$ we thus conclude that
$\varLambda _\psi \subset K$ we thus conclude that ![]() $\varLambda _{\varphi '} \subset K$.
$\varLambda _{\varphi '} \subset K$.
It therefore suffices to prove our lemma in two cases: (1) ![]() $f = \tau ^n$ and (2) the constant coefficient of
$f = \tau ^n$ and (2) the constant coefficient of ![]() $f$ is nonzero. In the case
$f$ is nonzero. In the case ![]() $f = \tau ^n$ the map
$f = \tau ^n$ the map ![]() $\sigma ^n$ defines a Galois-equivariant isomorphism of torsion modules
$\sigma ^n$ defines a Galois-equivariant isomorphism of torsion modules ![]() $\varphi [a] \xrightarrow {\smash {{ {\sim }}}} \psi [a]$ for all
$\varphi [a] \xrightarrow {\smash {{ {\sim }}}} \psi [a]$ for all ![]() $a \in A$. Invoking Lemma 2.4.4 we obtain a Galois-equivariant isomorphism
$a \in A$. Invoking Lemma 2.4.4 we obtain a Galois-equivariant isomorphism ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi ) \xrightarrow {\smash {{ {\sim }}}} {T}_{\text {ad},\bar {\mathfrak {p}}}(\psi )$, and the claim follows.
${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi ) \xrightarrow {\smash {{ {\sim }}}} {T}_{\text {ad},\bar {\mathfrak {p}}}(\psi )$, and the claim follows.
Finally, we consider the case when the constant coefficient of ![]() $f$ is not zero. We observed above that in this case the characteristic homomorphisms of
$f$ is not zero. We observed above that in this case the characteristic homomorphisms of ![]() $\varphi$ and
$\varphi$ and ![]() $\psi$ coincide. As a consequence there is an isogeny
$\psi$ coincide. As a consequence there is an isogeny ![]() $f'\colon \psi \to \varphi$ which is dual to
$f'\colon \psi \to \varphi$ which is dual to ![]() $f$ in the sense that
$f$ in the sense that ![]() $f' f = \varphi (a)$ for some nonzero
$f' f = \varphi (a)$ for some nonzero ![]() $a \in A$. Since the multiplication by
$a \in A$. Since the multiplication by ![]() $a$ is injective on
$a$ is injective on ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi )$ the isogeny
${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi )$ the isogeny ![]() $f$ induces a Galois-equivariant injective morphism
$f$ induces a Galois-equivariant injective morphism ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi ) \hookrightarrow {T}_{\text {ad},\bar {\mathfrak {p}}}(\psi )$. By definition of the conductor this implies that
${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi ) \hookrightarrow {T}_{\text {ad},\bar {\mathfrak {p}}}(\psi )$. By definition of the conductor this implies that ![]() $\operatorname {\mathfrak {f}}(\varphi /K) \leqslant \operatorname {\mathfrak {f}}(\psi /K)$.
$\operatorname {\mathfrak {f}}(\varphi /K) \leqslant \operatorname {\mathfrak {f}}(\psi /K)$.
The identity ![]() $f f' f = f \varphi (a) = \psi (a) f$ implies that
$f f' f = f \varphi (a) = \psi (a) f$ implies that ![]() $f f' = \psi (a)$ because the ring
$f f' = \psi (a)$ because the ring ![]() $K[\tau ]$ is a domain. Repeating the argument above we deduce an inequality
$K[\tau ]$ is a domain. Repeating the argument above we deduce an inequality ![]() $\operatorname {\mathfrak {f}}(\psi /K) \leqslant \operatorname {\mathfrak {f}}(\varphi /K)$, and the lemma follows.
$\operatorname {\mathfrak {f}}(\psi /K) \leqslant \operatorname {\mathfrak {f}}(\varphi /K)$, and the lemma follows.
The ramification filtration of the group ![]() $J_K$ changes in a nontrivial way when one passes to a finite separable extension
$J_K$ changes in a nontrivial way when one passes to a finite separable extension ![]() $L/K$. It is not generally true that
$L/K$. It is not generally true that ![]() $J_L^m$ maps into
$J_L^m$ maps into ![]() $J_K^m$, cf. the proof of Theorem 4.2.1 for a precise statement. The conductor thus depends on the choice of the field
$J_K^m$, cf. the proof of Theorem 4.2.1 for a precise statement. The conductor thus depends on the choice of the field ![]() $K$ which we reflect in the notation
$K$ which we reflect in the notation ![]() $\operatorname {\mathfrak {f}}(E/K)$. Note that we only consider conductors of Drinfeld modules of stable reduction under the extra assumption that the period lattice is defined over
$\operatorname {\mathfrak {f}}(E/K)$. Note that we only consider conductors of Drinfeld modules of stable reduction under the extra assumption that the period lattice is defined over ![]() $K$.
$K$.
Calculating the conductor is a hard problem in general. However, we have a full answer for a class of period lattices ![]() $\varLambda$.
$\varLambda$.
Theorem 4.1.13 Let ![]() $E$ be a Drinfeld module of stable reduction over
$E$ be a Drinfeld module of stable reduction over ![]() $\operatorname {Spec} K$ with period lattice
$\operatorname {Spec} K$ with period lattice ![]() $\varLambda$ defined over
$\varLambda$ defined over ![]() $K$. Suppose that elements
$K$. Suppose that elements ![]() $\lambda _1, \dotsc, \lambda _n$ generate an
$\lambda _1, \dotsc, \lambda _n$ generate an ![]() $A$-submodule of finite index in
$A$-submodule of finite index in ![]() $\varLambda$. We then have an inequality
$\varLambda$. We then have an inequality
If, in addition, the maximum ![]() $b = {\max } \|\lambda _i\|$ is prime to
$b = {\max } \|\lambda _i\|$ is prime to ![]() $p$ then the following hold.
$p$ then the following hold.
(1) The adelic monodromy representation
 $\rho \colon J_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ maps the ramification subgroup
$\rho \colon J_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ maps the ramification subgroup  $J_K^{b}$ to an infinite subgroup. In particular,
$J_K^{b}$ to an infinite subgroup. In particular,
 \[ \operatorname{\mathfrak{f}}(E/K) = {\max} \|\lambda_i\|. \]
\[ \operatorname{\mathfrak{f}}(E/K) = {\max} \|\lambda_i\|. \]
(2) For every prime
 $\mathfrak {p}$ different from the residual characteristic
$\mathfrak {p}$ different from the residual characteristic  $\bar {\mathfrak {p}}$ the
$\bar {\mathfrak {p}}$ the  $\mathfrak {p}$-adic monodromy representation
$\mathfrak {p}$-adic monodromy representation  $\rho _{\mathfrak {p}}\colon J_K \to \operatorname {GL}(T_\mathfrak {p} E)$ maps the subgroup
$\rho _{\mathfrak {p}}\colon J_K \to \operatorname {GL}(T_\mathfrak {p} E)$ maps the subgroup  $J_K^{b}$ to an infinite subgroup.
$J_K^{b}$ to an infinite subgroup.
Proof. Since the conductor is invariant under isogenies we are free to assume that the period lattice ![]() $\varLambda$ is generated by the vectors
$\varLambda$ is generated by the vectors ![]() $\lambda _1, \dotsc, \lambda _n$. The inequality
$\lambda _1, \dotsc, \lambda _n$. The inequality ![]() $\operatorname {\mathfrak {f}}(E/K) \leqslant {\max } \|\lambda _i\|$ then follows from Theorem 4.1.7.
$\operatorname {\mathfrak {f}}(E/K) \leqslant {\max } \|\lambda _i\|$ then follows from Theorem 4.1.7.
Next assume that the maximum ![]() $b = {\max } \|\lambda _i\|$ is prime to
$b = {\max } \|\lambda _i\|$ is prime to ![]() $p$ and let
$p$ and let ![]() $\lambda _i$ be a vector on which the maximum is achieved. Theorem 3.2.4(2) shows that the homomorphism
$\lambda _i$ be a vector on which the maximum is achieved. Theorem 3.2.4(2) shows that the homomorphism ![]() $[\lambda _i,\ )_{\text {ad}}$ maps the ramification subgroup
$[\lambda _i,\ )_{\text {ad}}$ maps the ramification subgroup ![]() $J_K^b$ surjectively onto
$J_K^b$ surjectively onto ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}} {D}$. Claim (1) is then a consequence of Lemma 4.1.3 and claim (2) follows since the natural projection
${T}_{\text {ad},\bar {\mathfrak {p}}} {D}$. Claim (1) is then a consequence of Lemma 4.1.3 and claim (2) follows since the natural projection ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}}{D} \twoheadrightarrow T_\mathfrak {p}{D}$ is surjective.
${T}_{\text {ad},\bar {\mathfrak {p}}}{D} \twoheadrightarrow T_\mathfrak {p}{D}$ is surjective.
One important consequence of this theorem is that all the values of the conductor not forbidden by Lemma 4.1.11 do actually occur.
Corollary 4.1.14 For every integer ![]() $m \geqslant 1$,
$m \geqslant 1$, ![]() $p \nmid m$, there exists a Drinfeld module over
$p \nmid m$, there exists a Drinfeld module over ![]() $\operatorname {Spec} K$ of rank
$\operatorname {Spec} K$ of rank ![]() $2$ and conductor
$2$ and conductor ![]() $m$. In particular, the conductor of a Drinfeld module can be arbitrarily large.
$m$. In particular, the conductor of a Drinfeld module can be arbitrarily large.
By analogy with the classical theory of lattices one defines the ![]() $i$th successive minimum
$i$th successive minimum ![]() $\mu _i(\varLambda )$ as the minimal real number
$\mu _i(\varLambda )$ as the minimal real number ![]() $b \geqslant 0$ such that the set of vectors
$b \geqslant 0$ such that the set of vectors ![]() $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant b\}$ generates an
$\{\lambda \in \varLambda,\:\|\lambda \| \leqslant b\}$ generates an ![]() $A$-submodule of rank at least
$A$-submodule of rank at least ![]() $i$. Theorem 4.1.13 implies that
$i$. Theorem 4.1.13 implies that
where ![]() $\mu _n(\varLambda )$ is the last successive minimum,
$\mu _n(\varLambda )$ is the last successive minimum, ![]() $n = \operatorname {rank} \varLambda$.
$n = \operatorname {rank} \varLambda$.
Finally, let us bring the lattice theory of § 1 to bear on the problem of estimating the conductor.
Theorem 4.1.15 Let ![]() $E$ be a Drinfeld module of stable reduction over
$E$ be a Drinfeld module of stable reduction over ![]() $\operatorname {Spec} K$ with period lattice
$\operatorname {Spec} K$ with period lattice ![]() $\varLambda$ defined over
$\varLambda$ defined over ![]() $K$. Let
$K$. Let ![]() $r$ be the rank of
$r$ be the rank of ![]() $E$ and set
$E$ and set ![]() $s: = r - \operatorname {rank}\varLambda$. Then we have an inequality,
$s: = r - \operatorname {rank}\varLambda$. Then we have an inequality,
where:
–
 $\operatorname {vol}(\varLambda )$ is the volume of the normed lattice
$\operatorname {vol}(\varLambda )$ is the volume of the normed lattice  $(\varLambda,\|\cdot \|^{{1}/{s}})$;
$(\varLambda,\|\cdot \|^{{1}/{s}})$;–
 $C = {|\kappa |}^{3g + 2f - 1}$;
$C = {|\kappa |}^{3g + 2f - 1}$;–
 $\kappa$ is the field of constants of the coefficient field
$\kappa$ is the field of constants of the coefficient field  $F$;
$F$;–
 $g$ is the genus of the coefficient field
$g$ is the genus of the coefficient field  $F$;
$F$;–
 $f$ is the degree of the place
$f$ is the degree of the place  $\infty$ over
$\infty$ over  $\kappa$.
$\kappa$.
Proof. Every nonzero period ![]() $\lambda \in \varLambda$ satisfies the inequality
$\lambda \in \varLambda$ satisfies the inequality ![]() $\|\lambda \|^{{1}/{s}} \geqslant 1$. Hence, Theorem 1.6.4 implies that the
$\|\lambda \|^{{1}/{s}} \geqslant 1$. Hence, Theorem 1.6.4 implies that the ![]() $A$-module
$A$-module ![]() $\varLambda$ is generated by the subset
$\varLambda$ is generated by the subset
In view of this fact, the bound on the conductor follows from Theorem 4.1.7.
Whenever ![]() $\operatorname {vol}(\varLambda ) \cdot C^{r-s} \ne 1$ one can tighten the bound in Theorem 4.1.15 by
$\operatorname {vol}(\varLambda ) \cdot C^{r-s} \ne 1$ one can tighten the bound in Theorem 4.1.15 by ![]() $1$ by appealing to Lemma 4.1.11.
$1$ by appealing to Lemma 4.1.11.
4.2 General results
Theorem 4.2.1 Let ![]() $E$ be a Drinfeld module of finite residual characteristic
$E$ be a Drinfeld module of finite residual characteristic ![]() $\bar {\mathfrak {p}}$ over
$\bar {\mathfrak {p}}$ over ![]() $\operatorname {Spec} K$ and let
$\operatorname {Spec} K$ and let ![]() $\rho \colon G_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ be its restricted adelic Tate module representation. Then there is a rational number
$\rho \colon G_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ be its restricted adelic Tate module representation. Then there is a rational number ![]() $u\geqslant 0$ such that
$u\geqslant 0$ such that ![]() $\rho (I_K^u) = 1$.
$\rho (I_K^u) = 1$.
Proof. Let ![]() $L\subset K^s$ be a finite Galois extension of
$L\subset K^s$ be a finite Galois extension of ![]() $K$ such that
$K$ such that ![]() $E$ has stable reduction over
$E$ has stable reduction over ![]() $\operatorname {Spec} L$ and the local period lattice of
$\operatorname {Spec} L$ and the local period lattice of ![]() $E$ is defined over
$E$ is defined over ![]() $L$. Theorem 4.1.7 shows that
$L$. Theorem 4.1.7 shows that ![]() $\rho (I_L^u) = 1$ for all rational numbers
$\rho (I_L^u) = 1$ for all rational numbers ![]() $u \gg 0$. We have a short exact sequence of groups
$u \gg 0$. We have a short exact sequence of groups
where ![]() $\varphi$ is the lower-to-upper reindexing function of the extension
$\varphi$ is the lower-to-upper reindexing function of the extension ![]() $L/K$ (see [Reference SerreSer68, Chapitre IV, § 3]). Taking a sufficiently large rational number
$L/K$ (see [Reference SerreSer68, Chapitre IV, § 3]). Taking a sufficiently large rational number ![]() $u$ we ensure that
$u$ we ensure that ![]() $\operatorname {Gal}(L/K)^{\varphi (u)} = 1$, and the claim follows.
$\operatorname {Gal}(L/K)^{\varphi (u)} = 1$, and the claim follows.
Theorem 4.2.2 Let ![]() $E$ be a Drinfeld module of finite residual characteristic
$E$ be a Drinfeld module of finite residual characteristic ![]() $\bar {\mathfrak {p}}$ and rank
$\bar {\mathfrak {p}}$ and rank ![]() $r$ over
$r$ over ![]() $\operatorname {Spec} K$. Suppose that the local period lattice of
$\operatorname {Spec} K$. Suppose that the local period lattice of ![]() $E$ has rank
$E$ has rank ![]() $1$. Then the group scheme
$1$. Then the group scheme ![]() $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ contains a closed subgroup scheme
$\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ contains a closed subgroup scheme ![]() $U \cong \smash {(\mathbf {G}_a)^{\times (r-1)}}$ such that the image of inertia is commensurable with
$U \cong \smash {(\mathbf {G}_a)^{\times (r-1)}}$ such that the image of inertia is commensurable with ![]() $U({A}_{\text {ad},\bar {\mathfrak {p}}})$.
$U({A}_{\text {ad},\bar {\mathfrak {p}}})$.
Proof. Since we are free to replace the field ![]() $K$ by a finite separable extension we assume that
$K$ by a finite separable extension we assume that ![]() $E$ has stable reduction and that its local period lattice
$E$ has stable reduction and that its local period lattice ![]() $\varLambda$ is defined over
$\varLambda$ is defined over ![]() $K$. As in § 4.1 we have a short exact sequence of Galois representations in finitely generated free
$K$. As in § 4.1 we have a short exact sequence of Galois representations in finitely generated free ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$-modules:
${A}_{\text {ad},\bar {\mathfrak {p}}}$-modules:
This defines an ![]() ${A}_{\text {ad},\bar {\mathfrak {p}}}$-module flag on the middle term. Let
${A}_{\text {ad},\bar {\mathfrak {p}}}$-module flag on the middle term. Let ![]() $U$ be the corresponding unipotent subgroup scheme of
$U$ be the corresponding unipotent subgroup scheme of ![]() $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$. By our assumption the period lattice
$\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$. By our assumption the period lattice ![]() $\varLambda$ is an invertible
$\varLambda$ is an invertible ![]() $A$-module. Hence, the group scheme
$A$-module. Hence, the group scheme ![]() $U$ is isomorphic to
$U$ is isomorphic to ![]() $(\mathbf {G}_a)^{\times d}$ where
$(\mathbf {G}_a)^{\times d}$ where
The image of inertia ![]() $\varGamma$ is contained in the subgroup
$\varGamma$ is contained in the subgroup ![]() $U({A}_{\text {ad},\bar {\mathfrak {p}}})$ since the representations
$U({A}_{\text {ad},\bar {\mathfrak {p}}})$ since the representations ![]() ${T}_{\text {ad},\bar {\mathfrak {p}}}{D}$ and
${T}_{\text {ad},\bar {\mathfrak {p}}}{D}$ and ![]() $\varLambda$ are unramified.
$\varLambda$ are unramified.
Pick a nonzero period ![]() $\lambda \in \varLambda$. As the period lattice
$\lambda \in \varLambda$. As the period lattice ![]() $\varLambda$ has rank
$\varLambda$ has rank ![]() $1$ the evaluation at
$1$ the evaluation at ![]() $\lambda$ defines an open embedding:
$\lambda$ defines an open embedding:
By Theorem 3.3.2 the homomorphism ![]() $[\lambda,\ )_{\text {ad}}$ has open image. Lemma 4.1.3 implies that the subgroup
$[\lambda,\ )_{\text {ad}}$ has open image. Lemma 4.1.3 implies that the subgroup ![]() $\varGamma$ is open in
$\varGamma$ is open in ![]() $U({A}_{\text {ad},\bar {\mathfrak {p}}}) \xrightarrow {\smash {{ {\sim }}}} \operatorname {Hom}_A(\varLambda,\,{T}_{\text {ad},\bar {\mathfrak {p}}}{D})$. Consequently, the index of
$U({A}_{\text {ad},\bar {\mathfrak {p}}}) \xrightarrow {\smash {{ {\sim }}}} \operatorname {Hom}_A(\varLambda,\,{T}_{\text {ad},\bar {\mathfrak {p}}}{D})$. Consequently, the index of ![]() $\varGamma$ in
$\varGamma$ in ![]() $U({A}_{\text {ad},\bar {\mathfrak {p}}})$ is finite.
$U({A}_{\text {ad},\bar {\mathfrak {p}}})$ is finite.
Acknowledgements
I would like to thank Nihar Gargava, Stefano Filipazzi, Ambrus Pál, Mihran Papikian, Federico Pellarin, Richard Pink, Maryna Viazovska and the anonymous reviewers of this paper.
This project arose from conversations with Ambrus Pál at a workshop of the National Center for Theoretical Sciences in Taipei. I would like to thank the NCTS for hospitality.
Conflicts of interest
None.
Financial support
This research is supported by an Ambizione grant of the Swiss National Science Foundation (project PZ00P2_202119). The initial investigation was performed when the author was supported by an ETH Zürich Postdoctoral Fellowship.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.