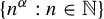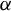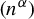1 Introduction and main results
Let
$(T^t)_{t\in {\mathbb {R}}}$
be a measure-preserving flow on a Lebesgue probability space
$(X,\Sigma , \mu )$
. Birkhoff’s pointwise ergodic theorem asserts that for any function
$f\in L^1(X)$
, the Cesàro averages
$({1}/{N})\sum _{n\in [N]}f(T^{n}x)$
converge for almost every x, where
$[N]=\{1,2,\ldots ,N\}$
. This classical result motivated others to study the ergodic averages along a sequence of positive real numbers
$(s_n)$
, that is,
$({1}/{N})\sum _{n\in [N]}f(T^{s_n}x)$
. In this paper, we will be concerned with the behavior of ergodic averages along
$(n^\alpha )$
where
$\alpha $
is a positive non-integer rational number. It was proved by Bergelson, Boshernitzan and Bourgain [Reference Bergelson, Boshernitzan and BourgainBBB94, Theorem B] that for any fixed positive non-integer rational
$\alpha $
, in every aperiodic system
$(X, \Sigma , \mu , T^t)$
, there exists
$f\in L^\infty $
such that the ergodic averages along
$(n^\alpha )$
, that is,
$({1}/{N})\sum _{n\in [N]}f(T^{n^\alpha }x)$
fail to converge almost everywhere (a.e.). Their proof is based on Bourgain’s entropy method. Later, the result was improved and the proof was simplified in [Reference KrengelJW94, Example 2.8]: it was proved that if the averages are taken along
$(n^{{a}/{b}})$
, where
$a,b\in {\mathbb {N}}$
and
$b\geq 2$
, then for any given
$\epsilon>0$
, there exists a set
$E\in \Sigma $
such that
$\mu (E)<\epsilon $
and, for almost every x, 
. The constant
$\delta $
depends on b and is explicitly given by
${1}/{\zeta (b)}$
, where
$\zeta (.) $
is the Riemann zeta function. For all
$b\geq 2$
,
$\delta $
lies in
$ (0,1).$
In this paper, we will prove a general result, Proposition 3.8, as a consequence of which we will prove the following theorem.
Theorem 1.1. Let
$\alpha $
be a fixed non-integer rational number. Then for every aperiodic dynamical system
$(X,\Sigma , \mu ,T^t)$
and every
$\epsilon>0$
, there exists a set
$E\in \Sigma $
such that
$\mu (E)<~\epsilon $
, and 
a.e. and 
a.e.
This result tells us that the extreme case of oscillation occurs for the averages along the sequence
$(n^\alpha )$
, when
$\alpha $
is a non-integer rational number.
Definition 1.2. Let
$1\leq p\leq \infty $
. A sequence
$(s_n)$
of positive real numbers is said to be pointwise good for
$L^p$
if for every system
$(X,\Sigma , \mu , T^t)$
and every
$f\in L^p(X)$
,
$\lim _{N\to \infty }({1}/{N})\sum _{n\in [N]}f(T^{s_n}x)$
exists for almost every
$x\in X.$
Definition 1.3. A sequence
$(s_n)$
of positive real numbers is said to be pointwise bad in
$L^p$
if for every aperiodic system
$(X,\Sigma , \mu , T^t)$
, there is an element
$f\in L^p(X)$
such that
$\lim _{N\to \infty } ({1}/{N})\sum _{n\in [N]}f(T^{s_n}x)$
does not exist for almost every
$x\in X.$
The behavior of ergodic averages along a subsequence of
$(n)$
has a rich history. First breakthrough result in this direction was due to Krengel [Reference LaVictoireKre71] who showed that there exists a sequence of positive integers which is pointwise bad for
$L^\infty $
. A few years later, Bellow proved in [Reference Bellow, Belley, Dubois and MoralesBel83] that any lacunary sequence, for example
$(s_n)=(2^n)$
, is pointwise bad for
$L^p$
when
$p\in [1,\infty )$
. At the other extreme, if a sequence grows slower than any positive power of n, for example
$(s_n)=((\log n)^c)$
,
$c>0$
, then it is also pointwise bad for
$L^\infty $
[Reference KrengelJW94, Theorem 2.16]. Bellow and Reinhold-Larsson proved in [Reference BellowBel89, Reference Rosenblatt and WierdlRei94] that whether a sequence will be pointwise good for
$L^p$
or not depends on the value of p. More precisely, they showed that for any given
$1\leq p<q\leq \infty $
, there are sequences
$(s_n)$
which are pointwise good for
$L^q$
but pointwise bad for
$L^p$
(see also [Reference Reinhold-LarssonPar11] for finer results in terms of Orlicz spaces). There are many instances where the behavior of the averages cannot be determined by either the growth rate of the sequence
$(s_n)$
or the value of p; instead one has to analyze the intrinsic arithmetic properties of the sequence
$(s_n)$
. One such curious example is
$(n^\alpha )$
. A celebrated result of Bourgain [Reference BourgainBou88, Theorem 2] says that the sequence
$(n^\alpha )$
is pointwise good for
$L^2$
when
$\alpha $
is a positive integer. This result is in a strong contrast to [Reference Bergelson, Boshernitzan and BourgainBBB94, Theorem B]. On the other hand,
$\lfloor (n^\alpha +\log n)\rfloor $
is known to be pointwise bad for
$L^2$
when
$\alpha $
is a positive integer [Reference Boshernitzan, Kolesnik, Quas and WierdlBos05, Theorem C]. It is interesting to compare Theorem 1.1 with [Reference Boshernitzan, Kolesnik, Quas and WierdlBos05, Theorem B] which says that
$\lfloor {n^{{3}/{2}}\rfloor }$
is pointwise good for
$L^2$
. In the same paper, one can find various interesting results about the behavior of averages along sequences which are modeled on functions from the Hardy field. After Bourgain’s result [Reference BourgainBou88, Theorem 2] was published, in a series of papers it was established that for any polynomial
$P(x)$
, the sequence
$P(n)$
and the sequence of primes are pointwise good for
$L^p$
, when
$p>1$
[Reference BuczolichBou89, Reference WierdlWie88]. However, they are pointwise bad for
$L^1$
[Reference BourgainBM10, Reference LindLaV11]. Thus, the
$L^1$
case turned out to be more subtle than the others. It was largely believed that there cannot be any sequence
$(s_n)$
which is pointwise good for
$L^1$
and satisfies
$(s_{n+1}-s_n) \to \infty $
as
$n \to \infty $
. Buczolich [Reference CalderónBuc07] inductively constructed a sophisticated example to disprove this conjecture. Later, it was shown in [Reference WierdlUZ07] that
$\lfloor n^c\rfloor $
,
$c\in (1,1.001)$
, is pointwise good for
$L^1$
. The current best result is due to Mirek [Reference ParrishMir15] who showed that
$\lfloor n^c\rfloor $
,
$c\in (1,{30}/{29})$
, is pointwise good for
$L^1$
; see also [Reference Urban and ZienkiewiczTro21]. It would be interesting to know if the above result can be extended to all positive non-integers c. For further exposition in this area, the reader is referred to the survey article [Reference TrojanRW95].
In our next theorem, we will give an example of a more general class of sequences which exhibit similar behavior.
Theorem 1.4. Fix a positive integer l. Let
$\alpha _i= {a_i}/{b_i}$
, for
$i\in [l]$
, be non-integer rational numbers with gcd
$(b_i,b_j)=1$
for
$i\neq j$
. Let
$S=(s_n)$
be the sequence obtained by rearranging the elements of the set
$\{n_1^{\alpha _1}n_2^{\alpha _2}\ldots n_l^{\alpha _l} :n_i\in {\mathbb {N}} \ \text {for all } i\in [l]\}$
in an increasing order. Then for every aperiodic dynamical system
$(X,\Sigma , \mu ,T^t)$
and every
$\epsilon>0$
, there exists a set
$E\in \Sigma $
such that
$\mu (E)<\epsilon $
and 
a.e. and 
a.e.
Theorem 1.1 is a special case of Theorem 1.4. The sequences considered in Theorem 1.4 indeed form a much larger class than the ones considered in Theorem 1.1. For example, Theorem 1.1 does not apply to the sequence
$(m^{{1}/{3}}n^{{2}/{5}} : m,n\in {\mathbb {N}})$
, but Theorem 1.4 does.
In Theorem 3.5 we will prove the Conze principle for flows.
The paper is organized as follows. In §2 we give some definitions. In §3 we prove the main results. In §4 we discuss some open problems.
2 Preliminaries
Let
$(X,\Sigma , \mu )$
be a Lebesgue probability space. That means
$\mu $
is a countably additive complete positive measure on
$\Sigma $
with
$\mu (X)=1$
, with the further property that the measure space is measure-theoretically isomorphic to a measurable subset of the unit interval with Lebesgue measure. By a flow
$\{T^t:t \in {\mathbb {R}}\}$
we mean a group of measurable transformations
$T^t : X\rightarrow X$
with
$T^0(x) = x$
,
$T^{t+s} = T^t\circ T^s$
,
$s,t \in {\mathbb {R}}$
. The flow is called measurable if the map
$(x,t) \rightarrow T^t(x)$
from
$X\times {\mathbb {R}}$
into X is measurable with respect to the completion of the product of
$\mu $
, the measure on X, and the Lebesgue measure on
${\mathbb {R}}$
. The flow will be called measure-preserving if it is measurable and each
$T^t$
satisfies
$\mu ({T^t}^{-1}A)=\mu (A)$
for all
$A\in \Sigma $
. The quadruple
$(X,\Sigma ,\mu , T^t)$
will be called a dynamical system. A measurable flow will be called aperiodic (free) if
$\mu \{x \mid T^t(x)=T^s(x) \text { for some } t\neq s\}=0.$
If the flow is aperiodic, then the quadruple will be called an aperiodic system.
We will use the following notation to denote the averages:
$$ \begin{align*} \mathbb{A}_{n\in [N]}f (T^{s_n}x)=\frac{1}{N}\displaystyle\sum_{n\in [N]}f(T^{s_n}x). \end{align*} $$
More generally, for a subset
$J\subset {\mathbb {N}}$
,
$$ \begin{align*} \mathbb{A}_{n\in J}f (T^{s_n}x):=\frac{1}{\# J}\displaystyle\sum_{n\in J}f(T^{s_n}x). \end{align*} $$
Before we go to the proof of our main results, let us give the following definitions.
Definition 2.1. Let
$0<\delta \leq 1.$
We say that a sequence
$(s_n)$
is
$\delta $
-sweeping out if in every aperiodic system
$(X,\Sigma , \mu , T^t)$
, for a given
$\epsilon>0$
, there is a set
$E\in \Sigma $
with
$\mu (E)<\epsilon $
such that 
for almost every
$x\in X$
. If
$\delta =1$
, then
$(s_n)$
is said to be strong sweeping out.
-
• The relative upper density of a subsequence
$B=(b_n)$
in
$A=(a_n)$
is defined by
$$ \begin{align*} \overline{{d}}_A(B):= \displaystyle \limsup_{N\to \infty }\frac{\#\{a_n\in B:n\in[N]\}}{N}. \end{align*} $$
-
• Similarly, the relative lower density of a subsequence
$B=(b_n)$
in
$A=(a_n)$
is defined by
$$ \begin{align*} \underline{{d}}_A(B):= \displaystyle \liminf_{N\to \infty }\frac{\#\{a_n\in B:n\in[N]\}}{N}.\end{align*} $$
If both the limits are equal, we just say relative density and denote it by
$d_A(B)$
.
Remark
-
(a) If a sequence
$(s_n)$
is
$\delta $
-sweeping out, then by Fatou’s lemma, it is pointwise bad for
$L^p$
,
$p\in [1,\infty ].$
If a sequence
$(s_n)$
contains a subsequence
$(b_n)$
of relative density
$\delta>0$
which is strong sweeping out, then
$(s_n)$
is
$\delta $
-sweeping out, and hence pointwise bad for
$L^p$
,
$p\in [1,\infty ]$
. -
(b) If
$(s_n)$
is strong sweeping out, then by [Reference Jones and WierdlJR79, Theorem 1.3], there exists a residual subset
$\Sigma _1$
of
$\Sigma $
in the symmetric pseudo-metric with the property that for all
$E\in \Sigma _1$
,(2.1)This, in particular, implies that for every
$\epsilon>0$
, there exists a set
$E\in \Sigma $
such that
$\mu (E)<\epsilon $
and E satisfies (2.1).
3 Proof of the main results
The proof of Theorems 1.1 and 1.4 has two main ideas, one is what we call here the grid method, which has its origins in [Reference del Junco and RosenblattJon04], and the other is partitioning a given sequence of real numbers into linearly independent pieces. Our plan is to prove the theorems as an application of Proposition 3.8. One of the main ingredients for the proof of Proposition 3.8 is the following theorem.
Theorem 3.1. Let
$(s_n)$
be a sequence of positive real numbers. Suppose that for any given
$\epsilon \in (0,1)$
,
$P_0>0$
and a finite constant C, there exist
$P>P_0$
and a dynamical system
$(\tilde {X},\beta , {\mathfrak {m}}, U^t)$
with a set
$\tilde {E}\in \beta $
such that
Then
$(s_n)$
is strong sweeping out.
Proof. This will follow from [Reference Akcoglu, Bellow, Jones, Losert, Reinhold-Larsson and WierdlAkc96, Theorem 2.2] and Proposition 3.2 below.
Let
$\unicode{x3bb} $
denote the Lebesgue measure on
${\mathbb {R}}$
.
-
• For a Lebesgue measurable subset B of
${\mathbb {R}}$
, we define the upper density of B by (3.2)
$$ \begin{align} \overline{d}(B)=\displaystyle\limsup_{J\to \infty}\frac{1}{J} \unicode{x3bb}(B\cap [0,J]). \end{align} $$
-
• Similarly, for a locally integrable function
$\phi $
on
${\mathbb {R}}$
, we define the upper density of the function by (3.3)
$$ \begin{align} \overline{d}(\phi)=\displaystyle\limsup_{J\to \infty}\frac{1}{J} \int_{[0,J]}\phi(t)\,dt. \end{align} $$
Proposition 3.2. Let
$(s_n)$
be a sequence of positive real numbers. Suppose there exist
$\epsilon \in (0,1)$
,
$P_0>0$
and a finite constant C such that for all P and Lebesgue measurable set
$E\subset {\mathbb {R}}$
,
Then for any dynamical system
$(\tilde {X},{\beta },{\mathfrak {m}},U^t)$
and for any
$\tilde {E}\in \beta $
we have
We will use here an argument similar to Calderón’s transference principle [Reference ConzeCal68].
Proof. Let
$P>P_0$
be an arbitrary integer. Choose
$\eta>0$
small. It will be sufficient to show that for any
$\tilde {E}\in \beta $
we have
To prove (3.6), we need the following lemma.
Lemma 3.3. Under the hypothesis of Proposition 3.2, there exists
$J_0=J_0(\eta )\in {\mathbb {N}}$
such that for every Lebesgue measurable set
$E\subset {\mathbb {R}}$
the following holds:
Proof. Let us assume that the conclusion is not true. Then for every integer
$J_k$
, there exists a Lebesgue measurable set
$E_k\subset {\mathbb {R}}$
such that
Fix such a
$J_k$
and
$E_k.$
Observe that the set
$E_k':= E_k\cap [0,J_k+s_P]$
also satisfies (3.8). Then for any
$J>J_k+s_P$
, we have
Letting
$J\to \infty $
, we get
But this contradicts our hypothesis (3.4). This finishes the proof of our lemma.
We now establish (3.6). Let
$\tilde {E}$
be an arbitrary element of
${\beta }$
. For a fixed element
$x\in \tilde {X}$
, define 
by
Applying (3.7) on the set
$E_x$
, we get
By definition of the sets
$E_x$
and
$\tilde {E}$
, we get
Substituting the above equality in (3.12), we get
Introducing the set
we can rewrite equation (3.13) as
which implies
Integrating the above equation with respect to the x variable, using (3.11) in the right-hand side and applying Fubini’s theorem, we get
By using the fact that
$U^t$
is measure-preserving we get
$$ \begin{align} {\mathfrak{m}} (B) J_0 \leq (C+\eta) {\mathfrak{m}}(\tilde{E}) J_0. \end{align} $$
This gives us that
$$ \begin{align} {\mathfrak{m}}(B)\leq (C+\eta) {\mathfrak{m}} (\tilde{E}), \end{align} $$
finishing the proof of the desired maximal inequality (3.6). This completes the proof.
One can generalize the above proposition as follows.
Proposition 3.4. Let
$(s_n)$
be a sequence of positive real numbers. Suppose there exists a finite constant C such that for all locally integrable functions
$\phi $
and
$\gamma>0$
we have
$$ \begin{align} \overline{d}\Big(t|\sup_{N} \displaystyle\mathbb{A}_{n\in [N]}\phi(s_n+t)\geq \gamma\Big)\leq \frac{C}{\gamma}\overline{d}(\lvert \phi \rvert). \end{align} $$
Then for any dynamical system
$(\tilde {X},{\beta },{\mathfrak {m}},U^t)$
and for any
$\tilde {f}\in L^1$
we have
$$ \begin{align} {\mathfrak{m}} (x|\sup_{ N} \displaystyle\mathbb{A}_{n\in [N]}{\tilde{f}}(U^{s_{n}}x)\geq \gamma )\leq \frac{C}{\gamma}\int_{\tilde{X}}\lvert \tilde{f}\rvert\,d{\mathfrak{m}}. \end{align} $$
The proof of this proposition is very similar to the proof of Proposition 3.2, hence we omit it.
The underlying principle of Theorem 3.1 is the Conze principle which has been widely used to prove many results related to the Birkhoff’s pointwise ergodic theorem. Originally, the theorem was proved for a single transformation system by Conze [Reference Jones and AssaniCon73]. Here we will prove a version of the theorem for flows. The theorem is not required for proving Proposition 3.8, but it is of independent interest.
Theorem 3.5. (Conze principle for flows)
Let
$S= (s_n)$
be a sequence of positive real numbers and
$(X,\Sigma ,\mu , T^t)$
be an aperiodic flow which satisfies the following maximal inequality: there exists a finite constant C such that for all
${f}\in L^1(X)$
and
$\gamma>0$
we have
$$ \begin{align} \mu (x|\sup_{N} \displaystyle\mathbb{A}_{n\in [N]}{{f}}(T^{s_{n}}x)\geq \gamma)\leq \frac{C}{\gamma}\int_{X} \lvert f\rvert\,d\mu. \end{align} $$
Then the above maximal inequality holds in every dynamical system with the same constant C.
For a Lebesgue measurable subset A of
${\mathbb {R}}$
, and
$F\in \Sigma $
, we will use the notation
$T^A(F)$
to denote the set
$\bigcup _{t\in A}T^t(F)$
. We will say that
$T^A(F)$
is disjoint if we have
$T^t(F)\cap T^s(F)~=~\emptyset $
for all
$t\neq s.$
Proof. We want to show that the maximal inequality (3.20) transfers to
${\mathbb {R}}$
. If we can show that, then Proposition 3.4 will finish the proof.
Let
$\phi $
be a measurable function. After a standard reduction, we can assume that
$\gamma =1$
and
$\phi $
is positive. It will be sufficient to show that for any fixed P we have
$$ \begin{align} \overline{d}\Big(t|\max_{N\leq P} \displaystyle\mathbb{A}_{n\in [N]}\phi(s_n+t)\geq 1\Big)\leq C\overline{d} (\phi). \end{align} $$
Define
$$ \begin{align} G:=\Big\{t: \max_{N\leq P}\mathbb{A}_{n\in [N]}\phi({s_{n}}+t)>1\Big\}. \end{align} $$
Let
$(L_n)$
be a sequence such that
$$ \begin{align} \overline{d}(G)=\lim_{n\to \infty} \frac{1}{L_n-s_P}\unicode{x3bb}([0,L_n-s_P]\cap G). \end{align} $$
Fix
$L_n$
large enough so that it is bigger than
$s_P$
. Then by applying the
${\mathbb {R}}$
-action version of the Rohlin tower [Reference MirekLin75, Theorem 1], we can find a set
$F\subset X$
, such that
$T^{[0,L_n]}(F)$
is disjoint, measurable and
$\mu (T^{[0,L_n]}F)>1-\eta $
, where
$\eta>0$
is small. It also has the additional property that if we define the map
$\nu $
by
$\nu (A):=\mu (T^A(F))$
for any Lebesgue measurable subset A of
$[0,L_n]$
, then
$\nu $
becomes a constant multiple of the Lebesgue measure.
Define
$f :X\to {\mathbb {R}}$
as follows:
$$ \begin{align*} f(x)= \begin{cases} \phi(t)&\text{when } x\in T^t(F),\\ 0&\text{when } x\not\in T^{[0,L_n]}(F). \end{cases} \end{align*} $$
Now we observe that for each
$x\in T^{t}(F)$
with
$t\in [0,L_n-s_P]$
and
$N\leq P$
we have
$$ \begin{align*} \max_{N\leq P}\frac{1}{N}\displaystyle\sum_{n\leq N}\phi({s_{n}}+t)=\max_{N\leq P}\frac{1}{N}\displaystyle\sum_{n\leq N}f(T^{s_{n}}x) \end{align*} $$
Substituting this into (3.20), we get
$$ \begin{align} \mu(x|x\in T^{t}(F) \text{ for some } t\in [0,L_n-s_P]\cap G)\leq C\int_X f\,d\mu. \end{align} $$
Then (3.24) can be rewritten as
$$ \begin{align} \mu(T^{[0,L_n-s_P]\cap G} (F))\leq C\int_X f\,d\mu. \end{align} $$
Applying the change-of-variable formula, we can rewrite (3.25) as
$$ \begin{align*} \nu([0,L_n-s_P]\cap G)&\leq C\int_{[0,L_n]} \phi(t)\,d\nu(t). \end{align*} $$
Since
$\nu $
is a constant multiple of the Lebesgue measure, we get
$$ \begin{align*} \unicode{x3bb}([0,L_n-s_P]\cap G)&\leq C\int_{[0,L_n]} \phi(t)\, dt. \end{align*} $$
Dividing both sides by
$(L_n-s_P)$
and taking limits inferior and superior, we have
$$ \begin{align*} \displaystyle\liminf_{n\to \infty} \frac{1}{L_n-s_P}\unicode{x3bb}([0,L_n-s_P]\cap G)&\leq C,\quad \displaystyle\limsup_{n\to \infty} \frac{L_n}{L_n-s_P}\frac{1}{L_n}\int_{[0,L_n]} \phi(t)\,dt. \end{align*} $$
This implies, by (3.23), that
$$ \begin{align*} \overline{d}(G)&\leq C\overline{d}(\phi). \end{align*} $$
This is the desired maximal inequality on
${\mathbb {R}}.$
We now invoke Proposition 3.4 to finish the proof.
We need the following two lemmas to prove Proposition 3.8.
Lemma 3.6. Let S be a finite subset of
${\mathbb {R}}$
such that S is linearly independent over
${\mathbb {Q}}$
. Suppose
${S}{\ =\ \ } \cdot \hspace {-8.4pt}\bigcup _{q\leq Q} {S}_{q}$
is a partition of S into Q sets. Then there is a positive integer r such that for every
$q\in [Q]$
,
$$ \begin{align} rs\in I_q \text{ (mod } 1)\quad \text{whenever } s\in {S}_{q}, \end{align} $$
where
$$ \begin{align} I_q:= \bigg(\frac{q-1}{Q},\frac{q}{Q}\bigg). \end{align} $$
Proof. The above lemma is a consequence of the well-known Kronecker diophantine theorem.
Let us introduce the following notation for stating our next lemma. Let
$\mathcal {P}$
denote the set of prime numbers. For a fixed positive integer m, we want to consider the linear independence of the set consisting of products of the form
$\prod _{p\in \mathcal {P}}p^{{v_p}/{m}}$
over
${\mathbb {Q}}$
, where only finitely many of the exponents
$v_p$
are non-zero. Let S be a possibly infinite collection of such products, that is,
$S= \{\prod _{p\in \mathcal {P}} p^{{v_{j,p}}/{m}}:j\in J\}$
, where J is a (countable) index set. We call S a good set if it satisfies the following two conditions.
-
(i) For any
$j\in J$
and
$p\in \mathcal {P}$
, if
$v_{j,p}\neq 0$
, then
$v_{j,p}\not \equiv 0$
(mod m). -
(ii) The vectors
${\textbf {v}}_j= ({v_{j,p}})_{p\in \mathcal {P}}$
,
$j\in J$
, of exponents are different (mod m). This just means that if
$i\ne j$
, then there is a
$p\in \mathcal {P}$
such that
$v_{j,p}\not \equiv v_{i,p}\pmod m$
.
Lemma 3.7. (Besicovitch reformulation)
Let m be a positive integer, and let the set S be good. Then S is a linearly independent set over the rationals.
Proof. Suppose, if possible, that there exist
$\unicode{x3bb} _i\in {\mathbb {Q}}, \text { for } \ i\in [N]$
, such that
$\sum _{i\leq N}\unicode{x3bb} _i s_i=0$
is a non-trivial relation in S. We can express this relation as
$P(p_1^{{1}/{m}},p_2^{{1}/{m}},\ldots ,p_r^{{1}/{m}})~=~0$
, where P is a polynomial, and for all
$i\in [r]$
,
$p_i$
is a prime divisor of
${s_j}^m$
for some
$j\in [N].$
Since S is a good set, we can reduce this relation to a relation
$P'(p_1^{{1}/{m}},p_2^{{1}/{m}},\ldots ,p_r^{{1}/{m}})=0$
such that each coefficient of
$P'$
is a non-zero constant multiple of the corresponding coefficient of P, and the degree of
$P'$
with respect to
$p_i^{{1}/{m}}$
is
$<m$
for all
$i\in [r].$
But this implies, by [Reference BesicovitchBes40, Corollary 1], that all coefficients of
$P'$
vanish. Hence, all the coefficients of P will also vanish. But this contradicts the non-triviality of the relation that we started with. This completes the proof.
Proposition 3.8. Let
$S=(s_n)$
be an increasing sequence of positive real numbers. Suppose S can be written as a disjoint union of
$(S_k)_{k=1}^\infty $
, that is,
$S=\cdot \hspace {-8.4pt}\bigcup _{k\in {\mathbb {N}}}S_{k}$
such that the following two conditions hold.
-
(a) (Density condition). The relative upper density of
$R_K := \bigcup _{k\in [K]}S_k$
goes to 1 as
$K\to \infty $
. -
(b) (Linearly independence condition). Each subsequence
$S_k$
of S is linearly independent over
${\mathbb {Q}}$
.
Then S is strong sweeping out.
Proof of Proposition 3.8
We will apply Theorem 3.1 to prove this result. So, let
$\epsilon \in (0,1), P_0$
and
$C>0$
be arbitrary. Choose
$\rho>1$
such that
$\delta :={\rho }{(1-\epsilon )}<1$
. By using condition (a), we can choose K large enough so that
$\overline {d}(R_K)> \delta .$
This implies that we can find a subsequence
$(s_{n_j})$
of
$(s_n)$
and
$N_0\in {\mathbb {N}}$
such that
$$ \begin{align} \frac{\#\{s_n\in R_K:n\leq n_j\}}{n_j}>\delta\quad \text{for all } j\geq N_0. \end{align} $$
Define
$C_K:=S\setminus R_K=\bigcup _{j>K}S_j$
.
Let P be a large number which will be determined later. For an interval
$J\subset [P]$
of indices, we consider the average
$\mathbb {A}_{n\in J}f(U^{s_n}x)$
, where
$U^t$
is a measure-preserving flow on a space which will be a torus with high enough dimensions for our purposes.
We let
$\tilde {S}$
be the truncation of the given sequence S up to the Pth term. Define
$\tilde {S}_k$
and
$\tilde {C}_K$
as the corresponding sections of
$S_k$
and
$C_K$
in
$\tilde {S}$
respectively, that is,
$$ \begin{align*} \tilde{S} &:= (s_n)_{n\in [P]}, \ \ \ \tilde{S}_k:= \tilde{S}\cap {S_k}\quad \text{for }k\in[K], \\ \tilde{C}_K &:= \tilde{S}\cap C_K. \end{align*} $$
The partition
$\tilde {S}_1, \tilde {S}_2,\ldots ,\tilde {S}_K, \tilde {C}_K$
of
$\tilde {S}$
naturally induces a partition of the index set
$[P]$
into
$K+1$
sets
$\mathcal {N}_k, k\leq K+1$
, where
$\tilde {S}_k$
corresponds to
$\mathcal {N}_k$
for
$k\in [K]$
and
$\tilde {C}_K$
corresponds to
$\mathcal {N}_{K+1}.$
The averages
$\mathbb {A}_{n\in J}f(U^{s_n}x)$
can be written as
$$ \begin{align} \displaystyle\mathbb{A}_{n\in J}f(U^{s_n}x)= \frac{1}{\# J}\sum_{k\leq {K+1}}\sum_{n\in J\cap \mathcal{N}_{k}}f(U^{s_n} {x}). \end{align} $$
By hypothesis (b) and Lemma 3.6, it follows that each
$\tilde {S}_k$
has the property that if it is partitioned into Q sets, so that
$\tilde {S}_k= \bigcup _{q\leq Q} \tilde {S}_{k,q}$
, then there is an integer r such that
$$ \begin{align} rs\in I_q \text{ mod } 1\quad \text{ for } s\in \tilde{S}_{k,q}\text{ and } q\leq Q. \end{align} $$
where
$$ \begin{align} I_q:= \bigg(\frac{q-1}{Q},\frac{q}{Q}\bigg). \end{align} $$
The space of action is K-dimensional torus
${\mathbb {T}}^K$
, subdivided into little K-dimensional cubes C of the form
$$ \begin{align} C= I_{q(1)}\times I_{q(2)}\times\cdots \times I_{q(k)} \quad\text{for some } q(k)\leq Q \text{ for } k\leq K. \end{align} $$
At this point, it is useful to introduce the following vectorial notation to describe these cubes C. For a vector
$\textsf {q}=(q(1),q(2),\ldots ,q(K))$
, with
$q(k)\leq Q$
, define
$$ \begin{align} I_{\textsf{q}}:= I_{q(1)}\times I_{q(2)}\times \cdots \times I_{q(K)}. \end{align} $$
Since each component
$q(k)$
can take the values
$1,2,\ldots ,Q$
, we divide
${\mathbb {T}}^K$
into
$Q^K$
cubes.
We also consider the ‘bad’ set E defined by
$$ \begin{align} E:= \displaystyle\bigcup_{k\leq K} (0,1)\times(0,1)\times\cdots \times \underbrace{(I_1\cup I_2)}_{k\text{th coordinate}}\times\cdots \times (0,1). \end{align} $$
Defining the set
$E_k$
by
$$ \begin{align} E_k:= (0,1)\times (0,1) \times \cdots \times \underbrace{(I_1\cup I_2)}_{k\text{th coordinate}}\times \cdots \times (0,1), \end{align} $$
we have
$$ \begin{align} E=\displaystyle\bigcup_{k\leq K}E_k\quad \text{and}\quad \unicode{x3bb}^{(K)}(E_k)\leq \frac{2}{Q}\quad\text{for every } k\leq K \end{align} $$
where
$\unicode{x3bb} ^{(K)}$
is the Haar-Lebesgue measure on
${\mathbb {T}}^K\!.$
By (3.36), we have
$$ \begin{align} \unicode{x3bb}^K(E)\leq \frac{2K}{Q}. \end{align} $$
Observe that by taking Q very large, one can make sure that the measure of the bad set is
$$ \begin{align} \unicode{x3bb}^{(K)}(E)<\frac{1}{C}. \end{align} $$
Now the idea is to have averages that move each of these little cubes into the supports of the set E. The two-dimensional version of the process is illustrated in Figure 1.
Figure 1 Illustration of the two-dimensional case. Here the ‘bad set’ E is the orange-colored region. Let
$(x_1,x_2)$
be an arbitrary point (which belongs to
$B_{6,3}$
in this case). We need to look at an average where
$r_1s_n\in ({4}/{10},{5}/{10})$
for all
$n\in \tilde {S}_1$
and
$r_2s_n\in ({7}/{10},{8}/{10})$
for all
$n\in \tilde {S}_2.$
Then it would give us
$(x_1,x_2)+(r_1s_n,r_2s_n)\in E$
for all
$n\in \tilde {S}_1\cup \tilde {S}_2$
. The picture suggests the name ‘grid method’.
Since we have
$Q^K$
little cubes, we need to have
$Q^K$
averages
$\mathbb {A}_J$
. This means we need to have
$Q^K$
disjoint intervals
$J_i$
of indices. The length of these intervals
$J_i$
needs to be ‘significant’. More precisely, we will choose
$J_i$
so that it satisfies the following two conditions.
-
(i)
(3.39)
$$ \begin{align} \ J_0=[1,P_0], \frac{\#J_i}{\sum\limits_{0\leq j\leq i}\#J_{j}}>\frac{1}{\rho}\quad \text{for all } i\in [Q^K]. \end{align} $$
-
(ii) If
$J_i=[N_{i},N_{i+1}],$
then
$(N_{i+1}-N_{i})$
is an element of the subsequence
$(n_j)$
and (3.40)
$$ \begin{align} (N_{i+1}-N_{i})>N_0\quad \text{for all } i\in [Q^K]. \end{align} $$
So we have
$Q^K$
little cubes
$C_i$
,
$i\leq Q^K$
, and
$Q^K$
intervals
$J_i$
,
$i\leq Q^K$
. We match
$C_i$
with
$J_i$
. The large number P can be taken to be the end-point of the last intervals
$J_{Q^K}.$
We know that each
$C_i$
is of the form
$$ \begin{align} C_i= I_{\textsf{q}_i}, \end{align} $$
for some K-dimensional vector
$\textsf {q}_i= (q_i(1),q_i(2),\ldots q_i(K)) $
with
$q_i(k)\leq Q$
for every
$k\leq K.$
The interval
$J_i$
is partitioned as
$$ \begin{align} J_i= \displaystyle\bigcup_{k\leq K+1}(J_i\cap \mathcal{N}_k). \end{align} $$
For a given
$k\leq K$
, let us define the set of indices
$\mathcal {N}_{k,q}$
, for
$q\leq Q$
, by
$$ \begin{align} \mathcal{N}_{k,q} := \bigcup\limits_{i\leq Q^K, q_i(k)=q} (J_i\cap \mathcal{N}_k). \end{align} $$
Since the sets
$\tilde {S}_{k,q} := \{s_n | n\in \mathcal {N}_{k,q}\}$
form a partition of
$\tilde {S}_k$
, by the argument of (3.30), we can find
$r_k$
so that
$$ \begin{align} r_ks_n\in I_{Q-q} \text{ (mod }1)\quad \text{for } n\in \mathcal{N}_{k,q}\quad\text{and}\quad q\leq Q. \end{align} $$
Define the flow
$U^t$
on the K-dimensional torus
${\mathbb {T}}^K$
by
$$ \begin{align} U^t(x_1,x_2,\ldots, x_K):= (x_1+r_1t,x_2+r_2t,\ldots , x_K+r_Kt). \end{align} $$
We claim that
This will imply that
To see this implication, let
$\textbf {x}\in {\mathbb {T}}^K$
and 
.
Assume that
$J_i=[N_i,N_{i+1}]$
. Then
where the second line holds since 
, and the third holds by (3.39). This proves (3.47).
Now let us prove our claim (3.46).
Let
$\textbf {x}\in C_i$
and consider the average 
. We have
by (3.45). If we can prove that for each
$k\in [K]$
,
$$ \begin{align} (x_1+r_1s_n,x_2+r_2s_n,\ldots, x_k+r_ks_n,\ldots, x_K+r_Ks_n)\in E_k\quad\text{if }n\in J_i\cap \mathcal{N}_k, \end{align} $$
then we will have
Using the notation
$J_i=[N_i,N_{i+1}]$
,
using (3.28) and (3.40) for the last inequality. We have proved (3.46).
We are yet to prove (3.48).
Since
$\textbf {x}\in C_i= I_{\textsf {q}}$
we have
$x_k\in I_{q_i(k)}$
for every k. By the definition of
$r_k$
in (3.44) we have
$r_ks_n\in I_{Q-q_i(k)}$
if
$n\in J_i\cap \mathcal {N}_k$
. It follows that
$$ \begin{align} x_k+r_ks_n\in I_{q_{i(k)}}+I_{Q-q_i(k)}\quad \text{if } n\in J_i\cap\mathcal{N}_k. \end{align} $$
Since
$I_{q_{i(k)}}+I_{Q-q_{i(k)}}\subset I_1\cup I_2$
, we get
$$ \begin{align} x_k+r_ks_n\in I_1\cup I_2\quad \text{if } n\in J_i\cap \mathcal{N}_k. \end{align} $$
By the definition of
$E_k$
in (3.35), this implies that
$$ \begin{align} (x_1+r_1s_n,x_2+r_2s_n,\ldots x_k+r_ks_n,\ldots, x_K+r_Ks_n)\in E_k \end{align} $$
as claimed.
Thus, what we have so far is the following: for every
$C>0,\epsilon \in (0,1)$
and
$P_0\in {\mathbb {N}}$
, there exist an integer
$P>P_0$
and a set E in the dynamical system
$({\mathbb {T}}^K,\Sigma ^{(K)},\unicode{x3bb} ^{(K)},U^t)$
such that
The right-hand side of this inequality is true by (3.38).
Now Theorem 3.1 finishes the proof.
We need the following definition to prove Theorem 1.1.
Definition 3.9. Let b be a fixed integer
$\geq 2$
. A positive integer n is said to be b-free if n is not divisible by the bth power of any integer greater than 1.
Proof of Theorem 1.1
If we can prove that the sequence
$(n^\alpha )$
is strong sweeping out, then part (b) of remark (at the end of §2) will give us the desired result.
To prove that the sequence
$(n^\alpha )$
is strong sweeping out, we want to apply Proposition 3.8 with
$S=(n^{\alpha })$
.
Observe that the set
$S_0:=\{s\in S: s \text { is an integer}\}$
has relative density
$0$
in the set S. Hence, we can safely delete
$S_0$
from S and rename the modified set as S. Let
$\alpha ={a}/{b} \text {with gcd}(a,b)=1 \text { and } b\geq 2$
.
By applying the fundamental theorem of arithmetic, one can easily prove that every positive integer n can be uniquely written as
$n={j^b}\tilde {n}$
, where
$j,\tilde {n}\in {\mathbb {N}}$
,
$\tilde {n}$
is b-free. This observation suggests us that we can partition the set S as follows.
Lemma 3.10.
$S{\ =\ \ }\cdot \hspace {-8.4pt}\bigcup _{k\in {\mathbb {N}}}S_{k}$
, where we define
$$ \begin{align} S _1:= \{n^{{a}/{b}}: n \text{ is }b\text{-}\mathrm{free}\}\quad\text{and}\quad S_k:=k^aS_1=\{k^a n^{{a}/{b}}:n\text{ is } b\text{-}\mathrm{free}\}. \end{align} $$
Proof. It can be easily seen that
$S=\bigcup _{k\in {\mathbb {N}}}S_{k}.$
To check the disjointness let, if possible, there exist
$s\in S_{k_1}\cap S_{k_2}, k_1\neq k_2$
. Then there exist b-free integers
$n_1,n_2$
such that
$$ \begin{align} s=k_{i}^a{n_i^{{a}/{b}}},\quad i=1,2. \end{align} $$
Without loss of any generality, we can assume gcd
$(k_1,k_2)=1$
.
Equation (3.53) implies that
$$ \begin{align} k_1^{b}n_1=k_2^{b}n_2. \end{align} $$
Observe that gcd
$(k_1,k_2)=1\!\implies \!\text {gcd}(k_1^b,k_2^b)=1$
. Hence, (3.54) can hold only if
$\mathrel {k_1^b \mid n_2}$
and
$\mathrel {k_2^b\mid n_1}$
. Since
$n_2$
is b-free,
$k_1^b$
can divide
$n_2$
only when
$k_1=1.$
Similarly,
$k_2^b$
can divide
$n_1$
only when
$k_2=1.$
But this contradicts our hypothesis
$k_1 \neq k_2$
.
We will be done if we can show that each
$S_{k}$
satisfies the hypothesis of Proposition 3.8. We need to show that the upper density of
$R_K := \bigcup _{k\in [K]}S_k$
goes to 1 as
$K\to \infty $
.
In fact, we will show that the lower density of
$R_K := \bigcup _{k\in [K]}S_k$
goes to 1 as
$K\to \infty $
. Let us look at the complement
$C_{K} := S\setminus R_{K}.$
It will be enough to show that the upper density of
$C_{K}$
goes to
$0$
as
$K\to \infty .$
An element
$n^\alpha $
of S belongs to
$C_{K}$
only when
$n^{\alpha }\in k^a S$
for some
$k>K$
. This means that there is
$k>K$
so that
$k^b \mid n$
. Hence, we have
$$ \begin{align} C_K\subset \bigcup\limits_{k>K}k^a S=\bigcup\limits_{k>K}k^a S_1=\bigcup\limits_{k>K} S_k. \end{align} $$
To see that the first equality of (3.55) is true, let
$ x\in \bigcup _{k>K}k^a S $
. Then we must have that
$x=k_1^a n^\alpha $
for some
$k_1>K.$
Write
$n=j^b \tilde {n}$
where
$\tilde {n}$
is b-free. Then
$x=(jk_1)^a\tilde {n}^\alpha $
. Since
$jk_1>K$
,
$x\in \bigcup _{k>K}k^a S_1.$
The reverse inclusion is obvious. We want to show that the upper density of
$A_K:=\bigcup _{k>K}S_k$
goes to
$0$
as
$K\to \infty .$
This would imply that the upper density of
$C_K$
also goes to
$0$
, implying that the lower density of its complement
$R_K$
goes to 1. We will see that we even have a rate of convergence of these lower and upper densities in terms of K.
Let us see why the upper density of
$A_K$
goes to
$0$
as
$K\to \infty $
.
We have
$$ \begin{align*} \#S(N)&:=\{n^\alpha\leq N:n\in {\mathbb{N}}\}\\ &=\lfloor{N^{a/b}}\rfloor,\\ \#S_k(N)&:=\{(k^bn)^\alpha\leq N:n\in {\mathbb{N}}\}\\ &=\bigg\lfloor{\frac{N^{a/b}}{k^b}}\bigg\rfloor. \end{align*} $$
Hence,
${\#S_k(N)}/{\#S(N)} \leq {1}/{k^b}$
.
We now have
$$ \begin{align*} \frac{\#A_K(N)}{\#S(N)}&=\frac{\#\left(\bigcup_{k>K} S_k(N)\right)}{\#S(N)}\\ &\leq \frac{\sum_{k>K}\#S_k(N)}{\#S_N}\\ &\leq \sum_{k>K}\frac{1}{k^b} \end{align*} $$
Since
$\sum _{k\geq K} {1}/{k^b} \to 0$
as
$K\to \infty $
, we must have that the upper density of
$A_K$
goes to
$0$
as
$K\to \infty $
. This proves that
$S_k$
satisfies the density condition.
To satisfy condition (b), first observe that every element
$s_j$
of
$S_1$
can be thought of as a product of the form
$p_1^{{c_1 a}/{b}}p_2^{{c_2a}/{b}}\ldots p_k^{{c_ka}/{b}}$
where the
$c_i$
depend on
$p_i$
and
$s_j$
for
$i\in [k]$
. We will apply Lemma 3.7 on the set
$S_1$
with
$m=b.$
To check (i), note that since
$S_1$
consists of b-free elements, we have
$0\leq c_i<b$
. Assume
$c_i>0$
. By assumption we have gcd
$(a,b)=1.$
This implies that
$ac_i\neq 0$
(mod b) for
$i\in [k]$
.
For (ii), let, if possible,
$s_1=p_1^{{c_1a}/{b}}p_2^{{c_2a}/{b}}\ldots p_k^{{c_ka}/{b}}$
and
$s_2=p_1^{{d_1a}/{b}}p_2^{{d_2a}/{b}}\ldots p_k^{{d_ka}/{b}}$
be two distinct elements of
$S_1$
satisfying
$ac_i=ad_i$
(mod b) for all
$i\in [k].$
This implies
$a(c_i-d_i)=0$
(mod b) for all
$i\in [k]\!\implies \!(c_i-d_i)=0$
(mod b) for all
$i\in [k].$
But this is not possible, since elements of
$S_1$
are b-free, and we must have
$c_i,d_i<b$
for all
$i\in [k].$
Hence, we conclude that
$S_1$
is a good set. Since
$S_k$
is an integer multiple of
$S_1$
, it follows that
$S_k$
is also linearly independent over
${\mathbb {Q}}$
. Thus condition (b) is also satisfied. This finishes the proof.
We now prove Theorem 1.4 with the help of Proposition 3.8. As before, it will be sufficient to show that the sequence
$S=(s_n)$
obtained by rearranging the elements of the set
$\{n_1^{\alpha _1}n_2^{\alpha _2}\ldots n_l^{\alpha _l} :n_i\in {\mathbb {N}}\text { for all } i\in [l]\}$
in an increasing order is strong sweeping out.
Proof of Theorem 1.4
Define
$$ \begin{align*} S_1:=\{n_1^{\alpha_1}n_2^{\alpha_2}\ldots n_l^{\alpha_l} :n_i\in{\mathbb{N}} \text{ such that } n_i \text{ is }b_i\text{ -free for all } i\in[l]\}. \end{align*} $$
First, let us see that the elements of
$S_1$
can be written uniquely. Suppose not. Then there are two different representation of an element:
$$ \begin{align} n_1^{\alpha_1}n_2^{\alpha_2}\ldots n_l^{\alpha_l}=m_1^{\alpha_1}m_2^{\alpha_2}\ldots m_l^{\alpha_l}. \end{align} $$
Let us introduce the notation
$$ \begin{align} \overline{b_i}=b_1b_2\ldots b_{i-1}b_{i+1}b_l. \end{align} $$
Equation (3.56) implies that
$$ \begin{align} n_1^{a_1\overline{b_1}}n_2^{a_2\overline{b_2}}\ldots n_l^{a_l\overline{b_l}}=m_1^{a_1\overline{b_1}}m_2^{b_2\overline{b_2}}\ldots m_l^{a_l\overline{b_l}}. \end{align} $$
After some cancellation if needed, we can assume that
$\gcd (n_i,m_i)=1.$
There exists i for which
$n_i>1$
, otherwise there is nothing to prove. Without loss of generality, let us assume that
$n_1>1$
and p is a prime factor of
$n_1$
. Let
$p^{c_i}$
be the highest power of p that divides
$m_i$
or
$n_i$
for
$i\in [l].$
Let us focus on the power of p in equation (3.58). We have
$$ \begin{align*} c_1 a_1 \overline{b_1}&=\pm c_2 a_2 \overline{b_2}\pm c_3 a_3 \overline{b_3}\pm \cdots \pm c_l a_l \overline{b_l}. \end{align*} $$
This implies that
$$ \begin{align*} c_1a_1\overline{b_1}&=0\quad (\text{mod}\ b_1). \end{align*} $$
Since
$(a_1\overline {b_1},b_1)=1$
, and
$c_1<b_1$
, we have
$c_1=0.$
This is a contradiction! This proves that
$n_i=1=m_i$
for all
$i\in [l].$
This finishes the proof that every element of
$S_1$
has a unique representation. Now let
$(e_k)$
be the sequence obtained by arranging the elements of the set
$\{\prod _{i\leq l} n_i^{b_i}, n_i\in {\mathbb {N}} \}$
in an increasing order. Define
$S_k:=e_kS_1=\{e_kn_1^{\alpha _1}n_2^{\alpha _2}\ldots n_l^{\alpha _l} :n_i\in ~{\mathbb {N}} \text { and } n_i \text { is }b_i\text { -free} \text { for all } i\in [l]\}.$
Next we will prove that
$S = \cdot \hspace {-8.4pt}\bigcup _{k\in {\mathbb {N}}} S_k$
. One can easily check that
$S=\bigcup _{k\in {\mathbb {N}}} S_k.$
To check the disjointness, we will use an argument similar to above. Suppose to the contrary that there exists
$k_1\neq k_2$
such that
$S_{k_1}=S_{k_2}.$
So we have
$$ \begin{align} e_{k_1} n_1^{\alpha_1}n_2^{\alpha_2}\ldots n_l^{\alpha_l}=e_{k_2} m_1^{\alpha_1}m_2^{\alpha_2}\ldots m_l^{\alpha_l}. \end{align} $$
This implies, using the same notation as before, that
$$ \begin{align} e_{k_1}^{b_1b_2\ldots b_l}n_1^{a_1\overline{b_1}}n_2^{a_2\overline{b_2}}\ldots n_l^{a_l\overline{b_l}}=e_{k_2}^{b_1b_2\ldots b_l}m_1^{a_1\overline{b_1}}m_2^{b_2\overline{b_2}}\ldots m_l^{a_l\overline{b_l}}. \end{align} $$
Assume without loss of generality that
$e_{k_1}>1$
,
$\gcd (e_{k_1},e_{k_2})=1$
and
$\gcd (n_i,n_j)=1$
for
$i\neq j.$
Let p be a prime which divides
$e_{k_1}$
. Assume
$p^{c_i}$
is the highest power of p that divides
$m_i$
or
$n_i$
, for
$i=1,2,\ldots l$
, and
$p^r$
is the highest power of p that divides
$e_{k_1}$
. We now focus on the power of p in (3.60). We have
$$ \begin{align*} rb_1b_2\ldots b_l&=\pm c_1 a_1 \overline{b_1}\pm c_2 a_2 \overline{b_2}\pm c_3 a_3 \overline{b_3}\pm \cdots \pm c_l a_l \overline{b_l}. \end{align*} $$
This implies that for all
$i\in [l]$
we have
$$ \begin{align*} c_ia_i\overline{b_i}&=0\ (\text{mod } b_i). \end{align*} $$
Since
$(a_i\overline {b_i},b_i)=1$
, and
$c_i<b_i$
, we get
$c_i=0\text { for all }i\in [l].$
This contradicts the assumption that
$p \mid e_{k_1}$
. Hence, we conclude that
$e_{k_1}=1.$
Similarly,
$e_{k_2}=1$
. This finishes the proof of disjointness of the
$S_k$
.
We now check the density condition. For any sequence A, denote by
$A(N)$
the set
$\{a\in A:a\leq N\}$
. As before, we will show that the lower density of
$B_K := \bigcup _{k\in [K]}S_k$
goes to 1 as
$K\to \infty $
. Let us look at the complement
$C_K:=S \setminus B_K$
. We want to show that the upper density of
$C_K$
goes to
$0$
as
$K \to \infty $
. Since the sets
$C_K$
are decreasing, it will be sufficient to show that the upper density of the subsequence
$C_M$
converges to
$0$
as
$M\to \infty $
, where
$M={e_K}^{a_1+a_2+\cdots +a_l}$
. But this is equivalent to saying that upper density of
$C_M$
converges to
$0$
as
$K\to \infty .$
This will follow from the following two lemmas.
Lemma 3.11.
$C_M(N)\subset \bigcup _{i\in [l]}\bigcup _{L\geq e_K}D_i^L(N)$
where
$$ \begin{align*} D_i^L(N):=\{n_1^{\alpha_1}n_2^{\alpha_2}\ldots n_{i-1}^{\alpha_{i-1}} (L^{b_i}n_i)^{\alpha_i} n_{i+1}^{\alpha_{i+1}} \ldots n_l^{\alpha_l}\leq N: n_j \in {\mathbb{N}} \text{ for }j\in[l] \}. \end{align*} $$
Proof. Let
$s=n_1^{\alpha _1}n_2^{\alpha _2}\ldots n_l^{\alpha _l}$
belong to
$C_{M}(N)$
. Write
$n_i=j_i^{b_i}\tilde {n_i}$
where
$\tilde {n_i}$
is
$b_i$
-free for
$i\in [l].$
Then we must have
$j_i\geq e_K$
for some
$i\in [l].$
To the contrary, suppose we have
$j_i<e_K$
for all i. Then
$j_1^{b_1}j_2^{b_2}\ldots j_l^{b_l}<{e_K}^{b_1+b_2+\cdots +b_l}=M$
. But this contradicts our hypothesis that
$s\in C_M(N).$
Lemma 3.12. For every fixed L and i,
$$ \begin{align} \frac{\#D_i^L(N)}{\#S(N)}\leq \frac{1}{L^{b_i}}. \end{align} $$
Proof. Fix
$n_j=r_j$
for
$j=1,2,\ldots ,i-1,i+1,\ldots ,l$
. Then
$$ \begin{align*} \#\{r_1^{\alpha_1}r_2^{\alpha_2}\ldots r_{i-1}^{\alpha_{i-1}} (L^{b_i}n_i)^{\alpha_i}r_{i+1}^{\alpha_{i+1}} \ldots r_l^{\alpha_l}\leq N: n_i \in {\mathbb{N}}\} =\bigg\lfloor{\frac{N^{{1}/{\alpha_i}}}{\kappa L^{b_i}}}\bigg\rfloor, \end{align*} $$
where
$\kappa =(r_1^{\alpha _1}r_2^{\alpha _2}\ldots r_{i-1}^{\alpha _{i-1}}r_{i+1}^{\alpha _{i+1}} \ldots r_l^{\alpha _l})^{{1}/{\alpha _i}}$
, and
$$\begin{align*}\#\{r_1^{\alpha_1}r_2^{\alpha_2}\ldots r_{i-1}^{\alpha_{i-1}} (n_i)^{\alpha_i} r_{i+1}^{\alpha_{i+1}}\ldots r_l^{\alpha_l}\leq N: n_i \in {\mathbb{N}}\}=\bigg\lfloor{\frac{N^{{1}/{\alpha_i}}}{\kappa}}\bigg\rfloor. \end{align*}$$
The proof follows by observing the following two equalities:
$$ \begin{align*} \#S{(N)}&=\#\{n_1^{\alpha_1}n_2^{\alpha_2}\ldots n_l^{\alpha_l}\leq N: n_j \in {\mathbb{N}} \text{ for }j\in[l] \}\\ &= \sum\#\{r_1^{\alpha_1}r_2^{\alpha_2}\ldots r_{i-1}^{\alpha_{i-1}} (n_i)^{\alpha_i} r_{i+1}^{\alpha_{i+1}}\ldots r_l^{\alpha_l}\leq N: n_i \in {\mathbb{N}}\}\end{align*} $$
and
$$ \begin{align*} \#D_i^L(N)&=\#\{n_1^{\alpha_1}n_2^{\alpha_2}\ldots n_{i-1}^{\alpha_{i-1}} (L^{b_i}n_i)^{\alpha_i} n_{i+1}^{\alpha_{i+1}} \ldots n_l^{\alpha_l}\leq N: n_j \in {\mathbb{N}} \text{ for }j\in[l] \}\\ &= \sum\#\{r_1^{\alpha_1}r_2^{\alpha_2}\ldots r_{i-1}^{\alpha_{i-1}} (L^{b_i}n_i)^{\alpha_i} r_{i+1}^{\alpha_{i+1}}\ldots r_l^{\alpha_l}\leq N: n_i \in {\mathbb{N}}\}, \end{align*} $$
where the summations are taken over all the
$(l-1)$
-tuple
$(r_1,r_2,\ldots ,r_{i-1},r_{i+1},\ldots ,r_l)$
such that their products
$r_1^{\alpha _1}r_2^{\alpha _2}\ldots r_{i-1}^{\alpha _{i-1}} r_{i+1}^{\alpha _{i+1}}$
are distinct.
Hence, the relative upper density of the set
$C_{M}$
in S is less than or equal to
$\sum _{i\in [l]}\sum _{L\geq e_K} {1}/{L^{b_i}}$
, which goes to
$0$
as
$K\to \infty .$
We now show that each
$S_k$
is linearly independent. It will be sufficient to show that
$S_1$
is linearly independent. After realizing every element
$s_j$
of
$S_1$
as
$\prod _{p\in \mathcal {P}} p^{{v_{j,p}}/{b_1b_2\ldots b_l}}$
, we apply Lemma 3.7 on
$S_1$
with
$m=b_1b_2\ldots b_l.$
(i) First let us show that for any given
$j_0\in J$
, and prime
$p_0\in \mathcal {P}$
, if
$v_{j_0,p_0}\neq 0$
, then
$v_{j_0,p_0}\not \equiv 0$
(mod m). By definition of the set
$S_1$
,
$v_{j_0,p_0}$
can be written as
$v_{j_0,p_0}=c_1a_1\overline {b_2}+c_2a_2\overline {b_2}+\cdots +c_la_l\overline {b_l}$
, where
$0\leq c_i<b_i$
, and
$c_i$
depends on
$s_{j_0,p_0}$
for
$i\in [l]$
. Here
$\overline {b_i}$
is same as in (3.57).
To the contrary, suppose
$v_{j_0,p_0}\equiv 0$
(mod m). Hence, we have
$$ \begin{align*} c_1a_1\overline{b_1}+c_2a_2\overline{b_2}+\cdots+c_la_l\overline{b_l}&\equiv 0 \text{ (mod }m).\end{align*} $$
This means that
$$ \begin{align*} c_1a_1\overline{b_1}+c_2a_2\overline{b_2}+\cdots+c_la_l\overline{b_l} &\equiv 0 \text{ (mod }b_i)\quad \text{for all }i\in [l]. \end{align*} $$
But this implies that
$$ \begin{align*} c_ia_i\overline{b_i}&\equiv 0 \text{ (mod }b_i)\quad \text{for all }i\in [l],\end{align*} $$
implying that
$$ \begin{align*} c_i&=0\quad \text{for all } i \in [l]. \end{align*} $$
So, we get
$$ \begin{align*} v_{j_0,p_0}&=0. \end{align*} $$
This is a contradiction! Hence, we conclude that if
$v_{j_0,p_0}\neq 0$
, then
$v_{j_0,p_0}\not \equiv 0$
(mod m).
(ii) Now let us assume that
$v_{j,p}\equiv v_{k,p}$
(mod
$m)$
, for all
$p~\in ~\mathcal {P}$
.
Write
$v_{j,p}=c_1a_1\overline {b_2}+c_2a_2\overline {b_2}+\cdots +c_la_l\overline {b_l}$
and
$v_{k,p}=d_1a_1\overline {b_2}+d_2a_2\overline {b_2}+\cdots +d_la_l\overline {b_l}$
, where
$0\leq c_i,d_i<b$
, and
$c_i$
depends on
$p,s_j$
and
$d_i$
depends on
$p,s_k$
for all
$i\in [l]$
. By assumption, we have
$$ \begin{align*} c_1a_1\overline{b_2}+c_2a_2\overline{b_2}+\cdots+c_la_l\overline{b_l}&\equiv d_1a_1\overline{b_2}+d_2a_2\overline{b_2}+\cdots+d_la_l\overline{b_l} \text{ (mod }m). \end{align*} $$
This implies that
$$ \begin{align*} (c_i-d_i)a_i\overline{b_i}&\equiv 0 \text{ (mod }b_i)\quad \text{for all } i\in [l].\end{align*} $$
Hence, we get
$$ \begin{align*} (c_i-d_i)&=0\quad \text{for all } i\in [l]. \end{align*} $$
So, we conclude that
$$ \begin{align*} v_{j,p}=v_{k,p}\quad \text{for all } p\in \mathcal{P}. \end{align*} $$
But we know that every element of
$S_1$
has a unique representation. Hence, we get
$j=k$
.
Thus we conclude that S is a good set and hence linearly independent over the rational. This completes the proof.
4 The case when
$\alpha $
is irrational: two open problems
We have proved that the sequence
$(n^\alpha )$
is strong sweeping out when
$\alpha $
is a non-integer rational number. For the case of irrational
$\alpha $
, it is known from [Reference Bergelson, Boshernitzan and BourgainBBB94, Reference KrengelJW94] that
$(n^\alpha )$
is strong sweeping out for all but countably many
$\alpha $
. However, the following questions are still open along these lines.
Problem 4.1. Find an explicit irrational
$\alpha $
, for which
$(n^\alpha )$
is strong sweeping out.
Problem 4.2. Is it true that for all irrational
$\alpha $
,
$(n^\alpha )$
is pointwise bad for
$L^2$
? If so, then is it true that
$(n^\alpha )$
is strong sweeping out?
If one can find an explicit
$\alpha $
for which
$(n^\alpha )$
is linearly independent over the rational, then obviously it will answer Problem 4.1. In fact, if we can find a suitable subsequence which is linearly independent over
${\mathbb {Q}}$
, then we can apply Proposition 3.8 to answer Problem 4.1.
It might be possible to apply Theorem 1.4 and some density argument to handle Problem 4.2.
Acknowledgements
The result is part of the author’s thesis. He is indebted to his advisor, Professor Máté Wierdl, for suggesting the problem and giving valuable inputs. The author is supported by the National Science Foundation under grant number DMS-1855745.
