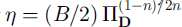Symbols and Notation
All superscripted asterisks represent dimensionless quantities. Lightfaced letters denote scalar quantities, boldfaced minuscules denote vectors and boldfaced majuscules denote second-order tensors. Exception: F represents a force vector.
Introduction
Glaciologists have long suspected that ice near the beds of temperate glaciers may be rheologically distinct from other glacier ice. From observations in subglacial cavities, Reference CarolCarol (1947) concluded that ice near the bed seemed more “plastic” (less viscous) than ice elsewhere. Since then, a basal ice layer that is texturally and structurally distinct has been observed beneath many glaciers (cf. references in Reference KnightKnight, 1997). In temperate glaciers this layer is typically decimeters to meters in thickness and is visually distinct from the ice above due to its higher sediment content. It may also have a different water content, texture and fabric. In addition, unlike ice higher in glaciers, it is subject to repeated, rapid changes in the state of stress as it flows past obstacles on the bed. All of these factors may influence its rheology.
The effect of sediment on ice rheology has been assessed in a few laboratory experiments (e.g. Reference Hooke, Dahlin and KauperHooke and others, 1972; Reference Baker and GerberichBaker and Gerberich, 1979; Reference Nickling and BennettNickling and Bennett, 1984; Reference LawsonLawson, 1996). Although there are no definitive conclusions, observations suggest that, in temperate ice, the presence of sediment softens the ice, probably because of the presence of a microscopic (or sub-microscopic) water layer around the sediment particles. Field observations and experiments on cores from ice sheets confirm that inclusions, microparticles and debris weaken ice which is at or near the melting temperature (e.g. Reference Fisher and KoernerFisher and Koerner, 1986; Reference Echelmeyer and WangEchelmeyer and Wang, 1987). These results, however, have not yielded precise estimates of the extent to which sediment reduces the viscosity of the ice, a critical parameter for modelling glaciers and ice sheets.
Experiments by Reference DuvalDuval (1977) demonstrated that ice viscosity is inversely related to water content. Liquid inclusions apparently enhance local melting and refreezing associated with recrystallization by acting as sinks and sources of heat (Reference Lliboutry and DuvalLliboutry and Duval, 1985). Observations suggest that the water content of basal ice may be anomalously high (Reference CarolCarol, 1947), as expected from high rates of strain-energy dissipation near the base of glaciers. These observations are in agreement with recent theories (Reference LliboutryLliboutry, 1993, Reference Lliboutry1996), so high water content may be an important control on the rheology of basal ice.
Anisotropic texture and fabric found in ice that has undergone large cumulative strains may reduce the effective ice viscosity. Strong single maximum fabric facilitates dislocation glide in the crystallographic basal planes. In contrast, ice with a multi-maximum fabric behaves isotropically. Analyses have shown that these fabrics are predominant near the bed (e.g. Reference HookeHooke, 1970; Reference AndertonAnderton, 1974; Reference Hooke and HudlestonHooke and Hudleston, 1980). In almost all of these studies, however, the fabric of the debrisladen basal ice layer was not measured because of the difficulty of making thin sections of such ice for measurements of c-axis orientation. Hence, the fabric of basal ice containing significant sediment concentrations is not well known. This technical difficulty has now been surmounted with the use of a diamond wire-saw technique (Reference TisonTison, 1994; Reference Tison, Thorsteinsson, Lorrain and KipfstuhlTison and others, 1994).
Finally, deformation of basal ice may be distinct from that elsewhere due to the varying, somewhat cyclic state of stress imposed on the ice by the bed roughness (Reference WeertmanWeertman, 1979; Reference LliboutryLliboutry, 1987). Because the state of stress is varying, it is seldom, if ever, symmetric with respect to the crystal fabric, as required for steady creep. As a result, the crystal fabric must be continuously adjusting to the changing stress field. Thus, rheological parameters determined in experiments carried out under steady laboratory conditions may not be appropriate when applied to basal ice.
In order to estimate the rheology of basal ice, an instrumented panel containing a flat-topped conical obstacle was mounted flush with the bedrock beneath 210 m of ice at Engabreen, a valley glacier in northern Norway. Simultaneous measurements of sliding speed, normal and shear stresses and temperature were obtained as dirty, temperate basal ice flowed past the obstacle. The experiments and measurements are discussed in Reference Cohen, Hooke, Iverson and KohlerCohen and others (2000). Herein, we use a three-dimensional finite-element model of ice flow past the obstacle to estimate the basal ice rheology. Preliminary measurements of water content, ice fabric and texture are used to interpret the results.
Summary of Field Measurements
Engabreen is a temperate valley glacier that drains ice from the Svartisen ice cap. The bedrock beneath the glacier is largely schist and gneiss. Access to the ice/bedrock interface is through tunnels in the bedrock excavated by the Norwegian Water Resources and Energy Administration (NVE) to tap meltwater for hydroelectric power generation. A tunnel off the main system is used for the sole purpose of research. This tunnel ends at the glacier bed beneath 210 m of ice. The bed can be accessed in two places: a horizontal tunnel with a door, and a 5 m high vertical shaft which opens onto a relatively planar section of the glacier bed. The instrumented panel was positioned at the top of this shaft, and measurements were made during two field efforts in April 1996 and November 1997.
Details of the measurements are given in Reference Cohen, Hooke, Iverson and KohlerCohen and others (2000). The main conclusions relevant here are:
-
(1) Normal stress and both sliding speed and direction changed from one year to the next, possibly because of changes in basal ice rheology triggered by changes in sediment concentration or water content.
-
(2) Regelation flow was negligible compared to viscous flow past the obstacle.
-
(3) Vertical melt rates were negligible compared to the sliding speed.
-
(4) Friction at the bed, estimated from Hallet’s (Reference Hallet1979, Reference Hallet1981) model, was only 5% of the total bed-parallel force exerted by the ice on the panel.
-
(5) There was no ice/bed separation on the lee side of the obstacle.
Description of Basal Ice
In 1994, Reference Jansson, Kohler and PohjolaJansson and others (1996) studied the ice sequence at the base of Engabreen. They retrieved a 1.6 m long core near the horizontal entrance. In this core, they distinguished four different units: clean blue ice, upper sediment-laden ice, cloudy ice and lower sediment-laden ice. The last of these rested on the bed and was about 0.13 m thick. None of the layers appeared to contain air bubbles. Sediment concentrations ranged from effectively zero in the cloudy and blue ice to as much as 25% by weight in the upper sediment-rich layer (10% by volume assuming an ice density of 917 kg m and a sediment density of 2650 kg m−3). Sediment concentration in the lower sediment-rich layer was 2–6% by volume, with concentration increasing near the bed.
During observations in 1996 and 1997, the four units described by Jansson and others could still be identified, although in 1997 the cloudy-ice layer thinned and disappeared a few meters up-glacier from the door. The thickness of the lower sediment-laden layer was found to vary spatially because of bedrock topography. It also varied temporally; above the shaft, it was 0.3 m thick in 1996, and 0.6 m thick in 1997. In 1997, debris concentration in this lower layer increased toward the bed, from 3% to 17% by volume. Debris concentration was also found to vary spatially. In samples collected from the lower layer, silty sediment was concentrated in small clots (also observed by Jansson and others). With increasing sediment concentration, the clots, which are no more than a couple of millimeters in diameter for the most part, collect into thin sediment layers (sometimes with and sometimes without visible interstitial ice), up to several millimeters thick, separated by layers or lenses of clean ice. These layers define a foliation which is generally parallel to the bed. Similar basal ice facies have been observed in other temperate glaciers (e.g. Reference Vivian and BocquetVivian and Bocquet, 1973; Reference Wold and ØstremWold and Østrem, 1979), in cold glaciers (e.g. Reference LawsonLawson, 1979; Reference Echelmeyer and WangEchelmeyer and Wang, 1987) and in ice sheets (e.g. Reference HookeHooke, 1970; Reference Gow, Epstein and SheehyGow and others, 1979).
In November 1997, tunnels in the blue ice near the door revealed numerous water pockets, similar to those described by Reference Jansson, Kohler and PohjolaJansson and others (1996). The water pockets found in 1997 were prolate ellipsoids, up to 2 m long, aligned with the ice-flow direction. In cross-section, they were flattened in the horizontal direction, with long axes ranging from 30 to 200 mm. The volume of these pockets was as high as 5% of the local ice volume. Some of these water pockets contained a small amount of sediment. Smaller water pockets, up to 10 mm long, were also found in the lower sediment-laden ice layer. These were not observed by Reference Jansson, Kohler and PohjolaJansson and others (1996). The total volume of water in these pockets was substantially smaller than in the blue ice above.
Numerical Model
The most commonly used constitutive equation for glacier ice is Nye’s generalization of Glen’s flow law (cf. Reference NyeNye, 1953, Reference Nye1957; Reference GlenGlen, 1958). Such a constitutive equation is that of an incompressible power-law fluid. This constitutive equation, however, cannot describe many of the observed characteristics of deforming ice. In particular, it has been noted (Reference WeertmanWeertman, 1979; Reference LliboutryLliboutry, 1987) that such an equation is inappropriate for ice deforming past obstacles, since a viscous fluid has no “memory” and therefore its constitutive equation cannot describe the phenomena of work-hardening and recovery observed during the transient stages of deformation of polycrystalline ice. However, owing to high stresses near our conical obstacle, the transient creep phase should last only a few hours at most, whereas ice takes > 1 day to pass the obstacle. Thus, adjustments to the transients should occur over time-spans that are short compared with the time it takes for ice to flow past the obstacle. In addition, the experiments at Engabreen did not yield sufficient data to consider a constitutive equation more complex than that of a two-parameter viscous fluid. In fact, because of the difficulty in accurately measuring, in situ, the sliding speed and the bed-parallel force, the data could not be used to estimate both material constants in the power-law fluid model. Instead, the pre-exponential factor in the power-law model was calculated as a function of the power-law exponent.
Constitutive equation
The constitutive equation for the deviatoric stress S for an incompressible power-law fluid is
where S = T + p
I, T is the Cauchy stress tensor, I is the identity tensor, p is an undetermined hydrostatic pressure due to the incompressibility constraint, and
is the stretching tensor with v the velocity vector. η is the viscosity function given by
where B is a pre-exponential factor, n is a power-law exponent, and
is the second invariant of D. B and n are two parameters commonly used in Glen’s flow law when it is written in the form
, where
and
,
being the second invariant of S. When n = 1, Equations (1) and (2) reduce to the constitutive equation of a Newtonian fluid with viscosity η = B/2. Equation (2) is empirical and has emerged as the simplest best fit to the large amount of data accumulated on the creep of polycrystalline ice in laboratory and glacier experiments (cf. Reference HookeHooke, 1981; Reference Lliboutry and DuvalLliboutry and Duval, 1985; Reference AlleyAlley, 1992).
Governing equations
Consider the steady, slow, isothermal flow of an incompressible power-law fluid past a rigid isolated obstacle on the bed of a glacier. In the present case, the obstacle is a flat-topped cone of height h and of radii r 0 at the base and r 1 at the top (cf. Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000, figs 4 and 5), with two camera housings, one on each side of the cone, protruding a distance h c above the base of the panel. The vertical plane that passes through the center of the cone, with one camera housing on each side, is the plane of symmetry of the instrumented panel. The bed surface around the obstacle is flat, and we assume that it is mathematically smooth. A Cartesian coordinate system (x, y, z) with basis (e x , e y , e z ) is chosen so that the base of the cone and the flat smooth bed surrounding the cone define the plane z = 0. The origin of the coordinate system is at the center of the base of the cone. The ice-flow direction, away from the obstacle, is parallel to the y axis. This axis is oriented at an angle φ to the plane of symmetry of the panel. The computational domain is a rectangular parallelepiped of length 2L, height H and width 2W, where H is much smaller than the ice thickness. The dynamical equations, to be solved in this domain, expressing the conservation of mass and momentum are
Boundary conditions
Boundary conditions need to be prescribed on all sides of the parallelepiped. On the bottom (bed), conditions of no friction and no melting–refreezing, which describe ice at the melting temperature sliding on a thin lubricating film of water, translate mathematically into zero tangential stress and zero normal velocity. The use of this boundary condition is substantiated by experimental data (Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000). A difficulty in modelling the flow in an artificially truncated domain is the choice of boundary conditions on surfaces within the ice mass, since nothing is known about the stresses or velocities on these boundaries. One of the simplest models consistent with the boundary conditions on the bed is to assume that at the inlet, the ice is moving with a constant, uniform speed v 0; at the top, the tangential stress and normal velocity are zero; at the outlet, the traction is zero; and on the sides, symmetric boundary conditions are used. We do not use periodic boundary conditions for the inlet and outlet flow, because there is only one isolated obstacle on the bed, located on a portion of the bed that is planar for several meters in every direction. Incidentally, using periodic boundary conditions does not change any of the results described below, because the inlet and outlet boundaries of the domain have been chosen far from the obstacle.
The dynamical Equations (3) and (4), together with the boundary conditions, form a system of non-linear (for n ≠ 1) partial differential equations for the velocity field v and pressure p as a function of position x.
Non-dimensionalization
The above system of partial differential equations contains three parameters: v 0, B and n. The remaining variables h, r 0, r 1, h c, H, W and L are geometrical constants that define the domain of computation. The non-dimensionalization of these equations leads to a simpler system with only one parameter, n. Let v = v 0 v *, and x = h 0 x *, where h 0 = 0.15 m is a reference length taken to be the initial height of the cone in the first field experiment, and quantities with an asterisk superscript are non-dimensional. Then, the Cauchy stress and the stretching tensors are given by
where
is a reference stress quantity and p 0 is a reference hydrostatic (far-field) pressure that must be determined from experimental data. Under these new non-dimensional quantities, the dynamical equations to be solved are
There is only one parameter in these dimensionless equations (not counting the domain geometry): n, the power-law exponent. Thus, our numerical calculations are independent of B and v 0. For each value of n, only one numerical solution is needed, a major computational advantage.
The force of gravity was not included in Equation (8). Had we included it, the gravitational term
would have appeared on the lefthand side of the equation. This term is the dimensionless ratio of gravitational to viscous forces. For ρ = 917 kg m−3, g = 9.81 m s−2, h 0 = 0.15 m, v 0 = 1.7 × 10−6 m s−1, n = 3 and B = 3 × 107 Pa s1/3 (see sections below), the numerical value for this term is 0.004. This is much smaller than the two other terms in Equation (8), which are of order 1. Physically, this is because we are considering the flow of only a very small part of the glacier above the panel. What drives the flow of this small volume of ice is not gravity but the force that the ice above exerts on it (the boundary conditions presuppose no longitudinal stresses). Of course, the ice above is driven by the gravitational force.
The non-dimensional boundary-value problem stated in Equations (8) and (9) was solved with the commercial software FIDAP using Galerkin’s finite-element method. Various three-dimensional meshes were constructed with different refinements using tri-quadratic basis functions for velocity and linear piecewise discontinuous basis functions for pressure. Each element has 9 nodes for velocity, or 27 unknowns, and 4 nodes/unknowns for pressure. The coarsest mesh had 5940 elements and 37 485 nodes. The finest mesh had 21650 elements and 148 461 nodes (Fig. 1). This discretization resulted in linear systems of ∼ 100 000 to ∼220 000 unknowns to be solved iteratively. Solutions were obtained on a CRAY C90 and an IBM RS6000 at the Minnesota Supercomputing Institute.
Fig. 1. (a) Finite-element mesh, (b) Detail of mesh on the obstacle.
Numerical results
The boundary-value problem was solved for three domain geometries representing the particular ice-flow direction and cone dimensions during the three experiments at Engabreen, one in April 1996 and two in November 1997. Table 1 gives the geometrical parameters describing the domain geometry for each of the experiments. All results shown below are dimensionless. Comparison between numerical values and measurements is deferred to the next section.
Table 1. Geometrical parameters for the computational domain, in meters
Velocity profile
The dimensionless speed above the obstacle is shown in Figure 2 as a function of n. Extrusion flow (flow velocity near the bed is higher than far-field velocity) begins for values of n between 1.5 and 2. This phenomenon was first documented by Reference CarolCarol (1947) in measurements of sliding velocity near a roche moutonnee, and later measured in the laboratory by Reference Hooke and IversonHooke and Iverson (1985). It has also been found in an analytical solution of ice sliding without friction past a hemisphere (Reference Lliboutry and RitzLliboutry and Ritz, 1978), in which the appearance of extrusion flow is at n = 1.5 precisely, and in numerical solutions of ice sliding over a sinusoidal bed (Reference GudmundssonGudmundsson, 1997). We were unable to observe whether extrusion flow was present above our obstacle.
Fig. 2. Dimensionless velocity profile computed from finite-element model for different values of n.
The speed at the ice/bed interface, along the center line x = 0, is shown in Figure 3 as a function of n. The speed decreases as the ice approaches the cone and reaches a minimum just before the cone. For n = 1 the speed near the cone is one-third of the far-field velocity. For n = 3 it is about one-half. The disturbance of the velocity field caused by the obstacle extends a greater distance from the obstacle for a Newtonian fluid. This is consistent with the analytical solution of Reference Lliboutry and RitzLliboutry and Ritz (1978) for flow past a hemisphere.
Fig. 3. Dimensionless speed along the ice/bed interface computed from finite-element model as a function of n. Small kinks are due to discontinuities in the velocity vectors at the corners of the obstacle; these give rise to numerical errors because corners are not fully resolved by the finite-element mesh.
Effective stresses
Figure 4a shows the dimensionless scalar quantity
for n = 1 and n = 3 for experiment 3 (
is the non-dimensional effective strain rate). The effective stress on the bed,
, can be calculated from the relation
From Figure 4a,
on the stoss side. With v
0 = 0.15 m d−1 = 1.74 × 10−6 m s−1, h
0 = 0.15 m, n = 3 and B = 3 × 107 Pa s1/3 (see next sections),
. This value for the effective stress is sufficiently high that transient creep should last only about an hour (Reference JackaJacka, 1984), which is much less than the time required for the ice to move past the cone.
Fig. 4. (a) Dimensionless effective strain rate, (b) dimensionless pressure and (c) dimensionless normal stress vector (on ice) on the bed for n = 1 (left panel) and n = 3 (right panel) computed from finite-element model. Flow is in the y direction. Because of the non-dimensionalization, lee-side pressures are negative, and lee-side normal stress vectors point toward the obstacle. In the experiments, the base of the cone is 0.25 m in diameter.
Pressure and normal stresses
Contours of the dimensionless pressure and normal traction on the obstacle are shown in Figure 4b and c, respectively, for n = 1 and n = 3. As ice flows past the cone, high pressures build up on the stoss side, with a zone of low pressure on the stoss side of the flat top of the cone. Since the flow is (almost) symmetric, the exact opposite is observed on the lee side of the cone.
The pressure on the ice/bed interface, along the center line x = 0, is shown in Figure 5 as a function of n. The peaks in pressure (there are also similar peaks in the normal stress curves) are due to the sharp edges at the base and top of the cone. At a perfect edge, the velocity is discontinuous. This results in a non-integrable discontinuity in normal stress in the continuum problem (cf. Reference BatchelorBatchelor, 1967, p. 226). This discontinuity is smoothed in the finite-element approximation, but mesh refinements worsen this effect. Of course in reality this discontinuity is not present, as the corners are not perfect.
Fig. 5. Dimensionless pressure along the ice/bed interface for n = 1, 1.5, 2, 3 and 4. Because of the non-dimensionalization, the far-field pressure is zero and lee-side pressures are negative. The real pressure p is calculated from the dimensionless pressure p * by multiplying by τ 0 and adding p 0. An explanation for the pressure peaks is given in the text.
Non-dimensional normal stresses on the stoss and lee sides of the cone at sites of pressure transducers where normal stresses were measured,
and
, respectively, are shown in Table 2 as a function of n. These are obtained by averaging the normal stress N
* over the area of the platens of the pressure transducers A
pt,
Table 2. Dimensionless normal stress
(stoss) and
(lee) calculated from finite-element model as a function of n for all three experiments
Because the obstacle is (almost) symmetrical, the values of
and
are (almost) equal and opposite. Negative values on the lee side are due to the assumption in the non-dimensional formulation that the far-field pressure is zero. These negative values do not mean that a cavity formed there. In fact, there are no separating streamlines or zones of recirculation in the flow, and hence no cavity forms on the lee side of the obstacle as was observed in the field experiments.
Force on panel
The dimensionless normal stress N * on the panel can be integrated over the entire area of the panel to obtain the dimensionless force F * that the ice exerts on the panel. In component form,
where
is the dimensionless area of the panel. The bed-parallel force is simply
The angle between the ice-flow direction and the direction of the bed-parallel force, (ψ = 0 since ϕ, the angle between the axis of symmetry of the panel and the ice-flow direction, is different from 0), is
The values of
,
and ψ as a function of n are given in Table 3.
is also shown in Figure 6 together with the dimensionless bed-parallel force on a hemisphere calculated by Reference Lliboutry and RitzLliboutry and Ritz (1978). This provides a check to our calculations, as the shape of the obstacle is not too dissimilar to that of a hemisphere. Not surprisingly,
is largest in experiment 1, when the camera housings on each side of the conical obstacle offer most resistance to flow owing to their high angle with the flow direction (ϕ = 30°). Similarly, the force on the panel is smallest for experiment 3, when the obstacle is smallest.
Table 3. Dimensionless bed-parallelforce,
, dimensionless vertical force,
, and the angle, in degrees, between the ice-flow direction and the bed-parallel force, ψ, as a function of n for the three experiments
Fig. 6. Dimensionless bed-parallel force,
computed from finite-element model as a function of n together with bed-parallel force on a hemisphere calculated from Reference Lliboutry and RitzLliboutry and Ritz (1978). For n = 1,
. For n = 3,
.
Comparison with Field Data
Results of the numerical model will now be compared with data from the field experiments, in which the bed-parallel force on the panel and normal stresses on the stoss and lee sides of the cone were measured. The objective is to obtain equations for estimating the value of B from the comparison between the numerical model and the field data. In this section, we establish relations between these measured quantities and the non-dimensional quantities from the numerical model. Again, dimensionless quantities are indicated with a superscript asterisk.
From Equation (5), the traction vector on the bed is
Because there are no shear stresses on the bed, T * n has been replaced by N * n, where N * is the non-dimensional normal stress. Both N * and n are functions of position on the bed. Integrating Equation (16) over the area of the panel yields the force F on the panel
To obtain the x, y and z components of F, we take the dot product of Equation (17) with the basis unit vectors e x , e y , and e z , and furthermore use the identities
(owing to the symmetry of the panel), and
where
is the non-dimensional area of the panel projected on the x−y plane. The components of F in the (x, y, z) coordinate system are then
where
, i = x, y, z is defined in Equation (13). The bed-parallel force (parallel to x−y plane) is
where
was defined in Equation (14). The true bed-parallel force, F
//, was not measured in the field experiments. Instead, the force exerted on a load cell mounted on the down-glacier side of the panel, F
m, was measured. F
// is related to F
m by (Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000, equation (4))
where μ is the friction coefficient between the instrumented panel and the plate beneath it (the absolute value of Fz is used because, in the numerical model, the vertical direction is up). In Cohen and others, Fz was estimated from the average normal stress on the stoss and lee sides of the cone. Here, we simply replace Fz by Equation (22). Then, equating (23) and (24), we obtain
In this equation, F
m and ϕ are measured quantities, μ = 0.1(Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000), h
0 and
are geometrical quantities, and all F
* are computed from the numerical model. ψ is given by Equation (15). τ
0 and p
0 are unknowns. Equation (25) forms one of the working equations from which B can be estimated, as B is indirectly present in τ
0.
From Equation (16), the relations between the measured normal stresses N
1 and N
2 on the stoss and lee sides of the cone, respectively, and the non-dimensional
and
, can be obtained by taking the dot product of the traction with the unit normal vector n:
Equations (26) and (27) form another pair of equations from which B can be estimated, again because B is indirectly present in τ 0.
Estimation of B
There are two independent ways of calculating the material constant B. In the first, p 0 is eliminated from Equations (26) and (27). Then, using Equation (7) for the definition of τ 0, we obtain
This method makes use only of the normal stress measurements on the surface of the cone. The second method is to solve for τ 0 in Equation (25), and using definition (7) obtain
where p 0 is obtained by eliminating τ 0 from Equations (26) and (27):
With this method, the normal stress measurements (through p
0) are used only to estimate the frictional force between the panel and the plate underneath. In Equations (28–30), all * quantities depend on n and on the flow geometry (except
which is the dimensionless panel area).
The far-field velocity, v 0, is determined as follows: for the experiments in 1997, we use the velocity measured 0.45 m above the bed by a dowel and cable (Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000); for the experiment in 1996, the velocity was measured on the side of the cone by a video camera looking through quartz-glass windows. The ice speed measured at this location is not the far-field velocity. To recover the far-field velocity, the measurement is scaled using the numerical model. For example, for n = 1, the dimensionless speed above the quartz-glass plate is 0.3. If the measured speed was v meas then the far-field speed is v 0 = v meas/0.3. Table 4 gives the values of the measured quantities (see Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000). Table 5 gives the values of B (1) and B (2) as a function of n for experiments 1–3. The two major sources of uncertainty in the calculations of B are the measurements of the sliding velocity (±20%) and the static coefficient of friction between the panel and the plate (±50%) (Reference Cohen, Hooke, Iverson and KohlerCohen and others, 2000). This gives an uncertainty of about ±20% for B (1), and about ±30–40% for B (2), depending on the value of n.
Table 4. Area of panel, reference length, and measured quantities
Table 5. Values of B(1) and B(2) in Pa s1/n as a function of n for each experiment
In Table 5, the value of B
(1) is always less than the value of B
(2). If our assumptions in the numerical model are correct, the two values of B should coincide for some value of n (within the limits of uncertainty). This would have allowed us to determine n directly. This, however, was not possible. The difference between B
(2) and B
(1) is >50% for n = 1, and >35% for n > 1; for n = 1 this exceeds the uncertainty in the measurements. For n > 1, some values of B
(1) and B
(2) overlap, but most do not. Of the key assumptions made in the model, namely, that ice is a power-law fluid and that it slides without friction on the bed, neglecting friction at the bed is probably responsible for the discrepancy in the two values of B. This friction is due to the interactions between sediment particles and the bed. An increase in friction at the bed will decrease the horizontal velocity gradient near the cone and cause
to decrease. This will increase B
(1). Such a simple reasoning cannot be used to predict the behavior of B
(2) because B
(2) depends on the total force on the obstacle
, which is the sum of the integrated normal and shear stress distributions. As the former decreases monotonically with increasing friction, the latter probably increases monotonically. Hence, one cannot predict how the sum will behave. Numerical solutions of ice flow past the obstacle with the no-slip condition at the bed indicate, however, that B
(2) < B
(1). Therefore, it is reasonable to assume that the two values of B will be equal for some intermediate frictional force. In Reference Cohen, Hooke, Iverson and KohlerCohen and others (2000), friction on the panel was calculated using the model of Reference HalletHallet (1979, Reference Hallet1981) and was found to be only about 5% of the total bed-parallel force. It appears that friction at the bed, however small, does affect the estimation of B. Friction was not included in the numerical model because of the uncertainty associated with friction laws and because our data could not provide a means of evaluating these laws.
Another important observation is that in experiment 1 (1996) the values of B are smaller than in experiments 2 and 3 (1997). This is due to the lower normal stresses and bed-parallel force measured in 1996. The difference between experiments 1 and 2 is about 20% for B (1) and about 25% for B (2). This is about equal to the error in the calculation of B (1) and slightly less than the error in B (2); hence it is possible that the change in B from one year to the next is just measurement error. However, changes in normal stresses, ice speed and direction were real. Reference Cohen, Hooke, Iverson and KohlerCohen and others (2000) suggested that these changes were due to variations in sediment concentration or water content which changed the basal ice rheology.
Discussion
In Table 6, the values of B for n = 3 obtained herein are compared with other measurements obtained from laboratory and field experiments and from comparison of velocity data with numerical models of glacier flow. Except for our measurements, all data are for clean ice. The values obtained by Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others (1998) and Reference GudmundssonGudmundsson (1999) are substantially higher than others. Both of these values were obtained from large-scale three-dimensional ice models as the best fit to velocity data. Values of B are smallest for laboratory experiments (Reference DuvalDuval, 1977; Reference Budd and JackaBudd and Jacka, 1989) and intermediate for tunnel-closure (Reference NyeNye, 1953) and borehole-tilting experiments (Reference Raymond and ColbeckRaymond, 1980). Ice at the bed of two Norwegian glaciers appears to be softer than that measured elsewhere. Both in Reference HagenHagen (1986) and in Reference KohlerKohler (1993), the data are obtained from closure of boreholes in clean ice. The experiments were done at the bed of Bondhusbreen beneath 160 m of ice and at the bed of Engabreen beneath 200 m of ice. Our debris-rich ice at Engabreen appears to be softer than clean temperate glacier or laboratory ice. The weakness of the debris-rich ice may be due to one or more of the following: high water content, high sediment content, texture or preferred fabric orientation.
Table 6. Comparison of B for n = 3 in Pa s1/3 with other values of B for clean temperate ice
Effect of water content
Reference CohenCohen (1999) measured the water content in the sediment-laden ice and in the cloudy-ice layer above it. Although there is a large margin of error, cloudy-ice was found to contain about 1% water, while sediment-laden ice near the bed contained >2.0%. Reference DuvalDuval (1977) noted that water content plays an extremely important role in controlling the viscosity of temperate ice. An empirical equation relating B to the water content is given in Reference Lliboutry and DuvalLliboutry and Duval (1985, equation (32)). In our notation this equation is
where B is in units of bars and years, θ is the temperature in °C and w is the water content in%. For θ = 0°C and w = 0%, B = 6.8 × 107 Pa s1/3. Using this equation, and assuming θ = 0°C, the water content for B = 4.1 × 107 Pa s1/3 (upper bound for experiments in 1997) is w = 1.9%, while for B = 3.2 × 107 Pa s1/3 (upper bound for 1996) it is w = 4.7%. The first value is reasonable, although it is already beyond the range of validity of Equation (31). For lower bounds of B, the results do not make any sense. Hence, although water plays an important role in lowering the value of B, it does not appear to be sufficient, by itself, to explain our results.
Effect of fabric and texture
Samples of cloudy ice and debris-rich ice above the bed were collected near the door. Thin sections were made by J.-L. Tison at the Université Libre de Bruxelles, Belgium, using the diamond wire-saw apparatus, and analyzed by Reference CohenCohen (1999). c-axis orientations were determined on a Rigs by stage following standard procedures (Reference LangwayLangway, 1958).
Fabric in the basal ice sequence changes gradually from a strong three-maximum one in the cloudy-ice layer to an isotropic fabric in the sediment-laden ice where sediment concentrations are highest. Hence, the hypothesis that the softness of the ice is due to a strong preferred orientation is unfounded. As sediment concentration increases near the bed, the thin sediment layers become thicker, more continuous and more frequent. In addition, average crystal cross-sectional area decreases from 50 mm2 in the clean ice to 7 mm2 in the dirty ice, perhaps because sediment grains act as pinning points, inhibiting boundary migration (Reference Nicolas and PoirierNicolas and Poirier, 1976, p. 167). Between sediment layers are bands of clean ice. Ice crystals in the clean bands commonly span the distance between sediment layers. In some cases, an ice crystal will extend across such a sediment layer. This is more common in samples with lower sediment concentration where sediment layers are often discontinuous. In a few instances, a crystal extending across such a sediment layer shows evidence of shearing along the sediment layer.
Owing to intermolecular interactions (Reference Dash, Fu and WettlauferDash and others, 1995), water is present around sediment particles and at the interface between a sediment layer and a clean-ice band. This thin water film will lubricate these interfaces. We hypothesize that sediment layers with unbound water surrounding them act as weak shear planes. This was suggested by Reference Echelmeyer and WangEchelmeyer and Wang (1987) for cold ice near the melting temperature. As implied by the shearing of an ice crystal spanning such a layer, preferential sliding apparently occurs on these planes, causing significant weakening of the ice. Further studies of fabric and texture evolution as ice flows past obstacles are needed to confirm this hypothesis.
Conclusions
A three-dimensional finite-element model was used to analyze field measurements obtained in 1996 and 1997 by Reference Cohen, Hooke, Iverson and KohlerCohen and others (2000) at the bed of Engabreen as dirty basal ice flowed past an instrumented obstacle. Comparison of the results from the numerical model with the measured normal stress across the obstacle, on the one hand, and the measured bed-parallel force, on the other, yielded two estimates of the pre-exponential factor B. These two estimates gave different values of B, probably because friction at the bed, although small as estimated from Hallet’s (Reference Hallet1979, Reference Hallet1981) theory in Reference Cohen, Hooke, Iverson and KohlerCohen and others (2000), was not included in the model. Hence, a range of B values was obtained. For n = 3, B was between 1.9 × 107 and 3.2 × 107 Pa s1/3 in 1996, and between 2.2 × 107 and 4.1 × 107 Pa s1/3 in 1997. Different values were obtained in 1996 and in 1997 due to variations in the quantities measured in the field. It is not clear whether these differences reflect real differences in the characteristics of the basal ice. All these values are lower than measurements obtained elsewhere for clean temperate glacier and laboratory ice. The value of the power-law exponent, n, could not be determined, in part owing to small frictional forces between the ice and the bed that were not taken into account in the numerical model.
Despite high water content (>1%), the enhanced melting-refreezing mechanism around liquid inclusions in clean ice proposed by Reference Lliboutry and DuvalLliboutry and Duval (1985) is, by itself, not sufficient to explain the low values of B. Fabric studies reveal that the sediment-laden ice is almost isotropic, indicating that weak ice is not the result of a strong preferred orientation. Instead, the combined measurements of water content and of fabric and texture of the sediment-laden ice suggest another deformation mechanism for the weak ice layer, previously put forward by Reference Echelmeyer and WangEchelmeyer and Wang (1987): sediments found to collect in layers a couple of millimeters thick are separated by layers of ice of similar thickness; unbound water at the sediment/ice interface acts as a lubricant and enhances sliding along these layers, thereby significantly lowering the ice viscosity.
Acknowledgements
This work was supported by U.S. National Science Foundation grants OPP-9423422 and OPP-9713383, the Norwegian Water Resources and Energy Administration (NVE) and a Gibson Fellowship and a Doctoral Dissertation Fellowship from the University of Minnesota. Computer resources were provided by the Minnesota Supercomputing Institute. I thank J.-L. Tison for helping with the fabric measurements using the diamond wire-saw apparatus. I thank R. Hooke and N. Iverson for helpful discussions and a thorough review of an earlier version of the paper. This paper also benefited from comments from H. Blatter, G. Gudmundsson and J. Walder.
