1. Introduction
Marker-assisted selection (MAS) can be based on molecular markers in linkage equilibrium with quantitative trait loci (QTLs) (LE-MAS), molecular markers in linkage disequilibrium with QTL (LD-MAS), or on selection of the actual mutations causing the QTL effect (Gene-MAS). All three types of MAS are currently being used in the livestock industries (Dekkers, Reference Dekkers2004). For example, Plastow et al. (Reference Plastow, Sasaki, Yu, Deeb, Prall, Siggens and Wilson2003) reported the use of LD-MAS and Gene-MAS for reproduction, feed intake, growth, body composition and meat quality in commercial lines of pigs, and national genetic evaluation programmes based on LE-MAS are available to dairy breeding organizations in both France (Boichard et al., Reference Boichard, Fritz, Rossignol, Boscher, Malafosse and Colleau2002) and Germany (Bennewitz et al., Reference Bennewitz, Reinsch, Szyda, Reinhardt, Kuhn, Schwerin, Erhardt, Weimann, Kalm and van der Honing2003).
Following the sequencing of the bovine genome, thousands of single nucleotide polymorphism (SNP) markers are now available, creating the possibility of implementing LD-MAS directly using significant SNPs from genome-wide association studies. A key question for the implementation of LD-MAS in this way is how many markers surrounding each QTL should be used in marker haplotypes so that the marker haplotypes are in sufficient LD with the QTL to accurately predict the QTL effects. Grapes et al. (Reference Grapes, Dekkers, Rothschild and Fernando2004) compared the accuracy of fine mapping QTLs with single markers and marker haplotypes. While the accuracies of MAS and of fine mapping are not equivalent, they are determined by similar parameters, including the level of linkage disequilibrium between markers or marker haplotypes, and the number of phenotypic records per marker allele or per haplotype. Grapes et al. (Reference Grapes, Dekkers, Rothschild and Fernando2004) concluded that using haplotypes rather than single markers gave only limited extra accuracy of fine mapping QTLs in previously defined QTL regions in simulated data. This result would be appealing if the same were true for the accuracy of MAS, as the implementation of MAS would be considerably simplified if haplotyping is not required. However, the generality of the result is likely to depend on population parameters such as the density of markers and extent of LD in the population. Furthermore Grapes et al. (Reference Grapes, Dekkers, Rothschild and Fernando2004) assumed that a requirement of haplotype analysis would be the collection of additional marker genotypes on relatives, to allow haplotype construction. They therefore compared results from single-marker analysis with twice as many markers as used in the haplotype analysis. Extra genotyping is not necessary when dense markers are available: provided the marker map is sufficiently dense, haplotypes can be constructed with a very high level of accuracy even in the absence of family information (Stephens et al., Reference Stephens, Smith and Donnelly2001).
With the aim of determining whether haplotyping prior to marker-assisted selection is worthwhile in cattle with currently available marker maps, we used the extent of LD in an Angus cattle data set, consisting of 9323 genome-wide SNPs genotyped in 379 Angus cattle, to predict the accuracy of MAS that could be achieved in the same population from either single markers or marker haplotypes. The data were used to simulate the LD between markers and a QTL by randomly selecting one SNP to act as a surrogate QTL, and then calculating the proportion of variance at the surrogate QTL that was explained by the other markers. This proportion of variance explained is used in an analytical formula to give the accuracy of MAS with any number of phenotypic records from the same population. This approach allowed us to assess the advantage of haplotyping given the actual extent and pattern of LD in our population, avoiding the need to simulate data with assumptions about past population size and other parameters that drive LD.
2. Materials and methods
The animals were selected from a research project based at Trangie Agricultural Research Centre in NSW, Australia. All animals were of Angus breed with sire and dam pedigree records. Animals born from 1993 to 2000 were selected for high or low post-weaning residual feed intake, a measure of feed efficiency. The original project design has been reported by Arthur et al. (Reference Arthur, Archer, Johnston, Herd, Richardson and Parnell2001). Approximately equal numbers of the extreme high and low residual feed intake animals were selected for SNP genotyping. Care was then taken to ensure that, where possible, animals were in half-sib groups of 2 or more and not exceeding 10. Not more than 3 animals were selected from each sire group for further analysis to avoid over-representation of sire haplotypes, leaving 249 animals. The animals were genotyped for 9323 SNP markers, using the Parallele technology. These SNPs were largely discovered as a result of the bovine genome sequencing project (http://www.ncbi.nlm.nih.gov/projects/genome/guide/cow/); other SNPs were discovered as the result of assembly of expressed sequence tags (Hawken et al., Reference Hawken, Barris, McWilliam and Dalrymple2004). Distances between SNPs were estimated by mapping the SNPs to the human genome (Goddard et al., Reference Goddard, Chamberlain and Hayes2006). The SNPs were not spaced evenly across the genome (Goddard et al., Reference Goddard, Chamberlain and Hayes2006). In particular, there were often multiple SNPs within the same sequence read (e.g. the sequence produced from a sequencing machine, usually of approximately 700 bp) followed by large gaps.
The extent of marker–marker LD in the data was used as an indication of the extent of marker–QTL LD we could expect in the data set. The parameter r 2 is a measure of LD that describes the proportion of QTL variance that would be explained by a marker if one of the markers were actually a QTL (Hill & Robertson, Reference Hill and Robertson1968). To determine the extent of LD in the Angus population, r 2 was calculated for all possible syntenic marker pairs and plotted against distance.
The accuracy of LD-MAS using marker haplotypes depends on: (1) the extent of LD between the marker haplotypes and the QTL, (2) the number of haplotypes in the population, (3) the number of individuals that are phenotyped for the trait and genotyped for the markers, and (4) the accuracy with which haplotypes can be predicted for individuals (which depends on SNP density and availability of genotypes on relatives). Points 2, 3 and 4 together determine the accuracy with which the mean of each marker haplotype is estimated.
We attempted to determine the additional genetic variance, if any, captured by using marker haplotypes rather than single markers. A SNP was randomly selected from the 9323 SNPs to act as a surrogate QTL. The 1, 2, 4 or 6 of the closest markers surrounding this ‘QTL’ were identified. Haplotype frequencies of the 2, 4 or 6 marker haplotypes were estimated using PHASE (Stephens et al., Reference Stephens, Smith and Donnelly2001). The single marker giving the highest r 2 value (calculated following Hill & Robertson, Reference Hill and Robertson1968) to the surrogate QTL was also selected, and called the best marker. The closest single marker was called the nearest marker. SNPs in the same sequence read as the ‘QTL’ SNP were discarded, as such SNPs are unlikely to be representative of the distribution of distances between SNPs and QTL.
Zhao et al. (Reference Zhao, Nettleton, Soller and Dekkers2005) give an expression for the proportion of QTL variance explained by a multi-allelic marker:

where P(A i) is the frequency of allele A i, P(Q) is the frequency of the first QTL allele, and P(Q/A i) is the frequency of the first QTL allele given the A i allele at the marker is observed, and the marker has n alleles. If we assume that the haplotypes are derived without error, then this equation can also be used to calculate the proportion of QTL variance explained by marker haplotypes, r 2(h, q), considering that haplotypes of multiple markers are equivalent to a single multiple allelic marker. The validity of the assumption that haplotypes can be derived without error is addressed in Section 3. Then n is the number of unique haplotypes observed in the population, A i is the frequency of the ith haplotype, and P(Q/A i) is the frequency of the first QTL allele given haplotype A i is observed. In our data, we observe, for example, the proportion of haplotype A i that carry the Q allele at the QTL allele, e.g. P(Q and A i), rather than the conditional probabilities P(Q/A i). If we substitute
in (1) we get

We also corrected the proportion of the QTL variance explained by the haplotypes for the effect of sampling a limited number of haplotypes as (following Hayes et al., Reference Hayes, Visscher, McPartlan and Goddard2003):
where n is number of unique haplotypes, and N is the number of haplotypes (2 times the number of animals, 498) in the sample, and r calc2 is calculated from (1).
Phenotype data can be used to estimate the effect of each haplotype using the model:
where y ij is the phenotype of animal j carrying haplotype i, h i is the effect of haplotype i, and e ij is a random error term. The variance of e ij was V (e)=Iσe2 and the variance of the haplotype effects was V (h)=Iσh2. Then the accuracy of estimating the haplotype effects is given by
where λ=σe2/σh2 and there are T phenotypic records. Note that r(h, ![]() ) can be evaluated at any value of T, not only the actual number of records in Angus data. The variance σh2 is equal to r 2(h, q) σQ2, where σQ2 is variance explained by the QTL.
) can be evaluated at any value of T, not only the actual number of records in Angus data. The variance σh2 is equal to r 2(h, q) σQ2, where σQ2 is variance explained by the QTL.
The accuracy of marker-assisted selection using haplotypes is then the accuracy with which the haplotypes estimate the QTL allele effects:
As an example of the accuracy of MAS that could be expected when a large population of animals are genotyped, we calculated the accuracy of MAS with 500, 1000 or 2000 phenotypic records and a value of λ was chosen given the proportion of QTL variance accounted for by the haplotype effects and such that each QTL accounted for 1·5% of the error variance. Two hundred and fifty replicates were performed. A replicate consists of randomly choosing a SNP to be a surrogate QTL, selecting the 1 to 6 markers surrounding the QTL, and evaluating the above expression.
We also evaluated the accuracy of multiple regression of multiple SNP genotypes to predict the alleles of the SNP chosen to be the surrogate QTL. To do this, we used the genotype of the surrogate QTL as the y variable, and the genotypes at the 2, 4 or 6 surrounding SNPs as the x variables. In the X matrix, there was a column for each SNP with the number of 2 alleles carried by each animal. The y variable was then predicted based on the estimated effects of the surrounding SNPs. A value for r 2(g, q), where g are the SNP genotypes, was calculated as ![]() .
.
3. Results and discussion
The distance between adjacent SNPs was on average 300 kb; however, there were large numbers of SNPs separated by much smaller distances (Fig. 1 A). This reflected the method of discovery of the SNP. Subsequent results refer to SNPs not in the same sequence read (for details see Section 2). The average value of r 2 for adjacent markers was 0·10, and for best SNP pair was 0·20. The distribution of r 2 values for adjacent markers and best SNP pairs is shown in Fig. 1 B. The average r 2 declined rapidly with distance (Fig. 1C).
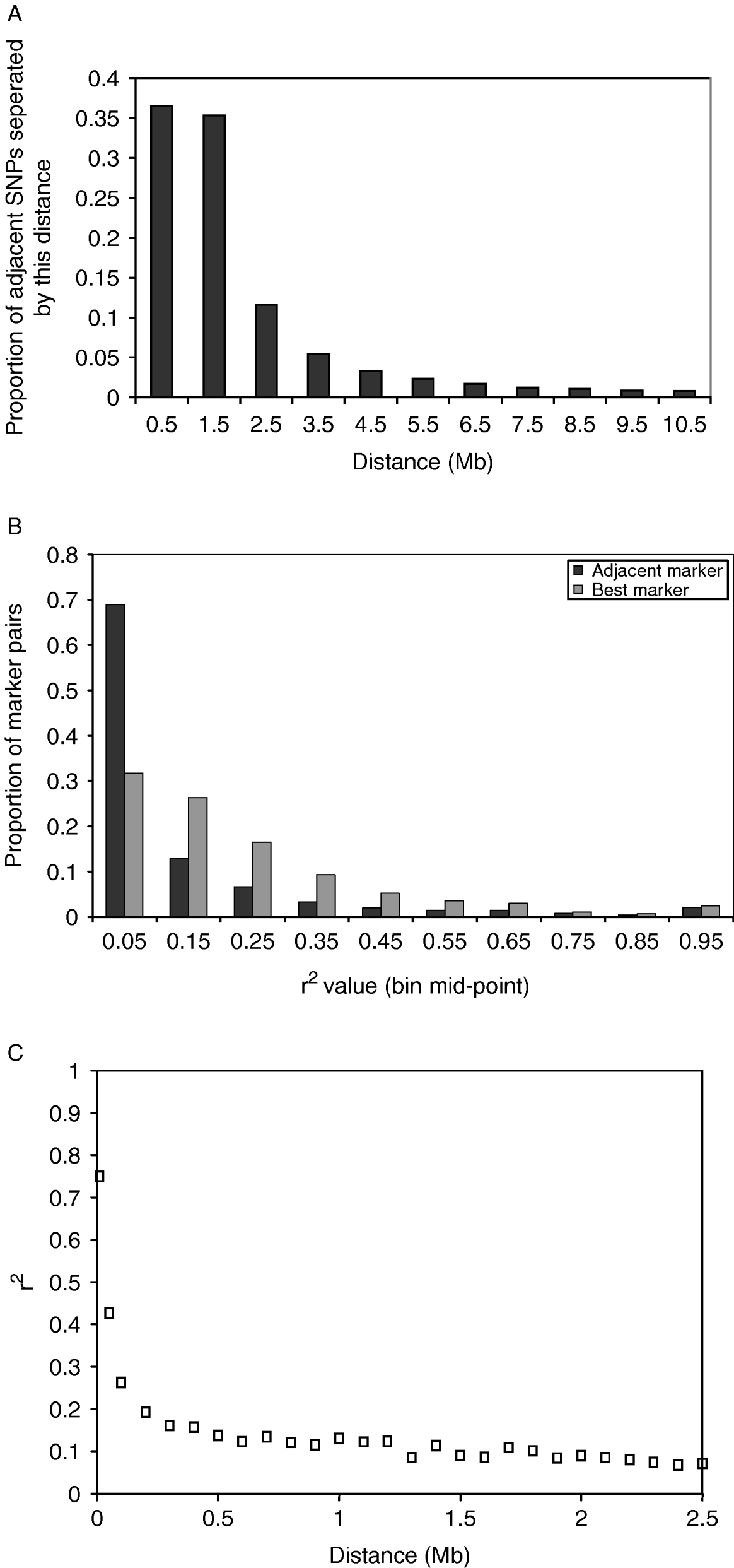
Fig. 1. (A) Distribution of distances between adjacent SNPs, including SNPs in the same sequence read. In the analysis that follows, only one SNP per sequence read is considered. (B) Distribution of r 2 values between adjacent SNP pairs and for the SNP pair for each SNP with the highest r 2. The values plotted are the proportion of SNP pairs with r 2 values in bins of 0·1. For example, the first point is the proportion of SNP pairs with r 2 values between 0 and 0·1. (C) Decline of average r 2 values for SNP pairs within bins of distance between the SNPs where the bins are multiples of 100 kb distance.
The proportion of QTL variance explained increased as the number of markers in the haplotype increased (Table 1). The increase in the proportion of QTL variance explained when moving from 2 marker haplotypes to 4 marker haplotypes and from 4 marker haplotypes to 6 marker haplotypes was substantial. The best SNP explained a higher proportion of QTL variance than the 2 marker haplotypes, but less than the 4 marker haplotypes.
Table 1. Proportion of QTL variance explained by marker haplotypes and observed number of unique haplotypes in the Angus data set

The proportion of QTL variance using multiple regression of SNP genotypes was 0·09, 0·18 and 0·22 with 2, 4 and 6 SNP genotypes fitted, respectively. These values are considerably lower than was achieved using haplotypes with the same number of SNPs (Table 1).
As the number of markers in the haplotypes increased, the observed number of unique haplotypes in the population also increased, indicating that a larger number of phenotypic records would be required to estimate the effect of each haplotype accurately. As the number of phenotypic records increased, the accuracy of estimating QTL effects from marker haplotypes increased, up to 0·58 in the case of 6 marker haplotypes with 2000 phenotypic records (Fig. 2). Although the proportion of QTL variance explained by the marker haplotypes does increase with an increasing number of markers, the number of haplotype effects which must be estimated also increases. In the case of the best marker, the proportion of QTL variance explained is similar to that from two marker haplotypes; however, only two effects must be estimated. The result is an accuracy of predicting QTL effects close to that achieved with 4 marker haplotypes.
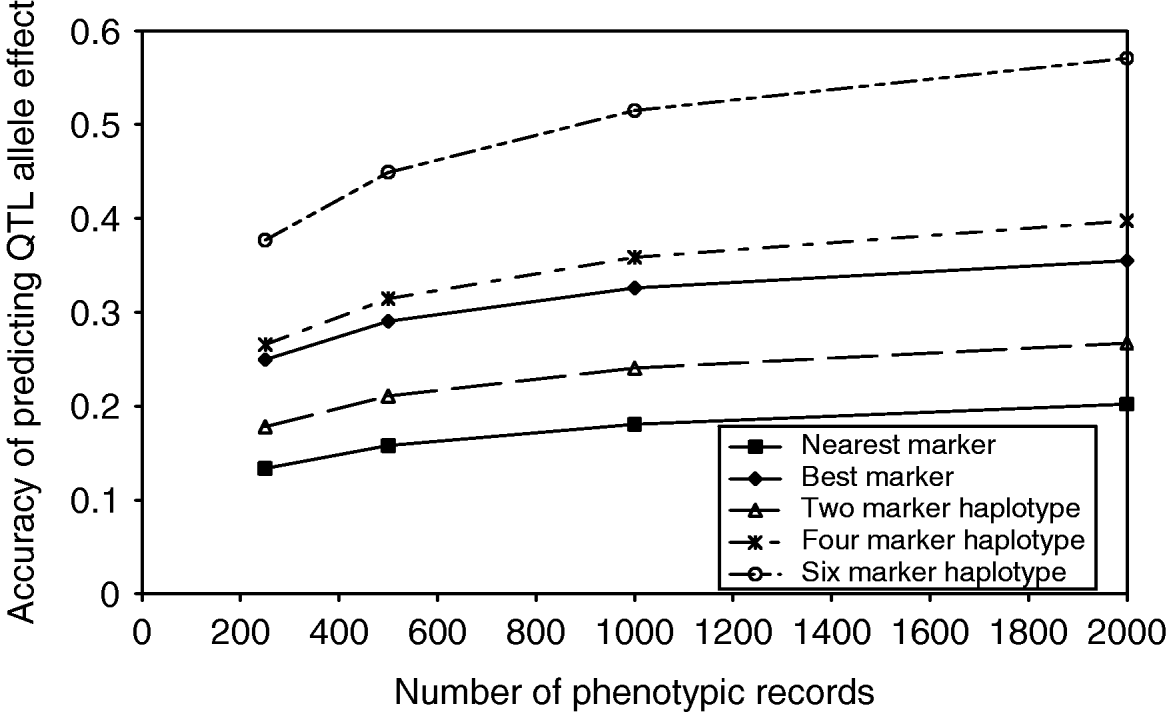
Fig. 2. Accuracy of predicting haplotype effects with an increasing number of markers in the haplotype and an increasing number of phenotypic records.
We can gain some insight into the impact of uncertainty of haplotype assignment on the accuracy of MAS with marker haplotypes by comparing results for the square of the regression of individual animal haplotypes on the genotype of the surrogate SNP with the proportion of QTL variance explained from (2), which is derived assuming the haplotypes are assigned without error. For 4 marker haplotypes, these were 0·25 and 0·28, respectively, indicating losses due to inaccurate haplotype assignment were relatively small in our data set. In general, the uncertainty of haplotype assignment and its effect will depend on the structure of the data set used, so generalizing the accuracy of haplotype assignment is difficult.
Our results suggest useful LD (e.g. r 2>0·2) extends on average only 50 kb in the Angus population. This is a much shorter distance for the extent of useful LD than has been proposed previously (Farnir et al., Reference Farnir, Coppieters, Arranz, Berzi, Cambisano, Grisart, Karim, Marcq, Moreau, Mni, Nezer, Simon, Vanmanshoven, Wagenaar and Georges2000; Tenesa et al., Reference Tenesa, Knott, Ward, Smith, Williams and Visscher2003). However previous estimates were based on D′ rather than r 2, and D′ overestimates the level of r 2 (Zhao et al., Reference Zhao, Nettleton, Soller and Dekkers2005). Secondly, our estimates are the average r 2 within a distance interval and do not display the maximum r 2 within a given distance. Recent estimates on the extent of LD in cattle based on r 2 are in agreement with our results (Goddard et al., Reference Goddard, Chamberlain and Hayes2006; Spelman & Coppieters, Reference Spelman and Coppieters2006).
In our data set, gains in the accuracy of MAS were achieved when haplotypes of markers were used rather than single markers. These results concur with those of Pe'er et al. (Reference Pe'er, de Bakker, Maller, Yelensky, Altshuler and Daly2006). They used empirical genotype data from the human International HapMap Project to evaluate the extent to which the sets of SNPs contained on three whole-genome genotyping arrays capture common SNPs across the genome. They concluded that limited inclusion of specific haplotype tests in association analysis can increase the fraction of common variants captured (as evaluated by r 2 between haplotypes and the common variants) by 25–100%. However, these specific haplotype tests were based on pre-selection of ‘tagging SNPs’ which capture 90% of the variation in SNP genotypes in a defined chromosome region. Use of tagging SNPs reduces the number of effects that need to be estimated compared with haplotypes, increasing the power of the test. De Bakker et al. (Reference de Bakker, Yelensky, Pe'er, Gabriel, Dalym and Altshuler2005) compared the power of exhaustive haplotype search and single SNP analysis to detect a surrogate QTL (a randomly chosen SNP from a panel of SNPs), where power was a function of the r 2 between the haplotypes or single marker and the surrogate QTL. They found that the use of haplotypes only increased power if the minimum allele frequency of the surrogate QTL was less than 5%; otherwise use of haplotypes actually decreased power. In the human data, however, the density of SNPs is very much higher than in our data. Even accounting for the increased effective population size of humans relative to QTLs, the average level of LD between adjacent SNPs is very much greater in the human data.
In our results, using the marker with the highest LD with the surrogate QTL did give accuracies almost as high as using 4 marker haplotypes. This result is attractive because it does not assume that the QTL position is known without error. Rather, it applies to the situation where a genome scan has been performed and the most significant SNP in a region is subsequently used in MAS. Zhao et al. (Reference Zhao, Fernando and Dekkers2007) found in simulated data that using the best marker could do as well as or better than marker haplotypes for QTL detection. They only observed an advantage of haplotypes over marker genotypes with large sample size (1000) and a relatively low density of SNPs (e.g. 6 markers per 11 cM with N e=100). While the accuracy of MAS and the power to detect QTLs in a genome-wide association study is not equivalent due to the testing of multiple markers in QTL mapping, both are driven by the LD between markers and QTLs and the number of phenotypic records available to estimate the QTL effects. In our results we did see an increase in accuracy above that achieved with the best marker if 6 marker haplotypes were used. Our marker density (average marker spacing ∼1·5 Mb when markers in the same read are removed) would be most similar to the lowest density of markers that Zhao et al. (Reference Zhao, Fernando and Dekkers2007) simulated. And as Zhao et al. (Reference Zhao, Fernando and Dekkers2007) also observed, the advantage of haplotypes over marker genotypes was larger when sample size was increased (or the disadvantage was reduced).
Our results demonstrate that even with 6 marker haplotypes, the accuracy of predicting QTL effects was only 0·58. Both this result and the limited extent of LD suggest the density of markers is not sufficient to take the results directly to LD-MAS. Either additional SNPs must be found in QTL regions or denser maps in the order of 30 000 markers are required, extrapolating the levels of r 2 we have observed. If the density of markers were increased, both single markers or haplotypes would account for a greater proportion of the QTL variance, and lead to increased accuracy of MAS. For example, Hayes et al. (Reference Hayes, Bowman and Goddard2001) found in simulations that with the extent of LD similar to that observed in the Angus data set and 2000 phenotypic records, 11 markers in 1 cM would result in haplotypes explaining 98% of the QTL variance, and an accuracy of estimating QTL effects from marker haplotypes of 0·84. The results of Zhao et al. (Reference Zhao, Fernando and Dekkers2007) suggest that as marker density is increased, the advantage of haplotypes over single markers will be reduced. A large number of phenotypic records (at least 2000) will be required to accurately estimate the effects of the QTL before LD-MAS is implemented.
The contribution by Paul Arthur, New South Wales Department of Primary Industries and Meat and Livestock Australia, to the generation of cattle and phenotypes is gratefully acknowledged.





