1. Introduction
It has been pointed out by several authors that meltwater retention has a significant effect on the surface mass balance of the Greenland ice sheet (e.g. Reference Pfeffer, Illangasekare and MeierPfeffer and others, 1990,Reference Pfeffer, Meier and Illangasekare1991; Reference ReehReeh, 1991; Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994). The process of meltwater infiltration and eventual refreezing in the snowpack causes the total runoff to be smaller than the total melt. Not accounting for it would overestimate the sea-level contribution from the Greenland ice sheet resulting from temperature changes. In this paper we investigate how this ˚excess" (Reference Pfeffer, Meier and IllangasekarePfeffer and others, 1991) can be treated in large-scale parameterizations of the mass balance. Our objective is to identify the boundaries of the excess and to find out whether treatments proposed in the literature are sufficiently accurate for large-scale modeling, or whether a more sophisticated model should be used to study the effects of mass-balance changes on sea level.
The surface mass balance is defined as the difference between total accumulation (snowfall, rainfall, sublimation, etc.) and total runoff. The latter can arise from rainfall, snowmelt, ice melt from refrozen snowmelt (superimposed ice), and/or ice melt from old ice layers. Total runoff can, however, not be set equal to the sum of these four terms, because part of the meltwater can be upheld on the ice sheet during the melting season. For the ice-melt terms, relief of the terrain is an important factor, as part of the runoff can be temporarily stored in lakes in surface hollows that have no drainage. Here we will concentrate on the retention of rainfall and snowmelt before runoff takes place. As described by Reference ColbeckColbeck (1975), this process is mainly a consequence of refreezing of percolating meltwater through new or old snow layers, and of capillary forces in the upper snow layers that retain the meltwater until the end of the melting season. The latter water refreezes during the winter and produces an impermeable layer in the water-saturated zone.
However, even in the percolation zone, the possibility exists that meltwater from the water-saturated zone will penetrate to form an impermeable layer. The latter effect was modelled by Reference Marsh and WooMarsh and Woo (1984), whereas Reference Pfeffer, Meier and IllangasekarePfeffer and others (1991) developed two models to describe the refreezing process of infiltrating meltwater. Reference Pfeffer, Meier and IllangasekarePfeffer and others (1991) also determined to what extent the retention effect can influence the mass balance of the Greenland ice sheet and its effect on global sea level in a warmer climate by assigning minimal and maximal bounds. Assuming a linear temperature rise of 4°C over 150 years, they found that the effect can reduce the Greenland contribution to sea-level rise by 4–4.3 cm, or about half of the total sea-level rise assuming a static mass-balance sensitivity of ≈0.30mm ˚C–1a–1 1 (Reference Warrick, le Provost, Meier, Oerlemans, Woodworth, Houghton, Meira Filho, Callander, Harris, Kattenberg and MaskellWarrick and others, 1996). However, this value takes into account only the excess above the runoff line. In this paper, we extend the calculation to the entire ice sheet. First we calculate the melt for the Greenland ice sheet and determine the fraction which is retained. We then compare different retention models and examine them in the light of the ice-sheet mass balance and its response to climate change. This comparison crucially relies on the concepts of ˚potential" and ˚effective" retention fractions introduced in the text.
2. Melt Model
In order to calculate the mass budget of the Greenland ice sheet, we need a method of determining the amount of energy available for melt. Here, we use an improved version of the positive degree-day model described in Reference Huybrechts and de WoldeHuybrechts and de Wolde (1999). First, the total amount of positive degree-days, which provides the melt ˚energy", was calculated semi-analytically by making use of the mathematical properties of the governing probability function, using parametenzations for surface temperature as a function of latitude, surface elevation and time of year. The expected positive degree, EPD, is calculated as follows:

where Tm is the mean daily temperature (°C), a is the standard deviation of the daily temperature taking into account the daily cycle and random weather fluctuations, and the function β–(Tm/<7) contains the standard normal distribution function 4≥ and the standard normal density function f , which relations can be accurately fitted using an exponential function:

The total annual amount of expected positive degree-days, EPDD, which represent a melt potential is then found by numerical integration of Equation (1) over lyear. Assuming that a is time-independent, this gives:
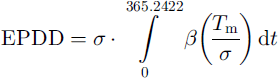
for which monthly time-steps provided sufficient accuracy. The above method represents a significant gain in efficiency compared to previous calculations of the positive-degree-days sum, because a time-consuming numerical integration of a double integral can be avoided (e.g. Reference Huybrechts, Letreguilly and ReehHuybrechts and others 1991)
We used an updated gridded dataset for surface elevation derived from satellite altimetry (Reference EkholmEkholm, 1996) that was shown to be a critical input to the calculation of the total melt in earlier work (Reference Reeh and StarzerReeh and Starzer, 1996; Van de Wal and Reference EkholmEkholm, 1996). The updated precipitation map was derived from the Reference Ohmura and ReehOhmura and Reeh (1991) distribution by including the results of recent shallow-ice-core studies obtained from traverses undertaken by the Alfred Wegener Institute in the northern part of the ice sheet during the mid-1990s (Reference Jung-RothenhäuslerJung-Rothenhausler, 1998). The fraction of total precipitation falling as rain was calculated as being proportional to the time fraction during which surface temperature rises above 1°C. This fraction of precipitation was added to the total snowmelt in subsequent calculations to make up for the total amount of water available for retention. All calculations were performed on a 5 km grid and took into account area factors arising from map distortions by using the appropriate map projection formulas.
The melt-and-runoff model was calibrated by regionally matching the mass balance to available observations of equilibrium-line altitude, calving rates and bottom melting rates, details of which are to be presented elsewhere. Particular attention was paid to obtaining a balance between runoff and accumulation in southwestern sectors where iceberg calving is virtually absent, and to approximately matching runoff in the north with recent estimates of accumulation rates, bottom melting rates and calving rates (Reference HigginsHiggins, 1991; Reference Rignot, Gogineni, Krabill and EkholmRignot and others, 1997; Reference Reeh, Mayer, Miller, Thomsen and WeidickReeh and others, 1999). This was done successfully by using the following spatially uniform values: a = 4.2°C, degree-day factor for snowmelt = 2.7 mm ˚C–1d–1, and degree-day factor for ice melt = 72 mm ˚C–16 d–1. These degree-day factors are in water equivalent and are all within the range of previous studies (e.g. Reference Huybrechts, Letreguilly and ReehHuybrechts and others, 1991; Greve, in press) and observations (Reference BraithwaiteBraithwaite, 1995). With these values, the average equilibrium-line altitude (ELA) was 1157 m and regionally did not deviate by >100m from about a dozen observations found in the literature (Reference HaeberliHaeberli, 1985; Reference Weidick, Bøggild and KnudsenWeidick and others, 1992; Reference Haeberli, Hoelzle, Suter and FrauenfelderHaeberli and others, 1998). The procedure relies on the assumption that the Greenland ice sheet is in steady state, which is not necessarily correct, but the imbalance is probably not much more than 15% of the total mass input either way (Reference Warrick, le Provost, Meier, Oerlemans, Woodworth, Houghton, Meira Filho, Callander, Harris, Kattenberg and MaskellWarrick and others, 1996).
3. Retention Masses
To compare the different treatments of the retention effect, it is helpful to introduce several concepts related to the meltwater in the snowpack. We define the ˚available water mass", Wr} as the maximum amount of water that can be retained provided enough energy is available. Wτ is in fact equal to the liquid fraction (snowmelt and rainfall) of the annual precipitation. Because we do not consider storage changes or net changes in lateral meltwater fluxes through the snowpack, the available water mass is limited by the annual precipitation. The ˚potential retention mass", Pτ, is the maximum amount of liquid water that can be retained by the end of the melting season by any of the possible processes, provided enough mass is available. Finally, the ˚effective retention mass", Eτ, is the amount of water that is effectively retained by the end of the melting season as a result of the retention process. A physical mechanism can take place only to the extent that energy and mass are available in sufficient quantities. Therefore, Eτ is the minimum of Wτ and Pτ and is also limited by the annual precipitation.
We define the retention mass as the sum of (i) the capillary water that remains in the snowpack until the end of the melt season and subsequently refreezes, (ii) the meltwater that refreezes to form superimposed ice and remains until the end of the melting season, and (iii) the refrozen meltwater that melts again and runs off later in the melting season. This definition excludes capillary water that is upheld in snow layers that eventually melt in the same year, because its liquid-water content escapes to the ocean.
Strictly speaking, fraction (iii) should not be included in the retention mass either, since it does not contribute to the accumulation and therefore represents runoff during the same year. However, we include it in our comparison of the retention models because it is energetically compatible with the formulation of the degree-day model. The sum of positive degree-days that is used to melt the refrozen meltwater during the same year is not available for melting old ice, so any difference in retention mass in our definition is reflected in an identical change in runoff or surface mass balance. One can argue also that, energy-wise, melting, refreezing and remelting during the same season makes no difference, because the latent heat released on the intermediate refreezing goes to warming the surrounding snow, reducing the thermal demand to warm that snow to 0°C. But this is only partly true since the warmed layers do not melt away everywhere. These subtleties are, however, beyond the capabilities of our existing melt-and-runoff model, because it has no proper thermodynamic treatment of the upper snow and ice layers and because their temperature is not accounted for in the sum of positive degree-days available for melting.
4. Retention Fractions
The three quantities defined above are strongly related to the annual precipitation. To distinguish the retention mechanism from their precipitation dependency, we will consider these quantities as fractions of the total annual precipitation P. The ˚available-water fraction", wr = Wτ/P, is thus the sum of the snowmelt and rainfall divided by the annual precipitation. Likewise, the ˚effective-retention fraction", ετ = ET/P, is the sum of the capillary water at the end of the melt season plus all of the meltwater that refreezes (including the fraction that remelts and runs off), divided by the total precipitation. The ˚potential-retention fraction", Pr, is the potential retention mass divided by the total annual precipitation. By implication, the following relation holds: ετ=min(ρτ,wt)≤1.
5. The Different Retention Models
The various methods documented in the literature that deal with the retention process can conveniently be defined by the way the potential-retention fraction can be established. The potential-retention fraction ρτ is closely related to the "PMAX" introduced by Reference ReehReeh (1991), which denotes the melt fraction of the annual snowfall that needs to refreeze before runoff occurs, and which was set to 0.6 on an intuitive basis. From a physical point of view, the potential-retention fraction can also be based either on the refreezing process (Reference OerlemansOerlemans, 1991), on capillary forces in the snowpack (Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994) or on a combination of both processes (Reference Pfeffer, Meier and IllangasekarePfeffer and others, 1991).
We can therefore define four different retention models:
-
(i) pr_ρ0.0: this is the lower-bound model in which no retention takes place, and against which the importance of the other treatments can be assessed:
-
(ii) pr_pmax: this is the model in which a constant and uniform fraction of the snowmelt, but not of the rain, is retained by any of the possible processes (cf Reference ReehReeh, 1991):
where snfr is the snow fraction of the yearly precipitation, and the factor 0.6 is equal to the PMAX as defined by Reference ReehReeh (1991). A maximum retention model, in which Pr = 1, was not considered, as it is not physically meaningful. Assuming that the previous summer surface acts as an impermeable layer, the free pore space in the snowpack cannot absorb more meltwater than the difference between the ice and snow densities can allow for (Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994).
-
(iii)pr_d2m: this model is based on a simple thermo-dynamic parameterization of the refreezing process (Reference Huybrechts and de WoldeHuybrechts and de Wolde, 1999):

where c and L are specific heat capacity and latent heat of fusion of ice, respectively, T is the mean annual temperature (°C below freezing; zero otherwise), P is the mean annual total precipitation (ma–1w.e.) and d is a typical thickness (m) of the thermal active layer that is raised to the melting point by the latent heat released by the refreezing meltwater. Calibrating the expression with mass-balance observations at the equilibrium line in central West Greenland suggests that d has a value of «2 m (Reference AmbachAmbach, 1963; Reference OerlemansOerlemans, 1991).
-
(iv) pr_capil: this is the most comprehensive model that takes into account both the refreezing process and the capillary suction effect of the snowpack (Reference Pfeffer, Meier and IllangasekarePfeffer and others, 1991):

where M is the total snowmelt (m a–1 w. e.), ρ0 = 300 kg m–3 and ρ e = 960 kg m–3 are the densities of dry snow and water-saturated wet snow, respectively, the thickness d of the thermal active layer providing the cold content is set equal to the annual snow accumulation rate C (m a"1 w.e.), and snfr = C/P. The formulation of this model puts a large emphasis on the effect of meltwater infiltration on the density of wet snow in establishing conditions for runoff. These processes are discussed in more detail in Reference Pfeffer, Meier and IllangasekarePfeffer and others (1991).
6. Comparison of Retention Fractions of Different Models
The available-water fraction expresses the liquid part of the annual precipitation (snowmelt and rainfall) that may be retained provided that the retention potential is large enough (Fig. 1), and is thus independent of the retention model. Values are close to zero over much of the accumulation zone above 2500 m a.s.L, and increase to unity below the equilibrium line.

Fig. 1. The annual amount of liquid water (snowmelt and rainfall)available for retention expressed as a fraction of the total annual precipitation (wr)
The potential-retention fractions for the models pr_pmax, Pr_d2m and pr_capil are shown in Figure 2. It can be seen that the more physically based models exhibit large spatial variations. The pattern for pr–pmax, on the other hand, is more constant and is 0.5–0.6 over most of the ice sheet. A minimum of Pr slightly below 0.4 is observed near the snouts of outlet glaciers in the extreme south, meaning that up to one-third of the annual precipitation there consists of rain. The distribution of ρτ for model pr_d2m mainly reflects the inverse of the precipitation pattern, and is further modulated by temperature. Pr values are unity only in the dry and relatively cold northeastern part of the ice sheet, because the cold content of the upper 2 m is sufficient to refreeze all of the annual snowfall and rain, if any. In the wetter and relatively milder southern part of the ice sheet, Pr values are ≤ 50% because the cold content of the upper ice-sheet layer is insufficient to refreeze all of the melt, and because the area receives more precipitation.
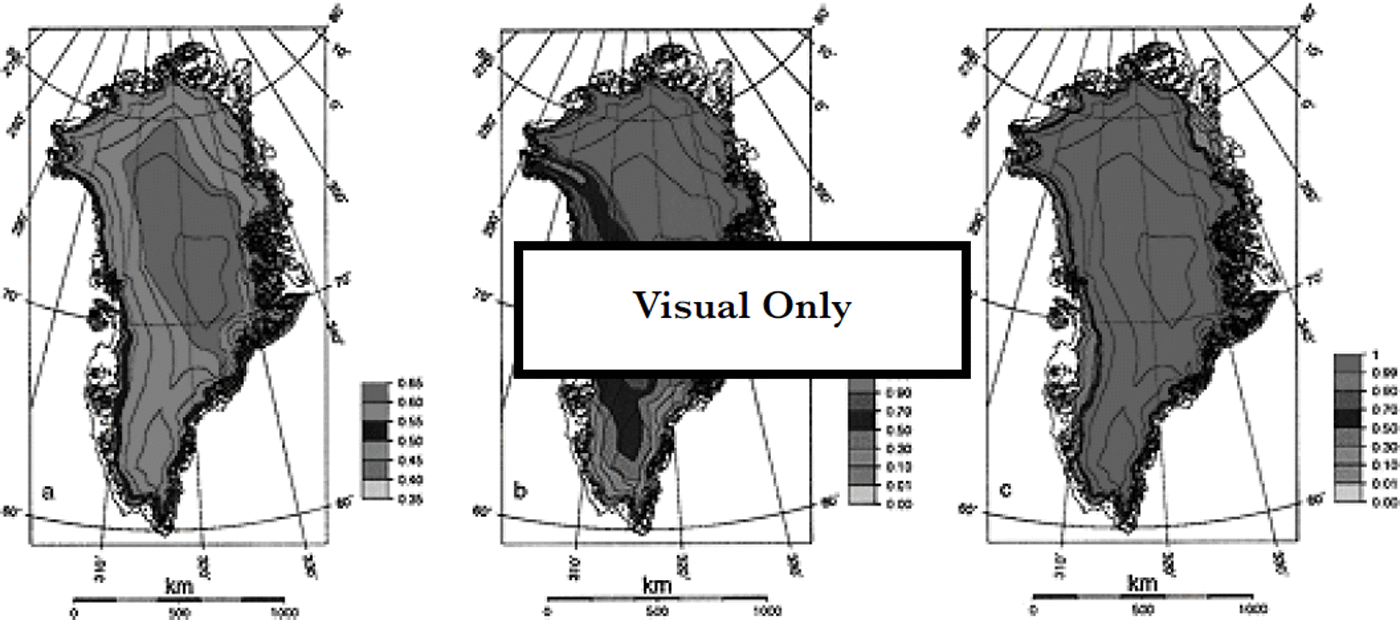
Fig. 2. The potential-retention fraction pr for the various retention models tested in this paper, expressing infraction of the annual precipitation that can potentially be retained. (a) Pr–max: constant fraction of the snowfall; (b)Pr_d2m: thermal active layer 2 m thick; ( c) pr_caρil: capillary retention and meltwater refreezing. Mote the different colour scale for model Pr–max. The pattern of px for the fourth model (Pr–0.0) is uniformly zero, so does not need to be shown. See text for more details on the various retention models. Elevation contours are 500 m apart.
The pattern of Pr for model pr_capil is very different, and is mainly linked to temperature, and thus elevation. The effect of temperature is twofold. Higher temperatures imply melting rates near or above the annual snowfall rate, so most or all of the snow cover will disappear, and little or no capillary water is able to survive until the end of the melting season. In that case, the thermodynamic refreezing effect dominates, which is proportional to (negative) temperature but becomes small for annual temperatures approaching the melting point. For lower temperatures, there will be less or negligible melting, and the combined capacity of capillary retention and meltwater refreezing in the snowpack is more than sufficient to refreeze all of the melt, if any. The result is a potential-retention fraction distribution that exhibits a sharp gradient between values of approximately unity above the 1500–2000 m contour, where virtually no rain occurs, and values of ≤ 10% in the ablation area, where only the thermodynamic refreezing effect plays a role as all of the annual snowfall runs off during the summer.
The large differences in the Px for the various models provide different amounts of retained meltwater only in those areas where enough meltwater is produced to cause runoff, i.e. along the margin of the ice sheet. These differences are displayed in Figure 3, and show the effective-retention fractions for the models pr–pmax, pr–d2m and pr_capil. The pattern of the effective-retention fraction ετ is in fact the local minimum value of the available-water fraction shown in Figure 1 and the potential-retention fraction shown in Figure 2. For the model pr_capil it appears that ετ reaches a maximum at the upper ice-sheet limit where runoff occurs, where it is 0.6–0.7. Incidentally, this is at the same location as the observations on which the models pr–pmax (Reference ReehReeh, 1991) and pr–d2m (Reference Huybrechts and de WoldeHuybrechts and de Wolde, 1999) are based. For model pr–pmax, the effective-retention fraction deviates from the Pr value of 0.6 above the runoff line, where the snowmelt drops below 60% of the annual snowfall. The pattern of ετ below the runoff line in model pr–d2m deviates entirely from the other models because it depends on the precipitation rate.
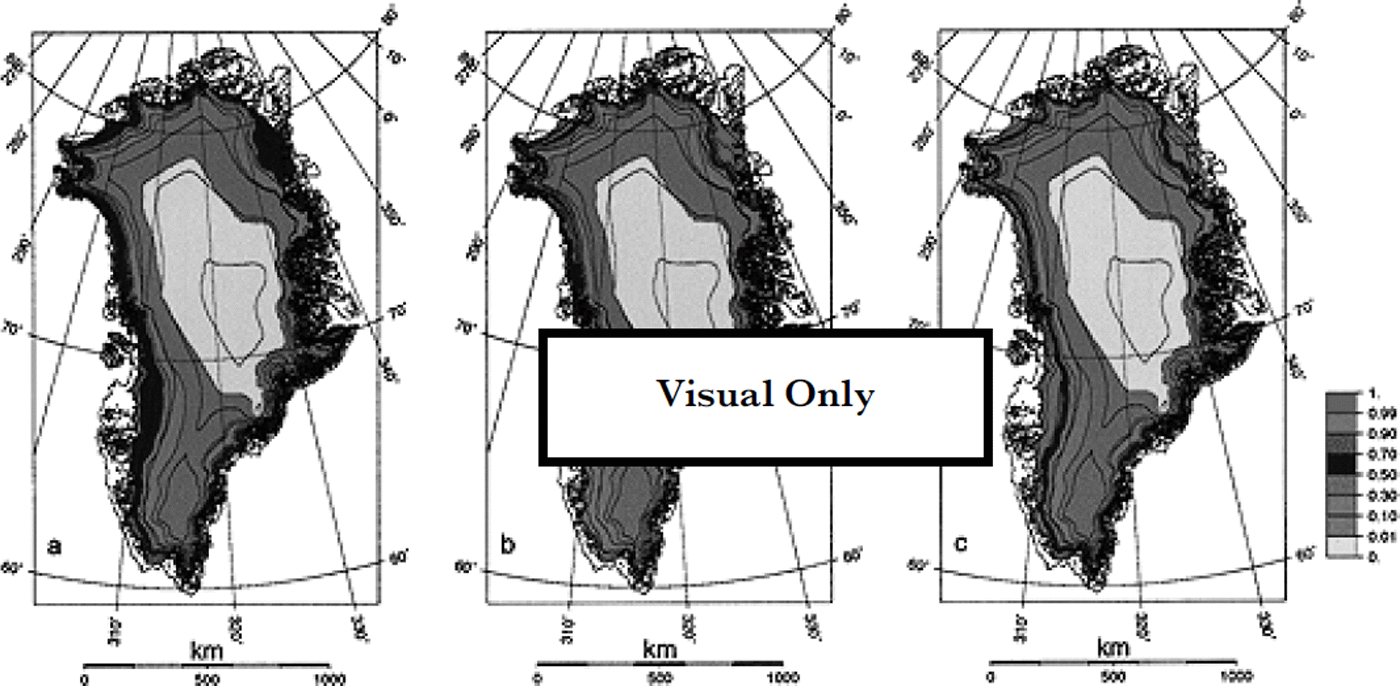
Fig. 3. The effective-retentionfractions ex for the various retention models, expressing the fraction of the annual precipitation that was effectively retained during the melting season, (a) Pr–Pmax: constant fraction of the snowfall; (b) Pr–d2m: thermal active layer 2 m thick; ( c) pr_caρil: capillary retention and meltwater refreezing. Elevation contours are 500 m apart.
Based on these results, it appears that it may be a gross simplification to assume a constant value for PMAX = ρτ/snfr. However, it is also striking that both of the more physically based models seem to yield a ρτ value around 0.6 in the area where it matters most, namely, around the runoff line, where it is nearly identical to PMAX because the snow fraction is about unity. A similar value of 0.58 was experimentally established by Reference Braithwaite, Laternser and PfefferBraithwaite and others (1994) in the lower accumulation area of the ice sheet near Paakitsoq, West Greenland. On the other hand, the refreezing part of the pr_capil model depends crucially on the thickness, d, of the thermal active layer providing the cold content, which was set equal to the thickness of the annual snow layer. Although it can reasonably be assumed that the infiltration depth of the meltwater is determined by the annual snow accumulation because the surface of the previous year is impermeable, meltwater will also conduct heat in the underlying ice layers. To account for this effect, a comprehensive calculation of the temperature profile of the upper ice and snow layers is required, but this would be beyond the simplicity sought in a parameterization involving many gridpoints over many time-steps in numerical ice-sheet simulations.
7. The Glaciological Facies
Various authors have tried to make a classification of ice-sheet surfaces according to the amount of surface melting and the characteristics of the mass balance (Reference BensonBenson, 1962; Reference MüllerMüller, 1962). Figure 4 shows a map of the various zones based on the retention model pr_capil. The Greenland ice sheet is a particularly interesting example because the whole sequence of glaciological zones (or facies) is represented at its surface.

Fig. 4. Glaciological zones on the Greenland ice sheet delimitedby retention model pr_capil. a: dry-snow zone; b: percolation zone; c: wet-snow zone; d: slush zone; e: superimposed-ice zone;/: ablation zone. See text for a full explanation of these glaciological zones. Elevation contours are 500 m apart.
The largest zone is the dry-snow zone, where no melting occurs even during the summer. Because the melt model produces a finite amount of meltwater even for very low temperatures (Equation (1)), we defined the dry-snow limit by the mean annual isotherm of –27°G, which gives a good fit to the measurements described in Reference BensonBenson (1962). An almost equally large area is formed by the percolation zone, where all surface melt refreezes immediately and no capillary water occurs because the firn temperature does not reach the melting point. Further downslope is the wet-snow zone, where capillary water is upheld in the liquid phase, but the firn is not entirely saturated and there is consequently no runoff. On average, the upper limit of this zone is at 2500 m a.s.l. in the south and around 1500 m a.s.l. in the extreme north. The wet-snow zone is separated from the slush zone by the runoff line. Here the potential and effective retention fractions as defined earlier are identical; below this limit, runoff occurs. In the slush zone, not all of the snow is transformed into meltwater, but there is runoff. The lower separation of the slush zone is the snowline, which represents the lowest elevation where snow survives during the summer melt season.
Below the slush zone is the superimposed-ice zone, which consists of a continuous mass of refrozen meltwater that survives at the surface, but this zone is so narrow that it is hardly visible in Figure 4. We define this zone as the area where all of the annual snow has melted and refrozen meltwater remains at the surface at the end of the melt season. Below the superimposed ice is the ablation zone, where the annual surface mass balance is negative and which is separated from the accumulation zone (positive mass balance) by the equilibrium line. According to the recalibrated mass-balance model, the ELA ranges from slightly over 1500 m in the southwest to ≤ 1000 m along the northern coast. Deviations from the general north-south trend result from strong precipitation gradients on the eastern side of the ice sheet. The ELA is at about 1300 m at around 77° N in the dry northeastern region and drops below 1000 m at the wet southeastern margin of the Greenland ice sheet. In general, the runoff line is 100–200 m higher than the equilibrium line.
These zones can help to validate passive microwave satellite data which are able to distinguish between zones of dry snow (no melt) and differing degrees of wet snow (Reference Abdalati and StefFenAbdalati and Steffen, 1997). However, a direct comparison between the model and reality is complicated by the fact that there is in reality a large interannual variability in the areal melt extent, whereas Figure 4 refers to a static situation.
8. The Surface Mass-Balance Components
For present-day conditions, the recalibrated mass-balance model with retention model pr_capil predicts a total annual precipitation of 542.27 km3 a"1 w.e. on the conterminous
Greenland ice sheet (excluding small ice caps and local glaciers not connected to the main ice sheet). With a total area of 1.691 × 106 km2, this gives a specific mean precipitation of 32.1 cm a"1 w.e. The larger part of the precipitation consists of snow (520.85 km3 a"1 w.e.), with the remainder falling as rain (21.42 km3 a"1 w.e.). By the end of the melt season, the model predicts that 409.70 km3 a"1 w. e. of the total precipitation remains in the solid phase, or about 75%; the total amount of liquid water (snowmelt and rain) available for retention Wτ is likewise 132.57 km3 a"1 w.e.
Table 1 lists values of the corresponding retention components for the four different models considered in this paper. Total retention for the models pr_d2m and pr_capil is all between the limits set by models pr.p0.0 (no retention, ρτ = 0) and pr_pmax (an equivalent 60% of the snow accumulation can be retained). Depending on the model chosen, it appears that between 45% (pr_capil) and 69% (pr_pmax) of the available water is retained during the summer. Compared to the experiment without retention, total runoff is 18% (pr_capil), 21% (pr_d2m) and 27% (pr_pmax) lower, meaning that runoff would be overestimated, on average, by as much as a quarter if meltwater retention were not taken into account in the mass balance.
Table 1. Terms of the Greenland mass balance (km3 a–1 w.e.) from the various models. The total precipitation is 542.27 km3 a–1
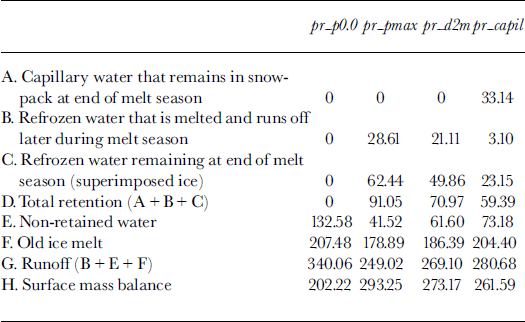
Overall, the three models produce rather similar amounts of total retention and runoff. Incidentally, if the fraction of refrozen meltwater that melts again and runs off later in the melting season is excluded from the retention mass, the agreement is even larger and the three methods produce a comparable amount of retained meltwater of between 49.86 km3 a"1 (pr_d2m) and 62.44 km3 a"1 (pr_pmax), (cf Table 1). Even if the total range of the retention volume is not so large among the various models, individual retention components vary much more. For example, the inclusion of the effect of capillary water in model pr_capil is largely compensated by a reduction of the amount of refrozen meltwater. This was expected because in model pr_capil only the annual snow layer absorbs the latent heat released by the refreezing meltwater, rather than the fixed 2 m layer in model pr_d2m. Also the various models differ much more on a regional basis, as became evident from the patterns of the effective-retention fractions. Total runoff from the Greenland ice sheet was found to be between 46% (pr_pmax) and 52% (pr_capil) of total precipitation.
9. Mass-Balance Sensitivity
Another important aspect of the mass balance is its sensitivity to temperature changes (Fig. 5; Table 2). To exactly balance the surface mass balance (total runoff equals total precipitation), a uniform temperature rise of between 1.70°C (pr.p0.0, i.e. no meltwater retention) and 2.61°C (pr_pmax, i.e. maximum retained water equal to 60% of the annual snowfall) is required. For the other models pr_d2m and pr_capil, the corresponding warmings are 2.38° and 2.25°C, respectively. In these calculations, it is assumed that precipitation rates change by 5% for every °C of temperature change, as was done in previous studies (Reference Huybrechts and de WoldeHuybrechts and de Wolde, 1999). Without the concomitant change in precipitation rate, the limits for a balanced surface budget are between 1.39°C (pr_ρ0.0) and 2.09°C (pr_pmax).
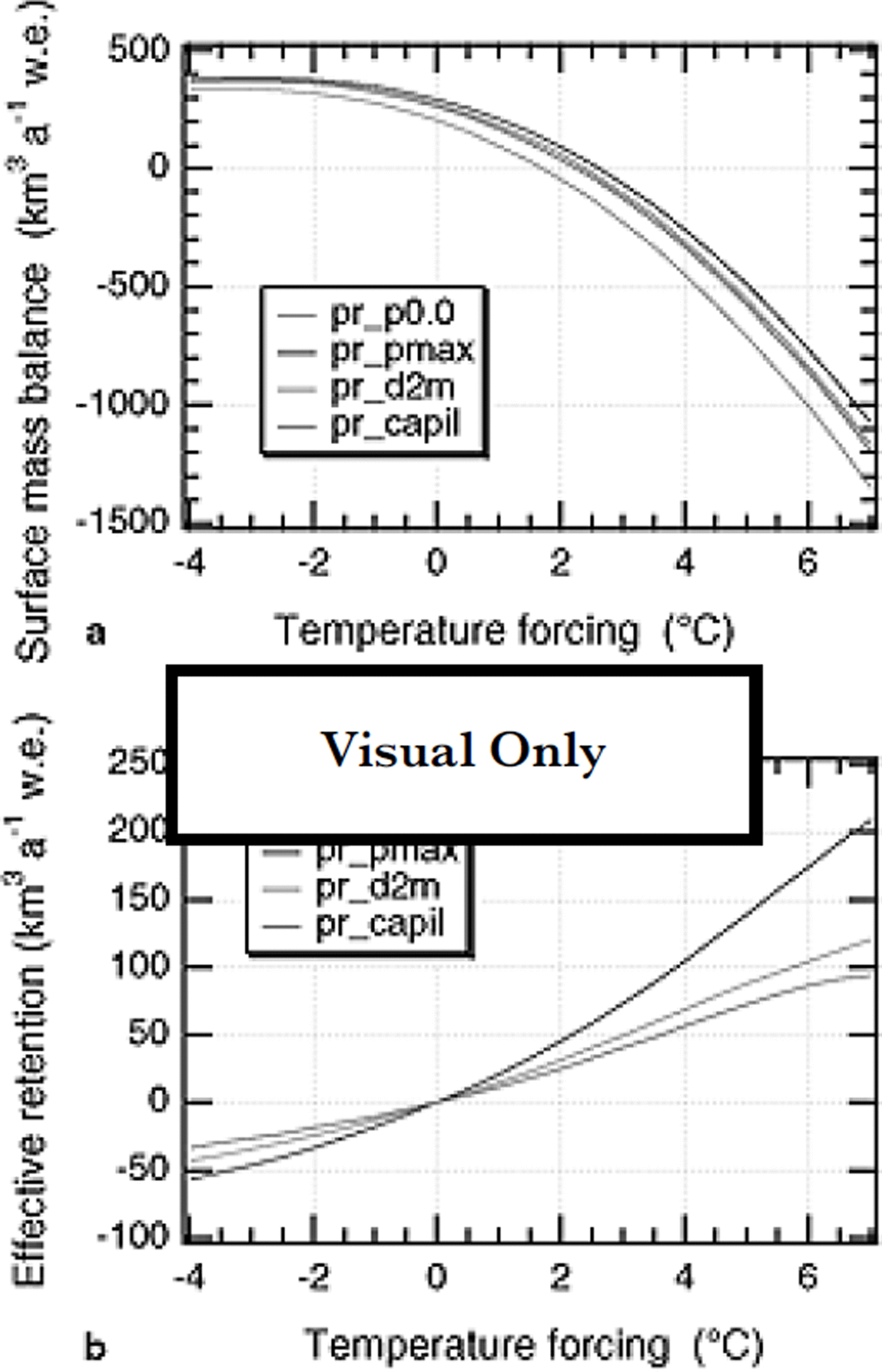
Fig. 5. Sensitivity of the total surface mass balance (a) and of the effective-retention component (b) to a uniform temperature change. These results include the effect of a 5% precipitation change for every °C of temperature change. The effective retention is shown relative to the present. Pr_ ρ0.0: no retention; pr–Pmax: constant fraction of the snowfall; Pr_d2m: thermal active layer 2 m thick; pr_capil: capillary retention and meltwater refreezing.
Table 2. Sensitivity of mass-balance components for the different retention models
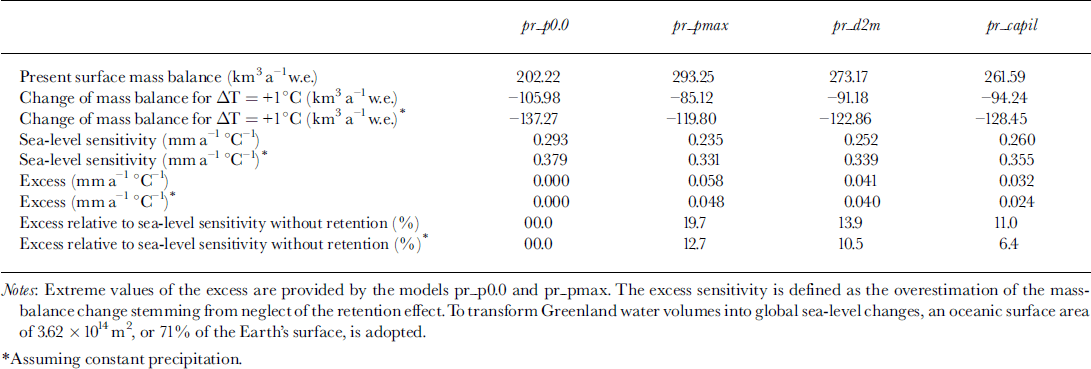
For a temperature rise of 1 ° C the decrease of mass balance varies between 85.12 km3 a"1 (pr_pmax) and 105.98 km3 a"1 (pr_ρ0.0) if precipitation rates rise by 5% as well. For constant precipitation, the change of mass balance (or runoff) is about 35% larger (Table 2). This means that the effect of including meltwater retention is about half of the precipitation effect, if one assumes that precipitation rates are roughly proportional to the humidity content of the overlying air column. On the other hand, it is noteworthy that the spread of the overall sensitivities between the models pr_pmax, pr_d2m and pr_capil is smaller than the spread of the respective retention masses diagnosed for the present state. Including meltwater retention is responsible for an excess sensitivity of 6–20% of the mass-balance sensitivity without meltwater retention.
Expressed in equivalent global sea-level changes, the sensitivity of the best mass-balance model for a +1° C warming is +0.355 mm a"1 with constant precipitation, and +0.260 mm a"1 including the temperature dependence of the precipitation rate. These values are within the range of previous estimates (Reference Van de WalVan de Wal, 1996; Reference Warrick, le Provost, Meier, Oerlemans, Woodworth, Houghton, Meira Filho, Callander, Harris, Kattenberg and MaskellWarrick and others, 1996), but tend to be at the higher end. Reference Van de WalVan de Wal (1996) finds a value of +0.34 mm ˚ C–1–6 a–1 for a similar calculation with an energy-balance model and +0.31 mm ˚ C–1 a–1 for a calculation with a positive degree-day model, but Van de Wal and Reference EkholmEkholm (1996) remark that their sensitivities are probably overestimated by 20% compared to calculations with the improved surface-elevation dataset used in this paper.
Finally, it should be remarked that the sensitivities found in this paper probably represent a conservative estimate of the retention effect in a warming climate. If glaciological zones move up on the ice sheet, it is conceivable that additional transient effects will occur because old permeable firn layers need to be saturated before other processes can take place that will ultimately lead to runoff.
10. Conclusions
It is clear that the retention process has a significant effect on meltwater runoff when the mass balance of the Greenland ice sheet and its impact on global sea level under a changing climate are calculated. From the models compared in this paper, it is found that runoff would be overestimated by about one-fifth if meltwater retention were not taken into account. Overall, the three models pr_pmax, pr_d2m and pr_capil produced comparable amounts of total retention and total runoff to within, respectively, 20% and 5% of their mutual average. Also their sensitivities for a +1˚C warming were quite similar. In order to obtain a global estimate of the mass balance, it may therefore be sufficient to work with a retention model with a fixed fraction of the snowfall, but then a lower value is suggested compared to the values 0.5–0.7 one usually finds near the runoff line. For an optimal PMAX value of 0.291 the global results and their sensitivity are identical to the most comprehensive model including meltwater refreezing and capillary water to within 1 %. However, the latter model includes more realistic physics and has a spatial variation not described by the other treatments, but could still be improved by fine-tuning of the thickness of the thermal active layer participating in the refreezing process.
Acknowledgements
We are grateful to S. Ekholm and F. Jung-Rothenhausler for providing their datasets on surface elevation and accumulation rate. Constructive comments from T. Pfeffer and an anonymous referee helped to clarify the text and were much appreciated. The authors wish to thank the Belgian Federal Office for Scientific, Technical and Cultural Affairs (Prime Minister’s Services, Programme Global Change and Sustainable Development, contract No. CG/DD/09) and the European Union Framework IV project ˚Climate Change and Sea Level" (ENV4-CT095-0124) for their support.









