No CrossRef data available.
Article contents
TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES
Published online by Cambridge University Press: 15 February 2024
Abstract
In this paper, we obtain the 
$H^{p_1}\times H^{p_2}\times H^{p_3}\to H^p$ boundedness for trilinear Fourier multiplier operators, which is a trilinear analogue of the multiplier theorem of Calderón and Torchinsky [4]. Our result improves the trilinear estimate in [22] by additionally assuming an appropriate vanishing moment condition, which is natural in the boundedness into the Hardy space 
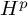$H^p$ for 
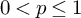$0<p\le 1$.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 5 , September 2024 , pp. 2217 - 2278
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Baernstein, A. II and Sawyer, E. T., ‘Embedding and multiplier theorems for
${H}^p\left({\mathbb{R}}^n\right)$
’, Mem. Amer. Math. Soc. 318 (1985).Google Scholar
${H}^p\left({\mathbb{R}}^n\right)$
’, Mem. Amer. Math. Soc. 318 (1985).Google ScholarBurkholder, D. L., Gundy, R. F. and Silverstein, M. L., ‘A maximal function characterization of the class
${H}^{p}$
’, Trans. Amer. Math. Soc. 157 (1971), 137–153.Google Scholar
${H}^{p}$
’, Trans. Amer. Math. Soc. 157 (1971), 137–153.Google ScholarCalderón, A. P., ‘An atomic decomposition of distributions in parabolic
${H}^p$
spaces’, Adv. Math. 25 (1977), 216–225.CrossRefGoogle Scholar
${H}^p$
spaces’, Adv. Math. 25 (1977), 216–225.CrossRefGoogle ScholarCalderón, A. P. and Torchinsky, A., ‘Parabolic maximal functions associated with a distribution, II’, Adv. Math. 24 (1977), 101–171.CrossRefGoogle Scholar
Coifman, R. R. and Meyer, Y., ‘Commutateurs d’ intégrales singulières et opérateurs multilinéaires’, Ann. Inst. Fourier (Grenoble) 28 (1978), 177–202.CrossRefGoogle Scholar
Cruze-Uribe, D. and Nguyen, H. V., ‘Multilinear multipliers and singular integrals with smooth kernels on Hardy spaces’, Tran. Amer. Math. Soc. 374 (2021), 3801–3825
CrossRefGoogle Scholar
Fefferman, C. and Stein, E. M., ‘
${H}^p$
spaces of several variables’, Acta Math. 129 (1972), 137–193.CrossRefGoogle Scholar
${H}^p$
spaces of several variables’, Acta Math. 129 (1972), 137–193.CrossRefGoogle ScholarFrazier, M. and Jawerth, B., ‘Decomposition of Besov spaces’, Indiana Univ. Math. J. 34 (1985), 777–799.CrossRefGoogle Scholar
Frazier, M. and Jawerth, B., ‘The
$\varphi$
-transform and applications to distribution spaces’, in Function Spaces and Applications, Lecture Notes in Math., vol. 1302 (Springer-Verlag, New York/Berlin, 1988), 223–246.CrossRefGoogle Scholar
$\varphi$
-transform and applications to distribution spaces’, in Function Spaces and Applications, Lecture Notes in Math., vol. 1302 (Springer-Verlag, New York/Berlin, 1988), 223–246.CrossRefGoogle ScholarFrazier, M. and Jawerth, B., ‘A discrete transform and decomposition of distribution spaces’, J. Funct. Anal. 93 (1990), 34–170.CrossRefGoogle Scholar
Fujita, M. and Tomita, N., ‘Weighted norm inequalities for multilinear Fourier multipliers’, Trans. Amer. Math. Soc. 364 (2012), 6335–6353.CrossRefGoogle Scholar
Grafakos, L., He, D. and Honzík, P., ‘The Hörmander multiplier theorem II: The bilinear local
${L}^2$
case’, Math. Z. 289 (2018), 875–887.CrossRefGoogle Scholar
${L}^2$
case’, Math. Z. 289 (2018), 875–887.CrossRefGoogle ScholarGrafakos, L., He, D., Honzík, P. and Nguyen, H. V., ‘The Hörmander multiplier theorem I: The linear case revisited’, Illinois J. Math. 61 (2017), 25–35.CrossRefGoogle Scholar
Grafakos, L., Miyachi, A., Nguyen, H. V. and Tomita, N., ‘Multilinear Fourier multipliers with minimal Sobolev regularity, II’, J. Math. Soc. Japan 69 (2017), 529–562.CrossRefGoogle Scholar
Grafakos, L., Miyachi, A. and Tomita, N., ‘On multilinear Fourier multipliers of limited smoothness’, Can. J. Math. 65 (2013), 299–330.CrossRefGoogle Scholar
Grafakos, L., Nakamura, S., Nguyen, H. V. and Sawano, Y., ‘Conditions for boundedness into Hardy spaces’, Math. Nachr. 292 (2019), 2383–2410.CrossRefGoogle Scholar
Grafakos, L., Nakamura, S., Nguyen, H. V. and Sawano, Y., ‘Multiplier condition for boundedness into Hardy spaces’, Ann. Inst. Fourier (Grenoble) 71 (2021), 1047–1064.CrossRefGoogle Scholar
Grafakos, L. and Nguyen, H. V., ‘Multilinear Fourier multipliers with minimal Sobolev regularity, I’, Colloq. Math. 144 (2016), 1–30.CrossRefGoogle Scholar
Grafakos, L. and Park, B., ‘Sharp Hardy space estimates for multipliers’, Int. Math. Res. Not. 2022 (2022), 10403–10430.CrossRefGoogle Scholar
Grafakos, L. and Slavíková, L., ‘A sharp version of the Hörmander multiplier theorem’, Int. Math. Res. Not. 15 (2019), 4764–4783.CrossRefGoogle Scholar
Hörmander, L., ‘Estimates for translation invariant operators in
${L}_p$
spaces’, Acta Math. 104 (1960), 93–140.CrossRefGoogle Scholar
${L}_p$
spaces’, Acta Math. 104 (1960), 93–140.CrossRefGoogle ScholarLee, J., Heo, Y., Hong, S., Lee, J. B., Park, B., Park, Y. and Yang, C., ‘The Hörmander multiplier theorem for
$n$
-linear operators’, Math. Ann. 381 (2021), 499–555.CrossRefGoogle Scholar
$n$
-linear operators’, Math. Ann. 381 (2021), 499–555.CrossRefGoogle ScholarMihlin, S. G., ‘On the multipliers of Fourier integrals’, Dokl. Akad. Nauk SSSR (N.S.) 109 (1956), 701–703 (Russian).Google Scholar
Miyachi, A. and Tomita, N., ‘Minimal smoothness conditions for bilinear Fourier multipliers’, Rev. Mat. Iberoam. 29 (2013), 495–530.CrossRefGoogle Scholar
Park, B., ‘Fourier multiplier theorems for Triebel–Lizorkin spaces’, Math. Z. 293 (2019), 221–258.CrossRefGoogle Scholar
Park, B., ‘Fourier multipliers on a vector-valued function space’, Constr. Approx. 55 (2022), 705–741.CrossRefGoogle Scholar
Park, B., ‘On the failure of multilinear multiplier theorem with endpoint smoothness conditions’, Potential Anal. 56 (2022), 87–96.CrossRefGoogle Scholar
Seeger, A., ‘A limit case of the Hörmander multiplier theorem’, Monatsh. Math. 105 (1988), 151–160.CrossRefGoogle Scholar
Seeger, A., ‘Estimates near
${L}^1$
for Fourier multipliers and maximal functions’, Arch. Math. (Basel) 53 (1989), 188–193.CrossRefGoogle Scholar
${L}^1$
for Fourier multipliers and maximal functions’, Arch. Math. (Basel) 53 (1989), 188–193.CrossRefGoogle ScholarSeeger, A. and Trebels, W., ‘Embeddings for spaces of Lorentz–Sobolev type’, Math. Ann. 373 (2019), 1017–1056.CrossRefGoogle Scholar
Stein, E. M., Harmonic Analysis, Real Variable Methods, Orthogonality, and Oscillatory Integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Tomita, N., ‘A Hörmander type multiplier theorem for multilinear operators’, J. Func. Anal. 259 (2010), 2028–2044.CrossRefGoogle Scholar
Uchiyama, A., ‘Characterization of
${H}^p\left({\mathbb{R}}^n\right)$
in terms of generalized Littlewood–Paley
$g$
-function’, Studia Math. 81 (1985), 135–158.CrossRefGoogle Scholar
${H}^p\left({\mathbb{R}}^n\right)$
in terms of generalized Littlewood–Paley
$g$
-function’, Studia Math. 81 (1985), 135–158.CrossRefGoogle ScholarYamazaki, M., ‘A quasi-homogeneous version of paradifferential operators, I. Boundedness on spaces of Besov type’, J. Fac. Sci. Univ. Tokyo Sect. IA, Math. 33 (1986), 131–174.Google Scholar