Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-16T20:05:32.887Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Jones polynomial modulo primes

Part of: Low-dimensional topology

Published online by Cambridge University Press:  15 August 2023

Valeriano Aiello ,
Sebastian Baader  and
Livio Ferretti
Valeriano Aiello
Affiliation:
University of Bern, Sidlerstrasse 5, CH-3012 Bern, Switzerland
Sebastian Baader*
Affiliation:
University of Bern, Sidlerstrasse 5, CH-3012 Bern, Switzerland
Livio Ferretti
Affiliation:
University of Bern, Sidlerstrasse 5, CH-3012 Bern, Switzerland
*
Corresponding author: Sebastian Baader; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive an upper bound on the density of Jones polynomials of knots modulo a prime number 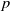$p$, within a sufficiently large degree range: 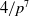$4/p^7$. As an application, we classify knot Jones polynomials modulo two of span up to eight.

Keywords

Jones polynomialknot

MSC classification

Secondary: 57M27: Invariants of knots and 3-manifolds
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 3 , September 2023 , pp. 730 - 734
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birman, J. S. and Lin, X.-S., Knot polynomials and Vassiliev’s invariants, Invent. Math. 111(2) (1993), 225–270.Google Scholar
Eliahou, S. and Fromentin, J., A remarkable 20-crossing tangle, J. Knot Theory Ramif. 26(14) (2017), 1750091.Google Scholar
Ganzell, S., Local moves and restrictions on the Jones polynomial, J. Knot Theory Ramif. 23(2) (2014), 1450011.Google Scholar
Jones, V. F. R., A polynomial invariant for knots via von Neumann algebras, Bull. Am. Math. Soc. (N.S.) 12(1) (1985), 103–111.Google Scholar
Livingston, C. and Moore, A. H., KnotInfo: Table of Knot Invariants. Available at https://knotinfo.math.indiana.edu (accessed 13 April 2022).Google Scholar
Przytycki, J. H., 3-coloring and other elementary invariants of knots. In Knot Theory (Warsaw, 1995), Banach Center Publications, vol. 42 (Polish Academy of Sciences, Institute of Mathematics, Warsaw, 1998), 275–295.Google Scholar
Rolfsen, D., Knots and Links, Mathematics Lecture Series, vol. 7 (Publish or Perish, Inc., Berkeley, CA, 1976).Google Scholar