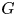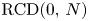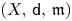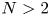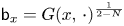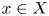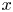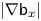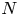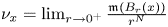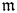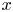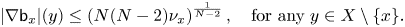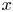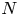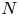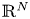1. Introduction
1.1. Green function and concerned problems in the smooth framework
In the classical PDE theory, the (positive) Green function $G_x$![]() at the pole $x$
at the pole $x$![]() of the Laplace operator on the $N$
of the Laplace operator on the $N$![]() -dimensional Euclidean space $\mathbb {R}^N$
-dimensional Euclidean space $\mathbb {R}^N$![]() is the solution to the heat equation
is the solution to the heat equation
as measures, where $\delta _x$![]() is the Dirac measure at $x$
is the Dirac measure at $x$![]() . In the case when $N\geqslant 2$
. In the case when $N\geqslant 2$![]() , it is well-known that this equation is solved by
, it is well-known that this equation is solved by

where $\mathsf {d}_x(\cdot )$![]() is the Euclidean distance function from $x$
is the Euclidean distance function from $x$![]() and $\omega _N:=\pi ^{\frac {N}{2}}\Gamma (\frac {N}{2}+1)^{-1}$
and $\omega _N:=\pi ^{\frac {N}{2}}\Gamma (\frac {N}{2}+1)^{-1}$![]() is the volume of a unit ball $B_1(0_N)$
is the volume of a unit ball $B_1(0_N)$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() .
.
We can also discuss the Green functions for more general classes of spaces along the same line. For instance, it is known that for an $N$![]() -dimensional complete Riemannian manifold $(M^N,\,g)$
-dimensional complete Riemannian manifold $(M^N,\,g)$![]() ($N\geqslant 2$
($N\geqslant 2$![]() ) with non-negative Ricci curvature, the existence of the (global) Green function $G$
) with non-negative Ricci curvature, the existence of the (global) Green function $G$![]() is equivalent to the following non-parabolic assumption:
is equivalent to the following non-parabolic assumption:
where $B_r(x)$![]() denotes the open ball centred at $x$
denotes the open ball centred at $x$![]() of radius $r$
of radius $r$![]() with respect to the induced distance $\mathsf {d}$
with respect to the induced distance $\mathsf {d}$![]() by $g$
by $g$![]() , and $\mathop {\mathrm {Vol}}$
, and $\mathop {\mathrm {Vol}}$![]() denotes the Riemannian volume measure by $g$
denotes the Riemannian volume measure by $g$![]() . See [Reference Varopoulos56] by Varopoulos for the details. In this case, it is well-known that the following asymptotic behaviour for the Green function $G_x$
. See [Reference Varopoulos56] by Varopoulos for the details. In this case, it is well-known that the following asymptotic behaviour for the Green function $G_x$![]() at the pole $x \in M^N$
at the pole $x \in M^N$![]() holds as $\mathsf {d}_x\rightarrow 0^+$
holds as $\mathsf {d}_x\rightarrow 0^+$![]() :
:

This fact indicates that in the case when $N\geqslant 3$![]() , the function
, the function
should be a counterpart of the distance function from $x$![]() up to a multiplication of a dimensional positive constant;
up to a multiplication of a dimensional positive constant;
Colding [Reference Colding16] proved the sharp gradient estimate for $\mathsf {b}_x$![]() and the rigidity as follows.
and the rigidity as follows.
Theorem 1.1 Theorem 3.1 of [Reference Colding16]
Let $(M^N,\,g)$![]() be an $N$
be an $N$![]() -dimensional ($N \geqslant 3$
-dimensional ($N \geqslant 3$![]() ), complete and non-parabolic Riemannian manifold with non-negative Ricci curvature and let $x\in M^N$
), complete and non-parabolic Riemannian manifold with non-negative Ricci curvature and let $x\in M^N$![]() . Then we have the following.
. Then we have the following.
(1) (Sharp gradient estimate) We have
(1.7)\begin{equation} |\nabla \mathsf{b}_x|(z)\leqslant (N(N-2)\omega_N)^\frac{1}{N-2} \end{equation}for any $z \in M^N \setminus \{x\}$
 .
.(2) (Rigidity) $(M^N,\,g)$
 is isometric to the $N$
is isometric to the $N$ -dimensional Euclidean space $\mathbb {R}^N$
-dimensional Euclidean space $\mathbb {R}^N$ with $\mathsf {b}_x=(N(N-2)\omega _N)^\frac {1}{N-2}\mathsf {d}_x$
with $\mathsf {b}_x=(N(N-2)\omega _N)^\frac {1}{N-2}\mathsf {d}_x$ if the equality of (1.7) holds for some $z \in M^N \setminus \{x\}$
if the equality of (1.7) holds for some $z \in M^N \setminus \{x\}$ .
.
Note that Colding used the normalized one, $(N(N-2)\omega _N)^\frac {1}{2-N}G_x^\frac 1{2-N}$![]() , as the definition of $\mathsf {b}_x$
, as the definition of $\mathsf {b}_x$![]() . Thus the sharp upper bound in [Reference Colding16] was exactly $1$
. Thus the sharp upper bound in [Reference Colding16] was exactly $1$![]() instead of the right-hand-side of (1.7). See the footnote $4$
instead of the right-hand-side of (1.7). See the footnote $4$![]() in [Reference Colding16].
in [Reference Colding16].
In particular the rigidity indicates that $\mathsf {b}_x$![]() exactly coincides with $(N(N-2)\omega _N)^\frac {1}{N-2} \mathsf {d}_x$
exactly coincides with $(N(N-2)\omega _N)^\frac {1}{N-2} \mathsf {d}_x$![]() if and only if the manifold is Euclidean. Given this rigidity result, it is natural to ask whether the quantitative almost rigidity result is satisfied or not:
if and only if the manifold is Euclidean. Given this rigidity result, it is natural to ask whether the quantitative almost rigidity result is satisfied or not:
(A) If $|\nabla \mathsf {b}_x|(y)$
 is close to the sharp upper bound $(N(N-2)\omega _N)^\frac {1}{N-2}$
is close to the sharp upper bound $(N(N-2)\omega _N)^\frac {1}{N-2}$ at some point $y \in M^N \setminus \{x\}$
at some point $y \in M^N \setminus \{x\}$ , then can we conclude that the manifold is pointed Gromov–Hausdorff (pGH) close to $\mathbb {R}^N$
, then can we conclude that the manifold is pointed Gromov–Hausdorff (pGH) close to $\mathbb {R}^N$ ?
?
It is worth mentioning that
whenever $y \to x$![]() . Therefore in order to give a positive answer to the question (Q), we need to find an additional assumption on $y$
. Therefore in order to give a positive answer to the question (Q), we need to find an additional assumption on $y$![]() .
.
We are now in a position to introduce the first main result of the paper.
Theorem 1.2 Almost rigidity
For any integer $N \geqslant 3$![]() , all $0<\varepsilon <1$
, all $0<\varepsilon <1$![]() , $0< r< R$
, $0< r< R$![]() , $1 \leqslant p <\infty$
, $1 \leqslant p <\infty$![]() and $\varphi \in L^1([0,\,\infty ),\, \mathscr {H}^1)$
and $\varphi \in L^1([0,\,\infty ),\, \mathscr {H}^1)$![]() there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, R,\, p,\, \varphi )>0$
there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, R,\, p,\, \varphi )>0$![]() such that if an $N$
such that if an $N$![]() -dimensional ($N \geqslant 3$
-dimensional ($N \geqslant 3$![]() ) complete Riemannian manifold with non-negative Ricci curvature $(M^N,\, g)$
) complete Riemannian manifold with non-negative Ricci curvature $(M^N,\, g)$![]() satisfies
satisfies
for some $x \in M^N$![]() and that
and that
holds for some $y \in \overline {B}_R(x) \setminus B_r(x)$![]() . Then we have
. Then we have
and

in particular
where $\mathsf {d}_{\mathrm {pmGH}}$![]() denotes any fixed distance metrizing the pointed measured Gromov–Hausdorff (pmGH) convergence.
denotes any fixed distance metrizing the pointed measured Gromov–Hausdorff (pmGH) convergence.
As explained around (1.8), the lower bound $r$![]() in theorem 1.10 cannot be dropped in order to get (1.11). On the other hand, it is known that if the asymptotic $N$
in theorem 1.10 cannot be dropped in order to get (1.11). On the other hand, it is known that if the asymptotic $N$![]() -volume $V_{M^N}$
-volume $V_{M^N}$![]() defined by
defined by
is close to $\omega _N$![]() , then $(M^N,\, \mathsf {d},\, \mathop {\mathrm {Vol}},\, x)$
, then $(M^N,\, \mathsf {d},\, \mathop {\mathrm {Vol}},\, x)$![]() is pmGH close to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, \mathscr {H}^N,\, 0_N)$
is pmGH close to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, \mathscr {H}^N,\, 0_N)$![]() , quantitatively. See [Reference Colding15] by Colding. Note that the converse statement is not true even in the case when the metric is Ricci flat with the maximal volume growth (namely $V_{M^N}>0$
, quantitatively. See [Reference Colding15] by Colding. Note that the converse statement is not true even in the case when the metric is Ricci flat with the maximal volume growth (namely $V_{M^N}>0$![]() ).
).
In connection with this observation, it is natural to ask whether the conclusion (1.11) in the theorem above can be improved to be that $V_{M^N}$![]() is close to $\omega _N$
is close to $\omega _N$![]() , or not. However a simple blow-up argument on a fixed manifold which is not isometric to $\mathbb {R}^N$
, or not. However a simple blow-up argument on a fixed manifold which is not isometric to $\mathbb {R}^N$![]() allows us to conclude that the desired improvement is impossible, see also remark 4.5.
allows us to conclude that the desired improvement is impossible, see also remark 4.5.
As another possible improvement in the theorem above, it is also natural to ask whether the case when $p=\infty$![]() in (1.13) is satisfied or not, namely
in (1.13) is satisfied or not, namely
However we can also see that this improvement is impossible (thus the improvement of (1.12) to the case when $p=\infty$![]() is also impossible) via Gromov–Hausdorff limits. See subsection 5.1.
is also impossible) via Gromov–Hausdorff limits. See subsection 5.1.
The observation above allows us to say that theorem 1.2 is sharp. Finally let us introduce an immediate corollary.
Corollary 1.3 For any integer $N \geqslant 3$![]() , all $0<\varepsilon <1$
, all $0<\varepsilon <1$![]() and $v>0$
and $v>0$![]() there exists $\delta :=\delta (N,\, \varepsilon,\, v)>0$
there exists $\delta :=\delta (N,\, \varepsilon,\, v)>0$![]() such that if an $N$
such that if an $N$![]() -dimensional ($N \geqslant 3$
-dimensional ($N \geqslant 3$![]() ) complete Riemannian manifold with non-negative Ricci curvature $(M^N,\, g)$
) complete Riemannian manifold with non-negative Ricci curvature $(M^N,\, g)$![]() satisfies $V_{M^N} \geqslant v$
satisfies $V_{M^N} \geqslant v$![]() and (1.10) for some sequence $y_i \in M^N(i=1,\,2,\,\ldots )$
and (1.10) for some sequence $y_i \in M^N(i=1,\,2,\,\ldots )$![]() with $\mathsf {d}(x,\, y_i)\to \infty$
with $\mathsf {d}(x,\, y_i)\to \infty$![]() , then
, then
In particular, in addition, if $\varepsilon$![]() is sufficiently small depending only on $N$
is sufficiently small depending only on $N$![]() and $v$
and $v$![]() , then $M^N$
, then $M^N$![]() is diffeomorphic to $\mathbb {R}^N$
is diffeomorphic to $\mathbb {R}^N$![]() .
.
Note that the existence of such sequence $y_i$![]() in the corollary above cannot be replaced by the existence of only one point which is far from $x$
in the corollary above cannot be replaced by the existence of only one point which is far from $x$![]() . See remark 4.7.
. See remark 4.7.
The results above are justified via a non-smooth geometric analysis with Ricci curvature bounded below. Moreover the results above are generalized to such a non-smooth framework, so-called $\operatorname {RCD}$![]() spaces. In the next section let us provide a brief introduction on $\operatorname {RCD}$
spaces. In the next section let us provide a brief introduction on $\operatorname {RCD}$![]() spaces.
spaces.
1.2. Non-smooth space with Ricci curvature bounded below; $\operatorname {RCD}$ spaces
spaces
In the first decade of this century, Lott–Villani [Reference Lott and Villani46] and Sturm [Reference Sturm53, Reference Sturm54] introduced the notion of $\operatorname {CD}(K,\,N)$![]() spaces independently as a concept of metric measure spaces with Ricci curvature bounded below by $K\in \mathbb {R}$
spaces independently as a concept of metric measure spaces with Ricci curvature bounded below by $K\in \mathbb {R}$![]() and dimension bounded above by $N\in [1,\,\infty ]$
and dimension bounded above by $N\in [1,\,\infty ]$![]() in some synthetic sense via the optimal transportation theory. For instance, in the case when $N$
in some synthetic sense via the optimal transportation theory. For instance, in the case when $N$![]() is an integer, $\mathbb {R}^N$
is an integer, $\mathbb {R}^N$![]() with any norm and the Lebesgue measure $\mathscr L^N$
with any norm and the Lebesgue measure $\mathscr L^N$![]() satisfies the $\operatorname {CD}(0,\, N)$
satisfies the $\operatorname {CD}(0,\, N)$![]() condition. Note that this is not ‘Riemannian’ whenever the norm does not come from an inner product and that Gigli found a ‘Riemannian’ notion on general metric measure spaces, so-called infinitesimally Hilbertianity, in [Reference Gigli32], which allows us to meet the Dirichlet form theory from the metric measure geometry. It is worth mentioning that $N$
condition. Note that this is not ‘Riemannian’ whenever the norm does not come from an inner product and that Gigli found a ‘Riemannian’ notion on general metric measure spaces, so-called infinitesimally Hilbertianity, in [Reference Gigli32], which allows us to meet the Dirichlet form theory from the metric measure geometry. It is worth mentioning that $N$![]() is not necessarily to be an integer in general.
is not necessarily to be an integer in general.
After a pioneer work of Gigli–Kuwada–Ohta [Reference Gigli, Kuwada and Ohta27] on Alexandrov spaces, Ambrosio–Gigli–Savaré (in the case when $N=\infty$![]() ) and Gigli (in the case when $N<\infty$
) and Gigli (in the case when $N<\infty$![]() ) introduced $\operatorname {RCD}(K,\, N)$
) introduced $\operatorname {RCD}(K,\, N)$![]() spaces (or $\operatorname {RCD}$
spaces (or $\operatorname {RCD}$![]() spaces for short) by adding the infinitesimally Hilbertianity to the $\operatorname {CD}$
spaces for short) by adding the infinitesimally Hilbertianity to the $\operatorname {CD}$![]() condition, see [Reference Ambrosio, Gigli and Savaré2, Reference Gigli33]. It is known that $\operatorname {RCD}$
condition, see [Reference Ambrosio, Gigli and Savaré2, Reference Gigli33]. It is known that $\operatorname {RCD}$![]() spaces include weighted Riemannian manifolds with Bakry–Émery Ricci curvature bounded below, Ricci limit spaces, and Alexandrov spaces [Reference Petrunin51, Reference Zhang and Zhu57] by Petrunin and Zhang-Zhu. The study is hugely developed, see for instance [Reference Ambrosio8, Reference Gigli35] as nice surveys.
spaces include weighted Riemannian manifolds with Bakry–Émery Ricci curvature bounded below, Ricci limit spaces, and Alexandrov spaces [Reference Petrunin51, Reference Zhang and Zhu57] by Petrunin and Zhang-Zhu. The study is hugely developed, see for instance [Reference Ambrosio8, Reference Gigli35] as nice surveys.
As explained in the previous subsection, we will mainly discuss an $\operatorname {RCD}(0,\, N)$![]() space $(X,\,\mathsf {d},\,\mathfrak {m})$
space $(X,\,\mathsf {d},\,\mathfrak {m})$![]() for some finite $N >2$
for some finite $N >2$![]() satisfying the non-parabolic assumption:
satisfying the non-parabolic assumption:
Then, as in the smooth case, the global Green function $G=G^X$![]() can be defined by the integration of the heat kernel $p(x,\,y,\,t)$
can be defined by the integration of the heat kernel $p(x,\,y,\,t)$![]() :
:
and it is proved in [Reference Bruè and Semola12] by Bruè–Semola that $G$![]() is well-defined with $G(x,\,\cdot )\in W^{1,1}_{\mathrm {loc}}(X,\,\mathsf {d},\,\mathfrak {m})$
is well-defined with $G(x,\,\cdot )\in W^{1,1}_{\mathrm {loc}}(X,\,\mathsf {d},\,\mathfrak {m})$![]() for any $x\in X$
for any $x\in X$![]() . A typical example of $\operatorname {RCD}(0,\, N)$
. A typical example of $\operatorname {RCD}(0,\, N)$![]() spaces is
spaces is
whose Green function $G$![]() satisfies the following expression from the pole/origin $0$
satisfies the following expression from the pole/origin $0$![]() ;
;
See proposition 3.8. It is worth mentioning that (1.19) is the $N$![]() -metric measure cone over a single point (definition 2.7).
-metric measure cone over a single point (definition 2.7).
1.3. Main results and organization of this paper
In order to introduce main results of this paper, fix an $\operatorname {RCD}(0,\,N)$![]() space $(X,\,\mathsf {d},\,\mathfrak {m})$
space $(X,\,\mathsf {d},\,\mathfrak {m})$![]() for some finite $N >2$
for some finite $N >2$![]() satisfying the non-parabolic assumption (1.17). Moreover we also fix a point $x\in X$
satisfying the non-parabolic assumption (1.17). Moreover we also fix a point $x\in X$![]() whose $N$
whose $N$![]() -volume density $\nu _x$
-volume density $\nu _x$![]() is finite;
is finite;
where the positivity is a direct consequence of the Bishop–Gromov inequality.
Remark 1.4 The origin of the $\operatorname {RCD}(0,\, N)$![]() space (1.19) satisfies (1.21), more generally (1.21) is satisfied at the pole of any $N$
space (1.19) satisfies (1.21), more generally (1.21) is satisfied at the pole of any $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space. It is worth mentioning that (1.21) is also satisfied at any point if the space is non-collapsed, namely $\mathfrak {m}=\mathscr {H}^N$
space. It is worth mentioning that (1.21) is also satisfied at any point if the space is non-collapsed, namely $\mathfrak {m}=\mathscr {H}^N$![]() because of the Bishop inequality, where $\mathscr {H}^N$
because of the Bishop inequality, where $\mathscr {H}^N$![]() denotes the $N$
denotes the $N$![]() -dimensional Hausdorff measure (see definition 2.4).
-dimensional Hausdorff measure (see definition 2.4).
Defining $\mathsf {b}_x$![]() by (1.5) in this setting, let us ask whether a similar rigidity result as in theorem 1.1 is justified even in this setting, or not. The main difficulty to realize this consist of two parts;
by (1.5) in this setting, let us ask whether a similar rigidity result as in theorem 1.1 is justified even in this setting, or not. The main difficulty to realize this consist of two parts;
• a priori, $|\nabla \mathsf {b}_x|$
 makes only $\mathfrak {m}$
makes only $\mathfrak {m}$ -a.e. sense;
-a.e. sense;• as observed in (1.20), in general, the constancy of $|\nabla \mathsf {b}_x|$
 does not imply an isomorphism to a Euclidean space.
does not imply an isomorphism to a Euclidean space.
The first main result in this setting are stated as follows, which allow us to overcome the first issue above.
Theorem 1.5 Pointwise properties on $|\nabla \mathsf {b}_x|$![]() ; theorems 3.15 and 3.22
; theorems 3.15 and 3.22
We have the following.
(1) (Canonical representative of $|\nabla \mathsf {b}_x|$
 ) For any $z \in X$
) For any $z \in X$ , the limit;
(1.22)\begin{equation} \lim_{r\to 0^+}{\unicode{x2A0D}}_{B_r(z)}|\nabla \mathsf{b}_x|\mathrm{d}\mathfrak{m} \in [0, \infty) \end{equation}exists. Denoting by $|\nabla \mathsf {b}_x|^*(z)$
, the limit;
(1.22)\begin{equation} \lim_{r\to 0^+}{\unicode{x2A0D}}_{B_r(z)}|\nabla \mathsf{b}_x|\mathrm{d}\mathfrak{m} \in [0, \infty) \end{equation}exists. Denoting by $|\nabla \mathsf {b}_x|^*(z)$
 (or $|\nabla \mathsf {b}_x|(z)$
(or $|\nabla \mathsf {b}_x|(z)$ for short if there is no confusion) the limit, we see that any point is a Lebesgue point of $|\nabla \mathsf {b}_x|$
for short if there is no confusion) the limit, we see that any point is a Lebesgue point of $|\nabla \mathsf {b}_x|$ , namely
(1.23)\begin{equation} \lim_{r \to 0^+}{\unicode{x2A0D}}_{B_r(z)}\left| |\nabla \mathsf{b}_x|-|\nabla \mathsf{b}_x|^*(z)\right| \mathrm{d} \mathfrak{m} =0, \quad \forall\ z \in X. \end{equation}
, namely
(1.23)\begin{equation} \lim_{r \to 0^+}{\unicode{x2A0D}}_{B_r(z)}\left| |\nabla \mathsf{b}_x|-|\nabla \mathsf{b}_x|^*(z)\right| \mathrm{d} \mathfrak{m} =0, \quad \forall\ z \in X. \end{equation}
(2) (Upper semicontinuity) The function $|\nabla \mathsf {b}_x|^*$
 is upper semicontinuous on $X$
is upper semicontinuous on $X$ .
.(3) (Sharp pointwise gradient estimate) We have
(1.24)\begin{equation} |\nabla \mathsf{b}_x|^*(z) \leqslant \mathscr C_N\nu_x^\frac{1}{N-2}, \quad \forall\ z \in X \end{equation}and (1.25)\begin{equation} |\nabla \mathsf{b}_x|^*(x)= \mathscr C_N\nu_x^\frac{1}{N-2}, \end{equation}where
(1.25)\begin{equation} |\nabla \mathsf{b}_x|^*(x)= \mathscr C_N\nu_x^\frac{1}{N-2}, \end{equation}where (1.26)\begin{equation} \mathscr C_N:=\left(N(N-2)\right)^{\frac{1}{N-2}}. \end{equation}In particular $\mathsf {b}_x$
(1.26)\begin{equation} \mathscr C_N:=\left(N(N-2)\right)^{\frac{1}{N-2}}. \end{equation}In particular $\mathsf {b}_x$
 with $\mathsf {b}_x(x):=0$
with $\mathsf {b}_x(x):=0$ is $\mathscr C_N\nu _x^\frac {1}{N-2}$
is $\mathscr C_N\nu _x^\frac {1}{N-2}$ -Lipschitz on $X$
-Lipschitz on $X$ with the (global) Lipschitz constant $\mathscr C_N\nu _x^\frac {1}{N-2}$
with the (global) Lipschitz constant $\mathscr C_N\nu _x^\frac {1}{N-2}$ .
.
Let us introduce the second main result overcoming the second issue above, see definition 2.7 for $N$![]() -metric measure cones.
-metric measure cones.
Theorem 1.6 Rigidity; theorem 4.1
If
for some $z \in X \setminus \{x\}$![]() , then $(X,\, \mathsf {d},\, \mathfrak {m})$
, then $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is isomorphic to the $N$
is isomorphic to the $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space, in particular, $|\nabla \mathsf {b}_x|^*\equiv \mathscr C_N\nu _x^\frac {1}{N-2}$
space, in particular, $|\nabla \mathsf {b}_x|^*\equiv \mathscr C_N\nu _x^\frac {1}{N-2}$![]() .
.
Combining the results above with the compactness of non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces with respect to the pmGH convergence (theorem 3.11), we obtain the following almost rigidity result
spaces with respect to the pmGH convergence (theorem 3.11), we obtain the following almost rigidity result
Theorem 1.7 Almost rigidity; theorem 4.3
For all $N >2$![]() , $0<\varepsilon <1$
, $0<\varepsilon <1$![]() , $v>0$
, $v>0$![]() , $0< r< R<\infty$
, $0< r< R<\infty$![]() and $\varphi \in L^1([0,\,\infty ),\, \mathscr {H}^1)$
and $\varphi \in L^1([0,\,\infty ),\, \mathscr {H}^1)$![]() there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, R,\, \varphi )>0$
there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, R,\, \varphi )>0$![]() such that if a pointed non-parabolic $\operatorname {RCD}(0,\, N)$
such that if a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() satisfies (1.21),
satisfies (1.21),
and
hold for some $z \in B_R(x)\setminus B_r(x)$![]() , then $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
, then $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() $\varepsilon$
$\varepsilon$![]() -pmGH close to the $N$
-pmGH close to the $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space.
space.
In particular, in theorem 1.7, if we further assume that $N$![]() is an integer and that the point $x$
is an integer and that the point $x$![]() admits an $N$
admits an $N$![]() -dimensional Euclidean tangent cone (which is trivial in the manifold case), then the $N$
-dimensional Euclidean tangent cone (which is trivial in the manifold case), then the $N$![]() -metric measure cone stated in theorem 1.7 can be replaced by the $N$
-metric measure cone stated in theorem 1.7 can be replaced by the $N$![]() -dimensional Euclidean space, which gives a positive answer to the question (Q) even in the $\operatorname {RCD}$
-dimensional Euclidean space, which gives a positive answer to the question (Q) even in the $\operatorname {RCD}$![]() setting.
setting.
In the next subsection let us provide the outlines of the proofs of the results above.
1.4. Outline of the proofs and organization of the paper
In order to prove theorem 1.5, we will study a drifted Laplace operator $\mathscr L$![]() defined by
defined by
Then we follow arguments by Colding in [Reference Colding16] to get the $\mathscr L$![]() -subharmonicity of $|\nabla \mathsf {b}_x|^2$
-subharmonicity of $|\nabla \mathsf {b}_x|^2$![]() and the ($\Delta$
and the ($\Delta$![]() -)subharmonicity of $|\nabla \mathsf {b}_x|^2G(x,\, \cdot )$
-)subharmonicity of $|\nabla \mathsf {b}_x|^2G(x,\, \cdot )$![]() (proposition 3.21) via the Bochner inequality appearing in the definition of $\operatorname {RCD}$
(proposition 3.21) via the Bochner inequality appearing in the definition of $\operatorname {RCD}$![]() spaces (see (2.8)). Combining their subharmonicities with regularity results on subharmonic functions on PI spaces [Reference Björn and Björn9] proves (1) and (2) of the theorem. To prove the remaining statements, (3), we recall that the Green function from the pole on the $N$
spaces (see (2.8)). Combining their subharmonicities with regularity results on subharmonic functions on PI spaces [Reference Björn and Björn9] proves (1) and (2) of the theorem. To prove the remaining statements, (3), we recall that the Green function from the pole on the $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space can be explicitly calculated (proposition 3.8) as in (1.20) and that any tangent cone at $x$
space can be explicitly calculated (proposition 3.8) as in (1.20) and that any tangent cone at $x$![]() whose $N$
whose $N$![]() -volume density is finite is isomorphic to such a metric measure cone (corollary 2.9) because of a result of De Philippis–Gigli [Reference De Philippis and Gigli19]. Then, combining them with blow-up arguments at the base point $x$
-volume density is finite is isomorphic to such a metric measure cone (corollary 2.9) because of a result of De Philippis–Gigli [Reference De Philippis and Gigli19]. Then, combining them with blow-up arguments at the base point $x$![]() based on the stability of the Laplacian [Reference Ambrosio and Honda3] by Ambrosio and the first named author, we obtain (3), where the $\mathscr L$
based on the stability of the Laplacian [Reference Ambrosio and Honda3] by Ambrosio and the first named author, we obtain (3), where the $\mathscr L$![]() -subharmonicity of $|\nabla \mathsf {b}_x|^2$
-subharmonicity of $|\nabla \mathsf {b}_x|^2$![]() plays a role here again.
plays a role here again.
In order to prove the rigidity result, theorem 1.6, we use the strong maximum principle for $\mathscr L$![]() -subharmonic, upper semicontinuous functions to get the constancy of $|\nabla \mathsf {b}_x|^2$
-subharmonic, upper semicontinuous functions to get the constancy of $|\nabla \mathsf {b}_x|^2$![]() . Then the explicit calculation of $\Delta \mathsf {b}_x$
. Then the explicit calculation of $\Delta \mathsf {b}_x$![]() allows us to apply a rigidity result of Gigli–Violo [Reference Gigli and Violo31] to prove theorem 1.6.
allows us to apply a rigidity result of Gigli–Violo [Reference Gigli and Violo31] to prove theorem 1.6.
Let us emphasize that under realizing the results above, we are also able to obtain a convergence result of the Green functions with respect to the pmGH convergence, in particular, as a corollary, the $W^{1,p}$![]() -strong convergence of $\mathsf {b}_x$
-strong convergence of $\mathsf {b}_x$![]() is proved for any finite $p<\infty$
is proved for any finite $p<\infty$![]() (corollary 3.23). After establishing compactness results on non-parabolic $\operatorname {RCD}(0,\, N)$
(corollary 3.23). After establishing compactness results on non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces with respect to pmGH convergence (theorem 3.11), the $W^{1,p}$
spaces with respect to pmGH convergence (theorem 3.11), the $W^{1,p}$![]() -convergence result allows us to show the almost rigidity, theorem 1.7, via a contradiction. Then the main results stated in the smooth framework, theorem 1.2 and corollary 1.3, are corollaries of the results for RCD spaces.
-convergence result allows us to show the almost rigidity, theorem 1.7, via a contradiction. Then the main results stated in the smooth framework, theorem 1.2 and corollary 1.3, are corollaries of the results for RCD spaces.
Finally we show the sharpness of theorem 1.2 via observing the $3$![]() -metric measure cone, $C(\mathbb {S}^2(r))$
-metric measure cone, $C(\mathbb {S}^2(r))$![]() for some $r<1$
for some $r<1$![]() which is close to $1$
which is close to $1$![]() , where $\mathbb {S}^2(r)$
, where $\mathbb {S}^2(r)$![]() denotes the round sphere of radius $r$
denotes the round sphere of radius $r$![]() in $\mathbb {R}^3$
in $\mathbb {R}^3$![]() centred at the origin. See subsection 5.1.
centred at the origin. See subsection 5.1.
The organization of the paper is as follows. Section 2 is devoted to fixing the notations/conventions and the introduction on $\operatorname {RCD}$![]() spaces, in particular, about $N$
spaces, in particular, about $N$![]() -metric measure cones. In § 3, we study the Green function on a non-parabolic $\operatorname {RCD}(0,\, N)$
-metric measure cones. In § 3, we study the Green function on a non-parabolic $\operatorname {RCD}(0,\, N)$![]() space, where the starting point is a work by Bruè–Semola [Reference Bruè and Semola12]. One of the main purposes in this section is to prove theorem 1.5. Section 4 is devoted to proving the rigidity/almost rigidity results. In § 5, we provide simple examples which show that our results are sharp. In the final section, § 6, we provide proofs of regularity results about $\mathscr L$
space, where the starting point is a work by Bruè–Semola [Reference Bruè and Semola12]. One of the main purposes in this section is to prove theorem 1.5. Section 4 is devoted to proving the rigidity/almost rigidity results. In § 5, we provide simple examples which show that our results are sharp. In the final section, § 6, we provide proofs of regularity results about $\mathscr L$![]() -subharmonic functions directly coming from the general theory of PI spaces [Reference Björn and Björn9]. This part makes the paper to be more self-contained.
-subharmonic functions directly coming from the general theory of PI spaces [Reference Björn and Björn9]. This part makes the paper to be more self-contained.
2. Preliminary
2.1. Notation and convention
Let us fix general conventions and geometric/analytic notations:
• We denote by $C(a_1,\,a_2,\,\ldots,\,a_k)$
 a positive constant only dependent on $a_1,\,a_2,\,\ldots,\, a_k$
a positive constant only dependent on $a_1,\,a_2,\,\ldots,\, a_k$ , which may vary from line to line unless otherwise stated.
, which may vary from line to line unless otherwise stated.• For a metric space $(X,\,\mathsf {d})$
 , denote by
, denote by
– $B_r(x):=\{y\in X\mathop |\mathsf {d}(x,\,y)< r\}$
 and $\overline {B}_r(x):=\{y\in X\mathop |\mathsf {d}(x,\,y)\leqslant r\}$
and $\overline {B}_r(x):=\{y\in X\mathop |\mathsf {d}(x,\,y)\leqslant r\}$ ;
;– $\operatorname {Lip}(X,\,\mathsf {d})$
 the collection of all Lipschitz functions on $(X,\,\mathsf {d})$
the collection of all Lipschitz functions on $(X,\,\mathsf {d})$ .
.
• We say that a triple $(X,\,\mathsf {d},\,\mathfrak {m})$
 is a metric measure space if $(X,\,\mathsf {d})$
is a metric measure space if $(X,\,\mathsf {d})$ is a complete and separable metric space and $\mathfrak {m}$
is a complete and separable metric space and $\mathfrak {m}$ is a locally finite Borel measure which is fully supported on $X$
is a locally finite Borel measure which is fully supported on $X$ .
.• Whenever we discuss on a metric measure space $(X,\,\mathsf {d},\, \mathfrak {m})$
 , we identify two objects which coincide except for a $\mathfrak {m}$
, we identify two objects which coincide except for a $\mathfrak {m}$ -negligible set.
-negligible set.• For a metric measure space $(X,\,\mathsf {d},\,\mathfrak {m})$
 , let $\mathcal {A}$
, let $\mathcal {A}$ be a collection of functions defined on an open subset $U$
be a collection of functions defined on an open subset $U$ of $X$
of $X$ . Then we denote by
. Then we denote by
– $\mathcal {A}_+:=\{f\in \mathcal {A}\mathop |f\geqslant 0\ \ \text {for }\mathfrak {m}\text {-a.e.}\}$
 ;
;– $\mathcal {A}_\mathrm {loc}:=\{f:U \to \mathbb {R} \mathop {|} {f\chi _{B_r(x)}\in \mathcal {A}} \,\text {for any }B_r(x)\text { with }\overline {B}_r(x) \subset U\}$
 ;
;– $\mathcal {A}_c:=\{f\in \mathcal {A}\mathop |\text {The support of }f,\, \operatorname {supp} f,\,\text { is compact and is included in }U\}.$

 , $\operatorname {Lip}_c(U,\,\mathsf {d})$
, $\operatorname {Lip}_c(U,\,\mathsf {d})$ , $W^{1,p}_{\mathrm {loc}}(U,\, \mathsf {d},\, \mathfrak {m})$
, $W^{1,p}_{\mathrm {loc}}(U,\, \mathsf {d},\, \mathfrak {m})$ , etc., make sense.
, etc., make sense.
2.2. Definition of $\operatorname {RCD}(K,\,N)$ space and heat kernel
space and heat kernel
Let $(X,\,\mathsf {d},\,\mathfrak {m})$![]() be a metric measure space. We define the local Lipschitz constant at $x$
be a metric measure space. We define the local Lipschitz constant at $x$![]() of a function $f$
of a function $f$![]() defined on $X$
defined on $X$![]() as follows:
as follows:
where $\mathop {\mathrm {lip}} f(x)$![]() is interpreted as $0$
is interpreted as $0$![]() if $x$
if $x$![]() is isolated. For any $f\in L^{2}(X,\, \mathfrak {m})$
is isolated. For any $f\in L^{2}(X,\, \mathfrak {m})$![]() , the Cheeger energy of $f$
, the Cheeger energy of $f$![]() is defined by
is defined by

The Sobolev space $W^{1,2}(X,\,\mathsf {d},\,\mathfrak {m})$![]() Footnote 1 is the collection of $L^2(X,\, \mathfrak {m})$
Footnote 1 is the collection of $L^2(X,\, \mathfrak {m})$![]() -functions with finite Cheeger energy, equipped with the $W^{1,2}$
-functions with finite Cheeger energy, equipped with the $W^{1,2}$![]() -norm
-norm
For any $f \in W^{1,2}(X,\, \mathsf {d},\, \mathfrak {m})$![]() , by taking a minimizing sequence $\{f_i\}_i$
, by taking a minimizing sequence $\{f_i\}_i$![]() in the right-hand-side of (2.2), we can find the optimal $L^2$
in the right-hand-side of (2.2), we can find the optimal $L^2$![]() -function denoted by $|\nabla f|$
-function denoted by $|\nabla f|$![]() , called the minimal relaxed slope of $f$
, called the minimal relaxed slope of $f$![]() , realizing the Cheeger energy, namely
, realizing the Cheeger energy, namely
We say that $(X,\,\mathsf {d},\,\mathfrak {m})$![]() is infinitesimally Hilbertian if $W^{1,2}(X,\,\mathsf {d},\,\mathfrak {m})$
is infinitesimally Hilbertian if $W^{1,2}(X,\,\mathsf {d},\,\mathfrak {m})$![]() is a Hilbert space. In this case, we set
is a Hilbert space. In this case, we set
which is symmetric and bi-linear in $\mathfrak {m}$![]() -a.e. sense (see for instance [Reference Gigli and Pasqualetto29, Theorem 4.3.3] for several equivalent definitions of infinitesimal Hilbertianity). Moreover then we can define the (linear) Laplacian as follows; we denote by $D(\Delta )$
-a.e. sense (see for instance [Reference Gigli and Pasqualetto29, Theorem 4.3.3] for several equivalent definitions of infinitesimal Hilbertianity). Moreover then we can define the (linear) Laplacian as follows; we denote by $D(\Delta )$![]() the set of all $f \in W^{1,2}(X,\, \mathsf {d},\, \mathfrak {m})$
the set of all $f \in W^{1,2}(X,\, \mathsf {d},\, \mathfrak {m})$![]() such that there exists $h\in L^2(X,\, \mathfrak {m})$
such that there exists $h\in L^2(X,\, \mathfrak {m})$![]() such that
such that
Since such $h$![]() is unique whenever it exists, we shall denote by $\Delta f$
is unique whenever it exists, we shall denote by $\Delta f$![]() . We are now in a position to give the definition of $\operatorname {RCD}$
. We are now in a position to give the definition of $\operatorname {RCD}$![]() spaces.
spaces.
Definition 2.1 $\operatorname {RCD}$![]() -space
-space
We say that $(X,\,\mathsf {d},\,\mathfrak {m})$![]() is an $\operatorname {RCD}(K,\,N)$
is an $\operatorname {RCD}(K,\,N)$![]() space for some $K\in \mathbb {R}$
space for some $K\in \mathbb {R}$![]() and $N\geqslant 1$
and $N\geqslant 1$![]() if the following four conditions are satisfied.
if the following four conditions are satisfied.
(1) (Volume growth bound) There exist $C>0$
 and $x \in X$
and $x \in X$ such that
(2.7)\begin{equation} \mathfrak{m}(B_r(x))\leqslant Ce^{Cr^2}, \quad \forall\ r>0. \end{equation}
such that
(2.7)\begin{equation} \mathfrak{m}(B_r(x))\leqslant Ce^{Cr^2}, \quad \forall\ r>0. \end{equation}
(2) (Infinitesimal Hilbertianity) $(X,\, \mathsf {d},\, \mathfrak {m})$
 is infinitesimally Hilbertian.
is infinitesimally Hilbertian.(3) (Sobolev-to-Lipschitz property) Any $f\in W^{1,2}(X,\,\mathsf {d},\,\mathfrak {m})$
 with $|\nabla f|\leqslant L$
with $|\nabla f|\leqslant L$ for $\mathfrak {m}$
for $\mathfrak {m}$ -a.e. admits an $L$
-a.e. admits an $L$ -Lipschitz representative.
-Lipschitz representative.(4) (Bochner's inequality) For any $f\in D(\Delta )$
 with $\Delta f\in W^{1,2}(X,\,\mathsf {d},\,\mathfrak {m})$
with $\Delta f\in W^{1,2}(X,\,\mathsf {d},\,\mathfrak {m})$ and any $\varphi \in D(\Delta )\cap L^\infty _+(X,\, \mathfrak {m})$
and any $\varphi \in D(\Delta )\cap L^\infty _+(X,\, \mathfrak {m})$ with $\Delta \varphi \in L^\infty (X,\, \mathfrak {m})$
with $\Delta \varphi \in L^\infty (X,\, \mathfrak {m})$ , it holds that
(2.8)\begin{equation} \frac 1 2\int_X \Delta\varphi|\nabla f|^2\, \mathrm{d}\mathfrak{m}\geqslant\int_X \varphi\left(\frac{(\Delta f)^2}{N}+\langle\nabla f,\nabla\Delta f\rangle+K|\nabla f|^2\right)\, \mathrm{d}\mathfrak{m}. \end{equation}
, it holds that
(2.8)\begin{equation} \frac 1 2\int_X \Delta\varphi|\nabla f|^2\, \mathrm{d}\mathfrak{m}\geqslant\int_X \varphi\left(\frac{(\Delta f)^2}{N}+\langle\nabla f,\nabla\Delta f\rangle+K|\nabla f|^2\right)\, \mathrm{d}\mathfrak{m}. \end{equation}
There are also several equivalent characterizations of $\operatorname {RCD}(K,\,N)$![]() -conditions, see [Reference Ambrosio, Mondino and Savaré7, Reference Cavalletti and Milman13, Reference Erbar, Kuwada and Sturm25]. We refer to [Reference Ambrosio8] as a good survey for the theory of $\operatorname {RCD}$
-conditions, see [Reference Ambrosio, Mondino and Savaré7, Reference Cavalletti and Milman13, Reference Erbar, Kuwada and Sturm25]. We refer to [Reference Ambrosio8] as a good survey for the theory of $\operatorname {RCD}$![]() spaces.
spaces.
Let us also mention that there exist local notions above, including the domain $D(\Delta,\, U)$![]() of the local Laplacian defined on an open subset $U$
of the local Laplacian defined on an open subset $U$![]() of $X$
of $X$![]() , the local Sobolev space $W^{1,2}(U,\, \mathsf {d},\, \mathfrak {m})$
, the local Sobolev space $W^{1,2}(U,\, \mathsf {d},\, \mathfrak {m})$![]() and so on.Footnote 2 In the sequel we immediately use them, see for instance [Reference Ambrosio and Honda3, Reference Björn and Björn9, Reference Heinonen, Koskela, Shanmugalingam and Tyson38] for the details.
and so on.Footnote 2 In the sequel we immediately use them, see for instance [Reference Ambrosio and Honda3, Reference Björn and Björn9, Reference Heinonen, Koskela, Shanmugalingam and Tyson38] for the details.
We here recall the precise definitions of the heat flow and the heat kernel on an $\operatorname {RCD}(K,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m})$
space $(X,\, \mathsf {d},\, \mathfrak {m})$![]() for some $K \in \mathbb {R}$
for some $K \in \mathbb {R}$![]() and some finite $N \geqslant 1$
and some finite $N \geqslant 1$![]() . For any $f \in L^2(X,\, \mathfrak {m})$
. For any $f \in L^2(X,\, \mathfrak {m})$![]() , there exists a unique locally absolutely continuous (or equivalently, smooth, in this setting, (see [Reference Gigli and Pasqualetto29])) curve $h_{\cdot }f:(0,\, \infty ) \to L^2(X,\, \mathfrak {m})$
, there exists a unique locally absolutely continuous (or equivalently, smooth, in this setting, (see [Reference Gigli and Pasqualetto29])) curve $h_{\cdot }f:(0,\, \infty ) \to L^2(X,\, \mathfrak {m})$![]() , called the heat flow starting at $f$
, called the heat flow starting at $f$![]() , such that $h_tf \to f$
, such that $h_tf \to f$![]() in $L^2(X,\, \mathfrak {m})$
in $L^2(X,\, \mathfrak {m})$![]() as $t \to 0^+$
as $t \to 0^+$![]() and that $h_tf \in D(\Delta )$
and that $h_tf \in D(\Delta )$![]() for any $t>0$
for any $t>0$![]() with
with
Then, thanks to [Reference Sturm53, Reference Sturm54] with the Bishop–Gromov inequality and the Poincaré inequality which will be explained in the next subsection 2.3, the heat flow can be written by the integral of a unique continuous kernel $p=p_X:X \times X \times (0,\, \infty ) \to (0,\, \infty )$![]() , called the heat kernel of $(X,\,\mathsf {d},\,\mathfrak {m})$
, called the heat kernel of $(X,\,\mathsf {d},\,\mathfrak {m})$![]() . Namely, for all $f\in L^2(X,\, \mathfrak {m})$
. Namely, for all $f\in L^2(X,\, \mathfrak {m})$![]() , we have $h_tf \in C(X)$
, we have $h_tf \in C(X)$![]() with
with
Note that the heat kernel $p$![]() can be characterized by using the dual heat flow $\tilde h_t$
can be characterized by using the dual heat flow $\tilde h_t$![]() acting on the space of all Borel probability measures with finite quadratic moments $\mathcal {P}_2(X)$
acting on the space of all Borel probability measures with finite quadratic moments $\mathcal {P}_2(X)$![]() ;
;
where $\mathbf {\delta }_x$![]() is the Dirac measure at $x$
is the Dirac measure at $x$![]() .
.
Let us write a formula on the heat kernel under a rescaling, which directly follows from the definition; for all $a,\, b >0$![]() , the $\operatorname {RCD}(a^{-2}K,\, N)$
, the $\operatorname {RCD}(a^{-2}K,\, N)$![]() space
space
satisfies
In order to keep our presentation short, we assume that the readers are familiar with basics on the $\operatorname {RCD}$![]() theory, including pointed measured Gromov–Hausdorff (pmGH) convergence, its metrization $\mathsf {d}_{\mathrm {pmGH}}$
theory, including pointed measured Gromov–Hausdorff (pmGH) convergence, its metrization $\mathsf {d}_{\mathrm {pmGH}}$![]() , stability/compactness of $\operatorname {RCD}$
, stability/compactness of $\operatorname {RCD}$![]() spaces with respect to $\mathsf {d}_{\mathrm {pmGH}}$
spaces with respect to $\mathsf {d}_{\mathrm {pmGH}}$![]() , and functional convergence with respect to $\mathsf {d}_{\mathrm {pmGH}}$
, and functional convergence with respect to $\mathsf {d}_{\mathrm {pmGH}}$![]() . We refer a recent nice survey [Reference Gigli35] about this topic (see also [Reference Ambrosio and Honda3, Reference Ambrosio and Honda5, Reference Gigli, Mondino and Savaré28]).
. We refer a recent nice survey [Reference Gigli35] about this topic (see also [Reference Ambrosio and Honda3, Reference Ambrosio and Honda5, Reference Gigli, Mondino and Savaré28]).
Let us end this subsection by introducing the following two notions with related results.
Definition 2.2 Tangent cone
A pointed $\operatorname {RCD}(0,\,N)$![]() space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y,\,y)$
space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y,\,y)$![]() is said to be a tangent cone of $(X,\,\mathsf {d},\,\mathfrak {m})$
is said to be a tangent cone of $(X,\,\mathsf {d},\,\mathfrak {m})$![]() at $x \in X$
at $x \in X$![]() (or tangent cone at infinity of $(X,\, \mathsf {d},\, \mathfrak {m})$
(or tangent cone at infinity of $(X,\, \mathsf {d},\, \mathfrak {m})$![]() in the case when $K=0$
in the case when $K=0$![]() , respectively) if there exists a sequence $r_i\to 0^+$
, respectively) if there exists a sequence $r_i\to 0^+$![]() (or $r_i \to \infty$
(or $r_i \to \infty$![]() , respectively) such that
, respectively) such that
Moreover a point $x \in X$![]() is called $k$
is called $k$![]() -regular if any tangent cone at $x$
-regular if any tangent cone at $x$![]() is isomorphic to the $k$
is isomorphic to the $k$![]() -dimensional Euclidean space $(\mathbb {R}^k,\, \mathsf {d}_{\mathrm {Euc}},\, \omega _k^{-1}\mathscr {H}^k,\, 0_k)$
-dimensional Euclidean space $(\mathbb {R}^k,\, \mathsf {d}_{\mathrm {Euc}},\, \omega _k^{-1}\mathscr {H}^k,\, 0_k)$![]() .
.
Remark 2.3 We often use $\frac {\mathfrak {m}}{r_i^k}$![]() for some $k \geqslant 1$
for some $k \geqslant 1$![]() instead of using $\frac {\mathfrak {m}}{\mathfrak {m} (B_{r_i}(x))}$
instead of using $\frac {\mathfrak {m}}{\mathfrak {m} (B_{r_i}(x))}$![]() in the definition above, and we also call such limit a tangent cone.
in the definition above, and we also call such limit a tangent cone.
It is proved in [Reference Bruè and Semola12] if $X$![]() is not a single point, then there exists a unique integer $k$
is not a single point, then there exists a unique integer $k$![]() at most $N$
at most $N$![]() such that for $\mathfrak {m}$
such that for $\mathfrak {m}$![]() -a.e. $x \in X$
-a.e. $x \in X$![]() , $x$
, $x$![]() is $k$
is $k$![]() -regular. We call $k$
-regular. We call $k$![]() the essential dimension of $(X,\, \mathsf {d},\, \mathfrak {m})$
the essential dimension of $(X,\, \mathsf {d},\, \mathfrak {m})$![]() (see also [Reference Colding and Naber18, Reference Deng22]). It is known that the essential dimension is at most the Hausdorff dimension, however in general they do not coincide. See [Reference Pan and Wei49]. The following is defined in [Reference De Philippis and Gigli20] as a synthetic counterpart of volume non-collapsed Ricci limit spaces.
(see also [Reference Colding and Naber18, Reference Deng22]). It is known that the essential dimension is at most the Hausdorff dimension, however in general they do not coincide. See [Reference Pan and Wei49]. The following is defined in [Reference De Philippis and Gigli20] as a synthetic counterpart of volume non-collapsed Ricci limit spaces.
Definition 2.4 Non-collapsed space
We say that $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is non-collapsed if $\mathfrak {m}=\mathscr {H}^N$
is non-collapsed if $\mathfrak {m}=\mathscr {H}^N$![]() .
.
It is known that any non-collapsed $\operatorname {RCD}$![]() space has nicer properties rather than that of general $\operatorname {RCD}$
space has nicer properties rather than that of general $\operatorname {RCD}$![]() spaces, including a fact that $N$
spaces, including a fact that $N$![]() must be an integer, and the Bishop inequality in the case when $K=0$
must be an integer, and the Bishop inequality in the case when $K=0$![]() ;
;
It is worth mentioning that $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is non-collapsed, up to multiplying a positive constant to the reference measure, if the essential dimension is equal to $N$
is non-collapsed, up to multiplying a positive constant to the reference measure, if the essential dimension is equal to $N$![]() , or $N$
, or $N$![]() is an integer with the existence of an $N$
is an integer with the existence of an $N$![]() -regular point. See [Reference Brena, Gigli, Honda and Zhu10] (and [Reference Honda40]).
-regular point. See [Reference Brena, Gigli, Honda and Zhu10] (and [Reference Honda40]).
2.3. Geometric and analytic inequalities on $\operatorname {RCD}(0,\, N)$ spaces
spaces
Let us recall several inequalities on an $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m})$
space $(X,\, \mathsf {d},\, \mathfrak {m})$![]() for some finite $N \ge 1$
for some finite $N \ge 1$![]() . Fix $x \in X$
. Fix $x \in X$![]() . The Bishop–Gromov inequality states
. The Bishop–Gromov inequality states
See [Reference Lott and Villani46] and [Reference Sturm53, Reference Sturm54] for the proof. Based on this inequality we introduce;
Definition 2.5 $N$![]() -volume density and asymptotic $N$
-volume density and asymptotic $N$![]() -volume
-volume
The $N$![]() -volume density at $x$
-volume density at $x$![]() , denoted by $\nu _x$
, denoted by $\nu _x$![]() , is defined by
, is defined by
Moreover the asymptotic $N$![]() -volume, denoted by $V_X$
-volume, denoted by $V_X$![]() , is defined by
, is defined by
Note that the Bishop–Gromov inequality (2.16) implies the existence of the both right-hand-sides of (2.17) and (2.18), that $V_X$![]() does not depend on the choice of $x\in X$
does not depend on the choice of $x\in X$![]() and that $\nu _x\ge V_X$
and that $\nu _x\ge V_X$![]() .
.
Remark 2.6 Let us provide a formula on the $N$![]() -volume density under a rescaling; for all $a,\, b >0$
-volume density under a rescaling; for all $a,\, b >0$![]() , the $N$
, the $N$![]() -volume density $\tilde \nu _{\tilde x}$
-volume density $\tilde \nu _{\tilde x}$![]() of the pointed non-parabolic $\operatorname {RCD}(0,\, N)$
of the pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(\tilde X,\, \tilde{\mathsf {d}},\, \tilde{\mathfrak {m}},\, \tilde x) :=(X,\, a\mathsf {d},\, b\mathfrak {m},\, x)$
space $(\tilde X,\, \tilde{\mathsf {d}},\, \tilde{\mathfrak {m}},\, \tilde x) :=(X,\, a\mathsf {d},\, b\mathfrak {m},\, x)$![]() satisfies
satisfies
In particular $\tilde \nu _{\tilde x}=\nu _x$![]() if $b=a^N$
if $b=a^N$![]() , which will play a role later. Note that similarly we have $V_{\tilde X}=\frac {b}{a^N}V_X$
, which will play a role later. Note that similarly we have $V_{\tilde X}=\frac {b}{a^N}V_X$![]() .
.
Next let us recall Gaussian estimates on the heat kernel $p$![]() established in [Reference Jiang, Li and Zhang43]; for any $0<\varepsilon <1$
established in [Reference Jiang, Li and Zhang43]; for any $0<\varepsilon <1$![]() , there exists $C(N,\, \varepsilon )>1$
, there exists $C(N,\, \varepsilon )>1$![]() such that
such that
and
Finally let us recall the following Poincaré inequality proved in [Reference Rajala52];

where
denotes the integral average for any measurable set $A$![]() with positive and finite measure.
with positive and finite measure.
When $N>2$![]() , the Poincaré inequality combining with the Bishop–Gromov inequality (2.16) implies the self-improved Poincaré inequality:
, the Poincaré inequality combining with the Bishop–Gromov inequality (2.16) implies the self-improved Poincaré inequality:

Moreover if $f\in W^{1,2}_0(B_r(x),\,\mathsf {d},\,\mathfrak {m})$![]() and $X$
and $X$![]() is non-compact, then we have a more convenient corollary usually referred as Sobolev inequality:
is non-compact, then we have a more convenient corollary usually referred as Sobolev inequality:

which plays a central role to get various properties on differential operators including the Laplacian and a drifted Laplace operator $\mathscr {L}$![]() in § 6. See for instance [Reference Björn and Björn9, Reference Hajłasz and Koskela37] for the details.
in § 6. See for instance [Reference Björn and Björn9, Reference Hajłasz and Koskela37] for the details.
2.4. Metric measure cone and rigidity
In this subsection, we introduce known rigidity results to an $N$![]() -metric measure cone whose definition is as follows. In the sequel, we fix a finite $N >2$
-metric measure cone whose definition is as follows. In the sequel, we fix a finite $N >2$![]() .
.
Definition 2.7 $N$![]() -metric measure cone
-metric measure cone
The ( $N$![]() -)metric measure cone $(C(Y),\,\mathsf {d}_{C(Y)},\,\mathfrak {m}_{C(Y)})$
-)metric measure cone $(C(Y),\,\mathsf {d}_{C(Y)},\,\mathfrak {m}_{C(Y)})$![]() over an $\operatorname {RCD}(N-2,\,N-1)$
over an $\operatorname {RCD}(N-2,\,N-1)$![]() space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y)$
space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y)$![]() is defined by
is defined by

where $\mathrm {d} r=\mathcal {L}^1$![]() is the $1$
is the $1$![]() -dimensional Lebesgue measure. Denote by $O_Y:=[(0,\, y)]$
-dimensional Lebesgue measure. Denote by $O_Y:=[(0,\, y)]$![]() the pole of $C(Y)$
the pole of $C(Y)$![]() .
.
Note that in the definition above, if $(Y,\, \mathsf {d}_Y,\, \mathfrak {m}_Y)$![]() is non-collapsed, then $(C(Y),\, \mathsf {d}_{C(Y)},\, \mathfrak {m}_{C(Y)})$
is non-collapsed, then $(C(Y),\, \mathsf {d}_{C(Y)},\, \mathfrak {m}_{C(Y)})$![]() is also non-collapsed because we can easily check by definition
is also non-collapsed because we can easily check by definition
This remark will play a role in subsection 5.1.
The following results are fundamental results for $N$![]() -metric measure cones, where (1) is due to [Reference Ketterer44, Corollary 1.3] and (2) is obtained in [Reference De Philippis and Gigli19, Theorem 1.1] and [Reference Gigli and Violo31, Theorem 5.1].
-metric measure cones, where (1) is due to [Reference Ketterer44, Corollary 1.3] and (2) is obtained in [Reference De Philippis and Gigli19, Theorem 1.1] and [Reference Gigli and Violo31, Theorem 5.1].
Theorem 2.8 Rigidity
We have the following.
(1) The $N$
 -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$ space is an $\operatorname {RCD}(0,\, N)$
space is an $\operatorname {RCD}(0,\, N)$ space.
space.(2) Let $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
 be a pointed $\operatorname {RCD}(0,\, N)$
be a pointed $\operatorname {RCD}(0,\, N)$ space. Then the following three conditions are equivalent:
space. Then the following three conditions are equivalent:
(a) $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
 is isomorphic to the $N$
is isomorphic to the $N$ -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$ space with the pole;
space with the pole;(b) there exists $f \in D_{\mathrm {loc}}(\Delta )$
 such that $\Delta f=2N$
such that $\Delta f=2N$ holds (in particular $f$
holds (in particular $f$ must be locally Lipschitz because of [Reference Ambrosio, Mondino and Savaré6, Reference Jiang42]), that $f$
must be locally Lipschitz because of [Reference Ambrosio, Mondino and Savaré6, Reference Jiang42]), that $f$ is positive on $X \setminus \{x\}$
is positive on $X \setminus \{x\}$ with $f(x)=0$
with $f(x)=0$ , and that $|\nabla \sqrt {2f}|^2=1$
, and that $|\nabla \sqrt {2f}|^2=1$ (moreover then $f$
(moreover then $f$ is equal to $\frac {1}{2}\mathsf {d}(x,\, \cdot )^2$
is equal to $\frac {1}{2}\mathsf {d}(x,\, \cdot )^2$ );
);(c) the function
(2.28)\begin{equation} R \mapsto \frac{\mathfrak{m}(B_R(x))}{R^N} \end{equation}is constant.
The following is a well-known result which will play a central role in the paper.
Corollary 2.9 We have the following.
(1) If an $\operatorname {RCD}(0,\, N)$
 space $(X,\, \mathsf {d},\, \mathfrak {m})$
space $(X,\, \mathsf {d},\, \mathfrak {m})$ has the finite $N$
has the finite $N$ -volume density $\nu _x<\infty$
-volume density $\nu _x<\infty$ at a point $x \in X$
at a point $x \in X$ , then any tangent cone at $x$
, then any tangent cone at $x$ is isomorphic to the $N$
is isomorphic to the $N$ -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$ space.
space.(2) If an $\operatorname {RCD}(0,\, N)$
 space $(X,\, \mathsf {d},\, \mathfrak {m})$
space $(X,\, \mathsf {d},\, \mathfrak {m})$ has the positive asymptotic $N$
has the positive asymptotic $N$ -volume $V_X>0$
-volume $V_X>0$ , then any tangent cone at infinity is isomorphic to the $N$
, then any tangent cone at infinity is isomorphic to the $N$ -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$ space.
space.
Proof. We give only a proof of (1) because (2) is similar. Denoting by $\tilde{\mathfrak {m}},\, \tilde x$![]() the reference measure, the base point, respectively on a tangent cone, it easily follows from the finiteness $\nu _x<\infty$
the reference measure, the base point, respectively on a tangent cone, it easily follows from the finiteness $\nu _x<\infty$![]() that
that
Thus (2) of theorem 2.8 allows us to conclude.
Let us recall the explicit description on the heat kernel on an $N$![]() -metirc measure cone.
-metirc measure cone.
Proposition 2.10 Let $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() be isomorphic to the $N$
be isomorphic to the $N$![]() -metric measure cone with the pole over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone with the pole over an $\operatorname {RCD}(N-2,\, N-1)$![]() space. Then we have
space. Then we have
and
where
Proof. It follows by definitions 2.5 and 2.7 that (2.30) holds. On the other hand, (2.31) is a direct consequence of [Reference Kuwada and Li45, Proposition 4.10] with (2.11) and (2) of theorem 2.8. See [Reference Huang41, Proposition 2.13] for a more general result (see also [Reference Ding23, Theorem 6.20] and [Reference Taylor55, Section 8]).
3. Green function
In this section we discuss the Green function on a non-parabolic $\operatorname {RCD}(0,\, N)$![]() space.
space.
3.1. Non-parabolic $\operatorname {RCD}(0,\, N)$ space
space
Throughout the section, we fix an $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m})$
space $(X,\, \mathsf {d},\, \mathfrak {m})$![]() for some finite $N >2$
for some finite $N >2$![]() , which is not necessarily an integer. Let us start by introducing the following fundamental notion due to [Reference Bruè and Semola12] in our framework.
, which is not necessarily an integer. Let us start by introducing the following fundamental notion due to [Reference Bruè and Semola12] in our framework.
Definition 3.1 Non-parabolic $\operatorname {RCD}(0,\,N)$![]() space
space
$(X,\, \mathsf {d},\, \mathfrak {m})$![]() is said to be non-parabolic if for some point $x\in X$
is said to be non-parabolic if for some point $x\in X$![]() (and thus for any $x\in X$
(and thus for any $x\in X$![]() ),
),
It is trivial that $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is non-parabolic if $V_X>0$
is non-parabolic if $V_X>0$![]() because of the Bishop–Gromov inequality. In the sequel we assume that $(X,\, \mathsf {d},\, \mathfrak {m})$
because of the Bishop–Gromov inequality. In the sequel we assume that $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is non-parabolic. Note that the diameter must be infinite, thus it is non-compact. Then we can define the Green function as follows.
is non-parabolic. Note that the diameter must be infinite, thus it is non-compact. Then we can define the Green function as follows.
Definition 3.2 Green function
The Green function $G=G^X$![]() of the non-parabolic $\operatorname {RCD}(0,\, N)$
of the non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m})$
space $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is defined by
is defined by

where $\mathrm {diag}(X):=\{(x,\,x) \in X \times X | x \in X\}$![]() . In the following we write $G_x^X(\cdot )=G_x(\cdot ):=G(x,\,\cdot ):X\setminus \{x\}\rightarrow (0,\, \infty )$
. In the following we write $G_x^X(\cdot )=G_x(\cdot ):=G(x,\,\cdot ):X\setminus \{x\}\rightarrow (0,\, \infty )$![]() .
.
In the sequel, we fix $x \in X$![]() . It is proved in (the proof of) [Reference Bruè and Semola12, Lemma 2.5] that $G_x$
. It is proved in (the proof of) [Reference Bruè and Semola12, Lemma 2.5] that $G_x$![]() is harmonic on $X \setminus \{x\}$
is harmonic on $X \setminus \{x\}$![]() and that $G_x \in W^{1,1}_{\mathrm {loc}}(X,\,\mathsf {d},\,\mathfrak {m})$
and that $G_x \in W^{1,1}_{\mathrm {loc}}(X,\,\mathsf {d},\,\mathfrak {m})$![]() holds with
holds with
for any $f \in D_c(\Delta )$![]() with $\Delta f \in L^{\infty }(X,\, \mathfrak {m})$
with $\Delta f \in L^{\infty }(X,\, \mathfrak {m})$![]() . In order to introduce quantitative estimates on $G_x$
. In order to introduce quantitative estimates on $G_x$![]() , let us prepare the following auxiliary functions for all $x\in X$
, let us prepare the following auxiliary functions for all $x\in X$![]() and $r\in (0,\,\infty )$
and $r\in (0,\,\infty )$![]() ;
;
It is easy to see that both $F$![]() and $H$
and $H$![]() are continuous with respect to the two variables $(x,\, r) \in X \times (0,\, \infty )$
are continuous with respect to the two variables $(x,\, r) \in X \times (0,\, \infty )$![]() . Note that Bishop–Gromov inequality (2.16) shows for any $r>0$
. Note that Bishop–Gromov inequality (2.16) shows for any $r>0$![]()
Let us provide formulae on their asymptotics.
Lemma 3.3 The following asymptotic properties hold as $r\rightarrow 0$![]() :
:
Moreover the following asymptotic properties hold as $r \to \infty$![]() :
:
where the limits of (3.8) and of (3.9) can be understood as $\infty$![]() in the case when $V_X=0$
in the case when $V_X=0$![]() .
.
Proof. We only show (3.6) under assuming $\nu _x<\infty$![]() because the others can follow from similar arguments. The Bishop–Gromov inequality (2.16) shows that the map
because the others can follow from similar arguments. The Bishop–Gromov inequality (2.16) shows that the map
is non-decreasing with $I_x(r)\geqslant 0$![]() . Thus fixing $r_0>0$
. Thus fixing $r_0>0$![]() , we have for any $0< r< r_0$
, we have for any $0< r< r_0$![]() ,
,
Write $F_x(r)$![]() as
as
Then by (3.11) the first term of the right-hand-side can be estimated as follows.
Thus

For any $\varepsilon \in (0,\,1)$![]() , we can let $r=\varepsilon r_0$
, we can let $r=\varepsilon r_0$![]() and thus
and thus

Letting $\varepsilon \rightarrow 0$![]() completes the proof of (3.6).
completes the proof of (3.6).
We are now in a position to introduce estimates on $G$![]() by $F,\, H$
by $F,\, H$![]() given in [Reference Bruè and Semola12, Proposition 2.3] after [Reference Grigor'yan36] in the smooth setting.
given in [Reference Bruè and Semola12, Proposition 2.3] after [Reference Grigor'yan36] in the smooth setting.
Proposition 3.4 There exists $C=C(N)>1$![]() such that
such that
and
Since $F_x(r)\rightarrow 0$![]() as $r\rightarrow \infty$
as $r\rightarrow \infty$![]() , we have immediately the following.
, we have immediately the following.
Corollary 3.5 We have $G_x(y)\rightarrow 0$![]() as $\mathsf {d}(x,\,y)\rightarrow \infty$
as $\mathsf {d}(x,\,y)\rightarrow \infty$![]() .
.
Let us define the main target on the paper.
Definition 3.6 Smoothed distance function $\mathsf {b}_x$![]()
Define a function $\mathsf {b}_x^X=\mathsf {b}_x$![]() on $X \setminus \{x\}$
on $X \setminus \{x\}$![]() by
by
We provide formulae related to $\mathsf {b}_x$![]() , which will play roles later.
, which will play roles later.
Lemma 3.7 We have
and
Proof. Because
and thus
where we used the fact that $G_x$![]() is harmonic on $X \setminus \{x\}$
is harmonic on $X \setminus \{x\}$![]() .
.
We give the explicit formula for the smoothed distance function for an $N$![]() -metric measure cone. Although this is well-known (see for instance [Reference Bruè, Deng and Semola11, Lemma 2.7]), let us provide a proof for readers’ convenience.
-metric measure cone. Although this is well-known (see for instance [Reference Bruè, Deng and Semola11, Lemma 2.7]), let us provide a proof for readers’ convenience.
Proposition 3.8 Green function on $N$![]() -metric measure cone
-metric measure cone
If $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() is isomorphic to the $N$
is isomorphic to the $N$![]() -metric measure cone with the pole over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone with the pole over an $\operatorname {RCD}(N-2,\, N-1)$![]() space, then we have
space, then we have
In particular
where
Proof. Thanks to proposition 2.10, we know

Finally let us provide formulae on the functions above, $F,\, G,\, H$![]() and $\mathsf {b}$
and $\mathsf {b}$![]() under rescalings, which will play roles later.
under rescalings, which will play roles later.
Lemma 3.9 For all $a,\, b>0$![]() , consider the rescaled non-parabolic $\operatorname {RCD}(0,\, N)$
, consider the rescaled non-parabolic $\operatorname {RCD}(0,\, N)$![]() space;
space;
Then the Green function $G^{\tilde X}_{\tilde x}$![]() , the corresponding auxiliary functions $F^{\tilde X}_{\tilde x},\, H^{\tilde X}_{\tilde x}$
, the corresponding auxiliary functions $F^{\tilde X}_{\tilde x},\, H^{\tilde X}_{\tilde x}$![]() , and the smoothed distance function $\mathsf {b}^{\tilde X}_x$
, and the smoothed distance function $\mathsf {b}^{\tilde X}_x$![]() of the rescaled space satisfy
of the rescaled space satisfy
and

In particular, if $b=a^N$![]() , then
, then
and
Proof. The formula for $G$![]() is a direct consequence of (2.13). Moreover it implies (3.29). On the other hand, since
is a direct consequence of (2.13). Moreover it implies (3.29). On the other hand, since

we have the desired formula for $F$![]() . Similarly we have the remaining results.
. Similarly we have the remaining results.
3.2. Convergence
In this subsection we discuss the convergence of non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces with respect to the pmGH topology. Let us introduce an elementary lemma.
spaces with respect to the pmGH topology. Let us introduce an elementary lemma.
Lemma 3.10 Let
be a pmGH convergent sequence of $\operatorname {RCD}(0,\, N)$![]() spaces for some finite $N \geqslant 1$
spaces for some finite $N \geqslant 1$![]() . Then we have
. Then we have
and
Proof. We give only a proof of (3.35) because the proof (3.34) is similar (moreover this is valid even in the case of negative lower bounds on Ricci curvature. See also [Reference Lytchak and Stadler47, Subsection 2.3]). For fixed $r>0$![]() , we have
, we have
which shows
Then letting $r \to \infty$![]() completes the proof of (3.35).
completes the proof of (3.35).
Next let us provide a compactness result as follows. In the sequel we fix a finite $N >2$![]() . Note that if $F_x(1)\le \tau <\infty$
. Note that if $F_x(1)\le \tau <\infty$![]() , then
, then
thus
This observation plays a role at the beginning of the proof of the following.
Theorem 3.11 Compactness of non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces
spaces
Let $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i, x_i)$![]() be a sequence of pointed non-parabolic $\operatorname {RCD}(0,\, N)$
be a sequence of pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces with
spaces with
and
Then after passing to a subsequence, $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i,\, x_i)$![]() pmGH converge to a pointed $\operatorname {RCD}(0,\, N)$
pmGH converge to a pointed $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() with the lower semicontinuity of $F_{x_i}$
with the lower semicontinuity of $F_{x_i}$![]() in the sense that
in the sense that
In particular $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is non-parabolic.
is non-parabolic.
Proof. Note that (3.41) gives a uniform positive lower (upper, respectively) bound on $\mathfrak {m}_i(B_1(x_i))$![]() because of (3.39). Thus, thanks to the compactness of $\operatorname {RCD}$
because of (3.39). Thus, thanks to the compactness of $\operatorname {RCD}$![]() spaces with respect to the pmGH topology (see for instance [Reference Ambrosio, Gigli and Savaré1, Theorem 6.11], [Reference Erbar, Kuwada and Sturm25, Theorem 5.3.22], [Reference Gigli, Mondino and Savaré28, Theorem 7.2], [Reference Lott and Villani46, Theorem 5.19], and [Reference Sturm53, Theorem 4.20]), after passing to a subsequence, $(X_i,\,\mathsf {d}_i,\,\mathfrak {m}_i,\,x_i)$
spaces with respect to the pmGH topology (see for instance [Reference Ambrosio, Gigli and Savaré1, Theorem 6.11], [Reference Erbar, Kuwada and Sturm25, Theorem 5.3.22], [Reference Gigli, Mondino and Savaré28, Theorem 7.2], [Reference Lott and Villani46, Theorem 5.19], and [Reference Sturm53, Theorem 4.20]), after passing to a subsequence, $(X_i,\,\mathsf {d}_i,\,\mathfrak {m}_i,\,x_i)$![]() pmGH converge to a pointed $\operatorname {RCD}(0,\, N)$
pmGH converge to a pointed $\operatorname {RCD}(0,\, N)$![]() space $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$
space $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$![]() . Observe that for all $r \leqslant s$
. Observe that for all $r \leqslant s$![]() , we have
, we have
which implies
Letting $s\rightarrow \infty$![]() , we have (3.42).
, we have (3.42).
Note that (3.40) is satisfied if
Because if $\nu _x \leqslant \nu <\infty$![]() , then
, then
by the Bishop–Gromov inequality. Compare the following theorem with [Reference Bruè, Deng and Semola11, Proposition 2.3].
Theorem 3.12 Convergence of Green functions
Let us consider a pmGH convergent sequence of pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces
spaces
Then the following conditions are equivalent.
(1) The functions $f_i(s):=\frac {s}{\mathfrak {m}_i(B_s(x_i))}$
 converge in $L^1([1,\, \infty ),\, \mathscr {H}^1)$
converge in $L^1([1,\, \infty ),\, \mathscr {H}^1)$ to the function $f(s):=\frac {s}{\mathfrak {m}(B_s(x))}$
to the function $f(s):=\frac {s}{\mathfrak {m}(B_s(x))}$ as $i \to \infty$
as $i \to \infty$ .
.(2) $F_{x_i}(1) \to F_x(1)$
 .
.(3) For any finite $p\geqslant 1$
 , $G_{x_i}$
, $G_{x_i}$ $W^{1,p}_{\mathrm {loc}}$
$W^{1,p}_{\mathrm {loc}}$ -strongly, and locally uniformly converge to $G_x$
-strongly, and locally uniformly converge to $G_x$ on $X \setminus \{x\}$
on $X \setminus \{x\}$ . Or equivalently $\mathsf {b}_{x_i}$
. Or equivalently $\mathsf {b}_{x_i}$ $W^{1,p}_{\mathrm {loc}}$
$W^{1,p}_{\mathrm {loc}}$ -strongly, and locally uniformly converge to $\mathsf {b}_x$
-strongly, and locally uniformly converge to $\mathsf {b}_x$ on $X\setminus \{x\}$
on $X\setminus \{x\}$ , where we say that a sequence of functions $f_i:X_i\setminus \{x_i\} \to \mathbb {R}$
, where we say that a sequence of functions $f_i:X_i\setminus \{x_i\} \to \mathbb {R}$ locally uniformly converge to a function $f:X \setminus \{x\} \to \mathbb {R}$
locally uniformly converge to a function $f:X \setminus \{x\} \to \mathbb {R}$ if under fixing isometric embeddings $\iota _i:X_i \hookrightarrow Y,\, \iota :X \hookrightarrow Y$
if under fixing isometric embeddings $\iota _i:X_i \hookrightarrow Y,\, \iota :X \hookrightarrow Y$ into a common proper metric space $(Y,\, \mathsf {d}_Y)$
into a common proper metric space $(Y,\, \mathsf {d}_Y)$ realizing (3.47), for any compact subset $A \subset X \setminus \{x\}$
realizing (3.47), for any compact subset $A \subset X \setminus \{x\}$ and any $\epsilon \in (0,\, 1)$
and any $\epsilon \in (0,\, 1)$ , there exist $\delta \in (0,\, 1)$
, there exist $\delta \in (0,\, 1)$ and $i_0 \in \mathbb {N}$
and $i_0 \in \mathbb {N}$ such that $|f_i(z_i)-f(z)|<\epsilon$
such that $|f_i(z_i)-f(z)|<\epsilon$ holds for all $z_i \in X_i$
holds for all $z_i \in X_i$ and $z \in A$
and $z \in A$ whenever $\mathsf {d}_Y(\iota _i(z_i),\, \iota (z))<\delta$
whenever $\mathsf {d}_Y(\iota _i(z_i),\, \iota (z))<\delta$ and $i \ge i_0$
and $i \ge i_0$ .
.
Proof. The key point is:
• it is proved in [Reference Ambrosio, Honda and Tewodrose4, Theorem 3.3] that
(3.48)\begin{equation} p_{X_i}(y_i,z_i,t_i)\to p_X(y,z,t) \end{equation}holds for all convergent sequences of $t_i \to t$
 in $(0,\, \infty )$
in $(0,\, \infty )$ and of $y_i,\, z_i \in X_i \to y, z \in X$
and of $y_i,\, z_i \in X_i \to y, z \in X$ , respectively.
, respectively.
Based on the above, let us start giving the proof. The implication from (1) to (2) is trivial. Assume that (2) holds. Thanks to (3.48) and (2.20) with the assumption, we know $\int _r^Rp_i(x_i,\, y_i,\,t)\mathrm {d} t \to \int _r^Rp(x,\, y,\, t)\mathrm {d} t$![]() and thus $F_{x_i}(R) \to F_x(R)$
and thus $F_{x_i}(R) \to F_x(R)$![]() for any $R \geqslant 1$
for any $R \geqslant 1$![]() . In particular for any $0<\varepsilon <1$
. In particular for any $0<\varepsilon <1$![]() there exists $R\geqslant 1$
there exists $R\geqslant 1$![]() such that $F_{x_i}(R) + F_x(R)<\varepsilon$
such that $F_{x_i}(R) + F_x(R)<\varepsilon$![]() for any $i$
for any $i$![]() . On the other hand, for any fixed convergent sequence $y_i \in X_i$
. On the other hand, for any fixed convergent sequence $y_i \in X_i$![]() to $y \in X$
to $y \in X$![]() with $x \neq y$
with $x \neq y$![]() , by (2.20), we know that there exists $0< r<1$
, by (2.20), we know that there exists $0< r<1$![]() such that
such that
The observation above allows us to conclude the pointwise convergence $G_{x_i}(y_i) \to G_x(y)$![]() . Then the locally uniform convergence comes from this with a locally uniform Lipschitz bound (3.17). Moreover since $G_{x_i}$
. Then the locally uniform convergence comes from this with a locally uniform Lipschitz bound (3.17). Moreover since $G_{x_i}$![]() is harmonic on $X_i\setminus \{x_i\}$
is harmonic on $X_i\setminus \{x_i\}$![]() , it follows from the stability of Laplacian, [Reference Ambrosio and Honda3, Theorem 4.4], that the $W^{1,2}_{\mathrm {loc}}$
, it follows from the stability of Laplacian, [Reference Ambrosio and Honda3, Theorem 4.4], that the $W^{1,2}_{\mathrm {loc}}$![]() -strong convergence of the Green functions holds. Finally the improvement to the $W^{1,p}_{\mathrm {loc}}$
-strong convergence of the Green functions holds. Finally the improvement to the $W^{1,p}_{\mathrm {loc}}$![]() -strong convergence is justified by combining this with (3.17) (see also [Reference Honda39]). Thus we have (3).
-strong convergence is justified by combining this with (3.17) (see also [Reference Honda39]). Thus we have (3).
Finally let us prove the remaining implication from (3) to (1). Thanks to corollary 3.5, for any $0<\varepsilon <1$![]() there exists $R\geqslant 1$
there exists $R\geqslant 1$![]() such that $G_x(y)<\varepsilon$
such that $G_x(y)<\varepsilon$![]() for any $y \in X \setminus B_{R}(x)$
for any $y \in X \setminus B_{R}(x)$![]() . Fix $y \in X \setminus B_{2R}(x)$
. Fix $y \in X \setminus B_{2R}(x)$![]() and take $y_i \in X_i$
and take $y_i \in X_i$![]() converging to $y$
converging to $y$![]() . Then our assumption allows us to conclude $G_{x_i}(y_i)<2\varepsilon$
. Then our assumption allows us to conclude $G_{x_i}(y_i)<2\varepsilon$![]() for any sufficiently large $i$
for any sufficiently large $i$![]() . Thus by (3.16), we have
. Thus by (3.16), we have
On the other hand, as discussed above, we can prove that $f_i$![]() converges in $L^1([1,\, r),\, \mathscr {H}^1)$
converges in $L^1([1,\, r),\, \mathscr {H}^1)$![]() to $f$
to $f$![]() for any finite $r>1$
for any finite $r>1$![]() . This with (3.50) implies (1) because $\varepsilon$
. This with (3.50) implies (1) because $\varepsilon$![]() is arbitrary.
is arbitrary.
Compared with theorem 3.11, it is natural to ask whether the second condition above can be replaced by a weaker one; $\sup _iF_{x_i}(1)$![]() , or not. However this improvement is impossible by observing a simple example discussed in subsection 5.2. In this sense theorem 3.11 is sharp.
, or not. However this improvement is impossible by observing a simple example discussed in subsection 5.2. In this sense theorem 3.11 is sharp.
Let us give corollaries of theorem 3.12. See also [Reference Bruè, Deng and Semola11, Corollary 2.4].
Corollary 3.13 We have
and
Proof. We prove only (3.51) via a blow-up argument because the proof of (3.52) is similar via a blow-down argument, where the case when $\nu _x=\infty$![]() or $V_X=0$
or $V_X=0$![]() directly follows from lemma 3.3 with (3.16).
directly follows from lemma 3.3 with (3.16).
Take a convergent sequence $y_i \in X \setminus \{x\} \to x$![]() , let $r_i:=\mathsf {d}(x,\, y_i)$
, let $r_i:=\mathsf {d}(x,\, y_i)$![]() and consider rescaled $\operatorname {RCD}(0,\, N)$
and consider rescaled $\operatorname {RCD}(0,\, N)$![]() spaces;
spaces;
Then since
thanks to theorem 3.11, after passing to a subsequence, $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i,\, x_i)$![]() pmGH converge to a tangent cone $(W,\, \mathsf {d}_W,\, \mathfrak {m}_W,\, w)$
pmGH converge to a tangent cone $(W,\, \mathsf {d}_W,\, \mathfrak {m}_W,\, w)$![]() at $x$
at $x$![]() , which is isomorphic to the non-parabolic $N$
, which is isomorphic to the non-parabolic $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space with the finite volume density $\nu _w=\nu _x$
space with the finite volume density $\nu _w=\nu _x$![]() (see (2.30)). By proposition 3.8 we know $F_w(1)=\frac {1}{(N-2)\nu _w} (=\lim _{i \to \infty }F_{x_i}(1)$
(see (2.30)). By proposition 3.8 we know $F_w(1)=\frac {1}{(N-2)\nu _w} (=\lim _{i \to \infty }F_{x_i}(1)$![]() by (3.54)) and
by (3.54)) and
After passing to a subsequence again, we find the limit point $z$![]() of $y_i \in X_i$
of $y_i \in X_i$![]() (thus $\mathsf {d}_W(w,\, z)=1$
(thus $\mathsf {d}_W(w,\, z)=1$![]() ). Then theorem 3.12 shows
). Then theorem 3.12 shows
which completes the proof because $y_i$![]() is arbitrary.
is arbitrary.
The next corollary gives an equi-convergent result on $\mathsf {b}$![]() . Note that this corollary can be improved later under adding a uniform upper bound on the $N$
. Note that this corollary can be improved later under adding a uniform upper bound on the $N$![]() -volume density. See corollary 3.27.
-volume density. See corollary 3.27.
Corollary 3.14 For all $N >2$![]() , $0<\varepsilon <1$
, $0<\varepsilon <1$![]() , $0< r< R<\infty$
, $0< r< R<\infty$![]() , $v>0$
, $v>0$![]() , $1 \leqslant p<\infty$
, $1 \leqslant p<\infty$![]() and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$
and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$![]() there exists $\delta =\delta (N,\,\varepsilon,\, r,\, R,\, v,\, p,\, \varphi )>0$
there exists $\delta =\delta (N,\,\varepsilon,\, r,\, R,\, v,\, p,\, \varphi )>0$![]() such that if two pointed non-parabolic $\operatorname {RCD}(0,\, N)$
such that if two pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i,\, x_i) (i=1,\,2)$
spaces $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i,\, x_i) (i=1,\,2)$![]() satisfy $\mathfrak {m}_i(B_1(x_i)) \leqslant v$
satisfy $\mathfrak {m}_i(B_1(x_i)) \leqslant v$![]() ,
,
and
then

for all $\delta r\leqslant s\leqslant (1-\delta )r$![]() and $y_i \in B_R(x_i) \setminus B_r(x_i)$
and $y_i \in B_R(x_i) \setminus B_r(x_i)$![]() satisfying that $y_1$
satisfying that $y_1$![]() $\delta$
$\delta$![]() -close to $y_2$
-close to $y_2$![]() with respect to (3.58).
with respect to (3.58).
Proof. In order to simplify our arguments below, we give a proof only in the case when $p=2$![]() because the general case is similar after replacing $W^{1,2}$
because the general case is similar after replacing $W^{1,2}$![]() -convergence by $W^{1, p_i}$
-convergence by $W^{1, p_i}$![]() -convergence for a convergent sequence $p_i \to p$
-convergence for a convergent sequence $p_i \to p$![]() .
.
The proof is done by a strandard contradiction argument based on the compactness of $\operatorname {RCD}$![]() spaces with respect to the pmGH convergence. Namely if the assertion is not satisfied, then there exist sequences of;
spaces with respect to the pmGH convergence. Namely if the assertion is not satisfied, then there exist sequences of;
• pointed non-parabolic $\operatorname {RCD}(0,\, N)$
 spaces $(X_{j, i},\, \mathsf {d}_{j, i},\, \mathfrak {m}_{j, i},\, x_{j, i})$
spaces $(X_{j, i},\, \mathsf {d}_{j, i},\, \mathfrak {m}_{j, i},\, x_{j, i})$ with $\mathfrak {m}_{j,i}(B_1 (x_{j, i}))\leqslant v$
with $\mathfrak {m}_{j,i}(B_1 (x_{j, i}))\leqslant v$ ,
(3.60)\begin{equation} f_{j, i}(s):=\frac{s}{\mathfrak{m}_{j, i}(B_s(x_{j, i}))}\leqslant \varphi(s),\quad \text{for }\mathscr{H}^1\text{-a.e. }s \in [1, \infty) \end{equation}and
,
(3.60)\begin{equation} f_{j, i}(s):=\frac{s}{\mathfrak{m}_{j, i}(B_s(x_{j, i}))}\leqslant \varphi(s),\quad \text{for }\mathscr{H}^1\text{-a.e. }s \in [1, \infty) \end{equation}and (3.61)\begin{equation} \mathsf{d}_{\mathrm{pmGH}}\left((X_{1, i}, \mathsf{d}_{1, i}, \mathfrak{m}_{1, i}, x_{1, i}), (X_{2, i}, \mathsf{d}_{2, i}, \mathfrak{m}_{2, i}, x_{2, i})\right) \to 0; \end{equation}
(3.61)\begin{equation} \mathsf{d}_{\mathrm{pmGH}}\left((X_{1, i}, \mathsf{d}_{1, i}, \mathfrak{m}_{1, i}, x_{1, i}), (X_{2, i}, \mathsf{d}_{2, i}, \mathfrak{m}_{2, i}, x_{2, i})\right) \to 0; \end{equation}
• points $y_{j, i} \in B_R(x_{j, i}) \setminus B_r(x_{j, i})$
 satisfying that $y_{1, i}$
satisfying that $y_{1, i}$ is $\varepsilon _i$
is $\varepsilon _i$ -close to $y_{2, i}$
-close to $y_{2, i}$ for some $\varepsilon _i \to 0^+$
for some $\varepsilon _i \to 0^+$ and that
(3.62)\begin{equation} \inf_i\left( \left| \mathsf{b}_{x_{1, i}}(y_{1, i})-\mathsf{b}_{x_{2, i}}(y_{2, i})\right|+\left|{\unicode{x2A0D}}_{B_s(y_{1, i})}|\nabla \mathsf{b}_{x_{1,i}}|^2\mathrm{d} \mathfrak{m}_{1, i} - {\unicode{x2A0D}}_{B_s(y_{2, i})}|\nabla \mathsf{b}_{x_{2, i}}|^2\mathrm{d} \mathfrak{m}_{2, i}\right|\right)>0. \end{equation}
and that
(3.62)\begin{equation} \inf_i\left( \left| \mathsf{b}_{x_{1, i}}(y_{1, i})-\mathsf{b}_{x_{2, i}}(y_{2, i})\right|+\left|{\unicode{x2A0D}}_{B_s(y_{1, i})}|\nabla \mathsf{b}_{x_{1,i}}|^2\mathrm{d} \mathfrak{m}_{1, i} - {\unicode{x2A0D}}_{B_s(y_{2, i})}|\nabla \mathsf{b}_{x_{2, i}}|^2\mathrm{d} \mathfrak{m}_{2, i}\right|\right)>0. \end{equation}
Theorem 3.11 shows that after passing to a subsequence, $(X_{j, i},\, \mathsf {d}_{j, i},\, \mathfrak {m}_{j, i},\, x_{j, i})$![]() pmGH-converge to a pointed non-parabolic $\operatorname {RCD}(0,\, N)$
pmGH-converge to a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() . With no loss of generality we can assume that $y_{j, i}$
. With no loss of generality we can assume that $y_{j, i}$![]() converge to a point $y \in \overline {B}_R(x) \setminus B_r(x)$
converge to a point $y \in \overline {B}_R(x) \setminus B_r(x)$![]() . Moreover the dominated convergence theorem with (3.60) yields that $f_{j,i}(s)$
. Moreover the dominated convergence theorem with (3.60) yields that $f_{j,i}(s)$![]() $L^1$
$L^1$![]() -strongly converge to $f(s):=\frac {s}{\mathfrak {m} (B_s(x))}$
-strongly converge to $f(s):=\frac {s}{\mathfrak {m} (B_s(x))}$![]() in $L^1([1,\, \infty ),\, \mathscr {H}^1)$
in $L^1([1,\, \infty ),\, \mathscr {H}^1)$![]() . Thus theorem 3.12 allows us to conclude
. Thus theorem 3.12 allows us to conclude

which contradicts (3.62).
3.3. Canonical representative of $|\nabla \mathsf {b}_x|$ and drifted Laplace operator $\mathscr L$
and drifted Laplace operator $\mathscr L$
Throughout this subsection we continue to argue under the same assumptions as in the previous subsection, namely we fix a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() . A main result of this subsection is the following.
. A main result of this subsection is the following.
Theorem 3.15 Canonical pointwise representative of $|\nabla \mathsf {b}_x|$![]()
The limit
exists for any $z \in X \setminus \{x\}$![]() . Denoting by $|\nabla \mathsf {b}_x|^*(z)$
. Denoting by $|\nabla \mathsf {b}_x|^*(z)$![]() the square root of the limit, we have the following.
the square root of the limit, we have the following.
(1) $|\nabla \mathsf {b}_x|^*$
 is upper semicontinuous.
is upper semicontinuous.(2) Any point $z \in X \setminus \{x\}$
 is a Lebesgue point of $|\nabla \mathsf {b}_x|^*$
is a Lebesgue point of $|\nabla \mathsf {b}_x|^*$ ;
(3.65)\begin{equation} {\unicode{x2A0D}}_{B_r(z)}\left||\nabla \mathsf{b}_x|^*-|\nabla \mathsf{b}_x|^*(z)\right|\mathrm{d} \mathfrak{m} \to 0. \end{equation}
;
(3.65)\begin{equation} {\unicode{x2A0D}}_{B_r(z)}\left||\nabla \mathsf{b}_x|^*-|\nabla \mathsf{b}_x|^*(z)\right|\mathrm{d} \mathfrak{m} \to 0. \end{equation}
(3) We see that
(3.66)\begin{equation} |\nabla \mathsf{b}_x|^*(z)=\limsup_{y\rightarrow z} |\nabla \mathsf{b}_x|^*(y),\quad \forall z\in X \setminus \{x\}. \end{equation}
It is worth mentioning that in the proof of the theorem above, we immediately show
Actually theorem 3.15 with (3.67) is a direct consequence of the subharmonicity of $|\nabla \mathsf {b}_x|^2G_x$![]() stated in proposition 3.21 and general results on PI spaces in [Reference Björn and Björn9, Section 8.5]. Thus in the rest of this subsection, we focus on introducing the subharmonicity and its drifted ones which play important roles later.
stated in proposition 3.21 and general results on PI spaces in [Reference Björn and Björn9, Section 8.5]. Thus in the rest of this subsection, we focus on introducing the subharmonicity and its drifted ones which play important roles later.
Remark 3.16 Let us recall the following well-known fact; if $x$![]() is a Lebesgue point of a locally bounded function $f$
is a Lebesgue point of a locally bounded function $f$![]() defined on an open subset $U$
defined on an open subset $U$![]() of a PI space $(X,\, \mathsf {d},\, \mathfrak {m})$
of a PI space $(X,\, \mathsf {d},\, \mathfrak {m})$![]() , then
, then
for all $\varphi,\, \psi \in C(\mathbb {R})$![]() with $\psi (0)=0$
with $\psi (0)=0$![]() . In particular $x$
. In particular $x$![]() is also a Lebesgue point of $\varphi \circ f$
is also a Lebesgue point of $\varphi \circ f$![]() . In order to prove the theorem above, we will apply this fact as $f=|\nabla \mathsf {b}_x|^2$
. In order to prove the theorem above, we will apply this fact as $f=|\nabla \mathsf {b}_x|^2$![]() , $\varphi (t)=\sqrt {|t|}$
, $\varphi (t)=\sqrt {|t|}$![]() and $\psi (t)=|t|$
and $\psi (t)=|t|$![]() with the following arguments.
with the following arguments.
Consider the following drifted Laplace operator $\mathscr L$![]() by
by
See definition 3.18 for the precise definition. It should be emphasized that Colding studied $\mathscr L$![]() in [Reference Colding16] deeply in the smooth framework in order to prove the pointwise rigidity result, (2) of theorem 1.1 (see [Reference Colding and Minicozzi17] for applications).
in [Reference Colding16] deeply in the smooth framework in order to prove the pointwise rigidity result, (2) of theorem 1.1 (see [Reference Colding and Minicozzi17] for applications).
In the sequel, we follow his arguments, but extra delicate treatments on $\mathscr L$![]() are necessary in our setting because of lack of the smoothness. Firstly let us estimate the drifted term of (3.69) as follows.
are necessary in our setting because of lack of the smoothness. Firstly let us estimate the drifted term of (3.69) as follows.
Proposition 3.17 We have
In particular
Proof. By theorem 3.4,
On the other hand by definition we have
Combining this with (3.72) completes the proof.
Let us recall the sub/super harmonicity of a function $f$![]() on an open subset $\Omega$
on an open subset $\Omega$![]() of $X$
of $X$![]() . We say that $f$
. We say that $f$![]() is sub (or super, respectively) harmonic on $\Omega$
is sub (or super, respectively) harmonic on $\Omega$![]() if $f \in W^{1,2}_{\mathrm {loc}}(\Omega,\, \mathsf {d},\, \mathfrak {m})$
if $f \in W^{1,2}_{\mathrm {loc}}(\Omega,\, \mathsf {d},\, \mathfrak {m})$![]() with
with
for any $\varphi \in (\mathrm {Lip}_c)_+(\Omega,\, \mathsf {d})$![]() . It directly follows that $f$
. It directly follows that $f$![]() is sub (or super, respectively) harmoninc on $\Omega$
is sub (or super, respectively) harmoninc on $\Omega$![]() if $f \in D_{\mathrm {loc}}(\Delta,\, \Omega )$
if $f \in D_{\mathrm {loc}}(\Delta,\, \Omega )$![]() with $\Delta f \geqslant 0$
with $\Delta f \geqslant 0$![]() (or $\Delta f \leqslant 0$
(or $\Delta f \leqslant 0$![]() , respectively). See also [Reference Peng, Zhang and Zhu50].
, respectively). See also [Reference Peng, Zhang and Zhu50].
Based on this observation, we are now in a position to define the $\mathscr L$![]() -operator precisely as follows.
-operator precisely as follows.
Definition 3.18 $\mathscr L$![]() -operator and $\mathscr L$
-operator and $\mathscr L$![]() -sub/super harmonicity
-sub/super harmonicity
Let $\Omega$![]() be an open subset in $X \setminus \{x\}$
be an open subset in $X \setminus \{x\}$![]() .
.
(1) ($\mathscr L$
 -operator) For $u \in D_{\mathrm {loc}}(\Delta,\,\Omega )$
-operator) For $u \in D_{\mathrm {loc}}(\Delta,\,\Omega )$ , let
(3.75)\begin{equation} \mathscr Lu:=\Delta u+2\langle\nabla\log G_x,\nabla u\rangle \in L^2_{\mathrm{loc}}(\Omega, \mathfrak{m}). \end{equation}
, let
(3.75)\begin{equation} \mathscr Lu:=\Delta u+2\langle\nabla\log G_x,\nabla u\rangle \in L^2_{\mathrm{loc}}(\Omega, \mathfrak{m}). \end{equation}
(2) ($\mathscr L$
 -sub/super harmonicity) A function $u \in W^{1,2}_{\mathrm {loc}}(\Omega,\, \mathsf {d},\, \mathfrak {m})$
-sub/super harmonicity) A function $u \in W^{1,2}_{\mathrm {loc}}(\Omega,\, \mathsf {d},\, \mathfrak {m})$ is said to be $\mathscr L$
is said to be $\mathscr L$ -sub (or super, respectively) harmonic on $\Omega$
-sub (or super, respectively) harmonic on $\Omega$ if
(3.76)\begin{equation} \int_\Omega -\langle\nabla u,\nabla \varphi\rangle\mathrm{d}\mathfrak{m}_{G_x}\geqslant 0,\quad \text{(or }\leqslant 0,\text{ respectively)} \end{equation}for any $\varphi \in (\mathrm {Lip}_c)_+(\Omega,\, \mathsf {d})$
if
(3.76)\begin{equation} \int_\Omega -\langle\nabla u,\nabla \varphi\rangle\mathrm{d}\mathfrak{m}_{G_x}\geqslant 0,\quad \text{(or }\leqslant 0,\text{ respectively)} \end{equation}for any $\varphi \in (\mathrm {Lip}_c)_+(\Omega,\, \mathsf {d})$
 , where $\mathfrak {m}_{G_x}$
, where $\mathfrak {m}_{G_x}$ is the weighted Borel measure on $X$
is the weighted Borel measure on $X$ defined by
(3.77)\begin{equation} \mathfrak{m}_{G_x}(A):=\int_AG_x^2\mathrm{d} \mathfrak{m}. \end{equation}
defined by
(3.77)\begin{equation} \mathfrak{m}_{G_x}(A):=\int_AG_x^2\mathrm{d} \mathfrak{m}. \end{equation}
Remark 3.19 The $\mathscr L$![]() -operator can be defined as a measure valued one; for any $u \in D(\mathbf \Delta,\, \Omega )$
-operator can be defined as a measure valued one; for any $u \in D(\mathbf \Delta,\, \Omega )$![]() , define
, define
where $D(\mathbf \Delta,\, \Omega )$![]() is the domain of the measure valued Laplacian, see [Reference Gigli and Pasqualetto29, Reference Gigli34] for the detail. Then, even in the measure valued case, $\mathscr L$
is the domain of the measure valued Laplacian, see [Reference Gigli and Pasqualetto29, Reference Gigli34] for the detail. Then, even in the measure valued case, $\mathscr L$![]() -sub/super harmonicity are also well-defined, and weak/strong maximum principles are justified. See also [Reference Gigli and Rigoni30, Reference Gigli and Violo31]. Although we avoid to use the measure valued Laplacian/$\mathscr L$
-sub/super harmonicity are also well-defined, and weak/strong maximum principles are justified. See also [Reference Gigli and Rigoni30, Reference Gigli and Violo31]. Although we avoid to use the measure valued Laplacian/$\mathscr L$![]() -operator for simplicity in our presentation, however, for our main target in the sequel, $|\nabla \mathsf {b}_x|^2$
-operator for simplicity in our presentation, however, for our main target in the sequel, $|\nabla \mathsf {b}_x|^2$![]() , the measure valued $\mathscr L$
, the measure valued $\mathscr L$![]() -operator, $\mathscr {L}|\nabla \mathsf {b}_x|^2$
-operator, $\mathscr {L}|\nabla \mathsf {b}_x|^2$![]() is well-defined.
is well-defined.
In connection with this, it is easy to see that $u$![]() is $\mathscr L$
is $\mathscr L$![]() -sub (or $\mathscr L$
-sub (or $\mathscr L$![]() -super, respectively) harmonic on $\Omega$
-super, respectively) harmonic on $\Omega$![]() if and only if for any $\varphi \in (\mathrm {Lip}_c)_+(\Omega,\, \mathsf {d})$
if and only if for any $\varphi \in (\mathrm {Lip}_c)_+(\Omega,\, \mathsf {d})$![]() ,
,
This observation will be a starting point in § 6.
Let us introduce a standard integration-by-parts formula for $\mathfrak {m}_{G_x}$![]() .
.
Proposition 3.20 Let $\Omega$![]() be an open subset in $X \setminus \{x\}$
be an open subset in $X \setminus \{x\}$![]() and let $u \in D_{\mathrm {loc}}(\Delta,\,\Omega )$
and let $u \in D_{\mathrm {loc}}(\Delta,\,\Omega )$![]() . Then
. Then
for any $\varphi \in \mathrm {Lip}_c(\Omega,\, \mathsf {d})$![]() . In particular $u$
. In particular $u$![]() is $\mathscr L$
is $\mathscr L$![]() -sub (or super, respectively) harmonic on $\Omega$
-sub (or super, respectively) harmonic on $\Omega$![]() if $\mathscr L u \geqslant 0$
if $\mathscr L u \geqslant 0$![]() (or $\mathscr L u \leqslant 0$
(or $\mathscr L u \leqslant 0$![]() , respectively).
, respectively).
Proof. The proof is quite standard;

We are now in a position to prove a main result in this subsection, recall that the subharmonicity of $|\nabla \mathsf {b}_x|^2G_x$![]() with results in [Reference Björn and Björn9, Section 8.5] implies theorem 3.15 (we can find the corresponding regularity results for the $\mathscr L$
with results in [Reference Björn and Björn9, Section 8.5] implies theorem 3.15 (we can find the corresponding regularity results for the $\mathscr L$![]() -operator in § 6).
-operator in § 6).
Proposition 3.21 Subharmonicity of gradient of $\mathsf {b}_x$![]()
We see that $|\nabla \mathsf {b}_x|^2G_x$![]() is subharmonic on $X \setminus \{x\}$
is subharmonic on $X \setminus \{x\}$![]() and that $|\nabla \mathsf {b}_x|^2$
and that $|\nabla \mathsf {b}_x|^2$![]() is $\mathscr L$
is $\mathscr L$![]() -subharmonic on $X \setminus \{x\}$
-subharmonic on $X \setminus \{x\}$![]() .
.
Proof. First of all, we claim that $|\nabla \mathsf {b}_x|^2\in W^{1,2}_{\mathrm {loc}}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$![]() . For any compact set $K\subset X\setminus \{x\}$
. For any compact set $K\subset X\setminus \{x\}$![]() , we can take a good cut-off function $\eta \in (\operatorname {Lip}_c)_+(X,\, \mathsf {d})\cap D(\Delta )$
, we can take a good cut-off function $\eta \in (\operatorname {Lip}_c)_+(X,\, \mathsf {d})\cap D(\Delta )$![]() such that $\eta \equiv 1$
such that $\eta \equiv 1$![]() in $K$
in $K$![]() , $\operatorname {supp}\eta \subset X\setminus \{x\}$
, $\operatorname {supp}\eta \subset X\setminus \{x\}$![]() and $|\nabla \eta |+|\Delta \eta |< C$
and $|\nabla \eta |+|\Delta \eta |< C$![]() (see [Reference Mondino and Naber48, Lemma 3.2] for such an existence). Letting $h:=\eta \mathsf {b}_x$
(see [Reference Mondino and Naber48, Lemma 3.2] for such an existence). Letting $h:=\eta \mathsf {b}_x$![]() , then [Reference Gigli34, Propositions 3.3.18 and 3.3.22] shows that $|\nabla h|^2\in W^{1,2}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$
, then [Reference Gigli34, Propositions 3.3.18 and 3.3.22] shows that $|\nabla h|^2\in W^{1,2}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$![]() , which implies $|\nabla \mathsf {b}_x|^2\in W^{1,2}_{\mathrm {loc}}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$
, which implies $|\nabla \mathsf {b}_x|^2\in W^{1,2}_{\mathrm {loc}}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$![]() because $K$
because $K$![]() is arbitrary.
is arbitrary.
Next recalling

for all $\psi \in \mathrm {Lip}_c(X\setminus \{x\},\, \mathsf {d})$![]() , $f \in D_{\mathrm {loc}}(\Delta,\, X\setminus \{x\})$
, $f \in D_{\mathrm {loc}}(\Delta,\, X\setminus \{x\})$![]() and $h \in W^{1,2}_{\mathrm {loc}}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$
and $h \in W^{1,2}_{\mathrm {loc}}(X\setminus \{x\},\, \mathsf {d},\, \mathfrak {m})$![]() , we apply this as $f=\mathsf {b}_x^2,\, h=|\nabla \mathsf {b}_x|^2$
, we apply this as $f=\mathsf {b}_x^2,\, h=|\nabla \mathsf {b}_x|^2$![]() to get
to get

where we used (3.20). On the other hand, since $\mathsf {b}_x^2|\nabla \mathsf {b}_x|^2=\frac {|\nabla \mathsf {b}_x^2|^2}{4}$![]() , the Bochner inequality allows us to estimate the left-hand-side above as follows;
, the Bochner inequality allows us to estimate the left-hand-side above as follows;

where we used (3.20) again. Therefore it follows from (3.83) and (3.84) that
Let us prove that this inequality (3.85) implies the conclusions. Actually as done in (3.83) and (3.84), it follows from Leibniz’ rule thatFootnote 3

holds, where $\varphi =\mathsf {b}_x^{-2}G_x^2\psi$![]() , which proves the $\mathscr L$
, which proves the $\mathscr L$![]() -subharmonicity of $|\nabla \mathsf {b}_x|^2$
-subharmonicity of $|\nabla \mathsf {b}_x|^2$![]() on $X\setminus \{x\}$
on $X\setminus \{x\}$![]() .
.
Similarly we haveFootnote 4

where $\varphi =\psi \mathsf {b}_x^{-N}$![]() , which proves the subharmonicity of $|\nabla \mathsf {b}_x|^2G_x$
, which proves the subharmonicity of $|\nabla \mathsf {b}_x|^2G_x$![]() on $X \setminus \{x\}$
on $X \setminus \{x\}$![]() .
.
In the sequel, we will use the simplified notation $|\nabla \mathsf {b}_x|=|\nabla \mathsf {b}_x|^*$![]() for the simplicity on our presentations. In § 6, we will also provide the fundamental properties on the $\mathscr L$
for the simplicity on our presentations. In § 6, we will also provide the fundamental properties on the $\mathscr L$![]() -operator with the proofs, including the strong maximum principle, which comes from the general theory on PI spaces. They will play important roles in the sequel.
-operator with the proofs, including the strong maximum principle, which comes from the general theory on PI spaces. They will play important roles in the sequel.
3.4 Sharp gradient estimate on $\mathsf {b}_x$
Fix a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() and assume that the $N$
and assume that the $N$![]() -volume density $\nu _x$
-volume density $\nu _x$![]() at $x$
at $x$![]() is finite;
is finite;
Note that this condition does not imply that the essential dimension is equal to $N$![]() because of an example; $([0,\,\infty ),\, \mathsf {d}_{\mathrm {Euc}},\, r^{N-1}\mathrm {d} r)$
because of an example; $([0,\,\infty ),\, \mathsf {d}_{\mathrm {Euc}},\, r^{N-1}\mathrm {d} r)$![]() is an $\operatorname {RCD}(0,\, N)$
is an $\operatorname {RCD}(0,\, N)$![]() space with the finite $N$
space with the finite $N$![]() -volume density at the origin.
-volume density at the origin.
The main result of this section is the following. Recall $\mathscr C_N=(N(N-2))^{\frac {1}{N-2}}$![]() .
.
Theorem 3.22 Sharp gradient estimate of $\mathsf {b}_x$![]()
We have
Proof. The proof is divided into several steps as follows.
Step 1. Let us prove that $|\nabla \mathsf {b}_x|\in L^\infty (X,\,\mathfrak {m})$![]() . By calculus rules
. By calculus rules
Let

Plugging in (3.51), (3.17) and (3.7) we see that
Thus we can take $r$![]() sufficiently small such that
sufficiently small such that
On the other hand, combining (3.92) with theorem 3.4 yields that for $\mathfrak {m}$![]() -a.e. $y\in X\setminus \{x\}$
-a.e. $y\in X\setminus \{x\}$![]() , we have
, we have
Note that it holds that $sH_x(s)\leqslant F_x(s)$![]() for any $s\in [1,\,\infty )$
for any $s\in [1,\,\infty )$![]() . Thus, choosing $R$
. Thus, choosing $R$![]() sufficiently large, then for any $y\in X\setminus B_R(x)$
sufficiently large, then for any $y\in X\setminus B_R(x)$![]() , we have
, we have

because of (3.8). Moreover it follows from the continuity of right-hand-side of (3.96) that $|\nabla \mathsf {b}_x|$![]() is bounded $\mathfrak {m}$
is bounded $\mathfrak {m}$![]() -a.e. in $\overline {B_R(x)}\setminus B_r(x)$
-a.e. in $\overline {B_R(x)}\setminus B_r(x)$![]() , which is a compact subset. Therefore $|\nabla \mathsf {b}_x|\in L^\infty (X,\,\mathfrak {m})$
, which is a compact subset. Therefore $|\nabla \mathsf {b}_x|\in L^\infty (X,\,\mathfrak {m})$![]() .
.
Step 2. Let us prove that $|\nabla \mathsf {b}_x|(y) \le C_{\mathrm {opt},\, x}$![]() for any $y \in X \setminus \{x\}$
for any $y \in X \setminus \{x\}$![]() .
.
Fix $0< r< R$![]() and choose arbitrarily $\varepsilon >0$
and choose arbitrarily $\varepsilon >0$![]() . By corollary 3.5, we can find $R_0>R$
. By corollary 3.5, we can find $R_0>R$![]() sufficiently large such that
sufficiently large such that
Take $0< r_0< r$![]() with
with
Let $L:=\big \||\nabla \mathsf {b}_x|\big \|_{L^\infty (X,\mathfrak {m})}$![]() and set
and set
which is upper semicontinuous and subharmonic on $X\setminus \{x\}$![]() because of proposition 3.21.
because of proposition 3.21.
Let $\Omega :=B_{R_0}(x)\setminus \overline {B_{r_0}(x)}$![]() . Applying the weak maximum principle for upper semicontinuous subharmonic functions [Reference Gigli and Violo31, Proposition 1.15], we see that
. Applying the weak maximum principle for upper semicontinuous subharmonic functions [Reference Gigli and Violo31, Proposition 1.15], we see that
which proves
This observation allows us to conclude that $|\nabla \mathsf {b}_x| \leqslant C_{\mathrm {opt},\, x}$![]() for $\mathfrak {m}$
for $\mathfrak {m}$![]() -a.e. after letting $\varepsilon \to 0^+$
-a.e. after letting $\varepsilon \to 0^+$![]() under fixing $r,\, R$
under fixing $r,\, R$![]() . Thus by theorem 3.15 we know that $|\nabla \mathsf {b}_x|(y) \leqslant C_{\mathrm {opt},\, x}$
. Thus by theorem 3.15 we know that $|\nabla \mathsf {b}_x|(y) \leqslant C_{\mathrm {opt},\, x}$![]() for any $y \in X \setminus \{x\}$
for any $y \in X \setminus \{x\}$![]() .
.
Step 3. We claim that $C_{\mathrm {opt},\, x}=\mathscr C_N\nu _x^{\frac {1}{N-2}}$![]() , where this completes the proof. Thanks to (2.30), proposition 3.8 and theorem 3.12, we know that for any $0<\delta <1$
, where this completes the proof. Thanks to (2.30), proposition 3.8 and theorem 3.12, we know that for any $0<\delta <1$![]()
Take $y_i \to x$![]() satisfying $|\nabla \mathsf {b}_x|(y_i) \to C_{\mathrm {opt},\, x}$
satisfying $|\nabla \mathsf {b}_x|(y_i) \to C_{\mathrm {opt},\, x}$![]() and let $r_i:=\mathsf {d}(x,\, y_i)$
and let $r_i:=\mathsf {d}(x,\, y_i)$![]() and consider rescaled spaces;
and consider rescaled spaces;
Applying the weak Harnack inequality for $\mathscr L$![]() -superharmonic functions, proposition 6.5, to a lower semicontinuous $\mathscr L$
-superharmonic functions, proposition 6.5, to a lower semicontinuous $\mathscr L$![]() -superharmonic function $C_{\mathrm {opt},\, x}^2-|\nabla \mathsf {b}_{x}^{X_i}|^2 \geqslant 0$
-superharmonic function $C_{\mathrm {opt},\, x}^2-|\nabla \mathsf {b}_{x}^{X_i}|^2 \geqslant 0$![]() , we have
, we have

where $p=p(N)>0$![]() . Thus recalling $|\nabla \mathsf {b}_x| \in L^{\infty }(X\setminus \{x\},\, \mathfrak {m})$
. Thus recalling $|\nabla \mathsf {b}_x| \in L^{\infty }(X\setminus \{x\},\, \mathfrak {m})$![]() , it holds that
, it holds that

namely

On the other hand, (3.103) implies

Thus by (3.107) and (3.108) we have $C_{\mathrm {opt},\, x}=\mathscr C_N\nu _x^{\frac {1}{N-2}}$![]() .
.
We provide direct consequences of theorem 3.22. Firstly we improve theorems 3.12 and 3.15 removing the singular base point.
Corollary 3.23 Improvement of the convergence of $\mathsf {b}$![]()
Let us consider a pmGH convergent sequence of pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces
spaces
with (3.45) and $F_{x_i}(1) \to F_x(1)$![]() . Then $\mathsf {b}_{x_i}$
. Then $\mathsf {b}_{x_i}$![]() $W^{1,p}_{\mathrm {loc}}$
$W^{1,p}_{\mathrm {loc}}$![]() -strongly, and locally uniformly converge to $\mathsf {b}_x$
-strongly, and locally uniformly converge to $\mathsf {b}_x$![]() on $X$
on $X$![]() for any $p<\infty$
for any $p<\infty$![]() .
.
Proof. Note

Since the right-hand-side of (3.110) is small if $\varepsilon$![]() is small, combining this with theorem 3.12 completes the proof.
is small, combining this with theorem 3.12 completes the proof.
Corollary 3.24 Let $\mathsf {b}_x(x):=0$![]() . Then $\mathsf {b}_x$
. Then $\mathsf {b}_x$![]() is $\mathscr C_N\nu _x^{\frac {1}{N-2}}$
is $\mathscr C_N\nu _x^{\frac {1}{N-2}}$![]() -Lipschitz with the Lipschitz constant $\mathscr C_N\nu _x^{\frac {1}{N-2}}$
-Lipschitz with the Lipschitz constant $\mathscr C_N\nu _x^{\frac {1}{N-2}}$![]() . Moreover letting
. Moreover letting
we have the same conclusions as in theorem 3.15 with (3.67) even for the base point $z=x$![]() . More strongly, we have for any $p<\infty$
. More strongly, we have for any $p<\infty$![]() .
.
In particular, $|\nabla \mathsf {b}_x|(y_i) \to \mathscr C_N\nu _x^{\frac {1}{N-2}}$![]() for some convergent sequence $y_i \to x$
for some convergent sequence $y_i \to x$![]() .
.
Proof. Thanks to (3.16) and (3.6), putting $\mathsf {b}_x(x):=0$![]() gives a unique continuous extention of $\mathsf {b}_x$
gives a unique continuous extention of $\mathsf {b}_x$![]() on $X$
on $X$![]() . Since $\{x\}$
. Since $\{x\}$![]() is null with respect to the $2$
is null with respect to the $2$![]() -Sobolev capacity because of the finiteness of $\nu _x$
-Sobolev capacity because of the finiteness of $\nu _x$![]() (see [Reference Björn and Björn9]), we know $\mathsf {b}_x \in W^{1, 2}_{\mathrm {loc}}(X,\, \mathsf {d},\, \mathfrak {m})$
(see [Reference Björn and Björn9]), we know $\mathsf {b}_x \in W^{1, 2}_{\mathrm {loc}}(X,\, \mathsf {d},\, \mathfrak {m})$![]() . Then the first statement comes from arguments in the last step in the proof of theorem 3.22 with the (local) Sobolev-to-Lipschitz property and corollary 3.23. Moreover corollary 3.23 with proposition 3.8 allows us to obtain (3.112).
. Then the first statement comes from arguments in the last step in the proof of theorem 3.22 with the (local) Sobolev-to-Lipschitz property and corollary 3.23. Moreover corollary 3.23 with proposition 3.8 allows us to obtain (3.112).
As the final application of theorem 3.22, we determine the small scale asymptotics of the gradient of the Green function.
Corollary 3.25 We have
Proof. Since (3.51), (3.92) and corollary 3.24 yield (under a suitable limit $y \to x$![]() )
)

we conclude.
Next we provide an asymptotic formula as $y \to \infty$![]() .
.
Corollary 3.26 Sharp gradient asymptotics
For any $p<\infty$![]() we have
we have
therefore
In particular
equivalently
holds for some sequence $y_i \in X$![]() with $\mathsf {d}(x,\, y_i) \to \infty$
with $\mathsf {d}(x,\, y_i) \to \infty$![]() .
.
Proof. Firstly we discuss the case when $V_X=0$![]() . Then we can follow the same arguments as in the proof of [Reference Colding16, Theorem 2.12]. Namely we can estimate as $\mathsf {d}(x,\, y) \to \infty$
. Then we can follow the same arguments as in the proof of [Reference Colding16, Theorem 2.12]. Namely we can estimate as $\mathsf {d}(x,\, y) \to \infty$![]() ,
,

where we used the gradient estimates on positive harmonic functions obtained in [Reference Jiang42, Theorem 1.2] in the first inequality above and we also used (3.8) and (3.16) in the last inequality and in the limit. Thus we obtain the conclusion in this case.
Next we consider the case when $V_X>0$![]() . The first statement, (3.115), is a direct consequence of corollary 3.23 and (2) of corollary 2.9. The remaining one (3.117) (or (3.118)) follows from an argument similar to the proof of corollary 3.25.
. The first statement, (3.115), is a direct consequence of corollary 3.23 and (2) of corollary 2.9. The remaining one (3.117) (or (3.118)) follows from an argument similar to the proof of corollary 3.25.
Based on corollary 3.23, we can prove the following whose proof is the same to that of corollary 3.14. Thus we omit the proof.
Corollary 3.27 For all $N >2$![]() , $0<\varepsilon <1$
, $0<\varepsilon <1$![]() , $0<\tau <1$
, $0<\tau <1$![]() , $v>0$
, $v>0$![]() , $1 \leqslant p<\infty$
, $1 \leqslant p<\infty$![]() and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$
and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$![]() there exists $\delta =\delta (N,\,\varepsilon,\, \tau,\, v,\, p,\, \varphi )>0$
there exists $\delta =\delta (N,\,\varepsilon,\, \tau,\, v,\, p,\, \varphi )>0$![]() such that if two pointed non-parabolic $\operatorname {RCD}(0,\, N)$
such that if two pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() spaces $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i,\, x_i) (i=1,\,2)$
spaces $(X_i,\, \mathsf {d}_i,\, \mathfrak {m}_i,\, x_i) (i=1,\,2)$![]() satisfy $\nu _{x_i} \leqslant v<\infty$
satisfy $\nu _{x_i} \leqslant v<\infty$![]() ,
,
and
then

for all $\tau \leqslant s\leqslant \tau ^{-1}$![]() and $y_i \in B_{\tau ^{-1}}(x_i)$
and $y_i \in B_{\tau ^{-1}}(x_i)$![]() satisfying that $y_1$
satisfying that $y_1$![]() $\delta$
$\delta$![]() -close to $y_2$
-close to $y_2$![]() with respect to (3.121).
with respect to (3.121).
Finally let us end this section by giving the following corollary which generalizes [Reference Fogagnolo, Mazzieri and Pinamonti26, Theorem 3.5] to the RCD setting. This corollary is pointed out by the reviewer. We thank the reviewer.
Corollary 3.28 The function $f_x:(0,\, \infty ) \to [0,\, \infty )$![]() defined by
defined by
is monotone non-increasing, where recall that we assume $\nu _x<\infty$![]() . Moreover we have
. Moreover we have
and
Proof. For the first statement, we just follow the proof of [Reference Fogagnolo, Mazzieri and Pinamonti26, Theorem 3.5]. Namely our goal is to prove for any $t>0$![]()
because then for any $s \le t$![]() we have
we have
which completes the proof of the first statement. Thus let us focus on the proof of (3.126). Note that $G_x$![]() is $\mathcal {L}$
is $\mathcal {L}$![]() -harmonic on $X \setminus \{x\}$
-harmonic on $X \setminus \{x\}$![]() . Fixing a sufficiently large $T>t$
. Fixing a sufficiently large $T>t$![]() , consider an $\mathcal {L}$
, consider an $\mathcal {L}$![]() -subharmonic function $\varphi$
-subharmonic function $\varphi$![]() on $X \setminus \{x\}$
on $X \setminus \{x\}$![]() defined by
defined by

It is trivial that $\varphi \le 0$![]() holds on $\{ \mathsf {b}_x =t \} \cup \{\mathsf {b}_x= T\}$
holds on $\{ \mathsf {b}_x =t \} \cup \{\mathsf {b}_x= T\}$![]() . Thus the strong maximum principle, proposition 6.7, shows $\varphi \le 0$
. Thus the strong maximum principle, proposition 6.7, shows $\varphi \le 0$![]() on $\{t \leqslant \mathsf {b}_x \leqslant T\}$
on $\{t \leqslant \mathsf {b}_x \leqslant T\}$![]() . Then letting $T \to \infty$
. Then letting $T \to \infty$![]() proves (3.126).
proves (3.126).
On the other hand (3.124) is a direct consequence of theorem 3.22 and corollary 3.24. Thus let us focus on the proof of (3.125). The proof is divided into the following $2$![]() cases.
cases.
Case 1: $V_X=0$![]() .
.
By the same argument as in (3.97), we see that for any $\epsilon >0$![]() , there exists $R>1$
, there exists $R>1$![]() such that
such that
holds for any $y \in X \setminus B_R(x)$![]() , namely we have $\limsup _{\mathsf {d}_x(y) \to \infty }|\nabla \mathsf {b}_x|(y) \leqslant C(N) V_X=0$
, namely we have $\limsup _{\mathsf {d}_x(y) \to \infty }|\nabla \mathsf {b}_x|(y) \leqslant C(N) V_X=0$![]() which proves (3.124) in this case.
which proves (3.124) in this case.
Case 2: $V_X>0$![]() .
.
In this case the proof is similar to Step 3 of the proof of theorem 3.22 with (3.126). Let $C_{\mathrm {opt},\, \infty }:=\lim _{t \to \infty }f_x(t)$![]() . Take $x_t \in \{\mathsf {b}_x=t\}$
. Take $x_t \in \{\mathsf {b}_x=t\}$![]() with $|\nabla \mathsf {b}_x|(x_t)=f_x(t)$
with $|\nabla \mathsf {b}_x|(x_t)=f_x(t)$![]() , and let $0\epsilon _t:=f_x(t)^2-C_{\mathrm {opt},\, \infty }^2\geqslant 0$
, and let $0\epsilon _t:=f_x(t)^2-C_{\mathrm {opt},\, \infty }^2\geqslant 0$![]() . Note that $C_{\mathrm {opt},\, \infty }^2-|\nabla \mathsf {b}_x|^2 +\varepsilon _t \geqslant 0$
. Note that $C_{\mathrm {opt},\, \infty }^2-|\nabla \mathsf {b}_x|^2 +\varepsilon _t \geqslant 0$![]() holds on $\{\mathsf {b}_x\geqslant t\}$
holds on $\{\mathsf {b}_x\geqslant t\}$![]() .
.
On the other hand, thanks to (3.52), for any sufficiently large $t>1$![]() , we have $B_{\delta t}(x_t) \subset \{\mathsf {b}_x\geqslant \frac {t}{2}\}$
, we have $B_{\delta t}(x_t) \subset \{\mathsf {b}_x\geqslant \frac {t}{2}\}$![]() , where $\delta =\delta (N,\, V_X)$
, where $\delta =\delta (N,\, V_X)$![]() is a positive constant depending only on $N,\, V_X$
is a positive constant depending only on $N,\, V_X$![]() . In particular
. In particular
Then, after a rescaling $t^{-1}\mathsf {d},\, \mathfrak {m} (B_t(x))^{-1}\mathfrak {m}$![]() , applying the weak Harnack inequality for $\mathcal {L}$
, applying the weak Harnack inequality for $\mathcal {L}$![]() -superharmonic function, proposition 6.5, to $C_{\mathrm {opt},\, \infty }^2-|\nabla \mathsf {b}_x|^2 +\varepsilon _{\frac {t}{2}} \geqslant 0$
-superharmonic function, proposition 6.5, to $C_{\mathrm {opt},\, \infty }^2-|\nabla \mathsf {b}_x|^2 +\varepsilon _{\frac {t}{2}} \geqslant 0$![]() , we have as $t \to \infty$
, we have as $t \to \infty$![]()

for some $p=p(N)>0$![]() , namely
, namely

Combining this with (3.116) yields $C_{\mathrm {opt},\, \infty }=\mathscr C_NV_X^{\frac {1}{N-2}}$![]() which completes the proof of (3.125).
which completes the proof of (3.125).
4. Rigidity to $N$ -metric measure cone
-metric measure cone
We are now in a position to prove the main results. Fix a finite $N >2$![]() .
.
4.1. Rigidity
Let us prove the desired rigidity result based on theorems 3.15 and 3.22 (see (3.25) for the definition of $\mathscr C_N$![]() ).
).
Theorem 4.1 Rigidity to $N$![]() -metric measure cone
-metric measure cone
Let $(X,\,\mathsf {d},\,\mathfrak {m},\, x)$![]() be a pointed non-parabolic $\operatorname {RCD}(0,\,N)$
be a pointed non-parabolic $\operatorname {RCD}(0,\,N)$![]() space with the finite $N$
space with the finite $N$![]() -volume density $\nu _x<\infty$
-volume density $\nu _x<\infty$![]() . If there exists a point $y \in X\setminus \{x\}$
. If there exists a point $y \in X\setminus \{x\}$![]() such that
such that
then $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$![]() is isomorphic to the $N$
is isomorphic to the $N$![]() -metric measure cone with the pole over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone with the pole over an $\operatorname {RCD}(N-2,\, N-1)$![]() space.
space.
Proof. First of all, let us prove that $X \setminus \{x\}$![]() is connected. Let $U$
is connected. Let $U$![]() be a connected component of $X\setminus \{x\}$
be a connected component of $X\setminus \{x\}$![]() . As mentioned in the beginning of the proof of corollary 3.24, since $\{x\}$
. As mentioned in the beginning of the proof of corollary 3.24, since $\{x\}$![]() has a null $2$
has a null $2$![]() -capacity, the indicator function $\chi _U$
-capacity, the indicator function $\chi _U$![]() of $U$
of $U$![]() is in $H^{1,2}_{\mathrm {loc}}(X,\, \mathsf {d},\, \mathfrak {m})$
is in $H^{1,2}_{\mathrm {loc}}(X,\, \mathsf {d},\, \mathfrak {m})$![]() with $|\nabla \chi _U|=0$
with $|\nabla \chi _U|=0$![]() . Thus the (local) Sobolev-to-Lipschitz property shows $\chi _U= 1$
. Thus the (local) Sobolev-to-Lipschitz property shows $\chi _U= 1$![]() for $\mathfrak {m}$
for $\mathfrak {m}$![]() -a.e., which implies $X\setminus \{x\}=U$
-a.e., which implies $X\setminus \{x\}=U$![]() . Thus $X\setminus \{x\}$
. Thus $X\setminus \{x\}$![]() is connected.
is connected.
Then applying the strong maximum principle, proposition 6.7, for $|\nabla \mathsf {b}_x|^2$![]() yields $|\nabla \mathsf {b}_x|\equiv \mathscr C_N\nu _x^\frac {1}{N-2}$
yields $|\nabla \mathsf {b}_x|\equiv \mathscr C_N\nu _x^\frac {1}{N-2}$![]() in $X \setminus \{x\}$
in $X \setminus \{x\}$![]() . Letting $u:={\mathsf {b}_x^2}/ (2\mathscr C_N^2\nu _x^\frac {2}{N-2})$
. Letting $u:={\mathsf {b}_x^2}/ (2\mathscr C_N^2\nu _x^\frac {2}{N-2})$![]() , we have $|\nabla \sqrt {2u}|^2=1$
, we have $|\nabla \sqrt {2u}|^2=1$![]() and thus, by (3.20), $\Delta u=N$
and thus, by (3.20), $\Delta u=N$![]() for $\mathfrak {m}$
for $\mathfrak {m}$![]() -a.e. These observations allow us to apply [Reference Gigli and Violo31, Theorem 5.1] (see also Theorem 2.8) to get the conclusion.
-a.e. These observations allow us to apply [Reference Gigli and Violo31, Theorem 5.1] (see also Theorem 2.8) to get the conclusion.
In particular, when restricted to points with Euclidean tangent spaces, theorem 4.1 implies an interesting corollary; compare with [Reference Colding16, Theorem 3.1].
Corollary 4.2 We have the following.
(1) Let $(X,\,\mathsf {d},\,\mathfrak {m})$
 be a non-parabolic $\operatorname {RCD}(0,\,N)$
be a non-parabolic $\operatorname {RCD}(0,\,N)$ space for some integer $N \geqslant 3$
space for some integer $N \geqslant 3$ with the finite $N$
with the finite $N$ -volume density $\nu _x<\infty$
-volume density $\nu _x<\infty$ at an $N$
at an $N$ -regular point $x$
-regular point $x$ . If there exists $z\in X \setminus \{x\}$
. If there exists $z\in X \setminus \{x\}$ such that $|\nabla \mathsf {b}_x|(z)=\mathscr C_N\nu _x^{\frac {1}{N-2}}$
such that $|\nabla \mathsf {b}_x|(z)=\mathscr C_N\nu _x^{\frac {1}{N-2}}$ holds, then $(X,\,\mathsf {d},\, \mathfrak {m})$
holds, then $(X,\,\mathsf {d},\, \mathfrak {m})$ is isometric to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, c\mathscr {H}^N)$
is isometric to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, c\mathscr {H}^N)$ for some positive constant $c >0$
for some positive constant $c >0$ .
.(2) If a non-parabolic non-collapsed $\operatorname {RCD}(0,\, N)$
 space $(X,\, \mathsf {d},\, \mathscr {H}^N)$
space $(X,\, \mathsf {d},\, \mathscr {H}^N)$ for some integer $N \geqslant 3$
for some integer $N \geqslant 3$ with the finite $N$
with the finite $N$ -volume density $\nu _x<\infty$
-volume density $\nu _x<\infty$ at a point $x \in X$
at a point $x \in X$ satisfies $|\nabla \mathsf {b}_x|(z) \ge \mathscr C_N \omega _N^{\frac {1}{N-2}}$
satisfies $|\nabla \mathsf {b}_x|(z) \ge \mathscr C_N \omega _N^{\frac {1}{N-2}}$ for some $z \in X \setminus \{x\}$
for some $z \in X \setminus \{x\}$ , then $(X,\, \mathsf {d},\, \mathscr {H}^N)$
, then $(X,\, \mathsf {d},\, \mathscr {H}^N)$ is isometric to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, \mathscr {H}^N)$
is isometric to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, \mathscr {H}^N)$ .
.
Proof. Let us prove (1). Theorem 4.1 yields that $(X,\, \mathsf {d},\, \mathfrak {m})$![]() is isomorphic to an $N$
is isomorphic to an $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space. In particular it must be isomorphic to a tangent cone at $x$
space. In particular it must be isomorphic to a tangent cone at $x$![]() . Thus we conclude.
. Thus we conclude.
Next let us prove (2). The sharp gradient estimate, theorem 3.22, yields
thus $x$![]() is an $N$
is an $N$![]() -regular point because of [Reference De Philippis and Gigli20, Corollary 1.7] (recall (2.15)). Then the conclusion follows from the first statement (1).
-regular point because of [Reference De Philippis and Gigli20, Corollary 1.7] (recall (2.15)). Then the conclusion follows from the first statement (1).
4.2. Almost rigidity
Finally, let us prove the following almost rigidity theorem of $\mathsf {b}_x$![]() :
:
Theorem 4.3 Almost rigidity
For all $N>2$![]() , $0<\varepsilon <1$
, $0<\varepsilon <1$![]() , $0< r< R<\infty$
, $0< r< R<\infty$![]() , $\nu >0$
, $\nu >0$![]() , $1\leqslant p<\infty$
, $1\leqslant p<\infty$![]() and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$
and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$![]() there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, R,\, \nu,\, p,\, \varphi )>0$
there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, R,\, \nu,\, p,\, \varphi )>0$![]() such that if a pointed non-parabolic $\operatorname {RCD}(0,\,N)$
such that if a pointed non-parabolic $\operatorname {RCD}(0,\,N)$![]() space $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$
space $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$![]() satisfies $\nu _x\leqslant \nu$
satisfies $\nu _x\leqslant \nu$![]() ,
,
and
for some $z\in \overline {B}_R(x)\setminus B_r(x)$![]() , then we have
, then we have

and there exists an $\operatorname {RCD}(N-2,\,N-1)$![]() space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y)$
space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y)$![]() such that
such that
Proof. As in the proof of corollary 3.14, it is enough to consider the case when $p=2$![]() . Then the proof is done by a contradiction, thus assume the conclusion fails. Then there exist sequences of positive numbers $\delta _i\to 0^+$
. Then the proof is done by a contradiction, thus assume the conclusion fails. Then there exist sequences of positive numbers $\delta _i\to 0^+$![]() and of pointed $\operatorname {RCD}(0,\,N)$
and of pointed $\operatorname {RCD}(0,\,N)$![]() spaces $(X_i,\,\mathsf {d}_i,\,\mathfrak {m}_i,\,x_i)$
spaces $(X_i,\,\mathsf {d}_i,\,\mathfrak {m}_i,\,x_i)$![]() such that $\nu _{x_i} \leqslant \nu$
such that $\nu _{x_i} \leqslant \nu$![]() , $\frac {s}{\mathfrak {m}_i(B_s(x_i))} \leqslant \varphi (s)$
, $\frac {s}{\mathfrak {m}_i(B_s(x_i))} \leqslant \varphi (s)$![]() for $\mathscr {H}^1$
for $\mathscr {H}^1$![]() -a.e. $s \in [1,\, \infty )$
-a.e. $s \in [1,\, \infty )$![]() , that
, that
and that for any $\operatorname {RCD}(N-2,\,N-1)$![]() space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y)$
space $(Y,\,\mathsf {d}_Y,\,\mathfrak {m}_Y)$![]() , we have
, we have
or

Theorem 3.11 allows us to conclude that after passing to a subsequence, $(X_i,\,\mathsf {d}_i,\,\mathfrak {m}_i,\,x_i)$![]() pmGH converge to a pointed non-parabolic $\operatorname {RCD}(0,\, N)$
pmGH converge to a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$
space $(X,\,\mathsf {d},\,\mathfrak {m},\,x)$![]() , and $\nu _{x_i} \to \mu$
, and $\nu _{x_i} \to \mu$![]() for some $\mu \in [0,\, \infty )$
for some $\mu \in [0,\, \infty )$![]() . On the other hand, the lower semicontinuity of $N$
. On the other hand, the lower semicontinuity of $N$![]() -volume densities (3.34) implies
-volume densities (3.34) implies
Consider $\mathscr L$![]() -superharmonic lower semicontinuous functions on $X_i\setminus \{x_i\}$
-superharmonic lower semicontinuous functions on $X_i\setminus \{x_i\}$![]() ;
;
Fix $0< s<\frac {r}{4}$![]() . Applying the weak Harnack inequality, proposition 6.5, to the nonegatively valued $\mathscr L$
. Applying the weak Harnack inequality, proposition 6.5, to the nonegatively valued $\mathscr L$![]() -superharmonic function $u_i$
-superharmonic function $u_i$![]() , we have
, we have

where $p=p(N,\, s)>0$![]() . Thus recalling that $u_i$
. Thus recalling that $u_i$![]() is uniformly bounded, we have
is uniformly bounded, we have
Note that with no loss of generality we can assume that $z_i$![]() converge to a point $z \in \overline {B}_R(x)\setminus B_r(x)$
converge to a point $z \in \overline {B}_R(x)\setminus B_r(x)$![]() . Moreover the dominated convergence theorem yields the convergence of $\frac {s}{\mathfrak {m}_i(B_s(x_i))}$
. Moreover the dominated convergence theorem yields the convergence of $\frac {s}{\mathfrak {m}_i(B_s(x_i))}$![]() to $\frac {s}{\mathfrak {m} (B_s(x))}$
to $\frac {s}{\mathfrak {m} (B_s(x))}$![]() in $L^1([1,\, \infty ),\, \mathscr {H}^1)$
in $L^1([1,\, \infty ),\, \mathscr {H}^1)$![]() . Thus theorem 3.12 shows that $\mathsf {b}_{x_i}$
. Thus theorem 3.12 shows that $\mathsf {b}_{x_i}$![]() $W^{1,2}$
$W^{1,2}$![]() -strongly converge to $\mathsf {b}_{x}$
-strongly converge to $\mathsf {b}_{x}$![]() on $B_{2s}(z)$
on $B_{2s}(z)$![]() . Therefore (4.13) with (4.10) implies
. Therefore (4.13) with (4.10) implies
In particular theorem 3.22 shows $\mu =\lim _{i\to \infty }\nu _{x_i}=\nu _x$![]() and
and
Thus, theorem 4.1 allows us to conclude that the limit space is isomorphic to the $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space, which contradicts (4.8) and (4.9).
space, which contradicts (4.8) and (4.9).
Next we provide an almost rigidity to a Euclidean space on a non-collapsed space.
Corollary 4.4 For any integer $N\geqslant 3$![]() , all $0<\varepsilon <1$
, all $0<\varepsilon <1$![]() , $0< r< R$
, $0< r< R$![]() and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$
and $\varphi \in L^1([1,\, \infty ),\, \mathscr {H}^1)$![]() there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, \varphi )>0$
there exists $\delta :=\delta (N,\, \varepsilon,\, r,\, \varphi )>0$![]() such that if a pointed non-parabolic non-collapsed $\operatorname {RCD}(0,\,N)$
such that if a pointed non-parabolic non-collapsed $\operatorname {RCD}(0,\,N)$![]() space $(X,\,\mathsf {d},\,\mathscr {H}^N,\,x)$
space $(X,\,\mathsf {d},\,\mathscr {H}^N,\,x)$![]() satisfies
satisfies
and
for some $y \in \overline {B}_R(x) \setminus B_r(x)$![]() , then $(X,\, \mathsf {d},\, \mathscr {H}^N,\, x)$
, then $(X,\, \mathsf {d},\, \mathscr {H}^N,\, x)$![]() is $\varepsilon$
is $\varepsilon$![]() - pmGH close to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, \mathscr {H}^N,\, 0_N)$
- pmGH close to $(\mathbb {R}^N,\, \mathsf {d}_{\mathbb {R}^N},\, \mathscr {H}^N,\, 0_N)$![]() .
.
Proof. The first statement is a direct consequence of (the proof of) theorem 4.3 with the Bishop inequality $\nu _x \leqslant \omega _N$![]() .
.
Remark 4.5 Let us remark that the conclusion of corollary 4.4 cannot be replaced by a stronger one;
Find an open $N$![]() -manifold $(M^N,\, g)$
-manifold $(M^N,\, g)$![]() with the maximal volume growth which is not isometric to $\mathbb {R}^N$
with the maximal volume growth which is not isometric to $\mathbb {R}^N$![]() (for instance the Eguchi-Hanson metric on the cotangent bundle $T^*\mathbb {S}^2$
(for instance the Eguchi-Hanson metric on the cotangent bundle $T^*\mathbb {S}^2$![]() of $\mathbb {S}^2$
of $\mathbb {S}^2$![]() gives such an example with vanishing Ricci curvature, see [Reference Eguchi and Hanson24]). Then since the tangent cone at infinity is not isometric to $\mathbb {R}^N$
gives such an example with vanishing Ricci curvature, see [Reference Eguchi and Hanson24]). Then since the tangent cone at infinity is not isometric to $\mathbb {R}^N$![]() , the asymptotic $N$
, the asymptotic $N$![]() -volume $V_{M^N}$
-volume $V_{M^N}$![]() is away from $\omega _N$
is away from $\omega _N$![]() . Fix $x \in M^N$
. Fix $x \in M^N$![]() . Take any convergent sequence $x_i \to x$
. Take any convergent sequence $x_i \to x$![]() with $x_i \neq x$
with $x_i \neq x$![]() and then recall
and then recall
Thus considering the rescaled distance $\mathsf {d}_i:=\mathsf {d}(x,\, y_i)^{-1}\mathsf {d}$![]() , the pointed Riemannian manifolds $(M^N,\, \mathsf {d}_i,\, x)$
, the pointed Riemannian manifolds $(M^N,\, \mathsf {d}_i,\, x)$![]() satisfies (4.19) for some $y_i \in \partial B_1^{\mathsf {d}_i}(x)$
satisfies (4.19) for some $y_i \in \partial B_1^{\mathsf {d}_i}(x)$![]() , but the asymptotic $N$
, but the asymptotic $N$![]() -volume is away from $\omega _N$
-volume is away from $\omega _N$![]() because of the scale invariance of $V_{M^N}$
because of the scale invariance of $V_{M^N}$![]() . In particular (4.18) is not satisfied in this case.
. In particular (4.18) is not satisfied in this case.
In connection with this remark, we prove the following.
Theorem 4.6 For any integer $N \geqslant 3$![]() , all $0<\varepsilon <1$
, all $0<\varepsilon <1$![]() and $\tau >0$
and $\tau >0$![]() there exists $\delta =\delta (N,\, \varepsilon,\, \tau )>0$
there exists $\delta =\delta (N,\, \varepsilon,\, \tau )>0$![]() such that if a pointed non-parabolic non-collapsed $\operatorname {RCD}(0,\,N)$
such that if a pointed non-parabolic non-collapsed $\operatorname {RCD}(0,\,N)$![]() space $(X,\,\mathsf {d},\,\mathscr {H}^N,\,x)$
space $(X,\,\mathsf {d},\,\mathscr {H}^N,\,x)$![]() satisfies $V_X \geqslant \tau$
satisfies $V_X \geqslant \tau$![]() and
and
for some sequence $y_i\in X$![]() with $\mathsf {d}(x,\, y_i)\to \infty$
with $\mathsf {d}(x,\, y_i)\to \infty$![]() , then
, then
In particular if $\varepsilon$![]() is sufficiently small depending only on $N$
is sufficiently small depending only on $N$![]() and $\tau$
and $\tau$![]() , then $X$
, then $X$![]() is homeomorphic to $\mathbb {R}^N$
is homeomorphic to $\mathbb {R}^N$![]() , moreover in addition, if $X$
, moreover in addition, if $X$![]() is smooth, then the homeomorphism can be improved to be a diffeomorphism.
is smooth, then the homeomorphism can be improved to be a diffeomorphism.
Proof. Let $r_i:=\mathsf {d}(x,\, y_i)$![]() and consider a rescaled pointed non-parabolic non-collapsed $\operatorname {RCD}(0,\, N)$
and consider a rescaled pointed non-parabolic non-collapsed $\operatorname {RCD}(0,\, N)$![]() space;
space;
Recalling (3.30) we have for any $r \geqslant 1$![]()
where we used (3.5) in the final inequality. Thus corollary 4.4 allows us to conclude that $(X_i,\, \mathsf {d}_i,\, \mathscr {H}^N_{\mathsf {d}_i},\, x_i)$![]() is pmGH close to the $N$
is pmGH close to the $N$![]() -dimensional Euclidean space. In particular a tangent cone at infinity is also pmGH close to the $N$
-dimensional Euclidean space. In particular a tangent cone at infinity is also pmGH close to the $N$![]() -dimensional Euclidean space. Therefore the volume convergence result, [Reference De Philippis and Gigli20, Theorem 1.3], implies (4.21). Thus we get the first statement. The remaining statements come from this with the same arguments as in [Reference Cheeger and Colding14, Theorems A.1.11].
-dimensional Euclidean space. Therefore the volume convergence result, [Reference De Philippis and Gigli20, Theorem 1.3], implies (4.21). Thus we get the first statement. The remaining statements come from this with the same arguments as in [Reference Cheeger and Colding14, Theorems A.1.11].
Remark 4.7 In the theorem above, in order to get the same conclusion, we cannot replace the existence of divergent points by the existence of a point which is far from $x$![]() . The reason is the same to remark 4.5.
. The reason is the same to remark 4.5.
5. Examples
In this section we see that theorems 3.12 and 4.3 are sharp via simple examples. Moreover we also discuss a related sharpness and open problems.
5.1. Sharpness I
In this subsection we prove that theorem 4.3 is sharp, namely this cannot be improved to the case when $p=\infty$![]() . The following arguments also allow us to conclude that (1.12) and (1.13) in theorem 1.2 are also sharp.
. The following arguments also allow us to conclude that (1.12) and (1.13) in theorem 1.2 are also sharp.
Step 1. Consider $\mathbb {S}^2(r):=\{x \in \mathbb {R}^3 | |x|_{\mathbb {R}^3}=r\}$![]() for $r<1$
for $r<1$![]() with the standard Riemannian metric and denote by $X=C(\mathbb {S}^2(r))$
with the standard Riemannian metric and denote by $X=C(\mathbb {S}^2(r))$![]() the $3$
the $3$![]() -metric measure cone with the $3$
-metric measure cone with the $3$![]() -dimensional Hausdorff measure $\mathscr {H}^3_X (=\mathfrak {m}_{C(\mathbb {S}^2(r))})$
-dimensional Hausdorff measure $\mathscr {H}^3_X (=\mathfrak {m}_{C(\mathbb {S}^2(r))})$![]() . Assume that $r$
. Assume that $r$![]() is close to $1$
is close to $1$![]() , and take a point $y \in X$
, and take a point $y \in X$![]() which is close to the pole $x \in X$
which is close to the pole $x \in X$![]() with $x \neq y$
with $x \neq y$![]() . Since $(X,\, \mathsf {d},\, \mathscr {H}^3,\, y)$
. Since $(X,\, \mathsf {d},\, \mathscr {H}^3,\, y)$![]() is pmGH close to the $3$
is pmGH close to the $3$![]() -dimensional Euclidean space, theorem 4.3 yields that
-dimensional Euclidean space, theorem 4.3 yields that
is small, where the Lipschitz constant can be calculated by $(3(3-2)\omega _3)^{\frac {1}{3-2}}=4\pi$![]() .
.
On the other hand, we have

because of the same trick observed in [Reference De Philippis and Zimbrón21]. Namely, thanks to lemmas 3.7, 3.9 and the stability of the Laplacian [Reference Ambrosio and Honda3, Theorem 4.4], under any blow-up at $x$![]() , $\mathsf {b}_x$
, $\mathsf {b}_x$![]() $W^{1,2}_{\mathrm {loc}}$
$W^{1,2}_{\mathrm {loc}}$![]() -strongly converge to a linear growth harmonic function on $C(\mathbb {S}^2(r))$
-strongly converge to a linear growth harmonic function on $C(\mathbb {S}^2(r))$![]() . Recalling that any such function must be a constant because $r<1$
. Recalling that any such function must be a constant because $r<1$![]() , we have (5.2).
, we have (5.2).
Then recalling the upper semicontinuity of $|\nabla \mathsf {b}_y|$![]() , we know that $|\nabla \mathsf {b}_y|$
, we know that $|\nabla \mathsf {b}_y|$![]() is small around $x$
is small around $x$![]() . In particular
. In particular
near $x$![]() , thus
, thus
Step 2. Let
be a pmGH convergent sequence of pointed $\operatorname {RCD}(K,\, N)$![]() spaces and let $f_i \in L^{\infty }(B_R(x_i),\, \mathfrak {m}_i)$
spaces and let $f_i \in L^{\infty }(B_R(x_i),\, \mathfrak {m}_i)$![]() $L^p$
$L^p$![]() -strongly converge to $f \in L^{\infty }(B_R(x),\, \mathfrak {m})$
-strongly converge to $f \in L^{\infty }(B_R(x),\, \mathfrak {m})$![]() for any $p<\infty$
for any $p<\infty$![]() with $\sup _i\|f_i\|_{L^{\infty }}<\infty$
with $\sup _i\|f_i\|_{L^{\infty }}<\infty$![]() . Then
. Then
Because for any $p<\infty$![]() , since
, since

letting $p \to \infty$![]() completes the proof of (5.6).
completes the proof of (5.6).
Step 3. Let us consider $X=C(\mathbb {S}^2(r))$![]() again as in Step 1. Note that it is easy to find a sequence of manifolds of dimension $3$
again as in Step 1. Note that it is easy to find a sequence of manifolds of dimension $3$![]() , $(M^3_i,\, g_i,\, \mathscr {H}^3,\, y_i)$
, $(M^3_i,\, g_i,\, \mathscr {H}^3,\, y_i)$![]() , pmGH-converge to $(X,\, \mathsf {d},\, \mathscr {H}^3,\, y)$
, pmGH-converge to $(X,\, \mathsf {d},\, \mathscr {H}^3,\, y)$![]() (actually $(X,\, \mathsf {d},\, \mathscr {H}^3,\, x)$
(actually $(X,\, \mathsf {d},\, \mathscr {H}^3,\, x)$![]() is the tangent cone at infinity of a $3$
is the tangent cone at infinity of a $3$![]() -dimensional complete Riemannian manifold $(M^3,\, g)$
-dimensional complete Riemannian manifold $(M^3,\, g)$![]() with $V_{M^3}=V_X>0$
with $V_{M^3}=V_X>0$![]() ). Then applying (5.6) for $f_i=4\pi -|\nabla \mathsf {b}_{y_i}|,\, f=4\pi -|\nabla \mathsf {b}_y|$
). Then applying (5.6) for $f_i=4\pi -|\nabla \mathsf {b}_{y_i}|,\, f=4\pi -|\nabla \mathsf {b}_y|$![]() with corollary 3.23 implies
with corollary 3.23 implies
This observation shows that we cannot improve theorem 4.3 to the case when $p=\infty$![]() .
.
5.2. Sharpness II
In the rest two subsections 5.2 and 5.3, we prove that several results we obtained previously under assuming;
do not hold if we replace (5.9) by a weaker one;
based on examples discussed in the previous subsection. Namely the assumption (5.9) is sharp in these results.
The first one is about theorem 3.12, namely we provide an example of pmGH convergent sequences of non-parabolic $\operatorname {RCD}(0,\,3)$![]() spaces whose Green functions do not converge to the limit one, though the corresponding $F_{x_i}(1)$
spaces whose Green functions do not converge to the limit one, though the corresponding $F_{x_i}(1)$![]() are bounded.
are bounded.
For fixed $0< r<1$![]() ,Footnote 5 let $X=C(\mathbb {S}^2(r))$
,Footnote 5 let $X=C(\mathbb {S}^2(r))$![]() with the pole $x$
with the pole $x$![]() , the cone distance $\mathsf {d}=\mathsf {d}_{C(\mathbb {S}^2(r))}$
, the cone distance $\mathsf {d}=\mathsf {d}_{C(\mathbb {S}^2(r))}$![]() and the $3$
and the $3$![]() -dimensional Hausdorff measure $\mathscr {H}^3_X$
-dimensional Hausdorff measure $\mathscr {H}^3_X$![]() . For any $R>0$
. For any $R>0$![]() , let us denote by $X_R$
, let us denote by $X_R$![]() the glued space of a closed ball $\overline {B}_R(x)$
the glued space of a closed ball $\overline {B}_R(x)$![]() and a cylinder $\partial B_R(x) \times [0,\, \infty )$
and a cylinder $\partial B_R(x) \times [0,\, \infty )$![]() along the boundary $\partial B_R(x):=\{y\in X|\mathsf {d} (x,\, y)=R\}$
along the boundary $\partial B_R(x):=\{y\in X|\mathsf {d} (x,\, y)=R\}$![]() . Then it is trivial that both $X$
. Then it is trivial that both $X$![]() and $X_R$
and $X_R$![]() with the canonical intrinsic distance $\mathsf {d}_R$
with the canonical intrinsic distance $\mathsf {d}_R$![]() can be canonically realized as boundaries $\partial D,\, \partial D_R$
can be canonically realized as boundaries $\partial D,\, \partial D_R$![]() of closed convex subsets $D,\, D_R$
of closed convex subsets $D,\, D_R$![]() in $\mathbb {R}^4$
in $\mathbb {R}^4$![]() with $x=0_4$
with $x=0_4$![]() and $D_R \subset D$
and $D_R \subset D$![]() , respectively. In particular $(X_R,\, \mathsf {d}_R,\, \mathscr {H}^3_{X_R})$
, respectively. In particular $(X_R,\, \mathsf {d}_R,\, \mathscr {H}^3_{X_R})$![]() is an $\operatorname {RCD}(0,\, 3)$
is an $\operatorname {RCD}(0,\, 3)$![]() space. Note that $(X_R,\, \mathsf {d}_R,\, \mathscr {H}^3_{X_R})$
space. Note that $(X_R,\, \mathsf {d}_R,\, \mathscr {H}^3_{X_R})$![]() is not non-parabolic.
is not non-parabolic.
Under the conventions above, denote by $\pi _R:X \to X_R$![]() the canonical projection in $\mathbb {R}^4$
the canonical projection in $\mathbb {R}^4$![]() (thus $\pi _R|_{\overline {B}_R(x)}=\mathrm {id}_{\overline {B}_R(x)}$
(thus $\pi _R|_{\overline {B}_R(x)}=\mathrm {id}_{\overline {B}_R(x)}$![]() ). For any $0\leqslant t \leqslant 1$
). For any $0\leqslant t \leqslant 1$![]() , define $\pi _{R, t}:X \to D$
, define $\pi _{R, t}:X \to D$![]() by $\pi _{R, t}(y):=(1-t)y+t\pi _R(y)$
by $\pi _{R, t}(y):=(1-t)y+t\pi _R(y)$![]() , and put $X_{R, t}:=\pi _{R, t}(X)$
, and put $X_{R, t}:=\pi _{R, t}(X)$![]() which is also the boundary of a covex closed subset in $\mathbb {R}^4$
which is also the boundary of a covex closed subset in $\mathbb {R}^4$![]() .
.
Choose $R_{0}>1$![]() with
with
because of the non-parabolicity of $(X,\, \mathsf {d},\, \mathscr {H}^3_X)$![]() . Fix $R \geqslant R_{0}^2$
. Fix $R \geqslant R_{0}^2$![]() . Since
. Since
because $(X_R,\, \mathsf {d}_R,\, \mathscr {H}^3_{X_R})$![]() is not non-parabolic, we can find $t_{R} \in (0,\, 1)$
is not non-parabolic, we can find $t_{R} \in (0,\, 1)$![]() with
with

Then let us consider a pmGH-convergent sequence of non-parabolic $\operatorname {RCD}(0,\, 3)$![]() spaces;
spaces;
where $\mathsf {d}_{R, t_{R}}$![]() denotes the canonical intrinsic distance on $X_{R, t_{R}}$
denotes the canonical intrinsic distance on $X_{R, t_{R}}$![]() . Since
. Since

Theorem 3.12 tells us that the Green functions do not converge to the limit one. Actually we can see this directly as follows.
Fix $y \in X\setminus \{x\}$![]() . Then for any sufficiently large $R$
. Then for any sufficiently large $R$![]() , Gaussian estimates (2.20) show
, Gaussian estimates (2.20) show

for some $C>1$![]() . Thus letting $R \to \infty$
. Thus letting $R \to \infty$![]() with Fatou's lemma and (3.48) yields
with Fatou's lemma and (3.48) yields
5.3. Sharpness III
The final sharpness result is related to corollary 3.27. An immediate consequence of corollary 3.27 states that if a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$
space $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() with the finite $N$
with the finite $N$![]() -volume density $\nu _x<\infty$
-volume density $\nu _x<\infty$![]() is pmGH-close to the $N$
is pmGH-close to the $N$![]() -metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$
-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$![]() space, then $|\nabla \mathsf {b}_x|$
space, then $|\nabla \mathsf {b}_x|$![]() attains the maximum $\mathscr C_N\nu _x^{\frac {1}{N-2}}$
attains the maximum $\mathscr C_N\nu _x^{\frac {1}{N-2}}$![]() almostly at some point which is bounded and away from $x$
almostly at some point which is bounded and away from $x$![]() , whenever (5.9) holds. In the sequel we prove that (5.9) cannot be replaced by (5.10) to get the same conclusion.
, whenever (5.9) holds. In the sequel we prove that (5.9) cannot be replaced by (5.10) to get the same conclusion.
To do so, under the same notations as in subsection 5.2, let us discuss the behaviour of $\mathsf {b}_x^{X_{R, t_R}}$![]() as $R \to \infty$
as $R \to \infty$![]() . Our claim is that if $r$
. Our claim is that if $r$![]() is small, then there exists no sequence $y_{R_i} \in X_{R_i, t_{R_i}}$
is small, then there exists no sequence $y_{R_i} \in X_{R_i, t_{R_i}}$![]() as $R_i \to \infty$
as $R_i \to \infty$![]() such that $y_{R_i}$
such that $y_{R_i}$![]() is bounded and is away from $x$
is bounded and is away from $x$![]() and that
and that
The proof is done by a contradiction. If such sequence $y_{R_i}$![]() exists, then after passing to a subsequence, with no loss of generality we can assume that $y_{R_i}$
exists, then after passing to a subsequence, with no loss of generality we can assume that $y_{R_i}$![]() converge to some $y \in X\setminus \{x\}$
converge to some $y \in X\setminus \{x\}$![]() and that $\mathsf {b}_{x}^{X_{R_i},\, t_{R_i}}$
and that $\mathsf {b}_{x}^{X_{R_i},\, t_{R_i}}$![]() locally uniformly converge to some $\tilde{\mathsf {b}} \in \mathrm {Lip}(X,\, \mathsf {d})$
locally uniformly converge to some $\tilde{\mathsf {b}} \in \mathrm {Lip}(X,\, \mathsf {d})$![]() . Note that thanks to lemma 3.7 and the stability of the Laplacian [Reference Ambrosio and Honda3, Theorem 4.4], we know that $\tilde{\mathsf {b}} \in D(\Delta,\, X \setminus \{x\})$
. Note that thanks to lemma 3.7 and the stability of the Laplacian [Reference Ambrosio and Honda3, Theorem 4.4], we know that $\tilde{\mathsf {b}} \in D(\Delta,\, X \setminus \{x\})$![]() and $\tilde{\mathsf {b}}^2\in D(\Delta )$
and $\tilde{\mathsf {b}}^2\in D(\Delta )$![]() hold with
hold with
On the other hand, applying a weak Harnack inequality, theorem 6.5, for $(3\nu _x)^2-|\nabla \mathsf {b}_x^{X_{R_i, t_{R_i}}}|^2$![]() as in (3.105) proves
as in (3.105) proves
for all $0< r< R<\infty$![]() . Thus we know
. Thus we know
Then since $\tilde{\mathsf {b}}^2-(3\nu _x)^2\mathsf {d}_x^2$![]() is a harmonic function on $X$
is a harmonic function on $X$![]() with polynomial growth of degree at most $2$
with polynomial growth of degree at most $2$![]() , any such function must be a constant if $r$
, any such function must be a constant if $r$![]() is small. Thus we have $\tilde{\mathsf {b}}^2=(3\nu _x)^2\mathsf {d}_x^2+d$
is small. Thus we have $\tilde{\mathsf {b}}^2=(3\nu _x)^2\mathsf {d}_x^2+d$![]() for some $d \in \mathbb {R}$
for some $d \in \mathbb {R}$![]() . Since $\tilde{\mathsf {b}}(x)=0$
. Since $\tilde{\mathsf {b}}(x)=0$![]() by definition, we know $d=0$
by definition, we know $d=0$![]() , namely
, namely
In particular we have ${\tilde{\mathsf {b}}}^{-1}=G^X_x$![]() which contradicts (5.17). Thus the observation above allows us to conclude for all $0< r_1< r_2<\infty$
which contradicts (5.17). Thus the observation above allows us to conclude for all $0< r_1< r_2<\infty$![]()
6. Appendix; analysis on a drifted Laplace operator $\mathscr L$
In this appendix, we provide detailed proofs of the regularity results for $\mathscr L$![]() -sub/super harmonic functions (recall definition 3.18), coming directly from the general theory on PI spaces. It is emphasized that these techniques can be applied to more general operators, including, of course, our Laplacian $\Delta$
-sub/super harmonic functions (recall definition 3.18), coming directly from the general theory on PI spaces. It is emphasized that these techniques can be applied to more general operators, including, of course, our Laplacian $\Delta$![]() . We refer [Reference Björn and Björn9, Section 8.5] as a main reference on this topic.
. We refer [Reference Björn and Björn9, Section 8.5] as a main reference on this topic.
Let $(X,\, \mathsf {d},\, \mathfrak {m},\, x)$![]() be a pointed non-parabolic $\operatorname {RCD}(0,\, N)$
be a pointed non-parabolic $\operatorname {RCD}(0,\, N)$![]() space. The first result is about the weak Harnack inequality for $\mathscr L$
space. The first result is about the weak Harnack inequality for $\mathscr L$![]() -subharmonic functions. This is justified by applying [Reference Björn and Björn9, Theorem 8.4] to an (incomplete) metric measure space $(B_{100r}(y),\, \mathsf {d},\, \mathfrak {m}_{G_x})$
-subharmonic functions. This is justified by applying [Reference Björn and Björn9, Theorem 8.4] to an (incomplete) metric measure space $(B_{100r}(y),\, \mathsf {d},\, \mathfrak {m}_{G_x})$![]() because of (3.16) and (3.70).
because of (3.16) and (3.70).
Proposition 6.1 Weak Harnack inequality for $\mathscr L$![]() -subharmonic functions
-subharmonic functions
Let $u$![]() be an $\mathscr L$
be an $\mathscr L$![]() -subharmonic function on a ball $B_{100r}(y)$
-subharmonic function on a ball $B_{100r}(y)$![]() for some $r \leqslant 1$
for some $r \leqslant 1$![]() with $B_{100r}(y) \subset X\setminus B_s(x)$
with $B_{100r}(y) \subset X\setminus B_s(x)$![]() for some $s \leqslant 1$
for some $s \leqslant 1$![]() . Then for all $k\in \mathbb {R}$
. Then for all $k\in \mathbb {R}$![]() and $p>1$
and $p>1$![]() , there exists $C=C(N,\,s,\,p)>0$
, there exists $C=C(N,\,s,\,p)>0$![]() such thatFootnote 6
such thatFootnote 6

Proof. First let us assume that $p>2$![]() . For arbitrary $l>0$
. For arbitrary $l>0$![]() , let $\hat u=\hat u_k:=(u+k)_+$
, let $\hat u=\hat u_k:=(u+k)_+$![]() , and denote by $\bar u=\bar u_{k,l}:=\min \{\hat u_k,\,l\}$
, and denote by $\bar u=\bar u_{k,l}:=\min \{\hat u_k,\,l\}$![]() . For $\frac 1 2 r\leqslant r_1< r_2\leqslant r$
. For $\frac 1 2 r\leqslant r_1< r_2\leqslant r$![]() , take the cutoff function
, take the cutoff function
Then we have $0\leqslant \eta \leqslant 1$![]() , $|\nabla \eta |\leqslant \frac 1{r_2-r_1}$
, $|\nabla \eta |\leqslant \frac 1{r_2-r_1}$![]() in $B_{r_2}(y)$
in $B_{r_2}(y)$![]() , $\eta \equiv 1$
, $\eta \equiv 1$![]() in $B_{r_1}(y)$
in $B_{r_1}(y)$![]() , and $\eta \equiv 0$
, and $\eta \equiv 0$![]() outside $B_{r_2}(y)$
outside $B_{r_2}(y)$![]() . For any $\beta > p-2>0$
. For any $\beta > p-2>0$![]() , define
, define
By direct calculation
Substitute $\varphi =v$![]() in (3.79),
in (3.79),
Let $E_k:=\{u\geqslant -k\}$![]() , noting that $\hat u\equiv 0$
, noting that $\hat u\equiv 0$![]() outside $E_k$
outside $E_k$![]() , the integrand above vanishes in $B_{r_2}(y)\setminus E_k$
, the integrand above vanishes in $B_{r_2}(y)\setminus E_k$![]() . Using Young's inequality, noticing that fact that $|\nabla \hat u|=|\nabla u|$
. Using Young's inequality, noticing that fact that $|\nabla \hat u|=|\nabla u|$![]() in $E_k$
in $E_k$![]() ,
,
Combining (6.6), (6.7) and (6.8), it holds that
Set $w:=\bar u^\frac \beta 2\hat u$![]() , noting that $\hat u\geqslant \bar u$
, noting that $\hat u\geqslant \bar u$![]() and $|\nabla \bar u|$
and $|\nabla \bar u|$![]() vanishes in $\{\hat u> l\}$
vanishes in $\{\hat u> l\}$![]() , it is easy to check
, it is easy to check
Therefore,
By the Sobolev inequality

where $\xi =\xi (N):=\frac {N}{N-2}$![]() . Recall that $|\nabla \log G_x|^2$
. Recall that $|\nabla \log G_x|^2$![]() is bounded above by $C(N,\, s)$
is bounded above by $C(N,\, s)$![]() , by the choice of $\eta$
, by the choice of $\eta$![]() ,
,

For any $\gamma >2$![]() and $t\in [\frac 1 2r,\,r]$
and $t\in [\frac 1 2r,\,r]$![]() , set the quantity
, set the quantity

Then (6.13) yields that

where we used the following fact from Bishop–Gromov inequality:
Let $\beta _n=p\xi ^n-2>0$![]() , $\gamma _n:=\beta _n+2>2$
, $\gamma _n:=\beta _n+2>2$![]() , $t_n:=(2^{-1}+2^{-n-1})r$
, $t_n:=(2^{-1}+2^{-n-1})r$![]() , iterating (6.15),
, iterating (6.15),

Let $n\rightarrow \infty$![]() , recalling by definition
, recalling by definition
it holds that
Since the right-handed side of the inequality is independent on $l$![]() , we may let $l\rightarrow \infty$
, we may let $l\rightarrow \infty$![]() , namely
, namely
which finishes the proof under the assumption $p>2$![]() .
.
The case where $1< p\leqslant 2$![]() can be treated via a similar iteration process provided $\hat {u} \in L^\infty (B_r(y),\,\mathfrak {m})$
can be treated via a similar iteration process provided $\hat {u} \in L^\infty (B_r(y),\,\mathfrak {m})$![]() . Indeed, for any $\beta >p-1>0$
. Indeed, for any $\beta >p-1>0$![]() , we can choose a simpler test function without truncation:
, we can choose a simpler test function without truncation:
which can further simplify the proof. Here we omit the details.
Next let us discuss about $\mathscr L$![]() -superharmonic functions. The corresponding results for PI spaces can be found in [Reference Björn and Björn9, Theorem 8.10]. In order to establish a weak Harnack inequality for $\mathscr L$
-superharmonic functions. The corresponding results for PI spaces can be found in [Reference Björn and Björn9, Theorem 8.10]. In order to establish a weak Harnack inequality for $\mathscr L$![]() -superharmonic functions, we first recall the definition of bounded mean oscillating (BMO) functions on metric measure spaces and John–Nirenberg's lemma.
-superharmonic functions, we first recall the definition of bounded mean oscillating (BMO) functions on metric measure spaces and John–Nirenberg's lemma.
Definition 6.2 BMO
Let $(X,\,\mathsf {d},\,\mathfrak {m})$![]() be a measure-doubling metric measure space, namely there exists a constant $C_d>0$
be a measure-doubling metric measure space, namely there exists a constant $C_d>0$![]() such that
such that
For any open subset $\Omega \subset X$![]() and any function $f\in L^1_{\mathrm {loc}}(\Omega,\,\mathfrak {m})$
and any function $f\in L^1_{\mathrm {loc}}(\Omega,\,\mathfrak {m})$![]() , we set
, we set
where the supremum is taken over all open balls $B$![]() with $B\subset \Omega$
with $B\subset \Omega$![]() . The class of BMO functions on $\Omega$
. The class of BMO functions on $\Omega$![]() is the collection
is the collection
Remark 6.3 Note that the doubling assumption is naturally fulfilled for $\operatorname {RCD}(0,\,N)$![]() spaces because of the Bishop–Gromov inequality. In particular, in this case, the doubling constant $C_d$
spaces because of the Bishop–Gromov inequality. In particular, in this case, the doubling constant $C_d$![]() is only dependent on $N$
is only dependent on $N$![]() .
.
John–Nirenberg's lemma we refer is stated as follows, see [Reference Björn and Björn9, Theorem 3.20].
Theorem 6.4 John–Nirenberg's lemma
Let $(X,\, \mathsf {d},\, \mathfrak {m})$![]() be as in definition 6.2 and let $f \in \mathrm {BMO}(B_{5r}(x))$
be as in definition 6.2 and let $f \in \mathrm {BMO}(B_{5r}(x))$![]() for some $x\in X$
for some $x\in X$![]() and $r>0$
and $r>0$![]() . Then for any $0<\varepsilon \leqslant A:=\log 2/(4C_d^{15})$
. Then for any $0<\varepsilon \leqslant A:=\log 2/(4C_d^{15})$![]() ,
,
We are now in a position to prove a weak Harnack inequality (see [Reference Björn and Björn9, Theorem 8.10]).
Proposition 6.5 Weak Harnack inequality for $\mathscr L$![]() -superharmonic functions
-superharmonic functions
Let $u$![]() be a non-negatively valued $\mathscr L$
be a non-negatively valued $\mathscr L$![]() -superharmonic function on a ball $B_{100r}(y)$
-superharmonic function on a ball $B_{100r}(y)$![]() for some $r \leqslant 1$
for some $r \leqslant 1$![]() with $B_{100r}(y) \subset X\setminus B_s(x)$
with $B_{100r}(y) \subset X\setminus B_s(x)$![]() for some $s \leqslant 1$
for some $s \leqslant 1$![]() . Then there exist $p=p(N,\, s)>0$
. Then there exist $p=p(N,\, s)>0$![]() and $C=C(N,\, s)>1$
and $C=C(N,\, s)>1$![]() such that
such that

Proof. First let us assume $u$![]() is bounded away from $0$
is bounded away from $0$![]() . For any fixed $\varepsilon >0$
. For any fixed $\varepsilon >0$![]() , there exists a piecewise linear function $\psi$
, there exists a piecewise linear function $\psi$![]() in the form
in the form
where $a_i<0$![]() , such that
, such that
Applying proposition 6.1 to $\psi \circ (u+\varepsilon )$![]() , we obtain that for any $p>0$
, we obtain that for any $p>0$![]() ,
,

Letting $\varepsilon \rightarrow 0$![]() , we obtain that
, we obtain that

Now it suffices to show that there exists some $p=p(N,\,s)>0$![]() such that
such that
On the other hand, recalling (3.79), we can establish an analogue of (6.11) similarly as in the proof of proposition 6.1 for $w:=\log u$![]() treating the test function $v:=\eta ^2$
treating the test function $v:=\eta ^2$![]()
where $\eta$![]() is any cut-off function with $\operatorname {supp} \eta \subset B_{100r}(y)$
is any cut-off function with $\operatorname {supp} \eta \subset B_{100r}(y)$![]() . Thus choosing $\eta$
. Thus choosing $\eta$![]() with $\eta \equiv 1$
with $\eta \equiv 1$![]() on $B_{50r}(y)$
on $B_{50r}(y)$![]() , we obtain
, we obtain
Thus using the Poincaré inequality (2.22), for any $z\in B_{10r}(y)$![]() and $r'<20r$
and $r'<20r$![]() , we have
, we have

which implies
On the other hand, for this $C(N,\, s)$![]() in (6.35), applying John–Nirenberg's lemma, theorem 6.4, to $w$
in (6.35), applying John–Nirenberg's lemma, theorem 6.4, to $w$![]() with $\varepsilon :=A \cdot C(N,\, s)/2$
with $\varepsilon :=A \cdot C(N,\, s)/2$![]() (recall $A$
(recall $A$![]() is taken as a dimensional constant in this setting), we have
is taken as a dimensional constant in this setting), we have
where
Thus

By (6.30),

Therefore, recalling our choice of $\varepsilon$![]() and (6.35), we have the desired inequality.
and (6.35), we have the desired inequality.
Finally let us assume $u$![]() is not bounded away from $0$
is not bounded away from $0$![]() . We can consider $u_\delta =u+\delta$
. We can consider $u_\delta =u+\delta$![]() $(\delta >0)$
$(\delta >0)$![]() instead, and then let $\delta \downarrow 0$
instead, and then let $\delta \downarrow 0$![]() .
.
We are now in a position to introduce a regularity result on ($\mathscr L$![]() -)superharmonic functions. See [Reference Björn and Björn9, Subsection 8.5], in particular, proposition 8.24 therein.
-)superharmonic functions. See [Reference Björn and Björn9, Subsection 8.5], in particular, proposition 8.24 therein.
Proposition 6.6 Let $u$![]() be as in proposition 6.1. Assume that $u$
be as in proposition 6.1. Assume that $u$![]() is locally bounded. Then there exists a unique representative $\bar u$
is locally bounded. Then there exists a unique representative $\bar u$![]() of $u$
of $u$![]() such that every $z\in B_{100r}(y)$
such that every $z\in B_{100r}(y)$![]() is a Lebesgue point of $\bar u$
is a Lebesgue point of $\bar u$![]() . Moreover $\bar u$
. Moreover $\bar u$![]() is upper semi-continuous satisfying that for any $z\in B_{100r}(y)$
is upper semi-continuous satisfying that for any $z\in B_{100r}(y)$![]()
Indeed, such a representative can be realized by
Proof. Let $\bar u$![]() be as in (6.41). Firstly, since it is easily checked that the set $\{z\mathop | \bar u(z)< a\}$
be as in (6.41). Firstly, since it is easily checked that the set $\{z\mathop | \bar u(z)< a\}$![]() is open for any $a \in \mathbb {R}$
is open for any $a \in \mathbb {R}$![]() , $\bar u$
, $\bar u$![]() is upper semicontinuous.
is upper semicontinuous.
Secondly, let us check $\bar u= u$![]() $\mathfrak {m}$
$\mathfrak {m}$![]() -a.e. Take a Lebesgue point $z\in B_{100r}(y)$
-a.e. Take a Lebesgue point $z\in B_{100r}(y)$![]() of $u$
of $u$![]() . Since $u$
. Since $u$![]() is locally bounded, we have
is locally bounded, we have
For any $\varepsilon >0$![]() , there exists $r_0>0$
, there exists $r_0>0$![]() such that for all $0<\rho < r_0$
such that for all $0<\rho < r_0$![]() , $B_\rho (z)\subset B_{100r}(y)$
, $B_\rho (z)\subset B_{100r}(y)$![]() and
and

where $p$![]() is as in proposition 6.1. Applying proposition 6.1 proves
is as in proposition 6.1. Applying proposition 6.1 proves

Thus $\bar u(z)\leqslant u(z)$![]() . On the other hand
. On the other hand
We obtain that $\bar u(z)=u(z)$![]() . Thus the Lebesgue differentiation theorem allows us to conclude $\bar u=u$
. Thus the Lebesgue differentiation theorem allows us to conclude $\bar u=u$![]() for $\mathfrak {m}$
for $\mathfrak {m}$![]() -a.e. Moreover, observe that
-a.e. Moreover, observe that
therefore we obtain (6.40).
Thirdly, let us show that every point in the domain is a Lebesgue point of $\bar u$![]() . Without loss of generality we may assume $0<\bar u<1$
. Without loss of generality we may assume $0<\bar u<1$![]() in $B_{100r}(y)$
in $B_{100r}(y)$![]() since $u$
since $u$![]() is locally bounded. Fix any $z\in B_{100r}(y)$
is locally bounded. Fix any $z\in B_{100r}(y)$![]() . For any $\varepsilon >0$
. For any $\varepsilon >0$![]() with $u(z)<1-\varepsilon$
with $u(z)<1-\varepsilon$![]() , by the upper semicontinuity, there exists $\rho >0$
, by the upper semicontinuity, there exists $\rho >0$![]() sufficiently small such that $0< u(w)< u(z)+\varepsilon <1$
sufficiently small such that $0< u(w)< u(z)+\varepsilon <1$![]() for any $w\in B_\rho (z)$
for any $w\in B_\rho (z)$![]() . Let $v:=-u+u(z)+\varepsilon$
. Let $v:=-u+u(z)+\varepsilon$![]() , then $0< v<1$
, then $0< v<1$![]() in $B_\rho (z)$
in $B_\rho (z)$![]() . Applying the weak Harnack inequality (6.26) to $v$
. Applying the weak Harnack inequality (6.26) to $v$![]() , there exist $p=p(N,\,s)>0$
, there exist $p=p(N,\,s)>0$![]() and $C=C(N,\,s)>0$
and $C=C(N,\,s)>0$![]() such that
such that

Letting $\rho \rightarrow 0$![]() , we conclude because $\varepsilon$
, we conclude because $\varepsilon$![]() is arbitrary.
is arbitrary.
Finally, the uniqueness is obvious because every point in the domain is a Lebesgue point.
In view of this, we always assume that any $\mathscr L$![]() -subharmonic function $u$
-subharmonic function $u$![]() is actually the canonical representative as obtained in proposition 6.6. Therefore, for example, by (6.40), the ‘$\mathrm {ess\ sup}$
is actually the canonical representative as obtained in proposition 6.6. Therefore, for example, by (6.40), the ‘$\mathrm {ess\ sup}$![]() ’ in proposition 6.1 (‘$\mathrm {ess\ inf}$
’ in proposition 6.1 (‘$\mathrm {ess\ inf}$![]() ’ in proposition 6.5, respectively) can be replaced by ‘$\sup$
’ in proposition 6.5, respectively) can be replaced by ‘$\sup$![]() ’ (‘$\inf$
’ (‘$\inf$![]() ’, respectively). Under this convention, finally let us provide the strong maximum principle for $\mathscr L$
’, respectively). Under this convention, finally let us provide the strong maximum principle for $\mathscr L$![]() -subharmonic functions.
-subharmonic functions.
Proposition 6.7 Strong maximum principle for $\mathscr L$![]() -subharmonic functions
-subharmonic functions
Let $u$![]() be a $\mathscr L$
be a $\mathscr L$![]() -subharmonic function on a connected open subset $\Omega$
-subharmonic function on a connected open subset $\Omega$![]() in $X \setminus \{x\}$
in $X \setminus \{x\}$![]() . If its supremum in $\Omega$
. If its supremum in $\Omega$![]() attains at a point in $\Omega$
attains at a point in $\Omega$![]() , then $u$
, then $u$![]() is constant.
is constant.
Proof. Denote by $A:=\sup _\Omega u$![]() and put $D:=\{x \in \Omega |u(x)=A\}$
and put $D:=\{x \in \Omega |u(x)=A\}$![]() . It is trivial that $D$
. It is trivial that $D$![]() is closed in $\Omega$
is closed in $\Omega$![]() . On the other hand, for any $y \in D$
. On the other hand, for any $y \in D$![]() , applying proposition 6.5 to $\bar u=A-u$
, applying proposition 6.5 to $\bar u=A-u$![]() proves
proves

namely $\bar u=0$![]() $\mathfrak {m}$
$\mathfrak {m}$![]() -a.e. in $B_{2r}(y)$
-a.e. in $B_{2r}(y)$![]() for any sufficiently small $r>0$
for any sufficiently small $r>0$![]() , thus $\bar u \equiv A$
, thus $\bar u \equiv A$![]() on $B_{2r}(y)$
on $B_{2r}(y)$![]() because of the lower semicontinuity of $\bar u$
because of the lower semicontinuity of $\bar u$![]() . This shows that $D$
. This shows that $D$![]() is open in $\Omega$
is open in $\Omega$![]() , Thus $D=\Omega$
, Thus $D=\Omega$![]() because $\Omega$
because $\Omega$![]() is connected.
is connected.
Acknowledgements
The both authors would like to thank Zhangkai Huang for fruitful discussions and valuable suggestions. They also wish to thank Daniele Semola for valuable comments on the preliminary version. Moreover we are grateful to the reviewer for his/her very careful reading of the paper and for giving us valuable suggestions for the revision, especially inspiring us to realize corollary 3.28. The first named author acknowledges supports of the Grant-in-Aid for Scientific Research (B) of 20H01799, the Grant-in-Aid for Scientific Research (B) of 21H00977 and Grant-in-Aid for Transformative Research Areas (A) of 22H05105. The second named author acknowledges the supports from JST SPRING Grant Number: JPMJSP2114 and JSPS KAKENHI Grant Number: JP23KJ0204.