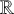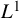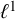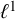1 Introduction
Let X be a pointed metric space: a metric space equipped with some fixed basepoint. The Banach space of Lipschitz functions
![]() $X \to \mathbb {R}$
vanishing at the basepoint has a canonical predual
$X \to \mathbb {R}$
vanishing at the basepoint has a canonical predual
![]() $\operatorname {\mathrm {LF}}(X)$
, called the Lipschitz free space, or just free space, of X. One of the main problems in the field is to determine when
$\operatorname {\mathrm {LF}}(X)$
, called the Lipschitz free space, or just free space, of X. One of the main problems in the field is to determine when
![]() $\operatorname {\mathrm {LF}}(X)$
isomorphically embeds into an
$\operatorname {\mathrm {LF}}(X)$
isomorphically embeds into an
![]() $L^1$
-space (a Banach space of the form
$L^1$
-space (a Banach space of the form
![]() $L^1(Y,\Sigma ,\mu )$
for some measure space
$L^1(Y,\Sigma ,\mu )$
for some measure space
![]() $(Y,\Sigma ,\mu )$
), or more strongly when
$(Y,\Sigma ,\mu )$
), or more strongly when
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to an
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to an
![]() $L^1$
-space (see [Reference Godard29, Reference Freeman and Gartland28], [Reference Weaver48,
$L^1$
-space (see [Reference Godard29, Reference Freeman and Gartland28], [Reference Weaver48,
![]() $\S$
8.6] for some examples and [Reference Kalton33,
$\S$
8.6] for some examples and [Reference Kalton33,
![]() $\S$
8], [Reference Khot and Naor35, Reference Naor and Schechtman41, Reference Dilworth, Kutzarova and Ostrovskii21, Reference Baudier, Gartland and Schlumprecht9] for some nonexamples). The isometric version of this question has an elegant but rigid solution:
$\S$
8], [Reference Khot and Naor35, Reference Naor and Schechtman41, Reference Dilworth, Kutzarova and Ostrovskii21, Reference Baudier, Gartland and Schlumprecht9] for some nonexamples). The isometric version of this question has an elegant but rigid solution:
![]() $\operatorname {\mathrm {LF}}(X)$
isometrically embeds into an
$\operatorname {\mathrm {LF}}(X)$
isometrically embeds into an
![]() $L^1$
-space if and only if X isometrically embeds into an
$L^1$
-space if and only if X isometrically embeds into an
![]() $\mathbb {R}$
-tree ([Reference Godard29, Theorem 4.2]; see also [Reference Aliaga, Petitjean and Procházka3]). However, the isomorphic category permits much greater geometric flexibility; for any infinite, compact, doublingFootnote 1 space
$\mathbb {R}$
-tree ([Reference Godard29, Theorem 4.2]; see also [Reference Aliaga, Petitjean and Procházka3]). However, the isomorphic category permits much greater geometric flexibility; for any infinite, compact, doublingFootnote 1 space
![]() $(X,d)$
and exponent
$(X,d)$
and exponent
![]() $\alpha \in (0,1)$
, the snowflake space
$\alpha \in (0,1)$
, the snowflake space
![]() $(X,d^\alpha )$
has free space isomorphic to
$(X,d^\alpha )$
has free space isomorphic to
![]() $\ell ^1$
(see [Reference Weaver48, Theorem 8.49]).
$\ell ^1$
(see [Reference Weaver48, Theorem 8.49]).
The main goal of this article is to build out the theory of
![]() $L^1$
-embeddings of free spaces and to apply the theory to identify the isomorphism type of
$L^1$
-embeddings of free spaces and to apply the theory to identify the isomorphism type of
![]() $\operatorname {\mathrm {LF}}(X)$
for several choice metric spaces X: finite Nagata-dimensional snowflake spaces, hyperbolic n-space
$\operatorname {\mathrm {LF}}(X)$
for several choice metric spaces X: finite Nagata-dimensional snowflake spaces, hyperbolic n-space
![]() $\mathbb {H}^n$
, and finitely generated Gromov hyperbolic groups. Toward this end, the principal role is played by stochastic biLipschitz embeddings: random maps
$\mathbb {H}^n$
, and finitely generated Gromov hyperbolic groups. Toward this end, the principal role is played by stochastic biLipschitz embeddings: random maps
![]() $\phi : X \to Y$
between pointed metric spaces
$\phi : X \to Y$
between pointed metric spaces
![]() $(X,d_X,p),(X,d_Y,q)$
for which there exists
$(X,d_X,p),(X,d_Y,q)$
for which there exists
![]() $L<\infty $
such that, for every
$L<\infty $
such that, for every
![]() $x,y \in X$
, it holds that
$x,y \in X$
, it holds that
-
○
 $d_Y(\phi (x),\phi (y)) \geq L^{-1}d_X(x,y)$
almost surely,
$d_Y(\phi (x),\phi (y)) \geq L^{-1}d_X(x,y)$
almost surely, -
○
 $\mathbb {E}[d_Y(\phi (x),\phi (y))] \leq Ld_X(x,y)$
, and
$\mathbb {E}[d_Y(\phi (x),\phi (y))] \leq Ld_X(x,y)$
, and -
○
 $\phi (p) = q$
almost surely.
$\phi (p) = q$
almost surely.
See
![]() $\S $
3.1 for the precise definition of a random map and for further discussion on stochastic embeddings. In the theoretical computer science literature, there is already an established finitary version of stochastic biLipschitz embeddings (first introduced in [Reference Bartal8], but not under this name), and this version is especially well-studied when the target spaces are tree metrics ([Reference Alon, Karp, Peleg and West4, Reference Fakcharoenphol, Rao and Talwar27, Reference Schlumprecht and Tresch45]). In this finitary setting, a stochastic biLipschitz embedding into tree metrics is known, among other things, to induce an isomorphic embedding of the Lipschitz free space into an
$\S $
3.1 for the precise definition of a random map and for further discussion on stochastic embeddings. In the theoretical computer science literature, there is already an established finitary version of stochastic biLipschitz embeddings (first introduced in [Reference Bartal8], but not under this name), and this version is especially well-studied when the target spaces are tree metrics ([Reference Alon, Karp, Peleg and West4, Reference Fakcharoenphol, Rao and Talwar27, Reference Schlumprecht and Tresch45]). In this finitary setting, a stochastic biLipschitz embedding into tree metrics is known, among other things, to induce an isomorphic embedding of the Lipschitz free space into an
![]() $L^1$
-space with controlled distortion ([Reference Baudier, Motakis, Schlumprecht and Zsák10, Corollary 6.5]). In this article, we extend the purview of stochastic embeddings to the infinite setting and obtain the analogous result that a stochastic biLipschitz embedding into an
$L^1$
-space with controlled distortion ([Reference Baudier, Motakis, Schlumprecht and Zsák10, Corollary 6.5]). In this article, we extend the purview of stochastic embeddings to the infinite setting and obtain the analogous result that a stochastic biLipschitz embedding into an
![]() $\mathbb {R}$
-tree induces an isomorphic embedding of the free space into an
$\mathbb {R}$
-tree induces an isomorphic embedding of the free space into an
![]() $L^1$
-space. Subsequently, we work toward constructing such embeddings for certain Gromov hyperbolic spaces. In our proofs, a major role is played by Bonk-Schramm’s hyperbolic fillings [Reference Bonk and Schramm12], a construction which provides an inverse functor to the Gromov boundary functor. In addition to the intrinsic interest in understanding the free spaces of hyperbolic spaces, we were motivated by an application to the theory of group actions on Banach spaces (as described in [Reference Candido, Cúth and Doucha16, Question 1]), and we are able to conclude that every infinite, finitely generated hyperbolic group admits a proper, uniformly Lipschitz affine action on
$L^1$
-space. Subsequently, we work toward constructing such embeddings for certain Gromov hyperbolic spaces. In our proofs, a major role is played by Bonk-Schramm’s hyperbolic fillings [Reference Bonk and Schramm12], a construction which provides an inverse functor to the Gromov boundary functor. In addition to the intrinsic interest in understanding the free spaces of hyperbolic spaces, we were motivated by an application to the theory of group actions on Banach spaces (as described in [Reference Candido, Cúth and Doucha16, Question 1]), and we are able to conclude that every infinite, finitely generated hyperbolic group admits a proper, uniformly Lipschitz affine action on
![]() $\ell ^1$
.
$\ell ^1$
.
We will now state precisely our main results and describe in more detail their proofs and the overall structure of the article. We also compare the present work to the related article [Reference Krauthgamer and Lee36] on stochastic biLipschitz embeddability of hyperbolic spaces into trees.
1.1 Main results, outline of their proofs and structure of article
Following this introductory section,
![]() $\S $
2 establishes the background on Lipschitz free spaces, metric spaces of finite Nagata dimension, Gromov hyperbolic spaces and their boundaries, and
$\S $
2 establishes the background on Lipschitz free spaces, metric spaces of finite Nagata dimension, Gromov hyperbolic spaces and their boundaries, and
![]() $\mathbb {R}$
-trees and ultrametric spaces that are necessary for the remainder of the article. The results of
$\mathbb {R}$
-trees and ultrametric spaces that are necessary for the remainder of the article. The results of
![]() $\S $
2 are generally known and not particularly new. However, there are a few important facts – Theorem 2.2, Corollary 2.6 and Lemma 2.8 – that do not appear in the literature to the level of specificity we require, and so we include their full proofs here.
$\S $
2 are generally known and not particularly new. However, there are a few important facts – Theorem 2.2, Corollary 2.6 and Lemma 2.8 – that do not appear in the literature to the level of specificity we require, and so we include their full proofs here.
Next, we obtain in
![]() $\S $
3 our base result, Theorem A (via Theorem 3.3), that stochastic biLipschitz embeddings into
$\S $
3 our base result, Theorem A (via Theorem 3.3), that stochastic biLipschitz embeddings into
![]() $\mathbb {R}$
-trees induce isomorphic embeddings into
$\mathbb {R}$
-trees induce isomorphic embeddings into
![]() $L^1$
-spaces. Under the additional hypothesis of properness,Footnote 2 we can use existing results in Lipschitz free space theory described in
$L^1$
-spaces. Under the additional hypothesis of properness,Footnote 2 we can use existing results in Lipschitz free space theory described in
![]() $\S $
2.3 to get a surjective isomorphism to an
$\S $
2.3 to get a surjective isomorphism to an
![]() $L^1$
-space. Recall that a metric space is purely 1-unrectifiable if it admits no biLipschitz embedding from a positive measure subset of
$L^1$
-space. Recall that a metric space is purely 1-unrectifiable if it admits no biLipschitz embedding from a positive measure subset of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Theorem A (Theorem 3.3).
Let X be an infinite, proper, pointed metric space. If X stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree, then
$\mathbb {R}$
-tree, then
![]() $\operatorname {\mathrm {LF}}(X) \approx L^1$
or
$\operatorname {\mathrm {LF}}(X) \approx L^1$
or
![]() $\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
, with the latter isomorphism holding if and only if the completion of X is purely 1-unrectifiable.
$\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
, with the latter isomorphism holding if and only if the completion of X is purely 1-unrectifiable.
Here and in what follows, we use the notation ‘
![]() $V\approx W$
’ to assert the existence of an isomorphism between two Banach spaces
$V\approx W$
’ to assert the existence of an isomorphism between two Banach spaces
![]() $V,W$
.
$V,W$
.
The subsequent sections
![]() $\S $
4–5 are aimed at producing stochastic biLipschitz embeddings of certain classes of Gromov hyperbolic spaces into
$\S $
4–5 are aimed at producing stochastic biLipschitz embeddings of certain classes of Gromov hyperbolic spaces into
![]() $\mathbb {R}$
-trees. Our method of proof proceeds by analyzing the corresponding problem on the Gromov boundary. Since ultrametric spaces are the boundaries of
$\mathbb {R}$
-trees. Our method of proof proceeds by analyzing the corresponding problem on the Gromov boundary. Since ultrametric spaces are the boundaries of
![]() $\mathbb {R}$
-trees, we are led to seek conditions on which the boundary of a hyperbolic metric space – which can be any bounded, complete metric space – will stochastic biLipschitzly embed into an ultrametric space. This is the content of
$\mathbb {R}$
-trees, we are led to seek conditions on which the boundary of a hyperbolic metric space – which can be any bounded, complete metric space – will stochastic biLipschitzly embed into an ultrametric space. This is the content of
![]() $\S $
4. It turns out that spaces of finite Nagata dimension provide a natural setting for this problem, and the main result of
$\S $
4. It turns out that spaces of finite Nagata dimension provide a natural setting for this problem, and the main result of
![]() $\S $
4 (Theorem 4.16) concerns these spaces. When we combine Theorem 4.16 with Theorem A, we obtain the next main theorem of the article.
$\S $
4 (Theorem 4.16) concerns these spaces. When we combine Theorem 4.16 with Theorem A, we obtain the next main theorem of the article.
Theorem B. Let
![]() $(X,d)$
be an infinite, compact, finite Nagata-dimensional metric space. Then for every
$(X,d)$
be an infinite, compact, finite Nagata-dimensional metric space. Then for every
![]() $\alpha \in (0,1)$
, the metric space
$\alpha \in (0,1)$
, the metric space
![]() $(X,d^\alpha )$
admits a stochastic biLipschitz embedding (for every choice of basepoint) into a pointed ultrametric space, and
$(X,d^\alpha )$
admits a stochastic biLipschitz embedding (for every choice of basepoint) into a pointed ultrametric space, and
![]() $\operatorname {\mathrm {LF}}(X,d^\alpha ) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(X,d^\alpha ) \approx \ell ^1$
.
Proof. Let
![]() $\alpha \in (0,1)$
. Equip
$\alpha \in (0,1)$
. Equip
![]() $(X,d^\alpha )$
with any basepoint. Then by Theorem 4.16, there is a stochastic biLipschitz embedding of
$(X,d^\alpha )$
with any basepoint. Then by Theorem 4.16, there is a stochastic biLipschitz embedding of
![]() $(X,d^\alpha )$
into a pointed ultrametric space. Since ultrametric spaces isometrically embed into
$(X,d^\alpha )$
into a pointed ultrametric space. Since ultrametric spaces isometrically embed into
![]() $\mathbb {R}$
-trees, there is a stochastic biLipschitz embedding of
$\mathbb {R}$
-trees, there is a stochastic biLipschitz embedding of
![]() $(X,d^\alpha )$
into a pointed
$(X,d^\alpha )$
into a pointed
![]() $\mathbb {R}$
-tree. Then since
$\mathbb {R}$
-tree. Then since
![]() $(X,d^\alpha )$
has purely 1-unrectifiable completion,Footnote 3 we have by Theorem A that
$(X,d^\alpha )$
has purely 1-unrectifiable completion,Footnote 3 we have by Theorem A that
![]() $\operatorname {\mathrm {LF}}(X,d^\alpha ) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(X,d^\alpha ) \approx \ell ^1$
.
It holds that
![]() $\operatorname {\mathrm {LF}}(X,d^{\alpha }) \approx \ell ^1$
whenever
$\operatorname {\mathrm {LF}}(X,d^{\alpha }) \approx \ell ^1$
whenever
![]() $(X,d)$
is an infinite, compact, doubling metric space and
$(X,d)$
is an infinite, compact, doubling metric space and
![]() $\alpha \in (0,1)$
(see [Reference Weaver48, Theorem 8.49]). However, for distortion functions
$\alpha \in (0,1)$
(see [Reference Weaver48, Theorem 8.49]). However, for distortion functions
![]() $\omega : [0,\infty ) \to [0,\infty )$
(see
$\omega : [0,\infty ) \to [0,\infty )$
(see
![]() $\S $
4.3 for the definition) satisfying
$\S $
4.3 for the definition) satisfying
![]() $\lim _{t\to 0}\frac {t^\alpha }{\omega (t)} = 0$
for all
$\lim _{t\to 0}\frac {t^\alpha }{\omega (t)} = 0$
for all
![]() $\alpha \in (0,1)$
, for example, when
$\alpha \in (0,1)$
, for example, when
![]() $\omega (t) = \log (\frac {1}{t})^{-1}$
for t sufficiently small, the space
$\omega (t) = \log (\frac {1}{t})^{-1}$
for t sufficiently small, the space
![]() $(X,\omega \circ d)$
generally fails to be doubling. As far as we are aware, at the time of this writing, the validity of statement
$(X,\omega \circ d)$
generally fails to be doubling. As far as we are aware, at the time of this writing, the validity of statement
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
for such
$\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
for such
![]() $\omega $
remained an open question (see [Reference Weaver48, page 294]). But, since post-composition with a distortion function
$\omega $
remained an open question (see [Reference Weaver48, page 294]). But, since post-composition with a distortion function
![]() $\omega $
does not change the Nagata dimension (see Lemma 4.18), we are able to invoke Theorem B and prove in Theorem 4.21 that whenever
$\omega $
does not change the Nagata dimension (see Lemma 4.18), we are able to invoke Theorem B and prove in Theorem 4.21 that whenever
![]() $(X,d)$
is an infinite, compact, finite Nagata-dimensional metric space and
$(X,d)$
is an infinite, compact, finite Nagata-dimensional metric space and
![]() $\omega $
is a distortion function with
$\omega $
is a distortion function with
![]() $\omega (t) = \log (\frac {1}{t})^{-1}$
for t sufficiently small (see Example 4.20), the isomorphism
$\omega (t) = \log (\frac {1}{t})^{-1}$
for t sufficiently small (see Example 4.20), the isomorphism
holds.
In
![]() $\S $
5, we return to the problem of constructing stochastic biLipschitz embeddings of hyperbolic spaces X into
$\S $
5, we return to the problem of constructing stochastic biLipschitz embeddings of hyperbolic spaces X into
![]() $\mathbb {R}$
-trees. Our objective is to understand specifically when this problem can be answered by stochastically embedding
$\mathbb {R}$
-trees. Our objective is to understand specifically when this problem can be answered by stochastically embedding
![]() $\partial X$
, the boundary of X, into an ultrametric space. This type of problem falls squarely within the realm of hyperbolic fillings, which are constructions of hyperbolic metric spaces with prescribed boundaries. The hyperbolic filling technique we find most fitting for our purposes is the one of Bonk-Schramm [Reference Bonk and Schramm12], as described in
$\partial X$
, the boundary of X, into an ultrametric space. This type of problem falls squarely within the realm of hyperbolic fillings, which are constructions of hyperbolic metric spaces with prescribed boundaries. The hyperbolic filling technique we find most fitting for our purposes is the one of Bonk-Schramm [Reference Bonk and Schramm12], as described in
![]() $\S $
2.5. With this apparatus in mind, we are able to identify ‘log-stochastic biLipschitz embeddings’ as the correct notion to study for boundaries of hyperbolic spaces. A log-stochastic biLipschitz embedding between pointed metric spaces is defined in the same way as a stochastic biLipschitz embedding, but with the weaker condition
$\S $
2.5. With this apparatus in mind, we are able to identify ‘log-stochastic biLipschitz embeddings’ as the correct notion to study for boundaries of hyperbolic spaces. A log-stochastic biLipschitz embedding between pointed metric spaces is defined in the same way as a stochastic biLipschitz embedding, but with the weaker condition
replacing
![]() $\mathbb {E}[d_Y(\phi (x),\phi (y))] \leq Ld_X(x,y)$
(this is indeed weaker by Jensen’s inequality). See
$\mathbb {E}[d_Y(\phi (x),\phi (y))] \leq Ld_X(x,y)$
(this is indeed weaker by Jensen’s inequality). See
![]() $\S $
5 for a more precise discussion of log-stochastic biLipschitz embeddings. The fundamental theorem on these embeddings is Theorem C (via Theorem 5.7). Recall that a metric space
$\S $
5 for a more precise discussion of log-stochastic biLipschitz embeddings. The fundamental theorem on these embeddings is Theorem C (via Theorem 5.7). Recall that a metric space
![]() $(X,d)$
is uniformly discrete if there exists
$(X,d)$
is uniformly discrete if there exists
![]() $\theta> 0$
such that
$\theta> 0$
such that
![]() $d(x,y) \geq \theta $
for all
$d(x,y) \geq \theta $
for all
![]() $x\neq y \in X$
, and is locally finite if all its bounded sets are finite. See
$x\neq y \in X$
, and is locally finite if all its bounded sets are finite. See
![]() $\S $
2.1 for the definition of rough biLipschitz embedding and
$\S $
2.1 for the definition of rough biLipschitz embedding and
![]() $\S $
2.5 for the definition of visual metric spaces.
$\S $
2.5 for the definition of visual metric spaces.
Theorem C (Theorem 5.7).
Let A be an infinite, uniformly discrete, locally finite, pointed metric space, and let X be a visual, hyperbolic, pointed metric space. If A rough biLipschitzly embeds into X and
![]() $\partial X$
log-stochastic biLipschitzly embeds (for every choice of basepoint) into a bounded, pointed ultrametric space, then A stochastic biLipschitzly embeds into a pointed
$\partial X$
log-stochastic biLipschitzly embeds (for every choice of basepoint) into a bounded, pointed ultrametric space, then A stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree and
$\mathbb {R}$
-tree and
![]() $\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
As an application of Theorem C, we show through Corollary 6.4 in
![]() $\S $
6 that the free space over hyperbolic n-space
$\S $
6 that the free space over hyperbolic n-space
![]() $\mathbb {H}^n$
is isomorphic to the free space over Euclidean n-space
$\mathbb {H}^n$
is isomorphic to the free space over Euclidean n-space
![]() $\mathbb {R}^n$
. See
$\mathbb {R}^n$
. See
![]() $\S $
6 for background on the space
$\S $
6 for background on the space
![]() $\mathbb {H}^n$
.
$\mathbb {H}^n$
.
Theorem D (Corollary 6.4).
![]() $\operatorname {\mathrm {LF}}(\mathbb {H}^n) \approx \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
.
$\operatorname {\mathrm {LF}}(\mathbb {H}^n) \approx \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
.
The proof of Theorem D can be summarized as follows: we establish in Lemma 6.2 a general local-to-global criterion for finite Nagata-dimensional spaces X, which states that
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of the
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of the
![]() $\ell ^1$
-sum
$\ell ^1$
-sum
![]() $\left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{r}(a))\right ) \oplus \operatorname {\mathrm {LF}}(A)$
, where
$\left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{r}(a))\right ) \oplus \operatorname {\mathrm {LF}}(A)$
, where
![]() $0<r<\infty $
is some fixed radius and
$0<r<\infty $
is some fixed radius and
![]() $A \subseteq X$
is a uniformly discrete subset. We can then apply this lemma to
$A \subseteq X$
is a uniformly discrete subset. We can then apply this lemma to
![]() $X = \mathbb {H}^n$
and use the fact that any infinite, uniformly discrete
$X = \mathbb {H}^n$
and use the fact that any infinite, uniformly discrete
![]() $A \subseteq \mathbb {H}^n$
satisfies the hypotheses of Theorem C to obtain that
$A \subseteq \mathbb {H}^n$
satisfies the hypotheses of Theorem C to obtain that
![]() $\operatorname {\mathrm {LF}}(\mathbb {H}^n)$
is isomorphic to a complemented subspace of
$\operatorname {\mathrm {LF}}(\mathbb {H}^n)$
is isomorphic to a complemented subspace of
![]() $\left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{r}(a))\right ) \oplus \ell ^1$
. We can then use existing free space theory and the fact that
$\left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{r}(a))\right ) \oplus \ell ^1$
. We can then use existing free space theory and the fact that
![]() $B_{r}(a)$
is uniformly (in
$B_{r}(a)$
is uniformly (in
![]() $a \in A$
) biLipschitz equivalent to a ball in
$a \in A$
) biLipschitz equivalent to a ball in
![]() $\mathbb {R}^n$
to obtain
$\mathbb {R}^n$
to obtain
![]() $\operatorname {\mathrm {LF}}(\mathbb {H}^n) \approx \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
.
$\operatorname {\mathrm {LF}}(\mathbb {H}^n) \approx \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
.
In the final section,
![]() $\S $
7, we apply Theorem C and [Reference Bonk and Schramm12, Embedding Theorem 1.1] and prove in Lemma 7.1 that every infinite, finitely generated hyperbolic group
$\S $
7, we apply Theorem C and [Reference Bonk and Schramm12, Embedding Theorem 1.1] and prove in Lemma 7.1 that every infinite, finitely generated hyperbolic group
![]() $\Gamma $
stochastic biLipschitzly embeds into a pointed
$\Gamma $
stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree and thus satisfies
$\mathbb {R}$
-tree and thus satisfies
This answers [Reference Candido, Cúth and Doucha16, Question 1]. In particular, we get Theorem E (via Theorem 7.2) as an immediate consequence. The unfamiliar reader may consult [Reference Nowak43] for the definition of proper, uniformly Lipschitz affine actions.
Theorem E (Theorem 7.2).
For every infinite hyperbolic group
![]() $\Gamma $
and finite generating set
$\Gamma $
and finite generating set
![]() $S \subseteq \Gamma $
, there exists an isometric affine action
$S \subseteq \Gamma $
, there exists an isometric affine action
![]() $\alpha $
of
$\alpha $
of
![]() $\Gamma $
on a Banach space V isomorphic to
$\Gamma $
on a Banach space V isomorphic to
![]() $\ell ^1$
such that the orbit map
$\ell ^1$
such that the orbit map
![]() $\gamma \mapsto \alpha (\gamma )(0)$
is an isometric embedding
$\gamma \mapsto \alpha (\gamma )(0)$
is an isometric embedding
![]() $\Gamma \hookrightarrow V$
(with respect to the S-word metric). In particular, every hyperbolic group admits a proper, uniformly Lipschitz affine action on
$\Gamma \hookrightarrow V$
(with respect to the S-word metric). In particular, every hyperbolic group admits a proper, uniformly Lipschitz affine action on
![]() $\ell ^1$
.
$\ell ^1$
.
Theorem E fits into a line of research inspired by a conjecture of Shalom positing that every hyperbolic group admits a proper, uniformly Lipschitz affine action on
![]() $\ell ^2$
([Reference Cherix17, Open Problem 14], [Reference Nowak43, Conjecture 35]). We are very grateful to Michal Doucha for bringing this problem to our attention and explaining the role of Lipschitz free space theory (see the paragraph following [Reference Candido, Cúth and Doucha16, Question 1]). We briefly mention in
$\ell ^2$
([Reference Cherix17, Open Problem 14], [Reference Nowak43, Conjecture 35]). We are very grateful to Michal Doucha for bringing this problem to our attention and explaining the role of Lipschitz free space theory (see the paragraph following [Reference Candido, Cúth and Doucha16, Question 1]). We briefly mention in
![]() $\S $
7 other recent work concerning this problem.
$\S $
7 other recent work concerning this problem.
1.2 Relationship to existing work
In [Reference Krauthgamer and Lee36, Theorem 5.4], Krauthgamer and Lee proved that for finite subsets X of certain visual hyperbolic metric spaces satisfying a type of local doubling condition (which holds for
![]() $\mathbb {H}^n$
), X admits a stochastic biLipschitz embedding into a ‘tree of neighborhoods’ of X. A tree of neighborhoods is constructed by gluing together balls
$\mathbb {H}^n$
), X admits a stochastic biLipschitz embedding into a ‘tree of neighborhoods’ of X. A tree of neighborhoods is constructed by gluing together balls
![]() $B_\tau (x_i) \subseteq X$
in a tree-like fashion, which amounts to the same process as described in [Reference Weaver48, Lemma 3.12]. By [Reference Weaver48, Lemma 3.12], the free space of this tree of neighborhoods is isomorphic to the (finite)
$B_\tau (x_i) \subseteq X$
in a tree-like fashion, which amounts to the same process as described in [Reference Weaver48, Lemma 3.12]. By [Reference Weaver48, Lemma 3.12], the free space of this tree of neighborhoods is isomorphic to the (finite)
![]() $\ell ^1$
-sum
$\ell ^1$
-sum
![]() $\oplus ^1_i \operatorname {\mathrm {LF}}(B_\tau (x_i))$
. We believe that this argument could be substituted for
$\oplus ^1_i \operatorname {\mathrm {LF}}(B_\tau (x_i))$
. We believe that this argument could be substituted for
![]() $\S $
4–5 in the proofs of Theorem D and (1.2), allowing us to (potentially) obtain those results more quickly. However, we opt for the current approach for at least two reasons. First, like the present article, the proof of [Reference Krauthgamer and Lee36, Theorem 5.4] uses boundary methods in an essential way, but the boundary itself does not explicitly appear in the statement of that theorem. In the present article, it is our desire to flesh out a more complete picture of the precise relationship between
$\S $
4–5 in the proofs of Theorem D and (1.2), allowing us to (potentially) obtain those results more quickly. However, we opt for the current approach for at least two reasons. First, like the present article, the proof of [Reference Krauthgamer and Lee36, Theorem 5.4] uses boundary methods in an essential way, but the boundary itself does not explicitly appear in the statement of that theorem. In the present article, it is our desire to flesh out a more complete picture of the precise relationship between
![]() $\partial X$
and the stochastic biLipschitz embeddability of X into trees. We believe that this is accomplished (at least partially) in
$\partial X$
and the stochastic biLipschitz embeddability of X into trees. We believe that this is accomplished (at least partially) in
![]() $\S $
5 with Theorem 5.7, and as a consequence, this theorem provides a blackbox that could find future use in proving stochastic biLipschitz embeddability of a hyperbolic metric space into a tree. Second, on the way to proving Theorem D and (1.2), we are able to establish (1.1) as a byproduct. As previously discussed, this result answers the open problem described in [Reference Weaver48, page 294].
$\S $
5 with Theorem 5.7, and as a consequence, this theorem provides a blackbox that could find future use in proving stochastic biLipschitz embeddability of a hyperbolic metric space into a tree. Second, on the way to proving Theorem D and (1.2), we are able to establish (1.1) as a byproduct. As previously discussed, this result answers the open problem described in [Reference Weaver48, page 294].
2 Preliminaries
2.1 Metric spaces and maps between them
Whenever
![]() $(X,d)$
is a metric space and
$(X,d)$
is a metric space and
![]() $A,B \subseteq X$
are nonempty subsets, we write
$A,B \subseteq X$
are nonempty subsets, we write
![]() $\operatorname {\mathrm {diam}}(A) := \sup _{a,b \in A} d(a,b) \in [0,\infty ]$
and
$\operatorname {\mathrm {diam}}(A) := \sup _{a,b \in A} d(a,b) \in [0,\infty ]$
and
![]() $\operatorname {\mathrm {dist}}(A,B) := \inf _{a\in A, b \in B}d(a,b) \in [0,\infty )$
. If
$\operatorname {\mathrm {dist}}(A,B) := \inf _{a\in A, b \in B}d(a,b) \in [0,\infty )$
. If
![]() $B = \{b\}$
is a singleton, we condense notation and write
$B = \{b\}$
is a singleton, we condense notation and write
![]() $\operatorname {\mathrm {dist}}(A,b)$
for
$\operatorname {\mathrm {dist}}(A,b)$
for
![]() $\operatorname {\mathrm {dist}}(A,\{b\})$
. If
$\operatorname {\mathrm {dist}}(A,\{b\})$
. If
![]() $x \in X$
and
$x \in X$
and
![]() $r \geq 0$
, we write
$r \geq 0$
, we write
![]() $B_r(x)$
for the closed ball
$B_r(x)$
for the closed ball
![]() $\{y \in X: d(x,y) \leq r\}$
.
$\{y \in X: d(x,y) \leq r\}$
.
Let
![]() $(X,d_X),(Y,d_Y)$
be metric spaces and
$(X,d_X),(Y,d_Y)$
be metric spaces and
![]() $f: X \to Y$
a map. Then f is L-Lipschitz (for some
$f: X \to Y$
a map. Then f is L-Lipschitz (for some
![]() $L<\infty $
) if for all
$L<\infty $
) if for all
![]() $x,y\in X$
, it holds that
$x,y\in X$
, it holds that
![]() $d_Y(f(x),f(y)) \leq Ld_X(x,y)$
. The minimal such L is called the Lipschitz constant of f and is denoted by
$d_Y(f(x),f(y)) \leq Ld_X(x,y)$
. The minimal such L is called the Lipschitz constant of f and is denoted by
![]() $\operatorname {\mathrm {Lip}}(f)$
. The map f is a biLipschitz embedding of distortion D if f is injective and there exists a scaling factor
$\operatorname {\mathrm {Lip}}(f)$
. The map f is a biLipschitz embedding of distortion D if f is injective and there exists a scaling factor
![]() $s\in (0,\infty )$
such that f is
$s\in (0,\infty )$
such that f is
![]() $sD$
-Lipschitz and
$sD$
-Lipschitz and
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $s^{-1}$
-Lipschitz. If f is also surjective, then it is a biLipschitz equivalence. BiLipschitz embeddings and equivalences of distortion 1 are isometric embeddings and isometries, respectively. The map f is a rough biLipschitz embedding (or quasi-isometric embedding) if there are
$s^{-1}$
-Lipschitz. If f is also surjective, then it is a biLipschitz equivalence. BiLipschitz embeddings and equivalences of distortion 1 are isometric embeddings and isometries, respectively. The map f is a rough biLipschitz embedding (or quasi-isometric embedding) if there are
![]() $K,L<\infty $
such that
$K,L<\infty $
such that
![]() $L^{-1}d_X(x,y) - K \leq d_Y(f(x),f(y)) \leq Ld_X(x,y) + K$
for all
$L^{-1}d_X(x,y) - K \leq d_Y(f(x),f(y)) \leq Ld_X(x,y) + K$
for all
![]() $x,y \in X$
. If, in addition, the image of f is coarsely dense, meaning there exists
$x,y \in X$
. If, in addition, the image of f is coarsely dense, meaning there exists
![]() $C<\infty $
such that
$C<\infty $
such that
![]() $\operatorname {\mathrm {dist}}(f(X),y) < C$
for every
$\operatorname {\mathrm {dist}}(f(X),y) < C$
for every
![]() $y \in Y$
, then f is a rough biLipschitz equivalence (or quasi-isometry). If there exist
$y \in Y$
, then f is a rough biLipschitz equivalence (or quasi-isometry). If there exist
![]() $\alpha \in (0,\infty )$
and
$\alpha \in (0,\infty )$
and
![]() $L<\infty $
such that
$L<\infty $
such that
![]() $L^{-1}d_X(x,y) \leq d_Y(f(x),f(y))^\alpha \leq Ld_X(x,y)$
for all
$L^{-1}d_X(x,y) \leq d_Y(f(x),f(y))^\alpha \leq Ld_X(x,y)$
for all
![]() $x,y \in X$
, then f is a snowflake embedding. Surjective snowflake embeddings are called snowflake equivalences. Note that snowflake embeddings (and thus biLipschitz embeddings) are always measurableFootnote 4 since they are continuous, but rough biLipschitz embeddings need not be measurable (indeed, any map between two bounded metric spaces is a rough biLipschitz equivalence).
$x,y \in X$
, then f is a snowflake embedding. Surjective snowflake embeddings are called snowflake equivalences. Note that snowflake embeddings (and thus biLipschitz embeddings) are always measurableFootnote 4 since they are continuous, but rough biLipschitz embeddings need not be measurable (indeed, any map between two bounded metric spaces is a rough biLipschitz equivalence).
2.2 Banach and Bochner-Lebesgue spaces
Let
![]() $T: V \to W$
be a linear map between Banach spacesFootnote 5 and
$T: V \to W$
be a linear map between Banach spacesFootnote 5 and
![]() $C<\infty $
. The map T is C-bounded if it is C-Lipschitz, T is a C-isomorphic embedding if it is biLipschitz with distortion C, and T is a C-isomorphism if it is a surjective C-isomorphic embedding. We will use the notation ‘
$C<\infty $
. The map T is C-bounded if it is C-Lipschitz, T is a C-isomorphic embedding if it is biLipschitz with distortion C, and T is a C-isomorphism if it is a surjective C-isomorphic embedding. We will use the notation ‘
![]() $V \approx W$
’ to indicate that there exists an isomorphism between V and W. Linear maps that are 1-isomorphic embeddings or 1-isomorphisms are linear isometric embeddings and linear isometries, respectively. A subspace
$V \approx W$
’ to indicate that there exists an isomorphism between V and W. Linear maps that are 1-isomorphic embeddings or 1-isomorphisms are linear isometric embeddings and linear isometries, respectively. A subspace
![]() $U \subseteq W$
is C-complemented if there exists a C-bounded linear map
$U \subseteq W$
is C-complemented if there exists a C-bounded linear map
![]() $R: W \to U$
such that
$R: W \to U$
such that
![]() $R(u) = u$
for every
$R(u) = u$
for every
![]() $u \in U$
. It holds that V is
$u \in U$
. It holds that V is
![]() $C_1$
-isomorphic to a
$C_1$
-isomorphic to a
![]() $C_1$
-complemented subspace of
$C_1$
-complemented subspace of
![]() $W\ \iff $
there exist
$W\ \iff $
there exist
![]() $C_2$
-bounded linear maps
$C_2$
-bounded linear maps
![]() $T: V \to W$
and
$T: V \to W$
and
![]() $R: W \to V$
such that
$R: W \to V$
such that
![]() $R \circ T = id_V$
(we say that R retracts T)
$R \circ T = id_V$
(we say that R retracts T)
![]() $\iff $
there exists a Banach space U such that
$\iff $
there exists a Banach space U such that
![]() $U \oplus V$
is
$U \oplus V$
is
![]() $C_3$
-isomorphic to W, where in each equivalence,
$C_3$
-isomorphic to W, where in each equivalence,
![]() $C_{i+1}$
depends only on
$C_{i+1}$
depends only on
![]() $C_{i}$
and vice versa. We will use the notation ‘
$C_{i}$
and vice versa. We will use the notation ‘
![]() $V\overset {\mathrm {c}}{\hookrightarrow } W$
’ to indicate that V is isomorphic to a complemented subspace of W. Here and in the sequel, whenever
$V\overset {\mathrm {c}}{\hookrightarrow } W$
’ to indicate that V is isomorphic to a complemented subspace of W. Here and in the sequel, whenever
![]() $\{(V_\lambda ,\|\cdot \|_\lambda )\}_{\lambda \in \Lambda }$
is an indexed family of Banach spaces, we denote the
$\{(V_\lambda ,\|\cdot \|_\lambda )\}_{\lambda \in \Lambda }$
is an indexed family of Banach spaces, we denote the
![]() $\ell ^1$
-sum of the family by
$\ell ^1$
-sum of the family by
![]() $\oplus ^1_{\lambda \in \Lambda } V_\lambda $
, or just
$\oplus ^1_{\lambda \in \Lambda } V_\lambda $
, or just
![]() $\oplus _{\lambda \in \Lambda } V_\lambda $
without the ‘1’ in the superscript. That is,
$\oplus _{\lambda \in \Lambda } V_\lambda $
without the ‘1’ in the superscript. That is,
![]() $\oplus ^1_{\lambda \in \Lambda } V_\alpha $
consists of all
$\oplus ^1_{\lambda \in \Lambda } V_\alpha $
consists of all
![]() $\Lambda $
-indexed generalized sequences
$\Lambda $
-indexed generalized sequences
![]() $(\boldsymbol {v}_\lambda )_{\lambda \in \Lambda }$
,
$(\boldsymbol {v}_\lambda )_{\lambda \in \Lambda }$
,
![]() $\boldsymbol {v}_\lambda \in V_\lambda $
, with finite norm
$\boldsymbol {v}_\lambda \in V_\lambda $
, with finite norm
![]() $\|(\boldsymbol {v}_\lambda )_{\lambda \in \Lambda }\| := \sum _{\lambda \in \Lambda } \|\boldsymbol {v}_\lambda \|_\lambda $
. Whenever each of two Banach spaces
$\|(\boldsymbol {v}_\lambda )_{\lambda \in \Lambda }\| := \sum _{\lambda \in \Lambda } \|\boldsymbol {v}_\lambda \|_\lambda $
. Whenever each of two Banach spaces
![]() $V,W$
is C-isomorphic to a C-complemented subspace of the other, and one of the two, say V, is C-isomorphic to its countable
$V,W$
is C-isomorphic to a C-complemented subspace of the other, and one of the two, say V, is C-isomorphic to its countable
![]() $\ell ^1$
-sum
$\ell ^1$
-sum
![]() $\oplus ^1_{n\in \mathbb {N}} V$
, then the Pełczyński decomposition method yields a
$\oplus ^1_{n\in \mathbb {N}} V$
, then the Pełczyński decomposition method yields a
![]() $C'$
-isomorphism
$C'$
-isomorphism
![]() $V \approx W$
, where
$V \approx W$
, where
![]() $C'$
depends only on C [Reference Benyamini and Lindenstrauss11, Proposition F.9].
$C'$
depends only on C [Reference Benyamini and Lindenstrauss11, Proposition F.9].
As previously stated, a Banach space is an
![]() $L^1$
-space if it equals the Lebesgue space
$L^1$
-space if it equals the Lebesgue space
![]() $L^1(\Omega ,\mathcal {F},\mu )$
for some measure space
$L^1(\Omega ,\mathcal {F},\mu )$
for some measure space
![]() $(\Omega ,\mathcal {F},\mu )$
. When
$(\Omega ,\mathcal {F},\mu )$
. When
![]() $\Omega $
equals
$\Omega $
equals
![]() $[0,1]$
equipped with the Borel
$[0,1]$
equipped with the Borel
![]() $\sigma $
-algebra and Lebesgue measure, we abbreviate
$\sigma $
-algebra and Lebesgue measure, we abbreviate
![]() $L^1(\Omega ,\mathcal {F},\mu )$
by
$L^1(\Omega ,\mathcal {F},\mu )$
by
![]() $L^1$
. When
$L^1$
. When
![]() $\Omega $
equals
$\Omega $
equals
![]() $\mathbb {N}$
equipped with the power set
$\mathbb {N}$
equipped with the power set
![]() $\sigma $
-algebra and counting measure, we abbreviate
$\sigma $
-algebra and counting measure, we abbreviate
![]() $L^1(\Omega ,\mathcal {F},\mu )$
by
$L^1(\Omega ,\mathcal {F},\mu )$
by
![]() $\ell ^1$
. It holds that any separable subspace of an
$\ell ^1$
. It holds that any separable subspace of an
![]() $L^1$
-space is contained in a separable
$L^1$
-space is contained in a separable
![]() $L^1$
-subspace (see, for example, [Reference Ostrovskii44, Fact 1.20]), and any separable, infinite dimensional
$L^1$
-subspace (see, for example, [Reference Ostrovskii44, Fact 1.20]), and any separable, infinite dimensional
![]() $L^1$
-space is isomorphic to
$L^1$
-space is isomorphic to
![]() $L^1$
or to
$L^1$
or to
![]() $\ell ^1$
[Reference Johnson and Lindenstrauss32, page 15].
$\ell ^1$
[Reference Johnson and Lindenstrauss32, page 15].
Let
![]() $(\Omega ,\mathcal {F},\mu )$
be a measure space,
$(\Omega ,\mathcal {F},\mu )$
be a measure space,
![]() $(V,\|\cdot \|)$
a Banach space, and
$(V,\|\cdot \|)$
a Banach space, and
![]() $g: \Omega \to V$
a function. We say that g is Bochner measurable if g is the
$g: \Omega \to V$
a function. We say that g is Bochner measurable if g is the
![]() $\mu $
-almost everywhere pointwise limit of a sequence of simple functions, where a function is simple if it belongs to the linear span of the indicator functions
$\mu $
-almost everywhere pointwise limit of a sequence of simple functions, where a function is simple if it belongs to the linear span of the indicator functions
![]() $\{\mathsf {1}_Fv\}_{F\in \mathcal {F},v\in V}$
. The function g is weakly measurable if
$\{\mathsf {1}_Fv\}_{F\in \mathcal {F},v\in V}$
. The function g is weakly measurable if
![]() $\lambda \circ g: \Omega \to \mathbb {R}$
is measurable for every
$\lambda \circ g: \Omega \to \mathbb {R}$
is measurable for every
![]() $\lambda \in V^*$
. The function g is essentially-separably-valued if there exist a separable subspace
$\lambda \in V^*$
. The function g is essentially-separably-valued if there exist a separable subspace
![]() $S \subseteq V$
and a
$S \subseteq V$
and a
![]() $\mu $
-null set N such that
$\mu $
-null set N such that
![]() $g(\omega ) \in S$
for every
$g(\omega ) \in S$
for every
![]() $\omega \in \Omega \setminus N$
. Pettis’s measurability theorem [Reference Diestel, Uhl and Pettis20, Theorem 1.2] characterizes Bochner measurable functions as exactly those that are weakly measurable and essentially-separably-valued. Since Bochner measurability immediately implies measurability and measurability immediately implies weak measurability, it holds that a function is Bochner measurable if and only if it is measurable and essentially-separably-valued. This latter characterization is the one we will most frequently use throughout the article. The set of Bochner measurable functions g with finite norm
$\omega \in \Omega \setminus N$
. Pettis’s measurability theorem [Reference Diestel, Uhl and Pettis20, Theorem 1.2] characterizes Bochner measurable functions as exactly those that are weakly measurable and essentially-separably-valued. Since Bochner measurability immediately implies measurability and measurability immediately implies weak measurability, it holds that a function is Bochner measurable if and only if it is measurable and essentially-separably-valued. This latter characterization is the one we will most frequently use throughout the article. The set of Bochner measurable functions g with finite norm
![]() $\|g\|_{L^1(\Omega ;V)} := \int _\Omega \|g\| d\mu < \infty $
forms a Banach space (the Bochner-Lebesgue space), denoted by
$\|g\|_{L^1(\Omega ;V)} := \int _\Omega \|g\| d\mu < \infty $
forms a Banach space (the Bochner-Lebesgue space), denoted by
![]() $L^1(\Omega ,\mathcal {F},\mu ;V)$
, or just
$L^1(\Omega ,\mathcal {F},\mu ;V)$
, or just
![]() $L^1(\Omega ;V)$
if the
$L^1(\Omega ;V)$
if the
![]() $\sigma $
-algebra and measure are understood. Also, if
$\sigma $
-algebra and measure are understood. Also, if
![]() $V=\mathbb {R}$
, we compress notation again and just write
$V=\mathbb {R}$
, we compress notation again and just write
![]() $L^1(\Omega ,\mathcal {F},\mu )$
or
$L^1(\Omega ,\mathcal {F},\mu )$
or
![]() $L^1(\Omega )$
. Simple functions are dense in
$L^1(\Omega )$
. Simple functions are dense in
![]() $L^1(\Omega ;V)$
, and thus, the integral
$L^1(\Omega ;V)$
, and thus, the integral
![]() $\int _\Omega h d\mu $
, which is defined in the obvious way for simple functions h, admits a unique continuous extension to all
$\int _\Omega h d\mu $
, which is defined in the obvious way for simple functions h, admits a unique continuous extension to all
![]() $h \in L^1(\Omega ;V)$
. Furthermore, if A is a dense subset of V, then the set of simple functions
$h \in L^1(\Omega ;V)$
. Furthermore, if A is a dense subset of V, then the set of simple functions
![]() $\Omega \to A$
taking values in A is dense in
$\Omega \to A$
taking values in A is dense in
![]() $L^1(\Omega ;V)$
. Using this fact, it is easy to prove that whenever
$L^1(\Omega ;V)$
. Using this fact, it is easy to prove that whenever
![]() $(\Omega ',\mathcal {F}',\mu ')$
is a second measure space,
$(\Omega ',\mathcal {F}',\mu ')$
is a second measure space,
![]() $L^1(\Omega ,\mathcal {F},\mu ;L^1(\Omega ',\mathcal {F}',\mu '))$
is canonically linearly isometric to
$L^1(\Omega ,\mathcal {F},\mu ;L^1(\Omega ',\mathcal {F}',\mu '))$
is canonically linearly isometric to
![]() $L^1(\Omega \times \Omega ',\mathcal {F}\otimes \mathcal {F}',\mu \otimes \mu ')$
. This implies that if V is an
$L^1(\Omega \times \Omega ',\mathcal {F}\otimes \mathcal {F}',\mu \otimes \mu ')$
. This implies that if V is an
![]() $L^1$
-space, then
$L^1$
-space, then
![]() $L^1(\Omega ;V)$
is another
$L^1(\Omega ;V)$
is another
![]() $L^1$
-space. If
$L^1$
-space. If
![]() $\mu $
is a probability measure, we will often use probabilistic notation and denote
$\mu $
is a probability measure, we will often use probabilistic notation and denote
![]() $\int _\Omega h d\mu $
by
$\int _\Omega h d\mu $
by
![]() $\mathbb {E}_{\omega \in \Omega }[h_\omega ]$
,
$\mathbb {E}_{\omega \in \Omega }[h_\omega ]$
,
![]() $\mathbb {E}_\omega [h_\omega ]$
, or just
$\mathbb {E}_\omega [h_\omega ]$
, or just
![]() $\mathbb {E}[h]$
. We refer the reader to [Reference Diestel, Uhl and Pettis20] for further background on Bochner-Lebesgue spaces.
$\mathbb {E}[h]$
. We refer the reader to [Reference Diestel, Uhl and Pettis20] for further background on Bochner-Lebesgue spaces.
2.3 Lipschitz free spaces
A pointed set is a set X equipped with some distinguished basepoint
![]() $x_0 \in X$
. A pointed metric space is a metric space
$x_0 \in X$
. A pointed metric space is a metric space
![]() $(X,d)$
such that X is a pointed set. We adopt the following important convention throughout the article:
$(X,d)$
such that X is a pointed set. We adopt the following important convention throughout the article:
Every subset of a vector space containing 0 will automatically be considered as a pointed metric space with basepoint 0.
A map between pointed sets is basepoint-preserving if it maps the basepoint of the domain to the basepoint of the codomain. Given a pointed metric space X, we denote by
![]() $\operatorname {\mathrm {Lip}}_0(X)$
the vector space of basepoint-preserving Lipschitz functions
$\operatorname {\mathrm {Lip}}_0(X)$
the vector space of basepoint-preserving Lipschitz functions
![]() $f:X\to \mathbb {R}$
. The vector space
$f:X\to \mathbb {R}$
. The vector space
![]() $\operatorname {\mathrm {Lip}}_0(X)$
becomes a Banach space when equipped with the norm
$\operatorname {\mathrm {Lip}}_0(X)$
becomes a Banach space when equipped with the norm
![]() $\|f\|_{\operatorname {\mathrm {Lip}}_0(X)} := \operatorname {\mathrm {Lip}}(f)$
. There is a canonical isometric embedding
$\|f\|_{\operatorname {\mathrm {Lip}}_0(X)} := \operatorname {\mathrm {Lip}}(f)$
. There is a canonical isometric embedding
![]() $\delta : X \hookrightarrow \operatorname {\mathrm {Lip}}_0(X)^*$
given by the pointwise evaluation map:
$\delta : X \hookrightarrow \operatorname {\mathrm {Lip}}_0(X)^*$
given by the pointwise evaluation map:
![]() $\delta (x) := \delta _x$
for
$\delta (x) := \delta _x$
for
![]() $x \in X$
, where
$x \in X$
, where
![]() $\delta _x(f) := f(x)$
for
$\delta _x(f) := f(x)$
for
![]() $f \in \operatorname {\mathrm {Lip}}_0(X)$
. The closed linear span of
$f \in \operatorname {\mathrm {Lip}}_0(X)$
. The closed linear span of
![]() $\delta (X)$
in
$\delta (X)$
in
![]() $\operatorname {\mathrm {Lip}}_0(X)^*$
is called the Lipschitz free space, or just free space, of X, which we denote by
$\operatorname {\mathrm {Lip}}_0(X)^*$
is called the Lipschitz free space, or just free space, of X, which we denote by
![]() $\operatorname {\mathrm {LF}}(X)$
, or by
$\operatorname {\mathrm {LF}}(X)$
, or by
![]() $\operatorname {\mathrm {LF}}(X,d)$
when we want to emphasize the metric. The isometry type of
$\operatorname {\mathrm {LF}}(X,d)$
when we want to emphasize the metric. The isometry type of
![]() $\operatorname {\mathrm {LF}}(X)$
is independent of the chosen basepoint, and thus, we omit it from the notation. The dual space of
$\operatorname {\mathrm {LF}}(X)$
is independent of the chosen basepoint, and thus, we omit it from the notation. The dual space of
![]() $\operatorname {\mathrm {LF}}(X)$
is
$\operatorname {\mathrm {LF}}(X)$
is
![]() $\operatorname {\mathrm {Lip}}_0(X)$
, and the induced weak
$\operatorname {\mathrm {Lip}}_0(X)$
, and the induced weak
![]() $^*$
topology on bounded subsets of
$^*$
topology on bounded subsets of
![]() $\operatorname {\mathrm {Lip}}_0(X)$
is the topology of pointwise convergence. By the Krein-Smulian theorem, a bounded linear map
$\operatorname {\mathrm {Lip}}_0(X)$
is the topology of pointwise convergence. By the Krein-Smulian theorem, a bounded linear map
![]() $T: \operatorname {\mathrm {Lip}}_0(X) \to V^*$
is the adjoint of a linear map
$T: \operatorname {\mathrm {Lip}}_0(X) \to V^*$
is the adjoint of a linear map
![]() $T_*: V \to \operatorname {\mathrm {LF}}(X)$
if and only if
$T_*: V \to \operatorname {\mathrm {LF}}(X)$
if and only if
![]() $T(f_\alpha )$
weak
$T(f_\alpha )$
weak
![]() $^*$
converges to
$^*$
converges to
![]() $T(f)$
whenever
$T(f)$
whenever
![]() $f_\alpha $
is a bounded net in
$f_\alpha $
is a bounded net in
![]() $\operatorname {\mathrm {Lip}}_0(X)$
converging pointwise to f. In this case,
$\operatorname {\mathrm {Lip}}_0(X)$
converging pointwise to f. In this case,
![]() $T_*$
is unique and called the preadjoint of T. Whenever
$T_*$
is unique and called the preadjoint of T. Whenever
![]() $f: X \to E$
is a basepoint-preserving Lipschitz map into a Banach space, there exists a unique bounded linear map
$f: X \to E$
is a basepoint-preserving Lipschitz map into a Banach space, there exists a unique bounded linear map
![]() $T_f: \operatorname {\mathrm {LF}}(X) \to E$
satisfying
$T_f: \operatorname {\mathrm {LF}}(X) \to E$
satisfying
![]() $T_f(\delta _x) = f(x)$
for every
$T_f(\delta _x) = f(x)$
for every
![]() $x \in X$
, and the operator norm of
$x \in X$
, and the operator norm of
![]() $T_f$
is
$T_f$
is
![]() $\operatorname {\mathrm {Lip}}(f)$
. We call
$\operatorname {\mathrm {Lip}}(f)$
. We call
![]() $T_f$
the induced linear map of f. If
$T_f$
the induced linear map of f. If
![]() $Y \subseteq X$
contains the basepoint, the formal identity map
$Y \subseteq X$
contains the basepoint, the formal identity map
![]() $\operatorname {\mathrm {LF}}(Y) \to \operatorname {\mathrm {LF}}(X)$
is a linear isometric embedding, and it is surjective if and only if Y is dense in X. This follows from the (Whitney-)McShane extension theorem, which states that every Lipschitz map
$\operatorname {\mathrm {LF}}(Y) \to \operatorname {\mathrm {LF}}(X)$
is a linear isometric embedding, and it is surjective if and only if Y is dense in X. This follows from the (Whitney-)McShane extension theorem, which states that every Lipschitz map
![]() $Y \to \mathbb {R}$
extends to a Lipschitz map
$Y \to \mathbb {R}$
extends to a Lipschitz map
![]() $X \to \mathbb {R}$
with the same Lipschitz constant. Other standard facts we will use are that
$X \to \mathbb {R}$
with the same Lipschitz constant. Other standard facts we will use are that
![]() $\operatorname {\mathrm {LF}}(X)$
is separable if and only if X is separable and that biLipschitz embeddings (resp. equivalences)
$\operatorname {\mathrm {LF}}(X)$
is separable if and only if X is separable and that biLipschitz embeddings (resp. equivalences)
![]() $X \to Y$
of distortion
$X \to Y$
of distortion
![]() $C<\infty $
induce C-isomorphic embeddings (resp. equivalences)
$C<\infty $
induce C-isomorphic embeddings (resp. equivalences)
![]() $\operatorname {\mathrm {LF}}(X) \to \operatorname {\mathrm {LF}}(Y)$
. See [Reference Weaver48, Chapter 3] for a standard reference on Lipshitz free spaces, and note that these spaces are also referred to as Arens-Eells spaces in that text and elsewhere.
$\operatorname {\mathrm {LF}}(X) \to \operatorname {\mathrm {LF}}(Y)$
. See [Reference Weaver48, Chapter 3] for a standard reference on Lipshitz free spaces, and note that these spaces are also referred to as Arens-Eells spaces in that text and elsewhere.
The class of Lipschitz free spaces often exhibits qualitative behavior similar to that of the class of
![]() $L^1$
-spaces. For example, the following dichotomy in
$L^1$
-spaces. For example, the following dichotomy in
![]() $L^1$
-spaces holds: either
$L^1$
-spaces holds: either
![]() $L^1(\Omega )$
contains a complemented subspace isomorphic to
$L^1(\Omega )$
contains a complemented subspace isomorphic to
![]() $L^1$
, or it has the Radon-Nikodym property (see [Reference Diestel, Uhl and Pettis20, Chapter III,
$L^1$
, or it has the Radon-Nikodym property (see [Reference Diestel, Uhl and Pettis20, Chapter III,
![]() $\S$
1, Definition 3] for the definition), with the latter property holding if and only if
$\S$
1, Definition 3] for the definition), with the latter property holding if and only if
![]() $\Omega $
is purely atomic. The same dichotomy holds in Lipschitz free spaces, with the property of pure 1-unrectifiability taking the place of pure atomicity.
$\Omega $
is purely atomic. The same dichotomy holds in Lipschitz free spaces, with the property of pure 1-unrectifiability taking the place of pure atomicity.
Lemma 2.1 (almost Theorem C, [Reference Aliaga, Gartland, Petitjean and Procházka2]).
Let X be a metric space. Then the following dichotomy holds: either
![]() $\operatorname {\mathrm {LF}}(X)$
contains a complemented subspace isomorphic to
$\operatorname {\mathrm {LF}}(X)$
contains a complemented subspace isomorphic to
![]() $L^1$
, or
$L^1$
, or
![]() $\operatorname {\mathrm {LF}}(X)$
has the Radon-Nikodym property, with the latter property holding if and only if the completion of X is purely 1-unrectifiable.
$\operatorname {\mathrm {LF}}(X)$
has the Radon-Nikodym property, with the latter property holding if and only if the completion of X is purely 1-unrectifiable.
Proof. Assume that
![]() $\operatorname {\mathrm {LF}}(X)$
fails to have the Radon-Nikodym property. Then by [Reference Aliaga, Gartland, Petitjean and Procházka2, Theorem C],
$\operatorname {\mathrm {LF}}(X)$
fails to have the Radon-Nikodym property. Then by [Reference Aliaga, Gartland, Petitjean and Procházka2, Theorem C],
![]() $\overline {X}$
is not purely 1-unrectifiable, where
$\overline {X}$
is not purely 1-unrectifiable, where
![]() $\overline {X}$
is the completion of X. Hence, there is a positive measure subset
$\overline {X}$
is the completion of X. Hence, there is a positive measure subset
![]() $A \subseteq \mathbb {R}$
and a biLipschitz embedding
$A \subseteq \mathbb {R}$
and a biLipschitz embedding
![]() $f: A \to \overline {X}$
. Since Nagata dimension (see
$f: A \to \overline {X}$
. Since Nagata dimension (see
![]() $\S $
2.4 for background) is nonincreasing under biLipschitz embeddings and the Nagata dimension of
$\S $
2.4 for background) is nonincreasing under biLipschitz embeddings and the Nagata dimension of
![]() $\mathbb {R}$
is 1, the Nagata dimension of
$\mathbb {R}$
is 1, the Nagata dimension of
![]() $f(A)$
is at most 1. Then by [Reference Freeman and Gartland28, Lemma 3.2],
$f(A)$
is at most 1. Then by [Reference Freeman and Gartland28, Lemma 3.2],
![]() $\operatorname {\mathrm {LF}}(f(A))$
is complemented in
$\operatorname {\mathrm {LF}}(f(A))$
is complemented in
![]() $\operatorname {\mathrm {LF}}(\overline {X}) = \operatorname {\mathrm {LF}}(X)$
. Since f is biLipschitz,
$\operatorname {\mathrm {LF}}(\overline {X}) = \operatorname {\mathrm {LF}}(X)$
. Since f is biLipschitz,
![]() $\operatorname {\mathrm {LF}}(f(A)) \approx \operatorname {\mathrm {LF}}(A)$
, and by [Reference Godard29, Corollary 3.4],
$\operatorname {\mathrm {LF}}(f(A)) \approx \operatorname {\mathrm {LF}}(A)$
, and by [Reference Godard29, Corollary 3.4],
![]() $\operatorname {\mathrm {LF}}(A) \approx L^1$
.
$\operatorname {\mathrm {LF}}(A) \approx L^1$
.
With the previous dichotomy lemma in hand, we can obtain a positive solution to the Complemented Subspace of
![]() $L^1$
Problem – which asserts that separable, complemented subspaces of
$L^1$
Problem – which asserts that separable, complemented subspaces of
![]() $L^1$
-spaces are isomorphic to
$L^1$
-spaces are isomorphic to
![]() $L^1$
-spaces (see [Reference Alspach and Odell5, page 129]) – when restricted to the class of Lipschitz free spaces.
$L^1$
-spaces (see [Reference Alspach and Odell5, page 129]) – when restricted to the class of Lipschitz free spaces.
Theorem 2.2. Let X be an infinite separable metric space. If
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
![]() $L^1$
-space, then
$L^1$
-space, then
![]() $\operatorname {\mathrm {LF}}(X) \approx L^1$
or
$\operatorname {\mathrm {LF}}(X) \approx L^1$
or
![]() $\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
, with the latter isomorphism holding if and only if the completion of X is purely 1-unrectifiable.
$\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
, with the latter isomorphism holding if and only if the completion of X is purely 1-unrectifiable.
Proof. Assume that
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
![]() $L^1$
-space. Since X is separable, we may assume that this
$L^1$
-space. Since X is separable, we may assume that this
![]() $L^1$
-space is
$L^1$
-space is
![]() $L^1$
. By Lemma 2.1, we only need to consider the cases where
$L^1$
. By Lemma 2.1, we only need to consider the cases where
![]() $\operatorname {\mathrm {LF}}(X)$
contains a complemented subspace isomorphic to
$\operatorname {\mathrm {LF}}(X)$
contains a complemented subspace isomorphic to
![]() $L^1$
or
$L^1$
or
![]() $\operatorname {\mathrm {LF}}(X)$
has the Radon-Nikodym property, with the latter case holding if and only if the completion of X is purely 1-unrectifiable. In the first case, it follows from the Pełczyński decomposition method that
$\operatorname {\mathrm {LF}}(X)$
has the Radon-Nikodym property, with the latter case holding if and only if the completion of X is purely 1-unrectifiable. In the first case, it follows from the Pełczyński decomposition method that
![]() $\operatorname {\mathrm {LF}}(X) \approx L^1$
. In the second case, it follows from the Lewis-Stegall theorem [Reference Diestel, Uhl and Pettis20, Theorem IV.5.3] that
$\operatorname {\mathrm {LF}}(X) \approx L^1$
. In the second case, it follows from the Lewis-Stegall theorem [Reference Diestel, Uhl and Pettis20, Theorem IV.5.3] that
![]() $\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
.
2.4 Nagata dimension and Lipschitz extensions
Let X be a metric space. A Nagata cover of dimension
![]() $n\in \mathbb {N}$
, constant
$n\in \mathbb {N}$
, constant
![]() $\gamma <\infty $
, and scale
$\gamma <\infty $
, and scale
![]() $s>0$
is a cover
$s>0$
is a cover
![]() $\mathcal {C}$
of X such that
$\mathcal {C}$
of X such that
![]() $\operatorname {\mathrm {diam}}(C) \leq \gamma s$
for every
$\operatorname {\mathrm {diam}}(C) \leq \gamma s$
for every
![]() $C \in \mathcal {C}$
and, for every
$C \in \mathcal {C}$
and, for every
![]() $A \subset X$
with
$A \subset X$
with
![]() $\operatorname {\mathrm {diam}}(A) \leq s$
, it holds that
$\operatorname {\mathrm {diam}}(A) \leq s$
, it holds that
![]() $|\{C \in \mathcal {C}: C \cap A \neq \emptyset \}| \leq n+1$
(where
$|\{C \in \mathcal {C}: C \cap A \neq \emptyset \}| \leq n+1$
(where
![]() $|S|$
denotes the cardinality of a set S). It is not hard to see that such a cover exists if and only if there exists a cover
$|S|$
denotes the cardinality of a set S). It is not hard to see that such a cover exists if and only if there exists a cover
![]() $B_1,B_2,\dots B_{n+1}$
of X such that each
$B_1,B_2,\dots B_{n+1}$
of X such that each
![]() $B_i$
is the union of a family of sets that is
$B_i$
is the union of a family of sets that is
![]() $\gamma s$
-bounded and s-separated, meaning
$\gamma s$
-bounded and s-separated, meaning
![]() $B_i = \bigcup _{\lambda \in \Lambda _i} B_i^\lambda $
, where
$B_i = \bigcup _{\lambda \in \Lambda _i} B_i^\lambda $
, where
![]() $\operatorname {\mathrm {diam}}(B_i^{\lambda _1}) \leq \gamma s$
and
$\operatorname {\mathrm {diam}}(B_i^{\lambda _1}) \leq \gamma s$
and
![]() $\operatorname {\mathrm {dist}}(B_i^{\lambda _1},B_i^{\lambda _2})> s$
for all
$\operatorname {\mathrm {dist}}(B_i^{\lambda _1},B_i^{\lambda _2})> s$
for all
![]() $\lambda _1 \neq \lambda _2 \in \Lambda _i$
. In this case, the sets
$\lambda _1 \neq \lambda _2 \in \Lambda _i$
. In this case, the sets
![]() $\{B_i^\lambda \}_{i=1,\lambda \in \Lambda _i}^{n+1}$
form a Nagata cover. A metric space X has (Assouad-)Nagata dimension
$\{B_i^\lambda \}_{i=1,\lambda \in \Lambda _i}^{n+1}$
form a Nagata cover. A metric space X has (Assouad-)Nagata dimension
![]() $n \in \mathbb {N}$
with constant
$n \in \mathbb {N}$
with constant
![]() $\gamma < \infty $
if, for every
$\gamma < \infty $
if, for every
![]() $s>0$
, there exists a Nagata cover of dimension n, constant
$s>0$
, there exists a Nagata cover of dimension n, constant
![]() $\gamma $
, and scale s. If such an n and
$\gamma $
, and scale s. If such an n and
![]() $\gamma $
exist, we say that X has finite Nagata dimension. We also call
$\gamma $
exist, we say that X has finite Nagata dimension. We also call
![]() $\gamma $
the n-Nagata-dimensional constant of X.
$\gamma $
the n-Nagata-dimensional constant of X.
The article of Lang and Schlichenmeier [Reference Lang and Schlichenmaier37] (and references therein) contains some foundational results on Nagata dimension. For example, Nagata dimension is nonincreasing under snowflake embeddings ([Reference Lang and Schlichenmaier37, Lemma 2.1]), the Nagata dimension of an open subset of
![]() $\mathbb {R}^n$
is n ([Reference Lang and Schlichenmaier37, page 3626]), every doubling space has finite Nagata dimension ([Reference Lang and Schlichenmaier37, Lemma 2.3]), ultrametric spaces have Nagata dimension 0, and nontrivial
$\mathbb {R}^n$
is n ([Reference Lang and Schlichenmaier37, page 3626]), every doubling space has finite Nagata dimension ([Reference Lang and Schlichenmaier37, Lemma 2.3]), ultrametric spaces have Nagata dimension 0, and nontrivial
![]() $\mathbb {R}$
-trees have Nagata dimension 1 (see
$\mathbb {R}$
-trees have Nagata dimension 1 (see
![]() $\S $
2.6 for these last two statements). The most important result of [Reference Lang and Schlichenmaier37] for us concerns extensions of Lipschitz functions. Let us say that a metric space Z is Lipschitz
$\S $
2.6 for these last two statements). The most important result of [Reference Lang and Schlichenmaier37] for us concerns extensions of Lipschitz functions. Let us say that a metric space Z is Lipschitz
![]() $\infty $
-connected with constant
$\infty $
-connected with constant
![]() $L<\infty $
if for every Banach space V, every Lipschitz map
$L<\infty $
if for every Banach space V, every Lipschitz map
![]() $f: S_V \to Z$
extends to an
$f: S_V \to Z$
extends to an
![]() $L\operatorname {\mathrm {Lip}}(f)$
-Lipschitz map
$L\operatorname {\mathrm {Lip}}(f)$
-Lipschitz map
![]() $B_V \to Z$
(where, as usual,
$B_V \to Z$
(where, as usual,
![]() $S_V$
denotes the unit sphere and
$S_V$
denotes the unit sphere and
![]() $B_V$
the unit ball of V). Theorem 1.6 of [Reference Lang and Schlichenmaier37] implies that every Lipschitz map
$B_V$
the unit ball of V). Theorem 1.6 of [Reference Lang and Schlichenmaier37] implies that every Lipschitz map
![]() $f: M \to Z$
from a closed subset
$f: M \to Z$
from a closed subset
![]() $M \subseteq Y$
of a metric space of finite Nagata dimension into a Lipschitz
$M \subseteq Y$
of a metric space of finite Nagata dimension into a Lipschitz
![]() $\infty $
-connected metric space Z extends to a Lipschitz map
$\infty $
-connected metric space Z extends to a Lipschitz map
![]() $\overline {f}: Y \to Z$
, where
$\overline {f}: Y \to Z$
, where
![]() $\operatorname {\mathrm {Lip}}(\overline {f})$
depends only on the relevant data of
$\operatorname {\mathrm {Lip}}(\overline {f})$
depends only on the relevant data of
![]() $Y,Z,f$
.
$Y,Z,f$
.
Lemma 2.3 (Theorem 1.6, [Reference Lang and Schlichenmaier37]).
Let Y be a metric space of Nagata dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
,
$\gamma <\infty $
,
![]() $M \subseteq Y$
a closed subset, and Z a Lipschitz
$M \subseteq Y$
a closed subset, and Z a Lipschitz
![]() $\infty $
-connected metric space with constant
$\infty $
-connected metric space with constant
![]() $L<\infty $
. Then for every Lipschitz map
$L<\infty $
. Then for every Lipschitz map
![]() $f: M \to Z$
, there exists an
$f: M \to Z$
, there exists an
![]() $L'\operatorname {\mathrm {Lip}}(f)$
-Lipschitz extension
$L'\operatorname {\mathrm {Lip}}(f)$
-Lipschitz extension
![]() $\overline {f}: Y \to Z$
, where
$\overline {f}: Y \to Z$
, where
![]() $L'$
depends only on
$L'$
depends only on
![]() $n,\gamma ,L$
.
$n,\gamma ,L$
.
We will use Lemma 2.3 in the proof of Lemma 2.5 to build uniform-bounded Lipschitz extension operators on metrics spaces of finite Nagata dimension, which will be defined shortly.
Let
![]() $K<\infty $
,
$K<\infty $
,
![]() $(Y,d)$
a metric space, and
$(Y,d)$
a metric space, and
![]() $M \subseteq Y$
a closed subset. We call a map
$M \subseteq Y$
a closed subset. We call a map
![]() $y \mapsto \mu _y: Y \to \operatorname {\mathrm {LF}}(M)$
a convex K-random projection onto M if, for every
$y \mapsto \mu _y: Y \to \operatorname {\mathrm {LF}}(M)$
a convex K-random projection onto M if, for every
![]() $y,z \in Y$
and
$y,z \in Y$
and
![]() $m \in M$
,
$m \in M$
,
-
○
 $\mu _y \in \overline {\mathrm{conv}}(\delta (M))$
,
$\mu _y \in \overline {\mathrm{conv}}(\delta (M))$
, -
○
 $\mu _m = \delta _m$
, and
$\mu _m = \delta _m$
, and -
○
 $\|\mu _y-\mu _z\|_{\operatorname {\mathrm {LF}}} \leq Kd(y,z)$
,
$\|\mu _y-\mu _z\|_{\operatorname {\mathrm {LF}}} \leq Kd(y,z)$
,
where
![]() $\overline {\mathrm{conv}}(S)$
denotes the closed convex hull of a subset S of a Banach space. Convex K-random projections were defined in [Reference Ambrosio and Puglisi6] under the name K-strong random projections to distinguish them from the larger class of K-random projections which include all maps satisfying the second and third items but not necessarily the first. We use the term ‘convex’ in place of ‘strong’, as the former is a bit more descriptive.
$\overline {\mathrm{conv}}(S)$
denotes the closed convex hull of a subset S of a Banach space. Convex K-random projections were defined in [Reference Ambrosio and Puglisi6] under the name K-strong random projections to distinguish them from the larger class of K-random projections which include all maps satisfying the second and third items but not necessarily the first. We use the term ‘convex’ in place of ‘strong’, as the former is a bit more descriptive.
Let
![]() $K,L<\infty $
, X a pointed metric space, and
$K,L<\infty $
, X a pointed metric space, and
![]() $M \subseteq X$
a closed subset containing the basepoint. We call
$M \subseteq X$
a closed subset containing the basepoint. We call
![]() $E: \operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(X)$
a K-Lipschitz-bounded linear extension operator if it is a K-bounded linear map and
$E: \operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(X)$
a K-Lipschitz-bounded linear extension operator if it is a K-bounded linear map and
![]() $E(f)(m) = f(m)$
for every
$E(f)(m) = f(m)$
for every
![]() $f \in \operatorname {\mathrm {Lip}}_0(M)$
and
$f \in \operatorname {\mathrm {Lip}}_0(M)$
and
![]() $m \in M$
. If additionally,
$m \in M$
. If additionally,
![]() $\|E(f)\|_\infty \leq L \|f\|_\infty $
for every
$\|E(f)\|_\infty \leq L \|f\|_\infty $
for every
![]() $f \in \operatorname {\mathrm {Lip}}_0(M)$
(where, as usual,
$f \in \operatorname {\mathrm {Lip}}_0(M)$
(where, as usual,
![]() $\|f\|_\infty := \sup _{m\in M}|f(m)|$
), then E is L-uniform-bounded. We say that X has the K-Lipschitz-bounded linear extension property if for every closed subset
$\|f\|_\infty := \sup _{m\in M}|f(m)|$
), then E is L-uniform-bounded. We say that X has the K-Lipschitz-bounded linear extension property if for every closed subset
![]() $M \subseteq X$
containing the basepoint, there exists a K-Lipschitz-bounded linear extension operator
$M \subseteq X$
containing the basepoint, there exists a K-Lipschitz-bounded linear extension operator
![]() $E: \operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(X)$
. If E can additionally be chosen to be L-uniform-bounded, then X has the K-Lipschitz-bounded, L-uniform-bounded linear extension property.
$E: \operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(X)$
. If E can additionally be chosen to be L-uniform-bounded, then X has the K-Lipschitz-bounded, L-uniform-bounded linear extension property.
Lemma 2.4. Let
![]() $(Y,d)$
be a pointed metric space,
$(Y,d)$
be a pointed metric space,
![]() $M \subseteq Y$
a closed subset containing the basepoint, and
$M \subseteq Y$
a closed subset containing the basepoint, and
![]() $K<\infty $
. If Y admits a convex K-random projection onto M, then there exists a K-Lipschitz-bounded, 1-uniform-bounded linear extension operator
$K<\infty $
. If Y admits a convex K-random projection onto M, then there exists a K-Lipschitz-bounded, 1-uniform-bounded linear extension operator
![]() $\operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(Y)$
.
$\operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(Y)$
.
Proof. Assume that there exists a convex K-random projection
![]() $y \mapsto \mu _y:\ Y \to \overline {\mathrm{conv}}(\delta (M))\ \subseteq \operatorname {\mathrm {LF}}(M)$
. Define
$y \mapsto \mu _y:\ Y \to \overline {\mathrm{conv}}(\delta (M))\ \subseteq \operatorname {\mathrm {LF}}(M)$
. Define
![]() $E: \operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(Y)$
by
$E: \operatorname {\mathrm {Lip}}_0(M) \to \operatorname {\mathrm {Lip}}_0(Y)$
by
![]() $E(f)(y) := f(\mu _y)$
. Then for all
$E(f)(y) := f(\mu _y)$
. Then for all
![]() $y,z \in Y$
and
$y,z \in Y$
and
![]() $m \in M$
,
$m \in M$
,
![]() $|E(f)(y)-E(f)(z)| \leq \operatorname {\mathrm {Lip}}(f)\|\mu _y-\mu _z\|_{\operatorname {\mathrm {LF}}} \leq K\operatorname {\mathrm {Lip}}(f)d(y,z)$
and
$|E(f)(y)-E(f)(z)| \leq \operatorname {\mathrm {Lip}}(f)\|\mu _y-\mu _z\|_{\operatorname {\mathrm {LF}}} \leq K\operatorname {\mathrm {Lip}}(f)d(y,z)$
and
![]() $E(f)(m) = f(\delta _m) = f(m)$
. Therefore, E is a K-Lipschitz-bounded linear extension operator. Next, we verify 1-uniform-boundedness.
$E(f)(m) = f(\delta _m) = f(m)$
. Therefore, E is a K-Lipschitz-bounded linear extension operator. Next, we verify 1-uniform-boundedness.
Let
![]() $f\in \operatorname {\mathrm {Lip}}_0(M)$
and
$f\in \operatorname {\mathrm {Lip}}_0(M)$
and
![]() $y \in Y$
. It is immediate that
$y \in Y$
. It is immediate that
![]() $|f(\nu )| \leq \|f\|_{\infty }$
for any
$|f(\nu )| \leq \|f\|_{\infty }$
for any
![]() $\nu \in \operatorname {\mathrm {conv}}(\delta (M)) \subseteq \operatorname {\mathrm {LF}}(M)$
, and by Lipschitz continuity of f, the inequality remains valid for
$\nu \in \operatorname {\mathrm {conv}}(\delta (M)) \subseteq \operatorname {\mathrm {LF}}(M)$
, and by Lipschitz continuity of f, the inequality remains valid for
![]() $\nu \in \overline {\mathrm{conv}}(\delta (M))$
. Therefore, since
$\nu \in \overline {\mathrm{conv}}(\delta (M))$
. Therefore, since
![]() $\mu _y \in \overline {\mathrm{conv}}(\delta (M))$
, we have that
$\mu _y \in \overline {\mathrm{conv}}(\delta (M))$
, we have that
![]() $|E(f)(y)| = |f(\mu _y)| \leq \|f\|_\infty $
. Since
$|E(f)(y)| = |f(\mu _y)| \leq \|f\|_\infty $
. Since
![]() $y \in Y$
was arbitrary, we get
$y \in Y$
was arbitrary, we get
![]() $\|E(f)\|_\infty \leq \|f\|_\infty $
.
$\|E(f)\|_\infty \leq \|f\|_\infty $
.
The next lemma we present can, in many cases, be deduced by combining established results (specifically, one could apply [Reference Naor and Silberman42, Lemma 5.1], [Reference Lee and Naor39, Theorem 4.1], [Reference Lee and Naor39, Lemma 3.8], and [Reference Ambrosio and Puglisi6, Theorem 2.10]). However, we found there to be less technical overhead in citing Lemma 2.3 and then filling in the remaining details ourselves.
Lemma 2.5. Let Y be a metric space of Nagata dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
. Then there exists
$\gamma <\infty $
. Then there exists
![]() $K<\infty $
, depending only on
$K<\infty $
, depending only on
![]() $n,\gamma $
, such that Y admits a convex K-random projection onto every closed subset.
$n,\gamma $
, such that Y admits a convex K-random projection onto every closed subset.
Proof. Let
![]() $M \subseteq Y$
be closed. By definition of convex K-random projections, we need to find a K-Lipschitz map
$M \subseteq Y$
be closed. By definition of convex K-random projections, we need to find a K-Lipschitz map
![]() $Y \to \overline {\mathrm{conv}}(\delta (M))$
extending the isometric embedding
$Y \to \overline {\mathrm{conv}}(\delta (M))$
extending the isometric embedding
![]() $\delta : M \to \operatorname {\mathrm {LF}}(M)$
, where K depends only on
$\delta : M \to \operatorname {\mathrm {LF}}(M)$
, where K depends only on
![]() $n,\gamma $
. By Lemma 2.3, it is enough to verify that every closed convex subset of a Banach space is Lipschitz
$n,\gamma $
. By Lemma 2.3, it is enough to verify that every closed convex subset of a Banach space is Lipschitz
![]() $\infty $
-connected with universal constant (we will get a constant of 4).
$\infty $
-connected with universal constant (we will get a constant of 4).
Let V be a Banach space and C a closed convex subset of some Banach space. Let
![]() $f: S_V \to C$
be a Lipschitz map. By composing with translations, it suffices to assume that
$f: S_V \to C$
be a Lipschitz map. By composing with translations, it suffices to assume that
![]() $0 \in f(S_V)$
. We will define the Lipschitz extension
$0 \in f(S_V)$
. We will define the Lipschitz extension
![]() $\overline {f}: B_V \to C$
on
$\overline {f}: B_V \to C$
on
![]() $B_V \setminus \{0\}$
, and then by Lipschitz continuity and completeness of C, it will extend to a map on all of
$B_V \setminus \{0\}$
, and then by Lipschitz continuity and completeness of C, it will extend to a map on all of
![]() $B_V$
with the same Lipschitz constant.
$B_V$
with the same Lipschitz constant.
There is a homeomorphism from
![]() $B_V \setminus \{0\}$
to
$B_V \setminus \{0\}$
to
![]() $(0,1] \times S_V$
given by
$(0,1] \times S_V$
given by
![]() $v \mapsto (\|v\|, \frac {v}{\|v\|})$
with inverse
$v \mapsto (\|v\|, \frac {v}{\|v\|})$
with inverse
![]() $(t,\theta ) \mapsto t\theta $
. By the reverse triangle inequality,
$(t,\theta ) \mapsto t\theta $
. By the reverse triangle inequality,
![]() $\|s\theta - t\eta \| \geq |t-s|$
, and then applying the reverse triangle inequality again, one can get
$\|s\theta - t\eta \| \geq |t-s|$
, and then applying the reverse triangle inequality again, one can get
![]() $\|s\theta - t\eta \| \geq \max \{s,t\}\|\theta -\eta \| - |t-s|$
. Averaging these yields
$\|s\theta - t\eta \| \geq \max \{s,t\}\|\theta -\eta \| - |t-s|$
. Averaging these yields
We define
![]() $\overline {f}$
on
$\overline {f}$
on
![]() $t\theta $
by
$t\theta $
by
![]() $\overline {f}(t\theta ) := tf(\theta )$
. This is well-defined because C is convex,
$\overline {f}(t\theta ) := tf(\theta )$
. This is well-defined because C is convex,
![]() $t \in [0,1]$
, and
$t \in [0,1]$
, and
![]() $0 \in f(S_V) \subseteq C$
, and it obviously extends f. It remains to bound the Lipschitz constant of
$0 \in f(S_V) \subseteq C$
, and it obviously extends f. It remains to bound the Lipschitz constant of
![]() $\overline {f}$
. Let
$\overline {f}$
. Let
![]() $t\theta ,s\eta \in B_V\setminus \{0\}$
. Then by the triangle inequality, and the fact that
$t\theta ,s\eta \in B_V\setminus \{0\}$
. Then by the triangle inequality, and the fact that
![]() $\|f\|_\infty \leq 2\operatorname {\mathrm {Lip}}(f)$
(since
$\|f\|_\infty \leq 2\operatorname {\mathrm {Lip}}(f)$
(since
![]() $0 \in f(S_V)$
and
$0 \in f(S_V)$
and
![]() $\operatorname {\mathrm {diam}}(S_V) = 2$
), we get
$\operatorname {\mathrm {diam}}(S_V) = 2$
), we get
Combining (2.1) and (2.2) yields
![]() $\operatorname {\mathrm {Lip}}(\overline {f}) \leq 4\operatorname {\mathrm {Lip}}(f)$
.
$\operatorname {\mathrm {Lip}}(\overline {f}) \leq 4\operatorname {\mathrm {Lip}}(f)$
.
Combining these two lemmas, we obtain the following:
Corollary 2.6. Let Y be a pointed metric space of finite Nagata dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
. Then there exists
$\gamma <\infty $
. Then there exists
![]() $K<\infty $
, depending only on
$K<\infty $
, depending only on
![]() $n,\gamma $
, such that Y has the K-Lipschitz bounded, 1-uniform bounded linear extension property.
$n,\gamma $
, such that Y has the K-Lipschitz bounded, 1-uniform bounded linear extension property.
2.5 Hyperbolic metric spaces
We mainly follow the presentation of hyperbolic metric spaces and their boundaries as given in Bonk-Schramm [Reference Bonk and Schramm12]. For more comprehensive accounts of this material, see [Reference Buyalo and Schroeder15] or [Reference Bridson and Haefliger13, Chapter III.H].
Let
![]() $(X,d)$
be a metric space and
$(X,d)$
be a metric space and
![]() $x,y,p \in X$
. The Gromov product of
$x,y,p \in X$
. The Gromov product of
![]() $x,y$
with respect to p is defined by
$x,y$
with respect to p is defined by
Let
![]() $\delta \in [0,\infty )$
. Then X is said to be
$\delta \in [0,\infty )$
. Then X is said to be
![]() $\delta $
-hyperbolic if for all
$\delta $
-hyperbolic if for all
![]() $x,y,z,p \in X$
,
$x,y,z,p \in X$
,
The space X is Gromov hyperbolic, or just hyperbolic, if it is
![]() $\delta $
-hyperbolic for some
$\delta $
-hyperbolic for some
![]() $\delta \in [0,\infty )$
.
$\delta \in [0,\infty )$
.
Suppose
![]() $(X,d)$
is a hyperbolic space. A sequence
$(X,d)$
is a hyperbolic space. A sequence
![]() $\{x_i\}_{i=1}^\infty \subseteq X$
is said to converge at
$\{x_i\}_{i=1}^\infty \subseteq X$
is said to converge at
![]() $\infty $
if for some (equivalently, for all)
$\infty $
if for some (equivalently, for all)
![]() $p \in X$
,
$p \in X$
,
![]() $\lim _{i,j\to \infty } (x_i|x_j)_p = \infty $
. Two sequences
$\lim _{i,j\to \infty } (x_i|x_j)_p = \infty $
. Two sequences
![]() $\{x_i\}_{i=1}^\infty , \{y_i\}_{i=1}^\infty \subseteq X$
converging at
$\{x_i\}_{i=1}^\infty , \{y_i\}_{i=1}^\infty \subseteq X$
converging at
![]() $\infty $
are equivalent if for some (equivalently, for all)
$\infty $
are equivalent if for some (equivalently, for all)
![]() $p \in X$
,
$p \in X$
,
![]() $\lim _{i\to \infty } (x_i|y_i)_p = \infty $
.
$\lim _{i\to \infty } (x_i|y_i)_p = \infty $
.
This is an equivalence relation on the set of sequences converging at
![]() $\infty $
by hyperbolicity, and the set of equivalences classes is called the Gromov boundary, or just boundary, of X, denoted by
$\infty $
by hyperbolicity, and the set of equivalences classes is called the Gromov boundary, or just boundary, of X, denoted by
![]() $\partial X$
. The Gromov product of
$\partial X$
. The Gromov product of
![]() $\xi ,\upsilon \in \partial X$
with respect to
$\xi ,\upsilon \in \partial X$
with respect to
![]() $p \in X$
is defined by
$p \in X$
is defined by
A metric d on
![]() $\partial X$
is said to be visual if there exist
$\partial X$
is said to be visual if there exist
![]() $p \in X$
,
$p \in X$
,
![]() $\varepsilon> 0$
, and
$\varepsilon> 0$
, and
![]() $C< \infty $
such that
$C< \infty $
such that
![]() $C^{-1}e^{-\varepsilon (\xi |\upsilon )_p} \leq d(\xi ,\upsilon ) \leq Ce^{-\varepsilon (\xi |\upsilon )_p}$
(in Bonk-Schramm, the set of visual metrics is called the canonical B-structure on
$C^{-1}e^{-\varepsilon (\xi |\upsilon )_p} \leq d(\xi ,\upsilon ) \leq Ce^{-\varepsilon (\xi |\upsilon )_p}$
(in Bonk-Schramm, the set of visual metrics is called the canonical B-structure on
![]() $\partial X$
[Reference Bonk and Schramm12, page 282]). Visual metrics on
$\partial X$
[Reference Bonk and Schramm12, page 282]). Visual metrics on
![]() $\partial X$
always exist and are unique up to snowflake equivalence, and it is clear from the definition that any metric snowflake equivalent to a visual metric is also visual. Thus, we always equip
$\partial X$
always exist and are unique up to snowflake equivalence, and it is clear from the definition that any metric snowflake equivalent to a visual metric is also visual. Thus, we always equip
![]() $\partial X$
with some visual metric, and we may unambiguously assert that
$\partial X$
with some visual metric, and we may unambiguously assert that
![]() $\partial X$
satisfies or fails a metric property P as long as P is invariant under snowflake equivalences (for example, having Nagata dimension
$\partial X$
satisfies or fails a metric property P as long as P is invariant under snowflake equivalences (for example, having Nagata dimension
![]() $n\in \mathbb {N}$
). The boundary of a hyperbolic space is always bounded and complete. Under the additional hypothesis of visibility, which will be described in the next paragraph, the boundary of a hyperbolic space completely determines the hyperbolic space up to rough biLipschitz equivalence. This theory was worked out in full by Bonk and Schramm [Reference Bonk and Schramm12].
$n\in \mathbb {N}$
). The boundary of a hyperbolic space is always bounded and complete. Under the additional hypothesis of visibility, which will be described in the next paragraph, the boundary of a hyperbolic space completely determines the hyperbolic space up to rough biLipschitz equivalence. This theory was worked out in full by Bonk and Schramm [Reference Bonk and Schramm12].
Let
![]() $(X,d)$
be a metric space,
$(X,d)$
be a metric space,
![]() $K<\infty $
, and
$K<\infty $
, and
![]() $I = [0,b]$
or
$I = [0,b]$
or
![]() $I = [0,\infty )$
. The image of I under a map
$I = [0,\infty )$
. The image of I under a map
![]() $f: I \to X$
satisfying
$f: I \to X$
satisfying
![]() $|s-t| - K \leq d(f(s),f(t)) \leq |s-t| + K$
is called a K-rough geodesic if
$|s-t| - K \leq d(f(s),f(t)) \leq |s-t| + K$
is called a K-rough geodesic if
![]() $I = [0,b]$
and a K-rough geodesic ray if
$I = [0,b]$
and a K-rough geodesic ray if
![]() $I = [0,\infty )$
. If
$I = [0,\infty )$
. If
![]() $I = [0,b]$
, the points
$I = [0,b]$
, the points
![]() $f(0),f(b)$
are called the endpoints of the rough geodesic, and if
$f(0),f(b)$
are called the endpoints of the rough geodesic, and if
![]() $I = [0,\infty )$
, the point
$I = [0,\infty )$
, the point
![]() $f(0)$
is called the origin of the rough geodesic ray. A metric space is K-roughly geodesic if every pair of points are the endpoints of some K-rough geodesic. A geodesic is a 0-rough geodesic, and similar definitions hold for geodesic rays and geodesic metric spaces. A metric space is visual if there exists (equivalently, for all)
$f(0)$
is called the origin of the rough geodesic ray. A metric space is K-roughly geodesic if every pair of points are the endpoints of some K-rough geodesic. A geodesic is a 0-rough geodesic, and similar definitions hold for geodesic rays and geodesic metric spaces. A metric space is visual if there exists (equivalently, for all)
![]() $p \in X$
and there exists
$p \in X$
and there exists
![]() $K' <\infty $
such that X is the union of all
$K' <\infty $
such that X is the union of all
![]() $K'$
-rough geodesic rays originating from p.
$K'$
-rough geodesic rays originating from p.
Let
![]() $(Z,d_Z)$
be a bounded metric space. The (Bonk-Schramm) hyperbolic filling of Z is the set
$(Z,d_Z)$
be a bounded metric space. The (Bonk-Schramm) hyperbolic filling of Z is the set
(note that
![]() $\operatorname {\mathrm {Hyp}}(Z)$
is called Con
$\operatorname {\mathrm {Hyp}}(Z)$
is called Con
![]() $(Z)$
in [Reference Bonk and Schramm12]) equipped with the metric
$(Z)$
in [Reference Bonk and Schramm12]) equipped with the metric
 $$ \begin{align} \rho_Z((z,h),(z',h')) := 2\log\left(\dfrac{d_Z(z,z')+h \vee h'}{\sqrt{hh'}}\right), \end{align} $$
$$ \begin{align} \rho_Z((z,h),(z',h')) := 2\log\left(\dfrac{d_Z(z,z')+h \vee h'}{\sqrt{hh'}}\right), \end{align} $$
where here and in the sequel,
![]() $\log $
denotes the natural logarithm and
$\log $
denotes the natural logarithm and
![]() $h \vee h'$
denotes
$h \vee h'$
denotes
![]() $\max \{h,h'\}$
. Note that
$\max \{h,h'\}$
. Note that
![]() $\rho _Z$
induces the product topology on
$\rho _Z$
induces the product topology on
![]() $Z \times (0,\operatorname {\mathrm {diam}}(Z)]$
. By [Reference Bonk and Schramm12, Theorem 7.2],
$Z \times (0,\operatorname {\mathrm {diam}}(Z)]$
. By [Reference Bonk and Schramm12, Theorem 7.2],
![]() $\operatorname {\mathrm {Hyp}}(Z)$
is always a visual hyperbolic metric space. If
$\operatorname {\mathrm {Hyp}}(Z)$
is always a visual hyperbolic metric space. If
![]() $f: Z \to Y$
is any map to another bounded metric space with
$f: Z \to Y$
is any map to another bounded metric space with
![]() $\operatorname {\mathrm {diam}}(Z) \leq \operatorname {\mathrm {diam}}(Y)$
, then there is an induced map
$\operatorname {\mathrm {diam}}(Z) \leq \operatorname {\mathrm {diam}}(Y)$
, then there is an induced map
![]() $\operatorname {\mathrm {Hyp}}(f): \operatorname {\mathrm {Hyp}}(Z) \to \operatorname {\mathrm {Hyp}}(Y)$
defined by
$\operatorname {\mathrm {Hyp}}(f): \operatorname {\mathrm {Hyp}}(Z) \to \operatorname {\mathrm {Hyp}}(Y)$
defined by
The salient feature of hyperbolic fillings is that, in the visual case, they invert Gromov boundaries up to rough biLipschitz equivalence.
Lemma 2.7 (Theorem 8.2, [Reference Bonk and Schramm12]).
If X is a visual hyperbolic metric space, then X and
![]() $\operatorname {\mathrm {Hyp}}(\partial X)$
are roughly biLipschitz equivalent.
$\operatorname {\mathrm {Hyp}}(\partial X)$
are roughly biLipschitz equivalent.
2.6 Ultrametric spaces and
 $\mathbb {R}$
-trees
$\mathbb {R}$
-trees
A subset of a topological space is an arc if it is homeomorphic to
![]() $[0,1]$
. The points in the image of
$[0,1]$
. The points in the image of
![]() $\{0,1\}$
under any such homeomorphism are called the endpoints of the arc. A metric space X is an
$\{0,1\}$
under any such homeomorphism are called the endpoints of the arc. A metric space X is an
![]() $\mathbb {R}$
-tree if any two points
$\mathbb {R}$
-tree if any two points
![]() $x,y \in X$
are the endpoints of a unique arc, denoted
$x,y \in X$
are the endpoints of a unique arc, denoted
![]() $[x,y]$
, and this arc is a geodesic. It holds that a metric space is an
$[x,y]$
, and this arc is a geodesic. It holds that a metric space is an
![]() $\mathbb {R}$
-tree if and only if it is geodesic and 0-hyperbolic (This follows, for example, from [Reference Evans26, Theorem 3.40]), and every 0-hyperbolic metric space isometrically embeds into an
$\mathbb {R}$
-tree if and only if it is geodesic and 0-hyperbolic (This follows, for example, from [Reference Evans26, Theorem 3.40]), and every 0-hyperbolic metric space isometrically embeds into an
![]() $\mathbb {R}$
-tree (see [Reference Evans26, Theorem 3.38]). For future reference, we note that
$\mathbb {R}$
-tree (see [Reference Evans26, Theorem 3.38]). For future reference, we note that
![]() $(X,d)$
is
$(X,d)$
is
![]() $0$
-hyperbolic if and only if it satisfies the 4-point condition
$0$
-hyperbolic if and only if it satisfies the 4-point condition
for all
![]() $w,x,y,z \in X$
(see [Reference Bridson and Haefliger13, page 410] or [Reference Evans26, Lemma 3.12]). The convex hull of a subset
$w,x,y,z \in X$
(see [Reference Bridson and Haefliger13, page 410] or [Reference Evans26, Lemma 3.12]). The convex hull of a subset
![]() $S \subseteq T$
of an
$S \subseteq T$
of an
![]() $\mathbb {R}$
-tree is the set
$\mathbb {R}$
-tree is the set
![]() $\cup _{s,t \in S} [s,t]$
. The convex hull of S is itself an
$\cup _{s,t \in S} [s,t]$
. The convex hull of S is itself an
![]() $\mathbb {R}$
-tree, and it is separable whenever S is separable. Consequently, any separable 0-hyperbolic metric space isometrically embeds into a separable
$\mathbb {R}$
-tree, and it is separable whenever S is separable. Consequently, any separable 0-hyperbolic metric space isometrically embeds into a separable
![]() $\mathbb {R}$
-tree. The Nagata dimension of any nontrivial
$\mathbb {R}$
-tree. The Nagata dimension of any nontrivial
![]() $\mathbb {R}$
-tree (one that contains more than one point) is 1 with constant
$\mathbb {R}$
-tree (one that contains more than one point) is 1 with constant
![]() $\gamma \leq 5$
(indeed, by the proofs of [Reference Lang and Schlichenmaier37, Lemma 3.1, Theorem 3.2],
$\gamma \leq 5$
(indeed, by the proofs of [Reference Lang and Schlichenmaier37, Lemma 3.1, Theorem 3.2],
![]() $\gamma \leq 4\gamma _{\mathbb {R}}+1$
, where
$\gamma \leq 4\gamma _{\mathbb {R}}+1$
, where
![]() $\gamma _{\mathbb {R}}$
1-Nagata-dimensional constant of
$\gamma _{\mathbb {R}}$
1-Nagata-dimensional constant of
![]() $\mathbb {R}$
, which is easily seen to be 1). The Lipschitz free space of any
$\mathbb {R}$
, which is easily seen to be 1). The Lipschitz free space of any
![]() $\mathbb {R}$
-tree is linearly isometric to an
$\mathbb {R}$
-tree is linearly isometric to an
![]() $L^1$
-space [Reference Godard29, Corollary 3.3].
$L^1$
-space [Reference Godard29, Corollary 3.3].
A metric d on a set U is called an ultrametric if the inequality
holds for every
![]() $u,v,w \in U$
. In this case, the pair
$u,v,w \in U$
. In this case, the pair
![]() $(U,d)$
(or just U if d is understood) is called an ultrametric space. A metric space is biLipschitz equivalent to an ultrametric space if and only if it is snowflake equivalent to an ultrametric space if and only if it has Nagata dimension 0 (see, for example, [Reference Brodskiy, Dydak, Higes and Mitra14, Theorem 3.3]). Every ultrametric space is 0-hyperbolic and thus isometrically embeds into an
$(U,d)$
(or just U if d is understood) is called an ultrametric space. A metric space is biLipschitz equivalent to an ultrametric space if and only if it is snowflake equivalent to an ultrametric space if and only if it has Nagata dimension 0 (see, for example, [Reference Brodskiy, Dydak, Higes and Mitra14, Theorem 3.3]). Every ultrametric space is 0-hyperbolic and thus isometrically embeds into an
![]() $\mathbb {R}$
-tree. The Lipschitz free space of any infinite, separable ultrametric space is isomorphic to
$\mathbb {R}$
-tree. The Lipschitz free space of any infinite, separable ultrametric space is isomorphic to
![]() $\ell ^1$
[Reference Cúth and Doucha18, Theorem 2].
$\ell ^1$
[Reference Cúth and Doucha18, Theorem 2].
It is well-known that the Gromov boundary of an
![]() $\mathbb {R}$
-tree is (biLipschitz equivalent to) an ultrametric space (see, for example, [Reference Ibragimov31, page 320]). In the proof of Theorem C (via Theorem 5.7), we will need a converse statement that the hyperbolic filling of a bounded, complete ultrametric space is roughly biLipschitz equivalent to an
$\mathbb {R}$
-tree is (biLipschitz equivalent to) an ultrametric space (see, for example, [Reference Ibragimov31, page 320]). In the proof of Theorem C (via Theorem 5.7), we will need a converse statement that the hyperbolic filling of a bounded, complete ultrametric space is roughly biLipschitz equivalent to an
![]() $\mathbb {R}$
-tree. This fact is also well-known (see, for example, [Reference Martínez-Pérez40, Proposition 3.2]), but we will require the rough biLipschitz map from the Bonk-Schramm filling
$\mathbb {R}$
-tree. This fact is also well-known (see, for example, [Reference Martínez-Pérez40, Proposition 3.2]), but we will require the rough biLipschitz map from the Bonk-Schramm filling
![]() $\operatorname {\mathrm {Hyp}}(U)$
to the
$\operatorname {\mathrm {Hyp}}(U)$
to the
![]() $\mathbb {R}$
-tree to be measurable and to map separable sets to separable sets. This is proved in the next lemma. The
$\mathbb {R}$
-tree to be measurable and to map separable sets to separable sets. This is proved in the next lemma. The
![]() $\mathbb {R}$
-tree is constructed using a common hyperbolic filling technique similar to [Reference Buyalo and Schroeder15, Chapter 6].
$\mathbb {R}$
-tree is constructed using a common hyperbolic filling technique similar to [Reference Buyalo and Schroeder15, Chapter 6].
Lemma 2.8. Let U be a bounded ultrametric space. Then there exist an
![]() $\mathbb {R}$
-tree T and a rough biLipschitz embedding
$\mathbb {R}$
-tree T and a rough biLipschitz embedding
![]() $\operatorname {\mathrm {Hyp}}(U) \to T$
that is measurable, maps separable subsets to separable subsets, and has coarsely dense image (and therefore
$\operatorname {\mathrm {Hyp}}(U) \to T$
that is measurable, maps separable subsets to separable subsets, and has coarsely dense image (and therefore
![]() $\operatorname {\mathrm {Hyp}}(U)$
is roughly biLipschitz equivalent to T).
$\operatorname {\mathrm {Hyp}}(U)$
is roughly biLipschitz equivalent to T).
For this proof, we need to recall some definitions. Let
![]() $\theta>0$
. A subset A of a metric space
$\theta>0$
. A subset A of a metric space
![]() $(X,d)$
is
$(X,d)$
is
![]() $\theta $
-separated if
$\theta $
-separated if
![]() $d(a,b)> \theta $
for all
$d(a,b)> \theta $
for all
![]() $a \neq b \in A$
. A maximal
$a \neq b \in A$
. A maximal
![]() $\theta $
-separated subset of a metric space is one that is
$\theta $
-separated subset of a metric space is one that is
![]() $\theta $
-separated and not properly contained in any other
$\theta $
-separated and not properly contained in any other
![]() $\theta $
-separated subset. Equivalently, a
$\theta $
-separated subset. Equivalently, a
![]() $\theta $
-separated subset
$\theta $
-separated subset
![]() $A \subseteq X$
is maximal if
$A \subseteq X$
is maximal if
![]() $\{B_\theta (a)\}_{a\in A}$
is a cover of X. By Zorn’s lemma, any point in a metric space is contained in some maximal
$\{B_\theta (a)\}_{a\in A}$
is a cover of X. By Zorn’s lemma, any point in a metric space is contained in some maximal
![]() $\theta $
-separated subset. Note that a subset of a metric space is uniformly discrete if and only if it is
$\theta $
-separated subset. Note that a subset of a metric space is uniformly discrete if and only if it is
![]() $\theta $
-separated for some
$\theta $
-separated for some
![]() $\theta>0$
.
$\theta>0$
.
Proof of Lemma 2.8.
First, we observe that once a rough biLipschitz embedding
![]() $f: \operatorname {\mathrm {Hyp}}(U) \to T'$
into an
$f: \operatorname {\mathrm {Hyp}}(U) \to T'$
into an
![]() $\mathbb {R}$
-tree
$\mathbb {R}$
-tree
![]() $(T',d)$
has been produced, the image will automatically be coarsely dense in its convex hull T (which is another
$(T',d)$
has been produced, the image will automatically be coarsely dense in its convex hull T (which is another
![]() $\mathbb {R}$
-tree) due to the fact that
$\mathbb {R}$
-tree) due to the fact that
![]() $\operatorname {\mathrm {Hyp}}(U)$
is coarsely path-connected. More precisely, by [Reference Bonk and Schramm12, Theorem 7.2],
$\operatorname {\mathrm {Hyp}}(U)$
is coarsely path-connected. More precisely, by [Reference Bonk and Schramm12, Theorem 7.2],
![]() $\operatorname {\mathrm {Hyp}}(U)$
is roughly geodesic, and thus for each
$\operatorname {\mathrm {Hyp}}(U)$
is roughly geodesic, and thus for each
![]() $x,y \in \operatorname {\mathrm {Hyp}}(U)$
, we can find a sequence of points
$x,y \in \operatorname {\mathrm {Hyp}}(U)$
, we can find a sequence of points
![]() $\{x_i\}_{i=0}^m \subseteq \operatorname {\mathrm {Hyp}}(U)$
such that
$\{x_i\}_{i=0}^m \subseteq \operatorname {\mathrm {Hyp}}(U)$
such that
![]() $x_0 = x$
,
$x_0 = x$
,
![]() $x_m = y$
, and for each
$x_m = y$
, and for each
![]() $1 \leq i \leq m$
,
$1 \leq i \leq m$
,
![]() $\rho _U(x_{i-1},x_i) \leq K'$
for some
$\rho _U(x_{i-1},x_i) \leq K'$
for some
![]() $K' < \infty $
(independent of
$K' < \infty $
(independent of
![]() $x,y$
). Then since f is roughly Lipschitz,
$x,y$
). Then since f is roughly Lipschitz,
![]() $d(f(x_{i-1}),f(x_i)) \leq K$
for some
$d(f(x_{i-1}),f(x_i)) \leq K$
for some
![]() $K<\infty $
(independent of
$K<\infty $
(independent of
![]() $x,y$
). Hence, the K-neighborhood of
$x,y$
). Hence, the K-neighborhood of
![]() $f(\operatorname {\mathrm {Hyp}}(U))$
contains
$f(\operatorname {\mathrm {Hyp}}(U))$
contains
![]() $\cup _{i=1}^m [f(x_{i-1}),f(x_i)]$
. This letter set is a topological curve containing
$\cup _{i=1}^m [f(x_{i-1}),f(x_i)]$
. This letter set is a topological curve containing
![]() $\{f(x),f(y)\}$
, and hence by uniqueness of arcs in
$\{f(x),f(y)\}$
, and hence by uniqueness of arcs in
![]() $T'$
, it contains
$T'$
, it contains
![]() $[f(x),f(y)]$
. Since
$[f(x),f(y)]$
. Since
![]() $x,y \in \operatorname {\mathrm {Hyp}}(U)$
were arbitrary, this shows that
$x,y \in \operatorname {\mathrm {Hyp}}(U)$
were arbitrary, this shows that
![]() $f(\operatorname {\mathrm {Hyp}}(U))$
is K-coarsely dense in its convex hull. It remains to produce a rough biLipschitz embedding of
$f(\operatorname {\mathrm {Hyp}}(U))$
is K-coarsely dense in its convex hull. It remains to produce a rough biLipschitz embedding of
![]() $\operatorname {\mathrm {Hyp}}(U)$
into an
$\operatorname {\mathrm {Hyp}}(U)$
into an
![]() $\mathbb {R}$
-tree.
$\mathbb {R}$
-tree.
Let
![]() $d_U$
denote the metric on U and
$d_U$
denote the metric on U and
![]() $k_0 := \min \{k\in \mathbb {Z}: \operatorname {\mathrm {diam}}(U) \leq e^k\}$
. For this proof, it will be more convenient to not work with
$k_0 := \min \{k\in \mathbb {Z}: \operatorname {\mathrm {diam}}(U) \leq e^k\}$
. For this proof, it will be more convenient to not work with
![]() $\operatorname {\mathrm {Hyp}}(U)$
exactly as it is defined in (2.3), but instead to replace the underlying set
$\operatorname {\mathrm {Hyp}}(U)$
exactly as it is defined in (2.3), but instead to replace the underlying set
![]() $U \times (0,\operatorname {\mathrm {diam}}(U)]$
with the set
$U \times (0,\operatorname {\mathrm {diam}}(U)]$
with the set
![]() $U \times (0,e^{k_0}]$
. Obviously, the inclusion
$U \times (0,e^{k_0}]$
. Obviously, the inclusion
![]() $U \times (0,\operatorname {\mathrm {diam}}(U)] \subseteq U \times (0,e^{k_0}]$
is an isometric embedding when each set is equipped with the metric
$U \times (0,\operatorname {\mathrm {diam}}(U)] \subseteq U \times (0,e^{k_0}]$
is an isometric embedding when each set is equipped with the metric
![]() $\rho _U$
defined in (2.4). Therefore, to prove the lemma, we can take
$\rho _U$
defined in (2.4). Therefore, to prove the lemma, we can take
![]() $\operatorname {\mathrm {Hyp}}(U)$
to be the set
$\operatorname {\mathrm {Hyp}}(U)$
to be the set
![]() $U \times (0,e^{k_0}]$
equipped with the metric
$U \times (0,e^{k_0}]$
equipped with the metric
![]() $\rho _U$
.
$\rho _U$
.
For each
![]() $k \leq k_0$
, choose a maximal
$k \leq k_0$
, choose a maximal
![]() $e^k$
-separated subset
$e^k$
-separated subset
![]() $N_k$
of U. Note that
$N_k$
of U. Note that
![]() $N_k$
is countable whenever U is separable. Since
$N_k$
is countable whenever U is separable. Since
![]() $\operatorname {\mathrm {diam}}(U) \leq e^{k_0}$
,
$\operatorname {\mathrm {diam}}(U) \leq e^{k_0}$
,
![]() $N_{k_0}$
is a singleton. By maximality of
$N_{k_0}$
is a singleton. By maximality of
![]() $N_k$
, for any
$N_k$
, for any
![]() $u \in U$
, there exists
$u \in U$
, there exists
![]() $w \in N_k$
such that
$w \in N_k$
such that
![]() $d_U(u,w) \leq e^k$
. Additionally, for any
$d_U(u,w) \leq e^k$
. Additionally, for any
![]() $u_1,u_2 \in U$
and
$u_1,u_2 \in U$
and
![]() $w_1, w_2 \in N_k$
with
$w_1, w_2 \in N_k$
with
![]() $d_U(u_i,w_i) \leq e^k$
, the ultrametric inequality implies
$d_U(u_i,w_i) \leq e^k$
, the ultrametric inequality implies
Now, if
![]() $w_1 \neq w_2$
, then this inequality and the
$w_1 \neq w_2$
, then this inequality and the
![]() $e^k$
-separation of
$e^k$
-separation of
![]() $N_k$
imply
$N_k$
imply
![]() $\max \{e^k,d_U(u_1,u_2)\}\ = d_U(u_1,u_2)$
, and thus, we get
$\max \{e^k,d_U(u_1,u_2)\}\ = d_U(u_1,u_2)$
, and thus, we get
Obviously, this inequality also holds if
![]() $w_1=w_2$
. In particular, if we take
$w_1=w_2$
. In particular, if we take
![]() $u_1=u=u_2$
, this inequality shows that there is a unique
$u_1=u=u_2$
, this inequality shows that there is a unique
![]() $w \in N_k$
with
$w \in N_k$
with
![]() $d_U(u,w) \leq e^k$
. Putting this all together, we get that there exists a unique map
$d_U(u,w) \leq e^k$
. Putting this all together, we get that there exists a unique map
![]() $\pi _k: U \to N_k$
satisfying
$\pi _k: U \to N_k$
satisfying
and this map is 1-Lipschitz. One can quickly deduce from this that the tower property
holds for all
![]() $j \leq k \leq k_0$
, and additionally that
$j \leq k \leq k_0$
, and additionally that
for all
![]() $u \in N_k$
.
$u \in N_k$
.
Set
![]() $N := \cup _{k \leq k_0} (N_k \times \{e^k\}) \subseteq U \times (0,e^{k_0}] = \operatorname {\mathrm {Hyp}}(U)$
. Note that N is countable whenever U is separable. It can be quickly checked that for any two distinct elements
$N := \cup _{k \leq k_0} (N_k \times \{e^k\}) \subseteq U \times (0,e^{k_0}] = \operatorname {\mathrm {Hyp}}(U)$
. Note that N is countable whenever U is separable. It can be quickly checked that for any two distinct elements
![]() $x=(u_x,e^{k_x}),y=(u_y,e^{k_y})$
of N,
$x=(u_x,e^{k_x}),y=(u_y,e^{k_y})$
of N,
![]() $\rho _U(x,y) \geq 1$
if
$\rho _U(x,y) \geq 1$
if
![]() $k_x \neq k_y$
and
$k_x \neq k_y$
and
![]() $\rho _U(x,y) \geq 2\log (2)$
if
$\rho _U(x,y) \geq 2\log (2)$
if
![]() $k_x = k_y$
, and hence, in both cases we have
$k_x = k_y$
, and hence, in both cases we have
For each
![]() $x = (u_x,e^{k_x}), y = (u_y,e^{k_y}) \in N$
, define
$x = (u_x,e^{k_x}), y = (u_y,e^{k_y}) \in N$
, define
![]() $k(x,y) := \min \{k \geq k_x \vee k_y: \pi _k(u_x) = \pi _k(u_y)\}$
(note that this minimum is over a nonempty set since the range of
$k(x,y) := \min \{k \geq k_x \vee k_y: \pi _k(u_x) = \pi _k(u_y)\}$
(note that this minimum is over a nonempty set since the range of
![]() $\pi _{k_0}$
is a singleton). For future reference, we record a couple of facts. The definition of
$\pi _{k_0}$
is a singleton). For future reference, we record a couple of facts. The definition of
![]() $k(x,y)$
, (2.6), and the ultrametric inequality imply that
$k(x,y)$
, (2.6), and the ultrametric inequality imply that
and the definition of
![]() $k(x,y)$
and
$k(x,y)$
and
![]() $e^{k(x,y)-1}$
-separation of
$e^{k(x,y)-1}$
-separation of
![]() $N_{k(x,y)-1}$
imply that
$N_{k(x,y)-1}$
imply that
which in turn implies
Define the symmetric function
![]() $\rho _U^N$
on N by
$\rho _U^N$
on N by
One can use the definition of
![]() $k(x,y)$
and (2.8) to verify that
$k(x,y)$
and (2.8) to verify that
![]() $\rho _U^N(x,y) = 0$
if and only if
$\rho _U^N(x,y) = 0$
if and only if
![]() $x=y$
. Indeed,
$x=y$
. Indeed,
![]() $x=y \implies \rho _U^N(x,y) = 0$
is clear. Now suppose that
$x=y \implies \rho _U^N(x,y) = 0$
is clear. Now suppose that
![]() $\rho _U^N(x,y) = 0$
. Then
$\rho _U^N(x,y) = 0$
. Then
![]() $k(x,y) = \frac {k_x+k_y}{2}$
by the definition of
$k(x,y) = \frac {k_x+k_y}{2}$
by the definition of
![]() $\rho _U^N$
, and
$\rho _U^N$
, and
![]() $k(x,y) \geq k_x\vee k_y$
by the definition of
$k(x,y) \geq k_x\vee k_y$
by the definition of
![]() $k(x,y)$
. Together, these imply that
$k(x,y)$
. Together, these imply that
![]() $k(x,y) = k_x = k_y$
. Thus,
$k(x,y) = k_x = k_y$
. Thus,
![]() $u_x,u_y \in N_{k(x,y)}$
, which by (2.8) implies that
$u_x,u_y \in N_{k(x,y)}$
, which by (2.8) implies that
![]() $\pi _{k(x,y)}(u_x) = u_x$
and
$\pi _{k(x,y)}(u_x) = u_x$
and
![]() $\pi _{k(x,y)}(u_y) = u_y$
. Together with the definition of
$\pi _{k(x,y)}(u_y) = u_y$
. Together with the definition of
![]() $k(x,y)$
, this implies
$k(x,y)$
, this implies
![]() $u_x=u_y$
. Hence,
$u_x=u_y$
. Hence,
![]() $x=y$
. Since
$x=y$
. Since
![]() $\rho _U^N$
is integer-valued, we get as a consequence that
$\rho _U^N$
is integer-valued, we get as a consequence that
for all
![]() $x \neq y \in N$
. The remainder of the proof will proceed as follows. We will prove that
$x \neq y \in N$
. The remainder of the proof will proceed as follows. We will prove that
-
(i) there is a rough biLipschitz embedding
 $(\operatorname {\mathrm {Hyp}}(U),\rho _U) \to (N,\rho _U)$
that is measurable and maps separable subsets to separable subsets,
$(\operatorname {\mathrm {Hyp}}(U),\rho _U) \to (N,\rho _U)$
that is measurable and maps separable subsets to separable subsets, -
(ii) the identity map
 $(N,\rho _U) \to (N,\rho _U^N)$
satisfies the two-sided estimate
$(N,\rho _U) \to (N,\rho _U^N)$
satisfies the two-sided estimate
 $\frac {1}{3}\rho _U^N(x,y) \leq \rho _U(x,y) \leq (2\log (2)+1)\rho _U^N(x,y)$
for all
$\frac {1}{3}\rho _U^N(x,y) \leq \rho _U(x,y) \leq (2\log (2)+1)\rho _U^N(x,y)$
for all
 $x,y \in N$
, and
$x,y \in N$
, and -
(iii)
 $(N,\rho _U^N)$
is a 0-hyperbolic metric space.
$(N,\rho _U^N)$
is a 0-hyperbolic metric space.
Since 0-hyperbolic spaces isometrically embed into
![]() $\mathbb {R}$
-trees, the composition of the maps produced in these steps yields a rough biLipschitz embedding of
$\mathbb {R}$
-trees, the composition of the maps produced in these steps yields a rough biLipschitz embedding of
![]() $\operatorname {\mathrm {Hyp}}(U)$
into an
$\operatorname {\mathrm {Hyp}}(U)$
into an
![]() $\mathbb {R}$
-tree that is measurable and maps separable subsets to separable subsets.
$\mathbb {R}$
-tree that is measurable and maps separable subsets to separable subsets.
We begin with (i). The construction comes in two stages. We first define
![]() $U' := \cup _{k\leq k_0} (U \times \{e^k\}) \subseteq \operatorname {\mathrm {Hyp}}(U)$
and a map
$U' := \cup _{k\leq k_0} (U \times \{e^k\}) \subseteq \operatorname {\mathrm {Hyp}}(U)$
and a map
![]() $\pi ': \operatorname {\mathrm {Hyp}}(U) \to U'$
defined by
$\pi ': \operatorname {\mathrm {Hyp}}(U) \to U'$
defined by
Obviously, this map is measurable, maps separable subsets to separable subsets, and satisfies
It is easy to check that this inequality implies that
![]() $\pi '$
is a rough biLipschitz embedding. It therefore remains to construct a rough biLipschitz embedding
$\pi '$
is a rough biLipschitz embedding. It therefore remains to construct a rough biLipschitz embedding
![]() $\pi _N: U' \to N$
that is measurable and maps separable subsets to separable subsets. We define such a map by
$\pi _N: U' \to N$
that is measurable and maps separable subsets to separable subsets. We define such a map by
Since each
![]() $\pi _k$
is 1-Lipschitz, the map
$\pi _k$
is 1-Lipschitz, the map
![]() $\pi _N$
is 1-Lipschitz, and hence, it is also measurable and maps separable subsets to separable subsets. Additionally,
$\pi _N$
is 1-Lipschitz, and hence, it is also measurable and maps separable subsets to separable subsets. Additionally,
As before, such an inequality implies that
![]() $\pi _N$
is a rough biLipschitz embedding.
$\pi _N$
is a rough biLipschitz embedding.
We proceed to the proof of (ii). Let
![]() $x=(u_x,e^{k_x}),y=(u_y,e^{k_y})$
be distinct elements of N. Then we have the upper bound
$x=(u_x,e^{k_x}),y=(u_y,e^{k_y})$
be distinct elements of N. Then we have the upper bound
 $$ \begin{align*} \rho_U(x,y) &= 2\log\left(\frac{d_U(u_x,u_y)+e^{k_x} \vee e^{k_y}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &\overset{({2.10})}{\leq} 2\log\left(\frac{e^{k(x,y)}+e^{k_x} \vee e^{k_y}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &\leq 2\log\left(\frac{e^{k(x,y)}+e^{k(x,y)}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &= 2\log(2)+\rho_U^N(x,y) \\ &\overset{({2.12})}{\leq} (2\log(2)+1)\rho_U^N(x,y). \end{align*} $$
$$ \begin{align*} \rho_U(x,y) &= 2\log\left(\frac{d_U(u_x,u_y)+e^{k_x} \vee e^{k_y}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &\overset{({2.10})}{\leq} 2\log\left(\frac{e^{k(x,y)}+e^{k_x} \vee e^{k_y}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &\leq 2\log\left(\frac{e^{k(x,y)}+e^{k(x,y)}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &= 2\log(2)+\rho_U^N(x,y) \\ &\overset{({2.12})}{\leq} (2\log(2)+1)\rho_U^N(x,y). \end{align*} $$
For the lower bound, we need to split into two cases: (a)
![]() $0 < \rho _U^N(x,y) \leq 3$
and (b)
$0 < \rho _U^N(x,y) \leq 3$
and (b)
![]() $\rho _U^N(x,y) \geq 3$
. In case (a), we have
$\rho _U^N(x,y) \geq 3$
. In case (a), we have
and in case (b), we have
 $$ \begin{align*} \rho_U(x,y) &= 2\log\left(\frac{d_U(u_x,u_y)+e^{k_x} \vee e^{k_y}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &\overset{({2.11})}{>} 2\log\left(\frac{e^{k(x,y)-1}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &= \rho_U^N(x,y)-2 \\ &\geq \rho_U^N(x,y)-\frac{2}{3}\rho_U^N(x,y) \\ &= \frac{1}{3}\rho_U^N(x,y). \end{align*} $$
$$ \begin{align*} \rho_U(x,y) &= 2\log\left(\frac{d_U(u_x,u_y)+e^{k_x} \vee e^{k_y}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &\overset{({2.11})}{>} 2\log\left(\frac{e^{k(x,y)-1}}{\sqrt{e^{k_x}e^{k_y}}}\right) \\ &= \rho_U^N(x,y)-2 \\ &\geq \rho_U^N(x,y)-\frac{2}{3}\rho_U^N(x,y) \\ &= \frac{1}{3}\rho_U^N(x,y). \end{align*} $$
This finishes the proof of (ii).
We conclude by proving (iii). The first step toward this end is to prove that
![]() $k(\cdot ,\cdot )$
satisfies the inequality
$k(\cdot ,\cdot )$
satisfies the inequality
for every
![]() $x,y,z \in N$
. Let
$x,y,z \in N$
. Let
![]() $x=(u_x,e^{k_x}),y=(u_y,e^{k_y}),z=(u_z,e^{k_z}) \in N$
. Let
$x=(u_x,e^{k_x}),y=(u_y,e^{k_y}),z=(u_z,e^{k_z}) \in N$
. Let
![]() $k_* := \max \{k(x,z),k(x,y),k(y,z)\}$
. If
$k_* := \max \{k(x,z),k(x,y),k(y,z)\}$
. If
![]() $k_* \neq k(x,z)$
, then (2.13) is proved. Thus, we may assume that
$k_* \neq k(x,z)$
, then (2.13) is proved. Thus, we may assume that
![]() $k_* = k(x,z)$
. Suppose that (2.13) fails, and hence,
$k_* = k(x,z)$
. Suppose that (2.13) fails, and hence,
![]() $k(x,y),k(y,z) \leq k_*-1$
. This implies that
$k(x,y),k(y,z) \leq k_*-1$
. This implies that
![]() $k_x,k_y,k_z \leq k_*-1$
and, by (2.7), that
$k_x,k_y,k_z \leq k_*-1$
and, by (2.7), that
![]() $\pi _{k_*-1}(u_x) = \pi _{k_*-1}(u_y) = \pi _{k_*-1}(u_z)$
, which in turn implies that
$\pi _{k_*-1}(u_x) = \pi _{k_*-1}(u_y) = \pi _{k_*-1}(u_z)$
, which in turn implies that
![]() $k(x,z) \leq k_*-1$
. This contradicts
$k(x,z) \leq k_*-1$
. This contradicts
![]() $k_* = k(x,z)$
. Hence, (2.13) must hold.
$k_* = k(x,z)$
. Hence, (2.13) must hold.
We are now in a position to verify (2.5) for
![]() $\rho _U^N$
. Note that (2.5) already implies the triangle inequality, and thus, the proof of (iii) is complete upon verification of (2.5). It is immediate from the definition of
$\rho _U^N$
. Note that (2.5) already implies the triangle inequality, and thus, the proof of (iii) is complete upon verification of (2.5). It is immediate from the definition of
![]() $\rho _U^N$
and some simple cancellations that (2.5) is equivalent to
$\rho _U^N$
and some simple cancellations that (2.5) is equivalent to
for all
![]() $w,x,y,z \in N$
. Notice that (2.14) is invariant under each of the permutations
$w,x,y,z \in N$
. Notice that (2.14) is invariant under each of the permutations
![]() $w \leftrightarrow x$
and
$w \leftrightarrow x$
and
![]() $(w,x) \leftrightarrow (y,z)$
. We will use these symmetries in the ensuing argument to reduce the number of cases needing verification.
$(w,x) \leftrightarrow (y,z)$
. We will use these symmetries in the ensuing argument to reduce the number of cases needing verification.
Let
![]() $w,x,y,z \in N$
. By the
$w,x,y,z \in N$
. By the
![]() $(w,x) \leftrightarrow (y,z)$
symmetry, we may assume that
$(w,x) \leftrightarrow (y,z)$
symmetry, we may assume that
Applying (2.13), we have that
![]() $k(w,x) \leq \max \{k(w,y),k(x,y)\}$
. Using this and the
$k(w,x) \leq \max \{k(w,y),k(x,y)\}$
. Using this and the
![]() $w \leftrightarrow x$
symmetry (which preserves (2.15)), we may assume that
$w \leftrightarrow x$
symmetry (which preserves (2.15)), we may assume that
Applying (2.13) again, we have
In the case where (2.17) holds, we have
which verifies (2.14). We may now assume that (2.18) holds. Applying (2.13) yet again, we have that
In the case where (2.19) holds, we have
and in the case where (2.20) holds, we have
In both cases, (2.14) is proved.
3 Stochastic embeddings and Lipschitz free spaces
We begin this section by precisely defining random maps and various types of stochastic embeddings. Then in the proceeding subsection, we introduce a space of random Lipschitz functions on a pointed metric space X that naturally maps to
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
. This space of random Lipschitz functions will be needed to prove Theorem 3.1, which is the main contributory theorem toward Theorem 3.3 (which proves Theorem A). These theorems are proved in the last subsection.
$L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
. This space of random Lipschitz functions will be needed to prove Theorem 3.1, which is the main contributory theorem toward Theorem 3.3 (which proves Theorem A). These theorems are proved in the last subsection.
3.1 Random maps and stochastic embeddings
A random map from a pointed set
![]() $(X,x_0)$
to a pointed topological space
$(X,x_0)$
to a pointed topological space
![]() $(Y,y_0)$
is a
$(Y,y_0)$
is a
![]() $Y^X$
-valued random variable that is pointwise measurable: a measurable function from some probability space
$Y^X$
-valued random variable that is pointwise measurable: a measurable function from some probability space
![]() $(\Omega ,\mathcal {F},\mathbb {P})$
to the topological space
$(\Omega ,\mathcal {F},\mathbb {P})$
to the topological space
![]() $Y^X$
(equipped with the product topology). Sometimes we will denote a random map by
$Y^X$
(equipped with the product topology). Sometimes we will denote a random map by
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
, and other times we will suppress the underlying probabilistic data and just write
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
, and other times we will suppress the underlying probabilistic data and just write
![]() $\phi : X \to Y$
. There are two additional properties we require as part of the definition of random maps
$\phi : X \to Y$
. There are two additional properties we require as part of the definition of random maps
![]() $\phi $
. The first is that
$\phi $
. The first is that
![]() $\phi $
is pointwise essentially-separably-valued: for every
$\phi $
is pointwise essentially-separably-valued: for every
![]() $x \in X$
, there exists a separable subset
$x \in X$
, there exists a separable subset
![]() $S \subseteq Y$
and a
$S \subseteq Y$
and a
![]() $\mathbb {P}$
-null net N such that
$\mathbb {P}$
-null net N such that
![]() $\phi _\omega (x) \in S$
for every
$\phi _\omega (x) \in S$
for every
![]() $\omega \in \Omega \setminus N$
. This crucial technical requirement ensures Bochner measurability of associated Banach-space-valued functions defined in the next paragraph, and it is also needed for other basic constructions in this section. Of course, this condition is automatic if Y is itself separable, which will often be the case. The second is that
$\omega \in \Omega \setminus N$
. This crucial technical requirement ensures Bochner measurability of associated Banach-space-valued functions defined in the next paragraph, and it is also needed for other basic constructions in this section. Of course, this condition is automatic if Y is itself separable, which will often be the case. The second is that
![]() $\phi $
is almost surely basepoint-preserving, meaning that for
$\phi $
is almost surely basepoint-preserving, meaning that for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $\omega \in \Omega $
, it holds that
$\omega \in \Omega $
, it holds that
![]() $\phi _\omega (x_0) = y_0$
. This condition will be necessary to define an induced bounded linear map
$\phi _\omega (x_0) = y_0$
. This condition will be necessary to define an induced bounded linear map
![]() $T_\phi $
on
$T_\phi $
on
![]() $\operatorname {\mathrm {LF}}(X)$
when X and Y are pointed metric spaces. Whenever
$\operatorname {\mathrm {LF}}(X)$
when X and Y are pointed metric spaces. Whenever
![]() $W,X$
are pointed sets,
$W,X$
are pointed sets,
![]() $Y,Z$
are pointed topological spaces,
$Y,Z$
are pointed topological spaces,
![]() $f_1: W \to X$
is a basepoint-preserving map,
$f_1: W \to X$
is a basepoint-preserving map,
![]() $f_2: Y \to Z$
is a basepoint-preserving continuous map, and
$f_2: Y \to Z$
is a basepoint-preserving continuous map, and
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a random map, it holds that
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a random map, it holds that
![]() $\{f_2 \circ \phi _\omega \circ f_1: W \to Z\}_{\omega \in \Omega }$
is a random map.
$\{f_2 \circ \phi _\omega \circ f_1: W \to Z\}_{\omega \in \Omega }$
is a random map.
Let
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
be a random map between pointed metric spaces
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
be a random map between pointed metric spaces
![]() $(X,d_X)$
,
$(X,d_X)$
,
![]() $(Y,d_Y)$
and
$(Y,d_Y)$
and
![]() $D< \infty $
. The random map is D-Lipschitz in expectation if for every
$D< \infty $
. The random map is D-Lipschitz in expectation if for every
![]() $x,y\in X$
, the inequality
$x,y\in X$
, the inequality
![]() $\mathbb {E}_\omega [d_Y(\phi _\omega (x),\phi _\omega (y))] \leq D d_X(x,y)$
holds. In this case, there is an associated basepoint-preserving D-Lipschitz map
$\mathbb {E}_\omega [d_Y(\phi _\omega (x),\phi _\omega (y))] \leq D d_X(x,y)$
holds. In this case, there is an associated basepoint-preserving D-Lipschitz map
![]() $T_\phi : X \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
defined by
$T_\phi : X \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
defined by
![]() $T_\phi (x) := \{\delta _{\phi _\omega (x)}\}_{\omega \in \Omega }$
. The pointwise measurability and essential-separable-valuedness of
$T_\phi (x) := \{\delta _{\phi _\omega (x)}\}_{\omega \in \Omega }$
. The pointwise measurability and essential-separable-valuedness of
![]() $\phi $
, together with Pettis’s measurability theorem [Reference Diestel, Uhl and Pettis20, Theorem 1.2], ensure that
$\phi $
, together with Pettis’s measurability theorem [Reference Diestel, Uhl and Pettis20, Theorem 1.2], ensure that
![]() $T_\phi (x)$
is Bochner measurable. We also write
$T_\phi (x)$
is Bochner measurable. We also write
![]() $T_\phi $
to denote the induced D-bounded linear map
$T_\phi $
to denote the induced D-bounded linear map
![]() $\operatorname {\mathrm {LF}}(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
. The random map is a stochastic biLipschitz embedding of distortion D and scaling factor
$\operatorname {\mathrm {LF}}(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
. The random map is a stochastic biLipschitz embedding of distortion D and scaling factor
![]() $s\in (0,\infty )$
if
$s\in (0,\infty )$
if
![]() $\phi $
is
$\phi $
is
![]() $sD$
-Lipschitz in expectation and, for all
$sD$
-Lipschitz in expectation and, for all
![]() $x,y \in X$
, it holds that
$x,y \in X$
, it holds that
![]() $d_Y(\phi _\omega (x),\phi _\omega (y)) \geq sd_X(x,y)$
for
$d_Y(\phi _\omega (x),\phi _\omega (y)) \geq sd_X(x,y)$
for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $\omega \in \Omega $
. We refer to this latter property as almost-sure noncontractivity. We will see in Theorem 3.1 that this property implies that the induced map
$\omega \in \Omega $
. We refer to this latter property as almost-sure noncontractivity. We will see in Theorem 3.1 that this property implies that the induced map
![]() $T_\phi $
is a D-isomorphic embedding. If there are
$T_\phi $
is a D-isomorphic embedding. If there are
![]() $D,D',K<\infty $
such that, for every
$D,D',K<\infty $
such that, for every
![]() $x,y \in X$
, we have
$x,y \in X$
, we have
![]() $\mathbb {E}_\omega [d_Y(\phi _\omega (x),\phi _\omega (y))] \leq D d_X(x,y) + K$
and
$\mathbb {E}_\omega [d_Y(\phi _\omega (x),\phi _\omega (y))] \leq D d_X(x,y) + K$
and
![]() $d_Y(\phi _\omega (x),\phi _\omega (y)) \geq (D')^{-1}d_X(x,y)-K$
for
$d_Y(\phi _\omega (x),\phi _\omega (y)) \geq (D')^{-1}d_X(x,y)-K$
for
![]() $\mathbb {P}$
-a.e.
$\mathbb {P}$
-a.e.
![]() $\omega \in \Omega $
, then
$\omega \in \Omega $
, then
![]() $\phi $
is a stochastic rough biLipschitz embedding. If we can choose
$\phi $
is a stochastic rough biLipschitz embedding. If we can choose
![]() $D=D'=1$
, then
$D=D'=1$
, then
![]() $\phi $
is a stochastic rough isometric embedding.
$\phi $
is a stochastic rough isometric embedding.
Whenever X is countable and
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding, then by passing to a
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding, then by passing to a
![]() $\mathbb {P}$
-full-measure subset, we may assume that there exists a separable subset
$\mathbb {P}$
-full-measure subset, we may assume that there exists a separable subset
![]() $S \subseteq Y$
such that, for every
$S \subseteq Y$
such that, for every
![]() $\omega \in \Omega $
, it holds that
$\omega \in \Omega $
, it holds that
![]() $\phi _\omega (X) \subseteq S$
,
$\phi _\omega (X) \subseteq S$
,
![]() $\phi _\omega $
is basepoint-preserving, and
$\phi _\omega $
is basepoint-preserving, and
![]() $d_Y(\phi _\omega (x),\phi _\omega (y)) \geq (D')^{-1}d_X(x,y) - K$
for every
$d_Y(\phi _\omega (x),\phi _\omega (y)) \geq (D')^{-1}d_X(x,y) - K$
for every
![]() $x,y \in X$
. We will use this simple reduction in the proof of Lemma 3.5.
$x,y \in X$
. We will use this simple reduction in the proof of Lemma 3.5.
Whenever
![]() $W,X,Y,Z$
are pointed metric spaces,
$W,X,Y,Z$
are pointed metric spaces,
![]() $f_1: W \to X$
is a basepoint-preserving biLipschitz embedding,
$f_1: W \to X$
is a basepoint-preserving biLipschitz embedding,
![]() $f_2: Y \to Z$
is a basepoint-preserving biLipschitz embedding, and
$f_2: Y \to Z$
is a basepoint-preserving biLipschitz embedding, and
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding, it holds that
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding, it holds that
![]() $\{f_2 \circ \phi _\omega \circ f_1: W \to Z\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding. However, the situation is more delicate for rough biLipschitz embeddings. Suppose instead that
$\{f_2 \circ \phi _\omega \circ f_1: W \to Z\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding. However, the situation is more delicate for rough biLipschitz embeddings. Suppose instead that
![]() $f_1,f_2$
are rough biLipschitz embeddings and that
$f_1,f_2$
are rough biLipschitz embeddings and that
![]() $\{\phi _\omega \}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding. We still have that
$\{\phi _\omega \}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding. We still have that
![]() $\{\phi _\omega \circ f_1\}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding. However,
$\{\phi _\omega \circ f_1\}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding. However,
![]() $\{f_2 \circ \phi _\omega \}_{\omega \in \Omega }$
need not be a stochastic rough biLipschitz embedding. This is due to the fact that rough biLipschitz embeddings are generally not measurable, nor do they map separable subsets to separable subsets, so
$\{f_2 \circ \phi _\omega \}_{\omega \in \Omega }$
need not be a stochastic rough biLipschitz embedding. This is due to the fact that rough biLipschitz embeddings are generally not measurable, nor do they map separable subsets to separable subsets, so
![]() $\{f_2 \circ \phi _\omega \}_{\omega \in \Omega }$
can fail to be a random map. However, these are the only obstructions; if
$\{f_2 \circ \phi _\omega \}_{\omega \in \Omega }$
can fail to be a random map. However, these are the only obstructions; if
![]() $f_2$
is measurable and maps separable subsets to separable subsets, then
$f_2$
is measurable and maps separable subsets to separable subsets, then
![]() $\{f_2 \circ \phi _\omega \}_{\omega \in \Omega }$
is indeed a random map and thus a stochastic rough biLipschitz embedding. We will be using these facts throughout the next few sections.
$\{f_2 \circ \phi _\omega \}_{\omega \in \Omega }$
is indeed a random map and thus a stochastic rough biLipschitz embedding. We will be using these facts throughout the next few sections.
3.2 Spaces of random Lipschitz functions
Let X be a pointed metric space and
![]() $(\Omega ,\mathcal {F},\mathbb {P})$
a probability space. We write
$(\Omega ,\mathcal {F},\mathbb {P})$
a probability space. We write
![]() $L^\infty _{pwm}(\Omega ,\mathcal {F},\mathbb {P};\operatorname {\mathrm {Lip}}_0(X))$
to denote the vector space of random maps
$L^\infty _{pwm}(\Omega ,\mathcal {F},\mathbb {P};\operatorname {\mathrm {Lip}}_0(X))$
to denote the vector space of random maps
![]() $\{f_\omega : X \to \mathbb {R}\}_{\omega \in \Omega }$
having finite seminorm
$\{f_\omega : X \to \mathbb {R}\}_{\omega \in \Omega }$
having finite seminorm
 $$ \begin{align*} \|f\|_{L^\infty_{pwm}} := \sup_{x\neq y\in X} \operatorname*{\mbox{ess sup}}_{\omega\in\Omega} \dfrac{|f_\omega(y)-f_\omega(x)|}{d_X(x,y)}, \end{align*} $$
$$ \begin{align*} \|f\|_{L^\infty_{pwm}} := \sup_{x\neq y\in X} \operatorname*{\mbox{ess sup}}_{\omega\in\Omega} \dfrac{|f_\omega(y)-f_\omega(x)|}{d_X(x,y)}, \end{align*} $$
where the essential supremum is with respect to the
![]() $\mathbb {P}$
-null sets. The subscript
$\mathbb {P}$
-null sets. The subscript
![]() $pwm$
stands for ‘pointwise measurable’. Notice that the seminorm is also given by
$pwm$
stands for ‘pointwise measurable’. Notice that the seminorm is also given by
where the supremum is over all countable subsets
![]() $I\subseteq X$
. We will often abbreviate notation and simply write
$I\subseteq X$
. We will often abbreviate notation and simply write
![]() $L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
. We could create an honest normed vector space by identifying two functions whose difference has norm 0, but this offers no advantage as we will work with
$L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
. We could create an honest normed vector space by identifying two functions whose difference has norm 0, but this offers no advantage as we will work with
![]() $L^\infty _{pwm}(\Omega ,\mathcal {F},\mathbb {P};\operatorname {\mathrm {Lip}}_0(X))$
only through its image in
$L^\infty _{pwm}(\Omega ,\mathcal {F},\mathbb {P};\operatorname {\mathrm {Lip}}_0(X))$
only through its image in
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
, which we explain beginning in the next paragraph.
$L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
, which we explain beginning in the next paragraph.
There is a natural linear isometric map (not claimed to be surjective) from the seminormed space
![]() $L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
into the normed space
$L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
into the normed space
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
given by the pairing
$L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
given by the pairing
The definition of this expectation requires further explanation. Let
![]() $f = \{f_\omega \}_{\omega \in \Omega } \in L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
with
$f = \{f_\omega \}_{\omega \in \Omega } \in L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
with
![]() $\|f\|_{L^\infty _{pwm}} \leq 1$
and
$\|f\|_{L^\infty _{pwm}} \leq 1$
and
![]() $\mu = \{\mu _\omega \}_{\omega \in \Omega } \in L^1(\Omega ;\operatorname {\mathrm {LF}}(X))$
. First of all, since
$\mu = \{\mu _\omega \}_{\omega \in \Omega } \in L^1(\Omega ;\operatorname {\mathrm {LF}}(X))$
. First of all, since
![]() $\{\mu _\omega \}_{\omega \in \Omega }$
is Bochner-measurable, there exists a countable subset
$\{\mu _\omega \}_{\omega \in \Omega }$
is Bochner-measurable, there exists a countable subset
![]() $I\subseteq X$
(which we may assume contains the basepoint) such that
$I\subseteq X$
(which we may assume contains the basepoint) such that
![]() $\mathbb {P}_\omega (\mu _\omega \in \operatorname {\mathrm {LF}}(I)) = 1$
. By (3.1),
$\mathbb {P}_\omega (\mu _\omega \in \operatorname {\mathrm {LF}}(I)) = 1$
. By (3.1),
![]() $f_\omega \big |_I$
is 1-Lipschitz for
$f_\omega \big |_I$
is 1-Lipschitz for
![]() $\mathbb {P}$
-a.e.
$\mathbb {P}$
-a.e.
![]() $\omega \in \Omega $
. Therefore, for
$\omega \in \Omega $
. Therefore, for
![]() $\mathbb {P}$
-a.e.
$\mathbb {P}$
-a.e.
![]() $\omega $
, the pairing
$\omega $
, the pairing
![]() $f_\omega (\mu _\omega ) = f_\omega \big |_I(\mu _\omega )$
is the usual duality pairing
$f_\omega (\mu _\omega ) = f_\omega \big |_I(\mu _\omega )$
is the usual duality pairing
![]() $\operatorname {\mathrm {Lip}}_0(I) \to \operatorname {\mathrm {LF}}(I)^*$
, and we have that
$\operatorname {\mathrm {Lip}}_0(I) \to \operatorname {\mathrm {LF}}(I)^*$
, and we have that
![]() $|f_\omega (\mu _\omega )| \leq \|\mu _\omega \|_{\operatorname {\mathrm {LF}}}$
. Then since the map
$|f_\omega (\mu _\omega )| \leq \|\mu _\omega \|_{\operatorname {\mathrm {LF}}}$
. Then since the map
![]() $\omega \mapsto f_\omega (\mu _\omega )$
is measurable (it is the composition of the measurable map
$\omega \mapsto f_\omega (\mu _\omega )$
is measurable (it is the composition of the measurable map
![]() $\omega \mapsto (f_\omega ,\mu _\omega )$
with the jointly continuous map
$\omega \mapsto (f_\omega ,\mu _\omega )$
with the jointly continuous map
![]() $(g,\nu ) \mapsto g(\nu )$
, where the intermediate space is
$(g,\nu ) \mapsto g(\nu )$
, where the intermediate space is
![]() $B_{\operatorname {\mathrm {Lip}}_0(X)} \times \operatorname {\mathrm {LF}}(X)$
equipped with the weak
$B_{\operatorname {\mathrm {Lip}}_0(X)} \times \operatorname {\mathrm {LF}}(X)$
equipped with the weak
![]() $^*\ \times $
norm topology), the expectation
$^*\ \times $
norm topology), the expectation
![]() $\mathbb {E}_\omega [f_\omega (\mu _\omega )]$
is a well-defined real number with
$\mathbb {E}_\omega [f_\omega (\mu _\omega )]$
is a well-defined real number with
![]() $|\mathbb {E}_\omega [f_\omega (\mu _\omega )]| \leq \mathbb {E}_\omega [\|\mu _\omega \|_{\operatorname {\mathrm {LF}}}] = \|\mu \|_{L^1(\operatorname {\mathrm {LF}})}$
. This inequality demonstrates contractivity of the map.
$|\mathbb {E}_\omega [f_\omega (\mu _\omega )]| \leq \mathbb {E}_\omega [\|\mu _\omega \|_{\operatorname {\mathrm {LF}}}] = \|\mu \|_{L^1(\operatorname {\mathrm {LF}})}$
. This inequality demonstrates contractivity of the map.
To see that the map is isometric, let
![]() $f \in L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
with
$f \in L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
with
![]() $\|f\|_{L^\infty _{pwm}}> 1$
. Then we can find
$\|f\|_{L^\infty _{pwm}}> 1$
. Then we can find
![]() $x\neq y \in X$
and
$x\neq y \in X$
and
![]() $A \in \mathcal {F}$
with
$A \in \mathcal {F}$
with
![]() $\mathbb {P}(A)> 0$
such that
$\mathbb {P}(A)> 0$
such that
![]() $\dfrac {|f_\omega (y)-f_{\omega }(x)|}{d_X(x,y)}> 1$
for all
$\dfrac {|f_\omega (y)-f_{\omega }(x)|}{d_X(x,y)}> 1$
for all
![]() $\omega \in A$
. Hence, we can find
$\omega \in A$
. Hence, we can find
![]() $B \in \mathcal {F}$
with
$B \in \mathcal {F}$
with
![]() $B \subseteq A$
,
$B \subseteq A$
,
![]() $\mathbb {P}(B)> 0$
, and either
$\mathbb {P}(B)> 0$
, and either
![]() $f_\omega (y)-f_\omega (x)> d_X(x,y)$
for all
$f_\omega (y)-f_\omega (x)> d_X(x,y)$
for all
![]() $\omega \in B$
or
$\omega \in B$
or
![]() $f_\omega (y)-f_\omega (x) < -d_X(x,y)$
for all
$f_\omega (y)-f_\omega (x) < -d_X(x,y)$
for all
![]() $\omega \in B$
. Then
$\omega \in B$
. Then
![]() $\mu := \dfrac {\delta _y-\delta _x}{d_X(x,y)}\dfrac {\mathsf {1}_{B}}{\mathbb {P}(B)}$
is a norm-1 element of
$\mu := \dfrac {\delta _y-\delta _x}{d_X(x,y)}\dfrac {\mathsf {1}_{B}}{\mathbb {P}(B)}$
is a norm-1 element of
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(X))$
with
$L^1(\Omega ;\operatorname {\mathrm {LF}}(X))$
with
![]() $|f(\mu )|> 1$
. Throughout this section, we will always consider any function
$|f(\mu )|> 1$
. Throughout this section, we will always consider any function
![]() $\{f_\omega \}_{\omega \in \Omega } \in L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
as an element of
$\{f_\omega \}_{\omega \in \Omega } \in L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
as an element of
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
under this pairing. There are natural questions that arise concerning the closedness or density of the image of
$L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
under this pairing. There are natural questions that arise concerning the closedness or density of the image of
![]() $L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
in
$L^\infty _{pwm}(\Omega ;\operatorname {\mathrm {Lip}}_0(X))$
in
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
with respect to different topologies, but we do not pursue them here as they are unnecessary for the focus of the article.
$L^1(\Omega ;\operatorname {\mathrm {LF}}(X))^*$
with respect to different topologies, but we do not pursue them here as they are unnecessary for the focus of the article.
3.3 Stochastic embeddings into
 $\mathbb {R}$
-trees and isomorphisms to
$\mathbb {R}$
-trees and isomorphisms to
 $L^1$
-spaces
$L^1$
-spaces
In this subsection, we work toward our base result that stochastic biLipschitz embeddability of a pointed metric space into an
![]() $\mathbb {R}$
-tree implies that its free space is isomorphic to an
$\mathbb {R}$
-tree implies that its free space is isomorphic to an
![]() $L^1$
-space (Theorem 3.3). Following that theorem, there is one final lemma of the section (Lemma 3.5) that will be used to prove Theorem C (via Theorem 5.7). This lemma asserts that a stochastic rough biLipschitz embedding into an
$L^1$
-space (Theorem 3.3). Following that theorem, there is one final lemma of the section (Lemma 3.5) that will be used to prove Theorem C (via Theorem 5.7). This lemma asserts that a stochastic rough biLipschitz embedding into an
![]() $\mathbb {R}$
-tree can be upgraded to a stochastic biLipschitz embedding into an
$\mathbb {R}$
-tree can be upgraded to a stochastic biLipschitz embedding into an
![]() $\mathbb {R}$
-tree when the domain is countable and uniformly discrete. We begin with a general result and then successively specialize to cases where the target space has additional structure.
$\mathbb {R}$
-tree when the domain is countable and uniformly discrete. We begin with a general result and then successively specialize to cases where the target space has additional structure.
Theorem 3.1. Let
![]() $X,Y$
be pointed metric spaces and
$X,Y$
be pointed metric spaces and
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
a stochastic biLipschitz embedding of distortion
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
a stochastic biLipschitz embedding of distortion
![]() $D<\infty $
. Let
$D<\infty $
. Let
![]() $K,L,C<\infty $
. Then the following statements are true.
$K,L,C<\infty $
. Then the following statements are true.
-
(1) The induced linear map
 $T_\phi : \operatorname {\mathrm {LF}}(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
is a D-isomorphic embedding.
$T_\phi : \operatorname {\mathrm {LF}}(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
is a D-isomorphic embedding. -
(2) If Y has the K-Lipschitz-bounded, L-uniform-bounded linear extension property and X is compact, then there is a K-bounded linear map
 $R: L^1(\Omega ;\operatorname {\mathrm {LF}}(Y)) \to \operatorname {\mathrm {LF}}(X)$
retracting
$R: L^1(\Omega ;\operatorname {\mathrm {LF}}(Y)) \to \operatorname {\mathrm {LF}}(X)$
retracting
 $T_\phi $
.
$T_\phi $
. -
(3) If Y has the K-Lipschitz-bounded linear extension property and
 $\operatorname {\mathrm {LF}}(X)$
is C-complemented in
$\operatorname {\mathrm {LF}}(X)$
is C-complemented in
 $\operatorname {\mathrm {LF}}(X)^{**}$
, then there is a
$\operatorname {\mathrm {LF}}(X)^{**}$
, then there is a
 $CK$
-bounded linear map
$CK$
-bounded linear map
 $R: L^1(\Omega ;\operatorname {\mathrm {LF}}(Y)) \to \operatorname {\mathrm {LF}}(X)$
retracting
$R: L^1(\Omega ;\operatorname {\mathrm {LF}}(Y)) \to \operatorname {\mathrm {LF}}(X)$
retracting
 $T_\phi $
.
$T_\phi $
.
Proof. Write
![]() $d_X,x_0$
for the metric and basepoint on X, and
$d_X,x_0$
for the metric and basepoint on X, and
![]() $d_Y,y_0$
for the metric and basepoint on Y. By rescalingFootnote 6
$d_Y,y_0$
for the metric and basepoint on Y. By rescalingFootnote 6
![]() $d_Y$
and observing that Lipschitz free spaces over rescaled metrics are linearly isometric, we may assume that the scaling factor s in the definition of stochastic biLipschitz embedding equals 1. Let
$d_Y$
and observing that Lipschitz free spaces over rescaled metrics are linearly isometric, we may assume that the scaling factor s in the definition of stochastic biLipschitz embedding equals 1. Let
![]() $(\Omega ,\mathcal {F},\mathbb {P})$
denote the probability space underlying the stochastic biLipschitz embedding
$(\Omega ,\mathcal {F},\mathbb {P})$
denote the probability space underlying the stochastic biLipschitz embedding
![]() $\{\phi _\omega \}_{\omega \in \Omega }$
. The three statements of the theorem will be proved simultaneously in the following way: we will construct a set-theoretic map
$\{\phi _\omega \}_{\omega \in \Omega }$
. The three statements of the theorem will be proved simultaneously in the following way: we will construct a set-theoretic map
![]() $E_\infty : \operatorname {\mathrm {Lip}}_0(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))^*$
(thought of as a random extension operator) splitting
$E_\infty : \operatorname {\mathrm {Lip}}_0(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))^*$
(thought of as a random extension operator) splitting
![]() $T_\phi ^*$
(i.e.,
$T_\phi ^*$
(i.e.,
![]() $T_\phi ^* \circ E_\infty = id_{\operatorname {\mathrm {Lip}}_0(X)}$
). In the general case with no additional assumptions on Y or X, the map
$T_\phi ^* \circ E_\infty = id_{\operatorname {\mathrm {Lip}}_0(X)}$
). In the general case with no additional assumptions on Y or X, the map
![]() $E_\infty $
will not be linear but will satisfy
$E_\infty $
will not be linear but will satisfy
![]() $\|E_\infty (f)\|_{L^1(\operatorname {\mathrm {LF}})^*} \leq \operatorname {\mathrm {Lip}}(f)$
. In the proof, we will refer to this as ‘case (1)’, and we refer to inequalities of the form
$\|E_\infty (f)\|_{L^1(\operatorname {\mathrm {LF}})^*} \leq \operatorname {\mathrm {Lip}}(f)$
. In the proof, we will refer to this as ‘case (1)’, and we refer to inequalities of the form
![]() $\|E(h)\| \leq L\|h\|$
by saying that ‘E is L-bounded’, even if E is only a set-theoretic map between normed spaces and not linear. Statement (1) of the theorem then follows. In the case where Y is assumed to have the K-Lipschitz-bounded, L-uniform-bounded linear extension property and X is compact, the map
$\|E(h)\| \leq L\|h\|$
by saying that ‘E is L-bounded’, even if E is only a set-theoretic map between normed spaces and not linear. Statement (1) of the theorem then follows. In the case where Y is assumed to have the K-Lipschitz-bounded, L-uniform-bounded linear extension property and X is compact, the map
![]() $E_\infty $
will be linear, K-bounded, and weak
$E_\infty $
will be linear, K-bounded, and weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
continuous. We will refer to this as ‘case (2)’ in the proof. In this case, the preadjoint
$^*$
continuous. We will refer to this as ‘case (2)’ in the proof. In this case, the preadjoint
![]() $(E_\infty )_*$
serves as the retract R. In the case where Y is assumed to have the K-Lipschitz-bounded linear extension property, the map
$(E_\infty )_*$
serves as the retract R. In the case where Y is assumed to have the K-Lipschitz-bounded linear extension property, the map
![]() $E_\infty $
will be linear and K-bounded. We will refer to this as ‘case (3)’ in the proof. In this case, we then use the assumption that
$E_\infty $
will be linear and K-bounded. We will refer to this as ‘case (3)’ in the proof. In this case, we then use the assumption that
![]() $\operatorname {\mathrm {LF}}(X)$
is C-complemented in
$\operatorname {\mathrm {LF}}(X)$
is C-complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
to construct the retract R. We now proceed with the construction of the random extension operator
$\operatorname {\mathrm {LF}}(X)^{**}$
to construct the retract R. We now proceed with the construction of the random extension operator
![]() $E_\infty : \operatorname {\mathrm {Lip}}_0(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))^*$
.
$E_\infty : \operatorname {\mathrm {Lip}}_0(X) \to L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))^*$
.
Let
![]() $\mathcal {P}_{<\infty }(X)$
denote the directed set of finite subsets of X containing the basepoint, ordered by inclusion. Let
$\mathcal {P}_{<\infty }(X)$
denote the directed set of finite subsets of X containing the basepoint, ordered by inclusion. Let
![]() $\mathscr {A}$
denote the directed set of
$\mathscr {A}$
denote the directed set of
![]() $\sigma $
-subalgebras of
$\sigma $
-subalgebras of
![]() $\mathcal {F}$
, ordered by inclusion, consisting of those
$\mathcal {F}$
, ordered by inclusion, consisting of those
![]() $\mathcal {A}$
generated by some countable partition of
$\mathcal {A}$
generated by some countable partition of
![]() $\Omega $
. We consider
$\Omega $
. We consider
![]() $\mathcal {P}_{<\infty }(X) \times \mathscr {A}$
as a directed set equipped with its product preorder. Let
$\mathcal {P}_{<\infty }(X) \times \mathscr {A}$
as a directed set equipped with its product preorder. Let
![]() $(F,\mathcal {A}) \in \mathcal {P}_{<\infty }(X) \times \mathscr {A}$
, and suppose that
$(F,\mathcal {A}) \in \mathcal {P}_{<\infty }(X) \times \mathscr {A}$
, and suppose that
![]() $\mathcal {A}$
is generated by the countable partition
$\mathcal {A}$
is generated by the countable partition
![]() $\{A_i\}_{i=1}^\infty $
of
$\{A_i\}_{i=1}^\infty $
of
![]() $\Omega $
(so
$\Omega $
(so
![]() $\{A_i\}_{i=1}^\infty $
is the set of atoms of the purely atomic
$\{A_i\}_{i=1}^\infty $
is the set of atoms of the purely atomic
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}$
). For each atom
$\mathcal {A}$
). For each atom
![]() $A_i \in \mathcal {A}$
with
$A_i \in \mathcal {A}$
with
![]() $\mathbb {P}(A_i)> 0$
, choose
$\mathbb {P}(A_i)> 0$
, choose
![]() $\omega _{F,i} \in A_i$
such that
$\omega _{F,i} \in A_i$
such that
![]() $\phi _{\omega _{F,i}}(x_0) = y_0$
and
$\phi _{\omega _{F,i}}(x_0) = y_0$
and
for every
![]() $x,y \in F$
. We can make such a choice by the almost-sure basepoint preservation and almost-sure noncontractivity of
$x,y \in F$
. We can make such a choice by the almost-sure basepoint preservation and almost-sure noncontractivity of
![]() $\phi $
(recalling that
$\phi $
(recalling that
![]() $s=1$
), and the fact that F is finite (note that if F was uncountable, we may not be able to choose any
$s=1$
), and the fact that F is finite (note that if F was uncountable, we may not be able to choose any
![]() $\omega _{F,i} \in A_i$
with this property). Let
$\omega _{F,i} \in A_i$
with this property). Let
![]() $E_{F,i}: \operatorname {\mathrm {Lip}}_0(\phi _{\omega _{F,i}}(F)) \to \operatorname {\mathrm {Lip}}_0(Y)$
be an extension operator (noting that each subset
$E_{F,i}: \operatorname {\mathrm {Lip}}_0(\phi _{\omega _{F,i}}(F)) \to \operatorname {\mathrm {Lip}}_0(Y)$
be an extension operator (noting that each subset
![]() $\phi _{\omega _{F,i}}(F)$
contains the basepoint
$\phi _{\omega _{F,i}}(F)$
contains the basepoint
![]() $y_0$
). In case (1) with no assumption on Y,
$y_0$
). In case (1) with no assumption on Y,
![]() $E_{F,i}$
is constructed using the McShane extension theorem, and it is not linear but is 1-bounded. In cases (2)–(3) where Y is assumed to have the K-Lipschitz-bounded linear extension property,
$E_{F,i}$
is constructed using the McShane extension theorem, and it is not linear but is 1-bounded. In cases (2)–(3) where Y is assumed to have the K-Lipschitz-bounded linear extension property,
![]() $E_{F,i}$
is chosen to be K-bounded and linear. In case (2), we also choose
$E_{F,i}$
is chosen to be K-bounded and linear. In case (2), we also choose
![]() $E_{F,i}$
to be L-uniform-bounded.
$E_{F,i}$
to be L-uniform-bounded.
Define a map
![]() $E_{(F,\mathcal {A})}: \operatorname {\mathrm {Lip}}_0(X) \to L_{pwm}^\infty (\Omega ,\mathcal {A};\operatorname {\mathrm {Lip}}_0(Y))$
by
$E_{(F,\mathcal {A})}: \operatorname {\mathrm {Lip}}_0(X) \to L_{pwm}^\infty (\Omega ,\mathcal {A};\operatorname {\mathrm {Lip}}_0(Y))$
by
 $$ \begin{align*} E_{(F,\mathcal{A})}(f)_\omega := \sum_{i=1}^\infty E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})\mathsf{1}_{A_i}(\omega), \end{align*} $$
$$ \begin{align*} E_{(F,\mathcal{A})}(f)_\omega := \sum_{i=1}^\infty E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})\mathsf{1}_{A_i}(\omega), \end{align*} $$
where we consider
![]() $\phi _{\omega _{F,i}}^{-1}$
as a map from
$\phi _{\omega _{F,i}}^{-1}$
as a map from
![]() $\phi _{\omega _{F,i}}(F)$
to X, which is 1-Lipschitz by (3.2). Then
$\phi _{\omega _{F,i}}(F)$
to X, which is 1-Lipschitz by (3.2). Then
![]() $E_{(F,\mathcal {A})}$
is 1-bounded in case (1) and K-bounded and linear in cases (2)–(3). After composing with the natural pairing
$E_{(F,\mathcal {A})}$
is 1-bounded in case (1) and K-bounded and linear in cases (2)–(3). After composing with the natural pairing
![]() $L_{pwm}^\infty (\Omega ,\mathcal {A};\operatorname {\mathrm {Lip}}_0(Y)) \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
, we may consider
$L_{pwm}^\infty (\Omega ,\mathcal {A};\operatorname {\mathrm {Lip}}_0(Y)) \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
, we may consider
![]() $E_{(F,\mathcal {A})}$
as having values in the dual space
$E_{(F,\mathcal {A})}$
as having values in the dual space
![]() $L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
, and define the map
$L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
, and define the map
![]() $E_\infty : \operatorname {\mathrm {Lip}}_0(X) \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
by
$E_\infty : \operatorname {\mathrm {Lip}}_0(X) \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
by
where
![]() $\mathcal {U}$
is any fixed eventuality ultrafilterFootnote 7 on the directed set
$\mathcal {U}$
is any fixed eventuality ultrafilterFootnote 7 on the directed set
![]() $\mathcal {P}_{<\infty }(X)\times \mathscr {A}$
, and the limit is the
$\mathcal {P}_{<\infty }(X)\times \mathscr {A}$
, and the limit is the
![]() $\mathcal {U}$
-ultralimit with respect to the (compact) weak
$\mathcal {U}$
-ultralimit with respect to the (compact) weak
![]() $^*$
topology on the ball of radius
$^*$
topology on the ball of radius
![]() $K\operatorname {\mathrm {Lip}}(f)$
in
$K\operatorname {\mathrm {Lip}}(f)$
in
![]() $L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
. In case (1),
$L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^*$
. In case (1),
![]() $E_{\infty }$
is 1-bounded and (generally) nonlinear, and in cases (2)–(3),
$E_{\infty }$
is 1-bounded and (generally) nonlinear, and in cases (2)–(3),
![]() $E_{\infty }$
is linear and K-bounded.
$E_{\infty }$
is linear and K-bounded.
Our first order of business is to prove that
![]() $E_\infty $
splits
$E_\infty $
splits
![]() $T_\phi ^*$
. Fix
$T_\phi ^*$
. Fix
![]() $f \in \operatorname {\mathrm {Lip}}_0(X)$
and
$f \in \operatorname {\mathrm {Lip}}_0(X)$
and
![]() $x \in X$
. Let
$x \in X$
. Let
![]() $\varepsilon>0$
be arbitrary. Since
$\varepsilon>0$
be arbitrary. Since
![]() $\phi $
is pointwise essentially-separably-valued, there exists a separable subset
$\phi $
is pointwise essentially-separably-valued, there exists a separable subset
![]() $S \subseteq Y$
such that
$S \subseteq Y$
such that
![]() $\phi _\omega (x) \in S$
for
$\phi _\omega (x) \in S$
for
![]() $\mathbb {P}$
-a.e.
$\mathbb {P}$
-a.e.
![]() $\omega \in \Omega $
. Hence, we may find a countable, Borel measurable partition
$\omega \in \Omega $
. Hence, we may find a countable, Borel measurable partition
![]() $\{S_i\}_{i=1}^\infty $
of S such that
$\{S_i\}_{i=1}^\infty $
of S such that
![]() $\operatorname {\mathrm {diam}}(S_i)<\frac {\varepsilon }{K\operatorname {\mathrm {Lip}}(f)}$
for every i. Then since the map
$\operatorname {\mathrm {diam}}(S_i)<\frac {\varepsilon }{K\operatorname {\mathrm {Lip}}(f)}$
for every i. Then since the map
![]() $\omega \to \phi _\omega (x)$
is measurable and takes values in S almost surely, the preimage
$\omega \to \phi _\omega (x)$
is measurable and takes values in S almost surely, the preimage
![]() $\{G_i\}_{i=1}^\infty $
of
$\{G_i\}_{i=1}^\infty $
of
![]() $\{S_i\}_{i=1}^\infty $
under this map is a countable,
$\{S_i\}_{i=1}^\infty $
under this map is a countable,
![]() $\mathcal {F}$
-measurable partition of
$\mathcal {F}$
-measurable partition of
![]() $\Omega \setminus N$
for some
$\Omega \setminus N$
for some
![]() $\mathbb {P}$
-null set
$\mathbb {P}$
-null set
![]() $N\in \mathcal {F}$
. Let
$N\in \mathcal {F}$
. Let
![]() $\mathcal {G}$
be the
$\mathcal {G}$
be the
![]() $\sigma $
-subalgebra of
$\sigma $
-subalgebra of
![]() $\mathcal {F}$
generated by
$\mathcal {F}$
generated by
![]() $\{G_i,N\}_{i=1}^\infty $
, so that
$\{G_i,N\}_{i=1}^\infty $
, so that
![]() $\mathcal {G} \in \mathscr {A}$
. Then, for any
$\mathcal {G} \in \mathscr {A}$
. Then, for any
![]() $\mathcal {A} \in \mathscr {A}$
with
$\mathcal {A} \in \mathscr {A}$
with
![]() $\mathcal {A} \supseteq \mathcal {G}$
, for any atom
$\mathcal {A} \supseteq \mathcal {G}$
, for any atom
![]() $A_i \in \mathcal {A}$
with
$A_i \in \mathcal {A}$
with
![]() $\mathbb {P}(A_i)>0$
, and for any
$\mathbb {P}(A_i)>0$
, and for any
![]() $\omega ,\omega ' \in A_i$
, it holds that
$\omega ,\omega ' \in A_i$
, it holds that
Then we get the estimate
 $$ \begin{align*} &|T^*_\phi(E_\infty(f))(x) - f(x)| \\ &\hspace{6pt}= |E_\infty(f)(T_\phi(x)) - f(x)| \\ &\hspace{6pt}= \left|\left[\mathcal{U}\text{-}w^*\lim_{(F,\mathcal{A})\to\infty} E_{(F,\mathcal{A})}(f)\right](T_\phi(x)) - f(x)\right| \\ &\hspace{6pt}= \mathcal{U}\text{-}\lim_{(F,\mathcal{A})\to\infty} |E_{(F,\mathcal{A})}(f)(T_\phi(x)) - f(x)| \\ &\hspace{6pt}= \mathcal{U}\text{-}\lim_{(F,\mathcal{A})\to\infty} \left|\sum_{i=1}^\infty \int_{A_i} E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_\omega(x)) \mathrm{d}\mathbb{P}(\omega) - f(x)\right| \\ &\hspace{6pt}\leq \sup_{F\ni x, \mathcal{A}\supseteq\mathcal{G}} \sum_{i=1}^\infty \int_{A_i} |E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_\omega(x)) - E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_{\omega_{F,i}}(x))| \mathrm{d}\mathbb{P}(\omega) \\ &\hspace{12pt}\ + \sum_{i=1}^\infty \int_{A_i} | E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_{\omega_{F,i}}(x)) - f(x)| \mathrm{d}\mathbb{P}(\omega) \\ &\hspace{6pt}\leq \sup_{F\ni x,\mathcal{A}\supseteq\mathcal{G}} \sum_{i=1}^\infty \int_{A_i} K\operatorname{\mathrm{Lip}}(f)\frac{\varepsilon}{K\operatorname{\mathrm{Lip}}(f)} \mathrm{d}\mathbb{P}(\omega) + \sum_{i=1}^\infty \int_{A_i} | (f \circ \phi_{\omega_{F,i}}^{-1})(\phi_{\omega_{F,i}}(x)) - f(x)| \mathrm{d}\mathbb{P}(\omega) \\ &\hspace{6pt}= \varepsilon.\end{align*} $$
$$ \begin{align*} &|T^*_\phi(E_\infty(f))(x) - f(x)| \\ &\hspace{6pt}= |E_\infty(f)(T_\phi(x)) - f(x)| \\ &\hspace{6pt}= \left|\left[\mathcal{U}\text{-}w^*\lim_{(F,\mathcal{A})\to\infty} E_{(F,\mathcal{A})}(f)\right](T_\phi(x)) - f(x)\right| \\ &\hspace{6pt}= \mathcal{U}\text{-}\lim_{(F,\mathcal{A})\to\infty} |E_{(F,\mathcal{A})}(f)(T_\phi(x)) - f(x)| \\ &\hspace{6pt}= \mathcal{U}\text{-}\lim_{(F,\mathcal{A})\to\infty} \left|\sum_{i=1}^\infty \int_{A_i} E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_\omega(x)) \mathrm{d}\mathbb{P}(\omega) - f(x)\right| \\ &\hspace{6pt}\leq \sup_{F\ni x, \mathcal{A}\supseteq\mathcal{G}} \sum_{i=1}^\infty \int_{A_i} |E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_\omega(x)) - E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_{\omega_{F,i}}(x))| \mathrm{d}\mathbb{P}(\omega) \\ &\hspace{12pt}\ + \sum_{i=1}^\infty \int_{A_i} | E_{F,i}(f \circ \phi_{\omega_{F,i}}^{-1})(\phi_{\omega_{F,i}}(x)) - f(x)| \mathrm{d}\mathbb{P}(\omega) \\ &\hspace{6pt}\leq \sup_{F\ni x,\mathcal{A}\supseteq\mathcal{G}} \sum_{i=1}^\infty \int_{A_i} K\operatorname{\mathrm{Lip}}(f)\frac{\varepsilon}{K\operatorname{\mathrm{Lip}}(f)} \mathrm{d}\mathbb{P}(\omega) + \sum_{i=1}^\infty \int_{A_i} | (f \circ \phi_{\omega_{F,i}}^{-1})(\phi_{\omega_{F,i}}(x)) - f(x)| \mathrm{d}\mathbb{P}(\omega) \\ &\hspace{6pt}= \varepsilon.\end{align*} $$
Since
![]() $\varepsilon>0$
was arbitrary, this proves
$\varepsilon>0$
was arbitrary, this proves
![]() $T^*_\phi (E_\infty (f))(x) = f(x)$
. Since
$T^*_\phi (E_\infty (f))(x) = f(x)$
. Since
![]() $f \in \operatorname {\mathrm {Lip}}_0(X)$
and
$f \in \operatorname {\mathrm {Lip}}_0(X)$
and
![]() $x \in X$
were arbitrary, this proves
$x \in X$
were arbitrary, this proves
![]() $T_\phi ^* \circ E_\infty = id_{\operatorname {\mathrm {Lip}}_0(X)}$
. The proof of statement (1) is now complete, and from here on, we work in cases (2)–(3) where
$T_\phi ^* \circ E_\infty = id_{\operatorname {\mathrm {Lip}}_0(X)}$
. The proof of statement (1) is now complete, and from here on, we work in cases (2)–(3) where
![]() $E_\infty $
is linear and K-bounded.
$E_\infty $
is linear and K-bounded.
We focus on case (2) first, using the L-uniform-boundedness of
![]() $E_{F,i}$
and compactness of X to prove that
$E_{F,i}$
and compactness of X to prove that
![]() $E_\infty $
is weak
$E_\infty $
is weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
continuous. Let
$^*$
continuous. Let
![]() $f_{\alpha } \in B_{\operatorname {\mathrm {Lip}}_0(X)}$
be a net converging pointwise to
$f_{\alpha } \in B_{\operatorname {\mathrm {Lip}}_0(X)}$
be a net converging pointwise to
![]() $f \in B_{\operatorname {\mathrm {Lip}}_0(X)}$
. Then since X is compact,
$f \in B_{\operatorname {\mathrm {Lip}}_0(X)}$
. Then since X is compact,
![]() $f_\alpha \overset {\alpha \to \infty }{\to } f$
uniformly. We need to prove that, for every
$f_\alpha \overset {\alpha \to \infty }{\to } f$
uniformly. We need to prove that, for every
![]() $\mu = \{\mu _\omega \}_{\omega \in \Omega } \in L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
,
$\mu = \{\mu _\omega \}_{\omega \in \Omega } \in L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
,
![]() $E_\infty (f_\alpha )(\mu ) \overset {\alpha \to \infty }{\to } E_\infty (f)(\mu )$
. By replacing
$E_\infty (f_\alpha )(\mu ) \overset {\alpha \to \infty }{\to } E_\infty (f)(\mu )$
. By replacing
![]() $f_\alpha $
with
$f_\alpha $
with
![]() $f_\alpha -f$
, we may assume that
$f_\alpha -f$
, we may assume that
![]() $f=0$
. Since the linear functionals
$f=0$
. Since the linear functionals
![]() $E_\infty (f_\alpha )$
are uniformly (in
$E_\infty (f_\alpha )$
are uniformly (in
![]() $\alpha $
) bounded, it suffices to prove the desired convergence for all
$\alpha $
) bounded, it suffices to prove the desired convergence for all
![]() $\mu $
in a chosen subset of
$\mu $
in a chosen subset of
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
whose linear span is dense. Toward this end, we consider
$L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
whose linear span is dense. Toward this end, we consider
![]() $\mu $
of the form
$\mu $
of the form
![]() $\delta _y\mathsf {1}_B$
, where
$\delta _y\mathsf {1}_B$
, where
![]() $y \in Y$
and
$y \in Y$
and
![]() $B\in \mathcal {F}$
. Let
$B\in \mathcal {F}$
. Let
![]() $\varepsilon>0$
be arbitrary. Since
$\varepsilon>0$
be arbitrary. Since
![]() $f_\alpha \to 0$
uniformly, we may choose
$f_\alpha \to 0$
uniformly, we may choose
![]() $\alpha _0$
large enough so that for all
$\alpha _0$
large enough so that for all
![]() $\alpha \geq \alpha _0$
, we have
$\alpha \geq \alpha _0$
, we have
![]() $\|f_\alpha \|_\infty \leq \frac {\varepsilon }{L}$
. Then, for all
$\|f_\alpha \|_\infty \leq \frac {\varepsilon }{L}$
. Then, for all
![]() $\alpha \geq \alpha _0$
, we have
$\alpha \geq \alpha _0$
, we have
 $$ \begin{align*} \left|E_\infty(f_\alpha)(\delta_y\mathsf{1}_B)\right| &= \left|\left[\mathcal{U}\text{-}w^*\lim_{(F,\mathcal{A})\to\infty} E_{(F,\mathcal{A})}(f_\alpha)\right](\delta_y\mathsf{1}_B)\right| \\ &= \mathcal{U}\text{-}\lim_{(F,\mathcal{A})\to\infty} |E_{(F,\mathcal{A})}(f_\alpha)(\delta_y\mathsf{1}_B)| \\ &\leq \sup_{(F,\mathcal{A})} |E_{(F,\mathcal{A})}(f_\alpha)(\delta_y\mathsf{1}_B)| \\ &= \sup_{(F,\mathcal{A})} \left|\sum_{i=1}^\infty E_{F,i}(f_\alpha \circ \phi_{\omega_{F,i}}^{-1})(y) \mathbb{P}(A_i\cap B)\right| \\ &\leq \sup_{(F,\mathcal{A})} \sum_{i=1}^\infty \|E_{F,i}(f_\alpha \circ \phi_{\omega_{F,i}}^{-1})\|_\infty \mathbb{P}(A_i\cap B) \\ &\leq \sup_{(F,\mathcal{A})} \sum_{i=1}^\infty L\|f_\alpha\|_\infty \mathbb{P}(A_i\cap B) \\ &\leq \varepsilon\mathbb{P}(B) \leq \varepsilon. \end{align*} $$
$$ \begin{align*} \left|E_\infty(f_\alpha)(\delta_y\mathsf{1}_B)\right| &= \left|\left[\mathcal{U}\text{-}w^*\lim_{(F,\mathcal{A})\to\infty} E_{(F,\mathcal{A})}(f_\alpha)\right](\delta_y\mathsf{1}_B)\right| \\ &= \mathcal{U}\text{-}\lim_{(F,\mathcal{A})\to\infty} |E_{(F,\mathcal{A})}(f_\alpha)(\delta_y\mathsf{1}_B)| \\ &\leq \sup_{(F,\mathcal{A})} |E_{(F,\mathcal{A})}(f_\alpha)(\delta_y\mathsf{1}_B)| \\ &= \sup_{(F,\mathcal{A})} \left|\sum_{i=1}^\infty E_{F,i}(f_\alpha \circ \phi_{\omega_{F,i}}^{-1})(y) \mathbb{P}(A_i\cap B)\right| \\ &\leq \sup_{(F,\mathcal{A})} \sum_{i=1}^\infty \|E_{F,i}(f_\alpha \circ \phi_{\omega_{F,i}}^{-1})\|_\infty \mathbb{P}(A_i\cap B) \\ &\leq \sup_{(F,\mathcal{A})} \sum_{i=1}^\infty L\|f_\alpha\|_\infty \mathbb{P}(A_i\cap B) \\ &\leq \varepsilon\mathbb{P}(B) \leq \varepsilon. \end{align*} $$
Since
![]() $\varepsilon> 0$
was arbitrary, this shows
$\varepsilon> 0$
was arbitrary, this shows
![]() $E_\infty (f_\alpha )(\delta _y\mathsf {1}_B) \overset {\alpha \to \infty }{\to } 0$
, completing the proof of weak
$E_\infty (f_\alpha )(\delta _y\mathsf {1}_B) \overset {\alpha \to \infty }{\to } 0$
, completing the proof of weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
continuity. Then the preadjoint
$^*$
continuity. Then the preadjoint
![]() $(E_\infty )_*$
is K-bounded and satisfies
$(E_\infty )_*$
is K-bounded and satisfies
which implies
![]() $(E_\infty )_* \circ T_\phi = id_{\operatorname {\mathrm {LF}}(X)}$
. This completes the proof of statement (2).
$(E_\infty )_* \circ T_\phi = id_{\operatorname {\mathrm {LF}}(X)}$
. This completes the proof of statement (2).
We now find ourselves in case (3). In this final case, the lack of uniform-boundedness of
![]() $E_{F,i}$
prevents us from being able to prove weak
$E_{F,i}$
prevents us from being able to prove weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
continuity of
$^*$
continuity of
![]() $E_\infty $
, and hence, we cannot use a preadjoint
$E_\infty $
, and hence, we cannot use a preadjoint
![]() $(E_\infty )_*$
to retract
$(E_\infty )_*$
to retract
![]() $T_\phi $
. Naturally, the assumption that
$T_\phi $
. Naturally, the assumption that
![]() $\operatorname {\mathrm {LF}}(X)$
is complemented in
$\operatorname {\mathrm {LF}}(X)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
provides an alternate route. Define the
$\operatorname {\mathrm {LF}}(X)^{**}$
provides an alternate route. Define the
![]() $CK$
-bounded linear map
$CK$
-bounded linear map
![]() $R: L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y)) \to \operatorname {\mathrm {LF}}(X)$
by
$R: L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y)) \to \operatorname {\mathrm {LF}}(X)$
by
![]() $R := P \circ E_\infty ^* \circ J_Y$
, where
$R := P \circ E_\infty ^* \circ J_Y$
, where
![]() $P: \operatorname {\mathrm {LF}}(X)^{**} \to \operatorname {\mathrm {LF}}(X)$
is a C-bounded linear map retracting the canonical embedding
$P: \operatorname {\mathrm {LF}}(X)^{**} \to \operatorname {\mathrm {LF}}(X)$
is a C-bounded linear map retracting the canonical embedding
![]() $J_X: \operatorname {\mathrm {LF}}(X) \to \operatorname {\mathrm {LF}}(X)^{**} = \operatorname {\mathrm {Lip}}_0(X)^*$
, and
$J_X: \operatorname {\mathrm {LF}}(X) \to \operatorname {\mathrm {LF}}(X)^{**} = \operatorname {\mathrm {Lip}}_0(X)^*$
, and
![]() $J_Y: L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y)) \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^{**}$
is the canonical embedding. It is then immediate to verify that R retracts
$J_Y: L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y)) \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^{**}$
is the canonical embedding. It is then immediate to verify that R retracts
![]() $T_\phi $
. To see this, let us introduce the notation
$T_\phi $
. To see this, let us introduce the notation
![]() $J_{X^{**}}: \operatorname {\mathrm {LF}}(X)^{**} \to \operatorname {\mathrm {LF}}(X)^{****}$
and
$J_{X^{**}}: \operatorname {\mathrm {LF}}(X)^{**} \to \operatorname {\mathrm {LF}}(X)^{****}$
and
![]() $J_{Y^{**}}: L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^{**} \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^{****}$
for the canonical embeddings, and, letting
$J_{Y^{**}}: L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^{**} \to L^1(\Omega ,\mathcal {F};\operatorname {\mathrm {LF}}(Y))^{****}$
for the canonical embeddings, and, letting
![]() $J_{U}: U \to U^{**}$
denote the canonical embedding for a general Banach space U, recall that for any Banach spaces
$J_{U}: U \to U^{**}$
denote the canonical embedding for a general Banach space U, recall that for any Banach spaces
![]() $V,W$
and bounded linear map
$V,W$
and bounded linear map
![]() $S: V \to W$
, we have
$S: V \to W$
, we have
![]() $J_{V}^{**} \circ J_V = J_{V^{**}} \circ J_V$
and
$J_{V}^{**} \circ J_V = J_{V^{**}} \circ J_V$
and
![]() $S^{**} \circ J_V = J_W \circ S$
. Using these facts together with the definition of R and the identity
$S^{**} \circ J_V = J_W \circ S$
. Using these facts together with the definition of R and the identity
![]() $T_\phi ^* \circ E_\infty = id_{\operatorname {\mathrm {LF}}(X)^*}$
established above, we get
$T_\phi ^* \circ E_\infty = id_{\operatorname {\mathrm {LF}}(X)^*}$
established above, we get
 $$ \begin{align*} (R \circ T_\phi)^{**} \circ J_X &= P^{**} \circ E_\infty^{***} \circ J_Y^{**} \circ T_\phi^{**} \circ J_X \\ &= P^{**} \circ E_\infty^{***} \circ J_Y^{**} \circ J_Y \circ T_\phi \\ &= P^{**} \circ E_\infty^{***} \circ J_{Y^{**}} \circ J_Y \circ T_\phi \\ &= P^{**} \circ E_\infty^{***} \circ J_{Y^{**}} \circ T_\phi^{**} \circ J_X \\ &= J_X \circ P \circ E_\infty^{*} \circ T_\phi^{**} \circ J_X \\ &= J_X \circ P \circ J_X \\ &= J_X, \end{align*} $$
$$ \begin{align*} (R \circ T_\phi)^{**} \circ J_X &= P^{**} \circ E_\infty^{***} \circ J_Y^{**} \circ T_\phi^{**} \circ J_X \\ &= P^{**} \circ E_\infty^{***} \circ J_Y^{**} \circ J_Y \circ T_\phi \\ &= P^{**} \circ E_\infty^{***} \circ J_{Y^{**}} \circ J_Y \circ T_\phi \\ &= P^{**} \circ E_\infty^{***} \circ J_{Y^{**}} \circ T_\phi^{**} \circ J_X \\ &= J_X \circ P \circ E_\infty^{*} \circ T_\phi^{**} \circ J_X \\ &= J_X \circ P \circ J_X \\ &= J_X, \end{align*} $$
which implies
![]() $R \circ T_\phi = id_{\operatorname {\mathrm {LF}}(X)}$
.
$R \circ T_\phi = id_{\operatorname {\mathrm {LF}}(X)}$
.
We now specialize to the case where the target space has finite Nagata dimension and apply Corollary 2.6.
Corollary 3.2. Let X be a pointed metric space stochastic biLipschitzly embedding with distortion
![]() $D<\infty $
into a pointed metric space Y of finite Nagata dimension (say, dimension
$D<\infty $
into a pointed metric space Y of finite Nagata dimension (say, dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
). If X is compact or if
$\gamma <\infty $
). If X is compact or if
![]() $\operatorname {\mathrm {LF}}(X)$
is C-complemented in
$\operatorname {\mathrm {LF}}(X)$
is C-complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
, then
$\operatorname {\mathrm {LF}}(X)^{**}$
, then
![]() $\operatorname {\mathrm {LF}}(X)$
is D-isomorphic to a
$\operatorname {\mathrm {LF}}(X)$
is D-isomorphic to a
![]() $C'$
-complemented subspace of
$C'$
-complemented subspace of
![]() $L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
, where
$L^1(\Omega ;\operatorname {\mathrm {LF}}(Y))$
, where
![]() $C'$
depends only on
$C'$
depends only on
![]() $D,C,n,\gamma $
, and
$D,C,n,\gamma $
, and
![]() $\Omega $
is the probability space underlying the stochastic biLipschitz embedding.
$\Omega $
is the probability space underlying the stochastic biLipschitz embedding.
Proof. Assume that X is compact or that
![]() $\operatorname {\mathrm {LF}}(X)$
is C-complemented in
$\operatorname {\mathrm {LF}}(X)$
is C-complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
for some
$\operatorname {\mathrm {LF}}(X)^{**}$
for some
![]() $C<\infty $
. By Corollary 2.6, Y has the K-Lipschitz bounded, 1-uniform bounded linear extension property, where K depends only on
$C<\infty $
. By Corollary 2.6, Y has the K-Lipschitz bounded, 1-uniform bounded linear extension property, where K depends only on
![]() $n,\gamma $
. Then the conclusion follows from Theorem 3.1.
$n,\gamma $
. Then the conclusion follows from Theorem 3.1.
We now reach our base result, which essentially follows from Corollary 3.2, the fact that
![]() $\mathbb {R}$
-trees have finite Nagata dimension, and a widely used decomposition lemma of Kalton [Reference Kalton33, Lemma 4.2]. This lemma allows one, in many cases, to restrict to bounded subsets of a metric space to prove isomorphic properties of its free space.
$\mathbb {R}$
-trees have finite Nagata dimension, and a widely used decomposition lemma of Kalton [Reference Kalton33, Lemma 4.2]. This lemma allows one, in many cases, to restrict to bounded subsets of a metric space to prove isomorphic properties of its free space.
Theorem 3.3. Let X be an infinite, separable, pointed metric space and
![]() $D<\infty $
. If X stochastic biLipschitzly embeds with distortion D into a pointed
$D<\infty $
. If X stochastic biLipschitzly embeds with distortion D into a pointed
![]() $\mathbb {R}$
-tree, and if X is proper or
$\mathbb {R}$
-tree, and if X is proper or
![]() $\operatorname {\mathrm {LF}}(X)$
is complemented in
$\operatorname {\mathrm {LF}}(X)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
, then
$\operatorname {\mathrm {LF}}(X)^{**}$
, then
![]() $\operatorname {\mathrm {LF}}(X) \approx L^1$
or
$\operatorname {\mathrm {LF}}(X) \approx L^1$
or
![]() $\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
, with the latter isomorphism holding if and only if the completion of X is purely 1-unrectifiable.
$\operatorname {\mathrm {LF}}(X) \approx \ell ^1$
, with the latter isomorphism holding if and only if the completion of X is purely 1-unrectifiable.
Proof. Assume that X stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree with distortion
$\mathbb {R}$
-tree with distortion
![]() $D<\infty $
and that X is proper or that
$D<\infty $
and that X is proper or that
![]() $\operatorname {\mathrm {LF}}(X)$
is complemented in
$\operatorname {\mathrm {LF}}(X)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
. We will prove that
$\operatorname {\mathrm {LF}}(X)^{**}$
. We will prove that
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
![]() $L^1$
-space, and then the conclusion follows from Theorem 2.2.
$L^1$
-space, and then the conclusion follows from Theorem 2.2.
First we work in the case where
![]() $\operatorname {\mathrm {LF}}(X)$
is complemented in
$\operatorname {\mathrm {LF}}(X)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
. Since
$\operatorname {\mathrm {LF}}(X)^{**}$
. Since
![]() $\mathbb {R}$
-trees have Nagata dimension 1 with constant
$\mathbb {R}$
-trees have Nagata dimension 1 with constant
![]() $\gamma \leq 5$
and have free spaces linearly isometric to
$\gamma \leq 5$
and have free spaces linearly isometric to
![]() $L^1$
-spaces (see
$L^1$
-spaces (see
![]() $\S $
2.6 for each of these facts), Corollary 3.2 implies that
$\S $
2.6 for each of these facts), Corollary 3.2 implies that
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of an
![]() $L^1$
-space.
$L^1$
-space.
Now we work in the other case where X is proper. By [Reference Kalton33, Lemma 4.2], there is a sequence
![]() $\{B_n\}_{n\in \mathbb {Z}}$
of closed, bounded subsets of X, containing the basepoint, such that
$\{B_n\}_{n\in \mathbb {Z}}$
of closed, bounded subsets of X, containing the basepoint, such that
![]() $\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \oplus ^1_{n\in \mathbb {Z}} \operatorname {\mathrm {LF}}(B_n)$
, and thus, it suffices to prove that there exists
$\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \oplus ^1_{n\in \mathbb {Z}} \operatorname {\mathrm {LF}}(B_n)$
, and thus, it suffices to prove that there exists
![]() $C'<\infty $
such that
$C'<\infty $
such that
![]() $\operatorname {\mathrm {LF}}(B)$
is
$\operatorname {\mathrm {LF}}(B)$
is
![]() $C'$
-isomorphic to a
$C'$
-isomorphic to a
![]() $C'$
-complemented subspace of an
$C'$
-complemented subspace of an
![]() $L^1$
-space for every closed, bounded
$L^1$
-space for every closed, bounded
![]() $B \subseteq X$
containing the basepoint. Let
$B \subseteq X$
containing the basepoint. Let
![]() $B \subseteq X$
be closed, bounded and basepoint-containing. Then B is compact and stochastic biLipschitzly embeds into a pointed
$B \subseteq X$
be closed, bounded and basepoint-containing. Then B is compact and stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree with distortion D. Then we use Corollary 3.2 again to obtain that
$\mathbb {R}$
-tree with distortion D. Then we use Corollary 3.2 again to obtain that
![]() $\operatorname {\mathrm {LF}}(B)$
is D-isomorphic to a
$\operatorname {\mathrm {LF}}(B)$
is D-isomorphic to a
![]() $C'$
-complemented subspace of an
$C'$
-complemented subspace of an
![]() $L^1$
-space, where
$L^1$
-space, where
![]() $C'$
depends only on D.
$C'$
depends only on D.
Remark 3.4. It is plausible that the conclusion of Theorem 3.3 could hold without assuming that X is proper or that
![]() $\operatorname {\mathrm {LF}}(X)$
is complemented in
$\operatorname {\mathrm {LF}}(X)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X)^{**}$
. We expect that a proof of such a general result would need to engage more directly with the geometry of
$\operatorname {\mathrm {LF}}(X)^{**}$
. We expect that a proof of such a general result would need to engage more directly with the geometry of
![]() $\mathbb {R}$
-trees and would be decidedly more technical than the proof of Theorem 3.3 we provided.
$\mathbb {R}$
-trees and would be decidedly more technical than the proof of Theorem 3.3 we provided.
The final result of this section states that if X is countable and uniformly discrete, then a stochastic rough biLipschitz embedding of X into an
![]() $\mathbb {R}$
-tree can be upgraded to a stochastic biLipschitz embedding. This lemma will be used in the proof of Theorem 5.7.
$\mathbb {R}$
-tree can be upgraded to a stochastic biLipschitz embedding. This lemma will be used in the proof of Theorem 5.7.
Lemma 3.5. Let
![]() $(X,d_X,p)$
be a countable, uniformly discrete, pointed metric space. If X stochastic rough biLipschitzly embeds into a pointed
$(X,d_X,p)$
be a countable, uniformly discrete, pointed metric space. If X stochastic rough biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree, then X stochastic biLipschitzly embeds into a pointed
$\mathbb {R}$
-tree, then X stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree. Moreover, the distortion of the stochastic biLipschitz embedding depends only on the implicit constants of the stochastic rough biLipschitz embedding and the separation constant of X.
$\mathbb {R}$
-tree. Moreover, the distortion of the stochastic biLipschitz embedding depends only on the implicit constants of the stochastic rough biLipschitz embedding and the separation constant of X.
Proof. Let
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
be a random map into a separable subset Y of a pointed
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
be a random map into a separable subset Y of a pointed
![]() $\mathbb {R}$
-tree
$\mathbb {R}$
-tree
![]() $(T,d_T,q)$
and
$(T,d_T,q)$
and
![]() $D,D',K<\infty $
such that, for every
$D,D',K<\infty $
such that, for every
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $x,y \in X$
,
$x,y \in X$
,
![]() $d_T(\phi _\omega (x),\phi _\omega (y))\ \geq (D')^{-1}d_X(x,y) - K$
,
$d_T(\phi _\omega (x),\phi _\omega (y))\ \geq (D')^{-1}d_X(x,y) - K$
,
![]() $\phi _\omega (p) = q$
, and
$\phi _\omega (p) = q$
, and
![]() $\mathbb {E}_\omega [d_T(\phi _\omega (x),\phi _\omega (y))] \leq Dd_X(x,y) + K$
(we can ask for these things to happen for all
$\mathbb {E}_\omega [d_T(\phi _\omega (x),\phi _\omega (y))] \leq Dd_X(x,y) + K$
(we can ask for these things to happen for all
![]() $\omega \in \Omega $
due to countability of X). By replacing
$\omega \in \Omega $
due to countability of X). By replacing
![]() $d_T$
with
$d_T$
with
![]() $(D')^{-1}d_T$
, and noting that rescalings of
$(D')^{-1}d_T$
, and noting that rescalings of
![]() $\mathbb {R}$
-trees are still
$\mathbb {R}$
-trees are still
![]() $\mathbb {R}$
-trees, we may assume that
$\mathbb {R}$
-trees, we may assume that
![]() $D'=1$
. Furthermore, by replacing T with the convex hull of Y, we may assume that T is separable.
$D'=1$
. Furthermore, by replacing T with the convex hull of Y, we may assume that T is separable.
Let
![]() $N_X \subseteq X$
be a maximal
$N_X \subseteq X$
be a maximal
![]() $2K$
-separated subset of X containing p and
$2K$
-separated subset of X containing p and
![]() $N_T$
a maximal
$N_T$
a maximal
![]() $\frac {K}{6}$
-separated subset of T containing q. Then
$\frac {K}{6}$
-separated subset of T containing q. Then
![]() $N_X$
and
$N_X$
and
![]() $N_T$
are countable since
$N_T$
are countable since
![]() $X,T$
are separable. Equip each of these sets with a well-order coming from any bijection with
$X,T$
are separable. Equip each of these sets with a well-order coming from any bijection with
![]() $\mathbb {N}$
, and then define projections
$\mathbb {N}$
, and then define projections
![]() $\pi _X: X \to N_X$
and
$\pi _X: X \to N_X$
and
![]() $\pi _T: T \to N_T$
by
$\pi _T: T \to N_T$
by
![]() $\pi _X(x) = \min \{n\in N_X: d_X(n,x) \leq 2\operatorname {\mathrm {dist}}(N_X,x)\}$
and
$\pi _X(x) = \min \{n\in N_X: d_X(n,x) \leq 2\operatorname {\mathrm {dist}}(N_X,x)\}$
and
![]() $\pi _T(t) = \min \{n\in N_T: d_T(n,t) \leq 2\operatorname {\mathrm {dist}}(N_T,t)\}$
. By maximality of
$\pi _T(t) = \min \{n\in N_T: d_T(n,t) \leq 2\operatorname {\mathrm {dist}}(N_T,t)\}$
. By maximality of
![]() $N_X$
, it holds that
$N_X$
, it holds that
for every
![]() $x \in X$
, and hence,
$x \in X$
, and hence,
By the countability of
![]() $N_T$
, it is easily seen that
$N_T$
, it is easily seen that
![]() $\pi _T$
is measurable. The maximality of
$\pi _T$
is measurable. The maximality of
![]() $N_T$
implies that
$N_T$
implies that
![]() $d_T(\pi _T(t),t) \leq \frac {K}{3}$
for every
$d_T(\pi _T(t),t) \leq \frac {K}{3}$
for every
![]() $t \in T$
. Using this, together with
$t \in T$
. Using this, together with
![]() $2K$
-separation of
$2K$
-separation of
![]() $N_X$
, we have for any
$N_X$
, we have for any
![]() $n \neq m \in N_X$
and
$n \neq m \in N_X$
and
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align} \nonumber d_T(\pi_T(\phi_\omega(m)),\pi_T(\phi_\omega(n))) &\geq d_T(\phi_\omega(m),\phi_\omega(n)) - \frac{2K}{3} \\ \nonumber &\geq d_X(m,n) - K - \frac{2K}{3} \\ &\geq \frac{1}{6}d_X(m,n). \end{align} $$
$$ \begin{align} \nonumber d_T(\pi_T(\phi_\omega(m)),\pi_T(\phi_\omega(n))) &\geq d_T(\phi_\omega(m),\phi_\omega(n)) - \frac{2K}{3} \\ \nonumber &\geq d_X(m,n) - K - \frac{2K}{3} \\ &\geq \frac{1}{6}d_X(m,n). \end{align} $$
Additionally,
 $$ \begin{align} \nonumber \mathbb{E}_\omega[d_T(\pi_T(\phi_\omega(m)),\pi_T(\phi_\omega(n)))] &\leq \mathbb{E}_\omega[d_T(\phi_\omega(m),\phi_\omega(n))] + \frac{2K}{3} \\ \nonumber &\leq Dd_X(m,n) + K + \frac{2K}{3} \\ &\leq \left(D+\frac{5}{6}\right)d_X(m,n). \end{align} $$
$$ \begin{align} \nonumber \mathbb{E}_\omega[d_T(\pi_T(\phi_\omega(m)),\pi_T(\phi_\omega(n)))] &\leq \mathbb{E}_\omega[d_T(\phi_\omega(m),\phi_\omega(n))] + \frac{2K}{3} \\ \nonumber &\leq Dd_X(m,n) + K + \frac{2K}{3} \\ &\leq \left(D+\frac{5}{6}\right)d_X(m,n). \end{align} $$
This shows that
![]() $\{(\pi _T \circ \phi _\omega )\big |_{N_X}: N_X \to N_T\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding. We will next use the uniform discreteness assumption to extend this to all of X by precomposing with
$\{(\pi _T \circ \phi _\omega )\big |_{N_X}: N_X \to N_T\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding. We will next use the uniform discreteness assumption to extend this to all of X by precomposing with
![]() $\pi _X$
. However, we need to enlarge our target tree. There are many ways to do this – we prioritize simplicity of the exposition over optimization of the distortion constants involved. Toward this end, we employ a star-type construction.
$\pi _X$
. However, we need to enlarge our target tree. There are many ways to do this – we prioritize simplicity of the exposition over optimization of the distortion constants involved. Toward this end, we employ a star-type construction.
Define the metric space
![]() $(Z,d_Z)$
by
$(Z,d_Z)$
by
 $$ \begin{align*} Z &:= X \times N_T, \\ d_Z((x,m),(y,n)) & := \begin{cases} 0 & (x,m)=(y,n) \\ 1+d_T(m,n) & (x,m) \neq (y,n) \end{cases}. \end{align*} $$
$$ \begin{align*} Z &:= X \times N_T, \\ d_Z((x,m),(y,n)) & := \begin{cases} 0 & (x,m)=(y,n) \\ 1+d_T(m,n) & (x,m) \neq (y,n) \end{cases}. \end{align*} $$
One can verify that Z is countable, uniformly discrete and 0-hyperbolic since X is countable and
![]() $N_T$
is countable and 0-hyperbolic. Thus, Z is isometric to a countable, uniformly discrete subset of an
$N_T$
is countable and 0-hyperbolic. Thus, Z is isometric to a countable, uniformly discrete subset of an
![]() $\mathbb {R}$
-tree (see
$\mathbb {R}$
-tree (see
![]() $\S $
2.6). Equip Z with basepoint
$\S $
2.6). Equip Z with basepoint
![]() $(p,q)$
. We will show that the random map
$(p,q)$
. We will show that the random map
![]() $\{\psi _\omega : X \to Z\}_{\omega \in \Omega }$
given by
$\{\psi _\omega : X \to Z\}_{\omega \in \Omega }$
given by
is a stochastic biLipschitz embedding. First note that
![]() $\psi $
is indeed pointwise measurable and essentially-separably-valued since
$\psi $
is indeed pointwise measurable and essentially-separably-valued since
![]() $\pi _T$
is measurable and Z is countable. It is also basepoint-preserving since
$\pi _T$
is measurable and Z is countable. It is also basepoint-preserving since
![]() $p\in N_X$
and
$p\in N_X$
and
![]() $q\in N_T$
. Now let
$q\in N_T$
. Now let
![]() $\theta> 0$
such that
$\theta> 0$
such that
![]() $d_X(x,y)> \theta $
for every
$d_X(x,y)> \theta $
for every
![]() $x\neq y \in X$
. Let
$x\neq y \in X$
. Let
![]() $x\neq y \in X$
. We treat two cases: (i)
$x\neq y \in X$
. We treat two cases: (i)
![]() $\pi _X(x) = \pi _X(y)$
and (ii)
$\pi _X(x) = \pi _X(y)$
and (ii)
![]() $\pi _X(x) \neq \pi _X(y)$
. Assume case (i) holds. Then for every
$\pi _X(x) \neq \pi _X(y)$
. Assume case (i) holds. Then for every
![]() $\omega $
, we have
$\omega $
, we have
Likewise,
Now assume that we are in case (ii). Then by (3.5),
![]() $d_X(x,y) \leq 5d_X(\pi _X(x),\pi _X(y))$
. Thus, for every
$d_X(x,y) \leq 5d_X(\pi _X(x),\pi _X(y))$
. Thus, for every
![]() $\omega \in \Omega $
, we have
$\omega \in \Omega $
, we have
 $$ \begin{align*} d_{Z}(\psi_\omega(x),\psi_\omega(y)) &= 1+d_{T}(\pi_T(\phi_\omega(\pi_X(x))),\pi_T(\phi_\omega(\pi_X(y)))) \\ &\overset{({3.6})}{\geq} 1 + \frac{1}{6}d_X(\pi_X(x),\pi_X(y)) \\ &\geq 1 + \frac{1}{30}d_X(x,y) \\ &> \frac{1}{30}d_X(x,y). \end{align*} $$
$$ \begin{align*} d_{Z}(\psi_\omega(x),\psi_\omega(y)) &= 1+d_{T}(\pi_T(\phi_\omega(\pi_X(x))),\pi_T(\phi_\omega(\pi_X(y)))) \\ &\overset{({3.6})}{\geq} 1 + \frac{1}{6}d_X(\pi_X(x),\pi_X(y)) \\ &\geq 1 + \frac{1}{30}d_X(x,y) \\ &> \frac{1}{30}d_X(x,y). \end{align*} $$
Likewise,
 $$ \begin{align*} \mathbb{E}_\omega[d_{Z}(\psi_\omega(x),\psi_\omega(y))] &= 1 + \mathbb{E}_\omega[d_{T}(\pi_T(\phi_\omega(\pi_X(x))),\pi_T(\phi_\omega(\pi_X(y))))] \\ &\overset{({3.7})}{\leq} 1 + \left(D+\frac{5}{6}\right)d_X(\pi_X(x),\pi_X(y)) \\ &\overset{({3.3})}{\leq} 1 + \left(D+\frac{5}{6}\right)(d_X(x,y) + 8K) \\ &\leq \left(\theta^{-1}+\left(D+\frac{5}{6}\right)(1+8K\theta^{-1})\right)d_X(x,y).\\[-34pt] \end{align*} $$
$$ \begin{align*} \mathbb{E}_\omega[d_{Z}(\psi_\omega(x),\psi_\omega(y))] &= 1 + \mathbb{E}_\omega[d_{T}(\pi_T(\phi_\omega(\pi_X(x))),\pi_T(\phi_\omega(\pi_X(y))))] \\ &\overset{({3.7})}{\leq} 1 + \left(D+\frac{5}{6}\right)d_X(\pi_X(x),\pi_X(y)) \\ &\overset{({3.3})}{\leq} 1 + \left(D+\frac{5}{6}\right)(d_X(x,y) + 8K) \\ &\leq \left(\theta^{-1}+\left(D+\frac{5}{6}\right)(1+8K\theta^{-1})\right)d_X(x,y).\\[-34pt] \end{align*} $$
4 Stochastic embeddings into ultrametric spaces
The main result of this section is Theorem 4.16 (which proves Theorem B), stating the every nontrivial snowflake of a separable, bounded, finite Nagata-dimensional, pointed metric space X admits a stochastic biLipschitz embedding into a pointed ultrametric space. We begin the section by establishing the core geometric tool underlying Theorem 4.16, which is Theorem 4.3. This theorem gives the same conclusion as Theorem 4.16, but for
![]() $X = [0,1]$
. The construction we use in its proof is based on the proof of [Reference Weaver48, Theorem 8.43]. Indeed, we directly cite two of the intermediate lemmas from that text ([Reference Weaver48, Lemmas 8.39, 8.40]). In subsections
$X = [0,1]$
. The construction we use in its proof is based on the proof of [Reference Weaver48, Theorem 8.43]. Indeed, we directly cite two of the intermediate lemmas from that text ([Reference Weaver48, Lemmas 8.39, 8.40]). In subsections
![]() $\S $
4.1–4.2, we bootstrap our way up from
$\S $
4.1–4.2, we bootstrap our way up from
![]() $[0,1]$
to general separable, bounded, finite Nagata-dimensional spaces in Theorem 4.16. Finally, in
$[0,1]$
to general separable, bounded, finite Nagata-dimensional spaces in Theorem 4.16. Finally, in
![]() $\S $
4.3, we apply Theorem 4.16 to distortions of finite Nagata-dimensional spaces by p-concave functions, and obtain in Theorem 4.21 that the free spaces over such distortions (under some additional assumptions) are isomorphic to
$\S $
4.3, we apply Theorem 4.16 to distortions of finite Nagata-dimensional spaces by p-concave functions, and obtain in Theorem 4.21 that the free spaces over such distortions (under some additional assumptions) are isomorphic to
![]() $\ell ^1$
.
$\ell ^1$
.
Before getting to the proof of Theorem 4.3, we establish in Lemma 4.1 a compactness property concerning stochastic biLipschitz embeddings.
Lemma 4.1. Let
![]() $(X,d_X,p)$
be a pointed metric space,
$(X,d_X,p)$
be a pointed metric space,
![]() $(K,d_K,q)$
a pointed compact metric space,
$(K,d_K,q)$
a pointed compact metric space,
![]() $D<\infty $
, and
$D<\infty $
, and
![]() $s \in (0,1)$
. If there exists a dense basepoint-containing subset
$s \in (0,1)$
. If there exists a dense basepoint-containing subset
![]() $A \subseteq X$
such that every finite basepoint-containing subset of A stochastic biLipschitzly embeds into K with distortion D and scaling factor s, then X stochastic biLipschitzly embeds into K with distortion D and scaling factor s.
$A \subseteq X$
such that every finite basepoint-containing subset of A stochastic biLipschitzly embeds into K with distortion D and scaling factor s, then X stochastic biLipschitzly embeds into K with distortion D and scaling factor s.
Remark 4.2. To prove Lemma 4.1, it is helpful to reorient our view of stochastic biLipschitz embeddings. If X is a set, Y a separable metric space, and
![]() $\mathbb {P}$
a probability measure on
$\mathbb {P}$
a probability measure on
![]() $Y^X$
, then we get a random map
$Y^X$
, then we get a random map
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
, where the underlying probability space
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
, where the underlying probability space
![]() $\Omega $
is
$\Omega $
is
![]() $Y^X$
equipped with the Borel
$Y^X$
equipped with the Borel
![]() $\sigma $
-algebra and probability measure
$\sigma $
-algebra and probability measure
![]() $\mathbb {P}$
, and
$\mathbb {P}$
, and
![]() $\phi _\omega $
equals
$\phi _\omega $
equals
![]() $\omega $
. Conversely, suppose
$\omega $
. Conversely, suppose
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a random map into a separable space with underlying probability measure
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a random map into a separable space with underlying probability measure
![]() $\mathbb {P}$
. Then we can push
$\mathbb {P}$
. Then we can push
![]() $\mathbb {P}$
forward to a probability measure
$\mathbb {P}$
forward to a probability measure
![]() $\mathbb {P}_\phi $
on
$\mathbb {P}_\phi $
on
![]() $Y^X$
defined by
$Y^X$
defined by
![]() $\mathbb {P}_\phi (E) := \mathbb {P}_\omega (\phi _\omega \in E)$
. Therefore, up to equality in distribution, every random map
$\mathbb {P}_\phi (E) := \mathbb {P}_\omega (\phi _\omega \in E)$
. Therefore, up to equality in distribution, every random map
![]() $X \to Y$
can be taken to have underlying measurable space
$X \to Y$
can be taken to have underlying measurable space
![]() $Y^X$
(equipped with Borel
$Y^X$
(equipped with Borel
![]() $\sigma $
-algebra), and what determines the salient properties of the random map (e.g., if it is a stochastic biLipschitz embedding) is the probability measure on
$\sigma $
-algebra), and what determines the salient properties of the random map (e.g., if it is a stochastic biLipschitz embedding) is the probability measure on
![]() $Y^X$
.
$Y^X$
.
Proof of Lemma 4.1.
Assume that there is some dense subset
![]() $p\in A \subseteq X$
such that every finite subset of A, containing p, almost-sure basepoint-preservingly stochastic biLipschitzly embeds into K with distortion D and scaling factor s. For the following three sentences, fix a finite subset
$p\in A \subseteq X$
such that every finite subset of A, containing p, almost-sure basepoint-preservingly stochastic biLipschitzly embeds into K with distortion D and scaling factor s. For the following three sentences, fix a finite subset
![]() $p\in F \subseteq A$
. Let
$p\in F \subseteq A$
. Let
![]() $\pi _F: X \to F$
be any nearest neighbor projection map;
$\pi _F: X \to F$
be any nearest neighbor projection map;
![]() $\pi _F$
is any map
$\pi _F$
is any map
![]() $X \to F$
satisfying
$X \to F$
satisfying
![]() $d(x,\pi _F(x)) = \operatorname {\mathrm {dist}}(F,x)$
. Let
$d(x,\pi _F(x)) = \operatorname {\mathrm {dist}}(F,x)$
. Let
![]() $\{\phi ^F_\omega : F \to K\}_{\omega \in \Omega }$
be a stochastic biLipschitz embedding of distortion D with underlying probability space
$\{\phi ^F_\omega : F \to K\}_{\omega \in \Omega }$
be a stochastic biLipschitz embedding of distortion D with underlying probability space
![]() $(\Omega _F,\mathcal {F},\mathbb {P}^F)$
, and set
$(\Omega _F,\mathcal {F},\mathbb {P}^F)$
, and set
![]() $\psi _\omega ^F := \phi _\omega ^F \circ \pi _F: X \to K$
. Let
$\psi _\omega ^F := \phi _\omega ^F \circ \pi _F: X \to K$
. Let
![]() $\widetilde {\mathbb {P}}_F := \mathbb {P}^F_{\psi _F}$
denote the pushforward probability measures on
$\widetilde {\mathbb {P}}_F := \mathbb {P}^F_{\psi _F}$
denote the pushforward probability measures on
![]() $K^X$
as described in Remark 4.2. Then by the Riesz representation theorem and weak
$K^X$
as described in Remark 4.2. Then by the Riesz representation theorem and weak
![]() $^*$
-compactness, we can find a probability measure
$^*$
-compactness, we can find a probability measure
![]() $\widetilde {\mathbb {P}}_\infty $
on
$\widetilde {\mathbb {P}}_\infty $
on
![]() $K^X$
that is a weak
$K^X$
that is a weak
![]() $^*$
-subnet limit of the net of measures
$^*$
-subnet limit of the net of measures
![]() $\widetilde {\mathbb {P}}_F$
. Let us check that this probability measure yields (in the sense of Remark 4.2) an almost-sure basepoint-preserving stochastic biLipschitz embedding with distortion D and scaling factor s.
$\widetilde {\mathbb {P}}_F$
. Let us check that this probability measure yields (in the sense of Remark 4.2) an almost-sure basepoint-preserving stochastic biLipschitz embedding with distortion D and scaling factor s.
First we verify almost-sure basepoint preservation. For every
![]() $F \subseteq A$
finite with
$F \subseteq A$
finite with
![]() $p \in F$
, we have
$p \in F$
, we have
Since
![]() $F \ni p$
was arbitrary, this implies
$F \ni p$
was arbitrary, this implies
Hence, for
![]() $\widetilde {\mathbb {P}}_\infty $
-a.e.
$\widetilde {\mathbb {P}}_\infty $
-a.e.
![]() $\phi \in K^X$
,
$\phi \in K^X$
,
![]() $\phi (p) = q$
.
$\phi (p) = q$
.
Next we show almost-sure noncontractivity. Fix
![]() $x,y \in X$
. Let
$x,y \in X$
. Let
![]() $\Phi : K^X \to [0,\infty )$
be a nonnegative continuous function. Let
$\Phi : K^X \to [0,\infty )$
be a nonnegative continuous function. Let
![]() $\varepsilon> 0$
, and choose
$\varepsilon> 0$
, and choose
![]() $a,b \in A$
such that
$a,b \in A$
such that
![]() $d_X(x,a),d_X(y,b) < \frac {\varepsilon }{2s\|\Phi \|_\infty }$
, which exist since
$d_X(x,a),d_X(y,b) < \frac {\varepsilon }{2s\|\Phi \|_\infty }$
, which exist since
![]() $A \subseteq X$
is dense. For every
$A \subseteq X$
is dense. For every
![]() $F \subseteq A$
finite with
$F \subseteq A$
finite with
![]() $\{a,b\} \subseteq F$
, we have
$\{a,b\} \subseteq F$
, we have
 $$ \begin{align*} \int_{K^X} (d_K(\phi(x),\phi(y))-sd_X(x,y))&\Phi(\phi)\mathrm{d}\widetilde{\mathbb{P}}_F(\phi) \\ &= \int_{\Omega_F} (d_K(\psi_\omega^F(x),\psi_\omega^F(y))-sd_X(x,y))\Phi(\psi_\omega^F)\mathrm{d}\mathbb{P}^F(\omega) \\ &\geq \int_{\Omega_F} (sd_X(\pi_F(x),\pi_F(y))-sd_X(x,y))\Phi(\psi_\omega^F)\mathrm{d}\mathbb{P}^F(\omega) \\ &\geq \int_{\Omega_F} -\frac{s\varepsilon}{s\|\Phi\|_\infty}\Phi(\psi_\omega^F)\mathrm{d}\mathbb{P}^F(\omega) \geq -\varepsilon. \end{align*} $$
$$ \begin{align*} \int_{K^X} (d_K(\phi(x),\phi(y))-sd_X(x,y))&\Phi(\phi)\mathrm{d}\widetilde{\mathbb{P}}_F(\phi) \\ &= \int_{\Omega_F} (d_K(\psi_\omega^F(x),\psi_\omega^F(y))-sd_X(x,y))\Phi(\psi_\omega^F)\mathrm{d}\mathbb{P}^F(\omega) \\ &\geq \int_{\Omega_F} (sd_X(\pi_F(x),\pi_F(y))-sd_X(x,y))\Phi(\psi_\omega^F)\mathrm{d}\mathbb{P}^F(\omega) \\ &\geq \int_{\Omega_F} -\frac{s\varepsilon}{s\|\Phi\|_\infty}\Phi(\psi_\omega^F)\mathrm{d}\mathbb{P}^F(\omega) \geq -\varepsilon. \end{align*} $$
Since
![]() $F \supseteq \{a,b\}$
was arbitrary, this implies
$F \supseteq \{a,b\}$
was arbitrary, this implies
Since
![]() $\varepsilon>0$
was arbitrary, this implies
$\varepsilon>0$
was arbitrary, this implies
Since
![]() $\Phi : K^X \to [0,\infty )$
was arbitrary, this implies
$\Phi : K^X \to [0,\infty )$
was arbitrary, this implies
for
![]() $\widetilde {\mathbb {P}}_\infty $
-a.e.
$\widetilde {\mathbb {P}}_\infty $
-a.e.
![]() $\phi \in K^X$
. This proves almost-sure noncontractivity.
$\phi \in K^X$
. This proves almost-sure noncontractivity.
For the Lipschitz in expectation bound, we again let
![]() $\varepsilon> 0$
and choose
$\varepsilon> 0$
and choose
![]() $a,b \in A$
such that
$a,b \in A$
such that
![]() $d_X(x,a),d_X(y,b) < \frac {\varepsilon }{2sD}$
. We have, for every
$d_X(x,a),d_X(y,b) < \frac {\varepsilon }{2sD}$
. We have, for every
![]() $F \subseteq A$
finite with
$F \subseteq A$
finite with
![]() $\{a,b\} \subseteq F$
,
$\{a,b\} \subseteq F$
,
 $$ \begin{align*} \int_{K^X} d_K(\phi(x),\phi(y))\mathrm{d}\widetilde{\mathbb{P}}_F(\phi) &= \int_{\Omega_F} d_K(\phi_\omega^F(\pi_F(x)),\phi_\omega^F(\pi_F(y)))\mathrm{d}\mathbb{P}^F(\omega) \\ &\leq sDd_X(\pi_F(x),\pi_F(y)) \leq \varepsilon + sDd_X(x,y). \end{align*} $$
$$ \begin{align*} \int_{K^X} d_K(\phi(x),\phi(y))\mathrm{d}\widetilde{\mathbb{P}}_F(\phi) &= \int_{\Omega_F} d_K(\phi_\omega^F(\pi_F(x)),\phi_\omega^F(\pi_F(y)))\mathrm{d}\mathbb{P}^F(\omega) \\ &\leq sDd_X(\pi_F(x),\pi_F(y)) \leq \varepsilon + sDd_X(x,y). \end{align*} $$
Since
![]() $F \supseteq \{a,b\}$
was arbitrary, this implies
$F \supseteq \{a,b\}$
was arbitrary, this implies
Since
![]() $\varepsilon>0$
was arbitrary, this implies
$\varepsilon>0$
was arbitrary, this implies
The following theorem, stating that snowflakes of the unit interval
![]() $[0,1]$
stochastic biLipschitzly embed into ultrametric spaces, is the core geometric tool powering several of the main results of the article (Theorems B, D, E, via Theorem 4.16). It is essential here that the snowflake exponent is nontrivial (not equal to 1); see Remark 4.10.
$[0,1]$
stochastic biLipschitzly embed into ultrametric spaces, is the core geometric tool powering several of the main results of the article (Theorems B, D, E, via Theorem 4.16). It is essential here that the snowflake exponent is nontrivial (not equal to 1); see Remark 4.10.
Theorem 4.3. For every
![]() $\alpha \in (0,1)$
, the pointed metric space
$\alpha \in (0,1)$
, the pointed metric space
![]() $([0,1],|\cdot |^\alpha )$
stochastic biLipschitzly embeds into a compact, pointed ultrametric space with distortion
$([0,1],|\cdot |^\alpha )$
stochastic biLipschitzly embeds into a compact, pointed ultrametric space with distortion
![]() $D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
.
$D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
.
Proof. Let
![]() $\alpha \in (0,1)$
. For
$\alpha \in (0,1)$
. For
![]() $n \in \mathbb {N}$
, set
$n \in \mathbb {N}$
, set
![]() $D_n := \{j2^{-n}: j \in \mathbb {Z} \cap [0,2^n]\}$
to be the level-n dyadics. For
$D_n := \{j2^{-n}: j \in \mathbb {Z} \cap [0,2^n]\}$
to be the level-n dyadics. For
![]() $k \in \mathbb {N} \cup \{\infty \}$
, let
$k \in \mathbb {N} \cup \{\infty \}$
, let
![]() $\Gamma _k$
denote the set of sequences
$\Gamma _k$
denote the set of sequences
![]() $(\gamma _i)_{i=0}^k \in \Pi _{i=0}^{k} D_i$
with
$(\gamma _i)_{i=0}^k \in \Pi _{i=0}^{k} D_i$
with
![]() $|\gamma _{i}-\gamma _{i-1}| \leq 2^{-i}$
for
$|\gamma _{i}-\gamma _{i-1}| \leq 2^{-i}$
for
![]() $i \geq 1$
. We canonically extend any finite sequence
$i \geq 1$
. We canonically extend any finite sequence
![]() $\gamma \in \Gamma _k$
to an infinite (eventually constant) sequence
$\gamma \in \Gamma _k$
to an infinite (eventually constant) sequence
![]() $\overline {\gamma } \in \Gamma _\infty $
defined by
$\overline {\gamma } \in \Gamma _\infty $
defined by
![]() $\overline {\gamma }_i := \gamma _i$
if
$\overline {\gamma }_i := \gamma _i$
if
![]() $i \leq k$
and
$i \leq k$
and
![]() $\overline {\gamma }_i := \gamma _k$
if
$\overline {\gamma }_i := \gamma _k$
if
![]() $i \geq k$
, and we equip
$i \geq k$
, and we equip
![]() $\Gamma _k$
and
$\Gamma _k$
and
![]() $\Gamma _\infty $
with the constant 0 sequences as their basepoints. In this way, we get canonical basepoint-preserving injections
$\Gamma _\infty $
with the constant 0 sequences as their basepoints. In this way, we get canonical basepoint-preserving injections
![]() $E_k: \Gamma _k \to \Gamma _\infty $
, with the convention that
$E_k: \Gamma _k \to \Gamma _\infty $
, with the convention that
![]() $E_\infty : \Gamma _\infty \to \Gamma _\infty $
is the identity map. Equip each
$E_\infty : \Gamma _\infty \to \Gamma _\infty $
is the identity map. Equip each
![]() $\Gamma _k$
with a metric d defined by
$\Gamma _k$
with a metric d defined by
![]() $d(\gamma ,\eta ) := 2^{-i_{\gamma \eta }\alpha }$
, where
$d(\gamma ,\eta ) := 2^{-i_{\gamma \eta }\alpha }$
, where
![]() $i_{\gamma \eta } := \min \{i \in \mathbb {Z} \cap [0,k]: \gamma _i \neq \eta _i\}$
(with the convention
$i_{\gamma \eta } := \min \{i \in \mathbb {Z} \cap [0,k]: \gamma _i \neq \eta _i\}$
(with the convention
![]() $\min \emptyset = \infty $
). Note that the canonical injections are isometric: for every
$\min \emptyset = \infty $
). Note that the canonical injections are isometric: for every
![]() $k \in \mathbb {N} \cup \{\infty \}$
and
$k \in \mathbb {N} \cup \{\infty \}$
and
![]() $\gamma ,\eta \in \Gamma _k$
,
$\gamma ,\eta \in \Gamma _k$
,
![]() $d(E_k(\gamma ),E_k(\eta )) = d(\gamma ,\eta )$
. It is standard to verify that
$d(E_k(\gamma ),E_k(\eta )) = d(\gamma ,\eta )$
. It is standard to verify that
![]() $\Gamma _\infty $
equipped with this metric is a compact ultrametric space, and we omit that verification.
$\Gamma _\infty $
equipped with this metric is a compact ultrametric space, and we omit that verification.
In the ensuing proof, we will produce a stochastic biLipschitz embedding of
![]() $(D_k,|\cdot |^\alpha )$
into
$(D_k,|\cdot |^\alpha )$
into
![]() $\Gamma _k$
for each
$\Gamma _k$
for each
![]() $k \in \mathbb {N}$
with distortion
$k \in \mathbb {N}$
with distortion
![]() $D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
and scaling factor
$D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
and scaling factor
![]() $s=4^{-\alpha }$
. Since
$s=4^{-\alpha }$
. Since
![]() $\Gamma _k$
maps into
$\Gamma _k$
maps into
![]() $\Gamma _\infty $
isometrically, we get stochastic biLipschitz embeddings of each
$\Gamma _\infty $
isometrically, we get stochastic biLipschitz embeddings of each
![]() $(D_k,|\cdot |^\alpha )$
into
$(D_k,|\cdot |^\alpha )$
into
![]() $\Gamma _\infty $
with distortion
$\Gamma _\infty $
with distortion
![]() $D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
. Then by the compactness propertyFootnote 8 of Lemma 4.1, we get a stochastic biLipschitz embedding of
$D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
. Then by the compactness propertyFootnote 8 of Lemma 4.1, we get a stochastic biLipschitz embedding of
![]() $([0,1],|\cdot |^\alpha )$
into
$([0,1],|\cdot |^\alpha )$
into
![]() $\Gamma _\infty $
with the same distortion
$\Gamma _\infty $
with the same distortion
![]() $D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
.
$D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
.
Before constructing the stochastic biLipschitz embeddings, we first note that the condition
![]() $|\gamma _{i}-\gamma _{i-1}| \leq 2^{-i}$
implies that we may sum a geometric series to obtain for all
$|\gamma _{i}-\gamma _{i-1}| \leq 2^{-i}$
implies that we may sum a geometric series to obtain for all
![]() $k \geq 0$
(and
$k \geq 0$
(and
![]() $i_{\gamma \eta } \geq 1$
) the estimates
$i_{\gamma \eta } \geq 1$
) the estimates
![]() $|\gamma _k-\gamma _{i_{\gamma \eta }-1}|, |\eta _k-\eta _{i_{\gamma \eta }-1}| \leq 2^{1-i_{\gamma \eta }}$
, and hence,
$|\gamma _k-\gamma _{i_{\gamma \eta }-1}|, |\eta _k-\eta _{i_{\gamma \eta }-1}| \leq 2^{1-i_{\gamma \eta }}$
, and hence,
since
![]() $\gamma _{i_{\gamma \eta }-1} = \eta _{i_{\gamma \eta }-1}$
(and note that this inequality also holds trivially if
$\gamma _{i_{\gamma \eta }-1} = \eta _{i_{\gamma \eta }-1}$
(and note that this inequality also holds trivially if
![]() $i_{\gamma \eta } = 0$
).
$i_{\gamma \eta } = 0$
).
For
![]() $k \geq 0$
, consider
$k \geq 0$
, consider
![]() $\{-1,1\}^k$
as a probability space equipped with the uniform probability measure. We define a sequence of random maps
$\{-1,1\}^k$
as a probability space equipped with the uniform probability measure. We define a sequence of random maps
![]() $\{\phi _\varepsilon : D_k \to \Gamma _k\}_{\varepsilon \in \{-1,1\}^k}$
recursively (interpreting
$\{\phi _\varepsilon : D_k \to \Gamma _k\}_{\varepsilon \in \{-1,1\}^k}$
recursively (interpreting
![]() $\{-1,1\}^0$
as
$\{-1,1\}^0$
as
![]() $\{\emptyset \}$
) by
$\{\emptyset \}$
) by
and, for
![]() $k \geq 0$
,
$k \geq 0$
,
![]() $\varepsilon \in \{-1,1\}^k$
,
$\varepsilon \in \{-1,1\}^k$
,
![]() $\delta \in \{-1,1\}$
, and
$\delta \in \{-1,1\}$
, and
![]() $j2^{-k-1} \in D_{k+1}$
,
$j2^{-k-1} \in D_{k+1}$
,
 $$\begin{align*}\phi_{(\varepsilon,\delta)}(j2^{-k-1}) := \begin{cases} (\phi_\varepsilon(j2^{-k-1}),j2^{-k-1}) & j \text{ even} \\ (\phi_\varepsilon((j+\delta)2^{-k-1}),j2^{-k-1}) & j \text{ odd} \\ \end{cases}.\end{align*}$$
$$\begin{align*}\phi_{(\varepsilon,\delta)}(j2^{-k-1}) := \begin{cases} (\phi_\varepsilon(j2^{-k-1}),j2^{-k-1}) & j \text{ even} \\ (\phi_\varepsilon((j+\delta)2^{-k-1}),j2^{-k-1}) & j \text{ odd} \\ \end{cases}.\end{align*}$$
Observe that, for every
![]() $\varepsilon \in \{-1,1\}^k$
and
$\varepsilon \in \{-1,1\}^k$
and
![]() $x \in D_k$
,
$x \in D_k$
,
This says that
![]() $\phi (x)$
is almost surely a path ending at x. Combining (4.1) and (4.2) yields, for every
$\phi (x)$
is almost surely a path ending at x. Combining (4.1) and (4.2) yields, for every
![]() $\varepsilon \in \{-1,1\}^k$
and
$\varepsilon \in \{-1,1\}^k$
and
![]() $x,y \in D_k$
,
$x,y \in D_k$
,
Thus,
![]() $\phi : (D_k,|\cdot |^\alpha ) \to \Gamma _k$
is almost surely noncontractive with scaling factor
$\phi : (D_k,|\cdot |^\alpha ) \to \Gamma _k$
is almost surely noncontractive with scaling factor
![]() $s=4^{-\alpha }$
.
$s=4^{-\alpha }$
.
Let
![]() $k \geq 0$
. We next derive the recursive inequality
$k \geq 0$
. We next derive the recursive inequality
for the numbers
![]() $L_0 := 1$
and
$L_0 := 1$
and
As we will see, (4.3) will directly lead to an upper bound for the Lipschitz-in-expectation constant of
![]() $\phi $
.
$\phi $
.
Let
![]() $x \in D_{k} \setminus \{1\}$
. Then we have
$x \in D_{k} \setminus \{1\}$
. Then we have
 $$ \begin{align*} \mathbb{E}_{\varepsilon \in \{-1,1\}^{k+1}}&[d(\phi_\varepsilon(x),\phi_\varepsilon(x+2^{-k-1}))] \\ =\ & \frac{1}{2}\mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k+1}((\phi_\varepsilon(x),x),(\phi_\varepsilon(x),x+2^{-k-1}))] \\ &+ \frac{1}{2}\mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k+1}((\phi_\varepsilon(x),x),(\phi_\varepsilon(x+2^{-k}),x+2^{-k-1}))] \\ =\ & \frac{1}{2}2^{(-k-1)\alpha} + \frac{1}{2}\mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k}(\phi_\varepsilon(x),\phi_\varepsilon(x+2^{-k}))] \\ \leq\ & \frac{1}{2}2^{(-k-1)\alpha} + \frac{1}{2}L_k2^{-k\alpha} \\ =\ & \left(\frac{1}{2}+ 2^{\alpha-1}L_k\right)2^{(-k-1)\alpha}. \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\varepsilon \in \{-1,1\}^{k+1}}&[d(\phi_\varepsilon(x),\phi_\varepsilon(x+2^{-k-1}))] \\ =\ & \frac{1}{2}\mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k+1}((\phi_\varepsilon(x),x),(\phi_\varepsilon(x),x+2^{-k-1}))] \\ &+ \frac{1}{2}\mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k+1}((\phi_\varepsilon(x),x),(\phi_\varepsilon(x+2^{-k}),x+2^{-k-1}))] \\ =\ & \frac{1}{2}2^{(-k-1)\alpha} + \frac{1}{2}\mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k}(\phi_\varepsilon(x),\phi_\varepsilon(x+2^{-k}))] \\ \leq\ & \frac{1}{2}2^{(-k-1)\alpha} + \frac{1}{2}L_k2^{-k\alpha} \\ =\ & \left(\frac{1}{2}+ 2^{\alpha-1}L_k\right)2^{(-k-1)\alpha}. \end{align*} $$
Since
![]() $x \in D_{k} \setminus \{1\}$
was arbitrary, this proves (4.3). This recursion yields the explicit bound
$x \in D_{k} \setminus \{1\}$
was arbitrary, this proves (4.3). This recursion yields the explicit bound
Let
![]() $x,y \in D_k$
. By [Reference Weaver48, Lemma 8.40], there exists
$x,y \in D_k$
. By [Reference Weaver48, Lemma 8.40], there exists
![]() $\{x_i\}_{i=0}^n \subseteq [0,1]$
such that
$\{x_i\}_{i=0}^n \subseteq [0,1]$
such that
-
○
 $x_0 = x$
and
$x_0 = x$
and
 $x_n = y$
,
$x_n = y$
, -
○
 $\sum _{i=1}^n |x_i-x_{i-1}| \leq 4|y-x|$
, and
$\sum _{i=1}^n |x_i-x_{i-1}| \leq 4|y-x|$
, and -
○ there exists a sequence
 $i \mapsto m_i: \{1,2, \dots n\} \to \{0,1, \dots k\}$
that is at most 2-to-1 (the preimage of any point has cardinality at most 2) such that
$i \mapsto m_i: \{1,2, \dots n\} \to \{0,1, \dots k\}$
that is at most 2-to-1 (the preimage of any point has cardinality at most 2) such that
 $x_{i-1},x_i$
are consecutive points in
$x_{i-1},x_i$
are consecutive points in
 $D_{m_i}$
(
$D_{m_i}$
(
 $\{x_{i-1},x_i\} \subseteq D_{m_i}$
and
$\{x_{i-1},x_i\} \subseteq D_{m_i}$
and
 $(x_{i-1},x_i) \cap D_{m_i} = (x_i,x_{i-1}) \cap D_{m_i} = \emptyset $
).
$(x_{i-1},x_i) \cap D_{m_i} = (x_i,x_{i-1}) \cap D_{m_i} = \emptyset $
).
By the third item, there is a subset
![]() $J \subseteq \{0,1,\dots k\}$
(with
$J \subseteq \{0,1,\dots k\}$
(with
![]() $|J| = n$
, although this is not important) such that for any function
$|J| = n$
, although this is not important) such that for any function
![]() $h: [0,\infty ] \to [0,\infty )$
, the estimate
$h: [0,\infty ] \to [0,\infty )$
, the estimate
 $$ \begin{align*} \sum_{j\in J} h(2^{-j}) \leq \sum_{i=1}^n h(|x_i-x_{i-1}|) \leq 2\sum_{j\in J} h(2^{-j}) \end{align*} $$
$$ \begin{align*} \sum_{j\in J} h(2^{-j}) \leq \sum_{i=1}^n h(|x_i-x_{i-1}|) \leq 2\sum_{j\in J} h(2^{-j}) \end{align*} $$
holds. Applying this estimate for
![]() $h(t) = t^\alpha $
and
$h(t) = t^\alpha $
and
![]() $h(t) = t$
, applying [Reference Weaver48, Lemma 8.39], and using the second item above, we get
$h(t) = t$
, applying [Reference Weaver48, Lemma 8.39], and using the second item above, we get
 $$ \begin{align*} \sum_{i=1}^n |x_i-x_{i-1}|^\alpha &\leq 2\sum_{j\in J} 2^{-j\alpha} \\ &\leq \frac{2^{\alpha+1}}{2^\alpha-1}\left(\sum_{j\in J} 2^{-j}\right)^\alpha \\ &\leq \frac{2^{\alpha+1}}{2^\alpha-1}\left(\sum_{i=1}^n |x_i-x_{i-1}|\right)^\alpha \\ &\leq \frac{2^{3\alpha+1}}{2^\alpha-1}|y-x|^\alpha. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^n |x_i-x_{i-1}|^\alpha &\leq 2\sum_{j\in J} 2^{-j\alpha} \\ &\leq \frac{2^{\alpha+1}}{2^\alpha-1}\left(\sum_{j\in J} 2^{-j}\right)^\alpha \\ &\leq \frac{2^{\alpha+1}}{2^\alpha-1}\left(\sum_{i=1}^n |x_i-x_{i-1}|\right)^\alpha \\ &\leq \frac{2^{3\alpha+1}}{2^\alpha-1}|y-x|^\alpha. \end{align*} $$
With this bound and (4.4), we have
 $$ \begin{align*} \mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k}(\phi_\varepsilon(x),\phi_\varepsilon(y))] &\leq \sum_{i=1}^n \mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k}(\phi_\varepsilon(x_{i-1}),\phi_\varepsilon(x_{i}))] \\ &\overset{({4.4})}{\leq} \sum_{i=1}^n \frac{1}{2-2^\alpha} |x_i-x_{i-1}|^\alpha \\ &\leq \frac{2^{3\alpha+1}}{(2^\alpha-1)(2-2^\alpha)} |y-x|^\alpha. \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k}(\phi_\varepsilon(x),\phi_\varepsilon(y))] &\leq \sum_{i=1}^n \mathbb{E}_{\varepsilon \in \{-1,1\}^{k}}[d_{k}(\phi_\varepsilon(x_{i-1}),\phi_\varepsilon(x_{i}))] \\ &\overset{({4.4})}{\leq} \sum_{i=1}^n \frac{1}{2-2^\alpha} |x_i-x_{i-1}|^\alpha \\ &\leq \frac{2^{3\alpha+1}}{(2^\alpha-1)(2-2^\alpha)} |y-x|^\alpha. \end{align*} $$
Thus,
![]() $\phi $
is L-Lipschitz in expectation with
$\phi $
is L-Lipschitz in expectation with
![]() $L \leq \frac {2^{3\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
. Since the scaling factor is
$L \leq \frac {2^{3\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
. Since the scaling factor is
![]() $s = 4^{-\alpha }$
, we get that
$s = 4^{-\alpha }$
, we get that
![]() $\phi $
is a stochastic biLipschitz embedding of distortion D with
$\phi $
is a stochastic biLipschitz embedding of distortion D with
![]() $D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
.
$D \leq \frac {2^{5\alpha +1}}{(2^\alpha -1)(2-2^\alpha )}$
.
Remark 4.4. We expect that the construction used in the proof of Theorem 4.3 could be modified to produce a stochastic biLipschitz embedding of
![]() $(\mathbb {R},|\cdot |^\alpha )$
into an (unbounded) ultrametric space. The ultrametric space would need to consist of bi-infinite paths
$(\mathbb {R},|\cdot |^\alpha )$
into an (unbounded) ultrametric space. The ultrametric space would need to consist of bi-infinite paths
![]() $(\gamma _i)_{i=-\infty }^{\infty } \in \Pi _{i=-\infty }^{\infty } D_i$
, where
$(\gamma _i)_{i=-\infty }^{\infty } \in \Pi _{i=-\infty }^{\infty } D_i$
, where
![]() $D_i = 2^{-i}\mathbb {Z}$
. We chose not to pursue this direction here since we need only the bounded case
$D_i = 2^{-i}\mathbb {Z}$
. We chose not to pursue this direction here since we need only the bounded case
![]() $([0,1],|\cdot |^\alpha )$
for applications to
$([0,1],|\cdot |^\alpha )$
for applications to
![]() $\ell ^1$
-isomorphisms of Lipschitz free spaces.
$\ell ^1$
-isomorphisms of Lipschitz free spaces.
4.1
 $\ell ^{0+}$
-small subsets of
$\ell ^{0+}$
-small subsets of
 $\ell ^\infty $
$\ell ^\infty $
In this subsection, we expand the scope of Theorem 4.3 from
![]() $[0,1]$
to all
$[0,1]$
to all
![]() $\ell ^{0+}$
-small subsets of
$\ell ^{0+}$
-small subsets of
![]() $\ell ^\infty ([0,1])$
(Theorem 4.11). We begin by defining these terms.
$\ell ^\infty ([0,1])$
(Theorem 4.11). We begin by defining these terms.
Given a pointed metric space
![]() $(X,d,p)$
and indexing set J, we denote by
$(X,d,p)$
and indexing set J, we denote by
![]() $(\ell ^\infty (J;X,d,p),d_{J,\infty },p_{J,\infty })$
the pointed metric space with underlying set
$(\ell ^\infty (J;X,d,p),d_{J,\infty },p_{J,\infty })$
the pointed metric space with underlying set
![]() $\ell ^\infty (J;X,d,p) := \{\boldsymbol {x} \in X^J: \sup _{j\in J}d(\boldsymbol {x}_j,p) < \infty \}$
, metric
$\ell ^\infty (J;X,d,p) := \{\boldsymbol {x} \in X^J: \sup _{j\in J}d(\boldsymbol {x}_j,p) < \infty \}$
, metric
![]() $d_{J,\infty }(\boldsymbol {x},\boldsymbol {y}) := \sup _{j\in J}d(\boldsymbol {x}_j,\boldsymbol {y}_j)$
, and basepoint
$d_{J,\infty }(\boldsymbol {x},\boldsymbol {y}) := \sup _{j\in J}d(\boldsymbol {x}_j,\boldsymbol {y}_j)$
, and basepoint
![]() $(p_{J,\infty })_j := p$
for all
$(p_{J,\infty })_j := p$
for all
![]() $j \in J$
. As before, we will often suppress notation and simply write
$j \in J$
. As before, we will often suppress notation and simply write
![]() $\ell ^\infty (J;X,d,p)$
or
$\ell ^\infty (J;X,d,p)$
or
![]() $\ell ^\infty (J;X)$
. Additionally, when
$\ell ^\infty (J;X)$
. Additionally, when
![]() $J=\mathbb {N}$
, we further suppress notation and write
$J=\mathbb {N}$
, we further suppress notation and write
![]() $\ell ^\infty (X,d,p)$
or
$\ell ^\infty (X,d,p)$
or
![]() $\ell ^\infty (X)$
. Any bijection between indexing sets
$\ell ^\infty (X)$
. Any bijection between indexing sets
![]() $J_1 \to J_2$
induces a basepoint-preserving isometry
$J_1 \to J_2$
induces a basepoint-preserving isometry
![]() $\ell ^\infty (J_1;X) \to \ell ^\infty (J_2;X)$
.
$\ell ^\infty (J_1;X) \to \ell ^\infty (J_2;X)$
.
Definition 4.5. Let
![]() $(X,d)$
be a pointed metric space, J an indexing set, and
$(X,d)$
be a pointed metric space, J an indexing set, and
![]() $p>0$
. A subset
$p>0$
. A subset
![]() $S \subseteq \ell ^\infty (J;X)$
is said to be
$S \subseteq \ell ^\infty (J;X)$
is said to be
![]() $\ell ^p$
-small (with respect to
$\ell ^p$
-small (with respect to
![]() $d_{J,\infty }$
) with constant
$d_{J,\infty }$
) with constant
![]() $A_p<\infty $
if for every
$A_p<\infty $
if for every
![]() $\boldsymbol {x},\boldsymbol {y} \in S$
,
$\boldsymbol {x},\boldsymbol {y} \in S$
,
 $$ \begin{align*} \left(\sum_{j\in J} d(\boldsymbol{x}_j,\boldsymbol{y}_j)^p\right)^{\frac{1}{p}} \leq A_pd_{J,\infty}(\boldsymbol{x},\boldsymbol{y}). \end{align*} $$
$$ \begin{align*} \left(\sum_{j\in J} d(\boldsymbol{x}_j,\boldsymbol{y}_j)^p\right)^{\frac{1}{p}} \leq A_pd_{J,\infty}(\boldsymbol{x},\boldsymbol{y}). \end{align*} $$
We often refer to the least such
![]() $A_p$
as the
$A_p$
as the
![]() $\ell ^p$
-smallness constant of S. We say
$\ell ^p$
-smallness constant of S. We say
![]() $S \subseteq \ell ^\infty (J)$
is
$S \subseteq \ell ^\infty (J)$
is
![]() $\ell ^{0+}$
-small (with respect to
$\ell ^{0+}$
-small (with respect to
![]() $d_{J,\infty }$
) if it is
$d_{J,\infty }$
) if it is
![]() $\ell ^p$
-small for every
$\ell ^p$
-small for every
![]() $p>0$
.
$p>0$
.
Remark 4.6. Clearly, the notion of
![]() $\ell ^p$
-smallness is invariant with respect to reindexing; if
$\ell ^p$
-smallness is invariant with respect to reindexing; if
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are in bijection, then a subset
$J_2$
are in bijection, then a subset
![]() $S \subseteq \ell ^\infty (J_1;X)$
is
$S \subseteq \ell ^\infty (J_1;X)$
is
![]() $\ell ^p$
-small with constant
$\ell ^p$
-small with constant
![]() $A_p$
if and only if its induced image in
$A_p$
if and only if its induced image in
![]() $\ell ^\infty (J_2;X)$
is
$\ell ^\infty (J_2;X)$
is
![]() $\ell ^p$
-small with constant
$\ell ^p$
-small with constant
![]() $A_p$
. Of course, the same invariance therefore holds for
$A_p$
. Of course, the same invariance therefore holds for
![]() $\ell ^{0+}$
-smallness.
$\ell ^{0+}$
-smallness.
Note that if
![]() $p < \infty $
and X is separable, then any
$p < \infty $
and X is separable, then any
![]() $\ell ^p$
-small subset of
$\ell ^p$
-small subset of
![]() $\ell ^\infty (X)$
is separable as well.
$\ell ^\infty (X)$
is separable as well.
Example 4.7 (Uniformly finite support implies
 $\ell ^{0+}$
-smallness).
$\ell ^{0+}$
-smallness).
Suppose
![]() $(X,p)$
is a pointed metric space, J an indexing set, and
$(X,p)$
is a pointed metric space, J an indexing set, and
![]() $N\in \mathbb {N}$
. We denote by
$N\in \mathbb {N}$
. We denote by
![]() $\ell _{\operatorname {\mathrm {supp}}\leq N}^\infty (J;X)$
the subset of
$\ell _{\operatorname {\mathrm {supp}}\leq N}^\infty (J;X)$
the subset of
![]() $\ell ^\infty (J;X)$
consisting of elements
$\ell ^\infty (J;X)$
consisting of elements
![]() $\boldsymbol {x}$
for which
$\boldsymbol {x}$
for which
![]() $|\{j\in J: \boldsymbol {x}_j \neq p\}| \leq N$
. It is immediate to verify that
$|\{j\in J: \boldsymbol {x}_j \neq p\}| \leq N$
. It is immediate to verify that
![]() $\ell _{\operatorname {\mathrm {supp}}\leq N}^\infty (J;X)$
is
$\ell _{\operatorname {\mathrm {supp}}\leq N}^\infty (J;X)$
is
![]() $\ell ^q$
-small for every
$\ell ^q$
-small for every
![]() $q>0$
, with constant
$q>0$
, with constant
![]() $A_q \leq (2N)^{1/q}$
, and therefore is
$A_q \leq (2N)^{1/q}$
, and therefore is
![]() $\ell ^{0+}$
-small.
$\ell ^{0+}$
-small.
For any
![]() $\alpha \in (0,1)$
, observe that
$\alpha \in (0,1)$
, observe that
![]() $\ell ^\infty (J;X,d,p)$
and
$\ell ^\infty (J;X,d,p)$
and
![]() $\ell ^\infty (J;X,d^\alpha ,p)$
are the same set, but equipped with the different metrics
$\ell ^\infty (J;X,d^\alpha ,p)$
are the same set, but equipped with the different metrics
![]() $d_{J,\infty }$
and
$d_{J,\infty }$
and
![]() $(d^\alpha )_{J,\infty }$
, respectively, and observe the ‘commutation’ equality
$(d^\alpha )_{J,\infty }$
, respectively, and observe the ‘commutation’ equality
In the next lemma, we show that the notion of
![]() $\ell ^{0+}$
-smallness does not depend on
$\ell ^{0+}$
-smallness does not depend on
![]() $\alpha $
.
$\alpha $
.
Lemma 4.8. Let
![]() $(X,d,p)$
be a pointed metric space, J an indexing set, and
$(X,d,p)$
be a pointed metric space, J an indexing set, and
![]() $\alpha \in (0,1]$
Footnote 9. Let
$\alpha \in (0,1]$
Footnote 9. Let
![]() $S \subseteq \ell ^\infty (J;X,d,p)$
(which, as discussed above, is the same set as
$S \subseteq \ell ^\infty (J;X,d,p)$
(which, as discussed above, is the same set as
![]() $\ell ^\infty (J;X,d^\alpha ,p)$
). Then S is
$\ell ^\infty (J;X,d^\alpha ,p)$
). Then S is
![]() $\ell ^{0+}$
-small with respect to
$\ell ^{0+}$
-small with respect to
![]() $d_{J,\infty }$
if and only if it is
$d_{J,\infty }$
if and only if it is
![]() $\ell ^{0+}$
-small with respect to
$\ell ^{0+}$
-small with respect to
![]() $(d^\alpha )_{J,\infty }$
, where the set of
$(d^\alpha )_{J,\infty }$
, where the set of
![]() $\ell ^q$
-smallness constants of S with respect to
$\ell ^q$
-smallness constants of S with respect to
![]() $(d^\alpha )_{J,\infty }$
depends only on
$(d^\alpha )_{J,\infty }$
depends only on
![]() $\alpha $
and the set of
$\alpha $
and the set of
![]() $\ell ^q$
-smallness constants of S with respect to
$\ell ^q$
-smallness constants of S with respect to
![]() $d_{J,\infty }$
(and vice versa).
$d_{J,\infty }$
(and vice versa).
Proof. We only show the forward implication, as the reverse follows by the same argument. Assume that S is
![]() $\ell ^{0+}$
-small with respect to
$\ell ^{0+}$
-small with respect to
![]() $d_{J,\infty }$
. Let
$d_{J,\infty }$
. Let
![]() $q>0$
, and let
$q>0$
, and let
![]() $A_{\alpha q}<\infty $
be the
$A_{\alpha q}<\infty $
be the
![]() $\ell ^{\alpha q}$
-smallness constant of S with respect to
$\ell ^{\alpha q}$
-smallness constant of S with respect to
![]() $d_{J,\infty }$
. We will show that S is
$d_{J,\infty }$
. We will show that S is
![]() $\ell ^{q}$
-small with respect to
$\ell ^{q}$
-small with respect to
![]() $(d^\alpha )_{J,\infty }$
with constant
$(d^\alpha )_{J,\infty }$
with constant
![]() $A_{\alpha q}^\alpha <\infty $
. Let
$A_{\alpha q}^\alpha <\infty $
. Let
![]() $\boldsymbol {x},\boldsymbol {y} \in S$
. Then we have
$\boldsymbol {x},\boldsymbol {y} \in S$
. Then we have
 $$ \begin{align*} \left(\sum_{j\in J} d^\alpha(\boldsymbol{x}_j,\boldsymbol{y}_j)^q\right)^{\frac{1}{q}} = \left(\left(\sum_{j\in J} d(\boldsymbol{x}_j,\boldsymbol{y}_j)^{\alpha q}\right)^{\frac{1}{\alpha q}}\right)^\alpha \leq \left(A_{\alpha q}d_{J,\infty}(\boldsymbol{x},\boldsymbol{y})\right)^\alpha = A_{\alpha q}^\alpha (d^\alpha)_{J,\infty}(\boldsymbol{x},\boldsymbol{y}). \end{align*} $$
$$ \begin{align*} \left(\sum_{j\in J} d^\alpha(\boldsymbol{x}_j,\boldsymbol{y}_j)^q\right)^{\frac{1}{q}} = \left(\left(\sum_{j\in J} d(\boldsymbol{x}_j,\boldsymbol{y}_j)^{\alpha q}\right)^{\frac{1}{\alpha q}}\right)^\alpha \leq \left(A_{\alpha q}d_{J,\infty}(\boldsymbol{x},\boldsymbol{y})\right)^\alpha = A_{\alpha q}^\alpha (d^\alpha)_{J,\infty}(\boldsymbol{x},\boldsymbol{y}). \end{align*} $$
The following lemma states that stochastic biLipschitz embeddability of X into ultrametric spaces passes to
![]() $\ell ^1$
-small subsets of
$\ell ^1$
-small subsets of
![]() $\ell ^\infty (X)$
.
$\ell ^\infty (X)$
.
Lemma 4.9. Suppose
![]() $(X,d,p)$
is a pointed metric space that stochastic biLipschitzly embeds into a separable, pointed ultrametric space with distortion
$(X,d,p)$
is a pointed metric space that stochastic biLipschitzly embeds into a separable, pointed ultrametric space with distortion
![]() $D<\infty $
. Then every
$D<\infty $
. Then every
![]() $\ell ^1$
-small subset of
$\ell ^1$
-small subset of
![]() $\ell ^\infty (X)$
(containing the basepoint) with
$\ell ^\infty (X)$
(containing the basepoint) with
![]() $\ell ^1$
-smallness constant
$\ell ^1$
-smallness constant
![]() $A_1<\infty $
admits a stochastic biLipschitz embedding into a separable, pointed ultrametric space with distortion
$A_1<\infty $
admits a stochastic biLipschitz embedding into a separable, pointed ultrametric space with distortion
![]() $DA_1$
.
$DA_1$
.
Proof. Let
![]() $p_\infty \in S \subseteq \ell ^\infty (X)$
be
$p_\infty \in S \subseteq \ell ^\infty (X)$
be
![]() $\ell ^1$
-small with constant
$\ell ^1$
-small with constant
![]() $A_1<\infty $
. Let
$A_1<\infty $
. Let
![]() $\{\phi _\omega : X \to U\}_{\omega \in \Omega }$
be a stochastic biLipschitz embedding into a separable, pointed ultrametric space
$\{\phi _\omega : X \to U\}_{\omega \in \Omega }$
be a stochastic biLipschitz embedding into a separable, pointed ultrametric space
![]() $(U,\rho ,q)$
with distortion
$(U,\rho ,q)$
with distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s\in (0,1)$
. We form the pointed product space
$s\in (0,1)$
. We form the pointed product space
![]() $(\ell ^\infty (U),\rho _\infty ,q_\infty )$
. It is clear that the underlying metric space
$(\ell ^\infty (U),\rho _\infty ,q_\infty )$
. It is clear that the underlying metric space
![]() $(\ell ^\infty (U),\rho _\infty )$
is again an ultrametric space (but not separable). Let
$(\ell ^\infty (U),\rho _\infty )$
is again an ultrametric space (but not separable). Let
![]() $(\Omega ,\mathcal {F},\mathbb {P})$
be the probability space underlying the stochastic biLipschitz embedding. We will define our stochastic biLipschitz embedding over the power probability space
$(\Omega ,\mathcal {F},\mathbb {P})$
be the probability space underlying the stochastic biLipschitz embedding. We will define our stochastic biLipschitz embedding over the power probability space
![]() $(\Omega ^{\mathbb {N}},\otimes _{\mathbb {N}} \mathcal {F}, \otimes _{\mathbb {N}} \mathbb {P})$
. Define
$(\Omega ^{\mathbb {N}},\otimes _{\mathbb {N}} \mathcal {F}, \otimes _{\mathbb {N}} \mathbb {P})$
. Define
![]() $\{\boldsymbol {\Phi }_{\boldsymbol {\omega }}: S \to \ell ^\infty (U)\}_{\boldsymbol {\omega }\in \Omega ^{\mathbb {N}}}$
by
$\{\boldsymbol {\Phi }_{\boldsymbol {\omega }}: S \to \ell ^\infty (U)\}_{\boldsymbol {\omega }\in \Omega ^{\mathbb {N}}}$
by
![]() $\left (\boldsymbol {\Phi }_{\boldsymbol {\omega }}(\boldsymbol {x})\right )_n := \phi _{\boldsymbol {\omega }_n}(\boldsymbol {x}_n)$
. Let
$\left (\boldsymbol {\Phi }_{\boldsymbol {\omega }}(\boldsymbol {x})\right )_n := \phi _{\boldsymbol {\omega }_n}(\boldsymbol {x}_n)$
. Let
![]() $\boldsymbol {x},\boldsymbol {y} \in S$
. We do not know yet whether
$\boldsymbol {x},\boldsymbol {y} \in S$
. We do not know yet whether
![]() $\boldsymbol {\Phi }_{\boldsymbol {\omega }}$
is a random map. However, we will begin with an estimate of the expected Lipschitz constant, which will also help us verify that
$\boldsymbol {\Phi }_{\boldsymbol {\omega }}$
is a random map. However, we will begin with an estimate of the expected Lipschitz constant, which will also help us verify that
![]() $\boldsymbol {\Phi }_{\boldsymbol {\omega }}$
is indeed a random map.
$\boldsymbol {\Phi }_{\boldsymbol {\omega }}$
is indeed a random map.
 $$ \begin{align*} \mathbb{E}_{\boldsymbol{\omega}\in\Omega^{\mathbb{N}}}\left[\rho_\infty(\boldsymbol{\Phi}_{\boldsymbol{\omega}}(\boldsymbol{x}),\boldsymbol{\Phi}_{\boldsymbol{\omega}}(\boldsymbol{y}))\right] &\leq \mathbb{E}_{\boldsymbol{\omega}\in\Omega^{\mathbb{N}}}\left[\sum_{n\in\mathbb{N}}\rho(\phi_{\boldsymbol{\omega_n}}(\boldsymbol{x}_n),\phi_{\boldsymbol{\omega_n}}(\boldsymbol{y}_n))\right] \\ &= \sum_{n\in\mathbb{N}} \mathbb{E}_{\boldsymbol{\omega_n}\in\Omega}\left[\rho(\phi_{\boldsymbol{\omega_n}}(\boldsymbol{x}_n),\phi_{\boldsymbol{\omega_n}}(\boldsymbol{y}_n))\right] \\ &\leq \sum_{n\in\mathbb{N}} sDd(\boldsymbol{x}_n,\boldsymbol{y}_n) \\ &\leq sDA_1d_\infty(\boldsymbol{x},\boldsymbol{y}). \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\boldsymbol{\omega}\in\Omega^{\mathbb{N}}}\left[\rho_\infty(\boldsymbol{\Phi}_{\boldsymbol{\omega}}(\boldsymbol{x}),\boldsymbol{\Phi}_{\boldsymbol{\omega}}(\boldsymbol{y}))\right] &\leq \mathbb{E}_{\boldsymbol{\omega}\in\Omega^{\mathbb{N}}}\left[\sum_{n\in\mathbb{N}}\rho(\phi_{\boldsymbol{\omega_n}}(\boldsymbol{x}_n),\phi_{\boldsymbol{\omega_n}}(\boldsymbol{y}_n))\right] \\ &= \sum_{n\in\mathbb{N}} \mathbb{E}_{\boldsymbol{\omega_n}\in\Omega}\left[\rho(\phi_{\boldsymbol{\omega_n}}(\boldsymbol{x}_n),\phi_{\boldsymbol{\omega_n}}(\boldsymbol{y}_n))\right] \\ &\leq \sum_{n\in\mathbb{N}} sDd(\boldsymbol{x}_n,\boldsymbol{y}_n) \\ &\leq sDA_1d_\infty(\boldsymbol{x},\boldsymbol{y}). \end{align*} $$
This establishes the required Lipschitz-in-expectation upper bound (note that all the terms appearing inside the expectation above are indeed
![]() $\mathbb {R}$
-valued measurable random variables, so their expectation is well-defined). Furthermore, one can quickly examine the string of inequalities above with
$\mathbb {R}$
-valued measurable random variables, so their expectation is well-defined). Furthermore, one can quickly examine the string of inequalities above with
![]() $p_\infty $
in place of
$p_\infty $
in place of
![]() $\boldsymbol {x}$
and
$\boldsymbol {x}$
and
![]() $q_\infty $
in place of
$q_\infty $
in place of
![]() $\boldsymbol {\Phi }_{\boldsymbol {\omega }}(\boldsymbol {y})$
to get that
$\boldsymbol {\Phi }_{\boldsymbol {\omega }}(\boldsymbol {y})$
to get that
![]() $\boldsymbol {\Phi }$
is almost surely basepoint-preserving. We can use this to verify pointwise almost-sure measurability and separability. Examining the second and last terms in the string of estimates above applied to
$\boldsymbol {\Phi }$
is almost surely basepoint-preserving. We can use this to verify pointwise almost-sure measurability and separability. Examining the second and last terms in the string of estimates above applied to
![]() $\boldsymbol {y} = p_\infty $
, we get that there exists a
$\boldsymbol {y} = p_\infty $
, we get that there exists a
![]() $\otimes _{\mathbb {N}} \mathbb {P}$
-null set
$\otimes _{\mathbb {N}} \mathbb {P}$
-null set
![]() $N_{\boldsymbol {x}}$
(which depends on
$N_{\boldsymbol {x}}$
(which depends on
![]() $\boldsymbol {x}$
) such that, for every
$\boldsymbol {x}$
) such that, for every
![]() $\boldsymbol {\omega }\in \Omega ^{\mathbb {N}} \setminus N_{\boldsymbol {x}}$
,
$\boldsymbol {\omega }\in \Omega ^{\mathbb {N}} \setminus N_{\boldsymbol {x}}$
,
Thus, by redefining
![]() $\boldsymbol {\Phi }_{\boldsymbol {\omega }}(\boldsymbol {x})$
for
$\boldsymbol {\Phi }_{\boldsymbol {\omega }}(\boldsymbol {x})$
for
![]() $\boldsymbol {\omega } \in N_{\boldsymbol {x}}$
to equal
$\boldsymbol {\omega } \in N_{\boldsymbol {x}}$
to equal
![]() $q_\infty $
identically, we may assume that
$q_\infty $
identically, we may assume that
![]() $\boldsymbol {\Phi }(\boldsymbol {x})$
takes values in the subset
$\boldsymbol {\Phi }(\boldsymbol {x})$
takes values in the subset
 $$ \begin{align*} V := \left\{\boldsymbol{z} \in \ell^\infty(U): \sum_{n\in\mathbb{N}} \rho(\boldsymbol{z}_n,q) < \infty\right\}, \end{align*} $$
$$ \begin{align*} V := \left\{\boldsymbol{z} \in \ell^\infty(U): \sum_{n\in\mathbb{N}} \rho(\boldsymbol{z}_n,q) < \infty\right\}, \end{align*} $$
which is obviously separable since
![]() $(U,\rho )$
is separable. Thus,
$(U,\rho )$
is separable. Thus,
![]() $\{\boldsymbol {\Phi }_{\boldsymbol {\omega }}\}_{\boldsymbol {\omega }\in \Omega ^{\mathbb {N}}}$
takes values in the separable ultrametric space
$\{\boldsymbol {\Phi }_{\boldsymbol {\omega }}\}_{\boldsymbol {\omega }\in \Omega ^{\mathbb {N}}}$
takes values in the separable ultrametric space
![]() $(V,\rho _\infty )$
. Finally, we can also use this to verify pointwise measurability. Since
$(V,\rho _\infty )$
. Finally, we can also use this to verify pointwise measurability. Since
![]() $(V,\rho _\infty )$
is separable, its Borel
$(V,\rho _\infty )$
is separable, its Borel
![]() $\sigma $
-algebra is generated by the collection of balls
$\sigma $
-algebra is generated by the collection of balls
![]() $\{\boldsymbol {y}\in S: \sup _{n\in \mathbb {N}}\rho (\boldsymbol {z}_n,\boldsymbol {y}_n) \leq r\}$
, where
$\{\boldsymbol {y}\in S: \sup _{n\in \mathbb {N}}\rho (\boldsymbol {z}_n,\boldsymbol {y}_n) \leq r\}$
, where
![]() $\boldsymbol {z}$
ranges over all points in V and r over all radii in
$\boldsymbol {z}$
ranges over all points in V and r over all radii in
![]() $(0,\infty )$
. Hence, pointwise measurability follows from the observation that
$(0,\infty )$
. Hence, pointwise measurability follows from the observation that
![]() $\{\boldsymbol {\omega }\in \Omega ^{\mathbb {N}}: \sup _{n\in \mathbb {N}}\rho (\boldsymbol {z}_n,\phi _{\boldsymbol {\omega }_n}(\boldsymbol {x}_n)) \leq r\}$
is
$\{\boldsymbol {\omega }\in \Omega ^{\mathbb {N}}: \sup _{n\in \mathbb {N}}\rho (\boldsymbol {z}_n,\phi _{\boldsymbol {\omega }_n}(\boldsymbol {x}_n)) \leq r\}$
is
![]() $\otimes _{\mathbb {N}} \mathcal {F}$
-measurable.
$\otimes _{\mathbb {N}} \mathcal {F}$
-measurable.
It remains to check almost-sure noncontractivity. For each fixed
![]() $n\in \mathbb {N}$
, there is a
$n\in \mathbb {N}$
, there is a
![]() $\mathbb {P}$
-null set
$\mathbb {P}$
-null set
![]() $N_n$
such that, for all
$N_n$
such that, for all
![]() $\omega \in \Omega \setminus N_n$
,
$\omega \in \Omega \setminus N_n$
,
Then
![]() $\Pi _{n\in \mathbb {N}} (\Omega \setminus N_n)$
is a
$\Pi _{n\in \mathbb {N}} (\Omega \setminus N_n)$
is a
![]() $\otimes _{\mathbb {N}} \mathbb {P}$
-full-measure set, and for every
$\otimes _{\mathbb {N}} \mathbb {P}$
-full-measure set, and for every
![]() $\boldsymbol {\omega } \in \Pi _{n\in \mathbb {N}} (\Omega \setminus N_n)$
and every
$\boldsymbol {\omega } \in \Pi _{n\in \mathbb {N}} (\Omega \setminus N_n)$
and every
![]() $n\in \mathbb {N}$
, we have that
$n\in \mathbb {N}$
, we have that
Since
![]() $n \in \mathbb {N}$
was arbitrary, this implies that
$n \in \mathbb {N}$
was arbitrary, this implies that
for every
![]() $\boldsymbol {\omega } \in \Pi _{n\in \mathbb {N}} (\Omega \setminus N_n)$
.
$\boldsymbol {\omega } \in \Pi _{n\in \mathbb {N}} (\Omega \setminus N_n)$
.
Remark 4.10. Lemma 4.9 shows that the interval
![]() $[0,1]$
with the Euclidean metric cannot stochastic biLipschitzly embed into an ultrametric space. Indeed, suppose that it does. Then since
$[0,1]$
with the Euclidean metric cannot stochastic biLipschitzly embed into an ultrametric space. Indeed, suppose that it does. Then since
![]() $[0,1]^2$
is biLipschitzly contained inside the
$[0,1]^2$
is biLipschitzly contained inside the
![]() $\ell ^1$
-small subset
$\ell ^1$
-small subset
![]() $\ell _{\operatorname {\mathrm {supp}}\leq 2}^\infty ([0,1]) \subseteq \ell ^\infty ([0,1])$
, Lemma 4.9 implies that
$\ell _{\operatorname {\mathrm {supp}}\leq 2}^\infty ([0,1]) \subseteq \ell ^\infty ([0,1])$
, Lemma 4.9 implies that
![]() $[0,1]^2$
stochastic biLipschitzly embeds into an ultrametric space. Since ultrametric spaces isometrically embed into
$[0,1]^2$
stochastic biLipschitzly embeds into an ultrametric space. Since ultrametric spaces isometrically embed into
![]() $\mathbb {R}$
-trees, Theorem 3.3 implies that
$\mathbb {R}$
-trees, Theorem 3.3 implies that
![]() $\operatorname {\mathrm {LF}}([0,1]^2) \approx L^1$
, contradicting a result of Naor-Schechtman [Reference Naor and Schechtman41]. Together with Theorem 4.3, this shows that stochastic biLipschitz embeddability into ultrametric spaces is not preserved under snowflake equivalence.
$\operatorname {\mathrm {LF}}([0,1]^2) \approx L^1$
, contradicting a result of Naor-Schechtman [Reference Naor and Schechtman41]. Together with Theorem 4.3, this shows that stochastic biLipschitz embeddability into ultrametric spaces is not preserved under snowflake equivalence.
Combining Lemma 4.9 with Theorem 4.3 yields the next result.
Theorem 4.11. For every
![]() $\alpha \in (0,1)$
and every
$\alpha \in (0,1)$
and every
![]() $\ell ^{0+}$
-small subset of
$\ell ^{0+}$
-small subset of
![]() $S \subseteq \ell ^\infty ([0,1])$
containing the basepoint, there exists a stochastic biLipschitz embedding of
$S \subseteq \ell ^\infty ([0,1])$
containing the basepoint, there exists a stochastic biLipschitz embedding of
![]() $(S,\|\cdot \|_\infty ^\alpha )$
into a separable, pointed ultrametric space. Moreover, the distortion of the embedding depends only on
$(S,\|\cdot \|_\infty ^\alpha )$
into a separable, pointed ultrametric space. Moreover, the distortion of the embedding depends only on
![]() $\alpha $
and the
$\alpha $
and the
![]() $\ell ^p$
-smallness constants of S.
$\ell ^p$
-smallness constants of S.
Proof. Let
![]() $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
![]() $0 \in S \subseteq \ell ^\infty ([0,1])$
an
$0 \in S \subseteq \ell ^\infty ([0,1])$
an
![]() $\ell ^{0+}$
-small subset, and for each
$\ell ^{0+}$
-small subset, and for each
![]() $p\in (0,\infty )$
,
$p\in (0,\infty )$
,
![]() $A_p<\infty $
the
$A_p<\infty $
the
![]() $\ell ^p$
-smallness constant of S. The pointed metric space
$\ell ^p$
-smallness constant of S. The pointed metric space
![]() $(\ell ^\infty ([0,1]),(\|~\cdot ~\|_\infty )^\alpha ,0)$
is identical to the pointed product metric space
$(\ell ^\infty ([0,1]),(\|~\cdot ~\|_\infty )^\alpha ,0)$
is identical to the pointed product metric space
![]() $(\ell ^\infty ([0,1],|\cdot |^\alpha ),(|\cdot |^\alpha )_\infty ,0)$
(this is immediate – see also (4.5)), and by Lemma 4.8, S is still an
$(\ell ^\infty ([0,1],|\cdot |^\alpha ),(|\cdot |^\alpha )_\infty ,0)$
(this is immediate – see also (4.5)), and by Lemma 4.8, S is still an
![]() $\ell ^{0+}$
-small subset of this product space, with
$\ell ^{0+}$
-small subset of this product space, with
![]() $\ell ^p$
-smallness constants depending only on
$\ell ^p$
-smallness constants depending only on
![]() $\alpha $
and
$\alpha $
and
![]() $A_p$
. Therefore,
$A_p$
. Therefore,
![]() $(S,\|\cdot \|_\infty ^\alpha )$
is basepoint-preservingly isometric to an
$(S,\|\cdot \|_\infty ^\alpha )$
is basepoint-preservingly isometric to an
![]() $\ell ^{0+}$
-small subset of
$\ell ^{0+}$
-small subset of
![]() $\ell ^\infty ([0,1],|\cdot |^\alpha )$
, and then the desired conclusion follows from Theorem 4.3 and Lemma 4.9.
$\ell ^\infty ([0,1],|\cdot |^\alpha )$
, and then the desired conclusion follows from Theorem 4.3 and Lemma 4.9.
4.2 Threshold and snowflake embeddings
The goal of this subsection is to extend the conclusion of Theorem 4.11 from
![]() $\ell ^{0+}$
-small subsets of
$\ell ^{0+}$
-small subsets of
![]() $\ell ^\infty ([0,1])$
to all bounded, separable metrics spaces of finite Nagata dimension. We will accomplish this by proving that
$\ell ^\infty ([0,1])$
to all bounded, separable metrics spaces of finite Nagata dimension. We will accomplish this by proving that
![]() $(X,d^\alpha )$
admits a biLipschitz embedding into an
$(X,d^\alpha )$
admits a biLipschitz embedding into an
![]() $\ell ^{0+}$
-small subset of
$\ell ^{0+}$
-small subset of
![]() $\ell ^\infty ([0,1])$
whenever
$\ell ^\infty ([0,1])$
whenever
![]() $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
![]() $(X,d)$
is bounded, separable, and finite Nagata-dimensional (Lemma 4.14). Toward this end, we begin by recalling the notion of threshold embeddings. These types of maps have frequently appeared in embedding theory and were formally named in [Reference Ding, Lee and Peres22].
$(X,d)$
is bounded, separable, and finite Nagata-dimensional (Lemma 4.14). Toward this end, we begin by recalling the notion of threshold embeddings. These types of maps have frequently appeared in embedding theory and were formally named in [Reference Ding, Lee and Peres22].
A threshold embedding with distortion
![]() $C<\infty $
and scaling factor
$C<\infty $
and scaling factor
![]() $s\in (0,1)$
is a collection of maps
$s\in (0,1)$
is a collection of maps
![]() $\{\varphi _t: X \to Y\}_{t>0}$
between metric spaces
$\{\varphi _t: X \to Y\}_{t>0}$
between metric spaces
![]() $(X,d_X),(Y,d_Y)$
such that, for every
$(X,d_X),(Y,d_Y)$
such that, for every
![]() $x,y \in X$
and
$x,y \in X$
and
![]() $t>0$
,
$t>0$
,
-
○
 $d_X(x,y) \geq t \implies d_Y(\varphi _t(x),\varphi _t(y)) \geq st$
and
$d_X(x,y) \geq t \implies d_Y(\varphi _t(x),\varphi _t(y)) \geq st$
and -
○
 $d_Y(\varphi _t(x),\varphi _t(y)) \leq sC\min \{d_X(x,y),t\}$
.
$d_Y(\varphi _t(x),\varphi _t(y)) \leq sC\min \{d_X(x,y),t\}$
.
If X and Y are also pointed, then
![]() $\{\varphi _t\}_{t>0}$
is basepoint-preserving if
$\{\varphi _t\}_{t>0}$
is basepoint-preserving if
![]() $\varphi _t$
is basepoint-preserving for every
$\varphi _t$
is basepoint-preserving for every
![]() $t>0$
.
$t>0$
.
The proof of the next lemma is adapted from the proof of Assouad’s embedding theorem (e.g., [Reference Heinonen30, Proof of Theorem 3.15]).
Lemma 4.12. Let
![]() $(X,d_X,q)$
be a pointed metric space. If X basepoint-preservingly threshold embeds into an
$(X,d_X,q)$
be a pointed metric space. If X basepoint-preservingly threshold embeds into an
![]() $\ell ^{0+}$
-small subset
$\ell ^{0+}$
-small subset
![]() $S\subseteq \ell ^\infty ([0,\infty ))$
with distortion
$S\subseteq \ell ^\infty ([0,\infty ))$
with distortion
![]() $C<\infty $
, then for every
$C<\infty $
, then for every
![]() $\alpha \in (0,1)$
, the space
$\alpha \in (0,1)$
, the space
![]() $(X,d^\alpha ,q)$
admits a basepoint-preserving biLipschitz embedding of distortion
$(X,d^\alpha ,q)$
admits a basepoint-preserving biLipschitz embedding of distortion
![]() $L<\infty $
into an
$L<\infty $
into an
![]() $\ell ^{0+}$
-small subset
$\ell ^{0+}$
-small subset
![]() $S'\subseteq \ell ^\infty ([0,\infty ))$
, where L and the
$S'\subseteq \ell ^\infty ([0,\infty ))$
, where L and the
![]() $\ell ^p$
-smallness constants of
$\ell ^p$
-smallness constants of
![]() $S'$
depend only on
$S'$
depend only on
![]() $C,\alpha $
, and the
$C,\alpha $
, and the
![]() $\ell ^p$
-smallness constants of S.
$\ell ^p$
-smallness constants of S.
Proof. Let S be an
![]() $\ell ^{0+}$
-small subset of
$\ell ^{0+}$
-small subset of
![]() $\ell ^\infty ([0,\infty ))=\ell ^{\infty }(\mathbb {N};[0,\infty ))$
and
$\ell ^\infty ([0,\infty ))=\ell ^{\infty }(\mathbb {N};[0,\infty ))$
and
![]() $\{\boldsymbol {\varphi }_t: X \to S\}_{t>0}$
a basepoint-preserving threshold embedding with distortion
$\{\boldsymbol {\varphi }_t: X \to S\}_{t>0}$
a basepoint-preserving threshold embedding with distortion
![]() $C<\infty $
. By postcomposing with a dilation (which is basepoint-preserving and maps an
$C<\infty $
. By postcomposing with a dilation (which is basepoint-preserving and maps an
![]() $\ell ^p$
-small set to an
$\ell ^p$
-small set to an
![]() $\ell ^p$
-small set with the same smallness constant), we may assume that the scaling factor of the threshold embedding is
$\ell ^p$
-small set with the same smallness constant), we may assume that the scaling factor of the threshold embedding is
![]() $s=1$
. Let
$s=1$
. Let
![]() $\alpha \in (0,1)$
. By Remark 4.6, it suffices to embed into an
$\alpha \in (0,1)$
. By Remark 4.6, it suffices to embed into an
![]() $\ell ^{0^+}$
-small subset of
$\ell ^{0^+}$
-small subset of
![]() $\ell ^\infty (\mathbb {N} \times \mathbb {Z};[0,\infty ))$
. Define
$\ell ^\infty (\mathbb {N} \times \mathbb {Z};[0,\infty ))$
. Define
![]() $\boldsymbol {\psi }: X \to \ell ^\infty (\mathbb {N} \times \mathbb {Z};[0,\infty ))$
by
$\boldsymbol {\psi }: X \to \ell ^\infty (\mathbb {N} \times \mathbb {Z};[0,\infty ))$
by
![]() $\boldsymbol {\psi }(x)_{m,n} := 2^{n(\alpha -1)}(\boldsymbol {\varphi }_{2^n}(x))_m$
. Then to reach the desired conclusion, it suffices to prove that, for every
$\boldsymbol {\psi }(x)_{m,n} := 2^{n(\alpha -1)}(\boldsymbol {\varphi }_{2^n}(x))_m$
. Then to reach the desired conclusion, it suffices to prove that, for every
![]() $p>0$
, there exists
$p>0$
, there exists
![]() $C'<\infty $
depending only on
$C'<\infty $
depending only on
![]() $A_p,p,C,\alpha $
with
$A_p,p,C,\alpha $
with
 $$ \begin{align*} (C')^{-1} \left(\sum_{m\in\mathbb{N},n\in\mathbb{Z}} |\boldsymbol{\psi}_{m,n}(x)-\boldsymbol{\psi}_{m,n}(y)|^p\right)^{\frac{1}{p}} \leq d_X^\alpha(x,y) \leq 2^\alpha \sup_{m\in\mathbb{N},n\in\mathbb{Z}} |\boldsymbol{\psi}_{m,n}(x)-\boldsymbol{\psi}_{m,n}(y)| \end{align*} $$
$$ \begin{align*} (C')^{-1} \left(\sum_{m\in\mathbb{N},n\in\mathbb{Z}} |\boldsymbol{\psi}_{m,n}(x)-\boldsymbol{\psi}_{m,n}(y)|^p\right)^{\frac{1}{p}} \leq d_X^\alpha(x,y) \leq 2^\alpha \sup_{m\in\mathbb{N},n\in\mathbb{Z}} |\boldsymbol{\psi}_{m,n}(x)-\boldsymbol{\psi}_{m,n}(y)| \end{align*} $$
for every
![]() $x,y \in X$
. Let
$x,y \in X$
. Let
![]() $p>0$
and
$p>0$
and
![]() $A_p<\infty $
the
$A_p<\infty $
the
![]() $\ell ^p$
-smallness constant of S. Let
$\ell ^p$
-smallness constant of S. Let
![]() $x,y \in X$
and
$x,y \in X$
and
![]() $j \in \mathbb {Z}$
such that
$j \in \mathbb {Z}$
such that
![]() $2^j \leq d_X(x,y) \leq 2^{j+1}$
. We will prove the lower bound for
$2^j \leq d_X(x,y) \leq 2^{j+1}$
. We will prove the lower bound for
![]() $d_X^\alpha (x,y)$
first. We have
$d_X^\alpha (x,y)$
first. We have
 $$ \begin{align*} \Biggl(\sum_{m\in\mathbb{N},n\in\mathbb{Z}} & |\boldsymbol{\psi}_{m,n}(x)-\boldsymbol{\psi}_{m,n}(y)|^p\Biggr)^{\frac{1}{p}} = \left(\sum_{n\in\mathbb{Z}}2^{n(\alpha-1)p}\sum_{m\in\mathbb{N}} |(\boldsymbol{\varphi}_{2^n}(x))_m-(\boldsymbol{\varphi}_{2^n}(y))_m|^p\right)^{\frac{1}{p}} \\ &\leq \left(\sum_{n\in\mathbb{Z}}2^{n(\alpha-1)p} \left(A_p\|\boldsymbol{\varphi}_{2^n}(x)-\boldsymbol{\varphi}_{2^n}(y)\|_{\infty}\right)^p\right)^{\frac{1}{p}} \\ &\leq A_p\max\{2^{\frac{1}{p}-1},1\}\left(\sum_{n\leq j}2^{n(\alpha-1)p} \|\boldsymbol{\varphi}_{2^n}(x)-\boldsymbol{\varphi}_{2^n}(y)\|_{\infty}^p\right)^{\frac{1}{p}} \\ &\hspace{.3in} + A_p\max\{2^{\frac{1}{p}-1},1\}\left(\sum_{n\geq j+1}2^{n(\alpha-1)p} \|\boldsymbol{\varphi}_{2^n}(x)-\boldsymbol{\varphi}_{2^n}(y)\|_{\infty}^p\right)^{\frac{1}{p}} \\ &\leq A_p\max\{2^{\frac{1}{p}-1},1\} \left(\left(\sum_{n\leq j}2^{n(\alpha-1)p}C^p2^{np}\right)^{\frac{1}{p}} + \left(\sum_{n\geq j+1}2^{n(\alpha-1)p}C^p2^{(j+1)p}\right)^{\frac{1}{p}}\right) \\ &= A_pC\max\{2^{\frac{1}{p}-1},1\} \left(\left(\sum_{n\leq j}2^{\alpha pn}\right)^{\frac{1}{p}} + 2^{j+1}\left(\sum_{n\geq j+1}2^{(\alpha-1)pn}\right)^{\frac{1}{p}}\right) \\ &= A_pC\max\{2^{\frac{1}{p}-1},1\} \left(\left(\frac{2^{\alpha pj}}{1-2^{-\alpha p}}\right)^{\frac{1}{p}} + 2^{j+1}\left(\frac{2^{(\alpha-1)p(j+1)}}{1-2^{(\alpha-1)p}}\right)^{\frac{1}{p}}\right) \\ &= C'2^{\alpha j} \leq C'd^\alpha_X(x,y),\end{align*} $$
$$ \begin{align*} \Biggl(\sum_{m\in\mathbb{N},n\in\mathbb{Z}} & |\boldsymbol{\psi}_{m,n}(x)-\boldsymbol{\psi}_{m,n}(y)|^p\Biggr)^{\frac{1}{p}} = \left(\sum_{n\in\mathbb{Z}}2^{n(\alpha-1)p}\sum_{m\in\mathbb{N}} |(\boldsymbol{\varphi}_{2^n}(x))_m-(\boldsymbol{\varphi}_{2^n}(y))_m|^p\right)^{\frac{1}{p}} \\ &\leq \left(\sum_{n\in\mathbb{Z}}2^{n(\alpha-1)p} \left(A_p\|\boldsymbol{\varphi}_{2^n}(x)-\boldsymbol{\varphi}_{2^n}(y)\|_{\infty}\right)^p\right)^{\frac{1}{p}} \\ &\leq A_p\max\{2^{\frac{1}{p}-1},1\}\left(\sum_{n\leq j}2^{n(\alpha-1)p} \|\boldsymbol{\varphi}_{2^n}(x)-\boldsymbol{\varphi}_{2^n}(y)\|_{\infty}^p\right)^{\frac{1}{p}} \\ &\hspace{.3in} + A_p\max\{2^{\frac{1}{p}-1},1\}\left(\sum_{n\geq j+1}2^{n(\alpha-1)p} \|\boldsymbol{\varphi}_{2^n}(x)-\boldsymbol{\varphi}_{2^n}(y)\|_{\infty}^p\right)^{\frac{1}{p}} \\ &\leq A_p\max\{2^{\frac{1}{p}-1},1\} \left(\left(\sum_{n\leq j}2^{n(\alpha-1)p}C^p2^{np}\right)^{\frac{1}{p}} + \left(\sum_{n\geq j+1}2^{n(\alpha-1)p}C^p2^{(j+1)p}\right)^{\frac{1}{p}}\right) \\ &= A_pC\max\{2^{\frac{1}{p}-1},1\} \left(\left(\sum_{n\leq j}2^{\alpha pn}\right)^{\frac{1}{p}} + 2^{j+1}\left(\sum_{n\geq j+1}2^{(\alpha-1)pn}\right)^{\frac{1}{p}}\right) \\ &= A_pC\max\{2^{\frac{1}{p}-1},1\} \left(\left(\frac{2^{\alpha pj}}{1-2^{-\alpha p}}\right)^{\frac{1}{p}} + 2^{j+1}\left(\frac{2^{(\alpha-1)p(j+1)}}{1-2^{(\alpha-1)p}}\right)^{\frac{1}{p}}\right) \\ &= C'2^{\alpha j} \leq C'd^\alpha_X(x,y),\end{align*} $$
where
![]() $C'<\infty $
depends only on
$C'<\infty $
depends only on
![]() $A_p,p,C,\alpha $
, and not on
$A_p,p,C,\alpha $
, and not on
![]() $x,y$
. Note also that this bound and the fact that
$x,y$
. Note also that this bound and the fact that
![]() $\boldsymbol {\psi }$
is basepoint-preserving verifies that
$\boldsymbol {\psi }$
is basepoint-preserving verifies that
![]() $\boldsymbol {\psi }$
indeed takes values in
$\boldsymbol {\psi }$
indeed takes values in
![]() $\ell ^\infty (\mathbb {N}\times \mathbb {Z};[0,\infty ))$
. Establishing the upper bound for
$\ell ^\infty (\mathbb {N}\times \mathbb {Z};[0,\infty ))$
. Establishing the upper bound for
![]() $d_X^\alpha (x,y)$
is simpler:
$d_X^\alpha (x,y)$
is simpler:
 $$ \begin{align*} \sup_{m\in\mathbb{N},m\in\mathbb{Z}}|\boldsymbol{\psi}(x)_{m,n}-\boldsymbol{\psi}(y)_{m,n}| & \geq 2^{j(\alpha-1)}\|\boldsymbol{\varphi}_{2^j}(x)-\boldsymbol{\varphi}_{2^j}(y)\|_\infty \\ &\geq 2^{j(\alpha-1)}2^j \geq 2^{-\alpha}d_X^\alpha(x,y).\\[-34pt] \end{align*} $$
$$ \begin{align*} \sup_{m\in\mathbb{N},m\in\mathbb{Z}}|\boldsymbol{\psi}(x)_{m,n}-\boldsymbol{\psi}(y)_{m,n}| & \geq 2^{j(\alpha-1)}\|\boldsymbol{\varphi}_{2^j}(x)-\boldsymbol{\varphi}_{2^j}(y)\|_\infty \\ &\geq 2^{j(\alpha-1)}2^j \geq 2^{-\alpha}d_X^\alpha(x,y).\\[-34pt] \end{align*} $$
The proof of the following lemma is based on the proof of [Reference Lang and Schlichenmaier37, Theorem 1.6].
Lemma 4.13. For every
![]() $n\in \mathbb {N}$
, every separable pointed metric space X of Nagata dimension
$n\in \mathbb {N}$
, every separable pointed metric space X of Nagata dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
basepoint-preservingly threshold embeds with distortion
$\gamma <\infty $
basepoint-preservingly threshold embeds with distortion
![]() $C \leq 4\gamma $
into
$C \leq 4\gamma $
into
![]() $\ell ^\infty _{\operatorname {\mathrm {supp}}\leq N}([0,\infty ))$
for
$\ell ^\infty _{\operatorname {\mathrm {supp}}\leq N}([0,\infty ))$
for
![]() $N = 2(n+1)$
(see Example 4.7 for the definition of this set). Consequently, X basepoint-preservingly threshold embeds with distortion
$N = 2(n+1)$
(see Example 4.7 for the definition of this set). Consequently, X basepoint-preservingly threshold embeds with distortion
![]() $C \leq 4\gamma $
into an
$C \leq 4\gamma $
into an
![]() $\ell ^{0+}$
-small subset S of
$\ell ^{0+}$
-small subset S of
![]() $\ell ^\infty ([0,\infty ))$
, where the
$\ell ^\infty ([0,\infty ))$
, where the
![]() $\ell ^p$
-smallness constants of S depends only on
$\ell ^p$
-smallness constants of S depends only on
![]() $n,\gamma $
.
$n,\gamma $
.
Proof. We begin by noting that the second sentence follows from the first and the discussion in Example 4.7. We will now prove the first sentence.
Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $(X,d,p)$
be a pointed separable metric space of Nagata dimension
$(X,d,p)$
be a pointed separable metric space of Nagata dimension
![]() $n\in \mathbb {N}$
and constant
$n\in \mathbb {N}$
and constant
![]() $\gamma <\infty $
. By replacing
$\gamma <\infty $
. By replacing
![]() $\gamma $
with
$\gamma $
with
![]() $\max \{\frac {1}{2},\gamma \}$
, we may assume that
$\max \{\frac {1}{2},\gamma \}$
, we may assume that
![]() $\gamma \geq \frac {1}{2}$
. Let
$\gamma \geq \frac {1}{2}$
. Let
![]() $t>0$
. Let
$t>0$
. Let
![]() $\{B_i\}_{i\in \mathbb {N}}$
be a Nagata cover of dimension n, constant
$\{B_i\}_{i\in \mathbb {N}}$
be a Nagata cover of dimension n, constant
![]() $\gamma $
, and scale
$\gamma $
, and scale
![]() $s=(2\gamma )^{-1}t$
. We can choose this cover to be countable since X is separable. Define
$s=(2\gamma )^{-1}t$
. We can choose this cover to be countable since X is separable. Define
![]() $\boldsymbol {\varphi }_t: X \to \ell ^\infty ([0,\infty ))$
by
$\boldsymbol {\varphi }_t: X \to \ell ^\infty ([0,\infty ))$
by
![]() $(\boldsymbol {\varphi }_t(x))_i = \max \{0,(4\gamma )^{-1}t-\operatorname {\mathrm {dist}}(B_i,x)\}$
. Since distance-to-subset function are 1-Lipschitz and the pointwise maximum of 1-Lipschitz functions is 1-Lipschitz, we obviously have
$(\boldsymbol {\varphi }_t(x))_i = \max \{0,(4\gamma )^{-1}t-\operatorname {\mathrm {dist}}(B_i,x)\}$
. Since distance-to-subset function are 1-Lipschitz and the pointwise maximum of 1-Lipschitz functions is 1-Lipschitz, we obviously have
![]() $\|\boldsymbol {\varphi }_t(x)-\boldsymbol {\varphi }_t(y)\|_\infty \leq \max \{1,(4\gamma )^{-1}\}\min \{d(x,y),t\}$
for every
$\|\boldsymbol {\varphi }_t(x)-\boldsymbol {\varphi }_t(y)\|_\infty \leq \max \{1,(4\gamma )^{-1}\}\min \{d(x,y),t\}$
for every
![]() $x,y \in X$
.
$x,y \in X$
.
Suppose
![]() $x,y \in X$
with
$x,y \in X$
with
![]() $d(x,y) \geq t$
. Choose
$d(x,y) \geq t$
. Choose
![]() $j\in \mathbb {N}$
such that
$j\in \mathbb {N}$
such that
![]() $x \in B_j$
. Then
$x \in B_j$
. Then
![]() $\operatorname {\mathrm {dist}}(B_j,y) \geq d(x,y) - \operatorname {\mathrm {diam}}(B_j) \geq t/2$
, which implies
$\operatorname {\mathrm {dist}}(B_j,y) \geq d(x,y) - \operatorname {\mathrm {diam}}(B_j) \geq t/2$
, which implies
![]() $(\boldsymbol {\varphi }_t(x))_j = (4\gamma )^{-1}t$
and
$(\boldsymbol {\varphi }_t(x))_j = (4\gamma )^{-1}t$
and
![]() $(\boldsymbol {\varphi }_t(y))_j = 0$
(since
$(\boldsymbol {\varphi }_t(y))_j = 0$
(since
![]() $\gamma \geq \frac {1}{2}$
), and hence,
$\gamma \geq \frac {1}{2}$
), and hence,
![]() $\|\boldsymbol {\varphi }_t(x)-\boldsymbol {\varphi }_t(y)\|_\infty \geq (4\gamma )^{-1}t$
.
$\|\boldsymbol {\varphi }_t(x)-\boldsymbol {\varphi }_t(y)\|_\infty \geq (4\gamma )^{-1}t$
.
Finally, fix
![]() $x \in X$
, and let
$x \in X$
, and let
![]() $I_x = \{i\in \mathbb {N}: (\boldsymbol {\varphi }_t(x))_i \neq 0\}$
. We will show that
$I_x = \{i\in \mathbb {N}: (\boldsymbol {\varphi }_t(x))_i \neq 0\}$
. We will show that
![]() $|I_x| \leq n+1$
. By definition of
$|I_x| \leq n+1$
. By definition of
![]() $\boldsymbol {\varphi }_t$
and
$\boldsymbol {\varphi }_t$
and
![]() $I_x$
, we can find, for each
$I_x$
, we can find, for each
![]() $i \in I_x$
, a point
$i \in I_x$
, a point
![]() $y_i \in B_i$
such that
$y_i \in B_i$
such that
![]() $d(x,y_i) < (4\gamma )^{-1}t$
. Then the set
$d(x,y_i) < (4\gamma )^{-1}t$
. Then the set
![]() $\{y_i\}_{i\in I_x}$
has diameter at most
$\{y_i\}_{i\in I_x}$
has diameter at most
![]() $(2\gamma )^{-1}t$
, and hence, it can have nonempty intersection with
$(2\gamma )^{-1}t$
, and hence, it can have nonempty intersection with
![]() $B_i$
for at most
$B_i$
for at most
![]() $n+1$
values of
$n+1$
values of
![]() $i\in \mathbb {N}$
. Since it has nonempty intersection with
$i\in \mathbb {N}$
. Since it has nonempty intersection with
![]() $B_i$
for every
$B_i$
for every
![]() $i\in I_x$
, we have
$i\in I_x$
, we have
![]() $|I_x| \leq n+1$
.
$|I_x| \leq n+1$
.
The collection of maps
![]() $\{\boldsymbol {\varphi }_t: X \to \ell ^\infty ([0,\infty ))\}_{t>0}$
is thus a threshold embedding of distortion
$\{\boldsymbol {\varphi }_t: X \to \ell ^\infty ([0,\infty ))\}_{t>0}$
is thus a threshold embedding of distortion
![]() $\max \{1,4\gamma \}$
and scaling factor
$\max \{1,4\gamma \}$
and scaling factor
![]() $s=(4\gamma )^{-1}$
into
$s=(4\gamma )^{-1}$
into
![]() $\ell ^\infty _{\operatorname {\mathrm {supp}}\leq n+1}([0,\infty ))$
. However, it is not necessarily basepoint-preserving. To fix this, we simply instead consider the maps
$\ell ^\infty _{\operatorname {\mathrm {supp}}\leq n+1}([0,\infty ))$
. However, it is not necessarily basepoint-preserving. To fix this, we simply instead consider the maps
![]() $\{\boldsymbol {\varphi }_t - \boldsymbol {\varphi }_t(p)\}_{t>0}$
, which clearly form a threshold embedding with the same distortion and scaling factor into
$\{\boldsymbol {\varphi }_t - \boldsymbol {\varphi }_t(p)\}_{t>0}$
, which clearly form a threshold embedding with the same distortion and scaling factor into
![]() $\ell ^\infty _{\operatorname {\mathrm {supp}}\leq 2(n+1)}([0,\infty ))$
and map p to 0.
$\ell ^\infty _{\operatorname {\mathrm {supp}}\leq 2(n+1)}([0,\infty ))$
and map p to 0.
We next combine Lemmas 4.12 and 4.13.
Lemma 4.14. For every separable pointed metric space
![]() $(X,d,p)$
with finite Nagata dimension (dimension
$(X,d,p)$
with finite Nagata dimension (dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
) and
$\gamma <\infty $
) and
![]() $\alpha \in (0,1)$
, the pointed metric space
$\alpha \in (0,1)$
, the pointed metric space
![]() $(X,d^{\alpha },p)$
basepoint-preservingly biLipschitzly embeds into an
$(X,d^{\alpha },p)$
basepoint-preservingly biLipschitzly embeds into an
![]() $\ell ^{0+}$
-small subset S of
$\ell ^{0+}$
-small subset S of
![]() $\ell ^\infty ([0,\infty ))$
with distortion L, where L and the
$\ell ^\infty ([0,\infty ))$
with distortion L, where L and the
![]() $\ell ^q$
-smallness constants of S depend only on
$\ell ^q$
-smallness constants of S depend only on
![]() $n,\gamma ,\alpha $
. If
$n,\gamma ,\alpha $
. If
![]() $(X,d)$
is also bounded, then
$(X,d)$
is also bounded, then
![]() $(X,d^{\alpha },p)$
basepoint-preservingly biLipschitzly embeds into an
$(X,d^{\alpha },p)$
basepoint-preservingly biLipschitzly embeds into an
![]() $\ell ^{0+}$
-small subset S of
$\ell ^{0+}$
-small subset S of
![]() $\ell ^\infty ([0,1])$
(with the same distortion and
$\ell ^\infty ([0,1])$
(with the same distortion and
![]() $\ell ^q$
-smallness constants).
$\ell ^q$
-smallness constants).
Proof. Let
![]() $(X,d,p)$
be a pointed separable metric space with finite Nagata dimension and
$(X,d,p)$
be a pointed separable metric space with finite Nagata dimension and
![]() $\alpha \in (0,1)$
. The first sentence follows immediately from Lemmas 4.12 and 4.13.
$\alpha \in (0,1)$
. The first sentence follows immediately from Lemmas 4.12 and 4.13.
For the second sentence, assume that
![]() $(X,d)$
is bounded. Then
$(X,d)$
is bounded. Then
![]() $(X,d^\alpha )$
is also bounded, and thus, its image in
$(X,d^\alpha )$
is also bounded, and thus, its image in
![]() $\ell ^\infty ([0,\infty ))$
under the biLipschitz embedding must be contained in
$\ell ^\infty ([0,\infty ))$
under the biLipschitz embedding must be contained in
![]() $\ell ^\infty ([0,B])$
for some
$\ell ^\infty ([0,B])$
for some
![]() $B< \infty $
. By postcomposing with a rescaling (which is basepoint-preserving and does not affect the biLipschitz distortion), we can arrange the target space to be
$B< \infty $
. By postcomposing with a rescaling (which is basepoint-preserving and does not affect the biLipschitz distortion), we can arrange the target space to be
![]() $\ell ^\infty ([0,1])$
. Since the image of an
$\ell ^\infty ([0,1])$
. Since the image of an
![]() $\ell ^{0+}$
-small set under a rescaling is also
$\ell ^{0+}$
-small set under a rescaling is also
![]() $\ell ^{0+}$
-small with the same
$\ell ^{0+}$
-small with the same
![]() $\ell ^q$
-smallness constants (this fact is immediate from the definition), this proves the second sentence.
$\ell ^q$
-smallness constants (this fact is immediate from the definition), this proves the second sentence.
In the next lemma, we will see that the target ultrametric space of a stochastic biLipschitz embedding can always taken to be bounded when the domain is bounded.
Lemma 4.15. Suppose X is a pointed metric space that stochastic biLipschitzly embeds into a pointed ultrametric space
![]() $(U,d,q)$
with distortion
$(U,d,q)$
with distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s\in (0,\infty )$
. If X is bounded, then X stochastic biLipschitzly embeds into a bounded, pointed ultrametric space
$s\in (0,\infty )$
. If X is bounded, then X stochastic biLipschitzly embeds into a bounded, pointed ultrametric space
![]() $U'$
with distortion D and scaling factor s, and if U is separable, then
$U'$
with distortion D and scaling factor s, and if U is separable, then
![]() $U'$
can be taken separable as well.
$U'$
can be taken separable as well.
Proof. Let
![]() $\{\phi _\omega : X \to (U,d,q)\}_{\omega \in \Omega }$
be a stochastic biLipschitz embedding of distortion
$\{\phi _\omega : X \to (U,d,q)\}_{\omega \in \Omega }$
be a stochastic biLipschitz embedding of distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s\in (0,\infty )$
. Assume that X is bounded with
$s\in (0,\infty )$
. Assume that X is bounded with
![]() $|X| \geq 2$
(the conclusion of the lemma is obvious if
$|X| \geq 2$
(the conclusion of the lemma is obvious if
![]() $|X| \leq 1$
), and define a new function
$|X| \leq 1$
), and define a new function
![]() $\rho : U \times U \to [0,\infty )$
by
$\rho : U \times U \to [0,\infty )$
by
![]() $\rho (x,y) = \min \{\operatorname {\mathrm {diam}}(X),d(x,y)\}$
. It is not difficult to see that
$\rho (x,y) = \min \{\operatorname {\mathrm {diam}}(X),d(x,y)\}$
. It is not difficult to see that
![]() $\rho $
is an ultrametric on U such that
$\rho $
is an ultrametric on U such that
![]() $(U,\rho )$
is bounded,
$(U,\rho )$
is bounded,
![]() $(U,\rho )$
is separable whenever
$(U,\rho )$
is separable whenever
![]() $(U,d)$
is separable, and
$(U,d)$
is separable, and
![]() $\{\phi _\omega : X \to (U,\rho ,q)\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding of distortion
$\{\phi _\omega : X \to (U,\rho ,q)\}_{\omega \in \Omega }$
is a stochastic biLipschitz embedding of distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s\in (0,\infty )$
.
$s\in (0,\infty )$
.
Finally, we arrive at our next main result of the article, which, together with Theorem A, proves Theorem B.
Theorem 4.16. For every bounded, separable, pointed metric space
![]() $(X,d,p)$
with finite Nagata dimension (dimension
$(X,d,p)$
with finite Nagata dimension (dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
) and every
$\gamma <\infty $
) and every
![]() $\alpha \in (0,1)$
, the pointed space
$\alpha \in (0,1)$
, the pointed space
![]() $(X,d^\alpha ,p)$
admits a stochastic biLipschitz embedding of distortion
$(X,d^\alpha ,p)$
admits a stochastic biLipschitz embedding of distortion
![]() $D<\infty $
into a bounded, separable, pointed ultrametric space, where D depends only on
$D<\infty $
into a bounded, separable, pointed ultrametric space, where D depends only on
![]() $n,\gamma ,\alpha $
.
$n,\gamma ,\alpha $
.
Proof. Let
![]() $(X,d,p)$
be a bounded, separable, pointed metric space with Nagata dimension
$(X,d,p)$
be a bounded, separable, pointed metric space with Nagata dimension
![]() $n\in \mathbb {N}$
and constant
$n\in \mathbb {N}$
and constant
![]() $\gamma <\infty $
, and let
$\gamma <\infty $
, and let
![]() $\alpha \in (0,1)$
. By Lemma 4.14, there is a basepoint-preserving biLipschitz embedding of distortion
$\alpha \in (0,1)$
. By Lemma 4.14, there is a basepoint-preserving biLipschitz embedding of distortion
![]() $L<\infty $
of
$L<\infty $
of
![]() $(X,d^{\sqrt {\alpha }},p)$
into an
$(X,d^{\sqrt {\alpha }},p)$
into an
![]() $\ell^{0+}$
-small subset S of
$\ell^{0+}$
-small subset S of
![]() $\ell ^\infty ([0,1])$
, where L and the set of
$\ell ^\infty ([0,1])$
, where L and the set of
![]() $\ell^q$
-smallness constants of S depend only on
$\ell^q$
-smallness constants of S depend only on
![]() $n,\gamma ,\alpha $
. Then by Theorem 4.11, there is a stochastic biLipschitz embedding of distortion
$n,\gamma ,\alpha $
. Then by Theorem 4.11, there is a stochastic biLipschitz embedding of distortion
![]() $D<\infty $
of
$D<\infty $
of
![]() $(X,(d^{\sqrt {\alpha }})^{\sqrt {\alpha }},p) = (X,d^\alpha ,p)$
into a separable, pointed ultrametric space, where D depends only on
$(X,(d^{\sqrt {\alpha }})^{\sqrt {\alpha }},p) = (X,d^\alpha ,p)$
into a separable, pointed ultrametric space, where D depends only on
![]() $n,\gamma ,\alpha $
. By Lemma 4.15, we may assume that the ultrametric space is also bounded.
$n,\gamma ,\alpha $
. By Lemma 4.15, we may assume that the ultrametric space is also bounded.
Remark 4.17. If it could be established that
![]() $(\mathbb {R},|\cdot |^\alpha )$
stochastic biLipschitzly embeds into a separable (unbounded) ultrametric space for every
$(\mathbb {R},|\cdot |^\alpha )$
stochastic biLipschitzly embeds into a separable (unbounded) ultrametric space for every
![]() $\alpha < 1$
(see Remark 4.4), then the same argument used in the proof of Theorem 4.16 would show that for every
$\alpha < 1$
(see Remark 4.4), then the same argument used in the proof of Theorem 4.16 would show that for every
![]() $\alpha <1$
and separable metric space
$\alpha <1$
and separable metric space
![]() $(X,d)$
with finite Nagata dimension, the snowflake space
$(X,d)$
with finite Nagata dimension, the snowflake space
![]() $(X,d^\alpha )$
stochastic biLipschitzly embeds into a separable (unbounded) ultrametric space.
$(X,d^\alpha )$
stochastic biLipschitzly embeds into a separable (unbounded) ultrametric space.
4.3 Free spaces over distorted finite Nagata-dimensional spaces
We conclude this section by applying Theorem 4.16 to study the Lipschitz free space of finite Nagata-dimensional metric spaces distorted by a concave function. Our methods allow for a solution to an open problem of Weaver concerning distorted spaces that fail to be doubling (see Theorem 4.21 and the preceding discussion). We begin by recalling concave distortion functions, following [Reference Weaver48,
![]() $\S$
2.6].
$\S$
2.6].
We call a function
![]() $\omega : [0,\infty ) \to [0,\infty )$
a distortion function if
$\omega : [0,\infty ) \to [0,\infty )$
a distortion function if
![]() $\omega $
is continuous and concave,Footnote 10
$\omega $
is continuous and concave,Footnote 10
![]() $\omega (0) = 0$
, and
$\omega (0) = 0$
, and
![]() $\omega (t)> 0$
for
$\omega (t)> 0$
for
![]() $t> 0$
. Each distortion function
$t> 0$
. Each distortion function
![]() $\omega $
is subadditiveFootnote 11 and admits a unique extended positive number
$\omega $
is subadditiveFootnote 11 and admits a unique extended positive number
![]() $a \in (0,\infty ]$
such that
$a \in (0,\infty ]$
such that
![]() $\omega $
is strictly increasing on
$\omega $
is strictly increasing on
![]() $[0,a]$
(to be interpreted as
$[0,a]$
(to be interpreted as
![]() $[0,\infty )$
if
$[0,\infty )$
if
![]() $a=\infty $
) and then constant on
$a=\infty $
) and then constant on
![]() $[a,\infty )$
(interpreting
$[a,\infty )$
(interpreting
![]() $[\infty ,\infty )$
as the empty set). Because of this, we will unambiguously write
$[\infty ,\infty )$
as the empty set). Because of this, we will unambiguously write
![]() $\omega ^{-1}$
for the inverse of the homeomorphism
$\omega ^{-1}$
for the inverse of the homeomorphism
![]() $\omega \big |_{[0,a]}: [0,a] \to [0,\omega (a)]$
. Whenever
$\omega \big |_{[0,a]}: [0,a] \to [0,\omega (a)]$
. Whenever
![]() $\omega $
is a distortion function and d is a metric on X, the distorted function
$\omega $
is a distortion function and d is a metric on X, the distorted function
![]() $\omega \circ d$
is again a metric on X inducing the same topology as that of d. In the next lemma, we record the effect on Nagata dimension of metric distortion (see also [Reference Lang and Schlichenmaier37, Lemma 2.1] for a general result along these same lines).
$\omega \circ d$
is again a metric on X inducing the same topology as that of d. In the next lemma, we record the effect on Nagata dimension of metric distortion (see also [Reference Lang and Schlichenmaier37, Lemma 2.1] for a general result along these same lines).
Lemma 4.18. Suppose
![]() $(X,d)$
is a metric space of Nagata dimension n with constant
$(X,d)$
is a metric space of Nagata dimension n with constant
![]() $\gamma $
. Then for all distortion functions
$\gamma $
. Then for all distortion functions
![]() $\omega $
, the metric space
$\omega $
, the metric space
![]() $(X,\omega \circ d)$
has Nagata dimension n with constant at most
$(X,\omega \circ d)$
has Nagata dimension n with constant at most
![]() $2\gamma $
.
$2\gamma $
.
Proof. Let
![]() $\omega : [0,\infty ) \to [0,\infty )$
be a distortion function. Let
$\omega : [0,\infty ) \to [0,\infty )$
be a distortion function. Let
![]() $s \in [0,\operatorname {\mathrm {diam}}(X,\omega \circ d)]$
with
$s \in [0,\operatorname {\mathrm {diam}}(X,\omega \circ d)]$
with
![]() $s<\infty $
, and let
$s<\infty $
, and let
![]() $B_1,B_2,\dots B_{n+1}$
be a cover of X such that each
$B_1,B_2,\dots B_{n+1}$
be a cover of X such that each
![]() $B_i$
is the union of a family of sets that is
$B_i$
is the union of a family of sets that is
![]() $\gamma \omega ^{-1}(s)$
-bounded and
$\gamma \omega ^{-1}(s)$
-bounded and
![]() $\omega ^{-1}(s)$
-separated with respect to d.
$\omega ^{-1}(s)$
-separated with respect to d.
Then with respect to
![]() $\omega \circ d$
, these same families are
$\omega \circ d$
, these same families are
![]() $\omega (\gamma \omega ^{-1}(s))$
-bounded and s-separated. It remains to show that
$\omega (\gamma \omega ^{-1}(s))$
-bounded and s-separated. It remains to show that
![]() $\omega (\gamma \omega ^{-1}(s)) \leq 2\gamma s$
. By subadditivity and induction, it follows that
$\omega (\gamma \omega ^{-1}(s)) \leq 2\gamma s$
. By subadditivity and induction, it follows that
![]() $\omega (2^nt) \leq 2^n\omega (t)$
for every
$\omega (2^nt) \leq 2^n\omega (t)$
for every
![]() $n\in \mathbb {Z}$
and
$n\in \mathbb {Z}$
and
![]() $t \in [0,\infty )$
. Choose
$t \in [0,\infty )$
. Choose
![]() $n \in \mathbb {Z}$
such that
$n \in \mathbb {Z}$
such that
![]() $2^n \leq \gamma < 2^{n+1}$
. Then by monotonicity and subadditivity, we get
$2^n \leq \gamma < 2^{n+1}$
. Then by monotonicity and subadditivity, we get
For
![]() $p \in [1,\infty )$
, a distortion function
$p \in [1,\infty )$
, a distortion function
![]() $\omega $
is called p-concave if
$\omega $
is called p-concave if
![]() $\omega ^p$
is concave. In this case,
$\omega ^p$
is concave. In this case,
![]() $\omega ^p$
is also a distortion function. In the following lemma, we provide a condition for a sufficiently smooth distortion function to be p-concave.
$\omega ^p$
is also a distortion function. In the following lemma, we provide a condition for a sufficiently smooth distortion function to be p-concave.
Lemma 4.19. Suppose
![]() $p \in [1,\infty )$
and
$p \in [1,\infty )$
and
![]() $\omega $
is a distortion function that is continuously differentiable on
$\omega $
is a distortion function that is continuously differentiable on
![]() $(0,\infty )$
. If
$(0,\infty )$
. If
![]() $\omega "(t)$
exists and
$\omega "(t)$
exists and
 $\omega "(t) \leq (1-p)\dfrac {\omega '(t)^2}{\omega (t)}$
for all
$\omega "(t) \leq (1-p)\dfrac {\omega '(t)^2}{\omega (t)}$
for all
![]() $t \in (0,\infty ) \setminus D$
, where D is discrete, then
$t \in (0,\infty ) \setminus D$
, where D is discrete, then
![]() $\omega $
is p-concave.
$\omega $
is p-concave.
Proof. Assume that
![]() $\omega "(t)$
exists for all
$\omega "(t)$
exists for all
![]() $t\in (0,\infty ) \setminus D$
, where D is discrete. Since
$t\in (0,\infty ) \setminus D$
, where D is discrete. Since
we see that
![]() $\omega ^p$
is concave if and only if
$\omega ^p$
is concave if and only if
![]() $\frac {d^2}{dt^2}(\omega (t)^p) \leq 0$
for all
$\frac {d^2}{dt^2}(\omega (t)^p) \leq 0$
for all
![]() $t \in (0,\infty ) \setminus D$
if and only if
$t \in (0,\infty ) \setminus D$
if and only if
 $\omega "(t) \leq (1-p)\dfrac {\omega '(t)^2}{\omega (t)}$
for all
$\omega "(t) \leq (1-p)\dfrac {\omega '(t)^2}{\omega (t)}$
for all
![]() $t \in (0,\infty ) \setminus D$
.
$t \in (0,\infty ) \setminus D$
.
Example 4.20. Fix
![]() $p \in [1,\infty )$
. Define a distortion function
$p \in [1,\infty )$
. Define a distortion function
![]() $\omega _p: [0,\infty ) \to [0,\infty )$
by
$\omega _p: [0,\infty ) \to [0,\infty )$
by
 $$ \begin{align*} \omega_p(t) = \begin{cases} 0 & t=0 \\ \log(\frac{1}{t})^{-1} & 0 < t \leq e^{-p-1} \\ \left(\frac{pe^{p+1}t+1}{(p+1)^{p+1}}\right)^{\frac{1}{p}} & e^{-p-1} \leq t \end{cases}. \end{align*} $$
$$ \begin{align*} \omega_p(t) = \begin{cases} 0 & t=0 \\ \log(\frac{1}{t})^{-1} & 0 < t \leq e^{-p-1} \\ \left(\frac{pe^{p+1}t+1}{(p+1)^{p+1}}\right)^{\frac{1}{p}} & e^{-p-1} \leq t \end{cases}. \end{align*} $$
It is a slightly tedious but routine verification that
![]() $\omega _p$
is a distortion function, continuously differentiable on
$\omega _p$
is a distortion function, continuously differentiable on
![]() $(0,\infty )$
, which satisfies
$(0,\infty )$
, which satisfies
 $\omega _p"(t) \leq (1-p)\dfrac {\omega _p'(t)^2}{\omega _p(t)}$
for all
$\omega _p"(t) \leq (1-p)\dfrac {\omega _p'(t)^2}{\omega _p(t)}$
for all
![]() $t \in (0,\infty ) \setminus \{e^{-p-1}\}$
. Hence,
$t \in (0,\infty ) \setminus \{e^{-p-1}\}$
. Hence,
![]() $\omega _p$
is p-concave by Lemma 4.19.
$\omega _p$
is p-concave by Lemma 4.19.
It holds that
![]() $\operatorname {\mathrm {LF}}(X,d^{\alpha }) \approx \ell ^1$
whenever
$\operatorname {\mathrm {LF}}(X,d^{\alpha }) \approx \ell ^1$
whenever
![]() $(X,d)$
is an infinite, compact, doubling metric space and
$(X,d)$
is an infinite, compact, doubling metric space and
![]() $\alpha \in (0,1)$
([Reference Weaver48, Theorem 8.49]). However, for distortion functions
$\alpha \in (0,1)$
([Reference Weaver48, Theorem 8.49]). However, for distortion functions
![]() $\omega $
satisfying
$\omega $
satisfying
![]() $\lim _{t\to 0}\frac {t^\alpha }{\omega (t)} = 0$
for all
$\lim _{t\to 0}\frac {t^\alpha }{\omega (t)} = 0$
for all
![]() $\alpha \in (0,1)$
(such as
$\alpha \in (0,1)$
(such as
![]() $\omega = \omega _p$
from Example 4.20), the space
$\omega = \omega _p$
from Example 4.20), the space
![]() $(X,\omega \circ d)$
fails to be doubling, and the validity of statement
$(X,\omega \circ d)$
fails to be doubling, and the validity of statement
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
remained unknown (see [Reference Weaver48, page 294]). In the following theorem, we fill this gap for p-concave distortion functions, which includes Example 4.20 as a special case.
$\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
remained unknown (see [Reference Weaver48, page 294]). In the following theorem, we fill this gap for p-concave distortion functions, which includes Example 4.20 as a special case.
Theorem 4.21. Let
![]() $p \in (1,\infty )$
and let
$p \in (1,\infty )$
and let
![]() $\omega $
be a p-concave distortion function. Let
$\omega $
be a p-concave distortion function. Let
![]() $(X,d,q)$
be a bounded, separable, finite Nagata-dimensional pointed metric space. Then there exists
$(X,d,q)$
be a bounded, separable, finite Nagata-dimensional pointed metric space. Then there exists
![]() $D<\infty $
such that
$D<\infty $
such that
![]() $(X,\omega \circ d,q)$
stochastic biLipschitzly embeds into a bounded, separable, pointed ultrametric space with distortion D. Furthermore, if X is infinite and if X is compact or
$(X,\omega \circ d,q)$
stochastic biLipschitzly embeds into a bounded, separable, pointed ultrametric space with distortion D. Furthermore, if X is infinite and if X is compact or
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d)$
is complemented in
$\operatorname {\mathrm {LF}}(X,\omega \circ d)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d)^{**}$
, then
$\operatorname {\mathrm {LF}}(X,\omega \circ d)^{**}$
, then
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
.
Proof. Since
![]() $\omega ^p$
is a distortion function and
$\omega ^p$
is a distortion function and
![]() $(X,d)$
has finite Nagata dimension, the metric space
$(X,d)$
has finite Nagata dimension, the metric space
![]() $(X,\omega ^p \circ d)$
has finite Nagata dimension by Lemma 4.18. Therefore, by Theorem 4.16, the pointed snowflake space
$(X,\omega ^p \circ d)$
has finite Nagata dimension by Lemma 4.18. Therefore, by Theorem 4.16, the pointed snowflake space
![]() $(X,(\omega ^p \circ d)^{\frac {1}{p}},q) = (X,\omega \circ d,q)$
stochastic biLipschitzly embeds into a bounded, separable, pointed ultrametric space with distortion. This proves the first conclusion.
$(X,(\omega ^p \circ d)^{\frac {1}{p}},q) = (X,\omega \circ d,q)$
stochastic biLipschitzly embeds into a bounded, separable, pointed ultrametric space with distortion. This proves the first conclusion.
For the second conclusion, assume that X is infinite and that X is compact or
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d)$
is complemented in
$\operatorname {\mathrm {LF}}(X,\omega \circ d)$
is complemented in
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d)^{**}$
. Then since ultrametric spaces isometrically embed into
$\operatorname {\mathrm {LF}}(X,\omega \circ d)^{**}$
. Then since ultrametric spaces isometrically embed into
![]() $\mathbb {R}$
-trees, the first conclusion of this theorem, Theorem 3.3, and the fact that snowflake spaces
$\mathbb {R}$
-trees, the first conclusion of this theorem, Theorem 3.3, and the fact that snowflake spaces
![]() $(Y,d^\alpha )$
have purely 1-unrectifiable completion (whenever
$(Y,d^\alpha )$
have purely 1-unrectifiable completion (whenever
![]() $(Y,d)$
is a metric space and
$(Y,d)$
is a metric space and
![]() $\alpha \in (0,1)$
, see Proof of Theorem B) imply that
$\alpha \in (0,1)$
, see Proof of Theorem B) imply that
![]() $\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(X,\omega \circ d) \approx \ell ^1$
.
5 log-stochastic embeddings and hyperbolic fillings
In this section, we show how Bonk-Schramm hyperbolic fillings (see Lemma 2.7) can be used to induce stochastic embeddings between visual hyperbolic metric spaces from stochastic embeddings between their boundaries (Lemma 5.5). It turns out that for boundaries of hyperbolic spaces, the correct notion of stochastic embedding is a relaxation of stochastic biLipschitz embedding that we call ‘log-stochastic’ biLipschitz embeddings.
Definition 5.1. Let
![]() $(X,d_X),(Y,d_Y)$
be pointed metric spaces. A random map
$(X,d_X),(Y,d_Y)$
be pointed metric spaces. A random map
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a log-stochastic biLipschitz embedding of distortion
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a log-stochastic biLipschitz embedding of distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s\in (0,\infty )$
if, for all
$s\in (0,\infty )$
if, for all
![]() $x,y \in X$
,
$x,y \in X$
,
-
○
 $d_Y(\phi _\omega (x),\phi _\omega (y)) \geq sd_X(x,y)$
for almost every
$d_Y(\phi _\omega (x),\phi _\omega (y)) \geq sd_X(x,y)$
for almost every
 $\omega \in \Omega $
and
$\omega \in \Omega $
and -
○
 $\mathbb {E}_\omega \left [\log \left (d_Y(\phi _\omega (x),\phi _\omega (y))\right )\right ] \leq \log (sDd_X(x,y))$
.
$\mathbb {E}_\omega \left [\log \left (d_Y(\phi _\omega (x),\phi _\omega (y))\right )\right ] \leq \log (sDd_X(x,y))$
.
Remark 5.2. By Jensen’s inequality, a stochastic biLipschitz embedding of distortion D is a log-stochastic biLipschitz embedding of distortion D.
One of the main reasons that log-stochastic biLipschitz embeddings are the correct notion to study for Gromov boundaries is that, for certain target spaces, they are inherited under snowflake embeddings. The next lemma reveals this to be the case when the target class is ultrametric spaces. This is opposite the situation for stochastic biLipschitz embeddability into ultrametric spaces, which is not inherited snowflake embeddings (see Remark 4.10).
Lemma 5.3. If
![]() $(X,d_X), (Y,d_Y)$
are pointed metric spaces such that X basepoint-preservingly snowflake embeds into Y with exponent
$(X,d_X), (Y,d_Y)$
are pointed metric spaces such that X basepoint-preservingly snowflake embeds into Y with exponent
![]() $\alpha \in (0,\infty )$
and distortion
$\alpha \in (0,\infty )$
and distortion
![]() $L<\infty $
, and Y log-stochastic biLipschitzly embeds into a pointed ultrametric space U with distortion
$L<\infty $
, and Y log-stochastic biLipschitzly embeds into a pointed ultrametric space U with distortion
![]() $D<\infty $
, then X log-stochastic biLipschitzly embeds into a pointed ultrametric space
$D<\infty $
, then X log-stochastic biLipschitzly embeds into a pointed ultrametric space
![]() $U'$
with distortion
$U'$
with distortion
![]() $D^\alpha L$
and scaling factor
$D^\alpha L$
and scaling factor
![]() $s=1$
. Moreover, if U is separable or bounded, then
$s=1$
. Moreover, if U is separable or bounded, then
![]() $U'$
is separable or bounded, respectively.
$U'$
is separable or bounded, respectively.
Proof. Let
![]() $\alpha \in (0,\infty )$
,
$\alpha \in (0,\infty )$
,
![]() $L < \infty $
,
$L < \infty $
,
![]() $s\in (0,\infty )$
and
$s\in (0,\infty )$
and
![]() $f: X \to Y$
such that, for all
$f: X \to Y$
such that, for all
![]() $x,y \in X$
,
$x,y \in X$
,
![]() $sd_X(x,y) \leq d_Y(f(x),f(y))^\alpha \leq sLd_X(x,y)$
. Let
$sd_X(x,y) \leq d_Y(f(x),f(y))^\alpha \leq sLd_X(x,y)$
. Let
![]() $\{\phi _\omega : Y \to U\}_{\omega \in \Omega }$
be a log-stochastic biLipschitz embedding of distortion
$\{\phi _\omega : Y \to U\}_{\omega \in \Omega }$
be a log-stochastic biLipschitz embedding of distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $t\in (0,\infty )$
into a pointed ultrametric space
$t\in (0,\infty )$
into a pointed ultrametric space
![]() $(U,d_U,q)$
. Then the triple
$(U,d_U,q)$
. Then the triple
![]() $(U',d_{U'},q)$
defined by
$(U',d_{U'},q)$
defined by
![]() $U' := U$
and
$U' := U$
and
![]() $d_{U'} := s^{-1}(t^{-1}d_U)^{\alpha }$
is a pointed ultrametric space (which is separable or bounded if U is), and we will show that the composite
$d_{U'} := s^{-1}(t^{-1}d_U)^{\alpha }$
is a pointed ultrametric space (which is separable or bounded if U is), and we will show that the composite
![]() $\{id \circ \phi _\omega \circ f: X \to U'\}_{\omega \in \Omega }$
is a log-stochastic biLipschitz embedding of distortion
$\{id \circ \phi _\omega \circ f: X \to U'\}_{\omega \in \Omega }$
is a log-stochastic biLipschitz embedding of distortion
![]() $D^\alpha L$
and scaling factor
$D^\alpha L$
and scaling factor
![]() $1$
, where
$1$
, where
![]() $id: U \to U'$
is the identity map. First note that
$id: U \to U'$
is the identity map. First note that
![]() $\{id \circ \phi _\omega \circ f\}_{\omega \in \Omega }$
is clearly pointwise measurable and essentially-separably-valued since
$\{id \circ \phi _\omega \circ f\}_{\omega \in \Omega }$
is clearly pointwise measurable and essentially-separably-valued since
![]() $id$
is a homeomorphism. It is clearly almost surely basepoint-preserving as well. Let
$id$
is a homeomorphism. It is clearly almost surely basepoint-preserving as well. Let
![]() $x,y \in X$
. Then, for almost every
$x,y \in X$
. Then, for almost every
![]() $\omega $
,
$\omega $
,
 $$ \begin{align*} d_{U'}(id(\phi_\omega(f(x))),id(\phi_\omega(f(y)))) &= s^{-1}(t^{-1}d_{U}(\phi_\omega(f(x)),\phi_\omega(f(y))))^{\alpha} \\ &\geq s^{-1}d_{Y}(f(x),f(y))^{\alpha} \\ &\geq d_X(x,y). \end{align*} $$
$$ \begin{align*} d_{U'}(id(\phi_\omega(f(x))),id(\phi_\omega(f(y)))) &= s^{-1}(t^{-1}d_{U}(\phi_\omega(f(x)),\phi_\omega(f(y))))^{\alpha} \\ &\geq s^{-1}d_{Y}(f(x),f(y))^{\alpha} \\ &\geq d_X(x,y). \end{align*} $$
Next,
 $$ \begin{align*} \mathbb{E}_\omega[\log(d_{U'}&(id(\phi_\omega(f(x))),id(\phi_\omega(f(y)))))] \\ &= \mathbb{E}_\omega[\log(s^{-1}(t^{-1}d_{U}(\phi_\omega(f(x)),\phi_\omega(f(y))))^{\alpha})] \\ &= -\log(s) -\alpha\log(t) + \alpha\mathbb{E}_\omega[\log(d_{U}(\phi_\omega(f(x)),\phi_\omega(f(y))))] \\ &\leq -\log(s) -\alpha\log(t) + \alpha\log(tDd_{Y}(f(x),f(y))) \\ &= \log(s^{-1}D^\alpha d_{Y}(f(x),f(y))^\alpha) \\ &\leq \log(D^\alpha L d_{X}(x,y)).\\[-36pt] \end{align*} $$
$$ \begin{align*} \mathbb{E}_\omega[\log(d_{U'}&(id(\phi_\omega(f(x))),id(\phi_\omega(f(y)))))] \\ &= \mathbb{E}_\omega[\log(s^{-1}(t^{-1}d_{U}(\phi_\omega(f(x)),\phi_\omega(f(y))))^{\alpha})] \\ &= -\log(s) -\alpha\log(t) + \alpha\mathbb{E}_\omega[\log(d_{U}(\phi_\omega(f(x)),\phi_\omega(f(y))))] \\ &\leq -\log(s) -\alpha\log(t) + \alpha\log(tDd_{Y}(f(x),f(y))) \\ &= \log(s^{-1}D^\alpha d_{Y}(f(x),f(y))^\alpha) \\ &\leq \log(D^\alpha L d_{X}(x,y)).\\[-36pt] \end{align*} $$
Lemma 5.3 shows that the property of log-stochastic biLipschitz embeddability into (separable or bounded) ultrametric spaces is preserved under snowflake equivalences. Therefore, when X is a hyperbolic metric space, we may unambiguously say that
‘
![]() $\partial X$
log-stochastic biLipschitzly embeds into a bounded ultrametric space’
$\partial X$
log-stochastic biLipschitzly embeds into a bounded ultrametric space’
without making reference to any particular visual metric on
![]() $\partial X$
. We will make such a statement in Theorem 5.7 with this understanding in mind.
$\partial X$
. We will make such a statement in Theorem 5.7 with this understanding in mind.
The following result is an immediate corollary of Lemma 5.3 and Theorem 4.16 and provides our main example of spaces that log-stochastic biLipschitzly embed into ultrametric spaces. We omit the proof.
Corollary 5.4. Let Z be a bounded, separable, pointed metric space of finite Nagata dimension. Then Z log-stochastic biLipschitzly embeds into a separable, bounded, pointed ultrametric space.
The next result is the fundamental lemma of log-stochastic biLipschitz embeddings, and it should be seen as our motivation to define such a notion in the first place.
Lemma 5.5. If
![]() $\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a log-stochastic biLipschitz embedding of distortion
$\{\phi _\omega : X \to Y\}_{\omega \in \Omega }$
is a log-stochastic biLipschitz embedding of distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s=1$
of a pointed metric space
$s=1$
of a pointed metric space
![]() $(X,d_X,p)$
into a bounded, pointed metric space
$(X,d_X,p)$
into a bounded, pointed metric space
![]() $(Y,d_Y,q)$
, then
$(Y,d_Y,q)$
, then
![]() $\operatorname {\mathrm {diam}}(X) \leq \operatorname {\mathrm {diam}}(Y)$
and
$\operatorname {\mathrm {diam}}(X) \leq \operatorname {\mathrm {diam}}(Y)$
and
![]() $\{\operatorname {\mathrm {Hyp}}(\phi _\omega ): \operatorname {\mathrm {Hyp}}(X) \to \operatorname {\mathrm {Hyp}}(Y)\}_{\omega \in \Omega }$
is a stochastic rough isometric embedding with roughness constant
$\{\operatorname {\mathrm {Hyp}}(\phi _\omega ): \operatorname {\mathrm {Hyp}}(X) \to \operatorname {\mathrm {Hyp}}(Y)\}_{\omega \in \Omega }$
is a stochastic rough isometric embedding with roughness constant
![]() $K \leq 2\log (D)$
. Here,
$K \leq 2\log (D)$
. Here,
![]() $\operatorname {\mathrm {Hyp}}(X)$
can be equipped with basepoint
$\operatorname {\mathrm {Hyp}}(X)$
can be equipped with basepoint
![]() $(p,h)$
for any
$(p,h)$
for any
![]() $h \in (0,\operatorname {\mathrm {diam}}(X)]$
, and
$h \in (0,\operatorname {\mathrm {diam}}(X)]$
, and
![]() $\operatorname {\mathrm {Hyp}}(Y)$
is then equipped with basepoint
$\operatorname {\mathrm {Hyp}}(Y)$
is then equipped with basepoint
![]() $(q,h)$
.
$(q,h)$
.
Before proving this result, we need a simple lemma that essentially amounts to a calculus exercise.
Lemma 5.6. Let Z be a
![]() $(0,\infty )$
-valued random variable,
$(0,\infty )$
-valued random variable,
![]() $\alpha \in (0,\infty )$
, and
$\alpha \in (0,\infty )$
, and
![]() $D \in [1,\infty)$
such that
$D \in [1,\infty)$
such that
![]() $Z \geq \alpha $
almost surely and
$Z \geq \alpha $
almost surely and
![]() $\mathbb {E}[\log (Z)] \leq \log (D\alpha )$
(in particular,
$\mathbb {E}[\log (Z)] \leq \log (D\alpha )$
(in particular,
![]() $\log (Z)$
is integrable). Then for all
$\log (Z)$
is integrable). Then for all
![]() $\beta \in [0,\infty )$
,
$\beta \in [0,\infty )$
,
![]() $\mathbb {E}[\log (Z+\beta )] \leq \log (D(\alpha +\beta ))$
.
$\mathbb {E}[\log (Z+\beta )] \leq \log (D(\alpha +\beta ))$
.
Proof. Let
![]() $(\Omega ,\mathcal {F},\mathbb {P})$
denote the probability space underlying Z. Define
$(\Omega ,\mathcal {F},\mathbb {P})$
denote the probability space underlying Z. Define
![]() $f: [0,\infty ) \to \mathbb {R}$
by
$f: [0,\infty ) \to \mathbb {R}$
by
Then f is continuous on
![]() $[0,\infty )$
. For
$[0,\infty )$
. For
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $\omega \in \Omega $
, the function
$\omega \in \Omega $
, the function
![]() $\beta \mapsto \log (Z(\omega )+\beta )$
is differentiable on
$\beta \mapsto \log (Z(\omega )+\beta )$
is differentiable on
![]() $(0,\infty )$
with derivative
$(0,\infty )$
with derivative
![]() $\beta \mapsto (Z(\omega )+\beta )^{-1} \leq \alpha ^{-1}$
bounded uniformly in
$\beta \mapsto (Z(\omega )+\beta )^{-1} \leq \alpha ^{-1}$
bounded uniformly in
![]() $\omega $
. Therefore, by the mean value theorem and dominated convergence theorem, we have that f is differentiable on
$\omega $
. Therefore, by the mean value theorem and dominated convergence theorem, we have that f is differentiable on
![]() $(0,\infty )$
with
$(0,\infty )$
with
 $$ \begin{align*} f'(\beta) = \mathbb{E}[(Z+\beta)^{-1}] - (\alpha+\beta)^{-1} = \mathbb{E}\left[\frac{\alpha-Z}{(Z+\beta)(\alpha+\beta)}\right] \leq 0. \end{align*} $$
$$ \begin{align*} f'(\beta) = \mathbb{E}[(Z+\beta)^{-1}] - (\alpha+\beta)^{-1} = \mathbb{E}\left[\frac{\alpha-Z}{(Z+\beta)(\alpha+\beta)}\right] \leq 0. \end{align*} $$
Thus, f is decreasing on
![]() $[0,\infty )$
. Since
$[0,\infty )$
. Since
![]() $f(0) \leq 0$
by assumption, this implies
$f(0) \leq 0$
by assumption, this implies
![]() $f(\beta ) \leq 0$
for all
$f(\beta ) \leq 0$
for all
![]() $\beta \geq 0$
, which proves the lemma.
$\beta \geq 0$
, which proves the lemma.
Proof of Lemma 5.5.
Let
![]() $\{\phi _\omega : (X,d_X,p) \to (Y,d_Y,q)\}_{\omega \in \Omega }$
be a log-stochastic biLipschitz embedding of distortion
$\{\phi _\omega : (X,d_X,p) \to (Y,d_Y,q)\}_{\omega \in \Omega }$
be a log-stochastic biLipschitz embedding of distortion
![]() $D<\infty $
and scaling factor
$D<\infty $
and scaling factor
![]() $s=1$
between bounded, pointed metric spaces. Choose any
$s=1$
between bounded, pointed metric spaces. Choose any
![]() $h \in (0,\operatorname {\mathrm {diam}}(X)]$
, and equip
$h \in (0,\operatorname {\mathrm {diam}}(X)]$
, and equip
![]() $\operatorname {\mathrm {Hyp}}(X)$
with basepoint
$\operatorname {\mathrm {Hyp}}(X)$
with basepoint
![]() $(p,h)$
and
$(p,h)$
and
![]() $\operatorname {\mathrm {Hyp}}(Y)$
with basepoint
$\operatorname {\mathrm {Hyp}}(Y)$
with basepoint
![]() $(q,h)$
. First note that the almost-sure noncontractivity of
$(q,h)$
. First note that the almost-sure noncontractivity of
![]() $\{\phi _\omega \}_{\omega \in \Omega }$
ensures
$\{\phi _\omega \}_{\omega \in \Omega }$
ensures
![]() $\operatorname {\mathrm {diam}}(X) \leq \operatorname {\mathrm {diam}}(Y)$
, and thus,
$\operatorname {\mathrm {diam}}(X) \leq \operatorname {\mathrm {diam}}(Y)$
, and thus,
![]() $\operatorname {\mathrm {Hyp}}(\phi _\omega )$
is well-defined for each
$\operatorname {\mathrm {Hyp}}(\phi _\omega )$
is well-defined for each
![]() $\omega \in \Omega $
. Next, note that
$\omega \in \Omega $
. Next, note that
![]() $\{\operatorname {\mathrm {Hyp}}(\phi _\omega )\}_{\omega \in \Omega }$
is clearly pointwise measurable and essentially-separably-valued since, for each
$\{\operatorname {\mathrm {Hyp}}(\phi _\omega )\}_{\omega \in \Omega }$
is clearly pointwise measurable and essentially-separably-valued since, for each
![]() $h \in (0,\operatorname {\mathrm {diam}}(Y)]$
, the map
$h \in (0,\operatorname {\mathrm {diam}}(Y)]$
, the map
![]() $y \mapsto (y,h)$
taking Y into
$y \mapsto (y,h)$
taking Y into
![]() $\operatorname {\mathrm {Hyp}}(Y)$
is a homeomorphic embedding. It is also clearly almost surely basepoint-preserving.
$\operatorname {\mathrm {Hyp}}(Y)$
is a homeomorphic embedding. It is also clearly almost surely basepoint-preserving.
Let
![]() $(x,h) \neq (x',h') \in \operatorname {\mathrm {Hyp}}(X)$
. Then for almost every
$(x,h) \neq (x',h') \in \operatorname {\mathrm {Hyp}}(X)$
. Then for almost every
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align*} \rho_Y(\operatorname{\mathrm{Hyp}}(\phi_\omega)(x,h),\operatorname{\mathrm{Hyp}}(\phi_\omega)(x',h')) &= 2\log\left(\dfrac{d_Y(\phi_\omega(x),\phi_\omega(x')) + h \vee h'}{\sqrt{hh'}}\right) \\ &\geq 2\log\left(\dfrac{d_X(x,x') + h \vee h'}{\sqrt{hh'}}\right) \\ &= \rho_X((x,h),(x',h')). \end{align*} $$
$$ \begin{align*} \rho_Y(\operatorname{\mathrm{Hyp}}(\phi_\omega)(x,h),\operatorname{\mathrm{Hyp}}(\phi_\omega)(x',h')) &= 2\log\left(\dfrac{d_Y(\phi_\omega(x),\phi_\omega(x')) + h \vee h'}{\sqrt{hh'}}\right) \\ &\geq 2\log\left(\dfrac{d_X(x,x') + h \vee h'}{\sqrt{hh'}}\right) \\ &= \rho_X((x,h),(x',h')). \end{align*} $$
To prove that the stochastic roughness constant is
![]() $\leq 2\log (D)$
, we need to treat two cases: (i)
$\leq 2\log (D)$
, we need to treat two cases: (i)
![]() $x=x'$
and (ii)
$x=x'$
and (ii)
![]() $x \neq x'$
. In case (i), we have
$x \neq x'$
. In case (i), we have
 $$ \begin{align*} \mathbb{E}_\omega[\rho_Y(\operatorname{\mathrm{Hyp}}(\phi_\omega)(x,h),\operatorname{\mathrm{Hyp}}(\phi_\omega)(x',h'))] = \mathbb{E}_\omega\left[2\log\left(\frac{h \vee h'}{\sqrt{hh'}}\right)\right] = \rho_X((x,h),(x',h')). \end{align*} $$
$$ \begin{align*} \mathbb{E}_\omega[\rho_Y(\operatorname{\mathrm{Hyp}}(\phi_\omega)(x,h),\operatorname{\mathrm{Hyp}}(\phi_\omega)(x',h'))] = \mathbb{E}_\omega\left[2\log\left(\frac{h \vee h'}{\sqrt{hh'}}\right)\right] = \rho_X((x,h),(x',h')). \end{align*} $$
In case (ii), we apply Lemma 5.6 with
 $Z = \dfrac {d_Y(\phi _\omega (x),\phi _\omega (x'))}{\sqrt {hh'}}$
,
$Z = \dfrac {d_Y(\phi _\omega (x),\phi _\omega (x'))}{\sqrt {hh'}}$
,
 $\alpha = \dfrac {d_X(x,x')}{\sqrt {hh'}}$
,
$\alpha = \dfrac {d_X(x,x')}{\sqrt {hh'}}$
,
![]() $D=D$
, and
$D=D$
, and
 $\beta = \dfrac {h \vee h'}{\sqrt {hh'}}$
, we get
$\beta = \dfrac {h \vee h'}{\sqrt {hh'}}$
, we get
 $$ \begin{align*} \mathbb{E}_\omega[\rho_Y(\operatorname{\mathrm{Hyp}}(\phi_\omega)(x,h),\operatorname{\mathrm{Hyp}}(\phi_\omega)(x',h'))] &= \mathbb{E}_\omega\left[2\log\left(\dfrac{d_Y(\phi_\omega(x),\phi_\omega(x')) + h \vee h'}{\sqrt{hh'}}\right)\right] \\ &\leq 2\log\left(\dfrac{D(d_X(x,x') + h \vee h')}{\sqrt{hh'}}\right) \\ &= \rho_X((x,h),(x',h')) + 2\log(D).\\[-34pt] \end{align*} $$
$$ \begin{align*} \mathbb{E}_\omega[\rho_Y(\operatorname{\mathrm{Hyp}}(\phi_\omega)(x,h),\operatorname{\mathrm{Hyp}}(\phi_\omega)(x',h'))] &= \mathbb{E}_\omega\left[2\log\left(\dfrac{d_Y(\phi_\omega(x),\phi_\omega(x')) + h \vee h'}{\sqrt{hh'}}\right)\right] \\ &\leq 2\log\left(\dfrac{D(d_X(x,x') + h \vee h')}{\sqrt{hh'}}\right) \\ &= \rho_X((x,h),(x',h')) + 2\log(D).\\[-34pt] \end{align*} $$
When Lemma 5.5 holds with Y an ultrametric space, we can apply Lemmas 2.7 and 2.8 and get a general criterion for stochastic biLipschitz embeddability of uniformly discrete hyperbolic metric spaces into
![]() $\mathbb {R}$
-trees, which proves Theorem C. Observe that a uniformly discrete metric space is locally finite if and only if it is proper.
$\mathbb {R}$
-trees, which proves Theorem C. Observe that a uniformly discrete metric space is locally finite if and only if it is proper.
Theorem 5.7. Let A be an infinite, uniformly discrete, locally finite, pointed metric space, and let X be a visual, hyperbolic, pointed metric space. If A rough biLipschitzly embeds into X and
![]() $\partial X$
log-stochastic biLipschitzly embeds (for every choice of basepoint) into a bounded, pointed ultrametric space, then A stochastic biLipschitzly embeds into a pointed
$\partial X$
log-stochastic biLipschitzly embeds (for every choice of basepoint) into a bounded, pointed ultrametric space, then A stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree and
$\mathbb {R}$
-tree and
![]() $\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
Proof. Assume that there is a rough biLipschitz embedding
![]() $f_1: A \to X$
and, with respect to any basepoint in
$f_1: A \to X$
and, with respect to any basepoint in
![]() $\partial X$
, a log-stochastic biLipschitz embedding from
$\partial X$
, a log-stochastic biLipschitz embedding from
![]() $\partial X$
into a bounded, pointed ultrametric space. Denote the basepoint in A by p, and equip X with basepoint
$\partial X$
into a bounded, pointed ultrametric space. Denote the basepoint in A by p, and equip X with basepoint
![]() $f_1(p)$
.
$f_1(p)$
.
By Lemma 2.7, there is a rough biLipschitz embedding
![]() $f_2: X \to \operatorname {\mathrm {Hyp}}(\partial X)$
. Let
$f_2: X \to \operatorname {\mathrm {Hyp}}(\partial X)$
. Let
![]() $(p',h) := f_2(f_1(p))$
. Equip
$(p',h) := f_2(f_1(p))$
. Equip
![]() $\operatorname {\mathrm {Hyp}}(\partial X)$
with basepoint
$\operatorname {\mathrm {Hyp}}(\partial X)$
with basepoint
![]() $(p',h)$
and
$(p',h)$
and
![]() $\partial X$
with basepoint
$\partial X$
with basepoint
![]() $p'$
. Fix a visual metric d on
$p'$
. Fix a visual metric d on
![]() $\partial X$
, and let
$\partial X$
, and let
![]() $\{\phi _\omega : (\partial X,d,p') \to (U,d_U,q')\}_{\omega \in \Omega }$
be a log-stochastic biLipschitz embedding into a bounded, pointed ultrametric space U. Since rescalings of bounded ultrametric spaces are bounded and ultrametric, we may assume that the scaling factor of the embedding is
$\{\phi _\omega : (\partial X,d,p') \to (U,d_U,q')\}_{\omega \in \Omega }$
be a log-stochastic biLipschitz embedding into a bounded, pointed ultrametric space U. Since rescalings of bounded ultrametric spaces are bounded and ultrametric, we may assume that the scaling factor of the embedding is
![]() $s=1$
. Thus,
$s=1$
. Thus,
![]() $\operatorname {\mathrm {diam}}(\partial X) \leq \operatorname {\mathrm {diam}}(U)$
, and we equip
$\operatorname {\mathrm {diam}}(\partial X) \leq \operatorname {\mathrm {diam}}(U)$
, and we equip
![]() $\operatorname {\mathrm {Hyp}}(U)$
with basepoint
$\operatorname {\mathrm {Hyp}}(U)$
with basepoint
![]() $(q',h)$
.
$(q',h)$
.
By Lemma 5.5,
![]() $\{\operatorname {\mathrm {Hyp}}(\phi _\omega ): \operatorname {\mathrm {Hyp}}(\partial X) \to \operatorname {\mathrm {Hyp}}(U)\}_{\omega \in \Omega }$
is a stochastic rough isometric embedding. By Lemma 2.8, there is a measurable rough biLipschitz embedding
$\{\operatorname {\mathrm {Hyp}}(\phi _\omega ): \operatorname {\mathrm {Hyp}}(\partial X) \to \operatorname {\mathrm {Hyp}}(U)\}_{\omega \in \Omega }$
is a stochastic rough isometric embedding. By Lemma 2.8, there is a measurable rough biLipschitz embedding
![]() $f_3: \operatorname {\mathrm {Hyp}}(U) \to T$
into a pointed
$f_3: \operatorname {\mathrm {Hyp}}(U) \to T$
into a pointed
![]() $\mathbb {R}$
-tree T, which maps separable subsets to separable subsets. We equip T with basepoint
$\mathbb {R}$
-tree T, which maps separable subsets to separable subsets. We equip T with basepoint
![]() $f_3(q',h)$
. Then
$f_3(q',h)$
. Then
![]() $\{f_3 \circ \operatorname {\mathrm {Hyp}}(\phi _\omega ) \circ f_2 \circ f_1: A \to T\}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding. By Lemma 3.5, there is a stochastic biLipschitz embedding from A into a pointed
$\{f_3 \circ \operatorname {\mathrm {Hyp}}(\phi _\omega ) \circ f_2 \circ f_1: A \to T\}_{\omega \in \Omega }$
is a stochastic rough biLipschitz embedding. By Lemma 3.5, there is a stochastic biLipschitz embedding from A into a pointed
![]() $\mathbb {R}$
-tree, and then by Theorem 3.3,
$\mathbb {R}$
-tree, and then by Theorem 3.3,
![]() $\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
The last result of this section gives our main example of spaces stochastic biLipschitzly embedding into
![]() $\mathbb {R}$
-trees. It follows immediately from Theorem 5.7 and Corollary 5.4, and we omit the proof.
$\mathbb {R}$
-trees. It follows immediately from Theorem 5.7 and Corollary 5.4, and we omit the proof.
Corollary 5.8. Let A be an infinite, uniformly discrete, locally finite, pointed metric space, and let X be a visual, hyperbolic, pointed metric space. If A rough biLipschitzly embeds into X and
![]() $\partial X$
is separable and finite Nagata-dimensional, then A stochastic biLipschitzly embeds into a pointed
$\partial X$
is separable and finite Nagata-dimensional, then A stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree and
$\mathbb {R}$
-tree and
![]() $\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
In the next two sections, we will apply Corollary 5.8 to answer a couple of open questions.
6 The Lipschitz free space over
 $\mathbb {H}^n$
$\mathbb {H}^n$
Our first application of Corollary 5.8 answers [Reference Doucha and Kaufmann23, Question 7] concerning the isomorphism type of the free space over classic hyperbolic n-space
![]() $\mathbb {H}^n$
(Corollary 6.4). We recall the definition and basic properties of this space here, following [Reference Bridson and Haefliger13].
$\mathbb {H}^n$
(Corollary 6.4). We recall the definition and basic properties of this space here, following [Reference Bridson and Haefliger13].
Let
![]() $2 \leq n \in \mathbb {N}$
. Hyperbolic n-space
$2 \leq n \in \mathbb {N}$
. Hyperbolic n-space
![]() $\mathbb {H}^n$
is the unique simply connected, n-dimensional, complete Riemannian manifold with constant sectional curvature
$\mathbb {H}^n$
is the unique simply connected, n-dimensional, complete Riemannian manifold with constant sectional curvature
![]() $-1$
[Reference Bridson and Haefliger13, page 15]. By virtue of being a complete Riemannian manifold, it is proper and geodesic ([Reference Bridson and Haefliger13, Chapter I.3: Proposition 3.7, Corollary 3.20]). The exponential map at every point of
$-1$
[Reference Bridson and Haefliger13, page 15]. By virtue of being a complete Riemannian manifold, it is proper and geodesic ([Reference Bridson and Haefliger13, Chapter I.3: Proposition 3.7, Corollary 3.20]). The exponential map at every point of
![]() $\mathbb {H}^n$
is a diffeomorphism from
$\mathbb {H}^n$
is a diffeomorphism from
![]() $\mathbb {R}^n$
([Reference Bridson and Haefliger13, page 94]), and thus, by homogeneityFootnote 12 of
$\mathbb {R}^n$
([Reference Bridson and Haefliger13, page 94]), and thus, by homogeneityFootnote 12 of
![]() $\mathbb {H}^n$
([Reference Bridson and Haefliger13, Chapter I.2: Proposition 2.17]) and the fact that diffeomorphisms between Riemannian manifolds are biLipschitz on compact subsets, we have, for every
$\mathbb {H}^n$
([Reference Bridson and Haefliger13, Chapter I.2: Proposition 2.17]) and the fact that diffeomorphisms between Riemannian manifolds are biLipschitz on compact subsets, we have, for every
![]() $r<\infty $
, that there exist
$r<\infty $
, that there exist
![]() $L<\infty $
and a ball
$L<\infty $
and a ball
![]() $B \subseteq \mathbb {R}^n$
(equipped with the Euclidean metric) such that for every
$B \subseteq \mathbb {R}^n$
(equipped with the Euclidean metric) such that for every
![]() $x \in \mathbb {H}^n$
, the ball
$x \in \mathbb {H}^n$
, the ball
![]() $B_r(x) \subseteq \mathbb {H}^n$
(equipped with the hyperbolic metric) is biLipschitz equivalent to B with distortion L. Hyperbolic n-space is Gromov hyperbolic ([Reference Bridson and Haefliger13, Chapter III.H: Proposition 1.2]) and visual (this is most easily seen in the Poincaré ball model [Reference Bridson and Haefliger13, Proposition 6.8]). The Gromov boundary admits a visual metric such that
$B_r(x) \subseteq \mathbb {H}^n$
(equipped with the hyperbolic metric) is biLipschitz equivalent to B with distortion L. Hyperbolic n-space is Gromov hyperbolic ([Reference Bridson and Haefliger13, Chapter III.H: Proposition 1.2]) and visual (this is most easily seen in the Poincaré ball model [Reference Bridson and Haefliger13, Proposition 6.8]). The Gromov boundary admits a visual metric such that
![]() $\partial \mathbb {H}^n = S^{n-1}$
isometrically, where the latter space is the
$\partial \mathbb {H}^n = S^{n-1}$
isometrically, where the latter space is the
![]() $(n-1)$
-sphere
$(n-1)$
-sphere
![]() $\{x \in \mathbb {R}^n: \|x\|_2 =1\}$
equipped with (a multiple of) its usual geodesic metric ([Reference Bridson and Haefliger13, page 434]). In particular,
$\{x \in \mathbb {R}^n: \|x\|_2 =1\}$
equipped with (a multiple of) its usual geodesic metric ([Reference Bridson and Haefliger13, page 434]). In particular,
![]() $\partial \mathbb {H}^{n-1}$
is doubling, and thus separable and finite Nagata-dimensional. Because of this, we immediately deduce the following lemma from Corollary 5.8.
$\partial \mathbb {H}^{n-1}$
is doubling, and thus separable and finite Nagata-dimensional. Because of this, we immediately deduce the following lemma from Corollary 5.8.
Lemma 6.1. Let A be an infinite, uniformly discrete, locally finite pointed metric space. If A rough biLipschitzly embeds into
![]() $\mathbb {H}^n$
for some
$\mathbb {H}^n$
for some
![]() $2 \leq n \in \mathbb {N}$
, then A stochastic biLipschitzly embeds into a pointed
$2 \leq n \in \mathbb {N}$
, then A stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree and
$\mathbb {R}$
-tree and
![]() $\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
$\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
.
Finally,
![]() $\mathbb {H}^n$
has finite Nagata dimension [Reference Lang and Schlichenmaier37, Theorem 3.6].
$\mathbb {H}^n$
has finite Nagata dimension [Reference Lang and Schlichenmaier37, Theorem 3.6].
It was recently proved in [Reference Bargetz, Luggin and Russo7] (for
![]() $n=2,3,4$
) that there is a uniformly discrete subset
$n=2,3,4$
) that there is a uniformly discrete subset
![]() $A \subseteq \mathbb {H}^n$
such that
$A \subseteq \mathbb {H}^n$
such that
In Corollary 6.4, we remove the factor of
![]() $\operatorname {\mathrm {LF}}(A)$
and obtain
$\operatorname {\mathrm {LF}}(A)$
and obtain
As a first step toward obtaining (6.2) for every n, we establish isomorphisms of the type (6.1) in the more general setting where
![]() $\mathbb {H}^n$
is replaced by any separable space of finite Nagata dimension and
$\mathbb {H}^n$
is replaced by any separable space of finite Nagata dimension and
![]() $\mathbb {R}^n$
is replaced by a Carnot group. This is the content of Theorem 6.3 (see the paragraph preceding the theorem statement for a discussion on Carnot groups). We will require the following general lemma on finite Nagata-dimensional spaces in the proof of Theorem 6.3.
$\mathbb {R}^n$
is replaced by a Carnot group. This is the content of Theorem 6.3 (see the paragraph preceding the theorem statement for a discussion on Carnot groups). We will require the following general lemma on finite Nagata-dimensional spaces in the proof of Theorem 6.3.
Lemma 6.2. Let
![]() $(X,d)$
be a metric space of finite Nagata dimension. Then there exists
$(X,d)$
be a metric space of finite Nagata dimension. Then there exists
![]() $\lambda <\infty $
such that, for every scale
$\lambda <\infty $
such that, for every scale
![]() $s\in (0,\infty )$
and every maximal s-separated subset
$s\in (0,\infty )$
and every maximal s-separated subset
![]() $A \subseteq X$
, the free space
$A \subseteq X$
, the free space
![]() $\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of the
$\operatorname {\mathrm {LF}}(X)$
is isomorphic to a complemented subspace of the
![]() $\ell ^1$
-sum
$\ell ^1$
-sum
![]() $\left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{\lambda s}(a))\right ) \oplus \operatorname {\mathrm {LF}}(A)$
.
$\left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{\lambda s}(a))\right ) \oplus \operatorname {\mathrm {LF}}(A)$
.
Before proving the lemma, we need to recall the construction of quotient metrics and some results about their Lipschitz free spaces. Following [Reference Weaver48,
![]() $\S$
1.4], if
$\S$
1.4], if
![]() $(X,d)$
is a metric space and
$(X,d)$
is a metric space and
![]() $A \subseteq X$
a closed subset, the quotient set
$A \subseteq X$
a closed subset, the quotient set
![]() $X/A$
is defined by
$X/A$
is defined by
![]() $X/A := X/\sim $
, where
$X/A := X/\sim $
, where
![]() $x\sim y$
if and only if
$x\sim y$
if and only if
![]() $x,y\in A$
or
$x,y\in A$
or
![]() $x=y$
. We denote by
$x=y$
. We denote by
![]() $\pi : X \to X/A$
the canonical projection. We equip
$\pi : X \to X/A$
the canonical projection. We equip
![]() $X/A$
with the quotient metric defined by
$X/A$
with the quotient metric defined by
![]() $\rho (\pi (x),\pi (y)):=\min \{d(x,y),\operatorname {\mathrm {dist}}(E,x)+\operatorname {\mathrm {dist}}(E,y)\}$
(which is obviously well-defined on equivalence classes). The metric
$\rho (\pi (x),\pi (y)):=\min \{d(x,y),\operatorname {\mathrm {dist}}(E,x)+\operatorname {\mathrm {dist}}(E,y)\}$
(which is obviously well-defined on equivalence classes). The metric
![]() $\rho $
is the largest metric on
$\rho $
is the largest metric on
![]() $X/A$
such that
$X/A$
such that
![]() $\pi : X \to X/A$
is 1-Lipschitz. Whenever X is pointed and A contains the basepoint, we equip
$\pi : X \to X/A$
is 1-Lipschitz. Whenever X is pointed and A contains the basepoint, we equip
![]() $X/A$
with basepoint
$X/A$
with basepoint
![]() $\pi (A)$
. There is a weak
$\pi (A)$
. There is a weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
-continuous, surjective linear isometry from
$^*$
-continuous, surjective linear isometry from
![]() $\operatorname {\mathrm {Lip}}_0(X/A)$
(which equals
$\operatorname {\mathrm {Lip}}_0(X/A)$
(which equals
![]() $\operatorname {\mathrm {LF}}(X/A)^*$
) to the weak
$\operatorname {\mathrm {LF}}(X/A)^*$
) to the weak
![]() $^*$
-closed subspace
$^*$
-closed subspace
![]() $\operatorname {\mathrm {Lip}}_A(X) := \{f\in \operatorname {\mathrm {Lip}}_0(X): f(A) = \{0\}\}$
given by
$\operatorname {\mathrm {Lip}}_A(X) := \{f\in \operatorname {\mathrm {Lip}}_0(X): f(A) = \{0\}\}$
given by
![]() $g \mapsto g \circ \pi $
. Whenever
$g \mapsto g \circ \pi $
. Whenever
![]() $A \subseteq X$
has finite Nagata dimension (say, dimension
$A \subseteq X$
has finite Nagata dimension (say, dimension
![]() $n\in \mathbb {N}$
with constant
$n\in \mathbb {N}$
with constant
![]() $\gamma <\infty $
), it holds that
$\gamma <\infty $
), it holds that
![]() $\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(X/A)$
, where the isomorphism constant depends only on
$\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(X/A)$
, where the isomorphism constant depends only on
![]() $n,\gamma $
(e.g., [Reference Freeman and Gartland28, Lemma 3.2]). In particular, if X has finite Nagata dimension, then the isomorphism
$n,\gamma $
(e.g., [Reference Freeman and Gartland28, Lemma 3.2]). In particular, if X has finite Nagata dimension, then the isomorphism
![]() $\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(X/A)$
holds for every closed
$\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(X/A)$
holds for every closed
![]() $A \subseteq X$
, with isomorphism constant independent of A.
$A \subseteq X$
, with isomorphism constant independent of A.
Proof of Lemma 6.2.
Suppose X has Nagata dimension
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $s\in (0,\infty )$
be a scale and
$s\in (0,\infty )$
be a scale and
![]() $A \subseteq X$
a maximal s-separated subset. For this paragraph, let
$A \subseteq X$
a maximal s-separated subset. For this paragraph, let
![]() $\lambda $
denote an arbitrary constant in
$\lambda $
denote an arbitrary constant in
![]() $(0,\infty )$
. It will be chosen specifically later in the proof (independent of s). Since
$(0,\infty )$
. It will be chosen specifically later in the proof (independent of s). Since
![]() $\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(X/A)$
and
$\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(X/A)$
and
![]() $\operatorname {\mathrm {LF}}(B_{\lambda s}(a)) \approx \operatorname {\mathrm {LF}}(B_{\lambda s}(a) \cap A) \oplus \operatorname {\mathrm {LF}}(B_{\lambda s}(a)/(B_{\lambda s}(a) \cap A))$
for every
$\operatorname {\mathrm {LF}}(B_{\lambda s}(a)) \approx \operatorname {\mathrm {LF}}(B_{\lambda s}(a) \cap A) \oplus \operatorname {\mathrm {LF}}(B_{\lambda s}(a)/(B_{\lambda s}(a) \cap A))$
for every
![]() $a \in A$
(with isomorphism constants independent of
$a \in A$
(with isomorphism constants independent of
![]() $\lambda ,s,a$
– see preceding discussion), it suffices to show that
$\lambda ,s,a$
– see preceding discussion), it suffices to show that
![]() $\operatorname {\mathrm {LF}}(X/A) \overset {\mathrm {c}}{\hookrightarrow } \oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{\lambda s}(a)/(B_{\lambda s}(a) \cap A))$
. We will achieve this by constructing bounded, weak
$\operatorname {\mathrm {LF}}(X/A) \overset {\mathrm {c}}{\hookrightarrow } \oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_{\lambda s}(a)/(B_{\lambda s}(a) \cap A))$
. We will achieve this by constructing bounded, weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
-continuous linear maps
$^*$
-continuous linear maps
![]() $\operatorname {\mathrm {Lip}}_A(X) \overset {R}{\to } \oplus _{a\in A}^\infty \operatorname {\mathrm {Lip}}_{B_{\lambda s}(a) \cap A}(B_{\lambda s}(a)) \overset {T}{\to } \operatorname {\mathrm {Lip}}_A(X)$
such that
$\operatorname {\mathrm {Lip}}_A(X) \overset {R}{\to } \oplus _{a\in A}^\infty \operatorname {\mathrm {Lip}}_{B_{\lambda s}(a) \cap A}(B_{\lambda s}(a)) \overset {T}{\to } \operatorname {\mathrm {Lip}}_A(X)$
such that
![]() $T \circ R = id_{\operatorname {\mathrm {Lip}}_A(X)}$
, where the middle Banach space in this sequence is an
$T \circ R = id_{\operatorname {\mathrm {Lip}}_A(X)}$
, where the middle Banach space in this sequence is an
![]() $\ell ^\infty $
-sum. The map R is simply a sum of restriction maps:
$\ell ^\infty $
-sum. The map R is simply a sum of restriction maps:
![]() $R(f)_a := f\big |_{B_{\lambda s}(a)}$
. We will use a special Nagata covering and associated Lipschitz partition of unity to construct the retraction T of R.
$R(f)_a := f\big |_{B_{\lambda s}(a)}$
. We will use a special Nagata covering and associated Lipschitz partition of unity to construct the retraction T of R.
By [Reference Lang and Schlichenmaier37, Proposition 4.1(i)(ii)], there is a constant
![]() $\gamma <\infty $
(independent of s) such that X admits a Nagata cover
$\gamma <\infty $
(independent of s) such that X admits a Nagata cover
![]() $\{B_j\}_{j \in J}$
of dimension n, constant
$\{B_j\}_{j \in J}$
of dimension n, constant
![]() $\gamma $
, and scale s, and with the additional property that for every
$\gamma $
, and scale s, and with the additional property that for every
![]() $x\in X$
, there exists an index
$x\in X$
, there exists an index
![]() $j \in J$
such that
$j \in J$
such that
![]() $B_{s}(x) \subseteq B_{j}$
. For each
$B_{s}(x) \subseteq B_{j}$
. For each
![]() $a \in A$
, choose
$a \in A$
, choose
![]() $j_a \in J$
such that
$j_a \in J$
such that
![]() $B_s(a) \subseteq B_{j_a}$
. By this containment and maximality of A, the collection
$B_s(a) \subseteq B_{j_a}$
. By this containment and maximality of A, the collection
![]() $\{B_{j_a}\}_{a\in A}$
covers X. We repeat the construction used in the proof of Lemma 4.13. For each
$\{B_{j_a}\}_{a\in A}$
covers X. We repeat the construction used in the proof of Lemma 4.13. For each
![]() $a \in A$
, define
$a \in A$
, define
![]() $\varphi _a: X \to [0,1]$
by
$\varphi _a: X \to [0,1]$
by
![]() $\varphi _a(x) := \max \{0,1-2s^{-1}\operatorname {\mathrm {dist}}(B_{j_a},x)\}$
. As in the proof of Lemma 4.13, it holds that, for every
$\varphi _a(x) := \max \{0,1-2s^{-1}\operatorname {\mathrm {dist}}(B_{j_a},x)\}$
. As in the proof of Lemma 4.13, it holds that, for every
![]() $x\in X$
,
$x\in X$
,
-
○
 $\operatorname {\mathrm {Lip}}(\varphi _a) \leq 2s^{-1}$
for every a and
$\operatorname {\mathrm {Lip}}(\varphi _a) \leq 2s^{-1}$
for every a and -
○
 $\varphi _a(x) \neq 0$
for at most
$\varphi _a(x) \neq 0$
for at most
 $n+1$
values of a,
$n+1$
values of a,
and additionally, since
![]() $\{B_{j_a}\}_{a\in A}$
covers X,
$\{B_{j_a}\}_{a\in A}$
covers X,
-
○ there exists
 $a \in A$
with
$a \in A$
with
 $\varphi _a(x) = 1$
.
$\varphi _a(x) = 1$
.
Furthermore, for any
![]() $a \in A$
, since
$a \in A$
, since
![]() $a \in B_{j_a}$
and
$a \in B_{j_a}$
and
![]() $\operatorname {\mathrm {diam}}(B_{j_a}) \leq \gamma s$
, for any
$\operatorname {\mathrm {diam}}(B_{j_a}) \leq \gamma s$
, for any
![]() $x \in X$
with
$x \in X$
with
![]() $\varphi _a(x) \neq 0$
, it holds that
$\varphi _a(x) \neq 0$
, it holds that
![]() $d(a,x) \leq \operatorname {\mathrm {diam}}(B_{j_a}) + \operatorname {\mathrm {dist}}(B_{j_a},x) < \gamma s + \frac {s}{2} = (\gamma +\frac {1}{2})s$
. Thus,
$d(a,x) \leq \operatorname {\mathrm {diam}}(B_{j_a}) + \operatorname {\mathrm {dist}}(B_{j_a},x) < \gamma s + \frac {s}{2} = (\gamma +\frac {1}{2})s$
. Thus,
-
○
 $\operatorname {\mathrm {supp}}(\varphi _a) = \varphi _a^{-1}((0,1]) \subseteq B_{\lambda s}(a)$
, where
$\operatorname {\mathrm {supp}}(\varphi _a) = \varphi _a^{-1}((0,1]) \subseteq B_{\lambda s}(a)$
, where
 $\lambda := \gamma +\frac {1}{2}$
.
$\lambda := \gamma +\frac {1}{2}$
.
Together, these items imply that the functions
![]() $\{\psi _a: X \to \mathbb {R}\}_{a\in A}$
defined by
$\{\psi _a: X \to \mathbb {R}\}_{a\in A}$
defined by
are well-defined and satisfy, for every
![]() $a \in A$
,
$a \in A$
,
-
○
 $\psi _a(X) \subseteq [0,1]$
,
$\psi _a(X) \subseteq [0,1]$
, -
○
 $\operatorname {\mathrm {supp}}(\psi _a) \subseteq B_{\lambda s}(a)$
,
$\operatorname {\mathrm {supp}}(\psi _a) \subseteq B_{\lambda s}(a)$
, -
○
 $\operatorname {\mathrm {Lip}}(\psi _a) \leq Cs^{-1}$
, where C depends only on n, and
$\operatorname {\mathrm {Lip}}(\psi _a) \leq Cs^{-1}$
, where C depends only on n, and -
○
 $\sum _{a\in A}\psi _a \equiv 1$
.
$\sum _{a\in A}\psi _a \equiv 1$
.
Also, as for
![]() $\varphi _a$
,
$\varphi _a$
,
-
○ for each
 $x \in X$
, the set
$x \in X$
, the set
 $A_x := \{a \in A: \psi _a(x) \neq 0\}$
has cardinality at most
$A_x := \{a \in A: \psi _a(x) \neq 0\}$
has cardinality at most
 $n+1$
.
$n+1$
.
Now we define our operator T. Given
![]() $(f_a)_{a\in A} \in \oplus ^\infty _{a \in A}\operatorname {\mathrm {Lip}}_{B_{\lambda s}(a) \cap A}(B_{\lambda s}(a))$
, define
$(f_a)_{a\in A} \in \oplus ^\infty _{a \in A}\operatorname {\mathrm {Lip}}_{B_{\lambda s}(a) \cap A}(B_{\lambda s}(a))$
, define
![]() $T((f_a)_a): X \to \mathbb {R}$
by
$T((f_a)_a): X \to \mathbb {R}$
by
where we interpret the product
![]() $\psi _a(x)f_a(x)$
as 0 if
$\psi _a(x)f_a(x)$
as 0 if
![]() $x \notin B_{\lambda s}(a)$
. It is clear that
$x \notin B_{\lambda s}(a)$
. It is clear that
![]() $T((f_a)_a)$
vanishes on A. We will verify that
$T((f_a)_a)$
vanishes on A. We will verify that
![]() $T((f_a)_a)$
is Lipschitz and bound the operator norm of T. Once this has been established, it is clear that T is a weak
$T((f_a)_a)$
is Lipschitz and bound the operator norm of T. Once this has been established, it is clear that T is a weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
-continuous bounded linear map and that
$^*$
-continuous bounded linear map and that
![]() $T \circ R = id_{\operatorname {\mathrm {Lip}}_A(X)}$
since
$T \circ R = id_{\operatorname {\mathrm {Lip}}_A(X)}$
since
![]() $\sum _{a\in A} \psi _a \equiv 1$
.
$\sum _{a\in A} \psi _a \equiv 1$
.
Note that
![]() $\|f_a\|_{L^\infty (B_{\lambda s}(a))} \leq \operatorname {\mathrm {Lip}}(f_a)\lambda s$
since
$\|f_a\|_{L^\infty (B_{\lambda s}(a))} \leq \operatorname {\mathrm {Lip}}(f_a)\lambda s$
since
![]() $f_a(a) = 0$
. By the Lipschitz Leibniz rule, for each
$f_a(a) = 0$
. By the Lipschitz Leibniz rule, for each
![]() $a \in A$
, we have
$a \in A$
, we have
 $$ \begin{align*} \operatorname{\mathrm{Lip}}(\psi_a f_a) &\leq \|\psi_a\|_\infty\operatorname{\mathrm{Lip}}(f_a) + \operatorname{\mathrm{Lip}}(\psi_a)\|f_a\|_{L^\infty(B_{\lambda s}(a))} \\ &\leq \operatorname{\mathrm{Lip}}(f_a) + Cs^{-1}\operatorname{\mathrm{Lip}}(f_a)\lambda s \\ &= (1+C\lambda)\operatorname{\mathrm{Lip}}(f_a). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Lip}}(\psi_a f_a) &\leq \|\psi_a\|_\infty\operatorname{\mathrm{Lip}}(f_a) + \operatorname{\mathrm{Lip}}(\psi_a)\|f_a\|_{L^\infty(B_{\lambda s}(a))} \\ &\leq \operatorname{\mathrm{Lip}}(f_a) + Cs^{-1}\operatorname{\mathrm{Lip}}(f_a)\lambda s \\ &= (1+C\lambda)\operatorname{\mathrm{Lip}}(f_a). \end{align*} $$
Using this, we get, for every
![]() $x,y \in X$
,
$x,y \in X$
,
 $$ \begin{align*} |T((f_a)_a)(x) - T((f_a)_a)(y)| &= \left|\sum_{a\in A}\psi_a(x)f_a(x)-\sum_{a\in A}\psi_a(y)f_a(y)\right| \\ &\leq \sum_{a\in A_x \cup A_y}|\psi_a(x)f_a(x)-\psi_a(y)f_a(y)| \\ &\leq 2(n+1)(1+C\lambda)\sup_{a\in A}\operatorname{\mathrm{Lip}}(f_a)d(x,y).\\[-38pt] \end{align*} $$
$$ \begin{align*} |T((f_a)_a)(x) - T((f_a)_a)(y)| &= \left|\sum_{a\in A}\psi_a(x)f_a(x)-\sum_{a\in A}\psi_a(y)f_a(y)\right| \\ &\leq \sum_{a\in A_x \cup A_y}|\psi_a(x)f_a(x)-\psi_a(y)f_a(y)| \\ &\leq 2(n+1)(1+C\lambda)\sup_{a\in A}\operatorname{\mathrm{Lip}}(f_a)d(x,y).\\[-38pt] \end{align*} $$
A (subRiemannian) Carnot group is a special type of nilpotent Lie group equipped with a left-invariant subRiemannian metric, which is, in general, not Riemannian. Carnot groups are always complete and doubling. In particular, they are separable with finite Nagata dimension. The abelian examples are exactly the Euclidean spaces
![]() $\mathbb {R}^n$
equipped with an inner product. See [Reference Albiac, Ansorena, Cúth and Doucha1, page 7306] and [Reference Le Donne38] for further background. For us, the relevant free-space-theoretic features of a Carnot group G – due to Albiac, Ansorena, Cúth and Doucha – are that
$\mathbb {R}^n$
equipped with an inner product. See [Reference Albiac, Ansorena, Cúth and Doucha1, page 7306] and [Reference Le Donne38] for further background. For us, the relevant free-space-theoretic features of a Carnot group G – due to Albiac, Ansorena, Cúth and Doucha – are that
![]() $\operatorname {\mathrm {LF}}(G)$
is isomorphic to its countable
$\operatorname {\mathrm {LF}}(G)$
is isomorphic to its countable
![]() $\ell ^1$
-sum
$\ell ^1$
-sum
![]() $\oplus ^1_{n\in \mathbb {N}} \operatorname {\mathrm {LF}}(G)$
([Reference Albiac, Ansorena, Cúth and Doucha1, Corollaries 5.5, 5.6]) and
$\oplus ^1_{n\in \mathbb {N}} \operatorname {\mathrm {LF}}(G)$
([Reference Albiac, Ansorena, Cúth and Doucha1, Corollaries 5.5, 5.6]) and
![]() $\operatorname {\mathrm {LF}}(U) \approx \operatorname {\mathrm {LF}}(G)$
whenever
$\operatorname {\mathrm {LF}}(U) \approx \operatorname {\mathrm {LF}}(G)$
whenever
![]() $U \subseteq G$
is nonempty and open ([Reference Albiac, Ansorena, Cúth and Doucha1, Corollary 5.6]). We will use these features in the proof of the next theorem.
$U \subseteq G$
is nonempty and open ([Reference Albiac, Ansorena, Cúth and Doucha1, Corollary 5.6]). We will use these features in the proof of the next theorem.
Theorem 6.3. Let
![]() $(X,d)$
be a finite Nagata-dimensional metric space and G a Carnot group. Then the following statements hold.
$(X,d)$
be a finite Nagata-dimensional metric space and G a Carnot group. Then the following statements hold.
-
(1) If there exists a nonempty open subset of G that biLipschitzly embeds into X, then for any nonempty uniformly discrete subset
 $A \subseteq X$
,
$A \subseteq X$
,
 $\operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(G) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(X)$
.
$\operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(G) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(X)$
. -
(2) If X is separable and if there exist a constant
 $L<\infty $
and scale
$L<\infty $
and scale
 $t> 0$
such that
$t> 0$
such that
 $B_t(x)$
biLipschitzly embeds with distortion L into G for every
$B_t(x)$
biLipschitzly embeds with distortion L into G for every
 $x \in X$
, then there is a uniformly discrete subset
$x \in X$
, then there is a uniformly discrete subset
 $A \subseteq X$
such that
$A \subseteq X$
such that
 $\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(G)$
.
$\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(G)$
. -
(3) If (1) and (2) hold, and if
 $\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(G)$
for every nonempty uniformly discrete
$\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(G)$
for every nonempty uniformly discrete
 $A \subseteq X$
, then
$A \subseteq X$
, then
 $\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(G)$
.
$\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(G)$
.
Proof. For item (1), assume that a nonempty open subset
![]() $U \subseteq G$
biLipschitzly embeds into X, and let
$U \subseteq G$
biLipschitzly embeds into X, and let
![]() $A \subseteq X$
be a
$A \subseteq X$
be a
![]() $\theta $
-separated nonempty subset for some
$\theta $
-separated nonempty subset for some
![]() $\theta>0$
. By restricting the embedding
$\theta>0$
. By restricting the embedding
![]() $f: U \to X$
to an even smaller open subset, we may assume that
$f: U \to X$
to an even smaller open subset, we may assume that
![]() $\operatorname {\mathrm {diam}}(f(U)) \leq \theta /3$
. Then it must hold that
$\operatorname {\mathrm {diam}}(f(U)) \leq \theta /3$
. Then it must hold that
![]() $\operatorname {\mathrm {dist}}(f(U),A\setminus \{a_0\}) \geq \theta /3$
for some
$\operatorname {\mathrm {dist}}(f(U),A\setminus \{a_0\}) \geq \theta /3$
for some
![]() $a_0 \in A$
. Choose a basepoint
$a_0 \in A$
. Choose a basepoint
![]() $x_0 \in f(U)$
, and consider the new
$x_0 \in f(U)$
, and consider the new
![]() $\theta /3$
-separated set
$\theta /3$
-separated set
![]() $A' := (A \setminus \{a_0\}) \cup \{x_0\}$
equipped with basepoint
$A' := (A \setminus \{a_0\}) \cup \{x_0\}$
equipped with basepoint
![]() $x_0$
. It holds that
$x_0$
. It holds that
![]() $f(U) \cap A' = \{x_0\}$
and, for any
$f(U) \cap A' = \{x_0\}$
and, for any
![]() $x \in f(U)$
and
$x \in f(U)$
and
![]() $y \in A'$
,
$y \in A'$
,
![]() $d(x,x_0) + d(x_0,y) \leq 3d(x,y)$
. Hence, by [Reference Kaufmann34, Proposition 5.1],
$d(x,x_0) + d(x_0,y) \leq 3d(x,y)$
. Hence, by [Reference Kaufmann34, Proposition 5.1],
Furthermore, since
![]() $A \setminus \{a_0\} \subseteq A,A'$
and
$A \setminus \{a_0\} \subseteq A,A'$
and
![]() $|A \setminus (A \setminus \{a_0\})| = 1 = |A' \setminus (A \setminus \{a_0\})|$
, it follows that
$|A \setminus (A \setminus \{a_0\})| = 1 = |A' \setminus (A \setminus \{a_0\})|$
, it follows that
Then, since
![]() $\operatorname {\mathrm {LF}}(f(U)) \approx \operatorname {\mathrm {LF}}(U) \approx \operatorname {\mathrm {LF}}(G)$
, we can combine this with the previous two isomorphisms and obtain
$\operatorname {\mathrm {LF}}(f(U)) \approx \operatorname {\mathrm {LF}}(U) \approx \operatorname {\mathrm {LF}}(G)$
, we can combine this with the previous two isomorphisms and obtain
Finally, since
![]() $\operatorname {\mathrm {LF}}(f(U) \cup A') \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(X)$
(because X has finite Nagata dimension), item (1) is proved.
$\operatorname {\mathrm {LF}}(f(U) \cup A') \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(X)$
(because X has finite Nagata dimension), item (1) is proved.
For item (2), assume that X is separable and that there exist a constant
![]() $L<\infty $
and scale
$L<\infty $
and scale
![]() $t> 0$
such that
$t> 0$
such that
![]() $B_t(x)$
biLipschitzly embeds with distortion L into G for every
$B_t(x)$
biLipschitzly embeds with distortion L into G for every
![]() $x \in X$
. Let
$x \in X$
. Let
![]() $\lambda <\infty $
be the constant appearing in the conclusion of Lemma 6.2, and set
$\lambda <\infty $
be the constant appearing in the conclusion of Lemma 6.2, and set
![]() $s := t/\lambda $
. By Lemma 6.2, we have that
$s := t/\lambda $
. By Lemma 6.2, we have that
![]() $\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_t(a))\right ) \oplus \operatorname {\mathrm {LF}}(A)$
, where
$\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \left (\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_t(a))\right ) \oplus \operatorname {\mathrm {LF}}(A)$
, where
![]() $A \subseteq X$
is an s-separated subset. Then A must be countable since it is uniformly discrete and X is separable. Since each ball
$A \subseteq X$
is an s-separated subset. Then A must be countable since it is uniformly discrete and X is separable. Since each ball
![]() $B_t(a)$
biLipschitzly embeds into G with distortion L, and since G has finite Nagata dimension (since it is doubling), we have that
$B_t(a)$
biLipschitzly embeds into G with distortion L, and since G has finite Nagata dimension (since it is doubling), we have that
![]() $B_t(a)$
is L-isomorphic to a C-complemented subspace of
$B_t(a)$
is L-isomorphic to a C-complemented subspace of
![]() $\operatorname {\mathrm {LF}}(G)$
, where C does not depend on a. Then
$\operatorname {\mathrm {LF}}(G)$
, where C does not depend on a. Then
![]() $\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_t(a)) \overset {\mathrm {c}}{\hookrightarrow } \oplus ^1_{n\in \mathbb {N}} \operatorname {\mathrm {LF}}(G)$
, and this latter space is itself isomorphic to
$\oplus ^1_{a\in A}\operatorname {\mathrm {LF}}(B_t(a)) \overset {\mathrm {c}}{\hookrightarrow } \oplus ^1_{n\in \mathbb {N}} \operatorname {\mathrm {LF}}(G)$
, and this latter space is itself isomorphic to
![]() $\operatorname {\mathrm {LF}}(G)$
. This completes the proof of item (2).
$\operatorname {\mathrm {LF}}(G)$
. This completes the proof of item (2).
For item (3), assume that (1) and (2) hold and that
![]() $\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(G)$
for every uniformly discrete
$\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(G)$
for every uniformly discrete
![]() $A \subseteq X$
. Let
$A \subseteq X$
. Let
![]() $A \subseteq X$
be the uniformly discrete subset given by item (2). Then since
$A \subseteq X$
be the uniformly discrete subset given by item (2). Then since
![]() $\operatorname {\mathrm {LF}}(G) \approx \oplus _{n\in \mathbb {N}}^1 \operatorname {\mathrm {LF}}(G)$
, the Pełczyński decomposition method implies
$\operatorname {\mathrm {LF}}(G) \approx \oplus _{n\in \mathbb {N}}^1 \operatorname {\mathrm {LF}}(G)$
, the Pełczyński decomposition method implies
![]() $\operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(G) \approx \operatorname {\mathrm {LF}}(G)$
. Therefore, we have by items (1) and (2) that
$\operatorname {\mathrm {LF}}(A) \oplus \operatorname {\mathrm {LF}}(G) \approx \operatorname {\mathrm {LF}}(G)$
. Therefore, we have by items (1) and (2) that
![]() $\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(G) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(X)$
, and so another application of the Pełczyński decomposition method yields
$\operatorname {\mathrm {LF}}(X) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(G) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(X)$
, and so another application of the Pełczyński decomposition method yields
![]() $\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(G)$
.
$\operatorname {\mathrm {LF}}(X) \approx \operatorname {\mathrm {LF}}(G)$
.
Combining the preceding results yields the main result of this section, which proves Theorem D.
Corollary 6.4.
![]() $\operatorname {\mathrm {LF}}(\mathbb {H}^n) \approx \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
.
$\operatorname {\mathrm {LF}}(\mathbb {H}^n) \approx \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
.
Proof. We will show that the hypotheses of all three items of Theorem 6.3 are satisfied with
![]() $X = \mathbb {H}^n$
and
$X = \mathbb {H}^n$
and
![]() $G = \mathbb {R}^n$
. Indeed, the hypotheses of items (1) and (2) are satisfied by virtue of the fact that
$G = \mathbb {R}^n$
. Indeed, the hypotheses of items (1) and (2) are satisfied by virtue of the fact that
![]() $\mathbb {H}^n$
is a homogeneous n-dimensional Riemannian manifold. It remains to show that
$\mathbb {H}^n$
is a homogeneous n-dimensional Riemannian manifold. It remains to show that
![]() $\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
for every uniformly discrete subset
$\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
for every uniformly discrete subset
![]() $A \subseteq \mathbb {H}^n$
.
$A \subseteq \mathbb {H}^n$
.
Let
![]() $A \subseteq \mathbb {H}^n$
be uniformly discrete. Then A is locally finite since
$A \subseteq \mathbb {H}^n$
be uniformly discrete. Then A is locally finite since
![]() $\mathbb {H}^n$
is proper. If A is finite, then
$\mathbb {H}^n$
is proper. If A is finite, then
![]() $\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } V$
for every infinite dimensional Banach space V, so we may assume that A is infinite. Then by Lemma 6.1, we have
$\operatorname {\mathrm {LF}}(A) \overset {\mathrm {c}}{\hookrightarrow } V$
for every infinite dimensional Banach space V, so we may assume that A is infinite. Then by Lemma 6.1, we have
![]() $\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
. By [Reference Cúth, Doucha and Wojtaszczyk19, Theorem 1.1(i)],
$\operatorname {\mathrm {LF}}(A) \approx \ell ^1$
. By [Reference Cúth, Doucha and Wojtaszczyk19, Theorem 1.1(i)],
![]() $\ell ^1 \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
, completing the proof.
$\ell ^1 \overset {\mathrm {c}}{\hookrightarrow } \operatorname {\mathrm {LF}}(\mathbb {R}^n)$
, completing the proof.
7 Uniformly Lipschitz affine actions on
 $\ell ^1$
$\ell ^1$
As a second application of Corollary 5.8, we obtain, for every hyperbolic group, a proper, uniformly Lipschitz affine action on
![]() $\ell ^1$
. This generalizes a recent result of Druţu-Mackay [Reference Druţu and Mackay25, Theorem 1.6] (albeit without control on the Lipschitz constant of the action), which asserts the same conclusion under the additional assumption that the hyperbolic group is residually finite.Footnote 13 See also the recent work of Vergara [Reference Vergara47] where it is proved that every finitely generated hyperbolic group admits a proper, uniformly Lipschitz affine action on a subspace of
$\ell ^1$
. This generalizes a recent result of Druţu-Mackay [Reference Druţu and Mackay25, Theorem 1.6] (albeit without control on the Lipschitz constant of the action), which asserts the same conclusion under the additional assumption that the hyperbolic group is residually finite.Footnote 13 See also the recent work of Vergara [Reference Vergara47] where it is proved that every finitely generated hyperbolic group admits a proper, uniformly Lipschitz affine action on a subspace of
![]() $L^1$
. As explained in
$L^1$
. As explained in
![]() $\S $
1.1, this line of research is inspired by a conjecture of Shalom ([Reference Cherix17, Open Problem 14], [Reference Nowak43, Conjecture 35]).
$\S $
1.1, this line of research is inspired by a conjecture of Shalom ([Reference Cherix17, Open Problem 14], [Reference Nowak43, Conjecture 35]).
Lemma 7.1. Every infinite, finitely generated hyperbolic group stochastic biLipschitzly embeds into a pointed
![]() $\mathbb {R}$
-tree and has free space isomorphic to
$\mathbb {R}$
-tree and has free space isomorphic to
![]() $\ell ^1$
.
$\ell ^1$
.
Proof. Let
![]() $\Gamma $
be an infinite, finitely generated hyperbolic group. Then
$\Gamma $
be an infinite, finitely generated hyperbolic group. Then
![]() $\Gamma $
is uniformly discrete, and locally finite, and admits a rough biLipschitz embedding into
$\Gamma $
is uniformly discrete, and locally finite, and admits a rough biLipschitz embedding into
![]() $\mathbb {H}^n$
for some
$\mathbb {H}^n$
for some
![]() $2 \leq n \in \mathbb {N}$
by [Reference Bonk and Schramm12, Embedding Theorem 1.1]. Then the conclusion follows from Lemma 6.1.
$2 \leq n \in \mathbb {N}$
by [Reference Bonk and Schramm12, Embedding Theorem 1.1]. Then the conclusion follows from Lemma 6.1.
The last result of this article proves Theorem E.
Theorem 7.2. For every infinite hyperbolic group
![]() $\Gamma $
and finite generating set
$\Gamma $
and finite generating set
![]() $S \subseteq \Gamma $
, there exists an isometric affine action
$S \subseteq \Gamma $
, there exists an isometric affine action
![]() $\alpha $
of
$\alpha $
of
![]() $\Gamma $
on a Banach space V isomorphic to
$\Gamma $
on a Banach space V isomorphic to
![]() $\ell ^1$
such that the orbit map
$\ell ^1$
such that the orbit map
![]() $\gamma \mapsto \alpha (\gamma )(0)$
is an isometric embedding
$\gamma \mapsto \alpha (\gamma )(0)$
is an isometric embedding
![]() $\Gamma \hookrightarrow V$
(with respect to the S-word metric). In particular, every hyperbolic group admits a proper, uniformly Lipschitz affine action on
$\Gamma \hookrightarrow V$
(with respect to the S-word metric). In particular, every hyperbolic group admits a proper, uniformly Lipschitz affine action on
![]() $\ell ^1$
.
$\ell ^1$
.
Proof. Let
![]() $\Gamma $
be an infinite hyperbolic group with finite generating set
$\Gamma $
be an infinite hyperbolic group with finite generating set
![]() $S \subseteq \Gamma $
. We consider
$S \subseteq \Gamma $
. We consider
![]() $\Gamma $
as a pointed metric space with the left-invariant S-word metric and basepoint the identity element
$\Gamma $
as a pointed metric space with the left-invariant S-word metric and basepoint the identity element
![]() $1 \in \Gamma $
. By Lemma 7.1,
$1 \in \Gamma $
. By Lemma 7.1,
![]() $\operatorname {\mathrm {LF}}(\Gamma ) \approx \ell ^1$
. We will show that
$\operatorname {\mathrm {LF}}(\Gamma ) \approx \ell ^1$
. We will show that
![]() $V=\operatorname {\mathrm {LF}}(\Gamma )$
satisfies remaining properties.
$V=\operatorname {\mathrm {LF}}(\Gamma )$
satisfies remaining properties.
There is a natural affine isometric action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\operatorname {\mathrm {LF}}(\Gamma )$
, which is essentially due to the fact that
$\operatorname {\mathrm {LF}}(\Gamma )$
, which is essentially due to the fact that
![]() $X \mapsto \operatorname {\mathrm {LF}}(X)$
is functorial. Indeed, let W be the linear subspace spanned by
$X \mapsto \operatorname {\mathrm {LF}}(X)$
is functorial. Indeed, let W be the linear subspace spanned by
![]() $\{\delta _\gamma \}_{\gamma \in \Gamma } \subseteq \operatorname {\mathrm {LF}}(\Gamma ) \subseteq \operatorname {\mathrm {Lip}}_0(\Gamma )^*$
. Since W is dense in
$\{\delta _\gamma \}_{\gamma \in \Gamma } \subseteq \operatorname {\mathrm {LF}}(\Gamma ) \subseteq \operatorname {\mathrm {Lip}}_0(\Gamma )^*$
. Since W is dense in
![]() $\operatorname {\mathrm {LF}}(X)$
, it suffices to produce the affine isometric action on W. We define
$\operatorname {\mathrm {LF}}(X)$
, it suffices to produce the affine isometric action on W. We define
![]() $\alpha : \Gamma \times W \to W$
by
$\alpha : \Gamma \times W \to W$
by
![]() $\alpha (\gamma )\left (\sum _{\gamma '} c_{\gamma '}\delta _{\gamma '}\right ) := \sum _{\gamma '} c_{\gamma '}(\delta _{\gamma \gamma '}-\delta _\gamma ) + \delta _\gamma $
. The map
$\alpha (\gamma )\left (\sum _{\gamma '} c_{\gamma '}\delta _{\gamma '}\right ) := \sum _{\gamma '} c_{\gamma '}(\delta _{\gamma \gamma '}-\delta _\gamma ) + \delta _\gamma $
. The map
![]() $\alpha (\gamma ): W \to W$
is well-defined since
$\alpha (\gamma ): W \to W$
is well-defined since
![]() $\delta _1 = 0$
and
$\delta _1 = 0$
and
![]() $\{\delta _{\gamma '}\}_{\gamma '\neq 1}$
is linearly independent. It is also clearly affine and satisfies
$\{\delta _{\gamma '}\}_{\gamma '\neq 1}$
is linearly independent. It is also clearly affine and satisfies
![]() $\alpha (\delta _1) = id_W$
since
$\alpha (\delta _1) = id_W$
since
![]() $\delta _1 = 0$
. To check the associativity property, let
$\delta _1 = 0$
. To check the associativity property, let
![]() $\gamma _1,\gamma _2 \in \Gamma $
and
$\gamma _1,\gamma _2 \in \Gamma $
and
![]() $\sum _{\gamma '} c_{\gamma '}\delta _{\gamma '} \in W$
. Then we have
$\sum _{\gamma '} c_{\gamma '}\delta _{\gamma '} \in W$
. Then we have
 $$ \begin{align*} \alpha(\gamma_1)\alpha(\gamma_2)\left(\sum_{\gamma'} c_{\gamma'}\delta_{\gamma'}\right) &= \alpha(\gamma_1)\left(\sum_{\gamma'} c_{\gamma'}(\delta_{\gamma_2\gamma'}-\delta_{\gamma_2}) + \delta_{\gamma_2}\right) \\ &= \left(\sum_{\gamma'} c_{\gamma'}(\delta_{\gamma_1\gamma_2\gamma'}-\delta_{\gamma_1\gamma_2}) + (\delta_{\gamma_1\gamma_2} - \delta_{\gamma_1})\right) + \delta_{\gamma_1} \\ &= \sum_{\gamma'} c_{\gamma'}(\delta_{\gamma_1\gamma_2\gamma'}-\delta_{\gamma_1\gamma_2}) + \delta_{\gamma_1\gamma_2} \\ &= \alpha(\gamma_1\gamma_2)\left(\sum_{\gamma'} c_{\gamma'}\delta_{\gamma'}\right). \end{align*} $$
$$ \begin{align*} \alpha(\gamma_1)\alpha(\gamma_2)\left(\sum_{\gamma'} c_{\gamma'}\delta_{\gamma'}\right) &= \alpha(\gamma_1)\left(\sum_{\gamma'} c_{\gamma'}(\delta_{\gamma_2\gamma'}-\delta_{\gamma_2}) + \delta_{\gamma_2}\right) \\ &= \left(\sum_{\gamma'} c_{\gamma'}(\delta_{\gamma_1\gamma_2\gamma'}-\delta_{\gamma_1\gamma_2}) + (\delta_{\gamma_1\gamma_2} - \delta_{\gamma_1})\right) + \delta_{\gamma_1} \\ &= \sum_{\gamma'} c_{\gamma'}(\delta_{\gamma_1\gamma_2\gamma'}-\delta_{\gamma_1\gamma_2}) + \delta_{\gamma_1\gamma_2} \\ &= \alpha(\gamma_1\gamma_2)\left(\sum_{\gamma'} c_{\gamma'}\delta_{\gamma'}\right). \end{align*} $$
For each
![]() $\gamma \in \Gamma $
, it is easy to see that
$\gamma \in \Gamma $
, it is easy to see that
![]() $\alpha (\gamma ) = \pi (\gamma )^* + \delta _\gamma $
, where
$\alpha (\gamma ) = \pi (\gamma )^* + \delta _\gamma $
, where
![]() $\pi (\gamma ): \operatorname {\mathrm {Lip}}_0(\Gamma ) \to \operatorname {\mathrm {Lip}}_0(\Gamma )$
is the linear isometry defined by
$\pi (\gamma ): \operatorname {\mathrm {Lip}}_0(\Gamma ) \to \operatorname {\mathrm {Lip}}_0(\Gamma )$
is the linear isometry defined by
![]() $\pi (\gamma )(f)(x) := f(\gamma x) - f(\gamma )$
and
$\pi (\gamma )(f)(x) := f(\gamma x) - f(\gamma )$
and
![]() $\pi (\gamma )^*: \operatorname {\mathrm {Lip}}_0(\Gamma )^* \to \operatorname {\mathrm {Lip}}_0(\Gamma )^*$
is its adjoint. Hence,
$\pi (\gamma )^*: \operatorname {\mathrm {Lip}}_0(\Gamma )^* \to \operatorname {\mathrm {Lip}}_0(\Gamma )^*$
is its adjoint. Hence,
![]() $\alpha (\gamma )$
is an isometry. Finally, observe that the orbit map
$\alpha (\gamma )$
is an isometry. Finally, observe that the orbit map
![]() $\gamma \mapsto \alpha (\gamma )(0) = \delta _\gamma $
is the isometric embedding
$\gamma \mapsto \alpha (\gamma )(0) = \delta _\gamma $
is the isometric embedding
![]() $\delta : \Gamma \hookrightarrow \operatorname {\mathrm {LF}}(\Gamma )$
.
$\delta : \Gamma \hookrightarrow \operatorname {\mathrm {LF}}(\Gamma )$
.
The proper and uniformly Lipschitz affine action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^1$
is given by
$\ell ^1$
is given by
![]() $\gamma \cdot x := (T \circ \alpha (\gamma ) \circ T^{-1})(x)$
, where
$\gamma \cdot x := (T \circ \alpha (\gamma ) \circ T^{-1})(x)$
, where
![]() $T: \operatorname {\mathrm {LF}}(\Gamma ) \to \ell ^1$
is any linear isomorphism.
$T: \operatorname {\mathrm {LF}}(\Gamma ) \to \ell ^1$
is any linear isomorphism.
Acknowledgements
We are very grateful to the referee for their careful reading of the original submission of this article, for providing improved references and for detecting some incorrect proofs and suggesting their fixes.
Competing interest
The authors have no competing interest to declare.
Financial support
The author was supported by the National Science Foundation under Grant Number DMS-2342644.