Introduction
Erosion by glaciers is conventionally attributed to at least three basic mechanisms: abrasion, quarrying, and subglacial fluvial activity. For glaciers in calcareous terrains, subglacial dissolution of the bed is also a significant erosive mechanism, which often leaves a clearer imprint on the glacier bed than abrasion (Reference HalletHallet, 1976). There are numerous discussions of the relative importance of these erosional mechanisms in the literature (for summary see Reference FlintFlint, [c1971]; Reference AndrewsAndrews, [c1975]; Reference VivianVivian, 1975), but they all suffer from a lack of experimental data.
A fundamental understanding of the mechanics of glacial abrasion is essential for the study of erosion by glaciers. The intent of this paper is to present preliminary results of a quantitative model of glacial abrasion constructed in the context of modern glaciological views of processes occurring close to the bed. This model shares several important elements with the pioneering and comprehensive study made by Reference Boulton and CoatesBoulton (c1974]). He discusses the principal facets of glacial erosion and presents observations and theoretical considerations of the abrasion process and its dependence on the size distribution of debris in basal ice. In the present paper, a more complete view is developed of abrasion by single particles lodged in the ice; I arrive at quite different conclusions because there are fundamental differences in the modeling, particularly in the evaluation of forces between rock fragments and the glacier bed. This analysis models the abrasion under temperate glaciers with basal layers which contain only occasional rock fragments, as is often observed in subglacial cavities and as is reflected by the common scarcity of debris on extensive rock surfaces exposed by glacial retreat. There are however, numerous examples of glaciers with considerable debris in basal ice Reference Boulton and Coates(Boulton, [c1974]) and even with a subglacial drift (Reference Kamb, Kamb, Engelhardt and HarrisonKamb and others, 1979); the model does not simulate abrasion by such glaciers because it neglects particle interactions and the effect of debris on sliding.
It has long been recognized that glacial abrasion is due to rock fragments forced against, and dragged along, the glacier bed by sliding ice. The rate of abrasion depends primarilly on the effective force with which individual fragments are pressed against the bed, the flux of fragments over the bed, and the relative hardness of rocks in the ice and of the bed. In the model presented here, the rate of abrasion is taken to be proportional to the flux of rock particles that make contact with the bed, and to the particle–bed contact forces. Effects of relative rock hardnesses and the geometry of contact areas are incorporated in an effective constant of proportionality which is to be determined empirically. The analysis yields estimates of the rate of abrasion for a glacier bed of arbitrary, but low, roughness by rock fragments of a particular size. The more realistic case, in which rock fragments which vary widely in size abrade the bed, could be modeled by considering the effective abrasion-rate due to each narrow size range of particles and by summing the individual rates to obtain a total as in the study of Reference Boulton and CoatesBoulton ([c1974]). The interdependence of the concentration of fragments dragging on the bed and the rate of basal sliding and, hence, the rate of abrasion will be discussed in a subsequent paper.
In the abrasion process, striations are formed by the motion of rock asperities that locally deform and fracture the rock of the glacier bed and remove the debris. The deformation and fracture of rock requires large stress differences between the contact point and areas immediately adjacent to it. Where abrasion occurs, rock fragments are likely to be completely enveloped by pressurized ice or water except where they contact the bed. This implies that the basal pressure does not affect the stress differences which are important in the striation process, because it contributes equal stresses to contact areas and to the adjacent zones. The effective force of contact is then independent of basal pressure and, hence, of the glacier thickness; it is only dependent on the buoyant weight of rock particles and on the viscous drag induced by ice flow towards the glacier bed due to basal melting and longitudinal straining of basal ice. For particular rock types and concentrations of rock particles in the ice, calculations of the abrasion-rates reduce to evaluations of the effective force pressing particles against the bed and of the particle velocity. These assumptions render this model markedly different from and considerably more realistic than the analysis of Reference Boulton and CoatesBoulton ([c1974])
After a brief introduction to the quantitative characterization of glacial abrasion, the analysis presented here proceeds from an evaluation of the contact force between rock fragments and the glacier bed to an estimate of the rate at which rock fragments are transported alone the bed, and then to an expression for the rate of abrasion. Finally, the abrasion of a simple sinusoidal bed is discussed to shed light on the relative rates at which bed irregularities of different sizes would disappear under sustained abrasion.
Quantitative characterization of glacial abrasion
The rate of abrasion of the bed depends on the flux of particles in contact with the bed, on the force with which rock particles press against the bed, and on the relative hardness of the bed and the abrasive particles. Therefore, the simplest general expression for the rate of abrasion Ȧ of any portion of the bed, is
where α and n are empirical constants, D is the number of particles dragging along the bed per unit time and unit length perpendicular to the ice flow direction, and F is the effective force pressing particles against the bed. Simple experiments to simulate the abrasion of a rock surface by single rock fragments suggest that Equation (1), which is similar to that used by Reference Boulton and CoatesBoulton ([c1974), is valid. These, and similar experiments, can provide numerical values for α and n that depend on the hardnesses, and hence on the lithologies of the striator and the rock which is being striated, and on the shape of the striator point. Reliable and realistic values of these constants are, however, difficult to determine empirically because the experimental results are likely to depend sensitively on the experimental apparatus. Rock-to-rock friction experiments designed to study faulting (e.g. Dieterich, 1972), show that accumulations and sudden releases of stress, which are responsible for the stick–slip behavior, are sensitively dependent on the effective stiffness of the apparatus as well as on the pressure, temperature, and rates of displacement. Because such behavior is probably related to the fracturing, chipping, and gouging of striated rocks, realistic experiments to simulate abrasion should be conducted under conditions representative of those at the glacier bed, using fragments embedded in temperate ice moving at reasonable rates. A few experiments of this type have been conducted by Reference Boulton and CoatesBoulton ([c 1974]) in subglacial cavities and have yielded very interesting data on rates of abrasion. More such experiments ought to be conducted in a variety of subglacial situations, and special care ought to be given to determining the force with which particles press against the bed. The results of Reference MathewsMathews (1979) will be difficult to apply to actual abrasion by temperate glaciers because his experiments were conducted at temperatures well below zero, the sliding velocities were very high, and the confining pressures were low.
The particle flux D is the product of the particle velocity υp and the number of rock asperities protruding from the basal ice per unit area of the glacier sole, a measure of the rock concentration C r. Thus, the average thickness of rock removed by abrasion per unit time can be expressed as
All parameters in this expression are, in general, functions of position along the bed. In the analysis, expressions for υ p and F will be obtained for particles of specific sizes. The abrasion-rate due to each particle-size fraction can be obtained using the surface concentration of particles of that size range. The total abrasion-rate can then be obtained by summing individual rates.
Contact force between fragments and the glacier bed
The density difference between rocks and ice leads to a downward force on rock fragments equal to their buoyant weights. Basal melting, as well as longitudinal extension of basal ice, causes the ice to flow toward the bed, thereby moving fragments to the ice-rock interface and forcing them against the bed. An effective viscous drag is exerted on these particles as temperate ice moves around them by deformation and regelation. Where basal freezing occurs along lee surfaces, the ice flows away from the bed and decreases the force pressing particles against the bed; it could also lift particles from the ice-rock interface.
The drag on a particle, as temperate ice moves around it by regelation as well as by deformation, is analogous to the drag on a sphere moving slowly through temperate ice, a problem studied by Watts (unpublished). He shows that the drag force per unit cross-sectional area σ on a rigid isolated sphere forced through temperate ice, with Newtonian viscosity, is

where η is the effective viscosity of the ice, ʋr
is the velocity of the particle relative to the ice, R is the radius of the spherical particle, and R*
is a parameter, analogous to the transition wavelength in the bed-slip theory, which is referred to as the critical radius at which the drag per cross-sectional area is greatest. The motions of smaller and larger spheres through temperate ice are made easier by melting–regelation and viscous deformation, respectively. For rock particles, R*
is typically about 11cm (Watts, unpublished). It is noteworthy that the drag expression reduces to 4πηRυ
r for a large sphere when regelation is ineffective ![]() Stokes’ law for the viscous drag on a slowly moving sphere yields a similar result, but
Stokes’ law for the viscous drag on a slowly moving sphere yields a similar result, but ![]() times as large because, unlike the temperate-ice case, a no-slip boundary condition is imposed on the sphere surface.
times as large because, unlike the temperate-ice case, a no-slip boundary condition is imposed on the sphere surface.
The evaluation of the force exerted on a particle against the glacier bed as ice flows toward the bed is a problem which is similar to, but much more complicated than, that of drag on an isolated particle forced through an infinite body of temperate ice. Reference MorrisMorris (1979) recently showed that the analogous problem of the motion of a rigid cylinder near a rigid boundary through temperate ice cannot be solved with the boundary conditions conventionally used in glacier sliding and other regelation problems. Moreover, additional complications arise near to the bed because ice flow around particles is affected by steep velocity gradients associated with active sliding over a rough bed, the irregular shape of rock fragments in basal ice, and the likelihood of their being in close proximity to, and hence interfering with, other rocks. Nevertheless, it appears reasonable to assume, as a first approximation, that for basal ice with a fairly low debris concentration, the drag on a fragment at the glacier bed will be of the same order of magnitude as that on an isolated fragment forced through temperate ice with a velocity equal to the mean velocity around the fragment in basal ice. Making this approximation, the viscous drag on particles at t he glacier bed can be expressed by Equation (3).
More refined calculations do not seem warranted, especially in view of the fact that even for the simplest problem involving regelation—the motion of wires forced through temperate ice—the drag predicted by the same theory that leads to Equation (3) can differ greatly from observed values (Reference Drake and ShreveDrake and Shreve, 1973).
Using Equation (3), the force with which a rock fragment presses against the bed can be approximated as

The fragment is taken to be equivalent to a sphere of radius R, ρ r and ρ i are the densities of rock and ice, g is the gravitational acceleration, υn is the velocity component of the ice normal to the bed (positive toward the bed). The coordinate system used in these calculations is shown in Figure 1. The local down-glacier inclination of the bed θ depends on its overall slope ɸ averaged over tens of meters, as well as on the local slope γ, which is equal to tan−1 dz/dx of the rough surface. θ can be characterized as

where z(x) is the two-dimensional glacier bed profile. The first term in Equation (4) represents the buoyant weight of the fragment and the second is the approximate force contribution due to ice flowing toward the bed with a velocity υ n. The ice velocity normal to the bed can be expressed as
where ɷ re, ɷ 0, and ɷ s are the normal velocity components due respectively to regelation sliding, uniform melting (resulting from geothermal heating and sliding friction), and longitudinal straining. Assuming that, for ice with low debris content, glacier sliding is not appreciably affected by the rock fragments in the ice, ɷ re can be expressed in terms of the velocity components parallel to and perpendicular to the overall trend of bed, u and ɷ, as obtained in glacier-sliding theories. In terms of the formulation due to Reference NyeNye (1969),
where γ is the deviation of the local bed slope from the overall trend of the glacier bed. Geothermal heating and sliding friction are assumed to cause fairly uniform melting of the basal ice; reasonable estimates of the resulting melting-rate are on the order of 10 to 100 mm a−1 for normal glaciers (Reference WeertmanWeertman, 1969).

Fig. 1. Coordinate system. In a vertical cross-section parallel to the ice flow, the gently-undulating glacier bed slopes down-valley at a mean angle ϕ from the horizontal.
In addition to the plastic deformation associated directly with glacier sliding, basal ice may, in general, be straining on a large scale. The mean convergence rate of ice toward the bed due to large-scale uniform longitudinal extension of basal ice is

(assuming that the ice is incompressible and that the deformation is two dimensional), U is the mean sliding velocity and L is the distance from the bed. For this abrasion problem a suitable L is on the order of the radius of the abrading fragments.
Particle velocity
A particle embedded in basal ice will move when the viscous drag due to ice flowing past the particle at a velocity υ r together with the down-slope component of the buoyant weight exceeds the resistive frictional drag due to the fragments rubbing against the bed, that is, when

where µ is the effective coefficient of friction. Once in motion a rock fragment will tend to move at a rate υ p such that the equality in Equation (9) is satisfied; the viscous forces urging the particle forward will then be exactly compensated by the frictional drag of the particle on the bed. The velocity component of the ice tangential to the bed is
The following equation for the particle velocity is derived from Equation (9), noting that υ r = υ t—υ p

A general expression for the abrasion-rate can be obtained using Equations (2), (4), and (11) together with values of the ice velocity components locally tangential and normal to the bed, υ t and υ n respectively. These can be readily obtained using Nye’s bed-slip theory and Equations (6), (7), (8), and (10). Consider a temperate glacier sliding over an arbitrary bed whose profile parallel to the ice flow is defined as

Where ε is a dimensionless number much smaller than one which is used to ensure that the roughness of the bed is sufficiently low for the theory to be valid, αn are the Fourier amplitudes of the bed harmonics, and k 0 is the wave number. Assuming a Newtonian viscosity for the ice, the velocity component in the x direction, parallel to the overall trend of the bed is to first order (Reference NyeNye, 1969, p. 454)

where U is the mean sliding velocity. The velocity away from the bed, the z component, is

where

k* being the transition wave number, a fundamental material constant whose value is characteristically around 10 m−1 using a value for the effective viscosity of the ice of 105 Pa a (1 bar a).
In as much as the ice velocities vary with distance from the bed, the rate of ice flow around particles will not be uniform. A formal treatment of the drag on a particle as straining temperate ice moves past it does not, however, seem warranted. Instead, as a first approximation, the viscous drag is considered as equivalent to that due to ice flow with uniform velocity past a spherical inclusion, using a representative value of the ice velocity averaged over an ice thickness equal to the particle diameter. It is more convenient, however, to evaluate simply u and ɷ at z = R, rather than to use the spatial average i.e.

but this could be done with little difficulty in the numerical model, discussed later.
The concentration of particles in the ice C r as a function of position along the bed is not known. However, on intuitive grounds, it is expected to be highest where the flow of debris-laden ice toward the bed is fastest. One could, therefore, postulate that
where C 0 is the average debris concentration at the glacier sole and C is a proportionality constant dependent, in part, on the volumetric concentration of particles in the basal ice.
As can be seen from Equation (11), an increase in the contact force F reduces the velocity υ p of abrading particles. In fact, given a sufficiently large F, particles would be lodged against the bed, abrasion could cease, and rock debris would be deposited on the bed. Therefore, as was clearly recognized by Reference Boulton and CoatesBoulton ([c 1974]), abrasion-rates cannot be assumed to increase monotonically with increasing particle-bed contact forces.
The flow of ice toward the bed pressing rock fragments against the bed is generally the most important factor controlling the contact force. Figure 2 shows the relative magnitude of each of the components contributing to the contact force. Except for abrading rock fragments exceeding 0.2 m in diameter, the viscous-drag contribution is greater than the contribution due to the buoyant weight of fragments and basal pressures, even for very modest values of the normal velocity components. The curves in Figure 2 were obtained assuming that ice flows toward the bed at 10 and 100 mm a–1. Normal geothermal heating of a temperate glacier will by itself melt sufficient basal ice to induce a convergence of the ice and the bed of 10 mm a–1; local rates several orders of magnitude larger than this can be associated with sliding over small obstacles (< 0.5 m) on the glacier bed.

Fig. 2. Relative importance of the buoyant weight and the viscous drag, which control the effective contact force between fragments and the bed. The viscous-drag contribution is shown for two relatively low values of the basal melting-rate. The effective viscosity of the ice was taken to be 105 Pa a (1 bar a).
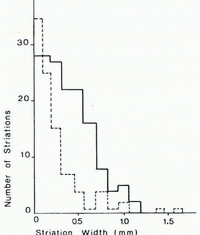
No direct data are available on actual fragment−bed contact forces. They can, however, be estimated from considerations of the widths of striations which reflect the size of the contact areas between rock fragments and the bed. The size of contact areas is in turn indicative of the contact force because, despite the wear on the fragments, actual contact is likely to be established only over small areas just large enough to support the load and to resist crushing of the asperities. The contact force will, therefore, tend to be about equal to the product of the crushing strength of the rock fragment and the area of contact. The widths of over a hundred striations were measured on specimens of Paleozoic limestone from the vicinities of Green Bay, Wisconsin, U.S.A. and Athabasca Glacier, Alberta, Canada. The results, shown in Figure 3, suggest that the majority of fragments were in light contact with the bed. The wider striations are one millimetre wide; this width corresponds to a contact area of about F/σ0 = 1 mm2 and to a contact force of 102N, using a crushing strength representative of limestones: σ0 = 102 MPa (103 bar) (Reference Handin and ClarkHandin, 1966, p. 273–74). This force is small but reasonable as it is equivalent to the buoyant weight of a rock particle, with a radius of about 10 cm, immersed in ice. Deep erosional gouges and particularly arcuate cracks on glaciated rock surfaces indicate much higher contact forces (Johnson, unpublished) presumably associated with the motion of very large rock fragments.

Fig. 3. Frequency distribution of the widths of 100 striations on each of two limestone slabs from glaciated carbonate terrains. These reflect small areas of contact and, hence, relatively small contact forces between rock fragments and the glacier bed. The solid and dashed curves correspond respectively to samples from the vicinity of Green Bay, Wisconsin, U.S.A. and of Athabasca Glacier, Alberta, Canada.
The model is suitable for calculating the abrasion-rate at every point of an arbitrary surface of low roughness and could, therefore, be used to simulate glacial abrasion and its spatial variability; starting with an initial surface, its evolution under abrasion could be simulated. One would start by defining or measuring the initial topography, Fourier analyzing it, computing the abrasion-rate at every point, and then displacing each point to represent an episode of abrasion, finally iterating through time.
An important motivation for modeling abrasion of rock surfaces is to understand better how the bed roughness changes when subjected to glacial erosion. This question is of particular importance in the context of glacier sliding and it has recently been addressed by Reference Johnson, Johnson, Melosh and KambJohnson and others (1976) on the basis of spectral power analyses of several profiles measured on former glacier beds. The rates at which bedforms of different sizes wear down through time, which control the evolution of the bed-roughness spectrum, can most readily be analyzed by simulating abrasion over simple sinusoids of different sizes.
Abrasion of sinusoidal beds
The velocity components tangent and normal to the bed, υ t and υ n respectively, are the main parameters needed in order to evaluate abrasion-rates. With a low-slope approximation (i.e. cos γ = 1 and sin γ = tan γ = dz/dx) and the bed surface described by z = α sin k 0 x, we use the u and ɷ velocity components of Reference NyeNye (1969) to get

and

To obtain a velocity which is representative of the average velocity around the particles of radius R, the velocities were calculated for a height above the bed of z = R. A numerical scheme was used to derive these velocities from which basis the contact force, the particle velocity, and finally the abrasion-rates were obtained. Figure 4 shows the computed abrasion-rates for different fragment sizes. The rate represents an average of rates calculated near the tops of the undulations, it is an intermediate value representative of the rate of abrasion of the entire surface. The abrasion coefficient α was taken to be on the order of 10–10 Pa–1 and n ≈ 1; these values were based on the preliminary results of rough experiments in which conical limestone samples striated saw-cut slabs of the same limestone. Because the model is limited to abrasion by sparse debris in the basal ice, the concentration of fragments projecting from the glacier sole was chosen arbitrarily to be one per square meter. This is probably equivalent to about one-tenth of the effective debris concentration at Glacier d’Argentière, as deduced from an abrasion experiment that Reference Boulton and CoatesBoulton ([c1974], p. 467) conducted there. An aluminum plate fixed to the bed under the glacier, which is sliding at ≈ 250 m a–1, was traversed and deeply striated by about 15 fragment asperities over a width transverse to the flow direction of ≈ 60 mm during a 30 d period. With the possibility that some fragments may contact the bed simultaneously at as many as three asperities, it appears reasonable that about ten fragments actually traversed and contacted the aluminum plate. Assuming that the mean particle velocity is approximately equal to the sliding velocity, the flux of fragments and their concentration are 3 mm–1 a–1 and 10 m–2 respectively.

Fig. 4. Dependence of the abrasion-rates on the effective radius of fragments and on the wavelength λ of bed undulations. The fragment concentration was taken to be one per square metre independent of size. No correction was made for the tendency for small particles to be more numerous than larger ones. The ice velocity and effective viscosity were 100 m a–1 and 105 Pa a (1 bar a).
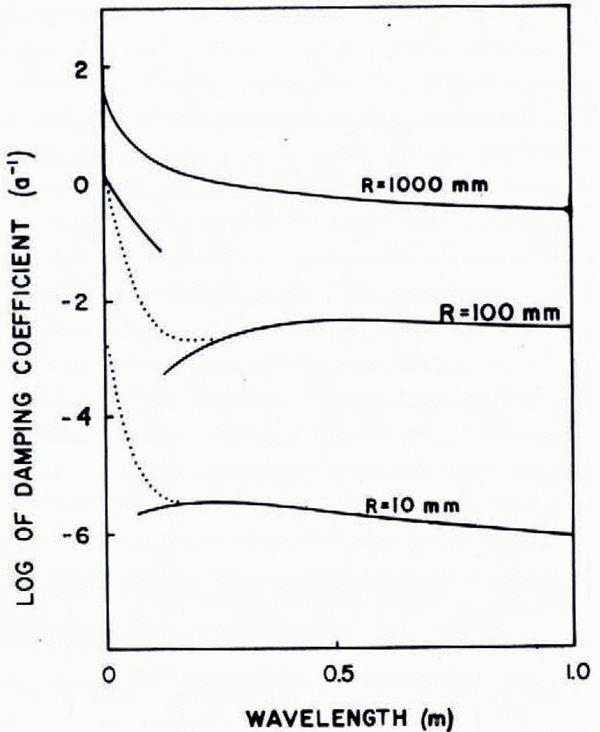
The rate of abrasion at a point does not determine the rate at which bedforms change in shape through time as a result of abrasion. Rather, a comparison is needed between the abrasion-rates calculated at the crest and at the troughs of bed undulations. The damping coefficient D, defined as the crest rate minus the trough rate normalized with the amplitude of the bed undulation, is a useful measure of the rate at which bedforms would disappear under abrasion. When D = 0 the abrasion is uniform, and the bedform is preserved; when D > 0 sustained abrasion wears down bed irregularities. As shown in Figure 5, D decreases with decreasing particle size and with increasing wavelength, except for very small particles and wavelengths. Hence, large rock fragments are most effective in wearing down bedrock bumps because the troughs suffer little wear. In fact, the rock fragments can be so large that they cannot make contact with the troughs, in which case only the crests will be abraded. The discontinuities in the damping curves (Fig. 5) are unrealistically abrupt. However, they do represent the transition between abrasion by large particles, which tends to be restricted to the crests of bed undulations of relatively short wavelengths, and abrasion by small particles, which can take place over the entire surface of larger bed undulations. Dotted lines in Figure 5 were drawn to suggest how the damping actually varies with wavelength.

Fig. 5. The rate at which irregularities in the glacier bed are damped by abrasion, as a function of the radius of the particles and the wavelength of irregularities parallel to the ice flow direction. The dotted lines suggest how the damping actually varies in the wavelength range where the numerical model yields an unrealistic discontinuity (see text). Parameters used in calculations are as indicated for Figure 4.
Conclusions
This model yields interesting new insights into the abrasion process, its controls, and its spatial variability. The viscous drag, induced by ice flow towards the bed due to basal melting, is generally the dominant process forcing particles against the bed. The glacier thickness appears to have no influence on abrasion through its control of basal pressures because they do not affect the differences in stress at or near the fragment–bed contact areas, yet it is these differences that control the rock deformation and fracture which are responsible for abrasion. For large particles (R > 0.5 m) the buoyant weight can contribute very significantly to the fragment–bed contact force.
The absolute rates of glacial abrasion can only be estimated roughly because few appropriate data are available to calculate abrasion coefficients and the concentration and size distribution of debris in basal ice. The spatial variability of abrasion can be calculated more reliably; it is such that irregularities of the glacial bed would invariably tend to disappear under sustained abrasion. Irregularities that are relatively short in the direction of ice flow tend to be particularly vulnerable to abrasion by large fragments (Fig. 5). The roughness of the glacier bed can only be maintained if other subglacial erosional processes effectively roughen the bed. The patterns of melting and freezing associated with regelation sliding are bound to affect greatly the patterns of abrasion because the flow of ice towards the bed appears to be the primary control of the contact force and, hence, of the abrasion-rate. For relatively low contact forces, abrasion ought to be strongest on surfaces facing up-glacier, particularly near their crest, and weakest along lee surfaces. This leads to the characteristic truncation of bed obstacles (Fig. 6) and to maximum abrasion near corners as observed by Reference Boulton and CoatesBoulton ([c1974]). Inasmuch as both the particle–bed contact force and the force urging particles along the bed result principally from viscous drag, the speed at which particles will be dragged along the bed depends simply on the relative magnitude of the ice velocity components parallel and perpendicular to the bed. Assuming, for simplicity, that the coefficient of rock-to-rock friction is about one, the force along the bed on a particle would about equal the particle–bed contact force. This implies that the relative velocity between the sliding ice and the rock ought to be approximately equal to the melting-rate. Therefore, particles ought to remain in motion, entrained in the ice, except when the sliding velocity slows to a low value equal to the melting-rate (10 mm a–1). This conclusion is not in accord with Reference Boulton and CoatesBoulton’s ([c1974], p. 52) suggestion that particles could lodge against a bed at sliding velocities up to 100 m a−1. His results apparently stem from a considerable overestimate of the particle–bed contact force which he views as depending dominantly upon the “effective normal pressure” around the fragments at the glacier base. If particles start to lodge, they would effectively increase the roughness of the glacier bed, thereby inducing continued lodgement. Deposition of lodgement till may, therefore, represent a fairly short-lived event when sliding velocity slows to rates equivalent to the mean basal melting-rate, perhaps as in the waning phase of a glaciation.

Fig. 6. A heavily abraded surface truncates a more steeply-inclined lee surface. Note contrasting abrasion character across the distinct break in slope. Abrasion is most pronounced where basal melting is fastest. Former ice flow direction is indicated by a 30 cm ruler.
On the larger scale, in areas where the geothermal heat flow or frictional heating are high or where the ice is extending, both the contact forces and the particle concentrations would tend to be relatively high. For a given mean particle velocity, abrasion ought to be relatively rapid in these areas. On intuitive grounds, Reference LliboutryLliboutry (1975) suggests that over-deepenings characteristic of glacier valleys are due to erosion by ice heavily laden with debris in these areas. However, if the debris concentration becomes too high in the basal ice, the sliding would be impeded and the flux of particles against the bed would be decreased, thereby slowing abrasion. Accordingly, relatively high sliding velocities as well as high debris content must be responsible for continued excavation of valley over-deepenings. It is stressed that the greater ice thickness in these areas would not favor lodgement of debris against the bed nor inhibit active abrasion there.
This analysis has been further developed to examine the interesting interdependence of the sliding velocity, the concentration of fragments projecting from the glacier sole, and the abrasion-rates. The resistance to glacier sliding induced by rock fragments per unit area of the bed is simply the product of the frictional resistance of one fragment moving against the bed µF and the surface concentration of particles in the basal ice Cr . Even for low debris concentrations, this rock-to-rock frictional resistance is significant compared to the normal range of shear stress at the base of temperate glaciers. These results will be presented in a subsequent paper.
Acknowledgements
I am pleased to acknowledge the competent assistance of Robert Anderson and Brian Aubry in several facets of this work. I gained a great deal from discussing glacial abrasion with them, as well as with Charles Raymond, Joseph Walder, Ray Fletcher, Chester Burrous, and Robert Rein. This manuscript was completed while I was visiting the Quaternary Research Center at the University of Washington in Seattle. I greatly appreciate the technical assistance I received from the Center, and particularly from Judy Hartman. Support for this work was provided by National Science Foundation Grant EAR77-13631.