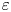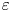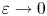1. Introduction
In this work we are concerned with the study of vector minimizers of the Allen–Cahn $\varepsilon$![]() -functional,
-functional,

where $\Omega \subset {\mathbb {R}}^n$![]() is an open set and $W$
is an open set and $W$![]() is a $N$
is a $N$![]() -well potential with $N$
-well potential with $N$![]() global minima.
global minima.
Let
Thus, $u_{\varepsilon } \in W^{1,2}(\Omega ; {\mathbb {R}}^m)$![]() is a weak solution of the system
is a weak solution of the system

We study the asymptotic behaviour of $u_\varepsilon$![]() within the framework of $\Gamma$
within the framework of $\Gamma$![]() -convergence. Moreover, we analyse the relationship between minimizers of the Allen–Cahn system and minimizing partitions subject to Dirichlet boundary conditions. For some particular assumptions on the limiting boundary conditions, we will prove uniqueness for the limiting geometric problem and we will determine the structure of the minimizers of the limiting functional.
-convergence. Moreover, we analyse the relationship between minimizers of the Allen–Cahn system and minimizing partitions subject to Dirichlet boundary conditions. For some particular assumptions on the limiting boundary conditions, we will prove uniqueness for the limiting geometric problem and we will determine the structure of the minimizers of the limiting functional.
1.1 Main results
Hypothesis on $W$![]() :
:
(H1) $W \in C^{1,\alpha }_{loc}({\mathbb {R}}^m ; [0,\,+ \infty )) \ ,\,\ \lbrace W=0 \rbrace = \lbrace a_1,\,a_2,\,...,\,a_N \rbrace \ ,\,\ N \in \mathbb {N} \ ,\, a_i$![]() are the global minima of $W$
are the global minima of $W$![]() . Assume also that
. Assume also that
Hypothesis on the Dirichlet data:
(H2)(i) $|g_{\varepsilon }| \leq M \ ,\, g_\varepsilon \stackrel {L^1(\Omega )}{\longrightarrow } g_0$![]() and $J_\varepsilon (g_\varepsilon,\, \Omega _{\rho _0} \setminus \Omega ) \leq C \ ,\,$
and $J_\varepsilon (g_\varepsilon,\, \Omega _{\rho _0} \setminus \Omega ) \leq C \ ,\,$![]() where $\partial \Omega$
where $\partial \Omega$![]() is Lipschitz and $\Omega _{\rho _0}$
is Lipschitz and $\Omega _{\rho _0}$![]() is a small dilation of $\Omega \ ,\,\ \rho _0 >1$
is a small dilation of $\Omega \ ,\,\ \rho _0 >1$![]() , in which $g_\varepsilon$
, in which $g_\varepsilon$![]() is extended $(C ,\,\ M \ \textrm {indep. of}\ \varepsilon )$
is extended $(C ,\,\ M \ \textrm {indep. of}\ \varepsilon )$![]() .
.
And either
(ii) $g_\varepsilon \in C^{1,\alpha }(\overline {\Omega }) \ ,\,\ | g_{\varepsilon } |_{1,\alpha } \leq \frac {M}{\varepsilon }$![]() and $\partial \Omega$
and $\partial \Omega$![]() is $C^2$
is $C^2$![]() , where we denote with $| \cdot |_{1, \alpha }$
, where we denote with $| \cdot |_{1, \alpha }$![]() as the $C^{1, \alpha }$
as the $C^{1, \alpha }$![]() norm.
norm.
Or (ii’) $g_\varepsilon \in H^1( \Omega )$![]() and $J_\varepsilon ( {u_\varepsilon },\, \Omega ) \leq C$
and $J_\varepsilon ( {u_\varepsilon },\, \Omega ) \leq C$![]() .
.
For $i \neq j \ ,\,\ i,\,j \in \lbrace 1,\,2,\,...,\,N \rbrace$![]() , let $U \in W^{1,2}( \mathbb {R};\mathbb {R}^m)$
, let $U \in W^{1,2}( \mathbb {R};\mathbb {R}^m)$![]() be the 1D minimizer of the action
be the 1D minimizer of the action

where $U$![]() is a connection that connects $a_i$
is a connection that connects $a_i$![]() to $a_j \ ,\,\ i,\,j \in \lbrace 1,\,2,\,...,\,N \rbrace$
to $a_j \ ,\,\ i,\,j \in \lbrace 1,\,2,\,...,\,N \rbrace$![]() .
.
The existence of such geodesics has been proved under minimal assumptions on the potential $W$![]() in [Reference Zuniga and Sternberg38].
in [Reference Zuniga and Sternberg38].
Let $J_\varepsilon$![]() defined in (1.1), we define
defined in (1.1), we define

where $\Omega \subset \Omega _{\rho _0}$![]() as in (H2)(i) and let
as in (H2)(i) and let
where $S_{ij}(u):= \partial ^* \lbrace u=a_i \rbrace \cap \partial ^* \lbrace u=a_j \rbrace \ ,\,\ u \in BV(\Omega ;\lbrace a_1,\,a_2,\,...,\,a_N \rbrace )$![]() and we denote as $\partial ^* \Omega _k$
and we denote as $\partial ^* \Omega _k$![]() the reduced boundary of $\Omega _k$
the reduced boundary of $\Omega _k$![]() .
.
Finally, we define the limiting functional subject to the limiting boundary conditions

We can write $J_\varepsilon,\,J_0,\, \tilde {J}_\varepsilon,\, \tilde {J}_0 : L^1(\Omega ; \mathbb {R}^n) \rightarrow \overline {\mathbb {R}}$![]() , where $\overline {\mathbb {R}} = \mathbb {R} \cup \lbrace \infty \rbrace$
, where $\overline {\mathbb {R}} = \mathbb {R} \cup \lbrace \infty \rbrace$![]() and the $\Gamma$
and the $\Gamma$![]() -convergence will be with respect to the $L^1$
-convergence will be with respect to the $L^1$![]() topology.
topology.
Our first main result is the following
Theorem 1.1 Let $J_{\varepsilon }$![]() be defined by (1.1) and $\tilde {J}_{\varepsilon } \ ,\,\ \tilde {J}_0$
be defined by (1.1) and $\tilde {J}_{\varepsilon } \ ,\,\ \tilde {J}_0$![]() defined in (1.5) and (1.7) respectively.
defined in (1.5) and (1.7) respectively.
Then
Remark 1.2 Note that the domain of $\tilde {J}_0$![]() is the closure of $\Omega$
is the closure of $\Omega$![]() , which means that there is a boundary term (see also (2.9) in [Reference Owen, Rubinstein and Sternberg32] for the analogue in the scalar case). More precisely, by proposition 3.5 and theorem 5.8 in [Reference Evans and Gariepy16] we can write
, which means that there is a boundary term (see also (2.9) in [Reference Owen, Rubinstein and Sternberg32] for the analogue in the scalar case). More precisely, by proposition 3.5 and theorem 5.8 in [Reference Evans and Gariepy16] we can write

The overview of the strategy of the proof of theorem 1.1 is as follows. First we observe that the $\Gamma$![]() -limit established in [Reference Baldo7], in particular theorem 2.5, holds also without the mass constraint (see theorem 2.2 in Preliminaries section). Next, we apply a similar strategy to that of [Reference Ansini, Braides and Chiadò Piat6, Theorem 3.7] in which there is a $\Gamma$
-limit established in [Reference Baldo7], in particular theorem 2.5, holds also without the mass constraint (see theorem 2.2 in Preliminaries section). Next, we apply a similar strategy to that of [Reference Ansini, Braides and Chiadò Piat6, Theorem 3.7] in which there is a $\Gamma$![]() -convergence result with boundary conditions in the scalar case which states that we can incorporate the constraint of Dirichlet values in the $\Gamma$
-convergence result with boundary conditions in the scalar case which states that we can incorporate the constraint of Dirichlet values in the $\Gamma$![]() -limit, provided that this $\Gamma$
-limit, provided that this $\Gamma$![]() -limit is determined. Since by theorem 2.2 we have that $J_\varepsilon \Gamma$
-limit is determined. Since by theorem 2.2 we have that $J_\varepsilon \Gamma$![]() -converges to $J_0$
-converges to $J_0$![]() , we establish the $\Gamma$
, we establish the $\Gamma$![]() -limit of $\tilde {J}_\varepsilon$
-limit of $\tilde {J}_\varepsilon$![]() , that is, the $\Gamma$
, that is, the $\Gamma$![]() -limit of the functional $J_\varepsilon$
-limit of the functional $J_\varepsilon$![]() with the constraint of Dirichlet values. For the proof of the $\Gamma$
with the constraint of Dirichlet values. For the proof of the $\Gamma$![]() -limit we can assume either (H2)(ii) or (H2)(ii’).
-limit we can assume either (H2)(ii) or (H2)(ii’).
Next, we study the solution of the geometric minimization problem that arises from the limiting functional.
In order to obtain precise information about the minimizer of the limiting functional $\tilde {J}_0 (u,\, \overline {B}_1) \ ,\, \ B_1 \subset \mathbb {R}^2$![]() , we impose that the limiting boundary conditions $g_0$
, we impose that the limiting boundary conditions $g_0$![]() have connected phases. So we assume,
have connected phases. So we assume,
(H2) (iii) Let $g_0 = \sum _{i=1}^3 a_i \ \chi _{I_i}(\theta ) \ ,\,\ \theta \in [0,\, 2 \pi ) \ ,\,\ I_i \subset [0,\, 2 \pi ) \ ,\,\ \cup _{i=1}^3 I_i = [0,\, 2 \pi )$![]() be the limit of $g_\varepsilon$
be the limit of $g_\varepsilon$![]() . Assume that $I_i$
. Assume that $I_i$![]() are connected and that
are connected and that

The assumption $\theta _0 < \frac {2 \pi }{3}$![]() arises from Proposition 3.2 in [Reference Morgan30] that we utilize for the proof (see proposition 2.5 in Preliminaries section) and guarantees that the boundary of the partition defined by the minimizer will be line segments meeting at a point inside $B_1$
arises from Proposition 3.2 in [Reference Morgan30] that we utilize for the proof (see proposition 2.5 in Preliminaries section) and guarantees that the boundary of the partition defined by the minimizer will be line segments meeting at a point inside $B_1$![]() .
.
Our second main result is the following
Theorem 1.3 Let $u_0 = a_1 \chi _{\Omega _1} +a_2 \chi _{\Omega _2} + a_3 \chi _{\Omega _3}$![]() be a minimizer of $\tilde {J}_0(u,\,\overline {B}_1)$
be a minimizer of $\tilde {J}_0(u,\,\overline {B}_1)$![]() subject to the limiting Dirichlet values (H2)(iii).
subject to the limiting Dirichlet values (H2)(iii).
Then the minimizer is unique and in addition,
For proving theorem 1.3, we first prove that the partition defined by $u_0$![]() is $(M,\,0,\, \delta )$
is $(M,\,0,\, \delta )$![]() -minimal as in Definition 2.1 in [Reference Morgan30] (see definition 2.4). This is proved by a comparison argument by defining a Lipschitz perturbation of the partition of the minimizer with strictly less energy. Then, by utilizing a uniqueness result for $(M,\, 0 ,\,\delta )$
-minimal as in Definition 2.1 in [Reference Morgan30] (see definition 2.4). This is proved by a comparison argument by defining a Lipschitz perturbation of the partition of the minimizer with strictly less energy. Then, by utilizing a uniqueness result for $(M,\, 0 ,\,\delta )$![]() -minimal sets in [Reference Morgan30] (see proposition 2.5), we can conclude that the minimizer of the limiting energy is unique and the boundaries of the partition that the minimizer defines are line segments meeting at $120^o$
-minimal sets in [Reference Morgan30] (see proposition 2.5), we can conclude that the minimizer of the limiting energy is unique and the boundaries of the partition that the minimizer defines are line segments meeting at $120^o$![]() degrees in an interior point of the unit disc.
degrees in an interior point of the unit disc.
In the last subsection, we note that the result in theorem 1.3 can be extended also to the mass constraint case (see [Reference Baldo7]). However, in this case the uniqueness will be up to rigid motions of the disc (see Theorems 3.6 and 4.1 in [Reference Canete and Ritore10]).
1.2 Previous fundamental contributions
We will now briefly introduce some of the well-known results in the scalar case. The notion of $\Gamma$![]() -convergence was introduced by De Giorgi and Franzoni in [Reference De Giorgi and Franzoni14] and in particular relates phase transition-type problems with the theory of minimal surfaces. One additional application of $\Gamma$
-convergence was introduced by De Giorgi and Franzoni in [Reference De Giorgi and Franzoni14] and in particular relates phase transition-type problems with the theory of minimal surfaces. One additional application of $\Gamma$![]() -convergence is the proof of existence of minimizers of a limiting functional, say $F_0$
-convergence is the proof of existence of minimizers of a limiting functional, say $F_0$![]() , by utilizing an appropriate sequence of functionals $F_\varepsilon$
, by utilizing an appropriate sequence of functionals $F_\varepsilon$![]() that we know they admit a minimizer and the $\Gamma$
that we know they admit a minimizer and the $\Gamma$![]() -limit of $F_\varepsilon$
-limit of $F_\varepsilon$![]() is $F_0$
is $F_0$![]() . And also vice versa ([Reference Kohn and Sternberg25]), we can obtain information for the $F_\varepsilon$
. And also vice versa ([Reference Kohn and Sternberg25]), we can obtain information for the $F_\varepsilon$![]() energy functional from the properties of minimizers of the limiting functional $F_0$
energy functional from the properties of minimizers of the limiting functional $F_0$![]() . We can think of this notion as a generalization of the Direct Method in the Calculus of Variations i.e. if $F_0$
. We can think of this notion as a generalization of the Direct Method in the Calculus of Variations i.e. if $F_0$![]() is lower semicontinuous and coercive we can take $F_\varepsilon = F_0$
is lower semicontinuous and coercive we can take $F_\varepsilon = F_0$![]() and then $\Gamma$
and then $\Gamma$![]() -lim $F_\varepsilon =F_0$
-lim $F_\varepsilon =F_0$![]() .
.
There are many other ways of thinking of this notion, such as a proper tool in finding the limiting functional among a sequence of functionals.
Let $X$![]() be the space of the measurable functions $u : \Omega \subset \mathbb {R}^n \rightarrow \mathbb {R}$
be the space of the measurable functions $u : \Omega \subset \mathbb {R}^n \rightarrow \mathbb {R}$![]() endowed with the $L^1$
endowed with the $L^1$![]() norm and
norm and

Let now $u_\varepsilon$![]() be a minimizer of $F_\varepsilon$
be a minimizer of $F_\varepsilon$![]() subject to a mass constraint, that is, $\int _{\Omega }u = V \in (0,\, |\Omega |)$
subject to a mass constraint, that is, $\int _{\Omega }u = V \in (0,\, |\Omega |)$![]() . The asymptotic behaviour of $u_\varepsilon$
. The asymptotic behaviour of $u_\varepsilon$![]() was first studied by Modica and Mortola in [Reference Modica and Mortola28] and by Modica in [Reference Modica27, Reference Modica29]. Also, later Sternberg [Reference Sternberg34] generalized these results for minimizers with volume constraint. Furthermore, Owen et al. in [Reference Owen, Rubinstein and Sternberg32] and Ansini et al. in [Reference Ansini, Braides and Chiadò Piat6], among others, studied the asymptotic behaviour of the minimizers subject to Dirichlet values for the scalar case.
was first studied by Modica and Mortola in [Reference Modica and Mortola28] and by Modica in [Reference Modica27, Reference Modica29]. Also, later Sternberg [Reference Sternberg34] generalized these results for minimizers with volume constraint. Furthermore, Owen et al. in [Reference Owen, Rubinstein and Sternberg32] and Ansini et al. in [Reference Ansini, Braides and Chiadò Piat6], among others, studied the asymptotic behaviour of the minimizers subject to Dirichlet values for the scalar case.
As mentioned previously, one of the most important outcomes of $\Gamma$![]() -convergence in the scalar phase transition-type problems is the relationship with minimal surfaces. More precisely, the well-known theorem of Modica and Mortola states that the $\varepsilon$
-convergence in the scalar phase transition-type problems is the relationship with minimal surfaces. More precisely, the well-known theorem of Modica and Mortola states that the $\varepsilon$![]() -energy functional of the Allen–Cahn equation $\Gamma$
-energy functional of the Allen–Cahn equation $\Gamma$![]() -converges to the perimeter functional that measures the perimeter of the interface between the phases (i.e. $\Gamma$
-converges to the perimeter functional that measures the perimeter of the interface between the phases (i.e. $\Gamma$![]() -$\textrm {lim} \ F_\varepsilon = F_0$
-$\textrm {lim} \ F_\varepsilon = F_0$![]() ). So the interfaces of the limiting problem will be minimal surfaces.
). So the interfaces of the limiting problem will be minimal surfaces.
This relationship is deeper as indicated in the De Giorgi conjecture (see [Reference De Giorgi15]) which states that the level sets of global entire solutions of the scalar Allen–Cahn equation that are bounded and strictly monotone with respect to $x_n$![]() are hyperplanes if $n \leq 8$
are hyperplanes if $n \leq 8$![]() . The relationship with the Bernstein problem for minimal graphs is the reason why $n \leq 8$
. The relationship with the Bernstein problem for minimal graphs is the reason why $n \leq 8$![]() appears in the conjecture. The $\Gamma$
appears in the conjecture. The $\Gamma$![]() -limit of the $\varepsilon$
-limit of the $\varepsilon$![]() -energy functional of the Allen–Cahn equation is a possible motivation behind the conjecture.
-energy functional of the Allen–Cahn equation is a possible motivation behind the conjecture.
In addition, Baldo in [Reference Baldo7] and Fonseca and Tartar in [Reference Fonseca and Tartar18] extended the $\Gamma$![]() -convergence analysis for the phase transition-type problems to the vector case subject to a mass constraint and the limiting functional measures the perimeter of the interfaces separating the phases, and thus there is a relationship with the problem of minimizing partitions. In § 5 we analyse this in the set up of Dirichlet boundary conditions. Furthermore, the general vector-valued coupled case has been thoroughly studied in the works of Borroso–Fonseca and Fonseca–Popovici in [Reference Cristina Barroso and Fonseca12] and [Reference Fonseca and Popovici17] respectively.
-convergence analysis for the phase transition-type problems to the vector case subject to a mass constraint and the limiting functional measures the perimeter of the interfaces separating the phases, and thus there is a relationship with the problem of minimizing partitions. In § 5 we analyse this in the set up of Dirichlet boundary conditions. Furthermore, the general vector-valued coupled case has been thoroughly studied in the works of Borroso–Fonseca and Fonseca–Popovici in [Reference Cristina Barroso and Fonseca12] and [Reference Fonseca and Popovici17] respectively.
There are many other fundamental contributions on the subject, such as the works of Gurtin [Reference Gurtin21, Reference Gurtin22], Gurtin and Matano [Reference Gurtin and Matano23] on the Modica–Mortola functional and its connection with materials science, the work of Hutchingson and Tonegawa on the convergence of critical points in [Reference Hutchinson and Tonegawa24], the work of Bouchitté [Reference Bouchitté8] and of Cristoferi and Gravina [Reference Cristoferi and Gravina13] on space-dependent wells and extensions on general metric spaces in the work of Ambrosio in [Reference Ambrosio5]. Several extensions to the non-local case and fractional setting have also been studied by Alberti-Bellettini in [Reference Alberti and Bellettini1], by Alberti-Bouchitté-Seppecher in [Reference Alberti, Bouchitté and Seppecher2] and by Savin-Valdinoci in [Reference Savin and Valdinoci33] among others.
2. Preliminaries
2.1 Specialized definitions and theorems for the $\Gamma$ -limit
-limit
First, we will define the supremum of measures that allow us to express the limiting functional in an alternative way. Let $\mu$![]() and $\nu$
and $\nu$![]() be two regular Borel measures on $\Omega$
be two regular Borel measures on $\Omega$![]() we denote by $\mu \bigvee \nu$
we denote by $\mu \bigvee \nu$![]() the smallest regular positive measure which is greater than or equal to $\mu$
the smallest regular positive measure which is greater than or equal to $\mu$![]() and $\nu$
and $\nu$![]() on all borel subsets of $\Omega$
on all borel subsets of $\Omega$![]() , for $\mu \ ,\,\ \nu$
, for $\mu \ ,\,\ \nu$![]() being two regular positive Borel measures on $\Omega.$
being two regular positive Borel measures on $\Omega.$![]() We have
We have

Now let

We will now provide a lemma from [Reference Ansini, Braides and Chiadò Piat6] that is crucial in the description of the behaviour of the $\Gamma$![]() -limit with respect to the set variable. Let $\Omega \subset \mathbb {R}^n$
-limit with respect to the set variable. Let $\Omega \subset \mathbb {R}^n$![]() be an open set. We denote by $\mathcal {A}_{\Omega }$
be an open set. We denote by $\mathcal {A}_{\Omega }$![]() the family of all bounded open subsets of $\Omega$
the family of all bounded open subsets of $\Omega$![]() .
.
Lemma 2.1 ([Reference Ansini, Braides and Chiadò Piat6]) Let $J_\varepsilon$![]() defined in (1.1). Then for every $\varepsilon >0$
defined in (1.1). Then for every $\varepsilon >0$![]() , for every bounded open set $U \ ,\,\ U' \ ,\,\ V$
, for every bounded open set $U \ ,\,\ U' \ ,\,\ V$![]() , with $U \subset \subset U'$
, with $U \subset \subset U'$![]() , and for every $u,\,v \in L^1_{loc}(\mathbb {R}^n)$
, and for every $u,\,v \in L^1_{loc}(\mathbb {R}^n)$![]() , there exists a cut-off function $\phi$
, there exists a cut-off function $\phi$![]() related to $U$
related to $U$![]() and $U'$
and $U'$![]() , which may depend on $\varepsilon \ ,\,\ U \ ,\,\ U' \ ,\,\ V \ ,\,\ u \ ,\,\ v$
, which may depend on $\varepsilon \ ,\,\ U \ ,\,\ U' \ ,\,\ V \ ,\,\ u \ ,\,\ v$![]() such that
such that
where $\delta _\varepsilon : L^1_{loc}(\mathbb {R}^n)^2 \times \mathcal {A}^3_{\Omega } \rightarrow [0,\, + \infty )$![]() are functions depending only on $\varepsilon$
are functions depending only on $\varepsilon$![]() and $J_\varepsilon$
and $J_\varepsilon$![]() such that
such that
whenever $U \ ,\,\ U' \ ,\,\ V \in \mathcal {A}_{\Omega } \ ,\,\ U \subset \subset U'$![]() and $u_\varepsilon \ ,\, \ v_\varepsilon \in L^1_{loc}(\mathbb {R}^n)$
and $u_\varepsilon \ ,\, \ v_\varepsilon \in L^1_{loc}(\mathbb {R}^n)$![]() have the same limit as $\varepsilon \rightarrow 0$
have the same limit as $\varepsilon \rightarrow 0$![]() in $L^1( (U' \setminus \overline {U}) \cap V )$
in $L^1( (U' \setminus \overline {U}) \cap V )$![]() and satisfy
and satisfy
The above result is Lemma 3.2 in [Reference Ansini, Braides and Chiadò Piat6] and has been proved in the scalar case. The proof also works in the vector case with minor modifications. In [Reference Ansini, Braides and Chiadò Piat6], there is an assumption on $W$![]() , namely $W \leq c( | u |^\gamma +1)$
, namely $W \leq c( | u |^\gamma +1)$![]() with $\gamma \geq 2$
with $\gamma \geq 2$![]() (see (2.2) in [Reference Ansini, Braides and Chiadò Piat6]). This assumption however is only utilized in the proof of lemma 2.1 above to apply the dominated convergence theorem in the last equation. In our case, this assumption is not necessary since $W(u_\varepsilon )$
(see (2.2) in [Reference Ansini, Braides and Chiadò Piat6]). This assumption however is only utilized in the proof of lemma 2.1 above to apply the dominated convergence theorem in the last equation. In our case, this assumption is not necessary since $W(u_\varepsilon )$![]() and $W (g_\varepsilon )$
and $W (g_\varepsilon )$![]() are uniformly bounded (see (H2)(i) and lemma 3.1). In fact, the only reason we assume in (H1) that $W(u) \geq c_1 | u |^2$
are uniformly bounded (see (H2)(i) and lemma 3.1). In fact, the only reason we assume in (H1) that $W(u) \geq c_1 | u |^2$![]() for $| u |>M$
for $| u |>M$![]() is to apply the above lemma.
is to apply the above lemma.
In [Reference Baldo7] it has been proved that $J_{\varepsilon } \ \Gamma$![]() -converges to $J_0$
-converges to $J_0$![]() with mass constraint, but it also holds without mass constraint (see theorem 2.5). We will point out this more clearly in the proof of theorem 1.1. In particular, it holds
with mass constraint, but it also holds without mass constraint (see theorem 2.5). We will point out this more clearly in the proof of theorem 1.1. In particular, it holds
Theorem 2.2 [Reference Baldo7]
Let $J_\varepsilon$![]() defined in (1.1) and $J_0$
defined in (1.1) and $J_0$![]() defined in (1.6). Then $\Gamma$
defined in (1.6). Then $\Gamma$![]() -$\lim _{\varepsilon \rightarrow 0} J_{\varepsilon }(u,\,\Omega ) = J_0(u,\, \Omega )$
-$\lim _{\varepsilon \rightarrow 0} J_{\varepsilon }(u,\,\Omega ) = J_0(u,\, \Omega )$![]() in $L^1(\Omega ; \mathbb {R}^m).$
in $L^1(\Omega ; \mathbb {R}^m).$![]() That is, for every $u \in L^1(\Omega ; \mathbb {R}^m)$
That is, for every $u \in L^1(\Omega ; \mathbb {R}^m)$![]() , we have the following two conditions:
, we have the following two conditions:
(i) If $\lbrace v_\varepsilon \rbrace \subset L^1(\Omega ; \mathbb {R}^m)$
 is any sequence converging to $u$
is any sequence converging to $u$ in $L^1$
in $L^1$ , then
(2.1)\begin{equation} \liminf_{\varepsilon \rightarrow 0} J_\varepsilon (v_\varepsilon, \Omega) \geq J_0 (u, \Omega), \end{equation}and
, then
(2.1)\begin{equation} \liminf_{\varepsilon \rightarrow 0} J_\varepsilon (v_\varepsilon, \Omega) \geq J_0 (u, \Omega), \end{equation}and
(ii) There exists a sequence $\lbrace w_\varepsilon \rbrace \subset L^1(\Omega ; \mathbb {R}^m)$
 converging to $u$
converging to $u$ in $L^1$
in $L^1$ such that
(2.2)\begin{equation} \lim_{\varepsilon \rightarrow 0} J_\varepsilon (w_\varepsilon, \Omega) = J_0 (u, \Omega). \end{equation}
such that
(2.2)\begin{equation} \lim_{\varepsilon \rightarrow 0} J_\varepsilon (w_\varepsilon, \Omega) = J_0 (u, \Omega). \end{equation}
Remark 2.3 We note that in [Reference Baldo7], there is also a technical assumption for the potential $W$![]() (see (1.2) in p.70). However, for the proof of the $\Gamma$
(see (1.2) in p.70). However, for the proof of the $\Gamma$![]() -limit this assumption is only utilized for the proof of the liminf inequality in order to obtain the equiboundedness of the minimizers $u_\varepsilon$
-limit this assumption is only utilized for the proof of the liminf inequality in order to obtain the equiboundedness of the minimizers $u_\varepsilon$![]() (see proof of (2.8) in [Reference Baldo7]). However, in our case we obtain equiboundedness from lemma 3.1 in the following section. Therefore, in our case this assumption is dismissed.
(see proof of (2.8) in [Reference Baldo7]). However, in our case we obtain equiboundedness from lemma 3.1 in the following section. Therefore, in our case this assumption is dismissed.
2.2 Specialized definitions and theorems for the geometric problem
In addition, we introduce the notion of $(M,\, 0 ,\,\delta )$![]() -minimality as defined in [Reference Morgan30] together with a proposition that certifies the shortest network connecting three given points in $\mathbb {R}^2$
-minimality as defined in [Reference Morgan30] together with a proposition that certifies the shortest network connecting three given points in $\mathbb {R}^2$![]() as uniquely minimizing in the context of $(M,\, 0 ,\,\delta )$
as uniquely minimizing in the context of $(M,\, 0 ,\,\delta )$![]() -minimal sets. This characterization is one of the ingredients for the solution of the geometric minimization problem in the last section. In fact, in [Reference Morgan30] the more general notion of $(M,\, \varepsilon,\,\delta )$
-minimal sets. This characterization is one of the ingredients for the solution of the geometric minimization problem in the last section. In fact, in [Reference Morgan30] the more general notion of $(M,\, \varepsilon,\,\delta )$![]() -minimality (or $(M,\, c r^\alpha,\,\delta )$
-minimality (or $(M,\, c r^\alpha,\,\delta )$![]() -minimality) is introduced and regularity results for such sets are established. Particularly, $(M,\, 0 ,\,\delta )$
-minimality) is introduced and regularity results for such sets are established. Particularly, $(M,\, 0 ,\,\delta )$![]() -minimality implies $(M,\, c r^\alpha,\,\delta )$
-minimality implies $(M,\, c r^\alpha,\,\delta )$![]() -minimality (see [Reference Morgan30]).
-minimality (see [Reference Morgan30]).
Definition 2.4 [Reference Morgan30]
Let $K \subset \mathbb {R}^n$![]() be a closed set and fix $\delta >0$
be a closed set and fix $\delta >0$![]() . Consider $S \subset \mathbb {R}^n \setminus K$
. Consider $S \subset \mathbb {R}^n \setminus K$![]() be a nonempty bounded set of finite $m$
be a nonempty bounded set of finite $m$![]() -dimensional Hausdorff measure. $S$
-dimensional Hausdorff measure. $S$![]() is $(M,\, 0 ,\,\delta )$
is $(M,\, 0 ,\,\delta )$![]() -minimal if $S = spt( \mathcal {H}^m \lfloor S) \setminus K$
-minimal if $S = spt( \mathcal {H}^m \lfloor S) \setminus K$![]() and
and
whenever

Proposition 2.5 [Reference Morgan30]
Let $K = \lbrace p_1,\,p_2 ,\,p_3 \rbrace$![]() be the vertices of a triangle in the open $\delta$
be the vertices of a triangle in the open $\delta$![]() -ball $B(0,\,\delta ) \subset \mathbb {R}^2$
-ball $B(0,\,\delta ) \subset \mathbb {R}^2$![]() , with largest angle $\theta$
, with largest angle $\theta$![]() for some fixed $\delta >0$
for some fixed $\delta >0$![]() . Then there exists a unique smallest $(M,\,0 ,\, \delta )$
. Then there exists a unique smallest $(M,\,0 ,\, \delta )$![]() -minimal set in $B(0,\,\delta )$
-minimal set in $B(0,\,\delta )$![]() with closure containing $K$
with closure containing $K$![]() , in particular:
, in particular:
Here by the ‘unique smallest’ we mean any other such $(M,\,0 ,\, \delta )$![]() -minimal set $S$
-minimal set $S$![]() has larger one-dimensional Hausdorff measure.
has larger one-dimensional Hausdorff measure.
We now state a well-known Bernstein-type theorem in $\mathbb {R}^2$![]() .
.
Theorem 2.6 [Reference Alikakos4]
Let $A$![]() be a complete minimizing partition in $\mathbb {R}^2$
be a complete minimizing partition in $\mathbb {R}^2$![]() with $N=3$
with $N=3$![]() (three phases), with surface tension coefficients satisfying
(three phases), with surface tension coefficients satisfying
Then $\partial A$![]() is a triod.
is a triod.
For a proof and related material we refer to [Reference White37] and the expository [Reference Alikakos4].
3. Basic lemmas
Lemma 3.1 For every critical point $u_{\varepsilon } \in W^{1,2}(\Omega ;\mathbb {R}^m)$![]() , satisfying (1.3) weakly together with assumptions (H1) and (H2)(i),(ii), it holds
, satisfying (1.3) weakly together with assumptions (H1) and (H2)(i),(ii), it holds
Proof. By linear elliptic theory, we have that $u_{\varepsilon } \in C^2(\Omega ;{\mathbb {R}}^m)$![]() (see e.g. Theorem 6.13 in [Reference Gilbarg and Trudinger19]). Set $v_{\varepsilon }(x) = |u_{\varepsilon }(x)|^2$
(see e.g. Theorem 6.13 in [Reference Gilbarg and Trudinger19]). Set $v_{\varepsilon }(x) = |u_{\varepsilon }(x)|^2$![]() , then
, then
Hence $\max _{\Omega } | u_{\varepsilon }|^2 \leq M^2$![]() .
.
On the other hand (from (H2)), $\max _{\partial \Omega } | u_{\varepsilon } | \leq M$![]() . Thus, $\max _{\overline {\Omega }} | u_{\varepsilon }| \leq M .$
. Thus, $\max _{\overline {\Omega }} | u_{\varepsilon }| \leq M .$![]()
For the gradient bound, consider the rescaled problem $y= \frac {x}{\varepsilon }$![]() , denote by $\tilde {u} \ ,\, \tilde {g}$
, denote by $\tilde {u} \ ,\, \tilde {g}$![]() the rescaled $u_{\varepsilon } \ ,\, g_{\varepsilon }$
the rescaled $u_{\varepsilon } \ ,\, g_{\varepsilon }$![]() , so by elliptic regularity (see e.g. Theorem 8.33 in [Reference Gilbarg and Trudinger19]),
, so by elliptic regularity (see e.g. Theorem 8.33 in [Reference Gilbarg and Trudinger19]),

Lemma 3.2 Let $u_\varepsilon$![]() defined in (1.2), then
defined in (1.2), then
$C$![]() independent of $\varepsilon >0$
independent of $\varepsilon >0$![]() , if $\Omega$
, if $\Omega$![]() is bounded.
is bounded.
Proof. Without loss of generality we will prove lemma 3.2 for $\Omega =B_1$![]() (or else we can cover $\Omega$
(or else we can cover $\Omega$![]() with finite number of unit balls and the outside part is bounded by (H2)(i)).
with finite number of unit balls and the outside part is bounded by (H2)(i)).
Substituting $y = \frac {x}{\varepsilon }$![]() ,
,

where $\tilde {u}_{\varepsilon } = u_{\varepsilon } (\varepsilon y)$![]() and for $\varepsilon = \frac {1}{R}$
and for $\varepsilon = \frac {1}{R}$![]() ,
,

So, $\tilde {u}_R$![]() is minimizer of $\tilde {J}_R (v) = \int _{B_R} (\frac {1}{2} |\nabla v|^2 + W(v) ) \,{\rm d}x$
is minimizer of $\tilde {J}_R (v) = \int _{B_R} (\frac {1}{2} |\nabla v|^2 + W(v) ) \,{\rm d}x$![]() .
.
By lemma 3.1 applied in $u_\varepsilon$![]() , it holds that $| \tilde {u}_R | ,\,| \nabla \tilde {u}_R |$
, it holds that $| \tilde {u}_R | ,\,| \nabla \tilde {u}_R |$![]() are uniformly bounded independent of $R$
are uniformly bounded independent of $R$![]() and via the comparison function (see [Reference Alikakos, Fusco and Smyrnelis3] p.135), for $R>1$
and via the comparison function (see [Reference Alikakos, Fusco and Smyrnelis3] p.135), for $R>1$![]()

we have
Thus
□
Lemma 3.3 Let $u_\varepsilon$![]() defined in (1.2), then $u_{\varepsilon } \stackrel {L^1}{\longrightarrow } u_0$
defined in (1.2), then $u_{\varepsilon } \stackrel {L^1}{\longrightarrow } u_0$![]() , along subsequences and $u_0 \in BV(\Omega ;\mathbb {R}^m)$
, along subsequences and $u_0 \in BV(\Omega ;\mathbb {R}^m)$![]() . Moreover, $u_0 = \sum _{i=1}^N a_i \chi _{\Omega _i} \ ,\,\ \mathcal {H}^{n-1}(\partial ^* \Omega _i) < \infty$
. Moreover, $u_0 = \sum _{i=1}^N a_i \chi _{\Omega _i} \ ,\,\ \mathcal {H}^{n-1}(\partial ^* \Omega _i) < \infty$![]() and $| \Omega \setminus \cup _{i=1}^N \Omega _i | =0$
and $| \Omega \setminus \cup _{i=1}^N \Omega _i | =0$![]() .
.
Proof. By lemma 3.1 we have that $u_\varepsilon$![]() is equibounded. Now arguing as in the proof of Proposition 4.1 in [Reference Baldo7] (see also remark 2.3), we obtain that $|| u_{\varepsilon } ||_{BV(\Omega ;\mathbb {R}^m)}$
is equibounded. Now arguing as in the proof of Proposition 4.1 in [Reference Baldo7] (see also remark 2.3), we obtain that $|| u_{\varepsilon } ||_{BV(\Omega ;\mathbb {R}^m)}$![]() is uniformly bounded, $u_\varepsilon \rightarrow u_0$
is uniformly bounded, $u_\varepsilon \rightarrow u_0$![]() in $L^1$
in $L^1$![]() along subsequences and also $u_0 \in BV(\Omega ; \mathbb {R}^m) .$
along subsequences and also $u_0 \in BV(\Omega ; \mathbb {R}^m) .$![]()
From lemma 3.2, it holds
Since $| u_{\varepsilon } | \leq M$![]() and $W$
and $W$![]() is continuous in $\overline {B}_M \subset {\mathbb {R}}^m \ \Rightarrow W( u_{\varepsilon }) \leq \tilde {M}$
is continuous in $\overline {B}_M \subset {\mathbb {R}}^m \ \Rightarrow W( u_{\varepsilon }) \leq \tilde {M}$![]() , by the dominated convergence theorem we obtain
, by the dominated convergence theorem we obtain

where $\chi _{\Omega _i}$![]() have finite perimeter since $u_0 \in BV( \Omega ;\mathbb {R}^m)$
have finite perimeter since $u_0 \in BV( \Omega ;\mathbb {R}^m)$![]() (see [Reference Evans and Gariepy16]).
(see [Reference Evans and Gariepy16]).
The proof of lemma 3.3 is complete.
Also, $g_0$![]() takes values on $\lbrace W=0 \rbrace$
takes values on $\lbrace W=0 \rbrace$![]() .
.
Lemma 3.4 Let $g_0$![]() be the limiting boundary condition of $g_\varepsilon$
be the limiting boundary condition of $g_\varepsilon$![]() .
.
Then

Proof. By (H2)(i),

So, arguing as in the proof of lemma 3.3, we have that $g_0 \in \lbrace W=0 \rbrace$![]() and we conclude.
and we conclude.
Proposition 3.5 It holds that

where $\phi _k (z) = \,{\rm d}(z,\,a_k) \ ,\,\ k=1,\,2,\,...,\,N,\,$![]() and $a_k$
and $a_k$![]() are the zeros of $W$
are the zeros of $W$![]() and $d$
and $d$![]() is the Riemannian metric derived from $W^{1/2}$
is the Riemannian metric derived from $W^{1/2}$![]() , that is
, that is

Proof. The proof can be found in proposition 2.2 in [Reference Baldo7].
Furthermore, reasoning as in the proof of proposition 2.2 in [Reference Baldo7] we have,

The above equation is an alternative way to express the limiting functional.
4. Proof of the $\Gamma$ -limit
-limit
Throughout the proof of the $\Gamma$![]() -limit we will assume (H1) and (H2)(i),(ii). The proof if we assume (H2)(ii’) instead of (H2)(ii) is similar with minor modifications.
-limit we will assume (H1) and (H2)(i),(ii). The proof if we assume (H2)(ii’) instead of (H2)(ii) is similar with minor modifications.
Proof Proof of theorem 1.1
We begin by proving the $\Gamma$![]() -$\liminf$
-$\liminf$![]() inequality.
inequality.
Let $u_\varepsilon \in L^1(\Omega ; \mathbb {R}^m)$![]() such that $u_\varepsilon \rightarrow u$
such that $u_\varepsilon \rightarrow u$![]() in $L^1(\Omega ; \mathbb {R}^m)$
in $L^1(\Omega ; \mathbb {R}^m)$![]() . If $u_\varepsilon \notin H^1_{loc}$
. If $u_\varepsilon \notin H^1_{loc}$![]() or $u_\varepsilon \neq g_\varepsilon$
or $u_\varepsilon \neq g_\varepsilon$![]() on $\Omega _{\rho _0} \setminus \Omega$
on $\Omega _{\rho _0} \setminus \Omega$![]() , where $\Omega \subset \Omega _{\rho _0}$
, where $\Omega \subset \Omega _{\rho _0}$![]() as in (H2)(i), then $\tilde {J}_\varepsilon (u_\varepsilon,\, \Omega ) = + \infty$
as in (H2)(i), then $\tilde {J}_\varepsilon (u_\varepsilon,\, \Omega ) = + \infty$![]() and the liminf inequality holds trivially. So, let $u_\varepsilon \in H^1_{loc}(\Omega ; \mathbb {R}^m)$
and the liminf inequality holds trivially. So, let $u_\varepsilon \in H^1_{loc}(\Omega ; \mathbb {R}^m)$![]() such that $u_\varepsilon \rightarrow u$
such that $u_\varepsilon \rightarrow u$![]() in $L^1$
in $L^1$![]() and $u_\varepsilon = g_\varepsilon$
and $u_\varepsilon = g_\varepsilon$![]() on $\Omega _{\rho _0} \setminus \Omega$
on $\Omega _{\rho _0} \setminus \Omega$![]() .
.
Let $\rho >1$![]() such that $\rho < \rho _0$
such that $\rho < \rho _0$![]() in (H2)(i), we have
in (H2)(i), we have
where $\partial \Omega _\rho \in C^2$![]() since it is a small dilation of $\Omega$
since it is a small dilation of $\Omega$![]() and there is a unique normal vector $\nu \perp \partial \Omega _{\rho }$
and there is a unique normal vector $\nu \perp \partial \Omega _{\rho }$![]() , such that each $x \in \partial \Omega$
, such that each $x \in \partial \Omega$![]() can be written as $x = y + \nu (y) d \ ,\,\ d = dist(x,\, \partial \Omega _{\rho })$
can be written as $x = y + \nu (y) d \ ,\,\ d = dist(x,\, \partial \Omega _{\rho })$![]() (see the Appendix in [Reference Gilbarg and Trudinger19]).
(see the Appendix in [Reference Gilbarg and Trudinger19]).
So,
by Fubini's Theorem and (H2)(i).
Hence, by (4.1), for every $u_{\varepsilon }$![]() converging to $u$
converging to $u$![]() in $L^1$
in $L^1$![]() such that $u_{\varepsilon }= g_{\varepsilon }$
such that $u_{\varepsilon }= g_{\varepsilon }$![]() on $\Omega _{\rho _0} \setminus \Omega$
on $\Omega _{\rho _0} \setminus \Omega$![]() and $\liminf _{\varepsilon \rightarrow 0} \tilde {J}_{\varepsilon } (u_{\varepsilon },\, \Omega ) < + \infty$
and $\liminf _{\varepsilon \rightarrow 0} \tilde {J}_{\varepsilon } (u_{\varepsilon },\, \Omega ) < + \infty$![]() , we have that
, we have that
Also, by the liminf inequality for $J_{\varepsilon }$![]() (see theorem 2.2 and (3.3)), we can obtain
(see theorem 2.2 and (3.3)), we can obtain
Thus, by (4.3) and (4.4), passing the limit as $\rho$![]() tends to $1$
tends to $1$![]() we have the liminf inequality
we have the liminf inequality
utilizing also the continuity of measures on decreasing sets.
We now prove the $\Gamma$![]() -limsup inequality. Let $u \in BV(\Omega ; \lbrace a_1,\,a_2,\,...,\,a_N \rbrace )$
-limsup inequality. Let $u \in BV(\Omega ; \lbrace a_1,\,a_2,\,...,\,a_N \rbrace )$![]() be such that $u = g_0$
be such that $u = g_0$![]() on $\Omega _{\rho _0} \setminus \Omega. \\$
on $\Omega _{\rho _0} \setminus \Omega. \\$![]() a) We first assume that $u = g_0$
a) We first assume that $u = g_0$![]() on $\Omega \setminus \Omega _{\rho _1}$
on $\Omega \setminus \Omega _{\rho _1}$![]() with $\rho _1 < 1$
with $\rho _1 < 1$![]() and $|\rho _1 -1|$
and $|\rho _1 -1|$![]() small.
small.
As we observe in the proof of Theorem 2.5 in [Reference Baldo7] the $\Gamma$![]() -limsup inequality for $J_\varepsilon$
-limsup inequality for $J_\varepsilon$![]() also holds without the mass constraint, see in particular the proof of Lemma 3.1 in [Reference Baldo7]. Since the $\Gamma$
also holds without the mass constraint, see in particular the proof of Lemma 3.1 in [Reference Baldo7]. Since the $\Gamma$![]() -liminf inequality holds, the $\Gamma$
-liminf inequality holds, the $\Gamma$![]() -limsup inequality is equivalent with
-limsup inequality is equivalent with
for some sequence $u_{\varepsilon }$![]() converging to $u$
converging to $u$![]() in $L^1(\Omega ;\mathbb {R}^m)$
in $L^1(\Omega ;\mathbb {R}^m)$![]() . So let $u_\varepsilon$
. So let $u_\varepsilon$![]() be a sequence converging to $u$
be a sequence converging to $u$![]() in $L^1(\Omega _{\rho _1};\mathbb {R}^m)$
in $L^1(\Omega _{\rho _1};\mathbb {R}^m)$![]() such that (4.6) is satisfied. In particular, $u_\varepsilon$
such that (4.6) is satisfied. In particular, $u_\varepsilon$![]() converges to $g_0$
converges to $g_0$![]() on $\Omega \setminus \Omega _{\rho _1}$
on $\Omega \setminus \Omega _{\rho _1}$![]() , where $\Omega _{\rho _1}$
, where $\Omega _{\rho _1}$![]() is a small contraction of $\Omega$
is a small contraction of $\Omega$![]() .
.
Now, utilizing the sequence $u_\varepsilon$![]() obtained from (4.6), we will modify it by a cut-off function so that the boundary condition is satisfied. By lemma 2.1, there exists a cut-off function $\phi$
obtained from (4.6), we will modify it by a cut-off function so that the boundary condition is satisfied. By lemma 2.1, there exists a cut-off function $\phi$![]() between $U= \Omega _{\frac {1+\rho _1}{2}}$
between $U= \Omega _{\frac {1+\rho _1}{2}}$![]() and $U'= \Omega$
and $U'= \Omega$![]() such that
such that
where $V = \Omega \setminus \overline {\Omega }_{\rho _1}$![]() and $g_\varepsilon$
and $g_\varepsilon$![]() is extended in $V$
is extended in $V$![]() trivially.
trivially.
By the assumptions on $u_\varepsilon$![]() and (H2) we also have
and (H2) we also have
Hence, again by lemma 2.1 we get
Note that the condition $\sup _{\varepsilon >0}( J_\varepsilon (u_\varepsilon,\,U') + J_\varepsilon (g_\varepsilon,\,V)) < + \infty$![]() in lemma 2.1 is satisfied. To be more precise, from lemma 3.2 it holds
in lemma 2.1 is satisfied. To be more precise, from lemma 3.2 it holds
and by (H2)(i),
where $\tilde {u}_{\varepsilon }= u_\varepsilon \phi + (1- \phi )g_\varepsilon$![]() and $\tilde {u}_{\varepsilon }= g_\varepsilon$
and $\tilde {u}_{\varepsilon }= g_\varepsilon$![]() in $\Omega _{\rho _0} \setminus \Omega. \\$
in $\Omega _{\rho _0} \setminus \Omega. \\$![]() b) In the general case we consider $\rho _1 <1$
b) In the general case we consider $\rho _1 <1$![]() and we define $u_{\rho _1}(x) = u(\frac {1}{\rho _1} x)$
and we define $u_{\rho _1}(x) = u(\frac {1}{\rho _1} x)$![]() and without loss of generality we may asume that the origin of $\mathbb {R}^n$
and without loss of generality we may asume that the origin of $\mathbb {R}^n$![]() belongs in $\Omega$
belongs in $\Omega$![]() .
.
By the previous case (a) and (1.6),

Since $u_{\rho _1}$![]() converges to $u$
converges to $u$![]() as $\rho _1$
as $\rho _1$![]() tends to $1$
tends to $1$![]() , if we denote
, if we denote
then by the lower semicontinuity of the $\Gamma$![]() -upper limit (see e.g. Proposition 1.28 in [Reference Braides9]) and (4.8),
-upper limit (see e.g. Proposition 1.28 in [Reference Braides9]) and (4.8),
Hence, by (4.5) and (4.9) we get the required equality (1.8).
5. Minimizing partitions and the structure of the minimizer
In this section, we begin with the basic definitions of minimizing partitions. Then we underline the relationship of minimizing partitions in $\mathbb {R}^2$![]() with the minimizers of the functional $\tilde {J}_0$
with the minimizers of the functional $\tilde {J}_0$![]() and we analyse the structure of the minimizer of $\tilde {J}_0$
and we analyse the structure of the minimizer of $\tilde {J}_0$![]() that we obtain from the $\Gamma$
that we obtain from the $\Gamma$![]() -limit. Utilizing a Bernstein-type theorem for minimizing partitions, we can explicitly compute the energy of the minimizer in proposition 5.5, and by regularity results in [Reference Morgan30], we can determine the precise structure of a minimizer subject to the limiting boundary conditions in theorem 1.3 and prove uniqueness. In subsection 5.2, we make some comments for the limiting minimizers in dimension three. Finally, in the last subsection, we note that we can extend these results to the mass constraint case.
-limit. Utilizing a Bernstein-type theorem for minimizing partitions, we can explicitly compute the energy of the minimizer in proposition 5.5, and by regularity results in [Reference Morgan30], we can determine the precise structure of a minimizer subject to the limiting boundary conditions in theorem 1.3 and prove uniqueness. In subsection 5.2, we make some comments for the limiting minimizers in dimension three. Finally, in the last subsection, we note that we can extend these results to the mass constraint case.
Let $\Omega \subset \mathbb {R}^n$![]() open, occupied by $N$
open, occupied by $N$![]() phases. Associated to each pair of phases $i$
phases. Associated to each pair of phases $i$![]() and $j$
and $j$![]() , there is a surface energy density $\sigma _{ij}$
, there is a surface energy density $\sigma _{ij}$![]() , with $\sigma _{ij}>0$
, with $\sigma _{ij}>0$![]() for $i \neq j$
for $i \neq j$![]() and $\sigma _{ij} = \sigma _{ji}$
and $\sigma _{ij} = \sigma _{ji}$![]() , with $\sigma _{ii}=0$
, with $\sigma _{ii}=0$![]() . Hence, if $A_i$
. Hence, if $A_i$![]() denoted the subset of $\Omega$
denoted the subset of $\Omega$![]() occupied by phase $i$
occupied by phase $i$![]() , then $\Omega$
, then $\Omega$![]() is the disjoint union
is the disjoint union
and the energy of the partition $A = \lbrace A_i \rbrace _{i=1}^N$![]() is
is
where $\mathcal {H}^{n-1}$![]() is the $(n-1)$
is the $(n-1)$![]() -Hausdorff measure in $\mathbb {R}^n$
-Hausdorff measure in $\mathbb {R}^n$![]() and $A_i$
and $A_i$![]() are sets of finite perimeter. If $\Omega$
are sets of finite perimeter. If $\Omega$![]() is unbounded, for example $\Omega =\mathbb {R}^n$
is unbounded, for example $\Omega =\mathbb {R}^n$![]() (we say then that $A$
(we say then that $A$![]() is complete), the quantity above in general will be infinity. Thus, for each $W$
is complete), the quantity above in general will be infinity. Thus, for each $W$![]() open, with $W \subset \subset \Omega$
open, with $W \subset \subset \Omega$![]() , we consider the energy
, we consider the energy
Definition 5.1 The partition $A$![]() is a minimizing $N$
is a minimizing $N$![]() -partition if given any $W \subset \subset \Omega$
-partition if given any $W \subset \subset \Omega$![]() and any $N$
and any $N$![]() -partition $A'$
-partition $A'$![]() of $\Omega$
of $\Omega$![]() with
with

we have
The symmetric difference $A_i \triangle A_i'$![]() is defined as their union minus their intersection, that is, $A_i \triangle A_i' = (A_i \cup A_i') \setminus (A_i \cap A_i')$
is defined as their union minus their intersection, that is, $A_i \triangle A_i' = (A_i \cup A_i') \setminus (A_i \cap A_i')$![]() .
.
To formulate the Dirichlet problem, we assume that $\partial \Omega$![]() is $C^1$
is $C^1$![]() and given a partition $C$
and given a partition $C$![]() of $\partial \Omega$
of $\partial \Omega$![]() up to a set of $\mathcal {H}^{n-1}$
up to a set of $\mathcal {H}^{n-1}$![]() -measure zero, we may prescribe the boundary data for $A$
-measure zero, we may prescribe the boundary data for $A$![]() :
:
Now the energy is minimized subject to such a prescribed boundary.
Remark 5.2 Note that the minimization of the functional $\tilde {J}_0(u,\, \Omega )$![]() is equivalent to minimizing the energy $E(A;\Omega )$
is equivalent to minimizing the energy $E(A;\Omega )$![]() under the appropriate Dirichlet conditions.
under the appropriate Dirichlet conditions.
In figure 1 we show a triod with angles $\theta _1,\, \theta _2,\, \theta _3$![]() , and the corresponding triangle with their supplementary angles $\hat {\theta }_i = \pi - \theta _i$
, and the corresponding triangle with their supplementary angles $\hat {\theta }_i = \pi - \theta _i$![]() . For these angles Young's law holds, that is,
. For these angles Young's law holds, that is,
Definition 5.3 Let $\mathcal {A}_{x_0} = \lbrace A_1,\,A_2,\,A_3 \rbrace$![]() be a $3$
be a $3$![]() -partition of $\mathbb {R}^2$
-partition of $\mathbb {R}^2$![]() such that $A_i$
such that $A_i$![]() is a single infinite sector emanating from the point $x_0 \in \mathbb {R}^2$
is a single infinite sector emanating from the point $x_0 \in \mathbb {R}^2$![]() with three opening angles $\theta _i$
with three opening angles $\theta _i$![]() that satisfy (5.4). We call as a triod $C_{tr}(x_0)$
that satisfy (5.4). We call as a triod $C_{tr}(x_0)$![]() the boundary of the partition $\mathcal {A}_{x_0}$
the boundary of the partition $\mathcal {A}_{x_0}$![]() , that is, $C_{tr}(x_0) = \lbrace \partial A_i \cap \partial A_j \rbrace _{1 \leq i < j \leq 3}$
, that is, $C_{tr}(x_0) = \lbrace \partial A_i \cap \partial A_j \rbrace _{1 \leq i < j \leq 3}$![]() .
.

Figure 1. In the left we show a triod with angles $\theta_1, \theta_2, \theta_3$![]() . In the right there is the corresponding triangle with supplementary angles $\hat{\theta}_1, \hat{\theta}_2, \hat{\theta}_3$
. In the right there is the corresponding triangle with supplementary angles $\hat{\theta}_1, \hat{\theta}_2, \hat{\theta}_3$![]() that satisfy the Young's law.
that satisfy the Young's law.
So, in other words, the triod is consisted of three infinite lines meeting at a point $x_0$![]() and their angles between the lines satisfy the Young's law (5.4) (see figure 1). As we see in theorem 2.6, the triod is the unique locally $3$
and their angles between the lines satisfy the Young's law (5.4) (see figure 1). As we see in theorem 2.6, the triod is the unique locally $3$![]() -minimizing partition of $\mathbb {R}^2$
-minimizing partition of $\mathbb {R}^2$![]() . The point $x_0$
. The point $x_0$![]() , i.e. the centre of the triod, is often called a triple junction point.
, i.e. the centre of the triod, is often called a triple junction point.
5.1 The structure of the minimizer in the disk
Throughout this section, we will assume that $\sigma _{ij} = \sigma >0$![]() for $i \neq j$
for $i \neq j$![]() , therefore we have by Young's law $\theta _i = \frac {2 \pi }{3} \ ,\,\ i=1,\,2,\,3$
, therefore we have by Young's law $\theta _i = \frac {2 \pi }{3} \ ,\,\ i=1,\,2,\,3$![]() . As a result of theorem 2.6, we expect that, by imposing the appropriate boundary conditions, the minimizer $u_0$
. As a result of theorem 2.6, we expect that, by imposing the appropriate boundary conditions, the minimizer $u_0$![]() of $\tilde {J}_0(u,\, \overline {B}_1) \ ,\, B_1 \subset \mathbb {R}^2$
of $\tilde {J}_0(u,\, \overline {B}_1) \ ,\, B_1 \subset \mathbb {R}^2$![]() which we obtain from the $\Gamma$
which we obtain from the $\Gamma$![]() -limit will be a triod with angles $\frac {2 \pi }{3}$
-limit will be a triod with angles $\frac {2 \pi }{3}$![]() restricted in $B_1$
restricted in $B_1$![]() and centred at a point $x \in B_1$
and centred at a point $x \in B_1$![]() .
.
We now recall Steiner's problem that gives us some geometric intuition about this fact.
Let us take three points $A ,\, \ B$![]() and $C$
and $C$![]() , arranged in any way in the plane. The problem is to find a fourth point $P$
, arranged in any way in the plane. The problem is to find a fourth point $P$![]() such that the sum of distances from $P$
such that the sum of distances from $P$![]() to the other three points is a minimum; that is, we require $AP + BP + CP$
to the other three points is a minimum; that is, we require $AP + BP + CP$![]() to be a minimum length.
to be a minimum length.
If the triangle $ABC$![]() possesses internal angles which are all less than $120^o$
possesses internal angles which are all less than $120^o$![]() , then $P$
, then $P$![]() is the point such that each side of the triangle, i.e. $AB ,\,\ BC$
is the point such that each side of the triangle, i.e. $AB ,\,\ BC$![]() and $CA$
and $CA$![]() , subtends an angle of $120^o$
, subtends an angle of $120^o$![]() at $P$
at $P$![]() . However, if one angle, say $A \hat {C} B$
. However, if one angle, say $A \hat {C} B$![]() , is greater than $120^o$
, is greater than $120^o$![]() , then $P$
, then $P$![]() must coincide with $C .$
must coincide with $C .$![]()
The Steiner's problem is a special case of the geometric median problem and has a unique solution whenever the points are not collinear. For more details and proofs, see [Reference Gilbert and Pollak20].
The problem of minimizing partitions subject to boundary conditions, in contrast to the mass constraint case, might not always admit a minimum, we provide an example in figure 2 below.

Figure 2. The geometric problem subject to such boundary conditions does not admit a minimum. However, the limiting functional admits a minimizer that forms a boundary layer.
However, a minimizer will exist for the minimization problem $\min _{u\in BV(\Omega ; \lbrace W=0 \rbrace )} \tilde {J}_0(u,\, \overline {\Omega })$![]() , for instance the one we obtain from the $\Gamma$
, for instance the one we obtain from the $\Gamma$![]() -limit, which will form a ‘boundary layer’ in the boundary of the domain instead of internal layer (i.e. the interface separating the phases). Particularly, in figure 2 above, $u_0 = a_1$
-limit, which will form a ‘boundary layer’ in the boundary of the domain instead of internal layer (i.e. the interface separating the phases). Particularly, in figure 2 above, $u_0 = a_1$![]() , a.e. will be a minimizer of $\tilde {J}_0$
, a.e. will be a minimizer of $\tilde {J}_0$![]() and
and

where $\partial \Omega _{AB}$![]() is the part of the boundary of $\Omega$
is the part of the boundary of $\Omega$![]() in which $g_0 = a_2$
in which $g_0 = a_2$![]() . When there are no line segments in the boundary of the domain or when $g_0$
. When there are no line segments in the boundary of the domain or when $g_0$![]() does not admit jumps nearby such line segments, then we expect that there are no boundary layers and the boundary term in the energy of $\tilde {J}_0$
does not admit jumps nearby such line segments, then we expect that there are no boundary layers and the boundary term in the energy of $\tilde {J}_0$![]() vanishes (see remark 1.2), otherwise we could find a minimizer with strictly less energy. In the cases where the boundary term vanishes we can write $\tilde {J}_0(u_0,\, \overline {\Omega }) = \tilde {J}_0(u_0,\,\Omega )$
vanishes (see remark 1.2), otherwise we could find a minimizer with strictly less energy. In the cases where the boundary term vanishes we can write $\tilde {J}_0(u_0,\, \overline {\Omega }) = \tilde {J}_0(u_0,\,\Omega )$![]() . This can be proved rigorously in the case where $\Omega = B_1$
. This can be proved rigorously in the case where $\Omega = B_1$![]() and assuming (H2)(iii), utilizing also proposition 2.5 as we will see in the proof of theorem 1.3.
and assuming (H2)(iii), utilizing also proposition 2.5 as we will see in the proof of theorem 1.3.
Remark 5.4 For the mass constraint case, by classical results of Almgren's improved and simplified by Leonardi in [Reference Leonardi26] for minimizing partitions with surface tension coefficients $\sigma _{ij}$![]() satisfying the strict triangle inequality (see (2.3)), $\Omega _j$
satisfying the strict triangle inequality (see (2.3)), $\Omega _j$![]() can be taken open with $\partial \Omega _j$
can be taken open with $\partial \Omega _j$![]() real analytic except possibly for a singular part with Hausdorff dimension at most $n-2$
real analytic except possibly for a singular part with Hausdorff dimension at most $n-2$![]() . Therefore, $\partial ^* \Omega _i \cap \partial ^* \Omega _j = \partial \Omega _i \cap \partial \Omega _j \ ,\,\ \mathcal {H}^{n-1}$
. Therefore, $\partial ^* \Omega _i \cap \partial ^* \Omega _j = \partial \Omega _i \cap \partial \Omega _j \ ,\,\ \mathcal {H}^{n-1}$![]() -a.e., where $u_0 = \sum _{i=1}^N a_i \chi _{\Omega _i}$
-a.e., where $u_0 = \sum _{i=1}^N a_i \chi _{\Omega _i}$![]() is the minimizer of $J_0$
is the minimizer of $J_0$![]() with a mass constraint. These regularity results have been stated by White in [Reference White36] but without providing a proof. Also, Morgan in [Reference Morgan31] has proved regularity of minimizing partitions in the plane subject to mass constraint. However, we deal with the problem with boundary conditions, so we cannot apply these regularity results.
with a mass constraint. These regularity results have been stated by White in [Reference White36] but without providing a proof. Also, Morgan in [Reference Morgan31] has proved regularity of minimizing partitions in the plane subject to mass constraint. However, we deal with the problem with boundary conditions, so we cannot apply these regularity results.
Notation: We set as $x_0 \in B_1$![]() the point such that the line segments starting from $p_i = \partial I_k \cap \partial I_l \ ,\,\ k \neq l \ ,\,\ i \in \lbrace 1,\,2,\,3 \rbrace \setminus \lbrace k,\,l \rbrace$
the point such that the line segments starting from $p_i = \partial I_k \cap \partial I_l \ ,\,\ k \neq l \ ,\,\ i \in \lbrace 1,\,2,\,3 \rbrace \setminus \lbrace k,\,l \rbrace$![]() and ending at $x_0$
and ending at $x_0$![]() meet all at angle $\frac {2 \pi }{3}$
meet all at angle $\frac {2 \pi }{3}$![]() (see (H2)(iii) and proposition 2.5). Also we denote by $C_0$
(see (H2)(iii) and proposition 2.5). Also we denote by $C_0$![]() the sum of the lengths of these line segments. The following proposition measures the energy of the limiting minimizer.
the sum of the lengths of these line segments. The following proposition measures the energy of the limiting minimizer.
Proposition 5.5 Let $(u_\varepsilon )$![]() be a minimizing sequence of $\tilde {J}_\varepsilon (u,\,B_1)$
be a minimizing sequence of $\tilde {J}_\varepsilon (u,\,B_1)$![]() . Then $u_\varepsilon \rightarrow u_0$
. Then $u_\varepsilon \rightarrow u_0$![]() in $L^1$
in $L^1$![]() along subsequence with $u_0 \in BV(B_1; \lbrace a_1,\,a_2,\,a_3 \rbrace )$
along subsequence with $u_0 \in BV(B_1; \lbrace a_1,\,a_2,\,a_3 \rbrace )$![]() and $u_0$
and $u_0$![]() is a minimizer of $\tilde {J}_0(u,\, \overline {B}_1)$
is a minimizer of $\tilde {J}_0(u,\, \overline {B}_1)$![]() subject to the limiting Dirichlet values (H2)(iii), where we extend $u$
subject to the limiting Dirichlet values (H2)(iii), where we extend $u$![]() by setting $u=g_0$
by setting $u=g_0$![]() on $\mathbb {R}^2 \setminus B_1$
on $\mathbb {R}^2 \setminus B_1$![]() .
.
In addition, we have
where $u_0 = a_1 \chi _{\Omega _1} +a_2 \chi _{\Omega _2} + a_3 \chi _{\Omega _3}.$![]()
Proof. From lemmas 3.2 and 3.3, it holds that if $u_\varepsilon$![]() is a minimizing sequence for $\tilde {J}_\varepsilon (u,\,B_1)$
is a minimizing sequence for $\tilde {J}_\varepsilon (u,\,B_1)$![]() , then $\tilde {J}_\varepsilon (u_\varepsilon,\,B_1) \leq C$
, then $\tilde {J}_\varepsilon (u_\varepsilon,\,B_1) \leq C$![]() and thus $u_\varepsilon \rightarrow u_0$
and thus $u_\varepsilon \rightarrow u_0$![]() in $L^1$
in $L^1$![]() along subsequence. The fact that $u_0$
along subsequence. The fact that $u_0$![]() is a minimizer of $\tilde {J}_0$
is a minimizer of $\tilde {J}_0$![]() is a standard fact from the theory of $\Gamma$
is a standard fact from the theory of $\Gamma$![]() -convergence. It can be seen as follows.
-convergence. It can be seen as follows.
Let $w \in BV(\overline {B_1},\, \lbrace a_1,\,a_2,\,a_3 \rbrace )$![]() such that $w = g_0$
such that $w = g_0$![]() on $\mathbb {R}^2 \setminus B_1$
on $\mathbb {R}^2 \setminus B_1$![]() , then from the limsup inequality in theorem 1.1, we have that there exists $w_\varepsilon \in H^1_{loc}(\mathbb {R}^2 ;\mathbb {R}^m) \ ,\,\ w_\varepsilon = g_\varepsilon$
, then from the limsup inequality in theorem 1.1, we have that there exists $w_\varepsilon \in H^1_{loc}(\mathbb {R}^2 ;\mathbb {R}^m) \ ,\,\ w_\varepsilon = g_\varepsilon$![]() on $\mathbb {R}^2 \setminus B_1$
on $\mathbb {R}^2 \setminus B_1$![]() such that $w_\varepsilon \rightarrow w$
such that $w_\varepsilon \rightarrow w$![]() in $L^1$
in $L^1$![]() and $\limsup _{\varepsilon \rightarrow 0} \tilde {J}_\varepsilon (w_\varepsilon,\,B_1) \leq \tilde {J}_0 (w,\, \overline {B}_1)$
and $\limsup _{\varepsilon \rightarrow 0} \tilde {J}_\varepsilon (w_\varepsilon,\,B_1) \leq \tilde {J}_0 (w,\, \overline {B}_1)$![]() . Now since $u_\varepsilon$
. Now since $u_\varepsilon$![]() is a minimizing sequence for $\tilde {J}_\varepsilon (u,\,B_1)$
is a minimizing sequence for $\tilde {J}_\varepsilon (u,\,B_1)$![]() and from the liminf inequality in theorem 1.1, we have
and from the liminf inequality in theorem 1.1, we have

For proving (5.5), we utilize theorem 2.6 (i.e. Theorem 2 in [Reference Alikakos4]). Since the triod is a minimizing 3-partition in $\mathbb {R}^2$![]() we have that for any $W \subset \subset \mathbb {R}^2$
we have that for any $W \subset \subset \mathbb {R}^2$![]() and any partition it holds that $E(A,\,W) \leq E(V,\,W)$
and any partition it holds that $E(A,\,W) \leq E(V,\,W)$![]() , where suppose that $A = \lbrace A_1,\,A_2,\,A_3 \rbrace$
, where suppose that $A = \lbrace A_1,\,A_2,\,A_3 \rbrace$![]() is the partition of the triod and $V = \lbrace V_1,\,V_2,\,V_3 \rbrace$
is the partition of the triod and $V = \lbrace V_1,\,V_2,\,V_3 \rbrace$![]() is a 3-partition in $\mathbb {R}^2 .$
is a 3-partition in $\mathbb {R}^2 .$![]()
We have $u_0 = a_1 \chi _{\Omega _1} +a_2 \chi _{\Omega _2} + a_3 \chi _{\Omega _3}$![]() such that $u_0 = g_0$
such that $u_0 = g_0$![]() on $\partial B_1$
on $\partial B_1$![]() and extend $u_0$
and extend $u_0$![]() in $\mathbb {R}^2$
in $\mathbb {R}^2$![]() , being the triod with $\theta _i = \frac {2 \pi }{3}$
, being the triod with $\theta _i = \frac {2 \pi }{3}$![]() in $\mathbb {R}^2 \setminus B_1$
in $\mathbb {R}^2 \setminus B_1$![]() centred at $x_0$
centred at $x_0$![]() . This defines a 3-partition in $\mathbb {R}^2$
. This defines a 3-partition in $\mathbb {R}^2$![]() , noted as $\tilde {\Omega } = \lbrace \tilde {\Omega }_i \rbrace _{i=1}^3$
, noted as $\tilde {\Omega } = \lbrace \tilde {\Omega }_i \rbrace _{i=1}^3$![]() . Since the triod is a minimizing 3-partition in the plane, we take any $W \subset \subset \mathbb {R}^2$
. Since the triod is a minimizing 3-partition in the plane, we take any $W \subset \subset \mathbb {R}^2$![]() such that $B_2 \subset \subset W$
such that $B_2 \subset \subset W$![]() and $\bigcup _{i=1}^3 (A_i \triangle \tilde {\Omega }_i) \subset \subset W$
and $\bigcup _{i=1}^3 (A_i \triangle \tilde {\Omega }_i) \subset \subset W$![]() , so we have
, so we have
where $A$![]() is the partition of the triod.
is the partition of the triod.
Now since
from the way we extended $u_0$![]() in $\mathbb {R}^2$
in $\mathbb {R}^2$![]() and
and
since $\partial A_i \cap \partial A_j \cap \overline {B}_1$![]() are line segments inside $B_1$
are line segments inside $B_1$![]() with sum of their lengths equals $C_0$
with sum of their lengths equals $C_0$![]() , we conclude
, we conclude

For the upper bound inequality $\sum _{1 \leq i < j \leq 3} \mathcal {H}^1(\partial ^* \Omega _i \cap \partial ^* \Omega _j \cap \overline {B}_1) \leq C_0$![]() , we consider as a comparison function $\tilde {u}= a_1 \chi _{A_1} +a_2 \chi _{A_2} + a_3 \chi _{A_3}$
, we consider as a comparison function $\tilde {u}= a_1 \chi _{A_1} +a_2 \chi _{A_2} + a_3 \chi _{A_3}$![]() , where $C_{tr}(x_0)= \lbrace A_1,\,A_2,\,A_3 \rbrace$
, where $C_{tr}(x_0)= \lbrace A_1,\,A_2,\,A_3 \rbrace$![]() is the partition of the triod centred at $x_0 \in B_1$
is the partition of the triod centred at $x_0 \in B_1$![]() and angles $\theta _i = \frac {2 \pi }{3}$
and angles $\theta _i = \frac {2 \pi }{3}$![]() (see definition 5.3).
(see definition 5.3).
Then $\tilde {u}$![]() satisfies the boundary condition $\tilde {u} = g_0$
satisfies the boundary condition $\tilde {u} = g_0$![]() on $\mathbb {R}^2 \setminus B_1$
on $\mathbb {R}^2 \setminus B_1$![]() and therefore by the minimality of $u_0$
and therefore by the minimality of $u_0$![]() we have
we have

Corollary 5.6 Assume for simplicity that $x_0$![]() in proposition 5.5 above is the origin of $\mathbb {R}^2$
in proposition 5.5 above is the origin of $\mathbb {R}^2$![]() . Then for every $R>0$
. Then for every $R>0$![]() the energy of the limiting minimizer will satisfy
the energy of the limiting minimizer will satisfy
In addition, there exists an entire minimizer in the plane and the partition that defines is a minimal cone.
Proof. Since $x_0$![]() is the origin of $\mathbb {R}^2$
is the origin of $\mathbb {R}^2$![]() , it holds that $C_0$
, it holds that $C_0$![]() in (5.5) equals $3$
in (5.5) equals $3$![]() . Arguing as in proposition 5.5 above we can similarly obtain a minimizer of $\tilde {J}_0 (u_0,\, \overline {B}_R)$
. Arguing as in proposition 5.5 above we can similarly obtain a minimizer of $\tilde {J}_0 (u_0,\, \overline {B}_R)$![]() that satisfies (5.10). By a diagonal argument the minimizer can be extended in the entire plane and will also satisfy
that satisfies (5.10). By a diagonal argument the minimizer can be extended in the entire plane and will also satisfy
Thus, the partition that it defines is a minimal cone (see [Reference White37] or [Reference Alikakos4]).
Finally, we will prove that the minimizer of $\tilde {J}_0$![]() in $\overline {B}_1$
in $\overline {B}_1$![]() is unique, that is, the only minimizer is the triod restricted to $B_1$
is unique, that is, the only minimizer is the triod restricted to $B_1$![]() centred at a point in $B_1 .$
centred at a point in $B_1 .$![]() In figure 3 below we provide the structure of the minimizer $u_0$
In figure 3 below we provide the structure of the minimizer $u_0$![]() obtained in theorem 1.3.
obtained in theorem 1.3.
Proof Proof of theorem 1.3
Firstly, we show that the minimizing partition of $B_1$![]() with respect to the boundary conditions defined from $g_0$
with respect to the boundary conditions defined from $g_0$![]() is a $(M,\,0,\,\delta )$
is a $(M,\,0,\,\delta )$![]() -minimal for $\delta >0$
-minimal for $\delta >0$![]() (see definition 2.4). If not, let $S$
(see definition 2.4). If not, let $S$![]() be the partition defined from $u_0$
be the partition defined from $u_0$![]() , we can find a Lipschitz function $\phi : \mathbb {R}^2 \rightarrow \mathbb {R}^2$
, we can find a Lipschitz function $\phi : \mathbb {R}^2 \rightarrow \mathbb {R}^2$![]() such that
such that
with

So if we consider the partition

then the boundary of the partition defined by $\tilde {S}$![]() will satisfy the boundary conditions (since dist$(W \cup \phi (W),\, \mathbb {R}^2 \setminus B_1) >0$
will satisfy the boundary conditions (since dist$(W \cup \phi (W),\, \mathbb {R}^2 \setminus B_1) >0$![]() ) and also $\mathcal {H}^1 (\tilde {S}) < \mathcal {H}^1(S)$
) and also $\mathcal {H}^1 (\tilde {S}) < \mathcal {H}^1(S)$![]() which contradicts the minimality of $S .$
which contradicts the minimality of $S .$![]()
Thus, by (H2)(iii) we apply proposition 2.5 and we have that the unique smallest $(M,\,0,\, \delta )$![]() -minimal set consists of three line segments from the three vertices defined from $g_0$
-minimal set consists of three line segments from the three vertices defined from $g_0$![]() (i.e. the jump points in $\partial B_1$
(i.e. the jump points in $\partial B_1$![]() ) meeting at $\frac {2 \pi }{3}$
) meeting at $\frac {2 \pi }{3}$![]() . The meeting point is unique and belongs in the interior of $B_1$
. The meeting point is unique and belongs in the interior of $B_1$![]() . Thus, $\partial \Omega _i \cap \partial \Omega _j = \partial ^* \Omega _i \cap \partial ^* \Omega _j$
. Thus, $\partial \Omega _i \cap \partial \Omega _j = \partial ^* \Omega _i \cap \partial ^* \Omega _j$![]() are line segments meeting at $\frac {2 \pi }{3}$
are line segments meeting at $\frac {2 \pi }{3}$![]() in an interior point of $B_1$
in an interior point of $B_1$![]() .
.
Corollary 5.7 Let $u_0 = a_1 \chi _{\Omega _1} +a_2 \chi _{\Omega _2} + a_3 \chi _{\Omega _3}$![]() be a minimizer of $\tilde {J}_0(u,\,\overline {B}_1)$
be a minimizer of $\tilde {J}_0(u,\,\overline {B}_1)$![]() subject to the limiting Dirichlet values $g_0( \theta ) = a_1 \chi _{(0, \frac {2 \pi }{3})} + a_2 \chi _{(\frac {2 \pi }{3} ,\, \frac {4 \pi }{3})} +a_3 \chi _{(\frac {4 \pi }{3} ,\, 2 \pi )}, \theta \in (0,\, 2\pi ) .$
subject to the limiting Dirichlet values $g_0( \theta ) = a_1 \chi _{(0, \frac {2 \pi }{3})} + a_2 \chi _{(\frac {2 \pi }{3} ,\, \frac {4 \pi }{3})} +a_3 \chi _{(\frac {4 \pi }{3} ,\, 2 \pi )}, \theta \in (0,\, 2\pi ) .$![]() Then $\partial \Omega _i \cap \partial \Omega _j$
Then $\partial \Omega _i \cap \partial \Omega _j$![]() are radi of $B_1 \ ,\,\ | \Omega _i |= \frac {1}{3}| B_1 |$
are radi of $B_1 \ ,\,\ | \Omega _i |= \frac {1}{3}| B_1 |$![]() and the minimizer is unique.
and the minimizer is unique.

Figure 3. Here is an example of a minimizer that we obtain in theorem 1.3.
In figure 4 above we illustrate the structure of the minimizer $u_0$![]() obtained in corollary 5.7.
obtained in corollary 5.7.

Figure 4. The singular set of the minimizer obtained in corollary 5.7 is consisted of three radii of the ball.
5.2 Minimizers in dimension three
In this subsection, we will briefly make some comments for the structure of minimizers in $\mathbb {R}^3$![]() . If we impose the appropriate boundary conditions in $B_R \subset \mathbb {R}^3$
. If we impose the appropriate boundary conditions in $B_R \subset \mathbb {R}^3$![]() and $\lbrace W=0 \rbrace = \lbrace a_1,\,a_2,\,a_3 \rbrace \ ,\,\ g_\varepsilon \rightarrow g_0 \ \textrm {in} \ L^1(B_R; \mathbb {R}^3)$
and $\lbrace W=0 \rbrace = \lbrace a_1,\,a_2,\,a_3 \rbrace \ ,\,\ g_\varepsilon \rightarrow g_0 \ \textrm {in} \ L^1(B_R; \mathbb {R}^3)$![]() such that the partition in $\partial B_R$
such that the partition in $\partial B_R$![]() defined by $g_0$
defined by $g_0$![]() is equal to the partition of $(C_{tr} \times \mathbb {R}) \cap \partial B_R$
is equal to the partition of $(C_{tr} \times \mathbb {R}) \cap \partial B_R$![]() , where $C_{tr}$
, where $C_{tr}$![]() is the triod as in figure 1 (with equal angles), then by Theorem 3 in [Reference Alikakos4], arguing as in proposition 5.5 (see also corollary 5.6), we can obtain
is the triod as in figure 1 (with equal angles), then by Theorem 3 in [Reference Alikakos4], arguing as in proposition 5.5 (see also corollary 5.6), we can obtain
which gives
where $\omega _2$![]() is the volume of the 2-dimensional unit ball (see [Reference White37]). That is, the partition that the minimizer defines can be extended to a minimal cone in $\mathbb {R}^3$
is the volume of the 2-dimensional unit ball (see [Reference White37]). That is, the partition that the minimizer defines can be extended to a minimal cone in $\mathbb {R}^3$![]() . Now since the only minimizing minimal cones are the triod and the tetrahedral cone (see [Reference Taylor35]), then the minimizer of $\tilde {J}_0$
. Now since the only minimizing minimal cones are the triod and the tetrahedral cone (see [Reference Taylor35]), then the minimizer of $\tilde {J}_0$![]() is such that $u_0 = \sum _{i=1}^3 a_i \chi _{\Omega _i}$
is such that $u_0 = \sum _{i=1}^3 a_i \chi _{\Omega _i}$![]() , where $\Omega = \lbrace \Omega _i \rbrace _{i=1}^3$
, where $\Omega = \lbrace \Omega _i \rbrace _{i=1}^3$![]() is the partition of $(C_{tr} \times \mathbb {R} ) \cap B_R$
is the partition of $(C_{tr} \times \mathbb {R} ) \cap B_R$![]() .
.
Similarly, if $\lbrace W=0 \rbrace = \lbrace a_1,\,a_2,\,a_3,\,a_4 \rbrace$![]() and we impose the Dirichlet conditions such that $g_0$
and we impose the Dirichlet conditions such that $g_0$![]() defines the partition of the tetrahedral cone intersection with $\partial B_R$
defines the partition of the tetrahedral cone intersection with $\partial B_R$![]() , then again $u_0 = \sum _{i=1}^4 a_i \chi _{\Omega _i}$
, then again $u_0 = \sum _{i=1}^4 a_i \chi _{\Omega _i}$![]() , where $\Omega = \lbrace \Omega _i \rbrace _{i=1}^4$
, where $\Omega = \lbrace \Omega _i \rbrace _{i=1}^4$![]() is the partition of the tetrahedral cone restricted in $B_R$
is the partition of the tetrahedral cone restricted in $B_R$![]() .
.
5.3 Minimizers in the disc for the mass constraint case
Throughout this subsection, we will assume that $a_i \ ,\, i=1,\,2,\,3,\,$![]() are affinely independent, that is, they are not contained in a single line. This can also be expressed as
are affinely independent, that is, they are not contained in a single line. This can also be expressed as

In addition, we consider that $m =(m_1,\,m_2) \in \mathbb {R}^2$![]() such that $m_1,\,m_2 >0$
such that $m_1,\,m_2 >0$![]() (as in [Reference Baldo7]).
(as in [Reference Baldo7]).
Let $u_0$![]() be a minimizer of $J_0(u,\,B_1) \ ,\,\ B_1 \subset \mathbb {R}^2$
be a minimizer of $J_0(u,\,B_1) \ ,\,\ B_1 \subset \mathbb {R}^2$![]() defined in (1.6) subject to the mass constraint
defined in (1.6) subject to the mass constraint
(i.e. the minimizer $u_0$![]() of Theorem p.70 in [Reference Baldo7]) and $\lbrace W=0 \rbrace = \lbrace a_1,\,a_2,\,a_3 \rbrace$
of Theorem p.70 in [Reference Baldo7]) and $\lbrace W=0 \rbrace = \lbrace a_1,\,a_2,\,a_3 \rbrace$![]() . Then $u_0 = \sum _{i=1}^3 a_i \chi _{\Omega _i}$
. Then $u_0 = \sum _{i=1}^3 a_i \chi _{\Omega _i}$![]() , where $\Omega _1,\,\Omega _2,\,\Omega _3$
, where $\Omega _1,\,\Omega _2,\,\Omega _3$![]() is a partition of $B_1$
is a partition of $B_1$![]() which minimizes the quantity
which minimizes the quantity
among all other partitions of $B_1$![]() such that $\sum _{i=1}^3 | \Omega _i | a_i = m .$
such that $\sum _{i=1}^3 | \Omega _i | a_i = m .$![]()
Theorem 5.8 Let $u_0$![]() be a minimizer of $J_0(u,\,B_1)$
be a minimizer of $J_0(u,\,B_1)$![]() as above and assume that
as above and assume that

Then
In particular, the boundary of the partition is consisted of three circular arcs or line segments meeting at an interior vertex at $120$![]() degrees angles, reaching orthogonally $\partial B_1$
degrees angles, reaching orthogonally $\partial B_1$![]() and so that the sum of geodesic curvature is zero.
and so that the sum of geodesic curvature is zero.
Proof. We have that $u_0 = \sum _{i=1}^3 a_i \chi _{\Omega _i}$![]() , where $\Omega _i$
, where $\Omega _i$![]() are such that $\sum _{i=1}^3 | \Omega _i | = | B_1 |$
are such that $\sum _{i=1}^3 | \Omega _i | = | B_1 |$![]() and $u_0$
and $u_0$![]() minimizes the quantity (5.13).
minimizes the quantity (5.13).
By assumption (5.14), since $u_0$![]() satisfies (5.12), we have
satisfies (5.12), we have

since $a_i$![]() are affinely independent.
are affinely independent.
Now by Theorem 4.1 in [Reference Canete and Ritore10] we conclude that the minimizer is a standard graph i.e. it is consisted of three circular arcs or line segments meeting at an interior vertex at $120$![]() degrees angles, reaching orthogonally $\partial B_1$
degrees angles, reaching orthogonally $\partial B_1$![]() and so that the sum of geodesic curvature is zero. So, $\partial ^* \Omega _i \cap \partial ^* \Omega _j = \partial \Omega _i \cap \partial \Omega _j$
and so that the sum of geodesic curvature is zero. So, $\partial ^* \Omega _i \cap \partial ^* \Omega _j = \partial \Omega _i \cap \partial \Omega _j$![]() are piecewise smooth.
are piecewise smooth.
Finally, the minimizer is unique up to rigid motions of the disc by Theorem 3.6 in [Reference Canete and Ritore10].
Note that in the case where $m = \frac {1}{3} | B_1 | \sum _{i=1}^3 c_i a_i$![]() , it holds that $| \Omega _i | = \frac {1}{3} | B_1 | \ ,\,\ i=1,\,2,\,3 \ ,\,\ \textrm {and} \partial \Omega _i \cap \partial \Omega _j$
, it holds that $| \Omega _i | = \frac {1}{3} | B_1 | \ ,\,\ i=1,\,2,\,3 \ ,\,\ \textrm {and} \partial \Omega _i \cap \partial \Omega _j$![]() are line segments meeting at the origin and the minimizer is unique up to rotations.
are line segments meeting at the origin and the minimizer is unique up to rotations.
Acknowledgements
I wish to thank my advisor Professor Nicholas Alikakos for his guidance and for suggesting this topic as a part of my thesis for the Department of Mathematics and Applied Mathematics at the University of Crete. Also, I would like to thank Professor P. Sternberg and Professor F. Morgan for their valuable comments on a previous version of this paper, which let to various improvements. Finally, I would like to thank the anonymous referee for their valuable suggestions, which not only enhanced the presentation but also significantly improved the quality of the paper by relaxing some of the assumptions in our results.