No CrossRef data available.
Published online by Cambridge University Press: 20 October 2023
We show that for every 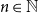 $n\in \mathbb N$ and
$n\in \mathbb N$ and 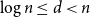 $\log n\le d\lt n$, if a graph
$\log n\le d\lt n$, if a graph 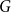 $G$ has
$G$ has 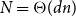 $N=\Theta (dn)$ vertices and minimum degree
$N=\Theta (dn)$ vertices and minimum degree 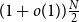 $(1+o(1))\frac{N}{2}$, then it contains a spanning subdivision of every
$(1+o(1))\frac{N}{2}$, then it contains a spanning subdivision of every  $n$-vertex
$n$-vertex 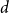 $d$-regular graph.
$d$-regular graph.