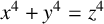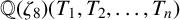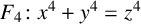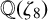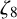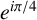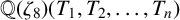1 Introduction
The problem of finding points on the Fermat quartic
$$ \begin{align*} F_4\colon x^4+y^4=z^4 \end{align*} $$
over number fields has been studied by several authors. Fermat showed that
$F_4$
only has trivial points over the rational numbers, where a trivial point on
$F_4$
is a point
$[x:y:z]$
with
$xyz=0$
. Aigner [Reference Aigner1] showed that if
$F_4$
has nontrivial points in a quadratic number field
${\mathbb {Q}}(\sqrt {d})$
, then
$d=-7$
. Faddeev [Reference Faddeev5] later found all points on
$F_4$
over all quadratic number fields and all cubic number fields. Bremner and Choudhry [Reference Bremner and Choudhry3] showed that
$F_4$
only has trivial points in any cyclic cubic number field. Recently, Ishitsuka et al. found all points on
$F_4$
over quadratic extensions of
${\mathbb {Q}}(\zeta _8)$
.
Theorem 1.1 (Ishitsuka et al. [Reference Ishitsuka, Ito and Oshita6, Theorem 7.3]).
There are
$188$
points on
$F_4$
defined over quadratic extensions of
${\mathbb {Q}}(\zeta _8)$
:
-
(A)
$12$
trivial points defined over
${\mathbb {Q}}(\zeta _8)$
:
$[1:\zeta _8^{j}:0], [0:\pm 1:1], [0:\pm {\zeta _8}^2:1]$
, and
$[\pm 1:0:1], [\pm {\zeta _8}^2:0:1 ], j=1,3,5,7$
; -
(B)
$48$
points defined over
${\mathbb {Q}}(2^{1/4}\zeta _8)$
:
$[2^{1/4}\zeta _8^{2i}:\zeta _8^{1+2j}:1], [\zeta _8^{1+2j}:2^{1/4}\zeta _8^{2i}:1]$
,
$[2^{-1/4}\zeta _8^{2i}:2^{-1/4}\zeta _8^{2j}:1], 0\leq i,j\leq 3$
; -
(C)
$32$
points defined over
${\mathbb {Q}}(\zeta _3,\zeta _8)$
:
$[\zeta _3\zeta _8^{1+2i}:\zeta _3^{2}\zeta _8^{1+2j}:1], [\zeta _3^2\zeta _8^{1+2i}:\zeta _3\zeta _8^{1+2j}:1]$
,
$0\leq i,j\leq 3$
; -
(D)
$96$
points defined over
${\mathbb {Q}}(\sqrt {-7},\zeta _8)$
:
$[\alpha \zeta _8^{2i}:\overline {\alpha }\zeta _8^{2j}:1], [\overline {\alpha }\zeta _8^{2i}:\alpha \zeta _8^{2j}:1]$
,
$[\overline {\alpha }\zeta _8^{7+2j}:\zeta _8^6:\alpha \zeta _8^{2i}],\ \ [\alpha \zeta _8^{7+2j}:\zeta _8^6:\overline {\alpha }\zeta _8^{2i}],\ \ [1\kern1.9pt{:}\kern1.9pt\alpha \zeta _8^{1+2i}\kern1.9pt{:}\kern1.9pt\overline {\alpha }\zeta _8^{2+2j}]$
,
$[1\kern1.9pt{:}\kern1.9pt\overline {\alpha }\zeta _8^{1+2i}\kern1.9pt{:}\kern1.9pt\alpha \zeta _8^{2+2j}], 0\kern2pt{\leq}\kern2pt i,j\kern2pt{\leq}\kern2pt 3$
,
where
$\zeta _3=e^{2i\pi /3}$
,
$\alpha =(1+\sqrt {-7})/2$
and
$\overline {\alpha }=(1-\sqrt {-7})/2$
.
In this paper, we give an alternative proof for Theorem 1.1 and its extension to rational function fields.
Theorem 1.2. There are
$188$
points on
$F_4$
defined over quadratic extensions of
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
. These points are the
$188$
points in Theorem 1.1.
Before moving on to the proof of Theorem 1.2, we note that our approach is completely different from the approach of Ishitsuka et al. In [Reference Ishitsuka, Ito and Oshita6], the authors use techniques from Galois representation theory and their proof relies on Rohrlich’s result [Reference Rohrlich11, Corollary 1, page 117] and Faddeev’s result [Reference Faddeev5, Section 3, page 1150]. This paper is modelled on Mordell’s paper [Reference Mordell9], where he reproved Faddeev’s result [Reference Faddeev5], see also [Reference Mordell10, Theorem 4, pages 116–118]. The advantage of Mordell’s approach is that it is simple, easy to use and concrete in calculations. For some other applications of this approach, see Li [Reference Li7] and Manley [Reference Manley8].
2 Some preliminary results
Lemma 2.1. Let k be a field of characteristic not
$2$
. Let
$K=k(T_1,T_2,\ldots ,T_n)$
be the function field over k generated by n algebraically independent variables
$T_1,T_2,\ldots ,T_n$
. Let E be the elliptic curve over K given by
$y^2=x^3+Ax+B$
, where
$A,B\in k$
. Then,
$E(K)=E(k)$
.
Proof. The following proof of Lemma 2.1 is due to Professor Andrew Bremner (personal communication). We use induction on n. When
$n=1$
, see Cohen [Reference Cohen4, Proposition 7.3.2, pages 487–488]. Assume that Lemma 2.1 is true for n. Let
${K=k(T_1,T_2,\ldots ,T_n)}$
. Consider the elliptic curve E over
$L=k(T_1,T_2,\ldots ,T_{n+1})$
given by
$y^2=x^3+Ax+B$
, where
$A,B\in k$
. Since
$L=K(T_{n+1})$
and
$k\subset K$
, by induction,
$$ \begin{align*}E(L)=E(K(T_{n+1}))=E(K)=E(k).\end{align*} $$
The proof is complete.
Lemma 2.1 enables us to verify Lemmas 2.2, 2.3 and 2.4 using MAGMA [Reference Bosma, Cannon and Playoust2].
Lemma 2.2. All
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
-points on
$y^2=2x(x^2+1)$
are
$$ \begin{align*}\infty,\, (0,0),\, (1,\pm 2),\, (\pm {\zeta_8}^2, 0),\, (-1, \pm 2{\zeta_8}^2),\end{align*} $$
$$ \begin{align*}({\zeta_8}^3+{\zeta_8}^2+{\zeta_8},\pm (2{\zeta_8}^3+2{\zeta_8}^2-2)),\, ({\zeta_8}^3-{\zeta_8}^2+{\zeta_8},\pm (2{\zeta_8}^2-2{\zeta_8}+2)),\end{align*} $$
$$ \begin{align*}(-({\zeta_8}^3+{\zeta_8}^2+{\zeta_8}),\pm (2{\zeta_8}^2+2{\zeta_8}+2)),\,(-({\zeta_8}^3-{\zeta_8}^2+{\zeta_8})),\pm (2{\zeta_8}^3-2{\zeta_8}^2+2)). \end{align*} $$
Lemma 2.3. All
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
-points on
$y^2=2x(x^2-1)$
are
$$ \begin{align*} \infty,\, (0,0),\, (\pm 1,0),\, ({\zeta_8}^2,\pm 2{\zeta_8}^3),\, (-{\zeta_8}^2,\pm 2{\zeta_8}),\end{align*} $$
$$ \begin{align*}({\zeta_8}^3-{\zeta_8}-1,\pm 2({\zeta_8}^3+2{\zeta_8}^2+2{\zeta_8})),\, ({\zeta_8}^3-{\zeta_8}+1,\pm (2{\zeta_8}^3-2{\zeta_8}+2)),\end{align*} $$
$$ \begin{align*}(-{\zeta_8}^3+{\zeta_8}+1,\pm (2{\zeta_8}^3-2{\zeta_8}-2)),\, (-{\zeta_8}^3+{\zeta_8}-1,\pm (2{\zeta_8}^3-2{\zeta_8}^2+2{\zeta_8})).\end{align*} $$
Lemma 2.4. All
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
-points on
$s^2=t^4-1$
are
$$ \begin{align*}\infty,\,(0 , \pm {\zeta_8}^2),\, (\pm 1, 0),\, (\pm {\zeta_8}^2, 0),\, (\pm {\zeta_8}, \pm ({\zeta_8}^3 + {\zeta_8}) ),\, (\pm {\zeta_8}^3 , \pm ({\zeta_8}^3 + {\zeta_8})). \end{align*} $$
3 Proof of Theorem 1.2
Let
$K={\mathbb {Q}}({\zeta _8})(T_1,T_2,\ldots ,T_n)$
. Let
$L=K(\sqrt {d})$
be a quadratic extension of K, where
$d\in K$
and
$\sqrt {d}\not \in K$
. Assume
$[x:y:z]\in F_4(L)$
.
If
$x=0$
, then
$y^4=z^4$
. Hence,
$$ \begin{align} [x:y:z]=[0:\pm 1:1], [0:\pm \zeta_8^2:1].\end{align} $$
Similarly, if
$y=0$
, then
$$ \begin{align} [x:y:z]=[\pm 1: 0:1], [\pm \zeta_8^2:0:1].\end{align} $$
If
$z=0$
, then
$x^4+y^4=0$
. Hence,
$$ \begin{align} [x:y:z]=[{\zeta_8}^j:1:0],\quad j=1,3,5,7.\end{align} $$
Note that the 12 points in (3.1), (3.2) and (3.3) are the 12 points in Theorem 1.1(A).
Assume
$xyz\neq 0$
. Let
$z=1$
. Then,
$$ \begin{align} x^4+y^4=1. \end{align} $$
Since
$x\neq 0$
,
$y^2\neq \pm 1$
. From (3.4),
$(1+y^2)/x^2=x^2/(1-y^2)$
. Let
$$ \begin{align} t=\dfrac{1+y^2}{x^2}\,\bigg(=\dfrac{x^2}{1-y^2}\bigg).\end{align} $$
Then,
$t\neq 0$
. If
$t=\pm \zeta _8^2$
, by (3.5),
$$ \begin{align*}-1=t^2=\dfrac{1+y^2}{x^2}\cdot \dfrac{x^2}{1-y^2}=\dfrac{1+y^2}{1-y^2}.\end{align*} $$
Hence,
$1+y^2=y^2-1$
, which is impossible. If
$t=\pm 1$
, by (3.5),
$$ \begin{align*}1=t^2=\dfrac{1+y^2}{x^2}\cdot \dfrac{x^2}{1-y^2}=\dfrac{1+y^2}{1-y^2}.\end{align*} $$
Hence,
$y=0$
, which is impossible. Therefore,
$$ \begin{align} t\not\in \{0, \pm 1, \pm \zeta_8^2\}. \end{align} $$
It follows from (3.4) and (3.5) that
$$ \begin{align} x^2=\dfrac{2t}{t^2+1},\quad y^2=\dfrac{t^2-1}{t^2+1},\end{align} $$
Let
$X=x(t^2+1)$
and
$Y=xy(t^2+1)$
. From (3.7),
$$ \begin{align} X^2=2t(t^2+1),\end{align} $$
$$ \begin{align} Y^2=2t(t^2-1).\end{align} $$
Case I:
$t\in K$
. Let
$X=u+v\sqrt {d}$
and
$Y=u_1+v_1\sqrt {d}$
, where
$u,v,u_1,v_1\in K$
. From (3.8),
$X^2,Y^2\in K$
. Since
$\sqrt {d}\not \in K$
,
$uv=u_1v_1=0$
.
Case I.1:
$v=0$
. Then,
$X=u\in K$
. Thus,
$(t,u)$
is a K-point on (3.8). Therefore, by Lemma 2.2,
$t=\pm ({\zeta _8}^3+{\zeta _8}^2+{\zeta _8}),\pm ({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})$
. If
$t={\zeta _8}^3+{\zeta _8}^2+{\zeta _8}$
, then
$$ \begin{align} [x:y:z]=[\pm {\zeta_8}^3:\pm \sqrt{{\zeta_8}-{\zeta_8}^3}:1].\end{align} $$
If
$t=-({\zeta _8}^3+{\zeta _8}^2+{\zeta _8})$
, then
$$ \begin{align} [x:y:z]=[\pm {\zeta_8}:\pm \sqrt{{\zeta_8}-{\zeta_8}^3}:1].\end{align} $$
If
$t={\zeta _8}^3-{\zeta _8}^2+{\zeta _8}$
, then
$$ \begin{align} [x:y:z]=[\pm {\zeta_8}:\pm \sqrt{{\zeta_8}^3-{\zeta_8}}:1 ].\end{align} $$
If
$t=-({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})$
, then
$$ \begin{align} [x:y:z]=[\pm {\zeta_8}^3:\pm \sqrt{{\zeta_8}^3-{\zeta_8}}:1]. \end{align} $$
Case I.2:
$v_1=0$
. Then,
$(t,u_1)$
is a K-point on (3.9). Therefore, by Lemma 2.3,
${t=\pm ({\zeta _8}^3-{\zeta _8}-1), \pm ({\zeta _8}^3-{\zeta _8}+1)}$
. If
$t={\zeta _8}^3-{\zeta _8}-1$
, then
$$ \begin{align} [x:y:z]=\bigg[{\pm} \sqrt{\dfrac{{\zeta_8}^3 - {\zeta_8}}{2}}:\pm \sqrt{\dfrac{{\zeta_8}-{\zeta_8}^3 }{2}}:1\bigg]. \end{align} $$
If
$t=-({\zeta _8}^3-{\zeta _8}-1)$
, then
$$ \begin{align} [x:y:z]=\bigg[{\pm} \sqrt{\dfrac{{\zeta_8} - {\zeta_8}^3}{2}}:\pm \sqrt{\dfrac{{\zeta_8}-{\zeta_8}^3 }{2}}:1\bigg].\end{align} $$
If
$t={\zeta _8}^3-{\zeta _8}+1$
, then
$$ \begin{align} [x:y:z]=\bigg[{\pm} \sqrt{\dfrac{{\zeta_8}^3 - {\zeta_8}}{2}}:\pm \sqrt{\dfrac{{\zeta_8}^3-{\zeta_8}}{2}}:1\bigg].\end{align} $$
If
$t=-({\zeta _8}^3-{\zeta _8}+1)$
, then
$$ \begin{align} [x:y:z]=\bigg[{\pm} \sqrt{\dfrac{{\zeta_8} - {\zeta_8}^3}{2}}:\pm \sqrt{\dfrac{{\zeta_8}^3-{\zeta_8}}{2}}:1\bigg].\end{align} $$
Case I.3:
$vv_1\neq 0$
. Since
$X^2,Y^2\in K$
and
$X,Y \notin K$
, we have
$u=u_1=0$
. It follows from (3.8) and (3.9) that
$dv^2=2t(t^2+1) \text { and } dv_1^2=2t(t^2-1)$
. Hence,
$$ \begin{align} s^2=(t^2+1)(t^2-1),\end{align} $$
where
$s=dvv_1/(2t) \in K$
. By Lemma 2.4,
$t=\pm \zeta _8,\pm \zeta _8^3$
. If
$t={\zeta _8}^3$
, then
$$ \begin{align} [x:y:z]=[\pm \sqrt{{\zeta_8}^3-{\zeta_8}}:\pm {\zeta_8}^3:1]. \end{align} $$
If
$t=-{\zeta _8}^3$
, then
$$ \begin{align} [x:y:z]=[\pm \sqrt{{\zeta_8}-{\zeta_8}^3}:\pm {\zeta_8}^3:1]. \end{align} $$
If
$t={\zeta _8}$
, then
$$ \begin{align} [x:y:z]=[\pm \sqrt{{\zeta_8}-{\zeta_8}^3}:\pm {\zeta_8}:1]. \end{align} $$
If
$t=-{\zeta _8}$
, then
$$ \begin{align} [x:y:z]=[\pm \sqrt{{\zeta_8}^3-{\zeta_8}}:\pm {\zeta_8}:1]. \end{align} $$
Note that the 48 points in (3.10), (3.11), (3.12), (3.13), (3.14), (3.15), (3.16), (3.17), (3.19), (3.20), (3.21) and (3.22) are the 48 points in Theorem (1.1)(B).
Case II:
$t\not \in K$
. Let
$P(T)\in K[T]$
be the monic minimal polynomial of t over K. Then,
$\mathrm {deg}P(T)=2$
.
Step 1: There exist
$a,b\in K$
such that
$X=at+b.$
By (3.8), the polynomial
$2T(T^2+1)-(aT+b)^2$
has a root
$T=t$
. Therefore, there exist
$c,d\in K$
such that
$$ \begin{align} 2T(T^2+1)-(aT+b)^2=P(T)(cT+d). \end{align} $$
Then,
$c=2$
and
$(-d/c, -ad/c+b)$
is a K-point on (3.8). Hence, by Lemma 2.3,
$$ \begin{align*}-d/c\in \{0, \pm 1, \pm {\zeta_8}^2, \pm ({\zeta_8}^3+{\zeta_8}^2+{\zeta_8}), \pm ({\zeta_8}^3-{\zeta_8}^2+{\zeta_8})\}.\end{align*} $$
Case 1.1:
$-d/c=0$
. Then,
$b=d=0$
. From (3.23),
$$ \begin{align} P(T)=T^2 - \dfrac{a^2}{2}T + 1.\end{align} $$
Case 1.2:
$-d/c=1$
. Then,
$d=-2$
and
$a+b=\pm 2$
. By changing the signs of a and b, we can assume that
$a+b=-2$
. From (3.23),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a^2}{2} + 1\bigg)T + \dfrac{a^2}{2} + 2a + 2.\end{align} $$
Case 1.3:
$-d/c=-1$
. Then,
$d=2$
and
${a-b=\pm 2 {\zeta _8}^2}$
. We can assume that
${a-b=2{\zeta _8}^2}$
. From (3.23),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a^2}{2} - 1\bigg)T - \dfrac{a^2}{2} - 2{\zeta_8}^2a + 2.\end{align} $$
Case 1.4:
$-d/c={\zeta _8}^2$
. Then,
$d=-2{\zeta _8}^2$
and
$b=-a{\zeta _8}^2$
. From (3.23),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a^2}{2} + {\zeta_8}^2\bigg)T + \dfrac{1}{2}{\zeta_8}^2a^2.\end{align} $$
Case 1.5:
$-d/c=-{\zeta _8}^2$
. Then,
$d=2{\zeta _8}^2$
and
$b=a{\zeta _8}^2$
. From (3.23),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a^2}{2} - {\zeta_8}^2\bigg)T - \dfrac{1}{2}{\zeta_8}^2a^2.\end{align} $$
Case 1.6:
$-d/c={\zeta _8}^3+{\zeta _8}^2+{\zeta _8}$
. Then,
$d=-2({\zeta _8}^3+{\zeta _8}^2+{\zeta _8})$
. It follows that
$$ \begin{align*} ({\zeta_8}^3+{\zeta_8}^2+{\zeta_8})a+b=\pm 2({\zeta_8}^3+{\zeta_8}^2-1). \end{align*} $$
We can assume that
$b=2({\zeta _8}^3+{\zeta _8}^2-1)-({\zeta _8}^3+{\zeta _8}^2+{\zeta _8})a$
. From (3.23),
$$ \begin{align} P(T)& =T^2 + \bigg({-}\dfrac{a^2}{2} + ({\zeta_8}^3 + {\zeta_8}^2 + {\zeta_8})\bigg)T + \dfrac{1}{2}({\zeta_8}^3 + {\zeta_8}^2 + {\zeta_8})a^2 \nonumber\\ & \quad + (-2{\zeta_8}^3 - 2{\zeta_8}^2 + 2)a + 2{\zeta_8}^3 - 2{\zeta_8} - 2. \end{align} $$
Case 1.7
$-d/c=-({\zeta _8}^3+{\zeta _8}^2+{\zeta _8})$
. Then,
$d=2({\zeta _8}^3+{\zeta _8}^2+{\zeta _8})$
. Then,
$$ \begin{align*}-({\zeta_8}^3+{\zeta_8}^2+{\zeta_8})a+b=\pm 2({\zeta_8}^2+{\zeta_8}+1).\end{align*} $$
We can assume that
$b=2({\zeta _8}^2+{\zeta _8}+1)+({\zeta _8}^3+{\zeta _8}^2+{\zeta _8})a$
. From (3.23),
$$ \begin{align} P(T)& = T^2 + \bigg({-}\dfrac{a^2}{2} - {\zeta_8}^3 - {\zeta_8}^2 - {\zeta_8}\bigg)T + \dfrac{1}{2}(-{\zeta_8}^3 - {\zeta_8}^2 - {\zeta_8})a^2 \nonumber\\ & \quad + (-2{\zeta_8}^2 - 2{\zeta_8} - 2)a + 2{\zeta_8}^3 - 2{\zeta_8} - 2. \end{align} $$
Case 1.8:
$-d/c={\zeta _8}^3-{\zeta _8}^2+{\zeta _8}$
. Then,
$d=-2({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})$
and
$$ \begin{align*}({\zeta_8}^3-{\zeta_8}^2+{\zeta_8})a+b=\pm 2({\zeta_8}^2-{\zeta_8}+1).\end{align*} $$
We can assume that
$$ \begin{align*}b=2({\zeta_8}^2-{\zeta_8}+1)-({\zeta_8}^3-{\zeta_8}^2+{\zeta_8})a.\end{align*} $$
From (3.23),
$$ \begin{align} P(T)& = T^2 + \bigg({-}\dfrac{a^2}{2} + ({\zeta_8}^3 - {\zeta_8}^2 + {\zeta_8})\bigg)T + \dfrac{1}{2}({\zeta_8}^3 - {\zeta_8}^2 + {\zeta_8})a^2 \nonumber\\ & \quad + (-2{\zeta_8}^2 + 2{\zeta_8} - 2)a - 2{\zeta_8}^3 + 2{\zeta_8} - 2. \end{align} $$
Case 1.9:
$-d/c=-({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})$
. Then,
$d=2({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})$
and
$$ \begin{align*}-({\zeta_8}^3-{\zeta_8}^2+{\zeta_8})a+b=\pm 2({\zeta_8}^3-{\zeta_8}^2+1).\end{align*} $$
We can assume that
$b=2({\zeta _8}^3-{\zeta _8}^2+1)+({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})a$
. From (3.23),
$$ \begin{align} P(T)& = T^2 + \bigg({-}\dfrac{a^2}{2} - {\zeta_8}^3 + {\zeta_8}^2 - {\zeta_8}\bigg)T + \dfrac{1}{2}(-{\zeta_8}^3 + {\zeta_8}^2 - {\zeta_8})a^2 \nonumber\\ & \quad + (-2{\zeta_8}^3 + 2{\zeta_8}^2 - 2)a - 2{\zeta_8}^3 + 2{\zeta_8} - 2. \end{align} $$
Step 2: There exist
$a_1,b_1\in K$
such that
$Y=a_1t+b_1$
. Then, (3.9) shows that the polynomial
$2T(T^2-1)-(a_1T+b_1)^2$
has a root
$T=t$
. Hence, there exist
$c_1,d_1\in K$
such that
$$ \begin{align} 2T(T^2-1)-(a_1T+b_1)^2=P(T)(c_1T+d_1).\end{align} $$
Thus,
$c_1=2$
and
$(-d_1/c_1,-a_1d_1/c_1+b_1)$
is a finite K-point on (3.9). Hence
$$ \begin{align*}-d_1/c_1\in \{0,\pm 1,\pm {\zeta_8}^2, \pm ({\zeta_8}^3-{\zeta_8}-1), \pm ({\zeta_8}^3-{\zeta_8}+1)\}.\end{align*} $$
Case 2.1:
$-d_1/c_1=0$
. Then,
$b_1=d_1=0$
. From (3.33),
$$ \begin{align} P(T)=T^2 - \dfrac{a_1^2}{2}T - 1.\end{align} $$
Case 2.2:
$-d_1/c_1=1$
. Then,
$d_1=-2$
and
$b_1=-a_1$
. From (3.33),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a_1^2}{2} + 1\bigg)T +\dfrac{a_1^2}{2}.\end{align} $$
Case 2.3:
$-d_1/c_1=-1$
. Then,
$d_1=2$
and
$b_1=a_1$
. From (3.33),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a_1^2}{2} - 1\bigg)T - \dfrac{a_1^2}{2}.\end{align} $$
Case 2.4:
$-d_1/c_1={\zeta _8}^3-{\zeta _8}-1$
. Then,
$d_1=-2({\zeta _8}^3-{\zeta _8}-1)$
and
$$ \begin{align*}({\zeta_8}^3-{\zeta_8}-1)a_1+b_1=\pm 2({\zeta_8}^3+{\zeta_8}^2+{\zeta_8}).\end{align*} $$
By changing the signs of
$a_1$
and
$b_1$
, we can assume that
$$ \begin{align*}b_1=2({\zeta_8}^3+{\zeta_8}^2+{\zeta_8})-({\zeta_8}^3-{\zeta_8}-1)a_1.\end{align*} $$
From (3.33),
$$ \begin{align} P(T)& =T^2 + \bigg({-}\dfrac{a_1^2}{2} + ({\zeta_8}^3 - {\zeta_8} - 1)\!\bigg)T + \dfrac{1}{2}({\zeta_8}^3 - {\zeta_8} - 1)a_1^2 \nonumber\\ & \quad + (-2{\zeta_8}^3 - 2{\zeta_8}^2 - 2{\zeta_8})a_1 - 2{\zeta_8}^3 + 2{\zeta_8} + 2. \end{align} $$
Case 2.5:
$-d_1/c_1=-({\zeta _8}^3-{\zeta _8}-1)$
. Then,
$d_1=2({\zeta _8}^3-{\zeta _8}-1)$
and
$$ \begin{align*}-({\zeta_8}^3-{\zeta_8}-1)a_1+b_1=\pm 2({\zeta_8}^3-{\zeta_8}-1).\end{align*} $$
We can assume that
$b_1=2({\zeta _8}^3-{\zeta _8}-1)+({\zeta _8}^3-{\zeta _8}-1)a_1$
. From (3.33),
$$ \begin{align} P(T)& = T^2 + \bigg({-}\dfrac{a_1^2}{2} - {\zeta_8}^3 + {\zeta_8} + 1\!\bigg)T + \dfrac{1}{2}(-{\zeta_8}^3 + {\zeta_8} + 1)a_1^2 \nonumber\\ & \quad + (-2{\zeta_8}^3 + 2{\zeta_8} + 2)a_1- 2{\zeta_8}^3 + 2{\zeta_8} + 2. \end{align} $$
Case 2.6:
$-d_1/c_1={\zeta _8}^2$
. Then,
$d_1=-2{\zeta _8}^2$
and
${\zeta _8}^2a_1+b_1=\pm 2{\zeta _8}^3$
. We can assume that
$b_1=2{\zeta _8}^3-a_1{\zeta _8}^2$
. From (3.33),
$$ \begin{align} P(T)=T^2 + \bigg({-}\dfrac{a_1^2}{2} + {\zeta_8}^2\bigg)T + \dfrac{1}{2}{\zeta_8}^2a_1^2 - 2{\zeta_8}^3a_1 - 2. \end{align} $$
Case 2.7:
$-d_1/c_1=-{\zeta _8}^2$
. Then,
$d_1=2{\zeta _8}^2$
and
$-{\zeta _8}^2a_1+b_1=\pm 2{\zeta _8}$
. We can assume that
$b_1=2{\zeta _8}+{\zeta _8}^2a_1$
. From (3.33),
$$ \begin{align} P(T)=T^2 - \bigg(\dfrac{a_1^2}{2}+ {\zeta_8}^2\bigg)T - \dfrac{1}{2}{\zeta_8}^2a_1^2 - 2{\zeta_8} a_1 - 2. \end{align} $$
Case 2.8:
$-d_1/c_1={\zeta _8}^3-{\zeta _8}+1$
. Then,
$d_1=-2({\zeta _8}^3-{\zeta _8}+1)$
and
$$ \begin{align*}({\zeta_8}^3-{\zeta_8}+1)a_1+b_1=\pm 2({\zeta_8}^3-{\zeta_8}+1).\end{align*} $$
We can assume that
$b_1=2({\zeta _8}^3-{\zeta _8}+1)-({\zeta _8}^3-{\zeta _8}+1)a_1$
. From (3.33),
$$ \begin{align} P(T)& = T^2 + \bigg({-}\dfrac{a_1^2}{2} + {\zeta_8}^3 - {\zeta_8} + 1\bigg)T + \dfrac{1}{2}({\zeta_8}^3 - {\zeta_8} + 1)a_1^2 \nonumber\\ & \quad + (-2{\zeta_8}^3 + 2{\zeta_8} - 2)a_1 + 2{\zeta_8}^3 - 2{\zeta_8} + 2. \end{align} $$
Case 2.9:
$-d_1/c_1=-({\zeta _8}^3-{\zeta _8}+1)$
. Then,
$d_1=2({\zeta _8}^3-{\zeta _8}+1)$
and
$$ \begin{align*}-({\zeta_8}^3-{\zeta_8}+1)a_1+b_1=\pm 2({\zeta_8}^3-{\zeta_8}^2+{\zeta_8}).\end{align*} $$
We can assume that
$b_1=2({\zeta _8}^3-{\zeta _8}^2+{\zeta _8})+({\zeta _8}^3-{\zeta _8}+1)a_1$
. From (3.33),
$$ \begin{align} P(T)& = T^2 + \bigg({-}\dfrac{a_1^2}{2} - {\zeta_8}^3 + {\zeta_8} - 1\bigg)T + \dfrac{1}{2}(-{\zeta_8}^3 + {\zeta_8} - 1)a_1^2 \nonumber\\ & \quad + (-2{\zeta_8}^3 + 2{\zeta_8}^2 - 2{\zeta_8})a_1 + 2{\zeta_8}^3 - 2{\zeta_8} + 2. \end{align} $$
Step 3: One polynomial from (3.24), (3.25), (3.26), (3.27), (3.28), (3.29), (3.30), (3.31) and (3.32) needs to match with one polynomial from (3.34), (3.35), (3.36), (3.37), (3.38), (3.39), (3.40), (3.41) and (3.42), resulting in 81 systems of equations in
$a,a_1$
. For each of these systems, MAGMA [Reference Bosma, Cannon and Playoust2] is used to find a and
$a_1$
. MAGMA codes are available from the author on request. Even though
$a,a_1\in K$
, each of these 81 systems of equations has coefficients in
${\mathbb {Q}}({\zeta _8})$
, so if a solution with
$a,a_1\in K$
exists, then
${a,a_1\in {\mathbb {Q}}({\zeta _8})}$
. Our computation shows that only 20 of these 81 systems have solutions and only 16 of these 20 systems give an irreducible polynomial
$P(T)$
. All of the remaining 61 systems have no solutions
$a,a_1\in {\mathbb {Q}}({\zeta _8})$
.
Case 3.1: (3.24) and (3.35). Then,
$$ \begin{align*}-\dfrac{a^2}{2}= -\dfrac{a_1^2}{2} + 1,\quad 1=\dfrac{a_1^2}{2}.\end{align*} $$
Thus,
$(a,a_1)=(0,\pm \sqrt {2})$
. Hence
$P(T)=T^2+1=(T+{\zeta _8}^2)(T-{\zeta _8}^2)$
, which is reducible in
$K[T]$
.
Case 3.2: (3.24) and (3.36). Then,
$$ \begin{align*}-\dfrac{a^2}{2}= -\dfrac{a_1^2}{2} - 1,\quad 1=-\dfrac{a_1^2}{2}.\end{align*} $$
Thus,
$(a,a_1)=(0,\pm \sqrt {-2})$
. Hence,
$P(T)=T^2+1=(T+{\zeta _8}^2)(T-{\zeta _8}^2)$
, which is reducible in
$K[T]$
.
Case 3.3: (3.25) and (3.35). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + 1=-\dfrac{a_1^2}{2} + 1,\quad \dfrac{a^2}{2} + 2a + 2=\dfrac{a_1^2}{2}.\end{align*} $$
Thus,
$(a,a_1)=(-1,\pm 1)$
. Hence,
$P(T)=T^2 + \tfrac 12T + \tfrac 12$
. So
$t^2+\tfrac 12t+\tfrac 12=0$
. Therefore,
$$ \begin{align} [x:y:z]=[\pm(2t+1):\pm 2t:1].\end{align} $$
Case 3.4: (3.25) and (3.36). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + 1=-\dfrac{a_1^2}{2} - 1,\quad \dfrac{a^2}{2} + 2a + 2=- \dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=(-2,0),\,(0,\pm 2{\zeta _8}^2)$
. The first solution gives
$P(T)=T^2-T$
, which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2+T+2$
. So
$t^2+t+2=0$
. Therefore,
$$ \begin{align} [x:y:z]=[\pm t: \pm (t+1){\zeta_8}^2 :1].\end{align} $$
Case 3.5: (3.25) and (3.39). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + 1=-\dfrac{a_1^2}{2} + {\zeta_8}^2,\quad \dfrac{a^2}{2} + 2a + 2=\dfrac{1}{2}{\zeta_8}^2a_1^2 - 2{\zeta_8}^3a_1 - 2.\end{align*} $$
Hence,
$(a,a_1)=({\zeta _8}^2-1,{\zeta _8}+{\zeta _8}^3),\,(-({\zeta _8}^2+3),3{\zeta _8}-{\zeta _8}^3)$
. The first solution gives
$$ \begin{align*}P(T)=T^2 + ({\zeta_8}^2 + 1)T + {\zeta_8}^2=(T+1)(T+{\zeta_8}^2),\end{align*} $$
which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2 -(3{\zeta _8}^2 + 3)T + {\zeta _8}^2$
. So
$t^2 -(3{\zeta _8}^2 + 3)t + {\zeta _8}^2=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[\pm \dfrac{({\zeta_8}^2 - 1)t + {\zeta_8}^2 + 3}{4} : \pm \dfrac{({\zeta_8}^3 + {\zeta_8})(t-3)}{4}:1\bigg].\end{align} $$
Case 3.6: (3.25) and (3.40). Then,
$$ \begin{align*}-\dfrac{a^2}{2}+1=-\dfrac{a_1^2}{2}-{\zeta_8}^2,\quad \dfrac{a^2}{2} + 2a + 2=- \dfrac{1}{2}{\zeta_8}^2a_1^2 - 2{\zeta_8} a_1 - 2.\end{align*} $$
Hence,
$(a,a_1)=(-{\zeta _8}^2-1,{\zeta _8}+{\zeta _8}^3),\,({\zeta _8}^2-3,3{\zeta _8}^3-{\zeta _8})$
. The first solution gives
$$ \begin{align*}P(T)=T^2 + (-{\zeta_8}^2 + 1)T - {\zeta_8}^2=(T+1)(T-{\zeta_8}^2),\end{align*} $$
which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2 + (3{\zeta _8}^2 - 3)T - {\zeta _8}^2$
. So
$t^2 + (3{\zeta _8}^2 - 3)t - {\zeta _8}^2=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[{\pm} \dfrac{({\zeta_8}^2 + 1)t + {\zeta_8}^2 - 3}{4}: \pm \dfrac{({\zeta_8}^3 + {\zeta_8})(t-3)}{4}:1\bigg].\end{align} $$
Case 3.7: (3.26) and (3.35). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - 1=-\dfrac{a_1^2}{2} + 1,\quad - \dfrac{a^2}{2} - 2{\zeta_8}^2a + 2=\dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=(2{\zeta _8}^2,0),\,(0,\pm 2)$
. The first solution gives
$P(T)=T^2+T= T(T+1)$
, which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2-T+2$
. So
$t^2-t+2=0$
. Therefore,
$$ \begin{align} [x:y:z]=[\pm t{\zeta_8}^2: (t-1){\zeta_8}^2:1]. \end{align} $$
Case 3.8: (3.26) and (3.36). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - 1=-\dfrac{a_1^2}{2} - 1,\quad - \dfrac{a^2}{2} - 2{\zeta_8}^2a + 2=- \dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=({\zeta _8}^2,\pm {\zeta _8}^2)$
. Therefore,
$P(T)=T^2-\tfrac 12T+\tfrac 12$
. So
$t^2-\tfrac 12t+\tfrac 12=0$
. Therefore,
$$ \begin{align} [x:y:z]=[\pm (2t-1){\zeta_8}^2: \pm 2t:1].\end{align} $$
Case 3.9: (3.26) and (3.39). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - 1=-\dfrac{a_1^2}{2} + {\zeta_8}^2,\quad - \dfrac{a^2}{2} + 2{\zeta_8}^2 a + 2= \dfrac{1}{2}{\zeta_8}^2 a_1^2 - 2{\zeta_8}^3 a_1 - 2.\end{align*} $$
Hence,
$(a,a_1)=({\zeta _8}^2-1,{\zeta _8}-{\zeta _8}^3),\,(3{\zeta _8}^2+1,3{\zeta _8}+{\zeta _8}^3)$
. The first solution gives
$$ \begin{align*}P(T)=T^2 + ({\zeta_8}^2 - 1)T - {\zeta_8}^2=(T-1)(T+{\zeta_8}^2),\end{align*} $$
which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2 + (-3{\zeta _8}^2 + 3)T - {\zeta _8}^2$
. So
$t^2 + (-3{\zeta _8}^2 + 3)t - {\zeta _8}^2=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[{\pm} \dfrac{({\zeta_8}^2 - 1)t +3{\zeta_8}^2 + 1}{4}: \pm \dfrac{({\zeta_8}^3 + {\zeta_8})(t +3)}{4}:1\bigg].\end{align} $$
Case 3.10: (3.26) and (3.40). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - 1=-\dfrac{a_1^2}{2} - {\zeta_8}^2,\quad - \dfrac{a^2}{2} + 2{\zeta_8}^2 a + 2= - \dfrac{1}{2}{\zeta_8}^2 a_1^2 - 2{\zeta_8} a_1 - 2.\end{align*} $$
Hence,
$(a,a_1)=({\zeta _8}^2+ 1,{\zeta _8}-{\zeta _8}^3),\,(3{\zeta _8}^2-1,{\zeta _8}+3{\zeta _8}^3)$
. The first solution gives
$$ \begin{align*}P(T)=T^2 + (-{\zeta_8}^2 - 1)T + {\zeta_8}^2=(T-1)(T-{\zeta_8}^2),\end{align*} $$
which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2 + (3{\zeta _8}^2 + 3)T + {\zeta _8}^2$
. So
$t^2 + (3{\zeta _8}^2 + 3)t + {\zeta _8}^2=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[{\pm} \dfrac{({\zeta_8}^2 + 1)t + (3{\zeta_8}^2 - 1)}{4}:\pm \dfrac{({\zeta_8}^3 + {\zeta_8})(t +3)}{4}:1\bigg].\end{align} $$
Case 3.11: (3.27) and (3.34). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + {\zeta_8}^2=-\dfrac{a_1^2}{2},\quad \dfrac{1}{2}{\zeta_8}^2a^2=-1.\end{align*} $$
Hence,
$(a,a_1)=(a,a_1)=(\pm \sqrt {2} \zeta _8, 0))$
. Therefore,
$P(T)=T^2-1$
, which is reducible in
$K[T]$
.
Case 3.12: (3.27) and (3.35). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + {\zeta_8}^2=-\dfrac{a_1^2}{2} + 1,\quad \dfrac{1}{2}{\zeta_8}^2 a^2=\dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=(\pm ({\zeta _8}+{\zeta _8}^3),\pm ({\zeta _8}^2-1))$
. Therefore,
$P(T)=T^2 + ({\zeta _8}^2 + 1)T - {\zeta _8}^2$
. So
$t^2 + ({\zeta _8}^2 + 1)t - {\zeta _8}^2=0$
. Therefore,
$$ \begin{align}\hspace{-27pt} [x:y:z]=\bigg[{\pm} \dfrac{({\zeta_8}^3 - {\zeta_8})(t+1)}{2}: \pm \dfrac{({\zeta_8}^3 - {\zeta_8})t -{\zeta_8}^3 - {\zeta_8})}{2}:1\bigg].\end{align} $$
Case 3.13: (3.27) and (3.36). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + {\zeta_8}^2=-\dfrac{a_1^2}{2} - 1,\quad \dfrac{1}{2}{\zeta_8}^2 a^2=-\dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=(\pm ({\zeta _8}^3-{\zeta _8}),\pm ({\zeta _8}^2-1))$
. Therefore,
$P(T)=T^2+({\zeta _8}^2-1)T+{\zeta _8}^2$
. So
$t^2+({\zeta _8}^2-1)t+{\zeta _8}^2=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[{\pm} \bigg(\dfrac{({\zeta_8}^3+ {\zeta_8})(1-t)}{2}\bigg):\pm \dfrac{({\zeta_8}^3 - {\zeta_8})t -{\zeta_8}^3 - {\zeta_8}}{2}:1\bigg].\end{align} $$
Case 3.14: (3.27) and (3.39). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + {\zeta_8}^2=-\dfrac{a_1^2}{2} + {\zeta_8}^2,\quad \dfrac{1}{2}{\zeta_8}^2 a^2=\dfrac{1}{2}{\zeta_8}^2 a_1^2 - 2{\zeta_8}^3 a_1 - 2.\end{align*} $$
Hence,
$(a,b)=(\pm {\zeta _8}, {\zeta _8})$
. Therefore,
$P(T)=T^2 + \tfrac 12{\zeta _8}^2 T - \tfrac 12$
. So
$t^2+\tfrac 12{\zeta _8}^2t-\tfrac 12=0$
. Therefore,
$$ \begin{align}[x:y:z]=\bigg[{\pm} \bigg({\zeta_8} t - \dfrac{{\zeta_8}^3}{2}\bigg): \pm \bigg({\zeta_8}^2 t - \dfrac{1}{2}\bigg) :1\bigg].\end{align} $$
Case 3.15: (3.27) and (3.40). Then,
$$ \begin{align*}-\dfrac{a^2}{2} + {\zeta_8}^2=-\dfrac{a_1^2}{2} - {\zeta_8}^2,\quad \dfrac{1}{2}{\zeta_8}^2 a^2=- \dfrac{1}{2}{\zeta_8}^2 a_1^2 - 2{\zeta_8} a_1 - 2.\end{align*} $$
Hence,
$(a,b)=(0, 2{\zeta _8}^3),\,(\pm 2{\zeta _8},0)$
. The first solution gives
$P(T)=T^2+{\zeta _8}^2T= T(T+{\zeta _8}^2)$
, which is reducible in
$K[T]$
. The second solution gives
$P(T)= T^2 - {\zeta _8}^2 T - 2$
. So
$t^2-{\zeta _8}^2t-2=0$
. Therefore,
$$ \begin{align}[x:y:z]=\bigg[{\pm} \bigg(\dfrac{1}{2}{\zeta_8} t - {\zeta_8}^3\bigg):\pm \dfrac{t}{2}:1\bigg]. \end{align} $$
Case 3.16: (3.28) and (3.34). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - {\zeta_8}^2=-\dfrac{a_1^2}{2},\quad - \dfrac{1}{2}{\zeta_8}^2 a^2= -1.\end{align*} $$
Hence,
$(a,a_1)=(\pm \sqrt {2} \zeta _8^3, 0)$
. Therefore,
$P(T)=T^2-1$
, which is reducible in
$K[T]$
.
Case 3.17: (3.28) and (3.35). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - {\zeta_8}^2=-\dfrac{a_1^2}{2} + 1,\quad - \dfrac{1}{2}{\zeta_8}^2 a^2= \dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=(\pm ({\zeta _8}+{\zeta _8}^3) ,\pm (1+{\zeta _8}^2))$
. Thus,
$P(T)=T^2+(1-{\zeta _8}^2)T+{\zeta _8}^2$
. So
$t^2+(1-{\zeta _8}^2)T+{\zeta _8}^2=0$
. Therefore,
$$ \begin{align}\hspace{-27pt} [x:y:z]=\bigg[{\pm} \dfrac{({\zeta_8}^3 - {\zeta_8})(t+1)}{2}:\ {\pm} \dfrac{({\zeta_8}^3 - {\zeta_8})t + {\zeta_8}^3 + {\zeta_8}}{2}:1\bigg].\end{align} $$
Case 3.18: (3.28) and (3.36). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - {\zeta_8}^2=-\dfrac{a_1^2}{2} - 1,\quad - \dfrac{1}{2}{\zeta_8}^2 a^2= - \dfrac{a_1^2}{2}.\end{align*} $$
Hence,
$(a,a_1)=(\pm ({\zeta _8}^3-{\zeta _8}) ,\pm ({\zeta _8}^2+1))$
. Thus,
$P(T)=T^2-({\zeta _8}^2+1)T-{\zeta _8}^2$
. So
$t^2-({\zeta _8}^2+1)t-{\zeta _8}^2=0$
. Therefore,
$$ \begin{align}\hspace{-27pt} [x:y:z]=\bigg[{\pm} \dfrac{({\zeta_8}+{\zeta_8}^3)(t-1)}{2}:\ {\pm} \dfrac{({\zeta_8}^3 - {\zeta_8})t + {\zeta_8}^3 + {\zeta_8}}{2}:1\bigg].\end{align} $$
Case 3.19: (3.28) and (3.39). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - {\zeta_8}^2=-\dfrac{a_1^2}{2} + {\zeta_8}^2,\quad - \dfrac{1}{2}{\zeta_8}^2 a^2= \dfrac{1}{2}{\zeta_8}^2 a_1^2 - 2{\zeta_8}^3 a_1 - 2.\end{align*} $$
Hence,
$(a,a_1)=(0,2{\zeta _8}),\, (\pm 2{\zeta _8}^3,0)$
. The first solution gives
$P(T)=T^2-{\zeta _8}^2T$
, which is reducible in
$K[T]$
. The second solution gives
$P(T)=T^2+{\zeta _8}^2T-2$
. So
$t^2+{\zeta _8}^2t-2=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[{\pm} \bigg(\dfrac{1}{2}{\zeta_8}^3 t - {\zeta_8}\bigg):\pm \dfrac{t}{2} :1\bigg].\end{align} $$
Case 3.20: (3.28) and (3.40). Then,
$$ \begin{align*}-\dfrac{a^2}{2} - {\zeta_8}^2=-\dfrac{a_1^2}{2} - {\zeta_8}^2,\quad - \dfrac{1}{2}{\zeta_8}^2 a^2= - \dfrac{1}{2}{\zeta_8}^2 a_1^2 - 2{\zeta_8} a_1 - 2.\end{align*} $$
Hence,
$(a,a_1)=(\pm {\zeta _8}^3,{\zeta _8}^3)$
. Thus,
$P(T)=T^2-\tfrac 12{\zeta _8}^2 T-\tfrac 12$
. So
$t^2-\tfrac 12{\zeta _8}^2t-\tfrac 12=0$
. Therefore,
$$ \begin{align} [x:y:z]=\bigg[{\pm} \bigg({\zeta_8}^3 t - \dfrac{{\zeta_8}}{2}\bigg):\pm \bigg({\zeta_8}^2 t + \dfrac{1}{2}\bigg):1\bigg].\end{align} $$
Note that the 32 points in (3.51), (3.52), (3.55) and (3.56) are the 32 points in Theorem 1.1(C) and the 96 points in (3.43), (3.44), (3.45), (3.46), (3.47), (3.48), (3.49), (3.50), (3.53), (3.54), (3.57) and (3.58) are the 96 points in Theorem 1.1(D).
The proof of Theorem 1.2 is complete.
Acknowledgement
The author is grateful to the referee for many suggestions to improve the presentation of the paper.
