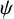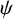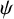1 Introduction
Khintchine’s theorem (1924) is a fundamental result in the metric theory of Diophantine approximation. It asserts that the Lebesgue measure of the set
of
![]() $\psi $
-approximable numbers is either zero or full according as the sum
$\psi $
-approximable numbers is either zero or full according as the sum
![]() $\sum _{q=1}^\infty \psi (q)$
converges or diverges. Here and throughout,
$\sum _{q=1}^\infty \psi (q)$
converges or diverges. Here and throughout,
![]() $\psi :\mathbb N\to {[0,\infty )}$
is a decreasing function such that
$\psi :\mathbb N\to {[0,\infty )}$
is a decreasing function such that
![]() $\psi (q)\to 0$
as
$\psi (q)\to 0$
as
![]() $q\to \infty $
, referred to as an approximating function. Throughout, we identify
$q\to \infty $
, referred to as an approximating function. Throughout, we identify
![]() ${\mathbb I}=[0, 1)$
.
${\mathbb I}=[0, 1)$
.
There are various higher dimensional generalisations of
![]() $W(\psi )$
leading to simultaneous, dual and multiplicative approximation. In this note, we are concerned with the dual (one linear form) and multiplicative problems on manifolds. We define the sets for the inhomogeneous setting which is considered to be more general than the homogeneous setting and where results are often more difficult to prove than in the homogeneous setting. Fix
$W(\psi )$
leading to simultaneous, dual and multiplicative approximation. In this note, we are concerned with the dual (one linear form) and multiplicative problems on manifolds. We define the sets for the inhomogeneous setting which is considered to be more general than the homogeneous setting and where results are often more difficult to prove than in the homogeneous setting. Fix
![]() ${\boldsymbol \theta }:=(\theta _1, \ldots , \theta _n)\in {\mathbb I}^n$
. Denote
${\boldsymbol \theta }:=(\theta _1, \ldots , \theta _n)\in {\mathbb I}^n$
. Denote
![]() $\mathbf x=(x_1, \ldots , x_n)\in \mathbb R^{n}, \mathbf p=(p_1, \ldots , p_n)\in \mathbb Z^n, \mathbf q=(q_1, \ldots , q_n)\in \mathbb Z^n$
and
$\mathbf x=(x_1, \ldots , x_n)\in \mathbb R^{n}, \mathbf p=(p_1, \ldots , p_n)\in \mathbb Z^n, \mathbf q=(q_1, \ldots , q_n)\in \mathbb Z^n$
and
![]() $\|\mathbf q\|:=\max \{|q_1|, \ldots , |q_n|\}$
. Define the sets
$\|\mathbf q\|:=\max \{|q_1|, \ldots , |q_n|\}$
. Define the sets
 $$ \begin{align*} {\mathcal S}^{\boldsymbol\theta}_n(\psi)&=\{\mathbf x\in{\mathbb I}^n: \max\limits_{1\leq i\leq n} |qx_i-p_i-\theta_i|<\psi(q) \ \text{for i.m.}\ (\mathbf p, q)\in\mathbb Z^{n+1}\setminus\{\mathbf 0\}\},\\ {\mathcal D}^{\boldsymbol\theta}_n(\psi)&=\{\mathbf x\in{\mathbb I}^n: |\mathbf q\cdot\mathbf x-p-\theta|<\psi(\|\mathbf q\|) \ \text{for i.m.} \ (p, \mathbf q)\in\mathbb Z^{n+1}\setminus\{\mathbf 0\} \}, \\ \Lambda^{\boldsymbol\theta}_n(\psi)&=\bigg\{\mathbf x\in{\mathbb I}^n: \prod\limits_{i=1}^n |qx_i-p_i-\theta_i|<\psi(q) \ \text{for i.m.} \ (\mathbf p, q)\in\mathbb Z^{n+1}\setminus\{\mathbf 0\} \bigg\}. \end{align*} $$
$$ \begin{align*} {\mathcal S}^{\boldsymbol\theta}_n(\psi)&=\{\mathbf x\in{\mathbb I}^n: \max\limits_{1\leq i\leq n} |qx_i-p_i-\theta_i|<\psi(q) \ \text{for i.m.}\ (\mathbf p, q)\in\mathbb Z^{n+1}\setminus\{\mathbf 0\}\},\\ {\mathcal D}^{\boldsymbol\theta}_n(\psi)&=\{\mathbf x\in{\mathbb I}^n: |\mathbf q\cdot\mathbf x-p-\theta|<\psi(\|\mathbf q\|) \ \text{for i.m.} \ (p, \mathbf q)\in\mathbb Z^{n+1}\setminus\{\mathbf 0\} \}, \\ \Lambda^{\boldsymbol\theta}_n(\psi)&=\bigg\{\mathbf x\in{\mathbb I}^n: \prod\limits_{i=1}^n |qx_i-p_i-\theta_i|<\psi(q) \ \text{for i.m.} \ (\mathbf p, q)\in\mathbb Z^{n+1}\setminus\{\mathbf 0\} \bigg\}. \end{align*} $$
Here and throughout, i.m. stands for infinitely many. The sets,
![]() $ {\mathcal S}^{\boldsymbol \theta }_n(\psi ), {\mathcal D}^{\boldsymbol \theta }_n(\psi )$
and
$ {\mathcal S}^{\boldsymbol \theta }_n(\psi ), {\mathcal D}^{\boldsymbol \theta }_n(\psi )$
and
![]() $ \Lambda ^{\boldsymbol \theta }_n(\psi )$
are called the set of simultaneous, dual and multiplicative
$ \Lambda ^{\boldsymbol \theta }_n(\psi )$
are called the set of simultaneous, dual and multiplicative
![]() $\psi $
-approximable points. A fundamental aim in Diophantine approximation is to quantify the ‘size’ of these sets in terms of Lebesgue measure, Hausdorff measure and Hausdorff dimension, which we generally refer to as the metrical theory. The metrical theory for the above sets, termed the independent variable setting, is relatively well developed as compared to the dependent variable theory (that is, when
$\psi $
-approximable points. A fundamental aim in Diophantine approximation is to quantify the ‘size’ of these sets in terms of Lebesgue measure, Hausdorff measure and Hausdorff dimension, which we generally refer to as the metrical theory. The metrical theory for the above sets, termed the independent variable setting, is relatively well developed as compared to the dependent variable theory (that is, when
![]() $\mathbf x$
is restricted to a manifold). Indeed, to estimate the size of the intersections of the above sets with a k-dimensional, nondegenerate submanifold
$\mathbf x$
is restricted to a manifold). Indeed, to estimate the size of the intersections of the above sets with a k-dimensional, nondegenerate submanifold
![]() $\mathcal M\subseteq \mathbb R^n$
is an intricate and challenging problem. However, some remarkable advances have been made. We state the latest results for all three sets in terms of Hausdorff measure. The Lebesgue measure or Hausdorff measure of the sets typically split into two parts: the convergence case and the divergence case. The convergence/divergence of the corresponding series depend upon the properties of the approximating function
$\mathcal M\subseteq \mathbb R^n$
is an intricate and challenging problem. However, some remarkable advances have been made. We state the latest results for all three sets in terms of Hausdorff measure. The Lebesgue measure or Hausdorff measure of the sets typically split into two parts: the convergence case and the divergence case. The convergence/divergence of the corresponding series depend upon the properties of the approximating function
![]() $\psi $
and/or dimension function g. Before we discuss the state of the art and our results, we briefly summarise the notation used. For the definitions of Hausdorff measure and dimension, see Section 1.5.
$\psi $
and/or dimension function g. Before we discuss the state of the art and our results, we briefly summarise the notation used. For the definitions of Hausdorff measure and dimension, see Section 1.5.
1.1 Notation
Throughout, by a dimension function g, we mean an increasing continuous function
![]() $g:\mathbb {R}\to \mathbb {R}$
with
$g:\mathbb {R}\to \mathbb {R}$
with
![]() $g(0)=0$
. By
$g(0)=0$
. By
![]() $\mathcal H^g$
-measure, we mean the g-dimensional Hausdorff measure which is proportional to the standard Lebesgue measure when
$\mathcal H^g$
-measure, we mean the g-dimensional Hausdorff measure which is proportional to the standard Lebesgue measure when
![]() $g(r)=r^n$
. In the case where the dimension function is of the form
$g(r)=r^n$
. In the case where the dimension function is of the form
![]() $g(r):=r^s$
for some
$g(r):=r^s$
for some
![]() $s < k$
,
$s < k$
,
![]() $\mathcal H^g$
is simply denoted as
$\mathcal H^g$
is simply denoted as
![]() $\mathcal H^s$
. For real quantities
$\mathcal H^s$
. For real quantities
![]() $A,B$
and a parameter t, we write
$A,B$
and a parameter t, we write
![]() $A \lesssim _t B$
if
$A \lesssim _t B$
if
![]() $A \leq c(t) B$
for a constant
$A \leq c(t) B$
for a constant
![]() $c(t)> 0$
that depends on t only (while A and B may depend on other parameters). We write
$c(t)> 0$
that depends on t only (while A and B may depend on other parameters). We write
![]() $A\asymp _{t} B$
if
$A\asymp _{t} B$
if
![]() $A\lesssim _{t} B\lesssim _{t} A$
. If the constant
$A\lesssim _{t} B\lesssim _{t} A$
. If the constant
![]() $c>0$
depends only on parameters that are constant throughout a proof, we simply write
$c>0$
depends only on parameters that are constant throughout a proof, we simply write
![]() $A\lesssim B$
and
$A\lesssim B$
and
![]() $B\asymp A$
.
$B\asymp A$
.
1.2 Dual approximation
The convergence Lebesgue measure result for
![]() ${\mathcal D}_n^{\mathbf {0}}\cap \mathcal M$
was established first in [Reference Beresnevich3] and then, for any nondegenerate manifold, in a generalised form in [Reference Bernik, Kleinbock and Margulis11]. The divergence Lebesgue measure was established for any nondegenerate manifold in [Reference Beresnevich, Bernik, Kleinbock and Margulis10]. The divergence case for the
${\mathcal D}_n^{\mathbf {0}}\cap \mathcal M$
was established first in [Reference Beresnevich3] and then, for any nondegenerate manifold, in a generalised form in [Reference Bernik, Kleinbock and Margulis11]. The divergence Lebesgue measure was established for any nondegenerate manifold in [Reference Beresnevich, Bernik, Kleinbock and Margulis10]. The divergence case for the
![]() $\mathcal H^g$
-measure of
$\mathcal H^g$
-measure of
![]() ${\mathcal D}_n^{\mathbf {0}}\cap \mathcal M$
was established in [Reference Beresnevich, Dickinson and Velani6] as a consequence of the ubiquity framework. Regarding the convergence case for
${\mathcal D}_n^{\mathbf {0}}\cap \mathcal M$
was established in [Reference Beresnevich, Dickinson and Velani6] as a consequence of the ubiquity framework. Regarding the convergence case for
![]() $\mathcal H^g$
-measure of
$\mathcal H^g$
-measure of
![]() ${\mathcal D}_n^{\mathbf {0}}\cap \mathcal M$
, progress has been made for various manifolds but not generalised as in the divergence case. The
${\mathcal D}_n^{\mathbf {0}}\cap \mathcal M$
, progress has been made for various manifolds but not generalised as in the divergence case. The
![]() $\mathcal H^g$
-measure for convergence for the parabola was proved in [Reference Hussain20] under some mild assumptions on the dimension function g, and then Huang [Reference Huang18] proved that
$\mathcal H^g$
-measure for convergence for the parabola was proved in [Reference Hussain20] under some mild assumptions on the dimension function g, and then Huang [Reference Huang18] proved that
![]() $\mathcal H^s({\mathcal D}_2^{\mathbf 0}(\psi )\cap {\mathcal C})=0$
for all nondegenerate planar curves
$\mathcal H^s({\mathcal D}_2^{\mathbf 0}(\psi )\cap {\mathcal C})=0$
for all nondegenerate planar curves
![]() ${\mathcal C}$
. We refer the reader to [Reference Badziahin, Harrap and Hussain1] for the inhomogeneous variant of Huang’s result.
${\mathcal C}$
. We refer the reader to [Reference Badziahin, Harrap and Hussain1] for the inhomogeneous variant of Huang’s result.
In a recent paper [Reference Hussain, Schleischitz and Simmons23], we (with David Simmons) proved the
![]() $\mathcal H^g$
-measure convergence result for hypersurfaces of dimension at least
$\mathcal H^g$
-measure convergence result for hypersurfaces of dimension at least
![]() $3$
for both homogeneous and inhomogeneous settings with a nonmonotonic multivariable approximating function. The results of [Reference Hussain, Schleischitz and Simmons23] have been extended in [Reference Hussain and Schleischitz21] to certain classes of nondegenerate sub-manifolds of co-dimension greater than one. For co-dimension two or three, examples of manifolds where the dependent variables can be chosen as quadratic forms are provided. In that paper, the method requires the manifold to have even dimension at least a minimum of four and half the dimension of the ambient space. Hence, the results of [Reference Hussain and Schleischitz21, Reference Hussain, Schleischitz and Simmons23] are not applicable to one-dimensional manifolds (curves). However, results of similar nature for the special class of Veronese curves have been obtained in [Reference Hussain, Schleischitz and Simmons22]. For general planar curves, the best result is due to Huang.
$3$
for both homogeneous and inhomogeneous settings with a nonmonotonic multivariable approximating function. The results of [Reference Hussain, Schleischitz and Simmons23] have been extended in [Reference Hussain and Schleischitz21] to certain classes of nondegenerate sub-manifolds of co-dimension greater than one. For co-dimension two or three, examples of manifolds where the dependent variables can be chosen as quadratic forms are provided. In that paper, the method requires the manifold to have even dimension at least a minimum of four and half the dimension of the ambient space. Hence, the results of [Reference Hussain and Schleischitz21, Reference Hussain, Schleischitz and Simmons23] are not applicable to one-dimensional manifolds (curves). However, results of similar nature for the special class of Veronese curves have been obtained in [Reference Hussain, Schleischitz and Simmons22]. For general planar curves, the best result is due to Huang.
Theorem 1.1 (Huang, [Reference Huang18])
Let
![]() $\psi $
be a decreasing approximating function and
$\psi $
be a decreasing approximating function and
![]() $s\in ~(0, 1]$
. Let
$s\in ~(0, 1]$
. Let
![]() ${\mathcal C}$
be any
${\mathcal C}$
be any
![]() $C^{(2)}$
planar curve which is nondegenerate everywhere except possibly on a set of zero Hausdorff s-measure. Then,
$C^{(2)}$
planar curve which is nondegenerate everywhere except possibly on a set of zero Hausdorff s-measure. Then,
 $$ \begin{align*} {\mathcal H}^s({\mathcal D}_2^{\mathbf 0}\cap{{\mathcal C}})=0\quad \mathrm{if } \sum_{q=1}^\infty\psi^{s}(q)q^{2-s}<\infty.\end{align*} $$
$$ \begin{align*} {\mathcal H}^s({\mathcal D}_2^{\mathbf 0}\cap{{\mathcal C}})=0\quad \mathrm{if } \sum_{q=1}^\infty\psi^{s}(q)q^{2-s}<\infty.\end{align*} $$
A natural problem is to extend Theorem 1.1 to
![]() ${\mathcal H}^g$
-measure on nondegenerate planar curves. By elaborating ideas presented by Huang [Reference Huang18], it is possible to do so with some restrictions on g.
${\mathcal H}^g$
-measure on nondegenerate planar curves. By elaborating ideas presented by Huang [Reference Huang18], it is possible to do so with some restrictions on g.
For convenience, we will assume that the planar curve
![]() ${\mathcal C}$
is the graph of a smooth map
${\mathcal C}$
is the graph of a smooth map
![]() $h:U\to \mathbb R$
, where
$h:U\to \mathbb R$
, where
![]() $U\subseteq \mathbb R$
is a connected bounded open set. Assume that the second derivative
$U\subseteq \mathbb R$
is a connected bounded open set. Assume that the second derivative
![]() $h^{\prime \prime }$
of the map h satisfies
$h^{\prime \prime }$
of the map h satisfies
Condition (I) was implicitly stated in Huang’s paper but, for clarity, we state it explicitly and for the
![]() ${\mathcal H}^g$
-measure. For a detailed discussion about the corresponding condition in higher dimensions, see [Reference Hussain, Schleischitz and Simmons23, Section 3]. We prove the following result.
${\mathcal H}^g$
-measure. For a detailed discussion about the corresponding condition in higher dimensions, see [Reference Hussain, Schleischitz and Simmons23, Section 3]. We prove the following result.
Theorem 1.2. Let
![]() $\psi $
be a decreasing approximating function. Let h be a
$\psi $
be a decreasing approximating function. Let h be a
![]() $C^{(2)}$
function satisfying condition (I) and let
$C^{(2)}$
function satisfying condition (I) and let
![]() ${\mathcal C}$
be the graph of h. Let g be a dimension function such that
${\mathcal C}$
be the graph of h. Let g be a dimension function such that
![]() $r\mapsto r^{-1}g(r)$
is decreasing and
$r\mapsto r^{-1}g(r)$
is decreasing and
![]() $r^{-1}g(r)\to \infty $
as
$r^{-1}g(r)\to \infty $
as
![]() $r\to 0$
. Assume that g has the property that, for some
$r\to 0$
. Assume that g has the property that, for some
![]() $\epsilon>0$
and for any
$\epsilon>0$
and for any
![]() $r\in (0,1)$
,
$r\in (0,1)$
,
Then,
 $$ \begin{align*}{\mathcal H}^g({\mathcal D}_2^{\mathbf 0}(\psi)\cap{\mathcal C})=0\quad\mbox{if } \sum_{q=1}^\infty q^2g\bigg(\frac{\psi(q)}{q}\bigg)<\infty.\end{align*} $$
$$ \begin{align*}{\mathcal H}^g({\mathcal D}_2^{\mathbf 0}(\psi)\cap{\mathcal C})=0\quad\mbox{if } \sum_{q=1}^\infty q^2g\bigg(\frac{\psi(q)}{q}\bigg)<\infty.\end{align*} $$
Observe that (1.1) becomes stronger as
![]() $\epsilon $
increases since
$\epsilon $
increases since
![]() $r<1$
and it does not make sense with exponent larger than
$r<1$
and it does not make sense with exponent larger than
![]() $1$
(that is, for
$1$
(that is, for
![]() $\epsilon>1/3$
) since the dimension of the curve is only 1. By combining Theorem 1.2 with the corresponding divergence theorem proved in [Reference Beresnevich, Dickinson and Velani6], we obtain the following complete dichotomy statement.
$\epsilon>1/3$
) since the dimension of the curve is only 1. By combining Theorem 1.2 with the corresponding divergence theorem proved in [Reference Beresnevich, Dickinson and Velani6], we obtain the following complete dichotomy statement.
Theorem 1.3. Let
![]() $\psi $
be a decreasing approximating function. Let h be a
$\psi $
be a decreasing approximating function. Let h be a
![]() $C^{(2)}$
function satisfying condition (I) and let
$C^{(2)}$
function satisfying condition (I) and let
![]() ${\mathcal C}$
be the graph of h. Let g be a dimension function such that
${\mathcal C}$
be the graph of h. Let g be a dimension function such that
![]() $r^{-1}g(r)$
is decreasing and
$r^{-1}g(r)$
is decreasing and
![]() $r^{-1}g(r)\to \infty $
as
$r^{-1}g(r)\to \infty $
as
![]() $r\to 0$
. Assume that g has the property (1.1). Then,
$r\to 0$
. Assume that g has the property (1.1). Then,
 $$ \begin{align*} {\mathcal H}^g( {\mathcal D}_2^{\mathbf 0}(\psi)\cap{\mathcal C})=\begin{cases} 0 & \mbox{if } \displaystyle\sum\limits_{q=1}^{\infty}g\bigg(\dfrac{\psi(q)}{q}\bigg)q^2<\infty,\\ \infty & \mbox{if } \displaystyle\sum\limits_{q=1}^{\infty}g\bigg(\dfrac{\psi(q)}{q}\bigg)q^2=\infty. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathcal H}^g( {\mathcal D}_2^{\mathbf 0}(\psi)\cap{\mathcal C})=\begin{cases} 0 & \mbox{if } \displaystyle\sum\limits_{q=1}^{\infty}g\bigg(\dfrac{\psi(q)}{q}\bigg)q^2<\infty,\\ \infty & \mbox{if } \displaystyle\sum\limits_{q=1}^{\infty}g\bigg(\dfrac{\psi(q)}{q}\bigg)q^2=\infty. \end{cases} \end{align*} $$
An immediate corollary of Theorem 1.3, which was proved explicitly in [Reference Baker2], is the following Hausdorff dimension result: for
![]() $\tau>2$
, if we write
$\tau>2$
, if we write
![]() ${\mathcal D}_2^{\mathbf 0} (\tau )$
for
${\mathcal D}_2^{\mathbf 0} (\tau )$
for
![]() ${\mathcal D}_2^{\mathbf 0} (q\to q^{-\tau })$
, we have
${\mathcal D}_2^{\mathbf 0} (q\to q^{-\tau })$
, we have
Moreover,
![]() $\mathcal H^s( {\mathcal D}_2^{\mathbf 0} (\tau ) \cap {\mathcal C})=\infty $
for
$\mathcal H^s( {\mathcal D}_2^{\mathbf 0} (\tau ) \cap {\mathcal C})=\infty $
for
![]() $s=3/(\tau +1)$
. To give a more subtle example, let
$s=3/(\tau +1)$
. To give a more subtle example, let
 $$ \begin{align} \log_{+}^{i}q=\underbrace{\log_{+}\cdots\log_+}_{i\text{ times}} q, \quad \log_{+}(q):= \max\{ 1, \log q\} \end{align} $$
$$ \begin{align} \log_{+}^{i}q=\underbrace{\log_{+}\cdots\log_+}_{i\text{ times}} q, \quad \log_{+}(q):= \max\{ 1, \log q\} \end{align} $$
and for some
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\tau>2$
and
$\tau>2$
and
![]() $\alpha _2,\ldots ,\alpha _t\in \mathbb R$
, let
$\alpha _2,\ldots ,\alpha _t\in \mathbb R$
, let
 $$ \begin{align*} \psi_\varepsilon(q)=q^{-\tau}\cdot (\log_{+} q)^{-\varepsilon}\prod_{i=2}^{t}(\log_{+}^{i}q)^{\alpha_i}. \end{align*} $$
$$ \begin{align*} \psi_\varepsilon(q)=q^{-\tau}\cdot (\log_{+} q)^{-\varepsilon}\prod_{i=2}^{t}(\log_{+}^{i}q)^{\alpha_i}. \end{align*} $$
Then we have the following exact logarithmic order statement for approximation on the parabola.
Corollary 1.4. Let
![]() $\varepsilon>0$
. Then for any fixed
$\varepsilon>0$
. Then for any fixed
![]() $\alpha _j$
and with
$\alpha _j$
and with
![]() $\psi _{\varepsilon }$
as defined above, there is a dimension function
$\psi _{\varepsilon }$
as defined above, there is a dimension function
![]() $g_\varepsilon $
such that
$g_\varepsilon $
such that
Consequently, the set
![]() $({\mathcal D}_2^{\mathbf 0}(\psi _0)\setminus {\mathcal D}_2^{\mathbf 0}(\psi _\varepsilon ))\cap {\mathcal C}$
is not empty and indeed uncountable.
$({\mathcal D}_2^{\mathbf 0}(\psi _0)\setminus {\mathcal D}_2^{\mathbf 0}(\psi _\varepsilon ))\cap {\mathcal C}$
is not empty and indeed uncountable.
We refer the reader to [Reference Beresnevich, Dickinson and Velani5, page 257] for explicit choices of
![]() $g_{\varepsilon }$
.
$g_{\varepsilon }$
.
1.3 Multiplicative approximation
For the set
![]() $ \Lambda ^{\boldsymbol \theta }_n(\psi )$
, hardly anything is known beyond a nondegenerate planar curve
$ \Lambda ^{\boldsymbol \theta }_n(\psi )$
, hardly anything is known beyond a nondegenerate planar curve
![]() ${\mathcal C}$
and this time, the most recent result is by Beresnevich and Velani [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9]. Even in the independent variable cases, most of the progress has been achieved quite recently (see for example [Reference Chow14, Reference Chow and Technau15, Reference Hussain and Simmons24]).
${\mathcal C}$
and this time, the most recent result is by Beresnevich and Velani [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9]. Even in the independent variable cases, most of the progress has been achieved quite recently (see for example [Reference Chow14, Reference Chow and Technau15, Reference Hussain and Simmons24]).
Theorem 1.5 (Beresnevich and Velani, [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9])
Let
![]() $\psi $
be any approximating function and
$\psi $
be any approximating function and
![]() $s\in (0, 1)$
. Let
$s\in (0, 1)$
. Let
![]() ${\mathcal C}$
be a
${\mathcal C}$
be a
![]() $C^{(3)}$
curve in
$C^{(3)}$
curve in
![]() $\mathbb R^2$
with nonzero curvature everywhere apart from a set of s-dimensional Hausdorff measure zero. Then,
$\mathbb R^2$
with nonzero curvature everywhere apart from a set of s-dimensional Hausdorff measure zero. Then,
 $$ \begin{align*} {\mathcal H}^s(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})=\begin {cases} 0 \ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty q^{1-s}\psi^s(q)<\infty, \\ \infty\ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty q^{1-s}\psi^s(q)=\infty. \end {cases} \end{align*} $$
$$ \begin{align*} {\mathcal H}^s(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})=\begin {cases} 0 \ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty q^{1-s}\psi^s(q)<\infty, \\ \infty\ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty q^{1-s}\psi^s(q)=\infty. \end {cases} \end{align*} $$
Note that the case
![]() $s=1$
is not covered by this theorem and represents a challenging open question. We refer the reader to [Reference Chow and Technau16] for further details.
$s=1$
is not covered by this theorem and represents a challenging open question. We refer the reader to [Reference Chow and Technau16] for further details.
We extend this theorem to the g-dimensional Hausdorff measure by combining arguments of this paper with arguments used by Beresnevich and Velani [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9]. For this improvement, we first introduce a condition on the dimension function g.
Condition G. For some
![]() $\alpha \in (0,1)$
, the dimension function g is such that
$\alpha \in (0,1)$
, the dimension function g is such that
![]() $g(t)\cdot t^{-\alpha }$
is nonincreasing. Equivalently, for this value of
$g(t)\cdot t^{-\alpha }$
is nonincreasing. Equivalently, for this value of
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
For power functions
![]() $g(t)=t^{s}$
with
$g(t)=t^{s}$
with
![]() $s\in (0,1)$
, the condition holds with
$s\in (0,1)$
, the condition holds with
![]() $\alpha =s$
. More generally, for example, we may consider any function of the form
$\alpha =s$
. More generally, for example, we may consider any function of the form
with the notation
![]() $\log _{+}$
as in (1.2). By a small twist of condition G, we can in fact take any
$\log _{+}$
as in (1.2). By a small twist of condition G, we can in fact take any
![]() $\gamma \in \mathbb R$
in the following results unless
$\gamma \in \mathbb R$
in the following results unless
![]() $\beta =0$
.
$\beta =0$
.
Theorem 1.6. Let
![]() $\psi $
be any approximating function. Let
$\psi $
be any approximating function. Let
![]() ${\mathcal C}$
be a
${\mathcal C}$
be a
![]() $C^{(3)}$
curve in
$C^{(3)}$
curve in
![]() $\mathbb R^2$
with nonzero curvature everywhere apart from a set of g-dimensional Hausdorff measure zero. Let g be a dimension function satisfying condition G. Then,
$\mathbb R^2$
with nonzero curvature everywhere apart from a set of g-dimensional Hausdorff measure zero. Let g be a dimension function satisfying condition G. Then,
 $$ \begin{align*} {\mathcal H}^g(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})=\begin {cases} 0 \ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty qg\bigg({\psi(q)\over q}\bigg)<\infty, \\ \infty\ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty qg\bigg({\psi(q)\over q}\bigg)=\infty. \end {cases} \end{align*} $$
$$ \begin{align*} {\mathcal H}^g(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})=\begin {cases} 0 \ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty qg\bigg({\psi(q)\over q}\bigg)<\infty, \\ \infty\ & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty qg\bigg({\psi(q)\over q}\bigg)=\infty. \end {cases} \end{align*} $$
1.4 Some remarks on simultaneous approximation
We first quote a result which is a combined statement of the divergence cases proven by Beresnevich [Reference Beresnevich4] for any nondegenerate manifolds and the convergence case for hypersurfaces by Huang [Reference Huang19].
Theorem 1.7 (Beresnevich–Huang)
Let
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $s>\tfrac 12(n-1)$
. Let
$s>\tfrac 12(n-1)$
. Let
![]() $\mathcal M$
denote a compact hypersurface in
$\mathcal M$
denote a compact hypersurface in
![]() $\mathbb R^n$
with nonvanishing Gaussian curvature except possibly on a set of zero Hausdorff s-measure. Let
$\mathbb R^n$
with nonvanishing Gaussian curvature except possibly on a set of zero Hausdorff s-measure. Let
![]() $\psi $
be an approximating function. Then,
$\psi $
be an approximating function. Then,
 $$ \begin{align*} {\mathcal H}^s( {{\mathcal S}}^{\mathbf 0}_n(\psi)\cap{\mathcal M})=\begin{cases} 0 & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty q^n\bigg(\frac{\psi(q)}{q}\bigg)^{s+1}< \infty,\\ \infty & \mbox {if } \displaystyle\sum\limits_{q}^\infty q^{n}\bigg(\frac{\psi(q)}{q}\bigg)^{s+1}=\infty. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathcal H}^s( {{\mathcal S}}^{\mathbf 0}_n(\psi)\cap{\mathcal M})=\begin{cases} 0 & \mbox{if } \displaystyle\sum\limits_{q=1}^\infty q^n\bigg(\frac{\psi(q)}{q}\bigg)^{s+1}< \infty,\\ \infty & \mbox {if } \displaystyle\sum\limits_{q}^\infty q^{n}\bigg(\frac{\psi(q)}{q}\bigg)^{s+1}=\infty. \end{cases} \end{align*} $$
The divergence part is valid for any nondegenerate analytical submanifold. Proving the convergence part, however, for any nondegenerate manifold represents a challenging problem and progress thus far has been limited to hypersurfaces and only for the s-dimensional Hausdorff measure with some limitations imposed on the real number s. Regarding the more general weighted settings, the
![]() $\mathcal H^g$
-measure on planar curves was established in [Reference Hussain and Yusupova25] and the lower bound of the Hausdorff dimension for any nondegenerate manifold in [Reference Beresnevich, Levesley and Ward7].
$\mathcal H^g$
-measure on planar curves was established in [Reference Hussain and Yusupova25] and the lower bound of the Hausdorff dimension for any nondegenerate manifold in [Reference Beresnevich, Levesley and Ward7].
It is possible to extend the convergence case of Theorem 1.7 to any g-Hausdorff measure without much effort by replacing the
![]() $\mathcal H^s$
-measure with
$\mathcal H^s$
-measure with
![]() $\mathcal H^g$
-measure for any dimension function g.
$\mathcal H^g$
-measure for any dimension function g.
Theorem 1.8 (Beresnevich–Huang)
Let g be a dimension function with
![]() $r^{-1}g(r)\to \infty $
as
$r^{-1}g(r)\to \infty $
as
![]() $r\to 0$
. Then, with notation and assumptions of Theorem 1.7,
$r\to 0$
. Then, with notation and assumptions of Theorem 1.7,
![]() ${\mathcal H}^{g}( {\mathcal S}^{\mathbf 0}_n(\psi )\cap {\mathcal M})=0$
as soon as
${\mathcal H}^{g}( {\mathcal S}^{\mathbf 0}_n(\psi )\cap {\mathcal M})=0$
as soon as
 $$ \begin{align*} \sum_{q=1}^{\infty} g\bigg(\frac{\psi(q)}{q}\bigg)q^{n-1}\psi(q)<\infty. \end{align*} $$
$$ \begin{align*} \sum_{q=1}^{\infty} g\bigg(\frac{\psi(q)}{q}\bigg)q^{n-1}\psi(q)<\infty. \end{align*} $$
However, extending the divergence case of Theorem 1.7 to an arbitrary dimension function is not that straightforward.
1.5 Hausdorff measure and dimension
For completeness, we give a very brief introduction to Hausdorff measures and dimension. For further details, see [Reference Bernik and Dodson12, Reference Falconer17].
Let
![]() $\Omega \subset \mathbb R^n$
. If
$\Omega \subset \mathbb R^n$
. If
![]() $0 < \rho \leq \infty $
, any finite or countable collection
$0 < \rho \leq \infty $
, any finite or countable collection
![]() $\{B_i\}$
of subsets of
$\{B_i\}$
of subsets of
![]() $\mathbb R^n$
such that
$\mathbb R^n$
such that
![]() $\Omega \subset \bigcup _i B_i$
and
$\Omega \subset \bigcup _i B_i$
and
![]() $\mathrm {diam} (B_i)\le \rho $
is called a
$\mathrm {diam} (B_i)\le \rho $
is called a
![]() $\rho $
-cover of
$\rho $
-cover of
![]() $\Omega $
. Let
$\Omega $
. Let
where the infimum is taken over all possible
![]() $\rho $
-covers
$\rho $
-covers
![]() $\{B_i\}$
of
$\{B_i\}$
of
![]() $\Omega $
. The g-dimensional Hausdorff measure of
$\Omega $
. The g-dimensional Hausdorff measure of
![]() $\Omega $
is defined to be
$\Omega $
is defined to be
The map
![]() $\mathcal H^g:\mathbb P(\mathbb R^n)\to [0,\infty ]$
defines an outer measure on all sets in
$\mathcal H^g:\mathbb P(\mathbb R^n)\to [0,\infty ]$
defines an outer measure on all sets in
![]() $\mathbb {R}^n$
, which becomes a proper measure when restricted to the subset of
$\mathbb {R}^n$
, which becomes a proper measure when restricted to the subset of
![]() $\mathcal H^g$
-measurable sets, that is, sets A that satisfy
$\mathcal H^g$
-measurable sets, that is, sets A that satisfy
![]() $\mathcal H^g(B)= {\mathcal H}^g(A\cap B)+\mathcal H^g(B\setminus A)$
for any
$\mathcal H^g(B)= {\mathcal H}^g(A\cap B)+\mathcal H^g(B\setminus A)$
for any
![]() $B\in \mathbb {R}^n$
. In the case that
$B\in \mathbb {R}^n$
. In the case that
![]() $g(r)=r^s \ (s\geq 0)$
, the measure
$g(r)=r^s \ (s\geq 0)$
, the measure
![]() $\mathcal H^g$
is denoted
$\mathcal H^g$
is denoted
![]() $\mathcal H^s$
and is called s-dimensional Hausdorff measure. For any set
$\mathcal H^s$
and is called s-dimensional Hausdorff measure. For any set
![]() $\Omega \subset \mathbb R^n$
, one can easily verify that there exists a unique critical value of s at which the function
$\Omega \subset \mathbb R^n$
, one can easily verify that there exists a unique critical value of s at which the function
![]() $s\mapsto \mathcal H^s(\Omega )$
‘jumps’ from infinity to zero. The value taken by s at this discontinuity is referred to as the Hausdorff dimension of
$s\mapsto \mathcal H^s(\Omega )$
‘jumps’ from infinity to zero. The value taken by s at this discontinuity is referred to as the Hausdorff dimension of
![]() $\Omega $
and denoted by
$\Omega $
and denoted by
![]() $\dim _{\mathcal H} \Omega $
; that is,
$\dim _{\mathcal H} \Omega $
; that is,
The countable collection
![]() $\{B_i\}$
is called a fine cover of
$\{B_i\}$
is called a fine cover of
![]() $\Omega $
if for every
$\Omega $
if for every
![]() $\rho>0$
, it contains a subcollection that is a
$\rho>0$
, it contains a subcollection that is a
![]() $\rho $
-cover of
$\rho $
-cover of
![]() $\Omega $
.
$\Omega $
.
We state the Hausdorff measure analogue of the famous Borel–Cantelli lemma (see [Reference Bernik and Dodson12, Lemma 3.10]) which will allow us to estimate the Hausdorff measure of certain sets via calculating the Hausdorff g-sum of a fine cover.
Lemma 1.9 (Hausdorff–Cantelli lemma)
Let
![]() $\{B_i\}\subset \mathbb R^n$
be a fine cover of a set
$\{B_i\}\subset \mathbb R^n$
be a fine cover of a set
![]() $\Omega $
and let g be a dimension function such that
$\Omega $
and let g be a dimension function such that
![]() $\sum _i g(\operatorname {\mathrm {diam}}(B_i))$
converges. Then,
$\sum _i g(\operatorname {\mathrm {diam}}(B_i))$
converges. Then,
![]() $\mathcal H^g(\Omega )=0.$
$\mathcal H^g(\Omega )=0.$
2 Proof of Theorem 1.2
To keep the length of the proof in control, where it is exactly the same as in [Reference Huang18], we only sketch it with reference to Huang’s paper. Since the aim is to extend Huang’s proof which is valid for s-dimensional Hausdorff measure to g-dimensional Hausdorff measure, we start by replacing the s-coverings with g-coverings until we encounter nontriviality. As established in [Reference Huang18, Proposition 1], we need to show the convergence of the series
 $$ \begin{align*} \sum_{(q_{1},q_{2},p)\in \mathbb{Z}^{3}} g(|\mu(q_{1},q_{2},p)|), \end{align*} $$
$$ \begin{align*} \sum_{(q_{1},q_{2},p)\in \mathbb{Z}^{3}} g(|\mu(q_{1},q_{2},p)|), \end{align*} $$
under our assumption. Here,
where
![]() $(t,h(t))$
for
$(t,h(t))$
for
![]() $t\in I$
is the local parametrisation of the curve
$t\in I$
is the local parametrisation of the curve
![]() ${\mathcal C}$
as a function,
${\mathcal C}$
as a function,
![]() $M=1+\max _{x\in I} \vert h^{\prime }(x)\vert $
and
$M=1+\max _{x\in I} \vert h^{\prime }(x)\vert $
and
![]() $q=\max \{|q_1|, |q_2|\}.$
We notice that Huang’s proof essentially works for general measures
$q=\max \{|q_1|, |q_2|\}.$
We notice that Huang’s proof essentially works for general measures
![]() $\mathcal H^g$
until we arrive at (3.15) in his paper, which corresponds to the case
$\mathcal H^g$
until we arrive at (3.15) in his paper, which corresponds to the case
![]() $(q_{1},q_{2})\in \Theta _{2}$
below. Define
$(q_{1},q_{2})\in \Theta _{2}$
below. Define
and distinguish two cases:
Let
![]() $(q_{1},q_{2})\in \Theta _{1}$
. Then using [Reference Huang18, Lemma 2],
$(q_{1},q_{2})\in \Theta _{1}$
. Then using [Reference Huang18, Lemma 2],
 $$ \begin{align*} \vert\mu(q_{1},q_{2},p)\vert \leq \frac{\psi(\vert q_{1}\vert)}{\vert q_{1}\vert}. \end{align*} $$
$$ \begin{align*} \vert\mu(q_{1},q_{2},p)\vert \leq \frac{\psi(\vert q_{1}\vert)}{\vert q_{1}\vert}. \end{align*} $$
Since for given
![]() $q_{1}$
there are only
$q_{1}$
there are only
![]() $\ll q_{1}^{2}$
choices for the pair
$\ll q_{1}^{2}$
choices for the pair
![]() $(p,q_{2})$
, the sum with
$(p,q_{2})$
, the sum with
![]() $(q_{1},q_{2})$
restricted to
$(q_{1},q_{2})$
restricted to
![]() $\Theta _{1}$
can be estimated as
$\Theta _{1}$
can be estimated as
 $$ \begin{align*} \sum_{p\in\mathbb Z, (q_{1},q_{2})\in\Theta_{1}} g(|\mu(q_{1},q_{2},p)|)\ll \sum_{q_{1}\in\mathbb Z, q_{1}\neq 0} g(\psi(q_{1})/\vert q_{1}\vert) q_{1}^{2}, \end{align*} $$
$$ \begin{align*} \sum_{p\in\mathbb Z, (q_{1},q_{2})\in\Theta_{1}} g(|\mu(q_{1},q_{2},p)|)\ll \sum_{q_{1}\in\mathbb Z, q_{1}\neq 0} g(\psi(q_{1})/\vert q_{1}\vert) q_{1}^{2}, \end{align*} $$
which converges by assumption.
We now treat the more delicate sum with
![]() $(q_{1},q_{2})\in \Theta _{2}$
. As in [Reference Huang18], we distinguish
$(q_{1},q_{2})\in \Theta _{2}$
. As in [Reference Huang18], we distinguish
![]() $p\neq p_{0}$
and
$p\neq p_{0}$
and
![]() $p= p_{0}$
, where
$p= p_{0}$
, where
![]() $p_{0}$
is defined by
$p_{0}$
is defined by
![]() $F(x_{0})-p_{0}\in (-1/2,1/2]$
, where
$F(x_{0})-p_{0}\in (-1/2,1/2]$
, where
![]() $F(x)=q_{1}x+q_{2}h(x)$
. Notice that
$F(x)=q_{1}x+q_{2}h(x)$
. Notice that
![]() $q_{1}/q_{2}\in [-2M,2M]$
since
$q_{1}/q_{2}\in [-2M,2M]$
since
![]() $(q_{1},q_{2})$
in
$(q_{1},q_{2})$
in
![]() $\Theta _{2}$
.
$\Theta _{2}$
.
When
![]() $p\neq p_{0}$
, proceeding as in [Reference Huang18] for a general dimension function g, we see that for fixed
$p\neq p_{0}$
, proceeding as in [Reference Huang18] for a general dimension function g, we see that for fixed
![]() $(q_{1},q_{2})\in \Theta _{2}$
and
$(q_{1},q_{2})\in \Theta _{2}$
and
![]() $q:= \max \{ \vert q_{1} \vert ,\vert q_{2}\vert \}$
,
$q:= \max \{ \vert q_{1} \vert ,\vert q_{2}\vert \}$
,
 $$ \begin{align*} \sum_{p\neq p_{0}} g(|\mu(q_{1},q_{2},p)|)\ll \sum_{p\neq p_{0}} g( \psi(q)\cdot |q(p-p_{0})|^{-1/2}). \end{align*} $$
$$ \begin{align*} \sum_{p\neq p_{0}} g(|\mu(q_{1},q_{2},p)|)\ll \sum_{p\neq p_{0}} g( \psi(q)\cdot |q(p-p_{0})|^{-1/2}). \end{align*} $$
For fixed q, we have
![]() $\ll q$
choices of
$\ll q$
choices of
![]() $(q_{1},q_{2})\in \Theta _{2}$
and
$(q_{1},q_{2})\in \Theta _{2}$
and
![]() $\vert p\vert \leq Cq=C\max \{\vert q_{1}\vert ,\vert q_{2}\vert \}$
for an absolute constant
$\vert p\vert \leq Cq=C\max \{\vert q_{1}\vert ,\vert q_{2}\vert \}$
for an absolute constant
![]() $C>0$
, so we have to show the convergence of
$C>0$
, so we have to show the convergence of
 $$ \begin{align*} S:=\sum_{q=1}^{\infty} \sum_{p\neq p_{0},\vert p\vert \leq Cq} q\cdot g( \psi(q)|q(p-p_{0})|^{-1/2}). \end{align*} $$
$$ \begin{align*} S:=\sum_{q=1}^{\infty} \sum_{p\neq p_{0},\vert p\vert \leq Cq} q\cdot g( \psi(q)|q(p-p_{0})|^{-1/2}). \end{align*} $$
We readily check that
 $$ \begin{align*} S\ll \sum_{q=1}^{\infty} \sum_{1\leq p \leq Cq} q\cdot g\bigg( \frac{\psi(q)}{q}\cdot \sqrt{q/p}\bigg). \end{align*} $$
$$ \begin{align*} S\ll \sum_{q=1}^{\infty} \sum_{1\leq p \leq Cq} q\cdot g\bigg( \frac{\psi(q)}{q}\cdot \sqrt{q/p}\bigg). \end{align*} $$
Observe that
Indeed, if
![]() $x>1$
, then by the assumption of the decay of
$x>1$
, then by the assumption of the decay of
![]() $r\mapsto r^{-1}g(r)$
, we have
$r\mapsto r^{-1}g(r)$
, we have
![]() $g(xy)/(xy)\leq g(y)/y$
or equivalently
$g(xy)/(xy)\leq g(y)/y$
or equivalently
![]() $g(xy)\leq xg(y)$
for any
$g(xy)\leq xg(y)$
for any
![]() $y>0$
, and if otherwise
$y>0$
, and if otherwise
![]() $0<x<1$
, then it follows trivially since g is increasing. Application of (2.1) with
$0<x<1$
, then it follows trivially since g is increasing. Application of (2.1) with
![]() $y=\psi (q)/q$
and
$y=\psi (q)/q$
and
![]() $x=\sqrt {q/p}$
yields
$x=\sqrt {q/p}$
yields
 $$ \begin{align*} S &\ll \sum_{q=1}^{\infty} q\cdot g\bigg(\frac{\psi(q)}{q}\bigg)\sum_{1\leq p \leq Cq} \max\bigg\{ \bigg(\frac{q}{p}\bigg)^{1/2}, 1\bigg\}. \end{align*} $$
$$ \begin{align*} S &\ll \sum_{q=1}^{\infty} q\cdot g\bigg(\frac{\psi(q)}{q}\bigg)\sum_{1\leq p \leq Cq} \max\bigg\{ \bigg(\frac{q}{p}\bigg)^{1/2}, 1\bigg\}. \end{align*} $$
We show that the inner sum is of order
![]() $\ll q$
. To see this, we split the sum over
$\ll q$
. To see this, we split the sum over
![]() $1\leq p \leq Cq$
into two sums, over
$1\leq p \leq Cq$
into two sums, over
![]() $1\leq p \leq q$
and
$1\leq p \leq q$
and
![]() $q< p \leq Cq$
. The sums can be estimated as
$q< p \leq Cq$
. The sums can be estimated as
 $$ \begin{align*} q^{1/2}\cdot\sum_{p=1}^{q} p^{-1/2} &\ll q^{1/2}\cdot\int_{1}^{q} p^{-1/2} \ll q^{1/2}\cdot q^{1/2}=q \end{align*} $$
$$ \begin{align*} q^{1/2}\cdot\sum_{p=1}^{q} p^{-1/2} &\ll q^{1/2}\cdot\int_{1}^{q} p^{-1/2} \ll q^{1/2}\cdot q^{1/2}=q \end{align*} $$
and
 $$ \begin{align*} \sum_{p=q+1}^{Cq} 1\ll q. \end{align*} $$
$$ \begin{align*} \sum_{p=q+1}^{Cq} 1\ll q. \end{align*} $$
Thus,
 $$ \begin{align*} \sum_{q=1}^{\infty} \sum_{p\neq p_{0},\vert p\vert \leq Cq} q\cdot g( \psi(q)|q(p-p_{0})|^{-1/2})\ll \sum_{q=1}^{\infty} q\cdot q g\bigg(\frac{\psi(q)}{q}\bigg)=\sum_{q=1}^{\infty} q^{2}g\bigg(\frac{\psi(q)}{q}\bigg), \end{align*} $$
$$ \begin{align*} \sum_{q=1}^{\infty} \sum_{p\neq p_{0},\vert p\vert \leq Cq} q\cdot g( \psi(q)|q(p-p_{0})|^{-1/2})\ll \sum_{q=1}^{\infty} q\cdot q g\bigg(\frac{\psi(q)}{q}\bigg)=\sum_{q=1}^{\infty} q^{2}g\bigg(\frac{\psi(q)}{q}\bigg), \end{align*} $$
where the rightmost series converges by assumption.
Now we treat the critical case
![]() $p=p_{0}$
. Proceeding as in [Reference Huang18] but for a general dimension function g, we have to show the convergence of
$p=p_{0}$
. Proceeding as in [Reference Huang18] but for a general dimension function g, we have to show the convergence of
 $$ \begin{align} \sum_{(q_{1},q_{2})\in \Theta_{2}} g(|\mu(q_{1},q_{2},p_{0})|), \end{align} $$
$$ \begin{align} \sum_{(q_{1},q_{2})\in \Theta_{2}} g(|\mu(q_{1},q_{2},p_{0})|), \end{align} $$
with
as defined above. Following the method of [Reference Huang18] of estimating (2.2) in this wider generality shows that to prove (2.2), it suffices to show that
 $$ \begin{align} \sum_{k\geq 1} (\psi(2^{k})^{1-\epsilon} 2^{2k}+ k2^{k})g\bigg(\sqrt{\frac{\psi(2^{k})}{2^{k}}}\bigg)< \infty. \end{align} $$
$$ \begin{align} \sum_{k\geq 1} (\psi(2^{k})^{1-\epsilon} 2^{2k}+ k2^{k})g\bigg(\sqrt{\frac{\psi(2^{k})}{2^{k}}}\bigg)< \infty. \end{align} $$
By assumption,
![]() $\sum _{q \geq 1} q^{2}g(\psi (q)/q)$
converges and thus
$\sum _{q \geq 1} q^{2}g(\psi (q)/q)$
converges and thus
 $$ \begin{align*} \sum_{k\geq 1} g\bigg(\frac{\psi(2^{k})}{2^{k}}\bigg) 2^{3k}<\infty. \end{align*} $$
$$ \begin{align*} \sum_{k\geq 1} g\bigg(\frac{\psi(2^{k})}{2^{k}}\bigg) 2^{3k}<\infty. \end{align*} $$
Hence, for all sufficiently large k,
This implies
![]() $\psi (2^k)<2^{-2k}$
, for sufficiently large k, because of the assumption that
$\psi (2^k)<2^{-2k}$
, for sufficiently large k, because of the assumption that
![]() $r^{-1}g(r)\to \infty $
as
$r^{-1}g(r)\to \infty $
as
![]() $r\to 0$
and the assumption of (1.1). Thus, we can estimate the argument of g above by
$r\to 0$
and the assumption of (1.1). Thus, we can estimate the argument of g above by
Assume (1.1), which is equivalent to
![]() $g(\!\sqrt {x})\leq x^{\gamma }$
for some
$g(\!\sqrt {x})\leq x^{\gamma }$
for some
![]() $\gamma>\tfrac 13$
, which we consider fixed in what follows. We see that the series in (2.3) can be bounded by
$\gamma>\tfrac 13$
, which we consider fixed in what follows. We see that the series in (2.3) can be bounded by
 $$ \begin{align*}\sum_{k\geq 1} (\psi(2^{k})^{1-\epsilon} 2^{2k}+ k2^{k})g\bigg(\sqrt{\frac{\psi(2^{k})}{2^{k}}}\bigg)\leq \sum_{k\geq 1} \psi(2^{k})^{1-\epsilon} 2^{2k-3k\gamma}+ \sum_{k\geq 1} k2^{k} 2^{-3k\gamma}.\end{align*} $$
$$ \begin{align*}\sum_{k\geq 1} (\psi(2^{k})^{1-\epsilon} 2^{2k}+ k2^{k})g\bigg(\sqrt{\frac{\psi(2^{k})}{2^{k}}}\bigg)\leq \sum_{k\geq 1} \psi(2^{k})^{1-\epsilon} 2^{2k-3k\gamma}+ \sum_{k\geq 1} k2^{k} 2^{-3k\gamma}.\end{align*} $$
The rightmost series is finite since
![]() $\gamma>\tfrac 13$
. Therefore, it suffices to show the convergence of the series
$\gamma>\tfrac 13$
. Therefore, it suffices to show the convergence of the series
![]() $ \sum _{k\geq 1} \psi (2^{k})^{1-\epsilon } 2^{2k-3k\gamma },$
which can be rewritten as
$ \sum _{k\geq 1} \psi (2^{k})^{1-\epsilon } 2^{2k-3k\gamma },$
which can be rewritten as
 $$ \begin{align} \sum_{k\geq 1} \bigg(\frac{\psi(2^{k})}{2^{k}}\bigg)^{1-\epsilon} 2^{3k-3k\gamma-k\epsilon}. \end{align} $$
$$ \begin{align} \sum_{k\geq 1} \bigg(\frac{\psi(2^{k})}{2^{k}}\bigg)^{1-\epsilon} 2^{3k-3k\gamma-k\epsilon}. \end{align} $$
Since
![]() $x\mapsto g(x)/x$
decreases for
$x\mapsto g(x)/x$
decreases for
![]() $x\in (0,1)$
, we have
$x\in (0,1)$
, we have
![]() $g(x)/x\geq g(1)/1$
, or equivalently
$g(x)/x\geq g(1)/1$
, or equivalently
![]() $g(x)\geq g(1)x$
. Thus, for any large k, the expression in (2.4) can be bounded by
$g(x)\geq g(1)x$
. Thus, for any large k, the expression in (2.4) can be bounded by
 $$ \begin{align*} \bigg(\frac{\psi(2^{k})}{2^{k}}\bigg)^{1-\epsilon}\leq \frac{1}{g(1)^{1-\epsilon}} g\bigg(\frac{\psi(2^{k})}{2^{k}}\bigg)^{1-\epsilon}\leq \frac{2^{-3k(1-\epsilon)}}{g(1)^{1-\epsilon}}. \end{align*} $$
$$ \begin{align*} \bigg(\frac{\psi(2^{k})}{2^{k}}\bigg)^{1-\epsilon}\leq \frac{1}{g(1)^{1-\epsilon}} g\bigg(\frac{\psi(2^{k})}{2^{k}}\bigg)^{1-\epsilon}\leq \frac{2^{-3k(1-\epsilon)}}{g(1)^{1-\epsilon}}. \end{align*} $$
For the sum over k of the products in (2.4) to converge, we require
![]() $3-3\gamma -\epsilon < 3 (1-\epsilon )$
or equivalently
$3-3\gamma -\epsilon < 3 (1-\epsilon )$
or equivalently
![]() $1-\gamma <1-\tfrac 23\epsilon $
, which by
$1-\gamma <1-\tfrac 23\epsilon $
, which by
![]() $\gamma>\tfrac 13$
is true as soon as
$\gamma>\tfrac 13$
is true as soon as
![]() $\epsilon <\tfrac 12$
. The claim is proved.
$\epsilon <\tfrac 12$
. The claim is proved.
3 Proof of Theorem 1.6
The proof of this theorem splits naturally into two parts: the divergence case and the convergence case.
3.1 The divergence case
The divergence case can be proven for any
![]() $C^2$
nondegenerate submanifold of
$C^2$
nondegenerate submanifold of
![]() $\mathbb R^n$
by using similar arguments to those in [Reference Hussain and Simmons24]. We first quote a result of Bugeaud.
$\mathbb R^n$
by using similar arguments to those in [Reference Hussain and Simmons24]. We first quote a result of Bugeaud.
Theorem 3.1 (Bugeaud, [Reference Bugeaud13])
Let
![]() $n\ge 1$
be an integer. Let
$n\ge 1$
be an integer. Let
![]() $\psi $
be an approximating function. Let g be a dimension function such that
$\psi $
be an approximating function. Let g be a dimension function such that
![]() $r^{-n}g(r)\to \infty $
as
$r^{-n}g(r)\to \infty $
as
![]() $r\to 0.$
Assume that
$r\to 0.$
Assume that
![]() $r\mapsto r^{1+n}g(2\psi (r)/r)$
and
$r\mapsto r^{1+n}g(2\psi (r)/r)$
and
![]() $r\mapsto r\psi ^n(r)$
are nonincreasing. Then,
$r\mapsto r\psi ^n(r)$
are nonincreasing. Then,
 $$ \begin{align*} {\mathcal H}^g( {\mathcal S}_n^{\boldsymbol\theta} (\psi))=\begin{cases} 0 & \textit{if } \displaystyle\sum\limits_{r=1}^\infty r^ng\bigg(\frac{2\psi(r)}{r}\bigg)< \infty,\\ \infty & \textit{if } \displaystyle\sum\limits_{r=1}^\infty r^ng\bigg(\frac{2\psi(r)}{r}\bigg)=\infty. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathcal H}^g( {\mathcal S}_n^{\boldsymbol\theta} (\psi))=\begin{cases} 0 & \textit{if } \displaystyle\sum\limits_{r=1}^\infty r^ng\bigg(\frac{2\psi(r)}{r}\bigg)< \infty,\\ \infty & \textit{if } \displaystyle\sum\limits_{r=1}^\infty r^ng\bigg(\frac{2\psi(r)}{r}\bigg)=\infty. \end{cases} \end{align*} $$
In fact, the monotonicity of
![]() $\psi $
is only needed in the divergence part and when
$\psi $
is only needed in the divergence part and when
![]() $n=1$
.
$n=1$
.
By Theorem 3.1, and since g is increasing,
 $$ \begin{align*}\mathcal H^g(\Lambda_1^{\theta_1}(\psi))=\mathcal H^g({\mathcal S}_1^{\theta_1}(\psi))= \infty \quad\mathrm{if } \sum\limits_{r=1}^{\infty}rg\bigg(\frac{\psi(r)}{r}\bigg)=\infty. \end{align*} $$
$$ \begin{align*}\mathcal H^g(\Lambda_1^{\theta_1}(\psi))=\mathcal H^g({\mathcal S}_1^{\theta_1}(\psi))= \infty \quad\mathrm{if } \sum\limits_{r=1}^{\infty}rg\bigg(\frac{\psi(r)}{r}\bigg)=\infty. \end{align*} $$
As in [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9], assume that the planar curve
![]() ${\mathcal C}:=\{(x, \mathcal F(x)): x\in I\}$
is the graph of a
${\mathcal C}:=\{(x, \mathcal F(x)): x\in I\}$
is the graph of a
![]() $C^{(3)}$
function
$C^{(3)}$
function
![]() $\mathcal F:I\to \mathbb R$
defined on a finite closed interval I and that
$\mathcal F:I\to \mathbb R$
defined on a finite closed interval I and that
![]() $\mathcal F^{\prime \prime }$
is continuous and nonvanishing on I. We may for simplicity assume
$\mathcal F^{\prime \prime }$
is continuous and nonvanishing on I. We may for simplicity assume
![]() $I={\mathbb I}=[0,1]$
.
$I={\mathbb I}=[0,1]$
.
Since any factor in the definition of
![]() $\Lambda _2^{{\boldsymbol \theta }}(\psi )$
can be trivially estimated from above by
$\Lambda _2^{{\boldsymbol \theta }}(\psi )$
can be trivially estimated from above by
![]() $1$
by a proper choice of numerators
$1$
by a proper choice of numerators
![]() $p_i$
within the definition of
$p_i$
within the definition of
![]() $\Lambda _2^{{\boldsymbol \theta }}(\psi )$
, we have the inclusion
$\Lambda _2^{{\boldsymbol \theta }}(\psi )$
, we have the inclusion
Since
![]() $\mathcal F\in C^{(1)}$
, we see that
$\mathcal F\in C^{(1)}$
, we see that
![]() $\mathcal F$
is locally bi-Lipschitz and therefore the map
$\mathcal F$
is locally bi-Lipschitz and therefore the map
![]() $x\mapsto (x, \mathcal F(x))$
preserves
$x\mapsto (x, \mathcal F(x))$
preserves
![]() $\mathcal H^g$
-measure. Thus, for any dimension function g,
$\mathcal H^g$
-measure. Thus, for any dimension function g,
Therefore,
 $$ \begin{align*}\mathcal H^g( {\mathcal C}\cap \Lambda_2^{{\boldsymbol\theta}} )=\infty \quad \mathrm{if } \sum\limits_{r=1}^{\infty}rg\bigg(\frac{\psi(r)}{r}\bigg)=\infty.\end{align*} $$
$$ \begin{align*}\mathcal H^g( {\mathcal C}\cap \Lambda_2^{{\boldsymbol\theta}} )=\infty \quad \mathrm{if } \sum\limits_{r=1}^{\infty}rg\bigg(\frac{\psi(r)}{r}\bigg)=\infty.\end{align*} $$
3.2 The convergence case
In this section, we prove the convergence case of Theorem 1.6, basically following [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9] with some twists towards the end. Assume that the series
![]() $\sum _q q g(\psi (q)/q)$
converges. Then, by the monotonicity of
$\sum _q q g(\psi (q)/q)$
converges. Then, by the monotonicity of
![]() $\psi $
and Cauchy condensation,
$\psi $
and Cauchy condensation,
 $$ \begin{align*} \sum_{q=1}^{\infty} q g(\psi(q)/q)\asymp \sum_{t=1}^{\infty} 2^{2t}g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)<\infty. \end{align*} $$
$$ \begin{align*} \sum_{q=1}^{\infty} q g(\psi(q)/q)\asymp \sum_{t=1}^{\infty} 2^{2t}g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)<\infty. \end{align*} $$
In particular, for large t,
Recall that the set
![]() $\Lambda _2^{\boldsymbol \theta }(\psi )$
can be written as
$\Lambda _2^{\boldsymbol \theta }(\psi )$
can be written as
 $$ \begin{align*} \bigg\{(x_1, x_2)\in{{\mathbb I}}^2: \bigg|x_1-\frac{p_1+\theta_1}{q}\bigg| \,\bigg|x_2-\frac{p_2+\theta_2}{q}\bigg|<\frac{\psi(q)}{q^2} \ \text{for i.m. }(p_1, p_2, q)\in\mathbb Z^{3}\setminus\{\mathbf 0\} \bigg\}.\end{align*} $$
$$ \begin{align*} \bigg\{(x_1, x_2)\in{{\mathbb I}}^2: \bigg|x_1-\frac{p_1+\theta_1}{q}\bigg| \,\bigg|x_2-\frac{p_2+\theta_2}{q}\bigg|<\frac{\psi(q)}{q^2} \ \text{for i.m. }(p_1, p_2, q)\in\mathbb Z^{3}\setminus\{\mathbf 0\} \bigg\}.\end{align*} $$
As in [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9], we note that for any
![]() $\ell \in \mathbb N$
, the set
$\ell \in \mathbb N$
, the set
![]() $\Lambda ^{\boldsymbol \theta }_2(\psi )\cap {\mathcal C}$
can be covered by the union over
$\Lambda ^{\boldsymbol \theta }_2(\psi )\cap {\mathcal C}$
can be covered by the union over
![]() $t\ge \ell $
of the sets
$t\ge \ell $
of the sets
 $$ \begin{align*}\bigcup_{2^t\leq q<2^{t+1}}\bigcup_{m\in\mathbb Z, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1}\bigcup_{p_1, p_2=-1}^q S_{\boldsymbol\theta}(q, m, t, p_{1},p_{2})\cap{\mathcal C},\end{align*} $$
$$ \begin{align*}\bigcup_{2^t\leq q<2^{t+1}}\bigcup_{m\in\mathbb Z, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1}\bigcup_{p_1, p_2=-1}^q S_{\boldsymbol\theta}(q, m, t, p_{1},p_{2})\cap{\mathcal C},\end{align*} $$
where
![]() $S_{\boldsymbol \theta }(q, m, t, p_{1},p_{2})$
is defined as the set of
$S_{\boldsymbol \theta }(q, m, t, p_{1},p_{2})$
is defined as the set of
![]() $(x_{1},x_{2})\in \mathbb {I}^{2}$
that satisfy
$(x_{1},x_{2})\in \mathbb {I}^{2}$
that satisfy
 $$ \begin{align*} \bigg\vert x_{1}-\frac{p_{1}+\theta_{1}}{q}\bigg\vert\leq \frac{2^{m}\sqrt{2\psi(2^{t})}}{2^{t}}, \quad \bigg\vert x_{2}-\frac{p_{2}+\theta_{2}}{q}\bigg\vert\leq \frac{2^{-m}\sqrt{2\psi(2^{t})}}{2^{t}}. \end{align*} $$
$$ \begin{align*} \bigg\vert x_{1}-\frac{p_{1}+\theta_{1}}{q}\bigg\vert\leq \frac{2^{m}\sqrt{2\psi(2^{t})}}{2^{t}}, \quad \bigg\vert x_{2}-\frac{p_{2}+\theta_{2}}{q}\bigg\vert\leq \frac{2^{-m}\sqrt{2\psi(2^{t})}}{2^{t}}. \end{align*} $$
(The sets depend on t as well; this is a small formal inaccuracy in [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9].)
By continuity and nonvanishing of
![]() $\mathcal F^{\prime \prime }$
, we see that
$\mathcal F^{\prime \prime }$
, we see that
![]() $\mathcal F^{\prime }$
has at most one local extremum. Hence, each set
$\mathcal F^{\prime }$
has at most one local extremum. Hence, each set
![]() ${\mathcal C}\cap S_{\boldsymbol \theta }(q, m, t, p_{1},p_{2})$
lies in the union of at most two boxes, that is, the projection to the first coordinate lies in two intervals. From a metrical point of view, we may without loss of generality assume that
${\mathcal C}\cap S_{\boldsymbol \theta }(q, m, t, p_{1},p_{2})$
lies in the union of at most two boxes, that is, the projection to the first coordinate lies in two intervals. From a metrical point of view, we may without loss of generality assume that
![]() $\mathcal F^{\prime }$
is increasing in
$\mathcal F^{\prime }$
is increasing in
![]() ${\mathbb I}$
so that there is in fact only one box. (Again, this argument closes a minor gap from [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9]). Then, since
${\mathbb I}$
so that there is in fact only one box. (Again, this argument closes a minor gap from [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9]). Then, since
![]() $|\mathcal F^{\prime \prime }|$
is bounded from below by a positive constant on the compact interval
$|\mathcal F^{\prime \prime }|$
is bounded from below by a positive constant on the compact interval
![]() ${\mathbb I}$
, it can easily be seen that
${\mathbb I}$
, it can easily be seen that
 $$ \begin{align*} \mathrm{diam}({\mathcal C}\cap S_{\boldsymbol\theta}(q, m, t, p_{1},p_{2}))\ll 2^{-\vert m\vert}\frac{\sqrt{\psi(2^{t})}}{2^{t}}. \end{align*} $$
$$ \begin{align*} \mathrm{diam}({\mathcal C}\cap S_{\boldsymbol\theta}(q, m, t, p_{1},p_{2}))\ll 2^{-\vert m\vert}\frac{\sqrt{\psi(2^{t})}}{2^{t}}. \end{align*} $$
Now we quote a result from [Reference Beresnevich, Vaughan and Velani8] that counts the number of rational points close to a nondegenerate curve. Since I is compact, this implies that
![]() $\mathcal F^{\prime \prime }$
is bounded between two positive constants. Given
$\mathcal F^{\prime \prime }$
is bounded between two positive constants. Given
![]() ${\boldsymbol \theta }\in \mathbb R^2, \delta>0$
and
${\boldsymbol \theta }\in \mathbb R^2, \delta>0$
and
![]() $Q\geq 1$
, consider the set
$Q\geq 1$
, consider the set
Let
![]() $N_{\boldsymbol \theta }(Q, \delta )=\#A_{\boldsymbol \theta }(Q, \delta )$
.
$N_{\boldsymbol \theta }(Q, \delta )=\#A_{\boldsymbol \theta }(Q, \delta )$
.
Theorem 3.2 [Reference Beresnevich, Vaughan and Velani8]
Let
![]() $\mathcal F\in C^{(3)}(I)$
, bounded on every
$\mathcal F\in C^{(3)}(I)$
, bounded on every
![]() $x\in I$
. If
$x\in I$
. If
![]() $\epsilon>0$
, then for any
$\epsilon>0$
, then for any
![]() $Q\geq 1$
and
$Q\geq 1$
and
![]() $0\leq \delta \leq 1/2$
,
$0\leq \delta \leq 1/2$
,
![]() $N_{\boldsymbol \theta }(Q, \delta )\ll \delta Q^2+ Q^{1+\epsilon }$
, where the implied constant is independent of
$N_{\boldsymbol \theta }(Q, \delta )\ll \delta Q^2+ Q^{1+\epsilon }$
, where the implied constant is independent of
![]() $\delta $
and Q.
$\delta $
and Q.
By using this theorem with
![]() $\delta =2^{|m|}\sqrt {\psi (2^t)}, Q=2^t$
, for every
$\delta =2^{|m|}\sqrt {\psi (2^t)}, Q=2^t$
, for every
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
So from the above cover,
 $$ \begin{align*} {\mathcal H}^{g}(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})\ll \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot (2^{\vert m\vert} \sqrt{\psi(2^{t})}2^{2t}+ 2^{(1+\epsilon)t}). \end{align*} $$
$$ \begin{align*} {\mathcal H}^{g}(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})\ll \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot (2^{\vert m\vert} \sqrt{\psi(2^{t})}2^{2t}+ 2^{(1+\epsilon)t}). \end{align*} $$
Until now, the method and calculations have not changed much from [Reference Beresnevich, Velani, Bhattacharya, Das, Ghosh and Shah9] with the exception of considering the g-measure instead of the s-measure. So the question is under what ‘nice’ conditions on g can we make the sum convergent, thus both sums
 $$ \begin{align*} S_1:= \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot 2^{\vert m\vert} \sqrt{\psi(2^{t})}2^{2t} \end{align*} $$
$$ \begin{align*} S_1:= \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot 2^{\vert m\vert} \sqrt{\psi(2^{t})}2^{2t} \end{align*} $$
and
 $$ \begin{align*} S_2:= \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot 2^{(1+\epsilon)t} \end{align*} $$
$$ \begin{align*} S_2:= \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot 2^{(1+\epsilon)t} \end{align*} $$
convergent. By (1.3), let
By the same geometric sum argument as in [Reference Beresnevich, Vaughan and Velani8],
 $$ \begin{align*} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1}2^{(1-\alpha) |m|} \ll (\sqrt{\psi(2^t)})^{\alpha-1}. \end{align*} $$
$$ \begin{align*} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1}2^{(1-\alpha) |m|} \ll (\sqrt{\psi(2^t)})^{\alpha-1}. \end{align*} $$
Using this estimate, along with (1.3) with
![]() $x,y$
as above, the sum
$x,y$
as above, the sum
![]() $S_1$
can be bounded by
$S_1$
can be bounded by
 $$ \begin{align*} S_1&= \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg)2^{\vert m\vert} \sqrt{\psi(2^{t})} 2^{2t} \\&\leq \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{-\alpha |m|} (\sqrt{\psi(2t)})^{-\alpha}\cdot 2^{\vert m\vert} \sqrt{\psi(2^{t})} 2^{2t} \\&= \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)\cdot 2^{2t} (\sqrt{\psi(2t)})^{(1-\alpha)} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1}2^{(1-\alpha) |m|} \\&\ll \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{2t}. \end{align*} $$
$$ \begin{align*} S_1&= \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg)2^{\vert m\vert} \sqrt{\psi(2^{t})} 2^{2t} \\&\leq \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{-\alpha |m|} (\sqrt{\psi(2t)})^{-\alpha}\cdot 2^{\vert m\vert} \sqrt{\psi(2^{t})} 2^{2t} \\&= \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)\cdot 2^{2t} (\sqrt{\psi(2t)})^{(1-\alpha)} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1}2^{(1-\alpha) |m|} \\&\ll \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{2t}. \end{align*} $$
The last sum converges by hypothesis and Cauchy condensation.
Now we bound the sum
![]() $S_2$
. Since the claim of the theorem becomes weaker if we increase
$S_2$
. Since the claim of the theorem becomes weaker if we increase
![]() $\psi $
, we may assume
$\psi $
, we may assume
or equivalently
Otherwise, we can just take the pointwise maximum of
![]() $\psi $
and the right-hand side function above whose sum over t converges as soon as
$\psi $
and the right-hand side function above whose sum over t converges as soon as
![]() $\varepsilon <1$
. Observe further that for given t,
$\varepsilon <1$
. Observe further that for given t,
for any
![]() $\varepsilon _0>0$
. Hence, given
$\varepsilon _0>0$
. Hence, given
![]() $\epsilon>0$
, we choose any
$\epsilon>0$
, we choose any
![]() $\varepsilon> \epsilon $
(for example,
$\varepsilon> \epsilon $
(for example,
![]() $\varepsilon =2\epsilon $
) and then we can choose
$\varepsilon =2\epsilon $
) and then we can choose
![]() $\epsilon _0>0$
small enough so that still
$\epsilon _0>0$
small enough so that still
We can therefore estimate
 $$ \begin{align*} S_2 &=\sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot 2^{(1+\epsilon)t} \\ &\le \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{t(1+\epsilon)} \psi(2^t)^{-\alpha/2} 2^{-\alpha |m|} \\ &\ll \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{t(1+\epsilon)} \psi(2^t)^{-\alpha/2} \cdot \#\{ m: 2^{|m|}\sqrt{\psi(2^t)}\leq 1 \} \\ &\ll \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{t(1+\epsilon)} 2^{t(1-\epsilon)} \\ &= \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{2t}. \end{align*} $$
$$ \begin{align*} S_2 &=\sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(2^{-\vert m\vert} \frac{\sqrt{\psi(2^{t})}}{2^{t}}\bigg) \cdot 2^{(1+\epsilon)t} \\ &\le \sum_{t=1}^{\infty} \sum_{m\in\mathbb{Z}, 2^{|m|}\sqrt{\psi(2^{t}) }\leq 1} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{t(1+\epsilon)} \psi(2^t)^{-\alpha/2} 2^{-\alpha |m|} \\ &\ll \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{t(1+\epsilon)} \psi(2^t)^{-\alpha/2} \cdot \#\{ m: 2^{|m|}\sqrt{\psi(2^t)}\leq 1 \} \\ &\ll \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{t(1+\epsilon)} 2^{t(1-\epsilon)} \\ &= \sum_{t=1}^{\infty} g\bigg(\frac{\psi(2^{t})}{2^{t}}\bigg)2^{2t}. \end{align*} $$
Again, the latter sum converges by Cauchy condensation. Hence, both sums converge and, thus, by the Hausdorff–Cantelli lemma,
 $$ \begin{align*}{\mathcal H}^{g}(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})=0 \quad\mbox{if and only if } \sum_q q g(\psi(q)/q)<\infty.\end{align*} $$
$$ \begin{align*}{\mathcal H}^{g}(\Lambda^{\boldsymbol\theta}_2(\psi)\cap{\mathcal C})=0 \quad\mbox{if and only if } \sum_q q g(\psi(q)/q)<\infty.\end{align*} $$