1. Introduction
Many micro-organisms live in environments characterized by currents (e.g. oceans, rivers, human intestines), and flow mediates many important microbial processes such as infection (Costerton, Stewart & Greenberg Reference Costerton, Stewart and Greenberg1999; Yawata et al. Reference Yawata, Nguyen, Stocker and Rusconi2016), uptake of nutrients (Musielak et al. Reference Musielak, Karp-Boss, Jumars and Fauci2009; Taylor & Stocker Reference Taylor and Stocker2012) and reproduction (Riffell & Zimmer Reference Riffell and Zimmer2007; Zimmer & Riffell Reference Zimmer and Riffell2011). Flow exerts forces and torques on micro-organisms that affect their motility dynamics and spatial distribution (Guasto, Rusconi & Stocker Reference Guasto, Rusconi and Stocker2012; Wheeler et al. Reference Wheeler, Secchi, Rusconi and Stocker2019). It also controls the transport of essential molecules including nutrients, oxygen and signals of mates and predators (Kim et al. Reference Kim, Ingremeau, Zhao, Bassler and Stone2016). Micro-organisms, in turn, can adapt their swimming behaviour to these physical and chemical gradients (Stocker et al. Reference Stocker, Seymour, Samadani, Hunt and Polz2008). Such interactions can lead to non-trivial phenomena such as rheotaxis (Hill et al. Reference Hill, Kalkanci, McMurry and Koser2007; Marcos et al. Reference Marcos, Fu, Powers and Stocker2012; Mathijssen et al. Reference Mathijssen, Figueroa-Morales, Junot, Clément, Lindner and Zöttl2019), gyrotaxis (De Lillo et al. Reference De Lillo, Cencini, Durham, Barry, Stocker, Climent and Boffetta2014; Borgnino et al. Reference Borgnino, Boffetta, De Lillo and Cencini2018) and chemotaxis (Locsei & Pedley Reference Locsei and Pedley2009; Stocker & Seymour Reference Stocker and Seymour2012), to name a few examples.
Even simple shear flows, when coupled to cell motility and morphology, can give rise to complex transport and cell motility behaviour (Durham, Kessler & Stocker Reference Durham, Kessler and Stocker2009; Rusconi, Guasto & Stocker Reference Rusconi, Guasto and Stocker2014; Ezhilan & Saintillan Reference Ezhilan and Saintillan2015; Gustavsson et al. Reference Gustavsson, Berglund, Jonsson and Mehlig2016). For instance, fluid shear can cause a torque that can rotate an elongated cell body and can result in accumulation of motile bacteria and phytoplankton in high-shear-rate regions of the flow (Rusconi et al. Reference Rusconi, Guasto and Stocker2014; Barry et al. Reference Barry, Rusconi, Guasto and Stocker2015; Ezhilan & Saintillan Reference Ezhilan and Saintillan2015). Near surfaces, shear flows can orient flagellated cells against the flow, causing bacteria and spermatozoa to swim upstream (Tung et al. Reference Tung, Ardon, Roy, Koch, Suarez and Wu2015; Zaferani, Cheong & Abbaspourrad Reference Zaferani, Cheong and Abbaspourrad2018; Mathijssen et al. Reference Mathijssen, Figueroa-Morales, Junot, Clément, Lindner and Zöttl2019). Away from surfaces, shear gradients can trap bottom-heavy gyrotactic swimmers at certain depth of water column, causing the formation of intense cell assemblages called ‘thin layers’ (Durham et al. Reference Durham, Kessler and Stocker2009, Reference Durham, Climent, Barry, De Lillo, Boffetta, Cencini and Stocker2013; Gustavsson et al. Reference Gustavsson, Berglund, Jonsson and Mehlig2016). In unsteady and/or complex flows, transport of micro-organisms shows intriguing phenomena such as aggregation, dispersion and pattern formation (Torney & Neufeld Reference Torney and Neufeld2007; Khurana, Blawzdziewicz & Ouellette Reference Khurana, Blawzdziewicz and Ouellette2011; Khurana & Ouellette Reference Khurana and Ouellette2012; Zhan et al. Reference Zhan, Sardina, Lushi and Brandt2014; Qin & Arratia Reference Qin and Arratia2022), but are less understood. In time-periodic flows, simulations show that elongated swimmers can be trapped or repelled by elliptic islands depending on their shape and swimming speed (Torney & Neufeld Reference Torney and Neufeld2007); such trapping effects can lead to a reduction in long-term swimmer transport (Khurana et al. Reference Khurana, Blawzdziewicz and Ouellette2011). Recent experiments and simulations show that microswimmers can be trapped, repelled or dispersed by vortices depending on the dimensionless path length and swimming speed (Qin & Arratia Reference Qin and Arratia2022). In isotropic turbulence, simulations show that elongated swimmers, while remaining rather uniformly distributed, exhibit preferential alignment with instantaneous Eulerian fields such as local velocity (Borgnino et al. Reference Borgnino, Gustavsson, De Lillo, Boffetta, Cencini and Mehlig2019), vorticity (Zhan et al. Reference Zhan, Sardina, Lushi and Brandt2014) and velocity gradient (Pujara, Koehl & Variano Reference Pujara, Koehl and Variano2018).
Recently, it has been shown that Lagrangian coherent structure (LCS) can be a useful concept to understand the transport properties of swimming micro-organisms in complex flows in both numerical simulations and experiments (Khurana & Ouellette Reference Khurana and Ouellette2012; Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Si & Fang Reference Si and Fang2021, Reference Si and Fang2022; Yoest et al. Reference Yoest, Buggeln, Doan, Johnson, Berman, Mitchell and Solomon2022). Simulations in chaotic flows show that elongated swimmers align with repelling LCSs of hyperbolic fixed points (Khurana & Ouellette Reference Khurana and Ouellette2012), while later numerical studies show that elongated active particles have a much stronger alignment with attracting LCSs (Si & Fang Reference Si and Fang2021, Reference Si and Fang2022), similar to passive elongated particles (Parsa et al. Reference Parsa, Guasto, Kishore, Ouellette, Gollub and Voth2011). Experimental investigations that examine the interactions of swimming organisms and flow LCSs are few but show some intriguing phenomena. Experiments in model porous media show that bacteria align and accumulate near attracting LCSs and induce filamentous density patterns (Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019). In time-periodic flows, experiments show that the accumulation of bacteria near the attracting LCSs can attenuate stretching and hinder large-scale transport, although small-scale mixing is locally enhanced (Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021). Most, if not all, previous studies focus on attracting and repelling LCSs associated with the flow hyperbolic fixed points. That is not surprising since one expects large levels of strain near or around those fixed points. Less understood are swimmer interactions with elliptic LCSs, i.e. vortex-like flow dynamical features (Haller Reference Haller2015; Farazmand & Haller Reference Farazmand and Haller2016; Haller et al. Reference Haller, Hadjighasem, Farazmand and Huhn2016). That is the focus of this manuscript.
Here, we experimentally investigate the effects of bacterial activity on the mixing and transport properties of a passive scalar in a time-periodic flow in experiments and simulations. We focus on the interaction of swimming bacteria (Escherichia coli) with the elliptic LCSs of the flow. Results show that such interaction leads to transport barriers through which the fluxes of the passive tracer are significantly reduced. By constructing the Poincaré map from velocimetry data, we show that these transport barriers coincide with the outermost member of elliptic LCSs, or namely, Lagrangian vortex boundaries (LVBs). We further test these results in numerical simulations and find that elliptic LCSs repel elongated swimmers and lead to swimmer accumulation outside (or swimmer depletion inside) the Lagrangian vortices. A simple mechanism shows that the repulsion of swimmers is due to the preferential alignment of elongated swimmers with the tangents of elliptic LCSs. Overall, these results can be useful in understanding the transport of micro-organisms in chaotic flows with elliptic dynamical features or non-trivial vortex structures.
2. Methods
Experiments are performed in the flow cell set-up where a 2-mm-thin conductive fluid layer is placed above an array of permanent magnets arranged in a disordered pattern (Voth, Haller & Gollub Reference Voth, Haller and Gollub2002; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021, Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2022). As a sinusoidal forcing (electrical current, 0.2 Hz frequency) is imposed on the fluid layer, the magnetic field induces a Lorentz force and creates spatially disordered vortex patterns (see flow field in figure 1c). The resulting flow is characterized by two parameters: the Reynolds number and the path length. The Reynolds number is defined as ![]() $Re=UL/\nu$, where
$Re=UL/\nu$, where ![]() $U=1.2$ mm s
$U=1.2$ mm s![]() $^{-1}$ is the average flow speed,
$^{-1}$ is the average flow speed, ![]() $L=6.0\ {\rm mm}$ is the characteristic length scale determined by the average spacing of the permanent magnets and
$L=6.0\ {\rm mm}$ is the characteristic length scale determined by the average spacing of the permanent magnets and ![]() $\nu =1.0$ mm
$\nu =1.0$ mm![]() $^2$ s
$^2$ s![]() $^{-1}$ is the fluid kinematic viscosity (water-like). The path length is the normalized mean displacement of a typical fluid parcel in one forcing period, defined as
$^{-1}$ is the fluid kinematic viscosity (water-like). The path length is the normalized mean displacement of a typical fluid parcel in one forcing period, defined as ![]() $p=UT/L$, where
$p=UT/L$, where ![]() $T=5$ s is the forcing period. Here, the Reynolds number and the path length are
$T=5$ s is the forcing period. Here, the Reynolds number and the path length are ![]() $Re\approx 7.2$,
$Re\approx 7.2$, ![]() $p\approx 1.0$; these conditions are known to lead to chaotic advection in this system (Voth et al. Reference Voth, Saint, Dobler and Gollub2003; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021).
$p\approx 1.0$; these conditions are known to lead to chaotic advection in this system (Voth et al. Reference Voth, Saint, Dobler and Gollub2003; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021).

Figure 1. Photographs of the dye concentration field for chaotic mixing in (a) buffer solution (![]() $\phi _b=0$) and (b) active suspension (
$\phi _b=0$) and (b) active suspension (![]() $\phi _b=0.5\,\%$). Images are taken at
$\phi _b=0.5\,\%$). Images are taken at ![]() $N=300$ periods after the start of the experiments. The imaged region is
$N=300$ periods after the start of the experiments. The imaged region is ![]() $60\ {\rm mm}\times 60\ {\rm mm}$; the scale bar represents 6 mm. The Reynolds number and path length of the flow are
$60\ {\rm mm}\times 60\ {\rm mm}$; the scale bar represents 6 mm. The Reynolds number and path length of the flow are ![]() $Re=7.2$ and
$Re=7.2$ and ![]() $p=1.0$, respectively. (c) Vorticity (colour code) and velocity (arrows) fields of the flow, corresponding the first peak of a time period. (d) Poincaré map of the flow in the same imaged region as the dye field. The map is coloured by the trajectory rotation average (TRA) calculated over 20 time periods.
$p=1.0$, respectively. (c) Vorticity (colour code) and velocity (arrows) fields of the flow, corresponding the first peak of a time period. (d) Poincaré map of the flow in the same imaged region as the dye field. The map is coloured by the trajectory rotation average (TRA) calculated over 20 time periods.
Two main types of experiments are performed: dye mixing and particle tracking velocimetry (PTV). Dye mixing experiments are performed by labelling half of the fluid layer with a passive dye tracer (![]() $6.25\times 10^{-5}$ M sodium fluorescein). Initially, the labelled and unlabelled portions are separated by a physical barrier. As the flow begins, the barrier is lifted, and the labelled fluid progressively penetrates the unlabelled portion with time. The dye concentration field is recorded by a complementary metal-oxide-semiconductor (CMOS) camera (Flare 4M180) at 5 frames s
$6.25\times 10^{-5}$ M sodium fluorescein). Initially, the labelled and unlabelled portions are separated by a physical barrier. As the flow begins, the barrier is lifted, and the labelled fluid progressively penetrates the unlabelled portion with time. The dye concentration field is recorded by a complementary metal-oxide-semiconductor (CMOS) camera (Flare 4M180) at 5 frames s![]() $^{-1}$ with a resolution of
$^{-1}$ with a resolution of ![]() $2000\times 2000$ pixels. Particle tracking experiments are performed by seeding the fluid with 100
$2000\times 2000$ pixels. Particle tracking experiments are performed by seeding the fluid with 100 ![]() $\mathrm {\mu }$m large fluorescent polystyrene particles; the Stokes number of these fluorescent particles is
$\mathrm {\mu }$m large fluorescent polystyrene particles; the Stokes number of these fluorescent particles is ![]() $O(10^{-4})$, indicating good tracer fidelity. Particle positions are recorded by the CMOS camera at 30 frames s
$O(10^{-4})$, indicating good tracer fidelity. Particle positions are recorded by the CMOS camera at 30 frames s![]() $^{-1}$ with a resolution of
$^{-1}$ with a resolution of ![]() $1200\times 1200$ pixels. Particle trajectories are obtained using an in-house tracking algorithm (Crocker & Grier Reference Crocker and Grier1996); these trajectories are then used to obtain the velocity fields from sixth-order polynomial fitting. Because the flow is time-periodic, we can combine particle positions at a given phase (relative to the forcing) to obtain up to 80 000 precise particle positions at each phase, which yields high spatial resolution (0.002 of the field of view), excellent temporal resolution (0.007 of a flow period) and velocities accurate to a few per cent. Two different velocity maps are obtained from separate experiments, one in the presence and the other in the absence of bacteria.
$1200\times 1200$ pixels. Particle trajectories are obtained using an in-house tracking algorithm (Crocker & Grier Reference Crocker and Grier1996); these trajectories are then used to obtain the velocity fields from sixth-order polynomial fitting. Because the flow is time-periodic, we can combine particle positions at a given phase (relative to the forcing) to obtain up to 80 000 precise particle positions at each phase, which yields high spatial resolution (0.002 of the field of view), excellent temporal resolution (0.007 of a flow period) and velocities accurate to a few per cent. Two different velocity maps are obtained from separate experiments, one in the presence and the other in the absence of bacteria.
Active suspensions are prepared by adding a strain (wild-type K12 MG1655) of E. coli to an aqueous buffer solution of 2 % KCl and 1 % NaCl by weight; the swimming motility of E. coli does not seem to be affected by the salts (Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021). The strain of E. coli has a swimming speed of 10–20 ![]() $\mathrm {\mu }$m s
$\mathrm {\mu }$m s![]() $^{-1}$ and a rod-shaped body of on average
$^{-1}$ and a rod-shaped body of on average ![]() $2\ \mathrm {\mu }$m length and
$2\ \mathrm {\mu }$m length and ![]() $0.5\ \mathrm {\mu }$m diameter. We note that the Péclet numbers of the bacteria and the dye are both considerably large, with
$0.5\ \mathrm {\mu }$m diameter. We note that the Péclet numbers of the bacteria and the dye are both considerably large, with ![]() $Pe_{b}=UL/D_b \sim O(10^6)$, and
$Pe_{b}=UL/D_b \sim O(10^6)$, and ![]() $Pe_{d}=UL/D_d \sim O(10^4)$, where
$Pe_{d}=UL/D_d \sim O(10^4)$, where ![]() $D_b$ and
$D_b$ and ![]() $D_d$ are the effective diffusivities of the swimming E. coli and the dye, respectively. Bacteria are cultured in Luria–Bertani (Lennox, Sigma-Aldrich) liquid media at
$D_d$ are the effective diffusivities of the swimming E. coli and the dye, respectively. Bacteria are cultured in Luria–Bertani (Lennox, Sigma-Aldrich) liquid media at ![]() $37\,^{\circ }$C overnight for 12 to 14 hours to attain a stationary phase of a number density of approximately
$37\,^{\circ }$C overnight for 12 to 14 hours to attain a stationary phase of a number density of approximately ![]() $10^9$ cells ml
$10^9$ cells ml![]() $^{-1}$. The stationary-phase culture is centrifuged at 5000 rev min
$^{-1}$. The stationary-phase culture is centrifuged at 5000 rev min![]() $^{-1}$ for 3.5 min and resuspended into the buffer solution to attain a number density of
$^{-1}$ for 3.5 min and resuspended into the buffer solution to attain a number density of ![]() $1.25\times 10^{10}$ cells ml
$1.25\times 10^{10}$ cells ml![]() $^{-1}$ or a bacterial volume fraction of
$^{-1}$ or a bacterial volume fraction of ![]() $\phi _b=0.5\,\%$. This bacterial volume fraction (
$\phi _b=0.5\,\%$. This bacterial volume fraction (![]() $\phi _b=0.5\,\%$) is considered dilute (Kasyap, Koch & Wu Reference Kasyap, Koch and Wu2014; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021), and large-scale collective behaviour/motion is not expected.
$\phi _b=0.5\,\%$) is considered dilute (Kasyap, Koch & Wu Reference Kasyap, Koch and Wu2014; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021), and large-scale collective behaviour/motion is not expected.
3. Results and discussion
3.1. Experimental results
Figures 1(a) and 1(b) show sample snapshots of dye mixing in the buffer solution (![]() $\phi _b=0\,\%$) and active suspension (
$\phi _b=0\,\%$) and active suspension (![]() $\phi _b=0.5\,\%$), respectively. Both snapshots are taken after
$\phi _b=0.5\,\%$), respectively. Both snapshots are taken after ![]() $N=300$ periods of forcing, with dye initially confined on the right-hand half of the images at
$N=300$ periods of forcing, with dye initially confined on the right-hand half of the images at ![]() $N=0$. The concentration field reveals complex patterns and underlying vortex structures, which are similar in the buffer and the active suspension. However, a main difference is the existence of regions devoid of dye near the centre of the vortex structures in the active suspension (figure 1b), while similar regions are dyed in the buffer case (figure 1a). The regions devoid of dye near the centre of the vortex appear primarily in the left-hand half of the image that is initially not covered with dye. This suggests that the interplay of microbial activity and vortex structures leads to (enhanced) transport barriers through which the dye fails to penetrate or penetrates much more slowly. A movie of the dye-mixing processes in the buffer and the active suspension are shown in supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.452.
$N=0$. The concentration field reveals complex patterns and underlying vortex structures, which are similar in the buffer and the active suspension. However, a main difference is the existence of regions devoid of dye near the centre of the vortex structures in the active suspension (figure 1b), while similar regions are dyed in the buffer case (figure 1a). The regions devoid of dye near the centre of the vortex appear primarily in the left-hand half of the image that is initially not covered with dye. This suggests that the interplay of microbial activity and vortex structures leads to (enhanced) transport barriers through which the dye fails to penetrate or penetrates much more slowly. A movie of the dye-mixing processes in the buffer and the active suspension are shown in supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.452.
To further understand the interaction between activity and vortex structures, we plot in figure 1(d) the flow Poincaré map obtained from PTV experiments. Lines in the map are stroboscopic particle trajectories that connect a particle's initial position to its next position after a period (![]() $T=5$ s). These trajectories are obtained by numerical integration of fluid particles in the experimentally measured velocity fields. The Poincaré map reveals several nested families of closed trajectories, whose behaviours mimic Kolmogorov–Arnold–Moser tori in Hamiltonian dynamical systems (Ottino Reference Ottino1989). These nested torus families define Lagrangian coherent vortices known as elliptic LCSs, with each torus acting as a barrier that blocks tracer (dye) transport within the vortex (Haller et al. Reference Haller, Katsanoulis, Holzner, Frohnapfel and Gatti2020; Katsanoulis et al. Reference Katsanoulis, Farazmand, Serra and Haller2020; Aksamit & Haller Reference Aksamit and Haller2022). Unlike hyperbolic LCSs, elliptic LCSs are rotation-dominated regions that do not experience substantial (fluid) stretching. We note that Lagrangian coherent vortices are fundamentally different from the vortices defined by Eulerian fields such as vorticity. While we find a striking correspondence between the dye-mixing patterns (figure 1a,b) and the Lagrangian coherent vortices on the Poincaré map (figure 1d), such similarity is absent for the Eulerian vorticity field in figure 1(c).
$T=5$ s). These trajectories are obtained by numerical integration of fluid particles in the experimentally measured velocity fields. The Poincaré map reveals several nested families of closed trajectories, whose behaviours mimic Kolmogorov–Arnold–Moser tori in Hamiltonian dynamical systems (Ottino Reference Ottino1989). These nested torus families define Lagrangian coherent vortices known as elliptic LCSs, with each torus acting as a barrier that blocks tracer (dye) transport within the vortex (Haller et al. Reference Haller, Katsanoulis, Holzner, Frohnapfel and Gatti2020; Katsanoulis et al. Reference Katsanoulis, Farazmand, Serra and Haller2020; Aksamit & Haller Reference Aksamit and Haller2022). Unlike hyperbolic LCSs, elliptic LCSs are rotation-dominated regions that do not experience substantial (fluid) stretching. We note that Lagrangian coherent vortices are fundamentally different from the vortices defined by Eulerian fields such as vorticity. While we find a striking correspondence between the dye-mixing patterns (figure 1a,b) and the Lagrangian coherent vortices on the Poincaré map (figure 1d), such similarity is absent for the Eulerian vorticity field in figure 1(c).
To quantitatively locate the elliptic LCSs, we calculate the TRA on the Poincaré map, as shown by the colour code in figure 1(d). The TRA characterizes the average angular velocity of a particle trajectory and is defined as
 \begin{equation} \overline{{\rm TRA}}_{0}^{N}(\boldsymbol{x}_0)=\frac{1}{NT} \sum_{i=0}^{N-1} \cos^{{-}1} \frac{\langle\dot{\boldsymbol{x}}_i, \dot{\boldsymbol{x}}_{i+1}\rangle}{|\dot{\boldsymbol{x}}_i||\dot{\boldsymbol{x}}_{i+1}|}. \end{equation}
\begin{equation} \overline{{\rm TRA}}_{0}^{N}(\boldsymbol{x}_0)=\frac{1}{NT} \sum_{i=0}^{N-1} \cos^{{-}1} \frac{\langle\dot{\boldsymbol{x}}_i, \dot{\boldsymbol{x}}_{i+1}\rangle}{|\dot{\boldsymbol{x}}_i||\dot{\boldsymbol{x}}_{i+1}|}. \end{equation}
Here, ![]() $\dot {\boldsymbol {x}}_i$ is a stroboscopic velocity related to the rate of change of the position of a particle on the Poincaré map and
$\dot {\boldsymbol {x}}_i$ is a stroboscopic velocity related to the rate of change of the position of a particle on the Poincaré map and ![]() $N$ is the number of periods over which the quantity is calculated. Although the TRA was originally defined for actual particle trajectories (Haller, Aksamit & Encinas-Bartos Reference Haller, Aksamit and Encinas-Bartos2021), we used it here for the stroboscopic trajectories in the extended phase space of the Poincaré map. We interpolate the values of the TRA onto a uniform spatial grid to obtain the TRA field (see supplementary movie 2). In two-dimensional flows, elliptic LCSs can be located from the closed convex contours of the TRA field (Haller et al. Reference Haller, Aksamit and Encinas-Bartos2021; Aksamit & Haller Reference Aksamit and Haller2022). Since elliptic LCSs are nested families, we identify the outermost convex TRA contours as the boundaries of Lagrangian coherent vortices, and the centroid of the innermost convex TRA contours as elliptic fixed points. For concision, we refer to the outermost members of elliptic LCSs as LVBs.
$N$ is the number of periods over which the quantity is calculated. Although the TRA was originally defined for actual particle trajectories (Haller, Aksamit & Encinas-Bartos Reference Haller, Aksamit and Encinas-Bartos2021), we used it here for the stroboscopic trajectories in the extended phase space of the Poincaré map. We interpolate the values of the TRA onto a uniform spatial grid to obtain the TRA field (see supplementary movie 2). In two-dimensional flows, elliptic LCSs can be located from the closed convex contours of the TRA field (Haller et al. Reference Haller, Aksamit and Encinas-Bartos2021; Aksamit & Haller Reference Aksamit and Haller2022). Since elliptic LCSs are nested families, we identify the outermost convex TRA contours as the boundaries of Lagrangian coherent vortices, and the centroid of the innermost convex TRA contours as elliptic fixed points. For concision, we refer to the outermost members of elliptic LCSs as LVBs.
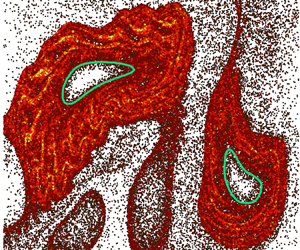
Figures 2(a) and 2(b) show the LVBs (green contours) and elliptic fixed point (red dots) identified from the TRA field, superimposed on dye-mixing patterns in the buffer and the active suspension, respectively. Although LVBs in chaotic flows are known to be transport barriers for convection (Haller et al. Reference Haller, Katsanoulis, Holzner, Frohnapfel and Gatti2020; Katsanoulis et al. Reference Katsanoulis, Farazmand, Serra and Haller2020; Aksamit & Haller Reference Aksamit and Haller2022), the LVBs in the buffer case (figure 2a) contain dye inside due to diffusion. On the other hand, the LVBs in the active case (figure 2b) enclose regions devoid of dye near the elliptic fixed points. This suggests that bacterial activity enhances the strength of LVBs as transport barriers in chaotic flows. We also notice some differences in the size and shape of the LVBs for the buffer and active cases. Since the LVBs are calculated from experimentally measured velocity fields, this indicates that microbial activity also modifies the underlying velocity field.

Figure 2. Enlarged photographs of the dye concentration field for (a) buffer and (b) active suspension, in the dashed square regions shown in figure 1. Green contours are LVBs identified from the TRA field and red dots are elliptic fixed points. (c) Dye flow rate, ![]() $\boldsymbol {J}$, as a function of time
$\boldsymbol {J}$, as a function of time ![]() $N$, for the vortex with the label ‘4’. Inset: time-averaged dye flow rate,
$N$, for the vortex with the label ‘4’. Inset: time-averaged dye flow rate, ![]() $\bar {\boldsymbol {J}}$, as a function of the vortex Reynolds number
$\bar {\boldsymbol {J}}$, as a function of the vortex Reynolds number ![]() $Re_\varGamma$, for the buffer (blue) and the active suspension (red). Different markers represent different vortices in the flow field. Error bars are standard deviations.
$Re_\varGamma$, for the buffer (blue) and the active suspension (red). Different markers represent different vortices in the flow field. Error bars are standard deviations.
To quantify the strength of the transport barriers, or the reduction in dye transport, we calculate the dye flow rate into the Lagrangian vortices using the following mass balance equation:
Here, ![]() $S(t)$ and
$S(t)$ and ![]() $B(t)$ denote the enclosed area and the contour of the LVBs,
$B(t)$ denote the enclosed area and the contour of the LVBs, ![]() $C$ is the dimensionless dye concentration field (normalized by the maximum fluorescence intensity),
$C$ is the dimensionless dye concentration field (normalized by the maximum fluorescence intensity), ![]() $D$ is the dye diffusivity,
$D$ is the dye diffusivity, ![]() $\boldsymbol {n}$ is the normal vector of LVBs,
$\boldsymbol {n}$ is the normal vector of LVBs, ![]() $\boldsymbol {v}$ is fluid velocity and
$\boldsymbol {v}$ is fluid velocity and ![]() $\boldsymbol {v}_{B}$ is the velocity induced by the motion and deformation of LVBs. The first and second terms on the right-hand side of (3.2) are the surface integrals of the dye fluxes through the LVBs due to diffusion and convection, respectively. The left-hand side of (3.2) gives a simple way to calculate dye flow rate as the rate of change of the total dye enclosed by the LVBs. Figure 2(c) shows the dye flow rate,
$\boldsymbol {v}_{B}$ is the velocity induced by the motion and deformation of LVBs. The first and second terms on the right-hand side of (3.2) are the surface integrals of the dye fluxes through the LVBs due to diffusion and convection, respectively. The left-hand side of (3.2) gives a simple way to calculate dye flow rate as the rate of change of the total dye enclosed by the LVBs. Figure 2(c) shows the dye flow rate, ![]() $\boldsymbol {J}$, as a function of time, for vortex with label ‘4’ in the buffer and the active suspension. We find a significant reduction of dye flow rate into the LVBs with bacterial activity, especially at earlier times (
$\boldsymbol {J}$, as a function of time, for vortex with label ‘4’ in the buffer and the active suspension. We find a significant reduction of dye flow rate into the LVBs with bacterial activity, especially at earlier times (![]() $N<150$). At later times (
$N<150$). At later times (![]() $N>200$), the dye flow rate in the active case is larger than that in the buffer, as a result of a larger diffusive flux due to large dye concentration gradients.
$N>200$), the dye flow rate in the active case is larger than that in the buffer, as a result of a larger diffusive flux due to large dye concentration gradients.
We now explore the generality of the reduction of dye flow rate in active suspensions. We start by calculating the circulation of a Lagrangian vortex, defined as
where ![]() $\omega _z$ denotes the vorticity component in the out-of-plane direction. We then define the the vortex Reynolds number as
$\omega _z$ denotes the vorticity component in the out-of-plane direction. We then define the the vortex Reynolds number as ![]() $Re_\varGamma = \vert \bar {\varGamma }\vert /\nu$, where
$Re_\varGamma = \vert \bar {\varGamma }\vert /\nu$, where ![]() $\bar {\varGamma }$ denotes the time-averaged circulation over a period, and the absolute value is included since
$\bar {\varGamma }$ denotes the time-averaged circulation over a period, and the absolute value is included since ![]() $\bar {\varGamma }$ can be positive or negative depending on the sign of the vorticity. We calculate
$\bar {\varGamma }$ can be positive or negative depending on the sign of the vorticity. We calculate ![]() $Re_\varGamma$ for each Lagrangian vortex in figure 2(a,b); the labels correspond to the magnitude of their
$Re_\varGamma$ for each Lagrangian vortex in figure 2(a,b); the labels correspond to the magnitude of their ![]() $Re_\varGamma$. The inset of figure 2(c) shows the time-averaged dye flow rate,
$Re_\varGamma$. The inset of figure 2(c) shows the time-averaged dye flow rate, ![]() $\bar {\boldsymbol {J}}$, as a function of the vortex Reynolds number
$\bar {\boldsymbol {J}}$, as a function of the vortex Reynolds number ![]() $Re_\varGamma$, for the buffer and active cases. We find that in both cases the average dye flow rates scale linearly with
$Re_\varGamma$, for the buffer and active cases. We find that in both cases the average dye flow rates scale linearly with ![]() $Re_\varGamma$. This is because both
$Re_\varGamma$. This is because both ![]() $\bar {\boldsymbol {J}}$ and
$\bar {\boldsymbol {J}}$ and ![]() $Re_\varGamma$ are linearly proportional to the area of the Lagrangian vortex. More importantly, however, we find that the slope of the scaling is larger in the buffer case compared with the active case. This result shows that the presence of bacteria enhances the barriers for scalar transport into the flow Lagrangian vortices.
$Re_\varGamma$ are linearly proportional to the area of the Lagrangian vortex. More importantly, however, we find that the slope of the scaling is larger in the buffer case compared with the active case. This result shows that the presence of bacteria enhances the barriers for scalar transport into the flow Lagrangian vortices.
3.2. Numerical simulations
To understand how swimming micro-organisms interact with an imposed time-periodic flow, we perform numerical simulations of swimming particles using the experimentally measured velocity field. Micro-organisms are modelled as axisymmetric ellipsoids with a constant swimming speed ![]() $v_s$, in the direction
$v_s$, in the direction ![]() $\boldsymbol {q}$ along their symmetry axis. The swimmer's position
$\boldsymbol {q}$ along their symmetry axis. The swimmer's position ![]() $\boldsymbol {x}$ is modelled as
$\boldsymbol {x}$ is modelled as
where ![]() $\boldsymbol {v}_f$ is experimentally measured fluid velocity in the active suspension, and
$\boldsymbol {v}_f$ is experimentally measured fluid velocity in the active suspension, and ![]() $v_s=20\ \mathrm {\mu }$m s
$v_s=20\ \mathrm {\mu }$m s![]() $^{-1}$ is the swimming speed of E. coli. As a control, simulations of elongated passive particles are also performed with
$^{-1}$ is the swimming speed of E. coli. As a control, simulations of elongated passive particles are also performed with ![]() $v_s=0$ in the velocity field measured in the buffer. The swimmer's orientation is described by Jeffery's equation (Jeffery & Filon Reference Jeffery and Filon1922)
$v_s=0$ in the velocity field measured in the buffer. The swimmer's orientation is described by Jeffery's equation (Jeffery & Filon Reference Jeffery and Filon1922)
where ![]() $\boldsymbol {D}$ and
$\boldsymbol {D}$ and ![]() $\boldsymbol {W}$ are the symmetric and skew-symmetric parts of the velocity gradient tensor,
$\boldsymbol {W}$ are the symmetric and skew-symmetric parts of the velocity gradient tensor, ![]() $\boldsymbol {\nabla }\boldsymbol {v}_f$. Here,
$\boldsymbol {\nabla }\boldsymbol {v}_f$. Here, ![]() $\varLambda = (1-\alpha ^2)/(1+\alpha ^2)$ is a shape factor, with
$\varLambda = (1-\alpha ^2)/(1+\alpha ^2)$ is a shape factor, with ![]() $\alpha$ being the swimmer's aspect ratio. We assume
$\alpha$ being the swimmer's aspect ratio. We assume ![]() $\alpha =0.25$ for rod-shaped E. coli, which leads to
$\alpha =0.25$ for rod-shaped E. coli, which leads to ![]() $\varLambda \approx 0.88$.
$\varLambda \approx 0.88$.
Initially, both passive and active particles are uniformly distributed in the flow field with random orientations. As simulations begin, passive and active particles begin to develop complex patterns following the morphology of Lagrangian vortices (supplementary movie 3). Figures 3(a) and 3(b) show the spatial distribution of passive and active particles at ![]() $N=150$, respectively. The colour code in the plots represents the local particle number density,
$N=150$, respectively. The colour code in the plots represents the local particle number density, ![]() $\rho _N$, normalized by the initial number density,
$\rho _N$, normalized by the initial number density, ![]() $\rho _0$. We find that active particles deplete within and aggregate outside the LVBs. This suggests that Lagrangian vortices repel elongated swimmers. By contrast, no depletion is observed for passive particles. Accumulation is not expected for passive particles in a two-dimensional incompressible flow, and aggregation of non-motile bacteria has not been observed in previous experiments (Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021). The accumulation of passive particles seen here is likely due to a small departure from an (ideal) divergence-free experimental velocity field (see supplementary materials). The passive particle simulation serves as a control to show that the repulsion of active particles by the Lagrangian vortices is not an intrinsic feature of the experimental velocity field itself. Rather, it is the result of the interaction between Lagrangian vortices and elongated swimmers.
$\rho _0$. We find that active particles deplete within and aggregate outside the LVBs. This suggests that Lagrangian vortices repel elongated swimmers. By contrast, no depletion is observed for passive particles. Accumulation is not expected for passive particles in a two-dimensional incompressible flow, and aggregation of non-motile bacteria has not been observed in previous experiments (Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021). The accumulation of passive particles seen here is likely due to a small departure from an (ideal) divergence-free experimental velocity field (see supplementary materials). The passive particle simulation serves as a control to show that the repulsion of active particles by the Lagrangian vortices is not an intrinsic feature of the experimental velocity field itself. Rather, it is the result of the interaction between Lagrangian vortices and elongated swimmers.

Figure 3. Spatial distributions of (a) passive particles, and (b) active particles, at time ![]() $N=150$. Particles are coloured by their normalized local number density,
$N=150$. Particles are coloured by their normalized local number density, ![]() $\rho _N/\rho _0$. Active particles are depleted from the vortex and accumulate outside the LVBs (green contours), while this depletion is not present for passive particles. (c) Radial distribution function
$\rho _N/\rho _0$. Active particles are depleted from the vortex and accumulate outside the LVBs (green contours), while this depletion is not present for passive particles. (c) Radial distribution function ![]() $g(r)$ calculated from the elliptic fixed points of the Lagrangian vortex with the label ‘4’; the dashed line is the nominal radius of the vortex. (d) Spatially averaged normalized number density within the LVBs,
$g(r)$ calculated from the elliptic fixed points of the Lagrangian vortex with the label ‘4’; the dashed line is the nominal radius of the vortex. (d) Spatially averaged normalized number density within the LVBs, ![]() $\langle \rho _N\rangle _S/\rho _0$, as a function of time
$\langle \rho _N\rangle _S/\rho _0$, as a function of time ![]() $N$ for the same vortex as in (c).
$N$ for the same vortex as in (c).
The repulsion of rod-shaped swimmers by the LVBs is quantified by the radial distribution function: ![]() $g(r)=\langle \rho _N (r)\rangle /\rho _0$, where the angle bracket denotes a radial average in all directions calculated from the elliptic fixed points. The function
$g(r)=\langle \rho _N (r)\rangle /\rho _0$, where the angle bracket denotes a radial average in all directions calculated from the elliptic fixed points. The function ![]() $g(r)$ represents the probability of finding a particle at a radial distance
$g(r)$ represents the probability of finding a particle at a radial distance ![]() $r$ from the elliptic fixed point of a Lagrangian vortex. Figure 3(c) shows
$r$ from the elliptic fixed point of a Lagrangian vortex. Figure 3(c) shows ![]() $g(r)$ for both passive and active particles in the Lagrangian vortex with the label ‘4’ in figure 2. The dashed line in figure 3(c) is a nominal radius of Lagrangian vortex, defined as
$g(r)$ for both passive and active particles in the Lagrangian vortex with the label ‘4’ in figure 2. The dashed line in figure 3(c) is a nominal radius of Lagrangian vortex, defined as ![]() $r_n=\sqrt {A_S/{\rm \pi} }$, where
$r_n=\sqrt {A_S/{\rm \pi} }$, where ![]() $A_S$ is the area enclosed by the LVBs. We find that the likelihood of finding an active particle within the nominal radius of a Lagrangian vortex is smaller than that of a passive particle and vice versa for outside the nominal radius. This result further corroborates the repulsion of elongated active particles by Lagrangian vortices.
$A_S$ is the area enclosed by the LVBs. We find that the likelihood of finding an active particle within the nominal radius of a Lagrangian vortex is smaller than that of a passive particle and vice versa for outside the nominal radius. This result further corroborates the repulsion of elongated active particles by Lagrangian vortices.
To quantify the time evolution of the repulsion of elongated swimmers, we calculate the average number density within the LVBs, ![]() $\langle \rho _N\rangle _S$, normalized by the initial number density
$\langle \rho _N\rangle _S$, normalized by the initial number density ![]() $\rho _0$. Figure 3(d) shows
$\rho _0$. Figure 3(d) shows ![]() $\langle \rho _N\rangle _S/\rho _0$ as a function of time
$\langle \rho _N\rangle _S/\rho _0$ as a function of time ![]() $N$. Results show that
$N$. Results show that ![]() $\langle \rho _N\rangle _S$ decreases non-monotonically with time for active particles, and drops to only 20 % of the initial number density
$\langle \rho _N\rangle _S$ decreases non-monotonically with time for active particles, and drops to only 20 % of the initial number density ![]() $\rho _0$ at
$\rho _0$ at ![]() $N=200$. This suggests that most active particles escape and accumulate outside the Lagrangian vortex as mixing progresses. In the control case,
$N=200$. This suggests that most active particles escape and accumulate outside the Lagrangian vortex as mixing progresses. In the control case, ![]() $\langle \rho _N\rangle _S$ for passive particles increases with time, which again suggests the repulsion of elongated particles by LVBs is not an intrinsic feature of the velocity field itself. Although symmetric and circular Eulerian vortices have been observed to repel elongated swimmers (Torney & Neufeld Reference Torney and Neufeld2007; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Qin & Arratia Reference Qin and Arratia2022), here we extend these results to a more general case of asymmetric and non-circular vortices from Lagrangian criteria.
$\langle \rho _N\rangle _S$ for passive particles increases with time, which again suggests the repulsion of elongated particles by LVBs is not an intrinsic feature of the velocity field itself. Although symmetric and circular Eulerian vortices have been observed to repel elongated swimmers (Torney & Neufeld Reference Torney and Neufeld2007; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Qin & Arratia Reference Qin and Arratia2022), here we extend these results to a more general case of asymmetric and non-circular vortices from Lagrangian criteria.
To gain further insights into how swimming particles are repelled by Lagrangian vortices, we plot the stroboscopic trajectories and orientations of passive and active particles as a function of time, as shown in figure 4(a). The Lagrangian vortices are illustrated by the TRA field (colour map); passive and active particles are shown as blue and red bars, respectively. The trajectories of the passive particles are blue, while the trajectories of the active particles are coloured by their normalized time or number of periods, ![]() $N/N_{tot}$, where
$N/N_{tot}$, where ![]() $N_{tot}$ is the total time duration of the trajectories. Despite sharing the same initial conditions for position and orientation, passive particles remain trapped in the Lagrangian vortices while active particles spiral outward with time and escape the vortices. We note that the swimming number of the active particles,
$N_{tot}$ is the total time duration of the trajectories. Despite sharing the same initial conditions for position and orientation, passive particles remain trapped in the Lagrangian vortices while active particles spiral outward with time and escape the vortices. We note that the swimming number of the active particles, ![]() $\varPhi =v_s/U$, is of the order of
$\varPhi =v_s/U$, is of the order of ![]() $10^{-2}$ in the simulations, suggesting that the swimming speed is fairly negligible compared with the flow speed. However, even such a (relatively) low swimming speed can drive active particles out of equilibrium and escape the Lagrangian vortices. That is, even small levels of swimming activity is enough to initiate the expulsion process. In addition, we find that the orientations of both passive and active particles tend to align with the level curves of the TRA field. Because the convex TRA contours locate the nested families of elliptic LCSs, this result indicates elongated particles – whether self-propelled or not – preferentially align with the members of elliptic LCSs. The difference is that the self-propulsion of active particles causes them to move outward and leave the vortices in a spiral manner.
$10^{-2}$ in the simulations, suggesting that the swimming speed is fairly negligible compared with the flow speed. However, even such a (relatively) low swimming speed can drive active particles out of equilibrium and escape the Lagrangian vortices. That is, even small levels of swimming activity is enough to initiate the expulsion process. In addition, we find that the orientations of both passive and active particles tend to align with the level curves of the TRA field. Because the convex TRA contours locate the nested families of elliptic LCSs, this result indicates elongated particles – whether self-propelled or not – preferentially align with the members of elliptic LCSs. The difference is that the self-propulsion of active particles causes them to move outward and leave the vortices in a spiral manner.

Figure 4. (a) Stroboscopic trajectories of passive (blue) and active (red) particles that are initially inside the Lagrangian vortices illustrated by the TRA field. While sharing the same initial condition, passive particles remain trapped in the vortices and active particles spiral outward and escape. The trajectories of active particles are coloured by their normalized time (or numbers of periods), ![]() $N/N_{{tot}}$, where
$N/N_{{tot}}$, where ![]() $N_{{tot}}$ is the total time duration of the trajectories. (b) The probability density functions (p.d.f.s) of the inner product of the particle orientation vector,
$N_{{tot}}$ is the total time duration of the trajectories. (b) The probability density functions (p.d.f.s) of the inner product of the particle orientation vector, ![]() $\boldsymbol {q}$, and the tangent vector of the elliptic LCSs in the direction of the vortex circulation,
$\boldsymbol {q}$, and the tangent vector of the elliptic LCSs in the direction of the vortex circulation, ![]() $\boldsymbol {t}$, as defined in the inset. The initial condition (
$\boldsymbol {t}$, as defined in the inset. The initial condition (![]() $N=0$) is approximately a uniform distribution for particles with random initial orientations. The p.d.f.s at a later time (
$N=0$) is approximately a uniform distribution for particles with random initial orientations. The p.d.f.s at a later time (![]() $N=50$) show that both passive and active particles preferentially align with members of elliptic LCSs at
$N=50$) show that both passive and active particles preferentially align with members of elliptic LCSs at ![]() $\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=\pm 1$. The p.d.f. of active particles is slightly biased towards the positive peak of
$\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=\pm 1$. The p.d.f. of active particles is slightly biased towards the positive peak of ![]() $\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=+1$. (c) Schematic of a ‘bacterial porous medium’ formed by cells aligning and accumulating outside a LVB. Dye transport is hindered as it diffuses through the porous media.
$\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=+1$. (c) Schematic of a ‘bacterial porous medium’ formed by cells aligning and accumulating outside a LVB. Dye transport is hindered as it diffuses through the porous media.
Next, we test the alignment of the elongated particles by calculating the inner product of the particle orientation vector, ![]() $\boldsymbol {q}$, and the tangent vector of the elliptic LCSs in the direction of vortex circulation,
$\boldsymbol {q}$, and the tangent vector of the elliptic LCSs in the direction of vortex circulation, ![]() $\boldsymbol {t}$. The inset of figure 4(b) shows a schematic of the two vectors. Since elliptic LCSs are nested families, we partition the elliptic LCSs into 10 members using the convex TRA contours. The inner product is calculated between the orientation vector of an elongated particle and the tangent of the nearest member of elliptic LCSs. Figure 4(b) shows p.d.f.s of
$\boldsymbol {t}$. The inset of figure 4(b) shows a schematic of the two vectors. Since elliptic LCSs are nested families, we partition the elliptic LCSs into 10 members using the convex TRA contours. The inner product is calculated between the orientation vector of an elongated particle and the tangent of the nearest member of elliptic LCSs. Figure 4(b) shows p.d.f.s of ![]() $\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}$ for both passive and active particles at two different times. At
$\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}$ for both passive and active particles at two different times. At ![]() $N=0$, the initial condition of the p.d.f.s shared by both passive and active particles is approximately a uniform distribution due to the random initial orientations. At a later time of
$N=0$, the initial condition of the p.d.f.s shared by both passive and active particles is approximately a uniform distribution due to the random initial orientations. At a later time of ![]() $N=50$, the p.d.f.s of both passive and active particles become bimodal at
$N=50$, the p.d.f.s of both passive and active particles become bimodal at ![]() $\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=\pm 1$, suggesting a parallel or antiparallel alignment between
$\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=\pm 1$, suggesting a parallel or antiparallel alignment between ![]() $\boldsymbol {q}$ and
$\boldsymbol {q}$ and ![]() $\boldsymbol {t}$. We find that the p.d.f. of active particles shows a slight bias towards the positive peak at
$\boldsymbol {t}$. We find that the p.d.f. of active particles shows a slight bias towards the positive peak at ![]() $\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=+1$, while the bias is not present for the p.d.f. of passive particles. This suggests that active particles prefer to swim parallel to the elliptic LCSs in the direction of vortex circulation rather than swimming against the circulation. The bias in parallel and antiparallel alignments is also found for active particles of different swimming speeds (see supplementary materials). The self-propulsion of active particles can cause them to travel towards the outer members of the elliptic LCSs in both parallel and antiparallel alignment configurations (see supplementary movie 4), resulting in the spiral escaping trajectories of the active particles shown in figure 4(a). Consequently, the interplay between self-propulsion and the alignment of elongated particles with elliptic LCSs leads to the depletion of active particles inside the elliptic LCSs, that is, the accumulation of active particles outside the LVBs. This accumulation of microswimmers outside the LVBs can further obstruct dye transport into the Lagrangian vortices, which is responsible for the observed transport barriers.
$\boldsymbol {q}\boldsymbol {\cdot }\boldsymbol {t}=+1$, while the bias is not present for the p.d.f. of passive particles. This suggests that active particles prefer to swim parallel to the elliptic LCSs in the direction of vortex circulation rather than swimming against the circulation. The bias in parallel and antiparallel alignments is also found for active particles of different swimming speeds (see supplementary materials). The self-propulsion of active particles can cause them to travel towards the outer members of the elliptic LCSs in both parallel and antiparallel alignment configurations (see supplementary movie 4), resulting in the spiral escaping trajectories of the active particles shown in figure 4(a). Consequently, the interplay between self-propulsion and the alignment of elongated particles with elliptic LCSs leads to the depletion of active particles inside the elliptic LCSs, that is, the accumulation of active particles outside the LVBs. This accumulation of microswimmers outside the LVBs can further obstruct dye transport into the Lagrangian vortices, which is responsible for the observed transport barriers.
3.3. Physical mechanism
We now propose a potential mechanism to explain the observed reduction in dye transport into Lagrangian vortices. We posit that the alignment and accumulation of bacteria outside the LVBs form an effective ‘bacterial porous medium’ that can impede the diffusion of dye molecules, as schematically shown in figure 4(c). In the absence of bacteria, dye should enter LVBs primarily by diffusion and marginally by inertial effect due to (low but) non-zero Reynolds number (![]() $Re\sim 10^1$). Here, we will focus on diffusive transport around the outside boundary of the LVBs where bacteria accumulate (figure 4c). The effective diffusivity of a molecular dye through a porous medium,
$Re\sim 10^1$). Here, we will focus on diffusive transport around the outside boundary of the LVBs where bacteria accumulate (figure 4c). The effective diffusivity of a molecular dye through a porous medium, ![]() $D_{{eff}}$, can be estimated as follows (Grathwohl Reference Grathwohl1998)
$D_{{eff}}$, can be estimated as follows (Grathwohl Reference Grathwohl1998)
where ![]() $D_0$ is the intrinsic diffusivity of the dye molecules,
$D_0$ is the intrinsic diffusivity of the dye molecules, ![]() $\epsilon$,
$\epsilon$, ![]() $\delta$ and
$\delta$ and ![]() $\tau$ are the porosity, constrictivity and tortuosity of the porous media, respectively. The porosity,
$\tau$ are the porosity, constrictivity and tortuosity of the porous media, respectively. The porosity, ![]() $\epsilon$, is the volume fraction of the void spaces (that is, pores) in the medium relative to its total volume;
$\epsilon$, is the volume fraction of the void spaces (that is, pores) in the medium relative to its total volume; ![]() $\epsilon$ ranges from 0 to 1. For our bacterial medium, the quantity
$\epsilon$ ranges from 0 to 1. For our bacterial medium, the quantity ![]() $\epsilon$ sums up to unity with the bacterial volume fraction
$\epsilon$ sums up to unity with the bacterial volume fraction ![]() $\phi _b$ such that
$\phi _b$ such that ![]() $\epsilon =1-\phi _b$. Bacterial accumulation around LVB leads to a local increase in
$\epsilon =1-\phi _b$. Bacterial accumulation around LVB leads to a local increase in ![]() $\phi _b$ of approximately tenfold (as shown by our simulations) such that
$\phi _b$ of approximately tenfold (as shown by our simulations) such that ![]() $\phi _{{LVB}}\approx 10\phi _b=0.05$. Thus, the porosity of the bacterial medium is
$\phi _{{LVB}}\approx 10\phi _b=0.05$. Thus, the porosity of the bacterial medium is ![]() $\epsilon = 1-\phi _{{LVB}}\approx 0.95$. This leads to only a 5 % decrease in
$\epsilon = 1-\phi _{{LVB}}\approx 0.95$. This leads to only a 5 % decrease in ![]() $D_{{eff}}$, which cannot account for the observed reduction in dye transport. Similarly, the constrictivity
$D_{{eff}}$, which cannot account for the observed reduction in dye transport. Similarly, the constrictivity ![]() $\delta$ is a dimensionless parameter ranging from 0 to 1, which captures the hindrance to which a diffusing substance is subjected to when travelling through narrow pores. It becomes important only if the size of the diffusing molecules is comparable to that of the pores (Stenzel et al. Reference Stenzel, Pecho, Holzer, Neumann and Schmidt2016; Bini et al. Reference Bini, Pica, Marinozzi and Marinozzi2019). Here, the pore size,
$\delta$ is a dimensionless parameter ranging from 0 to 1, which captures the hindrance to which a diffusing substance is subjected to when travelling through narrow pores. It becomes important only if the size of the diffusing molecules is comparable to that of the pores (Stenzel et al. Reference Stenzel, Pecho, Holzer, Neumann and Schmidt2016; Bini et al. Reference Bini, Pica, Marinozzi and Marinozzi2019). Here, the pore size, ![]() $O(1\ \mathrm {\mu }$m), is much greater than the molecular size,
$O(1\ \mathrm {\mu }$m), is much greater than the molecular size, ![]() $O$(1 nm), and therefore
$O$(1 nm), and therefore ![]() $\delta \approx 1$. Since the values of
$\delta \approx 1$. Since the values of ![]() $\delta$ and
$\delta$ and ![]() $\epsilon$ are close to unity, we do not expect them to play a significant role in the reduction of dye transport.
$\epsilon$ are close to unity, we do not expect them to play a significant role in the reduction of dye transport.
Next, we examine the role of tortuosity (![]() $\tau$), which compares the (tortuous) pathway of molecular diffusion in a porous medium with its pathway in an unrestricted medium (Bini et al. Reference Bini, Pica, Marinozzi and Marinozzi2019; da Silva et al. Reference da Silva, do Rocio Cardoso, Pabst Veronese and Mazer2022). The quantity
$\tau$), which compares the (tortuous) pathway of molecular diffusion in a porous medium with its pathway in an unrestricted medium (Bini et al. Reference Bini, Pica, Marinozzi and Marinozzi2019; da Silva et al. Reference da Silva, do Rocio Cardoso, Pabst Veronese and Mazer2022). The quantity ![]() $\tau$ can be defined as (Grathwohl Reference Grathwohl1998; Holzer et al. Reference Holzer, Wiedenmann, Münch, Keller, Prestat, Gasser, Robertson and Grobéty2013; da Silva et al. Reference da Silva, do Rocio Cardoso, Pabst Veronese and Mazer2022)
$\tau$ can be defined as (Grathwohl Reference Grathwohl1998; Holzer et al. Reference Holzer, Wiedenmann, Münch, Keller, Prestat, Gasser, Robertson and Grobéty2013; da Silva et al. Reference da Silva, do Rocio Cardoso, Pabst Veronese and Mazer2022)
where ![]() $L_0$ is the length of the straightest path and
$L_0$ is the length of the straightest path and ![]() $\langle L_s\rangle$ is the ensemble average of all possible tortuous path of diffusion. Note that
$\langle L_s\rangle$ is the ensemble average of all possible tortuous path of diffusion. Note that ![]() $\tau \ge 1$ since
$\tau \ge 1$ since ![]() $\langle L_s\rangle \ge L_0$. We consider the transverse diffusion of dye molecules across a bacterial porous medium, as sketched in figure 4(c), where
$\langle L_s\rangle \ge L_0$. We consider the transverse diffusion of dye molecules across a bacterial porous medium, as sketched in figure 4(c), where ![]() $x_1$ denotes the direction of the transverse diffusion and
$x_1$ denotes the direction of the transverse diffusion and ![]() $x_2$ denotes the direction of cell body alignment with the tangent of the elliptic LCSs. During the diffusion process, each time the (dye) molecule encounters an obstacle (i.e. a bacterium), its path will be deflected by on average half the body length of a bacterium,
$x_2$ denotes the direction of cell body alignment with the tangent of the elliptic LCSs. During the diffusion process, each time the (dye) molecule encounters an obstacle (i.e. a bacterium), its path will be deflected by on average half the body length of a bacterium, ![]() $l_E/2$. Also, dye diffusing a distance
$l_E/2$. Also, dye diffusing a distance ![]() $L_0$ (in the bacterial porous medium) will encounter bacterial cells on average
$L_0$ (in the bacterial porous medium) will encounter bacterial cells on average ![]() $L_0\sigma _N$ times, where
$L_0\sigma _N$ times, where ![]() $\sigma _N$ is the cell number density. We can then estimate the average transverse and longitudinal path lengths,
$\sigma _N$ is the cell number density. We can then estimate the average transverse and longitudinal path lengths, ![]() $\langle L_s\rangle _{11}$ and
$\langle L_s\rangle _{11}$ and ![]() $\langle L_s\rangle _{22}$, for the dye to diffuse across a distance
$\langle L_s\rangle _{22}$, for the dye to diffuse across a distance ![]() $L_0$ in the
$L_0$ in the ![]() $x_1$ and
$x_1$ and ![]() $x_2$ directions as
$x_2$ directions as
where ![]() $\alpha = d_E/l_E$ is the aspect ratio between the average cell diameter
$\alpha = d_E/l_E$ is the aspect ratio between the average cell diameter ![]() $d_E$ and cell length
$d_E$ and cell length ![]() $l_E$. For rod-shaped bacteria such as E. coli, we notice that
$l_E$. For rod-shaped bacteria such as E. coli, we notice that ![]() $\alpha <1$ and thus
$\alpha <1$ and thus ![]() $\langle L_s\rangle _{22}<\langle L_s\rangle _{11}$. This suggests that diffusion is anisotropic in the bacterial porous medium. We can now express the tortuosity for the transverse and longitudinal diffusion as
$\langle L_s\rangle _{22}<\langle L_s\rangle _{11}$. This suggests that diffusion is anisotropic in the bacterial porous medium. We can now express the tortuosity for the transverse and longitudinal diffusion as
In our experiments, the local bacterial volume fraction (around LVBs) is ![]() $\phi _{{LVB}}\approx 0.05$, which corresponds to a local cell number density of
$\phi _{{LVB}}\approx 0.05$, which corresponds to a local cell number density of ![]() $\rho _N \approx 1.25\times 10^{11}$ cells ml
$\rho _N \approx 1.25\times 10^{11}$ cells ml![]() $^{-1}$, and a local cell number density of
$^{-1}$, and a local cell number density of ![]() $\sigma _N \approx 5000$ cells cm
$\sigma _N \approx 5000$ cells cm![]() $^{-1}$. If we consider
$^{-1}$. If we consider ![]() $l_E$ to be the bacterium body length (
$l_E$ to be the bacterium body length (![]() ${\approx }2\ \mathrm {\mu }$m), then
${\approx }2\ \mathrm {\mu }$m), then ![]() $\tau _{11} = 1+\sigma _N l_E/2=1.5$. If instead we consider the ‘total’ bacterium length (cell body plus flagella),
$\tau _{11} = 1+\sigma _N l_E/2=1.5$. If instead we consider the ‘total’ bacterium length (cell body plus flagella), ![]() $L_{{total}}\approx 7\ \mathrm {\mu }$m (Patteson et al. Reference Patteson, Gopinath, Goulian and Arratia2015), then
$L_{{total}}\approx 7\ \mathrm {\mu }$m (Patteson et al. Reference Patteson, Gopinath, Goulian and Arratia2015), then ![]() $\tau _{11} = 1+\sigma _N L_{{total}}/2=2.75$. Using the above estimates, we expect
$\tau _{11} = 1+\sigma _N L_{{total}}/2=2.75$. Using the above estimates, we expect ![]() $1.5\le \tau _{11}\le 2.75$. The transverse effective diffusivity can be estimated using (3.6), and this yields
$1.5\le \tau _{11}\le 2.75$. The transverse effective diffusivity can be estimated using (3.6), and this yields ![]() $0.346\le D_{11}/D_0\le 0.633$. Therefore, a dye diffusing through this bacterial porous media would experience a 33 %–66 % decrease in the transverse effective diffusivity, which qualitatively corresponds to the decrease in dye transport into the LVBs. Note that (3.9a,b) estimates an anisotropic diffusivity,
$0.346\le D_{11}/D_0\le 0.633$. Therefore, a dye diffusing through this bacterial porous media would experience a 33 %–66 % decrease in the transverse effective diffusivity, which qualitatively corresponds to the decrease in dye transport into the LVBs. Note that (3.9a,b) estimates an anisotropic diffusivity, ![]() $D_{11}< D_{22}$, for rod-shaped bacteria (
$D_{11}< D_{22}$, for rod-shaped bacteria (![]() $\alpha <1$). Bacterial flagellar motion, in addition, can displace dye molecules farther in the
$\alpha <1$). Bacterial flagellar motion, in addition, can displace dye molecules farther in the ![]() $x_2$ direction, which would lead to an increase in
$x_2$ direction, which would lead to an increase in ![]() $D_{22}$. This would lead to a more complex behaviour than the one described here. Nevertheless, the concept of anisotropic diffusion in a bacterial porous media seems to capture, at least qualitatively, the observed decrease in scalar transport into the Lagrangian vortices.
$D_{22}$. This would lead to a more complex behaviour than the one described here. Nevertheless, the concept of anisotropic diffusion in a bacterial porous media seems to capture, at least qualitatively, the observed decrease in scalar transport into the Lagrangian vortices.
4. Conclusion
In this manuscript, we investigate the interaction between swimming micro-organisms and Lagrangian coherent vortices known as the elliptic LCSs in time-periodic flows in experiments and in simulations. Our results show that even small amounts of swimming activity can affect (i) the dynamics of active particles in the flow (figure 4) and consequently (ii) the mixing and transport of passive scalars (figure 1) in chaotic flows. Experiments show that the interaction between organisms and elliptic LCSs leads to transport barriers through which the tracer flux is significantly reduced. Using the Poincaré map and the TRA field, we show that these transport barriers coincide with outermost member of elliptic LCSs, or LVBs. To further understand the formation of the transport barriers, we perform numerical simulations of elongated microswimmers in experimentally measured velocity fields. Results show that elliptic LCSs can repel elongated swimmers and lead to swimmer accumulation outside LVBs. This accumulation of microswimmers effectively reduces the transport into elliptic LCSs. We further show that the interplay between self-propulsion and the preferential alignment of elongated particles with the tangents of elliptic LCSs leads swimmers to escape the Lagrangian vortices. Overall, our results allow quantitative prediction of the Lagrangian transport of micro-organisms and passive tracer quantities (e.g. temperature, oxygen and nutrients) in chaotic flows with non-trivial vortex structures. Although there have been previous studies on the interaction between micro-organisms and LCSs (Khurana & Ouellette Reference Khurana and Ouellette2012; Dehkharghani et al. Reference Dehkharghani, Waisbord, Dunkel and Guasto2019; Ran et al. Reference Ran, Brosseau, Blackwell, Qin, Winter and Arratia2021; Si & Fang Reference Si and Fang2021, Reference Si and Fang2022; Qin & Arratia Reference Qin and Arratia2022; Yoest et al. Reference Yoest, Buggeln, Doan, Johnson, Berman, Mitchell and Solomon2022), our work extends the study of micro-organism LCSs interaction to elliptic LCSs (i.e. vortex-like dynamical structures). From a practical perspective, our results may be useful in understanding the organic matter flux in the oceans, algal blooms in lakes and harmful bacterial infections.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.452.
Acknowledgements
We thank J.C. Burton, T. Solomon, K. Mitchell, S. Berman, D. Jerolmack, G.I. Park, A. Mathijssen, B.T. Maldonado and A. Théry for insightful discussions, and B. Blackwell for help with early work.
Funding
This work was supported by the National Science Foundation (NSF) grant number DMR-1709763.
Declaration of interests
The authors report no conflict of interest.