1. Introduction
In literature, various studies have been presented on high utility itemset mining (HUIM) (Liu et al., Reference Liu and Liao2005; Yao & Hamilton, Reference Yao and Hamilton2006) that considered the importance of the items, such as the unit profit of itemsets. Traditional HUIM approaches are designed for static quantitative datasets. In real-world situations, datasets are frequently updated dynamically, For instance, in tasks like market basket analysis and business decision-making, the datasets are modified incrementally by appending additional data dynamically. Extensive research has been conducted to develop efficient algorithms for discovering high utility itemsets (HUIs) from dynamically updated datasets. Traditional HUIM algorithms required processing datasets from scratch each time a new record was added. In contrast, incremental HUIM (iHUIM) updates and incrementally identifies HUIs without scanning the whole dataset, effectively reduce the cost associated with discovery of HUIs when new records are added. Over the past decade, various iHUIM algorithms have been introduced, primarily grouped into tree-based, pattern-growth-based, utility-list-based, projection-based, and pre-large-based approaches. However, there are still ample opportunities for designing efficient novel iHUIM algorithms, incorporating effective pruning strategies, data structures, and more.
An incremental mining approach for record insertions, named FUP-HU (Lin et al., Reference Lin, Lan and Hong2012) is designed for maintaining and updating the already obtained HUIs by FUP notion (Cheung et al. Reference Cheung, Han, Ng and Wong1996) and Two-phase algorithm (Liu et al., Reference Liu and Liao2005). However, it generates a substantial number of candidates and scans the dataset multiple times. Incremental and interactive utility tree (IIUT) (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009b) employs the pattern-growth method to resolve the issue of costly candidate generation in a level-wise manner. Nonetheless, the run-time of the IIUT algorithm also gets larger as the size of the dataset expands. Ahmed et al. (Reference Ahmed, Tanbeer, Jeong and Lee2009a) proposed an approach that presented three novel tree structures, namely Incremental high utility pattern lexicographic tree (IHUP
![]() $_L$
-Tree), IHUP transaction frequency tree (IHUP
$_L$
-Tree), IHUP transaction frequency tree (IHUP
![]() $_{TF}$
-Tree), and IHUP transaction-weighted utilization tree (IHUP
$_{TF}$
-Tree), and IHUP transaction-weighted utilization tree (IHUP
![]() $_{TWU}$
-Tree). These structures perform incremental and interactive HUPM and adhere to the ‘
$_{TWU}$
-Tree). These structures perform incremental and interactive HUPM and adhere to the ‘
![]() $ build \ once, \ mine \ many \ $
’ principle, enabling efficient mining of HUIs from incremental transaction datasets. However, the suggested method produces an excessive number of candidates when the dataset consists of lengthy transactions or when the minimum utility threshold is set exceedingly low. Moreover, IHUP-Tree proves to be a relatively efficient approach. This process requires the unnecessary generation of low-utility itemsets, which then require significant time for pruning. On the other hand, high utility patterns in incremental datasets (HUPID) growth (Yun & Ryang, Reference Yun and Ryang2014) efficiently mines patterns with reduced overestimated utility from incremental datasets using just a single dataset scan. Nonetheless, it requires an additional phase to find the actual HUIs from the candidate sets. In contrast, an incremental and interactive HUIM algorithm, namely incremental high utility itemset miner (IHUI-Miner) (Guo & Gao, Reference Guo and Gao2017), is designed to extract HUIs without the need of candidate generation. A new tree structure, called incremental high utility itemset tree (IHUI-Tree), has been introduced that tree organizes items in lexicographic order using the pattern-growth method and follows a bottom-up traversal approach.
$ build \ once, \ mine \ many \ $
’ principle, enabling efficient mining of HUIs from incremental transaction datasets. However, the suggested method produces an excessive number of candidates when the dataset consists of lengthy transactions or when the minimum utility threshold is set exceedingly low. Moreover, IHUP-Tree proves to be a relatively efficient approach. This process requires the unnecessary generation of low-utility itemsets, which then require significant time for pruning. On the other hand, high utility patterns in incremental datasets (HUPID) growth (Yun & Ryang, Reference Yun and Ryang2014) efficiently mines patterns with reduced overestimated utility from incremental datasets using just a single dataset scan. Nonetheless, it requires an additional phase to find the actual HUIs from the candidate sets. In contrast, an incremental and interactive HUIM algorithm, namely incremental high utility itemset miner (IHUI-Miner) (Guo & Gao, Reference Guo and Gao2017), is designed to extract HUIs without the need of candidate generation. A new tree structure, called incremental high utility itemset tree (IHUI-Tree), has been introduced that tree organizes items in lexicographic order using the pattern-growth method and follows a bottom-up traversal approach.
The efficient incremental high utility itemset (EIHI) miner (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) algorithm is designed to maintain HUIs within incremental datasets. However, it performs extra operations to construct new utility-lists for newly added data and merge them with the existing datasets. LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017) builds a global list-based structure with just one pass through the original dataset and then reorganizes this data structure by sorting the lists according to the ascending order of transaction-weighted utilization (TWU) values. But, the execution time and memory usage of this approach expand as the dataset size grows. In contrast, an efficient incremental HUIM algorithm named IIHUM (Indexed-list-based Incremental High utility pattern Mining) (Yun et al., Reference Yun, Nam, Lee and Yoon2019) adopts a novel indexed-list-based structure to incrementally mine HUIs without the need of candidate generation. The Id2HUP+ (Incremental direct discovery of high utility patterns) approach (Liu et al., Reference Liu, Ju, Zhang, Fung, Yang and Yu2019) employs a single-phase approach for incremental mining of HUIs from incremental datasets. A novel data structure named niCAUL (Newly Improved Chain of Accurate utility-lists) is designed to quickly update the dynamic datasets. IncCHUI (Incremental Closed high utility Itemset miner) (Dam et al. Reference Dam, Ramampiaro, Nørvåg and Duong2019) uses a novel incremental utility-list structure that is constructed and rearranged through a single pass of the dataset scan. However, it incurs memory overhead on some benchmark datasets, leading to higher memory consumption compared to benchmark algorithms, such as CHUI-Miner (Wu et al. Reference Wu, Fournier-Viger, Gu and Tseng2015), CLS-Miner (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2018), and EFIM-Closed (Fournier-Viger et al., Reference Fournier-Viger, Zida, Lin, Wu and Tseng2016). Extended HUI-miner (E-HUIM) (Pushp & Chand 2021) is proposed to generate and maintain the HUIs from the incremental datasets. Nevertheless, there is room for the development of more efficient data structures to enhance the mining process. The pre-large incremental high utility itemset (PRE-HUI) algorithm (Lin et al., Reference Lin, Gan, Hong and Pan2014), effectively preserves and modifies the obtained HUIs by integrating and updating the two-phase (Liu et al. Reference Liu and Liao2005) and pre-large concepts (Hong et al., Reference Hong, Wang and Tao2001). An efficient tree-based algorithm named PIHUP-MOD (Pre-large-based Incremental High Utility Pattern mining for transaction MODification) (Yun et al., Reference Yun, Kim, Ryu, Baek, Nam, Lee, Vo and Pedrycz2021) is proposed to mine HUIs from the modified datasets. This is achieved through the utilization of the pre-large concept. The PIHUP-MOD
![]() $_L$
-tree data structure (where L stands for lexicographic order) is designed for the extraction of pre-large and large patterns during the mining process. However, it proves to be a challenging task for users to define and set two thresholds. While numerous iHUIM algorithms have been introduced in the past, there exists a scarcity of documented surveys that offer a comprehensive overview and comparative assessment of their performance. The main purpose of this survey is to provide in-depth knowledge concerning the iHUIM algorithms.
$_L$
-tree data structure (where L stands for lexicographic order) is designed for the extraction of pre-large and large patterns during the mining process. However, it proves to be a challenging task for users to define and set two thresholds. While numerous iHUIM algorithms have been introduced in the past, there exists a scarcity of documented surveys that offer a comprehensive overview and comparative assessment of their performance. The main purpose of this survey is to provide in-depth knowledge concerning the iHUIM algorithms.
Differences from the existing survey
Within the existing literature, only two surveys (Gan et al., Reference Gan, Chun-Wei, Chao, Wang and Yu2018; Cheng et al., Reference Cheng, Han, Zhang, Li and Wang2021) concerning iHUIM have been identified. In 2017, Gan et al. (Reference Gan, Chun-Wei, Chao, Wang and Yu2018) presented a survey that organized iHUIM approaches into three primary classifications: Apriori-based, tree-based, and utility-list-based techniques. It provided an extensive overview of the latest state-of-the-art methods within the iHUIM domain. Additionally, the survey included a summary table, showing the characteristics of these state-of-the-art approaches. In 2021, Cheng et al. (Reference Cheng, Han, Zhang, Li and Wang2021) presented a survey of iHUIM approaches categorized by their storage structure. This survey categorized the available iHUIM approaches based on the manner in which they store data associated with itemsets and their utility values. The survey classifies the state-of-the-art methods into various groups, including tree-based, list-based, array-based, and alternative methods (e.g., hash-set-based approaches), based on the approach used to store information about items. This paper included a total of 19 papers across all categories. Additionally, it provided a comprehensive discussion of the characteristics, strengths, and weaknesses of the existing state-of-the-art methods. The survey outlined various potential future research directions in the field.
Our work discussed and analyzed several novel categories and features of the current state-of-the-art methods. The key contributions of this survey can be outlined as follows:
-
• The survey presents a novel taxonomy and categorized the existing approaches into various groups, including two-phase-based, pattern-growth-based, projection-based, utility-list-based, and pre-large-based methods.
-
• The paper provides a comprehensive overview that includes almost all features and characteristics of the current state-of-the-art methods.
-
• The survey also showcases a thorough summary table that includes outcomes, advantages, disadvantages, and future research directions for the latest state-of-the-art methods.
-
• Our work includes 27 state-of-the-art iHUIM approaches. This comparative analysis provides a more extensive and in-depth comparison compared to the other two existing surveys.
-
• The survey provides both a category-wise summary and a comprehensive consolidated overview of all the currently available state-of-the-art iHUIM methods.
-
• It also included a brief discussion on research possibilities and prospective directions.
The remainder of this study is structured in the following manner: Section 2 provides preliminaries and definitions that are essential for understanding the concept of iHUIM. Section 3 presents an in-depth analysis and summary of various iHUIM approaches. Section 4 discusses the comprehensive summary and analysis of all the current state-of-the-art methods. Section 5 presents several potential research opportunities and future directions. Lastly, Section 6 provides the conclusion of the study.
2. Preliminaries and definitions
Let
![]() $I=\{i_1,i_2,\ldots,i_n\}$
be a finite set of n items. Let the transactions
$I=\{i_1,i_2,\ldots,i_n\}$
be a finite set of n items. Let the transactions
![]() $T_1,T_2,\ldots,T_m$
take place in the dataset D with each transaction
$T_1,T_2,\ldots,T_m$
take place in the dataset D with each transaction
![]() $T_q \subseteq I$
. An itemset X is defined as a collection of k items
$T_q \subseteq I$
. An itemset X is defined as a collection of k items
![]() $\{i_1,i_2,\ldots,i_k\}$
, where k denotes the length of the itemset. An itemset X is considered to be included in a transaction
$\{i_1,i_2,\ldots,i_k\}$
, where k denotes the length of the itemset. An itemset X is considered to be included in a transaction
![]() $T_q$
if
$T_q$
if
![]() $X \subseteq T_q$
. Each item
$X \subseteq T_q$
. Each item
![]() $i_j$
within the transaction
$i_j$
within the transaction
![]() $T_q$
is linked to a purchase quantity, also called internal utility (presented by the numbers in brackets), represented as
$T_q$
is linked to a purchase quantity, also called internal utility (presented by the numbers in brackets), represented as
![]() $q(i_j,T_q)$
. Each item
$q(i_j,T_q)$
. Each item
![]() $i_j$
has relative importance and is also called an external utility (or unit profit) represented as
$i_j$
has relative importance and is also called an external utility (or unit profit) represented as
![]() $EU(i_j)$
. A user-defined minimum utility threshold is established and denoted as
$EU(i_j)$
. A user-defined minimum utility threshold is established and denoted as
![]() $\delta$
.
$\delta$
.
For instance, the transactional dataset includes six transactions
![]() $T_1,T_2,\ldots,T_6$
as illustrated in Table 1. Each transaction is associated with a set of items. The dataset consists of six items: A, B, C, D, E, and F. For instance, transaction
$T_1,T_2,\ldots,T_6$
as illustrated in Table 1. Each transaction is associated with a set of items. The dataset consists of six items: A, B, C, D, E, and F. For instance, transaction
![]() $T_1$
consists of four items A, C, D and F, each with internal utility of 2,3,5 and 1, respectively. Table 2 displays the external utility of each item. The items A, B, C, D, E, and F have external utility of 3, 7, 4, 3, 2, and 5, respectively.
$T_1$
consists of four items A, C, D and F, each with internal utility of 2,3,5 and 1, respectively. Table 2 displays the external utility of each item. The items A, B, C, D, E, and F have external utility of 3, 7, 4, 3, 2, and 5, respectively.
Table 1. A transactional dataset

Table 2. External utility value

Definition 2.1.
The utility of an item
![]() $i_j$
in a transaction
$i_j$
in a transaction
![]() $T_q$
is labelled as
$T_q$
is labelled as
![]() $U(i_j,T_q)$
and is defined as:
$U(i_j,T_q)$
and is defined as:
![]() $U(i_j,T_q)=$
$U(i_j,T_q)=$
![]() $q(i_j,T_q)$
$q(i_j,T_q)$
![]() $ \times EU(i_j) $
$ \times EU(i_j) $
For instance, the utility of an item A in a transaction
![]() $T_1$
is
$T_1$
is
![]() $U(A,T_1)=$
$U(A,T_1)=$
![]() $q(A,T_1)$
$q(A,T_1)$
![]() $ \times EU(A) $
$ \times EU(A) $
![]() $=2 \times 3=6$
. The utility of all items are displayed in the
$=2 \times 3=6$
. The utility of all items are displayed in the
![]() $4^{th}$
column of Table 3.
$4^{th}$
column of Table 3.
Table 3. Transaction utility in the original dataset
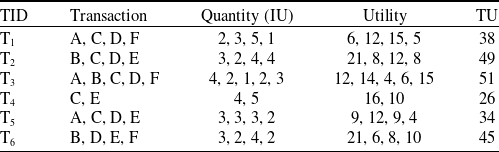
Definition 2.2
The utility of an itemset X in a transaction
![]() $T_q$
is denoted as
$T_q$
is denoted as
![]() $U(X,T_q)$
and is defined as:
$U(X,T_q)$
and is defined as:
![]() $U(X, T_q) = \sum_{i_j \in X \wedge X \subseteq T_q } U(i_j,T_q)$
$U(X, T_q) = \sum_{i_j \in X \wedge X \subseteq T_q } U(i_j,T_q)$
For instance, the utility of an itemset
![]() $\{A, C\}$
in a transaction
$\{A, C\}$
in a transaction
![]() $T_1$
is
$T_1$
is
![]() $U(\{A,C\},T_1)=$
$U(\{A,C\},T_1)=$
![]() $U(A,T_1)$
$U(A,T_1)$
![]() $+ U(C,T_1)$
$+ U(C,T_1)$
![]() $=6+12=18$
.
$=6+12=18$
.
Definition 2.3 The utility of an itemset X in a dataset D is indicated as U(X) and is defined as:
![]() $U(X) = \sum_{X \subseteq T_q \wedge T_q \in D } U(X,T_q)$
$U(X) = \sum_{X \subseteq T_q \wedge T_q \in D } U(X,T_q)$
For instance, the utility of an itemset
![]() $\{A, C\}$
in a dataset D is
$\{A, C\}$
in a dataset D is
![]() $U(\{A,C\}) =$
$U(\{A,C\}) =$
![]() $ U(\{A,C\},T_1) $
$ U(\{A,C\},T_1) $
![]() $ + U(\{A,C\},T_5)$
$ + U(\{A,C\},T_5)$
![]() $=18+21=39$
.
$=18+21=39$
.
Definition 2.4
The transaction utility of a transaction
![]() $T_q$
is represented as
$T_q$
is represented as
![]() $TU(T_q)$
and is defined as:
$TU(T_q)$
and is defined as:
![]() $TU(T_q) = \sum U(i_j,T_q)$
$TU(T_q) = \sum U(i_j,T_q)$
For instance, transaction utility of a transaction
![]() $T_1$
is
$T_1$
is
![]() $TU(T_1) =$
$TU(T_1) =$
![]() $ U(A,T_1) + $
$ U(A,T_1) + $
![]() $ U(C,T_1) +$
$ U(C,T_1) +$
![]() $ U(D,T_1) +$
$ U(D,T_1) +$
![]() $ U(F,T_1) $
$ U(F,T_1) $
![]() $ =6+12+15+5=38$
. The TU of all transactions are depicted in the
$ =6+12+15+5=38$
. The TU of all transactions are depicted in the
![]() $5\mathrm{th}$
column of Table 3.
$5\mathrm{th}$
column of Table 3.
Definition 2.5
The total utility of a dataset D is represented as
![]() $TU^{D}$
and is defined as:
$TU^{D}$
and is defined as:
![]() $TU^{D} = \sum_{T_q \in D} TU(T_q)$
$TU^{D} = \sum_{T_q \in D} TU(T_q)$
For instance, total utility of the original dataset D is
![]() $TU^{D} =$
$TU^{D} =$
![]() $ TU(T_1) + $
$ TU(T_1) + $
![]() $ TU(T_2) +$
$ TU(T_2) +$
![]() $ TU(T_3) +$
$ TU(T_3) +$
![]() $ TU(T_4) +$
$ TU(T_4) +$
![]() $ TU(T_5) +$
$ TU(T_5) +$
![]() $ TU(T_6) $
=
$ TU(T_6) $
=
![]() $38+49+51+26+34+45=243$
.
$38+49+51+26+34+45=243$
.
Definition 2.6
A minimum utility threshold
![]() $ \delta $
is determined by the percentage of the total utility of a dataset. The minimum utility value (
$ \delta $
is determined by the percentage of the total utility of a dataset. The minimum utility value (
![]() $min\_util$
) can be defined as:
$min\_util$
) can be defined as:
![]() $min\_util =$
$min\_util =$
![]() $ TU^{D} \times \delta$
$ TU^{D} \times \delta$
For instance,
![]() $\delta$
is 20%, then
$\delta$
is 20%, then
![]() $min\_util=$
$min\_util=$
![]() $ TU^{D} \times 0.2$
=
$ TU^{D} \times 0.2$
=
![]() $243 \times 0.2 $
$243 \times 0.2 $
![]() $=49$
.
$=49$
.
Definition 2.7
An itemset X, is designated as a high utility itemset in a dataset D if
![]() $U(X) \ge min\_util$
, otherwise itemset X is considered as a low utility itemset.
$U(X) \ge min\_util$
, otherwise itemset X is considered as a low utility itemset.
For instance,
![]() $\delta$
is 20% for the running example. The comprehensive list of high utility itemsets is displayed in Table 4.
$\delta$
is 20% for the running example. The comprehensive list of high utility itemsets is displayed in Table 4.
Table 4. High utility itemsets in original dataset for
![]() $ \delta $
= 20%
$ \delta $
= 20%
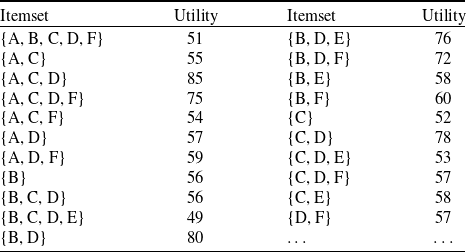
In high utility itemset mining, the utility value of an itemset does not follow the downward closure property (DCP). For instance, suppose
![]() $\delta$
is set at 20% that is 49, then itemset
$\delta$
is set at 20% that is 49, then itemset
![]() $\{A\}$
is a low utility itemset because
$\{A\}$
is a low utility itemset because
![]() $U(A)=27$
which is less than
$U(A)=27$
which is less than
![]() $min\_util$
. However, the superset of A, that is
$min\_util$
. However, the superset of A, that is
![]() $\{A, C\}$
is a high utility itemset because
$\{A, C\}$
is a high utility itemset because
![]() $U(\{A,C\})=55$
. In 2005, Liu et al. (Reference Liu and Liao2005) proposed transaction-weighted utilization (TWU) which can maintain DCP property.
$U(\{A,C\})=55$
. In 2005, Liu et al. (Reference Liu and Liao2005) proposed transaction-weighted utilization (TWU) which can maintain DCP property.
Definition 2.8 The TWU of an itemset X is represented as TWU(X) and is defined as:
![]() $TWU(X) = \sum_{X \subseteq T_q \wedge T_q \in D} TU(T_q)$
$TWU(X) = \sum_{X \subseteq T_q \wedge T_q \in D} TU(T_q)$
For instance, TWU of an itemset
![]() $\{A\}$
is
$\{A\}$
is
![]() $TWU(A)=$
$TWU(A)=$
![]() $ TU(T_1) + $
$ TU(T_1) + $
![]() $ TU(T_3) +$
$ TU(T_3) +$
![]() $ TU(T_5) $
$ TU(T_5) $
![]() $=38+51+34=123$
. Similarity, TWU of an itemset
$=38+51+34=123$
. Similarity, TWU of an itemset
![]() $\{A,C\}$
is
$\{A,C\}$
is
![]() $TWU(\{A,C\})=$
$TWU(\{A,C\})=$
![]() $TU(T_1)+$
$TU(T_1)+$
![]() $TU(T_5)=$
$TU(T_5)=$
![]() $38+34=72$
. TWU of all 1-itemsets are shown in
$38+34=72$
. TWU of all 1-itemsets are shown in
![]() $2\mathrm{nd}$
column of Table 5. Hence, in this example, TWU follows the DCP property.
$2\mathrm{nd}$
column of Table 5. Hence, in this example, TWU follows the DCP property.
Table 5. Transaction-weighted utilization and utility values of 1-itemsets in the original dataset
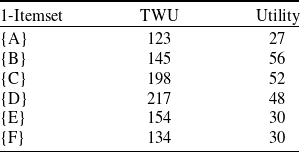
Property 1
(Transaction-weighted utilization based pruning) Let an itemset X, if TWU(X) is less than
![]() $min\_util$
, then the itemset X and all of its supersets are also low utility itemsets.
$min\_util$
, then the itemset X and all of its supersets are also low utility itemsets.
In accordance with the TWU based pruning, itemsets with a TWU value lower than the
![]() $min\_util$
, are removed from the search space and cannot be utilized to generate candidates. Later, utility-list based algorithms are presented (Liu & Qu, Reference Liu and Qu2012; Krishnamoorthy, Reference Krishnamoorthy2015). These algorithm introduced tighter pruning strategy than TWU-based strategy.
$min\_util$
, are removed from the search space and cannot be utilized to generate candidates. Later, utility-list based algorithms are presented (Liu & Qu, Reference Liu and Qu2012; Krishnamoorthy, Reference Krishnamoorthy2015). These algorithm introduced tighter pruning strategy than TWU-based strategy.
Definition 2.9
(Remaining utility of an itemset in a transaction). The remaining utility of itemset X in transaction
![]() $ T_q $
denoted by
$ T_q $
denoted by
![]() $ RU(X, T_q) $
is the sum of the utilities of all the items in
$ RU(X, T_q) $
is the sum of the utilities of all the items in
![]() $ T_q/X $
in
$ T_q/X $
in
![]() $ T_q $
where
$ T_q $
where
![]() $ RU(X, T_q) $
=
$ RU(X, T_q) $
=
![]() $ \sum_{i \in (T_q /X)} $
$ \sum_{i \in (T_q /X)} $
![]() $ U(i, T_q) $
(
Liu & Qu, Reference Liu and Qu2012
).
$ U(i, T_q) $
(
Liu & Qu, Reference Liu and Qu2012
).
Definition 2.10
(Utility-list structure). The utility-list structure contains three fields,
![]() $ T_{id}, iutil,$
and rutil. The
$ T_{id}, iutil,$
and rutil. The
![]() $ T_{id} $
indicates the transactions containing itemset X, iutil indicates the U(X), and the rutil indicates the remaining utility of itemset X is
$ T_{id} $
indicates the transactions containing itemset X, iutil indicates the U(X), and the rutil indicates the remaining utility of itemset X is
![]() $RU(X,T_q)$
(
Liu & Qu Reference Liu and Qu2012
).
$RU(X,T_q)$
(
Liu & Qu Reference Liu and Qu2012
).
Property 2
(Pruning search-space using remaining utility). For an itemset X, if the sum of
![]() $ U(X)+RU(X) $
is less than
$ U(X)+RU(X) $
is less than
![]() $min\_util $
, then itemset X and all its supersets are low utility itemsets. Otherwise, the itemset is eligible for HUIs. The details and proof of the remaining utility upper-bound (REU)-based upper-bound are given in Liu & Qu (Reference Liu and Qu2012).
$min\_util $
, then itemset X and all its supersets are low utility itemsets. Otherwise, the itemset is eligible for HUIs. The details and proof of the remaining utility upper-bound (REU)-based upper-bound are given in Liu & Qu (Reference Liu and Qu2012).
In the real-world, the transactional datasets are updated frequently and new transactions are added from time to time. Incremental datasets involve the integration of new transactions into the original dataset, resulting in more valuable real-world applications compared to conventional transactional datasets. Traditional algorithms require a substantial amount of time to find HUIs from incremental datasets, primarily due to the need to re-scan the whole updated dataset. To address this challenge, Yeh et al. (Reference Yeh, Chang and Wang2008) designed incremental dataset-based algorithms that eliminate the need for re-scanning the whole updated dataset.
The newly added transactions are displayed in Table 6. It comprises three transactions and includes six items from A to F. The utility values and transaction utility values in the updated dataset are displayed in Table 7. TWU and utility values of 1-itemsets of the whole dataset including newly added transactions, are displayed in Table 8. The final HUIs for the whole dataset are shown in Table 9. The minimum utility threshold
![]() $\delta$
is set to be 20% and the recalculated
$\delta$
is set to be 20% and the recalculated
![]() $min\_util$
is 70.
$min\_util$
is 70.
Table 6. New transactions

Table 7. Transaction utility of the newly added transactions
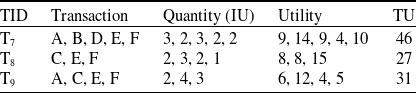
Table 8. TWU and utility values of 1-itemsets in whole dataset
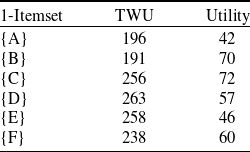
Table 9. HUIs of the whole dataset for
![]() $\delta $
= 20%
$\delta $
= 20%

3. Incremental high utility itemsets mining approaches
In literature, numerous iHUIM approaches are proposed to address the challenges posed by dynamic datasets, particularly when new transactions are added to the original dataset. This paper focuses on discussing the iHUIM algorithms highlighted within the taxonomy. The iHUIM algorithms are systematically classified into two-phase-based, pattern-growth-based, projection-based, utility-list-based, and pre-large-based categories. This comprehensive categorization is depicted in Figure 1.
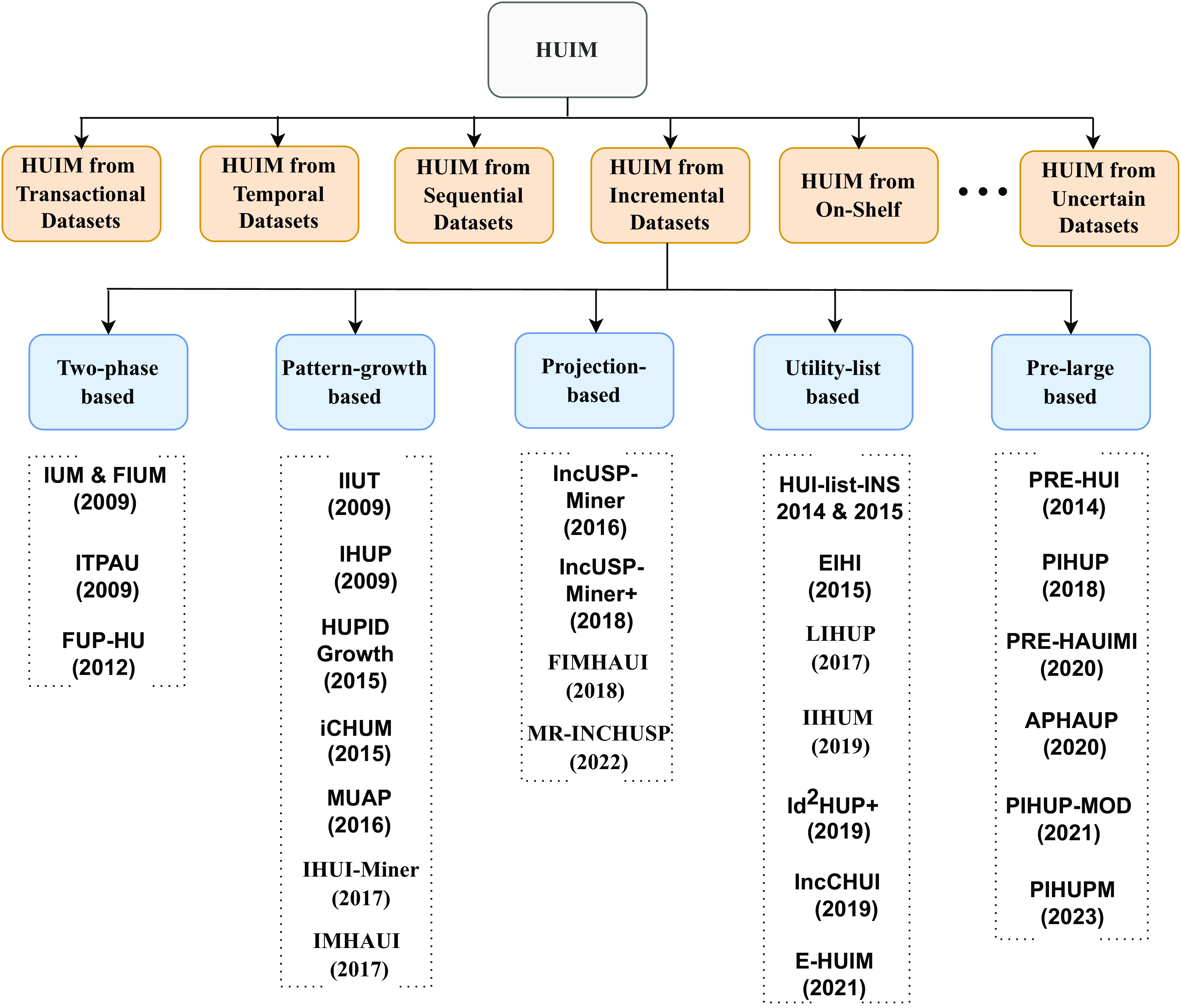
Figure 1. A taxonomy of incremental high utility itemsets mining approaches
3.1 Two-phase-based approaches
Traditional FIM algorithms (Agrawal et al., Reference Agrawal1993; Zaki, Reference Zaki2000) are designed to extract frequent itemsets using an user-defined support threshold. However, these algorithms are based on the frequency of occurrences within the dataset, which may not be adequate for identifying highly profitable itemsets. To resolve these issues, the concept of utility mining (Liu et al., Reference Liu and Liao2005; Yao & Hamilton, Reference Yao and Hamilton2006) is introduced. Utility mining can be viewed as an expansion of FIM, taking into account both sold quantity and unit profit of each itemset. These algorithms generate profitable itemsets instead of simple frequent itemsets. However, most of the traditional algorithms work on static datasets. In real-time systems, transactions are frequently added, removed, or changed in the dynamic environments. In this subsection, we discuss two-phase HUIM methods that mine the HUIs from the incremental datasets.
IUM and FIUM: Temporal mining is a sub-field of data mining focused on extracting interesting patterns from large temporal datasets (Li et al., Reference Li, Yeh and Chang2005b), while utility mining (Yao & Hamilton, Reference Yao and Hamilton2006) is used to find HUIs from transaction datasets. Both of these concepts can be integrated to produce significant results. To achieve this, Yeh et al. (Reference Yeh, Chang and Wang2008) conducted a study on incremental utility mining, focusing on the incremental extraction of high temporal utility itemsets (HTUIs) within a given time-period whether the TWU values of these time-periods from transactional datasets. Two effective approaches, namely incremental utility mining (IUM) and fast incremental utility mining (FIUM), are introduced to identify all the HTUIs. IUM is based on Two-phase (Liu et al., Reference Liu and Liao2005) and fast share measure (FSM) (Li et al., Reference Li, Yeh and Chang2005b) approaches, while FIUM is based on the ShFSM (Share-counted FSM) approach (Li et al., Reference Li, Yeh, Chang, Zhang, Tanaka, Yu, Wang and Li2005c). IUM initially, extracts 1-itemsets from partition 1 of the original dataset and checks whether their TWU values are less than the
![]() $min\_util$
threshold or not. If TWU of 1-itemsets
$min\_util$
threshold or not. If TWU of 1-itemsets
![]() $\ge$
$\ge$
![]() $min\_util$
, then these itemsets are saved in high TWU itemsets for partition 1. On the other hand, if utility of 1-itemsets
$min\_util$
, then these itemsets are saved in high TWU itemsets for partition 1. On the other hand, if utility of 1-itemsets
![]() $\ge$
$\ge$
![]() $min\_util$
, then these itemsets saved in HTUIs for partition 1. However, TWU of an itemset is always no less than its utility. Also, high TWU itemsets in partition 1 is a subset of high temporal utility itemsets in partition 1. The 1-itemsets in high TWU itemsets in partition 1 is used to generate level-2 candidates. This process continues until no candidate is generated in partition 1. The same procedure is applied to other partitions. Finally, it gives the complete set of HTUIs for the dataset.
$min\_util$
, then these itemsets saved in HTUIs for partition 1. However, TWU of an itemset is always no less than its utility. Also, high TWU itemsets in partition 1 is a subset of high temporal utility itemsets in partition 1. The 1-itemsets in high TWU itemsets in partition 1 is used to generate level-2 candidates. This process continues until no candidate is generated in partition 1. The same procedure is applied to other partitions. Finally, it gives the complete set of HTUIs for the dataset.
FIUM follows the same procedure as the IUM algorithm, with the primary difference is in the number of generated candidates. Both these algorithms use the TWU of the itemsets to reduce the number of candidates. The empirical findings proved that FIUM outperforms IUM concerning runtime on various
![]() $min\_util$
thresholds, both for real and synthetic datasets because FIUM takes less time to join the candidate itemsets. Both algorithms effectively search all HTUIs when new transactions are added into the original dataset. They not only search all HTUIs for a specific time-period but also search HUIs across the whole dataset. However, incremental utility mining finds it difficult when searching for HTUIs that have a large portion of utility in a specific time period. Furthermore, it does not specify information on the frequency of occurrence for itemsets within that particular period.
$min\_util$
thresholds, both for real and synthetic datasets because FIUM takes less time to join the candidate itemsets. Both algorithms effectively search all HTUIs when new transactions are added into the original dataset. They not only search all HTUIs for a specific time-period but also search HUIs across the whole dataset. However, incremental utility mining finds it difficult when searching for HTUIs that have a large portion of utility in a specific time period. Furthermore, it does not specify information on the frequency of occurrence for itemsets within that particular period.
ITPAU: The traditional HUIM algorithms (Liu et al., Reference Liu and Liao2005; Yao & Hamilton, Reference Yao and Hamilton2006) perform well only for the static datasets. Nevertheless, in real-time scenarios, the dataset is changing continually with the newly inserted transactions. Consequently, some HUIs may transition to low-utility itemsets and vice-versa, in the updated datasets. In address these challenges, Hong et al. (Reference Hong, Lee and Wang2009a) proposed an approach, called incremental two-phase average-utility mining (ITPAU), based on the Two-phase approach (Liu et al., Reference Liu and Liao2005). It’s purpose is to incrementally maintain the high average utility itemsets (HAUIs) in the incremental dataset. Based on the FUP notion (Cheung et al., Reference Cheung, Han, Ng and Wong1996), ITPAU joins the earlier extracted knowledge from the original dataset and the new information from recently added transactions to enhance mining performance. It employs a strategy, based on the Apriori approach (Agrawal et al., Reference Agrawal1993), to systematically identify HAUIs in a level-wise way. The DCP property is utilized to decrease the search space by removing low-utility itemsets earlier, thereby reducing the need for candidate generation at each level. To manage dataset changes resulting from newly added transactions, the concept of FUP (Cheung et al., Reference Cheung, Han, Ng and Wong1996) is employed to reduce the time required for reprocessing the whole updated dataset. ITPAU relies on four cases for the average-utility itemsets within the FUP framework. It performs two phases of incremental mining of these average-utility itemsets. During the first phase, average-utility upper-bound (AUUB) is employed to provide overestimated values for the itemsets. During the second phase, it calculates real average-utility values to extract HUBAUI (High Upper-Bound Average-Utility Itemsets).
The algorithm works as follows: first, it recomputes the minimum average-utility thresholds of new transactions and updated database, respectively. Then, it computes the utility value for each item in each new transaction. Afterwards, it identifies the maximal item-utility value in each new transaction. It generates k-itemsets (where k represents the counts of items in the currently processed itemsets.) and calculates their AUUB of k-itemsets from the new transactions. If AUUB of each k-itemset is not less than
![]() $min\_util$
of the new transaction, then put it in the set of HUBAUI of k-itemsets for the new transactions. If HUBAUI of k-itemsets does not appear in the new transaction, then update the AUUB. If HUBAUI of k-itemsets does not appear in the original dataset, then re-scan the original dataset to find AUUB of k-itemsets and update the original dataset. Repeat this procedure until no candidates are produced. In this way, the final HAUIs for the updated dataset are found. Experiments proved that ITPAU performs better than the state-of-the-art algorithm two-phase average-utility mining (TPAU) (Reference Hong, Lee and WangHong et al., 2009b
) in terms of runtime for updated datasets. ITPAU optimizes dataset scanning by computing the upper-bound of HUBAUI relative to the
$min\_util$
of the new transaction, then put it in the set of HUBAUI of k-itemsets for the new transactions. If HUBAUI of k-itemsets does not appear in the new transaction, then update the AUUB. If HUBAUI of k-itemsets does not appear in the original dataset, then re-scan the original dataset to find AUUB of k-itemsets and update the original dataset. Repeat this procedure until no candidates are produced. In this way, the final HAUIs for the updated dataset are found. Experiments proved that ITPAU performs better than the state-of-the-art algorithm two-phase average-utility mining (TPAU) (Reference Hong, Lee and WangHong et al., 2009b
) in terms of runtime for updated datasets. ITPAU optimizes dataset scanning by computing the upper-bound of HUBAUI relative to the
![]() $ min\_util$
threshold.
$ min\_util$
threshold.
FUP-HU: The traditional algorithms (Liu et al., Reference Liu and Liao2005; Yao & Hamilton, Reference Yao and Hamilton2006) consume a significant amount of computational time. To resolve this issue, the notion of FUP (Cheung et al. Reference Cheung, Han, Ng and Wong1996) is designed to update the obtained itemsets in the dynamic dataset. However, the process of re-scanning the original dataset consumes a significant amount of computational time. To further increase the mining performance, Lin et al. (Reference Lin, Lan and Hong2012) developed an incremental mining approach for record insertions, named FUP-HU. This method is based on the Two-phase (Liu et al., Reference Liu and Liao2005) and FUP concept (Cheung et al., Reference Cheung, Han, Ng and Wong1996) to effectively mine HUIs from the updated dataset. The method initially partitions the itemsets into four parts if they belong to the high TWU values of the itemsets in the original dataset and newly inserted transactions. To achieve this, the proposed method uses two-phase utility mining (Liu et al., Reference Liu and Liao2005) to search the TWU of itemsets and the corresponding actual utility values from the original datasets before incorporating additional transactions. First, it calculates the utility value for each item in every new transaction in the dataset. Then, it generates the k-itemsets and calculates their TWU from the new transactions. If TWU of each k-itemsets for the new transaction is no less than the
![]() $min\_util$
, then add it in the set of high TWU k-itemsets for the new transaction. Then, it generates the
$min\_util$
, then add it in the set of high TWU k-itemsets for the new transaction. Then, it generates the
![]() $(k+1)$
-itemsets from the set of high TWU k-itemsets in the updated datasets. Afterward, it calculates the actual utility value of itemsets for the new transactions. Finally, the HUIs for the whole updated database are generated. The experiments proved that the proposed approach performs better than the state-of-the-art approach Two-phase (Optimal) (Liu et al., Reference Liu and Liao2005) for various
$(k+1)$
-itemsets from the set of high TWU k-itemsets in the updated datasets. Afterward, it calculates the actual utility value of itemsets for the new transactions. Finally, the HUIs for the whole updated database are generated. The experiments proved that the proposed approach performs better than the state-of-the-art approach Two-phase (Optimal) (Liu et al., Reference Liu and Liao2005) for various
![]() $ min\_util$
thresholds in the updated dataset. This is because Two-phase (Optimal) performs the re-scanning of the updated dataset to discover HUIs in batch mode, resulting in a significant time overhead. In contrast, FUP-HU only re-scans the updated dataset for the newly inserted transactions, which significantly reduces the running time.
$ min\_util$
thresholds in the updated dataset. This is because Two-phase (Optimal) performs the re-scanning of the updated dataset to discover HUIs in batch mode, resulting in a significant time overhead. In contrast, FUP-HU only re-scans the updated dataset for the newly inserted transactions, which significantly reduces the running time.
Discussion
We have discussed two-phase-based HUIM algorithms (Liu et al. Reference Liu and Liao2005; Yao & Hamilton Reference Yao and Hamilton2006) for incremental datasets. Although the iHUIM algorithms (Yeh et al., Reference Yeh, Chang and Wang2008; Hong et al., Reference Hong, Lee and Wang2009a; Lin et al., Reference Lin, Lan and Hong2012) effectively address the limitations commonly associated with traditional HUIM algorithms. Nonetheless, they suffer from the same drawbacks as Apriori (Agrawal et al. Reference Agrawal1993) that produces more candidates and perform multiple dataset scans. The utilization of the FUP concept (Cheung et al., Reference Cheung, Han, Ng and Wong1996) reduces the number of re-scanning the original dataset, resulting in a reduced computational costs. In some cases, there can still be excessive re-scanning of original dataset, leading to significant computational overhead. Table 10 provides a comprehensive summary of two-phase iHUIM algorithms, encompassing key categories such as data structure, mining, pruning strategies, the state-of-the-art methods, and base methods. Table 11 provides an in-depth exploration of the theoretical aspects of two-phase iHUIM algorithms, including key categories such as outcomes, advantages and disadvantages, and future remarks.
Table 10. Characteristics and theoretical aspects of the Two-phase-based approaches

Table 11. Pros and cons of the Two-phase-based approaches

3.2 Pattern-growth-based approaches
Two-phase based iHUIM algorithms (Yeh et al., Reference Yeh, Chang and Wang2008; Hong et al., Reference Hong, Lee and Wang2009a; Lin et al., Reference Lin, Lan and Hong2012) extract the utility information in a level-wise fashion, thus suffering from excessive candidate’s generation and multiple dataset scans. To deal with these issues, pattern-growth-based iHUIM algorithms (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009b; Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a; Yun & Ryang, Reference Yun and Ryang2014; Zheng & Li, Reference Zheng and Li2015; Shao et al., Reference Shao, Meng and Cao2016; Guo & Gao, Reference Guo and Gao2017; Kim & Yun, Reference Kim and Yun2017) are introduced to efficiently extract the utility information in dynamic environments. These algorithms reduce the number of less promising candidates by mitigating the overestimation of their utilities (Liu et al., Reference Liu and Liao2005), thereby improving the mining performance. Efficient data structures are employed to handle newly added information without the need to process the whole dataset. This significantly minimizes the number of dataset scans as compared to level-wise incremental approaches (Yeh et al. Reference Yeh, Chang and Wang2008; Hong et al. Reference Hong, Lee and Wang2009a; Lin et al. Reference Lin, Lan and Hong2012). Furthermore, these methods significantly reduce redundant information, resulting in reduced storage space requirements and less execution times for the mining process. We here give the in-depth discussion of the pattern-growth-based iHUIM algorithms.
IIUT: Ahmed et al. (Reference Ahmed, Tanbeer, Jeong and Lee2009b) proposed an effective tree structure named IIUT (Incremental and Interactive Utility Tree), that employed a pattern-growth method to discover high utility itemsets without requiring the level-wise candidate generation. Incremental data can then be captured without re-structuring the process. It uses the ‘
![]() $build \ once, \ mine \ many$
’ characteristics, rendering it well-suited for interactive mining. The IIUT structure is designed according to the order of item appearances and performs two scans: (1) During the first scan, IIUT arranges items within a transaction based on their order of appearance and adds them to the leaf node of the tree. The header table is maintained in the form of an FP-tree (Han et al., Reference Han, Pei, Yin and Mao2004). (2) During the second scan, it maintains the TWU value in the header table and intermediate nodes of the tree. The adjacent links are preserved to efficiently traverse the tree. This, in turn, leads to a reduction in the time required for the mining process. The proposed tree structure is extremely efficient in the interactive and incremental mining of HUIs.
$build \ once, \ mine \ many$
’ characteristics, rendering it well-suited for interactive mining. The IIUT structure is designed according to the order of item appearances and performs two scans: (1) During the first scan, IIUT arranges items within a transaction based on their order of appearance and adds them to the leaf node of the tree. The header table is maintained in the form of an FP-tree (Han et al., Reference Han, Pei, Yin and Mao2004). (2) During the second scan, it maintains the TWU value in the header table and intermediate nodes of the tree. The adjacent links are preserved to efficiently traverse the tree. This, in turn, leads to a reduction in the time required for the mining process. The proposed tree structure is extremely efficient in the interactive and incremental mining of HUIs.
Figure 2 shows the incremental maintenance process of the proposed algorithm IIUT. In Step 1, the transaction database with their profit value is taken as an input. It consists six transactions
![]() $(T_1,\,T_2,\,T_3,\,T_4,\,T_5,\,T_6)$
and five items (a, b, c, d, e). In Step 2, the transactions are inserted into the H-table (Header-table) according to their appearance order, one at a time. The tree is constructed according to the FP-tree (Han et al., Reference Han, Pei, Yin and Mao2004). In Step 3, two groups of transactions Db1 and Db2 are added to the original database. The Db1 includes transactions
$(T_1,\,T_2,\,T_3,\,T_4,\,T_5,\,T_6)$
and five items (a, b, c, d, e). In Step 2, the transactions are inserted into the H-table (Header-table) according to their appearance order, one at a time. The tree is constructed according to the FP-tree (Han et al., Reference Han, Pei, Yin and Mao2004). In Step 3, two groups of transactions Db1 and Db2 are added to the original database. The Db1 includes transactions
![]() $(T_7,T_8)$
, while Db2 includes
$(T_7,T_8)$
, while Db2 includes
![]() $(T_9,T_{10})$
. Then, the tree is constructed from the updated database. In the same Step, the database is again updated by modifying the transactions
$(T_9,T_{10})$
. Then, the tree is constructed from the updated database. In the same Step, the database is again updated by modifying the transactions
![]() $(T_2,T_3)$
and deleting
$(T_2,T_3)$
and deleting
![]() $(T_5,T_9)$
. Finally, the tree is built based on its H-table from the updated database. Experiments proved that IIUT outperforms the state-of-the-art approaches, including Two-phase (Liu et al., Reference Liu and Liao2005), FUM (Fast Utility Mining) (Li et al., Reference Li, Yeh and Chang2008) and DCG
$(T_5,T_9)$
. Finally, the tree is built based on its H-table from the updated database. Experiments proved that IIUT outperforms the state-of-the-art approaches, including Two-phase (Liu et al., Reference Liu and Liao2005), FUM (Fast Utility Mining) (Li et al., Reference Li, Yeh and Chang2008) and DCG
![]() $+$
(Li et al., Reference Li, Yeh and Chang2008), an extended version of DCG (Direct Candidate Generation) algorithm (Li et al., Reference Li, Yeh and Chang2005a; Li et al., Reference Li, Yeh, Chang, Zhang, Tanaka, Yu, Wang and Li2005c), concerning runtime and number of promising candidates under various
$+$
(Li et al., Reference Li, Yeh and Chang2008), an extended version of DCG (Direct Candidate Generation) algorithm (Li et al., Reference Li, Yeh and Chang2005a; Li et al., Reference Li, Yeh, Chang, Zhang, Tanaka, Yu, Wang and Li2005c), concerning runtime and number of promising candidates under various
![]() $min\_util$
thresholds from the dense and sparse datasets.
$min\_util$
thresholds from the dense and sparse datasets.

Figure 2. Incremental maintenance process of IIUT
IHUP: The traditional HUIM algorithms (Yen et al., Reference Yen and Lee2005; Hong et al., Reference Hong, Lin and Wu2008) cannot deal with the incremental and interactive mining that includes addition, removal, or change of the transactions in the dynamic environment. Furthermore, these algorithms do not follow the ‘
![]() $build \ once, \ mine \ many \ $
’ characteristics. To address these challenges, Ahmed et al. (Reference Ahmed, Tanbeer, Jeong and Lee2009a) proposed three novel tree structures, namely Incremental HUI lexicographic Tree (IHUP
$build \ once, \ mine \ many \ $
’ characteristics. To address these challenges, Ahmed et al. (Reference Ahmed, Tanbeer, Jeong and Lee2009a) proposed three novel tree structures, namely Incremental HUI lexicographic Tree (IHUP
![]() $_L$
-Tree), IHUP transaction frequency tree (IHUP
$_L$
-Tree), IHUP transaction frequency tree (IHUP
![]() $_{TF}$
-Tree) and IHUP transaction-weighted utilization Tree (IHUP
$_{TF}$
-Tree) and IHUP transaction-weighted utilization Tree (IHUP
![]() $_{TWU}$
-Tree). These structures are specifically designed to enable incremental and interactive HUIM (High Utility Itemset Mining) while follow ‘
$_{TWU}$
-Tree). These structures are specifically designed to enable incremental and interactive HUIM (High Utility Itemset Mining) while follow ‘
![]() $build \ once, \ mine \ many \ $
’ property. This approach results in efficient HUI mining from incremental transaction datasets. These tree structures are based on the FP-Growth method (Han et al., Reference Han, Pei and Yin2000) and hold the DCP property (Agrawal et al., Reference Agrawal1993). They incorporate TWU of a pattern, which effectively avoid candidate generation in a level-wise manner. The first tree structure IHUP
$build \ once, \ mine \ many \ $
’ property. This approach results in efficient HUI mining from incremental transaction datasets. These tree structures are based on the FP-Growth method (Han et al., Reference Han, Pei and Yin2000) and hold the DCP property (Agrawal et al., Reference Agrawal1993). They incorporate TWU of a pattern, which effectively avoid candidate generation in a level-wise manner. The first tree structure IHUP
![]() $_L$
-Tree rely on the lexicographical order of items. It efficiently manages incremental data without the need of restructure functions. The second tree structure IHUP
$_L$
-Tree rely on the lexicographical order of items. It efficiently manages incremental data without the need of restructure functions. The second tree structure IHUP
![]() $_{TF}$
-Tree optimizes space by arranging items based on descending transaction frequency. The third tree structure IHUP
$_{TF}$
-Tree optimizes space by arranging items based on descending transaction frequency. The third tree structure IHUP
![]() $_{TWU}$
-Tree, is constructed to reduce the time required for the mining process, based on their TWU values in descending order.
$_{TWU}$
-Tree, is constructed to reduce the time required for the mining process, based on their TWU values in descending order.
In the first scan, the IHUP
![]() $_L$
-Tree is constructed, arranging items in lexicographic order. The order of items of IHUP
$_L$
-Tree is constructed, arranging items in lexicographic order. The order of items of IHUP
![]() $_L$
-Tree is not affected by changing the frequency of the items by performing the addition, deletion, and modification. Subsequently, the IHUP
$_L$
-Tree is not affected by changing the frequency of the items by performing the addition, deletion, and modification. Subsequently, the IHUP
![]() $_{TF}$
-Tree is derived from the IHUP
$_{TF}$
-Tree is derived from the IHUP
![]() $_L$
-Tree, utilizing the path-adjusting technique (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004) based on the bubble-sort method. The nodes in the IHUP
$_L$
-Tree, utilizing the path-adjusting technique (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004) based on the bubble-sort method. The nodes in the IHUP
![]() $_{TF}$
-Tree are organized in the descending order based on their transaction frequency. The advantage is that the items occur in numerous transaction can be placed in the upper section of the tree, resulting in the higher prefix-sharing nodes that, in turn, significantly reduce the size of the tree. These two tree structures face a significant drawback: they may inadvertently convert low-utility itemsets into HUIs, and vice-versa, resulting in a significant delay in the mining process. To address this issue, IHUP
$_{TF}$
-Tree are organized in the descending order based on their transaction frequency. The advantage is that the items occur in numerous transaction can be placed in the upper section of the tree, resulting in the higher prefix-sharing nodes that, in turn, significantly reduce the size of the tree. These two tree structures face a significant drawback: they may inadvertently convert low-utility itemsets into HUIs, and vice-versa, resulting in a significant delay in the mining process. To address this issue, IHUP
![]() $_{TWU}$
-Tree is designed in a same way as IHUP
$_{TWU}$
-Tree is designed in a same way as IHUP
![]() $_{TF}$
-Tree is constructed. IHUP
$_{TF}$
-Tree is constructed. IHUP
![]() $_{TF}$
-Tree keeps all promising candidates before the non-promising candidates. This tree structure is constructed from the IHUP
$_{TF}$
-Tree keeps all promising candidates before the non-promising candidates. This tree structure is constructed from the IHUP
![]() $_L$
-Tree using the path adjusting technique (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004) based on the bubble-sort method. The number of nodes involved in the mining process in IHUP
$_L$
-Tree using the path adjusting technique (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004) based on the bubble-sort method. The number of nodes involved in the mining process in IHUP
![]() $_{TWU}$
-Tree does not exceed that of the other two tree structures, leading to the significantly reduction in the mining time. During the second dataset scan, HUIs are mined. The proposed algorithms require just two dataset scans, regardless of the maximum length of candidate patterns. The experiments proved that the designed three structures perform better than Two-phase (Liu et al. Reference Liu and Liao2005), FUM (Li et al., Reference Li, Yeh and Chang2008), and DCG+ (Li et al., Reference Li, Yeh and Chang2008), concerning execution time, number of promising candidates, and scalability under different
$_{TWU}$
-Tree does not exceed that of the other two tree structures, leading to the significantly reduction in the mining time. During the second dataset scan, HUIs are mined. The proposed algorithms require just two dataset scans, regardless of the maximum length of candidate patterns. The experiments proved that the designed three structures perform better than Two-phase (Liu et al. Reference Liu and Liao2005), FUM (Li et al., Reference Li, Yeh and Chang2008), and DCG+ (Li et al., Reference Li, Yeh and Chang2008), concerning execution time, number of promising candidates, and scalability under different
![]() $ min\_util$
thresholds. However, IHUP
$ min\_util$
thresholds. However, IHUP
![]() $_L$
-Tree consumes a considerable amount of space. Both IHUP
$_L$
-Tree consumes a considerable amount of space. Both IHUP
![]() $_L$
-Tree and IHUP
$_L$
-Tree and IHUP
![]() $_{TF}$
-Tree have low-TWU itemsets appearing before high TWU itemsets, resulting in increased time delays. IHUP
$_{TF}$
-Tree have low-TWU itemsets appearing before high TWU itemsets, resulting in increased time delays. IHUP
![]() $_{TWU}$
-Tree overcomes the limitations of IHUP
$_{TWU}$
-Tree overcomes the limitations of IHUP
![]() $_L$
-Tree and IHUP
$_L$
-Tree and IHUP
![]() $_{TF}$
-Tree.
$_{TF}$
-Tree.
HUPID-Growth: Several HUIM algorithms (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a; Lin et al., Reference Lin, Lan and Hong2012) are proposed for incremental datasets to better emulate real-world characteristics. But, they produce excessive number of candidates and requiring multiple dataset scans, leading to a reduction in mining efficiency. In addition, these algorithms require excessive amount of runtime to extract candidates by their overestimated methods (Liu et al., Reference Liu and Liao2005). This situation becomes increasingly challenging as datasets gradually expand in a dynamic environment. Yun & Ryang (Reference Yun and Ryang2014) developed an efficient algorithm called HUPID-Growth (High Utility Patterns in Incremental Databases Growth) to extract HUIs from dynamic datasets. It focuses on mitigating overestimated utilities in the mining process. An efficient tree structure, called HUPID-Tree (High Utility Patterns in Incremental Datasets Tree), is proposed to effectively maintain details of the HUIs in the updated dataset, requiring just a single dataset scan. A header table is maintained in the HUPID-Tree to facilitate the tree traversal. Each record in the header table includes item name, TWU value and a link. These entries are sorted according to TWU descending order. The sorted entries are used effectively to traverse the tree. Furthermore, a data structure named TIList (Tail-node Information List) is employed in local trees by using the restructure method based on TWU (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a; Lin et al., Reference Lin, Lan and Hong2012). A TIList preserves information about the tail nodes in a global HUPID-Tree. It is used for restructuring the HUPID-Tree, resulting in the reduced overestimate utilities that, in turn, achieves efficient incremental HUIs mining.
The proposed algorithm is consists of two phases: (1) The first phase includes two steps. In the initial step, a global HUPID-Tree is built with a single scan. Subsequently, the data structure TIList is created using the restructure method, effectively reducing overestimated utilities in decreasing order of the TWU value. In the second step, candidates are generated, which significantly minimize the search space, enhances mining efficiency. (2) In the second phase, actual HUIs are extracted from the generated candidates. When the current database is updated by appending the new information to the database. Then, the proposed algorithm updates the existing tree with only added information without reconstructing the tree from the scratch. The proposed algorithm sorts the items in each added transaction as per the TWU decreasing order. Afterwards, it adds the transaction into the tree by computing the utility value to the tree. The proposed algorithm decreases overestimate utilities of nodes both in global and local trees, leading to the decrease in the number of candidates and search space. The proposed algorithm outperforms IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) and FUP-HU (Lin et al., Reference Lin, Lan and Hong2012) concerning execution time, memory usage, and the number of processed candidates, as demonstrated on retail and medical datasets. HUPID-Growth specifically performs well where datasets consist of a large number of lengthy transactions or when a low value for the
![]() $ min\_util $
threshold is employed.
$ min\_util $
threshold is employed.
iCHUM: The IHUP algorithm (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) failed to perform efficiently on incremental datasets containing a large number of itemsets. It retains redundant information, resulting in excessive processing times for unpromising candidates. Furthermore, it does not maintain the tree structure following the DCP (Liu et al., Reference Liu and Liao2005). To deal with these problems, Zheng & Li (Reference Zheng and Li2015) designed an efficient approach, named iCHUM (incremental Compressed High Utility Mining) to mine HUIs from incremental datasets. It employs high TWU values of items to construct and incrementally update the iCHUM-Tree structure, leading to a significant reduction of run-time. The iCHUM-Tree includes tree structure and header table. The iCHUM-Tree is constructed from the original database and the header table maintains the promising items whose TWU value is no less than
![]() $min\_util$
. The items are organized as per TWU decreasing order. Then, each reodered transaction is added in iCHUM-Tree.
$min\_util$
. The items are organized as per TWU decreasing order. Then, each reodered transaction is added in iCHUM-Tree.
The proposed algorithm updates the iCHUM-Tree when a new dataset is added to the original one. A recall item is one whose TWU value is no less than
![]() $min\_util$
in both original and updated databases. The nodes are reorder in the iCHUM-Tree and its header table by using bubble sort method (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004). The iCHUM-Tree is updated when all the items and the corresponding nodes are sorted in the iCHUM-Tree. The proposed algorithm includes four steps. Firstly, the algorithm constructs the iCHUM-Tree from the original dataset and collects the high TWU values of itemsets within that dataset. Secondly, when a new dataset is appended to the original dataset, the iCHUM-Tree undergoes an update process. Thirdly, the updated iCHUM-Tree becomes the input for the mining process, generates high TWU itemsets. Finally, it identifies actual HUIs from the candidates in the whole dataset. Experiments proved that iCHUM performs better than IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) concerning execution time on benchmark datasets, specifically for long transactions. However, the performance of iCHUM degrades as the number of recollected items increases.
$min\_util$
in both original and updated databases. The nodes are reorder in the iCHUM-Tree and its header table by using bubble sort method (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004). The iCHUM-Tree is updated when all the items and the corresponding nodes are sorted in the iCHUM-Tree. The proposed algorithm includes four steps. Firstly, the algorithm constructs the iCHUM-Tree from the original dataset and collects the high TWU values of itemsets within that dataset. Secondly, when a new dataset is appended to the original dataset, the iCHUM-Tree undergoes an update process. Thirdly, the updated iCHUM-Tree becomes the input for the mining process, generates high TWU itemsets. Finally, it identifies actual HUIs from the candidates in the whole dataset. Experiments proved that iCHUM performs better than IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) concerning execution time on benchmark datasets, specifically for long transactions. However, the performance of iCHUM degrades as the number of recollected items increases.
MUAP: In real-world scenarios, managers aim to maximize profits by considering actionable product. However, some of these products may not exhibit high frequency or utility in the datasets and are often considered for rejection. However, these actionable patterns are of great significance. Hence, extracting these itemsets as high-frequency or high utility patterns poses a challenging task. To resolve this challenge, Shao et al. (Reference Shao, Meng and Cao2016) developed a new structure for mining actionable patterns, namely, mining utility associated patterns (MUAP), the first of its kind, to discover the high utility incremental patterns and closely related itemsets by using a combination of criteria. The proposed algorithm utilizes a tree structure that combines utility growth and association rule mining. The proposed tree structure, named utility graph-tree (UG-tree), orderly analyses the connection between fundamental and derivative itemsets based on frequency and utility concepts. All branches whose utility decreases are discarded first time from the proposed UG-tree because the utility of the nodes may vary which means that the increment of the utility may be negative. The UG-tree involves two dataset scans. During the first scan, it generates itemsets and their corresponding TWU values based on transaction utility. In the second scan, it reorders transactions and generates their rebuilt transaction utility (RTU). RTU is the transaction utility of the rebuilt transaction.
Two efficient strategies are also designed to enhance the efficiency of the proposed structure. The global pruning strategy is designed to produce utility increase patterns with clusters from the given itemsets. The local strategy is designed for each cluster to identify patterns with the highest weighted value, considering a composite measure for utility growth and dependence computation. A combined mining approach is proposed to find the interesting patterns from the clusters of patterns. Two parameters namely, impact and confidence, are proposed to measure the interestingness of each combined pattern. The impact of the additional itemset is the impact factor to value the utility growth within each actionable combined pattern from the utility of the underlying itemset to the derivative itemset. On the other hand, the confidence is the measurement of the association relationship between the underlying itemset and the additional itemset. The results achieved by MUAP are satisfactory in terms of pattern utility from the dense and sparse datasets.
IHUI-Miner: IHUP approach (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) is developed to mine rule from incremental datasets while mitigating overestimated utility values. However, it suffers from two limitations: (1) Generates an excessive number of candidates and (2) Consumes more time to validate these candidates. To solve these limitations, Guo et al. developed an approach, called IHUI-Miner (Guo & Gao, Reference Guo and Gao2017) to extract HUIs without requiring for candidate generation. A novel tree structure, called IHUI-Tree (Incremental High Utility Itemset Tree), organizes items in lexicographic order (IHUI
![]() $_L$
-Tree), using the pattern-growth method and is traversed in a bottom-up manner. The details of the original dataset are represented using a 2D-array utility dataset (Zihayat & An, Reference Zihayat and An2014). The global IHUI
$_L$
-Tree), using the pattern-growth method and is traversed in a bottom-up manner. The details of the original dataset are represented using a 2D-array utility dataset (Zihayat & An, Reference Zihayat and An2014). The global IHUI
![]() $_L$
-Tree and the global utility dataset are initially constructed by scanning the original dataset. The DCP property of the dataset’s item prefix utility effectively reducing the search space. Prefix utility of an item is the summation of utility of the items of the prefix set in the database. It is used to estimate the true utility of an itemset in the database.
$_L$
-Tree and the global utility dataset are initially constructed by scanning the original dataset. The DCP property of the dataset’s item prefix utility effectively reducing the search space. Prefix utility of an item is the summation of utility of the items of the prefix set in the database. It is used to estimate the true utility of an itemset in the database.
If the prefix utility for an itemset is equal to or greater than
![]() $min\_util$
, then the following three steps are performed to compute the HUIs: (1) A conditional dataset is generated, and subsequently, conditional pattern tree and conditional utility dataset are constructed. (2) HUIs are extracted iteratively from the conditional pattern tree and the conditional utility dataset. (3) The information in global IHUI
$min\_util$
, then the following three steps are performed to compute the HUIs: (1) A conditional dataset is generated, and subsequently, conditional pattern tree and conditional utility dataset are constructed. (2) HUIs are extracted iteratively from the conditional pattern tree and the conditional utility dataset. (3) The information in global IHUI
![]() $_L$
-Tree and global utility dataset is updated. If the prefix utility of itemset is less than
$_L$
-Tree and global utility dataset is updated. If the prefix utility of itemset is less than
![]() $min\_util$
then only
$min\_util$
then only
![]() $3\mathrm{rd}$
step is performed. To generate the conditional dataset for an item in the global IHUI
$3\mathrm{rd}$
step is performed. To generate the conditional dataset for an item in the global IHUI
![]() $_L$
-Tree, the following steps are performed: (1) Node links are traced corresponding to an item in the global tree. (2) The obtained nodes are traced to their root, and all the paths corresponding to that item can be retrieved and collected into the item’s conditional dataset. Moreover, the utilities of items in the paths can also be collected from the global utility dataset with the node-link of the obtained nodes. The results proved that the IHUI-Miner performs better than IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) concerning the execution time. It is observed that the proposed approach is 1 to 2 orders of magnitude quicker than IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a).
$_L$
-Tree, the following steps are performed: (1) Node links are traced corresponding to an item in the global tree. (2) The obtained nodes are traced to their root, and all the paths corresponding to that item can be retrieved and collected into the item’s conditional dataset. Moreover, the utilities of items in the paths can also be collected from the global utility dataset with the node-link of the obtained nodes. The results proved that the IHUI-Miner performs better than IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) concerning the execution time. It is observed that the proposed approach is 1 to 2 orders of magnitude quicker than IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a).
IMHAUI: High average-utility itemsets mining (HAUIM) approaches (Hong et al., Reference Hong, Lee and Wang2011; Kim & Yun, Reference Kim and Yun2016) address the limitations of conventional HUIM methods by incorporating the concept of average-utility measure, thereby providing meaningful results to the users. However, these approaches scan the dataset twice and are suitable only for static datasets. To resolve these limitations, Kim & Yun (Reference Kim and Yun2017) designed an approach, called incremental mining of high average-utility itemsets (IMHAUI), utilizing the pattern-growth approach, to extract HAUIs from incremental datasets. A novel tree structure, called incremental high average utility itemset tree (IHAUI-Tree), is proposed to efficiently retain relevant information in incremental datasets while minimizing the number of dataset scans through the utilization of the node sharing effect. The algorithm also utilizes the path adjusting method (Koh & Shieh, Reference Koh, Shieh, Lee, Li, Whang and Lee2004) following restructuring techniques to generate a compressed IHAUI-Tree. It includes three basic steps: (1) node insert; (2) node exchange; and (3) node merge. In IHAUI-Tree, the AUUB value of any node is always no less than its child nodes. The path adjusting method is updated to restructure the IHAUI-Tree as per the descending order of AUUB, resulting in removing the irrelevant items from the construction of local trees and reducing the computational overhead in the mining process. This will result into the significant memory consumption to store the data in the IHAUI-Tree.
The proposed approach comprises the following functions: (1) IMHAUI function: This function is responsible for continuously processing the input transaction data. It calls for two other essential functions: ‘Restructure’ and ‘Mining,’ which restructure IHAUI-Tree and performs the mining process. (2) Restructure function: This function focuses on restructuring the IHAUI-Tree by decreasing the order of the optimum AUUB value. (3) Mining function: This function focuses on the mining candidate HAUIs using the pattern-growth method. It is observed that IMHAUI performs better than ITPAU (Hong et al., Reference Hong, Lee and Wang2009a) and HUPID-Growth (Yun & Ryang, Reference Yun and Ryang2014), concerning execution time and memory consumption. However, it requires additional processing time for candidate validation. There are lots of challenges to accelerating the mining process when new transactions are generated. The proposed approach extract conditional pattern base for each prefix itemset and constructs its local tree recursively. However, this recursive approach is negatively affects the execution efficiency.
Discussion
We have discussed pattern-growth-based iHUIM algorithms designed to extract relevant utility information in incremental environment. These algorithms overcome the limitations of two-phase-based iHUIM approaches by providing compact data structures and reducing redundant information, resulting in a significantly enhancing the mining performance. However, there are several issues: (1) It generates excessive number of candidates when dataset has long transactions or
![]() $ min\_util $
threshold is set quite low. (2) The substantial time required for candidate verification. (3) The performance of these algorithms can vary depending on the dataset size. Table 12 gives an overview of pattern-growth-based HUIM algorithms from the incremental datasets. The theoretical aspects of pattern-growth iHUIM algorithms, including their outcomes, advantages, disadvantages, and future considerations, are shown in Table 13.
$ min\_util $
threshold is set quite low. (2) The substantial time required for candidate verification. (3) The performance of these algorithms can vary depending on the dataset size. Table 12 gives an overview of pattern-growth-based HUIM algorithms from the incremental datasets. The theoretical aspects of pattern-growth iHUIM algorithms, including their outcomes, advantages, disadvantages, and future considerations, are shown in Table 13.
Table 12. Characteristics and theoretical aspects of the pattern-growth-based approaches
Table 13. Pros and cons of the pattern-growth-based approaches

3.3 Projection-based approaches
The pattern-growth-based iHUIM algorithms utilize tree-based structures to store previous mining information and avoid redundant re-computation when the original dataset is updated. However, this process consumes a high amount of memory as it produces a large number of tree nodes, resulting in considerable time overhead. Furthermore, the designed upper-bounds are not tighter, resulting in poor mining efficiency since they fail to efficiently prune the search space and reduce the number of less promising candidates. To address these challenges, projection-based iHUIM algorithms (Wang & Huang, Reference Wang and Huang2016; Wang & Huang, Reference Wang and Huang2018; Yildirim & Celik, Reference Yildirim and Celik2018; Saleti, Reference Saleti2021) are designed to extract profitable items from the incremental datasets. These approaches use tighter upper-bounds to reduce the less promising candidates, leading to improved mining performance. Moreover, they implement compact data structures for optimized storage space. Here we present in-depth overview of projection-based iHUIM algorithms, including their strengths and weaknesses.
IncUSP-Miner: Traditional HUSPM (High Utility Sequence Pattern mining) approaches (Yin et al., Reference Yin, Zheng and Cao2012; Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013) face challenges to address the mining issues of HUSPs (High Utility Sequence Patterns) from incremental datasets. When these algorithms are applied to incremental datasets, they encounter several challenges: (1) The utility of sequence does not follow DCP property. (2) A sequence may consist of multiple instances in each super-sequence, each with its utility. The tree structure stores redundant information when the dataset is updated, leading to excessive memory consumption and decreased runtime efficiency. (3) It requires scanning of whole dataset each time to identify new HUSPs. (4) The tree structure needs to be adjusted with each dataset update to guarantee the accuracy of the mining outcomes. To address these challenges, Wang & Huang (Reference Wang and Huang2016) developed an algorithm named IncUSP-Mine for incremental mining of HUSPs. A tight upper-bound, TSU (Tight Sequence Utility), is presented to enhance mining performance. TSU is tighter than PEU (Prefix-Extension Utility) (Wang et al. Reference Wang, Huang and Chen2016) and RSU (Reduced Sequence Utility) (Wang et al., Reference Wang, Huang and Chen2016) and it enhances the efficiency of the mining process. This approach eliminates sequences with low utility during the mining process. It comprises two main phases. The initial phase designed IncUSP-Miner algorithm (Wang & Huang, Reference Wang and Huang2016) utilizes TSU and PEU to discover HUSPs in the original dataset. It constructs all the nodes of the candidate pattern tree and extracts HUSPs from the root in a depth first search. During the incremental phase, a compact candidate pattern tree is used to further enhance mining efficiency. A candidate pattern tree is the expansion of the lexicographic tree that buffers a set of sequences in the database for incremental HUSP mining.
The proposed approach visits each node of candidate pattern tree using depth-first search and avoids nodes that do not appear in the updated sequences. To simplify the incremental HUSP mining process, a candidate pattern tree data structure retains all sequences with TSU values no less than the
![]() $min\_util$
. A compressed tree node structure is also presented to keep key details of the corresponding sequence that minimizes the need of additional computations. This strategy, based on the candidate pattern tree, is designed to minimize the computational load when a node is modified, thus the mining performance is improved. A node skipping strategy is also proposed that is used to safely skip some nodes in the tree structure without updating the database. Extensive experiments proved that IncUSP-Miner performs better than HUSP mining methods, USpan (Yin et al., Reference Yin, Zheng and Cao2012) and HUS-Span (Wang et al., Reference Wang, Huang and Chen2016), concerning the run-time under various
$min\_util$
. A compressed tree node structure is also presented to keep key details of the corresponding sequence that minimizes the need of additional computations. This strategy, based on the candidate pattern tree, is designed to minimize the computational load when a node is modified, thus the mining performance is improved. A node skipping strategy is also proposed that is used to safely skip some nodes in the tree structure without updating the database. Extensive experiments proved that IncUSP-Miner performs better than HUSP mining methods, USpan (Yin et al., Reference Yin, Zheng and Cao2012) and HUS-Span (Wang et al., Reference Wang, Huang and Chen2016), concerning the run-time under various
![]() $min\_util$
thresholds from the incremental datasets. The candidate pattern tree efficiently computes the utility and the proposed node skipping strategy avoids some nodes not necessary to be visited. However, it needs extra memory to construct the candidate pattern tree, leading to increased computational costs.
$min\_util$
thresholds from the incremental datasets. The candidate pattern tree efficiently computes the utility and the proposed node skipping strategy avoids some nodes not necessary to be visited. However, it needs extra memory to construct the candidate pattern tree, leading to increased computational costs.
IncUSP-Miner
![]() $^+$
: IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016) is the first projection-based work on incremental HUSP mining. The algorithm is further expanded by the same set of authors (Wang & Huang, Reference Wang and Huang2018). IncUSP-Miner
$^+$
: IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016) is the first projection-based work on incremental HUSP mining. The algorithm is further expanded by the same set of authors (Wang & Huang, Reference Wang and Huang2018). IncUSP-Miner
![]() $^+$
(Wang & Huang, Reference Wang and Huang2018) approach is developed to extract HUSPs from the incremental datasets and visits each node in the tree at the root in a depth first search way and skips those nodes that are not appearing in the updated sequences. The method provides a tighter upper-bound for sequence utility, named TSU (Tight Sequence Utility), to eliminate redundant recalculations in the mining process. TSU is tighter than the upper-bounds, PEU (Wang et al. Reference Wang, Huang and Chen2016) and RSU (Wang et al. Reference Wang, Huang and Chen2016), resulting in more efficient mining. A novel compact tree data structure named Candidate Pattern Tree, an extension of Lexicographic tree (Yin et al. Reference Yin, Zheng and Cao2012), is designed to store sequences with TSU values no less than
$^+$
(Wang & Huang, Reference Wang and Huang2018) approach is developed to extract HUSPs from the incremental datasets and visits each node in the tree at the root in a depth first search way and skips those nodes that are not appearing in the updated sequences. The method provides a tighter upper-bound for sequence utility, named TSU (Tight Sequence Utility), to eliminate redundant recalculations in the mining process. TSU is tighter than the upper-bounds, PEU (Wang et al. Reference Wang, Huang and Chen2016) and RSU (Wang et al. Reference Wang, Huang and Chen2016), resulting in more efficient mining. A novel compact tree data structure named Candidate Pattern Tree, an extension of Lexicographic tree (Yin et al. Reference Yin, Zheng and Cao2012), is designed to store sequences with TSU values no less than
![]() $min\_util$
in the original dataset. A candidate pattern tree supports the multiple database updates. Several pruning strategies, namely Auxiliary information update, Node skipping strategy, and Database scan reduction, are designed to reduce the need of dataset scans and computations whenever a node is inserted. Auxiliary information update strategy supports the multiple database updates. Node skipping strategy safely skips tree nodes that are not the instances of all sequences in database without updating the database. Database scan reduction strategy eliminates the need of multiple database scans These strategies significantly improves mining efficiency.
$min\_util$
in the original dataset. A candidate pattern tree supports the multiple database updates. Several pruning strategies, namely Auxiliary information update, Node skipping strategy, and Database scan reduction, are designed to reduce the need of dataset scans and computations whenever a node is inserted. Auxiliary information update strategy supports the multiple database updates. Node skipping strategy safely skips tree nodes that are not the instances of all sequences in database without updating the database. Database scan reduction strategy eliminates the need of multiple database scans These strategies significantly improves mining efficiency.
Extensive experiments are conducted to prove that IncUSP-Miner
![]() $^+$
outperforms USpan (Yin et al., Reference Yin, Zheng and Cao2012) and HUS-Span (Wang et al., Reference Wang, Huang and Chen2016), concerning both run-time and scalability from the dense and sparse datasets. IncUSP-Miner
$^+$
outperforms USpan (Yin et al., Reference Yin, Zheng and Cao2012) and HUS-Span (Wang et al., Reference Wang, Huang and Chen2016), concerning both run-time and scalability from the dense and sparse datasets. IncUSP-Miner
![]() $^+$
performs better than IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016), especially for dense datasets. However, both algorithms are not memory-efficient as compared to HUS-Span. This is due to the necessity of construction of candidate pattern trees and execution multiple dataset updates, which ultimately leading to higher computational demands as a new node inserted.
$^+$
performs better than IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016), especially for dense datasets. However, both algorithms are not memory-efficient as compared to HUS-Span. This is due to the necessity of construction of candidate pattern trees and execution multiple dataset updates, which ultimately leading to higher computational demands as a new node inserted.
FIMHAUI: The IMHAUI approach (Kim & Yun, Reference Kim and Yun2017), based on the IHAUI-Tree, is designed to extract HAUIs from incremental datasets. However, it recursively generates conditional pattern tree bases to build conditional local trees for candidate mining during the mining process. This extends the time needed to locate candidates and necessitates candidate verification during mining. To solve these problems, Yildirim & Celik (Reference Yildirim and Celik2018) developed FIMHAUI (Fast Incremental Mining of HAUIs) approach to extract HAUIs in incremental datasets. A new tree data structure named mIHAUI-Tree (modified IHAUI-Tree) is designed, an extension of IHAUI-Tree (Kim & Yun, Reference Kim and Yun2017), to keep the relevant details of transactions. Whenever a mining request occurs, the algorithm adjusts mIHAUI-Tree to maximize the node-sharing effect of mIHAUI-Tree. In subsequent step, it obtains the projected dataset in the next step. Finally, it employs transaction merging and dataset projection techniques to efficiently identify candidate itemsets.
FIMHAUI effectively decreases the required time to generate the candidates because each node N within IHAUI-Tree keeps relevant details about the transactions that intersect the path from root to node N. However, in mIHAUI-Tree, the AUUB value is only stored on the leaf nodes. The mIHAUI-Tree begins with empty root node and transactions are added in the alphabetical order of items. Then, a restructuring technique, based on the path-adjusting method (Kim & Yun Reference Kim and Yun2017), is applied to enhance the node-sharing effect of the tree. The algorithm employs merging techniques and dataset projection to efficiently identify candidate itemsets. A database sorting method is utilized to find the similar transactions in a linear time. It sorts the transaction in a lexicographic order in backwards way. Then, the projected dataset is extracted to combine the similar transactions by performing a single dataset scan.
Figure 3 shows the construction process of mIHAUI-Tree. In Step 1, the original database is taken that consists of seven transactions and a profit table is also taken with profit values of items. In Step 2, the utility of each transaction is considered according to their appearance order one by one and inserted into the header table. Then, the mIHAUI-Tree is constructed based on the alphabetic order of items
![]() $(A\gt B\gt C\gt D\gt E\gt F)$
. As the transaction utility is not appeared in the increasing order. To make in the ascending order, the items are rearranged
$(A\gt B\gt C\gt D\gt E\gt F)$
. As the transaction utility is not appeared in the increasing order. To make in the ascending order, the items are rearranged
![]() $(A\gt C\gt B\gt D\gt E\gt F)$
. In Step 3, the mIHAUI-Tree is restructured based on the header table. In Step 4, the database is updated by modifying the transactions
$(A\gt C\gt B\gt D\gt E\gt F)$
. In Step 3, the mIHAUI-Tree is restructured based on the header table. In Step 4, the database is updated by modifying the transactions
![]() $T_1,T_2,T_3$
in the original database. In the final Step, the mIHAUI-Tree is built from the restructured mIHAUI-Tree (Step 3) and updated database (Step 4). It has been observed that FIMHAUI performs better than IMHAUI (Kim & Yun, Reference Kim and Yun2017) concerning run-time under various
$T_1,T_2,T_3$
in the original database. In the final Step, the mIHAUI-Tree is built from the restructured mIHAUI-Tree (Step 3) and updated database (Step 4). It has been observed that FIMHAUI performs better than IMHAUI (Kim & Yun, Reference Kim and Yun2017) concerning run-time under various
![]() $min\_util$
thresholds from the dense and sparse datasets. However, it relies on the traditional AUUB model, thus required a validation phase to identify intended HAUIs.
$min\_util$
thresholds from the dense and sparse datasets. However, it relies on the traditional AUUB model, thus required a validation phase to identify intended HAUIs.
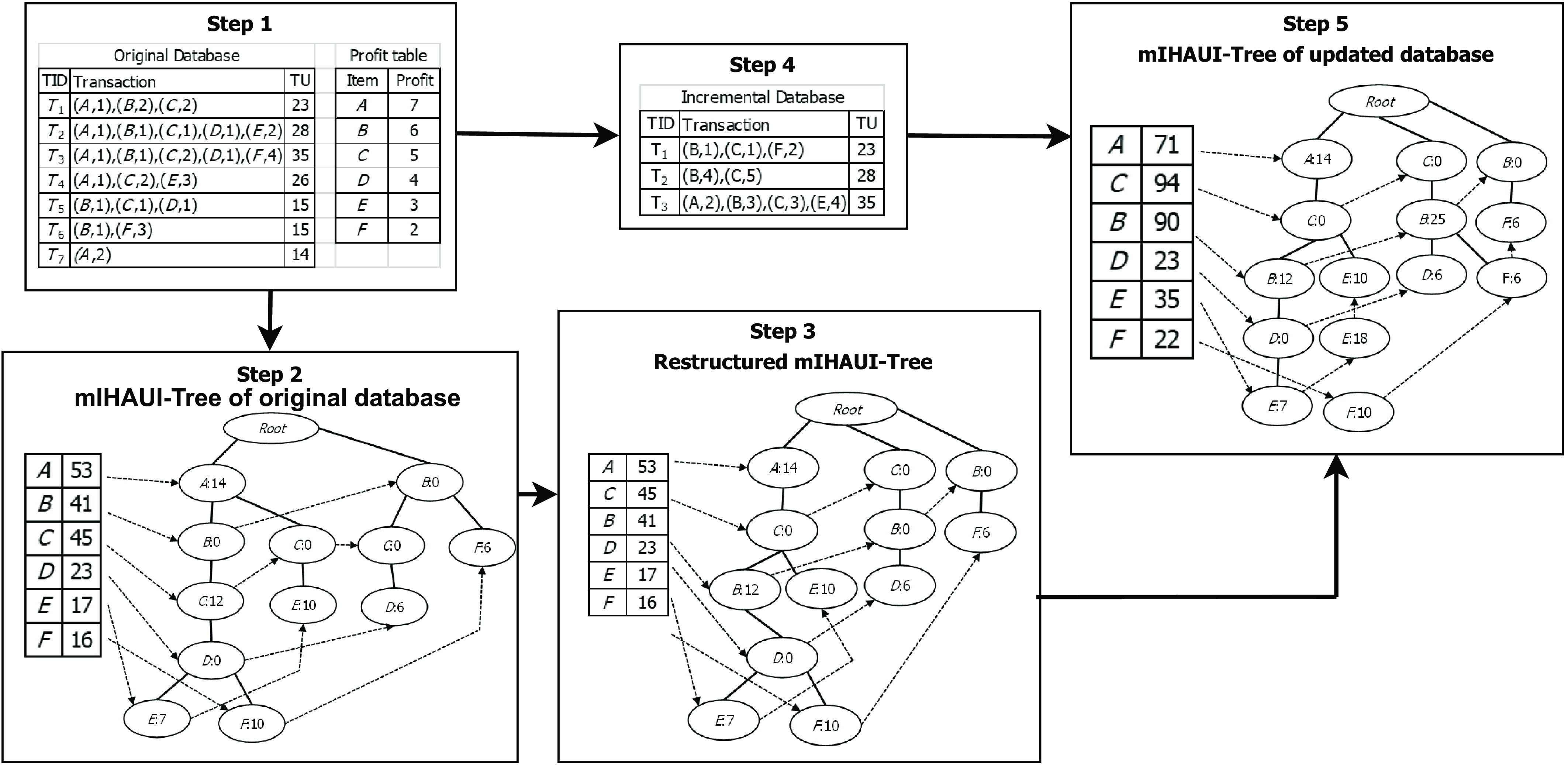
Figure 3. Construction process of mIHAUI-Tree
MR-INCHUSP: MapReduce is a distributed framework that follows a divide-and-conquer approach to deal with big data. A two-phase approach, named MR-INCSPM (MapReduce solution for Incremental Mining of Sequential Pattern Mining) (Saleti & Subramanyam, Reference Saleti and Subramanyam2019), is proposed to extract sequential patterns without the need for a complete dataset rescan. However, it does not include utility value, leading to failure to generate high profits in dynamic datasets. To address this limitation, Saleti (Reference Saleti2021) developed three-phase method, called MR-INCHUSP (INcremental algorithm for HUSP mining using MapReduce paradigm), the first of its kind, to find HUSPs from incremental datasets. MR-INCHUSP employs backward mining method, BSPinc (Backward mining for Incremental Sequential Patterns) (Lin et al., Reference Lin, Hsueh and Chan2009), to efficiently utilize the information obtained during previous mining processes. During the backward mining process, a new sequence is created by incorporating the item as a prefix to the existing pattern.
Two new data structures, namely RUTree (Reverse Utility Tree) and CURMAP (Co-occurrence Utility Reverse MAP), are proposed. RUTree quickly discovers utility information, thereby significantly minimizing the re-computation cost. On the other hand, CURMAP, based on the CMAP (Co-occurrence MAP) data structure (Fournier Viger et al., Reference Fournier Viger, Gomariz, Campos and Thomas2014), significantly minimizes the number of unpromising candidate sequences present in the input dataset. A pruning strategy, named TSU (Tight Sequence Utility), is adopted from Wang and Huang (Reference Wang and Huang2018) to extract HUSP from the incremental datasets. TSU represents the tighter upper-bound of sequence utility. A novel upper-bound, named CUUB (Co-occurrence Utility Upper-Bound), is designed to reduce the number of sequences prior to the utility computation. The novel sequence extension rules are further developed to enhance the mining performance.
MR-INCHUSP includes three MapReduce phases: (1) During the first phase, global utility and promising itemsets are kept in the distributed cache. (2) During the second phase, CURMAP structure is designed to generate candidates by using the backward extension approach. It also constructs RUTree nodes to efficiently generate all the local HUSPs using BSPinc approach. In RUTree, a sequence can manifest as either be itemset-extension or sequence-extension. An itemset-extension is created by prefixing an item to the initial itemset of the parent sequence. A sequence-extension relies on the backward extension method. The CURMAP structure based on the backward extension generates less number of candidate sequences. (3) During the third phase, the algorithm extracts the complete set of global HUSPs. Experiments proved the effectiveness of MR-INCHUSP as contrast to the non-incremental methods BigHUSP (Zihayat et al., Reference Zihayat, Hut, An and Hut2016) and HUSP-Spark (Srivastava et al., Reference Srivastava, Lin, Zhang and Li2021) concerning the run-time, memory consumption, and scalability. MR-INCHUSP takes less memory because of the inclusion of CURMAP structure. The efficient pruning strategies and sequence extension rules lead to significant scalability results.
Discussion
The projection-based iHUIM algorithms extract the useful, high utility information of itemsets from incremental datasets. These algorithms outperform the two-phase iHUIM and pattern-growth-based iHUIM algorithms concerning dataset scans, number of processed candidates, execution time, and scalability. However, they face several challenges: (1) Maintaining additional memory to store information about candidates’ pattern trees. (2) Requiring validation of candidates, which consumes a significant amount of time. (3) Applicable only for incremental datasets, while in real-world scenarios, transactions can also be removed or changed. (4) Designed to work with positive utility only, even though transactions in the business world can also have negative utility. The overview of the projection-based iHUIM algorithm is shown in Table 14, which includes details about data structures, output mining, pruning strategies, benchmark datasets, and base algorithms used in these approaches. Table 15 provides an overview of the theoretical aspects of projection-based HUIM methods when applied to incremental datasets.
Table 14. Characteristics and theoretical aspects of the projection-based approaches
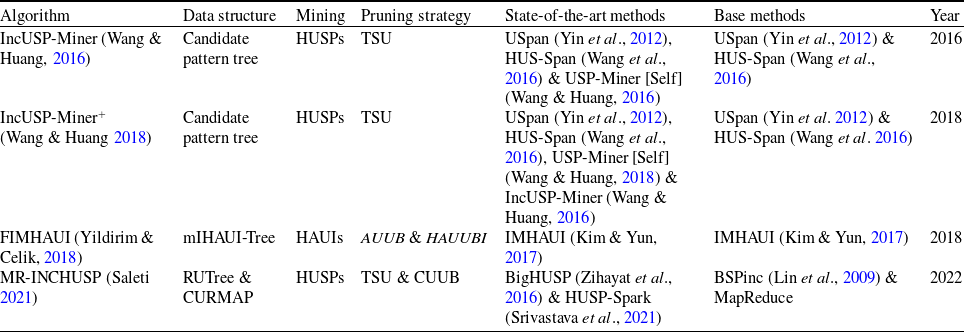
Table 15. Pros and cons of the projection-based approaches

3.4 Utility-list-based approaches
The projection-based iHUIM algorithms suffer from high memory overhead and more re-computational cost. Furthermore, candidate verification is performed to identify the low or high utility itemsets. Subsequently, the low-utility itemsets are pruned from the search space, which is a time-consuming process. To address these challenges, the utility-list-based iHUIM algorithms (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015; Yun et al., Reference Yun, Ryang, Lee and Fujita2017; Yun et al., Reference Yun, Nam, Lee and Yoon2019; Liu et al., Reference Liu, Ju, Zhang, Fung, Yang and Yu2019; Pushp & Chand, . 2021) are proposed. These algorithms aim to efficiently extract highly profitable itemsets from incremental datasets without the need for level-wise candidate generation. These algorithms utilize efficient data structures to reflect the newly added data using a restructuring technique. In this sub-section, we present utility-list-based and similar structure-based iHUIM algorithms and discuss their advantages and disadvantages along with a brief analysis.
HUI-list-INS: The traditional HUIM algorithms with transaction insertion (Ahmed et al. Reference Ahmed, Tanbeer, Jeong and Lee2009a; Lin et al., Reference Lin, Lan and Hong2012; Lin et al., Reference Lin, Gan, Hong and Pan2014) are designed to extract HUIs from incremental datasets. However, they require re-scanning the original dataset to maintain and update the HUIs. Furthermore, these level-wise-based approaches have a critical issue of the combinatorial explosion. To address these challenges, Lin et al. (Reference Lin, Gan, Hong and Pan2014) proposed a memory-based incremental approach, named HUI-list-INS to reduce the computation without the need for candidate generation. This approach is based on the HUI-Miner algorithm (Liu & Qu, Reference Liu and Qu2012) to construct the utility-list structures to mine HUIs with transaction insertion. It employs an EUCS (Estimated Utility Co-occurrence Structure) to enhance its efficiency. The EUCS structure keeps the relationship between 2-itemsets, leading to speed-up the computational speed. It is also used to prune the unpromising candidates, resulting in reduced search space for mining HUIs.
The utility-list structure is constructed prior to adding transactions to the original dataset. It stores both high transactional utility itemsets HTWUIs and the itemsets that are not high TWU itemsets from the original dataset. This allows for skipping the re-scanning of the dataset when new transactions are inserted. The utility-list structure efficiently stores the related information in a compressed way from the original dataset. The itemsets are stored in the increasing order of their TWU value using a depth-first manner. The enumeration tree and connections between 2-itemsets are utilized to accelerate computations. The pruning strategy, named EUCP (Estimated Utility Co-occurrence Pruning), is utilized to further maintain the relationship of 2-itemsets. This results the reduction of extended itemsets with lower utility without the need to reconstruct the utility-list structure.
HUI-list-INS shows high performance compared to Two-phase (Liu et al., Reference Liu and Liao2005) and the state-of-the-art FHM (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014) in the batch mode and other incremental approaches, namely FUP-HUI-INS (Lin et al., Reference Lin, Lan and Hong2012) and PRE-HUI-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) in the dynamic mode, with regards to the run-time, memory usage, and the generated patterns on the benchmark datasets. The proposed approach uses the pruning strategy to eliminate the unpromising candidates at the early stage, leading to high computational speed. It is observed that the proposed algorithm finds HUIs in an incremental dataset without the need to generate-and-test candidates in a level-wise way. However, the proposed algorithm requires a significant amount of memory in some cases because it stores more itemsets for the subsequent incremental datasets.
EIHI: The existing incremental algorithms (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a; Lin et al., Reference Lin, Gan, Hong and Pan2014) are very costly in terms of execution time. To address this issue, Fournier-Viger et al. (Reference Fournier-Viger, Lin, Gueniche and Barhate2015) proposed an approach named EIHI (Efficient Increment high utility Itemset miner) to extract HUIs from the incremental datasets. The main procedure works in the batches of the transactions, inspired by the FHM approach (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014). It receives input from the dataset along with
![]() $min\_util$
threshold and utility values. The proposed approach proceeds to scan the dataset to compute the TWU of each item. It subsequently recognizes itemsets having TWU, which is no less than
$min\_util$
threshold and utility values. The proposed approach proceeds to scan the dataset to compute the TWU of each item. It subsequently recognizes itemsets having TWU, which is no less than
![]() $min\_util$
. The dataset is scanned to calculate the TWU values for these items and sorted in ascending order according to their TWU values. The dataset is again scanned, and the items within transactions are reorganized according to the increasing order of their TWU values. The utility-list of each item of an itemset is constructed and this creates the EUCS structure (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014). The depth first search method is used to find the itemsets in a recursive manner and explores the search space to discover the complete set of HUIs.
$min\_util$
. The dataset is scanned to calculate the TWU values for these items and sorted in ascending order according to their TWU values. The dataset is again scanned, and the items within transactions are reorganized according to the increasing order of their TWU values. The utility-list of each item of an itemset is constructed and this creates the EUCS structure (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014). The depth first search method is used to find the itemsets in a recursive manner and explores the search space to discover the complete set of HUIs.
The proposed algorithm stores all itemsets in a trie-like structure called HUI-trie. In this structure, each itemset is represented by a path that originates from the root node and terminates at an intermediate or leaf node. Moreover, each node representing the last item of an itemset is associated with the utility of that itemset. Figure 4 shows the construction process of HUI-trie structure. Firstly, the original database consists of five transactions and seven items is taken as an input. Then, the user-defined
![]() $min\_util$
threshold is set to 30. Secondly, the complete set of HUIs are found. Finally, the HUI-tree structure is constructed where each item of a HUI is stored alphabetically. The searching of an item in a HUI-trie structure is efficient because it requires to visit only one path of the tree. The binary search method is used at each node when searching for the child node corresponding to the given item. EIHI is around two orders of magnitude faster as compared to the state-of-the-art algorithm HUI-list-INS (Lin et al. Reference Lin, Gan, Hong and Pan2014) with regards to the run-time under various
$min\_util$
threshold is set to 30. Secondly, the complete set of HUIs are found. Finally, the HUI-tree structure is constructed where each item of a HUI is stored alphabetically. The searching of an item in a HUI-trie structure is efficient because it requires to visit only one path of the tree. The binary search method is used at each node when searching for the child node corresponding to the given item. EIHI is around two orders of magnitude faster as compared to the state-of-the-art algorithm HUI-list-INS (Lin et al. Reference Lin, Gan, Hong and Pan2014) with regards to the run-time under various
![]() $min\_util$
thresholds. It is observed that EIHI exhibits greater scalability when it comes to handling a higher number of updates. However, it faces significant challenges in maintaining patterns within dynamic datasets.
$min\_util$
thresholds. It is observed that EIHI exhibits greater scalability when it comes to handling a higher number of updates. However, it faces significant challenges in maintaining patterns within dynamic datasets.
Figure 4. Construction process of HUI-trie structure
LIHUP: The traditional iHUIM algorithms suffer from excessive candidate generation and multiple dataset scans. These challenges have been effectively mitigated through utility-list-based methods (Lin et al. Reference Lin, Gan, Hong and Pan2014; Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015). These approaches enable the extraction of HUIs from the incremental dataset without the need for candidate generation. However, they are required to scan the dataset twice to determine the optimal order of TWU values, resulting in a time-consuming process. Yun et al. (Reference Yun, Ryang, Lee and Fujita2017) proposed an approach, named LIHUP, to mine HUIs from incremental datasets with just a single dataset scan. It is based on a utility-list structure that does not involve candidate generation. LIHUP solves the following challenges of the existing utility-list-based iHUIM approaches (Lin et al. Reference Lin, Gan, Hong and Pan2014; Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015): (1) The concept of overestimation (Liu et al., Reference Liu and Liao2005) causes performance degradation. (2) The approaches (Liu & Qu Reference Liu and Qu2012; Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014), based on utility-list structure, scan the dataset twice to mine the HUIs without generating candidates.
The proposed algorithm first builds the global-list data structure during a single dataset scan. It efficiently acquires the same pattern information by reorganizing the existing data structure according to the optimal sorting order, all without the need for additional database scans. If any new transaction is included in the previous database, the proposed algorithm scans the included data once, updates and restructures the data structure as per the TWU ascending order. Then, it mines all HUIs that satisfies the
![]() $min\_util$
threshold recursively from the data structure without candidate generation. The global-list structure includes details about the utility of candidate patterns, which are organized and maintained within a set of utility-lists based on the ascending order of the TWU value. After the construction and restructure of the global data structure, the proposed algorithm calculates the minimum utility by multiplying the total utility and user-defined threshold. It performs a series of operations to find the promising candidate pattern from the mining process. These series of operations are based on HUI-Miner (Liu & Qu, Reference Liu and Qu2012) with utility-lists.
$min\_util$
threshold recursively from the data structure without candidate generation. The global-list structure includes details about the utility of candidate patterns, which are organized and maintained within a set of utility-lists based on the ascending order of the TWU value. After the construction and restructure of the global data structure, the proposed algorithm calculates the minimum utility by multiplying the total utility and user-defined threshold. It performs a series of operations to find the promising candidate pattern from the mining process. These series of operations are based on HUI-Miner (Liu & Qu, Reference Liu and Qu2012) with utility-lists.
The utility-list is generated for each candidate itemset
![]() $\{i_p\}$
with a length of 1. Subsequently, the algorithm performs recursive mining of all HUIs, eliminating the need for candidates generation. The utility-list consists of entries that have the utility of patterns in the transactions containing
$\{i_p\}$
with a length of 1. Subsequently, the algorithm performs recursive mining of all HUIs, eliminating the need for candidates generation. The utility-list consists of entries that have the utility of patterns in the transactions containing
![]() $\{i_p\}$
. Consequently, the number of entries within the utility-list for
$\{i_p\}$
. Consequently, the number of entries within the utility-list for
![]() $\{i_p\}$
is similar to the number of transactions consisting of
$\{i_p\}$
is similar to the number of transactions consisting of
![]() $\{i_p\}$
in the given dataset. For each transaction,
$\{i_p\}$
in the given dataset. For each transaction,
![]() $T_d$
containing
$T_d$
containing
![]() $\{i_p\}$
, an entry having details of the utility of
$\{i_p\}$
, an entry having details of the utility of
![]() $\{i_p\}$
exists in the following three elements: (1) Transaction TD (TID) of the
$\{i_p\}$
exists in the following three elements: (1) Transaction TD (TID) of the
![]() $T_d$
. (2)
$T_d$
. (2)
![]() $T_d$
having
$T_d$
having
![]() $\{i_p\}$
pattern utility represented as
$\{i_p\}$
pattern utility represented as
![]() $u(i_p,T_d)$
. (3) Remaining utility in the
$u(i_p,T_d)$
. (3) Remaining utility in the
![]() $T_d$
after
$T_d$
after
![]() $\{i_p\}$
represented as
$\{i_p\}$
represented as
![]() $ru(i_p,T_d)$
. The experimental results showed that the proposed LIHUP algorithm works better than the existing state-of-the-art methods, IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) and HUPID (Yun & Ryang Reference Yun and Ryang2014), with regard to the run-time, memory usage, and scalability for the real and synthetic datasets.
$ru(i_p,T_d)$
. The experimental results showed that the proposed LIHUP algorithm works better than the existing state-of-the-art methods, IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) and HUPID (Yun & Ryang Reference Yun and Ryang2014), with regard to the run-time, memory usage, and scalability for the real and synthetic datasets.
IIHUM: Tree-based iHUIM algorithms (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a; Yun & Ryang, Reference Yun and Ryang2014) are designed to mine HUIs with less number of candidates and dataset scans. However, these algorithms suffer from high computation overhead because of the unpromising candidate generation in the mining process. Moreover, these approaches are not suitable for the large-scale incremental data because this is required to set the threshold value that may result into the generation of more number of candidate patterns. Furthermore, these tree-based approaches require two database scans to restructure the tree data structure which is a time-consuming process. To address these challenges, Yun et al. (Reference Yun, Nam, Lee and Yoon2019) proposed an efficient index-list based algorithm named IIHUM (Indexed-list-based Incremental High Utility pattern Mining) to effectively mine HUIs without the need of candidate generation. It uses the re-construct technique to accommodate incremental data with just a single dataset scan. The original dataset is first scanned to build the global-list structure. The list structures are then reorganized based on the ascending order of TWU, and the index information is appropriately reset. The proposed method reflects the new transactions data into the data structures constructed previously without the need to rescan the earlier processed data. This involves the recalculation of TWU values for items to construct the overall global structure. The updated data structures are then reorganized based on the modified TWU increasing order. Subsequently, the user specifies a threshold value, which is used to obtain the results for HUIs for the current incremental dataset. The proposed approach recursively generates the conditional list data structures from global data structures. Once all these recursive steps are completed, the user gets the complete set of HUIs without the need to verify candidates.
A novel data structure, named IIU-List (Incremental Indexed Utility-List), is designed to store the global data structures in the proposed algorithm. A global IIU-Lists is associated with each item in the original database. These global IIU-Lists are then restructured according to the ascending order of TWU, ensuring efficient extraction of HUIs from incremental data. If any new transaction is added to the original database, the proposed algorithm reads only added part and then reflects back into the previously constructed global IIU-Lists. The Remaining Utility values are accurately calculated for the computation of upper-bounds for the IIU-Lists to assess the validity of the respective patterns. The restructuring is performed to get the utility information of IIU-Lists whenever new transactions are added. Failure to update the remaining utility values during the restructuring of the IIU-List can lead to fatal pattern losses. The current global IIU-Lists are restructured when a request for the mining process comes, then the proposed algorithm obtains all the HUIs that satisfy the given threshold from the IIU-List data structure. As the data increases progressively, the low utlity patterns become HUIs and vice-versa. Furthermore, the
![]() $min\_util$
threshold may be changed by the users. Therefore, the proposed algorithm maintains and sorts all the items in the updated incremental database that are stored in the global IIU-Lists regardless of their TWU values.
$min\_util$
threshold may be changed by the users. Therefore, the proposed algorithm maintains and sorts all the items in the updated incremental database that are stored in the global IIU-Lists regardless of their TWU values.
The IIHUM algorithm performs well, compared to the state-of-the-art methods FUP-HU (Lin et al., Reference Lin, Lan and Hong2012), HUPID (Yun & Ryang, Reference Yun and Ryang2014) and LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017) with regards to the run-time, memory usage, and scalability for the various
![]() $min\_util$
thresholds. IIHUM gives a guarantee of stable memory usage as it does not perform any operations to generate the candidates and to verify them. IIHUM is highly efficient in extracting HUIs on non-binary incremental datasets, because of the indexed-list data structures. The proposed algorithm generates IIU-Lists data structures more efficiently during the recursive process and extracts no candidate patterns, leading to quickly extraction of HUIs.
$min\_util$
thresholds. IIHUM gives a guarantee of stable memory usage as it does not perform any operations to generate the candidates and to verify them. IIHUM is highly efficient in extracting HUIs on non-binary incremental datasets, because of the indexed-list data structures. The proposed algorithm generates IIU-Lists data structures more efficiently during the recursive process and extracts no candidate patterns, leading to quickly extraction of HUIs.
Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
: Two-phase iHUIM algorithms suffer from excessive candidate generation that leads to poor efficiency and scalability issues. On the other hand, one-phase incremental HUIM algorithms (Lin et al., Reference Lin, Gan, Hong and Pan2014; Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015; Yun et al., Reference Yun, Ryang, Lee and Fujita2017) perform costly join operations on the vertical data structure (Liu & Qu, Reference Liu and Qu2012; Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014), which are time-consuming and create bottlenecks in mining efficiency. To resolve these challenges, Liu et al. (Reference Liu, Ju, Zhang, Fung, Yang and Yu2019) proposed an approach named Id
$+$
: Two-phase iHUIM algorithms suffer from excessive candidate generation that leads to poor efficiency and scalability issues. On the other hand, one-phase incremental HUIM algorithms (Lin et al., Reference Lin, Gan, Hong and Pan2014; Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015; Yun et al., Reference Yun, Ryang, Lee and Fujita2017) perform costly join operations on the vertical data structure (Liu & Qu, Reference Liu and Qu2012; Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014), which are time-consuming and create bottlenecks in mining efficiency. To resolve these challenges, Liu et al. (Reference Liu, Ju, Zhang, Fung, Yang and Yu2019) proposed an approach named Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
(Incremental Direct Discovery of High Utility Patterns), based on the one-phase paradigm d
$+$
(Incremental Direct Discovery of High Utility Patterns), based on the one-phase paradigm d
![]() $^2$
HUP (Liu et al., Reference Liu, Wang and Fung2016) to mine for incremental HUI mining. The algorithm proposed four pruning strategies, namely relevance-based pruning, upper-bound-based pruning, absence-based pruning, and legacy-based pruning. Relevance-based pruning strategy eliminates the redundant items of a pattern when exploring the prefix extensions of that pattern. The utility of any prefix extension of a pattern is no more than the sum of the utility of the full prefix extension of that pattern with respect to every transaction in that transaction set of the database. This strategy suggests speedily recognizing all of the extensions of those patterns that are not new to the transactions, are pruned. Upper-bound-based pruning strategy prunes the prefix extensions of a pattern that do not belong to the HUIs. Absence-based pruning strategy prunes all the prefix extensions of a pattern that are absent in the incremental databases. This strategy efficiently determines whether a pattern is a HUIs in the original database or not, resulting in solving the scalability issues. Legacy-based pruning strategy quickly finds the patterns which are not in incremental databases and hence can be pruned.
$^2$
HUP (Liu et al., Reference Liu, Wang and Fung2016) to mine for incremental HUI mining. The algorithm proposed four pruning strategies, namely relevance-based pruning, upper-bound-based pruning, absence-based pruning, and legacy-based pruning. Relevance-based pruning strategy eliminates the redundant items of a pattern when exploring the prefix extensions of that pattern. The utility of any prefix extension of a pattern is no more than the sum of the utility of the full prefix extension of that pattern with respect to every transaction in that transaction set of the database. This strategy suggests speedily recognizing all of the extensions of those patterns that are not new to the transactions, are pruned. Upper-bound-based pruning strategy prunes the prefix extensions of a pattern that do not belong to the HUIs. Absence-based pruning strategy prunes all the prefix extensions of a pattern that are absent in the incremental databases. This strategy efficiently determines whether a pattern is a HUIs in the original database or not, resulting in solving the scalability issues. Legacy-based pruning strategy quickly finds the patterns which are not in incremental databases and hence can be pruned.
The procedure adopts hash tables to quickly merge the transactions because the hash tables organize all the utility-lists in such a way that the transactions consist the identical itemsets that are found in constant time and merge them into one utility-list. A novel data structure named niCAUL (newly improved Chain of Accurate utility-lists) is designed to efficiently update the dynamic dataset. The proposed niCAUL data structure improves CAUL(Chain of Accurate utility-lists) (Liu et al., Reference Liu, Wang and Fung2012; Liu et al., Reference Liu, Wang and Fung2016) for quickly computing the utility-lists by employing the hash tables to significantly merge the identical transactions and restoration of niCAUL after pseudo projection. The basic scheme revolves around enumerating patterns through prefix extensions of other patterns. These enumerated patterns are evaluated using upper-bound-based pruning, leading to a significant reduction in computational effort. This is useful for efficiently determining the utility of each enumerated pattern and identifying HUIs. In order to avoid redundant pattern enumeration, an imposed ordering is presented. This ordering enumerates the patterns that are of length 1 as the prefix extensions of the empty pattern (represented as
![]() $\{\}$
), patterns of length 2 as the prefix extensions of length 1 patterns, and so forth. Pattern enumeration follows a depth-first approach through prefix extensions. The niCAUL data structure is used to represent transaction sets that are supported by enumerated patterns, leading to effective pruning of the search space. This indicates that Id
$\{\}$
), patterns of length 2 as the prefix extensions of length 1 patterns, and so forth. Pattern enumeration follows a depth-first approach through prefix extensions. The niCAUL data structure is used to represent transaction sets that are supported by enumerated patterns, leading to effective pruning of the search space. This indicates that Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
visits significantly fewer candidates compared to EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015), HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014), and LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017). This is because niCAUI efficiently computes and quickly updates the dynamic datasets. This is accomplished through the merging of identical transactions. Id
$+$
visits significantly fewer candidates compared to EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015), HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014), and LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017). This is because niCAUI efficiently computes and quickly updates the dynamic datasets. This is accomplished through the merging of identical transactions. Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
exhibits the lowest memory consumption due to the utilization of pseudo-projection for computing the transaction set for each enumerated pattern.
$+$
exhibits the lowest memory consumption due to the utilization of pseudo-projection for computing the transaction set for each enumerated pattern.
The experimental results showed that Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
performs much better than the EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015), HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014), and LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017) algorithms with respect to the execution time, memory consumption, varying IR (Insertion Rate), number of visited candidates, and scalability on the benchmark datasets. The proposed algorithm is up to 2 orders of magnitude faster than the benchmark approached on the dense and sparse datasets. It is 3–4 orders of magnitude more efficient than compared algorithms. The proposed algorithm is 2 times faster as compared to the NoAbsence strategy, while it is up to 2–6 times faster when compared with NoLegancy strategy. It shows that Id
$+$
performs much better than the EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015), HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014), and LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017) algorithms with respect to the execution time, memory consumption, varying IR (Insertion Rate), number of visited candidates, and scalability on the benchmark datasets. The proposed algorithm is up to 2 orders of magnitude faster than the benchmark approached on the dense and sparse datasets. It is 3–4 orders of magnitude more efficient than compared algorithms. The proposed algorithm is 2 times faster as compared to the NoAbsence strategy, while it is up to 2–6 times faster when compared with NoLegancy strategy. It shows that Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
is the most efficient and scalable algorithm. This observation is based on the fact that scalability and efficiency are improved if legacy patterns are determined by contrasting the utilities rather than searching for saved patterns.
$+$
is the most efficient and scalable algorithm. This observation is based on the fact that scalability and efficiency are improved if legacy patterns are determined by contrasting the utilities rather than searching for saved patterns.
IncCHUI: In the literature, various CHUIM (Closed HUIM) algorithms (Wu et al., Reference Wu, Fournier-Viger, Gu and Tseng2015; Fournier-Viger et al., Reference Fournier-Viger, Zida, Lin, Wu and Tseng2016; Dam et al., Reference Dam, Li, Fournier-Viger and Duong2018) are designed to efficiently extract CHUIs (Closed HUIs) from transactional datasets. However, these algorithms cannot deal with incremental datasets where new transactions are inserted in the original dataset. To solve this issue, Dam et al., (Reference Dam, Ramampiaro, Nørvåg and Duong2019) designed an approach named IncCHUI (Incremental Closed high utility Itemset miner), the first of its kind, to extract CHUIs from incremental datasets. The authors presented an incremental utility-list structure based on the traditional utility-list structure (Liu & Qu, Reference Liu and Qu2012). This list structure consists of two traditional utility-lists that store information about itemset with respect to the original database and an updated database. The incremental utility-list of an itemset is constructed by intersecting the incremental utility-list of its subsets without the database scan. Therefore, it requires just one dataset scan to keep the relevant details of every single item present in the updated dataset. This procedure performs the operations in the linear time, resulting in a fast pruning process.
The proposed approach is based on the modified traditional utility-list. The updated dataset processes only those transactions that are newly inserted in the mining process. Furthermore, the proposed method implements early pruning of itemsets that haven’t been updated in the dataset. Another method is presented to ensure the integrity of lists by reconstructing them when a new transactions are inserted. The utility-list of the original dataset and the added transactions are integrated to form a single utility-list after each mining step. This list is subsequently utilized in another execution process for the next incremented dataset. The proposed algorithm effectively mines CHUIs from incremental datasets by using a utility-list structure. It scans the original dataset or modified parts only once to generate a list of single items. A global data structure, named global list is built that contains a set of incremental utility-lists where each list stores information of one single item in the incremental database. A CHT (Closed Hash Table) is used to store the discovered CHUIs. During the mining process, when a CHUI of an itemset P is obtained on the incremental dataset, the algorithm initially checks whether the itemset is already present in the CHT or not. If the itemset P is already in the CHT, then itemset P is obtained, and the algorithm proceeds to the original dataset. Subsequently, both its support and utility are updated. Conversely, if itemset P is not present in the CHT, it is inserted as a new CHUI.
The proposed algorithm outperforms existing methods (Lin et al., Reference Lin, Gan, Hong and Pan2014; Yun et al., Reference Yun, Ryang, Lee and Fujita2017) for several reasons: (1) The HUI-list-INS algorithm (Lin et al., Reference Lin, Gan, Hong and Pan2014) used the existing utility-list and constructed utility-lists of single items separately. The proposed utility-list structure consists of two parts: one is for the original dataset, and the other for the newly inserted transactions. (2) The proposed algorithm constructs the utility-list with a single dataset scan, whereas HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) required to scan the dataset twice to build its utility-list. (3) The proposed algorithm employs the fast and incremental utility-list construction procedure, contrasting with HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) and IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) which followed older and more costly construction methods for utility-lists. (4) The proposed method uses the modified utility-list to prune the candidates early. (5) A hash table is introduced to modify or add unique CHUIs in the mining process. The proposed method is more efficient than that of EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015). The proposed algorithm maintains the rank order of single items to preserve the HUI-tree in the original dataset. It uses the following three stages: (1) During the first stage, the original dataset and the newly added transactions are scanned. If required, the global list of one item and the closed hash table CHT are initialized. Subsequently, it establishes the overall order of the items. (2) During the second stage, the global list is stored according to the updated item order derived from the first stage. Subsequently, the list is validated through the appropriate procedure. (3) During the final stage, a recursive search technique is performed to effectively extract CHUIs. The resulting CHUIs are then appropriately stored in a closed table, along with the corresponding maintenance rule. IncCHUI outperforms the state-of-the-art batch algorithms, including CHUI-Miner (Wu et al. Reference Wu, Fournier-Viger, Gu and Tseng2015), CLS-Miner (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2018), and EFIM-Closed (Fournier-Viger et al., Reference Fournier-Viger, Zida, Lin, Wu and Tseng2016), in terms of runtime,
![]() $min\_util$
value, the number of added transactions, and scalability for both real and synthetic datasets. However, it consumes a lot of memory as compared to benchmark algorithms on some datasets.
$min\_util$
value, the number of added transactions, and scalability for both real and synthetic datasets. However, it consumes a lot of memory as compared to benchmark algorithms on some datasets.
E-HUIM: The iHUIM algorithms (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a; Lin et al., Reference Lin, Lan and Hong2012; Lin et al., Reference Lin, Gan, Hong and Pan2014) are proposed to extract HUIs from incremental datasets. However, the original dataset needs to be re-scanned to maintain and update the HUIs. Furthermore, these Apriori-based approaches suffer from a large number of candidate generations and multiple dataset scans. To address these issues, Pushp and Chand ( 2021) proposed an efficient algorithm named E-HUIM (Extended HUI-Miner) for mining HUIs from incremental datasets. The algorithm first scans the dataset to identify the single items that have high utility by constructing the utility-lists (Liu & Qu, Reference Liu and Qu2012) and EUCS data structure (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014). Each utility-list consists of the following three things for the transaction under consideration: (1) TID (Transaction ID), (2) iutil (Utility of itemset), and (3) rutil (Remaining utility). EUCS is constructed using an upper triangular matrix containing TWU values for itemsets.
The proposed approach takes the extensions of the itemsets that are promising candidates for HUIs mining. If the sum of the utility values of an itemset is no less than
![]() $min\_util$
, then it is considered as HUI and inserted into a trie-structure (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015). The itemset is further searched for the extensions only if the sum of iutil and rutil is no less than
$min\_util$
, then it is considered as HUI and inserted into a trie-structure (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015). The itemset is further searched for the extensions only if the sum of iutil and rutil is no less than
![]() $min\_util$
. It uses EUCS data structure to ensure that only those pairs of itemsets are considered for the extensions that have TWU values more than
$min\_util$
. It uses EUCS data structure to ensure that only those pairs of itemsets are considered for the extensions that have TWU values more than
![]() $min\_util$
. The EUCS data structure is based on the property which states that if the TWU of an itemset is less than
$min\_util$
. The EUCS data structure is based on the property which states that if the TWU of an itemset is less than
![]() $min\_util$
, then that itemset and its super-sets are to low utility itemsets. However, these itemsets may lead to overestimation and loss of accuracy in the final results. Therefore, a novel pruning technique is designed to prune the unpromising candidates to achieve optimization and improved mining efficiency. It adds the itemset to the extensions if and only if its utility is no less than
$min\_util$
, then that itemset and its super-sets are to low utility itemsets. However, these itemsets may lead to overestimation and loss of accuracy in the final results. Therefore, a novel pruning technique is designed to prune the unpromising candidates to achieve optimization and improved mining efficiency. It adds the itemset to the extensions if and only if its utility is no less than
![]() $min\_util$
. Moreover, the utility value is directly obtained from the utility-list of the itemset, resulting in the improved mining process without extra memory usage and run-time. E-HUIM utilizes the EIHI algorithm (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) to handle incremental datasets. The experimental results showed the effectiveness of the proposed algorithm compared to the state-of-the-art EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) method in terms of execution time, memory usage, number of processed transactions, and new HUI count from incremental datasets. The proposed algorithm demonstrated a substantial 60 percent improvement over the EIHI approach.
$min\_util$
. Moreover, the utility value is directly obtained from the utility-list of the itemset, resulting in the improved mining process without extra memory usage and run-time. E-HUIM utilizes the EIHI algorithm (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) to handle incremental datasets. The experimental results showed the effectiveness of the proposed algorithm compared to the state-of-the-art EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) method in terms of execution time, memory usage, number of processed transactions, and new HUI count from incremental datasets. The proposed algorithm demonstrated a substantial 60 percent improvement over the EIHI approach.
Table 16. Characteristics and theoretical aspects of the utility-list-based approaches
Table 17. Pros and cons of the utility-list-based approaches

Discussion
We have discussed the utility-list-based iHUIM algorithms to find the highly profitable itemsets in expanding datasets. However, several issues need to be addressed: (1) Additional utility-lists are needed to incorporate the added data into the original datasets, incurring high costs. (2) Variations in the performance of the proposed algorithms can occur as the dataset size changes. (3) These algorithms work only on the incremental datasets; however, there are lots of issues that occur when the transactions are deleted or modified in a dynamic environment. Table 16 gives the overview of utility-list-based iHUIM algorithms, while Table 17 presents the theoretical aspects of utility-list-based HUIM algorithms from the incremental datasets.
3.5 Pre-large-based approaches
The utility-list-based iHUIM algorithms perform better than the two-phase iHUIM, pattern-growth-based iHUIM, and projection-based iHUIM approaches concerning the number of dataset scans, efficient data structures, pruning strategies, number of processed candidates, and scalability in incremental environments. Nevertheless, the performance of the proposed algorithms exhibits substantial variability as the dataset size changes. Furthermore, when new data is added into the original dataset, the updated portion of the dataset needs to be scanned each time, resulting in significant time consumption. To solve the issues, pre-large-based iHUIM approaches (Lin et al., Reference Lin, Gan, Hong and Pan2014; Lee et al., Reference Lee, Yun, Lee and Yoon2018; Lin et al., Reference Lin, Pirouz, Djenouri, Cheng and Ahmed2020; Wu et al., Reference Wu, Teng, Lin, Fournier-Viger, Cheng, Fujita, Fournier-Viger, Ali and Sasaki2020c; Wu et al., Reference Wu, Teng, Lin and Cheng2020b) are developed to extract useful knowledge from incremental datasets. The pre-large notion (Hong et al., Reference Hong, Wang and Tao2001) is employed to avoid dataset scans in some cases when newly added data is inserted into the original dataset. In this sub-section, we provide an in-depth analysis about pre-large-based iHUIM approaches for the incremental datasets.
PRE-HUI: The pre-large notion (Hong et al., Reference Hong, Wang and Tao2001) is introduced to identify pre-large itemsets using upper-bound and lower-bound thresholds to prune unpromising candidates, resulting in reduced dataset scans. However, this approach incurs high computation and maintenance costs associated with dataset scans. The FUP-HUI algorithm (Lin et al., Reference Lin, Lan and Hong2012), based on the FUP method (Cheung et al., Reference Cheung, Han, Ng and Wong1996) discovered HUIs in an incremental way. However, it required more number of database scans if some itemsets are small in the original database, but large in a new added transaction. To solve the challenges, Lin et al. (Reference Lin, Gan, Hong and Pan2014) developed a Two-phase based incremental mining approach called PRE-HUI, based on the pre-large notion (Hong et al., Reference Hong, Wang and Tao2001). This approach is also designed to efficiently discover HUIs from incremental datasets. The DCP property of Two-phase approach (Liu et al., Reference Liu and Liao2005) is also utilized to decrease the number of candidates to accelerate the mining process. When new transactions are inserted in the original database, the proposed approach updates the obtained HUIs. The candidate 1-itemsets are first obtained with their TWUs and utility values. In PRE-HUI, a limited number of itemsets are re-scanned to maintain HUIs, reducing computational overhead compared to the batch method (Liu et al., Reference Liu and Liao2005). Additionally, upper-bound and lower-bound utility thresholds (Su and Sl) are employed to identify large and pre-large utility itemsets, respectively, leading to the optimization of the mining process. PRE-HUI efficiently manages both HTWU (High TWU) and PTWU (Pre-large TWU) to enhance the run-time of the mining process. Whenever new transactions are inserted into the original dataset, PRE-HUI categorizes itemsets into three parts, with a total of nine cases catering to large, pre-large, or small TWU in the original dataset. Each of these parts is managed individually to maintain the HUIs discovered thus far. Simultaneously, the TWUs and AU (Actual Utility) values of the generated candidates undergo updates concurrently. The candidate 2-itemsets are obtained from HTWU and PTWU candidate 1-itemsets. The same procedure is repeated until all HUIs are obtained.
Figure 5. Process of the proposed algorithm for transaction insertion
Figure 5 shows the process of the proposed algorithm for the transaction insertion. In Step 1, the original database includes eight transactions and five items. The items A, B, C, D and E have profit values 6,2,15,7 and 10, respectively. The total actual utility of all the transactions is 350 in the original database. The values of Su and Sl are set 30
![]() $\%$
and 20
$\%$
and 20
![]() $\%$
, respectively. In Step 2, both HTWU and PTWU itemsets are calculated based on the value of Su and Sl in the original database. In Step 3, four transactions
$\%$
, respectively. In Step 2, both HTWU and PTWU itemsets are calculated based on the value of Su and Sl in the original database. In Step 3, four transactions
![]() $t_9$
to
$t_9$
to
![]() $t_{12}$
are inserted into the original database. The actual utility of these new transactions is 210. The total actual utility of the updated database is
$t_{12}$
are inserted into the original database. The actual utility of these new transactions is 210. The total actual utility of the updated database is
![]() $350+210=560$
. In Step 4, HTWU 1-itemsets and PTWU 1-itemsets are calculated based on the nine cases of the original and updated databases. For example, an itemset
$350+210=560$
. In Step 4, HTWU 1-itemsets and PTWU 1-itemsets are calculated based on the nine cases of the original and updated databases. For example, an itemset
![]() $\{A\}$
is put into a small itemset because its ratio is
$\{A\}$
is put into a small itemset because its ratio is
![]() $108/560=19.30\%$
. On the other hand,
$108/560=19.30\%$
. On the other hand,
![]() $\{E\}$
is put into pre-large itemset because its ratio is
$\{E\}$
is put into pre-large itemset because its ratio is
![]() $162/560=28.90\%$
. However, both itemsets are HTWU in the original database. There are four cases: (1) If the ratio value of an 1-itemset is more than that of Su, then it is considered as large itemset. (2) If it is a smaller than Sl, then it will be small itemset. (3) If it is between Su and Sl, then it will be pre-large itemset. (4) The remaining 1-itemsets are added to the re-scan itemsets which have larger value than that of Su. Note that the remaining 1-itemsets are small itemsets in the original database. In Step 5, all the HTWU 1-itemsets and PTWU 1-itemsets are obtained along with their utility values. In Step 6, the same procedure is applied to obtain the complete set of HTWU and PTWU itemsets of the updated database. In the final Step, the HUIs are calculated based on the value of actual utility. For example, the itemset
$162/560=28.90\%$
. However, both itemsets are HTWU in the original database. There are four cases: (1) If the ratio value of an 1-itemset is more than that of Su, then it is considered as large itemset. (2) If it is a smaller than Sl, then it will be small itemset. (3) If it is between Su and Sl, then it will be pre-large itemset. (4) The remaining 1-itemsets are added to the re-scan itemsets which have larger value than that of Su. Note that the remaining 1-itemsets are small itemsets in the original database. In Step 5, all the HTWU 1-itemsets and PTWU 1-itemsets are obtained along with their utility values. In Step 6, the same procedure is applied to obtain the complete set of HTWU and PTWU itemsets of the updated database. In the final Step, the HUIs are calculated based on the value of actual utility. For example, the itemset
![]() $\{B\}$
is low-utility itemset because
$\{B\}$
is low-utility itemset because
![]() $44/560=7.90\%$
which is less than Sl. On the other hand, the itemset
$44/560=7.90\%$
which is less than Sl. On the other hand, the itemset
![]() $\{BCD\}$
is HUI because
$\{BCD\}$
is HUI because
![]() $173/560=30.90\%$
which is more than Su. Experiments proved that PRE-HUI performs better than FUP-HUI (Lin et al., Reference Lin, Lan and Hong2012) and Two-phase (Liu et al., Reference Liu and Liao2005) with regard to the run-time for the incremental datasets. The reason is that the proposed algorithm keeps both HTWU and PTWU to speed-up the running time. More PTWU can reduce more runtime when compared to the FUP-HUI and Two-Phase. Furthermore, PRE-HUI has been formally proven to be both complete and correct. However, the memory consumption of PRE-HUI is increased when the threshold value is decreased.
$173/560=30.90\%$
which is more than Su. Experiments proved that PRE-HUI performs better than FUP-HUI (Lin et al., Reference Lin, Lan and Hong2012) and Two-phase (Liu et al., Reference Liu and Liao2005) with regard to the run-time for the incremental datasets. The reason is that the proposed algorithm keeps both HTWU and PTWU to speed-up the running time. More PTWU can reduce more runtime when compared to the FUP-HUI and Two-Phase. Furthermore, PRE-HUI has been formally proven to be both complete and correct. However, the memory consumption of PRE-HUI is increased when the threshold value is decreased.
PIHUP: Lee et al. (Reference Lee, Yun, Lee and Yoon2018) developed an efficient method called PIHUP (Pre-large Incremental High Utility Patterns), based on pre-large notion (Hong et al., Reference Hong, Wang and Tao2001) to efficiently extract patterns from incremental datasets. During the first database scan, it builds initial-tree, header-list and tail-list. The tree is lexicographically ordered (named PIHUP
![]() $_L$
-tree). The header stores TWU of 1-itemsets, while tail-list creates links pointing to the nodes of PIHUP
$_L$
-tree). The header stores TWU of 1-itemsets, while tail-list creates links pointing to the nodes of PIHUP
![]() $_L$
-tree. Every node displays the most recent items from the newly added transactions. After constructing the tree, the header is rearranged in descending order based on TWU. After this, PIHUP
$_L$
-tree. Every node displays the most recent items from the newly added transactions. After constructing the tree, the header is rearranged in descending order based on TWU. After this, PIHUP
![]() $_L$
-tree is reorganized. The tail-list signifies that transactions with identical items constitute a single path. After obtaining a path, the extracted data is deleted from the tree. The path is rearranged and inserted into the tree without establishing a link from the tail-list. The mining process employs a divide-and-conquer method to extract large and pre-large candidate patterns from the PIHUP
$_L$
-tree is reorganized. The tail-list signifies that transactions with identical items constitute a single path. After obtaining a path, the extracted data is deleted from the tree. The path is rearranged and inserted into the tree without establishing a link from the tail-list. The mining process employs a divide-and-conquer method to extract large and pre-large candidate patterns from the PIHUP
![]() $_L$
-tree. A pattern tree is constructed from these candidate patterns. This pattern tree consists of the actual utility value of patterns. The patterns are categorized into three types: (1) large, (2) pre-large, and (3) small. Two values, namely upper-threshold (Su) and lower-threshold (Sl), are used to measure the threshold. Su is used to extract HUIs, whereas Sl is used to shrink the process of re-scanning when incremental data is processed. After building the tree, the headers are arranged in descending order according to TWU. Subsequently, the tree is reorganized in alignment with the sorted header. The patterns can be located more quickly in comparison to utilizing the list. The generated pattern tree is used to mine the HUIs.
$_L$
-tree. A pattern tree is constructed from these candidate patterns. This pattern tree consists of the actual utility value of patterns. The patterns are categorized into three types: (1) large, (2) pre-large, and (3) small. Two values, namely upper-threshold (Su) and lower-threshold (Sl), are used to measure the threshold. Su is used to extract HUIs, whereas Sl is used to shrink the process of re-scanning when incremental data is processed. After building the tree, the headers are arranged in descending order according to TWU. Subsequently, the tree is reorganized in alignment with the sorted header. The patterns can be located more quickly in comparison to utilizing the list. The generated pattern tree is used to mine the HUIs.
The mining process is carried out by systematically examining the prefix pattern one at a time. It builds the novel conditional pattern trees derived from the respective prefixes by selecting the items from the header sequentially. If the TWU value of an item is greater than or equal to
![]() $Su \times tu(D)$
, where tu(D) is a transaction in the database D, the item is stored as a large pattern, otherwise, it is recorded as pre-large pattern. The au (actual utility) values are computed and associated with the patterns during the database scan conducted after extracting all large and pre-large patterns. If au values of the generated large patterns is no less than
$Su \times tu(D)$
, where tu(D) is a transaction in the database D, the item is stored as a large pattern, otherwise, it is recorded as pre-large pattern. The au (actual utility) values are computed and associated with the patterns during the database scan conducted after extracting all large and pre-large patterns. If au values of the generated large patterns is no less than
![]() $Su \times tu(D)$
, then these patterns are HUIs. PIHUP performs better than PRE-HUI (Lin et al. Reference Lin, Gan, Hong and Pan2014) method concerning execution time, memory consumption, the number of itemsets, and scalability. PIHUP reduces redundant operations, resulting in a significant improvement in mining efficiency. However, it employs the anti-monotone property to generate candidate patterns. Even though overestimation techniques (Liu et al. Reference Liu and Liao2005) are employed to avoid the anti-monotone property, they may still generate unnecessary candidate patterns.
$Su \times tu(D)$
, then these patterns are HUIs. PIHUP performs better than PRE-HUI (Lin et al. Reference Lin, Gan, Hong and Pan2014) method concerning execution time, memory consumption, the number of itemsets, and scalability. PIHUP reduces redundant operations, resulting in a significant improvement in mining efficiency. However, it employs the anti-monotone property to generate candidate patterns. Even though overestimation techniques (Liu et al. Reference Liu and Liao2005) are employed to avoid the anti-monotone property, they may still generate unnecessary candidate patterns.
PRE-HAUIMI: The traditional HUIM algorithms suffer from two major problems: (1) the need to re-scan the dataset and (2) maintaining itemsets in the updated dataset. To address these issues, a level-wise HAUIM algorithm (Wu et al., Reference Wu, Teng, Lin, Yun and Chen2020a) is proposed, adopting pre-large notion (Hong et al., Reference Hong, Wang and Tao2001), to mine HAUIs in incremental datasets. Nevertheless, it incurs significant computational costs and lacks a theoretical proof of correctness and completeness for maintaining HAUIs throughout the mining process. To solve the challenges, Lin et al. (Reference Lin, Pirouz, Djenouri, Cheng and Ahmed2020) designed PRE-HAUIMI, relies on AUL (Average Utility-List) structure and pre-large notion (Hong et al., Reference Hong, Wang and Tao2001) of HAUIM, to find HAUIs from incremental datasets. The PAUUBI (Pre-large AUUB Itemsets) are utilized to show the correctness and completeness of discovered HAUIs. The AUL framework is implemented for the 1-HAUUBIs, and serves as a repository for the 1-PAUUBIs to aid in maintenance tasks. A join operation can be conveniently applied to generate k-itemsets of HAUIs, thereby surpassing level-wise methods.
The algorithm effectively manages the sets of 1-HAUUBIs and 1-PAUUBIs based on AUL structure and pre-large concept (Hong et al., Reference Hong, Wang and Tao2001). Furthermore, 1-PAUUBIs can serve as a buffer, reducing certain conditions, For example, making a direct transition from HAUUBI to minor patterns and vice-versa. The algorithm sets Su as upper-utility threshold and Sl as lower-utility threshold for PRE-HAUIMI. The AUL structure not only holds the 1-HAUUBIs, but also the 1-PAUUBIs. Although, it consumes extra memory, but it significantly reduces the number of database scans. If AUUB is no less than Su, then it is represented as 1-HAUUBI. If the value of AUUB is lies between Sl and Su, then it is considered as 1-PAUUBI. The AUL structure significantly improves efficiency of the mining process. The maintenance phase includes a safety bound to eliminate the necessity for dataset re-scans.
To determine k-itemsets (
![]() $k \ge 2$
) of promising candidates, the enumeration tree is built to reduce join operations by depth first search (DFS) method. The process of DFS is performed to decide whether to proceed with the superset (
$k \ge 2$
) of promising candidates, the enumeration tree is built to reduce join operations by depth first search (DFS) method. The process of DFS is performed to decide whether to proceed with the superset (
![]() $k+1$
)-itemsets of k-itemsets or not. An iterative join process is performed to create the AUL structure of k-itemsets to meet the requirement of their superset. This process is applied to all the remaining candidates. In this way, the final HUAIs are obtained by scanning the database. The experiments proved that PRE-HAUIMI outperforms HAUI-Miner (Lin et al., Reference Lin, Li, Fournier-Viger, Hong, Zhan and Voznak2016), IHAUPM (Incremental HAUPM) (Lin et al., Reference Lin, Ren, Fournier-Viger, Pan and Hong2018), and FUP (Cheung et al., Reference Cheung, Han, Ng and Wong1996) for the execution time, memory consumption, access patterns, and scalability. However, in some cases, where there are a significant number of processed itemsets within newly inserted transactions, constructing an AUL structure specifically for itemsets can be time-consuming, resulting in a high computational cost.
$k+1$
)-itemsets of k-itemsets or not. An iterative join process is performed to create the AUL structure of k-itemsets to meet the requirement of their superset. This process is applied to all the remaining candidates. In this way, the final HUAIs are obtained by scanning the database. The experiments proved that PRE-HAUIMI outperforms HAUI-Miner (Lin et al., Reference Lin, Li, Fournier-Viger, Hong, Zhan and Voznak2016), IHAUPM (Incremental HAUPM) (Lin et al., Reference Lin, Ren, Fournier-Viger, Pan and Hong2018), and FUP (Cheung et al., Reference Cheung, Han, Ng and Wong1996) for the execution time, memory consumption, access patterns, and scalability. However, in some cases, where there are a significant number of processed itemsets within newly inserted transactions, constructing an AUL structure specifically for itemsets can be time-consuming, resulting in a high computational cost.
APHAUP: Wu et al. (Reference Wu, Teng, Lin and Cheng2020b); Wu et al. (Reference Wu, Teng, Lin, Fournier-Viger, Cheng, Fujita, Fournier-Viger, Ali and Sasaki2020c) proposed an approach named APHAUP (Apriori-based HAUP with a pre-large concept), relies on the pre-large notion (Hong et al., Reference Hong, Wang and Tao2001) that is utilized to update the HAUIs obtained in the newly added transactions. APHAUP uses the pre-large concept to modify the new HAUIs discovered and decreases the time of the re-scanning process. It uses two novel upper-bounds to minimize the number of candidates, resulting in increased mining performance. A linked-list is introduced for incremental insertion of transactions, with each round requiring a maximum of one-time scanning. This structure ensures to decrease in the multiple database scans during the maintenance process. APHAUP includes two distinct cases: (1) First, it utilizes pre-large notion, which is performed for the incremental process. (2) Second, when the dataset dimension is expanded with additional transactions, necessitating a re-scan of the whole dataset.
A strict upper limit, referred to as pub (partial upper-bound), is introduced to reduce the upper-bound utility value of the itemsets. Also, a smaller upper-bound, named lpub is designed to decrease the size of candidates in the search space. The pmuub (partial maximal utility upper-bound), which is a tighter upper-bound than the AUUB, is designed to reduce the size of the component itemsets. Additionally, a sub-itemset called hpmuubi (High pmuub itemset) is introduced, which has a utility threshold higher than that of pmuub. The proposed algorithm selects a subset from hpmuubi, called lhpmuubi (lead-pmuub), and this selection is made using APHAUP. This lhpmuubi subset is highly efficient in reducing the size of candidate itemsets. Experimental results proved that APHAUP with lead-pmuub can decrease the run-time significantly when updating the obtained HAUIs as contrast to APHAUP with pmuub in dense datasets. Furthermore, APHAUP with pmuub is more than the number of determined candidates. It signifies that pre-large notion has great potential to increase the mining performance of HAUIs.
PIHUP-MOD: The utility pattern is quite useful in analyzing the time-series data in the IoT environment, where transaction modifications occur in dynamic datasets. The Apriori-based method using pre-large notion (Lin et al., Reference Lin, Hong, Gan, Chen and Li2015), needs to scan the database continuously, leading to taking lots of time when considering all cases to extract the pattern. To deal with the problems, Yun et al. (Reference Yun, Kim, Ryu, Baek, Nam, Lee, Vo and Pedrycz2021) developed tree-based approach called PIHUP-MOD (Pre-large-based Incremental HUIs mining for transaction MODification). This algorithm uncovers HUIs within the context of modified datasets. The PIHUP-MOD
![]() $_L$
-tree data structure (where T stands for transaction) is designed to extract the pre-large and large patterns for the mining process. A global PIHUP-MOD
$_L$
-tree data structure (where T stands for transaction) is designed to extract the pre-large and large patterns for the mining process. A global PIHUP-MOD
![]() $_T$
-tree is formed by scanning the database once. Each transaction is in lexicographic order and inserts into the global PIHUP-MOD
$_T$
-tree is formed by scanning the database once. Each transaction is in lexicographic order and inserts into the global PIHUP-MOD
![]() $_T$
-tree with their TWU value.
$_T$
-tree with their TWU value.
PIHUP-MOD includes three steps: (1) Firstly, during the full-scan step, the proposed algorithm scans the original dataset and builds the PIHUP-MOD
![]() $_T$
-tree data structure. (2) Secondly, during the mining step, it extracts pre-large and large patterns from PIHUP-MOD
$_T$
-tree data structure. (2) Secondly, during the mining step, it extracts pre-large and large patterns from PIHUP-MOD
![]() $_T$
-tree. Afterward, it generates a new pattern tree based on the TWU value and inserts it into the tree. It re-scans the original dataset to find the actual HUIs in the tree, which becomes the current pattern tree. (3) Finally, during the modification step, if there is any modification in the records, then it recalculates the utility values and updates the data structure. Subsequently, a new pattern tree is reconstructed for the whole dataset by scanning only the modified records. The proposed algorithm discovers the actual HUIs within the current pattern tree using the whole modified dataset. PIHUP-MOD performs better than UP-Growth+ (Tseng et al., Reference Tseng, Shie, Wu and Yu2013) and PRE-HUI-MOD (Lin et al., Reference Lin, Hong, Gan, Chen and Li2015) concerning the run-time, memory consumption, and scalability for dense and sparse datasets. However, it is difficult to set two thresholds Su and Sl of pre-large concept (Hong et al., Reference Hong, Wang and Tao2001) for efficient mining.
$_T$
-tree. Afterward, it generates a new pattern tree based on the TWU value and inserts it into the tree. It re-scans the original dataset to find the actual HUIs in the tree, which becomes the current pattern tree. (3) Finally, during the modification step, if there is any modification in the records, then it recalculates the utility values and updates the data structure. Subsequently, a new pattern tree is reconstructed for the whole dataset by scanning only the modified records. The proposed algorithm discovers the actual HUIs within the current pattern tree using the whole modified dataset. PIHUP-MOD performs better than UP-Growth+ (Tseng et al., Reference Tseng, Shie, Wu and Yu2013) and PRE-HUI-MOD (Lin et al., Reference Lin, Hong, Gan, Chen and Li2015) concerning the run-time, memory consumption, and scalability for dense and sparse datasets. However, it is difficult to set two thresholds Su and Sl of pre-large concept (Hong et al., Reference Hong, Wang and Tao2001) for efficient mining.
PIHUPM: The existing pre-large-based HUIM algorithm, named PIHUP (Lin et al., Reference Lin, Gan, Hong and Pan2014), relies on Apriori method or utilized tree structure. However, generating a large number of candidate patterns requires a substantial amount of time. Moreover, mining the desired patterns necessitates additional scans of the database. To overcome these problems, Kim et al. (Reference Kim, Lee, Ryu, Kim, Kim, Vo, Lin and Yun2023) developed an efficient pre-large-based approach called PIHUPM, first of its kind, to extract the HUIs without the need of candidate generation and additional database scans from the incremental database. The novel list data structure, named PIHUP-List, is developed to extract HUIs when new transactions are added to incremental database. PIHUP-List is divided into the following two lists: (1) During the database scan, a global PIHUP-List is generated to store data for 1-length items. (2) Combining two patterns results in the creation of a conditional PIHUP-List, which stores the data of patterns with a length greater than 1. The proposed PIHUP-List significantly reduces the number of database scans needed to produce the desired results. The PIHUP-List constructs the global PIHUP-List by scanning the original database just once. The global PIHUP-List is maintained to mine the large and pre-large patterns. The PIHUP-List is deleted after the completion of the mining process to utilize the memory in an efficient way. The DFS method is used for efficient memory consumption and pattern expansions.
PIHUPM includes the following four steps: (1) Construction: During this step, global list are constructed as per the lexicographic order when the original database is scanned. (2) Reconstruction: In this step, the previously configured global list structures are arranged in ascending order according to TWU value. (3) Mining: During this step, the large and pre-large patterns are obtained. (4) Pattern tree update: During this step, HUIs are obtained from the pattern tree. The proposed algorithm employs an improved pattern classification approach based on the actual utility calculation to efficiently manage the large and pre-large patterns. The algorithm suggested here employs a DFS-based pattern extension method incorporates pruning techniques for unpromising patterns and utilizes compact utility information storage to attain efficient and accurate patterns in a dynamic environment. The proposed approach is compared with PIHUP (Lin et al., Reference Lin, Gan, Hong and Pan2014), LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017), and EHMIN (Kim et al., Reference Kim, Ryu, Lee, Kim, Yoon, Vo, Chun-Wei Lin and Yun2022), concerning the run-time, threshold values, memory consumption, and scalability from benchmark datasets. The outcomes demonstrated the efficiency of the proposed algorithm in comparison to state-of-the-art methods. The proposed approach is more suitable for real-world problems. However, it takes more time during the re-scan process. Moreover, it takes more parameters to obtain the desired patterns.
Table 18. Characteristics and theoretical aspects of the pre-large-based approaches
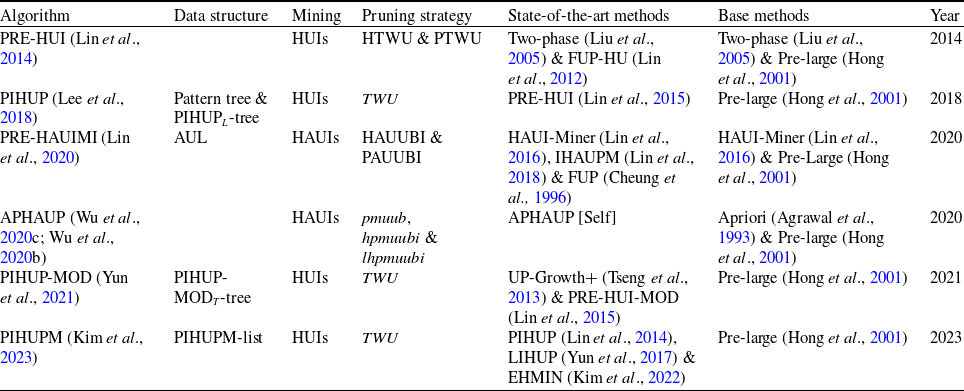
Discussion
We have discussed in-depth the pre-large-based iHUIM algorithms to extract high utility information by using pre-large notion that avoids to re-scan the updated dataset in some cases when the new data is inserted into the original dataset. However, two thresholds, Su and Sl need to be maintained, which is difficult to set for the users. In some cases, the newly added data is very large compared to the original dataset, leading to a degradation in mining performance. Table 18 outlines the detailed description of pre-large-based iHUIM algorithms. Table 19 highlights the theoretical aspects of pre-large-based HUIM approaches from the incremental datasets.
Table 19. Pros and cons of the pre-large-based approaches

4. Summary
Incremental data mining has emerged in recent years because the conventional HUIM algorithms are tailored for static datasets and encounter significant performance issues when handling incremental data. We provide an in-depth survey that falls into mainly four categories of iHUIM approaches: two-phase-based, projection-based, utility-list-based, and pre-large-based.
The IUM (Yeh et al., Reference Yeh, Chang and Wang2008) and FIUM (Yeh et al., Reference Yeh, Chang and Wang2008) algorithms are designed to identify itemsets with high temporal utility. IUM is a Two-phase algorithm (Liu et al., Reference Liu and Liao2005), and FIUM belongs to the ShFSM category (Li et al., Reference Li, Yeh, Chang, Zhang, Tanaka, Yu, Wang and Li2005c). FIUM uses the transaction-weighted downward closure property (Liu et al., Reference Liu and Liao2005). ITPAU (Hong et al., Reference Hong, Lee and Wang2009a) comes after FIUM and builds up on it. ITPAU is more efficient and is also implemented as a Two-phase method. IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) proposed three tree structures. IHUP
![]() $_L$
-Tree skips the functioning operations; IHUP
$_L$
-Tree skips the functioning operations; IHUP
![]() $_{TF}$
-Tree relies on the decreasing order of transaction frequency; and IHUP
$_{TF}$
-Tree relies on the decreasing order of transaction frequency; and IHUP
![]() $_{TWU}$
-Tree relies on the decreasing order of TWU values. It requires a maximum of two dataset scans to find HUIs. IIUT (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009b) proposes IIUT-Tree, which is based on the item’s appearance order. This approach follows a pattern-growth method and only requires two dataset scans. Tree structures prove highly effective and efficient in the extraction of HUIs. Then, FUP-HUI (Lin et al., Reference Lin, Lan and Hong2012) is introduced, which is based on the FUP method (Cheung et al., Reference Cheung, Han, Ng and Wong1996). This approach demonstrates faster performance in contrast to Two-phase method (Liu et al., Reference Liu and Liao2005) of batch mining. PRE-HUI algorithm (Lin et al., Reference Lin, Gan, Hong and Pan2014) relies on pre-large notion (Hong et al., Reference Hong, Wang and Tao2001). The algorithm divides the itemsets into a total of nine cases, taking into account both upper-bound and lower-bound utility. This approach outperforms FUP-HUI (Lin et al., Reference Lin, Lan and Hong2012).
$_{TWU}$
-Tree relies on the decreasing order of TWU values. It requires a maximum of two dataset scans to find HUIs. IIUT (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009b) proposes IIUT-Tree, which is based on the item’s appearance order. This approach follows a pattern-growth method and only requires two dataset scans. Tree structures prove highly effective and efficient in the extraction of HUIs. Then, FUP-HUI (Lin et al., Reference Lin, Lan and Hong2012) is introduced, which is based on the FUP method (Cheung et al., Reference Cheung, Han, Ng and Wong1996). This approach demonstrates faster performance in contrast to Two-phase method (Liu et al., Reference Liu and Liao2005) of batch mining. PRE-HUI algorithm (Lin et al., Reference Lin, Gan, Hong and Pan2014) relies on pre-large notion (Hong et al., Reference Hong, Wang and Tao2001). The algorithm divides the itemsets into a total of nine cases, taking into account both upper-bound and lower-bound utility. This approach outperforms FUP-HUI (Lin et al., Reference Lin, Lan and Hong2012).
HUI-list-INS (Lin et al. Reference Lin, Gan, Hong and Pan2014) is built upon HUI-Miner (Liu & Qu, Reference Liu and Qu2012), employing it to construct utility-list structures. The EUCS structure is utilized to accelerate mining performance. The EIHI algorithm (Fournier-Viger et al. Reference Fournier-Viger, Lin, Gueniche and Barhate2015) is based on HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) and is much faster than its predecessor. The iCHUM algorithm (Zheng & Li, Reference Zheng and Li2015) introduces a tree structure known as iCHUM-Tree, which is based on TWU values. It performs better than other algorithms, especially when a large number of transaction items are concerned. HUPID-Growth (Yun & Ryang, Reference Yun and Ryang2014) utilizes the HUPID-Tree structure, which is built with only a single dataset scan. This algorithm rectifies the problem of overestimated utilities that can occur in other local trees.
HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) adopts a memory-based incremental approach, outperforming the FHM algorithm (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014). It stores items from both HTWUIs and non-HTWUIs, eliminating the need for re-scanning the dataset during transaction insertions. In IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016), the extra sequences are removed that are not high utility in contrast with the prevailing HUSP mining approaches. A candidate pattern tree data structure is introduced in IncUSP-Miner. A compressed node structure is presented to keep the details of corresponding sequences to avoid computations. MUAP (Shao et al., Reference Shao, Meng and Cao2016) is based on frequency and utility concepts. It follows the global pruning strategy, and patterns are selected that have the highest weighted values. IHUI-Miner (Guo & Gao, Reference Guo and Gao2017) uses the IHUI-Tree data structure. This algorithm does not generate any candidate itemsets. Three steps are followed to compute HUIs in the case when the prefix utility is no less than
![]() $min\_util$
. After verification of itemsets, IHUI-Tree needs to be updated. On the other hand, LIHUP (Yun et al. Reference Yun, Ryang, Lee and Fujita2017) efficiently processes data with just a single dataset scan. This approach uses a list structure and entirely avoids candidate generation. It adeptly addresses the overestimation concept employed by FP-Growth (Han et al., Reference Han, Pei and Yin2000) and Apriori-based algorithms (Agrawal et al. Reference Agrawal1993). The optimized sorting order is determined post the construction phase. It follows the TWU descending order and performs better than HUPID (Yun & Ryang, Reference Yun and Ryang2014) and IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) algorithms, primarily due to its efficiency, which require only a single dataset scan.
$min\_util$
. After verification of itemsets, IHUI-Tree needs to be updated. On the other hand, LIHUP (Yun et al. Reference Yun, Ryang, Lee and Fujita2017) efficiently processes data with just a single dataset scan. This approach uses a list structure and entirely avoids candidate generation. It adeptly addresses the overestimation concept employed by FP-Growth (Han et al., Reference Han, Pei and Yin2000) and Apriori-based algorithms (Agrawal et al. Reference Agrawal1993). The optimized sorting order is determined post the construction phase. It follows the TWU descending order and performs better than HUPID (Yun & Ryang, Reference Yun and Ryang2014) and IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009a) algorithms, primarily due to its efficiency, which require only a single dataset scan.
IMHAUI (Kim & Yun, Reference Kim and Yun2017) uses a compact tree structure with a pattern-growth approach. It adopts the path-adjusting method to maintain the compression of the tree, adhering to the descending order of AUUB. The mining process consists of three functions. It outperforms other algorithms in terms of performance, although the validation of candidate itemsets remains a time-consuming task. IMHAUI (Kim & Yun, Reference Kim and Yun2017) increases the time required by recursively attracting conditional pattern bases. To deal with this issue, FIMHAUI (Yildirim & Celik, Reference Yildirim and Celik2018) is presented. A novel data structure named miHAUI-Tree is presented, which maximizes the node-sharing effect. Information is exclusively stored on the leaf nodes, and identical transactions are merged. Although it performs more efficiently than IMHAUI (Kim & Yun, Reference Kim and Yun2017), it still needs a validation phase to determine actual HAUIs. IncUSP-Miner
![]() $+$
(Wang & Huang, Reference Wang and Huang2018) is used for incremental mining of HUSPs. A new data structure, TSU, is proposed that reduces redundant re-computations. The candidate pattern tree is used to buffer sequences with high TSU values. This approach outperforms the USpan (Yin et al., Reference Yin, Zheng and Cao2012) and HUS-Span (Wang et al., Reference Wang, Huang and Chen2016) algorithms. USP-Miner (Wang & Huang, Reference Wang and Huang2016), IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016), and IncUSP-Miner
$+$
(Wang & Huang, Reference Wang and Huang2018) is used for incremental mining of HUSPs. A new data structure, TSU, is proposed that reduces redundant re-computations. The candidate pattern tree is used to buffer sequences with high TSU values. This approach outperforms the USpan (Yin et al., Reference Yin, Zheng and Cao2012) and HUS-Span (Wang et al., Reference Wang, Huang and Chen2016) algorithms. USP-Miner (Wang & Huang, Reference Wang and Huang2016), IncUSP-Miner (Wang & Huang, Reference Wang and Huang2016), and IncUSP-Miner
![]() $+$
(Wang & Huang, Reference Wang and Huang2018) require extra memory space. In contrast, PIHUP (Lee et al., Reference Lee, Yun, Lee and Yoon2018) employs a PIHUP-Tree which relied on pre-large notion (Hong et al., Reference Hong, Wang and Tao2001). This tree is lexicographically organized, and it utilizes Su and Sl as thresholds for measurement. The header is arranged in a descending order based on TWU values. Items are categorized into large, pre-large, and small values according to their TWU values. This method is better due to the pattern tree data structure. However, it becomes slow in the case of small insertion data. This algorithm still needs to maintain the anti-monotone property.
$+$
(Wang & Huang, Reference Wang and Huang2018) require extra memory space. In contrast, PIHUP (Lee et al., Reference Lee, Yun, Lee and Yoon2018) employs a PIHUP-Tree which relied on pre-large notion (Hong et al., Reference Hong, Wang and Tao2001). This tree is lexicographically organized, and it utilizes Su and Sl as thresholds for measurement. The header is arranged in a descending order based on TWU values. Items are categorized into large, pre-large, and small values according to their TWU values. This method is better due to the pattern tree data structure. However, it becomes slow in the case of small insertion data. This algorithm still needs to maintain the anti-monotone property.
MR-INCHUSP (Saleti, Reference Saleti2021) uses a backward mining approach (Lin et al., Reference Lin, Hsueh and Chan2009). A new data structure called CURMAP is proposed that deals with the combinatorial explosion. CURMAP efficiently handles pruning and memory consumption. INC-HUSP does not mine the dataset from scratch, and CURMAP efficiently reduces the number of candidate sequences. There are two MapReduce phases, and the stable sequence property is used in the second phase. This approach is better than previous MapReduce algorithms, exhibit good speed-up and linear scalability due to good practices. IIHUM (Yun et al., Reference Yun, Nam, Lee and Yoon2019) follows a global-list structure that follows the ascending order of TWU. This algorithm efficiently operates with just one dataset scan, eliminating the need for candidate checking. Additionally, it doesn’t require the extraction of candidates to recursively generate the ILU-lists from the built global-lists. This algorithm performs better compared with FUP-HU (Lin et al., Reference Lin, Lan and Hong2012), HUPID (Yun & Ryang, Reference Yun and Ryang2014), and LIHUP (Yun et al., Reference Yun, Ryang, Lee and Fujita2017) for the non-binary datasets. Id
![]() $^2$
HUP
$^2$
HUP
![]() $+$
(Liu et al., Reference Liu, Ju, Zhang, Fung, Yang and Yu2019) is introduced to improve upon the performance standard set up by EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) and HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) algorithms. It follows a one-phase paradigm and improves four types of pruning techniques. This algorithm makes use of hash tables and introduces a new data structure called niCAUL. This approach uses least memory because of the pseudo-projection. This performance enhancement is due to the fact that legacy patterns are determined by contrasting the utilities. The IncCHUI algorithm employs a CHT hash table to store CHUIs, and it efficiently constructs utility-lists in comparison to LIHUP and HUI-list-INS. This single-phase approach exhibits excellent scalability when compared to other algorithms.
$+$
(Liu et al., Reference Liu, Ju, Zhang, Fung, Yang and Yu2019) is introduced to improve upon the performance standard set up by EIHI (Fournier-Viger et al., Reference Fournier-Viger, Lin, Gueniche and Barhate2015) and HUI-list-INS (Lin et al., Reference Lin, Gan, Hong and Pan2014) algorithms. It follows a one-phase paradigm and improves four types of pruning techniques. This algorithm makes use of hash tables and introduces a new data structure called niCAUL. This approach uses least memory because of the pseudo-projection. This performance enhancement is due to the fact that legacy patterns are determined by contrasting the utilities. The IncCHUI algorithm employs a CHT hash table to store CHUIs, and it efficiently constructs utility-lists in comparison to LIHUP and HUI-list-INS. This single-phase approach exhibits excellent scalability when compared to other algorithms.
APHAUP (Wu et al., Reference Wu, Teng, Lin, Fournier-Viger, Cheng, Fujita, Fournier-Viger, Ali and Sasaki2020c; Wu et al., Reference Wu, Teng, Lin and Cheng2020b) is insertion-based approach that utilizes pre-large notion (Hong et al., Reference Hong, Wang and Tao2001). pub and ipub are upper-bounds designed to decrease the utility values and the size of candidates. These upper-bounds are implemented using a linked-list structure. APHAUP with ipub efficiently decreases the time when compared to APHUAP with pub, especially with dense datasets. PRE-HAUIMI (Lin et al., Reference Lin, Pirouz, Djenouri, Cheng and Ahmed2020) depends on the AUL structure and surpasses the level-wise method by employing an enumeration tree to minimize the number of required join operations. The itemsets are divided into nine cases according to the pre-large concept (Hong et al., Reference Hong, Wang and Tao2001). This approach outperforms HAUI-Miner (Lin et al., Reference Lin, Li, Fournier-Viger, Hong, Zhan and Voznak2016), IHAUPM (Lin et al., Reference Lin, Ren, Fournier-Viger, Pan and Hong2018), and FUP-based (Cheung et al., Reference Cheung, Han, Ng and Wong1996) algorithms. However, it may require more time to construct an AUL structure when dealing with large itemsets.
5. Research opportunities and future directions
In recent years, various approaches have been proposed to discover iHUIM; however, there are many challenges in this field. This section discusses important research opportunities and future directions for the iHUIM problem.
Closed patterns:
Mining closed HUIs is an important area of research. Closed patterns are compact but have complete information about items (Singh & Biswas, 2021). Decision-making based on compacted or not huge patterns is easier and more useful. Therefore, closed pattern mining from incremental datasets is desired compared to traditional iHUIM. In the literature, only one work (Dam et al., Reference Dam, Ramampiaro, Nørvåg and Duong2019) is available that mines closed iHUIM from incremental datasets.
Top-K patterns:
In traditional HUIM, a minimum utility threshold is always required to mine useful patterns. It is not easy for users to set the appropriate minimum utility threshold. To target this issue, k-value-based HUIM is introduced (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016). In top-k HUIM, users need to provide the value of kFootnote 1 instead of the minimum utility threshold. In literature, the T-HUDS (Zihayat & An, Reference Zihayat and An2014) approach is the only available work that finds top-k HUIM from data streams.
Multiple minimum utility threshold based pattern mining
Predicting the optimum minimum utility threshold is not an easy task for users. Therefore, multiple minimum utility threshold-based HUIM is proposed (Lin et al., Reference Lin, Hong, Gan, Chen and Li2015). It is easy for the user to give many (more than two) minimum utility thresholds instead of one appropriate one. In the literature, no work is available to mine HUIs from incremental or dynamic datasets.
Negative utility value-based pattern mining:
In real life, negative utility values occur very frequently. An item is called a negative item when it is given away for free with a set of items. In such a scenario, the free item becomes a negative item (Chu et al., Reference Chu, Tseng and Liang2009; Singh et al., . n.d.). Retailers and managers can make a better strategy to increase their overall profit by introducing negative utility (free items). In literature, only one work (Saleti, Reference Saleti2021) is available to mine iHUIs with negative utility.
High average utility pattern mining:
In traditional HUIM, the utility value of an itemset is calculated by simply summation of the utility value of each item in the itemset. Therefore, the total utility value of the itemset always increases as new items are added. Therefore, a large itemset may have an unreasonable estimate of the profit compared to the actual utility (Singh et al., Reference Singh, Kumar and Biswas2022). To overcome the limitation of HUIM, high average utility itemset (HAUI) mining has been introduced (Hong et al., Reference Hong, Lee and Wang2011). HAUI mining considers the utility value of an itemset and the length of an itemset. HAUI mining works on the average utility value of an itemset, such that the total utility of an itemset is divided by the length of the itemset. Therefore, the utility measures of HUIM cannot be directly applied to HAUI mining. In the future, it will be a big challenge to incorporate HAUI mining into the incremental datasets because the length of the itemset changes frequently as new transactions are inserted. In the future, it is a good area to explore.
Privacy preserving pattern mining:
The mining of privacy-preserving high utility itemsets (PPHUIM) is more realistic and useful compared to traditional HUIM (Gan et al., Reference Gan, Chun-Wei, Chao, Wang and Yu2018). Privacy-preserving hides sensitive items or information provided by the users. In traditional PPHUIM, dummy transactions are inserted instead of the information provided by the users. To find a more realistic HUIM, the incremental dataset area needs to be explored.
Other problems:
Some other extensions of HUIs from incremental datasets mine rich patterns in various ways, such as fuzzy HUIs mining, evolutionary computation-based HUIM (Kumar & Singh, Reference Kumar and Singh2022), complex and uncertain datasets, etc. The researchers can use the latest dataset compaction techniques to improve the performance of the algorithms.
Furthermore, artificial intelligence techniques such as deep learning, machine learning, reinforcement learning, and social intelligence can be employed to identify high utility itemsets (HUIs) from large-scale incremental datasets.
6. Conclusions
The iHUIM has become a significant focus in recent decades due to the performance issues faced by the earlier HUIM algorithms when dealing with dynamic datasets. This survey presented a brief discussion of various iHUIM approaches. The survey provided a taxonomy of the available approaches according to their data structure and utilized strategies like two-phase-based, pattern-growth-based, projection-based, utility-list-based, and pre-large-based methods. This survey provided a detailed category-wise analysis and summary of various iHUIM algorithms. Detailed comparison tables are presented, which include information on various iHUIM algorithms, like data structure used in the algorithm, mining strategy used, pruning strategy employed, their state-of-the-art methods, and the algorithms they are based on. The survey also described the outcome, pros and cons, and future directions of all the available state-of-the-art approaches. Additionally, the paper offers insights into research opportunities and potential future directions for iHUIM. The approaches analyzed in this survey can inspire various other related data mining tasks. The challenges encountered by iHUIM have been under scrutiny for over two decades. Nevertheless, active research is ongoing in this field, and these problems can be addressed in the future to enhance the efficiency of the algorithms under consideration.
Competing interests
The authors state that there are no conflicts of interest. This article provides a comprehensive overview of iHUIM approaches. No any Funding is received for this work.
Author contributions
K.S. formulated the concept for the analysis and introduced the taxonomy. R.K. developed the theory and conducted an analysis of the state-of-the-art approaches. R.K. furnished the data for Tables 10–19. K.S. executed the implementation of the example and the tables associated with the running example. R.K. conducted the analytical portion at Section 3. K.S. gathered all the necessary data. K.S. examined and revised the manuscript. Both authors participated in the analysis and made contributions to the final manuscript.
Ethical and informed consent for data used
The paper does not involve any studies with human or animal subjects.
Data availability and access
Our work does not have any data to explore. Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.





























