1 Introduction
Missing data is common in the social sciences. Researchers have traditionally confronted missing data by dropping all observations in the dataset for which the values of at least one variable are missing. This process of “listwise deletion” is inefficient, and frequently biased when the probability that an observation is missing is related to its true value. An alternative set of strategies attempts to use information contained within the observed data—including partially observed cases—to impute values for the missing data. Among the latter set of strategies, multiple imputation (Rubin Reference Rubin1987; Little and Rubin Reference Little and Rubin2002) has proven particularly influential.
Multiple imputation works by drawing repeated simulated datasets from a posterior distribution defined by the missing data conditional on the observed data, with parameters estimated from the observed data. For obvious reasons, much depends on the nature of the missingness relative to the complete data. If values are randomly omitted from the dataset, then the data are missing completely at random (MCAR). If the pattern of missingness can be predicted using other, observed data in the dataset, then data are missing at random (MAR). If the pattern of missingness cannot be predicted using the observed data in the dataset, and the pattern in missingness depends on the missing data itself, then data are missing not at random (MNAR), sometimes termed nonignorable (NI). Multiple imputation is more efficient than listwise deletion when data are MCAR, and both more efficient and less biased than listwise deletion when data are MAR. Both multiple imputation and listwise deletion are biased when data are MNAR. Table 1 summarizes what we know about the bias of listwise deletion and multiple imputation for different kinds of missing data.Footnote 1
Table 1. Bias in listwise deletion and multiple imputation.
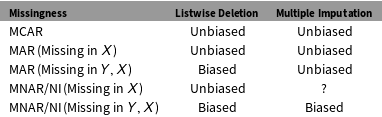
The last two rows in Table 1 are the focus of this letter.
Work that has popularized multiple imputation in political science recognizes that multiple imputation is biased when data are MNAR. However, the state of the art in the literature holds that multiple imputation is no worse than listwise deletion in this case.
Both listwise deletion and basic multiple imputation approaches can be biased under NI, in which case additional steps must be taken, or different models must be chosen, to ensure valid inferences. Thus, multiple imputation will normally be better than, and almost always not worse than, listwise deletion (King et al. Reference King, Honaker, Joseph and Scheve2001, 51, emphasis added).
However, when multiple imputation and listwise deletion are both biased, it does not follow that the bias in multiple imputation is generally lower than that of listwise deletion. Relatedly, Lall (Reference Lall2016, 419) writes:
the same conditions that cause multiple imputation to be severely biased also cause listwise deletion to be severely biased…. Since multiple imputation is always more efficient than listwise deletion, even in this worst-case scenario it is still the preferable strategy (emphasis added).
If multiple imputation were generally superior to listwise deletion for NI missing data, then researchers might prefer results from multiple imputation over results from listwise deletion when the true data generating process is unknown and the two return different findings.
This letter compares the performance of multiple imputation and listwise deletion for NI missing data in common data structures in the social sciences. Multiple imputation yields results that are almost always not better than listwise deletion. When data is missing in
$X$
, my simulation results confirm that multiple imputation is strictly worse than listwise deletion, even when missingness is NI. This is the case even when data are very nearly MAR. These results recommend caution when comparing the results from multiple imputation and listwise deletion when the true data generating process is unknown, complementing and amplifying the conclusions reached by Arel-Bundock and Pelc (Reference Arel-Bundock and Pelc2018), who focus on MAR data rather than NI missing data. Researchers using multiple imputation on still more complicated data structures should not conclude that multiple imputation is preferable to listwise deletion simply because they return different results.
2 A Basic Simulation Exercise
The data structure explored in this letter is a simple multiple regression model of the formFootnote 2
$$\begin{eqnarray}Y=\unicode[STIX]{x1D6FD}_{1}X_{1}+\unicode[STIX]{x1D6FD}_{2}X_{2}+\unicode[STIX]{x1D716}.\end{eqnarray}$$
In the initial exercise, data is missing only for
$X_{2}$
, so both
$X_{1}$
and
$Y_{1}$
are fully observed. In all simulations, I set
$\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}=5$
. The theoretical variable of interest is
$X_{2}$
, so the estimation problem is to estimate
$\unicode[STIX]{x1D6FD}_{2}$
. Restricting missingness to
$X_{2}$
only is the best case scenario for listwise deletion with MNAR data because under the assumption that (1) is the true data generating process, then listwise deletion is unbiased (see Little Reference Little1992, 1229; Arel-Bundock and Pelc Reference Arel-Bundock and Pelc2018). It serves as a useful benchmark from which to compare listwise deletion to multiple imputation, and then to build more complicated simulations.
To capture the possibility that there might be other useful variables in the dataset,
$X_{2}$
is modeled as a linear combination of two other variables and (possibly) an error term:
$$\begin{eqnarray}X_{2}=.5U_{1}+.5U_{2}+\unicode[STIX]{x1D702}.\end{eqnarray}$$
These are drawn following a rule that ensures that in expectation,
$X_{2}\sim N(0,1)$
: for values of
$q$
between 0 and approaching 1,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}\sim N(0,q) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{1},U_{2}\sim N(0,(1-q)/.5). & \displaystyle\end{eqnarray}$$
When
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}$
—the variance of
$\unicode[STIX]{x1D702}$
in (2)—is
$0$
, then
$X_{2}$
is an exact linear combination of
$U_{1}$
and
$U_{2}$
. Both
$X_{1}$
and
$\unicode[STIX]{x1D716}\sim N(0,1)$
, so by construction
$X_{1}$
and
$X_{2}$
are independent (this will be relaxed later). It is useful to observe that given this setup, with
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}=.2$
, the fully observed data contain a great deal of information about
$X_{2}$
, the variable that will be plagued by missingness. These are propitious conditions for using observed data to predict missing data.
To compare multiple imputation with listwise deletion, I first discard the lowest 20% of the values of
$X_{2}$
. I then run four standard analyses: one on the full data, one where I drop all observations that are missing, and then two multiple imputation analyses using the amelia package in R (Honaker, King, and Blackwell Reference Honaker, King and Blackwell2011), which I process through the zelig package (R Core Team Reference Choirat, Honaker, Imai, King and Lau2007). One includes the proxies
$U_{1},U_{2}$
and one omits them.
From there, I extract four quantities:
$\hat{b}_{2,\text{Full}}$
is the estimate when
$X_{2}$
is fully observed,
$\hat{b}_{2,\text{LD}}$
is the listwise deletion estimate (LD stands for listwise deletion),
$\hat{b}_{2,\text{NoProxies}}$
employs multiple imputation without including the proxy variable
$U_{1}$
or
$U_{2}$
, and
$\hat{b}_{2,\text{Proxies}}$
employs multiple imputation but includes the proxies.Footnote
3
To compare results, I repeat the above procedure 1000 times. Figure 1 displays the results of these 1000 simulations (left-hand side) alongside a density plot of the true versus simulated data in one run of the multiple imputation algorithm. The top left plot shows density plots of the four estimates of
$\hat{b}_{2}$
. The bottom left plot calculates the absolute error of each estimator, calculated as
$|\hat{b}_{2}-\unicode[STIX]{x1D6FD}_{2}|$
. Listwise deletion is unbiased, but less efficient than estimates with no missing data. Importantly, the two figures clearly show that multiple imputation is more biased than listwise deletion. And surprisingly, the inclusion of
$U_{1}$
and
$U_{2}$
does not help multiple imputation much, although the proxies do return estimates that are less biased than multiple imputation without proxies.
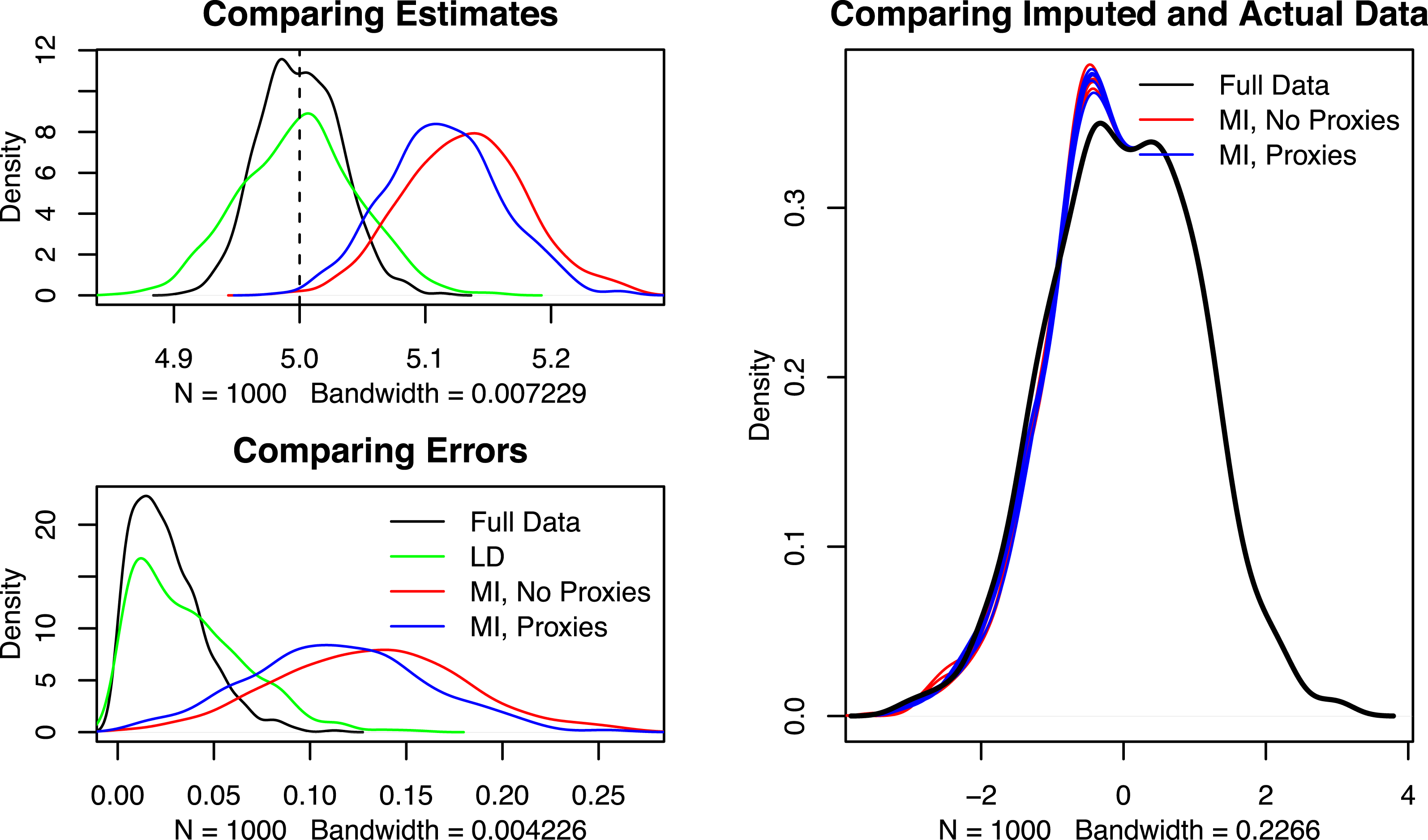
Figure 1. Simulation results.
Why would multiple imputation underperform listwise deletion? Because multiple imputation imputes values for the missing data by assuming that the complete data is representative of the missing data, it predicts the relationship between
$X_{2}$
and both
$Y$
and
$X_{1}$
without access to the lowest 20% of the observations for
$X_{2}$
. This produces a slightly biased prediction of the relationships among the three, and as a result a slightly biased prediction of the missing
$X_{2}$
(see the right side of Figure 1). Here, there is upward bias in the predictions of the missing
$X_{2}$
. Because listwise deletion is unbiased, in this case it will outperform multiple imputation.
To compare coverage rates for multiple imputation and listwise deletion, for each simulation I check whether the true value of
$\unicode[STIX]{x1D6FD}_{2}=5$
falls within two standard errors of the estimates
$\hat{b}_{2,\text{LD}}$
,
$\hat{b}_{2,\text{NoProxies}}$
, and
$\hat{b}_{2,\text{Proxies}}$
. The resulting coverage rates across the 1000 simulations are 95.3% for listwise deletion, 22.9% for multiple imputation without proxies, and 31.6% for multiple imputation with proxies.
Before proceeding, I pause here to reiterate that this result should be unsurprising: if missingness is purely a function of
$X_{2}$
then even when data are MNAR, listwise deletion is unbiased (see the proof in Allison (Reference Allison2002), footnote 1, p. 87). What is possibly surprising is that multiple imputation fares worse in this application than listwise deletion. Commenting on this issue, Allison (Reference Allison2014) observes that for NI missing data where missingness is unrelated to
$Y$
, missingness “certainly could lead to bias if you use standard implementations of multiple imputation.” The findings here suggest that the dangers of bias when using multiple imputation are not just “possible” (see Lall Reference Lall2016, footnote 17); they are substantial when missingness is confined to
$X$
. The results above also reveal that having proxy variables in the multiple imputation dataset that are known to be strongly predictive of the missing values does not help very much.
2.1 Variation: Missingness and the Informativeness of Proxies
To probe the performance of multiple imputation versus listwise deletion further, I repeat the above simulations, but vary the missingness on
$X_{2}$
by deleting from 10% to 90% of the data from
$X_{2}$
. For these simulations,
$P(\text{Missing})$
is a deterministic function of
$X_{2}$
: every observation lower than the cutoff threshold
$p$
is missing, and every observation above that threshold is fully observed. As a result,
$P(Y|X_{2}=\text{Observed})\neq P(Y|X_{2}=\text{Missing})$
, so data are MNAR, but simulated data are “closer to” MAR the lower the value of
$p$
is. The number of simulations is set at 1000 for each value of
$p$
.
Figure 2 displays the results. The top figure calculates the proportion of simulations of where the error of
$\hat{b}_{2,\text{NoProxies}}$
(or
$\hat{b}_{2,\text{Proxies}}$
) is greater than the error of
$\hat{b}_{2,\text{LD}}$
. The bottom left figure summarizes the empirical mean squared error (MSE),
$(\hat{b}_{2}-\unicode[STIX]{x1D6FD}_{2})^{2}$
, for the 1000 simulations of
$\hat{b}_{2,LD}$
,
$\hat{b}_{2,\text{NoProxies}}$
, and
$\hat{b}_{2,\text{Proxies}}$
across the values of
$p$
. And finally, the bottom right figure summarizes the coverage rates, which again correspond to the percentage of simulations in which
$\hat{b}_{2,\text{LD}}$
,
$\hat{b}_{2,\text{NoProxies}}$
, and
$\hat{b}_{2,\text{Proxies}}$
lie within two standard deviations of the true value of
$\unicode[STIX]{x1D6FD}_{2}$
. The top figure shows that although there are some simulations for which the multiple imputation estimate has lower error than the listwise deletion estimate, in most cases the error for multiple imputation exceeds that of listwise deletion. For both multiple imputation and listwise deletion, MSE is larger as missingness is larger. However, the average MSE for multiple imputation is higher, even with highly informative proxies included in the multiple imputation data, than it is for listwise deletion. When missingness is low, the three estimators fare comparably (although listwise deletion usually has lower MSE anyway), but as missingness increases the relative performance of multiple imputation declines faster than listwise deletion.
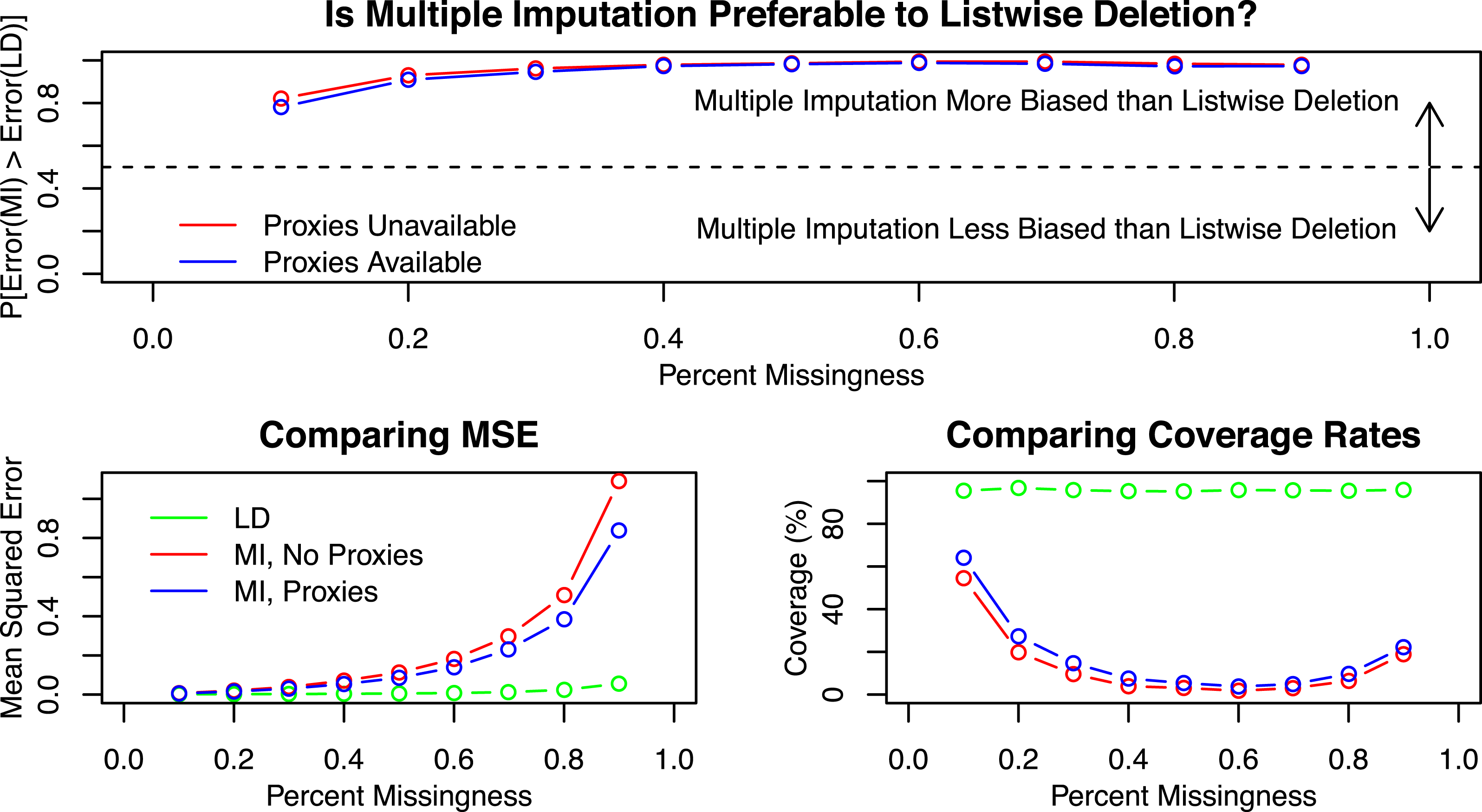
Figure 2. Simulation results by missingness.
I also vary the “informativeness” of the proxies. To do so, I fix
$p=.2$
, deleting the lowest 20% of the observations for
$X_{2}$
, but vary
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}$
from 0 to .9. Recall that when
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}=0$
then
$X_{2}$
is a perfect linear combination of
$U_{1}$
and
$U_{2}$
. In this case, the data are actually MAR when these proxies are included in multiple imputation. As
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}$
increases, the data depart ever more substantially from the MAR assumption.
Figure 3 below is identical to those above, but with
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}$
as the X-axis. It shows that when
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}=0$
, multiple imputation is superior to listwise deletion, as expected, because the data are MAR. However, with just the smallest bit of randomness, in this case as low as
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D702}}^{2}=.01$
, listwise deletion performs comparably to multiple imputation. As the data depart ever more systematically from MAR, the performance of multiple imputation relative to listwise deletion deteriorates as well.
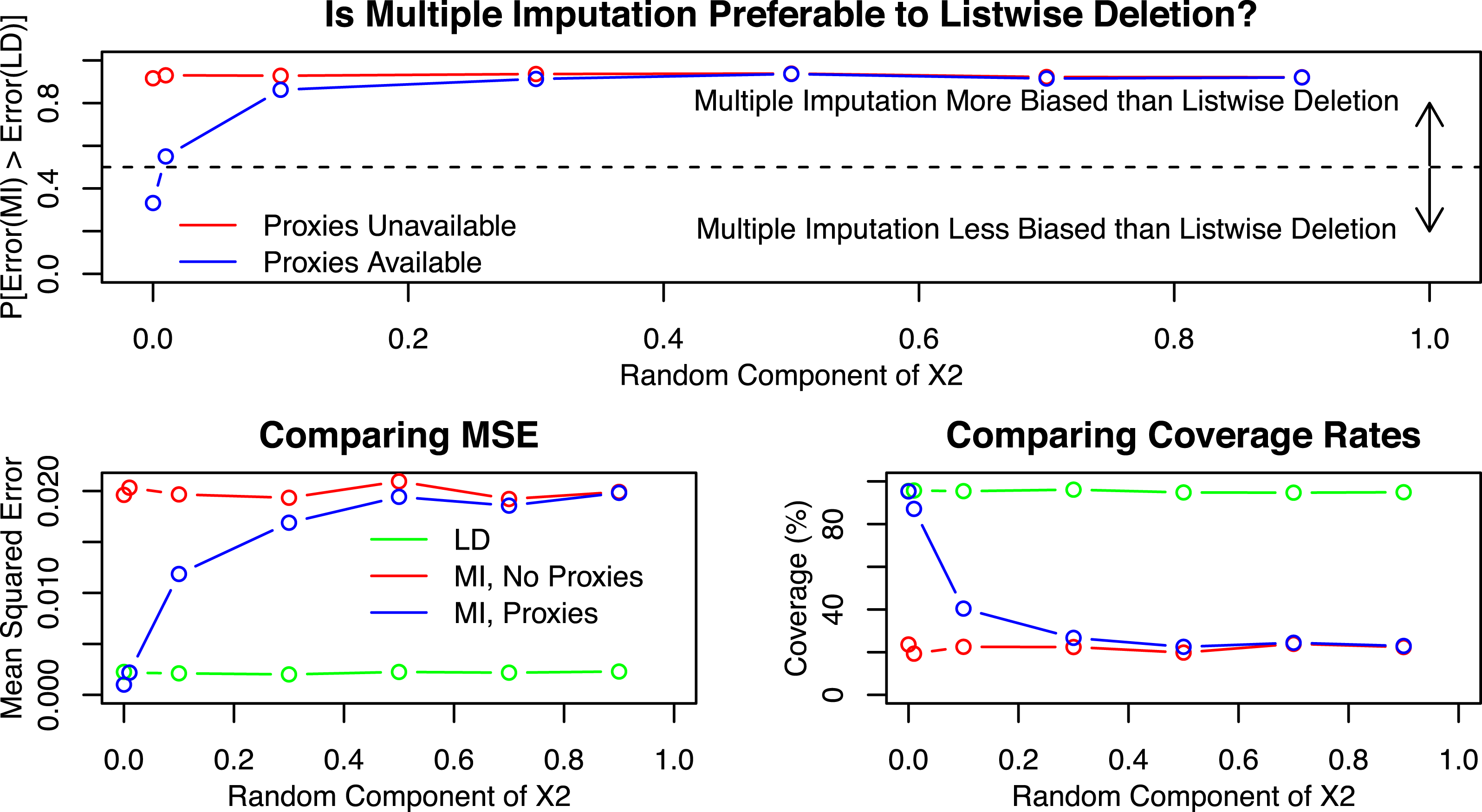
Figure 3. Simulation results by informativeness of the proxies.
3 Extended Simulations
In the Supplemental Appendix I introduce gradually more complicated data structures, and examine the relative performance of multiple imputation and listwise deletion using similar metrics. These extensions introduce probabilistic missingness in
$X_{2}$
, NI missingness in
$Y$
as well as
$X_{2}$
, missingness in
$X_{2}$
determined by the proxies
$U_{1},U_{2}$
rather than
$X_{2}$
itself, and allow
$X_{2}$
to be correlated with
$X_{1}$
. I also present an “exotic” multiple regression case with more independent variables, more kinds of missingness, discrete predictors, and non-normal distributions. In these simulations, multiple imputation performs relatively better than it does in the motivating case with missingness confined to
$X_{2}$
only, although in no simulations does multiple imputation outperform listwise deletion in terms of bias, efficiency, or coverage. Here, I entertain one particularly important example: a cluster randomized experiment with heterogeneous treatment effects.
3.1 A Cluster Randomized Example
In this example, the setup is a cluster randomized experiment where groups
$k$
are assigned to treatment
$T_{k}$
, and the researcher believes that there is an individual level characteristic
$D_{i}$
that differentiates the effect of
$T$
. Consider a model of individuals nested within villages with treatment assignment at the village level, and differences by ethnic group within the village; or students nested within schools with treatment assignment at the school level, and differences by gender within the school. The model to be estimated is
$$\begin{eqnarray}Y_{i}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FD}T_{k}+\unicode[STIX]{x1D6FE}D_{i}+\unicode[STIX]{x1D6FF}D_{i}\ast T_{k}+\unicode[STIX]{x1D719}_{k}+\unicode[STIX]{x1D716}_{i}.\end{eqnarray}$$
Fixed effects
$\unicode[STIX]{x1D719}_{k}$
are included but they are uncorrelated with
$T$
so their inclusion only increases efficiency. I set
$\unicode[STIX]{x1D6FC}=1$
and
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FF}=5$
for the simulations.
Missingness in
$Y$
depends on the value of
$D$
as well as the value of a fully observed pre-treatment covariate
$X$
. In the case of individuals within villages, consider
$Y$
to be a measure of political efficacy, and
$X$
a measure of income. Perhaps data on political efficacy is less likely to be recorded from ethnic group A versus ethnic group B, but in both cases is more likely to be recorded from higher-income individuals. Missingness is nonrandom, but confined to
$Y$
as a function of
$D$
and
$X$
:
$$\begin{eqnarray}\displaystyle P(\text{Missing}\,|D=1) & = & \displaystyle \unicode[STIX]{x1D6F7}(X+p+.25)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(\text{Missing}\,|D=0) & = & \displaystyle \unicode[STIX]{x1D6F7}(X+p-.05).\end{eqnarray}$$
As above,
$p$
varies across simulations in order to increase the overall level of missingness.
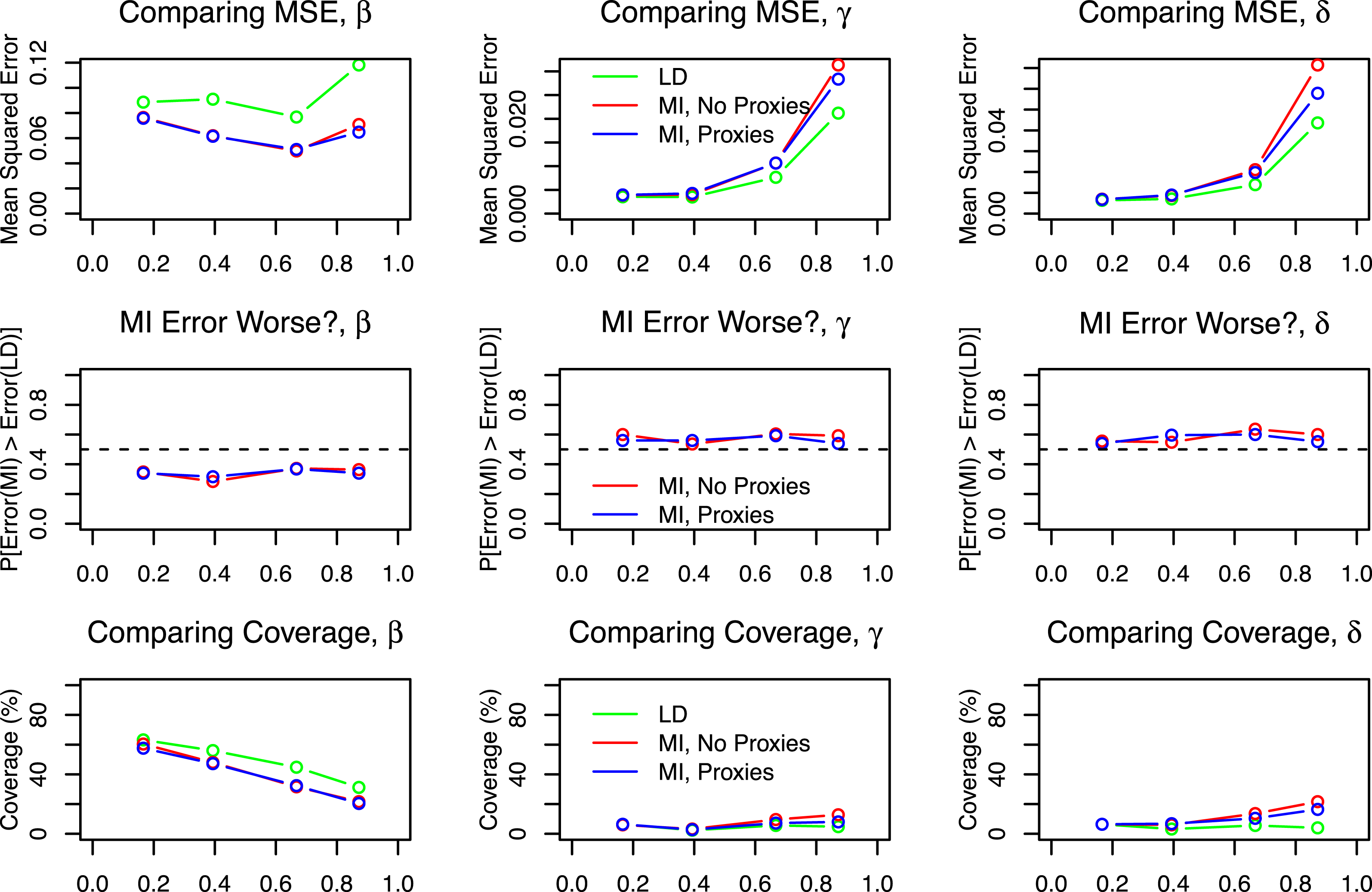
Figure 4. Simulation results from a cluster randomized experiment.
The results appear in Figure 4; in this example I compare performance for the parameters
$\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FE}$
, and
$\unicode[STIX]{x1D6FF}$
. In this example multiple imputation has a lower MSE than listwise deletion when estimating
$\unicode[STIX]{x1D6FD}$
but a higher MSE when estimating
$\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FF}$
. Coverage rates for
$\unicode[STIX]{x1D6FD}$
are the opposite: low, but better for listwise deletion when estimating
$\unicode[STIX]{x1D6FD}$
, and worse for listwise deletion when estimating
$\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FF}$
. Although neither listwise deletion nor multiple imputation performs particularly well by any metric, whether one prefers the former or the latter in this example depends both on the parameter of interest and the metric by which one compares them.
4 Application to Real Data
A final way to explore the effects of different strategies for handling missing data is to compare multiple imputation and listwise deletion using real-world data. To do so, I replicate the analysis of incumbency advantage in Indonesia’s legislative elections presented in Dettman, Pepinsky, and Pierskalla (Reference Dettman, Pepinsky and Pierskalla2017). I focus on Model 1 in Table 3 (p. 117), their baseline results that show the effects of incumbency and other variables on candidate vote share. Here, I confine my analysis to the relationship between incumbency, gender, and candidate age (as independent variables) and candidate vote share (as the dependent variable). A useful feature of Dettman, Pepinsky, and Pierskalla (Reference Dettman, Pepinsky and Pierskalla2017)’s data are that the dependent variable is highly skewed (median vote share is 0.48% and mean vote share is 1.19%) and the independent variable of interest is rare (433 out of 6043 or 7.2% of legislative candidates were incumbents). This mimics many real-world data problems, and thus allows me to explore a more realistic joint density using both listwise deletion and multiple imputation.
To simulate NI missingness, I generate a missing data situation in which data on incumbency status (the authors’ key theoretical variable of interest) is missing only among candidates who are not incumbents, and vote share is missing only among candidates who received the highest vote share. Specifically, I adopted the following procedure.
∙ I randomly select 25% of the observations in the dataset, and set Incumbency to missing when
$\mathit{Incumbency}=0$
.∙ I randomly select another 25% of the observations (with replacement, so some observations will be selected twice), and assign
$\text{Vote}~\text{Share}$
to missing if the candidate’s true vote share was in the highest quartile in the dataset.
I then estimate
$\hat{b}_{\text{Incumbency}}$
,
$\hat{b}_{\text{Gender}}$
, and
$\hat{b}_{\text{Age}}$
using both multiple imputation and listwise deletion. In this exercise I increase the number of imputed datasets substantially in the hopes of increasing the precision of the multiple imputation estimates: if 30% of the observations in a particular simulated dataset are missing, for example, I create and then analyze 30 imputed datasets. I repeat the above process 100 times, and display the results in Figure 5.
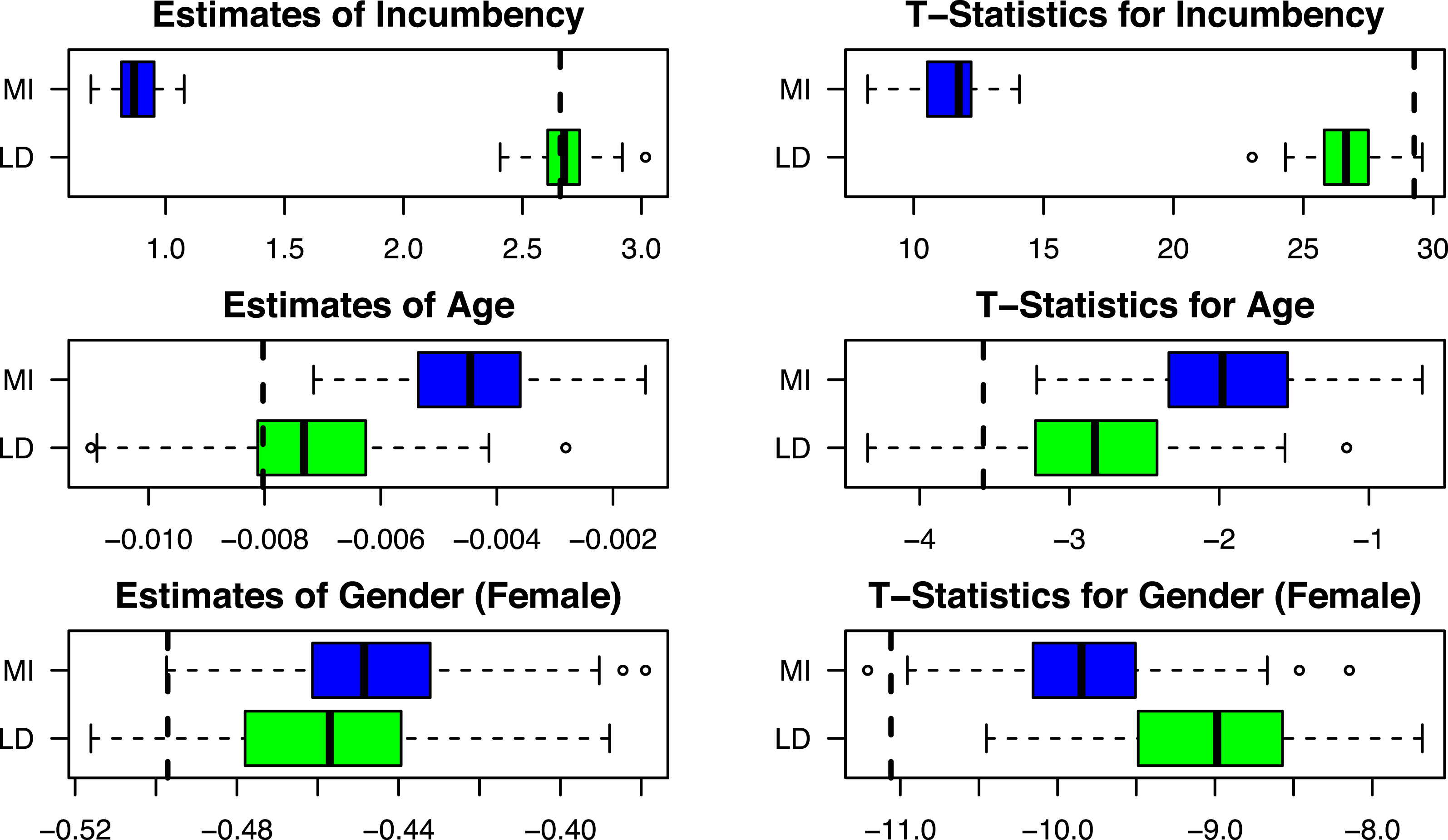
Figure 5. Replication of Dettman, Pepinsky, and Pierskalla (Reference Dettman, Pepinsky and Pierskalla2017).
The “true” coefficients and T-statistics estimated in Dettman, Pepinsky, and Pierskalla (Reference Dettman, Pepinsky and Pierskalla2017), Table 3 are plotted as black dotted lines. We discover that in general, multiple imputation underestimates
$\hat{b}_{\text{Incumbency}}$
by a factor of more than three—the median multiple imputation estimate is 0.87, whereas the true estimate is 2.66). Listwise deletion returns estimates of this key theoretical variable of interest that are roughly equivalent to the true estimate (the median listwise deletion estimate is 2.68), with T-statistics that are smaller but much closer to the true T-statistics.Footnote
4
In this case, given how large and statistically significant incumbency effects are in Indonesia’s legislative elections, an analysis using multiple imputation would still conclude that incumbency effects exist. But estimates of the magnitude of this effect will be much too small.
The same is not true for the estimates of
$\hat{b}_{\text{Age}}$
. Here, the effect of candidate age is statistically significant at the 95% level for 94% of the simulations using listwise deletion but only 51% of the simulations when using multiple imputation. In this particular case, then, multiple imputation is much more likely to result in Type-2 error than listwise deletion. Looking to
$\hat{b}_{\text{Gender}}$
, still another pattern emerges: here, both multiple imputation and listwise deletion perform about the same when estimating
$\hat{b}_{\text{Gender}}$
, but now listwise deletion has T-statistics that are relatively more conservative.
The results from this simulated missing data exercise amplify the discussion above. In this particular example, multiple imputation produces results that are significantly worse in terms of bias and precision than listwise deletion for the theoretical variable of interest. For two (fully observed) covariates, results are in one case worse, and in one case better (at least in terms of precision). Of course, only knowing the true values from the fully observed data allows us to compare the performance of the two. But this exercise clearly reveals that multiple imputation can change substantive conclusions in real-world applications, and in this case, those conclusions will frequently be more misleading than those that come from listwise deletion.
5 Conclusion
The conditions upon which multiple imputation is superior to listwise deletion are clear. When data are MAR multiple imputation is unbiased when listwise deletion is not; when data are MCAR both are unbiased but multiple imputation is more efficient. But as most authors recognize, real-world data are very unlikely to be MAR. Graham (Reference Graham2009, 567) argues, in fact, that “whether [data] is MNAR or not should never be the issue.” If, as he continues, “all missingness is MNAR (i.e., not purely MAR)”, then applied researchers must be careful using multiple imputation. Conclusions such as “multiple imputation is not seriously biased under MNAR if missingness is strongly related to observed data and thus approximates MAR” Lall (Reference Lall2016, 418) do not hold in most of the simulations presented above; and when multiple is least biased, listwise deletion is also least biased. Multiple imputation’s superiority over listwise deletion does not follow from the observation that both are biased.
Suppose, then, that the analyst finds herself in the situation where multiple imputation and listwise deletion present different results. Under what conditions would she conclude that the estimates from multiple imputation are superior to the estimates from listwise deletion? The possible answers are “if the missing data are MAR” or “if this is a type of data scenario in which nature of the NI missingness is such that multiple imputation generally performs better than listwise deletion.” I have not presented such a scenario because I have not discovered one, but it surely exists. The conclusion to draw is that multiple imputation cannot be applied agnostically when encountering missing data. Preferring multiple imputation over listwise deletion requires reference to the application-specific nature of the missing data.
Supplementary material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2018.18.
