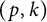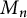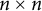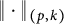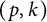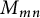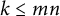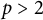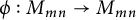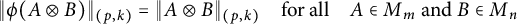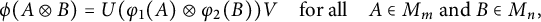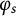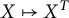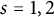1 Introduction
Throughout this paper, we denote by
![]() $M_{m,n}$
and
$M_{m,n}$
and
![]() $M_n$
the set of
$M_n$
the set of
![]() $m\times n$
and
$m\times n$
and
![]() $n\times n$
complex matrices, respectively. Denote by
$n\times n$
complex matrices, respectively. Denote by
![]() $H_n$
the set of all
$H_n$
the set of all
![]() $n\times n$
Hermitian matrices. For two matrices
$n\times n$
Hermitian matrices. For two matrices
![]() $A=(a_{ij})\in M_m$
and
$A=(a_{ij})\in M_m$
and
![]() $B\in M_n$
, their tensor product is defined to be
$B\in M_n$
, their tensor product is defined to be
![]() $A\otimes B=(a_{ij}B)$
, which is an
$A\otimes B=(a_{ij}B)$
, which is an
![]() $mn\times mn$
matrix. We denote by
$mn\times mn$
matrix. We denote by
and
Suppose
![]() $A\in M_{m,n}$
. The singular values of A are always denoted in decreasing order by
$A\in M_{m,n}$
. The singular values of A are always denoted in decreasing order by
![]() $s_1(A)\geq \cdots \geq s_{\ell }(A)$
, where
$s_1(A)\geq \cdots \geq s_{\ell }(A)$
, where
![]() $\ell =\min \{m,n\}$
. Given a real number
$\ell =\min \{m,n\}$
. Given a real number
![]() $p\geq 1$
and a positive integer
$p\geq 1$
and a positive integer
![]() $k\leq \min \{m,n\}$
, the
$k\leq \min \{m,n\}$
, the
![]() $(p,k)$
-norm of A is defined by
$(p,k)$
-norm of A is defined by
 $$ \begin{align*}\|A\|_{(p,k)}=\left[\sum\limits_{i=1}^ks_i^p(A)\right]^{ \frac{1}{p}}.\end{align*} $$
$$ \begin{align*}\|A\|_{(p,k)}=\left[\sum\limits_{i=1}^ks_i^p(A)\right]^{ \frac{1}{p}}.\end{align*} $$
The
![]() $(p,k)$
-norm, also known as the Ky Fan
$(p,k)$
-norm, also known as the Ky Fan
![]() $(p,k)$
-norm, was first recognized as a special class of unitarily invariant norms in the study of isometries by Grone and Marcus [Reference Grone and Marcus13] in their notable work from the 1970s. The
$(p,k)$
-norm, was first recognized as a special class of unitarily invariant norms in the study of isometries by Grone and Marcus [Reference Grone and Marcus13] in their notable work from the 1970s. The
![]() $(p,k)$
-norms encompass many commonly used norms. For instance, the
$(p,k)$
-norms encompass many commonly used norms. For instance, the
![]() $(1,k)$
-norm reduces to the Ky Fan k-norm, while the
$(1,k)$
-norm reduces to the Ky Fan k-norm, while the
![]() $(p,K)$
-norm, with
$(p,K)$
-norm, with
![]() $K = \min \{m,n\}$
, reduces to Schatten p-norm. Moreover, the Ky Fan
$K = \min \{m,n\}$
, reduces to Schatten p-norm. Moreover, the Ky Fan
![]() $1$
-norm, Ky Fan K-norm, and Shatten
$1$
-norm, Ky Fan K-norm, and Shatten
![]() $2$
-norm are also known as the spectral norm, the trace norm, and the Frobenius norm, respectively. Some earlier works exploring the fundamental properties of the
$2$
-norm are also known as the spectral norm, the trace norm, and the Frobenius norm, respectively. Some earlier works exploring the fundamental properties of the
![]() $(p,k)$
-norm can be found in [Reference Horn and Johnson14, Reference Kidman19, Reference Marcus, Kidman and Sandy24].
$(p,k)$
-norm can be found in [Reference Horn and Johnson14, Reference Kidman19, Reference Marcus, Kidman and Sandy24].
In addition to being a generalization of many well-known norms, the
![]() $(p,k)$
-norm itself has attracted extensive attention from researchers across various fields, particularly in the study of low-rank approximation (e.g., [Reference Doan and Vavasis5, Reference Jiang, Liu, Qi and Dai16, Reference Tanaka and Nakata30]). The application of the
$(p,k)$
-norm itself has attracted extensive attention from researchers across various fields, particularly in the study of low-rank approximation (e.g., [Reference Doan and Vavasis5, Reference Jiang, Liu, Qi and Dai16, Reference Tanaka and Nakata30]). The application of the
![]() $(p,k)$
-norm in quantum information science has also gained recent attention. Researchers in this field have explored the concept of the twisted commutators of two unitaries and focused on determining the minimum norm value of these twisted commutators. The authors in [Reference Chubb and Flammia3] succeeded in obtaining an explicit closed form for the minimum twisted commutation value with respect to the
$(p,k)$
-norm in quantum information science has also gained recent attention. Researchers in this field have explored the concept of the twisted commutators of two unitaries and focused on determining the minimum norm value of these twisted commutators. The authors in [Reference Chubb and Flammia3] succeeded in obtaining an explicit closed form for the minimum twisted commutation value with respect to the
![]() $(p,k)$
-norm. All these show the growing importance and relevance of the
$(p,k)$
-norm. All these show the growing importance and relevance of the
![]() $(p,k)$
-norm across various fields of study.
$(p,k)$
-norm across various fields of study.
Linear preserver problems concern the study of linear maps on matrices or operators preserving certain special properties. Since Frobenius gave the characterization of linear maps on
![]() $M_n$
that preserve the determinant of all matrices in 1897, a lot of linear preserver problems have been investigated (see [Reference Li and Pierce20, Reference Molnár26] and the references therein).
$M_n$
that preserve the determinant of all matrices in 1897, a lot of linear preserver problems have been investigated (see [Reference Li and Pierce20, Reference Molnár26] and the references therein).
The study of linear preservers on various matrix norms have been extensively explored since Schur [Reference Schur29] characterized linear maps on
![]() $M_n$
that preserve the spectral norm. This was followed by a series of subsequent results [Reference Arazy1, Reference Grone12, Reference Grone and Marcus13, Reference Li and Tsing23, Reference Russo27, Reference Russo28]. Notably, Li and Tsing [Reference Li and Tsing23] provided a complete characterization of linear maps that preserve the
$M_n$
that preserve the spectral norm. This was followed by a series of subsequent results [Reference Arazy1, Reference Grone12, Reference Grone and Marcus13, Reference Li and Tsing23, Reference Russo27, Reference Russo28]. Notably, Li and Tsing [Reference Li and Tsing23] provided a complete characterization of linear maps that preserve the
![]() $(p,k)$
-norms. They showed that linear maps on
$(p,k)$
-norms. They showed that linear maps on
![]() $M_{m,n}$
that preserve the
$M_{m,n}$
that preserve the
![]() $(p,k)$
-norms (except for the Frobenius norm) have the form
$(p,k)$
-norms (except for the Frobenius norm) have the form
for some unitary matrices
![]() $U\in M_m$
and
$U\in M_m$
and
![]() $V\in M_n.$
$V\in M_n.$
Traditional linear preserver problems deal with linear maps preserving certain properties of every matrix in the whole matrix space
![]() $M_n$
or
$M_n$
or
![]() $H_n$
. Recently, linear maps on
$H_n$
. Recently, linear maps on
![]() $M_{mn}$
or
$M_{mn}$
or
![]() $H_{mn}$
only preserving certain properties of matrices in
$H_{mn}$
only preserving certain properties of matrices in
![]() $M_m\otimes M_n$
or
$M_m\otimes M_n$
or
![]() $H_m\otimes H_n$
have been investigated. Friedland et al. [Reference Friedland, Li, Poon and Sze11] provided a characterization of linear maps on
$H_m\otimes H_n$
have been investigated. Friedland et al. [Reference Friedland, Li, Poon and Sze11] provided a characterization of linear maps on
![]() $H_m\otimes H_n$
that preserve the set of separable states in bipartite systems. The concept of separability is widely recognized as a fundamental and crucial aspect in the field of quantum information science. Johnston in his paper [Reference Johnston17] examined invertible linear maps on
$H_m\otimes H_n$
that preserve the set of separable states in bipartite systems. The concept of separability is widely recognized as a fundamental and crucial aspect in the field of quantum information science. Johnston in his paper [Reference Johnston17] examined invertible linear maps on
![]() $M_m\otimes M_n$
that preserve the set of rank one matrices with bounded Schmidt rank in both row and column spaces. Additionally, the author investigated linear maps on
$M_m\otimes M_n$
that preserve the set of rank one matrices with bounded Schmidt rank in both row and column spaces. Additionally, the author investigated linear maps on
![]() $M_m\otimes M_n$
that preserve the Schmidt k-norm, a norm induced by states with bounded Schmidt rank, which finds extensive application in the field of quantum information. For more details on the Schmidt k-norm, refer to [Reference Johnston and Kribs18].
$M_m\otimes M_n$
that preserve the Schmidt k-norm, a norm induced by states with bounded Schmidt rank, which finds extensive application in the field of quantum information. For more details on the Schmidt k-norm, refer to [Reference Johnston and Kribs18].
Note that
![]() $M_m\otimes M_n$
and
$M_m\otimes M_n$
and
![]() $H_m\otimes H_n$
are small subsets of
$H_m\otimes H_n$
are small subsets of
![]() $M_{mn}$
and
$M_{mn}$
and
![]() $H_{mn}$
. Researchers know much less information on such linear maps. So it is more difficult to characterize such linear maps. Along this line, linear maps on Hermitian matrices preserving the spectral radius were determined in [Reference Fošner, Huang, Li and Sze8]. Linear maps on complex matrices or Hermitian matrices preserving determinant were studied in [Reference Chooi and Kwa2, Reference Ding, Fošner, Xu and Zheng4, Reference Duffner and Cruz6]. Linear maps on complex matrices preserving numerical radius, k-numerical range, product numerical range, and rank-one matrices were characterized in [Reference Fošner, Huang, Li, Poon and Sze7, Reference Fošner, Huang, Li and Sze9, Reference Huang, Shi and Sze15, Reference Li, Poon and Sze21].
$H_{mn}$
. Researchers know much less information on such linear maps. So it is more difficult to characterize such linear maps. Along this line, linear maps on Hermitian matrices preserving the spectral radius were determined in [Reference Fošner, Huang, Li and Sze8]. Linear maps on complex matrices or Hermitian matrices preserving determinant were studied in [Reference Chooi and Kwa2, Reference Ding, Fošner, Xu and Zheng4, Reference Duffner and Cruz6]. Linear maps on complex matrices preserving numerical radius, k-numerical range, product numerical range, and rank-one matrices were characterized in [Reference Fošner, Huang, Li, Poon and Sze7, Reference Fošner, Huang, Li and Sze9, Reference Huang, Shi and Sze15, Reference Li, Poon and Sze21].
In [Reference Fošner, Huang, Li and Sze10], the authors characterized linear maps on
![]() $M_{mn}$
preserving the Ky Fan k-norm and the Schatten p-norm of the tensor products
$M_{mn}$
preserving the Ky Fan k-norm and the Schatten p-norm of the tensor products
![]() $A\otimes B$
for all
$A\otimes B$
for all
![]() $A\in M_m$
and
$A\in M_m$
and
![]() ${B\in M_n}$
. Despite the non-obvious connection to the field of quantum information, from a mathematical perspective, it is undeniably intriguing to consider the linear maps that preserve the
${B\in M_n}$
. Despite the non-obvious connection to the field of quantum information, from a mathematical perspective, it is undeniably intriguing to consider the linear maps that preserve the
![]() $(p,k)$
-norm of tensor products of matrices.
$(p,k)$
-norm of tensor products of matrices.
Therefore, in this paper, we aim to characterize linear maps
![]() $\phi $
on
$\phi $
on
![]() $M_{mn}$
such that for
$M_{mn}$
such that for
![]() $p>2$
and
$p>2$
and
![]() $1\leq k\leq mn$
,
$1\leq k\leq mn$
,
The comprehensive characterization in the bipartite systems will be presented in Section 2, while in Section 3, we will extend the results to multipartite systems.
2 Bipartite system
The linear maps on
![]() $M_{mn}$
satisfying (1.1) are determined by the following theorem.
$M_{mn}$
satisfying (1.1) are determined by the following theorem.
Theorem 2.1 Let
![]() $m,n \geq 2 $
be integers. Given a real number
$m,n \geq 2 $
be integers. Given a real number
![]() $p>2$
and a positive integer
$p>2$
and a positive integer
![]() $ k \leq mn$
, a linear map
$ k \leq mn$
, a linear map
![]() $\phi : M_{mn}\to M_{mn}$
satisfies
$\phi : M_{mn}\to M_{mn}$
satisfies
if and only if there exist unitary matrices
![]() $U,V \in M_{mn}$
such that
$U,V \in M_{mn}$
such that
where
![]() $\varphi _s$
is the identity map or the transposition map
$\varphi _s$
is the identity map or the transposition map
![]() $X\mapsto X^T$
for
$X\mapsto X^T$
for
![]() $s=1,2$
.
$s=1,2$
.
To prove the theorem, we need some notations and preliminary results. Denote by
![]() $\|A\|$
and
$\|A\|$
and
![]() $A^*$
the Frobenius norm and the conjugate transpose of the matrix A, respectively. Two matrices
$A^*$
the Frobenius norm and the conjugate transpose of the matrix A, respectively. Two matrices
![]() $A,B\in M_n$
are said to be orthogonal, denoted by
$A,B\in M_n$
are said to be orthogonal, denoted by
![]() $A\perp B$
, if
$A\perp B$
, if
![]() $A^*B=AB^*=0$
. Denote by
$A^*B=AB^*=0$
. Denote by
![]() $E_{ij}\in M_{m,n}$
the matrix whose
$E_{ij}\in M_{m,n}$
the matrix whose
![]() $(i,j)$
th entry is equal to one and all the other entries are equal to zero.
$(i,j)$
th entry is equal to one and all the other entries are equal to zero.
The eigenvalues of an
![]() $n\times n$
Hermitian matrix A are always denoted in decreasing order by
$n\times n$
Hermitian matrix A are always denoted in decreasing order by
![]() $\lambda _1(A)\geq \lambda _2(A)\geq \cdots \geq \lambda _n(A)$
. For
$\lambda _1(A)\geq \lambda _2(A)\geq \cdots \geq \lambda _n(A)$
. For
![]() $A,B\in H_n$
, we use the notation
$A,B\in H_n$
, we use the notation
![]() $A\geq B$
or
$A\geq B$
or
![]() $B\leq A$
to mean that
$B\leq A$
to mean that
![]() $A-B$
is positive semidefinite. Let
$A-B$
is positive semidefinite. Let
![]() $\mathbb {R}$
be the set of all real numbers. Rearrange the components of
$\mathbb {R}$
be the set of all real numbers. Rearrange the components of
![]() $x=(x_1,\ldots ,x_n)\in \mathbb {R}^n$
in decreasing order as
$x=(x_1,\ldots ,x_n)\in \mathbb {R}^n$
in decreasing order as
![]() $x_{[1]}\geq \cdots \geq x_{[n]}$
. For
$x_{[1]}\geq \cdots \geq x_{[n]}$
. For
![]() $x=(x_1,\ldots ,x_n),$
$x=(x_1,\ldots ,x_n),$
![]() $y=(y_1,\ldots ,y_n)\in \mathbb {R}^n$
, if
$y=(y_1,\ldots ,y_n)\in \mathbb {R}^n$
, if
 $$ \begin{align*}\sum_{i=1}^kx_{[i]}\leq \sum_{i=1}^ky_{[i]} \quad \text{for}\quad k=1,\ldots,n,\end{align*} $$
$$ \begin{align*}\sum_{i=1}^kx_{[i]}\leq \sum_{i=1}^ky_{[i]} \quad \text{for}\quad k=1,\ldots,n,\end{align*} $$
then we say x is weakly majorized by y and denote by
![]() $y\succ _w x$
or
$y\succ _w x$
or
![]() $x\prec _w y$
.
$x\prec _w y$
.
Notice that
![]() $x\mapsto x^{\gamma } (x\geq 0)$
is a convex function for any real number
$x\mapsto x^{\gamma } (x\geq 0)$
is a convex function for any real number
![]() $ \gamma \geq 1$
. One can easily conclude the following lemma.
$ \gamma \geq 1$
. One can easily conclude the following lemma.
Lemma 2.2 Let
![]() $a,b\in \mathbb {R}$
. If
$a,b\in \mathbb {R}$
. If
![]() $-a\leq b\leq a$
, then for any real number
$-a\leq b\leq a$
, then for any real number
![]() $\gamma \geq 1$
,
$\gamma \geq 1$
,
The following lemmas are crucial in our proof.
Lemma 2.3 [Reference McCarthy25, Lemma 2.1]
Let
![]() $A\in M_n$
be a positive semidefinite matrix. Then
$A\in M_n$
be a positive semidefinite matrix. Then
Lemma 2.4 [Reference Zhan31, Lemma 3.7]
Let
![]() $A\in M_n$
be a Hermitian matrix, and let
$A\in M_n$
be a Hermitian matrix, and let
![]() $k \leq n$
be a positive integer. Then
$k \leq n$
be a positive integer. Then
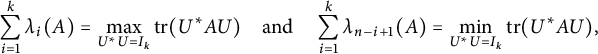 $$ \begin{align*} \sum_{i=1}^k\lambda_i(A)=\max\limits_{U^*U=I_k}\mathrm{tr}(U^*AU)\quad \text{and}\quad \sum_{i=1}^k\lambda_{n-i+1}(A)=\min\limits_{U^*U=I_k}\mathrm{tr}(U^*AU), \end{align*} $$
$$ \begin{align*} \sum_{i=1}^k\lambda_i(A)=\max\limits_{U^*U=I_k}\mathrm{tr}(U^*AU)\quad \text{and}\quad \sum_{i=1}^k\lambda_{n-i+1}(A)=\min\limits_{U^*U=I_k}\mathrm{tr}(U^*AU), \end{align*} $$
where
![]() $I_k$
is the identity matrix of order k and
$I_k$
is the identity matrix of order k and
![]() $U\in M_{n,k}$
.
$U\in M_{n,k}$
.
Lemma 2.5 [Reference Li, Šemrl and Sourour22, Lemma 1]
Let
![]() $A, B\in M_n$
. Then
$A, B\in M_n$
. Then
![]() $A\perp B$
if and only if there exist
$A\perp B$
if and only if there exist
![]() $\hat {A}\in M_m $
,
$\hat {A}\in M_m $
,
![]() $\hat {B}\in M_{n-m}$
and unitary matrices
$\hat {B}\in M_{n-m}$
and unitary matrices
![]() $U,V\in M_n$
such that
$U,V\in M_n$
such that
Lemma 2.6 Let
![]() $A, B,C\in M_{n}$
. If
$A, B,C\in M_{n}$
. If
![]() $(A+B)\perp C$
and
$(A+B)\perp C$
and
![]() $A\perp B$
, then
$A\perp B$
, then
Proof Since
![]() $A\perp B$
, we can apply Lemma 2.5 to conclude that there exist
$A\perp B$
, we can apply Lemma 2.5 to conclude that there exist
![]() $\hat {A}\in M_m $
,
$\hat {A}\in M_m $
,
![]() $\hat {B}\in M_{n-m}$
and unitary matrices
$\hat {B}\in M_{n-m}$
and unitary matrices
![]() $U,V\in M_n$
such that
$U,V\in M_n$
such that
Let
![]() $UCV$
be partitioned as
$UCV$
be partitioned as
 $$ \begin{align*}UCV=\begin{bmatrix} C_{11}&C_{12}\\ C_{21}&C_{22} \end{bmatrix} \end{align*} $$
$$ \begin{align*}UCV=\begin{bmatrix} C_{11}&C_{12}\\ C_{21}&C_{22} \end{bmatrix} \end{align*} $$
with
![]() $C_{11}\in M_m$
and
$C_{11}\in M_m$
and
![]() $C_{22}\in M_{n-m}.$
It follows from
$C_{22}\in M_{n-m}.$
It follows from
![]() $(A+B)\perp C$
that
$(A+B)\perp C$
that
that is,
 $$ \begin{align*}\begin{bmatrix} \hat{A}^*C_{11}&\hat{A}^*C_{12}\\ \hat{B}^{*}C_{21}&\hat{B}^{*}C_{22} \end{bmatrix}=0\quad \text{and}\quad \begin{bmatrix} \hat{A}C_{11}^*&\hat{A}C_{21}^*\\ \hat{B}C_{12}^*&\hat{B}C_{22}^* \end{bmatrix}=0. \end{align*} $$
$$ \begin{align*}\begin{bmatrix} \hat{A}^*C_{11}&\hat{A}^*C_{12}\\ \hat{B}^{*}C_{21}&\hat{B}^{*}C_{22} \end{bmatrix}=0\quad \text{and}\quad \begin{bmatrix} \hat{A}C_{11}^*&\hat{A}C_{21}^*\\ \hat{B}C_{12}^*&\hat{B}C_{22}^* \end{bmatrix}=0. \end{align*} $$
Then we have
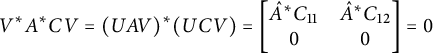 $$ \begin{align*}V^*A^*CV=(UAV)^*(UCV)= \begin{bmatrix} \hat{A}^*C_{11}&\hat{A}^*C_{12}\\ 0&0 \end{bmatrix}=0 \end{align*} $$
$$ \begin{align*}V^*A^*CV=(UAV)^*(UCV)= \begin{bmatrix} \hat{A}^*C_{11}&\hat{A}^*C_{12}\\ 0&0 \end{bmatrix}=0 \end{align*} $$
and
 $$ \begin{align*}UAC^*U^*=(UAV)\ (UCV)^*=\begin{bmatrix} \hat{A}C_{11}^*&\hat{A}C_{21}^*\\ 0&0 \end{bmatrix}=0 .\end{align*} $$
$$ \begin{align*}UAC^*U^*=(UAV)\ (UCV)^*=\begin{bmatrix} \hat{A}C_{11}^*&\hat{A}C_{21}^*\\ 0&0 \end{bmatrix}=0 .\end{align*} $$
Thus,
![]() $A^{*}C=0$
and
$A^{*}C=0$
and
![]() $AC^{*}=0$
, i.e.,
$AC^{*}=0$
, i.e.,
![]() $A\perp C$
. Similarly, we can also conclude that
$A\perp C$
. Similarly, we can also conclude that
![]() $B\perp C$
.
$B\perp C$
.
Lemma 2.7 Let
![]() $C,D\in M_n$
be two Hermitian matrices such that
$C,D\in M_n$
be two Hermitian matrices such that
![]() $-C\leq D\leq C$
and
$-C\leq D\leq C$
and
![]() $ k\leq n$
be a positive integer. Then, for any real number
$ k\leq n$
be a positive integer. Then, for any real number
![]() $ \gamma \geq 1$
,
$ \gamma \geq 1$
,
 $$ \begin{align} \sum_{i=1}^{k}\lambda_i^{\gamma}(C+D)+\sum_{i=1}^{k}\lambda_i^{\gamma}(C-D)\geq 2\sum_{i=1}^k\lambda_i^{\gamma}(C). \end{align} $$
$$ \begin{align} \sum_{i=1}^{k}\lambda_i^{\gamma}(C+D)+\sum_{i=1}^{k}\lambda_i^{\gamma}(C-D)\geq 2\sum_{i=1}^k\lambda_i^{\gamma}(C). \end{align} $$
Proof Let
![]() $U\in M_n$
be a unitary matrix such that
$U\in M_n$
be a unitary matrix such that
Denote by
![]() $u_i$
the ith column of U for
$u_i$
the ith column of U for
![]() $i=1,\ldots ,n$
. Let
$i=1,\ldots ,n$
. Let
![]() $\hat {U}=[u_1,u_2,\ldots ,u_k].$
Then, applying Lemma 2.4, we have
$\hat {U}=[u_1,u_2,\ldots ,u_k].$
Then, applying Lemma 2.4, we have
 $$ \begin{align*} \sum_{i=1}^k\lambda_{i}^{\gamma}(C+D)=\sum_{i=1}^k\lambda_{i}\big((C+D)^{\gamma}\big)\geq \mathrm{tr}(\hat{U}^*(C+D)^{\gamma}\hat{U}) \end{align*} $$
$$ \begin{align*} \sum_{i=1}^k\lambda_{i}^{\gamma}(C+D)=\sum_{i=1}^k\lambda_{i}\big((C+D)^{\gamma}\big)\geq \mathrm{tr}(\hat{U}^*(C+D)^{\gamma}\hat{U}) \end{align*} $$
and
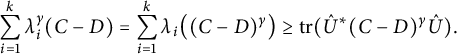 $$ \begin{align*}\quad \sum_{i=1}^k\lambda_{i}^{\gamma}(C-D)=\sum_{i=1}^k\lambda_{i}\big((C-D)^{\gamma}\big)\geq \mathrm{tr}(\hat{U}^*(C-D)^{\gamma}\hat{U}).\end{align*} $$
$$ \begin{align*}\quad \sum_{i=1}^k\lambda_{i}^{\gamma}(C-D)=\sum_{i=1}^k\lambda_{i}\big((C-D)^{\gamma}\big)\geq \mathrm{tr}(\hat{U}^*(C-D)^{\gamma}\hat{U}).\end{align*} $$
Since
![]() $-C\leq D\leq C$
, we have
$-C\leq D\leq C$
, we have
By Lemma 2.3, we have
for
![]() $i=1,\ldots ,n$
. Applying Lemma 2.2 with
$i=1,\ldots ,n$
. Applying Lemma 2.2 with
![]() $a=u_i^{*}Cu_i$
and
$a=u_i^{*}Cu_i$
and
![]() $b=u_i^{*}Du_i$
, we get
$b=u_i^{*}Du_i$
, we get
It follows from the above inequalities that
 $$ \begin{align*} \sum_{i=1}^k\lambda_{i}^{\gamma}(C+D)+\sum_{i=1}^k\lambda_{i}^{\gamma}(C-D)\geq& \mathrm{tr}(\hat{U}^*(C+D)^{\gamma}\hat{U})+\mathrm{tr}(\hat{U}^*(C-D)^{\gamma}\hat{U})\\ =&\sum_{i=1}^{k}u_i^{*}(C+D)^{\gamma}u_i+\sum_{i=1}^{k}u_i^{*}(C-D)^{\gamma}u_i \\ \geq&\sum_{i=1}^{k}(u_i^{*}(C+D)u_i)^{\gamma}+\sum_{i=1}^{k}(u_i^{*}(C-D)u_i)^{\gamma} \\ \geq& 2 \sum_{i=1}^{k}(u_i^{*}Cu_i)^{\gamma}=2\sum_{i=1}^k\lambda_i^{\gamma}(C). \\[-42pt] \end{align*} $$
$$ \begin{align*} \sum_{i=1}^k\lambda_{i}^{\gamma}(C+D)+\sum_{i=1}^k\lambda_{i}^{\gamma}(C-D)\geq& \mathrm{tr}(\hat{U}^*(C+D)^{\gamma}\hat{U})+\mathrm{tr}(\hat{U}^*(C-D)^{\gamma}\hat{U})\\ =&\sum_{i=1}^{k}u_i^{*}(C+D)^{\gamma}u_i+\sum_{i=1}^{k}u_i^{*}(C-D)^{\gamma}u_i \\ \geq&\sum_{i=1}^{k}(u_i^{*}(C+D)u_i)^{\gamma}+\sum_{i=1}^{k}(u_i^{*}(C-D)u_i)^{\gamma} \\ \geq& 2 \sum_{i=1}^{k}(u_i^{*}Cu_i)^{\gamma}=2\sum_{i=1}^k\lambda_i^{\gamma}(C). \\[-42pt] \end{align*} $$
Remark 2.8 The inequality (2.4) can be regarded as a generalization of the inequality (2.3) in Lemma 2.2. It is worth noting that if
![]() $-a\leq b\leq a$
, then
$-a\leq b\leq a$
, then
In our attempt to generalize this inequality, we aimed to obtain the following analogous inequality to (2.4):
 $$ \begin{align*}\sum_{i=1}^{k}\lambda_i^{\gamma}(C+D)+\sum_{i=1}^{k}\lambda_i^{\gamma}(C-D)\leq 2\sum_{i=1}^k\lambda_i^{\gamma}(C)\quad \text{for all }\quad 0<\gamma<1,\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{k}\lambda_i^{\gamma}(C+D)+\sum_{i=1}^{k}\lambda_i^{\gamma}(C-D)\leq 2\sum_{i=1}^k\lambda_i^{\gamma}(C)\quad \text{for all }\quad 0<\gamma<1,\end{align*} $$
where
![]() $1\leq k\leq n$
and
$1\leq k\leq n$
and
![]() $C,D\in M_n$
are Hermitian matrices such that
$C,D\in M_n$
are Hermitian matrices such that
![]() $C+D$
and
$C+D$
and
![]() $C-D$
are both positive semidefinite. However, it has been demonstrated that this inequality does not hold in general. A counterexample can be constructed by considering matrices C and D such that
$C-D$
are both positive semidefinite. However, it has been demonstrated that this inequality does not hold in general. A counterexample can be constructed by considering matrices C and D such that
![]() $C+D=\mathrm {diag}(1,1,3,3)$
and
$C+D=\mathrm {diag}(1,1,3,3)$
and
![]() $C-D=\mathrm {diag}(3,3,1,1)$
. In this case, we observe that
$C-D=\mathrm {diag}(3,3,1,1)$
. In this case, we observe that
![]() $\sum \limits _{i=1}^{2}\lambda _i^{\gamma }(C+D)+\sum \limits _{i=1}^{2}\lambda _i^{\gamma }(C-D)= 4\cdot 3^{\gamma }>2\sum \limits _{i=1}^2\lambda _i^{\gamma }(C)=4\cdot 2^{\gamma }.$
$\sum \limits _{i=1}^{2}\lambda _i^{\gamma }(C+D)+\sum \limits _{i=1}^{2}\lambda _i^{\gamma }(C-D)= 4\cdot 3^{\gamma }>2\sum \limits _{i=1}^2\lambda _i^{\gamma }(C)=4\cdot 2^{\gamma }.$
Corollary 2.9 Let
![]() $p>2$
be a real number, and let
$p>2$
be a real number, and let
![]() $ k\leq n$
be a positive integer. Then
$ k\leq n$
be a positive integer. Then
 $$ \begin{align} \|A+B\|_{(p,k)}^p+\|A-B\|_{(p,k)}^p\geq 2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(A^*A+B^*B) \end{align} $$
$$ \begin{align} \|A+B\|_{(p,k)}^p+\|A-B\|_{(p,k)}^p\geq 2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(A^*A+B^*B) \end{align} $$
for all
![]() $A,B\in M_n.$
$A,B\in M_n.$
Proof Notice that
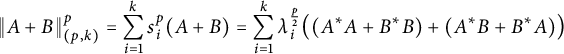 $$ \begin{align*}\|A+B\|_{(p,k)}^p=\sum_{i=1}^ks_i^p(A+B)=\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big((A^*A+B^*B)+(A^*B+B^*A)\big)\end{align*} $$
$$ \begin{align*}\|A+B\|_{(p,k)}^p=\sum_{i=1}^ks_i^p(A+B)=\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big((A^*A+B^*B)+(A^*B+B^*A)\big)\end{align*} $$
and
 $$ \begin{align*}\|A-B\|_{(p,k)}^p=\sum_{i=1}^ks_i^p(A-B)=\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big((A^*A+B^*B)-(A^*B+B^*A)\big).\end{align*} $$
$$ \begin{align*}\|A-B\|_{(p,k)}^p=\sum_{i=1}^ks_i^p(A-B)=\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big((A^*A+B^*B)-(A^*B+B^*A)\big).\end{align*} $$
Let
![]() $C=A^*A+B^*B$
and
$C=A^*A+B^*B$
and
![]() $D= A^*B+B^*A$
. Then
$D= A^*B+B^*A$
. Then
![]() $C+D=(A+B)^*(A+B)$
and
$C+D=(A+B)^*(A+B)$
and
![]() $C-D=(A-B)^*(A-B)$
are both positive semidefinite, that is,
$C-D=(A-B)^*(A-B)$
are both positive semidefinite, that is,
![]() $-C\leq D\leq C$
. Applying Lemma 2.7, we get (2.5).
$-C\leq D\leq C$
. Applying Lemma 2.7, we get (2.5).
Lemma 2.10 Let
![]() $A,B\in M_n$
be nonzero matrices, and let
$A,B\in M_n$
be nonzero matrices, and let
![]() $ 2\leq k\leq n$
be an integer. Given a real number
$ 2\leq k\leq n$
be an integer. Given a real number
![]() $p\geq 1,$
if
$p\geq 1,$
if
then
![]() $\mathrm {rank}(A+B)\leq k.$
$\mathrm {rank}(A+B)\leq k.$
Proof With the assumption that
![]() $A\perp B$
, we can assume that the largest k singular values of
$A\perp B$
, we can assume that the largest k singular values of
![]() $A+B$
are
$A+B$
are
![]() $s_1(A),\ldots ,s_{\ell }(A),s_1(B),\ldots ,s_{k-\ell }(B)$
for some
$s_1(A),\ldots ,s_{\ell }(A),s_1(B),\ldots ,s_{k-\ell }(B)$
for some
![]() $0\leq \ell \leq k$
. Then
$0\leq \ell \leq k$
. Then
 $$ \begin{align} \|A+B\|_{(p,k)}^p=\sum_{i=1}^{\ell}s_i^p(A)+\sum_{i=1}^{k-\ell}s_i^p(B)\leq \sum_{i=1}^{k}s_i^p(A)+\sum_{i=1}^{k}s_i^p(B). \end{align} $$
$$ \begin{align} \|A+B\|_{(p,k)}^p=\sum_{i=1}^{\ell}s_i^p(A)+\sum_{i=1}^{k-\ell}s_i^p(B)\leq \sum_{i=1}^{k}s_i^p(A)+\sum_{i=1}^{k}s_i^p(B). \end{align} $$
On the other hand, we have
 $$ \begin{align*}\|A+B\|_{(p,k)}^p=\|A\|_{(p,k)}^p+\|B\|_{(p,k)}^p=\displaystyle\sum_{i=1}^{k}s_i^p(A)+\displaystyle\sum_{i=1}^{k}s_i^p(B).\end{align*} $$
$$ \begin{align*}\|A+B\|_{(p,k)}^p=\|A\|_{(p,k)}^p+\|B\|_{(p,k)}^p=\displaystyle\sum_{i=1}^{k}s_i^p(A)+\displaystyle\sum_{i=1}^{k}s_i^p(B).\end{align*} $$
Thus, the equality in (2.6) holds, which implies
 $$ \begin{align} \sum_{i=1}^{\ell}s_i^p(A)=\sum_{i=1}^{k}s_i^p(A)\quad \text{and}\quad \sum_{i=1}^{k-\ell}s_i^p(B)=\sum_{i=1}^{k}s_i^p(B). \end{align} $$
$$ \begin{align} \sum_{i=1}^{\ell}s_i^p(A)=\sum_{i=1}^{k}s_i^p(A)\quad \text{and}\quad \sum_{i=1}^{k-\ell}s_i^p(B)=\sum_{i=1}^{k}s_i^p(B). \end{align} $$
Since A and B are both nonzero, we have
 $$ \begin{align*}\displaystyle\sum_{i=1}^{k}s_i^p(A)>0\quad \mathrm{and}\quad \displaystyle\sum_{i=1}^{k}s_i^p(B)>0,\end{align*} $$
$$ \begin{align*}\displaystyle\sum_{i=1}^{k}s_i^p(A)>0\quad \mathrm{and}\quad \displaystyle\sum_{i=1}^{k}s_i^p(B)>0,\end{align*} $$
which implies
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $k-\ell \geq 1$
, i.e.,
$k-\ell \geq 1$
, i.e.,
![]() $1\leq \ell \leq k-1.$
With (2.7), it follows that
$1\leq \ell \leq k-1.$
With (2.7), it follows that
 $$ \begin{align*} \sum_{i=\ell+1}^{k}s_i^p(A)=0\quad \text{and} \quad \displaystyle \sum_{i=k-\ell+1}^{k}s_k^p(B)=0, \end{align*} $$
$$ \begin{align*} \sum_{i=\ell+1}^{k}s_i^p(A)=0\quad \text{and} \quad \displaystyle \sum_{i=k-\ell+1}^{k}s_k^p(B)=0, \end{align*} $$
which implies
![]() $s_{\ell +1}(A)=0$
and
$s_{\ell +1}(A)=0$
and
![]() $s_{k-\ell +1}(B)=0.$
Therefore,
$s_{k-\ell +1}(B)=0.$
Therefore,
Since
![]() $A\perp B$
, we have
$A\perp B$
, we have
Lemma 2.11 Let
![]() $A, B\in M_n$
be two positive semidefinite matrices, let
$A, B\in M_n$
be two positive semidefinite matrices, let
![]() $\gamma>1$
be a real number, and let
$\gamma>1$
be a real number, and let
![]() $k\leq n$
be a positive integer. Suppose
$k\leq n$
be a positive integer. Suppose
 $$ \begin{align} \sum_{i=1}^{k}\lambda_{i}^{\gamma}(A+\alpha B)\leq \sum_{i=1}^{k}\lambda_i^{\gamma}(A)+\sum_{i=1}^{k}\lambda_i^{\gamma}(\alpha B) \quad \text{for all}\quad 0<\alpha<1 \end{align} $$
$$ \begin{align} \sum_{i=1}^{k}\lambda_{i}^{\gamma}(A+\alpha B)\leq \sum_{i=1}^{k}\lambda_i^{\gamma}(A)+\sum_{i=1}^{k}\lambda_i^{\gamma}(\alpha B) \quad \text{for all}\quad 0<\alpha<1 \end{align} $$
and
![]() $U^*AU=\mathrm {diag}(\lambda _1(A),\ldots ,\lambda _n(A))$
for some unitary matrix
$U^*AU=\mathrm {diag}(\lambda _1(A),\ldots ,\lambda _n(A))$
for some unitary matrix
![]() $U\in M_n$
.
$U\in M_n$
.
-
(a) If
 $\lambda _k(A)=0,$
then
$\lambda _k(A)=0,$
then
 $A\perp B$
.
$A\perp B$
. -
(b) If
 $\lambda _k(A)>0,$
then
$\lambda _k(A)>0,$
then
 $U^*BU=0_{k+\ell }\oplus \hat {B}$
with
$U^*BU=0_{k+\ell }\oplus \hat {B}$
with
 $\hat {B}\in M_{n-k-\ell }$
, where
$\hat {B}\in M_{n-k-\ell }$
, where
 $\ell $
is the largest integer such that
$\ell $
is the largest integer such that
 $\lambda _{k+\ell }(A)=\lambda _k(A)$
.
$\lambda _{k+\ell }(A)=\lambda _k(A)$
.
Proof Denote the ith diagonal entry of
![]() $U^*BU$
by
$U^*BU$
by
![]() $b_i.$
Then
$b_i.$
Then
![]() $\lambda _i(A)+\alpha b_{i}$
is the ith diagonal entry of
$\lambda _i(A)+\alpha b_{i}$
is the ith diagonal entry of
![]() $U^*(A+\alpha B)U$
. It follows that
$U^*(A+\alpha B)U$
. It follows that
Notice that
![]() $g(x)=x^{\gamma } (x>0)$
is an increasing convex function when
$g(x)=x^{\gamma } (x>0)$
is an increasing convex function when
![]() $\gamma>1$
. We can apply Theorem 3.26 in [Reference Zhan31] to obtain
$\gamma>1$
. We can apply Theorem 3.26 in [Reference Zhan31] to obtain
Thus,
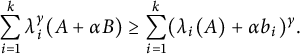 $\displaystyle \sum _{i=1}^{k}\lambda _{i}^{\gamma }(A+\alpha B)\geq \displaystyle \sum _{i=1}^{k}(\lambda _i(A)+\alpha b_i)^{\gamma }.$
With the assumption in (2.8), we can conclude that
$\displaystyle \sum _{i=1}^{k}\lambda _{i}^{\gamma }(A+\alpha B)\geq \displaystyle \sum _{i=1}^{k}(\lambda _i(A)+\alpha b_i)^{\gamma }.$
With the assumption in (2.8), we can conclude that
 $$ \begin{align} \sum_{i=1}^{k}(\lambda_i(A)+\alpha b_{i})^{\gamma} \leq \sum_{i=1}^{k}\lambda_i^{\gamma}(A)+\sum_{i=1}^{k}\lambda_i^{\gamma}(\alpha B)\quad \text{for all}\quad 0<\alpha<1. \end{align} $$
$$ \begin{align} \sum_{i=1}^{k}(\lambda_i(A)+\alpha b_{i})^{\gamma} \leq \sum_{i=1}^{k}\lambda_i^{\gamma}(A)+\sum_{i=1}^{k}\lambda_i^{\gamma}(\alpha B)\quad \text{for all}\quad 0<\alpha<1. \end{align} $$
Let
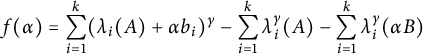 $f(\alpha )=\displaystyle \sum _{i=1}^{k}(\lambda _i(A)+\alpha b_{i})^{\gamma } -\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma }(A)-\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma }(\alpha B)$
be a function on
$f(\alpha )=\displaystyle \sum _{i=1}^{k}(\lambda _i(A)+\alpha b_{i})^{\gamma } -\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma }(A)-\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma }(\alpha B)$
be a function on
![]() $\alpha $
. Then we have
$\alpha $
. Then we have
 $$ \begin{align} f(\alpha)=f(0)+f^{'}(0)\alpha+o(\alpha)= \left[\sum_{i=1}^{k}\lambda_i^{\gamma-1}(A)b_{i}\gamma\right]\alpha+o(\alpha), \end{align} $$
$$ \begin{align} f(\alpha)=f(0)+f^{'}(0)\alpha+o(\alpha)= \left[\sum_{i=1}^{k}\lambda_i^{\gamma-1}(A)b_{i}\gamma\right]\alpha+o(\alpha), \end{align} $$
where a function
![]() $g(\alpha )=o(\alpha )$
means
$g(\alpha )=o(\alpha )$
means
![]() $ \lim \limits _{\alpha \to 0}\frac {g(\alpha )}{\alpha }=0$
. Since A and B are both positive semidefinite, we have
$ \lim \limits _{\alpha \to 0}\frac {g(\alpha )}{\alpha }=0$
. Since A and B are both positive semidefinite, we have
![]() $\lambda _i(A)\geq 0$
and
$\lambda _i(A)\geq 0$
and
![]() $ b_{i}\geq 0$
for all
$ b_{i}\geq 0$
for all
![]() $i=1,\ldots ,n.$
It follows that
$i=1,\ldots ,n.$
It follows that
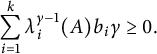 $\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma -1}(A)b_{i}\gamma \geq 0.$
We claim that
$\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma -1}(A)b_{i}\gamma \geq 0.$
We claim that
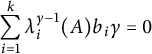 $\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma -1}(A)b_{i}\gamma =0$
. Otherwise,
$\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma -1}(A)b_{i}\gamma =0$
. Otherwise,
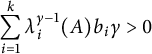 $\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma -1}(A)b_{i}\gamma>0$
leads to
$\displaystyle \sum _{i=1}^{k}\lambda _i^{\gamma -1}(A)b_{i}\gamma>0$
leads to
![]() $f(\alpha )>0$
when
$f(\alpha )>0$
when
![]() $\alpha>0$
is sufficiently small, which contradicts (2.9). It follows that
$\alpha>0$
is sufficiently small, which contradicts (2.9). It follows that
For the case
![]() $\lambda _k(A)=0$
, we may assume that
$\lambda _k(A)=0$
, we may assume that
![]() $ t$
is the largest integer such that
$ t$
is the largest integer such that
![]() ${\lambda _t(A)>0}$
. Then
${\lambda _t(A)>0}$
. Then
![]() $U^*AU=\mathrm {diag}(\lambda _1(A),\ldots ,\lambda _t(A))\oplus 0_{n-t}$
and
$U^*AU=\mathrm {diag}(\lambda _1(A),\ldots ,\lambda _t(A))\oplus 0_{n-t}$
and
![]() $b_i=0$
for
$b_i=0$
for
![]() $i=1,\ldots ,t.$
Recall that B is positive semidefinite. Thus,
$i=1,\ldots ,t.$
Recall that B is positive semidefinite. Thus,
![]() $U^*BU=0_{t}\oplus \hat {B}$
with
$U^*BU=0_{t}\oplus \hat {B}$
with
![]() $\hat {B}\in M_{n-t}.$
It follows that
$\hat {B}\in M_{n-t}.$
It follows that
![]() $A\perp B.$
$A\perp B.$
For the case
![]() $\lambda _k(A)>0,$
we first have
$\lambda _k(A)>0,$
we first have
![]() $b_i=0$
for all
$b_i=0$
for all
![]() $i=1,\ldots ,k$
. Since B is positive semidefinite, it follows that
$i=1,\ldots ,k$
. Since B is positive semidefinite, it follows that
![]() $U^*BU=0_k\oplus C$
with
$U^*BU=0_k\oplus C$
with
![]() $C\in M_{n-k}.$
Recall that
$C\in M_{n-k}.$
Recall that
![]() $\ell $
is the largest integer such that
$\ell $
is the largest integer such that
![]() $\lambda _{k+\ell }(A)=\lambda _k(A)$
. If
$\lambda _{k+\ell }(A)=\lambda _k(A)$
. If
![]() $\ell =0$
, then the proof is completed. If
$\ell =0$
, then the proof is completed. If
![]() $\ell>0$
, then for any
$\ell>0$
, then for any
![]() $i=k+1,\ldots ,k+\ell $
, replacing the role of
$i=k+1,\ldots ,k+\ell $
, replacing the role of
![]() $\lambda _k(A)+\alpha b_k$
with
$\lambda _k(A)+\alpha b_k$
with
![]() $\lambda _i(A)+\alpha b_i$
in the above argument, we can conclude
$\lambda _i(A)+\alpha b_i$
in the above argument, we can conclude
![]() $b_i=0$
. Thus, we have
$b_i=0$
. Thus, we have
![]() $b_i=0$
for
$b_i=0$
for
![]() $i=1,\ldots ,k+\ell .$
It follows that
$i=1,\ldots ,k+\ell .$
It follows that
![]() $U^*BU=0_{k+\ell }\oplus \hat {B}$
with
$U^*BU=0_{k+\ell }\oplus \hat {B}$
with
![]() $\hat {B}\in M_{n-k-\ell }$
.
$\hat {B}\in M_{n-k-\ell }$
.
Corollary 2.12 Let
![]() $T,S\in M_n$
be two matrices, let
$T,S\in M_n$
be two matrices, let
![]() $p>2$
be a real number, and let
$p>2$
be a real number, and let
![]() $k\leq n$
be a positive integer. Suppose
$k\leq n$
be a positive integer. Suppose
 $$ \begin{align*}\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S)\end{align*} $$
$$ \begin{align*}\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S)\end{align*} $$
and
 $$ \begin{align*}\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*+x^2SS^*)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2SS^*)\end{align*} $$
$$ \begin{align*}\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*+x^2SS^*)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2SS^*)\end{align*} $$
for all
![]() $0<x<1,$
and
$0<x<1,$
and
![]() $UTV=\mathrm {diag}(s_1(T),\ldots ,s_n(T))$
for some unitary matrices
$UTV=\mathrm {diag}(s_1(T),\ldots ,s_n(T))$
for some unitary matrices
![]() ${U,V\in M_n}$
.
${U,V\in M_n}$
.
-
(1) If
 $s_k(T)=0,$
then
$s_k(T)=0,$
then
 $T\perp S$
.
$T\perp S$
. -
(2) If
 $s_k(T)>0,$
then
$s_k(T)>0,$
then
 $ USV=0_{k+\ell }\oplus \hat {S}$
with
$ USV=0_{k+\ell }\oplus \hat {S}$
with
 $\hat {S}\in M_{n-k-\ell }$
, where
$\hat {S}\in M_{n-k-\ell }$
, where
 $\ell $
is the largest integer such that
$\ell $
is the largest integer such that
 $s_{k+\ell }(T)=s_k(T).$
$s_{k+\ell }(T)=s_k(T).$
Proof If
![]() $s_k(T)=0$
, then
$s_k(T)=0$
, then
![]() $\lambda _k(T^*T)=\lambda _k(TT^*)=0$
. We can use Lemma 2.11 twice to conclude that
$\lambda _k(T^*T)=\lambda _k(TT^*)=0$
. We can use Lemma 2.11 twice to conclude that
![]() $T^*T\perp S^*S$
and
$T^*T\perp S^*S$
and
![]() $TT^*\perp SS^*$
, and hence
$TT^*\perp SS^*$
, and hence
![]() $T\perp S.$
$T\perp S.$
If
![]() $s_k(T)>0$
, then we have
$s_k(T)>0$
, then we have
Notice that
![]() $\lambda _{i}(TT^*)=\lambda _{i}(T^*T)=s^2_i(T)$
for
$\lambda _{i}(TT^*)=\lambda _{i}(T^*T)=s^2_i(T)$
for
![]() $i=1,\ldots ,n$
. Thus,
$i=1,\ldots ,n$
. Thus,
and
![]() $\ell $
is the largest integer such that
$\ell $
is the largest integer such that
Then we use Lemma 2.11 twice to conclude that
It follows that
![]() $USV=0_{k+\ell }\oplus \hat {S}.$
$USV=0_{k+\ell }\oplus \hat {S}.$
The following result originates from the last two paragraphs of the proof of Theorem 2.1 in [Reference Fošner, Huang, Li and Sze10].
Lemma 2.13 Let
![]() $\phi :M_{mn}\to M_{mn}$
be a linear map. Suppose for any unitary matrix
$\phi :M_{mn}\to M_{mn}$
be a linear map. Suppose for any unitary matrix
![]() $X \in M_m$
and integer
$X \in M_m$
and integer
![]() $1\leq i\leq m$
, there exists a unitary matrix
$1\leq i\leq m$
, there exists a unitary matrix
![]() $W_X$
such that
$W_X$
such that
where
![]() $\varphi _{i,X}$
is the identity map or the transposition map and
$\varphi _{i,X}$
is the identity map or the transposition map and
![]() $W_I=I_{mn}$
. Then
$W_I=I_{mn}$
. Then
where
![]() $\varphi _1$
is a linear map and
$\varphi _1$
is a linear map and
![]() $\varphi _2$
is the identity map or the transposition map.
$\varphi _2$
is the identity map or the transposition map.
Proof For any real symmetric matrix
![]() $S\in M_n$
and any unitary matrix
$S\in M_n$
and any unitary matrix
![]() $X\in M_m$
,
$X\in M_m$
,
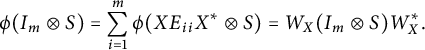 $$ \begin{align*}{\phi}(I_m\otimes S)=\sum_{i=1}^m{\phi}(XE_{ii}X^*\otimes S)={W}_X(I_m\otimes S){W}_X^*.\end{align*} $$
$$ \begin{align*}{\phi}(I_m\otimes S)=\sum_{i=1}^m{\phi}(XE_{ii}X^*\otimes S)={W}_X(I_m\otimes S){W}_X^*.\end{align*} $$
Since
![]() $W_I=I_{mn}$
, it follows that
$W_I=I_{mn}$
, it follows that
Thus,
![]() ${W}_X$
commutes with
${W}_X$
commutes with
![]() $I_m\otimes S$
for all real symmetric
$I_m\otimes S$
for all real symmetric
![]() $S\in M_n.$
This yields that
$S\in M_n.$
This yields that
![]() ${{W}_X=Z_X\otimes I_n}$
for some unitary matrix
${{W}_X=Z_X\otimes I_n}$
for some unitary matrix
![]() $Z_X\in M_m$
, and hence
$Z_X\in M_m$
, and hence
Define linear maps
![]() $\text {tr}_1 : M_{mn}\to M_{n}$
and
$\text {tr}_1 : M_{mn}\to M_{n}$
and
![]() $ \text {Tr}_1: M_{mn}\to M_{n}$
as
$ \text {Tr}_1: M_{mn}\to M_{n}$
as
for all
![]() $A\in M_m$
and
$A\in M_m$
and
![]() $B\in M_n.$
The map
$B\in M_n.$
The map
![]() $\text {tr}_1$
is also called the partial trace function in quantum science. Then
$\text {tr}_1$
is also called the partial trace function in quantum science. Then
Note that
![]() $\text {Tr}_1$
is linear and therefore continuous and the set
$\text {Tr}_1$
is linear and therefore continuous and the set
is connected. So, all the maps
![]() $\varphi _{i, X}$
are the same, and hence we can rewrite (2.11) as
$\varphi _{i, X}$
are the same, and hence we can rewrite (2.11) as
where
![]() $\varphi _2$
is the identity map or the transposition map. By the linearity of
$\varphi _2$
is the identity map or the transposition map. By the linearity of
![]() ${\phi }$
, it follows that
${\phi }$
, it follows that
for some linear map
![]() $\varphi _1.$
$\varphi _1.$
Now we are ready to present the proof of Theorem 2.1.
Proof of Theorem 2.1.
Notice that the
![]() $(p,k)$
-norm reduces to the spectral norm when
$(p,k)$
-norm reduces to the spectral norm when
![]() $k=1$
. It was shown in [Reference Fošner, Huang, Li and Sze10] that a linear map
$k=1$
. It was shown in [Reference Fošner, Huang, Li and Sze10] that a linear map
![]() $\phi $
preserves the spectral norm of tensor products
$\phi $
preserves the spectral norm of tensor products
![]() $A\otimes B$
for all
$A\otimes B$
for all
![]() $A\in M_m$
and
$A\in M_m$
and
![]() $B\in M_n$
if and only if
$B\in M_n$
if and only if
![]() $\phi $
has form
$\phi $
has form
![]() $A\otimes B\mapsto U(\varphi _1(A)\otimes \varphi _2(B))V$
for some unitary matrices
$A\otimes B\mapsto U(\varphi _1(A)\otimes \varphi _2(B))V$
for some unitary matrices
![]() $U,V\in M_{mn}$
, where
$U,V\in M_{mn}$
, where
![]() $\varphi _s$
is the identity map or the transposition map for
$\varphi _s$
is the identity map or the transposition map for
![]() $s=1,2$
. So we need only consider the case when
$s=1,2$
. So we need only consider the case when
![]() $k\geq 2$
in the following discussion. Since the sufficiency part is clear, we consider only the necessity part.
$k\geq 2$
in the following discussion. Since the sufficiency part is clear, we consider only the necessity part.
Suppose a linear map
![]() $\phi : M_{mn}\to M_{mn}$
satisfies (2.1) and
$\phi : M_{mn}\to M_{mn}$
satisfies (2.1) and
![]() $k \geq 2$
. We need the following three claims.
$k \geq 2$
. We need the following three claims.
Claim 1 For any unitary matrices
![]() $X\in M_m\text { and } Y\in M_n$
, we have
$X\in M_m\text { and } Y\in M_n$
, we have
and
for any possible
![]() $i,j,s$
with
$i,j,s$
with
![]() $j\neq s$
. Moreover,
$j\neq s$
. Moreover,
and
for any possible
![]() $i,j,s$
with
$i,j,s$
with
![]() $j\neq s $
.
$j\neq s $
.
Proof of Claim 1. For simplicity, we denote
We need to show
With the assumption in (2.1), we have
for all
![]() $F\in M_m$
and
$F\in M_m$
and
![]() $G\in M_n$
. It follows that
$G\in M_n$
. It follows that
for all
![]() $0<x<1$
. We can conclude from the above equalities that
$0<x<1$
. We can conclude from the above equalities that
Applying Corollary 2.9 with
![]() $A=T$
and
$A=T$
and
![]() $B=xS$
, we get
$B=xS$
, we get
 $$ \begin{align} \|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p\geq 2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S) \end{align} $$
$$ \begin{align} \|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p\geq 2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S) \end{align} $$
for all
![]() $0<x<1.$
Since
$0<x<1.$
Since
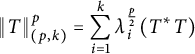 $\|T\|_{(p,k)}^p=\displaystyle \sum _{i=1}^k\lambda _i^{\frac {p}{2}}(T^*T)$
and
$\|T\|_{(p,k)}^p=\displaystyle \sum _{i=1}^k\lambda _i^{\frac {p}{2}}(T^*T)$
and
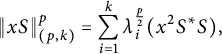 $\|xS\|_{(p,k)}^p=\displaystyle \sum _{i=1}^k\lambda _i^{\frac {p}{2}}(x^2S^*S),$
it follows from (2.12) and (2.13) that
$\|xS\|_{(p,k)}^p=\displaystyle \sum _{i=1}^k\lambda _i^{\frac {p}{2}}(x^2S^*S),$
it follows from (2.12) and (2.13) that
 $$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S) \end{align} $$
$$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S) \end{align} $$
for all
![]() $0<x<1.$
$0<x<1.$
Replacing the role of
![]() $(T,S)$
with
$(T,S)$
with
![]() $(T^*,S^*)$
in the above argument, we have
$(T^*,S^*)$
in the above argument, we have
 $$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*+x^2SS^*)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2SS^*) \end{align} $$
$$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*+x^2SS^*)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2SS^*) \end{align} $$
for all
![]() $0<x<1.$
We claim that
$0<x<1.$
We claim that
![]() $s_k(T)=0$
. Otherwise, suppose
$s_k(T)=0$
. Otherwise, suppose
![]() $s_k(T)>0$
. Then, by (2.14) and (2.15), we can apply Corollary 2.12 to conclude that there exist unitary matrices
$s_k(T)>0$
. Then, by (2.14) and (2.15), we can apply Corollary 2.12 to conclude that there exist unitary matrices
![]() $U,V\in M_{n}$
such that
$U,V\in M_{n}$
such that
where
![]() $\ell $
is the largest integer such that
$\ell $
is the largest integer such that
![]() $s_{k+\ell }(T)=s_k(T).$
Thus, there exists a sufficiently small number
$s_{k+\ell }(T)=s_k(T).$
Thus, there exists a sufficiently small number
![]() $t>0$
such that the largest k singular values of
$t>0$
such that the largest k singular values of
![]() $T+tS$
are
$T+tS$
are
![]() $s_1(T),\ldots ,s_k(T)$
. Since
$s_1(T),\ldots ,s_k(T)$
. Since
![]() $\|T\|_{(p,k)}^p=\|E_{ii}\otimes E_{jj}\|_{(p,k)}^p=1,$
we have
$\|T\|_{(p,k)}^p=\|E_{ii}\otimes E_{jj}\|_{(p,k)}^p=1,$
we have
 $$ \begin{align*}\|T+tS\|_{(p,k)}^p=\sum_{i=1}^ks_i^p(T+tS)=\sum_{i=1}^ks_i^p(T)=\|T\|_{(p,k)}^p=1,\end{align*} $$
$$ \begin{align*}\|T+tS\|_{(p,k)}^p=\sum_{i=1}^ks_i^p(T+tS)=\sum_{i=1}^ks_i^p(T)=\|T\|_{(p,k)}^p=1,\end{align*} $$
which contradicts the fact that
So, our claim is correct, that is,
![]() $s_k(T)=0.$
$s_k(T)=0.$
Now, applying Corollary 2.12 again, we have
![]() $T\perp S.$
Notice that
$T\perp S.$
Notice that
Applying Lemma 2.10 on S and T, we have
Similarly, we can also show that
and
for any possible
![]() $i,j,s$
with
$i,j,s$
with
![]() $j\neq s$
.
$j\neq s$
.
Claim 2 For any unitary matrices
![]() $X\in M_m\text { and } Y\in M_n$
, we have
$X\in M_m\text { and } Y\in M_n$
, we have
whenever
![]() $i\neq t.$
$i\neq t.$
Proof of Claim 2. For simplicity, we denote
We need to show
![]() $S\perp T.$
Applying Corollary 2.9 on T and
$S\perp T.$
Applying Corollary 2.9 on T and
![]() $xS$
, we get
$xS$
, we get
 $$ \begin{align} \|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p\geq 2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S) \end{align} $$
$$ \begin{align} \|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p\geq 2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S) \end{align} $$
for all
![]() $0<x<1.$
With the assumption in (2.1), we have
$0<x<1.$
With the assumption in (2.1), we have
-
(i)
 $\|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p=2\|T\|_{(p,k)}^p+2\|xS\|_{(p,k)}^p$
for the case
$\|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p=2\|T\|_{(p,k)}^p+2\|xS\|_{(p,k)}^p$
for the case
 $k\geq 4$
;
$k\geq 4$
; -
(ii)
 $\|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p=2\|T\|_{(p,k)}^p+\|xS\|_{(p,k)}^p$
for the case
$\|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p=2\|T\|_{(p,k)}^p+\|xS\|_{(p,k)}^p$
for the case
 $k=3$
;
$k=3$
; -
(iii)
 $\|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p=2\|T\|_{(p,k)}^p$
for the case
$\|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p=2\|T\|_{(p,k)}^p$
for the case
 $k=2.$
$k=2.$
So we can conclude that for any integer
![]() $k\geq 2$
,
$k\geq 2$
,
 $$ \begin{align} \nonumber \|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p&\leq 2\|T\|_{(p,k)}^p+2\|xS\|_{(p,k)}^p \\ &=2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S). \end{align} $$
$$ \begin{align} \nonumber \|T+xS\|_{(p,k)}^p+\|T-xS\|_{(p,k)}^p&\leq 2\|T\|_{(p,k)}^p+2\|xS\|_{(p,k)}^p \\ &=2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+2\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S). \end{align} $$
It follows that
 $$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S) \end{align} $$
$$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T+x^2S^*S)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(T^*T)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2S^*S) \end{align} $$
for all
![]() $0<x<1.$
The above observations also hold if
$0<x<1.$
The above observations also hold if
![]() $(T,S)$
is replaced by
$(T,S)$
is replaced by
![]() $(T^*,S^*)$
, that is,
$(T^*,S^*)$
, that is,
 $$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*+x^2SS^*)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2SS^*) \end{align} $$
$$ \begin{align} \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*+x^2SS^*)\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}(TT^*)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}(x^2SS^*) \end{align} $$
for all
![]() $0<x<1.$
$0<x<1.$
If
![]() $s_k(T)=0$
, then applying Corollary 2.12, we have
$s_k(T)=0$
, then applying Corollary 2.12, we have
![]() $T\perp S$
. Otherwise,
$T\perp S$
. Otherwise,
![]() $s_k(T)>0$
. Notice that Claim 1 implies
$s_k(T)>0$
. Notice that Claim 1 implies
![]() $\mathrm {rank}(T)\leq k.$
Thus, by (2.18) and (2.19), we can apply Corollary 2.12 to conclude that there exist unitary matrices
$\mathrm {rank}(T)\leq k.$
Thus, by (2.18) and (2.19), we can apply Corollary 2.12 to conclude that there exist unitary matrices
![]() $U,V\in M_{mn}$
such that
$U,V\in M_{mn}$
such that
It follows that
![]() $T\perp S.$
This completes the proof.
$T\perp S.$
This completes the proof.
Claim 3 For any unitary matrices
![]() $X\in M_m$
and
$X\in M_m$
and
![]() $Y\in M_n$
,
$Y\in M_n$
,
Proof of Claim 3. If
![]() $i=r$
or
$i=r$
or
![]() $j=s$
, then applying Claim 1 directly, we have
$j=s$
, then applying Claim 1 directly, we have
Next, we suppose that
![]() $i\neq r$
and
$i\neq r$
and
![]() $j\neq s$
. With Claim 1, we have
$j\neq s$
. With Claim 1, we have
and
With Claim 2, we have
Applying Lemma 2.6, we conclude from (2.20) and (2.22) that
Then, applying Lemma 2.6 again, we can conclude from (2.21) and (2.23) that
Now we prove that
![]() $\phi $
has the desired form (2.2). For any unitary matrix
$\phi $
has the desired form (2.2). For any unitary matrix
![]() $Y\in M_n$
, applying Claims 1 and 3, we know
$Y\in M_n$
, applying Claims 1 and 3, we know
is a set of
![]() $mn$
orthogonal matrices in
$mn$
orthogonal matrices in
![]() $M_{mn}$
. By Claim 1, each matrix in
$M_{mn}$
. By Claim 1, each matrix in
![]() $\mathscr {F}$
has exactly one nonzero singular value, which equals 1. Thus, there exist unitary matrices
$\mathscr {F}$
has exactly one nonzero singular value, which equals 1. Thus, there exist unitary matrices
![]() $U_Y,V_Y\in M_{mn}$
such that
$U_Y,V_Y\in M_{mn}$
such that
for all
![]() $ i=1,\ldots , m \text { and } j=1,\ldots , n.$
Without loss of generality, we may assume that
$ i=1,\ldots , m \text { and } j=1,\ldots , n.$
Without loss of generality, we may assume that
![]() $U_I=V_I=I_{mn}$
, i.e.,
$U_I=V_I=I_{mn}$
, i.e.,
for all
![]() $i=1,\ldots , m \text { and } j=1,\ldots , n.$
By (2.24) and (2.25), we have:
$i=1,\ldots , m \text { and } j=1,\ldots , n.$
By (2.24) and (2.25), we have:
-
(i)
 $I_{mn}=\phi (I_m\otimes I_n)=U_Y(I_m\otimes I_n)V_Y^*$
;
$I_{mn}=\phi (I_m\otimes I_n)=U_Y(I_m\otimes I_n)V_Y^*$
; -
(ii)
 $E_{ii}\otimes I_n=\phi (E_{ii}\otimes I_n)=U_Y(E_{ii}\otimes I_n)V_Y^* \text { for all } i=1,\ldots ,m.$
$E_{ii}\otimes I_n=\phi (E_{ii}\otimes I_n)=U_Y(E_{ii}\otimes I_n)V_Y^* \text { for all } i=1,\ldots ,m.$
It follows that
![]() $U_Y=V_Y$
and
$U_Y=V_Y$
and
![]() $U_Y$
commutes with
$U_Y$
commutes with
![]() $E_{ii}\otimes I_n$
for all
$E_{ii}\otimes I_n$
for all
![]() $i=1,\ldots , m$
. Therefore,
$i=1,\ldots , m$
. Therefore,
![]() $U_Y$
commutes with
$U_Y$
commutes with
![]() $E_{11}\otimes I_n+2E_{22}\otimes I_n+\cdots +mE_{mm}\otimes I_n,$
which implies that
$E_{11}\otimes I_n+2E_{22}\otimes I_n+\cdots +mE_{mm}\otimes I_n,$
which implies that
![]() $U_Y=\bigoplus \limits _{i=1}^{m}U_{i,Y}$
with unitary matrices
$U_Y=\bigoplus \limits _{i=1}^{m}U_{i,Y}$
with unitary matrices
![]() $U_{i,Y}\in M_n$
. It follows that
$U_{i,Y}\in M_n$
. It follows that
So far, we have showed that for any unitary matrix
![]() $Y\in M_n$
, there exists a unitary matrix
$Y\in M_n$
, there exists a unitary matrix
![]() $U_{i,Y}\in M_n$
depending on i and Y such that
$U_{i,Y}\in M_n$
depending on i and Y such that
By the linearity of
![]() $\phi $
, we conclude from the above equation that for any
$\phi $
, we conclude from the above equation that for any
![]() $i=1,\ldots , m$
, there exists a linear map
$i=1,\ldots , m$
, there exists a linear map
![]() $\psi _i$
such that
$\psi _i$
such that
Let
![]() $\hat {k}=\min \{k,n\}$
. Then it is easy to check that
$\hat {k}=\min \{k,n\}$
. Then it is easy to check that
for all
![]() $B\in M_n$
. That is,
$B\in M_n$
. That is,
![]() $\psi _i$
is a linear map on
$\psi _i$
is a linear map on
![]() $M_n$
preserving the
$M_n$
preserving the
![]() $(p,\hat {k})$
-norm. Thus, by Theorem 1 in [Reference Li and Tsing23],
$(p,\hat {k})$
-norm. Thus, by Theorem 1 in [Reference Li and Tsing23],
![]() $\psi _i$
has form
$\psi _i$
has form
![]() $B\mapsto W_i B\widetilde {W}_i$
or
$B\mapsto W_i B\widetilde {W}_i$
or
![]() $B\mapsto W_i B^T\widetilde {W}_i$
for some unitary matrices
$B\mapsto W_i B^T\widetilde {W}_i$
for some unitary matrices
![]() $W_i, \widetilde {W}_i\in M_n.$
Let
$W_i, \widetilde {W}_i\in M_n.$
Let
![]() $W=\bigoplus \limits _{i=1}^m W_i$
and
$W=\bigoplus \limits _{i=1}^m W_i$
and
![]() $\widetilde {W}=\bigoplus \limits _{i=1}^m\widetilde {W}_i$
. It follows that for any
$\widetilde {W}=\bigoplus \limits _{i=1}^m\widetilde {W}_i$
. It follows that for any
![]() ${i=1,\ldots , m,}$
${i=1,\ldots , m,}$
where
![]() $\varphi _i$
is the identity map or the transposition map. Recall that
$\varphi _i$
is the identity map or the transposition map. Recall that
![]() $I_{mn}=\phi (I_m\otimes I_n). $
Thus, we have
$I_{mn}=\phi (I_m\otimes I_n). $
Thus, we have
![]() $\widetilde {W} = W^*$
.
$\widetilde {W} = W^*$
.
Applying Claim 3 again, we can repeat the same argument above to show that for any unitary matrix
![]() $X \in M_m$
and any integer
$X \in M_m$
and any integer
![]() $1\leq i\leq m$
, there exists a unitary matrix
$1\leq i\leq m$
, there exists a unitary matrix
![]() $W_X$
such that
$W_X$
such that
where
![]() $\varphi _{i,X}$
is the identity map or the transposition map. We may further assume that
$\varphi _{i,X}$
is the identity map or the transposition map. We may further assume that
![]() $W_I=I_{mn}$
. Then, applying Lemma 2.13, we have
$W_I=I_{mn}$
. Then, applying Lemma 2.13, we have
where
![]() $\varphi _2$
is the identity map or the transposition map and
$\varphi _2$
is the identity map or the transposition map and
![]() $\varphi _1$
is a linear map on
$\varphi _1$
is a linear map on
![]() $M_m$
. Let
$M_m$
. Let
![]() $\widetilde {k}=\min \{k,m\}.$
It is easy to verify that
$\widetilde {k}=\min \{k,m\}.$
It is easy to verify that
![]() $\varphi _1$
is a linear map on
$\varphi _1$
is a linear map on
![]() $M_m$
preserving the
$M_m$
preserving the
![]() $(p,\widetilde {k})$
-norm. Hence,
$(p,\widetilde {k})$
-norm. Hence,
![]() $\varphi _1$
also has the form
$\varphi _1$
also has the form
![]() $A\mapsto UAV$
or
$A\mapsto UAV$
or
![]() $A\mapsto UA^TV$
for some unitary matrices
$A\mapsto UA^TV$
for some unitary matrices
![]() $U, V\in M_m$
. This completes the proof.
$U, V\in M_m$
. This completes the proof.
3 Multipartite system
In this section, we extend Theorem 2.1 to multipartite systems. The proof of the following lemma can be found in the proof of Theorem 3.1 in [Reference Fošner, Huang, Li and Sze10]. For completeness, we present it as follows.
Lemma 3.1 Given an integer
![]() $m\geq 2$
, let
$m\geq 2$
, let
![]() $n_i \geq 2 $
be integers for
$n_i \geq 2 $
be integers for
![]() $i=1,\ldots ,m$
and
$i=1,\ldots ,m$
and
![]() ${N=\prod \limits _{i=1}^{m}n_i}$
. Let
${N=\prod \limits _{i=1}^{m}n_i}$
. Let
![]() $\phi :M_N\to M_N$
be a linear map. Suppose for any unitary matrices
$\phi :M_N\to M_N$
be a linear map. Suppose for any unitary matrices
![]() $X_i\in M_{n_i}$
and any integers
$X_i\in M_{n_i}$
and any integers
![]() $ 1\leq j_i\leq n_i$
with
$ 1\leq j_i\leq n_i$
with
![]() $ 1\leq i\leq m-1$
, there exists a unitary matrix
$ 1\leq i\leq m-1$
, there exists a unitary matrix
![]() $W_X\in M_N$
depending on
$W_X\in M_N$
depending on
![]() $X=(X_1,\ldots ,X_{m-1})$
such that
$X=(X_1,\ldots ,X_{m-1})$
such that
 $$ \begin{align} \phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i} X_i^*\otimes B\right )= W_{X}\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes\varphi_{j_1,\ldots,j_{m-1},X}(B)\right )W_{X}^* \end{align} $$
$$ \begin{align} \phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i} X_i^*\otimes B\right )= W_{X}\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes\varphi_{j_1,\ldots,j_{m-1},X}(B)\right )W_{X}^* \end{align} $$
for all
![]() $B\in M_{n_m},$
where
$B\in M_{n_m},$
where
![]() $\varphi _{j_1,\ldots ,j_{m-1},X}$
is the identity map or the transposition map and
$\varphi _{j_1,\ldots ,j_{m-1},X}$
is the identity map or the transposition map and
![]() $W_X=I_N$
when
$W_X=I_N$
when
![]() $X=(I_{n_1},\ldots ,I_{n_{m-1}})$
. Then
$X=(I_{n_1},\ldots ,I_{n_{m-1}})$
. Then
where
![]() $\varphi _1$
is a linear map and
$\varphi _1$
is a linear map and
![]() $\varphi _2$
is the identity map or the transposition map.
$\varphi _2$
is the identity map or the transposition map.
Proof Considering all symmetric real matrices as in the proof of Lemma 2.13, one can conclude that there exists some unitary matrix
![]() $Z_{X}$
such that
$Z_{X}$
such that
 $$ \begin{align} \phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )= \left(Z_{X}\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\right )Z_{X}^*\right) \otimes \varphi_{j_1,\ldots,j_{m-1},X}(B) \end{align} $$
$$ \begin{align} \phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )= \left(Z_{X}\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\right )Z_{X}^*\right) \otimes \varphi_{j_1,\ldots,j_{m-1},X}(B) \end{align} $$
for all
![]() $B\in M_{n_m}$
and integers
$B\in M_{n_m}$
and integers
![]() $1\leq j_i\leq n_i $
with
$1\leq j_i\leq n_i $
with
![]() $ 1\leq i\leq m-1$
. Define linear maps
$ 1\leq i\leq m-1$
. Define linear maps
![]() $\mathrm {tr_1}:M_N\to M_{n_m}$
and
$\mathrm {tr_1}:M_N\to M_{n_m}$
and
![]() $\mathrm {Tr_1}:M_N\to M_{n_m}$
by
$\mathrm {Tr_1}:M_N\to M_{n_m}$
by
for all
![]() $A\in M_{n_1\cdots n_{m-1}}$
and
$A\in M_{n_1\cdots n_{m-1}}$
and
![]() $B\in M_{n_m}$
. Then
$B\in M_{n_m}$
. Then
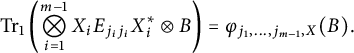 $$ \begin{align*}\mathrm{Tr_1}\left(\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )=\varphi_{j_1,\ldots,j_{m-1},X}(B).\end{align*} $$
$$ \begin{align*}\mathrm{Tr_1}\left(\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )=\varphi_{j_1,\ldots,j_{m-1},X}(B).\end{align*} $$
Notice that
![]() $\text {Tr}_1$
is linear and therefore continuous. Besides, the set
$\text {Tr}_1$
is linear and therefore continuous. Besides, the set
 $$ \begin{align} \nonumber \left\{\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\mid 1\leq j_i\leq n_i \text{ and } X_i\in M_{n_i} \text{ is unitary for }i=1,\ldots,m-1\right\} \\ =\left\{\bigotimes\limits_{i=1}^{m-1}x_ix_i^*\mid x_i\in \mathbb{C}^{n_i} \text{ with } x_i^*x_i=1 \text{ for }i=1,\ldots,m-1\right\} \end{align} $$
$$ \begin{align} \nonumber \left\{\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\mid 1\leq j_i\leq n_i \text{ and } X_i\in M_{n_i} \text{ is unitary for }i=1,\ldots,m-1\right\} \\ =\left\{\bigotimes\limits_{i=1}^{m-1}x_ix_i^*\mid x_i\in \mathbb{C}^{n_i} \text{ with } x_i^*x_i=1 \text{ for }i=1,\ldots,m-1\right\} \end{align} $$
is connected. So, all the maps
![]() $\varphi _{j_1,\ldots ,j_{m-1},X}$
are the same. Then (3.2) can be rewritten as
$\varphi _{j_1,\ldots ,j_{m-1},X}$
are the same. Then (3.2) can be rewritten as
 $$ \begin{align*}\phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )= \left(Z_{X}\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\right )Z_{X}^*\right) \otimes \varphi_{2}(B),\end{align*} $$
$$ \begin{align*}\phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )= \left(Z_{X}\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\right )Z_{X}^*\right) \otimes \varphi_{2}(B),\end{align*} $$
where
![]() $\varphi _2$
is the identity map or the transposition map. With the linearity of
$\varphi _2$
is the identity map or the transposition map. With the linearity of
![]() $\phi $
, it follows that
$\phi $
, it follows that
for some linear map
![]() $\varphi _1.$
$\varphi _1.$
Theorem 3.2 Given an integer
![]() $m\geq 2$
, let
$m\geq 2$
, let
![]() $n_i \geq 2 $
be integers for
$n_i \geq 2 $
be integers for
![]() $i=1,\ldots ,m$
and
$i=1,\ldots ,m$
and
![]() $N=\prod \limits _{i=1}^{m}n_i.$
Then, for any real number
$N=\prod \limits _{i=1}^{m}n_i.$
Then, for any real number
![]() $p>2$
and any positive integer
$p>2$
and any positive integer
![]() $k \leq N,$
a linear map
$k \leq N,$
a linear map
![]() $\phi : M_N \to M_N$
satisfies
$\phi : M_N \to M_N$
satisfies
for all
![]() $A_i\in M_{n_i}, i=1,\ldots ,m$
, if and only if there exist unitary matrices
$A_i\in M_{n_i}, i=1,\ldots ,m$
, if and only if there exist unitary matrices
![]() $U,V \in M_N$
such that
$U,V \in M_N$
such that
for all
![]() $A_i\in M_{n_i},i=1,\ldots ,m,$
where
$A_i\in M_{n_i},i=1,\ldots ,m,$
where
![]() $\varphi _i$
is the identity map or the transposition map
$\varphi _i$
is the identity map or the transposition map
![]() $A\mapsto A^T $
for
$A\mapsto A^T $
for
![]() $i=1,\ldots ,m$
.
$i=1,\ldots ,m$
.
Proof By Theorem 3.2 of [Reference Fošner, Huang, Li and Sze10], we know the result holds for
![]() $k=1$
. So we may assume
$k=1$
. So we may assume
![]() $k\ge 2$
.
$k\ge 2$
.
We use induction on m. By Theorem 2.1, the result holds for
![]() $m=2$
. Now suppose that
$m=2$
. Now suppose that
![]() $m\geq 3$
and the result holds for any
$m\geq 3$
and the result holds for any
![]() $(m-1)$
-partite system. We need to show that the result holds for any m-partite system.
$(m-1)$
-partite system. We need to show that the result holds for any m-partite system.
We first show that for any unitary matrices
![]() $X_i\in M_{n_i}, i=1,\ldots ,m,$
$X_i\in M_{n_i}, i=1,\ldots ,m,$
for any
![]() $(i_1,\ldots ,i_m)\neq (j_1,\ldots ,j_m).$
Without loss of generality, we need only to prove that (3.6) holds when
$(i_1,\ldots ,i_m)\neq (j_1,\ldots ,j_m).$
Without loss of generality, we need only to prove that (3.6) holds when
![]() $X_i=I_{n_i}$
for
$X_i=I_{n_i}$
for
![]() $i=1,\ldots ,m$
. By Lemma 2.6, it suffices to show that for any integer
$i=1,\ldots ,m$
. By Lemma 2.6, it suffices to show that for any integer
![]() $1\leq s\leq m,$
we have
$1\leq s\leq m,$
we have
 $$ \begin{align} \nonumber &\phi\left (\bigotimes\limits_{u=1}^{s-1}(E_{i_ui_u}+E_{j_uj_u})\otimes E_{i_si_s}\otimes \bigotimes\limits_{u=s+1}^mE_{i_ui_u}\right ) \\ &\qquad\qquad\qquad\perp \phi\left (\bigotimes\limits_{u=1}^{s-1}(E_{i_ui_u}+E_{j_uj_u})\otimes E_{j_sj_s}\otimes \bigotimes\limits_{u=s+1}^mE_{i_ui_u}\right ) \end{align} $$
$$ \begin{align} \nonumber &\phi\left (\bigotimes\limits_{u=1}^{s-1}(E_{i_ui_u}+E_{j_uj_u})\otimes E_{i_si_s}\otimes \bigotimes\limits_{u=s+1}^mE_{i_ui_u}\right ) \\ &\qquad\qquad\qquad\perp \phi\left (\bigotimes\limits_{u=1}^{s-1}(E_{i_ui_u}+E_{j_uj_u})\otimes E_{j_sj_s}\otimes \bigotimes\limits_{u=s+1}^mE_{i_ui_u}\right ) \end{align} $$
for all
![]() $\mathrm {i}=(i_1,\ldots ,i_m)$
and
$\mathrm {i}=(i_1,\ldots ,i_m)$
and
![]() $\mathrm {j}=(j_1,\ldots ,j_m)$
with
$\mathrm {j}=(j_1,\ldots ,j_m)$
with
![]() $i_u\neq j_u$
for
$i_u\neq j_u$
for
![]() $ u=1,\ldots , s.$
Denote by
$ u=1,\ldots , s.$
Denote by
![]() $A_s(\mathrm {i,j})$
and
$A_s(\mathrm {i,j})$
and
![]() $B_s(\mathrm {i,j})$
the two matrices in (3.7) accordingly. It is easy to check that for any integer
$B_s(\mathrm {i,j})$
the two matrices in (3.7) accordingly. It is easy to check that for any integer
![]() $1\leq s\leq m$
and real number
$1\leq s\leq m$
and real number
![]() $0<x<1$
,
$0<x<1$
,
 $$ \begin{align*} &\|A_s(\mathrm{i,j})+xB_s(\mathrm{i,j})\|_{(p,k)}^p+\|A_s(\mathrm{i,j}) -xB_s(\mathrm{i,j})\|_{(p,k)}^p\qquad\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\leq 2\|A_s(\mathrm{i,j})\|^p_{(p,k)}+2\|xB_s(\mathrm{i,j})\|^p_{(p,k)}.\notag \end{align*} $$
$$ \begin{align*} &\|A_s(\mathrm{i,j})+xB_s(\mathrm{i,j})\|_{(p,k)}^p+\|A_s(\mathrm{i,j}) -xB_s(\mathrm{i,j})\|_{(p,k)}^p\qquad\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\leq 2\|A_s(\mathrm{i,j})\|^p_{(p,k)}+2\|xB_s(\mathrm{i,j})\|^p_{(p,k)}.\notag \end{align*} $$
Then, applying the same argument as in the proof of Theorem 2.1, we conclude that for any integer
![]() $1\leq s \leq m$
and real number
$1\leq s \leq m$
and real number
![]() $0<x<1$
,
$0<x<1$
,
 $$ \begin{align} \nonumber &\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A_s^*(\mathrm{i,j})A_s(\mathrm{i,j}\big)+x^2B_s^*(\mathrm{i,j})B_s(\mathrm{i,j})\big) \\ &\qquad\qquad\qquad\qquad\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A^*_s(\mathrm{i,j})A_s(\mathrm{i,j})\big)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(x^2B_s^*(\mathrm{i,j})B_s(\mathrm{i,j})\big) \end{align} $$
$$ \begin{align} \nonumber &\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A_s^*(\mathrm{i,j})A_s(\mathrm{i,j}\big)+x^2B_s^*(\mathrm{i,j})B_s(\mathrm{i,j})\big) \\ &\qquad\qquad\qquad\qquad\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A^*_s(\mathrm{i,j})A_s(\mathrm{i,j})\big)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(x^2B_s^*(\mathrm{i,j})B_s(\mathrm{i,j})\big) \end{align} $$
and
 $$ \begin{align} \nonumber& \sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A_s(\mathrm{i,j})A^*_s(\mathrm{i,j})+x^2B_s(\mathrm{i,j})B_s^*(\mathrm{i,j})\big) \\&\qquad\qquad\qquad\qquad\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A_s(\mathrm{i,j})A^*_s(\mathrm{i,j})\big)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(x^2B_s(\mathrm{i,j})B^*_s(\mathrm{i,j})\big) \end{align} $$
$$ \begin{align} \nonumber& \sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A_s(\mathrm{i,j})A^*_s(\mathrm{i,j})+x^2B_s(\mathrm{i,j})B_s^*(\mathrm{i,j})\big) \\&\qquad\qquad\qquad\qquad\leq \sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(A_s(\mathrm{i,j})A^*_s(\mathrm{i,j})\big)+\sum_{i=1}^k\lambda_i^{\frac{p}{2}}\big(x^2B_s(\mathrm{i,j})B^*_s(\mathrm{i,j})\big) \end{align} $$
for all
![]() $\mathrm {i}=(i_1,\ldots ,i_m)$
and
$\mathrm {i}=(i_1,\ldots ,i_m)$
and
![]() $\mathrm {j}=(j_1,\ldots ,j_m)$
with
$\mathrm {j}=(j_1,\ldots ,j_m)$
with
![]() $i_u\neq j_u$
for
$i_u\neq j_u$
for
![]() $ u=1,\ldots , s.$
Now we distinguish two cases.
$ u=1,\ldots , s.$
Now we distinguish two cases.
Case 1. Suppose
![]() $k>2^{m-1}$
. Then
$k>2^{m-1}$
. Then
where
![]() $a_s=2^{s-1}$
for
$a_s=2^{s-1}$
for
![]() $s=1,\ldots ,m-1$
and
$s=1,\ldots ,m-1$
and
![]() $a_m=\min \{k-2^{m-1},2^{m-1}\}$
. We claim that
$a_m=\min \{k-2^{m-1},2^{m-1}\}$
. We claim that
Otherwise,
![]() $s_k(A_s(\mathrm {i,j}))>0$
for some
$s_k(A_s(\mathrm {i,j}))>0$
for some
![]() $1\leq s\leq m$
. Then, by (3.8) and (3.9), we can use the same argument as in Claim 1 in the proof of Theorem 2.1 to conclude that there exists a sufficiently small
$1\leq s\leq m$
. Then, by (3.8) and (3.9), we can use the same argument as in Claim 1 in the proof of Theorem 2.1 to conclude that there exists a sufficiently small
![]() $x>0$
such that
$x>0$
such that
which contradicts (3.10). Thus, (3.11) holds. Applying Corollary 2.12, we have
Case 2. Suppose
![]() $k\leq 2^{m-1}$
. Let
$k\leq 2^{m-1}$
. Let
![]() $s_0$
be the integer such that
$s_0$
be the integer such that
![]() $2^{s_0-1}< k\leq 2^{s_0}.$
We can use the same argument as in Case 1 to show that for any integer
$2^{s_0-1}< k\leq 2^{s_0}.$
We can use the same argument as in Case 1 to show that for any integer
![]() $1\leq s\leq s_0$
,
$1\leq s\leq s_0$
,
for all
![]() $\mathrm {i}=(i_1,\ldots ,i_m)$
and
$\mathrm {i}=(i_1,\ldots ,i_m)$
and
![]() $\mathrm {j}=(j_1,\ldots ,j_m)$
with
$\mathrm {j}=(j_1,\ldots ,j_m)$
with
![]() $i_u\neq j_u$
for
$i_u\neq j_u$
for
![]() $u=1,\ldots ,s.$
$u=1,\ldots ,s.$
Next, we use induction on s to prove that for any
![]() $s_0+1\leq s \leq m, \mathrm {i}=(i_1,\ldots ,i_m )$
and
$s_0+1\leq s \leq m, \mathrm {i}=(i_1,\ldots ,i_m )$
and
![]() $\mathrm {j}=(j_1,\ldots ,j_m)$
with
$\mathrm {j}=(j_1,\ldots ,j_m)$
with
![]() $i_u\neq j_u$
for
$i_u\neq j_u$
for
![]() $u=1,\ldots , s,$
there exist unitary matrices
$u=1,\ldots , s,$
there exist unitary matrices
![]() $U,V\in M_N$
depending on s and
$U,V\in M_N$
depending on s and
![]() $(\mathrm {i,j})$
such that
$(\mathrm {i,j})$
such that
First, by (3.12), we have
![]() $A_{s_0}(\mathrm {i,j})\perp B_{s_0}(\mathrm {i,j})$
and there exist unitary matrices
$A_{s_0}(\mathrm {i,j})\perp B_{s_0}(\mathrm {i,j})$
and there exist unitary matrices
![]() $U,V\in M_N$
and an integer
$U,V\in M_N$
and an integer
![]() $0\leq r< k$
such that
$0\leq r< k$
such that
and
with
![]() $a_1\geq \cdots \geq a_r>0$
and
$a_1\geq \cdots \geq a_r>0$
and
![]() $b_{r+1}\geq \cdots \geq b_N\geq 0$
. If
$b_{r+1}\geq \cdots \geq b_N\geq 0$
. If
![]() $a_1>1$
, then by (3.12), applying Lemma 2.6, we have
$a_1>1$
, then by (3.12), applying Lemma 2.6, we have
![]() $s_1\Big (\phi \Big (\bigotimes \limits _{u=1}^mE_{i_ui_u}\Big )\Big )>1$
for some
$s_1\Big (\phi \Big (\bigotimes \limits _{u=1}^mE_{i_ui_u}\Big )\Big )>1$
for some
![]() $(i_1,\ldots ,i_m)$
. It follows that
$(i_1,\ldots ,i_m)$
. It follows that
![]() $\Big \|\phi \Big (\bigotimes \limits _{u=1}^mE_{i_ui_u}\Big )\Big \|_{(p,k)}>1$
, which contradicts (3.4). Thus,
$\Big \|\phi \Big (\bigotimes \limits _{u=1}^mE_{i_ui_u}\Big )\Big \|_{(p,k)}>1$
, which contradicts (3.4). Thus,
![]() $a_1\leq 1$
, and similarly
$a_1\leq 1$
, and similarly
![]() $b_{r+1}\leq 1.$
Then we have
$b_{r+1}\leq 1.$
Then we have
 $$ \begin{align} \sum_{j=1}^ra_j^p+\sum_{j=r+1}^kb_j^p\leq k. \end{align} $$
$$ \begin{align} \sum_{j=1}^ra_j^p+\sum_{j=r+1}^kb_j^p\leq k. \end{align} $$
Clearly,
![]() $a_1\geq \cdots \geq a_r\geq xb_{r+1}\geq \cdots \geq xb_k$
are the largest k singular values of
$a_1\geq \cdots \geq a_r\geq xb_{r+1}\geq \cdots \geq xb_k$
are the largest k singular values of
![]() $A_{s_0}(\mathrm {i,j})+xB_{s_0}(\mathrm {i,j})$
for all
$A_{s_0}(\mathrm {i,j})+xB_{s_0}(\mathrm {i,j})$
for all
![]() $0<x\leq \frac {a_r}{b_{r+1}}$
. Hence,
$0<x\leq \frac {a_r}{b_{r+1}}$
. Hence,
 $$ \begin{align*}\|A_{s_0}(\mathrm{i,j})+xB_{s_0}(\mathrm{i,j})\|^p_{(p,k)}=\sum_{j=1}^ra_j^p+x^p\sum_{j=r+1}^kb_j^p\quad \text{for all}\quad 0< x\leq \frac{a_r}{b_{r+1}}.\end{align*} $$
$$ \begin{align*}\|A_{s_0}(\mathrm{i,j})+xB_{s_0}(\mathrm{i,j})\|^p_{(p,k)}=\sum_{j=1}^ra_j^p+x^p\sum_{j=r+1}^kb_j^p\quad \text{for all}\quad 0< x\leq \frac{a_r}{b_{r+1}}.\end{align*} $$
On the other hand, with (3.4), we have
It follows from the above two equations that
 $$ \begin{align*}\displaystyle\sum_{j=1}^ra_j^p=2^{s_0-1} \quad\mathrm{and}\quad \displaystyle\sum_{j=r+1}^kb_j^p=k-2^{s_0-1}.\end{align*} $$
$$ \begin{align*}\displaystyle\sum_{j=1}^ra_j^p=2^{s_0-1} \quad\mathrm{and}\quad \displaystyle\sum_{j=r+1}^kb_j^p=k-2^{s_0-1}.\end{align*} $$
Therefore,
![]() $ \sum _{j=1}^ra_j^p+ \sum _{j=r+1}^kb_j^p=k,$
i.e., the equality in (3.14) holds, which implies that
$ \sum _{j=1}^ra_j^p+ \sum _{j=r+1}^kb_j^p=k,$
i.e., the equality in (3.14) holds, which implies that
![]() $a_j=1$
for
$a_j=1$
for
![]() $j=1,\ldots ,r$
. Notice that
$j=1,\ldots ,r$
. Notice that
![]() $\|A_{s_0}(\mathrm {i,j})\|_{(p,k)}^p=2^{s_0-1}$
. Thus,
$\|A_{s_0}(\mathrm {i,j})\|_{(p,k)}^p=2^{s_0-1}$
. Thus,
![]() $r=2^{s_0-1},$
that is,
$r=2^{s_0-1},$
that is,
![]() $UA_{s_0}(\mathrm {i,j})V=I_{2^{s_0-1}}\oplus 0_{N-2^{s_0-1}}$
. Hence, (3.13) holds for
$UA_{s_0}(\mathrm {i,j})V=I_{2^{s_0-1}}\oplus 0_{N-2^{s_0-1}}$
. Hence, (3.13) holds for
![]() $s_0$
.
$s_0$
.
Suppose that (3.13) holds for
![]() $s-1$
with
$s-1$
with
![]() $s_0< s\leq m.$
We will show that (3.13) also holds for s. Notice that
$s_0< s\leq m.$
We will show that (3.13) also holds for s. Notice that
![]() $A_{s}(\mathrm {i,j})=A_{s-1}(\mathrm {\hat {i},\hat {j}})+B_{s-1}(\mathrm {\hat {i},\hat {j}})$
for some
$A_{s}(\mathrm {i,j})=A_{s-1}(\mathrm {\hat {i},\hat {j}})+B_{s-1}(\mathrm {\hat {i},\hat {j}})$
for some
![]() $\mathrm {\hat {i}}=(\hat {i}_1,\ldots ,\hat {i}_m)$
and
$\mathrm {\hat {i}}=(\hat {i}_1,\ldots ,\hat {i}_m)$
and
![]() $\mathrm {\hat {j}}=(\hat {j}_1,\ldots ,\hat {j}_m)$
with
$\mathrm {\hat {j}}=(\hat {j}_1,\ldots ,\hat {j}_m)$
with
![]() $\hat {i}_u\neq \hat {j}_u$
for
$\hat {i}_u\neq \hat {j}_u$
for
![]() $u=1,\ldots , s-1.$
By our assumption, we have
$u=1,\ldots , s-1.$
By our assumption, we have
for some unitary matrices
![]() $U,V\in M_N$
. It follows that
$U,V\in M_N$
. It follows that
Then, with (3.8) and (3.9), we apply Corollary 2.12 to conclude that
for some
![]() $\hat {B}\in M_{N-2^{s-1}}$
. It follows that
$\hat {B}\in M_{N-2^{s-1}}$
. It follows that
![]() $A_s(\mathrm {i,j})\perp B_s(\mathrm {i,j}).$
Now we have proved that (3.13) holds for s. Then we can conclude from the above discussion that for any
$A_s(\mathrm {i,j})\perp B_s(\mathrm {i,j}).$
Now we have proved that (3.13) holds for s. Then we can conclude from the above discussion that for any
![]() $s=1,\ldots ,m$
,
$s=1,\ldots ,m$
,
for all
![]() $\mathrm {i}=(i_1,\ldots ,i_m)$
and
$\mathrm {i}=(i_1,\ldots ,i_m)$
and
![]() $\mathrm {j}=(j_1,\ldots ,j_m)$
with
$\mathrm {j}=(j_1,\ldots ,j_m)$
with
![]() $i_u\neq j_u$
for
$i_u\neq j_u$
for
![]() $ u=1,\ldots , s,$
that is, (3.6) holds.
$ u=1,\ldots , s,$
that is, (3.6) holds.
It follows that for any unitary matrix
![]() $X_m\in M_{n_m}$
, there exist unitary matrices
$X_m\in M_{n_m}$
, there exist unitary matrices
![]() $U_{X_m}$
and
$U_{X_m}$
and
![]() $V_{X_m}$
such that
$V_{X_m}$
such that
 $$ \begin{align} \phi\left(\bigotimes\limits_{i=1}^{m-1} E_{j_ij_i}\otimes X_mE_{j_{m}j_{m}}X_m^*\right)= U_{X_m}(E_{j_1j_1}\otimes \cdots \otimes E_{j_mj_m})V_{X_m}^* \end{align} $$
$$ \begin{align} \phi\left(\bigotimes\limits_{i=1}^{m-1} E_{j_ij_i}\otimes X_mE_{j_{m}j_{m}}X_m^*\right)= U_{X_m}(E_{j_1j_1}\otimes \cdots \otimes E_{j_mj_m})V_{X_m}^* \end{align} $$
for all
![]() $ j_i=1,\ldots , n_i$
with
$ j_i=1,\ldots , n_i$
with
![]() $1 \leq i\leq m.$
For simplicity, we may assume that
$1 \leq i\leq m.$
For simplicity, we may assume that
![]() $U_{I}=V_{I}=I$
, i.e.,
$U_{I}=V_{I}=I$
, i.e.,
Then we have
![]() $\phi (I_N)=I_N$
. Applying a similar argument as in the last two paragraphs of the proof of Theorem 2.1, one can conclude from (3.15) and (3.16) that there are unitary matrices
$\phi (I_N)=I_N$
. Applying a similar argument as in the last two paragraphs of the proof of Theorem 2.1, one can conclude from (3.15) and (3.16) that there are unitary matrices
![]() $W,\widetilde {W}\in M_N$
such that for all
$W,\widetilde {W}\in M_N$
such that for all
![]() $ j_i=1,\ldots ,n_i$
with
$ j_i=1,\ldots ,n_i$
with
![]() $1\leq i\leq m-1$
,
$1\leq i\leq m-1$
,
 $$ \begin{align*}\phi\left(\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes B\right)= W\left(\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes \varphi_{j_1,\ldots,j_{m-1}}(B)\right)\widetilde{W},\end{align*} $$
$$ \begin{align*}\phi\left(\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes B\right)= W\left(\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes \varphi_{j_1,\ldots,j_{m-1}}(B)\right)\widetilde{W},\end{align*} $$
where
![]() $\varphi _{j_1,\ldots ,j_{m-1}}$
is the identity map or the transposition map. It follows that
$\varphi _{j_1,\ldots ,j_{m-1}}$
is the identity map or the transposition map. It follows that
![]() ${\phi (I_N)=W\widetilde {W}}$
. Recall that
${\phi (I_N)=W\widetilde {W}}$
. Recall that
![]() $\phi (I_N)=I_N$
and W and
$\phi (I_N)=I_N$
and W and
![]() $\widetilde {W}$
are both unitary matrices. We have
$\widetilde {W}$
are both unitary matrices. We have
![]() $\widetilde {W}=W^*.$
$\widetilde {W}=W^*.$
Following a similar argument as above, one can show that for any
![]() ${X=(X_1,\ldots ,X_{m-1})}$
and any integer
${X=(X_1,\ldots ,X_{m-1})}$
and any integer
![]() $ j_i=1,\ldots , n_i$
with
$ j_i=1,\ldots , n_i$
with
![]() $1\leq i\leq m-1$
, there exists a unitary matrix
$1\leq i\leq m-1$
, there exists a unitary matrix
![]() $W_X\in M_N$
such that
$W_X\in M_N$
such that
 $$ \begin{align} \phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )=W_X\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes\varphi_{j_1,\ldots,j_{m-1},X}(B)\right )W_X^* \end{align} $$
$$ \begin{align} \phi\left (\bigotimes\limits_{i=1}^{m-1}X_iE_{j_ij_i}X_i^*\otimes B\right )=W_X\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes\varphi_{j_1,\ldots,j_{m-1},X}(B)\right )W_X^* \end{align} $$
for all
![]() $B\in M_{n_m},$
where
$B\in M_{n_m},$
where
![]() $\varphi _{j_1,\ldots ,j_{m-1},X}$
is the identity map or transposition map. Denote
$\varphi _{j_1,\ldots ,j_{m-1},X}$
is the identity map or transposition map. Denote
![]() $\mathrm {I}=(I_{n_1},\ldots ,I_{n_{m-1}}).$
For simplicity, we may further assume that
$\mathrm {I}=(I_{n_1},\ldots ,I_{n_{m-1}}).$
For simplicity, we may further assume that
![]() $W_{\mathrm {I}}=I_N$
, i.e., for any integer
$W_{\mathrm {I}}=I_N$
, i.e., for any integer
![]() $j_i=1,\ldots , n_i$
with
$j_i=1,\ldots , n_i$
with
![]() $1\leq i\leq m-1$
,
$1\leq i\leq m-1$
,
 $$ \begin{align*} \phi\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes B\right )=\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes\varphi_{j_1,\ldots,j_{m-1},\mathrm{I}}(B)\quad \text{for all}\quad B\in M_{n_m}. \end{align*} $$
$$ \begin{align*} \phi\left (\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes B\right )=\bigotimes\limits_{i=1}^{m-1}E_{j_ij_i}\otimes\varphi_{j_1,\ldots,j_{m-1},\mathrm{I}}(B)\quad \text{for all}\quad B\in M_{n_m}. \end{align*} $$
Then we apply Lemma 3.1 to conclude that
for all
![]() $B\in M_{n_m}$
and
$B\in M_{n_m}$
and
![]() $A_i\in M_{n_i}$
,
$A_i\in M_{n_i}$
,
![]() $1\leq i\leq m-1$
, where
$1\leq i\leq m-1$
, where
![]() $\varphi _m$
is the identity map or the transposition map and
$\varphi _m$
is the identity map or the transposition map and
![]() $\psi $
is a linear map. Let
$\psi $
is a linear map. Let
![]() $\hat {k}=\min \Big \{k,\prod \limits _{i=1}^{m-1}n_i\Big \}.$
It is easy to check that
$\hat {k}=\min \Big \{k,\prod \limits _{i=1}^{m-1}n_i\Big \}.$
It is easy to check that
for all
![]() $A_i \in M_{n_i}, i=1,\ldots ,m-1.$
Then, by the induction hypothesis, we conclude that there exist unitary matrices
$A_i \in M_{n_i}, i=1,\ldots ,m-1.$
Then, by the induction hypothesis, we conclude that there exist unitary matrices
![]() $\widetilde {U}$
and
$\widetilde {U}$
and
![]() $\widetilde {V} $
such that
$\widetilde {V} $
such that
where
![]() $\varphi _i$
is the identity map or the transposition map for
$\varphi _i$
is the identity map or the transposition map for
![]() $i=1,\ldots ,m-1.$
Therefore,
$i=1,\ldots ,m-1.$
Therefore,
![]() $\phi $
has the desired form and the proof is completed.
$\phi $
has the desired form and the proof is completed.
4 Conclusion and remarks
In this paper, we determined the structures of linear maps on
![]() $M_{mn}$
that preserve the
$M_{mn}$
that preserve the
![]() $(p,k)$
-norms of tensor products of matrices for
$(p,k)$
-norms of tensor products of matrices for
![]() $p>2$
and
$p>2$
and
![]() $1\leq k\leq mn$
. Our study generalized the results in [Reference Fošner, Huang, Li and Sze10] concerning the maps preserving the Ky Fan k-norm and Schatten p-norms. Furthermore, we have also extended the result on bipartite systems to multipartite systems using mathematical induction.
$1\leq k\leq mn$
. Our study generalized the results in [Reference Fošner, Huang, Li and Sze10] concerning the maps preserving the Ky Fan k-norm and Schatten p-norms. Furthermore, we have also extended the result on bipartite systems to multipartite systems using mathematical induction.
The proofs of the main results in [Reference Fošner, Huang, Li and Sze10] heavily rely on Lemmas 2.2 and 2.7 from the same paper, which specifically address Ky Fan k-norms and Schatten p-norms. However, it is important to note that these two lemmas are not applicable for
![]() $(p,k)$
-norms. To overcome this limitation, we derived two inequalities involving the eigenvalues of Hermitian matrices and
$(p,k)$
-norms. To overcome this limitation, we derived two inequalities involving the eigenvalues of Hermitian matrices and
![]() $(p,k)$
-norms, which are presented in Lemma 2.7 and its corollary. These two inequalities play a crucial role in our proofs.
$(p,k)$
-norms, which are presented in Lemma 2.7 and its corollary. These two inequalities play a crucial role in our proofs.
To characterize linear maps that preserve the
![]() $(p, k)$
-norms of tensor products of matrices for
$(p, k)$
-norms of tensor products of matrices for
![]() $1< p\leq 2$
, we attempted to derive an analogue to the inequality (2.4). However, as demonstrated in Remark 2.8, this analogous inequality does not hold in general. Consequently, the techniques employed in this paper are not able to address the case
$1< p\leq 2$
, we attempted to derive an analogue to the inequality (2.4). However, as demonstrated in Remark 2.8, this analogous inequality does not hold in general. Consequently, the techniques employed in this paper are not able to address the case
![]() $1<p\leq 2$
. Therefore, novel approaches need to be introduced to tackle this particular scenario.
$1<p\leq 2$
. Therefore, novel approaches need to be introduced to tackle this particular scenario.