1. Introduction
The formation of the Antarctic ice sheet (AIS), placed by most workers at about 35×106 years ago, was a significant event in the climatic evolution of the Earth (Reference KennettKennett, 1977; Reference BarrettBarrett, 1996; Reference Barker, Barrett, Cooper and HuybrechtsBarker and others, 1999). There is ample geological evidence (especially the lack or abundance of ice-rafted detritus (IRD) in marine sediments) that the AIS has undergone significant fluctuations since that time. However, in Pleistocene times the greater part of the ice sheet was relatively stable, as witnessed by deep ice cores spanning a number of glacial cycles (e.g. Reference PetitPetit and others, 1999).
Many of the questions relating to the dynamics of the AIS and its interaction with climate can only be answered, if ever, by the use of numerical ice-sheet models with high spatial resolution (e.g. Reference OerlemansOerlemans, 1982; Reference HuybrechtsHuybrechts, 1993; Reference DeConto and PollardDeConto and Pollard, 2003). However, such studies require large amounts of central processing unit (CPU) time, especially when the ice-sheet model is coupled to a climate model. As a consequence, the possibilities of studying parameter sensitivity are limited. It is therefore useful to develop simpler models as well, with which the more robust characteristcs of the ice sheet can be studied for a wide range of parameter values.
The work presented here builds on Reference OerlemansOerlemans (2002), in which a simple axisymmetrical model for the AIS was constructed and used to simulate the history of the AIS over the last two glacial cycles. Meanwhile a more general formulation has been developed (Reference Oerlemans, Oerlemans and vanOerlemans, 2003), allowing the study of ice sheets in warmer climates. In this contribution, the more general model is applied to the AIS. The focus is on the relation between equilibrium states and atmospheric temperature.
As a further application, the model is applied to make a new interpretation of the deep-sea temperature record as inferred from δ18O values in ocean sediments. This record suggests that a general cooling took place during the last 50×106 years (e.g. Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others, 2001). Possible causes for this cooling include thermal isolation of Antarctica due to the rearrangement of ocean current as a consequence of continental drift (e.g. Reference KennettKennett, 1977; Reference Diester-Haas and ZahnDiester-Haas and Zahn, 1996; Reference Toggweiler and BjrnssonToggweiler and Bjrnsson, 2000), and declining levels of carbon dioxide in the atmosphere (e.g. Reference Pearson and PalmerPearson and Palmer, 2000).
No attempt is made in this paper to explain the Cenozoic cooling. The purpose is to derive a deep-sea temperature and ice-volume record that are mutually consistent.
2. Model
The model to be used is basically a continuity model, in which ice mechanics are not considered explicitly and the shape of the ice sheet is entirely determined by its size. The model has been documented in detail in Reference Oerlemans, Oerlemans and vanOerlemans (2003), so here only a brief summary is given.
The model is axisymmetric and the state variable is the ice-sheet radius R. The ice sheet rests on a bed that slopes linearly downwards from the centre of the continent into the ocean (the bed is linear in the undisturbed case, without an ice load). The ice-sheet surface is described by a parabolic profile (Fig. 1):
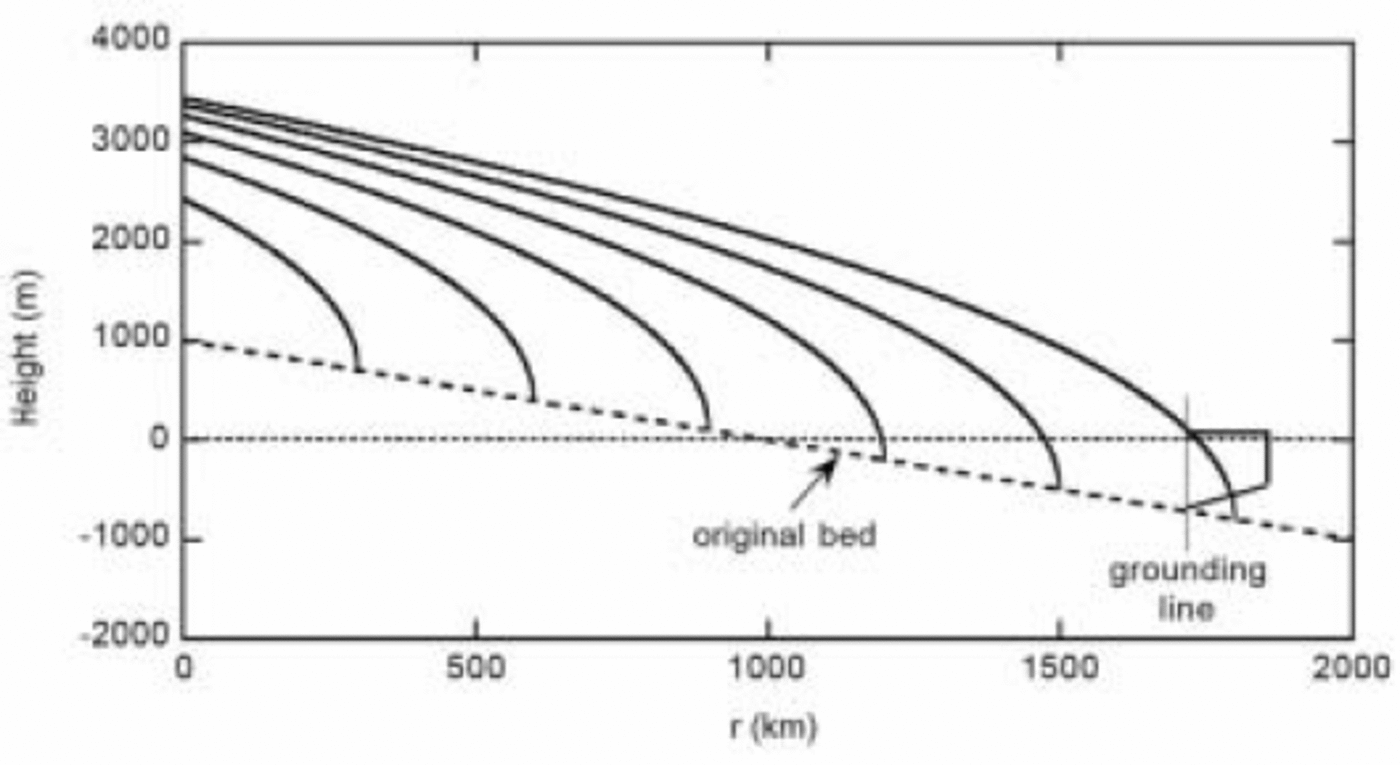
Fig. 1. Typical ice-sheet cross-sections as described by Equation (1).
Here r is the distance to the centre, h is the surface height, d0 is the undisturbed surface elevation at the centre, s is the undisturbed surface slope and μ is the profile parameter. The evolution of the ice sheet is governed bya continuity equation:
Here V is the ice volume, Btot is the total mass accumulating at the surface (accumulation minus runoff) and Fgr the ice flux across the grounding line. When the ice sheet ends on land, Fgr is zero, of course. Otherwise, it is assumed that the azimuthally averaged ice velocity at the grounding line is proportional to the water depth (with constant of proportionality f; Reference OerlemansOerlemans, 2002).
It is not difficult to take glacial isostatic effects into account (Reference Oerlemans, Oerlemans and vanOerlemans, 2003), as long as larger time-scales are considered (i.e. the time lag between loading and bed response, typically a few thousand years, can be neglected).
To study the state of the AIS in different climates requires a fairly universal formulation of the mass balance. Here the concept of the runoff line is used. Its altitude is denoted by hR. Above the runoff line, the specific balance B is constant and equal to A; below the runoff line the balance gradient (with respect to altitude) is constant. Therefore
Here β is the balance gradient (β < 0). Note that a simple relation exists between the altitude of the runoff line and the more commonly used altitude of the equilibrium line hE.
Mass-balance observations on glaciers around the world have shown that a distinct relation exists between the balance gradient and precipitation. One reason for this is that in an absolute sense altitudinal precipitation gradients are larger when precipitation is larger. Observed values of β range from about 0.009 m ice m–1 a–1 for glaciers in very maritime climates to as small as 0.001 m ice m–1 a–1 for very dry continental ice caps (Reference OerlemansOerlemans, 2001). A reasonable fit to observed data is given by
with ν = 0.006 μ–1/2 a–1/2.
With this description of the mass-balance field, an analytical expression can be derived for Btot (Reference Oerlemans, Oerlemans and vanOerlemans, 2003). The resulting equation for the total budget, i.e. the righthand side of Equation (2), is of a high order in R. Consequently, the equilibrium states cannot be found analytically. However, a standard numerical method does the job (e.g. Newton–Raphson or integration of the time-dependent equation).
3. Mass Balance and Climate
The next step is to relate the parameters A and hR to the climatic state. In the following, the mean Antarctic temperature reduced to sea level, denoted by Ta, will be used as the prime climatic parameter. Its current value will be taken as –18˚C. In fact, Ta is not so well defined since much depends on how surface temperature is reduced to sea level. The present-day annual mean temperature averaged over the Antarctic coastal stations is about –13˚C (e.g. Reference MüllerMüller, 1987).
As a first step the height of the runoff line is related to Ta by
The values of h0 and λ can be estimated from mass-balance studies. In Figure 2, results of a number of mass-balance (modelling) studies in different parts of the world are brought together, namely, from Severnaya Zemlya, Russian High Arctic (Reference DowdeswellDowdeswell and others, 2002), west Svalbard (Reference Fleming, Dowdeswell and OerlemansFleming and others, 1997), West Greenland (Reference Zuo and OerlemansZuo and Oerlemans, 1996; Reference Greuell, Denby, van de Wal and OerlemansGreuell and others, 2001), southern Norway (Reference OerlemansOerlemans, 1992) and the Alps (Reference Greuell and OerlemansGreuell and Oerlemans, 1986). In view of the low annual temperature, the runoff line on Severnaya Zemlya is remarkably high. This is related to the large annual temperature range here, and illustrates the uncertainty involved in using annual mean temperature. One may argue that it would be better to use summer temperature as a predictor as well, but this would introduce the problem of estimating changes in summer temperature in a much warmer climate. For the moment, the use of Equation (7) seems to be the best approach. A linear fit to the data points in Figure 2 yields h0 = 1471 m and λ=95 m K–1.
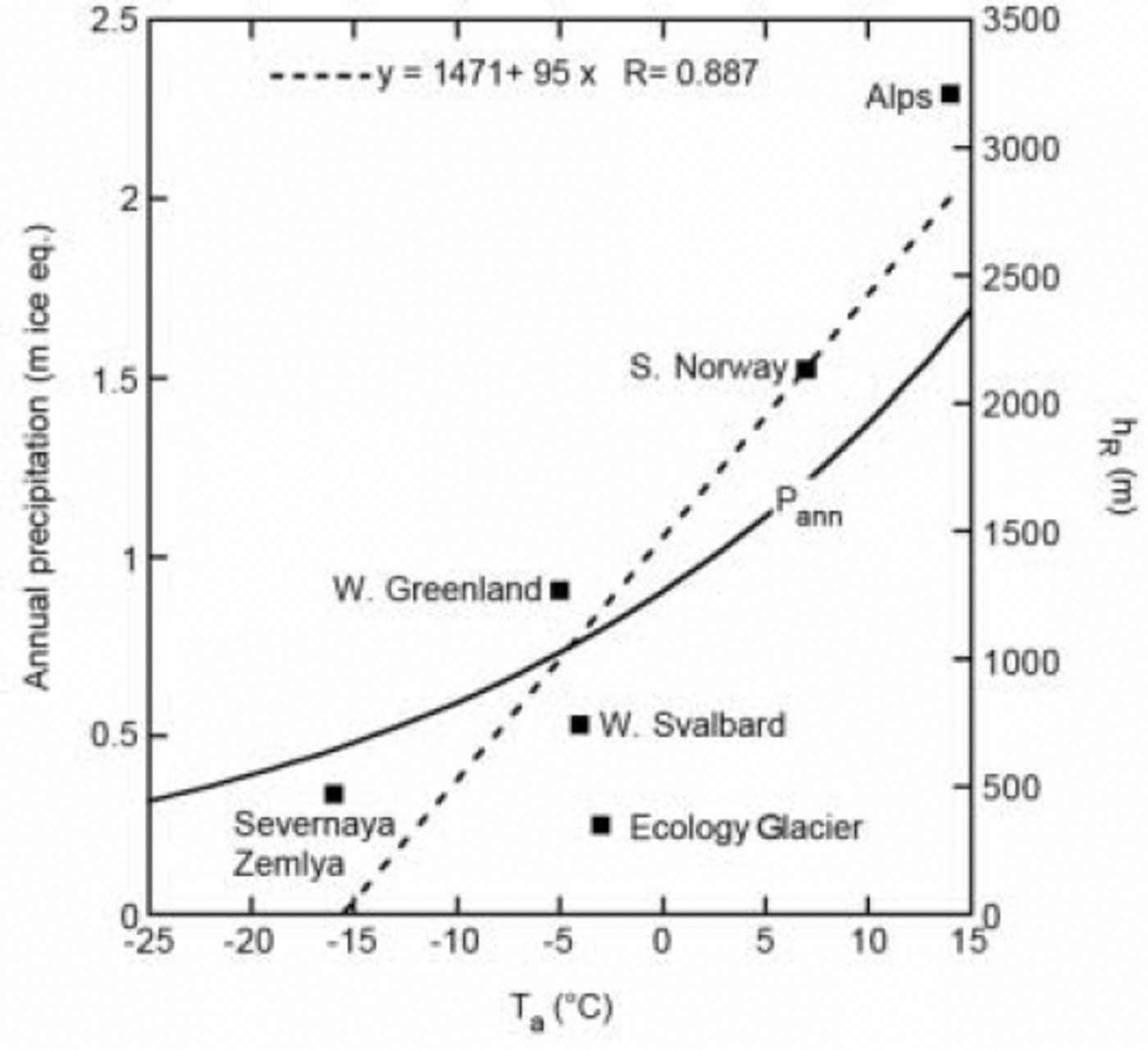
Fig. 2. Height of the runoff line (h R) estimated from studies in different glaciated regions, as a function of annual temperature reduced to sea level. The dashed line is the fit adopted in the present study. The solid line shows the relation between annual precipitation and annual temperature (excluding the feedback between ice-sheet size and accumulation rate).
Although the formation of precipitation is a matter of atmospheric dynamics, there is a strong relation between annual precipitation rates and atmospheric temperature.
This is due to the strong dependence of the moisture-holding capacity of the atmosphere on air temperature. When it is assumed that the precipitation rate is proportional to the columnar precipitable water, one can write (Oerlemans and Van der Veen, 1984, p. 140):
In this expression, P is the annual precipitation and P0 is the precipitation for a sea-level temperature of 0˚C. The coefficient κ depends on the characteristic depth of the atmospheric column. Here a constant value of κ=0.04 K–1 is used. The result is shown in Figure 2.
Ice sheets are among the driest places on Earth. Several processes make the deposition of snow on ice sheets more difficult when the ice sheets get bigger. This effect is taken into account by writing (Reference Oerlemans, Oerlemans and vanOerlemans, 2003)

So the accumulation rate drops off exponentially with the ice-sheet radius, with an e-folding length scale Rc. Values for P0 and Rc have been chosen such that the present-day total accumulation on the ice sheet is reproduced (P0=0.92m ice a–1, Rc = 2000 km).
By means of Equations (3–9) the mass balance has been modelled to a sufficient degree to study the response of the ice sheet to changes in annual mean temperature. The parameterization should be valid for a large range of temperatures. In the following the state of the ice sheet will be studied for –25 ≤ Ta ≤ 5˚C.
4. Equilibrium States for Different Temperatures
For the reference values of h0 and λ, the equilibrium states of the model are shown as a function of Ta in Figure 3. Starting in warm conditions and then gradually cooling the climate shows that an ice sheet is initiated when Ta drops below –6.5˚C. The ice sheet reaches its maximum size for Ta = –15.5˚C, which is only a few degrees above the temperature representing the current state (Ta=–18˚C). In fact, the model parameters were determined in such a way that the state calculated for the current temperature matches the observed state of the ice sheet in terms of area, volume and mass throughput (corresponding parameter values: μ = 9 μ1 / 2, f = 1.2 m a–1, d 0 = 760 m, s = 0.0006. When going back to a warm climate, hysteresis occurs, which is a well-known feature of ice-sheet models that include the height–mass-balance feedback. However, the ‘width’ of the hysteresis is rather small, only 2.5 K.
In Figure 3, equilibrium states as reported by Reference HuybrechtsHuybrechts (1993) are also shown. Huybrechts used a three-dimensional (3-D) thermomechanical model with a representation of the real orography. Compared to the equilibrium states of the present model, the shape of the curve is similar, but there is a shift along the temperature axis of about 6 K. Apparently, the simple model predicts a less stable AIS than the numerical model. The mass-balance scheme used by Reference HuybrechtsHuybrechts (1993) (and also the one used by Reference OerlemansOerlemans, 1982) predicts a smaller increase in melt rates for rising temperatures. In fact, the larger sensitivity of the mass balance to temperature change found in the present study implies that, for a warming of 5 K, conditions in the marginal zone of the AIS become similar to those now found in the high Arctic (Fig. 2).

Fig. 3. A comparison between equilibrium ice volumes and those obtained by Reference HuybrechtsHuybrechts (1993) with a 3-D thermomechanical ice-sheet model (black and open squares). Black squares refer to calculations with a large ice sheet as initial state; open squares refer to calculations with no ice as initial state. The dashed curve gives the solution for a different relation between runoff line and temperature (see text).
The question arises whether the difference in climate sensitivity is a consequence of the parameterization of the mass balance or rather due to the schematic geometry of the simple ice-sheet model. The dashed curve in Figure 3 shows the solution in the case that h0 in Equation (7) is set to 1200m instead of 1471 m. The curve shifts to higher temperatures, of course, and part of the difference between the present model and the Huybrechts model disappears. Therefore much seems to depend on how the mass balance is formulated, a point also stressed by Reference Barker, Barrett, Cooper and HuybrechtsBarker and others (1999). Nevertheless, the larger ice volumes seen in Reference HuybrechtsHuybrechts (1993) for high temperatures are most likely related to the fact that local ice sheets are generated on higher terrain. The simple model is not able to simulate this stage of Antarctic glaciation properly.
The components of the mass budget corresponding to the equilibrium states are shown in Figure 4. Apparently, the calving flux (F gr) remains small until the ice-sheet radius becomes larger than about 1300 km. For T a = –12°C, runoff and calving flux are about the same. A zero value of F gr for T a > –8.5°C should of course not be taken too literally, since the simple model is not able to simulate local active glaciers that will produce icebergs in limited areas.

Fig. 4. Ice-sheet radius (upper panel) and mass-budget components (lower panel) for the equilibrium states of Figure 3. F gr denotes the flux across the grounding line. The thin vertical line indicates the present state.
5. Regional Climate Feedback
In the previous section, the equilibrium states of the AIS were considered as a function of the Antarctic temperature Ta. However, this does not necessarily reflect the dependence of the ice volume on the global mean temperature. In the following an attempt is made to include the feedback between the ice sheet and the regional climate in a simple way.
Even when surface temperatures are reduced to sea level, the Antarctic region is colder than the Arctic region. For annual mean temperature this difference is 5–8 K (e.g. Reference Peixoto and OortPeixoto and Oort, 1992), depending on data source and how the sea level is reduced for the Antarctic continent. The most obvious way in which the AIS affects the regional climate is by reflecting a great deal of the solar energy back to space. Therefore it is assumed that the reduction of Ta due to the ice sheet is proportional to the ice-sheet area. This can be formulated as
Here Tgl is the global mean temperature (reduced to sea level), Δ is the difference between the global mean and Antarctic temperature in the absence of an ice sheet, η a feedback parameter and R ref the present-day radius of the ice sheet (1920 km). For η = 5K, the current value of Δ is about 27 K. In Figure 5 the equilibrium volume of the model ice sheet (upper branch) for the case with regional climate feedback is compared to the reference case. Ice volume is now plotted as a function of T gl, and the present state corresponds to T gl=14˚C. Clearly, the regional climate feedback has a significant effect. The dependence of ice volume on temperature becomes stronger now. Although there is little hard evidence that Equation (10) is a realistic representation of the regional Antarctic climate feedback, the result shows that such feedbacks can change the picture considerably, in particular for warmer climates.

Fig. 5. Steady-state ice volume for the reference case (dashed line) and for the case with regional climate feedback (solid line). T gl is the global mean temperature reduced to sea level.
6. Antarctic Ice Volume and Deep-Sea Temperature during the Cenozoic
The oxygen isotope signal in benthic foraminifera from deep-sea cores is mainly determined by deep-ocean temperature (T sea) and land-ice volume. Separating the temperature and ice-volume effect for the Cenozoic is a key step in understanding the long-term evolution of climate. Except for the last few million years, fluctuations in land-ice volume were determined mainly by the size of the AIS (Reference BarrettBarrett, 1996). The ice-sheet model described in this paper can be used to make a first-order estimate of the ice-volume effect in the benthic δ18O record. The method described below can be applied to any δ18O record. Here the composite record compiled by Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others (2001) is used (Fig. 6). This record suggests that after the Cenozoic climatic optimum of about 50 Myr ago deep-sea temperatures have declined steadily. Since most of the deeper ocean waters are generated in the high-latitude seas, changes in the proxy deep-sea temperature are normally assumed to reflect temperature changes at high (subpolar) latitudes. Here this interpretation of the δ18O record is used by assuming that the characteristic Antarctic temperature varies in proportion to the deep-sea temperature:

Fig. 6. The composite benthic δ18O curve from Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others (2001), sampled at a 0.1 Myr time resolution and including their temperature scale (at right). Glacial activity as inferred from various sources of geological information (e.g. Reference BarrettBarrett, 1996) is indicated at the top. The presence of smaller ice sheets is indicated by dashes, whereas a solid line refers to a full-grown ice sheet covering most of the Antarctic continent.
Δ0 denotes the typical temperature difference between the deep sea and the Antarctic continent in the absence of an ice sheet. Note that Equation (11) includes the regional climate feedback again, as discussed in section 5. The basis of the calculation is formed by the following equation:
Here T sea is the deep-sea temperature δ as commonly used in the interpretation of oxygen isotope records, and a, b, λ are suitable constants. Equation (12) is the simplest possible relation between variations in 18O in the ocean, temperature and ice volume. Commonly used values for a and b found in the literature are a = 2.625% and b = –0.25%K–1 (e.g. Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others, 2001). The value of λ has been set to 0.4×10–16%μ–3. This implies that the current volume of the AIS corresponds to a 1% shift in ocean 18O.
Deep-sea temperature and ice volume are now calculated from the following equations:
Here f represents symbolically the AIS model. At this point it should be mentioned that the temporal resolution of the deep-sea δ18O record used here is 0.1 Myr. Consequently, the model ice sheet is always in equilibrium. Equations (13) and (14) can be solved by a simple iterative method which is not described here. The 0.1 Myr sampling of the composite δ18O record also implies that the Pleistocene glacial cycles are not resolved. Therefore the δ18O curve is corrected for Northern Hemisphere ice by subtracting a value that increases linearly from zero at 2Myr ago to 0.8% in the late Pleistocene. It should be mentioned that the precise form of this correction is not relevant for the longer time-scales which are the subject of the present study.
The parameter Δ0 is now used as a control parameter. Its value should be determined in such a way that some constraints are met. First of all, the simulated ice volume should be in broad agreement with the marine geological record. This implies that a large ice sheet should form around 35 Myr ago, with significantly less extensive glacial activity 25–10 Myr ago. Then the final outcome of the integration should be an ice sheet that is close to the present-day ice sheet in terms of volume and mass throughput.
Calculated ice volumes for a range of values of Δ0 are shown in Figure 7. The curves for Δ0 = 8, 9 or 10 K all show a rapid growth of Antarctic ice around –34 Myr. However, only the simulation with Δ0 = 10 K produces a significant discharge of ice into the ocean in the period between –134 and –26 Myr (Fig. 8). Therefore this value of Δ0 is considered to be the most appropriate one. The corresponding deep-sea temperature is shown in Figure 8. It is clear that the ice-volume effect on the isotopic signal is quite substantial. After formation of the AIS the equivalent temperature effect of the ice volume varies between 1 and 4 K. The corrected deep-sea temperature curve shows that one cannot characterize the Cenozoic climate as having a gradual cooling trend as is sometimes stated. Between 25 and 10 Myr ago the climate was not colder than at the time of ice-sheet initiation. It is entirely because of the positive feedbacks (altitude–mass-balance feedback and regional climate feedback) that the AIS has been able to persist. The present model predicts that for a 3 K smaller difference between deep-sea temperature and Antarctic temperature, the initiation of a large ice sheet would have occurred only 5 Myr ago.

Fig. 7. Antarctic ice volume for the last 45 ×106 years calculated for different values of Δ0 (labels, in K).

Fig. 8. (a,b) Deep-sea temperature (a) and ice volume (b) derived from the composite benthic δ18O record of Reference Zachos, Pagani, Sloan, Thomas and BillupsZachos and others (2001). The curve labelled ‘not corrected’ is identical to the δ18O curve (Fig. 6). (c) The flux of ice into the ocean. This flux is considered to be a measure of the total amount of IRD deposited onto the ocean floor.
In Figure 3 it is shown that the relation between ice volume and climate depends very much on how the height of the runoff line is related to Antarctic temperature. However, with respect to the calculation of a corrected deep-sea temperature curve, this is not a great problem. Because the value of Δ0 is chosen in such a way that the Cenozoic ice-volume history is broadly matched, the effect of a different relation between h R and T a is compensated for by a different value of Δ0. This is illustrated in Figure 9. Here two calculations are compared. The solid line shows the derived deep-sea temperature for the reference case (the Δ0 = 10 K case from Fig. 8), whereas the dotted line corresponds to a calculation with Δ0 = 12 K and with h 0 in Equation (7) equal to 1200 m instead of 1471 m (so the latter case corresponds to the dashed line in Figure 3). Obviously, the difference between the calculated deep-sea temperature curves is very small.

Fig. 9. Calculated deep-sea temperatures for the reference case of Figure 8 (solid line) and for a different relation between runoff line and Antarctic temperature (dashed line).
7. Discussion
Given its simplicity, the axisymmetrical ice-sheet model seems to do a relatively good job. It reveals the basic dependence of total ice volume and the components of the mass budget on Antarctic temperature. Perhaps the model should first of all be seen as a learning tool, illustrating the overall constraints set by mass continuity on the evolution of the AIS. Notably, it shows in a transparent way how sensitive modelling results are to the particular choice of parameter values that describe the mass balance, especially for temperatures 5–10 K higher than today.
Nevertheless, the AIS model used in this study is very schematic. Simulations with more sophisticated models with spatial resolution have shown that glaciation of the Antarctic continent starts in different places, on topography that is considerably higher than the top of the cone used here (Reference OerlemansOerlemans, 1982; Reference HuybrechtsHuybrechts, 1993; Reference DeConto and PollardDeConto and Pollard, 2003). This probably explains why the (T a, volume) curve from Reference HuybrechtsHuybrechts (1993) is flatter than the one produced by the simple model (Fig. 3). Therefore the early stages of Antarctic glaciation are not captured by the simple model. In spite of this, the broad structure of the equilibrium solutions is rather similar to that in the 3-D numerical models, so the simple model can be used to make a quick survey of how different parameterizations of the mass balance work out on the size of the ice sheet. It is unfortunate that for 3-D models equilibrium states for different parameterizations of the mass-balance field have hardly been investigated. Consequently, a thorough comparison of the simple modelling approach with the output of models with spatial resolution remains difficult.
The deep-sea temperature and ice-volume curve derived here differs significantly from the results of Mg/Ca analysis in benthic forminiferal calcite (Lear and others, 2000). The corrected deep-sea temperature curve in Figure 8 shows no net cooling for the Miocene (25 to ~5Myr ago), whereas the Mg/Ca analysis suggests a net cooling of about 4 K during this period. Reference Lear, Elderfield and WilsonLear and others (2000) also derive an estimate of continental ice build-up by using the Mg/Ca temperature for T sea in Equation (1) and solve for ice volume. There is broad agreement between their ice-volume curve and the one derived in the present here, but there are also some differences. It remains unclear to what extent their result is consistent from the viewpoint of ice-sheet dynamics. Perhaps in the future it will be possible to use the information from the δ18O record as well as the Mg/Ca record in combination with a continental ice model.
In this study it is assumed that the parameter λ in Equation (1) is constant. This implies that the difference in mean isotopic composition of the oceans and the ice sheets does not change. In reality, the mean isotopic composition of an ice sheet depends mainly on two factors: (i) the mean altitude of the accumulation region, and (ii) the temperature difference between the moisture source and the characteristic temperature of the region in which the ice sheet is located. No attempt was made to handle such effects. Since the mean surface elevation of the ice sheet is calculated, a correction could be made. Factor (ii) is more difficult to deal with, unless it is assumed that the moisture source for Antarctic precipitation changes little through time. In future work a more sophisticated treatment of the isotopic composition of the ice sheet will be considered.
Acknowledgements
I am grateful to the reviewers and to R. Bintanja, R. van de Wal and D. Pollard for useful comments and suggestions. This paper is a contribution to the research programme on ‘Climate Change and Geodynamics’ of the Utrecht Centre of Geosciences.











